大学控制工程基础6系统误差分析
合集下载
控制工程基础6章
H(S) +
Xor(S)
+ N(S)
+
-
E(S)
G1(S)
G2(S)
X0(S)
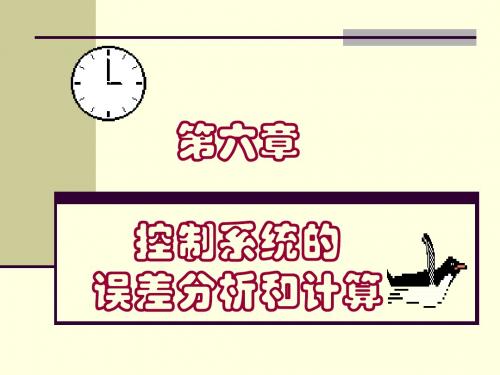
设xor (t )是控制系统希望的输出信号,而 xo (t ) 是实际的输出信号, 一般把二者之差定义为 误差信号,记做e(t), e(t) = xor (t ) - xo (t )
m(p) 是理想算子,是认为规 定的。一般情况下, m( s) =1/H(s)。
时的系统输出端的稳态误差。
1 2 例题:求下图所示系统 在1(t), t, 和 t 分别作用下的稳态误差 。 2
五、扰动引起的误差
+
G1(s) N(s) G2(s) Xo(s)
Xi(s) +
+
Y(s) H(s)
要想求稳态偏差,可以利用叠加原理,分别求
出给定信号Xi(s) 和N(s)单独作用时的偏差,然
2 2
对于0型系统,Ka=0,ess=
对于I型系统, Ka=0, ess=
对于II型系统, Ka=K, ess= 1/K 对于III型及以上系统, Ka= , ess= 0
0和I型系统不能跟踪单位斜坡输入,I I型系统能跟踪单 位斜坡输入但有静差,需要III型以上系统才能消除静差。
10 G 例:设有一非单位反馈控制系统, ( s) = s 1 H(s)=Kh,输入为单位阶跃。试求, Kh=1和0.1
结构形式 输入形 式
1 例:设单位反馈控制系统的 G( s) = ,输 2 Ts t 入信sint , 2 试求系统的稳态误差。
为什么? 因为:E(s) = s (s 2 2 )(s 1 ) T T 1 T s T 2 3 1 =- 2 2 2 2 2 2 2 2 1 T 1 s 2 T 1 s 2 T 1 s T 求拉式反变换 T
Xor(S)
+ N(S)
+
-
E(S)
G1(S)
G2(S)
X0(S)
设xor (t )是控制系统希望的输出信号,而 xo (t ) 是实际的输出信号, 一般把二者之差定义为 误差信号,记做e(t), e(t) = xor (t ) - xo (t )
m(p) 是理想算子,是认为规 定的。一般情况下, m( s) =1/H(s)。
时的系统输出端的稳态误差。
1 2 例题:求下图所示系统 在1(t), t, 和 t 分别作用下的稳态误差 。 2
五、扰动引起的误差
+
G1(s) N(s) G2(s) Xo(s)
Xi(s) +
+
Y(s) H(s)
要想求稳态偏差,可以利用叠加原理,分别求
出给定信号Xi(s) 和N(s)单独作用时的偏差,然
2 2
对于0型系统,Ka=0,ess=
对于I型系统, Ka=0, ess=
对于II型系统, Ka=K, ess= 1/K 对于III型及以上系统, Ka= , ess= 0
0和I型系统不能跟踪单位斜坡输入,I I型系统能跟踪单 位斜坡输入但有静差,需要III型以上系统才能消除静差。
10 G 例:设有一非单位反馈控制系统, ( s) = s 1 H(s)=Kh,输入为单位阶跃。试求, Kh=1和0.1
结构形式 输入形 式
1 例:设单位反馈控制系统的 G( s) = ,输 2 Ts t 入信sint , 2 试求系统的稳态误差。
为什么? 因为:E(s) = s (s 2 2 )(s 1 ) T T 1 T s T 2 3 1 =- 2 2 2 2 2 2 2 2 1 T 1 s 2 T 1 s 2 T 1 s T 求拉式反变换 T
第六章 控制系统误差分析与计算

23
6.3 综合分析
静态误差
提高系统的准确度,增加系统的抗干扰能力,必须增 大干扰作用点之前的回路的放大倍数K1,以及增加这 一段回路中积分环节的数目。 增加干扰作用点之后到输出量之间的放大系数K2,或 增加积分环节的数目,对减少干扰引起的误差是没有 好处的。
24
6.4
动态误差
系统的动态误差
6.1
2.系统偏差
误差的概念
系统误差e(t)与偏差ε(t)
系统偏差ε (t). E(s)是输入信号与反馈信号的差。 若输入信号xi(t)作为期望值,反馈信号b(t)作为实际 值。 则偏差: ε (t)= xi(t)- b(t) L变换: E(s)= Xi(s)- B(s) = Xi(s)-H(s) • Xo(s) ---(2)
系统误差:
E1(s) = Xor(s)- Xo(s) =Xi(s)/H(s)- Xo(s) =〔1/ H(s) - Gxi(s)〕•Xi(s)+(-GN(s))•N(s) = Φ xi(s) •Xi(s)+Φ N(s) •N(s)
可见,系统的误差不仅与系统的结构和参数有关,而且 8 与系统的输入和干扰的特性有关。
前面讲的是静态误差,是一个静态值。即当 t→∞时系统误差的极限值。 E(S)逆变换,是一个时间的函数。
时间在t→∞是一个有限的变化过程。 实际控制系统的稳态误差往往表现为时间的函数,----即动态误差。
25
6.4
例:如图系统:
动态误差
动态误差实例
其误差传递函数为:
Φxi(s)= E(s)/ Xi(s)=1/[1+G(s)H(s)]
13
6.3
静态误差
与输入有关的静态偏差
第六章 控制系统的误差分析和计算

解
+
E ( s)
10 s
X o ( s)
e ( s ) =
1 1 s = = 1 + G ( s ) 1 + 10 s + 10 s s ess = lim si iXi (s) s →0 s + 10 1 Xi ( s) = s s 1 ess = lim si i =0 s →0 s + 10 s
K a = lim s 2 iG ( s )
s →0
对0型系统 型系统
K a = lim s 2 i
s →0
K 0 (Ta s + 1)(Tb s + 1) (Tm s + 1) =0 (T1s + 1)(T2 s + 1) (Tn s + 1)
对Ⅰ型系统
K a = lim s 2 i
s →0
K1 (Ta s + 1)(Tb s + 1) (Tm s + 1) s (T1s + 1)(T2 s + 1) (Tn s + 1)
=0
自动控制原理
对Ⅱ型系统
K2 (Ta s +1)(Tb s +1)(Tms +1) Ka = lim s i 2 = K2 s→0 s (T1s +1)(T2s +1)(Tn s +1)
2
所以, 就是Ⅱ 所以,静态加速度误差系数 Ka 就是Ⅱ型系统的开环放大倍 对于Ⅲ型或高于Ⅲ型的系统, 数 K 2 。对于Ⅲ型或高于Ⅲ型的系统, K a 才为 ∞ 。 在单位加速度输入下 型系统, 对0型系统, ess = ∞ 型系统 型系统, 对Ⅰ型系统,
这就是求去单位反馈系统稳态误差的方法
+
E ( s)
10 s
X o ( s)
e ( s ) =
1 1 s = = 1 + G ( s ) 1 + 10 s + 10 s s ess = lim si iXi (s) s →0 s + 10 1 Xi ( s) = s s 1 ess = lim si i =0 s →0 s + 10 s
K a = lim s 2 iG ( s )
s →0
对0型系统 型系统
K a = lim s 2 i
s →0
K 0 (Ta s + 1)(Tb s + 1) (Tm s + 1) =0 (T1s + 1)(T2 s + 1) (Tn s + 1)
对Ⅰ型系统
K a = lim s 2 i
s →0
K1 (Ta s + 1)(Tb s + 1) (Tm s + 1) s (T1s + 1)(T2 s + 1) (Tn s + 1)
=0
自动控制原理
对Ⅱ型系统
K2 (Ta s +1)(Tb s +1)(Tms +1) Ka = lim s i 2 = K2 s→0 s (T1s +1)(T2s +1)(Tn s +1)
2
所以, 就是Ⅱ 所以,静态加速度误差系数 Ka 就是Ⅱ型系统的开环放大倍 对于Ⅲ型或高于Ⅲ型的系统, 数 K 2 。对于Ⅲ型或高于Ⅲ型的系统, K a 才为 ∞ 。 在单位加速度输入下 型系统, 对0型系统, ess = ∞ 型系统 型系统, 对Ⅰ型系统,
这就是求去单位反馈系统稳态误差的方法
第六章 控制系统的误差分析和计算.ppt

6.2 输入引起的稳态误差
6.2.1 误差传递函数与稳态误差
➢单位反馈控制系统
输入引起的系统的误差传递函数为
E(s) 1 Xi(s) 1G(s)
则
E(s) 1 1G(s)
Xi(s)
X i sE(s)源自G(s)X o s
图6-2 单位反馈系统
根据终值定理 e ss lt ie m (t) ls i0s m (E s) ls i0s m 1 G 1 (s)X i(s)
这就是求取输入引起的单位反馈系统稳态误差的方法.需要注意的 是,终值定理只有对有终值的变量有意义.如果系统本身不稳定,用 终值定理求出的值是虚假的.故在求取系统稳态误差之前,通常应 首先判断系统的稳定性.
➢ 非单位反馈控制系统
输入引起的系统的偏差传递函数为:
sXi(s)Y(s)
1
1G(s)H(s)
控制系统的方块图如图6-1所示.实线部分与实际系统有对应关系, 而虚线部分则是为了说明概念额外画出的.
控制系统的误差信号的象函数是 E ( s )s X is X o s (6-1)
而
偏差信号的象函数是 (s)X is Y s
(6-2)
考虑Xi(s)与Y(s)近似相等,且Y(s)=H(s)Xo(s),得
一般情况下,H为常值,故这时:
e ss
ss
H
例6-1 某反馈控制系统如图6-4,当xi(t)=1(t)时,求稳态误差.
解:该系统为一阶惯性系统,系统稳定.误差传递函数为:
Es 1 1 s
Xi(s) 1G(s) 110 s10 s
而
X
i
(s)
1 s
则
e ss ls i0s m s s1X 0 i(s) ls i0s m s s11 s0 0
控制工程基础 第6章 控制系统的误差分析和计算

C0 (s)
N (s)
R(s) B(s)
(s)
-
G1 ( s )
+ G2 (s)
H (s)
e(s) -
C(s)
(b)
误差
C0(s) (s) N(s)
R(s)
1 H(s)
R1(s) C0(s)
E1(s(s))H(s)
E(s)
G1(s)
G2(s) C(s)
(c)
e(s) -+ (s)
H (s)
E(s)
因为偏差 (s) R(s) B(s) H (s)C0 (s) H (s)C(s) H (s)e(s)
这里 R(s) H (s)C0 (s) 是基于控制系统在理想工作情况下
(s) 0 得到的。
即当控制系统的偏差信号 (s) 0 时,该控制系统无调节控制
作用,此时的实际输出信号C(s)就是希望输出信号 C0 (s) 。
G(s)H(s)
i1 nv
sv (Tis 1)
i1
(4)稳态误差系数和稳态误差的总结 (系统在控制信号作用下)
此表概括了0型、Ⅰ型和Ⅱ型反馈控制系统在不同输入信号作用下的
稳态误差。在对角线上,稳态误差为有限值;在对角线以上部分,
稳态误差为无穷大;在对角线以下部分,稳态误差为零。由此表可
以得如下结论:
何改变系统结构?
(s)
- G1 K1
解:(1)给定作用下的误差传递函数为
RE (s)
(s)
R(s)
1
1
K1
K2 s
s s K1K2
当给定输入为单位阶跃输入时,稳态误差为
N (s)
+
G2
K2 s
控制工程实验-第6章

• II 型或高于 II 型的系统能准确地跟踪斜坡输入。
• 如果对具有速度函数性质的输入信号要求稳态 误差为零,则系统必须是 II 型或高于I单位加速度输入的稳态误差是
essls i0m s1G 1(s)s13s2G 1(s)
定义静态加速度误差系数为
Ka
lims2G(s) s0
在一个给定的系统中,输出量可以是位置、
速度、压力、温度等,然而,输出量的物理形式 对控制系统的分析并不重要,因此,可称系统输 出量是“位置”,输出量的变化率为“速度”等。
将阶跃、斜坡、加速度等输入信号称为广义 位置、速度、加速度信号。
静态位置误差系数
系统对单位阶跃输入的稳态误差是
11 1 essls i0m s1G(s)s1G(0)
一般情况下, H(s)H为常值,因此
ess ss H • 稳态误差取决于系统结构参数和输入信号 • 求解稳态误差首先必须判断系统的稳定性
6.2.2 静态误差系数
1、控制系统的类型
控制系统可以按照它们跟踪阶跃输入、 斜坡(速度)输入、加速度输入等信号的 能力来分类,因为实际的输入往往可以认 为是这些输入的组合,所以这样的分类是 合理的。由这些特定的输入所引起的稳态 误差的大小表征了系统的“优良度”。
控制工程基础
第六章 控制系统的误差分析
和计算
系统在达到稳态时,输出量与希望输 出量之间的误差称为稳态误差。稳态误差 是控制系统准确度的一种度量。
对于稳定的控制系统,它的稳态性能 一般是根据阶跃、速度或加速度输入所引 起的稳态误差来判断的。本章所研究的稳 态误差是由于系统不能很好地跟踪特定形 式的输入信号或者由于扰动作用而引起的 稳态误差,即系统原理性误差。
本节要点:
了解动态误差系数概念及计算动态 误差的方法。
• 如果对具有速度函数性质的输入信号要求稳态 误差为零,则系统必须是 II 型或高于I单位加速度输入的稳态误差是
essls i0m s1G 1(s)s13s2G 1(s)
定义静态加速度误差系数为
Ka
lims2G(s) s0
在一个给定的系统中,输出量可以是位置、
速度、压力、温度等,然而,输出量的物理形式 对控制系统的分析并不重要,因此,可称系统输 出量是“位置”,输出量的变化率为“速度”等。
将阶跃、斜坡、加速度等输入信号称为广义 位置、速度、加速度信号。
静态位置误差系数
系统对单位阶跃输入的稳态误差是
11 1 essls i0m s1G(s)s1G(0)
一般情况下, H(s)H为常值,因此
ess ss H • 稳态误差取决于系统结构参数和输入信号 • 求解稳态误差首先必须判断系统的稳定性
6.2.2 静态误差系数
1、控制系统的类型
控制系统可以按照它们跟踪阶跃输入、 斜坡(速度)输入、加速度输入等信号的 能力来分类,因为实际的输入往往可以认 为是这些输入的组合,所以这样的分类是 合理的。由这些特定的输入所引起的稳态 误差的大小表征了系统的“优良度”。
控制工程基础
第六章 控制系统的误差分析
和计算
系统在达到稳态时,输出量与希望输 出量之间的误差称为稳态误差。稳态误差 是控制系统准确度的一种度量。
对于稳定的控制系统,它的稳态性能 一般是根据阶跃、速度或加速度输入所引 起的稳态误差来判断的。本章所研究的稳 态误差是由于系统不能很好地跟踪特定形 式的输入信号或者由于扰动作用而引起的 稳态误差,即系统原理性误差。
本节要点:
了解动态误差系数概念及计算动态 误差的方法。
控制工程基础 (第15讲) 第六章 干扰引起的误差及动态误差系数 PPT课件

xi(1)
(t)
dxi (t) dt
a1
2a2t
x (2) i
(t
)
d
2 xi (t) dt 2
2a2
x (3) i
(t
)
d 3 xi (t) dt 3
0
e(t) 0.1(a1 2a2t) 0.18 • 2a2 0.1a1 0.36a2 0.2a2t
ess
lim e(t)
从结构上看,利用双通道原理:
(1)一条由干扰信号经 Gn (s) 、G1(s) 到达第二个相加点。
(2)一条由干扰信号直接到达相加点。
满足(6-19)条件后,两路信号在此点相加,大小相等, 方向相反,实现了全补偿。
由于G1(s)分母的s阶次一般比分子的s阶次高,故式(6-19) 的
条件在工程实践中只能近似地得到满足。
X o (s) G2 (s)
G(s)H (s) G1(s)G2 (s)H (s)
H (s)
ss1
lim
s0
sg1(s)
lim
s0
sg 1
1 G1(s)G2 (s)H
(s) gX i
(s)
控制工程基础
5
(2)由干扰信号 n(t) 产生的偏差,此时令 xi (t) 0
N(s)
2s)(s2
s 10) (s (s2 s 10)2
s
2
)(2s
1)
|s
0
10 100
0.1
控制工程基础
19
(2) e
控制系统的误差分析和计算

1 E s X i s 1 G s 1 e ss lim e t lim sE s lim s X i s t s0 s 0 1 G s
11
控制工程基础
第六章 控制系统的误差分析和计算
非单位反馈系统
1 X i s 1 G s H s
' '
( s) X or ( s) X o ( s) E ( s)
'
( s)
H ( s)
1 单位反馈系统H s 1,E s s E s s H ( s) H ( s) : 求稳态误差,应先求稳态偏差。
9
控制工程基础
n m
14
控制工程基础
第六章 控制系统的误差分析和计算
1、影响稳态误差的因素
G s K 1 s 1 2 s 1 v s T1 s 1T2 s 1
s 0
n m
e ss lim e ( t ) lim sE ( s )
t
输出量期望值的大小,即Xor(s)= Xi(s),由此得到:
( s) Xi ( s) H ( s) X 0 ( s) X or (s) X 0 (s) E (s)
单位反馈控制系统的偏差函数(s)和误差函数E(s)是相等的。
7
控制工程基础
第六章 控制系统的误差分析和计算
对于非单位负反馈控制系统,其输入量间接反映了输出量 期望值的大小,根据等效规则转变为单位负反馈控制系统。
Xi s
s
× -
( s)
Y s
G s
Xo s
H s
第6章_控制系统的误差分析和计算_6.3干扰引起的稳态误差

N (s ) R (s ) E (s )
-
G1 = K1
+
G2 =
K2 s
C (s )
(2)扰动作用下的误差传递函数为 K2 − E(s) − K2 s ΦNE (s) = = = N(s) 1+ K K2 s + K1K2 1 s 当扰动输入为单位阶跃输入时,稳态误差为
essn
1 − K2 1 1 = lim s ⋅ Φ NE ⋅ = lim s ⋅ ⋅ =− s →0 s s →0 s + K1 K 2 s K1
N (s )
X i (s )
ε (s )
B (s )
-
G1 ( s )
+
H (s )
G2 (s)
X o (s )
(2)稳态误差的计算 )
①给定作用下的偏差传递函数
N (s )
X i
X i (s )
-
G1 ( s )
+
H (s )
G2 (s)
X o (s )
ε (s )
ess = essr + essn 1 =− K1
(3)输入作用与扰动作用共同作用下的稳态误差为
N (s ) R (s ) E (s )
-
G1 =
K1 s
+
G2 =
K2 s
C (s )
(4)如果要求稳态误差为零,可以在G1中串联积分环节,令 K1 G1 = s 1 s2 1 essr = lim s ⋅ Φ RE ⋅ = lim s ⋅ 2 ⋅ =0 则有 s →0 s s →0 s + K1 K 2 s
④对于稳定的系统,采用拉氏变换的终值定理计算稳态偏差
控制系统的误差分析

6.2 输入引起的稳态误差
6.2.1 误差传递函数与稳态误差
先讨论单位反馈的控制系统,如图6-2所示。
Xi(s)X0(s)11 G G((ss))Xi(s)1GG (s()s)Xi(s) X i s
E(s)
G(s)
X o s
1G 1(s)Xi(s)
根据终值定理
图6-2 单位反馈系统
这就是求取输入引起的单位反馈系统稳态误差的方法。
ess
1 1Kp
1 1K
对于Ⅰ型或高于Ⅰ型以上系统
K p ls i0s K m ((T 1 1 s s 1 1 ))T (2 (2 s s 1 1 )) ((T m ns s 1 1 ) )
ess 0 可编辑ppt
6
(3) 静态速度误差系数Kv
当系统的输入为单位斜坡信号时r(t)=t·1(t),即R(s)
误差定义为控制系统希望的输出量与实际的输出量之差,记
做e(t),误差信号的稳态分量被称为稳态误差,或称为静态误差, 记作 。输入信号和反馈信号比较后的信号 也能反映系统误
差的大小,称之为偏差。应该指出,系统的误差信号e(t)与偏差 信号 ,在一般情况下并不相同(见图6-1)。
控制系统的误差信号的象函数是
essK1
对于Ⅱ型或Ⅱ型以上系统:
Kls i0m ssK ((T11ss 1 1))T ((22ss 1 1)) ((Tm nss 1 1))
ess0
可编辑ppt
,则有
7
(4) 静态加速度误差系数Ka
当系统输入为单位加速度信号时,即 r(t)1t21(t)R ,(s)1
2
s3
则系统稳态误差为
1
ess
lims s0 1G(s)
第六章 控制系统的误差分析

稳态误差系数和稳态误差
浙江理工大学机械与自动控制学院
控制工程基础
第六章 控制系统的误差分析
K ( i s 1)
m
0型系统的稳态误差
G (s)H(s) K ( i s 1) s
v m
(T s 1) V=0
i i 1
i 1 n v
K p lim G (s)H(s) lim
浙江理工大学机械与自动控制学院
控制工程基础
第六章 控制系统的误差分析
例1
ess lim s
s 0
1 (0.5s 1)(0.04s 1) R( s) lim s R( s ) s 0 (0.5s 1)(0.04s 1) 20 1 G( s) H ( s)
1 s
ess lim s
K j
20lg | G( jv ) H ( jv ) | 20lg | Kv / jv | 0dB
v Kv
浙江理工大学机械与自动控制学院
控制工程基础
第六章 控制系统的误差分析
• II型系统(稳态加速度误差系数)
低频段
G (s) H ( s)
K ( i s 1) s 2 (Ti s 1) i 1 2 a
t
1 '' e (0)r ' ' ( t ) 2!
1 1 1 r(t) r' (t) r' ' (t) k0 k1 k2 动态加速度误差系数
动态位置误差系数
动态速度误差系数
浙江理工大学机械与自动控制学院
控制工程基础
第六章 控制系统的误差分析
动态误差系数的长除法求取
s 0
第6章_控制系统的误差分析和计算_6.4减小系统误差的途径

Φ n ( s) = 0
G1 ( s )
即可以使得干扰信号N(s)所产生的输出信号C(s)=0,从而 N(s) C(s)=0 消除了干扰信号N(s)对输出信号C(s)的影响。 该系统由两个通道组成,属于复合控制系统。实际上,该 系统就是利用双通道原理,实现了对干扰信号N(s)的补偿作用。 一个通道是干扰信号N(s)直接到达相加点,另一个通道是干扰信 号N(s)经过Gc(s)G1(s)后到达同一个相加点。如果满足上述选择 Gc(s)G1(s)=-1,则从两个通道过来的干扰信号在此相加点处, 大小相等,方向相反,从而实现了干扰信号的全补偿。
《控制工程基础》 控制工程基础》
第6章 控制系统的误差分析和计算 6.4 减小系统误差的途径
为了减小系统误差,可以考虑以下途径: (1)反馈通道的精度对于减小系统误差至关 重要。反馈通道元部件的精度要高,避免在反馈通 道引入干扰。 (2)在系统稳定的前提下: 对于输入引起的误差,增大系统开环放大倍数 或提高系统型次,可以使之减小。 对于干扰引起的误差,在前向通道干扰点前加 积分器或增大放大倍数,可以使之减小。 (3)既要求稳态误差小,又要求良好的动态 性能,只靠加大开环放大倍数或串入积分环节不能 同时满足要求时,可以采用复合控制(顺馈)方法 对误差进行补偿。补偿的方式可分为按干扰补偿和 按输入补偿。
6.4.2 按输入补偿(顺馈补偿闭环控制) 按输入补偿(顺馈补偿闭环控制)
顺馈补偿闭环控制系统的典型结构如图所示,其中R(s) 是输入信号,C(s)是输出信号,E(s)是偏差,Gc(s)是顺馈补偿 通道传递函数。该系统由两个通道组成,属于复合控制系统。 一个通道是由G1(s)G2(s)组成的主控制通道,为闭环控制。另 一个通道是由Gc(s)G2(s)组成的顺馈补偿控制通道,为开环控 制。系统的输出不仅与系统的误差有关,而且还与补偿信号有 关。补偿信号所产生的作用,可以用来补偿原来的误差信号。
G1 ( s )
即可以使得干扰信号N(s)所产生的输出信号C(s)=0,从而 N(s) C(s)=0 消除了干扰信号N(s)对输出信号C(s)的影响。 该系统由两个通道组成,属于复合控制系统。实际上,该 系统就是利用双通道原理,实现了对干扰信号N(s)的补偿作用。 一个通道是干扰信号N(s)直接到达相加点,另一个通道是干扰信 号N(s)经过Gc(s)G1(s)后到达同一个相加点。如果满足上述选择 Gc(s)G1(s)=-1,则从两个通道过来的干扰信号在此相加点处, 大小相等,方向相反,从而实现了干扰信号的全补偿。
《控制工程基础》 控制工程基础》
第6章 控制系统的误差分析和计算 6.4 减小系统误差的途径
为了减小系统误差,可以考虑以下途径: (1)反馈通道的精度对于减小系统误差至关 重要。反馈通道元部件的精度要高,避免在反馈通 道引入干扰。 (2)在系统稳定的前提下: 对于输入引起的误差,增大系统开环放大倍数 或提高系统型次,可以使之减小。 对于干扰引起的误差,在前向通道干扰点前加 积分器或增大放大倍数,可以使之减小。 (3)既要求稳态误差小,又要求良好的动态 性能,只靠加大开环放大倍数或串入积分环节不能 同时满足要求时,可以采用复合控制(顺馈)方法 对误差进行补偿。补偿的方式可分为按干扰补偿和 按输入补偿。
6.4.2 按输入补偿(顺馈补偿闭环控制) 按输入补偿(顺馈补偿闭环控制)
顺馈补偿闭环控制系统的典型结构如图所示,其中R(s) 是输入信号,C(s)是输出信号,E(s)是偏差,Gc(s)是顺馈补偿 通道传递函数。该系统由两个通道组成,属于复合控制系统。 一个通道是由G1(s)G2(s)组成的主控制通道,为闭环控制。另 一个通道是由Gc(s)G2(s)组成的顺馈补偿控制通道,为开环控 制。系统的输出不仅与系统的误差有关,而且还与补偿信号有 关。补偿信号所产生的作用,可以用来补偿原来的误差信号。
第六章 系统的稳态误差(第十五讲)

j 1 m i 1 n −ν
ν
, n≥m
(6(6-11)
06-7-20
控制工程基础
13
K:系统开环增益
ν = 0 0型系统 Ι型系统 ν : 为系统中含有的积分环节数ν = 1 ν = ΙΙ型系统 2 ν > 2时,ΙΙ型以上的系统,实际上很难使之稳定,所以这种类型的 系统在控制工程中一般不会碰到。
06720控制工程基础23静态位置误差系数静态加速度误差系数误差系数类型静态速度误差系数不同类型系统误差系数表06720控制工程基础24输入类型有关开环传递函数有就越小与系统稳态误差静态误差系数不同类型系统稳态误差表06720控制工程基础254多种典型函数组合信号作用下的稳态误差对于线性系统在多种典型函数组合信号的作用如
1 s +1.6 E(s) = Xi (s) = 2 1+ G(s) s +1.6s + 4
0.2
0
-0.2
ess = lims • E(s) = 0
s−0
-0.4
-0.6
Xi (s)
_
ωn2 S(S+2ξωn)
Xo (s)
-0.8
-1
0
100
200
300
400
500
600
图6-4 标准形式的二阶系统方块图
lim
lim
lim
误差为零,即系统能够很好地跟踪阶跃输入,稳态精度很高。 误差为零,即系统能够很好地跟踪阶跃输入,稳态精度很高。
06-7-20 控制工程基础 10
例2 二阶系统在单位阶跃输入作用下的响应的误差曲线
Φ(s) = 4 s2 +1.6s + 4
G(s) = 4 s(s +1.6)
ν
, n≥m
(6(6-11)
06-7-20
控制工程基础
13
K:系统开环增益
ν = 0 0型系统 Ι型系统 ν : 为系统中含有的积分环节数ν = 1 ν = ΙΙ型系统 2 ν > 2时,ΙΙ型以上的系统,实际上很难使之稳定,所以这种类型的 系统在控制工程中一般不会碰到。
06720控制工程基础23静态位置误差系数静态加速度误差系数误差系数类型静态速度误差系数不同类型系统误差系数表06720控制工程基础24输入类型有关开环传递函数有就越小与系统稳态误差静态误差系数不同类型系统稳态误差表06720控制工程基础254多种典型函数组合信号作用下的稳态误差对于线性系统在多种典型函数组合信号的作用如
1 s +1.6 E(s) = Xi (s) = 2 1+ G(s) s +1.6s + 4
0.2
0
-0.2
ess = lims • E(s) = 0
s−0
-0.4
-0.6
Xi (s)
_
ωn2 S(S+2ξωn)
Xo (s)
-0.8
-1
0
100
200
300
400
500
600
图6-4 标准形式的二阶系统方块图
lim
lim
lim
误差为零,即系统能够很好地跟踪阶跃输入,稳态精度很高。 误差为零,即系统能够很好地跟踪阶跃输入,稳态精度很高。
06-7-20 控制工程基础 10
例2 二阶系统在单位阶跃输入作用下的响应的误差曲线
Φ(s) = 4 s2 +1.6s + 4
G(s) = 4 s(s +1.6)
大学控制工程基础课件第4章6系统误差分析

湿度变化:影响设备或元件的 稳定性和可靠性
振动和冲击:使设备或元件产 生疲劳或变形
电磁干扰:影响设备的正常工 作和测量精度
人为因素误差:由于操作人员主观或客观原因导致的误差,如测量方法不准确、读数误差等。 仪器设备误差:由于仪器设备本身缺陷或使用不当导致的误差,如传感器精度不高、放大器失真 等。 信号源误差:由于信号源本身特性或外部干扰导致的误差,如输入信号不稳定、电磁干扰等。
选择依据:选择合适的测量方法需要考虑被测量的性质、测量环境、测量要求等因素。例如,对于温度、压力等物理量的 测量,可以选择使用热电偶、压力传感器等测量仪器;对于化学成分的测量,可以选择使用光谱分析、色谱分析等技术。
注意事项:在选择合适的测量方法时,需要注意以下几点。首先,需要了解各种测量方法和技术的基本原理和误差特性;其次,需要 根据实际情况进行选择,不能盲目追求高精度;最后,需要定期对测量仪器进行校准和维护,以确保其准确性和可靠性。
PPT,a click to unlimited possibilities
01 单 击 添 加 目 录 项 标 题 02 系 统 误 差 概 述 03 系 统 误 差 的 来 源 04 系 统 误 差 的 消 除 方 法 05 系 统 误 差 的 分 析 与 处 理 06 系 统 误 差 的 实 例 分 析
正
测量设备的精度 等级
测量设备的老化 与磨损
测量设备的校准 与维护
测量设备的选择 与配置
测量方法选择不当:导致测量结果偏离真实值 测量设备误差:设备本身存在的误差,如传感器、仪表等 操作不当:测量过程中操作不规范或错误操作导致误差 环境因素影响:如温度、湿度、振动等环境因素对测量结果的影响
温度变化:导致设备或元件性 能发生变化
控制工程基础 第6章 控制系统的误差分析和计算

② 扰动作用下的偏差传递函数
C(s)
B(s)
N (s) G2 (s)
+Leabharlann H (s)(s) 1
G1 ( s )
NE (s)
(s)
N (s)
G2 (s)H (s) 1 G1(s)G2 (s)H (s)
③ 给定和扰动同时作用下的偏差表达式
(s) RE (s)R(s) NE (s)N(s)
R(s)
(2)稳态误差系数的概念
➢单位阶跃输入
R(s) 1 s
定义:
essss
lim s s0 1
1 G(s)H (s)
1 s
1
lim
1 G(s)H (s)
1 1 K
p
稳态位置 误差系数
s0
➢单位斜坡输入
R(s) 1 s2
定义: 稳态速度
e
ssss
lim
s0
s
1
1 G(s)H(s)
1 s2
1 lim sG(s)H(s)
(s)
我
们
将
偏
偏差
6.2 输入引起的稳态误差
6.2.1 误差传递函数与稳态误差
稳态误差的计算:一般要先求稳态偏差 , 根据拉普拉斯变换的终值定理:
对于单位反馈系统
例: 设单位反馈系统的开环传递函数为G(s) 1 ,试求当输入信号为 Ts
r(t) 1 t 2时,控制系统的稳态误差值。 2
由终值定理
当系统的输入信号由位置、速度和加速度等分量 组成时,即
下面再说明几个问题。 用稳态误差系数Kp、Kv和Ka表示的稳态误差分别 被称为位置误差、速度误差和加速度误差,都表示 系统的过渡过程结束后,虽然输出能够跟踪输入,
第六章 控制系统的误差分析与计算.
T T 1
2 2
cost
T 2 2 T 1
2 2
sin t
第三章 时域分析法
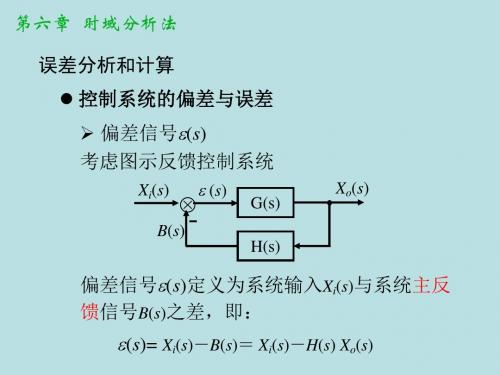
稳态输出为:
ess (t ) T T 1
2 2
cost
T 2 2 T 1
2 2
sin t
而如果采用拉氏变换的终值定理求解,将得 到错误得结论:
Ts ess lim s 0 2 2 s0 Ts 1 s
此例表明,输入信号不同,系统的稳态误差 也不相同。
第三章 时域分析法 稳态误差系数 稳态误差系数的概念
稳态位置误差(偏差)系数 单位阶跃输入时系统的稳态偏差
ss
1 1 1 lim s X i (s) lim s0 1 G( s) H ( s) s0 1 G( s) H ( s) 1 K p
G( s) H ( s) K (1s 1)( 2 s 1)( m s 1) s 2 (T1s 1)(T2 s 1)(Tnv s 1)
1 0 1 K p
K p lim G( s) H ( s)
s0
ss
K v lim sG ( s) H ( s)
s 0
ss
ss
1 0 Kv
1 1 Ka K
K a lim s G(s) H (s) K
s0
2
第三章 时域分析法
表1、系统的稳态误差系数单位阶 跃输入
1 1 K
稳态偏差 单位速 度输入 单位加速 度输入
0型
I型 II型
第六章 时域分析法 误差分析和计算 控制系统的偏差与误差 偏差信号(s) 考虑图示反馈控制系统
Xi(s)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
位置指 令
控制器
摩擦、变 形等
速度控 制模块
传播 路径
输出位移
位置检测 图a 进给伺服系统结构
图b 某机床进给系统结构参数
§4.6系统误差分析
机械控制工程基础
解:设ess1、ess2分别由R(s)、N(s)引起。
(1)、R(s)作用时,N(s)=0 ,
R(s) E (s) 4 E (s) 1 4s 1 1
,E1
(s)
1
R(s) U (s)V
(s)
(2)、N(s)作用时,R(s)=0
,E2
(s)
1
N (s)V (s) U (s)V (s)
e ss1 ess 2
e e e
ss
ss1
ss 2
§4.6系统误差分析
机械控制工程基础
例2 已知数控机床进给伺服系统结构图(a),在图(b)中
设R(s)=N(s)=1/s,计算机床系统稳态误差。
例2 补充:机械系统时间响应的作图方法
§4.6系统误差分析
一、 误差与稳态误差 1、误差信号
机械控制工程基础
如图有: E(s) R(s) H (s)C(s)
误差信号定义为输入与反馈信号之差,反映系统精度。
2、稳态误差信号
e lime(t)
ss
t
稳态误差是误差信号的稳态分量。
§4.6系统误差分析
阶跃响应图,其中:
ss
s0
1
s GH
1 s2
s0
1 s sGH
s0
1。 sGH
令 K v lims G(s)H (s),称为速度误差系数。 s0
机械控制工程基础
2
t 3)输入为加速度信号时, (t) (t 0)
x X i
2
1
(s)
i
s3
,
e lim 则
s
ss s0 1 GH
1 s3
lim s0
s2
1
s2
机械控制工程基础
3、稳态误差计算方法
用终值定理求稳态误差 :
ess
lime(t)
t
lim
s0
s E(s)
因为 E(s) R(s) E(s)G(s)H (s)
E(s) R(s) 1 G(s)H (s)
e (s)
E(s) R(s)
1
1 G(s)H (s)
ess
lime(t)
t
lim
s0
s E(s)
ess1
lim
s0
s
s(Ts 1) s(Ts 1) K
A s
0
r(t) A t
s(Ts 1) A A
e ss 2
lim s s0
s(Ts 1)
K
s2
K
r(t) A t2 2
s(Ts 1) A
ess 3
lim
s0
s
s(Ts 1)
K
s3
机械控制工程基础
二、系统类型和误差系数
E(s) X i(s) H (s) X o(s)
GH
lim s0
s2
1 GH
。
令 K a lims2G(s)H (s),称为加速度误差系数。 s0
2、考察系统结构对稳态偏差的影响:
G s T T 设开环传函
(s) GH
K
K(
s 1).....( s 1)
1
m
,
(
s 1).....(
1
n s 1)
m, n分别为分子、分母的阶次, 为
积分环节数目。K为开环放大倍数。
lim s R(s) s0 1 G(s)H (s)
lim
s0
s
e
(s)
R(
s)
机械控制工程基础
§4.6系统误差分析
例 1 系统结构图如右图所示,求 r(t)分别为A·1(t), At, At2/2时系
统的稳态误差。
解:
e
(s)
E(s) R(s)
s(Ts 1) s(Ts 1) K
r(t) A1(t)
机械控制工程基础
§4 系统的瞬态响应与误差分析
§4.1 §4.2 §4.3 §4.5 §4.6
时间响应 一阶系统的时间响应 二阶系统的时间响应 瞬态响应的性能指标 系统误差分析
机械控制工程基础
§4.6 系统误差分析
主要内容
一、误差与稳态误差 1、误差信号 2、稳态误差 3、稳态误差计算方法 例1
二、系统类型和误差系数 三、扰动作用下稳态误差分析
型次
稳态误差
1
0
1 K
0
1 K
1
0
0
K
机械控制工程基础
结论: 1)提高系统型次,可减小或消除系统的稳态偏差。 2)增大系统开环增益,有利于减小系统的稳态偏差。
机械控制工程基础
§4.6系统误差分析
三、扰动作用下系统稳态误差分析
分析:设ess1、ess2分别由R(s)、N(s)引起。
(1)、R(s)作用时,N(s)=0
E1 ( s)
4s 1 s(5 4s)
ess1
lim s0
s
E1 (s)
4s 1 lim s0 5 4s
1 5
(2)、N(s)作用时,R(s)=0 ,
E (s) 4 N(s) 0 E (s)
2 4s 1 3s 1
2
ess 2
lim
s0
s
E2 (s)
1 5
1 1
E2
(s)
s 1
3s 4
1
4s 1
X i(s) H (s) E(s) G(s)
E(s)
1 1 GH
X
i
(s)
Xi(s)
E(s) G(s)
- Xb(s)
H(s)
Xo(s)
e 稳态误差 ss
lime(t) t
lims s0
E(s)
lsim0 1
s GH
X
i
(s)
机械控制工程基础
1、误差系数
ess
lsim0 1
s GH
X
i
(s)
1)输入为单位阶跃信号时,xi
(t)
1(t
0)
X
i
(s)
1 s
,
e 则 ss
lsim0 1s GHຫໍສະໝຸດ 1 slsim0 1
1 GH
。
令 K p limG(s)H (s),称为位置误差系数。 s0
x X 2)输入为斜坡信号时, (t) t(t 0) i
i
(s)
1 s2
,
e lim lim lim 则
当 0、1、2时,分别称为0型、型、 型系统。
机械控制工程基础
误差系数
K
p
limGH s0
lim s0
K
s
K lim lim
v
sGH
K
1
s
s0
s0
K lims lim s
a s0
2 GH
s0
K
2
误差
系统 系数 K p K v K a
型次
0
K0 0
K 0
K
系统 系统输入 单位阶跃 斜坡 加速度
e e e 0
ss
ss1
ss 2
机械控制工程基础
补充:机械系统时间响应作图方法
作二阶系统
w 6 n
G(s)
s2
w2 n
2wn s
w2 n
0.7
在Matlab下编M文件: wn=6; kesi=0.7; figure(1) num=wn.^2; den=[1 2*kesi*wn wn.^2]; step(num,den) title('step response')
