圆综合练习题
中考数学总复习《圆的综合题》练习题(附答案)
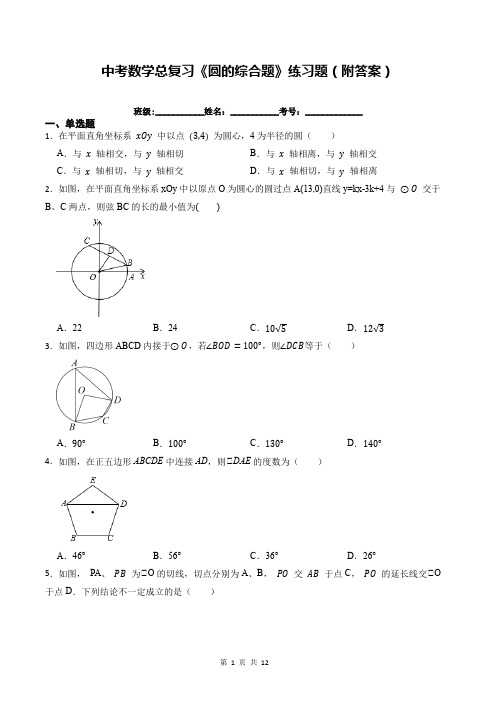
中考数学总复习《圆的综合题》练习题(附答案)班级:___________姓名:___________考号:_____________一、单选题1.在平面直角坐标系xOy中以点(3,4)为圆心,4为半径的圆()A.与x轴相交,与y轴相切B.与x轴相离,与y轴相交C.与x轴相切,与y轴相交D.与x轴相切,与y轴相离2.如图,在平面直角坐标系xOy中以原点O为圆心的圆过点A(13,0)直线y=kx-3k+4与⊙O交于B、C两点,则弦BC的长的最小值为()A.22B.24C.10√5D.12√33.如图,四边形ABCD内接于⊙O,若∠BOD=100°,则∠DCB等于()A.90°B.100°C.130°D.140°4.如图,在正五边形ABCDE中连接AD,则∠DAE的度数为()A.46°B.56°C.36°D.26°5.如图,PA、PB为∠O的切线,切点分别为A、B,PO交AB于点C,PO的延长线交∠O 于点D.下列结论不一定成立的是()A.△BPA为等腰三角形B.AB与PD相互垂直平分C.点A,B都在以PO为直径的圆上D.PC为△BPA的边AB上的中线6.如图,四边形ABCD内接于半径为6的∠O中连接AC,若AB=CD,∠ACB=45°,∠ACD=12∠BAC,则BC的长度为()A.6 √3B.6 √2C.9 √3D.9 √27.如图,点A,B,D,C是∠O上的四个点,连结AB,CD并延长,相交于点E,若∠BOD=20°,∠AOC=90°,则∠E的度数为()A.30°B.35°C.45°D.55°8.∠ABC中∠C=Rt∠,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB,BC分别交于点E,D,则AE的长为()A.95B.125C.185D.3659.如图,AB为∠O的直径,点C在∠O上,若∠B=60°,则∠A等于()A.80°B.50°C.40°D.30°10.两个圆的半径分别是2cm和7cm,圆心距是5cm,则这两个圆的位置关系是() A.外离B.内切C.相交D.外切11.已知正三角形的边长为12,则这个正三角形外接圆的半径是()A.B.C.D.12.一个扇形的弧长为4π,半径长为4,则该扇形的面积为()A.4πB.6πC.8πD.12π二、填空题13.在Rt∠ABC中∠C=90°,AB=5,BC=4,求内切圆半径14.如图,∠C过原点,且与两坐标轴分别交于点A,点B,点A的坐标为(0,3),M是第三象限内弧OB上一点,∠BMO=120°,则∠C的半径为.15.一个立体图形的三视图如图所示,根据图中数据求得这个立体图形的侧面积为.16.一个半径为5cm的球形容器内装有水,若水面所在圆的直径为8cm,则容器内水的高度为cm.17.如图,在直角坐标系中以点P为圆心的圆弧与x轴交于A,B两点,已知P(4,2)和A(2,0),则点B的坐标是.18.下面是“作一个30°角”的尺规作图过程.已知:平面内一点A.求作:∠A,使得∠A=30°.作法:如图①作射线AB;②在射线AB取一点O,以O为圆心,OA为半径作圆,与射线AB相交于点C;③以C为圆心,OC C为半径作弧,与⊙O交于点D,作射线AD.则∠DAB即为所求的角.请回答:该尺规作图的依据是.三、综合题19.如图,在△ABC中AC=BC=BD,点O在AC边上,OC为⊙O的半径,AB是⊙O 的切线,切点为点D,OC=2,OA=2√2.(1)求证:BC是⊙O的切线;(2)求阴影部分的面积.20.如图,△ABC内接于⊙O,CD是直径,∠CBG=∠BAC,CD与AB相交于点E,过点E作EF⊥BC,垂足为F,过点O作OH⊥AC,垂足为H,连接BD、OA.(1)求证:直线BG与⊙O相切;(2)若BEOD=54,求EFAC的值.21.如图,四边形ABCD 内接于∠O,BD是∠O的直径,过点A作∠O的切线AE交CD的延长线于点E,DA平分∠BDE.(1)求证:AE∠CD;(2)已知AE=4cm,CD=6cm,求∠O的半径.22.如图,∠O是∠ABC的外接圆,BC为∠O的直径,点E为∠ABC的内心,连接AE并延长交∠O 于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.(1)求证:DB=DE;(2)求证:直线CF为∠O的切线.23.公元前5世纪,古希腊哲学家阿那克萨哥拉因“亵渎神灵罪”而被投人监狱,在狱中他对方铁窗和圆月亮产生了兴趣.他不断变换观察的位置,一会儿看见圆比正方形大,一会儿看见正方形比圆大,于是伟大的古希腊尺规作图几何三大问题之--的化圆为方问题诞生了:作一个正方形,使它的面积等于已知圆的面积(1)设有一个半径为√3的圆,则这个圆的周长为,面积为,作化圆为方得到的正方形的边长为(计算结果保留π)(2)由于对尺规作图的限制(只能有限次地使用没有刻度的直尺和圆规进行作图),包括化圆为方在内的几何三大问题都已被证明是不可能的.但若不受标尺的限制,化圆为方并非难事。
初三数学圆的综合的专项培优练习题(含答案)及答案解析

初三数学圆的综合的专项培优练习题(含答案)及答案解析一、圆的综合1.如图,四边形OABC 是平行四边形,以O 为圆心,OA 为半径的圆交AB 于D ,延长AO 交O 于E ,连接CD ,CE ,若CE 是⊙O 的切线,解答下列问题:(1)求证:CD 是⊙O 的切线;(2)若BC=4,CD=6,求平行四边形OABC 的面积.【答案】(1)证明见解析(2)24【解析】试题分析:(1)连接OD ,求出∠EOC=∠DOC ,根据SAS 推出△EOC ≌△DOC ,推出∠ODC=∠OEC=90°,根据切线的判定推出即可;(2)根据切线长定理求出CE=CD=4,根据平行四边形性质求出OA=OD=4,根据平行四边形的面积公式=2△COD 的面积即可求解.试题解析:(1)证明:连接OD ,∵OD=OA ,∴∠ODA=∠A ,∵四边形OABC 是平行四边形,∴OC ∥AB ,∴∠EOC=∠A ,∠COD=∠ODA ,∴∠EOC=∠DOC ,在△EOC 和△DOC 中,OE OD EOC DOC OC OC =⎧⎪∠=∠⎨⎪=⎩∴△EOC ≌△DOC (SAS ),∴∠ODC=∠OEC=90°,即OD ⊥DC ,∴CD 是⊙O 的切线;(2)由(1)知CD 是圆O 的切线,∴△CDO 为直角三角形,∵S △CDO =12CD•OD , 又∵OA=BC=OD=4,∴S△CDO=12×6×4=12,∴平行四边形OABC的面积S=2S△CDO=24.2.如图,⊙M交x轴于B、C两点,交y轴于A,点M的纵坐标为2.B(﹣33,O),C(3,O).(1)求⊙M的半径;(2)若CE⊥AB于H,交y轴于F,求证:EH=FH.(3)在(2)的条件下求AF的长.【答案】(1)4;(2)见解析;(3)4.【解析】【分析】(1)过M作MT⊥BC于T连BM,由垂径定理可求出BT的长,再由勾股定理即可求出BM的长;(2)连接AE,由圆周角定理可得出∠AEC=∠ABC,再由AAS定理得出△AEH≌△AFH,进而可得出结论;(3)先由(1)中△BMT的边长确定出∠BMT的度数,再由直角三角形的性质可求出CG 的长,由平行四边形的判定定理判断出四边形AFCG为平行四边形,进而可求出答案.【详解】(1)如图(一),过M作MT⊥BC于T连BM,∵BC是⊙O的一条弦,MT是垂直于BC的直径,∴BT=TC=123∴124;(2)如图(二),连接AE,则∠AEC=∠ABC,∵CE⊥AB,∴∠HBC+∠BCH=90°在△COF中,∵∠OFC+∠OCF=90°,∴∠HBC=∠OFC=∠AFH,在△AEH和△AFH中,∵AFH AEHAHF AHE AH AH∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△AEH≌△AFH(AAS),∴EH=FH;(3)由(1)易知,∠BMT=∠BAC=60°,作直径BG,连CG,则∠BGC=∠BAC=60°,∵⊙O的半径为4,∴CG=4,连AG,∵∠BCG=90°,∴CG⊥x轴,∴CG∥AF,∵∠BAG=90°,∴AG⊥AB,∵CE⊥AB,∴AG∥CE,∴四边形AFCG为平行四边形,∴AF=CG=4.【点睛】本题考查的是垂径定理、圆周角定理、直角三角形的性质及平行四边形的判定与性质,根据题意作出辅助线是解答此题的关键.3.如图,⊙O的半径为6cm,经过⊙O上一点C作⊙O的切线交半径OA的延长于点B,作∠ACO的平分线交⊙O于点D,交OA于点F,延长DA交BC于点E.(1)求证:AC∥OD;(2)如果DE⊥BC,求»AC的长度.【答案】(1)证明见解析;(2)2π.【解析】试题分析:(1)由OC=OD,CD平分∠ACO,易证得∠ACD=∠ODC,即可证得AC∥OD;(2)BC切⊙O于点C,DE⊥BC,易证得平行四边形ADOC是菱形,继而可证得△AOC是等边三角形,则可得:∠AOC=60°,继而求得弧AC的长度.试题解析:(1)证明:∵OC=OD,∴∠OCD=∠ODC.∵CD平分∠ACO,∴∠OCD=∠ACD,∴∠ACD=∠ODC,∴AC∥OD;(2)∵BC切⊙O于点C,∴BC⊥OC.∵DE⊥BC,∴OC∥DE.∵AC∥OD,∴四边形ADOC 是平行四边形.∵OC=OD,∴平行四边形ADOC是菱形,∴OC=AC=OA,∴△AOC是等边三角形,∴∠AOC=60°,∴弧AC的长度=606180π⨯=2π.点睛:本题考查了切线的性质、等腰三角形的判定与性质、菱形的判定与性质以及弧长公式.此题难度适中,注意掌握数形结合思想的应用.4.如图,△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,交BC于点E(BE>EC),且BD=23.过点D作DF∥BC,交AB的延长线于点F.(1)求证:DF为⊙O的切线;(2)若∠BAC=60°,DE=7,求图中阴影部分的面积.【答案】(1)详见解析;(2)32π.【解析】【分析】(1)连结OD,根据垂径定理得到OD⊥BC,根据平行线的性质得到OD⊥DF,根据切线的判定定理证明;(2)连结OB,连结OD交BC于P,作BH⊥DF于H,证明△OBD为等边三角形,得到∠ODB=60°,3PE,证明△ABE∽△AFD,根据相似三角形的性质求出AE,根据阴影部分的面积=△BDF的面积-弓形BD的面积计算.【详解】证明:(1)连结OD,∵AD平分∠BAC交⊙O于D,∴∠BAD=∠CAD,∴»»BD CD=,∴OD⊥BC,∵BC∥DF,∴OD⊥DF,∴DF为⊙O的切线;(2)连结OB,连结OD交BC于P,作BH⊥DF于H,∵∠BAC=60°,AD平分∠BAC,∴∠BAD=30°,∴∠BOD=2∠BAD=60°,∴△OBD为等边三角形,∴∠ODB=60°,3,∴∠BDF=30°,∵BC∥DF,∴∠DBP=30°,在Rt△DBP中,PD=123,3,在Rt△DEP中,∵37∴22(7)(3)=2,∵OP⊥BC,∴BP=CP=3,∴CE=3﹣2=1,∵∠DBE=∠CAE,∠BED=∠AEC,∴△BDE∽△ACE,∴AE:BE=CE:DE,即AE:5=17,∴57∵BE∥DF,∴△ABE∽△AFD,∴BE AE DF AD=,即5757125DF=,解得DF=12,在Rt△BDH中,BH=12BD=3,∴阴影部分的面积=△BDF的面积﹣弓形BD的面积=△BDF的面积﹣(扇形BOD的面积﹣△BOD的面积)=22160(23)3123(23)23604π⨯⨯⨯--⨯ =93﹣2π.【点睛】考查的是切线的判定,扇形面积计算,相似三角形的判定和性质,圆周角定理的应用,等边三角形的判定和性质,掌握切线的判定定理,扇形面积公式是解题的关键.5.如图1,是用量角器一个角的操作示意图,量角器的读数从M点开始(即M点的读数为0),如图2,把这个量角器与一块30°(∠CAB=30°)角的三角板拼在一起,三角板的斜边AB与量角器所在圆的直径MN重合,现有射线C绕点C从CA开始沿顺时针方向以每秒2°的速度旋转到与CB,在旋转过程中,射线CP与量角器的半圆弧交于E.连接BE.(1)当射线CP经过AB的中点时,点E处的读数是,此时△BCE的形状是;(2)设旋转x秒后,点E处的读数为y,求y与x的函数关系式;(3)当CP旋转多少秒时,△BCE是等腰三角形?【答案】(1)60°,直角三角形;(2)y=4x(0≤x≤45);(3)7.5秒或30秒【解析】【分析】(1)根据圆周角定理即可解决问题;(2)如图2﹣2中,由题意∠ACE=2x,∠AOE=y,根据圆周角定理可知∠AOE=2∠ACE,可得y=2x(0≤x≤45);(3)分两种情形分别讨论求解即可;【详解】解:(1)如图2﹣1中,∵∠ACB=90°,OA=OB,∴OA=OB=OC,∴∠OCA=∠OAC=30°,∴∠AOE=60°,∴点E处的读数是60°,∵∠E=∠BAC=30°,OE=OB,∴∠OBE=∠E=30°,∴∠EBC=∠OBE+∠ABC=90°,∴△EBC是直角三角形;故答案为60°,直角三角形;(2)如图2﹣2中,∵∠ACE=2x,∠AOE=y,∵∠AOE=2∠ACE,∴y=4x(0≤x≤45).(3)①如图2﹣3中,当EB=EC时,EO垂直平分线段BC,∵AC⊥BC,∵EO∥AC,∴∠AOE=∠BAC=30°,∠AOE=15°,∴∠ECA=12∴x=7.5.②若2﹣4中,当BE=BC时,易知∠BEC=∠BAC=∠BCE=30°,∴∠OBE=∠OBC=60°,∵OE=OB,∴△OBE是等边三角形,∴∠BOE=60°,∴∠AOB=120°,∠ACB=60°,∴∠ACE=12∴x=30,综上所述,当CP旋转7.5秒或30秒时,△BCE是等腰三角形;【点睛】本题考查几何变换综合题、创新题目、圆周角定理、等腰三角形的判定和性质等知识,解题的关键是理解题意,学会用分类讨论的思想思考问题,属于中考压轴题.6..如图,△ABC中,∠ACB=90°,∠A=30°,AB=6.D是线段AC上一个动点(不与点A 重合),⊙D与AB相切,切点为E,⊙D交射线..DC于点F,过F作FG⊥EF交直线..BC于点G,设⊙D的半径为r.(1)求证AE=EF;(2)当⊙D与直线BC相切时,求r的值;(3)当点G落在⊙D内部时,直接写出r的取值范围.【答案】(1)见解析,(2)r=3,(3)63 3r<<【解析】【分析】(1)连接DE,则∠ADE=60°=∠DEF+∠DFE,而∠DEF=∠DFE,则∠DEF=∠DFE=30°=∠A,即可求解;(2)如图2所示,连接DE,当圆与BC相切时,切点为F,∠A=30°,AB=6,则BF=3,AD=2r,由勾股定理,即可求解;(3)分点F在线段AC上、点F在线段AC的延长线上两种情况,分别求解即可.【详解】解:设圆的半径为r;(1)连接DE,则∠ADE=60°=∠DEF+∠DFE,而∠DEF=∠DFE,则∠DEF=∠DFE=30°=∠A,∴AE=EF;(2)如图2所示,连接DE,当圆与BC相切时,切点为F∠A=30°,AB=6,则BF=3,AD=2r ,由勾股定理得:(3r )2+9=36,解得:r=3; (3)①当点F 在线段AC 上时,如图3所示,连接DE 、DG ,333,3933FC r GC FC r =-==-②当点F 在线段AC 的延长线上时,如图4所示,连接DE 、DG ,333,3339FC r GC FC r ===-两种情况下GC 符号相反,GC 2相同,由勾股定理得:DG 2=CD 2+CG 2,点G 在圆的内部,故:DG2<r2,即:22(332)(339)2r r r +-<整理得:25113180r r -+<6335r <<【点睛】本题考查了圆的综合题:圆的切线垂直于过切点的半径;利用勾股定理计算线段的长.7.如图1,等腰直角△ABC 中,∠ACB=90°,AC=BC ,过点A ,C 的圆交AB 于点D ,交BC 于点E ,连结DE(1)若AD=7,BD=1,分别求DE ,CE 的长(2)如图2,连结CD ,若CE=3,△ACD 的面积为10,求tan ∠BCD(3)如图3,在圆上取点P 使得∠PCD=∠BCD (点P 与点E 不重合),连结PD ,且点D 是△CPF 的内心①请你画出△CPF ,说明画图过程并求∠CDF 的度数②设PC=a ,PF=b ,PD=c ,若(a-2c )(b-2c )=8,求△CPF 的内切圆半径长.【答案】(1)DE=1,CE=322)tan ∠BCD=14;(3)①135°;②2. 【解析】 【分析】(1)由A 、C 、E 、D 四点共圆对角互补为突破口求解;(2)找∠BDF 与∠ODA 为对顶角,在⊙O 中,∠COD=2∠CAD ,证明△OCD 为等腰直角三角形,从而得到∠EDC+∠ODA=45°,即可证明∠CDF=135°;(3)过点D 做DH CB ⊥于点H ,以D 为圆心,DH 为半径画圆,过点P 做D e 切线PF 交CB 的延长线于点F ,结合圆周角定理得出∠CPD=∠CAD=45°,再根据圆的内心是三角形三个内角角平分线的交点,得出∠CPF=90°,然后根据角平分线性质得出114522DCF CFD PCF PFC ∠+∠=∠+∠=︒,最后再根据三角形内角和定理即可求解;证明∠DCF+∠CFD=45°,从而证明∠CPF 是直角,再求证四边形PKDN 是正方形,最后以△PCF 面积不变性建立等量关系,结合已知(2c )(2c )=8,消去字母a ,b 求出c 值,即求出△CPF 2c . 【详解】 (1)由图可知:设BC=x .在Rt △ABC 中,AC=BC .由勾股定理得: AC 2+BC 2=AB 2,∵AB=AD+BD ,AD=7,BD=1, ∴x 2+x 2=82, 解得:x=42.∵⊙O 内接四边形,∠ACD=90°, ∴∠ADE=90°, ∴∠EDB=90°, ∵∠B=45°,∴△BDE 是等腰直角三形. ∴DE=DB , 又∵DB=1, ∴DE=1, 又∵CE=BC-BE , ∴CE=42232-=. (2)如图所示:在△DCB 中过点D 作DM ⊥BE ,设BE=y ,则DM=12y , 又∵CE=3,∴BC=3+y , ∵S △ACB =S ACD +S DCB ,∴()1114242103y y 222⨯=+⨯+⨯, 解得:y=2或y=-11(舍去). ∴EM=1,CM=CE+ME=1+3=4, 又∵∠BCD=∠MCD ,∴tan ∠BCD=tan ∠MCD , 在Rt △DCM 中,tan ∠MCD=DM CM =14, ∴tan ∠BCD=14. (3)①如下图所示:过点D 做DH CB ⊥于点H ,以D 为圆心,DH 为半径画圆,过点P 做D e 切线PF 交CB 的延长线于点F .∵∠CAD=45°, ∴∠CPD=∠CAD=45°, 又∵点D 是CPF ∆的内心, ∴PD 、CD 、DF 都是角平分线,∴∠FPD=∠CPD =45°,∠PCD=∠DCF ,∠PFD=∠CFD ∴∠CPF=90° ∴∠PCF+∠PFC=90°∴114522DCF CFD PCF PFC ∠+∠=∠+∠=︒ ∴∠CDF=180°-∠DCF-∠CFD F=90°+45°=135°, 即∠CDF 的度数为135°. ②如下图所示过点D 分别作DK ⊥PC ,DM ⊥CF ,DN ⊥PF 于直线PC ,CF 和PF 于点K ,M ,N 三点, 设△PCF 内切圆的半径为m ,则DN=m ,∵点D 是△PCF 的内心, ∴DM=DN=DK ,又∵∠DCF+∠CFD+∠FDC=180°,∠FDC=45°, ∴∠DCF+∠CFD=45°,又∵DC ,DF 分别是∠PCF 和∠PFC 的角平分线, ∴∠PCF=2∠DCF ,∠PFC=2∠DFC , ∴∠PCF+∠PFC=90°, ∴∠CPF=90°.在四边形PKDN 中,∠PND=∠NPK=∠PKD=90°, ∴四边形PKDN 是矩形, 又∵KD=ND ,∴四边形PKDN 是正方形. 又∵∠MBD=∠BDM=45°, ∠BDM=∠KDP , ∴∠KDP=45°. ∵PC=a ,PF=b ,PD=c ,∴,∴NF=b -,CK=a -, 又∵CK=CM ,FM=FN ,CF=CM+FM , ∴CF=a b +, 又∵S △PCF =S △PDF +S △PDC +S △DCF ,∴1111ab a b (a b 2222=+++-),化简得:)2a b c c +-------(Ⅰ),又∵若(c )(c )=8化简得:()2ab a b 2c 8++=------(Ⅱ),将(Ⅰ)代入(Ⅱ)得:c 2=8,解得:c =c =-∴m=c 222==, 即△CPF 的内切圆半径长为2. 【点睛】本题考查圆的内接四边形性质,圆的内心,圆心角、圆周角,同弧(或等弧)之间的相互关系,同时也考查直角三角形,勾股定理,同角或等角的三角函数值相等和三角形的面积公式,正方形,对顶角和整式的运算等知识点;难点是作辅助线和利用等式求△CPF 的内切圆半径长.8.如图,四边形为菱形,且,以为直径作,与交于点.请仅用无刻度的直尺按下列要求画图.(保留作图痕迹)(1)在如图中,过点作边上的高.(2)在如图中,过点作的切线,与交于点.【答案】(1)如图1所示.(答案不唯一),见解析;(2)如图2所示.(答案不唯一),见解析.【解析】【分析】(1)连接AC交圆于一点F,连接PF交AB于点E,连接CE即为所求.(2)连接OF交BC于Q,连接PQ即为所求.【详解】(1)如图1所示.(答案不唯一)(2)如图2所示.(答案不唯一)【点睛】本题考查作图-复杂作图,菱形和圆的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.9.如图,△ABC中,AC=BC=10,cosC=35,点P是AC边上一动点(不与点A、C重合),以PA长为半径的⊙P与边AB的另一个交点为D,过点D作DE⊥CB于点E.(1)当⊙P与边BC相切时,求⊙P的半径.(2)连接BP交DE于点F,设AP的长为x,PF的长为y,求y关于x的函数解析式,并直接写出x的取值范围.(3)在(2)的条件下,当以PE长为直径的⊙Q与⊙P相交于AC边上的点G时,求相交所得的公共弦的长.【答案】(1)409R=;(2)25880320xy x xx=-++;(3)50105-.【解析】【分析】(1)设⊙P与边BC相切的切点为H,圆的半径为R,连接HP,则HP⊥BC,cosC=35,则sinC=45,sinC=HPCP=10RR-=45,即可求解;(2)首先证明PD∥BE,则EB BFPD PF=,即:2024588x yxxx-+--=,即可求解;(3)证明四边形PDBE为平行四边形,则AG=EP=BD,即:AB=DB+AD=AG+AD=45,即可求解.【详解】(1)设⊙P与边BC相切的切点为H,圆的半径为R,连接HP,则HP⊥BC,cosC=35,则sinC=45,sinC =HP CP =10R R -=45,解得:R =409; (2)在△ABC 中,AC =BC =10,cosC =35, 设AP =PD =x ,∠A =∠ABC =β,过点B 作BH ⊥AC ,则BH =ACsinC =8,同理可得:CH =6,HA =4,AB =45,则:tan ∠CAB =2, BP =228+(4)x -=2880x x -+,DA =25x ,则BD =45﹣25x , 如下图所示,PA =PD ,∴∠PAD =∠CAB =∠CBA =β,tanβ=2,则cosβ5,sinβ5, EB =BDcosβ=(525x )5=4﹣25x ,∴PD ∥BE ,∴EB BFPD PF=,即:2024588x y x xx -+--=,整理得:y 25xx 8x 803x 20-++(3)以EP 为直径作圆Q 如下图所示,两个圆交于点G,则PG=PQ,即两个圆的半径相等,则两圆另外一个交点为D,GD为相交所得的公共弦,∵点Q是弧GD的中点,∴DG⊥EP,∵AG是圆P的直径,∴∠GDA=90°,∴EP∥BD,由(2)知,PD∥BC,∴四边形PDBE为平行四边形,∴AG=EP=BD,∴AB=DB+AD=AG+AD=5设圆的半径为r,在△ADG中,AD=2rcosβ5DG5AG=2r,5=52r51+,则:DG550﹣5相交所得的公共弦的长为50﹣5【点睛】本题考查的是圆知识的综合运用,涉及到解直角三角形、勾股定理等知识,其中(3),要关键是根据题意正确画图,此题用大量的解直角三角形的内容,综合难度很大.10.如图,四边形ABCD是⊙O的内接四边形,AC为直径,»»BD AD=,DE⊥BC,垂足为E.(1)判断直线ED与⊙O的位置关系,并说明理由;(2)若CE=1,AC=4,求阴影部分的面积.【答案】(1)ED 与O e 相切.理由见解析;(2)2=33S π-阴影. 【解析】 【分析】(1)连结OD ,如图,根据圆周角定理,由»»BD AD =得到∠BAD =∠ACD ,再根据圆内接四边形的性质得∠DCE =∠BAD ,所以∠ACD =∠DCE ;利用内错角相等证明OD ∥BC ,而DE ⊥BC ,则OD ⊥DE ,于是根据切线的判定定理可得DE 为⊙O 的切线;(2)作OH ⊥BC 于H ,易得四边形ODEH 为矩形,所以OD =EH =2,则CH =HE ﹣CE =1,于是有∠HOC =30°,得到∠COD =60°,然后根据扇形面积公式、等边三角形的面积公式和阴影部分的面积=S 扇形OCD ﹣S △OCD 进行计算即可. 【详解】(1)直线ED 与⊙O 相切.理由如下:连结OD ,如图,∵»»BD AD =,∴∠BAD =∠ACD .∵∠DCE =∠BAD ,∴∠ACD =∠DCE .∵OC =OD ,∴∠OCD =∠ODC ,而∠OCD =∠DCE ,∴∠DCE =∠ODC ,∴OD ∥BC . ∵DE ⊥BC ,∴OD ⊥DE ,∴DE 为⊙O 的切线;(2)作OH ⊥BC 于H ,则四边形ODEH 为矩形,∴OD =EH .∵CE =1,AC =4,∴OC =OD =2,∴CH =HE ﹣CE =2﹣1=1.在Rt △OHC 中,∵OC =2,CH =1,∠OHC =90°,∠HOC =30°,∴∠COD =60°,∴阴影部分的面积=S 扇形OCD ﹣S △OCD26023360π⋅⋅=-•2223=π3-.【点睛】本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了扇形面积的计算.11.已知四边形ABCD 是⊙O 的内接四边形,∠DAB =120°,BC =CD ,AD =4,AC =7,求AB 的长度.【答案】AB =3. 【解析】 【分析】作DE ⊥AC ,BF ⊥AC ,根据弦、弧、圆周角、圆心角的关系,求得BC CD =u u u r u u u r,进而得到∠DAC =∠CAB =60°,在Rt △ADE 中,根据60°锐角三角函数值,可求得DE =23,AE =2,再由Rt △DEC 中,根据勾股定理求出DC 的长,在△BFC 和△ABF 中,利用60°角的锐角三角函数值及勾股定理求出AF 的长,然后根据求出的两个结果,由AB =2AF ,分类讨论求出AB 的长即可. 【详解】作DE ⊥AC ,BF ⊥AC ,∵BC =CD , ∴BC CD =u u u r u u u r, ∴∠CAB =∠DAC , ∵∠DAB =120°, ∴∠DAC =∠CAB =60°, ∵DE ⊥AC ,∴∠DEA =∠DEC =90°, ∴sin60°=4DE ,cos60°=4AE, ∴DE =3AE =2, ∵AC =7,∴CE =5,∴DC= ∴BC ,∵BF ⊥AC ,∴∠BFA =∠BFC =90°,∴tan60°=BF AF,BF 2+CF 2=BC 2, ∴BF,∴()2227AF +-=, ∴AF =2或AF =32, ∵cos60°=AF AB, ∴AB =2AF ,当AF =2时,AB =2AF =4,∴AB =AD ,∵DC =BC ,AC =AC ,∴△ADC ≌△ABC (SSS ),∴∠ADC =∠ABC ,∵ABCD 是圆内接四边形,∴∠ADC+∠ABC =180°,∴∠ADC =∠ABC =90°,但AC 2=49,2222453AD DC +=+=,AC 2≠AD 2+DC 2,∴AB =4(不合题意,舍去), 当AF =32时,AB =2AF =3, ∴AB =3.【点睛】 此题主要考查了圆的相关性质和直角三角形的性质,解题关键是构造直角三角形模型,利用直角三角形的性质解题.12.如图,BD 为△ABC 外接圆⊙O 的直径,且∠BAE =∠C .(1)求证:AE 与⊙O 相切于点A ;(2)若AE ∥BC ,BC =AC =2,求AD 的长.【答案】(1)证明见解析;(2)23【解析】【分析】(1)根据题目中已出现切点可确定用“连半径,证垂直”的方法证明切线,连接AO并延长交⊙O于点F,连接BF,则AF为直径,∠ABF=90°,根据同弧所对的圆周角相等,则可得到∠BAE=∠F,既而得到AE与⊙O相切于点A.(2))连接OC,先由平行和已知可得∠ACB=∠ABC,所以AC=AB,则∠AOC=∠AOB,从而利用垂径定理可得AH=1,在Rt△OBH中,设OB=r,利用勾股定理解得r=2,在Rt△ABD中,即可求得AD的长为3【详解】解:(1)连接AO并延长交⊙O于点F,连接BF,则AF为直径,∠ABF=90°,∵»»,AB AB∴∠ACB=∠F,∵∠BAE=∠ACB,∴∠BAE=∠F,∵∠FAB+∠F=90°,∴∠FAB+∠BAE=90°,∴OA⊥AE,∴AE与⊙O相切于点A.(2)连接OC,∵AE∥BC,∴∠BAE=∠ABC,∵∠BAE=∠ACB,∴∠ACB=∠ABC,∴AC=AB=2,∴∠AOC=∠AOB,∵OC=OB,∴OA⊥BC,∴CH=BH=1BC32在Rt△ABH中,AH=22AB BH-=1,在Rt△OBH中,设OB=r,∵OH2+BH2=OB2,∴(r﹣1)2+(3)2=r2,解得:r=2,∴DB=2r=4,在Rt△ABD中,AD=22BD AB-=2242-=23,∴AD的长为23.【点睛】本题考查了圆的综合问题,恰当的添加辅助线是解题关键.13.如图1,D是⊙O的直径BC上的一点,过D作DE⊥BC交⊙O于E、N,F是⊙O上的一点,过F的直线分别与CB、DE的延长线相交于A、P,连结CF交PD于M,∠C=12∠P.(1)求证:PA是⊙O的切线;(2)若∠A=30°,⊙O的半径为4,DM=1,求PM的长;(3)如图2,在(2)的条件下,连结BF、BM;在线段DN上有一点H,并且以H、D、C 为顶点的三角形与△BFM相似,求DH的长度.【答案】(1)证明见解析;(2)PM=32;(3)满足条件的DH的值为632-或122311+. 【解析】【分析】(1)如图1中,作PH ⊥FM 于H .想办法证明∠PFH=∠PMH ,∠C=∠OFC ,再根据等角的余角相等即可解决问题;(2)解直角三角形求出AD ,PD 即可解决问题;(3)分两种情形①当△CDH ∽△BFM 时,DH CD FM BF =. ②当△CDH ∽△MFB 时,DH CD FB MF=,分别构建方程即可解决问题; 【详解】(1)证明:如图1中,作PH ⊥FM 于H .∵PD ⊥AC ,∴∠PHM =∠CDM =90°,∵∠PMH =∠DMC ,∴∠C =∠MPH ,∵∠C =12∠FPM ,∴∠HPF =∠HPM , ∵∠HFP+∠HPF =90°,∠HMP+∠HPM =90°,∴∠PFH =∠PMH ,∵OF =OC ,∴∠C =∠OFC ,∵∠C+∠CMD =∠C+∠PMF =∠C+∠PFH =90°,∴∠OFC+∠PFC =90°,∴∠OFP =90°,∴直线PA 是⊙O 的切线. (2)解:如图1中,∵∠A =30°,∠AFO =90°,∴∠AOF =60°,∵∠AOF =∠OFC+∠OCF ,∠OFC =∠OCF ,∴∠C =30°,∵⊙O 的半径为4,DM =1,∴OA =2OF =8,CD 33,∴OD =OC ﹣CD =43,∴AD =OA+OD =8+43 =123 ,在Rt △ADP 中,DP =AD•tan30°=(12﹣3 )×33 =43 ﹣1, ∴PM =PD ﹣DM =4 3﹣2. (3)如图2中,由(2)可知:BF =12BC =4,FM =3BF =43 ,CM =2DM =2,CD =3 , ∴FM =FC ﹣CM =43﹣2,①当△CDH ∽△BFM 时,DH CD FM BF = , ∴ 3432=- ,∴DH =63- ②当△CDH ∽△MFB 时,DH CD FB MF =, ∴34432DH =- ,∴DH =1223+ , ∵DN =()22443833--=- ,∴DH <DN ,符合题意,综上所述,满足条件的DH 的值为63- 或1223+. 【点睛】本题考查圆综合题、切线的判定、解直角三角形、相似三角形的判定和性质等知识,解题的关键是熟练掌握基本知识,学会用分类讨论的思想思考问题.14.如图,是大半圆的直径,是小半圆的直径,点是大半圆上一点,与小半圆交于点,过点作于点. (1)求证:是小半圆的切线; (2)若,点在上运动(点不与两点重合),设,. ①求与之间的函数关系式,并写出自变量的取值范围;②当时,求两点之间的距离.【答案】(1)见解析;(2)①,,②两点之间的距离为或.【解析】【分析】(1)连接CO、CM,只需证到CD⊥CM.由于CD⊥OP,只需证到CM∥OP,只需证到CM 是△AOP的中位线即可.(2)①易证△ODC∽△CDP,从而得到CD2=DP•OD,进而得到y与x之间的函数关系式.由于当点P与点A重合时x=0,当点P与点B重合时x=4,点P在大半圆O上运动(点P不与A,B两点重合),因此自变量x的取值范围为0<x<4.②当y=3时,得到-x2+4x=3,求出x.根据x的值可求出CD、PD的值,从而求出∠CPD,运用勾股定理等知识就可求出P,M两点之间的距离.【详解】(1)连接,如图1所示∵是小半圆的直径,∴即∵∴∵∴∴,∵∴,∴∴.,即∵经过半径的外端,且∴直线是小半圆的切线.(2)①∵,,∴∴∴∽∴∴∵,,,∴当点与点重合时,;当点与点重合时,∵点在大半圆上运动(点不与两点重合),∴∴与之间的函数关系式为,自变量的取值范围是.②当时,解得,Ⅰ当时,如图2所示在中,∵,∴,∴∵,∴是等边三角形∵∴∴.Ⅱ当时,如图3所示,同理可得∵∴∴过点作,垂足为,连接,如图3所示∵,∴同理在中,∵,∴综上所述,当时,两点之间的距离为或.【点睛】考查了切线的判定、平行线的判定与性质、等边三角形的判定与性质、相似三角形的判定与性质、特殊角的三角函数值、勾股定理等知识,综合性比较强.15.如图,已知四边形ABCD内接于⊙O,点E在CB的延长线上,连结AC、AE,∠ACB=∠BAE=45°.(1)求证:AE是⊙O的切线;(2)若AB=AD,AC=32,tan∠ADC=3,求BE的长.【答案】(1)证明见解析;(2)52 BE【解析】试题分析:(1)连接OA、OB,由圆周角定理得出∠AOB=2∠ACB=90°,由等腰直角三角形的性质得出∠OAB=∠OBA=45°,求出∠OAE=∠OAB+∠BAE=90°,即可得出结论;(2)过点A 作AF ⊥CD 于点F,由AB=AD ,得到∠ACD =∠ACB =45°,在Rt △AFC 中可求得AF=3,在Rt △AFD 中求得DF =1,所以AB =AD = ,CD = CF +DF =4,再证明△ABE ∽△CDA ,得出BE AB DA CD =,即可求出BE 的长度; 试题解析:(1)证明:连结OA ,OB ,∵∠ACB =45°,∴∠AOB =2∠ACB = 90°,∵OA=OB ,∴∠OAB =∠OBA =45°,∵∠BAE =45°,∴∠OAE =∠OAB +∠BAE =90°,∴OA ⊥AE .∵点A 在⊙O 上,∴AE 是⊙O 的切线.(2)解:过点A 作AF ⊥CD 于点F ,则∠AFC =∠AFD =90°.∵AB=AD , ∴AB u u u r =AD u u u r∴∠ACD =∠ACB =45°,在Rt △AFC 中,∵AC =∠ACF =45°,∴AF=CF=AC ·sin ∠ACF =3,∵在Rt △AFD 中, tan ∠ADC=3AF DF =, ∴DF =1,∴AB AD ==且CD = CF +DF =4,∵四边形ABCD 内接于⊙O ,∴∠ABE =∠CDA ,∵∠BAE =∠DCA ,∴△ABE ∽△CDA , ∴BE AB DA CD=,∴10=,10∴5BE=.2。
圆的专项练习题

圆的专项练习题一、选择题(每题3分,共30分)1. 圆的周长公式是()。
A. C = πrB. C = 2πrC. C = 4πrD. C = πd2. 半径为5厘米的圆的周长是()厘米。
A. 31.4B. 15.7C. 62.8D. 94.23. 圆的面积公式是()。
A. S = πr²B. S = 2πrC. S = πrD. S = πd²4. 半径为3厘米的圆的面积是()平方厘米。
A. 9πB. 18πC. 28.26D. 56.525. 一个扇形的半径为4厘米,圆心角为30°,其面积是()平方厘米。
A. 2πB. 4πC. 6πD. 8π6. 圆的直径是半径的()倍。
A. 1B. 2C. 3D. 47. 圆的内接四边形的对角线()。
A. 互相垂直B. 互相平分C. 相等D. 互相垂直且相等8. 圆的切线在切点处与半径()。
A. 垂直B. 平行C. 重合D. 相交9. 圆的外切四边形的对边()。
A. 相等B. 互相垂直C. 平行D. 互相垂直且相等10. 圆的弧长公式是()。
A. L = rθB. L = πrθC. L = 2πrθD. L = πr/θ二、填空题(每题2分,共20分)11. 圆的周长是半径的________倍。
12. 如果圆的周长为40π厘米,那么它的半径是________厘米。
13. 一个圆的直径为10厘米,它的面积是________平方厘米。
14. 圆的内接正六边形的边长等于圆的________。
15. 圆的内接正三角形的边长是半径的________倍。
16. 圆的外切正六边形的边长等于圆的________。
17. 圆的外接正三角形的边长是半径的________倍。
18. 圆的切线与圆相切于一点,这一点叫做圆的________。
19. 圆的内切圆与外接圆的半径之和等于________。
20. 圆的内切正多边形的边数越多,其形状越接近于________。
2023年中考九年级数学高频考点提升练习--圆的综合题(含答案)
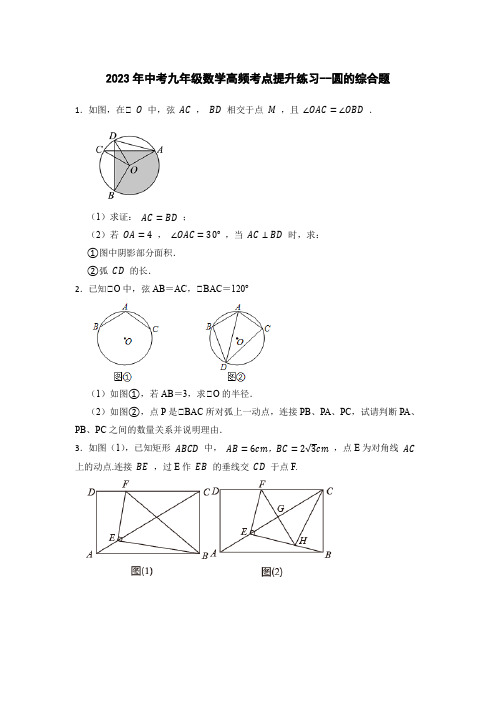
2023年中考九年级数学高频考点提升练习--圆的综合题1.如图,在⊙ O中,弦AC,BD相交于点M,且∠OAC=∠OBD.(1)求证:AC=BD;(2)若OA=4,∠OAC=30°,当AC⊥BD时,求:①图中阴影部分面积.②弧CD的长.2.已知⊙O中,弦AB=AC,⊙BAC=120°(1)如图①,若AB=3,求⊙O的半径.(2)如图②,点P是⊙BAC所对弧上一动点,连接PB、PA、PC,试请判断PA、PB、PC之间的数量关系并说明理由.3.如图(1),已知矩形ABCD中,AB=6cm,BC=2√3cm,点E为对角线AC 上的动点.连接BE,过E作EB的垂线交CD于点F.(1)探索BE与EF的数量关系,并说明理由.(2)如图(2),过F作AC垂线交AC于点G,交EB于点H,连接CH.若点E从A出发沿AC方向以2√3cm/s的速度向终点C运动,设E的运动时间为ts.①是否存在t,使得H与B重合?若存在,求出t的值;若不存在,说明理由;②t为何值时,△CFH是等腰三角形;③当CG=GH时,求△CGH的面积.4.如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.(1)求证:CD是⊙O的切线;(2)求证:⊙C=2⊙DBE.(3)若EA=AO=2,求图中阴影部分的面积.(结果保留π)5.定义:三角形一边上的点将该边分为两条线段,且这两条线段的积等于这个点到该边所对顶点连线的平方,则称这个点为三角形该边的“好点”.如图1,⊙ABC中,点D 是BC边上一点,连结AD,若AD2=BD⋅CD,则称点D是⊙ABC中BC边上的“好点”.(1)如图2,⊙ABC的顶点是4×3网格图的格点,请仅用直尺画出AB边上的一个“好点”.(2)⊙ABC中,BC=9,tanB=43,tanC=23,点D是BC边上的“好点”,求线段BD的长.(3)如图3,⊙ABC是⊙O的内接三角形,OH⊙AB于点H,连结CH并延长交⊙O于点D.①求证:点H是⊙BCD中CD边上的“好点”.②若⊙O的半径为9,⊙ABD=90°,OH=6,请直接写出CHDH的值.6.如图,⊙O为等边⊙ABC的外接圆,半径为2,点D在劣弧上运动(不与点A,B 重合),连接DA,DB,DC.(1)求证:DC是⊙ADB的平分线;(2)设四边形ADBC的面积为S,线段DC的长为x,试用含x的代数式表示S;(3)若点M,N分别在线段CA,CB上运动(不含端点),经过探究发现,点D 运动到每一个确定的位置,⊙DMN的周长有最小值t,随着点D的运动,t的值会发生变化,求所有t值中的最大值.7.在⊙ABC中,D,E分别是⊙ABC两边的中点,如果弧DE(可以是劣弧、优弧或半圆)上的所有点都在⊙ABC的内部或边上,则称弧DE为⊙ABC的中内弧.例如,图1中弧DE是⊙ABC其中的某一条中内弧.(1)如图2,在边长为4 √3的等边⊙ABC中,D,E分别是AB,AC的中点.画出⊙ABC的最长的中内弧DE,并直接写出此时弧DE的长;(2)在平面直角坐标系中,已知点A(2 √3,6),B(0,0),C(t,0),在⊙ABC中,D,E分别是AB,AC的中点.①若t=2 √3,求⊙ABC的中内弧DE所在圆的圆心P的纵坐标的取值范围;②请写出一个t的值,使得⊙ABC的中内弧DE所在圆的圆心P的纵坐标可以取全体实数值.8.如图,⊙O是⊙ABC的外接圆,AC是直径,过点O作OD⊙AB于点D,延长DO 交⊙O于点P,过点P作PE⊙AC于点E,作射线DE交BC的延长线于F点,连接PF.(1)若⊙POC=60°,AC=12,求劣弧PC的长;(结果保留π)(2)求证:OD=OE;(3)求证:PF是⊙O的切线.9.如图,点A和动点P在直线l上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O.点C在点P右侧,PC=4,过点C作直线m⊥l,过点O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=32CD,以DE,DF为邻边作矩形DEGF.设AQ=3x.(1)用关于x的代数式表示BQ=,DF=.(2)当点P在点A右侧时,若矩形DEGF的面积等于90,求AP的长.(3)当点P在点A右侧时,作直线BG交⊙O于点N,若BN的弦心距为1,求AP的长.10.如图,⊙ABC中,⊙ACB=90°,D是边AB上一点,且⊙A=2⊙DCB.E是BC边上的一点,以EC为直径的⊙O经过点D.(1)求证:AB是⊙O的切线;(2)若CD的弦心距为1,BE=EO,求BD的长.11.已知:A、B两点在直线l的同一侧,线段AO,BM均是直线l的垂线段,且BM 在AO的右边,AO=2BM,将BM沿直线l向右平移,在平移过程中,始终保持⊙ABP=90°不变,BP边与直线l相交于点P.(1)当P与O重合时(如图2所示),设点C是AO的中点,连接BC.求证:四边形OCBM是正方形;(2)请利用如图1所示的情形,求证:ABPB=OMBM;(3)若AO=2 √6,且当MO=2PO时,请直接写出AB和PB的长.12.(问题情境)如图①,小区A、B位于一条笔直的道路l的同侧,为了方便A,B两个小区居民投放垃圾,现在l上建一个垃圾分类站C,使得C与A,B的距离之比为2:1.(1)(初步研究)在线段AB上作出点C,使CACB=2.如图,做法如下:第一步:过点A作射线AM,以A为圆心,任意长为半径画弧,交AM于点P1;以P1为圆心,AP1长为半径画弧,交AM于点P2;以P2为圆心,AP1长为半径画弧,交AM于点P3.第二步:连接BP3,作∠AP2C=∠AP3B,交AB于点C.则点C即为所求.请证明所作的点C满足CACB=2.(2)(深入思考)如图,点C在线段AB上,点D在直线AB外,且DADB=CACB=2.求证:DC是∠ADB的平分线.(3)(问题解决)如图,已知点A,B和直线l,点C在线段AB上,且CACB=2.用直尺和圆规完成下列作图.(保留作图痕迹,不写作法)(⊙)在直线AB上作出点E(异于点C),使EAEB=2;(⊙)在直线l上作出点F,使FAFB=2.13.在矩形ABCD中,BC=2AB,点E是对角线AC上任意一点,过点E作AD的垂线分别交AD,BC于点F,G,作FH平行AC交CD于点H.(1)证明:EF=CH.(2)连结GH交AC于点K,若AE:CK=3,求AE:EK的值.(3)作⊙FGH的外接圆⊙O,且AB=1.①若⊙O与矩形的边相切时,求CH的长.②作点E关于GH的对称点E',当E'落在⊙O上时,直接写出⊙FGH的面积。
小学六年级圆的练习题综合

小学六年级圆的练习题综合圆单元练题(一)一、完成下表。
圆的半径r | 2cm | 4cm | 8cm |圆的直径d | 4cm | 8cm | 16cm |圆的周长C | 12.56cm | 25.12cm | 50.24cm |圆的面积S | 12.56cm² | 50.24cm² | 201.06cm² |二、想一想,填一填。
1、当圆规两脚间的距离为4厘米时,画出圆的周长是(12.56)厘米。
2、在一张长8厘米,宽12厘米的长方形纸上画一个最大的圆,这个圆的直径是(8cm),面积是(16π)平方厘米,周长是(8π)厘米。
3、一个车轮的直径是55厘米,车轮转动一周,大约前进(172.7)米。
4、一个环形的外圆直径是10cm,内圆直径是8cm,它的面积(9.42)cm²。
5、一个圆的半径扩大2倍,它的周长扩大(2)倍,面积扩大(4)倍。
6、把一个圆分成若干等份,剪开拼成一个近似的长方形。
这个长方形的长相当于(圆的周长),长方形的宽就是圆的(直径)。
因为长方形的面积是(πr²),所以圆的面积是(πr²)。
7、圆的直径是6厘米,它的周长是(18.84)厘米,面积是(28.27)平方厘米。
8、圆的周长是25.12分米,它的面积是(50.24)平方分米。
9、甲圆半径是乙圆半径的3倍,甲圆的周长是乙圆周长的(3)倍,甲圆面积是乙圆面积的(9)倍。
10、一个圆的半径是8厘米,这个圆面积的3/4是(48π)平方厘米。
11、周长相等的长方形、正方形、圆,(圆)面积最大。
12、圆的半径由6厘米增加到9厘米,圆的面积增加了(63π-36π=27π)平方厘米。
13、要在一个边长为10厘米的正方形纸板里剪出一个最大的圆,剩下的面积是(100-25π)平方厘米。
14、用圆规画一个圆,如果圆规两脚之间的距离是7厘米,画出的这个圆的周长是(14π)厘米。
这个圆的面积是(49π)平方厘米。
中考数学《圆的综合题》专项练习题及答案

中考数学《圆的综合题》专项练习题及答案一、单选题1.如图,在一块正三角形飞镖游戏板上画一个正六边形(图中阴影部分),假设飞镖投中游戏板上的每一点是等可能的(若投中边界或没有投中游戏板,则重投1次),任意投掷飞镖1次,则飞镖投中阴影部分的概率为()A.13B.49C.12D.232.如图,AB为⊙O的直径,弦DC垂直AB于点E,⊙DCB=30°,EB=3,则弦AC的长度为()A.3 √3B.4√3C.5√3D.6√33.如图,AB是⊙O的弦,半径OC⊙AB于点D,且AB=6cm,OD=4cm。
则DC的长为()A.cm B.1cm C.2cm D.5cm4.如图,四边形ABCD内接于⊙ O,AB为⊙ O的直径,∠ABD=20∘,则∠BCD的度数是()A.90°B.100°C.110°D.120°5.如图,点A,B,C,D都在⊙O上,AC,BD相交于点E,则⊙ABD=()A.⊙ACD B.⊙ADB C.⊙AED D.⊙ACB6.如图,在⊙O中,弦AB⊙CD,若⊙ABC=40°,则⊙BOD=()A.20°B.40°C.50°D.80°7.下列判断结论正确的有()(1)直径是圆中最大的弦.(2)长度相等的两条弧一定是等弧.(3)面积相等的两个圆是等圆.(4)同一条弦所对的两条弧一定是等弧.(5)圆上任意两点间的部分是圆的弦.A.1个B.2个C.3个D.4个8.已知如图,PA、PB切⊙O于A,B,MN切⊙O于C,交PB于N;若PA=7.5cm,则⊙PMN的周长是()A.7.5cm B.10cm C.15cm D.12.5cm9.若小李同学掷出的铅球在场地航砸出一个直径为10厘米,深2厘米的小坑,则该铅球的直径为()A.20厘米B.19.5厘米C.14.5厘米D.10厘米10.如图,如果从半径为9cm的圆形纸片剪去13圆周的一个扇形,将留下的扇形(阴影部分)围成一个圆锥(接缝处不重叠),那么这个圆锥的高为()A.6cm B.5√3cm C.8cm D.3√5cm11.如图,△ABC内接于⊙O,∠B=65o,∠C=70o,若BC=2√2,则弧BC长为()A.πB.√2πC.2πD.√2π12.如下图,点B,C,D在⊙O上,若⊙BCD=130°,则⊙BOD的度数是()A.96°B.98°C.102°D.100°二、填空题13.如图,在扇形AOB中,OA=4,⊙AOB=90°,点P是弧AB上的动点,连接OP,点C是线段OP的中点,连接BC并延长交OA于点D,则图中阴影部分面积最小值为.14.如图,在边长为√2的正方形ABCD中,分别以四个顶点为圆心,以边长为半径画弧,分别与正方形的边和对角线相交,则图中阴影部分的面积为(结果保留π).15.如图,⊙ABC的顶点A,B,C均在⊙O上,若⊙ABC+⊙AOC=90°,则⊙AOC的大小是.16.如图:⊙O为⊙ABC的内切圆,⊙C=90°,AO的延长线交BC于点D,AC=4,CD=1,则⊙O的半径为.17.如图,在正八边形ABCDEFGH中,AC、GC是两条对角线,则tan⊙ACG=.18.如图,菱形ABCD中,已知AB=2,∠DAB=60°将它绕着点A逆时针旋转得到菱形ADEF,使AB与AD重合,则点C运动的路线CE⌢的长为.三、综合题19.如图,AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C,点D为AP的中点,连结AC.求证:(1)⊙P=⊙BAC(2)直线CD是⊙O的切线.20.如图,以△ABC的边AB为直径的⊙O交AC于点F,点E是BF⌢的中点,连接BE并延长交AC于点D,若∠CBD=12∠CAB.(1)求证:BC是⊙O的切线;(2)若⊙O的半径为2,cos∠BAC=25,求CD的长.21.如图,⊙O是⊙ABC的外接圆,AC是O的直径,BD=BA=12,BC=5,BE⊙DC,交D的延长线于点E,BD交直径AC于点F.(1)求证:⊙BCA=⊙BAD.(2)求证:BE是⊙O的切线.(3)若BD平分⊙ABC,交⊙O于点D,求AD的长.22.如图,⊙OAB中,OA=OB=10cm,⊙AOB=80°,以点O为圆心,半径为6cm的优弧弧MN分别交OA,OB于点M,N.(1)点P在右半弧上(⊙BOP是锐角),将OP绕点O逆时针旋转80°得OP′.求证:AP=BP′;(2)点T在左半弧上,若AT与弧相切,求A T的长.23.如图,有一直径是√2米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,则:(1)AB的长为米;(2)用该扇形铁皮围成一个圆锥,所得圆锥的底面圆的半径为米.⌢的中点,CE⊥AB于点E,BD交CE于点F.24.如图,AB是⊙O的直径,C是BD(1)求证:CF=BF;(2)若CD﹦5,AC﹦12,求⊙O的半径和CE的长.参考答案1.【答案】D2.【答案】D3.【答案】B4.【答案】C5.【答案】A6.【答案】D7.【答案】B8.【答案】C9.【答案】C10.【答案】D11.【答案】A12.【答案】D13.【答案】4π−8√3314.【答案】4-π15.【答案】60°16.【答案】0.817.【答案】118.【答案】2√33π19.【答案】(1)解:证明:∵AB是⊙O的直径∴⊙ACB=90°∴⊙ACP=90°∴⊙P+⊙CAP=90°∵AP⊙O是切线∴⊙BAP=90°即⊙CAP+⊙BAC=90°∴⊙P=⊙BAC;(2)解:∵CD是Rt⊙PAC斜边PA的中线∴CD=AD∴⊙DCA=⊙DAC连接OC∵OC=OA∴⊙OCA=⊙OAC∴⊙DCO=⊙DAO=90°∴CD是⊙O的切线.20.【答案】(1)证明:连接AE,如图所示:∵AB是⊙O的直径∴∠AEB=90°∴∠BAE+∠ABE=90°.∵点E为弧BF的中点∴EF⌢=EB⌢∴∠BAE=∠DAE=12∠CAB.又∵∠CBD=12∠CAB∴∠BAE=∠CBD∴∠CBD+∠ABE=90°∴AB⊥CB∴BC是⊙O的切线.(2)解:∵∠BAE=∠DAE,∠AED=∠AEB=90°∴∠ADE=∠ABE∴AD=AB=2×2=4.∵cos∠BAC=2 5∴在Rt△ABC中即4AC=25,得AC=10∴CD=AC−AD=10−4=6.21.【答案】(1)证明:∵BD=BA ∴∠BDA=∠BAD.∵∠BCA=∠BDA∴∠BCA=∠BAD.(2)证明:连结OB,如图∵∠BCA=∠BAD又∵∠BCE=∠BAD∴∠BCA=∠BCE∵OB=OC∴∠BCO=∠CBO∴∠BCE=∠CBO∴OB//ED.∵BE⊥ED∴EB⊥BO.∴BE是⊙O的切线.(3)解:∵AC是⊙O的直径∴∠ABC=90°∴AC=√AB2+BC2=√122+52=13.∵∠BDE=∠CAB∴△BED∽△CBA∴BDAC=DEAB,即1213=DE12∴DE=14413∴BE=√BD2−DE2=6013∴CE=√BC2−BE2=2513∴CD=DE−CE=119 13∵BD平分⊙ABC ∴∠CBD=∠ABD∴AD=CD=119 13.22.【答案】(1)证明:∵⊙AOB=⊙POP′=80°∴⊙AOB+⊙BOP=⊙POP′+⊙BOP即⊙AOP=⊙BOP′在⊙AOP 与⊙BOP′中 OA=OB ⊙AOP=⊙BOP OP=OP′∴⊙AOP⊙⊙BOP′ ∴AP=BP′(2)解:∵A T 与弧相切,连结OT .∴OT⊙A T在Rt⊙AOT 中,根据勾股定理得,A T= √OA 2−OT 2 ∵OA=10,OT=6 ∴AT=823.【答案】(1)1 (2)1424.【答案】(1)证明:∵AB 是 ⊙O 的直径∴∠ACB =90° ∴∠A +∠ABC =90° 又∵CE ⊥AB ∴∠CEB =90° ∴∠BCE +∠ABC =90° ∴∠BCE =∠A∵C 是 BD ⌢ 的中点 ∴CD⌢=CB ⌢ ∴∠DBC =∠A ∴∠DBC =∠BCE ∴CF =BF(2)解:∵CD⌢=CB ⌢,CD =5 ∴∠DBC =∠BDC∴BC=CD=5∵∠ACB=90°∴AB=√AC2+BC2=√122+52=13∴AO=6.5∵∠BCE=∠A,∠ACB=∠CEB=90°∴△CEB⊙ △ACB∴CE=AC⋅BCAB=12×513=6013故⊙O的半径为6.5,CE的长是6013.第11页共11。
苏教版五年级数学(下册)圆的综合练习题

苏教版五年级数学(下册)圆的综合练习题圆单元练习题(一)一、完成下表。
圆的半径r2cm圆的直径d2cm8cm圆的周长C18.84cm圆的面积S二、想一想,填一填。
1、当圆规两脚间的距离为4厘米时,画出圆的周长是()厘米。
2、在一张长8厘米,宽12厘米的长方形纸上画一个最大的圆,这个圆的直径是(),面积是(),周长是()。
3、一个车轮的直径是55厘米,车轮转动一周,大约前进()米。
4、一个环形的外圆直径是10cm,内圆直径是8cm,它的面积()cm2。
5、一个圆的半径扩大2倍,它的周长扩大()倍,面积扩大()倍。
6、把一个圆分成若干等份,剪开拼成一个近似的长方形。
这个长方形的长相当于(),长方形的宽就是圆的()。
因为长方形的面积是(),所以圆的面积是().7、圆的直径是6厘米,它的周长是(),面积是()。
8、圆的周长是25.12分米,它的面积是()。
10、周长相称的长方形、正方形、圆,()面积最大。
11、圆的半径由6厘米增加到9厘米,圆的面积增加了()平方厘米。
12、要在一个边长为10厘米的正方形纸板里剪出一个最大的圆,剩下的面积是()。
13、要在底面半径是12厘米的圆柱形水桶表面打上一个铁丝箍,接头部分是8厘米,需用铁丝()厘米。
14、用圆规画一个圆,假如圆规两脚之间的距离是7厘米,画出的这个圆的周长是()厘米。
这个圆的面积是()平方厘米。
15、有大小两个圆,大圆直径是小圆半径的4倍,小圆与大圆周长的比是(),小圆与大圆面积的比是()。
16、一个半圆半径是r,它的周长是()。
三、请你来当小裁判。
1、圆心决定圆的位置,半径决定圆的大小。
()2、当圆的半径等于2分米时,这个圆的周长和面积相等。
()3、一个圆的面积和一个正方形的面积相等,它们的周长一定也相等. ()4、同一个圆的直径一定是半径的2倍。
()5、两端都在圆上的线段,直径是最长的一条。
()6、半圆的周长是圆周长的一半。
()四、选一选。
(挑选精确答案的序号填在括号里)1、圆周率π()3.14。
圆综合练习(提优)-2020-2021学年九年级数学上册同步课堂帮帮帮(苏科版)(解析版)

圆综合练习(提优)一.选择题1.如图,⊙O是△ABC的外接圆,半径为2cm,若BC=2cm,则∠A的度数为()A.30°B.25°C.15°D.10°【解答】A【解析】连接OB和OC,∵圆O半径为2,BC=2,∴△OBC为等边三角形,∴∠BOC=60°,∴∠A=30°,故选A.2.刘徽是中国古代卓越的数学家之一,他在《九章算术》中提出了“割圆术”,即用内接或外切正多边形逐步逼近圆来近似计算圆的面积,设圆O的半径为1,若用圆O的外切正六边形的面积来近似估计圆O的面积,那么圆O的面积估计值是()A.√3B.2√3C.πD.2π【解答】B【解析】根据题意画出图形,如图所示,∵六边形ABCDEF为正六边形,∴△ABO是等边三角形,∵圆O的半径为1,∴OM=1,∴BM=AM=√33,∴AB=2√33,∴S=6S△ABO=6×12×2√33×1=2√3.答:圆O的面积估计值是2√3.故选B.3.如图,将边长为3的正方形铁丝框ABCD,变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形ADB的面积为()A.3 B.6 C.9 D.3π【解答】C【解析】∵正方形ABCD的边长为3,∴AB=BC=CD=AD=3,即DCB̂的长是3+3=6,∴扇形DAB的面积是12×6×3=9,故选C.4.如图,⊙O中,若OA⊥BC、∠AOB=66°,则∠ADC的度数为()A.33°B.56°C.57°D.66°【解答】A【解析】如图,连接OC,OB.∵OA⊥BC,̂=AĈ,∴AB∴∠AOC=∠AOB=66°,∠AOC=33°,∴∠ADC=12故选A.5.如图,已知⊙O的半径为5,弦AB、CD所对的圆心角分别是∠AOB、∠COD,若∠AOB与∠COD互补,弦CD=6,则点O到弦AB的距离为()A.6 B.8 C.3 D.4【解答】C【解析】延长CO交⊙O于E,连接DE,过O作OF⊥DE于F,OH⊥CD于H,OG⊥AB于G,线段OG的长是点O 到弦AB的距离,∵∠COD和∠DOE互补,∠COD和∠AOB互补,∴∠DOE=∠AOB,∴DE=AB,OF=OG,∵OH⊥DC,CD=6,OH过O,DC=3,∠OHD=∠OHC=90°,∴DH=HC=12由勾股定理得:OH=√OD2−DH2=√52−32=4,∵OC=OE,DH=HC,OH=4,∴DE=2OH=8,∵OF⊥DE,OF过O,DE=4,∴DF=EF=12在Rt△DFO中,由勾股定理得:OF=√OD2−DF2=√52−42=3,∴OG=OF=3,即点O到AB的距离是3,故选C.6.如图,△ABC是等腰直角三角形,AC=BC=2,以斜边AB上的点O为圆心的圆分别与AC、BC相切于点E、F,与AB分别相交于点G、H,且EH的延长线与CB的延长线交于点D,则CD的长为()A.2√2−1 B.2√2C.√2+1 D.2√2−12【解答】C【解析】如右图所示,连接OE、OF,∵⊙O与AC、BC切于点E、F,∴∠OEC=∠OFC=90°,OE=OF,又∵△ABC是等腰直角三角形,∴∠C=90°,∴四边形CEOF是正方形,∴OE∥BC,又∵以斜边AB上的点O为圆心的圆分别与AC、BC相切于点E、F,OE=OF,∴O在∠ACB的角平分线上,∵AC=BC,∴O是AB中点,∴AE=CE,又∵AC=2,∴AE=CE=1,∴OE=OF=CE=1,∴OH=1,∵OE∥CD,∴△OEH∽△BDH,∴OEOH =DBBH,又∵AB=√AC2+BC2=2√2,∴OB=√2,∴11=√2−1,∴BD=√2−1,∴CD=2+BD=√2+1,故选C.7.如图,四边形ABCD内接于⊙O,AB=CB,∠BAC=30°,BD=√3,则AD+CD的值为()A .3B .2√3C .√3+1D .不能确定【解答】A【解析】如图,过点B 作BE ⊥AD 于E ,BF ⊥DC 交DC 的延长线于F .∵AB =BC ,∴AB̂=BC ̂, ∴∠BDE =∠BDF ,∵∠DEB =∠DFB =90°,DB =DB ,∴△BDE ≌△BDF (AAS ),∴BE =BF ,DE =DF ,∵∠AEB =∠F =90°,BA =BC ,BE =BF ,∴Rt △BEA ≌Rt △BFC (HL ),∴AE =CF ,∴AD +DC =DE +AE +DF ﹣CF =2DF ,∵∠BDF =∠BAC =30°,BD =√3,∴BF =12BD =√32, ∴DF =√BD 2−BF 2=√(√3)2−(√32)2=32,∴DA +DC =3,故选A .8. 如图,Rt △ACB 中,∠C =90°,AC =6,BC =8,半径为1的⊙O 与AC ,BC 相切,当⊙O 沿边CB 平移至与AB 相切时,则⊙O 平移的距离为( )A.3 B.4 C.5 D.6【解答】B【解析】∵Rt△ACB中,∠C=90°,AC=6,BC=8,∴AB=10,设⊙O与AC相切于D,与BC相切于H,平移后的⊙O′与AB相切于F,与BC相切于E,连接OH,O′D,则点O在O′D上,连接O′F,EO′并延长交AB于G,∴四边形CDOH是正方形,四边形OHEO′是矩形,∴OD=OH=O′E=O′F=CD=CH=1,OO′=HE,∴EG⊥BC,∵∠C=90°,∴EG∥AC,∴∠FGE=∠A,∵∠GFO′=∠C=90°,∴∠O′FG∽∠BCA,∴O′FBC =O′GAB,∴18=O′G10,∴O′G=54,∴EG=94,∵GE∥AC,∴△BGE∽△BAC,∴BEBC =EGAC,∴BE8=946,∴BE=3,∴OO′=HE=BC﹣CH﹣BE=8﹣1﹣3=4,∴⊙O平移的距离为4,故选B.9.如图,已知⊙O的半径为10,A、B是⊙O上的两点,∠AOB=90°,C是射线OB上一个动点,连结AC 并延长交⊙O于点D,过点D作DE⊥OD交OB的延长线于点E.当∠A从30°增大到60°时,弦AD在圆内扫过的面积是()A.100π3−25√3B.50π3C.64π3−16√3D.50π3−25√3【解答】B【解析】过点D作AO的垂线,交AO的延长线于F.当∠A=30°时,∠DOF=60°,DF=OD•sin60°=10×√32=5√3,S弓形ABD=120π⋅102360−12×10×5√3=1003π﹣25√3,当∠A=60°时,过点D'作D'F⊥OA于F',连接OD',∠D 'OF '=60°,D 'F '=5√3,S 弓形ABD '=60⋅π⋅102360−12×10×5√3=503π﹣25√3, ∴S =1003π﹣25√3−(503π﹣25√3)=503π.故选B .10.如图,在 O 中,AB̂=AC ̂,BC =6.AC =3√10,I 是△ABC 的内心,则线段OI 的值为( )A .1B .√10−3C .5−√10D .13√10【解答】C【解析】如图,连接AO ,延长AO 交BC 于H ,连接OB .∵AB ̂=AC ̂,∴AB =AC ,AH ⊥BC ,∴BH =CH =3,∴AH =√AC 2−CH 2=√(3√10)2−32=9,设OA =OB =x ,在Rt △BOH 中,∵OB 2=OH 2+BH 2,∴x 2=(9﹣x )2+32,∴x =5,∴OH =AHAO =9﹣5=4,∵S △ABC =12•BC •AH =12•(AB +AC +BC )•IH ,=√10−1,∴IH=6+6√10∴OI=OH﹣IH=4﹣(√10−1)=5−√10,故选C.11.如图,在等腰直角△ABC中,斜边AB的长度为8,以AC为直径作圆,点P为半圆上的动点,连接BP,取BP的中点M,则CM的最小值为()A.3√5B.2√5−√3C.√10−√2D.3√2−√5【解答】C【解析】如图,连接PA、PC,取AB、BC的中点E、F,连接EF、EM、FM,取EF的中点O,连接OM,OC,CM.∵AC是直径,∴∠APC=90°,∵BE=EA,BM=MP,∴EM∥PA,同理FM∥PC,∴∠BME=∠BPA,∠BMF=∠BPC,∴∠BME+∠BMF=∠BPA+∠BPC=90°,∴∠EMF=90°,̂,(EF为直径的半圆,图中红线部分)∴点M的轨迹是EF∵BC=AC,∠ACB=90°,AB=8,∴AC=BC=4√2,∵AE=EB,BF=CF=2√2,∴EF=12AC=2√2,EF∥AC,∴∠EFB=∠EFC=∠ACB=90°,OE=OF=OM=√2,∴OC=√OF2+CF2=√(√2)2+(2√2)2=√10,∵CM≥OC﹣OM,∴CM≥√10−√2故选C.12.如图,AB是⊙O的直径,点D,C在⊙O上,∠DOC=90°,AD=√2,BC=1,则⊙O的半径为()A.√3B.√52C.√102D.√2+12【解答】C【解析】如图延长DO交⊙O于E,作EF⊥CB交CB的延长线于F,连接BE、EC.∵∠AOD=∠BOE,∴AD̂=BÊ,∴AD=BE=√2,∵∠DOC=∠COE=90°,OC=OB=OE,∴∠OCB=∠OBC,∠OBE=∠OEB,∴∠CBE=12(360°﹣90°)=135°,∴∠EBF=45°,∴△EBF是等腰直角三角形,∴EF=BF=1,在Rt△ECF中,EC=√EF2+CF2=√12+22=√5,∵△OCE 是等腰直角三角形,∴OC =√2=√102. 故选C .二.填空题13.如图,在矩形ABCD 中,AB =1,AD =√3,连接BD ,以点C 为圆心,CD 为半径作弧DF ,与BD 交于点E ,则图中阴影部分的面积是 .【解答】112π−2−√34【解析】连接CE ,过C 作CF ⊥DE 于F ,∵在矩形ABCD 中,AB =1,AD =√3,∴∠A =∠DCF =90°,DC =AB =1,BC =AD =√3,∴tan ∠BDC =BC CD =√31=√3,∴∠BDC =60°,∵CD =CE ,∴△DCE 是等边三角形,∴∠DCE =60°,DE =CD =CE =1,∵CF ⊥DE ,∴DF =EF =12DE =12×1=12,由勾股定理得:CF =√CD 2−DF 2=√12−(12)2=√32, ∴扇形DCE 和△DCE 围成的弓形的面积S =S 扇形DCE ﹣S △DCE =60π×12360−12×1×√32=16π−√34,∴阴影部分的面积=S 扇形DCF ﹣S △DCF ﹣S 弓形=90π×12360−12×1×1−(16π−√34)=112π−2−√34, 故答案为112π−2−√34.14.如图,在正方形ABCD 中,AB =2,分别以B 、C 为圆心,以AB 的长为半径作弧,则阴影部分的面积为 .【解答】2√3−23π【解析】∵在正方形ABCD 中,AB =2,分别以B 、C 为圆心,以AB 的长为半径作弧,∴∠DCB =90°,BC =AB =2,弧对应的半径是2,如图,连接BE 、CE ,∵BC =CE =BE =2,∴△BEC 是等边三角形,∴∠EBC =∠ECB =60°,∴∠DCE =30°,S 弓形=S 扇形EBC ﹣S △EBC =60π×22360−12×2×√3=23π−√3, ∴阴影部分的面积S =2(S 扇形DCE ﹣S 弓形)=2×[30π×22360−(23π−√3)]=2√3−23π.15.如图,点P 为⊙O 外一点,过点P 作⊙O 的切线PA 、PB ,点A 、B 为切点,连接AO 并延长交PB 的延长线于点C ,过点C 作CD ⊥PO ,交PO 的延长线于点D .已知PA =6,AC =8,则CD 的长为 .【解答】2√5【解析】连接OB,如图,∵PA、PB为⊙O的切线,∴PB=PA=6,OB⊥PC,OA⊥PA,∴∠CAP=∠CBO=90°,在Rt△APC中,PC=√62+82=10,∴BC=PC﹣PB=4,设⊙O的半径为r,则OA=OB=r,OC=8﹣r,在Rt△BCO中,42+r2=(8﹣r)2,解得r=3,∴OA=3,OC=5,在Rt△OPA中,OP=√32+62=3√5,∵CD⊥PO,∴∠CDO=90°,∵∠COD=∠POA,∠CDO=∠PAO,∴△COD∽△POA,∴CD:PA=OC:OP,即CD:6=5:3√5,∴CD=2√5.故答案为2√5.16.如图,AB是⊙O的直径,点C,D,E都在⊙O上,∠1=55°,则∠2=°.【解答】35【解析】如图,连接AD.∵AB是直径,∴∠ADB=90°,∵∠1=∠ADE,∴∠1+∠2=90°,∵∠1=55°,∴∠2=35°,故答案为35.17.如图,正方形ABCD的边长为4,点E是AB边上一个动点,点F是CD边上一个动点,且AE=CF,过点B作BG⊥EF于点G,连接AG,则AG长的最小值是.【解答】√10−√2【解析】设正方形的中心为O,可证EF经过O点.连结OB,取OB中点M,连结MA,MG,则MA,MG为定长,过点M作MH⊥AB于H.则MH=BH=1,AH=3,OB=√2,由勾股定理可得MA=√10,MG=12∵AG≥AM﹣MG=√10−√2,当A,M,G三点共线时,AG最小=√10−√2,故答案为√10−√2.18.如图,正五边形ABCDE内接于半径为4的圆O,作OF⊥BC交⊙O于点F,连结FA,FB,则FA•FB的值为.【解答】16【解析】连接OA,OB,OB交AF于J.∵OF⊥BC,̂=CF̂,∴BF∵五边形ABCDE是正五边形,∴∠AOB=72°,∠BOF=36°,∴∠AOF=108°,∵OA=OF,∴∠OAF=∠OFA=∠FOJ=36°,∴OJ=JF,∵AO=AJ,OB=OF,∠OAJ=∠FOB,∴△AOJ≌△OFB(SAS),∴OJ=BF,∵∠OFJ=∠AFO,∠FOJ=∠OAF,∴△FOJ∽△FAO,∴FOFA =FJOF,∴OF2=FJ•FA,∵FJ=OJ=FB,∴FA•FB=OF2=16.故答案为16.19.如图,在平面直角坐标系xOy中,与y轴相切的⊙M与x轴交于A、B两点,AC为⊙M直径,AC=10,AB=6,连结BC,点P为劣弧BĈ上点,点Q为线段AB上点,且MP⊥MQ,MP与BC交于点N.则当NQ平分∠MNB时,点P坐标是.【解答】(495,135)【解析】设⊙M与y轴相切于E,连接EM并延长交BC于H,过P作PF⊥x轴于F,延长FP交EH于D,∵AC为⊙M直径,∴BC⊥AB,∵AC=10,AB=6,∴BC=8,∵⊙M与y轴相切,∴EM⊥y轴,∴四边形OEDF是矩形,∴OE =BH =DF ,ED =OF ,ED ∥OF ,∵AM =CM ,∴MH =12AB =3,BH =DF =4,∵MP ⊥MQ ,NQ 平分∠MNB ,∴MN =BN ,设MN =BN =x ,∴NH =4﹣x ,∵MH 2+HN 2=MN 2,∴x 2=32+(4﹣x )2,解得:x =258,∴MN =BN =258, ∴HN =78, ∵HN ∥PD ,∴△MHN ∽△MDP ,∴MH MD =HN PD =MN MP , ∴3MD =78PD =2585, ∴MD =245,PD =75, ∴DE =EM +MD =495,PF =DF ﹣PD =135, ∴点P 坐标是(495,135),故答案为(495,135).20.如图,PA 、PB 切⊙O 于A 、B 两点,连接OP 交AB 于点C ,交弧AB 于点D ,∠APB =70°,点Q 为优弧AmB上一点,OQ∥PB,则∠OQA的大小为.【解答】10°【解析】如图,连接OA.∵PA,PB是⊙O的切线,∴∠OPB=∠OPA=1∠APB=35°,PA⊥OA,2∴∠OAP=90°,∴∠POA=90°﹣35°=55°,∵OQ∥PB,∴∠POQ=180°﹣∠OPB=145°,∴AOQ=360°﹣145°﹣55°=160°,∵OQ=OA,(180°﹣∠AOQ)=10°,∴∠OQA=∠OAQ=12故答案为10°.21.如图,等边△ABC中,AB=2,点D是以A为圆心,半径为1的圆上一动点,连接CD,取CD的中点E,连接BE,则线段BE的最大值与最小值之和为.【解答】2√3【解析】延长CB到T,使得BT=BC,连接AT,DT,AD.∵△ABC是等边三角形,∴BA=BC=AC=BT=2,∠ACB=60°,∴∠CAT=90°,∴AT=CT•sin60°=2√3,∵AD=1,∴2√3−1≤DT≤2√3+1,∵CB=BT,CE=DE,∴BE=12DT,∴2√3−12≤BE≤2√3+12,∴线段BE的最大值与最小值之和为2√3,故答案为2√3.22.如图,等腰△ABC中,底边BC长为8,腰长为6,点D是BC边上一点,过点B作AC的平行线与过A、B、D三点的圆交于点E,连接DE,则DE的最小值是.【解答】2√5【解析】如图,连接AE,AD,OE,OD,作AJ⊥BC于J,OK⊥DE于K.∵BE∥AC,∴∠EBC+∠C=180°,∵∠EBC+∠EAD=180°,∴∠EAD=∠C,∵∠EOD=2∠EAD,∴∠EOD=2∠C=定值,∴⊙O的半径最小时,DE的值最小,∴当AB是⊙O的直径时,DE的值最小,∵AB=AC=6,AJ⊥BC,∴BJ=CJ=4,∴AJ=√AC2−CJ2=√62−42=2√5,∵OK⊥DE,∴EK=DK,∵AB=6,∴OE=OD=3,∵∠EOK=∠DOK=∠C,∴sin∠EOK=sin∠C=√53,∴EK3=√53,∴EK=√5,∴DE=2√5,∴DE的最小值为2√5.故答案为2√5.三.解答题23.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,交BC于F.(1)若∠ABC=40°,∠C=80°,求∠CBD的度数;(2)求证:DB=DE;(3)若AB=6,AC=4,BC=5,求DE的长.【解答】(1)30°;(2)见解析;(3)2√2【解析】(1)∵∠ABC=40°,∠C=80°,∴∠BAC=180°﹣40°﹣80°=60°,∵点E是△ABC的内心,∠BAC=30°,∴∠CAD=∠BAD=12∴∠CBD=∠CAD=30°.答:∠CBD的度数为30°;(2)证明:如图,连接BE,∴∠1=∠2,∠3=∠4,∵∠2=∠6,∴∠1=∠6,∵∠5=∠1+∠3,∠DBE=∠6+∠4=∠1+∠3,∴∠5=∠DBE,∴DB=DE;(3)∵∠1=∠2,AB=6,AC=4,BC=5,∴ABAC =BFCF=32,∴BF=3,CF=2,∵∠6=∠2,∠D=∠C,∴△BDF∽△ACF,∴BDDF =ACCF=42=2,BFAF=DFCF,∴DF=12BD,DF•AF=BF•CF=6,∵∠1=∠2=∠6,∠BDF=∠ADB,∴△DBF∽△DAB,∴BDDA =DFBD,∴BD2=DF•DA=DF(AF+DF)=DF•AF+DF2=6+(12BD)2,解得BD=2√2,∴DE=BD=2√2.答:DE的长为2√2.24.如图,已知⊙O是等边三角形ABC的外接圆,点D在圆上,在CD的延长线上有一点F,使DF=DA,AE ∥BC交CF于E.(1)求证:EA是⊙O的切线;(2)判断BD与CF的数量关系?说明理由.【解答】(1)见解析;(2)BD=CF 【解析】(1)证明:如图,连接AO,∵⊙O是等边三角形ABC的外接圆,∴AO平分∠BAC,∴∠OAC=12∠BAC=30°,∵AE∥BC,∴∠CAE=∠BCA=60°,∴∠OAE=∠OAC+∠CAE=90°,∴OA⊥AE,∴EA为⊙O的切线;(2)BD=CF,理由如下:∵△ABC为正三角形,∴AB=AC,∠BAC=∠ABC=60°;∵A、B、C、D四边共圆,∴∠ADF=∠ABC=60°,∵DF=DA,∴△ADF为正三角形,∴∠DAF=60°=∠BAC,∴∠BAC+∠CAD=∠DAF+∠CAD,即∠BAD=∠CAF,在△BAD与△CAF中,{BA=CA∠BAD=∠CAF AD=AF,∴△BAD≌△CAF(SAS),∴BD=CF.所以BD与CF的数量关系为相等.25.如图,AB为⊙O的直径,C、D为圆上的两点,OC∥BD,弦AD与BC,OC分别交于E、F.(1)求证:AĈ=CD̂;(2)若CE=1,EB=3,求⊙O的半径.【解答】(1)见解析;(2)√5【解析】(1)证明:∵AB是圆的直径,∴∠ADB=90°,∵OC∥BD,∴∠AFO=∠ADB=90°,∴OC⊥AD∴AĈ=CD̂.(2)连接AC,如图,∵AĈ=CD̂,∴∠CAD=∠ABC,∵∠ECA=∠ACB,∴△ACE∽△BCA,∴ACBC =CEAC,∴AC2=CE•CB,即AC2=1×(1+3),∴AC=2,∵AB是圆的直径,∴∠ACB=90°,∴AB=√AC2+BC2=√22+42=2√5,∴⊙O的半径为√5.26.如图,在△ABC中,AC=BC,以BC为直径作⊙O,交AC于点M,作CD⊥AC交AB延长线于点D,E为CD 上一点,且BE=DE.(1)证明:BE为⊙O的切线;(2)若AM=8,AB=8√5,求BE的长.【解答】(1)见解析;(2)BE=15【解析】(1)证明:∵CD⊥AC,∴∠ACD=90°,∴∠A+∠D=90°,∵AC=BC,BE=DE,∴∠A=∠ABC,∠D=∠DBE,∴∠ABC+∠DBE=90°,∴∠CBE=180°﹣90°=90°,∴CB⊥BE,∴BE为⊙O的切线;(2)连接BM,∵BC为⊙O的直径,∴BM⊥AC,∵AM=8,AB=8√5,∴BM=√AB2−AM2=16,∵AC=BC,∴CM=BC﹣AM=BC﹣8,∵BC2=BM2+CM2,∴BC2=162+(BC﹣8)2,∴BC=20,∴AC=BC=20,∵BM⊥AC,AC⊥CD,∴BM∥CD,∴∠MBC=∠BCE,∵∠BMC=∠CBM=90°,∴△BMC∽△CBE,∴CMBE =BMBC,∴12BE =1620,∴BE=15.27.如图,在平行四边形ABCD中,AC是对角线,∠CAB=90°,以点A为圆心,以AB的长为半径作⊙A,交BC边于点E,交AC于点F,连接DE.(1)求证:DE与⊙A相切;(2)若∠ABC=60°,AB=4,求阴影部分的面积.【解答】(1)见解析;(2)4√3−4π3【解析】(1)证明:连接AE,∵四边形ABCD是平行四边形,∴AD =BC ,AD ∥BC ,∴∠DAE =∠AEB ,∵AE =AB ,∴∠AEB =∠ABC ,∴∠DAE =∠ABC ,∴△AED ≌△BAC (SAS ),∴∠DEA =∠CAB ,∵∠CAB =90°,∴∠DEA =90°,∴DE ⊥AE ,∵AE 是⊙A 的半径,∴DE 与⊙A 相切;(2)∵∠ABC =60°,AB =AE =4,∴△ABE 是等边三角形,∴AE =BE ,∠EAB =60°,∵∠CAB =90°,∴∠CAE =90°﹣∠EAB =90°﹣60°=30°,∠ACB =90°﹣∠B =90°﹣60°=30°,∴∠CAE =∠ACB ,∴AE =CE ,∴CE =BE ,∴S △ABC =12AB •AC =12×4×4√3=8√3,∴S △ACE =12S △ABC =12×8√3=4√3, ∵∠CAE =30°,AE =4,∴S 扇形AEF =30π×AE 2360=30π×42360=4π3,∴S 阴影=S △ACE ﹣S 扇形AEF =4√3−4π3.28.如图,四边形ABCD中,∠B=∠D=90°,∠C=60°,⊙O过点D,与AB相切于点A,与CD相交于点E,且AB=DE.(1)求证:BC与⊙O相切;(2)若⊙O的半径为5,求四边形ABCD的面积.【解答】(1)见解析;(2)50+50√33【解析】(1)连接AE,∵∠D=90°,∴AE是⊙O的直径,过O作OF⊥BC于F,∵AB是⊙O的切线,∴∠OAB=90°,∵∠B=90°,∴∠OAB=∠B=∠OFB=90°,∴四边形ABFO是矩形,∴AB=OF,∵∠B=∠D=90°,∠C=60°,∴∠DAB=120°,∴∠DAE=30°,∴DE =12AE =AO , ∵AB =DE ,∴OF =OA ,∴BC 与⊙O 相切;(2)由(1)知,AB =AO =5,AE =10,过E 作EH ⊥BC 于H ,则BH =AE =10,EH =AB =5,∵∠C =60°,∴CH =√33EH =5√33, ∴BC =10+5√33, 在Rt △ADE 中,∵DE =AB =5,∴AD =√3DE =5√3,∴四边形ABCD 的面积=12×5√3×5+12(10+10+5√33)×5=50+50√33.29.如图,Rt △ABC 中,∠ABC =90°,以AB 为直径的⊙O 交AC 于点D ,E 是BC 的中点,连接DE 、OE .(1)判断DE 与⊙O 的位置关系并说明理由.(2)若⊙O 半径r =3,DE =4,求AD 的长.【解答】(1)相切;(2)AD =185【解析】(1)连接OD 、BD ,如图所示.∵点O 为AB 的中点,点E 为BC 的中点,∴OE∥AC,且AC=2OE,∴∠A=∠BOE.又∵∠BOD=2∠A,∴∠DOE=∠A=∠BOE.在△BOE和△DOE中,{OB=OD∠BOE=∠DOE OE=OE,∴△BOE≌△DOE(SAS),∴∠ODE=∠OBE=90°,∴DE与⊙O相切;(2)∵AB为⊙O的直径,∴BD⊥AC,∴∠ADB=∠BDC=90°,∴∠ADB=∠ABC,∴∠A+∠ABD=∠A+∠C=90°,∴∠ABD=∠C,∴△ABD∽△ACB,∴ABAD =ACAB,∵AB=6,BC=2DE=8,∴AC=10,∴AB2=AD•AC,∴62=AD×10,∴AD=185.30.如图,⊙O为△ABC的外接圆,D为OC与AB的交点,E为线段OC延长线上一点,且∠EAC=∠ABC.(1)求证:直线AE是⊙O的切线.(2)若D为AB的中点,CD=6,AB=16①求⊙O的半径;②求△ABC的内心到点O的距离.【解答】(1)见解析;(2)①25;②53【解析】(1)证明:连接AO,并延长AO交⊙O于点F,连接CF∵AF是直径∴∠ACF=90°∴∠F+∠FAC=90°,∵∠F=∠ABC,∠ABC=∠EAC∴∠EAC=∠F∴∠EAC+∠FAC=90°∴∠EAF=90°,且AO是半径∴直线AE是⊙O的切线.(2)①如图,连接AO,∵D为AB的中点,OD过圆心,∴OD⊥AB,AD=BD=12AB=8,∵AO2=AD2+DO2,∴AO2=82+(AO﹣6)2,∴AO=253,∴⊙O的半径为253;②如图,作∠CAB的平分线交CD于点H,连接BH,过点H作HM⊥AC,HN⊥BC,∵OD⊥AB,AD=BD∴AC=BC,且AD=BD∴CD平分∠ACB,且AH平分∠CAB∴点H是△ABC的内心,且HM⊥AC,HN⊥BC,HD⊥AB∴MH=NH=DH在Rt△ACD中,AC=√AD2+CD2=√82+62=10=BC,∵S△ABC=S△ACH+S△ABH+S△BCH,∴12×16×6=12×10×MH+12×16×DH+12×10×NH,∴DH=83,∵OH=CO﹣CH=CO﹣(CD﹣DH),∴OH=253−(6−83)═5.。
备考2020年中考数学复习专题 《圆》综合练习题(含答案)

备考2020年中考数学复习专题《圆》综合练习题一.选择题1.如图,一个小圆沿着一个五边形的边滚动,如果五边形的各边长都和小圆的周长相等,那么当小圆滚动到原来位置时,小圆自身滚动的圈数是()A.4 B.5 C.6 D.102.如图,在⊙O中,弦AB长6cm,圆心O到AB的距离是3cm,⊙O的半径是()A.3cm B.C.4cm D.3.如图为球形灯笼的截面图,过圆心的CD垂直弦AB于D,AB=2dm,CD=4dm,则⊙O半径为()A.2dm B.dm C.dm D.dm4.下列判断中不正确的是()A.半圆是弧,但弧不一定是半圆B.平分弦的直径垂直于弦C.在平面内,到圆心的距离等于半径的点都在圆上D.在同圆或等圆中,相等的圆心角所对的弦相等5.如图,点A、B、C在⊙O上,D是的中点,若∠ACD=20°,则∠AOB的度数为()A.60°B.70°C.80°D.90°6.在菱形ABCD中,记∠ABC=∠α(0°<∠α<90°),菱形的面积记作S,菱形的周长记作C,若AD=2,则()A.C与∠α的大小有关B.当∠α=45°时,S=C.A,B,C,D四个点可以在同一个圆上D.S随∠α的增大而增大7.如图在一次游园活动中有个投篮游戏,活动开始时四个人A、B、C、D在距篮筐P都是5米处站好,篮球放在AC和BD的交点O处,已知取篮球时A要走6米,B要走3米,C要走2米,则D要走()A.2米B.3米C.4米D.5米8.⊙O半径为5,圆心O的坐标为(0,0),点P的坐标为(3,4),则点P与⊙O的位置关系是()A.点P在⊙O内B.点P在⊙O上C.点P在⊙O外D.点P在⊙O上或外9.给定下列条件可以确定一个圆的是()A.已知圆心B.已知半径C.已知直径D.不在同一直线上三点10.如图,△ABC是⊙O的内接三角形,半径OE⊥AB,垂足为点F,连结弦AE,已知OE =1,则下面的结论:①AE2+BC2=4 ②sin∠ACB=③cos∠B=,其中正确的是()A.①②B.①③C.②③D.②11.若半径为5m的圆,其圆心到直线的距离是5m,则直线和圆的位置关系为()A.相离B.相交C.相切D.无法确定12.如图,圆上有A、B、C三点,直线l与圆相切于点A,CD平分∠ACB,且与l交于点D,若=80°,=60°,则∠ADC的度数为()A.80°B.85°C.90°D.95°二.填空题13.如图,在正方形纸片ABCD中,EF∥AD,M,N是线段EF的六等分点,若把该正方形纸片卷成一个圆柱,使点A与点D重合,此时,底面圆的半径为2cm,则此时M、N两点间的距离是cm.14.如图,⊙O的半径OA垂直于弦BC,垂足是D,OA=5,AD:OD=1:4,则BC的长为.15.在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在墙壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”问题题意为:如图,有一圆柱形木材埋在墙壁中,不知其直径大小.用锯去锯这木材,锯口深1寸(即CD=1寸),锯道长1尺(即AB=1尺),问这圆形木材直径是多少?(注:1尺=10寸)由此,可求出这圆形木材直径为为寸.16.′如图,在平面直角坐标系xOy中,扇形OAB的圆心角∠AOB=60°,点A在x轴正半轴上且OA=2,带你C为弧AB的中点,D为半径OA上一点,点A关于直线CD的对称点为E,若点E落在扇形OAB内(不含边界),则点E的横坐标x取值范围为.17.如图,以等边△ABC的一边AB为直径的半圆O交AC于点D,交BC于点E,若AB =4,则阴影部分的面积是.18.在一个圆内接四边形ABCD中,已知∠A=100°,则∠C的度数为.三.解答题19.如图AB=3cm,用图形表示:到点A的距离小于2cm,且到点B的距离不小于2cm 的所有点的集合(用阴影表示,注意边界上的点是否在集合中,如果在,用实线表示,如果不在,则用虚线表示).20.如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.21.一条排水管的截面如图所示,已知排水管的半径OA=10m,水面宽AB=12m,某天下雨后,水管水面上升了2m,求此时排水管水面的宽CD.22.如图,已知⊙O的弦AB,E,F是弧AB上两点,=,OE、OF分别交于AB于C、D两点,求证:AC=BD.23.如图,CD为⊙O的弦,P为⊙O上一点,OP∥CD,∠PCD=15°(1)求∠POC的度数;(2)若=,AB⊥CD,点A在CD的上方,直接写出∠BPA的度数.24.如图,四边形ABCD内接于⊙O,∠ABC=135°,AC=4,求⊙O的半径长.25.已知圆O,弦AB、CD相交于点M.(1)求证:AM•MB=CM•MD;(2)若M为CD中点,且圆O的半径为3,OM=2,求AM•MB的值.参考答案一.选择题1.解:因为五边形的各边长都和小圆的周长相等,所以小圆在每一边上滚动正好一周,在五条边上共滚动了5周.由于每次小圆从五边形的一边滚动到另一边时,都会翻转72°,所以小圆在五个角处共滚动一周.因此,总共是滚动了6周.故选:C.2.解:如图所示,由题意知OC=3,且OC⊥AB,∵AB=6,∴AC=AB=3,则OA===3,故选:B.3.解:∵过圆心的CD垂直弦AB于D,AB=2dm,CD=4dm,∴BD=AD=1dm,在Rt△ODB中,OD2+DB2=OB2,即(4﹣r)2+12=r2,解得:r=dm,故选:C.4.解:A、半圆是弧,但弧不一定是半圆,正确;B、平分弦的直径垂直于弦,不正确.需要添加条件:此弦非直径;C、在平面内,到圆心的距离等于半径的点都在圆上,正确;D、在同圆或等圆中,相等的圆心角所对的弦相等,正确,故选:B.5.解:连接OD,∴∠AOD=2∠ACD,∵D是的中点,∴∠AOB=2∠AOD=4∠ACD=80°,故选:C.6.【解答】解:A、错误.菱形的周长=8,与∠α的大小无关;B、错误,∠α=45°时,菱形的面积=2•2•sin45°=2;C、错误,A,B,C,D四个点不在同一个圆上;D、正确.∵0°<α<90°,S=菱形的面积=2•2•sinα,∴菱形的面积S随α的增大而增大.故选:D.7.解:根据题意得:A、B、C、D在以P为圆心,半径是5米的圆上.∴OA•OC=OB•OD,即6×2=3×OD.解得OD=4.故选:C.8.解:∵点P的坐标为(3,4),∴由勾股定理得,点P到圆心O的距离==5,∴点P在⊙O上,故选B.9.解:A、不能确定.因为半径不确定,故不符合题意;B、不能确定.因为圆心的位置不确定,故不符合题意;C、不能确定,因为圆心的位置不确定,故不符合题意;D.不在同一直线上三点可以确定一个圆.故符合题意;故选:D.10.解:连接AO,延长AO交⊙O于M,连接BM、CM、EM.∵AM是直径,∴∠AEM=90°,∴AE2+EM2=AM2,∴AE2+EM2=4,显然无法判定BC=EM,故①错误,∵∠ACB=∠AMB,∴sin∠ACB=sin∠AMB==,故②正确,∵∠ABC=∠AMC,∴cos∠ABC=cos∠AMC==,显然无法判断CM=AE,故③错误,故选:D.11.解:根据圆心到直线的距离等于圆的半径,则直线和圆相切.故选:C.12.解:设圆心为O,连接OA、OC,∵=80°,=60°,∴∠AOC=140°,∠ACB=40°,∵OA=OC,∴∠OAC=20°,∵直线l与圆相切于点A,∴OA⊥l,∴∠OAD=90°,∴∠CAD=70°,∵CD平分∠ACB,∴∠ACD=∠ACB=20°,∴∠ADC=180°﹣∠CAD﹣∠ACD=90°,故选:C.二.填空题(共6小题)13.解:根据题意得:EF=BC,MN=EF,把该正方形纸片卷成一个圆柱,使点A与点D重合,则线段BC形成一半径为2cm的圆,线段BC是圆的周长,BC=EF=2π×2=4π,∴的长=EF==,∴n=120°,即∠MON=120°,∵OM=ON,∴∠M=30°,过O作OG⊥MN于G,∵OM=2,∴OG=1,MG=,∴MN=2MG=2,故答案为:2.14.解:连接OB,∵OA=5,AD:OD=1:4,∴AD=1,OD=4,OB=5,在Rt△ODB中,由勾股定理得:OB2=OD2+BD2,52=42+BD2,解得:BD=3,∵OD⊥BC,OD过O,∴BC=2BD=6,故答案为:6.15.解:延长CD,交⊙O于点E,连接OA,由题意知CE过点O,且OC⊥AB,则AD=BD=AB=5(寸),设圆形木材半径为r,则OD=r﹣1,OA=r,∵OA2=OD2+AD2,∴r2=(r﹣1)2+52,解得r=13,所以⊙O的直径为26寸,故答案为:26.16.解:当点E落在半径OA上时,连接OC,如下图1所示,∵∠ADC=90°,∠AOB=60°,点C为弧AB的中点,点A(2,0),∴∠COD=30°,OA=OC=2,∴CD=OC•sin30°=2×=1,∴OD=O C•cos30°=2×=,∴AD=OA﹣OD=2﹣,∵DE=DA,∴OE=OD﹣OE=﹣(2﹣)=2﹣2,即点E的坐标为(2﹣2,0);当点E落在半径OB上时,连接OC,CD,如图2所示,由已知可得,CE=CA=CB,由上面的计算可知,OE=2﹣2,∴点E的横坐标为:(2﹣2)×cos60°=﹣1,点E的纵坐标为:(2﹣2)×sin60°=3﹣,∴E(﹣1,3﹣),∴满足条件的点E的横坐标x取值范围为﹣1<x<2﹣2.故答案为﹣1<x<2﹣2.17.解:如图,连接OD,OE,DE.∵△ABC是等边三角形,∴∠A=∠B=60°,∵OA=OD=OB=OE=2,∴△AOD,∠EOB都是等边三角形,∴∠AOD=∠EOB=60°,∴∠DOE=60°,△DOE是等边三角形,∴∠DOE=∠EOB,∴弓形DE与弓形BE的面积相等,∵CD=DE=CE=2,∴△CDE是等边三角形,∴S阴=S△CDE=×22=,故答案为.18.解:∵四边形ABCD是⊙O的内接四边形,∴∠C+∠A=180°,∴∠C=180°﹣100°=80°.故答案为:80°三.解答题(共7小题)19.解:到点A的距离小于2cm,且到点B的距离不小于2cm的所有点的集合如图所示:20.解:过O作OF⊥CD,交CD于点F,连接OD,∴F为CD的中点,即CF=DF,∵AE=2,EB=6,∴AB=AE+EB=2+6=8,∴OA=4,∴OE=OA﹣AE=4﹣2=2,在Rt△OEF中,∠DEB=30°,∴OF=OE=1,在Rt△ODF中,OF=1,OD=4,根据勾股定理得:DF==,则CD=2DF=2.21.解:如图:作OE⊥AB于E,交CD于F,∵AB=12m,OE⊥AB,OA=1m,∴OE=8m.∵水管水面上升了2m,∴OF=8﹣2=6m,∴CF==8m,∴CD=16m.22.证明:连接OA、OB,∵OA=OB,∴∠A=∠B,∵=,∴∠AOC=∠BOD,在△AOC和△BOD中,,∴△AOC≌△BOD,∴AC=BD.23.解:(1)∵OP∥CD,∴∠OPC=∠PCD=15°,∵OP=OC,∴∠OPC=∠OCP=15°,∴∠OCD=30°.(2)①如图1中,当AB在点O的左侧时,连接PA,PB,OD,OA,OB.∵OC=OD,∴∠OCD=∠ODC=30°,∴∠COD=120°,∵=,∴∠AOB=∠COD=120°,∴∠APB=∠AOB=60°.②如图2中,当AB在点O的右侧时,同法可得∠ACB=60°,∵∠APB+∠ACB=180°,∴∠APB=120°,综上所述,∠APB=60°或120°.24.解:∵四边形ABCD内接于⊙O,∠ABC=135°,∴∠D=180°﹣∠ABC=45°,∴∠AOC=2∠D=90°,∵OA=OC,且AC=4,∴OA=OC=AC=2,即⊙O的半径长为2.25.解:(1)连接AD、BC.∵∠A=∠C,∠D=∠B,∴△ADM∽△CBM∴即AM•MB=CM•MD.(2)连接OM、OC.∵M为CD中点,∴OM⊥CD在Rt△OMC中,∵OC=3,OM=2 ∴CD=CM===由(1)知AM•MB=CM•MD.∴AM•MB=•=5.。
九年级数学圆的综合的专项培优练习题(含答案)附答案解析

九年级数学圆的综合的专项培优练习题(含答案)附答案解析一、圆的综合1.如图,△ABC 是⊙O 的内接三角形,点D 在BC uuu r 上,点E 在弦AB 上(E 不与A 重合),且四边形BDCE 为菱形.(1)求证:AC=CE ;(2)求证:BC 2﹣AC 2=AB•AC ;(3)已知⊙O 的半径为3.①若AB AC =53,求BC 的长; ②当AB AC为何值时,AB•AC 的值最大?【答案】(1)证明见解析;(2)证明见解析;(3)2;②32【解析】 分析:(1)由菱形知∠D=∠BEC ,由∠A+∠D=∠BEC+∠AEC=180°可得∠A=∠AEC ,据此得证;(2)以点C 为圆心,CE 长为半径作⊙C ,与BC 交于点F ,于BC 延长线交于点G ,则CF=CG=AC=CE=CD ,证△BEF ∽△BGA 得BE BG BF BA =,即B F•BG=BE•AB ,将BF=BC-CF=BC-AC 、BG=BC+CG=BC+AC 代入可得; (3)①设AB=5k 、AC=3k ,由BC 2-AC 2=AB•AC 知6k ,连接ED 交BC 于点M ,Rt △DMC 中由DC=AC=3k 、MC=126k 求得22CD CM -3,可知OM=OD-3,在Rt △COM 中,由OM 2+MC 2=OC 2可得答案.②设OM=d ,则MD=3-d ,MC 2=OC 2-OM 2=9-d 2,继而知BC 2=(2MC )2=36-4d 2、AC 2=DC 2=DM 2+CM 2=(3-d )2+9-d 2,由(2)得AB•AC=BC 2-AC 2,据此得出关于d 的二次函数,利用二次函数的性质可得答案. 详解:(1)∵四边形EBDC 为菱形,∴∠D=∠BEC ,∵四边形ABDC 是圆的内接四边形,∴∠A+∠D=180°,又∠BEC+∠AEC=180°,∴∠A=∠AEC ,∴AC=CE;(2)以点C为圆心,CE长为半径作⊙C,与BC交于点F,于BC延长线交于点G,则CF=CG,由(1)知AC=CE=CD,∴CF=CG=AC,∵四边形AEFG是⊙C的内接四边形,∴∠G+∠AEF=180°,又∵∠AEF+∠BEF=180°,∴∠G=∠BEF,∵∠EBF=∠GBA,∴△BEF∽△BGA,∴BE BGBF BA=,即BF•BG=BE•AB,∵BF=BC﹣CF=BC﹣AC、BG=BC+CG=BC+AC,BE=CE=AC,∴(BC﹣AC)(BC+AC)=AB•AC,即BC2﹣AC2=AB•AC;(3)设AB=5k、AC=3k,∵BC2﹣AC2=AB•AC,∴6k,连接ED交BC于点M,∵四边形BDCE是菱形,∴DE垂直平分BC,则点E、O、M、D共线,在Rt△DMC中,DC=AC=3k,MC=126k,∴223CD CM k-=,∴OM=OD﹣DM=33k,在Rt△COM中,由OM2+MC2=OC2得(33)2+6k)2=32,解得:k=33或k=0(舍),∴62;②设OM=d,则MD=3﹣d,MC2=OC2﹣OM2=9﹣d2,∴BC 2=(2MC )2=36﹣4d 2,AC 2=DC 2=DM 2+CM 2=(3﹣d )2+9﹣d 2,由(2)得AB•AC=BC 2﹣AC 2=﹣4d 2+6d+18=﹣4(d ﹣34)2+814, ∴当d=34,即OM=34时,AB•AC 最大,最大值为814, ∴DC 2=272, ∴AC=DC=362, ∴AB=964,此时32AB AC =. 点睛:本题主要考查圆的综合问题,解题的关键是掌握圆的有关性质、圆内接四边形的性质及菱形的性质、相似三角形的判定与性质、二次函数的性质等知识点.2.已知AB ,CD 都是O e 的直径,连接DB ,过点C 的切线交DB 的延长线于点E . ()1如图1,求证:AOD 2E 180∠∠+=o ;()2如图2,过点A 作AF EC ⊥交EC 的延长线于点F ,过点D 作DG AB ⊥,垂足为点G ,求证:DG CF =;()3如图3,在()2的条件下,当DG 3CE 4=时,在O e 外取一点H ,连接CH 、DH 分别交O e 于点M 、N ,且HDE HCE ∠∠=,点P 在HD 的延长线上,连接PO 并延长交CM 于点Q ,若PD 11=,DN 14=,MQ OB =,求线段HM 的长.【答案】(1)证明见解析(2)证明见解析(3)37【解析】【分析】(1)由∠D +∠E =90°,可得2∠D +2∠E =180°,只要证明∠AOD =2∠D 即可;(2)如图2中,作OR ⊥AF 于R .只要证明△AOR ≌△ODG 即可;(3)如图3中,连接BC 、OM 、ON 、CN ,作BT ⊥CL 于T ,作NK ⊥CH 于K ,设CH 交DE于W .解直角三角形分别求出KM ,KH 即可;【详解】()1证明:如图1中,O Q e 与CE 相切于点C ,OC CE ∴⊥,OCE 90∠∴=o ,D E 90∠∠∴+=o ,2D 2E 180∠∠∴+=o ,AOD COB ∠∠=Q ,BOC 2D ∠∠=,AOD 2D ∠∠=,AOD 2E 180∠∠∴+=o .()2证明:如图2中,作OR AF ⊥于R .OCF F ORF 90∠∠∠===o Q ,∴四边形OCFR 是矩形,AF//CD ∴,CF OR =,A AOD ∠∠∴=,在AOR V 和ODG V 中,A AOD ∠∠=Q ,ARO OGD 90∠∠==o ,OA DO =,AOR ∴V ≌ODG V ,OR DG ∴=,DG CF ∴=,()3解:如图3中,连接BC 、OM 、ON 、CN ,作BT CL ⊥于T ,作NK CH ⊥于K ,设CH 交DE 于W .设DG 3m =,则CF 3m =,CE 4m =,OCF F BTE 90∠∠∠===o Q ,AF//OC//BT ∴,OA OB =Q ,CT CF 3m ∴==,ET m ∴=,CD Q 为直径,CBD CND 90CBE ∠∠∠∴===o ,E 90EBT CBT ∠∠∠∴=-=o ,tan E tan CBT ∠∠∴=,BT CT ET BT∴=, BT 3m m BT∴=, BT 3m(∴=负根已经舍弃),3m tan E 3∠∴== E 60∠∴=o ,CWD HDE H ∠∠∠=+Q ,HDE HCE ∠∠=,H E 60∠∠∴==o ,MON 2HCN 60∠∠∴==o ,OM ON =Q ,OMN ∴V 是等边三角形,MN ON ∴=,QM OB OM ==Q ,MOQ MQO ∠∠∴=,MOQ PON 180MON 120∠∠∠+=-=o o Q ,MQO P 180H 120∠∠∠+=-=o o , PON P ∠∠∴=,ON NP 141125∴==+=,CD 2ON 50∴==,MN ON 25==,在Rt CDN V 中,2222CN CD DN 501448=-=-=,在Rt CHN V 中,CN 48tan H 3HN HN∠===, HN 163∴=,在Rt KNH V 中,1KH HN 832==,3NK HN 24==, 在Rt NMK V 中,2222MK MN NK 25247=-=-=,HM HK MK 837∴=+=+.【点睛】本题考查圆综合题、全等三角形的判定和性质、平行线的性质、勾股定理、等边三角形的判定和性质、锐角三角函数等知识,添加常用辅助线,构造全等三角形或直角三角形解题的关键.3.已知O e 的半径为5,弦AB 的长度为m ,点C 是弦AB 所对优弧上的一动点. ()1如图①,若m 5=,则C ∠的度数为______o ;()2如图②,若m 6=.①求C ∠的正切值;②若ABC V 为等腰三角形,求ABC V 面积.【答案】()130;()2C ∠①的正切值为34;ABC S 27=V ②或43225. 【解析】【分析】 ()1连接OA ,OB ,判断出AOB V 是等边三角形,即可得出结论;()2①先求出10AD =,再用勾股定理求出8BD =,进而求出tan ADB ∠,即可得出结论;②分三种情况,利用等腰三角形的性质和垂径定理以及勾股定理即可得出结论.【详解】()1如图1,连接OB ,OA ,OB OC 5∴==,AB m 5==Q ,OB OC AB ∴==,AOB ∴V 是等边三角形,AOB 60∠∴=o , 1ACB AOB 302∠∠∴==o , 故答案为30;()2①如图2,连接AO 并延长交O e 于D ,连接BD ,AD Q 为O e 的直径,AD 10∴=,ABD 90∠=o ,在Rt ABD V 中,AB m 6==,根据勾股定理得,BD 8=,AB 3tan ADB BD 4∠∴==, C ADB ∠∠=Q ,C ∠∴的正切值为34; ②Ⅰ、当AC BC =时,如图3,连接CO 并延长交AB 于E ,AC BC =Q ,AO BO =,CE ∴为AB 的垂直平分线,AE BE 3∴==,在Rt AEO V 中,OA 5=,根据勾股定理得,OE 4=,CE OE OC 9∴=+=,ABC 11S AB CE 692722∴=⨯=⨯⨯=V ; Ⅱ、当AC AB 6==时,如图4,连接OA 交BC 于F ,AC AB =Q ,OC OB =,AO ∴是BC 的垂直平分线,过点O 作OG AB ⊥于G ,1AOG AOB 2∠∠∴=,1AG AB 32==, AOB 2ACB ∠∠=Q ,ACF AOG ∠∠∴=,在Rt AOG V 中,AG 3sin AOG AC 5∠==, 3sin ACF 5∠∴=, 在Rt ACF V 中,3sin ACF 5∠=, 318AF AC 55∴==,24CF 5∴=, ABC 111824432S AF BC 225525∴=⨯=⨯⨯=V ; Ⅲ、当BA BC 6==时,如图5,由对称性知,ABC 432S 25=V .【点睛】圆的综合题,主要圆的性质,圆周角定理,垂径定理,等腰三角形的性质,三角形的面积公式,用分类讨论的思想解决问题是解本题的关键.4.如图,AB 为O e 的直径,弦//CD AB ,E 是AB 延长线上一点,CDB ADE ∠=∠. ()1DE 是O e 的切线吗?请说明理由;()2求证:2AC CD BE =⋅.【答案】(1)结论:DE 是O e 的切线,理由见解析;(2)证明见解析.【解析】【分析】(1)连接OD ,只要证明OD DE ⊥即可;(2)只要证明:AC BD =,CDB DBE V V ∽即可解决问题.【详解】()1解:结论:DE 是O e 的切线.理由:连接OD .CDB ADE ∠=∠Q ,ADC EDB ∴∠=∠,//CD AB Q ,CDA DAB ∴∠=∠,OA OD =Q ,OAD ODA ∴∠=∠,ADO EDB ∴∠=∠,AB Q 是直径,90ADB ∴∠=o ,90ADB ODE ∴∠=∠=o ,DE OD ∴⊥,DE ∴是O e 的切线.()2//CD AB Q ,ADC DAB ∴∠=∠,CDB DBE ∠=∠,AC BD ∴=n n, AC BD ∴=,DCB DAB ∠=∠Q ,EDB DAB ∠=∠,EDB DCB ∴∠=∠,CDB ∴V ∽DBE V ,CD DB BD BE∴=, 2BD CD BE ∴=⋅,2AC CD BE ∴=⋅.【点睛】本题考查相似三角形的判定和性质、圆周角定理、切线的判定等知识,解题的关键是学会添加常用辅助线,准确寻找相似三角形解决问题,属于中考常考题型.5.在⊙O 中,点C 是AB u u u r 上的一个动点(不与点A ,B 重合),∠ACB=120°,点I 是∠ABC 的内心,CI 的延长线交⊙O 于点D ,连结AD,BD .(1)求证:AD=BD.(2)猜想线段AB与DI的数量关系,并说明理由.(3)若⊙O的半径为2,点E,F是»AB的三等分点,当点C从点E运动到点F时,求点I 随之运动形成的路径长.【答案】(1)证明见解析;(2)AB=DI,理由见解析(3)23【解析】分析:(1)根据内心的定义可得CI平分∠ACB,可得出角相等,再根据圆周角定理,可证得结论;(2)根据∠ACB=120°,∠ACD=∠BCD,可求出∠BAD的度数,再根据AD=BD,可证得△ABD是等边三角形,再根据内心的定义及三角形的外角性质,证明∠BID=∠IBD,得出ID=BD,再根据AB=BD,即可证得结论;(3)连接DO,延长DO根据题意可知点I随之运动形成的图形式以D为圆心,DI1为半径的弧,根据已知及圆周角定理、解直角三角形,可求出AD的长,再根据点E,F是弧AB ⌢的三等分点,△ABD是等边三角形,可证得∠DAI1=∠AI1D,然后利用弧长的公式可求出点I 随之运动形成的路径长.详解:(1)证明:∵点I是∠ABC的内心∴CI平分∠ACB∴∠ACD=∠BCD∴弧AD=弧BD∴AD=BD(2)AB=DI理由:∵∠ACB=120°,∠ACD=∠BCD∴∠BCD=×120°=60°∵弧BD=弧BD∴∠DAB=∠BCD=60°∵AD=BD∴△ABD是等边三角形,∴AB=BD,∠ABD=∠C∵I是△ABC的内心∴BI平分∠ABC∴∠CBI=∠ABI∵∠BID=∠C+∠CBI,∠IBD=∠ABI+∠ABD∴∠BID=∠IBD∴ID=BD∵AB=BD∴AB=DI(3)解:如图,连接DO,延长DO根据题意可知点I随之运动形成的图形式以D为圆心,DI1为半径的弧∵∠ACB=120°,弧AD=弧BD∴∠AED=∠ACB=×120°=60°∵圆的半径为2,DE是直径∴DE=4,∠EAD=90°∴AD=sin∠AED×DE=×4=2∵点E,F是弧AB ⌢的三等分点,△ABD是等边三角形,∴∠ADB=60°∴弧AB的度数为120°,∴弧AM、弧BF的度数都为为40°∴∠ADM=20°=∠FAB∴∠DAI1=∠FAB+∠DAB=80°∴∠AI1D=180°-∠ADM-∠DAI1=180°-20°-80°=80°∴∠DAI1=∠AI1D∴AD=I1D=2∴弧I1I2的长为:点睛:此题是一道圆的综合题,有一定的难度,熟记圆的相关性质与定理,并对圆中的弦、弧、圆心角、圆周角等进行灵活转化是解题关键,注意数形结合思想的渗透.6.如图,AB是⊙O的直径,PA是⊙O的切线,点C在⊙O上,CB∥PO.(1)判断PC与⊙O的位置关系,并说明理由;(2)若AB=6,CB=4,求PC的长.【答案】(1)PC是⊙O的切线,理由见解析;(235 2【解析】试题分析:(1)要证PC是⊙O的切线,只要连接OC,再证∠PCO=90°即可.(2)可以连接AC,根据已知先证明△ACB∽△PCO,再根据勾股定理和相似三角形的性质求出PC的长.试题解析:(1)结论:PC是⊙O的切线.证明:连接OC∵CB∥PO∴∠POA=∠B,∠POC=∠OCB∵OC=OB∴∠OCB=∠B∴∠POA=∠POC又∵OA=OC,OP=OP∴△APO≌△CPO∴∠OAP=∠OCP∵PA是⊙O的切线∴∠OAP=90°∴∠OCP=90°∴PC是⊙O的切线.(2)连接AC∵AB是⊙O的直径∴∠ACB=90°(6分)由(1)知∠PCO=90°,∠B=∠OCB=∠POC∵∠ACB=∠PCO∴△ACB∽△PCO∴∴.点睛:本题考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.同时考查了勾股定理和相似三角形的性质.7.如图,在RtΔABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.(1)求证:AE=BF;(2)连接EF,求证:∠FEB=∠GDA;(3)连接GF,若AE=2,EB=4,求ΔGFD的面积.【答案】(1)(2)见解析;(3)9【解析】分析:(1)连接BD,由三角形ABC为等腰直角三角形,求出∠A与∠C的度数,根据AB 为圆的直径,利用圆周角定理得到∠ADB为直角,即BD垂直于AC,利用直角三角形斜边上的中线等于斜边的一半,得到AD=DC=BD=12AC,进而确定出∠A=∠FBD,再利用同角的余角相等得到一对角相等,利用ASA得到三角形AED与三角形BFD全等,利用全等三角形对应边相等即可得证;(2)连接EF ,BG ,由三角形AED 与三角形BFD 全等,得到ED =FD ,进而得到三角形DEF 为等腰直角三角形,利用圆周角定理及等腰直角三角形性质得到一对同位角相等,利用同位角相等两直线平行,再根据平行线的性质和同弧所对的圆周角相等,即可得出结论;(3)由全等三角形对应边相等得到AE =BF =1,在直角三角形BEF 中,利用勾股定理求出EF 的长,利用锐角三角形函数定义求出DE 的长,利用两对角相等的三角形相似得到三角形AED 与三角形GEB 相似,由相似得比例,求出GE 的长,由GE +ED 求出GD 的长,根据三角形的面积公式计算即可.详解:(1)连接BD .在Rt △ABC 中,∠ABC =90°,AB =BC ,∴∠A =∠C =45°. ∵AB 为圆O 的直径,∴∠ADB =90°,即BD ⊥AC ,∴AD =DC =BD =12AC ,∠CBD =∠C =45°,∴∠A =∠FBD .∵DF ⊥DG ,∴∠FDG =90°,∴∠FDB +∠BDG =90°.∵∠EDA +∠BDG =90°,∴∠EDA =∠FDB .在△AED 和△BFD 中,A FBD AD BD EDA FDB ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△AED ≌△BFD (ASA ),∴AE =BF ; (2)连接EF ,BG . ∵△AED ≌△BFD ,∴DE =DF .∵∠EDF =90°,∴△EDF 是等腰直角三角形,∴∠DEF =45°. ∵∠G =∠A =45°,∴∠G =∠DEF ,∴GB ∥EF ,∴∠FEB =∠GBA . ∵∠GBA =∠GDA ,∴∠FEB =∠GDA ;(3)∵AE =BF ,AE =2,∴BF =2.在Rt △EBF 中,∠EBF =90°,∴根据勾股定理得:EF 2=EB 2+BF 2.∵EB =4,BF =2,∴EF∵△DEF 为等腰直角三角形,∠EDF =90°,∴cos ∠DEF =DEEF. ∵EF=∴DE=2. ∵∠G =∠A ,∠GEB =∠AED ,∴△GEB ∽△AED ,∴GE AE =EBED,即GE •ED =AE •EB ,∴GE =8,即GE,则GD =GE +ED∴11192252S GD DF GD DE =⨯⨯=⨯⨯==.点睛:本题属于圆综合题,涉及的知识有:全等三角形的判定与性质,相似三角形的判定与性质,勾股定理,圆周角定理,以及平行线的判定与性质,熟练掌握判定与性质是解答本题的关键.8.如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;(2)若D为线段NB的中点,求证:直线CD是⊙M的切线.【答案】(1) B(,2).(2)证明见解析.【解析】试题分析:(1)在Rt△ABN中,求出AN、AB即可解决问题;(2)连接MC,NC.只要证明∠MCD=90°即可试题解析:(1)∵A的坐标为(0,6),N(0,2),∴AN=4,∵∠ABN=30°,∠ANB=90°,∴AB=2AN=8,∴由勾股定理可知:NB=,∴B(,2).(2)连接MC,NC∵AN是⊙M的直径,∴∠ACN=90°,∴∠NCB=90°,在Rt△NCB中,D为NB的中点,∴CD=NB=ND,∴∠CND=∠NCD,∵MC=MN,∴∠MCN=∠MNC,∵∠MNC+∠CND=90°,∴∠MCN+∠NCD=90°,即MC⊥CD.∴直线CD是⊙M的切线.考点:切线的判定;坐标与图形性质.9.在平面直角坐标系中,已知点A(2,0),点B(0,),点O(0,0).△AOB绕着O顺时针旋转,得△A'OB',点A、B旋转后的对应点为A',B',记旋转角为α.(Ⅰ)如图1,A'B'恰好经过点A时,求此时旋转角α的度数,并求出点B'的坐标;(Ⅱ)如图2,若0°<α<90°,设直线AA'和直线BB'交于点P,求证:AA'⊥BB';(Ⅲ)若0°<α<360°,求(Ⅱ)中的点P纵坐标的最小值(直接写出结果即可).【答案】(Ⅰ)α=60°,B'(3,);(Ⅱ)见解析;(Ⅲ)点P纵坐标的最小值为﹣2.【解析】【分析】(Ⅰ)作辅助线,先根据点A(2,0),点B(0,),确定∠ABO=30°,证明△AOA'是等边三角形,得旋转角α=60°,证明△COB'是30°的直角三角形,可得B'的坐标;(Ⅱ)依据旋转的性质可得∠BOB'=∠AOA'=α,OB=OB',OA=OA',即可得出∠OBB'=∠OA'A=(180°﹣α),再根据∠BOA'=90°+α,四边形OBPA'的内角和为360°,即可得到∠BPA'=90°,即AA'⊥BB';(Ⅲ)作AB的中点M(1,),连接MP,依据点P的轨迹为以点M为圆心,以MP=AB=2为半径的圆,即可得到当PM∥y轴时,点P纵坐标的最小值为﹣2.【详解】解:(Ⅰ)如图1,过B'作B'C⊥x轴于C,∵OA=2,OB=2,∠AOB=90°,∴∠ABO=30°,∠BAO=60°,由旋转得:OA=OA',∠A'=∠BAO=60°,∴△OAA'是等边三角形,∴α=∠AOA'=60°,∵OB=OB'=2,∠COB'=90°﹣60°=30°,∴B'C =OB’=,∴OC=3,∴B'(3,),(Ⅱ)证明:如图2,∵∠BOB'=∠AOA'=α,OB=OB',OA=OA',∴∠OBB'=∠OA'A=(180°﹣α),∵∠BOA'=90°+α,四边形OBPA'的内角和为360°,∴∠BPA'=360°﹣(180°﹣α)﹣(90°+α)=90°,即AA'⊥BB';(Ⅲ)点P纵坐标的最小值为-2.理由是:如图,作AB的中点M(1,),连接MP,∵∠APB=90°,∴点P的轨迹为以点M为圆心,以MP=AB=2为半径的圆,除去点(2,2),∴当PM⊥x轴时,点P纵坐标的最小值为﹣2.【点睛】本题属于几何变换综合题,主要考查了旋转的性质,含30°角的直角三角形的性质,四边形内角和以及圆周角定理的综合运用,解决问题的关键是判断点P的轨迹为以点M为圆心,以MP 为半径的圆.10..如图,△ABC中,∠ACB=90°,∠A=30°,AB=6.D是线段AC上一个动点(不与点A重合),⊙D与AB相切,切点为E,⊙D交射线..BC于..DC于点F,过F作FG⊥EF交直线点G,设⊙D的半径为r.(1)求证AE=EF;(2)当⊙D与直线BC相切时,求r的值;(3)当点G落在⊙D内部时,直接写出r的取值范围.【答案】(1)见解析,(2)r=3,(3)63 3r<<【解析】【分析】(1)连接DE,则∠ADE=60°=∠DEF+∠DFE,而∠DEF=∠DFE,则∠DEF=∠DFE=30°=∠A,即可求解;(2)如图2所示,连接DE,当圆与BC相切时,切点为F,∠A=30°,AB=6,则BF=3,AD=2r,由勾股定理,即可求解;(3)分点F在线段AC上、点F在线段AC的延长线上两种情况,分别求解即可.【详解】解:设圆的半径为r;(1)连接DE,则∠ADE=60°=∠DEF+∠DFE,而∠DEF=∠DFE,则∠DEF=∠DFE=30°=∠A,∴AE=EF;(2)如图2所示,连接DE,当圆与BC相切时,切点为F∠A=30°,AB=6,则BF=3,AD=2r,由勾股定理得:(3r)2+9=36,解得:3(3)①当点F 在线段AC 上时,如图3所示,连接DE 、DG ,333,3933FC r GC FC r =-==- ②当点F 在线段AC 的延长线上时,如图4所示,连接DE 、DG ,333,3339FC r GC FC r ===-两种情况下GC 符号相反,GC 2相同,由勾股定理得:DG 2=CD 2+CG 2,点G 在圆的内部,故:DG2<r2, 即:22(332)(339)2r r r +-<整理得:25113180r r -+<6335r <<【点睛】本题考查了圆的综合题:圆的切线垂直于过切点的半径;利用勾股定理计算线段的长.11.如图,⊙O 是△ABC 的外接圆,AB 是直径,过点O 作OD ⊥CB ,垂足为点D ,延长DO 交⊙O 于点E ,过点E 作PE ⊥AB ,垂足为点P ,作射线DP 交CA 的延长线于F 点,连接EF ,(1)求证:OD=OP;(2)求证:FE是⊙O的切线.【答案】(1)证明见解析;(2)证明见解析.【解析】试题分析:(2)证明△POE≌△ADO可得DO=EO;(3)连接AE,BE,证出△APE≌△AFE即可得出结论.试题解析:(1)∵∠EPO=∠BDO=90°∠EOP=∠BODOE=OB∴△OPE≌△ODB∴OD="OP"(2)连接EA,EB∴∠1=∠EBC∵AB是直径∴∠AEB=∠C=90°∴∠2+∠3=90°∵∠3=∠DEB∵∠BDE=90°∴∠EBC+∠DEB=90°∴∠2=∠EBC=∠1∵∠C=90°∠BDE=90°∴CF∥OE∴∠ODP=∠AFP∵OD=OP∴∠ODP=∠OPD∵∠OPD=∠APF∴∠AFP=∠APF∴AF=AP 又AE=AE∴△APE≌△AFE∴∠AFE=∠APE=90°∴∠FED=90°∴FE是⊙O的切线考点:切线的判定.12.如图,点B在数轴上对应的数是﹣2,以原点O为原心、OB的长为半径作优弧AB,使点A在原点的左上方,且tan∠AOB=3,点C为OB的中点,点D在数轴上对应的数为4.(1)S扇形AOB=(大于半圆的扇形);(2)点P是优弧AB上任意一点,则∠PDB的最大值为°(3)在(2)的条件下,当∠PDB最大,且∠AOP<180°时,固定△OPD的形状和大小,以原点O为旋转中心,将△OPD顺时针旋转α(0°≤α≤360°)①连接CP,AD.在旋转过程中,CP与AD有何数量关系,并说明理由;②当PD∥AO时,求AD2的值;③直接写出在旋转过程中,点C到PD所在直线的距离d的取值范围.【答案】(1)103π(2)30(3)①AD=2PC②20+83或20+83③1≤d≤3【解析】【分析】(1)利用扇形的面积公式计算即可.(2)如图1中,当PD与⊙O相切时,∠PDB的值最大.解直角三角形即可解决问题.(3)①结论:AD=2PC.如图2中,连接AB,AC.证明△COP∽△AOD,即可解决问题.②分两种情形:如图3中,当PD∥OA时,设OD交⊙O于K,连接PK交OC于H.求出PC即可.如图④中,当PA∥OA时,作PK⊥OB于K,同法可得.③判断出PC的取值范围即可解决问题.【详解】(1)∵tan∠AOB=3,∴∠AOB=60°,∴S扇形AOB=23002103603ππ⋅⋅=(大于半圆的扇形),(2)如图1中,当PD与⊙O相切时,∠PDB的值最大.∵PD是⊙O的切线,∴OP⊥PD,∴∠OPD =90°, ∵21sin 42OP PDO OD ∠=== ∴∠PDB =30°, 同法当DP ′与⊙O 相切时,∠BDP ′=30°,∴∠PDB 的最大值为30°.故答案为30.(3)①结论:AD =2PC .理由:如图2中,连接AB ,AC .∵OA =OB ,∠AOB =60°,∴△AOB 是等边三角形,∵BC =OC ,∴AC ⊥OB ,∵∠AOC =∠DOP =60°,∴∠COP =∠AOD ,∵2AO OD OC OP==, ∴△COP ∽△AOD , ∴2AD AO PC OC==, ∴AD =2PC . ②如图3中,当PD ∥OA 时,设OD 交⊙O 于K ,连接PK 交OC 于H .∵OP =OK ,∠POK =60°,∴△OPK 是等边三角形,∵PD∥OA,∴∠AOP=∠OPD=90°,∴∠POH+∠AOC=90°,∵∠AOC=60°,∴∠POH=30°,∴PH=12OP=1,OH=3PH=3,∴PC=2222PH CH1(13)523+=++=+,∵AD=2PC,∴AD2=4(5+23)=20+83.如图④中,当PA∥OA时,作PK⊥OB于K,同法可得:PC2=12+(3﹣1)2=5﹣23,AD2=4PC2=20﹣83.③由题意1≤PC≤3,∴在旋转过程中,点C到PD所在直线的距离d的取值范围为1≤d≤3.【点睛】本题属于圆综合题,考查了切线的性质,相似三角形的判定和性质,旋转变换,勾股定理,等边三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题.13.如图,已知AB是⊙O的直径,BC是弦,弦BD平分∠ABC交AC于F,弦DE⊥AB于H,交AC于G.①求证:AG=GD;②当∠ABC满足什么条件时,△DFG是等边三角形?③若AB=10,sin∠ABD=35,求BC的长.【答案】(1)证明见解析;(2)当∠ABC=60°时,△DFG是等边三角形.理由见解析;(3)BC 的长为145. 【解析】【分析】 (1)首先连接AD ,由DE ⊥AB ,AB 是O e 的直径,根据垂径定理,即可得到¶¶AD AE =,然后根据在同圆或等圆中,同弧或等弧所对的圆周角相等,证得∠ADE =∠ABD ,又由弦BD 平分∠ABC ,可得∠DBC =∠ABD ,根据等角对等边的性质,即可证得AG=GD ;(2)当∠ABC=60°时,△DFG 是等边三角形,根据半圆(或直径)所对的圆周角是直角与三角形的外角的性质,易求得∠DGF=∠DFG=60°,即可证得结论;(3)利用三角函数先求出tan ∠ABD 34=,cos ∠ABD =45,再求出DF 、BF ,然后即可求出BC.【详解】(1)证明:连接AD ,∵DE ⊥AB ,AB 是⊙O 的直径,∴¶¶AD AE =,∴∠ADE =∠ABD ,∵弦BD 平分∠ABC ,∴∠DBC =∠ABD ,∵∠DBC =∠DAC ,∴∠ADE =∠DAC ,∴AG =GD ;(2)解:当∠ABC =60°时,△DFG 是等边三角形.理由:∵弦BD 平分∠ABC ,∴∠DBC =∠ABD =30°,∵AB 是⊙O 的直径,∴∠ACB =90°,∴∠CAB =90°﹣∠ABC =30°,∴∠DFG =∠FAB+∠DBA =60°,∵DE ⊥AB ,∴∠DGF =∠AGH =90°﹣∠CAB =60°,∴△DGF 是等边三角形;(3)解:∵AB 是⊙O 的直径,∴∠ADB =∠ACB =90°,∵∠DAC =∠DBC =∠ABD ,∵AB =10,sin ∠ABD =35, ∴在Rt △ABD 中,AD =AB•sin ∠ABD =6,∴BD8,∴tan ∠ABD =34AD BD ,cos ∠ABD =4=5BD AB , 在Rt △ADF 中,DF =AD•tan ∠DAF =AD•tan ∠ABD =6×34=92, ∴BF =BD ﹣DF =8﹣92=72, ∴在Rt △BCF 中,BC =BF•cos ∠DBC =BF•cos ∠ABD =72×45=145. ∴BC 的长为:145.【点睛】此题考查了圆周角定理、垂径定理、直角三角形的性质、三角函数的性质以及勾股定理等知识.此题综合性较强,难度较大,解题的关键是掌握数形结合思想与转化思想的应用,注意辅助线的作法.14.如图,AB 是半圆⊙O 的直径,点C 是半圆⊙O 上的点,连接AC ,BC ,点E 是AC 的中点,点F 是射线OE 上一点.(1)如图1,连接FA ,FC ,若∠AFC =2∠BAC ,求证:FA ⊥AB ;(2)如图2,过点C 作CD ⊥AB 于点D ,点G 是线段CD 上一点(不与点C 重合),连接FA ,FG ,FG 与AC 相交于点P ,且AF =FG .①试猜想∠AFG 和∠B 的数量关系,并证明;②连接OG ,若OE =BD ,∠GOE =90°,⊙O 的半径为2,求EP 的长.【答案】(1)见解析;(2)①结论:∠GFA =2∠ABC .理由见解析;②PE 3. 【解析】【分析】 (1)证明∠OFA =∠BAC ,由∠EAO +∠EOA =90°,推出∠OFA +∠AOE =90°,推出∠FAO =90°即可解决问题.(2)①结论:∠GFA=2∠ABC.连接FC.由FC=FG=FA,以F为圆心FC为半径作⊙F.因为»»=,推出∠GFA=2∠ACG,再证明∠ACG=∠ABC.AG AG②图2﹣1中,连接AG,作FH⊥AG于H.想办法证明∠GFA=120°,求出EF,OF,OG即可解决问题.【详解】(1)证明:连接OC.∵OA=OC,EC=EA,∴OF⊥AC,∴FC=FA,∴∠OFA=∠OFC,∵∠CFA=2∠BAC,∴∠OFA=∠BAC,∵∠OEA=90°,∴∠EAO+∠EOA=90°,∴∠OFA+∠AOE=90°,∴∠FAO=90°,∴AF⊥AB.(2)①解:结论:∠GFA=2∠ABC.理由:连接FC.∵OF垂直平分线段AC,∴FG=FA,∵FG=FA,∴FC=FG=FA,以F为圆心FC为半径作⊙F.∵»»AG AG=,∴∠GFA=2∠ACG,∵AB是⊙O的直径,∴∠ACB =90°,∵CD ⊥AB ,∴∠ABC +∠BCA =90°,∵∠BCD +∠ACD =90°,∴∠ABC =∠ACG ,∴∠GFA =2∠ABC .②如图2﹣1中,连接AG ,作FH ⊥AG 于H .∵BD =OE ,∠CDB =∠AEO =90°,∠B =∠AOE ,∴△CDB ≌△AEO (AAS ),∴CD =AE ,∵EC =EA ,∴AC =2CD .∴∠BAC =30°,∠ABC =60°,∴∠GFA =120°,∵OA =OB =2,∴OE =1,AE =,BA =4,BD =OD =1, ∵∠GOE =∠AEO =90°,∴OG ∥AC , 323DG OG ∴==, 22221AG DG AD ∴=+=, ∵FG =FA ,FH ⊥AG ,∴AH =HG 21∠AFH =60°, ∴AF =27sin 603AH ︒=, 在Rt △AEF 中,EF 2213AF AE -=, ∴OF =OE +EF =43 , ∵PE ∥OG , ∴PE EF OG 0F=,∴1342333PE,∴PE=36.【点睛】圆综合题,考查了垂径定理,勾股定理,圆周角定理,全等三角形的判定和性质,锐角三角函数,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.15.如图1,⊙O的直径AB=12,P是弦BC上一动点(与点B,C不重合),∠ABC=30°,过点P作PD⊥OP交⊙O于点D.(1)如图2,当PD∥AB时,求PD的长;(2)如图3,当弧DC=弧AC时,延长AB至点E,使BE=12AB,连接DE.①求证:DE是⊙O的切线;②求PC的长.【答案】(1)26;(2)①证明见解析;②33﹣3.【解析】试题分析:(1)根据题意首先得出半径长,再利用锐角三角三角函数关系得出OP,PD的长;(2)①首先得出△OBD是等边三角形,进而得出∠ODE=∠OFB=90°,求出答案即可;②首先求出CF的长,进而利用直角三角形的性质得出PF的长,进而得出答案.试题解析:(1)如图2,连接OD,∵OP⊥PD,PD∥AB,∴∠POB=90°,∵⊙O的直径AB=12,∴OB=OD=6,在Rt△POB中,∠ABC=30°,∴OP=OB•tan30°=6×=2,在Rt△POD中,PD===;(2)①如图3,连接OD,交CB于点F,连接BD,∵,∴∠DBC=∠ABC=30°,∴∠ABD=60°,∵OB=OD,∴△OBD是等边三角形,∴OD⊥FB,∵BE=AB,∴OB=BE,∴BF∥ED,∴∠ODE=∠OFB=90°,∴DE是⊙O的切线;②由①知,OD⊥BC,∴CF=FB=OB•cos30°=6×=3,在Rt△POD中,OF=DF,∴PF=DO=3(直角三角形斜边上的中线,等于斜边的一半),∴CP=CF﹣PF=3﹣3.考点:圆的综合题。
《圆的认识(二)》综合练习题3
圆的认识(二)综合练习题3一、单选题1.图()中的两个圆组成的图形有无数条对称轴。
A. B. C. D.2.下面图形中,对称轴最多的是()。
A. B. C. D.3.下列图形中,()的对称轴数量最少。
A. 圆B. 等边三角形C. 长方形D. 正方形4.半圆的对称轴有()条。
A. 1B. 2C. 4D. 无数5.下面各图形中,对称轴最多的是()。
A. 正方形B. 圆C. 等腰三角形D. 等边三角形6.从对称轴数量的角度考虑,下面()图形与其他图形不是同一类。
A. 扇形B. 等腰梯形C. 圆D. 半圆7.如下图所示,4个等圆的圆心连线正好是正方形,图中有()条对称轴。
A. 2B. 4C. 6D. 8二、填空题8. 有________条对称轴的四边形是正方形。
9.圆的对称轴有________条,圆的对称轴必须经过________ 。
10.有________条对称轴。
11.把7根粗细相同的圆柱形木棒捆成一捆,其截面图如右图所示,这个图形有________条对称轴。
三、解答题12. 画出下面各图形的对称轴。
13. 小明将一张正方形纸对折两次,如下图所示,并在中央点打孔,再将它展开,请画出展开后的图形。
14. 图中,圆的半径是多少厘米?圆的直径是多少厘米?答案解析部分一、单选题1.B2. B3. C4. A5. B6. C7. B二、填空题8. 4 9. 无数;圆心10. 4 11. 6三、解答题12.解:如图:13.14. 4厘米;8厘米。
圆的专项练习题

圆的专项练习题一、选择题1. 圆的周长公式是()。
A. C = πdB. C = 2πrC. C = πrD. C = 2πd2. 圆的面积公式是()。
A. S = πr²B. S = 2πrC. S = πdD. S = πd²3. 半径为5厘米的圆的周长是()厘米。
A. 31.4B. 15.7C. 62.8D. 3144. 半径为3厘米的圆的面积是()平方厘米。
A. 28.26B. 9C. 4.5D. 285. 圆的直径是半径的()倍。
A. 2B. 1/2C. 1/3D. 3二、填空题6. 半径为2厘米的圆的周长是________厘米。
7. 半径为4厘米的圆的面积是________平方厘米。
8. 如果一个圆的周长是31.4厘米,那么它的半径是________厘米。
9. 一个圆的直径是8厘米,那么它的半径是________厘米。
10. 如果一个圆的面积是78.5平方厘米,那么它的半径是________厘米。
三、计算题11. 一个圆形花坛的直径是20米,求这个花坛的周长和面积。
12. 一个圆形的钟表的半径是10厘米,求这个钟表的周长和面积。
13. 一个圆形水池的半径是15米,如果沿着水池的边缘铺设一条1米宽的小路,求这条小路的面积。
四、应用题14. 一个圆形的花园,半径为10米,现在要在花园周围铺设一条宽2米的环形小路,求这条小路的面积。
15. 一个圆形的水池,半径为5米,现在要在水池的中心建造一个圆形的喷泉,喷泉的半径为2米,求喷泉占据的面积。
五、解答题16. 某工厂需要制作一个圆形的金属盖子,直径为1米,求这个盖子的周长和面积。
17. 一个圆形的花坛,半径为15米,现在要在花坛的周围铺设一条宽1米的环形小路,求这条小路的面积。
18. 一个圆形的操场,半径为30米,如果沿着操场的边缘铺设一条宽5米的跑道,求这条跑道的面积。
六、证明题19. 证明:在一个圆中,任意两个直径所夹的圆心角相等。
九年级《圆》综合练习题

九年级《圆》综合练习题1、下列命题中,正确的是()A.平分弦的直线必垂直于这条弦 B.垂直于弦的直线必过圆心 C.平分弦的直径必垂直于这条弦,并且平分这条弦所对的两条弧 D.垂直平分弦的直线必平分这条弦所对的弧2、半径为5的圆内有两条平行弦,分别长6和8,则两弦间的距离为()A.1B.4C.7D.1或73、三角形的外心是三条()的交点. A.高 B.垂直平分线 C.角平分线 D.中线4、已知等腰△ABC的腰AB=4厘米,若以A为圆心,2厘米为半径的圆与BC相切,则∠BAC等于A.30°B.60°C.90°D.120°5、如图9-13,PA切⊙O于A,PB切⊙O于B,∠APB=90°,OP=4,则⊙O的半径长为()A.2 B.4 C. D.26、△ABC中,AB=3,AC=4,∠A=90°,把△ABC绕直线AC旋转一周,得到一个圆锥,其表面积为S1,把△ABC 绕直线AB旋转一周,得到一个圆锥,其表面积为S2,则S1∶S2等于()A.2∶3B.3∶4C.4∶9D.39∶567、若⊙O的半径为8,点P在⊙O内部,则线段PO的长度范围是________________.8、△ABC中,AB=AC=10厘米,BC=12厘米,若要剪一张圆形纸片盖住这个三角形,则这个圆形纸片的最小半径是_____________厘米.9、⊙O的直径为10,且O到直线l的距离为8,则直线l与⊙O的位置关系是________________.10、两圆的半径之比为4∶3,外切时两圆圆心距是28厘米,则两圆内切时的圆心距为___________________.11、任意一个五边形,以每个顶点为圆心作半径为R的等圆,如图9-14所示,则阴影部分面积为___________________.12、粮仓的顶部是一个圆锥形,其底面周长为32米,母线长为7米,为防雨需在粮仓顶部铺上油毡,需用________________平方米的油毡.(不计接头)13、如图9-15,一个残破的圆轮,为了再制作一个同样大小的圆轮,请用圆规、直尺作出它的圆心和半径.14、在半径为5厘米的圆中有一个内接等腰三角形,等腰三角形的底边长为8厘米,求等腰三角形的周长.15、如图9-16,已知两同心圆,大圆的弦AB切小圆于M,若环形的面积为9π,求AB的长.16、已知AB为⊙O的直径,P为AB弧的中点.(1)若⊙O′与⊙O外切于点P(见图9-17甲),AP,BP的延长线分别交⊙O′于点C、D,连结CD,则△PCD是_____________三角形;(2)⊙O′与⊙O相交于点P,Q(见图9-17乙),连结AQ、BQ并延长分别交⊙O′于点E、F,请选择下列两个问题中的一个作答:问题一:判断△PEF的形状,并证明你的结论;问题二:判断线段AE与BF的关系,并证明你的结论.我选择问题_____________________________,结论:_______________________________.证明:甲乙17、实践探究如图,某工地工人为了用起重机吊起两根半径为10厘米和30厘米的钢管,需要先用钢丝绳把两根钢管扎紧,问扎紧这两根钢管的钢丝绳至少要多长?(打节部分不计,精确到0.1厘米)。
圆的周长和面积综合练习题

圆的周长和面积综合练习题圆的周长和面积(一)一、细心填写:1、圆是平面上的一种()图形,围成圆的()的长叫做圆的周长。
在小小的圆中,它们的周长总是各自圆直径的()倍多一些,我们把这个固定的数叫做(),用字母()表示,它是一个()小数,在()和()之间,在计算时,一般只取它的近似值()。
2、一个圆的直径扩大2倍,它的半径扩大()倍,它的周长扩大()倍。
3、两个圆的半径的比是2:3,它们直径的比是(),周长的比是()。
二、求圆的周长:d=5厘米d=2.4分米d=3米r=2米r=4分米r=1厘米3米12厘米三、解决问题:1、XXX沿直径6.4米的圆形花圃边走一周,需要走多少米?2、一捆电线绕了9圈,每圈直径都是48厘米,这捆电线长多少米?3、在一块半径20米的圆形花坛周围围一圈篱笆。
篱笆长多少米?4、一种自行车轮胎的外直径60厘米,XXX骑车车轮每分钟转动100周。
她骑车每分钟行使多少米?5、两个小圆的周长的和与大圆的周长相比,哪个长?(单位:厘米)6 10圆的周长和面积(二)一、判断是不是:1、圆的周长是这个圆的直径的3.14倍。
2、XXX的圆周率比大圆的圆周率小。
3、把一张圆形纸片对折若干次,所有折痕相交于圆心。
4、圆的半径扩大3倍,它的直径就扩大6倍。
5、半圆的周长即是圆周长的一半。
二、填表:半径(分米)28直径(分米)312周长(分米)18.8462.83、办理题目:1、一个圆形花坛的直径是2.2米,它的周长多少米?2、一个圆形水池的半径6米。
XXX沿着水池边走了5圈,一共走了多少米?3、XXX家圆桌的直径1.2米,买铝合金条把桌边包起来,要买多少米铝合金条?4、一辆汽车从甲地去乙地,已行了全程的,这时距中点还有15千米。
已行了多少千米?5、建造一座污水处置惩罚厂,实际投资是计划的,比计划节省1.8万元。
计划投资几何万元?6、一段铁路,甲队独铺要10天完成,乙队独铺要15天完成。
目前两队合铺,完成时,甲队铺了这段公路的几分之几?圆的周长和面积(三)一、细心填写:1、一个圆形花坛的半径2.25米,直径是()米,周长()米。
圆的面积综合练习题20

1.求下面各圆的面积。
⑴r=2cm (2)r=2.2cm (3)d=3.2cm2.求下面各圆的周长和面积。
1cm3.完成下表。
半径直径圆面积2cm7cm6cm50cm4.一个圆的直径是0.8cm,它的面积是多少?(1)d=16cm (2)r=1.8cm (3)r=2.8cm2.求下面各圆的周长和面积。
6cm3.完成下表。
半径直径圆面积9cm1cm10cm90cm4.一个圆的半径是2.4cm,它的面积是多少?2.求下面各圆的周长和面积。
5. 8cm3.完成下表。
半径直径圆面积8cm1cm10cm40cm4.一个圆的半径是2.4cm,它的面积是多少?2.求下面各圆的周长和面积。
4.8cm3.完成下表。
半径直径圆面积8cm5cm10cm80cm4.一个圆的直径是2.8cm,它的面积是多少?⑴r=12cm (2)r=3.2cm (3)r=2.8cm2.求下面各圆的周长和面积。
6cm3.完成下表。
半径直径圆面积5cm5cm4cm80cm4.一个圆的半径是3.2cm,它的面积是多少?(1)d=2cm (2)r=2cm ⑶r=1.6cm2.求下面各圆的周长和面积。
4.2cm3.完成下表。
半径直径圆面积7 cm8cm4cm40cm4.一个圆的直径是1.6cm,它的面积是多少?1.6cm3.完成下表。
半径直径圆面积3cm6cm10cm20cm4.一个圆的半径是2.8cm,它的面积是多少?2.求下面各圆的周长和面积。
8cm 0.2cm3.完成下表。
半径直径圆面积2cm8cm8cm80cm4.一个圆的半径是1.2cm,它的面积是多少?圆的面积综合练习题。
(完整版)苏教版五年级数学(下册)圆的综合练习题

圆单元练习题(一)一、完成下表。
二、想一想,填一填。
1、当圆规两脚间的距离为4厘米时,画出圆的周长是()厘米。
2、在一张长8厘米,宽12厘米的长方形纸上画一个最大的圆,这个圆的直径是(),面积是(),周长是()。
3、一个车轮的直径是55厘米,车轮转动一周,大约前进()米。
4、一个环形的外圆直径是10cm,内圆直径是8cm,它的面积() cm2。
5、一个圆的半径扩大2倍,它的周长扩大()倍,面积扩大()倍。
6、把一个圆分成若干等份,剪开拼成一个近似的长方形。
这个长方形的长相当于(),长方形的宽就是圆的()。
因为长方形的面积是(),所以圆的面积是().7、圆的直径是6厘米,它的周长是(),面积是()。
8、圆的周长是25.12分米,它的面积是()。
9、甲圆半径是乙圆半径的3倍,甲圆的周长是乙圆周长的(),甲圆面积是乙圆面积的()。
10、一个圆的半径是8厘米,这个圆面积的3/4 是()平方厘米。
10、周长相等的长方形、正方形、圆,()面积最大。
11、圆的半径由6厘米增加到9厘米,圆的面积增加了()平方厘米。
12、要在一个边长为10厘米的正方形纸板里剪出一个最大的圆,剩下的面积是()。
13、要在底面半径是12厘米的圆柱形水桶外面打上一个铁丝箍,接头部分是8厘米,需用铁丝()厘米。
14、用圆规画一个圆,如果圆规两脚之间的距离是7厘米,画出的这个圆的周长是()厘米。
这个圆的面积是()平方厘米。
15、有大小两个圆,大圆直径是小圆半径的4倍,小圆与大圆周长的比是(),小圆与大圆面积的比是()。
16、一个半圆半径是r,它的周长是()。
三、请你来当小裁判。
1、圆心决定圆的位置,半径决定圆的大小。
()2、当圆的半径等于2分米时,这个圆的周长和面积相等。
()3、一个圆的面积和一个正方形的面积相等,它们的周长一定也相等. ()4、同一个圆的直径一定是半径的2倍。
()5、两端都在圆上的线段,直径是最长的一条。
()6、半圆的周长是圆周长的一半。
圆的综合练习(四)

6、下面是学校操场跑道示意图。每条跑道宽 1m。体育课上小明和小华进行400m赛跑,小明 在里面的跑道,小华在外面的跑道。起跑时, 小华要在小明前面多少米才公平?
6、下面是学校操场跑道示意图。每条跑道宽 1m。体育课上小明和小华进行400m赛跑,小明 在里面的跑道,小华在外面的跑道。起跑时, 小华要在小明前面多少米才公平?
7、 (拓展题)从一个直径是4 cm的圆形纸片上剪下一 个最大的正方形剩下的边角料的面积是多少? (π值取 3.14)
思路分析:可根据题意画出图。由图可知,圆的面
积减去正方形的面积就是边角料的面积。已知圆的直 径,利用S=πr2可求出圆的面积。正方形的对角线是圆 的直径,可以把正方形看成是两个同底等高的三角形。 两个三角形的底是圆的直径,高是圆的半径,根据三角形 面积公式可求出三角形的面积。
宝剑锋自磨砺出,梅花香自苦寒来
教学目标
知识点梳理
典题精讲
1、下图涂色部分是一个圆环, 它的内圆半 径是10厘米,外圆半径是15厘米。它的面积 是多少? (π值取3.14)
拓展要点:圆环的意义和圆环的面积的计算方法
圆环是指两个半径不相等的同心圆之间的部分。 它由外圆和内圆组成。 环宽:外圆半径和内圆半径之差叫作环宽。 圆环面积计算公式: S= π R2- π r2= π (R2- r2)
规范解答:
圆的面积:(4÷2)2π=12. 56( cm2) 正方形的面积:4x(4÷2)÷2x2=8(cm2 ) 边角料的面积:12.56-8 =4.56( cm2) 答:剩下的边角料的面积是4.56 cm2。
9、(拓展题)下图中圆的周长是16.4cm,圆的面 积与长方形的面积正好相等。阴影部分的周长是 多少厘米? ( π值取3.14)
圆的综合训练题(同步练习)-六年级上册数学人教版

圆综合训练题一、填空题。
1、用一根铁丝围成一个圆,半径正好是10分米,如果把这根铁丝改围成一个正方形,它的边长是( )分米。
2、一个圆的周长是6.28分米,半圆的周长是( )分米。
3、在一个长6cm ,宽3cm 的长方形中画一个最大的半圆形,这个半圆形的周长是( ),面积是( )4、将一个直径8厘米的圆形纸片沿直径对折后,得到一个半圆,这个半圆的周长是( )厘米,面积是( )平方厘米。
5、小圆半径是大圆半径的31,小圆与大圆周长比是( ),面积比是( )。
6、大圆和小圆直径的比是3:2,小圆和大圆周长的比是( ),面积的比是( )。
7、甲乙两圆周长比是2:3,其中一个圆的面积是18,另一个圆的面积可能是( ),也可能是( )8、学校新建的运动场正在画跑道,要求终点相同,跑道的宽度是1.25米。
(注:π取3.14)外圈跑道的起跑线应该往前移( )米。
如果跑道的宽度是A 米,则起跑线应该往前移( )米。
9、一座钟的时针长3厘米,它的尖端在一昼夜里走过的路程是( )厘米。
10、一个闹钟的分针长5厘米,从12:00走到12:30,分针的分尖走过( )厘米。
11、把一个圆剪拼成一个近似的长方形,已知剪拼成的长方形的长是6.28厘米,宽为圆的半径,则原来圆的面积是( )平方厘米。
12、在一块长10分米、宽5分米的长方形铁板上,最多能截取( )个直径是2分米的圆形铁板。
13、一个钟表的分针长10㎝,从10时走到12时,分针走过了( )㎝。
14、圆的半径增加2倍,则圆的周长扩大( )倍,圆的面积增加( )倍。
15、大圆的直径是8cm,小圆的半径是2厘米,大圆和小圆的面积比是()小圆的与大圆的周长比值是()。
16、如图,把一个圆分成若干偶数等份,拼成一个近似的长方形,拼成的长方形的长是12.56cm,宽是圆的半径,那么这个圆的周长是()cm,面积是()cm2。
17、用同样长的铁丝分别围成一个长方形、正方形、圆,()的面积最大,()的面积最小。
六年级圆练习题

六年级圆练习题一、选择题1. 一个圆的直径是10cm,那么它的半径是多少?A. 5cmB. 10cmC. 20cmD. 15cm2. 已知一个圆的半径是8cm,求它的直径是多少?A. 4cmB. 16cmC. 12cmD. 8cm3. 若一个圆的半径为3cm,则它的周长是多少?A. 6cmB. 12cmC. 18cmD. 9cm4. 已知一个圆的直径是20cm,则它的周长是多少?A. 10cmB. 20cmC. 40cmD. 30cm5. 若一个圆的半径为6cm,则它的面积是多少?A. 12cm²B. 18cm²C. 36cm²D. 24cm²6. 已知一个圆的直径是14cm,则它的面积是多少?A. 154cm²B. 616cm²C. 307cm²D. 28cm²二、填空题1. 若一个圆的直径是12cm,则它的半径是________。
2. 若圆的半径是5cm,则它的直径是________。
3. 若一个圆的周长是20cm,则它的半径是________。
4. 若一个圆的周长是30cm,则它的直径是________。
5. 若一个圆的半径是7cm,则它的面积是________。
6. 若一个圆的直径是18cm,则它的面积是________。
三、计算题1. 一个圆的半径是14cm,求它的周长和面积。
2. 若一个圆的直径是18cm,求它的周长和面积。
3. 若一个圆的周长是36cm,求它的半径和面积。
4. 若一个圆的直径是20cm,求它的周长和面积。
5. 若一个圆的周长是24cm,求它的半径和面积。
6. 若一个圆的半径是8cm,求它的周长和面积。
四、解答题1. 请解释什么是圆的直径、半径、周长和面积?2. 请说明直径与半径的关系。
3. 请解释周长和面积的计算公式,并给出一个示例。
五、综合题小明的妈妈给他买了一个蛋糕,蛋糕的形状是一个半径为10cm的圆形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
O F A BC D EF EDCBOA CEBODFA圆综合练习题一、与圆有关的中档题:与圆有关的证明(证切线为主)和计算(线段长、面积、三角函数值、最值等)1. 如图,BD 为⊙O 的直径,AC 为弦,AB AC =,AD 交BC 于E ,2AE =,4ED =.(1)求证:ABE ADB △∽△,并求AB 的长; (2)延长DB 到F ,使BF BO =,连接FA ,判断直线FA 与⊙O 的位置关系,并说明理由. 2. 已知:如图,以等边三角形ABC 一边AB 为直径的⊙O 与边AC 、BC 分别交于点D 、E ,过点D 作DF ⊥BC ,垂足为F .(1)求证:DF 为⊙O 的切线;(2)若等边三角形ABC 的边长为4,求DF 的长;(3)求图中阴影部分的面积.3、如图,已知圆O 的直径AB 垂直于弦CD 于点E ,连接CO 并延长交AD 于点F ,且CF AD ⊥.(1)请证明:E 是OB 的中点; (2)若8AB =,求CD 的长.4.如图,AB 是⊙O 的直径,点C 在⊙O 上,∠BAC = 60?,P 是OB 上一点,过P 作AB 的垂线与AC 的延长线交于点Q ,连结OC ,过点C 作OC CD ⊥交PQ 于点D . (1)求证:△CDQ 是等腰三角形; (2)如果△CDQ ≌△COB ,求BP :PO 的值.5. 已知:如图, BD 是半圆O 的直径,A 是BD 延长线上的一点,BC ⊥AE ,交AE的延长线于点C , 交半圆O 于点E ,且E 为»DF的中点. (1)求证:AC 是半圆O 的切线; (2)若662AD AE ==,,求BC 的长.6.如图,ABC △内接于⊙O ,过点A 的直线交⊙O 于点P ,交BC 的延长线于点D ,且AB 2=AP ·AD(1)求证:AB AC =;(2)如果60ABC ∠=o,⊙O 的半径为1,且P 为弧AC 的中点,求AD 的长.7.如图,在△ABC 中,∠C =90°, AD 是∠BAC 的平分线,O 是AB 上一点, 以OA 为半径的⊙O 经过点D .(1)求证: BC 是⊙O 切线; (2)若BD =5, DC =3, 求AC 的长.OPDC BOABA BCDE OGFOQP CB AG FE D C O B A第13题图8.如图,AB 是⊙O 的直径,CD 是⊙O 的一条弦,且CD⊥AB 于E ,连结AC 、OC 、BC.(1)求证:∠ACO=∠BCD;(2)若BE=2,CD=8,求AB 和AC 的长.9.如图,已知BC 为⊙O 的直径,点A 、F 在⊙O 上,BC AD ⊥,垂足为D ,BF 交AD 于E ,且BE AE =. (1)求证:AF AB =;(2)如果3sin =∠FBC ,54=AB ,求AD 的长.10.如图,已知直径与等边ABC ∆的高相等的圆O 分别与边AB 、BC 相切于点D 、E ,边AC 过圆心O 与圆O 相交于点F 、G 。
(1) 求证:DE AC P ;(2) 若ABC ∆的边长为a ,求ECG ∆的面积. 11.如图,在△ABC 中,∠BCA =90°,以BC 为直径的⊙O 交AB 于点P ,Q 是AC的中点.(1)请你判断直线PQ 与⊙O 的位置关系,并说明理由;(2)若∠A =30°,AP =23,求⊙O 半径的长. 12.如图,已知点A 是⊙O 上一点,直线MN 过点A ,点B是MN 上的另一点,点C 是OB 的中点, 12AC OB =,若点P 是⊙O 上的一个动点,且∠30OBA =o,AB =23时,求△APC 的面积的最大值.13.如图,等腰△ABC 中,AB =AC =13,BC =10,以AC 为直径作⊙O 交BC 于点D ,交AB 于点G ,过点D 作⊙O 的切线交AB 于点E ,交AC 的延长线与点F . (1)求证:EF ⊥AB ; (2)求co s∠F 的值. 14.(应用性问题)已知:如图,为了测量一种圆形零件的精度,在 加工流水线上设计了用两块大小相同,且含有30°的直角三角尺按图 示的方式测量. (1)若⊙O 分别与AE 、AF 交于点B 、C ,且AB=AC ,若⊙O 与AF 相切.求证: ⊙O 与AE 相切;(2)在满足(1)的情况下,当B、C分别为AE 、AF 的三分之一点时,且AF =3,求»BC的弧长. 二、圆与相似综合A BCM NOPFB CE GOEB 15.已知:如图,⊙O 的内接△ABC 中,∠BAC=45°,∠ABC =15°,AD ∥OC 并交BC 的延长线于D ,OC 交AB 于E. (1)求∠D 的度数;(2)求证:2AC AD CE =⋅; (3)求BCCD的值. 16.如图⑴,⊙O 的直径为AB ,过半径OA 的中点G 作弦AB CE ⊥,在BC 上取一点D ,分别作直线ED CD 、,交直线AB 于点M F 、. ⑴求COA ∠和FDM ∠的度数; ⑵求证:FDM ∆∽COM ∆;⑶如图⑵,若将垂足改取为半径上任意一点,点改取在 上,仍作直线ED CD 、,分别交直线AB 于点M F 、. 试判断:此时是否仍有FDM ∆∽COM ∆成立若成立请证明你的结论;若不成立,请说明理由。
三、圆与三角函数综合 17.已知⊙O 过点D (4,3),点H 与点D 关于y 轴对称,过H 作⊙O 的切线交y 轴于点A (如图1)。
⑴求⊙O 半径;⑵求sin HAO ∠的值;⑶如图2,设⊙O 与y 轴正半轴交点P ,点E 、F 是线段OP 上的动点(与P 点不重合),联结并延长DE 、DF 交⊙O 于点B 、C ,直线BC 交y 轴于点G ,若DEF ∆是以EF 为底的等腰三角形,试探索sin CGO ∠的大小怎样变化请说明理由。
四、圆与二次函数(或坐标系)综合18、如图,⊙M 的圆心在x 轴上,与坐标轴交于A (0,3)、B (-1,0),抛物线233y x bx c =-++经过A 、B 两点.(1) 求抛物线的函数解析式;(2) 设抛物线的顶点为P .试判断点P 与⊙M 的位置关系,并说明理由;(3) 若⊙M 与y 轴的另一交点为D ,则由线段PA 、图1图2O xy D(4,3)AHCF E P BG OxyD(4,3)图1图2线段PD 及弧ABD 围成的封闭图形PABD 的面积是多少19.如图,在平面直角坐标系中,O 是原点,以点C (1,1)为圆心,2为半径作圆,交x 轴于A ,B 两点,开口向下的抛物线经过点A ,B ,且其顶点P 在⊙C 上. (1)求∠ACB 的大小;(2)写出A ,B 两点的坐标; (3)试确定此抛物线的解析式;(4)在该抛物线上是否存在一点D ,使线段OP 与CD 互相平分若存在,求出点D 的坐标;若不存在,请说明理由.20.(以圆为幌子,二次函数为主的代几综合题)如图,半径为1的⊙1O 与x 轴交于A B 、两点,圆心1O 的坐标为(20),,二次函数2y x bx c =-++的图象经过A B 、两点,其顶点为F .(1)求b c ,的值及二次函数顶点F 的坐标;(2)将二次函数2y x bx c =-++的图象先向下平移1个单位, 再向左平移2个单位,设平移后图象的顶点为C ,在经过点B 和点()0,3D -的直线l 上是否存在一点P ,使PAC ∆的周长最小,若存在,求出点P 的坐标;若不存在,请说明理由. 五、以圆为背景的探究性问题21.下图中, 图(1)是一个扇形OAB ,将其作如下划分:第一次划分: 如图(2)所示,以OA 的一半OA 1的长为半径画弧交OA 于点A 1,交OB 于点B 1,再作∠AOB 的平分线,交»AB 于点C ,交¼11A B 于点C 1, 得到扇形的总数为6个,分别为: 扇形OAB 、扇形OAC 、扇形OCB 、扇形OA 1B 1、扇形OA 1C 1、扇形OC 1B 1;第二次划分: 如图(3)所示,在扇形OC 1B 1中, 按上述划分方式继续划分, 即以OC 1的一半OA 2的长为半径画弧交OC 1于点A 2,交OB 1于点B 2,再作∠B 1OC 1的平分线,交¼11B C 于点D 1,交¼22A B 于点D 2,可以得到扇形的总数为11个;第三次划分: 如图(4)所示,按上述划分方式继续划分;…… 依次划分下去.(1)根据题意, 完成右边的表格;xyABO-245-1-32-1-21O 1(2)根据右边的表格, 请你判断按上述划分方式, 能否得到扇形的总数为2008个? 为什么?(3)若图(1)中的扇形的圆心角∠AOB=m °,且扇形的半径OA 的长为R .我们把图(2)第一次划分的图形中,扇形11OA C (或扇形11OC B )称为第一次划分的最小扇形,其面积记为S 1;把图(3)第二次划分的最小扇形面积记为S 2;……,把第n 次划分的最小扇形面积记为S n..求1n n S S -的值.22.圆心角定理是“圆心角的度数与它所对的弧的度数相等”,记作»AOB AB ∠@两B ,两 请一、与圆有关的中档题:与圆有关的证明(证切线为主)和计算(线段长、面积、三角函数值、最值等)1. 如图,BD 为⊙O 的直径,AC 为弦,AB AC =,AD 交BC 于E ,2AE =,4ED =.(1)求证:ABE ADB △∽△,并求AB 的长;(2)延长DB 到F ,使BF BO =,连接FA ,判断直线FA 与⊙O 的位置关系,并说明理由. 1.解:AB AC =Q ,ABC C ∴=∠∠C D =Q ∠∠,ABC D ∴=∠∠. 又BAE DAB =Q ∠∠,ABE ADB ∴△∽△. AB AEAD AB∴=. ()()224212AB AD AE AE ED AE ∴==+=+⨯=g g .AB ∴=(舍负).(2)直线FA 与O e 相切.连接OA .BD Q 为O e 的直径,90BAD ∴=o ∠.(2)∵OAD ∆是等边三角形,∴CD =AD =AO =21AB =2.Rt CDF ∆中,∠CDF =30°,∴CF =21CD =1. ∴DF =322=-CF CD .(3)连接OE ,由(2)同理可知E 为CB 中点,∴2=CE .∵1=CF ,∴1=EF . ∴233)(21=⋅+=DF OD EF S FDOE直角梯形.CEFA∴ππ323602602=⨯=DOES 扇形.∴π32233-=-DOE FDOE S S 扇形直角梯形. 3、如图,已知圆O 的直径AB 垂直于弦CD 于点E ,连接CO 并延长交AD 于点F ,且CF AD ⊥.(1)请证明:E 是OB 的中点; (2)若8AB =,求CD 的长. 3、(1)证明:连接AC ,如图CF AD ⊥Q ,AE CD ⊥且CF AE ,过圆心O»»AC AD ∴=,»»AC CD =,ACD ∴△是等边三角形. 30FCD ∴∠=o在Rt COE △中,12OE OC =,12OE OB ∴=∴点E 为OB 的中点(2)解:在OCE t ∆R 中8AB =Q ,142OC AB ∴==又BE OE =Q ,2OE ∴= 4.如图,AB 是⊙O 的直径,点C 在⊙O 上,∠BAC = 60?,P 是OB 上一点,过P 作AB 的垂线与AC 的延长线交于点Q ,连结OC ,过点C 作OC CD ⊥交PQ 于点D .(1)求证:△CDQ 是等腰三角形; (2)如果△CDQ ≌△COB ,求BP :PO 的值.4. (1)证明:由已知得∠ACB =90°,∠ABC =30°,∴∠Q =30°,∠BCO =∠ABC =30°. ∵CD ⊥OC ,∴∠DCQ =∠BCO =30°,∴∠DCQ =∠Q ,∴△CDQ 是等腰三角形. (2)解:设⊙O 的半径为1,则AB =2,OC =1,AC =121=AB ,BC =3. ∵等腰三角形CDQ 与等腰三角形COB 全等,∴CQ =BC =3.∵AQ =AC +CQ =1+3,AP =23121+=AQ , ∴BP =AB -AP =2332312-=+- PO =AP -AO =2131231-=-+, ∴BP ∶PO =3.5. 已知:如图, BD 是半圆O 的直径,A 是BD 延长线上的一点,BC ⊥AE ,交AE的延长线于点C , 交半圆O 于点E ,且E 为»DF的中点. (1)求证:AC 是半圆O 的切线;(2)若6AD AE ==,BC 的长.5.解:(1)连接OE , ∵E 为»DF的中点,∴»»DE EF =. ∴ OBE CBE ∠=∠. ∵OE OB =,∴OEB OBE ∠=∠.∴ OEB CBE ∠=∠.∴OE ∥BC. ∵BC ⊥AC , ∴∠C=90°. ∴ ∠AEO =∠C =90°. 即OE ⊥AC . 又OE 为半圆O 的半径,∴ AC 是半圆O 的切线. (2)设O e 的半径为x ,∵OE AC ⊥,∴222(6)x x +-=. ∴3x =. ∴12AB AD OD OB =++=.7.如图,在△ABC 中,∠C =90°, AD 是∠BAC 的平分线,O 是AB 上一点, 以OA 为半径的⊙O 经过点D .(1)求证: BC 是⊙O 切线;(2)若BD =5, DC =3, 求AC 的长. 7.(1)证明: 如图1,连接OD . ∵ OA =OD , AD 平分∠BAC , ∴ ∠ODA =∠OAD , ∠OAD =∠CAD .∴ ∠ODA =∠CAD .∴ OD //AC . ∴ ∠ODB =∠C =90?.∴ BC 是⊙O 的切线. 图1(2)解法一: 如图2,过D 作DE ⊥AB 于E .∴ ∠AED =∠C =90?.又∵ AD =AD , ∠EAD =∠CAD ,∴ △AED ≌△ACD . ∴ AE =AC , DE =DC =3.在Rt △BED 中,∠BED =90?,由勾股定理,得 BE =422=-DE BD . 图2设AC =x (x >0), 则AE =x .在Rt △ABC 中,∠C =90?, BC =BD +DC =8, AB =x +4, 由勾股定理,得x 2 +82= (x +4) 2.解得x =6. 即 AC =6. 解法二: 如图3,延长AC 到E ,使得AE =AB .∵ AD =AD , ∠EAD =∠BAD ,∴ △AED ≌△ABD .∴ ED =BD=5.在Rt △DCE 中,∠DCE =90?, 由勾股定理,得 CE =422=-DC DE . ………… ……………5分 图3在Rt △ABC 中,∠ACB =90?, BC =BD +DC =8, 由勾股定理,得 AC 2+BC 2= AB 2.即 AC 2 +82=(AC +4) 2.解得 AC =6.8.如图,AB 是⊙O 的直径,CD 是⊙O 的一条弦,且CD⊥AB 于E ,连结AC 、OC 、BC.(1)求证:∠ACO=∠BCD;(2)若BE=2,CD=8,求AB 和AC 的长.8、证明:(1)连结BD ,∵AB 是⊙O 的直径,CD⊥AB,∴. ∴∠A=∠2.又∵OA=OC,∴∠1=∠A.∴∠1=∠2.即:∠ACO=∠BCD.解:(2)由(1)问可知,∠A=∠2,∠AEC=∠CE B.∴△ACE∽△CBE. ∴.CEAEBE CE =∴CE 2=BE·AE. 又CD=8,∴CE=DE=4.∴AE=8.∴AB=10.∴AC=.548022==+CE AE9.如图,已知BC 为⊙O 的直径,点A 、F 在⊙O 上,BC AD ⊥,垂足为D ,BF 交AD 于E ,且BE AE =. CA OB E B DC AO EABCD EO GFO G FH ABCDE(1)求证:AF AB =;(2)如果53sin =∠FBC ,54=AB ,求AD 的长.9.解:(1)延长AD 与⊙O 交于点G .∵ 直径BC ⊥弦AG 于点D ,∴. ∴ ∠AFB =∠BAE .∵ AE =BE ,∴ ∠ABE =∠BAE .∴ ∠ABE =∠AFB . ∴ AB =AF .(2)在Rt △EDB 中,sin ∠FBC =5=BE .设ED =3x ,BE =5x ,则AE =5x ,AD =8x ,在Rt △EDB 中,由勾股定理得BD =4x . 在Rt △ADB 中,由勾股定理得BD 2+AD 2=AB 2. ∵ AB =45,∴ 222)54()8()4(=+x x . ∴ x =1(负舍).∴ AD =8x =8.10.如图,已知直径与等边ABC ∆的高相等的圆O 分别与边AB 、BC 相切于点D 、E ,边AC 过圆心O 与圆O 相交于点F 、G 。
