2013年高二新课程数学(新课标人教A版)课件选修1-2《1.1回归分析的基本思想及其初步应用》
人教a版高中数学选修1-2课件:第一章1.1回归分析的基本思想及其初步应用

(1)作出散点图,并求线性回归方程; (2)求出 R2; (3)进行残差分析.
解:(1)散点图如图所示.
-x =16×(5+10+15+20+25+30)=17.5,
-y
=
1 6
×
(7.25
+
8.12
D.若变量 y 和 x 之间的相关系数 r=-0.936 2,则 变量 y 与 x 之间具有线性相关关系
解析:R2 的值越大,说明残差平方和越小,也就是 模型的拟合效果越好,因此 C 是不正确的.
答案:C
类型 2 线性回归分析(互动探究) [典例 2] 为研究重量 x(单位:克)对弹簧长度 y(单位: 厘米)的影响,对不同重量的 6 个物体进行测量,数据如 下表所示:
3.刻画回归效果的方式
[思考尝试·夯基]
1.思考判断(正确的打“√”,错误的打“×”) (1)求线性回归方程前可以不进行相关性检验.( ) (2)在残差图中,纵坐标为残差,横坐标可以选为样 本编号.( ) (3)利用线性回归方程求出的值是准确值.( ) 答案:(1)× (2)√ (3)×
2.如图四个散点图中,适合用线性回归模型拟合其 中两个变量的是( )
第一章 统计案例
1.1 回归分析的基本思想 及其初步应用
[学习目标] 1.了解随机误差、残差、残差分析的概 念(重点). 2.会求线性回归方程. 3.会用残差分析判 断线性回归模型的拟合效果. 4.通过对典型案例的探 究,了解回归分析的基本思想方法和初步应用(重点、难 点).
[知识提炼·梳理]
答案:①②③
类型 1 概念的理解和判断(自主研析)
新课标人教A版高中数学选修1-2 《1.1 回归分析的基本思想及其初步应用》(共45张PPT)

n
n
ˆ = 0.849是回归直线的斜率的估计值,说明身高x b 每增加1个单位,体重y就增加0.849个单位,这表明体重 与身高具有正的线性相关关系.
图1.1 1
ˆ 和a ˆ, 未知参数 b 和 a 的最小二乘估计分别为 b 其计算公式如下:
ˆ b
x
i 1 n
n
i
x yi y
i
x
i 1
x
,
2
ˆ x, ˆ = y-b a
1 1 其中 x = xi ,y = yi . x,y 称为样本点 的 中心 . n i=1 n i=1
思考:如何发现数据中的错误?如何衡量模型的拟 合效果? 可以通过残差发现原始数据中的可疑数据,判 断所建立模型的拟合效果.下表列出了女大学生身 高和体重的原始数据以及相应的残差数据.
编号 1 2 3 4 170 5 6 7 155 8 170
身 高 / cm 165
165 157
175 165
体 重 / kg 48 57Fra bibliotek50 54 64 61 43 59 ˆ 6 .373 2 .627 2 .419 4 .618 1 .137 6 .627 2 .883 0 .382 残 差e
我们可以利用图形来分析残差特性.作图时纵 坐标为残差, 横坐标可以选为样本编号, 或身高数据, 或 体重估计值等, 这样作出的图形为残差图.下图 是以 样本编号为横坐标的残差图.
所以 ,对身高为 172 cm的女大学生 , 由回归方程可以 预报其体重为 ˆ = 0.849 172 - 85.712 = 60.316 ( kg) . y
人教版高中数学选修1-2(A版)课件:第一章 1.1回归分析的基本思想及其初步应用 (共93张PPT)

昨日的明天是今天。明天的昨日是今天。为什么要计较于过去呢(先别急着纠正我的错误,你确实可以在评判过去中学到许多)。但是我发现有的人过分地瞻前顾后了。为 何不想想“现在”呢?为何不及时行乐呢?如果你的回答是“不”,那么是时候该重新考虑一下了。成功的最大障碍是惧怕失败。这些句子都教育我们:不要惧怕失败。如 果你失败了他不会坐下来说:“靠,我真失败,我放弃。”并且不是一个婴儿会如此做,他们都会反反复复,一次一次地尝试。如果一条路走不通,那就走走其他途径,不 断尝试。惧怕失败仅仅是社会导致的一种品质,没有人生来害怕失败,记住这一点。宁愿做事而犯错,也不要为了不犯错而什么都不做。不一定要等到时机完全成熟才动手。 开头也许艰难,但是随着时间的流逝,你会渐渐熟悉你的事业。世上往往没有完美的时机,所以当你觉得做某事还不是时候,先做起来再说吧。喜欢追梦的人,切记不要被 梦想主宰;善于谋划的人,切记空想达不到目标;拥有实干精神的人,切记选对方向比努力做事重要。太阳不会因为你的失意,明天不再升起;月亮不会因为你的抱怨,今 晚不再降落。蒙住自己的眼睛,不等于世界就漆黑一团;蒙住别人的眼睛,不等于光明就属于自己!鱼搅不浑大海,雾压不倒高山,雷声叫不倒山岗,扇子驱不散大雾。鹿 的脖子再长,总高不过它的脑袋。人的脚指头再长,也长不过他的脚板。人的行动再快也快不过思想!以前认为水不可能倒流,那是还没有找到发明抽水机的方法;现在认 为太阳不可能从西边出来,这是还没住到太阳从西边出来的星球上。这个世界只有想不到的,没有做不到的!不是井里没有水,而是挖的不够深;不是成功来的慢,而是放 弃速度快。得到一件东西需要智慧,放弃一样东西则需要勇气!终而复始,日月是也。死而复生,四时是也。奇正相生,循环无端,涨跌相生,循环无端,涨跌相生,循环 无穷。机遇孕育着挑战,挑战中孕育着机遇,这是千古验证了的定律!种子放在水泥地板上会被晒死,种子放在水里会被淹死,种子放到肥沃的土壤里就生根发芽结果。选
高中数学人教A版选修1-2第一章回归分析的基本思想及其初步应用课件

高中数学人教A版选修1-2第一章回归 分析的 基本思 想及其 初步应 用课件 【精品 】
高中数学人教A版选修1-2第一章回归 分析的 基本思 想及其 初步应 用课件 【精品 】
残差图的制作及作用
1、坐标纵轴为残差变量,横轴可以有不同的选择; 2、若模型选择的正确,残差图中的点应该分布在以横
轴为心的带形区域; 3、对于远离横轴的点,要特别注意。
34 157 170
50 54
2.419 -4.618
5 175
64
1.137
678 165 155 170
61 43 59
6.627 -2.883 0.382
(一)我们可以利用图形来分析残差特性,作图时纵坐标为 残差,横坐标可以选为样本编号,或身高数据,或体重估计值 等,这样作出的图形称为残差图。
探索2:在这些点附近可画直线不止一条,哪条直 线最能代表x与y之间的关系呢?
探究
对于一组具有线性相关关系的数据 (x1, y1), (x2 , y2 ),..., (xn , yn ),
我们知道其回归方程的截距和斜率的最小二乘估计公式分别为:
^
^
a y b x,......(1)
n
n
y ^
编号 1
2
身高 165 165 /cm
体重/kg 48 57
残差 -6.373 2.627
34 157 170
50 54
2.419 -4.618
5 175
64
1.137
678 165 155 170
61 43 59
6.627 -2.883 0.382
(一)我们可以利用图形来分析残差特性,作图时纵坐标为 残差,横坐标可以选为样本编号,或身高数据,或体重估计值 等,这样作出的图形称为残差图。
高中数学人教a版选修1-2课件:第一章 1.1 回归分析的基本思想及其初步应用

(3)线性回归模型 线性回归模型用 y=bx+a+e 来表示,其中 a 和 b 为模型 的 未知参数,e 称为随机误差. (4)刻画回归效果的方式 残差 把随机误差的估计值^ e i 称为相应 于点(xi,yi)的残差 作图时纵坐标为 残差 ,横坐标 残差图 可以选为样本编号,或身高数 据,或体重估计值等,这样作出 的图形称为残差图
(2)所有的两个相关变量都可以求回归 方程吗?
Hale Waihona Puke 提示:不一定.2.归纳总结,核心必记 (1)回归分析 回归分析是对具有 相关关系 的两个变量进行统计分 析的一种常用方法. (2)回归直线方程 方程^ y =^ b x+^ a 是两个具有线性相关关系的变量的一 组数据(x1,y1),(x2,y2),…,(xn,yn)的回归方程,其中^ a, ^ b 是待定参数,其最小二乘估计分别为:
xiyi 60 160 300 300 560 1 380
5 25 250 所以, x = =5, y = =50, x2 i =145, 5 5 i= 1
xiyi=1 380.
i= 1
5
x- y xiyi-5- 于是可得^ b=
i= 1 5 2 x2 i -5 x i= 1
5
1 380-5×5×50 = =6.5, 2 145-5×5 ^ a =- y -^ b- x =50-6.5×5=17.5. 所以所求的线性回归方程为^ y =6.5x+17.5.
n 2 (2)计算 x , y , xi , xiyi; i= 1 i= 1
n
(3)代入公式计算^ a ,^ b 的值; (4)写出线性回归方程.
讲一讲 1.(链接教材 P2-例 1)某种产品的广告费用支出 x 与 销售额 y(单位:百万元)之间有如下的对应数据: x/百万元 2 4 5 6 8
2013年高二数学(人教A版选修1-2)课件1.1《回归分析的基本思想及其初步应用》

②省略了一些因素的影响产生的误差;
③观测与计算产生的误差.
(3)残差分析是回归分析的一种方法. (4)用相关指数R2来刻画回归效果. R2越大,意味着残差平方和越小,即模型的拟 合效果越好;R2越小,残差平方和越大,即模
3.建立回归模型的基本步骤
(1)确定研究对象,明确哪个变量是解释变量, 哪个变量是预报变量.
残差平
残差平方和为
n
(yi-y^ )2,残差平方和
越小
,模型
i=1
方和
拟合效果越好
n
yi-y^ i2
i=1
相关指 R2=1-
,R2 表示 解释 变量对 预报 变量变
数 R2
n
yi- y 2
i=1
化的贡献率,R2 越接近于 1,表示回归的效果越好
想一想:回归分析中,利用线性回归方程求出的 函数值一定是真实值吗?为什么?
[思路探索] 先利用散点图分析物理成绩与数学成 绩是否线性相关,若相关再利用线性回归模型求 解.
解 (1)散点图如图.
(2) x =15×(88+76+73+66+63)=73.2, y =15×(78+65+71+64+61)=67.8.
5
xiyi=88×78+76×65+73×71+66×64+63×61=25 054.
高中新课标数学人教A版选修1-2课件:1.1 回归分析的基本思想及初步应用 .1

∑ i=1 xi- x yi- y ^ ^ ^ ^ ^ (1)回归直线方程:y=bx+a,其中:b ,a= y
i =1
n
xi- x 2
n
1n 1n ^ -b x , x =ni∑ ∑ =1xi, y =ni =1yi. (2)变量样本点中心:( x , y ),回归直线过样本点的中心. (3)线性回归模型:y=bx+a+e,其中 e 称为随机误差,a 和 b 是 模型的未知参数,自变量 x 称为解释变量,因变量 y 称为预报变量.
目标导航 1.能知道用回归分析处理两个变量之间的不确定关系的统计方法. 2ห้องสมุดไป่ตู้会利用散点图分析两个变量是否存在相关关系;会用残差及 R2 来刻 画线性回归模型的拟合效果. 3.能记住建立回归模型的方法和步骤;能知道如何利用线性回归模型 求非线性回归模型.
1 新知识· 预习探究 知识点一 线性回归模型 阅读教材 P2~P4 探究,完成下列问题.
误差是有的,但并不意味着预报值没有使用价值,它是预报变量 的可能取值的平均值,每一个真实值都在预报值的左右. 可以利用残差(特别是残差平方和)来描述回归模型的回归效果, 如果残差很小,说明样本点几乎全部分布在回归方程上,这时的回归 方程能很好地刻画两变量间的关系. 3.残差平方和的效果 n 残差平方和∑ ^ e2 i 越小,回归模型刻画两变量之间的关系越好;残
2.残差^ e的意义 残差^ e是随机误差 e 的估计量,^ ei 是相应于点(xi,yi)的 ei 的估计 值.可以通过残差发现原始数据中的可疑数据,判断所建立模型的拟 合效果,残差的绝对值越小,拟合效果越好. n n n 2 2 ^ ^ ^xi-a ^)2 称为残差平方 残差平方和:∑ ei =∑ (yi-yi) =∑ (yi-b
人教A版高中选修1-2《1.1回归分析的基本思想及其初步应用》课件

2 y - y i
n
=1-0=1.
1
2
3
4
5
解析
答案
4.面对竞争日益激烈的消费市场,众多商家不断扩大自己的销售市场, 以降低生产成本 .某白酒酿造企业市场部对该企业 9 月份的产品销量 x(单 位:千箱 ) 与单位成本 y( 单位:元 ) 的资料进行线性回归分析,结果如下:
6 6 7 2 x =2, y =71, xi =79, xiyi=1 481.则销量每增加 1 000 箱,单位成 i=1 i=1
^
a= y -b x =4-2×1.5=1, 故y=2x+1.
^
^
1
2
3
4
5
解答
回归分析的步骤
规律与方法
(1)确定研究对象,明确哪个变量是解释变量,哪个变量是预报变量;
(2)画出确定好的解释变量和预报变量的散点图,观察它们之间的关系
(如是否存在线性关系等);
(3)由经验确定回归方程的类型(如果呈线性关系,则选用线性回归方程 y=bx+a);
^ ^ ^
(4)按一定规则估计回归方程中的参数; (5)得出结果后分析残差图是否有异常(个别数据对应的残差过大,或残 差呈现不随机的规律性等),若存在异常,则检查数据是否有误或模型是 否合适等.
本课结束
R2=1-
i=1
2 y - y i
,R2表示 解释 变量对于 预报 变量变
化的贡献率,R2越接近于1,表示回归的效果越好
题型探究
类力x和判断力y进行统计分析,得下表
数据: x y 6 2 8 3 10 5 12 6
(1)请画出上表数据的散点图;
答案
3.若一组观测值(x1,y1),(x2,y2),…,(xn,yn)之间满足yi=bxi+a+ei 1 (i=1,2,…,n),且ei恒为0,则R2为_____.
数学选修1-2人教新课标a版1.1回归分析的基本思想及其初步.
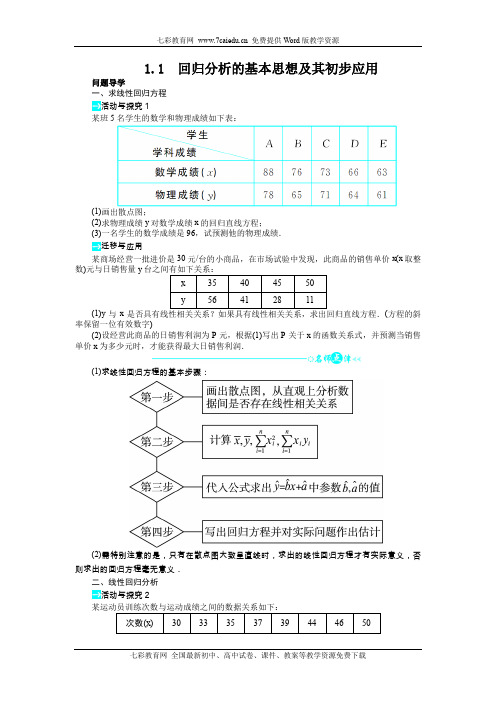
1.1 回归分析的基本思想及其初步应用问题导学一、求线性回归方程活动与探究1某班5名学生的数学和物理成绩如下表:(1)画出散点图;(2)求物理成绩y对数学成绩x的回归直线方程;(3)一名学生的数学成绩是96,试预测他的物理成绩.迁移与应用某商场经营一批进价是30元/台的小商品,在市场试验中发现,此商品的销售单价x(x取整数)元与日销售量y(1)y与x(方程的斜率保留一位有效数字)(2)设经营此商品的日销售利润为P元,根据(1)写出P关于x的函数关系式,并预测当销售单价x为多少元时,才能获得最大日销售利润.(1)求线性回归方程的基本步骤:(2)需特别注意的是,只有在散点图大致呈直线时,求出的线性回归方程才有实际意义,否则求出的回归方程毫无意义.二、线性回归分析活动与探究2(1)(2)求出线性回归方程;(3)作出残差图,并说明模型的拟合效果; (4)计算R 2,并说明其含义.迁移与应用且知x 与y“相关指数R 2、残差图”在回归分析中的作用:(1)相关指数R 2是用来刻画回归效果的,由R 2=1-∑ni =1(y i -y ^i )2∑n i =1(y i -y )2可知,R 2越大,意味着残差平方和越小,也就是说模型的拟合效果就越好.(2)残差图也是用来刻画回归效果的,判断依据是:残差点比较均匀地分布在水平带状区域中,带状区域越窄,说明模型拟合精度越高,回归方程预报的精度也越高.三、非线性回归分析活动与探究3(1)作出x 与y(2)建立x 与y 的关系,预报回归模型并计算残差; (3)利用所得模型,预报x =40时y 的值.迁移与应用试建立y 关于x非线性回归问题有时并不给出经验公式,这时我们可以画出已知数据的散点图,把它与学过的各种函数(幂函数、指数函数、对数函数等)图象作比较,挑选一种跟这些散点拟合得最好的函数,然后采用适当的变量置换,把问题化为线性回归分析问题,使之得到解决.答案: 课前·预习导学 【预习导引】1.(1)确定性 非确定性 (2)相关(3)121()()()niii nii x x yy x x ==---∑∑ y -b ^x (x ,y ) (4)随机误差 解释变量 预报变量预习交流1 D2.y i -bx i -a y i -y ^i y i -b ^x i -a ^3.1-∑ni =1(y i -y ^i )2∑ni =1(y i -y )2 预习交流2 提示:散点图可以说明变量间有无线性相关关系,但只能粗略地说明两个变量之间关系的密切程度,而相关指数R 2能精确地描述两个变量之间的密切程度.预习交流3 提示:(1)回归方程只适用于所研究的样本的总体. (2)所建立的回归方程一般都有时间性.(3)样本取值的范围会影响回归方程的适用范围.(4)不能期望回归方程得到的预报值就是预报变量的精确值.事实上,它是预报变量的可能取值的平均值.课堂·合作探究 【问题导学】活动与探究1 思路分析:先画散点图,分析物理与数学成绩是否有线性相关关系,若相关,再利用线性回归模型求解预报变量.解:(1)散点图如图所示.(2)因为x =15×(88+76+73+66+63)=73.2,y =15×(78+65+71+64+61)=67.8,∑5i =1x i y i =88×78+76×65+73×71+66×64+63×61=25 054,∑5i =1x 2i =882+762+732+662+632=27 174.所以b ^=∑5i =1x i y i -5x y ∑5i =1x 2i -5x 2=25 054-5×73.2×67.827 174-5×73.22≈0.625,a ^=y -b ^x ≈67.8-0.625×73.2=22.05.所以y 对x 的回归直线方程是y ^=0.625x +22.05.(3)x =96,则y ^=0.625×96+22.05≈82,即可以预测他的物理成绩是82.迁移与应用 解:(1)散点图如图所示,从图中可以看出这些点大致分布在一条直线附近,因此两个变量线性相关.设回归直线为y ^=b ^x +a ^, 由题知x =42.5,y =34,则求得b ^=∑4i =1(x i -x )(y i -y )∑4i =1(x i -x )2=-370125≈-3. a ^=y -b ^x =34-(-3)×42.5=161.5.∴y ^=-3x +161.5.(2)依题意有P =(-3x +161.5)(x -30) =-3x 2+251.5x -4 845=-3⎝⎛⎭⎫x -251.562+251.5212-4 845.∴当x =251.56≈42时,P 有最大值,约为426.即预测销售单价为42元时,能获得最大日销售利润.活动与探究2 思路分析:先画出散点图,确定是否具有线性相关关系,求出回归方程,再求出残差,确定模型的拟合效果和R 2的含义.解:(1)作出该运动员训练次数(x )与成绩(y )之间的散点图,如图所示,由散点图可知,它们之间具有线性相关关系.(2)x =39.25,y =40.875,∑i =18x 2i =12 656,∑i =18y 2i =13 731,∑i =18x i y i =13 180,∴b ^=∑8i =1(x i -x )(y i -y )∑8i =1(x i -x )2=∑i =18x i y i -8x y∑i =18x 2i -8x2≈1.041 5,a ^=y -b ^x =-0.003 875,∴线性回归方程为y ^=1.041 5x -0.003 875.(3)作残差图如图所示,由图可知,残差点比较均匀地分布在水平带状区域中,说明选用的模型比较合适.(4)计算得相关指数R 2=0.985 5,说明了该运动员成绩的差异有98.55%是由训练次数引起的.迁移与应用 解:x =15×(14+16+18+20+22)=18,y =15×(12+10+7+5+3)=7.4,∑5i =1x 2i =142+162+182+202+222=1 660, ∑5i =1y 2i =122+102+72+52+32=327, ∑5i =1x i y i =14×12+16×10+18×7+20×5+22×3=620,∴b ^=∑5i =1x i y i -5x y ∑5i =1x 2i -5x 2=620-5×18×7.41 660-5×182=-1.15.∴a ^=7.4+1.15×18=28.1,∴y 对x 的回归直线方程为y ^=-1.15x +28.1.∴∑5i =1(y i -y ^i ) 2=0.3,∑i =1(y i -y )2=53.2, R 2=1-∑5i =1(y i -y ^)2∑5i =1(y i -y )2≈0.994. ∴R 2≈0.994,拟合效果较好.活动与探究3 思路分析:先由数值表作出散点图,然后根据散点的形状模拟出近似函数,进而转化为线性函数,由数值表求出回归函数.解:(1)作出散点图如图所示,从散点图中可以看出x 与y 不具有线性相关关系,根据已有知识可以发现样本点分布在某一条指数函数曲线y =c 1e c 2x 的周围,其中c 1,c 2为待定的参数.(2)对两边取对数把指数关系变为线性关系,令z =ln y ,则变换后的样本点应分布在直线z =bx +a ,a =ln c 1,b =c 2的周围,这样就可以利用线性回归模型来建立y 与x 之间的非线性回归方程了,数据可以转化为:求得回归直线方程为z =0.272x -3.849,∴y ^=e 0.272x -3.849.迁移与应用 解:画出散点图如图所示.根据散点图可知y 与x 近似地呈反比例函数关系,设y =k x ,令t =1x ,则y =kt ,原数据变为:由散点图可以看出y 与t 呈近似的线性相关关系.列表如下:所以t =1.55,y =7.2.所以b ^=∑5i =1t i y i -5t y∑5i =1t 2i -5t 2≈4.134 4.a ^=y -b ^t ≈0.8, 所以y ^=4.134 4t +0.8.所以y 关于x 的回归方程是y ^=4.134 4x +0.8. 当堂检测1.有下列说法:①线性回归分析就是由样本点去寻找一条直线,使它贴近这些样本点的数学方法; ②利用样本点的散点图可以直观判断两个变量的关系是否可以用线性关系表示; ③通过回归方程=+y b ax 及其回归系数b,可以估计和观测变量的取值和变化趋势;④因为由任何一组观测值都可以求得一个回归直线方程,所以没有必要进行相关性检验. 其中正确说法的个数是( ).A .1B .2C .3D .4答案:C 解析:①反映的正是最小二乘法思想,故正确. ②反映的是画散点图的作用,也正确.③反映的是回归模型y =bx +a +e ,其中e 为随机误差,故也正确.④是不正确的,在求回归方程之前必须进行相关性检验,以确定两变量的关系.2.在两个变量y 与x 的回归模型中,分别选择了4个不同的模型.它们的相关指数R 2如下,其中拟合效果最好的模型是( ).A .模型1的相关指数R 2为0.98B .模型2的相关指数R 2为0.80C .模型3的相关指数R 2为0.50D .模型4的相关指数R 2为0.25答案:A 解析:相关指数R 2越接近于1,则该模型的拟合效果就越好,精度越高. 3.设有一个回归方程y=2-1.5x ,则变量x 增加1个单位时,( ).A .y 平均增加1.5个单位B .y 平均增加2个单位C .y 平均减少1.5个单位D .y 平均减少2个单位答案:C 解析:∵b=-1.5<0,∴x 增加1个单位时,y 平均减少1.5个单位.4.若施肥量x (kg)与小麦产量y (kg)之间的回归直线方程为y=250+4x ,当施肥量为50 kg时,预计小麦产量为________.答案:450 kg 解析:将x =50代入回归方程得y=450 kg .5.若对于变量y 与x 的10组统计数据的回归模型中,相关指数R 2=0.95,又知残差平方和为120.53,那么1021()ii yy =-∑的值为__________.答案:2 410.6 解析:依题意有0.95=1-1021120.53()ii y y =-∑,所以1021()ii y y =-∑=2 410.6.。
高二数学人教A版选修1-2课件:1.1 回归分析的基本思想及其初步应用

知识精要
典题例解
迁移应用
由图可知,残差点比较均匀地分布在水平带状区域中,说明选用的模型比较合适. (4)计算得相关指数R2=0.985 5,说明了该运动员成绩的差异有98.55%是由训练次数引起的.
一 二三
知识精要
典题例解
迁移应用
为了研究三月下旬的平均气温x(℃)与四月二十日前棉花害虫化蛹高峰日y(日)的关系,某地观察了2008年至 2013年间的情况,得到下面数据表:
一 二三
知识精要
【例2】 某运动员训练次数与运动成绩之间的数据关系如下:
典题例解
迁移应用
训练次数(x) 30 33 35 37 39 44 46 50
成绩(y)
30 34 37 39 42 46 48 51
(1)作出散点图; (2)求出线性回归方程; (3)作出残差图,并说明模型的拟合效果; (4)计算R2,并说明其含义. 思路分析:先画出散点图,确定是否具有线性相关关系,求出回归方程,再求出残差,确定模型的拟合效果和R2 的含义.
其估计值为
���^��������� =yi-���^��������� =yii=-���1^���,2x,…i-���,^n���,,
���^���称������ 为相应于点(xi,yi)的残差.
目标导航
预习导引
1234
3.回归模型拟合效果的刻画
类别 特点
残差图法
残差点比较均匀 地落在水平的带 状区域中,说明选 用的模型比较合 适,这样的带状区 域的宽度越窄,说 明模型拟合精度 越高
5
∑ ���������2��� =882+762+732+662+632=27 174.
1.1.1《回归分析》课件(新人教版A选修1-2) 公开课一等奖课件

语文
小魔方站作品 盗版必究
谢谢您下载使用!
更多精彩内容,微信扫描二维码获取
扫描二维码获取更多资源
附赠 中高考状元学习方法
前
言
高考状元是一个特殊的群体,在许多 人的眼中,他们就如浩瀚宇宙里璀璨夺目 的星星那样遥不可及。但实际上他们和我 们每一个同学都一样平凡而普通,但他们 有是不平凡不普通的,他们的不平凡之处 就是在学习方面有一些独到的个性,又有 着一些共性,而这些对在校的同学尤其是 将参加高考的同学都有一定的借鉴意义。
y a bx
其中a+bx是确定性函数, 是随机误差
注: 产生的主要原因:
(1)所用确定性函数不恰当; (2)忽略了某些因素的影响; (3)观测误差。
对于线性回归模型
y a bx
应注意以下两个问题: I 模型的合理性; II 在模型合理的情况下,如何估计a,b.
8
8 4.50 21.06 13.08 168.5 64 560.1 204
3、回归分析的基本步骤:
画散点图
求回归方程
预报、决策
1. 2. 3. 4.
数学3——统计 画散点图 求出b,a的值。 求回归直线方程 用回归直线方程解决应用问题
思考:在时刻x=9s时,质点运动位置一定 是22.6287cm吗? 4、线性回归模型
选修1-2
(一)
必修3(第二章 统计)知识结构
收集数据
(随机抽样)
整理、分析数据 估计、推断 用样本估计总体 变量间的相关关系
简 单 随 机 抽 样
分 层 抽 样
系 统 抽 样
用样本 的频率 分布估 计总体 分布
用样本 数字特 征估计 总体数 字特征
2013年高二新课程数学(新课标人教A版)教案选修1-2《1.1回归分析的基本思想及其初步应用》3

1.1回归分析的基本思想及其初步应用(三)教学要求:通过典型案例的探究,进一步了解回归分析的基本思想、方法及初步应用.教学重点:通过探究使学生体会有些非线性模型通过变换可以转化为线性回归模型,了解在解决实际问题的过程中寻找更好的模型的方法.教学难点:了解常用函数的图象特点,选择不同的模型建模,并通过比较相关指数对不同的模型进行比较. 教学过程:一、复习准备:1. 给出例3:一只红铃虫的产卵数y 和温度x 有关,现收集了7组观测数据列于下表中,试建立y 与x 之间的回归方程.2. 讨论:观察右图中的散点图,发现样本点并没有分布在某个带状区域内,即两个变量不呈线性相关关系,所以不能直接用线性回归方程来建立两个变量之间的关系.二、讲授新课:1. 探究非线性回归方程的确定: ① 如果散点图中的点分布在一个直线状带形区域,可以选线性回归模型来建模;如果散点图中的点分布在一个曲线状带形区域,就需选择非线性回归模型来建模.② 根据已有的函数知识,可以发现样本点分布在某一条指数函数曲线y =2C 1e x C 的周围(其中12,c c 是待定的参数),故可用指数函数模型来拟合这两个变量. ③ 在上式两边取对数,得21ln ln y c x c =+,再令ln z y =,则21ln z c x c =+,而z 与x 间的关线的附近,因此可以用线性回归方程来拟合. ④ 利用计算器算得 3.843,0.272a b =-=,z 与x 间的线性回归方程为0.272 3.843z x =-,因此红铃虫的产卵数对温度的非线性回归方程为0.272 3.843x y e -=.⑤ 利用回归方程探究非线性回归问题,可按“作散点图→建模→确定方程”这三个步骤进行.其关键在于如何通过适当的变换,将非线性回归问题转化成线性回归问题. 2. 小结:用回归方程探究非线性回归问题的方法、步骤. 三、巩固练习:为了研究某种细菌随时间天数x /天繁殖个数(1)用天数作解释变量,繁殖个数作预报变量,作出这些数据的散点图;(2)试求出预报变量对解释变量的回归方程.(答案:所求非线性回归方程为0.69 1.112ˆy=e x +.)。
推荐-高中数学人教A版选修1-2课件1.1 回归分析的基本思想及其初步应用(1)

重难聚焦
1.相关关系与函数关系的区别与联系是什么? 剖析:(1)两者之间的区别. ①相关关系是一种非确定性关系.如人的身高与年龄、商品的销 售额与广告费等都是相关关系.而函数关系中的两个变量是一种 确定性关系.如正方形的面积S与边长x之间的关系S=x2就是函数关 系,即对于边长x的每一个确定的值,面积S都有唯一确定的值与之 对应. ②函数关系是一种因果关系,而相关关系不一定是因果关系. (2)两者之间的联系. 相关关系与函数关系有着密切的联系,在一定条件下可以相互转 化.例如正方形的面积S与其边长x之间虽然是一种确定性关系,但 在每次测量时,由于测量误差等原因,其数值大小又表现出一种随 机性,而对于具有相关关系的两个变量来说,当求得其回归直线方 程后,我们又可以用一种确定的关系对这两个变量间的关系进行 估计.
=
^
������ ������
+ ^������至少经过点(x1,y1),(x2,y2),…,(xn,yn)中的一个点;
^ ^ ^ ^ ������
③直线������
=
������ ������
+ ������的斜率为������
=
������=∑1������������������������ -������������ ������=∑������1���������2��� -������������2
i=1
^5
∴
������
=
������=∑1������������������������-5������ ������=∑51���������2��� -5������2
������
=
620-5×18×7.4 1 660-5×182
人教新课标版数学高二人A选修1-2课件1.1回归分析的基本思想

31
解 由题意得 y =50. 由甲模型可得 yi-y^ i 与 yi- y 的关系如下表:
yi-y^ i -0.5 -3.5 10 -6.5 0.5
yi- y -20 -10 10 0 20
5
^
5
∴∑
i=1
(yi-y
i)2=155,i∑=1
(yi- y )2=1 000,
1.1 回归分析的基本思想及其初步应用
1.1 回归分析的基本思想及其初步应用
36
(2)建立x与y的关系,预报回归模型并计算残差; 解 对两边取对数把指数关系变为线性关系,令z=ln y,则有变 换后的样本点应分布在直线z=bx+a(a=ln c1,b=c2)的周围, 这样就可以利用线性回归模型来建立y与x之间的非线性回归方程 了,数据可以转化为
n
n
xi- x yi- y xiyi-n x y
i=1 n
xi- x 2
i=1
=
n
xi2-n x 2
,a^= y -b^ x ,其中( x , y )称
i=1
i=1
为样本点的中心.
1.1 回归分析的基本思想及其初步应用
7
(4)线性回归模型 y=bx+a+e,其中 a 和 b 是模型的未知参数,e
34
要点三 非线性回归分析 例3 下表为收集到的一组数据:
x 21 23 25 27 29 32 35 y 7 11 21 24 66 115 325 (1)作出x与y的散点图,并猜测x与y之间的关系;
1.1 回归分析的基本思想及其初步应用
35
解 作出散点图如下图,从散点图可以看出x与y不具有线性相 关关系,根据已有知识可以发现样本点分布在某一条指数函数 曲线y=c1ec2x 的周围,其中c1,c2为待定的参数.
人教A版高中数学选修1-2课件《1.1回归分析的基本思想及其初步应用》ppt8

2、现实生活中存在着大量的相关关系。
如:人的身高与年龄; 产品的成本与生产数量; 商品的销售额与广告费; 家庭的支出与收入。等等
回归分析的内容与步骤:
回归分析通过一个变量或一些变量的变化解释 另一变量的变化。
思考:
如何刻画预报变量(体重)的变化?这个变化在多大程度上 与解析变量(身高)有关?在多大程度上与随机误差有关?
编号 身高/cm 体重/kg
1
2
3
4
5
6
7
8
165 165 157 170 175 165 155 170
48 57 50 54 64 61 43 59
例如,编号为6的女大学生的体重并没有落在水平直线上,她的体重为61kg。解析 变量(身高)和随机误差共同把这名学生的体重从54.5kg“推”到了61kg,相差6.5kg, 所以6.5kg是解析变量和随机误差的组合效应。
机误差。
思考: 产生随机误差项e的原因是什么?
随机误差e的来源(可以推广到一般):
1、忽略了其它因素的影响:影响身高 y 的因素不只 是体重 x,可能还包括遗传基因、饮食习惯、生 长环境等因素;
2、用线性回归模型近似真实模型所引起的误差; 3、身高 y 的观测误差。
以上三项误差越小,说明我们的回归模型的拟合 效果越好。
n
n
bˆ =i=1i(n=x1i(-xxi)-(xy)i2-y) =
xiyi - nxy
i=1 n
xi2 - nx2
,
Hale Waihona Puke i=1aˆ =y-bˆx.
其中x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解 x =15(14+16+18+20+22)=18, y =15(12+10+7+5+3)=7.4,
5
x2i =142+162+182+202+222=1 660,
i=1
5
xiyi=14×12+16×10+18×7+20×5+22×3=620,
i=1
5
xiyi-5 x y
i=1
所以b^ =
6
6
x2i =2 275,xiyi=1 076.2
i=1
i=1
计算得,b^≈0.183,a^≈6.285,
所求回归直线方程为y^=0.183x+6.285.
•(2)列表如下:
yi-y^i 0.05 0.005 -0.08 -0.045 0.04 0.025 yi- y -2.24 -1.37 -0.54 0.41 1.41 2.31
• (1)画出数据对应的散点图; • (2)求线性回归方程,并在散点图中加上回归
直线; • (3)据(2)的结果估计当房屋面积为150 m2时的
销售价格.
解 (1)数据对应的散点图如下图所示:
(2) x =15i=51xi=109,i=51 (xi- x )2=1 570,
5
y =23.2, (xi- x )(yi- y )=308.
y 7 11 21 24 66 115 325
• (1)作出x与y的散点图,并猜测x与y之间的关 系;
• (2)建立x与y的关系,预报回归模型并计算残 差;
• (3)利用所得模型,预报x=40时y的值.
•
(1)画出散点图或进行相关性检验,确
定两变量x、y是否线性相关.由散点图得x、y之
间的回归模型.
•规律方法 当资料点较少时,也可以利用残差表 进行残差分析,注意计算数据要认真细心,残差 分析要全面.
• 【变式2】 已知某种商品的价格x(元)与需求量 y(件)之间的关系有如下一组数据:
x 14 16 18 20 22 y 12 10 7 5 3
• 求y对x的回归直线方程,并说明回归模型拟 合效果的好坏.
物理成绩(y) 78 65 71 64 61
•(1)画出散点图;
•(2)求物理成绩y对数学成绩x的回归直线方程;
•(3)一名学生的数学成绩是96,试预测他的物理成 绩.
•[思路探索] 先利用散点图分析物理成绩与数学成 绩是否线性相关,若相关再利用线性回归模型求 解.
解 (1)散点图如图.
(2) x =15×(88+76+73+66+63)=73.2, y =15×(78+65+71+64+61)=67.8.
6
所以
(yi-y^ i)2≈0.013
6
18,
(yi- y )2=14.678 4.
i=1
i=1
所以,R2=1-01.40.16378184≈0.999 1, 回归模型的拟合效果较好.
•(3)由残差表中的数值可以看出第3个样本点的残 差比较大,需要确认在采集这个数据的时候是否 有人为的错误,如果有的话,需要纠正数据,重 新建立回归模型;由表中数据可以看出残差点比 较均匀地落在不超过0.15的狭窄的水平带状区域中, 说明选用的线性回归模型的精度较高,由以上分 析可知,弹簧长度与拉力成线性关系.
i=1
≈0.625.
a^= y -b^ x ≈67.8-0.625×73.2=22.05. 所以 y 对 x 的回归直线方程是 y^=0.625x+22.05. (3)x=96,则y^=0.625×96+22.05≈82, 即可以预测他的物理成绩是 82.
•规律方法 (1)散点图是定义在具有相关关系的两 个变量基础上的,对于性质不明确的两组数据, 可先作散点图,在图上看它们有无关系,关系的 密切程度,然后再进行相关回归分析.
•[思路探索] 作残差分析时,一般从以下几个方面 予以说明:(1)散点图;(2)相关指数;(3)残差图中 的异常点和样本点的带状分布区域的宽窄.
解 (1)散点图如图
x =16(5+10+15+20+25+30)=17.5, y =16(7.25+8.12+8.95+9.90+10.9+11.8)≈9.487,
数 R2
n
yi- y 2
i=1
化的贡献率,R2 越接近于 1,表示回归的效果越好
•想一想:回归分析中,利用线性回归方程求出的 函数值一定是真实值吗?为什么?
•提示 不一定是真实值,利用线性回归方程求的 值,在很多时候是个预报值,例如,人的体重与 身高存在一定的线性关系,但体重除了受身高的 影响外,还受其他因素的影响,如饮食,是否喜 欢运动等.
• 2.回归模型的选择,特别是非线性回归模 型.(难点、易错点)
• 自学导引
• 1.回归分析
•
回归分析是相对关具关系有
的两个变量进行
统计分析的一种常用方法.
• 2.线性回归模型
• (1)由散点图易发现,样本点散布在某一条
直线附近,而不是一条直线上,不能用一次函
数y=bx+a描述它们之间的关系,因此用线性
•1.1 回归分析的基本思想及其初步应用
•【课标要求】 •1.了解随机误差、残差、残差分析的概念; •2.会用残差分析判断线性回归模型的拟合 效果;
•3.掌握建立回归模型的步骤; •4.通过对典型案例的探究,了解回归分析 的基本思想方法
• 和初步应用.
• 【核心扫描】
• 1.利用散点图分析两个变量是否存在相关关 系,求线性回归方程.(重点)
等,这样作出的图形称为残差图
残差 图法
残差点比较均匀地落在水平的带状区域内,说明选 用的模型比较适合,这样的带状区域的宽度越窄, 说明模型拟合精度越高
残差平
残差平方和为
n
(yi-y^ )2,残差平方和
越小
,模型
i=1
方和
拟合效果越好
n
yi-y^ i2
i=1
相关指 R2=1-
,R2 表示 解释 变量对 预报 变量变
拟合效果越好;R2越小,残差平方和越大,即
3.建立回归模型的基本步骤
•(1)确定研究对象,明确哪个变量是解释变量, 哪个变量是预报变量.
•(2)画出确定好的解释变量和预报变量的散点图, 观察它们之间的关系(如是否存在线性关系等).
•(3)由经验确定回归方程的类型(如我们观察到 数据呈线性关系,则选用线性回归方程).
n
xi- x 2
n
x2i -n x 2
i=1
i=1
其中 x =1ni=n1xi, y =1ni=n1yi,( x , y )称为样本点的中心.
•(3)解释变量和预报变量
•线性回归模型与一次函数模型的不同之处是增加
了随机误自差变项量xe,因变随量机y误由差e
和
共同确定,即自变量x只解释部分y的变化,在统
• 题型二 线性回归分析
• 【例2】 为研究重量x(单位:克)对弹簧长度 y(单位:厘米)的影响,对不同重量的6个物体 进行测量,数据如下表所示:
•
x 5 10 15 20 25 30
y 7.25 8.12 8.95 9.90 10.9 11.8
• (1)作出散点图并求线性回归方程; • (2)求出R2; • (3)进行残差分析.
• 则u=nv+b,图象为一直线.
• ②y=cax(a>0,c>0)(指数型函数)
名师点睛 1.线性回归方程
(1)在分析两个变量的相关关系时,可根据样本数据散点图确定 两个变量之间是否存在相关关系,然后利用最小二乘法求出回 归直线方程. (2)求线性回归方程^y=b^x+a^的关键是求未知参数a^和b^,其中b^ 可借助于计算器求出,因为a^= y -b^ x ,即 y =b^ x +a^,所以点 ( x ,y )一定满足线性回归方程,即回归直线一定过点( x ,y ).
•(2)进行拟合,预报回归模型,求回归方程.
•[规范解答] (1)作出散点图如下图,从散点图可以 看出x与y不具有线性相关关系,根据已有知识可 以发现样本点分布在某一条指数函数曲线y= c1ec2x的周围,其中c1、c2为待定的参数.(4分)
5
所以,
(yi-y^ i)2=0.3,
5
(yi- y )2=53.2,
i=1
i=1
5
yi-y^ i2
i=1
R2=1-
≈0.994,
5
yi- y 2
i=1
所以回归模型的拟合效果很好.
• 题型三 非线性回归分析 • 【例3】 下表为收集到的一组数据:
x 21 23 25 27 29 32 35
5
=62106-605-×51×8×1872.4=-1.15.
x2i -5 x 2
i=1
a^ =7.4+1.15×18=28.1, 所以所求回归直线方程是:y^=-1.15x+28.1. 列出残差表:
yi-y^i 0 0.3 -0.4 -0.1 0.2 yi- y 4.6 2.6 -0.4 -2.4 -4.4
•3.刻画回归效果的方式
残差
数据点和它在回归直线上相应位置的差异(yi-y^i)是随机 误差.称e^i=yi-y^i 为残差,e^i 称为相应于点(xi,yi)的残
n
差.
(yi-y^ i)2
称为残差平方和
i=1
利用图形来分析残差特性,作图时纵坐标为 残差 ,横 残差图 坐标可以选为样本编号 ,或 身高数据 ,或体重估计值
•(2)求回归直线方程,首先应注意到,只有在散点 图大致呈线性时,求出的回归直线方程才有实际 意义,否则,求出的回归直线方程毫无意义.
• 【变式1】 以下是某地搜集到的新房屋的销售 价格y和房屋的面积x的数据:
房屋面积/m2 115 110 80 135 105
