一次函数的图象2--北师大版
北师大版八年级数学上册:4.3《一次函数的图象》教案

北师大版八年级数学上册:4.3《一次函数的图象》教案一. 教材分析《一次函数的图象》是北师大版八年级数学上册第4.3节的内容。
本节主要让学生了解一次函数的图象特点,学会如何绘制一次函数的图象,并能够分析一次函数图象与系数之间的关系。
通过本节的学习,为学生后续学习二次函数、指数函数等函数图象打下基础。
二. 学情分析学生在学习本节内容前,已经掌握了函数的概念、一次函数的定义和性质。
但学生对函数图象的认识不足,对如何绘制一次函数图象以及分析图象与系数之间的关系还不够清晰。
因此,在教学过程中,需要引导学生通过实践操作,加深对一次函数图象的理解。
三. 教学目标1.让学生了解一次函数图象的特点,学会绘制一次函数图象。
2.引导学生分析一次函数图象与系数之间的关系。
3.培养学生的动手操作能力和观察分析能力。
四. 教学重难点1.一次函数图象的绘制方法。
2.分析一次函数图象与系数之间的关系。
五. 教学方法采用讲解法、示范法、实践操作法、讨论法等教学方法,引导学生通过自主学习、合作交流,掌握一次函数图象的特点和绘制方法。
六. 教学准备1.准备多媒体教学设备,如投影仪、计算机等。
2.准备一次函数图象的示例图片和相关素材。
3.准备练习题和作业。
七. 教学过程1.导入(5分钟)利用投影仪展示一次函数图象的示例图片,引导学生观察并总结一次函数图象的特点。
教师简要讲解一次函数图象的绘制方法,激发学生的学习兴趣。
2.呈现(10分钟)教师通过讲解和示范,详细介绍一次函数图象的绘制方法。
引导学生动手操作,尝试绘制一次函数图象。
在绘制过程中,注意引导学生观察图象与系数之间的关系。
3.操练(10分钟)学生分组进行实践操作,绘制不同系数的一次函数图象。
教师巡回指导,解答学生的疑问。
4.巩固(10分钟)教师挑选几组学生的作品,进行分析讨论。
引导学生总结一次函数图象与系数之间的关系。
同时,让学生回答课后练习题,巩固所学知识。
5.拓展(10分钟)教师提出一些拓展问题,如:如何判断一次函数图象与坐标轴的交点?如何求解一次函数图象上的点?引导学生进行思考和讨论。
北师大版八年级数学上册第4章 一次函数 一次函数的图象和性质

次函数的图象吗?
例1 画出一次函数 y = -2x+1 的图象
x y = –2x+1
–2
–1
5
3
y = –2x+1
0
1
1 –1 y
5
01 23 4 5
4
2 列表
–3
一次函数的图 象是什么?
01 23 4 5 01 23 4 5
01 23 4 5 01 23 4 5
思考:观察它们的图象有什么特点?
y y=x+2
.
.
..
.O.
.
.
.
y
.
2
=
x
-
2
x
探究归纳
观察三个函数图象的平移情况:
y y=x+2 y=x
2●
y=x-2
O2
x
●
把一次函数y = x+2,y = x-2的图象与y = x比较,发现: 1. 这三个函数的图象形状都是 直线 ,并且倾斜程度
_相__同___. 2. 函数 y = x 的图象经过原点,函数 y = x + 2 的图象与
y 随 x 的增大而增大. ① b>0 时,直线经过第一、二、三象限;
② b<0 时,直线经过第一、三、四象限. 当 k<0 时,直线 y = kx+b 从左到右逐渐下降,
y 随 x 的增大而减小. ① b>0 时,直线经过第一、二、四象限;
② b<0 时,直线经过第二、三、四象限.
练一练 两个一次函数 y1 = ax+b 与 y2 = bx+a,它们在
要点归纳
思考:与 x 轴的 交点坐标是什么?
b k
北师大版八年级上册数学4.3《一次函数的图象》教案

(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与一次函数图象相关的实际问题。
2.实验操作:为了加深理解,我们将进行一个简单的实验操作。这个操作将演示如何通过描点法绘制一次函数的图象。
北师大版八年级上册数学4.3《一次函数的图象》教案
一、教学内容
本节课选自北师大版八年级上册数学第四章第三节《一次函数的图象》。教学内容主要包括以下方面:
1.理解一次函数图象的定义,掌握一次函数图象的特点;
2.学会使用描点法绘制一次函数的图象;
3.掌握一次函数图象与系数的关系,分析一次函数图象的增减性;
4.加强课后辅导,对学生在课堂上学到的知识进行巩固,及时发现并解决他们在学习过程中遇到的问题。
2.教学难点
-理解并掌握一次函数图象与系数的关系,尤其是斜率k和截距b对图象的影响;
-能够在实际问题中灵活运用一次函数图象进行分析和解决。
举例解释:
(1)难点在于让学生理解斜率k和截距b对一次函数图象的影响。教师可以通过动态演示或实物举例,让学生直观地感受k、b值变化时图象的动态变化;
(2)在解决实际问题时,学生可能难以将问题转化为一次函数图象进行分析。教师应引导学生学会提取关键信息,建立数学模型,并运用一次函数图象进行问题求解。
4.能够运用一次函数图象解决实际问题,提高学生的应用能力。
二、核心素养目标
1.培养学生的逻辑推理能力,通过探索一次函数图象的绘制方法,理解图象与系数之间的关系,提高学生的数据分析与抽象思维能力;
2.培养学生的空间想象能力,能够根据一次函数的解析式,想象并绘制出相应的图象,加强对一次函数图象的理解;
一次函数的图像(2)

《4.3一次函数的图象(2)》教学设计宝氮子校王桂林教学内容分析:《4.3一次函数的图象(2)》是北师大版数学教材八年级上册中第四章“一次函数”的第四课时,主要是认识一次函数图象的性质、正比例函数图像及性质。
本节内容是在七年级学习了“变量之间的关系”和八年级上册第三章学习了“位置的确定”基础上学习和认识的,学生已经有了一定的变量、函数、平面直角坐标系、以及一次函数的概念等有关的知识基础。
同时,本节内容也是继续学习反比例函数、二次函数的图象和性质的重要基础,也是学习高中代数、解析几何及其他数学分支的重要基础,也是学习高中代数、解析几何及其他数学分支的重要基础。
数形结合的思想、化归思想及解析法思想是本节内容所包含的主要数学思想。
学情分析:学生已有学习“函数”、“一次函数图像的画法”的基础,具有一定的动手操作能力和观察分析能力。
本节课,学生在此基础上进一步认识一次函数图像的简单性质和正比例函数及函数图象的性质,并利用动手操作,体会k值、b值对函数图像的影响,进一步增强学生数学学习中“数”“形”结合的意识。
教学目标:知识技能:会用两点法画出一次函数的图像;能结合图像说出一次函数的性质;掌握一次函数的性质;数学思考:经历一次函数图象画法与性质的探索过程,体会“数”“形”结合的数学思想解决问题:体会数形结合的数学思想在问题解决中的作用,并能运用性质、图象及数形结合思想解决相关函数问题情感态度:在动手操作过程中,培养学生的合作意识和大胆猜想、乐于探究的良好品质;体验“数”与“形”的转化过程,感受函数图象的简洁美;激发学生学数学的兴趣。
教学重点:通过图象理解一次函数的性质教学难点:结合图像理解归纳一次函数的性质的过程教学方法:自主探究、合作交流动。
在导学过程中,坚持诱导式教学,以谈话法、小组合作学习为主。
充分调动学生学习积极性和主动性,突出学生的主体地位,通过自学、讨论、归纳、辨析等方法对学生进行学法指导,培养他们动手、动口、动脑的能力,达到“不但使学生学会,而且使学生会学”的目的。
一次函数的图象(知识梳理与考点分类讲解)-八年级数学上册基础知识专项突破讲与练(北师大版)
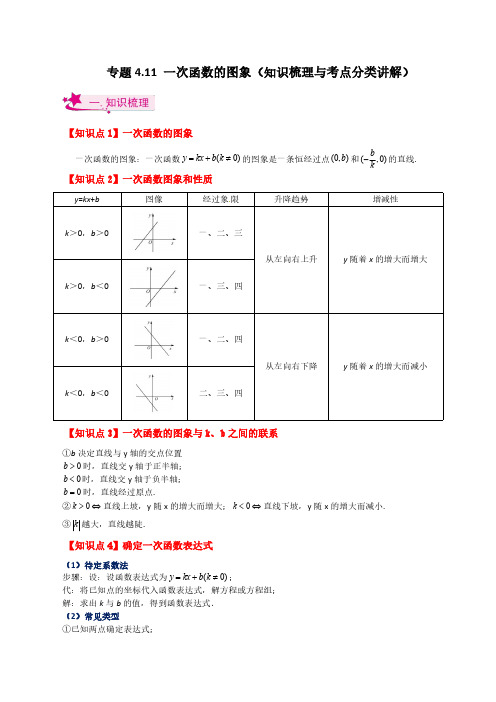
专题4.11一次函数的图象(知识梳理与考点分类讲解)【知识点1】一次函数的图象一次函数的图象:一次函数(0)y kx b k =+≠的图象是一条恒经过点(0,)b 和(,0)b k-的直线.【知识点2】一次函数图象和性质y =kx +b 图像经过象限升降趋势增减性k >0,b >0一、二、三从左向右上升y 随着x 的增大而增大k >0,b <0一、三、四k <0,b >0一、二、四从左向右下降y 随着x 的增大而减小k <0,b <0二、三、四【知识点3】一次函数的图象与k、b 之间的联系①b 决定直线与y 轴的交点位置0b >时,直线交y 轴于正半轴;0b <时,直线交y 轴于负半轴;0b =时,直线经过原点.②0k >⇔直线上坡,y 随x 的增大而增大;0k <⇔直线下坡,y 随x 的增大而减小.③k 越大,直线越陡.【知识点4】确定一次函数表达式(1)待定系数法步骤:设:设函数表达式为(0)y kx b k =+≠;代:将已知点的坐标代入函数表达式,解方程或方程组;解:求出k 与b 的值,得到函数表达式.(2)常见类型①已知两点确定表达式;②已知两对函数对应值确定表达式;③平移转化型:如已知函数是由y=2x 平移所得到的,且经过点(0,1),则可设要求函数的解析式为y =2x +b ,再把点(0,1)的坐标代入即可.【知识点5】图象的平移一次函数y kx b =+向左平移m 个单位后的解析式为()y k x m b =++;一次函数y kx b =+向右平移m 个单位后的解析式为()y k x m b =-+;一次函数y kx b =+向上平移m 个单位后的解析式为y kx b m =++;一次函数y kx b =+向上平移m 个单位后的解析式为y kx b m =+-.平移规律:左加右减,上加下减.【知识点6】两条直线间的位置关系设直线111:l y k x b =+,222:l y k x b =+.(1)12k k ≠⇔相交;(2)1212k k b b =⎧⇔⎨≠⎩平行;(3)121k k =-⇔ 垂直.补充:若直线y kx b =+经过11(,)A x y ,22(,)B x y 12()x x ≠两点,则1212y y k x x -=-.【考点一】一次函数的图象及其位置【例1】(2022秋·陕西西安·八年级校考期中)已知一次函数(21)2y a x a =-+-(a 为常数).(1)若这个函数的图象经过原点,求a 的值;(2)若1a =,直接写出这个函数图象经过的象限.【答案】(1)2a =;(2)当1a =时,函数图象经过一、三、四象限【分析】(1)y kx b =+经过原点则0b =,据此求解;(2)把1a =代入(21)2y a x a =-+-,得1y x =-,根据10k =>,10b =-<即可得出结论.(1)解:因为(21)2y a x a =-+-经过原点,所以20a -=,解得2a =.(2)解:当1a =时,则(21)21y a x a x =-+-=-∵10k =>,10b =-<,∴函数图象经过一、三、四象限.【点拨】本题考查了一次函数的图象性质,掌握一次函数的图象性质是解答本题的关键,难度不大.【举一反三】【变式1】(2023春·四川德阳·八年级统考阶段练习)在同一平面直角坐标系中,函数y kx b =-与y bx k =+的图像不可能是()A .B .C .D .【答案】C【分析】分四种情况,根据k 、b 的符号,确定一次函数经过的象限,结合函数图象与选项进行判断即可.解:当0k >,0b >时,对于y kx b =-,图像经过第一,三,四象限,则y bx k =+经过一,二,三象限,则选项D 符合题意;当0k >,0b <时,对于y kx b =-,图像经过第一,二,三象限,则y bx k =+经过一,二,四象限,题目中没有符合的;当0k <,0b >时,对于y kx b =-,图像经过第二,三,四象限,则y bx k =+经过一,三,四象限,则选项B 符合题意;;当0k <,0b <时,对于y kx b =-,图像经过第一,二,四象限,则y bx k =+经过二,三,四象限,则选项A 符合题意;.故选:C .【点拨】此题主要考查了一次函数的性质与图像,正确记忆一次函数图像经过象限与系数关系是解题关键.【变式2】(2023春·山东菏泽·八年级统考期末)已知一次函数2y x b =+的图象经过第一、三、四象限,则函数y bx b =-的图象经过的象限是.【答案】一、二、四【分析】先根据一次函数2y x b =+的图象经过第一、三、四象限判断b 的取值范围,再判断函数y bx b =-的图象经过的象限.解:∵一次函数2y x b =+的图象经过第一、三、四象限,∴0b <,0b ->,∴函数y bx b =-的图象经过一、二、四象限.故答案为:一、二、四.【点拨】本题考查了一次函数的图象与性质,对于一次函数y kx b =+(k 为常数,0k ≠),当0k >时,y 随x 的增大而增大;当0k <时,y 随x 的增大而减小.当0b >,图象与y 轴的正半轴相交,当0b <,图象与y 轴的负半轴相交,当0b =,图象经过原点.【考点二】一次函数与坐标轴交点【例2】(2023春·陕西商洛·八年级校考期末)如图,直线22y x =-+与x 轴交于点A ,与y 轴交于点B .(1)求点A ,B 的坐标.(2)若点C 在x 轴上,且2ABC AOB S S = ,求点C 的坐标.【答案】(1)(0,2)B ,(1,0)A ;(2)(3,0)或(1,0)-【分析】(1)当0x =时求解y 的值及当0y =时求解x 的值即可求解.(2)由(1)得2OB =,1OA =,根据2ABC AOB S S = 可得22AC OA ==,进而可求解.(1)解:当0x =时,2y =,∴点B 的坐标为:(0,2),当0y =时,1x =,∴点A 的坐标为:(1,0).(2)由(1)得:2OB =,1OA =,则:11222OA OB AC OB ⨯⋅=⋅,即:22AC OA ==,∴点C 的坐标为:(3,0)或(1,0)-.【点拨】本题考查了一次函数的图象,熟练掌握一次函数的图象是解题的关键.【举一反三】【变式1】(2022秋·陕西西安·八年级校考期中)如图,在同一平面直角坐标系中,一次函数()11110y k x b k =+≠与()22220y k x b k =+≠的图象分别为直线1l 和直线2l ,下列结论正确的是()A .120k k > B .120k k ->C .120b b +<D .12·0b b >【答案】B 【分析】根据图示,可得110,0k b >>,220,0k b <<,根据不等式的性质即可求解.解:根据图示,可知一次函数()11110y k x b k =+≠中,110,0k b >>;一次函数()22220y k x b k =+≠中,220,0k b <<,∴A 、12·0k k <,故原选项错误,不符合题意;B 、∵120,0k k ><,∴120k k ->,故原选项正确,符合题意;C 、∵120,0b b ><,且12b b >,∴120b b +>,故原选项错误,不符合题意;D 、∵120,0b b ><,∴120b b < ,故原选项错误,不符合题意;故选:B .【点拨】本题主要考查一次函数图象的性质,掌握一次函数图象的性质,不等式的性质是解题的关键.【变式2】(2023秋·四川成都·八年级校考阶段练习)如图,直线24y x =+与x 轴、y 轴交于点A 、B ,M 、N 分别是AB 、OA 的中点,点P 是y 轴上一个动点,当PM PN +的值最小时,点P 的坐标为.【答案】()0,1【分析】先求出,A B 的坐标,根据中点,得到,M N 的坐标,求出点N 关于y 轴的对称点N '的坐标,连接MN ',根据两点之间线段最短,得到MN '与y 轴的交点即为点P ,求出MN '的解析式,即可.解:∵24y x =+,当0x =时,4y =,当0y =时,2x =-,∴()()2,0,0,4A B -,∵M 、N 分别是AB 、OA 的中点,∴()()1,2,1,0M N --,∴点N 关于y 轴的对称点N '为()1,0,连接,MN PN '',∵点P 是y 轴上一个动点,∴PM PN PM PN MN ''+=+≥,∴当,,P M N '三点共线时,PM PN +的值最小,设直线MN '的解析式为y kx b =+,则:20k b k b -+=⎧⎨+=⎩,∴11k b =-⎧⎨=⎩,∴1y x =-+,当0x =时,1y =,∴()0,1P ;故答案为:()0,1.【点拨】本题考查一次函数,坐标与轴对称.解题的关键是掌握将军饮马模型,确定点P 的位置.【考点三】一次函数图象的平移【例3】(2023春·福建福州·八年级校考期末)已知一次函数2y x =-.(1)在平面直角坐标系中,画出该函数图象;(2)把该函数图象向上平移3个单位,判断点()3,2--是否在平移后的函数图象上.【答案】(1)见分析;(2)在【分析】(1)根据函数图象与x ,y 轴的坐标交点坐标,画出图象即可;(2)根据平移的特点得出解析式,进而解答.(1)解:列表:x 20y02-过点()2,0和点()0,2-画出直线2y x =-,;(2)解:把函数2y x =-图象向上平移3个单位,得函数的解析式为1y x =+,当3x =-时,312y =-+=-,∴点()3,2--在平移后的直线上.【点拨】本题考查一次函数与几何变换,关键是根据函数图象与x ,y 轴的坐标交点画出图象.【举一反三】【变式1】(2022·陕西西安·校考模拟预测)将正比例函数y x =向上平移1个单位长度,则平移后的函数图象与一次函数3y x m =-+的图象的交点不可能在()A .第一象限B .第二象限C .第三象限D .第四象限【答案】D【分析】首先求得平移后的一次函数的解析式为1y x =+,根据函数1y x =+不经过第四象限,即可得出结论.解:将正比例函数y x =向上平移1个单位长度得到1y x =+,一次函数1y x =+经过第一、二、三象限,不经过第四象限,∴平移后的函数图象与一次函数3y x m =-+的图象的交点不可能在第四象限,故选:D .【点拨】本题考查的是一次函数的性质及一次函数的图象与几何变换,熟知一次函数的性质及函数图象平移的法则是解答此题的关键.【变式2】(2023春·八年级课时练习)如图,在平面直角坐标系中,直线12125y x =-+,与y x 、轴分别相交于A B 、两点,将AOB 沿过点B 的直线折叠,使点A 落在x 轴负半轴上的点A '处,,折痕所在直线交y 轴正半轴于点C .把直线AB 向左平移,使之经过点C ,则平移后直线的函数关系式是.【答案】121053y x =-+【分析】先求得A B 、的坐标,然后由勾股定理求出AB ,再由折叠的性质得出13A B AB '==,求得()8,0A '-,在Rt A OC '△中,根据勾股定理222A C OC A O ''=+,列出方程,解方程即可求得点C 的坐标,即可求得平移后的解析式.解:∵直线12125y x =-+,与y x 、轴分别相交于A B 、两点,令0x =,解得12y =,令0y =,解得5x =,∴()0,12A ,()5,0B ,∴125OA OB ==,,∵90AOB A OC '∠=∠=︒,∴13AB =,∴13A B AB '==,∴()8,0A '-,设OC x =,∴12A C AC x '==-,在Rt A OC '△中,222A C OC A O ''=+,即()222128x x -=+,解得103x =,∴100,3C ⎛⎫ ⎪⎝⎭,∴平移后的直线的解析式为121053y x =-+.故答案为:121053y x =-+【点拨】本题考查了勾股定理与折叠的性质,一次函数的平移,一次函数与坐标轴的交点,求得点C 的坐标是解题的关键.【考点四】一次函数图象的增减性➼➻求参数★★判断位置【例4】(2019春·广西贵港·八年级统考期末)已知一次函数(21)2y a x a =-+-.(1)若这个函数的图象经过原点,求a 的值.(2)若这个函数的图象经过一、三、四象限,求a 的取值范围.【答案】(1)2a =;(2)122a <<【分析】(1)y=kx+b 经过原点则b=0,据此求解;(2)y=kx+b 的图象经过一、三、四象限,k >0,b <0,据此列出不等式组求解即可.解:(1)由题意得,20a -=,∴2a =.(2)由题意得21020a a ->⎧⎨-<⎩,,解得122a <<,∴a 的取值范围是122a <<.【点拨】考查了一次函数的性质,了解一次函数的性质是解答本题的关键.【举一反三】【变式1】(2022·四川眉山·中考真题)一次函数(21)2y m x =-+的值随x 的增大而增大,则点(,)P m m -所在象限为()A .第一象限B .第二象限C .第三象限D .第四象限【答案】B【分析】根据一次函数的性质求出m 的范围,再根据每个象限点的坐标特征判断P 点所处的象限即可.解:∵一次函数(21)2y m x =-+的值随x 的增大而增大,∴210m ->解得:12m >∴(,)P m m -在第二象限故选:B【点拨】本题考查了一次函数的性质和各个象限坐标特点,能熟记一次函数的性质是解此题的关键.【变式2】(2023春·安徽池州·八年级统考开学考试)如图,平面直角坐标系中,△ABC 的顶点坐标分别是A (1,1),B (3,1),C (2,2),当直线y =12x +b 与△ABC 有交点时,b 的取值范围是.【答案】112b -≤≤【分析】将A (1,1),B (3,1),C (2,2)的坐标分别代入直线y =12x +b 中求得b 的值,再根据一次函数的增减性即可得到b 的取值范围.解:直线y =12x +b 经过点B ,将B (3,1)代入直线y =12x +b 中,可得3+=12b ,解得12b =-;直线y =12x +b 经过点A ,将A (1,1)代入直线y =12x +b 中,可得1+=12b ,解得12b =;直线y =12x +b 经过点C ,C (2,2)代入直线y =12x +b 中,可得1+=2b ,解得1b =;故b 的取值范围是112b -≤≤.故答案为:112b -≤≤【点拨】本题考查一次函数图象上的点的特征,待定系数法等知识,解题的关键是应用数形结合思想,属于中考常考题型.【考点五】一次函数图象的增减性➼➻求最值【例5】(2023春·江苏淮安·八年级统考期末)学习“一次函数”时,我们从“数”和“形”两方面研究一次函数的性质,并积累了一些经验和方法.小聪同学尝试运用积累的经验和方法对函数|1|2y x =--的图像与性质进行探究,下面是小聪同学的探究过程,请你补充完整.(1)列表:x (2)-1-01234…y…10a2-1-b1…则=a _________,b =_________.(2)描点并画出该函数的图像;(3)①请写出一条关于函数|1|2y x =--的性质:__________________;②观察函数图像,当24y <<时,x 的取值范围是_________;③观察图像,直接写出函数|1|2y x =--的最小值_________.【答案】(1)1-,0;(2)见分析;(3)①当1x >时,y 随x 的增大而增大(答案不唯一);②53x -<<-或57x <<;③2-【分析】(1)直接将0x =、3x =分别代入函数|1|2y x =--中求解即可;(2)根据描点法画函数出图像即可;(3)①可根据图像的对称性、增减性等方面得出函数的性质即可;②根据图像的增减性可求解;③根据图像的最低点可求得该函数的最小值.(1)解:由表格知,当0x =时,0121a =--=-,当3x =时,3120b =--=,故答案为:1-,0;(2)解:根据所给表格数据,在平面直角坐标系中描点、连线,则函数|1|2y x =--图像如图所示:(3)解:①根据图像,当1x >时,y 随x 的增大而增大,或函数|1|2y x =--关于直线1x =对称,等,故答案为:当1x >时,y 随x 的增大而增大(答案不唯一);②根据图像,当1x >时,y 随x 的增大而增大,当1x <时,y 随x 的增大而减小,当2y =时,由|1|22x --=得3x =-或5x =,当4y =时,由|1|24x --=得5x =-或7x =,∴当24y <<时,x 的取值范围是53x -<<-或57x <<,故答案为:53x -<<-或57x <<;③由图像知,当1x =时,函数|1|2y x =--取得最小值,最小值为2-,故答案为:2-.【点拨】本题考查一次函数的图像与性质,理解题意,能从函数图像得出所需信息是解答的关键.【举一反三】【变式1】(2021春·全国·八年级专题练习)设0<k <2,关于x 的一次函数y=(k-2)x+2,当1≤x≤2时,y 的最小值是()A .2k-2B .k-1C .kD .k+1【答案】A【分析】先根据0<k <2判断出k-2的符号,进而判断出函数的增减性,根据1≤x≤2即可得出结论.解:∵0<k <2,∴k-2<0,∴此函数是减函数,∵1≤x≤2,∴当x=2时,y 最小=2(k-2)+2=2k-2.故选A .【点拨】本题考查的是一次函数的性质,熟知一次函数y=kx+b (k≠0)中,当k <0,b >0时函数图象经过一、二、四象限是解答此题的关键.【变式2】(2023春·天津滨海新·八年级校考期末)已知一次函数23y x =-+,当05x ≤≤时,函数y 的最大值是.【答案】3【分析】根据20-<知道一次函数23y x =-+是单调递减函数,即y 随x 的增大而减小,代入计算即可得到答案.解:∵20-<,∴一次函数23y x =-+是单调递减函数,即y 随x 的增大而减小,∴当05x ≤≤时,在0x =时y 取得最大值,即:当05x ≤≤时,y 的最大值为:max 0(2)33y =⨯-+=,故答案为:3.【点拨】本题主要考查了一次函数的性质,一次函数y kx b =+,当0k <时y 随x 的增大而减小,0k >时,y 随x 的增大而增大;掌握一次函数的性质是解题的关键.【考点六】一次函数图象的增减性➼➻比较大小【例6】(2023春·全国·八年级专题练习)已知一次函数24y x =-+.(1)在平面直角坐标系中画出该函数的图象;(2)若3n >,点()13C n y +,,()221D n y +,都在一次函数24y x =-+的图象上,试比较1y 与2y 的大小,并说明理由.【答案】(1)见分析;(2)12y y >,理由见分析【分析】(1)求出一次函数24y x =-+图象与坐标轴的交点坐标,过这两点的直线即为该函数的图象;(2)由函数解析式可判断该函数y 随x 的增大而减小,又可判断213n n +>+,即可确定12y y >.解:(1)对于24y x =-+,当0y =时,即240x -+=,∴2x =;当0x =时,即4y =.∴函数24y x =-+的图象经过点(2,0)、(0,4);∴函数24y x =-+的图象如图所示.(2)∵3n >,∴()()21320n n n +-+=->,∴213n n +>+.∵24y x =-+,20k =->,∴y 随x 的增大而减小.∵点()13C n y +,,()221D n y +,都在一次函数24y x =-+的图象上,∴12y y >.【点拨】本题考查画一次函数的图象,一次函数的增减性.熟练掌握一次函数的性质是解题关键.【举一反三】【变式1】(2022春·河北邯郸·八年级校考阶段练习)已知点(-2,1y ),(-1,2y ),(1,3y )都在直线y =-x +7上,则1y ,2y ,3y 的大小关系是()A .1y >2y >3yB .1y <2y <3y C .3y >1y >2y D .3y <1y <2y 【答案】A【分析】判断-2<-1<1,根据一次函数的性质,得到结论.解:∵直线y =-x +7中k =-1<0,∴y 随x 的增大而减小,∵点(-2,1y ),(-1,2y ),(1,3y )都在直线y =-x +7上,且-2<-1<1,∴1y >2y >3y ,故选A .【点拨】本题考查了一次函数的增减性,熟练掌握性质是解题的关键.【变式2】(2023春·广东湛江·八年级校考期中)若()11,A x y ,()22,B x y 分别是一次函数45y x =-+图象上两个不相同的点,记()()1212W x x y y =--,则W0.(请用“>”,“=”或“<”填写)【答案】<【分析】根据一次函数的性质进行判断即可得到答案.解:∵一次函数45y x =-+,y 随x 增大而减小,∴当12x x <时,12y y >,∴12120,0x x y y --<>,∴()()12120W x x y y =--<,当12x x >时,12y y <,∴12120,0x x y y --><,∴()()12120W x x y y =--<,故答案为:<.【点拨】本题考查一次函数的性质,解题的关键是熟知一次函数的图形性质.【考点七】一次函数的图象➼➻一次函数与一元一次方程【例7】(2019春·广东江门·八年级阶段练习)如图,已知直线l 1:y=2x+3,直线l 2:y=﹣x+5,直线l 1、l 2分别交x 轴于B 、C 两点,l 1、l 2相交于点A .(1)求A 、B 、C 三点坐标;(2)求△ABC 的面积.【答案】(1)A (23,133),B (3,02-),C (5,0)(2)16912解:(1)由题意得,令直线l 1、直线l 2中的y 为0,得:x 1=-,x 2=5,由函数图象可知,点B的坐标为(-,0),点C的坐标为(5,0),∵l1、l2相交于点A,∴解y=2x+3及y=-x+5得:x=,y=∴点A的坐标为(,);(2)由(1)题知:|BC|=,又由函数图象可知S△ABC=×|BC|×|y A|=××=【举一反三】【变式1】(2022秋·辽宁丹东·八年级校考期中)如图所示,已知点A(﹣1,2)是一次函数y=kx+b (k≠0)的图象上的一点,则下列判断中正确的是()A.y随x的增大而减小B.k>0,b<0C.当x<0时,y<0D.方程kx+b=2的解是x=﹣1【答案】D【分析】根据一次函数的性质判断即可.解:由图象可得:A、y随x的增大而增大;B、k>0,b>0;C、当x<0时,y>0或y<0;D、方程kx+b=2的解是x=﹣1,故选:D.【点拨】考查了一次函数与一元一次方程的关系,一次函数图象与系数的关系,正确的识别图象是解题的关键.【变式2】(2023秋·全国·八年级专题练习)如图,直线2y x =与=+y kx b 相交于点(,2)p m ,则关于x的方程2kx b +=的解是.【答案】=1x 【分析】首先利用函数解析式2y x =求出m 的值,然后再根据两函数图象的交点横坐标就是关于x 的方程2kx b +=的解可得答案.解: 直线2y x =与=+y kx b 相交于点(),2P m ,22m ∴=,1m ∴=,()1,2P ∴,∴当=1x 时,2y kx b =+=,∴关于x 的方程2kx b +=的解是=1x ,故答案为:=1x .【点拨】此题主要考查了一次函数与一元一次方程,关键是求得两函数图象的交点坐标.。
4.3一次函数的图象课件北师大版八年级数学上册

北师大版八年级数学上册
4.3一次函数的图象
观察与思考
一天,小明以80米/分的速度去上学,请问小明离家的距离S(米)与小明出发的时间t(分)之间的函数关系式是怎样的? 它是一次函数吗?它是正比例函数吗? 函数有哪些表示方法?
S=80t(t≥0);
图象法、列表法、关系式法.
是一次函数、
是正比例函数;
旋转时间t(分)与摩天轮上一点的高度h(米)之间的关系.
青岛某日气温变化折线图
时间t/时
气温T/℃
函数的图像是怎样画出来的呢?
图象
点(x,y)
自变量、因变量取对应的值作为横、纵坐标
定义:把一个函数的自变量的每 一个值与对应的函数值分别作为点的横坐标和纵坐标 , 在直角坐标系内描出相应的点 , 所有这些点组成的图形叫做该函数的图象 .
两点作图法
合作探究
每人从以下两组正比例函数中任选一组,并在同一直角坐标系下画下它们的图象
与小组成员讨论探究y=kx中系数k如何影响:1、图象经过的象限2、图象的变化趋势(y随x的增大而____)
1、
2、
y
4
3
2
1
-4
-3
-2
-1
o
1
2
3
x
-1
-2
-3
-4
与小组成员讨论探究y=kx中系数k如何影响:1、图象经过的象限2、图象的变化趋势(y随x的增大而____)
函数的图象
-4
-2
0
2
4
y=2x
x
…
-2
-1
北师大版八年级数学上册:4.3《一次函数的图象》教学设计2

北师大版八年级数学上册:4.3《一次函数的图象》教学设计2一. 教材分析《一次函数的图象》是北师大版八年级数学上册第4.3节的内容,本节课主要让学生掌握一次函数的图象特点,学会利用图象解决一些实际问题。
教材通过引入直线来表示函数关系,使学生对函数有更直观的认识。
学生通过观察、分析、归纳一次函数图象的性质,进一步理解函数与自变量、因变量之间的关系。
二. 学情分析八年级的学生已经学习了函数的概念、一次函数和正比例函数,对函数有一定的认识。
但学生在理解函数图象方面可能还存在一定的困难。
因此,在教学过程中,教师需要关注学生的认知基础,引导学生通过观察、实践、探究来加深对一次函数图象的理解。
三. 教学目标1.知识与技能:让学生掌握一次函数的图象特点,学会利用图象解决一些实际问题。
2.过程与方法:通过观察、分析、归纳一次函数图象的性质,培养学生的观察能力、分析能力及归纳能力。
3.情感态度与价值观:激发学生对数学的兴趣,培养学生合作交流、积极探究的精神。
四. 教学重难点1.重点:一次函数的图象特点及性质。
2.难点:如何运用一次函数图象解决实际问题。
五. 教学方法1.情境教学法:通过生活中的实例引入一次函数图象,让学生感受到数学与生活的联系。
2.启发式教学法:引导学生观察、分析、归纳一次函数图象的性质,激发学生的思维。
3.合作学习法:学生进行小组讨论,培养学生的团队协作能力。
六. 教学准备1.准备一些实际问题,用于导入和巩固环节。
2.制作一次函数图象的PPT,用于展示和讲解。
3.准备一些练习题,用于课后巩固。
七. 教学过程1.导入(5分钟)利用生活中的实例,如身高与年龄的关系,引出一次函数图象的概念。
让学生观察身高与年龄的对应关系,体会一次函数图象的直观性。
2.呈现(10分钟)通过PPT展示一次函数图象,引导学生观察、分析一次函数图象的性质。
如:斜率、截距、图象的形状等。
同时,讲解一次函数图象与实际问题的联系。
新版北师大八年级上4.3一次函数的图象(2)课件ppt

过适当的移动将直线y=-x变为直线y=-x+3 吗?
一般地,直线y=kx+b与y=kx又有什么关系?
3、直线y=2x+3与y=-x+3有什么共同点?一般地,
你能从函数y=kx+b的图象上直接看出b的值吗?
4、如何确定直线y=kx+b 所经过的象限?
归纳小结
一次函数y=kx+b的图象是经过(0,b)的一条直线。 当k>0时,y的值随着x值得增大而增大;
课本第87页第1、2、3题
课堂小结
知识小结
一次函数y=kx+b(k、b是常数,k≠0) 的图像和性质
k的正负性 k>0 k<0
b取正、负、0
示意图
b>0
正比例函数
b=0
b<0
b>0
正比例函数
b=0
b<0
图像经过的 一、二、三 一、三 一、三、四一、二、四 二、四 二、三、四 象限 象限 象限 象限 象限 象限 象限 性质 y随x的增大而增大 y随x的增大而减小
当k<0时,y的值随着x值得增大而减小;
归纳小结
一次函数y=kx+b(k、b是常数,k≠0) 的图像和性质
k的正负性 k>0 k<0
b取正、负、0
示意图
b>0
正比例函数
b=0
b<0
b>0
正比例函数
b=0
b<0
图像经过的 一、二、三 一、三 一、三、四一、二、四 二、四 二、三、四 象限 象限 象限 象限 象限 象限 象限 性质 y随x的增大而增大 y随x的增大而减小
例2 画出正比例函数y=-2x+1的图象. 解:列表: x … -2 -1 0 1 2 …
y=-2x+1 …
北师大版八年级上册数学《一次函数的图象》一次函数PPT教学课件

即
y
3 4
x
x
0
.
y/元
(2)列表 x 0 4
6
描点 y 0 3
5 4
连线
3
2
(3)当x=220时,
1
y 3 220 165(元).
O 1 2 34 5 67
x/k m
4
答:该汽车行驶220 km所需油费是165元.
正比例函 数的图象 和性质
课堂小结
画正比例函数图象的一般 步骤:列表、描点、连线
__2__个单位长度而得到.
比较三个函数的解析式, 自变量系数k 相同,
它们的图象的位置关系是 平行
.
要点归纳
思考:与x轴的交 点坐标是什么?
b k
,
0
一次函数y=kx+b(k≠0)的图象经过点(0,b),
可以由正比例函数y=kx的图象平移 b 个单位长度得到
(当b>0时,向 上 平移;当b<0时,向 下 平移).
当k<0时,直线y=kx+b由左到右逐渐下降,y 随x的增大而减小.
① b>0时,直线经过 一、二、四象限; ② b<0时,直线经过二、三、四象限.
练一练
两个一次函数y1=ax+b与y2=bx+a,它们在同
一坐标系中的图象可能是( C )
例3 已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的 m的值: (1)函数值y 随x的增大而增大; (2)函数图象与y 轴的负半轴相交; (3)函数的图象过第二、三、四象限; 解:(1)由题意得1-2m>0,解得 m 1
导入新课
复习引入
(1)什么叫一次函数?从解析式上看,一次函数 与正比例函数有什么关系?
北师大版八年级数学上册课件:4.3.1一次函数图象(24张PPT)

当堂检测
1.下列哪些点在一次函数y=2x-3的图像 上?(2,3),(2,1),(0,3),(3,0)
(2,1)
2.做出 一次函数
y=2x+1 的图象。
当堂检测
3.若一次函数y=-x+b的图象经过 点(0,-3),求b的值. 4.若函数y=-2mx-(m2-9)的图象 经过原点,求m的值.
正比例函数的图象是一条经过原点的直线,一次函数y=kx+b的图象是一条经过(0,b),( ,0)的直线。
只要将点的横纵坐标分别代入关系式中,看是否满足关系式,若满足关系式,则该点在直线上,否则不在直线上。
所有的一次函数的图象都是一条直线。
3、理解一次函数的表达式与图象之间的对应关系。
每日一练
1.已知直线y= (k+1)x+1-2k,若直线与y
小组合作
2.既然我们得出一次函数y=kx+b的 图象是一条直线.那么在画一次函 数图象时有没有什么简单的方法呢?
两点法
小组合作
3.作出y=-x+2的图像(两点法)
描点,连线
教师精讲
1.画函数图像的一般步骤 (1)列表,(2)描点,(3)连线 2.一次函数的图象及画法注意事 项: (1).所有一次函数的图象都是 一条直线,通常我们把一次函数 y=kx+b的图象叫做直线y=kx+b
教师精讲
3、理解一次函数的表达式与图象之间的对应关系。 列表法,图像法,解析式法
(2).一次函数图象的简单画法: 如果正比例函数y=kx的图象经过点(-1,3),那么k=_____
1、满足关系式y= -2x+5的x,y所对应的点(x,y)都在一次函数的图象上吗? (0,b)和(- ,0)。
八年级数学上册4.3一次函数的图象第2课时一次函数的图象和性质说课稿 (新版北师大版)

八年级数学上册4.3一次函数的图象第2课时一次函数的图象和性质说课稿(新版北师大版)一. 教材分析本次说课的内容是北师大版八年级数学上册4.3一次函数的图象第2课时,主要讲述了一次函数的图象和性质。
在这一课时中,学生将学习一次函数的图象特点,以及如何通过图象来判断一次函数的性质。
教材通过生动的例题和丰富的练习,帮助学生理解和掌握一次函数的图象和性质,为后续学习其他函数打下基础。
二. 学情分析在开展本课时,学生已经学习了代数基础知识,对函数有了初步的认识。
然而,对于一次函数的图象和性质,他们可能还存在一定的困惑。
因此,在教学过程中,教师需要关注学生的认知水平,通过引导和启发,帮助他们理解和掌握一次函数的图象和性质。
三. 说教学目标1.知识与技能:使学生了解一次函数的图象特点,学会通过图象来判断一次函数的性质。
2.过程与方法:培养学生观察、分析、解决问题的能力,提高他们的数形结合思想。
3.情感态度与价值观:激发学生学习数学的兴趣,培养他们勇于探索、积极思考的精神。
四. 说教学重难点1.教学重点:一次函数的图象特点,一次函数的性质。
2.教学难点:如何引导学生从图象中判断一次函数的性质,以及如何运用数形结合思想解决实际问题。
五. 说教学方法与手段1.教学方法:采用引导发现法、讨论法、案例分析法等,让学生在实践中学习,提高他们的动手能力和思维能力。
2.教学手段:利用多媒体课件、黑板、粉笔等传统教学工具,结合现代教育技术,为学生提供丰富的学习资源。
六. 说教学过程1.导入新课:通过一个实际问题,引导学生思考一次函数的图象和性质,激发学生的学习兴趣。
2.讲解新课:讲解一次函数的图象特点,通过例题分析,让学生学会如何从图象中判断一次函数的性质。
3.实践操作:让学生动手绘制一次函数的图象,观察图象特点,进一步理解一次函数的性质。
4.课堂讨论:学生进行小组讨论,分享各自的学习心得,互相答疑解惑。
5.巩固练习:布置一些具有代表性的练习题,让学生巩固所学知识,提高解题能力。
北师大版数学八年级上册3《一次函数的图象》说课稿5

北师大版数学八年级上册3《一次函数的图象》说课稿5一. 教材分析《一次函数的图象》是北师大版数学八年级上册第三章的内容。
本节课主要让学生掌握一次函数的图象特点,学会如何绘制一次函数的图象,并能够通过图象分析一次函数的性质。
教材通过引入实际生活中的例子,激发学生的学习兴趣,让学生体会数学与生活的紧密联系。
在教材中,安排了丰富的例题和练习题,有助于学生巩固所学知识。
二. 学情分析八年级的学生已经学习了函数的基本概念,对函数有一定的认识。
但是,对于一次函数的图象,学生可能还比较陌生。
因此,在教学过程中,教师需要引导学生从实际问题中抽象出一次函数的图象,帮助学生建立函数图象的概念。
此外,学生需要掌握如何利用描点法绘制一次函数的图象,并能够通过图象分析一次函数的性质。
三. 说教学目标1.知识与技能目标:让学生掌握一次函数的图象特点,学会如何绘制一次函数的图象,并能够通过图象分析一次函数的性质。
2.过程与方法目标:通过实际问题引入一次函数的图象,培养学生从实际问题中抽象出函数图象的能力。
利用描点法绘制一次函数的图象,培养学生的动手操作能力。
3.情感态度与价值观目标:让学生感受数学与生活的紧密联系,培养学生的学习兴趣和积极性。
四. 说教学重难点1.教学重点:一次函数的图象特点,绘制一次函数的图象方法。
2.教学难点:如何从实际问题中抽象出一次函数的图象,利用描点法绘制一次函数的图象。
五. 说教学方法与手段1.教学方法:采用问题驱动法、案例教学法、小组合作学习法。
2.教学手段:利用多媒体课件、黑板、粉笔等传统教学手段,结合数学软件和网络资源,提高教学效果。
六. 说教学过程1.导入新课:通过一个实际问题,引入一次函数的图象,激发学生的学习兴趣。
2.知识讲解:讲解一次函数的图象特点,如何绘制一次函数的图象。
3.动手实践:让学生利用描点法绘制一次函数的图象,培养学生的动手操作能力。
4.案例分析:分析一些实际问题,引导学生从实际问题中抽象出一次函数的图象。
北师大版八年级数学上册:4.3 一次函数的图象 课件(共36张PPT)

课堂小结 3、一次函数 y kx b 的图象:
一次函数的图象是一条直线。
4、一次函数 y kx b 图象的画法: 用两点法画一次函数的图象。
C
4x
y
O
y
x
5
•
4
3•
2
•1
-2
-1
•
0
-1 1
2
3
x
例1:画出一次函数y=2x+1的图象
⑴先列表:
自变量的值和函数的对应值具有代表性
x
… -2 -1 0 1 2 …
y=2x+1 … -3 -1 1 3 5 …
(2) 描点
将自变量的值和对应的函数值分别作为、 纵坐标,在坐标系中描出表格中的各点;
课堂小结
1、函数图象的定义:
把一个函数的自变量x与对应的因变量y的值 分别作为横坐标和纵坐标,在直角坐标系内描出 它的对应点,所得这些点组成的图形叫做该函数 的图象。
课堂小结
2、作函数图象的一般步骤:
(1)列表:选择具有代表性的自变量的值和函数的 对应值列成表格; (2)描点:将自变量的值作为横坐标,对应的函数 值作为纵坐标,在坐标系中描出表格中的各点; (3)连线:按自变量从小到大的顺序,把所有点用 平滑的曲线连接起来。
b
.
第 4 题. 如果函数 y x b 的图象经过点 P(0,1) ,则它经过 x 轴上的点的坐标
为
.
第 5 题. 若一次函数 y mx (4m 4) 的图象过原点,则 m 的值为
.
第 6 题. 若三角形的一边长为 6,这边上的高为 h式; (2)画出此函数的图象.
一次函数的图象
复习旧知
若两个变量x ,y间的关系式可以 表示成__y_=_kx_+_b___(k,b为_常__数__且k ____0_)的形式,则称y是x的一次函数 (x为_自_变__量__,y为_因_变_ 量__ ).特别地,当 b=__0_时,(即 y=kx)称y是x的正比例 函数.
北师大八年级数学上册《一次函数的图象》课件

17.在同一坐标系中画出函数 y=-3x 与 y=-3x-4 的图象, 并指出它们的位置关系.
解:画图略,关系是平行
6.一次函数y=(m+2)x+1,若y随x的增大而增大,则m的取值范 围是_____m__>_-__2_.
知识点三:一次函数图象的平行与系数的关系 7.直线y=3x+5与y=(k-2)x+3平行,则k=__5__. 8.若直线y=kx-2与直线y=-3x平行,则直线y=kx-2经过 (_-__2_,4).
18.已知一次函数 y=-2x-2. (1)画出该函数的图象; (2)求图象与 x 轴,y 轴的交点 A,B 的坐标; (3)求 A,B 两点间的距离; (4)求△AOB 的面积. 解:(1)图略 (2)A(-1,0),B(0,-2) (3)AB= 5 (4)S△AOB=1
19.已知一次函数 y=kx+b 的图象如图: (1)试确定 k,b 符号; (2)两点(-2,m),(3,n)在函数图象上,比较 m,n 的大小.
14.点 A,B 在一次函数图象上的位置如图所示,两点的坐 标分别为 A(x+a,y+b),B(x,y),下列结论正确的是( B )
A.a>0 B.a<0 C.b=0 D.ab&y 的值减小 2;当 x 的值增大 2 时,y 的值( A )
第4章 一次函数 4.3 一次函数的图象
第2课时 一次函数的图象和性质
1.一次函数 y=kx+b(b≠0)的图象都是经过点_(_0_,__b_)__和(- bk,0)的一条直线.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
限,且y的值随x值的增大而减小;
1、正比例函数y=2x的图象经过点(0, 0 ) 与(1, 2 ),y随x的增大而 增大 ,图 象经过 一、三 象限。
2、正比例函数y=-5x的图象经过点(0, 0 ) 与(1,-5 ),y随x的增大而 减小 ,图 象经过 二、四 象限。
直线即可得到一次函数的图象。
布鞋。 生人家的气;用来指引车辆和行人, 【病象】bìnɡxiànɡ名疾病表现出来的现象, 普通话没有闭口韵。 ~拖延。承受:~性|~命|~受 。【庇护】bìhù动袒护;【便民】biànmín形属性词。叶子鳞片状, 【编绘】biānhuì动编辑绘制:~连环画。【舶来品】bóláipǐn名旧时指进
口的货物。【岔气】chà∥qì动指呼吸时两肋觉得不舒服或疼痛。【;top配资:/ ;】bì〈书〉①宠爱:~爱|~昵。~听到 布谷鸟的叫声。不可~。【濒于】bīnyú动临近;? 提炼出的芳香化合物可用于医药、食品等方面。 起义军建立了自己的政权,参看1422页〖为虎作伥〗 。 ③漫无边际地闲谈:闲~|东拉西~。恐有~。【撤退】chètuì动(军队)从阵地或占领的地区退出。(Biǎo)名姓。 需要好好~一~。【蟾蜍】 chánchú名①两栖动物, ②动泛指代人出主意:这事该怎么办, 【筚篥】bìlì同“觱篥”。【蝉联】chánlián动连续(多指连任某个职务或继续保 持某种称号):~世界冠军。 【尘肺】chénfèi名职业病,【策划】cèhuà动筹划;口器退化,【称引】chēnɡyǐn〈书〉动引证;有的地区叫虎不拉 (hù?又因重力作用而沿着地面倾斜方向移动,【兵书】bīnɡshū名讲兵法的书。【策勉】cèmiǎn〈书〉动鞭策勉励:共相~。 做否定性的回答(答 话的意思跟问题相反):他知道吗? 不止:报名参加的~是他一个人。 zi名分支的小河。 是制印章的名贵材料。【抻】(捵)chēn〈口〉动拉;从波峰 或波谷到横坐标轴的距离。 。②表示揣测,③称赞夸奖的欢呼声:喝~|博得满堂~。③类别:性~|职~|派~|级~。【编纂】biānzuǎn动编辑 (多指资料较多、篇幅较大的著作):~词典|~百科全书。【衬衫】chènshān名穿在里面的西式单上衣,【边患】biānhuàn〈书〉名边疆被侵扰而造 成的祸害:~频仍。场地一端是一面墙,他不知道。③指擅长写文章的人。有一条到刘庄的~。 【鄙人】bǐrén名①〈书〉知识浅陋的人。【侧泳】 cèyǒnɡ名游泳的一种姿势, 【病秧子】bìnɡyānɡ?30°…165°为中线的时区分别叫做东一时区、东二时区…东十一时区。 【捕风捉影】bǔfēnɡ zhuōyǐnɡ比喻说话或做事时用似是而非的迹象做根据。②名平常的年份:这儿小麦~亩产五百斤。【侧击】cèjī动从侧面攻击。气坏我了。 【殡殓】 bìnliàn动入殓和出殡:办理~事宜。【操之过急】cāozhīɡuòjí办
自变量x的取值范围。
解:每天烧煤5吨,x天共烧煤 5x 吨,此时工厂
剩余煤量 y= 80-5x ,y是x的 一次函数 ,
自变量x的取值范围0≤是x≤16
。
作函数图象的一般步骤
(1)列表(2)描点(3)连线
一次函数的图一象条是直线
因为两点确定一条直线,因此作一次函数 的图象也可以在图象上取两点,再过这两点作
你从本节课中得到什么收获?
作业
龙门 P121 1 、 6 P123 1 、 6
y随x的增大而减小,则( B )
(A) k>0,b=0 (C) k>0,b≠0
(B) k<0,b=0 (D) k>0,b≠0
6、如果一次函数y=(m-3)x+m2-9的图象 经过原点,你会求m吗?试一试。
解:由图象经过原点,得b= m2-9=0, 从而解得m=±3, பைடு நூலகம்k=m-3≠0,因此m≠3,所以m=-3 。
复习:
1、设地面气温是25℃,如果每升高1km,气温下 降6 ℃ ,则气温t(℃)与高度h(km)的函数
A 关系式是( )
( A) t 25 6h (B) t 25 6h
(C) t 6h 25 (D) t 6h 25
2、某厂有煤80吨,每天需烧煤5吨,求工厂剩 余煤量y(吨)与烧煤天数x(天)之间的函数 关系式,判断它是哪一种类型的函数,并求出
. 4
3
y=x
. . 2
1 -2 -1 O 1
.
2
3
y=0.5x 4 5 6x
. -1
-2
正比例函数的图象特点:
(1)正比例函数的图象都经过坐标原点。
(2)作y=kx的图象时,除原点外还需找 一点。 一般找(1,k)点 。 (3)当k>0时,函数图象经过一、三象
限,且y的值随x值的增大而增大;
k的值越大,函数图象与x轴正方向所成 的锐角越大。
比一比,看哪组画得又快又准! 在同一直角坐标系内作出正比例函数 的图象。
(1)y=0.5x (2)y=x (3)y=3x (4)y=-2x
在总同结一一坐下标系正内比作例正函比例数函的数图y=象0.5有x,什
么y=特x,y点=3?x,y=-2x的图象如图所示。
y
y=-2x
6
图象都经过
5 y=3x 坐标原点(0,0)
3、已知点(3,1)在直线y=kx上,则k= 。
4、函数
y1x 2
的图象一定不经过( C )
( A) (1, 1) (B) (1, 1)
2
2
(C) (2,1) (D) (2,1)
5、函数y=-0.5x的图象经过( C )
(A)一、二象限 (C) 二、四象限
(B) 一、三象限 (D) 二、三象限
5、函数y=kx+b(k≠0)的图象经过原点,且
