安徽省淮南市2016届高三第一次模拟数学(理)试题
2016年安徽省淮南市高考一模数学试卷(理科)【解析版】
2016年安徽省淮南市高考数学一模试卷(理科)一、选择题1.(5分)复数的虚部是()A.i B.﹣i C.1D.﹣12.(5分)已知集合U={1,2,3,4},B={1,2,3},且A∩B={1,2},则满足条件的A的个数为()A.1B.2C.3D.43.(5分)下面的程序框图能判断任意输入的数x的奇偶性.其中判断框内的条件是()A.m=0B.m=1C.x=0D.x=14.(5分)函数f(x)=2sin(ωx+φ)的部分图象如图所示,则ω,φ的值分别是()A.2,﹣B.2,﹣C.4,﹣D.4,5.(5分)经过抛物线y=x2的焦点和双曲线﹣=1的右焦点的直线方程为()A.x+48y﹣3=0B.x+80y﹣5=0C.x+3y﹣3=0D.x+5y﹣5=0 6.(5分)设a=log32,b=log52,c=log23,则()A.a>c>b B.b>c>a C.c>a>b D.c>b>a 7.(5分)O是平面上一定点,A、B、C是平面上不共线的三个点,动点P满足,λ∈[0,+∞),则P的轨迹一定通过△ABC的()A.外心B.内心C.重心D.垂心8.(5分)如图,有一圆柱形无盖水杯,其轴截面ABCD是边长为2的正方形,P是BC的中点,现有一只蚂蚁位于外壁A处,内壁P处有一粒米,则这只蚂蚁取得米粒所经过的最短路程是()A.B.π+1C.D.9.(5分)已知{a n}中,,且{a n}是递增数列,则实数的取值范围是()A.(﹣2,+∞)B.[﹣2,+∞)C.(﹣3,+∞)D.[﹣3,+∞)10.(5分)椭圆C:+=1的左,右顶点分别为A1,A2,点P在C上,且直线P A2斜率的取值范围是[﹣2,﹣1],那么直线P A1斜率的取值范围是()A.[,]B.[,]C.[,1]D.[,1] 11.(5分)如图,是某多面体的三视图,则该多面体的体积为()A.B.C.D.12.(5分)设正实数x,y,z满足x2﹣3xy+4y2﹣z=0,则当取得最小值时,x+2y﹣z的最大值为()A.0B.C.2D.二、填空题13.(5分)过平面区域内一点P作圆O:x2+y2=1的两条切线,切点分别为A,B,记∠APB=α,当α最小时,此时点P坐标为.14.(5分)已知过点M(﹣3,﹣3)的直线l被圆x2+y2+4y﹣21=0所截得的弦长为8,则直线l的方程为.15.(5分)定义在[﹣2,2]上的偶函数f(x)在[﹣2,0]上为增,若满足f(1﹣m)<f(m),则m的取值范围是.16.(5分)设函数y=f(x)的图象与y=2x+a的图象关于y=﹣x+1对称,且f (﹣3)+f(﹣7)=1,则a的值为.三.解答题17.(12分)在△ABC中,B=,AC=,求AB+BC的最大值并判断取得最大值时△ABC的形状.18.(12分)在公差为d的等差数列{a n}中,已知a1=10,且a1,2a2+2,5a3成等比数列.(Ⅰ)求d,a n;(Ⅱ)若d<0,求|a1|+|a2|+|a3|+…+|a n|.19.(12分)如图,在斜三棱柱ABC﹣A1B1C1中,A1B⊥AC,且A1B=AC=5,AA1=BC=13,且AB=12.(1)求证:平面ABB1A1⊥平面ACC1A1;(2)求二面角A﹣BB1﹣C的正切值的大小.20.(12分)已知点A(2,0),椭圆E:(a>b>0)的离心率为,F是椭圆E的上焦点,直线AF的斜率为,O为坐标原点.(1)求E的方程;(2)设过点A的动直线l与E相交于点P,Q两点,当△OPQ的面积最大时,求l的方程.21.(12分)已知函数f(x)=xlnx+(2a﹣1)x﹣ax2﹣a+1,(1)若,求f(x)的单调区间;(2)若x∈[1,+∞)时恒有f(x)≤0,求a的取值范围.四.选做题,以下三题任选一题22.(10分)已知函数f(x)=sin(x﹣ϕ)cos(x﹣ϕ)﹣cos2(x﹣ϕ)+(0≤ϕ≤)为偶函数.(I)求函数的最小正周期及单调减区间;(II)把函数的图象向右平移个单位(纵坐标不变),得到函数g(x)的图象,求函数g(x)的对称中心.23.已知p:|1﹣|<2;q:x2﹣2x+1﹣m2<0;若¬p是¬q的充分非必要条件,求实数m的取值范围.24.在直角坐标系xOy中,已知点A(1,1),B(2,3),C(3,2),点P(x,y)在△ABC三边围成的区域(含边界)上.(Ⅰ)若++=,求||;(Ⅱ)设=m+n(m,n∈R),用x,y表示m﹣n,并求m﹣n的最大值.2016年安徽省淮南市高考数学一模试卷(理科)参考答案与试题解析一、选择题1.(5分)复数的虚部是()A.i B.﹣i C.1D.﹣1【解答】解:=,则复数的虚部是1,故选:C.2.(5分)已知集合U={1,2,3,4},B={1,2,3},且A∩B={1,2},则满足条件的A的个数为()A.1B.2C.3D.4【解答】解:∵U={1,2,3,4},B={1,2,3},且A∩B={1,2},∴满足条件的A可能为{1,2},{1,2,4}共2个,故选:B.3.(5分)下面的程序框图能判断任意输入的数x的奇偶性.其中判断框内的条件是()A.m=0B.m=1C.x=0D.x=1【解答】解:由程序框图所体现的算法可知判断一个数是奇数还是偶数,看这个数除以2的余数是1还是0.由图可知应该填m=1.故选:B.4.(5分)函数f(x)=2sin(ωx+φ)的部分图象如图所示,则ω,φ的值分别是()A.2,﹣B.2,﹣C.4,﹣D.4,【解答】解:由函数的图象可知T==π,ω==2.x=时,y=2,可得:2sin(2×+φ)=2,由五点法作图可知φ=﹣.故选:A.5.(5分)经过抛物线y=x2的焦点和双曲线﹣=1的右焦点的直线方程为()A.x+48y﹣3=0B.x+80y﹣5=0C.x+3y﹣3=0D.x+5y﹣5=0【解答】解:抛物线y=x2的焦点坐标为(0,1),双曲线﹣=1的右焦点的坐标为(5,0),∴所求直线方程为即x+5y﹣5=0.故选:D.6.(5分)设a=log32,b=log52,c=log23,则()A.a>c>b B.b>c>a C.c>a>b D.c>b>a【解答】解:由题意可知:a=log32∈(0,1),b=log52∈(0,1),c=log23>1,所以a=log32,b=log52=,所以c>a>b,故选:C.7.(5分)O是平面上一定点,A、B、C是平面上不共线的三个点,动点P满足,λ∈[0,+∞),则P的轨迹一定通过△ABC的()A.外心B.内心C.重心D.垂心【解答】解:∵、分别表示向量、方向上的单位向量∴+的方向与∠BAC的角平分线一致又∵,∴=λ(+)∴向量的方向与∠BAC的角平分线一致∴一定通过△ABC的内心故选:B.8.(5分)如图,有一圆柱形无盖水杯,其轴截面ABCD是边长为2的正方形,P是BC的中点,现有一只蚂蚁位于外壁A处,内壁P处有一粒米,则这只蚂蚁取得米粒所经过的最短路程是()A.B.π+1C.D.【解答】解:侧面展开后得矩形ABCD,其中AB=π,AD=2问题转化为在CD 上找一点Q使AQ+PQ最短作P关于CD的对称点E,连接AE,令AE与CD交于点Q,则得AQ+PQ的最小值就是AE为.故选:D.9.(5分)已知{a n}中,,且{a n}是递增数列,则实数的取值范围是()A.(﹣2,+∞)B.[﹣2,+∞)C.(﹣3,+∞)D.[﹣3,+∞)【解答】解:∵{a n}是递增数列,∴∀n∈N*,a n+1>a n,∴(n+1)2+λ(n+1)>n2+λn,λ>﹣(2n+1),∴λ>﹣3.故选:C.10.(5分)椭圆C:+=1的左,右顶点分别为A1,A2,点P在C上,且直线P A2斜率的取值范围是[﹣2,﹣1],那么直线P A1斜率的取值范围是()A.[,]B.[,]C.[,1]D.[,1]【解答】解:由椭圆C:+=1可知其左顶点A1(﹣2,0),右顶点A2(2,0).设P(x0,y0)(x0≠±2),则得=﹣.∵=,=kP A 1=,∴=•==﹣.∵直线P A 2斜率的取值范围是[﹣2,﹣1], ∴直线P A 1斜率的取值范围是[,] 故选:A .11.(5分)如图,是某多面体的三视图,则该多面体的体积为( )A .B .C .D .【解答】解:根据几何体的三视图,得;该几何体为棱长是2的正方体,截去两个相同的三棱锥(底面直角三角形的直角边为2和2,高为1);,再截去一个三棱柱(底面直角三角形的直角边为2和2,高为2)而得到,其直观图如图所示,∴该多面体的体积为:2×2×2﹣2×﹣2×(2××)=.故选:B .12.(5分)设正实数x ,y ,z 满足x 2﹣3xy +4y 2﹣z =0,则当取得最小值时,x +2y ﹣z 的最大值为( )A.0B.C.2D.【解答】解:∵x2﹣3xy+4y2﹣z=0,∴z=x2﹣3xy+4y2,又x,y,z为正实数,∴=+﹣3≥2﹣3=1(当且仅当x=2y时取“=”),即x=2y(y>0),∴x+2y﹣z=2y+2y﹣(x2﹣3xy+4y2)=4y﹣2y2=﹣2(y﹣1)2+2≤2.∴x+2y﹣z的最大值为2.故选:C.二、填空题13.(5分)过平面区域内一点P作圆O:x2+y2=1的两条切线,切点分别为A,B,记∠APB=α,当α最小时,此时点P坐标为(﹣4,﹣2).【解答】解:如图阴影部分表示,确定的平面区域,当P离圆O最远时,α最小,此时点P坐标为:(﹣4,﹣2),故答案为::(﹣4,﹣2).14.(5分)已知过点M(﹣3,﹣3)的直线l被圆x2+y2+4y﹣21=0所截得的弦长为8,则直线l的方程为4x+3y+21=0或x=﹣3.【解答】解:圆x2+y2+4y﹣21=0的圆心为(0,﹣2),半径r==5,当直线l的斜率不存在时,直线方程为x=﹣3,联立,得或,∴直线l:x=﹣3被圆x2+y2+4y﹣21=0所截得的弦长为8,成立;当直线l的斜率存在时,设直线l:y=k(x+3)﹣3,圆心(0,﹣2)到直线y=k(x+3)﹣3的距离d==,∵过点M(﹣3,﹣3)的直线l被圆x2+y2+4y﹣21=0所截得的弦长为8,∴由勾股定理得:,即25=+16,解得k=﹣,∴直线l:,整理,得:4x+3y+21=0.综上直线l的方程为:4x+3y+21=0或x=﹣3.故答案为:4x+3y+21=0或x=﹣3.15.(5分)定义在[﹣2,2]上的偶函数f(x)在[﹣2,0]上为增,若满足f(1﹣m)<f(m),则m的取值范围是.【解答】解:因为f(x)是定义在[﹣2,2]上的偶函数,所以不等式f(1﹣m)<f(m)等价于:f(|1﹣m|)<f(|m|),因为f(x)在[﹣2,0]上为增函数,所以,解得﹣1≤m<,即m的取值范围是,故答案为:.16.(5分)设函数y=f(x)的图象与y=2x+a的图象关于y=﹣x+1对称,且f (﹣3)+f(﹣7)=1,则a的值为2.【解答】解:设函数y=f(x)的任意点的坐标为(x,y),关于y=﹣x+1对称点的坐标(m,n),则(m,n)在y=2x+a的图象上,,解得m=1﹣y,n=1﹣x,代入y=2x+a可得:1﹣x=21﹣y+a,即:y=log2(1﹣x)﹣a﹣1,函数y=f(x)=log2(1﹣x)﹣a﹣1,∵f(﹣3)+f(﹣7)=1,∴log24﹣a﹣1+log28﹣a﹣1=1,解得,a=2,故答案为:2.三.解答题17.(12分)在△ABC中,B=,AC=,求AB+BC的最大值并判断取得最大值时△ABC的形状.【解答】(本题满分为12分)解:∵B=,AC=,∴在△ABC中,根据==,得AB=•sin C=sin C=2sin C,∴同理BC=2sin A,∴AB+BC=2sin C+2sin A,…(4分)=2sin C+2sin(π﹣C)=,…(8分)当C=,可得AB+BC的最大值为,…(10分)取最大值时,因而△ABC是等边三角形.…(12分)18.(12分)在公差为d的等差数列{a n}中,已知a1=10,且a1,2a2+2,5a3成等比数列.(Ⅰ)求d,a n;(Ⅱ)若d<0,求|a1|+|a2|+|a3|+…+|a n|.【解答】解:(Ⅰ)由题意得,即,整理得d2﹣3d﹣4=0.解得d=﹣1或d=4.当d=﹣1时,a n=a1+(n﹣1)d=10﹣(n﹣1)=﹣n+11.当d=4时,a n=a1+(n﹣1)d=10+4(n﹣1)=4n+6.所以a n=﹣n+11或a n=4n+6;(Ⅱ)设数列{a n}的前n项和为S n,因为d<0,由(Ⅰ)得d=﹣1,a n=﹣n+11.则当n≤11时,.当n≥12时,|a1|+|a2|+|a3|+…+|a n|=﹣S n+2S11=.综上所述,|a1|+|a2|+|a3|+…+|a n|=.19.(12分)如图,在斜三棱柱ABC﹣A1B1C1中,A1B⊥AC,且A1B=AC=5,AA1=BC=13,且AB=12.(1)求证:平面ABB1A1⊥平面ACC1A1;(2)求二面角A﹣BB1﹣C的正切值的大小.【解答】证明:(1)在△ABC中,∵AB2+AC2=BC2,∴AC⊥AB,…(2分)又∵A1B⊥AC且A1B、AC是面ABB1A1内的两条相交直线,∴AC⊥平面ABB1A1,..…(4分)又AC⊂平面ACC1A1,∴平面ABB1A1⊥平面ACC1A1.…(5分)解:(2)在△ABC中,∵,∴A1B⊥AB,又∵A1B⊥AC且AB、AC是面ABC内的两条相交直线,∴A1B⊥面ABC,…(7分)∴以B为原点,BA为x轴,在平面ABC中过B作BA的垂线为y轴,BA1为z 轴,建立如图所示的空间直角坐标系,则B(0,0,0),A(12,0,0),C(12,5,0),A1(0,0,5),由,得B1(﹣12,0,5),…(8分)取平面ABB1A1的一个法向量=(0,1,0),设平面BCC1B1的一个法向量,由,得取x=5,则…(10分)∴cos<>==﹣,设A﹣BB1﹣C的大小为θ,则,.∴二面角A﹣BB1﹣C的正切值的大小为…(12分)20.(12分)已知点A(2,0),椭圆E:(a>b>0)的离心率为,F是椭圆E的上焦点,直线AF的斜率为,O为坐标原点.(1)求E的方程;(2)设过点A的动直线l与E相交于点P,Q两点,当△OPQ的面积最大时,求l的方程.【解答】解:(1)由e=,可得:,即,设F(0,c),则,,又a2﹣b2=c2=3,∴a2=4,b2=1,∴E的方程是;(2)设l的方程为x=my+2,设P(x1,y1),Q(x2,y2),由得(4m2+1)y2+16my+12=0,y1+y2=﹣,y1y2=,△=(16m)2﹣4×12×(4m2+1)=16(4m2﹣3)>0,=,令,则,而当且仅当t=2,≤1.即时等号成立,此时S△OPQ∴当△OPQ的面积最大时,求l的方程为,即.21.(12分)已知函数f(x)=xlnx+(2a﹣1)x﹣ax2﹣a+1,(1)若,求f(x)的单调区间;(2)若x∈[1,+∞)时恒有f(x)≤0,求a的取值范围.【解答】解:(1)函数f(x)=xlnx+(2a﹣1)x﹣ax2﹣a+1的导数为f′(x)=lnx﹣2a(x﹣1),当时,f′(x)=lnx﹣(x﹣1),令g(x)=lnx﹣(x﹣1),则.x∈(0,1)时g′(x)>0;x∈(1,+∞)时g′(x)<0.∴g(x)≤g(1)=0,即f′(x)≤0(只在x=1处取等号)∴f(x)的单减区间是(0,+∞);(2)f′(x)=lnx﹣2a(x﹣1),令f′(x)=0,则lnx=2a(x﹣1)且函数lnx在x=1处的切线为y=x﹣1,由(1)知,时,f(x)在[1,+∞)上单减且f(1)=0,∴f(x)≤0,合题意;当a>时,数形结合知,f(x)在[1,+∞)上仍单减且f(1)=0,∴f(x)≤0,合题意;当0<a<时,数形结合知,∃x0>1,使得f′(x0)=0.即x∈(1,x0)时f′(x)>0,f(x)在(1,x0)上单增,f(x)>f(1)=0,不合题意;当a≤0时,数形结合知,x∈(1,+∞)时,f′(x)>0,f(x)在(1,+∞)上单增,f(x)>f(1)=0,不合题意.综上,若x∈[1,+∞)时恒有f(x)≤0,则a的取值范围是.四.选做题,以下三题任选一题22.(10分)已知函数f(x)=sin(x﹣ϕ)cos(x﹣ϕ)﹣cos2(x﹣ϕ)+(0≤ϕ≤)为偶函数.(I)求函数的最小正周期及单调减区间;(II)把函数的图象向右平移个单位(纵坐标不变),得到函数g(x)的图象,求函数g(x)的对称中心.【解答】解:(I)函数f(x)=sin(x﹣ϕ)cos(x﹣ϕ)﹣cos2(x﹣ϕ)+=sin(2x﹣2φ)﹣(2cos2φ﹣1)=sin(2x﹣2φ)﹣cos(2x﹣2φ)=sin(2x﹣2φ)函数f(x)为偶函数,则﹣2φ=kπ,k∈z∵0≤ϕ≤∴φ=∴f(x)=sin(2x﹣π)=﹣sin2x∴函数的最小正周期T==π令2x∈[﹣+2kπ,+2kπ]k∈Z解得:﹣+kπ≤x≤+kπ∴函数f(x)的单调递减区间为[﹣+kπ,+kπ]k∈Z(II)由(I)知f(x)=﹣sin2x由题意知g(x)=﹣sin[2(x﹣)]=﹣sin(2x﹣)令2x﹣=kπ(k∈Z),则x=+(k∈Z),∴函数的对称中心坐标为(+,0)(k∈Z).23.已知p:|1﹣|<2;q:x2﹣2x+1﹣m2<0;若¬p是¬q的充分非必要条件,求实数m的取值范围.【解答】解:p:|1﹣|<2即为p:﹣2<x<10,q:x2﹣2x+1﹣m2<0即为(x﹣1)2<m2,即q:1﹣|m|<x<1+|m|,又¬p是¬q的充分非必要条件,所以q是p的充分非必要,∴(两式不能同时取等)得到|m|≤3,满足题意,所以m的范围为[﹣3,3].24.在直角坐标系xOy中,已知点A(1,1),B(2,3),C(3,2),点P(x,y)在△ABC三边围成的区域(含边界)上.(Ⅰ)若++=,求||;(Ⅱ)设=m+n(m,n∈R),用x,y表示m﹣n,并求m﹣n的最大值.【解答】解:(Ⅰ)∵A(1,1),B(2,3),C(3,2),++=,∴(1﹣x,1﹣y)+(2﹣x,3﹣y)+(3﹣x,2﹣y)=0∴3x﹣6=0,3y﹣6=0∴x=2,y=2,即=(2,2)∴(Ⅱ)∵A(1,1),B(2,3),C(3,2),∴,∵=m+n,∴(x,y)=(m+2n,2m+n)∴x=m+2n,y=2m+n∴m﹣n=y﹣x,令y﹣x=t,由图知,当直线y=x+t过点B(2,3)时,t取得最大值1,故m﹣n的最大值为1.。
2016年合肥市第一次模拟考试 理科数学汇编

2016年淮南市高三数学一模理科试题一、选择题1. 复数2+i1-2i 的虚部是 ( )A .1 B.-1 C .-i D .I 【答案】A【考查方向】本题主要考查了复数的运算与复数的相关概念,常考复数的运算、复数的相关概念(模、共轭复数、纯虚数、实部、虚部及其几何意义。
【易错点】本题易在复数运算上出错和虚部概念出错。
【解题思路】直接由复数运算求出()()()()ii i i +++52122,再找到其虚部为1; 【解析】由i i =-+2122.已知集合U ( ) 【答案】B【解题思路】1A A ∉3,,2{}4的子集个数。
【解析】由由全集A ,故A 可以为{}{}4,2,1,2,13.下面的程序框图(如图所示)能判断任意输入的数x 的奇偶性:A 【答案】 D 选项。
4. 函数f (x )=2sin(ωx +φ)⎝ ⎛⎭⎪⎫ω>0,-π2<φ<π2的部分图象如图所示,则ω,φ的值分别是 ( )A .2,-π3B .2,-π6C .4,-π6D .4,π3【答案】A【考查方向】本题主要考查了由三角函数的图象和性质求解析式,在近几年的各省高考题出现的频率较高,常与三角恒等变形公式,函数单调性、周期性、对称型、奇偶性等知识点交汇命题。
【易错点】1、本题易在对性质理解不到位没有办法求出w 的值 。
2、本题在求ϕ上应全最值点,也易忽略题目所给ϕ的范围。
【解题思路】1、由图可知ππππ=⇒=⎪⎭⎫ ⎝⎛--=T T 43312543,进出求出22==T w π; 2、把点⎪⎭⎫⎝⎛2,125π代入()x f 得Z k k ∈+=+⇒=⎪⎭⎫⎝⎛+,2265165sin ππϕπϕπ,即3,22,,23πϕπϕπππϕ-=⇒<<-∈+-=结合Z k k 。
故选A5. 经过抛物线y =14x 2的焦点和双曲线x 217-y28=1的右焦点的直线方程为( )A .x +48y -3=0B .x +80y -5=0C .x +3y -3=0D .x +5y -5=0【答案】D【考查方向】本题主要考查了圆锥曲线的一些基本概念(焦点)和求直线方程,圆锥曲线常考求方程、离心率的值或范围、中点弦,切线方程、面积计算和函数的最值问题 【易错点】本题易在抛物线方程是否标准上求焦点出错; 【解题思路】1、把抛物线方程化成标准型,再求出其焦点;2、再求出双曲线的右焦点,进而求出直线方程;【解析】把抛物线方程化成标准型为:y x 42=,故其焦点为()1,0P ,而双曲线的焦点为()0,5Q ,故所求直线方程为x +5y -5=0;故选D6.设3log 2a =,5log 2b =,2log 3c =,则( ) A.a c b >> B.b c a >> C. c a b >> D. c b a >> 【答案】C【考查方向】本题主要考查了函数值大小的比较,常见比较大小的方法有作差法、作商法、单调性法、中间值法、图象法等;【易错点】本题易在思路的寻找上迷失。
安徽省淮南市高考数学一诊试卷(理科)

安徽省淮南市高考数学一诊试卷(理科)姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)(2020·大庆模拟) 已知集合,,则下列结论正确的是()A .B .C .D .2. (2分)(2020·漯河模拟) 若复数z满足,则()A .B .C .D .3. (2分)用随机数表法进行抽样有以下几个步骤:①将总体中的个体编号;②获取样本号码;③选定开始的数字,这些步骤的先后顺序应为A . ①②③B . ③②①C . ①③②D . ③①②4. (2分)已知两个不同的平面α,和两条不重合的直线m,n,则下列四种说法正确的为()A . 若m∥n,nα,则m∥αB . 若m⊥n,m⊥α,则n∥αC . 若mα,n,α∥,则m,n为异面直线D . 若α⊥,m⊥α,n⊥,则m⊥n5. (2分) (2019高二上·集宁月考) 已知等差数列的前项和为,且,数列满足,则数列的前9项和为()A . 20B . 80C . 166D . 1806. (2分)(2020·梅河口模拟) 如图,某几何体的三视图是由三个边长为2的正方形和其内部的一些虚线构成的,则该几何体的体积为()A .B .C . 6D . 与点O的位置有关7. (2分)(2018·孝义模拟) 已知点是直线上的动点,由点向圆引切线,切点分别为,,且,若满足以上条件的点有且只有一个,则()A .B .C .D .8. (2分) (2016高二下·黔南期末) 按照如图的程序运行,已知输入x的值为2+log23,则输出y的值为()A . 7B . 11C . 12D . 249. (2分)设实数x,y满足:,则z=x﹣3y的最大值为()A . ﹣2B . ﹣8C . 4D . 210. (2分) (2019高一上·昌吉月考) 将函数的图象向右平移个周期后,所得图象对应的函数为()A .B .C .D .11. (2分)(2017·泸州模拟) 过抛物线C:y2=2px(p>0)焦点F的直线l与C相交于A,B两点,与C的准线交于点D,若|AB|=|BD|,则直线l的斜率k=()A .B . ±3C .D .12. (2分)(2018高一上·台州期末) 已知函数是定义在上的单调函数,且,则的值为()A .B .C .D . 4二、填空题 (共4题;共4分)13. (1分) (2016高三上·长春期中) 如图,边长为1的菱形ABCD,∠ABC=60°,E为AB中点,F为AD中点,则 =________.14. (1分)(2018·上海) 在(1+x)7的二项展开式中,x²项的系数为________。
安徽省示范高中高三数学第一次联考试题 理(扫描版)

安徽省示范高中2016届高三数学第一次联考试题理(扫描版)2016届安徽省示范高中高三第一次联考理数参考答案一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.C 【解析】因为错误!未找到引用源。
,错误!未找到引用源。
,所以错误!未找到引用源。
.2.A 【解析】错误!未找到引用源。
,因为复数在第一象限,所以错误!未找到引用源。
,解得错误!未找到引用源。
,故选A.3.B 【解析】全称命题的否定,要把量词任意改为存在,且否定结论,故非错误!未找到引用源。
为:存在错误!未找到引用源。
,错误!未找到引用源。
.4. C 【解析】根据题意,三角形F1F2P是以F1F2为斜边的直角三角形,设|F2P|=m,|F1P|=2m,则由双曲线定义可得m=2a,所以错误!未找到引用源。
,即错误!未找到引用源。
,则错误!未找到引用源。
,故一条渐近线方程是错误!未找到引用源。
.5.D 【解析】由题意知错误!未找到引用源。
,所以错误!未找到引用源。
,故选D.6.A 【解析】二项式错误!未找到引用源。
的通项公式为错误!未找到引用源。
,其中错误!未找到引用源。
,所以错误!未找到引用源。
,解得错误!未找到引用源。
.7.B【解析】可行域为错误!未找到引用源。
及其内部,三个顶点分别为错误!未找到引用源。
,当错误!未找到引用源。
过点错误!未找到引用源。
时取得最小值,此时错误!未找到引用源。
.8. C 【解析】由三视图的俯视图、正视图和侧视图可还原的空间几何体一个四棱锥M-ABCD,如图所示,由勾股定理计算CD=5,即知底面是边长为5的正方形ABCD,补形为三棱柱,则所求的几何体的体积:错误!未找到引用源。
×3×4×5-错误!未找到引用源。
=20.9.C 【解析】由流程图可知,错误!未找到引用源。
,只要错误!未找到引用源。
,就再一次进入循环体循环,直到首次出现错误!未找到引用源。
2016届高三上学期第一次联考数学(理)试题 Word版含答案

2016届高三第一次联考数学试题(理科)第I 卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的. 1.已知集合22{230},{log (1)2}A x x x B x x =--≥=-<,则()..R A B = A .()1,3 B .()1,3- C .()3,5 D . ()1,5- 2.命题“若220x y +=,则0x y ==”的否命题为A .若220x y +=,则0x ≠且0y ≠ B .若220x y +=,则0x ≠或0y ≠ C .若220x y +≠,则0x ≠且0y ≠ D .若220x y +≠,则0x ≠或0y ≠3.欧拉公式cos sin ixe x i x =+(i 为虚数单位)是由瑞士著名数学家欧拉发明的,它将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,它在复变函数论里占有非常重要的地位,被誉为“数学中的天桥”,根据欧拉公式可知,2ie 表示的复数在复平面中位于 A .第一象限 B .第二象限 C .第三象限 D .第四象限4.函数222,1,()log (1),1,x x f x x x ⎧-≤=⎨->⎩则52f f ⎡⎤⎛⎫= ⎪⎢⎥⎝⎭⎣⎦A .12-B .1-C .5-D .125.等差数列{}n a 前n 项和为n S ,且20162015120162015S S=+,则数列{}n a 的公差为A .1B .2C .2015D .20166.若ln 2,5a b == 01,s i n 4c x d x π=⎰,则,,a b c 的大小关系 A .a b c << B .b a c << C .c b a << D .b c a <<7.已知1sin cos 63παα⎛⎫--= ⎪⎝⎭,则cos 23πα⎛⎫+= ⎪⎝⎭A .518B .-518C .79D .-798.已知某几何体的三视图的侧视图是一个正三角形,如图所示,则该几何体的 体积等于A .B .C .D .9.已知函数()()()21sin ,02f x x ωω=->的周期为π,若将其图象沿x 轴向右平移a 个单位()0a >,所得图象关于原点对称,则实数a 的最小值为A .πB .34π C .2π D .4π 10.如图所示,在正六边形ABCDEF 中,点P 是△CDE 内(包括边界)的一个动点,设(),AP AF AB R λμλμ=+∈,则λμ+的取值范围是A .3,42⎡⎤⎢⎥⎣⎦ B .[]3,4 C .35,22⎡⎤⎢⎥⎣⎦ D .3,24⎡⎤⎢⎥⎣⎦11.若一个四棱锥底面为正方形,顶点在底面的射影为正方形的中心,且该四棱锥的体积为9,当其外接球表面积最小时,它的高为A .3B .C .D . 12.关于函数()2ln f x x x=+,下列说法错误的是 A .2x =是()f x 的极小值点B .函数()y f x x =-有且只有1个零点C .存在正实数k ,使得()f x kx >恒成立D .对任意两个正实数12,x x ,且21x x >,若()()12f x f x =,则124x x +>第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4个小题,每小题5分,共20分.13.已知平面直角坐标系中,b ()3,4=,a b ⋅3=-,则向量a 在向量b 的方向上的投影是________. 14.若函数()1,021,20x x f x x -<≤⎧=⎨--≤≤⎩,()()[],2,2g x f x ax x =+∈-为偶函数,则实数a =_________.15.设实数x ,y 满足约束条件202x y y x -≥⎧⎪⎨≥-⎪⎩,则2z x y =+的最大值为________.16.如图所示,已知ABC ∆中,90C ∠= ,6,8AC BC ==,D 为边AC 上 的一点,K 为BD 上的一点,且ABC KAD AKD ∠=∠=∠,则DC =________.第16题图第10题图-12三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)在等比数列{}n a 中,3339,S 22a ==. (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)设2216log n nb a +=,且{}n b 为递增数列,若11n n n c b b +=⋅,求证:12314n c c c c ++++< .18.(本小题满分12分)如图,ABC ∆中,三个内角B 、A 、C 成等差数列,且10,15AC BC ==. (Ⅰ)求ABC ∆的面积; (Ⅱ)已知平面直角坐标系xOy,点()10,0D ,若函数()s i n ()(0,0,)2f x M x M π=ω+ϕ>ω>ϕ<的图象经过A 、C 、D 三点,且A 、D 为()f x 的图象与x 轴相邻的两个交点,求()f x 的解析式.19. (本小题满分12分)如图,已知长方形ABCD中,AB =AD =M 为DC 的中点.将ADM ∆沿AM 折起,使得平面ADM ⊥平面ABCM .(Ⅰ)求证:AD BM ⊥;(Ⅱ)若点E 是线段DB 上的一动点,问点E 在何位置时,二面角E AM D --.20. (本小题满分12分)小明同学制作了一个简易的网球发射器,可用于帮忙练习定点接发球,如图1所示,网球场前半区、后半区总长为23.77米,球网的中间部分高度为0.914米,发射器固定安装在后半区离球网底部8米处中轴线上,发射方向与球网底部所在直线垂直.为计算方便,球场长度和球网中间高度分别按24米和1米计算,发射器和网球大小均忽略不计.如图2所示,以发射器所在位置为坐标原点建立平面直角坐标系xOy ,x 轴在地平面上的球场中轴线上,y 轴垂直于地平面,单位长度为1米.已知若不考虑球网的影响,网球发射后的轨迹在方程2211(1)(0)280y kx k x k =-+>表示的曲线上,其中k 与发射方向有关.发射器的射程是指网球落地点的横坐标.(Ⅰ)求发射器的最大射程;(Ⅱ)请计算k 在什么范围内,发射器能将球发过网(即网球飞行到球网正上空时,网球离地距离大于1米)?若发射器将网球发过球网后,在网球着地前,小明要想在前半区中轴线的正上空选择一个离地面2.55米处的击球点正好击中网球,试问击球点的横坐标a 最大为多少?并请说明理由.21. (本小题满分12分)已知函数()e ,xf x x R =∈.(Ⅰ)若直线y kx =与()f x 的反函数的图象相切,求实数k 的值;(Ⅱ)设,a b R ∈,且()()()(),,,,22f a f b f a f b a b a b A f B C a b +-+⎛⎫≠===⎪-⎝⎭试比较,,A B C 三者的大小,并说明理由.第19题图第20题图图1图2第18题图第22题图请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分.答时用2B 铅笔在答题卡上把所选题目的题号涂黑.22.(本小题满分10分)选修4-1几何证明选讲如图,BC 是圆O 的直径,点F 在弧BC 上,点A 为弧BF 的中点,作AD BC ⊥于点D ,BF 与AD 交于点E ,BF 与AC 交于点G .(Ⅰ)证明:AE BE =; (Ⅱ)若9,7AG GC ==,求圆O 的半径.23.(本小题满分10分)选修4-4极坐标与参数方程已知曲线C 的极坐标方程为2sin cos 10ρθρθ+=,将曲线1cos :sin x C y αα=⎧⎨=⎩(α为参数)经过伸缩变换32x xy y'=⎧⎨'=⎩后得到曲线2C .(Ⅰ)求曲线2C 的参数方程; (Ⅱ)若点M 在曲线2C 上运动,试求出M 到曲线C 的距离的最小值.24.(本小题满分10分)选修4-5不等式证明选讲已知函数()1020f x x x =-+-,且满足()1010f x a <+(a R ∈)的解集不是空集.(Ⅰ)求实数a 的取值集合A ; (Ⅱ)若,,b A a b ∈≠求证:abbaa b a b >.数学试题(理科)参考答案一、选择题 ADBAB DCCDB AC二、填空题 35- 12- 10 73三、解答题17. (1)1q =时,32n a =; ………………2分1q ≠时,116()2n n a -=⋅- ………………4分(2)由题意知:116()2n n a -=⋅- ………………6分∴2116()4n n a +=⋅∴2n b n = ………………8分 ∴111111()2(2n 2)4(n 1)41n c n n n n ===-⋅+⋅++ ………………10分∴123111(1)414n c c c c n ++++=-<+ ………………12分 18. (1)在△ABC 中,60B = ………………1分 由余弦定理可知:2222c o s 60a b c b c =+- ………………2分∴2101250c c --=5c A B ∴== ………………4分 又∵10cos605AO =⋅=BO ∴=125(5633)22ABC S ∴=+⨯= . ………………6分(2)T=2×(10+5)=30,∴15πω= ………………8分∵(5)Msin((5))015f π-=⋅-+ϕ=s i n ()03π∴-+ϕ=,,3k k Z π∴-+ϕ=π∈2πϕ< ,3π∴ϕ=。
安徽省示范高中2016届高三第一次联考数学(理)试题(扫描版)(附答案)

2016届安徽省示范高中高三第一次联考理数参考答案一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.C 【解析】因为2{|0}{|01}A x x x x x x =+≥=≥≤-或,{|55}{|1}x B x x x =≥=≥,所以{|1}A B x x ⋂=≥.2.A 【解析】1(1)(1)(1)(1)1(1)(1)2ai ai i a a i z i i i +++-++===--+,因为复数在第一象限,所以 1010a a ->⎧⎨+>⎩,解得11a -<<,故选A. 3.B 【解析】全称命题的否定,要把量词任意改为存在,且否定结论,故非p 为:存在0x >,34log log x x ≤.4. C 【解析】 根据题意,三角形F 1F 2P 是以F 1F 2为斜边的直角三角形,设|F 2P|=m ,|F 1P|=2m ,则由双曲线定义可得m=2a ,所以222(2)(4)(2)a a c +=,即225a c =,则2b a ===,故一条渐近线方程是2b y x x a ==. 5.D 【解析】由题意知2tan log 164θ==,所以2sin 22sin 2tan 8cos cos θθθθθ===,故选D. 6.A 【解析】二项式5()a x -的通项公式为515()r r r r T C a x -+=-,其中2323235()10T C a x a x =-=,所以3210270a a ==,解得3a =.7.B 【解析】可行域为ABC ∆及其内部,三个顶点分别为(0,4)(0,1)(2,0)A B C 、、,当y x z -=过点A 时取得最小值,此时min 044z =-=-.8. C 【解析】由三视图的俯视图、正视图和侧视图可还原的空间几何体一个四棱锥M-ABCD ,如图所示,由勾股定理计算CD=5,即知底面是边长为5的正方形ABCD ,补形为三棱柱,则所求的几何体的体积: 12×3×4×5-1134532⨯⨯⨯⨯=20. 9.C 【解析】由流程图可知,57923S n =+++++ ,只要480S <,就再一次进入循环体循环,直到首次出现2011S ≥,才跳出循环体,输出x ,程序结束.由2579234480S n n n =+++++=+≥ 得20n ≥,所以220343x =⨯+=.10.D 【解析】如图,4,2AB AD CD ===,所以AC BC ==AC BC ⊥.取AC 的中点为E ,AB 的中点为O ,连接DE,OE,OC ,因为三棱锥D ABC -体积最大,所以平面DCA ⊥平面ABC ,此时容易计算出OD=2,即OD=OB=OA=OC=2,故O 是外接球的球心,OA 是球的半径,于是三棱锥D ABC -外接球的表面积是24216ππ⨯=.11.B 【解析】()2015sin 2016cos )f x x x x ϕ=-=-,其中2016tan 2015ϕ=,且02πϕ<<,因为()f x 一个对称中心为(,0)a ,所以()sin 0a ϕ-=,∴ ()a k k Z ϕπ-=∈,即()a k k Z πϕ=+∈.由2016tan 2015ϕ=,可知1tan ϕ<02πϕ<<,所以43ππϕ<<,于是可得 ()43k a k k Z ππππ+<<+∈,故当0k =时,43a ππ<<,选B.12.C 【解析】因为()f x 是R 上的奇函数,所以22()()()g x x f x x f x -=-=-,所以2()()g x x f x =是奇函数.由对任意正实数x 满足()2()xf x f x '>-,可得()2()xf x f x '>-,即2()2()x f x xf x '>-,即2()2()0x f x xf x '+>,即()0g x '>,所以2()()g x x f x =在(0,)+∞上是增函数,而(0)0g =,故2()()g x x f x =在R 上是增函数,于是由()(13)g x g x <-得13x x <-,即14x <. 二、填空题:本大题共4小题,每小题5分.13. 5 【解析】因为2(4,3)-a +b =,所以(2)5+⋅=a b a .14. 4230x y --= 【解析】易知点1(1,)2P 在此圆的内部,当且仅当直线AB PC ⊥时,ACB ∠最小,此时1AB PC k k =-,而1112012PC k -==--,则2AB k =,故直线l 的方程为4230x y --=. 15. 15 【解析】若甲同学分配到A 工厂,则其余3人应安排到B ,C 两个工厂,一共有2232C A 种分配方案.若甲同学分配到B 工厂,则又分为两类:一是其余3人安排到A ,C 两个工厂,而A 工厂只能安排1名同学,所以一共有13C 种分配方案;二是从其余3人中选出1人安排到B 工厂,其余2人安排到A,C 工厂,所以一共有1232C A 种分配方案.综上,共有221123233215C A C C A ++=种不同的分配方案.16.【解析】以AB 为x 轴,线段AB 的垂直平分线为y 轴建立平面直角坐标系.设C(x,y),则A(-1,0),B(1,0),由题意得2222(1)(1)10x y x y +++-+=,即224x y +=,故点C 的轨迹为圆(除去与x 轴的两个交点),易知1||22ABC C S AB y ∆=⋅≤.此时最大的边长为AC BC ==三、解答题:解答应写出文字说明,证明过程或演算步骤.17.解:(Ⅰ)由于1{}n a 为等差数列,若设其公差为d ,则32711118,4a a a ==⋅, 1128d a +=,11111(6)4d d a a +=+,解得112,3d a ==, ………3分 于是123(1)nn a =+-,整理得131n a n =-; ………5分 (Ⅱ)由(1)得11111()(31)(32)33132n n n b a a n n n n +===--+-+, ………7分 所以1111111()3255831322(32)n n S n n n =-+-++-=-++ . ………10分 18.【解析】(Ⅰ)()sin )(cos sin )2sin cos 222222x x x x x x f x =-++22sin )sin 22x x x =-+sin x x =+)cos 23sin 21(2x x +=)3sin(2π+=x . …………4分 所以)(x f 的最小正周期为π2. ……………6分(Ⅱ) 将)(x f 的图象向右平移6π个单位,得到函数)(x g 的图象, ∴⎥⎦⎤⎢⎣⎡+-=-=3)6(sin 2)6()(πππx x f x g )6sin(2π+=x , ………8分 由22()262k x k k Z πππππ-≤+≤+∈,可得222()33k x k k Z ππππ-≤≤+∈, 所以单调递增区间为2[2,2]()33k k k Z ππππ-+∈. ………12分 19.(Ⅰ)证明:∵PA ⊥平面ABC ,∴PA BC ⊥又AC BC ⊥,∴BC ⊥平面PAC ;又∵//BC DE ,∴DE ⊥面PAC . ………5分(Ⅱ)解:因为//MN DE ,结合(Ⅰ)中结论,∴MN ⊥平面PAC ,∴,MN FM MN DM ⊥⊥,∴FMD ∠即为二面角F MN D --的平面角. ………7分由条件可得: 1260,30,,23APC ACP FM CD ︒︒∠=∠===,∴DM FD ====,………9分 ∴在FMD ∆中,1731cos FMD +-∠== .………12分 20.解:依题意,这4个人中,每个人去淘宝网购物的概率为13,去京东商城购物的概率为23.设“这4个人中恰有i 人去淘宝网购物”为事件(0,1,2,3,i A i =,则4412()()()(0,1,2,3,4)33i i i i P A C i -==. (Ⅰ)这4个人中恰有1人去淘宝网购物的概率 113141232()()()3381P A C ==.………5分 (II )易知X 的所有可能取值为0,3,4.(第19题) A D P BC F E M N0044400444121216117(0)()()()()()()3333818181P X P A P A C C ==+=+=+=, 1133311344121232840(3)()()()()()()3333818181P X P A P A C C ==+=+=+=, 222241224(4)()()()3381P X P A C ====. ………8分 所以X 的分布列是随机变量ξ的数学期望0348181813EX =⨯+⨯+⨯=. ………12分21. (Ⅰ)解:设椭圆C 的方程为22221(0)x y a b a b+=>>,则12c a =,又抛物线214x y =的焦点为(1,0),所以1c =,所以234,3a b ==,所以椭圆C 的方程为22143x y +=. ……………5分 (Ⅱ)证明:设直线AB 的方程为:1122111,(,),(,),(,)x ty A x y B x y A x y '=+-,直线A B '与x 轴的交点为0(,0)M x .,,A B M ' 三点共线,12112101210121,1()y y y y y y x x x x x t y t y y ++∴=∴=-----,化简整理可得1201221ty y x y y =++ …………① ……………8分联立221431x y x ty ⎧+=⎪⎨⎪=+⎩,消去x 得:22121226(43)690,,43t t y ty y y y y t -++-=∴+=⋅=+ 2943t -+ …………②……………10分将②代入①得:20292431314643tt x tt -+=+=+=-+,即直线A B '过x 轴的另一个定点(4,0)M .证毕.……………12分22.解:(Ι)当1a =时,()(5)cos sin (0)f x x x x x π=--≤≤,则()cos (5)sin cos (5)sin 0f x x x x x x x '=---=-≥,所以()f x 在[0,]π上单调递增,又(0)50,()50f f ππ=-<=->,所以()f x 在[0,]π上只有1个的零点.………………4分(Ⅱ)()cos (5)sin cos (5)sin f x a x ax x a x ax x '=---=-(0)x π≤≤,令()0f x '=,取其中的50,,x a π=. ………………5分 (1)若5a π≥,即50a π<≤,则()f x 在(0,)π上恒有()0f x '>,于是()f x 在 [0,]π上单调递增,则此时最大值为()()(0)10g a f f a ππ=-=-. ………………6分(2)50a π<<,即5a π>,则当50x a <<时,()0f x '>,当5x a π<<时,()0f x '<, 所以()f x 在5[0,]a 上单调递增,在5[,]a π上单调递减. 又因为(0)50,()50f f a ππ=-<=->,所以(0)()10f f a ππ-=-+ .…………8分 ① 若(0)()100f f a ππ-=-+<,即510a ππ<≤,则此时的最大值为55()()(0)sin 5g a f f a a a=-=-+; ②若(0)()100f f a ππ-=-+>,即10a π>,则此时的最大值为55()()()sin 5g a f f a a a a ππ=-=--+.综上所述,()g a 的表达式为510(0)5510()sin 5()510sin 5()a x g a a a a a a a a ππππππ⎧-<≤⎪⎪⎪=-+<≤⎨⎪⎪--+>⎪⎩ . ………………12分。
2016届安徽省示范高中高三第一次大联考数学理科

与很多的竞技项目不一样,高尔夫与其说是一场与他人的抗衡,更像是一次自己与自己的较量,它需要足够的耐心和专注,锻炼一个人独立思虑的能力,培育一个人踊跃进步的心态。
有人形容高尔夫的18 洞就仿佛人生,阻碍重重,崎岖不停。
但是一旦踏上了球场,你就一定集中注意力,独立面对照赛中可能出现的各样困难,而且肩负全部结果。
或许,经常还会碰到这样的状况:你刚才还在为抓到一个小鸟球而喝彩雀跃,下一刻狂风就把小白球吹跑了;或许你才在上一个洞吞了柏忌,下一个洞你就为抓了老鹰而喜悦不已。
这说明,在高尔夫球场上,短暂的当先其实不代表最后的成功;而一时的落伍也不意味着通盘失败。
困难,而且肩负全部结果。
或许,经常还会碰到这样的状况:你刚才还在为抓到一个小鸟球而喝彩雀跃,下一刻狂风就把小白球吹跑了;或许你才在上一个洞吞了柏忌,下一个洞你就为抓了老鹰而喜悦不已。
这说明,在高尔夫球场上,短暂的当先其实不代表最后的成功;而一时的落伍也不意味着通盘失败。
只有依靠毅力,坚持究竟,才有可能成为最后的赢家。
这些磨炼与考验使成长中的青少年得益匪浅。
在各种困难,而且肩负全部结果。
或许,经常还会碰到这样的状况:你刚才还在为抓到一个小鸟球而喝彩雀跃,下一刻狂风就把小白球吹跑了;或许你才在上一个洞吞了柏忌,下一个洞你就为抓了老鹰而喜悦不已。
这说明,在高尔夫球场上,短暂的当先其实不代表最后的成功;而一时的落伍也不意味着通盘失败。
只有依靠毅力,坚持究竟,才有可能成为最后的赢家。
这些磨炼与考验使成长中的青少年得益匪浅。
在各种困难,而且肩负全部结果。
或许,经常还会碰到这样的状况:你刚才还在为抓到一个小鸟球而喝彩雀跃,下一刻狂风就把小白球吹跑了;或许你才在上一个洞吞了柏忌,下一个洞你就为抓了老鹰而喜悦不已。
这说明,在高尔夫球场上,短暂的当先其实不代表最后的成功;而一时的落伍也不意味着通盘失败。
只有依靠毅力,坚持究竟,才有可能成为最后的赢家。
这些磨炼与考验使成长中的青少年得益匪浅。
安徽省淮南市2016届高三第一次模拟理科综合试卷.pdf

。
III.为摆脱对石油的过度依赖,科研人员将煤液化制备汽油,并设计了汽油燃料电池,电池工作原理如右图所示
:一个电极通入氧气,另一电极通入汽油蒸气,电解质是掺杂了Y2O3的ZrO2晶体,它在高温下能传导O2—。
(5)以己烷(C6H14)代表汽油,写出该电池工作时的负极反应方程式
。
(6)已知一个电子的电量是1.602×10—19C,用该电池电解饱和食盐水,当电路中通过1.929×104C的电量时,生
g·cm-3(不
需要化简)。
31、(15分)
姜黄素是从姜科植物中提取的一种色素,它的主要药理作用有抗氧化、保肝护肝、抑制肿瘤生长等,它具有对称性
结构。
已知:①E、G能发生银镜反应
②R-CHO+R’-CH2-CHO +H2O(R、R’表示烃基或氢)
请根据以上信息回答下列问题:
(1)A的名称是
成标况下氢气的体积为
L。
(化学选做题:请考生在第30、31题中任选一题作答,如果多做,则按所做的第一题给分)
30、(15分)
碳、氮、氟、硅、铜等元素的化合物广泛存在于自然界,回答下列问题:
(1)氮气分子中σ键和π键的比值为
;基态铜原子的电子排布式为
。
(2)C、N、F三种元素第一电离能由大到小的顺序为
;试剂X的名称
。
(2)F到G的反应类型
;Y分子中的官能团名称
。
(3)E→F的化学反应方程式
。
(4)J(C8H8O3)的同分异构体中同时满足如下条件:①能与NaHCO3反应,②能使FeCl3溶液显色,共有
(不考虑立体异构体)种,其中苯环上的一氯代物有两种的同分异构体的结构简式
。
(5)参考上述合成路线,设计一条由 和乙醛为起始原料(其他无机试剂可任选),制备的合成路线,合成路线
安徽省淮南市高考数学一模试卷(理科)

安徽省淮南市高考数学一模试卷(理科)姓名:________班级:________成绩:________一、 选择题: (共 12 题;共 24 分)1. (2 分) 已知全集 U={1,2,3,4,5,6,7},集合 A={2,4,6},集合 B={1,3,5,7},则等于( )A . {2,4,6}B . {1,3,5}C . {2,4,5}D . {2,5}2. (2 分) (2020·河南模拟) 已知复数 满足 A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限,则复平面内与复数 对应的点在( )3. (2 分) (2019·深圳模拟) 设 为等差数列 的前 项和.若,公差为( )A . -2B . -1C.1D.24. (2 分) 下列判断,正确的是( )A . 平行于同一平面的两直线平行第 1 页 共 14 页,则 的B . 垂直于同一直线的两直线平行 C . 垂直于同一平面的两平面平行 D . 垂直于同一平面的两直线平行5. (2 分) 已知正四棱锥的各棱棱长都为 , 则正四棱锥的外接球的表面积为( ) A. B. C. D.6. (2 分) (2019 高一上·玉溪期中) 已知 可能是( ),则函数与函数的图象A. B.C.第 2 页 共 14 页D.7. (2 分) 如右图所示的算法流程图中(注:“A=1”也可写成“A:=1”或“ 第 3 个输出的数”, 均表示赋值语句),是 A.1B. C.2D. 8. (2 分) 某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了 5 次试验,收集数据如 下: 加工零件 x(个) 10 20 30 40 50 加工时间 y(分钟) 64 69 75 82 90 经检验,这组样本数据具有线性相关关系,那么对于加工零件的个数 x 与加工时间 y 这两个变量,下列判断正 确的是( ) A . 成正相关,其回归直线经过点(30,75) B . 成正相关,其回归直线经过点(30,76) C . 成负相关,其回归直线经过点(30,76)第 3 页 共 14 页D . 成负相关,其回归直线经过点(30,75)9. (2 分) (2017·四川模拟) 函数 f(x)=sinωx(ω>0),对任意实数 x 有,那么=( )A.aB.C. D . ﹣a10. (2 分) (2018 高一下·伊通期末) 已知定义在 上的偶函数在,则不等式成立的概率是( ),且 上单调递增,若A. B. C. D.11. (2 分) 已知双曲线 C1: ﹣ =1(a>0,b>0)的离心率为 2,若抛物线 C2:y2=2px(p>0)的焦点 到双曲线 C1 的渐近线的距离是 2,则抛物线 C2 的方程是( )A . =8xB. = xC. = x D . =16x12. (2 分) 设,,, 则( )第 4 页 共 14 页A. B. C. D.二、 填空题: (共 4 题;共 5 分)13. (1 分) (2016 高一下·南市期末) 关于平面向量 , , ,有下列三个命题: ①若 • = • ,则 = ; ②若| • |=| |•| |,则 ∥ ;③ =(﹣1,1)在 =(3,4)方向上的投影为 ; ④非零向量 和 满足| |=| |=| ﹣ |,则 与 + 的夹角为 60°. 其中真命题的序号为________(写出所有真命题的序号)14. (1 分) 在的展开式中, 项的系数为________.(结果用数值表示)15. (2 分) (2018 高二上·嘉兴月考) 数列 满足,,其前 项和为 ,则(1) (2)________; ________.16. (1 分) 设变量 x,y 满足约束条件三、 解答题: (共 7 题;共 65 分), 则目标函数 z= 的最小值为________17. (10 分) (2016 高二上·开鲁期中) 已知顶点在单位圆上的△ABC 中,角 A、B、C 所对的边分别为 a、b、 c,且 b2+c2=a2+bc.(1) 求角 A 的大小;(2) 若 b2+c2=4,求△ABC 的面积.第 5 页 共 14 页18. (10 分) (2015 高二上·安庆期末) 如图,平面 ABEF⊥平面 ABC,四边形 ABEF 为矩形,AC=BC.O 为 AB 的中点,OF⊥EC.(1) 求证:OE⊥FC:(2) 若时,求二面角 F﹣CE﹣B 的余弦值.19. (10 分) (2016·襄阳模拟) 在汶川大地震后对唐家山堰塞湖的抢险过程中,武警官兵准备用射击的方法 引爆从湖坝上游漂流而下的一个巨大的汽油罐.已知只有 5 发子弹,第一次命中只能使汽油流出,第二次命中才能引爆.每次射击是相互独立的,且命中的概率都是 .(1) 求油罐被引爆的概率;(2) 如果引爆或子弹打光则停止射击,设射击次数为 ξ.求 ξ 的分布列及数学期望 E(ξ).( 结果用分数 表示)20. (10 分) (2018·全国Ⅲ卷文) 已知斜率为 的中点为的直线 与椭圆交于两点,线段(1) 证明:(2) 设 为 的右焦点, 为 上一点,且,证明:21. (10 分) (2018 高三上·定远期中) 已知函数 f(x)=ax3-3ax,g(x)=bx2+clnx,且 g(x)在点(1,g(1)) 处的切线方程为 2y-1=0.(1) 求 g(x)的解析式;(2) 设函数 G(x)=若方程 G(x)=a2 有且仅有四个解,求实数 a 的取值范围.第 6 页 共 14 页22. (10 分) (2017·孝义模拟) 已知在直角坐标系 xOy 中,以 O 为极点,x 轴正半轴为极轴建立极坐标系,曲线 C1 的参数方程为:,曲线 C2 的极坐标方程为:ρ2(1+sin2θ)=8,(1) 写出 C1 和 C2 的普通方程;(2) 若 C1 与 C2 交于两点 A,B,求|AB|的值.23. (5 分) 有一块铁皮零件,其形状是由边长为 30cm 的正方形截去一个三角形 ABF 所得的五边形 ABCDE, 其中 AF=8cm,BF=6cm,如图所示.现在需要用这块材料截取矩形铁皮 DMPN,使得矩形相邻两边分别落在 CD,DE 上, 另一顶点 P 落在边 CB 或 BA 边上.设 DM=xcm,矩形 DMPN 的面积为 ycm2 .(1)试求出矩形铁皮 DMPN 的面积 y 关于 x 的函数解析式,并写出定义域;(2)试问如何截取(即 x 取何值时),可使得到的矩形 DMPN 的面积最大?第 7 页 共 14 页一、 选择题: (共 12 题;共 24 分)1-1、 2-1、 3-1、 4-1、 5-1、 6-1、 7-1、 8-1、 9-1、 10-1、 11-1、 12-1、二、 填空题: (共 4 题;共 5 分)13-1、 14-1、 15-1、参考答案第 8 页 共 14 页15-2、 16-1、三、 解答题: (共 7 题;共 65 分)17-1、17-2、18-1、第 9 页 共 14 页18-2、 19-1、第 10 页 共 14 页19-2、20-1、20-2、21-1、21-2、22-1、22-2、23-1、。
安徽省淮南市2016届高三第一次模拟数学(理)试题 含答案
2016年淮南市高三数学一模理科试题一、选择题1。
复数错误!的虚部是 ( )A .1 B.-1 C .-i D .i2.已知集合{}1,2,3,4U =,{}1,2,3B =,且{}1,2A B ⋂=,则满足条件的A 的个数为( ) A 。
1 B.2 C 。
3 D 。
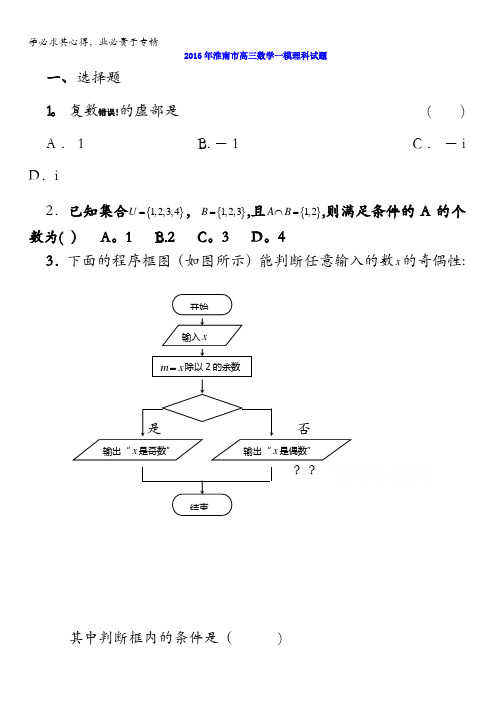
43.下面的程序框图(如图所示)能判断任意输入的数x 的奇偶性:是 否??其中判断框内的条件是( )输入xx m =除以2的余数输出“x 是奇数”开始 输出“x 是偶数”结束(),ABAC OP OA ABACλ→→→→→→=++A .0=mB 。
0=x C. 1=x D 。
1=m4. 函数f (x )=2sin (ωx +φ)错误!的部分图象如图所示,则ω,φ的值分别是( )A .2,-错误!B .2,-错误!C .4,-错误!D .4,错误!5. 经过抛物线y =错误!x 2的焦点和双曲线错误!-错误!=1的右焦点的直线方程为( )A .x +48y -3=0B .x +80y -5=0C .x +3y -3=0D .x +5y -5=06.设3log 2a =,5log 2b =,2log 3c =,则( ) A 。
a c b >> B.b c a >> C.c a b >>D.c b a >>7. O 是平面上一定点,A 、B 、C 平面上不共线的三点,动点P 满足[)0,λ∈+∞ 则P 点的轨迹一定经过∆ABC的( )221111222243831633A 。
外心 B 。
内心 C.重心 D 。
垂心8.如图,有一圆柱开口容器(下表面封闭),其轴截面是边长为2的正方形,P 是BC A 处,内壁P ) A 。
B.1π+C.; D.9。
已知{}na 中,2nan nλ=+,且{}na 是递增数列,则实数的取值范围是( )A.(2,)-+∞;B 。
[2,)-+∞ C. (3,)-+∞ D. [3,)-+∞10。
2016年安徽省淮南市高考数学一模试卷(理科)(解析版)
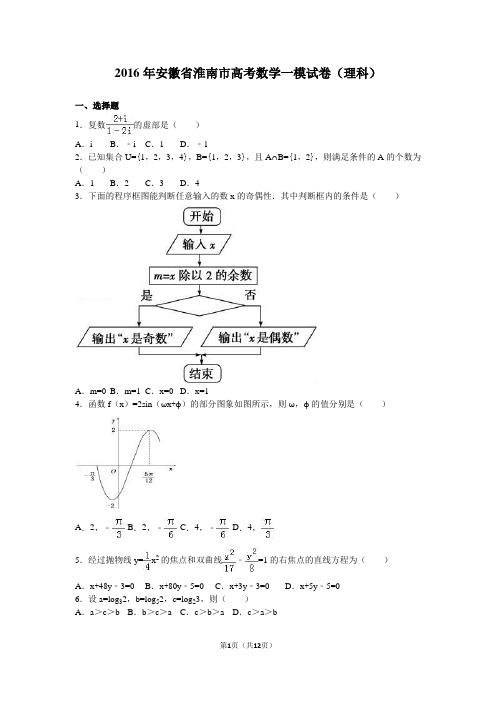
2016年安徽省淮南市高考数学一模试卷(理科)一、选择题1.复数的虚部是()A.i B.﹣i C.1 D.﹣12.已知集合U={1,2,3,4},B={1,2,3},且A∩B={1,2},则满足条件的A的个数为()A.1 B.2 C.3 D.43.下面的程序框图能判断任意输入的数x的奇偶性.其中判断框内的条件是()A.m=0 B.m=1 C.x=0 D.x=14.函数f(x)=2sin(ωx+φ)的部分图象如图所示,则ω,φ的值分别是()A.2,﹣ B.2,﹣ C.4,﹣ D.4,5.经过抛物线y=x2的焦点和双曲线﹣=1的右焦点的直线方程为()A.x+48y﹣3=0 B.x+80y﹣5=0 C.x+3y﹣3=0 D.x+5y﹣5=06.设a=log32,b=log52,c=log23,则()A.a>c>b B.b>c>a C.c>b>a D.c>a>b7.O是平面上一定点,A、B、C是平面上不共线的三个点,动点P满足,λ∈[0,+∞),则P的轨迹一定通过△ABC的()A.外心 B.内心 C.重心 D.垂心8.如图,有一圆柱形无盖水杯,其轴截面ABCD是边长为2的正方形,P是BC的中点,现有一只蚂蚁位于外壁A处,内壁P处有一粒米,则这只蚂蚁取得米粒所经过的最短路程是()A.B.π+1 C.D.9.已知{a n}中,,且{a n}是递增数列,则实数的取值范围是()A.(﹣2,+∞)B.[﹣2,+∞)C.(﹣3,+∞)D.[﹣3,+∞)10.椭圆C: +=1的左,右顶点分别为A1,A2,点P在C上,且直线PA2斜率的取值范围是[﹣2,﹣1],那么直线PA1斜率的取值范围是()A.[,]B.[,]C.[,1]D.[,1]11.如图,是某多面体的三视图,则该多面体的体积为()A.B.C.D.12.设正实数x,y,z满足x2﹣3xy+4y2﹣z=0,则当取得最小值时,x+2y﹣z的最大值为()A.0 B.C.2 D.二、填空题13.过平面区域内一点P作圆O:x2+y2=1的两条切线,切点分别为A,B,记∠APB=α,当α最小时,此时点P坐标为.14.已知过点M(﹣3,﹣3)的直线l被圆x2+y2+4y﹣21=0所截得的弦长为8,则直线l的方程为.15.定义在[﹣2,2]上的偶函数f(x)在[﹣2,0]上为增,若满足f(1﹣m)<f(m),则m的取值范围是.16.设函数y=f(x)的图象与y=2x+a的图象关于y=﹣x+1对称,且f(﹣3)+f(﹣7)=1,则a的值为.三.解答题17.在△ABC中,B=,AC=,求AB+BC的最大值并判断取得最大值时△ABC的形状.18.在公差为d的等差数列{a n}中,已知a1=10,且a1,2a2+2,5a3成等比数列.(Ⅰ)求d,a n;(Ⅱ)若d<0,求|a1|+|a2|+|a3|+…+|a n|.19.如图,在斜三棱柱ABC﹣A1B1C1中,A1B⊥AC,且A1B=AC=5,AA1=BC=13,且AB=12.(1)求证:平面ABB1A1⊥平面ACC1A1;(2)求二面角A﹣BB1﹣C的正切值的大小.20.已知点A(2,0),椭圆E:(a>b>0)的离心率为,F是椭圆E的上焦点,直线AF的斜率为,O为坐标原点.(1)求E的方程;(2)设过点A的动直线l与E相交于点P,Q两点,当△OPQ的面积最大时,求l的方程.21.已知函数f(x)=xlnx+(2a﹣1)x﹣ax2﹣a+1,(1)若,求f(x)的单调区间;(2)若x∈[1,+∞)时恒有f(x)≤0,求a的取值范围.四.选做题,以下三题任选一题22.已知函数f(x)=sin(x﹣ϕ)cos(x﹣ϕ)﹣cos2(x﹣ϕ)+(0≤ϕ≤)为偶函数.(I)求函数的最小正周期及单调减区间;(II)把函数的图象向右平移个单位(纵坐标不变),得到函数g(x)的图象,求函数g (x)的对称中心.23.已知p:|1﹣|<2;q:x2﹣2x+1﹣m2<0;若¬p是¬q的充分非必要条件,求实数m的取值范围.24.在直角坐标系xOy中,已知点A(1,1),B(2,3),C(3,2),点P(x,y)在△ABC三边围成的区域(含边界)上.(Ⅰ)若++=,求||;(Ⅱ)设=m+n(m,n∈R),用x,y表示m﹣n,并求m﹣n的最大值.2016年安徽省淮南市高考数学一模试卷(理科)一、选择题1.【解答】解:=,则复数的虚部是1,故选:C2.【解答】解:∵U={1,2,3,4},B={1,2,3},且A∩B={1,2},∴满足条件的A可能为{1,2},{1,2,4}共2个,故选:B.3.【分析】本题考查了选择结构,由程序框图所体现的算法可知判断一个数是奇数还是偶数,看这个数除以2的余数是1还是0,从而得到判断框条件.【解答】解:由程序框图所体现的算法可知判断一个数是奇数还是偶数,看这个数除以2的余数是1还是0.由图可知应该填m=1.故选B4.【分析】利用函数的周期求解ω,然后利用五点法作图求解φ即可.【解答】解:由函数的图象可知T==π,ω==2.x=时,y=2,可得:2sin(2×+φ)=2,由五点法作图可知φ=﹣.故选:A.5.【分析】求出抛物线y=x2的焦点坐标、双曲线﹣=1的右焦点,即可求出直线方程.【解答】解:抛物线y=x2的焦点坐标为(0,1),双曲线﹣=1的右焦点的坐标为(5,0),∴所求直线方程为即x+5y﹣5=0.故选:D.6.【分析】判断对数值的范围,然后利用换底公式比较对数式的大小即可.【解答】解:由题意可知:a=log32∈(0,1),b=log52∈(0,1),c=log23>1,所以a=log32,b=log52=,所以c>a>b,故选:D.7.【分析】先根据、分别表示向量、方向上的单位向量,确定+的方向与∠BAC的角平分线一致,再由可得到=λ(+),可得答案.【解答】解:∵、分别表示向量、方向上的单位向量∴+的方向与∠BAC的角平分线一致又∵,∴=λ(+)∴向量的方向与∠BAC的角平分线一致∴一定通过△ABC的内心故选B.8.【分析】画出圆柱的侧面展开图,根据对称性,求出AQ+PQ的最小值就是AE的长,求解即可.【解答】解:侧面展开后得矩形ABCD,其中AB=π,AD=2问题转化为在CD上找一点Q 使AQ+PQ最短作P关于CD的对称点E,连接AE,令AE与CD交于点Q,则得AQ+PQ的最小值就是AE为.故选:D.9.【分析】由于{a n}是递增数列,可得∀n∈N*,a n+1>a n,即(n+1)2+λ(n+1)>n2+λn,解出利用数列的单调性即可得出.【解答】解:∵{a n}是递增数列,∴∀n∈N*,a n+1>a n,∴(n+1)2+λ(n+1)>n2+λn,λ>﹣(2n+1),∴λ>﹣3.故选:C.10.【分析】由椭圆C: +=1可知其左顶点A1(﹣2,0),右顶点A2(2,0).设P(x0,y0)(x0≠±2),代入椭圆方程可得=﹣,利用斜率计算公式可得,再利用已知给出的直线PA2斜率的取值范围是[﹣2,1],即可解出.【解答】解:由椭圆C: +=1可知其左顶点A1(﹣2,0),右顶点A2(2,0).设P(x0,y0)(x0≠±2),则得=﹣.∵=,=kPA1=,∴=•==﹣.∵直线PA2斜率的取值范围是[﹣2,﹣1],∴直线PA1斜率的取值范围是[,]故选:A.11.【分析】根据几何体的三视图,得出该几何体为棱长是2的正方体,截去两个相同的三棱锥,再截去一个三棱柱(底面直角三角形的直角边为2和2,高为2)而得到,画出它的直观图,即可求其体积.【解答】解:根据几何体的三视图,得;该几何体为棱长是2的正方体,截去两个相同的三棱锥(底面直角三角形的直角边为2和2,高为1);,再截去一个三棱柱(底面直角三角形的直角边为2和2,高为2)而得到,其直观图如图所示,∴该多面体的体积为:2×2×2﹣2×﹣2×(2××)=.故选:B.12.【分析】将z=x2﹣3xy+4y2代入,利用基本不等式化简即可求得x+2y﹣z的最大值.【解答】解:∵x2﹣3xy+4y2﹣z=0,∴z=x2﹣3xy+4y2,又x,y,z为正实数,∴=+﹣3≥2﹣3=1(当且仅当x=2y时取“=”),即x=2y(y>0),∴x+2y﹣z=2y+2y﹣(x2﹣3xy+4y2)=4y﹣2y2=﹣2(y﹣1)2+2≤2.∴x+2y﹣z的最大值为2.故选:C.13.(﹣4,﹣2).【分析】先依据不等式组,结合二元一次不等式(组)与平面区域的关系画出其表示的平面区域,再利用圆的方程画出图形,确定α最小时点P的位置即可.【解答】解:如图阴影部分表示,确定的平面区域,当P离圆O最远时,α最小,此时点P坐标为:(﹣4,﹣2),故答案为::(﹣4,﹣2).14.4x+3y+21=0或x=﹣3.【分析】求出圆x2+y2+4y﹣21=0的圆心、半径,当直线l的斜率不存在时,直线方程为x=﹣3,成立;当直线l的斜率存在时,设直线l:y=k(x+3)﹣3,求出圆心(0,﹣2)到直线y=k(x+3)﹣3的距离,由过点M(﹣3,﹣3)的直线l被圆x2+y2+4y﹣21=0所截得的弦长为8,利用勾股定理能求出直线l的方程.【解答】解:圆x2+y2+4y﹣21=0的圆心为(0,﹣2),半径r==5,当直线l的斜率不存在时,直线方程为x=﹣3,联立,得或,∴直线l:x=﹣3被圆x2+y2+4y﹣21=0所截得的弦长为8,成立;当直线l的斜率存在时,设直线l:y=k(x+3)﹣3,圆心(0,﹣2)到直线y=k(x+3)﹣3的距离d==,∵过点M(﹣3,﹣3)的直线l被圆x2+y2+4y﹣21=0所截得的弦长为8,∴由勾股定理得:,即25=+16,解得k=﹣,∴直线l:,整理,得:4x+3y+21=0.综上直线l的方程为:4x+3y+21=0或x=﹣3.故答案为:4x+3y+21=0或x=﹣3.15..【分析】根据偶函数的性质等价转化所求的不等式,利用函数的单调性和定义域,列出关于m的不等式组,再求出m的取值范围.【解答】解:因为f(x)是定义在[﹣2,2]上的偶函数,所以不等式f(1﹣m)<f(m)等价于:f(|1﹣m|)<f(|m|),因为f(x)在[﹣2,0]上为增函数,所以,解得﹣1≤m<,即m的取值范围是,故答案为:.16.2.【分析】先求出函数y=f(x)的解析式,再由f(﹣3)+f(﹣7)=1,问题得以解决.【解答】解:设函数y=f(x)的任意点的坐标为(x,y),关于y=﹣x+1对称点的坐标(m,n),则(m,n)在y=2x+a的图象上,,解得m=1﹣y,n=1﹣x,代入y=2x+a可得:1﹣x=21﹣y+a,即:y=log2(1﹣x)﹣a﹣1,函数y=f(x)=log2(1﹣x)﹣a﹣1,∵f(﹣3)+f(﹣7)=1,∴log24﹣a﹣1+log28﹣a﹣1=1,解得,a=2,故答案为:2.三.解答题17.【分析】根据正弦定理可得AB=2sinC,BC=2sinA,从而利用三角函数恒等变换的应用可求AB+BC=,利用正弦函数的图象和性质即可得解.【解答】(本题满分为12分)解:∵B=,AC=,∴在△ABC中,根据==,得AB=•sinC=sinC=2sinC,∴同理BC=2sinA,∴AB+BC=2sinC+2sinA,…=2sinC+2sin(π﹣C)=,…当C=,可得AB+BC的最大值为,…取最大值时,因而△ABC是等边三角形.…18.【分析】(Ⅰ)直接由已知条件a1=10,且a1,2a2+2,5a3成等比数列列式求出公差,则通项公式a n可求;(Ⅱ)利用(Ⅰ)中的结论,得到等差数列{a n}的前11项大于等于0,后面的项小于0,所以分类讨论求d<0时|a1|+|a2|+|a3|+…+|a n|的和.【解答】解:(Ⅰ)由题意得,即,整理得d2﹣3d﹣4=0.解得d=﹣1或d=4.当d=﹣1时,a n=a1+(n﹣1)d=10﹣(n﹣1)=﹣n+11.当d=4时,a n=a1+(n﹣1)d=10+4(n﹣1)=4n+6.所以a n=﹣n+11或a n=4n+6;(Ⅱ)设数列{a n}的前n项和为S n,因为d<0,由(Ⅰ)得d=﹣1,a n=﹣n+11.则当n≤11时,.当n≥12时,|a1|+|a2|+|a3|+…+|a n|=﹣S n+2S11=.综上所述,|a1|+|a2|+|a3|+…+|a n|=.19.【分析】(1)推导出AC⊥AB,A1B⊥AC,从而AC⊥平面ABB1A1,由此能证明平面ABB1A1⊥平面ACC1A1.(2)以B为原点,BA为x轴,在平面ABC中过B作BA的垂线为y轴,BA1为z轴,建立空间直角坐标系,利用向量法能求出二面角A﹣BB1﹣C的正切值.【解答】证明:(1)在△ABC中,∵AB2+AC2=BC2,∴AC⊥AB,…又∵A1B⊥AC且A1B、AC是面ABB1A1内的两条相交直线,∴AC⊥平面ABB1A1,..…又AC⊂平面ACC1A1,∴平面ABB1A1⊥平面ACC1A1.…解:(2)在△ABC中,∵,∴A1B⊥AB,又∵A1B⊥AC且AB、AC是面ABC内的两条相交直线,∴A1B⊥面ABC,…∴以B为原点,BA为x轴,在平面ABC中过B作BA的垂线为y轴,BA1为z轴,建立如图所示的空间直角坐标系,则B(0,0,0),A(12,0,0),C(12,5,0),A1(0,0,5),由,得B1(﹣12,0,5),…取平面ABB1A1的一个法向量=(0,1,0),设平面BCC1B1的一个法向量,由,得取x=5,则…∴cos<>==﹣,设A﹣BB1﹣C的大小为θ,则,.∴二面角A﹣BB1﹣C的正切值的大小为…20.【分析】(1)运用椭圆的离心率公式和直线的斜率公式,以及a,b,c的关系,解方程可得椭圆方程;(2)设l的方程为x=my+2,设P(x1,y1),Q(x2,y2),联立椭圆方程,运用韦达定理和弦长公式,判别式大于0,运用三角形的面积公式,由基本不等式可得最大值,即可得到m,进而得到直线方程.【解答】解:(1)由e=,可得:,即,设F(0,c),则,,又a2﹣b2=c2=3,∴a2=4,b2=1,∴E的方程是;(2)设l的方程为x=my+2,设P(x1,y1),Q(x2,y2),由得(4m2+1)y2+16my+12=0,y1+y2=﹣,y1y2=,△=(16m)2﹣4×12×(4m2+1)=16(4m2﹣3)>0,=,令,则,而当且仅当t=2,即时等号成立,此时S△OPQ≤1.∴当△OPQ的面积最大时,求l的方程为,即.21.【分析】(1)求出f(x)的导数,令g(x)=lnx﹣(x﹣1),求出g(x)的导数,可得单调区间和最值,进而得到f(x)的单调区间;(2)求出导数,对a讨论,当时,当a>时,当0<a<时,结合函数的单调性,即可得到所求a的范围.【解答】解:(1)函数f(x)=xlnx+(2a﹣1)x﹣ax2﹣a+1的导数为f′(x)=lnx﹣2a(x﹣1),当时,f′(x)=lnx﹣(x﹣1),令g(x)=lnx﹣(x﹣1),则.x∈(0,1)时g′(x)>0;x∈(1,+∞)时g′(x)<0.∴g(x)≤g(1)=0,即f′(x)≤0(只在x=1处取等号)∴f(x)的单减区间是(0,+∞);(2)f′(x)=lnx﹣2a(x﹣1),令f′(x)=0,则lnx=2a(x﹣1)且函数lnx在x=1处的切线为y=x﹣1,由(1)知,时,f(x)在[1,+∞)上单减且f(1)=0,∴f(x)≤0,合题意;当a>时,数形结合知,f(x)在[1,+∞)上仍单减且f(1)=0,∴f(x)≤0,合题意;当0<a<时,数形结合知,∃x0>1,使得f′(x0)=0.即x∈(1,x0)时f′(x)>0,f(x)在(1,x0)上单增,f(x)>f(1)=0,不合题意;当a≤0时,数形结合知,x∈(1,+∞)时,f′(x)>0,f(x)在(1,+∞)上单增,f(x)>f(1)=0,不合题意.综上,若x∈[1,+∞)时恒有f(x)≤0,则a的取值范围是.22.【分析】(I)把函数解析式第一项利用二倍角的正弦函数公式化简,第二项利用二倍角的余弦函数公式化简,合并整理后,再利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,即为函数解析式的最简形式,即可求出最小正周期以及单调区间;(II)由题意根据平移变换求出函数的解析式,然后求出函数的对称中心即可.【解答】解:(I)函数f(x)=sin(x﹣ϕ)cos(x﹣ϕ)﹣cos2(x﹣ϕ)+=sin(2x﹣2φ)﹣(2cos2φ﹣1)=sin(2x﹣2φ)﹣cos(2x﹣2φ)=sin(2x﹣2φ)函数f(x)为偶函数,则﹣2φ=kπ,k∈z∵0≤ϕ≤∴φ=∴f(x)=sin(2x﹣π)=﹣sin2x∴函数的最小正周期T==π令2x∈[﹣+2kπ, +2kπ]k∈Z 解得:﹣+kπ≤x≤+kπ∴函数f(x)的单调递减区间为[﹣+kπ, +kπ]k∈Z(II)由(I)知f(x)=﹣sin2x由题意知g(x)=﹣sin[2(x﹣)]=﹣sin(2x﹣)令2x﹣=kπ(k∈Z),则x=+(k∈Z),∴函数的对称中心坐标为(+,0)(k∈Z).23.【分析】¬p是¬q的充分非必要条件,所以q是p的充分非必要条件,求出p、q的范围进而求解.【解答】解:p:|1﹣|<2即为p:﹣2<x<10,q:x2﹣2x+1﹣m2<0即为(x﹣1)2<m2,即q:1﹣|m|<x<1+|m|,又¬p是¬q的充分非必要条件,所以q是p的充分非必要,∴(两式不能同时取等)得到|m|≤3,满足题意,所以m的范围为[﹣3,3].24.【分析】(Ⅰ)先根据++=,以及各点的坐标,求出点p的坐标,再根据向量模的公式,问题得以解决;(Ⅱ)利用向量的坐标运算,先求出,,再根据=m+n,表示出m﹣n=y﹣x,最后结合图形,求出m﹣n的最小值.【解答】解:(Ⅰ)∵A(1,1),B(2,3),C(3,2),++=,∴(1﹣x,1﹣y)+(2﹣x,3﹣y)+(3﹣x,2﹣y)=0∴3x﹣6=0,3y﹣6=0∴x=2,y=2,即=(2,2)∴(Ⅱ)∵A(1,1),B(2,3),C(3,2),∴,∵=m+n,∴(x,y)=(m+2n,2m+n)∴x=m+2n,y=2m+n∴m﹣n=y﹣x,令y﹣x=t,由图知,当直线y=x+t过点B(2,3)时,t 取得最大值1,故m﹣n的最大值为1.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016年淮南市高三数学一模理科试题一、选择题1. 复数2+i1-2i 的虚部是 ( )A .1 B.-1 C .-i D .i2.已知集合{}1,2,3,4U =,{}1,2,3B =,且{}1,2A B ⋂=,则满足条件的A 的个数为( ) A.1 B.2 C.3 D.43.下面的程序框图(如图所示)能判断任意输入的数x 的奇偶性:其中判断框内的条件是( ) A .0=m B. 0=xC. 1=xD. 1=m4. 函数f (x )=2sin(ωx +φ)⎝ ⎛⎭⎪⎫ω>0,-π2<φ<π2的部分图象如图所示,则ω,φ的值分别是 ( )(),AB ACOP OA AB ACλ→→→→→→=++A .2,-π3 B .2,-π6C .4,-π6D .4,π35. 经过抛物线y =14x 2的焦点和双曲线x 217-y28=1的右焦点的直线方程为( )A .x +48y -3=0B .x +80y -5=0C .x +3y -3=0D .x +5y -5=06.设3log 2a =,5log 2b =,2log 3c =,则( ) A.a c b >> B.b c a >> C. c a b >> D. c b a >> 7. O 是平面上一定点,A 、B 、C 平面上不共线的三点,动点P 满足[)0,λ∈+∞ 则P 点的轨迹一定经过∆ABC 的( )A.外心B.内心C.重心D.垂心8.如图,有一圆柱开口容器(下表面封闭),其轴截面是边长为2的正方形,P 是BC的中点,现有一只蚂蚁位于外壁A 处,内壁P 处有一粒米,则这只蚂蚁取得米粒的所经过的最短路程是( )1π+9. 已知{}n a 中,2n a n n λ=+,且{}n a 是递增数列,则实数的取值范围是( ) A. (2,)-+∞; B. [2,)-+∞ C. (3,)-+∞ D. [3,)-+∞10. 椭圆C: 22143x y +=的左、右顶点分别为1A , 2A ,点P 在C 上且直线2PA 斜率的取值范围是[]2,1--,那么直线1PA 斜率的取值范围是 ( )A.1324⎡⎤⎢⎥⎣⎦,B. 112⎡⎤⎢⎥⎣⎦, C. 3384⎡⎤⎢⎥⎣⎦, D.314⎡⎤⎢⎥⎣⎦,2211112222438316311. 如图,是某多面体的三视图, 则该多面体的体积为( )A. B. C. D. 正视图 侧视图俯视图12. 设正实数,,x y z 满足22340x xy y z -+-=,则当zxy取得最大值时,2x y z +-的最大值为( )A.0B. 2C.98 D.94二、填空题13. 过平面区域202020x y y x y -+≥⎧⎪+≥⎨⎪++≤⎩内一点P 作圆22:1O x y +=的两条切线,切点分别为,A B ,记APB α∠=,当α最小时,点P 坐标为 。
14. 已知过点(3,3)M --的直线l 被圆224210x y y ++-=所截得的弦长为8,则直线l 的方程为 。
15.定义在上的偶函数f(x)在上为增,若满足f(1-m) <f(m),则m 的取值范围是 . 16.设函数()y f x =的图象与2x a y +=的图象关于1y x =-+对称,且(3)(7)1f f -+-=,则a 的值为 。
17. 在△ABC 中,B =3π,AC =3,求AB +BC 的最大值并判断取得最大值时△ABC 的形状。
C 1B 1A 1CBA18. 在公差为d 的等差数列{}n a 中,已知110a =,且123,22,5a a a +成等比数列. (1)求d, n a(2)若d<0,求|1a |+|2a |+|3a |+…+|n a |.19.如图,在斜三棱柱111ABC A B C -中,1A B AC ⊥,且15A B AC ==,113AA BC ==,且12AB =。
(1)求证:平面11ABB A ⊥平面11ACC A ;(2)求二面角1A BB C --的正切值的大小。
20.已知点A (2,0),椭圆E :22221y x a b +=(a >b >0)的离心率为2,F 是椭圆E的上焦点,直线AF的斜率为2-,O 为坐标原点。
(1)求E 的方程;(2)设过点A 的动直线l 与E 相交于点P ,Q 两点,当OPQ ∆的面积最大时,求l 的方程。
21.已知函数2()ln (21)1f x x x a x ax a =+---+,(1)若12a =,求()f x 的单调区间; (2)若[1,)x ∈+∞时恒有()0f x ≤,求a 的取值范围。
22.以下三题任选一题①已知函数f(x)= 3 2sin()cos()cos ()x x x ϕϕϕ----+12( 02πϕ≤≤)为偶函数.(1)求函数f(x)的最小正周期及单调减区间; (2)把函数f(x)的图像向右平移6π个单位(纵坐标不变),得到函数g(x)的图像,求函数g(x)的对称中心.②已知1:13x p --<2;22:21q x x m -+-<0,若p ⌝是q ⌝的充分非必要条件,求实数m 的取值范围.3C π=③在直角坐标系xOy 中,已知点A (1,1),B (2,3),C (3,2),点P (x ,y )在△ABC 三边围成的区域(含边界)上.(1)若PA →+PB →+PC →=0 ,求|OP →|;(2)设OP →=mAB →+nAC →(m ,n ∈R),用x ,y 表示m -n ,并求m -n 的最大值.2016年淮南市高三数学一模理科试题答案一、选择题1. A 2. B 3. D 4. A. 5. D 6. C 7.B 8.D 9.C 10. C 11. B 12. B 二、填空题13.(-4,-2) 14. 4x+3y+21=0或x=-3 15. 211〈≤-m 16. 217. 解:在△ABC 中,根据AB sin C =AC sin B =BC sin A ,得AB =AC sin B ·sin C =332sin C =2sin C ,同理BC =2sin A ,因此AB +BC =2sin C +2sin A .......................................... 4分 =2sin C+2sin(23π-C )=)6C π+,......................................................................... 8分 因此AB +BC 的最大值为. ........................................................................................ 10分取最大值时, ,因而△ABC 是等边三角形............................................................ 12分18. 解(1)由题意得,5a 3·a 1=(2a 2+2)2, ..................................................... 2分 d 2-3d-4=0,解得d=-1或d=4, ........................................................................ 4分所以n a =-n+11或n a =4n+6. ........................................................................... 5分(2)设数列{n a }前n 项和为n S , 因为d<0,所以d=-1,n a =-n+11, ....................................................................6分则n ≤11时,|a 1|+|a 2|+|a 3|+…+|n a |=n S =-12n 2+212n; ................. 8分 n ≥12时,|a 1|+|a 2|+…+|a 11|+|a 12|+…+|n a | =a 1+a 2+…+a 11-a 12-…-n a =S 11-(n S -S 11) = -n S +2S 11=12n 2-212n+110. ................................................................... 10分综上所述,|a 1|+|a 2|+…+|n a |=22121,11,22121110,12.22≤≥⎧-+⎪⎪⎨⎪-+⎪⎩n n n n n n ..........................12分xB 19.(1)证明:在ABC ∆中,222AB AC BC += ,AC AB ∴⊥,............................................................................................................. 2分又 1A B AC ⊥且1A B 、AC 是面11ABB A 内的两条相交直线,AC ∴⊥平面11ABB A ,.............................................................................................. 4分 又AC ⊂平面11ACC A ,∴平面11ABB A ⊥平面11ACC A ;............................................................................... 5分(2)在ABC ∆中,22211A B AB AA += ,1A B AB ∴⊥,又 1AB A C ⊥且AB 、AC 是面ABC 内的两条相交直线,1A B ∴⊥面ABC ,...................................................... 7分因而,可建立如图所示的坐标系:则B (0,0,0),A (12,0,0),C (12,5,0),1(0,0,5)A ,由11BB AA = 得1(12,0,5)B -,...............................................................8分取平面11ABB A 的一个法向量1(0,1,0)n =, 设平面BCC 1B 1的一个法向量2(,,)n x y z =,由⎩⎨⎧=⋅=⋅.0;0212BC n BB n 得 1250;1250.x z x y -+=⎧⎨+=⎩取5x =,则2(5,12,12)n =-........................................................................... 10分∴111122cos ,n n n n n n ⋅==⋅设1A BB C --的大小为θ,则31312cos =θ,13tan 12θ=.∴二面角1A BB C --的正切值的大小为1312................................................. 12分 20.解:(1)222234a b e a -==,2214b a =,................................................ 2分 设F (0,c),则2c -=,c =a 2-b 2=c 2=3 ∴224,1,a b == ∴E 的方程是2214y x +=.................................................................................. 4分(2)设l 的方程为2x my =+,设1122(,),(,)P x y Q x y ,由222,1.4x my y x =+⎧⎪⎨+=⎪⎩得22(41)16120m y my +++=,........................................... 6分222(16)412(41)16(43)m m m ∆=-⨯⨯+=->0,1212122OPQS y y y y ∆=⨯⨯-=-==........... 10分令t =,则24444OPQ t S t t t∆==++,而44t t +≥当且仅当2t =,即m =时等号成立,此时1OPQ S ∆≤.∴当OPQ ∆的面积最大时,求l 的方程为2x y =+, 即240x -=.......................................................................................... 12分21.解:(1)'()ln 2(1)f x x a x =--当12a =时,'()ln (1)f x x x =--.................................................................. 2分令()ln (1)g x x x =--,则'11()1x g x x x-=-=. (0,1)x ∈时'()g x >0;(1,)x ∈+∞时'()g x <0.∴()(1)0g x g ≤=,即'()0f x ≤(只在1x =处取等号) ∴()f x 的单减区间是(0,)+∞;........................................................................4分(2)'()ln 2(1)f x x a x =--,令'()0f x =,则ln 2(1)x a x =-且函数ln x 在1x =处的切线为1y x =-,由(1)知,12a =时, ()f x 在[1,)+∞上单减且(1)0f =, ∴()0f x ≤,合题意. ....................................................................................... 6分当a >12时,数形结合知,()f x 在[1,)+∞上仍单减且(1)0f =, ∴()0f x ≤,合题意. ....................................................................................... 8分当0<a <12时,数形结合知,0x ∃>1,使得'0()0f x =.即0(1,)x x ∈时'()f x >0,()f x 在0(1,)x 上单增,()f x >(1)0f =,不合题意. ......................................... 10分当a ≤0时,数形结合知,(1,)x ∈+∞时,'()f x >0,()f x 在(1,)+∞上单增,()f x >(1)0f =,不合题意.综上,若[1,)x ∈+∞时恒有()0f x ≤,则a 的取值范围是12a ≥................................................................................. 12分22.解析: (1)f(x)=32sin(2x -2φ)-cos 2x-2φ +12+12=32sin(2x -2φ)-12cos(2x -2φ)=sin(2x -2φ-6π).................................... 2分 ∵函数f(x)为偶函数,∴2φ+6π=k π+2π,k ∈Z. ∴φ=2k π+6π,k ∈Z.又∵0≤φ≤2π,∴φ=6π.∴f(x)=sin(2x -3π-6π)=-cos2x...................................................................... 4分∴f(x)的最小正周期为T =22ππ=.......................................................................... 5分由2k ππ-≤2x≤2k π,k ∈Z ,得k π-2π≤x≤k π,k ∈Z. ∴f(x)的单调减区间为[k π-2π,k π](k ∈Z).................................................... 7分(2)函数f(x)=-cos2x 的图像向右平移6π个单位,得到 g(x)=-cos2(x -6π)的图像,即g(x)=-cos(2x -3π)................................. 8分 令2x -3π=k π+2π,k ∈Z ,∴5212k x ππ=+,k ∈Z. ∴g(x)的对称中心为(5212k ππ+,0),k ∈Z. ......................................................... 10分23.解:113x --<2⇔-2<x <10,............................................................ 2分 记{A x =-2<x <10},B {x =2221x x m -+-<0},由题知,B , .... A............................................................................................ 4分记,22()21f x x x m =-+-则(2)0,(10)0.f f -≥⎧⎨≥⎩即2290,810.m m ⎧-≥⎪⎨-≥⎪⎩ 解此不等式组得,33m -≤≤........................................................................... 8分经检验3m =±时上等式组中两不等式的等号不同时成立.∴m 的取值范围是33m -≤≤………….......................................................... 10分24.解:(1)∵PA →+PB →+PC →=0 ,又PA →+PB →+PC →=(1-x ,1-y )+(2-x ,3-y )+(3-x ,2-y )=(6-3x ,6-3y ), ∴⎩⎪⎨⎪⎧6-3x =0,6-3y =0,解得⎩⎪⎨⎪⎧x =2,y =2,.............................................................................................. 2分即OP →=(2,2),故|OP →|=2 2........................................................................................... 4分其它方法参考给分.(2)∵OP →=mAB →+nAC →,∴(x ,y )=(m +2n ,2m +n ),∴⎩⎪⎨⎪⎧x =m +2n ,y =2m +n ,两式相减得,m -n =y -x ,............................................................................................. 8分令y-x=t,由图知,当直线y=x+t过点B(2,3)时,t取得最大值1,故m-n的最大值为1. ............................................................................. ....................... 10分其它方法参考给分.。
