三角形内角和为180°-动态图
合集下载
人教版初中八年级数学上册-三角形内角和定理PPT课件

三角形内角和定理三角形的内角和等于1800
1
02
3
03
3
B l
A
l 1
2 C
A 1
B
C
如图,在△ABC 中, ∠BAC =40°, ∠B = 75°,AD 是△ABC 的角平分线.求∠ADB 的度数 .
解:
由∠BAC=40°,AD是△ ABC的角平分线 得∠BAD= ∠BAC=20°. 在△ ABD 中,
小结
1 三角形内角和定理三角形的内角和等于1800
2 运用三角形内角和定理解决相关的求角度问题.
老师:当图儿ຫໍສະໝຸດ A∠ADB =180°-∠B-∠BAD = 180° - 75°- 20°=85°.
C D B
下列各组角是同一个三角形的内角吗?为什么? 3°, 150°, 27° ( 是 )
口答
60°, 40°, 90° ( 不是)
30°, 60°, 50° ( 不是)
填空 (1)在△ABC中,∠A=35°,∠ B=43 °则∠ C= 102. ° (2)在△ABC中, ∠A :∠B:∠C=2:3:4则∠A = 40 ° ∠ B= 60 ° ∠ C= 80 °.
老师:当图儿
想一想:关于角涉及到180°的有哪些知识?
A
B
C
在小学,我们怎么发现“三角形三个内角的和等于180°”的呢 ?
方法1:度量
A
方法2:折叠
B
C
方法3:剪拼图
3
" 01
1
2
3
" 02
3
" 03
从剪拼中受到什么启发,如何证明“三角形内角和等于180°”呢?
A
l
312
1
02
3
03
3
B l
A
l 1
2 C
A 1
B
C
如图,在△ABC 中, ∠BAC =40°, ∠B = 75°,AD 是△ABC 的角平分线.求∠ADB 的度数 .
解:
由∠BAC=40°,AD是△ ABC的角平分线 得∠BAD= ∠BAC=20°. 在△ ABD 中,
小结
1 三角形内角和定理三角形的内角和等于1800
2 运用三角形内角和定理解决相关的求角度问题.
老师:当图儿ຫໍສະໝຸດ A∠ADB =180°-∠B-∠BAD = 180° - 75°- 20°=85°.
C D B
下列各组角是同一个三角形的内角吗?为什么? 3°, 150°, 27° ( 是 )
口答
60°, 40°, 90° ( 不是)
30°, 60°, 50° ( 不是)
填空 (1)在△ABC中,∠A=35°,∠ B=43 °则∠ C= 102. ° (2)在△ABC中, ∠A :∠B:∠C=2:3:4则∠A = 40 ° ∠ B= 60 ° ∠ C= 80 °.
老师:当图儿
想一想:关于角涉及到180°的有哪些知识?
A
B
C
在小学,我们怎么发现“三角形三个内角的和等于180°”的呢 ?
方法1:度量
A
方法2:折叠
B
C
方法3:剪拼图
3
" 01
1
2
3
" 02
3
" 03
从剪拼中受到什么启发,如何证明“三角形内角和等于180°”呢?
A
l
312
《三角形内角和》教学课件ppt

平角
知识讲解
有什么方法能验证你们的想法?说一说,做一
做。
1
2
213
3
三角形内角和等于180°。
知识讲解
试一试。 猜一猜,可能是什么三角形?
80° 60° 40°
锐角三角形
180°-60°-40°=80°
根据三角形的内角和等于180°,且已知三角 形中两个角的度数,可以求出第三个角的度 数,从而判断该三角形是什么三角形。
A
B 75° 28° C35°AB20° 45°
∠A= 77° ∠C= 55° ∠B= 115°
小结
通过今天的学习你收获了什么?
三角形内角和
课前导入
我的三个内角的 和一定比你大。
是这样吗?
知识讲解
小组活动,每人准备一个三角形,量一 量,填一填。
说一说:你发现了什么?
大小、形状不同的三角形,它们 三个内角的和都是180°左右。
实际上,三角形的三个内角和就是180°, 只是因为测量有误差……
知识讲解
有什么方法能验证你们的想法?说一说, 做一做。
知识讲解
试一试。 猜一猜,可能是什么三角形?
等边三角形
80°60° 60°60°4600°°
锐角三角形
新知探究 试一试。 猜一猜,可能是什么三角形?
直角三角形
10900°° 606°0° 230°
钝角三角形
练习
1.三角形内角和等于多少?回顾探索与交 流的过程。
练习
2.填出下面各角的度数。 C
知识讲解
有什么方法能验证你们的想法?说一说,做一
做。
1
2
213
3
三角形内角和等于180°。
知识讲解
试一试。 猜一猜,可能是什么三角形?
80° 60° 40°
锐角三角形
180°-60°-40°=80°
根据三角形的内角和等于180°,且已知三角 形中两个角的度数,可以求出第三个角的度 数,从而判断该三角形是什么三角形。
A
B 75° 28° C35°AB20° 45°
∠A= 77° ∠C= 55° ∠B= 115°
小结
通过今天的学习你收获了什么?
三角形内角和
课前导入
我的三个内角的 和一定比你大。
是这样吗?
知识讲解
小组活动,每人准备一个三角形,量一 量,填一填。
说一说:你发现了什么?
大小、形状不同的三角形,它们 三个内角的和都是180°左右。
实际上,三角形的三个内角和就是180°, 只是因为测量有误差……
知识讲解
有什么方法能验证你们的想法?说一说, 做一做。
知识讲解
试一试。 猜一猜,可能是什么三角形?
等边三角形
80°60° 60°60°4600°°
锐角三角形
新知探究 试一试。 猜一猜,可能是什么三角形?
直角三角形
10900°° 606°0° 230°
钝角三角形
练习
1.三角形内角和等于多少?回顾探索与交 流的过程。
练习
2.填出下面各角的度数。 C
三角形内角和定理ppt

现代数学的发展与应用
03
定理的证明方法
三角形内角和等于180度的几何证明方法是通过将三角形分割成两个等腰三角形,然后利用等腰三角形的性质来证明。
三角形内角和等于180度的几何证明方法也可以通过利用平行线的性质,将三角形的三个内角转化成同一直线上的三个内角,然后利用等角定理来证明。
几何证明方法
三角形内角和等于180度的代数证明方法是通过在三角形中任取一个顶点,向其他两个顶点连线,将三角形分成三个直角三角形,然后利用勾股定理来证明。
定理在数学、工程、物理学等许多学科中都有广泛的应用,同时也是许多几何问题证明的基本工具之一。
重要性及应用领域
现代数学中,三角形内角和定理的证明方法有很多种,其中较为常见的是代数方法、三角函数方法、向量方法等。
代数方法是通过代入三角形的三个内角,利用三角函数的和差公式进行证明;三角函数方法则是利用三角函数恒等变换的性质进行证明;向量方法则是通过建立直角坐标系,用向量表示三角形的三个顶点,再利用向量的加减运算进行证明。
三角形内角和定理的推广
平分线的应用
等边三角形的特殊性质
双曲线的应用
定理的拓展形式
03
在计算机科学中的应用
在计算机科学中,三角形内角和定理可以用来判断一个点是否在多边形内部。
定理在其他领域的应用
01
工程设计中的应用
在工程设计中,三角形内角和定理经常被用来确定角度和长度之间的关系。
02
在物理学中的应用
定理的妙用
个人观点与思考
THANKS
感谢观看
定理在数学中的地位
三角形内角和定理是数学中严谨证明和推理的典范,对于数学教育也有着重要的意义。
定理的推广与深化
01
新人教版四年级数学下册《三角形的内角和》PPT

顶角是96°,两个底角都是(180° - 96°)÷2=42°。 (3)一个直角三角形,其中一个锐角是40°。
一个锐角是40°,另一个锐角是90°-40°=50°, 还有一个角是90°。
5.爸爸给小红买了一个等腰 三角形的风筝。风筝的一 个 底 角 是 70° ,0° 答:风筝的顶角是 40°。
剪拼法
1
拼成了一个平角。
2
3
那直角三角形和钝角三角形呢?
折一折
2
折成了一个平角。
2
1
1
33
转化法
4 3
1
2
4 3
1
2
任意三角形的内角和是180 °。
1. 在右图中,∠1=140°,∠3=25°。求∠2 的度数。
∠1+∠2+∠3=180° ∠2=180°-∠1-∠3
=180°-140°-25° =15°
6.猜一猜。
(1) 在三角形中,一个角是直角, 另外两个角可能各是多少度?
30°和60°
(2)
三角形的两条边分别是3cm 和4cm,另一条边可能是多
少厘米(取整厘米数)?
5cm
通过今天的学习你有什么收获?
任意三角形的内角和是180°。
2.算出下面各个未知角的度数。
180°-65°-37° 180°-90°-30° 180°-20°-25°
=78°
=60°
=135°
3. 把下面这个三角形沿虚线剪成两个小三角 形,每个小三角形的内角和是多少度?
180°
4.求出下列三角形各个角的度数。 (1)一个等边三角形。
每个角都是60°。 (2)一个等腰三角形,顶角是96°。
三角形的内角和
1
一个锐角是40°,另一个锐角是90°-40°=50°, 还有一个角是90°。
5.爸爸给小红买了一个等腰 三角形的风筝。风筝的一 个 底 角 是 70° ,0° 答:风筝的顶角是 40°。
剪拼法
1
拼成了一个平角。
2
3
那直角三角形和钝角三角形呢?
折一折
2
折成了一个平角。
2
1
1
33
转化法
4 3
1
2
4 3
1
2
任意三角形的内角和是180 °。
1. 在右图中,∠1=140°,∠3=25°。求∠2 的度数。
∠1+∠2+∠3=180° ∠2=180°-∠1-∠3
=180°-140°-25° =15°
6.猜一猜。
(1) 在三角形中,一个角是直角, 另外两个角可能各是多少度?
30°和60°
(2)
三角形的两条边分别是3cm 和4cm,另一条边可能是多
少厘米(取整厘米数)?
5cm
通过今天的学习你有什么收获?
任意三角形的内角和是180°。
2.算出下面各个未知角的度数。
180°-65°-37° 180°-90°-30° 180°-20°-25°
=78°
=60°
=135°
3. 把下面这个三角形沿虚线剪成两个小三角 形,每个小三角形的内角和是多少度?
180°
4.求出下列三角形各个角的度数。 (1)一个等边三角形。
每个角都是60°。 (2)一个等腰三角形,顶角是96°。
三角形的内角和
1
PPT 图形旋转 指针 90度 180度 三角形 教程 演示
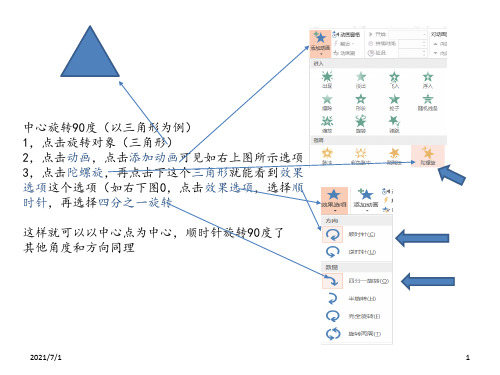
出现效果选项,点击效果选项,点 击顺时针,点击四分之一旋转就完成了 (这个步骤其实就是中心旋转90度(以 三角形为例)的步骤)
图六 图七 图八
2021/7/1
图九
3
以上方法中旋转角度调节可以通过选择四 分之一旋转、半目标再点
击添加动画重复以上步骤,添加一个逆时 针旋转的动画即可(右图)
图三
图四 图五
2021/7/1
2
5,双击三角形B(注意是只点击B三角 形),单击右键(这时你会看到如右图 样式、填充、轮廓、剪切、复制等这些 选项,如果不是则双击三角形B后重试 一次),(见图六、图七)然后将三角 形B的填充和样式都选择空白,这时三 角形B就看不见了,成透明的了(见图 八)。
6,单击组合图(图九),点击动画,点 击添加动画,点击陀螺旋
1
图一 图二
绕一点旋转(以三角形为例,O点为定点) 1,画一个三角形A,点击此三角形选中, Ctrl+C,Ctrl+V进行复制粘贴,现在就有了两 个三角形A和B 2,双击三角形B,在工具栏中(右上角)找到 旋转,点击旋转、垂直旋转就旋转了180度 3,移动三角形B使定点O重合(绕O点旋转) 4,按住Ctrl键,同时用鼠标分别点击三角形A 和B同时选中A、B两个三角形,然后点击鼠标 右键,选择组合再点击组合,这样两个三角形 就成了一个组合了
触发方式,开始时间,持续时间也可以调 节(如右图)
2021/7/1
4
结束语
若有不当之处,请指正,谢谢!
中心旋转90度(以三角形为例) 1,点击旋转对象(三角形) 2,点击动画,点击添加动画可见如右上图所示选项 3,点击陀螺旋,再点击下这个三角形就能看到效果 选项这个选项(如右下图0,点击效果选项,选择顺 时针,再选择四分之一旋转
图六 图七 图八
2021/7/1
图九
3
以上方法中旋转角度调节可以通过选择四 分之一旋转、半目标再点
击添加动画重复以上步骤,添加一个逆时 针旋转的动画即可(右图)
图三
图四 图五
2021/7/1
2
5,双击三角形B(注意是只点击B三角 形),单击右键(这时你会看到如右图 样式、填充、轮廓、剪切、复制等这些 选项,如果不是则双击三角形B后重试 一次),(见图六、图七)然后将三角 形B的填充和样式都选择空白,这时三 角形B就看不见了,成透明的了(见图 八)。
6,单击组合图(图九),点击动画,点 击添加动画,点击陀螺旋
1
图一 图二
绕一点旋转(以三角形为例,O点为定点) 1,画一个三角形A,点击此三角形选中, Ctrl+C,Ctrl+V进行复制粘贴,现在就有了两 个三角形A和B 2,双击三角形B,在工具栏中(右上角)找到 旋转,点击旋转、垂直旋转就旋转了180度 3,移动三角形B使定点O重合(绕O点旋转) 4,按住Ctrl键,同时用鼠标分别点击三角形A 和B同时选中A、B两个三角形,然后点击鼠标 右键,选择组合再点击组合,这样两个三角形 就成了一个组合了
触发方式,开始时间,持续时间也可以调 节(如右图)
2021/7/1
4
结束语
若有不当之处,请指正,谢谢!
中心旋转90度(以三角形为例) 1,点击旋转对象(三角形) 2,点击动画,点击添加动画可见如右上图所示选项 3,点击陀螺旋,再点击下这个三角形就能看到效果 选项这个选项(如右下图0,点击效果选项,选择顺 时针,再选择四分之一旋转
四年级下册数学课件 - 三角形的内角和 西师大版(共23张PPT) (1)

西师版小学数学四年级下册
《魔术师,你来当》
三角形内角和是180°的验证方法
执教:刘丽华 自贡市汇东实验学校
西师版小学数学四年级下册四单元
《魔术师,你来当》
三角形内角和是180°的验证方法
探究步骤
猜想 验证 归纳 应用
1
2
3
3
1
2
3
1
2
锐角三角形 直角三角形
3 1
2 钝角三角形
锐角三角形
1
1
2
2
3
3
∠1=90°则∠2+∠3=90°
1
2
1
2
3
锐角三角形
3
探究步骤
猜想 验证 归纳 应用
探究步骤
猜想 验证 归纳 应用
31Biblioteka 23∠1+∠2+∠3=180°
锐角三角形的内角和是180°
直角三角形
3
3
1
2
∠1+∠2+∠3=180°
直角三角形的内角和是180°
钝角三角形
3 1
3 2
∠1+∠2+∠3=180°
钝角三角形的内角和是180°
3
1
2 锐角三角形
3
1
2 直角三角形
3 1
2 钝角三角形
钝角三角形
1
1
2
2
3
3
直角三角形
《魔术师,你来当》
三角形内角和是180°的验证方法
执教:刘丽华 自贡市汇东实验学校
西师版小学数学四年级下册四单元
《魔术师,你来当》
三角形内角和是180°的验证方法
探究步骤
猜想 验证 归纳 应用
1
2
3
3
1
2
3
1
2
锐角三角形 直角三角形
3 1
2 钝角三角形
锐角三角形
1
1
2
2
3
3
∠1=90°则∠2+∠3=90°
1
2
1
2
3
锐角三角形
3
探究步骤
猜想 验证 归纳 应用
探究步骤
猜想 验证 归纳 应用
31Biblioteka 23∠1+∠2+∠3=180°
锐角三角形的内角和是180°
直角三角形
3
3
1
2
∠1+∠2+∠3=180°
直角三角形的内角和是180°
钝角三角形
3 1
3 2
∠1+∠2+∠3=180°
钝角三角形的内角和是180°
3
1
2 锐角三角形
3
1
2 直角三角形
3 1
2 钝角三角形
钝角三角形
1
1
2
2
3
3
直角三角形
人教版《三角形的内角和》公开课课件12

任意直角三角形的内角和是180
(1623—1662)
长方形的四个角都是直角,所以长方形的内角和
2、用你们喜欢的方法验证(三角形内角和是180度),并进行小组交流,得出结论。
应为:90°×4=360°。
考考你:你知道下面的三角形各个角的度数吗?
沿高可以将任意三角形分成两个直角三角形。
考考你:你知道下面的三角形各个角的度数吗?
顶角是多少度?
第十五页,编辑于星期四:十六点 三十一分。
400
1800-700 -700 =1100 -700 =400
700
700 1800-700×2
的一一个个等底腰角三是角7形00的,风它筝的,顶它==4108000 -1400
角是多少度?
答:它的顶角是400。
第十六页,编辑于星期四:十六点 三十一分。
我是等腰三角 形,顶角是96
任意直角三角形的内角和是180 90°-40°=50°
1、钝角三角形的内角和大于锐角三角形的内角和。
度
我有一个锐
角是40度
180°÷3=60°
(180°-96°) ÷2=42°
90°-40°=50° 第十四页,编辑于星期四:十六点 三十一分。
一个等腰三角形的风筝, 它的一个底角是700,它的
三角形内角和等于180 ° (选了什么图形 用了哪些方法验证 结论是什么) 长方形的四个角都是直角,所以长方形的内角和
90°-40°=50°
1、钝角三角形的内角和大于锐角三角形的内角和。 三角形内角和是180°。 3、直角三角形的两个锐角和是90度。 1、钝角三角形的内角和大于锐角三角形的内角和。 3、直角三角形的两个锐角和是90度。 (1623—1662)
三角形的内角 ppt

三角形的内角
主讲人: 30号
学习任务
• 了解三角形的内角 • 会用平行线的性质与平角的定义证明三 角形内角和等于180 ° • 学会解决与角有关的实际问题 • 初步培养学生的说理能力
内角三兄弟之争
在一个直角三角形里住着三个内角,平 时,它们三兄弟非常团结。可是有一天,老 二突然不高兴,发起脾气来,它指着老大说: “你凭什么度数最大,我也要和你一样 大!”“不行啊!”老大说:“这是不可能 的,否则,我们这个家就再也围不起来 了……”“为什么?” 老二很纳闷。
三角形的内角和等于1800.
证明:过A作EF∥Bc 所以∠B=∠2( 两直线平行,内错角相等 ) 同理 E ∠C=∠1( 两直线平行,内错角相等 )
A
F
1
因为∠2+∠1+∠BAC=180°( 平角定义 ) 所以∠B+∠C+∠BAC=180°
l
2
B
C
三角形的内角和等于1800.
A
E
1
2
B
C
D
0. 三角形的内角和等于1;∠B +∠C =180°
B C
想一想
问题:有什么方法可以得到180
1.平角的度数是180
°
°
°
2.两直线平行,同旁内角的和是
180
3.邻补角的和是180 ° 从刚才拼角的过程你能想出 证明的方法吗?
三角形的三个内角和是180°
图1
图2
刚才拼角的过程你能想出证明的方法吗?
D
E
北 500
C
北 B
400
A
动动脑:还有其
他的解法吗?
北 北 D A C F
E
主讲人: 30号
学习任务
• 了解三角形的内角 • 会用平行线的性质与平角的定义证明三 角形内角和等于180 ° • 学会解决与角有关的实际问题 • 初步培养学生的说理能力
内角三兄弟之争
在一个直角三角形里住着三个内角,平 时,它们三兄弟非常团结。可是有一天,老 二突然不高兴,发起脾气来,它指着老大说: “你凭什么度数最大,我也要和你一样 大!”“不行啊!”老大说:“这是不可能 的,否则,我们这个家就再也围不起来 了……”“为什么?” 老二很纳闷。
三角形的内角和等于1800.
证明:过A作EF∥Bc 所以∠B=∠2( 两直线平行,内错角相等 ) 同理 E ∠C=∠1( 两直线平行,内错角相等 )
A
F
1
因为∠2+∠1+∠BAC=180°( 平角定义 ) 所以∠B+∠C+∠BAC=180°
l
2
B
C
三角形的内角和等于1800.
A
E
1
2
B
C
D
0. 三角形的内角和等于1;∠B +∠C =180°
B C
想一想
问题:有什么方法可以得到180
1.平角的度数是180
°
°
°
2.两直线平行,同旁内角的和是
180
3.邻补角的和是180 ° 从刚才拼角的过程你能想出 证明的方法吗?
三角形的三个内角和是180°
图1
图2
刚才拼角的过程你能想出证明的方法吗?
D
E
北 500
C
北 B
400
A
动动脑:还有其
他的解法吗?
北 北 D A C F
E
