中考数学第21讲-矩形菱形正方形(含答案)
2013-2014中考数学专题复习学生版第二十一讲 矩形 菱形 正方形

第二十一讲矩形菱形正方形【基础知识回顾】一、矩形:1、定义:有一个角是角的平行四边形叫做矩形2、矩形的性质:⑴矩形的四个角都⑵矩形的对角线3、矩形的判定:⑴用定义判定⑵有三个角是直角的是矩形⑶对角线相等的是矩形【名师提醒:1、矩形是对称图形,对称中心是,矩形又是对称图形,对称轴有条2、矩形被它的对角线分成四个全等的三角形和两对全等的三角形3、矩形中常见题目是对角线相交成600或1200角时,利用直角三角形、等边三角形等图形的性质解决问题】二、菱形:1、定义:有一组邻边的平行四边形叫做菱形2、菱形的性质:⑴菱形的四条边都⑵菱形的对角线且每条对角线3、菱形的判定:⑴用定义判定⑵对角线互相垂直的是菱形⑶四条边都相等的是菱形【名师提醒:1、菱形既是对称图形,也是对称图形,它有条对称轴,分别是2、菱形被对角线分成四个全等的三角形和两对全等的三角形3、菱形的面积可以用平行四边形面积公式计算,也可以用两对角线积的来计算4、菱形常见题目是内角为1200或600时,利用等边三角形或直角三角形的相关知识解决的题目】三、正方形:1、定义:有一组邻边相等的是正方形,或有一个角是直角的是正方形2、性质:⑴正方形四个角都都是角,⑵正方形四边条都⑶正方形两对角线、且每条对角线平分一组内角3、判定:⑴先证是矩形,再证⑵先证是菱形,再证【名师提醒:1、菱形、正方形具有平行四边形的所有性质,正方形具有以上特殊四边形的所有性质。
这四者之间的关系可表示为:2、正方形也既是对称图形,又是对称图形,有条对称轴3、几种特殊四边形的性质和判定都是从、、三个方面来看的,要注意它们的区别和联系】【重点考点例析】点评:本题考查了矩形的对边相等,四个角都是直角的性质,锐角三角函数,勾股定理的应用,根据正切值设出未知数并表示出图形中的各线段是解题的关键,也是本题的难点. 对应训练A .12B .3C .23D .2考点二:和菱形有关的对角线、周长、面积的计算问题 AC :BD=1:2,则AO :BO= ,菱形ABCD 的面积S= .凉山州点评:本题考查了菱形性质和勾股定理,注意:菱形的对角线互相垂直平分,菱形的四条边对应训练2.(2013•凉山州)如图,菱形ABCD 中,∠B=60°,AB=4,则以AC 为边长的正方形ACEF 的周长为( )A .14B .15C .16D .17CF的长.对应训练3.(2013•三明)如图①,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.(1)求证:△BCP≌△DCP;(2)求证:∠DPE=∠ABC;(3)把正方形ABCD改为菱形,其它条件不变(如图②),若∠ABC=58°,则∠DPE= 度.考点四:四边形综合性题目点评:本题是运动型几何综合题,考查了相似三角形、全等三角形、正方形、等腰三角形、命题证明等知识点.解题要点是:(1)明确动点的运动过程;(2)明确运动过程中,各组成线段、三角形之间的关系;(3)运用分类讨论的数学思想,避免漏解.对应训练4.(2013•营口)如图1,△ABC为等腰直角三角形,∠ACB=90°,F是AC边上的一个动点(点F与A、C不重合),以CF为一边在等腰直角三角形外作正方形CDEF,连接BF、AD.(1)①猜想图1中线段BF、AD的数量关系及所在直线的位置关系,直接写出结论;②将图1中的正方形CDEF,绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图2、图3的情形.图2中BF交AC于点H,交AD于点O,请你判断①中得到的结论是否仍然成立,并选取图2证明你的判断.(2)将原题中的等腰直角三角形ABC改为直角三角形ABC,∠ACB=90°,正方形CDEF 改为矩形CDEF,如图4,且AC=4,BC=3,CD=43,CF=1,BF交AC于点H,交AD 于点O,连接BD、AF,求BD2+AF2的值.【聚焦山东中考】1.(2013•威海)如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是()A.BC=AC B.CF⊥BF C.BD=DF D.AC=BF枣庄2.(2013•枣庄)如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC,以DE为边作正方形DEFG,点G在边CD上,则DG的长为()A B.C D3.(2013•临沂)如图,菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则△AEF的面积是.烟台4.(2013•烟台)如图,正方形ABCD的边长为4,点E在BC上,四边形EFGB也是正方形,以B为圆心,BA长为半径画»AC,连结AF,CF,则图中阴影部分面积为.其中正确的序号是(把你认为正确的都填上).6.(2013•济宁)如图1,在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE.(1)求证:AF=BE;(2)如图2,在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?并说明理由.7.(2013•青岛)已知:如图,在矩形ABCD中,M,N分别是边AD、BC的中点,E,F 分别是线段BM,CM的中点.(1)求证:△ABM≌△DCM;(2)判断四边形MENF是什么特殊四边形,并证明你的结论;(3)当AD:AB= 时,四边形MENF是正方形(只写结论,不需证明)8.(2013•淄博)矩形纸片ABCD中,AB=5,AD=4.(1)如图1,四边形MNEF是在矩形纸片ABCD中裁剪出的一个正方形.你能否在该矩形中裁剪出一个面积最大的正方形,最大面积是多少?说明理由;(2)请用矩形纸片ABCD剪拼成一个面积最大的正方形.要求:在图2的矩形ABCD中画出裁剪线,并在网格中画出用裁剪出的纸片拼成的正方形示意图(使正方形的顶点都在网格的格点上).9.(2013•济南)(1)如图1,已知△ABC,以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接BE,CD,请你完成图形,并证明:BE=CD;(尺规作图,不写做法,保留作图痕迹);(2)如图2,已知△ABC,以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE,CD,BE与CD有什么数量关系?简单说明理由;(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:如图3,要测量池塘两岸相对的两点B,E的距离,已经测得∠ABC=45°,∠CAE=90°,AB=BC=100米,AC=AE,求BE的长.【备考真题过关】一、选择题1.(2013•铜仁地区)下列命题中,真命题是()A.对角线相等的四边形是矩形B.对角线互相垂直的四边形是菱形C.对角线互相平分的四边形是平行四边形D.对角线互相垂直平分的四边形是正方形2.(2013•宜宾)矩形具有而菱形不具有的性质是()A.两组对边分别平行B.对角线相等C.对角线互相平分D.两组对角分别相等3.(2013•随州)如图,在菱形ABCD中,∠BAD=120°.已知△ABC的周长是15,则菱形ABCD的周长是()A.25 B.20 C.15 D.10重庆4.(2013•重庆)如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为()A.6cm B.4cm C.2cm D.1cm 5.(2013•南充)如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是()A.12 B.24 C.D.•巴中6.(2013•巴中)如图,菱形ABCD的两条对角线相交于O,若AC=6,BD=4,则菱形ABCD 的周长是()A.24 B.16 C.D.7.(2013•茂名)如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=2,则AC的长是()A.2 B.4 C.2 D.8.(2013•成都)如图,将矩形ABCD沿对角线BD折叠,使点C和点C′重合,若AB=2,则C′D的长为()A.1 B.2 C.3 D.4茂名9.(2013•包头)如图,四边形ABCD和四边形AEFC是两个矩形,点B在EF边上,若矩形ABCD和矩形AEFC的面积分别是S1、S2的大小关系是()A.S1>S2B.S1=S2C.S1<S2D.3S1=2S2扬州10.(2013•扬州)如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC 于点F,垂足为E,连接DF,则∠CDF等于()A.50°B.60°C.70°D.80°11.(2013•绵阳)如图,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于点H,且DH与AC交于G,则GH=()A.2825cm B.2120cm C.2815cm D.2521cm雅安12.(2013•雅安)如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.其中正确结论有()个.A.2 B.3 C.4 D.5二、填空题13.(2013•宿迁)如图,一个平行四边形的活动框架,对角线是两根橡皮筋.若改变框架的形状,则∠α也随之变化,两条对角线长度也在发生改变.当∠α为度时,两条对角线长度相等.无锡∠B=60°,则菱形的面积为.攀枝花3则tanE= .苏州19.(2013•苏州)如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后交AB于E,若BC=4,△AOE的面积为5,则sin∠BOE的值为.北京21.(2013•北京)如图,O是矩形ABCD的对角线AC的中点,M是AD的中点.若AB=5,舟山23.(2013•舟山)如图,正方形ABCD的边长为3,点E,F分别在边AB、BC上,AE=BF=1,点P从点C运动到点D时,线段O1O2中点G的运动路径的长是.荆州25.(2013•荆州)如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得三、解答题26.(2013•南通)如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE.求证:四边形BCDE是矩形.27.(2013•广州)如图,四边形ABCD是菱形,对角线AC与BD相交于O,AB=5,AO=4,求BD的长.28.(2013•厦门)如图所示,在正方形ABCD中,点G是边BC上任意一点,DE⊥AG,垂足为E,延长DE交AB于点F.在线段AG上取点H,使得AG=DE+HG,连接BH.求证:∠ABH=∠CDE.29.(2013•黔东南州)如图,在正方形ABCD中,点M是对角线BD上的一点,过点M作ME∥CD交BC于点E,作MF∥BC交CD于点F.求证:AM=EF.30.(2013•铁岭)如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.(1)求证:四边形AEBD是矩形;(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.31.(2013•南宁)如图,在菱形ABCD中,AC为对角线,点E、F分别是边BC、AD的中点.(1)求证:△ABE≌△CDF;(2)若∠B=60°,AB=4,求线段AE的长.32.(2013•贵阳)已知:如图,在菱形ABCD中,F是BC上任意一点,连接AF交对角线BD于点E,连接EC.(1)求证:AE=EC;(2)当∠ABC=60°,∠CEF=60°时,点F在线段BC上的什么位置?说明理由.(2)若点E是AB的中点,设∠DCF=α,求sinα的值.35.(2013•绥化)已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B,C重合).以AD为边做正方形ADEF,连接CF(1)如图1,当点D在线段BC上时.求证CF+CD=BC;(2)如图2,当点D在线段BC的延长线上时,其他条件不变,请直接写出CF,BC,CD 三条线段之间的关系;(3)如图3,当点D在线段BC的反向延长线上时,且点A,F分别在直线BC的两侧,其他条件不变;①请直接写出CF,BC,CD三条线段之间的关系;②若正方形ADEF的边长为22,对角线AE,DF相交于点O,连接OC.求OC的长度.36.(2013•盘锦)如图,正方形ABCD的边长是3,点P是直线BC上一点,连接PA,将线段PA绕点P逆时针旋转90°得到线段PE,在直线BA上取点F,使BF=BP,且点F与点E在BC同侧,连接EF,CF.(1)如图 ,当点P在CB延长线上时,求证:四边形PCFE是平行四边形;(2)如图 ,当点P在线段BC上时,四边形PCFE是否还是平行四边形,说明理由;(3)在(2)的条件下,四边形PCFE的面积是否有最大值?若有,请求出面积的最大值及此时BP长;若没有,请说明理由.。
2025年中考数学总复习培优训第21课时 矩形、菱形、正方形

线 AC 于点 E.则点 E 的坐标为( B )
A. 1,52
B. (1,2)
C.. [2024 包头]如图,在矩形 ABCD 中,E,F 是边 BC 上两点,
且 BE=EF=FC,连接 DE,AF,DE 与 AF 相交于点 G,连接
BG.若 AB=4,BC=6,则 sin∠GBF 的值为( A )
课时对应练
又∵∠A=∠M=90°,∴△AHE≌△MFG.∴MF=AH=2. ∴S△FCG=12×2CG=CG. 若△FCG 的面积能等于 1,则 CG=1,∴DG=CD-CG=5. ∵DH=AD-AH=4,∴GH= DG2+DH2= 41. ∴EH=GH= 41.∴AE= EH2-AH2= 37. ∵AB=6< 37,∴点 E 不在线段 AB 上, ∴△FCG 的面积不能等于 1.
速度沿 OA,BC 向终点 A,C 移动. 当移动时间为 4 秒时,AC·EF
的值为( D )
A. 10
B. 9 10
C. 15
D. 30
课时对应练
9. 在菱形ABCD中,对角线AC,BD相交于点O,请添加一个条 件:∠__A__B_C_=__9_0_°_(_答__案__不__唯__一__) _,使得菱形ABCD为正方形.
课时对应练
12. [2023台州]如图,在矩形ABCD中,AB=4,AD=6.在边AD 上取一点E,使BE=BC,过点C作CF⊥BE,垂足为点F,则 BF的长为__2___5___.
课时对应练
13. [2024陕西改编]如图,正方形CEFG的顶点G在正方形ABCD 的边CD上,AF与DC交于点H,若AB=6,CE=2,则DH的 长为____3____.
课时对应练
19. [2024北京]如图,在正方形ABCD中,点E在AB上,AF⊥DE 于点F,CG⊥DE于点G.若AD=5,CG=4,则△AEF的面积 为___28_7____.
中考数学真题-矩形菱形正方形

矩形菱形正方形姓名:__________________ 班级:______________ 得分:_________________一、单选题1.(2021·四川成都市·中考真题)如图,四边形ABCD 是菱形,点E ,F 分别在,BC DC 边上,添加以下条件不能判定ABE ADF ≌的是( )A .BE DF =B .BAE DAF ∠=∠C .AE AD = D .AEB AFD ∠=∠2.(2021·四川遂宁市·中考真题)如图,在矩形ABCD 中,AB =5,AD =3,点E 为BC 上一点,把△CDE 沿DE 翻折,点C 恰好落在AB 边上的F 处,则CE 的长是( )A .1B .43C .32D .53 3.(2021·重庆中考真题)如图,正方形ABCD 的对角线AC ,BD 交于点O ,M 是边AD 上一点,连接OM ,过点O 做ON △OM ,交CD 于点N .若四边形MOND 的面积是1,则AB 的长为( )A .1B 2C .2D .224.(2021·四川凉山彝族自治州·中考真题)下列命题中,假命题是( )A .直角三角形斜边上的中线等于斜边的一半B .等腰三角形顶角的平分线,底边上的中线,底边上的高相互重合C .若AB BC =,则点B 是线段AC 的中点D .三角形三条边的垂直平分线的交点叫做这个三角形的外心5.(2021·四川泸州市·中考真题)下列命题是真命题的是( )A .对角线相等的四边形是平行四边形B .对角线互相平分且相等的四边形是矩形C .对角线互相垂直的四边形是菱形D .对角线互相垂直平分的四边形是正方形6.(2021·浙江温州市·中考真题)由四个全等的直角三角形和一个小正方形组成的大正方形ABCD 如图所示.过点D 作DF 的垂线交小正方形对角线EF 的延长线于点G ,连结CG ,延长BE 交CG 于点H .若2AE BE =,则CG BH 的值为( )A .32B .2C .3107D .3557.(2021·安徽中考真题)如图,在菱形ABCD 中,2AB =,120A ∠=︒,过菱形ABCD 的对称中心O 分别作边AB ,BC 的垂线,交各边于点E ,F ,G ,H ,则四边形EFGH 的周长为( )A .33+B .223+C .23+D .123+ 8.(2021·重庆中考真题)如图,把含30°的直角三角板PMN 放置在正方形ABCD 中,30PMN ∠=︒,直角顶点P 在正方形ABCD 的对角线BD 上,点M ,N 分别在AB 和CD 边上,MN 与BD 交于点O ,且点O 为MN 的中点,则AMP ∠的度数为( )A .60°B .65°C .75°D .80°9.(2021·四川乐山市·中考真题)如图,已知点P 是菱形ABCD 的对角线AC 延长线上一点,过点P 分别作AD 、DC 延长线的垂线,垂足分别为点E 、F .若120ABC ∠=︒,2AB =,则PE PF -的值为( )A .32B .3C .2D .5210.(2021·四川自贡市·中考真题)如图,在正方形ABCD 中,6AB =,M 是AD 边上的一点,:1:2AM MD =.将BMA △沿BM 对折至BMN △,连接DN ,则DN 的长是( )A .52B .58C .3D .5511.(2021·浙江绍兴市·中考真题)如图,菱形ABCD 中,60B ∠=︒,点P 从点B 出发,沿折线BC CD -方向移动,移动到点D 停止.在ABP △形状的变化过程中,依次出现的特殊三角形是( )A .直角三角形→等边三角形→等腰三角形→直角三角形B .直角三角形→等腰三角形→直角三角形→等边三角形C .直角三角形→等边三角形→直角三角形→等腰三角形D .等腰三角形→等边三角形→直角三角形→等腰三角形12.(2021·陕西中考真题)如图,在菱形ABCD 中,60ABC ∠=︒,连接AC 、BD ,则AC BD的值为( )A .12B .22C .32D .33二、填空题13.(2021·山东临沂市·中考真题)数学知识在生产和生活中被广泛应用,下列实例所应用的最主要的几何知识,说法正确的是___(只填写序号).△射击时,瞄准具的缺口、准星和射击目标在同一直线上,应用了“两点确定一条直线”;△车轮做成圆形,应用了“圆是中心对称图形”;△学校门口的伸缩门由菱形而不是其他四边形组成,应用了“菱形的对角线互相垂直平分”;△地板砖可以做成矩形,应用了“矩形对边相等”.14.(2021·四川泸州市·中考真题)如图,在边长为4的正方形ABCD 中,点E 是BC 的中点,点F 在CD 上,且CF =3BF ,AE ,BF 相交于点G ,则AGF 的面积是________.15.(2021·四川成都市·中考真题)如图,在矩形ABCD 中,4,8AB AD ==,点E ,F 分别在边,AD BC 上,且3AE =,按以下步骤操作:第一步,沿直线EF 翻折,点A 的对应点'A 恰好落在对角线AC 上,点B 的对应点为'B ,则线段BF 的长为_______;第二步,分别在,'EF A B ¢上取点M ,N ,沿直线MN 继续翻折,使点F 与点E 重合,则线段MN 的长为_______.16.(2021·江苏扬州市·中考真题)如图,在ABC 中,AC BC =,矩形DEFG 的顶点D 、E 在AB 上,点F 、G 分别在BC 、AC 上,若4CF =,3BF =,且2DE EF =,则EF 的长为________.17.(2021·云南中考真题)已知ABC 的三个顶点都是同一个正方形的顶点,ABC ∠的平分线与线段AC 交于点D .若ABC 的一条边长为6,则点D 到直线AB 的距离为__________.18.(2021·山东泰安市·中考真题)如图,将矩形纸片ABCD 折叠(AD AB >),使AB 落在AD 上,AE 为折痕,然后将矩形纸片展开铺在一个平面上,E 点不动,将BE 边折起,使点B 落在AE 上的点G 处,连接DE ,若DE EF =,2CE =,则AD 的长为________.19.(2021·江苏连云港市·中考真题)如图,菱形ABCD 的对角线AC 、BD 相交于点O ,OE AD ⊥,垂足为E ,8AC =,6BD =,则OE 的长为______.20.(2021·四川南充市·中考真题)如图,点E 是矩形ABCD 边AD 上一点,点F ,G ,H 分别是BE ,BC ,CE 的中点,3AF =,则GH 的长为________.21.(2021·四川凉山彝族自治州·中考真题)菱形ABCD 中,对角线10, 24AC BD ==,则菱形的高等于___________.22.(2021·重庆中考真题)如图,在菱形ABCD 中,对角线12AC =,16BD =,分别以点A ,B ,C ,D 为圆心,12AB 的长为半径画弧,与该菱形的边相交,则图中阴影部分的面积为__________.(结果保留π)23.(2021·四川遂宁市·中考真题)如图,正方形ABCD 中,点E 是CD 边上一点,连结BE ,以BE 为对角线作正方形BGEF ,边EF 与正方形ABCD 的对角线BD 相交于点H ,连结AF ,有以下五个结论:△ABF DBE ∠=∠;△ABF DBE ∽;△AF BD ⊥;△22BG BH BD =;△若:1:3CE DE =,则:17:16BH DH =,你认为其中正确是_____(填写序号)24.(2021·湖北十堰市·中考真题)如图,O 是矩形ABCD 的对角线AC 的中点,M 是AD 的中点,若AB=5,AD=12,则四边形ABOM 的周长为_______.25.(2021·浙江绍兴市·中考真题)图1是一种矩形时钟,图2是时钟示意图,时钟数字2的刻度在矩形ABCD 的对角线BD 上,时钟中心在矩形ABCD 对角线的交点O 上.若30cm AB =,则BC 长为_______cm (结果保留根号).26.(2021·湖北黄冈市·中考真题)如图,正方形ABCD 中,1AB =,连接AC ,ACD ∠的平分线交AD 于点E ,在AB 上截取AF DE =,连接DF ,分别交CE ,AC 于点G ,H ,点P 是线段GC 上的动点,PQ AC ⊥于点Q ,连接PH .下列结论:△CE DF ⊥;△DE DC AC +=;△3EA =;△PH PQ +的最小值是22.其中所有正确结论的序号是_____.27.(2021·湖南衡阳市·中考真题)如图1,菱形ABCD的对角线AC与BD相交于点O,P、Q两点同时从---,点Q的运O点出发,以1厘米/秒的速度在菱形的对角线及边上运动.点P的运动路线为O A D O ---.设运动的时间为x秒,P、Q间的距离为y厘米,y与x的函数关系的图象大致如动路线为O C B O-段上运动且P、Q两点间的距离最短时,P、Q两点的运动路程之和为__________图2所示,当点P在A D厘米.28.(2021·湖南株洲市·中考真题)《蝶几图》是明朝人戈汕所作的一部组合家具的设计图(蜨,同“蝶”),它的基本组件为斜角形,包括长斜两只、右半斜两只、左半斜两只、闺一只、小三斜四只、大三斜两只,△和CBD为“大三斜”组共十三只(图△中的“様”和“隻”为“样”和“只”).图△为某蝶几设计图,其中ABD件(“一様二隻”的大三斜组件为两个全等的等腰直角三角形),已知某人位于点P处,点P与点A关于直线∠=︒,则D C PADQDQ对称,连接CP、DP.若24∠=___________度.29.(2021·江苏苏州市·中考真题)如图,四边形ABCD 为菱形,70ABC ∠=︒,延长BC 到E ,在DCE ∠内作射线CM ,使得15ECM ∠=︒,过点D 作DF CM ⊥,垂足为F ,若5DF =,则对角线BD 的长为______.(结果保留根号)30.(2021·浙江金华市·中考真题)如图,在平面直角坐标系中,有一只用七巧板拼成的“猫”,三角形△的边BC 及四边形△的边CD 都在x 轴上,“猫”耳尖E 在y 轴上.若“猫”尾巴尖A 的横坐标是1,则“猫”爪尖F 的坐标是___________.三、解答题31.(2021·四川广安市·中考真题)如图,四边形ABCD 是菱形,点E 、F 分别在边AB 、AD 的延长线上,且BE DF =.连接CE 、CF . 求证:CE CF =.32.(2021·江苏扬州市·中考真题)如图,在ABC 中,BAC ∠的角平分线交BC 于点D ,//,//DE AB DF AC .(1)试判断四边形AFDE 的形状,并说明理由;(2)若90BAC ∠=︒,且22AD =,求四边形AFDE 的面积.33.(2021·浙江金华市·中考真题)已知:如图,矩形ABCD 的对角线,AC BD 相交于点O ,120,2BOC AB ∠=︒=.(1)求矩形对角线的长.(2)过O 作OE AD ⊥于点E ,连结BE .记ABE α∠=,求tan α的值.34.(2021·江苏连云港市·中考真题)如图,点C 是BE 的中点,四边形ABCD 是平行四边形. (1)求证:四边形ACED 是平行四边形;(2)如果AB AE =,求证:四边形ACED 是矩形.35.(2021·四川凉山彝族自治州·中考真题)如图,在四边形ABCD 中,90ADC B ∠=∠=︒,过点D 作DE AB ⊥于E ,若DE BE =.(1)求证:DA DC =;(2)连接AC 交DE 于点F ,若30,6ADE AD ∠=︒=,求DF 的长.36.(2021·四川遂宁市·中考真题)如图,在平行四边形ABCD 中,对角线AC 与BD 相交于点O ,过点O 的直线EF 与BA 、DC 的延长线分别交于点E 、F . (1)求证:AE =CF ;(2)请再添加一个条件,使四边形BFDE 是菱形,并说明理由.37.(2021·四川自贡市·中考真题)如图,在矩形ABCD中,点E、F分别是边AB、CD的中点.求证:DE=BF.⨯的正方形网格中,网格线的交点称为格点,B在格点上,38.(2021·浙江嘉兴市·中考真题)如图,在77每一个小正方形的边长为1.(1)以AB为边画菱形,使菱形的其余两个顶点都在格点上(画出一个即可).(2)计算你所画菱形的面积.∠是锐角,E是BC边上的动点,将射线39.(2021·浙江丽水市·中考真题)如图,在菱形ABCD中,ABCAE 绕点A 按逆时针方向旋转,交直线CD 于点F .(1)当AE BC EAF ABC ,^Ð=Ð时, △求证:AE AF =;△连结BD EF ,,若25EF BD =,求ABCDAEF菱形SS的值;(2)当12EAF BAD ∠=∠时,延长BC 交射线AF 于点M ,延长DC 交射线AE 于点N ,连结AC MN ,,若42AB AC ==,,则当CE 为何值时,AMN 是等腰三角形.40.(2021·安徽中考真题)学生到工厂劳动实践,学习制作机械零件.零件的截面如图阴影部分所示,已知四边形AEFD 为矩形,点B 、C 分别在EF 、DF 上,90ABC ∠=︒,53BAD ∠=︒,10AB cm =,6BC cm =.求零件的截面面积.参考数据:sin 530.80︒≈,cos530.60︒≈.41.(2021·四川眉山市·中考真题)如图,在等腰直角三角形ABC 中,90ACB ∠=︒,25AC BC ==,边长为2的正方形DEFG 的对角线交点与点C 重合,连接AD ,BE . (1)求证:≌ACD BCE V V ;(2)当点D 在ABC 内部,且90ADC ∠=︒时,设AC 与DG 相交于点M ,求AM 的长;(3)将正方形DEFG 绕点C 旋转一周,当点A 、D 、E 三点在同一直线上时,请直接写出AD 的长.42.(2021·浙江嘉兴市·中考真题)小王在学习浙教版九上课本第72页例2后,进一步开展探究活动:将一个矩形ABCD 绕点A 顺时针旋转()090αα︒<≤︒,得到矩形'''AB C D[探究1]如图1,当90α=︒时,点'C 恰好在DB 延长线上.若1AB =,求BC 的长.[探究2]如图2,连结'AC ,过点'D 作'//'D M AC 交BD 于点M .线段'D M 与DM 相等吗?请说明理由.[探究3]在探究2的条件下,射线DB 分别交'AD ,'AC 于点P ,N (如图3),MN ,PN 存在一定的数量关系,并加以证明.。
中考数学热身 矩形、菱形、正方形(含解析)-人教版初中九年级全册数学试题

矩形、菱形、正方形一、填空题1.矩形的两条对角线的一个交角为60°,两条对角线的长度的和为8cm,则这个矩形的一条较长边为cm.2.边长为5cm的菱形,一条对角线长是6cm,则另一条对角线的长是cm.3.正方形的一条对角线长为2,则它的面积为.4.已知菱形的两对角线长分别为6cm和8cm,则菱形的面积为cm2.二、选择题5.下列命题中,真命题是()A.两条对角线垂直的四边形是菱形B.对角线垂直且相等的四边形是正方形C.两条对角线相等的四边形是矩形D.两条对角线相等的平行四边形是矩形6.平行四边形ABCD中,AC、BD是两条对角线,如果添加一个条件,即可推出平行四边形ABCD是矩形,那么这个条件是()A.AB=BC B.AC=BD C.AC⊥BD D.AB⊥BD7.如图,把矩形ABCD沿EF对折后使两部分重合,若∠1=50°,则∠AEF=()A.110°B.115°C.120°D.130°8.如图,沿虚线EF将平行四边形ABCD剪开,则得到的四边形ABFE是()A.梯形 B.平行四边形C.矩形 D.菱形三、解答题9.如图,菱形的对角线BD,AC的长分别是6和8,求菱形的周长与面积.10.如图,在四边形ABCD中,点E是线段AD上的任意一点(E与A,D不重合),G,F,H分别是BE,BC,CE的中点.(1)证明:四边形EGFH是平行四边形;(2)在(1)的条件下,若EF⊥BC,且EF=BC,证明:平行四边形EGFH是正方形.11.如图,菱形ABCD中,BE⊥AD,BF⊥CD,E、F为垂足,AE=ED,求∠EBF的度数.12.如图,四边形ABCD是矩形,E是AB上一点,且DE=AB,过C作CF⊥DE,垂足为F.(1)猜想:AD与CF的大小关系;(2)请证明上面的结论.13.已知:如图,D是△ABC的BC边上的中点,DE⊥AC,DF⊥AB,垂足分别是E、F,且BF=CE.(1)求证:△ABC是等腰三角形;(2)当∠A=90°时,试判断四边形AFDE是怎样的四边形,证明你的结论.14.如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.(1)求证:EO=FO;(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.矩形、菱形、正方形参考答案与试题解析一、填空题1.矩形的两条对角线的一个交角为60°,两条对角线的长度的和为8cm,则这个矩形的一条较长边为2cm.【考点】矩形的性质.【分析】根据矩形的性质推出OA=OB,证出等边△OAB,求出BA,根据勾股定理求出BC即可得到答案.【解答】解:∵四边形ABCD是矩形,∴AC=BD,OA=OC,OD=OB,∴OA=OB,∵∠AOB=60°,∴△AOB是等边三角形,∴OA=OB=AB=AC=2(cm),∵四边形ABCD是矩形,∴AB=CD=2cm,∠ABC=90°,在△ABC中,由勾股定理得:BC===2(cm),∴AD=BC=2(cm).故答案是:2.【点评】本题主要考查对矩形的性质,等边三角形的性质和判定,勾股定理等知识点的理解和掌握,能求出AB的长是解此题的关键.2.边长为5cm的菱形,一条对角线长是6cm,则另一条对角线的长是8 cm.【考点】勾股定理;菱形的性质.【专题】压轴题.【分析】根据菱形的对角线互相垂直平分,得已知对角线的一半是3.根据勾股定理,得要求的对角线的一半是4,则另一条对角线的长是8.【解答】解:在菱形ABCD中,AB=5,AC=6,因为对角线互相垂直平分,所以∠AOB=90°,AO=3,在RT△AOB中,BO==4,∴BD=2BO=8.【点评】注意菱形对角线的性质:菱形的对角线互相垂直平分.熟练运用勾股定理.3.正方形的一条对角线长为2,则它的面积为 2 .【考点】正方形的性质.【专题】计算题.【分析】根据正方形的性质利用勾股定理可求得其边长,从而就不难求得其面积.【解答】解:由题意得,正方形的边长为,故面积为2.故答案为2.【点评】主要考查到正方形的性质和面积的求法.要注意:正方形的对角线和正方形的两条相邻的边构成等腰直角三角形.4.已知菱形的两对角线长分别为6cm和8cm,则菱形的面积为24 cm2.【考点】菱形的性质.【专题】计算题.【分析】根据菱形的面积等于两对角线乘积的一半求得其面积即可.【解答】解:由已知得,菱形的面积等于两对角线乘积的一半即:6×8÷2=24cm2.故答案为:24.【点评】此题主要考查菱形的面积等于两条对角线的积的一半.二、选择题5.下列命题中,真命题是()A.两条对角线垂直的四边形是菱形B.对角线垂直且相等的四边形是正方形C.两条对角线相等的四边形是矩形D.两条对角线相等的平行四边形是矩形【考点】菱形的判定;矩形的判定;正方形的判定.【分析】本题要求熟练掌握平行四边形、菱形、矩形、正方形的性质以及之间的相互联系.【解答】解:A、两条对角线垂直并且相互平分的四边形是菱形,故选项A错误;B、对角线垂直且相等的平行四边形是正方形,故选项B错误;C、两条对角线相等的平行四边形是矩形,故选项C错误;D、根据矩形的判定定理,两条对角线相等的平行四边形是矩形,为真命题,故选项D正确;故选D.【点评】本题考查的是普通概念,熟练掌握基础的东西是深入研究的必要准备.6.平行四边形ABCD中,AC、BD是两条对角线,如果添加一个条件,即可推出平行四边形ABCD是矩形,那么这个条件是()A.AB=BC B.AC=BD C.AC⊥BD D.AB⊥BD【考点】矩形的判定;平行四边形的性质.【专题】证明题;压轴题.【分析】根据对角线相等的平行四边形是矩形判断.【解答】解:A、是邻边相等,可得到平行四边形ABCD是菱形,故不正确;B、是对角线相等,可推出平行四边形ABCD是矩形,故正确;C、是对角线互相垂直,可得到平行四边形ABCD是菱形,故不正确;D、无法判断.故选B.【点评】本题主要考查的是矩形的判定定理.但需要注意的是本题的知识点是关于各个图形的性质以及判定.7.如图,把矩形ABCD沿EF对折后使两部分重合,若∠1=50°,则∠AEF=()A.110°B.115°C.120°D.130°【考点】翻折变换(折叠问题).【专题】压轴题.【分析】根据折叠的性质,对折前后角相等.【解答】解:根据题意得:∠2=∠3,∵∠1+∠2+∠3=180°,∴∠2=(180°﹣50°)÷2=65°,∵四边形ABCD是矩形,∴AD∥BC,∴∠AEF+∠2=180°,∴∠AEF=180°﹣65°=115°.故选B.【点评】本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.8.如图,沿虚线EF将平行四边形ABCD剪开,则得到的四边形ABFE是()A.梯形 B.平行四边形C.矩形 D.菱形【考点】剪纸问题.【专题】操作型.【分析】对于此类问题,学生只要亲自动手操作,答案就会很直观地呈现.【解答】解:由于EF的位置是不确定的,只能得到所求的四边形的一组对边平行,所以是梯形.故选A.【点评】本题主要考查学生的动手能力及空间想象能力.三、解答题9.如图,菱形的对角线BD,AC的长分别是6和8,求菱形的周长与面积.【考点】菱形的性质.【分析】根据菱形的对角线可以求得菱形ABCD的面积,根据菱形对角线互相垂直平分的性质,可以求得BO=OD,AO=OC,在Rt△AOB中,根据勾股定理可以求得AB的长,即可求菱形ABCD的周长.【解答】解:菱形的对角线BD,AC的长分别是6和8,则菱形的面积为×6×8=24,菱形对角线互相垂直平分,∴BO=OD=3,AO=OC=4,∴AB==5,故菱形的周长为20,答:菱形的周长为20,面积为24.【点评】本题考查了菱形面积的计算,考查了勾股定理在直角三角形中的运用,考查了菱形各边长相等的性质,本题中根据勾股定理计算AB的长是解题的关键.10.如图,在四边形ABCD中,点E是线段AD上的任意一点(E与A,D不重合),G,F,H分别是BE,BC,CE的中点.(1)证明:四边形EGFH是平行四边形;(2)在(1)的条件下,若EF⊥BC,且EF=BC,证明:平行四边形EGFH是正方形.【考点】正方形的判定;三角形中位线定理;平行四边形的判定.【专题】证明题.【分析】通过中位线定理得出GF∥EH且GF=EH,所以四边形EGFH是平行四边形;当添加了条件EF ⊥BC,且EF=BC后,通过对角线相等且互相垂直平分(EF⊥GH,且EF=GH)就可证明是正方形.【解答】证明:(1)∵G,F分别是BE,BC的中点,∴GF∥EC且GF=EC.又∵H是EC的中点,EH=EC,∴GF∥EH且GF=EH.∴四边形EGFH是平行四边形.(2)连接GH,EF.∵G,H分别是BE,EC的中点,∴GH∥BC且GH=BC.又∵EF⊥BC且EF=BC,又∵EF⊥BC,GH是三角形EBC的中位线,∴GH∥BC,∴EF⊥GH,又∵EF=GH.∴平行四边形EGFH是正方形.【点评】主要考查了平行四边形的判定和正方形的性质.正方形对角线的特点是:对角线互相垂直;对角线相等且互相平分;每条对角线平分一组对角.11.如图,菱形ABCD中,BE⊥AD,BF⊥CD,E、F为垂足,AE=ED,求∠EBF的度数.【考点】菱形的性质.【专题】计算题.【分析】首先连接BD,根据菱形的四条边都相等,可得AB=BC=CD=AD;又由BE⊥AD,AE=ED,可得AB=AD=BD,所以∠A=60°,可得∠ADC=120°,即可得∠EBF的度数.【解答】解:连接BD,∵BE⊥AD,AE=ED,∴AB=BD,∵四边形ABCD是菱形,∴AB=BC=CD=AD,AD∥BC,AB∥CD,∴AB=AD=BD,∴∠A=60°,∴∠ADC=120°,∵BE⊥AD,BF⊥CD,∴∠BED=∠BFD=90°,∴∠EBF=60°.【点评】此题考查了菱形的性质:菱形的四条边都相等.还考查了线段垂直平分线的性质.此题比较简单,解题要细心.12.如图,四边形ABCD是矩形,E是AB上一点,且DE=AB,过C作CF⊥DE,垂足为F.(1)猜想:AD与CF的大小关系;(2)请证明上面的结论.【考点】矩形的性质;全等三角形的判定与性质.【专题】探究型.【分析】由全等三角形的判定定理直接可证△ADE≌△FCD,即证AD=CF.【解答】解:(1)AD=CF.(2分)(2)证明:∵四边形ABCD是矩形,∴CD∥AE,AB=CD,∴∠AED=∠FDC,∵DE=AB,∴DE=AB=CD.又∵CF⊥DE,∴∠CFD=∠A=90°.(4分)∴△ADE≌△FCD(AAS).(5分)∴AD=CF.(6分)【点评】三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.13.已知:如图,D是△ABC的BC边上的中点,DE⊥AC,DF⊥AB,垂足分别是E、F,且BF=CE.(1)求证:△ABC是等腰三角形;(2)当∠A=90°时,试判断四边形AFDE是怎样的四边形,证明你的结论.【考点】全等三角形的判定与性质;正方形的判定.【专题】几何综合题.【分析】先利用HL判定Rt△BDF≌Rt△CDE,从而得到∠B=∠C,即△ABC是等腰三角形;由已知可证明它是矩形,因为有一组邻边相等即可得到四边形AFDE是正方形.【解答】(1)证明:∵DE⊥AC,DF⊥AB,∴∠BFD=∠CED=90°,又∵,∴Rt△BDF≌Rt△CDE(HL),∴∠B=∠C.∴△ABC是等腰三角形;(2)解:四边形AFDE是正方形.证明:∵∠A=90°,DE⊥AC,DF⊥AB,∴四边形AFDE是矩形,又∵Rt△BDF≌Rt△CDE,∴DF=DE,∴四边形AFDE是正方形.【点评】此题主要考查学生对全等三角形的判定和性质及正方形的判定方法的掌握情况.判别一个四边形为正方形主要根据正方形的概念,途经有两种:①先说明它是矩形,再说明有一组邻边相等;②先说明它是菱形,再说明它有一个角为直角.14.如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.(1)求证:EO=FO;(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.【考点】矩形的判定.【专题】几何综合题.【分析】(1)根据平行线性质和角平分线性质,以及由平行线所夹的内错角相等易证.(2)根据矩形的判定方法,即一个角是直角的平行四边形是矩形可证.【解答】(1)证明:∵CE平分∠ACB,∴∠1=∠2,又∵MN∥BC,∴∠1=∠3,∴∠3=∠2,∴EO=CO,同理,FO=CO,∴EO=FO.(2)解:当点O运动到AC的中点时,四边形AECF是矩形.理由:∵EO=FO,点O是AC的中点.∴四边形AECF是平行四边形,∵CF平分∠BCA的外角,∴∠4=∠5,又∵∠1=∠2,∴∠2+∠4=×180°=90°.即∠ECF=90°,∴四边形AECF是矩形.【点评】本题涉及矩形的判定定理,解答此类题的关键是要突破思维定势的障碍,运用发散思维,多方思考,探究问题在不同条件下的不同结论,挖掘它的内在联系,向“纵、横、深、广”拓展,从而寻找出添加的条件和所得的结论.。
中考数学试题-矩形、菱形、正方形试题及答案
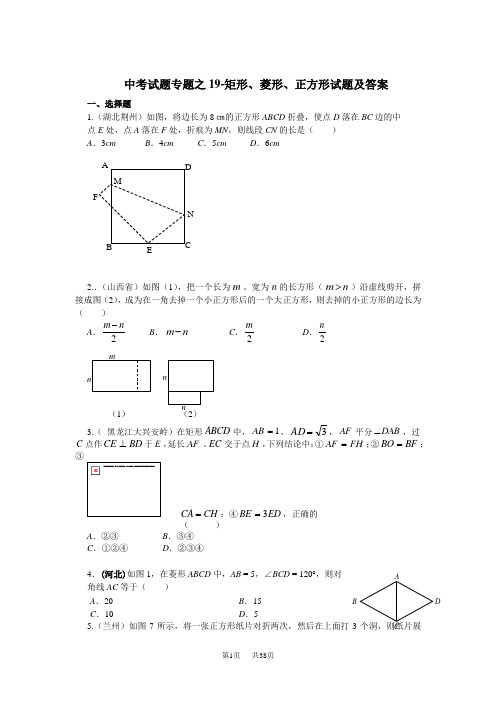
中考试题专题之19-矩形、菱形、正方形试题及答案一、选择题1.(湖北荆州)如图,将边长为8㎝的正方形ABCD 折叠,使点D 落在BC 边的中 点E 处,点A 落在F 处,折痕为MN ,则线段CN 的长是( ) A .3cm B .4cm C .5cm D .6cm2..(山西省)如图(1),把一个长为、宽为的长方形()沿虚线剪开,拼接成图(2),成为在一角去掉一个小正方形后的一个大正方形,则去掉的小正方形的边长为( ) A .B .C .D .3.( 黑龙江大兴安岭)在矩形ABCD 中,1=AB ,3=AD ,AF 平分DAB ∠,过C 点作BD CE ⊥于E ,延长AF 、EC 交于点H ,下列结论中:①FH AF =;②BF BO =;③CH CA =;④ED BE 3=,正确的( ) A .②③ B .③④ C .①②④D .②③④4.(河北)如图1,在菱形ABCD 中,AB = 5,∠BCD = 120°,则对 角线AC 等于( ) A .20B .15C .10D .55.(兰州)如图7所示,将一张正方形纸片对折两次,然后在上面打3个洞,则纸片展m n m n >2m n -m n -2m2nmnnn (2)(1)N M FEBABAC D开后是6.(济南)如图,矩形ABCD 中,35AB BC ==,.过对角线交点O 作OE AC ⊥交AD 于E ,则AE 的长是( ) A .1.6 B .2.5 C .3 D .3.47.(凉山州)如图,将矩形ABCD 沿对角线BD 折叠,使C 落在C '处,BC '交AD 于E ,则下列结论不一定成立的是( )A .AD BC '=B .EBD EDB ∠=∠C .ABE CBD △∽△ D .sin AEABE ED∠=8.(济宁市)“赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形.如图,是一“赵爽弦图”飞镖板,其直角三角形的两条直角边的长分别是2和4.小明同学距飞镖板一定距离向飞镖板投掷飞镖(假设投掷的飞镖均扎在飞镖板上), 则投掷一次飞镖扎在中间小正方形区域(含边线)的概率是 A .12 B . 14 C . 15D .9.(衡阳市) 如图,菱形ABCD 的周长为20cm ,DE ⊥AB ,垂足为E ,54A cos =,则下列结论中正确 的个数为( )①DE =3cm ; ②EB =1cm ; ③2A BCD 15S cm =菱形. A .3个B .2个C .1个D .0个C D C 'A BEA .B .C .D .10.(衡阳市)如图,矩形纸片ABCD 中,AB =4,AD =3,折叠纸片使AD 边与对角线BD 重合,折痕为DG ,则AG 的长为( ) A .1 B .34 C .23D .211.(广西南宁)如图2,将一个长为10cm ,宽为8cm 的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为( ) A .210cmB .220cmC .240cmD .280cm12.(宁波市)如图,菱形ABCD 中,对角线AC 、BD 相交于点O ,M 、N 分别是边AB 、AD 的中点,连接OM 、ON 、MN ,则下列叙述正确的是( ) A .△AOM 和△AON 都是等边三角形 B .四边形MBON 和四边形MODN 都是菱形C .四边形AMON 与四边形ABCD 是位似图形 D .四边形MBCO 和四边形NDCO 都是等腰梯形AB CDEA ′G DB CAABCD图2DBCANM O13.(桂林百色)如图,正方形ABCD 的边长为2,将长为2的线段QR 的两端放 在正方形的相邻的两边上同时滑动.如果Q 点从A 点出发,沿 图中所示方向按A →B →C →D →A 滑动到A 止,同时点R 从B 点 出发,沿图中所示方向按B →C →D →A →B 滑动到B 止,在这个 过程中,线段QR 的中点M 所经过的路线围成的图形的面积为 ( ).A .2B .C .D .14.(河池)已知菱形的边长和一条对角线的长均为2cm ,则菱形的面积为( ) A . 23cmB . 24cmC .2 D .215.(杭州市)如图,在菱形ABCD 中,∠A =110°,E ,F 分别是边AB 和BC 的中点,EP ⊥CD 于点P ,则∠FPC =( ) A .35° B .45° C .50° D .55°16.(义乌)如图,一块砖的外侧面积为x ,那么图中残留部分墙面的面积为 A .4x A .12x A .8x A .16x17.(台湾) 如图(八),长方形ABCD 中,E 点在上,且平分∠BAC 。
2024成都中考数学复习专题 矩形、菱形、正方形的性质与判定(含答案)

2024成都中考数学复习专题矩形、菱形、正方形的性质与判定基础题1. (2023上海)在四边形ABCD中,AD∥BC,AB=C D.下列说法能使四边形ABCD为矩形的是()A. AB∥CDB. AD=BCC. ∠A=∠BD. ∠A=∠D2. (2023自贡)如图,边长为3的正方形OBCD两边与坐标轴正半轴重合,点C的坐标是()A. (3,-3)B. (-3,3)C. (3,3)D. (-3,-3)第2题图3. (2022玉林)若顺次连接四边形ABCD各边的中点所得的四边形是正方形,则四边形ABCD 的两条对角线AC,BD一定是()A. 互相平分B. 互相垂直C. 互相平分且相等D. 互相垂直且相等4. (2023深圳)如图,在平行四边形ABCD中,AB=4,BC=6,将线段AB水平向右平移a 个单位长度得到线段EF,若四边形ECDF为菱形时,则a的值为()第4题图A. 1B. 2C. 3D. 45. (2023十堰)如图,将四根木条用钉子钉成一个矩形框架ABCD,然后向左扭动框架,观察所得四边形的变化.下面判断错误的是()A. 四边形ABCD由矩形变为平行四边形B. 对角线BD的长度减小C. 四边形ABCD的面积不变D. 四边形ABCD的周长不变第5题图6. 如图,菱形ABCD中,点E,F分别为AB,BC的中点,EF=2,BD=8,则该菱形的面积为()第6题图A. 12B. 16C. 20D. 327. (2023杭州)如图,矩形ABCD的对角线AC,BD相交于点O.若∠AOB=60°,则ABBC=()A. 12 B.3-12 C.32 D.33第7题图8. (2023大庆)将两个完全相同的菱形按如图方式放置,若∠BAD=α,∠CBE=β,则β=()第8题图A. 45°+12α B. 45°+32αC. 90°-12αD. 90°-32α 9. (2023河北)如图,在Rt △ABC 中,AB =4,点M 是斜边BC 的中点,以AM 为边作正方形AMEF .若S 正方形AMEF =16,则S △ABC =( ) A. 4 3 B. 8 3 C. 12 D. 16第9题图10. [新考法—条件开放](2023齐齐哈尔)如图,在四边形ABCD 中,AD =BC ,AC ⊥BD 于点O .请添加一个条件:________,使四边形ABCD 成为菱形.第10题图 11. (2023怀化)如图,点P 是正方形ABCD 的对角线AC 上的一点,PE ⊥AD 于点E ,PE =3.则点P 到直线AB 的距离为________.第11题图12. (2023绍兴)如图,在菱形ABCD 中,∠DAB =40°,连接AC ,以点A 为圆心,AC 长为半径作弧,交直线AD 于点E ,连接CE ,则∠AEC 的度数是________.第12题图13. (2023河南)矩形ABCD 中,M 为对角线BD 的中点,点N 在边AD 上,且AN =AB =1.当以点D ,M ,N 为顶点的三角形是直角三角形时,AD 的长为________.14. [新考法—条件开放](2023十堰)如图,▱ABCD 的对角线AC ,BD 交于点O ,分别以点B ,C 为圆心,12AC ,12BD 长为半径画弧,两弧交于点P ,连接BP ,CP . (1)试判断四边形BPCO 的形状,并说明理由;(2)请说明当▱ABCD 的对角线满足什么条件时,四边形BPCO 是正方形?第14题图15. 如图,在平行四边形ABCD 中,点E ,F 分别在边BC ,AD 上,且BE =DF ,连接AE ,CF ,EH ⊥CF 于点H ,FG ⊥AE 于点G .(1)判断四边形EGFH 的形状,并说明理由;(2)若AE =5,tan ∠DAE =2,EG =2GF ,求AG 的长.第15题图拔高题16. (2022青羊区模拟)我们规定菱形与正方形接近程度称为“接近度”,设菱形相邻两个内角的度数分别为α,β,将菱形的“接近度”定义为|α-β|,于是|α-β|越小,菱形越接近正方形.第16题图①若菱形的一个内角为80°,则该菱形的“接近度”为________;②当菱形的“接近度”等于________时,菱形是正方形.课时2基础题1. (2023湘潭)如图,菱形ABCD中,连接AC,BD,若∠1=20°,则∠2的度数为()A. 20°B. 60°C. 70°D. 80°第1题图2. 如图,在菱形ABCD中,AC,BD为菱形的对角线,∠DBC=60°,BD=10,点F为BC 中点,则EF的长为()第2题图A. 3B. 4C. 5D. 63. 如图所示,将一张矩形纸片沿虚线对折两次,当剪刀与纸片的夹角∠ABC=45°时,已知AB=4 cm,则剪下来图形的周长为()第3题图A. 4 cmB. 4 2 cmC. 16 cmD. 16 2 cm4. (2022青岛改编)如图,O 为正方形ABCD 对角线AC 的中点,△ACE 为等边三角形.若AB =2,则OE 的长度为________.第4题图5. [新考法—数学文化](2023内江)出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一.如图,在矩形ABCD 中,AB =5,AD =12,对角线AC 与BD 交于点O ,点E 为BC 边上的一个动点,EF ⊥AC ,EG ⊥BD ,垂足分别为点F ,G ,则EF +EG =________.第5题图6. (2023天津)如图,在边长为3的正方形ABCD 的外侧,作等腰三角形ADE ,EA =ED =52.第6题图(1)△ADE 的面积为________;(2)若F 为BE 的中点,连接AF 并延长,与CD 相交于点G ,则AG 的长为________.7. (2023内江)如图,在△ABC 中,D 是BC 的中点,E 是AD 的中点,过点A 作AF ∥BC 交CE 的延长线于点F .(1)求证:F A =BD ;(2)连接BF ,若AB =AC ,求证:四边形ADBF 是矩形.第7题图8. (2023兰州)如图,矩形ABCD的对角线AC与BD相交于点O,CD∥OE,直线CE是线段OD的垂直平分线,CE分别交OD,AD于点F,G,连接DE.(1)判断四边形OCDE的形状,并说明理由;(2)当CD=4时,求EG的长.第8题图拔高题9. (2023绍兴改编)如图,在矩形ABCD中,O为对角线BD的中点,∠ABD=60°,动点E 在线段OB上,动点F在线段OD上,点E,F同时从点O出发,分别向终点B,D运动,且始终保持OE=OF.点E关于AD,AB的对称点为E1,E2;点F关于BC,CD的对称点为F1,F2.当E,F,O三点重合时,当点E,F分别为OB,OD的中点时,当E,F分别运动到B,D两点时,四边形E1E2F1F2形状的变化依次是()第9题图A. 菱形→平行四边形→矩形B. 菱形→矩形→菱形C. 平行四边形→矩形→平行四边形D. 平行四边形→菱形→正方形10. (2023武侯区二诊节选)如图①,在矩形ABCD中,AD=nAB(其中n>1),点P是AD边上一动点(点P不与点A重合),点E是AB边的中点,连接PE,将矩形ABCD沿直线PE进行翻折,其顶点A翻折后的对应点为O,连接PO并延长,交BC边于点F(点F不与点C重合),过点F作∠PFC的平分线FG,交矩形ABCD的边于点G.(1)求证:PE∥FG;(2)如图②,在点P运动过程中,若E,O,G三点在同一条直线上时,点G与点D刚好重合,求n的值.图①图②第10题图参考答案与解析1. C2. C 【解析】∵正方形的边长为3,∴DC =BC =3,DC 与BC 分别垂直于y 轴和x 轴.∵点C 在第一象限,∴点C 的坐标为(3,3).3. D 【解析】如解图,E ,F ,G ,H 分别为AB ,BC ,CD ,DA 的中点,则EH ∥DB ∥GF ,HG ∥AC ∥EF ,EF =12 AC ,FG =12BD ,∴四边形EFGH 为平行四边形.要使其为正方形,即EF ⊥FG ,FE =FG ,则AC ⊥BD ,AC =BD ,即对角线一定互相垂直且相等.第3题解图4. B 【解析】∵四边形ABCD 是平行四边形,∴AB ∥CD ,CE ∥FD ,CD =AB =4.∵将线段AB 水平向右平移得到线段EF ,∴AB ∥EF ∥CD ,∴四边形ECDF 为平行四边形,当CD =CE =4时,▱ECDF 为菱形,此时a =BE =BC -CE =6-4=2.5. C 【解析】将四根木条用钉子钉成一个矩形框架ABCD ,然后向左扭动框架,∵两组对边的长度分别相等,∴四边形ABCD 是平行四边形,故A 正确,∵向左扭动框架,∴BD 的长度减小,故B 正确;∵平行四边形ABCD 的底不变,高变小了,∴平行四边形ABCD 的面积变小,故C 错误;∵平行四边形ABCD 的四条边长度不变,∴四边形ABCD 的周长不变,故D 正确.6. B 【解析】如解图,连接AC ,∵点E ,F 分别为AB ,BC 的中点,∴EF 是△ABC 的中位线,∴AC =2EF =4.∵四边形ABCD 是菱形,∴AC ⊥BD ,∴S 菱形ABCD =12 AC ·BD =12×4×8=16.第6题解图7. D 【解析】∵四边形ABCD 是矩形,∴OA =OB =OC =OD ,∠ABC =90°,∴∠OBC =∠OCB .∵∠AOB =60°,∴∠ACB =12 ∠AOB =30°,∴AB BC =tan ∠ACB =tan 30°=33. 8. D 【解析】∵四边形ABCD 和四边形BGHF 是完全相同的菱形,∴∠DBE =∠BAD =α,AB =AD ,∠ABD =∠CBD =∠CBE +∠DBE =β+α.∴∠ADB =∠ABD =β+α.∵∠BAD +∠ADB +∠ABD =180°,∴α+β+α+β+α=180°,∴β=90°-32α. 9. B 【解析】∵S 正方形AMEF =16,∴AM =4.∵M 是斜边BC 的中点,∴AM 是Rt △ABC 斜边上的中线,∴BC =2AM =8.在Rt △ABC 中,由勾股定理,得AC =BC 2-AB 2 =43 ,∴S △ABC =12 AB ·AC =12×4×43 =83 . 10. AD ∥BC (答案不唯一) 【解析】当AD ∥BC ,AD =BC 时,四边形ABCD 为平行四边形,又∵AC ⊥BD ,∴四边形ABCD 是菱形.11. 3 【解析】如解图,过点P 作PF ⊥AB 于点F ,∵四边形ABCD 是正方形,AC 是对角线,∴∠DAC =∠BAC .∵PE ⊥AD ,PF ⊥AB ,∴∠AEP =∠AFP .∵AP =AP ,∴△AEP ≌△AFP (AAS),∴PE =PF .∵PE =3,∴点P 到直线AB 的距离为PF =3.第11题解图12. 10°或80° 【解析】如解图,以点A 为圆心,AC 长为半径作弧,交直线AD 于点E 和E ′.在菱形ABCD 中,∠DAC =∠BAC ,∵∠DAB =40°,∴∠DAC =20°.∵AC =AE ,∴∠AEC =(180°-20°)÷2=80°.∵AE ′=AC ,∴∠AE ′C =∠ACE ′=10°.综上所述,∠AEC 的度数是10°或80°.第12题解图 13. 2或2 +1 【解析】分两种情况,①当∠DNM =90°时,如解图①,则MN ∥AB ,∴AN BM=AD BD.∵M 是BD 的中点,∴BD =2BM ,∴AD =2AN =2;②当∠DMN =90°时,如解图②,连接BN ,∵M 是BD 的中点,∠DMN =90°,∴BN =DN =AB 2+AN 2 =12+12 =2 ,∴AD =2 +1.综上所述,AD 的长为2或2 +1.图①图②第13题解图14. 解:(1)四边形BPCO 为平行四边形.理由如下:由作法得,BP =12 AC ,CP =12BD , ∵四边形ABCD 为平行四边形,∴OC =12 AC ,OB =12BD, ∴OC =BP ,OB =CP ,∴四边形BPCO 为平行四边形.(2)当▱ABCD 的对角线垂直且相等时,四边形BPCO 为正方形.理由:∵AC ⊥BD ,∴四边形BPCO 为矩形,∵AC =BD ,∴OB =OC ,∴四边形BPCO 为正方形.15. 解:(1)四边形EGFH 是矩形.理由如下:∵四边形ABCD 是平行四边形,∴AD =BC ,AD ∥BC .∵BE =DF ,∴AD -DF =BC -BE ,∴AF =CE ,∴四边形AECF 是平行四边形,∴AE ∥CF ,∴∠AEH +∠FHE =180°.∵EH ⊥CF ,FG ⊥AE ,∴∠FGE =∠FHE =∠GEH =90°,∴四边形EGFH 是矩形;(2)∵FG ⊥AE ,∴∠AGF =90°.在Rt △AGF 中,tan ∠DAE =GF AG=2, ∴GF =2AG .∵EG =2GF ,∴EG =4AG .∵AE =AG +EG =5,∴AG =1,即AG 的长为1.16. 20°;0° 【解析】①∵菱形相邻两个内角的度数和为180°,∴α+β=180°,即80°+β=180,解得β=100°,∴该菱形的“接近度”为|α-β|=|80°-100°|=20°;②∵当α=β=90°时,菱形是正方形,∴|α-β|=0°时,菱形是正方形.课时21. C 【解析】∵四边形ABCD 是菱形,∴AB ∥CD ,AC ⊥BD ,∴∠DCA =∠1=20°,∴∠2=90°-∠DCA =70°.2. C 【解析】∵四边形ABCD 是菱形,∴BC =DC ,BE =DE ,∵∠DBC =60°,∴△BDC是等边三角形,∴CD =BD =10.∵点F 为BC 中点,∴EF =12CD =5. 3. D 【解析】由折叠可知,剪下的图形两条对角线互相垂直且平分,此时图形为菱形,∵∠ABC =45°,∴剪下的图形有一个角为90°,∴有一个角为90°的菱形是正方形,∵AB =4 cm ,根据勾股定理得BC =42 cm ,故剪下来图形的周长为4×42 =16 2 cm. 4. 6 【解析】∵四边形ABCD 为正方形,AB =2,∴AC =22 .∵O 为正方形ABCD 对角线AC 的中点,△ACE 为等边三角形,∴∠AOE =90°,∴AC =AE =22 ,AO =2 ,∴OE=6 .5. 6013【解析】如解图,连接OE ,∵四边形ABCD 是矩形,∴∠BAD =90°, AB =CD =5,AD =BC =12.在Rt △ABD 中,BD =AB 2+AD 2 =13.∴AC =BD =13.∵AC 与BD 交于点O ,∴AO =CO =BO =DO =132 .∵S △BCO =14 S 四边形ABCD =14×12×5=15,∴S △BCO =S △BEO +S △CEO =12 BO ·EG +12 CO ·EF =12 ×132 (EG +EF )=15,∴EF +EG =15×413 =6013.第5题解图6. (1)3 【解析】(1)如解图,过点E 作EM ⊥AD 于点M ,∵△ADE 是等腰三角形,EA =ED =52 ,AD =3,∴AM =12 AD =32,∴EM =AE 2-AM 2 =(52)2-(32)2 =2,∴S △ADE =12 AD ·EM =12 ×3×2=3. (2)13 【解析】如解图,延长EM 交AG 于点N ,∵∠BAD =∠AME =90°,∴AB ∥NE ,∴∠ABF =∠FEN ,∠BAF =∠ENF .又∵点F 为BE 中点,∴BF =EF ,∴△AFB ≌△NFE ,∴EN =BA =3.由(1)知,EM =2,∴NM =1.∵∠NMD =∠ADC =90°,且M 为AD 中点,∴NM ∥GD ,∴NM 为△AGD 的中位线,∴GD =2NM =2,∴AG =AD 2+GD 2 =13 .第6题解图7. 证明:(1)∵AF ∥BC ,∴∠AFE =∠DCE .又∵E 是AD 的中点,∴AE =DE .在△AFE 和△DCE 中,∵ ⎩⎪⎨⎪⎧∠AFE =∠DCE ,∠AEF =∠DEC ,AE =DE ,∴△AFE≌△DCE,∴AF=DC.又∵D是BC的中点,∴BD=CD,∴AF=BD;(2)∵AB=AC,∴△ABC是等腰三角形.又∵D是BC的中点,∴∠ADB=90°,由(1)知F A=BD,又∵F A∥BD,∴四边形ADBF是平行四边形.又∵∠ADB=90°,∴四边形ADBF是矩形.8. 解:(1)四边形OCDE为菱形,理由如下:∵CE是线段OD的垂直平分线,∴OF=DF,OC=DC.∵CD∥OE,∴∠EOF=∠CDF.∵∠EFO=∠CFD,∴△OFE≌△DFC,∴OE=CD,∴四边形OCDE是平行四边形.又∵OC=CD,∴四边形OCDE是菱形;(2)∵四边形ABCD是矩形,∴DO=OC=OA,由(1)可知,OC=DC,∴OC=DO=CD,∴△OCD 是等边三角形,∴∠DCO =∠CDO =60°,∴∠FDG =90°-60°=30°.∵四边形OCDE 是菱形,∴∠DEC =∠DCE =30°,∠CGD =90°-∠DCE =60°,∴∠EDG =30°,∴DG =EG .∵CD =4,∴tan ∠DCG =DG CD =DG 4, ∴DG =4·tan 30°=4×33 =433, ∴EG =433. 9. B 【解析】∵四边形ABCD 为矩形,∠ABD =60°,∴∠CDF =60°,∠EDA =∠CBD =30°.∵OE =OF ,O 为对角线BD 的中点,∴DF =EB .由对称的性质得DF =DF 2,BF =BF 1,BE =BE 2,DE =DE 1,∠F 2DC =∠CDF =60°,∠EDA =∠E 1DA =30°,∠F 1BC =∠FBC =30°,∴E 1F 2=E 2F 1,∠E 1DB =60°,∠F 1BD =60°,∴DE 1∥BF 1,∴E 1F 2∥E 2F 1,∴四边形E 1E 2F 1F 2是平行四边形,如解图①,当E ,F ,O 三点重合时,DO =BO ,∴DE 1=DF 2=AE 1=AE 2,即E 1E 2=E 1F 2,∴四边形E 1E 2F 1F 2是菱形,如解图②,当E ,F 分别为OB ,OD 的中点时,设DB =4,则DF 2=DF =1,DE 1=DE =3,在Rt △ABD 中,AB =2,AD =23 ,连接AE ,易得AE =32 AB =3 ,根据对称性可得AE 1=AE =3 ,∵AD 2=12,DE 21 =9,AE 21 =3,即AD 2=AE 21 +DE 21 ,∴△DE 1A 是直角三角形,且∠E 1=90°,∴四边形E 1E 2F 1F 2是矩形;如解图③,当F ,E 分别与D ,B 重合时,△BE 1D ,△BDF 1都是等边三角形,则四边形E 1E 2F 1F 2是菱形,∴在这三个位置时,四边形E 1E 2F 1F 2形状的变化依次是菱形→矩形→菱形.图①图②图③第9题解图10. (1)证明:由翻折知,∠APE=∠OPE,∵FG平分∠PFC,∴∠PFG=∠CFG.∵AD∥BC,∴∠APF=∠CFP,∴∠EPF=∠PFG,∴PE∥FG;(2)解:由翻折知,EA=EO,∠EOP=90°.∵E,O,D三点在同一条直线上,∴∠DOF=∠EOF=∠C=90°.又∵DF=DF,∠OFG=∠CFG,∴△DOF≌△DCF(AAS),∴DO=DC=AB.∵E是AB的中点,∴设EA=EB=EO=a,∴OD=CD=AB=2a,∴DE=OE+OD=3a.在Rt△ADE中,由勾股定理,得AD2+AE2=DE2,∴AD=(3a)2-a2=22a.∵AD=nAB,∴22a=2na,∴n=2.。
中考数学专题训练:矩形、菱形、正方形(附参考答案)

中考数学专题训练:矩形、菱形、正方形(附参考答案)1.下列命题正确的是( )A .正方形的对角线相等且互相平分B .对角互补的四边形是平行四边形C .矩形的对角线互相垂直D .一组邻边相等的四边形是菱形2.如图,D ,E ,F 分别是△ABC 各边的中点,则以下说法错误的是( )A .△BDE 和△DCF 的面积相等B .四边形AEDF 是平行四边形C .若AB =BC ,则四边形AEDF 是菱形D .若∠A =90°,则四边形AEDF 是矩形3.如图,在正方形ABCD 中,E ,F 分别是AB ,BC 的中点,CE ,DF 交于点G ,连接AG .下列结论:①CE =DF ;②CE ⊥DF ;③∠AGE =∠CDF .其中正确的结论是( )A .①②B .①③C .②③D .①②③4.如图,平行四边形ABCD 的对角线AC ,BD 相交于点O ,E 为BC 的中点,连接EO 并延长交AD 于点F ,∠ABC =60°,BC =2AB .下列结论:①AB ⊥AC ;②AD =4OE ;③四边形AECF 是菱形;④S △BOE =14S △ABC .其中正确结论的个数是( )A .4B .3C .2D .15.如图,在矩形ABCD中,AB=6 cm,BC=9 cm,点E,F分别在边AB,BC上,AE=2 cm,BD,EF交于点G.若G是EF的中点,则BG的长为______cm.6.如图,在菱形ABCD中,AC,BD为菱形的对角线,∠DBC=60°,BD=10,点F为BC的中点,则EF的长为_____.7.已知四边形ABCD是正方形,点E在边DA的延长线上,连接CE交AB于点G,过点B作BM⊥CE,垂足为点M,BM的延长线交AD于点F,交CD的延长线于点H.(1)如图1,求证:CE=BH;(2)如图2,若AE=AB,连接CF,在不添加任何辅助线情况下,请直接写出图2中的四个三角形(△AEG除外),使写出的每个三角形都与△AEG全等.8.如图,在菱形ABCD中,E,F,G,H分别是AB,BC,CD,AD上的点,且BE =BF=CG=AH.若菱形的面积等于24,BD=8,则EF+GH=_____.9.如图,在矩形ABCD中,点E在DC上,DE=BE,AC与BD相交于点O,BE与AC相交于点F.(1)若BE平分∠CBD,求证:BF⊥AC;(2)找出图中与△OBF相似的三角形,并说明理由;(3)若OF=3,EF=2,求DE的长度.10.(1)如图1,在矩形ABCD中,点E,F分别在边DC,BC上,AE⊥DF,垂足为点G.求证:△ADE∽△DCF.【问题解决】(2)如图2,在正方形ABCD中,点E,F分别在边DC,BC上,AE=DF,延长BC 到点H,使CH=DE,连接DH.求证:∠ADF=∠H.【类比迁移】(3)如图3,在菱形ABCD中,点E,F分别在边DC,BC上,AE=DF=11,DE=8,∠AED=60°,求CF的长.参考答案1.A 2.C 3.A 4.D5.√13 6.5 7.(1)证明略 (2)略8.6解析:如图,连接AC ,交BD 于点O ,∵四边形ABCD 是菱形,BD =8,∴AB =BC =AD =CD ,AC ⊥BD ,AO =OC =12AC ,BO =OD =12BD =4. ∵S 菱形ABCD =12AC ·BD =24,∴AC =6,∴AO =3,∴AB =√AO 2+BO 2=5=AD .∵BE =BF =CG =AH ,∴AE =CF =DH =DG ,∴BE AE =BF CF ,∴EF ∥AC .同理可得GH ∥AC ,设BE =BF =CG =AH =a ,则有DH =5-a ,∵EF ∥AC ,∴△BEF ∽△BAC ,∴BE AB =EF AC ,即a 5=EF 6,∴EF =65a ,同理可得DH DA =GH CA ,即5−a 5=GH 6,∴GH =6-65a ,∴EF +GH =6.9.(1)证明略(2)与△OBF相似的三角形有△ECF,△BAF,理由略(3)DE=3+√1910.(1)证明:∵四边形ABCD是矩形,∴∠C=∠ADE=90°,∴∠CDF+∠DFC=90°.∵AE⊥DF,∴∠DGE=90°,∴∠CDF+∠AED=90°,∴∠AED=∠DFC,∴△ADE∽△DCF.(2)证明:∵四边形ABCD是正方形,∴AD=DC,AD∥BC,∠ADE=∠DCF=90°.∵AE=DF,∴Rt△ADE≌Rt△DCF(HL),∴DE=CF.∵CH=DE,∴CF=CH.∵点H在BC的延长线上,∴∠DCH=∠DCF=90°.又∵DC=DC,∴△DCF≌△DCH(SAS),∴∠DFC=∠H.∵AD∥BC,∴∠ADF=∠DFC,∴∠ADF=∠H.(3)解:如图3,延长BC至点G,使CG=DE=8,连接DG,∵四边形ABCD是菱形,∴AD=DC,AD∥BC,∴∠ADE=∠DCG,∴△ADE≌△DCG(SAS),∴∠DGC=∠AED=60°,AE=DG. ∵AE=DF,∴DG=DF,∴△DFG是等边三角形,∴FG=DF=11.∵CF+CG=FG,∴CF=FG-CG=11-8=3,即CF的长为3.。
中考数学复习四边形

判定 2.有三个角是直角的四边形是矩形; 3.对角线__相__等____的平行四边形是矩形.
图 21-2
皖考解读
考点聚焦
皖考探究
当堂检测
第21课时┃ 多边形与平行四边形
探究三 平行四边形的判定
命题角度: 1.从对边判定四边形是平行四边形; 2.从对角判定四边形是平行四边形; 3.从对角线判定四边形是平行四边形.
皖考解读
考点聚焦
皖考探究
当堂检测
第21课时┃ 多边形与平行四边形
例 3 [2012·泰州] 如图 21-3,四边形 ABCD 中,AD ∥BC,AE⊥AD 交 BD 于点 E,CF⊥BC 交 BD 于点 F, 且 AE=CF.求证:四边形 ABCD 是平行四边形.
当堂检测
第21课时┃ 多边形与平行四边形
考点聚焦
考点1 多边形
多边 形的 定义
在同一平面内,不在同一直线上的一些线段 __首__尾____顺次相接组成的图形叫做多边形.
多边 形
1.n 边形的内角和为_(_n_-__2_)_·1_8_0_°__. 2.任意多边形的外角和为__3__6_0_°__.
的性 质
皖考解读
考点聚焦
皖考探究
当堂检测
第21课时┃ 多边形与平行四边形
两条平 在两条平行线中一条直线上任意一点到另一条 行线间 直线上的距离叫做两条平行线间的距离. 的距离 夹在两条平行线间的平行线段__相__等____.
2020年中考数学一轮专项复习——矩形、菱形、正方形(含解析)

第3题图A. 20 °B.302020年中考数学一轮专项复习一一矩形、菱形、正方形课时1 矩形■基础过关1. (2019重庆模拟)下列关于矩形对角线的说法中,正确的是 ( )A.对角线相互垂直B.面积等于对角线乘积的一半C.对角线平分一组对角D.对角线相等2 . (2019临沂)如图,在?ABCD 中,M, N 是BD 上两点,个条件,使四边形 AMCN 是矩形,这个条件是()B. MB= MOD. / AMB = Z CNDBM = DN,连接 AM, MC , CN, NA.添加一1A. OM =2ACC. BD± AC3 .如图,将矩形纸片 数为( )ABCD 沿BD 折叠,得到△ BCD, CD 与AB 交于点E.若/1 = 35°,则/ 2的度第2题图5.如图,矩形 ABCD 中,A (-2, 0), B (2, 0), C (2, 2),将AB 绕点A 旋转,使点 B 落在边CD 上的点E 处,则点E 的坐标为()B. (2击,2) D. (2^3-2, 2)4. (2019贵阳模拟)如图,在矩形ABCD ( ) ABCD 中,AE 平分/ BAD,交边BC 于点E,若ED=5, EC=3,则A. 11B. 14C. 22D. 28A.(a 2) C. (1 ,6.如图,在矩形ABCD 中,对角线 AC 与BD 相交于点 O,过点A 作BD 的垂线,垂足为E.已知/ EAD= 3/BAE,则/ EAO 的度数为(A . 22.5B. 67.5C. 45°D. 60°7 . (2020原创)如图,点O 是矩形 则^ BOE 的周长为()ABCD 对角线 AC 的中点,OE // AB 交AD 于点E.若AB=6, BC=8,A. 10B. 8 + 2^5C. 8+2^13D. 14E第4题图第5题图4第6题图10.(人教八下P55练习2题)如图,?ABCD的对角线AC、BD交于点O, △ OAB是等边三角形,AB =4.(1)求证:四边形ABCD是矩形;(2)求四边形ABCD的面积.8. (2018遵义)如图,点P是矩形ABCD的对角线AC上一点, 点E, F,连接PB、PD.若AE=2, PF = 8.则图中阴影部分的面积为过点P作EF // BC,分别交AB, CD于A. 10 8.12 C. 16D. 189.(2019徐州)如图,矩形ABCD中,AC、BD交于点O, M、N分别为BC、OC的中点,若MN = 4, 则AC的长为第7题图第8题图第9题图第10题图11 . (2019怀化)已知:如图,在?ABCD中,AEXBC, CFXAD, E, F分别为垂足.⑴求证:△ ABE^A CDF ;(2)求证:四边形AECF是矩形.第11题图12 . (2019连云港)如图,在^ ABC中,AB = AC>AABC沿着BC方向平移得到△ DEF ,其中点E在边BC上,DE 与AC相交于点O.(1)求证:△ OEC为等腰三角形;(2)连接AE、DC、AD,当点E在什么位置时,四边形AECD为矩形,并说明理由.第12题图1 . (2019台州)如图,有两张矩形纸片 ABCD 和EFGH, AB=EF =2 cm, BC = FG=8 cm 把纸片 ABCD 交叉叠放在纸片 EFGH 上,使重叠部分为平行四边形,且点 D 与点G 重合,当两张纸片交叉所成的角 “最 小时,tan a 等于()2 .如图,在矩形 ABCD 中,AB = 4, BC = 6, E 是矩形内部的一个动点,且 AEXBE,则线段CE 的最 小值为.A.B. 2C. 187D.8_15;1 DB EC F第1题图第2题图立满分冲关1. (2019眉山模拟)如图,在矩形ABCD中,E是AD边的中点,BEXAC,垂足为点F,连接DF ,分析下列四个结论:① CF = 3AF;②AB=DF;③DF = ^BC;④S四边形CDEF^S MBF.其中正确白结论有( )第1题图A . 1个B,2个C,3个D,4个【错误结论纠正】请将错误结论改正确.2 .如图,在矩形ABCD中,ZBAC=30°,对角线AC, BD交于点O, / BCD的平分线CE分别交AB, BD于点E, H,连接OE.(1)求/ BOE的度数;(2)若BC=1,求^ BCH的面积;(3)求S A CHO :S^BHE的值.H E第2题图课时2菱形(建议时间:40分钟)名■基础过关1. (2019玉林)菱形不具备的性质是()A.是轴对称图形B.是中心对称图形C.对角线互相垂直D.对角线一定相等2. (2019 河北)如图,菱形ABCD 中,/ D= 150°,则/ 1 =()A.30 °B. 25 °C. 20 °D. 15 °DB第2题图3. (2019襄阳)如图,分别以线段AB的两个端点为圆心,大于AB的一半的长为半径画弧,两弧分别交于C, D两点,连接AC, BC, AD, BD,则四边形ADBC一定是()A.正方形B.矩形第3题图4. (2019呼和浩特)已知菱形的边长为3,较短的一条对角线的长为2,则该菱形较长的一条对角线的长为()A.2 2B. 2 . 5C. 4 2D. 2 . 105. (2019宁夏)如图,四边形ABCD的两条对角线相交于点O,且互相平分.添加下列条件,仍不能判定四边形ABCD为菱形的是()A.AC± BDB.AB = ADC.AC= BDD./ ABD = Z CBD,4第5题图6 . (2019赤峰)如图,菱形ABCD的周长为20,对角线AC、BD相交于点O, E是CD的中点,则OE 的长是()A. 2.5B. 3第6题图7. (2019天津)如图,四边形ABCD 为菱形,A, B两点的坐标分别是(2, 0), (0, 1),点C, D在坐标轴上,则菱形ABCD的周长等于(y6D第7题图A. 5B.4 3C.4 5D. 208 . (2019永州)如图,四边形ABCD的对角线相交于点O,且点。
中考数学复习 几何专题:矩形、菱形(含答案)

2021中考数学 几何专题:矩形、菱形一、选择题(本大题共10道小题) 1. 如图所示,P 是菱形ABCD 的对角线AC 上一动点,过P 垂直于AC 的直线交菱形ABCD 的边于M 、N 两点,设AC =2,BD =1,AP =x ,△AMN 的面积为y ,则y 关于x 的函数图象的大致形状是()2. 关于▱ABCD的叙述,正确的是( )A . 若AB ⊥BC ,则▱ABCD 是菱形 B . 若AC ⊥BD ,则▱ABCD 是正方形 C . 若AC =BD ,则▱ABCD 是矩形 D . 若AB =AD ,则▱ABCD 是正方形3. (2020·武威)如图所示的木制活动衣帽架是由三个全等的菱形构成,根据实际需要可以调节AE 间的距离.若AE 间的距离调节到60cm ,菱形的边长AB =20cm ,则∠DAB 的度数是( )A .90°B .100°C .120°D .150°4. (2020·牡丹江)如图,在菱形OABC 中,点B 在x 轴上,点A 的坐标为(2,23),将菱形绕点O 旋转,当点A 落在x 轴上时,点C 的对应点的坐标为 ( )A .(2,23)--或(23,2)-B .(2,23)C .(2,23)-D .(2,23)--或(2,23)BCA y5. (2020·黄冈)若菱形的周长为16,高为2,则菱形两邻角的度数之比为()A.4∶1 B.5∶1 C.6∶1 D.7∶16. (2020·乐山)如图,在菱形ABCD中,AB=4,∠BAD=120°,O是对角线BD的中点,过点O作OE⊥CD于E,连接OA,则四边形AOED的周长为()A.9+2 3 B.9+ 3 C.7+2 3 D.87. 如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F.在下列结论中,不一定正确的是()A. △AFD≌△DCEB. AF=12ADC. AB=AFD. BE=AD-DF8. (2020·黔东南州)若菱形ABCD的一条对角线长为8,边CD的长是方程x2﹣10x+24=0的一个根,则该菱形ABCD的周长为()A.16 B.24 C.16或24 D.489. (2020·邵阳)将一张矩形纸片ABCD按如图所示操作:(1)将DA沿DP向内折叠,使点A落在点A1处,(2)将DP沿DA1向内继续折叠,使点P落在点P1处,折痕与边AB交于占M.若P1M⊥AB,则∠DP1M的大小是()A.135°B. 120°C. 112.5°D.115°10. (2020·绥化)如图,在R t△ABC中,CD为斜边AB的中线,过点D作DE⊥AC 于点E,延长DE至点F,使EF=DE,连接AF,CF,点G在线段CF上,连接EG,且∠CDE+∠EGC=180°,FG=2,GC=3.下列结论:①DE=12BC;②四边形DBCF是平行四边形;③EF=EG;④BC=5是( )A.1个B.2个C.3个D.4个二、填空题(本大题共6道小题)11. 如图,在菱形ABCD中,AB=5,AC=8,则菱形的面积是________.12. 如图,延长矩形ABCD的边BC至点E,使CE=BD,连接AE.如果∠ADB =30°,则∠E=________度.13. 在菱形ABCD中,∠A=30°,在同一平面内,以对角线BD为底边作顶角为120°的等腰三角形BDE,则∠EBC的度数为________.14. (2020·四川甘孜州)如图,有一张长方形纸片ABCD,AB=8cm,BC=10cm,点E为CD上一点,将纸片沿AE折叠,BC的对应边B'C'恰好经过点D,则线段DE的长为__________cm.15. 如图,在△ABC中,AC=BC=2,AB=1,将它沿AB翻折得到△ABD,则四边形ADBC的形状是形,点P,E,F分别为线段AB,AD,DB上的任意一点,则PE+PF的最小值是.GFDCB16. 如图,在矩形纸片ABCD 中,AB =6,BC =10.点E 在CD 上,将△BCE 沿BE 折叠,点C 恰落在边AD 上的点F 处;点G 在AF 上,将△ABG 沿BG 折叠,点A 恰落在线段BF 上的点H 处.有下列结论:①∠EBG =45°;②△DEF ∽△ABG ;③S △ABG =32S △FGH ;④AG +DF =FG . 其中正确的是______________.(把所有正确结论的序号都选上)三、解答题(本大题共5道小题)17. 如图,对折矩形纸片ABCD ,使AB 与DC 重合,得到折痕MN ,将纸片展平;再一次折叠,使点D 落到MN 上的点F 处,折痕AP 交MN 于E ;延长PF 交AB 于G .求证: (1)△AFG ≌△AFP ; (2)△APG 为等边三角形.18. 如图,将▱ABCD的边AB 延长至点E ,使BE=AB ,连接BD ,DE ,EC ,DE交BC 于点O.(1)求证:△ABD ≌△BEC ;(2)若∠BOD=2∠A ,求证:四边形BECD 是矩形.19. 已知:如图,在菱形ABCD 中,点E ,F 分别在边BC ,CD 上,且BE=DF ,连结AE ,AF.求证:AE=AF.20. 如图,已知△ABC 中,AB =AC ,把△ABC 绕A 点沿顺时针方向旋转得到△ADE ,连接BD 、CE 交于点F. (1)求证:△AEC ≌△ADB ; (2)若AB =2,∠BAC =45°,当四边形ADFC 是菱形时,求BF 的长.21. 如图,⊙O 的直径AB =4,C 为⊙O 上一点,AC =2.过点C 作⊙O 的切线DC ,P 点为优弧CBA ︵上一动点(不与A 、C 重合). (1)求∠APC 与∠ACD 的度数;(2)当点P 移动到劣弧CB ︵的中点时,求证:四边形OBPC 是菱形; (3)当PC 为⊙O 的直径时,求证:△APC 与△ABC 全等.中考数学 几何专题:矩形、菱形-答案一、选择题(本大题共10道小题)1. 【答案】C 【解析】本题考查菱形的性质、相似三角形的性质、函数的图象和二次函数的图象和性质. 解题思路:设AC 、BD 交于点O ,由于点P 是菱形ABCD的对角线AC 上一动点,所以0<x <2.当0<x <1时,△AMN ∽△ABD ⇒APAO =MN BD ⇒x 1=MN 1⇒MN =x ⇒y =12x 2.此二次函数的图象开口向上,对称轴是x =0,此时y 随x 的增大而增大. 所以B 和D 均不符合条件.当1<x <2时,△CMN∽△CBD ⇒CP CO =MN BD ⇒2-x 1=MN 1⇒MN =2-x ⇒y =12x(2-x)=-12x 2+x.此二次函数的图象开口向下,对称轴是x =1,此时y 随x 的增大而减小. 所以A 不符合条件.综上所述,只有C 是符合条件的.2. 【答案】C 【解析】逐项分析如下表:选项 逐项分析 正误 A 有一个角是直角的平行四边形是矩形,不是菱形 ×B对角线互相垂直的平行四边形是菱形,不一定是正方形×C对角线相等的平行四边形是矩形√D有一组邻边相等的平行四边形是菱形,不一定是正方形×3. 【答案】连结AE,∵AE间的距离调节到60cm,木制活动衣帽架是由三个全等的菱形构成,∴AC=20cm,∵菱形的边长AB=20cm,∴AB=BC=20cm,∴AC=AB=BC,∴△ACB是等边三角形,∴∠B=60°,∴∠DAB=120°.故选:C.4. 【答案】D【解析】菱形OABC中,点A的坐标为(2,23),所以OA=4,∠A=∠C=60°,分类讨论,①若顺时针旋转,旋转后的图形如图1所示,则OC=OA=4,∠C=60°,可求出点C对应点的坐标为(-2,-23);②若逆时针旋转,旋转后的图形如图2所示,则OC=OA=4,∠C=60°,可求出点C对应点的坐标为(2,23).5. 【答案】B【解析】本题考查了菱形的性质及锐角三角函数等知识.由菱形的周长为16可得其边长为4,而高为2,即转化为已知某一直角三角形的斜边为4,一直角边yxABCOyxAB CO图1图2为2,求该直角三角形的锐角.由sin α=2142=,可得锐角α=30°,所以该菱形的两邻角为150°和30°,两邻角之比5∶1,因此本题选B . 6. 【答案】B【解析】由已知及菱形的性质求得∠ABD =∠CDB =30º,AO ⊥BD ,利用含30º的直角三角形边的关系分别求得AO 、DO 、OE 、DE ,进而求得四边形AOED 的周长.∵四边形ABCD 是菱形,O 是对角线AC 的中点,∴AO ⊥BD ,AD =AB =4,AB ∥DC ;∵∠BAD =120º,∴∠ABD =∠ADB =∠CDB =30º;∵OE ⊥DC ,∴在R t △AOD 中,AD =4,AO =12AD =2,DO =AD 2-AO 2=23;在R t △DEO 中,OE =12OD =3,DE =AD 2-AO 2=3,∴四边形AOED 的周长为AO+OE +DE +AD =2+3+3+4=9+3. B 【解析】逐项分析如下表: 选项 逐项分析 正误A ∵四边形ABCD 是矩形,AF ⊥DE ,∴∠C =90°=∠AFD ,AD ∥BC ,∴∠ADF =∠CED ,∵AD =DE ,∴△AFD ≌△DCE (AAS)√B 只有当∠ADF =30°时,才有AF =12AD 成立× C 由△AFD ≌△DCE 可知,AF =DC ,∵矩形ABCD 中,AB=DC ,∴AB =AF√D ∵△AFD ≌△DCE ,∴DF =CE ,∴BE =BC -CE =AD -DF √ 8. 【答案】B【解析】解方程x 2﹣10x +24=0得(x ﹣4)(x ﹣6)=0,∴x =4,或x =6,分两种情况:①当AB =AD =4时,4+4=8,不能构成三角形;②当AB =AD =6时,6+6>8,即可得出菱形ABCD 的周长为4AB =24.9. 【答案】C【解析】本题考查了折叠问题、三角形内角和定理、矩形的性质,由折叠前后对应角相等且190∠=PMA 可先求出145∠=∠=DMP DMA ,进一步求出45ADM ∠=,再由折叠可求出122.5∠=∠=∠=MDP ADP PDM ,最后在1∆DPM 中由三角形内角和定理即可求解.解:由折叠知,190∠=PMA , ∴145∠=∠=DMP DMA ,即45ADM ∠=, 由折叠可得,∴1122.52∠=∠=∠=∠=MDP ADP PDM ADM , ∴在1∆DPM 中,1=1804522.5112.5∠--=DPM ,因此本题选C . 10. 【答案】D【解析】(1)∵DF ⊥AC ,BC ⊥AC ,∴DE ∥BC .∵点D 是AB 的中点,∴点E是AC 的中点.∴DE =12BC .可见结论①正确.(2)∵AC 与DF 互相垂直平分,∴四边形ADCF 是菱形.∴FC AD .∴FC DB .∴四边形DBCF 是平行四边形.可见结论②正确. (3)∵∠CDE +∠EGC =180°,∠EGF +∠EGC =180°,∴∠CDE =∠EGC .由菱形的性质得∠CDE =∠EFG ,∴∠EGF =∠EFG .∴EF =EG .可见结论③正确.(4)易知△FEG ∽△FCD ,∴FEFC=FGFD ,即FE·FD =FC·FG .∴2DE2=2×5,DE =5.∴BC =2DE =25.可见结论④正确.综上所述,正确结论有4个,故选D .二、填空题(本大题共6道小题)11. 【答案】24 【解析】如解图,连接BD 交AC 于点O ,∵四边形ABCD 是菱形,AB =5,AC =8,且菱形的对角线互相垂直平分,∴OA =4,在Rt △AOB中,由勾股定理得OB =3,∴BD =6,∴S 菱形ABCD =12AC ·BD =12×8×6=24.解图12. 【答案】15【解析】如解图,连接AC.∵四边形ABCD 是矩形,∴AD =BC ,AC =BD ,又∵AB =BA ,∴△DAB ≌△CBA(SSS ),∴∠ACB =∠ADB =30°,∵CE =BD ,∴AC =CE ,∴∠E =∠CAE =12∠ACB =15°.解图13. 【答案】105°或45° 【解析】如解图,∵四边形ABCD 是菱形,∠A =30°,∴∠ABC =150°,∠ABD =∠DBC =75°,且顶角为120°的等腰三角形的底角是30°.分为以下两种情况:(1)当点E 在△ABD 内时,∠E 1BC =∠E 1BD +∠DBC =30°+75°=105°;(2)当点E 在△DBC 内时,∠E 2BC =∠DBC -∠E 2BD =75°-30°=45°.综上所述,∠EBC 的度数为105°或45°.解图14. 【答案】5【解析】本题考查了矩形的性质,轴对称的性质,勾股定理.∵长方形纸片ABCD ,AB =8,BC =10,∴AB '=8,AD =10,B 'C '=10.在R t △ADB '中,由勾股定理,得DB '=6.∴DC '=4. 设DE =x ,则CE =C 'E =8-x .在R t △C 'DE 中,由勾股定理,得DE 2=EC '2+DC '2即x 2=(8-x )2+42.∴x =5.即线段DE 的长为5cm .461088-x x 108C'B'D A BCE15. 【答案】菱[解析]∵AC=BC ,∴△ABC 是等腰三角形.将△ABC 沿AB 翻折得到△ABD ,∴AC=BC=AD=BD ,∴四边形ADBC 是菱形. ∵△ABC 沿AB 翻折得到△ABD ,∴△ABC 与△ABD 关于AB 成轴对称.如图所示,作点E 关于AB 的对称点E',连接PE',根据轴对称的性质知AB 垂直平分EE',∴PE=PE', ∴PE +PF=PE'+PF ,当E',P ,F 三点共线,且E'F ⊥AC 时,PE +PF 有最小值,该最小值即为平行线AC 与BD 间的距离.作CM ⊥AB 于M ,BG ⊥AD 于G ,由题知AC=BC=2,AB=1,∠CAB=∠BAD , ∴cos ∠CAB=cos ∠BAD ,即=,∴AG=, 在Rt △ABG 中,BG===,由对称性可知BG 长即为平行线AC ,BD 间的距离, ∴PE +PF 的最小值=.16. 【答案】①③④ 【解析】由折叠的性质得,∠CBE =∠FBE ,∠ABG =∠FBG ,∴∠EBG =∠FBE +∠FBG =12×90°=45°,故①正确;由折叠的性质得,BF =BC =10,BA =BH =6,∴HF =BF -BH =4,AF =BF 2-BA 2=102-62=8,设GH =x ,则GF =8-x ,在Rt △GHF 中,x 2+42=(8-x)2,∴x =3,∴GF =5,∴AG =3,同理在Rt △FDE 中,由FD 2=EF 2-ED 2,得ED =83,EF =103,∴EDFD =43≠AB AG =2,∴△DEF 与△ABG 不相似,故②不正确;S △ABG =12×3×6=9,S △FGH =12×3×4=6,∴S △ABG S △FGH =96=32,故③正确;∵AG =3,DF =AD -AF =2,∴FG=5,∴AG +DF =FG =5,故④正确.综上,答案是①③④.三、解答题(本大题共5道小题)17. 【答案】证明:(1)∵对折矩形纸片ABCD ,使AB 与CD 重合,得到折痕MN , ∴MN ∥AB ,M ,N 分别为AD ,BC 中点,由平行线的性质可知PF=GF . 由折叠的性质得∠PF A=∠GF A=90°, ∴△AFG ≌△AFP (SAS).(2)∵△AFG ≌△AFP ,∴AP=AG ,∠2=∠3. 又∵∠2=∠1,∴∠1=∠2=∠3.又∵∠1+∠2+∠3=90°,∴3∠2=90°,∴∠2=30°,∠P AG=2∠2=60°,∴△APG 为等边三角形.18. 【答案】[解析](1)根据平行四边形的判定与性质得到四边形BECD 为平行四边形,然后由SSS 推出两三角形全等即可;(2)欲证明四边形BECD 是矩形,只需推出BC=ED即可.证明:(1)在▱ABCD 中,AD=BC ,AB=CD ,AB ∥CD ,则BE ∥CD. 又∵BE=AB ,∴BE=DC ,∴四边形BECD 是平行四边形,∴BD=EC.在△ABD 与△BEC 中,∴△ABD ≌△BEC (SSS).(2)由(1)知四边形BECD 是平行四边形,则OD=OE ,OC=OB.∵四边形ABCD 是平行四边形,∴∠A=∠BCD ,即∠A=∠OCD.又∵∠BOD=2∠A ,∠BOD=∠OCD +∠ODC ,∴∠OCD=∠ODC ,∴OC=OD ,∴BC=ED ,∴平行四边形BECD 是矩形.19. 【答案】 ∵四边形ABCD 是菱形,∴AB=AD ,∠B=∠D ,∵BE=DF ,∴△ABE ≌△ADF ,∴AE=CF .20. 【答案】(1)证明:∵△ADE 是由△ABC 绕点A 沿顺时针方向旋转而得, ∴AD =AB ,AE =AC ,∠BAC =∠DAE ,(1分)∵AB =AC ,∴AD =AB =AE =AC ,∠EAC =∠DAB ,在△AEC 和△ADB 中∵⎩⎨⎧AD = AE∠EAC =∠DAB AB =AC,∴△AEC ≌△ADB(SAS ).(3分)(2)解:当四边形ADFC 是菱形时,AC =DF ,AC ∥DF , ∴∠BAC =∠ABD ,又∵∠BAC =45°,∴∠ABD =45°,(5分)又∵△ADE 是由△ABC 绕点A 沿顺时针方向旋转而得, ∴AD =AB ,∴∠DAB =90°,(6分)又∵AB =2,由勾股定理可得:BD =AD 2+AB 2=2AB =22, 在菱形ADFC 中,DF =AD =AB =2,∴BF =BD -DF =22-2.(8分)21. 【答案】(1)解:∵AC =2,OA =OB =OC =12AB =2,∴AC =OA =OC ,∴△ACO 为等边三角形,∴∠AOC =∠ACO =∠OAC =60°,∴∠APC =12∠AOC =30°,又∵DC 与⊙O 相切于点C ,∴OC ⊥DC ,∴∠DCO =90°,∴∠ACD =∠DCO -∠ACO =90°-60°=30°;解图(2)证明:如解图,连接PB ,OP ,∵AB 为直径,∠AOC =60°,∴∠COB =120°,当点P 移动到CB ︵的中点时,∠COP =∠POB =60°,∴△COP 和△BOP 都为等边三角形,∴OC =CP =OB =PB ,∴四边形OBPC 为菱形;(3)证明:∵CP 与AB 都为⊙O 的直径,∴∠CAP =∠ACB =90°,在Rt △ABC 与Rt △CP A 中,⎩⎨⎧AB =CP AC =AC, ∴Rt △ABC ≌Rt △CP A (HL).。
中考数学一轮复习特殊的平行四边形——矩形、菱形、正方形专题培优、能力提升复习讲义(含答案)

)
A.若 AB⊥ BC,则 ABCD是菱形 B.若 AC⊥ BD,则 ABCD是正方形
C.若 AC=BD,则 ABCD是矩形 D.若 AB=AD,则 ABCD是正方形
【答案】 C.
【解析】
试题分析:根据矩形的判定可得 A、C 项应是矩形;根据菱形的判定可得 B、D 项应是菱形 , 故答案选 C.
考点:矩形、菱形的判定 .
主要考查学生运用定理进行推理的能力.
【举一反三】
如图,正方形 ABCD的边长为 1 , AC、BD是对角线,将 △DCB绕点 D顺时针旋转 450 得到 △DGH,
HG交 AB于点 E ,连接 DE交 AC于点 F ,连接 FG,则下列结论:
①四边形 AEGF是菱形
②△ AED≌△ GED见解析;( 2)四边形 ABEF是菱形,理由详见解析 . 【解析】
( 2)四边形 ABEF是菱形;理由如下: ∵四边形 ABCD是平行四边形, ∴ AD∥ BC, ∴∠ DAE=∠ AEB, ∵ AE平分∠ BAD, ∴∠ BAE=∠ DAE, ∴∠ BAE=∠ AEB, ∴ BE=AB, 由( 1)得: AF=AB, ∴ BE=AF, 又∵ BE∥ AF, ∴四边形 ABEF是平行四边形,
. 对于菱形的判定,若可证出四边形为平行
四边形,则可证一组邻边相等或对角线互相垂直;若相等的边较多,则可证四条边都相等
.
【举一反三】
1. 如图,四边形 ABCD是菱形, AC 8 , DB 6 , DH AB 于 H,则 DH等于
A. 24 5
B . 12 5
C
.5 D .4
D
C
【答案】 A. 【解析】
【答案】证明见解析 . 【解析】
考点:正方形的判定;全等三角形的判定与性质.
中考数学真题《矩形菱形正方形》专项测试卷(附答案)

中考数学真题《矩形菱形正方形》专项测试卷(附答案)学校:___________班级:___________姓名:___________考号:___________(39题)一 、单选题1.(2023·湖南·统考中考真题)如图,菱形ABCD 中 连接AC BD , 若120∠=︒,则2∠的度数为( )A .20︒B .60︒C .70︒D .80︒2.(2023·湖南常德·统考中考真题)如图1 在正方形ABCD 中 对角线AC BD 、相交于点O E F 分别为AO DO 上的一点 且EF AD ∥ 连接,AF DE .若15FAC ∠=︒,则AED ∠的度数为( )A .80︒B .90︒C .105︒D .115︒3.(2023·湖南常德·统考中考真题)下列命题正确的是( )A .正方形的对角线相等且互相平分B .对角互补的四边形是平行四边形C .矩形的对角线互相垂直D .一组邻边相等的四边形是菱形4.(2023·浙江·统考中考真题)如图,在菱形ABCD 中 160AB DAB =∠=︒,,则AC 的长为( )A .12 B .1 C 3D 35.(2023·上海·统考中考真题)在四边形ABCD 中 ,AD BC AB CD =∥.下列说法能使四边形ABCD 为矩形的是( )A .AB CD B .AD BC = C .A B ∠=∠D .A D ∠=∠6.(2023·浙江宁波·统考中考真题)如图,以钝角三角形ABC 的最长边BC 为边向外作矩形BCDE 连结,AE AD 设AED △ ABE ACD 的面积分别为12,,S S S 若要求出12S S S --的值 只需知道( )A .ABE 的面积B .ACD 的面积C .ABC 的面积D .矩形BCDE 的面积7.(2023·湖南·统考中考真题)如图所示 在矩形ABCD 中 AB AD > AC 与BD 相交于点O 下列说法正确的是( )A .点O 为矩形ABCD 的对称中心B .点O 为线段AB 的对称中心C .直线BD 为矩形ABCD 的对称轴 D .直线AC 为线段BD 的对称轴8.(2023·四川宜宾·统考中考真题)如图,边长为6的正方形ABCD 中 M 为对角线BD 上的一点 连接AM 并延长交CD 于点P .若PM PC =,则AM 的长为( )A .()331B .()3332C .)631D .()6332 9.(2023·四川乐山·统考中考真题)如图,菱形ABCD 的对角线AC 与BD 相交于点O E 为边BC 的中点 连结OE .若68AC BD ==,,则OE =( )A .2B .52C .3D .410.(2023·甘肃武威·统考中考真题)如图,将矩形ABCD 对折 使边AB 与DC BC 与AD 分别重合 展开后得到四边形EFGH .若2AB = 4BC =,则四边形EFGH 的面积为( )A .2B .4C .5D .611.(2023·浙江绍兴·统考中考真题)如图,在矩形ABCD 中 O 为对角线BD 的中点 60ABD ∠=︒.动点E 在线段OB 上 动点F 在线段OD 上 点,E F 同时从点O 出发 分别向终点,B D 运动 且始终保持OE OF =.点E 关于,AD AB 的对称点为12,E E 点F 关于,BC CD 的对称点为12,F F .在整个过程中 四边形1212E E F F 形状的变化依次是( )A .菱形→平行四边形→矩形→平行四边形→菱形B .菱形→正方形→平行四边形→菱形→平行四边形C .平行四边形→矩形→平行四边形→菱形→平行四边形D .平行四边形→菱形→正方形→平行四边形→菱形12.(2023·重庆·统考中考真题)如图,在正方形ABCD 中 O 为对角线AC 的中点 E 为正方形内一点 连接BE BE BA = 连接CE 并延长 与ABE ∠的平分线交于点F 连接OF 若2AB =,则OF 的长度为( )A .2B 3C .1D 2二 解答题13.(2023·湖南怀化·统考中考真题)如图,矩形ABCD 中 过对角线BD 的中点O 作BD 的垂线EF分别交AD BC 于点E F .(1)证明:BOF DOE ≌△△(2)连接BE DF 证明:四边形EBFD 是菱形.14.(2023·湖北随州·统考中考真题)如图,矩形ABCD 的对角线AC BD 相交于点O ,DE AC CE BD .(1)求证:四边形OCED 是菱形(2)若32BC DC ==, 求四边形OCED 的面积.15.(2023·湖南永州·统考中考真题)如图,已知四边形ABCD 是平行四边形其对角线相交于点O 3,8,5OA BD AB ===.(1)AOB 是直角三角形吗?请说明理由(2)求证:四边形ABCD 是菱形.16.(2023·新疆·统考中考真题)如图,AD 和BC 相交于点O 90ABO DCO ∠=∠=︒ OB OC =.点E F 分别是AO DO 的中点.(1)求证:OE OF =(2)当30A ∠=︒时 求证:四边形BECF 是矩形.17.(2023·云南·统考中考真题)如图,平行四边形ABCD 中 AE CF 、分别是BAD BCD ∠∠、的平分线且E F 、分别在边BC AD 、上 AE AF =.(1)求证:四边形AECF 是菱形(2)若60ABC ∠=︒ ABE 的面积等于3 求平行线AB 与DC 间的距离.18.(2023·四川遂宁·统考中考真题)如图,四边形ABCD 中 AD BC ∥ 点O 为对角线BD 的中点 过点O 的直线l 分别与AD BC 所在的直线相交于点E F .(点E 不与点D 重合)(1)求证:DOE BOF ≌(2)当直线l BD ⊥时 连接BE DF 试判断四边形EBFD 的形状 并说明理由.19.(2023·浙江嘉兴·统考中考真题)如图,在菱形ABCD 中 AE BC ⊥于点E AF CD ⊥于点F连接EF(1)求证:AE AF =(2)若=60B ∠︒ 求AEF ∠的度数.20.(2023·湖北鄂州·统考中考真题)如图,点E 是矩形ABCD 的边BC 上的一点 且AE AD =.(1)尺规作图(请用2B 铅笔):作DAE ∠的平分线AF 交BC 的延长线于点F 连接DF .(保留作图痕迹 不写作法)(2)试判断四边形AEFD 的形状 并说明理由.21.(2023·吉林长春·统考中考真题)将两个完全相同的含有30︒角的直角三角板在同一平面内按如图所示位置摆放.点A E B D 依次在同一直线上 连结AF CD .(1)求证:四边形AFDC 是平行四边形(2)己知6cm BC 当四边形AFDC 是菱形时.AD 的长为__________cm .22.(2023·湖南张家界·统考中考真题)如图,已知点A D C B 在同一条直线上 且AD BC = AE BF ==.CE DF(1)求证:AE BF∥=时求证:四边形DECF是菱形.(2)若DF FC23.(2023·湖南郴州·统考中考真题)如图,四边形ABCD是平行四边形.(1)尺规作图作对角线AC的垂直平分线MN(保留作图痕迹)(2)若直线MN分别交AD BC于E F两点求证:四边形AFCE是菱形AC BD交于点O分别以点,B C为圆心24.(2023·湖北十堰·统考中考真题)如图,ABCD的对角线,11,22AC BD 长为半径画弧 两弧交于点P 连接,BP CP .(1)试判断四边形BPCO 的形状 并说明理由(2)请说明当ABCD 的对角线满足什么条件时 四边形BPCO 是正方形?25.(2023·四川内江·统考中考真题)如图,在ABC 中 D 是BC 的中点 E 是AD 的中点 过点A 作AF BC ∥交CE 的延长线于点F .(1)求证:AF BD =(2)连接BF 若AB AC = 求证:四边形ADBF 是矩形.26.(2023·湖南岳阳·统考中考真题)如图,点M 在ABCD 的边AD 上 BM CM = 请从以下三个选项中①12∠=∠ ①AM DM = ①34∠∠= 选择一个合适的选项作为已知条件 使ABCD 为矩形.(1)你添加的条件是_________(填序号)(2)添加条件后 请证明ABCD 为矩形.27.(2023·四川乐山·统考中考真题)如图,在Rt ABC △中 90C ∠=︒ 点D 为AB 边上任意一点(不与点A B 重合) 过点D 作DE BC ∥ DF AC ∥ 分别交AC BC 于点E F 连接EF .(1)求证:四边形ECFD 是矩形(2)若24CF CE ==, 求点C 到EF 的距离.28.(2023·浙江台州·统考中考真题)如图,四边形ABCD 中 AD BC ∥ A C ∠=∠ BD 为对角线.(1)证明:四边形ABCD 是平行四边形.(2)已知AD AB > 请用无刻度的直尺和圆规作菱形BEDF 顶点E F 分别在边BC AD 上(保留作图痕迹 不要求写作法).三 填空题29.(2023·黑龙江齐齐哈尔·统考中考真题)如图,在四边形ABCD 中 AD BC = AC BD ⊥于点O .请添加一个条件:______ 使四边形ABCD 成为菱形.30.(2023·辽宁大连·统考中考真题)如图,在菱形ABCD 中 AC BD 、为菱形的对角线60,10DBC BD ︒∠== 点F 为BC 中点,则EF 的长为_______________.31.(2023·福建·统考中考真题)如图,在菱形ABCD 中 1060AB B ︒=∠=,,则AC 的长为___________.32.(2023·浙江绍兴·统考中考真题)如图,在菱形ABCD 中 40DAB ∠=︒ 连接AC 以点A 为圆心 AC 长为半径作弧 交直线AD 于点E 连接CE ,则AEC ∠的度数是________.33.(2023·甘肃武威·统考中考真题)如图,菱形ABCD 中 60DAB ∠=︒ BE AB ⊥ DF CD ⊥ 垂足分别为B D 若6cm AB =,则EF =________cm .34.(2023·山东聊城·统考中考真题)如图,在ABCD 中 BC 的垂直平分线EO 交AD 于点E 交BC 于点O 连接BE CE 过点C 作CF BE ∥ 交EO 的延长线于点F 连接BF .若8AD = 5CE =,则四边形BFCE 的面积为______..35.(2023·湖北十堰·统考中考真题)如图,在菱形ABCD 中 点E F G H 分别是AB BC CD AD 上的点 且BE BF CG AH === 若菱形的面积等于24 8BD =,则EF GH +=___________________.36.(2023·四川内江·统考中考真题)出入相补原理是我国古代数学的重要成就之一 最早是由三国时期数学家刘徽创建.“将一个几何图形 任意切成多块小图形 几何图形的总面积保持不变 等于所分割成的小图形的面积之和”是该原理的重要内容之一 如图,在矩形ABCD 中 5AB = 12AD = 对角线AC 与BD 交于点O 点E 为BC 边上的一个动点 EF AC ⊥ EG BD ⊥ 垂足分别为点F G ,则EF EG +=___________.37.(2023·山东滨州·统考中考真题)如图,矩形ABCD 的对角线,AC BD 相交于点O 点,E F 分别是线段,OB OA 上的点.若,5,1,3AE BF AB AF BE ====,则BF 的长为___________.38.(2023·山东枣庄·统考中考真题)如图,在正方形ABCD 中 对角线AC 与BD 相交于点O E 为BC 上一点 7CE = F 为DE 的中点 若CEF △的周长为32,则OF 的长为___________.39.(2023·浙江台州·统考中考真题)如图,矩形ABCD 中 4AB = 6AD =.在边AD 上取一点E 使BE BC = 过点C 作CF BE ⊥ 垂足为点F ,则BF 的长为________.参考答案一 单选题1.(2023·湖南·统考中考真题)如图,菱形ABCD 中 连接AC BD , 若120∠=︒,则2∠的度数为( )A .20︒B .60︒C .70︒D .80︒【答案】C 【分析】根据菱形的性质可得,BD AC AB CD ⊥∥,则1,290ACD ACD ∠=∠∠+∠=︒ 进而即可求解.【详解】解:①四边形ABCD 是菱形①,BD AC AB CD ⊥∥①1,290ACD ACD ∠=∠∠+∠=︒①120∠=︒①2902070∠=︒-︒=︒,故选:C .【点睛】本题考查了菱形的性质 熟练掌握是菱形的性质解题的关键.2.(2023·湖南常德·统考中考真题)如图1 在正方形ABCD 中 对角线AC BD 、相交于点O E F 分别为AO DO 上的一点 且EF AD ∥ 连接,AF DE .若15FAC ∠=︒,则AED ∠的度数为( )A .80︒B .90︒C .105︒D .115︒【答案】C 【分析】首先根据正方形的性质得到45OAD ODA ∠=∠=︒ AO DO = 然后结合EF AD ∥得到OE OF = 然后证明出()SAS AOF DOE △≌△ 最后利用三角形内角和定理求解即可.【详解】①四边形ABCD 是正方形①45OAD ODA ∠=∠=︒ AO DO =①EF AD ∥①45OEF OAD ∠=∠=︒ 45OFE ODA ∠=∠=︒①OEF OFE ∠=∠①OE OF =又①90AOF DOE ∠=∠=︒ AO DO =①()SAS AOF DOE △≌△①15ODE FAC ∠=∠=︒①30ADE ODA ODE ∠=∠-∠=︒①180105AED OAD ADE ∠=︒-∠-∠=︒故选:C .【点睛】此题考查了正方形的性质 全等三角形的性质和判定 等腰直角三角形三角形的性质等知识 解题的关键是熟练掌握以上知识点.3.(2023·湖南常德·统考中考真题)下列命题正确的是( )A .正方形的对角线相等且互相平分B .对角互补的四边形是平行四边形C .矩形的对角线互相垂直D .一组邻边相等的四边形是菱形【答案】A【分析】根据正方形 平行四边形 矩形 菱形的各自性质和构成条件进行判断即可.【详解】A 正方形的对角线相等且互相垂直平分 描述正确B 对角互补的四边形不一定是平行四边形 只是内接于圆 描述错误C 矩形的对角线不一定垂直 但相等 描述错误D 一组邻边相等的平行四边形才构成菱形 描述错误.故选:A .【点睛】本题考查平行四边形 矩形 菱形 正方形的性质和判定 解题的关键是熟悉掌握各类特殊四边形的判定和性质.4.(2023·浙江·统考中考真题)如图,在菱形ABCD 中 160AB DAB =∠=︒,,则AC 的长为( )A .12B .1C 3D 3【答案】D 【分析】连接BD 与AC 交于O .先证明ABD △是等边三角形 由AC BD ⊥ 得到1302OAB BAD ∠=∠=︒ 90AOB ∠=︒ 即可得到1122OB AB == 利用勾股定理求出AO 的长度 即可求得AC 的长度.【详解】解:连接BD 与AC 交于O .①四边形ABCD 是菱形①AB CD ∥ AB AD = AC BD ⊥ 12AO OC AC ==①60DAB ∠=︒ 且AB AD =①ABD △是等边三角形①AC BD ⊥ ①1302OAB BAD ∠=∠=︒ 90AOB ∠=︒ ①1122OB AB == ①2222111322AO AB OB ⎛⎫-= ⎪⎭=-⎝ ①23AC AO ==故选:D .【点睛】此题主要考查了菱形的性质 勾股定理 等边三角形的判定和性质 30︒角所对直角边等于斜边的一半 关键是熟练掌握菱形的性质.5.(2023·上海·统考中考真题)在四边形ABCD 中 ,AD BC AB CD =∥.下列说法能使四边形ABCD 为矩形的是( )A .AB CD B .AD BC = C .A B ∠=∠D .A D ∠=∠【答案】C【分析】结合平行四边形的判定和性质及矩形的判定逐一分析即可.【详解】A :AB CD ,AD BC AB CD =∥∴ABCD 为平行四边形而非矩形故A 不符合题意B :AD BC = ,AD BC AB CD =∥∴ABCD 为平行四边形而非矩形故B 不符合题意C :AD BC ∥180A B ∴∠+∠=︒A B ∠=∠∴90A B ∠=∠=︒AB CD =∴ABCD 为矩形故C 符合题意D :AD BC ∥180A B ∴∠+∠=︒A D ∠=∠180D B ∴∠+∠=︒∴ABCD 不是平行四边形也不是矩形故D 不符合题意故选:C .【点睛】本题主要考查平行线的性质 平行四边形的判定和性质及矩形的判定等知识 熟练掌握以上知识并灵活运用是解题的关键.6.(2023·浙江宁波·统考中考真题)如图,以钝角三角形ABC 的最长边BC 为边向外作矩形BCDE 连结,AE AD 设AED △ ABE ACD 的面积分别为12,,S S S 若要求出12S S S --的值 只需知道( )A .ABE 的面积B .ACD 的面积C .ABC 的面积D .矩形BCDE 的面积【答案】C【分析】过点A 作FG BC ∥ 交EB 的延长线于点F DC 的延长线于点G 易得:,,FG BC AF BE AG CD =⊥⊥ 利用矩形的性质和三角形的面积公式 可得1212BCDES S S +=矩形 再根据1212ABC ABC BCDE BCDE S S S S S S S -=+-=+矩形矩形 得到12ABC S S S S -=- 即可得出结论.【详解】解:过点A 作FG BC ∥ 交EB 的延长线于点F DC 的延长线于点G①矩形BCDE①,,BC BE BC CD BE CD ⊥⊥=①,FG BE FG CD ⊥⊥①四边形BFGC 为矩形①,,FG BC AF BE AG CD =⊥⊥①1211,22S BE AF S CD AG =⋅=⋅①()12111222BCDE BE AF AG BE B S C S S =+=⋅=+矩形又1212ABC ABC BCDE BCDE S S S S S S S -=+-=+矩形矩形①121122ABC ABC BCDE BCDE S S S S S S S =+---=矩形矩形 ①只需要知道ABC 的面积即可求出12S S S --的值故选C .【点睛】本题考查矩形的性质 求三角形的面积.解题的关键是得到1212BCDES S S +=矩形 7.(2023·湖南·统考中考真题)如图所示 在矩形ABCD 中 AB AD > AC 与BD 相交于点O 下列说法正确的是( )A .点O 为矩形ABCD 的对称中心B .点O 为线段AB 的对称中心C .直线BD 为矩形ABCD 的对称轴D .直线AC 为线段BD 的对称轴【答案】A 【分析】由矩形ABCD 是中心对称图形 对称中心是对角线的交点 线段AB 的对称中心是线段AB 的中点 矩形ABCD 是轴对称图形 对称轴是过一组对边中点的直线 从而可得答案.【详解】解:矩形ABCD 是中心对称图形 对称中心是对角线的交点 故A 符合题意线段AB 的对称中心是线段AB 的中点 故B 不符合题意矩形ABCD 是轴对称图形 对称轴是过一组对边中点的直线故C D 不符合题意故选A【点睛】本题考查的是轴对称图形与中心对称图形的含义 矩形的性质 熟记矩形既是中心对称图形也是轴对称图形是解本题的关键.8.(2023·四川宜宾·统考中考真题)如图,边长为6的正方形ABCD 中 M 为对角线BD 上的一点 连接AM 并延长交CD 于点P .若PM PC =,则AM 的长为( )A .()331B .()3332C .)631D .()6332 【答案】C【分析】先根据正方形的性质 三角形全等的判定证出ADM CDM ≅ 根据全等三角形的性质可得DAM DCM ∠=∠ 再根据等腰三角形的性质可得CMP DCM ∠=∠ 从而可得30DAM ∠=︒ 然后利用勾股定理 含30度角的直角三角形的性质求解即可得. 【详解】解:四边形ABCD 是边长为6的正方形6,90,45AD CD ADC ADM CDM ∴==∠=︒∠=∠=︒在ADM △和CDM 中 45DM DM ADM CDM AD CD =⎧⎪∠=∠=︒⎨⎪=⎩()SAS ADM CDM ∴≅DAM DCM ∴∠=∠PM PC =CMP DCM ∴∠=∠22APD CMP DCM DCM DAM ∴∠=∠+∠=∠=∠又18090APD DAM ADC ∠+∠=︒-∠=︒30DAM ∴∠=︒设PD x =,则22AP PD x == 6PM PC CD PD x ==-=-2236AD AP PD x ∴=-= 解得3x =663PM x ∴=-=- 243AP x ==(()43623631AM AP PM ∴=-=-= 故选:C .【点睛】本题考查了正方形的性质 勾股定理 含30度角的直角三角形的性质 等腰三角形的性质等知识点 熟练掌握正方形的性质是解题关键.9.(2023·四川乐山·统考中考真题)如图,菱形ABCD 的对角线AC 与BD 相交于点O E 为边BC 的中点 连结OE .若68AC BD ==,,则OE =( )A .2B .52C .3D .4【答案】B 【分析】先由菱形的性质得AC BD ⊥ 116322OC AC ==⨯= 118422OB BD ==⨯= 再由勾股定理求出5BC = 然后由直角 三角形斜边的中线等于斜边的一半求解.【详解】解:①菱形ABCD①AC BD ⊥ 116322OC AC ==⨯= 118422OB BD === ①由勾股定理 得225BC OB OC =+=①E 为边BC 的中点 ①1155222OE BC ==⨯= 故选:B .【点睛】本考查菱形的性质 勾股定理 直角三角形的性质 熟练掌握菱形的性质 直角三角形的性质是解题的关键.10.(2023·甘肃武威·统考中考真题)如图,将矩形ABCD 对折 使边AB 与DC BC 与AD 分别重合 展开后得到四边形EFGH .若2AB = 4BC =,则四边形EFGH 的面积为( )A .2B .4C .5D .6【答案】B 【分析】由题意可得四边形EFGH 是菱形 2FH AB == 4GE BC == 由菱形的面积等于对角线乘积的一半即可得到答案.【详解】解:①将矩形ABCD 对折 使边AB 与DC BC 与AD 分别重合 展开后得到四边形EFGH①EF GH ⊥ EF 与GH 互相平分①四边形EFGH 是菱形①2FH AB == 4GE BC ==①菱形EFGH 的面积为1124422FH GE ⋅=⨯⨯=. 故选:B【点睛】此题考查了矩形的折叠 菱形的判定和性质等知识 熟练掌握菱形的面积等于对角线乘积的一半是解题的关键.11.(2023·浙江绍兴·统考中考真题)如图,在矩形ABCD 中 O 为对角线BD 的中点 60ABD ∠=︒.动点E 在线段OB 上 动点F 在线段OD 上 点,E F 同时从点O 出发 分别向终点,B D 运动 且始终保持OE OF =.点E 关于,AD AB 的对称点为12,E E 点F 关于,BC CD 的对称点为12,F F .在整个过程中 四边形1212E E F F 形状的变化依次是( )A .菱形→平行四边形→矩形→平行四边形→菱形B .菱形→正方形→平行四边形→菱形→平行四边形C .平行四边形→矩形→平行四边形→菱形→平行四边形D .平行四边形→菱形→正方形→平行四边形→菱形【答案】A【分析】根据题意 分别证明四边形1212E E F F 是菱形 平行四边形 矩形 即可求解.【详解】①四边形ABCD 是矩形①AB CD ∥ 90BAD ABC ∠=∠=︒①60BDC ABD ∠=∠=︒ 906030ADB CBD ∠=∠=︒-︒=︒①OE OF = OB OD =①DF EB =①对称①21DF DF BF BF ==, 21,BE BE DE DE ==①1221E F E F =①对称①260F DC CDF ∠=∠=︒ 130EDA E DA ∠=∠=︒①160E DB ∠=︒同理160F BD ∠=︒①11DE BF ∥①1221E F E F ∥①四边形1212E E F F 是平行四边形如图所示当,,E F O 三点重合时 DO BO =①1212DE DF AE AE ===即1212E E E F =①四边形1212E E F F 是菱形如图所示 当,E F 分别为,OD OB 的中点时设4DB =,则21DF DF == 13DE DE ==在Rt △ABD 中 2,23AB AD ==连接AE AO①602ABO BO AB ∠=︒==,①ABO 是等边三角形①E 为OB 中点①AE OB ⊥ 1BE = ①22213AE - 根据对称性可得13AE AE =①2221112,9,3AD DE AE ===①22211AD AE DE =+①1DE A 是直角三角形 且190E ∠=︒①四边形1212E E F F 是矩形当,F E 分别与,D B 重合时 11,BE D BDF 都是等边三角形,则四边形1212E E F F 是菱形①在整个过程中 四边形1212E E F F 形状的变化依次是菱形→平行四边形→矩形→平行四边形→菱形 故选:A .【点睛】本题考查了菱形的性质与判定 平行四边形的性质与判定 矩形的性质与判定 勾股定理与勾股定理的逆定理 轴对称的性质 含30度角的直角三角形的性质 熟练掌握以上知识是解题的关键. 12.(2023·重庆·统考中考真题)如图,在正方形ABCD 中 O 为对角线AC 的中点 E 为正方形内一点 连接BE BE BA = 连接CE 并延长 与ABE ∠的平分线交于点F 连接OF 若2AB =,则OF 的长度为( )A .2B 3C .1D 2【答案】D 【分析】连接AF 根据正方形ABCD 得到AB BC BE == 90ABC ∠=︒ 根据角平分线的性质和等腰三角形的性质 求得45BFE ∠=︒ 再证明ABF EBF ≌ 求得90AFC ∠=︒ 最后根据直角三角形斜边上的中点等于斜边的一半 即可求出OF 的长度.【详解】解:如图,连接AF四边形ABCD 是正方形AB BE BC ∴== 90ABC ∠=︒ 222AC ==BEC BCE ∴∠=∠1802EBC BEC ∴∠=︒-∠290ABE ABC EBC BEC ∴∠=∠-∠=∠-︒ BF 平分ABE ∠1452ABF EBF ABE BEC ∴∠=∠=∠=∠-︒45BFE BEC EBF ∴∠=∠-∠=︒在BAF △与BEF △,AB EB ABF EBF BF BF =⎧⎪∠=∠⎨⎪=⎩()SAS BAF BEF ∴△≌△45BFE BFA ∴∠=∠=︒90AFC BAF BFE ∴∠=∠+∠=︒O 为对角线AC 的中点122OF AC ∴= 故选:D .【点睛】本题考查了等腰三角形的判定和性质 三角形内角和定理 正方形的性质 直角三角形特征 作出正确的辅助线 求得45BFE ∠=︒是解题的关键.二 解答题13.(2023·湖南怀化·统考中考真题)如图,矩形ABCD 中 过对角线BD 的中点O 作BD 的垂线EF 分别交AD BC 于点E F .(1)证明:BOF DOE ≌△△(2)连接BE DF 证明:四边形EBFD 是菱形.【答案】(1)见解析 (2)见解析【分析】(1)根据矩形的性质得出AD BC ∥,则12,34∠=∠∠=∠ 根据O 是BD 的中点 可得BO DO = 即可证明()AAS BOF DOE ≌△△(2)根据BOF DOE ≌△△可得ED BF = 进而可得四边形EBFD 是平行四边形 根据对角线互相垂直的四边形是菱形 即可得证.【详解】(1)证明:如图所示①四边形ABCD 是矩形①AD BC ∥①12,34∠=∠∠=∠①O 是BD 的中点①BO DO =在BOF 与DOE 中1234BO DO ∠=∠⎧⎪∠=∠⎨⎪=⎩①()AAS BOF DOE ≌△△(2)①BOF DOE ≌△△①ED BF =又①ED BF ∥①四边形EBFD 是平行四边形①EF BD ⊥①四边形EBFD 是菱形.【点睛】本题考查了矩形的性质 全等三角形的性质与判定 菱形的判定 熟练掌握特殊四边形的性质与判定是解题的关键.14.(2023·湖北随州·统考中考真题)如图,矩形ABCD 的对角线AC BD 相交于点O ,DE AC CE BD .(1)求证:四边形OCED 是菱形(2)若32BC DC ==, 求四边形OCED 的面积.【答案】(1)见解析 (2)3【分析】(1)先根据矩形的性质求得OC OD = 然后根据有一组邻边相等的平行四边形是菱形分析推理 (2)根据矩形的性质求得OCD 的面积 然后结合菱形的性质求解.【详解】(1)解:①DE AC CE BD ∥,∥ ①四边形OCED 是平行四边形又①矩形ABCD 中 OC OD =①平行四边形OCED 是菱形(2)解:矩形ABCD 的面积为326BC DC ⋅=⨯=①OCD 的面积为13642⨯= ①菱形OCED 的面积为3232⨯=. 【点睛】本题考查矩形的性质 菱形的判定 属于中考基础题 掌握矩形的性质和菱形的判定方法 正确推理论证是解题关键.15.(2023·湖南永州·统考中考真题)如图,已知四边形ABCD 是平行四边形 其对角线相交于点O 3,8,5OA BD AB ===.(1)AOB 是直角三角形吗?请说明理由(2)求证:四边形ABCD 是菱形.【答案】(1)AOB 是直角三角形 理由见解析.(2)见解析【分析】(1)根据平行四边形对角线互相平分可得142BO BD == 再根据勾股定理的逆定理 即可得出结论(2)根据对角线互相垂直的平行四边形是菱形 即可求证.【详解】(1)解:AOB 是直角三角形 理由如下:①四边形ABCD 是平行四边形 ①142BO BD ==①222222345OA OB AB +=+==①AOB 是直角三角形.(2)证明:由(1)可得:AOB 是直角三角形①90AOB ∠=︒即AC BD ⊥①四边形ABCD 是平行四边形①四边形ABCD 是菱形.【点睛】本题主要考查了平行四边形的性质 勾股定理的逆定理 菱形的判定 解题的关键是掌握平行四边形对角线互相平分 对角线互相垂直的平行四边形是菱形.16.(2023·新疆·统考中考真题)如图,AD 和BC 相交于点O 90ABO DCO ∠=∠=︒ OB OC =.点E F 分别是AO DO 的中点.(1)求证:OE OF =(2)当30A ∠=︒时 求证:四边形BECF 是矩形.【答案】(1)见解析 (2)见解析【分析】(1)直接证明()ASA AOB DOC ≌△△ 得出OA OD = 根据E F 分别是AO DO 的中点 即可得证(2)证明四边形BECF 是平行四边形 进而根据30A ∠=︒ 推导出BOE △是等边三角形 进而可得BC EF = 即可证明四边形BECF 是矩形.【详解】(1)证明:在AOB 与DOC △中90ABO DCO OB OCAOB DOC ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩①()ASA AOB DOC ≌△△①OA OD =又①E F 分别是AO DO 的中点①OE OF =(2)①OB OC OF OE ==,①四边形BECF 是平行四边形 22BC OB EF OE ==,①E 为AO 的中点 90∠=︒ABO①EB EO EA ==①30A ∠=︒①60BOE ∠=︒①BOE △是等边三角形①OB OE =①BC EF =①四边形BECF 是矩形.【点睛】本题考查了全等三角形的性质与判定 等边三角形的性质与判定 矩形判定 熟练掌握以上知识是解题的关键.17.(2023·云南·统考中考真题)如图,平行四边形ABCD 中 AE CF 、分别是BAD BCD ∠∠、的平分线 且E F 、分别在边BC AD 、上 AE AF =.(1)求证:四边形AECF 是菱形(2)若60ABC ∠=︒ ABE 的面积等于3 求平行线AB 与DC 间的距离.【答案】(1)证明见解析 (2)3【分析】(1)先证AD BC ∥ 再证AE FC 从而四边形AECF 是平行四边形 又AE AF = 于是四边形AECF 是菱形(2)连接AC 先求得60BAE DAE ABC ∠∠∠===︒ 再证AC AB ⊥9030ACB ABC EAC ∠∠∠=︒-=︒= 3AB AC= 得3AB AC = 再证AE BE CE == 从而根据面积公式即可求得AC =43 【详解】(1)证明:①四边形ABCD 是平行四边形①AD BC ∥ BAD BCD ∠∠=①BEA DAE ∠∠=①AE CF 、分别是BAD BCD ∠∠、的平分线①BAE DAE ∠∠==12BAD ∠ BCF ∠=12BCD ∠①DAE BCF BEA ∠∠∠==①AE FC①四边形AECF 是平行四边形①AE AF =①四边形AECF 是菱形(2)解:连接AC①AD BC ∥ 60ABC ∠=︒①180120BAD ABC ∠∠=︒-=︒①60BAE DAE ABC ∠∠∠===︒①四边形AECF 是菱形①EAC ∠=1230DAE ∠=︒①90BAC BAE EAC ∠∠∠=+=︒①AC AB ⊥ 9030ACB ABC EAC ∠∠∠=︒-=︒=①AE CE = tan 30tan AB ACB AC ︒=∠=3AB AC= ①3AB AC = ①BAE ABC ∠∠=①AE BE CE ==①ABE 的面积等于43 ①211338322ABC S AC AB AC AC AC =⋅=== ①平行线AB 与DC 间的距离AC =43【点睛】本题考查了平行四边形的判定及性质 菱形的判定 角平分线的定义 等腰三角形的判定 三角函数的应用以及平行线间的距离 熟练掌握平行四边形的判定及性质 菱形的判定 角平分线的定义 等腰三角形的判定 三角函数的应用以及平行线间的距离等知识是解题的关键.18.(2023·四川遂宁·统考中考真题)如图,四边形ABCD 中 AD BC ∥ 点O 为对角线BD 的中点 过点O 的直线l 分别与AD BC 所在的直线相交于点E F .(点E 不与点D 重合)(1)求证:DOE BOF ≌(2)当直线l BD ⊥时 连接BE DF 试判断四边形EBFD 的形状 并说明理由.【答案】(1)见解析 (2)四边形EBFD 为菱形 理由见解析【分析】(1)根据AAS 证明DOE BOF ≌即可(2)连接EB FD 根据DOE BOF ≌ 得出ED BF = 根据ED BF ∥ 证明四边形EBFD 为平行四边形 根据EF BD ⊥ 证明四边形EBFD 为菱形即可.【详解】(1)证明:①点O 为对角线BD 的中点①BO DO =①AD BC ∥①ODE OBF ∠=∠ OED OFB ∠=∠在DOE 和BOF 中ODE OBF OED OFB BO DO ∠=∠⎧⎪∠=∠⎨⎪=⎩①()AAS DOE BOF ≌(2)解:四边形EBFD 为菱形 理由如下:连接EB FD 如图所示:根据解析(1)可知 DOE BOF ≌①ED BF =①ED BF ∥①四边形EBFD 为平行四边形①l BD ⊥ 即EF BD ⊥①四边形EBFD 为菱形.【点睛】本题主要考查了三角形全等的判定和性质 菱形的判定 平行线的性质 解题的关键是熟练掌握三角形全等的判定方法和菱形的判定方法.19.(2023·浙江嘉兴·统考中考真题)如图,在菱形ABCD 中 AE BC ⊥于点E AF CD ⊥于点F 连接EF(1)求证:AE AF =(2)若=60B ∠︒ 求AEF ∠的度数.【答案】(1)证明见解析 (2)60︒【分析】(1)根据菱形的性质的三角形全等即可证明AE AF =.(2)根据菱形的性质和已知条件可推出BAD ∠度数 再根据第一问的三角形全等和直角三角形的性质可求出BAE ∠和DAF ∠度数 从而求出EAF ∠度数 证明了等边三角形AEF 即可求出AEF ∠的度数.【详解】(1)证明:菱形ABCD,AB AD B D ∴=∠=∠又,AE BC AF CD ⊥⊥90AEB AFD ∴∠=∠=︒.在AEB △和AFD △中AEB AFD B DAB AD ∠=∠⎧⎪∠=∠⎨⎪=⎩(AAS)ABE ADF ∴≌.AE AF ∴=.(2)解:菱形ABCD180B BAD ∴∠+∠=︒=60B ∠︒120BAD ∴∠=︒.又90,60AEB B ∠=︒∠=︒30BAE =∴∠︒.由(1)知ABE ADF ≌30BAE DAF ∴∠=∠=︒.120303060EAF ∴∠=︒-︒-︒=︒. =AE AFAEF ∴等边三角形.60AEF ∴∠=︒.【点睛】本题考查了三角形全等 菱形的性质 等边三角形的性质 解题的关键在于熟练掌握全等的方法和菱形的性质.20.(2023·湖北鄂州·统考中考真题)如图,点E 是矩形ABCD 的边BC 上的一点 且AE AD =.(1)尺规作图(请用2B 铅笔):作DAE ∠的平分线AF 交BC 的延长线于点F 连接DF .(保留作图痕迹 不写作法)(2)试判断四边形AEFD 的形状 并说明理由.【答案】(1)见解析 (2)四边形AEFD 是菱形 理由见解析【分析】(1)根据题意结合尺规作角平分线的方法作图即可(2)根据矩形的性质和平行线的性质得出DAF AFE ∠=∠ 结合角平分线的定义可得EFA EAF ∠=∠,则AE EF = 然后根据平行四边形和菱形的判定定理得出结论.【详解】(1)解:如图所示:(2)四边形AEFD 是菱形理由:①矩形ABCD 中 AD BC ∥①DAF AFE ∠=∠①AF 平分DAE ∠①DAF EAF ∠=∠①EFA EAF ∠=∠①AE EF =①AE AD =①AD EF =①AD EF ∥①四边形AEFD 是平行四边形又①AE AD =①平行四边形AEFD 是菱形.【点睛】本题主要考查了尺规作角平分线 矩形的性质 平行线的性质 等腰三角形的判定 平行四边形的判定以及菱形的判定等知识 熟练掌握相关判定定理和性质定理是解题的关键.21.(2023·吉林长春·统考中考真题)将两个完全相同的含有30︒角的直角三角板在同一平面内按如图所示位置摆放.点A E B D 依次在同一直线上 连结AF CD .(1)求证:四边形AFDC 是平行四边形(2)己知6cm BC 当四边形AFDC 是菱形时.AD 的长为__________cm .【答案】(1)见解析 (2)18【分析】(1)由题意可知ACB DFE △≌△易得AC DF = 30CAB FDE ∠=∠=︒即AC DF ∥ 依据一组对边平行且相等的四边形是平行四边形可证明(2)如图,在Rt ACB △中 由30︒角所对的直角边等于斜边的一半和直角三角形锐角互余易得212cm AB BC == 60ABC ∠=︒ 由菱形得对角线平分对角得30CDA FDA ∠=∠=︒ 再由三角形外角和易证BCD CDA ∠=∠即可得6cm BC BD 最后由AD AB BD =+求解即可.【详解】(1)证明:由题意可知ACB DFE △≌△AC DF =∴ 30CAB FDE ∠=∠=︒AC DF ∥∴四边形AFDC 地平行四边形(2)如图,在Rt ACB △中 90ACB ∠=︒ 30CAB ∠=︒ 6cm BC212cm AB BC ∴== 60ABC ∠=︒四边形AFDC 是菱形AD ∴平分CDF ∠30CDA FDA ∴∠=∠=︒ABC CDA BCD ∠=∠+∠603030BCD ABC CDA ∴∠=∠-∠=︒-︒=︒BCD CDA ∴∠=∠6cm BC BD ∴==18cm AD AB BD ∴=+=故答案为:18.【点睛】本题考查了全等三角形的性质 平行四边形的判定 菱形的性质 30︒角所对的直角边等于斜边的一半和直角三角形锐角互余 三角形外角及等角对等边 解题的关键是熟练掌握相关知识综合求解. 22.(2023·湖南张家界·统考中考真题)如图,已知点A D C B 在同一条直线上 且AD BC = AE BF = CE DF =.。
中考数学总复习:矩形、菱形、正方形ppt专题课件

第 二 十 二 讲
第 二 十 三 讲
【思路点拨】 (1)证明全等时应避免把对应边找错. (2)因 s i n ∠E D F =
EF DE
第 二 十 四 讲
, 结合(1)求 E F , D E 的长.
复习目标
知识回顾
重点解析
探究拓展
真题演练
【自主解答】 ( 1) 证明: 在矩形 A B C D 中, BC = AD , A D ∥B C , ∠B = 90°. ∴∠D A F = ∠A E B . ∵D F ⊥A E , AE= BC , ∴∠A F D = 90°= ∠B . 又∵A E = A D . ∴△A B E ≌△D F A .
第 二 十 四 讲
复习目标
知识回顾
重点解析
探究拓展
真题演练
名 称
定义与判定 1. 有一个角是直角, 一组邻边相等 的 2. 一组邻边相等的 3. 一个角是直角的 4. 对角线相等且 形 的平行四边
性质
第 二 十 二 讲
1. 对角线与边的夹角为 度 2. 面积等于边长的 3. 面积等于对角线
第 二 十 三 讲
第 二 十 四 讲
复习目标
知识回顾
重点解析
探究拓展
真题演练
➡特别提示: 矩形、 菱形、 正方形都是特殊的平行四边形, 它们都具有平行四 边形的性质, 但又有它们独特的性质.
第 二 十 二 讲
【答案】2. 直角 3. 相等 1. 直角 4. 中心对称图形 1. 相等 2. 四边形 3. 平行四边形 2. 平分 3. 一半 4. 轴对称 1. 平行四边形 2. 矩形 3. 菱形 4. 垂直 1. 45 2. 平方 3. 平方的一半
复习目标
中考一轮复习--第21讲 矩形、菱形、正方形

考法1
考法2
考法3
对应练1(课本习题改编)下列命题,其中是真命题的为( D )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.对角线互相垂直的四边形是菱形
C.对角线相等的四边形是矩形
D.一组邻边相等的矩形是正方形
考法1
考法2
考法3
对应练2(2019·内蒙古通辽)如图,在矩形ABCD中,AD=8,对角线
∵AD2+AB2=BD2,∴64+AB2=4AB2,
8 3
.
3
∴AB=
考法1
考法2
考法3
对应练3
(2018·甘肃白银)已知矩形ABCD中,E是AD边上一个动点,点
F,G,H分别是BC,BE,CE的中点.
(1)求证:△BGF≌△FHC;
(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.
∴OD= 2,
∴直线 l∥AC 并且到 D 的距离为 3,同理,在点 D 的另一侧还有一条
直线满足条件,
故共有 2 条符合题意的直线 l.故选 B.
考法1
考法2
考法3
矩形的性质和判定
例1(2018·合肥行知学校模拟)如图,已知▱ABCD,延长AB到E使
BE=AB,连接BD,ED,EC,若ED=AD.
AC与BD相交于点O,AE⊥BD,垂足为点E,且AE平分∠BAC,则AB的
8 3
长为 3
.
解析:∵四边形ABCD是矩形,
∴AO=CO=BO=DO,∵AE平分∠BAO,
∴∠BAE=∠EAO,且AE=AE,∠AEB=∠AEO,
∴△ABE≌△AOE(ASA),
∴AO=AB,且AO=OB,
【2022】苏教版中考数学精编专题《平行四边形、矩形、正方形、菱形》(含答案解析)

【苏教版】中考数学精编专题汇编专题1平行四边形、矩形、菱形、正方形学校:___________姓名:___________班级:___________1.【江苏省南京市中考二模】下列命题中假命题是( ) A 、两组对边分别相等的四边形是平行四边形 B 、两组对角分别相等的四边形是平行四边形C 、一组对边平行一组对角相等的四边形是平行四边形D 、一组对边平行一组对边相等的四边形是平行四边形D 、例如等腰梯形,满足一组对边平行一组对边相等,但它不是平行四边形,所以是个假命题.正确. 故选D .【考点定位】命题与定理.2.【江苏省江阴市中考】如图,菱形ABCD 中,对角线AC 交BD 于O ,AB =8, E 是CD 的中点,则OE 的长等于( )A.2B.3C.4D.5 【答案】C.B【解析】已知菱形ABCD ,根据菱形的性质可得AB=BC=8,OB=OD ,又因E 是CD 的中点,所以OE 为△DBC 的中位线,根据三角形的中位线定理可得OE=BC=4.故选C. 【考点定位】菱形的性质;三角形的中位线定理.3. 【江苏省常州市中考】如图,▱ABCD 的对角线AC 、BD 相交于点O ,则下列说法一定正确的是( )A .AO =ODB .AO ⊥ODC .AO =OCD .AO ⊥AB 【答案】C .【考点定位】平行四边形的性质.4.【江苏省徐州市中考】如图,菱形中,对角线AC 、BD 交于点O ,E 为AD 边中点,菱形ABCD 的周长为28,则OE 的长等于( )【考点定位】菱形的性质.215. 【江苏省徐州市中考模拟】15.如图,四边形ABCD 中,E ,F ,G ,H 分别是边AB 、BC 、CD 、DA 的中点.若四边形EFGH 为菱形,则对角线AC 、BD 应满足条件 .【答案】AC=BD .【考点定位】1.菱形的性质;2.三角形中位线定理.6.【江苏省徐州市中考模拟】将两块全等的含30°角的三角尺如图1摆放在一起,设较短直角边为1,如图2,将Rt△BCD 沿射线BD 方向平移,在平移的过程中,当点B的移动距离为时,四边ABC 1D 1为矩形;当点B 的移动距离为 时,四边形ABC1D 1为菱形.【解析】当点B 的移动距离为时,∠C 1BB 1=60°,则∠ABC 1=90°,根据有一直角的平行四边形是矩形,可判定四边形ABC 1D 1为矩形;当点B 的移动距离为时,D 、B1两点重合,根据对角线互相垂直平分的四边形是菱形,可判定四边形ABC 1D 1为菱形.333如图:【考点定位】1.菱形的判定;2.矩形的判定;3.平移的性质.7. 【江苏省淮安市中考】如图,A,B两地被一座小山阻隔,为测量A,B两地之间的距离,在地面上选一点C,连接CA,CB,分别取CA,CB的中点D、E,测得DE的长度为360米,则A、B两地之间的距离是米.【答案】720.【考点定位】1.三角形中位线定理;2.应用题.8.【江苏省无锡市中考】如图,已知矩形ABCD的对角线长为8cm,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH的周长等于 cm.【答案】16.【解析】根据三角形的中位线定理和矩形对角线相等的性质可证得四边形EFGH是菱形,且故答案为:16.【考点定位】三角形的中位线定理;矩形的性质;菱形的判定及性质.9.【江苏省中考模拟】已知:如图,在平行四边形ABCD中,点E、F在AC上,且AE=CF.求证:四边形BEDF是平行四边形.【答案】证明见解析.【解析】试题分析:根据平行四边形的性质,可得对角线互相平分,根据对角线互相平分的四边形是平行四边形,可得证明结论.试题解析:证明:如图,连接 BD设对角线交于点O.∵四边形ABCD是平行四边形,∴OA=OC,OB=OD.∵AE=CF,OA﹣AE=OC﹣CF,∴OE=OF.∴四边形BEDF是平行四边形.【考点定位】平行四边形的判定与性质.10.【江苏省常州市中考】如图,在▱ABCD中,∠BCD=120°,分别延长DC、BC到点E,F,使得△BCE和△CDF 都是正三角形.(1)求证:AE=AF;(2)求∠EAF的度数.【答案】(1)证明见试题解析;(2)60°.【考点定位】1.全等三角形的判定与性质;2.等边三角形的性质;3.平行四边形的性质.专题2 圆的有关计算及圆的综合学校:___________姓名:___________班级:___________1.【江苏省南通市九年级上学期期末】如图,⊙O 中,OA ⊥BC ,∠A OB=52°,则∠ADC 的度数为( )A .36°B .26°C . 38°D .46°【答案】D . 【解析】故选D.【考点定位】1.圆周角定理;2.垂径定理.2.【江苏省江阴市九年级下学期期中】一个圆锥底面直径为2,母线为4,则它的侧面积为( ) A . B.C .D .【答案】C.【解析】根据圆锥的侧面积公式S=πrl 可得这个圆锥的侧面积为π×1×4=4π.故选C. 【考点定位】圆锥的侧面积公式.3.【江苏省苏州市区中考】如图,⊙O 上A 、B 、C 三点,若∠B=50,∠A=20°,则∠AOB 等于( ) A 、30° B 、50° C 、70° D 、60°【答案】D .2π12π4π8π【解析】先根据圆周角定理得出∠ACB=∠AOB ,再由三角形内角和定理即可得出结论.∵∠AOB 与∠ACB是同弧所对的圆心角与圆周角,∠B=50,∠A=20°,∴∠ACB=∠AOB .∴180°-∠AOB-∠A=180°-∠ACB-∠B ,即180°-∠AOB-20°=180°-∠AOB-50°,解得∠AOB=60°.故选D .【考点定位】圆周角定理.4.【江苏省南通市九年级上学期期末】某个圆锥的侧面展开图形是一个半径为6cm ,圆心角为120°的扇形,则这个圆锥的底面半径为( )cm . A 、2B 、3C 、4D 、5【答案】A .故选A.【考点定位】弧长的计算.5.【江苏省苏州市中考一模】如图,AB 是⊙O 的切线,切点为B ,AO 交⊙O 于点C ,且AC=OC ,若⊙O 的半径为5,则图中阴影部分的面积是 .. 【解析】直接利用切线的性质结合勾股定理得出AB 的长,再利用锐角三角函数关系得出∠BOC 的度数,结合阴影部分的面积为:S △OBA -S 扇形BOC 求出即可.连接OB ,∵AB 是⊙O 的切线,切点为B ,∴∠OBBA=90°,∵AC=OC ,⊙O 的半径为5,∴AC=5,AB=5,∴∠A=30°,则∠BOC=60°,∴图中阴影部分的面积为:S △OBA -S 扇形BOC =×BO ×AB-.故答案为:121212625π312605360π⨯536225π. 【考点定位】1.扇形面积的计算;2.切线的性质.6.【江苏省徐州中考】13.圆锥底面圆的半径为3m ,其侧面展开图是半圆,则圆锥母线长为 m. 【答案】6.【考点定位】圆锥的计算.7.【江苏省中考】已知扇形的圆心角为120°,弧长为6π,则扇形的面积是 . 【答案】27π.【考点定位】扇形面积的计算.8.【江苏省南京市中考二模】已知等腰△ABC 中,AB=AC=13cm ,BC=10cm ,则△ABC 的内切圆半径为 cm . 【答案】. 【解析】如图,设△ABC 的内切圆半径为r ,由勾股定理得AD=12,再由切线长定理得AE=8,根据勾股定理求得r 即可.如图,∵AB=AC=13cm ,BC=10cm ,∴BD=5cm ,∴AD=12cm ,根据切线长定理,AE=AB-BE=AB-BD=13-5=8,设△ABC 的内切圆半径为r ,∴AO=12-r ,∴(12-r )2-r 2=64,解得r=.故答案为:. 【考点定位】1.三角形的内切圆与内心;2.等腰三角形的性质.9.【江苏省苏州中考一模】如图所示,D 是以AB 为直径的半圆O 上的一点,C 是弧AD 的中点,点M 在AB 上,AD 与CM 交于点N ,CN=AN .625π103103103(1)求证:CM⊥AB;(2)若BD=2,求半圆的直径.【答案】(1)证明见解析;(2)6.【解析】试题解析:(1)证明:如图1,连接BC,则∠ACB=90°,∵CN=AN,∴∠NCA=∠NAC,∴∠MCA=∠DAC,∵C是弧AD的中点,∴∠ABC=∠DAC,∴∠MCA=∠ABC,∵∠CAB=∠BAC,∴△ABC∽△ACM,∴∠AMC=90°,∴CM⊥AB;(2)解:如图2,连接CD,作CE⊥BD,交BD的延长线于E,在△CMB与△BCE中,,【考点定位】1.相似三角形的判定与性质;2,全等三角形的判定与性质;2.圆周角定理.10.【江苏省无锡市中考】已知:如图,AB 为⊙O 的直径,点C 、D 在⊙O 上,且BC =6cm ,AC =8cm ,∠ABD =45º.(1)求BD 的长;(2)求图中阴影部分的面积.【答案】(1)BD =52cm;(2)S 阴影=25π-504cm 2. 【解析】MBC CBE CMB CEB BC BC ∠=∠∠=∠=⎧⎪⎨⎪⎩【考点定位】圆周角定理的推论;勾股定理;扇形的面积公式.专题3 图形的变换、视图与投影学校:___________姓名:___________班级:___________1. 【江苏省苏州市中考一模】下列腾讯QQ表情中,不是轴对称图形的是()【答案】C.【解析】根据轴对称图形的概念求解.A、是轴对称图形,故本选项错误;B、是轴对称图形,故本选项错误;C、不是轴对称图形,故本选项正确;D、是轴对称图形,故本选项错误.故选C.【考点定位】轴对称图形.2.【江苏省徐州市中考模拟】下列图形中,既是中心对称图形又是轴对称图形的是()【答案】D.【考点定位】1.中心对称图形;2.轴对称图形.3. 【江苏省淮安市中考】如图所示物体的主视图是()A. B. C. D.【答案】C.【考点定位】简单组合体的三视图.4.【江苏省常州市中考】下列“慢行通过,注意危险,禁止行人通行,禁止非机动车通行”四个交通标志图(黑白阴影图片)中为轴对称图形的是()A. B. C. D.【答案】B.故选B.【考点定位】轴对称图形.5.【江苏省常州市中考】将一张宽为4cm的长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形,则这个三角形面积的最小值是【答案】8cm2 .故答案为:8cm 2.【考点定位】1.翻折变换(折叠问题);2.最值问题.6.【江苏省江阴市中考】如图,Rt ΔABC 中,AB=9,BC=6,∠B=900,将ΔABC 折叠,使A 点与BC 的中点D 重合,折痕为MN ,则线段BN的长为【答案】 4. 【解析】 故答案为:4.【考点定位】翻折变换;勾股定理. 7.【江苏省苏州市区中考】在R t △ABC 中,斜边AB=4,∠B=60°,将△ABC 绕点B 旋转60°,顶点C 运动的路线长是 (结果保留π).【答案】.【解析】将△ABC 绕点B 旋转60°,顶点C 运动的路线长是就是以点B 为圆心,B C 为半径所旋转的弧,根据弧长公式即可求得.∵AB=4,∴BC=2,所以弧长=.故答案为:. 【考点定位】1.弧长的计算;2.旋转的性质.8.【江苏省扬州市2015年中考数学试题】如图,已知Rt △ABC 中,∠ABC =90°,AC =6,BC =4,将△ABC 绕直角顶点C 顺时针旋转90°得到△DEC ,若点F 是DE 的中点,连接AF ,则AF = 23π602180π⨯=23π23π【答案】5【考点定位】旋转的性质9.【江苏省徐州市中考】如图,在方格纸上建立平面直角坐标系,每个小正方形的边长为1.(1)画出△AOB关于x轴对称的△A1OB1.(2)画出将△AOB绕点O顺时针旋转90°的△A2OB2,并判断△A1OB1和△A2OB2在位置上有何关系?若成中心对称,请直接写出对称中心坐标;如成轴对称,请直接写出对称轴的函数关系式.(3)若将△AOB绕点O旋转360°,试求出线段AB扫过的面积.【答案】(1)画图见解析;(2)画图见解析;△A1OB1和△A2OB2是轴对称关系,对称轴为:y=﹣x.(3)2.5π.【解析】试题解析:(1)如图所示:.(2)如图所示:△A1OB1和△A2OB2是轴对称关系,对称轴为:y=﹣x.(3)过点O作OE⊥AB,线段AB2﹣π()2=5π﹣2.5π=2.5π. 【考点定位】1.作图-旋转变换;2.扇形面积的计算;3.作图-轴对称变换.10.【江苏省南京市中考二模试题】△ABC 中,AB=AC=10,BC=12,矩形DEFG 中,EF=4,FG >12.(1)如图①,点A 是FG 的中点,FG ∥BC ,将矩形DEFG 向下平移,直到DE 与BC 重合为止.要研究矩形DEFG 与△ABC 重叠部分的面积,就要进行分类讨论,你认为如何进行分类,写出你的分类方法(无需求重叠部分的面积).(2)如图②,点B 与F 重合,E 、B 、C 在同一直线上,将矩形DEFG 向右平移,直到点E 与C 重合为止.设矩形DEFG 与△ABC 重叠部分的面积为y ,平移的距离为x .①求y 与x 的函数关系式,并写出自变量的取值范围;②在给定的平面直角坐标系中画出y 与x 的大致图象,并在图象上标注出关键点坐标.2【考点定位】几何变换综合题.。
2020年中考数学二轮专题——矩形、菱形、正方形(含详细解答)

2020年中考数学二轮专题——矩形、菱形、正方形基础过关1. (2019无锡)下列结论中,矩形具有而菱形不一定具有的性质是()A. 内角和为360°B. 对角线相互平分C. 对角线相等D. 对角线互相垂直2. (2019娄底)顺次连接菱形四边中点得到的四边形是()A. 平行四边形B. 菱形C. 矩形D. 正方形3. (2019重庆A卷)下列命题正确的是()A.有一个角是直角的平行四边形是矩形B.四条边相等的四边形是矩形C.有一组邻边相等的平行四边形是矩形D.对角线相等的四边形是矩形4. (2019青羊区二诊)在菱形ABCD中,对角线AC、BD交于点O,下列说法错误的是()A.AB∥DC B.OC=OBC.AC⊥BD D.OA=OC5. (2019毕节)如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD的面积为()A. 3B. 3C. 5D. 5第5题图6. (2019天津)如图,四边形ABCD为菱形,A,B两点的坐标分别是(2,0),(0,1),点C,D在坐标轴上,则菱形ABCD的周长等于()A. 5B. 4 3C. 4 5D. 20第6题图7. (2019呼和浩特)已知菱形的边长为3,较短的一条对角线的长为2,则该菱形较长的一条对角线的长为()A. 2 2B. 2 5C. 4 2D. 2108. (2019临沂)如图,在▱ABCD中,M,N是BD上的两点,BM=DN,连接AM,MC,CN,N A.添加一个条件,使四边形AMCN 是矩形,这个条件是( )A. OM =12ACB. MB =MOC. BD ⊥ACD. ∠AMB =∠CND第8题图9. 如图,在正方形ABCD 外侧,作等边△ADE ,AC ,BE 相交于点F ,则∠BFC 为( ) A. 75°B. 60°C. 55°D. 45°第9题图10. 如图,在矩形ABCD 中,点E 在BC 上,AE =AD ,DF ⊥AE ,垂足为F ,若∠FDC =30°,且AB =3,则AD 的长为( )A .3B .4C .5D .6第10题图11. (2019贵阳)如图,菱形ABCD 的周长是4 cm ,∠ABC =60°,那么这个菱形的对角线AC 的长是( ) A. 1 cmB. 2 cmC. 3 cmD. 4 cm第11题图12. (2019德阳)已知▱ABCD 的对角线AC 、BD 相交于点O ,△AOD 是等边三角形,且AD =4,则AB 等于( )A. 2B. 4C. 2 3D. 4 313. (2019河池)如图,在正方形ABCD 中,点E ,F 分别在BC ,CD 上,BE =CF ,则图中与∠AEB 相等的角的个数是( )A. 1B. 2C. 3D. 4第13题图14. 如图,在矩形ABCD 中,AB =12,BC =16,点E 是BC 的中点,点F 是边CD 上的任意一点,则AF +EF 的最小值为( )A .12B .14C .12 5D .14 5第14题图15. (2019兰州)如图,边长为2的正方形ABCD 的对角线AC 与BD 交于点O ,将正方形ABCD 沿直线DF 折叠,点C 落在对角线BD 上的点E 处,折痕DF 交AC 于点M ,则OM =( )A.12B.22C.3-1D.2-1第15题图16. (2019金华)如图,矩形ABCD 的对角线交于点O ,已知AB =m ,∠BAC =∠α,则下列结论错误..的是( )A. ∠BDC =∠αB. BC =m ·tan αC. AO =m 2sin αD. BD =m cos α第16题图17. (2019台州)如图,有两张矩形纸片ABCD 和EFGH ,AB =EF =2 cm ,BC =FG =8 cm.把纸片ABCD 交叉叠放在纸片EFGH 上,使重叠部分为平行四边形,且点D 与点G 重合,当两张纸片交叉所成的角α最小时,tan α等于( )A. 14B. 12C. 817D. 815第17题图18.(2019绍兴)正方形ABCD的边AB上有一动点E,以EC为边作矩形ECFG,且边FG过点D,在点E从点A移动到点B的过程中,矩形ECFG的面积()A. 先变大后变小B. 先变小后变大C. 一直变大D. 保持不变第18题图19. (2019双流区一诊)一个菱形的周长为20 cm,一条对角线长为6 cm,则这个菱形的面积是______cm2.20. (2019扬州)如图,已知点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M、N分别是DC、DF的中点,连接MN.若AB=7,BE=5,则MN=________.第20题图21.(2019徐州)如图,矩形ABCD中,AC、BD交于点O、M、N分别为BC、OC的中点.若MN=4,则AC的长为________.第21题图22. (2019菏泽)如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是________.第22题图23.如图,在矩形ABCD中,AB=6,BC=8,过对角线交点O作EF⊥AC交AD于点E,交BC于点F,则DE 的长是________.第23题图24. (2019北京)如图,在菱形ABCD 中,AC 为对角线,点E ,F 分别在AB ,AD 上,BE =DF ,连接EF . (1)求证:AC ⊥EF ;(2)延长EF 交CD 的延长线于点G ,连接BD 交AC 于点O .若BD =4,tan G =12,求AO 的长.第24题图25. (2019云南)如图,四边形ABCD 中,对角线AC 、BD 相交于点O ,AO =OC ,BO =OD ,且∠AOB =2∠OA D.(1)求证:四边形ABCD 是矩形;(2)若∠AOB ∶∠ODC =4∶3,求∠ADO 的度数.第25题图能力提升1. (2019烟台)如图,面积为24的▱ABCD中,对角线BD平分∠ABC,过点D作DE⊥BD交BC的延长线于点E,DE=6,则sin∠DCE的值为()A. 2425 B.45 C.34 D.1225第1题图2. (2019安徽)如图,在正方形ABCD中,点E,F将对角线AC三等分,且AC=12.点P在正方形的边上,则满足PE+PF=9的点P的个数是()A. 0B. 4C. 6D. 8第2题图3. (2019黄石)如图,矩形ABCD中,AC与BD相交于点E,AD∶AB=3∶1,将△ABD沿BD折叠,点A的对应点为F,连接AF交BC于点G,且BG=2,在AD边上有一点H,使得BH+EH的值最小,此时BHCF=()A.32 B.233 C.62 D.32第3题图4.(2019遵义)如图,平行四边形纸片ABCD的边AB,BC的长分别是10 cm和7.5 cm,将其四个角向内对折后,点B与点C重合于点C′,点A与点D重合于点A′.四条折痕围成一个“信封四边形”EHFG,其顶点分别在平行四边形ABCD的四条边上,则EF=________cm.第4题图5. (2019海南)如图,在边长为1的正方形ABCD中,E是边CD的中点,点P是边AD上一点(与点A、D不重合),射线PE与BC的延长线交于点Q.(1)求证:△PDE≌△QCE;(2)过点E作EF∥BC交PB于点F,连接AF,当PB=PQ时.①求证:四边形AFEP是平行四边形;②请判断四边形AFEP是否为菱形,并说明理由.第5题图6. (2019双流区一诊)如图①,菱形ABCD中,点P是CD的中点,∠BCD=60°,射线AP交BC的延长线于点E,射线BP交DE于点K,点O是线段BK的中点.(1)求证:△ADP≌△ECP;(2)若BP=n·PK,试求出n的值;(3)作BM⊥AE于点M,作KN⊥AE于点N,连接MO、NO,如图②,请证明△MON是等腰三角形,并求出∠MON的度数.第6题图满分冲关1. (2019新都区一诊)如图,直线l 经过正方形ABCD 的顶点A ,先分别过此正方形的顶点B 、D 作BE ⊥l 于点E 、DF ⊥l 于点F ,然后再以正方形的对角线的交点O 为端点,引两条相互垂直的射线分别与AD 、CD 交于点G 、H 两点.若EF =25,S △ABE =2,则线段GH 长度的最小值是______.第1题图2. (2018本溪)在菱形ABCD 中,∠BAD =120°,点O 为射线CA 上的动点,作射线OM 与直线BC 相交于点E ,将射线OM 绕点O 逆时针旋转60°,得到射线ON ,射线ON 与直线CD 相交于点F .(1)如图①,点O 与点A 重合时,点E ,F 分别在线段BC ,CD 上,请直接写出CE ,CF ,CA 三条线段之间的数量关系;(2)如图②,点O 在CA 的延长线上,且OA =13AC ,E ,F 分别在线段BC 的延长线和线段CD 的延长线上,请写出CE ,CF ,CA 三条线段之间的数量关系,并说明理由;(3)点O 在线段AC 上,若AB =6,BO =27,当CF =1时,请直接写出BE 的长.参考答案基础过关1. C2. C 【解析】顺次连接任意四边形的四边中点,得到四边形一定是平行四边形,如果原四边形的对角线相等,则可得中点四边形的邻边相等,即是菱形;如果原四边形的对角线互相垂直,则可得中点四边形的邻边垂直,即是矩形.因为菱形的对角线互相垂直,所以它的中点四边形是矩形.3.A 【解析】根据矩形的判定定理可知,有一个角是直角的平行四边形是矩形,故A 正确;四条边相等的四边形是菱形,不是矩形,故B 错误;有一组邻边相等的平行四边形是菱形,不是矩形,故C 错误;对角线相等的平行四边形是矩形,故D 错误.4. B 【解析】∵四边形ABCD 是菱形,∴AB ∥CD ,AC ⊥BD ,OA =OC ,故A ,C ,D 正确.5. B 【解析】在Rt △BCE 中,BC =22-12=3,∴正方形ABCD 的面积为(3)2=3.6. C 【解析】∵A (2,0),B (0,1),∴OA =2,OB =1,在Rt △AOB 中,由勾股定理得AB =22+12=5,∵四边形ABCD 为菱形,∴菱形ABCD 的周长为4AB =4 5.7. C 【解析】菱形对角线相互垂直且平分,因此另一条对角线长为2×32-1=4 2.8. A 【解析】∵四边形ABCD 是平行四边形,∴OB =OD ,OA =OC .∵BM =DN ,∴OM =ON ,∴四边形AMCN 是平行四边形.当OM =12AC 时,MN =AC ,∴四边形AMCN 是矩形.9. B 【解析】∵四边形ABCD 是正方形,∴∠BAD =90°,AB =AD ,∠BAF =45°,∵△ADE 是等边三角形,∴∠DAE =60°,AD =AE ,∴∠BAE =90°+60°=150°,AB =AE ,∴∠ABE =∠AEB =12(180°-150°)=15°,∴∠BFC =∠BAF +∠ABE =45°+15°=60°,故选B .10. D 【解析】∵四边形ABCD 是矩形,∴AD ∥BC ,∴∠AEB =∠DAF ,又∵DF ⊥AE ,∴∠DF A =∠B ,又∵AE =AD ,∴△ADF ≌△EAB ,∴DF =AB .∵∠ADF +∠FDC =90°,∠DAF +∠ADF =90°,∴∠FDC =∠DAF =30°,∴AD =2DF =2AB =6.11. A 【解析】∵菱形ABCD 的周长是4 cm ,∴AB =BC =CD =DA =1 cm ,又∵∠ABC =60°,∴△ABC 是等边三角形,∴AC =AB =BC =1 cm .12.D 【解析】在平行四边形ABCD 中,∵△AOD 为等边三角形,即OA =OD =AD =4,∴AC =BD =8,∴平行四边形ABCD 是矩形,∴由勾股定理得AB =4 3.13. C 【解析】四边形ABCD 是正方形,∴AD ∥BC ,∴∠DAE =∠AEB .∵BE =CF ,∠ABE =∠BCF ,AB =BC ∴△ABE ≌△BCF (SAS),∴∠BFC =∠AEB .∵AB ∥CD ,∴∠ABF =∠BFC =∠AEB .∴与∠AEB 相等的角有3个.14.C 【解析】如解图,作点E 关于直线CD 的对称点E ′,连接AE ′交CD 于点F ,此时AF +EF 的最小值为AE ′的长.∵在矩形ABCD 中,AB =12,BC =16,E 是BC 的中点,∴BE =CE =CE ′=8,∴BE ′=24,∴AE ′=AB 2+BE ′2=122+242=12 5.第14题解图15. D 【解析】∵四边形ABCD 是正方形,∴∠CBE =∠DCM =45°,BC =CD = 2.∴AC =BD =2.∴OC =1.由折叠的性质知,DE =CD =2,CF =EF ,∴BE =2-2,∠DFC =90°.∴∠CDM +∠DCE =90°.又∠BCE +∠DCE =90°,∴∠BCE =∠CDM . ∴△BCE ≌△CDM .∴CM =BE =2- 2.∴OM =OC -CM =1-(2-2)=2-1.16. C 【解析】∵四边形ABCD 是矩形,∴AC =BD ,且OD =OC ,∠ABC =90°,∴∠BDC =∠OCD =∠BAO =∠α,tan α=BC AB =BC m ,sin α=BC AC =BC 2AO ,cos α=AB AC =m AC ,∴BC =m ·tan α,AO =BC 2sin α,AC =m cos α,而BD =AC ,BC ≠m ,∴BD =m cos α,AO ≠m2sin α∴A 、B 、D 正确,C 错误.17.D 【解析】如解图,当B 、E 重合时, α最小,∵在△BMF 和△DMC 中,⎩⎪⎨⎪⎧∠BMF =∠DMC ∠F =∠C BF =DC ,∴△BMF ≌△DMC (AAS),∴BM =DM ,设FM =x ,则DM =BM =8-x ,在Rt △BFM 中,由勾股定理得22+x 2=(8-x )2,解得x =154,∴tan α=BF FM =2154=815.第17题解图18. D 【解析】如解图,连接DE ,∵在正方形ABCD 中,S △DEC =12AD ·CD =12S 正方形ABCD ,在长方形ECFG 中,S △DEC =12×EC ·GE =12S 矩形ECFG ,而点E 从点A 移动到点B 的过程中,三角形DEC 的面积保持不变,∴矩形ECFG 的面积保持不变.第18题解图19. 24 【解析】如解图,在菱形ABCD 中,BD =6.∵菱形的周长为20,BD =6,∴AB =5,BO =3,∴AO =52-32=4,AC =8.∴S 菱形ABCD =12×6×8=24.第19题解图20.132 【解析】 如解图,连接FC ,则MN =12CF ,在Rt △CFG 中,FG =5,CG =5+7=12,∴FC =52+122=13,∴MN =132.第20题解图21. 16 【解析】在△OBC 中,根据三角形中位线等于它所对的第三边的一半,得到OB =2MN =8,又根据矩形的性质:对角线相等且互相平分,得到AC =BD =2OB =16.22. 85 【解析】如解图,连接BD 交AC 于点O ,∵四边形ABCD 是正方形,AC 是对角线,∴CD =AD ,∠DAE =∠DCF =45°,BD ⊥AC . ∵AE =CF , ∴△DAE ≌△DCF (SAS), ∴DE =DF ,同理可证:DE =BE ,BE =BF ,∴四边形BEDF 是菱形,∵AC =8,AO =OD ,AE =2,∴OE =2,OD =4,∴DE =OD 2+OE 2=42+22=2 5.∴四边形BEDF 的周长为4DE =8 5.第22题解图23. 74 【解析】如解图,连接EC ,∵OA =OC ,EF ⊥AC ,∴EC =AE ,设DE =x ,则EC =AE =8-x ,根据勾股定理可得(8-x )2=x 2+62,解得x =74.∴DE 的长为74.第23题解图24. (1)证明:∵四边形ABCD 是菱形, ∴AB =AD ,∴∠BAC =∠DAC . ∵AB =AD ,BE =DF ,∴AB -BE =AD -DF ,即AE =AF . ∴△AEF 是等腰三角形. 又∵∠BAC =∠DAC , ∴AC ⊥EF ;(2)解:由题意作解图如下, ∵四边形ABCD 是菱形,∴AC ⊥BD ,AB ∥CD ,OB =12BD =12×4=2.∴∠G =∠AEG .由(1)知EF ⊥AC .又∵BD ⊥AC . ∴EF ∥BD .∴∠AEG =∠ABO . ∴∠G =∠ABO .∵tan G =12,∴tan ∠ABO =AO OB =12.∴AO =OB ·tan ∠ABO =2×12=1.第24题解图25. (1)证明:∵AO =OC ,BO =OD , ∴四边形ABCD 是平行四边形.又∵∠AOB =2∠OAD ,∠AOB 是△AOD 的外角, ∴∠AOB =∠OAD +∠ADO . ∴∠OAD =∠ADO . ∴AO =OD .又∵AC =AO +OC =2AO ,BD =BO +OD =2OD , ∴AC =BD .∴四边形ABCD 是矩形;(2)解:设∠AOB =∠DOC =4x ,∠ODC =3x ,则∠ODC =∠OCD =3x . 在△ODC 中,∠DOC +∠OCD +∠CDO =180°, ∴4x +3x +3x =180°, 解得x =18°.∴∠ODC =3×18°=54°.∴∠ADO =90°-∠ODC =90°-54°=36°.能力提升1. A 【解析】如解图,连接AC 交BD 于点O ,过点D 作DF ⊥BE 于点F .∵BD 平分∠ABC ,∴∠ABD =∠CBD .∵四边形ABCD 是平行四边形,∴BC ∥AD . ∴∠ADB =∠CBD .∴∠ABD =∠ADB .∴AB =AD . ∴▱ABCD 是菱形. ∴AO 垂直平分BD . ∵DE ⊥BD ,∴OC ∥DE .∴OC =12DE =12×6=3.∵菱形ABCD 的面积为24,∴BD =8. ∴BO =4. ∴BC =DC =5.∵DF ·BC =24,∴DF =245. ∴sin ∠DCE =DF DC =2425.第1题解图2. D 【解析】如解图,∵点E ,F 将对角线AC 三等分,且AC =12,∴AE =EF =FC =4,当P 点在AD 上时,作E 点关于AD 的对称点E ′,连接E ′F ,则AE ′=AE =4,当P 点运动至E ′F 和AD 交点时,PE +PF 具有最小值,由对称性可知∠E ′AF =90°,此时E ′F =(AE ′)2+AF 2=42+82=45<9,当P 点和A 点重合时,过点E 作EG ⊥AD ,垂足为G ,PE +PF =AE +AF =12,当P 点和D 点重合时,连接DF ,∵AD =CD ,∠DAE =∠DCF ,AE =CF ,∴△AED ≌△CFD (SAS),∴DE =DF ,∴PE +PF =2DE =2EG 2+DG 2=2×(22)2+(42)2=410.∵45<9<12,45<9<410,∴在AD 上有两个位置存在PE +PF =9,同理在其余三边上各有两种情况,故正方形四条边上共存在8个位置使得PE +PF =9,∴满足条件的P 点有8个.第2题解图3. B 【解析】∵矩形ABCD 中,AD ∶AB =3∶1,∴∠ADB =30°,又△ABD 沿BD 折叠,点A 的对应点为F ,∴∠ADB =∠BDF =30°,∠ABD =∠DBF =60°,AD =FD ,AB =BF ,∴∠CDF =30°,△ADF 为等边三角形,DF =AF ,∴∠BAF =12(180°-∠ABD -∠DBF )=30°=∠CDF ,又DC =AB ,∴△ABF ≌△DCF ,∴CF =BF ,在Rt △ABG 中,ABG =90°,∠BAG =30°,BG =2,∴AB =23,∴CF =23,如解图,延长BA 到B ′使AB ′=AB ,连接EB ′交AD 于H ,根据对称性可知此时点H 即为满足BH +EH 的值最小的H 点.∵∠ADB =30°,∴AB =BE =ED ,又∵AB ′=AB =BE =AE ,∴△BB ′E 为直角三角形,在Rt △BEH 和Rt △BAH 中,BH =BH ,BE =BA ,∴Rt △BEH ≌Rt △BAH ,∴∠ABH =30°,∴BH =AB cos ∠ABH=4,∴BH CF =423=233.第3题解图4. 10 【解析】根据折叠的性质可得△CFH ≌△C ′FH ,△DFG ≌△A ′FG ,△AEG ≌△A ′EG ,△HBE ≌△HC ′E ,∵四边形HFGE 是矩形,∴HF =EG ,FG =HE ,∴△CFH ≌△C ′FH ≌△AEG ≌△A ′EG ,△DFG ≌△A ′FG ≌△HBE ≌△HC ′E ,∴EF =A ′F + A ′E =FD +AE = FD +CF =CD =AB =10 cm .5. (1)证明:∵四边形ABCD 是正方形, ∴∠D =∠BCD =90°. ∴∠ECQ =90°=∠D . ∵E 是CD 的中点, ∴DE =CE .又∵∠DEP =∠CEQ , ∴△PDE ≌△QCE (ASA);(2)①证明:如解图,由(1)可知△PDE ≌△QCE , ∴PE =QE =12PQ .又∵EF ∥BC , ∴PF =FB =12PB .∵PB =PQ , ∴PF =PE . ∴∠1=∠2.∵四边形ABCD 是正方形, ∴∠BAD =90°.在Rt △ABP 中,∵F 是PB 的中点, ∴AF =12BP =FP .∴∠3=∠4.又∵AD ∥BC ,EF ∥BC , ∴AD ∥EF . ∴∠1=∠4.∴∠2=∠3. 又∵PF =FP ,∴△APF ≌△EFP (AAS). ∴AP =EF . 又∵AP ∥EF ,∴四边形AFEP 是平行四边形;第5题解图②解:四边形AFEP 不是菱形,理由如下: 设PD =x ,则AP =1-x . 由(1)可知△PDE ≌△QCE . ∴CQ =PD =x . ∴BQ =BC +CQ =1+x .∵点E ,F 分别是PQ ,PB 的中点, ∵EF 是△PBQ 的中位线. ∴EF =12BQ =1+x 2.由①可知AP =EF . 即1-x =1+x 2,解得x =13.∴PD =13,AP =23.在Rt △PDE 中,∵DE =12,∴PE =PD 2+DE 2=136. ∵AP ≠PE .∴四边形AFEP 不是菱形.6. (1)证明:∵四边形ABCD 为菱形, ∴AD ∥BC ,∴∠DAP =∠CEP ,∠ADP =∠ECP , 在△ADP 和△ECP 中,⎩⎪⎨⎪⎧∠DAP =∠CEP ∠ADP =∠ECP DP =CP, ∴△ADP ≌△ECP (AAS);(2)解:如解图①,过点P 作PI ∥CE 交DE 于点I , 则PI CE =DPDC ,又点P 是CD 的中点, ∴PI CE =12, ∵△ADP ≌△ECP , ∴AD =CE , ∴KP KB =PI BE =14, ∴BP =3PK , ∴n =3;第6题解图①(3)解:如解图②,过点O 作OG ⊥AE 于点G , ∵BM ⊥AE 于点M ,KN ⊥AE 于点N , ∴BM ∥OG ∥KN , ∵点O 是线段BK 的中点, ∴MG =NG ,又∵OG ⊥MN , ∴OM =ON ,即△MON 是等腰三角形,由题意得,△BPC ,△AMB ,△ABP 为直角三角形, 设BC =2,则CP =1,由勾股定理得,BP =3, 则AP =7,根据三角形面积公式,BM =2217, ∴MP =377.易得PB =3PO ,∴OG =13BM =22121,MG =23MP =277,tan ∠MOG =MGOG =3,∴∠MOG =60°,∴∠MON 的度数为120°.第6题解图②满分冲关1. 6 【解析】由题易证△ABE ≌△DAF .∵GO ⊥HO ,易得△AGO ≌△DHO ,∴GO =HO .∴△GHO 为等腰直角三角形.∴当GO 最小时,GH 取得最小值.令AF =a ,AE =b ,则BE =a ,DF =b ,∴a +b =25,12a ·b =2,∴AB 2=a 2+b 2=12.∴AB =23.∴当GO ⊥AD 时,GO 有最小值,此时OG ∥AB ,∵O 为BD 中点,∴OG 为△ABD 的中位线,∴GO =12AB =3,∴GO 的最小值为3,∴GH 最小值为 6.2. 解:(1)CA =CE +CF ;【解法提示】∵在菱形ABCD 中,∠BAD =120°, ∴∠DAC =∠ACB =∠D =60°. 又∵∠EAF =60°, ∴∠DAF =∠CAE . ∵AD =CD 且∠D =60°,∴△ACD 是等边三角形,AD =AC , ∴△ADF ≌△ACE , ∴DF =CE .又∵CA =CD =DF +CF , ∴CA =CE +CF . (2)CF -CE =43CA ,理由:如解图①,过点O 作OG ∥AD ,交CF 于点G , ∵四边形ABCD 是菱形, ∴AB =BC =CD =DA . ∵∠BAD =120°, ∴∠B =∠ADC =60°,∴△ABC 和△ADC 都为等边三角形. ∵OG ∥AD ,∴∠OGC =∠ADC =∠ACD =60°, ∴△OGC 为等边三角形,∴OC =OG ,∠OCE =∠OGF =180°-60°=120°. ∵∠COE =∠GOF =60°-∠EOG ,∴△OCE ≌△OFG , ∴FG =CE . ∵CF =GF +CG , ∴CF -CE =CO . ∵AO =13CA ,∴OC =43CA ,∴CF -CE =43CA ;第2题解图①(3)BE 的长为1或3或5.【解法提示】连接BD 交AC 于点I ,①如解图②,当点O 在AI 上时,过点O 作OP ⊥BC 于点P ,作OQ ⊥CD 于点Q , 又∵菱形ABCD 中,AC 平分∠BCD , ∴OP =OQ .∵∠POQ =360°-120°-90°×2=60°, ∴∠EOF =∠POQ , ∴∠EOP =∠FOQ . 又∵∠OPE =OQF =90°, ∴△EOP ≌△FOQ , ∴EP =FQ .在Rt △AIB 中,AB =6,∠BAI =60°, ∴BI =AB ·sin60°=3 3. 在Rt △BIO 中, BO =27,BI =33, ∴OI =OB 2-BI 2=1. 又∵CI =12AC =3,∴OC =3+1=4, ∴CP =CQ =12OC =2.又∵CF =1,∴EP =FQ =1,∴BE =BC -CP -EP =6-2-1=3;第2题解图②②如解图③,当点O 在AI 上,点F 在线段DC 的延长线上时,过点O 作OP ⊥BC 于点P ,过点O 作OQ ⊥CD 于点Q ,同理可得EP =QF ,OC =4,CQ =CP =2, ∵CF =1,∴QF =CQ +CF =3,∴BE =CB -CP -PE =6-2-3=1;第2题解图③③如解图④,当点O 在IC 上时,由①知OC =3-1=2, 又∵CF =1,∠ACD =60°, ∴OF ⊥CD ,∴∠OEC =360°-60°-120°-90°=90°, ∴EC =12OC =1,∴BE =6-1=5;第2题解图④④如解图⑤,当点O 在IC 上,点F 在线段DC 的延长线上时,过点O 作OP ⊥BC 于点P ,过点O 作OQ ⊥CD 于点Q ,同理可得QF =PE ,OC =2,CP =CQ =1,QF =CQ +CF =2,∴BE =BC -EP -CP =6-2-1=3; 综上所述,BE 的长为1或3或5.第2题解图⑤。
2013年中考数学第五单元四边形

第21讲┃ 多边形与平行四边形
14.如图21-8,E、F是平行四边形ABCD对角线BD上 的两点,给出下列三个条件:①BE=DF;②∠AEB= ∠DFC;③AF∥EC.请你从中选择一个适当的条件 ________,使四边形AECF是平行四边形,并证明你的结 论.
图21-8
第21讲┃ 多边形与平行四边形
第21讲 多边形与平行四边形 第22讲 矩形、菱形、正方形(一) 第23讲 矩形、菱形、正方形(二) 第24讲 梯形
第21讲
多边形与平行四 边形
第21讲┃ 多边形与平行四边形
┃考点自主梳理与热身反馈 ┃ 考点1 多边形及其性质
(n-2)×180° 内角和 n边形内角和为______________ 360° 多边形 外角和 任意多边形的外角和为________ nn-3 的性质 多边形 n边形共有____________条对角线 2 对角线 相等 相等 各个角________,各条边________ 定义 的多边形叫正多边形 正多边形 正多边形都是轴对称图形,边数为 对称性 偶数的正多边形也是中心对称图形
4.下列性质中,平行四边形不一定具备的是(D ) A.对边相等 B.对角相等 C.对角线互相平分 D.是轴对称图形 5.平行四边形ABCD的对角线交于点O,下列结论错误的 是( C ) A.平行四边形ABCD是中心对称图形 B.△AOB≌△COD C.△AOB≌△BOC D.△AOB与△BOC的面积相等
图21-2
第21讲┃ 多边形与平行四边形
8.如图21-3,平行四边形ABCD的对角线AC、BD相交 于点O,EF过点O与AD、BC分别相交于点E、F,求证: OE=OF.
证明:∵四边形ABCD为平行四边形, ∴AD∥BC,OA=OC, ∴∠EAO=∠FCO,∠AEO=∠CFO, ∴△AEO≌△CFO, ∴OE=OF.
中考数学专项训练 矩形、菱形与正方形(含解析)

矩形、菱形与正方形一、选择题1.矩形具有而菱形不具有的性质是()A.两组对边分别平行 B.对角线相等C.对角线互相平分D.两组对角分别相等2.如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是()A.矩形 B.菱形 C.正方形D.梯形3.如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND是菱形,则等于()A.B.C.D.4.如图,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于点H,且DH与AC交于G,则GH=()A. cm B. cm C. cm D. cm5.如图所示,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,错误的有()A.1个B.2个C.3个D.4个二、填空题6.若菱形的两条对角线分别为2和3,则此菱形的面积是.7.在矩形ABCD中,对角线AC、BD相交于点O,若∠AOB=60°,AC=10,则AB= .8.如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=110°,则∠α= .9.如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是.10.如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+.其中正确的序号是(把你认为正确的都填上).三、解答题(共40分)11.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.(1)线段BD与CD有什么数量关系,并说明理由;(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.12.如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.(1)求证:四边形BCFE是菱形;(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.13.如图1,在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE.(1)求证:AF=BE;(2)如图2,在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?并说明理由.14.如图,在边长为3的正方形ABCD中,点E是BC边上的点,BE=1,∠AEP=90°,且EP交正方形外角的平分线CP于点P,交边CD于点F,(1)的值为;(2)求证:AE=EP;(3)在AB边上是否存在点M,使得四边形DMEP是平行四边形?若存在,请给予证明;若不存在,请说明理由.矩形、菱形与正方形参考答案与试题解析一、选择题1.矩形具有而菱形不具有的性质是()A.两组对边分别平行 B.对角线相等C.对角线互相平分D.两组对角分别相等【考点】矩形的性质;菱形的性质.【分析】根据矩形与菱形的性质对各选项分析判断后利用排除法求解.【解答】解:A、矩形与菱形的两组对边都分别平行,故本选项错误;B、矩形的对角线相等,菱形的对角线不相等,故本选项正确;C、矩形与菱形的对角线都互相平分,故本选项错误;D、矩形与菱形的两组对角都分别相等,故本选项错误.故选B.【点评】本题考查了矩形的性质,菱形的性质,熟记两图形的性质是解题的关键.2.如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是()A.矩形 B.菱形 C.正方形D.梯形【考点】旋转的性质;矩形的判定.【分析】根据旋转的性质可得AE=CE,DE=EF,再根据对角线互相平分的四边形是平行四边形判断出四边形ADCF是平行四边形,然后利用等腰三角形三线合一的性质求出∠ADC=90°,再利用有一个角是直角的平行四边形是矩形解答.【解答】解:∵△ADE绕点E旋转180°得△CFE,∴AE=CE,DE=EF,∴四边形ADCF是平行四边形,∵AC=BC,点D是边AB的中点,∴∠ADC=90°,∴四边形ADCF是矩形.故选:A.【点评】本题考查了旋转的性质,矩形的判定,主要利用了对角线互相平分的四边形是平行四边形,有一个角是直角的平行四边形是矩形的判定方法,熟练掌握旋转变换只改变图形的位置不改变图形的形状与大小是解题的关键.3.如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND是菱形,则等于()A.B.C.D.【考点】勾股定理;菱形的性质;矩形的性质.【分析】首先由菱形的四条边都相等与矩形的四个角是直角,即可得到直角△ABM中三边的关系.【解答】解:∵四边形MBND是菱形,∴MD=MB.∵四边形ABCD是矩形,∴∠A=90°.设AB=x,AM=y,则MB=2x﹣y,(x、y均为正数).在Rt△ABM中,AB2+AM2=BM2,即x2+y2=(2x﹣y)2,解得x=y,∴MD=MB=2x﹣y=y,∴==.故选:C.【点评】此题考查了菱形与矩形的性质,以及直角三角形中的勾股定理.解此题的关键是注意数形结合思想与方程思想的应用.4.如图,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于点H,且DH与AC交于G,则GH=()A. cm B. cm C. cm D. cm【考点】菱形的性质;勾股定理;解直角三角形.【分析】先求出菱形的边长,然后利用面积的两种表示方法求出DH,在Rt△DHB中求出BH,然后得出AH,利用tan∠HAG的值,可得出GH的值.【解答】解:∵四边形ABCD是菱形,对角线AC=8cm,BD=6cm,∴AO=4cm,BO=3cm,在Rt△AOB中,AB==5cm,∵BD×AC=AB×DH,∴DH=cm,在Rt△DHB中,BH==cm,则AH=AB﹣BH=cm,∵tan∠HAG===,∴GH=AH=cm.故选:B.【点评】本题考查了菱形的性质、解直角三角形及三角函数值的知识,注意菱形的面积等于对角线乘积的一半,也等于底乘高.5.如图所示,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,错误的有()A.1个B.2个C.3个D.4个【考点】正方形的性质.【分析】根据四边形ABCD是正方形及CE=DF,可证出△ADE≌△BAF,则得到:①AE=BF,以及△ADE 和△BAF的面积相等,得到;④S△AOB=S四边形DEOF;可以证出∠ABO+∠BAO=90°,则②AE⊥BF一定成立.错误的结论是:③AO=OE.【解答】解:∵四边形ABCD是正方形,∴CD=AD∵CE=DF∴DE=AF∴△ADE≌△BAF∴AE=BF(故①正确),S△ADE=S△BAF,∠DEA=∠AFB,∠EAD=∠FBA∵S△AOB=S△BAF﹣S△AOF,S四边形DEOF=S△ADE﹣S△AOF,∴S△AOB=S四边形DEOF(故④正确),∵∠ABF+∠AFB=∠DAE+∠D EA=90°∴∠AFB+∠EAF=90°∴AE⊥BF一定成立(故②正确).假设AO=OE,∵AE⊥BF(已证),∴AB=BE(线段垂直平分线上的点到线段两端点的距离相等),∵在Rt△BCE中,BE>BC,∴AB>BC,这与正方形的边长AB=BC相矛盾,∴,假设不成立,AO≠OE(故③错误);故错误的只有一个.故选:A.【点评】本题考查了正方形的四条边都相等,每一个角都是直角的性质,全等三角形的判定与性质,综合题但难度不大,求出△ADE≌△BAF是解题的关键,也是本题的突破口.二、填空题6.若菱形的两条对角线分别为2和3,则此菱形的面积是 3 .【考点】菱形的性质.【分析】菱形的面积是对角线乘积的一半,由此可得出结果即可.【解答】解:由题意,知:S菱形=×2×3=3,故答案为:3.【点评】本题考查了菱形的面积两种求法:(1)利用底乘以相应底上的高;(2)利用菱形的特殊性,菱形面积=×两条对角线的乘积;具体用哪种方法要看已知条件来选择.7.在矩形ABCD中,对角线AC、BD相交于点O,若∠AOB=60°,AC=10,则AB= 5 .【考点】含30度角的直角三角形;矩形的性质.【分析】根据矩形的性质,可以得到△AOB是等边三角形,则可以求得OA的长,进而求得AB的长.【解答】解:∵四边形ABCD是矩形,∴OA=OB又∵∠AOB=60°∴△AOB是等边三角形.∴AB=OA=AC=5,故答案是:5.【点评】本题考查了矩形的性质,正确理解△AOB是等边三角形是关键.8.如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=110°,则∠α= 20°.【考点】旋转的性质;矩形的性质.【分析】根据矩形的性质得∠B=∠D=∠BAD=90°,根据旋转的性质得∠D′=∠D=90°,∠4=α,利用对顶角相等得到∠1=∠2=110°,再根据四边形的内角和为360°可计算出∠3=70°,然后利用互余即可得到∠α的度数.【解答】解:如图,∵四边形ABCD为矩形,∴∠B=∠D=∠BAD=90°,∵矩形ABCD绕点A顺时针旋转得到矩形AB′C′D′,∴∠D′=∠D=90°,∠4=α,∵∠1=∠2=110°,∴∠3=360°﹣90°﹣90°﹣110°=70°,∴∠4=90°﹣70°=20°,∴∠α=20°.故答案为:20°.【点评】本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了矩形的性质.9.如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是10 .【考点】轴对称﹣最短路线问题;正方形的性质.【分析】由正方形性质的得出B、D关于AC对称,根据两点之间线段最短可知,连接DE,交AC于P,连接BP,则此时PB+PE的值最小,进而利用勾股定理求出即可.【解答】解:如图,连接DE,交AC于P,连接BP,则此时PB+PE的值最小.∵四边形ABCD是正方形,∴B、D关于AC对称,∴PB=PD,∴PB+PE=PD+PE=DE.∵BE=2,AE=3BE,∴AE=6,AB=8,∴DE==10,故PB+PE的最小值是10.故答案为:10.【点评】本题考查了轴对称﹣最短路线问题,正方形的性质,解此题通常是利用两点之间,线段最短的性质得出.10.如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+.其中正确的序号是①②④(把你认为正确的都填上).【考点】正方形的性质;全等三角形的判定与性质;等边三角形的性质.【专题】压轴题.【分析】根据三角形的全等的知识可以判断①的正误;根据角角之间的数量关系,以及三角形内角和为180°判断②的正误;根据线段垂直平分线的知识可以判断③的正误,利用解三角形求正方形的面积等知识可以判断④的正误.【解答】解:∵四边形ABCD是正方形,∴AB=AD,∵△AEF是等边三角形,∴AE=AF,在Rt△ABE和Rt△ADF中,,∴Rt△ABE≌Rt△ADF(HL),∴BE=DF,∵BC=DC,∴BC﹣BE=CD﹣DF,∴CE=CF,∴①说法正确;∵CE=CF,∴△ECF是等腰直角三角形,∴∠CEF=45°,∵∠AEF=60°,∴∠AEB=75°,∴②说法正确;如图,连接AC,交EF于G点,∴AC⊥EF,且AC平分EF,∵∠CAF≠∠DAF,∴DF≠FG,∴BE+DF≠EF,∴③说法错误;∵EF=2,∴CE=CF=,设正方形的边长为a,在Rt△ADF中,AD2+DF2=AF2,即a2+(a﹣)2=4,解得a=,则a2=2+,S正方形ABCD=2+,④说法正确,故答案为:①②④.【点评】本题主要考查正方形的性质的知识点,解答本题的关键是熟练掌握全等三角形的证明以及辅助线的正确作法,此题难度不大,但是有一点麻烦.三、解答题(共40分)11.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.(1)线段BD与CD有什么数量关系,并说明理由;(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.【考点】矩形的判定;全等三角形的判定与性质.【专题】证明题.【分析】(1)根据两直线平行,内错角相等求出∠AFE=∠DCE,然后利用“角角边”证明△AEF和△DEC全等,根据全等三角形对应边相等可得AF=CD,再利用等量代换即可得证;(2)先利用一组对边平行且相等的四边形是平行四边形证明四边形AFBD是平行四边形,再根据一个角是直角的平行四边形是矩形,可知∠ADB=90°,由等腰三角形三线合一的性质可知必须是AB=AC.【解答】解:(1)BD=CD.理由如下:依题意得AF∥BC,∴∠AFE=∠DCE,∵E是AD的中点,∴AE=DE,在△AEF和△DEC中,,∴△AEF≌△DEC(AAS),∴AF=CD,∵AF=BD,∴BD=CD;(2)当△ABC满足:AB=AC时,四边形AFBD是矩形.理由如下:∵AF∥BD,AF=BD,∴四边形AFBD是平行四边形,∵AB=AC,BD=CD(三线合一),∴∠ADB=90°,∴▱AFBD是矩形.【点评】本题考查了矩形的判定,全等三角形的判定与性质,平行四边形的判定,是基础题,明确有一个角是直角的平行四边形是矩形是解本题的关键.12.如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.(1)求证:四边形BCFE是菱形;(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.【考点】菱形的判定与性质;三角形中位线定理.【分析】从所给的条件可知,DE是△ABC中位线,所以DE∥BC且2DE=BC,所以BC和EF平行且相等,所以四边形BCFE是平行四边形,又因为BE=FE,所以是菱形;∠BCF是120°,所以∠EBC为60°,所以菱形的边长也为4,求出菱形的高面积就可求.【解答】(1)证明:∵D、E分别是AB、AC的中点,∴DE∥BC且2DE=BC,又∵BE=2DE,EF=BE,∴EF=BC,EF∥BC,∴四边形BCFE是平行四边形,又∵BE=FE,∴四边形BCFE是菱形;(2)解:∵∠BCF=120°,∴∠EBC=60°,∴△EBC是等边三角形,∴菱形的边长为4,高为2,∴菱形的面积为4×2=8.【点评】本题考查菱形的判定和性质以及三角形中位线定理,以及菱形的面积的计算等知识点.13.如图1,在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE.(1)求证:AF=BE;(2)如图2,在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?并说明理由.【考点】正方形的性质;全等三角形的判定与性质.【专题】证明题.【分析】(1)根据正方形的性质可得AB=AD,∠BAE=∠D=90°,再根据同角的余角相等求出∠ABE=∠DAF,然后利用“角边角”证明△ABE和△DAF全等,再根据全等三角形的证明即可;(2)过点A作AF∥MP交CD于F,过点B作BE∥NQ交AD于E,然后与(1)相同.【解答】(1)证明:在正方形ABCD中,AB=AD,∠BAE=∠D=90°,∴∠DAF+∠BAF=90°,∵AF⊥BE,∴∠ABE+∠BAF=90°,∴∠ABE=∠DAF,∵在△ABE和△DAF中,,∴△ABE≌△DAF(ASA),∴AF=BE;(2)解:MP与NQ相等.理由如下:如图,过点A作AF∥MP交CD于F,过点B作BE∥NQ交AD于E,∵AB∥CD,AD∥BC,∴四边形AMPF与四边形BNQE是平行四边形,∴AF=PM,BE=NQ,∵在正方形ABCD中,AB=AD,∠BAE=∠D=90°,∴∠DAF+∠BAF=90°,∵AF⊥BE,∴∠ABE+∠BAF=90°,∴∠ABE=∠DAF,∵在△ABE和△DAF中,,∴△ABE≌△DAF(ASA),∴AF=BE;∴MP=NQ.【点评】本题考查了正方形的性质,全等三角形的判定与性质,主要利用了正方形的四条边都相等,每一个角都是直角的性质,同角的余角相等的性质,利用三角形全等证明相等的边是常用的方法之一,要熟练掌握并灵活运用.14.如图,在边长为3的正方形ABCD中,点E是BC边上的点,BE=1,∠AEP=90°,且EP交正方形外角的平分线CP于点P,交边CD于点F,(1)的值为;(2)求证:AE=EP;(3)在AB边上是否存在点M,使得四边形DMEP是平行四边形?若存在,请给予证明;若不存在,请说明理由.【考点】正方形的性质;全等三角形的判定与性质;平行四边形的判定.【分析】(1)由正方形的性质可得:∠B=∠C=90°,由同角的余角相等,可证得:∠BAE=∠CEF,根据同角的正弦值相等即可解答;(2)在BA边上截取BK=BE,连接KE,根据角角之间的关系得到∠AKE=∠ECP,由AB=CB,BK=BE,得AK=EC,结合∠KAE=∠CEP,证明△AKE≌△ECP,于是结论得出;(3)作DM⊥AE于AB交于点M,连接ME、DP,易得出DM∥EP,由已知条件证明△ADM≌△BAE,进而证明MD=EP,四边形DMEP是平行四边形即可证出.【解答】(1)解:∵四边形ABCD是正方形,∴∠B=∠D,∵∠AEP=90°,∴∠BAE=∠FEC,在Rt△ABE中,AE==,∵sin∠BAE==sin∠FEC=,∴=,解法二:由上得∠BAE=∠FEC,∵∠BAE=∠FEC,∠B=∠DCB,∴△ABE∽△ECF,∴=,(2)证明:在BA边上截取BK=BE,连接KE,∵∠B=90°,BK=BE,∴∠BKE=45°,∴∠AKE=135°,∵CP平分外角,∴∠DCP=45°,∴∠ECP=135°,∴∠AKE=∠ECP,∵AB=CB,BK=BE,∴AB﹣BK=BC﹣BE,即:AK=EC,由第一问得∠KAE=∠CEP,∵在△AKE和△ECP中,,∴△AKE≌△ECP(ASA),∴AE=EP;(3)答:存在.证明:作DM⊥AE交AB于点M,则有:DM∥EP,连接ME、DP,∵在△ADM与△BAE中,,∴△ADM≌△BAE(ASA),∴MD=AE,∵AE=EP,∴MD=EP,∴MD EP,∴四边形DMEP为平行四边形.【点评】此题考查了相似三角形的判定与性质,全等三角形的判定与性质以及正方形的性质等知识.此题综合性很强,图形比较复杂,解题的关键是注意数形结合思想的应用与辅助线的准确选择.。
2014中考复习备战策略_数学PPT第21讲_矩形、菱形、正方形

BD=CD, BF=CE,
∴Rt△DFB≌Rt△DEC. ∴DE=DF.
(2)四边形 AFDE 是正方形. 证明: ∵DE⊥ AC, DF⊥ AB, ∴∠ AFD= ∠ AED= 90° . 又 ∵∠ A= 90° . ∴四边形 AFDE 是矩形. 又 ∵ DF= DE, ∴四边形 AFDE 是正方形.
A.14
B.15
C.16
D.17
解析:∵四边形 ABCD 为菱形, AB= 4, ∴ BC= AB= 4.∵∠ABC= 60° , ∴△ABC 是等边三角形, ∴ AC= AB= 4.∴ C 正方形 ACEF=4×4=16.故选 C.
5.(2013· 扬州)如图,在菱形 ABCD 中,∠BAD= 80° , AB 的垂直平分线交对角线 AC 于点 F, 垂足为 E, 连接 DF,则∠CDF 等于( B )
考点二 平行四边形、矩形、菱形、正方形的关系
温馨提示 1.矩形、 菱形和正方形都具有平行四边形的所有性 质 .2.平行四边形及特殊平行四边形的有关知识点比较 多,要想做到准确而不混淆就要从 “边、角、对角线、 对称性 ”这四个方面来研究它们的性质和判定,多用 数形结合法,掌握它们的区别与联系,把握它们的特 征是关键 .
B. 2 5- 1 D. 1 + 2
解析: 由题意可先尝试画出符合条件的图形如图所 示,然后根据面积相等,
可得 (x+ y)y= x ,将 y= 2 代入,可得 x - 2x- 4= 0,解得 x1= 1+ 5, x2= 1- 5(舍去 ).故选 C.
2
2
8.(2013· 南京)设边长为 3 的正方形的对角线长为 a,下列关于 a 的四种说法:①a 是无理数;②a 可以用 数轴上的一个点来表示;③ 3<a<4;④a 是 18 的算术 平方根.其中,所有正确说法的序号是( A.①④ C.①②④ B.②③ D.①③④ C )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考数学专题复习第二十一讲矩形菱形正方形
【基础知识回顾】
一、矩形:
1、定义:有一个角是角的平行四边形叫做矩形
2、矩形的性质:
⑴矩形的四个角都
⑵矩形的对角线
3、矩形的判定:
⑴用定义判定
⑵有三个角是直角的是矩形
⑶对角线相等的是矩形
【提醒:1、矩形是对称到对称中心是又是对称图形对称轴有条
2、矩形被它的对角线分成四个全等的三角形和两个全等的三角形
3、矩形中常见题目是对角线相交成600或1200角时,利用直角三角形、等边三角形等知识解决问题】
菱形:
1、定义:有一组邻边的平行四边形叫做菱形
2、菱形的性质:⑴菱形的四条边都
⑵菱形的对角线且每条对角线
3、菱形的判定:⑴用定义判定
⑵对角线互相垂直的是菱形
⑶四条边都相等的是菱形
【提醒:1、菱形即是对称图形,也是对称图形,它有条对称轴,分别是
2、菱形被对角线分成四个全等的三角形和两对全等的三角形
3、菱形的面积可以用平行四边形面积公式计算,也可以用两对角线积的来计算
4、菱形常见题目是内角为1200或600时,利用等边三角形或直角三角形知识洁具的题目】
三、正方形:
1、定义:有一组邻边相等的是正方形,或有一个角是直角的是正方形
2、性质:⑴正方形四个角都都是角,
⑵正方形四边条都
⑶正方形两对角线、且每条对角线平分一组内角
3、判定:⑴先证是矩形,再证
⑵先证是菱形,再证
【提醒:菱形、正方形具有平行四边形的所有性质,正方形具有以上特殊四边形的所有性质。
这四者之间的关系可表示为:
⑴正方形也即是对称图形,又是对称图形,有条对称轴
⑵几种特殊四边形的性质和判定都是从、、三个方面来看的,要注意它们的和联系】
【重点考点例析】
考点一:和矩形有关的折量问题
例1 如图,四边形ABCD是矩形,对角线AC、BD相交于点O,BE∥AC交DC的延长线于点E.
(1)求证:BD=BE;
(2)若∠DBC=30°,BO=4,求四边形ABED的面积.
对应训练
1.如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB 于点F,∠AED=2∠CED,点G是DF的中点,若BE=1,AG=4,则AB的长
为.
考点二:和菱形有关的对角线、周长、面积的计算问题
例2 如图,菱形ABCD的周长为20cm,且tan∠ABD=3
4
,则菱形ABCD的面
积为cm2.
对应训练
2.如图,已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm,AE⊥BC 于点E,则AE的长是()
A.53cm B.25cm C.48
5
cm D.
24
5
cm
考点三:和正方形有关的证明题
例3 如图,在正方形ABCD中,对角线AC、BD相交于点O,E、F分别在OD、OC上,且DE=CF,连接DF、AE,AE的延长线交DF于点M.
求证:AM⊥DF.
对应训练
12.如图,在正方形ABCD中,等边三角形AEF的顶点E、F分别在BC和CD 上.
(1)求证:CE=CF;
(2)若等边三角形AEF的边长为2,求正方形ABCD的周长.
考点四:四边形综合性题目
例4 如图,正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕顶点A 旋转,在旋转过程中,当BE=DF时,∠BAE的大小可以是.
对应训练
4.以边长为2的正方形的中心O为端点,引两条相互垂直的射线,分别与正方形的边交于A、B两点,则线段AB的最小值是.
【聚焦中考】
2.已知:如图,四边形ABCD的对角线AC、BD交于点O,BE⊥AC于E,DF ⊥AC于F,点O既是AC的中点,又是EF的中点.
(1)求证:△BOE≌△DOF;
(2)若OA=1
2
BD,则四边形ABCD是什么特殊四边形?说明理由.
3.如图,在▱ABCD中,AE,CF分别是∠BAD和∠BCD的平分线,添加一个条件,仍无法判断四边形AECF为菱形的是()
A.AE=AF B.EF⊥AC C.∠B=60°D.AC是∠EAF的平分线
4.如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
求证:四边形OCED是菱形.
5.(如图,AD是△ABC的角平分线,过点D作DE∥AB,DF∥AC,分别交AC、AB于点E和F.
(1)在图中画出线段DE和DF;
(2)连接EF,则线段AD和EF互相垂直平分,这是为什么?
【备考真题过关】
一、选择题
1.如图,矩形ABCD的对角线AC=8cm,∠AOD=120°,则AB的长为()A.3cm B.2cm C.2 3 D.4cm
2.若顺次连接四边形ABCD各边的中点所得四边形是矩形,则四边形ABCD一定是()
A.矩形B.菱形
C.对角线互相垂直的四边形D.对角线相等的四边形
3.如图,菱形ABCD中,AC=8,BD=6,则菱形的周长是()
A.20 B.24 C.28 D.40
4.顺次连接矩形四边中点所得的四边形一定是()
A.正方形B.矩形C.菱形D.等腰梯形
5.如图,菱形ABCD的周长为24cm,对角线AC、BD相交于O点,E是AD 的中点,连接OE,则线段OE的长等于()
A.3cm B.4cm C.2.5cm D.2cm
6.如图,菱形ABCD的两条对角线相交于O,若AC=6,BD=4,则菱形的周长是()
A.24 B.16 C.413D.23
7.如图,菱形ABCD和菱形ECGF的边长分别为2和3,∠A=120°,则图中阴影部分的面积是()
A.3B.2 C.3 D.2
8.如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:
①△BDF≌△DCE;②∠BMD=120°;③△AMH是等边三角形;④S
四边形ABCD
= 3
4
AM2.
其中正确结论的个数是()
A.1 B.2 C.3 D.4
9.如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,
CE、DF交于点O.下列结论:①∠DOC=90°,②OC=OE,③tan∠OCD=4
3
,
④S
△ODC =S
四边形BEOF
中,正确的有()
A.1个B.2个C.3个D.4个
10.如图,边长为a 的正方形ABCD 绕点A 逆时针旋转30°得到正方形A ′B ′C ′D ′,图中阴影部分的面积为( )
A .212a
B .233a
C .23(1)4a -
D .23(1)3a -
二、填空题
11.如图,矩形ABCD 中,AB=2,AD=4,AC 的垂直平分线EF 交AD 于点E 、交BC 于点F ,则EF= .
11.5
12.如图,在平面直角坐标系中,矩形OABC 的对角线AC 平行于x 轴,边OA 与x 轴正半轴的夹角为30°,OC=2,则点B 的坐标是 .
13.如图,在矩形ABCD 中,对角线AC 、BD 相交于O ,DE ⊥AC 于E ,∠EDC :∠EDA=1:2,且AC=10,则DE 的长度是 .
14.如图,Rt△ABC中,∠C=90°,AC=BC=6,E是斜边AB上任意一点,作EF⊥AC于F,EG⊥BC于G,则矩形CFEG的周长是.
16.我们把顺次连接四边形四条边的中点所得的四边形叫中点四边形.现有一个对角线分别为6cm和8cm的菱形,它的中点四边形的对角线长是.
17.菱形的两条对角线长分别为6和8,则这个菱形的周长为.18.如图,在菱形ABCD中,对角线AC、BD相交于点O,AC=12,BD=16,E 为AD中点,点P在x轴上移动,小明同学写出了两个使△POE为等腰三角形的P点坐标(-5,0)和(5,0).请你写出其余所有符合这个条件的P点坐标.
19.如图,在菱形ABCD中,点E、F分别是BD、CD的中点,EF=6cm,则AB= cm.
20.如图,菱形ABCD的边长为8cm,∠A=60°,DE⊥AB于点E,DF⊥BC 于点F,则四边形BEDF的面积为cm2.
21.如图,正方形的边长为2,以各边为直径在正方形内画半圆,则图中阴影部分的面积为(结果保留两位有效数字,参考数据π≈3.14)
22.如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6 2,则另一直角边BC的
长为.
三、解答题
23.如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点N,连接BM,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
24.如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作▱ABDE,连接AD,EC.
(1)求证:△ADC≌△ECD;
(2)若BD=CD,求证:四边形ADCE是矩形.
25.已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.
①求证:CD=AN;
②若∠AMD=2∠MCD,求证:四边形ADCN是矩形.
27.如图,△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,连接AD.求证:四边形ACFD是菱形.
28.已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
(1)若CE=1,求BC的长;
(2)求证:AM=DF+ME.。
