其他正交变换
3 正交矩阵及正交变换

正交矩阵及正交变换一、正交矩阵定义1 如果n 阶方阵A 满足T T AA A A E==( 即 ) 1TA A -=称 A 为正交矩阵. 性质 设A ,B 都是n 阶正交矩阵,则(1) |A |=±1;(2) A T , A -1, AB 也是正交矩阵.一、正交矩阵正交矩阵举例cos sin .sin cos A θθθθ-⎛⎫= ⎪⎝⎭(2) 旋转矩阵(1) n 阶单位矩阵 ;n E一、正交矩阵定理1 矩阵A 为正交矩阵的充分必要条件是 A 的行(列)向量组为规范正交向量组. 证明 设11121121222212,n n n n nn n a a a a a a A a a a ααα⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭一、正交矩阵()1212,,,T T T T n n AA E Eαααααα⎛⎫ ⎪ ⎪=⇔= ⎪ ⎪ ⎪⎝⎭121111222212T T T n T T T n T T T n n n n Eαααααααααααααααααα⎛⎫ ⎪ ⎪⇔= ⎪ ⎪ ⎪⎝⎭()1,;,1,2,,0,T j i i j i j n i j αα=⎧⇔==⎨≠⎩当当二、正交变换性质 正交变换保持向量的长度不变. 证明 ,y Px =设为正交变换T y y y =则有定义2 若P 为正交矩阵,则线性变换 y=Px 称为正交变换.T T Px x P =.Tx x x ==三、举例判别下列矩阵是否为正交矩阵.11213(1)12112.13121A -⎛⎫ ⎪=- ⎪ ⎪-⎝⎭解 ,021********≠⨯+⨯⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-⨯所以它不是正交矩阵.考察矩阵的第一列和第二列,由于 例1三、举例1111222211112222(2)110022110022B ⎛⎫-- ⎪ ⎪ ⎪-- ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭,,.B B 的每个列向量都是单位向量且两两正交所以是正交矩阵解谢谢!。
9.4正交变换

必要性。若 σ 是正交变换,由定理9.4.2知 σα1 , σα 2 , 也是V的一个标准正交基。 故A是正交矩阵。
定理9.4.3 设 σ 是n维欧氏空间V的一个线性变换。 σ 是 正交变换的充要条件是:σ 关于V的任意标准正交基的矩阵是正 交矩阵。 证明: 设 α1 , α 2 , , α n 是V的一个标准正交基,则 (σα1 , σα 2 , , σα n ) = (α1 , α 2 z ) = ( x, y, − z ) = x 2 + y 2 + z 2 = ( x, y, z )
定理9.4.1 设 σ 是n维欧氏空间V的一个线性变换。 σ 是 正交变换的充要条件是: σ 保持向量的内积不变。 证明:必要性。 如果 σ 是正交变换,即对 ∀α ∈ V , σα = α , ∀α , β ∈ V , 则有: (σα , σα ) = (α , α ), (σβ , σβ ) = ( β , β ),
§9.4
正交变换
§9.4
正交变换
一、正交变换的定义及性质 二、正交变换的类型
第九章 欧几里得空间
线性空间的线性变换,实际上是保持向量线性运算的变换。 在欧氏空间中,除了向量的线性运算外,还有向量的度量性质, 因此有必要讨论保持度量关系不变的线性变换。其中保持长度 不变的线性变换无疑是重要的。 例9.4.1 在欧氏空间 R 2 中有一个坐标旋转变换,在把平面 围绕原点逆时针旋转 θ 角之后,平面上向量之间什么关系保持 不变? 向量的长度、向量的夹角、向量的距离等保持不变。 能否在一般欧氏空间也找到具有这种性质的线性变换? 这种线性变换就是本节要研究的正交变换。
σ −1 仍是V的一个正交变换。 解: 正交变换 σ 在任一标准正交基下的矩阵是正交矩阵, 正交矩阵是可逆的,所以 σ 是可逆变换。
信号变换与处理分析

函数的傅里叶变换
傅里叶变换是把图像从空间域转换到频率域, 即将空间域中复杂的卷积运算转化为频率域中简单 的乘积运算。 应用:在频率域中可以有效的实现图像增强、特征 提取、 图像恢复、纹理分析与水印嵌入等。
1.傅里叶变换的定义:
正 变 换 : 函 数f (t )的 一 维 傅 里 叶 变 换 定 义
参考书目 1、现代信号处理技术,武汉大学出版社;吴正国 夏立 尹为民 ,2003。 2、基于计算机的信号处理实践,电子工业出版社;栾晓明,2006。 3、现代信号处理,清华大学出版社; 张贤达,1995。
信号变换与处理
信号变换与处理
数字信号处理的流程:
信号变换与处理
数字信号处理的一些应用:
数字信号处理的一些应用:图像处理
遥感图像自动分类
气象云图 气象预报
信号变换与处理
数字信号处理的一些应用:雷达
军事应用 目标跟踪
数字信号处理的一些应用:交通辅助
如车牌识别等。
数字信号处理的一些应用:文化娱乐
(1)计算机合成图像 (2)动画制作 (3)广告设计
计算机合成图像
计算机合成图像
动画
广告设计
娱乐
信号变换与处理
百闻不如一见
One picture is worth more than ten thousand words.
Anonymous
什么是图像
“像”是人的视觉系 统对图的接收在大 脑中形成的印像或 认识
“像”是人的感觉
“图”是物体投 射光或反射光 图像是两者的结合 的分布
“图”是客观存在的
什么是图像?
其中,F (u)
R2(u) I 2(u),
(u)
arctg
欧几里得空间中的正交基与正交变换

欧几里得空间中的正交基与正交变换欧几里得空间是一个重要的数学概念,它涉及到向量、点、线和平面等几何图形的性质与关系。
在欧几里得空间中,正交基和正交变换是其中两个重要的概念。
本文将对欧几里得空间中的正交基和正交变换进行探讨,旨在帮助读者更好地理解和应用这两个概念。
一、正交基在欧几里得空间中,正交基是指一组向量中的每两个向量都相互垂直。
更具体地说,如果向量v₁、v₂、...、vₙ满足vᵀᵢ·vₙ=0(其中1≤i≠j≤n,vᵀ表示向量的转置),则称这组向量为正交基。
正交基的一个重要性质是它们是线性无关的,这意味着没有任何一个向量可以表示成其他向量的线性组合。
因此,正交基可以作为欧几里得空间的一个基础,用来描述和计算向量的性质和关系。
在实际应用中,正交基有着广泛的应用。
例如,在计算机图形学中,使用正交基可以轻松地描述和转换三维空间中的物体位置和方向;在信号处理中,正交基可以用来表示和处理复杂的信号和波形;在机器学习中,正交基可以用来降低数据的维度和提取有效特征等。
二、正交变换正交变换是指在欧几里得空间中保持向量长度和夹角不变的线性变换。
简单来说,正交变换是一种保持形状不变的变换。
正交变换的一个重要特性是它可以保持向量的正交性。
也就是说,如果两个向量在变换前相互垂直,那么它们在变换后仍然相互垂直。
这一性质使得正交变换在几何学和物理学中得到广泛应用。
常见的正交变换包括旋转、反射和投影等。
通过这些变换,我们可以改变向量的方向、位置和维度等属性,从而得到新的向量和图形。
正交变换还有一些特殊的性质。
例如,正交变换的逆变换是它本身的转置矩阵。
这个性质使得正交变换比较容易求解和应用。
结语正交基和正交变换是欧几里得空间中的两个重要概念,它们在数学、物理和工程等领域中都有着广泛的应用。
正交基可以作为描述和计算向量性质的基础,而正交变换可以保持向量的长度和夹角不变,用于改变和操作向量的属性。
通过理解和应用正交基和正交变换,我们可以更好地理解欧几里得空间中的几何性质,并且能够应用于各个领域的实际问题。
n维欧氏空间上正交变换的分类

论文题目《正交变换的分类》N维欧氏空间上正交变换的分类摘要:本文通过对正交变换的概念以及正交变换的一些定理进行定义,再逐步了解n维欧氏空间上的正交变换。
最后讨论普通几何空间中正交变换的类型。
最终掌握欧氏空间、性质、判别及其初步分类.关键字:欧氏空间正交变换分类1.1 正交变换的概念定义1设V是一个欧氏空间,σ是V的一个变换.若σ保持向量的内积不变,即∀α,β∈V,都有〈σ(α),σ(β)〉=〈α,β〉(1) 则称σ是V上的一个正交变换.从定义1容易看出,V的正交变换保持向量的长度不变,保持两个非零向量的夹角不变,保持正交性不变.命题1.1欧氏空间V上的正交变换σ一定是线性变换.证先证∀α,β∈V, 有σ(α+β)=σ(α)+σ(β).事实上,〈σ(α+β)-(σ(α)+σ(β)),σ(α+β)-(σ(α)+σ(β))〉=|σ(α+β)|2-2〈σ(α+β),σ(α)+σ(β)〉+|σ(α)+σ(β)|2=|α+β|2-2〈σ(α+β),σ(α)〉-2〈σ(α+β),σ(β)〉+|σ(α)|2 +|σ(β)|2+2〈σ(α),σ(β)〉=|α+β|2-2〈α+β, α〉-2〈α+β, β〉+|α|2+|β|2+2〈α,β〉=|α+β|2-2〈α+β,α+β〉+|α+β|2=0,所以σ保持加法运算.同理可证σ(kα)=kσ(α),∀α∈V,k∈R.故σ是V的一个线性变换.从命题1.1和定义1容易得出,正交变换保持两个向量之间的距离不变.命题1.2欧氏空间V上的正交变换σ一定是单射.因此,有限维欧氏空间的正交变换是可逆变换.证因为〈σ(α),σ(α)〉=〈α,α〉,所以∀α∈Kerσ⇔σ(α)=θ⇔〈σ(α),σ(α)〉=0⇔〈α,α〉=0⇔α=θ.从而Kerσ=0.因此σ是单射.此时,当dim V=n,则σ是满射,所以σ是双射,故σ可逆.注意到欧氏空间V的任一自同构σ均保持内积不变,因此由命题1.2立得推论1.1有限维欧氏空间V的变换σ是正变变换的充分且必要条件为σ是欧氏空间V的自同构.我们可从另外一个角度来刻画正交变换,即定理1.1欧氏空间V到自身上的变换σ是正交变换的充分且必要条件为σ是保持向量的长度不变的线性变换.证必要性从定义1和命题1.1立即得到.充分性设σ∈End V,且保持向量的长度不变,则∀α,β∈V,有〈σ(α+β),σ(α+β)〉=〈α+β,α+β〉.(2)(2)式的左边、右边分别为,||)(),(2|||) (|)(),(2|)(|)()(),()(2222ββσασαβσβσασασβσασβσασ++=++=++|α|2+2〈α,β〉+|β|2.所以,〈σ(α),σ(β)〉=〈α,β〉.故σ是正交变换. 显然,欧氏空间V的任两正交变换σ,τ的乘积仍然是正交变换.1.2 n维欧氏空间的正交变换定理1.2设σ是n维欧氏空间V的一个线性变换,则下列陈述彼此等价:1)σ是正交变换;2)若α1,…,αn是V的一个标准正交基,则σ(α1),…,σ(αn)也是V的标准正交基;3)σ在V的任意一个标准正交基下的矩阵是正交矩阵.证1)⇒2) 因为〈σ(αi),σ(αj)〉=〈αi,αj〉=δij,i,j=1,2,…,n;且σ(αi)≠θ,i=1,…,n.所以σ(α1),…,σ(αn)是V的一个标准正交基.2)⇒3) 任取V的一个标准正交基α1,…,αn.由假设知σ(α1),…,σ(αn)也是V的标准正交基.从而由基α1,…,αn到基σ(α1),…,σ(αn)的过渡矩阵A是正交矩阵,即σ(α1,…,αn)=( α1,…,αn)A.(3) (3)式说明σ在基α1,…,αn下的矩阵是A,故3)成立.3)⇒1) 取V的一个标准正交基α1,…,αn,设σ在这个基下的矩阵是正交矩阵A.∀α=(α1,…,αn)X,β=(α1,…,αn)Y∈V,则σ(α)=(α1,…,αn)(AX),σ(β)=( α1,…,αn)(AY).由于α1,…,αn是V的标准正交基,所以〈σ(α),σ(β)〉=(AX)'(AY)= X' (A'A)Y= X'Y=〈α,β〉.因此σ是正交变换.据上,在标准正交基下,n维欧氏空间V的正交变换与实n阶正交矩阵一一对应.因而可利用正交矩阵将正交变换分类.注意到正交矩阵的行列式等于1或-1.因此,行列式等于1的正交变换称为旋转,或者称为第一类的;行列式等于-1的正交变换称为第二类的.n维向量空间的任意一个n-1维子空间称为一个超平面.例1在欧氏空间V中取一个标准正交基α1,…,αn.定义V上的一个线性变换σ,使得σ(α1)=-α1,σ(αi)= αi,i=2,…,n,则σ在基α1,…,αn下的矩阵为A=diag(-1,I n-1).显然A是正交矩阵,因此σ是正交变换.由于|A| = -1,因此σ是第二类的.这个正交变换是关于超平面W=L(α2,…,αn)的一个镜面反射(参见本节习题第2题).1.3 普通几何空间中正交变换的类型下面讨论几何空间V 2和V 3的正交变换有哪些类型?设σ是V 2的一个正交变换,σ在V 2的一个标准正交基{γ1,γ2}下的矩阵是U =⎪⎭⎫ ⎝⎛d c b a , 则U 是一个正交矩阵.因此a 2+c 2=1,b 2+d 2=1,ab +cd =0. (4)由第一个等式,存在一个角ω使a =cos ω,c =±sin ω.由于cos ω=cos(±ω),±sin ω=sin (±ω),因此可设a =cos ϕ,c =sin ϕ.这里ϕ=ω或-ω.同理,由(4)的第二个等式,存在一个角ψ,使b =cos ψ,d =sin ψ.将a ,b ,c ,d 代入(4)的第三个等式得cos ϕcos ψ+sin ϕsin ψ=0,或cos(ϕ-ψ)=0.最后等式表明,ϕ-ψ是2π的一个奇数倍.于是 cos ψ= sin ϕ,sin ψ =±cos ϕ.所以⎪⎭⎫ ⎝⎛-=ϕϕϕϕcos sin sin cos U ,或⎪⎭⎫ ⎝⎛-=ϕϕϕϕcos sin sin cos U . 对前一情形,σ是将V 2的每一向量旋转角ϕ的旋转;对后一情形,σ将V 2中以(x ,y )为坐标的向量变成以(x cos ϕ+y sin ϕ,x sin ϕ-y cos ϕ)为坐标的向量.这时σ是关于直线y =⎪⎭⎫ ⎝⎛2tan ϕx 的反射. 这样,V 2的正交变换或者是一个旋转,或者是关于一条过原点的直线的反射.若是后一情形,可以取V 2的一个标准正交基{β2,β3},使σ在基{β1,β2}下的矩阵为⎪⎭⎫ ⎝⎛-1001. 现在设σ是V 3的一个正交变换,σ的特征多项式是一个实系数三次多项式,因而至少有一个实根r .令γ1是σ的属于特征值r 的一个特征向量,并且取γ1是一个单位向量.再添加单位向量γ2,γ3使{γ1,γ2,γ3}是V 3的一个标准正交基.则可设σ在这个基下的矩阵为⎪⎪⎪⎭⎫ ⎝⎛=d c b a t s r U 00. 由于U 是正交矩阵,则有r 2=1,rs =rt =0,从而r =±1,s =t =0.于是⎪⎪⎪⎭⎫ ⎝⎛±=d c b a U 00001. 由U 的正交性推出,矩阵⎪⎭⎫ ⎝⎛d c b a 是一个二阶正交矩阵.由上面的讨论,存在一个角ϕ使⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛ϕϕϕϕϕϕϕϕcos sin sin cos cos sin sin cos 或c c b a . 在前一情形,⎪⎪⎪⎭⎫ ⎝⎛-±=ϕϕϕϕcos sin 0sin cos 0001U . 在后一情形,根据对V 2的正交变换的讨论,我们可以取V 3的一个标准正交基{γ1 ,β2 , β3 }使σ在这个基的矩阵是T =⎪⎪⎪⎭⎫ ⎝⎛-±100010001. 若在T 中左上角的元素是1,则重新排列基向量,σ在基{β3, β2 ,γ1}的矩阵是⎪⎪⎪⎭⎫ ⎝⎛-100010001. 若左上角的元素是-1,则σ在基{β2 , β3 ,1γ}下的矩阵是⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛--ππππcos sin 0sin cos 0001100010001. 这样,V 3的任意正交变换σ在某一标准正交基{α1,α2,α3}下的矩阵是下列三种类型之一:⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛-100010001cos sin 0sin cos 0001,ϕϕϕϕ, 或⎪⎪⎪⎭⎫ ⎝⎛--ϕϕϕϕcos sin 0sin cos 0001=⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛-100010001cos sin 0sin cos 0001ϕϕϕϕ. 在第一种情形,σ是绕通过α1的直线L (α1)的一个旋转;在第二种情形,σ是关于平面L (α2,α3)的反射;第三种情形,σ是前两种变换的合成.参考文献1. 张禾瑞.高等代数.第五版.高等教育出版社。
数字图像处理数字图像处理第二章(第六讲)KL变换、其他正交变换

第二章 常用的数学变换
2.6其他正交变换 —离散沃尔什-哈达玛变换(WHT)
1 1 1 1 1 1 1 1
1
1
1
1
1
1
1
1
1 1 1 1 1 1 1 1
H8
1 22
1 1
1 1
1 1
1 1
1
1 1
1
1 1 1 1
1
1
1
1 1
1
1
1
1 1 1 1 1 1 1 1
1
1
1
1
1
2.6其他正交变换 —离散沃尔什-哈达玛变换(WHT)
1893年法国数学家哈达玛总结前人研究只包含+1和-1的正交矩 阵结果,形成哈达玛矩阵,既简单又有规律
1923年美国数学家沃尔什提出Walsh函数,具有特点 函数取值仅有两个(0,1或-1,+1) 由Walsh函数构成的Walsh函数集,具备正交性和完备性
种是按照哈达玛排列来定义。由于哈达玛排序的沃尔什函数是由2n (n=0,1,2,…)阶哈达玛矩阵(Hadamard Matrix)得到的,而
哈达玛矩阵的最大优点在于它具有简单的递推关系, 即高阶矩阵可 用两个低阶矩阵的克罗内克积求得,因此在此只介绍哈达玛排列定 义的沃尔什变换。
第二章 常用的数学变换
0.443(60) 0.742(70) 0.376(62) 0.106(50)
119.53
国家级精品资源共享课
第二章 常用的数学变换
第二章 常用的数学变换
2.1 引言 2.2 空域变换 2.3 频率域变换 2.4 离散余弦变换 2.5 KL变换 2.6 其他正交变换
第二章 常用的数学变换
关于正交变换的分类

实数域上正交变换的分类一、正交变换定义1.1 设A是欧氏空间V的一个线性变换,若A保持向量的内积不变,即对于任意的α,βεV都有(Aɑ,Aβ) = (ɑv,β),则称A为V的正交变换.二、等价条件定理2.1 设A是n维欧氏空间V的一个线性变换,则下列命题等价:1)A是正交变换;2)A保持向量的长度不变,即对于V,|Aα|=|ɑ|;3)A把V的规范正交基变为V的规范正交基;4)A在规范正交基下的矩阵是正交矩阵.⇒2)对于αεV, 由证:1)(Aɑ,Aɑ)=(ɑ,ɑ),即得:|Aɑ|=|ɑ|2)⇒3)设ε1,ε2,…,εn是V的任一规范正交基,记εi+εj=ɑεV.由|Aɑ|=|ɑ|或(Aɑ,Aɑ)=(ɑ,ɑ)得(A(εi+εj),A(εi+εj))=(εi+εj,εi+εj)而(A(εi+εj),A(εi+εj))=(Aεi,Aεi)+2(Aεi,Aεj)+(Aεj,Aεj)=(εi ,εi)+2(εi ,εj)+(εj ,εj)(εi+εj,εi+εj )=(εi ,εi)+2(εi ,εj)+(εj ,εj)故 A ε1,A ε2,…,A εn 是V 的一组规范正交基. 3)⇒4)设ε1,ε2,…,εn 是V的规范正交基,A(ε1,ε2,…,εn)=(A ε1, A ε2,…,A εn)= (ε1,ε2,…,εn)A由3), A ε1,A ε2,…,A εn 是0,(,)(,)1,i j i j i j A A i j εεεε≠⎧∴==⎨=⎩V的规范正交基,故A可看作是由规范正交基ε1,ε2,…,εn到规范正交基Aε1,Aε2,…,Aεn的过渡矩阵,A是正交矩阵.4) 1)设ε1,ε2,…,εn是V 的规范正交基,且A在此基下的矩阵A为正交矩阵.由(Aε1,Aε2,…,Aεn)= (ε1,ε2,…,εn)A,知Aε1,Aε2,…,Aεn也是V的规范正交基,设α=x1ε1+x2ε2+……x nεn,Β=y1ε1+y2ε2+……y nεn,Aɑ=x1Aε1+x2Aε2+…+xnAεnAβ=y1Aε1+y2Aε2+…+ynAεn (Aα,Aβ)= x1y1+x2y2+…+xnyn(α,β)= x1y1+x2y2+…+xnyn 所以 (A α,A β)=(α,β),故A 为正交变换.三、规范正交基到规范正交基的过渡矩阵。
正交变换

§1 定义与基本性质 §2 标准正交基 §3 同构 §4 正交变换 §5 子空间 §6 对称矩阵的标准形 §7 向量到子空间的 距离─ 距离─最小二乘法 §8酉空间介绍
§9.4 正交变换
一、一般欧氏空间中的正交变换 二、n 维欧氏空间中的正交变换
§9.4 正交变换
一、一般欧氏空间中的正交变换
§9.4 正交变换
(
)
{
i= j i≠ j
(2)若线性变换 σ 使V的标准正交基 ε 1 , ε 2 ,L , ε n 变 ) 的标准正交基
成标准正交基 σ (ε 1 ),σ (ε 2 ),L ,σ (ε n ) ,则 σ 为V的正 的正 交变换. 交变换. 证:任取 α , β ∈ V ,设
α = x1ε 1 + x2ε 2 + L xnε n β = y1ε 1 + y2ε 2 + L ynε n ,
∴ σ 是正交变换. 是正交变换.
§9.4 正交变换
再证明( ) 再证明(2)与(3)等价. )等价.
( 2) ⇒ ( 3)
Q σ (α ) − σ ( β ) = σ (α − β ),
∴ d ( σ (α ),σ ( β ) ) = σ (α ) − σ ( β ) = σ (α − β ) = α − β = d (α , β )
即,(σε 1 ,σε 2 ,L ,σε n ) = ( ε 1 , ε 2 ,L , ε n ) A 由于当A是正交矩阵时, 也是V的 由于当 是正交矩阵时,σε 1 ,σε 2 ,L ,σε n 也是 的 是正交矩阵时 标准正交基, 标准正交基, 为正交变换. 再由 1 即得 σ 为正交变换.
§9.4 正交变换
欧式空间正交变换的分类

欧式空间正交变换的分类欧氏空间正交变换的分类在多维空间里保持长度不变的正交变换无疑是重要的,但这种变换在多维空间下的可操作性我们还并不清楚,下面,我们从课本出发,把二、三维空间下的正交变换推广到五维空间定义:欧式空间v的一个线性变换σ叫做一个正交变换,如果对于任一ξ∈v都存有∣σ(ξ)∣=∣ξ∣正交变换的基本性质:欧式空间v的一个线性变换σ是正交变换的充要条件是:对于v任意向量ξ,η,=。
设v就是一个n佩欧式空间,σ就是v的一个线性变换。
如果σ就是v正交变换,那么σ把v的任一一个规范拓扑基仍变为的一个规范拓扑基为。
反过来,如果σ把v的某一规范拓扑基为仍旧变为的一个规范拓扑基为,那么σ就是v的一个正交变换。
n维欧式空间v的一个正交变换σ关于v的任意规范的矩阵是一个正交矩阵。
反过来,如果v的一个线性变换关于某一个规范正交基的矩阵是单位阵,那么该线性变换σ是一个正交变换。
将v2的一个向量转动一个角ϕ的正交变换关于v2的任一规范拓扑基的矩阵就是⎛cosϕ-sinϕ⎛sinϕcosϕ⎛⎛⎛⎛在平面h内取两个正交的单位向量γ1,γ2,在取一个垂直于h的单位向量γ3,那么{γ1,γ2,γ3}是v3的一个规范正交基。
关于这个基的矩阵是010⎛。
以上两00-1⎛⎛⎛个都是正交矩阵。
设立σ就是v2的一个正交变换。
σ关于v2的一个规范拓扑基u=γ2}的矩阵是⎛cb⎛⎛,那么就是一个正交矩阵。
于是⎛d⎛a2+b2=1,b2+d2=1,ab+cd=0(2)存有第一个等式,存有一个角α并使a=cosα,c=sinα.由于cosα=cos(±α),±sinα=sin(±α)因此可以而令a=cosϕ,c=sinϕ这里ϕ=α或-α同理,由(2)的第二个等式,存在一个角ψ使b=cosψ,d=sinψ.将a,b,c,d代入(2)的第三个等式得cosϕcosψ+sinϕsinψ=0,或cos(ϕ-ψ)=0.最后等式表明,ϕ-ψ是的一个基数倍。
数字图像处理 第三讲 正交变换

正交变换
6、二维卷积定理
f ( x, y ) g ( x, y ) F (u, v) G (u, v) f ( x, y ) g ( x, y ) F (u, v) G (u, v)
7、相关定理
f ( x, y ) g ( x, y ) F (u, v) G * (u, v) f ( x, y ) g ( x, y ) F (u, v) G (u, v)
二维离散傅立叶变换对可表示为:
ux vy f ( x, y) exp j 2 N x 0 y 0 u, v 0,1,2,, N 1 1 F (u, v) N
N 1 N 1
ux vy F (u, v) exp j 2 N u 0 v 0 x, y 0,1,2,, N 1 1 f ( x, y ) N
x 0 y 0
N 1 N 1
ux vy f ( x, y) exp j 2 N exp j 2 mx ny x 0 y 0 当m,n为整数时, j 2 mx ny 为单位值 exp
N 1 N 1
正交变换
8、平均值 二维离散函数的平均值定义为:
1 f ( x, y ) 2 N
f ( x, y)
x 0 y 1
N 1 N 1
将u=0,v=0代入二维离散傅立叶变换式中有:
1 F 0,0 2 N
f ( x, y) f ( x, y)
x 0 y 1
N 1 N 1
u mN x v nN y f ( x, y ) exp j 2 N
F (u mN , v nN ) F (u , v)
第8章:信号处理中常用的正交变换

(1) A 1 A T ; AA 1 AA T I ;
(2)对 N 维离散信号 x N M , 存在正交变换 A ,
0
Ax ( Ax ) T Axx T A T Axx T A 1
1
N
i为特征值, Ai为特征向量。
(3)正交变换的结果,可以 看成向量在标准正交基 底上的投影,
x'1,Nm1 x'2,Nm1
x'm,1 x'm,2 x'm,3 x'm,i x'm,Nm1
x ˆjmm i,m n{ 1 ji,N n{ j 1 }} k l 1 x j'k,l j 1 , ,N
有趣发现:相位不变。
阶次与截止频率?
K—L 变换 (K arhunen--Loeve)
是分解系数 或信号的变换
由 x 1,2,L,N 正变换
由 1,2,L,N x 反变换
Step 1:
设想另有一组向量
ˆ1,ˆ2,L ,ˆN
满足:
i,ˆj
i
j
1 0
ij ij
双正交关系( biorthogonality)
Step2:做内积
N
x nn
n1
N
x,ˆ j nn,ˆj n1
N
[A]i,j N 2j1/2sin j(i1)(N21)(j1)2
i,j0,1,L,N1
i 是方程 taN n()co (1 s) (22) si2n c)(os)( 的根
1
1
tan(N)0
有: jj/N , j 0 ,1 , ,N 1
由:
j (1 2 )(1 2c o s (j)2 )
及算子 A N N
M正交变换和仿射变换
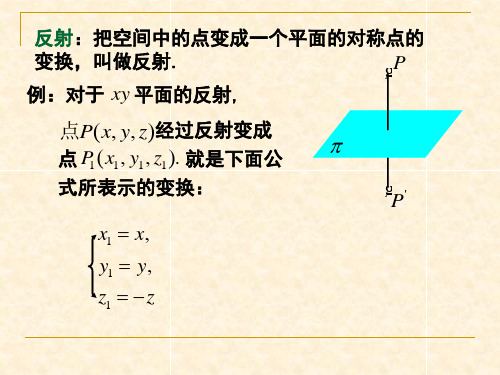
如果保持所有的点不动,即是一个恒等变换
那 么 就 有 = , 这 和 不 是 刚 体 运 动 矛 盾 .所 以
所以不能保持所有的点不动.
设 P 是 的 动 点 , 记 P ' = ( P ).
由 于 是 正 交 变 换 , 所 以 的 不 动 点 都 会 位 于 PP ' 的 垂 直 平 分 面 P上 .
设 P1 , P2 , P3 是 直 线 l 上 的 三 点 , 经 过 仿 射 变 换 变 成 直 线 l ' 上 ' ' ' ' ' ' ' ' 的 三 点 P1 , P2 , P3 .如 果 P1 P 2 P2 P3 , P1 P2 P2 P3 , 要 证 明 = '
,
那 么 是 一 个 保 持 A ' B ' C ' 不 变 的 正 交 变 换
A ' B ' C ' A ' B ' C '.
同 时 , ( P ) ( ( P ))
-1
正交变换
( ( P )) ( P ),
这 表 明 = .
例 题 2: 分 别 对 于 两 个 相 交 平 面பைடு நூலகம்的 两 个 反 射 的 乘 积 是一个旋转.
作业
7,10,11
复习:坐标变换
旧 坐 标 系 [ O , e1 , e 2 , e 3 ]
O ( a1 , a 2 , a 3 )
'
新 坐 标 系 [ O , e1 , e 2 , e 3 ] ' O O a 1 e1 a 2 e 2 a 3 e 3 .
线性代数课件7-3正交变换

05
正交变换在信号处理中的 应用
信号分解与合成原理介绍
信号分解
将复杂信号分解为一系列简单信 号的过程,这些简单信号通常是 正交基函数的线性组合。
信号合成
将分解得到的简单信号按照一定 规则重新组合,以恢复或逼近原 始信号的过程。
正交基函数
一组满足正交性条件的函数,用 于表示信号空间中的任意信号。 常见的正交基函数包括正弦函数、 余弦函数、小波基函数等。
曲线和曲面形状描述及性质分析
曲线形状描述
通过正交变换可以对曲线进行形 状描述,如曲线的弯曲程度、拐 点等性质可以通过正交变换进行
分析。
曲面形状描述
正交变换也可以用于曲面的形状描 述,如曲面的弯曲程度、法线方向 等性质可以通过正交变换进行分析。
性质分析
通过正交变换可以分析曲线和曲面 的性质,如曲线的长度、曲面的面 积等性质可以通过正交变换进行计 算和分析。
小波变换原理及实现方法
小波变换原理
小波变换是一种时频分析方法,通过伸缩和 平移小波基函数来匹配信号的局部特性。与 傅里叶变换相比,小波变换具有更好的时频 分辨率和局部化特性,适用于非平稳信号的 分析和处理。
实现方法
小波变换的实现包括连续小波变换(CWT) 和离散小波变换(DWT)两种方法。CWT 通过连续变化的小波基函数对信号进行匹配, 可以得到信号的时频分布;DWT则通过离 散化的小波基函数对信号进行分解和重构, 可以实现信号的压缩和去噪等应用。
通过正交变换得到的标准型具有唯一性,即不依赖于正交矩阵的选择。
02
正交变换的求解方法
施密特正交化过程
01 选择一组线性无关的向量作为起始向量组。
02
对起始向量组进行施密特正交化,得到一组 正交向量组。
图像信号的正交变换

定义
哈达玛变换是一种离散数学中的正交 变换,它将一个有限维的实数向量空 间映射到其自身,并保持向量的欧几 里得范数不变。
应用
哈达玛变换在图像处理、信号处理、数 据压缩等领域有广泛应用,特别是在图 像压缩编码中,可以有效地去除图像中 的冗余信息,提高图像压缩效率。
凯泽变换
定义
凯泽变换是一种离散数学中的正交变换,它将一个有限维的实数向量空间映射到其自身,并保持向量的欧几里得 范数不变。
小波变换在图像处理中的应用
01
02
03
图像压缩
小波变换可以将图像分解 成不同频率和方向的子图 像,从而去除冗余信息, 实现高效的图像压缩。
图像增强
通过调比度、锐 度等。
图像去噪
小波变换能够检测到图像 中的噪声,并通过滤波器 去除噪声,提高图像质量。
图像信号的正交变换
目
CONTENCT
录
• 正交变换简介 • 傅里叶变换 • 离散余弦变换 • 小波变换 • 其他正交变换方法
01
正交变换简介
正交变换的定义
正交变换是一种线性变换,它将输入信号从一种表示形式转换到 另一种表示形式,同时保持信号的能量不变。
正交变换具有正交性,即变换的逆变换与原变换是相互正交的, 这意味着逆变换可以恢复出原始信号。
对于连续信号,傅里叶变换可以表示为积分形式。
傅里叶变换的基本思想是,任何周期函数都可以由 一组正弦和余弦函数构成,而每个正弦和余弦函数 都有一个频率。
傅里叶变换的性质
线性性
如果 $f(t)$ 和 $g(t)$ 是两个信号,且 $a$ 和 $b$ 是常数,那么 $a f(t) + b g(t)$ 的傅里叶变 换等于 $a F(w) + b G(w)$,其中 $F(w)$ 和 $G(w)$ 分别是 $f(t)$ 和 $g(t)$ 的傅里叶变换。
第二章 正交变换、K-L变换与离散余弦变换

从数学的观点看,“集合”等效于空间。比如, 实数集合构成一维实数空间,记为R1,复数集合 构成一维复数空间,记为C1。 一般我们研究的是带有一定规律的“空间”,最 常见的是“线性空间”。粗略的说,线性空间指 这样一种集合,其中任意两元素的线性组合得到 集合内的另一元素。 把集合中的元素和信号之间建立对应关系,我们 就可以把线性空间理解为信号矢量空间。
1.2 常见的线性空间
N维实数空间RN和N维复数空间CN 连续时间信号空间L,定义在复数或实数域 上,时间变量为实数:无穷维空间 离散时间信号空间l,定义在复数或实数域 上,自变量为整数:无穷维空间或有限维 空间
1.3 范数(norm)
范数是矢量长度的度量,与信号的能量特性 相关 线性空间中元素x的范数以符号||x||表示,满 足以下公理 (1)半正定性: x ≥ 0 , x = 0 iff x=0 (2)正齐性: (3)三角不等式:
2.3 H空间中的正交变换
设X和Y为两个H空间,矢量x∈X,矢量 y∈Y,若将x变换到y,有关系式 y = Ax A为线性算子,完成的是线性变换,若有 < Ax, Ax > = < x , x > = < y, y >,则变换 前后,二阶范数保持不变,这是一种正 交变换,正交变换保持了变换前后的能 量相同。
4.3 2N点FFT来实现DCT
令x(n)=0,n=N,…2N-1 DCT可写成(k>0)
X c (k ) =
2π j nk 2 N 1 2N 2 jk π / 2 N Re{ e ∑0 x 2 N ( n ) e N n=
上式告诉我们,计算一个N点的DCT可通过 2N点FFT来实现,步骤是:
第二章 正交变换、 正交变换、K-L变换 与离散余弦变换
第四章正交变换1

对图像的旋转变换和傅里叶变换的顺序是可交换的
第四章 正交变换
14
傅里叶变换(离散)
8. 卷积定理:空域中的卷积等价于频域中的相乘
9. 相关定理:空域中f ( x, y) 与 g ( x, y ) 的相等等价于频域中 F (u, v) 的共轭与 G (u, v) 相乘 自相关:
互相关:
第四章 正交变换
n0
快速傅里叶变换(FFT)
令
W e
j
2 N
,W 1 e
x ( n )W
j
2 N
,
傅里叶变换对表示为:
1 x (n) N
N 1 n0
X ( m)
N 1 n0
mn
X ( m)W mn
第四章 正交变换
21
傅里叶变换(离散)
快速傅里叶变换(FFT)
将 X (m) x(n)W mn 展开可得到如下算式:
第四章 正交变换
33
傅里叶变换(离散)
(2) 对偶节点的计算
如: x1 ( 0) 和 x1 ( 4 ) 就是一对对偶节点,因为它们均来源于 x(0)和x(4)。对偶节点的计算也就是求出在每次迭代中对 偶节点的间隔或者节距。由流程图可见,第一次迭代的 N N 节距为 ,第二次迭代的节距为 4 ,第三次迭代的节距 N 2 为 3 等等。由以上分析可得到如下对偶节点的计算方法。
这种算法的蝶式流程图如下(a)和(b)所示 ,其中图(a)输入
为顺序的,运算结果是乱序的;图(b)输入为乱序的,运算结 果是顺序的。
第四章 正交变换 26
傅里叶变换(离散)
第四章 正交变换
27
傅里叶变换(离散)
第四章 正交变换
正交变换第二基本定理-概念解析以及定义

正交变换第二基本定理-概述说明以及解释1.引言1.1 概述正交变换作为线性代数中的重要概念,具有广泛的应用和深远的理论意义。
本文将重点阐述正交变换的第二基本定理,包括其基本定义、性质和在实际应用中的重要性。
通过对正交变换的深入讨论,可以加深对其理论内涵的理解,同时也可以帮助读者更好地掌握正交变换在实际问题中的应用技巧。
在论述正交变换的基础理论和实际应用的基础上,本文还将展望未来正交变换在数学和工程领域的发展趋势,为读者提供对正交变换研究的全面认识和深入理解。
1.2 文章结构文章结构部分的内容应该包括对整篇文章的大体结构进行说明,指明各个部分的主题和相互之间的关系。
可以简要介绍每个章节的内容和讨论重点,同时提前点明全文的重点和主题,让读者对整篇文章的结构有一个清晰的了解。
例如:文章结构部分:本文主要包括引言、正文和结论三个部分。
在引言部分,我们将对正交变换进行基本概念的介绍,以及本文的目的和意义进行阐述。
在正文部分,将详细介绍正交变换的基本概念、第二基本定理以及在实际应用中的意义。
在结论部分,将总结正交变换的重要性,强调第二基本定理的作用,并展望正交变换在未来的发展。
通过这样的结构,读者能够清晰地了解到整篇文章的内容和主题,为后续的阅读打下基础。
1.3 目的本文旨在探讨正交变换的第二基本定理,通过对正交变换的基本概念和第二基本定理的详细阐述,以及在实际应用中的意义进行深入分析,旨在通过全面解析正交变换的重要性和第二基本定理的作用,展望正交变换在未来的发展,为读者提供全面的理论知识和实际应用价值的启发。
希望通过本文的阐述,能够使读者对正交变换有更深入的理解,并为相关领域的学习和研究提供有益的参考。
2.正文2.1 正交变换的基本概念正交变换是线性代数和几何学中非常重要的概念,它描述了一个向量空间中的变换,在这种变换下,向量的长度和角度保持不变。
简单来说,正交变换是指在欧几里德空间中保持向量长度和夹角不变的线性变换。
正交变换

《正交变换的分类》一.概述正交变换是一种保持长度不变的线性变换(数域F中一个空间V 到自身的映射),在解析几何平面内保持这种关系或是等价关系或是全等关系。
其中包括平移、旋转、对折、或者是其中的组合等。
那么在欧氏空间(基本理论中有其概念)中,也会有如此的形式将一个向量经过某种途径将其变化而保持其长度不变。
在欧氏空间中实现这一变化和几何平面中几乎相同,它包括反射,旋转和这两种的组合,有限维数(两维以上)的空间中,这一变化可以实现,但是,实践起来并不容易。
以一个简单例子引入,如图:αβ向量βα,在平面上采取了反射(或对称)变换使得βα=,这是平面中的实例。
那么在欧氏空间中,实现正交变换(反射,旋转还有而者的组合)会在论文中从二维和三维空间中步步引入。
二. 基础知识与理论基础 1. 正交变换的定义欧氏空间V 的一个线性变换叫δ作一个正交变换,如果对于任意V ∈ξ都有:|)(ξδ|=|ξ|2. 欧氏空间的概念设V 是实数域R 上一个向量空间。
如果对于V 中任意一对向量ηξ,有一个确定的记作<ηξ,>的实数与他们对应,叫作向量ξ与η的内积(或标量积),并且下列条件被满足:(i)<ηξ,>=<ξη,>(ii)<ζηξ,+>=<ζξ,>+<ζη,> (iii)<a ηξ,>=a<ηξ,> (iv)当0≠ξ时,<ξξ,>>0这里ζηξ,,是V 中任意向量,a 是任意实数,那么V 叫作这个内积来说的一个欧氏空间。
3. 正交矩阵n 维欧氏空间一个规范正交基到另外 一个规范正交基的过渡矩阵是一个正交矩阵。
有以下结论:UU T =U T U=I, U -1=U T4. 特征多项式定义设A=(a ij )是数域F 上一个n 阶矩阵。
行列式:f A (x)=det(XI-A)=1...312111an a a a x ----annx n a na n a ----................3...............2..............1.............. 叫作矩阵A 的特征矩阵多项式。
正交变换原理讲解PPT

高了通信干线的传输效率,同时也可使计算机实时处理音频、视频信息,以保证播放出高
质量的视频、音频节目成为可能。用于声音图象数据压缩的编码方法甚多。
13
第一组
感谢观看
用这些少量的数据同样表述原有的信息。对这些系数进行量化、编码,就
可以达到压缩编码的目的。
正交变换应是可逆的,但是由于利用系数分布集中的特点,当舍去集
中区域外的那些系数后的逆变换就会产生一定的误差。一个好的正交变换 ,
舍去集中区域外的系数值后,进行的逆变换得到的图象和声音与原先图象
和声音质量相差不大。这就达到了在基本保质的前提下较大的提高数据压
那么称为正交矩阵,简称正交阵。
4. 若为正交矩阵,则线性变换 = 称为正交变换。设
= 为正交变换,则
有
y =
= = = .
由于 表示向量的长度,相当于线段的长度,
因此 y = 说明经正交变换线段长度不变。
4
Part 01
1.2 数字信号处理中的正交变换:
低次分量之中(M<N)。
(3)最佳特性
K-L变换是在均方误差测度下,失真最小的一种变换,其失真为被略去的各分量之和。
由于这一特性,K-L变换被称为最佳变换。许多其他变换都将K-L变换作为性能上比较的
参考标准。
(4)无快速算法,且变换矩阵随不同的信号样值集合而不同。
这是K-L变换的一个缺点,是K-L变换实际应用中的一个很大障碍。
正
交
变
换
的
性
质
1. 正交变换的基向量即是其对偶基向量。
2. 展开系数是信号在基向量上的准确投影。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C x E ( x x )(x 现了信号向量 x各分量之间的相关性。
二、K – L变换
设0,1, ,N 1为Cx的特征值 则 K L变换y Ax满足
0 C y ACx AT
1
N 1
非正弦类变换
变换(WHT ) Walsh Hadam ard Haar变换( HRT ) 斜变换(SLT)
K - L变换
最佳变换
二、K – L变换
K – L变换主要用于信号的数据压缩 正弦信号可以仅用三个参数决定(幅值、频率、相 位),如果可以仅传输这三个参数,就可以实现最大 限度数据压缩。 一般的信号可能具有冗余,即数据中具有相关性。 为了压缩数据,可以通过滤除信号中的相关性而达到。 K-L变换的思路是:寻找正交矩阵A,使得y=Ax除 去相关性。
二、K – L变换
设信号 x [ x(0), x(1),, x( N 1)] 其协方差矩阵为
c00 c 10 c N 1, 0 c01 c11 c N 1,1 c0, N 1 c1, N 1 c N 1, N 1
可以证明,C N的行、列向量满足 0 ck , cn 1 kn k n
因此,DCT是正交变换。在一定条件下, DCT是K-L变换的很好近似。
四、离散正弦变换(DST)
给定序列x(n),n=1,2,…,N,其正弦变换及其反变换分别定义为
X s (k ) x ( n)
2 N 1 nk x(n) sin( ), N 1 n 0 N 1 2 N 1 nk X s (k ) sin( ),, N 1 n 0 N 1
k 0,1,, N 1 n 1,2,, N
这样,若x(n)为实数,则其 DST也是实数, 因此,DST也避免了复数运算。将 上式写为矩阵形式 X s SN x
三、离散正弦变换(DST)
当N 8时,可以写出
sin 9 2 2 sin S8 9 9 sin 8 9
2 9 4 sin 9 16 sin 9 sin
8 9 16 sin 9 64 sin 9 sin
同样可以证明, S N的行、列向量满足 0 sk , sn 1 kn k n
因此,DST是正交变换。在一定条件下, DST也是K-L变换的很好近似。
2.4 其他常用正交变换
一、正交变换
二、K-L变换
三、离散余弦变换(DCT) 四、离散正弦变换
一、正交变换
1 信号的正交分解 2 正交变换的性质
3 正交变换的种类
一、正交变换
1 信号的正交分解
设
1,2, N 为N维线性空间X中的一组向量
x X , 可以将x按上述向量组 (2.4.1)
三、离散余弦变换(DCT)
当N 8时,可以写出 1 2 cos 1 16 C8 8 7 2 cos 16 3 2 cos 16 21 2 cos 16 1 15 2 cos 16 105 2 cos 16 1
T
1
因此,正交变换的反变换不需要求逆,编程容易, 运算速度快,便于实时实现
一、正交变换
2、正交变换的性质
性质2:正交变换保持变换前后信号的能量不变。
x x(n) x (n) x x
2 n
n n k n k
k
n k n k n k (n k )
令 则当 d
2
L
ˆ x, x
n 1
ˆ xx ˆ xx
2
ˆ xx
n n
ˆ 取最小值 时,d 2 x, x
因此,正交变换分解具有最小平方逼近性质
一、正交变换 3、正交变换的种类
DFT 离散傅立叶变换 DST 正弦类变换 离散正弦变换 离散余弦变换DCT
三、离散余弦变换(DCT)
给定序列x(n),n=0,1,…,N-1,其余弦变换定义为
1 X c (0) N X c (k )
x ( n)
n 0
N 1
2 N 1 (2n 1)k x(n) cos , N n 0 2N
K 0,1,, N 1
这样,若x(n)为实数,则其DCT也是实数, 因此,DCT避免了复数运算。将上 式写为矩阵形式 X c CN x
n k n k
n
2 n n
2
因此,正交变换满足Parsecal定理,称为“保范”变换
一、正交变换
2、正交变换的性质
性质3:正交变换分解具有最小平方逼近性质。
设
x n n
n 1
N
假定我们取前 L个向量1 , 2 ,, L来逼近x,则有
ˆ n n x
设X、Y为两个向量空间,算子 A将X 中的元素x映射到Y中的y,即
y Ax
若有 Ax, Ax y, y x, x
则称算子A是正交变换。
正交变换的意义是:信 号变换前后能量不变 即成立Parseval 公式
一、正交变换
2、正交变换的性质
性质1:若正交变换存在,则反变换存在且唯一
y Ax x A y A y
N
如果1,2, n 线性独立,则称之为 X中的一组基。
对任意 进行分解,即 x n n
n 1
当1,2, ,n两两相互正交时, (2.4.1)称为信号x的正交分解
3 3
2
2
1
1
信号的正交分解
若空间X中的任一元素都可由一 组向量
n 作正交分解,则称 n 是完备的。
二、K – L变换
K-L变换具有如下优点 ① 完全除去了原信号的相关性
②进行数据压缩时,将y(n)截短所得信号均方误差最小
③ 信号经K-L变换后,若将N个特征值按大小顺序排列, 则将y(n)舍去一段后,可以保留原信号的最大能量
因此,K-L变换被称为最佳变换
K-L变换的缺点: 目前没有K-L变换的快速算法,特征值的计算比较困难。 因此人们寻找具有接近K-L变换的良好性质,又具有快速 算法的变换。
