专题二.滑块滑板的临界问题docx
物理滑块滑板问题总结

物理滑块滑板问题总结在物理学中,滑块滑板问题是一个经典的力学问题,它涉及到物体在斜面上的运动和受力分析。
通过对滑块滑板问题的总结和分析,我们可以更好地理解物体在斜面上的运动规律,为解决类似问题提供参考和指导。
本文将对物理滑块滑板问题进行总结,包括问题的基本概念、运动规律、受力分析和相关公式推导,希望能够对读者有所帮助。
首先,我们来看滑块滑板问题的基本概念。
滑块滑板问题是指一个物体沿着倾斜的滑板或斜面运动的问题。
在这个问题中,我们需要考虑物体在斜面上的加速度、受力情况以及最终的运动轨迹。
通过对滑块滑板问题的分析,我们可以了解到斜面对物体的影响,以及如何利用斜面来改变物体的运动状态。
其次,我们需要了解滑块滑板问题的运动规律。
根据牛顿运动定律,物体在斜面上的运动受到重力、支持力和摩擦力等多个力的作用。
通过对这些力的分析,我们可以得出物体在斜面上的加速度和速度变化规律,从而更好地理解物体在斜面上的运动情况。
另外,滑块滑板问题的受力分析也是非常重要的。
在这个问题中,我们需要分析物体受到的各种力,包括重力、支持力和摩擦力等。
通过对这些力的分析,我们可以计算出物体在斜面上的加速度和速度,从而得出物体的最终运动状态。
最后,我们可以通过相关公式推导来进一步理解滑块滑板问题。
通过对滑块滑板问题的相关公式推导,我们可以得出物体在斜面上的运动规律,包括加速度、速度和位移等。
这些公式可以帮助我们更好地理解滑块滑板问题,为解决类似问题提供参考和指导。
综上所述,物理滑块滑板问题是一个经典的力学问题,通过对它的总结和分析,我们可以更好地理解物体在斜面上的运动规律,为解决类似问题提供参考和指导。
希望本文对读者有所帮助,谢谢阅读!。
木板滑块模型中的临界值问题分析

木板滑块模型中的临界值问题分析在高中研究力与运动的关系时,经常遇到滑块与木板模型的问题,涉及到两物体的受力分析、物体相对运动的分析、能量转化等问题综合性较强.近年全国高考理综课标卷都对该问题进行了考查,通过高考试题分析和得分情况来看,学生对该问题的难点理解还是存在很大问题。
此类题是高中物理学习的重点和难点,很好地考查了考生对摩擦力知识、动力学知识的掌握情况以及图像的识读能力和分析能力,对物理教学提出了能力培养的要求。
其中的一个难点就是模型中的临界状态分析,笔者将通过以下情境来分析木板滑块模型中的临界值问题。
模型一:恒力作用木板,木板叠放在光滑水平面上情境1.已知木板的质量为mB ,物块的质量为mA,物块A和木板B之间的动摩擦因数为μ,物块和木板之间的最大静摩擦力近似等于滑动摩擦力,恒力作用于木板,木板放在光滑水平面上,试讨论恒力多大时物块和木板发生滑动及相对运动各自的加速度?分析:先确定临界值,即刚好使A、B发生相对滑动的F值。
可先分析木块A,对A:,由于B对A的摩擦力的最大值为最大静摩擦力,所以A向右运动存在最大加速度,若B也是以此最大加速度加速,这就是A、B即将发生相对滑动的临界状态。
临界状态:对A:,对A、B整体:联立可得临界值讨论:(1)若,A、B一起加速,(2)若F>F,A、B发生相对滑动,,模型二:恒力作用木块,木板叠放在光滑水平面上情境2.已知木板的质量为mB ,物块的质量为mA,物块A和木板B之间的动摩擦因数为μ,物块和木板之间的最大静摩擦力近似等于滑动摩擦力,恒力作用于物块,木板放在光滑水平面上,试讨论恒力多大时物块和木板发生滑动及相对运动各自的加速度?分析:先确定临界值,经例1分析可知,当A、B间恰好达到最大静摩擦力时,为临界状态。
临界状态:对B:,对A、B整体:联立可得临界值讨论:(1)若,A、B一起加速,(2)若F>F,A、B发生相对滑动,,例题1、如图所示,木块A、B静止叠放在光滑水平面上,A的质量为m,B的质量为2m。
滑块木板模型的临界条件总结

滑块木板模型的临界条件总结
滑块木板模型是一种用于研究结构动力学的简单模型,它可以用来模拟结构的振动和稳定性。
滑块木板模型的临界条件是指在滑块木板模型中,当滑块木板模型的参数达到一定的值时,结构的振动和稳定性会发生变化。
首先,滑块木板模型的临界条件之一是滑块木板模型的振动频率。
当滑块木板模型的振动频率达到一定的值时,结构的振动和稳定性会发生变化。
其次,滑块木板模型的临界条件之二是滑块木板模型的振幅。
当滑块木板模型的振幅达到一定的值时,结构的振动和稳定
性会发生变化。
最后,滑块木板模型的临界条件之三是滑块木板模型的振动模式。
当滑块
木板模型的振动模式达到一定的值时,结构的振动和稳定性会发生变化。
总之,滑块木板模型的临界条件包括滑块木板模型的振动频率、振幅和振动模式。
当滑块木板模型的参数达到一定的值时,结构的振动和稳定性会发生变化,从而影响结构的性能。
因此,在研究结构动力学时,必须考虑滑块木板模型的临界条件,以确保结构的安全性和
可靠性。
专题二.滑块滑板的临界问题docx

专题二:滑块滑板和临界问题1.模型特点:上、下叠放两个物体,并且两物体在摩擦力的相互作用下发生相对滑动.2.建模指导,解此类题的基本思路:(1)分析滑块和木板的受力情况,根据牛顿第二定律分别求出滑块和木板的加速度;(2)对滑块和木板进行运动情况分析,找出滑块和木板之间的位移关系或速度关系,建立方程。
特别注意滑块和木板的位移都是相对地面的位移。
3.分析滑块—木板模型问题时应掌握的技巧(1).分析题中滑块、木板的受力情况,求出各自的加速度.(2).画好运动草图,找出位移、速度、时间等物理量间的关系.(3).知道每一过程的末速度是下一过程的初速度.(4).两者发生相对滑动的条件:A.摩擦力为滑动摩擦力.B二者加速度不相等.例1.(2016·江苏泰州期末)如图所示,在光滑平面上有一静止小车,小车质量为M=5 kg,小车上静止地放置着质量为m=1 kg的木块,木块和小车间的动摩擦因数为μ=0.2,用水平恒力F拉动小车,下列关于木块的加速度a m和小车的加速度a M,可能正确的有( )A. a m=1 m/s2,a M=1 m/s2B.a m=1 m/s2,a M=2 m/s2C.a m=2 m/s2,a M=4 m/s2D.a m=3 m/s2,a M=5 m/s2例2.(2016·河北省衡水中学调研)如图甲所示,A、B两物体叠放在一起放在光滑的水平面上,B物体从静止开始受到一个水平变力的作用,该力与时间的关系如图乙所示,运动过程中A、B始终保持相对静止。
则在0~2t0时间内,下列说法正确的是( )A.t0时刻, A、B间的静摩擦力最大,加速度最小B.t0时刻,A、B的速度最大C.0时刻和2t0时刻,A、B间的静摩擦力最大D.2t0时刻,A、B离出发点最远,速度为0例3.如图所示,质量为M的长木板位于光滑水平面上,质量为m的物块静止在长木板上,两者之间的动摩擦因数为μ,现对物块m施加水平向右的恒力F,若恒力F使长木板与物块出现相对滑动,施加力F的最小值为(重力加速度大小为g,物块与长木板之间的最大静摩擦力等于两者之间的滑动摩擦力)()。
专题:“滑块-滑板”问题的综合求解-课件

【精讲精析】(1)设滑块冲上传送带时的速度为v,在弹簧弹开过程中,
由机械能守恒:Ep=1 mv2
①
2
设滑块在传送带上做匀减速运动的加速度大小为a,
一、滑块与滑板结合问题 1
【例证1】如图所示,AB为半径R=0.8m的 4光滑圆 弧轨道,下端B恰与小车右端平滑对接。小车质量 M=3kg,车长L=2.06m,车上表面距地面的高度h=0.2m,现有一质量m=1kg的滑块, 由轨道顶端无初速度释放,滑到B端后冲上小车。已知地面光滑,滑块与小车上 表面间的动摩擦因数μ=0.3,当车运动了t0=1.5s时,车被地面装置锁定。 (g=10m/s2)。试求: (1)滑块到达B端时,轨道对它支持力的大小。 (2)车被锁定时,车右端距轨道B端的距离。 (3)从车开始运动到被锁定的过程中,滑块与车面间由于摩擦而产生的内能大小。
C.2.5s 2J
D.2.5s 8J
【解析】选C。小物体刚放上去时做匀加速运动,加速度为a=μg=
2m/s2,当速度达到v=2m/s时与传送带相对静止,此时运动的时间t1= av=1s,物体的位移x1= v2t=1 1m,传送带的位移x2=vt1=2m,所以摩擦生 热Q=μmg(x2-x1)=2J;以后小物体匀速运动的时间t2l=vx1 =1.5s,所 用总时间t=t1+t2=2.5s。选项C正确。
答案:(1) 12mv02+μmgL
(2)μmgL-mv0(
v
2 0
2gL-v0
)
四、“滑块+滑板”与图像结合问题 【例证4】如图甲,长木板A放在光滑的水平面上,质量为m=2kg的另一 物体B以水平速度v0=2m/s滑上原来静止的长木板A的表面。由于A、B 间存在摩擦,之后A、B速度随时间变化情况如图乙所示,则下列说法错 误的是( )
滑块与滑板类问题的解题分析

起 保持相对静 止做加速度 大小为嘞: 1 m, S 2 的匀减 速运动 。 由 = 里 得: 此过 程滑 板 的位 移 大 小 为 : :
一
a v-
= 2 m。滑板在 水平 面 上滑行 的距 离 为 。 慨 =
运动过程 的关键。两者之间的摩擦力变化存在一个 临界状态 , 滑块 和滑板之间开始发生相对滑动 , 它们 之 间存在滑动摩擦力 , 当二者速度相 等后 , 它们之间 没有摩擦力 , 保持相对静止一起 匀速运动 。 求 出二者
( M+ m) m。
对滑块苗 半顿第二定律可得 : m 嘞 = 2 N 。 由于此 m 。 F 4 N , 几何关系可得 : 滑块在滑板上滑行 的距离为S = x 一 = 时 滑板 对滑块 的最大摩 擦力 的大小为厂 f < f z , 所以假设成立, 即滑块和滑板速度柏等后 它们 t vo
由 = — y O - I — - V t f 得 :滑板 匀加速运动 的位 移大小 为
号 拄 l m 。
由 : — y O - O — - V  ̄ £ 得 :滑 块 匀 加 速 运 动 的位 移 大 小 为
2
Vo +V
F
滑 块 和 滑板 速 度 相 等 后 ,不 妨 假 设 它们 一起 保 持相对静止做加速度大小为 的匀减速运动 ,对 滑 块 和滑 板整 体 由牛 顿第 二定 律 可得 : ( M+ m) g =
藩 2
1 g 2m/ s 2 o
以 假 设 不 成 立 滑 块 在
。
匀减速直线运动,滑板先做加速度大小为 的匀加
速 直线 运动 , 经 过£ s 滑 块 和 滑 板 有 共 同 速 度 。 对 滑块 由牛 顿第 二定 律 可 得 : , n mⅡ I ’解 得 :
动力学中的滑块—滑板模型

解此类题的基本思路:
(1)分析滑块和木板的受力情况,根据牛顿第二定律分别 求出滑块和木板的加速度;
(2)对滑块和木板进行运动情况分析,找出滑块和木板之 间的位移关系或速度关系,建立方程.特别注意滑块和木板 的位移都是相对地面的位移.
*
4
动力学中的滑块—滑板模型
知识梳理
3.两种位移关系:(相对滑动的位移关系)
滑块由滑板的一端运动到另一端的过程中,若滑块和滑
板同向运动F ,位移之差等F于板长;反向运动时,位移之和等
x
于板长.
1
x2
L
x2
L
x1
L
4.考试题型: (1)选择题:包括文字选择题与图象选择题;
(2)计算题:主要有关于滑块和滑板间是否存在相对滑动 的分析计算、使滑块与滑板间发生相对滑动的临界力的计算 (即外力的作用范围问题);其它临界问题的分析计算等。
2k
kt f
,之后A的加速度 a A m A
随时间增大,
木板B以不变的加速度 a B
f 2m A
做匀加速直线运动.从
以上分析可知,C正确.故选C.
19
动力学中的滑块—滑板模型
方三法、滑指块导在滑板上不滑下的临界条件:
滑块滑到滑板一端时,滑块和滑板两者速度相同.
方法指导
20
动力学中的滑块—滑板模型
2.此类试题由于研究对象多、受力分析困难,运动过程复杂, 往往会使考生“手忙脚乱”,“顾此失彼”导致丢分。是 学生比较容易感到“头疼”的一类试题。因此探究并掌握 此类试题的分析技巧和解题方法是十分必要的。
*
3
动力学中的滑块—滑板模型
知识梳理
1.模型特点:
课题滑板和滑块 (相对滑动的两个物体)问题的解题思路
fs 2 =
1 1 2 m2 v′ 2 − m2 v2 2 2
(3)
S2 (4)
d
它们的位置关系是 s1 − s 2 = d 由 fd =
1 1 1 2 2 m1v1 + m2 v 2 − (m1 + m2 )v ′ 2 2 2 2
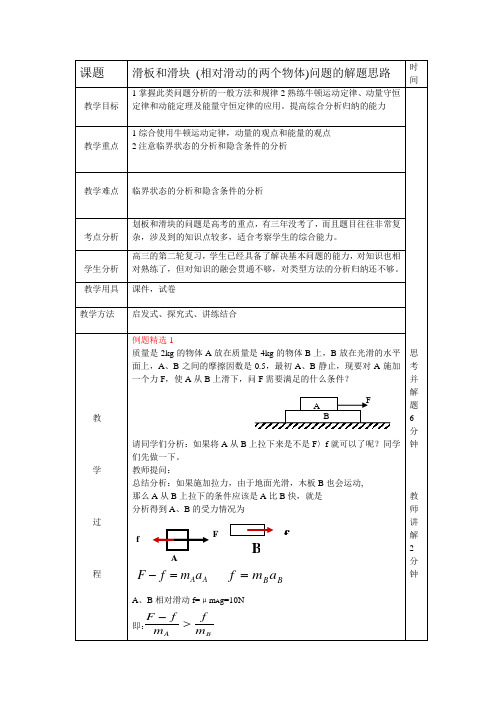
即 fd = Q 例题精选 3: 一个质量为 M、 长为 L 的长方形木板 B 放在光滑的水平地 面上,在它的右端放一个质量为 m 的小木块 A,m<M,现以地面为参 照系,给 A 和 B 以大小相等、方向相反的初速度,使 A 开始向左运动, B 开始向右运动,最后 A 刚好没离开滑板 B, (1) 若已知 A 和 B 的初速度的大小是 v0 求他们最后的速度大小和 方向 (2) 若初速度的大小未知,求小木块向左到达的最远处离出发点的 距离(在地面上观察) V0 B A V0 独 立 解 题 6 分 钟
Q=
1 1 1 2 2 m1v1 + m2 v 2 − (m1 + m2 )v ′ 2 (1) 2 2 2
V 两个物体的运动位移情况如图 对小物体,根据动能定理有 V2 (2) S1 教 师 分 V’ 析 点 评 3 分 钟
− fs1 =
1 1 2 m1v ′ 2 − m1v1 2 2
对于长木板,根据动能定理有
学生分析 教学用具 教学方法
教
思 考 并 解 题 6 分 钟
学
过
f A
程
F
Bቤተ መጻሕፍቲ ባይዱ
f = mB a B
f
F − f = mAa A
F − f f > m A mB
教 师 讲 解 2 分 钟
A、B 相对滑动 f=μmAg=10N 即:
滑块-木板、临界问题

滑块-木板、临界问题一.选择题(共1小题)1.如图所示,质量均为m的A、B两物体叠放在竖直轻质弹簧上并保持静止,用大小等于mg的恒力F向上拉B,当运动距离为h时B与A分离.下列说法正确的是()A.B和A刚分离时,弹簧长度等于原长B.B和A刚分离时,它们的加速度为gC.弹簧的劲度系数等于D.在B和A分离前,它们先做加速运动后做减速运动二.多选题(共3小题)2.如图所示,劲度系数为k的轻弹簧下端系一个质量为m的小球A,小球被水平挡板P托住使弹簧长度恰为自然长度(小球与挡板不粘连),然后使挡板P以恒定的加速度a(a <g)竖直向下做匀加速直线运动,对小球从开始运动直至到达最低点的过程,用t表示与挡板分离所经历的时间,用x表示小球速度最大时弹簧的伸长量,则()A.t=B.t=C.x=0D.x=3.如图所示,A、B两物块的质量分别为2m和m,静止叠放在水平地面上.A、B间的动摩擦因数为μ,B与地面间的动摩擦因数为μ.最大静摩擦力等于滑动摩擦力,重力加速度为g.现对B施加一水平拉力F,则()A.当F<2μmg时,A、B相对地面静止B.当F=μmg时,A的加速度为μgC.当F>3μmg时,A相对B滑动D.无论F为何值,A的加速度不会超过μg4.如图所示,光滑水平面上放置质量分别为m、2m的A、B两个物体,A、B间的最大静摩擦力为μmg,现用水平拉力F拉B,使A、B以同一加速度运动,则拉力F的可能值为()A.2μmg B.3μmg C.4μmg D.5μmg三.计算题(共2小题)5.如图所示,长为L=2m、质量为M=4kg、下表面光滑的薄木板(厚度不计)放在水平地面上,处于静止状态。
现对木板施加大小为F=14N的水平向右的恒力,同时在木板右端轻放一个大小不计、质量为m=1kg的小物块。
物块与木板及物块与地面间的动摩擦因数均为μ=0.2,取g=10m/s2.求(1)物块及木板的加速度大小(2)物块滑离木板时的速度大小;(3)物块停止运动时,木板右端与物块的间距△x6.如图所示,有两个高低不同的水平面,高水平面光滑,低水平面粗糙。
应用动力学方法解决“滑块——滑板”模型问题 讲义

应用动力学方法解决“滑块——滑板”模型问题[核心精讲]滑块——滑板模型是近几年来高考考查的热点,涉及摩擦力的分析判断、牛顿运动定律、匀变速运动等主干知识,能力要求较高,滑块和滑板的位移关系、速度关系是解答滑块——滑板模型的切入点,前一运动阶段的末速度是下一运动阶段的初速度,解题过程中必须以地面为参考系.1.模型特点:滑块(视为质点)置于滑板上,滑块和滑板均相对地面运动,且滑块和滑板在摩擦力的相互作用下发生相对滑动.2.运动学分析:无临界速度时,滑块与滑板分离,确定相等时间内的位移关系解题;有临界速度时,滑块与滑板不分离,假设速度相等后加速度相同,由整体法求解系统的共同加速度,再由隔离法用牛顿第二定律求滑块与滑板间的摩擦力f ,如果该摩擦力不大于最大静摩擦力说明假设成立,则整体列式解题;如果该摩擦力大于最大静摩擦力说明假设不成立,则分别列式;确定相等时间内的位移关系解题.3.动力学分析:判断滑块与滑板是否发生相对滑动是解决这类问题的一个难点,通常采用整体法、隔离法和假设法等.往往先假设两者相对静止,由牛顿第二定律求出它们之间的摩擦力f ,与最大静摩擦力f m 进行比较.若f <f m ,则不会发生相对滑动;反之,将发生相对滑动.从运动学角度看,滑块与滑板的速度和加速度不等,则会发生相对滑动.[范例] (20分)(2015·高考全国卷Ⅰ)一长木板置于粗糙水平地面上,木板左端放置一小物块;在木板右方有一墙壁,木板右端与墙壁的距离为4.5 m ,如图甲所示.t =0时刻开始,小物块与木板一起以共同速度向右运动,直至t =1 s 时木板与墙壁碰撞(碰撞时间极短).碰撞前后木板速度大小不变,方向相反;运动过程中小物块始终未离开木板.已知碰撞后1 s 时间内小物块的v -t 图线如图乙所示.木板的质量是小物块质量的15倍,重力加速度大小g 取10 m/s 2.求:(1)木板与地面间的动摩擦因数μ1及小物块与木板间的动摩擦因数μ2; (2)木板的最小长度;(3)木板右端离墙壁的最终距离.[解析] (1)规定向右为正方向.木板与墙壁相碰前,小物块和木板一起向右做匀变速运动,设加速度为a 1,小物块和木板的质量分别为m 和M .由牛顿第二定律得-μ1(m +M )g =(m +M )a 1①(1分)由题图乙可知,木板与墙壁碰撞前瞬间的速度v 1=4 m/s ,由运动学公式得v 1=v 0+ a 1t 1②(1分) x 0=v 0t 1+12a 1t 21③(1分)式中,t 1=1 s ,x 0=4.5 m 是木板碰撞前的位移,v 0是小物块和木板开始运动时的速度.联立①②③式和题给条件得μ1=0.1 ④(1分)在木板与墙壁碰撞后,木板以初速度为-v 1向左做匀变速运动,小物块以初速度v 1向右做匀变速运动.设小物块的加速度为a 2,由牛顿第二定律得-μ2mg =ma 2⑤(1分)由题图乙可得a 2=v 2-v 1t 2-t 1⑥(1分)式中,t 2=2 s ,v 2=0,联立⑤⑥式和题给条件得 μ2=0.4.⑦(1分)(2)设碰撞后木板的加速度为a 3,经过时间Δt ,木板和小物块刚好具有共同速度v 3.由牛顿第二定律及运动学公式得μ2mg +μ1(M +m )g =Ma 3⑧(1分) v 3=-v 1+a 3Δt ⑨(1分) v 3=v 1+a 2Δt⑩(1分)碰撞后至木板和小物块刚好达到共同速度的过程中,木板运动的位移为 x 1=-v 1+v 32Δt⑪(1分) 小物块运动的位移为x 2=v 1+v 32Δt⑫(1分) 小物块相对木板的位移为Δx =x 2-x 1⑬(1分)联立④⑥⑦⑧⑨⑩⑪⑫⑬式,并代入数值得 Δx =6.0 m⑭(1分)因为运动过程中小物块没有脱离木板,所以木板的最小长度应为6.0 m .(1分) (3)在小物块和木板具有共同速度后,两者向左做匀变速运动直至停止,设加速度为a 4,此过程中小物块和木板运动的位移为x 3.由牛顿第二定律及运动学公式得μ1(m +M )g =(m +M )a 4⑮(1分) 0-v 23=2a 4x 3⑯(1分)碰后木板运动的位移为x=x1+x3 ⑰(1分)联立④⑥⑦⑧⑨⑩⑪⑮⑯⑰式,并代入数值得x=-6.5 m(1分)木板右端离墙壁的最终距离为6.5 m.(1分)[答案](1)0.10.4(2)6.0 m(3)6.5 m(1)规范要求书写物理表达式要以课本原始公式为依据,牛顿第二定律的表达式为F合=ma,要分步列式,尽量不要列综合式,否则容易失分;符号使用要规范,与题目提供的符号要一致,再者木板和物块的加速度不同,若都用a表示不加以区分,将不得分.(2)评分细则第(1)问7分,①~⑦式各1分.第(2)问8分,⑧~⑭式各1分.第(3)问5分,⑮~⑰式各1分.题目中给出的符号解析中必须要一致,若μ1、μ2用错,则扣结果分.无单位、单位错误,相应的得分点不给分.(用其他方法求解,正确的,参照上述答案酌情给分)[预测押题]1.如图甲所示,质量为M的长木板,静止放置在粗糙水平地面上,有一个质量为m、可视为质点的物块,以某一水平初速度从左端冲上木板.从物块冲上木板到物块和木板达到共同速度的过程中,物块和木板的v-t图象分别如图乙中的折线acd和bcd所示,a、b、c、d点的坐标分别为a(0,10)、b(0,0)、c(4,4)、d(12,0).根据v-t图象,求:(1)物块冲上木板做匀减速直线运动的加速度大小a1,木板开始做匀加速直线运动的加速度大小a2,达到共同速度后一起做匀减速直线运动的加速度大小a3;(2)物块质量m与长木板质量M之比;(3)物块相对长木板滑行的距离Δx.解析:(1)由v -t 图象可求出物块冲上木板做匀减速直线运动的加速度大小a 1=10-44m/s 2=1.5 m/s 2,木板开始做匀加速直线运动的加速度大小a 2=4-04m/s 2=1 m/s 2,达到共同速度后一起做匀减速直线运动的加速度大小a 3=4-08m/s 2=0.5 m/s 2.(2)对物块冲上木板匀减速阶段:μ1mg =ma 1 对木板向前匀加速阶段:μ1mg -μ2(m +M )g =Ma 2 物块和木板达到共同速度后向前匀减速阶段: μ2(m +M )g =(M +m )a 3 以上三式联立可得m M =32.(3)由v -t 图象可以看出,物块相对于长木板滑行的距离Δx 对应图中△abc 的面积,故Δx =10×4×12m =20 m.答案:(1)1.5 m/s 2 1 m/s 2 0.5 m/s 2 (2)32(3)20 m 2.(2017·湖北七市联考)如图所示,可视为质点的物体A 叠放在长木板B 上,A 、B 的质量分别为m 1=10 kg 、m 2=10 kg ,B 长为L =16 m ,开始时A 在B 的最右端;A 与B 、B 与地之间的动摩擦因数分别为μ1=0.4、μ2=0.4;现将一水平恒力F =200 N 作用在B 上,使A 、B 由静止开始运动,当A 恰好运动到B 的中点时撤去外力F ,g 取10 m/s 2.求:(1)力F 作用的时间及此时B 前进的距离; (2)撤去外力F 后B 还能走多远?解析:(1)力F 开始作用时,设A 、B 的加速度分别为a 1、a 2, 对A :μ1m 1g =m 1a 1,a 1=4 m/s 2 对B :F -μ1m 1g -μ2(m 1+m 2)g =m 2a 2, a 2=8 m/s 2,设力F 作用的时间为t ,对应此时A 、B 的速度为v A 、v B 则有12a 2t 2-12a 1t 2=12L代入数据得,t =2 s ,v A=8 m/s,v B=16 m/s此时B前进的距离为x B=12a2t2=16 m.(2)撤去外力F后,对A有μ1m1g=m1a3,a3=4 m/s2对B有μ1m1g+μ2(m1+m2)g=m2a4,a4=12 m/s2设A、B经过时间t1达到共同速度v1则有v A+a3t1=v B-a4t1解得:t1=0.5 s,v1=10 m/s此过程中B前进的距离为x1=v2B-v212a4=6.5 mA、B共速后一起匀减速的加速度为a5μ2(m1+m2)g=(m1+m2)a5,a5=4 m/s2此时B前进的距离为x2=v 2 12a5=12.5 m 撤去F后B前进的总距离为x=x1+x2=19 m.答案:(1)2 s16 m(2)19 m。
滑块-滑板模型

滑块、滑板模型专题【学习目标】1、能正确的隔离法、整体法受力分析2、能正确运用牛顿运动学知识求解此类问题3、能正确运用动能定理和功能关系求解此类问题。
【自主学习】1、处理滑块与滑板类问题的基本思路与方法是什么?2、滑块与滑板存在相对滑动的临界条件是什么?3、滑块滑离滑板的临界条件是什么?【合作探究 精讲点拨】例题:如图所示,滑块A 的质量m =1kg ,初始速度向右v 1=8.5m/s ;滑板B 足够长,其质量M =2kg ,初始速度向左v 2=3.5m/s 。
已知滑块A 与滑板B 之间动摩擦因数μ1=0.4,滑板B 与地面之间动摩擦因数μ2=0.1。
取重力加速度g =10m/s 2。
且两者相对静止时,速度大小:,s m v /5 ,在两者相对运动的过程中:问题(1):刚开始a A 、a B1问题(2):B 向左运动的时间t B1及B 向左运动的最大位移S B2问题(3):A 向右运动的时间t 及A 运动的位移S A问题(4):B 运动的位移S B 及B 向右运动的时间t B2问题(5):A 对B 的位移大小△S 、A 在B 上的划痕△L 、A 在B 上相对B 运动的路程x A问题(6):B 在地面的划痕L B 、B 在地面上的路程x B问题(7):摩擦力对A 做的功W fA 、摩擦力对A 做的功W fB 、系统所有摩擦力对A 和B 的总功W f问题(8):A 、B 间产生热量Q AB 、B 与地面产生热量Q B 、系统因摩擦产生的热量Q问题(9):画出两者在相对运动过程中的示意图和v -t 图象练习:如图为某生产流水线工作原理示意图.足够长的工作平台上有一小孔A ,一定长度的操作板(厚度可忽略不计)静止于小孔的左侧,某时刻开始,零件(可视为质点)无初速地放上操作板的中点,同时操作板在电动机带动下向右做匀加速直线运动,直至运动到A 孔的右侧(忽略小孔对操作板运动的影响),最终零件运动到A 孔时速度恰好为零,并由A 孔下落进入下一道工序.已知零件与操作板间的动摩擦因数μ1=0.05,零件与与工作台间的动摩擦因数μ2=0.025,不计操作板与工作台间的摩擦.重力加速度g=10m/s2.求:(1)操作板做匀加速直线运动的加速度大小;(2)若操作板长L=2m ,质量M=3kg ,零件的质量m=0.5kg ,则操作板从A 孔左侧完全运动到右侧的过程中,电动机至少做多少功?【总结归纳】【针对训练】A工作台v v 0图1、光滑水平地面上叠放着两个物体A 和B ,如图所示.水平拉力F 作用在物体B 上,使A 、B 两物体从静止出发一起运动.经过时间t ,撤去拉力F ,再经过时间t ,物体A 、B 的动能分别设为EA 和EB ,在运动过程中A 、B 始终保持相对静止.以下有几个说法:①EA +EB 等于拉力F 做的功;②EA +EB 小于拉力F 做的功;③EA 等于撤去拉力F 前摩擦力对物体A 做的功;④EA 大于撤去拉力F 前摩擦力对物体A 做的功。
一轮复习物理专题专题动力学中的滑块滑板问题

文档来源为 :从网络收集整理 .word 版本可编辑 .欢迎下载支持 .专题 :动力学中的滑块 —滑板模型1、模型特点:上、下叠放两个物体,并且两物体在摩擦力的相互作用下发生相对滑动.2、考点:“滑块 - 木板”类问题,具有涉及考点多(运动学公式、牛顿运动定律、功能关系等) ,情境丰富,设问灵活,解法多样,思维量高等特点,是一类选拔功能极强的试题,也是新课标力学常考的试题。
3、解题思路:( 1)动力学关系 : 受力分析注意摩擦的作用是相互的,灵活运用整体法和隔离法分析,根据牛顿第二定律分别求出滑块和木板的加速度;而出现最大加速度时往往是运动过程出现 临界转折的关键点。
( 2)运动关系:恰好“滑落”或“不滑落”常为找时间关系列位移方程,一般为同向运动位移差为板长,反向运动位移之和为板长。
( 3)能量关系:相互摩擦机械能损失转化为内能,常用能量守恒△ E=f 滑 X 相对。
( 4)区分选修 3-5 动量守恒中的滑块滑板: 要满足动量守恒必不受外力,一般无外界拉力和地面摩擦力。
【典例 1】【临界问题】木板 M 静止在光滑水平面上,木板上放着一个小滑块 m ,与木板之间的动摩擦因数 μ,为了使得 m能从 M 上滑落下来,求下列两种情况下力F 的大小范围。
Fm m F方法归纳:是否滑动的关键在于是否达到最大静摩擦,MM关键在最大静摩擦及最大加速度判断比较【变式一】图所示,在光滑的水平地面上有一个长为L ,质量为 M=4kg 的木板 A ,在木板的左端有一个质量为m=2kg 的小物体 B ,A 、B 之间的动摩擦因数为 μ=0.2 ,当对 B 施加水平向右的力 F 作用时 ( 设 A 、B 间的最大静摩擦力大小与滑动摩擦力大小相等 ) ,( 1)若 F=5N ,则 A 、B 加速度分别为多大?( 2)若 F=10N ,则 A 、B 加速度分别为多大?( 3)在( 2)的条件下,若力 F 作用时间 t =3s , B 刚好到达木板 A 的右端,则木板长 L 应为多少? 【变式二】【 2011·理综课标 I 第 21 题】 如图, 在光滑水平面上有一质量为m 的足够长的木板,其上叠放1一质量为 m 的木块。
粗糙和光滑地面滑块滑板模型临界条件

粗糙和光滑地面滑块滑板模型临界条件示例文章篇一:哎呀,我的天呐!今天老师给我们讲了一个超级神奇的东西,叫“粗糙和光滑地面滑块滑板模型临界条件”。
这名字一听,是不是觉得超级复杂,超级难懂?其实刚开始我也是这么想的!上课的时候,老师就像个魔法师一样,在黑板上画呀画,嘴里还不停地说:“同学们,你们看啊,这粗糙的地面就像是长满刺的小怪兽,会使劲儿抓住滑板,不让它滑得太快。
而光滑的地面呢,就像给滑板铺了一条超级顺滑的跑道,让它能飞一样地冲出去!” 我在下面听得一愣一愣的,心里想:“这到底是啥意思呀?”我同桌小李可积极了,他举着手问老师:“老师,那到底怎么才能知道什么时候滑板会在粗糙地面上停下来,什么时候又能在光滑地面上一直冲呢?”老师笑着说:“这就是我们要研究的临界条件啦!”然后老师又开始讲一堆公式和原理,我感觉我的脑袋都要被这些东西塞满啦!我忍不住跟后面的小王嘀咕:“这也太难了吧,感觉像是在解一个超级大的谜团!”小王也点点头说:“就是就是,我都快被绕晕了!”老师好像听到了我们的抱怨,他说:“同学们别着急,咱们慢慢来。
就像你们学骑自行车,一开始也觉得很难,但是多练习就会啦!” 听老师这么一说,我好像又有点信心了。
后来老师给我们做了实验,拿了一个小滑块和一块滑板,在粗糙的地面和光滑的地面上分别试了试。
我们都瞪大了眼睛看着,哇,真的好神奇!在粗糙地面上,滑块没滑多远就停了,而在光滑地面上,它滑出去好远好远。
这时候我突然明白了,原来这个临界条件就像是一个神秘的开关,控制着滑块和滑板的行动。
如果我们能掌握这个开关,就能知道它们会怎么运动啦!现在想想,虽然一开始觉得这个“粗糙和光滑地面滑块滑板模型临界条件”特别难,特别让人头疼,但是通过老师的讲解和实验,好像也没有那么可怕啦!我觉得只要我们认真学,多思考,多做实验,就一定能搞明白这个神秘的东西!你们说是不是呀?示例文章篇二:哎呀呀,这题目可真够复杂的!粗糙和光滑地面,滑块滑板模型,还有临界条件?这对我这个小学生来说,可真是个大难题呢!先来说说粗糙地面吧。
牛顿第二定律之滑块与滑板问题(含解析)

1一 无外力F 的板块问题分析【知识构建】1. 地面光滑,即板和地面的μ2=0,2.地面粗糙,即A 和B 的动摩擦因数μ1板和地面的动摩擦因数μ2, (1)μ1>μ2(2)μ1<μ211mg ma μ=()()23+M m g M m a μ+=23.板和快都有初速度【总结】μ1>μ2 μ1<μ211a v t =3【典例分析】 1、地面光滑【例1】 (多选)(2021·深圳第二外国语学校高一开学考试)如图甲所示,长木板A 静止在光滑水平面上,另一质量为2kg 的物体B (可看作质点)以水平速度v 0=3 m/s 滑上长木板A 的表面。
由于A 、B 间存在摩擦,之后的运动过程中A 、B 的速度图像如图乙所示。
g 取10 m/s 2,下列说法正确的是( )A .长木板A 、物体B 所受的摩擦力均与运动方向相反 B .A 、B 之间的动摩擦因数μ=0.2C .长木板A 的长度可能为L =0.8 mD .长木板A 的质量是4kg 【答案】BD【详解】A .由题意可知,A 木板的运动方向与其摩擦力方向相同,故A 错误;B .由图象知B 的加速度大小为2231m/s 2m/s 1B a -==对B 进行分析有:μm B g =m B a B ,可解得:μ=0.2故B 正确;C .由题意可知,木块B 尚未滑出木板A ,则临界条件为当AB 具有共同速度时,B 恰好滑到A 的右端,设A 、B 物体位移量分别为s A 、s B ,加速度分别为a A 、a B ,由图可知a A =1m/s 2,a B =2m/s 2,A 的长度为L ,则有:22011,,22A A B B B A s a t s v t a t s s L ==--=联立上式可解得L =1.5m ,即L ≥1.5m 即可,故C 错误;D .由μm B g =m A a A ,μm B g =m B a B 联立两式可解得:21A B BA a m a m ==即A 物体的质量是B 物体的两倍,长木板A 的质量是4kg ,故D 正确;故选BD 。
2020年高考物理素养提升专题02 动力学中的“滑块-滑板”模型(解析版)

素养提升微突破02 动力学中的“滑块-滑板”模型——构建模型,培养抽象思维意识“滑块-滑板”模型“滑块-滑板”模型涉及两个物体,并且物体间存在相对滑动。
叠放在一起的滑块和木板,它们之间存在着相互作用力,在其他外力作用下它们或加速度相同,或加速度不同,无论哪种情况受力分析和运动过程分析都是关键,特别是对相对运动条件的分析。
本模型深刻体现了物理运动观念、相互作用观念的核心素养。
【2019·新课标全国Ⅲ卷】如图(a),物块和木板叠放在实验台上,物块用一不可伸长的细绳与固定在实验台上的力传感器相连,细绳水平。
t=0时,木板开始受到水平外力F的作用,在t=4 s时撤去外力。
细绳对物块的拉力f随时间t变化的关系如图(b)所示,木板的速度v与时间t的关系如图(c)所示。
木板与实验台之间的摩擦可以忽略。
重力加速度取g=10 m/s2。
由题给数据可以得出A.木板的质量为1 kgB.2 s~4 s内,力F的大小为0.4 NC.0~2 s内,力F的大小保持不变D.物块与木板之间的动摩擦因数为0.2【答案】AB【解析】结合两图像可判断出0~2 s物块和木板还未发生相对滑动,它们之间的摩擦力为静摩擦力,此过程力F等于f,故F在此过程中是变力,即C错误;2~5 s内木板与物块发生相对滑动,摩擦力转变为滑动摩擦力,由牛顿运动定律,对2~4 s和4~5 s列运动学方程,可解出质量m为1 kg,2~4 s内的力F 为0.4 N,故A、B正确;由于不知道物块的质量,所以无法计算它们之间的动摩擦因数μ,故D错误。
【素养解读】本题以木板为研究对象,通过f-t与v-t图像对运动过程进行受力分析、运动分析,体现了物理学科科学推理的核心素养。
一、水平面上的滑块—滑板模型水平面上的滑块—滑板模型是高中参考题型,一般采用三步解题法:【典例1】如图所示,质量m=1 kg 的物块A放在质量M=4 kg的木板B的左端,起初A、B静止在水平地面上。
滑块与滑板类问题

板块的临界问题【例1】木板M静止在光滑水平面上,木板上放着一个小滑块m,与木板之间的动摩擦因数μ,为了使得m能从M上滑落下来,求下列各种情况下力F的大小范围。
解析(1)m与M刚要发生相对滑动的临界条件:①要滑动:m与M间的静摩擦力达到最大静摩擦力;②未滑动:此时m与M加速度仍相同。
受力分析如图,先隔离m,由牛顿第二定律可得:a=μmg/m=μg再对整体,由牛顿第二定律可得:F0=(M+m)a解得:F0=μ(M+m) g所以,F的大小范围为:F>μ(M+m)g(2)受力分析如图,先隔离M,由牛顿第二定律可得:a=μmg/M再对整体,由牛顿第二定律可得:F0=(M+m)a解得:F0=μ(M+m) mg/M所以,F的大小范围为:F>μ(M+m)mg/M板块的动力学问题【例2】如图所示,有一块木板静止在光滑水平面上,木板质量M=4kg,长L=1.4m.木板右端放着一个小滑块,小滑块质量m=1kg,其尺寸远小于L,它与木板之间的动摩擦因数μ=0.4,g=10m/s2,(1)现用水平向右的恒力F作用在木板M上,为了使得m能从M上滑落下来,求F的大小范围.(2)若其它条件不变,恒力F=22.8N,且始终作用在M上,求m在M上滑动的时间.[解析](1)小滑块与木板间的滑动摩擦力f=μFN=μmg=4N…………①滑动摩擦力f是使滑块产生加速度的最大合外力,其最大加速度a1=f/m=μg=4m/s2…②当木板的加速度a2> a1时,滑块将相对于木板向左滑动,直至脱离木板F-f=m a2>m a1 F> f +m a1=20N …………③即当F>20N,且保持作用一般时间后,小滑块将从木板上滑落下来。
(2)当恒力F=22.8N时,木板的加速度a2',由牛顿第二定律得F-f=Ma2' 解得:a2'=4.7m/s2………④设二者相对滑动时间为t,在分离之前小滑块:x1=? a1t2 …………⑤木板:x1=? a2't2 …………⑥又有x2-x1=L …………⑦解得:t=2s …………⑧【例3】质量m=1kg的滑块放在质量为M=1kg的长木板左端,木板放在光滑的水平面上,滑块与木板之间的动摩擦因数为0.1,木板长L=75cm,开始时两者都处于静止状态,如图所示,试求:(1)用水平力F0拉小滑块,使小滑块与木板以相同的速度一起滑动,力F0的最大值应为多少?(2)用水平恒力F拉小滑块向木板的右端运动,在t=0.5s内使滑块从木板右端滑出,力F应为多大?(3)按第(2)问的力F的作用,在小滑块刚刚从长木板右端滑出时,滑块和木板滑行的距离各为多少?(设m与M之间的最大静摩擦力与它们之间的滑动摩擦力大小相等)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题二:滑块滑板和临界问题1.模型特点:上、下叠放两个物体,并且两物体在摩擦力的相互作用下发生相对滑动.2.建模指导,解此类题的基本思路:(1)分析滑块和木板的受力情况,根据牛顿第二定律分别求出滑块和木板的加速度;(2)对滑块和木板进行运动情况分析,找出滑块和木板之间的位移关系或速度关系,建立方程。
特别注意滑块和木板的位移都是相对地面的位移。
3.分析滑块—木板模型问题时应掌握的技巧(1).分析题中滑块、木板的受力情况,求出各自的加速度.(2).画好运动草图,找出位移、速度、时间等物理量间的关系.(3).知道每一过程的末速度是下一过程的初速度.(4).两者发生相对滑动的条件:A.摩擦力为滑动摩擦力.B二者加速度不相等.例1.(2016·江苏泰州期末)如图所示,在光滑平面上有一静止小车,小车质量为M=5 kg,小车上静止地放置着质量为m=1 kg的木块,木块和小车间的动摩擦因数为μ=0.2,用水平恒力F拉动小车,下列关于木块的加速度a m和小车的加速度a M,可能正确的有( )A. a m=1 m/s2,a M=1 m/s2B.a m=1 m/s2,a M=2 m/s2C.a m=2 m/s2,a M=4 m/s2D.a m=3 m/s2,a M=5 m/s2例2.(2016·河北省衡水中学调研)如图甲所示,A、B两物体叠放在一起放在光滑的水平面上,B物体从静止开始受到一个水平变力的作用,该力与时间的关系如图乙所示,运动过程中A、B始终保持相对静止。
则在0~2t0时间内,下列说法正确的是( )A.t0时刻, A、B间的静摩擦力最大,加速度最小B.t0时刻,A、B的速度最大C.0时刻和2t0时刻,A、B间的静摩擦力最大D.2t0时刻,A、B离出发点最远,速度为0例3.如图所示,质量为M的长木板位于光滑水平面上,质量为m的物块静止在长木板上,两者之间的动摩擦因数为μ,现对物块m施加水平向右的恒力F,若恒力F使长木板与物块出现相对滑动,施加力F的最小值为(重力加速度大小为g,物块与长木板之间的最大静摩擦力等于两者之间的滑动摩擦力)()。
A.μmg(1+M/m)B.μmg(1+ m/M)C.μmgD.μMg例4.(2016湖北武汉联考)如图1所示,在光滑水平面上叠放着甲、乙两物体。
现对甲施加水平向右的拉力F,通过传感器可测得甲的加速度a随拉力F变化的关系如图2所示。
已知重力加速度g=10 m/s2,由图线可知()A.甲的质量m A=2kg B.甲的质量m A=6kgC.甲、乙间的动摩擦因数μ=0.2D.甲、乙间的动摩擦因数μ=0.6例5.如图甲所示,质量为M=2kg的木块静止在光滑水平面上,可视为质点的物块(质量设为m)从木块左侧沿木板表面水平冲上木板。
物块和木板的速度-时间图像如图乙所示,g=10m/s2,结合图像,下列说法正确的是()A可求解物块在t=2 s时的位移5mB可求解物块与木板间的动摩擦因数μ=0.2C可求解物块的质量m=2kgD可求解木板的长度L=2m例6.(新课标理综第21题).如图,在光滑水平面上有一质量为m1的足够长的木板,其上叠放一质量为m2的木块。
假定木块和木板之间的最大静摩擦力和滑动摩擦力相等。
现给木块施加一随时间t增大的水平力F=kt(k是常数),木板和木块加速度的大小分别为a1和a2,下列反映a1和a2变化的图线中正确的是()例7.(2016.苏州高三)如图所示,足够长的木板A禁止放置于水平面上,小物块B以初速度V0从木板左侧滑上木板,关于此后A、B两物块运动的V-t图像可能是()例8.如图所示,静止在光滑水平面上的木板B的质量M = 2.0 kg、长度L = 2.0 m。
铁块A 静止于木板的右端,其质量m = 1.0 kg,与木板间的动摩擦因数μ = 0.2,并可看作质点。
现给木板B施加一个水平向右的恒定拉力F = 8 N,使木板从铁块下方抽出,试求:(取g = 10 m/s2)(1)抽出木板所用的时间;(2)抽出木板时,铁块和木板的速度大小;(3)抽木板过程中克服摩擦力使系统增加的内能。
例9:一小圆盘静止在桌布上,位于一方桌的水平桌面的中央。
桌布的一边与桌的AB边重合,如图,已知盘与桌布间的动摩擦因数为μl,盘与桌面间的动摩擦因数为μ2。
现突然以恒定加速度a将桌布抽离桌面,加速度方向是水平的且垂直于AB边。
若圆盘最后未从桌面掉下,则加速度a满足的条件是什么?(以g表示重力加速度)例10.如图所示, 木板静止于水平地面上, 在其最右端放一可视为质点的木块. 已知木块的质量m =1 kg, 木板的质量M =4 kg, 长L =2.5 m, 上表面光滑, 下表面与地面之间的动摩擦因数μ=0.2.现用水平恒力F =20 N 拉木板, g 取10 m/s 2 , 求: (1)木板加速度的大小;(2)要使木块能滑离木板, 水平恒力F 作用的最短时间;(3)如果其他条件不变, 假设木板的上表面也粗糙, 其上表面与木块之间的动摩擦因数为μ 1 =0.3, 欲使木板能从木块的下方抽出, 需对木板施加的最小水平拉力;(4)若木板的长度、木块质量、木板的上表面与木块之间的动摩擦因数、木板与地面间的动摩擦因数都不变, 只将水平恒力增加为30 N, 则木块滑离木板需要多长时间?例11.如图所示,质量M =1kg 的木板静止在粗糙的水平地面上,木板与地面间的动摩擦因数μ1=0.1,在木板的左端放置一个质量m =1 kg 、大小可以忽略的铁块,铁块与木板间的动摩擦因数μ2=0.4,取g =10 m/s 2,试求: (1)若木板长L =1 m ,在铁块上加一个水平向右的恒力F =8 N ,经过多长时间铁块运动到木板的右端?(2)若在木板(足够长)的左端施加一个大小从零开始连续增加的水平向左的拉力F ,认为最大静摩擦力等于滑动摩擦力,在图中画出铁块受到的摩擦力F f 随F 变化的图象.(设木板足够长)(3)若在铁块上的右端施加一个大小从零开始连续增加的水平向左的力F ,通过分析和计算后,请在图中画出铁块受到木板的摩擦力f 2随拉力F 大小变化的图像。
(设木板足够长)专题二:滑块滑板和临界问题答案例1.(2016·江苏泰州期末)如图所示,在光滑平面上有一静止小车,小车质量为M=5 kg,小车上静止地放置着质量为m=1 kg的木块,木块和小车间的动摩擦因数为μ=0.2,用水平恒力F拉动小车,下列关于木块的加速度a m和小车的加速度a M,可能正确的有( )A. a m=1 m/s2,a M=1 m/s2B.a m=1 m/s2,a M=2 m/s2C.a m=2 m/s2,a M=4 m/s2D.a m=3 m/s2,a M=5 m/s2例2.(2016·河北省衡水中学调研)如图甲所示,A、B两物体叠放在一起放在光滑的水平面上,B物体从静止开始受到一个水平变力的作用,该力与时间的关系如图乙所示,运动过程中A、B始终保持相对静止。
则在0~2t0时间内,下列说法正确的是( )A.t0时刻, A、B间的静摩擦力最大,加速度最小B.t0时刻,A、B的速度最大C.0时刻和2t0时刻,A、B间的静摩擦力最大D.2t0时刻,A、B离出发点最远,速度为0例3.如图所示,质量为M的长木板位于光滑水平面上,质量为m的物块静止在长木板上,两者之间的动摩擦因数为μ,现对物块m施加水平向右的恒力F,若恒力F使长木板与物块出现相对滑动,施加力F的最小值为(重力加速度大小为g,物块与长木板之间的最大静摩擦力等于两者之间的滑动摩擦力)()。
A.μmg(1+M/m)B.μmg(1+ m/M)C.μmgD.μMg例4.(2016湖北武汉联考)如图1所示,在光滑水平面上叠放着甲、乙两物体。
现对甲施加水平向右的拉力F,通过传感器可测得甲的加速度a随拉力F变化的关系如图2所示。
已知重力加速度g=10 m/s2,由图线可知()A.甲的质量m A=2kg B.甲的质量m A=6kgC.甲、乙间的动摩擦因数μ=0.2D.甲、乙间的动摩擦因数μ=0.6例5.如图甲所示,质量为M=2kg的木块静止在光滑水平面上,可视为质点的物块(质量设为m)从木块左侧沿木板表面水平冲上木板。
物块和木板的速度-时间图像如图乙所示,g=10m/s2,结合图像,下列说法正确的是()A可求解物块在t=2 s时的位移5mB可求解物块与木板间的动摩擦因数μ=0.2C可求解物块的质量m=2kgD可求解木板的长度L=2m例6.(新课标理综第21题).如图,在光滑水平面上有一质量为m1的足够长的木板,其上叠放一质量为m2的木块。
假定木块和木板之间的最大静摩擦力和滑动摩擦力相等。
现给木块施加一随时间t增大的水平力F=kt(k是常数),木板和木块加速度的大小分别为a1和a 2,下列反映a 1和a 2变化的图线中正确的是( A )例7.(2016.苏州高三)如图所示,足够长的木板A 禁止放置于水平面上,小物块B 以初速度V0从木板左侧滑上木板,关于此后A 、B 两物块运动的V-t 图像可能是( AD )例8.如图所示,静止在光滑水平面上的木板B 的质量M = 2.0 kg 、长度L = 2.0 m 。
铁块A 静止于木板的右端,其质量m = 1.0 kg ,与木板间的动摩擦因数μ = 0.2,并可看作质点。
现给木板B 施加一个水平向右的恒定拉力F = 8 N ,使木板从铁块下方抽出,试求:(取g =10 m/s 2)(1)抽出木板所用的时间;(2)抽出木板时,铁块和木板的速度大小;(3)抽木板过程中克服摩擦力使系统增加的内能。
例3 (1)2.0 s (2)4 m/s 6 m/s (3)4 J例9:一小圆盘静止在桌布上,位于一方桌的水平桌面的中央。
桌布的一边与桌的AB 边重合,如图,已知盘与桌布间的动摩擦因数为μl ,盘与桌面间的动摩擦因数为μ2。
现突然以恒定加速度a 将桌布抽离桌面,加速度方向是水平的且垂直于AB 边。
若圆盘最后未从桌面掉下,则加速度a 满足的条件是什么?(以g 表示重力加速度)【解析】由牛顿第二定律:μl mg=ma l (注:在地面坐标系求解,没有什么惯性系的事!!) ①由运动学知识:v 12=2a l x 1 ②2.桌布从突然以恒定加速度a 开始抽动至圆盘刚离开桌布这段时间内做匀加速运动的过程。
设桌布从盘下抽出所经历时间为t ,在这段时间内桌布移动的距离为x1, 由运动学知识:x =at 2③x1=a 1t 2④而x=L+x1 ⑤3.圆盘离开桌布后在桌面上做匀减速直线运动的过程。
设圆盘离开桌布后在桌面上作匀减速运动,以a2表示加速度的大小,运动x2后便停下,由牛顿第二定律:μ2mg =ma 2 ⑥ 由运动学知识:v 12=2a 2 x 2 ⑦ 盘没有从桌面上掉下的条件是:x2≤L —x1 ⑧由以上各式解得:≥⑨例10.如图所示, 木板静止于水平地面上, 在其最右端放一可视为质点的木块. 已知木块的质量m =1 kg, 木板的质量M =4 kg, 长L =2.5 m, 上表面光滑, 下表面与地面之间的动摩擦因数μ=0.2.现用水平恒力F =20 N 拉木板, g 取10 m/s 2 , 求: (1)木板加速度的大小;(2)要使木块能滑离木板, 水平恒力F 作用的最短时间;(3)如果其他条件不变, 假设木板的上表面也粗糙, 其上表面与木块之间的动摩擦因数为21212121a g 12212μμμμ+μ 1 =0.3, 欲使木板能从木块的下方抽出, 需对木板施加的最小水平拉力;(4)若木板的长度、木块质量、木板的上表面与木块之间的动摩擦因数、木板与地面间的动摩擦因数都不变, 只将水平恒力增加为30 N, 则木块滑离木板需要多长时间?解析(1)木板受到的摩擦力Ff=μ(M+m)g=10 N木板的加速度a==2.5 m/s2. (2分)(2)设拉力F作用时间t后撤去F撤去后,木板的加速度为a′=-=-2.5 m/s2 (2分)木板先做匀加速运动,后做匀减速运动,且a=-a′,故at2=L解得t=1 s,即F作用的最短时间为1 s. (2分)(3)设木块的最大加速度为a木块,木板的最大加速度为a木板,则μ1mg=ma木(2分)得a木块=μ1g=3 m/s2对木板:F1-μ1mg-μ(M+m)g=Ma木板(2分)木板能从木块的下方抽出的条件为a木板>a木块解得F1>25 N.(2分)(4)木块的加速度a木块′=μ1g=3 m/s2 (1分)木板的加速度a木板′==4.25 m/s2 (1分)木块滑离木板时,两者的位移关系为x木板-x木块=L,即a木板′t2-a木块′t2=L (2分)代入数据解得t=2 s.(2分)例11.如图所示,质量M=1kg的木板静止在粗糙的水平地面上,木板与地面间的动摩擦因数μ1=0.1,在木板的左端放置一个质量m=1 kg、大小可以忽略的铁块,铁块与木板间的动摩擦因数μ2=0.4,取g=10 m/s2,试求:(1)若木板长L=1 m,在铁块上加一个水平向右的恒力F=8 N,经过多长时间铁块运动到木板的右端?(2)若在木板(足够长)的左端施加一个大小从零开始连续增加的水平向左的拉力F,认为最大静摩擦力等于滑动摩擦力,在图中画出铁块受到的摩擦力F f随F变化的图象.(设木板足够长)(3)若在铁块上的右端施加一个大小从零开始连续增加的水平向左的力F,通过分析和计算后,请在图中画出铁块受到木板的摩擦力f2随拉力F大小变化的图像。
