高三数学-【数学】山东省聊城水城中学2018届高三上学期学段检测(理)14 精品
最新-2018届高三理科数学4月份高考模拟卷及答案【山东

山东省聊城市2018 年 高 考 模 拟 试 题数学试题(理)注意事项:1.本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,满分150分。
考试时间120分钟2.答第Ⅰ卷前,考生务必用黑色签字笔将自己的姓名、准考证号、考试科目涂写在答题卡和试题纸上。
3.第I 卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,答案不能答在试题卷上。
4.第II 卷写在答题纸对应区域内,严禁在试题卷或草纸上答题。
5.考试结束后,将答题卡和答题纸一并交回。
参考公式:①如果事件A 在一次试验中发生概率是P ,那么n 次独立重复试验中恰好发生k 次的概率Pn (k )=C knPk (1-P )n -k 。
②棱柱的体积公式:V=sh (s 底面积,h 为高)。
③K 2统计量的表达式K 2=))())()(()(2d b c a d c b a bc ad n ++++-。
第Ⅰ卷(选择题 共60分)一、选择题(本大题共12小题,每小题5分;共60分。
在每小题给出的四个选项中,选出一个符合题目要求的选项。
) 1.给定下列结论:其中正确的个数是 ( )①用20㎝长的铁丝折成的矩形最大面积是25㎝2;②命题“所有的正方形都是矩形”的否定是“所有的正方形都不是矩形”;③函数y=2-x 与函数y=log 21x 的图像关于直线y=x 对称。
A .0B .1C .2D .32.已知{}*∈==Nn i y y M n ,|2(其中i 为虚数单位),,11lg |⎭⎬⎫⎩⎨⎧-+==xx y x N{},,1|2R x x x P ∈>=则以下关系中正确的是( )A .P N M =⋃B .N P MC R ⋃=C .M N P =⋂D .Φ=⋂)(N P C R3.若a>2,则函数131)(23+-=ax x x f 在区间(0,2)上恰好有 ( )A .0个零点B .1个零点C .2个零点D .3个零点 4.如果执行如图所示的程序框图,那么输出的S= ( )A .1B .100101C .10099 D .99985.在ABCABC∆︒︒=︒︒=∆则已知向量中),27cos 2,63cos 2(),72cos ,18(cos ,的面积等于( )A .22B .42 C .23 D .26.2018年北京奥运会期间,计划将5名志愿者分配到3个不同的奥运场馆参加接待工作,每个场馆至少分配一名志愿者的方案种数为 ( ) A .540 B .300 C .150 D .180 7.某个几何体的三视图如图所示,则该几何体的体积是 ( )A .32B .3C .433 D .233 8.两个正数a 、b 的等差中项是5,等比例中项是4,若a>b ,则双曲线122=-by a x 的离心率e 等于( )A .23B .25 C .5017 D .39.给出下列四个命题,其中正确的一个是 ( )A .在线性回归模型中,相关指数R 2=0.80,说明预报变量对解释变量的贡献率是80% B .在独立性检验时,两个变量的2×2列表中对角线上数据的乘积相差越大,说明这两个变量没有关系成立的可能性就越大C .相关指数R 2用来刻画回归效果,R 2越小,则残差平方和越大,模型的拟合效果越好D .随机误差e 是衡量预报精确度的一个量,它满足E (e )=0 10.已知函数),0()0,()(,4)(2+∞⋃-∞-=是定义在x g x x f 上的奇函数,当x>0时,)()(,log )(2x g x f y x x g ⋅==则函数的大致图象为( )11.已知在平面直角坐标系),(),1,2(),1,1(),2,1(),0,0(,y x M C B A O xOy 动点中--满足条件⎪⎩⎪⎨⎧≤⋅≤≤⋅≤-,21,22OA OM 则⋅的最大值为( )A .-1B .0C .3D .412.一支足球队每场比赛获胜(得3分)的概率为a ,与对手踢平(得1分)的概率为b ,负于对手(得0分)的概率为c (a ,b ,c ∈(0,1)),已知该足球队进行一场比赛得分的期望是1,则ba 311+的最小值为 ( )A .316 B .314C .317D .310第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4个小题,每小题4分,共16分。
山东省聊城水城中学届高三上学期学段检测-基本能力doc

山东省聊城水城中学2010届高三上学期学段检测化学试题审稿:李翠玲说明:1.本试卷包括第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
满分100分,考试时间90分钟。
2.请将第Ⅰ卷的正确选项用2B铅笔涂在答题卡上,考试结束只收答题卡和第Ⅱ卷。
可能用到的相对原子质量H:1 C:12 N:14 O:16第Ⅰ卷(选择题,共45分)选择题(本题15包括小题,每小题3分,共45分。
每小题只有一个选项符合题意。
)1.下列对化学反应的认识错误的是()A.会引起化学键的变化B.必然引起物质状态的变化C.会产生新的物质D.会伴随着能量的变化2.用0.01 mol·L—1的NaOH溶液完全中和下列同物质的量浓度溶液各100 mL,需NaOH溶液体积最大的是()A.盐酸B.硫酸C.高氯酸D.醋酸3.一定量的稀硫酸跟过量铁粉反应,为了减缓反应速率,又不影响生产氢气的总量,可向稀硫酸中加入适量的()A.(固体) B.(固体)C.(溶液)D.(固体)4.将锌粒投入一定浓度的稀H2SO4中,实际反应速率和时间的关系与下图最接近的是()5B.第三周期元素的最高正化合价等于它所在的族序数C.六种元素,c元素单质的化学性质最不活泼D.a、b的最高价氧化物对应水化物的碱性依次增强6.取五等份NO2,分别加入温度不同、容积相同的恒荣密闭容器中,发生反应:;△H<0在相同反应时间间隔内,分别测定不同容器中NO2的百分含量(NO2%)并作出其随反应温度(T)变化的关系图,下列示意图中,可能与实验结果相符的是()7.能使反应:发生的是()A.铜片作阴、阳极,电解B.铁片作正极,Cu片作负极,作电解质溶液的原电池C.用铜片作阴、阳极,电解NaOH溶液D.铜锌合金在潮湿空气中发生电化学腐蚀8.把0.6 mol气体X和0.4 mol气体Y混合于2.0 L密闭容器中,发生如下反应:3X(g)+Y(g)nZ(g)+2W(g)测得5min末时,生成0.2 mol W,又知以Z表示的平均反应速率为0.01 mol·(L·min)—1则n值是()A.1 B.2 C.3 D.49.的稀溶液可作手术刀的消毒液,已知:熔融状态的不能导电,的稀溶液有弱的导电能力,则下列关于的叙述不正确的是()A.是电解质B.是盐C.是离子化合物D.是共价化合物10.下列离子方程式书写正确的是()A.与溶液反应:B.溶液与浓氨水(过量)反应:C.ZnS与CuSO4溶液反应::D.铜与溶液反应::11.已知:S(s)+O 2(g)SO2(g),△H=—297.23kJ·mol—1。
山东省聊城市2018届高三下学期第一次模拟考试数学(理)试卷(含解析)

山东省聊城市2018届高三第一次模拟考试数学试题(理科)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
1. 已知集合,,则()A. B. C. D.【答案】A【解析】.故选A.2. 设复数,则()A. 4B. 2C.D. 1【答案】C【解析】,故选C.3. 设等差数列的前项和为,若,,则数列的公差为()A. 2B. 3C. 4D. 5【答案】B【解析】,故公差.故选B.4. 我国三国时期的数学家赵爽为了证明勾股定理创制了一幅“勾股圆方图”,该图是由四个全等的直角三角形组成,它们共同围成了一个如图所示的大正方形和一个小正方形.设直角三角形中一个锐角的正切值为3.在大正方形内随机取一点,则此点取自小正方形内的概率是()A. B. C. D.【答案】D【解析】不妨设两条直角边为,故斜边,即大正方形的边长为,小正方形边长为,故概率为.5. 设等比数列的各项均为正数,其前项和为,则“”是“数列是递增数列”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】C【解析】由得,故是递增数列,反之也成立,所以为充要条件.选C.6. 已知直线与抛物线:相交于,两点,若线段的中点为,则直线的方程为()A. B. C. D.【答案】D【解析】设,代入抛物线得,两式相减得,即,即直线的斜率为,由点斜式得,化简得,故选D. 7. 已知函数,不等式的解集为()A. B. C. D.【答案】A【解析】由于,所以函数为奇函数,且为单调递增函数,故,所以,故选A.8. 已知双曲线:的右焦点到渐近线的距离为4,且在双曲线上到的距离为2的点有且仅有1个,则这个点到双曲线的左焦点的距离为()A. 2B. 4C. 6D. 8【答案】D【解析】双曲线焦点到渐近线的距离为,所以.双曲线上到的距离为2的点有且仅有1个,即双曲线右顶点到右焦点的距离为,故,由于,解得,右顶点到左焦点的距离为,故选D.9. 执行如图所示的程序框图,若输出的结果为1.5,则输入的值应为()A. 4.5B. 6C. 7.5D. 9【答案】B【解析】,判断是,,判断是,,判断是, ,判断否,输出,故选B.10. 在中,边上的中线的长为2,点是所在平面上的任意一点,则的最小值为()A. 1B. 2C. -2D. -1【答案】C【解析】建立如图所示的平面直角坐标系,使得点D在原点处,点A在y轴上,则.设点P的坐标为,则,故,当且仅当时等号成立.所以的最小值为.选C.11. 如图是某几何体的三视图,其中俯视图为等边三角形,正视图为等腰直角三角形,若该几何体的各个顶点都在同一个球面上,则这个球的体积与该几何体的体积的比为()A. B. C. D.【答案】C【解析】设底边长和高为,则三棱锥的体积为.底面外接圆半径,故几何体外接球的半径为,体积为.故比值为.故选C.12. 已知函数恰有3个零点,则实数的取值范围为()A. B. C. D.【答案】A【解析】,在上单调递减.若,则在上递增,那么零点个数至多有一个,不符合题意,故.故需当时,且,使得第一段有一个零点,故.对于第二段,,故需在区间有两个零点,,故在上递增,在上递减,所以,解得.综上所述,【点睛】本小题主要考查函数的图象与性质,考查含有参数的分段函数零点问题的求解策略,考查了利用导数研究函数的单调区间,极值,最值等基本问题.其中用到了多种方法,首先对于第一段函数的分析利用了分离常数法,且直接看出函数的单调性.第二段函数利用的是导数来研究图像与性质.13. 设,满足约束条件,则的最大值为__________.【答案】4【解析】,画出可行域如下图所示,由图可知,目标函数在点处取得最大值为.[点睛]本小题主要考查线性规划的基本问题,考查了指数的运算. 画二元一次不等式或表示的平面区域的基本步骤:①画出直线(有等号画实线,无等号画虚线);②当时,取原点作为特殊点,判断原点所在的平面区域;当时,另取一特殊点判断;③确定要画不等式所表示的平面区域.14. 某工厂从生产的一批产品中随机抽出一部分,对这些产品的一项质量指标进行了检测,整理检测结果得到如下频率分布表:据此可估计这批产品的此项质量指标的方差为__________.【答案】144【解析】由题意得这批产品的此项质量指标的平均数为,故方差为.答案:点睛:在频率分布直方图中平均数的估计值等于每个小矩形的面积乘以矩形底边中点横坐标之和,在频率分布表中平均数的估计值等于每个分组的中点值乘以该组频率之和.利用类似的方法也可根据频率分布直方图或频率分布表求得方差.15. 的展开式中常数项为__________.【答案】672【解析】表示9个相乘,从这9个中选取6个且只取其中的,从剩余的3个中只取,相乘后即可得到常数项,故常数项为.答案:16. 若函数在开区间内,既有最大值又有最小值,则正实数的取值范围为__________.【答案】【解析】,其中,,故,解得,故,解得.17. 已知数列满足,.(Ⅰ)证明:是等比数列;(Ⅱ)求数列的前项和.【答案】(Ⅰ)证明见解析;(Ⅱ).【解析】(Ⅰ)递推公式是型时,通常等式两边同时加,构成新的等比数列,(Ⅱ)求和时采用分组求和的方法,其中是差比数列,采用错位想减法。
山东省聊城市2018届高三一模考试数学(理)试卷(含答案)

2018年聊城市高考模拟试题理科数学(一)第Ⅰ卷(选择题 共60分)一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知集合2{|1}A x x =<,{|lg(1)0}B x x =+≥,则A B =I ( ) A .[0,1) B .(1,)-+∞ C .(0,1) D .(1,0]-2.设复数2(1)1i z i-=+,则z =( )A .4B .2C .2D .13.设等差数列{}n a 的前n 项和为n S ,若13104S =,65a =,则数列{}n a 的公差为( ) A .2 B .3 C .4 D .54.我国三国时期的数学家赵爽为了证明勾股定理创制了一幅“勾股圆方图”,该图是由四个全等的直角三角形组成,它们共同围成了一个如图所示的大正方形和一个小正方形.设直角三角形中一个锐角的正切值为3.在大正方形内随机取一点,则此点取自小正方形内的概率是( )A .110 B .15 C .310 D .255.设等比数列{}n a 的各项均为正数,其n 前项和为n S ,则“1921202S S S +>”是“数列{}n a 是递增数列”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件6.已知直线l 与抛物线C :24y x =相交于A ,B 两点,若线段AB 的中点为(2,1),则直线l 的方程为( )A .1y x =-B .25y x =-+C .3y x =-+D .23y x =- 7.已知函数()(1010)xxf x x -=-,不等式(12)(3)0f x f -+>的解集为( ) A .(,2)-∞ B .(2,)+∞ C .(,1)-∞ D .(1,)+∞8.已知双曲线C :22221(0,0)x y a b a b-=>>的右焦点2F 到渐近线的距离为4,且在双曲线C 上到2F 的距离为2的点有且仅有1个,则这个点到双曲线C 的左焦点1F 的距离为( ) A .2 B .4 C .6 D .8 9.执行如图所示的程序框图,若输出的结果为1.5,则输入k 的值应为( )A .4.5B .6C .7.5D .910.在ABC ∆中,BC 边上的中线AD 的长为2,点P 是ABC ∆所在平面上的任意一点,则PA PB PA PC ⋅+⋅u u u r u u u r u u u r u u u r的最小值为( )A .1B .2C .-2D .-111.如图是某几何体的三视图,其中俯视图为等边三角形,正视图为等腰直角三角形,若该几何体的各个顶点都在同一个球面上,则这个球的体积与该几何体的体积的比为( )A .73π B .289π C 147π.43π12.已知函数3,21(),20x xa x x f x a e x x ⎧--≤-⎪⎪+=⎨⎪--<<⎪⎩恰有3个零点,则实数a 的取值范围为( )A .11,3e ⎛⎫-- ⎪⎝⎭ B .211,e e ⎛⎫--⎪⎝⎭ C .221,3e ⎡⎫--⎪⎢⎣⎭ D .21,33⎡⎫--⎪⎢⎣⎭第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4个小题,每小题5分,共20分)13.设x ,y 满足约束条件102020x y x y x y -+≥⎧⎪-≤⎨⎪+≤⎩,则12()16x y z =的最大值为 .14.某工厂从生产的一批产品中随机抽出一部分,对这些产品的一项质量指标进行了检测,整理检测结果得到如下频率分布表:质量指标分组[10,30)[30,50)[50,70]频率0.10.60.3据此可估计这批产品的此项质量指标的方差为 . 15.2922()y x x ++的展开式中常数项为 . 16.若函数()sin()4f x m x π=+2x -在开区间7(0,)6π内,既有最大值又有最小值,则正实数m 的取值范围为 .三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分17.已知数列{}n a 满足12a =-,124n n a a +=+. (Ⅰ)证明:{4}n a +是等比数列; (Ⅱ)求数列{}n a 的前n 项和n S .18.某教育培训中心共有25名教师,他们全部在校外住宿.为完全起见,学校派专车接送教师们上下班.这个接送任务承包给了司机王师傅,正常情况下王师傅用34座的大客车接送教师.由于每次乘车人数不尽相同,为了解教师们的乘车情况,王师傅连续记录了100次的乘车人数,统计结果如下: 乘车人数 1516171819202122232425频数2441016201612862以这100次记录的各乘车人数的频率作为各乘车人数的概率.(Ⅰ)若随机抽查两次教师们的乘车情况,求这两次中至少有一次乘车人数超过18的概率; (Ⅱ)有一次,王师傅的大客车出现了故障,于是王师傅准备租一辆小客车来临时送一次需要乘车的教师.可供选择的小客车只有20座的A 型车和22座的B 型车两种,A 型车一次租金为80元,B 型车一次租金为90元.若本次乘车教师的人数超过了所租小客车的座位数,王师傅还要付给多出的人每人20元钱供他们乘出租车.以王师傅本次付出的总费用的期望值为依据,判断王师傅租哪种车较合算?19.如图,四棱锥P ABCD -中,PAD ∆为等边三角形,且平面PAD ⊥平面ABCD ,22AD BC ==,AB AD ⊥,AB BC ⊥.(Ⅰ)证明:PC BC ⊥;(Ⅱ)若直线PC 与平面ABCD 所成角为60o,求二面角B PC D --的余弦值.20.已知圆224x y +=经过椭圆C :22221(0)x y a b a b+=>>的两个焦点和两个顶点,点(0,4)A ,M ,N 是椭圆C 上的两点,它们在y 轴两侧,且MAN ∠的平分线在y 轴上,AM AN ≠.(Ⅰ)求椭圆C 的方程; (Ⅱ)证明:直线MN 过定点. 21.已知函数()22xf x e kx =--.(Ⅰ)讨论函数()f x 在(0,)+∞内的单调性;(Ⅱ)若存在正数m ,对于任意的(0,)x m ∈,不等式()2f x x >恒成立,求正实数k 的取值范围.(二)选考题:共10分.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.选修4-4:坐标系与参数方程在直角坐标系xOy 中,圆C 的普通方程为2246120x y x y +--+=.在以坐标原点为极点,x 轴正半轴为极轴的极坐标系中,直线l 的极坐标方程为sin()4πρθ+=(Ⅰ)写出圆C 的参数方程和直线l 的直角坐标方程;(Ⅱ)设直线l 与x 轴和y 轴的交点分别为A 、B ,P 为圆C 上的任意一点,求PA PB ⋅u u u r u u u r的取值范围.23.选修4-5:不等式选讲已知函数()22f x x a a =++,a R ∈.(Ⅰ)若对于任意x R ∈,()f x 都满足()(3)f x f x =-,求a 的值; (Ⅱ)若存在x R ∈,使得()21f x x a ≤--+成立,求实数a 的取值范围.2018年聊城市高考模拟 理科数学(一)答案一、选择题1-5: ACBDC 6-10: DADBC 11、12:CA二、填空题13. 4 14. 144 15. 672 16. 23m <<+三、解答题17.解:(Ⅰ)∵12a =-,∴142a +=,∵124n n a a +=+,∴1428n n a a ++=+2(4)n a =+, ∴1424n n a a ++=+,∴{4}n a +是以2为首项,2为公比的等比数列.(Ⅱ)由(Ⅰ),可知42n n a +=,∴24nn a =-.∴12n n S a a a =++⋅⋅⋅+2(24)(24)=-+-(24)n+⋅⋅⋅+-2(222)4nn =++⋅⋅⋅+-2(12)412n n -=--1224n n +=--.∴1242n n S n +=--.18.解:(Ⅰ)由题意得,在一次接送中,乘车人数超过18的概率为0.8. 记“抽查的两次中至少有一次乘车人数超过18”为事件A ,则()1(10.8)P A =--(10.8)0.96-=.即抽查的两次中至少有一次乘车人数超过18的概率为0.96.(Ⅱ)设X 表示租用A 型车的总费用(单位:元),则X 的分布列为800.561000.16EX =⨯+⨯1200.121400.08+⨯+⨯1600.061800.0299.6+⨯+⨯=.设Y 表示租用B 型车的总费用(单位:元),则Y 的分布列为900.841100.08EX =⨯+⨯1300.061500.0295.2+⨯+⨯=.因此以王师傅本次付出的总费用的期望值为依据,租B 型车较合算. 19.证明:(Ⅰ)取AD 的中点为O ,连接PO ,CO , ∵PAD ∆为等边三角形,∴PO AD ⊥.底面ABCD 中,可得四边形ABCO 为矩形,∴CO AD ⊥, ∵PO CO O =I ,∴AD ⊥平面POC , ∵PC ⊂平面POC,∴AD PC ⊥. 又//AD BC ,所以BC PC ⊥.(Ⅱ)由面PAD ⊥面ABCD ,PO AD ⊥,∴PO ⊥平面ABCD ,可得OP ,OD ,OC 两两垂直,又直线PC 与平面ABCD 所成角为60o ,即60PCO ∠=o , 由2AD =,知PO =,得1CO =.建立如图所示的空间直角坐标系O xyz -,则P ,(0,1,0)D ,(1,0,0)C ,(1,1,0)B -,(0,1,0)BC =u u u r ,(1,0,PC =u u u r ,(1,1,0)CD =-u u u r, 设平面PBC 的一个法向量为(,,)n x y z =r . ∴00y x =⎧⎪⎨=⎪⎩,令1z =,则n=r ,设平面PDC 的一个法向量为(',',')m x y z =u r, ∴''0''0x y x -=⎧⎪⎨=⎪⎩,令'1z =,则m =u r , cos ,m n<>u r r m n m n ⋅=u r ru r r 7==, ∵二面角B PC D --为钝角,∴二面角B PC D --的余弦值为7-.20.解:(Ⅰ)圆224x y +=与x 轴交点(2,0)±即为椭圆的焦点,圆224x y +=与y 轴交点(0,2)±即为椭圆的上下两顶点,所以2c =,2b =.从而22a =因此椭圆C 的方程为:22184x y +=. (Ⅱ)设直线MN 的方程为y kx m =+.由22184y kx mx y =+⎧⎪⎨+=⎪⎩,消去y 得222(21)4280k x kmx m +++-=.设11(,)M x y ,22(,)N x y ,则122421kmx x k +=-+,21222821m x x k -=+. 直线AM 的斜率1114y k x -=14m k x -=+; 直线AN 的斜率2224y k x -=24m k x -=+. 12k k +=1212(4)()2m x x k x x -++2(4)(4)228m km k m --=+-216(1)28k m m -=-. 由MAN ∠的平分线在y 轴上,得120k k +=.又因为AM AN ≠,所以0k ≠, 所以1m =.因此,直线MN 过定点(0,1).21.解:(Ⅰ)'()2xf x e k =-,(0,)x ∈+∞,当2k ≤时,因为22xe >,所以'()0f x >,这时()f x 在(0,)+∞内单调递增.当2k >时,令'()0f x >得ln2k x >;令'()0f x <得0ln 2k x <<. 这时()f x 在(0,ln )2k 内单调递减,在(ln ,)2k+∞内单调递增.综上,当2k ≤时,()f x 在(0,)+∞内单调递增, 当2k >时,()f x 在(0,ln )2k内单调递减,在(ln,)2k+∞内单调递增. (Ⅱ)①当02k <≤时,因为()f x 在(0,)+∞内单调递增,且(0)0f =,所以对于任意的(0,)x m ∈,()0f x >.这时()2f x x >可化为()2f x x >,即2(2)20x e k x -+->.设()2(2)2xg x e k x =-+-,则'()2(2)xg x e k =-+,令'()0g x =,得2ln2k x +=,因为2ln 02k +>,所以()g x 在2(0,ln )2k +单调递减.又因为(0)0g =,所以当2(0,ln )2k x +∈时,()0g x <,不符合题意.②当2k >时,因为()f x 在(0,ln )2k内单调递减,且(0)0f =,所以存在00x >,使得对于任意的0(0,)x x ∈都有()0f x <.这时()2f x x >可化为()2f x x ->,即2(2)20xe k x -+-+>.设()2(2)2xh x e k x =-+-+,则'()2(2)xh x e k =-+-.(i )若24k <≤,则'()0h x <在(0,)+∞上恒成立,这时()h x 在(0,)+∞内单调递减, 又因为(0)0h =,所以对于任意的0(0,)x x ∈都有()0h x <,不符合题意. (ii )若4k >,令'()0h x >,得2ln 2k x -<,这时()h x 在2(0,ln )2k -内单调递增,又因为(0)0h =,所以对于任意的2(0,ln)2k x -∈,都有()0h x >, 此时取02min{,ln }2k m x -=,对于任意的(0,)x m ∈,不等式()2f x x >恒成立.综上,k 的取值范围为(4,)+∞.22.解:(Ⅰ)圆C 的参数方程为2cos 3sin x y θθ=+⎧⎨=+⎩(θ为参数).直线l 的直角坐标方程为20x y +-=.(Ⅱ)由直线l 的方程20x y +-=可得点(2,0)A ,点(0,2)B .设点(,)P x y ,则PA PB ⋅u u u r u u u r(2,)(,2)x y x y =--⋅--.2222x y x y =+--2412x y =+-.由(Ⅰ)知2cos 3sin x y θθ=+⎧⎨=+⎩,则PA PB ⋅u u u r u u u r 4sin 2cos 4θθ=++)4θϕ=++.因为R θ∈,所以44PA PB -≤⋅≤+u u u r u u u r23.解:(Ⅰ)因为()(3)f x f x =-,x R ∈,所以()f x 的图象关于32x =对称. 又()2||22a f x x a =++的图象关于2a x =-对称,所以322a -=,所以3a =-. (Ⅱ)()21f x x a ≤--+等价于2210x a x a ++-+≤. 设()g x =221x a x a ++-+,则min ()(2)(21)g x x a x a =+--+1a a =++. 由题意min ()0g x ≤,即10a a ++≤. 当1a ≥-时,10a a ++≤,12a ≤-,所以112a -≤≤-; 当1a <-时,(1)0a a -++≤,10-≤,所以1a <-, 综上12a ≤-.。
聊城水城中学高三上学期学段检测-数学文

山东省聊城水城中学2010届高三上学期学段检测数学试题(文)本试题考试时间120分钟,满分150分。
审稿:李翠玲一、选择题(本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合要求的。
请将正确答案的序号涂在和题卡上或填写在答题纸的相应表格里)1.设集合,则实数a的组成的集合Q是()A.{3,5} B.{0,3,5}C.D.2.如果函数上是单调递增的,则实数a的取值范围是()A.B.C.D.3.定义在R上的奇函数的值为()A.-1 B.0 C.1 D.24.设,则()A.B.C.D.5.平面向量= ()A.4 B.3 C.2 D.6.函数是()A.最小正周期为π的奇函数B.最小正周期为π的偶函数C.最小正周期为2π的奇函数D.最小正周期为2π的偶函数7.已知,其中A、B、C三点共线,则满足条件的x()A.不存在B.有一个C.有两个D.以上情况均有可能8.若函数在(1,2)内有极小值,则实数a的取值范围是()A.B.C.D.9.函数的零点所在的区间是()A.(1,2)B.(2,e)C.(e,3)D.(3,4)10.已知的值是()A.B.C.D.11.设变量x,y,z满足约束条件,则目标函数z=2x+3y的最小值是()A.6 B.7 C.8 D.1312.函数的一段图象如图所示,则的值为()A.0 B.-2C.2 D.不确定二、填空题(本大题共4小题,每小题4分,满分16分。
请将答案填在答题纸的相应空格上)13.设A、B为非空集合,定义集合,若= 。
14.函数,若= 。
15.若△ABC的三内角A、B、C所对的边分别为a、b、c,已知向量,B的大小为。
16.函数的图象恒过定点A,若点A在一次函数的图象上,其中的最小值为。
三、解答题(本大题共6个小题,满分74分。
解答时应写出必要的文字说明、证明过程或演算步骤。
请在答题纸的指定区域内作答。
)17.(本题满分12分)在中,边a,b是方程的两根,且(1)求角C的度数;(2)求边c的长及的面积。
高三上学期第一次教学质量诊断性考试理科数学试题 Word版含答案

泸州市高2018级第一次教学质量诊断性考试数学(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页,第Ⅱ卷3至4页.共150分.考试时间120分钟. 注意事项:1.答题前,先将自己的姓名、准考证号填写在试卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置.2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题的答案标号涂黑.3.填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内,作图题可先用铅笔绘出,确认后再用0.5毫米黑色签字笔描清楚,写在试题卷、草稿纸和答题卡上的非答题区域均无效. 4.考试结束后,请将本试题卷和答题卡一并上交. 第Ⅰ卷(选择题共60分)一、选择题:本大题共有12个小题,每小题5分,共60分.每小题给出的四个选项中,只有一项是符合要求的.1.已知集合{}240A x x x =-≤,{}21,B x x n n ==-∈N ,则A B ⋂=( ) A .{}3B .{}1,3C .{}1,3,4D .{}1,2,3,42.“sin cos αα=”是“cos20α=”的( ) A .充分但不必要条件 B .必要但不充分条件 C .充要条件D .既不充分也不必要条件3.已知3log 5a =,1ln 2b =, 1.11.5c -=,则a ,b ,c 的大小关系正确的是( ) A .b c a <<B .b a c <<C .a c b <<D .a b c <<4.我国的5G 通信技术领先世界,5G 技术的数学原理之一是著名的香农(Shannon )公式,香农提出并严格证明了“在被高斯白噪声干扰的信道中,计算最大信息传送速率C 的公式2log 1S C W N ⎛⎫=⋅+⎪⎝⎭”,其中W 是信道带宽(赫兹),S 是信道内所传信号的平均功率(瓦),N 是信道内部的高斯噪声功率(瓦),其中SN叫做信噪比.根据此公式,在不改变W 的前提下,将信噪比从99提升至λ,使得C 大约增加了60%,则λ的值大约为(参考数据:0.210 1.58≈) A .1559B .3943C .1579D .25125.右图为某旋转体的三视图,则该几何体的侧面积为( )A .10πB .8πC .9πD6.定义在R 上的函数()f x 满足(2)()f x f x +=,(2)()f x f x -=,当[]0,1x ∈时,2()f x x =,则函数()f x 的图象与()g x x =的图象的交点个数为( ) A .3B .4C .5D .67.A ,B 是函数()2sin (0)6f x x πωω⎛⎫=+> ⎪⎝⎭的图象与x 轴的两个交点,且A ,B 两点间距离的最小值为3π,则ω的值为( ) A .2B .3C .4D .58.函数3e ex xxy -=+(其中e 是自然对数的底数).的图象大致为( ) A . B .C .D .9.如图,在长方体1111ABCD A B C D -中,E ,F 分别为11C D ,11B C 的中点,O ,M 分别为BD ,EF 的中点,则下列说法错误的是( )A .四点B ,D ,E ,F 在同一平面内 B .三条直线BF ,DE ,1CC 有公共点 C .直线1A C 与直线OF 不是异面直线D .直线1A C 上存在点N 使M ,N ,O 三点共线 10.已知方程22log 0xx --=的两根分别为1x ,2x ,则下列关系正确的是(A .1212x x <<B .122x x >C .1201x x <<D .121x x =11.已知三棱锥A BCD -中,平面ABD ⊥平面BCD ,且ABD △和BCD △都是边长为2的等边三角形,则该三棱锥的外接球表面积为( ) A .4π B .163π C .8π D .203π12.已知函数321()(0)3f x ax x a =+>,若存在实数0(1,0)x ∈-,且012x ≠-,使()012f x f ⎛⎫=- ⎪⎝⎭,则实数a 的取值范围为( ) A .2,53⎛⎫ ⎪⎝⎭B .2,3(3,5)3⎛⎫⋃⎪⎝⎭C .18,67⎛⎫⎪⎝⎭D .18,4(4,6)7⎛⎫⋃⎪⎝⎭第Ⅱ卷(非选择题共90分) 注意事项:(1)非选择题的答案必须用0.5毫米黑色签字笔直接答在答题卡上,作图题可先用铅笔绘出,确认后再用0.5毫米黑色签字笔描清楚,答在试题卷和草稿纸上无效. (2)本部分共10个小题,共90分.二、填空题(本大题共4小题,每小题5分,共20分.把答案填在答题纸上)13.已知函数23,0()21,0x x x f x x +≤⎧=⎨+>⎩,则()()1f f -的值为______.14.曲线[]()sin 0,y x x π=∈与x 轴所围成的图形面积为______.15.在平面直角坐标系xOy 中,角α与角β均以Ox 为始边,它们的终边关于y 轴对称.若1tan 3α=,则tan()αβ-=______.16.如图,棱长为1的正方体1111ABCD A B C D -中,P 为线段1A B 上的动点(不含端点),给出下列结论:①平面11A D P ⊥平面1A AP ; ②多面体1CDPD 的体积为定值; ③直线1D P 与BC 所成的角可能为3π; ④1APD △可能是钝角三角形.其中正确结论的序号是______(填上所有正确结论的序号).三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. (一)必考题:共60分.17.已知函数2()2cos 12xf x x =-+.(Ⅰ)若()6f παα⎛⎫=+⎪⎝⎭,求tan α的值; (Ⅱ)若函数()f x 图象上所有点的纵坐标保持不变,横坐标变为原来的12倍得函数()g x 的图象,且关于x 的方程()0g x m -=在0,2π⎡⎤⎢⎥⎣⎦上有解,求m 的取值范围. 18.已知曲线()sin f x kx x b =+在点,22f ππ⎛⎫⎛⎫ ⎪⎪⎝⎭⎝⎭处的切线方程为230x y --=.(Ⅰ)求k ,b 的值; (Ⅱ)判断函数()f x 在区间0,2π⎛⎫⎪⎝⎭上零点的个数,并证明. 19.ABC △的内角A ,B ,C 的对边分别为a ,b ,c .已知sin()sin 2B Ca A B c ++=. (Ⅰ)求A ;(Ⅱ)已知1b =,3c =,且边BC 上有一点D 满足3ABD ADC S S =△△,求AD .20.如图,在四棱锥S ABCD -中,底面ABCD 是菱形,G 是线段AB 上一点(不含A ,B ),在平面SGD 内过点G 作//GP 平面SBC 交SD 于点P .(Ⅰ)写出作GP 的步骤(不要求证明); (Ⅱ)若3BAD π∠=,2AB SA SB SD ====,P 是SD 的中点,求平面SBC 与平面SGD 所成锐二面角的余弦值.21.已知函数1()ln f x x m x m x=---,其中[]1,e m ∈,e 是自然对数的底数. (Ⅰ)求函数()f x 的单调递增区间; (Ⅱ)设关于x 的不等式1()ln f x x x kx n x≤--+对[]1,e x ∀∈恒成立时k 的最大值为[](),1,e c k n ∈∈R ,求n c +的取值范围.(二)选考题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分. 22.选修4-4:坐标系与参数方程在平面直角坐标系xOy 中,曲线1C 是圆心在()0,2,半径为2的圆,曲线2C 的参数方程为4x ty t π⎧=⎪⎨⎛⎫=- ⎪⎪⎝⎭⎩(t 为参数且02t π≤≤),以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系. (Ⅰ)求曲线1C 的极坐标方程;(Ⅱ)若曲线2C 与坐标轴交于A ,B 两点,点P 为线段AB 上任意一点,直线OP 与曲线1C 交于点M (异于原点),求OM OP的最大值.23.选修4-5:不等式选讲若0a >,0b >,且223a b ab ++=,已知ab 的最小值为k . (Ⅰ)求k 的值(Ⅱ)若0x ∃∈R 使得关于x 的不等式2x m x k -+-≤成立,求实数m 的取值范围.泸州市高2018级第一次教学质量诊断性考试数学(理科)参考答案及评分意见评分说明:1.本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分参考制订相应的评分细则.2.对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度.可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右侧所注分数,表示考生正确做到这一步应得的累加分数. 4.只给整数分数,选择题和填空题不给中间分. 一、选择题二、填空题13.3; 14.2; 15.34; 16.①②④. 三、解答题:17.解:(Ⅰ)因为2()2cos 12x f x x =-+cos x x =-2sin 6x π⎛⎫=- ⎪⎝⎭,因为()6f παα⎛⎫=+⎪⎝⎭,所以sin 6παα⎛⎫-= ⎪⎝⎭,所以1sin cos 22ααα-=,即cos αα-=,所以tan 9α=-; (Ⅱ)把()f x 图象上所有点横坐标变为原来的12倍得到函数()g x 的图象, 所以函数()g x 的解析式为()(2)2sin 26g x f x x π⎛⎫==-⎪⎝⎭, 关于x 的方程()0g x m -=在0,2π⎡⎤⎢⎥⎣⎦上有解求m 范围, 等价于求()g x 在0,2π⎡⎤⎢⎥⎣⎦上的值域, 因为02x π≤≤,所以52666x πππ-≤-≤, 所以1()2g x -≤≤,故m 的取值范围为[]1,2-. 18.解:(Ⅰ)因为()sin cos f x k x kx x '=+, 所以sin cos 2222f k k k ππππ⎛⎫'=+⨯=⎪⎝⎭, 又因为sin 2222k f k b b ππππ⎛⎫=⨯+=+⎪⎝⎭, 曲线()f x 在点,22f ππ⎛⎫⎛⎫ ⎪⎪⎝⎭⎝⎭处的切线方程为230x y --=. 所以2k =,3b =-; (Ⅱ)()f x 在0,2π⎛⎫⎪⎝⎭上有且只有一个零点, 因为()2sin 2cos f x x x x '=+,当0,2x π⎛⎫∈ ⎪⎝⎭时,()0f x '>, 所以()f x 在0,2x π⎛⎫∈ ⎪⎝⎭上为单调递增函数且图象连续不断, 因为(0)30f =-<,302f ππ⎛⎫=->⎪⎝⎭,所以()f x 在0,2π⎛⎫⎪⎝⎭上有且只有一个零点. 19.解:(Ⅰ)由A B C x ++=可得:sin()sin()sin A B C C π+=-=,sinsin cos 222B C A Aπ+-==, 又sin()sin 2B C a A B c ++=,得sin cos 2Aa C c =,由正弦定理得sin sin sin cos 2AA C C =,因为sin 0C ≠,所以sin cos 2A A =, 所以2sincos cos 222A A A =,因为022A π<<,所以cos 02A≠, 所以1sin 22A =,即26A π=,所以3A π=.(Ⅱ)解法一:设ABD △的AB 边上的高为1h ,ADC △的AC 边上的高为2h , 因为3ABD ADC S S =△△,3c =,1b =, 所以1211322c h b h ⋅=⨯⋅, 所以12h h =,AD 是ABC △角A 的内角平分线,所以30BAD ∠=︒, 因为3ABD ADC S S =△△,可知34ABD ABC S S =△△, 所以131sin 30sin 60242AB AD AB AC ⨯⨯︒=⨯⨯⨯︒,所以AD =. 解法二:设03BAD παα⎛⎫∠=<<⎪⎝⎭,则3DAC πα∠=-,因为3ABD ADC S S =△△,3c =,1b =, 所以11sin 3sin 223c AD b AD παα⎛⎫⨯⨯=⨯⨯⨯- ⎪⎝⎭, 所以sin sin 3παα⎛⎫=-⎪⎝⎭,所以1sin cos sin 22ααα=-,tan 3α∴=,因为03πα<<,所以30BAD ∠=︒,3ABD ADC S S =△△,可知34ABD ABC S S =△△, 所以131sin 30sin 60242AB AD AB AC ⨯⨯︒=⨯⨯⨯︒,所以AD =.解法三:设AD x =,BDA α∠=,则ADC πα∠=-,在ABC △中,由3c =,1b =及余弦定理可得:2222cos a b c bc A =+-,所以a =因为3ABD ADC S S =△△,可知3BD DC ==在ABD △中2222cos AB BD AD BD AD α=+-⋅⋅,即2639cos 16AD AD α=+⋅在ADC △中,271cos()16AD AD πα=+⋅-,即271cos 162AD AD α=++⋅⋅,所以4AD =. 20.解:(Ⅰ)第一步:在平面ABCD 内过点G 作//GH BC 交CD 于点H ; 第二步:在平面SCD 内过点H 作//HP SC 交SD 于P ; 第三步:连接GP ,GP 即为所求.(Ⅱ)解法一:因为P 是SD 的中点,//HP SC ,所以H 是CD 的中点,而//GH BC ,所以G 是AB 的中点,连接AC ,GD 交于O ,连SO ,设S 在底面ABCD 的射影为M , 因为SA SB SD ==,所以MA MB MD ==,即M 为ABD △的外心, 所以M 与O 重合,因为OD =2SD =,所以SO =,23OC AC ==,过O 作//OE GB 交BC 于E ,分别以OG ,OE ,OS 为x ,y ,z 轴建立空间直角坐标系,则S ⎛ ⎝⎭,B ⎫⎪⎪⎝⎭,2,0C ⎛⎫ ⎪ ⎪⎝⎭,所以3SB ⎛=⎝⎭,()BC =-,设平面SBC 的法向量为(,,)nx y z =, 则303330n SB x y zn BC y ⎧⋅=+-=⎪⎨⎪⋅=-+=⎩,取z =,则1x =,y =所以(1,3,n =因为SO ⊥平面ABD ,所以平面SDG ⊥平面ABD ,又AB DG ⊥, 所以GB ⊥平面SGD ,故()0,1,0GB =为平面SGD 的法向量,设平面SBC 与平面SGD 所成锐二面角的大小为θ, 则3cos 26n GB n GBθ⋅===, 故平面SBC 与平面SGD 所成锐二面角的余弦值为2. 解法二:延长DG ,CB 交于I ,连接SI ,因为//GP 平面SBC ,平面SBC ⋂平面SGD SI =,GP ⊂平面SGD ,所以//GP SI , 又P 是SD 的中点,则G 是DI 的中点,又//GB DC ,所以B 是CI 的中点, 故IB BC SB ==,所以IS SC ⊥,因为SO ⊥平面ABD ,所以平面SDG ⊥平面ABD , 又AB DG ⊥,所以GB ⊥平面SGD ,所以CD ⊥平面SGD ,所以CD SI ⊥,即SI ⊥平面SDC ,所以CSD ∠为二面角C SI D --的平面角,在Rt CSD △中,2SD CD ==,故4CSD π∠=故平面SBC 与平面SGD 所成的锐二面角的余弦值为2.21.解:(Ⅰ)因为[]()1()ln 0,1,e f x x m x m x m x =--->∈, 所以22211()1m x mx f x x x x -+'=+-=,因为0x >,[]1,e m ∈, 所以①当240m ∆=-≤即12m ≤≤时,()f x 的增区间为(0,)+∞,②当240m ∆=->即2m e <≤时,方程210x mx -+=的两根为:1x =,2x =, ()f x 的增区间为()10,x ,()2,x +∞,综上①当12m ≤≤时,()f x 的增区间为(0,)+∞,②当2e m <≤时,()f x 的增区间为⎛ ⎝⎭,⎫+∞⎪⎪⎝⎭; (Ⅱ)原不等式分(1ln )ln m x x x x n k x+-++⇔≤, 因为[]1,e m ∈,[]1,e x ∈,所以(1ln )ln 1ln ln m x x x x n x x x x n x x+-+++-++≥, 令1ln ln ()x x x x n g x x+-++=,即2ln ()x x n g x x -+-'=,令()ln p x x x n =-+-,即1()10p x x'=-+>, 所以()p x 在[]1,e x ∈上递增;①当(1)0p ≥,即1n ≤时,因为[]1,e n ∈,所以1n =,当[]1,e x ∈,()0p x ≥,即()0g x '≥,所以()g x 在[]1,e 上递增, 所以min ()(1)c g x g n ===,故22n c n +==;②当(e)0p ≤即[]e 1,e n ∈-时,因为[]1,e x ∈,()0p x ≤,即()0g x '≤,所以()g x 在[]1,e 上递减,所以min 2()(e)e n c g x g +===, 故212e ,e 1e ee n n c n +⎡⎤+=+∈+++⎢⎥⎣⎦; ③当(1)(e)0p p <,即(1,e 1)n ∈-时,因为()ln p x x x n =-+-在[]1,e 上递增,所以存在唯一实数0(1,e)x ∈,使得()00p x =,即00ln n x x =-, 则当()01,x x ∈时,()0p x <,即()0g x '<;当()0,e x x ∈时,()0p x >,即()0g x '>,故()g x 在()01,x 上单减,()0,e x 上单增,所以()0000min 00001ln ln 1()ln x x x x n c g x g x x x x +-++====+, 所以00000011ln ln n c x x x x x x +=++-=+, 设()0001()(1,e)u x x x x =+∈,则2020011()10x u x x x -'=-=>, 所以()u x 在[]1,e 上递增,所以12,e e n c ⎛⎫+∈+ ⎪⎝⎭.综上所述,22,e 1e n c ⎡⎤+∈++⎢⎥⎣⎦. 22.解:(Ⅰ)解法一:设曲线1C 与过极点且垂直于极轴的直线相交于异于极点的点E ,设曲线1C 上任意点(,)F ρθ,连接OF ,EF ,则OF EF ⊥,在OEF △中,4cos 4sin 2πρθθ⎛⎫=-= ⎪⎝⎭; 解法二:曲线1C 的直角坐标方程为22(2)4x y +-=,即2240x y y +-=,所以曲线1C 的极坐标方程为4sin ρθ=; (Ⅱ)曲线2C的参数方程为4x t y t π⎧=⎪⎨⎛⎫=- ⎪⎪⎝⎭⎩,因为曲线2C 与两坐标轴相交,所以点(2,0)A ,(0,2)B ,所以线段AB 的极坐标方程为cos sin 2002πρθρθθ⎛⎫+-=≤≤ ⎪⎝⎭, 12sin cos OP ρθθ==+,24sin OM ρθ==, sin cos 4sin 2OM OP θθθ+=⨯22sin 2sin cos θθθ=+ 1cos2sin 2θθ=-+214πθ⎛⎫=-+ ⎪⎝⎭, 所以当38πθ=时,OM OP1.23.解:(Ⅰ)由3222ab a b =++≥,2320-≥,≥3≤-(舍去), 当且仅当1a =,2b =时取得“=”,即k 的最小值为2;(Ⅱ)由2k =,2()(2)2x m x x m x m -+-≥---=-, 因为0x ∃∈R 使得关于x 的不等式2x m x k -+-≤成立, 所以22m -≤,解得:222m -≤-≤,即m 的取值范围是[]0,4.。
2018年山东省聊城市高考一模数学试卷(理科)【解析版】

大正方形和一个小正方形.设直角三角形中一个锐角的正切值为 3.在大正方
形内随机取一点,则此点取自小正方形内的概率是( )
A.
B.
C.
D.
5.(5 分)设等比数列{an}的各项均为正数,其 n 前项和为 Sn,则“S19+S21>2S20”
是“数列{an}是递增数列”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
6.(5 分)已知直线 l 与抛物线 C:y2=4x 相交于 A,B 两点,若线段 AB 的中点
为(2,1),则直线 l 的方程为( )
A.y=x﹣1
B.y=﹣2x+5
C.y=﹣x+3
D.y=2x﹣3
7.(5 分)已知函数 f(x)=|x|(10x﹣10﹣x),不等式 f(1﹣2x)+f(3)>0 的
A.2
B.4
C.6
D.8
9.(5 分)执行如图所示的程序框图,若输出的结果为 1.5,则输入 k 的值应为
()
A.4.5
B.6
C.7.5
D.9
10.(5 分)在△ABC 中,BC 边上的中线 AD 的长为 2,点 P 是△ABC 所在平面
上的任意一点,则
的最小值为( )
A.1
B.2
C.﹣2
D.﹣1
11.(5 分)如图是某几何体的三视图,其中俯视图为等边三角形,正视图为等
数
频数 2 4 4 10 16 20 16 12 8 6 2 以这 100 次记录的各乘车人数的频率作为各乘车人数的概率. (Ⅰ)若随机抽查两次教师们的乘车情况,求这两次中至少有一次乘车人数超过
18 的概率; (Ⅱ)有一次,王师傅的大客车出现了故障,于是王师傅准备租一辆小客车来临
数学理科试卷·2018届山东省聊城市高三一模考试Word版含答案

2018年聊城市高考模拟试题理科数学(一)第Ⅰ卷(选择题 共60分)一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知集合2{|1}A x x =<,{|lg(1)0}B x x =+≥,则AB =( )A .[0,1)B .(1,)-+∞C .(0,1)D .(1,0]-2.设复数2(1)1i z i-=+,则z =( )A .4B .2C .13.设等差数列{}n a 的前n 项和为n S ,若13104S =,65a =,则数列{}n a 的公差为( ) A .2 B .3 C .4 D .54.我国三国时期的数学家赵爽为了证明勾股定理创制了一幅“勾股圆方图”,该图是由四个全等的直角三角形组成,它们共同围成了一个如图所示的大正方形和一个小正方形.设直角三角形中一个锐角的正切值为3.在大正方形内随机取一点,则此点取自小正方形内的概率是( )A .110 B .15 C .310 D .255.设等比数列{}n a 的各项均为正数,其n 前项和为n S ,则“1921202S S S +>”是“数列{}n a 是递增数列”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件6.已知直线l 与抛物线C :24y x =相交于A ,B 两点,若线段AB 的中点为(2,1),则直线l 的方程为( )A .1y x =-B .25y x =-+C .3y x =-+D .23y x =- 7.已知函数()(1010)x x f x x -=-,不等式(12)(3)0f x f -+>的解集为( ) A .(,2)-∞ B .(2,)+∞ C .(,1)-∞ D .(1,)+∞8.已知双曲线C :22221(0,0)x y a b a b-=>>的右焦点2F 到渐近线的距离为4,且在双曲线C上到2F 的距离为2的点有且仅有1个,则这个点到双曲线C 的左焦点1F 的距离为( ) A .2 B .4 C .6 D .8 9.执行如图所示的程序框图,若输出的结果为1.5,则输入k 的值应为( )A .4.5B .6C .7.5D .910.在ABC ∆中,BC 边上的中线AD 的长为2,点P 是ABC ∆所在平面上的任意一点,则PA PB PA PC ⋅+⋅的最小值为( )A .1B .2C .-2D .-1 11.如图是某几何体的三视图,其中俯视图为等边三角形,正视图为等腰直角三角形,若该几何体的各个顶点都在同一个球面上,则这个球的体积与该几何体的体积的比为( )A .73π B .289π C .43π12.已知函数3,21(),20x x a x x f x a e x x ⎧--≤-⎪⎪+=⎨⎪--<<⎪⎩恰有3个零点,则实数a 的取值范围为( )A .11,3e ⎛⎫-- ⎪⎝⎭ B .211,e e ⎛⎫--⎪⎝⎭ C .221,3e ⎡⎫--⎪⎢⎣⎭ D .21,33⎡⎫--⎪⎢⎣⎭第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4个小题,每小题5分,共20分)13.设x ,y 满足约束条件102020x y x y x y -+≥⎧⎪-≤⎨⎪+≤⎩,则12()16x yz =的最大值为 .14.某工厂从生产的一批产品中随机抽出一部分,对这些产品的一项质量指标进行了检测,整理检测结果得到如下频率分布表:据此可估计这批产品的此项质量指标的方差为 . 15.2922()y x x ++的展开式中常数项为 . 16.若函数()sin()4f x m x π=+x 在开区间7(0,)6π内,既有最大值又有最小值,则正实数m 的取值范围为 .三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分17.已知数列{}n a 满足12a =-,124n n a a +=+. (Ⅰ)证明:{4}n a +是等比数列; (Ⅱ)求数列{}n a 的前n 项和n S .18.某教育培训中心共有25名教师,他们全部在校外住宿.为完全起见,学校派专车接送教师们上下班.这个接送任务承包给了司机王师傅,正常情况下王师傅用34座的大客车接送教师.由于每次乘车人数不尽相同,为了解教师们的乘车情况,王师傅连续记录了100次的乘车人数,统计结果如下:以这100次记录的各乘车人数的频率作为各乘车人数的概率.(Ⅰ)若随机抽查两次教师们的乘车情况,求这两次中至少有一次乘车人数超过18的概率; (Ⅱ)有一次,王师傅的大客车出现了故障,于是王师傅准备租一辆小客车来临时送一次需要乘车的教师.可供选择的小客车只有20座的A 型车和22座的B 型车两种,A 型车一次租金为80元,B 型车一次租金为90元.若本次乘车教师的人数超过了所租小客车的座位数,王师傅还要付给多出的人每人20元钱供他们乘出租车.以王师傅本次付出的总费用的期望值为依据,判断王师傅租哪种车较合算?19.如图,四棱锥P ABCD -中,PAD ∆为等边三角形,且平面PAD ⊥平面ABCD ,22AD BC ==,AB AD ⊥,AB BC ⊥.(Ⅰ)证明:PC BC ⊥;(Ⅱ)若直线PC 与平面ABCD 所成角为60,求二面角B PC D --的余弦值.20.已知圆224x y +=经过椭圆C :22221(0)x y a b a b+=>>的两个焦点和两个顶点,点(0,4)A ,M ,N 是椭圆C 上的两点,它们在y 轴两侧,且MAN ∠的平分线在y 轴上,AM AN ≠.(Ⅰ)求椭圆C 的方程; (Ⅱ)证明:直线MN 过定点. 21.已知函数()22xf x e kx =--.(Ⅰ)讨论函数()f x 在(0,)+∞内的单调性;(Ⅱ)若存在正数m ,对于任意的(0,)x m ∈,不等式()2f x x >恒成立,求正实数k 的取值范围.(二)选考题:共10分.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.选修4-4:坐标系与参数方程在直角坐标系xOy 中,圆C 的普通方程为2246120x y x y +--+=.在以坐标原点为极点,x 轴正半轴为极轴的极坐标系中,直线l 的极坐标方程为sin()4πρθ+=(Ⅰ)写出圆C 的参数方程和直线l 的直角坐标方程;(Ⅱ)设直线l 与x 轴和y 轴的交点分别为A 、B ,P 为圆C 上的任意一点,求PA PB ⋅的取值范围.23.选修4-5:不等式选讲已知函数()22f x x a a =++,a R ∈.(Ⅰ)若对于任意x R ∈,()f x 都满足()(3)f x f x =-,求a 的值; (Ⅱ)若存在x R ∈,使得()21f x x a ≤--+成立,求实数a 的取值范围.2018年聊城市高考模拟 理科数学(一)答案一、选择题1-5: ACBDC 6-10: DADBC 11、12:CA二、填空题13. 4 14. 144 15. 672 16. 23m <<三、解答题17.解:(Ⅰ)∵12a =-,∴142a +=,∵124n n a a +=+,∴1428n n a a ++=+2(4)n a =+, ∴1424n n a a ++=+,∴{4}n a +是以2为首项,2为公比的等比数列.(Ⅱ)由(Ⅰ),可知42n n a +=,∴24n n a =-. ∴12n n S a a a =++⋅⋅⋅+2(24)(24)=-+-(24)n+⋅⋅⋅+-2(222)4nn =++⋅⋅⋅+-2(12)412n n -=--1224n n +=--. ∴1242n n S n +=--.18.解:(Ⅰ)由题意得,在一次接送中,乘车人数超过18的概率为0.8. 记“抽查的两次中至少有一次乘车人数超过18”为事件A ,则()1(10.8)P A =--(10.8)0.96-=.即抽查的两次中至少有一次乘车人数超过18的概率为0.96.(Ⅱ)设X 表示租用A 型车的总费用(单位:元),则X 的分布列为800.561000.16EX =⨯+⨯1200.121400.08+⨯+⨯1600.061800.0299.6+⨯+⨯=.设Y 表示租用B 型车的总费用(单位:元),则Y 的分布列为900.841100.08EX =⨯+⨯1300.061500.0295.2+⨯+⨯=.因此以王师傅本次付出的总费用的期望值为依据,租B 型车较合算. 19.证明:(Ⅰ)取AD 的中点为O ,连接PO ,CO , ∵PAD ∆为等边三角形,∴PO AD ⊥.底面ABCD 中,可得四边形ABCO 为矩形,∴CO AD ⊥, ∵POCO O =,∴AD ⊥平面POC ,∵PC ⊂平面POC ,∴AD PC ⊥. 又//AD BC ,所以BC PC ⊥.(Ⅱ)由面PAD ⊥面ABCD ,PO AD ⊥,∴PO ⊥平面ABCD ,可得OP ,OD ,OC 两两垂直,又直线PC 与平面ABCD 所成角为60,即60PCO ∠=, 由2AD =,知PO =,得1CO =.建立如图所示的空间直角坐标系O xyz -,则P ,(0,1,0)D ,(1,0,0)C ,(1,1,0)B -,(0,1,0)BC =,(1,0,PC =,(1,1,0)CD =-,设平面PBC 的一个法向量为(,,)n x y z =.∴00y x =⎧⎪⎨=⎪⎩,令1z =,则(3,0,1)n =, 设平面PDC 的一个法向量为(',',')m x y z =,∴''0''0x y x -=⎧⎪⎨=⎪⎩,令'1z =,则(3,m =, cos ,m n <>m n m n⋅===∵二面角B PC D --为钝角,∴二面角B PC D--的余弦值为20.解:(Ⅰ)圆224x y +=与x 轴交点(2,0)±即为椭圆的焦点,圆224x y +=与y 轴交点(0,2)±即为椭圆的上下两顶点,所以2c =,2b =.从而a =因此椭圆C 的方程为:22184x y +=. (Ⅱ)设直线MN 的方程为y kx m =+.由22184y kx mx y =+⎧⎪⎨+=⎪⎩,消去y 得222(21)4280k x kmx m +++-=.设11(,)M x y ,22(,)N x y ,则122421km x x k +=-+,21222821m x x k -=+.直线AM 的斜率1114y k x -=14m k x -=+; 直线AN 的斜率2224y k x -=24m k x -=+. 12k k +=1212(4)()2m x x k x x -++2(4)(4)228m km k m --=+-216(1)28k m m -=-. 由MAN ∠的平分线在y 轴上,得120k k +=.又因为AM AN ≠,所以0k ≠, 所以1m =.因此,直线MN 过定点(0,1).21.解:(Ⅰ)'()2xf x e k =-,(0,)x ∈+∞,当2k ≤时,因为22xe >,所以'()0f x >,这时()f x 在(0,)+∞内单调递增.当2k >时,令'()0f x >得ln2k x >;令'()0f x <得0ln 2k x <<.这时()f x 在(0,ln )2k 内单调递减,在(ln,)2k+∞内单调递增. 综上,当2k ≤时,()f x 在(0,)+∞内单调递增, 当2k >时,()f x 在(0,ln )2k 内单调递减,在(ln,)2k+∞内单调递增. (Ⅱ)①当02k <≤时,因为()f x 在(0,)+∞内单调递增,且(0)0f =,所以对于任意的(0,)x m ∈,()0f x >.这时()2f x x >可化为()2f x x >,即2(2)20x e k x -+->.设()2(2)2x g x e k x =-+-,则'()2(2)x g x e k =-+,令'()0g x =,得2ln2k x +=,因为2ln02k +>,所以()g x 在2(0,ln )2k +单调递减.又因为(0)0g =,所以当2(0,ln )2k x +∈时,()0g x <,不符合题意. ②当2k >时,因为()f x 在(0,ln )2k内单调递减,且(0)0f =,所以存在00x >,使得对于任意的0(0,)x x ∈都有()0f x <.这时()2f x x >可化为()2f x x ->, 即2(2)20x e k x -+-+>.设()2(2)2x h x e k x =-+-+,则'()2(2)x h x e k =-+-.(i )若24k <≤,则'()0h x <在(0,)+∞上恒成立,这时()h x 在(0,)+∞内单调递减, 又因为(0)0h =,所以对于任意的0(0,)x x ∈都有()0h x <,不符合题意.(ii )若4k >,令'()0h x >,得2ln 2k x -<,这时()h x 在2(0,ln)2k -内单调递增,又因为(0)0h =,所以对于任意的2(0,ln )2k x -∈,都有()0h x >, 此时取02min{,ln }2k m x -=,对于任意的(0,)x m ∈,不等式()2f x x >恒成立. 综上,k 的取值范围为(4,)+∞.22.解:(Ⅰ)圆C 的参数方程为2cos 3sin x y θθ=+⎧⎨=+⎩(θ为参数).直线l 的直角坐标方程为20x y +-=.(Ⅱ)由直线l 的方程20x y +-=可得点(2,0)A ,点(0,2)B . 设点(,)P x y ,则PA PB ⋅(2,)(,2)x y x y =--⋅--.2222x y x y =+--2412x y =+-.由(Ⅰ)知2cos 3sin x y θθ=+⎧⎨=+⎩,则PA PB ⋅4sin 2cos 4θθ=++)4θϕ=++.因为R θ∈,所以44PA PB -≤⋅≤+23.解:(Ⅰ)因为()(3)f x f x =-,x R ∈,所以()f x 的图象关于32x =对称. 又()2||22a f x x a =++的图象关于2a x =-对称,所以322a -=,所以3a =-. (Ⅱ)()21f x x a ≤--+等价于2210x a x a ++-+≤. 设()g x =221x a x a ++-+,则min ()(2)(21)g x x a x a =+--+1a a =++. 由题意min ()0g x ≤,即10a a ++≤. 当1a ≥-时,10a a ++≤,12a ≤-,所以112a -≤≤-; 当1a <-时,(1)0a a -++≤,10-≤,所以1a <-, 综上12a ≤-.。
山东聊城市水城中学等差数列单元测试题含答案 百度文库

一、等差数列选择题1.等差数列{}n a 的前n 项和为n S ,已知58a =,36S =,则107S S -的值是( )A .48B .60C .72D .242.南宋数学家杨辉《详解九张算法》和《算法通变本末》中,提出垛积公式,所讨论的高阶等差数列与一般等差数列不同,前后两项之差不相等,但是逐项差数之差或者高次成等差数列.在杨辉之后一般称为“块积术”.现有高阶等差数列,其前7项分别1,7,15,27,45,71,107,则该数列的第8项为( ) A .161B .155C .141D .1393.在等差数列{}n a 中,3914a a +=,23a =,则10a =( ) A .11B .10C .6D .34.已知n S 为等差数列{}n a 的前n 项和,3518a S +=,633a a =+,则n a =( ) A .1n -B .nC .21n -D .2n5.数列{}n a 为等差数列,11a =,34a =,则通项公式是( ) A .32n -B .322n - C .3122n - D .3122n + 6.已知数列{}n a 为等差数列,2628a a +=,5943a a +=,则10a =( ) A .29B .38C .40D .587.已知数列{}n a 是公差不为零的等差数列,且1109a a a +=,则12910a a a a ++⋅⋅⋅+=( ) A .278B .52C .3D .48.已知等差数列{}n a 的前n 项和为n S ,31567a a a +=+,则23S =( ) A .121B .161C .141D .1519.已知各项不为0的等差数列{}n a 满足26780a a a -+=,数列{}n b 是等比数列,且77b a =,则3810b b b =( )A .1B .8C .4D .210.已知等差数列{}n a 的公差d 为正数,()()111,211,n n n a a a tn a t +=+=+为常数,则n a =( )A .21n -B .43n -C .54n -D .n11.在函数()y f x =的图像上有点列{},n n x y ,若数列{}n x 是等比数列,数列{}n y 是等差数列,则函数()y f x =的解析式可能是( )A .3(4)f x x =+B .2()4f x x =C .3()4xf x ⎛⎫= ⎪⎝⎭D .4()log f x x =12.冬春季节是流感多发期,某地医院近30天每天入院治疗流感的人数依次构成数列{}n a ,已知11a =,22a=,且满足()211+-=+-nn n a a (n *∈N ),则该医院30天入院治疗流感的共有( )人A .225B .255C .365D .46513.设等差数列{}n a 的前n 项之和为n S ,已知10100S =,则47a a +=( ) A .12B .20C .40D .10014.“中国剩余定理”又称“孙子定理”,1852年英国来华传教伟烈亚力将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年,英国数学家马西森指出此法符合1801年由高斯得出的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.“中国剩余定理”讲的是一个关于整除的问题,现有这样一个整除问题:将正整数中能被3除余2且被7除余2的数按由小到大的顺序排成一列,构成数列{} n a ,则5a =( ) A .103B .107C .109D .10515.设等差数列{}n a 的公差d ≠0,前n 项和为n S ,若425S a =,则99S a =( ) A .9 B .5 C .1 D .5916.设等差数列{}n a 的前n 和为n S ,若()*111,m m a a a m m N +-<<->∈,则必有( )A .0m S <且10m S +>B .0m S >且10m S +>C .0m S <且10m S +<D .0m S >且10m S +<17.若数列{}n a 满足121()2n n a a n N *++=∈,且11a =,则2021a =( ) A .1010 B .1011 C .2020D .202118.已知数列{x n }满足x 1=1,x 2=23,且11112n n n x x x -++=(n ≥2),则x n 等于( ) A .(23)n -1B .(23)n C .21n + D .12n + 19.已知数列{}n a 的前n 项和为n S ,且()11213n n n n S S a n +++=+-+,现有如下说法:①541a a =;②222121n n a a n ++=-;③401220S =. 则正确的个数为( ) A .0B .1C .2D .320.设等差数列{}n a 的前n 项和为n S ,若2938a a a +=+,则15S =( ) A .60B .120C .160D .240二、多选题21.等差数列{}n a 的前n 项和为n S ,1385a a S +=,则下列结论一定正确的是( ) A .100a = B .911a a =C .当9n =或10时,n S 取得最大值D .613S S =22.题目文件丢失!23.题目文件丢失! 24.题目文件丢失!25.著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一列数:1,1,2,3,5,…,其中从第三项起,每个数等于它前面两个数的和,后来人们把这样的一列数组成的数列{}n a 称为“斐波那契数列”,记S n 为数列{}n a 的前n 项和,则下列结论正确的是( ) A .68a = B .733S =C .135********a a a a a ++++=D .22212201920202019a a a a a +++= 26.设等差数列{}n a 的前n 项和为n S .若30S =,46a =,则( ) A .23n S n n =- B .2392-=n n nSC .36n a n =-D .2n a n =27.等差数列{}n a 的前n 项和为n S ,若10a >,公差0d ≠,则( ) A .若59S >S ,则150S > B .若59S =S ,则7S 是n S 中最大的项 C .若67S S >, 则78S S >D .若67S S >则56S S >.28.记n S 为等差数列{}n a 前n 项和,若81535a a = 且10a >,则下列关于数列的描述正确的是( ) A .2490a a += B .数列{}n S 中最大值的项是25S C .公差0d >D .数列{}na 也是等差数列29.已知数列{}n a 为等差数列,则下列说法正确的是( ) A .1n n a a d +=+(d 为常数) B .数列{}n a -是等差数列 C .数列1n a ⎧⎫⎨⎬⎩⎭是等差数列 D .1n a +是n a 与2n a +的等差中项30.已知等差数列{}n a 的前n 项和为S n (n ∈N *),公差d ≠0,S 6=90,a 7是a 3与a 9的等比中项,则下列选项正确的是( ) A .a 1=22B .d =-2C .当n =10或n =11时,S n 取得最大值D .当S n >0时,n 的最大值为21【参考答案】***试卷处理标记,请不要删除一、等差数列选择题 1.A 【分析】根据条件列方程组,求首项和公差,再根据107891093S S a a a a -=++=,代入求值. 【详解】由条件可知114832362a d a d +=⎧⎪⎨⨯+=⎪⎩,解得:102a d =⎧⎨=⎩, ()10789109133848S S a a a a a d -=++==+=.故选:A 2.B 【分析】画出图形分析即可列出式子求解. 【详解】所给数列为高阶等差数列,设该数列的第8项为x ,根据所给定义:用数列的后一项减去前一项得到一个新数列,得到的新数列也用后一项减去前一项得到一个新数列,即得到了一个等差数列,如图:由图可得:3612107y x y -=⎧⎨-=⎩ ,解得15548x y =⎧⎨=⎩.故选:B. 3.A 【分析】利用等差数列的通项公式求解1,a d ,代入即可得出结论. 【详解】由3914a a +=,23a =, 又{}n a 为等差数列, 得39121014a a a d +=+=,213a a d =+=,解得12,1a d ==, 则101+92911a a d ==+=; 故选:A. 4.B 【分析】根据条件列出关于首项和公差的方程组,求解出首项和公差,则等差数列{}n a 的通项公式可求. 【详解】因为3518a S +=,633a a =+,所以11161218523a d a d a d +=⎧⎨+=++⎩,所以111a d =⎧⎨=⎩,所以()111n a n n =+-⨯=, 故选:B. 5.C 【分析】根据题中条件,求出等差数列的公差,进而可得其通项公式. 【详解】因为数列{}n a 为等差数列,11a =,34a =, 则公差为31322a a d -==, 因此通项公式为()33111222n a n n =+-=-. 故选:C. 6.A 【分析】根据等差中项的性质,求出414a =,再求10a ; 【详解】因为{}n a 为等差数列,所以264228a a a +==, ∴414a =.由59410a a a a +=+43=,得1029a =, 故选:A. 7.A 【分析】根据数列{}n a 是等差数列,且1109a a a +=,求出首项和公差的关系,代入式子求解. 【详解】因为1109a a a +=, 所以11298a d a d +=+,即1a d =-,所以()11295101019927278849a a a a a d a a d d a d ++⋅⋅⋅+====++. 故选:A 8.B 【分析】由条件可得127a =,然后231223S a =,算出即可. 【详解】因为31567a a a +=+,所以15637a a a =-+,所以1537a d =+,所以1537a d -=,即127a =所以231223161S a == 故选:B 9.B 【分析】根据等差数列的性质,由题中条件,求出72a =,再由等比数列的性质,即可求出结果. 【详解】因为各项不为0的等差数列{}n a 满足26780a a a -+=,所以27720a a -=,解得72a =或70a =(舍);又数列{}n b 是等比数列,且772b a ==,所以33810371178b b b b b b b ===.故选:B. 10.A 【分析】由已知等式分别求出数列的前三项,由2132a a a =+列出方程,求出公差,利用等差数列的通项公式求解可得答案. 【详解】11a =,()()1211n n n a a tn a ++=+,令1n =,则()()121211a a t a +=+,解得21a t =-令2n =,则()()2322121a a t a +=+,即()2311t a t -=-,若1t =,则20,1a d ==,与已知矛盾,故解得31a t =+{}n a 等差数列,2132a a a ∴=+,即()2111t t -=++,解得4t =则公差212d a a =-=,所以()1121n a a n d n =+-=-. 故选:A 11.D【分析】把点列代入函数解析式,根据{x n }是等比数列,可知1n nx x +为常数进而可求得1n n y y +-的结果为一个与n 无关的常数,可判断出{y n }是等差数列. 【详解】对于A ,函数3(4)f x x =+上的点列{x n ,y n },有y n =43n x +,由于{x n }是等比数列,所以1n nx x +为常数, 因此1n n y y +-=()()()()114343441n n n n n x x x x x q +++-+=-=-这是一个与n 有关的数,故{y n }不是等差数列;对于B ,函数2()4f x x =上的点列{x n ,y n },有y n =24n x ,由于{x n }是等比数列,所以1n nx x +为常数,因此1n n y y +-=()222214441n n n x x x q +-=-这是一个与n 有关的数,故{y n }不是等差数列;对于C ,函数3()4xf x ⎛⎫= ⎪⎝⎭上的点列{x n ,y n },有y n =3()4n x ,由于{x n }是等比数列,所以1n nx x +为常数, 因此1n n y y +-=133()()44n n x x+-=33()()144n qx⎡⎤-⎢⎥⎣⎦,这是一个与n 有关的数,故{y n }不是等差数列;对于D ,函数4()log f x x =上的点列{x n ,y n },有y n =4log n x,由于{x n }是等比数列,所以1n nx x +为常数, 因此1n n y y +-=114444log log log log n n n nx x x x q ++-==为常数,故{y n }是等差数列;故选:D . 【点睛】 方法点睛:判断数列是不是等差数列的方法:定义法,等差中项法. 12.B 【分析】直接利用分类讨论思想的应用求出数列的通项公式,进一步利用分组法求出数列的和 【详解】解:当n 为奇数时,2n n a a +=, 当n 为偶数时,22n n a a +-=,所以13291a a a ==⋅⋅⋅==,2430,,,a a a ⋅⋅⋅是以2为首项,2为公差的等差数列,所以30132924301514()()1515222552S a a a a a a ⨯=++⋅⋅⋅++++⋅⋅⋅+=+⨯+⨯=, 故选:B 13.B 【分析】由等差数列的通项公式可得47129a a a d +=+,再由1011045100S a d =+=,从而可得结果. 【详解】 解:1011045100S a d =+=,12920a d ∴+=, 4712920a a a d ∴+=+=.故选:B. 14.B 【分析】根据题意可知正整数能被21整除余2,即可写出通项,求出答案. 【详解】根据题意可知正整数能被21整除余2,21+2n a n ∴=, 5215+2107a ∴=⨯=.故选:B. 15.B 【分析】由已知条件,结合等差数列通项公式得1a d =,即可求99S a . 【详解】4123425S a a a a a =+++=,即有13424a a a a ++=,得1a d =,∴1999()452a a S d ⨯+==,99a d =,且0d ≠, ∴995S a =. 故选:B 16.D 【分析】由等差数列前n 项和公式即可得解. 【详解】由题意,1110,0m m a a a a ++>+<, 所以1()02m m m a a S +=>,111(1)()02m m m a a S ++++=<. 故选:D. 17.B 【分析】根据递推关系式求出数列的通项公式即可求解. 【详解】 由121()2n n a a n N *++=∈,则11()2n n a a n N *+=+∈, 即112n n a a +-=, 所以数列{}n a 是以1为首项,12为公差的等差数列, 所以()()11111122n n a a n d n +=+-=+-⨯=, 所以2021a =2021110112+=. 故选:B 18.C 【分析】由已知可得数列1n x ⎧⎫⎨⎬⎩⎭是等差数列,求出数列1n x ⎧⎫⎨⎬⎩⎭的通项公式,进而得出答案.【详解】由已知可得数列1n x ⎧⎫⎨⎬⎩⎭是等差数列,且121131,2x x ==,故公差12d = 则()1111122n n n x +=+-⨯=,故21n x n =+故选:C 19.D 【分析】由()11213n n n n S S a n +++=+-+得到()11132n n n a a n ++=-+-,再分n 为奇数和偶数得到21262k k a a k +=-+-,22165k k a a k -=+-,然后再联立递推逐项判断. 【详解】因为()11213n n n n S S a n +++=+-+,所以()11132n n n a a n ++=-+-,所以()212621k k a a k +=-+-,()221652k k a a k -=+-, 联立得:()212133k k a a +-+=, 所以()232134k k a a +++=, 故2321k k a a +-=,从而15941a a a a ===⋅⋅⋅=,22162k k a a k ++=-,222161k k a a k ++=++,则222121k k a a k ++=-,故()()()4012345383940...S a a a a a a a a =++++++++,()()()()234538394041...a a a a a a a a =++++++++,()()201411820622k k =+⨯=-==∑1220,故①②③正确. 故选:D 20.B 【分析】根据等差数列的性质可知2938a a a a +=+,结合题意,可得出88a =,最后根据等差数列的前n 项和公式和等差数列的性质,得出()11515815152a a S a +==,从而可得出结果.【详解】解:由题可知,2938a a a +=+,由等差数列的性质可知2938a a a a +=+,则88a =,故()1158158151521515812022a a a S a +⨯====⨯=. 故选:B.二、多选题21.ABD 【分析】由题意利用等差数列的通项公式、求和公式可得19a d =-,结合等差数列的性质,逐一判断即可得出结论. 【详解】∵等差数列{}n a 的前n 项和为n S ,1385a a S +=, ∴()111875282a a d a d ⨯++=+,解得19a d =-, 故10190a a d =+=,故A 正确;∵918a a d d d =+=-=,11110a a d d =+=,故有911a a =,故B 正确; 该数列的前n 项和()21119222n n n n S na d d d n -=+=-⋅ ,它的最值,还跟d 的值有关,故C 错误; 由于61656392S a d d ⨯=+=-,131131213392S a d d ⨯=+=-,故613S S =,故D 正确,故选:ABD.【点睛】思路点睛:利用等差数列的通项公式以及前n 项和公式进行化简,直接根据性质判断结果. 22.无23.无24.无25.ABD【分析】根据11a =,21a =,21n n n a a a ++=+,计算可知,A B 正确;根据12a a =,342a a a =-,564a a a =-,786a a a =-,,201920202018a a a =-,累加可知C 不正确;根据2121a a a =,222312312()a a a a a a a a =-=-,233423423()a a a a a a a a =-=-,244534534()a a a a a a a a =-=-,,220192019202020182019202020182019()a a a a a a a a =-=-,累加可知D 正确.【详解】依题意可知,11a =,21a =,21n n n a a a ++=+,312112a a a =+=+=,423123a a a =+=+=,534235a a a =+=+=,645358a a a =+=+=,故A 正确;7565813a a a =+=+=,所以712345671123581333S a a a a a a a =++++++=++++++=,故B 正确; 由12a a =,342a a a =-,564a a a =-,786a a a =-,,201920202018a a a =-,可得13572019a a a a a +++++=242648620202018a a a a a a a a a +-+-+-++-2020a =,故C 不正确; 2121a a a =,222312312()a a a a a a a a =-=-,233423423()a a a a a a a a =-=-,244534534()a a a a a a a a =-=-,,220192019202020182019202020182019()a a a a a a a a =-=-,2222212342019a a a a a +++++122312342345342019202020182019a a a a a a a a a a a a a a a a a a =+-+-+-+-20192020a a =, 所以22212201920202019a a a a a +++=,故D 正确. 故选:ABD.【点睛】本题考查了数列的递推公式,考查了累加法,属于中档题.26.BC【分析】由已知条件列方程组,求出公差和首项,从而可求出通项公式和前n 项和公式【详解】解:设等差数列{}n a 的公差为d ,因为30S =,46a =,所以113230236a d a d ⨯⎧+=⎪⎨⎪+=⎩,解得133a d =-⎧⎨=⎩, 所以1(1)33(1)36n a a n d n n =+-=-+-=-,21(1)3(1)393222n n n n n n n S na d n ---=+=-+=, 故选:BC27.BC【分析】根据等差数列的前n 项和性质判断.【详解】A 错:67895911415000S a a a a a S a S ⇒+++<>⇒+<⇒<;B 对:n S 对称轴为n =7;C 对:6770S S a >⇒<,又10a >,887700a S a d S ⇒⇒<<⇒<>;D 错:6770S S a >⇒<,但不能得出6a 是否为负,因此不一定有56S S >.故选:BC .【点睛】关键点点睛:本题考查等差数列的前n 项和性质,(1)n S 是关于n 的二次函数,可以利用二次函数性质得最值;(2)1n n n S S a -=+,可由n a 的正负确定n S 与1n S -的大小;(3)1()2n n n a a S +=,因此可由1n a a +的正负确定n S 的正负.【分析】根据已知条件求得1,a d 的关系式,然后结合等差数列的有关知识对选项逐一分析,从而确定正确选项.【详解】依题意,等差数列{}n a 中81535a a =,即()()1137514a d a d +=+,1149249,2a d a d =-=-. 对于A 选项,24912490a a a d +=+=,所以A 选项正确. 对于C 选项,1492a d =-,10a >,所以0d <,所以C 选项错误. 对于B 选项,()()149511122n a a n d d n d n d ⎛⎫=+-=-+-=- ⎪⎝⎭,令0n a ≥得51510,22n n -≤≤,由于n 是正整数,所以25n ≤,所以数列{}n S 中最大值的项是25S ,所以B 选项正确. 对于D 选项,由上述分析可知,125n ≤≤时,0n a ≥,当26n ≥时,0n a <,且0d <.所以数列{}na 的前25项递减,第26项后面递增,不是等差数列,所以D 选项错误. 故选:AB【点睛】等差数列有关知识的题目,主要把握住基本元的思想.要求等差数列前n 项和的最值,可以令0n a ≥或0n a ≤来求解.29.ABD【分析】由等差数列的性质直接判断AD 选项,根据等差数列的定义的判断方法判断BC 选项.【详解】A.因为数列{}n a 是等差数列,所以1n n a a d +-=,即1n n a a d +=+,所以A 正确;B. 因为数列{}n a 是等差数列,所以1n n a a d +-=,那么()()()11n n n n a a a a d ++---=--=-,所以数列{}n a -是等差数列,故B 正确; C.111111n n n n n n n n a a d a a a a a a ++++---==,不是常数,所以数列1n a ⎧⎫⎨⎬⎩⎭不是等差数列,故C 不正确;D.根据等差数列的性质可知122n n n a a a ++=+,所以1n a +是n a 与2n a +的等差中项,故D 正确.故选:ABD【点睛】本题考查等差数列的性质与判断数列是否是等差数列,属于基础题型.30.BC【分析】分别运用等差数列的通项公式和求和公式,解方程可得首项和公差,可判断A ,B ;由配方法,结合n 为正整数,可判断C ;由S n >0解不等式可判断D .【详解】由公差60,90d S ≠=,可得161590a d +=,即12530a d +=,①由a 7是a 3与a 9的等比中项,可得2739a a a =,即()()()2111628a d a d a d +=++,化简得110a d =-,②由①②解得120,2a d ==-,故A 错,B 对; 由()()22121441201221224n S n n n n n n ⎛⎫=+-⨯-=-=--+ ⎪⎝⎭ *n N ∈,可得10n =或11时,n S 取最大值110,C 对;由S n >0,解得021n <<,可得n 的最大值为20,D 错;故选:BC【点睛】本题考查等差数列的通项公式和求和公式的运用,考查方程思想和运算能力,属于基础题.。
【高三数学试题精选】2018高考数学(理)一模考试题(聊城市含答案)

2018高考数学(理)一模考试题(聊城市含答案)
5 c 1
11如图是某几何体的三视图,其中俯视图为等边三角形,正视图为等腰直角三角形,若该几何体的各个顶点都在同一个球面上,则这个球的体积与该几何体的体积的比为()
A. B. c. D.
12已知函数恰有3个零点,则实数的取值范围为()
A. B. c. D.
第Ⅱ卷(非选择题共90分)
二、填空题(本大题共4个小题,每小题5分,共5不等式选讲
已知函数,
(Ⅰ)若对于任意,都满足,求的值;
(Ⅱ)若存在,使得成立,求实数的取值范围
10 DADBc 11、12cA
二、填空题
13 4 14 144 15 672 16
三、解答题
17解(Ⅰ)∵ ,∴ ,
∵ ,∴ ,
∴ ,∴ 是以2为首项,2为比的等比数列
(Ⅱ)由(Ⅰ),可知,∴
∴
∴
18解(Ⅰ)由题意得,在一次接送中,乘车人数超过18的概率为08
记“抽查的两次中至少有一次乘车人数超过18”为事,则。
山东省聊城水城中学2010届高三数学理上学期学段检测新人教版

2009-2010学年度高三第一学期学段检测数 学 试 题(理)本试题考试时间120分钟,满分150分。
一、选择题(本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合要求的。
请将正确答案的序号涂在和题卡上或填写在答题纸的相应表格里) 1.已知全集U=R ,集合)()(},1|{},2|{A C B B C A x x B x x A U U ⋃⋃≤=>= 则=( ) A .φB .}21|{≥<x x x 或C .}21|{<≤x xD .}21|{≤<x x2.已知直线y=kx 是曲线x x y ln 212+=在x=e 处的切线,则k 的值为 ( )A .ee 1+B .ee 1- C .e 2 D .03.不等式211<x 的解集是( )A .)2,(-∞B .),2(+∞C .(0,2)D .),2()0,(+∞⋃-∞4.已知定义在R 上的奇函数),0()(+∞在区间x f 上单调递增,若ABC f ∆=,0)21(的内角满足0)(cos ≤A f ,则角A 的取值范围是( )A .],32[ππB .]2,3[ππC .]2,3[ππ∪ ],32[ππ D .]32,3[ππ5.已知)(02R x OC x OB x OA ∈=-⋅+⋅,其中A 、B 、C 三点共线,则满足条件的x ( ) A .不存在 B .有一个C .有两个D .以上情况均有可能6.已知定义域为R 的函数),8()(+∞在x f 上为减函数,且)8(+x f 为偶函数,则 ( ) A .)7()6(f f > B .)9()6(f f >C .)9()7(f f >D .)10()7(f f >7.已知函数)0,4()4sin()(ππP x y x f y 的图象关于点的图象和+==对称,现将)(x f 的图象向左平移4π个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数)(x g y =的图象,则)(x g y =的表达式为( )A .x y 41sin-=B .x y cos 41=-=C .)44sin(π--=x yD .)44cos(π--=x y8.已知二次函数c bx ax x f ++=2)(的导数为,0)0('),('>f x f 对任意实数x 都有0)(≥x f ,则)0(')1(f f 的最小值为 ( )A .23 B .2C .25 D .39.函数)0,0)(cos()(>>+=ωϕωA x A x f 的部分图象如图所示,则+++)3()2()1(f f f )2009(f + 的值为 ( )A .2B .22-C .7D .010.已知函数12||4)(-+=x x f 的定义域为[a ,b],其中a 、b ∈Z ,且a <b 。
山东省聊城市某重点高中2018-2018学年高三上学期期初分班教学测试理科数学试题 Word版含答案

山东省聊城市某重点高中2018-2018学年高三上学期期初分班教学测试理科数学试题 考试时间:100分钟;注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷<选择题)一、选择题1.已知集合{}0,2|>==x y y M x ,{}2|lg(2)N x y x x ==-,则N M 为< )<A )(1,2) (B> ),1(+∞ (C> ),2[+∞ (D> ),1[+∞2.执行如图所示的程序框图,则输出的k 的值为 < )<A )4 <B )5<C )6<D )73.一个几何体的三视图如图所示,且其侧视图是一个等边三角形,则这个几何的体积为< )<A)(4π+<C <D 4.在△ABC 中,∠C =90°,∠B =30°,AC=1,M 为 AB 中点,将△ACM 沿 CM 折起,使 A 、B 间的距离为 M 到面 ABC 的距离为< )fGTPy9ZyYz<A )12<B <C )1 <D )325.椭圆22221(0)x y a b a b +=>>的左、右焦点分别为F1、F2,P 是椭圆上的一点,2:a l x c=-,且PQ l ⊥,垂足为Q ,若四边形12PQF F 为平行四边形,则椭圆的离心率的取值范围是< )fGTPy9ZyYz<A ) 1(,1)2<B )1(0)2, <C )(0 <D )1)6.如图,已知球O 是棱长为1的正方体ABCB-A1B1C1D1的内切球,则平面ACD1截球O 的截面面积为< )fGTPy9ZyYz<A ) 6π <B )3π <C )6( D ) 3 7.已知服从正态分布N<μ,2σ)的随机变量在区间<σμ-,σμ+),<σμ2-,σμ2+),和<σμ3-,σμ3+)内取值的概率分别为68.3%,95.4%,和99.7%.某校为高一年级1000名新生每人定制一套校服,经统计,学生的身高<单位:cm )服从正态分布<165,52),则适合身高在155~175cm 范围内的校服大约要定制< )fGTPy9ZyYz A. 683套 B. 954套 C. 972套 D. 997套fGTPy9ZyYz 8.6)3(y x +的二项展开式中,42y x 项的系数是< )A. 45B. 90C. 135D. 270fGTPy9ZyYz 9.投掷一枚骰子,若事件A={点数小于5},事件B={点数大于2},则P<B|A )= < )A. 51B. 41C. 31D. 21fGTPy9ZyYz10.已知某一随机变量X 的概率分布如下,且E<X )=6.9,则a 的值为 ( >A. 5B. 6C. 7D. 8fGTPy9ZyYz 11.函数||x y x x=+的图象是< )12.函数()f x 是定义在R 上的偶函数,且对任意的x R ∈,都有(2)()f x f x +=.当01x ≤≤时,2()f x x =.若直线y x a =+与函数()y f x =的图象有两个不同的公共点,则实数a 的值为< )fGTPy9ZyYz A. n ()n ∈Z B. 2n ()n ∈Z C. 2n 或124n - ()n ∈Z D. n 或14n -()n ∈Z第II 卷<非选择题)二、填空题13.设集合R A ⊆,如果R x ∈0满足:对任意0>a ,都存在A x ∈,使得a x x <-<||00,那么称0x 为集合A 的一个聚点,则在下列集合中:<1)-+z z ;<2)-+R R ;(3>⎭⎬⎫⎩⎨⎧∈=*,1|N n n x x ;(4>⎭⎬⎫⎩⎨⎧∈+=*,1|N n n n x x ,以0为聚点的集合有 fGTPy9ZyYz <写出所有你认为正确的结论的序号). 14.若复数iiz 2131-+=<i 是虚数单位),则z 的模z = . 15.电脑系统中有个“扫雷”游戏,要求游戏者标出所有的雷,游戏规则是:一个方块下面有一个雷或没有雷,如果无雷,掀开方块下面就会标有数字<如果数字是0,常省略不标),此数字表明它周围的方块中雷的个数<至多八个),如图甲中的“3”表示它的周围八个方块中有且仅有3个雷.图乙是张三玩的游戏中的局部,根据图乙中信息,上方第一行左起七个方块中<方块上标有字母),能够确定下面一定没有雷的方块有 ,下面一定有雷的方块有 .<请填入所有选定方块上的字母)fGTPy9ZyYz图甲 图乙16.设20lg ()3ax f x x t dt ⎧⎪=⎨+⎪⎰ 00x x >≤,若((1))1f f =,则a = .三、解答题17.在△ABC 中,,,a b c 分别为三个内角,,A B C 的对边,锐角B 满足sin B =. <Ⅰ)求2sin 2cos 2A CB ++的值; <Ⅱ) 若b =ac 取最大值时,求cos()3A π+的值.18.如图,在三棱锥P -ABC 中,PA =PB =AB =2,BC =3,∠ABC =90°,平面PAB ⊥平面ABC ,D 、E 分别为AB 、AC 中点.fGTPy9ZyYz<Ⅰ)求证:DE ∥平面PBC ; <Ⅱ)求证:AB ⊥PE ;<Ⅲ)求二面角A -PB -E 的大小.PA BCED19.已知函数)0()(>+=t xt x x f 和点)0 , 1(P ,过点P 作曲线)(x f y =的两条切线PM 、PN ,切点分别为M 、N . <Ⅰ)设)(t g MN =,试求函数)(t g 的表达式;<Ⅱ)是否存在t ,使得M 、N 与)1 , 0(A 三点共线.若存在,求出t 的值;若不存在,请说明理由.<Ⅲ)在<Ⅰ)的条件下,若对任意的正整数n ,在区间]64 , 2[nn +内总存在1+m 个实数m a a a ,,,21 ,1+m a ,使得不等式)()()()(121+<+++m m a g a g a g a g 成立,求m 的最大值.20.已知圆1C 的参数方程为=cos =sin x y ϕϕ⎧⎨⎩<ϕ为参数),以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,圆2C 的极坐标方程为2cos()3πρθ=+.fGTPy9ZyYz <Ⅰ)将圆1C 的参数方程化为普通方程,将圆2C 的极坐标方程化为直角坐标方程;<Ⅱ)圆1C 、2C 是否相交,若相交,请求出公共弦的长;若不相交,请说明理由. 21.在对某校高一学生体育选修工程的一次调查中,共调查了160人,其中女生85人,男生75人.女生中有60人选修排球,其余的人选修篮球;男生中有20人选修排球,其余的人选修篮球.<每人必须选一项,且只能选一项)fGTPy9ZyYz 根据以上数据建立一个2×2的列联表;能否在犯错误的概率不超过0.001的前提下认为性别与体育选修工程有关?参考公式及数据:))()()(()(22d b c a d c b a bc ad n K ++++-=,其中d c b a n +++=.22.下面四个图案,都是由小正三角形构成,设第n 个图形中所有小正三角形边上黑点的总数为)(n f .图1 图2 图3 图4fGTPy9ZyYz <1)求出)2(f ,)3(f ,)4(f ,)5(f ;<2)找出)(n f 与)1(+n f 的关系,并求出)(n f 的表达式; <3)求证:362512)(3117)3(3115)2(3113)1(311+++++++++n n f f f f (*N n ∈>.参考答案1.A【解读】试题分析:因为,{}}1y=yxM x,=yy={|>,2|>{}222==-=->=-<=<<,|lg(2){x|20}{|20}{|02}N x y x x x x x x x x x所以,NM =(1,2),选A。
山东省聊城市某重点高中高三上学期期初分班教学测试理科数学试题Word版含答案

山东省聊城市某重点高中2018-2018 学年高三上学期期初分班教案测试理科数学试卷考试时间: 100 分钟;题号一二三总分得分注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第 I 卷(选择题)评卷人得分一、选择题1.已知集合M y | y2x , x 0 ,N x | y lg(2 x x2 ) ,则 M N 为()( A)(1,2)(B)(1,)(C) [2, )(D)[1,)2.执行如图所示的程序框图,则输出的k 的值为()开始k=0s=0否s<100?是s=s+2 s输出k=k+1结束( A)4(B)5k(C)6(D)73.一个几何体的三视图如图所示,且其侧视图是一个等边三角形,则这个几何的体积为()(A)(4) 3(B)(4) 3 3(C)(8) 3(D)(8) 3364.在△ ABC中,∠ C =90 °,∠ B =30 °, AC=1 , M 为 AB 中点,将△ ACM 沿 CM 折起,使 A、 B 间的距离为 2 ,则M到面ABC的距离为()(A)12( B)32(C)1(D)32x2y21(a b0) 的左、右焦点分别为F1、 F2, P 是椭圆上的一点,5 .椭圆b2a2l : x a2,且 PQ l ,垂足为 Q ,若四边形PQF1F2为平行四边形,则椭圆的离心率c的取值范围是()( A)11( C)2(D)2 ( ,1)(B),),,(0)(22(01)226.如图,已知球O 是棱长为 1 的正方体 ABCB-A1B 1C1D1的内切球,则平面 ACD 1截球 O 的截面面积为()( A)(B)(C)6( D )37.已知服从正态分布 N(2)的随机变量在区间(,),,( 2 ,2),和( 3 , 3 )内取值的概率分别为68.3%, 95.4%,和 99.7%.某校为高一年级1000名新生每人定制一套校服,经统计,学生的身高(单位: cm)服从正态分布(165, 52),则适合身高在155~175cm 范围内的校服大约要定制()A. 683 套B. 954 套C. 972 套D. 997 套8.( x 3 y)6的二项展开式中,x 2 y4项的系数是()A. 45B. 90C. 135D. 2709.投掷一枚骰子,若事件A={ 点数小于5} ,事件B={ 点数大于2} ,则 P(B|A )=()1111A. B. C. D.543210.已知某一随机变量 X 的概率分布如下,且 E( X) =6.9,则 a 的值为 ()X4a9P m0.20.5A. 5B. 6C. 7D. 811.函数y | x |x的图象是()x12.函数f ( x)是定义在R上的偶函数,且对任意的x R ,都有 f ( x 2) f ( x) .当0 x 1 时,f (x)x2.若直线y x a 与函数 y f ( x) 的图象有两个不同的公共点,则实数 a 的值为()A. n n ZB. 2n n ZC. 2n或2n 1n Z D. n或n1n Z44第 II 卷(非选择题)评卷人得分二、填空题0 | x x 0 | a ,那么称 x 0 为集合 A 的一个聚点,则在下列集合中:( 1) z z ;( 2) RR 。
水城县第一中学2018-2019学年上学期高三数学10月月考试题含解析
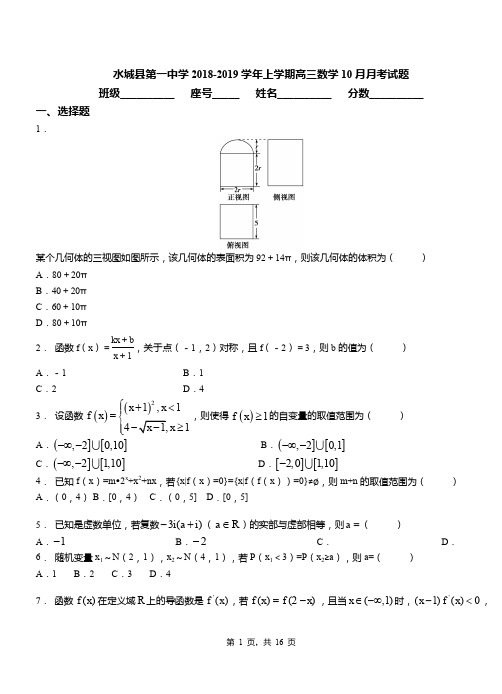
水城县第一中学2018-2019学年上学期高三数学10月月考试题 班级__________ 座号_____ 姓名__________ 分数__________一、选择题1.某个几何体的三视图如图所示,该几何体的表面积为92+14π,则该几何体的体积为( ) A .80+20π B .40+20π C .60+10π D .80+10π2. 函数f (x )=kx +bx +1,关于点(-1,2)对称,且f (-2)=3,则b 的值为( )A .-1B .1C .2D .43. 设函数()()21,141x x f x x ⎧+<⎪=⎨≥⎪⎩,则使得()1f x ≥的自变量的取值范围为( )A .(][],20,10-∞-B .(][],20,1-∞-C .(][],21,10-∞-D .[][]2,01,10-4. 已知f (x )=m •2x +x 2+nx ,若{x|f (x )=0}={x|f (f (x ))=0}≠∅,则m+n 的取值范围为( ) A .(0,4) B .[0,4) C .(0,5] D .[0,5]5. 已知是虚数单位,若复数)(3i a i +-(R a ∈)的实部与虚部相等,则=a ( )A .1-B .2-C .D . 6. 随机变量x 1~N (2,1),x 2~N (4,1),若P (x 1<3)=P (x 2≥a ),则a=( )A .1B .2C .3D .47. 函数()f x 在定义域R 上的导函数是'()f x ,若()(2)f x f x =-,且当(,1)x ∈-∞时,'(1)()0x f x -<,设(0)a f =,b f =,2(log 8)c f =,则( )A .a b c <<B .a b c >>C .c a b <<D .a c b <<8. 若直线l 的方向向量为=(1,0,2),平面α的法向量为=(﹣2,0,﹣4),则( ) A .l ∥α B .l ⊥αC .l ⊂αD .l 与α相交但不垂直9. 某校在暑假组织社会实践活动,将8名高一年级学生,平均分配甲、乙两家公司,其中两名英语成绩优秀学生不能分给同一个公司;另三名电脑特长学生也不能分给同一个公司,则不同的分配方案有( ) A .36种 B .38种 C .108种 D .114种10.已知{}n a 是等比数列,25124a a ==,,则公比q =( ) A .12-B .-2C .2D .1211.已知点P 是抛物线y 2=2x 上的一个动点,则点P 到点M (0,2)的距离与点P 到该抛物线准线的距离之和的最小值为( )A .3B .C .D .12.如果点P (sin θcos θ,2cos θ)位于第二象限,那么角θ所在象限是( )A .第一象限B .第二象限C .第三象限D .第四象限二、填空题13.命题“若1x ≥,则2421x x -+≥-”的否命题为.14()23k x =-+有两个不等实根,则的取值范围是 . 15.等差数列{}n a 的前项和为n S ,若37116a a a ++=,则13S 等于_________. 16.设有一组圆C k :(x ﹣k+1)2+(y ﹣3k )2=2k 4(k ∈N *).下列四个命题: ①存在一条定直线与所有的圆均相切; ②存在一条定直线与所有的圆均相交; ③存在一条定直线与所有的圆均不相交; ④所有的圆均不经过原点.其中真命题的代号是 (写出所有真命题的代号).三、解答题17.(本小题满分12分)菜农为了蔬菜长势良好,定期将用国家规定的低毒杀虫农药对蔬菜进行喷洒,以防止害虫的危害,待蔬菜成熟时将采集上市销售,但蔬菜上仍存有少量的残留农药,食用时可用清水清洗干净,下表是用清水x(1(2)若用解析式y =cx 2+d 作为蔬菜农药残量与用水量的回归方程,求其解析式;(c ,a 精确到0.01);附:设ωi =x 2i ,有下列数据处理信息:ω=11,y =38,(ωi -ω)(y i -y )=-811, (ωi -ω)2=374,对于一组数据(x 1,y 1),(x 2,y 2),…,(x n ,y n ),其回归直线方程y =bx +a 的斜率和截距的最小二乘估计分别为(3)为了节约用水,且把每千克蔬菜上的残留农药洗净估计最多用多少千克水.(结果保留1位有效数字)18.(本小题满分13分)如图,已知椭圆22:14x C y +=的上、下顶点分别为,A B ,点P 在椭圆上,且异于点,A B ,直线,AP BP 与直线:2l y =-分别交于点,M N ,(1)设直线,AP BP 的斜率分别为12,k k ,求证:12k k ⋅为定值;(2)求线段MN 的长的最小值;(3)当点P 运动时,以MN 为直径的圆是否经过某定点?请证明你的结论.【命题意图】本题主要考查椭圆的标准方程及性质、直线与椭圆的位置关系,考查考生运算求解能力,分析问题与解决问题的能力,是中档题.19.【徐州市第三中学2017~2018学年度高三第一学期月考】为了制作广告牌,需在如图所示的铁片上切割出一个直角梯形,已知铁片由两部分组成,半径为1的半圆O 及等腰直角三角形EFH ,其中FE FH ⊥,为裁剪出面积尽可能大的梯形铁片ABCD (不计损耗),将点,A B 放在弧EF 上,点,C D 放在斜边EH 上,且////AD BC HF ,设AOE θ∠=.(1)求梯形铁片ABCD 的面积S 关于θ的函数关系式;(2)试确定θ的值,使得梯形铁片ABCD 的面积S 最大,并求出最大值.20.(本题12分)在锐角ABC ∆中,内角A ,B ,C 所对的边分别为,,,且2sin a B =.111] (1)求角A 的大小;(2)若6a =,8b c +=,求ABC ∆的面积.21.在平面直角坐标系xoy 中,已知圆C 1:(x+3)2+(y ﹣1)2=4和圆C 2:(x ﹣4)2+(y ﹣5)2=4 (1)若直线l 过点A (4,0),且被圆C 1截得的弦长为2,求直线l 的方程(2)设P 为平面上的点,满足:存在过点P 的无穷多对互相垂直的直线l 1和l 2,它们分别与圆C 1和C 2相交,且直线l 1被圆C 1截得的弦长与直线l 2被圆C 2截得的弦长相等,求所有满足条件的点P 的坐标.22.已知椭圆C :+=1(a >b >0)的左,右焦点分别为F 1,F 2,该椭圆的离心率为,以原点为圆心,椭圆的短半轴长为半径的圆与直线y=x+相切.(Ⅰ)求椭圆C 的方程;(Ⅱ)如图,若斜率为k (k ≠0)的直线l 与x 轴,椭圆C 顺次交于P ,Q ,R (P 点在椭圆左顶点的左侧)且∠RF 1F 2=∠PF 1Q ,求证:直线l 过定点,并求出斜率k 的取值范围.水城县第一中学2018-2019学年上学期高三数学10月月考试题(参考答案)一、选择题1. 【答案】【解析】解析:选D.该几何体是在一个长方体的上面放置了半个圆柱.依题意得(2r ×2r +12πr 2)×2+5×2r ×2+5×2r +πr ×5=92+14π,即(8+π)r 2+(30+5π)r -(92+14π)=0, 即(r -2)[(8+π)r +46+7π]=0, ∴r =2,∴该几何体的体积为(4×4+12π×22)×5=80+10π.2. 【答案】【解析】解析:选B.设点P (m ,n )是函数图象上任一点,P 关于(-1,2)的对称点为Q (-2-m ,4-n ),则⎩⎪⎨⎪⎧n =km +b m +14-n =k (-2-m )+b-1-m,恒成立.由方程组得4m +4=2km +2k 恒成立, ∴4=2k ,即k =2,∴f (x )=2x +b x +1,又f (-2)=-4+b -1=3,∴b =1,故选B. 3. 【答案】A 【解析】考点:分段函数的应用.【方法点晴】本题主要考查了分段函数的应用,其中解答中涉及到不等式的求解,集合的交集和集合的并集运算,着重考查了学生分析问题和解答问题的能力,以及推理与运算能力,属于中档试题,本题的解答中,根据分段函数的分段条件,列出相应的不等式,通过求解每个不等式的解集,利用集合的运算是解答的关键. 4. 【答案】B【解析】解:设x1∈{x|f(x)=0}={x|f(f(x))=0},∴f(x1)=f(f(x1))=0,∴f(0)=0,即f(0)=m=0,故m=0;故f(x)=x2+nx,f(f(x))=(x2+nx)(x2+nx+n)=0,当n=0时,成立;当n≠0时,0,﹣n不是x2+nx+n=0的根,故△=n2﹣4n<0,故0<n<4;综上所述,0≤n+m<4;故选B.【点评】本题考查了函数与集合的关系应用及分类讨论的思想应用,同时考查了方程的根的判断,属于中档题.5.【答案】A考点:复数运算.6.【答案】C【解析】解:随机变量x1~N(2,1),图象关于x=2对称,x2~N(4,1),图象关于x=4对称,因为P(x1<3)=P(x2≥a),所以3﹣2=4﹣a,所以a=3,故选:C.【点评】本题主要考查正态分布的图象,结合正态曲线,加深对正态密度函数的理解.7.【答案】C【解析】考点:函数的对称性,导数与单调性.【名师点睛】函数的图象是研究函数性质的一个重要工具,通过函数的图象研究问题是数形结合思想应用的不可或缺的重要一环,因此掌握函数的图象的性质是我们在平常学习中要重点注意的,如函数()f x 满足:()()f a x f a x +=-或()(2)f x f a x =-,则其图象关于直线x a =对称,如满足(2)2()f m x n f x -=-,则其图象关于点(,)m n 对称. 8. 【答案】B【解析】解:∵ =(1,0,2),=(﹣2,0,4),∴=﹣2,∴∥, 因此l ⊥α. 故选:B .9. 【答案】A【解析】解:由题意可得,有2种分配方案:①甲部门要2个电脑特长学生,则有3种情况;英语成绩优秀学生的分配有2种可能;再从剩下的3个人中选一人,有3种方法. 根据分步计数原理,共有3×2×3=18种分配方案.②甲部门要1个电脑特长学生,则方法有3种;英语成绩优秀学生的分配方法有2种;再从剩下的3个人种选2个人,方法有33种,共3×2×3=18种分配方案. 由分类计数原理,可得不同的分配方案共有18+18=36种, 故选A .【点评】本题考查计数原理的运用,根据题意分步或分类计算每一个事件的方法数,然后用乘法原理和加法原理计算,是解题的常用方法.10.【答案】D 【解析】试题分析:∵在等比数列}{a n 中,41,2a 52==a ,21,81q 253=∴==∴q a a .考点:等比数列的性质.11.【答案】B【解析】解:依题设P 在抛物线准线的投影为P ′,抛物线的焦点为F ,则F(,0),依抛物线的定义知P 到该抛物线准线的距离为|PP ′|=|PF|, 则点P 到点M (0,2)的距离与P 到该抛物线准线的距离之和,d=|PF|+|PM|≥|MF|==.即有当M ,P ,F三点共线时,取得最小值,为.故选:B . 【点评】本题主要考查抛物线的定义解题,考查了抛物线的应用,考查了学生转化和化归,数形结合等数学思想.12.【答案】D【解析】解:∵P (sin θcos θ,2cos θ)位于第二象限,∴sin θcos θ<0,cos θ>0, ∴sin θ<0, ∴θ是第四象限角. 故选:D .【点评】本题考查了象限角的三角函数符号,属于基础题.二、填空题13.【答案】若1x <,则2421x x -+<- 【解析】试题分析:若1x <,则2421x x -+<-,否命题要求条件和结论都否定. 考点:否命题. 14.【答案】53,124⎛⎤ ⎥⎝⎦ 【解析】试题分析:作出函数y =()23y k x =-+的图象,如图所示,函数y =的图象是一个半圆,直线()23y k x =-+的图象恒过定点()2,3,结合图象,可知,当过点()2,0-时,303224k -==+,当直线()23y k x =-+2=,解得512k =,所以实数的取值范围是53,124⎛⎤⎥⎝⎦.111]考点:直线与圆的位置关系的应用.【方法点晴】本题主要考查了直线与圆的位置关系的应用,其中解答中涉及到点到直线的距离公式、两点间的斜率公式,以及函数的图像的应用等知识点的综合考查,着重考查了转化与化归思想和学生的分析问题和解答问题的能力,属于中档试题,本题的解答中把方程的根转化为直线与半圆的交点是解答的关键. 15.【答案】26 【解析】试题分析:由题意得,根据等差数列的性质,可得371177362a a a a a ++==⇒=,由等差数列的求和11313713()13262a a S a +===.考点:等差数列的性质和等差数列的和. 16.【答案】 ②④【解析】解:根据题意得:圆心(k ﹣1,3k ),圆心在直线y=3(x+1)上,故存在直线y=3(x+1)与所有圆都相交,选项②正确; 考虑两圆的位置关系,圆k :圆心(k ﹣1,3k ),半径为k 2,圆k+1:圆心(k ﹣1+1,3(k+1)),即(k ,3k+3),半径为(k+1)2,两圆的圆心距d==,两圆的半径之差R ﹣r=(k+1)2﹣k 2=2k+,任取k=1或2时,(R ﹣r >d ),C k 含于C k+1之中,选项①错误; 若k 取无穷大,则可以认为所有直线都与圆相交,选项③错误;将(0,0)带入圆的方程,则有(﹣k+1)2+9k 2=2k 4,即10k 2﹣2k+1=2k 4(k ∈N*),因为左边为奇数,右边为偶数,故不存在k 使上式成立,即所有圆不过原点,选项④正确. 则真命题的代号是②④. 故答案为:②④【点评】本题是一道综合题,要求学生会将直线的参数方程化为普通方程,会利用反证法进行证明,会利用数形结合解决实际问题.三、解答题17.【答案】 【解析】解:(1)根据散点图可知,x 与y 是负相关. (2)根据提供的数据,先求数据(ω1,y 1),(ω2,y 2),(ω3,y 3),(ω4,y 4),(ω5,y 5)的回归直线方程,y =cω+d ,=-811374≈-2.17, a ^=y -c ^ω=38-(-2.17)×11=61.87.∴数据(ωi ,y i )(i =1,2,3,4,5)的回归直线方程为y =-2.17ω+61.87, 又ωi =x 2i ,∴y 关于x 的回归方程为y =-2.17x 2+61.87.(3)当y =0时,x =61.872.17=6187217≈5.3.估计最多用5.3千克水.18.【答案】【解析】(1)易知()()0,1,0,1A B -,设()00,P x y ,则由题设可知00x ≠ ,∴ 直线AP 的斜率0101y k x -=,BP 的斜率0201y k x +=,又点P 在椭圆上,所以 20014x y +=,()00x ≠,从而有200012200011114y y y k k x x x -+-⋅===-.(4分)19.【答案】(1)()21sin cos S θθ=+,其中02πθ<<.(2)6πθ=时,max S =【解析】试题分析:(1)求梯形铁片ABCD 的面积S 关键是用θ表示上下底及高,先由图形得AOE BOF θ∠=∠=,这样可得高2cos AB θ=,再根据等腰直角三角形性质得()1cos sin AD θθ=-+,()1cos sin BC θθ=++最后根据梯形面积公式得()2AD BC ABS +⋅=()21sin cos θθ=+,交代定义域02πθ<<.(2)利用导数求函数最值:先求导数()'f θ()()22sin 1sin 1θθ=--+,再求导函数零点6πθ=,列表分析函数单调性变化规律,确定函数最值试题解析:(1)连接OB ,根据对称性可得AOE BOF θ∠=∠=且1OA OB ==, 所以1cos sin AD θθ=-+,1cos sin BC θθ=++,2cos AB θ=, 所以()2AD BC ABS +⋅=()21sin cos θθ=+,其中02πθ<<.考点:利用导数求函数最值【方法点睛】利用导数解答函数最值的一般步骤:第一步:利用f′(x )>0或f′(x )<0求单调区间;第二步:解f′(x )=0得两个根x 1、x 2;第三步:比较两根同区间端点的大小;第四步:求极值;第五步:比较极值同端点值的大小. 20.【答案】(1)3π=A ;(2)337=∆ABC S . 【解析】试题分析:(1)利用正弦定理AaB b sin sin =及b B a 3sin 2=,便可求出A sin ,得到A 的大小;(2)利用(1)中所求A 的大小,结合余弦定理求出bc 的值,最后再用三角形面积公式求出1sin 2ABC S bc A ∆=值.试题解析:(1)由b B a 3sin 2=及正弦定理AaB b sin sin =,得23sin =A .…………分因为A 为锐角,所以3π=A .………………分(2)由余弦定理A bc c b a cos 2222-+=,得3622=-+bc c b ,………………分又8=+c b ,所以328=bc ,………………分 所以3372332821sin 21=⨯⨯==∆A bc S ABC.………………12分 考点:正余弦定理的综合应用及面积公式. 21.【答案】 【解析】【分析】(1)因为直线l 过点A (4,0),故可以设出直线l 的点斜式方程,又由直线被圆C 1截得的弦长为2,根据半弦长、半径、弦心距满足勾股定理,我们可以求出弦心距,即圆心到直线的距离,得到一个关于直线斜率k 的方程,解方程求出k 值,代入即得直线l 的方程.(2)与(1)相同,我们可以设出过P 点的直线l 1与l 2的点斜式方程,由于两直线斜率为1,且直线l 1被圆C 1截得的弦长与直线l 2被圆C 2截得的弦长相等,故我们可以得到一个关于直线斜率k 的方程,解方程求出k 值,代入即得直线l 1与l 2的方程.【解答】解:(1)由于直线x=4与圆C 1不相交;∴直线l 的斜率存在,设l 方程为:y=k (x ﹣4)(1分)圆C 1的圆心到直线l 的距离为d ,∵l 被⊙C 1截得的弦长为2 ∴d==1(2分) d=从而k (24k+7)=0即k=0或k=﹣∴直线l 的方程为:y=0或7x+24y ﹣28=0(5分) (2)设点P (a ,b )满足条件,由题意分析可得直线l 1、l 2的斜率均存在且不为0, 不妨设直线l 1的方程为y ﹣b=k (x ﹣a ),k ≠0 则直线l 2方程为:y ﹣b=﹣(x ﹣a )(6分)∵⊙C 1和⊙C 2的半径相等,及直线l 1被圆C 1截得的弦长与直线l 2被圆C 2截得的弦长相等, ∴⊙C 1的圆心到直线l 1的距离和圆C 2的圆心到直线l 2的距离相等即=(8分)整理得|1+3k+ak ﹣b|=|5k+4﹣a ﹣bk|∴1+3k+ak ﹣b=±(5k+4﹣a ﹣bk )即(a+b ﹣2)k=b ﹣a+3或(a ﹣b+8)k=a+b ﹣5 因k 的取值有无穷多个,所以或(10分)解得或这样的点只可能是点P1(,﹣)或点P2(﹣,)(12分)22.【答案】【解析】(Ⅰ)解:椭圆的左,右焦点分别为F1(﹣c,0),F2(c,0),椭圆的离心率为,即有=,即a=c,b==c,以原点为圆心,椭圆的短半轴长为半径的圆方程为x2+y2=b2,直线y=x+与圆相切,则有=1=b,即有a=,则椭圆C的方程为+y2=1;(Ⅱ)证明:设Q(x1,y1),R(x2,y2),F1(﹣1,0),由∠RF1F2=∠PF1Q,可得直线QF1和RF1关于x轴对称,即有+=0,即+=0,即有x1y2+y2+x2y1+y1=0,①设直线PQ:y=kx+t,代入椭圆方程,可得(1+2k2)x2+4ktx+2t2﹣2=0,判别式△=16k2t2﹣4(1+2k2)(2t2﹣2)>0,即为t2﹣2k2<1②x1+x2=,x1x2=,③y1=kx1+t,y2=kx2+t,代入①可得,(k+t)(x1+x2)+2t+2kx1x2=0,将③代入,化简可得t=2k,则直线l的方程为y=kx+2k,即y=k(x+2).即有直线l恒过定点(﹣2,0).将t=2k代入②,可得2k2<1,解得﹣<k<0或0<k<.则直线l的斜率k的取值范围是(﹣,0)∪(0,).【点评】本题考查椭圆的方程和性质,主要是离心率的运用,注意运用直线和圆相切的条件,联立直线方程和椭圆方程,运用韦达定理,考查化简整理的运算能力,属于中档题和易错题.。
山东省聊城市高三上学期期末数学试卷(理科)

山东省聊城市高三上学期期末数学试卷(理科)姓名:________ 班级:________ 成绩:________一、选择题 (共8题;共16分)1. (2分) (2016高一上·普宁期中) 指数函数f(x)=(a﹣1)x在R上是增函数,则a的取值范围是()A . a>1B . a>2C . 0<a<1D . 1<a<22. (2分)如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A'DE是△ADE绕DE旋转过程中的一个图形,则下列命题中正确的是()①FA'⊥DE;②BC∥平面A'DE;③三棱锥A'﹣FED的体积有最大值.A . ①B . ①②C . ①②③D . ②③3. (2分) (2018高一下·大连期末) 将函数的图像向左平移个周期(即最小正周期)后,所得图像对应的函数为()A .B .C .D .4. (2分) (2018高一上·广西期末) 一个几何体的三视图如图所示,则该几何体的侧面积为()A .B .C .D .5. (2分)正项递增等比数列{}中,,则该数列的通项公式为()A .B .C .D .6. (2分)直线x+y+1=0与圆的位置关系是()A . 相交B . 相离C . 相切D . 不能确定7. (2分) (2017高二上·汕头月考) 已知,则方程实数根的个数为()A . 7B . 6C . 5D . 48. (2分)“成都七中”四个字按逆时针排列在1,2,3,4号位置如图所示:,第一次前后排调位,第二次左右调位,依次交替进行下去,那么第2014次互换后,“七”字对应的位置是()A . 编号1B . 编号2C . 编号3D . 编号4二、填空题 (共7题;共7分)9. (1分) (2019高二上·哈尔滨月考) 双曲线的离心率是________.10. (1分) (2017高三上·张掖期末) 如图,在△ABC中,AB=5,AC=9,若O为△ABC内一点,且满足||=| |=| |,则• 的值是________.11. (1分)(2018·河北模拟) 已知满足,则的取值范围是________.12. (1分) (2017高一上·乌鲁木齐期末) 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ| )的部分图像如图所示,则函数y=f(x)对应的解析式为________13. (1分) (2017高一上·延安期末) 在正方体ABCD﹣A1B1C1D1中,异面直线AD1 , B1C所成的角的度数为________.14. (1分)若直线l:(a>0,b>0)经过点(1,2)则直线l在x轴和y轴的截距之和的最小值是________15. (1分) (2019高二下·荆门期末) 关于曲线C:,给出下列五个命题:①曲线C关于直线y=x对称;②曲线C关于点对称;③曲线C上的点到原点距离的最小值为;④当时,曲线C上所有点处的切线斜率为负数;⑤曲线C与两坐标轴所围成图形的面积是 .上述命题中,为真命题的是________.(将所有真命题的编号填在横线上)三、解答题 (共5题;共45分)16. (5分)(2017·仁寿模拟) 在△ABC中,角A、B、C所对的边为a、b、c,且满足cos2A﹣cos2B=2cos(A ﹣)cos(A+ ).(Ⅰ)求角B的值;(Ⅱ)若b= ≤a,求2a﹣c的取值范围.17. (10分) (2015高三上·盘山期末) 如图,△ABC是边长为4的等边三角形,△ABD是等腰直角三角形,AD⊥BD,平面ABC⊥平面ABD,且EC⊥平面ABC,EC=2.(1)求证:AD⊥BE(2)求平面AEC和平面BDE所成锐二面角的余弦值.18. (10分)(2018·大新模拟) 已知数列为单调递增数列,,其前项和为,且满足.(1)求数列的通项公式;(2)若数列,其前项和为,若成立,求的最小值.19. (5分)(2017·天津) 已知椭圆 + =1(a>b>0)的左焦点为F(﹣c,0),右顶点为A,点E的坐标为(0,c),△EFA的面积为.(14分)(I)求椭圆的离心率;(II)设点Q在线段AE上,|FQ|= c,延长线段FQ与椭圆交于点P,点M,N在x轴上,PM∥QN,且直线PM与直线QN间的距离为c,四边形PQNM的面积为3c.(i)求直线FP的斜率;(ii)求椭圆的方程.20. (15分) (2018高一上·舒兰月考) 设函数,是定义域为的奇函数.(1)确定的值;(2)若,函数,,求的最小值;(3)若,是否存在正整数,使得对恒成立?若存在,请求出所有的正整数;若不存在,请说明理由.参考答案一、选择题 (共8题;共16分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、二、填空题 (共7题;共7分)9-1、10-1、11-1、12-1、13-1、14-1、15-1、三、解答题 (共5题;共45分)16-1、17-1、17-2、18-1、18-2、19-1、20-1、20-2、20-3、第11 页共11 页。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018-2018学年度高三第一学期学段检测数 学 试 题(理)本试题考试时间120分钟,满分150分。
一、选择题(本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合要求的。
请将正确答案的序号涂在和题卡上或填写在答题纸的相应表格里) 1.已知全集U=R ,集合)()(},1|{},2|{A C B B C A x x B x x A U U ⋃⋃≤=>= 则=( ) A .φB .}21|{≥<x x x 或C .}21|{<≤x xD .}21|{≤<x x2.已知直线y=kx 是曲线x x y ln 212+=在x=e 处的切线,则k 的值为 ( )A .ee 1+B .ee 1- C .e 2 D .03.不等式211<x 的解集是( )A .)2,(-∞B .),2(+∞C .(0,2)D .),2()0,(+∞⋃-∞4.已知定义在R 上的奇函数),0()(+∞在区间x f 上单调递增,若ABC f ∆=,0)21(的内角满足0)(cos ≤A f ,则角A 的取值范围是 ( )A .],32[ππB .]2,3[ππ C .]2,3[ππ∪ ],32[ππ D .]32,3[ππ5.已知)(02R x OC x OB x OA ∈=-⋅+⋅,其中A 、B 、C 三点共线,则满足条件的x ( )A .不存在B .有一个C .有两个D .以上情况均有可能6.已知定义域为R 的函数),8()(+∞在x f 上为减函数,且)8(+x f 为偶函数,则 ( ) A .)7()6(f f > B .)9()6(f f >C .)9()7(f f >D .)10()7(f f >7.已知函数)0,4()4sin()(ππP x y x f y 的图象关于点的图象和+==对称,现将)(x f 的图象向左平移4π个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数)(x g y =的图象,则)(x g y =的表达式为 ( )A .x y 41sin-=B .x y cos 41=-=C .)44sin(π--=x y D .)44cos(π--=x y8.已知二次函数c bx ax x f ++=2)(的导数为,0)0('),('>f x f 对任意实数x 都有0)(≥x f ,则)0(')1(f f 的最小值为 ( )A .23B .2C .25 D .39.函数)0,0)(cos()(>>+=ωϕωA x A x f 的部分图象如图所示,则+++)3()2()1(f f f )2009(f + 的值为 ( )A .2B .22-C .7D .010.已知函数12||4)(-+=x x f 的定义域为[a ,b],其中a 、b ∈Z ,且a <b 。
若函数)(x f 的值域为[0,1],则满足条件整数对(a ,b )共有( )个A .2B .5C .6D8.11. 已知点A(2,3),B(--3,--2).若直线l 过点P(1,1)且与线段AB 相交,则直线l 的斜率k 的取值范围是 ( )A. 2≥k 或43≤k B. 243≤≤k C.43≥k D. 2≤k12.设函数)(),(x g x f 的定义域分别为F 、G ,且F G 。
若对任意的F x ∈,都有)()(x f x g =,则称)()(x f x g 为在G上的一个“延拓函数”。
已知函数)()(),0(2)(x f x g x x f x 为若≤=在R 上一个延拓函数,且g (x )是偶函数,则函数g(x )的解析式是 ( )A .||2)(x x g =B .||log )(2x x g =≠ ⊂C .||)21()(x x g =D .||log )(21x x g =二、填空题(本大题共4个小题,每小题4分,满分16分。
请将答案填在答题纸的相应空格。
) 13.若△ABC 的三内角A 、B 、C 所对的边分别为a 、b 、c ,已知向量)(c b a p ++=,∠-=+--=则若|,|||),,(q p q p a c b a q B 的大小为 。
14.不等式0|32|)1(2≥---x x x 的解集为 。
15.已知=∈=ααππαα2cos 2sin ),,2(,53sin 则且 。
16.函数)10(1)1(log ≠>+-=a a x y a 且的图象恒过定点A ,若点A 在一次函数n mx y +=的图象上,其中nm n m 21,0,0+>>则的最小值为 。
三、解答题(本大题共6个小题,满分74分。
解答时应写出必要的文字说明、证明过程或演算步骤,请在答题纸的指定区域内作答。
) 17.(本题满分12分) 解关于x 的不等式:.0)(322>++-a x a a x 18.(本题满分12分)如图所示,角A 为钝角,且53sin =A ,点P 、Q 分别在角A 的两边上。
(1)AP=5,PQ=53,求AQ 的长; (2)设)2sin(,1312cos ,,βααβα+==∠=∠求且AQP APQ 的值。
19.(本题满分12分)已知),3,3(A O 是原点,点⎪⎪⎩⎪⎪⎨⎧≥≥+-≤-0.02303),(y y x y x y x P 满足(1)求||OA OP OA ⋅的最大值;(2)求||OP OP OA z ⋅=的取值范围。
20.(本题满分12分)诺贝尔奖发放方式为:每年一闪,把奖金总额平均分成6份,奖励在6项(物理、化学、文学、经济学、生理学和医学、和平)为人类作出最有益贡献的人,每年发放奖金的总金额是基金在该年度所获利息的一半,另一半利息用于基金总额,以便保证奖金数逐年增加。
假设基金平均年利率为%24.6=r 。
资料显示:1999年诺贝尔奖发放后基金总额约为19800万美元。
设)(x f 表示为第)(*N x x ∈年诺贝尔奖发放后的基金总额(1999年记为)1(f ,2000年记为)2(f ,……,依次类推)(1)用)1(f 表示)2(f 与)3(f ,并根据所求结果归纳出函数)(x f 的表达式; (2)试根据)(x f 的表达式判断网上一则新闻“2018年度诺贝尔奖各项奖金高达150万美元”是否为真,并说明理由。
(参考数据:36.10312.1,83.10624.11010==)21.(本题满分12分)定义:两个连续函数(图象不间断))(),(x g x f 在区间[a ,b]上都有意义,我们称函数|)()(|x g x f +在[a ,b]上的最大值叫做函数)()(x g x f 与在区间[a ,b]上的“绝对和”。
(1)试求函数)4)(2()()(2-+==x x x x g x x f 与在闭区间[-2,2]上的“绝对和”; (2)设2)(4)(x x f m x x h m =+-=及都是定义在闭区间[1,3]上,记)()(x f x h m 与的“绝对和”为D m ,如果)(m D 的最小值是)()(),(00x h x f m D m 可用则称“替代”,试求0m 的值,使)(x f 可用)(0x h m “替代”。
22.(本题满分14分)定义),0(,,)1(),(+∞∈+=y x x y x F y(1)令函数))94(log ,1()(22+-=x x F x f 的图象为曲线c 1,曲线c 1与y 轴交于点A(0,m ),过坐标原点O 作曲线c 1的切线,切点为B (n ,t )(n >0)设曲线c 1 在点A 、B 之间的曲线段与OA 、OB 所围成图形的面积为S ,求S 的值;(2)当).,(),(,,*x y F y x F y x N y x ><∈证明时且参考答案一、选择题DADCC DBBAB A C 二、填空题: 13.3π 14.}11|{-=≥x x x 或 15.23-16.8三、解答题:17.解:0))((2>--a x a x①当1,02<><x a x a 或时 …………2分 ②当0,0≠=x a 时…………4分 ③当2,10a x a x a <><<或时 …………6分 ④当1,1≠=x a 时 …………8分 ⑤当a x a x a <>>或时2,1…………10分综上,当10><a a 或时,不等式解集为}|{2a x a x x <>或当a=0时,不等式解集为}0|{≠x x当}|{,102a x a x x a <><<或不等式解集为时 当a=1时,不等式解集为}1|{≠x x …………12分 18.解:(1)A ∠ 是钝角,54cos ,53sin -=∴=A A …………2分在A AQ AP AQ AP PQ APQ cos 2,222⋅-+=∆中)54(5225452-⋅⨯-+=∴AQ AQ…………4分 解得AQ=2或AQ=-10(舍) 即AQ=2 …………6分 (2)由135sin ,1312cos ==αα得…………8分又54cos )cos(,53sin )sin(=-=+==+A A βαβα …………10分)sin(cos )cos(sin )](sin[)2sin(βααβααβααβα+++=++=+∴ 655653131254135=⋅+⋅=…………12分19.解:作出可行域如图。
(1),cos ||||AOP OP OA OP OA ∠⋅=⋅它表示OA P OA OP 作过上的投影在,的垂线PH ,显然当P 移动到OA OP ,),B (y x y x 在时的交点得3102303=+-=-上的投影最大。
…………5分此时62||||π=∠=∠==AOB AOP ,OB OP3c o s ||||=∠⋅∴A OB OB OA OP OA 的最大值为…………7分(2)AOP AOP OA OP OP OA ∠=∠=⋅∴cos 32cos ||||…………9分]65,6[ππ∈∠AOP…………10分]3,3[]6cos 32,65cos32[||-=∈⋅∴ππOP OP OA …………12分20.解:由题意知:2%)12.31)(1(%24.6)1(21%)24.61)(1()2(+=⋅-+=f f f f…………4分%)12.31)(1(%24.6)2(21%)4.61)(2()3(+=⋅-+=f f f f )(%)12.31(19800)(*1N x x f x ∈+=∴-…………6分(2)2018年诺贝尔奖发放后基金总额为26100%)12.31(19800)10(=+=f…………9分2018的度诺贝尔奖各项金额为136%24.6)10(2161≈⋅⋅f (万美元)…………11分 与150万美元相比少了约14万美元,∴是假新闻…………12分21.解:(1)令,8)4)(2()()()(232x x x x x x x x g x f x F --=-++=+=则).2)(43(823)('2-+=--=x x x x x F…………2分)('),(x F x F 随x 的值的变化情况如下表x-2 )34,2(--34-)2,34(- 2 )('x F + 0-)(X F4极大27176-12由表可知F (x )的值域为].27176,12[-…………4分故]2,2[|)()(|-+在x f x f 上的最大值为12。
