华东理工大学高数下第14章
华理高数答案(下)

第 9 章(之 1) (总第 44 次)
教学内容:§9.1 微分方程基本概念 *1. 微分方程 2( y ) 9 y y 5xy 的阶数是
3 7
( (D)7.
0.
解: 方程变形为
y
2 1 1 y 2 ,是一阶线性非齐次方程,其通解为 x x x
ye
2 2 1 1 x dx x dx c ( ) e dx 2 x x
1 x2
c 1 1 1 1 1 1 c ( 2 ) x 2 dx 2 c x 2 x 2 2 x x x 2 x x
y C cos 2 x 1 C sin 2 x ,实质上只有一个任意常数;
(D)中的函数确实有两个独立的任意常数,而且经验算它也确实是方程的解. *3.在曲线族 y c1e c2 e 中,求出与直线 y x 相切于坐标原点的曲线.
x x
2
解
根据题意条件可归结出条件 y(0) 0, y (0) 1,
2
解:分离变量 2 ye y dy xe 2 x dx ,两边积分就得到了通解
ey
2
1 1 1 ( xe 2 x e 2 x dx) ( xe 2 x e 2 x ) c . 2 2 2
(3) (2 x 1)e y y 2e y 4 0 .
ey d y dx 解: , y 2x 1 2e 4
2
为 y y (2 x yy ) .
2
华东理工大学级(下)高等数学期中考试试卷(学分)解答

华东理工大学级(下)高等数学期中考试试卷(学分)解答————————————————————————————————作者:————————————————————————————————日期:华东理工大学2013–2014学年第二学期《高等数学(下)11学分》课程期中考试试卷 2014.4开课学院:理学院, 专业:大面积, 考试形式:闭卷,所需时间 120 分钟考生姓名: 学号: 班级 任课教师题序 一二三四五六总分得分 阅卷人注 意:试 卷 共 两 页 六 大 题一.填空题(本大题共11小题,每小题4分,共44分):1、微分方程222'y x e yx y -=的通解为 。
答:C e xe e xx y +-=22412122、微分方程0''9)4(=+y y 的通解为 。
答:x C x C x C C y 3sin 3cos 4321+++=3、函数 zxy u )(= 对变量x 的偏导数 =x u 。
答:12)(--=z x xy x yz u 4、设 ))arctan(,,(xyz e y xze f u zy+=,其中f 关于所有变量有一阶连续偏导数, 则=∂∂yu。
答:3222211f zy x xz f f xze y u y +++=∂∂ 5、设函数z z x y =(,)由方程 ),(yzxz f z = 所确定,其中f 关于所有变量有一阶连续偏导数,则∂∂zy= 。
答:21222yf f xy y zf ---6、设1)(-=⋅⨯c b a ρρρ,则=+⨯+⋅)]()[(c b b a b ρρρρϖ 。
答: 17、函数)ln(22z y x u ++=在点)1,0,1(处最大的方向导数等于 。
答:228、微分方程 0'2''=+y xy 的通解=y 。
答: 21C xC y +-= 9、设平面π过直线⎩⎨⎧=+-=++04,05:z x z y x L 则原点到平面π距离d 的范围是 。
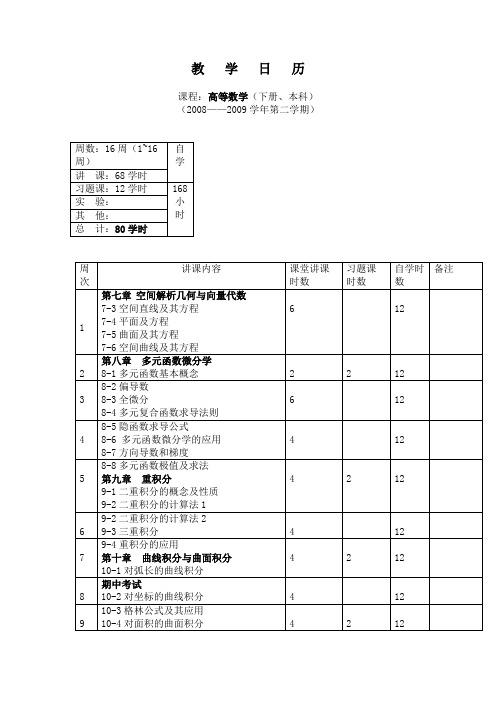
华南理工大学高等数学(下) 教学日历
2
12
15
12-4一阶线性微分方程
12-5全微分方程
12-6可降阶的高阶微分方程
12-7高阶线性微分方程
6
12
16
12-8常系数齐次线性微分方程
12-9常系数非齐次线性微分方程
4
12
17
公益劳动一周
18
学期总复习
12
19
20
考试周
教材:《高等数学》(1、同济大学主编第五版,2、华南理工大学陈凤平等主编,3、华南理工大学王全迪等主编讲
4
2
12
6
9-2二重积分的计算法2
9-3三重积分
4
12
7
9-4重积分的应用
第十章曲线积分与曲面积分
10-1对弧长的曲线积分
4
2
12
8
期中考试
10-2对坐标的曲线积分
4
12
9
10-3格林公式及其应用
10-4对面积的曲面积分
4
2
12
10
10-5对坐标的曲面积分
10-6高斯公式通量与散度
4
12
11
10-6斯托克斯公式环流量与旋度
第十一章无穷级数
11-1常数项级数的概念和性质
4
2
12
12
11-2常数项级数审敛法
11-3幂级数
4
12
13
11-4函数展成幂级数
11-5函数幂级数展开式的应用
11-7傅里叶级数
11-8一般周期函数的傅里叶级数
6
12
14
第十二章微分方程
12-1微分方程的基本概念
12-2可分离变量的微分方程
2005-2006高数下(8学分)期末试题A及解答

华东理工大学2005-2006学年高等数学下(8学分)期末考试试卷A 2006.6一. 填空题(每小题4分, 共36分) 1.一阶微分方程0)21(22=-+'y x y x 的通解是y =____________.2.微分方程052=+'+''y y y 满足初始条件3)0(,1)0(='=y y 的特解为y =___________.3.已知ABC ∆的三个顶点为)2,3,4(),4,3,2(),1,1,1(C B A =, 则ABC ∆的面积S =_______.4.已知)0,2,2(),1,,0(-=ππB A , 则函数)sin(2yz e u x =在点A 处沿方向B A方向 导数A lu |∂∂=_______.5.空间曲线)(),(z g y y f x ==(其中g f ,是可微函数)上对应于0z z =点的切线方程是_____________________6.设函数)(⋅f 具有二阶连续导数, ),(⋅⋅g 具有二阶连续偏导数, ),()(z xyz g z xy f u ++=,则zx u ∂∂∂2=_____________.7.二次积分dy e dx xy ⎰⎰-2222的值等于______________.8.某公司生产产品A , 当生产到第x 个单位的边际成本是34)(+='x x c (万元/单位), 其固定成本是100万元, 则生产量为10单位时的平均成本等于_______(万元/单位). 9.设22224|),,{(y x z y x z y x --≤≤+=Ω, 则Ω的体积V =________. 10.函数)1ln(),,(2z x ye z y x f z ++=在点)0,1,1(P 处的梯度)(P gradf ________.二. 选择题(每小题4分, 共32分)1. 微分方程1+=-''x e y y 的一个特解应具有形式(式中b a ,为常数), ( ) (A)b ae x +; (B)b axe x +; (C)bx ae x +; (D)bx axe x +.2.函数),(y x f y =在点),(00y x 处具有偏导数),(00y x f x , ),(00y x f y 是该函数在点),(00y x 可微的()(A)充要条件; (B)必要条件; (C)充分条件; (D)既非充分条件也非必要条件.3.已知非零向量b a,满足||||b a b a +=-,则必成立的是 ( )(A)b a b a +=-; (B)b a =; (C)0=⨯b a ; (D)0=⋅b a.4.下列广义积分中收敛的是( ) (A)dx xx e⎰1ln 1; (B)dx xx e⎰+∞ln 1; (C)dxxx e⎰+∞ln 1; (D)dxxx e⎰12ln 1.5*.二元函数⎪⎩⎪⎨⎧=≠+=)0,0(),(,0)0,0(),(,),(22y x y x y x xyy x f 在)0,0(点处( )(A)连续且偏导数存在; (B)连续, 偏导数不存在;(C)不连续, 偏导数存在; (D)不连续, 偏导数不存在三. (本题8分) 设函数yz e x u =, 而)(x z z =与)(y z z =分别是由方程1=-xz e z 与2sin =-y z e z所确定,计算yux u ∂∂∂∂,. 四. (本题6分)曲线过点)1,1(, 其上任一点与原点的距离平方等于该点横坐标与该点的法线在x 轴上截距的乘积的两倍, 求曲线方程.五. (本题6分) 计算数列极限2)1tan511(lim 2nn nn-+∞→.六. (本题8分)在曲面1:=++∑z y x 上作一切平面, 使它与三个坐标面所围成的四面体体积最大, 求切平面方程.七、(本题8分)设1D 是由抛物线22x y =和直线2,==x a x 及0=y 所围成的平面区域,2D 是由抛物线22x y =和直线a x y ==,0所围成的平面区域, 其中20<<a .(1)求1D 绕x 轴旋转而生成的旋转体体积)(1a V , 求2D 绕x 轴旋转而生成的旋转体体积)(1a V ; (2)当a 取何值时, )()(21a V a V +取得最大值? 并求此最大值. 八、设函数)(x f 在]1,0[上连续, 2)(1=⎰dx x f , 证明:3)(1)(11)(≥⋅⎰⎰dx x f dx ex f x f .华东理工大学2005-2006学年第二学期《高等数学(下)》课程期终考试试卷参考答案与评分标准一.填空题(每小题4分,共40分)1.cx x +-2||ln 1 2.)2si n (cos x x e y x +=- 3. 62 4.32π+5.1)()()()]([)]([000000z z z g z g y z g z g f z g f x -='-='⋅'- 6. 22321221g zx g zy g zf y -+-''7. 41--e 8. 33 9.二.选择题(每小题4分,共32分):5.C;A ; 4.D; 3.;B 2.;1.B三.xz xyeexu yzyz∂∂+=∂∂,yz xyexze yu yzyz∂∂+=∂∂而xe z xz z-=∂∂,ye z z yz zsin cos -=∂∂, ------------------------------------------------(2分xe xyzeex z zyzyz-+=∂∂, ------------------------------------------------(2分)ye xyzexzeyz zyzyzsin -+=∂∂, -----------------------------------------(2分)四.曲线在点),(y x 处的法线方程为: )(1x X y y Y -'-=-,令0=Y , 得曲线在x 轴上截距为: y y x X '+=,根据题意得: )(222y y x x y x '+=+或 x y xy y -=-'212, 1)1(=y , -------------( 2分)令2y z =,x z xdxdz -=-1 ------------(3分))())(()1()1(2c x x c dx ex ez y dxxdxx+-=+-==⎰⎰-⎰--, -------------------------------------(3分)由1)1(=y , 得2=c ,所求曲线为)2(2x x y -=或.222x y x =+ ----------------------------(1分)六.(本题8分)曲面∑在点),,(000z y x 处的切平面方程为:0)(1)(1)(1000000=-+-+-z z z y y y x x x , -------------------------------(2分),100=++z z y y x x ,截距分别为000,,z y x ,问题为求xyz V 61=在条件1000=++z y x 下的最大值, ---------(2分)令 )1(6100-+++=z y x xyz L λ,⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=-++==+==+==+=010212102121,02121z y x L zzxy L yy xz L xx yz L zy yxλλλ, 解得: 91===z y x ,-----------------------------------------(3分)因为问题的最大值存在,故91===z y x 就是最大值点,此时截距为31000===z y x ,所求切平面为: 31=++z y x . --------------------------(1分)七、)32(54)2()(52221a dx x a V a-==⎰ππ, -------------------------(2分)422222)(a dx x x a V aππ=⋅=⎰, -------------------------(2分)设)()()(21a V a V a V +=, 令 0)1(4)(3=-='a a a V π, 得唯一驻点: 1=a , ----(2分)当10<<a 时, 0)(>'a V ; 当21<<a 时, 0)(<'a V ;故当1=a 时, )()()(21a V a V a V +=取到最大值π5129)1(=V . --------------------(2分) 八、dx x f dx e x f x f ⎰⎰⋅110)()(1)(dy y f dx ex f x f ⎰⎰⋅=11)()(1)(⎰⎰=Dx f dxdy ey f x f )()()(,其中}10,10|),{(≤≤≤≤=y x y x D , --------------------(2)又dx x f dy ey f y f ⎰⎰⋅=11)()(1)(⎰⎰=Dy f dxdy ex f y f )()()(,所以dx x f dx ex f x f ⎰⎰⋅11)()(1)(⎰⎰+=Dy f x f dxdy ex f y f ey f x f ])()()()([21)()(⎰⎰+≥Dy f x f dxdye)]()([21--------------------(2)⎰⎰++≥Ddxdy y f x f ]2)()(1[3)(21)(2111111=++≥⎰⎰⎰⎰dy y f dx dy dx x f . ----------(2)填空题解答:1. 0)21(22=-+'y x y x , 是可分离变量微分方程,分离变量得: dx xx dy y )12(2-=, 积分得: c x x y--=-||ln 12,化简为:cx x +-2||ln 1.2. 特征方程: 0522=++λλ, 解得: i 212542222,1±-=⨯-±-=λ,故通解为: )2si n (co s x x e y x +=-. 3.|}1,2,3{}3,2,1{|21||21⨯=⨯=AB AC S 6216641621|}4,8,4{|21=++=--=.4.}1,2,2{--=B A , 32cos =α,32cos -=β, 31cos -=γ ,0|)sin(2|2==∂∂A xA exy x xu ,1|)cos(|2-==∂∂A xA eyz z yu ,π-==∂∂A xeyz y zu |)cos(2,γβαcos |cos |cos |A A A zu yu xu lu ∂∂+∂∂+∂∂=∂∂=323132)1(320ππ+=-⨯+-⨯-+⨯.。
数学分析课后习题答案--高教第二版(陈纪修)--14章

a
ww
2
2π ( (1 + a 4 ) 3 − 1) 。 3a 2
w. kh d
= 2b ∫ sin t a 2 + (b 2 − a 2 ) cos 2 t dt
0
πHale Waihona Puke aw .解质量 m = ∫ ρds = b ∫0 sin t a 2 sin 2 t + b 2 cos 2 t dt
2π
co m
Σ
∫∫ ( x
Σ
2
+ y + z )dS = ∫∫ a dS = 4πa 4 ,
2 2 2 Σ
所以
⎛ x2 y2 z2 ⎞ 13 13 4 2 ⎜ ∫∫ ⎜ 2 + 3 + 4⎟ ⎟dS = 12 ∫∫ x dS = 9 πa 。 ⎠ Σ ⎝ Σ 1 (6)由对称性,有 ∫∫ x 3 dS = 0 , ∫∫ y 2 dS = ∫∫ ( x 2 + y 2 )dS ,再由 2 Σ Σ Σ 1 zdS = ∫∫ ( x 2 + y 2 )dS ,得到 ∫∫ 2 Σ Σ
⎧ x = (b + a cos φ ) cos ϕ , ⎪ (6) 环面 ⎨ y = (b + a cos φ ) sin ϕ , 0 ≤ φ ≤ 2π , 0 ≤ ϕ ≤ 2π , 其中 0 < a < b 。 ⎪ z = a sin φ , ⎩
解(1) A = ∫∫ 1 + a 2 ( x 2 + y 2 )dxdy
4. 求下列第一类曲面积分: (1) ∫∫ ( x + y + z )dS ,其中∑是左半球面 x 2 + y 2 + z 2 = a 2 , y ≤ 0 ;
华东理工大学高等数学(下册)第11章作业答案

第 11 章(之1)(总第59次)教材容:§11.1多元函数 1.解下列各题:**(1). 函数f x y x y (,)ln()=+-221连续区域是 ⎽⎽⎽⎽⎽⎽⎽ . 答:x y 221+>**(2). 函数f x y xy x y x y x y (,)=++≠+=⎧⎨⎪⎩⎪222222000, 则( )(A) 处处连续 (B) 处处有极限,但不连续(C) 仅在(0,0)点连续 (D) 除(0,0)点外处处连续 答:(A )**2. 画出下列二元函数的定义域: (1)=u y x -;解:定义域为:{}x y y x ≤),(,见图示阴影部分:(2))1ln(),(xy y x f +=;解:{}1),(->xy y x ,第二象限双曲线1-=xy 的上方,第四象限双曲线1-=xy 的下方(不包括边界,双曲线1-=xy 用虚线表示).(3)yx yx z +-=. 解:()()⎩⎨⎧-≠≥⇔⎩⎨⎧≠+≥+-⇔≥+-y x y x y x y x y x y x y x 000.***3. 求出满足22,y x x y y x f -=⎪⎭⎫ ⎝⎛+的函数()y x f ,. 解:令⎪⎩⎪⎨⎧=+=x yt y x s , ∴⎪⎩⎪⎨⎧+=+=t st y t s x 11∴()()()t t s t t s s t s f +-=+-=111,22222, 即 ()()y y x y x f +-=11,2. ***4. 求极限:()()220,0,11limyx xy y x +-+→.解:()()()()()22222222112111110yx xy y x yx xy xyyx xy ++++≤+++=+-+≤()011222→+++=xy y x (()()0,0,→y x ) ∴()()011lim220,0,=+-+→yx xy y x .**5. 说明极限()()22220,0, lim y x y x y x +-→不存在.解:我们证明()y x ,沿不同的路径趋于()0,0时,极限不同.首先,0=x 时,极限为()()1lim 2222220,0,0-=-=+-→=y y y x y x y x x ,其次,0=y 时,极限为()()1lim 2222220,0,0==+-→=x x y x y x y x y ,故极限()()22220,0,y y lim +-→x x y x 不存在.**6. 设112sin ),(-+=xy x y y x f ,试问极限),(lim )0,0(),(y x f y x →是否存在?为什么?解:不存在,因为不符合极限存在的前提,在)0,0(点的任一去心邻域函数112sin ),(-+=xy x y y x f 并不总有定义的,x 轴与y 轴上的点处函数),(y x f 就没有定义.***7. 试讨论函数z x yxy=+-arctan1的连续性. 解:由于arctan x yxy+-1是初等函数,所以除xy =1以外的点都连续,但在xy =1上的点处不连续.**8. 试求函数f x y xyx y(,)sin sin =+22ππ的间断点.解:显然当(,)(,),x y m n m n Z =∈时,f x y (,)没定义,故不连续. 又f x y xyx y(,)sin sin =+22ππ是初等函数. 所以除点(,)m n (其中m n Z ,∈)以外处处连续.第 11 章(之2) (总第60次)教材容:§11.2 偏导数 [§11.2.1]**1.解下列各题: (1)函数32),(y x y x f +=在)0,0(点处 ( )(A ))0,0(x f '和)0,0(y f '都存在; (B ))0,0(x f '和)0,0(y f '都不存在; (C ))0,0(x f '存在,但)0,0(y f '不存在; (D ))0,0(x f '不存在,但)0,0(y f '存在. 答:(D ).(2) 设z x y xy =+-()arcsin2,那么∂∂z y (!,)2= ( )(A) 0 ; (B) 1; (C)π2; (D)π4. 答:(D).(3)设()xy y x f =,,则=)0,0('x f ______,=)0,0('y f __________.解:由于0)0,(=x f ,0)0,0('=∴x f ,同理 0)0,0('=y f .**2. 设z x y x y e xy =-+++2322ln , 求 z z x y ,. 解:z x x y ye x xy=+++1322, z y x yxe y xy =-+++2322.**3. 求函数xyz arctan =对各自变量的偏导数. 解:2222,y x xz y x y z yx +=+-=.**4. 设f x y x x y x y x y (,)ln()=++≠+=⎧⎨⎩222222200,求f f x y (,),(,)0000.解:f x x x x x (,)limln 000022==→, f yy y (,)lim 000000=-=→.***5. 求曲线⎩⎨⎧=+-=122x y xy x z 在()1,1,1点处切线与y 轴的夹角.解:由于曲线在平面1=x ,故由 ()()()121,11,1=+-=y x z y ,得切线与y 轴的夹角为 41arctan π=.[也可求出切向量为{}1,1,0]∴夹角={}{}422arccos12110,1,01,1,0arccos 22π==+.***6. 设函数ϕ(,)x y 在点)0,0(连续,已知函数f x y x y x y (,)(,)=-ϕ在点)0,0(偏导数)0,0(x f '存在,(1)证明ϕ(,)000=; (2)证明)0,0(y f '也一定存在.解:(1)lim(,)(,)lim (,)∆∆∆∆∆∆∆x x f x f x x x x→→-=000000ϕ, 因为)0,0(x f '存在,所以 lim (,)lim(,)∆∆∆∆∆∆∆∆x x x x x x x x→+→-⋅=-⋅0000ϕϕ 即 ϕϕ(,)(,)0000=-, 故 ϕ(,)000=.(2)由于ϕ(,)x y 在点)0,0(连续,且ϕ(,)000=,所以0→∆y 时,),0(y ∆ϕ是无穷小量,而yy ∆∆是有界量,所以0),0(lim )0,0(),0(lim00=∆∆∆=∆-∆→∆→∆yy y y f y f x y ϕ,即0)0,0(='y f .第 11 章(之3) (总第61次)教材容:§11.2 偏导数 [§11.2.2 ~ 11.2.4]**1. 求函数()x y z x z y x f sh ch ,,-=的全微分,并求出其在点()2ln ,1,0=P 处的梯度向量.解:()()()x y d z x d z y x df sh ch ,,-=()zdzx xdy dx x y z xdxy xdy zdz x zdx sh sh ch ch ch sh sh ch +--=--+=∴()()dx z y x df 41,,2ln ,1,0=, ()()⎭⎬⎫⎩⎨⎧=∇0,0,41,,2ln ,1,0z y x f . **2.求函数xyyx z -+=1arctan的全微分: 解:xyyx d dz -+=1arctan)arctan (arctan y x d +=2211)(arctan )(arctan y dy x dx y d x d +++=+=**3. 设z xy xy =-sec ()ln()21,求d z .解:222)]1[ln()]1d[ln()(sec )](d[sec )]1[ln(d ----=xy xy xy xy xy z)]d d (1)(sec )d d )(tan()(sec 2)1[ln()]1[ln(1222y x x y xy xy y x x y xy xy xy xy +--+--= )1(ln )(cos )1()d d ](1)1)(tan()1ln(2[22--+---=xy xy xy y x x y xy xy xy .**4. 利用df f ≈∆,可推出近似公式:()()()y x df y x f y y x x f ,,,+≈∆+∆+, 并利用上式计算()()2203.498.2+的近似值.解:由于()()()y x df y x f y y x x f ,,,+≈∆+∆+, 设()22,y x y x f +=,03.0,02.0,4,3=∆-=∆==y x y x ,于是 ()2222,yx y y x x yx ydy xdx y x df +∆+∆=++=,()()22,,yx y y x x y x f y y x x f +∆+∆+≈∆+∆+,∴()()()()012.54303.0402.034303.498.2222222=++-++≈+.***5.已知圆扇形的中心角为60=α,半径为cm r 20=,如果α增加了 1,r 减少了1cm ,试用全微分计算面积改变量的近似值. 解:180212παrS =, ))(2(3602ααπd r dr dS +=,∴ )(4533.17)3601)20(360)1(60202(22cm dS S -=⨯+-⨯⨯⨯=≈∆π.***6. 计算函数()()z y x z y x f 32ln ,,++=在点()0,2,1=P 处沿给定方向k j i l-+=2 的方向导数Plf∂∂.解:zy x f zy x f zy x f z y x 323,322,321++=++=++=,⎭⎬⎫⎩⎨⎧-=61,61,62l e ,∴ 65161,61,6253,52,51=⎭⎬⎫⎩⎨⎧-⋅⎭⎬⎫⎩⎨⎧=⋅∇=∂∂l Pe f lf.***7. 函数z xy=++arctan 11在(0,0)点处沿哪个方向的方向导数最大,并求此方向导数的值. 解:∂∂z xx y y(,)(,)0020011111112=+++⎛⎝ ⎫⎭⎪⋅+=, ∂∂z yx y x y (,)(,)()00220011111112=+++⎛⎝ ⎫⎭⎪⋅-++⎡⎣⎢⎤⎦⎥=-,{}{}∂∂ααααϕz l =+-=-⋅=1212121122cos ()sin ,cos ,sin cos , 其中ϕ为{} l =cos ,sin αα与 g =-⎧⎨⎩⎫⎬⎭1212,的夹角,所以ϕ=0时,即l 与g 同向时,方向导数取最大值∂∂z l =22.**8. 对函数 xyze z y xf =),,( 求出 ),,(z y x f ∇ 以及 )3,2,1(f ∇.解: {}xyz xyz xyzxye xze yze f ,,=∇,{}2,3,6)3,2,1(6e f =∇.**9. 求函数z y x z y x f 1)(),,(+=在点)21,21,21(-+=e e P 处的梯度. 解:⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧++-++=∇--)ln()(,)(1,)(1211111y x z y x y x z y x z f z z z , {}24,2,2)21,21,21(e e e e ef -=-+∇.***10. 讨论函数⎪⎩⎪⎨⎧=+≠+++=0,00,1sin ),(22222222y x y x y x y x y x f 在点(0,0)处的连续性,可导性和可微性.解:因为 lim (,)lim sin(,)x y x y f x y x y x y f →→→→=++==022221000,所以f x y (,)在点(0,0)连续.因为 lim(,)(,)lim sin ()∆∆∆∆∆∆∆x x f x f x x x x →→+-=00200001, 极限不存在,f x y (,)在(0,0)处不可导,从而在(0,0)处不可微.第 11 章(之4)(总第62次)教材容:§11.3 复合函数微分法;§11.4 隐函数微分法**1.解下列各题:(1) 若函数),(v u f 可微,且有x x x x x f ++=3422),(及122),(22 +-='x x x x f u ,则),(2 x x f v '= ( )(A) 1222++x x(B) xx x 21322++ (C) 1222+-x x(D) 1322++x x答:(A)(2)设函数z z x y =(,)由方程xy z x y z 2=++所确定,则∂∂zy=_________. 答: 2112xyz xy-- .(3)方程yzx z ∂∂=∂∂3,在变量代换y x u 3+=,y x v +=3下,可得新方程为_______. 答:0=∂∂uz.**2. 设u x y z x r y r z r =++===222,cos sin ,sin sin ,cos θϕθϕϕ求∂∂∂∂θ∂∂ϕu r u u ,,.解:()∂∂θϕθϕϕurx y z r =++=2222cos sin sin sin cos ,0)sin cos (2]sin )sin ([2=+-=ϕθθϕ∂θ∂r y r x u,0sin 2)cos sin (2)cos cos (2=-+=ϕϕθϕθ∂ϕ∂r z r y r x u.**3. 一直圆锥的底半径以3s cm /的速率增加,高h 以5s cm /的速率增加,试求r=15cm ,h=25cm 时其体积的增加速率. 解:h r V 231π=, s cm h r dtdVdtdhr dt dr rh dt dh h V dt dr r V dt dV /11252515313232πππ===+=⋅∂∂+⋅∂∂=*4. 设,3y e z x -=而4,sin t y t x ==,求dtdz. 解:32334cos y t t e dtdy z dt dx z dt dz xy x -=+=.**5. 若)(22y x f xy z -=,证明:z y z x y z y x x z xy 2222+=∂∂+∂∂. 解:22222,2ff xy xf z f f y x yf z y x '+='-=, 则 z y z x fy x xy yz x z xy y x 222222)(+=+=+. **6. 设 )cos ,,(2x xy ye xe f u x y =,求du yux u ,,∂∂∂∂. 解:3221)2sin cos (f x xy x y f ye f e xux y -++=∂∂ , 3221cos xf x f e f xe yux y ++=∂∂, [][]dy xf x f e f xe dx f x xy x y f ye f e du x y x y 32213221cos )2sin cos (+++-++=.**7. 求由方程y z z x ln =所确定的函数),(y x z z =的偏导数yz x z ∂∂∂∂,. 解:zx zyz y zx zFz Fx z x +=---=-=21,yz xy z z z x y Fz Fy z y +=---=-=2211.**8. 设,0),,(=+xz z y xy F 试求dz yzx z ,,∂∂∂∂. 解:,0),,(=+xz z y xy F 两边对x 求导,得 0)(321=+++x x xz z F F z yF , 解得 3231xF F zF yF z x ++-=,两边对y 求导,得 0)1(321=+++y y xz F z F xF . 解得3221xF F F xF z y ++-= ,所以dy xF F F xF dx xF F zF yF dz 32213231++-++-=.***9. 函数z z x y =(,)由方程F x x y z z xy (,,)+++=1所确定,其中F 具有连续一阶偏导数,F F 230+≠,求∂∂z x 和∂∂z y. 解:F x x y z F z y x x y F 1230d (d d d )(d d d )++++++=,d ()d ()d z F F yF x F xF yF F =-+++++1232323,∂∂z x F F yF F F =-+++12323, ∂∂z y F xF F F =-++2323. ***10. 求由方程z xyz aa 3330-=≠()所确定的隐函数z z x y =(,)在坐标原点处沿由向量{}a =--12,所确定的方向的方向导数. 解:当x y ==00,时,z a 00=≠.0,0)0,0(2)0.0()0,0(2)0.0(=-==-=xyz xz yz xyz yz xz ∂∂∂∂,0=∂∂∴az.***11. 设)0(,1,022≠+=+=-y x xv yu yv xu 求yv y u x v x u ∂∂∂∂∂∂∂∂,,,. 解: ⎪⎪⎩⎪⎪⎨⎧=∂∂+∂∂+=∂∂-∂∂+00x v x x u y v xv y x u x u ⎪⎪⎩⎪⎪⎨⎧+--=∂∂++-=∂∂⇒2222y x yu xv x v y x yv xu x u类似地 ⎪⎪⎩⎪⎪⎨⎧=∂∂+∂∂+=∂∂--∂∂00y v x y u y u y v y v y ux ⎪⎪⎩⎪⎪⎨⎧++-=∂∂+--=∂∂⇒2222y x yv xu yv y x xv yu y u第 11 章 (之5)(总第63次)教材容:§11.5 多元函数微分法在几何上的应用**1. 曲面x y z xyz x z 2222426-+--+=在点)2,1,0(=A 处的切平面方程为 ( ) (A )31223110()()x y z -+--+= (B )3234x y z +-= (C )032213=--+-+z y x (D )x y z 31223=-=-- 答:(A).**2.设函数F x y z (,,)可微,曲面F x y z (,,)=0过点)0,1,2(-=M ,且F F F x y z (,,),(,,),(,,)210521022103-=-=--=-.过点M 作曲面的一个法向量n ,已知n 与x 轴正向的夹角为钝角,则n 与z 轴正向的夹角γ=______ . 答:π3.***3. 设曲线x t y t z t =+=-=+2131223,,在t =-1对应点处的法平面为S ,则点)1,4,2(-=P 到S 的距离d =______ .答:2.**4. 求曲线ct z t b y t a x L ===,sin ,cos :在点)2,0,(0c a M π=处的切线和法平面方程. 解:,0sin 00=-===t t t a dt dx,cos 00b t b dt dy t t =-=== cdtdzt ==0.∴切线方程为:⎪⎩⎪⎨⎧-==⇔-=-=-c c z by ax c c z b y a x ππ2200,法平面方程为:0)2(=-+c z c by π.***5. 求曲线6,11:==++xyz zx yz xy L 在点)3,2,1(0=M 处的切线和法平面方程.解:设 11),,(-++=zx yz xy z y x F ,6),,(-=xyz z y x G ,)()()(),(),(2x y z z x yz z y xz xz yz z x zy y x G F +-=+-+=++=∂∂,)()()(),(),(2z y x y x xz z x xy xy zx x y z x z y G F -=+-+=++=∂∂,)()()(),(),(2x z y z y xy y x zy zyxy z y y x x z G F -=+-+=++=∂∂.∴8),(),(,1),(),(,9),(),(0=∂∂-=∂∂-=∂∂M M M x z G F z y G F y x G F ,∴切线方程为938211--=-=--z y x , 法平面方程为 ()()()()()0948211=--+-+--z y x ,即 01298=-+-z y x .***6. 求曲面4416222x y z ++=在点1,22,1(-=P )处的法线在yOz 平面上投影方程.解:曲面在点1,22,1(-=P )处的法线方向向量{}{}2,2,248,24,8-=-=→n ,法线方程为:x y z -=-=+-1222212.法线在yOz 平面上投影方程为212220-+=-=z y x .***7.求曲线x t y t z t ===3223,,上的点,使曲线在该点处的切线平行于平面x y z +-=21.解:设所求的点对应于t t =0,则对应的切线方向向量为: {}3,4,3020t t s =→.因为→s 垂直于平面法向量{}1,2,1-=→n ,所以0383020=-+=⋅→→t t n s , 解得:t 013=和t 03=-.所求点为:127291,,⎛⎝ ⎫⎭⎪和(,,)--27189.**8.求曲面xyz 6=上平行于平面.06236=+--z y x 的切平面方程. 解:26,6xyy z xyx z -=∂∂-=∂∂, ∴由条件,得:⎪⎩⎪⎨⎧-=-==⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫-=--=-=-32121366622z y x k k x y k yx∴切平面方程为:,0)3(2)2(3)1(6=+-+--z y x 即 018236=---z y x .***9.求函数22y x ez +=在点),(000y x M =沿过该点的等值线的外法线方向的方向导数.解:等值线方程为x y x y 220202+=+, 在),(000y x M =处的法线斜率为 00x y k =,即法线方向向量为 },1{00x y n =或},{00y x ,方向余弦为:cos cos αβ=+=+x x yy x y0020200202,∂∂zn e x x x y e y y x y x y x y =⋅⋅++⋅⋅+++0202020222000202000202=⋅++202020202e x y x y .***10. 求函数z y x =+sin 在⎪⎭⎫⎝⎛=1,2πP 点沿 a 方向的方向导数,其中 a 为曲线x t y t ==22sin ,cos π在t =π6处的切向量(指向t 增大的方向). 解:tan d d sin cos αππππ==-=-==y xt tt t 66222,1sin 11cos 22+-=+=ππαπα,,221sin 210sin 2cos 1,21,21,21,2=+==+=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛ππππ∂∂∂∂xy yz xy x xz ,,所以 ∂∂πππz a =⨯++⨯-+011122122()()1222+-=ππ.***11. 设f y z g z (,),()都是可微函数,求曲线x f y z y g z ==⎧⎨⎩(,)()在对应于z z =0点处的切线方程和法平面方程.解:z z =0对应点()f g z z g z z [(),],(),0000, 对应的切线方向向量:{}S f g z z g z f g z z g z y z ='+'[(),]()[(),],(),0000001.切线方程:x f g z z f g z z g z f g z z y g z g z z z y z -'+=-'=-[(),][(),]()[(),]()()0000000000,法平面方程: {}{}f g z z g z f g z z x f g z z y z [(),]()[(),][(),]0000000'+-+'-+-=g z y g z z z ()[()]()0000.****12. 在函数yx u 11+=的等值线中哪些曲线与椭圆16822=+y x 相切?解:对等值线 y x u 110+= 两边微分得 022=--ydy x dx , 即 22x y dx dy -=, 同样对16822=+y x 两边微分,有yx dx dy 8-=, 令y xxy 822-=-,得 y x 2=,代入16822=+y x ,得 32,34±=±=y x ,∴ 433110±=+=y x u .***13. 试证明曲面3a xyz =上任一点处的切平面在三个坐标轴上截距之积为定值.解:由3a xyz =, 得 xya z 3=,∴在点),,(000z y x 处法向量为:⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧-1,,02030203x y a y x a, ∴切平面为:0)()(0020300203=-+-+-z z y y y x a x x y x a ,又 ∵3000a z y x =, ∴ 切平面方程化为:1333000=++z zy y x x , ∴ 截距之积为: 30002727a z y x =(定值).***14. 证明曲面0,=⎪⎭⎫⎝⎛----c z b y c z a x F 的所有切平面都通过一个定点,这里F u v (,)具有一阶连续偏导数.解:曲面上点(,,)x y z 000处的切平面法向量:[]n F z c F z c z c x a F y b F =-----+-⎧⎨⎩⎫⎬⎭10200201021,,()()()[]{}=-----+-10201020102()(),(),()()z c z c F z c F x a F y b F . 切平面方程为: ()()()()z c F x x z c F y y 010020--+--[]0)()()(02010=--+--z z F b y F a x .易知x a y b z c ===,,满足上述方程,即曲面的所有切平面都通过定点(,,)a b c .第 11 章 (之6)(总第64次)教学容:§11.6泰勒展开1.填空:*(1)设u xy yx=+,则∂∂22u x =________ .答:32xy. *(2)设u x xy =ln ,则∂∂∂2ux y= _________.答:y1. *(3)设u x y y x =+22sin cos ,则∂∂∂2ux y= _________ .答: x y y x sin 2cos 2-.*(4)设u x yxy=+-arctan 1,则∂∂∂2u x y =_______ .答:0 .**(5)设z e y e y xx=+-sin cos ,则∂∂∂∂2222z x zy+= _________.答:0.**2.设z f x u =(,)具有连续的二阶偏导数,而u xy =,求∂∂22zx.解:z f yf x x u =+, z f yf y f xx xx xu uu =++22.**3.设z x xy =ln(),求∂∂∂32zx y.解一: z x yy =, z yyx =1, z yx 20=.解二: z xy x =+ln()1, z xx 21=, z yx 20=.**4.设)2,21(),()(4322xy z y x xf xy f y z 求+=. 解:)(3)()('43434324y x f y x y x f xy f y z x ++=,,4)("3)('124)('2)(")('4334343433333432423yx y x f y x y x f y x x y y x f yx xy f y xy f y z xy ⋅++⋅+⋅+=∴)2("24)2('12)2('4)2("32)2('32)2,21(f f f f f z xy ++++= )2("56)2('48f f +=.**5.函数y y x =()由方程x xy y 2221+-=所确定,求22d d xy. 解:xy yx y x y x x y -+=-+-=2222d d ,222)())(1())(1(d d x y y x y x y y x y -+-'--'+= 322)()2(2x y y xy x --+-=3)(2y x -=. ***6.求方程 zy ez x +=+ 所确定的函数),(y x z z =z=z(x,y)的所有的二阶偏导数.解:xz e x z z y ∂∂⋅=∂∂++1, ∴ 11-=∂∂+zy e x z .3222)1()1(--=-∂∂⋅-=∂∂++++z y zy zy z y e e e x ze x z, 因为 )1(y z e y z zy ∂∂+=∂∂+, ∴zy z y z y e e e y z +++-+-=-=∂∂1111. 则 3222)1()1()1(z y z y z y z y e e e yze y z ++++-=-+∂∂=∂∂, 322)1()1()1(z y z y z y z y e e e yze yx z ++++--=-+∂∂-=∂∂∂, 322)1()1(-=-∂∂=∂∂∂++++z y z y z y zy e e e x ze x y z .***7.对于由方程0),,(=z y x F 确定的隐函数),(y x z =,试求 22xz ∂∂.解:由公式zx F F x z-=∂∂两边对x 求偏导数,得。
华东理工高数期中考试题

华东理工大学2008–2009学年第一学期《 高等数学(上)11学分》期中考试试卷 2008.10开课学院:_理学院_ ,考试形式:_闭卷_,所需时间: 120 分钟考生姓名: 学号: 班级: 任课老师:注意:试卷共3大张,6大题一. (本题8分)设⎩⎨⎧+=-=21ln arctan t y t t x ,计算dx dy 和22dx y d 。
二. (本题8分)设函数⎩⎨⎧≥+<=0),ln(;0,)(x b ax x e x f x 处处可导,求正数b a ,。
三. (本题8分)设)(x f 有二阶导数,且0)('≠x f ,)(y g x =与)(x f y =互为反函数,试用)(''),('x f x f 来表示)(''y g 。
四. (本题8分)设函数)(x f 在]1,0[上连续,在)1,0(内可导,且0)1(=f ,证明:存在)1,0(∈ξ,使得 0arctan )(')1()(2=++ξξξξf f 。
五.填空题(每小题4分,共48分):1、设)(x f y =和)(x g y =互为反函数,则函数))(1)(1(x f x f g y +-=的反函数为 my 。
2、计算心形线θρcos 1-=在2πθ=对应点处的切线方程(直角坐标形式)为 my 。
3、设)(x y y =是由方程312e e eye y x -=-+确定的隐函数,则==)2,1(),(y x dxdy y 。
4、设b a ,为常数,且1)1(lim 2=-+++∞→x bx ax x ,则=+b a 3 。
5、设常数0>α,且)0(~+→++x x x x x α,则=α 8 。
6、计算极限=+-∞→)arctan(cos )arctan(cos limx x x x x 1 。
7、设e x x x y +=,则==1x dx dy e+1 。
高数下模拟试卷

华东理工大学继续教育学院成人教育《高等数学》(下)(本科136学时)练习试卷(1)一、单项选择题1、设xy e y z 2=,则=)1,1(dz 答( ) (A ))3(dy dx e + (B ))3(dy dx e -(C ))2(dy dx e + (D ))2(dy dx e -2、设方程0yz z 3y 2x 2222=-++确定了函数z=z (x ,y ),则=∂∂xz答( ) (A )y z x -64 (B )zy x64- (C )y z y +64 (D )yz y-643、平面0D Cz By Ax =+++过y 轴,则 答( ) (A )A=D=0 (B )B=0,0D ≠ (C )0D ,0B == (D )C=D=04、设u =(0,0)ux∂=∂ 答( )(A )等于0 (B )不存在 (C )等于1- (D )等于15、极限 00s i n l i mx y xyx→→= 答( ) (A )不存在 (B )1 (C )0 (D )∞二、填空题1、设函数)ln(sin 22y x y z +=,则=∂∂yz2、改变积分⎰⎰e x dy y x f dx1ln 0),(的积分次序,⎰⎰e x dy y x f dx 1ln 0),( =3、积分=+⎰-112)25(dx x x4、函数ln()arcsinyz y x x=-+ 的定义域为 5、曲线段 3223y x =(38)x ≤≤的弧长s =三、解答下列各题 1、求微分方程 y y dxdyx ln = 的通解。
2、计算二重积分:⎰⎰+Dd y x σ)23(, 其中D 是由曲线2x y =及直线y=1所围成的区域。
3、判别级数∑∞=+132n nn 的敛散性。
4、设),(2zy y x f u =,其中f 为可微函数 ,求,u uy x ∂∂∂∂。
5、计算定积分 2sin x xdx π⎰6、求过点(0,1,2)M -且平行于直线113211x y z -+-==-的直线方程。
合工大高数下(复习)

注:① 两类曲线积分之间的联系
L
P ( x , y )d x Q( x , y )d y P ( x , y )cos Q( x , y )cos d s
② 运用积分曲线方程简化计算!
§3 格林公式
Q P P ( x , y )d x Q( x , y )d y d L x y D 注:① L 封闭正向(补) ;② P ( x , y ), Q ( x , y ) 在 D 内偏导连续(挖) !
f ( x , y )d y d y
c
d
2 ( y)
1 ( y)
f ( x , y )d x
注:选择积分次序(根据积分区域特点、被积函数特点) 交换积分次序! ② 利用极坐标:
f ( x , y )d f (r cos , r sin )r d r d
x x(t ) ① y y( t ) 在 M 0 x ( t 0 ), y ( t 0 ), z ( t 0 ) 的切向量: x ( t 0 ), y ( t 0 ), z ( t 0 ) z z( t ) x x F ( x, y, z ) 0 ② y y( x ) 在 M 0 ( x0 , y0 , z0 ) 的切向量: 1, y( x0 ), z ( x0 ) G( x, y, z ) 0 z z( x )
x x区域连续! §3 偏导数 分段函数在分段点处的偏导数:
f x ( x0 , y0 ) lim
f ( x 0 x , y0 ) f ( x 0 , y0 ) x 0 x f ( x 0 , y 0 y ) f ( x 0 , y0 ) f y ( x0 , y0 ) lim y 0 y
华东理工大学高等数学作业答案第10章

即
2 2 2 cos , 则 cos 3 3 ,即 a 与 b 的夹角为 . 4 4
0 ,所以
** 9.在 yz 平面内求模为 10 的向量 b,使它和向量 a 8i 4 j 3k 垂直. 解:∵ 向量 b 在 yz 平面内, ∵ b a,
∴ 可设坐标为
0, y, z ,
∴ b a 0 , ∴ 4 y 3z 0 , 或 z 8, y 6 ,
即: 0, y , z 8,4,3 0 , 又 b
y 2 z 2 10 , ∴ z 8, y 6 ,
∴向量 b 的坐标为: 0,6,8 或
OA OC , | OB | | OA | | OC | ,
则有 AB OB OA ,
B
CB OB OC OB OA , AB CB (OB OA) (OB OA) | OB | 2 | OA | 2 0 ,
2q 0, 2
p 1 0 ,即 q 2, p 1 , 2
2 q 5 3 p 1 , , ), 2 2 2
故 C 点的坐标为 (0,1,0) ,即交点的坐标为 (0,1,0) .
**3.设 A,B 两点的坐标分别为 0,2,1, 1,0,1 .求 (1)向量 AB 的模; (2)向量 AB 的方向余弦;
即: u v ,
2 p 4 , 1 0 q 向量 u 与 v 垂直时,
∴
∴ p 0, q 2 ,
u v 0,
∴ 2 1 p 0 4 q 0 . ∴q
2006-2007高数下(8学分)期末试题A及解答

华东理工大学2006-2007学年高等数学下(8学分)期末考试试卷A 2007.7一. 填空题(每小题4分, 共36分) 1.微分方程22x x e xy y -=+'满足初始条件0)0(=y 的特解为y =____________. 2.微分方程09)4(=''+y y 的通解为y =________________.3.1||||==b a , a 与b 夹角等于3π, 则|32|b a -=_____________.4.过直线⎩⎨⎧=-=+21:z y y x L 且平行于}4,1,2{--=l 的平面方程是____________5.设),4()(2)4(t e t f t F -+=, 其中1),(C y x f ∈且有a f =-)1,2(及b f =-')1,2(1, c f =-')1,2(2, 则)0(F '=______________6.设函数),(y x z z =由方程xz xy e z y x -=-+32确定, 则)0,0(dz =_____________.7.σd y x y x y x ⎰⎰≤++++12222222)(1)(=______________.8.广义积分dx x x ⎰+∞+1)1(1=_______________. 9.极坐标系下心脏线)cos 1(2ϑρ+=所围成区域D 的面积为A =_______________.二. 选择题(每小题4分, 共32分)1.椭圆122≤+y x 绕x 轴和y 轴旋转所得的体积分别是上x V 和y V , 则 ( ) (A)y x V V 49=; (B)y x V V 32=; (C)y x V V 94=; (D)y x V V 23=.2.函数Cx y =是微分方程032=+'-''y y x y x 的 ( ) (A)通解; (B)特解; (C)是解, 但既不是通解, 也不是特解; (D)以上都不对.3.若a 与b不平行, 且μλ≠, 则b a λ+与b a μ+ ( ) (A)必不平行; (B)模不相等; (C)必不垂直(正交); (D)不排除有平行的可能性; 4.“函数),(y x f 在),(00y x 点两个一阶偏导数都存在”是“函数),(y x f 在),(00y x 点 可微”的 ( ) (A)充分条件, 但不是必要条件; (B)必要条件, 但不是充分条件;(C)必要条件; (D)既不是充分条件, 也不是必要条件.5.设2C f ∈, ),,2(xz z y y x f u -+=, 则yx u∂∂∂2= ( )(A)131122f z f ''+''; (B)23131122f z f z f ''+''+''; (C)2313121122f z f z f f ''+''+''+''; (D)23131211222f z f z f f ''+''+''+'' 6.C f ∈, 则⎰⎰ϑϑπρρρρϑρϑcos 2sec 40)sin ,cos (d f d = ( )(A)⎰⎰--111102),(y dx y x f dy ; (B)⎰⎰-22121),(x x dy y x f dx ; (C)⎰⎰-22020),(x x dy y x f dx ; (D)⎰⎰-+211110),(y dx y x f dy .7.下列极限中等于0的是 ( ) (A)dx e n nn xn ⎰+∞→12lim ; (B)dx e n nn xn ⎰+∞→12lim ; (C)dx e n nn xn ⎰+∞→12lim ; (D)dx e n nn xn ⎰+∞→1222lim .8.边际成本等于边际收益是利润最大的 ( )(A)充要条件; (B)充分条件, 非必要条件;(C)必要条件, 非充分条件; (D)既不是必要条件, 也不是充分条件.三. (本题8分) 微分方程y y y y ''='+''2)(2满足初始条件2)0(=y , 3)0(='y 的特解.四. (本题8分)求曲线⎩⎨⎧-=++=++3zx yz xy z y x L :上的点P , 使L 在点P 处的切线平行与平面0=-+z y x .五. (本题8分) 利用夹逼性准则求极限)332211(lim 2222nn nn n n n n n n n ++++++++++++∞→ . 六. (本题8分)求有二阶连续导数的函数)0)((>t t f , 使)(22y x f u +=满足12222=∂∂+∂∂y ux u .华东理工大学2006-2007学年第二学期《高等数学(下)》课程期终考试试卷参考答案与评分标准一.填空题(每小题4分,共36分)1.)1e (e2--x x 2.x C x C x C C 3sin 3cos 4321+++ 3.7 4. 123=++z y x5. )8(3c b a - 6. y xd 20d 1+ 7. )122(3-π8. 2ln 9. π6二.选择题(每小题4分,共32分):8.C. 7.C; 6.D; 5.B; B; 4.A; 3.; C 2.; 1.D三.以y p '=为新未知函数,暂以y 为新自变量,原方程可化为 p ypy 2d d )1(=----(2分)解得 21)1(-=y C p ------------------------------------------------(2分)由32==y p可得31=C ---------------------------------------------------------------------------(1分)由2)1(3-='y y 解得x C y 3112-=----------------------------------------------------------(2分) 根据条件2)0(=y 可得12=C ,即x y 3111-=-或xxy 3132--=------------------------(1分) 四.因为{}1,1,11=→n ,{}y x x z z y n +++=→,,2,所以切向量为 {}y x x z z y n n t ---=⨯=→→→,,21 --------------------------( 3分){}{}y x y x x z z y l t lt =⇒=-⋅---⇒=⋅⇒⊥→→→→1,1,1.,0 ------------(3分)代入原曲线方程(组)得⎩⎨⎧-=+=+32,022zx x z x 解得)2,1,1(1-=P 和)2,1,1(2--=P -------(2分)五.(本题8分)记kn kn b k ++=2,n k ,,3,2,1 =,并记n n b b b a +++= 21, 适当放大缩小可得11122++≤≤++=n n n b n n n n k ,n k ,,3,2,1 =, 所以 n k n Q n n n n a n n P =⎪⎪⎭⎫⎝⎛++≤≤⎪⎭⎫ ⎝⎛=112----------------------------------------------------(5分) 而1lim lim ==∞→∞→n n n n Q P ,根据夹逼准则可得1lim =∞→k n a -------------------------------------(3分)六.(本题8分)记22y x t +=,则有)(t f u =,所以tx t f x u ⋅'=∂∂)(,t y t f y u⋅'=∂∂)(-------------------------------(1分) 322222)()(ty t f t x t f x u ⋅'+⋅''=∂∂,322222)()(t x t f t y t f y u ⋅'+⋅''=∂∂---------(2分) 原方程可化为 1)(1)(='+''t f tt f ---------------------------------------------------------(1分) 以)(t f p '=为新的未知函数,仍然以x 为自变量,得到新方程为11=+'p tp ------------------------------------------------(2分)解得t C t p t f 121)(+==',从而有212ln 21)(C t C t t f ++=--------------------------(2分)。
高数下课本详解答案(合工大版)

习题8-11.自点(),,P a b c 分别作各坐标面和各坐标轴的垂线,写出各垂足的坐标.解在,,xoy yoz zox 坐标面上的垂足坐标分别为(),,0a b 、()0,,b c 、(),0,a c ,在x 轴、y 轴、z 轴上垂足的坐标分别为(),0,0a 、()0,,0b 、()0,0,c .2.已知三角形个的三个顶点的坐标分别为()4,1,9A 、()10,1,6B -、()2,4,3C ,求该三角形的三边长度,此三角形由何特点?解7AB ==,7AC ==,BC =由于AB AC =,且222AB ACBC +=,故此三角形为等腰直角三角形.3.在z 轴上求与点()4,1,7P -和点()3,5,2Q -等距离的点的坐标.解设z 轴上的点为()0,0,M z,则MP MQ=即=,解得149z =,故点为140,0,9M ⎛⎫ ⎪⎝⎭.4.求到两定点()1,2,1A -和()2,1,2B -等距离的点(),,M x y z 的轨迹.解由于MA MB =,从而有=解得26630x y z +--=.5.设平行四边形的两条对角线向量为a 和b,求其四条边向量.解如意8-1所示,由向量加减法的平行四边形法则有,,c d a c d b ⎧+=⎪⎨-=⎪⎩ 故2a b c += ,2a b d -=,即平行四边形的四条边向量为2a b + 、2a b + 、2a b - 、2a b- .(图8-1)(图8-2)6.设A 、B 、C 、D 是一个四面体的顶点,M 、N 分别是边AB 、CD 的中点,证明:()12MN AD BC =+.证如图8-2所示,AD DN AN +=,BC CN BN += ,AN AM MN -= ,BN BM MN -= ,又DN CN =- ,AM BM =- ,于是22AN BN AD BC MN ++==.7.已知两点()A 和()3,0,2B ,计算向量AB 的模、方向余弦、方向角及与AB平行的单位向量.解由于{}1,AB =-,则有2AB = ,1cos 2α=-,cos 2β-,1cos 2γ=-,方向角为23πα=,34πβ=,3πγ=,与AB 平行的单位向量为121,,222⎧⎫⎪⎪±--⎨⎬⎪⎪⎩⎭.8.设358a i j k =++,27b i j k =--,求向量23c a b =+在x 轴上的投影及在z 轴上的分向量.解23945c a b i j k =+=+-,故c 在x 轴上的投影为9,在z 轴上的分向量为5k - .9.一向量的终点在点()2,1,7B -,它在x 轴、y 轴及z 轴上的投影依次为4,4-和7,求这向量的起点A 的坐标.解设起点(),,A x y z ,由{}{}2,1,74,4,7AB x y z =----=-解得()2,3,0A -.10.设{}3,5,1a =- ,{}2,2,3b = ,{}4,1,3c =-- ,求与a b c +-平行的单位向量.解{}1,8,5a b c +-=,故与a b c +-平行的单位向量为±.11.设5AB a b =+ ,618BC a b =-+ ,()8CD a b =-,试证A 、B 、D 三点共线.证因为()()6188210BD BC CD a b a b a b=+=-++-=+()252a b AB=+=所以AB平行BD ,即A 、B 、D 三点共线.12.已知向量AB 的模为10,与x 轴正向夹角为4π,与y 轴正向夹角为3π,求向量AB .解设向量AB的方向余弦为cos α、cos β、cos γ,由于4πα=,3πβ=,222cos cos cos 1αβγ++=,得1cos 2γ=±于是向量{}211cos ,cos ,cos 10,,222AB AB αβγ⎫⎪==±⎨⎬⎪⎪⎩⎭.习题8-21.设4a i j k =+-,22b i j k =-+ ,求(1)()()22a b a b +⋅-;(2)()()22a b a b +⨯- ;(3)a 与b 夹角.解(1)a =,3b =,4a b ⋅=-()()222223230a b a b a a b b +⋅-=-⋅-=;(2)114794221i j k a b i j k⨯=-=----()()225354520a b a b a b i j k +⨯-=-⨯=++;(3)设a 与b夹角为θ,则cos9a ba bθ⋅===-arccos9θ⎛⎫=-⎪⎪⎝⎭.2.已知向量a 和b相互垂直,且1a=,b=,求(1)()()a b a b+⋅-;(2)()()a b a b+⨯-;(3)()a b+与()a b-夹角.解(1)()()22222a b a b a b a a b b a b+⋅-=+⋅-⋅-=-=-;(2)()()2a b a b a a b a a b b b a b+⨯-=⨯+⨯-⨯+⨯=-⨯=(3)()a b+与()a b-夹角为θ,则()()()()21cos42a b a ba b a bθ+⋅--===-+-,故23πθ=.3.已知13a=,19b=,24a b+=,求a b-.解()()2222a b a b a b a a b b+=+⋅+=+⋅+()()2222a b a b a b a a b b-=-⋅-=-⋅+两式相加,得()22222a b a b a b-=+-+()2222131924484=+-=,22a b-=.4.已知()1,1,2A-、()5,6,2B-、()1,3,1C-,求:(1)同时与AB及AC垂直的单位向量;(2)三角形ABC的面积ABCS∆;(3)B点到边AC的距离d.解(1){}4,5,0AB=-,{}0,4,3AC=-,450151216043i j kAB AC i j k⨯=-=++-故同时与AB 及AC 垂直的单位向量为{}115,12,1625AB AC AB AC⨯±=±⨯;(2)12522ABC S AB AC ∆=⨯=;(3)由于1122ABC S AB AC AC d ∆=⨯=⋅,且5AC = ,则5d =.5.设平行四边形的对角线2c a b =+ ,34d a b =- ,其中1a =,2b = ,且a b ⊥ ,求平行四边形的面积.解设平行四边形的两邻边分别为m 、n,则c m n =+ ,d m n =-,从而()()1142222m c d a b a b =+=-=-,()()1126322n c d a b a b =-=-+=-+ ,55sin 102S m n a b a b π=⨯=⨯== .6.已知向量a 、b 、c两两垂直,且1a = ,2b = ,3c = ,求向量s a b c =++ 的长度,以及s 分别与a 、b 、c的夹角.解()()222214s a b c a b c a b c =++⋅++=++=,于是s =cos ,s a s a s a⎛⎫⋅===⎪⎝⎭cos ,s b s b s b ⎛⎫⋅== ⎪ ⎪⎝⎭cos ,s c s c s c ⎛⎫⋅== ⎪⎝⎭所以,s a arc ⎛⎫= ⎪⎝⎭,s b arc ⎛⎫= ⎪ ⎪⎝⎭,,s c arc ⎛⎫= ⎪⎝⎭7.试用向量证明直径上的圆周角是直角.证取圆心为原点建立坐标系如图8-3所示,则圆周方程为222x y R +=,在圆周上任取一点(),A x y ,直径BC ,(),0B R -,(),0C R ,().AB R x y =--- ,().AC R x y =--则()()22220AB AC R x R x y R x y ⋅=---+=-++=故AB AC ⊥,即直径BC 所对应的圆周角为直角,由圆周关于任意一条直径都对称的性质知,直径所对应的圆周角是直角.(图8-3)8.判断下列两组向量a 、b 、c是否共面:(1){}2,1,3a =- ,{}1,0,5b =- ,{}1,1,4c =-;(2){}4,2,1a =- ,{}2,6,3b =- ,{}1,4,1c =-.解(1)21310540114abc -⎡⎤=-=≠⎣⎦- ,故a 、b 、c 不共面;(2)4212630141abc -⎡⎤=-=⎣⎦-,故a 、b 、c共面.9.计算顶点()2,1,1A -、()5,5,4B 、()3,2,1C -、()4,1,3D 的四面体的体积.解{}3,6,3AB = ,{}1,3,1AC =- ,{}2,2,2AD =,则四面体的体积为36311132366222V ABAC AD ⎡⎤==-=⎣⎦ .10.如果存在向量c同时满足11a c b ⨯= ,22a c b ⨯= ,证明:12210a b a b ⋅+⋅= .证由于()()12211221a b a b a a c a a c ⋅+⋅=⋅⨯+⋅⨯ ()()2112a c a a c a =⨯⋅+⨯⋅ [][]2112a ca a ca =+ [][]21210a ca a ca =-=习题8-3.1.求出满足下列条件的各平面方程:(1)过点()2,1,1-且与平面32120x y z -+-=平行;(2)过三点()1,1,1-、()2,2,2--、()1,1,2-;(3)过点()2,1,2,且分别垂直于平面32x y z ++=和平面3241x y z +-=;(4)平行x 轴且过两点()1,0,1和()1,1,0;(5)通过z 轴和点()3,1,2-.解(1)设所求平面的法向量n ,可取平面的法向量为{}3,2,1n =-故过点()2,1,1-平面方程为()()()322110x y z ---++=,即3230x y z -+-=;(2)由三点式平面方程知,所求平面方程为1113330023x y z --+--=-即320x y z --=;(3)设所求平面的法向量n ,{}11,3,1n = ,{}23,2,4n =-{}1213114,7,7324i j kn n n =⨯==---,则所求平面方程为()()()14271720x y z --+---=,即250x y z -+-=;(4)设平面的一般式方程为0Ax By Cz D +++=,由于平面平行x 轴,且点()1,0,1、()1,1,0在平面上,从而有000A A C D A B D =⎧⎪++=⎨⎪++=⎩解得0A =,B D =-,C D =-,且0D ≠,故平面方程为10y z +-=;(5)设过z 轴的平面为0Ax By +=,且点()3,1,2-在平面上,则由30A B -=,得3B A =,且0A ≠所以平面方程为30x y +=.2.求平面2260x y z -++=与各坐标面的夹角的余弦.解平面的法向量{}2,2,1n =- ,取xoy 坐标面的法向量{}10,0,1n =,yoz 坐标面的法向量{}21,0,0n = ,zox 坐标面的法向量{}30,1,0n =,则平面与xoy 、yoz 、zox 各坐标面的夹角余弦分别为1cos 3α=,2cos 3β=,22cos 33γ-==.3.求过点()0,1,0-和()0,0,1,且与xoy 坐标面成3π角的平面.解设平面的一般式方程为0Ax By Cz D +++=,从而有0,0,cos ,3B D C D π⎧⎪-+=⎪⎪+=⎨⎪⎪=⎪⎩得,A B D C D ⎧=⎪=⎨⎪=-⎩于是,所求平面方程为10y z +-+=.4.在z 轴上求一点P ,使它到点()1,2,0M -与到平面:32690x y z π-+-=有相等的距离.解设z 轴上点()0,0,P z,则PM =又()1,2,0M -到:3269x y z π-+-=的距离为697z d -=则有697z -=,即2131081640z z ++=,解得2z =-或8213z =-,故所求点为()0,0,2-或820,0,13⎛⎫-⎪⎝⎭.5.试求平面270x y z -+-=与平面2110x y z ++-=的夹角平分面的方程.解设(),,M x y z 为该平面上任取的一点,那么M到两平面的距离相等,即有于是有()27211x y z x y z -+-=±++-故所求平面方程为240x y z --+=或60x z +-=.6.设从原点到平面1x y za b c++=的距离为ρ,试证明:22221111a b c ρ++=,并由此求点(),,a b c 到该平面的距离.证由点到平面的距离公式知ρ=1ρ=,即22221111a b c ρ++=.点(),,a b c到平面的距离2d ρ=.7.判别平面:3210x y z π+-+=与下列各平面之间的位置关系:(1)1:3210x y z π+--=;(2)2:520x y z π-++=;(3)3:2310x y z π-+-=.解(1)取平面π法向量{}1,3,2n =- ,1π法向量{}11,3,2n =-,由于n与1n 的坐标成比例,故n 与1n平行,且d ==;(2)取平面2π法向量{}25,1,1n =-,由于20n n ⋅= ,故2n n ⊥,即两平面相互垂直;(3)取平面3π法向量{}32,3,1n =-,两平面夹角余弦339cos 14n n n n θ⋅==所以两平面斜交,夹角9arccos14θ=.习题8-4.1.求满足下列条件的各直线方程:(1)过两点()13,2,1M -和()21,0,2M -;(2)过点()4,2,1-且平行于直线230,510,x y y z --=⎧⎨--=⎩平行;(3)过点()1,2,2-且垂直于平面3210x y z +-+=.解(1)直线的方向向量可取{}124,2,1s M M ==-于是直线方程为321421x y z -+-==-,(2)直线的方向向量可取{}1202,1,5051i j k s =-=-则直线方程为421215x y z -+-==;(3)平面法向量{}3,2,1n =- ,直线的方向向量可取{}3,2,1sn ==-于是直线方程为122321x y z -+-==-.2.用对称式方程和参数方程表示下列直线10,2340.x y z x y z +++=⎧⎨-++=⎩解直线的方向向量{}1114,1,3213ij k s ==---,可在直线上取一点()1,0,2A -,则直线的对称式方程和参数方程分别为12413x y z -+==--,14,4,2 3.x t y z t =+⎧⎪=-⎨⎪=--⎩3.求过点()0,1,2M 且与直线11112x y z --==-垂直相交的直线方程.解过点()0,1,2M 且垂直直线L 的平面方程为()()()01220x y z ---+-=即230x y z -+-=解方程组230,11,112x y z x y z -+-=⎧⎪⎨--==⎪⎩-,得直线与平面的交点为131,,122M ⎛⎫⎪⎝⎭由此可得121,,122s MM ⎧⎫==--⎨⎬⎩⎭,故所求直线方程为12312x y z --==--.4.求直线240,3290.x y z x y z -+=⎧⎨---=⎩在平面41x y z -+=上的投影直线的方程.解设过直线240,3290.x y z x y z -+=⎧⎨---=⎩的平面束方程为()()243290x y z x y z λ-++---=,(λ为非零常数)即()()()2341290x y z λλλλ+-++--=,上述平面法向量为{}23,4,12n λλλ=+--- ,已知平面法向量为{}14,1,1n =-选择λ使1n n ⊥,即()()()()234411210λλλ+⋅-+⋅-+-⋅=,解得1311λ=-故得与已知平面垂直的平面为1731371170x y z +--=则所求投影直线为1731371170,4 1.x y z x y z +--=⎧⎨-+=⎩5.求过点()3,1,2M -且通过直线43521x y z-+==的平面方程.解()4,3,0P -为直线上的一点,直线的方向向量为{}5,2,1s =,则平面的法向量{}1428,9,22521i j kn MP s =⨯=-=- 故所求平面方程为()()()83912220x y z --+-++=即8922590x y z ---=.6.已知平面220x y z +--=及平面外一点()2,1,4M -,求点M 关于已知平面的对称点N .解过点()2,1,4M -且垂直于平面220x y z +--=的直线方程为214121x y z +--==-设M 关于已知平面的对称点(),,N x y z ,则有214,121x y z +--⎧==⎪-⎪=解得0,5,2,x y z =⎧⎪=⎨⎪=⎩即对称点()0,5,2N .7.设0M 是直线L 外一点,M 是直线L 上任意一点,且直线的方向向量为s ,试证:点0M 到直线L 的距离为0d ⨯=MM s s.证设向量0MM 与直线L 的方向向量s 的夹角为θ,则00000sin MM s MM s MM MM MM ssd θ⨯⨯==⋅=.8.求点()03,1,2M -到直线10,240,x y z x y z +-+=⎧⎨-+-=⎩的距离.解直线的方向向量{}1110,3,3211=-=---ij ks ,在直线上取一点()1,2,0M -,则{}02,1,2=---MM ,{}02123,6,6033⨯=---=----i j kMM s 所以0322d ⨯===MM s s.习题8-51.指出下列方程在平面解析几何中和空间解析几何中分别表示什么图形:(1)1x y +=;(2)22y x =;(3)222x y R +=;(4)22149x y -=.解(1)在平面解析几何表示直线,空间解析几何中表示平面;(2)在平面解析几何表示抛物线,空间解析几何中表示抛物柱面;(3)在平面解析几何表示圆,空间解析几何中表示圆柱面;(4)在平面解析几何表示双曲线,空间解析几何中表示双曲柱面.2.说明下列旋转曲面是怎样形成的:(1)2221x y z --=;(2)()222z a x y -=+.解(1)将xoy 平面上双曲线221x y -=绕x 轴旋转一周;(2)将yoz 平面上直线z y a =+绕z 轴旋转一周.3.根据常数k 的不同取值,分别讨论下列方程所表示的曲面是什么曲面.(1)22x ky z +=;(2)222x y z k +-=.解(1)当0k >时,为椭圆抛物面,特别地当1k =时为旋转抛物面,当0k =时,为抛物柱面,当0k <时,为双曲面;(2)当0k >时,为旋转单叶双曲面,当0k =时,为圆锥面,当0k <时,为旋转双叶双曲面.4.作出下列曲面所围成的图形:(1)22,1z x y z =+=;(2)z =,z ;(3)0x =,0y =,0z =,1x y +=,226x y z +=-;(4)2y x =,1x y z ++=,0z =.解(1)见图8-4;(2)见图8-5(图8-4)(图8-5)(3)见图8-6;(4)见图8-7(图8-6)(图8-7)习题8-61.将空间曲线222,:1,z x y x z ⎧=+Γ⎨+=⎩转换成母线平行于坐标轴的柱面的交线方程.解曲线Γ等价于212,1,y x x z ⎧=-⎨+=⎩,表示母线平行于z 轴的柱面212y x =-与母线平行于y 轴的柱面1x z +=的交线,或等价于221,1,y z x z ⎧=-⎨+=⎩,表示母线平行于x 轴的柱面221y z =-与母线平行于y 轴的柱面1x z +=的交线.2.将下列曲线的一般方程转化为参数式方程:(1)()22221,11,z x y x y ⎧=--⎪⎨-+=⎪⎩(2)2229,,x y z y x ⎧++=⎨=⎩.解(1)曲线的参数方程为1cos ,sin ,2sin ,2x t y t t z ⎧⎪=+⎪=⎨⎪⎪=⎩(02t π≤≤);(2)曲线的参数方程为,,3sin ,2x t y t t z ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩(02t π≤≤).3.试分别确定常数,,B C D 的各组值,使得平面0By Cz D ++=与圆锥面222z x y =+的截痕为:(1)一点;(2)一条直线;(3)两条相交直线(4)圆;(5)双曲线.解(1)取0B D ==,1C =,则平面0z =与圆锥面的截痕为一点()0,0,0;(2)取1B C ==,0D =,则平面0y z +=与圆锥面的截痕为一条直线0,0;y z x +=⎧⎨=⎩(3)取1B =,0C D ==,则平面0y =与圆锥面的截痕为为两条直线0,,y z x =⎧⎨=⎩和0,;y z x =⎧⎨=-⎩(4)取0B =,1C =,1D =-,则平面1z =与圆锥面的截痕为圆221,1;x y z ⎧+=⎨=⎩(5)取1B =,0C =,1D =-,则平面1y =与圆锥面的截痕为为双曲线221,1;z x y ⎧-=⎨=⎩4.求下列曲线在三个坐标面上的投影曲线方程:(1)22,1;z x y z x ⎧=+⎨=+⎩(2)cos ,sin ,2.x y z θθθ=⎧⎪=⎨⎪=⎩解(1)消去z 得曲线在xoy 面投影曲线方程:2210,0;y y x z ⎧+--=⎨=⎩消去x 得曲线在yoz 面投影曲线方程:22310,0;y z z x ⎧+-+=⎨=⎩消去y 得曲线在zox 面投影曲线方程:1,0;x z y +=⎧⎨=⎩(2)消去z 得曲线在xoy 面投影曲线方程:221,0;x y z ⎧+=⎨=⎩消去x 得曲线在yoz 面投影曲线方程:sin20;z y x ⎧=⎪⎨⎪=⎩消去y 得曲线在zox 面投影曲线方程:cos ,20.z x y ⎧=⎪⎨⎪=⎩5.求由旋转抛物面22z x y =+与222z x y =--围成的立体在三个坐标面上的投影区域.解立体在xoy 面投影区域(){}22,1xy D x y xy =+≤,立体在yoz 面投影区域(){}22,2,11yz D y z yz y y =≤≤--≤≤,立体在zox 面投影区域(){}22,2,11zx D x z xz x x =≤≤--≤≤总复习题八1.填空题(1)设()2a b c ⨯⋅= ,则()()()a b b c c a ⎡⎤+⨯+⋅+=⎣⎦;(2)设{}2,1,2a = ,{}4,1,10b =- ,c b a λ=- ,且a c ⊥,则λ=;(3)yoz 平面的圆()222,0,y b z a x ⎧-+=⎪⎨=⎪⎩(0b a >>)绕z 轴旋转一周所得环面的方程为;(4)点()2,1,0M 到平面3450x y z ++=的距离d=;(5)设有直线1158:121x y z L --+==-与26,:23,x y L y z -=⎧⎨+=⎩则1L 与2L 的夹角为.(1)答案“4”.解()()()()24a b b c c a a b c ⎡⎤+⨯+⋅+=⨯⋅=⎣⎦;(2)答案“3”.解{}42,1,102c b a λλλλ=-=---- ,由a c ⊥ ,()()()2421121020λλλ⋅-+⋅--+⋅-=,解得3λ=;(3)答案“()()2222222224x y z b a b x y +++-=+”.解绕z轴旋转环面的方程为()222b z a -+=,即222222x y b z a +±++=所以()()2222222224x y z b a b x y +++-=+(4)答案解d ;(5)答案“3π”.解1L 和2L 的方向向量分别为{}11,2,1s =-和{}21,1,2s =-- 则12121cos 2s s s s θ⋅== ,3πθ=.2.选择题(1)直线11:213x y z L +-==-与平面:1x y z π--=的关系为();(A )L 在π上(B )L 平行π但L 不在π上(C )L π⊥(D )一般斜交(2)两条直线111:201x y z L --==-与22:112x y z L +==的关系为();(A )平行(B )相交但不垂直(C )垂直相交(D )异面直线(3)直线方程23,1,x y z x y z --=⎧⎨+-=⎩可化为();(A )21213x y z -+==-(B )114213x y z +++==-(C )12213x y z ++==(D )122213x y z -+-==-(4)旋转曲面22z x y =+不是由平面曲线()旋转而成的.(A )2,0,z y x ⎧=⎨=⎩绕z 轴(B )2,0,z x y ⎧=⎨=⎩绕z 轴(C )2,,z xy x y =⎧⎨=⎩绕z 轴(D ),,z xy x y =⎧⎨=⎩绕z 轴.(1)答案选(B ).解直线L 的方向向量{}2,1,3s =-,()1,0,1M -为直线L 上一点,平面π的法向量为{}1,1,1n =--,显然0s n ⋅=,且点()1,0,1M -不在平面π上,故L 平行π但L 不在π上;(2)答案“C ”.解1L 、2L 的方向向量分别为{}12,0,1s =- 、{}21,1,2s = ,则120s s ⋅=,直线1L 与2L 垂直,又()11,1,0M 、()20,0,2M -分别为1L 、2L 上的点,且12122011120112s s M M -⎡⎤==⎣⎦---,即1L 、2L 在同一平面上;(3)答案选(C ).解直线的方向向量{}2112,1,3111i j k s =--=-,()0,1,2--为直线上一点,故选(C );(4)答案选(D ).解在曲线,:,z xy L x y =⎧⎨=⎩上任取一点()0000,,M x y z ,设(),,M x y z 是0M 绕z 轴旋转轨迹上任一点,则有20000,z z x y x ⎧===⎪==故得旋转曲面方程为()2212z x y =+.3.已知2c a b =+ ,d a b λ=+ ,2a = ,1b = ,且a b ⊥,求:(1)λ为何值时,c d ⊥;(2)λ为何值时,以,c d为邻边所围成的平行四边形的面积为6.解(1)由于c d ⊥ ,则0c d ⋅=,即()()22220a b a b a b λλ+⋅+=+= 解得2λ=-;(2)由题设条件知6c d ⨯=而()()()22c d a b a b a bλλ⨯=+⨯+=-⨯则有()22sin 222c d a b a b πλλλ⨯=-⨯=-=- 所以226λ-=,5λ=或1λ=-.4.设一平面通过从点()1,1,1-到直线10,0,y z x -+=⎧⎨=⎩的垂线,且与平面0z =垂直,求此平面方程.解过点()1,1,1M -且与直线10,:0,y z L x -+=⎧⎨=⎩垂直的平面1π的方程为()()()0111110x y z ⋅-+⋅++⋅-=,即y z +=解方程组10,0,0,y z x y z -+=⎧⎪=⎨⎪+=⎩得直线L 与平面1π的交点1110,,22M ⎛⎫ ⎪⎝⎭,平面0z =的法向量{}10,0,1n = ,则所求平面的法向量可取为111001,1,0211122ij kn n M M ⎧⎫=⨯==⎨⎬⎩⎭-所以所求平面方程为()()11102x y -++=,即210x y ++=.5.求通过直线3220,260,x y x y z -+=⎧⎨--+=⎩且与点()1,2,1的距离为1的平面方程.解设过直线3220,260,x y x y z -+=⎧⎨--+=⎩的平面束方程为()()322260x y x y z λ-++--+=(λ为非零常数)即()()321260x y z λλλλ+-+-++=,由点()1,2,1到平面的距离为1,即1d =解得2λ=-或3λ=-,所以所求平面方程为22100x y z ++-=或43160y z +-=.6.在xoy 面上求过原点,且与直线x y z ==的夹角为3π的直线方程.解设所求直线L 方程为,0,y Ax z =⎧⎨=⎩即10x y zA ==,直线L 的方向向量{}1,,0s A= 由题意知1cos32π==,得4A =-于是,所求直线方程为(40,0,xy z ⎧+=⎪⎨=⎪⎩或(40,0.x y z ⎧+=⎪⎨=⎪⎩7.求通过点()1,2,3--,平行于平面62350x y z --+=,且又与直线13x -=1325y z +-=-相交的直线方程.解过点()1,2,3M--作已知平面的平行平面,此平面方程为()()()6122330x y z +---+=即62310x y z --+=求此平面与已知直线的交点,由62310,113,325x y z x y z t --+=⎧⎪-+-⎨===⎪-⎩解得0t =,交点为()01,1,3M -,故所求直线的法向量为{}02,3,6s MM ==-所求直线方程为123236x y z +-+==-.8.确定常数k 的值,使得平面y kz =与椭球面222241xy z ++=的交线为圆.解平面与椭球面的交线222241,:,x y z y kz ⎧++=Γ⎨=⎩等价于方程组()22222241,:,x y k z y kz ⎧++-=⎪Γ⎨=⎪⎩要使交线为圆,只须242k-=,即k =,交线为2221,2.x y z y ⎧++=⎪⎨⎪=⎩9.求曲面2221x y z ++=和()()222111x y z -+-+=的交线在yoz 平面上的投影曲线方程.解由题设两曲面的方程消去x ,得交线在yoz 平面上的投影柱面方程22220y y z -+=所求投影曲线方程为22220,0.y y z x ⎧-+=⎨=⎩10.求两曲面22z x =与z =所围立体在三个坐标面上的投影区域.解两曲面的交线在xoy 面上的投影柱面为()2211x y -+=,则投影区域为()(){}22,11xy D x y x y =-+≤,两曲面的交线在yoz 面上的投影柱面为222112z y ⎛⎫-+=⎪⎝⎭,则投影区域为()222,112yz z D y z y ⎧⎫⎛⎫⎪⎪=-+≤⎨⎬ ⎪⎝⎭⎪⎪⎩⎭,两曲面的交线在zox 面上的投影柱面为z 和z x =,则投影区域为(){,zx D x z x z =≤≤.11.画出下列曲面所围立体的图形:(1)22z xy =+,1x =,1y =,0z =;(2)z xy =,0z =,1x y +=;(3)22z xy =+,2y x =,1y =,0z =;(4)2y x =,212y x =,1x z +=,0z =.解(1)见图8-8;(2)见图8-9;(图8-8)(图8-9)(3)见图8-10;(4)见图8-11.(图8-10)(图8-11)习题9-11指出下列平面点集中,那些是开集、闭集、有界集、连通集、开区域以及闭区域?并分别求其聚点和边界点:(1)22{(,)|0<1}x y x +y <;(2){(,)|}x y y x >;(3){(,)|2,2,2}x y x y x y ≤≤+≥;(4)2222{(,)|1}{(,)|(1)1}x y x y x y x y +>⋂+-≤.解(1)为有界开区域;聚点为集合22{(,)|1}x y x +y ≤,边界点为集合22{(,)|=1}{(0,0)}x y x +y ⋃;(2)为无界的开区域;聚点为集合{(,)|}x y y x ≥,边界点为集合{(,)|,}x y y x x =-∞<<+∞;(3)为有界闭区域;聚点集合为该区域上所有点,边界点集合为三个直线段{(,)|2,02}x y x y =≤≤与{(,)|2,02}x y y x =≤≤及{(,)|2,02}x y x y x +=≤≤的并集;(4)为有界连通集合;聚点为2222{(,)|1}{(,)|(1)1}x y x y x y x y +≥⋂+-≤,边界点为圆弧221{(,)|1,2x y x y y +=≥及圆弧221{(,)|(1)1,}2x y x y y +-=≥的并集.2.证明:点0P 为点集E 的聚点的充分必要条件是点0P 的任意邻域内都至少含有一个点集E 中异于0P 的点.证明:“⇒”由聚点的定义即可得;“⇐”取101(,){|01}U P P P P δδ=<<=(其中0P P 表示点0P 与点P 的距离),则111(,)P U P E δ∃∈⋂,记20112P P δ=,则202(,)P U P E δ∃∈⋂ ,依此类推,由数学归纳法可知对于每个正整数n ,均可取到点01101111(,),22n n n n n P U P E P P δδ----∈⋂=≤ ,由此可得一个两两均不相同的点列{}n P ,若0δ>,因lim 0n n δ→∞=,则k δ∃使得k δδ<,那么当n k ≥时必有0(,)n P U P δ∈,即在0(,)U P δ中比含有集合E 的无穷多个点,因此点0P 为点集E 的聚点.3.求下列各函数值:(1)设22(,)2x y f x y xy-=,求(,1)x f y ;(2)设22(,)y xf x y x y xye =+-,求(,)f tx ty ;(3)设(,)3f x y x y =+,求(,(,))f x f x y ;(4)设(,,)v u v f u v w u w +=+,求(,,)f x y x y xy +-;(5)设22(,)y f x y x y x+=-,求(,)f x y .解(1)2221(,1)(,)22x y x x y f f x y x y xy y⎛⎫- ⎪-⎝⎭===;(2)222222(,)(,)yxf tx ty t x t y t xye t f x y =+-=;(3)(,(,))3(3)49f x f x y x x y x y =++=+;(4)2(,,)()()x y x f x y x y xy x y xy -+-=++;(5)设,,,11y u uv u x y v x y x v v =+===++,222(1)(,)111u uv u v f u v v v v -⎛⎫⎛⎫=-=⎪ ⎪+++⎝⎭⎝⎭,2(1)(,)1x y f x y y-=+.4.设1)z f =+-,若当1y =时,z x =,求函数()f u 及(,)z z x y =的表达式.解由题设有11),1)1x f f x =+=-,令1u =,则2(1)x u =+,所以有2()2f u u u =+,相应的有(,)1z z x y x ==-.5.求下列函数的定义域:(1)(,)f x y =;(2)(,)ln()f x y y x =-+;(3)22221(,)arcsin 4x y f x y x y+=+-;(4)(,,)f x y z =解(1){(,)|}D x y y x y =-<<;(2)22{(,)|0,,1}D x y x y x x y =≥>+<;(3)22{(,)|4,}D x y x y y x =+≤≠;(4)222{(,,)|1,D x y z x y z z =++<>.习题9-21.证明:2222001lim()sin0x y x y x y →→+=+.证明0ε∀>,因为2222221()sinx y x y x y+≤++,取δ=当0δ<<时,则有2222221()sin 0x y x y x y ε+-≤+<+,因此有2222001lim()sin 0x y x y x y →→+=+.2.求下列极限:(1)201ln()lim 2x x y e y x y →→++;(2)220x y →→(3)100lim(1sin )xyx y xy →→-;(4)22()lim ()x y x y x y e-+→+∞→+∞+解(1)原式0ln(1)ln 21e +==;(2)原式220220lim 21()2x y x y x y →→+==--+;(3)原式sin 11sin 00lim (1sin )xyxyxyx y xy e ---→→⎡⎤=-=⎢⎥⎢⎥⎣⎦;(4)原式222()()lim (2),lim lim 0,lim lim 0u x y x y x y x y u x y x x x x y y y x y x y x y u x ye e e e e e e =+++→+∞→+∞→+∞→+∞→+∞→+∞→+∞++=-⋅======,原式0=.3.证明下列极限不存在:(1)22400lim x y xy x y →→+;(2)2222200lim ()x y x y x y x y →→+-.解(1)当取点(,)P x y 沿曲线2:C y kx =趋于点(0,0)O 时则有222422000lim lim 1x x y xy kx k x y x kx k →→→==+++,k 取值不同,则该极限值不同,因此该极限不存在;(2)当取点(,)P x y 沿直线y x =趋于点(0,0)O 时则有2222200lim 1()x y x y x y x y →→=+-,而当取点(,)P x y 沿直线0y =趋于点(0,0)O 时则有2222200lim 0()x y x y x y x y →→=+-,因沿不同方向取极限,则该极限值不同,故该极限不存在.4.讨论下列函数的连续性:(1)22(,)y xf x y y x+=-;(2)22,(,)(0,0),(,)0,(,)(0,0);xyx y x yf x y x y ⎧≠⎪+=⎨⎪≠⎩(3),)(0,0),(,)0,(,)(0,0);x y f x y x y ≠=≠⎩(4)(,,)f x y z =.解(1)函数的定义域为2{(,)|}D x y y x =≠,它在D 内处处连续,抛物线2:C y x =上的点均为它的间断点;(2)函数在全平面内处处有定义,它在区域{(,)|(,)(0,0)}D x y x y =≠内处处连续,由于00lim (,)x y f x y →→不存在,故(0,0)O 是它的间断点;(3)当(,)(0,0)x y ≠时,函数显然是连续的,又00lim0(0,0)x y f →→==,所以它在(0,0)O 处也连续,因此该函数在全平面内处处连续;(4)函数(,,)f x y z 的定义域为222{(,,)|14}x y z x y z Ω=<++<,在定义域内(,,)f x y z处处连续,在球面2221x y z ++=及2224x y z ++=上函数间断.5.设二元函数(,)f x y 在有界闭区域E 上连续,点(,),1,2,,i i x y E i n ∈=⋅⋅⋅,证明至少存在一点(,)E ξη∈,使得1122(,)(,)(,)(,)n n f x y f x y f x y f nξη++⋅⋅⋅+=.证明令112211(,)min{(,)},(,)max{(,)}i i i i i i i i i ni nm f x y f x y M f x y f x y ≤≤≤≤====,则有(,),1,2,,i i m f x y M i n≤≤=⋅⋅⋅,由此可得1(,)ni i i mn f x y Mn=≤≤∑,即1(,)niii f x y m M n=≤≤∑.(1)若m M =,则1122(,)(,)(,)n n f x y f x y f x y ==⋅⋅⋅=,取11(,)(,)x y ξη=即可;(2)若m M <,则有1(,)niii f x y m M n=<<∑,由连续函数介值定理知至少存在一点(,)E ξη∈,使得1122(,)(,)(,)(,)n n f x y f x y f x y f nξη++⋅⋅⋅+=.习题9-31.求下列函数的一阶偏导数:(1)2tan()cos ()z x y xy =++;(2)arctanx yz x y+=-;(3)ln(z x =+;(4)(1)yz xy =+.解(1)22sec ()2cos()sin()sec ()sin(2)zx y y xy xy x y y xy x∂=+-=+-∂,由对称性可知2sec ()sin(2)zx y x xy y ∂=+-∂;(2)22222212,()1zy y z xxx y x y y x yx y x y ∂--∂=⋅==∂-+∂+⎛⎫++ ⎪-⎝⎭;(3)z z xy ∂∂==∂∂;(4)21(1),(1)[ln(1)]1y y z z xyy xy xy xy x y xy-∂∂=+=+++∂∂+.2.求下列函数在指定点的偏导数:(1)(,)sin(2)xf x y ex y -=+,求(0,)4x f π'及(0,)4y f π';(2)22(,)(2)arccos f x y x y x =++-,求(2,)y f y '.解(1)(0,)4(0,)[(cos(2)sin(2)]1,(0,)044x x y f e x y x y f πππ-''=+-+=-=;(2)()2(2,)42y f y yy ''=+=.3.求下列函数的二阶偏导数:(1)2cos ()z ax by =+;(2)z =;(3)arctan 1x yz xy+=-;(4)z yu x =,求2ux z ∂∂∂及22u y ∂∂.解(1)2cos()sin()sin 2(),sin 2()z za ax by ax by a ax byb ax by x y∂∂=-++=-+=-+∂∂,22222222cos 2(),2cos(),2cos 2()z z z a ax by ab ax by b ax by x x y y ∂∂∂=-+=-+=-+∂∂∂∂.(2)2222222222222222,,,()()z x z y z y x z xy x x y x x y x x y x y x y ∂∂∂-∂-====∂+∂+∂+∂∂+,2222222()z x y y x y ∂-=∂+;(3)22211()1(1)111z xy y x y xxy x x y xy ∂-++=⋅=∂-+⎛⎫++ ⎪-⎝⎭,由对称性可知211z y y ∂=∂+,22222222222,0,(1)(1)z x z z yx x x y y y ∂-∂∂-===∂+∂∂∂+;(4)2222112224ln ln 2ln ln ,,,zzzzy y y yu z u y z x u z x u yz x z x x x x x x y x z y y y y y --∂∂+∂∂+===-=∂∂∂∂∂.4.求下列函数的指定高阶偏导数:(1)ln()z x xy =,求32z x y ∂∂∂及32z x y ∂∂∂;(2)u x y z αβγ=,求3ux y z∂∂∂∂.解(1)23232222111ln()1,,0,,z z z z z xy x x x x y x y y x y y∂∂∂∂∂=+====-∂∂∂∂∂∂∂∂;(2)23111111,,u u u x y z x y z x y z x x y x y zαβγαβγαβγααβαβγ------∂∂∂===∂∂∂∂∂∂.5.设322,(,)(0,0),(,)20,(,)(0,0),xy x y f x y x y x y ⎧≠⎪=+⎨⎪=⎩求(0,0)xyf ''及(0,0)yx f ''.解(,0)(0,0)(0,0)lim0,0x x f x f f y x →-'==≠时,0(,)(0,)1(0,)lim 2x x f x y f y f y y x →-'==,(0,)(0,0)1(0,0)lim 2x x xyy f y f f y →''-''==,0(0,)(0,0)(0,0)lim 0,0y x f y f f x y→-'==≠时,0(,)(,0)(,0)lim 0y y f x y f x f x y →-'==,0(,0)(0,0)(0,0)lim 0y y yx x f x f f x→''-''==.6.已知二元函数(,)z z x y =在区域{(,)|0}D x y x =>内有定义,且满足3,(1,)cos z x y z y y x x∂+==∂,试求(,)z x y .解由3z x yx x∂+=∂可得31(,)ln ()3z x y x y x C y =++,由(1,)cos z y y =可得1()cos 3C y y =-,因而31(,)(1)ln cos 3z x y x y x y =-++.7.分别讨论下列函数在点的连续性和可偏导性:(1)222,(,)(0,0),(,)0,(,)(0,0);xy x y f x y x y x y ⎧≠⎪=+⎨⎪=⎩(2)(,)f x y =(3)2222,(,)(0,0),(,)1,(,)(0,0).x y x y f x y x yx y ⎧-≠⎪=+⎨⎪=⎩解(1)因为22212xy y x y ≤+,所以22200lim 0x y xy x y →→=+,因此该函数在点(0,0)处连续,又[][]0(0,0)(,0)0,(0,0)(0,)0x y x x f f x f f y ==''''====,因而该函数在(0,0)处存在偏导数;(2)因00(0,0)x y f →→==,因而该函数在点(0,0)处连续,而0(0,0)limx x x f x→'=不存在,同理(0,0)y f '也不存在,因而该函数在(0,0)处不存在偏导数;(3)当取点(,)P x y 沿直线y kx =趋于点(0,0)O 时,则有222222001lim 1x y x y k x y k →→--=++,由于k 取不同值时,上述极限不一样,故222200lim x y x y x y →→-+不存在,因而该函数点(0,0)处不连续,(,0)(0,0)(0,)(0,0)(0,0)lim0,(0,0)limx y x y f x f f y f f f xy→→--''===∞,故在点(0,0)处偏导数(0,0)x f '存在,而偏导数(0,0)y f '不存在.8.考察函数2244,(,)(0,0),(,)0,(,)(0,0),x y x y f x y x y x y ⎧≠⎪=+⎨⎪=⎩并回答下列问题:(1)(,)f x y 在点(0,0)处是否有二阶偏导数;(2)(,)x f x y '与(,)y f x y '在点(0,0)处是否连续.解(1)2444422(3),(,)(0,0),(,)()0,(,)(0,0),x xy x y x y f x y x y x y ⎧-≠⎪'=+⎨⎪≠⎩2444422(3),(,)(0,0),(,)()0,(,)(0,0),y x y y x x y f x y x y x y ⎧-≠⎪'=+⎨⎪≠⎩0(,0)(0,0)(0,0)lim 0x x xx y f x f f x →''-''==0(0,)(0,0)(0,0)lim 0y yyy f y f f y→''-''==,0(0,)(0,0)(0,0)lim 0x x xyy f y f f y→''-''==.(2)当取点(,)P x y沿直线(y kx k =≠趋于点(0,0)O 时则有2442444242000002(3)2(13)lim (,)lim lim ()(1)x x x x y y xy x y k k f x y x y x k →→→→→--'===∞++,故(,)x f x y '在点(0,0)处不连续,同理可证(,)y f x y '点(0,0)处也不连续.9.设arctan y u z x =,证明2222220u u ux y z∂∂∂++=∂∂∂.证明222221,1uy yz z y xx x y x∂--=⋅⋅=∂++222222()u xyz x x y ∂=∂+,同理有222222()u xyzy x y ∂-=∂+,22arctan ,0u y uz x z∂∂==∂∂,所以有2222222222222200()()u u u xyz xyz x y z x y x y ∂∂∂++=-+=∂∂∂++.10.证明:如果(,)f x y 在区域D 内偏导数(,)x f x y '与(,)y f x y '有界,则函数(,)f x y 在区域D 内连续.证明因为(,)x f x y '与(,)y f x y '在D 内有界,所以0M ∃>,对(,)x y D ∀∈均有(,),(,)x y f x y M f x y M ''≤≤,设000(,)P x y D ∈,则0δ∃>,当ρδ=<时有00(,)x x y y D +∆+∆∈,记100200(,),(,)P x x y P x x y y +∆+∆+∆,则线段01P P 与12PP 必完全属于D 内,由Lagrange 中值定理知0000(,)(,)f x x y y f x y +∆+∆-00000000[(,)(,)][(,)(,)]f x x y y f x x y f x x y f x y =+∆+∆-+∆++∆-001020(,)(,)y x f x x y y y f x x y x θθ''=+∆+∆∆++∆∆,0000(,)(,)()f x x y y f x y M x y +∆+∆-≤∆+∆,由夹逼准则可知00000lim[(,)(,)]0x y f x x y y f x y ∆→∆→+∆+∆-=,即函数(,)f x y 在点000(,)P x y 处连续,由点000(,)P x y 的任意性可知,函数(,)f x y 在区域D 内处处连续.习题9-41.求函数22z x xy y =+-在点000(,)P x y 处当自变量,x y 分别取得增量,x y ∆∆时相应的全增量及全微分.解222200000000()()()()()z x x x x y y y y x x y y ∆=+∆++∆+∆-+∆--+2200000000(2)(2),d (2)(2)x y x x y y x x y y y x y x x y y =+∆+-∆+∆+∆∆-∆=+∆+-∆.2.求下列函数的全微分:(1)yz yx =;(2)arctan y z x=;(3)2222x y z x y-=+;(4)u =.解(1)21d d (1ln )d y y z y x x x x y -=++;(2)22d d d y x x yz x y -+=+;(3)2224(d d )d ()xy y x x y z x y -=+;(4)d u =3.试证:(,)f x y =在点(0,0)处连续,偏导数存在,但不可微.证明000(0,0)x y f →→==,因而函数(,)f x y 在点(0,0)处连续,00(,0)(0,0)(0,)(0,0)(0,0)lim0,(0,0)lim 0x y x y f x f f y f f f x y→→--''====,因而函数(,)f x y 在点(0,0)处偏导数存在,又00limx x y y →→→→''---=不存在,故该函数在点(0,0)处不可微.4.设221sin ,(,)(0,0),(,)0,(,)(0,0).xy x y x y f x y x y ⎧≠⎪+=⎨⎪=⎩证明:(1)(0,0),(0,0)x y f f ''存在;(2)(,),(,)x y f x y f x y ''在点(0,0)处不连续;(3)(,)f x y 在点(0,0)处可微.解(1)00(,0)(0,0)(0,)(0,0)lim0,(0,0)lim 0y x y f x f f y f f x y→→--'====,因此(0,0)x f ',(0,0)y f '存在;(2)222222220000121lim (,)lim[sin cos ]()x x x y y x y f x y y x y x y x y →→→→'=-+++不存在,因而(,)x f x y '在(0,0)处不连续,又222222220000121lim (,)lim[sin cos ]()y x x y y xy f x y x x y x y x y →→→→'=-+++不存在,因此(,)x f x y '在(0,0)处也不连续;(3)22001sin lim0x x y y xy x y →→→→''---==,因而函数(,)f x y 在点(0,0)处可微.5的近似值.解令22(,)(,)(,)x y f x y f x y f x y ''===,则有(1.02,1.97)(1,2)(1,2)0.02(1,2)(0.03)x y f f f f ''=≈+⨯+⨯-130.022(0.03) 2.952=+⨯+⨯-=.6.设有一无盖的圆柱形容器,容器的壁与底厚均为0.1cm ,内高为20cm ,内半径为4cm ,求容器外壳体积的近似值.解若圆柱体的底半径为r ,高为h ,则体积为2V hr π=,223d 22 3.144200.1 3.1440.155.3cm V V rh r r h ππ∆≈=∆+∆=⨯⨯⨯⨯+⨯⨯=.。
华东理工 高等数学 作业解答 第14章

,其中 L 是从 O(0,0)沿曲线
,到 B (0,2).
108
x dx 2 xydy ,其中 L 是由 y x 与 y x 2 构成的简单闭曲线. x 1 x 解: dx 2 xydy L x 1 1 0 x x ( 4 x 4 )dx ( x)dx 0 x 1 1 x 1
教学内容: § 14.2 格林公式(续) 1. 选择题
114
**(1) 曲线积分
的值
(
)
(A) 与曲线 L 及起点、终点均有关; (B) 与曲线 L 无关,仅与其起点及终点有关; (C) 与曲线 L 及起点无关,仅与终点无关; (D) 与曲线 L 及起点终点都无关. 答: (B)
**(2) 设 C 是从 A (1,1)到 B (2,3)的直线,则
第 14 章 (之 1) (总第 75 次)
教学内容: § 14.1 第二型曲线积分 **1.设 L :
x cos x , y sin t ,
0t
2
, 则 x 2 ydy y 2 xdx
L
(
)
(A)
cos t
2 0
sin t sin t cos t dt ;
0
t2 t5 dt (1 t 3 ) 3
a2 2
0
t2 a2 1 a2 dt 6 (1 t 3 ) 0 6 (1 t 3 ) 2
4.在下列各题中适当补上一条曲线,使积分路径成闭曲线,再考虑用格林公式: **(1)
xy sin x sin y dx x
w fds
L
L
x y dx 2 dy 2 x y x y2
第十四章 典型习题解答与提示

第十四章 导数与微分典型习题解答与提示习 题 14-11.(1)()()002sinsin cos cos 22cos lim lim sin 2x x x x xx x x x x x x→→+-+-'===-V V V V V V V ; (2)()()()0[]lim x a x x b ax b ax b a x→++-+'+==V V V 。
2.(1)()0A f x '=-;(2)()0A f '=,这是因为:左端()()()00lim00x f x f f x →-'==-;(3)()02A f x '=,这是因为:左端()()()()()000000lim 2x f x x f x f x x f x f x x x →+---⎡⎤'=+=⎢⎥⎣⎦-V V V V V 。
3.(1)34y x '=; (2)1323y x -'=; (3)32y x -'=-; (4)16115516,5y x y x '==。
4.()212m s s υ'==。
5.(1)所求切线方程为1y =-,法线方程为32x π=; (2)所求切线方程为1223y x π⎫-=--⎪⎝⎭,法线方程为123y x π⎫-=-⎪⎭; (3)所求切线方程为1y x -=,法线方程为1y x -=-。
6.割线斜率为212191431y y k x x --===--,因为2y x '=,令4y '=,得2x =,即抛物线上过()2,4点的切线平行于已知割线。
7.因为2y x '=,令4y '=,得82,3x y =±=±,所以过点882,,2,33⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭处的切线平行于直线45y x =+,令9y '=,所以3,9x y =±=±,所以过点()()3,9,3,9--处的切线垂直于已知直线930x y ++=。
华东理工大学高等数学答案第章

第2章 (之1)第2次作业教学内容: §2.1 导数概念**1. 设x x x f 2)(3+=,试用导数定义求)(x f '.解:lim ()()lim()()∆∆∆∆∆∆∆x x f x x f x x x x x x x xx→→+-=+++--003322 =+322x .**2. 试用导数定义计算下列函数的导数:(1)xx f 1)(=, 求)1(f '; (2)()38t t g -=,求()2g '; (3)()t t t -=23ϕ,求()1-'ϕ.解:(1)x f x f f x ∆-∆+='→∆)1()1(lim )1(0=+-→lim ∆∆∆x x x 0111=-+=-→lim ∆∆x x0111.(2) ()()()tt g t t g t g t ∆-∆+='→∆0lim()[][]()()tt t t t t t t t t t t t t t t t t t ∆∆+∆+∆+-=∆∆+-=∆--∆+-=→∆→∆→∆32233033033033lim lim 88lim()22033lim t t t t t ∆-∆--=→∆23t -=,即 ()23t t g -=', ()122-='∴g .(3) ()()()tt t t t t ∆-∆+='→∆ϕϕϕ0lim()()[][]ttt t t t t t ∆--∆+-∆+=→∆22033limttt t t t ∆∆-∆+∆=→∆2036lim()16136lim 0-=-∆+=→∆t t t t , ()16-='∴t t ϕ, ()71-=-'ϕ.**3. 求曲线22x y = 在点 ()2,1=P 处的切线方程.解:曲线在点P 处切线的斜率为 4122lim21=--→x x x , 所以切线方程为 ()214+-=x y .**4. 化学反应速率通常是以单位时间内反应物浓度的减少或生成物浓度的增加来表征。
东华理工大学高等数学A练习册答案(下)(学生用)

第7章 微分方程§7.5 可降阶的高阶微分方程一、填空题答:1. 2121ln arctan C x C x x x y +++-= 2.22121C x x e C y x +--= 3.121C xy C e =+二、 y =C 1ln x +C 2 . 三、 22x x y -=.§7.6 高阶线性微分方程一、判断题1.( √ )2.( ╳ )3.( √ ) 二、选择题答:1.C 2.C 3.C 4.B§7.7 常系数齐次线性微分方程一、判断题1.( √ )2.( ╳ )3.( ╳ ) 二、填空题1、y =C 1e x +C 2e-2x2、 t t e C e C x 252251t +=, 3、 y =e -3x (C 1cos2x +C 2sin2x ).4、 y =C 1+C 2x +C 3e x +C 4xe x5、y =e 2x sin3x三、选择题答:1.B 2.B 3.A 4.C 5.B四、求下列微分方程(1) y =C 1+C 2e 4x . (2) y =e 2x (C 1cos x +C 2sin x ). (3) y =C 1+C 2x +C 3e x +C 4xe x . (4))2(21x e y x+=-.§7.8 常系数非齐次线性微分方程一、填空题 答:1、x x xe e C e C y ++=-2211,2、x xe x C x C e y x x 2cos 41)2sin 2cos (21-+=.3、x x x y 2sin 31sin 31cos +-+-= 4、x xx y cos 2sin 21+= 二、选择题答:1.D 2.B 3.A 4.C 5.D 6.D三、)323(2221x x e e C e C y x x x -++=--- 四、 2527521++-=x x e e y . 第12章 无穷级数§12.1 常数项级数的概念与性质一、判断题答:1. √2. √ 3. ×4. ×5. √ 6. √ 二、填空题答:1. 1/2、3/8 、5/16 2. [(-1)^(n-1)]*[(n+1)/n] 3. [x^(n/2)]*(1/2*n!) 4. 0 三、选择题答:1.C 2.A 3.C 4.C四、判定下列级数的收敛性(1)级数收敛. (2) 该级数发散. (3) 级数发散.§12.2 常数项级数的审敛法一、判断题答:1. √ 2. × 3. √4.√ 5√6. ×7. √8. √9.√ 二、填空题答:1.P>1 2. {}n s 有界 3. 绝对收敛 4. 收敛5.1lim 0n nn u u u +=⎧⎨>⎩三、选择题答:1. D 2.C 3.D 4.A 5.C四、用比较审敛法或极限形式的比较审敛法判定下列级数的收敛性: (1) 级数发散. (4) 级数收敛.五、用比值审敛法判定下列级数的收敛性: (1) 级数发散. (2) 级数收敛.六、用根值审敛法判定下列级数的收敛性:(1) 级数收敛; (2) 当b <a 时级数收敛, 当b >a 时级数发散. 七、 (1) 此级数是收敛的. 条件收敛的. (2) 级数收敛, 并且绝对收敛.§12.3 幂级数一、判断题答:1. √ 2. √ 3. √ 4. √ 5. × 二、填空题答:1.[-1/2、1/2] 2. [-1,5) 3. (-1,1) ,11ln21xx+- 4. 绝对收敛三、选择题 答:1.D 2.B 3 D四、求下列幂级数的收敛域:(1) 收敛域为(-1, 1). (2) 收敛域为[-1, 1]. 五、利用逐项求导或逐项积分, 求下列级数的和函数: (1) ()S x 21(11)(1)x x =-<<-. (2) ()S x 11ln (11)21x x x+=-<<- . 提示: 由)0()()(0S x S dx x S x-='⎰得⎰'+=xdx x S S x S 0)()0()(.§12.4 函数展开成幂级数一、判断题答:1. √2. × 3. × 二、填空题 1. 答:1.11ln 2(1)2nn nn x n ∞-=+-∑ ,(-2,2 ] 2. 1111()(4)23nn n n x ∞++=-+∑ ,(-6,-2) 3.)( ])3()!12(3)3()!2(1[)1(211202+∞<<-∞++++-+∞=∑x x n x n n n n nππ 三、选择题答:1.B 2.C 3.C四、(1) 210sh (21)!n n x x n -∞==-∑, x ∈(-∞, +∞). (2) 212212sin (1)(2)!n n n n x x n -∞=⋅=-∑ x ∈(-∞, +∞). 五、∑=<<--=n n n n x x x 0)60( )33()1(311.§12.5 函数的幂级数展开式的应用一、填空题答:1.3. ; 2、)( !4cos2cos 02+∞<<-∞=∑∞=x x n n x e n n nx π.§12.7 傅立叶级数一、判断题 答:1. × 2. √3.√4.√二、填空题 1.5 2. ,n n a b - 3. nx nx f n sin 1)(1∑∞==(0<x ≤π), 级数在x =0处收敛于0. 三、选择题答:1.A 2.C 3.B 4A 5.B四、∑∞=+--+=121cos 141)1(422cos n n nx n x ππ(-π≤x ≤π). 五、正弦级数为nx n n nx f n n sin ]2)2()1[(4)(1323∑∞=---=ππ(0≤x <π), 级数在x =0处收敛于0.余弦级数为 nx nx f n n cos )1(832)(122∑∞=-+=π(0≤x ≤π).§12.8 一般周期函数的傅里叶级数一、 ∑∞=+-+=12122cos )1(11211)(n n x n n x f ππ, x ∈(-∞, +∞).二、正弦级数13218(1)2[(1)1]{}sin2n n n n xn n πππ+∞=---+∑, x ∈[0, 2). 余弦级数:221416(1)cos 32n n n xn ππ∞=-+∑, x ∈[0, 2].第8章 空间解析几何与向量代数§8.1 向量及其线性运算一、判断题。
曲面的第二基本形式

§2.3 曲面的第二基本形式一、曲面的第二基本形式二、曲面曲线的曲率三、Dupin指标线四、曲面的渐近方向和共轭方向五、曲面的主方向和曲率线六、曲面的主曲率、Gauss曲率和平均曲率七、曲面在一点邻近的结构八、Gauss映射一、曲面的第二基本形式SQπn单位法向量δ(,)(,)(,),uu u v u v L r u v n =⋅ 其中,uv M r n =⋅ .vv N r n =⋅222II d d 2d d d ,n r L u M u v N v ==++ 曲面的第二基为本形式称(,),(,),(,).L u v M u v N u v 称为曲面的第二类基本量PP '2II d d n r n ⋅⇒=-=例P114-23. Meusnier(梅尼埃)定理00.P C P C ΓΓΓΓ曲面曲线在给定点的曲率中心就是与曲线具有共同切线的法截线上同一个点的曲率中心在曲线的密切平面上的投影Meusnier 定理揭示了平面截线与法截线之间的联系.请理解课本内容后及时独立地完成如下作业!P114: 3,4, 5补充作业题32.3.2.()(,)()()C r u R u v r u vr u '=+ 求类曲线的切线面().u v c c +=上的曲线为常数的法曲率2.3.1.(,)(cos ,sin ,sin 2)r u v u v u v v =求曲面的第一类基本形式和第二类基本形式.4. 根据Dupin指标线的形状对切点进行分类(1)椭圆点20LN M ->(2)双曲点20LN M -<(3)抛物点2,,0LN M L M N ⎧-=⎨⎩不同时为(4)平点0L M N ===Dupin 指标线不存在请理解课本内容后及时独立地完成如下作业!P115: 24补充作业题232.3.3.(,)(,,)r u v u v u v =+ 求曲面上的抛物点、.椭圆点和双曲点的集合2.渐近曲线每一点的切方向都是渐近方向的曲面曲线.渐近曲线的微分方程22L u v u M u v u v N u v v++=(,)d2(,)d d(,)d0P93 命题1如果曲面上有直线则它一定是曲面的渐近曲线,. P94 命题2曲面在渐近曲线上一点处的切平面一定是渐近曲线的密切平面.3. 渐近网如果曲面上的点都是双曲点,则每个点处都有两个不相切的渐近方向,在曲面上会有两族渐近曲线,称曲面上这两族曲线为的渐近网.P94 命题30.L N≡≡曲纹坐标网为渐近网的充要条件是.此时渐近曲线的微分方程就渐近网的微分方程是4. 共轭方向直径一族平行弦的中点的轨迹.直径AB 的共轭直径AB 平行于的弦的中点的轨迹.Dupin ,,.P P 设曲面上点处的某两个切方向所在的某直线段是点处指标线的共轭直径则称这两个切方向互共轭曲面的为共轭方向相共轭方向的等价定义(d)d :d (δ)δ:δ.d δ(d δd δ)d δ0P P P L u u M u v v u N P u v u v v v +++===曲面的共轭曲面上点处的两个切方向和为当方向当且仅共轭其他等价定义d δ0n r ⋅=⇔ d 0n r δ⇔⋅= 渐近方向为自共轭方向.,,.如果曲面上的两族曲线使得过曲面上的每一点此两族曲线的两条曲线的切方向都是共轭方向则称这曲面的族曲线为共轭网两5. 共轭网共轭网的微分方程(已知一族曲线, 求它的共轭曲线族)(,)d δ(,)(d δd δ)(,)d δ0.L u v u u M u v u v v u N u v v v +++=P96 命题4(,)0.M u v ≡曲纹坐标网为共轭网的充要条件是2. 主方向判别定理(Rodrigues(罗德里格斯)定理)(d)(d :d )d d ;u v n r λλ=∃=是主方向的充要条件是使,(d).n n k k λ=-在上述条件下有其中为沿方向的法曲率曲率线网及其应用(Ref: Spectral Quadrangulation with Orientation and Alignment Control)(Ref: Extracting lines of curvature from noisy point clouds,,.对于曲面上任意两族不相切的曲线族都可以通过参数选择使其成为曲纹坐标网,,,特别地在不含脐点的曲面上可以经过参数选择使曲率线网成为曲纹坐标网.P99 命题5(,)(,)0.F u v M u v ≡≡曲面上的曲纹坐标网是曲率线网的充要条件是例如(,)(()cos ,()sin ,()),0,r t t t t F M θϕθϕθψ=≡≡在旋转面中它的曲纹坐标网就是曲率线网.请理解课本内容后及时独立地完成如下作业!P114: 13补充作业题求曲面上的脐点xyz2.3.5.1.六、曲面的主曲率、Gauss 曲率和平均曲率1. 主曲率主方向上曲面上一点处的法曲率.沿曲率线即:曲面方向的上一点处法曲率.2. Euler 公式()法曲率随着切方向变化映的规律反2212cos sin n k k k θθ=+SπP1k 2k nk θ请理解课本内容后及时独立地完成如下作业!补充作业题2.3.6.2.xy z =求双曲抛物面的两个主曲率之比122.3.7.(cos ,sin ,)Gauss ,.r u v u v u v K H k k =+求螺旋面的曲率、平均曲率和主曲率2.3.8.,Gauss .S S K H 证明:如果曲面上的渐近曲线网的夹角是常数则曲面的曲率和平均曲率的平方成比例P114: 18.1()d 2()d nP开口向下的抛物线开口向上的抛物线开口向下的抛物线)00(,2)πθπθ+-(2π-1(d 2()d nP。
华东理工大学 高等数学下 课件PPT ch14-2

C 正弦级数与余弦级数
定理 设f ( x)是分段光滑的周期为2的函数,
(1)当f ( x)为奇函数时,其傅立叶系数
an 0,(n 0,1,2,)
bn
2
0
f ( x) sin nxdx.
(n 1,2,3,)
和函数s( x)的图象为:
2y
3
4
x
当0 x 2,有
o
2
x 2(sin x sin 2 x sin 3 x sin 4 x ).
2
3
4
例2 周期为2的周期函数在[0,2)上的表达式为f ( x) x2 .
求其傅立叶级数,并画 出傅立叶级数的和函数 的图形。
解:
1
a0
2 x 2dx 8 2 .
0
3
an
1
2
f ( x) cos nxdx
0
1 2 x 2 cos nxdxx
2
sin nx n
2
x
cos nx n2
sin nx 2
n2 0
4 n2
(n 1,2,)
bn
1
2 x 2 sin nxdx
0
1
x
2
(
cos nx n
)
sin nx 2x n2
cos nx 2( n3
常用公式:sin k 0,cos k (1)k .
B 函数的傅立叶展开 定理( 1 Dirichlet收敛定理)
若周期为2函数f ( x)在长为2的闭区间上分段光滑,
则其傅立叶级数每一点 都收敛,且收敛到
f ( x 0) f ( x 0) . 2
即
a0 2
ak
k 1
