标准斜齿轮传动的强度计算
(整理)标准斜齿圆柱齿轮传动的强度计算
研究,可用
式中为斜齿轮传动的端面重合度
图<标准圆柱齿轮传动的端面重合度>
斜齿轮的纵向重合度可按以下公式计算:
斜齿轮计算中的载荷系数,其中使用系数
与齿向载荷分布系数的查取与直齿轮相同;动载系数可由图<动载系数值>中查取;齿间载荷分配系数与可根据斜齿轮的精度等级、齿面硬化情况和载荷大小由表<齿间载荷分配系数>中查取。
(三)齿根弯曲疲劳强度计算
如下图所示,斜齿轮齿面上的接触线为一斜线。
受载时,齿轮的失效形式为局部折断。
斜齿轮的弯曲强度,若按轮齿局部
斜齿轮的计算载荷要比直齿轮的多计入一个参数劳强度公式为:
、
ZH称为区域系数。
上右图为法面压力角αn=20°的标准齿轮的ZH值。
于是得
同前理,由上式可得
应该注意,对于斜齿圆柱齿轮传动,因齿面上的接触线是倾斜的(如右图),所以在同一齿面上就会有齿顶面(其上接触线段为e1P)与齿根面(其上接触线段为e2P)同时参与啮合的情况(直齿轮传动,齿面上的接触线与轴线平行,就没有这种现象)。
如前所述,齿轮齿顶面比齿恨面具有较高的接触疲劳强度。
设小齿轮的齿面接触疲劳强度比大齿轮的高(即小齿轮的材料
较好,齿面硬度较高),那么,当大齿轮的齿根面产生点蚀,e2 P一段接触线已不能在承受原来所分担的载荷,而要部分地由齿顶面上的e1P一段接触线来承担时,因同一齿面上,齿顶面的接触疲劳强度较高,所以即使承担的载荷有所增大,只要还
为,当>1.23应取=1.23。
标准斜齿轮计算公式

标准斜齿轮计算公式标准斜齿轮是机械传动中常见的齿轮类型之一,其齿廓为斜线齿廓,主要用于传递轴的旋转运动和功率传递。
在设计和计算标准斜齿轮时,需要考虑齿廓的形状、齿轮参数、齿轮传动的力学性能等方面。
下面将介绍标准斜齿轮计算公式的相关内容。
1. 齿廓计算公式:标准斜齿轮的齿廓形状可以通过齿轮生成方法来确定,常见的齿廓有直线齿廓、圆弧齿廓等。
其中,直线齿廓是应用最广泛的一种齿廓形状。
- 直线齿廓计算公式:直线齿廓的计算公式主要包括齿顶圆直径、齿根圆直径、齿顶高度、齿根高度等参数的计算。
以下为直线齿廓计算公式的参考内容:齿顶高度:h_a = m + c齿根高度:h_f = m齿顶圆直径:d_a = m * (z + 2)齿根圆直径:d_f = m * (z + 0.95)齿顶圆直径角:α_a = arctan(tan(α) / cos(β))齿根圆直径角:α_f = arctan(tan(α) / cos(β))其中,m为模数,c为齿顶高度系数,z为齿数,α为压力角,β为齿顶圆螺线角。
2. 齿轮参数计算公式:标准斜齿轮的齿轮参数包括齿数、模数、压力角等。
齿轮参数的选择和计算直接影响到齿轮传动的性能。
- 模数计算公式:模数是齿轮参数中的一个重要指标,其计算公式如下:m = d / z其中,d为齿轮的分度圆直径,z为齿数。
- 压力角计算公式:压力角是齿轮接触线与传动力矢的夹角,常见的压力角有20°、22.5°、25°等。
压力角的计算公式如下:cos(α) = (r1 + r2) / (m * z1)其中,r1为动力齿轮的齿顶圆半径,r2为从动齿轮的齿顶圆半径,z1为动力齿轮的齿数。
3. 力学性能计算公式:标准斜齿轮在传递功率时,需要考虑其力学性能,如齿面接触疲劳强度、齿根弯曲疲劳强度、齿面接触应力等。
- 齿面接触疲劳强度计算公式:齿面接触疲劳强度是齿轮耐久性的重要指标,其计算公式如下:Z_H = H * Z_E * Z_Hv * Z_Hp其中,H为传递功率,Z_E为冲击系数,Z_Hv为齿宽影响系数,Z_Hp为可靠性系数。
齿轮传动强度设计计算

直齿轮箱尺寸变化影响传动强度分析阮超传递:功率P,转速n,扭矩T齿轮:齿数Z,齿宽b,模数m,材料强度σ 强度公式: 弯曲 T∝b(Zm)mσ 接触 T∝b(Zm)2σ2(体积关联) 条件变化: 1.齿轮箱外形尺寸不变,n2=3600r/min, m2=4mm,求P2? 弯曲 模数变化4/3,转速变化3600/3000, P2=120*4/3KW 接触 体积不变,转速变化3600/3000,P2=120KW;弯曲变化机理:齿形变大 接触变化机理:P=T*n/9550已知:功率P1=100KW,转速n1=3000r/min,模数m1=3mm直齿轮箱尺寸变化影响传动强度分析阮超传递:功率P,转速n,扭矩T齿轮:齿数Z,齿宽b,模数m,材料强度σ 强度公式: 弯曲 T∝b(Zm)mσ 接触 T∝b(Zm)2σ2(体积关联) 条件变化: 2.齿轮箱齿数不变,n2=3600r/min, m2=4mm,求P2? 弯曲 模数变化4/3,转速变化3600/3000, P =120*(4/3) KW 接触 模数变化4/3,转速变化3600/3000, P =120*(4/3) KW2 2 2 2弯曲变化机理:力臂和曲率半径增大 接触变化机理:单位齿宽负载和直径增大已知:功率P1=100KW,转速n1=3000r/min,模数m1=3mm直齿轮箱尺寸变化影响传动强度分析阮超传递:功率P,转速n,扭矩T齿轮:齿数Z,齿宽b,模数m,材料强度σ 强度公式: 弯曲 T∝b(Zm)mσ 接触 T∝b(Zm)2σ2(体积关联) 条件变化: 3.齿轮箱尺寸放大4/3倍,n2=3600r/min, 求P2? 弯曲 模数变化4/3,转速变化3600/3000, P =120*(4/3) KW 接触 模数变化4/3,转速变化3600/3000, P =120*(4/3) KW2 2 3 3弯曲变化机理:齿宽b,模数m增大 接触变化机理:齿宽b,模数m增大已知:功率P1=100KW,转速n1=3000r/min,模数m1=3mm直齿轮箱尺寸变化影响传动强度分析阮超传递:功率P,转速n,扭矩T齿轮:齿数Z,齿宽b,模数m,材料强度σ 强度公式: 弯曲 T∝b(Zm)mσ 接触 T∝b(Zm)2σ2(体积关联) 条件变化: 4.齿轮材料选用1.2倍σ,n2=3600r/min, 求P2? 弯曲 模数变化4/3,转速变化3600/3000, P =120*1.2KW 接触 模数变化4/3,转速变化3600/3000, P =120*(1.2) KW2 2 2弯曲变化机理:材料增强 接触变化机理:材料增强已知:功率P1=100KW,转速n1=3000r/min,模数m1=3mm。
齿轮传动的强度设计计算

1. 齿面接触疲劳强度的计算齿面接触疲劳强度的计算中,由于赫兹应力是齿面间应力的主要指标,故把赫兹应力作为齿面接触应力的计算基础,并用来评价接触强度。
齿面接触疲劳强度核算时,根据设计要求可以选择不同的计算公式。
用于总体设计和非重要齿轮计算时,可采用简化计算方法;重要齿轮校核时可采用精确计算方法。
分析计算表明,大、小齿轮的接触应力总是相等的。
齿面最大接触应力一般出现在小轮单对齿啮合区内界点、节点和大轮单对齿啮合区内界点三个特征点之一。
实际使用和实验也证明了这一规律的正确。
因此,在齿面接触疲劳强度的计算中,常采用节点的接触应力分析齿轮的接触强度。
强度条件为:大、小齿轮在节点处的计算接触应力均不大于其相应的许用接触应力,即:⑴圆柱齿轮的接触疲劳强度计算1)两圆柱体接触时的接触应力在载荷作用下,两曲面零件表面理论上为线接触或点接触,考虑到弹性变形,实际为很小的面接触。
两圆柱体接触时的接触面尺寸和接触应力可按赫兹公式计算。
两圆柱体接触,接触面为矩形(2axb),最大接触应力σHmax位于接触面宽中线处。
计算公式为:接触面半宽:最大接触应力:•F——接触面所受到的载荷•ρ——综合曲率半径,(正号用于外接触,负号用于内接触)•E1、E2——两接触体材料的弹性模量•μ1、μ2——两接触体材料的泊松比2)齿轮啮合时的接触应力两渐开线圆柱齿轮在任意一处啮合点时接触应力状况,都可以转化为以啮合点处的曲率半径ρ1、ρ2为半径的两圆柱体的接触应力。
在整个啮合过程中的最大接触应力即为各啮合点接触应力的最大值。
节点附近处的ρ虽然不是最小值,但节点处一般只有一对轮齿啮合,点蚀也往往先在节点附近的齿根表面出现,因此,接触疲劳强度计算通常以节点为最大接触应力计算点。
参数直齿圆柱齿轮斜齿圆柱齿轮节点处的载荷为综合曲率半径为接触线的长度为,3)圆柱齿轮的接触疲劳强度将节点处的上述参数带入两圆柱体接触应力公式,并考虑各载荷系数的影响,得到:接触疲劳强度的校核公式为:接触疲劳强度的设计公式为:•KA——使用系数•KV——动载荷系数•KHβ——接触强度计算的齿向载荷分布系数•KHα——接触强度计算的齿间载荷分配系数•Ft——端面内分度圆上的名义切向力,N;•T1——端面内分度圆上的名义转矩,N.mm;•d1——小齿轮分度圆直径,mm;•b ——工作齿宽,mm,指一对齿轮中的较小齿宽;•u ——齿数比;•ψd——齿宽系数,指齿宽b和小齿轮分度圆直径的比值(ψd=b/d1)。
斜齿轮

式中:YFa、YSa应按当量齿数zv=z/cos3查表确定 斜齿轮螺旋角影响系数Yβ的数值可查图确定
标准斜齿圆柱齿轮强度计算
四、齿面接触疲劳强度计算 斜齿轮齿面接触强度仍以节点处的接触应
标准斜齿圆柱齿轮强度计算4
力为代表,将节点处的法面曲率半径rn代入计 算。法面曲率半径以及综合曲率半径有以下关 系为: rt d sin t
L
L
因此,
b cos b
KFt KFt KFn pca bα L cos t cos b bα cos t cos b
载荷系数的计算与直齿轮相同,即:K=KA Kv Kα Kβ
标准斜齿圆柱齿轮强度计算
三、齿根弯曲疲劳强度计算 斜齿轮齿面上的接触线为一斜线。受载时,
标准斜齿圆柱齿轮强度计算3
轮齿的失效形式为局部折断(如右图)。
强度计算时,通常以斜齿轮的当量齿轮为对
象,借助直齿轮齿根弯曲疲劳计算公式,并引入
斜齿轮螺旋角影响系数Yβ,得: 校核计算公式: F
斜齿圆柱齿轮轮齿受载及折断KFtYFaYSa Y bmnα
F
2 KT1Y cos 2 YFaYSa 设计计算公式:m n 3 2 F d z1 α
KT1 H 2 3 R 1 0.5R d1 u
设计计算公式: d1 2.923 (
H
ZE
)2
KT1 R 1 0.5R 2 u
齿轮的结构设计
齿轮的结构设计 通过强度计算确定出了齿轮的齿数z、模数m、齿宽B、螺旋角、分度圆直 径d 等主要尺寸。
2
dα
u H
斜齿轮的[H]
标准锥齿轮传动的强度计算
标准锥齿轮传动的强度计算

在综合考虑齿轮几何尺寸,毛坯,材料,加工方法,使用 要求及经济性等各方面因素的基础上,按齿轮的直径大小,选 定合适的结构形式,再根据推荐的经验数据进行结构尺寸计算 。
常见齿轮结构形式
⑴ 齿轮轴 ⑵ 实心式结构 ⑶ 腹板式结构 ⑷ 轮辐式结构
标准锥齿轮传动的强度计算
1 设计参数
直齿锥齿轮传动是以大端参数为标准值,强度计算时,是 以锥齿轮齿宽中点处的当量齿轮作为计算时的依据。
轴交角∑,齿数比u,齿 数z1、z2,锥距R,分 度圆锥角δ1、 δ2,分度 圆直径d1、d2,齿宽中点 处即平均分度圆的直径为
dm1、dm2,当量齿轮 齿数zv1、zv2,当量齿轮 的分度圆直径dv1、dv2,
很显然,当两齿轮平均齿宽处两当量齿轮在节点上的啮 合曲率半径为:
从而可得到 :
若将上式(综合曲率表达式)及uv=u2、 等式代入赫兹公式,并令接触线长度L=b,得到:
若α=20°,则得到: 校核式 设计式
§10-10 齿轮的结构设计
通过强度计算确定出了齿轮的齿数z、模数m、齿宽B、螺
旋角b、分度圆直径d 等主要尺寸。
常见齿轮结构形式
⑴齿轮轴
直径较小的钢质齿轮,当齿根圆直径与轴径 接近时,可以将齿轮与轴做成一体,称为齿轮轴
圆柱齿轮轴
圆锥齿轮轴
圆柱齿轮轴
圆柱齿轮e<2mt
圆锥齿轮轴
< (对锥齿轮指小端)
圆锥齿轮轴பைடு நூலகம்
e
⑵实心式结构
< 160mm
实心式圆柱齿轮
但航空齿轮为减轻重量, 腹板式结构。
实心式圆锥齿轮 < 160mm 时,有时也设计为
斜齿圆柱齿轮传动的强度计算

一、齿轮的受力分析
直齿轮法面与端面重合受力分析比较简单,而斜齿轮转呈螺旋状,垂直轮齿的法平面与端面成β角。
在上图中Fn 分解为:
Fr --径向力指向轴心
Ft --圆周力,主动轮上与受力点方向速度相反,从动轮与速度相同
Fa --轴向力(方向根据左右手定则)
已知主动轮上驱动力矩T1时,有:
二、计算载荷
斜齿轮计算载荷:
式中:
Ft --主动轮上所受圆周力;
K--载荷系数;
b--齿轮宽度;
εα --斜齿轮端面重合度
三、齿根弯曲疲劳强度计算
当接触线通过齿顶边缘时,齿根出现最大弯曲应力,对斜齿轮很难用解析法进行精确计算。
斜齿轮齿根弯曲强度借助当量齿轮概念,直接应用直齿轮的公式。
校核与设计式:
式中:
K、T1、b、Фd 、d1、mn 、εα 同前;
Y β --螺旋角影响系数,根据β查表
YFa --斜齿轮齿形系数,按当量齿轮查表
Ysa --斜齿轮应力集中系数
四、齿面接触疲劳强度计算
以斜齿轮的法面参数代入进行计算。
校核与设计式:
(end)。
斜齿轮设计计算过程

斜齿轮设计计算过程斜齿轮是一种常见的传动装置,具有传递大转矩、平稳运转、精度高等优点,在各种机械设备中广泛应用。
斜齿轮的设计计算涉及到齿轮的基本几何参数、载荷计算、传动比选择等方面。
下面将详细介绍斜齿轮设计计算的过程。
一、齿轮的基本几何参数设计1.模数的选择:模数是斜齿轮设计的重要参数,它是齿轮齿数与分度圆直径之比。
根据所要传递的功率、速度和转矩大小,选择合适的模数。
通常,模数的选择与齿数有关,齿数多则模数小,齿数少则模数大。
2.齿数的确定:齿数与模数有关,一般模数越大,齿数越少。
齿数的确定是通过传动比和传动效率来选择的。
传动比是输入轴的转速与输出轴的转速之比,传动效率是指输入功率与输出功率之比。
3.齿轮齿宽的确定:齿轮齿宽的确定主要与所要传递的功率及轴向载荷有关。
齿宽一般比轴向载荷要大一些,通常为2-3倍。
4.齿轮齿数的选择:齿数的选择要注意齿轮尺寸、密度与传动比之间的关系,并根据啮合角、齿侧力系数等因素进行计算。
5.齿轮齿形修正:齿形修正是为了解决齿轮啮合中的啮合误差,提高传动效率和齿轮的寿命。
齿形修正一般采用弯曲齿形法。
二、载荷计算1.受力分析:首先需要确定齿轮在工作过程中所受的载荷类型和方向。
常见的载荷有径向力、轴向力和弯矩。
2.力的计算:根据齿轮传动的理论公式,计算齿轮所受的各个力的大小,并确定其作用点位置。
3.强度计算:根据齿轮所受载荷的大小和方向,采用材料的抗弯强度、接触强度等指标进行强度计算,判断齿轮的强度是否满足要求。
三、传动比选择根据所要传递的转速和转矩大小,选择合适的传动比。
一般情况下,传动比应选择为整数或近似值,以便于加工制造和传动装置的调整。
四、传动系统的优化设计在完成基本的几何参数设计和载荷计算后,可以对传动系统进行优化设计。
包括选取合适的传动方式、齿轮材料的选择、齿轮的热处理等。
五、齿轮加工制造根据已完成的设计计算结果,制定相应的加工工艺和技术要求,进行齿轮的加工制造。
齿轮疲劳强度计算公式

齿轮疲劳强度计算公式齿轮疲劳强度是评价齿轮工作可靠性和耐久性的重要参数。
根据齿轮的传动方式不同,其强度计算公式也有所区别。
以下将介绍常见的副伞齿轮对齿轮疲劳强度的计算公式及其相关参考内容,帮助读者了解和应用相关知识。
副伞齿轮是一种常见的齿轮传动类型,其传动公式及工作原理较为简单清晰。
对于副伞齿轮而言,齿轮疲劳强度的计算可基于AGMA(美国齿轮制造商协会)标准进行推导。
常用的副伞齿轮疲劳强度计算公式包括以下几种:1. 根据AGMA 2001标准计算常规弯曲疲劳强度公式:Sf = (Y*F*Zi*Kv*Ko*Ks) / [(R*V*Sw*hv)^(1/n)]其中,Sf为弯曲疲劳强度,Y为几何系数,F为载荷系数,Zi为齿数影响系数,Kv为速度系数,Ko为工况系数,Ks为大小系数,R为齿轮传动比,V为线速度,Sw为底隙磨损系数,hv为齿顶高度,n为齿数。
2. 按照AGMA 2101-D04标准计算循环弯曲疲劳强度公式:Sf = 1.355(De2/mi)^2*(fen*Zi*Kv*Ks)*Kr*Ks其中,Sf为弯曲疲劳强度,De为最大有效齿轮外径,mi为模数,fen为等效载荷系数,Zi为齿数影响系数,Kv为速度系数,Ks为大小系数,Kr为可靠性系数。
3. 考虑曲轴轴向载荷的综合疲劳强度计算公式公式:S = Km * (σHb / Yn) * КF * kh * J * Kv * Ko * KB * KR* KT其中,S为综合疲劳强度,Km为可靠度系数,σHb为齿根弯曲接触应力,Yn为弯曲疲劳极限,КF为载荷比例系数,kh为动荷载系数,J为几何修正系数,Kv为速度系数,Ko为工况系数,KB为尺寸系数,KR为可靠性系数,KT为温度系数。
以上是常见的副伞齿轮疲劳强度计算公式,根据具体应用需求可选取适用的公式进行计算。
需要注意的是,齿轮疲劳强度的计算不仅依赖于传动方式和材料性质,还受到载荷、速度、尺寸、工况等多种因素的影响,因此在实际应用中应综合考虑各个因素进行计算,以确保齿轮的可靠性和耐久性。
齿面 硬度 强度计算公式

齿面硬度强度计算公式摘要,本文介绍了齿面硬度和强度的计算公式,通过分析齿轮的材料、几何形状和工作条件等因素,计算出齿轮的硬度和强度,为齿轮设计和选型提供了理论依据。
引言。
齿轮是一种常见的传动装置,广泛应用于机械设备中。
齿轮的硬度和强度是影响其使用性能和寿命的重要因素。
通过计算齿轮的硬度和强度,可以为齿轮的设计和选型提供理论依据,保证齿轮在工作条件下具有足够的耐用性和可靠性。
一、齿面硬度计算公式。
齿面硬度是指齿轮齿面的硬度,通常用洛氏硬度(HRC)来表示。
齿面硬度的计算公式如下:HRC = 185 / (T + 18)。
其中,T为齿轮的表面硬度(HB)。
在实际应用中,可以根据齿轮的材料和热处理工艺来确定齿轮的表面硬度,然后通过上述公式计算出齿面硬度,从而评估齿轮的耐磨性和耐用性。
二、齿面强度计算公式。
齿面强度是指齿轮齿面的承载能力,通常用齿面接触应力来表示。
齿面强度的计算公式如下:σH = (2KmF) / (bd)。
其中,σH为齿面接触应力(MPa),Km为齿轮载荷分布系数,F为齿轮传递的力(N),b为齿轮的面宽(mm),d为齿轮的分度圆直径(mm)。
在实际应用中,可以根据齿轮的工作条件和载荷来确定齿轮的载荷分布系数和传递的力,然后通过上述公式计算出齿面接触应力,从而评估齿轮的承载能力和工作可靠性。
三、影响齿面硬度和强度的因素。
1. 材料选择,齿轮的材料直接影响其硬度和强度,通常选择高强度和高硬度的合金钢或表面经过渗碳渗氮处理的材料。
2. 几何形状,齿轮的模数、齿数、齿宽等几何参数会影响其齿面硬度和强度,通常通过几何设计来优化齿轮的硬度和强度。
3. 热处理工艺,热处理工艺可以提高齿轮的硬度和强度,包括淬火、渗碳、渗氮等工艺。
4. 工作条件,齿轮在不同的工作条件下承受不同的载荷和速度,这会影响其齿面硬度和强度的要求。
四、应用实例。
以某型号齿轮为例,其材料为20CrMnTi合金钢,经过渗碳淬火处理,齿轮的模数为3,齿数为20,齿宽为30mm,分度圆直径为60mm,工作条件下承受的力为5000N。
斜齿轮计算公式大全

斜齿轮计算公式大全斜齿轮是一种常见的传动装置,其计算公式涉及到许多参数和变量。
在工程设计和制造过程中,掌握斜齿轮计算公式是非常重要的。
本文将为大家详细介绍斜齿轮计算公式大全,希望能对大家有所帮助。
1. 基本参数。
在计算斜齿轮时,首先需要了解一些基本参数,包括模数、齿数、压力角、齿宽等。
这些参数将直接影响到斜齿轮的设计和计算。
模数是指齿轮齿数与齿轮直径的比值,通常用m表示。
齿数即为齿轮上的齿的数量,用z表示。
压力角是齿轮齿面上与基圆切线的夹角,用α表示。
齿宽即为齿轮齿面的宽度,用b表示。
2. 齿轮啮合传动比。
齿轮啮合传动比是指齿轮啮合时,从动齿轮齿数与动齿轮齿数之比。
在计算斜齿轮时,需要根据实际情况计算齿轮啮合传动比,以确定齿轮的设计参数。
3. 齿轮啮合角。
齿轮啮合角是指相邻两齿啮合时,它们的啮合线与轴线的夹角。
在斜齿轮的设计中,需要计算齿轮啮合角,以确定齿轮的啮合情况。
4. 齿轮啮合线速度。
齿轮啮合线速度是指齿轮啮合点上的线速度。
在设计斜齿轮时,需要计算齿轮啮合线速度,以确定齿轮的工作情况。
5. 齿轮啮合力。
齿轮啮合力是指齿轮啮合时所受的力。
在设计斜齿轮时,需要计算齿轮啮合力,以确定齿轮的强度和耐用性。
6. 齿轮啮合噪声。
齿轮啮合噪声是指齿轮啮合时产生的噪声。
在设计斜齿轮时,需要计算齿轮啮合噪声,以确定齿轮的工作环境。
7. 齿轮啮合温升。
齿轮啮合温升是指齿轮啮合时产生的温升。
在设计斜齿轮时,需要计算齿轮啮合温升,以确定齿轮的工作温度。
8. 齿轮啮合效率。
齿轮啮合效率是指齿轮啮合时的能量传递效率。
在设计斜齿轮时,需要计算齿轮啮合效率,以确定齿轮的能量传递情况。
总结。
斜齿轮计算公式涉及到许多参数和变量,包括基本参数、齿轮啮合传动比、齿轮啮合角、齿轮啮合线速度、齿轮啮合力、齿轮啮合噪声、齿轮啮合温升、齿轮啮合效率等。
在设计斜齿轮时,需要根据实际情况计算这些参数和变量,以确定齿轮的设计参数和工作情况。
希望本文所介绍的斜齿轮计算公式大全能对大家有所帮助。
斜齿轮设计计算

斜齿轮设计计算
斜齿轮设计通常包括以下几个步骤:
1. 基本参数确定:包括传动比、中心距、轮齿数量等。
这些参数需要根据传动需求和具体应用来确定。
2. 齿数计算:根据传动比和轮齿数量,使用公式计算主动轮和从动轮的齿数。
3. 齿宽计算:根据传动功率、传动速度和齿数,使用公式计算齿宽。
4. 齿廓计算:根据齿数和齿宽,选择合适的齿廓形状,如直线齿廓、圆弧齿廓等。
5. 齿距计算:根据齿宽和齿廓形状,使用公式计算齿距。
6. 齿轮材料选择:根据传动功率、工作环境和设计寿命要求,选择合适的齿轮材料。
7. 齿轮强度计算:使用齿轮强度公式,计算齿轮的强度,包括扭矩强度和接触强度。
8. 齿轮几何误差计算:根据齿廓曲线和齿距,计算齿轮的几何误差,包括齿顶间距误差、齿宽误差等。
以上仅为斜齿轮设计的常用步骤,具体的设计计算方法和公式
可以根据具体需求和标准来确定。
在实际设计过程中,还需要考虑材料强度、齿面处理、润滑方式等因素,以确保齿轮的可靠性和性能。
斜齿轮的参数及齿轮计算

斜齿轮的参数及齿轮计算斜齿轮是一种常见的传动装置,主要用于实现两个交叉轴之间的转动传递。
斜齿轮的参数与齿轮计算是设计斜齿轮传动所必备的基本步骤之一、本文将介绍斜齿轮的参数以及齿轮计算的相关知识,并详细解释如何进行齿轮设计与计算。
一、斜齿轮的参数1. 模数(Module):模数是斜齿轮的一个重要参数,代表齿轮大圆与齿数之比。
模数一般以毫米为单位,常见的模数有0.5、1、1.5、2、2.5等。
模数越大,齿轮尺寸越大,传动能力越强。
2. 齿数(Number of Teeth):齿数是指齿轮上的齿的数量,用N表示。
齿数决定了齿厚、齿宽等参数,可以根据传动比、模数和其他要求进行计算确定。
3. 压力角(Pressure Angle):压力角是齿轮上任意一点的轮齿延长线与与该点处相切的准线之间的夹角。
常用的压力角有20°、14.5°、25°等,其中20°和25°的最常见。
选择合适的压力角可以提高齿轮传动的平稳性和效率。
4. 齿宽(Face Width):齿宽是指齿轮上两相邻齿顶之间的距离。
齿宽大小应根据传递的转矩大小、使用环境等因素进行综合考虑与计算。
二、齿轮计算齿轮计算是根据给定的参数和需求,对齿轮的尺寸、传动比等进行计算和设计。
齿轮计算通常包括以下步骤:1.传动比计算:根据实际应用需求和设计要求,计算传动比。
传动比可以根据两个斜齿轮的齿数N1、N2来计算,传动比等于齿数比N2/N12.齿数计算:确定斜齿轮的齿数。
齿数一般根据传动比和模数来计算,可使用公式N=(Z1/Z2)*(Z2/Z1)。
3.齿轮尺寸计算:通过使用已知的参数,计算齿轮的尺寸。
齿轮尺寸计算包括齿顶高度、齿根高度、齿厚、齿槽宽度等。
4.齿轮间隙计算:齿轮间隙是两个齿轮啮合时齿顶与齿根之间的距离,用来保证齿轮运转时的正常啮合。
齿轮间隙的计算需要根据齿轮的尺寸和齿轮材料的热胀冷缩系数进行计算。
5.齿数修正:根据使用要求和实际制造条件,对齿数进行修正。
斜齿轮公式计算公式表

斜齿轮公式计算公式表
斜齿轮是一种常见的机械传动元件,其公式计算可以涉及到多
个方面。
首先,我们可以从几何参数入手,斜齿轮的齿数、模数、
压力角等参数可以通过一定的公式计算得出。
其次,斜齿轮的传动
比和传动效率也是重要的计算指标,可以通过相关的公式进行计算。
另外,斜齿轮的强度和耐磨性等参数也需要通过相应的公式来计算。
最后,斜齿轮的啮合角、齿顶间隙、齿根间隙等几何参数也需要通
过公式计算来确定。
在实际应用中,斜齿轮的计算公式涉及到几何学、力学、材料
力学等多个学科的知识。
例如,斜齿轮的啮合角可以通过以下公式
计算,tan(啮合角)=(tan(压力角)-((cos(齿轮螺旋角)+cos(齿
轮螺旋角))tan(齿顶圆压力角)))/(1+sin(齿轮螺旋角)sin(齿
轮螺旋角))。
传动比可以通过齿数的比值来计算,传动效率可以通
过齿轮副的设计参数和工作条件来计算。
而斜齿轮的强度计算则需
要考虑齿面载荷、齿根载荷等因素,可以通过相关的公式进行计算。
总之,斜齿轮的公式计算涉及到多个方面的参数和指标,需要
综合运用几何学、力学、材料力学等知识来进行计算。
在实际应用
中,需要根据具体的设计要求和工作条件来选择合适的公式进行计算,以确保斜齿轮传动的可靠性和稳定性。
标准斜齿轮传动的强度计算

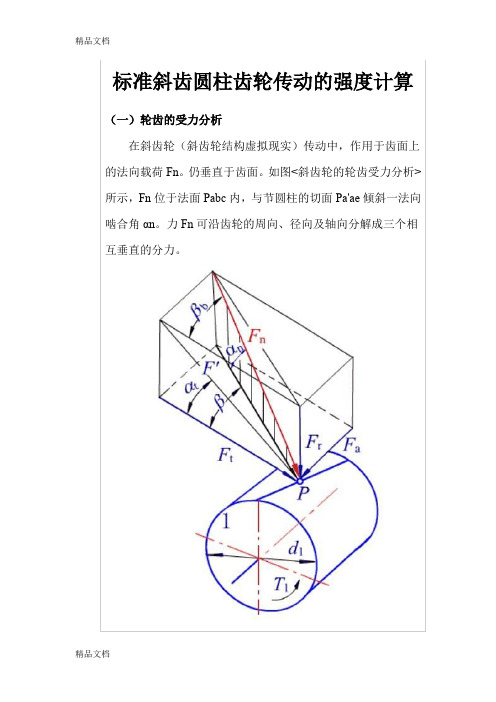
标准斜齿轮传动的强度计算(一)轮齿的受力分析如图10-24所示,在斜齿轮传动中,法向力n F 仍垂直于齿面,作用于主动轮上的n F 位于法面内,与节圆柱的切面呈法向啮合角n α,力n F 可沿齿轮的轴向、径向及轴向分解成三个相互垂直的分力。
各力的大小为:⎪⎪⎪⎩⎪⎪⎪⎨⎧=====b t t n t n t a n t r tF F F F F F F d T F βαβαββαcos cos cos cos tan cos tan 211 (10-14) 各力的方向:径向力指向各自中心;圆周力在主动轮上与运动方向相反,在从动轮上与运动方向相同;主动轮上的轴向力用左右手定则,即左旋用左手,右旋用右手,四指的指向与其转向相同,则拇指的指向即为轴向力的方向。
对从动轮,由于12a a F F -=,或采用左右手定则,拇指的指向与方向相反。
为分析方便,可用平面图来表示受力情况。
如下所示:n 1 n 2F r1 F r2F a1 F a2F a1从上面的计算知:轴向力a F 与βtan 成正比,为不使轴承承受大的轴向力,β不宜过大,一般︒=12~8β;人字齿有两个轴向力且大小相等,方向相反,故可取较大值,一般︒=40~15β。
(二)计算载荷由于轮齿上的计算载荷与啮合区的实际接触线的长度有关,在斜齿轮的轮齿上啮合线为斜线,且可能有几对齿同时啮合,故接触线的总长为所有啮合齿上接触线的长度之和,这个总和可用βεαcos b 来表示。
因此, t t b t bt n ca b KF b KF L KF p αεβαβεααcos cos cos cos === (10-15) αε为端面重合度,可按图10-26查取。
斜齿轮的纵向重合度可用如下公式计算:()βφπβεβtan 318.0sin 1Z m b d n ==计算载荷系数βαK K K K K v a =,各系数的查取可参考直齿轮。
(三)齿根弯曲强度的计算如右图所示,斜齿轮齿面上的接触线为一斜线。
标准斜齿轮计算公式

标准斜齿轮计算公式在机械传动中,斜齿轮是常用的传动方式之一,它具有结构简单、传递能力强、传递效率高等优点。
在设计中,需要计算斜齿轮的参数,以确保传动的准确性和可靠性。
下面将介绍斜齿轮计算的相关公式和参考内容。
1. 齿数计算公式:斜齿轮的齿数是设计中最基本的参数之一,可以根据齿轮传动的所需传输比和模数来计算。
公式:z1 = z2 * i其中,z1和z2分别为齿轮1和齿轮2的齿数,i为齿轮的传动比,通常为整数。
2. 中心距计算公式:中心距是斜齿轮传动中的另一个重要参数,决定了齿轮的相对位置。
公式:a = (dz1 + dz2) / 2其中,a为齿轮的中心距,d为齿轮的分度圆直径,z1和z2为齿轮的齿数。
3. 齿厚计算公式:齿厚是指齿轮上齿槽的宽度,也是斜齿轮的重要参数之一。
公式:bw = a * cos(β)其中,bw为齿厚,a为齿轮的中心距,β为齿轮的斜角。
4. 模数计算公式:模数是设计斜齿轮的一个重要参数,它决定了齿轮传动的几何形状和尺寸。
公式:m = d / z其中,m为模数,d为齿轮的分度圆直径,z为齿轮的齿数。
除了上述计算公式之外,设计斜齿轮还需要考虑齿轮的动力学参数、强度计算等方面的内容。
以下是一些参考内容,供设计师在斜齿轮计算中参考使用:1. GB/T 10095-2001《斜齿轮的几何标准》:该标准规定了斜齿轮的几何图形、尺寸和公差等基本要求,是设计斜齿轮的重要参考资源。
2. GB/T 10096-2001《斜齿轮计算手册》:该手册详细介绍了斜齿轮的计算方法和公式,并给出了实例,可以帮助设计师更好地进行斜齿轮的设计和选型。
3. ISO 6336《齿轮传动-计算法》:该国际标准规定了齿轮传动的计算方法和公式,包括斜齿轮的计算内容,是齿轮传动设计的重要参考依据。
4. 机械设计手册:机械设计手册是机械工程师常用的参考书之一,其中包含了大量的齿轮传动计算公式和实例,对斜齿轮的设计和计算提供了全面的指导。
斜齿轮弯曲强度公式

斜齿轮弯曲强度公式斜齿轮是一种常见的齿轮类型,它在机械传动系统中得到了广泛的应用。
斜齿轮的弯曲强度是机械传动系统设计中的一个重要参数,它反映了斜齿轮在工作中承受弯曲应力的能力。
了解斜齿轮的弯曲强度公式可以帮助我们更好地设计和选型斜齿轮,提高机械传动系统的稳定性和可靠性。
一、斜齿轮的基本概念斜齿轮是指齿轮的齿线方向与齿轮轴线不垂直,而是成一个夹角。
夹角的大小称为螺旋角,用β表示。
根据螺旋角的方向,斜齿轮可分为左旋和右旋两种类型。
二、斜齿轮的弯曲强度斜齿轮在工作中,其齿部受到很大的弯曲应力,这种弯曲应力的大小与齿轮的几何参数、材料、转速等因素有关。
根据弹性力学理论,斜齿轮的弯曲强度可以表示为:σ = K ×σ′× Ym × Zm × [σ]其中,σ表示斜齿轮的弯曲强度;K表示弯曲强度系数,它与齿轮的几何参数、材料等因素有关;σ′表示齿轮的接触应力,即齿轮在接触区内的应力;Ym表示弯曲强度计算系数,它与齿轮的几何参数、转速等因素有关;Zm表示弯曲强度计算系数,它与齿轮的几何参数、转速等因素有关;[σ]表示齿轮材料的许用应力。
三、斜齿轮弯曲强度公式的推导弯曲强度计算系数的确定根据齿轮传动的原理,斜齿轮在工作中主要受到弯曲应力和接触应力两种作用。
弯曲应力的大小与齿轮的几何参数、材料、转速等因素有关,接触应力的大小与齿轮的几何参数、工作压力等因素有关。
因此,弯曲强度系数K可以通过以下公式计算:K = K1 × K2 × K3 × K4其中,K1表示弯曲系数,它与齿轮的几何参数、材料等因素有关;K2表示工作系数,它与工作压力、工作压力位置等因素有关;K3表示转速系数,它与齿轮的转速等因素有关;K4表示温度系数,它与齿轮的工作温度等因素有关。
弯曲强度计算系数的具体值弯曲强度计算系数K的具体值可以根据实际情况查表得到。
根据不同的设计条件和参数,弯曲强度计算系数K可以取不同的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
标准斜齿轮传动的强度计算
(一)轮齿的受力分析
如图10-24所示,在斜齿轮传动中,法向力n F 仍垂直于齿面,作用于主动轮上的n F 位于法面内,与节圆柱的切面呈法向啮合角n α,力n F 可沿齿轮的轴向、径向及轴向分解成三个相互垂直的分力。
各力的大小为:
⎪⎪⎪⎩
⎪⎪⎪⎨⎧=
====b
t t
n t
n t a n
t r t F F F F F F F d T F βαβ
αββ
αcos cos cos cos tan cos tan 21
1
(10-14)
各力的方向:径向力指向各自中心;圆周力在主动轮上与运动方向相反,在从动轮上与运动方向相同;主动轮上的轴向力用左右手定则,即左旋用左手,右旋用右手,四指的指向与其转向相同,则拇指的指向即为轴向力的方向。
对从动轮,由于12a a F F -=,或采用左右手定则,拇指的指向与方向相反。
为分析方便,可用平面图来表示受力情况。
如下所示:
n
从上面的计算知:轴向力a F 与βtan 成正比,为不使轴承承受大的轴向力,β
不宜过大,一般︒=12~8β;人字齿有两个轴向力且大小相等,方向相反,故可取较大值,一般︒=40~15β。
(二)计算载荷
由于轮齿上的计算载荷与啮合区的实际接触线的长度有关,在斜齿轮的轮齿上啮合线为斜线,且可能有几对齿同时啮合,故接触线的总长为所有啮合齿上接触线的长度之和,这个总和可用β
εα
cos b 来表示。
因此,
t
t b
t b
t
n ca b KF b KF L
KF p αεβαβεααcos cos cos cos =
=
=
(10-15)
αε为端面重合度,可按图10-26查取。
斜齿轮的纵向重合度可用如下公式
计算:
)β
φπβ
εβtan 318.0sin 1Z m b d n =
=
计算载荷系数βαK K K K K v a =,各系数的查取可参考直齿轮。
(三)齿根弯曲强度的计算
如右图所示,斜齿轮齿面上的接触线为一斜线。
受载时,齿轮的失效形式为局部折断。
斜齿轮的弯曲强度,若按轮齿局部折断分析则较繁。
现对比直齿轮的弯曲强度计算,仅就其计算特点作必要的说明。
首先,斜齿轮的计算载荷要比直齿轮的多计入一个参数
,其次还应计入反映螺旋角β对轮齿弯曲强度影响的因素,即计
入螺旋角影响系数Y β。
由上述特点,可得斜齿轮轮齿的弯曲疲劳强度公式为:
[]F
n sa Fa t F
bm Y Y Y KF σ
εσ
α
β
≤=
(10-16)
为校核公式。
[]
3
2
112F sa
Fa d Y Y Z Y KT m σεφα
β
⋅
≥
mm (10-17)
为设计公式。
βY 的大小可查图10-28;Fa Y 、Sa Y 可近似地按当量齿数由表10-5查取。
(四)齿面接触强度的计算
仿直齿轮的计算,只是曲率半径有变化,同时,由于螺旋角的影响,区域系数也变化,
t t b H Z ααβcos sin cos 2=,大小可查图10-30。
综合起来,齿面接触强度的计算公式为:
[]H H E t H Z Z u
u bd KF σεσα
≤⋅±
⋅=
11 (10-20)
为校核计算公式。
[]3
2
1112⎪⎪⎭
⎫
⎝⎛⋅±⋅≥
H H
E d Z Z u u KT d σεφα (10-21) 为设计计算公式。
各量的单位同前。
(五)注意
和直齿轮相比,斜齿轮的计算有以下几点不同: 1.计入了端面重合度αε的影响;
2.计入了螺旋角的影响;
3.用当量齿数来查取某些系数;
4.在接触强度的设计计算中,代入的许同应力值不同,说明如下: 在斜齿轮传动中,由于齿面上的接触线倾斜,使得在同一齿面上,就会有齿顶面(其上接触线段为P e 1)与齿根面(接触线段为P e 2)同时参与啮合(在直齿轮中接触线与轴线平行,无此现象)。
由实践得知,同一齿面上,往往齿根面先发生点蚀,然后才扩展到齿顶面,也即齿顶面比齿根面具有较高的接触疲劳强度。
设小齿轮的齿面接触强度比大齿轮的高(即小齿轮的材料好,
齿面硬度高,[][]21H H σσ>)。
因为大小齿轮的实际接触应力相等,故小齿轮的接触强度高,因此当大齿轮的齿根面产生点蚀,P e 2段已不能承担原来所分担的载荷,而要部分地由齿顶面上的P e 1来承担(因法向力始终不变)。
又因同一齿面上齿顶面的接触强度高,即使承担的载荷有所增大,只要未超出其承载能力,大齿轮的齿顶面上仍不会出现点蚀。
同时因小齿轮的接触强度高,与大齿轮齿顶面啮合的小齿轮的齿根面,也未因载荷的增大而出现点蚀,这说明:在斜齿轮传动中,当大齿轮的齿根面出现点蚀时,并不导致传动的失效,因此,斜齿轮的接触疲劳强度同时取决于大小齿轮。
实用中,计算公式中的[][][]221H H H σσσ+=,当[][]223.1H H σσ>时,因为二者相差较大,应按[][]223.1H H σσ=代入。
为软齿面的许用接触应力。
5.区域系数H z 和螺旋角β有关。
通过例题10-1、10-2、
10-3,比较计算结果,有如下两个特点:
1.在工作条完全相同的情况下,采用斜齿轮传动比直齿轮传动的几何尺寸小,或者说,斜齿轮传动比直齿轮传动具有较大的承载能力;
2.硬齿面齿轮传动明显比软齿面齿轮传动的几何尺寸小,因此硬齿面齿轮传动得到了较广泛的应用。
