函数概念测试题(一)
函数概念及其表示方法测试题
函数的概念及表示方法测试题A 卷 基础在线一．填空题（本大题共10小题，每题5分） 1. 若函数2()2f x x x =-，则)3(f =________． 1.3 提示：2(3)3233f .2.函数422--=x x y 的定义域________．515050()2x t2.2x x提示：2402x x，故定义域为2x x .. ①29()3x f x x ，()3g x x ；②2()()f x x ，2()g x x ；③21()3f x x；242()3x g x xx；④2()()f x x ，()g x x .3.提示：①29()3,(3)3x f x x x x ，()3g x x 定义域为全体实数，两个函数定义域不同；②2()()(0)f x x x ，2(),g x x x xR ，两函数解析式不同；③21()()3f x x R x，24221()(0)33x g x xx x x 两函数定义域不同；④两函数解析式相同，定义域也相同故两函数为同一函数.4. 若函数2(1)f x +的定义域为[2,1)-，则函数()f x 的定义域为________． 4. [0,5] 提示：由题意可知204x ，则2015x ，故函数()f x 的定义域为[0,5].5. 下列图象中能表示函数y ＝()f x 的有 ．① ② ③ ④5.①④．提示：根据函数的定义可判断。
6.函数221,[1,3)y x x x =--∈-的值域为_______． 6. [2,2] 提示：该二次函数开口方向向上，对称轴为1x ，故函数的最小值为2，当1x时，函数有最大值为2，故函数的值域为[2,2].7.定义运算,,,,a ab abb ab 则对任意x R ，函数()1f x x 的解析式为 .7. 1,1(),1x f x x x提示：若1x ，则()1f x ；若1x ，则()f x x .8.若函数2()1f x x ，()2g x x，则[(2)]f g .8.17 提示：由题意(2)224g ，则2[(2)](4)4117f g f .9.若函数()f x 满足()()()f x f y f xy ，且(3)f a ，(2)f b ，则(36)f .9.22a b 提示：由题意知(6)(2)(3)f f f ab，则22(36)(6)(6)f f f ab ab a b .10.若(2),2()1,2f x x f x xx，则(0)f 的值为 .10.1 提示：由题意(0)(02)(2)211f f f .二．解答题（本大题共3小题）13.已知A 、B 两地相距150千米，某人开汽车以60千米/小时的速度从A 地到达B 地，在B 地停留1小时后以50千米/小时的速度返回A 地，求汽车离开A 地的距离x 表示为时间t （小时）的函数表达式. 13.解析：由题意当52t时，60x t ，当5722t时，则150x ，当71322t时，715050()325502xtt 。
初中数学函数基础知识基础测试题(1)
初中数学函数基础知识基础测试题(1)一、选择题1．下列各曲线中，表示y 是x 的函数的是（ ）A ．B ．C ．D ．【答案】B【解析】【分析】根据函数的意义即可求出答案．【详解】解：根据函数的意义可知：对于自变量x 的任何值，y 都有唯一的值与之相对应，所以B 正确．故选：B ．【点睛】此题考查函数图象的概念．解题关键在于要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件，结合实际意义得到正确的结论．函数的意义反映在图象上简单的判断方法是：做垂直x 轴的直线在左右平移的过程中与函数图象只会有一个交点．2．如图，在矩形ABCD 中，AB 4=，BC 6=，当直角三角板MPN 的直角顶点P 在BC 边上移动时，直角边MP 始终经过点A ，设直角三角板的另一直角边PN 与CD 相交于点Q.BP x =，CQ y =，那么y 与x 之间的函数图象大致是( )A ．B ．C ．D ．【答案】D【解析】试题解析：设BP =x ，CQ =y ，则AP 2=42+x 2，PQ 2=（6-x ）2+y 2，AQ 2=（4-y ）2+62； ∵△APQ 为直角三角形，∴AP 2+PQ 2=AQ 2，即42+x 2+（6-x ）2+y 2=（4-y ）2+62，化简得：y =−14x 2+32x 整理得：y=−14(x −3)2+94 根据函数关系式可看出D 中的函数图象与之对应．故选D ．【点睛】本题考查的是动点变化时，两线段对应的变化关系，重点是找出等量关系，即直角三角形中的勾股定理．3．如图，在ABC ∆中，90C =o ∠，30B ∠=o ，10AB cm =，P Q 、两点同时从点A 分别出发，点P 以2/cm s 的速度，沿A B C →→运动，点Q 以1/cm s 的速度，沿A C B →→运动，相遇后停止，这一过程中，若P Q 、两点之间的距离PQ y =，则y 与时间t 的关系大致图像是（ ）A ．B ．C ．D ．【答案】A【解析】【分析】根据题意分当05t ≤≤、5t >时两种情况，分别表示出PQ 的长y 与t 的关系式，进而得出答案．【详解】解：在ABC ∆中，90C =o ∠，30B ∠=o ，AB=10,∴AC=5, 12AC AB =， I. 当05t ≤≤时，P 在AB 上，Q 在AC 上，由题意可得：2AP t =，AQ t =，依题意得：12AQ AP =， 又∵A A ∠=∠∴APQ ABC V :V , ∴90AQP C ∠=∠=︒则3PQ t =，II.当5t >，P 、Q 在BC 上，由题意可得：P 走过的路程是2t ，Q 走过的路程是t ， ∴15533PQ t =+-,故选：A ．【点睛】此题主要考查了动点问题的函数图象，正确理解PQ 长与时间是一次函数关系，并得出函数关系式是解题关键．4．已知圆锥的侧面积是8πcm 2，若圆锥底面半径为R （cm ），母线长为l （cm ），则R 关于l 的函数图象大致是（ ）A ．B ．C ．D ．【答案】A【解析】【分析】根据圆锥的侧面展开图是扇形、扇形面积公式列出关系式，根据反比例函数图象判断即可．【详解】 解：由题意得，12×2πR×l ＝8π， 则R ＝8lπ， 故选A ．【点睛】 本题考查的是圆锥的计算、函数图象，掌握圆锥的圆锥的侧面积的计算公式是解题的关键．5．下列说法：①函数6y x =-x 的取值范围是6x >；②对角线相等的四边形是矩形；③正六边形的中心角为60︒；④对角线互相平分且相等的四边形是菱形；⑤计算92|-的结果为7：⑥相等的圆心角所对的弧相等；1227理数．其中正确的个数有（ ）A ．1个B ．2个C ．3个D ．4个【答案】B【解析】【分析】根据正多边形和圆，无理数的定义，二次根式的加减运算，菱形的判定，矩形的判定，函数自变量的取值范围解答即可．【详解】解：①函数6y x =-x 的取值范围是6x ≥；故错误；②对角线相等且互相平分的四边形是矩形；故错误；③正六边形的中心角为60°；故正确；④对角线互相平分且垂直的四边形是菱形；故错误；⑤计算9的结果为1；故错误；⑥同圆或等圆中，相等的圆心角所对的弧相等；故错误； 122723333==是无理数；故正确．故选：B ．【点睛】本题考查了正多边形和圆，无理数的定义，二次根式的加减运算，菱形的判定，矩形的判定，函数自变量的取值范围，熟练掌握各知识点是解题的关键．6．如图所示，菱形ABCD 中，直线l ⊥边AB ，并从点A 出发向右平移，设直线l 在菱形ABCD 内部截得的线段EF 的长为y ，平移距离x ＝AF ，y 与x 之间的函数关系的图象如图2所示，则菱形ABCD 的面积为（ ）A ．3B 3C ．3D ．3【答案】C【解析】【分析】 将图1和图2结合起来分析，分别得出直线l 过点D ，B 和C 时对应的x 值和y 值，从而得出菱形的边长和高，从而得其面积．【详解】解：由图2可知，当直线l 过点D 时，x ＝AF ＝a ，菱形ABCD 的高等于线段EF 的长，此时y ＝EF 3；直线l 向右平移直到点F 过点B 时，y 3；当直线l 过点C 时，x ＝a +2，y ＝0∴菱形的边长为a +2﹣a ＝2∴当点E 与点D 重合时，由勾股定理得a 2+23)＝4∴a ＝1 3∴菱形的面积为3故选：C ．【点睛】本题是动点函数图象问题，将图形的运动与函数图象结合起来分析，是解决此类问题的关键，7．如图，在ABC ∆中，AB AC =，MN 是边BC 上一条运动的线段（点M 不与点B 重合，点N 不与点C 重合），且12MN BC =，MD BC ⊥交AB 于点D ，NE BC ⊥交AC 于点E ，在MN 从左至右的运动过程中，设BM x =，BMD ∆的面积减去CNE ∆的面积为y ，则下列图象中，能表示y 与x 的函数关系的图象大致是（ ）A ．B ．C ．D ．【答案】A【解析】【分析】设a ＝12BC ，∠B ＝∠C ＝α，求出CN 、DM 、EN 的长度，利用y ＝S △BMD −S △CNE ，即可求解． 【详解】 解：设a ＝12BC ，∠B ＝∠C ＝α，则MN ＝a ， ∴CN ＝BC−MN−BM ＝2a−a−x ＝a−x ，DM ＝BM·tanB ＝x·tanα，EN ＝CN•tanC ＝（a−x ）·tanα， ∴y ＝S △BMD −S △CNE ＝12（BM·DM−CN·EN ）＝()()221tan tan 222x a x a tan x a ααα⋅⎡⎤⋅-⋅=⎣⎦--， ∵2a tan α⋅为常数， ∴上述函数图象为一次函数图象的一部分，故选：A ．【点睛】本题考查了动点问题的函数图象、等腰三角形的性质、解直角三角形、图形面积等知识点．解题关键是深刻理解动点的函数图象，了解图象中关键点所代表的实际意义，理解动点的完整运动过程．8．小丽早上步行去车站然后坐车去学校，下列能近似的刻画她离学校的距离随时间变化的大致图象是()A．B．C．D．【答案】D【解析】【分析】根据上学，可得离学校的距离越来越小，根据开始步行，可得距离变化慢，后来坐车，可得距离变化快．【详解】解：A、距离越来越大，选项错误；B、距离越来越小，但前后变化快慢一样，选项错误；C、距离越来越大，选项错误；D、距离越来越小，且距离先变化慢，后变化快，选项正确；故选：D．【点睛】本题考查了函数图象，观察距离随时间的变化是解题关键．9．在同一条道路上，甲车从A地到B地，乙车从B地到A地，乙先出发，图中的折线段表示甲、乙两车之间的距离y（千米）与行驶时间x（小时）的函数关系的图象，下列说法错误的是（）A．乙先出发的时间为0.5小时B．甲的速度是80千米/小时C．甲出发0.5小时后两车相遇D．甲到B地比乙到A地早112小时【答案】D【解析】试题分析：A．由图象横坐标可得，乙先出发的时间为0.5小时，正确，不合题意；B．∵乙先出发，0.5小时，两车相距（100﹣70）km，∴乙车的速度为：60km/h，故乙行驶全程所用时间为：=（小时），由最后时间为1.75小时，可得乙先到到达A地，故甲车整个过程所用时间为：1.75﹣0.5=1.25（小时），故甲车的速度为：100÷1.25 =80（km/h），故B选项正确，不合题意；C．由以上所求可得，甲出发0.5小时后行驶距离为：40km，乙车行驶的距离为：60km，40+60=100，故两车相遇，故C选项正确，不合题意；D．由以上所求可得，乙到A地比甲到B地早：1.75﹣=（小时），故此选项错误，符合题意．故选D．考点：函数的图象．10．父亲节当天，学校“文苑”栏登出了某同学回忆父亲的小诗：“同辞家门赴车站，别时叮咛语千万，学子满载信心去，老父怀抱希望还．”如果用纵轴y表示父亲和学子在行进中离家的距离，横轴t表示离家的时间，下面与上述诗意大致相吻合的图像是()A．B．C．D．【答案】B【解析】【分析】正确理解函数图象即可得出答案．【详解】解：同辞家门赴车站，父亲和学子的函数图象在一开始的时候应该一样，当学子离开车站出发，离家的距离越来越远，父亲离开车站回家，离家越来越近．故选B．【点睛】首先应理解函数图象的横轴和纵轴表示的量，再根据实际情况来判断函数图象．11．某工厂加工一批零件，为了提高工人工作积极性，工厂规定每名工人每天薪金如下：生产的零件不超过a件，则每件3元，超过a件，超过部分每件b元，如图是一名工人一天获得薪金y（元）与其生产的件数x（件）之间的函数关系式，则下列结论错误的（）A．a=20B．b=4C．若工人甲一天获得薪金180元，则他共生产45件．D．人乙一天生产40（件），则他获得薪金140元【答案】C【解析】【分析】根据题意和函数图象可以求得a、b的值，从而可以判断选项A和B是否正确，根据C和D的数据可以分别计算出题目中对应的数据是否正确，从而可以解答本题．【详解】解：由题意和图象可得，a＝60÷3＝20，故选项A正确，b＝（140−60）÷（40−20）＝80÷20＝4，故选项B正确，若工人甲一天获得薪金180元，则他共生产：20＋180602030504-=+=（件），故选项C错误；由图象可知，工人乙一天生产40（件），他获得的薪金为：140元，故选项D正确，故选：C．【点睛】本题考查函数图象的应用，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．12．如图甲，在四边形ABCD中，AD//BC，∠C=90°动点P从点C出发沿线段CD向点D运动.到达点D即停止，若E、F分别是AP、BP的中点，设CP=x,△PEF的面积为y，且y与x 之间的函数关系的图象如图乙所示，则线段AB长为（）A．22B．23C．25D．26【答案】C【解析】【分析】根据三角形中位线定理，得到S△PEF=14S△ABP，由图像可以看出当x为最大值CD=4时，S△PEF=2，可求出AD=4，当x为0时，S△PEF=3，可求出BC=6；过点A作AG⊥BC于点G，根据勾股定理即可得解.【详解】解：∵E、F分别为AP、BP的中点，∴EF∥AB，EF=12 AB，∴S△PEF=14S△ABP，根据图像可以看出x的最大值为4，∴CD=4，∵当P在D点时，△PEF的面积为2，∴S△ABP=2×4=8，即S△ABD=8，∴AD=24ABDSV=284⨯=4，当点P在C点时，S△PEF=3，∴S△ABP=3×4=12，即S△ABC=12，∴BC=24ABCSV=2124⨯=6，过点A作AG⊥BC于点G，∴∠AGC=90°，∵AD∥BC，∴∠ADC+∠BCD=180°，∵∠BCD=90°，∴∠ADC=180°-90°=90°，∴四边形AGCD是矩形，∴CG=AD=4，AG=CD=4，∴BG=BC-CG=6-4=2，∴AB=2242=25.故选C.【点睛】本题主要考查了动点的函数问题，三角形中位线定理，勾股定理.13．一辆慢车从甲地匀速行驶至乙地，一辆快车同时从乙地出发匀速行驶至甲地，两车之间的距离y（千米）与行驶时间x（小时）的对应关系如图所示，下列叙述正确的是（）A．甲乙两地相距1200千米B．快车的速度是80千米∕小时C．慢车的速度是60千米∕小时D．快车到达甲地时，慢车距离乙地100千米【答案】C【解析】【分析】（1）由图象容易得出甲乙两地相距600千米；（2）由题意得出慢车速度为60010=60（千米/小时）；设快车速度为x千米/小时，由图象得出方程60×4+4x=600，解方程即可；（3）求出快车到达的时间和慢车行驶的路程，即可得出答案.【详解】解:（1）由图象得：甲乙两地相距600千米,故选项A错;（2）由题意得：慢车总用时10小时，∴慢车速度为：60010=60（千米/小时）；设快车速度为x千米/小时，由图象得：60×4+4x=600，解得：x=90，∴快车速度为90千米/小时，慢车速度为60千米/小时；选项B错误，选项C正确；（3）快车到达甲地所用时间：60020903小时，慢车所走路程：60×203=400千米，此时慢车距离乙地距离：600-400=200千米，故选项D错误.故选C【点睛】本题考核知识点：函数图象. 解题关键点：从图象获取信息，由行程问题基本关系列出算式.14．如图，两块完全重合的正方形纸片，如果上面的一块绕正方形的中心O逆时针0°～90°的旋转，那么旋转时露出的△ABC的面积（S）随着旋转角度（n）的变化而变化，下面表示S与n关系的图象大致是（）A．B．C．D．【答案】B【解析】【分析】注意分析y随x的变化而变化的趋势，而不一定要通过求解析式来解决．【详解】旋转时露出的△ABC的面积（S）随着旋转角度（n）的变化由小到大再变小．故选B．【点睛】考查动点问题的函数图象问题，关键要仔细观察．15．甲、乙两同学骑自行车从A地沿同一条路到B地，已知乙比甲先出发，他们离出发地的距离S（km）和骑行时间t（h）之间的函数关系如图所示，给出下列说法：①他们都骑行了20km；②乙在途中停留了0.5h；③甲、乙两人同时到达目的地；④相遇后，甲的速度小于乙的速度．根据图象信息，以上说法正确的有（）A．1个B．2个C．3个D．4个【答案】B【解析】试题分析：根据图象上特殊点的坐标和实际意义即可作出判断．由图可获取的信息是：他们都骑行了20km；乙在途中停留了0.5h；相遇后，甲的速度＞乙的速度，所以甲比乙早0.5小时到达目的地，所以（1）（2）正确．故选B．考点：本题考查的是学生从图象中读取信息的数形结合能力点评：同学们要注意分析其中的“关键点”，还要善于分析各图象的变化趋势．16．如图所示：边长分别为1和2的两个正方形，其一边在同一水平线上，小正方形沿该水平线自左向右匀速穿过大正方形，设穿过的时间为t，大正方形内除去小正方形部分的面积为S（阴影部分），那么S与t的大致图象应为（）A．B．C．D．【答案】A【解析】【分析】【详解】解：根据题意，设小正方形运动速度为v，由于v分为三个阶段，①小正方形向右未完成穿入大正方形，=⨯-⨯=-≤．S vt vt vt2214(1)②小正方形穿入大正方形但未穿出大正方形，22113S=⨯-⨯=，③小正方形穿出大正方形，22(11)3(1)S vt vt vt =⨯-⨯-=+≤，∴符合变化趋势的是A 和C ，但C 中面积减小太多不符合实际情况，∴只有A 中的符合实际情况．故选A ．17．甲乙两同学同时从400m 环形跑道上的同一点出发，同向而行，甲的速度为6/m s ，乙的速度为4/m s ，设经过xs 后，跑道上两人的距离（较短部分）为ym ，则y 与x 0300x ≤≤之间的关系可用图像表示为（ ）A ．B ．C ．D ．【答案】C【解析】【分析】根据同向而行，二人的速度差为642/m s -=，二人间的最长距离为200，最短距离为0，从而可以解答本题．【详解】二人速度差为642/m s -=，100秒时，二人相距2×100=200米，200秒时，二人相距2×200=400米，较短部分的长度为0，300秒时，二人相距2×300=600米，即甲超过乙600-400=200米．∴()201004002(100200)2400(200300)x x y x x x x ⎧≤≤⎪=-<≤⎨⎪-<≤⎩，函数图象均为线段，只有C 选项符合题意．故选：C ．【点睛】本题考查了利用函数的图象解决实际问题以及动点问题的函数图象，正确理解函数图象表示的意义，理解问题的过程，就能够通过图象得到函数问题的相应解决．18．甲、乙两人沿相同的路线由A 地到B 地匀速前进，A 、B 两地间的路程为20km ．他们前进的路程为s (km)，甲出发后的时间为t (h)，甲、乙前进的路程与时间的函数图象如图所示．根据图象信息，下列说法正确的是（ ）A ．甲的速度是4km/hB ．乙的速度是10km/hC ．乙比甲晚出发1hD ．甲比乙晚到B 地3h【答案】C【解析】甲的速度是：20÷4=5km/h ；乙的速度是：20÷1=20km/h ； 由图象知，甲出发1小时后乙才出发，乙到2小时后甲才到，故选C ．19．如图1，点F 从菱形ABCD 的项点A 出发，沿A －D －B 以1cm/s 的速度匀速运动到点B ．图2是点F 运动时，△FBC 的面积y (m 2)随时间x (s)变化的关系图象，则a 的值为( )A ．5B ．2C ．52D ．5【答案】C【解析】【分析】 过点D 作DE BC ⊥于点E 由图象可知，点F 由点A 到点D 用时为as ，FBC ∆的面积为2acm ．求出DE=2，再由图像得5BD =BE=1，再在DEC Rt △根据勾股定理构造方程，即可求解．【详解】解：过点D 作DE BC ⊥于点E由图象可知，点F 由点A 到点D 用时为as ，FBC ∆的面积为2acm ．AD BC a ∴== ∴12DE AD a =g 2DE ∴=由图像得，当点F 从D 到B 时，用5s5BD ∴=Rt DBE V 中， 2222(5)21BE BD DE =-=-=∵四边形ABCD 是菱形，1EC a ∴=-，DC a =DEC Rt △中，2222(1)a a =+-解得52a =故选：C ．【点睛】本题综合考查了菱形性质和一次函数图象性质，要注意函数图象变化与动点位置之间的关系，解答此题关键根据图像关键点确定菱形的相关数据．20．已知：在ABC ∆中， 10,BC BC =边上的高5h =，点E 在边AB 上，过点E 作//EF BC 交AC 边于点F ．点D 为BC 上一点，连接DE DF 、．设点E 到BC 的距离为x ，则DEF ∆的面积S 关于x 的函数图象大致为（ ）A ．B ．C．D．【答案】D【解析】【分析】判断出△AEF和△ABC相似，根据相似三角形对应边成比例列式求出EF，再根据三角形的面积列式表示出S与x的关系式，然后得到大致图象选择即可．【详解】解：∵EF∥BC，∴△AEF∽△ABC，∴55EF x BC-=，∴EF=55x-•10=10-2x，∴S=12（10-2x）•x=-x2+5x=-（x-52）2+254，∴S与x的关系式为S=-（x-52）2+254（0＜x＜5），纵观各选项，只有D选项图象符合．故选：D．【点睛】此题考查动点问题函数图象，相似三角形的性质，求出S与x的函数关系式是解题的关键．。
必修一函数测试题
必修一函数测试题一、选择题（每题3分，共15分）1. 函数f(x) = 3x^2 - 2x + 1的图像关于哪条直线对称？A. x = 0B. x = 1C. x = -1/3D. x = 1/32. 若函数f(x) = x^3 - 2x^2 + x - 2在区间[-1, 2]上是增函数，则下列哪个选项是正确的？A. f(-1) < f(2)B. f(-1) > f(2)C. f(-1) = f(2)D. 无法确定3. 函数y = √(x^2 + 1)的值域是：A. (-∞, 0]B. [0, +∞)C. (-1, 1)D. [1, +∞)4. 已知函数f(x) = 2x - 3，求f(5)的值是：A. 7B. 4C. 1D. 05. 对于函数f(x) = ax + b，若f(1) = 0且f(2) = 5，求a和b的值分别是：A. a = 5, b = -5B. a = -5, b = 5C. a = 1, b = -1D. a = -1, b = 1二、填空题（每题2分，共10分）6. 若函数f(x) = x^2 + 2x + 3的顶点坐标是________。
7. 函数y = 2x + 3与x轴的交点坐标是________。
8. 函数y = 1/x的图像在第________象限是单调递增的。
9. 若函数f(x) = √x在区间[0, +∞)上是单调递增的，则f(4)与f(9)的大小关系是f(4)________f(9)。
10. 函数y = |x - 2| + 3的图像与y轴的交点坐标是________。
三、解答题（共25分）11. 求函数f(x) = x^3 - 6x^2 + 9x + 2的极值点，并判断其单调性。
（10分）12. 已知函数f(x) = x^2 - 4x + 4，求其在区间[0, 6]上的值域。
（7分）13. 给定函数f(x) = 2x - 1，请证明对于所有x > 0，都有f(x) > x。
初中数学函数基础知识经典测试题含答案(1)
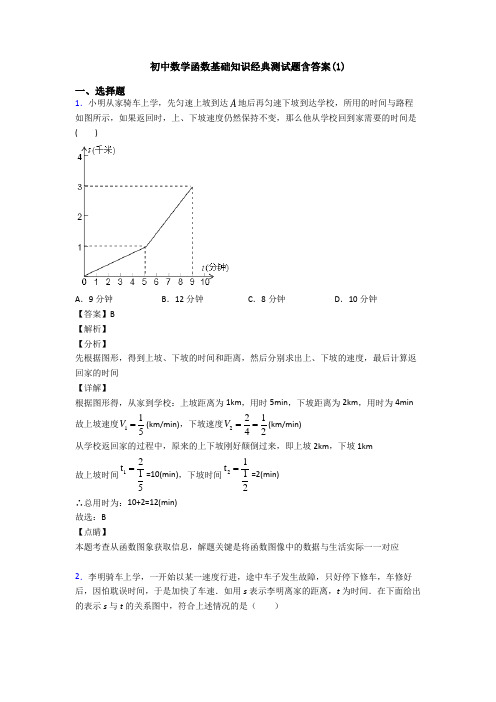
初中数学函数基础知识经典测试题含答案(1)一、选择题1．小明从家骑车上学，先匀速上坡到达A 地后再匀速下坡到达学校，所用的时间与路程如图所示，如果返回时，上、下坡速度仍然保持不变，那么他从学校回到家需要的时间是( )A ．9分钟B ．12分钟C ．8分钟D ．10分钟【答案】B【解析】【分析】 先根据图形，得到上坡、下坡的时间和距离，然后分别求出上、下坡的速度，最后计算返回家的时间【详解】根据图形得，从家到学校：上坡距离为1km ，用时5min ，下坡距离为2km ，用时为4min 故上坡速度115V =(km/min)，下坡速度22142V ==(km/min) 从学校返回家的过程中，原来的上下坡刚好颠倒过来，即上坡2km ，下坡1km 故上坡时间12t 15==10(min)，下坡时间21t 12==2(min) ∴总用时为：10+2=12(min)故选：B【点睛】 本题考查从函数图象获取信息，解题关键是将函数图像中的数据与生活实际一一对应2．李明骑车上学，一开始以某一速度行进，途中车子发生故障，只好停下修车，车修好后，因怕耽误时间，于是加快了车速．如用s 表示李明离家的距离，t 为时间．在下面给出的表示s 与t 的关系图中，符合上述情况的是（ ）A．B．C．D．【答案】C【解析】【分析】先弄清题意，再分析路程和时间的关系.【详解】∵停下修车时，路程没变化，观察图象，A、B、D的路程始终都在变化，故错误；C、修车是的路程没变化，故C正确；故选：C．【点睛】考核知识点：函数的图象.理解题意看懂图是关键.3．下列各曲线中表示y是x的函数的是（）A．B．C．D．【答案】D【解析】根据函数的意义可知：对于自变量x的任何值，y都有唯一的值与之相对应，故D正确．故选D．4．如图，边长为 2 的正方形ABCD，点P从点A出发以每秒 1 个单位长度的速度沿A D C--的路径向点 C 运动，同时点 Q 从点 B 出发以每秒 2 个单位长度的速度沿∆的面B C D A---的路径向点 A运动，当点 Q 到达终点时，点P停止运动，设PQC积为S，运动时间为t秒，则能大致反映S与t的函数关系的图象是（）A ．B ．C ．D ．【答案】C【解析】【分析】 分三种情况求出解析式，即可求解．【详解】当0≤t≤1时，即当点Q 在BC 上运动，点P 在AD 上运动时，()2222212S t t =⨯⨯-=-， ∴该图象y 随x 的增大而减小，当1＜t≤2时，即当点Q 在CD 上运动时，点P 在AD 上运动时，()()21222322S t t t t =--=-+-， ∴该图象开口向下， 当2＜t≤3，即当点Q 在AD 上运动时，点P 在DC 上运动时，()()21424682S t t t t =--=-+- ∴该图象开口向下，故选：C ．【点睛】本题考查了动点问题的函数图象，求出分段函数解析式是本题的关键．5．若A(﹣3，y 1)、B(0，y 2)、C(2，y 3)为二次函数y ＝（x+1）2+1的图象上的三点，则y 1、y 2、y 3的大小关系是（ ）A ．y 1＜y 2＜y 3B ．y 2＜y 1＜y 3C ．y 3＜y 1＜y 2D ．y 1＜y 3＜y 2【答案】B【解析】【分析】把三个点的坐标代入二次函数解析式分别计算出则y 1、y 2、y 3的值，然后进行大小比较．【详解】解：∵A （﹣3，y 1）、B （0，y 2）、C （2，y 3）为二次函数y ＝（x+1）2+1的图象上的三点，∴y 1＝（﹣3+1）2+1＝5，y 2＝（0+1）2+1＝2，y 3＝（2+1）2+1＝10，∴y 2＜y 1＜y 3．故选：B．【点睛】本题考查了比较函数值大小的问题，掌握二次函数的性质、代入法是解题的关键．6．小丽早上步行去车站然后坐车去学校，下列能近似的刻画她离学校的距离随时间变化的大致图象是()A．B．C．D．【答案】D【解析】【分析】根据上学，可得离学校的距离越来越小，根据开始步行，可得距离变化慢，后来坐车，可得距离变化快．【详解】解：A、距离越来越大，选项错误；B、距离越来越小，但前后变化快慢一样，选项错误；C、距离越来越大，选项错误；D、距离越来越小，且距离先变化慢，后变化快，选项正确；故选：D．【点睛】本题考查了函数图象，观察距离随时间的变化是解题关键．7．弹簧挂上物体后会伸长，现测得一弹簧的长度y（厘米）与所挂物体的质量x（千克）之间有如下关系：物体质量x/千克 0 1 2 3 4 5 …弹簧长度y/厘米10 10.5 11 11.5 12 12.5 …下列说法不正确的是（）A．x与y都是变量，其中x是自变量，y是因变量B ．弹簧不挂重物时的长度为0厘米C ．在弹性范围内，所挂物体质量为7千克时，弹簧长度为13.5厘米D ．在弹性范围内，所挂物体质量每增加1千克弹簧长度增加0.5厘米【答案】B【解析】试题分析：根据图表数据可得，弹簧的长度随所挂重物的质量的变化而变化，并且质量每增加1千克，弹簧的长度增加0.5cm ，然后对各选项分析判断后利用排除法．解：A 、x 与y 都是变量，且x 是自变量，y 是因变量，正确，不符合题意；B 、弹簧不挂重物时的长度为10cm ，错误，符合题意；C 、在弹性范围内，所挂物体质量为7千克时，弹簧长度为10+0.5×7=13.5，正确，不符合题意；D 、在弹性范围内，所挂物体质量每增加1千克弹簧长度增加0.5厘米，正确，不符合题意．故选B ．点评：本题考查了函数关系的确认，常量与变量的确定，读懂图表数据，并从表格数据得出正确结论是解题的关键，是基础题，难度不大．8．在平面直角坐标系中有三个点的坐标：()()0,2,2,01(),3A B C ---，，从、、A B C 三个点中依次取两个点，求两点都落在抛物线2y x x 2=--上的概率是（ ）A ．13B ．16C ．12D ．23【答案】A【解析】【分析】先画树状图展示所有6种等可能的结果数，再找出两点都落在抛物线2y x x 2=--上的结果数，然后根据概率公式求解．【详解】解：在()()0,2,2,01(),3A B C ---，三点中，其中AB 两点在2y x x 2=--上， 根据题意画图如下：共有6种等可能的结果数，其中两点都落在抛物线2y x x 2=--上的结果数为2， 所以两点都落在抛物线2y x x 2=--上的概率是2163=； 故选：A ．【点睛】本题考查了列表法或树状图法和函数图像上点的特征．通过列表法或树状图法展示所有等可能的结果求出n，再从中选出符合事件A或B的结果数目m，然后根据概率公式求出事件A或B的概率．也考查了二次函数图象上点的坐标特征．9．如图，矩形ABCD中，P为CD中点，点Q为AB上的动点（不与,A B重合）．过Q作QM PA⊥于M，QN PB⊥于N．设AQ的长度为x，QM与QN的长度和为y．则能表示y与x之间的函数关系的图象大致是（）A．B．C．D．【答案】D【解析】【分析】根据三角形面积得出S△PAB=12PE•AB；S△PAB=S△PQB+S△PAQ=12QN•PB+12PA•MQ，进而得出y=PE ABPB，即可得出答案．【详解】解：连接PQ，作PE⊥AB垂足为E，∵过Q作QM⊥PA于M，QN⊥PB于N，∴S△PAB=12 PE•AB；S△PAB=S△PQB+S△PAQ=12QN•PB+12PA•MQ，∵矩形ABCD中，P为CD中点，∴PA=PB，∵QM与QN的长度和为y，∴S△PAB=S△PQB+S△PAQ=12QN•PB+12PA•MQ=12PB（QM+QN）=12PB•y，∴S△PAB=12PE•AB=12PB•y，∴y=PE AB PB⋅，∵PE=AD，∴PE，AB，PB都为定值，∴y的值为定值，符合要求的图形为D，故选：D．【点睛】此题考查了矩形的性质，三角形的面积，动点函数的图象，根据已知得出y=PE ABPB⋅，再利用PE=AD，PB，AB，PB都为定值是解题关键．10．木杆AB斜靠在墙壁上，当木杆的上端A沿墙壁NO竖直下滑时，木杆的底端B也随之沿着射线OM方向滑动．下列图中用虚线画出木杆中点P随之下落的路线，其中正确的是（）A．B．C．D．【答案】D【解析】解：如右图，连接OP ，由于OP 是Rt △AOB 斜边上的中线，所以OP=12AB ，不管木杆如何滑动，它的长度不变，也就是OP 是一个定值，点P 就在以O 为圆心的圆弧上，那么中点P 下落的路线是一段弧线．故选D ．11．如图，矩形ABCD 的周长是28cm ，且AB 比BC 长2cm ．若点P 从点A 出发，以1/cm s 的速度沿A D C →→方向匀速运动，同时点Q 从点A 出发，以2/cm s 的速度沿A B C →→方向匀速运动，当一个点到达点C 时，另一个点也随之停止运动．若设运动时间为()t s ，APQ V 的面积为()2cm S ，则()2cm S 与()t s 之间的函数图象大致是（ ）A ．B ．C ．D ．【答案】A【解析】【分析】先根据条件求出AB 、AD 的长，当0≤t≤4时，Q 在边AB 上，P 在边AD 上，如图1，计算S 与t 的关系式，分析图像可排除选项B 、C ；当4＜t≤6时，Q 在边BC 上，P 在边AD 上，如图2，计算S 与t 的关系式，分析图像即可排除选项D ，从而得结论．【详解】解：由题意得2228AB BC +=，2AB BC =+，可解得8AB =，6BC =，即6AD =，①当0≤t≤4时，Q 在边AB 上，P 在边AD 上，如图1，S △APQ =211222AP AQ t t t ==g g ， 图像是开口向上的抛物线，故选项B 、C 不正确；②当4＜t≤6时，Q 在边BC 上，P 在边AD 上，如图2，S △APQ =118422AP AB t t =⨯=g ， 图像是一条线段，故选项D 不正确；故选：A ．【点睛】本题考查了动点问题的函数图象，根据动点P 和Q 的位置的不同确定三角形面积的不同，解决本题的关键是利用分类讨论的思想求出S 与t 的函数关系式．12．甲、乙两同学骑自行车从A 地沿同一条路到B 地，已知乙比甲先出发，他们离出发地的距离S （km ）和骑行时间t （h ）之间的函数关系如图所示，给出下列说法：①他们都骑行了20km ；②乙在途中停留了0.5h ；③甲、乙两人同时到达目的地；④相遇后，甲的速度小于乙的速度．根据图象信息，以上说法正确的有（ ）A ．1个B ．2个C ．3个D ．4个【答案】B【解析】 试题分析：根据图象上特殊点的坐标和实际意义即可作出判断．由图可获取的信息是：他们都骑行了20km ；乙在途中停留了0.5h ；相遇后，甲的速度＞乙的速度，所以甲比乙早0.5小时到达目的地，所以（1）（2）正确．故选B ．考点：本题考查的是学生从图象中读取信息的数形结合能力点评：同学们要注意分析其中的“关键点”，还要善于分析各图象的变化趋势．13．如图所示：边长分别为1和2的两个正方形，其一边在同一水平线上，小正方形沿该水平线自左向右匀速穿过大正方形，设穿过的时间为t，大正方形内除去小正方形部分的面积为S（阴影部分），那么S与t的大致图象应为（）A．B．C．D．【答案】A【解析】【分析】【详解】解：根据题意，设小正方形运动速度为v，由于v分为三个阶段，①小正方形向右未完成穿入大正方形，=⨯-⨯=-≤．S vt vt vt2214(1)②小正方形穿入大正方形但未穿出大正方形，22113S=⨯-⨯=，③小正方形穿出大正方形，=⨯-⨯-=+≤，22(11)3(1)S vt vt vt∴符合变化趋势的是A和C，但C中面积减小太多不符合实际情况，∴只有A中的符合实际情况．故选A．14．2019年，中国少年岑小林在第六届上海国际交互绳大赛上，破“30秒内单脚单摇轮换跳次数最多”吉尼斯世界纪录！实践证明1分钟跳绳的最佳状态是前20秒频率匀速增加，最后10秒冲刺，中间频率保持不变，则跳绳频率（次/秒）与时间（秒）之间的关系可以用下列哪幅图来近似地刻画（）A．B．C．D．【答案】C【解析】【分析】根据前20秒频率匀速增加，最后10秒冲刺，中间频率保持不变判断图象即可．【详解】:秒频率保持不变，排除选项A和D，再根据最后10秒冲解：根据题意可知，中间2050刺，频率是增加的，排除选项B，因此，选项C正确．故选：C．【点睛】本题考查的知识点是一次函数的实际应用，理解题意是解此题的关键．15．均匀地向一个容器注水，最后把容器注满，在注水过程中，水面高度h随时间t的变化规律如图所示（图中OABC为折线），这个容器的形状可以是（）A．B．C．D．【答案】D【解析】试题分析：注水量一定，函数图象的走势是稍陡，平，陡；那么速度就相应的变化，跟所给容器的粗细有关．则相应的排列顺序就为D ．故选D ．考点：函数的图象．16．当实数x 的取值使得2x -有意义时，函数41y x =+中y 的取值范围是( ) A ．7y ≥-B ．9y ≥C ．9y <-D ．7y <-【答案】B【解析】【分析】根据二次根式有意义易得x 的取值范围，代入所给函数可得y 的取值范围．【详解】解：由题意得20x -≥，解得2x ≥， 419x ∴+≥，即9y ≥．故选：B ．【点睛】本题考查了函数值的取值的求法；根据二次根式被开方数为非负数得到x 的取值是解决本题的关键．17．如图是某蓄水池的横断面示意图，分为深水池和浅水池，如果向这个蓄水池以固定的流量注水，下面能大致表示水的最大深度h 与时间t 之间的关系的图象是（ ）A ．B ．C ．D ．【答案】C【解析】【分析】首先看图可知，蓄水池的下部分比上部分的体积小，故h 与t 的关系变为先快后慢．【详解】根据题意和图形的形状，可知水的最大深度h 与时间t 之间的关系分为两段，先快后慢。
高一数学必修一第三章函数的概念与性质单元测试卷(1)
2019-2020 7-年必修第•册第三章函数的概念与性质注It 事項，1. 答題询・先将白己的姓准考证号轨写在试題卷和答軀卡上.并 将准考证号条形码粘贴在答Ifi 卡上的損定位BL2. 选样題的作答：毎小Ifi 选出答窠后•用2B 把答题卡上对f-zJKII 的答案标号涂黑・写在试腿卷.苹横纸和答硒卡上的非答题区域沟无效.3. 非选择腿的作答：用签字笔直接答在告腿卡上对应的诈胚区域内・ 写在试題卷.◎毎紙和答腿卡上的非答軀区域均无效.4. 韦试结束后.请称本试軀卷和答腿卡•并上交.两个函《（的对应法则不相同・・・・不ft∣∏j •个曲散.对于B ・Vy = （√7χ的定义域[0、+x ）・ y≈∖x ∖的定义域为R ・・・・樽个函数不处冋•个负敘• 对于C ・7y = -的定文城为R H Λ≠O ・）U.｛的定义域为Rfl-v≠O.X对应法则相同・・・・两个rttt ⅛冋•个附散・——一.堆择JB 本大忌共12个小每小題5分.共60分.在每小題给出的四个选 M 中.只有一刁是符合題目要求的）1.下列备对换散中•图盘完全相同的足＜A- y=χ与）'=壮何「 C. y =-与〉=XOX rn%] CB. y = (√Γ∕⅛>∙=∣χ∣ D.【鮮析】对于A ・・・・y = X 的定义域为R ・ y=(3√T∣)1rft 定文域为R ・x+1 = X=Z I对干D ・>=：二的定文域Z 如厂:严5≡Z定义域不相冋…•・不是冋∙φ⅛ft.T —5 " O勺【弊析】要使噱式' •解得x>-且Λ≠2・ [Λ-2≠0 2 做幣数的定义域为[∣.2 ∣U(2,+x)・3. iT ⅛tt∕(A)的定义域为[T,4]∙则函散/(2ΛT)的定义域为《>【TTtJA【林桁】V /(X)的定义域为[-L4]・・・・/(2.\—1)満足一1<2Λ-1<4.解⅛O<Λ<- 4.甬数〉• = =的处(XA.[>B.C ・[∣,2^∪(2,+∞)【答案】BD. (-x.2)∪(2,+∞)2.甬数〉U的定义域册(B. [-7,习C.,∙∙∕(2x -l)的定义域为【解析】= i-⅛⅛H⅛ia・ llll⅛B・ C・X⅛Λ = 1时..r-κ 0・Ay=-L-1< O •图線在X轴的下方.故选A.2 X5・cl⅛∕(Λ∙)½R匕的卩!函数・且^ix>O时J (X) = A(I-X) •則当.YO时. Λ-υ= <>A. -V(X-I)B. .v(x-l)C. -.V(Λ+1)D. .v(x+l)【答案】C【弊析】・・・/(刀址R上的偶函散・・•・/(-Q =/CO・S A < O・-Λ >0・ WJ/(-V)= -XI+x) = f(x)・・•・Λ <0时.J∖x)的解析式⅛∕(.v) = -v(l+.v)・6. ⅛tt∕ω=Γ +6' ve^2l 則/(.0 的4iλffi和姐小tfl分别为() [.V+7,Λ∈[-1,1)A. 10. 6B. 10. 8C. S ・ 6D. 10. 7 【答案】A【解析】由题意得・⅛l<x≤2时.7≤∕(x)≤10:⅛-l≤x<l时.6<∕(.v)<S・所以的域大値为10.曲小仪为6・Y•— r γV Ao.■ '•-为奇函散•则实救α的值为()-r+ατ, x<0A. 2B. -2C. 1D. -1 【答知B 【解析I=/CV)为命甬数・・•・/(-E = ・/(“)・~↑x<0时.—.v>O ・:、f(x) = -/(-.V)= -<.v2 + 2x) = -V:-2.Y ・又.r<0 时./(X) = -X= + ax ・Λ a≈-2 ・S.若/(e・&C0均兄定义在R上的旳散・W i f(X)和都肚何隨数啜的()A.充分而不必妾条件B.吒要Ifti不充分条件C.充要条件D. BI不充分也不必妾条件【答知A【解析】W∕ω fπ^(Λ)βι⅛偶甫敘.WJA-V) =/(x)^(-Λ)= ^r(X)./(-.υ∙^(-A)=^(X)./(.V)・即.充分性或立：-I /(Λ)= X^(Λ)=2x时.AT(A)-Z(X)足偶曲散.但ft/W和g(x)祁不定PI用数.必耍性不成立・・・・“几。
高中数学 1.2.1函数的概念同步测试 新人教A版必修1-新人教A版高一必修1数学试题
第一章1.21.2.1函数的概念基础巩固一、选择题1．下列四种说法中，不正确的是( )A ．在函数值域中的每一个数，在定义域中都至少有一个数与之对应B ．函数的定义域和值域一定是无限集合C ．定义域和对应关系确定后，函数的值域也就确定了D ．若函数的定义域中只含有一个元素，则值域也只含有一个元素 [答案] B2．f (x )＝1＋x ＋x1－x 的定义域是( )A ．[－1，＋∞)B ．(－∞，－1]C ．RD ．[－1,1)∪(1，＋∞)[答案] D[解析] ⎩⎪⎨⎪⎧1＋x ≥01－x ≠0，解得⎩⎪⎨⎪⎧x ≥－1，x ≠1，故定义域为[－1,1)∪(1，＋∞)，选D.3．各个图形中，不可能是函数y ＝f (x )的图象的是( )[答案] A[解析] 因为垂直x 轴的直线与函数y ＝f (x )的图象至多有一个交点，故选A. 4．(2015·曲阜二中月考试题)集合A ＝{x |0≤x ≤4}，B ＝{y |0≤y ≤2}，下列不表示从A 到B 的函数是( )A ．f x →y ＝12xB ．f x →y ＝13xC ．f x →y ＝23xD ．f x →y ＝x[答案] C[解析] 对于选项C ，当x ＝4时，y ＝83＞2不合题意．故选C.5．下列各组函数相同的是( )A ．f (x )＝x 2－1x －1与g (x )＝x ＋1B ．f (x )＝－2x 3与g (x )＝x ·－2xC ．f (x )＝2x ＋1与g (x )＝2x 2＋xxD ．f (x )＝|x 2－1|与g (t )＝t 2－12[答案] D[解析] 对于A.f (x )的定义域是(－∞，1)∪(1，＋∞)，g (x )的定义域是R ，定义域不同，故不是相同函数；对于B.f (x )＝|x |·－2x ，g (x )＝x ·－2x 的对应法则不同；对于C ，f (x )的定义域为R 与g (x )的定义域是{x |x ≠0}，定义域不同，故不是相同函数；对于D.f (x )＝|x 2－1|，g (t )＝|t 2－1|，定义域与对应关系都相同，故是相同函数，故选D.6．函数y ＝f (x )的图象与直线x ＝a 的交点个数有( ) A ．必有一个 B ．一个或两个 C ．至多一个 D ．可能两个以上[答案] C[解析] 当a 在f (x )定义域内时，有一个交点，否则无交点． 二、填空题 7．已知函数f (x )＝11＋x，又知f (t )＝6，则t ＝________. [答案] －56[解析] f (t )＝1t ＋1＝6.∴t ＝－568．用区间表示下列数集： (1){x |x ≥1}＝________； (2){x |2＜x ≤4}＝________； (3){x |x ＞－1且x ≠2}＝________.[答案] (1)[1，＋∞) (2)(2,4] (3)(－1,2)∪(2，＋∞) 三、解答题9．求下列函数的定义域，并用区间表示：(1)y ＝x ＋12x ＋1－1－x ；(2)y ＝5－x|x |－3.[分析] 列出满足条件的不等式组⇒解不等式组⇒求得定义域[解析] (1)要使函数有意义，自变量x 的取值必须满足⎩⎪⎨⎪⎧x ＋1≠01－x ≥0，解得x ≤1且x ≠－1，即函数定义域为{x |x ≤1且x ≠－1}＝(－∞，－1)∪(－1,1]．(2)要使函数有意义，自变量x 的取值必须满足⎩⎪⎨⎪⎧5－x ≥0|x |－3≠0，解得x ≤5，且x ≠±3，即函数定义域为{x |x ≤5，且x ≠±3}＝(－∞，－3)∪(－3,3)∪(3,5]． [规律总结] 定义域的求法：(1)如果f (x )是整式，那么函数的定义域是实数集R ；(2)如果f (x )是分式，那么函数的定义域是使分母不为0的实数的集合；(3)如果f (x )为偶次根式，那么函数的定义域是使根号内的式子大于或等于0的实数的集合；(4)如果f (x )是由几个部分的数学式子构成的，那么函数的定义域是使各部分式子都有意义的实数的集合．(5)如果函数有实际背景，那么除符合上述要求外，还要符合实际情况． 函数定义域要用集合或区间形式表示，这一点初学者易忽视． 10．已知函数f (x )＝x ＋3＋1x ＋2. (1)求函数的定义域； (2)求f (－3)，f (23)的值；(3)当a ＞0时，求f (a )，f (a －1)的值．[解析] (1)使根式x ＋3有意义的实数x 的集合是{x |x ≥－3}，使分式1x ＋2有意义的实数x 的集合是{x |x ≠－2}，所以这个函数的定义域是{x |x ≥－3}∩{x |x ≠－2}＝{x |x ≥－3，且x ≠－2}． (2)f (－3)＝－3＋3＋1－3＋2＝－1； f (23)＝23＋3＋123＋2＝113＋38＝38＋333. (3)因为a ＞0，故f (a )，f (a －1)有意义．f (a )＝a ＋3＋1a ＋2；f (a －1)＝a －1＋3＋1a －1＋2＝a ＋2＋1a ＋1.能力提升一、选择题1．给出下列从A 到B 的对应：①A ＝N ，B ＝{0,1}，对应关系是：A 中的元素除以2所得的余数 ②A ＝{0,1,2}，B ＝{4,1,0}，对应关系是f ：x →y ＝x 2③A ＝{0,1,2}，B ＝{0,1，12}，对应关系是f ：x →y ＝1x其中表示从集合A 到集合B 的函数有( )个．( ) A ．1 B ．2 C ．3 D ．0 [答案] B[解析] 由于③中，0这个元素在B 中无对应元素，故不是函数，因此选B. 2．(2012·高考某某卷)下列函数中，不满足：f (2x )＝2f (x )的是( ) A ．f (x )＝|x | B ．f (x )＝x －|x | C ．f (x )＝x ＋1 D ．f (x )＝－x[答案] C[解析] f (x )＝kx 与f (x )＝k |x |均满足：f (2x )＝2f (x )得：A ，B ，D 满足条件． 3．(2014～2015惠安中学月考试题)A ＝{x |0≤x ≤2}，B ＝{y |1≤y ≤2}，下列图形中能表示以A 为定义域，B 为值域的函数的是( )[答案] B[解析] A 、C 、D 的值域都不是[1,2]，故选B. 4．(2015·某某高一检测)函数f (x )＝11－2x 的定义域为M ，g (x )＝x ＋1的定义域为N ，则M ∩N ＝( )A ．[－1，＋∞)B ．[－1，12)C ．(－1，12)D ．(－∞，12)[答案] B 二、填空题5．若函数f (x )的定义域为[2a －1，a ＋1]，值域为[a ＋3,4a ]，则a 的取值X 围是________．[答案] (1,2)[解析] 由区间的定义知⎩⎪⎨⎪⎧2a －1＜a ＋1，a ＋3＜4a ⇒1＜a ＜2.6．函数y ＝f (x )的图象如图所示，那么f (x )的定义域是________；其中只与x 的一个值对应的y 值的X 围是________．[答案] [－3,0]∪[2,3] [1,2)∪(4,5] [解析] 观察函数图象可知f (x )的定义域是[－3,0]∪[2,3]；只与x 的一个值对应的y 值的X 围是[1,2)∪(4,5]． 三、解答题7．求下列函数的定义域： (1)y ＝31－1－x；(2)y ＝x ＋10|x |－x；(3)y ＝2x ＋3－12－x ＋1x.[解析] (1)要使函数有意义，需⎩⎨⎧1－x ≥0，1－1－x ≠0⇔⎩⎪⎨⎪⎧x ≤1，x ≠0⇔x ≤1且x ≠0，所以函数y ＝31－1－x的定义域为(－∞，0)∪(0,1]．(2)由⎩⎪⎨⎪⎧x ＋1≠0，|x |－x ≠0得⎩⎪⎨⎪⎧x ≠－1，|x |≠x ，∴x ＜0且x ≠－1，∴原函数的定义域为{x |x ＜0且x ≠－1}． (3)要使函数有意义，需⎩⎪⎨⎪⎧2x ＋3≥0，2－x ＞0，x ≠0.解得－32≤x ＜2且x ≠0，所以函数y ＝2x ＋3－12－x ＋1x 的定义域为[－32，0)∪(0,2)．[点评] 求给出解析式的函数的定义域的步骤为：(1)列出使函数有意义的x 所适合的式子(往往是一个不等式组)；(2)解这个不等式组；(3)把不等式组的解表示成集合(或者区间)作为函数的定义域．8．已知函数f (x )＝1＋x 21－x 2，(1)求f (x )的定义域． (2)若f (a )＝2，求a 的值．(3)求证：f ⎝ ⎛⎭⎪⎫1x＝－f (x )． [解析] (1)要使函数f (x )＝1＋x 21－x 2有意义，只需1－x 2≠0，解得x ≠±1，所以函数的定义域为{x |x ≠±1}． (2)因为f (x )＝1＋x21－x2，且f (a )＝2，所以f (a )＝1＋a 21－a 2＝2，即a 2＝13，解得a ＝±33. (3)由已知得f ⎝ ⎛⎭⎪⎫1x ＝1＋⎝ ⎛⎭⎪⎫1x 21－⎝ ⎛⎭⎪⎫1x 2＝x 2＋1x 2－1，－f (x )＝－1＋x 21－x 2＝x 2＋1x 2－1， ∴f ⎝ ⎛⎭⎪⎫1x ＝－f (x )．。
函数与极限测试题及答案一
函数与极限测试题（一）一、 填空题 二、1、若1ln 11ln x f x x+⎛⎫=⎪-⎝⎭，则()f x =_____。
三、2、函数()f x 的定义域为[],a b ，则()21f x -的定义域为_____。
四、3、若0x →时，无穷小221ln 1x x -+与2sin 2a 等价，则常数a =_____。
五、4、设()()21lim 1n n x f x nx →∞-=+，则()f x 的间断点为x =_____。
六、 单选题七、 1、当0x →时，变量211sinx x是（ ） 八、A 、无穷小B 、无穷大九、 C 、有界的，但不是无穷小 D 、无界的，也不是无穷大 十、2、设函数()bx xf x a e=+在(),-∞+∞上连续，且()lim 0x f x →-∞=，则常数,a b 满足（ ）十一、 A 、0,0a b << B 、0,0a b >> 十二、 C 、0,0a b ≥< D 、0,0a b ≤> 十三、 3、设()232xxf x =+-，则当0x →时（ ）十四、 A 、()f x 与x 是等价无穷小 B 、()f x 与x 是同阶但非等价无穷小 十五、 C 、()f x 是x 的高阶无穷小 D 、()f x 是x 的低阶无穷小十六、 4、设对任意的x ，总有()()()x f x g x ϕ≤≤，且()()lim 0x g x x ϕ→∞-=⎡⎤⎣⎦，则()lim x f x →∞为（ ）十七、 A 、存在且等于零 B 、存在但不一定等于零十八、 C 、一定不存在 D 、不一定存在 十九、 例：()()()11,,221x x f x x g x x x x ϕ==+=+++ 二十、 求下列极限 二十一、1、2241limsin x x x x x+-+、()221212lim 1xx x x x -→⎛⎫ ⎪+⎝⎭二十二、确定,a b 的值，使()322ln 101tan 1sin 011ln 01ax x x x f x bx x x x x x x ⎧+⎪<+-+⎪⎪==⎨⎪-+⎪>++⎪⎩在(),-∞+∞内连续。
人教高中数学 第三章 函数概念与性质 单元测试(含答案)
人教高中数学函数概念与性质一、单选题1．下列函数中，在其定义域内既是增函数又是奇函数的是（ ）A．y=x2B．y=―log2x C．y=3x D．y=x3+x 2．若幂函数f(x)=xα的图象经过点(3，3)，则α的值为（ ）A．2B．-2C．12D．―123．若f[g(x)]=6x+3且g(x)=2x+1，则f(x)的解析式为（ ）A．3B．3x C．3(2x+1)D．6x+14．已知函数y=f（x+2）的定义域为（0，2），则函数y=f（log2x）的定义域为（ ）A．（﹣∞，1）B．（1，4）C．（4，16）D．（14，1）5．下列各组函数中，表示同一函数的是（ ）A．f（x）=x和g（x）=(x)2B．f（x）=|x|和g（x）=3x3C．f（x）=x|x|和g（x）={x2(x>0)―x2(x<0)D．f（x）=x2―1x―1和g（x）=x+1，（x≠1）6．已知函数f(x)={2x+1,x≤0|ln x|,x>0,则方程f[f(x)]=3的实数根的个数是（ ）A．2B．3C．4D．57．连续函数f(x)是定义在(―1，1)上的偶函数，当x≠0时，x f′(x)>0.若f(a+1)―f(2a)>0，则a的取值范围是（ ）A．(―13，1)B．(―12，0)C．(―12，1)D．(―13，0)8．已知函数f(x)是定义在R上的偶函数，且在(―∞，0)上单调递减，若a=f(log215)，b=f( log24.1)，c=f(20.8)，则a，b，c的大小关系是（ ）A．a<b<c B．b<a<c C．c<a<b D．c<b<a二、多选题9．下列函数中既是奇函数又在定义域上是单调函数的有（ ）A．y=1x2B．y=―x3C．y=x|x|D．y=x+1x10．给出定义：若m―12<x≤m+12（m∈Z），则称m为离实数x最近的整数，记作{x}=m.在此基础上给出下列关于函数f(x)=|x―{x}|的四个结论，其中正确的是（ ）A．函数y=f(x)的定义域为R，值域为[0，12]B．函数y=f(x)的图象关于直线x=k2（k∈Z）对称C．函数y=f(x)是偶函数D．函数y=f(x)在[―12，12]上单调递增11．设函数f(x)=ln|x+2|―ln|x―2|，则（ ）A．f(x)的定义域为(―∞，―2)∪(2，+∞)B．f(x)的值域为RC．f(x)在(―∞，―2)单调递增D．f(x)在(2，+∞)单调递减12．定义：若对于定义域内任意x，总存在正常数a，使得f(x+a)>f(x)恒成立，则称函数f(x)为“a距”增函数，以下判断正确的有（ ）A．函数f(x)=3x(x∈R)是“a距”增函数B．函数f(x)=2x―x(x>0)是“1距”增函数C．若函数f(x)=x3―14x+4(x∈R)是“a距”增函数，则a的取值范围是(0，1)D．若函数f(x)=2x2+k|x|(x∈(―1，+∞))是“2距”增函数，则k的取值范围是(―2，+∞)三、填空题13．幂函数f（x）图象过（2，4），则幂函数f（x）= ．14．已知函数f（x）= 2x―3x+1的图象关于点P中心对称，则点P的坐标是 ．15．设函数g(x)满足g(x+2)=2x+3，则g(x)的解析式为 .16．设函数f（x）= {1，x≥0―1，x<0，g（x）= x2e2f（x﹣1），则函数g（x）的递增区间是 ．四、解答题17．已知f(x)为二次函数，且f(x)的两个零点为1和3，g(x)为幂函数，且y=f(x)和y=g(x)都经过点(4，2)．（1）求函数y=g(f(x))的定义域；（2）当x∈[1，16]时，求函数y=f(g(x))的值域．18．已知函数f(x)=x2+ax+bx(a,b∈R)．（1）若函数f(x)为奇函数，求实数a的值；（2）当a=2，b=1时，求函数f(x)在区间(0,+∞)上的最小值．19．已知f（x）=x|x﹣a|+2x﹣3，其中a∈R（1）当a=4，2≤x≤5时，求函数f （x ）的最大值和最小值，并写出相应的x 的值．（2）若f （x ）在R 上恒为增函数，求实数a 的取值范围．20．已知二次函数f （x ）=ax 2+bx+1，（a ＞0）， F (x )={f (x )，x >0―f (x )，x <0 若f （﹣1）=0且对任意实数x 均有f （x ）≥0成立（1）求F （x ）的表达式；（2）当x ∈[﹣2，2]时，g （x ）=f （x ）﹣kx 是单调函数，求k 的取值范围． 21．某企业投入81万元经销某产品，经销时间共60个月，市场调研表明，该企业在经销这个产品期间第x 个月的利润 f (x )={1(1≤x ≤20，x ∈N ∗)110x (21≤x ≤60，x ∈N ∗) （单位：万元），为了获得更多的利润，企业将每月获得的利润投入到次月的经营中，记第x 个月的当月利润率 g (x )=第x 个月的利润第x 个月前的资金总和 ，例如： g (3)=f (3)81+f (1)+f (2) ． （1）求g （10）；（2）求第x 个月的当月利润率g （x ）；（3）该企业经销此产品期间，哪个月的当月利润率最大，并求该月的当月利润率． 22．已知定义域为 R 的函数 f (x )=ℎ(x )+n ―2ℎ(x )―2是奇函数， ℎ(x ) 为指数函数且 ℎ(x ) 的图象过点 (2，4) .（1）求 f (x ) 的表达式；（2）若对任意的 t ∈[―1，1] .不等式 f (t 2―2a )+f (at ―1)≥0 恒成立，求实数 a 的取值范围； （3）若方程 f (|x 2+3x |)+f (―a |x ―1|)=0 恰有2个互异的实数根，求实数 a 的取值集合.答案解析部分1．【答案】D2．【答案】C3．【答案】B4．【答案】C5．【答案】D6．【答案】D7．【答案】D8．【答案】D9．【答案】B,C10．【答案】A,B,C11．【答案】B,D12．【答案】A,B,D13．【答案】x 214．【答案】（﹣1，2）15．【答案】g (x )=2x ―116．【答案】（﹣∞，0]，[1，2]17．【答案】（1）解：设 f (x )=a (x ―1)(x ―3) ，（ a ≠0 ） 又 y =f (x ) 过点 (4，2) ，∴2=a (4―1)(4―3) ，∴a =23 ，∴f (x )=23(x ―1)(x ―3) ，设 g (x )=x α ，由 y =g (x ) 都经过点 (4，2) 知， 2=4α ，∴α=12 ，∴g (x )=x ，y =g (f (x ))=23(x ―1)(x ―3) ，∴23(x ―1)(x ―3)≥0 ，∴x ≥3 或 x ≤1 ，∴函数的定义域为 (―∞，1]∪[3，+∞) ．（2）令 t =g (x )=x ，∵x ∈[1，16] ，∴t ∈[1，4] ，所以 y =f (g (x ))=23(t 2―4t +3)=23[(t ―2)2―1] ，当 t =2 时， y min =―23 ； t =4 时， y max =2 ，所以函数的值域为[―23，2]．18．【答案】（1）解：函数f(x)=x2+ax+bx的定义域为{x|x≠0}，若函数f(x)为奇函数，则f(―x)=―f(x)成立，即(―x)2+a(―x)+b―x=―x2+ax+bx，即2ax=0恒成立，因为x≠0，所以a=0；（2）解：当a=2，b=1时，函数f(x)=x2+2x+1x =x+1x+2，因为x>0，所以f(x)=x+1x +2≥2x⋅1x+2=4，当且仅当x=1x，即x=1时等号成立，则函数f(x)取得最小值为4.19．【答案】（1）解：∵f（x）=x|x﹣a|+2x﹣3，∴当a=4时，f(x)=x|x―4|+2x―3={―x2+6x―3，2≤x≤4x2+2x―3，4<x≤5；作图如下：由图知，当x=5时，f（x）max=f（5）=52﹣2×5﹣3=12；当x=2或4时，f（x）min=f（2）=f（4）=﹣22+6×2﹣3=5，（2）解：f(x)={―x2+(a+2)x―3，x≤ax2+(2―a)x―3，x>a，∵f（x）在R上恒为增函数，∴{a+22≥aa―22≤a，解得﹣2≤a≤2．∴实数a的取值范围是[﹣2，2]．20．【答案】（1）解：∵f（x）=ax2+bx+1（a＞0），f（﹣1）=0且对任意实数x均有f（x）≥0成立；∴x=﹣b2a=﹣1，且a﹣b+1=0；即{b=2aa―b+1=0，解得{a=1b=2；∴f（x）=x2+2x+1，∴F（x）= {x2+2x+1(x>0)―x2―2x―1(x<0)（2）解：∵f（x）=x2+2x+1，∴g（x）=f（x）﹣kx=x2+（2﹣k）x+1，∵g（x）在[﹣2，2]上是单调函数，∴x= ―(2―k)2应满足：―(2―k)2≥2，或―(2―k)2≤﹣2，即k≥6，或k≤﹣2；∴k的取值范围是{k|k≤﹣2，或k≥6}21．【答案】（1）解：由题意得：f（1）=f（2）=f（3）=…═f（9）=f（10）=1g（x）=f(10)81+f(1)+⋯f(9)= 181+1+⋯+1= 190（2）解：当1≤x≤20时，f（1）=f（2）═f（x﹣1）=f（x）=1∴g（x）=f(x)81+f(1)+⋯f(x―1)= 181+1+⋯+1= 181+(x―1)=1x+80．当21≤x≤60时，g（x）=f(x)81+f(1)+⋯+f(20)+f(21)+⋯+f(x―1)=110x81+f(1)+⋯f(x―1)=110x81+20+2110+⋯+x―110=110x101+12(2110+x―110)(x―21)=110x101+(x―21)(x+20)20=2xx2―x+1600∴当第x个月的当月利润率g(x)={1x+80(1≤x≤20，x∈N∗)2xx2―x+1600(21≤x≤60，x∈N∗)（3）解：当1≤x≤20时，g(x)=1x+80是减函数，此时g（x）的最大值为g(1)=181当21≤x≤60时，g(x)=2xx2―x+1600=2x+1600x―1≤221600―1=279当且仅当x=1600x时，即x=40时，g(x)max=279，又∵279>181，∴当x=40时，g(x)max=279所以，该企业经销此产品期间，第40个月的当月利润率最大，最大值为279 22．【答案】（1）由题意，设ℎ(x)=a x，因为ℎ(x)过点(2，4)，可得a2=4，解得a=2，即ℎ(x)=2x，所以f(x)=2x+n―2x+1―2，又因为f(x)为奇函数，可得f(0)=0，即f(0)=20+n―2―2=0，解答n=―1，经检验，符合f(x)=―f(―x)，所以f(x)=―2x+12x+1+2.（2）由函数f(x)=―2x+12x+1+2=―12+12x+1，可得f(x)在R上单调递减，又因为f(x)为奇函数，因为f(t2―2a)+f(at―1)≥0，即f(t2―2a)≥f(1―at)，所以t2―2a≤1―at，即t2+at―1―2a≤0，又因为对任意的t∈[―1，1]，不等式f(t2―2a)+f(at―1)≥0恒成立，令g(t)=t2+at―1―2a，即g(t)≤0对任意的t∈[―1，1]恒成立，可得{g(―1)≤0g(1)≤0，即{(―1)2+a×(―1)―1―2a≤012+a―1―2a≤0，解得a≥2，所以实数a的取值范围为[0，+∞).（3）由于f(x)为奇函数，所以由f(|x2+3x|)+f(―a|x―1|)=0，可得f(|x2+3x|)=f(a|x―1|)，又因为f(x)在R上递减，即|x2+3x|=a|x―1|，显然x≠1，所以a=|x2+3xx―1|，令t=x―1，则a=|t+4t+5|，又由当t>0时，t+4t +5≥2t⋅4t+5=9，当且仅当t=4t时，即t=2时等号成立；当t<0时，t+4t +5=―[(―t)+4―t]+5≤―2(―t)⋅4(―t)+5=1，当且仅当―t=―4t时，即t=―2时等号成立，方程有2个互异实数根，画出y=|t+4t+5|的图象，如图所示，由图可得，实数a的取值集合为{a|1<a<9或a=0}。
集合与函数概念单元测试题经典(含答案)
Equation Chapter 1 Section 1【1】第一章集合与函数概念测试题 一：选择题 1、下列集合中与集合{21,}x x k k N +=+∈不相等的是（ ）A ．{23,}x x k k N =+∈B ．{41,}x x k k N +=±∈C ．{21,}x x k k N =+∈D ．{23,3,}x x k k k Z =-≥∈2、图中阴影部分所表示的集合是（）A.B∩［CU(A ∪C)］B.(A ∪B) ∪(B ∪C)C.(A ∪C)∩(CUB)D.［C U(A∩C)］∪B3、已知集合2{1}A y y x ==+，集合2{26}B x y x ==-+，则A B =（ ）A ．{(,)1,2}x y x y ==B ．{13}x x ≤≤C ．{13}x x -≤≤D ．∅4、已知集合2{40}A x x =-=，集合{1}B x ax ==，若B A ⊆，则实数a 的值是（ ）A ．0B ．12±C ．0或12±D ．0或125、已知集合{1,2,3,}A a =，2{3,}B a =，则使得Φ=B A C U )(成立的a 的值的个数为（ ）A ．2B ．3C ．4D ．56、设A 、B 为两个非空集合，定义{(,),}A B a b a A b B ⊕=∈∈，若{1,2,3}A =，{2,3,4}B =，则A B ⊕中的元素个数为 （ ）A ．3B ．7C ．9D ．127、已知A 、B 两地相距150千米，某人开汽车以60千米/小时的速度从A 地到达B 地，在B 地停留1小时后再以50千米/小时的速度返回A 地，把汽车离开A 地的距离x 表示为时间t （小时）的函数表达式是（ ）A ．x=60tB ．x=60t+50C ．x=⎩⎨⎧>-≤≤)5.3(,50150)5.20(,60t t t tD ．x=⎪⎩⎪⎨⎧≤<--≤<≤≤)5.65.3(),5.3(50150)5.35.2(,150)5.20(,60t t t t t 8、已知g(x)=1-2x,f[g(x)]=)0(122≠-x x x ,则f(21)等于（ ） A ．1B ．3C ．15D ．309、函数y=xx ++-1912是（ ） A ．奇函数 B ．偶函数 C ．既是奇函数又是偶函数 D ．非奇非偶数10、设函数f (x)是（－∞，+∞）上的减函数，又若a ∈R ，则（ ）A ．f(a)>f(2a)B ．f(a2)<f(a)C ．f(a2+a)<f(a)D ．f(a2+1)<f(a)二、填空题11、设集合A={23≤≤-x x },B={x 1122-≤≤-k x k },且A ⊇B ，则实数k 的取值范围是.12、已知x ∈[0,1],则函数y=x x --+12的值域是.13、设函数x y 111+=的定义域为___________________;值域为_____________________________.14、设f(x)是定义在R 上的偶函数，在区间（－∞，0）上单调递增，且满足, 22(25)(21)f a a f a a -+-<++求实数a 的取值范围_______________。
函数测试题1
函数测试题1一、选择题(本大题共10个小题，每小题5分，共50分) 1．函数y ＝x 2－2x 的定义域为{0,1,2,3}，那么其值域为( A ．{－1,0,3} B ．{0,1,2,3}C ．{y |－1≤y ≤3}D ．{y |0≤y ≤3} 2．函数f (x )＝1x －x 的图像关于( )A ．y 轴对称B ．直线y ＝－x 对称C ．坐标原点对称D ．直线y ＝x 对称3．汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车，若把这一过程中汽车的行驶路程s 看作时间t 的函数，其图像可能是( )4．函数y ＝f (x )的图像与直线x ＝a (a ∈R)的交点有( )A ．至多有一个B ．至少有一个C ．有且仅有一个D ．有一个或两个以上5．若函数y ＝f (x )，x ∈R 是奇函数，且f (1)<f (2)，则必有( )A ．f (－1)<f (－2)B ．f (－1)>f (－2)C ．f (－1)＝f (1)D ．f (－2)＝f (1)6．函数y ＝x 2＋bx ＋c (x ∈[0，＋∞))是单调函数，则有( )A ．b ≥0B ．b ≤0C ．c ≥0D ．c ≤07.幂函数y ＝f (x )图像如图，那么此函数为( )A ．y ＝x －2B ．y ＝x 32C ．y ＝x 12D ．y ＝x 238．(2011·安徽高考)设f (x )是定义在R 上的奇函数，当x ≤0时，f (x ) ＝2x 2－x ， 则f (1)＝( )A ．－3B ．－1C ．1D ．39．(2011·浙江高考)设函数f (x )＝⎩⎪⎨⎪⎧－x ，x ≤0，x 2，x ＞0.若f (α)＝4，则实数α＝( )A ．－4或－2B ．－4或2C ．－2或4D ．－2或210．定义在R 上的偶函数在[0,7]上是增函数，又f (7)＝6，则f (x )( )A ．在[－7,0]上是增函数，且最大值是6B ．在[－7,0]上是减函数，且最大值是6C ．在[－7,0]上是增函数，且最小值是6D ．在[－7,0]上是减函数，且最小值是6二、填空题(本大题共4小题，每小题5分，共20分) 11．若函数f (x )＝⎩⎪⎨⎪⎧x －12， x >0，－2， x ＝0，(x ＋3)12， x <0，则f (f (f (0)))＝________.12．若函数f (x )＝x 2－|x ＋a |为偶函数，则实数a ＝________. 13．函数y ＝－x 2＋2x ＋3的值域为________．14.设函数y ＝f (x )是偶函数，它在[0,1]上的图像如图，则它在[－1,0]上的解析式为________．三、解答题(本大题共4个小题，共50分)15．(12分)已知f (x )是定义在[－1,2)上的增函数，若f (a －1)>f (1－3a )，求实数a 的取值范围．16．(12分)已知二次函数f (x )满足条件f (0)＝1及f (x ＋1)－f (x )＝2x . (1)求f (x )的解析式；(2)求f (x )在区间[－1,1]上的最值．17．(12分)已知函数f (x )＝ax 2＋23x ＋b 是奇函数，且f (2)＝53.(1)求实数a ，b 的值；(2)判断函数f (x )在(－∞，－1]上的单调性，并加以证明．18．(14分)小张周末自己驾车旅游，早上八点从家出发，驾车3个小时后到达景区停车场，期间由于交通等原因，小张的车所走的路程s (单位：km)与离家的时间t (单位：h)的函数关系为s (t )＝－5t ·(t －13)．由于景区内不能驾车，小张把车停在景区停车场．在景区玩到16点，小张开车从停车场以60 km/h的速度沿原路返回．(1)求这天小张的车所走的路程s(单位：km)与离家时间t(单位：h)的函数解析式；(2)在距离小张家60 km处有一加油站，求这天小张的车途经该加油站的时间。
函数测试题及答案大全
函数测试题及答案大全一、选择题1. 下列哪个选项不是函数的基本特征？A. 有确定的名称B. 有固定的参数列表C. 可以返回多个值D. 有确定的返回类型答案：C2. 在Python中，以下哪项是定义函数的正确语法？A. def function_name(parameters):B. function_name(parameters):C. define function_name(parameters):D. function function_name(parameters):答案：A3. 以下哪个选项正确描述了函数调用的过程？A. 函数定义后立即执行B. 函数定义后需要显式调用才会执行C. 函数定义后，系统自动调用D. 函数定义后，只能在其他函数内部调用答案：B二、填空题4. 在C语言中，函数声明通常放在___________。
答案：源文件的顶部5. 函数的参数可以是值传递，也可以是___________。
答案：引用传递6. 在JavaScript中，可以通过___________关键字定义一个匿名函数。
答案：function三、简答题7. 描述什么是递归函数，并给出一个简单的例子。
答案：递归函数是指在函数体内调用自身的函数。
递归函数通常用于解决可以分解为相似子问题的问题。
例如，计算阶乘的函数：```function factorial(n) {if (n === 0) return 1;return n * factorial(n - 1);}```8. 函数重载是什么？请简述其在面向对象编程中的作用。
答案：函数重载是指在同一个作用域内，允许存在多个同名函数，只要它们的参数列表不同（参数的类型、数量或顺序不同）。
在面向对象编程中，函数重载允许同一个操作符或方法应用于不同类型的对象，提高了代码的灵活性和可读性。
四、编程题9. 编写一个Python函数，实现对列表中的元素进行排序，并返回排序后的列表。
函数(一)综合测试题
函数（一）综合测试题一、选择题1、若点A（-3，n）在x轴上，则点B（n-1，n+1）在（）A．第一象限B．第二象限C．第三象限D．第四象限2、下列各曲线中表示y是x的函数的是（）A．B．C．D．3、在直角坐标系中，点M，N在同一个正比例函数图象上的是（）A．M（2，-3），N（-4，6）B．M（-2，3），N（4，6）C．M（-2，-3），N（4，-6）D．M（2，3），N（-4，6）4、已知点A（a，1）与点A′（-5，b）是关于原点O的对称点，则a+b的值为（）A．1 B．5 C．6 D．45、线段MN是由线段EF经过平移得到的，若点E（-1，3）的对应点M（2，5），则点F（-3，-2）的对应点N的坐标是（）A．（-1，0）B．（-6，0）C．（0，-4）D．（0，0）6、一次函数y=kx-（2-b）的图象如图所示，则k和b的取值范围是（）A．k＞0，b＞2 B．k＞0，b＜2 C．k＜0，b＞2 D．k＜0，b＜27、当k＞0时，反比例函数y= kx和一次函数y=kx+2的图象大致是（）A．A．C．D．8、已知反比例函数y= 12mx的图象上有两点A（x1，y1），B（x2，y2），当x1＜0＜x2时，有y1＜y2，则m的取值范围是（）A．m＜0 B．m＞0 C．m＜12D．m＞129、如图，经过点B（-2，0）的直线y=kx+b与直线y=4x+2相交于点A（-1，-2），4x+2＜kx+b＜0的解集为（）A．x＜-2 B．-2＜x＜-1 B．-2＜x＜-1 D．x＞-110、如图，在边长为2的正方形ABCD 中剪去一个边长为1的小正方形CEFG ，动点P 从点A 出发，沿A →D →E →F →G →B 的路线绕多边形的边匀速运动到点B 时停止（不含点A 和点B ），则△ABP 的面积S 随着时间t 变化的函数图象大致是（ ）A ．B ．C ．D ．二、填空题 11、在函数y=3x -+12x -中，自变量x 的取值范围是____ 12、若点A （1，-3），B （m ，3）在同一反比例函数的图象上，则m 的值是____13、如图，若在象棋棋盘上建立直角坐标系，使“帅”位于点（-3，-2），“炮”位于点（-2，0），则“兵”位于的点的坐标为____14、如图，A 、B 两点在双曲线y=4x上，分别经过A 、B 两点向轴作垂线段，已知S 阴影=1，则S 1+S 2=____15、已知关系x ，y 的二元一次方程3ax+2by=0和5ax-3by=19化成的两个一次函数的图象的交点坐标为（1，-1），则a=____，b=___16、已知m 是整数，且一次函数y=（m+4）x+m+2的图象不过第二象限，则m=____17、已知函数y=ax 和y=4a x-的图象有两个交点，其中一个交点的横坐标为1，则两个函数图象的交点坐标为____18、如图，在平面直角坐标系中，一动点从原点O出发，沿着箭头所示方向，每次移动1个单位，依次得到点P1（0，1），P2（1，1），P3（1，0），P4（1，-1），P5（2，-1），P6（2，0），…，则点P60的坐标为____三、解答题19、常用的确定物体位置的方法有两种．如图，在4×4个边长为1的正方形组成的方格中，标有A，B两点．请你用两种不同方法表述点B相对点A的位置20、已知y关于x的一次函数y=（2m2-32）x3-（n-3）x2+（m-n）x+m+n．（1）若该一次函数的y值随x的值的增大而增大，求该一次函数的表达式，并在如图所示的平面直角坐标系中画出该一次函数的图象；（2）若该一次函数的图象经过点（-2，13），求该函数的图象与坐标轴围成的三角形的面积21、如图，在矩形OABC中，OA=3，OC=2，F是AB上的一个动点（F不与A，B重合），过点F的反比例函数y=kx（k＞0）的图象与BC边交于点E．（1）当F为AB的中点时，求该函数的解析式；（2）当k为何值时，△EFA的面积最大，最大面积是多少22、如图，已知在平面直角坐标系xOy中，O是坐标原点，点A（2，5）在反比例函数y=k x的图象上，过点A的直线y=x+b交反比例函数y=kx的图象于另一点B．（1）求k和b的值；（2）求△OAB的面积23、心理学家研究发现，一般情况下，一节课40分钟中，学生的注意力随教师讲课的变化而变化．开始上课时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的稳定状态，随后学生的注意力开始分散．经过实验分析可知，学生的注意力指标数y随时间x（分钟）的变化规律如下图所示（其中AB、BC分别为线段，CD为双曲线的一部分）：（1）开始上课后第五分钟时与第三十分钟时相比较，何时学生的注意力更集中？（2）一道数学竞赛题，需要讲19分钟，为了效果较好，要求学生的注意力指标数最低达到36，那么经过适当安排，老师能否在学生注意力达到所需的状态下讲解完这道题目参考答案一、选择题1、A2、D3、A4、D5、D6、B7、C8、C9、B10、B二、填空题11、x≥312、-113、（-5，1），14、615、a=2，b=316、：-3或-217、（1，2）和（-1，-2）．18、（20，0）．三、解答题19、解：方法1：用有序实数对（a，b）表示．比如：以点A为原点，水平方向为x轴，建立直角坐标系，则B（3，3）．方法2：用方向和距离表示．比如：B点位于A点的东北方向（北偏东45°等均可），距离A点3 2处20、解：（1）∵y关于x的一次函数y=（2m2-32）x3-（n-3）x2+（m-n）x+m+n，∴2m2-32=0，n-3=0，解得：m=±4，n=3，又∵该一次函数的y值随x的值的增大而增大，∴m-n＞0，则m=4，n=3，∴该一次函数的表达式为：y=x+7，如图所示：；（2）∵该一次函数的图象经过点（-2，13），∴y=-7x-1，如图所示：，当x=0，则y=-1，当y=0，则x=-17，故该函数的图象与坐标轴围成的三角形的面积为12×1×17=11421、解：（1）∵在矩形OABC中，OA=3，OC=2，∴B（3，2），∵F为AB的中点，∴F。
高一数学必修1《集合与函数概念》测试卷(含答案)
第一章《集合与函数概念》测试卷（一）考试时间：120分钟满分：150分一.选择题.(本大题共12小题，每小题5分，共60分) 1.下列叙述正确的是（ ）A.函数的值域就是其定义中的数集BB.函数()y f x =的图像与直线x m =至少有一个交点C.函数是一种特殊的映射D.映射是一种特殊的函数2.如果{}1A x x =>-，则下列结论正确的是（） A.0A ⊆ B.{}0A ⊆ C.{}0A ∈ D.A ∅∈3.设()(21)f x a x b =-+在R 上是减函数，则有（ ） A.12a ≥B.12a ≤C.12a >D.12a < 4.定义在R 上的偶函数()f x ，对任意1x ，2x ∈[)0,+∞12()x x ≠，有1212()()0f x f x x x -<-，则有（）A.(3)(2)(1)f f f <-<B.(1)(2)(3)f f f <-<C.(2)(1)(3)f f f -<<D.(3)(1)(2)f f f <<-5.若奇函数()f x 在区间[]1,3上为增函数，且有最小值0，则它在区间[]3,1--上（） A.是减函数，有最小值0B.是增函数，有最小值0C.是减函数，有最大值0D.是增函数，有最大值06.设:f x x →是集合A 到集合B 的映射，若{}2,0,2A =-，则A B 等于（）A.{}0B.{}2C.{}0,2D.{}2,0-7.定义两种运算：a b ab ⊕=，22a b a b ⊗=+，则函数3()33xf x x ⊕=⊗-为（）A.奇函数B.偶函数C.既不是奇函数又不是偶函数D.既是奇函数又是偶函数 8.若函数()f x 是定义域在R 上的偶函数，在(),0-∞上是减函数，且(2)0f -=，则使()0f x <的x 的取值范围为（） A.()2,2- B.()()2,00,2- C.()(),22,-∞-+∞ D.(][),22,-∞-+∞9.函数()xf x x x=+的图像是（ ） 10.设()f x 是定义域在R 上的奇函数，(2)()f x f x +=-，当01x <≤时，()f x x =，则(7.5)f 的值为（ ）A. -0.5B. 0.5C. -5.5D.7.511.已知2(21)1f x x -+=+，且(21)f x -+的定义域为[)2,1-，则()f x 的解析式为（ ）A.)51(,452141)(2≤<--+=x x x x f B.)51(,452141)(2≤<-+-=x x x x f C.21153()(0)4242f x x x x =+-<≤， D.21153()(0)4242f x x x x =-+<≤，12.已知函数()f x 是定义在R 上的不恒为零的偶函数，且对任意实数x 都有(1)(1)()xf x x f x +=+，则5(())2f f 的值是（ ）A.0B.12C.1D.52二．填空题.（本大题共4小题，每小题5分，共20分）13.已知1()x f x +=()f x 的定义域为.14.设函数(1)()()x x a f x x++=为奇函数，则a 的值为.15.设22,1(),12x x f x x x +≤-⎧=⎨-<<⎩，若()f x =3，则x 的值为.16.关于函数()()1(),,00,f x x x x=-∈-∞+∞，有下列四个结论：○1()f x 的值域为R ； ○2()f x 是定义域上的增函数； ○3对任意的()(),00,x ∈-∞+∞，都有()()0f x f x -+=成立；○4()f x 与20()x x g x x x=-表示同一个函数.把你认为正确的结论的序号填写到横线上.三．解答题.（本大题共6小题，其中17题10分，其余5个小题每题12分，共70分）17.设函数()f x 是定义域在R 上的奇函数，当0x >时，2()331f x x x =-+-，求()f x 在R 上的解析式. 18.已知集合{}{}13,22A x x B x m x m -≤≤=-≤≤+=. （1）若{}03AB x x =≤≤，求实数m 的值（2）若R A C B ⊆，求实数m 的取值范围.19.二次函数()f x 的最小值为1，且(0)(2)3f f ==. （1）求()f x 的解析式；（2）若()f x 在区间[]2,1a a +上不单调，求a 的取值范围.20.某商场国庆节期间搞促销活动，规定：顾客购物总金额不超过800元，不享受任何折扣；如果顾（1）试写出y x 关于的函数解析式； （2）若30y =，求此人购物实际所付金额. 21.已知函数2()2(1)f x x a x a =+-+. （1）当1a =-时，求()f x 在[]3,3-上的值域; （2）求()f x 在区间[]3,3-上的最小值. 22.已知2()1ax b f x x +=+是定义域在()1,1-上的奇函数，且12()25f =. （1）求()f x 的解析式；（2）判断()f x 的单调性，并证明你的结论； （3）解不等式(22)()0f t f t -+<.第一章《集合与函数概念》答案解析一.选择题.(本大题共12小题，每小题5分，共60分) CBDAD CAADA BA 二.填空题.（本大题共4小题，每小题5分，共20分） 13.[)()()1,11,22,-+∞或者{}11,2x x x x ≥-≠≠且14. -1 16.①③三.解答题.（本大题共6小题，其中17题10分，其余5个小题每题12分，共70分）2222217.0,0()3()3()1331()()()331()(0)0331,0()0,0331,0x x f x x x x x f x f x f x x x f x R f x x x f x x x x x <->∴-=--+--=---∴=--=++∴=⎧++<⎪∴==⎨⎪-+->⎩解：设则是奇函数又是上的奇函数{}()()2018.(1)2232.(2),2,2232153,35,U U m m m m B C B x x m x m A C Bm m m m m -=⎧⇒=⎨+≥⎩∴≠∅=<->+⊆∴->+<-><-∴-∞-+∞解：由题意得: 的值为 由题意知:则或或 得到或 的取值范围为22219.(1)(0)(2)3()1()1()(1)1(0)(0)132()2(1)1,()243211(2)02112f f f x x f x f x a x a f a a f x x f x x x a a a a a a ==∴=∴=-+>=+==∴=-+=-+<+⎧⇒<<⎨<<+⎩∴解： 二次函数的对称轴为 又有最小值 设 由得 即 由题意得: 的取值范围102⎛⎫⎪⎝⎭为， 0,080020.(1):(800)5%,800130025(1300)10%,1300(2)305005%2525(1300)10%30,135013503013201320x y x x x x x x ≤≤⎧⎪=-⨯<≤⎨⎪+-⨯>⎩>⨯=∴+-⨯==∴-=∴解：由题意得 解得 此人购物实际所付金额为元.[](][][]2min 21.(1)1()41()2()-3,22,3()=(2)5(3)20,(3)4()3,3-5,20(2)()113,4a f x x x f x x f x f x f f f f x f x x a a a =-=--∴=∴∴=--==-∴-=--<->解：当时, 的对称轴为 在上单调递减,在上单调递增 ／ 又在上的值域为 的对称轴为 ①当即时 [][](][]min 2min()-33()=(3)155313,24()-3,11,3()=(1)3113,2()-33f x f x f a a a f x a a f x f a a a a a f x f ∴-=--≤-≤-≤≤--∴-=-+--><-∴ 在，上单调递增 ／ ②当即时在上单调递减,在上单调递增／ ③当即时 在，上单调递减 min 2min ()=(3)7+37+3,2()=31,24155,4x f a a a f x a a a a a =<-⎧⎪-+--≤≤⎨⎪->⎩／ 综上所述，／()()22212121222.(1)()1,1(0)0()112()2522,115()12()1(2)()-1,1,(1,1),,()()f x f baxf x x f aa xf x x f x x x x x x f x f x -∴==∴=+=∴==+∴=+∈-<-=解：是上的奇函数又 解得 在上单调递增.证明:任意取且则()1212122222121212221212121212()(1)11(1)(1)110,10,10,10()()0,()()()-1,1(3)(22)()0x x x x x x x x x x x x x x x x x f x f x f x f x f x f t f t ---=++++-<<<∴-<->+>+>∴-<<∴-+<∴即 在上单调递增. ()()(22)()()1,1()()(22)()(2)()1,122121221,2311f t f t f x f t f t f t f t f x t tt t t -<--∴-=-∴-<---<-⎧⎪∴-<-<<<⎨⎪-<-<⎩ 易知是上的奇函数 又由知是上的增函数 解得。
高一数学新教材人教版必修一第三章函数的概念与性质测试卷含答案
（Ⅲ）若 f (x) 在区间[2, ) 上单调递增,求实数 a 的取值范围.
19.（本小题满分 12 分）
已知函数
f
(x)
ax x2
b 1
是定义在
(1,1)
上奇函数,
且 f (1) 3 .
3 10
（Ⅰ）判断函数 f (x) 在 (1,1) 上的单调性，并用
定义证明；
（Ⅱ）若实数 t 满足 f (2t 1) f (t 1) 0 ，求实
4
5.令 t 1 x 0, 则 y 2 2t2 t 2(t 1)2 17 17
4 88
6.
y
x(x 2),(x x(x 2),(
2) x 2)
，作出图象即可.
7.函数 f (x) ax 2a 1,(a 0) 在 (0, ) 上单 x
调递增,又 m2 1 0,m2 m 3 0
x3 数,则实数 a 的取值范围是
15.已知函数 f (x) x5 3x3 5x 3 ,若 f (a) f (a 2) 6 ，则实数 a 的取值范围是
16.已知 m R ,函数 f (x) x 3 m m 在[2, x 1
5] 上的最大值是 5 ,则 m 的取值范围是
三、解答题：（写出必要的文字说明，推理过程或 演算步骤） 17.（本小题满分 10 分） 设函数 f (x) ax2 (b 2)x 3 . （Ⅰ）若 f (1) 3 ，且 a 0,b 0 ,求 b 1 的最
9.已知奇函数 y f (x) 的图象关于直线 x 2 对称,
且 f (m) 3,且 f (m 4) 的值为（ ）
A. 3
B. 0
C. 3
D. 1
3
10.已知函数 f (x 1) 是偶函数,且 x 1 时, f (x) 单调递减,设 a f ( 1),b f (3),c f (0) ，则 a,
函数测试题1
函数检测1一、选择题1.函数y ＝2－x ＋1（x ＞0）的反函数是（ ）A.y ＝log211-x ，x ∈（1，2） B.y ＝－1og211-x ，x ∈（1，2） C.y ＝log211-x ，x ∈（1，2]D.y ＝－1og211-x ，x ∈（1，2]2.已知(31)4,1()log ,1a a x a x f x x x -+<⎧=⎨>⎩是(,)-∞+∞上的减函数，那么a 的取值范围是( )（A ）(0,1) （B ）1(0,)3 （C ）11[,)73 （D ）1[,1)73.在下列四个函数中，满足性质：“对于区间(1,2)上的任意1212,()x x x x ≠，1221|()()|||f x f x x x -<-恒成立”的只有( )（A ）1()f x x =（B ）()||f x x = （C ）()2xf x = （D ）2()f x x =4.已知()f x 是周期为2的奇函数，当01x <<时，()l g f x x =设63(),(),52a f b f ==5(),2c f =则( )（A ）a b c << （B ）b a c << （C ）c b a << （D ）c a b <<5.函数23()lg(31)1x f x x x =++-的定义域是( )A.1(,)3-+∞B.1(,1)3- C. 11(,)33- D. 1(,)3-∞- 6、下列函数中，在其定义域内既是奇函数又是减函数的是( )A.3,y x x R =-∈ B. sin ,y x x R =∈ C. ,y x x R =∈ D. x1() ,2y x R =∈7、函数()y f x =的反函数1()y f x -=的图像与y 轴交于点(0,2)P （如右图所示），则方程()0f x =在[1,4]上的根是x =( )xy 1-2431()y f x -=OA.4B.3C. 2D.18、设()f x 是R 上的任意函数，则下列叙述正确的是( )(A)()()f x f x -是奇函数 (B)()()f x f x -是奇函数(C) ()()f x f x --是偶函数 (D) ()()f x f x +-是偶函数9、已知函数x y e =的图象与函数()y f x =的图象关于直线y x =对称，则( )A ．()22()x f x e x R =∈ B ．()2ln 2ln (0)f x x x => C ．()22()x f x e x R =∈ D ．()2ln ln2(0)f x x x =+>10、设1232,2()((2))log (1) 2.x e x f x f f x x -⎧⎪=⎨-≥⎪⎩＜，则的值为， ( )(A)0 (B)1 (C)2 (D)311、对a ，b ∈R ，记max{a ，b}＝⎩⎨⎧≥b a b ba a ＜,,，函数f （x ）＝max{|x ＋1|，|x －2|}(x ∈R)的最小值是( )(A)0 (B)12 (C) 32 (D)312、关于x 的方程222(1)10x x k ---+=，给出下列四个命题：①存在实数k ，使得方程恰有2个不同的实根； ②存在实数k ，使得方程恰有4个不同的实根； ③存在实数k ，使得方程恰有5个不同的实根； ④存在实数k ，使得方程恰有8个不同的实根；其中假命题的个数是( )A ．0B ．1C ．2D ．3二、填空题13.函数()f x 对于任意实数x 满足条件()()12f x f x +=，若()15,f =-则()()5f f =_______________。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
函数概念测试题（一）
一、精心选一选（每小题3分，共24分） 1．下列关系中的两个量，成反比例的是（ ）
A ．压力一定时，压强与受力面积
B ．面积一定时，矩形周长与一边长
C ．读一本书，已读的页数与余下的页数
D ．某人年龄与体重
2．计划修建铁路l （Km ），铺轨天数为t （d ），每日铺轨量s （km/d ），则在下列三个结论中，正确的是（ ）
①当l 一定时，t 是s 的反比例函数；②当t 一定时，l 是s 的反比例函数；③当s 一定时，l 是t 的反比例函数．
A ．仅①
B ．仅②
C ．仅③
D ．①②③ 3．一定质量的干松木，当它的体积V=23
m 时，它的密度ρ=0.5×3
10kg/3
m ，则ρ与V 的函数关系是（ ）
A ．V 100=ρ（V ＞0）
B ．V 1000
=
ρ（V ＞0） C ．1000+=V ρ（V ＞0） D ．V
500
=ρ（V ＞0）
4．在温度不变的情况下，气球内气体的压强P （Pa ）与它的体积V （3
m ）的乘积是一个常数k ，即k PV =（k 为常数，0>k ），下列图象能正确反映P 和V 之间的函数关系的是（ ）
5．下列各问题中，两个变量之间的关系不是反比例函数的是（ ） A ．小明完成100m 赛跑时，时间t （s ）与他跑步平均速度v （m/s ）之间的关系 B ．矩形的面积为10，它的长x 与宽y 之间的关系
C ．一个玻璃容器的体积为30L 时，所盛液体的质量m 与所盛液体的体积V 之间的关系
D ．压力为600N 时，压强P 与受力面积S 之间的关系
6．一辆汽车从相距60km 的甲地驶往乙地，则行驶的速度v （km/h ）与所用时间t （h ）的函数关系式为（ ）
A ．v=60t
B ．t
v 60
=
A B C D
C ．60
t
v =
D ．t v +=60 7．面积为2的△ABC ，一边长为x ，这边上的高为y ，则y 与x 的变化规律用图象表示大致是（ ）
8．两位同学在描述同一反比例函数的图象时，甲同学说：“这个反比例函数图象上任意一点到两坐标轴的距离之积都是3．”乙同学说：“这个反比例函数的图象与直线y=x 有两个交点．”你认为这两位同学所描述的反比例函数的解析式是（ ）
A ．x
y 3
=
B ．x y 3-=
C ．x y 3-=
D ．x y 3=
二、细心填一填（每题3分，共24分）
9．在体积为20的圆柱中，底面积S 关于高h 的函数关系式是 ．
10．已知广州市的土地面积是74342
km ，人均占有的土地面积S （单位：2
km /人）随全市人口n （单位：人）的变化而变化，则S 与n 的函数关系式是 ．
11．我们学习过的反比例函数，例如，当矩形面积S 一定时，长a 是宽b 的反比例函数，其函数关系式可以写成b
S
a =
（S 为常数，S ≠0）．甲、乙两地相距100千米，汽车从甲地去乙地的速度y （千米/时）与时间t （时）之间的关系式是 ，若速度y 增大10千米时，则时间可少用 时（用式子表示）．
12．收音机刻度盘的波长l 和频率f 分别是用米（m ）和千赫兹（KHz ）为单位标刻的，波长l 和频率f 满足关系式l
f 300000
=
，这说明波长l 越大，频率f 就越 ． 13．一定体积的面团做成拉面，面条的总长度y （cm ）是面条横截面积（粗细）x （2
cm ）的反比例函数．假设它的图象如图所示，则y 与x 的函数关系式为 ．
14．某物体对地面的压力为定值，物体对地面的压强P （Pa ）与受力面积S （2
m ）之间的函数关系如图所示．当某物体的受力面积S=202
m 时，则该物体对地面的压强是 帕．
15．若正方形AOBC 的边OA 、OB 在坐标轴上，顶点C 在第一象限且在反比例函数x
y 1
=的图象上，则点C 的坐标是 ．
A B C D
2
2
4
4
1
1 2
2
16.一块蓄电池的电压为定值，使用此蓄电池为电源时，电流I （A ）与电阻R （Ω）之间的函数关系如图所示，如果此蓄电池为电源的电器限制电流不得超过10A ，那么此用电器的可变电阻应 ．
三、专心解一解（共52分）
17．（5分）一司机驾驶汽车从甲地去乙地，以80千米/时的平均速度用6小时到达目的地．
（1）当他按原路匀速返回时，求汽车速度v （千米/时）与时间t （小时）之间的函数关系式；
（2）如果该司机匀速返回时，用了4.8小时，求返回时的速度．
18．（6分）某服装厂承揽一项生产夏凉小衫1600件的任务，计划用t （t ＞4）天完成． （1）写出每天生产夏凉小衫w （件）与生产时间t （天）之间的函数关系式； （2）由于气温提前升高，上见与服装厂商议调整计划，决定提前4天交货，那么服装厂每天要多做多少件夏凉小衫才能完成任务．
19．（7分）要求取消市场上使用杆秤的呼声越来越高．原因在于，一些不法商贩在卖货时将秤砣挖空，或更换较小的秤砣，使秤砣变轻，从而欺骗顾客．
（1）如图所示，对于同一物体，哪个用了较轻的秤砣？
（2）在称同一物体时，秤砣到支点的距离y 与所用秤砣质量x 之间满足 关系． （3）当秤砣变轻时，称得的物体变重，这正好符合哪个函数的哪些性质？
20．（7分）人的视觉机能受运动速度的影响很大，行驶中司机在驾驶室内观察前方物体时是动态的，车速增加，视野变窄．当车速为50千米/时时，视野为80度．如果视野f （度）是车速v （千米/时）的反比例函数，求f 、v 之间的关系式，并计算当车速为100千
第13题图
P （0.04，3200）
y （cm ）
x （cm 2）
第14题图
2 4 6 8
10 4
8 10
P/Pa
S/m 2 第16题图
8
R/Ω
I/A
2
①
②
第19题图
米/时时视野的度数．
21．（8分）某汽车的功率P 为一定值，汽车行驶的速度v （米/秒）与它所受的牵引力F （牛）之间的函数关系式如图所示．
（1）这辆汽车的功率是多少瓦？请写出这一函数关系式； （2）当它所受牵引力为1200牛时，汽车的速度为多少米/秒？ （3）如果限定汽车的速度不超过30米/秒，则F 在什么范围内？
22．（9分）如图所示，学校生物兴趣小组的同学们用围栏围了一个面积为24平方米的矩形饲养场地ABCD ，设BC 为x 米，AB 为y 米．
（1）求y 与x 的函数关系式；
（2）延长BC 至E ，使CE 比BC 少1米，围成一个新的矩形ABEF ，结果场地的面积增加了16平方米，求BC 的长．
23．（10分）水产公司有一种海产品共2104千克，为寻求合适的销售价格，进行了8天试销，试销情况如下：
第1天 第2天 第3天 第4天 第5天 第6天 第7天 第8天 销售x （元/千克） 400
250
240
200
150
125
120
销售量y （千克）
30 40 48 60 80 96 100
观察表中数据，发现可以用反比例函数刻画这种海产品的每天销售量y （千克）与销售价格x 之间的关系．现假定在这批海产品的销售中，每天的销售量y （千克）与销售价格x （元/千克）之间都满足这一关系．
（1）写出这个反比例函数的关系式，并补全表格；
（2）在试销8天后，公司决定将这种海产品的销售价格定为150元/千克，并且每天都按这个价格销售，那么余下这些海产品预计再用多少天可以全部售出？
（牛）
（米/秒）
第21题图
B C E
A D F
第22题图。