学而思寒假七年级尖子班讲义第6讲含参不等式(组)
(word完整版)学而思寒假七年级尖子班讲义第1讲平行线四大模型(1)

目录Contents第1讲平行线四大模型 (1)第2讲实数三大概念 (17)第3讲平面直角坐标系 (33)第4讲坐标系与面积初步 (51)第5讲二元一次方程组进阶 (67)第6讲含参不等式〔组〕 (79)1 平行线四大模型知识目标目标一熟练掌握平行线四大模型的证实目标二熟练掌握平行线四大模型的应用目标三掌握辅助线的构造方法,熟悉平行线四大模型的构造秋季回忆平行线的判定与性质1、平行线的判定根据平行线的定义,如果平面内的两条直线不相交,就可以判断这两条直线平行,但是,由于直线无限延伸,检验它们是否相交有困难,所以难以直接根据定义来判断两条直线是否平行,这就需要更简单易行的判定方法来判定两直线平行.判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简称:同位角相等,两直线平行.判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简称:内错角相等,两直线平行,判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简称:同旁内角互补,两直线平行,假设/ 1 = 72,那么AB// CD 〔同位角相等,两直线平行〕;假设/ 1 = 7 3,那么AB// CD 〔内错角相等,两直线平行〕;假设/ 1+ /4= 180°,那么AB//CD 〔同旁内角互补,两直线平行〕.另有平行公理推论也能证实两直线平行:平行公理推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.2、平行线的性质利用同位角相等,或者内错角相等,或者同旁内角互补,可以判定两条直线平行.反过来,如果两条直线平行,当它们被第三条直线所截,得到的同位角、内错角、同旁内角也有相应的数量关系,这就是平行线的性质.性质1:两条平行线被第三条直线所截,同位角相等.简称:两直线平行,同位角相等性质2:两条平行线被第三条直线所截,内错角相等简称:两直线平行,内错角相等性质3:两条平行线被第三条直线所截,同旁内角互补.简称:两直线平行,同旁内角互补本讲进阶平行线四大模型模型一“铅笔〞模型点P在EF右侧,在AB、CD内部结论 1 :假设AB // CD,贝U/ P+Z AEP + ZPFC =3 60° ;结论2:假设/ P+/AEP+/PFC= 360°,贝U AB//CD.模型二“猪ET模型〔M模型〕点P在EF左侧,在AB、CD内部“猪蹄〞模型结论 1 :假设AB // CD,贝U/ P=/AEP + /CFP ;结论 1 :假设AB // CD ,贝U/ P=Z AEP-ZCFP 或/ P=/ CFP-/AEP; 结论2:假设/ P=/AEP- / CFP 或/ P=/CFP- / AEP,贝U AB // CD.模型四“骨折〞模型点P在EF左侧,在AB、CD外部“骨折〞模型结论 1 :假设AB // CD ,贝U/ P=Z CFP- / AEP 或/ P=Z AEP-/ CFP ; 结论2:假设/ P= ZCFP- / AEP 或/ P= ZAEP- / CFP,贝U AB // CD.稳固练习平行线四大模型证实(1) AE // CF ,求证/ P +/AEP +/ PFC = 360(2) / P=Z AEP+ZCFP,求证AE//CF.(3) AE//CF,求证/ P=/AEP-/CFP.(4) ZP= ZCFP -/AEP,求证AE //CF .模块一平行线四大模型应用例1(1)如图,a//b, M、N分别在a、b上,P为两平行线间一点,那么/ l + /2+/3= .(2)如图,AB//CD,且/ A=25° , / 0=45°,那么/ E 的度数是(3)如图, AB// DE, /ABC=80° , / 0DE =140°,那么/ B0D= .A* ---------------------- rB (4)如图,射线AC//BD, / A= 70° , / B= 40°,那么/ P=(1)如下图,AB//CD, /E=37° , / 0= 20 °,那么/ EAB 的度数为(2) (七一中学2021-2021七下3月月考)如图,AB // CD, / B=30° , / O=/ C.那么/ 0=例2如图, AB//DE, BF、DF分别平分/ ABC、/ CDE,求/ C、/ F的关系.练如图, AB//DE, /FBC = 1/ABF, /FDC = 1/FDE. n n⑴假设n=2,直接写出/ C、/ F的关系 ;(2)假设n=3,试探冗/ C、/F的关系;(3)直接写出/ C、/ F的关系 (用含n的等式表示)如图, AB//CD, BE 平分/ABC, DE 平分 / ADC .求证:/ E= 2 (/A+/C).如图,己知AB//DE, BF、DF分别平分/ ABC、/ CDE ,求/ C、/ F的关系.例4如图,/ 3==/1+/2,求证:/ A+/B+/C+/D=180〔武昌七校2021-2021七下期中〕如图, ABXBC, AE 平分/ BAD 交BC 于E, AEXDE , / 1+ / 2= 90° ,M、N分别是BA、CD的延长线上的点,/ EAM和/ EDN的平分线相交于点F那么/ F的度数为〔〕A. 120° B.135° C. 145°D,150°模块二平行线四大模型构造例5如图,直线AB//CD, / EFA= 30° , / FGH = 90 /GHM = . ,/ HMN =30° , / CNP= 50°,那么如图,直线AB//CD, / EFG =100° , / FGH =140°,那么/ AEF+ ZCHG =例6/ B =25° , / BCD=45° , / CDE =30 ° , Z E=l0°,求证:AB // EF .练AB // EF,求/ 1- / 2+/3+/4 的度数.⑴如图⑴, MA i//NA n,探索/ A i、/A2、…、/ A n, / B i、/ B2…/B n-1之间的关系.(2)如图(2),己知MA i// NA4,探索/ A i、/ A2、/ A3、/ A4, / B i、/ B2之间的关系.(3)如图(3),MA i// NA n,探索/ A i、/ A2、…、/ A n之间的关系.如下图,两直线AB//CD平行,求/ i+/2+/3+/4+/5+/6.挑战压轴题(粮道街2021—2021七下期中)如图1,直线AB//CD, P是截线MN上的一点,MN与CD、AB分别交于E、F.(1)假设/EFB=55° , / EDP= 30°,求/ MPD 的度数;(2)当点P在线段EF上运动时,/ CPD与/ ABP的平分线交于Q,问:一Q-是否为定值?假设是定值, 请DPB求出定值;假设不是,说明其范围;(3)当点P在线段EF的延长线上运动时,/ CDP与/ ABP的平分线交于Q,问——的值足否认值,请DPB在图2中将图形补充完整并说明理由.图1 图2第一讲平行线四大模型〔课后作业〕1.如图,AB // CD // EF , EH^CD 于 H ,贝U/ BAC+/ACE +/CEH 等于〔〕.3 .如图 3,己知 AE// BD, / 1=130° , / 2=30 ° ,贝U/ C=4 .如图,直线 AB//CD, /C =115° , / A= 25 ° ,那么/ E=5 .如阁所示,AB// CD, / l=l l0° , / 2=120° ,那么/ 后6 .如下图, AB// DF, /D =116° , / DCB=93° ,那么/ B=A.180°B.270°C.360°2.(武昌七校 2021-2021七下期中) D. 450假设 AB // CD , / CDF =-/ CDE, 3 / ABF = - Z ABE,3贝叱 E: / F=( ).A. 2: 1B. 3: 1C. 4: 3AE7.如图,将三角尺的直角顶点放在直线 a 上,a// b. Z 1=50° , Z 2 =60°,那么/ 3的度数为8.如图,AB//CD, EP± FP,/1=30° , / 2=20°.那么/F的度数为9 .如图,假设AB//CD, ZBEF=70°,求/ B+/F+/C 的度数.10 .,直线AB// CD.(1)如图l, / A、/C、/ AEC之间有什么关系?请说明理由;(2)如图2, / AEF、/ EFC、/ FCD之间有什么关系?请说明理由;(3)如图3, / A、/ E、/ F、/ G、/ H、/ O、/ C 之间的关是—FA第11页共11。
人教版七年级数学寒假高分班讲义
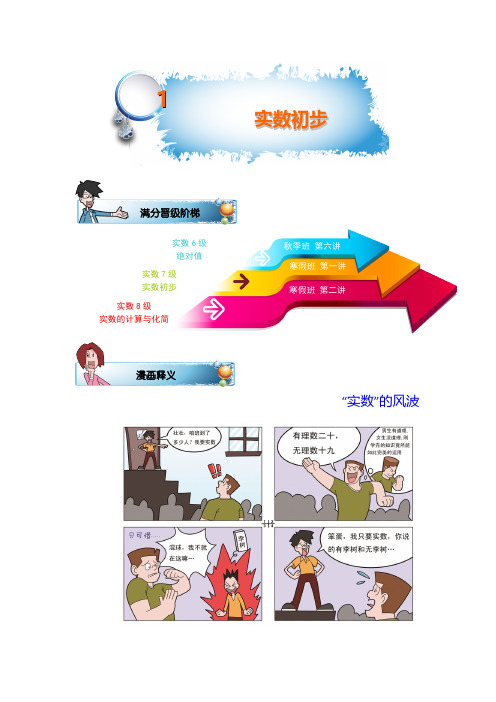
A.1 个
B.2 个
C.3 个
D.4 个
第十四种品格:信念
品格教育—信念
信念是脊梁,支撑着不倒的灵魂;信念是明灯,照耀着期盼的心灵;信念是路 标,指引着前进的方向。信念之于人生,如同舵手之于航船,航船没有舵手,就会 在大海中迷失方向。信念之于人生,如同羽翼之于飞鸟,飞鸟没有羽翼,就不能展 翅飞翔。 【信念的三个层次】 一、相信自己,相信别人;(故事 1、2) 二、勇于挑战,相信自己一定能成功;(故事 3、4) 三、坚持自己的理想与信念,用一生去追求.(故事 5、6)
标 与性质
实数
例 6;例 7;演练 5
模块一 平方根的定义与性质
知识导航
定义
平方根的概念: 如果一个数的平方等于 a ,那么这个数叫 做 a 的平方根.也就是说,若 x2 a ,则 x 就叫做 a 的平方根. 平方根的表示:一个非负数 a 的平方根可
示例剖析
22 4 , 2 就叫做 4 的平方根
二元一次方程定义:通过化简后,只有两个 未知数,并且未知数的项的次数都是 1 ,系数都 不是 0 的整式方程.
二元一次方程的解:使二元一次方程左右两 边的值相等的一对未知数的值,叫做这个二元一 次方程的一个解.
示例剖析
2x 3y, x y 5,
a b 1, m n ; 35
x 1
y
4
是方程
知识模块二 立方根的定义及性质 课后演练
【演练3】 求下列各数的立方根
1
5
0.216
8
立方
根
64 3 125
12
【演练4】 已知 5x 32 的立方根是 2 ,求 x 17 的平方根.
9 3
33
知识模块三 实数 课后演练
七年级数学培优辅导讲义(共十讲80页)

第一讲有理数的巧算有理数运算是中学数学中一切运算的基础.它要求同学们在理解有理数的有关概念、法则的基础上,能根据法则、公式等正确、迅速地进行运算.不仅如此,还要善于根据题目条件,将推理与计算相结合,灵活巧妙地选择合理的简捷的算法解决问题,从而提高运算能力,发展思维的敏捷性与灵活性.1.括号的使用在代数运算中,可以根据运算法则和运算律,去掉或者添上括号,以此来改变运算的次序,使复杂的问题变得较简单.例1计算:分析中学数学中,由于负数的引入,符号“+”与“-”具有了双重涵义,它既是表示加法与减法的运算符号,也是表示正数与负数的性质符号.因此进行有理数运算时,一定要正确运用有理数的运算法则,尤其是要注意去括号时符号的变化.注意在本例中的乘除运算中,常常把小数变成分数,把带分数变成假分数,这样便于计算.例2计算下式的值:211×555+445×789+555×789+211×445.分析直接计算很麻烦,根据运算规则,添加括号改变运算次序,可使计算简单.本题可将第一、第四项和第二、第三项分别结合起来计算.解原式=(211×555+211×445)+(445×789+555×789)=211×(555+445)+(445+555)×789=211×1000+1000×789=1000×(211+789)=1 000 000.说明加括号的一般思想方法是“分组求和”,它是有理数巧算中的常用技巧.例3计算:S=1-2+3-4+…+(-1)n+1·n.分析不难看出这个算式的规律是任何相邻两项之和或为“1”或为“-1”.如果按照将第一、第二项,第三、第四项,…,分别配对的方式计算,就能得到一系列的“-1”,于是一改“去括号”的习惯,而取“添括号”之法.解 S=(1-2)+(3-4)+…+(-1)n+1·n.下面需对n的奇偶性进行讨论:当n为偶数时,上式是n/2个(-1)的和,所以有当n为奇数时,上式是(n-1)/2个(-1)的和,再加上最后一项(-1)n+1·n=n,所以有例4在数1,2,3,…,1998前添符号“+”和“-”,并依次运算,所得可能的最小非负数是多少?分析与解因为若干个整数和的奇偶性,只与奇数的个数有关,所以在1,2,3,…,1998之前任意添加符号“+”或“-”,不会改变和的奇偶性.在1,2,3,…,1998中有1998÷2个奇数,即有999个奇数,所以任意添加符号“+”或“-”之后,所得的代数和总为奇数,故最小非负数不小于1.现考虑在自然数n,n+1,n+2,n+3之间添加符号“+”或“-”,显然n-(n+1)-(n+2)+(n+3)=0.这启发我们将1,2,3,…,1998每连续四个数分为一组,再按上述规则添加符号,即(1-2-3+4)+(5-6-7+8)+…+(1993-1994-1995+1996)-1997+1998=1.所以,所求最小非负数是1.说明本例中,添括号是为了造出一系列的“零”,这种方法可使计算大大简化.2.用字母表示数我们先来计算(100+2)×(100-2)的值:(100+2)×(100-2)=100×100-2×100+2×100-4=1002-22.这是一个对具体数的运算,若用字母a代换100,用字母b代换2,上述运算过程变为(a+b)(a-b)=a2-ab+ab-b2=a2-b2.于是我们得到了一个重要的计算公式(a+b)(a-b)=a2-b2,①这个公式叫平方差公式,以后应用这个公式计算时,不必重复公式的证明过程,可直接利用该公式计算.例5计算 3001×2999的值.解 3001×2999=(3000+1)(3000-1)=30002-12=8 999 999.例6计算 103×97×10 009的值.解原式=(100+3)(100-3)(10000+9)=(1002-9)(1002+9)=1004-92=99 999 919.例7计算:分析与解直接计算繁.仔细观察,发现分母中涉及到三个连续整数:12 345,12 346,12 347.可设字母n=12 346,那么12 345=n-1,12 347=n+1,于是分母变为n2-(n-1)(n+1).应用平方差公式化简得n2-(n2-12)=n2-n2+1=1,即原式分母的值是1,所以原式=24 690.例8计算:(2+1)(22+1)(24+1)(28+1)(216+1)(232+1).分析式子中2,22,24,…每一个数都是前一个数的平方,若在(2+1)前面有一个(2-1),就可以连续递进地运用(a+b)(a-b)=a2-b2了.解原式=(2-1)(2+1)(22+1)(24+1)(28+1)×(216+1)(232+1)=(22-1)(22+1)(24+1)(28+1)(216+1)×(232+1)=(24-1)(24+1)(28+1)(216+1)(232+1)=……=(232-1)(232+1)=264-1.例9计算:分析在前面的例题中,应用过公式(a+b)(a-b)=a2-b2.这个公式也可以反着使用,即a2-b2=(a+b)(a-b).本题就是一个例子.通过以上例题可以看到,用字母表示数给我们的计算带来很大的益处.下面再看一个例题,从中可以看到用字母表示一个式子,也可使计算简化.例10计算:我们用一个字母表示它以简化计算.3.观察算式找规律例11某班20名学生的数学期末考试成绩如下,请计算他们的总分与平均分.87,91,94,88,93,91,89,87,92,86,90,92,88,90,91,86,89,92,95,88.分析与解若直接把20个数加起来,显然运算量较大,粗略地估计一下,这些数均在90上下,所以可取90为基准数,大于90的数取“正”,小于90的数取“负”,考察这20个数与90的差,这样会大大简化运算.所以总分为90×20+(-3)+1+4+(-2)+3+1+(-1)+(-3)+2+(-4)+0+2+(-2)+0+1+(-4)+(-1)+2+5+(-2)=1800-1=1799,平均分为 90+(-1)÷20=89.95.例12 计算1+3+5+7+…+1997+1999的值.分析观察发现:首先算式中,从第二项开始,后项减前项的差都等于2;其次算式中首末两项之和与距首末两项等距离的两项之和都等于2000,于是可有如下解法.解用字母S表示所求算式,即S=1+3+5+…+1997+1999.①再将S各项倒过来写为S=1999+1997+1995+…+3+1.②将①,②两式左右分别相加,得2S=(1+1999)+(3+1997)+…+(1997+3)+(1999+1)=2000+2000+…+2000+2000(500个2000)=2000×500.从而有 S=500 000.说明一般地,一列数,如果从第二项开始,后项减前项的差都相等(本题3-1=5-3=7-5=…=1999-1997,都等于2),那么,这列数的求和问题,都可以用上例中的“倒写相加”的方法解决.例13计算 1+5+52+53+…+599+5100的值.分析观察发现,上式从第二项起,每一项都是它前面一项的5倍.如果将和式各项都乘以5,所得新和式中除个别项外,其余与原和式中的项相同,于是两式相减将使差易于计算.解设S=1+5+52+…+599+5100,①所以5S=5+52+53+…+5100+5101.②②—①得4S=5101-1,说明如果一列数,从第二项起每一项与前一项之比都相等(本例中是都等于5),那么这列数的求和问题,均可用上述“错位相减”法来解决.例14 计算:分析一般情况下,分数计算是先通分.本题通分计算将很繁,所以我们不但不通分,反而利用如下一个关系式来把每一项拆成两项之差,然后再计算,这种方法叫做拆项法.解由于所以说明本例使用拆项法的目的是使总和中出现一些可以相消的相反数的项,这种方法在有理数巧算中很常用.练习一1.计算下列各式的值:(1)-1+3-5+7-9+11-…-1997+1999;(2)11+12-13-14+15+16-17-18+…+99+100;(3)1991×1999-1990×2000;(4)4726342+472 6352-472 633×472 635-472 634×472 636;(6)1+4+7+ (244)2.某小组20名同学的数学测验成绩如下,试计算他们的平均分.81,72,77,83,73,85,92,84,75,63,76,97,80,90,76,91,86,78,74,85.第二讲绝对值绝对值是初中代数中的一个基本概念,在求代数式的值、化简代数式、证明恒等式与不等式,以及求解方程与不等式时,经常会遇到含有绝对值符号的问题,同学们要学会根据绝对值的定义来解决这些问题.下面我们先复习一下有关绝对值的基本知识,然后进行例题分析.一个正实数的绝对值是它本身;一个负实数的绝对值是它的相反数;零的绝对值是零.即绝对值的几何意义可以借助于数轴来认识,它与距离的概念密切相关.在数轴上表示一个数的点离开原点的距离叫这个数的绝对值.结合相反数的概念可知,除零外,绝对值相等的数有两个,它们恰好互为相反数.反之,相反数的绝对值相等也成立.由此还可得到一个常用的结论:任何一个实数的绝对值是非负数.例1 a,b为实数,下列各式对吗?若不对,应附加什么条件?(1)|a+b|=|a|+|b|;(2)|ab|=|a||b|;(3)|a-b|=|b-a|;(4)若|a|=b,则a=b;(5)若|a|<|b|,则a<b;(6)若a>b,则|a|>|b|.解 (1)不对.当a,b同号或其中一个为0时成立.(2)对.(3)对.(4)不对.当a≥0时成立.(5)不对.当b>0时成立.(6)不对.当a+b>0时成立.例2设有理数a,b,c在数轴上的对应点如图1-1所示,化简|b-a|+|a+c|+|c-b|.解由图1-1可知,a>0,b<0,c<0,且有|c|>|a|>|b|>0.根据有理数加减运算的符号法则,有b-a<0,a+c<0,c-b<0.再根据绝对值的概念,得|b-a|=a-b,|a+c|=-(a+c),|c-b|=b-c.于是有原式=(a-b)-(a+c)+(b-c)=a-b-a-c+b-c=-2c.例3已知x<-3,化简:|3+|2-|1+x|||.分析这是一个含有多层绝对值符号的问题,可从里往外一层一层地去绝对值符号.解原式=|3+|2+(1+x)||(因为1+x<0)=|3+|3+x||=|3-(3+x)|(因为3+x<0)=|-x|=-x.解因为 abc≠0,所以a≠0,b≠0,c≠0.(1)当a,b,c均大于零时,原式=3;(2)当a,b,c均小于零时,原式=-3;(3)当a,b,c中有两个大于零,一个小于零时,原式=1;(4)当a,b,c中有两个小于零,一个大于零时,原式=-1.说明本例的解法是采取把a,b,c中大于零与小于零的个数分情况加以解决的,这种解法叫作分类讨论法,它在解决绝对值问题时很常用.例5若|x|=3,|y|=2,且|x-y|=y-x,求x+y的值.解因为|x-y|≥0,所以y-x≥0,y≥x.由|x|=3,|y|=2可知,x<0,即x=-3.(1)当y=2时,x+y=-1;(2)当y=-2时,x+y=-5.所以x+y的值为-1或-5.例6若a,b,c为整数,且|a-b|19+|c-a|99=1,试计算|c-a|+|a-b|+|b-c|的值.解 a,b,c均为整数,则a-b,c-a也应为整数,且|a-b|19,|c-a|99为两个非负整数,和为1,所以只能是|a-b|19=0且|c-a|99=1,①或|a-b|19=1且|c-a|99=0.②由①有a=b且c=a±1,于是|b-c|=|c-a|=1;由②有c=a且a=b±1,于是|b-c|=|a-b|=1.无论①或②都有|b-c|=1且|a-b|+|c-a|=1,所以|c-a|+|a-b|+|b-c|=2.解依相反数的意义有|x-y+3|=-|x+y-1999|.因为任何一个实数的绝对值是非负数,所以必有|x-y+3|=0且|x+y-1999|=0.即由①有x-y=-3,由②有x+y=1999.②-①得2y=2002, y=1001,所以例8 化简:|3x+1|+|2x-1|.分析本题是两个绝对值和的问题.解题的关键是如何同时去掉两个绝对值符号.若分别去掉每个绝对值符号,则是很容易的事.例如,化简|3x+1|,只要考虑3x+1的正负,即可去掉绝对值符号.这里我们为三个部分(如图1-2所示),即这样我们就可以分类讨论化简了.原式=-(3x+1)-(2x-1)=5x;原式=(3x+1)-(2x-1)=x+2;原式=(3x+1)+(2x-1)=5x.即说明解这类题目,可先求出使各个绝对值等于零的变数字母的值,即先求出各个分界点,然后在数轴上标出这些分界点,这样就将数轴分成几个部分,根据变数字母的这些取值范围分类讨论化简,这种方法又称为“零点分段法”.例9已知y=|2x+6|+|x-1|-4|x+1|,求y的最大值.分析首先使用“零点分段法”将y化简,然后在各个取值范围内求出y的最大值,再加以比较,从中选出最大者.解有三个分界点:-3,1,-1.(1)当x≤-3时,y=-(2x+6)-(x-1)+4(x+1)=x-1,由于x≤-3,所以y=x-1≤-4,y的最大值是-4.(2)当-3≤x≤-1时,y=(2x+6)-(x-1)+4(x+1)=5x+11,由于-3≤x≤-1,所以-4≤5x+11≤6,y的最大值是6.(3)当-1≤x≤1时,y=(2x+6)-(x-1)-4(x+1)=-3x+3,由于-1≤x≤1,所以0≤-3x+3≤6,y的最大值是6.(4)当x≥1时,y=(2x+6)+(x-1)-4(x+1)=-x+1,由于x≥1,所以1-x≤0,y的最大值是0.综上可知,当x=-1时,y取得最大值为6.例10设a<b<c<d,求|x-a|+|x-b|+|x-c|+|x-d|的最小值.分析本题也可用“零点分段法”讨论计算,但比较麻烦.若能利用|x-a|,|x-b|,|x-c|,|x-d|的几何意义来解题,将显得更加简捷便利.解设a,b,c,d,x在数轴上的对应点分别为A,B,C,D,X,则|x-a|表示线段AX之长,同理,|x-b|,|x-c|,|x-d|分别表示线段BX,CX,DX之长.现要求|x-a|,|x-b|,|x-c|,|x-d|之和的值最小,就是要在数轴上找一点X,使该点到A,B,C,D四点距离之和最小.因为a<b<c<d,所以A,B,C,D的排列应如图1-3所示:所以当X在B,C之间时,距离和最小,这个最小值为AD+BC,即(d-a)+(c-b).例11若2x+|4-5x|+|1-3x|+4的值恒为常数,求x该满足的条件及此常数的值.分析与解要使原式对任何数x恒为常数,则去掉绝对值符号,化简合并时,必须使含x的项相加为零,即x的系数之和为零.故本题只有2x-5x+3x=0一种情况.因此必须有|4-5x|=4-5x且|1-3x|=3x-1.故x应满足的条件是此时原式=2x+(4-5x)-(1-3x)+4=7.练习二1.x是什么实数时,下列等式成立:(1)|(x-2)+(x-4)|=|x-2|+|x-4|;(2)|(7x+6)(3x-5)|=(7x+6)(3x-5).2.化简下列各式:(2)|x+5|+|x-7|+|x+10|.3.若a+b<0,化简|a+b-1|-|3-a-b|.4.已知y=|x+3|+|x-2|-|3x-9|,求y的最大值.5.设T=|x-p|+|x-15|+|x-p-15|,其中0<p<15,对于满足p≤x≤15的x 来说,T的最小值是多少?6.已知a<b,求|x-a|+|x-b|的最小值.7.不相等的有理数a,b,c在数轴上的对应点分别为A,B,C,如果|a-b|+|b-c|=|a-c|,那么B点应为( ).(1)在A,C点的右边;(2)在A,C点的左边;(3)在A,C点之间;(4)以上三种情况都有可能.第三讲求代数式的值用具体的数代替代数式里的字母进行计算,求出代数式的值,是一个由一般到特殊的过程.具体求解代数式值的问题时,对于较简单的问题,代入直接计算并不困难,但对于较复杂的代数式,往往是先化简,然后再求值.下面结合例题初步看一看代数式求值的常用技巧.例1求下列代数式的值:分析上面两题均可直接代入求值,但会很麻烦,容易出错.我们可以利用已经学过的有关概念、法则,如合并同类项,添、去括号等,先将代数式化简,然后再求值,这样会大大提高运算的速度和结果的准确性.=0-4a3b2-a2b-5=-4×13×(- 2)2- 12×(-2)-5=-16+2-5=-19.(2)原式=3x2y-xyz+(2xyz-x2z)+4x2?[3x2y-(xyz-5x2z)]=3x2y-xyz+2xyz-x2z+4x2z-3x2y+(xyz-5x2z)=(3x2y-3x2y)+(-xyz+2xyz+xyz)+(-x2z+4x2z-5x2z)=2xyz-2x2z=2×(-1)×2×(-3)-2×(-1)2×(-3)=12+6=18.说明本例中(1)的化简是添括号,将同类项合并后,再代入求值;(2)是先去括号,然后再添括号,合并化简后,再代入求值.去、添括号时,一定要注意各项符号的变化.例2已知a-b=-1,求a3+3ab-b3的值.分析由已知条件a-b=-1,我们无法求出a,b的确定值,因此本题不能像例1那样,代入a,b的值求代数式的值.下面给出本题的五种解法.解法1由a-b=-1得a=b-1,代入所求代数式化简a3+3ab-b3=(b-1)3+3(b-1)b-b3=b3-3b2+3b-1+3b2-3b-b3=-1.说明这是用代入消元法消去a化简求值的.解法2因为a-b=-1,所以原式=(a3-b3)+3ab=(a-b)(a2+ab+b2)+3ab=-1×(a2+ab+b2)+3ab=-a2-ab-b2+3ab=-(a2-2ab+b2)=-(a-b)2=-(-1)2=-1.说明这种解法是利用了乘法公式,将原式化简求值的.解法3 因为a-b=-1,所以原式=a3-3ab(-1)-b3=a3-3ab(a-b)-b3=a3-3a2b+3ab2-b3=(a-b)3=(-1)3=-1.说明这种解法巧妙地利用了-1=a-b,并将3ab化为-3ab(-1)=-3ab(a-b),从而凑成了(a-b)3.解法4 因为a-b=-1,所以(a-b)3=(-1)3=1,即 a3+3ab2-3a2b-b3=-1,a3-b3-3ab(a-b)=-1,所以 a3-b3-3ab(-1)=-1,即 a3-b3+3ab=-1.说明这种解法是由a-b=-1,演绎推理出所求代数式的值.解法 5a3+3ab-b3=a3+3ab2-3a2b-b3-3ab2+3a2b+3ab=(a-b)3+3ab(a-b)+3ab=(-1)3+3ab(-1)+3ab=-1.说明这种解法是添项,凑出(a-b)3,然后化简求值.通过这个例题可以看出,求代数式的值的方法是很灵活的,需要认真思考,才能找到简便的算法.在本例的各种解法中,用到了几个常用的乘法公式,现总结如下:(a+b)2=a2+2ab+b2;(a-b)2=a2-2ab+b2;(a+b)3=a3+3a2b+3ab2+b3;(a-b)3=a3-3a2b+3ab2-b3;a3+b3=(a+b)(a2-ab+b2);a3-b3=(a-b)(a2+ab+b2).解由已知,xy=2(x+y),代入所求代数式中,消去xy,然后化简.所以解因为a=3b,所以c=5a=5×(3b)=15b.将a,c代入所求代数式,化简得解因为(x-5)2,|m|都是非负数,所以由(1)有由(2)得y+1=3,所以y=2.下面先化简所求代数式,然后再代入求值.=x2y+5m2x+10xy2=52×2+0+10×5×22=250例6如果4a-3b=7,并且3a+2b=19,求14a-2b的值.分析此题可以用方程组求出a,b的值,再分别代入14a-2b求值.下面介绍一种不必求出a,b的值的解法.解 14a-2b=2(7a-b)=2[(4a+3a)+(-3b+2b)]=2[(4a-3b)+(3a+2b)]=2(7+19)=52.|x|+|x-1|+|x-2|+|x-3|+|x-4|+|x-5|的值.分析所求代数式中六个绝对值的分界点,分别为:0,1,2,据绝对值的意义去掉绝对值的符号,将有3个x和3个-x,这样将抵消掉x,使求值变得容易.原式=x+(x-1)+(x-2)-(x-3)-(x-4)-(x-5)=-1-2+3+4+5=9.说明实际上,本题只要x的值在2与3之间,那么这个代数式的值就是9,即它与x具体的取值无关.例8若x:y:z=3:4:7,且2x-y+z=18,那么x+2y-z的值是多少?分析 x:y:z=3:4:7可以写成的形式,对于等比,我们通常可以设它们的比值为常数k,这样可以给问题的解决带来便利.x=3k,y=4k,z=7k.因为2x-y+z=18,所以2×3k-4k+7k=18,所以k=2,所以x=6,y=8,z=14,所以x+2y-z=6+16-14=8.例9已知x=y=11,求(xy-1)2+(x+y-2)(x+y-2xy)的值.分析本题是可直接代入求值的.下面采用换元法,先将式子改写得较简洁,然后再求值.解设x+y=m,xy=n.原式=(n-1)2+(m-2)(m-2n)=(n-1)2+m2-2m-2mn+4n=n2-2n+1+4n-2m-2mn+m2=(n+1)2-2m(n+1)+m2=(n+1-m)2=(11×11+1-22)2=(121+1-22)2=1002=10000.说明换元法是处理较复杂的代数式的常用手法,通过换元,可以使代数式的特征更加突出,从而简化了题目的表述形式.练习三1.求下列代数式的值:(1)a4+3ab-6a2b2-3ab2+4ab+6a2b-7a2b2-2a4,其中a=-2,b=1;的值.3.已知a=3.5,b=-0.8,求代数式|6-5b|-|3a-2b|-|8b-1|的值.4.已知(a+1)2-(3a2+4ab+4b2+2)=0,求 a,b的值.5.已知第四讲一元一次方程方程是中学数学中最重要的内容.最简单的方程是一元一次方程,它是进一步学习代数方程的基础,很多方程都可以通过变形化为一元一次方程来解决.本讲主要介绍一些解一元一次方程的基本方法和技巧.用等号连结两个代数式的式子叫等式.如果给等式中的文字代以任何数值,等式都成立,这种等式叫恒等式.一个等式是否是恒等式是要通过证明来确定的.如果给等式中的文字(未知数)代以某些值,等式成立,而代以其他的值,则等式不成立,这种等式叫作条件等式.条件等式也称为方程.使方程成立的未知数的值叫作方程的解.方程的解的集合,叫作方程的解集.解方程就是求出方程的解集.只含有一个未知数(又称为一元),且其次数是1的方程叫作一元一次方程.任何一个一元一次方程总可以化为ax=b(a≠0)的形式,这是一元一次方程的标准形式(最简形式).解一元一次方程的一般步骤:(1)去分母;(2)去括号;(3)移项;(4)合并同类项,化为最简形式ax=b;(5)方程两边同除以未知数的系数,得出方程的解.一元一次方程ax=b的解由a,b的取值来确定:(2)若a=0,且b=0,方程变为0·x=0,则方程有无数多个解;(3)若a=0,且b≠0,方程变为0·x=b,则方程无解.例1解方程解法1从里到外逐级去括号.去小括号得去中括号得去大括号得解法2按照分配律由外及里去括号.去大括号得化简为去中括号得去小括号得例2已知下面两个方程3(x+2)=5x,①4x-3(a-x)=6x-7(a-x) ②有相同的解,试求a的值.分析本题解题思路是从方程①中求出x的值,代入方程②,求出a的值.解由方程①可求得3x-5x=-6,所以x=3.由已知,x=3也是方程②的解,根据方程解的定义,把x=3代入方程②时,应有4×3-3(a-3)=6×3-7(a-3),7(a-3)-3(a-3)=18-12,例3已知方程2(x+1)=3(x-1)的解为a+2,求方程2[2(x+3)-3(x-a)]=3a的解.解由方程2(x+1)=3(x-1)解得x=5.由题设知a+2=5,所以a=3.于是有2[2(x+3)-3(x-3)]=3×3,-2x=-21,例4解关于x的方程(mx-n)(m+n)=0.分析这个方程中未知数是x,m,n是可以取不同实数值的常数,因此需要讨论m,n取不同值时,方程解的情况.解把原方程化为m2x+mnx-mn-n2=0,整理得 m(m+n)x=n(m+n).当m+n≠0,且m=0时,方程无解;当m+n=0时,方程的解为一切实数.说明含有字母系数的方程,一定要注意字母的取值范围.解这类方程时,需要从方程有唯一解、无解、无数多个解三种情况进行讨论.例5解方程(a+x-b)(a-b-x)=(a2-x)(b2+x)-a2b2.分析本题将方程中的括号去掉后产生x2项,但整理化简后,可以消去x2,也就是说,原方程实际上仍是一个一元一次方程.解将原方程整理化简得(a-b)2-x2=a2b2+a2x-b2x-x2-a2b2,即 (a2-b2)x=(a-b)2.(1)当a2-b2≠0时,即a≠±b时,方程有唯一解(2)当a2-b2=0时,即a=b或a=-b时,若a-b≠0,即a≠b,即a=-b时,方程无解;若a-b=0,即a=b,方程有无数多个解.例6已知(m2-1)x2-(m+1)x+8=0是关于x的一元一次方程,求代数式199(m+x)(x-2m)+m的值.解因为(m2-1)x2-(m+1)x+8=0是关于x的一元一次方程,所以m2-1=0,即m=±1.(1)当m=1时,方程变为-2x+8=0,因此x=4,代数式的值为199(1+4)(4-2×1)+1=1991;(2)当m=-1时,原方程无解.所以所求代数式的值为1991.例7 已知关于x的方程a(2x-1)=3x-2无解,试求a的值.解将原方程变形为2ax-a=3x-2,即 (2a-3)x=a-2.由已知该方程无解,所以例8 k为何正数时,方程k2x-k2=2kx-5k的解是正数?来确定:(1)若b=0时,方程的解是零;反之,若方程ax=b的解是零,则b=0成立.(2)若ab>0时,则方程的解是正数;反之,若方程ax=b的解是正数,则ab>0成立.(3)若ab<0时,则方程的解是负数;反之,若方程ax=b的解是负数,则ab<0成立.解按未知数x整理方程得(k2-2k)x=k2-5k.要使方程的解为正数,需要(k2-2k)(k2-5k)>0.看不等式的左端(k2-2k)(k2-5k)=k2(k-2)(k-5).因为k2≥0,所以只要k>5或k<2时上式大于零,所以当k<2或k>5时,原方程的解是正数,所以k>5或0<k<2即为所求.例9若abc=1,解方程解因为abc=1,所以原方程可变形为化简整理为化简整理为说明像这种带有附加条件的方程,求解时恰当地利用附加条件可使方程的求解过程大大简化.例10若a,b,c是正数,解方程解法1原方程两边乘以abc,得到方程ab(x-a-b)+bc(x-b-c)+ac(x-c-a)=3abc.移项、合并同类项得ab[x-(a+b+c)]+bc[x-(a+b+c)]+ac[x-(a+b+c)]=0,因此有[x-(a+b+c)](ab+bc+ac)=0.因为a>0,b>0,c>0,所以ab+bc+ac≠0,所以x-(a+b+c)=0,即x=a+b+c为原方程的解.解法2将原方程右边的3移到左边变为-3,再拆为三个“-1”,并注意到其余两项做类似处理.设m=a+b+c,则原方程变形为所以即x-(a+b+c)=0.所以x=a+b+c为原方程的解.说明注意观察,巧妙变形,是产生简单优美解法所不可缺少的基本功之一.例11设n为自然数,[x]表示不超过x的最大整数,解方程:分析要解此方程,必须先去掉[ ],由于n是自然数,所以n与(n+1)…,n[x]都是整数,所以x必是整数.解根据分析,x必为整数,即x=[x],所以原方程化为合并同类项得故有所以x=n(n+1)为原方程的解.例12已知关于x的方程且a为某些自然数时,方程的解为自然数,试求自然数a的最小值.解由原方程可解得a最小,所以x应取x=160.所以所以满足题设的自然数a的最小值为2.练习四1.解下列方程:*2.解下列关于x的方程:(1)a2(x-2)-3a=x+1;4.当k取何值时,关于x的方程3(x+1)=5-kx,分别有:(1)正数解;(2)负数解;(3)不大于1的解.第五讲方程组的解法二元及多元(二元以上)一次方程组的求解,主要是通过同解变形进行消元,最终转化为一元一次方程来解决.所以,解方程组的基本思想是消元,主要的消元方法有代入消元和加减消元两种,下面结合例题予以介绍.例1解方程组解将原方程组改写为由方程②得x=6+4y,代入①化简得11y-4z=-19.④由③得2y+3z=4.⑤④×3+⑤×4得33y+8y=-57+16,所以 y=-1.将y=-1代入⑤,得z=2.将y=-1代入②,得x=2.所以为原方程组的解.说明本题解法中,由①,②消x时,采用了代入消元法;解④,⑤组成的方程组时,若用代入法消元,无论消y,还是消z,都会出现分数系数,计算较繁,而利用两个方程中z的系数是一正一负,且系数的绝对值较小,采用加减消元法较简单.解方程组消元时,是使用代入消元,还是使用加减消元,要根据方程的具体特点而定,灵活地采用各种方法与技巧,使解法简捷明快.例2解方程组解法1由①,④消x得由⑥,⑦消元,得解之得将y=2代入①得x=1.将z=3代入③得u=4.所以解法2由原方程组得所以x=5-2y=5-2(8-2z)=-11+4z=-11+4(11-2u)=33-8u=33-8(6-2x)=-15+16x,即x=-15+16x,解之得x=1.将x=1代入⑧得u=4.将u=4代入⑦得z=3.将z=3代入⑥得y=2.所以为原方程组的解.解法3①+②+③+④得x+y+z+u=10,⑤由⑤-(①+③)得y+u=6,⑥由①×2-④得4y-u=4,⑦⑥+⑦得y=2.以下略.说明解法2很好地利用了本题方程组的特点,解法简捷、流畅.例3解方程组分析与解注意到各方程中同一未知数系数的关系,可以先得到下面四个二元方程:①+②得x+u=3,⑥②+③得y+v=5,⑦③+④得z+x=7,⑧④+⑤得u+y=9.⑨又①+②+③+④+⑤得x+y+z+u+v=15.⑩⑩-⑥-⑦得z=7,把z=7代入⑧得x=0,把x=0代入⑥得u=3,把u=3代入⑨得y=6,把y=6代入⑦得v=-1.所以为原方程组的解.例4解方程组解法1①×2+②得由③得代入④得为原方程组的解.为原方程组的解.说明解法1称为整体处理法,即从整体上进行加减消元或代入消为换元法,也就是干脆引入一个新的辅助元来代替原方程组中的“整体元”,从而简化方程组的求解过程.例5已知分析与解一般想法是利用方程组求出x,y,z的值之后,代入所求的代数式计算.但本题中方程组是由三个未知数两个方程组成的,因此无法求出x,y,z的确定有限解,但我们可以利用加减消元法将原方程组变形.①-②消去x得①×3+②消去y得①×5+②×3消去z得例6已知关于x,y的方程组分别求出当a为何值时,方程组(1)有唯一一组解;(2)无解;(3)有无穷多组解.分析与一元一次方程一样,含有字母系数的一次方程组求解时也要进行讨论,一般是通过消元,归结为一元一次方程ax=b的形式进行讨论.但必须特别注意,消元时,若用含有字母的式子去乘或者去除方程的两边时,这个式子的值不能等于零.解由①得2y=(1+a)-ax,③将③代入②得(a-2)(a+1)x=(a-2)(a+2).④(1)当(a-2)(a+1)≠0,即a≠2且a≠-1时,方程④有因而原方程组有唯一一组解.(2)当(a-2)(a+1)=0且(a-2)(a+2)≠0时,即a=-1时,方程④无解,因此原方程组无解.(3)当(a-2)(a+1)=0且(a-2)(a+2)=0时,即a=2时,方程④有无穷多个解,因此原方程组有无穷多组解.例7已知关于x,y的二元一次方程(a-1)x+(a+2)y+5-2a=0,当a每取一个值时,就有一个方程,而这些方程有一个公共解,试求出这个公共解.解法1根据题意,可分别令a=1,a=-2代入原方程得到一个方程组将x=3,y=-1代入原方程得(a-1)·3+(a+2)·(-1)+5-2a=0.所以对任何a值都是原方程的解.说明取a=1为的是使方程中(a-1)x=0,方程无x项,可直接求出y值;取a=-2的道理类似.解法2可将原方程变形为a(x+y-2)-(x-2y-5)=0.由于公共解与a无关,故有例8甲、乙两人解方程组原方程的解.分析与解因为甲只看错了方程①中的a,所以甲所得到的解4×(-3)-b×(-1)=-2.③a×5+5×4=13.④解由③,④联立的方程组得所以原方程组应为练习五1.解方程组2.若x1,x2,x3,x4,x5满足方程组试确定3x4+2x5的值.3.将式子3x2+2x-5写成a(x+1)2+b(x+1)+c的形式,试求4.k为何值时,方程组有唯一一组解;无解;无穷多解?5.若方程组的解满足x+y=0,试求m的值.第六讲一次不等式(不等式组)的解法不等式和方程一样,也是代数里的一种重要模型.在概念方面,它与方程很类似,尤其重要的是不等式具有一系列基本性质,而且“数学的基本结果往往是一些不等式而不是等式”.本讲是系统学习不等式的基础.下面先介绍有关一次不等式的基本知识,然后进行例题分析.1.不等式的基本性质这里特别要强调的是在用一个不等于零的数或式子去乘(或去除)不等式时,一定要注意它与等式的类似性质上的差异,即当所乘(或除)的数或式子大于零时,不等号方向不变(性质(5));当所乘(或除)的数或式子小于零时,不等号方向要改变(性质(6)).2.区间概念在许多情况下,可以用不等式表示数集和点集.如果设a,b为实数,且a<b,那么(1)满足不等式a<x<b的数x的全体叫作一个开区间,记作(a,b).如图1-4(a).(2)满足不等式a≤x≤b的数x的全体叫作一个闭区间,记作[a,b].如图1-4(b).(3)满足不等式a<x≤b(或a≤x<b)的x的全体叫作一个半开半闭区间,记作(a,b](或[a,b)).如图1-4(c),(d).3.一次不等式的一般解法一元一次不等式像方程一样,经过移项、合并同类项、整理后,总可以写成下面的标准型:ax>b,或ax<b.为确定起见,下面仅讨论前一种形式.一元一次不等式ax>b.(3)当a=0时,用区间表示为(-∞,+∞).例1解不等式解两边同时乘以6得12(x+1)+2(x-2)≥21x-6,化简得-7x≥-14,两边同除以-7,有x≤2.所以不等式的解为x≤2,用区间表示为(-∞,2].例2求不等式的正整数解.正整数解,所以原不等式的正整数解为x=1,2,3.例3解不等式分析与解因y2+1>0,所以根据不等式的基本性质有例4解不等式为x+2>7,解为x>5.这种错误没有考虑到使原不等式有意义的条件:x≠6.解将原不等式变形为解之得所以原不等式的解为x>5且x≠6.例5已知2(x-2)-3(4x-1)=9(1-x),且y<x+9,试比较解首先解关于x的方程得x=-10.将x=-10代入不等式得y<-10+9,即y<-1.例6解关于x的不等式:解显然a≠0,将原不等式变形为3x+3-2a2>a-2ax,即(3+2a)x>(2a+3)(a-1).说明对含有字母系数的不等式的解,也要分情况讨论.例7已知a,b为实数,若不等式(2a-b)x+3a-4b<0解由(2a-b)x+3a-4b<0得(2a-b)x<4b-3a.。
初一下册不等式含参

初一下册不等式含参初一下册不等式含参一、引言不等式是数学中的一个重要概念,通过不等式我们可以研究数的大小关系。
在初一下册数学学习中,我们接触到了不等式含参这个新的概念。
不等式含参的学习,不仅可以提高我们的逻辑思维能力,还能够帮助我们理解和解决实际问题。
二、基本概念不等式含参是指在不等式中含有带有参数的表达式。
参数是不确定的数,可以取不同的值,从而使得不等式的解集发生变化。
例如,不等式 |2x - 3| > a 可以称为一个不等式含参,其中 x 是参数,a是给定常数。
当我们确定了不同的 a 值时,不等式的解集也会随之改变。
三、解决方法解决不等式含参的问题,一般需要进行以下几个步骤:1. 化简:首先,我们需要对不等式进行化简,将其转化为简洁的形式。
例如,使用绝对值不等式的性质,可以将 |2x - 3| > a 化简为 2x - 3 > a 或者 2x - 3 < -a。
2. 分类讨论:根据化简得到的不等式,我们可以将其分成几种情况进行讨论。
例如,当 a > 0 时,将 2x - 3 > a 分成 x > (a+3)/2 和 x < (3-a)/2 两种情况。
3. 求解:接下来,我们需要解决每个分类讨论中的不等式。
通过运用代数运算和性质,将不等式化简为 x 的区间表示形式。
例如,在第一种情况 x > (a+3)/2 中,可以化简为 x > (a+3)/2。
4. 综合解集:最后,我们需要将每个分类的解集综合起来,得到不等式含参的解集。
综合解集时,需要考虑各个分类的交集或并集。
四、应用示例不等式含参可以帮助我们解决许多实际问题。
例如,在经济学中,我们可以利用不等式含参来分析商品价格的涨跌幅度。
在生活中,我们可以通过不等式含参来研究食品或药品的安全问题。
五、总结初一下册不等式含参是一个重要的数学概念,在我们的学习中扮演着重要的角色。
通过学习不等式含参,我们可以锻炼逻辑思维能力,理解和解决实际问题。
含参不等式

不等式一、不含参的二次不等式(1)3x2﹣4x+1<0;(2)﹣x2+4x+5>0.(3)x2+x﹣12≤0;(4)﹣4x2+4x﹣1<0;(5)5x2﹣7x+3≤0.(6)x2+2x﹣3>0.(7)x2﹣6x+9≤0二、解集为空集或者是R的不等式1.已知函数f(x)=x2+ax+6.(Ⅱ)若不等式f(x)>0的解集为R,求实数a的取值范围.2.已知关于x的不等式kx2﹣2x+6k<0(k≠0),(1)若不等式的解集为R,求k的取值范围;(2)若不等式的解集为∅,求k的取值范围.3.若不等式mx2+2mx﹣4<2x2+4x对任意x均成立,求实数m的取值范围.4.已知关于x的不等式kx2﹣2x+3k<0.(2)若不等式的解集为∅,求实数k的取值范围.5.若不等式kx2﹣2x+6k<0(k≠0).(2)若不等式解集是R,求k的取值.三、二次项系数不含参可以十字相乘1.解关于x的不等式2.解关于x的不等式x2+x﹣m(m﹣1)>0(m∈R).3.解关于x的不等式(x﹣1)(x+a)≥0.4.解关于x的不等式x2﹣(3m+1)x+m(2m+1)<0.5.解关于x的不等式x2+(a﹣2)x﹣2a≥0(a∈R).6.解关于x的不等式x2﹣2ax+a2﹣1<0(a∈R).7.解不等式x2﹣(a+)x+1<0(a≠0)8.解下列关于x的不等式:56x2+ax﹣a2<0.四、二次项系数含参可以十字相乘1.解关于x的不等式(ax﹣1)(x﹣1)<0.2.解关于x的不等式[(m+3)x﹣1](x+1)>0(m∈R).3.解关于x的不等式ax2+(a﹣2)x﹣2≥0(a≥0)4.解关于x的不等式ax2﹣(2a+1)x+2<0.5.解不等式mx2+(m2﹣1)x﹣m≥0.6.解关于x的不等式mx2+(2m﹣1)x﹣2>0.7.解关于x的不等式:a(a﹣1)x2﹣(2a﹣1)x+1>0,其中α∈R.8.已知a∈R,解关于x的不等式(a+1)x2+(2a+3)x+a+2<0.9.解含参数a的一元二次不等式:(a﹣2)x2+(2a﹣1)x+6>0.五、二次项不含参但不能十字相乘的1.解关于x的不等式x2+2x+a>0.。
学而思初中数学课程规划
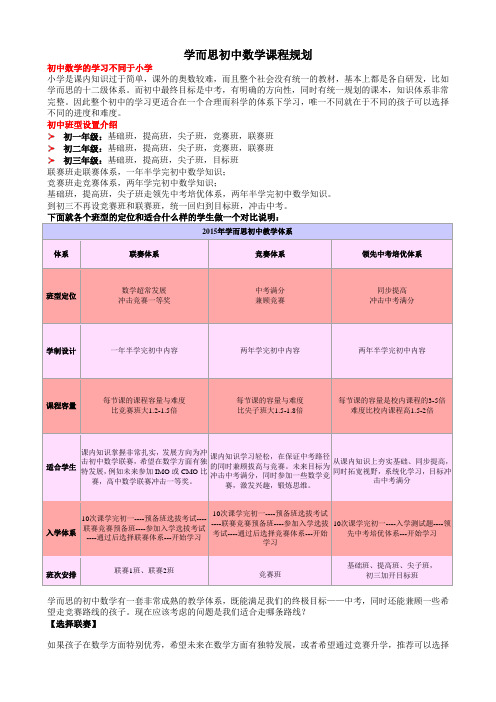
学而思初中数学课程规划初中数学的学习不同于小学小学是课内知识过于简单,课外的奥数较难,而且整个社会没有统一的教材,基本上都是各自研发,比如学而思的十二级体系。
而初中最终目标是中考,有明确的方向性,同时有统一规划的课本,知识体系非常完整。
因此整个初中的学习更适合在一个合理而科学的体系下学习,唯一不同就在于不同的孩子可以选择不同的进度和难度。
初中班型设置介绍初一年级:基础班,提高班,尖子班,竞赛班,联赛班初二年级:基础班,提高班,尖子班,竞赛班,联赛班初三年级:基础班,提高班,尖子班,目标班联赛班走联赛体系,一年半学完初中数学知识;竞赛班走竞赛体系,两年学完初中数学知识;基础班,提高班,尖子班走领先中考培优体系,两年半学完初中数学知识。
到初三不再设竞赛班和联赛班,统一回归到目标班,冲击中考。
下面就各个班型的定位和适合什么样的学生做一个对比说明:2015年学而思初中教学体系体系联赛体系竞赛体系领先中考培优体系班型定位数学超常发展冲击竞赛一等奖中考满分兼顾竞赛同步提高冲击中考满分学制设计一年半学完初中内容两年学完初中内容两年半学完初中内容课程容量每节课的课程容量与难度比竞赛班大1.2-1.5倍每节课的容量与难度比尖子班大1.5-1.8倍每节课的容量是校内课程的3-5倍难度比校内课程高1.5-2倍适合学生课内知识掌握非常扎实,发展方向为冲击初中数学联赛,希望在数学方面有独特发展,例如未来参加IMO或CMO比赛,高中数学联赛冲击一等奖。
课内知识学习轻松,在保证中考路径的同时兼顾拔高与竞赛。
未来目标为冲击中考满分,同时参加一些数学竞赛,激发兴趣,锻炼思维。
从课内知识上夯实基础、同步提高,同时拓宽视野,系统化学习,目标冲击中考满分入学体系10次课学完初一----预备班选拔考试----联赛竞赛预备班----参加入学选拔考试----通过后选择联赛体系---开始学习10次课学完初一----预备班选拔考试----联赛竞赛预备班----参加入学选拔考试----通过后选择竞赛体系---开始学习10次课学完初一----入学测试题----领先中考培优体系---开始学习班次安排联赛1班、联赛2班竞赛班基础班、提高班、尖子班,初三加开目标班学而思的初中数学有一套非常成熟的教学体系,既能满足我们的终极目标——中考,同时还能兼顾一些希望走竞赛路线的孩子。
七年级数学竞赛联赛班讲义 第六讲 不等式(组)与高斯方程(无答案)

第 六 讲 不等式(组)与高斯方程【知识要点】一、 定义:x 为实数,y 为不超过x 的最大整数,则有y=[x].[x]也叫做x 的整数部分,用{x}表示x 的小数部分,{x}=x-[x],0≤{x}<1;二、 性质:1、 x-1<[x]≤x ;0≤{x}<1;2、 0≤x-[x]<1;3、 n 为整数,则[x+n]=[x]+n.【新知讲授】例一、设[]x 表示不小于x 的最小整数,如[][][][]3.44,44,3.84, 3.83===-=-.则下列结论中:①[]x x ≤;②[]1x x +<;③[]x x =只有x 为整数才成立;④[][]22x x +=+;⑤[][]22x x -=-;⑥[][]22x x =;⑦[]22x x ⎡⎤=⎢⎥⎣⎦不成立的结论( ). (A)不超过3个 (B)恰为4个 (C)刚好为5个 (D)至少有6个 例二、[]x 表示不大于x 的最大整数,解方程53[]42x x +=.例三、解方程:(1)[2]32x x +=-; (2)56157[]85x x +-=.例四、解方程: (1)3[]6{}1x x -=- (2)53{}6x x -=.例五、对于数x ,符号[x ]表示不大于x 的最大整数.例如,[3.14]=3,[-7.59]=-8,则满足关系式[773+x ]=4的x 的整数值有( ). (A )6个(B )5个 (C )4个 (D )3个例六、若[x]=5,[y]=-3,[z]=-1,则[x-y-z]所有可能的取值的个数是( ). (A)2个(B)3个 (C)4个 (D)5个例七、正整数n 满足n ≤2012,且[][][]236n n n n ++=,则满足条件的正整数n 的个数是 .例八、设[]x 表示不大于x 的最大整数,若222221111123414152341415S =+++++,则[]S 的值为 .例八、For a real number a ,let []a denote the maximum integer which does not exceed a .For example ,[3.1]=3,[-1.5]=-2,[0.7]=0. Now let 1()1x f x x +=-,then [2][3][99][100]f f f f +++= .(英汉小词典real number :实数;the maximum integer which does not exceed :不超过的最大整数)例九、实数x 、y 满足[][2]1[]1y x x y x =+--⎧⎨=+⎩,则x+y 的取值范围是( ).(A)整数 (B)9<x+y<10 (C)9≤x+y<10 (D)9<x+y≤10例十、设19202191[][][][]546100100100100x x x x++++++++=L L,求]100[x的值.例十一、若x、y、z满足[]{}0.9[]{}0.2{}[] 1.3x y zx y zx y z++=-⎧⎪++=⎨⎪++=⎩,其中[]a表示不大于a的最大整数,{}[]a a a=-,求x、y、z的值. 【赛题解密】1.解方程:1[31]22x x+=-. 2.解方程:551[]23x x-+=.3.解方程:1751[]52x x +-=. 4.解方程:53[]4x x +=.5.解方程:35{}6x x -=. 6.解方程:2[]5{}4x x -=.7.][x 表示不大于x 的最大整数,那么方程50][43=+x x 的解为 .。
含参不等式以及含参不等式组的解法知识分享

含参不等式以及含参不等式组的解法
含参不等式以及含参不等式组的解法
不等式在中考中的运用,往往掺杂参数来增加难度,我们只要读清楚题目找到解题思路便能迎刃而解了。
本节课我们就重点讲讲如何读题去寻找解题思路。
含参不等式:
解不等式5(x-1)<3x+1
通过去括号、移项、合并同类项等一系列运算可以求出解为:x<3 求不等式57x -<3
2-x 的最小整数解. 通过去括号、移项、合并同类项等一系列运算可以求出解为:x>
831,故可以得出最小整数为4.
那么含参不等式如下:
在这些需要讨论的情况下,等号最后讨论才方便,不会讨论重合。
例题:1、求不等式kx+2>2x-3的解集
移项、合并同类项、讨论取值
2、(1)求不等式解集mx+a>nx+b
移项、合并同类项、讨论取值
(2)(m-1)x>a2+1对于任意x都成立,则参数m的值为
2、解关于x 的不等式组⎩
⎨⎧+->+-<-8)21(563x m x mx mx mx
3、如果一元一次不等式组⎪⎩⎪⎨⎧≥≤≤-a
x x 432
(1)有解,求a 的取值范围。
(2)无解,求a 的取值范围。
(3)有且只有一个解,求a 的取值范围。
(4)只有两个整数解,求a 的取值范围。
学而思新初一数学培优讲义word版(全年级章节培优-绝对经典)

第1讲 与有理数有关的概念 考点·方法·破译1.了解负数的产生过程,能够用正、负数表示具有相反意义的量. 2.会进行有理的分类,体会并运用数学中的分类思想.3.理解数轴、相反数、绝对值、倒数的意义.会用数轴比较两个有理数的大小,会求一个数的相反数、绝对值、倒数. 经典·考题·赏析【例1】写出下列各语句的实际意义⑴向前-7米⑵收人-50元⑶体重增加-3千克 【解法指导】用正、负数表示实际问题中具有相反意义的量.而相反意义的量包合两个要素:一是它们的意义相反.二是它们具有数量.而且必须是同类两,如“向前与自后、收入与支出、增加与减少等等”解:⑴向前-7米表示向后7米⑵收入-50元表示支出50元⑶体重增加-3千克表示体重减小3千克.【变式题组】01.如果+10%表示增加10%,那么减少8%可以记作( ) A . -18% B . -8% C . +2% D . +8% 02.(金华)如果+3吨表示运入仓库的大米吨数,那么运出5吨大米表示为( ) A . -5吨 B . +5吨 C . -3吨 D . +3吨 03.(山西)北京与纽约的时差-13(负号表示同一时刻纽约时间比北京晚).如现在是北京时间l5:00,纽约时问是____【例2】在-227,π,0.033.3这四个数中有理数的个数( )A . 1个B . 2个C . 3个D . 4个【解法指导】有理数的分类:⑴按正负性分类,有理数0⎧⎧⎨⎪⎩⎪⎪⎨⎪⎧⎪⎨⎪⎩⎩正整数正有理数正分数负整数负有理数负份数;按整数、分数分类,有理数⎧⎧⎪⎪⎨⎪⎪⎪⎨⎩⎪⎧⎪⎨⎪⎩⎩正整数整数0负整数正分数分数负分数;其中分数包括有限小数和无限循环小数,因为π=3.1415926…是无限不循环小数,它不能写成分数的形式,所以π不是有理数,-227是分数0.033.3是无限循环小数可以化成分数形式,0是整数,所以都是有理数,故选C . 【变式题组】01.在7,0.1 5,-12,-301.31.25,-18,100.l ,-3 001中,负分数为 ,整数为 ,正整数 .02.(河北秦皇岛)请把下列各数填入图中适当位置 15,-19,215,-138,0.1.-5.32,123, 2.333【例3】(宁夏)有一列数为-1,12,-13,14.-15,16,…,找规律到第2007个数是 .【解法指导】从一系列的数中发现规律,首先找出不变量和变量,再依变量去发现规律.击归纳去猜想,然后进行验证.解本题会有这样的规律:⑴各数的分子部是1;⑵各数的分母依次为1,2,3,4,5,6,…⑶处于奇数位置的数是负数,处于偶数位置的数是正数,所以第2007个数的分子也是1.分母是2007,并且是一个负数,故答案为-12007.【变式题组】 01.(湖北宜宾)数学解密:第一个数是3=2 +1,第二个数是5=3 +2,第三个数是9=5+4,第四十数是17=9+8…观察并精想第六个数是 . 02.(毕节)毕选哥拉斯学派发明了一种“馨折形”填数法,如图则?填____. 03.(茂名)有一组数l ,2,5,10,17,26…请观察规律,则第8个数为____. 【例4】(2008年河北张家口)若l +m 2的相反数是-3,则m 的相反数是____.【解法指导】理解相反数的代数意义和几何意义,代数意义只有符号不同的两个数叫互为相反数.几何意义:在数轴上原点的两旁且离原点的距离相等的两个点所表示的数叫互为相反数,本题m2=-4,m =-8【变式题组】 01.(四川宜宾)-5的相反数是( ) A .5 B . 15 C . -5 D . -1502.已知a 与b 互为相反数,c 与d 互为倒数,则a +b +cd =______03.如图为一个正方体纸盒的展开图,若在其中的三个正方形A 、B 、C 内分别填人适当的数,使得它们折成正方体.若相对的面上的两个数互为相反数,则填人正方形A 、B 、C 内的三个数依次为( )A . - 1 ,2,0B . 0,-2,1C . -2,0,1D . 2,1,0 【例5】(湖北)a 、b 为有理数,且a >0,b <0,|b|>a ,则a,b 、-a,-b 的大小顺序是( ) A . b <-a <a <-b B . –a <b <a <-b C . –b <a <-a <b D . –a <a <-b <b【解法指导】理解绝对值的几何意义:一个数的绝对值就是数轴上表示a 的点到原点的距离,即|a|,用式子表示为|a|=0)0(0)(0)a a a a a >⎧⎪=⎨⎪-<⎩(.本题注意数形结合思想,画一条数轴标出a 、b,依相反数的意义标出-b,-a,故选A .【变式题组】 01.推理①若a =b ,则|a|=|b|;②若|a|=|b|,则a =b ;③若a ≠b ,则|a |≠|b|;④若|a |≠|b|,则a ≠b ,其中正确的个数为( )A . 4个B . 3个C . 2个D . 1个02.a 、b 、c 三个数在数轴上的位置如图,则|a|a +|b|b +|c|c = .03.a 、b 、c 为不等于O 的有理散,则a |a|+b |b|+c|c|的值可能是____.【例6】(江西课改)已知|a -4|+|b -8|=0,则a+bab的值.【解法指导】本题主要考查绝对值概念的运用,因为任何有理数a 的绝对值都是非负数,即|a |≥0.所以|a -4|≥0,|b -8|≥0.而两个非负数之和为0,则两数均为0.解:因为|a -4|≥0,|b -8|≥0,又|a -4|+|b -8|=0,∴|a -4|=0,|b -8|=0即a -4=0,b -8=0,a =4,b =8.故a+b ab =1232=38【变式题组】01.已知|a|=1,|b|=2,|c|=3,且a >b >c ,求a +b +C . 02.(毕节)若|m -3|+|n +2|=0,则m +2n 的值为( ) A . -4 B . -1 C . 0 D . 403.已知|a|=8,|b|=2,且|a -b|=b -a ,求a 和b 的值 【例7】(第l8届迎春杯)已知(m +n)2+|m|=m ,且|2m -n -2|=0.求mn 的值.【解法指导】本例关键是通过分析(m +n)2+|m|的符号,挖掘出m 的符号特征,从而把问题转化为(m +n)2=0,|2m -n -2|=0,找到解题途径. 解:∵(m +n )2≥0,|m |≥O∴(m +n)2+|m |≥0,而(m +n)2+|m|=m ∴ m ≥0,∴(m +n)2+m =m ,即(m +n)2=0 ∴m +n =O ① 又∵|2m -n -2|=0 ∴2m -n -2=0 ②由①②得m =23,n =-23,∴ mn =-49【变式题组】01.已知(a +b)2+|b +5|=b +5且|2a -b –l|=0,求a -B . 02.(第16届迎春杯)已知y =|x -a|+|x +19|+|x -a -96|,如果19<a <96.a ≤x ≤96,求y 的最大值. 演练巩固·反馈提高01.观察下列有规律的数12,16,112,120,130,142…根据其规律可知第9个数是( )A .156 B . 172 C . 190 D . 111002.(芜湖)-6的绝对值是( )A . 6B . -6C . 16D . -1603.在-227,π,8..0.3四个数中,有理数的个数为( )A . 1个B . 2个C . 3个D . 4个 04.若一个数的相反数为a +b ,则这个数是( )A . a -bB . b -aC . –a +bD . –a -b05.数轴上表示互为相反数的两点之间距离是6,这两个数是( ) A . 0和6 B . 0和-6 C . 3和-3 D . 0和3 06.若-a 不是负数,则a( )A . 是正数B . 不是负数C . 是负数D . 不是正数 07.下列结论中,正确的是( )①若a =b,则|a|=|b| ②若a =-b,则|a|=|b| ③若|a|=|b|,则a =-b ④若|a|=|b|,则a =bA . ①②B . ③④C . ①④D . ②③08.有理数a 、b 在数轴上的对应点的位置如图所示,则a 、b ,-a ,|b|的大小关系正确 的是( )A . |b|>a >-a >bB . |b| >b >a >-aC . a >|b|>b >-aD . a >|b|>-a >b09.一个数在数轴上所对应的点向右移动5个单位后,得到它的相反数的对应点,则这个数是____.10.已知|x +2|+|y +2|=0,则xy =____.11.a 、b 、c 三个数在数轴上的位置如图,求|a|a +|b|b +|abc|abc +|c|c12.若三个不相等的有理数可以表示为1、a 、a +b 也可以表示成0、b 、ba 的形式,试求a 、b 的值.13.已知|a|=4,|b|=5,|c|=6,且a >b >c ,求a +b -C .14.|a|具有非负性,也有最小值为0,试讨论:当x 为有理数时,|x -l|+|x -3|有没有最小值,如果有,求出最小值;如果没有,说明理由.15.点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为|AB|.当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a-b| 当A、B两点都不在原点时有以下三种情况:①如图2,点A、B都在原点的右边|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|;②如图3,点A、B都在原点的左边,|AB|=|OB|-|OA|=|b|-|a|=-b-(-a)=|a-b|;③如图4,点A、B在原点的两边,|AB|=|OB|-|OA|=|b|-|a|=-b-(-a)=|a-b|;综上,数轴上A、B两点之间的距离|AB|=|a-b|.回答下列问题:⑴数轴上表示2和5的两点之间的距离是, 数轴上表示-2和-5的两点之间的距离是, 3,数轴上表示1和-3的两点之间的距离是 4;⑵数轴上表示x和-1的两点分别是点A和B,则A、B之间的距离是|x+1|,如果|AB|=2,那么x=1或3;⑶当代数式|x+1|+|x-2|取最小值时,相应的x的取值范围是7.培优升级·奥赛检测01.(重庆市竞赛题)在数轴上任取一条长度为199919的线段,则此线段在这条数轴上最多能盖住的整数点的个数是( )A . 1998B . 1999C . 2000D . 2001 02.(第l8届希望杯邀请赛试题)在数轴上和有理数a 、b 、c 对应的点的位置如图所示,有下列四个结论:①abc <0;②|a -b|+|b -c|=|a -c|;③(a -b )(b -c)(c -a)>0;④|a|<1-bc .其中正确的结论有( )A . 4个B . 3个C . 2个D . 1个03.如果a 、b 、c 是非零有理数,且a +b +c =0.那么a |a|+b |b|+c |c|+abc|abc|的所有可能的值为( )A . -1B . 1或-1C . 2或-2D . 0或-2 04.已知|m|=-m ,化简|m -l|-|m -2|所得结果( )A . -1B . 1C . 2m -3D . 3- 2m05.如果0<p <15,那么代数式|x -p|+|x -15|+|x -p -15|在p ≤x ≤15的最小值( ) A . 30 B . 0 C . 15 D . 一个与p 有关的代数式 06.|x +1|+|x -2|+|x -3|的最小值为 .07.若a >0,b <0,使|x -a|+|x -b|=a -b 成立的x 取值范围 . 08.(武汉市选拔赛试题)非零整数m 、n 满足|m|+|n|-5=0所有这样的整数组(m ,n)共有 组09.若非零有理数m 、n 、p 满足|m|m +|n|n +|p|p =1.则2mnp|3mnp|= .10.(19届希望杯试题)试求|x -1|+|x -2|+|x -3|+…+|x -1997|的最小值.11.已知(|x +l|+|x -2|)(|y -2|+|y +1|)(|z -3|+|z +l|)=36,求x +2y +3的最大值和最小值.12.电子跳蚤落在数轴上的某点k0,第一步从k0向左跳1个单位得k1,第二步由k1向右跳2个单位到k2,第三步由k2向左跳3个单位到k3,第四步由k3向右跳4个单位到k4…按以上规律跳100步时,电子跳蚤落在数轴上的点k100新表示的数恰好19.94,试求k0所表示的数.13.某城镇,沿环形路上依次排列有五所小学,它们顺扶有电脑15台、7台、1l台、3台,14台,为使各学校里电脑数相同,允许一些小学向相邻小学调出电脑,问怎样调配才能使调出的电脑总台数最小?并求出调出电脑的最少总台数.第02讲有理数的加减法考点·方法·破译1.理解有理数加法法则,了解有理数加法的实际意义.2.准确运用有理数加法法则进行运算,能将实际问题转化为有理数的加法运算.3.理解有理数减法与加法的转换关系,会用有理数减法解决生活中的实际问题.4.会把加减混合运算统一成加法运算,并能准确求和.经典·考题·赏析【例1】(河北唐山)某天股票A开盘价18元,上午11:30跌了1.5元,下午收盘时又涨了0.3元,则股票A这天的收盘价为()A.0.3元B.16.2元C.16.8元D.18元【解法指导】将实际问题转化为有理数的加法运算时,首先将具有相反意义的量确定一个为正,另一个为负,其次在计算时正确选择加法法则,是同号相加,取相同符号并用绝对值相加,是异号相加,取绝对值较大符号,并用较大绝对值减去较小绝对值.解:18+(-1.5)+(0.3)=16.8,故选C.【变式题组】01.今年陕西省元月份某一天的天气预报中,延安市最低气温为-6℃,西安市最低气温2℃,这一天延安市的最低气温比西安低()A.8℃B.-8℃C.6℃D.2℃02.(河南)飞机的高度为2400米,上升250米,又下降了327米,这是飞机的高度为__________03.(浙江)珠穆朗玛峰海拔8848m,吐鲁番海拔高度为-155 m,则它们的平均海拔高度为__________【例2】计算(-83)+(+26)+(-17)+(-26)+(+15)【解法指导】应用加法运算简化运算,-83与-17相加可得整百的数,+26与-26互为相反数,相加为0,有理数加法常见技巧有:⑴互为相反数结合一起;⑵相加得整数结合一起;⑶同分母的分数或容易通分的分数结合一起;⑷相同符号的数结合一起.解:(-83)+(+26)+(-17)+(-26)+(+15)=[(-83)+(-17)]+[(+26)+(-26)]+15=(-100)+15=-85【变式题组】01.(-2.5)+(-312)+(-134)+(-114)02.(-13.6)+0.26+(-2.7)+(-1.06)03.0.125+314+(-318)+1123+(-0.25)【例3】计算111112233420082009++++⨯⨯⨯⨯【解法指导】依111(1)1n n n n =-++进行裂项,然后邻项相消进行化简求和.解:原式=1111111(1)()()()2233420082009-+-+-++-=111111112233420082009-+-+-++-=112009-=20082009【变式题组】01.计算1+(-2)+3+(-4)+ … +99+(-100)02.如图,把一个面积为1的正方形等分成两个面积为12的长方形,接着把面积为12的长方形等分成两个面积为14的正方形,再把面积为14的正方形等分成两个面积为18的长方形,如此进行下去,试利用图形揭示的规律计算11111111248163264128256+++++++=__________.【例4】如果a <0,b >0,a +b <0,那么下列关系中正确的是( ) A .a >b >-b >-a B .a >-a >b >-b C .b >a >-b >-a D .-a >b >-b >a【解法指导】紧扣有理数加法法则,由两加数及其和的符号,确定两加数的绝对值的大小,然后根据相反数的关系将它们在同一数轴上表示出来,即可得出结论. 解:∵a <0,b >0,∴a +b 是异号两数之和又a +b <0,∴a 、b 中负数的绝对值较大,∴| a |>| b |将a 、b 、-a 、-b 表示在同一数轴上,如图,则它们的大小关系是-a >b >-b >a 【变式题组】01.若m>0,n<0,且| m |>| n |,则m+n ________ 0.(填>、<号)02.若m<0,n>0,且| m |>| n |,则m+n ________ 0.(填>、<号)03.已知a<0,b>0,c<0,且| c |>| b |>| a |,试比较a、b、c、a+b、a+c的大小【例5】425-(-33311)-(-1.6)-(-21811)【解法指导】有理数减法的运算步骤:⑴依有理数的减法法则,把减号变为加号,并把减数变为它的相反数;⑵利用有理数的加法法则进行运算.解:425-(-33311)-(-1.6)-(-21811)=425+33311+1.6+21811=4.4+1.6+(33311+21811)=6+55=61【变式题组】01.21511 ()()()()(1) 32632 --+---+-+02.434-(+3.85)-(-314)+(-3.15)03.178-87.21-(-43221)+1531921-12.79【例6】试看下面一列数:25、23、21、19…⑴观察这列数,猜想第10个数是多少?第n个数是多少?⑵这列数中有多少个数是正数?从第几个数开始是负数?⑶求这列数中所有正数的和.【解法指导】寻找一系列数的规律,应该从特殊到一般,找到前面几个数的规律,通过观察推理、猜想出第n个数的规律,再用其它的数来验证.解:⑴第10个数为7,第n个数为25-2(n-1)⑵∵n=13时,25-2(13-1)=1,n=14时,25-2(14-1)=-1故这列数有13个数为正数,从第14个数开始就是负数.⑶这列数中的正数为25,23,21,19,17,15,13,11,9,7,5,3,1,其和=(25+1)+(23+3)+…+(15+11)+13=26×6+13=169【变式题组】01.(杭州)观察下列等式1-12=12,2-25=85,3-310=2710,4-417=6417…依你发现的规律,解答下列问题.⑴写出第5个等式;⑵第10个等式右边的分数的分子与分母的和是多少?02.观察下列等式的规律9-1=8,16-4=12,25-9=16,36-16=20⑴用关于n(n≥1的自然数)的等式表示这个规律;⑵当这个等式的右边等于2008时求n.【例7】(第十届希望杯竞赛试题)求12+(13+23)+(14+24+34)+(15+25+35+45)+…+(150+250+…+4850+4950)【解法指导】观察式中数的特点发现:若括号内在加上相同的数均可合并成1,由此我们采取将原式倒序后与原式相加,这样极大简化计算了.解:设S=12+(13+23)+(14+24+34)+…+(150+250+…+4850+4950)则有S=12+(23+13)+(34+24+14)+…+(4950+4850+…+250+150)将原式和倒序再相加得2S=12+12+(13+23+23+13)+(14+24+34+34+24+14)+…+(150+250+…+4850+4950+4950+4850+…+250+150)即2S=1+2+3+4+…+49=49(491)2⨯+=1225∴S=1225 2【变式题组】01.计算2-22-23-24-25-26-27-28-29+21002.(第8届希望杯试题)计算(1-12-13-…-12003)(12+13+14+…+12003+12004)-(1-12-13-…-12004)(12+13+14+…+12003)演练巩固·反馈提高01.m是有理数,则m+|m|()A.可能是负数B.不可能是负数C.比是正数D.可能是正数,也可能是负数02.如果|a|=3,|b|=2,那么|a+b|为()A. 5 B.1 C.1或5 D.±1或±503.在1,-1,-2这三个数中,任意两数之和的最大值是()A. 1 B.0 C.-1 D.-304.两个有理数的和是正数,下面说法中正确的是()A.两数一定都是正数B.两数都不为0C.至少有一个为负数D.至少有一个为正数05.下列等式一定成立的是()A.|x|-x =0 B.-x-x =0 C.|x|+|-x| =0 D.|x|-|x|=006.一天早晨的气温是-6℃,中午又上升了10℃,午间又下降了8℃,则午夜气温是()A.-4℃B.4℃C.-3℃D.-5℃07.若a<0,则|a-(-a)|等于()A.-a B.0 C.2a D.-2a08.设x是不等于0的有理数,则||||2x xx-值为()A.0或1 B.0或2 C.0或-1 D.0或-2 09.(济南)2+(-2)的值为__________10.用含绝对值的式子表示下列各式:⑴若a<0,b>0,则b-a=__________,a-b=__________⑵若a>b>0,则|a-b|=__________⑶若a<b<0,则a-b=__________11.计算下列各题:⑴23+(-27)+9+5 ⑵-5.4+0.2-0.6+0.35-0.25⑶-0.5-314+2.75-712⑷33.1-10.7-(-22.9)-|-2310|12.计算1-3+5-7+9-11+…+97-9913.某检修小组乘汽车沿公路检修线路,规定前进为正,后退为负,某天从A地出发到收工时所走的路线(单位:千米)为:+10,-3,+4,-2,-8,+13,-7,+12,+7,+5⑴问收工时距离A地多远?⑵若每千米耗油0.2千克,问从A地出发到收工时共耗油多少千克?14.将1997减去它的12,再减去余下的13,再减去余下的14,再减去余下的15……以此类推,直到最后减去余下的11997,最后的得数是多少?15.独特的埃及分数:埃及同中国一样,也是世界著名的文明古国,古代埃及人处理分数与众不同,他们一般只使用分子为1的分数,例如13+115来表示25,用14+17+128表示37等等.现有90个埃及分数:12,13,14,15, (1)90,191,你能从中挑出10个,加上正、负号,使它们的和等于-1吗?培优升级·奥赛检测01.(第16届希望杯邀请赛试题)1234141524682830-+-+-+-+-+-+-等于( ) A .14B .14-C .12D .12-02.自然数a 、b 、c 、d 满足21a +21b +21c +21d =1,则31a +41b +51c +61d 等于( ) A .18B .316C .732D .156403.(第17届希望杯邀请赛试题)a 、b 、c 、d 是互不相等的正整数,且abcd =441,则a +b +c +d 值是( ) A .30 B .32 C .34 D .3604.(第7届希望杯试题)若a =1995199519961996,b =1996199619971997,c =1997199719981998,则a 、b 、c大小关系是( )5343332313A .a <b <c B .b <c <a C .c <b <a D .a <c <b05.11111(1)(1)(1)(1)(1)1324351998200019992001+++++⨯⨯⨯⨯⨯的值得整数部分为( )A .1B .2C .3D .4 06.(-2)2004+3×(-2)2003的值为( ) A .-22003 B .22003 C .-22004 D .2200407.(希望杯邀请赛试题)若|m|=m +1,则(4m +1)2004=__________08.12+(13+23)+(14+24+34)+ … +(160+260+…+5960)=__________ 09.19191976767676761919-=__________10.1+2-22-23-24-25-26-27-28-29+210=__________ 11.求32001×72002×132003所得数的末位数字为__________ 12.已知(a +b)2+|b +5|=b +5,且|2a -b -1|=0,求aB .13.计算(11998-1)(11997-1) (11996-1) … (11001-1) (11000-1)14.请你从下表归纳出13+23+33+43+…+n3的公式并计算出13+23+33+43+…+1003的值.第03讲 有理数的乘除、乘方考点·方法·破译1.理解有理数的乘法法则以及运算律,能运用乘法法则准确地进行有理数的乘法运算,会利用运算律简化乘法运算.2.掌握倒数的概念,会运用倒数的性质简化运算.3.了解有理数除法的意义,掌握有理数的除法法则,熟练进行有理数的除法运算.4.掌握有理数乘除法混合运算的顺序,以及四则混合运算的步骤,熟练进行有理数的混合运算.5.理解有理数乘方的意义,掌握有理数乘方运算的符号法则,进一步掌握有理数的混合运算.经典·考题·赏析【例1】计算⑴11()24⨯-⑵1124⨯⑶11()()24-⨯-⑷25000⨯⑸3713 ()()(1)() 5697 -⨯-⨯⨯-【解法指导】掌握有理数乘法法则,正确运用法则,一是要体会并掌握乘法的符号规律,二是细心、稳妥、层次清楚,即先确定积的符号,后计算绝对值的积.解:⑴11111 ()() 24248⨯-=-⨯=-⑵11111() 24248⨯=⨯=⑶11111 ()()() 24248 -⨯-=+⨯=⑷250000⨯=⑸3713371031 ()()(1)()() 569756973 -⨯-⨯⨯-=-⨯⨯⨯=-【变式题组】01.⑴(5)(6)-⨯-⑵11()124-⨯⑶(8)(3.76)(0.125)-⨯⨯-⑷(3)(1)2(6)0(2)-⨯-⨯⨯-⨯⨯-⑸111112(2111)42612-⨯-+-02.24(9)5025-⨯3.1111(2345)()2345⨯⨯⨯⨯---04.111 (5)323(6)3333 -⨯+⨯+-⨯【例2】已知两个有理数a、b,如果ab<0,且a+b<0,那么()A.a>0,b<0 B.a<0,b>0C.a、b异号D.a、b异号且负数的绝对值较大【解法指导】依有理数乘法法则,异号为负,故a、b异号,又依加法法则,异号相加取绝对值较大数的符号,可得出判断.解:由ab<0知a、b异号,又由a+b<0,可知异号两数之和为负,依加法法则得负数的绝对值较大,选D.【变式题组】01.若a+b+c=0,且b<c<0,则下列各式中,错误的是()A.a+b>0 B.b+c<0 C.ab+ac>0 D.a+bc>002.已知a+b>0,a-b<0,ab<0,则a___________0,b___________0,|a|___________|b|.03.(山东烟台)如果a+b<0,ba>,则下列结论成立的是()A.a>0,b>0 B.a<0,b<0 C.a>0,b<0 D.a<0,b>0 04.(广州)下列命题正确的是()A.若ab>0,则a>0,b>0 B.若ab<0,则a<0,b<0C.若ab=0,则a=0或b=0 D.若ab=0,则a=0且b=0 【例3】计算⑴(72)(18)-÷-⑵11(2)3÷-⑶13()()1025-÷⑷0(7)÷-【解法指导】进行有理数除法运算时,若不能整除,应用法则1,先把除法转化成乘法,再确定符号,然后把绝对值相乘,要注意除法与乘法互为逆运算.若能整除,应用法则2,可直接确定符号,再把绝对值相除.解:⑴(72)(18)72184 -÷-=÷=⑵1733 1(2)1()1()3377÷-=÷-=⨯-=-⑶131255 ()()()() 10251036 -÷=-⨯=-⑷0(7)0÷-=【变式题组】01.⑴(32)(8)-÷-⑵112(1)36÷-⑶10(2)3÷-⑷13()(1)78÷-02.⑴12933÷⨯⑵311()(3)(1)3524-⨯-÷-÷⑶530()35÷-⨯03.113()(10.2)(3) 245÷-+-÷⨯-【例4】(茂名)若实数a、b满足a ba b+=,则abab=___________.【解法指导】依绝对值意义进行分类讨论,得出a、b的取值范围,进一步代入结论得出结果.解:当ab>0,2(0,0)2(0,0)a ba ba ba b>>⎧+=⎨-<<⎩;当ab<0,a ba b+=,∴ab<0,从而abab=-1.【变式题组】01.若k是有理数,则(|k|+k)÷k的结果是()A.正数B.0 C.负数D.非负数02.若A.b都是非零有理数,那么aba ba b ab++的值是多少?03.如果x yx y+=,试比较xy-与xy的大小.【例5】已知223(2),1 x y=-=-⑴求2008xy的值;⑵求32008xy的值.【解法指导】na表示n个a相乘,根据乘方的符号法则,如果a为正数,正数的任何次幂都是正数,如果a是负数,负数的奇次幂是负数,负数的偶次幂是正数.解:∵223(2),1 x y=-=-⑴当2,1x y==-时,200820082(1)2xy=-=当2,1x y=-=-时,20082008(2)(1)2xy=-⨯-=-⑵当2,1x y ==-时,332008200828(1)x y ==- 当2,1x y =-=-时,3320082008(2)8(1)x y -==--【变式题组】 01.(北京)若2(2)0m n m -+-=,则nm 的值是___________.02.已知x 、y 互为倒数,且绝对值相等,求()n nx y --的值,这里n 是正整数.【例6】(安徽)2007年我省为135万名农村中小学生免费提供教科书,减轻了农民的负担,135万用科学记数法表示为( )A .0.135×106B .1.35×106C .0.135×107D .1.35×107 【解法指导】将一个数表示为科学记数法的a×10n 的形式,其中a 的整数位数是1位.故答案选B .【变式题组】 01.(武汉)武汉市今年约有103000名学生参加中考,103000用科学记数法表示为( ) A .1.03×105 B .0.103×105 C .10.3×104 D .103×103 02.(沈阳)沈阳市计划从2008年到2012年新增林地面积253万亩,253万亩用科学记数法表示正确的是( )A .25.3×105亩B .2.53×106亩C .253×104亩D .2.53×107亩 【例7】(上海竞赛)222222221299110050002200500010050009999005000k k k ++⋅⋅⋅++⋅⋅⋅+-+-+-+-+【解法指导】找出21005000k k -+的通项公式=22(50)50k -+原式=2222222222221299(150)50(250)50(50)50(9950)50k k ++⋅⋅⋅++⋅⋅⋅+-+-+-+-+ =222222222222199298[][](150)50(9950)50(250)50(9850)50++++⋅⋅⋅+-+-+-+-+ 222222222495150[](4950)50(5150)50(5050)50++-+-+-+=49222+1++⋅⋅⋅+个=99【变式题组】3333+++=( ) 2+4+6++10042+4+6++10062+4+6++10082+4+6++2006⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅A.31003B.31004C.1334D.1100002.(第10届希望杯试题)已知111111111. 2581120411101640+++++++=求11111111 2581120411101640---+--++的值.演练巩固·反馈提高01.三个有理数相乘,积为负数,则负因数的个数为()A.1个B.2个C.3个D.1个或3个02.两个有理数的和是负数,积也是负数,那么这两个数()A.互为相反数B.其中绝对值大的数是正数,另一个是负数C.都是负数D.其中绝对值大的数是负数,另一个是正数03.已知abc>0,a>0,ac<0,则下列结论正确的是()A.b<0,c>0 B.b>0,c<0 C.b<0,c<0 D.b>0,c>0 04.若|ab|=ab,则()A.ab>0 B.ab≥0 C.a<0,b<0 D.ab<005.若a、b互为相反数,c、d互为倒数,m的绝对值为2,则代数式a bm cdm+-+的值为()A.-3 B.1 C.±3 D.-3或106.若a>1a,则a的取值范围()A.a>1 B.0<a<1 C.a>-1 D.-1<a<0或a>107.已知a、b为有理数,给出下列条件:①a+b=0;②a-b=0;③ab<0;④1 ab=-,其中能判断a、b互为相反数的个数是()A.1个B.2个C.3个D.4个08.若ab≠0,则a ba b+的取值不可能为()A.0 B.1 C.2 D.-209.1110(2)(2)-+-的值为()A .-2B .(-2)21C .0D .-21010.(安徽)2010年一季度,全国城镇新增就业人数289万人,用科学记数法表示289万正确的是( )A .2.89×107B .2.89×106C .2.89×105D .2.89×104 11.已知4个不相等的整数a 、b 、c 、d ,它们的积abcd =9,则a +b +c +d =___________. 12.21221(1)(1)(1)n n n +--+-+-(n 为自然数)=___________.13.如果2xy x y+=,试比较xy -与xy 的大小.14.若a 、b 、c 为有理数且1a b ca b c++=-,求abc abc的值.15.若a 、b 、c 均为整数,且321a b c a -+-=.求a c cb b a-+-+-的值.培优升级·奥赛检测01.已知有理数x 、y 、z 两两不相等,则,,x y y z z xy z z x x y ------中负数的个数是( )A .1个B .2个C .3个D .0个或2个02.计算12345211,213,217,2115,2131-=-=-=-=-=⋅⋅⋅归纳各计算结果中的个位数字规律,猜测201021-的个位数字是( )A .1B .3C .7D .5 03.已知23450ab c d e <,下列判断正确的是( )A .abcde <0B .ab2cd4e <0C .ab2cde <0D .abcd4e <004.若有理数x 、y 使得,,,xx y x y xy y +-这四个数中的三个数相等,则|y|-|x|的值是( )A .12-B .0C .12D .3205.若A =248163264(21)(21)(21)(21)(21)(21)(21)+++++++,则A -1996的末位数字是( )A .0B .1C .7D .906.如果20012002()1,()1a b a b+=--=,则20032003a b+的值是()A.2 B.1 C.0 D.-107.已知5544332222,33,55,66a b c d====,则a、b、c、d大小关系是()A.a>b>c>d B.a>b>d>c C.b>a>c>d D.a>d>b>c08.已知a、b、c都不等于0,且a b c abca b c abc+++的最大值为m,最小值为n,则2005()m n+=___________.09.(第13届“华杯赛”试题)从下面每组数中各取一个数将它们相乘,那么所有这样的乘积的总和是___________.第一组:15,3,4.25,5.753-第二组:11 2,315 -第三组:5 2.25,,412-10.一本书的页码从1记到n,把所有这些页码加起来,其中有一页码被错加了两次,结果得出了不正确的和2002,这个被加错了两次的页码是多少?11.(湖北省竞赛试题)观察按下列规律排成一列数:11,12,21,13,22,31,14,23,3 2,41,15,24,23,42,51,16,…(*),在(*)中左起第m个数记为F(m),当F(m)=12001时,求m的值和这m个数的积.12.图中显示的填数“魔方”只填了一部分,将下列9个数:11,,1,2,4,8,16,32,6442填入方格中,使得所有行列及对角线上各数相乘的积相等,求x的值.13.(第12届“华杯赛”试题)已知m、n都是正整数,并且111111(1)(1)(1)(1)(1)(1);2233A m m =-+-+⋅⋅⋅-+ 111111(1)(1)(1)(1)(1)(1).2233B n n =-+-+⋅⋅⋅-+证明:⑴11,;22m n A B m n ++==⑵126A B -=,求m 、n 的值.第04讲 整式 考点·方法·破译1.掌握单项式及单项式的系数、次数的概念.2.掌握多项式及多项式的项、常数项及次数等概念. 3.掌握整式的概念,会判断一个代数式是否为整式.4.了解整式读、写的约定俗成的一般方法,会根据给出的字母的值求多项式的值. 经典·考题·赏析【例1】判断下列各代数式是否是单项式,如果不是请简要说明理由,如果是请指出它的系数与次数.【解法指导】 理解单项式的概念:由数与字母的积组成的代数式,单独一个数或一个字母也是单项式,数字的次数为0,是常数,单项式中所有字母指数和叫单项式次数. 解:⑴不是,因为代数式中出现了加法运算; ⑵不是,因为代数式是与x 的商; ⑶是,它的系数为π,次数为2;⑷是,它的系数为32-,次数为3.【变式题组】01.判断下列代数式是否是单项式02.说出下列单项式的系数与次数【例2】 如果与都是关于x 、y 的六次单项式,且系数相等,求m 、n的值.【解法指导】单项式的次数要弄清针对什么字母而言,是针对x或y或x、y等是有区别的,该题是针对x与y而言的,因此单项式的次数指x、y的指数之和,与字母m无关,此时将m看成一个要求的已知数.解:由题意得【变式题组】01.一个含有x、y的五次单项式,x的指数为3.且当x=2,y=-1时,这个单项式的值为32,求这个单项式.02.(毕节)写出含有字母x、y的五次单项式______________________.【例3】已知多项式⑴这个多项式是几次几项式?⑵这个多项式最高次项是多少?二次项系数是什么?常数项是什么?【解法指导】n个单项式的和叫多项式,每个单项式叫多项式的项,多项式里次数最高项的次数叫多项式的次数.解:⑴这个多项式是七次四项式;(2)最高次项是,二次项系数为-1,常数项是1.【变式题组】01.指出下列多项式的项和次数⑴(2)02.指出下列多项式的二次项、二次项系数和常数项⑴(2)【例4】多项式是关于x的三次三项式,并且一次项系数为-7.求m+n-k的值【解法指导】多项式的次数是单项式中次数最高的次数,单项式的系数是数字与字母乘积中的数字因数.解:因为是关于x的三次三项式,依三次知m=3,而一次项系数为-7,即-(3n+1)=-7,故n=2.已有三次项为,一次项为-7x,常数项为5,又原多项式为三次三项式,故二次项的系数k=0,故m+n-k=3+2-0=5.【变式题组】01.多项式是四次三项式,则m的值为()A.2 B.-2 C.±2 D.±102.已知关于x、y的多项式不含二次项,求5a-8b的值.03.已知多项式是六次四项式,单项式的次数与这个多项式的次数相同,求n的值.【例5】已知代数式的值是8,求的值.【解法指导】由,现阶段还不能求出x的具体值,所以联想到整体代入法. 解:由得由(3【变式题组】01.(贵州)如果代数式-2a+3b+8的值为18,那么代数式9b-6a+2的值等于()A.28 B.-28 C.32 D.-3202.(同山)若,则的值为_______________.03.(潍坊)代数式的值为9,则的值为______________.【例6】证明代数式的值与m的取值无关.【解法指导】欲证代数式的值与m的取值无关,只需证明代数式的化简结果不出现字母即可.证明:原式=∴无论m的值为何,原式值都为4.∴原式的值与m的取值无关.【变式题组】01.已知,且的值与x无关,求a的值.02.若代数式的值与字母x的取值无关,求a、b的值.【例7】(北京市选拔赛)同时都含有a、b、c,且系数为1的七次单项式共有()个A.4 B.12 C.15 D.25【解法指导】首先写出符合题意的单项式,x、y、z都是正整数,再依x+y+z=7来确定x、y、z的值.解:为所求的单项式,则x、y、z都是正整数,且x+y+z=7.当x=1时,y=1,2,3,4,5,z =5,4,3,2,1.当x=2时,y=1,2,3,4,z=4,3,2,1. 当x=3时,y=1,2,3,z=3,2,1.当x=4时,y =1,2,z=2,1.当x=5时,y=z=1.所以所求的单项式的个数为5+4+3+2+1=15,故选C.【变式题组】01.已知m、n是自然数,是八次三项式,求m、n值.02.整数n=___________时,多项式是三次三项式.演练巩固·反馈提高01.下列说法正确的是()A.是单项式B.的次数为5 C.单项式系数为0 D.是四次二项02.a表示一个两位数,b表示一个一位数,如果把b放在a的右边组成一个三位数.则这个三位数是()A.100b+a B.10a+b C.a+b D.100a+b03.若多项式的值为1,则多项式的值是()A.2 B.17 C.-7 D.704.随着计算机技术的迅猛发展,电脑价格不断降低,某品牌电脑原售价为n元,降低m 元后,又降低20%,那么该电脑的现售价为()A.B.C.D.05.若多项式是关于x的一次多项式,则k的值是()A.0 B.1 C.0或1 D.不能确定06.若是关于x、y的五次单项式,则它的系数是____________.07.电影院里第1排有a个座位,后面每排都比前排多3个座位,则第10排有_______个座位.08.若,则代数式xy+mn值为________.09.一项工作,甲单独做需a天完成,乙单独做需b天完成,如果甲、乙合做7天完成工作量是____________.10.(河北)有一串单项式(1)请你写出第100个单项式;⑵请你写出第n个单项式.11.(安徽)一个含有x、y的五次单项式,x的指数为3,且当x=2,y=-1时,这个单项式值为32,求这个单项式.12.(天津)已知x=3时多项式的值为-1,则当x=-3时这个多项式的值为多少?13.若关于x、y的多项式与多项式的系数相同,并且最高次项的系数也相同,求a-b的值.14.某地电话拨号入网有两种方式,用户可任取其一.A:计时制:0.05元/分B:包月制:50元/月(只限一部宅电上网).此外,每种上网方式都得加收通行费0.02元/分.⑴某用户某月上网时间为x小时,请你写出两种收费方式下该用户应该支付的费用;(2)若某用户估计一个月内上网时间为20小时,你认为采用哪种方式更合算.培优升级·奥赛检测01.(扬州)有一列数,从第二个数开始,每一个数都等于1与它前面那个数的倒数的差.若,则为()A.2007 B.2 C.D.-102.(华师一附高招生)设记号*表示求a、b算术平均数的运算,即,则下列等式中对于任意实数a、b、c都成立的是()①②③④A.①②③B.①②④C.①③④D.②④03.已知,那么在代数式中,对任意的a、b,对应的代数式的值最大的是()A.B.C.D.04.在一个地球仪的赤道上用铁丝箍半径增大1米,需增加m米长的铁丝,假设地球的赤道上一个铁丝箍,同样半径增大1米,需增加n米长的铁丝,则m与n大小关系()A.m>n B.m<n C.m=n D.不能确定05.(广安)已知_____________.06.某书店出售图书的同时,推出一项租书业务,每租看一本书,租期不超过3天,每天租金a元,租期超过3天,从第4天开始每天另加收b元,如果租看1本书7天归还,那么租金为____________元.07.已知=_____________.08.有理数a、b、c在数轴上的位置如图所示,化简后的结果是______________.09.已知=______________.。
不等式讲义知识点详解+例题+习题(含详细答案)(最新整理)

不等式讲义最新考纲:1.理解绝对值的几何意义,并了解下列不等式成立的几何意义及取等号的条件:(1)|a +b |≤|a |+|b |(a ,b ∈R ).(2)|a -b |≤|a -c |+|c -b |(a ,b ∈R ).2.会利用绝对值的几何意义求解以下类型的不等式:|ax +b |≤c ,|ax +b |≥c ,|x -c |+|x -b |≥a .3.了解柯西不等式的几种不同形式,理解它们的几何意义,并会证明.4.通过一些简单问题了解证明不等式的基本方法:比较法、综合法、分析法、反证法、放缩法、数学归纳法.1.含有绝对值的不等式的解法(1)|f (x )|>a (a >0)⇔f (x )>a 或f (x )<-a ;(2)|f (x )|<a (a >0)⇔-a <f (x )<a ;(3)对形如|x -a |+|x -b |≤c ,|x -a |+|x -b |≥c 的不等式,可利用绝对值不等式的几何意义求解.2.含有绝对值的不等式的性质|a |-|b |≤|a ±b |≤|a |+|b |.问题探究:不等式|a |-|b |≤|a ±b |≤|a |+|b |中,“=”成立的条件分别是什么?提示:不等式|a |-|b |≤|a +b |≤|a |+|b |,右侧“=”成立的条件是ab ≥0,左侧“=”成立的条件是ab ≤0且|a |≥|b |;不等式|a |-|b |≤|a -b |≤|a |+|b |,右侧“=”成立的条件是ab ≤0,左侧“=”成立的条件是ab ≥0且|a |≥|b |.3.基本不等式定理1:设a ,b ∈R ,则a 2+b 2≥2ab .当且仅当a =b 时,等号成立.定理2:如果a 、b 为正数,则≥,当且仅当a =b 时,等号成立.a +b 2ab 定理3:如果a 、b 、c 为正数,则≥,当且仅当a =b =c 时,a +b +c 33abc 等号成立.定理4:(一般形式的算术—几何平均值不等式)如果a 1、a 2、…、a n 为n 个正数,则≥,当且仅当a 1=a 2=…=a n 时,等号成立.a 1+a 2+…+a nn n a 1a 2…a n 4.柯西不等式(1)柯西不等式的代数形式:设a ,b ,c ,d 为实数,则(a 2+b 2)·(c 2+d 2)≥(ac +bd )2,当且仅当ad =bc 时等号成立.(2)若a i ,b i (i ∈N *)为实数,则()()≥(i b i )2,当且仅当b i =0(i =n ∑i =1a 2i n ∑i =1b 2i n ∑i =1a 1,2,…,n )或存在一个数k ,使得a i =kb i (i =1,2,…,n )时,等号成立.(3)柯西不等式的向量形式:设α,β为平面上的两个向量,则|α|·|β|≥|α·β|,当且仅当这两个向量同向或反向时等号成立.1.判断正误(在括号内打“√”或“×”)(1)对|a +b |≥|a |-|b |当且仅当a >b >0时等号成立.( )(2)对|a -b |≤|a |+|b |当且仅当ab ≤0时等号成立.( )(3)|ax +b |≤c (c >0)的解等价于-c ≤ax +b ≤c .( )(4)不等式|x -1|+|x +2|<2的解集为Ø.( )(5)若实数x 、y 适合不等式xy >1,x +y >-2,则x >0,y >0.( )[答案] (1)× (2)√ (3)√ (4)√ (5)√2.不等式|2x -1|-x <1的解集是( )A .{x |0<x <2}B .{x |1<x <2}C .{x |0<x <1}D .{x |1<x <3}[解析] 解法一:x =1时,满足不等关系,排除C 、D 、B ,故选A.解法二:令f (x )=Error!则f (x )<1的解集为{x |0<x <2}.[答案] A3.设|a |<1,|b |<1,则|a +b |+|a -b |与2的大小关系是( )A .|a +b |+|a -b |>2B .|a +b |+|a -b |<2C .|a +b |+|a -b |=2D .不能比较大小[解析] |a +b |+|a -b |≤|2a |<2.[答案] B4.若a ,b ,c ∈(0,+∞),且a +b +c =1,则++的最大值为( )a b c A .1 B . 2C. D .23[解析] (++)2=(1×+1×+1×)2≤ (12+12+12)(a +b +c )a b c a b c =3.当且仅当a =b =c =时,等号成立.13∴(++)2≤3.a b c ++的最大值为.故应选C.a b c 3[答案] C5.若存在实数x 使|x -a |+|x -1|≤3成立,则实数a 的取值范围是________.[解析] 利用数轴及不等式的几何意义可得x 到a 与到1的距离和小于3,所以a 的取值范围为-2≤a ≤4.[答案] -2≤a ≤4考点一 含绝对值的不等式的解法解|x -a |+|x -b |≥c (或≤c )型不等式,其一般步骤是:(1)令每个绝对值符号里的代数式为零,并求出相应的根.(2)把这些根由小到大排序,它们把定义域分为若干个区间.(3)在所分区间上,去掉绝对值符号组成若干个不等式,解这些不等式,求出它们的解集.(4)这些不等式解集的并集就是原不等式的解集.解绝对值不等式的关键是恰当的去掉绝对值符号.(1)(2015·山东卷)不等式|x -1|-|x -5|<2的解集是( )A .(-∞,4)B .(-∞,1)C .(1,4)D .(1,5)(2)(2014·湖南卷)若关于x 的不等式|ax -2|<3的解集为Error!,则a =________.[解题指导] 切入点:“脱掉”绝对值符号;关键点:利用绝对值的性质进行分类讨论.[解析] (1)当x <1时,不等式可化为-(x -1)+(x -5)<2,即-4<2,显然成立,所以此时不等式的解集为(-∞,1);当1≤x ≤5时,不等式可化为x -1+(x -5)<2,即2x -6<2,解得x <4,又1≤x ≤5,所以此时不等式的解集为[1,4);当x >5时,不等式可化为(x -1)-(x -5)<2,即4<2,显然不成立,所以此时不等式无解.综上,不等式的解集为(-∞,4).故选A.(2)∵|ax -2|<3,∴-1<ax <5.当a >0时,-<x <,与已知条件不符;1a 5a当a =0时,x ∈R ,与已知条件不符;当a <0时,<x <-,又不等式的解集为Error!,故a =-3.5a 1a[答案] (1)A (2)-3用零点分段法解绝对值不等式的步骤:(1)求零点;(2)划区间、去绝对值号;(3)分别解去掉绝对值的不等式;(4)取每个结果的并集,注意在分段时不要遗漏区间的端点值.对点训练已知函数f (x )=|x +a |+|x -2|.(1)当a =-3时,求不等式f (x )≥3的解集;(2)若f (x )≤|x -4|的解集包含[1,2],求a 的取值范围.[解] (1)当a =-3时,f (x )=Error!当x ≤2时,由f (x )≥3得-2x +5≥3,解得x ≤1;当2<x <3时,f (x )≥3无解;当x ≥3时,由f (x )≥3得2x -5≥3,解得x ≥4;所以f (x )≥3的解集为{x |x ≤1或x ≥4}.(2)f (x )≤|x -4|⇔|x -4|-|x -2|≥|x +a |.当x ∈[1,2]时,|x -4|-|x -2|≥|x +a |⇔4-x -(2-x )≥|x +a |⇔-2-a ≤x ≤2-a .由条件得-2-a ≤1且2-a ≥2,即-3≤a ≤0.故满足条件的a 的取值范围为[-3,0].考点二 利用绝对值的几何意义或图象解不等式对于形如|x -a |+|x -b |>c 或|x -a |+|x -b |<c 的不等式,利用绝对值的几何意义或者画出左、右两边函数的图象去解不等式,更为直观、简捷,它体现了数形结合思想方法的优越性.|x -a |+|x -b |的几何意义是数轴上表示x 的点与点a 和点b 的距离之和,应注意x 的系数为1.(1)(2014·重庆卷)若不等式|x -1|+|x +2|≥a 2+a +2对任意实数x 恒成立,12则实数a 的取值范围是________.(2)不等式|x +1|-|x -2|>k 的解集为R ,则实数k 的取值范围是__________.[解题指导] 切入点:绝对值的几何意义;关键点:把恒成立问题转化为最值问题.[解析] (1)∵|x -1|+|x +2|≥|(x -1)-(x -2)|=3,∴a 2+a +2≤3,解得≤a ≤.12-1174-1+174即实数a 的取值范围是.[-1-174,-1+174](2)解法一:根据绝对值的几何意义,设数x ,-1,2在数轴上对应的点分别为P ,A ,B ,则原不等式等价于PA -PB >k 恒成立.∵AB =3,即|x +1|-|x -2|≥-3.故当k <-3时,原不等式恒成立.解法二:令y =|x +1|-|x -2|,则y=Error!要使|x+1|-|x-2|>k恒成立,从图象中可以看出,只要k<-3即可.故k<-3满足题意.[答案] (1) (2)(-∞,-3)[-1-174,-1+174]解含参数的不等式存在性问题,只要求出存在满足条件的x即可;不等式的恒成立问题,可转化为最值问题,即f(x)<a恒成立⇔a>f(x)max,f(x)>a恒成立⇔a<f(x)min.对点训练(2015·唐山一模)已知函数f(x)=|2x-a|+a,a∈R,g(x)=|2x-1|.(1)若当g(x)≤5时,恒有f(x)≤6,求a的最大值;(2)若当x∈R时,恒有f(x)+g(x)≥3,求a的取值范围.[解] (1)g(x)≤5⇔|2x-1|≤5⇔-5≤2x-1≤5⇔-2≤x≤3;f(x)≤6⇔|2x-a|≤6-a⇔a-6≤2x-a≤6-a⇔a-3≤x≤3.依题意有,a-3≤-2,a≤1.故a的最大值为1.(2)f(x)+g(x)=|2x-a|+|2x-1|+a≥|2x-a-2x+1|+a=|a-1|+a,当且仅当(2x-a)(2x-1)≤0时等号成立.解不等式|a-1|+a≥3,得a的取值范围是[2,+∞).考点三 不等式的证明与应用不等式的证明方法很多,解题时既要充分利用已知条件,又要时刻瞄准解题目标,既不仅要搞清是什么,还要搞清干什么,只有兼顾条件与结论,才能找到正确的解题途径.应用基本不等式时要注意不等式中等号成立的条件.(2015·新课标全国卷Ⅱ)设a ,b ,c ,d 均为正数,且a +b =c +d ,证明:(1)若ab >cd ,则+>+;a b c d (2)+>+是|a -b |<|c -d |的充要条件.a b c d [解题指导] 切入点:不等式的性质;关键点:不等式的恒等变形.[证明] (1)因为(+)2=a +b +2,(+)2=c +d +2,a b ab c d cd 由题设a +b =c +d ,ab >cd 得(+)2>(+)2.a b c d +>+.a b c d (2)①若|a -b |<|c -d |,则(a -b )2<(c -d )2,即(a +b )2-4ab <(c +d )2-4cd .因为a +b =c +d ,所以ab >cd .由(1)得+>+.a b c d +>+,则(+)2>(+)2,即a b c d a b c d a +b +>c +d +2.ab cd 因为a +b =c +d ,所以ab >cd .于是(a -b )2=(a +b )2-4ab <(c +d )2-4cd =(c -d )2.因此|a -b |<|c -d |.+>+是|a -b |<|c -d |的充要条件.a b c d分析法是证明不等式的重要方法,当所证不等式不能使用比较法且与重要不等式、基本不等式没有直接联系,较难发现条件和结论之间的关系时,可用分析法来寻找证明途径,使用分析法证明的关键是推理的每一步必须可逆.对点训练(2014·新课标全国卷Ⅱ)设a 、b 、c 均为正数,且a +b +c =1.证明:(1)ab +bc +ac ≤;13(2)++≥1.a 2b b 2c c 2a[证明] (1)由a 2+b 2≥2ab ,b 2+c 2≥2bc ,c 2+a 2≥2ca 得a 2+b 2+c 2≥ab +bc +ca .由题设得(a +b +c )2=1,即a 2+b 2+c 2+2ab +2bc +2ca =1.所以3(ab +bc +ca )≤1,即ab +bc +ca ≤.13(2)因为+b ≥2a ,+c ≥2b ,+a ≥2c ,a 2b b 2c c 2a故+++(a +b +c )≥2(a +b +c ),a 2b b 2c c 2a即++≥a +b +c .a 2b b 2c c 2a所以++≥1.a 2b b 2c c 2a———————方法规律总结————————[方法技巧]1.绝对值不等式求解的根本方向是去除绝对值符号.2.绝对值不等式在求与绝对值运算有关的最值问题时需灵活运用,同时还要注意等号成立的条件.3.在证明不等式时,应根据命题提供的信息选择合适的方法与技巧.如在使用柯西不等式时,要注意右边为常数.[易错点睛]1.对含有参数的不等式求解时,分类要完整.2.应用基本不等式和柯西不等式证明时要注意等号成立的条件.课时跟踪训练(七十)一、填空题1.不等式|2x -1|<3的解集为__________.[解析] |2x -1|<3⇔-3<2x -1<3⇔-1<x <2.[答案] (-1,2)2.若不等式|kx -4|≤2的解集为{x |1≤x ≤3},则实数k =__________.[解析] ∵|kx -4|≤2,∴-2≤kx -4≤2,∴2≤kx ≤6.∵不等式的解集为{x |1≤x ≤3},∴k =2.[答案] 23.不等式|2x +1|+|x -1|<2的解集为________.[解析] 当x ≤-时,原不等式等价为-(2x +1)-(x -1)<2,即-3x <2,x >-12,此时-<x ≤-.当-<x <1时,原不等式等价为(2x +1)-(x -1)<2,即x <0,23231212此时-<x <0.当x ≥1时,原不等式等价为(2x +1)+(x -1)<2,即3x <2,x <,此1223时不等式无解,综上,原不等式的解为-<x <0,即原不等式的解集为.23(-23,0)[答案] (-23,0)4.已知关于x 的不等式|x -1|+|x |≤k 无解,则实数k 的取值范围是__________.[解析] ∵|x -1|+|x |≥|x -1-x |=1,∴当k <1时,不等式|x -1|+|x |≤k 无解,故k <1.[答案] (-∞,1)5.(2015·西安统考)若关于实数x 的不等式|x -5|+|x +3|<a 无解,则实数a 的取值范围是________.[解析] |x -5|+|x +3|≥|(x -5)-(x +3)|=8,故a ≤8.[答案] (-∞,8]6.(2015·重庆卷)若函数f (x )=|x +1|+2|x -a |的最小值为5,则实数a =__________.[解析] 当a =-1时,f (x )=3|x +1|≥0,不满足题意;当a <-1时,f (x )=Error!f (x )min =f (a )=-3a -1+2a =5,解得a =-6;当a >-1时,f (x )=Error!f (x )min =f (a )=-a +1+2a =5,解得a =4.[答案] -6或47.若关于x 的不等式|a |≥|x +1|+|x -2|存在实数解,则实数a 的取值范围是__________.[解析] ∵f (x )=|x +1|+|x -2|=Error!∴f (x )≥3.要使|a |≥|x +1|+|x -2|有解,∴|a |≥3,即a ≤-3或a ≥3.[答案] (-∞,-3]∪[3,+∞)8.已知关于x 的不等式|x -a |+1-x >0的解集为R ,则实数a 的取值范围是__________.[解析] 若x -1<0,则a ∈R ;若x -1≥0,则(x -a )2>(x -1)2对任意的x ∈[1,+∞)恒成立,即(a -1)[(a +1)-2x ]>0对任意的x ∈[1,+∞)恒成立,所以Error!(舍去)或Error!对任意的x ∈[1,+∞]恒成立,解得a <1.综上,a <1.[答案] (-∞,1)9.设a ,b ,c 是正实数,且a +b +c =9,则++的最小值为__________.2a 2b 2c[解析] ∵(a +b +c )(2a +2b +2c )=[()2+()2+()2]a b c [(2a )2+(2b )2+(2c )2]≥2=18,(a ·2a +b ·2b +c ·2c )∴++≥2,∴++的最小值为2.2a 2b 2c 2a 2b 2c[答案] 210.(2014·陕西卷)设a ,b ,m ,n ∈R ,且a 2+b 2=5,ma +nb =5,则 m 2+n 2的最小值为________.[解析] 由柯西不等式,得(a 2+b 2)(m 2+n 2)≥(am +bn )2,即5(m 2+n 2)≥25,∴m 2+n 2≥5,当且仅当an =bm 时,等号成立.∴的最小值为.m 2+n 25[答案] 511.对任意x ,y ∈R ,|x -1|+|x |+|y -1|+|y +1|的最小值为__________.[解析] ∵|x -1|+|x |+|y -1|+|y +1|=(|1-x |+|x |)+(|1-y |+|1+y |)≥|(1-x )+x |+|(1-y )+(1+y )|=1+2=3,当且仅当(1-x )·x ≥0,(1-y )·(1+y )≥0,即0≤x ≤1,-1≤y ≤1时等号成立,∴|x -1|+|x |+|y -1|+|y +1|的最小值为3.[答案] 312.若不等式|x +1|-|x -4|≥a +,对任意的x ∈R 恒成立,则实数a 的取4a值范围是________.[解析] 只要函数f (x )=|x +1|-|x -4|的最小值不小于a +即可.由于||x +1|4a-|x -4||≤|(x +1)-(x -4)|=5,所以-5≤|x +1|-|x -4|≤5,故只要-5≥a +即4a可.当a >0时,将不等式-5≥a +整理,得a 2+5a +4≤0,无解;当a <0时,4a将不等式-5≥a +整理,得a 2+5a +4≥0,则有a ≤-4或-1≤a <0.综上可知,4a实数a 的取值范围是(-∞,-4]∪[-1,0).[答案] (-∞,-4]∪[-1,0)二、解答题13.已知不等式2|x -3|+|x -4|<2a .(1)若a =1,求不等式的解集;(2)若已知不等式的解集不是空集,求a 的取值范围.[解] (1)当a =1时,不等式即为2|x -3|+|x -4|<2,若x ≥4,则3x -10<2,x <4,∴舍去;若3<x <4,则x -2<2,∴3<x <4;若x ≤3,则10-3x <2,∴<x ≤3.83综上,不等式的解集为Error!.(2)设f (x )=2|x -3|+|x -4|,则f (x )=Error!作出函数f (x )的图象,如图所示.由图象可知,f (x )≥1,∴2a >1,a >,即a 的取值范围为.12(12,+∞)14.(2015·新课标全国卷Ⅰ)已知函数f (x )=|x +1|-2|x -a |,a >0.(1)当a =1时,求不等式f (x )>1的解集;(2)若f (x )的图象与x 轴围成的三角形面积大于6,求a 的取值范围.[解] (1)当a =1时,f (x )>1化为|x +1|-2|x -1|-1>0.当x ≤-1时,不等式化为x -4>0,无解;当-1<x <1时,不等式化为3x -2>0,解得<x <1;23当x ≥1时,不等式化为-x +2>0,解得1≤x <2.所以f (x )>1的解集为Error!.(2)由题设可得,f (x )=Error!所以函数f (x )的图象与x 轴围成的三角形的三个顶点分别为A ,B (2a +1,0),C (a ,a +1),△ABC 的面积为(a +1)2.(2a -13,0)23由题设得(a +1)2>6,故a >2.23所以a 的取值范围为(2,+∞).15.设函数f (x )=|x -1|+|x -a |.(1)若a =-1,解不等式f (x )≥3;(2)如果∀x ∈R ,f (x )≥2,求a 的取值范围.[解] (1)当a =-1时,f (x )=|x -1|+|x +1|,f (x )=Error!作出函数f (x )=|x -1|+|x +1|的图象.由图象可知,不等式f (x )≥3的解集为Error!.(2)若a =1,f (x )=2|x -1|,不满足题设条件;若a <1,f (x )=Error!f (x )的最小值为1-a ;若a >1,f (x )=Error!f (x )的最小值为a -1.∴对于∀x ∈R ,f (x )≥2的充要条件是|a -1|≥2,∴a 的取值范围是(-∞,-1]∪[3,+∞).16.(2015·福建卷)已知a >0,b >0,c >0,函数f (x )=|x +a |+|x -b |+c 的最小值为4.(1)求a +b +c 的值;(2)求a 2+b 2+c 2的最小值.1419[解] (1)因为f (x )=|x +a |+|x -b |+c ≥|(x +a )-(x -b )|+c =|a +b |+c ,当且仅当-a ≤x ≤b 时,等号成立.又a >0,b >0,所以|a +b |=a +b ,所以f (x )的最小值为a +b +c .又已知f (x )的最小值为4,所以a +b +c =4.(2)由(1)知a +b +c =4,由柯西不等式得(4+9+1)≥(14a 2+19b 2+c 2)2=(a +b +c )2=16,(a 2×2+b 3×3+c ×1)即a 2+b 2+c 2≥.141987当且仅当==,12a 213b 3c 1即a =,b =,c =时等号成立.8718727故a 2+b 2+c 2的最小值为.141987。
学而思七年级数学下1-10讲

学而思七年级数学下1-10讲第一讲、整式第二讲同底数幂的乘法、幂的乘方与积的乘方第三讲同底数幂的除法与整式的乘除第四讲整式的除法第五讲平方差公式第六讲完全平方公式第七讲、整式的除法第八讲测试第九讲中考经典第十讲平行线与相交线余角与补角第一讲、整式知识要点:1、单项式的意义:数与字母的乘积的代数式叫做单项式。
(单独的一个数或字母也是单项式) 2b 与 2b的区别2、单项式中的数字因数叫做叫做这个单项式的系数3、单项式中所有字母的指数和叫做叫做这个单项式的次数。
4、几个单项式的和叫做多项式5、组成多项式的每一个单项式叫做多项式的项6、多项式里此数目最高的项的次数,就是这个多项式的次数。
7、整式的意义:单项式和多项式统称为整式。
(分母中含有字母的代数式不是整式)8、整式的加减:求几个整式的和或差的运算,运算结果仍是整式9、整式加减的一般步骤:(1)去括号;(2)合并同类项10、整体代入法:11、整式的运算对数的运算的指导性作用:例1、填空题:(1)单项式213x -的系数是,次数是;(2)单项式222a b c-的系数是,次数是;(3)单项式 22x y z π的系数是,次数是;例2、填空:(1)多项式23x +是次项式,最高次项是,常数项是。
(2)多项式43923101232x y x x y -++是次项式,最高次项的系数是,常数项是。
例3 、已知多项式4212331534a x y xy x y +--+(1)求多项式中各项的系数与次数。
(2)若多项式是8次三项式,求a 的值例4、(1)25ax -与24x a -的差是(2)与2421x x ++的差是24x2例5、若2,3xy x y =-+=,求代数式[](310)5(223xy y x xy y x++-+-的值。
例6、证明:对于任意一个三位数字,交换它的百位数和个位数又得到一个一个数,两个数相减,所得结果能被99整除。
例7、甲、乙两种服装的成本共600元,商店老板为获取利润,决定将甲种服装按60%的利润率定价,在实际出售时,两种服装均按八五折出售。
含参不等式解法

例2.解关于x 的不等式:x 2-ax-2a 2<0例3.解关于x 的不等式:2a x a x --<0(a ∈R)例4.解关于x 的不等式:2)1(--x x a >1 (a >0)例5.解关于x 的不等式:22---x x x a >0练习:均值不等式的解法:5.若实数x,y 满足11122=+yx ,则222y x +有( ) A.最大值223+ B. 最小值223+ C. 最小值6 D.最小值610.若14<<-x ,则2222)(2-+-=x x x x f 有( ) A.最小值1 B. 最大值1 C. 最小值-1 D.最大值-113.函数1)(+=x x x f 的最大值为( ) A.52 B. 21 C. 22 D. 1 18.若0>x ,则xx 2+的最小值为 (1)已知0,0>>b a ,且14=+b a ,求ab 的最大值;(2)已知2>x ,求24-+x x 的最小值;(3)已知0,0>>y x ,且1=+y x ,求y x 94+的最小值.1. 凑系数当40<<x 时,求的最大值)28(x x y -=。
2. 凑项。
当 ,45<x 求函数54124)(-+-=x x x f 的最大值3. 拆项。
求)1(,11072-≠+++=x x x x y 的值域。
4. 整体代换(遇到1了)已知a>0, b>0, b a t b a 11,12+==+求的最小值。
5. 换元法 求函数522++=x x y 的最大值6. 试着取平方看看: 求函数)2521(,2512<<-+-=x x x y 的最大值。
【练习】1. 若,20<<x 求)36(x x y -=的最大值。
2. 求函数)3(,31>+-=x x x y 的最小值。
3. 求函数)1(,182>-+=x x x y 的最小值。
学而思初一数学秋季班第6讲.含参一元一次方程的解法.尖子班.教师版

解方程满分晋级阶梯漫画释义6含参一元一次 方程的解法方程4级 方程中的设元 方程3级含参一元一次方程的解法方程2级 二元一次方程组的 概念及基本解法题型切片(四个) 对应题目题型目标 复杂一元一次方程 例1;例2;练习1; 同解一元一次方程 例3;例8;练习2; 含参一元一次方程 例4;例5;练习3;练习4 绝对值方程例6;例7;练习5;练习6对于复杂的一元一次方程,在求解过程中通常会采用一些特殊的求解方法,需要同学们掌握,如:解一元一次方程中()ax bx a b x +=+的应用.【引例】 解方程:111123452345x x x x +++=+++. 【解析】 法一:1111111123452345x ⎛⎫+++=+++ ⎪⎝⎭,所以1x =;法二:111102345x x x x ----+++=,1111()(1)02345x +++-=,所以1x =.【点评】 注意传递给学生两种解决此类问题的思路.【例1】 ⑴解方程:2152234x x +--=.(西城期末) ⑵解方程:1123(23)(32)11191313x x x -+-+=【解析】 ⑴ 去分母(方程两边同乘以12),得 4(21)3(52)24x x +--=.去括号,得 8415624x x +-+=. 移项,得 8152446x x -=--. 合并同类项,得 714x -=. 系数化为1,得 2x =-.∴ 原方程的解是 2x =-.⑵ 原方程可变为111(23)(23)(23)0111913x x x ---+-=,即111(23)0111319x ⎛⎫+--= ⎪⎝⎭, 又1110111319+-≠,所以230x -=,即32x =. 点评:若0ab =,则0a =或0b =.复杂一元一次方程思路导航题型切片【例2】 解方程:2009122320092010x xx+++=⨯⨯⨯【解析】 1112009122320092010x ⎛⎫+++= ⎪⨯⨯⨯⎝⎭,1120092010x ⎛⎫-= ⎪⎝⎭即200920092010x =, 故2010x =.若两个一元一次方程的解有等量关系,先分别求出这两个方程的解,再通过数量关系列等式. 两个解的数量关系有很多种,比如相等、互为相反数、多几倍等等.【引例】 当m =________时,方程5443x x +=-的解和方程2(1)2(2)x m m +-=-的解相同.(北京四中期中考试)【解析】 法一:方程5443x x +=-的解为7x =-,方程2(1)2(2)x m m +-=-的解为362m x -=.由题意解相同,所以3672m --=,解得83m =-. 法二:方程5443x x +=-的解为7x =-,把7x =-代入2(1)2(2)x m m +-=-中,求得83m =-.【点评】同解方程问题,先分别求出这两个方程的解,再让解相等,或求出一个方程的解,把解代入另一个方程.【例3】 ⑴已知:关于x 的方程42x k -=与()322x k +=的解相同,求k 的值及相同的解.(石景山期末)⑵若关于x 的方程5342x x =-和12524ax ax x -=+有相同的解,求a 的值. ⑶若()40k m x ++=和(2)10k m x --=是关于x 的同解方程,求2km-的值.【解析】 ⑴ 22643k k +-=,解得6k =,2x ∴= ⑵ 方程5342x x =-的解为8x =-,把8x =-代入12524a x ax x -=+中,求得12a =.⑶ 法一:方程()40k m x ++=的解为4x k m-=+,方程(2)10k m x --=的解为12x k m =-,所以412k m k m -=+-,所以3m k =,所以523k m -=-. 法二:方程(2)10k m x --=等号两边乘以4-得(48)40m k x -+=,故同解一元一次方程思路导航48k m m k +=-,523k m -=-.当方程的系数用字母表示时,这样的方程称为含字母系数的方程,含字母系数的方程总能化成ax b =的形式,方程ax b =的解根据a b ,的取值范围分类讨论.① 当0a ≠时,方程有唯一解bx a=.② 当0a =且0b =时,方程有无数个解,解是任意数. ③ 当0a =且0b ≠时,方程无解.【引例】 当a ,b 时,方程1ax x b +=-有唯一解;当a ,b 时,方程1ax x b +=-无解;当a ,b 时,方程1ax x b +=-有无穷多个解. 【解析】 1a b ≠,为任意数;11a b =≠-,;11a b ==-,. 【例4】 ⑴ 已知:关于x 的方程32ax x b +=-有无数多个解,试求2011()5aba b x x a b a b+-=-++ 的解.⑵ 若a 、b 为定值,关于x 的一元一次方程2236kx a x bk+--=,无论k 为何值时,它的解总是1x =,求23a b +的值.(北师大附中期中)【解析】 ⑴ 原方程整理为(2)3a x b -=--,因为当20a -=且30b --=该方程有无数多组解,所以23a b ==-,,故把23a b ==-,代入2011()5aba b x x a b a b+-=-++得610x x --=, 解得107x =-.⑵ 方程2236kx a x bk+--=可化为:(41)212k x a bk -++=,由该方程总有解1x =可知41212k a bk -++=,即(4)132b k a +=-,又k 为任意值,故401320b a +=⎧⎨-=⎩,231a b +=.【例5】 解关于x 的方程()()134m x n x m -=-【解析】 去分母,化简可得:(43)43m x mn m -=-当34m ≠时,方程的解为4343mn mx m -=-;当34m =,34n =时,解为任意值;思路导航含参一元一次方程当34m =,34n ≠时,方程无解.绝对值符号中含有未知数的方程叫绝对值方程,解绝对值方程的基本方法是:去掉绝对值符号,把绝对值方程转化为一般的方程求解1.形如ax b c +=的方程,可分如下三种情况讨论: ⑴0c <,则方程无解;⑵0c =,则根据绝对值的定义可知,0ax b +=; ⑶0c >,则根据绝对值的定义可知,ax b c +=±. 2.形如ax b cx d +=+型的绝对值方程的解法:首先根据绝对值的定义得出,()ax b cx d +=±+,且0cx d +≥;分别解方程ax b cx d +=+和()ax b cx d +=-+,然后将得出的解代入0cx d +≥检验即可. 3.含多重绝对值符号的绝对值方程的解法:主要方法是根据定义,逐层去掉绝对值.【引例】 解绝对值方程:15x -=【解析】 15x -=可知,15x -=或15x -=-,故6x =或4x =-.【例6】 若关于x 的方程230x m -+=无解,340x n -+=只有一个解,450x k -+=有两个解,下列选项正确的是( )A .m n k <<B .m n k ≤≤C .m n k >>D .m n k ≥≥【解析】 C .【例7】 解绝对值方程:⑴ 4812x +=⑵ 4329x x +=+⑶ 方程125x x -++=的解是 .(北京四中期中)【解析】 ⑴由4812x +=可知,4812x +=±,故1x =或5x =-.⑵方程4329x x +=+可化为,43(29)x x +=±+,且290x +≥,解方程4329x x +=+可得,3x =;解方程43(29)x x +=-+可得,2x =-,代入检验可知,3x =,2x =-均满足题意.⑶法一:1x -与2x +的零点分别是1x =和2x =-.由“零点分段法”,分情况讨论: 若2x <-,则原方程可化为(1)25x x ---+=(),解得32x =-<-,满足题意,故3x =-是原方程的解;若21x -≤≤,则原方程可化为(1)25x x --++=(),无解;若1x >,则原方程可化为(1)25x x -++=(),解得21x =>,满足题意,故2x =也思路导航绝对值方程是方程的解.综上:方程125x x -++=的解为3x =-或2x =. 法二:用绝对值的几何意义画数轴即可解决.【选讲题】【例8】 已知:333n x m n p ++-=与2321m x m np --+=-都是关于x 的一元一次方程,且它们的解互为相反数,求关于x 的方程115x p -+=的解.(人大附中期中练习)【解析】 由题意可知,312211n n m m +==-⎧⎧⇒⎨⎨-==⎩⎩,故题中的两个方程变为1x p +=和42x p -=,由上述两个方程的解互为相反数可知,114205p p p -++=⇒=-,故方程115x p -+=变为1111655x x --=⇒-=,从而可知,5x =-或7x =.训练1. 方程3x a b x b c x c a c a b ------++=中,若11100abc a b c≠++≠,则x = . 【解析】 .x a b c =++训练2. 解关于x 方程:4x a b c x b c d x a c d x a b dd a b c------------+++=【解析】 原方程可变()()()()0x a b c d x a b c d x a b c d x a b c d d a b c -+++-+++-+++-++++++=也就是1111[()]0x a b c d a b c d ⎛⎫+++-+++= ⎪⎝⎭当11110a b c d +++=时,原方程有无穷多个解; 当11110a b c d+++≠时,原方程的解为:x a b c d =+++.训练3. 已知关于x 的方程1(1)12x k -=-的解与351148x k x +--=的解相同,求k 的值.【解析】 由 1(1)12x k -=-得 122x k -=- 12x k -=- 12x k =-+ 由351148x k x +--=得()()23518x k x +--=62518x k x +-+= 72x k =-∵两个方程的解相同, ∴1272k k -+=- ∴2k =.训练4. ⑴ 方程158x x -++=的解是 .⑵ 解绝对值方程:35162x x ---= 【解析】 ⑴2x =或6x =-.⑵35162x x ---=或6-,即3572x x -=-或3552x x -=+ 当70x -≥时(即7x ≥),3502x ->,3572x x -=-化为3572x x -=-,解得9x =-.当50x +≥时(5x -≥),若还有3502x -≥(即53x ≥),3552x x -=+,解得15x =.当50x +≥时(5x -≥),若还有3502x -<(即5<3x ),3552x x -=--,解得1x =-.检验这三个解9x =-(舍去),故15x =,1x =-.复杂一元一次方程 巩固练习【练习1】 解方程:0.130.41200.20.5x x +--=【解析】 10x =-. (提示:含有小数的一元一次方程在求解过程中通常是先将小数化成整数)两个一元一次方程解的关系问题 巩固练习【练习2】 已知关于x 的方程3242a x x x ⎡⎤⎛⎫--= ⎪⎢⎥⎝⎭⎣⎦与3151128x a x +--=有相同的解,求a 的值及方程的解.【解析】 把a 当常数,方程3242a x x x ⎡⎤⎛⎫--= ⎪⎢⎥⎝⎭⎣⎦的解为37x a =,方程3151128x a x +--=的解为27221a x -=, 故3272721a a -=,解得2711a =,所以8177x =.(同解方程问题)含字母系数的一元一次方程 巩固练习【练习3】 已知关于x 的方程2(1)(5)3a x a x b -=-+无解,那么a = ,b .【解析】 2253ax a x ax b -=-+,即(35)23a x a b -=+,故350a -=且230a b +≠,即53a =,复习巩固109b ≠-. 【练习4】 如果关于x 的方程2(3)15(23)326kx x +++=有无数个解,求k 值. 【解析】 原方程整理得(410)0k x -=,由方程有无数个解得4100k -=,52k =.绝对值方程 巩固练习【练习5】 解方程:3548x -+=【解析】 3548x -+=或8-(舍),即354x -=,所以354x -=或4-,即39x =或31x =,故3x =或13x =.【练习6】 方程147x x -++=的解是 .2x =或5x =-.每个人的成功都有秘诀,那你知道爱因斯坦的成功公式是什么?数学史第十三种品格:公平不要羡慕别人的生活,别人不见得比你活得好,世间是公平的,每个人都有自己的欢乐和痛苦。
含参不等式以及含参不等式组的解法

含参不等式以及含参不等式组的解法不等式在中考中的运用,往往掺杂参数来增加难度,我们只要读清楚题目找到解题思路便能迎刃而解了。
本节课我们就重点讲讲如何读题去寻找解题思路。
含参不等式:解不等式5(x-1)<3x+1通过去括号、移项、合并同类项等一系列运算可以求出解为:x<3 求不等式57x -<32-x 的最小整数解. 通过去括号、移项、合并同类项等一系列运算可以求出解为:x>831,故可以得出最小整数为4.那么含参不等式如下:解含参不等式ax<b若解ax ≤b 呢分类情况 解集情况解集情况a>0时 X<a b X ≤a b a<0时 X>abX ≥aba=0时若b>0,则解集为任意数 若b ≥0,则解集为任意数 若b ≤0,则这个不等式无解若b<0,则这个不等式无解在这些需要讨论的情况下,等号最后讨论才方便,不会讨论重合。
例题:1、求不等式kx+2>2x-3的解集 移项、合并同类项、讨论取值2、(1)求不等式解集mx+a>nx+b 移项、合并同类项、讨论取值(2)(m-1)x>a 2+1对于任意x 都成立,则参数m 的值为 练习 :1、求不等式kx+2>3的解集2、(1)求不等式mx-2<-7-nx 的解集 (2)求不等式m 2x+1<-x+5的解集3、关于x 的方程5x-2m=-4-x 的解满足2<x<10,求m 的取值范围。
含参不等式组:观察下列不等式组的解集 ⎩⎨⎧>>31x x⎩⎨⎧<<31x x ⎩⎨⎧<>31x x ⎩⎨⎧><31x x 同大取大 同小取小 大小小大中间找 大大小小无限了 例题:1、(1)求不等式x-a )(x-b )>0的解集。
(2)求不等式320-x +518-x +716-x +914-x +1112-x >5的解集。
不等式含参题型及解题方法初一下册

不等式含参题型及解题方法初一下册不等式含参是初中数学中的一个重要内容,熟练掌握不等式含参的题型及解题方法对于学习数学有很大的帮助。
本文将从不等式的基本概念、不等式含参的基本形式和解题方法等方面展开介绍,旨在帮助学生掌握不等式含参的相关知识。
一、不等式的基本概念不等式是数学中的一个重要概念,它是指两个数之间的大小关系。
不等式中常见的符号有“<”(小于)、“>”(大于)、“≤”(小于等于)和“≥”(大于等于),分别表示“小于”、“大于”、“小于等于”和“大于等于”的关系。
例如,3 < 5表示3小于5;8 > 6表示8大于6;4 ≤ 5表示4小于等于5;7 ≥ 5表示7大于等于5。
在不等式中,两个数之间用不等号连接,不等式的左边称为左端,右边称为右端。
二、不等式含参的基本形式不等式含参是指在不等式中含有未知数(或变量),通常以字母表示。
不等式含参的基本形式可以分为一元一次不等式和二元一次不等式两种。
1.一元一次不等式一元一次不等式是指未知数的最高次数为1的不等式。
其一般表示形式为ax + b > c(或ax + b < c),其中a、b、c为常数,a ≠ 0。
例如,2x + 3 > 7就是一个一元一次不等式,其中未知数为x。
解一元一次不等式的基本方法是通过一系列的化简和推导,最终确定未知数的取值范围。
具体解题步骤可分为以下几步:(1)将不等式化简为形如ax > b(或ax < b)的形式;(2)确定未知数的取值范围,并得出结论。
2.二元一次不等式二元一次不等式是指含有两个未知数的一次不等式。
其一般表示形式为ax + by > c(或ax + by < c),其中a、b、c为常数,且a ≠ 0,b ≠ 0。
例如,3x + 2y ≤ 6就是一个二元一次不等式,其中未知数为x 和y。
解二元一次不等式的基本方法是通过一系列的化简和推导,最终确定两个未知数的取值范围。
上海学而思校内同步课七年级数学第6-10讲

【例1】若方程ຫໍສະໝຸດ xx 3x
2
4
1
x2
xm x 12
无解,则
m
的值为(
)
A. m 10 B. m 24 C. m 10 或 m 24 D.不存在
1. 裂项法
【例2】
解方程: 1 1 1 3 x2 x x2 3x 2 x2 5x 6 2
【例2】 多项式 2x3 3x 4 除以 x 3 的余数为
.
【例3】 分解因式: 2x3 x2 5x 2
【例4】 分解因式: x3 3x2 8x 6 【例5】 分解因式: 2x3 5x2 6x 3
第七讲
因式分解进阶方法(五)
待定系数法
如果两个多项式恒等,则左右两边同类项的系数相等. 即,如果 an xn an1xn1 an2 xn2 a1x1 a0 bn xn bn1xn1 bn2 xn2 b1x1 b0 那么 an bn , an1 bn1 ,…, a1 b1 , a0 b0 .
2. 分离整系数
【例3】 解方程: x2 x 3 1 2x2 5x 4
x 1
2x 3
3. 部分通分法 【例4】 解方程: x 1 x 6 x 2 x 5
x2 x7 x3 x6
第九讲
分式化简与求值
【例1】
当
x
1 2
时,求代数式
x2 x2
6 1
x x
1 1
1
x2
2x x2 x
4
的值
【例2】
先化简,再求值:
(3a
4a 12 4)(a
2)
[a
不等式含参问题

含参不等式专题一.利用基本性质对比求解.已知关于x 的不等式()132>--x a 的解集为24-<a x ,则a 的取值范围是; 二.已知解集求参数的值1.关于x 的不等式22521-≥-x x 与不等式3x 的解集相同,则=a 2.若关于x 的不等式1232->-a a x 与5<a x的解相同,则=a3.若关于x 的不等式132≤--ax x 的解集在数轴上表示如图所示,则=a三.利用解的范围构造不等式求解1.关于x 的不等式32521+≥-x x 的解都是012≤+-a x 的解,则a 的取值范围是 2.关于x 的不等式1232+≤-a a x 的解都是1215312≥+--x x 的解,则a 的取值范围是4.借助数轴求解例4.不等式a x ≤3只有2个正整数解,则a 的最小值为变式:已知不等式02≥+a x 的负整数解恰好有1-、2-、3-,则a 的取值范围是 三、方程(组)与不等式的联手解答 1.方程联手不等式例1.若关于x 的方程44232+-=-x m m x 的解不小于3187m--,求m 的最小值。
变式1:已知025253=+-++b a a ,求关于x 的不等式()()241213--<+-x b x ax 的最小非负整数解; 变式2:若不等式()()716825+-<+-x x 的最小整数解是关于x 的方程32=-ax x 的解,求aa 144-的值。
2.方程组联手不等式 例1.已知方程组⎩⎨⎧-=++=-8423332m y x m y x 的解满足15<+y x ,则m 的取值范围是变式:已知方程组⎩⎨⎧=+=-a y x y x 624的解满足3<-y x ,则a 的取值范围是四、含有两个参数不等式解集的解法例1.已知关于x 的不等式()n m x n m 52>--的解集为413<x ,求关于x 的不等式()n m x n m +>-的解集。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第6讲:含参不等式(组)
知识目标
目标一:掌握含参不等式(组)的解法,理解分类讨论的本质原因 目标二:掌握已知不等式(组)的解集,求参数的值(或范围)的解法 目标三:掌握不等式组整数解问题的解法,理解等号的取舍原则 1.不等式的性质
性质1:不等式两边都加上(或减去)同一个数(或式子),不等号方向不变.
如果a >b ,那么a ±c >b ±c ; 如果a <b ,那么a ±c <b ±c .
性质2:不等式两边都乘以(或除以)同一个正数,不等号方向不变.
如果a >b ,并且c >0,那么ac >bc (或
a b
c c
>); 性质3:不等式两边都乘以(或除以)同一个负数,不等号方向不变. 2.解一元一次不等式
去分母→去括号→移项→合并同类项(化成为ax <b 或ax >b 的形式)→系数化为1(化成a
b
x a b x <
或>的形式).
例如:
112x +->1
3
x x --
解:去分母,得:3(x +1)﹣6>6x ﹣2(x ﹣1) 去括号,得: 3x +3﹣6>6x ﹣2x +2 移项,得: 3x ﹣6x +2x >2+6﹣3 合并同类项,得 ﹣x >5 系数化为1,得 x <5 3
4.解一元一次不等式组的步骤
(1)第一步:求分解.分别解不等式组中的每一个不等式,求出它们的解集;
(2)第二步:求公解.将每一个不等式的解集画在同一条数轴上,并确定其公共部分;
(3)第三步:写组解.将第二步所确定的公共部分用不等式表示出来,就是原不等式组的解集. 5.解
解一元一次不等式组步骤示例:
23113
5 212x x x x +≤+⎧⎪
⎨+->-⎪⎩①②
解:解不等式①,得8x ≤
解不等式②,得4
5
x >
把不等式和的解集在数轴上表示出来(如下图)
所以这个不等式组的解集是
4
85
x <≤. 巩固练习:解不等式(组)
(1)解不等式,并把它的解集在数轴上表示出来.
①12(2)55x x -≤-
②5113
x x -->
(2)解一元一次不等式组,并把它的解集在数轴上表示出来.
①3(2)4
2115
2x x x x --≥⎧⎪
-+⎨<⎪⎩ ②21315x x -≤≤-
模块一:解含参不等式(组)——未知参数的取值范围题型一:解含参不等式——未知参数的取值范围
例1:(1)解下列关于x的不等式:
①2x>a-1 ②ax-1<3
③ax≥b ④(a-1)x≤b+2
(2)解关于x的不等式25
3
mx-
-
32
2
x+
≤1.
(3)解关于x的不等式2mx+3<3x+n.
练:解关于x的不等式3x+2≥a(x-1).
题型二:解含参不等式组——依据数轴分类讨论
例2:解关于x的不等式组:
2 326
2(1)11
x a x
x x
+⎧
-
⎪
⎨
⎪+-⎩
>
>
练:求关于x 的不等式组:0122
3x a x x x -<⎧⎪
-+⎨+<⎪⎩的解集.
拓:解关于x 的不等式组:(2)3
9(1)98a x x a x ax ->-⎧⎨+>+⎩
模块二:求参数的值或范围——已知不等式(组)的解集
题型一:求参数的值——已知不等式的解集
例3:关于x 的不等式3m -2x <5的解集是x >2,求m 的平方根.
练:关于x 的不等式组2
223
x
a x
b ⎧+≥⎪⎨⎪-⎩<的解集为0≤x <1,求a +b 的值.
例4:已知关于x 的不等式(4a -3b )x >2b -a 的解集为x <4
9,求ax >b 的解集.
练:(武昌区2015-2016七下期末)已知关于x 的不等式(2a -b )x +a -5b >0的解集为x <10
7
,求关于
x 的不等式bx >b -a 的解集为( )
A .x >-2
B .x <3
C .x <-23
D .x >-3
2
题型二:求参数的范围——已知不等式组的解集
例5:
(1)若不等式组⎩⎨⎧x >3
x >a
的解集是x >3,则a 的取值范围是_________.
若不等式组⎩⎨⎧x >3
x ≥a
的解集是x >3,则a 的取值范围是_________.
若不等式组⎩⎨⎧x ≥3
x >a
的解集是x ≥3,则a 的取值范围是_________.
若不等式组⎩⎨⎧x ≥3
x ≥a
的解集是x ≥3,则a 的取值范围是_________.
(2)若不等式组⎩⎨⎧x >3
x <a
无解,则a 的取值范围是_________.
若不等式组⎩⎨⎧x >3
x ≤a
无解,则a 的取值范围是_________.
若不等式组⎩⎨⎧x ≥3
x <a
无解,则a 的取值范围是_________.
若不等式组⎩⎨⎧x ≥3
x ≤a
无解,则a 的取值范围是_________.
练:(1)不等式组951
1x x x m ì+<+ïí>+ïî
的解集是x >2,求m 的取值范围.
(2)若不等式组1
21x m x m ì<+ïí>-ïî
无解,求m 的取值范围.
(3)已知关于x的不等式组
2
1
x
x
x a
ì<
ïï
>-
í
ï
>
ïî
的解集为-1<x<2,求a取值范围.
拓:若不等式2x<4的解集使关于x的一次不等式(a-1)x<a+5恒成立,求a的取值范围.
题型三:整数解问题
例6:
(1)已知关于x的不等式组
321
x a
x
ì-?
ï
í
->-
ïî
的整数解只有四个,求a的取值范围.
(2)已知关于x的不等式组
2
2
3
32
44
x
x a
x
ì-
>
ï
ï
í
+
ï
>-
ï
î
的整数解只有五个,求a的取值范围.
练:已知关于x的不等式组
320
x a
x
ì-?
ï
í
->
ïî
的整数解只有六个,求a的取值范围.
【疯狂训练】 (1)(汉阳区2015-2016七下期末)
若不等式组191
112
3x a x x ì+<ï
í+++?ï
î有解,则实数a 的取值范围是( ). A .a <-36 B .a ≤-36 C .a >-36 D .a ≥-36
(2)(外校2015-2016七下期末)
若不等式组841
x x x m ì+<-ïí>ïî
的解集是x >3,则m 的取值范围是( ).
A .m ≥3
B .m =3
C .m ≤3
D .m <3
(3)(江汉区2015-2016七下期末)
已知a 、b 为常数,若ax +b >0的解集为2
3
x >,则bx -a <0的解集是 .
(4)(武昌区2015-2016七下期末)已知关于x 的不等式组30217
x a x ì+<ïí+?ïî的所有整数解的和为-7,则a 的
取值范围是 .
拓:解关于x 的不等式:
①215x +? ②21x +?
③123x ?? ④143x x +?
第6讲:含参不等式(组)【课后作业】
1.若关于x 的不等式2(1)20a x a --+>的解集为2x <,求a 的值.
2.不等式组3
x x a
≥-⎧⎨>⎩的解集为3x ≥-,求a 的取值范围.
3.己知关于x 的不等式组20
12
x m x +>⎧⎨-<⎩有四个整数解,求m 的取值范围.
4.关于x 的不等式组25
53
32
x x x x a +⎧>-⎪⎪⎨+⎪<+⎪⎩只有五个整数解,求a 的取值范围.
5.解关于x 的不等式:
(1)235ax x +≥+ (2)(1)2a x x ->-
6.(梅苑中学2015-2016七下期中)在平面直角坐标系中, △ABC的三个顶点A(-1,0),B(-5,0),C (-3,4), 点P(0,m)为y轴上一动点.若△ABC的面积大于△ABP的面积, 求m的取值范围.。
