2019-2020年中考数学思维方法讲义:第5讲 解直角三角形专题
2019-2020学年度九年级数学讲义:解直角三角形及其应用

2019-2020学年度九年级数学讲义:解直角三角形及其应用【学习目标】1.了解解直角三角形的含义,会综合运用平面几何中有关直角三角形的知识和锐角三角函数的定义解直角三角形;2.会运用有关解直角三角形的知识解决实际生活中存在的解直角三角形问题.【要点梳理】要点一、解直角三角形在直角三角形中,由已知元素(直角除外)求未知元素的过程,叫做解直角三角形.在直角三角形中,除直角外,一共有5个元素,即三条边和两个锐角.设在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,则有:①三边之间的关系:a2+b2=c2(勾股定理).②锐角之间的关系:∠A+∠B=90°.③边角之间的关系:,,,,,.④,h为斜边上的高.要点诠释:(1)直角三角形中有一个元素为定值(直角为90°),是已知值.(2)这里讲的直角三角形的边角关系指的是等式,没有包括其他关系(如不等关系).(3)对这些式子的理解和记忆要结合图形,可以更加清楚、直观地理解.要点二、解直角三角形的常见类型及解法已知条件解法步骤Rt△ABC两边两直角边(a,b)由求∠A,∠B=90°-∠A,斜边,一直角边(如c,a) 由求∠A,∠B=90°-∠A,一边一角一直角边和一锐角锐角、邻边(如∠A,b)∠B=90°-∠A,,锐角、对边(如∠A,a)∠B=90°-∠A,,斜边、锐角(如c,∠A)∠B=90°-∠A,,要点诠释:1.在遇到解直角三角形的实际问题时,最好是先画出一个直角三角形的草图,按题意标明哪些元素是已知的,哪些元素是未知的,然后按先确定锐角、再确定它的对边和邻边的顺序进行计算.2.若题中无特殊说明,“解直角三角形”即要求出所有的未知元素,已知条件中至少有一个条件为边.要点三、解直角三角形的应用解直角三角形的知识应用很广泛,关键是把实际问题转化为数学模型,善于将某些实际问题中的数量关系化归为直角三角形中的边角关系是解决实际应用问题的关键.解这类问题的一般过程是:(1)弄清题中名词、术语的意义,如仰角、俯角、坡度、坡角、方向角等概念,然后根据题意画出几何图形,建立数学模型.(2)将已知条件转化为几何图形中的边、角或它们之间的关系,把实际问题转化为解直角三角形的问题.(3)根据直角三角形(或通过作垂线构造直角三角形)元素(边、角)之间的关系解有关的直角三角形.(4)得出数学问题的答案并检验答案是否符合实际意义,得出实际问题的解.拓展:在用直角三角形知识解决实际问题时,经常会用到以下概念:(1)坡角:坡面与水平面的夹角叫做坡角,用字母表示.坡度(坡比):坡面的铅直高度h和水平距离的比叫做坡度,用字母表示,则,如图,坡度通常写成=∶的形式.(2)仰角、俯角:视线与水平线所成的角中,视线中水平线上方的叫做仰角,在水平线下方的叫做俯角,如图.(3)方位角:从某点的指北方向线按顺时针转到目标方向的水平角叫做方位角,如图①中,目标方向PA,PB,PC的方位角分别为是40°,135°,245°.(4)方向角:指北或指南方向线与目标方向线所成的小于90°的水平角,叫做方向角,如图②中的目标方向线OA,OB,OC,OD的方向角分别表示北偏东30°,南偏东45°,南偏西80°,北偏西60°.特别如:东南方向指的是南偏东45°,东北方向指的是北偏东45°,西南方向指的是南偏西45°,西北方向指的是北偏西45°.要点诠释:1.解直角三角形实际是用三角知识,通过数值计算,去求出图形中的某些边的长或角的大小,最好画出它的示意图.2.非直接解直角三角形的问题,要观察图形特点,恰当引辅助线,使其转化为直角三角形或矩形来解.3.解直角三角形的应用题时,首先弄清题意(关键弄清其中名词术语的意义),然后正确画出示意图,进而根据条件选择合适的方法求解.【典型例题】 类型一、解直角三角形1.在Rt △ABC 中,∠C =90°,a 、b 、c 分别是∠A 、∠B 、∠C 的对边,根据下列条件,解这个直角三角形.(1)∠B=60°,a =4; (2)a =1,3b =.【答案与解析】(1)∠A =90°-∠B =90°-60°=30°.由tan bB a =知,tan 4tan 6043b a B ==⨯=°. 由cos a B c =知,48cos cos 60a c B ===°. (2)由tan 3bB a==得∠B =60°,∴ ∠A =90°-60°=30°.∵ 222a b c +=,∴ 2242c a b =+==.【总结升华】解直角三角形的两种类型是:(1)已知两边;(2)已知一锐角和一边.解题关键是正确选择边角关系.常用口诀:有弦(斜边)用弦(正弦、余弦),无弦(斜边)用切(正切).(1)首先用两锐角互余求锐角∠A,再利用∠B的正切、余弦求b、c的值;(2)首先用正切求出∠B的值,再求∠A的值,然后由正弦或余弦或勾股定理求c的值.举一反三:【变式】(1)已知∠C=90°,a=23,b=2 ,求∠A、∠B和c;(2)已知sinA=23, c=6 ,求a和b;【答案】(1)c=4;∠A=60°、∠B=30°;(2)a=4;b=252.(2015•湖北)如图,AD是△ABC的中线,tanB=,cosC=,AC=.求:(1)BC的长;(2)sin∠ADC的值.【答案与解析】解:过点A作AE⊥BC于点E,∵cosC=,∴∠C=45°,在Rt△ACE中,CE=AC•cosC=1,∴AE=CE=1,在Rt△ABE中,tanB=,即=,∴BE=3AE=3,∴BC=BE+CE=4;(2)∵AD是△ABC的中线,∴CD=BC=2,∴DE=CD﹣CE=1,∵AE⊥BC,DE=AE,∴∠ADC=45°,∴sin∠ADC=.【总结升华】正确作出辅助线构造直角三角形是解题的关键,注意锐角三角函数的概念的正确应用.类型二、解直角三角形在解决几何图形计算问题中的应用3.(2016•盐城)已知△ABC中,tanB=,BC=6,过点A作BC边上的高,垂足为点D,且满足BD:CD=2:1,则△ABC面积的所有可能值为.【思路点拨】分两种情况,根据已知条件确定高AD的长,然后根据三角形面积公式即可求得.【答案】8或24.【解析】解:如图1所示:∵BC=6,BD:CD=2:1,∴BD=4,∵AD⊥BC,tanB=,∴=,∴AD=BD=,∴S△ABC=BC•AD=×6×=8;如图2所示:∵BC=6,BD:CD=2:1,∴BD=12,∵AD⊥BC,tanB=,∴=,∴AD=BD=8,∴S△ABC=BC•AD=×6×8=24;综上,△ABC面积的所有可能值为8或24,故答案为8或24.【总结升华】本题考查了解直角三角形,以及三角函数的定义,三角形面积,分类讨论思想的运用是本题的关键.举一反三:【变式】(2015•河南模拟)如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=,则AD的长为多少?【答案与解析】解:作DE⊥AB于E,如图,∵∠C=90°,AC=BC=6,∴△ACB为等腰直角三角形,AB=AC=6,∴∠A=45°,在Rt△ADE中,设AE=x,则DE=x,AD=x,在Rt△BED中,tan∠DBE==,∴BE=5x,∴x+5x=6,解得x=,∴AD=×=2.类型三、解直角三角形在解决实际生活、生产问题中的应用4.某过街天桥的截面图为梯形,如图所示,其中天桥斜面CD 的坡度为1:3i =(i =1:3是指铅直高度DE 与水平宽度CE 的比),CD 的长为10 m ,天桥另一斜面AB 的坡角∠ABC =45°.(1)写出过街天桥斜面AB 的坡度; (2)求DE 的长;(3)若决定对该过街天桥进行改建,使AB 斜面的坡度变缓,将其45°坡角改为30°,方便过路群众,改建后斜面为AF ,试计算此改建需占路面的宽度FB 的长(结果精确到.0.01 m). 【答案与解析】(1)作AG ⊥BC 于G ,DE ⊥BC 于E ,在Rt △AGB 中,∠ABG =45°,AG =BG . ∴ AB 的坡度1AGi BG'==. (2)在Rt △DEC 中,∵ 3tan 3DE C EC ∠==,∴ ∠C =30°. 又∵ CD =10 m .∴ 15m 2DE CD ==. (3)由(1)知AG =BG =5 m ,在Rt △AFG 中,∠AFG =30°,tan AGAFG FG∠=,即3535FB =+,解得535 3.66(m)FB =-=. 答:改建后需占路面的宽度FB 的长约为3.66 m .【总结升华】(1)解梯形问题常作出它的两条高,构造直角三角形求解.(2)坡度是坡面的铅直高度与水平宽度的比,它等于坡角的正切值.5.腾飞中学在教学楼前新建了一座“腾飞”雕塑.为了测量雕塑的高度,小明在二楼找到一点C ,利用三角板测得雕塑顶端A 点的仰角为30°,底部B 点的俯角为45°,小华在五楼找到一点D ,利用三角板测得A 点的俯角为60°(如图所示).若已知CD 为10米,请求出雕塑AB 的高度.(结果精确到0.1米,参考数据3=1.73).【答案与解析】过点C 作CE ⊥AB 于E .∵ ∠D =90°-60°=30°,∠ACD =90°-30°=60°, ∴ ∠CAD =180°-30°-60°=90°.∵ CD =10,∴ AC =12CD =5. 在Rt △ACE 中,AE =AC ·sin ∠ACE =5×sin 30°=52, CE =AC ·cos ∠ACE =5×cos 30°=532,在Rt △BCE 中,∵ ∠BCE =45°, ∴ 5553(31)222AB AE BE =+=+=+≈6.8(米). ∴ 雕塑AB 的高度约为6.8米.【总结升华】此题将实际问题抽象成数学问题是解题关键,从实际操作(用三角形板测得仰角、俯角)过程中,提供作辅助线的方法,同时对仰角、俯角等概念不能模糊.。
2020年中考数学考点梳理:相似三角形和解直角三角形

知识点:一、比例线段1、比:选用同一长度单位量得两条线段。
a 、b 的长度分别是m 、n ,那么就说这两条线段的比是a :b =m :n (或nm b a =) 2、比的前项,比的后项:两条线段的比a :b 中。
a 叫做比的前项,b 叫做比的后项。
说明:求两条线段的比时,对这两条线段要用同一单位长度。
3、比例:两个比相等的式子叫做比例,如dc b a = 4、比例外项:在比例d cb a =(或a :b =c :d )中a 、d 叫做比例外项。
5、比例内项:在比例d cb a =(或a :b =c :d )中b 、c 叫做比例内项。
6、第四比例项:在比例dcb a =(或a :b =c :d )中,d 叫a 、b 、c 的第四比例项。
7、比例中项:如果比例中两个比例内项相等,即比例为abb a =(或a:b=b:c 时,我们把b 叫做a 和d 的比例中项。
8、比例线段:在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么,这四条线段叫做成比例线段,简称比例线段。
9、比例的基本性质:如果a :b =c :d 那么ad =bc 逆命题也成立,即如果ad =bc ,那么a :b =c :d10、比例的基本性质推论:如果a :b=b :d 那么b 2=ad ,逆定理是如果b 2=ad 那么a :b=b :c 。
说明:两个论是比积相等的式子叫做等积式。
比例的基本性质及推例式与等积式互化的理论依据。
11、合比性质:如果d c b a =,那么d dc b b a +=+ 12.等比性质:如果n m d c b a ===K ,(0≠+++m d b Λ),那么ban d b m c a =++++++ΛΛ说明:应用等比性质解题时常采用设已知条件为k ,这种方法思路单一,方法简单不易出错。
13、黄金分割把一条线段分成两条线段,使较长的线段是原线段与较小的线段的比例中项,叫做把这条线段黄金分割。
中考数学专题复习第5讲解直角三角形

解直角三角形教学目标:1.掌握解直角三角形的类型和方法 2掌握解直角三角形的应用。
教学重难点:重点:解直角三角形的方法 难点:解直角三角形的应用。
教学过程:【基础知识回顾】一、 锐角三角函数定义:在Rt △ABC 中,∠C=900, ∠A 、∠B 、∠C 的对边分别为a 、b 、c ,则∠A 的正弦可表示为:sinA= ,∠A 的余弦可表示为cosA= ∠A 的正切:tan A= ,它们统称为∠A 的锐角三角函数【提醒:1、sinA 、∠cosA 、tanA 表示的是一个整体,是两条线段的比,没有单位,这些比值只与 有关,与直角三角形的 无关2、取值范围 <sinA< , cosA< ,tanA> 】【提醒:1、三个特殊角的三角函数值都是根据定义应用直角三角形性质算出来的,要在理解的基础上结合表格进行记忆2、正弦和正切值随着角度的增大而 余弦值随着角度的增大而3、几个特殊关系:⑴sinA+cos 2A= ,tanA=sin A( )⑵若∠A+∠B=900,则sinA= ,tanA.tanB= 】 三、解直角三角形:1、定义:由直角三角形中除直角外的 个已知元素,求出另外 个未知元素的过程叫解直角三角形2、解直角三角形的依据:Rt ∠ABC 中,∠C=900 三边分别为a 、b 、c ⑴三边关系: ⑵两锐角关系⑶边角之间的关系:sinAcosA tanA sinB cosB tanB 【提醒:解直角三角形中已知的两个元素应至少有一个是当没有直角三角形时应注意构造直角三角形,再利用相应的边角关系解决】3、解直角三角形应用中的有关概念⑴仰角和俯角:如图:在图上标上仰角和俯角铅直水平线⑵坡度坡角:如图:斜坡AB 的垂直度h 和水平宽度l 的比叫做坡度,用i 表示,即i= 坡面与水平面得夹角为 用字母α表示,则i=tanα=hl。
⑶方位角:是指南北方向线与目标方向所成的小于900的水平角 如图:OA 表示 OB 表示 OC 表示OD 表示 (也可称东南方向)3、 利用解直角三角形知识解决实际问题的一般步骤:⑴把实际问题抓化为数学问题(画出平面图形,转化为解直角三角形的问题)⑵根据条件特点,选取合适的锐角三角函数去解直角三角形 ⑶解出数学问题答案,从而得到实际问题的答案【提醒:在解直角三角形实际应用中,先构造符合题意的三角形,解题的关键是弄清在哪个直角三角形中用多少度角的哪种锐角三角函数解决】 【重点考点例析】考点一:锐角三角函数的概念例1 (2013•贵阳)如图,P 是∠α的边OA 上一点,点P 的坐标为(12,5),则tan α等于( ) A .513B .1213C .512D .125对应训练 1.(2013•宿迁)如图,将∠AOB 放置在5×5的正方形网格中,则tan ∠AOB 的值是( )A .23B .32C D1.B考点二:特殊角的三角函数值tanA=tan30°=对应训练2.(2013•重庆)计算6tan45°-2cos60°的结果是()A.B.4 C.D.52.D考点三:化斜三角形为直角三角形对应训练3.(2013•陕西)如图,四边形ABCD的对角线AC,BD相交于点O,且BD平分AC.若BD=8,AC=6,∠BOC=120°,则四边形ABCD的面积为.(结果保留根号)3.考点四:解直角三角形的应用例4 (2013•舟山)某学校的校门是伸缩门(如图1),伸缩门中的每一行菱形有20个,每个菱形边长为30厘米.校门关闭时,每个菱形的锐角度数为60°(如图2);校门打开时,每个菱形的锐角度数从60°缩小为10°(如图3).问:校门打开了多少米?(结果精确到1米,参考数据:sin5°≈0.0872,cos5°≈0.9962,sin10°≈0.1736,cos10°≈0.9848).思路分析:先求出校门关闭时,20个菱形的宽即大门的宽;再求出校门打开时,20个菱形的宽即伸缩门的宽;然后将它们相减即可.解:如图,校门关闭时,取其中一个菱形ABCD.根据题意,得∠BAD=60°,AB=0.3米.∵在菱形ABCD中,AB=AD,∴△BAD是等边三角形,∴BD=AB=0.3米,∴大门的宽是:0.3×20≈6(米);如图,校门打开时,取其中一个菱形A1B1C1D1.根据题意,得∠B1A1D1=10°,A1B1=0.3米.∵在菱形A1B1C1D1中,A1C1⊥B1D1,∠B1A1O1=5°,∴在Rt△A1B1O1中,B1O1=sin∠B1A1O1•A1B1=sin5°×0.3=0.02616(米),∴B1D1=2B1O1=0.05232米,∴伸缩门的宽是:0.05232×20=1.0464米;∴校门打开的宽度为:6-1.0464=4.9536≈5(米).故校门打开了5米.点评:本题考查了菱形的性质,解直角三角形的应用,难度适中.解题的关键是把实际问题转化为数学问题,只要把实际问题抽象到解直角三角形中,一切将迎刃而解.对应训练【聚焦山东高考】1的坡比为A.12 B.C.D.2.A3.(2013•潍坊)一渔船在海岛A南偏东20°方向的B处遇险,测得海岛A与B的距离为20海里,渔船将险情报告给位于A处的救援船后,沿北偏西80°方向向海岛C靠近,同时,从A处出发的救援船沿南偏西10°方向匀速航行,20分钟后,救援船在海岛C处恰好追上渔船,那么救援船航行的速度为()A./小时B.30海里/小时C./小时D./小时3.D4.(2013•东营)某校研究性学习小组测量学校旗杆AB的高度,如图在教学楼一楼C处测得旗杆顶部的仰角为60°,在教学楼三楼D处测得旗杆顶部的仰角为30°,旗杆底部与教学楼一楼在同一水平线上,已知每层楼的高度为3米,则旗杆AB的高度为米.地北偏西t A>tan11°≈0.19)4【备考真题过关】一、选择题1.(2013•天津)tan60°的值等于()A.1 B C D.21.C2.(2013•温州)如图,在△ABC中,∠C=90°,AB=5,BC=3,则sinA的值是()A.34B.43C.35D.452.C中,∠C=90°,若A.12B.13C.3D.133.D4.(2013•乐山)如图,在直角坐标系中,P是第一象限内的点,其坐标是(3,m),且OPA.5B.4C.5D.34.AA.B.0 C.D.25.BA.30°B.45°C.60°D.90°6.D7.(2013•宁夏)如图是某水库大坝横断面示意图.其中AB、CD分别表示水库上下底面的水平线,∠ABC=120°,BC的长是50m,则水库大坝的高度h是()A.B.25m C.D m7.A8.(2013•山西)如图,某地修建高速公路,要从B地向C地修一座隧道(B、C在同一水平面上).为了测量B、C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升100m 到达A处,在A处观察B地的俯角为30°,则B、C两地之间的距离为()A.B.C.D8.A10.(2013•淮安)sin30°的值为.10.111.412.(2013•铜仁地区)如图,在直角三角形ABC中,∠C=90°,AC=12,AB=13,则sinB 的值等于.12.1213.14.215.(2013•荆门)如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,过D点作AB的垂线交AC于点E,BC=6,sinA= 35,则DE= .15.15 416.(2013•成都)如图,某山坡的坡面AB=200米,坡角∠BAC=30°,则该山坡的高BC的长为米.16.10017.(2013•十堰)如图,在小山的东侧A点有一个热气球,由于受西风的影响,以30米/分的速度沿与地面成75°角的方向飞行,25分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,则小山东西两侧A、B两点间的距离为米.17.18.(2013•荆州)如图,在高度是21米的小山A处没得建筑物CD顶部C处的仰角为30°,底部D处的俯角为何45°,则这个建筑物的高度CD= 米(结果可保留根号)三、解答题DC=AD=1A O=OH÷sin如图,过点E作EG⊥AD于G,。
解直角三角形完整版PPT课件

余弦或正切函数计算得出。
已知一边和一角求另一边
02
在直角三角形中,已知一边长和一个锐角大小可以求出另一边
长,通过正弦、余弦或正切函数计算得出。
解直角三角形的实际应用
03
例如测量建筑物高度、计算航海距离等。
三角函数在实际问题中应用
测量问题
在测量问题中,可以利用三角函数计算高度、距离等未知量。例如,利用正切函数可以计算 山的高度或者河的宽度。
直角三角形重要定理
勾股定理
如上所述,勾股定理描述了直角三角 形三边之间的数量关系。
射影定理
相似三角形判定定理
若两个直角三角形的对应角相等,则 这两个直角三角形相似。根据此定理, 可以推导出一些重要的直角三角形性 质和定理。
射影定理涉及直角三角形中斜边上的 高与斜边及两直角边之间的数量关系。
02
三角函数在解直角三角形中应用
• 性质:正弦、余弦函数值域为[-1,1],正切函数值域为R;正弦、余弦函 数在第一象限为正,第二象限正弦为正、余弦为负,第三象限正弦、余 弦都为负,第四象限余弦为正、正弦为负;正切函数在第一、三象限为 正,第二、四象限为负。
利用三角函数求边长和角度
已知两边求角度
01
在直角三角形中,已知两边长可以求出锐角的大小,通过正弦、
注意单位换算和精确度
在求解过程中,要注意单位换算和精确度的控制,避免因单位或精 度问题导致答案错误。
拓展延伸:非直角三角形解法简介
锐角三角形和钝角三角形的解法
对于非直角三角形,可以通过作高线或利用三角函数等方法将其转化为直角三角形进行 求解。
三角形的边角关系和面积公式
了解三角形的边角关系和面积公式,有助于更好地理解和解决非直角三角形问题。
解直角三角形ppt课件

在经济学中,经常需要进行复利计算。虽然复利计算本身与解直角三角形没有直接关系, 但是可以通过构造类似直角三角形的数学模型并求解,得到复利计算的精确结果。
06
解直角三角形的拓展与延伸
斜三角形的解法探讨
斜三角形的定义与性质
斜三角形是指一个三角形中不包含直角的情况。其性质包 括三角形的内角和为180度,以及三边关系等。
工程问题中的解直角三角形
土木工程中的坡度计算
在土木工程中,经常需要计算坡度,即斜坡的倾斜程度。 通过构造直角三角形并求解,可以得到精确的坡度值。
机械工程中的力学分析
在机械工程中,经常需要对物体进行力学分析。通过构造 直角三角形并利用三角函数求解,可以得到物体受到的力 的大小和方向。
电气工程中的相位差计算
在电气工程中,经常需要计算两个交流信号之间的相位差 。通过构造直角三角形并求解,可以得到精确的相位差值 。
其他实际问题中的解直角三角形
航海问题中的航向和航程计算
在航海问题中,经常需要计算航向和航程。通过构造直角三角形并求解,可以得到精确的 航向和航程值。
物理学中的矢量合成与分解
在物理学中,经常需要对矢量进行合成与分解。通过构造直角三角形并利用三角函数求解 ,可以得到合成或分解后的矢量的大小和方向。
在直角三角形中,已知任意两边长,可以利用勾股定理求出 第三边长。
已知角度和一边求另一边
在直角三角形中,已知一个锐角和一条边长,可以利用三角 函数和勾股定理求出另一条边长。
勾股定理在实际问题中的应用
测量问题
在测量问题中,可以利用 勾股定理解决距离、高度 等测量问题。
工程问题
在工程问题中,可以利用 勾股定理解决角度、长度 等计算问题。
中考数学复习讲义课件 专题5 几何与图形实际应用

解:过点 C 作 CF⊥AE 于点 F.则 FC=AD=20m,AF=DC. 在 Rt△ACF 中,∠EAC=22°. ∵tan∠EAC=FACF=tan22°≈25,∴DC=AF≈52FC=50(m). 在 Rt△ABD 中,∠ABD=∠EAB=67°. ∵tan∠ABD=ABDD=tan67°≈152,∴BD≈152AD=235(m). ∴BC=DC-BD=50-235≈41.7(m). 答:大桥 BC 的长约为 41.7m.
4.(2021·怀化)政府将要在某学校大楼前修一座大桥.如图,宋老师测得大 楼的高是 20m,大楼的底部 D 处与将要修的大桥 BC 位于同一水平线上, 宋老师又上到楼顶 A 处测得 B 和 C 的俯角∠EAB,∠EAC 分别为 67°和 22°,宋老师说现在我能算出将要修的大桥 BC 的长了.同学们:你知道宋 老师是怎么算的吗?请写出计算过程.(结果精确到 0.1m,其中 sin67°≈ 1123,cos67°≈153,tan67°≈152,sin22°≈38,cos22°≈1156,tan22°≈25)
解:设 BN 的长为 x 米,则 BM=x+1.1+2.8-1.5=x+2.4(米). 由题意,得∠CND=∠ANB,∠CDN=∠ABN=90°. ∴△CND∽△ANB.∴ CADB=DBNN.同理,△EMF∽△AMB.∴AEBF=FBMM. ∵EF=CD,∴DBNN=FBMM,即1x.1=x+1.52.4. ∴x=6.6.∵CADB=DBNN,∴A1.B6=16..16.∴AB=9.6(米).
答:点 C 到弦 AB 所在直线的距离约为 6.64 米.
8.某新农村乐园设置了一个秋千场所,如图所示,秋千拉绳 OB 的长为 3m, 静止时,踏板到地面距离 BD 的长为 0.6m(踏板厚度忽略不计).为安全起见, 乐园管理处规定:儿童的“安全高度”为 hm,成人的“安全高度”为 2m.(计 算结果精确到 0.1m)
中考知识大串讲 几何图形 第五讲 解直角三角形

例1(2013•常德)如图,在△ABC中,AD是BC边上的高,AE是BC边
上的中线,∠C=45°,sinB= (1)求BC的长;
1 3
,AD=1.
(2)求tan∠DAE的值.
类型一:锐角三角函数在斜三角形中的应用——转化为解直角三角形
例2(20பைடு நூலகம்3•呼和浩特)如图,A、B两地之间有一座山,汽车原来从A地到B地经
MB 12,B 30, M 90,求MC
B 30,M =90
C
C
tan B=tan30= MC MB
D
3 = MC 3 12
MC 4 3
M
A
B
M
B
CD MC MD 4 3 4
类型一:锐角三角函数在斜三角形中的应用——转化为解直角三角形
考点聚焦
考查频率 考查题型 命题特点
方法点拨
1、知识结构:
sin
cos
tan
2、解直角三角形的依据
B c
a A bC
3、概念解析
(3)方位角
北30°A
西 45°O
东
B南
铅 垂 线
视线
仰角 俯角
水平线
视线
4、特殊角函数值
30°,45°,60°的三角函数值
sin
cos
tan
D
海上有一座灯塔P,一客轮以60海里 / 时的速度由西向东航行,行 至A处时测得灯塔P在北偏东60方向,继续航行40分钟后,到B处 又测得灯塔P在北偏东30方向. (1)客轮在B处距离灯塔P多少海里? (2)若在灯塔周围30海里有暗礁,客轮继续向东航行是否由触礁危险?
类型三:坡角坡度问题——转化为解直角三角形
初中数学解直角三角形综合讲义

1 B 初中数学解直角三角形综合讲义一、理解概念1.产生的背景:直角三角形中三边和三角的数量关系2 明确概念:解直角三角形阐述概念:在直角三角形中,除直角外,一共有5个元素,即三条边和2个锐角。
由直角三角形中除直角外的已知元素,求出所有未知元素的过程,叫做解直角三角形定对象:特殊的求解过程定角度:已知元素新事物:求出未知元素举例:在△举例:在△ABC ABC 中,∠中,∠C C 为直角,∠为直角,∠A A ,∠,∠B B ,∠,∠C C 所对的边分别为a ,b ,c ,且c=287.4c=287.4,,∠B=42B=42°°6′,解这个直角三角形。
解:(1)∠)∠A=90A=90A=90°°- 42- 42°°6′=47=47°°5454′′(2)∵)∵ cosB= cosB=c a, , ∴∴a=c cosB=287.4a=c cosB=287.4××0.74200.7420≈≈213.3 (3)∵)∵ sinB= sinB=cb, , ∴∴b=c sinB=287.4b=c sinB=287.4××0.67040.6704≈≈192.7二、研究概念1.1.条件:条件:直角三角形2.2.构成和本质构成和本质 [ [边边] ] 两条直角边两条直角边 [ [角角] ] 有一个直角有一个直角 [ [角角]] 两锐角互余两锐角互余3.3.特征:特征: [[角角] ] 两锐角互余,∠两锐角互余,∠两锐角互余,∠A+A+A+∠∠B=90B=90°°[边] ] 勾股定理,勾股定理,勾股定理,a a 2+b 2=c2[等式的性质等式的性质] a ] a 2 =c 2—b2b 2=c 2—a2勾股定理逆定理[ [边、角边、角边、角] ] ] 锐角三角函数锐角三角函数 [ [重要线段重要线段重要线段] ] ] 直角三角形斜边上的中线等于斜边的一半直角三角形斜边上的中线等于斜边的一半[圆] ] 直角三角形三顶点共圆,圆心是斜边的中点直角三角形三顶点共圆,圆心是斜边的中点 [ [特殊角特殊角特殊角] 30] 30] 30°角所对的直角边是斜边的一半°角所对的直角边是斜边的一半 45 45°角所对的直角边是斜边的°角所对的直角边是斜边的22倍4.4.下位下位无5.5.应用:应用:三、例题讲解1、在R t R t△△ABC 中,中,AD AD 是斜边BC 上的高,如果BC= a BC= a,∠,∠,∠B=B=α,那么AD 等于等于 (( )) ((A 级)级) A A、、 asin 2α B B、、acos 2α C C、、asin αcos α D D、、asin αtan α 对象:对象:对象:R t R t R t△△ABC 中,中,AD AD AD 角度:角度:角度: 三角函数三角函数三角函数分析:分析:R t R t R t△△ABC cosB=BC AB cos α= aAB AB= a AB= a··cos αR t R t△△ABD sin α=ABADAD= sin α·AB AD= asin αcos α2、 正方形ABCD 中,对角线BD 上一点P ,BP∶PD=1∶2,且P 到边的距离为2,则正方形的边长是,则正方形的边长是 ,BD=对象:正方形ABCD 对角线BD 上的点P P 角度:角度:角度: 直角三角形直角三角形 分析:设P 到边的距离为PE PE。
中考数学一轮复习第四章几何初步第5节直角三角形与勾股定理试题

2019-2020年中考数学一轮复习第四章几何初步第5节直角三角形与勾股定理试题课标呈现指引方向1.了解直角三角形的概念,探索并掌握直角三角形的性质定理:直角三角形的两个锐角互余,直角三角形斜边上的中线等于斜边的一半。
掌握有两个角互余的三角形是直角三角形。
2.探索勾股定理及其逆定理,并能运用它们解决一些简单的实际问题。
考点梳理夯实基础1.直角三角形的性质:(1)直角三角形的两个锐角;【答案】互余(2)勾股定理:若直角三角形的两条直角边分别为a,b,斜边为c,那么;【答案】a2+b2=c2(3)直角三角形斜边上的中线等于;【答案】斜边的一半(4)直角三角形中,30°角所对的直角边等于.【答案】斜边的一半2.直角三角形的判定:(1)勾股定理逆定理:如果三角形的三边a,b,c满足a2+b2=c2,那么这个三角形是直角三角形;(2)如果三角形一边上的中线等于这边的,那么这个三角形是直角三角形.【答案】一半3.勾股数:可以构成直角三角形三边的一组正整数.常见的勾股数有:(3,4,5)、(5,12,13)、(7,24,25)、(8,15,17)…以及(3n,4n,5n)、(5n,12n,13n)、(7n,24n,25n)、(8n,15n,17n)…(n为正整数)考点精析专项突破考点一勾股定理和勾股定理的逆定理【例1】(1)(xx临沂)如图,将一矩形纸片ABCD折叠,使两个顶点A,C重合,折痕为FG.若AB=4,BC=8,则△ABF的面积为_____________.【答案】6解题点拨:本题考查矩形的性质,折叠的性质,勾股定理等,根据勾股定理列出方程是解题的关键.①先利用矩形的性质和折叠的性质得出∠B=90°,AF=FC;②然后利用勾股定理列方程求出BF的长;③再用三角形面积公式求出三角形的面积.(2)(xx武汉)如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=,则BD的长为___________【答案】解题点拨:连接AC,过点D作BC边上的高,交BC延长线于点H.在Rt△ABC中,AB=3,BC=4,∴AC=5,又CD=10,DA=5,可知△ACD为直角三角形,且∠ACD=90°,易证△ABC ∽△CHD.则CH=6,DH=8,从而在Rt△BHD中易求BD.考点二性质“直角三角形斜边上的中线等于斜边的一半”的运用【例3】如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E.连接AC交DE于点F,点G为AF的中点.∠ACD=2∠ACB.若DG=3,EC=1.求DE的长.解题点拨:综合考查了勾股定理、等腰三角形的判定与性质和直角三角形斜边上的中线,解题的关键是证明CD=DG=3.鼹:∵AD∥BC,DE⊥BC,∴DE⊥AD,∠CAD=∠ACB∵点G为AF的中点,∴DG=AG,∴∠GAD=∠GDA,∴∠CGD=2∠CAD,∵∠ACD=2∠ACB,∴∠ACD=∠CGD,∴CD=DG=3,在Rt△CED中,DE==2.考点三性质“直角三角形中,30°角所对的直角边等于斜边的一半”的运用【例4】(xx西宁)如图,OP平分∠AOB,∠AOP=15°,PC∥OA,PD⊥OA于点D,PC=4,则PD=.【答案】2解题点拨:作PE⊥OB于E,根据角平分线的性质可得PE=PD.根据平行线的性质可得∠BCP=∠AOB=30°,由直角三角形中30°的角所对的直角边等于斜边的一半,可求得PE,即可求得PD.课堂训练当堂检测1.(xx南京)下列长度的三条线段能组成直角三角形的是 ( )A.3,4,4 B.3,4,5C.3,4,6 D.3,4,7【答案】B2.(xx滨州)如图,在直角∠O的内部有一滑动杆AB,当端点A沿直线AO向下滑动时,端点B会随之自动地沿直线OB向左滑动,如果滑动杆从图中AB处滑动到处,那么滑动杆的中点C所经过的路径是 ( )A.直线的一部分B.圆的一部分C.双曲线的一部分D.抛物线的一部分第2题【答案】B3.(xx黄冈)如图,在矩形ABCD中,点E,F分别在边CD,BC上,且DC=3DE=3a,将矩形沿直线EF折叠,使点C恰好落在AD边上的点P处,则FP=.【答案】2a第3题4.(xx重庆A)如图1,在△ABC中,∠ACB= 90°,∠BAC=60°,点E是∠BAC角平分线上一点,过点E作AE的垂线,过点A作AB的垂线,两垂线交于点D,连接DB,点F是BD 的中点,DH⊥AC,垂足为H,连接EF,HF.(1)如图1,若点H是AC的中点,AC=2,求AB,BD的长:(2)如图1,求证:HF=EF;(3)如图2,连接CF,CE,猜想:△CEF是否是等边三角形?若是,请证明;若不是,请说明理由,图1 图2第4题【答案】解:(1)∵在△ABC中,∠ACB=90°,∠BAC=60°,AC=2,∴AB===4.∵AD⊥AB.∴∠DAH=30°.∵点H是AC的中点,∴AH=AC=.∴在△ADH中.AD===2.∴在△ADB中,根据勾股定理,得BD===2.(2)如答图1,连接AF,易证:△DAE≌△ADH(AAS),∴DH=AE.∵∠FDH=∠FDA-∠HDA=∠FDA-60°=(90°-∠FBA)-60°=30°-∠FBA,∴∠EAF=∠FDH.又∵点F是BD的中点,即AF是Rt△ABD斜边上的中线,∴AF=DF.∴△DHF≌△AEF(SAS).∴HF=EF.(3)△CEF为等边三角形,证明如下:如答图2,取AB的中点M,连接CM、FM,在Rt△ADE中,AD=2AE,∵FM是△ABD的中位线.∴AD=2FM.∴FM=AE.易证△ACM为等边三角形,∴AC=CM,∠ACM=60°.∵∠CAE=∠CAB=30°,∠CMF=∠AMF-∠AMC=30°,∴∠CAE=∠CMF.∴△ACE≌△MCF(SAS).∴CE=CF,∠ACE=∠MCF.∴∠ECF=∠ECM+∠MCF=∠ECM+∠ACE=60°.∴△CEF为等边三角形.图1 图2第4题答案图中考达标模拟自测A组基础训练一、选择题1.(xx连云港)如图1,分别以直角三角形三边为边向外作等边三角形,面积分别为S1、S2、S3;如图2,分别以直角三角形三个顶点为圆心,三边长为半径向外作圆心角相等的扇形,面积分别为S4、S5、S6.其中S1=16,S2=45 ,S5=11,S6=14,则S3+S4= ( ) A.8 B.64 C.54 D.48图1 图2第1题【答案】C2.(xx海南)如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿着直线AD对折,点C落在点E的位置.如果BC=6,那么线段BE的长度为 ( )A.6 B.6 C.2 D.3第2题【答案】D3.如图,在△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线,若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是 ( )A.B.4 C.D.5第3题【答案】C4.(xx泰安)如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE.延长BG交CD于点F.若AB=6,BC=4,则FD的长为 ( )A.2 B.4 C.B D.2第4题【答案】B二、填空题5.(xx随州)如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=BD,连接DM、DN、MN.若AB=6,则DN=.第5题【答案】36.(xx温州)七巧板是我们祖先的一项卓越创造,被誉为“东方魔板”,小明利用七巧板(如图1所示)中各板块的边长之间的关系拼成一个凸六边形(如图2所示),则该凸六边形的周长是cm.图1 图2第6题【答案】(32+16)7.(xx连云港)如图1,将正方形纸片ABCD对折,使AB与CD重合,折痕为EF.如图2,展开后再折叠一次,使点C与点E重合,折痕为GH,点B的对应点为点M.EM交AB于N.若AD=2.则MN=图1 图2第7题【答案】三、解答题8.已知,如图,在△ABC中,∠ACB=90°,点D为AB中点,连接CD.点E为边AC上一点,过点E作EF∥AB,交CD于点F,连接EB,取EB的中点G,连接DG、FG..(1)求证:EF=CF;(2)求证:FG⊥DG.第8题【答案】证明:(1)∵在R△ACB中,D为AB中点∴DA=DC=DB∴∠A=∠1∵EF∥AB∴∠2=∠A∴∠1=∠2∴CF=EF.(2)延长FG,交AB于点H∵EF∥AB∴∠FEG=∠GBH∵G为EB中点∴EG=GB又∵∠FGE=∠HGB∴△EFG≌△BHG∴FG=GH,EF=HB=CF∴DC-CF=DB-HB即DF=DH∴DG⊥FG.第8题答案图9.(xx黄石)在△ABC中,AB=AC,∠BAC=2∠DAE= 90°.(1)如图1,若点D关于直线AE的对称点为F,求证:DE2=BD2+CE2:(2)如图2,点E在BC的延长线上,则等式DE2=BD2+CE2还能成立吗?请说明理由.图1 图2第9题【答案】解:(1)∵点D关于直线AE的对称点为F,∴EF=DE,AF=AD,∵∠BAC=90°,∴∠BAD=90°-∠CAD,∠CAF=∠DAE+∠EAF-∠CAD=45°+45°-∠CAD=90°-∠CAD,∴∠BAD=∠CAF,在△ABD和△ACF中,AB AC BAD CAF AD AF∴△ABD≌△ACF(SAS),∴CF=BD,∠ACF=∠B,∵△ABC是等腰直角三角形,∴∠B=∠ACB=45°,∴∠ECF=∠ACB+∠ACF=45°+45°=90°,在Rt△CEF中,由勾股定理得,EF2=CF2+CE2,所以,DE2=BD2+CE2;(2) DE2=BD2+CE2还能成立.理由如下:作点D关于AE的对称点F,连接EF、CF,由轴对称的性质得,EF=DE,AF=AD,∵∠BAC=90°,∴∠BAD=90°-∠CAD,∠CAF=∠DAE+∠EAF-∠CAD=45°+45°-∠CAD=90°-∠CAD,∴∠BAD=∠CAF,在△ABD和△ACF中,AB AC BAD CAF AD AF∴△ABD≌△ACF(SAS),∴CF=BD,∠ACF=∠B,∵△ABC是等腰直角三角形,∴∠B=∠ACB=45°,∴∠ECF=∠ACB+∠ACF=45°+45°=90°,在Rt△CEF中,由勾股定理得,EF2=CF2+CE2,所以,DE2=BD2+CE2.第9题答案图B组提高练习10.(xx东营)在△ABC中,AB=10,AC=2,BC边上的高AD=6,则另一边BC等于 ( ) A.10 B.8 C.6或10 D.8或10【答案】C(提示:在图①中,由勾股定理,得BD===8;CD===2;∴BC=BD+CD=8+2=10.在图②中,由勾股定理,得BD===8;CD===2;∴BC=BD-CD=8-2=6.)图①图②11.(xx资阳)如图,在等腰直角△ABC中,∠ACB=90°,CO⊥AB于点O,点D、E分别在边AC、BC上,且AD=CE,连结DE交CO于点P,给出以下结论:①△DOE是等腰直角三角形:②∠CDE=∠COE;③若AC=1,则四边形CEOD的面积为,其中所有正确结论的序号是.【答案】①②③(提示:①如图,∵∠ACB=90°,AC=BC,CO⊥AB,∴AO=OB=OC,∠A=∠B=∠ACO=∠BCO=45°,∴△ADO≌△CEO,∴DO=OE,∠AOD=∠COE,∴∠AOC=∠DOE =90°,∴△DOE是等腰直角三角形.故①正确.②∵∠DCE+∠DOE=180°,∴D、C、E、O四点共圆,∴∠CDE=∠COE,故②正确.③∵AC=BC=1,∴S△ABC=×1×1=,S四边形DCEO=S△DOC+S△CEO=S△CDO+S△ADO=S△AOC=S△ABC=,故③正确.)12.△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF.连接CF.(1)观察猜想如图1.当点D在线段BC上时,①BC与CF的位置关系为:.②BC,CD,CF之间的数量关系为:;(将结论直接写在横线上)(2)数学思考如图2,当点D在线段CB的延长线上时,结论②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.(3)拓展延伸如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2,CD=BC,请求出GE的长.图1 图2 图3 第12题【答案】解:(1)垂直,BC=CD+CF.(2)不成立,BC=CD-CF.∵正方形ADEF中,AD=AF,∵∠BAC=∠DAF=90°,∴∠BAD=∠CAF,∵AD=AF,AB=AC,∴△DA B≌△FAC,∴∠ABD=∠ACF,CF=BD∴∠ACF-∠ACB=90°,即CF⊥BD;∵BC=CD-BD,∴BC=CD-CF.(3)过A作AH⊥BC于H,过E作EM⊥BD于M,EN⊥CF于N,∵∠BAC=90°,AB=AC,∴BC=AB=4,AH=BC=2,∴CD=BC=1,CH=BC=2,∴DH=3.由(2)证得BC⊥CF,CF=BD=5,∵四边形ADEF是正方形,∴AD=DE,∠ADE=90°,∵BC⊥CF,EM⊥BD,EN⊥CF,∴四边形CMEN是矩形,∴NE=CM,EM=CN,∵∠AHD=∠ADE=∠EMD=90°,∴∠ADH+∠EDM=∠EDM+∠DEM=90°,∴∠ADH=∠DEM,∴△ADH≌△DEM,∴EM=DH=3,DM=AH=2,∴CN=EM=3,EN=CM=3,∵∠ABC= 45°,∴∠BGC=45°,∴△BCG是等腰直角三角形,∴CG=BC=4,∴GN=1,∴EG==.第12题答案图&28171 6E0B 渋27194 6A3A 樺37994 946A 鑪37548 92AC 銬GU20943 51CF 减NuHzc36655 8F2F 輯。
2019年中考数学复习第5章图形的相似与解直角三角形第20课时锐角三角函数与解直角三角形精讲试题word版本
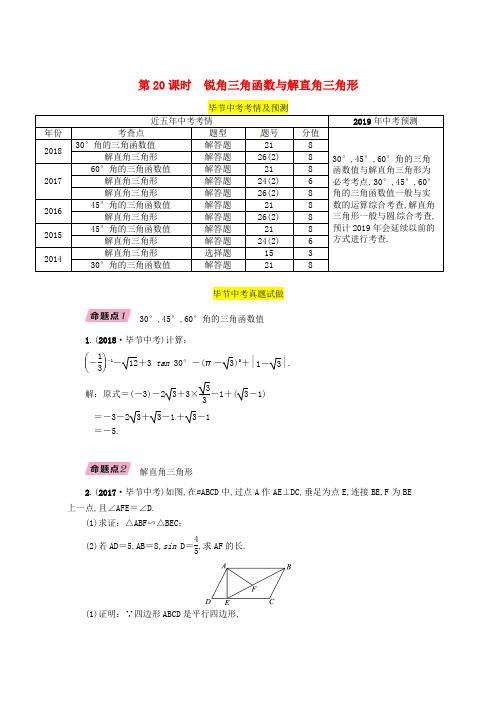
第20课时锐角三角函数与解直角三角形题号,30三角形一般与圆综合考查毕节中考真题试做30°,45°,60°角的三角函数值1.(2018·毕节中考)计算:⎝⎛⎭⎪⎫-13-1-12+3 tan 30°-(π-3)0+||1-3.解:原式=(-3)-23+3×33-1+(3-1)=-3-23+3-1+3-1=-5.解直角三角形2.(2017·毕节中考)如图,在▱ABCD中,过点A作AE⊥DC,垂足为点E,连接BE,F为BE上一点,且∠AFE=∠D.(1)求证:△ABF∽△BEC;(2)若AD=5,AB=8,sin D=45,求AF的长.(1)证明:∵四边形ABCD是平行四边形,∴AB ∥CD,AD ∥BC,AD =BC. ∴∠D +∠C =180°,∠ABF =∠BEC. ∵∠AFB +∠AFE =180°,∠AFE =∠D, ∴∠C =∠AFB. ∴△ABF ∽△BEC ; (2)解:∵AE ⊥DC,AB ∥DC, ∴∠AED =∠BAE =90°.在Rt △ADE 中,AE =AD·sin D =5×45=4.在Rt △ABE 中,根据勾股定理,得 BE =AE2+AB2=42+82=4 5. ∵△ABF ∽△BEC, ∴AF BC =AB BE , 即AF 5=845,∴AF =2 5.毕节中考考点梳理锐角三角函数的概念特殊角的三角函数值\ 锐角α α解直角三角形1.(2018·柳州中考)如图,在Rt △ABC 中,∠C =90°,BC =4,AC =3,则sin B =ACAB =( A )A .35B .45C .37D .34(第1题图)(第3题图)2.若∠A+∠B =90°,则下列各式成立的是( D )A .sin A =cos AB .tan A +tan B =1C .sin A =sin BD .sin A =cos B3.(2018·广州中考)如图,旗杆高AB =8 m ,某一时刻,旗杆影子长BC =16 m ,则tan C =__12__.4.(2018·滨州中考)在△ABC 中,∠C =90°,若tan A =12,则sin B =55.(2018·贵阳中考)如图①,在Rt △ABC 中,以下是小亮探究a sin A 与bsin B之间关系的方法:∵sin A =a c ,sin B =bc,∴c =a sin A ,c =bsin B ,∴a sin A =b sin B. 根据你掌握的三角函数知识.在图②的锐角△ABC 中,探究a sin A ,b sin B ,c sin C之间的关系,并写出探究过程.解:a sin A =b sin B =c sin C .证明如下:过A 作AD ⊥BC 于点D,过B 作BE ⊥AC 于点E.在Rt △ABD 中,sin B =ADc ,即AD =c si n B.在Rt △ADC 中,sin C =ADb ,即AD =b sin C.∴c sin B =b sin C,即b sin B =csin C .同理可得a sin A =csin C ,则a sin A =b sin B =csin C.6.(2018·遵义中考)如图,吊车在水平地面上吊起货物时,吊绳BC 与地面保持垂直,吊臂AB 与水平线的夹角为64°,吊臂底部A 距地面1.5 m .(计算结果精确到0.1 m ,参考数据sin 64°≈0.90,cos 64°≈0.44,tan 64°≈2.05)(1)当吊臂底部A 与货物的水平距离AC 为5 m 时,吊臂AB 的长为______m ; (2)如果该吊车吊臂的最大长度AD 为20 m ,那么从地面上吊起货物的最大高度是多少?(吊钩的长度与货物的高度忽略不计)解:(1)在Rt △ABC 中,∠BAC =64°,AC =5, ∴AB =ACcos 64°≈5÷0.44≈11.4.∴吊臂AB 的长为11.4 m .故应填:11.4; (2)过点D 作DH ⊥地面于点H,交水平线于点E.在Rt △ADE 中,AD =20,∠DAE =64°,EH =1.5,∴DE =sin 64°×AD ≈20×0.90=18.0,即DH =DE +EH ≈18.0+1.5=19.5.答:从地面上吊起货物的最大高度是19.5 m .中考典题精讲精练30°,45°,60°角的三角函数值例1 (2018·广安中考)计算:⎝ ⎛⎭⎪⎫13-2+|3-2|-12+6 cos 30°+(π-3.14)0.【解析】对照30°,45°,60°角的三角函数值表,然后按照实数的运算方法计算出结果.【答案】解:原式=9+2-3-23+6×32+1=12.解直角三角形例2 (2018·潍坊中考)如图,点M 是正方形ABCD 边CD 上一点,连接AM,作DE ⊥AM 于点E,BF ⊥AM 于点F,连接BE.(1)求证:AE =BF ;(2)已知AF =2,四边形ABED 的面积为24,求∠EBF 的正弦值.【解析】(1)由正方形的性质,可得BA =AD,∠BAD =90°.由DE ⊥AM,BF ⊥AM,可得∠ABF =∠DAE.对于△ABF 和△DAE,可由AAS 得到△ABF ≌△DAE,结论可证;(2)设AE =x,由(1)中结论可得BF =x,DE =AF =2.利用S 四边形ABED=S △ABE +S △ADE 可列方程求出x 得到EF 的长.在Rt △BFE 中利用勾股定理可求出BE 的长.最后利用正弦的定义可求结果.【答案】(1)证明:∵四边形ABCD 为正方形, ∴BA =AD,∠BAD =90°. ∵DE ⊥AM 于点E,BF ⊥AM 于点F, ∴∠AFB =∠DEA =90°,∴∠ABF +∠BAF =90°,∠DAE +∠BAF =90°, ∴∠ABF =∠DAE. 在△ABF 和△DAE 中, ⎩⎪⎨⎪⎧∠AFB=∠DEA,∠ABF=∠DAE,AB =DA ,∴△ABF ≌△DAE(AAS ),∴BF =AE ; (2)解:设AE =x,则BF =x,DE =AF =2. ∵四边形ABED 的面积为24, ∴12·x·x +12·x·2=24, 解得x 1=6,x 2=-8(舍去),∴EF =x -2=4. 在Rt △BEF 中,BE =42+62=213, ∴sin ∠EBF =EF BE =4213=21313.解直角三角形的应用例3 (2018·烟台中考)汽车超速行驶是交通安全的重大隐患,为了有效降低交通事故的发生,许多道路在事故易发路段设置了区间测速.如图,学校附近有一条笔直的公路l,其间设有区间测速,所有车辆限速40 km /h .数学实践活动小组设计了如下活动:在l 上确定A,B 两点,并在AB 路段进行区间测速.在l 外取一点P,作PC ⊥l,垂足为点C.测得PC =30 m ,∠APC =71°,∠BPC =35°.上午9时测得一汽车从点A 到点B 用时6 s ,请你用所学的数学知识说明该车是否超速.(参考数据:sin 35°≈0.57,cos 35°≈0.82,tan 35°≈0.70,sin 71°≈0.95,cos 71°≈0.33,tan 71°≈2.90)【解析】先根据角的正切分别得出AC =PC tan ∠APC,BC =PC tan ∠BPC,再根据线段的和与差得出AB 的长,继而根据速度=路程时间,求得该车通过AB 路段的车速.若该车通过AB 路段的车速超过40 km /h ,则该车超速;否则,该车没有超速.【答案】解:在Rt △APC 中,AC =PC tan ∠APC =30 tan 71°≈30×2.90=87. 在Rt △BPC 中,BC =PC tan ∠BPC =30 tan 35°≈30×0.70=21, 则AB =AC -BC =87-21=66, ∴该汽车的实际速度为666=11(m /s ).又∵40 km /h ≈11.1 m /s ,11<11.1, ∴该车没有超速.1.计算:|-2|-(2 019+2)0+⎝ ⎛⎭⎪⎫12-1+2 cos 30°-27.解:原式=2-1+2+2×32-33=3+3-3 3 =3-2 3.2.如图,在△ABC 中,∠BAC =90°,AB =AC,点D 为边AC 的中点,DE ⊥BC 于点E,连接BD,则tan ∠DBC 的值为( A )A .13B .2-1C .2- 3D .143.(2018·扬州中考)如图,在平行四边形ABCD 中,DB =DA,点F 是AB 的中点,连接DF 并延长,交CB 的延长线于点E,连接AE.(1)求证:四边形AEBD 是菱形;(2)若DC =10,tan ∠DCB =3,求菱形AEBD 的面积. (1)证明:∵四边形ABCD 是平行四边形, ∴AD ∥CE,∴∠DAF =∠EBF. ∵∠AFD =∠BFE,AF =FB, ∴△AFD ≌△BFE,∴AD =BE.∵AD ∥EB,∴四边形AEBD 是平行四边形. 又∵DB =DA,∴四边形AEBD 是菱形; (2)解:∵四边形ABCD 是平行四边形, ∴CD =AB =10,AB ∥CD, ∴∠ABE =∠DCB,∴tan ∠ABE =tan ∠DCB =3. ∵四边形AEBD 是菱形, ∴AB ⊥DE,AF =FB,EF =DF, ∴tan ∠ABE =EFBF =3.∵BF =102,∴EF =3102,∴DE =310. ∴S 菱形AEBD =12AB·D E =1210×310=15.4.如图,一块三角形空地上种植草皮绿化,已知AB =20 m ,AC =30 m ,∠A =150°,草皮的售价为a 元/m 2,则购买草皮至少需要( C )A .450a 元B .225a 元C .150a 元D .300a 元(第4题图)(第5题图)5.一个公共房门前的台阶高出地面 1.2 m ,台阶拆除后,换成供轮椅行走的斜坡,数据如图所示,则下列关系或说法正确的是( B )A .斜坡AB 的坡度是10° B .斜坡AB 的坡度是tan 10°C .AC =1.2 tan 10° mD.AB=1.2cos 10°m6.(2018·重庆中考A卷)如图,旗杆及升旗台的剖面和教学楼的剖面在同一平面上,旗杆与地面垂直,在教学楼底部E点处测得旗杆顶端的仰角∠AED=58°,升旗台底部到教学楼底部的距离DE=7 m,升旗台坡面CD的坡度i=1∶0.75,坡长CD=2 m,若旗杆底部到坡面CD的水平距离BC=1 m,则旗杆AB的高度约为(参考数据:sin 58°≈0.85,cos 58°≈0.53,tan 58°≈1.6)( B )A.12.6 mB.13.1 mC.14.7 mD.16.3 m。
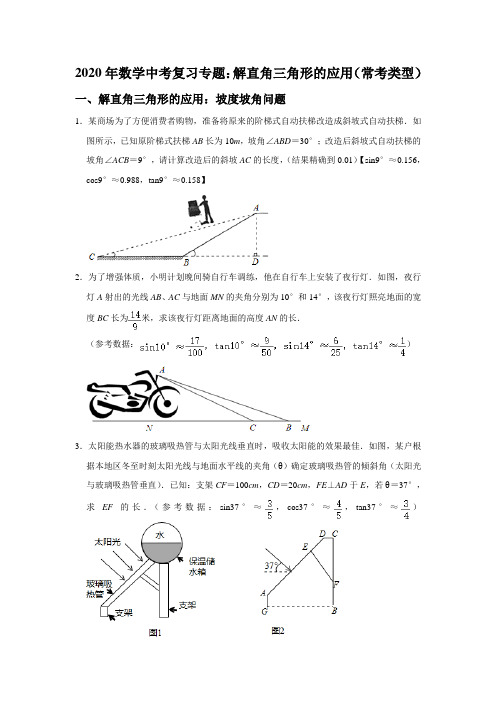
2020年数学中考复习专题:解直角三角形的应用(常考类型)(附答案)
2020年数学中考复习专题:解直角三角形的应用(常考类型)一、解直角三角形的应用:坡度坡角问题1.某商场为了方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯.如图所示,已知原阶梯式扶梯AB长为10m,坡角∠ABD=30°;改造后斜坡式自动扶梯的坡角∠ACB=9°,请计算改造后的斜坡AC的长度,(结果精确到0.01)【sin9°≈0.156,cos9°≈0.988,tan9°≈0.158】2.为了增强体质,小明计划晚间骑自行车调练,他在自行车上安装了夜行灯.如图,夜行灯A射出的光线AB、AC与地面MN的夹角分别为10°和14°,该夜行灯照亮地面的宽度BC长为米,求该夜行灯距离地面的高度AN的长.(参考数据:)3.太阳能热水器的玻璃吸热管与太阳光线垂直时,吸收太阳能的效果最佳.如图,某户根据本地区冬至时刻太阳光线与地面水平线的夹角(θ)确定玻璃吸热管的倾斜角(太阳光与玻璃吸热管垂直).已知:支架CF=100cm,CD=20cm,FE⊥AD于E,若θ=37°,求EF的长.(参考数据:sin37°≈,cos37°≈,tan37°≈)4.公园内一凉亭,凉亭顶部是一圆锥形的顶盖,立柱垂直于地面,在凉亭内中央位置有一圆形石桌,某数学研究性学习小组,将此凉亭作为研究对象,并绘制截面示意图,其中顶盖母线AB与AC的夹角为124°,凉亭顶盖边缘B、C到地面的距离为2.4米,石桌的高度DE为0.6米,经观测发现:当太阳光线与地面的夹角为42°时,恰好能够照到石桌的中央E处(A、E、D三点在一条直线上),请你求出圆锥形顶盖母线AB的长度.(结果精确到0.1m)(参考数据:sin62°≈0.88,tan42°≈0.90)5.自开展“全民健身运动”以来,喜欢户外步行健身的人越来越多,为方便群众步行健身,某地政府决定对一段如图1所示的坡路进行改造.如图2所示,改造前的斜坡AB=200米,坡度为1:;将斜坡AB的高度AE降低AC=20米后,斜坡AB改造为斜坡CD,其坡度为1:4.求斜坡CD的长.(结果保留根号)6.汛期即将来临,为保证市民的生命和财产安全,市政府决定对一段长200米且横断面为梯形的大坝用土石进行加固.如图,加固前大坝背水坡坡面从A至B共有30级阶梯,平均每级阶梯高30cm,斜坡AB的坡度i=1:1;加固后,坝顶宽度增加2米,斜坡EF的坡度i=1:,问工程完工后,共需土石多少立方米?(计算土石方时忽略阶梯,结果保留根号)7.如图是某市一座人行天桥的示意图,天桥离地面的高BC是10米,坡面AC的倾斜角∠CAB=45°,在距A点10米处有一建筑物HQ.为了方便行人推车过天桥,市政府部门决定降低坡度,使新坡面DC的倾斜角∠BDC=30°,若新坡面下D处与建筑物之间需留下至少3米宽的人行道,问该建筑物是否需要拆除?(计算最后结果保留一位小数).(参考数据:=1.414,=1.732)二、解直角三角形的应用:仰角俯角问题8.如图,某地有甲、乙两栋建筑物,小明于乙楼楼顶A点处看甲楼楼底D点处的俯角为45°,走到乙楼B点处看甲楼楼顶E点处的俯角为60°,已知AB=6m,DE=10m.求乙楼的高度AC的长.(参考数据:≈1.41,≈1.73,精确到0.1m.)9.水城门位于淀浦河和漕港河三叉口,是环城水系公园淀浦河梦蝶岛区域重要的标志性景观.在课外实践活动中,某校九年级数学兴趣小组决定测量该水城门的高.他们的操作方法如下:如图,先在D处测得点A的仰角为20°,再往水城门的方向前进13米至C处,测得点A的仰角为31°(点D、C、B在一直线上),求该水城门AB的高.(精确到0.1米)(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)10.某校九年级数学兴趣小组的学生进行社会实践活动时,想利用所学的解直角三角形的知识测量教学楼的高度,他们先在点D处用测角仪测得楼顶M的仰角为30°,再沿DF方向前行40米到达点E处,在点E处测得楼项M的仰角为45°,已知测角仪的高AD为1.5米.请根据他们的测量数据求此楼MF的高.(结果精到0.1m,参考数据:≈1.414,≈1.732,≈2.449)11.国庆期间,小明和爸爸妈妈去开元寺参观,对东西塔这对中国现存最高也是最大的石塔赞叹不已,也对石塔的高度产生了浓厚的兴趣.小明进行了以下的测量:他到与西塔距离26米的一栋大楼处,在楼底A处测得塔顶B的仰角为60°,再到楼顶C处测得塔顶B的仰角为30°.那么你能帮小明计算西塔BD和大楼AC的高度吗?12.如图,学校教学楼上悬挂一块长为3m的标语牌,即CD=3m.数学活动课上,小明和小红要测量标语牌的底部点D到地面的距离.测角仪支架高AE=BF=1.2m,小明在E 处测得标语牌底部点D的仰角为31°,小红在F处测得标语牌顶部点C的仰角为45°,AB=5m,依据他们测量的数据能否求出标语牌底部点D到地面的距离DH的长?若能,请计算;若不能,请说明理由(图中点A,B,C,D,E,F,H在同一平面内)(参考数据:tan31°≈0.60,sin31°≈0.52,cos31°≈0.86)13.某地为打造宜游环境,对旅游道路进行改造.如图是风景秀美的观景山,从山脚B到山腰D沿斜坡已建成步行道,为方便游客登顶观景,欲从D到A修建电动扶梯,经测量,山高AC=154米,步行道BD=168米,∠DBC=30°,在D处测得山顶A的仰角为45°.求电动扶梯DA的长(结果保留根号).14.我国于2019年6月5日首次完成运载火箭海上发射,这标志着我国火箭发射技术达到了一个崭新的高度.如图,运载火箭从海面发射站点M处垂直海面发射,当火箭到达点A处时,海岸边N处的雷达站测得点N到点A的距离为8千米,仰角为30°.火箭继续直线上升到达点B处,此时海岸边N处的雷达测得B处的仰角增加15°,求此时火箭所在点B处与发射站点M处的距离.(结果精确到0.1千米)(参考数据:≈1.41,≈1.73)三、解直角三角形的应用:方向角问题15.如图,A,B两市相距150km,国家级风景区中心C位于A市北偏东60°方向上,位于B市北偏西45°方向上.已知风景区是以点C为圆心、50km为半径的圆形区域.为了促进旅游经济发展,有关部门计划修建连接A,B两市的高速公路,高速公路AB是否穿过风景区?通过计算加以说明.(参考数据:≈1.73)16.如图,某市郊外景区内一条笔直的公路l经过A、B两个景点,景区管委会又开发了风景优美的景点C.经测量,C位于A的北偏东60°的方向上,C位于B的北偏东30°的方向上,且AB=10km.(1)求景点B与C的距离;(2)求景点A与C的距离.(结果保留根号)17.如图,轮船在A处观测灯塔C位于北偏东70°方向上,轮船从A处以每小时30海里的速度沿南偏东50°方向匀速航行,1小时后到达码头B处,此时观测灯塔C位于北偏东25°方向上,求灯塔C与码头B之间的距离(结果保留根号).18.如图为某海域示意图,其中灯塔D的正东方向有一岛屿C.一艘快艇以每小时20nmile 的速度向正东方向航行,到达A处时得灯塔D在东北方向上,继续航行0.3h,到达B处时测得灯塔D在北偏东30°方向上,同时测得岛屿C恰好在B处的东北方向上,此时快艇与岛屿C的距离是多少?(结果精确到1nmile.参考数据:≈1.41,≈1.73,≈2.45)19.如图,海上观察哨所B位于观察哨所A正北方向,距离为25海里.在某时刻,哨所A 与哨所B同时发现一走私船,其位置C位于哨所A北偏东53°的方向上,位于哨所B 南偏东37°的方向上.(1)求观察哨所A与走私船所在的位置C的距离;(2)若观察哨所A发现走私船从C处以16海里/小时的速度向正东方向逃窜,并立即派缉私艇沿北偏东76°的方向前去拦截,求缉私艇的速度为多少时,恰好在D处成功拦截.(结果保留根号)(参考数据:sin37°=cos53°≈,cos37°=sin53°≈,tan37°≈,tan76°≈4)20.某海域有A,B,C三艘船正在捕鱼作业,A船突然出现故障,向B,C两船发出紧急求救信号,此时C船位于B船的北偏西81°方向,距B船36海里的海域,A船位于B船的北偏东24°方向,同时又位于C船的北偏东69°方向.(1)求∠ACB的度数;(2)B船以每小时30海里的速度前去救援,问多长时间能到出事地点(结果精确到0.01小时.参考数据:≈1.414,≈1.732).21.如图,已知甲地在乙地的正东方向,因有大山阻隔,由甲地到乙地需要绕行丙地.已知丙地位于甲地北偏西30°方向,距离甲地460km,丙地位于乙地北偏东66°方向,现要打通穿山隧道,建成甲乙两地直达高速公路,如果将甲、乙、丙三地当作三个点A、B、C,可抽象成图(2)所示的三角形,求甲乙两地之间直达高速线路的长AB(结果用含非特殊角的三角函数和根式表示即可).参考答案一、解直角三角形的应用:坡度坡角问题1.【解答】解:在Rt△ABD中,∠ABD=30°,AB=10m,∴AD=AB sin∠ABD=10×sin30°=5(m),在Rt△ACD中,∠ACD=9°,sin9°=,∴AC==≈32.05(m),答:改造后的斜坡AC的长度为32.05米.2.【解答】解:解:过点A作AD⊥MN于点D,在Rt△ADB与Rt△ACD中,由锐角三角函数的定义可知:tan10°===,tan14°==,故4AD=DC,则=,解得:AD=1,答:该夜行灯距离地面的高度AN的长为1m.3.【解答】解:地面水平线与吸热管夹角∠1与θ互余,延长ED交BC的延长线于点H,则∠H=θ=37°,在Rt△CDH中,HC=,∴HF=HC+CF=+CF,在Rt△EFM中,EF=(+CF)•sin37°≈=76答:EF的长为76cm.4.【解答】解:如图,连接BC、AE,交于点O,则AE⊥BC.由题意,可知OE=2.4﹣0.6=1.8,∠OBE=42°,∠BAO=∠BAC=62°.在Rt△OBD中,∵tan∠OBE=,∴OB=≈=2.在Rt△OAB中,∵sin∠OAB=,∴AB=≈≈2.3(m).答:圆锥形顶盖母线AB的长度约为2.3米.5.【解答】解:∵∠AEB=90°,AB=200,坡度为1:,∴tan∠ABE=,∴∠ABE=30°,∴AE=AB=100,∵AC=20,∴CE=80,∵∠CED=90°,斜坡CD的坡度为1:4,∴,即,解得,ED=320,∴CD==米,答:斜坡CD的长是米.6.【解答】解:过A作AH⊥BC于H,过E作EG⊥BC于G,则四边形EGHA是矩形,∴EG=AH,GH=AE=2,∵斜坡AB的坡度i=1:1,∴AH=BH=30×30=900cm=9米,∴BG=BH﹣HG=7,∵斜坡EF的坡度i=1:,∴FG=9,∴BF=FG﹣BG=9﹣7,∴S梯形ABFE=(2+9﹣7)×9=,∴共需土石为×200=900(9﹣5)立方米.7.【解答】解:由题意知,AH=10米,BC=10米,在Rt△ABC中,∵∠CAB=45°,∴AB=BC=10米在Rt△DBC中,∵∠CDB=30°,∴DB==10(米)∵DH=AH﹣DA=AH﹣(DB﹣AB)=10﹣10+10=20﹣10≈2.7(米)∴建筑物需要拆除.二、解直角三角形的应用:仰角俯角问题8.【解答】解:如图,过点E作EF⊥AC于F,则四边形CDEF为矩形,∴EF=CD,CF=DE=10,设AC=xm,则CD=EF=xm,BF=(x﹣16)m,在Rt△BEF中,∠EBF=60°,tan∠EBF=,∴=,∴x=24+8≈37.8m答:乙楼的高度AC的长约为37.8m.9.【解答】解:由题意得,∠ABD=90°,∠D=20°,∠ACB=31°,CD=13,在Rt△ABD中,∵tan∠D=,∴BD==,在Rt△ABC中,∵tan∠ACB=,∴BC==,∵CD=BD﹣BC,∴13=,解得AB≈11.7米.答:水城门AB的高为11.7米.10.【解答】解:设MC=x,∵∠MAC=30°,∴在Rt△MAC中,AC===x.∵∠MBC=45°,∴在Rt△MCB中,MC=BC=x,又∵AB=DE=40,∴AC﹣BC=AB=40,即x﹣x=40,解得:x=20+20≈54.6,∴MF=MC+CF=54.6+1.5=56.1(米),答:楼MF的高56.1米.11.【解答】解:作CE⊥BD于E,则四边形ACED为矩形,∴CE=AD=26,AC=DE,在Rt△BAD中,tan∠BAD=,则BD=AD•tan∠BAD=26,在Rt△BCE中,tan∠BCE=,则BE=CE•tan∠BCE=,∴AC=DE=BD﹣BE=,答:西塔BD的高度为26米,大楼AC的高度为米.12.【解答】解:能,理由如下:延长EF交CH于N,则∠CNF=90°,∵∠CFN=45°,∴CN=NF,设DN=xm,则NF=CN=(x+3)m,∴EN=5+(x+3)=x+8,在Rt△DEN中,tan∠DEN=,则DN=EN•tan∠DEN,∴x≈0.6(x+8),解得,x=12,则DH=DN+NH=12+1.2=13.2(m),答:点D到地面的距离DH的长约为13.2m.13.【解答】解:作DE⊥BC于E,则四边形DECF为矩形,∴FC=DE,DF=EC,在Rt△DBE中,∠DBC=30°,∴DE=BD=84,∴FC=DE=84,∴AF=AC﹣FC=154﹣84=70,在Rt△ADF中,∠ADF=45°,∴AD=AF=70(米),答:电动扶梯DA的长为70米.14.【解答】解:如图所示:连接MN,由题意可得:∠AMN=90°,∠ANM=30°,∠BNM =45°,AN=8km,在直角△AMN中,MN=AN•cos30°=8×=4(km).在直角△BMN中,BM=MN•tan45°=4km≈6.9km.答:此时火箭所在点B处与发射站点M处的距离约为6.9km.三、解直角三角形的应用:方向角问题15.【解答】解:高速公路AB不穿过风景区.过点C作CH⊥AB于点H,如图所示.根据题意,得:∠CAB=30°,∠CBA=45°,在Rt△CHB中,∵tan∠CBH==1,∴CH=BH.设BH=tkm,则CH=tkm,在Rt△CAH中,∵tan∠CAH==,∴AH=tkm.∵AB=150km,∴t+t=150,∴t=75﹣75≈75×1.73﹣75=54.75.∵54.75>50,∴高速公路AB不穿过风景区.16.【解答】解:(1)过点C作CD⊥直线l,垂足为D,如图所示.根据题意,得:∠CAD=30°,∠CBD=60°.设CD=xkm.在Rt△ACD中,cot∠CAD==,∴AD=xkm;在Rt△BCD中,cot∠CBD==,sin∠CBD==,∴BD=xkm,BC=xkm.∴AB=AD﹣BD=x=10,∴x=5,∴BC=x=10km.(2)在Rt△ACD中,sin∠CAD==,∴AC=2CD=10km.17.【解答】解:过点B作BD⊥AC,交AC于点D由题意知,AB=30海里,∠DAB=60°,∠ABC=50°+25°=75°,∴∠C=45°在Rt△ABD中,∵sin∠DAB=,∴sin60°=∴BD=海里在Rt△BCD中,∵sin∠C=,∴sin45°=∴BC=海里答:灯塔C与码头B之间的距离为海里.18.【解答】解:过点D作DE⊥AB于点E,过点C作CF⊥AB于点F,如图所示.则DE∥CF,∠DEA=∠CF A=90°.∵DC∥EF,∴四边形CDEF为平行四边形.又∵∠CFE=90°,∴▱CDEF为矩形,∴CF=DE.根据题意,得:∠DAB=45°,∠DBE=60°,∠CBF=45°.设DE=x(nmile),在Rt△DEA中,∵tan∠DAB=,∴AE==x(nmile).在Rt△DEB中,∵tan∠DBE=,∴BE==x(nmile).∵AB=20×0.3=6(nmile),AE﹣BE=AB,∴x﹣x=6,解得:x=9+3,∴CF=DE=(9+3)nmile.在Rt△CBF中,sin∠CBF=,∴BC===9+3≈20(nmile).答:此时快艇与岛屿C的距离约为20nmile.19.【解答】解:(1)在△ABC中,∠ACB=180°﹣∠B﹣∠BAC=180°﹣37°﹣53°=90°.在Rt△ABC中,sin B=,∴AC=AB•sin37°=25×=15(海里).答:观察哨所A与走私船所在的位置C的距离为15海里;(2)过点C作CM⊥AB于点M,由题意易知,D、C、M在一条直线上.在Rt△AMC中,CM=AC•sin∠CAM=15×=12,AM=AC•cos∠CAM=15×=9.在Rt△AMD中,tan∠DAM=,∴DM=AM•tan76°=9×4=36,∴AD===9,CD=DM﹣CM=36﹣12=24.设缉私艇的速度为x海里/小时,则有=,解得x=6.经检验,x=6是原方程的解.答:当缉私艇的速度为6海里/小时时,恰好在D处成功拦截.20.【解答】解:(1)∵BD∥CE,∴∠DBC+∠ECB=180°,∴∠ECB=180°﹣81°=99°,∴∠ACB=99°﹣69°=30°;(2)如图,作BH⊥AC,垂足为H.在△ABC中,∠CAB=180°﹣81°﹣24°﹣30°=45°.∵∠ACB=30°,∴在Rt△BCH中,BH=BC=18,∵在Rt△ABH中,sin∠CAB=,∴AB===18.则B船到A船出事地点的时间是:≈≈0.85(小时).答:B船约0.85小时能到达A船出事地点.21.【解答】解:过点C作CD⊥AB于点D,∵丙地位于甲地北偏西30°方向,距离甲地460km,.在Rt△ACD中,∠ACD=30°,∴AD=AC=230km.CD=AC=230km.∵丙地位于乙地北偏东66°方向,在Rt△BDC中,∠CBD=24°,∴BD==(km).∴AB=BD+AD=230+(km).答:公路AB的长为(230+)km.。
2019-2020年中考数学分类解直角三角形

【答案】 解 : 在 Rt ECD 中, tan DEC = DC .
EC
DC
30
B
∴EC=
≈
40 ( m ).
tan DEC 0.75
在 Rt BAC 中,∠ BCA= 45°,∴ BA CA
D h
在 Rt BAE 中, tan BEA = BA .∴ h
0.75.∴ h 120( m ).
37 45°
C
A
B
(连云港)如图,自 来水厂 A 和村庄 B 在小河 l 的两侧,现要在 A,B间铺设一知输水管道.为了搞好工程
预算,需测算出 A, B 间的距离.一小船在点 P 处测得 A 在正北方向, B 位于南偏东 24.5 °方向,前行
1200m,到达点 Q处,测得 A位于北偏东 49°方向, B位于南偏西 41°方向.
(贵阳市)如图,
可.能.是 (A) 3.5
ABC 中, C 90 , AC 3 , B 30 ,点 P 在 BC 边上的动点,则 AP 长不.
( B) 4.2
( C) 5.8
(D) 7
A
(昆明市)如图,在
C
P
30°( B
(第 7题图)
Rt△ABC中,∠ ACB=90°, BC=3,AC= 15 ,AB 的垂直平分线 ED 交 BC 的延长线与 D
(黄石市)东方山是鄂东南地区的佛教圣地,月亮山是黄荆山脉第二高峰,山顶上有黄石电视塔。据黄石地 理资料记载:东方山海拔 453.20 米,月亮山海拔 442.00 米,一飞机从东方山到月亮山方向水平飞行,
(哈尔滨市)已知:正方形 ABCD的边长为 2,点 P 是直线 CD上一点,若 DP=1,则 tan ∠ BPC 的值是 (海南)如图 l0 ,在菱形 ABCD中,∠ A=60°,点 P、 Q分别在边 AB、 BC上,且 AP=BQ.
2019-2020年中考数学 知识点聚焦 第十九章 解直角三角形

以用面积(拼图)证明,其中拼图法是最常见的一种方法,验证如下: 现有四块直角边长为a ,b ,斜边长为c 的直角三角形纸板,请从中取出若干块进行拼图(需画出所拼的图形),证明勾股定理。
证法1:如图所示,∵=4+S S S 大正方形三角形小正方形, ∴()221=4+-2c ab b a ⨯,∴222=+c a b 。
证法2:如图所示,∵=2+S S S 梯形小三角形大三角形,∴()()2111++=2+222a b a b ab c ⨯, 整理,得222+=a b c 。
证法3:如图所示,∵=4+S S S 大正方形三角形小正方形, ∴()221=4+2a+b ab c ⨯,整理,得222+=a b c 。
c cb b a acbbaacbb b baa aa知能解读(二)勾股定理的应用勾股定理揭示了直角三角形的三边关系,其应用有:(1)已知两边求第三边;(2)证明三角形中的某些线段的平方关系;(3的线段。
知能解读(三)勾股定理的逆定理如果三角形的三边长a ,b ,c 满足222+=a b c ,那么这个三角形是直角三角形。
点拨勾股定理的逆定理是判定三角形是直角三角形的一个依据。
知能解读(四)勾股数一般地,能够成为直角三角形三条边长的三个正常数称为勾股数,当k 为正整数时,下列各组数都是常见勾股数:}{3,4,5k k k ,}{5,12,13k k k ,}{8,15,17k k k ,}{7,24,25k k k ,}{9,40,41k k k 等。
如当=1k 时,}{3,4,5k k k 是一组勾股数:当=2k 时,}{6,8,10也是一组勾股数。
点拨求勾股数的方法:(1)如果a 是大于1的奇数,b ,c 是两个连续自然数,且有2=+a b c ,则a ,b ,c 是一组勾股数;(2)如果a ,b ,c 为一组勾股数,则na ,nb ,nc 也是一组勾股数,其中()>1n n 为自然数。
河南省2019年中考数学总复习第四章三角形第五节解直角三角形及其应用课件201812253108

第五节 解直角三角形及其应用命题角度❶ 母子型例1(2017·河南)如图所示,我国两艘海监船A,B在南海海域巡航,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船C,此时B船在A船的正南方向5海里处,A船测得渔船C在其南偏东45°方向,B船测得渔船C在其南偏东53°方向.已知A船的航速为30海里/小时,B船的航速为25海里/小时,问C船至少要等待多长时间才能得到救援?(参考数据:sin 53°≈ , cos 53°≈ ,tan 53°≈, ≈1.41)【分析】可考虑作CE⊥AB于E.设AE=EC=x,则BE长可求,在Rt△BCE中,根据tan 53°=,可列关系式,求出x,再求出BC、AC,分别求出A、B两船到C的时间,即可解决问题.【自主解答】解:如解图,作CE⊥AB于E.在Rt△ACE中,∵∠A=45°,∴AE=EC,设AE=EC=x,则BE=x-5,在Rt△BCE中,∴tan 53°= .∴ = ,解得x=20,∴AE=EC=20,∴AC=20 ≈28.2,BC= ≈25,∴A船到渔船C的时间为 =0.94小时,B船到C渔船的时间 =1小时,∴C船至少要等待0.94小时才能得到救援.(2014·河南)在中俄“海上联合—2014”反潜演习中,我军舰A测得潜艇C的俯角为30°,位于军舰A正上方 1 000 米的反潜直升机B测得潜艇C的俯角为68°.试根据以上数据求出潜艇C离开海平面的下潜深度.(结果保留整数.参考数据:sin 68°≈0.9,cos 68°≈0.4,tan 68°≈2.5,≈1.7)解:如解图,过点C作CD⊥AB,交BA的延长线于点D,则AD即为潜艇C的下潜深度.根据题意,得∠ACD=30°,∠BCD=68°.设AD=x,则BD=BA+AD=1 000+x.在Rt△ACD中,命题角度❷ 背靠背型例2(2016·河南)如图,小东在教学楼距地面9米高的窗口C 处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°,升旗时,国旗上端悬挂在距地面2.25米处.若国旗随国歌声冉冉升起,并在国歌播放45秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度匀速上升?(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)【分析】通过解Rt△BCD和Rt△ACD分别求得BD、AD的长度,则得AB的长度,则根据题意得到整个过程中旗子上升的高度,由“速度= ”进行解答即可.【自主解答】解:如解图,在Rt△BCD中,BD=9米,∠BCD =45°,则BD=CD=9米.在Rt△ACD中,CD=9米,∠ACD=37°,则AD=CD·tan37°≈9×0.75=6.75(米).所以,AB=AD+BD=15.75米,整个过程中旗子上升高度是:15.75-2.25=13.5(米),∵耗时45秒,∴上升速度v= =0.3(米/秒).答:国旗应以0.3米/秒的速度匀速上升.(2018·昆明)小婷在放学路上,看到隧道上方有一块宣传“中国-南亚博览会”的竖直标语牌CD.她在A点测得标语牌顶端D处的仰角为42°,测得隧道底端B处的俯角为30°(B,C,D在同一条直线上),AB=10 m,隧道高6.5 m(即BC=6.5 m),求标语牌CD的长(结果保留小数点后一位).(参考数据:sin 42°≈0.67,cos 42°≈0.74,tan 42°≈0.90, ≈1.73)解:如解图,作AE⊥BD于E.在Rt△AEB中,∵∠EAB=30°,AB=10(m),∴BE= AB=5(m),AE=5 (m),在Rt△ADE中,DE=AE·tan42°≈7.79(m),∴BD=DE+BE≈12.79(m),∴CD=BD-BC=12.79-6.5≈6.3(m),答:标语牌CD的长约为6.3 m.。
2019年中考数学第五章图形的认识5.6解直角三角形(讲解部分)素材

第五章 图形的认识 3 9
140
������������������������������������������������������������������������������������������������������������������������������������������������������������
∵ 在 Rt△AQD 中,AQ = AD2 +DQ2 = 21 k,
������������������������������������������������������������������������������������������������������������������������������������������������������������������
例 2 (2017 吉林,21,7 分) 如图,一枚运载火箭从距雷达 站 C 处5 km的地面 O 处发射,当火箭到达点 A,B 时,在雷达站 C 处测得点 A,B 的仰角分别为 34°,45°,其中点 O,A,B 在同一条 直线上.求 A,B 两点间的距离( 结果精确到 0.1 km) .
( 参考数据:sin 34° = 0.56,cos 34° = 0.83,tan 34° = 0.67)
铅锤 P 处的水深 h.
æ
2
72
1ö
ç 参考数据:sin
è
8°≈10 ,cos
8°≈
10
,tan
8°≈
7
÷
ø
解析 由题意,得∠AOC = 90°,OC = 5 km.
在 Rt△AOC 中,
∵
tan
初三解直角三角形数学知识点讲解

2019年初三解直角三角形数学知识点讲解
鉴于数学知识点的重要性,小编为您提供了这篇2019
年初三解直角三角形数学知识点讲解,希望对同学们的数学有所帮助。
★重点★解直角三角形
☆ 内容提要☆
一、三角函数
1.定义:在Rt△ABC中,C=Rt,则sinA= ;cosA= ;tgA= ;ctgA= .
2. 特殊角的三角函数值:
0 30 45 60 90
sin
cos
tg /
ctg /
3. 互余两角的三角函数关系:sin(90-)=cos
4. 三角函数值随角度变化的关系
5.查三角函数表
二、解直角三角形
1. 定义:已知边和角(两个,其中必有一边)所有未知的边和角。
2. 依据:①边的关系:
②角的关系:A+B=90
③边角关系:三角函数的定义。
注意:尽量避免使用中间数据和除法。
三、对实际问题的处理
1. 俯、仰角:
2.方位角、象限角:
3.坡度:
4.在两个直角三角形中,都缺解直角三角形的条件时,可用列方程的办法解决。
四、应用举例(略)
这篇2019年初三解直角三角形数学知识点讲解是精品小编精心为同学们准备的,祝大家学习愉快!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
68 CEABD状元廊学校秋季班数学思维方法讲义之五 年级:九年级2019-2020年中考数学思维方法讲义:第5讲 解直角三角形专题【考点透视】一、锐角三角函数与解直角三角形:1.锐角三角函数的定义,通过画图找出直角三角形中边角关系;2.准确记忆30°、45°、60°的三角函数值并进行计算;已知三角函数值求相应锐角;3.三角函数与直角三角形的相关应用. 二、几何直线型:1、利用有关三角形、平行四边形、特殊平行四边形(矩形、菱形、正方形)、梯形等的性质、判定及其相关结论进行相关计算推理;2、解决几何图形的三大变换问题。
【思想方法】1、本专题所研究的锐角三角函数,所涉及的角都是锐角,研究这样的角,可以与直角三角形直接联系起来。
利用直角三角形的边角关系求图形中的某些边或角时,都是通过数值计算,这是数形结合的一种方式。
所以在分析问题时,最好画出它的平面或截面示意图,按照图中边角关系去进行计算,便于解答、防止出错。
有些图形虽然不是直角三角形,但可添加适当的辅助线把它们分割成一些直角三角形和矩形,如等腰三角形、梯形等问题。
从而可以运用直角三角形的有关知识去解决这些图形中求边角的问题。
2、“一招制胜”——分离图形法【精彩知识】考点1:有关三角函数的重要概念【例1】(1)如图所示正方形网格中,每个小正方形的边长都相等,点A 、B 、C 、D 都在这些小正方形的顶点上,线段AB 与CD 相交于P ,则tan ∠BPD 的值为 。
(2)已知△ABC 中,∠A 、∠B 是锐角,且sin A =135,tan B =2,AB =29cm,则ABC S ∆= .变式训练:1.(泰安市)直角三角形纸片的两直角边长分别为 6,8,现将ABC △如图那样折叠,使点A 与点B 重合,折痕为DE ,则tan CBE ∠的值是( ) A .247B.724D .132. 如图,已知△ABC ,AB =AC =1,∠A =36°,∠ABC 的平分线BD 交AC于点D ,则AD 的长是 ,cos A 的值是 .(结果保留根号)考点2: 有关三角函数的计算【例2】已知α是锐角,且sin(α+15°)=2,计算114c o s (3.14)t a n 3απα-⎛⎫--++ ⎪⎝⎭的值。
变式训练:计算:20113015(1)()(cos68)338sin 602π---+++-考点3: 锐角三角函数之间的关系及三角函数增减性 【例3】若0°<α<45°,且sin αcos α= 1673,则sin α的值为 。
变式训练:1.已知α为锐角,下列结论:<>+=11sin cos αα <2>如果α>︒45,那么sin cos αα><3>如果cos α>12,那么α<︒60 <4>(sin )sin αα-=-112其中正确的有( )A. 1个B. 2个C. 3个D. 4个2. 已知m 为实数,且sin α、cos α是方程0132=+-mx x 的两根,则αα44cos sin +的值为 。
考点4:解直角三角形【例4】如图,在梯形ABCD 中,AB ∥CD ,∠BCD =90°,且AB =1,BC =2,tan∠ADC =2. (1)求证:DC =BC ;(2)E 是梯形内一点,F 是梯形外一点,且∠EDC =∠FBC ,DE =BF ,试判断△ECF 的形状,并证明你的结论;(3)在(2)的条件下,当BE :CE =1:2,∠BEC =135°时,求sin∠BFE 的值.【例5】如图,为了测量某山AB 的高度,小明先在山脚下C 点测得山顶A 的仰角为45°,然后沿坡角为30°的斜坡走100米到达D 点,在D 点测得山顶A 的仰角为30°,求山AB ≈1.73)【例6】如图,在某海域内有三个港口A 、D 、C .港口C 在港口A 北偏东60方向上,港口D 在港口A 北偏西60方向上.一艘船以每小时25海里的速度沿北偏东30的方向驶离A 港口3小时后到达B 点位置处,此时发现船舱漏水,海水以每5分钟4吨的速度渗入船内.当船舱渗入的海水总量超过75吨时,船将沉入海中.同时在B 处测得港口C 在B 处的南偏东75方向上.若船上的抽水机每小时可将8吨的海水排出船外,问此船在B 处至少应以怎样的航行速度驶向最近的港口停靠,才能保证船在抵达港口前不会沉没(要求计算结果保留根号)?并指出此时船的航行方向.变式训练:如图,在东西方向的海岸线l 上有一长为1千米的码头MN ,在码头西端M 的正西方向30 千米处有一观察站O .某时刻测得一艘匀速直线航行的轮船位于O 的北偏西30°方向,且与O 相距千米的A 处;经过40分钟,又测得该轮船位于O 的正北方向,且与O 相距20千米的B 处.(1)求该轮船航行的速度;(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN 靠岸?请说明理由.(参考数据:,)【能力拓展】【例7】在平面直角坐标系xOy 中,已知抛物线y=2(1)(0)a x c a ++>与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,其顶点为M ,若直线MC 的函数表达式为3y kx =-,与x 轴的交点为N ,且COS ∠BCO =10。
(1)求此抛物线的函数表达式;(2)在此抛物线上是否存在异于点C 的点P ,使以N 、P 、C 为顶点的三角形是以NC 为一条直角边的直角三角形?若存在,求出点P 的坐标:若不存在,请说明理由;(3)过点A 作x 轴的垂线,交直线MC 于点Q .若将抛物线沿其对称轴上下平移,使抛物线与线段NQ 总有公共点,则抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?【例8】(1)如图①,在菱形ABCD 和菱形BEFG 中,点A 、B 、E 在同一条直线上,P 是线段DF 的中点,连结PG 、PC 。
若∠ABC =∠BEF =60°,试探究PG 与PC 的位置关系及PC PG的值; (2)将图①中的菱形BEFG 绕B 点顺时针旋转,使菱形BEFG 的对角线BF 恰好与菱形ABCD 的边AB 在同一条直线上,原问题中的其他条件不变(如图②),(1)中的两个结论是否发生变化?写出你的猜想并加以证明;(3)在图①中若∠ABC =∠BEF =2α(0°<α<90°),将菱形BEFG 绕B 点顺时针旋转任意角度,原问题中的其他条件不变请直接写出PC PG = (用含α的式子表示)CBAD图① 图②【以练励学】1. 如图,Rt△ABC 中,∠C =90°,AC =BC ,AC =6,D 是AC 上一点, tan∠DBA =15,则AD 的长为( )2、小明是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板如图位置摆放,A 、B 、C 在同一直线上,EF ∥AD ,∠A =∠EDF =90°,∠C =45°,∠E =60°,量得DE =8,试求BD 的长。
3、综合实践课上,小明所在小组要测量护城河的宽度。
如图所示是护城河的一段,两岸ABCD ,河岸AB 上有一排大树,相邻两棵大树之间的距离均为10米.小明先用测角仪在河岸CD 的M 处测得∠α=36°,然后沿河岸走50米到达N 点,测得∠β=72°。
请你根据这些数据帮小明他们算出河宽FR (结果保留两位有效数字).(参考数据:sin 36°≈0.59,cos 36°≈0.81,tan36°≈0.73,sin 72°≈0.95,cos 72°≈0.31,tan72°≈3.08)4、我市在规划沿江新城期间,欲拆江岸边的一根电线杆AB (如图),已知距电线杆AB 水平距离14米处是河岸,即BD =14米,该河岸的坡面CD 的坡角∠CDF 的正切值为2(即tan∠CDF =2),岸高CF 为2米,在坡顶C 处测得杆顶A 的仰角为30°,D 、E 之间是宽2米的人行道,请你通过计算说明在拆除电线杆AB 时,为确保安全,是否将此人行道封上?(在地面上以点B 为圆心,以AB 长为半径的圆形区域为危险区)5、在矩形ABCD 和矩形CEFG 中,已知k CECGAB AD ==,连结DE 与AF 交于点P ,连结CP . (1)如图1,当k =1时,点B 、C 、E 在一条直线上,求DEAF的值。
(2)如图2,当k =1,并将图1中的矩形CEFG 绕点C 顺时针旋转一定的角度时,① 求DEAF的值;② 求证:CP ⊥AF 。
(3)如图3,当k≠1时,请直接写出DEAF的值(用含k 的式子表示)。
图1 图2 图3【例5】解:过D 作DE⊥BC 于E ,作DF⊥AB 于F,设AB=x ,在Rt△DEC 中,∠DCE=30°,CD=100, ∴DE=50,在Rt△ABC 中,∠ACB=45°,∴BC=x。
则AF=AB-BF=AB -DE=x -50,DF=BE=BC +CE=x +在Rt△AFD中,∠ADF=30°,tan30°=AFFD=。
∴x 503236.5=≈((米)。
答:山AB 的高度约为236.5米。
变式:解:(1)过点A 作AC ⊥OB 于点C。
由题意,得 OA=OB=20千米,∠AOC=30°。
∴11AC=OA=22⨯=。
∵在Rt △AOC 中OC=OA•cos ∠AOC=2(千米), ∴BC=OC ﹣OB=30﹣20=10(千米)。
∴在Rt △ABC 中,20=(千米)。
∴轮船航行的速度为:40203060÷=(千米/时)。
【例7】解:(1) 在Rt △OCE 中,OE =OCtan ∠OCE 35=∴点E(0,。
设直线AC 的函数解析式为y =kx +0+=,解得:k =35-。
∴直线AC 的函数解析式为y =3x 5-+ (2) 在Rt △OGE 中,tan ∠EOG =tan ∠OCE =EG 3GO 5=,设EG =3t ,OG =5t ,,∴,得t =2。
∴EG =6,OG =10。
∴OEG 11S OG EG=106=3022∆⋅⋅⨯⨯=/ (3) 存在。
①当点Q 在AC 上时,点Q 即为点G , 如图1,作∠FOQ 的角平分线交CE 于点P1, 由△OP 1F ≌△OP 1Q ,则有P 1F ⊥x 轴, 由于点P 1在直线AC 上,当x =10时,y =31065-⨯+=∴点P 1(10,6)。
