信号与线性系统课件 第十一节
合集下载
信号与线性系统_吴大正_教材课件

s ( t ) f1 ( t ) f 2 ( t ) P ( t ) f1 ( t ) f 2 ( t )
第 1 章 信号与系统的基本概念
同样,若有两个离散信号f1(k)和f2(k),则其和信号s(k)与 积信号p(k)可表示为
s ( k ) f1 ( k ) f 2 ( k ) P ( k ) f1 ( k ) f 2 ( k )
解 一般说来,在t轴尺度保持不变的情况下,信号 f(at+b)(a≠0)的波形可以通过对信号f(t)波形的平移、翻转(若
a<0)和展缩变换得到。根据变换操作顺序不同,可用多种方法
画出f(1-2t)的波形。 (1) 按“翻转-展缩-平移”顺序。 首先将f(t)的波形进行翻 转得到如图1.3-6(b)所示的f(-t)波形。然后,以坐标原点为中心, 将f(-t)波形沿t轴压缩1/2,得到f(-2t)波形如图1.3-6(c)所示。由 于f(1-2t)可以改写为
f(-t+1)波形。最后,将f(-t+1)波形压缩1/2得到f(1-2t)的波形。
信号波形的变换过程如图1.3-7所示。
第 1 章 信号与系统的基本概念
f (t ) f (t + 1)
1 -2 -1 0 -1 1 2 t -1
1
0 -1
1
t
(a )
(b )
f (- t + 1)
f (1 - 2 ) t
第 1 章 信号与系统的基本概念
f1 (t ) A 1 f2 (t ) A f3 (t )
-2
-1
0
1
2
t
o
t
o
t0
t
-A
(a )
(b )
第一章信号与线性系统吴大正教材课件

第 1 章 信号与系统的基本概念
二、信号的分类
1. 连续信号与离散信号
连续信号:一个信号,如果在某个时间区间内除有限个间断点 外都有定义, 就称该信号在此区间内为连续时间信号, 简称 连续信号。 这里“连续”一词是指在定义域内 (除有限个间断 点外)信号变量是连续可变的。至于信号的取值,在值域内可 以是连续的,也可以是跳变的。
第 1 章 信号与系统的基本概念
离散信号: 仅在离散时刻点上有定义的信号称为离散时间信 号,简称 离散信号 。这里“离散”一词表示自变量只取离散 的数值,相邻离散时刻点的间隔可以是相等的,也可以是不 相等的。在这些离散时刻点以外,信号无定义。信号的值域 可以是连续的, 也可以是不连续的。
定义在等间隔离散时刻点上的离散信号也称为序列, 通 常记为f(k),其中k称为序号。与序号 m相应的序列值 f(m)称为 信号的第m个样值。 例如:
f2 (t)
?
? (t)
?
??1(t ?
?
0)
??0(t ? 0)
图1.1-2(c)表示一个延时的单边指数信号, 其表达式为
f3 (t)
?
?? Ae?? ?
(t (t? t0 )
?
t0 )
??0
(t ? t0 )
式中,A是常数, α>0。信号变量 t在定义域(-∞, ∞)内连续变 化,信号f3(t)在值域[0, A) 上连续取值。注意,f3(t)在t=t0处 有间断点。
第 1 章 信号与系统的基本概念
极限 :对于间断点处的信号值一般不作定义,这样做不会影响 分析结果。如有必要, 也可按高等数学规定,定义信号 f(t)在 间断点 t0处的信号值等于其左极限 f(t0-)与右极限 f(t0+)的算术平 均值, 即
信号与线性系统分析课件

04 线性系统的响应
系统的冲激响应
冲激响应定义
01
冲激响应是线性系统对单位冲激函数的响应,反映了系统对瞬
时作用的响应特性。
冲激响应计算
02
通过求解线性系统的微分方程或差分方程,可以得到系统的冲
激响应。
冲激响应的物理意义
03
冲激响应可以理解为系统内部能量的传播和分布,是分析系统
动态特性的重要手段。
卷积积分定义
卷积积分是信号处理中常用的一种运算,用于描述两个函数的相互作用。在线性系统中 ,卷积积分用于描述系统的输出与输入之间的关系。
卷积积分的计算
卷积积分的计算涉及到函数乘积的积分,常用的计算方法包括离散卷积和离散化卷积等 。
卷积积分的物理意义
卷积积分可以理解为系统对输入信号的处理和转换能力,是分析系统动态特性的重要手 段。在信号处理中,卷积积分常用于信号滤波、预测和控制系统设计等领域。
03 信号的傅里叶分析
傅里叶级数
傅里叶级数定义
将周期信号表示为无穷多个正弦和余弦函数 的线性组合。
复指数形式
使用复指数函数来表示周期信号。
三角函数形式
使用正弦和余弦函数来表示周期信号。
傅里叶级数的应用
用于分析信号的频率成分和幅度变化。
傅里叶变换
01
02
03
傅里叶变换定义
将时域信号转换为频域信 号,表示信号的频率分布 。
傅里叶变换的性质
线性、时移、频移、共轭 、对称等性质。
傅里叶变换的应用
用于信号处理、图像处理 、通信等领域。
频域分析
频域分析定义
通过分析信号的频率成分 来理解信号的特征和性质 。
频域分析的应用
用于信号滤波、调制解调 、频谱分析等领域。
信号与线性系统(管致中)

1 p 1 p
1 d t p x(t )d x(t ) p dt
?
t dx(t ) 1 p x(t ) x() dt p
1 p =1 p
dx (t ) dy (t ) dt dt
当且仅当x() 0时等号成立
x(t ) y (t ) C
注:初始条件
rzs (0 ) 0, rzs ' (0 ) 0
零输入响应和零状态响应
r (t )(全响应) rzi (t )(零输入响应 rzs (t(零状态响应) ) )
2. 用叠加积分的方法求解零状态响应:原理——系统的叠加性
若f1 (t ) r1 (t ),f 2 (t ) r2 (t )
转移算子:
N ( p) r (t ) e (t ) D( p)
N ( p) H ( p) D( p)
转移算子描述了响应函数和激励函数在时域中的关系
2-2 系统方程的算子表示法
二、算子多项式的运算法则 1、代数运算:
( p a)( p b) p 2 (a b) p ab
B0不可解
i f (t ) (B0 t )e2t
i(t ) in (t ) i f (t ) (C1 B0 )e2t C2e3t tet
其中待定常数C1+B0,C2由初始条件确定:
i(0) C1 B0 C2 1 1, C1 B0 2, C2 1
(杜阿美积分,卷积积分)
零输入响应 自然响应
零状态响应 受迫响应
对于一个稳定的系统而言,系统的零输入响应必然是
自然响应的一部分
零状态响应中又可以分为自然响应和受迫响应两部分。 零输入响应和零状态响应中的自然响应部分和起来构 成总的自然响应,零状态响应中有外加激励源作用产生的 响应是受迫响应
信号与线性系统ppt课件
⑸ 深刻理解单位冲激响应h(t)的意义,并会求解。
⑹ 深刻理解卷积积分的定义、运算规律及主要性质,能会求解卷积积分。
⑺ 会应用卷积积分法求线性时不变系统的零状态响应rzs(t)。
第二章 连续时间系统的时域分析
§2.1 引 言 §2.2 系统方程的算子表示法 §2.3 系统的零输入响应 § 2.4 奇异函数 §2.5 信号的脉冲分解 §2.6 阶跃响应和冲激响应 §2.7 叠加积分 §2.8 卷积及其性质 §2.9 线性系统响应时域求解
零输入响应和零状态响应分量;
暂态响应分量和稳态响应分量。
2. 变换域法
系统方程为高阶微分方程或激励信号是较为复杂的函数,利 用时域法求解方程十分困难。为求解方程常采用变换域的方法。
即将自变量从时间变量变换为频率变量、复频率变量等. 如:傅氏变换、拉氏变化等
将求系统的微分方程转换求代数方程
零输入响应和零状态响应的求解
§2.1 引 言
系统分析的基本任务是在给定系统和输入的条件下,求解系统的输出响应。
连续时间系统的分析方法: 时域分析法;变换域分析法
连续时间系统的时域分析法:
在系统的整个分析过程都在连续时间域进行,即所涉及的函 数自变量均为连续时间 t 的一种分析方法。
连续时间系统的变换域分析法:
为便于求解方程而将时间变量变换成其他变量。
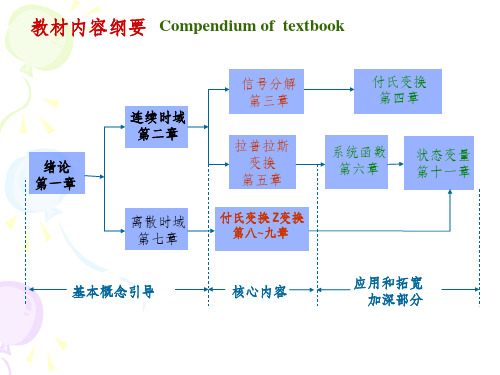
绪论 第一章
连续时域 第二章
离散时域 第七章
信号分解 第三章
付氏变换 第四章
拉普拉斯 变换
第五章
系统函数 第六章
状态变量 第十一章
付氏变换 Z变换 第八~九章
基本概念引导
核心内容
应用和拓宽 加深部分
第二章 连续时间系统的时域分析
⑹ 深刻理解卷积积分的定义、运算规律及主要性质,能会求解卷积积分。
⑺ 会应用卷积积分法求线性时不变系统的零状态响应rzs(t)。
第二章 连续时间系统的时域分析
§2.1 引 言 §2.2 系统方程的算子表示法 §2.3 系统的零输入响应 § 2.4 奇异函数 §2.5 信号的脉冲分解 §2.6 阶跃响应和冲激响应 §2.7 叠加积分 §2.8 卷积及其性质 §2.9 线性系统响应时域求解
零输入响应和零状态响应分量;
暂态响应分量和稳态响应分量。
2. 变换域法
系统方程为高阶微分方程或激励信号是较为复杂的函数,利 用时域法求解方程十分困难。为求解方程常采用变换域的方法。
即将自变量从时间变量变换为频率变量、复频率变量等. 如:傅氏变换、拉氏变化等
将求系统的微分方程转换求代数方程
零输入响应和零状态响应的求解
§2.1 引 言
系统分析的基本任务是在给定系统和输入的条件下,求解系统的输出响应。
连续时间系统的分析方法: 时域分析法;变换域分析法
连续时间系统的时域分析法:
在系统的整个分析过程都在连续时间域进行,即所涉及的函 数自变量均为连续时间 t 的一种分析方法。
连续时间系统的变换域分析法:
为便于求解方程而将时间变量变换成其他变量。
绪论 第一章
连续时域 第二章
离散时域 第七章
信号分解 第三章
付氏变换 第四章
拉普拉斯 变换
第五章
系统函数 第六章
状态变量 第十一章
付氏变换 Z变换 第八~九章
基本概念引导
核心内容
应用和拓宽 加深部分
第二章 连续时间系统的时域分析
11信号讲义与系统

讨论
0, 0 直流
0, 0 等幅
0, 0 升指数信号 0, 0 增幅振荡
0,
0
衰 减 指 数 信 号
0,
0
衰减
4.抽样信号(Sampling Signal)
Sa(t) sint t
Sat
1
2π
性质
t
πO π
3π
① SatSat,偶函数
11信号与系统
精品
第一章 绪 论
§ 1.1 信号与系统
•信号(signal) •系统(system) •信号理论与系统理论
信号(Signal)
•信号(Signal):带有信息(如语言、音乐、图像、数据等)的 随时间(和空间)变化的物理量或物理现象。是消息的表现形式 与传送载体。信号是单个或多个独立变量的函数。 •消息(Message):是信号的具体内容。在通信系统中,一般将 语言、文字、图像或数据统称为消息。 •信息(Information):一般指消息中赋予人们的新知识、新概 念,定义方法复杂,将在后续课程中研究。 •例如电信号传送声音、图像、文字等。 •电信号是应用最广泛的物理量,如电压、电流、电荷、磁通等。
t00
0
t0
欧拉(Euler)公式
sin t1 ejt ejt 2j
cost1ejt ejt 2
e jt co t sjsitn
3.复指数信号
f (t) Kest
( t )
Ke t cos t jKet sin t
s j 为复数,称为复频率
, 均 为 实 常 数
的量 1/纲 , s的 为量 ra 纲 d为 /s
信号理论与系统理论
信号分析:研究信号的基本性能,如信号 信号理论 信号传输 的描述、性质等。
信号与线性系统PPT教学课件

2、信号的接入特性及定义域的表达
2.1.3 阶跃信号的应用
2、信号的接入特性及定义域的表达
2.1.4 冲激信号的定义
冲激信号:
t 0,t 0
tdt 1
2.1.4 冲激信号的性质
1、抽样特性
f t t f 0 t f t t t0 f t0 t t0
2.1.4 冲激信号的性质
1.1 信号的基本概念
3、信号总是以下面的形式传输: 信源 通过 信道 到达 信宿 甲(语言) (空气) 乙(耳朵)
信号的特性:(时间特性 频率特性)
一般地说 :信号是时间的函数;有一定的波形。 任一信号具有其自身特有的频率组成,所以信号 也是频率的函数。
1.2 信号的分类
1.确定性信号和随机信号 按信号是否可预知划分,可以将信号分为确定性信号和随 机信号。 2.连续时间信号和离散时间信号 按信号是否是时间的连续函数划分,将信号分为连续时间 信号和离散时间信号。
1.确定信号与随机信号
(a)
(b)
2.连续时间信号与离散时间信号
f (t)
f (k)
-1
0 t1
t -4 -3 0 1 2 k
3.周期信号与非周期信号
周期信号是指依一定时间间隔周而复始,且无始 无终的信号,表达式可写为
f t f t nT
n 0,复始的特性。非 周期信号也可以看作为周期为无穷大的周期信号
1.3 系统的定义和分类
3、系统的模拟和联结
系统的模拟
1.4 信号与系统分析概要
1、信号的分析 信号分析的内容及方法有多种,本教材主要描
述了时域法和频域法。 2、系统的分析
系统的分析方法也有时域法和频域法。对连续 时间系统的分析主要采用卷积法,而离散时间系 统则采用卷积和的方法;
2.1.3 阶跃信号的应用
2、信号的接入特性及定义域的表达
2.1.4 冲激信号的定义
冲激信号:
t 0,t 0
tdt 1
2.1.4 冲激信号的性质
1、抽样特性
f t t f 0 t f t t t0 f t0 t t0
2.1.4 冲激信号的性质
1.1 信号的基本概念
3、信号总是以下面的形式传输: 信源 通过 信道 到达 信宿 甲(语言) (空气) 乙(耳朵)
信号的特性:(时间特性 频率特性)
一般地说 :信号是时间的函数;有一定的波形。 任一信号具有其自身特有的频率组成,所以信号 也是频率的函数。
1.2 信号的分类
1.确定性信号和随机信号 按信号是否可预知划分,可以将信号分为确定性信号和随 机信号。 2.连续时间信号和离散时间信号 按信号是否是时间的连续函数划分,将信号分为连续时间 信号和离散时间信号。
1.确定信号与随机信号
(a)
(b)
2.连续时间信号与离散时间信号
f (t)
f (k)
-1
0 t1
t -4 -3 0 1 2 k
3.周期信号与非周期信号
周期信号是指依一定时间间隔周而复始,且无始 无终的信号,表达式可写为
f t f t nT
n 0,复始的特性。非 周期信号也可以看作为周期为无穷大的周期信号
1.3 系统的定义和分类
3、系统的模拟和联结
系统的模拟
1.4 信号与系统分析概要
1、信号的分析 信号分析的内容及方法有多种,本教材主要描
述了时域法和频域法。 2、系统的分析
系统的分析方法也有时域法和频域法。对连续 时间系统的分析主要采用卷积法,而离散时间系 统则采用卷积和的方法;
信号与线性系统 绪论完美版PPT

y(n) 数字信号处理器
D/A变换器
ya (t)
xa (t)
T 2T y(n)
x(n)7 5Biblioteka 443t0
1234
n -1 -3
ya (t )
0 1234
n
二. 数字信号处理的实现方法
1.软件实现方法(优缺点分析) 按照原理和算法,编写程序在通用计算机上实现。
2.硬件实现方法(优缺点分析) 按照具体的要求和算法,设计硬件结构图,用乘法器、加 法器、延时器、控制器、存储器以及输入输出接口部件 实现的一种方法。
3.专用计算机(DSP芯片) 目前发展最快、应用最广的一种方法。
三. 数字信号处理的特点
与模拟信号处理(ASP)相比,数字信号处理具有如
依自变量和函数值的连续与否:模拟信号;
下特点: 程佩青, 清华大学出版社
依周期性:周期信号; 非周期信号。
▪ 精度高 它是采用数值计算的方法,完成对信号的处理,而模拟信号处理是通过一些模拟器件(晶体管、电阻、电容、电感等),完成对信号
讲授内容
1.时域离散信号和时域离散系统 2.时域离散信号和系统的频域分析 3.离散傅里叶变换(DFT) 4.快速傅里叶变换(FFT) 5.时域离散系统的基本网络结构与
状态变量分析法 6.IIR DF (无限脉冲响应数字滤波器)的设计 7.FIR DF (有限脉冲响应数字滤波器)的设计
绪论
一. 数字信号处理的基本概念
对数字信号进行加工/运算处理,以实现某种需要的功能。它 是采用数值计算的方法,完成对信号的处理,而模拟信号处理是 通过一些模拟器件(晶体管、电阻、电容、电感等),完成对信 号的处理。
数字信号处理是在模拟信号处理的
基础上发展起来的,数字信号处理系统 也可以处理模拟信号。
信号与系统课件-绪论:信号与系统

周期信号
f (t)
f (t)
A
- T T o T
T
2
2
-A
…
…
t
-4 -2 0
246
k
上一页
2022/1/13
信号与线性系统分析——绪论、信号与系统
17
纵轴对称:余弦(偶函数)
f t f t
T
原点对称:正弦(奇函数)
T
f t f t
o
Tt
T
o
t
半波重叠:偶次波 (偶谐函数)ftT 2
f
(c)
上一页 返 回
2022/1/13
信号与线性系统分析——绪论、信号与系统
14
信号的分类(二) 因 果:t < 0 时,f ( t ) ≡ 0 非因果:对任何 t < 0 或 t > 0,f (t)≠0 反因果:t > 0 时,f (t) ≡ 0
如:连续信号、离散信号
上一页 返 回
2022/1/13
o t0 (c)
12
t t 2022/1/13
信号与线性系统分析——绪论、信号与系统
13
离散信号
f1(k )
… -8
-6
-4
-2
A
5 6 78 01 2 3 4
… k
f2(k ) 2 1
-A (a)
f3(k ) A
- 3 - 1 01 23 4
k
-1
- 3 - 1 01 2 3 4 5 6 k
(b)
信号与线性系统分析——绪论、信号与系统
目录
§1.1 绪 言 §1.2 信 号 §1.3 信号的基本运算 §1.4 阶跃函数和冲激函数 §1.5 系统的描述 §1.6 系统的特性和分析方法
信号与线性系统课件

频谱图
介绍使用频谱图来可视化信号 在频域中的能量分布。
傅里叶级数和傅里叶变换
1
傅里叶级数
学习傅里叶级数的原理和应用,包括拆解周期信号和频率分量的计算。
2
傅里叶变换
深入研究傅里叶变换的概念,揭示其将时域信号转换为频域表示的强大能力。
3
离散傅里叶变换
介绍离散傅里叶变换的定义、性质和在数字信号处理中的应用。
信号与线性系统课件
欢迎来到信号与线性系统课件!本课程涵盖信号与系统的多个关键概念,包 括信号分类、傅里叶变换、系统特性和滤波器设计等内容。
信号的概念和分类
信号概念
介绍信号的定义和基本属性,以及信号在实 际应用中的重要性。
周期信号和非周期信号
介绍周期信号和非周期信号的定义、周期性 质和周期函数的应用。
3 视频信号处理4 通源自信号处理介绍视频信号处理的内容,如视频压缩、 视频分析和视频编解码。
解释通信信号处理的重要性和实际应用, 如调制解调和信道编码。
滤波器的概念和分类
1
模拟滤波器和数字滤波器
2
比较模拟滤波器和数字滤波器的特点、
设计方法和应用领域。
3
滤波器的定义
阐述滤波器的基本概念和功能,以及 在信号处理中的作用。
FIR滤波器和IIR滤波器
介绍FIR滤波器和IIR滤波器的定义、性 质和在实际系统中的应用。
信号的采样和量化
信号采样
学习信号采样的原理、采样率 选择和采样定理的应用。
连续信号与离散信号
探讨连续信号和离散信号的区别、特点和应 用领域。
能量信号和功率信号
比较能量信号和功率信号的特点,并探讨它 们在信号处理中的重要性。
信号的时域表示和频域表示
第一章信号与线性系统吴大正教材课件.ppt

第 1 章 信号与系统的基本概念 例 1试判断下列信号是否为周期信号。若是,确定其周期。 (1) f1(t)=sin 2t+cos 3t (2) f2(t)=cos 2t+sinπt 解 我们知道,如果两个周期信号x(t)和y(t)的周期具有公 倍数,则它们的和信号
f(t)=x(t)+y(t) 仍然是一个周期信号, 其周期是x(t)和y(t)周期的最小公倍数。
第 1 章 信号与系统的基本概念
f1(t) A
f2(t) 1
f3(t) A
-2 -1
01
2t
o
-A
t
o t0
t
(a)
(b)
(c)
图 1.1-2 连续信号 图1.1-2(a)是正弦信号,其表达式
f1(t) Asin(t)
第 1 章 信号与系统的基本概念
图1.1-2(b)是单位阶跃信号, 通常记为ε(t),其表达式为
第 1 章 信号与系统的基本概念
二、信号的分类
1. 连续信号与离散信号
连续信号:一个信号,如果在某个时间区间内除有限个间断点 外都有定义, 就称该信号在此区间内为连续时间信号,简称 连续信号。 这里“连续”一词是指在定义域内(除有限个间断 点外)信号变量是连续可变的。至于信号的取值,在值域内可 以是连续的,也可以是跳变的。
量E为
E lim
2
f (t) 2dt
2
P lim 1
注意:为方便起见,有时将信号f(t)或f(k)的自变量省略,简记 为f(·), 表示信号变量允许取连续变量或者离散变量,即用f(·) 统一表示连续信号和离散信号。
第 1 章 信号与系统的基本概念 2. 一个连续信号f(t),若对所有t均有
《信号与系统 》PPT课件
一、系统的定义 二、系统的分类及性质
1.6 系统的描述
一、连续系统 二、离散系统
1.7 LTI系统分析方法概
述
二、冲激函数
点击目录 ,进入相关章节
a
10
第1-10页
■
信号与系统 电子教案
第一章 信号与系统
1.1 绪言
思考问题:什么是信号?什么是系统?为什么把这两 个概念联系在一起?
一、信号的概念
1. 消息(message):
a
26
第1-26页
■
信号与系统 电子教案
1.2 信号的描述和分类
4.能量信号与功率信号
将信号f (t)施加于1Ω电阻上,它所消耗的瞬时功率 为| f (t) |2,在区间(–∞ , ∞)的能量和平均功率定义为
(1)信号的能量E
def
E
f (t) 2 dt
(2)信号的功率P
def
Pl
i
m1
TT
29
第1-29页
■
信号与系统 电子教案
1.3 信号的基本运算
二、信号的时间变换运算
1. 反转
演示
将 f (t) → f (– t) , f (k) → f (– k) 称为对信号f (·) 的反转或反折。从图形上看是将f (·)以纵坐标为轴反 转180o。如
f (t) 1
反转 t → - t
1
f (- t )
看成系统。它们所传送的语音、音乐、图像、文字
等都可以看成信号。信号的概念与系统的概念常常
紧密地联系在一起。 系统的基本作用是对输入 输入信号
信号进行加工和处理,将其转 换为所需要的输出信号。
激励
系统
演示
1.6 系统的描述
一、连续系统 二、离散系统
1.7 LTI系统分析方法概
述
二、冲激函数
点击目录 ,进入相关章节
a
10
第1-10页
■
信号与系统 电子教案
第一章 信号与系统
1.1 绪言
思考问题:什么是信号?什么是系统?为什么把这两 个概念联系在一起?
一、信号的概念
1. 消息(message):
a
26
第1-26页
■
信号与系统 电子教案
1.2 信号的描述和分类
4.能量信号与功率信号
将信号f (t)施加于1Ω电阻上,它所消耗的瞬时功率 为| f (t) |2,在区间(–∞ , ∞)的能量和平均功率定义为
(1)信号的能量E
def
E
f (t) 2 dt
(2)信号的功率P
def
Pl
i
m1
TT
29
第1-29页
■
信号与系统 电子教案
1.3 信号的基本运算
二、信号的时间变换运算
1. 反转
演示
将 f (t) → f (– t) , f (k) → f (– k) 称为对信号f (·) 的反转或反折。从图形上看是将f (·)以纵坐标为轴反 转180o。如
f (t) 1
反转 t → - t
1
f (- t )
看成系统。它们所传送的语音、音乐、图像、文字
等都可以看成信号。信号的概念与系统的概念常常
紧密地联系在一起。 系统的基本作用是对输入 输入信号
信号进行加工和处理,将其转 换为所需要的输出信号。
激励
系统
演示
信号与系统分析PPT全套课件可修改全文

1.系统的初始状态
根据各电容及电感的状态值能够确定在 t 0
时刻系统的响应及其响应的各阶导数
( y(0 ) k 1, 2 , , n 1)
称这一组数据为该系统的初始状态。
2.系统的初始值
一般情况下,由于外加激励的作用或系统内 部结构和参数发生变化,使得系统的初始值与 初始状态不等,即:
y(0 ) y(0 )
自由响应又称固有响应,它反映了系统本身 的特性,取决于系统的特征根; 强迫响应又称强制响应,是与激励相关的响 应。 利用经典法可以直接求得自由响应与强迫响 应,强迫响应即特解
先求得系统的零输入响应和零状态响应,并 获得系统的全响应;
然后利用系统特性与自由响应、激励与强迫 响应的关系可以间接得到自由响应和强迫响应。
t
f (t) (t)dt f (0) (t)dt
f (0) (t)dt f (0)
(1)
0
t
ห้องสมุดไป่ตู้(3)偶函数
(4)
(at)
1 a
(t)
f (t) (t) ( f (0))
(5) (t)与U (t)的关系
0
t
1.2 基本信号及其时域特性
单位冲激偶信号 '(t)
f (t) 1/
f ' (t) (1/ )
第2章 连续系统的时域分析
2.1 LTI连续系统的模型 2.2 LTI连续系统的响应 2.3 冲激响应与阶跃响应 2.4 卷积与零状态响应
2.1 LTI连续系统的模型
2.1.1 LTI连续系统的数学模型 2.1.2 LTI连续系统的框图
返回首页
2.1.1 LTI连续系统的数学模型
对于任意一个线性时不变电路,当电路结构 和组成电路的元件参数确定以后, 根据元件的伏安关系和基尔霍夫定律,可以 建立起与该电路对应的动态方程。
信号与线性系统ppt

年VIP
月VIP
连续包月VIP
VIP专享文档下载特权
享受60次VIP专享文档下载特权,一 次发放,全年内有效。
VIP专享文档下载特权自VIP生效起每月发放一次, 每次发放的特权有效期为1个月,发放数量由您购买 的VIP类型决定。
每月专享9次VIP专享文档下载特权, 自VIP生效起每月发放一次,持续有 效不清零。自动续费,前往我的账号 -我的设置随时取消。
2.1 信号的描述
1、典型信号 (1) 复指数信号
f t Aest
t
式中, s j , A,与且都是实数
2.1 信号的描述
2、抽样信号
Sat sin t
t
2.1 信号的描述
3、奇异信号
(a)
(b)
(c)
2.1.3 阶跃信号的应用
1、矩形方波的描述
2.1.3 阶跃信号的应用
其他特 VIP专享精彩活动
权
VIP专属身份标识
开通VIP后可以享受不定期的VIP随时随地彰显尊贵身份。
专属客服
VIP专属客服,第一时间解决你的问题。专属客服Q全部权益:1.海量精选书免费读2.热门好书抢先看3.独家精品资源4.VIP专属身份标识5.全站去广告6.名
路漫漫其修远兮,吾将上下而求索!
豫 章 故 郡 , 洪都新 府。星 分翼轸 ,地接 衡庐。 襟三江 而带五 湖,控 蛮荆而 引瓯越 。物华 天宝, 龙光射 牛斗之 墟;人 杰地灵 ,徐孺 下陈蕃 之榻。 雄州雾 列,俊 采星驰 。台隍 枕夷夏 之交, 宾主尽 东南之 美。都 督阎公 之雅望 ,棨戟 遥 临 ; 宇 文 新 州之懿 范,襜 帷暂驻 。十旬 休假, 胜友如 云;千 里逢迎 ,高朋 满座。 腾蛟起 凤,孟 学士之 词宗; 紫电青 霜,王 将军之 武库。 家君作 宰,路 出名区 ;童子 何知, 躬逢胜 饯。 时 维 九 月 , 序属三 秋。潦 水尽而 寒潭清 ,烟光 凝而暮 山紫。 俨骖騑 于上路 ,访风 景于崇 阿;临 帝子之 长洲, 得天人 之旧馆 。层峦 耸翠, 上出重 霄;飞 阁流丹 ,下临 无地。 鹤汀凫 渚,穷 岛屿之 萦回; 桂殿兰 宫,即 冈峦之 体势。 披 绣 闼 , 俯 雕甍, 山原旷 其盈视 ,川泽 纡其骇 瞩。闾 阎扑地 ,钟鸣 鼎食之 家;舸 舰迷津 ,青雀 黄龙之 舳。云 销雨霁 ,彩彻 区明。 落霞与 孤鹜齐 飞,秋 水共长 天一色 。渔舟 唱晚, 响穷彭 蠡之滨 ;雁阵 惊寒, 声断衡 阳之浦 。 遥 襟 甫 畅 , 逸兴遄 飞。爽 籁发而 清风生 ,纤歌 凝而白 云遏。 睢园绿 竹,气 凌彭泽 之樽; 邺水朱 华,光 照临川 之笔。 四美具 ,二难 并。穷 睇眄于 中天, 极娱游 于暇日 。天高 地迥, 觉宇宙 之无穷 ;兴尽 悲来, 识盈虚 之有数 。望长 安 于 日 下 , 目 吴会于 云间。 地势极 而南溟 深,天 柱高而 北辰远 。关山 难越, 谁悲失 路之人 ?萍水 相逢, 尽是他 乡之客 。怀帝 阍而不 见,奉 宣室以 何年? 嗟 乎 ! 时 运 不齐, 命途多 舛。冯 唐易老 ,李广 难封。 屈贾谊 于长沙 ,非无 圣主; 窜梁鸿 于海曲 ,岂乏 明时? 所赖君 子见机 ,达人 知命。 老当益 壮,宁 移白首 之心? 穷且益 坚,不 坠青云 之志。 酌贪泉 而觉爽 ,处涸 辙以犹 欢。北 海 虽 赊 , 扶 摇 可接; 东隅已 逝,桑 榆非晚 。孟尝 高洁, 空余报 国之情 ;阮籍 猖狂, 岂效穷 途之哭 ! 勃 , 三 尺 微 命,一 介书生 。无路 请缨, 等终军 之弱冠 ;有怀 投笔, 慕宗悫 之长风 。舍簪 笏于百 龄,奉 晨昏于 万里。 非谢家 之宝树 ,接孟 氏之芳 邻。他 日趋庭 ,叨陪 鲤对; 今兹捧 袂,喜 托龙门 。杨意 不逢, 抚凌云 而自惜 ;钟期 既 遇 , 奏 流 水 以何惭 ? 呜 乎 ! 胜 地 不常, 盛筵难 再;兰 亭已矣 ,梓泽 丘墟。 临别赠 言,幸 承恩于 伟饯; 登高作 赋,是 所望于 群公。 敢竭鄙 怀,恭 疏短引 ;一言 均赋, 四韵俱 成。请 洒潘江 ,各倾 陆海云 尔: 滕 王 高 阁 临 江渚, 佩玉鸣 鸾罢歌 舞。 画 栋 朝 飞 南 浦云, 珠帘暮 卷西山 雨。 闲 云 潭 影 日 悠悠, 物换星 移几度 秋。 阁 中 帝 子 今 何在? 槛外长 江空自 流。
信号与线性系统分析(第四版)--吴大正课件.

第 20 页
离散周期信号举例2
例 判断下列序列是否为周期信号,若是,确定其周期。 (1)f1(k) = sin(3πk/4) + cos(0.5πk) (2)f2(k) = sin(2k)
解 (1)sin(3πk/4) 和cos(0.5πk)的数字角频率分别为 β1 = 3π/4 rad, β2 = 0.5π rad 由于2π/ β1 = 8/3, 2π/ β2 = 4为有理数,故它们的周期 分别为N1 = 8 , N2 = 4,故f1(k) 为周期序列,其周期为 N1和N2的最小公倍数8。 (2)sin(2k) 的数字角频率为 β1 = 2 rad;由于2π/ β1 = π为无理数,故f2(k) = sin(2k)为非周期序列 。
如:ε(t)是功率信号; tε(t)、 e t为非功率非能量信号;
δ(t)是无定义的非功率非能量信号。
第 25 页
5.一维信号和多维信号
一维信号: 只由一个自变量描述的信号,如语音信号。
多维信号: 由多个自变量描述的信号,如图像信号。 还有其他分类,如:
实信号与复信号 左边信号与右边信号 因果信号和反因果信号
③ S t ) 0 a ,t ( n π , n 1 , 2 , 3
④ sitd n tπ, sitd n tπ
⑤
0t
2
limSat)(0
t
t
⑥ sit)n sπ c itn ( π t
t
第 31 页
§1.3 信号的基本运算
两信号的相加和相乘 信号的时间变化
➢ 平移 ➢ 反转 ➢ 尺度变换 信号的微分和积分
第7页
通信系统 为传送消息而装设的全套技术设备
信信
信信
信
信信
离散周期信号举例2
例 判断下列序列是否为周期信号,若是,确定其周期。 (1)f1(k) = sin(3πk/4) + cos(0.5πk) (2)f2(k) = sin(2k)
解 (1)sin(3πk/4) 和cos(0.5πk)的数字角频率分别为 β1 = 3π/4 rad, β2 = 0.5π rad 由于2π/ β1 = 8/3, 2π/ β2 = 4为有理数,故它们的周期 分别为N1 = 8 , N2 = 4,故f1(k) 为周期序列,其周期为 N1和N2的最小公倍数8。 (2)sin(2k) 的数字角频率为 β1 = 2 rad;由于2π/ β1 = π为无理数,故f2(k) = sin(2k)为非周期序列 。
如:ε(t)是功率信号; tε(t)、 e t为非功率非能量信号;
δ(t)是无定义的非功率非能量信号。
第 25 页
5.一维信号和多维信号
一维信号: 只由一个自变量描述的信号,如语音信号。
多维信号: 由多个自变量描述的信号,如图像信号。 还有其他分类,如:
实信号与复信号 左边信号与右边信号 因果信号和反因果信号
③ S t ) 0 a ,t ( n π , n 1 , 2 , 3
④ sitd n tπ, sitd n tπ
⑤
0t
2
limSat)(0
t
t
⑥ sit)n sπ c itn ( π t
t
第 31 页
§1.3 信号的基本运算
两信号的相加和相乘 信号的时间变化
➢ 平移 ➢ 反转 ➢ 尺度变换 信号的微分和积分
第7页
通信系统 为传送消息而装设的全套技术设备
信信
信信
信
信信
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
26
频分/时分复用的结合
FDMA/TDMA信道分派(channel assignment)
信号与系统,©2014春 郭红星
2014/5/7 Lecture 11-傅里叶分析法在通信中的应用
27
频分/时分复用结合的应用
GSM的帧结构(frame structure)
信号与系统,©2014春 郭红星
②
从硬件看,频分复用的每一信号产生不同的载波, 从硬件看 频分复用的每 信号产生不同的载波 系统复杂;而时分复用则简单,易于大规模集成 ; , 时分复用不会产生信号间的串扰,而频分复用由 于有谐波失真,易于产生信号间的串扰,但时分 复用容易产生码间串扰
信号与系统,©2014春 郭红星
③
2014/5/7 Lecture 11-傅里叶分析法在通信中的应用
2
1 4
( 0 )
1
0
1 4
2 0
0
0
2 0
G ( )
2014/5/7 Lecture 11-傅里叶分析法在通信中的应用
19
m
m
信号与系统,©2014春 郭红星
抑制载波调幅方案的分析
要求精确的同步,即要求接收端解调器所加的 载波信号, 必须与发送端调制器中所使用的 载波信号严格地同频同相 锁相环 载波信号严格地同频同相-锁相环
复用
H 1 ( )
cos1t
H 2 ( )
HL
cos 2t
3
HL
x3 (t )
cos t
3
H 3 ( )
HL cos t
24
利用正弦幅度调制的频分多路复用和解复用的原理图
信号与系统,©2014春 郭红星
2014/5/7 Lecture 11-傅里叶分析法在通信中的应用
关键是有什么样的系统频率特性
H ( j) H ( j) e
2014/5/7 Lecture 11-傅里叶分析法在通信中的应用 信号与系统,©2014春 郭红星
j ( )
33
无失真传输的条件
e(t)
r(t)
system
时域: r (t ) ke(t t0 ) 频域:令 e(t ) E ( j ), ) E ( j ) R ( j )
30
视频信号失真测试
2014/5/7 Lecture 11-傅里叶分析法在通信中的应用
信号与系统,©2014春 郭红星
31
无失真传输的系统要求
从系统函数的意义上讲:输出仅是输 从系统函数的意义上讲 输出仅是输 入的线性放大和延时,则系统输出波 形无失真 (t ) r (t ) K (t t0 ) h(t )
15
§4.5 .5调制与解调
调制的功能和目的:
①
进行频率变换,以利于信号的发送 进行频率变换 以利于信号的发送 和信道中的传输 实现信道的复用 提高通信系统的抗干扰性能
② ③
调制方法: • 调幅 调幅-调频-调相 调频 调相
信号与系统,©2014春 郭红星
2014/5/7 Lecture 11-傅里叶分析法在通信中的应用
m
m
1 1 G0 ( ) G ( ) [G ( 2 0 ) G ( 2 0 )] 2 4
2014/5/7 Lecture 11-傅里叶分析法在通信中的应用 信号与系统,©2014春 郭红星
18
解调过程的频域分析
1 2
0
( 0 )
0 0
信号与系统,©2014春 郭红星
2014/5/7 Lecture 11-傅里叶分析法在通信中的应用
21
发送载波的调幅及其解调波形
2014/5/7 Lecture 11-傅里叶分析法在通信中的应用
信号与系统,©2014春 郭红星
22
§4.6 .6 频分复用与时分复用
多路复用:在同一个传输信道内,同时 多路复用 在同 个传输信道内 同时 传输多路不同信号的概念和方法。
a) ) b) c)
频分复用(FDMA) 时分复用(TDMA) 码分复用(CDMA)
2014/5/7 Lecture 11-傅里叶分析法在通信中的应用
信号与系统,©2014春 郭红星
23
频分复用
载频调制
x1 (t )
解复用
同步解调
x 2 (t )
理 cos1t y 想 y 信 cos 2t 道
m
0
信号与系统,©2014春 郭红星
0
17
2014/5/7 Lecture 11-傅里叶分析法在通信中的应用
同步解调
g (t ) cos 0t
相乘
g 0 (t )
低通
g (t )
cos 0t
g 0 (t ) [ g (t ) cos 0 t ] cos 0 t 1 g (t )(1 cos 2 0 t ) 2 1 1 g (t ) g (t ) cos 2 0 t 2 2
导 体
J r
a L
接 地
发射机(时 变电信号)
导体上电流的大小和相位 分布是不均匀的和时变的
信号与系统,©2014春 郭红星
14
讨论
声音信号能直接发送吗? 直接发送引起的问题
功率太大 速度太慢 天线太长 相互干扰太厉害 ……
信号与系统,©2014春 郭红星
2014/5/7 Lecture 11-傅里叶分析法在通信中的应用
见P192
否则
g 0 (t ) [ g (t ) cos 0t ] cos(0t ) 1 g (t )(cos cos( 20t )) 2 1 1 g (t ) cos g (t ) cos( 20t ) 2 2
2014/5/7 Lecture 11-傅里叶分析法在通信中的应用 信号与系统,©2014春 郭红星
信号与系统,©2014春 郭红星
4
音频的波形与频谱
2014/5/7 Lecture 10-信号通过系统的频域分析方法
信号与系统,©2014春 郭红星
5
音频的波形与频谱
2014/5/7 Lecture 10-信号通过系统的频域分析方法
信号与系统,©2014春 郭红星
6
音频的波形与频谱
2014/5/7 Lecture 10-信号通过系统的频域分析方法
16
载波抑制调制
相乘 调制 cos 0t
信号
g (t )
f (t ) g (t ) cos 0t
1 F() G() *[ ( 0 ) ( 0 )] 2 1 [G( 0 ) G( 0 )] 2
G ( )
载波 信号
F ( )
m
无失真传输
4.8节-Good、better、best
幅度失真和相位失真 线性失真和非线性失真 相位时延和群时延 信号与系统频域分析的应用
信号与系统,©2014春 郭红星
2014/5/7 Lecture 11-傅里叶分析法在通信中的应用
3
音频的波形与频谱
2014/5/7 Lecture 10-信号通过系统的频域分析方法
时变电流或 加速运动的 电荷向空间 辐射电磁波 研究设计产 生能满足各 种应用要求 的电磁波 作为信息的载体应用于 通信、广播、电视
V
I
电 磁 波
作为探求未知物质世界 作 物 的手段应用于雷达、导 航、遥测、遥感和遥控 能量存在的一种形式 能量存在的 种形式
电磁波辐射问题
2014/5/7 Lecture 11-傅里叶分析法在通信中的应用 信号与系统,©2014春 郭红星
t0
e ( t ) e
jt
dt
2014/5/7 Lecture 11-傅里叶分析法在通信中的应用
ke ( t t ) e 0
jt
dt
信号与系统,©2014春 郭红星
34
无失真传输的条件
令 x t t0 R ( j ) ke k
j t 0
信号与系统,©2014春 郭红星
7
Lena彩色图像
2014/5/7 Lecture 10-信号通过系统的频域分析方法
信号与系统,©2014春 郭红星
8
Lena灰度图像
2014/5/7 Lecture 10-信号通过系统的频域分析方法
信号与系统,©2014春 郭红星
9
Lena灰度图像的频谱图
2014/5/7 Lecture 10-信号通过系统的频域分析方法
2014/5/7 Lecture 11-傅里叶分析法在通信中的应用
28
码分复用
CDMA 系统的发送和接收
信号与系统,©2014春 郭红星
2014/5/7 Lecture 11-傅里叶分析法在通信中的应用
29
ቤተ መጻሕፍቲ ባይዱ
图像失真
正常
失真
2014/5/7 Lecture 11-傅里叶分析法在通信中的应用
信号与系统,©2014春 郭红星
信号与系统,©2014春 郭红星
10
Barbara灰度图像
2014/5/7 Lecture 11-傅里叶分析法在通信中的应用
信号与系统,©2014春 郭红星
11
Barbara灰度图像的频谱图
2014/5/7 Lecture 11-傅里叶分析法在通信中的应用
