第四章 线性方程组与向量组的线性相关性(第一讲)
向量组的线性相关性

则称向量 b 能由向量组 A 的线性表示.
引言
问题1:给定向量组 A,零向量是否可以由向量组 A 线性表 示?
问题2:如果零向量可以由向量组 A 线性表示,线性组合的 系数是否不全为零?
P.83 定理1 的结论:
a2l
b21
b22
aml bl1 bl 2
b1n
b2n
bln
b11 b12
b1n
则
c1,c2,
, cn a1, a2 ,
, al
b21
b22
b2n
bl1 bl 2
bln
结论:矩阵 C 的列向量组能由矩阵 A 的列向量组线性表示, B 为这一线性表示的系数矩阵.
当 a 不是零向量时,线性无关.
向量组 A:a1, a2, …, am (m ≥2) 线性相关,也就是向量组 A 中,至少有一个向量能由其余 m-1 个向量线性表示.
设有向量组 A:a1, a2, …, am 及 B:b1, b2, …, bl , 若向量组 B 能由向量组 A 线性表示,即
b1 k11a1 k21a2 b2 k12a1 k22a2
km1am km2am
bl k1la1 k2la2 kmlam
线性表示的 系数矩阵
k11 k12
b1 1 0 0
b2
0
1
0
b
b3
b1
0
b2
0
b3
1
bn 0 0 0
0
0
bn
0
1
b1 1 0 0
高等数学线性代数教材目录

高等数学线性代数教材目录第一章行列式1.1 行列式的引入1.2 二阶和三阶行列式的计算1.3 行列式的性质和性质的应用1.4 行列式的性质证明第二章矩阵和向量2.1 矩阵的概念和基本运算2.2 矩阵的转置和逆2.3 向量的线性相关性和线性无关性2.4 向量组的秩和极大线性无关组第三章矩阵的运算3.1 矩阵的加法和减法3.2 矩阵的数乘3.3 矩阵的乘法3.4 矩阵的特殊类型第四章线性方程组4.1 线性方程组的概念和解的分类4.2 齐次线性方程组和非齐次线性方程组的解 4.3 线性方程组的向量表示第五章向量空间5.1 向量空间的定义和例子5.2 向量子空间和子空间的概念5.3 向量空间的线性组合和生成子空间5.4 基和维数第六章矩阵的特征值和特征向量6.1 特征值和对角化6.2 特征多项式和特征方程6.3 相似矩阵和相似对角矩阵6.4 实对称矩阵的对角化第七章线性变换7.1 线性变换的概念和性质7.2 线性变换的矩阵表示7.3 线性变换的特征值和特征向量7.4 线性变换的相似、迹和行列式第八章内积空间8.1 内积的定义和性质8.2 欧几里得空间和具有内积的实向量空间8.3 向量的正交性和正交子空间8.4 施密特正交化方法第九章广义特征值问题9.1 广义特征值问题的引入9.2 广义特征值的计算9.3 广义特征值与相似变换9.4 对称矩阵的广义特征值问题与对角化第十章特殊矩阵的标准形式10.1 对称矩阵的对角化10.2 正定矩阵和正定二次型10.3 实对称矩阵的正交对角化10.4 复数矩阵的标准型这是《高等数学线性代数》教材的目录, 包含了十个章节,每个章节中有相应的小节来详细介绍相关内容。
这本教材综合了高等数学和线性代数的知识,旨在帮助读者掌握线性代数的基本概念、理论和方法,以及应用于实际问题的能力。
希望读者通过学习这本教材,能够系统地理解和应用线性代数的知识,为今后的学习和研究打下坚实的基础。
线性代数第四章

§3 向量组的秩
定义5 设有向量组 A, 如果在A中能选出 r个向量a1 , a 2 , , a r, 满足(1) 向量组A0 : a1 , a 2 , , a r 线性无关; ( 2) 向量组中 任意r 1个向量(如果A中有r 1个向量的话 )都线性相关 , 那么称向量组 A0 是向量组 A的一个最大线性无关向 量组(简 称最大无关组 ), 最大无关组所含向量个 数r称为向量组 A 的秩, 记为RA .
a T (a1 , a2 ,, an )
二、向量的运算
三、向量组
定义 由若干个同维数的列向 量(或同维数的行向量 )构成 的集合称为向量组 . a11 a12 a1n a21 a22 a 2 n A a a a m2 mn m1 A (1 , 2 , , n ) , 其中 j (a1 j , a 2 j , , a mj )T T T A ( , , , ) , 其中 1 2 m i ( a i 1 , a i 2 , , a in )
向量组B : b1 , b2 , , bl 能由向量组向量 A : a1 , a2 , , am 线性表示 R( A) R( A, B ) 有矩阵K, 使得B AK 矩阵方程 AX B有解
例( P 86例 3) 设n维 向 量 组 A : a1 , a 2 , , a m 构 成n m 矩 阵 A ( a1 , a 2 , , a m ),n阶 单 位 矩 阵 E (e1 , e 2 , , e n )的 列 向 量 称 为n维 单 位 坐 标 向 量 .证 明 : n 维 单 位 坐 标 向 量 e1 , e 2 , , e n能 由 向 量 组 A线 性 表 示 的 充 要 条 件 是 R( A) n.
第四章、向量组的线性相关性(文经)

15
说明:两个向量线性相关的几何意义是这两个向量共线,
三个向量线性相关的几何意义是这三个向量共面。
例1 判断向量组
其中, i是 n 阶单位矩阵的第 i 列 (i 1,2,, n) 解: 对任意的一组数k1,k2,…,kn都有
20
例3 判断向量组 1= ( 1, -1, 1)T, 2= ( 2, 0, -2)T, 3=( 2, -1, 0)T的线性相关性。
解:对矩阵 A 1, 2, 3 做初等行变换化为行阶梯型
1 2 2 1 A 1, 2, 3 = -1 0 -1 0 1 -2 0 0 2 2 0 2 1 0
答: 01 0 2 0 m 1 2 i 01 0 2 1 i 0 i 1 0 m
9
例如:
2 1 0 0 0 5 0 1 0 0 , 1 , 2 , 3 , 4 3 0 0 1 0 0 0 0 0 1
§2
向量组的线性相关性
定义1 对于 向量组 1 , 2 ,, m ,如果存在一组不 全为零的数 k1,k2,…,km,使 k11 k2 2 km m
则称该向量组线性相关 反之,如果只有在 k1=k2=…=km=0时上式才成立,就 称向量组 1 , 2 ,, m 线性无关。 向量组具有的线性相关或线性无关的性质称为向量 组的线性相关性 注意: 讨论向量组的线性相关性,一般是指该向量组要含有
西北工业大学《线性代数》课件-第四章 向量组的线性相关性

b
b2
bm
三、两向量相等
设向量
α (a1, a2 ,, ak )
β (b1, b2 ,, bl )
则
α β k l 且 ai bi
(i 1,2,, k)
四、零向量
分量都是0的向量称为零向量,记做 0,即
0 (0,0,,0).
五、向量的线性运算
⒈ 加法 设
α (a1, a2 ,, an )
2 2 2 ( )2
几何解释:三角形两边 之和大于第三边
α
β
α β
⒊ 夹角 设 与 是n维非零向量,则其夹角定义为
arccos [ , ]
arccos
a1b1 a2b2 anbn
a12 a22 an2 b12 b22 bn2
(0 )
定义的合理性:由不等式 (5) α, β α β
2
➢ 非零向量单位化
设 0 ,单位化向量
0
则有 0 1且 0与 同向.
九、小结
1. n维向量的定义; 2. n维向量的运算规律;
§4.2 向量组的线性相关性
一、线性相关与线性无关
1. 线性组合 定义4.6 设 ,1,2,,m均为n维向量,若有一组 数 k1, k2 ,, km ,使得
⑶ 数量积:a b a b cos
bx
(a
x
,
a
y
,
az
)
by bz
axbx a yby azbz
向量内积及 与模,夹角关系
矩阵乘积表示
可用作内积定义
⑷ 模: a aa
模的定义
三维向量全体构成的集合,称为三维向量空间.记做 R3
解析几何
向量
第四章 向量组的线性相关性总结

第四章 向量组的线性相关性§1 n 维向量概念一、向量的概念定义1 n 个有次序的数12,,,n a a a 所组成的数组称为n 维向量,这n 个数称为该向量的n 个分量,第i 个数i a 称为第i 个分量.注1分量全为实数的向量称为实向量.分量不全为实数的向量称为复向量. 注2 n 维向量可以写成一行的形式()12,,,n a a a a =,出可以写成一列的形式12n a a a a ⎛⎫⎪ ⎪= ⎪ ⎪⎝⎭,前者称为行向量,而后者称为列向量.行向量可看作是一个1n ⨯矩阵,故又称行矩阵;而列向量可看作一个1n ⨯矩阵,故又称作列矩阵.因此它们之间的运算就是矩阵之间的运算,从而符合矩阵运算的一切性质.向量之间的运算只涉及到线性运算和转置运算.为叙述方便,特别约定:在不特别声明时说到的向量均为列向量,行向量视为列向量的转置.注3 用小写黑体字母,,,a b αβ 等表示列向量,用,,,T T T T a b αβ表示行向量. 例1 设123(1,1,0),(0,1,1),(3,4,0)T T T v v v ===,求12v v -及12332v v v +-.解 12v v -(1,1,0)(0,1,1)T T =-(10,11,01)T =---(1,0,1)T =-12332v v v +-3(1,1,0)2(0,1,1)(3,4,0)T T T =+-(31203,31214,30210)T =⨯+⨯-⨯+⨯-⨯+⨯-(0,1,2)T =定义 设v 为n 维向量的集合,如果集合v 非空,且集合v 对于加法与数乘两种运算封闭(即若α∈v,β∈v ,有α+β∈v ;若α∈v, k ∈R ,有k α∈v ),称v 为向量空间。
§2 向量组的线性相关性一、向量组的线性组合 定义3 给定向量组A :12,,,m a a a ,对于任何一组实数12,,,m k k k ,称向量1122m m a a a k k k +++ 为向量组A 的一个线性组合,12,,,m k k k 称为这个线性组合的系数.定义4 给定向量组A :12,,,m a a a 和向量b ,若存在一组实数12,,,m λλλ,使得1122m m a a a b λλλ=+++则称向量b 是向量组A 的一个线性组合,或称向量b 可由向量组A 线性表示.注1任一个n 维向量12n a a a a ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭都可由n 维单位向量组12,,,n e e e 线性表示:1122n n a a a a e e e =+++ .注2向量b 可由向量组A :12,,,n a a a 线性表示(充要条件)⇔方程组1122n n a a a x x x b +++=有解m n A x b ⨯⇔=有解()(,)R A R A b ⇔=注3 由于线性方程组的解分为:无解,有唯一解,有无穷多解三种情况,所以向量β由向量12,,,n a a a 线性表示的情形也分为三种:不能线性表示,唯一线性表示,无穷多种线性表示,且线性表示式中的系数就是对应线性方程组的解。
《向量组线性相关性》课件

示。
向量组线性相关性的定义
向量组线性相关性
如果存在不全为零的标量$k_1, k_2, ldots, k_n$,使得$sum_{i=1}^{n} k_i mathbf{a}_i = mathbf{0}$,则称向量组$mathbf{a}_1, mathbf{a}_2, ldots, mathbf{a}_n$线性相关。
详细描述:利用向量组线性相关性,可以对矩阵进行分 解,如奇异值分解、QR分解等,为解决实际问题提供 有效工具。
详细描述:通过向量组线性相关性,可以进一步研究矩 阵的特征值和特征向量,从而深入了解矩阵的性质。
向量组线性相关性在优化理论中的应用
总结词
约束优化问题
详细描述
在优化理论中,向量组线性相关性可以用于描述和解决 一系列约束优化问题,如线性规划、二次规划等。
THANKS
[ 感谢观看 ]
判定定理
如果存在不全为零的标量$k_1, k_2, ldots, k_n$,使得 $sum_{i=1}^{n} k_i mathbf{a}_i = mathbf{0}$,则向量组 $mathbf{a}_1, mathbf{a}_2, ldots, mathbf{a}_n$线性相关 。
反例
如果对于任何不全为零的标量$k_1, k_2, ldots, k_n$,都有 $sum_{i=1}^{n} k_i mathbf{a}_i neq mathbf{0}$,则向量 组$mathbf{a}_1, mathbf{a}_2, ldots, mathbf{a}_n$线性无 关。
向量组的线性组合与线性相关性

线性组合的几何意义
几何解释
在几何上,线性组合可以表示为向量 的平移和伸缩变换。通过改变标量的 值,可以得到不同的线性组合结果, 从而描绘出不同的几何图形。
应用
线性组合在解析几何、计算机图形学 等领域有广泛应用,如通过线性组合 表示平面上的点、线、面等几何对象 。
PART 03
线性相关与线性无关
REPORTING
性质
线性组合满足交换律、结合律、分配律等基本的数学运算规 则。
线性组合的几何意义
几何解释
在几何上,线性组合可以表示为向量 的平移和伸缩变换。通过改变标量的 值,可以得到不同的线性组合结果, 从而描绘出不同的几何图形。
应用
线性组合在解析几何、计算机图形学 等领域有广泛应用,如通过线性组合 表示平面上的点、线、面等几何对象 。
PART 01
引言
REPORTING
WENKU DESIGN
PART 01
引言
REPORTING
WENKU DESIGN
目的和背景
研究向量组的线性组合与线性相关性的目的
揭示向量组内部元素间的依赖关系,为向量空间的理论研究和实际应用提供基础 。
线性组合与线性相关性的重要性
在数据分析、机器学习、图像处理等领域中,向量组的线性组合与线性相关性是 理解数据结构和特征提取的关键。
关;否则,线性无关。
行列式法
对于$n$个$n$维向量,可以 构造一个$n$阶行列式。如果 行列式为零,则向量组线性 相关;否则,线性无关。
线性相关与线性无关的判断方法
观察法
通过观察向量组是否包含零 向量或是否共线/共面来判断 其线性相关性。包含零向量 或共线/共面的向量组必定线
性相关。
第4章向量组的线性相关性

[定义]若向量组A与B能相互线性表示 则称这两个向量组等价。
➢矩阵等价与向量组等价的关系
若矩阵A与B 行等价 则这两个矩阵的行向量组等价 若矩阵A与B 列等价 则这两个矩阵的列向量组等价
➢向量组等价的判据 [定理4-2]推论:向量组 A a1, a2, , an 与向量组 B : b1,b2, ,bm 等价的充要条件是R(A)R(B)=R(A B) 。
分量全为实数的向量称为实向量, 例如 (1,2,3,,n)
分量全为复数的向量称为复向量。 例如 (1 2i,2 3i,,n (n 1)i)
第四章 向量组的线性相关性
2、向量的表示
n维向量写成一列,称为列向量(即列矩阵),
通常用 a, b,, 等表示,如:
a1
a
a2
an
n维向量写成一行,称为行向量(即行矩阵),
1 1 1 1
1 0 3 2
~ ~ B
1 2
2 1
1 4
0
3
r
0
1
2
1
r
0
1
2
1
0 0 0 0
0 0 0 0
2
3
0
1
0
0
0
0
0
0
0
0
R(A) R(B) 2
向量b能由向量组 a1, a2, a3 线性表示。
第四章 向量组的线性相关性
由B最简形可得线性方程组 (a1,a2,a3)x b即Ax b 解为
(a11 a12 a1n)
(a21 a22 a2n)
(am1 am2 amn)
第四章 向量组的线性相关性
2、向量组的线性组合
第四章线性方程组与向量组的线性相关性

4 x1 6 x2 2x3 2
2
x1
x2
x3 1
1 1 1 2
1 1 1 2
➢
解
( A, b)
4
6
2
2
22rr13rr32
0
4
4
4
2 1 1 1
0 3 1 3
r2 (
1)
4
1 0
1 1
1 2
1 0 0 1
1
1
3rr22 rr31 0
1
1
1
0 3 1 3
➢ 记:A (aij )mn, x ( x1, x2, , xn )T , b ( b1, b2, , bm )T, 称A为系数矩阵,x为未知列,b为常数列, 则线性方程组可写成矩阵形式 Ax=b
§1 消元法与线性方程组的相容性
➢ 设n元线性方程组 Ax=b,若A按列分块为 A=(1, 2, … ,n),则方程组可写成向量形式
线性代数 第四章
第四章 线性方程组与向量组的线性相关性
➢ 本章教学内容 ➢ §1 消元法与线性方程组的相容性 ➢ §2 向量组的线性相关性 ➢ §3 向量组的秩 矩阵的行秩与列秩 ➢ §4 线性方程组解的结构
§1 消元法与线性方程组的相容性
➢ 本节教学内容 ➢ 1.线性方程组的概念 ➢ 2. Cramer(克莱姆)法则 ➢ 3.用消元法解线性方程组
x3 1
11 2
x1 1, x2 1, x3 0. 2 1 2
A 4 6 2 8 0, D1 2 6 2 8,
2 1 1
1 1 1
1 2 2 D2 4 2 2 8,
2 1 1
1 1 2 D3 4 6 2 0,
第四章 线性方程组 一、主要内容

性线性方程组 A' AX = A' B 必有解.
5.证明:方程 Bn×s X = b 有解的充分必要条件是从 B'Y = 0 一定能推出 b'Y = 0 .
6.设齐次线性方程组
a11 x1 + a12 x2 + L + a1n xn = 0, a21 x1 + a22 x2 + L + a2n xn = 0, LLLLLLLLLL LL an1 x1 + an2 x2 + L + ann xn = 0
二、训练题 一、填空题
1.线性方程组 AX = b 无解,且 r( A) = 3, 则 r( AMb) = ____ .
⎧
2.若方程组
⎪ ⎨
x1 + 2x2 − x3 = λ − 1 3x2 − x3 = λ − 2
⎪⎩λx2 − x3 = λ2 − 6λ + 10
有无穷多解,则 λ = ____ .
秩为( )。
二、判断说明题
1.齐次线性方程组 ⎪⎨⎧λxx11
+ x2 + λ2 x3 = 0 + λx2 + x3 = 0 的系数矩阵为
A,若存在三阶矩阵 B
≠
0. 使
⎪ ⎩
x1 + x2
+ λx3
=0
得 AB = 0, 则 λ = 1, 且 B = 0.
2.非齐次线性方程组 AX = b 有解,若其解不唯一,则必有无穷多个解.
多组解;
(3) 若 r( A) ≠ r( A) , 则该方程组无解. 2、齐次线性方程组解的结构
定理 4.5-2 设有齐次线性方程组
线性代数考研讲义完整版(完整资料).doc

【最新整理,下载后即可编辑】考研数学线性代数讲义目录第一讲基本概念线性方程组矩阵与向量初等变换和阶梯形矩阵线性方程组的矩阵消元法第二讲行列式完全展开式化零降阶法其它性质克莱姆法则第三讲矩阵乘法乘积矩阵的列向量和行向量矩阵分解矩阵方程逆矩阵伴随矩阵第四讲向量组线性表示向量组的线性相关性向量组的极大无关组和秩矩阵的秩第五讲方程组解的性质解的情况的判别基础解系和通解第六讲特征向量与特征值相似与对角化特征向量与特征值—概念,计算与应用相似对角化—判断与实现附录一内积正交矩阵施密特正交化实对称矩阵的对角化第七讲二次型二次型及其矩阵可逆线性变量替换实对称矩阵的合同标准化和规范化惯性指数正定二次型与正定矩阵附录二向量空间及其子空间附录三两个线性方程组的解集的关系附录四06,07年考题第一讲 基本概念1.线性方程组的基本概念线性方程组的一般形式为: a 11x 1+a 12x 2+…+a 1n x n =b 1,a 21x 1+a 22x 2+…+a 2n x n =b 2,… … … …a m1x 1+a m2x 2+…+a mn x n =b m ,其中未知数的个数n 和方程式的个数m 不必相等.线性方程组的解是一个n 维向量(k 1,k 2, …,k n )(称为解向量),它满足:当每个方程中的未知数x i 都用k i 替代时都成为等式.线性方程组的解的情况有三种:无解,唯一解,无穷多解.对线性方程组讨论的主要问题两个:(1)判断解的情况.(2)求解,特别是在有无穷多接时求通解.b 1=b 2=…=b m =0的线性方程组称为齐次线性方程组.n 维零向量总是齐次线性方程组的解,称为零解.因此齐次线性方程组解的情况只有两种:唯一解(即只要零解)和无穷多解(即有非零解).把一个非齐次线性方程组的每个方程的常数项都换成0,所得到的齐次线性方程组称为原方程组的导出齐次线性方程组,简称导出组.2.矩阵和向量(1)基本概念矩阵和向量都是描写事物形态的数量形式的发展.由m ⨯n 个数排列成的一个m 行n 列的表格,两边界以圆括号或方括号,就成为一个m ⨯n 型矩阵.例如2 -1 0 11 1 1 0 22 5 4 -2 93 3 3 -1 8是一个4⨯5矩阵.对于上面的线性方程组,称矩阵a 11 a 12 … a 1n a 11 a 12 … a 1nb 1A = a 21 a 22 … a 2n 和(A |)= a 21 a 22 … a 2n b 2… … … … … … …a m1 a m2 … a mn a m1 a m2 … a mnb m为其系数矩阵和增广矩阵. 增广矩阵体现了方程组的全部信息,而齐次方程组只用系数矩阵就体现其全部信息.一个矩阵中的数称为它的元素,位于第i 行第j 列的数称为(i,j)位元素.元素全为0的矩阵称为零矩阵,通常就记作0.两个矩阵A 和B 相等(记作A =B ),是指它的行数相等,列数也相等(即它们的类型相同),并且对应的元素都相等.由n 个数构成的有序数组称为一个n 维向量,称这些数为它的分量.书写中可用矩阵的形式来表示向量,例如分量依次是a 1,a 2,⋯ ,a n 的向量可表示成a 1(a 1,a 2,⋯ ,a n )或 a 2 ,┆a n请注意,作为向量它们并没有区别,但是作为矩阵,它们不一样(左边是1⨯n 矩阵,右边是n ⨯1矩阵).习惯上把它们分别称为行向量和列向量.(请注意与下面规定的矩阵的行向量和列向量概念的区别.)一个m ⨯n 的矩阵的每一行是一个n 维向量,称为它的行向量; 每一列是一个m 维向量, 称为它的列向量.常常用矩阵的列向量组来写出矩阵,例如当矩阵A 的列向量组为1,2,⋯ ,n 时(它们都是表示为列的形式!)可记A =(1,2,⋯ ,n ).矩阵的许多概念也可对向量来规定,如元素全为0的向量称为零向量,通常也记作0.两个向量和相等(记作=),是指它的维数相等,并且对应的分量都相等.(2) 线性运算和转置线性运算是矩阵和向量所共有的,下面以矩阵为例来说明.加(减)法:两个m ⨯n 的矩阵A 和B 可以相加(减),得到的和(差)仍是m ⨯n 矩阵,记作A +B (A -B ),法则为对应元素相加(减).数乘: 一个m ⨯n 的矩阵A 与一个数c 可以相乘,乘积仍为m ⨯n 的矩阵,记作c A ,法则为A 的每个元素乘c.这两种运算统称为线性运算,它们满足以下规律:① 加法交换律: A +B =B +A .② 加法结合律: (A +B )+C =A +(B +C ).③ 加乘分配律: c(A +B )=c A +c B .(c+d)A =c A +d A .④ 数乘结合律: c(d)A =(cd)A .⑤ c A =0⇔ c=0 或A =0.转置:把一个m ⨯n 的矩阵A 行和列互换,得到的n ⨯m 的矩阵称为A 的转置,记作A T (或A ').有以下规律:① (A T )T = A .② (A +B )T =A T +B T .③ (c A )T =c A T .转置是矩阵所特有的运算,如把转置的符号用在向量上,就意味着把这个向量看作矩阵了.当是列向量时, T 表示行向量,当是行向量时, T 表示列向量.向量组的线性组合:设1,2,…,s 是一组n 维向量, c 1,c 2,…,c s 是一组数,则称c 11+c 22+…+c s s 为1,2,…,s 的(以c 1,c 2,…,c s 为系数的)线性组合.n 维向量组的线性组合也是n 维向量.(3) n 阶矩阵与几个特殊矩阵行数和列数相等的矩阵称为方阵,行列数都为n 的矩阵也常常叫做n 阶矩阵.把n 阶矩阵的从左上到右下的对角线称为它对角线.(其上的元素行号与列号相等.)下面列出几类常用的n 阶矩阵,它们都是考试大纲中要求掌握的.对角矩阵: 对角线外的的元素都为0的n 阶矩阵.单位矩阵: 对角线上的的元素都为1的对角矩阵,记作E (或I ).数量矩阵: 对角线上的的元素都等于一个常数c 的对角矩阵,它就是c E.上三角矩阵: 对角线下的的元素都为0的n阶矩阵.下三角矩阵: 对角线上的的元素都为0的n阶矩阵.对称矩阵:满足A T=A矩阵.也就是对任何i,j,(i,j)位的元素和(j,i)位的元素总是相等的n阶矩阵.(反对称矩阵:满足A T=-A矩阵.也就是对任何i,j,(i,j)位的元素和(j ,i)位的元素之和总等于0的n阶矩阵.反对称矩阵对角线上的元素一定都是0.)3. 矩阵的初等变换和阶梯形矩阵矩阵有以下三种初等行变换:①交换两行的位置.②用一个非0的常数乘某一行的各元素.③把某一行的倍数加到另一行上.(称这类变换为倍加变换)类似地, 矩阵还有三种初等列变换,大家可以模仿着写出它们,这里省略了. 初等行变换与初等列变换统称初等变换.阶梯形矩阵:一个矩阵称为阶梯形矩阵,如果满足:①如果它有零行,则都出现在下面.②如果它有非零行,则每个非零行的第一个非0元素所在的列号自上而下严格单调递增.把阶梯形矩阵的每个非零行的第一个非0元素所在的位置称为台角.简单阶梯形矩阵:是特殊的阶梯形矩阵,特点为:③台角位置的元素为1.④并且其正上方的元素都为0.每个矩阵都可以用初等行变换化为阶梯形矩阵和简单阶梯形矩阵.这种运算是在线性代数的各类计算题中频繁运用的基本运算,必须十分熟练.请注意: 1.一个矩阵用初等行变换化得的阶梯形矩阵并不是唯一的,但是其非零行数和台角位置是确定的.2. 一个矩阵用初等行变换化得的简单阶梯形矩阵是唯一的.4. 线性方程组的矩阵消元法线性方程组的基本方法即中学课程中的消元法:用同解变换把方程组化为阶梯形方程组(即增广矩阵为阶梯形矩阵的方程组).线性方程组的同解变换有三种:①交换两个方程的上下位置.②用一个非0的常数乘某个方程.③把某个方程的倍数加到另一个方程上.以上变换反映在增广矩阵上就是三种初等行变换.线性方程组求解的基本方法是消元法,用增广矩阵或系数矩阵来进行,称为矩阵消元法. 对非齐次线性方程组步骤如下:(1)写出方程组的增广矩阵(A|),用初等行变换把它化为阶梯形矩阵(B|γ).(2)用(B|γ)判别解的情况:如果最下面的非零行为(0,0, ⋯,0|d),则无解,否则有解.有解时看非零行数r(r不会大于未知数个数n),r=n时唯一解;r<n时无穷多解.(推论:当方程的个数m<n时,不可能唯一解.)(3)有唯一解时求解的初等变换法:去掉(B|γ)的零行,得到一个n×(n+1)矩阵(B0|γ0),并用初等行变换把它化为简单阶梯形矩阵(E|η),则η就是解.对齐次线性方程组:(1)写出方程组的系数矩阵A,用初等行变换把它化为阶梯形矩阵B.(2)用B判别解的情况:非零行数r=n时只有零解;r<n时有非零解(求解方法在第五章讲). (推论:当方程的个数m<n时,有非零解.)讨论题1.设A是n阶矩阵,则(A) A是上三角矩阵⇒A是阶梯形矩阵.(B) A是上三角矩阵⇐A是阶梯形矩阵.(C) A是上三角矩阵⇔A是阶梯形矩阵.(D) A是上三角矩阵与A是阶梯形矩阵没有直接的因果关系.2.下列命题中哪几个成立?(1) 如果A是阶梯形矩阵,则A去掉任何一行还是是阶梯形矩阵.(2) 如果A是阶梯形矩阵,则A去掉任何一列还是是阶梯形矩阵.(3) 如果(A|B)是阶梯形矩阵,则A也是阶梯形矩阵.(4) 如果(A|B)是阶梯形矩阵,则B也是阶梯形矩阵.(5) 如果 A 是阶梯形矩阵,则A和B都是阶梯形矩阵.B第二讲行列式一.概念复习1. 形式和意义形式:用n 2个数排列成的一个n 行n 列的表格,两边界以竖线,就成为一个n 阶行列式:a 11 a 12 … a 1na 21 a 22 … a 2n… … … .a n1 a n2 … a nn 如果行列式的列向量组为1,2, … ,n ,则此行列式可表示为|1,2, … ,n |.意义:是一个算式,把这n 2个元素按照一定的法则进行运算,得到的数值称为这个行列式的值.请注意行列式和矩阵在形式上和意义上的区别.当两个行列式的值相等时,就可以在它们之间写等号! (不必形式一样,甚至阶数可不同.)每个n 阶矩阵A 对应一个n 阶行列式,记作|A |.行列式这一讲的的核心问题是值的计算,以及判断一个行列式的值是否为0.2. 定义(完全展开式)2阶和3阶行列式的计算公式:a 11 a 12a 21 a 22 = a 11a 22-a 12a 21 .a 11 a 12 a 13a 21 a 22 a 23 = a 11a 22a 33+ a 12a 23a 31+ a 13a 21a 32-a 13a 22a 31- a 11a 23a 32-a 12a 21a 33.a 31 a 32 a 33一般地,一个n 阶行列式a 11 a 12 … a 1na 21 a 22 … a 2n… … …a n1 a n2 … a nn 的值是许多项的代数和,每一项都是取自不同行,不同列的n 个元素的乘积,其一般形式为:n nj j j a a a 2121,这里把相乘的n 个元素按照行标的大小顺序排列,它们的列标j 1j 2…j n 构成1,2, …,n 的一个全排列(称为一个n 元排列),共有n!个n 元排列,每个n 元排列对应一项,因此共有n!个项.所谓代数和是在求总和时每项先要乘+1或-1.规定(j 1j 2…j n )为全排列j 1j 2…j n 的逆序数(意义见下面),则项nnj j j a a a 2121所乘的是.)1()(21n j j j τ-全排列的逆序数即小数排列在大数右面的现象出现的个数. 逆序数可如下计算:标出每个数右面比它小的数的个数,它们的和就是逆序数.例如求436512的逆序数: 0023********,(436512)=3+2+3+2+0+0=10.至此我们可以写出n 阶行列式的值:a 11 a 12 … a 1na 21 a 22 … a 2n =.)1(21212121)(nn n nj j j j j j j j j a a a τ-∑ … … …a n1 a n2 … a nn这里∑nj j j 21表示对所有n 元排列求和.称此式为n 阶行列式的完全展开式.用完全展开式求行列式的值一般来说工作量很大.只在有大量元素为0,使得只有少数项不为0时,才可能用它作行列式的计算.例如对角行列式,上(下)三角行列式的值就等于主对角线上的元素的乘积,因为其它项都为0.2. 化零降阶法把n 阶行列式的第i 行和第j 列划去后所得到的n-1阶行列式称为(i,j)位元素a ij 的余子式,记作M ij .称A ij =(-1)i+j M ij 为元素a ij 的代数余子式.定理(对某一行或列的展开)行列式的值等于该行(列)的各元素与其代数余子式乘积之和.命题 第三类初等变换(倍加变换)不改变行列式的值.化零降阶法 用命题把行列式的某一行或列化到只有一个元素不为0,再用定理.于是化为计算一个低1阶的行列式.化零降阶法是实际计算行列式的主要方法,因此应该熟练掌握.3.其它性质行列式还有以下性质:① 把行列式转置值不变,即|A T |=|A | .② 某一行(列)的公因子可提出.于是, |c A |=c n |A |.③ 对一行或一列可分解,即如果某个行(列)向量则原行列式等于两个行列式之和,这两个行列式分别是把原行列式的该行(列)向量换为或所得到的行列式.例如 |,1+2|=|,1|+|,2|.④ 把两个行(列)向量交换, 行列式的值变号.⑤ 如果一个行(列)向量是另一个行(列)向量的倍数,则行列式的值为0.⑥ 某一行(列)的各元素与另一行(列)的对应元素的代数余子式乘积之和=0.⑦ 如果A 与B 都是方阵(不必同阶),则A * = A O =|A ||B |.O B * B范德蒙行列式:形如1 1 1 (1)a 1 a 2 a 3 … a na 12 a 22 a 32 … a n 2… … … …a 1n-i a 2n-i a 3n-i … a n n-i的行列式(或其转置).它由a 1,a 2 ,a 3,…,a n 所决定,它的值等于).(i j ji a a -∏< 因此范德蒙行列式不等于0⇔ a 1,a 2 ,a 3,…,a n 两两不同.对于元素有规律的行列式(包括n 阶行列式),常常可利用性质简化计算,例如直接化为三角行列式等.4.克莱姆法则克莱姆法则 应用在线性方程组的方程个数等于未知数个数n (即系数矩阵为n 阶矩阵)的情形.此时,如果它的系数矩阵的行列式的值不等于0,则方程组有唯一解,这个解为(D 1/D, D 2/D,⋯,D n /D),这里D 是系数行列式的值, D i 是把系数行列式的第i 个列向量换成常数列向量所得到的行列式的值.说明与改进:按法则给的公式求解计算量太大,没有实用价值.因此法则的主要意义在理论上,用在对解的唯一性的判断,而在这方面法则不够. 法则的改进:系数行列式不等于0是唯一解的充分必要条件.实际上求解可用初等变换法:对增广矩阵(A |)作初等行变换,使得A 变为单位矩阵:(A |)→(E |η),η就是解.用在齐次方程组上 :如果齐次方程组的系数矩阵A 是方阵,则它只有零解的充分必要条件是|A |≠0.二. 典型例题1.利用性质计算元素有规律的行列式例1① 2 a a a a ②1+x 1 1 1③1+a 1 1 1a 2 a a a 1 1+x 1 12 2+a 2 2a a 2 a a . 1 1 1+x 1 .3 3 3+a 3 .a a a 2 a 1 1 1 1+x4 4 4 4+aa a a a 2例2 1 2 3 4 52 3 4 5 13 4 5 1 2 .4 5 1 2 35 1 2 3 4例31+x1 1 111 1 .1 1+x211 1 1+x31 1 1 1+x4例4 a 0 b c0 a c b .b c a 0c b 0 a例5 1-a a 0 0 0-1 1-a a 0 00 -1 1-a a 0 . (96四)0 0 -1 1-a a0 0 0 -1 1-a2. 测试概念与性质的题例6 x3-3 1 -3 2x+2多项式f(x)= -7 5 -2x 1 ,求f(x)的次数和最高次项的系数.X+3 -1 3 3x 2-29 x 3 6 -6例7 求 x-3 a -1 4f(x)= 5 x-8 0 –2 的x 4和x 3的系数.0 b x+1 12 2 1 x例8 设4阶矩阵A =(, 1, 2 ,3),B =(, 1, 2 ,3),|A |=2, |B |=3 ,求|A +B | .例9 a b c d已知行列式 x -1 -y z+1 的代数余子式A 11=-9,A 12=3,A 13=-1,A 14=3,求x,y,z.1 -z x+3 yy-2 x+1 0 z+3例10 求行列式 3 0 4 0 的第四行各元素的余子式的和.(01)2 2 2 20 -7 0 05 3 -2 23.几个n 阶行列式两类爪形行列式及其值:例11 a 1 a 2 a 3 … a n-1 a nb 1c 2 0 … 0 0证明 0 b 2 c 3 0 0 =11111(1)n i i i i n i b b a c c --+=-∑.… … … …0 0 0 … b n-1 c n提示: 只用对第1行展开(M 1i 都可直接求出).例12 a 0 a 1 a 2 … a n-1 a nb 1c 1 0 … 0 0证明 b 2 0 c 2 … 0 0 =011111n n i i i i i n i i a c c c a b c c -+==-∑∏.… … … …b n … 0c n提示: 只用对第1行展开(M 1i 都可直接求出).另一个常见的n 阶行列式:例13 证明a+b b 0 … 0 0a a+b b … 0 0… … … … = 110n n n n i i i a b a b a b ++-=-=-∑(当a ≠b 时).0 0 0 … a+b b0 0 0 a a+b提示:把第j 列(行)的(-1)j-1倍加到第1列(行)上(j=2,…,n),再对第1列(行)展开.4.关于克莱姆法则的题例14设有方程组x 1+x 2+x 3=a+b+c,ax 1+bx 2+cx 3=a 2+b 2+c 2,bcx 1+acx 2+abx 3=3abc.(1)证明此方程组有唯一解的充分必要条件为a,b,c 两两不等.(2)在此情况求解.参考答案例1 ①(2+4a)(2-a)4.② x 3(x+4). ③ a 3(a+10).例2 1875.例3 x 1x 2x 3x 4+x 2x 3x 4+x 1x 3x 4+x 1x 2x 4+x 1x 2x 3.例4 (a+b+c)(a+b-c)(a-b+c)(a-b-c).例5 1-a+a 2-a 3+a 4-a 5.例6 9,-6例7 1,-10.例8 40.例9 x=0,y=3,z=-1.例10 -28.例14 x 1=a,x 2=b,x 3=c..第三讲 矩阵一.概念复习1. 矩阵乘法的定义和性质定义2.1 当矩阵A 的列数和B 的行数相等时,和A 和B 可以相乘,乘积记作AB . AB 的行数和A 相等,列数和B 相等. AB 的(i,j)位元素等于A 的第i 个行向量和B 的第j 个列向量(维数相同)对应分量乘积之和.设 a 11 a 12 … a 1n b 11 b 12 … b 1s c 11c 12 … c 1sA = a 21 a 22 … a 2nB = b 21 b 22 … b 2sC =AB =c 21 c 22 … c 2s… … … … … …… … …a m1 a m2 … a mn ,b n1 b n2 … b ns ,c m1c m2 … c ms ,则c ij =a i1b 1j +a i2b 2j +…+a in b nj .矩阵的乘法在规则上与数的乘法有不同:① 矩阵乘法有条件.② 矩阵乘法无交换律.③ 矩阵乘法无消去律,即一般地由AB =0推不出A =0或B =0.由AB =AC 和A ≠0推不出B =C .(无左消去律)由BA =CA 和A ≠0推不出B =C . (无右消去律)请注意不要犯一种常见的错误:把数的乘法的性质简单地搬用到矩阵乘法中来.矩阵乘法适合以下法则:① 加乘分配律 A (B +C )= AB +AC , (A +B )C =AC +BC .② 数乘性质 (c A )B =c(AB ).③ 结合律 (AB )C = A (BC ).④ (AB )T =B T A T .2. n 阶矩阵的方幂和多项式任何两个n 阶矩阵A 和B 都可以相乘,乘积AB 仍是n 阶矩阵.并且有行列式性质:|AB |=|A ||B |.如果AB =BA ,则说A 和B 可交换.方幂 设k 是正整数, n 阶矩阵A 的k 次方幂A k 即k 个A的连乘积.规定A 0=E .显然A 的任何两个方幂都是可交换的,并且方幂运算符合指数法则:① A k A h = A k+h .② (A k )h = A kh .但是一般地(AB )k 和A k B k 不一定相等!n 阶矩阵的多项式设f(x)=a m x m +a m-1x m-1+…+a 1x+a 0,对n 阶矩阵A 规定f(A )=a m A m +a m-1A m-1+…+ a 1A +a 0E .称为A 的一个多项式.请特别注意在常数项上加单位矩阵E .乘法公式 一般地,由于交换性的障碍,小代数中的数的因式分解和乘法公式对于n 阶矩阵的不再成立.但是如果公式中所出现的n 阶矩阵互相都是乘法交换的,则乘法公式成立.例如当A 和B 可交换时,有:(A ±B )2=A 2±2AB +B 2;A 2-B 2=(A +B )(A -B )=(A +B )(A -B ).二项展开式成立: B AC B A -=∑=+1)(等等.前面两式成立还是A 和B 可交换的充分必要条件.同一个n 阶矩阵的两个多项式总是可交换的. 一个n 阶矩阵的多项式可以因式分解.3. 分块法则矩阵乘法的分块法则是简化矩阵乘法的一种方法.对两个可以相乘的矩阵A 和B ,可以先用纵横线把它们切割成小矩阵(一切A的纵向切割和B 的横向切割一致!),再用它们来作乘法.(1)两种常见的矩阵乘法的分块法则A 11 A 12B 11 B 12 = A 11B 11+A 12B 21 A 11B 12+A 12B 22A 21 A 22B 21 B 22 A 21B 11+A 22B 21 A 21B 12+A 22B 22要求A ij 的列数B jk 和的行数相等.准对角矩阵的乘法:形如A 1 0 0A = 0 A 2 0… … …0 0 … A n的矩阵称为准对角矩阵,其中A 1,A 2,…,A k 都是方阵.两个准对角矩阵A 1 0 ... 0 B 1 0 0A = 0 A 2 ... 0 , B = 0 B 2 0… … … … … …0 0 … A k 0 0 … B k如果类型相同,即A i 和B i 阶数相等,则A 1B 1 0 0AB = 0 A 2B 2 … 0 .… … …0 0 … A k B k(2)乘积矩阵的列向量组和行向量组设A 是m ⨯n 矩阵B 是n ⨯s 矩阵. A 的列向量组为1,2,…,n ,B的列向量组为1,2,…,s , AB 的列向量组为1,2,…,s ,则根据矩阵乘法的定义容易看出(也是分块法则的特殊情形):① AB 的每个列向量为:i =A i ,i=1,2,…,s.即A (1,2,…,s )= (A 1,A 2,…,A s ).② =(b 1,b 2,…,b n )T ,则A = b 11+b 22+…+b n n .应用这两个性质可以得到:如果i =(b 1i ,b 2i ,…,b ni )T ,则i =A I =b 1i 1+b 2i 2+…+b ni n .即:乘积矩阵AB 的第i 个列向量i 是A 的列向量组1,2,…,n 的线性组合,组合系数就是B 的第i 个列向量i的各分量.类似地, 乘积矩阵AB 的第i 个行向量是B 的行向量组的线性组合,组合系数就是A 的第i 个行向量的各分量.以上规律在一般教材都没有强调,但只要对矩阵乘法稍加分析就不难得出.它们无论在理论上和计算中都是很有用的.(1) 当两个矩阵中,有一个的数字很简单时,直接利用以上规律写出乘积矩阵的各个列向量或行向量,从而提高了计算的速度.(2) 利用以上规律容易得到下面几个简单推论:用对角矩阵从左侧乘一个矩阵,相当于用的对角线上的各元素依次乘此矩阵的各行向量; 用对角矩阵从右侧乘一个矩阵,相当于用的对角线上的各元素依次乘此矩阵的各列向量.数量矩阵k E乘一个矩阵相当于用k乘此矩阵;单位矩阵乘一个矩阵仍等于该矩阵.两个同阶对角矩阵的相乘只用把对角线上的对应元素相乘.求对角矩阵的方幂只需把对角线上的每个元素作同次方幂.(3) 矩阵分解:当一个矩阵C的每个列向量都是另一个A的列向量组的线性组合时,可以构造一个矩阵B,使得C=AB.例如设A=(α,β,γ), C=(α+2β-γ,3α-β+γ,α+2γ),令1 3 1B= 2 -1 0 ,则C=AB.-1 1 2(4) 初等矩阵及其在乘法中的作用对单位矩阵E作一次初等(行或列)变换,所得到的矩阵称为初等矩阵.有三类初等矩阵:E(i,j):交换E的i,j两行(或列)所得到的矩阵.E(i(c)):用非0数c乘E的第i行(或列)所得到的矩阵.也就是把E的对角线上的第i个元素改为c.E(i,j(c))(i≠j):把E的第j行的c倍加到第i行上(或把第i列的c 倍加到第j列上)所得到的矩阵, 也就是把E的(i,j)位的元素改为c.命题对矩阵作一次初等行(列)变换相当于用一个相应的初等矩阵从左(右)乘它.4. 矩阵方程和可逆矩阵(伴随矩阵)(1) 矩阵方程矩阵不能规定除法,乘法的逆运算是解下面两种基本形式的矩阵方程:(I) AX=B.(II) XA=B.这里假定A是行列式不为0的n阶矩阵,在此条件下,这两个方程的解都是存在并且唯一的.(否则解的情况比较复杂.)当B只有一列时,(I)就是一个线性方程组.由克莱姆法则知它有唯一解.如果B有s列,设B=(1,2,…,s),则X也应该有s 列,记X=(X1,X2,…,X s),则有AX i=i,i=1,2,…,s,这是s个线性方程组.由克莱姆法则,它们都有唯一解,从而AX=B有唯一解.这些方程组系数矩阵都是A,可同时求解,即得(I)的解法:将A和B并列作矩阵(A|B),对它作初等行变换,使得A变为单位矩阵,此时B变为解X.(A|B)→(E|X)(II)的解法:对两边转置化为(I)的形式:A T X T=B T.再用解(I)的方法求出X T,转置得X..(A T|B T)→(E|X T)矩阵方程是历年考题中常见的题型,但是考试真题往往并不直接写成(I)或(II)的形式,要用恒等变形简化为以上基本形式再求解.(2) 可逆矩阵的定义与意义定义设A是n阶矩阵,如果存在n阶矩阵B,使得AB=E, BA=E,则称A为可逆矩阵.此时B是唯一的,称为A的逆矩阵,通常记作A-1.如果A可逆,则A在乘法中有消去律:AB=0⇒B=0;AB=AC⇒B=C.(左消去律);BA=0⇒B=0;BA=CA⇒B=C. (右消去律)如果A可逆,则A在乘法中可移动(化为逆矩阵移到等号另一边):AB=C⇔B=A-1C. BA=C⇔B=CA-1.由此得到基本矩阵方程的逆矩阵解法:(I) AX=B的解X=A-1B .(II) XA=B的解X= BA-1.这种解法想法自然,好记忆,但是计算量比初等变换法大(多了一次矩阵乘积运算).(3) 矩阵可逆性的判别与性质定理n阶矩阵A可逆⇔|A|≠0.证明“⇒”对AA-1=E两边取行列式,得|A||A-1|=1,从而|A|≠0. (并且|A-1|=|A|-1.)“⇐”因为|A|≠0,矩阵方程AX=E和XA=E都有唯一解.设B,C分别是它们的解,即AB=E,CA=E. 事实上B=C(B=EB=CAB=CE=C),于是从定义得到A可逆.推论如果A和B都是n阶矩阵,则AB=E⇔BA=E.于是只要AB=E(或BA=E)一式成立,则A和B都可逆并且互为逆矩阵.可逆矩阵有以下性质:①如果A可逆,则A-1也可逆,并且(A-1)-1=A.A T也可逆,并且(A T)-1=(A-1)T.当c≠0时, c A也可逆,并且(c A)-1=c-1A-1.对任何正整数k, A k也可逆,并且(A k)-1=(A-1)k.(规定可逆矩阵A的负整数次方幂A-k=(A k)-1=(A-1)k.)② 如果A 和B 都可逆,则AB 也可逆,并且(AB )-1=B -1A -1.(请自己推广到多个可逆矩阵乘积的情形.)初等矩阵都是可逆矩阵,并且E (i,j)-1= E (i,j), E (i(c))-1=E (i(c -1)), E (i,j(c))-1= E (i,j(-c)).(4) 逆矩阵的计算和伴随矩阵① 计算逆矩阵的初等变换法当A 可逆时, A -1是矩阵方程AX =E 的解,于是可用初等行变换求A -1:(A |E )→(E |A -1)这个方法称为求逆矩阵的初等变换法.它比下面介绍的伴随矩阵法简单得多.② 伴随矩阵若A 是n 阶矩阵,记A ij 是|A |的(i,j)位元素的代数余子式,规定A的伴随矩阵为A 11 A 21 … A n1A *= A 12 A 22 … A n2 =(A ij )T .… … …A 1n A 2n … A mn请注意,规定n 阶矩阵A 的伴随矩阵并没有要求A 可逆,但是在A 可逆时, A *和A -1有密切关系.基本公式: AA *=A *A =|A |E .于是对于可逆矩阵A ,有A -1=A */|A |, 即A *=|A |A -1.因此可通过求A *来计算A -1.这就是求逆矩阵的伴随矩阵法.和初等变换法比较, 伴随矩阵法的计算量要大得多,除非n=2,一般不用它来求逆矩阵.对于2阶矩阵a b * d -bc d = -c a ,因此当ad-bc ≠0时,a b -1 d -bc d = -c a (ad-bc) .伴随矩阵的其它性质:①如果A是可逆矩阵,则A*也可逆,并且(A*)-1= A/|A|=(A-1)*.② |A*|=|A|n-1.③ (A T)*=(A*)T.④ (c A)*=c n-1A*.⑤ (AB)*=B*A*;(A k)*=(A*)k.⑥当n>2时,(A*)*=|A|n-2A;n=2时,(A*)*=A.二典型例题1.计算题例1=(1,-2,3) T,=(1,-1/2,1/3)T, A= T,求A6.讨论:(1)一般地,如果n阶矩阵A=T,则A k=(T)k-1A=(tr A)k-1A .(2)乘法结合律的应用:遇到形如T的地方可把它当作数处理.① 1 -1 1T= -1 1 -1 ,求T.(2003一)②设=(1,0,-1)T, A=T,求|a E-A n|.③n维向量=(a,0,⋯,0,a)T, a<0, A=E-T, A-1=E+a-1T,求a. (03三,四)④n维向量=(1/2,0,⋯,0,1/2)T,A=E-T,B=E+2T,求AB. (95四)⑤A=E-T,其中,都是n维非零列向量,已知A2=3E-2A,求T.例2(1999三) 1 0 1设A = 0 2 0 ,求A n-2A n-1.(n>1)例3 1 0 0设A = 1 0 1 ,(1)证明当n>1时A n =A n-2+A 2-E . (2) 求A n .例4设A 为3阶矩阵, 1,2,3是线性无关的3维列向量组,满足 A1=1+2+3, A 2=22+3,A 3=22+33.求作矩阵B ,使得A (1,2,3)=(1,2,3)B . (2005年数学四)例5设3阶矩阵A =(1,2,3),|A |=1,B =(1+2+3,1+22+33,1+42+93),求|B |.(05)例6 3维向量1,2,3,1,2,3满足1+3+21-2=0,31-2+1-3=0,2+3-2+3=0,已知1,2,3|=a,求|1,2,3|.例7设A 是3阶矩阵, 是3维列向量,使得P =(,A ,A 2)可逆,并且A 3=3A -2A 2.又3阶矩阵B 满足A =PBP -1.(1)求B .(2)求|A +E |.(01一)2 1 0例8 3阶矩阵A ,B 满足ABA *=2BA *+E ,其中A = 1 2 0 ,求|B |.(04一)0 0 1例9 3 -5 1设3阶矩阵A = 1 -1 0 , A -1XA =XA +2A ,求X .-1 0 2例10 1 1 -1设3阶矩阵A = -1 1 1 , A *X =A -1+2X ,求X .1 -1 1例11 4阶矩阵A ,B 满足ABA -1=BA -1+3E ,已知1 0 0 0A *= 0 1 0 0 ,求B . (00一)1 0 1 00 -3 0 8例12 3 0 0 1 0 0已知A = 2 1 0 , B = 0 0 0 , XA +2B =AB +2X ,求X 11.2 13 0 0 -1例13 设1=(5,1,-5)T ,2=(1,-3,2)T ,3=(1,-2,1)T ,矩阵A满足A 1=(4,3) T , A 2=(7,-8) T , A 3=(5,-5) T ,求A .2.概念和证明题例14 设A 是n 阶非零实矩阵,满足A *=A T .证明:(1)|A |>0.(2)如果n>2,则|A |=1.例15 设矩阵A =(a ij )3 3满足A *=A T ,a 11,a 12,a 13为3个相等的正数,则它们为(A) 3/3.(B) 3. (C)1/3. (D) 3. (2005年数学三)例16 设A和B都是n阶矩阵,C= A0 ,则C*=0 B(A) |A|A* 0 . (B) |B|B * 0 .0 |B|B * 0 |A|A*(C) |A|B* 0 . (D ) |B|A* 0 .0 |B|A* 0 |A|B*例17 设A是3阶矩阵,交换A的1,2列得B,再把B的第2 列加到第3 列上,得C.求Q,使得C=AQ.例18 设A是3阶可逆矩阵,交换A的1,2行得B,则(A) 交换A*的1,2行得到B*.(B) 交换A*的1,2列得到B*.(C) 交换A*的1,2行得到-B*.(D) 交换A*的1,2列得到-B*.(2005年)例19 设A是n阶可逆矩阵, 交换A的i,j行得到B.(1) 证明B可逆.(2) 求AB-1.例20设n阶矩阵A满足A2+3A-2E=0.(1)证明A可逆,并且求A-1.(2)证明对任何整数c,A-c E可逆.讨论: 如果f(A)=0,则(1) 当f(x)的常数项不等于0时,A可逆.(2) f(c)≠0时,A-c E可逆.(3) 上述两条的逆命题不成立.例21设是n维非零列向量,记A=E-T.证明(1) A2=A⇔T =1.(2)T =1⇒ A不可逆. (96一)讨论: (2)的逆命题也成立.例22 设A,B都是n阶矩阵,证明E-AB可逆⇔ E-BA可逆.例23设3阶矩阵A,B满足AB=A+B.(1) 证明A-E可逆.(2) 设 1 -3 0B= 2 1 0 ,求A.0 0 2 (91)例24设A,B是3阶矩阵, A可逆,它们满足2A-1B=B-4E.(1) 证明A-2E可逆.(2) 设 1 -2 0B= 1 2 0 ,求A.0 0 2 (2002)例25设n阶矩阵A,B满足AB=a A+b B.其中ab≠0,证明(1) A-b E和B-a E都可逆.(2) A可逆⇔ B可逆.(3) AB=BA.例26设A,B都是n阶对称矩阵,E+AB可逆,证明(E+AB)-1A 也是对称矩阵.例27 设A,B都是n阶矩阵使得A+B可逆,证明(1) 如果AB=BA,则B(A+B)-1A=A(A+B)-1B.(2) 如果A.B都可逆,则B(A+B)-1A=A(A+B)-1B.(3) 等式B(A+B)-1A=A(A+B)-1B总成立.例28设A,B,C都是n阶矩阵,满足B=E+AB,C=A+CA,则B-C 为(A) E.(B) -E. (C) A. (D) -A. (2005年数学四)参考答案1 -1/2 1/3例1 35A=35 -2 1 –2/3 .3 -3/2 1①3.②a2(a-2n). ③-1. ④E. ⑤4.例2 O.例 3 (1)提示:A n=A n-2+A2-E⇔A n-2(A2-E)=A2-E ⇔A(A2-E)=A2-E.(2)n=2k时, 1 0 0A n = k 1 0 .k 0 1n=2k+1时, 1 0 0A n = k+1 0 1 .k 1 0例4 1 0 0B= 1 2 2 .1 1 3例5 2.例6 –4a.例7 0 0 0B= 1 0 3 . |E+A|=-40 1 -2例8 1/9.例9 -6 10 4X= -2 4 2 .-4 10 0例10 1 1 0(1/4) 0 1 1 .1 0 1例11 6 0 0 0B= 0 6 0 0 .6 0 6 00 3 0 -1例12 1 0 02 0 0 .6 -1 -1例13 2 -1 1-4 -2 -5 .例15 (A).例16 (D).例17 0 1 1Q= 1 0 0 .0 0 1例18 (D).例19E(i,j).例22提示:用克莱姆法则.例如证明 ,即在E-AB可逆时证明齐次方程组(E-BA)X=0只有零解.例23 1 1/2 0A= -1/3 1 0 .0 0 2例24 0 2 0A= -1 -1 0 .0 0 -2例25 提示:计算(A-b E)(B-a E).例28 (A).第四讲向量组的线性关系与秩一.概念复习1. 线性表示关系 设1,2,…,s 是一个n 维向量组.如果n 维向量等于1,2,…,s 的一个线性组合,就说可以用1,2,…,s 线性表示.如果n 维向量组1,2,…,t 中的每一个都可以可以用1,2,…,s 线性表示,就说向量 1,2,…,t 可以用1,2,…,s 线性表示.判别“是否可以用1,2,…,s 线性表示? 表示方式是否唯一?”就是问:向量方程x 11+x 22+…+x s s =是否有解?解是否唯一?用分量写出这个向量方程,就是以1,2,…,s为增广矩阵的线性方程组.反之,判别“以A 为增广矩阵的线性方程组是否有解?解是否唯一?”的问题又可转化为“是否可以用A 的列向量组线性表示? 表示方式是否唯一?”的问题.向量组之间的线性表示问题与矩阵乘法有密切关系: 乘积矩阵AB 的每个列向量都可以表示为A 的列向量组的线性组合,从而AB 的列向量组可以用A 的列向量组线性表示;反之,如果向量组1,2,…,t 可以用1,2,…,s 线性表示,则矩阵(1,2,…,t )等于矩阵(1,2,…,s )和一个s ⨯t 矩阵C 的乘积. C 可以这样构造: 它的第i 个列向量就是i 对1,2,…,s 的分解系数(C 不是唯一的).向量组的线性表示关系有传递性,即如果向量组1,2,…,t 可以用1,2,…,s 线性表示,而1,2,…,s 可以用γ1,γ2,…,γr 线性表示,则1,2,…,t 可以用γ1,γ2,…,γr 线性表示.当向量组1,2,…,s 和1,2,…,t 互相都可以表示时就说它们等价并记作1,2,…,s ≅1,2,…,t. 等价关系也有传递性.。
第四章-向量组及其线性组合

线性代数——第 4章
定理2 定理
向量组B能由向量组 线性表示 向量组 能由向量组A线性表示 能由向量组 ⇔ R(A) = R(A, B).
推论 向量组 A : a1 ,a2 , ...,am 与向量组 B : b1 ,b2 , ...,bn 等价⇔ 等价⇔ R(A) = R(B) = R(A, B)
定义3 定义3
设有两个向量组 A : α 1 ,α 2 ,L ,α m 及 B : β 1 , β 2 ,L , β s .
线性表示, 若 B 组中的每个向量都能由 向量组 A 线性表示,则 称 向量组 B能由向量组 A 线性表示 . 若向量组 A 与向 量组 B 能相互线性表示,则称 这两个 向量组等价. 能相互线性表示, 向量组等价.
学习本章要特别注意: 学习本章要特别注意 方程语言、矩阵语言、几何语言之间的转换。 方程语言、矩阵语言、几何语言之间的转换。 突出的典型问题是对关系式
(b1 , b2 , b3 ,⋅ ⋅ ⋅, bl ) = (a1, a2 , a3 ,⋅ ⋅ ⋅am ) K m×l
即
B = AK
所作的解释: 所作的解释: 方程语言: 是矩阵方程Ax= 的一个解 K是矩阵方程 的一个解; 方程语言: 是矩阵方程 =B的一个解; 矩阵语言: 是 与 的乘积矩阵 的乘积矩阵; 矩阵语言:B是A与K的乘积矩阵; 几何语言: 向量组B能由向量组 线性表出, 能由向量组A线性表出 几何语言: 向量组 能由向量组 线性表出, K是这一表示的系数矩阵 是这一表示的系数矩阵
同时, 同时, C的行向量组能由 B的行向量组线性表示 , A 为这一表示的系数矩阵 :
γ 1T a11 T γ 2 a 21 M = M T γ a m m1 a12 a 22 M am 2 L a1 s β 1 T T L a 2 s β 2 M M T L a ms β s
第四章向量组的线性相关性

若记 A ( 2, , 和 B ( b ,b B 1, m) 1,b 2, s ). 能由 A 线性表示,即对每个向 量 bj ( j 1 ,2 , ,s)存 在数 k k ,使 1j ,k 2j , mj
b k k k j 1 j 1 2 j2 mj m
个有次序的数 a ,a , ,a 所组成的 1 2 n 定义1 n 组称为 n 维向量,这 n 个数称为该向量 n 个分量
第 i 个数 a i 个分量 . i称为第
分Hale Waihona Puke 全为实数的向量称为实向量,分量中有复数的向量称为复向量.
2、n 维向量的表示方法
n 维向量写成一行,称为行向量,也就是行 T T T T 矩阵,通常用 a,b, , 等表示,如: T a ( a , a , , a ) 1 2 n n 维向量写成一列,称为列向量,也就是列 ,b , , 矩阵,通常用 a 等表示,如: a1 a2 a an
T
a 1n a 2n a in a mn
T 1 T 2
T i
T m
, …, m 称为矩阵A的行向量组.
反之,由有限个向量所组成的向量组可以构 成一个矩阵.
构 成 一 个 n m 矩 阵
m 个 n 维 列 向 量 所 组 成 的 向 量 组 ,2 , ,m , 1
条件是矩阵 A ( , , , ) 的秩等于矩阵 1 2 m
四、等价向量组
定义2设有两个向量组 A: ,m及 B: 1, 2, , s. 1, 2,
若 B 组中的每个向量都能由 向量组 A 线性表示,则 称 A 与向 向量组B 能由向量组A 线性表示 .若向量组 量组 B 能相互线性表示,则称 这两个 向量组等价.
线性代数-课后答案(第四章)

第四章 向量组的线性相关性1. 设v 1=(1, 1, 0)T , v 2=(0, 1, 1)T , v 3=(3, 4, 0)T , 求v 1-v 2及3v 1+2v 2-v 3.解 v 1-v 2=(1, 1, 0)T -(0, 1, 1)T=(1-0, 1-1, 0-1)T=(1, 0, -1)T .3v 1+2v 2-v 3=3(1, 1, 0)T +2(0, 1, 1)T -(3, 4, 0)T =(3⨯1+2⨯0-3, 3⨯1+2⨯1-4, 3⨯0+2⨯1-0)T=(0, 1, 2)T .2. 设3(a 1-a )+2(a 2+a )=5(a 3+a ), 求a , 其中a 1=(2, 5, 1, 3)T , a 2=(10, 1, 5, 10)T , a 3=(4, 1, -1, 1)T .解 由3(a 1-a )+2(a 2+a )=5(a 3+a )整理得)523(61321a a a a -+=])1 ,1 ,1 ,4(5)10 ,5 ,1 ,10(2)3 ,1 ,5 ,2(3[61T T T --+==(1, 2, 3, 4)T .3. 已知向量组A : a 1=(0, 1, 2, 3)T , a 2=(3, 0, 1, 2)T , a 3=(2, 3, 0, 1)T ;B : b 1=(2, 1, 1, 2)T , b 2=(0, -2, 1, 1)T , b 3=(4, 4, 1, 3)T , 证明B 组能由A 组线性表示, 但A 组不能由B 组线性表示.证明 由www.kh da w.c o m⎪⎪⎪⎭⎫⎝⎛-=312123111012421301402230) ,(B A ⎪⎪⎪⎭⎫ ⎝⎛-------971820751610402230421301~r ⎪⎪⎪⎭⎫⎝⎛------531400251552000751610421301 ~r⎪⎪⎪⎭⎫ ⎝⎛-----000000531400751610421301~r 知R (A )=R (A , B )=3, 所以B 组能由A 组线性表示.由⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛-=000000110201110110220201312111421402~~r r B 知R (B )=2. 因为R (B )≠R (B , A ), 所以A 组不能由B 组线性表示.4. 已知向量组A : a 1=(0, 1, 1)T , a 2=(1, 1, 0)T ;B : b 1=(-1, 0, 1)T , b 2=(1, 2, 1)T , b 3=(3, 2, -1)T , 证明A 组与B 组等价.证明 由⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛--=000001122010311112201122010311011111122010311) ,(~~r r A B ,知R (B )=R (B , A )=2. 显然在A 中有二阶非零子式, 故R (A )≥2, 又R (A )≤R (B , A )=2, 所以R (A )=2, 从而R (A )=R (B )=R (A , B ). 因此A 组与B 组等价.www.kh da w.co m5. 已知R (a 1, a 2, a 3)=2, R (a 2, a 3, a 4)=3, 证明 (1) a 1能由a 2, a 3线性表示; (2) a 4不能由a 1, a 2, a 3线性表示.证明 (1)由R (a 2, a 3, a 4)=3知a 2, a 3, a 4线性无关, 故a 2, a 3也线性无关. 又由R (a 1, a 2, a 3)=2知a 1, a 2, a 3线性相关, 故a 1能由a 2, a 3线性表示.(2)假如a 4能由a 1, a 2, a 3线性表示, 则因为a 1能由a 2, a 3线性表示, 故a 4能由a 2, a 3线性表示, 从而a 2, a 3, a 4线性相关, 矛盾.因此a 4不能由a 1, a 2, a 3线性表示.6. 判定下列向量组是线性相关还是线性无关: (1) (-1, 3, 1)T , (2, 1, 0)T , (1, 4, 1)T ; (2) (2, 3, 0)T , (-1, 4, 0)T , (0, 0, 2)T .解 (1)以所给向量为列向量的矩阵记为A . 因为 ⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=000110121220770121101413121~~r r A ,所以R (A )=2小于向量的个数, 从而所给向量组线性相关.(2)以所给向量为列向量的矩阵记为B . 因为 022*******12||≠=-=B ,所以R (B )=3等于向量的个数, 从而所给向量组线性相无关.7. 问a 取什么值时下列向量组线性相关? a 1=(a , 1, 1)T , a 2=(1, a , -1)T , a 3=(1, -1, a )T .www.kh da w.c o m解 以所给向量为列向量的矩阵记为A . 由)1)(1(111111||+-=--=a a a aa a A知, 当a =-1、0、1时, R (A )<3, 此时向量组线性相关. 8. 设a 1, a 2线性无关, a 1+b , a 2+b 线性相关, 求向量b 用a 1, a 2线性表示的表示式. 解 因为a 1+b , a 2+b 线性相关, 故存在不全为零的数λ1, λ2使λ1(a 1+b )+λ2(a 2+b )=0,由此得 2211121122121211)1(a a a a b λλλλλλλλλλλλ+--+-=+-+-=,设211λλλ+-=c , 则 b =c a 1-(1+c )a 2, c ∈R .9. 设a 1, a 2线性相关, b 1, b 2也线性相关, 问a 1+b 1, a 2+b 2是否一定线性相关?试举例说明之.解 不一定.例如, 当a 1=(1, 2)T , a 2=(2, 4)T , b 1=(-1, -1)T , b 2=(0, 0)T 时, 有a 1+b 1=(1, 2)T +b 1=(0, 1)T , a 2+b 2=(2, 4)T +(0, 0)T =(2, 4)T , 而a 1+b 1, a 2+b 2的对应分量不成比例, 是线性无关的.10. 举例说明下列各命题是错误的:(1)若向量组a 1, a 2, ⋅ ⋅ ⋅, a m 是线性相关的, 则a 1可由a 2, ⋅ ⋅ ⋅,www.kh da w.c o ma m 线性表示.解 设a 1=e 1=(1, 0, 0, ⋅ ⋅ ⋅, 0), a 2=a 3= ⋅ ⋅ ⋅ =a m =0, 则a 1, a 2, ⋅ ⋅ ⋅, a m 线性相关, 但a 1不能由a 2, ⋅ ⋅ ⋅, a m 线性表示.(2)若有不全为0的数λ1, λ2, ⋅ ⋅ ⋅, λm 使λ1a 1+ ⋅ ⋅ ⋅ +λm a m +λ1b 1+ ⋅ ⋅ ⋅ +λm b m =0成立, 则a 1, a 2, ⋅ ⋅ ⋅, a m 线性相关, b 1, b 2, ⋅ ⋅ ⋅, b m 亦线性相关.解 有不全为零的数λ1, λ2, ⋅ ⋅ ⋅, λm 使 λ1a 1+ ⋅ ⋅ ⋅ +λm a m +λ1b 1+ ⋅ ⋅ ⋅ +λm b m =0,原式可化为λ1(a 1+b 1)+ ⋅ ⋅ ⋅ +λm (a m +b m )=0.取a 1=e 1=-b 1, a 2=e 2=-b 2, ⋅ ⋅ ⋅, a m =e m =-b m , 其中e 1, e 2, ⋅ ⋅ ⋅, e m 为单位坐标向量, 则上式成立, 而a 1, a 2, ⋅ ⋅ ⋅, a m 和b 1, b 2, ⋅ ⋅ ⋅, b m 均线性无关.(3)若只有当λ1, λ2, ⋅ ⋅ ⋅, λm 全为0时, 等式λ1a 1+ ⋅ ⋅ ⋅ +λm a m +λ1b 1+ ⋅ ⋅ ⋅ +λm b m =0才能成立, 则a 1, a 2, ⋅ ⋅ ⋅, a m 线性无关, b 1, b 2, ⋅ ⋅ ⋅, b m 亦线性无关.解 由于只有当λ1, λ2, ⋅ ⋅ ⋅, λm 全为0时, 等式由λ1a 1+ ⋅ ⋅ ⋅ +λm a m +λ1b 1+ ⋅ ⋅ ⋅ +λm b m =0成立, 所以只有当λ1, λ2, ⋅ ⋅ ⋅, λm 全为0时, 等式λ1(a 1+b 1)+λ2(a 2+b 2)+ ⋅ ⋅ ⋅ +λm (a m +b m )=0成立. 因此a 1+b 1, a 2+b 2, ⋅ ⋅ ⋅, a m +b m 线性无关.取a 1=a 2= ⋅ ⋅ ⋅ =a m =0, 取b 1, ⋅ ⋅ ⋅, b m 为线性无关组, 则它们满足以上条件, 但a 1, a 2, ⋅ ⋅ ⋅, a m 线性相关.www.kh da w.c o m(4)若a 1, a 2, ⋅ ⋅ ⋅, a m 线性相关, b 1, b 2, ⋅ ⋅ ⋅, b m 亦线性相关, 则有不全为0的数, λ1, λ2, ⋅ ⋅ ⋅, λm 使λ1a 1+ ⋅ ⋅ ⋅ +λm a m =0, λ1b 1+ ⋅ ⋅ ⋅ +λm b m =0同时成立.解 a 1=(1, 0)T , a 2=(2, 0)T , b 1=(0, 3)T , b 2=(0, 4)T ,λ1a 1+λ2a 2 =0⇒λ1=-2λ2, λ1b 1+λ2b 2 =0⇒λ1=-(3/4)λ2,⇒λ1=λ2=0, 与题设矛盾.11. 设b 1=a 1+a 2, b 2=a 2+a 3, b 3=a 3+a 4, b 4=a 4+a 1, 证明向量组b 1, b 2, b 3, b 4线性相关. 证明 由已知条件得 a 1=b 1-a 2, a 2=b 2-a 3, a 3=b 3-a 4, a 4=b 4-a 1, 于是 a 1 =b 1-b 2+a 3=b 1-b 2+b 3-a 4=b 1-b 2+b 3-b 4+a 1, 从而 b 1-b 2+b 3-b 4=0,这说明向量组b 1, b 2, b 3, b 4线性相关.12. 设b 1=a 1, b 2=a 1+a 2, ⋅ ⋅ ⋅, b r =a 1+a 2+ ⋅ ⋅ ⋅ +a r , 且向量组a 1,a 2, ⋅ ⋅ ⋅ , a r 线性无关, 证明向量组b 1, b 2, ⋅ ⋅ ⋅ , b r 线性无关. 证明 已知的r 个等式可以写成⎪⎪⎪⎭⎫⎝⎛⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=⋅⋅⋅100110111) , , ,() , , ,(2121r r a a a b b b , www.kh da w.c o m上式记为B =AK . 因为|K |=1≠0, K 可逆, 所以R (B )=R (A )=r , 从而向量组b 1, b 2, ⋅ ⋅ ⋅ , b r 线性无关.13. 求下列向量组的秩, 并求一个最大无关组: (1)a 1=(1, 2, -1, 4)T , a 2=(9, 100, 10, 4)T , a 3=(-2, -4, 2, -8)T ; 解 由⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛----=000000010291032001900820291844210141002291) , ,(~~321r r a a a ,知R (a 1, a 2, a 3)=2. 因为向量a 1与a 2的分量不成比例, 故a 1, a 2线性无关, 所以a 1, a 2是一个最大无关组.(2)a 1T =(1, 2, 1, 3), a 2T =(4, -1, -5, -6), a 3T =(1, -3, -4, -7).解 由⎪⎪⎪⎭⎫⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛------⎪⎪⎪⎭⎫⎝⎛------=00000059014110180590590141763451312141) , ,(~~321r r a a a , 知R (a 1T , a 2T , a 3T )=R (a 1, a 2, a 3)=2. 因为向量a 1T 与a 2T 的分量不成比例, 故a 1T , a 2T 线性无关, 所以a 1T , a 2T 是一个最大无关组.14. 利用初等行变换求下列矩阵的列向量组的一个最大无关组:(1); ⎪⎪⎪⎭⎫⎝⎛4820322513454947513253947543173125www.kh da w.c o m解 因为⎪⎪⎪⎭⎫ ⎝⎛482032251345494751325394754317312513143~r r r r --123r r -34rr -132rr -23rr +⎪⎪⎪⎭⎫ ⎝⎛5310531032104317312523~r r -⎪⎪⎪⎭⎫ ⎝⎛00003100321043173125, 所以第1、2、3列构成一个最大无关组.(2). ⎪⎪⎪⎭⎫⎝⎛---14011313021512012211解 因为⎪⎪⎪⎭⎫ ⎝⎛---1401131302151201221114~r r -⎪⎪⎪⎭⎫ ⎝⎛------222015120151201221143~r r ↔⎪⎪⎪⎭⎫ ⎝⎛---00000222001512012211, 所以第1、2、3列构成一个最大无关组.15. 设向量组(a , 3, 1)T , (2, b , 3)T , (1, 2, 1)T , (2, 3, 1)T的秩为2, 求a , b .解 设a 1=(a , 3, 1)T , a 2=(2, b , 3)T , a 3=(1, 2, 1)T , a 4=(2, 3, 1)T . 因为⎪⎪⎭⎫ ⎝⎛----⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=52001110311161101110311131********) , , ,(~~2143b a a b a b a r r a a a a ,而R (a 1, a 2, a 3, a 4)=2, 所以a =2, b =5.www.kh da w.co m16. 设a 1, a 2, ⋅ ⋅ ⋅, a n 是一组n 维向量, 已知n 维单位坐标向量e 1, e 2,⋅ ⋅ ⋅, e n 能由它们线性表示, 证明a 1, a 2, ⋅ ⋅ ⋅, a n 线性无关. 证法一 记A =(a 1, a 2, ⋅ ⋅ ⋅, a n ), E =(e 1, e 2,⋅ ⋅ ⋅, e n ). 由已知条件知, 存在矩阵K , 使E =AK .两边取行列式, 得|E |=|A ||K |.可见|A |≠0, 所以R (A )=n , 从而a 1, a 2, ⋅ ⋅ ⋅, a n 线性无关.证法二 因为e 1, e 2,⋅ ⋅ ⋅, e n 能由a 1, a 2, ⋅ ⋅ ⋅, a n 线性表示, 所以R (e 1, e 2,⋅ ⋅ ⋅, e n )≤R (a 1, a 2, ⋅ ⋅ ⋅, a n ),而R (e 1, e 2,⋅ ⋅ ⋅, e n )=n , R (a 1, a 2, ⋅ ⋅ ⋅, a n )≤n , 所以R (a 1, a 2, ⋅ ⋅ ⋅,a n )=n , 从而a 1, a 2, ⋅ ⋅ ⋅, a n 线性无关.17. 设a 1, a 2, ⋅ ⋅ ⋅, a n 是一组n 维向量, 证明它们线性无关的充分必要条件是: 任一n 维向量都可由它们线性表示.证明 必要性: 设a 为任一n 维向量. 因为a 1, a 2, ⋅ ⋅ ⋅, a n 线性无关, 而a 1, a 2, ⋅ ⋅ ⋅, a n , a 是n +1个n 维向量, 是线性相关的, 所以a 能由a 1, a 2, ⋅ ⋅ ⋅, a n 线性表示, 且表示式是唯一的.充分性: 已知任一n 维向量都可由a 1, a 2, ⋅ ⋅ ⋅, a n 线性表示,故单位坐标向量组e 1, e 2, ⋅ ⋅ ⋅, e n 能由a 1, a 2, ⋅ ⋅ ⋅, a n 线性表示, 于是有n =R (e 1, e 2, ⋅ ⋅ ⋅, e n )≤R (a 1, a 2, ⋅ ⋅ ⋅, a n )≤n ,即R (a 1, a 2, ⋅ ⋅ ⋅, a n )=n , 所以a 1, a 2, ⋅ ⋅ ⋅, a n 线性无关.www.kh da w.c o m18. 设向量组a 1, a 2, ⋅ ⋅ ⋅, a m 线性相关, 且a 1≠0, 证明存在某个向量a k (2≤k ≤m ), 使a k 能由a 1, a 2, ⋅ ⋅ ⋅, a k -1线性表示.证明 因为a 1, a 2, ⋅ ⋅ ⋅, a m 线性相关, 所以存在不全为零的数λ1, λ2, ⋅ ⋅ ⋅, λm , 使λ1a 1+λ2a 2+ ⋅ ⋅ ⋅ +λm a m =0,而且λ2, λ3,⋅ ⋅ ⋅, λm 不全为零. 这是因为, 如若不然, 则λ1a 1=0, 由a 1≠0知λ1=0, 矛盾. 因此存在k (2≤k ≤m ), 使λk ≠0, λk +1=λk +2= ⋅ ⋅ ⋅ =λm =0,于是λ1a 1+λ2a 2+ ⋅ ⋅ ⋅ +λk a k =0,a k =-(1/λk )(λ1a 1+λ2a 2+ ⋅ ⋅ ⋅ +λk -1a k -1),即a k 能由a 1, a 2, ⋅ ⋅ ⋅, a k -1线性表示.19. 设向量组B : b 1, ⋅ ⋅ ⋅, b r 能由向量组A : a 1, ⋅ ⋅ ⋅, a s 线性表示为(b 1, ⋅ ⋅ ⋅, b r )=(a 1, ⋅ ⋅ ⋅, a s )K , 其中K 为s ⨯r 矩阵, 且A 组线性无关.证明B 组线性无关的充分必要条件是矩阵K 的秩R (K )=r .证明 令B =(b 1, ⋅ ⋅ ⋅, b r ), A =(a 1, ⋅ ⋅ ⋅, a s ), 则有B =AK .必要性: 设向量组B 线性无关.由向量组B 线性无关及矩阵秩的性质, 有 r =R (B )=R (AK )≤min{R (A ), R (K )}≤R (K ), 及 R (K )≤min{r , s }≤r .www.kh da w.c o m因此R (K )=r .充分性: 因为R (K )=r , 所以存在可逆矩阵C , 使为K 的标准形. 于是⎪⎭⎫⎝⎛=O E KC r (b 1, ⋅ ⋅ ⋅, b r )C =( a 1, ⋅ ⋅ ⋅, a s )KC =(a 1, ⋅ ⋅ ⋅, a r ). 因为C 可逆, 所以R (b 1, ⋅ ⋅ ⋅, b r )=R (a 1, ⋅ ⋅ ⋅, a r )=r , 从而b 1, ⋅ ⋅ ⋅, b r 线性无关.20. 设⎪⎩⎪⎨⎧+⋅⋅⋅+++=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅+⋅⋅⋅++=+⋅⋅⋅++=-1321312321 n n nn ααααβαααβαααβ, 证明向量组α1, α2, ⋅ ⋅ ⋅, αn 与向量组β1, β2, ⋅ ⋅ ⋅, βn 等价.证明 将已知关系写成⎪⎪⎪⎪⎭⎫ ⎝⎛⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=⋅⋅⋅0111101111011110) , , ,() , , ,(2121n n αααβββ, 将上式记为B =AK . 因为0)1()1(0111101111011110||1≠--=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=-n K n , 所以K 可逆, 故有A =BK -1. 由B =AK 和A =BK -1可知向量组α1, α2,⋅ ⋅ ⋅, αn 与向量组β1, β2, ⋅ ⋅ ⋅, βn 可相互线性表示. 因此向量组α1,www.k h da w.c o mα2, ⋅ ⋅ ⋅, αn 与向量组β1, β2, ⋅ ⋅ ⋅, βn 等价.21. 已知3阶矩阵A 与3维列向量x 满足A 3x =3A x -A 2x , 且向量组x , A x , A 2x 线性无关.(1)记P =(x , A x , A 2x ), 求3阶矩阵B , 使AP =PB ;解 因为AP =A (x , A x , A 2x ) =(A x , A 2x , A 3x ) =(A x , A 2x , 3A x -A 2x ) ⎪⎪⎭⎫⎝⎛-=110301000) , ,(2x x x A A ,所以⎪⎪⎭⎫⎝⎛-=110301000B .(2)求|A |.解 由A 3x =3A x -A 2x , 得A (3x -A x -A 2x )=0. 因为x , A x , A 2x 线性无关, 故3x -A x -A 2x ≠0, 即方程A x =0有非零解, 所以R (A )<3,|A |=0.22. 求下列齐次线性方程组的基础解系:(1)⎪⎩⎪⎨⎧=-++=-++=++-02683054202108432143214321x x x x x x x x x x x x ;解 对系数矩阵进行初等行变换, 有 ⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛---=00004/14/3100401 2683154221081~r A ,于是得www.kh da w.co m⎩⎨⎧+=-=43231)4/1()4/3(4x x x x x .取(x 3, x 4)T =(4, 0)T , 得(x 1, x 2)T =(-16, 3)T ; 取(x 3, x 4)T =(0, 4)T , 得(x 1, x 2)T =(0, 1)T .因此方程组的基础解系为 ξ1=(-16, 3, 4, 0)T , ξ2=(0, 1, 0, 4)T .(2)⎪⎩⎪⎨⎧=-++=-++=+--03678024530232432143214321x x x x x x x x x x x x .解 对系数矩阵进行初等行变换, 有⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛----=000019/719/141019/119/201 367824531232~r A ,于是得⎩⎨⎧+-=+-=432431)19/7()19/14()19/1()19/2(x x x x x x .取(x 3, x 4)T =(19, 0)T , 得(x 1, x 2)T =(-2, 14)T ;取(x 3, x 4)T =(0, 19)T , 得(x 1, x 2)T =(1, 7)T . 因此方程组的基础解系为ξ1=(-2, 14, 19, 0)T , ξ2=(1, 7, 0, 19)T .(3)nx 1 +(n -1)x 2+ ⋅ ⋅ ⋅ +2x n -1+x n =0.解 原方程组即为x n =-nx 1-(n -1)x 2- ⋅ ⋅ ⋅ -2x n -1.取x 1=1, x 2=x 3= ⋅ ⋅ ⋅ =x n -1=0, 得x n =-n ;取x 2=1, x 1=x 3=x 4= ⋅ ⋅ ⋅ =x n -1=0, 得x n =-(n -1)=-n +1;www.kh da w.c o m⋅ ⋅ ⋅ ;取x n -1=1, x 1=x 2= ⋅ ⋅ ⋅ =x n -2=0, 得x n =-2. 因此方程组的基础解系为 ξ1=(1, 0, 0, ⋅ ⋅ ⋅, 0, -n )T ,ξ2=(0, 1, 0, ⋅ ⋅ ⋅, 0, -n +1)T , ⋅ ⋅ ⋅,ξn -1=(0, 0, 0, ⋅ ⋅ ⋅, 1, -2)T .23. 设⎪⎭⎫ ⎝⎛--=82593122A , 求一个4⨯2矩阵B , 使AB =0, 且 R (B )=2. 解 显然B 的两个列向量应是方程组AB =0的两个线性无关的解. 因为, ⎪⎭⎫ ⎝⎛---⎪⎭⎫ ⎝⎛--=8/118/5108/18/101 82593122~rA 所以与方程组AB =0同解方程组为.⎩⎨⎧+=-=432431)8/11()8/5()8/1()8/1(x x x x x x 取(x 3, x 4)T =(8, 0)T , 得(x 1, x 2)T =(1, 5)T ;取(x 3, x 4)T =(0, 8)T , 得(x 1, x 2)T =(-1, 11)T . 方程组AB =0的基础解系为ξ1=(1, 5, 8, 0)T , ξ2=(-1, 11, 0, 8)T . 因此所求矩阵为. ⎪⎪⎪⎭⎫⎝⎛-=800811511B www.kh da w.co m24. 求一个齐次线性方程组, 使它的基础解系为ξ1=(0, 1, 2, 3)T , ξ2=(3, 2, 1, 0)T .解 显然原方程组的通解为⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛01233210214321k k x x x x , 即, (k ⎪⎩⎪⎨⎧=+=+==142132********k x k k x k k x k x 1, k 2∈R ),消去k 1, k 2得⎩⎨⎧=+-=+-023032431421x x x x x x , 此即所求的齐次线性方程组.25. 设四元齐次线性方程组I : , II :⎩⎨⎧=-=+004221x x x x ⎩⎨⎧=+-=+-00432321x x x x x x . 求: (1)方程I 与II 的基础解系; (2) I 与II 的公共解.解 (1)由方程I 得.⎩⎨⎧=-=4241x x x x 取(x 3, x 4)T =(1, 0)T , 得(x 1, x 2)T =(0, 0)T ;取(x 3, x 4)T =(0, 1)T , 得(x 1, x 2)T =(-1, 1)T . 因此方程I 的基础解系为ξ1=(0, 0, 1, 0)T , ξ2=(-1, 1, 0, 1)T . 由方程II 得.⎩⎨⎧-=-=43241x x x x x 取(x 3, x 4)T =(1, 0)T , 得(x 1, x 2)T =(0, 1)T ;www.kh da w.c o m取(x 3, x 4)T =(0, 1)T , 得(x 1, x 2)T =(-1, -1)T . 因此方程II 的基础解系为ξ1=(0, 1, 1, 0)T , ξ2=(-1, -1, 0, 1)T . (2) I 与II 的公共解就是方程III : ⎪⎩⎪⎨⎧=+-=+-=-=+00004323214221x x x x x x x x x x的解. 因为方程组III 的系数矩阵, ⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫⎝⎛---=000210010101001 1110011110100011~r A 所以与方程组III 同解的方程组为⎪⎩⎪⎨⎧==-=4342412x x x x x x .取x 4=1, 得(x 1, x 2, x 3)T =(-1, 1, 2)T , 方程组III 的基础解系为ξ=(-1, 1, 2, 1)T . 因此I 与II 的公共解为x =c (-1, 1, 2, 1)T , c ∈R .26. 设n 阶矩阵A 满足A 2=A , E 为n 阶单位矩阵, 证明R (A )+R (A -E )=n .证明 因为A (A -E )=A 2-A =A -A =0, 所以R (A )+R (A -E )≤n . 又R (A -E )=R (E -A ), 可知R (A )+R (A -E )=R (A )+R (E -A )≥R (A +E -A )=R (E )=n ,由此R (A )+R (A -E )=n .www.kh da w.c o m27. 设A 为n 阶矩阵(n ≥2), A *为A 的伴随阵, 证明⎪⎩⎪⎨⎧-≤-===2)( 01)( 1)( *)(n A R n A R n A R n A R 当当当.证明 当R (A )=n 时, |A |≠0, 故有 |AA *|=||A |E |=|A |≠0, |A *|≠0, 所以R (A *)=n .当R (A )=n -1时, |A |=0, 故有 AA *=|A |E =0,即A *的列向量都是方程组A x =0的解. 因为R (A )=n -1, 所以方程组A x =0的基础解系中只含一个解向量, 即基础解系的秩为1. 因此R (A *)=1.当R (A )≤n -2时, A 中每个元素的代数余子式都为0, 故A *=O , 从而R (A *)=0. 28. 求下列非齐次方程组的一个解及对应的齐次线性方程组的基础解系:(1)⎪⎩⎪⎨⎧=+++=+++=+3223512254321432121x x x x x x x x x x ;解 对增广矩阵进行初等行变换, 有⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛=2100013011080101 322351211250011~r B . 与所给方程组同解的方程为⎪⎩⎪⎨⎧=+=--=213 843231x x x x x . www.kh da w.c o m当x 3=0时, 得所给方程组的一个解η=(-8, 13, 0, 2)T . 与对应的齐次方程组同解的方程为⎪⎩⎪⎨⎧==-=043231x x x x x . 当x 3=1时, 得对应的齐次方程组的基础解系ξ=(-1, 1, 1, 0)T .(2)⎪⎩⎪⎨⎧-=+++-=-++=-+-6242163511325432143214321x x x x x x x x x x x x .解 对增广矩阵进行初等行变换, 有⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛-----=0000022/17/11012/17/901 6124211635113251~r B .与所给方程组同解的方程为⎩⎨⎧--=++-=2)2/1((1/7)1)2/1()7/9(432431x x x x x x .当x 3=x 4=0时, 得所给方程组的一个解 η=(1, -2, 0, 0)T .与对应的齐次方程组同解的方程为⎩⎨⎧-=+-=432431)2/1((1/7))2/1()7/9(x x x x x x . 分别取(x 3, x 4)T =(1, 0)T , (0, 1)T , 得对应的齐次方程组的基础解系ξ1=(-9, 1, 7, 0)T . ξ2=(1, -1, 0, 2)T .www.kh da w.co m29. 设四元非齐次线性方程组的系数矩阵的秩为3, 已知η1, η2, η3是它的三个解向量. 且η1=(2, 3, 4, 5)T , η2+η3=(1, 2, 3, 4)T ,求该方程组的通解.解 由于方程组中未知数的个数是4, 系数矩阵的秩为3, 所以对应的齐次线性方程组的基础解系含有一个向量, 且由于η1, η2, η3均为方程组的解, 由非齐次线性方程组解的结构性质得2η1-(η2+η3)=(η1-η2)+(η1-η3)= (3, 4, 5, 6)T为其基础解系向量, 故此方程组的通解:x =k (3, 4, 5, 6)T +(2, 3, 4, 5)T , (k ∈R ).30. 设有向量组A : a 1=(α, 2, 10)T , a 2=(-2, 1, 5)T , a 3=(-1, 1, 4)T , 及b =(1, β, -1)T , 问α, β为何值时 (1)向量b 不能由向量组A 线性表示;(2)向量b 能由向量组A 线性表示, 且表示式唯一;(3)向量b 能由向量组A 线性表示, 且表示式不唯一, 并求一般表示式.解 ⎪⎪⎭⎫ ⎝⎛---=11054211121) , , ,(123βαb a a a ⎪⎪⎭⎫ ⎝⎛-+++---βαβαα34001110121 ~r .(1)当α=-4, β≠0时, R (A )≠R (A , b ), 此时向量b 不能由向量组A 线性表示.(2)当α≠-4时, R (A )=R (A , b )=3, 此时向量组a 1, a 2, a 3线性无关, 而向量组a 1, a 2, a 3, b 线性相关, 故向量b 能由向量组A 线性表示, 且表示式唯一.www.kh da w.c o m(3)当α=-4, β=0时, R (A )=R (A , b )=2, 此时向量b 能由向量组A 线性表示, 且表示式不唯一. 当α=-4, β=0时,⎪⎪⎭⎫ ⎝⎛----=1105402111421) , , ,(123b a a a ⎪⎪⎭⎫⎝⎛--000013101201 ~r ,方程组(a 3, a 2, a 1)x =b 的解为, c ∈R .⎪⎪⎭⎫⎝⎛--+=⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛c c c c x x x 1312011132321因此 b =(2c +1)a 3+(-3c -1)a 2+c a 1,即 b = c a 1+(-3c -1)a 2+(2c +1)a 3, c ∈R .31. 设a =(a 1, a 2, a 3)T , b =(b 1, b 2, b 3)T , c =(c 1, c 2, c 3)T , 证明三直线l 1: a 1x +b 1y +c 1=0,l 2: a 2x +b 2y +c 2=0, (a i 2+b i 2≠0, i =1, 2, 3) l 3: a 3x +b 3y +c 3=0,相交于一点的充分必要条件为: 向量组a , b 线性无关, 且向量组a , b , c 线性相关.证明 三直线相交于一点的充分必要条件为方程组⎪⎩⎪⎨⎧=++=++=++000333222111c y b x a c y b x a c y b x a , 即⎪⎩⎪⎨⎧-=+-=+-=+333222111c y b x a c y b x a c y b x a有唯一解. 上述方程组可写为x a +y b =-c . 因此三直线相交于一www.kh da w.c o m点的充分必要条件为c 能由a , b 唯一线性表示, 而c 能由a , b 唯一线性表示的充分必要条件为向量组a , b 线性无关, 且向量组a , b , c 线性相关.32. 设矩阵A =(a 1, a 2, a 3, a 4), 其中a 2, a 3, a 4线性无关,a 1=2a 2- a 3. 向量b =a 1+a 2+a 3+a 4, 求方程A x =b 的通解. 解 由b =a 1+a 2+a 3+a 4知η=(1, 1, 1, 1)T 是方程A x =b 的一个解.由a 1=2a 2- a 3得a 1-2a 2+a 3=0, 知ξ=(1, -2, 1, 0)T 是A x =0的一个解. 由a 2, a 3, a 4线性无关知R (A )=3, 故方程A x =b 所对应的齐次方程A x =0的基础解系中含一个解向量. 因此ξ=(1, -2, 1, 0)T 是方程A x =0的基础解系.方程A x =b 的通解为x =c (1, -2, 1, 0)T +(1, 1, 1, 1)T , c ∈R .33. 设η*是非齐次线性方程组A x =b 的一个解, ξ1, ξ2, ⋅ ⋅ ⋅,ξn -r ,是对应的齐次线性方程组的一个基础解系, 证明: (1)η*, ξ1, ξ2, ⋅ ⋅ ⋅, ξn -r 线性无关;(2)η*, η*+ξ1, η*+ξ2, ⋅ ⋅ ⋅, η*+ξn -r 线性无关.证明 (1)反证法, 假设η*, ξ1, ξ2, ⋅ ⋅ ⋅, ξn -r 线性相关. 因为ξ1, ξ2, ⋅ ⋅ ⋅, ξn -r 线性无关, 而η*, ξ1, ξ2, ⋅ ⋅ ⋅, ξn -r 线性相关, 所以η*可由ξ1, ξ2, ⋅ ⋅ ⋅, ξn -r 线性表示, 且表示式是唯一的, 这说明η*也是齐次线性方程组的解, 矛盾.(2)显然向量组η*, η*+ξ1, η*+ξ2, ⋅ ⋅ ⋅, η*+ξn -r 与向量组η*, w w w .k h d a w .c o mξ1, ξ2, ⋅ ⋅ ⋅, ξn -r 可以相互表示, 故这两个向量组等价, 而由(1)知向量组η*, ξ1, ξ2, ⋅ ⋅ ⋅, ξn -r 线性无关, 所以向量组η*, η*+ξ1, η*+ξ2, ⋅ ⋅ ⋅, η*+ξn -r 也线性无关.34. 设η1, η2, ⋅ ⋅ ⋅, ηs 是非齐次线性方程组A x =b 的s 个解, k 1, k 2, ⋅ ⋅ ⋅, k s 为实数, 满足k 1+k 2+ ⋅ ⋅ ⋅ +k s =1. 证明x =k 1η1+k 2η2+ ⋅ ⋅ ⋅ +k s ηs也是它的解.证明 因为η1, η2, ⋅ ⋅ ⋅, ηs 都是方程组A x =b 的解, 所以 A ηi =b (i =1, 2, ⋅ ⋅ ⋅, s ),从而 A (k 1η1+k 2η2+ ⋅ ⋅ ⋅ +k s ηs )=k 1A η1+k 2A η2+ ⋅ ⋅ ⋅ +k s A ηs =(k 1+k 2+ ⋅ ⋅ ⋅ +k s )b =b .因此x =k 1η1+k 2η2+ ⋅ ⋅ ⋅ +k s ηs 也是方程的解.35. 设非齐次线性方程组A x =b 的系数矩阵的秩为r , η1, η2, ⋅ ⋅ ⋅, ηn -r +1是它的n -r +1个线性无关的解. 试证它的任一解可表示为x =k 1η1+k 2η2+ ⋅ ⋅ ⋅ +k n -r +1ηn -r +1, (其中k 1+k 2+ ⋅ ⋅ ⋅ +k n -r +1=1). 证明 因为η1, η2, ⋅ ⋅ ⋅, ηn -r +1均为A x =b 的解, 所以ξ1=η2-η1, ξ2=η3-η1, ⋅ ⋅ ⋅, ξn -r =η n -r +1-η1均为A x =b 的解. 用反证法证: ξ1, ξ2, ⋅ ⋅ ⋅, ξn -r 线性无关. 设它们线性相关, 则存在不全为零的数λ1, λ2, ⋅ ⋅ ⋅, λn -r , 使得 λ1ξ1+ λ2ξ2+ ⋅ ⋅ ⋅ + λ n -r ξ n -r =0, w ww .k h d a w .c o m即 λ1(η2-η1)+ λ2(η3-η1)+ ⋅ ⋅ ⋅ + λ n -r (ηn -r +1-η1)=0, 亦即 -(λ1+λ2+ ⋅ ⋅ ⋅ +λn -r )η1+λ1η2+λ2η3+ ⋅ ⋅ ⋅ +λ n -r ηn -r +1=0, 由η1, η2, ⋅ ⋅ ⋅, ηn -r +1线性无关知-(λ1+λ2+ ⋅ ⋅ ⋅ +λn -r )=λ1=λ2= ⋅ ⋅ ⋅ =λn -r =0,矛盾. 因此ξ1, ξ2, ⋅ ⋅ ⋅, ξn -r 线性无关. ξ1, ξ2, ⋅ ⋅ ⋅, ξn -r 为A x =b 的一个基础解系.设x 为A x =b 的任意解, 则x -η1为A x =0的解, 故x -η1可由ξ1, ξ2, ⋅ ⋅ ⋅, ξn -r 线性表出, 设x -η1=k 2ξ1+k 3ξ2+ ⋅ ⋅ ⋅ +k n -r +1ξn -r =k 2(η2-η1)+k 3(η3-η1)+ ⋅ ⋅ ⋅ +k n -r +1(ηn -r +1-η1), x =η1(1-k 2-k 3 ⋅ ⋅ ⋅ -k n -r +1)+k 2η2+k 3η3+ ⋅ ⋅ ⋅ +k n -r +1ηn -r +1. 令k 1=1-k 2-k 3 ⋅ ⋅ ⋅ -k n -r +1, 则k 1+k 2+k 3 ⋅ ⋅ ⋅ -k n -r +1=1, 于是 x =k 1η1+k 2η2+ ⋅ ⋅ ⋅ +k n -r +1ηn -r +1.36. 设V 1={x =(x 1, x 2, ⋅ ⋅ ⋅, x n )T | x 1, ⋅ ⋅ ⋅, x n ∈R 满足x 1+x 2+ ⋅ ⋅ ⋅ +x n =0}, V 2={x =(x 1, x 2, ⋅ ⋅ ⋅, x n )T | x 1, ⋅ ⋅ ⋅, x n ∈R 满足x 1+x 2+ ⋅ ⋅ ⋅ +x n =1}, 问V 1, V 2是不是向量空间?为什么?解 V 1是向量空间, 因为任取α=(a 1, a 2, ⋅ ⋅ ⋅, a n )T ∈V 1, β=(b 1, b 2, ⋅ ⋅ ⋅, b n )T ∈V 1, λ∈∈R ,有 a 1+a 2+ ⋅ ⋅ ⋅ +a n =0, b 1+b 2+ ⋅ ⋅ ⋅ +b n =0,从而 (a 1+b 1)+(a 2+b 2)+ ⋅ ⋅ ⋅ +(a n +b n )=(a 1+a 2+ ⋅ ⋅ ⋅ +a n )+(b 1+b 2+ ⋅ ⋅ ⋅ +b n )=0, λa 1+λa 2+ ⋅ ⋅ ⋅ +λa n =λ(a 1+a 2+ ⋅ ⋅ ⋅ +a n )=0, w w w .k h d a w .c o m所以 α+β=(a 1+b 1, a 2+b 2, ⋅ ⋅ ⋅, a n +b n )T ∈V 1, λα=(λa 1, λa 2, ⋅ ⋅ ⋅, λa n )T ∈V 1. V 2不是向量空间, 因为任取 α=(a 1, a 2, ⋅ ⋅ ⋅, a n )T ∈V 1, β=(b 1, b 2, ⋅ ⋅ ⋅, b n )T ∈V 1,有 a 1+a 2+ ⋅ ⋅ ⋅ +a n =1,b 1+b 2+ ⋅ ⋅ ⋅ +b n =1,从而 (a 1+b 1)+(a 2+b 2)+ ⋅ ⋅ ⋅ +(a n +b n ) =(a 1+a 2+ ⋅ ⋅ ⋅ +a n )+(b 1+b 2+ ⋅ ⋅ ⋅ +b n )=2, 所以 α+β=(a 1+b 1, a 2+b 2, ⋅ ⋅ ⋅, a n +b n )T ∉V 1.37. 试证: 由a 1=(0, 1, 1)T , a 2=(1, 0, 1)T , a 3=(1, 1, 0)T 所生成的向量空间就是R 3. 证明 设A =(a 1, a 2, a 3), 由020********||≠-==A , 知R (A )=3, 故a 1, a 2, a 3线性无关, 所以a 1, a 2, a 3是三维空间R 3的一组基, 因此由a 1, a 2, a 3所生成的向量空间就是R 3.38. 由a 1=(1, 1, 0, 0)T , a 2=(1, 0, 1, 1)T 所生成的向量空间记作V 1,由b 1=(2, -1, 3, 3)T , b 2=(0, 1, -1, -1)T 所生成的向量空间记作V 2, 试证V 1=V 2.证明 设A =(a 1, a 2), B =(b 1, b 2). 显然R (A )=R (B )=2, 又由 w w w .k h d a w .c o m, ⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛---=0000000013100211 1310131011010211) ,(~r B A 知R (A , B )=2, 所以R (A )=R (B )=R (A , B ), 从而向量组a 1, a 2与向量组b 1, b 2等价. 因为向量组a 1, a 2与向量组b 1, b 2等价, 所以这两个向量组所生成的向量空间相同, 即V 1=V 2.39. 验证a 1=(1, -1, 0)T , a 2=(2, 1, 3)T , a 3=(3, 1, 2)T 为R 3的一个基, 并把v 1=(5, 0, 7)T , v 2=(-9, -8, -13)T 用这个基线性表示. 解 设A =(a 1, a 2, a 3). 由06230111321|) , ,(|321≠-=-=a a a , 知R (A )=3, 故a 1, a 2, a 3线性无关, 所以a 1, a 2, a 3为R 3的一个基. 设x 1a 1+x 2a 2+x 3a 3=v 1, 则 ⎪⎩⎪⎨⎧=+=++-=++723053232321321x x x x x x x x , 解之得x 1=2, x 2=3, x 3=-1, 故线性表示为v 1=2a 1+3a 2-a 3. 设x 1a 1+x 2a 2+x 3a 3=v 2, 则 ⎪⎩⎪⎨⎧-=+-=++--=++1323893232321321x x x x x x x x , 解之得x 1=3, x 2=-3, x 3=-2, 故线性表示为v 2=3a 1-3a 2-2a 3. w ww .k h d a w .c o m40. 已知R 3的两个基为 a 1=(1, 1, 1)T , a 2=(1, 0, -1)T , a 3=(1, 0, 1)T , b 1=(1, 2, 1)T , b 2=(2, 3, 4)T , b 3=(3, 4, 3)T . 求由基a 1, a 2, a 3到基b 1, b 2, b 3的过渡矩阵P . 解 设e 1, e 2, e 3是三维单位坐标向量组, 则⎪⎪⎭⎫ ⎝⎛-=111001111) , ,() , ,(321321e e e a a a , 1321321111001111) , ,() , ,(-⎪⎪⎭⎫ ⎝⎛-=a a a e e e , 于是 ⎪⎪⎭⎫ ⎝⎛=341432321) , ,() , ,(321321e e e b b b ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=-341432321111001111) , ,(1321a a a , 由基a 1, a 2, a 3到基b 1, b 2, b 3的过渡矩阵为⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=-1010104323414323211110011111P .w w w .k h d a w .c o m。
最新-线性代数-向量组的线性相关性-PPT文档资料

5
【例 1】设 1 2 3 0T ,1 1 2 1 0T , 2 3 0 1 1T 。问 能否由1,2线性表示?
1 3 1
解:设
x11
x22,则 x1
2 来自1x2
0 1
2
,即
3
i k 1 1 k 2 2 k i 1 i 1 k i 1 i 1 k m m
即
k 1 1 k 2 2 k i 1 i 1 ( 1 ) i k i 1 i 1 k m m 0
{PAGE}
2
定义 2:
设1 ,2 ,,m是向量组,若其中至少有一个向量可以 由其余向量线性表出,则称此向量组线性相关,否 则称为线性无关。
{PAGE}
3
方程组的向量表示形式
=x11 x22
b1 a11
a12
xm m
b2
§2 向量组的线性相关性
本节主要内容: 向量组的线性相关性 向量组线性相关性的判定
{PAGE}
1
一 向量组线性相关的概念
定义 1:
1)一组同维的列(行)向量组称为向量组。
2)若向量 k11 k22 ks s , 则称向量 可由向量1 ,2 ,, s线性表示, 其中k1 ,k2 ,,ks是数, k11 k22 ks s称为1 ,2 ,, s的线性组合。
k i 1 k i 1 k i i 1 k i i 1
k m k i m
所以至少有一个向量可由其余m 1个向量线性表示。
向量组的线性表示与线性相关性
向量组等价结论:向量组A : a1 ,a2 , ,am与B : b1,b2 , ,bl 等价的充分必要条件是: R( A) R(B) R( A, B)
分析:由定理2和向量组等价定义易推出结论成立
不等式推论: 若向量B : b1,b2, ,bs能由向量组A : a1,a2, ,am 线性表示,则: R( A) R(a1,a2, ,am ) R(B) R(b1,b2, ,bs )
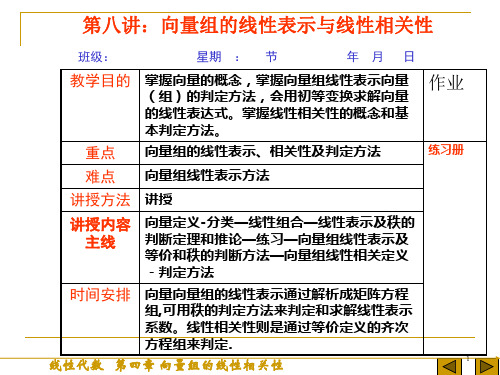
班级:
星期 : 节
年月 日
教学目的 重点
掌握向量的概念,掌握向量组线性表示向量 (组)的判定方法,会用初等变换求解向量 的线性表达式。掌握线性相关性的概念和基 本判定方法。
向量组的线性表示、相关性及判定方法
作业
练习册
难点 向量组线性表示方法
讲授方法 讲授
讲授内容 主线
向量定义-分类—线性组合—线性表示及秩的 判断定理和推论—练习—向量组线性表示及 等价和秩的判断方法—向量组线性相关定义 -判定方法
给定向量组 A :a1, a2 , , am 和向量 b , 如果存在一组数 1, 2 , , m , 使
b 1a1 2a2 m am ,
则向量b 是向量组 A 的线性组合, 这时称向量 b能由向量组 A 线性表示。 线性表示的关键是线性表示系数的存在与求解
线性代数 第四章 向量组的线性相关性
这是s个同系数A的方程组AX1 b1, AX2 b2 , , AXs bs , 写成矩阵形式,即: ( AX1, AX2 , , AXs ) (b1,b2 , ,bs ), 令X ( X1, X2 , , X s ), B (b1,b2 , ,bs ),则上式成 矩阵方程组: AX B
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§1 消元法与线性方程组的相容性
1.1 线性方程组的相容性与 线性方程组的相容性与Cramer法则 法则 1,线性方程组的表示法 , 一般地,n个未知量 个方程的线性方程组可以表示为 一般地, 个未知量m个方程的线性方程组可以表示为 个未知量
a11 x1 + a12 x2 + L + a1n xn = b1 , a x + a x +L+ a x = b , 21 1 22 2 2n n 2 LLLLLLLLLL am1 x1 + am 2 x2 + L + amn xn = bm ,
3,线性方程组的相容性 设非齐次方程组Ax=b ,其中A=(aij)m×n,且R(A)=r. 不妨设矩阵A的前r列中有r阶的非零子式,对增广矩阵 B=(A,b)施以初等行的换法变换,将非零子式所在的行调整 到前r行,再经过若干次初等行变换将B化43;1 1 O M M O 0 cr-1,r+1 初等 1 cr ,r+1 B = ( A, b) → ( C , d ) = 0 行变换 0 M 0
L
c1n M cr-1,n crn 0 0 M 0
L L L L
d1 M d r-1 dr , d r+1 0 M 0
它所对应的与原方程组Ax=b 的同解方程组为
c1r +1 xr +1 + L x1 + x2 + c2 r +1 xr +1 + L L L L L L L L L L xr + crr +1 xr +1 + L + c1n xn = d1 , + c2n xn = d2 , L L L L + crn xn = dr , 0 = dr +1 , 0 L 0 = L = 0, L 0.
所以方程组的解为x1= -1,x2= -1,x3= 0.
1.2
用消元法解线性方程组
1,同解方程组 定义1.1 若线性方程组A1x=b1都是线性方程组A2x=b2 定义 的解;反之, A2x=b2的解也都是A1x=b1的解,则称线性方 程组A1x=b1与A2x=b2是同解方程组. 2,消元法 线性方程组的求解过程是不断寻求化简的同解方程组 的过程.其实质上是对方程组的增广矩阵施行初等行变换, 使其变成行阶梯形矩阵 行阶梯形矩阵.在该阶梯形矩阵非零行所对应的 行阶梯形矩阵 方程中,越下面的方程所含的未知量个数越少.正是利用 这一点,最后求出方程组的解.这种求解线性方程组的方 法称之为消元法 消元法. 消元法
1 1 1 2 1 1 1 0 2 1 0 0 1 ×r3 0 1 1 1 0 1 0 1 0 1 0 1. r2 +r 2 1 → → → r3 +r2 r +r 0 0 2 0 3 1 0 0 1 0 0 0 1 0
1 ( )×r2 2 3r2 +r3
于是得方程组的解为x1= -1,x2= -1,x3= 0.
显然R(A)= 2 , R(B)=3,故方程组无解.
定理1.2 n元非齐次线性方程组Ax=b 有无穷多解的充 定理 分必要条件是R(A) <n. 推论1.1 n元非齐次线性方程组Ax=b 有惟一解的充分 推论 必要条件是R(A) =n. 定理1.1主要用于判别方程组Ax=b 是否有解,而定理 1.2则主要用于判别相容的线性方程组Ax=b 有多少解.特 别当b =0时,定理1.2仍然成立.成为判别齐次线性方程组 Ax=0 有非零解的条件 . 定理1.3 n元齐次线性方程组Ax=0 有非零解的充分必 定理 要条件是R(A) <n. 推论1.2 n个未知数n个方程的齐次线性方程组Ax=0 推论 仅有零解的充分必要条件是|A| ≠0 .
0 5 3 A = 4 6 2 = 4 10 6 = 2 = 8, 3 1 2 1 1 2 3 1
由于|A|≠0,所以方程组有唯一解.又因为
2 1 1 1 1 2 1 2 1 D1 = 2 6 2 = 8, D2 = 4 2 2 = 8, D3 = 4 6 2 = 0, 1 1 1 2 1 1 2 1 1
例2
用消元法解线性方程组 x1 + x2 + x3 = 2, 4 x1 6 x2 2 x3 = 2, 2 x x + x3 = 1. 2 1
解 对方程组的增广矩阵 B 施以初等行变换
1 1 1 2 1 1 1 2 1 × r2 4 6 2 2 0 2 2 2 2 B= r 23r++r2r → 1 3 2 1 1 1 0 3 1 3
x1 = d1 c1,r +1 xr +1 L c1n xn , x = d c x L c x , 2 2 2,r +1 r +1 2n n xr = d r cr ,r +1 xr +1 L crn xn .
由此可见,任给xr+1,xr+2,…,xn的一组值,就可以确定 x1,x2, …,xr的值,从而得到方程组的一个解.此时方 程组有无穷多个解.其解的表达式为
(1)
其中x 个未知量, 其中 1,x2,…, xn 是方程组的 n 个未知量,aij (i =1, 2, …, m; j = 1, 2, …, n)是第 i 个方程中的第 j 个未知量的系数, 个未知量的系数, 是第 个方程的常数项. bi (i =1, 2, …, m) 是第 i 个方程的常数项.若记
由于bi在Dj中的代数余子式为Aij,将Dj按第 j 列展开,得 Dj=b1A1j+ b2A2j+…+ bnAnj, j=1,2,…,n. 于是 D1 D 1 2 x= , A M Dn 即方程组(1)的唯一解 x j = , j=1,2,…,n .这就是 A 著名的Cramer法则. Cramer法则 n个未知数n个方程的线性方程组Ax=b , 法则 若|A| ≠0,则方程组有唯一解
例4 试判断λ取何值时,方程组
λ x1 + x2 + x3 = 0, x1 + λ x2 + x3 = 0, x + x + λx = 0 3 1 2
有非零解? 解 由于方程组的系数行列式
x1 c1r +1 c1n d1 x c c d 2 2 r +1 2n 2 M M M M xr = xr +1 crr +1 + L + xn crn + d r . xr +1 1 0 0 M M M M x 0 1 0 n
= 1, = 2, = 3
解 对方程组的增广矩阵B施以初等行变换 1 2 3 1 1 B = ( A, b) = 3 1 5 3 2 2 1 2 2 3
1 2 3 1 1 1 2 3 1 1 0 5 4 0 1→ 0 5 4 0 1 . → 0 5 4 0 1 0 0 0 0 2
4, Cramer法则 , 法则 我们先来看一种特殊的情形, 我们先来看一种特殊的情形,设 m = n,且 |A| ≠0, , , 即方阵A可逆 由于其逆是惟一的, 可逆, 即方阵 可逆,由于其逆是惟一的,所以方程组有惟一解 x = A-1b, 其中
A11 A 1 12 1 A = A M A1n
xj = Dj A , j = 1, 2,L , n.
Dj
其中Dj为以 b 代替|A|中的第 j 列所得到的行列式.
例1 解线性方程组 x1 + x2 4 x1 6 x2 2 x x 2 1
+ x3 2 x3 + x3
= 2, = 2, = 1.
解 方程组的系数行列式 1 1 1 1 0
上述表达式称为方程组的通解 xr+1,xr+2,…,xn称 通解, 通解 为一组自由的未知量 自由的未知量. 自由的未知量 综合以上的讨论,得出如下的定理. 定理1.1 n元非齐次线性方程组Ax=b 有解的充分必要 定理 条件是R(A) = R(A,b).
例3 试判明非齐次线性方程组
是否有解?
x1 2 x2 + 3 x3 x4 3x1 x2 + 5 x3 3x4 2 x + x + 2 x 2 x 3 4 1 2
为方程组(1)的解向量 解向量,或说 x = ξ 是Ax=b 的解. 解向量 解
3,线性方程组的相容性 线性方程组的相容性 当一个线性方程组的未知量个数为 n 时,就说该方程 元线性方程组. 组为一个 n 元线性方程组. 当线性方程组有解时,就说该方程组是相容的, 相容的 当线性方程组有解时,就说该方程组是相容的,否则 就说它是不相容的 不相容的. 就说它是不相容的. 满足( ) 若 x = ξ ≠ 0 满足(4)式,则称 x = ξ 是齐次线性方程 组的一个非零解 组的一个非零解. 显然,齐次线性方程组总是相容的.那末, 显然,齐次线性方程组总是相容的.那末,非齐次的 线性方程组在什么条件下才相容呢? 线性方程组在什么条件下才相容呢?
从而
A21 L An1 A22 L An 2 , M M A2 n L Ann
1 x= A
1 = A
A11 A21 L An1 b1 A A22 L An 2 b2 12 M M M M A1n A2 n L Ann bn b1 A11 + b2 A21 + L + bn An1 b A + b A + L + b A n n2 1 12 2 22 . M b1 A1n + b2 A2 n + L + bn Ann
x1 b1 a11 a12 L a1n x a b a22 L a2 n 21 , x = 2, b = 2 , A= M M M M M am1 am 2 L amn xn bm 按矩阵的乘法和矩阵相等的定义,(1)式可以写成 Ax = b (2) 其中m×n 矩阵 A 是线性方程组(1)的 系数矩阵, 系数矩阵, m×(n+1) 矩阵 B= (A,b)是方程组的 增广矩阵 增广矩阵. 设 A 按列分块为 A = (α1 , α 2 ,Lα n ) ,(1)也可表为 x1α1 + x2α 2 + L + xnα n = b. (3) 当b≠0时,即b1, b2,…, bm不全为零时,相应的方程组 称为非齐次线性方程组 非齐次线性方程组.当b=0时,即b1=b2=…=bm=0时, 非齐次线性方程组 齐次线性方程组,即 相应的方程组称为齐次线性方程组 齐次线性方程组 Ax = 0. (4) .
