第三章 管路,孔口和管嘴的水力计算(1)
《管道的水力计算》PPT课件

(1)按ΣQi=0分配流量 从A点和最远点F点分配,可假设
(2)计算各管段损失并填表 注意正负号 hi SiQi2
(3)计算校正流量ΔQ
注意公共段CD
环网计算表
环 管 假定流
路 段 量Qi
Si
管段校 校正后 校正后
hi
hi /Qi
ΔQ
正流量 的流量Qi 的hi
AB +0.15 59.76 +1.3346 8.897
vB2 2g
zA
zB
pA pB
g
v
2 A
2g
1 vB2Biblioteka 2gH0——作用水头
H0
1
vB2 2g
流速
vB
1
1
2gH0 2gH0
对锐缘进口的管嘴,ζ=0.5, 1 0.82
1 0.5
流量 Q vB A A 2gH0 A 2gH0
Qi 0 b.由流量确定各管段管径
d 4Qi ve
ve——经济流速(规范要求)
c.由控制线确定作用压力
p pi pc Spi Qi2 pc 或 H hi hc Shi Qi2 hc
d.阻力平衡,调整支管管径
(2)管网布置和作用压力已定,求di——校核计 算,扩建管网
短管的作用水头
H0
1
l d
v2 2g
1→突扩ζ=1,H0→H
H l v2
d 2g
v2
4Q
d
2
2
代入,得
5.3 短管水力计算——学习材料

学习单元三、短管水力计算一、管流概述在水利土木工程和日常生活中,经常用管道来输送液体,如水利工程中的有压引水隧洞、有压泄洪隧洞、水电站的压力管道、灌溉工程中的虹吸管和倒虹吸管、抽水机的吸水管和压水管、建筑或城市给排水工程中的自来水管、通风热水管道、石油工程中的输油管、人体中的血管等,都是常见的有压管流。
有压管流一般都采用圆形管道输送。
水流运动的特点是:整个断面被液体所充满,没有自由液面,管道的整个边壁上都受动水压强作用,而且一般不等于大气压强。
因此,管流又称为有压流。
管道中的断面如果未被水冲满,则不能视为有压流,是无压流动(明渠流动)根据管道中水流的沿程水头损失、局部水头损失及流速水头所占的比重不同,管流可分为长管流动和短管流动。
长管即管道中水流的沿程水头损失较大,而局部水头损失和流速水头很小,此两项之和只占沿程水头损失5%以下,以致可以忽略不计。
一般自来水管可视为长管。
短管即管道中局部水头损失与流速水头两项之和占沿程水头损失的5%以上,水力计算时不能忽略,必须一起考虑在内。
虹吸管、倒虹吸管、坝内泄水管、抽水机的吸水管等,均可按短管计算。
特别需要指出的是,长管和短管并不是按管道的长度分类的,即使很长的管道,局部水头损失和流速水头不能忽略时,仍应按短管计算。
根据水流运动要素随时间是否变化,可分为有压恒定流和有压非恒定流。
当管中任一点的水流运动要素不随时间而改变时,即为有压恒定流,否则为有压非恒定流。
本课程主要研究有压恒定流的计算。
本节先介绍短管流动下图5-6表示一段短管的自由出流过程。
列1-1断面和2-2断面的能量方程,有:212222201-+=+w h gv g v H αα令0212H gv H =+α,称为作用水头。
又有∑∑+=-j f w h h h 21。
因此g v d lH 2)(220∑++=ξλα取 12=α 则g v dlH 2)1(2∑++=ξλ图5-6 短管的自由出流管中流速0211gH dl v ∑++=ξλ通过管道流量 002211gH A gH A dl Q c μξλ=++=∑式中 ∑++=ξλμdl c 11称为管道系统的流量系数。
水力学常用知识讲解(笔记)

《水力学》学习指南第一章绪 论(一)液体的主要物理性质1.惯性与重力特性:掌握水的密度ρ和容重γ;2.粘滞性:液体的粘滞性是液体在流动中产生能量损失的根本原因。
描述液体内部的粘滞力规律的是牛顿内摩擦定律 :注意牛顿内摩擦定律适用范围:1)牛顿流体, 2)层流运动3.可压缩性:在研究水击时需要考虑。
4.表面张力特性:进行模型试验时需要考虑。
下面我们介绍水力学的两个基本假设: (二)连续介质和理想液体假设1.连续介质:液体是由液体质点组成的连续体,可以用连续函数描述液体运动的物理量。
2.理想液体:忽略粘滞性的液体。
(三)作用在液体上的两类作用力第二章 水静力学水静力学包括静水压强和静水总压力两部分内容。
通过静水压强和静水总压力的计算,我们可以求作用在建筑物上的静水荷载。
(一)静水压强:主要掌握静水压强特性,等压面,水头的概念,以及静水压强的计算和不同表示方法。
1.静水压强的两个特性:(1)静水压强的方向垂直且指向受压面(2)静水压强的大小仅与该点坐标有关,与受压面方向无关,2.等压面与连通器原理:在只受重力作用,连通的同种液体内, 等压面是水平面。
(它是静水压强计算和测量的依据)3.重力作用下静水压强基本公式(水静力学基本公式)p=p 0+γh 或 其中 : z —位置水头,p/γ—压强水头(z+p/γ)—测压管水头请注意,“水头”表示单位重量液体含有的能量。
4.压强的三种表示方法:绝对压强p ′,相对压强p , 真空度p v , ↑ 它们之间的关系为:p= p ′-p a p v =│p │(当p <0时p v 存在)↑相对压强:p=γh,可以是正值,也可以是负值。
要求掌握绝对压强、相对压强和真空度三者的概念和它们之间的转换关系。
1pa(工程大气压)=98000N/m 2=98KN/m2下面我们讨论静水总压力的计算。
计算静水总压力包括求力的大小、方向和作用点,受压面可以分为平面和曲面两类。
孔口,管嘴出流和有压管路

流量计算公式的形式以及流量系数的数值均相同
不同点
两者的作用水头在计量时有所不同,自由出流时是指上游水 池液面至下游出口中心的高度,而淹没出流时则指得是上下 游水位差。
出口位置处的总水头线和测压管水头线的画法不同
短管水力计算的内容
四类问题 已知水头H、管径d,计算通过流量Q;
校核输水 能力
已知流量Q、管径d,计算作用水头H,以确定水箱、水塔水位 标高或水泵扬程H值;
经济流速——在选用时应使得给水的总成本(包括铺设水管的 建筑费、泵站建筑费、水塔建筑费及抽水经常运转费之总和) 最小的流速。
一般的中、小直径的管路大致为:
——当直径 d=100-400mm,经济流速 v =0.6~1.0m/s ——当直径 d400mm,经济流速 v =1.0~1.4m/s
3
2g
(H下3 2
H
32 上
)
b为宽 d为高
如果用孔口中心高度H作为孔口作用水头,将孔口断面 各点的压强水头视为相等,按小孔口计算的流量为
Q bd 2gH
大孔口的流量系数
孔口形状和水流收缩情况
全部不完善收缩 底部无收缩,侧向收缩较大 底部无收缩,侧向收缩较小 底部无收缩,侧向收缩极小
流量系数
圆柱形短管内形成收缩,然后又逐渐扩大
H 0 0v02 0 0 v 2 v 2 ,
2g
2g 2g
H0
1
vB2
2g
流速
vB
1
1
2gH0 2gH0
对锐缘进口的管嘴,ζ=0.5, 1 0.82
1 0.5
流量
Q vB A A 2gH0 n A 2gH0
第三章管路,孔口和管嘴的水力计算(3)

1
Ac A2
vc2 2g
vc2 2g
h h1c hc2 1
vc2 2g
将h表达式代入能量方程,并注意到v0 v2 0
z 1 vc2
2g
vc
1
1
2gz 2gz (3-47)
式中 为淹没出流的速度系数,与自由出流流速
系数 的表达式相同
9
淹没出流的流量为:
q vc Ac A 2gz A 2gz
v0
v C
D A AC
c
C
5
O
将其代入能量方程可得:
H0
1
vc2
2g
vc
1
1
2gH0 2gH0 (3-44)
1 为流速系数,与有关,由实验确定, 1
对完善收缩的小孔口,一般取 0.97。
孔口自由出流的流量为:Q vc Ac
vc 2gH0 ; Ac A
6
所以有: Q A 2gH0 A 2gH0 (3-45)
Ⅰ
验确定式中的系数。
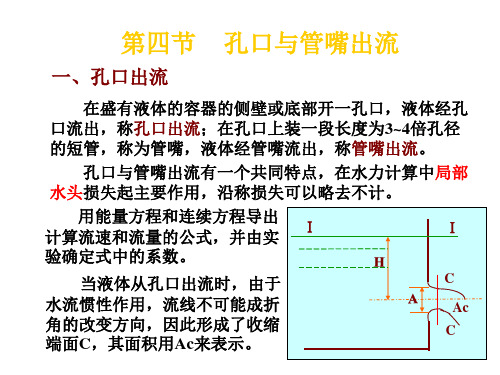
当液体从孔口出流时,由于
C
水流惯性作用,流线不可能成折
Ac
角的改变方向,因此形成了收缩
端面C,其面积用Ac来表示。
C
1
1、孔口出流的分类
小孔口出流:D/H >10为小孔口
大孔口出流:D/H<10为大孔口,
D/H 为孔口直径与水头的比值。
恒定出流、非恒定出:
自由出流、淹没出流:在大气中的出流为自由出流;
并且:
式中 是流量系数,其值常由实验确定。
对于完善收缩的圆形小孔口, 0.64, 0.97
0.97 0.64 0.62
对于其它情况,可查经验公式。对于大孔口的自由 出流的流速及流量仍可采用公式(3-44)和(3-45)计 算,只是相应的水头应近似取为孔口形心处的值,具体 的流量系数也与小孔口出流不同,大孔口的流量系数值 见表3-7。
流体力学名词解释和简答题

流体力学名词解释和问答题一、绪论1.连续介质假设:把流体当作是由密集质点构成的、内部无空隙的连续体来研究,这就是连续介质假设。
或 连续介质:由密集质点构成的、内部无空隙的连续体。
2.表面力:通过直接接触作用在所取流体表面上的力。
3.质量力:作用在流体内每个质点上,大小与流体质点质量成正比的力。
4. 粘性:是流体在运动过程中抵抗剪切变形的能力,是产生机械能损失的根源。
或粘性是流体的内摩擦特性。
或相邻流层在发生相对运动时产生内摩擦力的性质。
5.理想流体:指无粘性,动力粘度0=μ或运动粘度0=ν的流体。
6.不可压缩流体:流体的每个质点在运动全过程中,密度不变化的流体。
(1)什么是理想流体?为什么要引入理想流体的概念?(2)试从力学分析的角度,比较流体与固体对外力抵抗能力的差别。
二、流体静力学1.真空度:指绝对压强不足当地大气压的差值,即相对压强的负值。
2.相对压强:以当地大气压为基准起算的压强。
3.绝对压强:以没有气体分子存在的完全真空为基准起算的压强。
4.测压管水头:gp z ρ+称为测压管水头,是单位重量流体具有的总势能。
或,位置高度(或位置水头)与测压管高度(压强水头)之和。
5.帕斯卡原理:在平衡状态下,液体任一点压强的变化将等值地传到其他各点。
6.等压面:流体中压强相等的空间点构成的面(平面或曲面)。
7.阿基米德原理:液体作用于潜体(或浮体)上的总压力,只有铅垂向上的浮力,大小等于所排的液体重量,作用线通过潜体的几何中心。
(1)简述静止流体中应力的特性。
(2)何为压力体?压力体的作用是什么?如何确定压力体?(3)试述液体静力学基本方程C gp z =+ρ及其各项的物理和几何意义? 三、流体动力学1.流线:表示某时刻流动方向的曲线,曲线上各质点的速度矢量都与该曲线相切。
2.迹线:流体质点在一段时间内的运动轨迹称为迹线。
3.水力坡度:粘性流体的总水头线沿程单调下降的快慢程度,亦即单位流程内的水头损失。
流体力学--第3章习题

1
1 2 2
解: (1)列两自由液面的伯努利方程,只计沿 程损失,得到
H hf
2
64 l v 32lQ 128 lQ hf 4 Re d 2 g gd 4 gd 4
校核流态
2.73 0.006 Re 1918 2320 6 8.54 10 vd
层流
沿程阻力系数
一、选择题
C 1. 圆管紊流过渡区的沿程阻力系数________ 。 A. 与雷诺数Re有关; B. 与管壁相对粗糙度△/d有关; C. 与Re和△/d有关; D. 与Re和管长l有关。 B 2. 圆管紊流粗糙区的沿程阻力系数________ 。 A. 与雷诺数Re有关; B. 与管壁相对粗糙度△/d有关; C. 与Re和△/d有关; D. 与Re和管长l有关。
解: 列橡皮管进, 出口两端伯努利方程:
pm
L v2 ( ) d 2g
2 pm
v
L d
2 5.49 105 5.024m s
18 1000 (7.5 0.024 ) 0.012
6. 长管输送液体只计沿程损失,已知 H=127.4m, L=500m, 管路末端可用水头 h=2H/3,管路末端 可用功率为 1000Kw, λ=0.024,求管路的输送流量 与管路直径。
3. 圆管层流,实测管轴线上流速为4m/s,则断面平 均流速为: C A. 4m/s B. 3.2m/s C. 2m/s D. 1m/s
二、计算题
1. ρ=0.85g/cm3、v=0.18cm2/s的油在管径为100mm的 管中以 v =6.35cm/s的速度作层流运动, 求(1)管中心处的最大流速; (2)在离管中心r=20mm处的流速; (3)沿程阻力系数λ ; (4)管壁切应力τ0及每1000km管长的水头损失。
管路孔口和管嘴的水力计算

再列干管与支管2之间的能量方程,用同样的方法求干管
流量q与支管2流量q2之间的关系,此时有:
40
v22 2g
h 2
8q22
g 2d24
h 2
d
1 50m
1
h 2
l
d
v2 2g
2l2
d2
v22 2g
三
v22 2g
l
d
8q2
g 2d 4
2l2
d2
三
8q22
g 2d24
e
q, l, d
q1,l1, d1 2
l
d
8q2
g 2d 4
1
1l1
d1
三
8q12
g 2d14
由此式得:
q1
30 1
l
d
1l1
d1
8q2
g 2d
三
4
g 2d14
8
30
150 0.8
9.8
8q2 3.142
0.84
9.8
3.142
0.64
8
1
200 0.6
1
1.5
9
q1
30 37.82q2 1.6 213.331
c
(C)式给出了干管流量q与支管1流量q1之间的关系。
再来计算一次近似的1, 2和 ,为此先计算近似
的Re, Re1 和Re2
12
Re
4q
d
4 3.77 3.14106 0.8
6 106
Re1
4q1
d1
4 2.233 3.14106 0.6
4.72 106
Re 2
4q2
第三章 管路,孔口和管嘴的水力计算(3)
C
D
C
vc
3~4D
v
15
三、变水头孔口出流
变水头出流是非定常问题, 变水头出流是非定常问题,但在水位随时间变化的速 率较小的情况下,如果把整个水头变化范围分为若干等份, 率较小的情况下,如果把整个水头变化范围分为若干等份, 则在每一等份可近似看作定常,通常称这种为准定常流。 则在每一等份可近似看作定常,通常称这种为准定常流。 如图所示, 如图所示,容器内自由表面积为 Ω ,在dt时段内水 时段内水 头的增量为dH, 头的增量为 ,则dt时段 时段 内孔口的泄水量为: 内孔口的泄水量为:
2ΩH t= µA 2gH
(3-52) )
表明非定常流的 泄水时间等于相 同水头下定常泄 放同样体积所需 时间的两倍。 时间的两倍。
17
H+
O
2 α0v0
αv
2 0 0
1
H
2g
1
H0 C D
2g
= H0为 口 总 头 孔 的 水 ;
2
Байду номын сангаас
vc 令 ω =ζ h 2g
ζ为 口 局 阻 系 孔 的 部 力 数
O
v0
A
AC C
5
vc
将其代入能量方程可得: 将其代入能量方程可得:
2 vc ∴H0 = (1+ζ ) 2g 1 ∴vc = 2gH0 = ϕ 2gH0 1+ζ
l1
l1 < 3a l2 > 3b
不 完 善 完善收缩 收 l2 缩
无收缩
4
以孔口中心的水平面为基准面,列断面 与收缩断 以孔口中心的水平面为基准面,列断面1-1与收缩断 之间的能量方程: 面C-C之间的能量方程 之间的能量方程
武大水力学习题+答案第三章

第三章水动力学基础1、渐变流与急变流均属非均匀流。
( )2、急变流不可能是恒定流。
( )3、总水头线沿流向可以上升,也可以下降。
( )4、水力坡度就是单位长度流程上的水头损失。
( )5、扩散管道中的水流一定是非恒定流。
( )6、恒定流一定是均匀流,非恒定流一定是非均匀流。
( )7、均匀流流场内的压强分布规律与静水压强分布规律相同。
( )8、测管水头线沿程可以上升、可以下降也可不变。
( )9、总流连续方程v1A1 = v2A2对恒定流和非恒定流均适用。
( )10、渐变流过水断面上动水压强随水深的变化呈线性关系。
( )11、水流总是从单位机械能大的断面流向单位机械能小的断面。
( )12、恒定流中总水头线总是沿流程下降的,测压管水头线沿流程则可以上升、下降或水平。
( )13、液流流线和迹线总是重合的。
( )14、用毕托管测得的点流速是时均流速。
( )15、测压管水头线可高于总水头线。
( )16、管轴高程沿流向增大的等直径管道中的有压管流,其管轴压强沿流向增大。
( )17、理想液体动中,任意点处各个方向的动水压强相等。
( )18、恒定总流的能量方程z1 + p1/g + v12/2g = z2 +p2/g + v22/2g +h w1- 2 ,式中各项代表( )(1) 单位体积液体所具有的能量;(2) 单位质量液体所具有的能量;(3) 单位重量液体所具有的能量;(4) 以上答案都不对。
19、图示抽水机吸水管断面A─A动水压强随抽水机安装高度h的增大而( )(1) 增大(2) 减小(3) 不变(4) 不定h1与h2的关系为( ) (1) h>h(2) h<h(3) h1 = h2(4) 无法确定( )(1) 测压管水头线可以上升也可以下降(2) 测压管水头线总是与总水头线相平行(3) 测压管水头线沿程永远不会上升(4) 测压管水头线不可能低于管轴线22、图示水流通过渐缩管流出,若容器水位保持不变,则管内水流属( )(3) 恒定非均匀流(4) 非恒定非均匀流( )(1) 逐渐升高(2) 逐渐降低(3) 与管轴线平行(4) 无法确定24、均匀流的总水头线与测压管水头线的关系是( )(1) 互相平行的直线;(2) 互相平行的曲线;(3) 互不平行的直线;(4) 互不平行的曲线。
水力学计算公式

❖常用消能方式:底流消能、条流消能和面 流消能
❖水流衔接形式
当ht<hc' '
当ht= hc' ' 当ht> hc' '
远驱水跃 临界水跃 淹没水跃
第三十三页,共36页。
水力学重点及难点
❖底流消能降低护坦消力池设计 (1)消力池深d (2)消力池长度的计算 (由于消力池末端
池壁的作用,消力池中水跃长度比自由水 跃Lj短) Lk=(0.7~0.8)Lj
第十三页,共36页。
水力学重点及难点
② 能量方程应用注意事项: 选择统一基准面便于计算、选计算断面、 选典型点计算测压管水(压强计算采用统 一标准)
能量方程应用:
孔口恒定出流 、 毕托管、文丘里 流量计 、管嘴出流
第十四页,共36页。
能量方程图示
掌握总头线、测压管水头线、水力坡度的 概念及水头线的绘制。
第十七页,共36页。
Chapter 4 水力学重点及难点
❖ 液体的两种流态和判别 雷诺实验 层流 —液体质点互相不混掺的层 状流动。 紊流 —存在涡体质点互相混掺的 流动。
❖ 流态的判别:雷诺数Re
Re<Rek 层流 ;Re>Rek 紊流
雷诺数是重要的无量纲数,它的物理意义 表示惯性力与粘滞力的比值。
表示土壤渗透能力的大小 适用范围:恒定均匀层流渗流
第三十五页,共36页。
水力学重点及难点
❖ 恒定无压渐变渗流基本公式 —杜比公式
v k dH ds
dH J
ds
式中:H—测压管水头,(或称为水面高 程), J—渗透坡降。(对于渐变渗流,同 一过水断面上的渗透坡降可以认为是常数, 因此同一渗流断面上各点的流速为定值。)
第三章 管路孔口和管嘴的水力计算(3N)PPT课件

H l 30030m, 10 10
qK HK 30K 1,
l
300 10
K g 2d 5 8
由于 取决 R和 e于壁面 ,但状 流况 量,无 不法 知R确 道 e,定 时
故须采,先 用假 试 0设 算 .0,2 则 法 :有
K 9.83.1420.85 14.1 80.2
2
qK11.1 4 14.4m 63/s
h
l
d
8q2
g2d4
0 .01 1 0 8 .35 59 .0 8 8 3 .1 0 .2 2 4 20 .3 4 1.9 8 m
所以泵的扬程为: H 1 1 0 .9 8 2.9 m 8
所以泵的功率为:
P oH il 9 q. 2 4 2 2 .9 8 1 0 .2 5 .3 K 3 W
三
g2d24
8
代入已知数据得:
q2
4037.82q2 3.36602
f
12
根据流动的连续性有: qq1q2
g
将(C)与(f)代入(g)得:
q
1 3.6 0 32.7 8 1.32 3q 32 1
4 03.7 82q2 3.36610
h
采用逐次逼近法求解,假设 12 0 .0 2 ,q 1 m 3/s
q1.73 3 15.4(8m3/s) 10
4
例题5:
如图所示:带泵管路用 来将油液从低位油箱打 入高位
油箱,两油箱均为敞口 ,自由液面差为 10 m, 钢管管路 总长 l 150 m,直径 d 30 cm,
油的重度 9221 .4 N m3 , 粘 度 10 6 m2 s 。试问:
当想保证管路中有
凝土管,
孔口、管嘴出流和有压管流

H0
2v2 2
2g
hw
1 v l d
由此得到管道的流量为
2 gH o
A Q l d
2 gH o
由该式 看出,管道的流量取决于H0、A和Hw。A由管径
的大小决定,Hw按第四章水头损失计算方法求得。
若
1 1.0 代入式 v l d
hw h f h j
1
pa
该式说明短管水流在 自由出流的情况下, 其作用水头H0 一部分 消耗于水流的沿程水 1 头损失和局部水头损 失,另一部分转化为 管道2-2断面的流速水头。
v1
H HP v 2 H
v2
闸门
2
对于等直径管 , 管中流速为常数v, 所以v2=v,代入上式 ,取α2=α,得
1)短管自由出流
液体经短管流动流入大气后,流束四周受到大气压的 作用,称这种流动为短管自由出流,图示为一短管自由出流。
液流从水箱 进入管径为d, 装有一个阀门并 带有两个弯头的 管路,管路总长 度为 l。
1 pa
v1
1
H HP v 2 H
v2
闸门
2
取出口中心高程的水平面为基准面 0-0,断面1-1 取在 管道入口上游水流满足渐变流条件处,2-2断面则取在管流 出口处,对断面1-1至断面2-2 的水流建立能量方程:
可见, 同一短管在自由出流和淹没出流的情况下,
其流量计算公式的形式及μc的数值均相同,但作用水头
H0 的计量基准不同,淹没出流时作用水头是以下游水面 为基准 ,自由出流时是以通过管道出口断面中心点的水
平面为基准。
3)、短管的水力计算问题
短管的水力计算包括以下几类问题: ①已知作用水头、断面尺寸和局部阻碍的组成,计算 管道输水能力,求流量; ② 已知管线的布置和必需输送的流量(设计 流量), 求所需水头(例如:设计水箱、 水塔的水位标高H、水泵 的扬程H等); ③ 已知管线布置,设计流量及作用水头,求管径d; ④ 分析计算沿管道各过水断面的压强。
孔口、管嘴和管道的流动计算方法

vB2
2g
流速
1
vB 1
2gH 0 2gH 0
对锐缘进口的管嘴,ζ=0.5, 1 0.82
10.5
流量 Q vBAA2g0 H A2g0 H
0.82
真空的抽吸作用,流量增加
2.管嘴正常使用条件 防止气蚀 列C-C、B-B断面能量方程
pgC 2vC g2 pgB 2vB g2 hw
hw
l d
pagpCzCz11 l1ldl121 CHhv7~8m
d 12
最大安装高度
1l1
hmaxzCz1hv
d
l1l2
1C Hhv
d 1不计,损失线性下降,总水
头线与测压管水头线重合
单位长阻抗——比阻a
aH
SH L
28d5g
s2/m6
HLaHQ2
H 0z1z2H
收缩断面流速
1
vC 11
2gH 0 2gH 0
孔口流量
QvCACvCACA2gH 0
与自由出流一致
气体: 作用压力
p0p1p2
v1 2v2 2 2
(略去高差)
流速 v 2 p0
流量 Q A 2 p0
p0 0 排气
p0 0 吸气
应用:孔板流量计
H 0z1z2p1 gp2v1 22 gv2 2 g p
伸管嘴 流量大
0.04 0.98 1 0.98
4.例:水箱中用一带薄壁孔口的板隔开,孔口及两出 流管嘴直径均为d=100mm,为保证水位不变,流入水 箱左边的流量Q=80L/s,求两管嘴出流的流量q1、q2
解:设孔口的流量为q
qA2gh 1h2
对管嘴
q1 1A 2gh1
管路、孔口和管嘴的水力计算

第二节 管路的水力计算
一、流动阻力及能量损失的两种形式 二、圆管的层流运动 三、沿程阻力系数 四、局部阻力系数 五、管路的水力计算
第三节 圆管中的层流流动
不可压缩流体在一半径为R的水平放置等截面圆 管中作定常层流运动,现在分析这一流动的有 关力学特征。
工程中也可取2000,即
层流: Re 2320 湍流: Re 2320
当过流断面是非圆断面时,
Re vR
或
Re vde
R是水力半径, de 是水力直径, de 4R
用R计算的临界雷诺数 Rec 580
层流: Re 580
湍流: Re 580
例1. 一等径圆管内径d=100mm,流通运动粘 度ν=1.306×10-6m2/s的水,求管中保持层流流 态的最大流量。
p
gh f
l
d
v 2
2
540Pa
第五节 局部水头损失
当水流流过流程中的阀门、弯头、扩散段、收缩段等 局部障碍时,具有粘性的水流将在这些障碍处脱离固 体表面产生耗能严重的旋涡,这是产生局部损失的主 要原因,另外,旋涡随主流下移也将引起下游一定范 围内水流机械能减少。
流动处于湍流水力光滑区
0.3164 Re0.25
0.0348
沿程水头损失
hf
l
d
v2 2g
1000 1.212 0.0348
0.2 19.6
12.99m油柱
例3. 有一镀锌铁管,l=40m,d=0.2m, △=0.15mm, 输送干空气,其密度ρ=1.2kg/m3,运动粘度ν=15.7× 10-6m2/s,测得风量Q=1700m3/h,气流的沿程损失为多 少?
第章 孔口管嘴与管路流动

①有压管道:管内表压不等于零( p 0 ),供水、煤气、通风、 电站引水管。
②无压管道(涵管):管内表压等于零( p 0),非满管流动 (如排水管道,管内存在自由液面的情况)。
2019年2月12日星期二
流体力学
设备和热动
2.短管和长管 都不能忽略不计的管道;
Tianjin Institute of Urban Construction
Tianjin Institute of Urban Construction
对A—A液面与C—C断面列能量方程:
pA
H
2 A A
2g
pc
c c2
2g
he
he hm
c2
2g
若令
H0 H
p A pC
2 A A
2g
H 0 ( c )
短管是指管路中水流的流速水头和局部水头损失
长管是指流速水头与局部损失之和远小于沿程损失,
在计算中可以忽略的管道。一般认为(局部水头损失 +流
速水头)<5%的沿程水头损失,可以按长管计算。
需要注意的是:长管和短管不是完全按管道的长短来区分的。 将有压管道按长管计算,可以简化计算过程。但在不能判断流速 水头与局部水头损失之和远小于沿程水头损失之前,按短管计算
c2
2g
出口流速:
1 c c
2 gH 0 2 gH 0
H0称为作用水头,是促使出流的全部能量,包括 A、 C间的位 差、压差和上游速度头, 0.97 ~ 0.98 称为流速系数。
孔口出流量 :
Ac 其中, A
Q cAc A 2 gH 0 A 2 gH 0
孔口、管嘴和管道的流动计算方法(ppt 74页)

h2 hh1 A点连续性方程
q1q2 Q 解得 q12.79 L/s q21.2L 1/s
(2)当h是多少时,由低位油箱流出的q2=0? 令q2=0,解得h=1.27m
(3)当h>1.27m时会出现什么情况?
会出现高位油箱向低位油箱倒灌的现象
(4)当z为多高,高位油箱泄空后空气不会进入泵 内,且又可使低位油箱可泄空?
H0——作用水头
H0
1
vB2
2g
流速
1
vB 1
2gH 0 2gH 0
对锐缘进口的管嘴,ζ=0.5, 1 0.82
10.5
流量 Q vBAA2g0 H A2g0 H
0.82
真空的抽吸作用,流量增加
2.管嘴正常使用条件 防止气蚀 列C-C、B-B断面能量方程
g
0.75H0
允许真空值 H0的极限值
hv7m
H00.7759.3m
——管嘴正常使用条件之一
l3~4d ——管嘴正常使用条件之二
3.管嘴的种类 (a)圆柱外伸管嘴; (b)圆柱内伸管嘴 ; (c)外伸收缩型管嘴 ; (d)外伸扩张型管嘴 ; (e)流线型外伸管嘴
类型
特点
ζφε μ
1→突扩ζ=1,H0→H
H l v2
d 2g
v2
4Q
d
2
2
代入,得
8 l
H
d
2d4g
Q2
SH——管路阻抗 S2/m5
HSHQ2
8 l
p
d
2d4
Q2
Sp kg/m7
p SpQ2 类比电路:S→R H(p)→U Q2→I
管嘴的水力计算

要保证水泵的真空值不超过规定的允许值,就必须按水泵最大允 许真空值(一般不超过6-7m)计算水泵允许安装高度H允。
以等截面容器为例,设容器截面积为w,无补给水,初始水头为 H1,终止水头为H2,要求泄流时间为T。
设某一时刻水头为H,在dt时段 内水位变化值为dH,体积变化 值为wdt,应等于dt时段内从孔 口流出的液体体积。
Qdt A 2gHdt Wdt
T dt H2 w dh H1 A 2g h
教学基本要求
1、了解有压管流的基本特点。掌握孔口、管嘴的水力 计算;
2、掌握短管(水泵、虹吸管)的水力计算方法; 3、了解复杂管道的特点和计算方法,重点掌握串联管
道和并联管道的水力计算。 4、了解有压管道中的水击现象和水击传播过程。
孔口出流:在贮水池、水箱等容器侧壁上开一孔口,水经孔口流 出的水力现象。
管嘴出流:在孔口上连接长度为3-4倍孔径的短管,水流经此短管 并在出口断面满管流出的水力现象。 有压管流:流体沿管道满管流动的水力现象。
H
H
H
相同点:有压流动。
不同点: 孔口出流只有局部损失; 管嘴出流虽有沿程损失,但与局部损失相比很小,可以忽略。 有压管流沿流动方向有一定的边界长度,水头损失包括沿程损 失和局部损失。
vc
1
c 0
2gH0
2 gH 0
1 c 0
ψ称为孔口的流速系数,一般取αc=1
流量 Q Ac 2gH0 A 2gH0 A 2gH0 μ称为孔口流量系数。
实验测得孔口流速系数:φ= 0.97~0.98
孔口的局部阻力系数: 0
1
2
1
1 0.9 72
通常可用自由出流与淹没出流计算公式解决以下三类问题: 已知流量Q,管径d,管长L等,求水头H(或Z); 已知水头H(或Z),管径d,管长L等,求流量Q; 已知流量Q,水头H,管长L等,求管径d。
第三章 管路,孔口和管嘴的水力计算(1)

l v2 hf = λ L 达 L 西公式 d 2g 其 :hf : 程水头损 ; 中 沿 失
λ :沿程阻力系数;
沿程阻力系数和管道内表面的粗糙度有关, 沿程阻力系数和管道内表面的粗糙度有关,是一个无量纲 由实验确定。 数,由实验确定。 11
2、局部阻力与局部损失 、
粘性流体流经各种局部障碍装置如阀门、弯头、 粘性流体流经各种局部障碍装置如阀门、弯头、 变截面管等时, 变截面管等时,由于过流断面在局部地区发生急剧变 从而引起速度的大小和方向也发生急剧变化, 化,从而引起速度的大小和方向也发生急剧变化,质 局部阻力。 点间进行动量交换而产生的阻力称为局部阻力 点间进行动量交换而产生的阻力称为局部阻力。流体 为克服局部阻力而损失掉的机械能称为局部损失 局部损失。 为克服局部阻力而损失掉的机械能称为局部损失。
紊流
lg vc lg vc ′
lg v
14
对于紊流: 对于紊流:
lg hf = lg k2 + tanθ lg v
lg hf
m=1.75-2.0
∴hf = k2v
= lg k2 + mlg v
m
m=1
其中: m =1.75 ~ 2
表示紊流沿程水头损失与流速的 1.75~2次方成正比。可见沿程水头 次方成正比。 次方成正比 损失与流动形态密切相关,因此, 损失与流动形态密切相关,因此, 欲确定损失,必先判定流态。 欲确定损失,必先判定流态。
2
一、雷诺实验: 雷诺实验:
3
1、层流状态:所有流 、层流状态: 体质点做定向有规则的 运动。 运动。
(a)
2、过渡状态:颜色水 、过渡状态: 开始抖动, 开始抖动,直线形状遭 到破坏。 到破坏。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
2
对于水平等直径管: 对于水平等直径管:
z1 = z2, v1 = v2,α1 = α2, hω = hf
1
L
2
13
p1 − p2 ∴hf = ρg
可知测管液面高度差即为流体自1截 可知测管液面高度差即为流体自 截 面流向2截面的沿程水头损失 截面的沿程水头损失。 面流向 截面的沿程水头损失。
de =
4A
χ
A− 过 断 面 ; χ − 湿 o 水 面 积 周
vde
故对非圆形管道: Re =
υ
9
第二节 流动阻力及能量损失的两种形式
本节主要讨论阻力及损失, 本节主要讨论阻力及损失,工程中必须解决阻 力及损失的确定问题。 力及损失的确定问题。
阻力; 流体层之间的相对运动 粘性切应力 阻力; 阻力损失不可逆地转化为能量损失。 阻力消耗机械能 阻力损失不可逆地转化为能量损失。 流动阻力一般是指流体与固体边界相互作用, 流动阻力一般是指流体与固体边界相互作用,而产生的 平行于流动方向的作用力。 平行于流动方向的作用力。
16
一、运动微分方程
如图所示, 长度为L的圆柱流束 的圆柱流束, 如图所示,在圆管中取一半径为 r ,长度为 的圆柱流束, 定常流动中,作用在圆柱流束上的外力在Y方向的投影之 在定常流动中,作用在圆柱流束上的外力在 方向的投影之 和应为零。 和应为零。即:
( p1 − p2 )πr
2
− 2πrlτ = 0
(
)
π∆pR4 π∆pd4 所 以 q= = 8µl 128µl
管中平均流速为:
dr
q ∆p 2 v= = R A 8µl
19
r 3 ) 管中最大 速度在 = 0处, 由( −10 得: vmax ∆pR = 4µl
2
因此
四、切应力
vmax v= 2
将式( -10 3 )代入牛顿内摩擦公式,可得圆管中的切应力 分布。即: dv ∆pr τ = −µ = dr 2l 切应力的分布规律见右图o
局部损失用hj表示:
v2 hj = ζ 2g 式中 为局部 ζ 阻力系数 ,是一 个由实验 确定的 无量纲数 。
12
3、总的水头损失:
hω = ∑hf + ∑hj
4、沿程损失与流态的关系
水头损失 叠加公式
在雷诺管上取1、2两截面,相距为L,现讨论沿程水头损失 在雷诺管上取 、 两截面,相距为 , 两截面 与流速的关系。 与流速的关系。 两断面列伯努利方程: 对1、2两断面列伯努利方程: 、 两断面列伯努利方程
∆p 2 对( − 9 3 )积分得:v = − r +C 4µl
()rFra bibliotekvmax
∆pR = 4µl
2
表明断面速度为旋转抛物面 分布 max 在管轴上o ,v
18
V
三、流量与断面平均速度
由 ( -9 可 算 过 面 流 q : 式 3 ) 计 通 断 的 量
q = ∫ 2πrvdr = ∫
0
R
R
0
∆p 2 2 R − r 2πrdr 4µl
(或 c )怎 变 , Re′ = v 样 化 c
′ vcd
υ
或Rec =
vcd
υ
却 一 的o 是 定
Re =
vd
υ
vd 将 这一无量纲数,称为雷诺数。
υ
5
1883年 雷诺试验表明: 圆管中恒 1883 年 , 雷诺试验表明 : 圆管中 恒 定流动的流态转化取决 于雷诺数 vd
Re =
d 是圆管直径,v 是断面平均流速, 是流体的运动粘性系数。 是圆管直径, 是断面平均流速, 是流体的运动粘性系数。
lg hf
n=1.75-2.0
雷 分 在 种 态 ,测 v 诺 别 两 流 下 定 与 f 的 系o h 关
n=1
o
对于层流:
lg hf = lg k1 + tan 45 lg v = lg k1v
lgk1
lgk2
层流
∴hf = k1v
表示层流沿程水头损失与流速的 一次方成正比。 一次方成正比。
过 渡 区
紊流
lg vc lg vc ′
lg v
14
对于紊流: 对于紊流:
lg hf = lg k2 + tanθ lg v
lg hf
m=1.75-2.0
∴hf = k2v
= lg k2 + mlg v
m
m=1
其中: m =1.75 ~ 2
表示紊流沿程水头损失与流速的 1.75~2次方成正比。可见沿程水头 次方成正比。 次方成正比 损失与流动形态密切相关,因此, 损失与流动形态密切相关,因此, 欲确定损失,必先判定流态。 欲确定损失,必先判定流态。
υ
υ
实际流体的流动之所以会呈现出两种不同的型态是扰动因素 与粘性稳定作用之间对比和抗衡的结果。 与粘性稳定作用之间对比和抗衡的结果。针对圆管中恒定流动 的情况,容易理解: 的情况,容易理解:减小 d ,减小 v ,加大 三种途径都是 有利于流动稳定的。综合起来看,小雷诺数流动趋于稳定, 有利于流动稳定的。综合起来看,小雷诺数流动趋于稳定,而 大雷诺数流动稳定性差,容易发生紊流现象。 大雷诺数流动稳定性差,容易发生紊流现象。
五、动能及动量修正系数
动能: = α
v3dA ∫
A
v A
3
=2
4 动量: = 2 = β v A 3
A
22
v2dA ∫
六、沿程阻力与沿程水头损失
对等直径圆管1、 断面列伯努利方程 断面列伯努利方程, 对等直径圆管 、2断面列伯努利方程,得:
α1v12 α2v22 p1 − p2 − z2 + + hω = hf = z1 + 2g 2g ρg
′ 上临界雷诺数 ReC 12000-40000
ReC = 2320 下临界雷诺数
从 流 紊 时 雷 数 为 临 雷 数 ec 层 变 流 的 诺 称 上 界 诺 R
′
8
从紊流变层流时的雷诺数称为下临界雷诺数Rec
一般以下临界雷诺系数 作为层流、 一般以下临界雷诺系数Rec作为层流、湍流流态的 下临界雷诺系数 判别标准。 判别标准。 Rec<2320时,管中是层流。 时 管中是层流。 Rec>2320时,管中是湍流。 时 管中是湍流。 对于非圆形截面之过流,实验结果仍然成立, 对于非圆形截面之过流,实验结果仍然成立,只 是计算雷诺数时,对于非圆形断面的管道, 是计算雷诺数时,对于非圆形断面的管道,常以 进行计算。 当量直径 de 进行计算。
4
二、流态的判别
如果 径d及流 的运 管 体 动粘 υ一定 则 层 度 , 从 流变 流时 紊 的 均 平 速度 是一 的 此 度 也 定 , 速 称为 临界 度vc;从 上 速 ′ 紊 流 层流 平 变 的 均速 也是一 的 称为 临界 度 定 , 下 速度vc ,一 般 c 〉vc o v′ ′ 如 d或 改 ,则 c和 c也 之 变 但 ,无 d,υ, vc 果 υ 变 v′ v 随 改 , 是 论
υ
6
扰动因素
对比 抗衡
v
粘性稳定
d
υ
vd
Re =
υ
利于稳定
圆管中恒定流动的流态转化仅取决于雷诺数, 这是客观规律 圆管中恒定流动的流态转化仅取决于雷诺数 , 用无量纲量表达的又一例证,也是粘性相似准则的实际应用。 用无量纲量表达的又一例证,也是粘性相似准则的实际应用。
7
圆管中恒 定流动的流态发生转化时对应的雷诺数称为临界雷 圆管中 恒 诺数,又分为上临界雷诺数和下临界雷诺数。 诺数,又分为上临界雷诺数和下临界雷诺数。上临界雷诺数表示 超过此雷诺数的流动必为紊流,它很不确定, 超过此雷诺数的流动必为紊流,它很不确定,跨越一个较大的取 值范围。有实际意义的是下临界雷诺数, 值范围。有实际意义的是下临界雷诺数,表示低于此雷诺数的流 动必为层流,有确定的取值, 动必为层流,有确定的取值,圆管定常流动取为 ReC = 2320 层流 紊流 Re 层流 紊流 Re
lgk1
lgk2
层流
过 渡 区
紊流
lg vc lg vc ′
lg v
15
第三节 圆管的层流运动及其沿程损失
工程技术中常有层流现象出现,如石油输送、 工程技术中常有层流现象出现,如石油输送、 地下水渗流、液压传动与机械润滑等。 地下水渗流、液压传动与机械润滑等。 本节只讨论是不可压缩粘性流体在等截面水平 直圆管中的定常层流运动及其沿程损失 定常层流运动及其沿程损失。 直圆管中的定常层流运动及其沿程损失。
2
一、雷诺实验: 雷诺实验:
3
1、层流状态:所有流 、层流状态: 体质点做定向有规则的 运动。 运动。
(a)
2、过渡状态:颜色水 、过渡状态: 开始抖动, 开始抖动,直线形状遭 到破坏。 到破坏。
(b)
(c)
3、湍流状态:所有质 、湍流状态: 点作无规则不定向的 混杂运动, 混杂运动,也可称为 紊流状态。 紊流状态。
一、过流与绕流的概念
流体若在固体边界外部流过时叫绕流,在绕流问题中, 流体若在固体边界外部流过时叫绕流,在绕流问题中,关 绕流 固体边界所受的阻力( 心的是固体边界所受的阻力 如机翼、叶片等); 心的是固体边界所受的阻力(如机翼、叶片等); 流体若在固体边界内部流过时叫过流 在过流问题中, 过流, 流体若在固体边界内部流过时叫过流,在过流问题中,关 心的是流动的流体所受的阻力 流动的流体所受的阻力。 心的是流动的流体所受的阻力。
