导数中的双变量任意
导数中双变量问题的四种策略

导数中双变量问题的四种策略双变量问题的几种处理策略策略一:合并思想已知函数$f(x)=\ln x$的图像上任意不同的两点的中点为$A(x_1,y_1)$。
$B(x_2,y_2)$,线段$AB$的中点为$C(x,y)$,记直线$AB$的斜率为$k$,试证明:$k>f'(x)$。
解析:因为$f(x)=\ln x$,所以$f'(x)=\frac{1}{x}$。
又因为k=\frac{f(x_2)-f(x_1)}{x_2-x_1}=\frac{\ln x_2-\lnx_1}{x_2-x_1}=\frac{\ln\frac{x_2}{x_1}}{x_2-x_1}$$不妨设$x_2>x_1$,要比较$k$与$f(x)$的大小,即比较frac{\ln\frac{x_2}{x_1}}{x_2-x_1}\text{和}\frac{1}{x_1}$$的大小,即比较ln\left(\frac{x_2}{x_1}\right)^{\frac{1}{x_2-x_1}}\text{和}e^{\frac{1}{x_2-x_1}}$$的大小。
又因为$x_2>x_1$,所以frac{x_2-x_1}{x_2+1}<\ln\left(\frac{x_2}{x_1}\right)^{\frac{1}{x_2-x_1}}<\frac{x_2-x_1}{x_1}$$因此frac{x_2-x_1}{x_2+1}<k<\frac{x_2-x_1}{x_1}$$又因为$x_2>x_1$,所以$\frac{x_2-x_1}{x_2+1}>\frac{1}{2}$,因此$k>f'(x)$。
策略二:分离思想问题2:若$g(x)=\ln x+\frac{1}{x}$,求$a$的取值范围,使得对任意的$x_1,x_2\in(1,2)$,都有$g(x_2)-g(x_1)<-1$。
导数中双变量问题的四种策略

双变量问题的几种处理策略策略一:合的思想问题1:已知函数x x f ln )(=的图象上任意不同的两点,,线段的中点为,记直线的斜率为,试证明:.解析:因为∴, ∴,又 不妨设 , 要比较与的大小,即比较与的大小, 又∵,∴ 即比较与的大小.令,则, ∴在上位增函数.又,∴, ∴,即二:分的思想问题2:若1ln )(++=x a x x g ,且对任意的(]2,1,21∈x x ,,都有,求a 的取值范围.解析∵ ,∴由题意得在区间(]2,1上是减函数. ∴ ()11,y x A ()22,y x B AB),(00y x C AB k )(0x f k '>x x f ln )(=xx f 1)(='210021)(x x x x f +=='121212121212ln ln ln )()(x x x x x x x x x x x f x f k -=--=--=12x x >k )(0x f '1212lnx x x x -212x x +12x x >12lnx x 1)1(2)(212122112+-=+-x x x x x x x x )1(1)1(2ln )(≥+--=x x x x x h 0)1()1()1(41)(222≥+-=+-='x x x x x x h )(x h [)+∞,1112>x x 0)1()(12=>h x x h 1)1(2ln 121212+->x x x x x x )(0x f k '>21x x ≠1)()(1212-<--x x x g x g 1)()(1212-<--x x x g x g []0)()(121122<-+-+x x x x g x x g x x g x F +=)()(1)1(1)(2++-='x ax x F由在恒成立. 设,,则 ∴在上为增函数,∴.策略3:变得思想设函数x x x f ln )(=,若,求证 解析:, ,所以在上是增函数,上是减函数.因为,所以即,同理. 所以 又因为当且仅当“”时,取等号. 又,, 所以,所以, 所以:.问题4:已知函数()21ln ,2f x x x mx x m R =--∈,若函数()f x 有两个极值点12,x x ,求证: 212x x e >解析:欲证212x x e >,需证: 12ln ln 2x x +>,若()f x 有两个极值点12,x x ,即函数()'f x 有两个零点,又()'ln f x x mx =-, 所以12,x x 是方程()'0f x =的两个不同实根313)1()1(0)(222+++=+++≥⇒≤'xx x x x x a x F []2,1∈x =)(x m 3132+++x x x []2,1∈x 0312)(2>+-='xx x m )(x m []2,1227)2(=≥m a 1),1,1(,2121<+∈x x e x x 42121)(x x x x +<x x xx f x g ln )()(==e x x x g 1,0ln 1)(==+=),1(+∞e )(x g )1,0(e11211<+<<x x x e111212121ln )()ln()()(x x x g x x x x x x g =>++=+)ln(ln 211211x x x x x x ++<)ln(ln 212212x x x x x x ++<)ln()2()ln()(ln ln 2112212112122121x x x xx x x x x x x x x x x x +++=++++<+,421221≥++x x x x 21x x =1),1,1(,2121<+∈x x ex x 0)ln(21<+x x )ln(4)ln()2(21211221x x x x x x x x +≤+++)ln(4ln ln 2121x x x x +<+42121)(x x x x +<于是,有1122ln 0{ln 0x mx x mx -=-=,解得1212ln ln x x m x x +=+,另一方面,由1122ln 0{ln 0x mx x mx -=-=,得()2121ln ln x x m x x -=-,从而可得21122112ln ln ln ln x x x x x x x x -+=-+,于是()()222121111222111lnln ln ln ln 1x x x x x x x x x x x x x x ⎛⎫+ ⎪-+⎝⎭+==--.又120x x <<, 设21x t x =,则1t >.因此, ()121ln ln ln ,1t t x x t ++=-1t >. 要证12ln ln 2x x +>,即证:()1ln 2,11t t t t +>>-.即当1t >时,有()21ln 1t t t ->+. 设函数()()21ln ,11t h t t t t -=-≥+,则()()()()()()222212111011t t t h t t t t t +---'=-=≥++, 所以, ()h t 为()1,+∞上的增函数.注意到, ()10h =,因此, ()()10h t h ≥=.于是,当1t >时,有()21ln 1t t t ->+. 所以,有12ln ln 2x x +>成立, 212x x e >.问题5:x m x x x f x --=221ln )(已知函数,若()x f 有两个极值点x 1,x 2,(x 1<x 2),且x x x x x a 12112ln 2ln ->-恒成立,求整数a 的最大值。
导数中的双变量任意

导数中的双变量任意、存在恒成立问题解决方法:转化为最值问题处理●类型 一:若2211D x D x ∈∀∈∀,,)()(21x g x f >恒成立 ⇔ max 2min 1)()(x g x f >. 基本思想是:函数)(x f 的任一函数值均大于)(x g 的任一函数值,故只需max 2min 1)()(x g x f >即可. 几何解释如图一.例1、已知x x x f ln )(=,3)(2++-=ax x x g ,若对)0(1∞+∈∀,x ,]1[2e x ,∈∀使得)(21x f ≥)(2x g 成立,求实数a 的取值范围.【变式训练1】已知函数14341ln )(-+-=xx x x f ,42)(2-+-=bx x x g ,若)20(1,∈∀x , ]21[2,∈∀x ,不等式)(1x f ≥)(2x g 恒成立,求实数b 的取值范围.●类型 二:若2211D x D x ∈∃∈∃,,)()(21x g x f >恒成立 ⇔ min 2max 1)()(x g x f >. 基本思想是:函数)(x f 的某些函数值大于)(x g 的某些函数值,只要求有这样的函数值,不要求所有的函数值.故只需min 2max 1)()(x g x f >即可. 几何解释如图二.例2、已知a ≤2,设函数x a x x x f ln 1)(--=,ex x x g 1ln )(--=, 若在]1[e ,上存在21x x ,,使)(1x f ≥)(2x g 成立,求实数a 取值范围.【变式训练2】已知函数xx x g ln )(=,ax x g x f -=)()(. (1)求函数)(x g 的单调区间;(2)若函数)(x f 在(1,∞+)上是减函数,求实数a 的最小值;(3)若存在][221e e x x ,,∈,使得)(1x f ≤a x f +')(2成立,求实数a 取值范围.●类型 三:若2211D x D x ∈∃∈∀,,)()(21x g x f >恒成立 ⇔ min 2min 1)()(x g x f >. 基本思想是:函数)(x f 的任一函数值大于)(x g 的某些函数值,但并不要求大于)(x g 所有的函数值.故只需min 2min 1)()(x g x f >即可. 几何解释如图三.例3、已知函数x x x f 2)(2+=,m x g x -=)21()(. 若对]11[]21[21,,,-∈∃∈∀x x ,使得 )(1x f ≥)(2x g 成立,求实数m 取值范围.【变式训练3】已知函数)()(2R n m nx mx x f ∈+=,在1=x 取得极值2. (1)求)(x f 的解析式; (2)设函数x a x x g +=ln )(,若对]1[]11[21e x x ,,,∈∃-∈∀,使得)(2x g ≤27)(1+x f 成立,求实数a 的取值范围.●类型 四:若2211D x D x ∈∀∈∃,,)()(21x g x f >恒成立 ⇔ max 2max 1)()(x g x f >. 基本思想是:函数)(x f 的某些函数值大于)(x g 的任一函数值,只要求)(x f 有函数值大于)(x g 的函数值即可.故只需max 2max 1)()(x g x f >即可. 几何解释如图三.例4、已知函数,x ax x f ln )(+=,22)(2+-=x x x g . 若a 1->且]1[1e x ,∈∃,对 ]10[2,∈∀x ,使得)()(21x g x f >成立,求实数a 的取值范围.【变式训练4】已知函数xx x f 2ln )(-=,x x x f x g ln 62)()(-+=,设4)(2+-=mx x x h . 若)10(1,∈∃x ,对]21[2,∈∀x ,总有)(1x g ≥)(2x h 成立,求实数m 的取值范围.例4、【解析】:因为22)(2+-=x x x g ,]1,0[∈x ,易得2)0()(max ==g x g . 又x ax x f ln )(+=,x a x f 1)(+=',易知)(x f '在[1,e]上单调递减,∴]11[)(++∈'a e a x f ,,若a ≥e1-,则)(x f '>0,)(x f 在[1,e]上单调递增,1)()(max +==ae e f x f >2,解得a >e 1.若e a 11-<<-,)(x f 在(1,a 1-)上单调递增,在(a1-,e )上单调递减,)ln(1)1()(max a af x f ---=-=>2,得31e a ->,此时与e a 11-<<-矛盾. 综上所述,所求a 的取值范围是(+∞,1e ).。
导数题中“任意、存在”型的归纳辨析

导数题中“任意、存在”型的归纳辨析南昌外国语学校 梁懿涛导数题是高考题中的常客,而且大都以压轴题的面目出现,所以拿下导数题是迈入高分段的标志。
导数题虽年年有,但却悄然之中发生着些改变。
这其中,尤以关于“任意”、“存在”的内容最为明显。
“任意”、“存在”可以说是导数题最为明显的特色,从早期单一型,发展到现今的混合型。
下面对此作一归纳。
一.单一函数单一“任意”型例1.已知函数()ln()f x x x a =-+的最小值为0,其中0a >。
(1)求a 的值;(2)若对任意的[0,)x ∈+∞,有2()f x kx ≤成立,求实数k 的最小值。
解析:(1)1()x a f x x a+-'=+,()f x ∴在(,1)a a --单调递减,在(1,)a -+∞单调递增,所min ()f x (1)01f a a =-=⇒=。
(2)设2()ln()g x kx x x a =-++,则问题等价于()0g x ≥对[0,)x ∈+∞恒成立,即min ()0g x ≥。
因为当0k ≤时,x →+∞时,()f x →-∞,所以0k >。
由22(21)()1kx k x g x x +-'=+,若2104k k -->,则当21(0,)4k x k -∈-时,()0g x '<,()g x 单调递减,()(0)0g x g <=,矛盾。
从而2104k k--≤,解得12k ≥。
即实数k 的最小值是12。
点评:“任意”的意思是不管x 取给定集合中的哪一个值,得到的函数值都要满足给定的不等式,它有两种形式:“对任意的x A ∈,()()a f x >≥恒成立”等价于“当x A ∈时,max ()()a f x >≥”;“对任意的x A ∈,()()a f x <≤恒成立”等价于“当x A ∈时,min ()()a f x <≤”。
二.单一函数单一“存在”型例2. 已知函数2()ln f x a x x =+(a R ∈),若存在[1,]x e ∈,使得()(2)f x a x ≤+成立,求实数a 的取值范围。
导数中双变量处理策略教学提纲

导数中双变量处理策略导数-双变量问题处理策略1.构造函数利用单调性证明2.任意性与存在性问题3.整体换元—双变单4.极值点偏移【构造函数利用单调性证明】形式如:1212|()()|||f x f x m x x -≥-例1、设函数221()(2)ln (0)ax f x a x a x+=-+<. (1)讨论函数()f x 在定义域内的单调性;(2)当(3,2)a ∈--时,任意12,[1,3]x x ∈,12(ln 3)2ln 3|()()|m a f x f x +->-恒成立,求实数m 的取值范围.【任意与存在性问题】例2、 已知函数()2a f x x x=+,()ln g x x x =+,其中0a >. (1)若函数()x f y =在[]e ,1上的图像恒在()x g y =的上方,求实数a 的取值范围. (2)若对任意的[]12,1x x e ∈,(e 为自然对数的底数)都有()1f x ≥()2g x 成立, 求实数a 的取值范围.【整体换元——双变单】例3、已知函数x x x f ln )(=的图象为曲线C , 函数b ax x g +=21)(的图象为直线l . (Ⅰ) 当3,2-==b a 时, 求)()()(x g x f x F -=的最大值;(Ⅱ) 设直线l 与曲线C 的交点的横坐标分别为21,x x , 且21x x ≠, 求证:2)()(2121>++x x g x x .【对称轴问题12x x +的证明】例4、已知函数11()(x x f x x e --=∈R).⑴求函数()f x 的单调区间和极值;⑵已知函数()y g x =对任意x 满足()(4)g x f x =-,证明:当2x >时,()();f x g x >⑶如果12x x ≠,且12()()f x f x =,证明:12 4.x x +>【实战演练】1.已知函数f (x )=21x 2-ax +(a -1)ln x ,1a >. (1)讨论函数()f x 的单调性;(2)证明:若5a <,则对任意x 1,x 2∈(0,)+∞,x 1≠x 2,有1212()()1f x f x x x ->--.2.设3x =是函数()()()23,x f x x ax b e x R -=++∈的一个极值点. (1)求a 与b 的关系式(用a 表示b ),并求()f x 的单调区间;(2)设()2250,4x a g x a e ⎛⎫>=+ ⎪⎝⎭,若存在[]12,0,4ξξ∈,使得()()121f g ξξ-< 成立,求a 的取值范围.3.已知函数21()ln (1)(0)2f x x ax a x a R a =-+-∈≠,. ⑴求函数()f x 的单调增区间;⑵记函数()F x 的图象为曲线C ,设点1122(,)(,)A x y B x y 、是曲线C 上两个不同点,如果曲线C 上存在点00(,)M x y ,使得:①1202x x x +=;②曲线C 在点M 处的切线平行于直线AB ,则称函数()F x 存在“中值相依切线”.试问:函数()f x 是否存在中值相依切线,请说明理由.4.(2018届高三咸阳市二模理科).已知函数2()2ln (,0)x f x x a R a a=-∈≠. (1)讨论函数()f x 的单调性;(2) 若函数()f x 有两个零点1x ,2x 12()x x <,且2a e =,证明:122x x e +>.。
导数中双变量处理策略

导数-双变量问题处理策略1.构造函数利用单调性证明2.任意性与存在性问题3.整体换元—双变单4.极值点偏移【构造函数利用单调性证明】形式如:1212|()()|||f x f x m x x -≥-例1、设函数221()(2)ln (0)ax f x a x a x+=-+<. (1)讨论函数()f x 在定义域内的单调性;(2)当(3,2)a ∈--时,任意12,[1,3]x x ∈,12(ln 3)2ln 3|()()|m a f x f x +->-恒成立,求实数m 的取值范围.【任意与存在性问题】例2、已知函数()2a f x x x=+,()ln g x x x =+,其中0a >. (1)若函数()x f y =在[]e ,1上的图像恒在()x g y =的上方,求实数a 的取值范围.(2)若对任意的[]12,1x x e ∈,(e 为自然对数的底数)都有()1f x ≥()2g x 成立, 求实数a 的取值范围.【整体换元——双变单】例3、已知函数x x x f ln )(=的图象为曲线C ,函数b ax x g +=21)(的图象为直线l . (Ⅰ)当3,2-==b a 时,求)()()(x g x f x F -=的最大值;(Ⅱ)设直线l 与曲线C 的交点的横坐标分别为21,x x ,且21x x ≠,求证:2)()(2121>++x x g x x .【对称轴问题12x x +的证明】例4、已知函数11()(x x f x x e --=∈R). ⑴求函数()f x 的单调区间和极值;⑵已知函数()y g x =对任意x 满足()(4)g x f x =-,证明:当2x >时,()();f x g x > ⑶如果12x x ≠,且12()()f x f x =,证明:12 4.x x +>【实战演练】1.已知函数f (x )=21x 2-ax +(a -1)ln x ,1a >. (1)讨论函数()f x 的单调性;(2)证明:若5a <,则对任意x 1,x 2∈(0,)+∞,x 1≠x 2,有1212()()1f x f x x x ->--. 2.设3x =是函数()()()23,x f x x ax b e x R -=++∈的一个极值点. (1)求a 与b 的关系式(用a 表示b ),并求()f x 的单调区间;(2)设()2250,4x a g x a e ⎛⎫>=+ ⎪⎝⎭,若存在[]12,0,4ξξ∈,使得()()121f g ξξ-<成立,求a 的取值范围.3.已知函数21()ln (1)(0)2f x x ax a x a R a =-+-∈≠,. ⑴求函数()f x 的单调增区间;⑵记函数()F x 的图象为曲线C ,设点1122(,)(,)A x y B x y 、是曲线C 上两个不同点,如果曲线C 上存在点00(,)M x y ,使得:①1202x x x +=;②曲线C 在点M 处的切线平行于直线AB ,则称函数()F x 存在“中值相依切线”.试问:函数()f x 是否存在中值相依切线,请说明理由.4.(2018届高三咸阳市二模理科).已知函数2()2ln (,0)x f x x a R a a=-∈≠. (1)讨论函数()f x 的单调性;(2)若函数()f x 有两个零点1x ,2x 12()x x <,且2a e =,证明:122x x e +>.。
函数与导数的 “双变量”问题探究

函数与导数的“双变量”问题探究一、问题提出近年来函数综合问题中,常常出现两个在一定范围内可以变化的量,即函数的双变量问题。
此问题经常结合不等式进行命题,主要考查学生转化与化归思想,考查学生对问题的转化及处理能力,此类问题难度较大,对学生的综合能力要求较高。
解决此类问题主要通过变元来解决,如何将两个变量转化为一个变量是此类问题解体的关键。
然后,再结合函数性质即可解决此类问题。
二、例题解说−x+alnx例1:已知函数f(x)=1x(1)讨论f(x)的单调性.<a−2.(2)若函数存在两个极值点x1,x2,证明f(x1)−f(x2)x1−x2小结1:消元,变量归一①若两个变量存在确定的关系,可以利用其中一个变量替换另一个变量,直接消元,将两个变量转化为一个变量.,x1x2,x1−②若两个变量不存在确定的关系,有时可以将两个变量之间的关系看成一个整体(比如x1x2x2,x1+x2),进行整体换元,将两个变量化为一个变量..例2:已知函数f(x)=e2x−2t(e x+x)+x2+2t2+1,求证f(x)≥32小结2:变换主元当两个变量之间没有关系,也不能看成一个整体时,主元的选择就显得尤为重要了,主元若选择得当,可以降低思维难度,可以将复杂的函数变为简单函数。
主元变换是将其中一个变量作为主元,其中一个变量作为参数。
例3:已知函数f(x)=1+2lnx.x2(1)求f(x)的单调区间(2)存在x1,x2∈(1,+∞)且x1≠x2,使|f(x1)−f(x2)|≥k|lnx1−lnx2|成立,求k的取值范围.小结3:构造函数根据题中条件构造适当的函数,利用函数性质解决.,1],|f(x1)−f(x2)|≤b,求b的取值范围.例4:已知函数f(x)=xlnx+x,对∀x1,x2∈[1e3小结4:转化为最值根据题中条件将双变量问题转化为函数最值来处理,此类题型可以参考“恒成立”与“存在性”问题解题思路与方法.三、练习提升1.设函数f(x)=e mx+x2−mx.(1)证明:f(x)在(−∞,0)单调递减,在(0,+∞)单调递增;(2)若对于任意x1,x2∈[−1,1],都有|f(x1)−f(x2)|≤e−1,求m的取值范围.2.已知常数a>0,函数f(x)=ln(1+ax)−2xx+2.(1)讨论f(x)在区间(0,+∞)上的单调性;(2)若f(x)存在两个极值点x1,x2,且f(x1)+f(x2)>0,求a的取值范围.3.已知函数f(x)=lnx−ax+1−ax−1,(a∈R).(Ⅰ)当a≤12时,讨论f(x)的单调性;(Ⅱ)设g(x)=x2−2bx+4,当a=14时,若对任意x1∈(0,2),存在x2∈[1,2],使f(x1)≥g(x2),求实数b取值范围.4.已知函数f(x)=ln x+mx−2(m∈R).(1)讨论函数f(x)的单调性;(2)若函数f(x)存在两个零点分别为x1,x2(x1<x2),试求m的取值范围,并证明1x1+1x2>1e.5.已知函数f(x)=x ln x−2ax2+x,a∈R.(Ⅰ)若()f x在(0,+∞)内单调递减,求实数a的取值范围;(Ⅱ)若函数f(x)有两个极值点分别为x1,x2,证明:x1+x2>12a.6.已知函数f(x)=(x+2)ln x+ax2(a为常数)在x=1处的切线方程为y=4x−72. (1)求a的值,并讨论f(x)的单调性;(2)若f(x1)+f(x2)=1,求证x1x2≤1.函数与导数的“双变量”问题探究一、问题提出近年来函数综合问题中,常常出现两个在一定范围内可以变化的量,即函数的双变量问题。
双变量的“任意性”与 “存在性”五种题型的解题方法解析

1双变量的“任意性”与 “存在性”五种题型的解题方法 一、“存在=存在”型∃x 1∈D 1,∃x 2∈D 2,使得f (x 1)=g (x 2),等价于函数f (x )在D 1上的值域A 与函数g (x )在D 2上的值域B 的交集不为空集,即A ∩B ≠⌀.其等价转化的基本思想:两个函数有相等的函数值,即它们的值域有公共部分.【例1】 已知函数f (x )=x 2-23ax 3,a >0,x ∈R .g (x )=1x 2(1-x ).若∃x 1∈(-∞,-1],∃x 2∈-∞,-12 ,使得f (x 1)=g (x 2),求实数a 的取值范围.【解析】∵f (x )=x 2-23ax 3,∴f '(x )=2x -2ax 2=2x (1-ax ).令f '(x )=0,得x =0或x =1a .∵a >0,∴1a>0,∴当x ∈(-∞,0)时, f '(x )<0,∴f (x )在(-∞,-1]上单调递减, f (x )在(-∞,-1]上的值域为1+2a3,+∞ .∵g (x )=1x 2(1-x ),∴g '(x )=3x 2-2x (x 2-x 3)2=3x -2x 3(1-x )2.∵当x <-12时,g '(x )>0,∴g (x )在-∞,-12 上单调递增,∴g (x )<g -12 =83,∴g (x )在-∞,-12 上的值域为-∞,83.若∃x 1∈(-∞,-1],∃x 2∈-∞,-12 ,使得f (x 1)=g (x 2),则1+2a 3<83,a <52.故实数a 的取值范围是0,52.【变式1】 已知函数f (x )=-16x +112,0≤x ≤12,x 3x +1,12<x ≤1 和函数g (x )=a ·sin π6x -a +1(a >0),若存在x 1,x 2∈[0,1],使得f (x 1)=g (x 2)成立,则实数a 的取值范围是( )A.12,32 B.[1,2)C.12,2D.1,32【答案】选C 【解析】设函数f (x ),g (x )在[0,1]上的值域分别为A ,B ,则“存在x 1,x 2∈[0,1],使得f (x 1)=g (x 2)成立”等价于“A ∩B ≠⌀”.当0≤x ≤12时, f (x )=-16x +112单调递减,所以0≤f (x )≤112;当12<x ≤1时, f '(x )=x 2(2x +3)(x +1)2>0,所以f (x )=x 3x +1单调递增,112<f (x )≤12,故f (x )在[0,1]上的值域A =0,12.当x ∈[0,1]时,π6x ∈0,π6 ,y =sin π6x 在[0,1]上单调递增.又a >0,所以g (x )=a sin π6x -a +1在[0,1]上单调递增,其值域B =1-a ,1-a 2.2由A ∩B ≠⌀,得0≤1-a ≤12或0≤1-a 2≤12,解得12≤a ≤2.故选C .二、“任意=存在”型∀x 1∈D 1,∃x 2∈D 2,使得f (x 1)=g (x 2),等价于函数f (x )在D 1上的值域A 是函数g (x )在D 2上的值域B 的子集,即A ⊆B .其等价转化的基本思想:函数f (x )的任意一个函数值都与函数g (x )的某一个函数值相等,即f (x )的函数值都在g (x )的值域之中.【例2】 已知函数f (x )=4x 2-72-x,x ∈[0,1].(1)求f (x )的单调区间和值域;(2)设a ≥1,函数g (x )=x 3-3a 2x -2a ,x ∈[0,1].若对于任意的x 1∈[0,1],总存在x 0∈[0,1],使得g (x 0)=f (x 1)成立,求a 的取值范围.【解析】(1)f '(x )=-4x 2+16x -7(2-x )2=-(2x -1)(2x -7)(2-x )2,x ∈[0,1].令f '(x )=0,解得x =12或x =72(舍去).当x 变化时, f '(x ), f (x )的变化情况如下表所示:x 00,121212,11f '(x )-0+f (x )-72↘-4↗-3 所以f (x )的递减区间是0,12,递增区间是12,1 .f (x )min =f 12=-4,又f (0)=-72, f (1)=-3,所以f (x )max =f (1)=-3.故当x ∈[0,1]时, f (x )的值域为[-4,-3].(2)“对于任意的x 1∈[0,1],总存在x 0∈[0,1],使得g (x 0)=f (x 1)成立”等价于“在x ∈[0,1]上,函数f (x )的值域B 是函数g (x )的值域A 的子集,即B ⊆A ”.因为a ≥1,且g '(x )=3(x 2-a 2)<0,所以当x ∈[0,1]时,g (x )为减函数,所以g (x )的值域A =[1-2a -3a 2,-2a ].由B ⊆A ,得1-2a -3a 2≤-4且-2a ≥-3,又a ≥1,故1≤a ≤32.【变式2】 已知函数f (x )=x 2-23ax 3(a >0),x ∈R .(1)求f (x )的单调区间和极值;(2)若对于任意的x 1∈(2,+∞),都存在x 2∈(1,+∞),使得f (x 1)·f (x 2)=1.求a 的取值范围.【解析】 解析 (1)由已知,有f '(x )=2x -2ax 2(a >0).令f '(x )=0,解得x =0或x =1a .当x 变化时, f '(x ), f (x )的变化情况如下表:x(-∞,0)0,1a 1a 1a ,+∞3f '(x )-0+0-f (x )↘↗13a 2↘所以, f (x )的单调递增区间是0,1a;单调递减区间是(-∞,0),1a ,+∞ .当x =0时, f (x )有极小值,且极小值f (0)=0;当x =1a 时,f (x )有极大值,且极大值f 1a =13a2.(2)由f (0)=f 32a=0及(1)知,当x ∈0,32a 时, f (x )>0;当x ∈32a,+∞ 时, f (x )<0.设集合A ={f (x )|x ∈(2,+∞)},集合B =1f (x )|x ∈(1,+∞),f (x )≠0,则“对于任意的x 1∈(2,+∞),都存在x 2∈(1,+∞),使得f (x 1)·f (x 2)=1”等价于A ⊆B .显然,0∉B .下面分三种情况讨论:①当32a >2,即0<a <34时,由f 32a=0可知,0∈A ,而0∉B ,所以A 不是B 的子集.②当1≤32a ≤2,即34≤a ≤32时,有f (2)≤0,且此时f (x )在(2,+∞)上单调递减,故A =(-∞, f (2)),因而A ⊆(-∞,0);由f (1)≥0,有f (x )在(1,+∞)上的取值范围包含(-∞,0),即(-∞,0)⊆B .所以,A ⊆B .③当32a <1,即a >32时,有f (1)<0,且此时f (x )在(1,+∞)上单调递减,故B =1f (1),0,A =(-∞, f (2)),所以A 不是B 的子集.综上,a 的取值范围是34,32.三、“任意≥(≤、>、<)任意”型∀x 1∈D 1,∀x 2∈D 2,f (x 1)>g (x 2)恒成立,等价于f (x )min >g (x )max ,或等价于f (x )>g (x )max 恒成立,或等价于f (x )min >g (x )恒成立.其等价转化的基本思想是函数f (x )的任何一个函数值均大于函数g (x )的任何一个函数值.∀x 1∈D 1,∀x 2∈D 2,f (x 1)<g (x 2)恒成立,等价于f (x )max <g (x )min ,或等价于f (x )<g (x )min 恒成立,或等价于f (x )max <g (x )恒成立.其等价转化的基本思想是函数f (x )的任何一个函数值均小于函数g (x )的任何一个函数值.∀x 1∈D 1,∀x 2∈D 2,f (x 1)-g (x 2)>k 恒成立,等价于[f (x 1)-g (x 2)]min >k 恒成立,也等价于f (x )min-g (x )max >k .∀x 1∈D 1,∀x 2∈D 2,f (x 1)-g (x 2)<k 恒成立,等价于[f (x 1)-g (x 2)]max <k 恒成立,也等价于f (x )max-g (x )min <k .【例3】 设函数f (x )=x 3-x 2-3.(1)求f (x )的单调区间;(2)设函数g (x )=a x+x ln x ,如果对任意的x 1,x 2∈12,2,都有f (x 1)≤g (x 2)成立,求实数a 的取值范围.【解析】解析 (1)f '(x )=3x 2-2x .f '(x )>0时,x <0或x >23,f '(x )<0时,0<x <23.所以, f (x )的递增区间是(-∞,0),23,+∞;递减区间是0,23.4(2)由(1)知,函数f (x )在12,23 上单调递减,在23,2 上单调递增,而f 12=-258, f (2)=1,故f (x )在区间12,2上的最大值f (x )max =f (2)=1.“对任意的x 1,x 2∈12,2 ,都有f (x 1)≤g (x 2)成立”等价于“对任意的x ∈12,2,g (x )≥f (x )max 恒成立”,即当x ∈12,2时,g (x )=a x+x ln x ≥1恒成立,即a ≥x -x 2ln x 恒成立,记u (x )=x -x 2ln x 12≤x ≤2,则有a ≥u (x )max .u '(x )=1-x -2x ln x ,可知u '(1)=0.当x ∈12,1时,1-x >0,2x ln x <0,则u '(x )>0,所以u (x )在12,1上递增; 当x ∈(1,2)时,1-x <0,2x ln x >0,则u '(x )<0,所以u (x )在(1,2)上递减.故u (x )在区间12,2上的最大值u (x )max =u (1)=1,所以实数a 的取值范围是[1,+∞).【点拨】 (1)∀x 1∈D 1,∀x 2∈D 2,f (x 1)>g (x 2)恒成立,通常等价转化为f (x )min >g (x )max .这是两个独立变量--双变量问题,不等式两边f (x 1),g (x 2)中自变量x 1,x 2可能相等,也可能不相等;(2)对任意的x ∈[m ,n ],不等式f (x )>g (x )恒成立,通常等价转化为[f (x )-g (x )]min >0.这是单变量问题,不等式两边f (x ),g (x )的自变量x 相等.【变式3】 函数f (x )=mxx 2+1+1(m ≠0),g (x )=x 2e ax (a ∈R ).(1)直接写出函数f (x )的单调区间;(2)当m >0时,若对于任意的x 1,x 2∈[0,2], f (x 1)≥g (x 2)恒成立,求a 的取值范围.【解析】 (1)当m >0时,f (x )的递增区间是(-1,1);递减区间是(-∞,-1),(1,+∞).当m <0时,f (x )的递增区间是(-∞,-1),(1,+∞);递减区间是(-1,1).(2)当m >0时,“对于任意的x 1,x 2∈[0,2],f (x 1)≥g (x 2)恒成立”等价于“对于任意的x ∈[0,2],f (x )min ≥g (x )max 成立”.当m >0时,由(1)知,函数f (x )在[0,1]上单调递增,在[1,2]上单调递减,因为f (0)=1,f (2)=2m5+1>1,所以f (x )min =f (0)=1,故应满足1≥g (x )max .因为g (x )=x 2e ax ,所以g '(x )=(ax 2+2x )e ax .①当a =0时,g (x )=x 2,此时g (x )max =g (2)=4,不满足1≥g (x )max .②当a ≠0时,令g '(x )=0,得x =0或x =-2a .(i )当-2a≥2,即-1≤a <0时,在[0,2]上,g '(x )≥0,g (x )在[0,2]上单调递增,g (x )max =g (2)=4e 2a .由1≥4e 2a ,得a ≤-ln 2,所以-1≤a ≤-ln 2.(ii )当0<-2a <2,即a <-1时,在0,-2a上,g '(x )≥0,g (x )递增;在-2a ,2 上,g '(x )<0,g (x )递减.g (x )max =g -2a =4a 2e 2,由1≥4a 2e 2,得a ≤-2e ,所以a <-1.5(iii )当-2a<0,即a >0时,显然在[0,2]上,g '(x )≥0,g (x )单调递增,于是g (x )max =g (2)=4e 2a >4,此时不满足1≥g (x )max .综上,a 的取值范围是(-∞,-ln 2].四、“任意≥(≤、>、<)存在”型∀x 1∈D 1,∃x 2∈D 2,使得f (x 1)>g (x 2)成立,等价于f (x )min >g (x )min .其等价转化的基本思想是函数f (x )的任意一个函数值大于函数g (x )的某一个函数值,但并不要求大于函数g (x )的所有函数值.∀x 1∈D 1,∃x 2∈D 2,使得f (x 1)<g (x 2)成立,等价于f (x )max <g (x )max .其等价转化的基本思想是函数f (x )的任意一个函数值小于函数g (x )的某一个函数值,但并不要求小于函数g (x )的所有函数值.∀x 1∈D 1,∃x 2∈D 2,使得f (x 1)-g (x 2)>k 成立,等价于f (x )min -g (x )min >k .∀x 1∈D 1,∃x 2∈D 2,使得f (x 1)-g (x 2)<k 成立,等价于f (x )max -g (x )max <k .【例4】 函数f (x )=ln x -14x +34x-1,g (x )=x 2-2bx +4,若对任意的x 1∈(0,2),存在x 2∈[1,2],使得f (x 1)≥g (x 2)成立,求实数b 的取值范围.【解析】 “对任意的x 1∈(0,2),存在x 2∈[1,2],使得f (x 1)≥g (x 2)成立”等价于“f (x )在(0,2)上的最小值不小于g (x )在[1,2]上的最小值,即f (x )min ≥g (x )min (*)”.f '(x )=1x -14-34x 2=-(x -1)(x -3)4x 2,当x ∈(0,1)时, f '(x )<0, f (x )单调递减;当x ∈(1,2)时, f '(x )>0, f (x )单调递增.故当x ∈(0,2)时, f (x )min =f (1)=-12.又g (x )=(x -b )2+4-b 2,x ∈[1,2],①当b <1时,g (x )min =g (1)=5-2b >3,此时与(*)矛盾;②当b ∈[1,2]时,g (x )min =g (b )=4-b 2≥0,同样与(*)矛盾;③当b ∈(2,+∞)时,g (x )min =g (2)=8-4b ,由8-4b ≤-12,得b ≥178.综上,实数b 的取值范围是178,+∞ .【变式4】 已知函数f (x )=13x 3+x 2+ax .(1)若f (x )在区间[1,+∞)上单调递增,求a 的最小值;(2)若g (x )=x ex ,∀x 1∈12,2 ,∃x 2∈12,2 ,使得f '(x 1)≤g (x 2)成立,求a 的取值范围.【解析】 (1)由题设知f '(x )=x 2+2x +a ≥0,即a ≥-(x +1)2+1在[1,+∞)上恒成立,而y =-(x +1)2+1在[1,+∞)上单调递减,则y max =-3,∴a ≥-3,∴a min =-3.(2)“∀x 1∈12,2,∃x 2∈12,2 ,使f '(x 1)≤g (x 2)成立”等价于“x ∈12,2 时,f '(x )max ≤g (x )max 恒成立”.∵f '(x )=x 2+2x +a =(x +1)2+a -1在12,2上递增,∴f '(x )max =f '(2)=8+a ,又g '(x )=e x -xe x e 2x =1-x e x,6∴g (x )在(-∞,1)上递增,在(1,+∞)上递减.∴当x ∈12,2时,g (x )max =g (1)=1e ,由8+a ≤1e 得,a ≤1e -8,所以a 的取值范围是-∞,1e-8 .五、“存在≥(≤、>、<)存在”型若∃x 1∈D 1,∃x 2∈D 2,使得f (x 1)>g (x 2)成立,等价于f (x )max ≥g (x )min .其等价转化的基本思想是函数f (x )的某一个函数值大于函数g (x )的某一个函数值,即只要有这样的函数值即可.若∃x 1∈D 1,∃x 2∈D 2,使得f (x 1)<g (x 2)成立,等价于f (x )min <g (x )max .其等价转化的基本思想是函数f (x )的某一个函数值小于函数g (x )的某一个函数值,即只要有这样的函数值即可.若∃x 1∈D 1,∃x 2∈D 2,使得f (x 1)-g (x 2)>k 成立,等价于[f (x 1)-g (x 2)]max >k ,也等价于f (x )max-g (x )min >k .若∃x 1∈D 1,∃x 2∈D 2,使得f (x 1)-g (x 2)<k 成立,等价于[f (x 1)-g (x 2)]min <k ,也等价于f (x )min -g (x )max <k .【例5】 已知函数f (x )=4ln x -ax +a +3x(a ≥0).(1)直接写出函数f (x )的单调区间;(2)当a ≥1时,设g (x )=2e x -4x +2a ,若存在x 1,x 2∈12,2,使f (x 1)>g (x 2),求实数a 的取值范围.【解析】 (1)当a =0时,函数f (x )的递减区间为0,34,递增区间为34,+∞ .当0<a <1时,函数f (x )的递减区间为0,2--(a -1)(a +4)a,2+-(a -1)(a +4)a,+∞,递增区间为2--(a -1)(a +4)a ,2+-(a -1)(a +4)a.当a ≥1时, f (x )的递减区间为(0,+∞).(2)“存在x 1,x 2∈12,2 ,使f (x 1)>g (x 2)”等价于“ 当x ∈12,2时, f (x )max >g (x )min ”.由(1)知,当x ∈12,2时, f (x )max =f 12 =-4ln 2+32a +6,由g '(x )=2e x -4>0,得x >ln 2,所以g (x )在(0,ln 2)上单调递减,在(ln 2,+∞)上单调递增,故当x ∈12,2时,g (x )min =g (ln 2)=4-4ln 2+2a ,由f (x )max >g (x )min ,得-4ln 2+32a +6>4-4ln 2+2a ,又a ≥1,所以1≤a <4.【变式5】 设函数f (x )=xln x-ax .(1)若函数f (x )在(1,+∞)上为减函数,求实数a 的最小值;(2)若存在x 1,x 2∈[e ,e 2],使f (x 1)≤f '(x 2)+a 成立,求实数a 的取值范围.【解析】 (1)由题设知f '(x )=ln x -1(ln x )2-a ≤0在(1,+∞)上恒成立,则只需f '(x )max ≤0.又f '(x )=ln x -1(ln x )2-a =-1ln x -12 2+14-a ,7所以当1ln x =12,即x =e 2时, f '(x )max =14-a ,由14-a ≤0得a ≥14,故a 的最小值为14.(2)“存在x 1,x 2∈[e ,e 2],使f (x 1)≤f '(x 2)+a 成立”等价于“当x 1,x 2∈[e ,e 2]时, f (x 1)min ≤f '(x 2)max +a ”.由(1)知,当x ∈[e ,e 2]时, f '(x )max =f '(e 2)=14-a ,所以f '(x )max +a =14.则问题等价于“当x ∈[e ,e 2]时, f (x )min ≤14”.①当a ≥14时,由(1)得f '(x )max =14-a ≤0, f (x )在[e ,e 2]上为减函数,则f (x )min =f (e 2)=e 22-ae 2,由f (x )min ≤14,得a ≥12-14e 2.②当a <14时, f '(x )=-1ln x -12 2+14-a 在[e ,e 2]上的值域为-a ,14-a .(i )当-a ≥0,即a ≤0时, f '(x )≥0在[e ,e 2]恒成立,故f (x )在[e ,e 2]上为增函数,于是f (x )min =f (e )=e -ae ≥e >14,与f (x )min ≤14矛盾.(ii )当-a <0,即0<a <14时,由f '(x )的单调性和值域知,存在唯一的x 0∈(e ,e 2),使f '(x )=0,且满足:当x ∈(e ,x 0)时, f '(x )<0, f (x )为减函数;当x ∈(x 0,e 2)时, f '(x )>0, f (x )为增函数,所以f (x )min =f (x 0)=x 0ln x 0-ax 0≤14,x 0∈(e ,e 2).所以a ≥1ln x 0-14x 0>1ln e 2-14e >12-14=14,与0<a <14矛盾.综上,a 的取值范围是a ≥12-14e2.。
导数中的双变量问题

1、设函数 f(x) (2 a)lnx __ (ax(1)讨论函数f (x)在定义域内的单调性;⑵ 当 a ( 3, 2)时,任意 X i ,X 2 [1,3] , (m In 3)a 2l n3 | f(xj f(x 2)| 恒成立,求实数 m 的取值范围.2、已知二次函数g(x)对xR 都满足 g(x 1) g(1 x) x 2 2x 1 且 g(1)1,设函数19f (x) g(x ) ml nx ( mR , x 0).(I)求g(x)的表达式;(H)若 x R ,使f(x) 0成立,求实数m 的取值范围;(皿)设1 m e ,H(x) f(x) (m 1)x ,求证:对于 x b x ? [1,m],恒有 | H (xj H(X 2)| 1 . 3、 设x 3是函数f x x 2 ax b e 3 x , x R 的一个极值点. (1) 求a 与b 的关系式(用a 表示b ),并求f x 的单调区间;25(2) 设ao, g x a— e,若存在1, 20,4,使得f1g 21成立,求a的取值范围.4、 f (x) (x 2 ax b)e x (x R). (1)若a 2,b 2,求函数f(x)的极值;(2) 若x 1是函数f(x)的一个极值点,试求出a 关于b 的关系式(用a表示b ), 并确定f(x)的单调区间;(3) 在(2)的条件下,设a 0,函数g(x) (a 2 14)e x 4 .若存在1, 2 [0,4]使得 | f( 1)f( 2)l 1成立,求a 的取值范围.5、已知函数f x ax 3 bx 2 3x a,b R 在点1, f 1处的切线方程为y 2 0 . ⑴求函数f x 的解析式;导数 0) •⑵若对于区间2,2上任意两个自变量的值x1,x2都有f x1c,求实数c的最小值;⑶若过点M 2,m m 2可作曲线y f x的三条切线,求实数m的取值范围.16、设函数f(x) x aln x(a R).x⑴讨论函数f(x)的单调性;⑵若f(x)有两个极值点X i,X2,记过点A(X i, f(G), B(X2, f(X2))的直线斜率为k,问:是否存在a,使得k 2 a ?若存在,求出a的值;若不存在,请说明理由.7、已知函数f(x) ln x — ax2(a 1)x(a R, a 0).2⑴求函数f(x)的单调增区间;⑵记函数F(x)的图象为曲线C ,设点A(x1,y1),B(x2,y2)是曲线C上两个不同点,如果曲线C上存在点M(x0,y0),使得:①x0X2;②曲线C在点M处的切线平行于直2线AB,贝S称函数F(x)存在“中值相依切线”.试问:函数f(x)是否存在中值相依切线,请说明理由.&已知函数 f (x) (a 1)lnx ax .⑴试讨论f(x)在定义域内的单调性;⑵当a V—1时,证明:N,X2 (0,1),⑴:1)1.求实数m的取值范围.I X1 x2 |9、已知函数f(x) (a 1)lnx ax2 1.⑴讨论函数f(x)的单调性;⑵设a 1,如果对任意X1,X2 (0, ) , |f(xj f(x2) |> 4|X1 X2 |,求a的取值范围.1 210、已知函数f(x)=§x —ax+(a—1) lnx , a 1 .(1)讨论函数f(x)的单调性;11、 已知函数 f(x) x 1 aln x(a 0). (1) 确定函数y f(x)的单调性; (2)若对任意x 1,x 2 0,1,且x 1 x 2,都有| f (x 1) f(x 2)| 4|— — |,求实数a 的取 X ] x 2值范围。
双变量任意,存在性导数问题

值域法破解双变量压轴题的四种情形1基本原理.第1类.“任意=存在”型2211,D x D x ∈∃∈∀,使得)()(21x g x f =,等价于函数)(x f 在1D 上上的值域A 是函数)(x g 在2D 上的值域B 的子集,即B A ⊆.其等价转化的基本思想:函数)(x f 的任意一个函数值都与函数)(x g 的某一个函数值相等,即)(x f 的函数值都在)(x g 的值域之中.此类型出现频率最高.第2类.“存在=存在”型2211,D x D x ∈∃∈∃,使得)()(21x g x f =,等价于函数)(x f 在1D 上的值域A 与函数)(x g 在2D 上的值域B 的交集不为空集,即∅≠⋂B A .其等价转化的基本思想:两个函数有相等的函数值,即它们的值域有公共部分.第3类.“任意≥(≤、>、<)任意”型2211,D x D x ∈∀∈∀,使得)()(21x g x f ≥恒成立等价于max min )()(x g x f ≥.其等价转化的基本思想是函数)(x f 的任何一个函数值均大于函数)(x g 的任何一个函数值.同理,可得其他类型.第4类.m x f x f b a x x ≤-∈∀|)()(|],,[,2121型.由于闭区间上连续函数必有最值,故此类转化为m x f x f ≤-|)()(|min max ,解决掉双变量转化为求最值.2.典例分析第1类问题问题应用.例1.已知函数()()ln f x ax x a R =+∈.(1)若1a =,求曲线()y f x =在1x =处切线方程;(2)讨论()y f x =的单调性;(3)12a ≥-时,设()222g x x x =-+,若对任意[]11,2x ∈,均存在[]20,3x ∈,使得()()12f x g x =,求实数a 的取值范围.解析:(2)()f x 定义域为()0,∞+,()1'1ax a x f xx +=+=,当0a ≥时,()'0f x >恒成立,所以()f x 在()0,∞+上单调递增;当0a <时,10,x a ⎛⎫∈- ⎪⎝⎭时()'0f x >恒成立,1,x a ⎛⎫∈-+∞ ⎪⎝⎭时()'0f x <恒成立,所以()f x 在10,a ⎛⎫- ⎪⎝⎭上单调递增,在1,a ⎛⎫-+∞ ⎪⎝⎭上单调递减;综上述,当0a ≥时,()f x 在()0,∞+上单调递增;当0a <时,()f x 在10,a ⎛⎫- ⎪⎝⎭上单调递增,在1,a ⎛⎫-+∞ ⎪⎝⎭上单调递减.(3)由已知,转化为()f x 在[]1,2x ∈的值域M 和()g x 在[]0,3x ∈的值域N 满足:M N ⊆,易求[]1,5N =.又()1'1ax a x f xx +=+=且12a ≥-,()f x 在[]1,2x ∈上单调递增,故值域[],2ln 2M a a =+.所以152ln 2a a ≤⎧⎨≥+⎩,解得5ln 212a -≤≤,即5ln 21,2a -⎡⎤∈⎢⎥⎣⎦.第2类问题应用例2.已知曲线()y ln x m =+与x 轴交于点P ,曲线在点P 处的切线方程为()y f x =,且2)1(=f .(1)求()y f x =的解析式;(2)求函数()()xf xg x e =的极值;(3)设2(1)1()ln x a lnx h x x +-+=,若存在实数1[1x ∈,]e ,12[x e -∈,1],使得21222222()(1)h x x ln x a x lnx x <+-+成立,求实数a 的取值范围.解析:(1)曲线()y ln x m =+与x 轴交于点(1,0)P m -,1y x m'=+,∴曲线在点P 处的切线斜率111k m m==-+,可得切线方程为0(1)y x m -=--,f (1)2=,21(1)m ∴=--,解得2m =.()(12)y f x x ∴==--,即()1f x x =+.(2)函数()1()x x f x x g x e e +==,()x xg x e-'=,0x ∴>时,()0g x '<,此时函数()g x 单调递减;0x <时,()0g x '>,此时函数()g x 单调递增.0x ∴=是函数()g x 的极大值点,(0)1g =.(3)设21x m =,12[x e -∈ ,1],则[1m ∈,]e ,2222222(1)1(1)ln m a lnm x ln x a x lnx x m +-++-+=.2(1)1()ln x a lnx h x x +-+= ,∴2(1)1()ln m a lnm h m m+-+=.若存在实数1[1x ∈,]e ,12[x e -∈,1],使21222222()(1)h x x ln x a x lnx x <+-+成立,等价于:12()()h x h m <成立,[1m ∈,]e .即2()()min max h x h x <,[1x ∈,]e .令lnx t =,[1x ∈ ,]e ,则[0t ∈,1].22(1)1(1)1()tln x a lnx t a t h x x e +-++-+∴==,[0t ∈,1],(0)1h =,h (1)3ae -=.221[(1)1](1)()()t tt a t a t t t a h t e e +--+-+--'==,a的取值范围是(-∞,32)(32ee --⋃,)+∞.第3类情形应用实例例3.设函数()(0)kx f x xe k =≠.(1)讨论函数()f x 的单调性;(2)设2()24g x x bx =-+,当1k =时,若对任意的1x R ∈,存在2[1,2]x ∈,使得()()12f x g x ≥,求实数b 的取值范围.解析:(1)令()(1)0kx f x kx e '=+>,所以10kx +>,当0k >时,1x k >-,此时()f x 在1,k ⎛⎫-∞- ⎪⎝⎭上单调递减,在1,k ⎛⎫-+∞ ⎪⎝⎭上单调递增;当k 0<时,1x k <-,此时()f x 在1,k ⎛⎫-∞- ⎪⎝⎭上单调递增,在1,k ⎛⎫-+∞ ⎪⎝⎭上单调递减;(2)当1k =时,,()f x 在(),1-∞-上单调递减,在()1,-+∞单调递增.所以对任意1x R ∈,有()11(1)f x f e ≥-=-,又已知存在2[1,2]x ∈,使()()12f x g x ≥,所以()221,[1,2]g x x e -≥∈即存在2[1,2]x ∈,使21()24g x x bx e =-+≤-,即142e b x x-+≥+,又因为当[1,2]x ∈,14114,52e x x ee -+⎡⎤+∈++⎢⎥⎣⎦,所以1242b e ≥+,124b e ≥+,即实数b 的取值范围124b e ≥+.第4类情形应用实例例4.已知函数()()ln 0bf x a x x a =+≠.(1)当2b =时,若函数()f x 恰有一个零点,求实数a 的取值范围;(2)当0a b +=,0b >时,对任意121,,x x e e ⎡⎤∈⎢⎥⎣⎦,有()()122f x f x e -≤-成立,求实数b 的取值范围.解析:(1)定义域为()0,∞+,当2b =时,22()2a x af x x x x+'=+=;当0a >时,()0f x '>,()f x 为增函数,取10a x e -=,120()1(e )0a f x -=-+<,(1)10f =>所以0()(1)0f x f ⋅<,故此时恰有一个零点;当0a <时,令()0f x '=,x =0x <时,()0f x '<,所以()f x 在⎛ ⎝单调递减,x ()0f x '>,所以()f x 在⎫+∞⎪⎪⎭单调递增;要使函数恰有一个零点,需要ln 02af a ==,解得2a e =-,综上,实数a 的取值范围是2a e =-或0a >.(2)因为对任意121,x x e e ⎡⎤∈⎢⎥⎣⎦,有()()122f x f x e -≤-成立,且12max min ()()()()f x f x f x f x --≤,所以max min ()2(e )f x f x -≤-.因为0a b +=,所以=-a b ,所以()ln bf x b x x =-+,1(1)().b b b b x f x bx x x--'=-+=当01x <<时,()0f x '<,当1x >时,()0f x '>;所以函数在1[,1)e上单调递减,在(1,]e 上单调递增,min ()(1)1,f x f ==因为1()bf b e e -=+与()b f e b e =-+,所以max 1()max (),(e),e f x f f ⎧⎫=⎨⎬⎩⎭令1()(e)()e e 2,eb bg b f f b -=-=--则当0b >时,()220b b g b e e -'=+->-=,所以()g b 在()0,∞+上单调递增,故()(0)0g b g >=,所以1()()f e f e>,从而max ()e .bf x b =-+所以12b b e e -+-≤-,即10b e b e --+≤.令()e e 1(0)t t t t ϕ=--+>,则()e 1t t ϕ'=-.当0t >时,()0t ϕ'>,所以()t ϕ在()0,∞+上单调递增.又(1)0ϕ=,所以10b e b e --+≤,即()(1)b ϕϕ≤,解得1b ≤,所以b 的取值范围是(0,1].。
导数中的双变量问题解题策略(史上最全题型)

h(m)
(x
1)m
x2
1在m [2, 2]时的函数值恒为非负值
h(2) 0 h(2) 0
x
3或x
1
★对任意n N , 恒有(1 1 )2na e2 ,求实数a 的最大值. n
(1 1 )2na e2 ln(1 1 )2na ln e2 (2n a) ln(1 1 ) 2 (n a ) ln(1 1) 1
n
n
n
2
n
a 2
1 ln(1
1
)
n, 设G (
x)
1 ln(1
x)
1 x
,
x
0,1
n
G '(x)
(1
1 x) ln2 (1
x)
1 x2
(1 x) ln2 (1 x) x2 x2 (1 x) ln2 (1 x)
, 设h( x)
(1
x) ln2 (1
x) x2
h '(x) ln2 (1 x) 2ln(1 x) 2x, h ''(x) 2ln(1 x) x ,易得G(x)在0,1上单调递减
构造函数f (x) exm ln(m 1) 1 ln(x 1), x (m, ), m 0 f (x) exm 1 ex 1 (x 1)ex em 0在x (m, )上恒成立,
x 1 em x 1 (x 1)em f (x)在(m, )上递增 f (x) f (m) 0 当0 m n时,即f (n) enm ln(m 1) 1 ln(n 1) 0 enm ln(m 1) 1 ln(n 1)
要题设中的不等式恒成立,只需a ln a e 1成立便可,于是构造(a) a ln a e 1,
导数中双变量处理策略

导数中双变量处理策略在微积分中,导数是研究函数变化率的重要工具,它可以描述函数在给定点的局部变化情况。
通常情况下,我们将导数应用于单变量函数,即只含有一个自变量的函数。
然而,在实际问题中,我们经常需要处理含有两个自变量的双变量函数。
本文将介绍导数中的双变量处理策略,并讨论其中的相关概念和技巧。
首先,我们回顾一下单变量函数的导数。
对于函数f(x),它的导数可以定义为:f′(x) = lim┬(Δx→0)〖(f(x+Δx)−f(x))/Δx〗这个定义描述了当自变量x的变化趋近于0时,函数f(x)在给定点x 的变化率。
我们可以通过计算导数来确定函数在这一点的切线斜率,从而了解函数在这一点的局部性质。
对于含有两个自变量的双变量函数f(x,y),我们希望找到一个类似于单变量函数的导数。
这样,我们就可以通过计算导数来了解函数在特定点的变化情况。
经典的导数公式无法直接应用于双变量函数。
因此,我们引入偏导数的概念。
偏导数是指将函数f(x,y)对其中一个自变量求导时,将另一个自变量视为常数进行求导。
对于双变量函数f(x,y),它的偏导数可以分别表示为∂f/∂x和∂f/∂y。
其中,∂f/∂x表示对x的偏导数,∂f/∂y表示对y的偏导数。
求偏导数的方法与求一元函数导数的方法相似,只需要将另一个自变量视为常数即可。
在计算偏导数时,我们可以使用基本的导数法则,如加法法则、乘法法则和链式法则。
这些法则可以帮助我们计算复杂函数的偏导数。
对于含有多个自变量的函数,我们可以计算多个偏导数。
例如,对于双变量函数f(x,y),我们可以计算∂f/∂x和∂f/∂y的值。
这些偏导数可以描述函数在特定点的斜率以及函数在局部区域的变化情况。
在一些情况下,我们还可以计算交叉偏导数。
交叉偏导数表示在对一个自变量求偏导后,再对另一个自变量求偏导。
例如,我们可以计算∂²f/∂x∂y和∂²f/∂y∂x的值。
这些交叉偏导数可以描述函数在给定点的曲率以及函数在不同方向的变化情况。
导数中的双变量

导数中的双变量问题1.已知函数1)(+=x ax ϕ,a 为正常数.⑴若)(ln )(x x x f ϕ+=,且a29=,求函数)(x f 的单调增区间;⑵在⑴中当0=a 时,函数)(x f y =的图象上任意不同的两点()11,y x A ,()22,y x B ,线段AB 的中点为),(00y x C ,记直线AB 的斜率为k ,试证明:)(0x f k '>.⑶若)(ln )(x x x g ϕ+=,且对任意的(]2,0,21∈x x ,21x x ≠,都有1)()(1212-<--x x x g x g ,求a 的取值范围.解:⑴222)1(1)2()1(1)(++-+=+-='x x x a x x a x x f ∵a 29=,令0)(>'x f 得2>x 或210<<x ,∴函数)(x f 的单调增区间为),2(),21,0(+∞.⑵证明:当0=a 时x x f ln )(=∴x x f 1)(=', ∴210021)(x x x x f +==',又121212121212ln ln ln )()(x x x x x x x x x x x f x f k -=--=--= 不妨设12x x > , 要比较k 与)(0x f '的大小,即比较1212lnx x x x -与212x x +的大小,又∵12x x >,∴ 即比较12lnx x 与1)1(2)(212122112+-=+-x x x x x x x x 的大小.令)1(1)1(2ln )(≥+--=x x x x x h ,则0)1()1()1(41)(222≥+-=+-='x x x x x x h , ∴)(x h 在[)+∞,1上位增函数.又112>x x ,∴0)1()(12=>h x x h , ∴1)1(2ln 121212+->x x x x x x,即)(0x f k '>⑶∵ 1)()(1212-<--x x x g x g ,∴[]0)()(121122<-+-+x x x x g x x g 由题意得x x g x F +=)()(在区间(]2,0上是减函数.︒1 当x x a x x F x +++=≤≤1ln )(,21, ∴ 1)1(1)(2++-='x a x x F 由313)1()1(0)(222+++=+++≥⇒≤'x x x x x x a x F 在[]2,1∈x 恒成立.设=)(x m 3132+++x x x ,[]2,1∈x ,则0312)(2>+-='xx x m∴)(x m 在[]2,1上为增函数,∴227)2(=≥m a .︒2 当x x a x x F x +++-=<<1ln )(,10,∴ 1)1(1)(2++--='x a x x F 由11)1()1(0)(222--+=+++-≥⇒≤'x x x x x x a x F 在)1,0(∈x 恒成立设=)(x t 112--+xx x ,)1,0(∈x 为增函数,∴0)1(=≥t a综上:a 的取值范围为227≥a .2.设函数1()ln ().f x x a x a R x =--∈⑴讨论函数()f x 的单调性;⑵若()f x 有两个极值点12,x x ,记过点11(,()),A x f x 22(,())B x f x 的直线斜率为k ,问:是否存在a ,使得2k a =-?若存在,求出a 的值;若不存在,请说明理由.解:⑴()f x 的定义域为(0,).+∞22211'()1a x ax f x x x x-+=+-= 令2()1,g x x ax =-+其判别式2 4.a =-①当||2,0,'()0,a f x ≤≤≥时故()(0,)f x +∞在上单调递增.②当2a <-时,>0,g(x)=0的两根都小于0,在(0,)+∞上,'()0f x >,故()(0,)f x +∞在上单调递增.③当2a >时,>0,g(x)=0的两根为12x x ==,当10x x <<时, '()0f x >;当12x x x <<时,'()0f x <;当2x x >时,'()0f x >,故()f x 分别在12(0,),(,)x x +∞上单调递增,在12(,)x x 上单调递减. ⑵由⑴知,若()f x 有两个极值点12,x x ,则只能是情况③,故2a >. 因为1212121212()()()(ln ln )x x f x f x x x a x x x x --=-+--, 所以1212121212()()ln ln 11f x f x x x k a x x x x x x --==+---1212ln ln 2x x k ax x -=--若存在a ,使得2.k a =-则1212ln ln 1x x x x -=-.即1212ln ln x x x x -=-.再由⑴知,函数1()2ln h t t t t=--在(0,)+∞上单调递增,而21x >,所以222112ln 12ln10.1x x x -->--=这与(*)式矛盾.故不存在a ,使得2.k a =- 3.已知函数)0)(ln()(2>=a ax x x f .(1)若2)('x x f ≤对任意的0>x 恒成立,求实数a 的取值范围;(2)当1=a 时,设函数x x f x g )()(=,若1),1,1(,2121<+∈x x e x x ,求证42121)(x x x x +<解:(1)x ax x x f +=)ln(2)(',2)ln(2)('x x ax x x f ≤+=,即x ax ≤+1ln 2在0>x 上恒成立 设x ax x u -+=1ln 2)(,2,012)('==-=x xx u ,2>x 时,单调减,2<x 单调增,所以2=x 时,)(x u 有最大值.212ln 2,0)2(≤+≤a u ,所以20ea ≤<.(2)当1=a 时,x x xx f x g ln )()(==,e x x x g 1,0ln 1)(==+=,所以在),1(+∞e 上)(x g 是增函数,)1,0(e上是减函数. 因为11211<+<<x x x e,所以111212121ln )()ln()()(x x x g x x x x x x g =>++=+ 即)ln(ln 211211x x x x x x ++<,同理)ln(ln 212212x x x x x x ++<. 所以)ln()2()ln()(ln ln 2112212112122121x x x xx x x x x x x x x x x x +++=++++<+ 又因为,421221≥++x x x x 当且仅当“21x x =”时,取等号. 又1),1,1(,2121<+∈x x ex x ,0)ln(21<+x x , 所以)ln(4)ln()2(21211221x x x x x x x x +≤+++,所以)ln(4ln ln 2121x x x x +<+,所以:42121)(x x x x +<.4.设a R ∈,函数()ln f x x ax =-.(Ⅰ)若2a =,求曲线()y f x =在()1,2P -处的切线方程;(Ⅱ)若()f x 无零点,求实数a 的取值范围;(Ⅲ)若()f x 有两个相异零点12,x x ,求证: 212x x e ⋅>.解:在区间()0,+∞上,11()axf x a x x-'=-=. (1)当2a =时,(1)121f '=-=-,则切线方程为(2)(1)y x --=--,即10x y ++= (2)①若0a =,()ln f x x =有唯一零点1x =.②若0a <,则()0f x '>,()f x 是区间()0,+∞上的增函数,(1)0f a =->Q ,()(1)0a a a f e a ae a e =-=-<,(1)()0a f f e ∴⋅<,函数()f x 在区间()0,+∞有唯一零点.③若0a >,令()0f x '=得: 1x a=. 在区间1(0,)a上, ()0f x '>,函数()f x 是增函数;在区间1(,)a+∞上, ()0f x '<,函数()f x 是减函数; 故在区间()0,+∞上, ()f x 的极大值为11()ln 1ln 1f a a a=-=--. 由1()0,f a <即ln 10a --<,解得:1a e>. 故所求实数a 的取值范围是1(,)e+∞. (3) 设120,x x >>12()0,()0,f x f x ==Q 1122ln 0,ln 0x ax x ax ∴-=-=1212ln ln ()x x a x x ∴+=+,1212ln ln ()x x a x x -=-原不等式21212ln ln 2x x e x x ⋅>⇔+>12()2a x x ⇔+>121212ln ln 2x x x x x x -⇔>-+1122122()ln x x x x x x -⇔>+令12x t x =,则1t >,于是1122122()2(1)ln ln 1x x x t t x x x t -->⇔>++. 设函数2(1)()ln 1t g t t t -=-+(1)t >,求导得: 22214(1)()0(1)(1)t g t t t t t -'=-=>++ 故函数()g t 是()1,+∞上的增函数,()(1)0g t g ∴>=,即不等式2(1)ln 1t t t ->+成立, 故所证不等式212x x e ⋅>成立.5.已知函数32()(63)xf x x x x t e =-++,t R ∈.(1)若函数()y f x =依次在,,()x a x b x c a b c ===<<处取到极值.①求t 的取值范围;②若22a c b +=,求t 的值. (2)若存在实数[]0,2t ∈,使对任意的[]1,x m ∈,不等式 ()f x x ≤恒成立.求正整数m 的最大值.解:(1)①23232()(3123)(63)(393)xxxf x x x e x x x t e x x x t e '=-++-++=--++32()3,39303,,.f x x x x t a b c ∴--++=有个极值点有个根 322()393,'()3693(1)(3)g x x x x t g x x x x x =--++=--=+-令()(-,-1),(3,+)(-1,3)g x ∞∞在上递增,上递减. ()3824.(3)0g x t g ⎧∴∴-<<⎨<⎩g(-1)>0有个零点②,,()a b c f x 是的三个极值点3232393(x-a)(x-b)(x-c)=x ()()x x x t a b c x ab bc ac x abc ∴--++=-+++++-393a b c ab ac bc t abc++=⎧⎪∴++=-⎨⎪+=-⎩31(b (-1,3))2b ∴=-∈或舍1181a b t c ⎧=-⎪∴=∴=⎨⎪=+⎩. (2)不等式 ()f x x ≤,即32(63)x x x x t e x -++≤,即3263x t xe x x x -≤-+-. 转化为存在实数[]0,2t ∈,使对任意[]1,x m ∈,不等式3263x t xe x x x -≤-+-恒成立,即不等式32063x xe x x x -≤-+-在[]1,x m ∈上恒成立。
函数导数中双变量问题的四种转化化归思想

2012 年 第 8 期 数学通讯(上半月) 8-12处理函数双变量问题的六种解题思想吴享平(福建省厦门第一中学) 361000在解决函数综合题时, 我们经常会遇到在某个范围内都可以任意变动的双变量问题, 由 于两个变量都在变动,因此不知把那个变量当成自变量进行函数研究,从而无法展开思路, 造成无从下手的之感, 正因为如此, 这样的问题往往穿插在试卷压轴题的某些步骤之中, 是 学生感到困惑的难点问题之一, 本文笔者给出处理这类问题的六种解题思想, 希望能给同学 们以帮助和启发。
一、改变“主变量”思想例1.已知 f (x) x 2 mx 1 m,在|m| 2时 恒成立,求实数 x 的取值范围 .分析: 从题面上看,本题的函数式 f (x)是以 x 为主变量 ,但由于该题中的“恒”字是 相对于变量m 而言的,所以该题应把 m 当成主变量,而把变量 x 看成系数,我们称这种思 想方法为改变“主变量”思想。
解: x 2 mx 1 m m(x 1) x 2 1 0 在| m| 2时 恒成立,即关于 m 为自 变量的一次函数 h(m) (x 1)m x 21在 m [ 2,2] 时的函数值恒为非负值得 x x 2 22x x 33 00x3或 x 1。
对于题目所涉及的两个变元, 已知其中一个变元在题设给定范围内任意变动, 求另一个 变元的取值范围问题,这类问题我们称之为“假”双变元问题,这种“假”双变元问题,往 往会利用我们习以常的 x 字母为变量的惯性“误区”来设计,其实无论怎样设计,只要我们 抓住“任意变动的量”为主变量, “所要求范围的量”为常数,便可找到问题所隐含的自变 量,而使问题快速获解。
二、指定“主变量”思想例2 .已知 0 m n,试比较 e n m ln(m 1) 与1 ln(n 1)的大小,并给出证明m,n ,这里不妨把 m 当成常数,指定 n 为主变量 x ,解答如下xm解:构造函数 f (x) e x m ln(m 1) 1 ln(x 1),x [m, ) ,m 0,f (x)min f(m) 0,于是,当 0 m n 时,f (n) e n m ln(m 1) 1 ln(n 1) 0即 e n m ln(m 1) >1 ln(n 1)。
高考专题 导数双变量问题

导数专题——导数背景下双变量问题(内含极值点偏移)类型一 消参构造)(21x x f ±或者)(21x x f 化二元函数为一元函数处理 【例1】已知函数()()1ln a f x a x x a x+=--∈R . (1)求函数()f x 的单调区间;(2)当e a <<x 的方程()1a f ax ax+=-有两个不同的实数解12,x x ,求证:22124x x x x +<.【解析】(1)()f x 的定义域为(0)+∞,,()21a a f x x x +'=-221x ax ax -+++=()()211x x a x -+-+⎡⎤⎣⎦=.①当10a +>,即1a >-时,)1(0x a ∈+,,()0f x '>,1()x a ∈++∞,,()0f x '<, ∴函数()f x 的单调递增区间是(0)1a +,,单调递减区间是(1)a ++∞,. ②当10a +≤,即1a ≤-时,0()x ∈+∞,,()0f x '<,∴函数()f x 单调递减区间是(0)+∞,,无单调递增区间.(2)设()()1a g x f ax ax+=+()ln ln a a x x =+-, ()()()10a x g x x x-'∴=>. 当01x <<时,()0g x '>,函数()g x 在区间(0)1,上单调递增; 当1x >时,()0g x '<,函数()g x 在区间(1)+∞,上单调递减;()g x ∴在1x =处取得最大值.方程()1a f ax ax+=-有两个不同的实数解12x x ,. ∴函数()g x 的两个不同的零点12,x x ,一个零点比1小,一个零点比1大.不妨设1201x x <<<,由()10g x =,且()20g x =,得()11ln x ax =,且()22ln x ax =,则111x x e a =,221x x e a =,121221x x x x e a +∴=, 1212212121x x x x e x x a x x +∴=⋅++, 令12x x t +=,()te h t t=,()()221tt t e t e t e h t t t -⋅-'==. 12t x x =+,1201x x <<<,1t ∴>.()0h t '>.函数()h t 在区间(1)+∞,上单调递增,()()1h t h e >=,()12122212121x xx x e ex x a x x a+∴=⋅>++. e a <<2144e e a e ∴>=,121214x x x x ∴>+. 又120x x +>,12124x x x x ∴+<.【例2】已知函数)()(a ax e e x f x x +-=有两个极值点21,x x . (1)求a 的取值范围; (2)求证:21212x x x x +<.【解析】(1)因为)2()(ax e e x f x x -=',令0)(='x f ,即ax e x =2①当0=a 时,无解 ②当0≠a 时,x e x a =2,令x e x x g =)(,则x ex x g -='1)( 易得)(x g 在)1,(-∞上单调递增,在),1(+∞上单调递减又因为0)(,)(,,1)1(→+∞→-∞→-∞→=x g x x g x eg 时,时所以当ea 120<<,即e a 2>时,)(x f 有两个极值点.(2)由(1)设2110x x <<<,且有⎪⎩⎪⎨⎧==212122ax e ax e x x即1212x x e x x =-,两边取对,得1212ln x xx x =- 要证21212x x x x +<,即证))((ln212211221x x x x x x x x -+<,即211212ln 2x xx x x x -< 令)1(12>=t t x x ,只需证明01ln 2)(<+-=tt t t h 在),1(+∞上恒成立即可 由于0)1(112)(222<--=--='tt t t t h ,所以)(t h 在),1(+∞上单调递减, 即0)1()(=<h t h ,原式得证. 【例3】已知函数()ln )R (f x x ax a a =-+∈. (1)求函数()f x 的单调区间;(2)当1a =时,对任意的0m n <<,求证:()()()1n m f m m f n m--<+. 【解析】(1)()()110axf x a x xx-'=-=>. 当0a ≤时,()0f x '>恒成立,()f x ∴的单调递增区间为(0)+∞,,无单调递减区间;当0a >时,由()0f x '>得10x a<<,由()0f x '<,得1x a>,()f x ∴的单调递增区间为10,a ⎛⎫ ⎪⎝⎭单调递减区间为1,a ⎛⎫+∞ ⎪⎝⎭.(2)1a =时,()()ln 10f x x x x =-+>,由(1)知()f x 在()0,1上为增函数,在()1+∞,上为减函数,()()ln 110f x x x f ∴=-+≤=,ln 1x x ∴≤-,当且仅当1x =时,取“=”.()()f n f m -()()ln 1ln 1n n m m =-+--+()ln nn m m=--. ()11n m n m nm m m m--=-++ 0m n <<,11m ∴+>,0n m ->,1nm>.()1n m n m m -∴--<-+,∴只要证明ln1n nm m<-即可. 又1nm>,∴上式成立()()()1n m f n f m m m -∴-<+. 技巧二 借助极值点偏移处理双变量问题【例4】已知函数()2x af x e x c⎛⎫=-- ⎪⎝⎭,其定义域为(0)+∞,.(其中常数 2.71828e =…,是自然对数的底数)(1)求函数()f x 的单调递增区间;(2)若函数()f x 为定义域上的增函数,且()()124f x f x e +=-,证明:122x x +≥.【解析】(1)函数()2xa f x e x x ⎛⎫⎪⎝=-⎭-的定义域是()0,+∞,()()()221x e x x a f x x --'=.①若0a ≤,由()0f x '>,得1x >,∴函数()f x 的单调递增区间是()1,+∞.②若01a <<,由()0f x '>,得1x >或0x <<∴函数()f x 的单调递增区间是和.()1,+∞. ③若1a =,()()()22110x e x x f x x+-'=≥,∴函数()f x 的单调递增区间是()0,+∞.④若1a >,由()0f x '>,得x >01x <<,∴函数()f x 的单调递增区间是(0)1,和)+∞.综上,若0a ≤,函数()f x 的单调递增区间是(1)+∞,;若01a <<,函数()f x 的单调递增区间是和(1)+∞,; 若1a =,函数()f x 的单调递增区间是()0,+∞;若1a >,函数()f x 的单调递增区间是(0)1,和)+∞ (2)函数()f x 为定义域()0,+∞上的增函数,由(1)可知,1a =,()12x f x e x x ⎛⎫∴=--⎪⎝⎭. ()12f e =-,()()()12421f x f x e f ∴+=-=.不妨设1201x x <≤≤,欲证122x x +≥,只需证212x x ≥-, 即证()()212f x f x ≥-,又只需证()()1142e f x f x --≥-,即证()()1124f x f x e +-≤-令()()()2g x f x f x =+-,01x <≤,只需证()()1g x g ≤,()()()()2222221312x xe x x g x ex x x --⎡⎤+-'=--⎢⎥-⎢⎥⎣⎦, 1x e x ≥+.()()22221211x x e e x x --∴=≥-+=.()()2222132x e x xx x -+-∴--()2312xx x -≥+--()322312x x x x -++=-()()()2212102x x x x ---=≥-. ()()()()22222213102x xe x x g x ex x x --⎡⎤+-'∴=--≥⎢⎥-⎢⎥⎣⎦. ()g x ∴单调递增,即()()1g x g ≤,从而122x x +≥得证.【例5】已知函数2()(2)e (1)x f x x a x =-+-有两个零点. (1)求a 的取值范围;(2)设12,x x 是()f x 的两个零点,证明:122x x +<.【解析】(1)()0,+∞(2)当1x >时,'()0g x <,而(1)0g =,故当1x >时,()0g x <.从而22()(2)0g x f x =-<,故122x x +<.解析:(1)'()(1)e 2(1)(1)(e 2)x x f x x a x x a =-+-=-+. ①设0a =,则()(2)e ,()x f x x f x =-只有一个零点,②设0a >,则当(,1)x ∈-∞时,'()0f x <;当()1,x ∈+∞时,'()0f x >,所以()f x 在(),1-∞上单调递减,在()1,+∞上单调递增.又(1)e,(2)f f a =-=,取b 满足0b <且ln 2ab <,则223()(2)(1)022a f b b a b a b b ⎛⎫>-+-=-> ⎪⎝⎭, 故()f x 存在两个零点.③设0a <,由'()0f x =得1x =或ln(2)x a =-.若e 2a ≥-,则ln(2)1a -≤,故当()1,x ∈+∞时,'()0f x >,因此()f x 在()1,+∞上单调递增.又当1x ≤时,()0f x <,所以()f x 不存在两个零点.若e 2a <-,则ln(2)1a ->,故当(1,ln(2))x a ∈-时,'()0f x <;当(ln(2),)x a ∈-+∞时,'()0f x >.因此()f x 在(1,ln(2))a -单调递减,在(ln(2),)a -+∞单调递增。
第15讲 导数中函数中的双变量问题系列(学生版)2023年高考数学重难突破之导数、数列(全国通用)
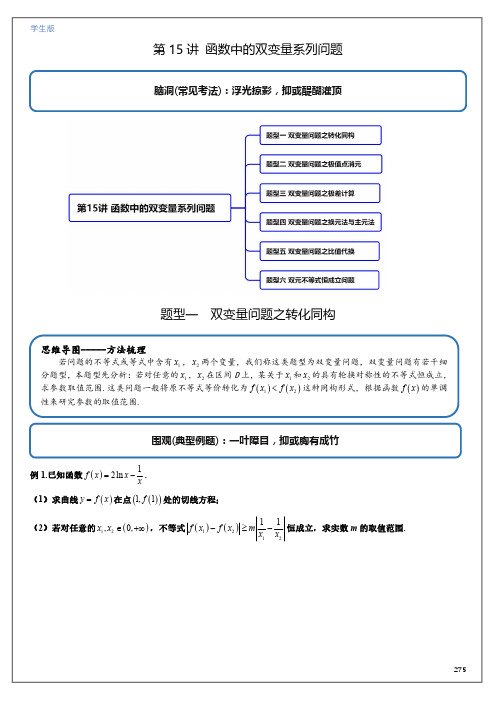
第15讲函数中的双变量系列问题
脑洞(常见考法):浮光掠影,抑或醍醐灌顶
题型一
双变量问题之转化同构
思维导图-----方法梳理
若问题的不等式或等式中含有1x ,2x 两个变量,我们称这类题型为双变量问题,双变量问题有若干细
分题型,本题型先分析:若对任意的1x ,2x 在区间D 上,某关于1x 和2x 的具有轮换对称性的不等式恒成立,求参数取值范围.这类问题一般将原不等式等价转化为()()12f x f x <这种同构形式,根据函数()f x 的单调性来研究参数的取值范围.
围观(典型例题):一叶障目,抑或胸有成竹
例1.已知函数()12ln f x x x
=-
.(1)求曲线()y f x =在点()()1,1f 处的切线方程;(2)若对任意的()12,0,x x ∈+∞,不等式()()1212
11
f x f x m
x x -≥-
恒成立,求实数m 的取值范围.
的单调性;
,且
的值;
双变量问题之极差计算
双变量问题之换元法与主元法
双变量问题之比值代换
套路(举一反三):手足无措,抑或从容不迫
的代数式取值范围”型,利用几何意义,转化为。
函数与导数重点题型04:双变量问题研究

重点题型四:“双变量”问题【问题分析】近年来函数综合问题中,常常出现两个在一定范围内可以变化的量,即函数的双变量问题。
此问题经常结合不等式进行命题,主要考查学生转化与化归思想,考查学生对问题的转化及处理能力,此类问题难度较大,对学生的综合能力要求较高。
解决此类问题主要通过变元来解决,如何将两个变量转化为一个变量是此类问题解体的关键。
然后,再结合函数性质即可解决此类问题。
【解题策略】解决此类问题常用以下四种策略:策略一:消元,变量归一 ①若两个变量存在确定的关系,可以利用其中一个变量替换另一个变量,直接消元,将两个变量转化为一个变量.②若两个变量不存在确定的关系,有时可以将两个变量之间的关系看成一个整体(比如x 1x 2,x 1x 2,x 1−x 2,x 1+x 2),进行整体换元,将两个变量化为一个变量.策略二:变换主元 当两个变量之间没有关系,也不能看成一个整体时,主元的选择就显得尤为重要了,主元若选择得当,可以降低思维难度,可以将复杂的函数变为简单函数。
主元变换是将其中一个变量作为主元,其中一个变量作为参数。
策略三:构造函数根据题中条件构造适当的函数,利用函数性质解决.策略四:转化为最值 根据题中条件将双变量问题转化为函数最值来处理,此类题型可以参考“恒成立”与“存在性”问题解题思路与方法.【典例赏析】例一:已知函数f (x )=1x −x +alnx(1)讨论f(x)的单调性.(2)若函数存在两个极值点x1,x2,证明f(x1)−f(x2)x1−x2<a−2. 试题分析:(1)略,参考重点题型一。
(2)由已知导函数f′(x)=−1x2−1+ax,整理后f′(x)=−x2−ax+1x2,极值点x1,x2即为方程x2−ax+1=0的两个根,x1x2=1,由此可以进行消元,只留一个变量。
解析:(1)略,参考重点题型一.(2)由(1)知a>2且x1x2=1.f(x1)−f(x2)=x2−x1x1x2−(x1−x2)+a(lnx1−lnx2).故f (x1)−f(x2)x1−x2=−2+a(lnx1−lnx2)x1−x2要证f (x1)−f(x2)x1−x2<a−2,即证(lnx1−lnx2)x1−x2<1.假设x1>1>x2>0,则只需证lnx1−lnx2<x1−x2.又x1x2=1,所以2 lnx1−x1+1x1<0.令g(x)=2 lnx−x+1x(x>1),由(1)知当a=2时,g(x)是单调递减的. 所以g(x)<g(1)=0所以 2 lnx1−x1+1x1<0成立,即f(x1)−f(x2)x1−x2<a−2成立.例二:已知函数f(x)=e2x−2t(e x+x)+x2+2t2+1,求证f(x)≥32.试题分析:题中主元为x,不等式f(x)≥32等价于e2x−2(e x+x)t+x2+2t2+1≥32。
导数中含两个变量问题 (1)

导数中含双变量问题1.设函数143)(2++=x x x f ,a x a x g +=26)(,其中31>a ; (1)求)(x f 的极值(2)若对任意],0[a x ∈ ,总存在相应的],0[,21a x x ∈,使得)()()(21x g x f x g ≤≤ 成立,求a 的取值范围;2.已知函数x f ex x f )1(2ln)('-= (1)求)1('f(2)求)(x f 的单调区间和极值;(3)设1≥a ,函数523)(22-+-=a ax x x g ,若对任意)1,0(0∈x ,总存在)2,0(1∈x ,使得)()(01x g x f =成立,求a 的取值范围.3.(已知函数52)4()(-+=x e a x f ,x e a ax x x g ---+=32)32()((1)若,1=a 求)(x g 的单调区间与极值;(2)求证:当6-<a 时,一定存在]5,0[,21∈x x ,使得40)()(21>-x g x f ;4.已知函数ax x ax x f -++=2)2121ln()((a 为常数,)0>a (1)若21=x 是函数)(x f 的一个极值点,求a 的值; (2)求证:当20≤<a 时,)(x f 在),21[+∞上是增函数; (3)若对任意的)2,1(∈a ,总存在]1,21[0∈x ,使不等式)1()(20a m x f ->成立,求实数m 的取值范围.5.已知x a x x f ln )(2-=在(1,2]上是增函数,x a x x g -=)(在(0,1]上是减函数。
(1)求a 的值;(2)设212)(xbx x -=ϕ在]1,0(上是增函数,且对于]1,0(内任意两个自变量t s ,,恒有)()(t s f ϕ≥成立,求实数b 的取值范围.(3)设xx x g x f x h 32)()()('+--=,求证:*)(2)(2)]([N n x h x h n n n ∈+≥+6.已知函数14)(2+=x x x f ,x a x x g +=ln )(,若对任意的]1,1[1-∈x ,总存在],1[2e x ∈,使得27)()(12+≤x f x g ,求实数a 的取值范围.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
导数中的双变量任意、存在恒成立问题
解决方法:转化为最值问题处理
●类型 一:若2211D x D x ∈∀∈∀,,)()(21x g x f >恒成立 ⇔ max 2min 1)()(x g x f >. 基本思想是:函数)(x f 的任一函数值均大于)(x g 的任一函数值,
故只需max 2min 1)()(x g x f >即可. 几何解释如图一.
例1、已知x x x f ln )(=,3)(2++-=ax x x g ,若对)0(1∞+∈∀,x ,
]1
[2e x ,∈∀使得)(21x f ≥)(2x g 成立,求实数a 的取值范围.
【变式训练1】已知函数14341ln )(-+-=x
x x x f ,42)(2-+-=bx x x g ,若)20(1,∈∀x , ]21[2,∈∀x ,不等式)(1x f ≥)(2x g 恒成立,求实数b 的取值范围.
●类型 二:若2211D x D x ∈∃∈∃,,)()(21x g x f >恒成立 ⇔ min 2max 1)()(x g x f >. 基本思想是:函数)(x f 的某些函数值大于)(x g 的某些函数值,
只要求有这样的函数值,不要求所有的函数值.
故只需min 2max 1)()(x g x f >即可. 几何解释如图二.
例2、已知a ≤2,设函数x a x x x f ln 1)(--=,e
x x x g 1ln )(--=, 若在]1
[e ,上存在21x x ,,使)(1x f ≥)(2x g 成立,求实数a 取值范围.
【变式训练2】已知函数x
x x g ln )(=,ax x g x f -=)()(. (1)求函数)(x g 的单调区间;
(2)若函数)(x f 在(1,∞+)上是减函数,求实数a 的最小值;
(3)若存在][221e e x x ,,∈,使得)(1x f ≤a x f +')(2成立,求实数a 取值范围.
●类型 三:若2211D x D x ∈∃∈∀,,)()(21x g x f >恒成立 ⇔ min 2min 1)()(x g x f >. 基本思想是:函数)(x f 的任一函数值大于)(x g 的某些函数值,
但并不要求大于)(x g 所有的函数值.
故只需min 2min 1)()(x g x f >即可. 几何解释如图三.
例3、已知函数x x x f 2)(2+=,m x g x -=)2
1()(. 若对]11[]21[21,,,-∈∃∈∀x x ,使得 )(1x f ≥)(2x g 成立,求实数m 取值范围.
【变式训练3】已知函数)()(2R n m n
x mx x f ∈+=,在1=x 取得极值2. (1)求)(x f 的解析式; (2)设函数x a x x g +
=ln )(,若对]1[]11[21e x x ,,,∈∃-∈∀,使得)(2x g ≤2
7)(1+
x f 成立,求实数a 的取值范围.
●类型 四:若2211D x D x ∈∀∈∃,,)()(21x g x f >恒成立 ⇔ max 2max 1)()(x g x f >. 基本思想是:函数)(x f 的某些函数值大于)(x g 的任一函数值,
只要求)(x f 有函数值大于)(x g 的函数值即可.
故只需max 2max 1)()(x g x f >即可. 几何解释如图三.
例4、已知函数,x ax x f ln )(+=,22)(2+-=x x x g . 若a 1->且]1
[1e x ,∈∃,对 ]10[2,∈∀x ,使得)()(21x g x f >成立,求实数a 的取值范围.
【变式训练4】已知函数x
x x f 2ln )(-=,x x x f x g ln 62)()(-+=,设4)(2+-=mx x x h . 若)10(1,
∈∃x ,对]21[2,∈∀x ,总有)(1x g ≥)(2x h 成立,求实数m 的取值范围.
例4、【解析】:因为22)(2
+-=x x x g ,]1,0[∈x ,易得2)0()(max ==g x g . 又x ax x f ln )(+=,x a x f 1)(+
=',易知)(x f '在[1,e]上单调递减,∴]11[)(++∈'a e a x f ,,若a ≥e
1-,则)(x f '>0,)(x f 在[1,e]上单调递增,1)()(max +==ae e f x f >2,解得a >e 1.若e a 11-<<-,)(x f 在(1,a 1-)上单调递增,在(a
1-,e )上单调递减,)ln(1)1()(max a a
f x f ---=-=>2,得31e a ->,此时与e a 11-<<-矛盾. 综上所述,所求a 的取值范围是(+∞,1e
).。
