有阻尼受迫振动系统的计算机仿真分析(1)
MATLAB系统仿真报告——有阻尼受迫振动系统

MATLAB系统仿真报告——有阻尼受迫振动系统摘要:本报告通过MATLAB系统仿真,研究了一维受阻尼受迫振动系统的运动规律。
首先建立了该系统的运动方程,然后通过数值计算方法进行了模拟,并进行了参数分析和振动图像绘制。
结果表明,阻尼系数和外力频率对系统的振动性质有重要影响,阻尼系数越大,振动幅度越小,外力频率的谐振区域越窄。
关键词:阻尼受迫振动系统,MATLAB系统仿真,运动方程,数值计算,参数分析。
1.引言阻尼受迫振动系统是振动学中的基础问题之一,具有很广泛的应用,如建筑物结构的抗震设计、电子设备的振动控制等。
通过数值计算方法对系统进行仿真研究,可以直观地了解系统的振动规律,为工程实际应用提供理论依据。
2.系统建模考虑一维阻尼受迫振动系统,其运动方程可表示为:m*x'' + b*x' + k*x = F0*cos(ω*t) (1)其中,m为质量,b为阻尼系数,k为弹性系数,F0为外力幅值,ω为外力频率。
将该二阶常微分方程转化为一阶微分方程组,得到:x'=v(2)v' = (F0*cos(ω*t) - b*v - k*x)/m (3)3.数值计算通过使用MATLAB的ode45函数,可以对方程组进行数值求解。
根据方程(2)和(3),定义函数damp_force_vibration来求解微分方程组的右侧项:function dx = damp_force_vibration(t, x)m=1;b=0.1;k=1;F0=1;omega = 0.5;dx = zeros(2,1);dx(1) = x(2);dx(2) = (F0*cos(omega*t) - b*x(2) - k*x(1))/m;end然后,使用ode45函数进行数值求解:tspan = [0 100]; % 时间范围x0=[00];%初始条件,位移和速度均为04.参数分析通过修改阻尼系数和外力频率的值,可以观察系统振动的不同特性。
1.4有阻尼的受迫振动解析

F0 it c k x x x e m m m
其中, 0
k m
系统的无阻尼固有频率;
系统的阻尼比;
c 2 km
i (t ) x ( t ) Ae 设非齐次方程的特解,即稳态响应:
2 A 2 e i (t ) i 2 0 Ae i (t ) 0 Aei (t )
2. s=1处,即 不同
区间单调上升的曲线;
1 0 2 时,共振,
的曲线共交于一点。
3. 小阻尼 0
s 1
0
时,激励力与位移同相; 时,激励力与位移反相;
s 1
,
l 例题:已知等效质量m且可简化于杆长 处,阻尼为c,弹簧刚度为k, 3 F (t ) F0 sin t ,水平位置平衡,试求: 1. 动力学微分方程;
第四节 有阻尼的受迫振动
一.
定义:
受迫振动:有阻尼的系统在外界控制的持续激 励作用下所产生的振动。 激励:外界力、基座运动所产生的惯性力。 响应:激励所引起的系统的振动状态。
非自治系统:显含时间变量的系统。
二.
有阻尼受迫振动
受激励力存在使得动力学方程成为非齐次方程:
cx kx F0 eit m x
9 F0 4c 9k sin t m m ml
(2)
0
9k k =3 m m
2c m
3F0 B k
2c 0 3 mk
9F 4c 9k 0 sin t m m ml
当 n时 振幅(最大摆角)
Amax B 3F0 3 mk 9F0 2 2kl 2c 4cl
2.
s=1(接近共振),且
阻尼受迫振动数据分析
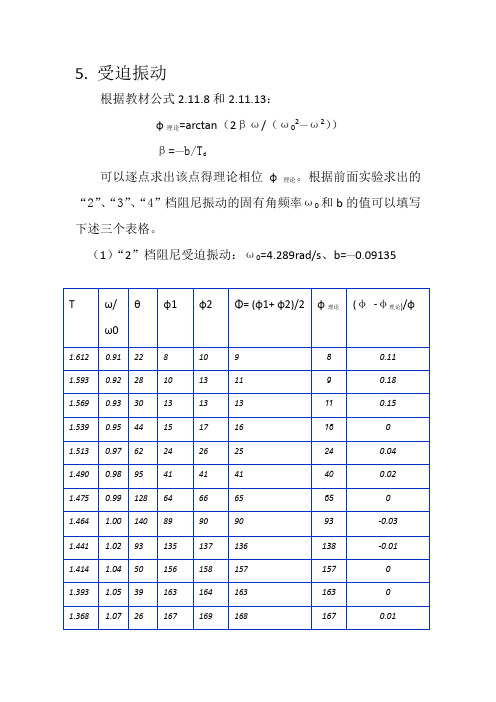
5. 受迫振动
根据教材公式2.11.8和2.11.13:
φ理论=arctan(2βω/(ω02—ω2))
β=—b/T d
可以逐点求出该点得理论相位φ理论。
根据前面实验求出的“2”、“3”、“4”档阻尼振动的固有角频率ω0和b的值可以填写下述三个表格。
(1)“2”档阻尼受迫振动:ω0=4.289rad/s、b=—0.09135
将上面的数据绘制成幅频特性曲线和相频特性曲线如下:
(2)“3”档阻尼受迫振动:ω0=4.289rad/s、b=—0.11837
将上面的数据绘制成幅频特性曲线和相频特性曲线如下:
(3)“4”档阻尼受迫振动:ω0=4.293rad/s、b=—0.15369
将上面的数据绘制成幅频特性曲线和相频特性曲线如下:
(3)不同阻尼状态下幅频特性曲线和相频特性曲线比较:
下面是三组不同阻尼状态下幅频特性曲线和相频特性曲线的
比较:。
MATLAB系统仿真报告——有阻尼受迫振动系统

一、 问题描述有阻尼受迫振动的结构及基本原理图一 有阻尼的受迫振动系统图1为有阻尼的受迫振动系统,质量为M ,摩擦系数为B , 弹簧倔强系数为K 。
拉力、摩擦力和弹簧力三都影响质量为M 的物体的加速度。
如果系统的能量守恒,且振动一旦发生,它就会持久的、等幅的一直进行下去。
但是,实际上所遇到的自由振动都是逐渐衰减直至最终停止,即系统存在阻尼。
阻尼有相对运动表面的摩擦力、液体与气体的介质阻力、电磁阻力以及材料变形时的内阻力等作用。
物体在驱动力作用下的振动是受迫振动。
二、 模型分析与建立利用牛顿运动定律,建立系统的力平衡微分方程如下:)(M 22t f Kx dt dxB dt x d =++(1)式中的f (t)是一个外加的激励力,如果 f (t) =F0 sin ωt ,则称为谐激励力,其中ω为外施激励频率,t 是持续时间。
故(1)式又可写成:wtF Kx dt dxB dt x d sin M 022=++ (2)(2)式是一个线性非齐次方程。
令B/M = 2n (n 为阻尼系数)),K/M=2nw (nw 为固有振动频率),ξ = n w n为相对阻尼系数或阻尼比,则(2)式可写为:)sin(2222wt h x w dt dx n dt dx n =++ (3)根据阻尼对系统振动的影响,振动响应分为弱阻尼(ξ<1)、(强阻尼ξ>1)和临界阻尼(ξ=1)三种情况。
这里仅讨论弱阻尼的情况。
在弱阻尼情况下的振动为响应:x=Ae-ξwnt sin ( 1-ξ2wn t +φ ) +A1 sin (wt+θ) (4) 谐迫振动的主要特性有:(1)式(4)包括瞬态与稳态响应两部分,其中瞬态响应是一个有阻尼的谐振。
振动频率为系统固有频率n w ,振幅A 与初相位角ψ决定初始条件,振幅的衰减按tw e n ε-规律,因此,振动持续时间决定于系统的阻尼比ε。
(2)谐振的稳态响应是一个简谐振动,其频率比等于激励力的频率w ,振幅为1A ,相位角为θ。
(完整word版)有阻尼自由系统的振动分析

有阻尼自由系统的振动分析实际系统振动时不可避免地存在阻力,因而在一定时间内振动逐渐衰减直至停止。
阻力有多种来源,例如两个物体之间的干摩擦阻力、气体或液体介质的阻力、有润滑剂的两个面之间的摩擦力、由于材料的粘弹性而产生的内部阻力等等。
在振动中这些阻力统称为阻尼。
其弹簧—质量系统模型图示如右图,因为有考虑到阻尼的影响故其运动方程应为:0ku(t)(t)u c (t)u m ...=++ (1) 或 0u(t)ω(t)u ξω2(t)u2=++ (2) 其中mc =ξω2 式(2)是一个常系数齐次线性微分方程 0222=++ωξωx x (3)其通解为 12-±-=ξωξωx由上可知,式(2)的解与ξ的大小有关。
对于ξ可分为以下四种情况简要讨论:1、临界阻尼情况(ξ=1或C=2m ω)在这种情况下特征方程的根是一对重根:X 1、2=-ω,式(2)的通解是 ])1([)(00t ut u e t u t ++=-ωω (4) 在这种情况下系统不发生振动。
临界阻尼就是不产生振动的最小阻尼。
2、超阻尼情况(ξ>1或C >2m ω) 此特征根是两个负实数。
通解为t sh u u t ch u e t u d dd t ωωξωωξω000[)(++=- (5) 式中12-=ξωωd ,这种阻尼过大系统的运动是按指数规律衰减的非周期运动。
3、负阻尼情况(ξ<0或C <0)阻尼本来是消耗能量的,负阻尼则表示系统在不断增加能量,这种情况下的运动是不稳定的,其振幅会越来越大,直到系统振动失效破坏。
4、低阻尼或小阻尼情况(ξ<1或C <2m ω)此时特征根是两个复数,式(2)的通解为)cos sin ()(000t u t u u e t u d d dt ωωωξωξω++=- (6) 式中21ξωω-=d ,由此可知,阻尼使系统自振频率减小,亦即使系统自振周期增大。
由上式可看出,阻尼式振幅按指数规律衰减。
阻尼受迫振动实验报告

一、实验目的1. 了解阻尼受迫振动的基本原理和实验方法。
2. 观察阻尼对受迫振动的影响,分析阻尼系数对振幅和振动频率的影响。
3. 通过实验验证共振现象,并研究共振频率与系统固有频率的关系。
二、实验原理阻尼受迫振动是指在外力作用下,阻尼对振动系统的影响。
在阻尼受迫振动中,系统的运动方程可以表示为:\[ m\frac{d^2x}{dt^2} + c\frac{dx}{dt} + kx = F_0\cos(\omega t) \]其中,\( m \) 为质量,\( c \) 为阻尼系数,\( k \) 为弹簧刚度系数,\( F_0 \) 为驱动力幅值,\( \omega \) 为驱动力角频率,\( x \) 为位移。
当驱动力频率 \( \omega \) 与系统固有频率 \( \omega_0 \) 相等时,系统产生共振,振幅达到最大值。
此时,阻尼系数 \( c \) 对振幅的影响显著。
三、实验仪器1. 阻尼振动实验装置:包括质量块、弹簧、阻尼器、驱动器、数据采集系统等。
2. 频率计:用于测量驱动器的频率。
3. 电脑:用于数据采集、处理和分析。
四、实验步骤1. 将质量块、弹簧和阻尼器组装成阻尼振动系统。
2. 使用驱动器对系统施加周期性外力,频率逐渐增加。
3. 使用数据采集系统记录振幅和频率随时间的变化。
4. 改变阻尼系数,重复实验步骤,观察振幅和频率的变化。
5. 分析实验数据,绘制振幅-频率曲线,研究共振现象。
五、实验结果与分析1. 随着驱动器频率的增加,振幅先增大后减小,出现共振现象。
2. 阻尼系数越大,振幅减小越快,共振现象越不明显。
3. 当驱动器频率等于系统固有频率时,振幅达到最大值,即共振现象。
4. 实验结果与理论分析基本一致。
六、结论1. 阻尼受迫振动是物理学中常见的振动形式,阻尼系数对振幅和振动频率有显著影响。
2. 共振现象是阻尼受迫振动的一个重要特性,共振频率与系统固有频率有关。
3. 通过实验,我们可以观察和分析阻尼受迫振动现象,加深对振动理论的理解。
阻尼受迫振动实验报告

阻尼受迫振动实验报告阻尼受迫振动实验报告引言:阻尼受迫振动是物理学中一个重要的研究领域,它涉及到物体在受到外力作用下的振动情况。
通过实验研究阻尼受迫振动的特性,我们可以更好地理解物体的振动行为,并且为实际应用提供有价值的参考。
实验目的:本实验的目的是通过测量和分析阻尼受迫振动的振幅和频率随时间的变化规律,探究阻尼对振动的影响,并验证阻尼对振动幅度和频率的影响关系。
实验装置和方法:实验中我们使用了一个弹簧振子和一个受迫振动装置。
首先,我们将弹簧振子固定在支架上,并调整弹簧的初始位置。
然后,我们将受迫振动装置连接到弹簧振子上,并调整振动频率和振幅。
接下来,我们使用传感器测量弹簧振子的振动幅度和频率,并记录下相关数据。
最后,我们分析数据,得出结论。
实验结果:通过实验测量和数据分析,我们得到了以下结果:随着时间的推移,弹簧振子的振幅逐渐减小,呈现出阻尼现象。
同时,振动频率也随时间推移而发生变化,频率逐渐减小。
这表明阻尼对振幅和频率都有影响。
讨论与分析:从实验结果中我们可以看出,阻尼对振幅和频率的影响是相互关联的。
当阻尼增大时,振幅减小的速度更快,同时频率的减小也更为明显。
这是因为阻尼力会抵消振动系统的动能,使振幅逐渐减小,同时也会减小振动系统的自由度,导致频率减小。
这一结果与阻尼受迫振动的理论预测相符。
此外,我们还发现在阻尼受迫振动中,当外力频率等于振动系统的固有频率时,振幅最大。
这是因为外力与振动系统的固有频率产生共振,能量传递最为有效,使振幅达到最大。
而当外力频率与振动系统的固有频率差距较大时,振幅会逐渐减小。
这一现象在实验中得到了验证。
结论:通过本次实验,我们验证了阻尼对振幅和频率的影响关系,并进一步认识到阻尼受迫振动的特性。
阻尼力会减小振幅和频率,而共振现象能够使振幅达到最大。
这些结果对于理解振动系统的行为和应用于实际工程中具有重要意义。
总结:阻尼受迫振动是物理学中一个重要的研究领域,通过实验研究阻尼对振幅和频率的影响,我们可以更好地理解振动系统的特性。
清华大学物理实验A1阻尼振动与受迫振动实验报告
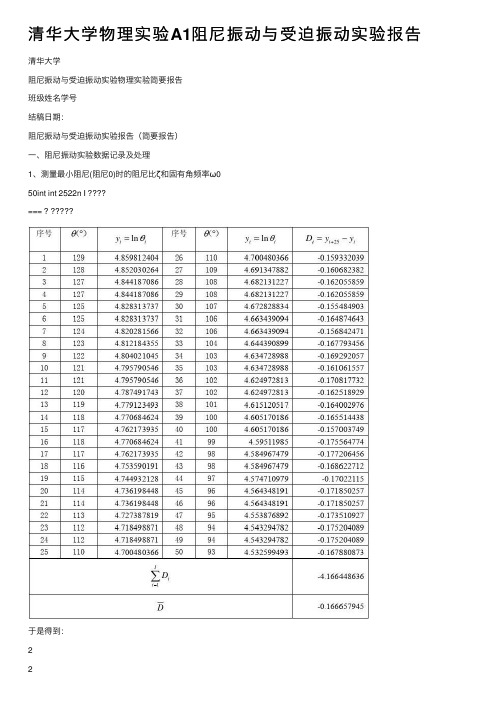
清华⼤学物理实验A1阻尼振动与受迫振动实验报告清华⼤学阻尼振动与受迫振动实验物理实验简要报告班级姓名学号结稿⽇期:阻尼振动与受迫振动实验报告(简要报告)⼀、阻尼振动实验数据记录及处理1、测量最⼩阻尼(阻尼0)时的阻尼⽐ζ和固有⾓频率ω050int int 2522n I=== ? ?????于是得到:22325221111()(ln ln )1-4.166448636(ln ln ) 6.666317818102525 IIi Ii i Ii i i i i i b D yy I IIθθθθ++==-+===-=-=?-==-?∑∑∑42.56547539510b -?===?由()0.5221b πζ--=--得到:31.06097683610ζ-===?2223/224(4)4 2.565475395104( 6.66631781810)4.0830*******b b πζπππ---?==?+=+-???=?从⽽可得-31.0610.04110ζ=±?()。
由上表,可得均值1.49428d T s =。
d -5-3T 1.4942810+0.001=1.014942810s=(0122 1.494284.204826965d T s ωππ-=?=??=0-46.79218621710ωω?===?⾓频率的不确定度为:00-3102.855996775100.0029s ωωωω-??==?≈由此,⾓频率为:()10 4.20480.0029s ω-=±2、测量其他2种阻尼的相关振动参数。
(1)阻尼110int int 522n I === ? ?221155221111()(ln ln )1-2.286548856(ln ln )0.0914619542455I Ii Ii i Ii i i i i i b D yy I IIθθθθ++==+===-=-=-==-∑∑∑0.0017005750.0017b ?===≈由()0.5221b πζ--=--得到:0.01455508013ζ===()()22323222224440.001700575440.0914********.70568914410b b ππζππ-?==?=++-??=?可得阻尼⽐:-21.4560.02710ζ=±?()由上表,可得均值 1.4964s d T =d -5-3T 1.496410+0.001=1.01496410s=0122 1.49644.199312323T s ωππ-=?=??=0-46.78281953410ωω?===? ⾓频率的不确定度为:0-4-3104.204826965 6.78281953410=2.848317766100.0029s ωωωω-??==≈⾓频率为:()10 4.19930.0029sω-=±()330.0914*******0.061121327351.49640.061121327351.1368160411061.1 1.210d b T βββ---=-=-=?===?∴=±?11.496416.360901230.0914*******16.360901230.304301882216.360.31d T b ττβττ==-=-=-?===∴=±1134.3522670834.35220.014555080130.63858498390.734.40.7Q Q Q ζ===≈??===≈∴=± (2)阻尼210int int 522n I === ? ?221155221111()(ln ln )1-3.122118769(ln ln )0.124884750855I Ii Ii i Ii i i i i i b D yy I IIθθθθ++==+===-=-=-==-∑∑∑0.0019389440.0020b ?===≈由()0.5221b πζ--=--得到:0.01987210049ζ===2223/223/222-4-44(4)40.0019389444(0.1248847508)3.0840******* 3.110b b πζπππ?==?+=+-??=?≈?这样,阻尼⽐为:-21.9870.03110ζ=±?()由上表可得: 1.4949s d T =d -5-3T 1.494910+0.001=1.01494910s=0122 1.49494.203910824T s ωππ-=?=??=0-46.78968749510ωω?===? ⾓频率不确定度为:0-4-3104.203910824 6.78968749510=2.854324075100.0029s ωωωω-??==≈⾓频率为:()10 4.20390.0029sω-=±()330.12488475080.0835********.49490.0835********.2982788281083.54 1.310d b T βββ---=-=-=?===?∴=±?111.9702364811.970236480.186025909111.970.19dT bττβτ==-=?===∴=±1125.1609033625.16220.019872100490.39049056720.3925.160.39Q Q Q ζ===≈??===≈∴=±下⾯将两个阻尼的部分振动参数的计算结果整理在表格中:⼆、受迫振动实验数据记录及处理测定受迫振动的幅频特性和相频特性曲线由于实验中途更换仪器,现直接给出实验⼆的1 04.288863691s ω-=①阻尼1②阻尼2根据表1和表2的数据,借助MATLAB计算机仿真,得到受迫振动的幅频特性曲线如图1所⽰。
仿真物理实验-受迫振动

受迫振动一、实验目的:本实验目的在于研究阻尼振动和受迫振动的特性,要求学生测量弹簧重物振动系统的阻尼常数,共振频率。
二、实验原理:受迫振动图1 受迫振动质量M的重物按图1放置在两个弹簧中间。
静止平衡时,重物收到的合外力为0。
当重物被偏离平衡位置时,系统开始振动。
由于阻尼衰减(例如摩擦力),最终系统会停止振动。
振动频率较低时,可以近似认为阻力与振动频率成线性关系。
作用在重物上的合力:其中 k1, k2是弹簧的倔强系数。
K = k+ k2是系统的等效倔强系数。
1x是重物偏离平衡位置的距离,是阻尼系数。
因此重物的运动方程可表示为:其中 and 。
在欠阻尼状态时() ,方程解为:A, 由系统初始态决定。
方程的解是一幅度衰减的谐振动,如图2所示。
图2 衰减振动振动频率是:(1)如果重物下面的弹簧由一个幅度为a的振荡器驱动,那么这个弹簧作用于重物的力是。
此时重物的运动方程为:方程的稳态解为:(2)其中。
图3显示振动的幅度与频率的关系。
图3 衰减振动幅度与振动频率关系弱阻尼情况下,当,振动的幅度会很大,最大值出现在:(3)幅度衰减一半的区域:(4)三、实验仪器:砝码挂钩、砝码、电子天平、弹簧、振荡器、信号发生器、米尺、秒表。
四、实验内容: 1.测量弹簧倔强系数。
(1)测量两根弹簧和砝码挂钩的质量。
在实验场景中单击鼠标右键弹出菜单,对挂钩和弹簧进行称重。
通过鼠标选择并砝码并拖放到电子天平上完成砝码的称重操作。
(2)按照实验原理中图1安装好振动系统,把较紧的弹簧放在面。
(3)在砝码盘上添加砝码并记录砝码挂钩的偏移。
使用砝码前先用电子天平称量砝码。
使用鼠标选择砝码,并把砝码拖放在需要的位置。
(4)画出质量m和挂钩偏移x的曲线,算出系统等效弹簧倔强系数K。
2.阻尼振动(1)调整挂钩上砝码质量,使弹簧的长度基本相等。
(2)计算振动系统的本征频率f o 。
(3)连接好信号发生器和振荡器,打开信号发生器,设定频率为f o 。
有阻尼体系受迫振动位移响应分析

有阻尼体系受迫振动位移响应分析引言振动是一种广泛存在于自然界和工程中的现象,其解析和分析对于工程设计和振动控制具有重要意义。
受迫振动是指在外力作用下物体产生的振动现象,而阻尼体系受迫振动位移响应分析则是对于这种受迫振动情况下体系的位移响应进行研究和分析。
本文将对有阻尼体系受迫振动位移响应分析进行探讨,分析受迫振动的基本特性,阻尼对振动的影响以及如何进行位移响应的分析。
一、受迫振动的基本特性受迫振动是指振动系统受到外部作用力的影响而产生的振动现象。
在实际工程中,受迫振动常常由于外部激励或者周期性作用力引起,比如机械系统中的激振器、电梯系统中的电动机等。
受迫振动的基本特性包括:振幅、频率和相位。
1. 振幅:受迫振动的振幅是指振动系统在外部作用力作用下最大的位移幅度。
振幅的大小取决于外部激励的大小和频率、振动系统的固有特性以及阻尼参数等。
2. 频率:受迫振动的频率是指振动系统在外部作用力的驱动下产生的振动频率。
频率与外部激励的频率有关,当外部激励的频率与振动系统的固有频率接近时,系统会产生共振现象,振幅将会变得非常大。
3. 相位:受迫振动的相位是指系统在受到外部激励驱动时位移的相位变化。
相位对于振动系统的稳定性和能量传递有重要影响。
在阻尼系统中,相位差可以描述外部激励与振动响应之间的关系。
二、阻尼对振动的影响阻尼是振动系统中的一种能量损耗机制,它可以减小振动系统的振幅,改变振动系统的频率响应特性,抑制共振现象,提高系统的稳定性。
在受迫振动中,阻尼对振动的影响主要体现在以下几个方面:1. 振幅的衰减:阻尼会使系统的振动幅度逐渐减小,最终趋于稳定。
阻尼比越大,振动幅度的衰减越快。
2. 频率响应特性:阻尼会改变振动系统的频率响应特性,使得系统的固有频率发生变化,从而影响系统的共振特性。
3. 稳定性和控制性能:适当的阻尼可以提高振动系统的稳定性,防止共振现象的产生;也可以改善振动系统的控制性能,使得系统的响应更加稳定和可控。
有阻尼体系受迫振动位移响应分析

有阻尼体系受迫振动位移响应分析阻尼体系受迫振动位移响应是指将一定大小和形式的外力作用于带有阻尼的体系中,来研究阻尼体系相应的位移变化。
在阻尼体系中,由于存在阻力作用,使振动体系的内能逐渐耗散,因此振幅会随时间的推移而减小,同时相角会发生改变,表现出阻尼现象。
受迫振动的基本方程为:$$m\ddot{x}+c\dot{x}+kx=F_c \sin \omega t$$其中,$m$表示振动体系的质量,$c$表示阻尼系数,$k$表示弹簧的劲度系数,$F_c$表示外力的大小,$\omega$表示外力的频率,$x$表示振动体系的位移。
从上式中可以看出,阻尼和弹簧对外力的作用方式是不同的,弹簧是以$x$的形式作用于振动体系,而阻尼则是以$\dot{x}$的形式作用于振动体系,这两种作用方式将使体系的振动方程解决起来变得更加困难。
在研究阻尼体系受迫振动位移响应时,通常会采用另一种形式的方程来描述系统的行为,即响应函数法。
响应函数法实质上是通过建立外力与体系响应的关系,来寻求解决受迫振动问题的方法。
响应函数法中的响应函数表示系统对于单位外力的谐振响应,因此通常用$X_0$来表示,其满足线性微分方程:在阻尼体系中,由于存在能量的散失现象,因此振幅会逐渐减小,为了描述振幅随时间的变化情况,可以引入阻尼比$\xi$,其定义为:$$\xi=\frac{c}{2\sqrt{mk}}$$阻尼比是描述体系耗散能力的一个比较重要的参数,它是阻尼系数$c$与振动体系固有频率$\sqrt{k/m}$的比值。
当外力的频率与系统固有频率相等时,响应函数的幅值达到最大,此时振动称为共振。
共振时的振幅与阻尼比密切相关,当阻尼比为0时,系统会发生无阻尼共振,振幅会无限增大;当阻尼比为1时,系统发生临界阻尼,振幅达到最大。
当阻尼比大于1时,系统进入过阻尼状态,振幅逐渐减小,最终趋于稳定。
通过分析响应函数,可以得到系统在任意频率下的响应情况,进而研究阻尼体系受迫振动的稳定性和动态特性。
有阻尼体系受迫振动位移响应分析

有阻尼体系受迫振动位移响应分析【摘要】有阻尼体系受迫振动是一个重要的研究领域,对于振动系统的稳定性和性能有着关键的影响。
本文首先介绍了有阻尼体系受迫振动的基本特性,包括振动的频率、振幅和相位等方面的特点。
接着分析了阻尼对受迫振动的影响,阻尼大小不同会导致振动系统响应的差异。
然后讨论了受迫振动的位移响应分析方法,包括理论推导和数值模拟两种方法。
我们还探讨了不同参数对振动响应的影响,包括阻尼比、激励频率和振动系统的质量等。
最后总结了阻尼对受迫振动的重要性,强调了未来研究需要进一步深入探讨阻尼对振动系统的影响,并提出了未来研究的展望。
这篇文章对于理解有阻尼体系受迫振动的主要特性和分析方法具有重要的参考价值。
【关键词】有阻尼体系、受迫振动、位移响应、影响、分析、数值模拟、参数、振动响应、重要性、未来研究、阻尼。
1. 引言1.1 研究背景阻尼是动力学系统中的一种重要参数,它对体系的振动特性有着重要的影响。
在实际工程中,许多系统都会受到外部激励而产生振动,这种受迫振动在自然界和工程领域都有广泛的应用。
受迫振动的研究往往需要考虑体系的阻尼特性,因为阻尼会影响振动系统的稳定性和能量衰减。
在过去的研究中,人们已经对受迫振动体系的响应进行了广泛的研究,但对于有阻尼体系受迫振动的位移响应分析仍有一定的局限性。
研究有阻尼体系受迫振动的位移响应具有重要意义,可以帮助我们更好地理解振动系统的动力学行为,并为工程实践提供理论支持。
在本文中,我们将探讨有阻尼体系受迫振动的基本特性、阻尼对受迫振动的影响、受迫振动的位移响应分析方法、受迫振动的数值模拟以及参数对振动响应的影响。
通过对这些内容的研究,我们可以更全面地认识阻尼在受迫振动中的作用,为相关领域的研究和应用提供理论依据。
1.2 研究意义有阻尼体系受迫振动位移响应分析的研究意义主要体现在以下几个方面:1.对于工程应用的重要性:在工程领域中,很多结构或系统都可能受到外部激励的影响而发生振动,而阻尼对于抑制振动、减小能量损耗具有至关重要的作用。
有阻尼体系受迫振动位移响应分析

有阻尼体系受迫振动位移响应分析阻尼体系受迫振动位移响应分析是一种研究机械系统动力学特性的方法,其主要目的是分析系统在受到外界力作用下的振动特性。
阻尼体系常见的有线性阻尼、非线性阻尼和viscoelastic阻尼等。
在阻尼体系受迫振动位移响应分析中,我们需要考虑系统的质量、刚度、阻尼以及外部力等因素。
在阻尼体系受迫振动位移响应分析中,我们通常使用微分方程来描述系统的动力学行为。
具体而言,我们可以通过Newton第二定律得到系统的运动方程。
对于一个一阶线性振动系统,其运动方程可以表示为:m*x''(t) + c*x'(t) + k*x(t) = F(t)m是系统的质量,x(t)是位移,c是阻尼系数,x'(t)是速度,k是系统的刚度,F(t)是外部力。
在阻尼体系受迫振动位移响应分析中,我们通常将外部力表示为F(t) = F0 * cos(ωt + φ),其中F0是振幅,ω是角频率,φ是相位差。
我们通过求解上述微分方程得到系统在受到外力作用下的位移响应x(t)。
在求解微分方程时,我们通常采用拉普拉斯变换、复频域分析或数值计算等方法。
通过这些方法,我们可以得到系统的传递函数、频率响应和相频特性等信息。
这些信息对于理解系统的动力学特性非常重要。
在阻尼体系受迫振动位移响应分析中,我们还可以通过绘制相图、相空间图和频谱分析图等来观察系统的动力学特性。
相图表示系统在相空间中的运动轨迹,可以直观地展示系统的稳定性和周期性。
频谱分析图可以帮助我们分析系统在不同频率下的响应情况。
阻尼体系受迫振动位移响应分析是研究机械系统动力学特性的重要方法。
通过该分析方法,我们可以了解系统在受到外力作用下的振动特性,对于优化系统设计和改善系统性能具有重要的指导意义。
有阻尼体系受迫振动位移响应分析

有阻尼体系受迫振动位移响应分析阻尼体系是由弹簧和阻尼器组成的振动系统,当该系统受到外界力的作用时,会产生位移响应。
分析阻尼体系的位移响应,可以帮助我们了解系统对不同外力的响应情况,从而对系统的工作性能进行评估和优化。
设阻尼体系的质量为m,弹簧的刚度为k,阻尼器的阻尼系数为c。
外界力F(t)作用在系统上,使系统发生位移。
我们可以通过求解系统的运动方程来分析阻尼体系的位移响应。
根据牛顿第二定律,可以得到阻尼体系的运动方程为:m d^2x/dt^2 + c dx/dt + kx = F(t)x表示位移,t表示时间。
方程左边是系统的惯性力和阻尼力,右边是外界力。
这是一个二阶线性常微分方程。
为了求解该方程,首先需要确定外界力。
外界力可以是一个确定的函数,也可以是一个随机变量。
根据外界力的不同取值情况,我们可以采用不同的方法来求解该方程。
1. 纯弹簧振动:当外界力F(t)为零时,即系统没有受到外力作用,只有弹簧的力和质量的惯性力在起作用。
这时,方程变为:该方程的解是一个简谐振动函数。
可以通过假设解为x = A cos (ωt + φ),其中A 为振幅,ω为角频率,φ为初相位,代入方程中解得:m ω^2 A cos (ωt + φ) + k A cos (ωt + φ) = 0整理后得到:m ω^2 + k = 0这是一个特征方程,其中ω为振动的固有频率。
通过求解该方程,可以得到固有频率ω,进而求得振幅A和初相位φ。
2. 纯阻尼振动:当外界力F(t)为零时,但系统中存在摩擦阻尼时,方程变为:这是一个含有二阶导数和一阶导数的常微分方程。
我们可以假设解为x = e^(λt),其中λ为待定常数,代入方程求解得到特征方程:通过求解该特征方程,可以得到特征根λ的值。
根据特征根的不同情况,可以分别得到过阻尼、临界阻尼和欠阻尼振动的解析表达式。
通过以上分析,我们可以得到阻尼体系受迫振动的位移响应。
根据实际情况,可以采用不同的数值方法进行数值模拟,从而更精确地求解位移响应。
有阻尼体系受迫振动位移响应分析

有阻尼体系受迫振动位移响应分析1. 引言振动是在物体受外力作用下产生的周期性的运动。
在实际的工程问题中,往往会遇到受迫振动的问题,即外界施加着周期性的力或位移而引起的振动现象。
而当受迫振动的物体存在阻尼时,振动的特性将会发生一些变化。
对于有阻尼体系受迫振动的位移响应进行分析和研究具有重要的意义。
2. 有阻尼体系受迫振动的基本方程对于有阻尼体系受迫振动的分析,首先需要建立受迫振动的基本方程。
考虑一个有阻尼的单自由度振动系统,系统的受迫振动可以表示为以下方程:m*x'' + c*x' + k*x = F0*cos(ω*t)m为系统的质量,c为阻尼系数,k为刚度,F0为外界施加的迫振动力的振幅,ω为外界力的角速度,x为系统的位移,x'为位移的一阶导数,x''为位移的二阶导数。
这个方程描述了阻尼体系受迫振动的基本特征,通过对这个方程进行分析可以得到系统的位移响应。
针对上述的受迫振动方程,我们可以通过解析方法得到系统的位移响应。
最常用的方法是采用叠加原则和复数法,通过解析得到系统的稳态和瞬态解。
对于稳态解,我们可以通过欧拉公式将其表示为:x(t) = A*cos(ω*t - φ)A和φ分别为振幅和相位,可以通过系统的初始条件和受迫振动的特性进行计算。
而对于瞬态解,我们可以通过拉普拉斯变换的方法得到系统的响应函数,从而得到系统的瞬态解。
有阻尼体系受迫振动的频率响应特性是描述系统响应的重要指标之一。
频率响应特性可以通过系统的传递函数来描述,传递函数可以通过对系统的受迫振动方程进行拉普拉斯变换得到。
通过对传递函数的分析,我们可以得到系统在不同频率下的频率响应特性。
具体来说,我们可以得到系统的共振频率、阻尼比对系统响应的影响,从而对系统进行频率特性的分析。
除了通过解析方法进行分析外,我们还可以通过数值模拟的方法来研究有阻尼体系受迫振动的位移响应。
数值模拟方法可以通过有限元分析、时域积分等方法来进行,通过对系统的微分方程进行离散化,我们可以得到系统在不同时间下的位移响应。
有阻尼体系受迫振动位移响应分析

有阻尼体系受迫振动位移响应分析阻尼体系受迫振动位移响应分析涉及到了物理学、数学等多个学科的知识,是一门非常复杂的学科。
阻尼体系是指受到阻尼力或阻尼扭矩影响的振动体系,其受迫振动位移响应是指在外部力的作用下,体系的振动位移随时间的变化情况。
阻尼体系受迫振动位移响应,通常都是通过分析阻尼振动的微分方程来研究的。
在分析的过程中,首先要确定阻尼体系的特征方程,然后通过特征方程解析出特征根,据此推导出阻尼振动的解析式。
阻尼体系的特征方程,一般都是由自由振动的动能和势能之和构成的。
如果阻尼体系受到一个周期性的外部力的作用,那么特征方程应该加上外部周期性力的作用。
在这个特征方程中,阻尼系数的影响必需明确地列出,同时这个方程的解析式中也必需有阻尼因子的影响。
根据阻尼振动的解析式,阻尼体系的受迫振动位移响应应该包括以下几个方面的内容:1.振幅在阻尼振动系统中,受迫振动的振幅一般都不是很大,因为阻尼系数的存在会削弱外部力的作用。
但是如果外部力的周期等于系统的固有周期,那么阻尼振动的振幅会呈现出共振现象,因此振幅的计算是非常关键的。
2.相位受迫振动位移响应的相位是指系统振动的相对位移,即一组振动波的“起点”位置。
相位的计算需要根据外部周期性力的相位以及振动系统的固有振动周期来进行计算。
3.频率受迫振动位移响应的频率是指振动系统产生振动的频率。
在阻尼振动系统中,由于阻尼作用的存在,在某个外部周期性力作用下,系统响应的频率不再是系统的固有频率,而是会逐渐趋近于外部周期性力的频率。
以上三个方面,是阻尼体系受迫振动位移响应分析中最为核心的内容。
在应用中,需要根据具体问题的不同,分别采取不同的计算方法来确定振幅、相位和频率等参数。
总之,阻尼体系受迫振动位移响应分析是一个涉及数学、物理学等多个学科知识的综合性分析问题。
在不同领域的应用中,也都需要根据自身的特点和需求来进行相应的分析和计算。
阻尼振动和受迫振动简介分析ppt课件.ppt

4
大学物理 第三次修订本
第6章 机械振动基础
受迫振动微分方程的稳态解为
x Acos(t ) 为驱动力角频率。
为受迫振动与驱动力之间的相位差。
A
f
(02 2 ) 4n22
tan
2n 02 2
受迫振动是谐振动,其角频率与驱动力
的角频率相同。
受迫振动的振幅 A, 以及它与驱动力间
的相位差,都与起始条件无关。
第6章 机械振动基础
令 / m 2n,2 k / m
d2 dt
x
2
2n
dx dt
2
x
0
n — 阻尼常量
阻尼振动运动方程
x Aent cos( 2 n2 t )
振幅衰减随时间按指数衰减。
角频率 2 n2
1
大学物理 第三次修订本
第6章 机械振动基础
x Aent cos(' t )
' 2 n2
r越接近于系统的 固有频率 0 ,同
时共振振幅 Ar也 越大。
共振频率
A 小阻尼
0阻尼
大阻尼
o
r0
P
7
大学物理 第三次修订本
第6章 机械振动基础
1940年11月,华盛顿州的Tacoma Narrows 桥, 由于桥面刚度太差,在45 mph风速的情形下,产 生“Galloping Gertie”(驰振).
三种阻尼情况
(1)小阻尼 2 n2
x 阻尼振动位移时间曲线
A
Aent
Aent cos t
O
t
( 0)
A
(2)大阻尼 2 n2 x
三种阻尼
b
(3)临界阻尼 2 n2
有阻尼系统受迫振动 振动力学课件

0
kl
k m2
l2 l
C
c
l
1
k m
l2 (1 ) l l2 1 2 l2 0
l 1
1 0
1 0
2 2
2
2k m
1 0
2 2
l2
l
2
l
1(1)
0
1 1
l2
l
2
l 1
11(2)
0
1
(1) l
1
(2)
1 l
1
1
l 1
1 l
本征值问题: M2 CP K 0
有非零解的充要条件: M 2 CP K 0
一般粘性阻尼系统的特征方程
2n 个特征值: 1, 2 , , 2n 实数或复数
一般粘性阻尼系统的特征方程 M 2 CP K 0
2n 个特征值: 1, 2 , , 2n 实数或复数
相对应,2n 个特征向量: 1 , 2 , , 2n
例题:
质量为3m、长为 的刚性板左端用铰链支承于地面,右端通过支
架支承于浮船支架的刚度系数为k,粘阻尼系数为c,浮船的质量为m。
水浪引起简谐激励力 (作业题4.21)
F上0 s,in作t用于浮船。求板的最大摆动角度。
解:两个自由度系统 , x
J k l xl c l x
mx k l x F0 sint c(l x)
M的、线K性组合,属于精确对角化矩阵,在实际中
证明:
Cp TC T M K T M T K
Mp Kp
对角阵
2. 弱非对角矩阵
忽略 C矩p 阵中的全部非对角元素 C p C pi
Cpij 0
但 C p相ij 对 C较P小j ,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有阻尼受迫振动的结构及基本原理1 Mx t( )f t( )图有阻尼的受迫振动系统1 图为有阻尼的受迫振动系统,质量为1M ,摩擦系数为B ,弹簧倔强系数为 K 。
拉力、摩擦力和弹簧力三个量都影响质量M 的加速度。
如果系统的能量守恒,且振动一旦发生,它就会持久的、等幅的一直进行下去。
但是,实际上所遇到的自由振动都是逐渐衰减直至最终停止,即系统存在阻尼。
阻尼有相对运动表面的摩擦力、液体与气体的介质阻力、电磁阻力以及材料变形时的内阻力等作用。
物体系统的数学模型2 利用牛顿运动定律,建立系统的力平衡微分方程如下:M d 2xdt 2B dxdt +Kx = f (t ()) 1式中的 f(t 是一个外加的激励力,如果)f (t ) =F 0 sin ωt ,则称为谐激励力,其中ω为外施激励频率,t 是持续时间。
故()式又可写成:1M d 2x dt 2 dxdt B+Kx = F 0 sin ωt () 2()式是一个线性非齐次方程。
令2B /M = 2n (n 为阻尼系数),K /M = 2nω (n ω n W n 为固有振动频率),ξ为相对= 阻尼系数或阻尼比,则()式可写为:2d 2x dt2 +2n dx dt +2n ω x=h sin (wt ()) 3根据阻尼对系统振动的影响,振动响应分为弱阻尼ξ(<、(强阻尼ξ>)和临界阻尼(ξ)三种情况。
这1)1=1里仅讨论弱阻尼的情况。
在弱阻尼情况下的振动为响应:有阻尼受迫振动系统的计算机仿真分析杨红(长江工程职业技术学院,湖北赤壁) 437302摘要: 介绍了一种基于环境下有阻尼受迫振动系统的仿真分析方法。
它是根据系统的数学模MATLAB/Simulink 型建立仿真模型,利用软件强大的仿真功能生成可视化的图形。
在物理学和控制理论等课程中,恰当运Simulink 用该技术来仿真,可加深对复杂振动系统的理解。
关键词:有阻尼受迫振动系统;;仿真MATLAB/Simulink 中图分类号:-O439 文献标识码: B 文章编号: -()--16730496200602005502Computer Simulation Analysis of Damped andForced Vibration SystemYANG Hong(Changjiang Vocational College, Chibi Hubei 437302 China)Abstract :Smulation analysis of MATLAB/Simulink-based damped and forced vibration system is introduced, in which visible pictures are formed on the basis of Simulink simulation model through the software's powerful simulation function. In the courses of physics and control theory, proper use of this technology can help to get a deeper understanding of complicated vibration system.Key words: damped and forced vibration system; MATLAB/Simulink; simulationx=Ae ξ-w n t 1-ξ2sin ( w n t +φ) +A 1 sin (θwt+()) 4谐迫振动的主要特性有:()式包括瞬态与稳态响应两部分,其中瞬态响应1(4)是一个有阻尼的谐振。
振动频率为系统固有频率ωn ,振幅A 与初相位角φ决定于初始条件,振幅的衰减按e ξ-n w t 规律,因此,振动持续时间决定于系统的阻尼比ξ。
()谐振的2稳态响应是一个简谐振动,其频率比等于激励力的频率ω,振幅为A 1,相位角为 θ。
()当外施激励频率等于系统固3有频率ωn时,系统发生位移共振,即振动位移最大。
将()式进行变换得:1Laplace MX (s ) S 2+BX (s ) S +KX (s ) =F (s )这样,该系统的传递函数为:H (s )X (s )F (s )1MS 2+BS +K (1/M )S 2+(B /M )S +(K /M ) = = = () 5仿真分析与步骤3 系统仿真是一种特殊的试验技术,其基本思想是利用物理的或数学的模型来类比模仿现实过程,以寻求对真实过程的认识,它在航天、航空、造船等方面有着广泛的应用,显示出巨大的社会效益和经济效益。
是Simulink 实现交互式动态系统建模、仿真和分析的一个集MATLAB 成图形环境,它使的功能得到进一步的扩展。
其MATLAB 主要特点是()实现了可视化建模。
()实现了多工作12环境间文件互用和数据交换。
()把理论研究和工程实现3有机结合在一起。
仿真分析的具体步骤为:①在MATLAB 窗口键入命令,打开模块库浏览器;②创simulink simulink 建新的模型文件;③设置模块的内部参数;④设置仿真参数。
本仿真采用系统默认设置;⑤仿真输出结果。
仿真分析实例4 如图所示,已知1K ,= 43.8N/S M ,=18.2kg B =1.49N/。
在的平台下,根据()式建立仿真S MATLAB simulink 3模型文件,如图所示。
另外,还可以根据系统传递函数建2立其模型文件,如图所示。
在设置模块的内部参数和仿真3参数后,就可以输出仿真结果。
图有阻尼受迫振动的模型之一2simulink图有阻尼受迫振动的模型之二3 simulink 仿真输出结果5 根据图,当输入激励力的频率2ω作如下变化时,将分别得到其振动响应。
()当激励力的频率1ω(小于系统固有频率=1rad/s nω =)时,其响应曲线如图所示。
还可以得到其1.5513rad/s 4速度和加速度的响应曲线,如图、图。
56图 4 ω的振动响应曲线=1 rad/s图 5 ω的速度响应曲线=1 rad/s图 6 ω的加速度响应曲线=1 rad/s图 7 ω的振动响应曲线=15rad/s ()当激励力的频率2ω(大于系统固有频率=15rad/s nω )时,其响应曲线如图所示。
=1.5513rad/s 7()当激励力的频率3ω等于系统固有频率nω 时,其响应曲线如图所示,即发生了共振现象。
8(下转第页)58图 8 ω=nω 的振动响应曲线=1.5513rad/s 杨红有阻尼受迫振动系统的计算机仿真分析这种方法从高等数学的角度出发,推导严谨,思路清晰,但从实际教学情况来看,对于高职生来讲,大部分学生对微积分就不大理解,以至于并不复杂的问题在他们眼里就成了难点,在他们难以接受的心理作用下,教师就很难将此方法解释清楚。
建议方法2图 2首先,取闸门前的部分水体为脱离体,如图2所示。
然后,对该水体进行受力分析,其上共有4个作用力:①铅直面A x上的水压力 P 1;②水平面 Z A 上的水压力P 2;③水体自重 G ;④受压曲面对水体的反作用力P 。
其中:①铅直面A x上的水压力 1P 为作用在平面壁上的静水总压力,可按作用在矩形平面壁上的静水总压力求解:1P = P c A x = S b②水平面A z上的水压力 P 2由图可知: 2P 2 = γz hA = γhl CF b = γS CFGH b ③水体自重 G = γV ECF =γS ECF b ;④受压曲面对水体的反作用力P 可分解为水平分力x P 和铅直分力P z 。
最后,分别对 x 、y 轴列平衡方程得:∑F x: = 0xP= 1P = cxP A =S b ∑yF:= 0P z= P 2- G = γ b (S HCFG -S ECF ) =γb S EFGH =γV EFGH用第二种方法可以推导出与前一种方法相同的结果,但是第二种方法根据《水力学》前修课程《工程力学》所学的内容很容易推导得出,较第一种方法好理解、易掌握,概念运用得少,解题思路清晰,还能与工程力学联系起来,将本专业的专业基础课融合在一起。
从实际教学情况来看,学生的学习兴趣要浓厚得多,教学效果较好。
运用时,即使同学们记不住该公式,自己也能快而准地推导出来。
(上接第页)56图动态系统的幅频特性曲线9 此外,还可以根据系统传递函数建立的模型文件求得其动态幅频特性曲线,如图所示。
显然,共振发生在频率9为ω处。
=1.5513rad/s运用建立振动系统的动态模型很简MATLAB/Simulink 单、直观,也比较容易得到所需的响应曲线,可以加深对复杂振动问题的理解。
参考文献:程守洙,江之永.普通物理学.北京:高等教育出[1] [M]版社,.1999陈晓平,李长杰.及其在电路与控制理论中的[2] MATLAB应用.合肥:中国科学技术大学出版社,.[M]2004陈怀琛等.及在电子信息课程中的应用.[3] MATLAB[M]北京:电子工业出版社,.2002尚涛等.工程计算可视化与实现.武汉:[4] MATLAB[M]武汉大学出版社,.2002王正林等.与控制系统仿真.北[5] MATLAB/Simulink[M]京:电子工业出版社,.2005邹林推导曲面壁上静水总压力计算公式的另类方法n。
