2020年人教版五年级上册数学六、2.三角形的面积附答案
人教版小学五年级数学上册 三角形与梯形的面积练习题及答案解析

三角形与梯形的面积1.三角形的底和高(1)如图,高CF对应的底边是边______;高BE对应的底边是边______。
(2)如右图,边AB上的高是线段______;边BC上的高是线段______。
(3)如图,高AF对应的底边是边______;高BD对应的底边是边______。
(4)如图,边AC上的高是线段______;边AB上的高是线段______。
(5)如图,高BE对应的底边是边______;高CD对应的底边是边______。
2.三角形的面积—与平行四边形等底等高(1)一个平行四边形的面积是7.2平方分米,与它等底等高的三角形的面积是______平方分米。
(2)一个平行四边形的面积是8.8平方厘米,与它等底等高的三角形的面积是______平方厘米。
(3)一个平行四边形的面积是3.6平方厘米,与它等底等高的三角形的面积是______平方厘米。
(4)图中BC=FG,平行四边形ABCD的面积为9.8平方分米,那么三角形EFG 的面积是______平方分米(5)图中BC=FG,平行四边形ABCD的面积为36.4平方厘米,那么三角形EFG 的面积是______平方厘米(6)图中平行四边形的面积为12.6平方厘米,那么三角形的面积是______平方厘米3.三角形与平行四边形(1)下图中平行四边形ABCD的面积是15.2平方厘米,AB=4cm,EC=2.5cm则阴影部分的面积是______平方厘米。
(2)下图中平行四边形ABCD的面积是15平方厘米,AB=5cm,EB=3cm则阴影部分的面积是______平方厘米。
(3)下图中平行四边形ABCD的面积是50平方厘米,则阴影部分的面积是______平方厘米。
(4)下图中平行四边形ABCD的面积是30平方厘米,AE=1.5cm,EB=4.5cm则阴影部分的面积是______平方厘米。
(5)如图,阴影部分面积是60平方厘米,EB=3厘米,三角形EDC中EC边上的高为15厘米,平行四边形的面积为______平方厘米。
人教版五年级数学上册练习二十二详细答案课件

练习二十二
2020/7/28
课本101页 练习二十二 1. 新丰小学有一块菜地,形状如右图。 这块菜地的面积是多少平方米?
33m
S = S平行四边形 + S三角形
50m
= 50×33 + 35×12÷2
= 1650 + 210
= 1860(m2)
答:这块菜地的面积是1860m2。
1cm
方法一:
满格的一共有13格, 不满格有20格。
13 + 20÷2
= 13 + 10 = 23(cm2)
课本102页 练习二十二 10. 请你采集几片树叶,利用方格纸估计叶子的面积。
3 7
方法二: S = ab
= 7×3 = 21(cm2)
1cm
你能像这样估一估手掌的面积吗?
1234 25 1 2 5 6 24 3 4 5 7 8 23 6 7 8 9 10 11
一个大写英文字母“A”。 它的面积是多少?
S = S大梯形 - S小梯形 - S三角形 =(2 + 10)×12÷2 - (4 + 6)×4÷2 - 3×4÷2 = 72 - 20 - 6 = 46(cm2) 答:它的面积是46cm2。
课本101页 练习二十二 6. 一个指示牌的形状是一个组合图形,
课本101页 练习二十二 4. 在一块梯形的地中间有一个长方形的
游泳池,其余的地方是草地。草地的 面积是多少平方米?
S = S梯形 - S长方形 =(40 + 70)×30÷2 - 30×15 = 1650 - 450 = 1200(m2)
答:草地的面积是1200m2。
课本101页 练习二十二 5. 小欣用一张红色不干胶剪了
人教版五年级数学上册第6单元不规则图形的面积的计算附答案
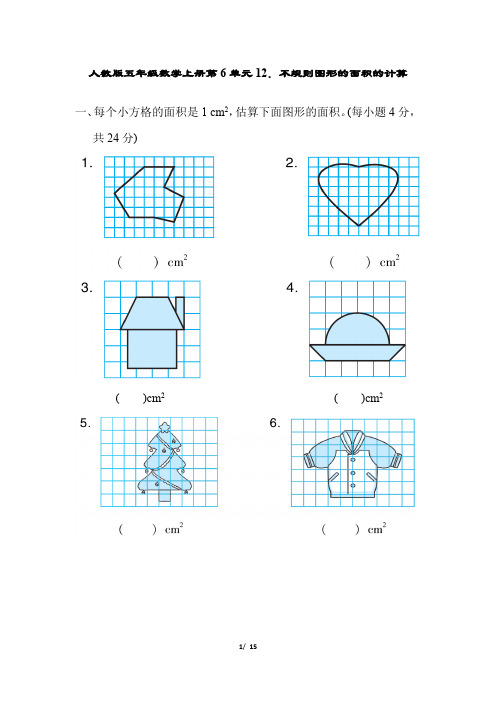
人教版五年级数学上册第6单元12.不规则图形的面积的计算一、每个小方格的面积是1 cm2,估算下面图形的面积。
(每小题4分,共24分)()cm2()cm2二、计算下面各图形的面积。
(单位:cm)(每小题6分,共24分)三、求阴影部分的面积。
(每小题6分,共12分)四、聪明的你,答一答。
(共40分)1.美术手工剪纸课中,乐乐剪了一个大写英文字母“E”,它的面积是多少?(单位:cm)(7分)2.几位“环保大使”用铁板给学校的草地做了一个标语牌(如图),请算出用了多少铁板?(7分)3.下图是一个占地6240平方米的花坛。
花坛两条平行的边分别是88米和42米。
请你算出这两条边的距离。
(6分)4.聪聪将一张长方形纸的一角如图折叠。
聪聪考大家:请求出阴影部分的面积。
(单位:dm)(6分)5.下图是一面墙,中间有一个长2 m,宽1.5 m的窗户,如果砌这面墙平均每平方米用160块砖,一共需要用多少块砖?(7分)6.雯雯家装修需要用下面的木板,木板形状如下图,一共需要多少平方米的木板?(7分)答案一、1.24 2.33 3.15 4.10 5.13 6.26二、1.200(cm2)2.20-9=11(cm)18×9+(18+30)×11÷2=162+264=426(cm2)3.6-2×2=2(cm)6×4-(2+1.5)×2÷2=24-3.5=20.5(cm2)4.11×8÷2+(11+22)×10÷2=209(cm2)三、1.15×10=150(平方厘米)5×(10-5)=25(平方厘米)5×(10-5)÷2=12.5(平方厘米)(15-5-5)×(10-5)÷2=12.5(平方厘米) 150-(25+12.5+12.5)=100(平方厘米) 2.8×8=64(dm2)6×6=36(dm2)(8+6)×6÷2=42(dm2)64+36-42=58(dm2)四、1.20-15=5(cm)15×5×3+25×5=75×3+125=350(cm2)答:它的面积是350 cm2。
2020-2021学年人教版数学五年级上册第六单元《多边形的面积》单元测试卷(一)

A.3×5÷2B.4×5÷2C.3×4D.以上都不对
3.一个三角形的底和高都扩大到原来的3倍,它的面积就扩大到原来的( )倍.
A.3B.6C.9D.27
4.把一个平行四边形活动框架拉成一个长方形,那么原来平行四边形与现在长方形相比( ).
A.周长不变、面积不变B.周长变了、面积不变
29.从一张硬纸板上剪下4个边长是5厘米的小正方形后(如下图所示),剩下的硬纸板可以做成一个没有盖的盒子,求剩下的硬纸板的面积。
30.某工厂的仓库里有一堆钢管,第一层有3根,第二层有5根,以后每层比上一层多2根,最下面一层有11根,这堆钢管共有多少根?
31.如图所示,一块梯形稻田,中间有一条水渠通过,水渠宽1米,
平行四边形活动框架拉成长方形之后,原来平行四边形的高比现在的长方形的高要小,但是对应的底的长度不变,又因为长方形是特殊的平行四边形,根据面积计算公式,平行四边形的面积=底×高,所以平行四边形的面积比长方形的面积要小。
所以一个平行四边形活动框架拉成长方形,原来平行四边形与现在长方形比较,周长不变,面积变了。
21.两个平行四边形的周长相等,但面积不一定相等。(_____)
22.长方形内画一个最大的三角形,三角形面积是长方形的一半.(____)
四、图形计算
23.求下面阴影部分的面积.(单位:cm)
五、作图题
24.在方格纸上画一个长方形和一个平行四边形,使它们的面积都与图中的平行四边形面积相等.
六、解答题
25.一块三角形小麦地,高是150米,底长200米,如果每公顷产小麦8.5吨,那么这块地一共可产小麦多少吨?
14.下图是一个边长为10cm的正方形框架,若将它拉成高是7cm的平行四边形,则面积减少(_____)cm2.
小学五年级上册数学《三角形面积的计算》教案(精选7篇)

小学五年级上册数学《三角形面积的计算》教案(精选7篇)小学五年级上册数学《三角形面积的计算》篇1教学内容:教材第9—10页例4、例5及“练一练”、“试一试”、“练习二”第6-9题。
教学目标:1.通过操作、观察、填表、讨论、归纳等数学活动,探索并掌握三角形的面积公式,能正确地计算三角形的面积,并应用公式解决简单的实际问题。
2.进一步体会转化方法的价值,培养自己应用已有知识解决新问题的能力,发展自己的空间观念和初步的推理能力。
教学重点:经历探究三角形面积计算公式的过程,理解并掌握三角形的面积计算公式。
教学难点:理解三角形面积公式的推导过程。
教学准备:多媒体、教材第115页的三角形。
探究方案:一、自主准备1.说一说:下面每个小方格表示1平方厘米,你知道涂色三角形的面积各是多少平方厘米吗?你是怎么想的?()()()2.思考:(1)三角形的面积与它拼成的平行四边形的面积有什么关系?(2)有没有直接计算三角形面积的方法呢?(3)假如要你探究三角形的面积,你打算把它转化成什么图形进行研究?我想转化成二、自主探究1.拼一拼:从课本第115页上选两个完全一样的三角形剪下来,看看能不能拼成平行四边形。
2.填一填:你剪下的两个完全一样的三角形能拼成平行四边形吗?如果能,拼成的平行四边形的面积和每个三角形的面积各是多少?请填写下表。
3.想一想(1)拼成平行四边形的两个三角形有什么关系?(2)拼成的平行四边形的底和高与原三角形的底和高有什么关系?每个三角形的面积与拼成的平行四边形的面积呢?(3)根据平行四边形的面积公式,怎样求三角形的面积?三、自主应用试一试:完成书上第10页的“试一试”。
四、自主质疑说一说:(1)三角形的面积公式是怎么推导的?你还有什么疑问?(2)你认为本节课应学会什么?教学过程:一、明确目标提问:同学们,通过自主学习,你知道今天的学习内容吗?(揭示课题)你认为本节课应学会什么?二、交流提升1.出示例4的方格图及其中的平行四边形。
五年级上册数学《三角形的面积》教案

五年级上册数学《三角形的面积》教案五年级上册数学《三角形的面积》教案4篇作为一名人民教师,常常需要准备教案,教案是教学蓝图,可以有效提高教学效率。
来参考自己需要的教案吧!下面是小编为大家整理的五年级上册数学《三角形的面积》教案,欢迎阅读与收藏。
五年级上册数学《三角形的面积》教案1教学内容:人教版小学数学教材五年级上册第91页主题图、92页例2、“做一做”,“你知道吗?”教学目标:1、知识与技能:探索并掌握三角形的面积公式,能正确计算三角形的面积,并能应用公式解决简单的实际问题2、过程与方法:是学生经历操作、观察、讨论、归纳等数学活动,进一步体会转化方法的价值,发展学生的空间观念和初步的推理能力。
3、情感态度与价值观:让学生在探索活动中获得积极的情感体验,进一步培养学生学习的兴趣。
教学重点:理解并掌握三角形面积的计算公式教学难点:理解三角形面积计算公式的推导过程考点分析:能根据具体情况应用三角形面积公式解决实际问题教学方法:创设情境——新知讲授——巩固总结——练习提高教学用具:多媒体课件、三角形学具教学过程:一、创设情境师:我们学校有一批小朋友要加入少先队了,学校为他们做了一批红领巾,要我们帮忙算算要用多少布。
同学们有没有信心帮学校解决这个问题?(屏幕出示红领巾图)师:同学们,红领巾是什么形状的?生:三角形的师:你们会算三角形的'面积吗?这节课我们就一起来研究,探索这个问题。
板书:三角形的面积二、新知探究1、课件出示一个平行四边形师:平行四边形的面积怎么计算?生:平行四边形的面积=底×高(板书:平行四边形的面积=底×高)师:平行四边形的面积公式是怎样得到的?生说推导过程师:在研究平行四边形的面积的时,我门是把平行四边形转化成学过的长方形来研究的,那三角形的面积你打算怎么研究呢?生1:我想把它转化成已学过的图形。
生2:我想看看三角形能不能转化成长方形或平行和四边形。
2、动手实验师:请同学们拿出准备好的学具:两个完全一样的锐角三角形,直角三角形,钝角三角形;一个长方型,一个平行四边形,你们可以利用这些图形进行操作研究,看哪一组能用多种方法发现三角形面积的计算公式。
全优卷 2020年人教版数学五年级上册 第六单元测试 提优卷附答案
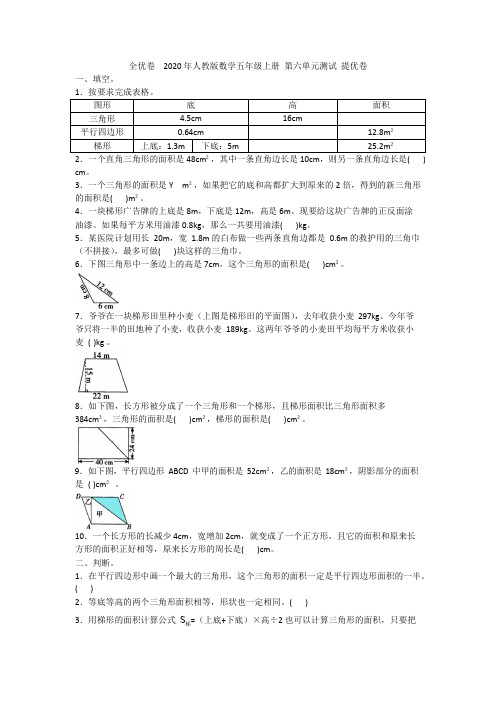
全优卷2020 年人教版数学五年级上册第六单元测试提优卷一、填空。
2.一个直角三角形的面积是48cm²,其中一条直角边长是10cm,则另一条直角边长是( ) cm。
3.一个三角形的面积是Y m²,如果把它的底和高都扩大到原来的2 倍,得到的新三角形的面积是( )m²。
4.一块梯形广告牌的上底是8m,下底是12m,高是6m。
现要给这块广告牌的正反面涂油漆。
如果每平方米用油漆0.8kg,那么一共要用油漆( )kg。
5.某医院计划用长20m,宽1.8m 的白布做一些两条直角边都是0.6m 的救护用的三角巾(不拼接),最多可做( )块这样的三角巾。
6.下图三角形中一条边上的高是7cm,这个三角形的面积是( )cm²。
7.爷爷在一块梯形田里种小麦(上图是梯形田的平面图),去年收获小麦297kg。
今年爷爷只将一半的田地种了小麦,收获小麦189kg。
这两年爷爷的小麦田平均每平方米收获小麦( )kg 。
8.如下图,长方形被分成了一个三角形和一个梯形,且梯形面积比三角形面积多384cm²,三角形的面积是( )cm²,梯形的面积是( )cm²。
9.如下图,平行四边形ABCD 中甲的面积是52cm²,乙的面积是18cm²,阴影部分的面积是( )cm² 。
10.一个长方形的长减少4cm,宽增加2cm,就变成了一个正方形,且它的面积和原来长方形的面积正好相等,原来长方形的周长是( )cm。
二、判断。
1.在平行四边形中画一个最大的三角形,这个三角形的面积一定是平行四边形面积的一半。
( )2.等底等高的两个三角形面积相等,形状也一定相同。
( )3.用梯形的面积计算公式S梯=(上底+下底)×高÷2 也可以计算三角形的面积,只要把梯形的上底看作0 即可。
( )4.求组合图形面积的唯一方法就是分割法,就是把组合图形分割成几个基本图形,然后再计算。
苏教版五年级上册数学分层作业设计2.2三角形的面积(附答案)

2.2 三角形的面积(练习)一、学习重难点1、学习重点:掌握三角形的面积公式,并能运用公式解决实际问题。
2、学习难点:理解三角形的面积公式的推导过程。
二、知识梳理1、三角形的面积计算公式的推导。
三角形的面积公式及用字母表示公式。
三角形的面积=底×高÷2如果用S表示三角形的面积,a表示三角形的底,h表示三角形的高,那么三角形的面积计算公式可以写成s=a×h÷22、三角形面积计算公式的应用。
运用三角形的面积计算公式解决简单的实际问题时,要做到“一找”“二算”。
一找:分析题意,找出已知什么,求什么。
二算:列式计算真题基础过关练一、选择题1.(2023秋·湖北荆门·五年级统考期末)一个三角形与一个平行四边形的面积相等,高也相等,三角形的底是6厘米,平行四边形的底是()厘米。
A.6B.3C.122.(2021秋·广东茂名·五年级统考期末)如图,三角形ABC的面积是32cm2,阴影部分的面积是()cm2。
A.48B.16C.643.(2022秋·甘肃酒泉·五年级统考期末)一个三角形的底不变,如果高扩大4倍,那么它的面积()。
A.扩大4倍B.扩大2倍C.无法确定4.(2020秋·辽宁沈阳·五年级统考期末)一个三角形和一个平行四边形的高相等,面积也相等。
如果平行四边形的底边是3cm,那么三角形的底是()厘米。
A.1.5B.3C.65.(2023秋·辽宁鞍山·五年级统考期末)下图中三角形()的面积可以用“4×3÷2”进行计算。
A.B.C.二、填空题6.(2023秋·山东枣庄·五年级统考期末)把一个长方形框架用力一拉,拉成一个平行四边形,与原来框架比,周长( ),面积( );如果拉成的平行四边形的面积是32cm2,与它等底等高的三角形的面积是( )cm2。
2020年人教版五年级上册数学六、4.组合图形的面积附答案

六、4.组合图形的面积一、填空乐园1.在一个上底是6厘米、下底是9厘米、高是4厘米的梯形中剪去一个最大的三角形,剩下的部分面积是( )平方厘米。
2.一个平行四边形,面积是54平方分米,如果高缩小到原来的21,要使面积不变,底应该( )。
3.三角形的底扩大a 倍,高扩大b 倍,面积扩大( )倍。
4.如图,要使三角形ABE 的面积是梯形AECD 面积的一半.BE 的长应是( )。
5.下面平行四边形的面积是15平方厘米,阴影部分的面积是( )平方厘米。
6.如图,现有6x6的方格,每个小方格的边长都是1,那么图中阴影部分的面积的总和等于( )。
7.如图,每两个相邻点之间的距离都是1厘米,三角形ABG 的面积是( ),梯形CDEF 的面积是( ),这个图形的面积是( )。
8.如图,每两个相邻的点之间的距离都是1厘米,平行四边形ABCE 的面积为( ),梯形ABDE 的面积为( )。
9.如图,若每个小正方形的面积都是1平方厘米,那么图中阴影部分的面积是( )平方厘米。
10.如图.每相邻三个点所形成的三角形都是面积为1的正三角形,则三角形ABC的面积为( )。
11.如图,平行四边形ABCD的底边DC长5 cm,直角三角形DCE的直角边EC长4厘米。
已知两块阴影部分的面积和比三角形EFG的面积大5平方厘米,则CF=( )厘米。
12.将一个正方形的一组对边各延长4厘米后,就成了一个长方形,这个长方形的面积比原来正方形的面积多32平方厘米,这个长方形的面积是原来正方形面积的( )倍。
二、判断快车1.两个等底等高的三角形都能拼成一个平行四边形。
( )2.在平行四边形内画一个三角形,三角形的面积一定等于平行四边形面积的一半。
( ) 3.两个面积相等的梯形,形状也一定相同。
( )4.梯形只有一条高,三角形有三条高。
( )5.两个完全一样的直角梯形可以拼成一个等腰梯形。
( )6.周长相等的两个平行四边形的面积不一定相等。
( )7.把一个长方形木框拉成平行四边形后,它的面积一定与原来长方形的面积相等。
全优卷 2020年人教版数学五年级上册 第六单元测试 提优卷附答案
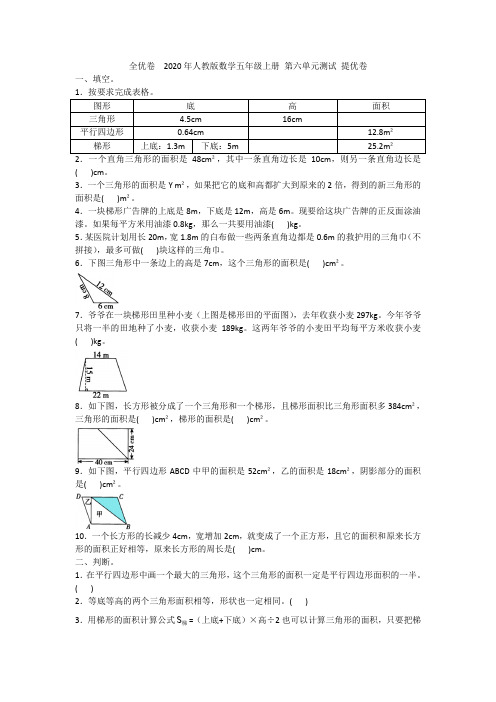
全优卷2020年人教版数学五年级上册第六单元测试提优卷一、填空。
2.一个直角三角形的面积是48cm²,其中一条直角边长是10cm,则另一条直角边长是( )cm。
3.一个三角形的面积是Y m²,如果把它的底和高都扩大到原来的2倍,得到的新三角形的面积是( )m²。
4.一块梯形广告牌的上底是8m,下底是12m,高是6m。
现要给这块广告牌的正反面涂油漆。
如果每平方米用油漆0.8kg,那么一共要用油漆( )kg。
5.某医院计划用长20m,宽1.8m的白布做一些两条直角边都是0.6m的救护用的三角巾(不拼接),最多可做( )块这样的三角巾。
6.下图三角形中一条边上的高是7cm,这个三角形的面积是( )cm²。
7.爷爷在一块梯形田里种小麦(上图是梯形田的平面图),去年收获小麦297kg。
今年爷爷只将一半的田地种了小麦,收获小麦189kg。
这两年爷爷的小麦田平均每平方米收获小麦( )kg。
8.如下图,长方形被分成了一个三角形和一个梯形,且梯形面积比三角形面积多384cm²,三角形的面积是( )cm²,梯形的面积是( )cm²。
9.如下图,平行四边形ABCD中甲的面积是52cm²,乙的面积是18cm²,阴影部分的面积是( )cm²。
10.一个长方形的长减少4cm,宽增加2cm,就变成了一个正方形,且它的面积和原来长方形的面积正好相等,原来长方形的周长是( )cm。
二、判断。
1.在平行四边形中画一个最大的三角形,这个三角形的面积一定是平行四边形面积的一半。
( )2.等底等高的两个三角形面积相等,形状也一定相同。
( )S=(上底+下底)×高÷2也可以计算三角形的面积,只要把梯3.用梯形的面积计算公式梯形的上底看作0即可。
( )4.求组合图形面积的唯一方法就是分割法,就是把组合图形分割成几个基本图形,然后再计算。
五年级上册数学多边形的面积知识精讲+易错练习(含答案)

五年级上册数学多边形的面积知识精讲+易错题过关练习(含答案)知识精讲:1.平行四边形面积公式推导:剪拼、平移平行四边形可以转化成一个长方形;长方形的长相当于平行四边形的底;长方形的宽相当于平行四边形的高;长方形的面积等于平行四边形的面积,因为长方形面积=长×宽,所以平行四边形面积=底×高。
2.三角形面积公式推导:旋转两个完全一样的三角形可以拼成一个平行四边形,平行四边形的底相当于三角形的底;平行四边形的高相当于三角形的高;平行四边形的面积等于三角形面积的2倍,因为平行四边形面积=底×高,所以三角形面积=底×高÷23.梯形面积公式推导:旋转4.两个完全一样的梯形可以拼成一个平行四边形。
平行四边形的底相当于梯形的上下底之和;平行四边形的高相当于梯形的高;平行四边形面积等于梯形面积的2倍,因为平行四边形面积=底×高,所以梯形面积=(上底+下底)×高÷25.等底等高的平行四边形面积相等;等底等高的三角形面积相等;等底等高的平行四边形面积是三角形面积的2倍。
6.长方形框架拉成平行四边形,周长不变,面积变小。
7.组合图形面积计算:必须转化成已学的简单图形。
当组合图形是凸出的,用虚线分割成几种简单图形,把简单图形面积相加计算。
当组合图形是凹陷的,用虚线补齐成一种最大的简单图形,用最大简单图形面积减几个较小的简单图形面积进行计算。
易错题过关练习(拔高篇)一、选择题1.下图中阴影部分的面积是48平方厘米,梯形的面积是()平方厘米。
A.95B.117C.138D.2762.如图所示,每个小正方形的面积是1平方厘米,涂色部分的面积是()平方厘米。
A.6B.7C.8D.93.晓东列出算式“13.5×17.5-(5+13.5)×(17.5-11)÷2”计算下面图形的面积,晓东的思考过程可以用()来表示。
A.B.C.D.4.如图所示,每个小方格的面积是1平方厘米,则阴影部分的面积大约是()平方厘米。
五年级数学上册 第六单元 多边形的面积同步奥数(附答案)

第六单元多边形的面积同步奥数1.平行四边形的面积例题1.如下图,已知平行四边形ABCD的周长是22.4厘米。
求平行四边形ABCD的面积是多少平方厘米? D A练习1.如图所示,平行四边形ABCD的周长是75厘米,以BC为底的高是14厘米,以CD为底的高是16厘米,求平行四边形ABCD的面积。
2.三角形的面积等积法:1.同底等高型:如果两个三角形的底相同,且能够证明出高相等,则这两个三角形面积相等。
2.同高等底型:如果两个三角形的高相同,且能够证明出底相等,则这两个三角形面积相等。
例题1.找出下图中哪些三角形的面积是相等的。
A D练习1.找出找出下图中哪些三角形的面积是相等的。
例题2.下图中的ABCD和CEFG分别是边长为8和6的正方形,连接BD、DF、FB形成△BDF,求阴影部分BDF的面积。
(单位:厘米)练习2.如图中大小正方形的边长分别是9厘米和5厘米,求阴影部分的面积。
例题3.在图中,正方形ABCD和正方形CEFG形AEG和三角形BDF的面积分别是多少?A D练习3.如图,甲、乙两图形都是正方形,它们的边长分别是5厘米和6厘米,求阴影部分的面积。
例题4.正方形ABCD的面积为9平方厘米,正方形EFGH的面积为64平方厘米。
如图所示,边BC落在EH上。
已知三角形ACG的面积为6.75平方厘米,则三角形ABE的面积为多少平方厘米?A D练习4.已知正方形ABCD边长为10,正方形BEFG边长为6,求阴影部分的面积。
A DB EC H例题5.如图所示,在四边形ABCD中,M和N分别是AB和CD的中点。
如果四边形ABCD的面积是40,那么BNDM的面积是多少? A练习5.如图所示,在四边形ABCD中,M和N分别是AD和BC的中点。
如果四边形ABCD的面积是28,那么BNDM的面积是多少? D3.梯形面积例题1.将一个底边BC长16厘米的直角三角形ABC向右平移6厘米,再向下平移1.5厘米,得到一个图形(如下图),求阴影部分的面积。
2020年人教版五年级上册数学六、1.平行四边形的面积附答案

六、1.平行四边形的面积一、填空乐园1.把一个平行四边形沿着( )割成两部分,通过( )法,可以把这两个部分拼成一个( )形,它的( )等于平行四边形的( ),它的( )等于平行四边形的( ),因为长方形的面积等于( ),所以平行四边形的面积等于( )。
因此平行四边形与拼成的长方形相比较( )变了,( )没变。
2.平行四边形的大小由它的( )和( )决定。
3.把一个长为10厘米、宽为8厘米的活动式长方形,拉成一个高为9厘米的平行四边形,拉成的平行四边形的面积是( )平方厘米。
4.一个平行四边形,相邻的两条边分别长为4厘米和6厘米.测得其中一条边上的高长为5厘米,这个平行四边形的面积是( )平方厘米。
5.把两根14厘米长的铁丝都在8厘米处弯折.然后摆成首尾相连的平行四边形,这个平行四边形的面积(填“>”“=”或“<”)( ) 48平方厘米。
6.一个平行四边形和一个长方形的面积都是72平方厘米,长方形长18厘米,是平行四边形高的2倍,平行四边形的底是( )厘米。
7.一个平行四边形割补后是一个正方形,正方形的周长是20厘米,这个平行四边形的面积是( )平方厘米。
8.一个平行四边形的底扩大2倍,高缩小2倍,面积( )。
9.一个平行四边形的面积是23平方米,底扩大2倍,高增加3倍,它的面积扩大( )倍,最后的面积是( )。
10.把一个长14分米、宽5分米的长方形拉成一个平行四边形,面积减少28平方分米,拉成的平行四边形的高是( )分米。
二、判断快车1.平行四边形的面积与长方形的面积相等。
( )2.两个面积相等的平行四边形,底和高也分别相等。
( )3.将一个长方形的铁丝框拉成一个平行四边形,它的面积和原来的长方形面积相等。
( ) 4.平行四边形的高扩大到原来的2倍,底不变,面积也扩大到原来的2倍。
( )5.等底等高的平行四边形面积相等。
( )6.平行四边形的底越长,它的面积越大。
( )三、选择超市1.一个平行四边形,底扩大6倍,高缩小2倍,那么这个平行四边形的面积( )A.扩大6倍B.缩小2倍C.面积不变D.扩大3倍2.如图,两个平行四边形的面积的关系是( )A. S₁>S₂B.S₁<S₂C.S₁=S₂D.无法比较3.要使平行四边形的面积不变,高扩大到原来的4倍,则底( )A .缩小到原来的41B .扩大到原来的4倍C .不变D .无法确定4.平行四边形的底缩小到原来的81,高扩大到原来的4倍,面积( ) A .缩小到原来的41B .扩大到原来的4倍c .缩小到原来的21D .扩大到原来的2倍5.把一个平行四边形框架拉成长方形,它的周长( ),面积( )A .比原来大B .比原来小C .和原来相等6.一个正方形的周长是24厘米,把它割补成一个平行四边形,这个平行四边形的面积是( )平方厘米。
人教版小学五年级上册数学《三角形的面积》教学设计(精选3篇)

人教版小学五年级上册数学《三角形的面积》教学设计(精选3篇)人教版小学五年级上册数学《三角形的面积》篇1教学目标:1.在实际情境中,认识计算梯形面积的必要性。
2.在自主探索活动中,经历推导梯形面积公式的过程。
3.能运用梯形面积的计算公式,解决相应的实际问题。
教学重点:理解并掌握梯形面积的计算公式。
教学难点:理解梯形面积计算公式的推导过程。
教具准备:各种梯形各两份,剪刀,。
教学过程:一、揭示课题,明确主题1. 生活中我们能找到许多平面图形,这个教室里有吗?2. 请大家看看这组图片,看看你发现了谁?找到了就立刻喊出它名字!出现次数最多的是……?(梯形)板书 2.梯形,四年级的时候我们已经认识它了,谁来介绍一下它。
3.今天,我们来更深入地了解这位朋友,研究梯形的面积。
(板书)二、回忆旧知,建立联系1. 面积,我们现在已经会计算哪些图形的面积了?他们计算方法你们还记得吗?(课件)2. 回忆一下,平行四边形和三角形的面积计算方法我们是怎样推导出来的?还记得吗?3. 同学们,我们在研究它们面积的计算时候,都用到了一种非常重要的数学思想——转化。
(板书)把要研究的图形转化成已经学过的图形来发现他们之间的联系,进而推导出面积计算的公式.这种思想,这节课我们也要用到。
三、转化梯形,推导公式(一)应用的需要引出猜想1.同学们喜欢什么体育运动?喜欢篮球吗?(课件出示篮球场地)你们知道这一处是什么区域吗?这是3秒钟限制区,是限制对方队员在这个区域内停留不能超过3秒钟。
2.但是梯形面积的计算方法我们还没有学过,你猜想梯形的面积可能与什么有关?你想怎样推导出梯形面积的计算方法呢?3.同学们都很有想法,那到底是不是像同学们想的那样呢?让我们来动手验证一下。
在动手操作之前,老师提出三点建议:(1)想想能把梯形转化成学过的什么图形。
(2)根据转化图形与梯形的关系,推导出梯形面积计算的方法。
(3)填写好汇报单,比一比,哪个小组的动作快。
五年级数学上册试题 -《6.多边形的面积》单元测试 人教版(含答案)

人教版五年级数学上册《6.多边形的面积》单元测试8一、单选题(总分:40分本大题共8小题,共40分)1.(本题5分)用四根小棒组成一个平行四边形,面积等于24平方厘米,捏住它的两个对角,把平行四边形拉成了一个长方形,这时面积()24平方厘米.A.大于B.等于C.小于D.无法确定2.(本题5分)如图中,阴影部分的面积占圆面积的()A.12.5%B.25%C.33.3%3.(本题5分)如图,图中每个圆的直径都为2cm,阴影部分的周长和的面积各是()A.2π-4 π-4B.4π 4πC.2π 4-πD.4 74.(本题5分)一个三角形的底是8厘米,高是5厘米,与它等底等高的平行四边形的面积是()平方厘米.A.40B.20C.10D.55.(本题5分)下面说法错误的是()A.循环小数都是无限小数B.除数大于1,商一定小于被除数C.梯形的面积等于平行四边形面积的一半D.用中位数表示一组数据的一般水平,比用平均数表示更合适6.(本题5分)如图,梯形甲的面积()梯形乙的面积.A.大于B.等于C.小于7.(本题5分)如图所示:E、F、G和H分别是梯形每条边的中点,那么下面有()图形的阴影部分面积是原来梯形面积的一半.A.4个B.3个C.2个D.1个8.(本题5分)梯形的上底减少4厘米,下底增加4厘米,高不变,那么梯形的面积()A.比原来小B.比原来大C.与原来相等二、填空题(总分:25分本大题共5小题,共25分)9.(本题5分)在一边靠水渠处,用篱笆围成一块直角梯形菜地(如图),已知三面篱笆总长27米,梯形的高为7米,则此菜地的面积是____平方米.10.(本题5分)如图,阴影部分的面积是8.7cm2,那么平行四边形的面积是____cm2.11.(本题5分)图中阴影部分的两段圆弧所对应的圆心分别为点A和点C,AE=4m,点B是AE的中点,那么阴影部分的周长是____m,面积是____m2(圆周率π取3).12.(本题5分)如图,周长为52厘米的“L”形纸片可沿虚线分成两个完全相同的长方形.如果最长的边长是16厘米,那么该“L”形纸片的面积是____平方厘米.13.(本题5分)已知△ABC的面积是180平方厘米,AC长18厘米,CE长8厘米,则阴影部分的面积是____平方厘米.三、解答题(总分:35分本大题共5小题,共35分)14.(本题7分)一个洗浴中心的指示牌(如图所示),求它的面积.15.(本题7分)如图,是大小两个正方形组成的图形,大正方形边长是8厘米,小正方形边长为6厘米,求阴影部分的面积.16.(本题7分)在一个边长是4厘米的正方形中画一个最大的圆,求阴影部分的面积是多少平方厘米.17.(本题7分)按照下页图的样子,在一平行四边形纸片上割去了甲、乙两个直角三角形.已知甲三角形两条直角边分别为4厘米和8厘米,乙三角形两条直角边分别为6厘米和12厘米.求阴影部分的面积.18.(本题7分)选择合适的条件,计算下面图形的面积.人教版五年级数学上册《6.多边形的面积》单元测试8参考答案与试题解析1.【答案】:A;【解析】:解:由于把平行四边形拉成长方形,平行四边形的高小于长方形的宽(或长),因此长方形的面积大于平行四边形的面积.故选A.2.【答案】:B;【解析】:解:90÷360=0.25=25%答:阴影部分的面积占圆的面积的25%.故选:B.3.【答案】:C;【解析】:解:(1)阴影部分的周长为:π×2=2π(厘米);(2)阴影部分的面积为:2×2-π(2÷1)2,=4-π(平方厘米);故选:C.4.【答案】:A;【解析】:解:8×5÷2×2=40÷2×2=40(平方厘米)答:与它等底等高平行四边形的面积是40平方厘米.故选:A.5.【答案】:C;【解析】:解:A、循环小数都是无限小数,说法正确;B、一个数(0除外)除以大于1的数,商小于这个数,所以除数大于1,商一定小于被除数说法正确;C、因为梯形的面积=(上底+下底)×高÷2,平行四边形的面积=底×高,若不知道二者的底和高的大小关系,则没法比较其面积大小,故原题说法错误;D、用中位数表示一组数据的一般水平,比用平均数表示更合适,说法正确;故选:C.6.【答案】:B;【解析】:解:据分析可知:梯形甲的面积等于梯形乙的面积.故选:B.7.【答案】:C;【解析】:解:第一个图形中,阴影部分的面积小于空白处的两个三角形的面积之和,即小于原梯形的面积的一半,第二个图形阴影部分还是一个梯形,上底和下底都是原梯形的上底和下底的一半,高不变,所以阴影部分的面积等于原梯形的面积的一半,第三个图形上下底中点的连线把梯形分成面积相等的两部分,但是右下方阴影部分减少了右下方空白处三角形的面积,所以阴影部分的面积小于原梯形的面积的一半,第四个图形,连接阴影内部的梯形的对角线,把阴影部分分成两部分,每部分都等于它所在的三角形的面积的一半,所以阴影部分的面积等于这个梯形的面积的一半,所以第二个图形和第四个图形的阴影部分面积是原来梯形面积的一半.故选:C.8.【答案】:C;【解析】:解:梯形的面积=(上底+下底)×高÷2,上底减少4厘米,下底增加4厘米,梯形上下底的和不变,所以梯形的面积不变.故选:C.9.【答案】:70;【解析】:解:(27-7)×7÷2,=20×7÷2,=140÷2,=70(平方米).答:梯形菜地的面积70平方米.故答案为:70.10.【答案】:17.4;【解析】:解:8.7×2=17.4(平方厘米)答:平行四边形的面积是17.4平方厘米.故答案为:17.4.11.【答案】:13;7;【解析】:解:阴影部分的周长:4+3×4×2÷4+3×2×2÷4,=4+6+3,=13(米);阴影部分的面积:3×42÷4+3×22÷4-2×4,=12+3-8,=7(平方米);答:阴影部分的周长是13米,面积是7平方米.故答案为:13、7.12.【答案】:120;【解析】:解:设分成的长方形的宽为x,那么分成的长方形的长为16-x,16+(16-x)+x+(16-x-x)+(16-x)+x=5264-2x=52,2x=12,x=6,分成的长方形的长为:16-6=10(厘米),长方形的面积为:10×6=60(平方厘米),“L”形纸片的面积为:60×2=120(平方厘米).故填:120.13.【答案】:288;【解析】:解:AF的长度:180×2÷18,=360÷18,=20(厘米);DE的长度:20-8=12(厘米),阴影部分的面积:(12+20)×18÷2,=32×18÷2,=576÷2,=288(平方厘米);答:阴影部分的面积是288平方厘米.故答案为:288.14.【答案】:解:50×24+(24+5×2)×(60-50)÷2=1200+34×10÷2=1200+170=1370(平方分米);答:它的面积是1370平方分米.;【解析】:指示牌是由长方形和三角形组成的,根据长方形和三角形的面积公式解答即可.15.【答案】:解:阴影部分的面积:6×6÷2=36÷2=18(平方厘米)答:阴影部分的面积是18平方厘米.;【解析】:如图所示,连接BD,则三角形ABD与三角形DBC等底等高,所以它们的面积相等,再分别减去公共部分三角形BDE的面积,剩余部分的面积仍然相等,即三角形ABE与三角形CDE的面积相等,于是阴影部分的面积就变成了小正方形的面积的一半,小正方形的边长已知,从而可以求出阴影部分的面积.16.【答案】:解:圆的面积:3.14×(4÷2)2=12.56(平方厘米);阴影部分的面积:4×4-12.56=3.44(平方厘米).答:阴影部分的面积是3.44平方厘米.;【解析】:这个圆的直径就是正方形的边长,再依据圆的面积公式即可求其面积;正方形的面积减圆的面积即为阴影部分的面积.17.【答案】:解:将甲、乙分别平移到如图位置,则平行四边形的面积就是两个长方形的面积之和,8×6+4×12-8×4÷2-12×6÷2,=48+48-16-36,=96-52,=44(平方厘米);答:阴影部分的面积是44平方厘米.;【解析】:如下图,将甲、乙分别平移到如图位置,则平行四边形的面积就是图中画红线的长方形的面积,即两个长方形面积之和,由此再根据三角形的面积公式S=ah÷2,求出甲、乙的面积,进而求出阴影部分的面积.18.【答案】:解:24×15=360(平方厘米)答:平行四边形的面积是360平方厘米.;【解析】:根据平行四边形的面积=底×高,找出平行四边形对应的底与高,代入数据即可解答.。
人教版五年级上册数学课课练:6.2 三角形的面积(附答案)

人教版五年级上册数学课课练
三角形的面积
1.用两个完全一样的三角形拼成一个平行四边形,已知每个三角形的面积是6.4dm2,拼成的平行四边形的面积是多少平方分米?
2.右图中,平行四边形的面积是8.8cm2,涂色部分的面积是多少平方厘米?
3.求下面各三角形的面积。
(单位:cm)
(1)(2)
(3)
4.一块三角形地,底是38m,高是27m,如果每平方米收小麦0.7kg,这块地可以收小麦多少千克?
答案提示
1.6.4×2=1
2.8(dm2)
答:拼成的平行四边形的面积是12.8平方分米。
2.8.8÷2=4.4(cm2)答:涂色部分的面积是4.4平方厘米。
3.(1)7×8.5÷2=29.75(cm2)
(2)8×6÷2=24(cm2)
(3)3×3÷2=4.5(cm2)
4.38×27÷2×0.7=359.1(kg)答:这块地可以收小麦359.1千克。
2020年人教版五年级上册数学六、3.梯形的面积附答案

3.梯形的面积一、填空乐园1.用两个完全一样的梯形可以拼成一个( ),它的高就是原来梯形的( ),它的底就是原来梯形的( )。
2.两个完全相同的直角梯形可以拼成一个( )形、( )形或( )形。
3.梯形的上底逐渐缩小,最后成为一点,这时梯形就变成( )形。
4.一个梯形的面积是164平方分米,上下底之和是32分米,这个梯形的高是( )分米。
5.一个梯形的面积是63平方厘米,高是15厘米,上底是2.4厘米,这个梯形的下底是( )厘米。
6.一堆钢管,每层之间相差一根,最上层6根,最下层14根,这堆钢管共有( )根。
7.在一个上底为12厘米、下底为18厘米、高是8厘米的梯形硬纸板中剪去一个边长分别为3厘米、4厘米、5厘米的直角三角形,剩下部分的面积是( )平方厘米。
8.一个高是4分米的直角梯形的面积是68平方分米,如果上底增加6分米,它就成了一个长方形,那么这个梯形的下底是( )分米。
9.一个梯形的上底扩大到原来的5倍,下底也扩大到原来的5倍,如果高不变,面积就扩大( )。
10. 一个直角梯形的下底是15厘米,如果下底缩短3厘米,原来的梯形就变成了正方形。
原来梯形的面积是( )平方厘米。
二、判断快车1.梯形的上底和下底各增加10厘米,面积就增加20 cm2。
( )2.梯形的面积等于平行四边形面积的一半。
( )3.一个梯形可以分割成一个三角形和一个平行四边形。
( )4.任何一个梯形都可以分成两个等高的三角形。
( )5.梯形的上下底越长,面积越大。
( )6.梯形的上底扩大到原来的2倍,下底也扩大到原来的2倍,高不变,它的面积扩大到原来的4倍。
( )7.梯形的上底减少4,下底增加4,高不变,那么梯形的面积与原来相等。
( )8.一个梯形的上底是4厘米,下底是5厘米,高是4厘米,它的面积就是80平方厘米。
( ) 三、选择超市1.能拼成一个平行四边形的是两个( )的梯形。
A.形状一样B.面积相等C.完全一样D.任意2.一堆圆木,上层有5根,下层有10根,每往下一层都比上层多1根,这堆圆木共有( )根。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六、2.三角形的面积
一、填空乐园
1.用两个( )的三角形拼成一个平行四边形,这个平行四边形的底是三角形的( ),高是三角形的( ),面积是三角形面积的( )。
2.一个三角形的底是4分米,高是3分米,面积是( )。
3.三角形的面积是56平方分米,高是8分米,三角形的底是( )分米。
4.一个三角形的面积是5.2平方厘米,与它等底等高的平行四边形的面积是( )平方厘米。
5.一个平行四边形与一个三角形等底等高,平行四边形的面积比三角形的面积大10平方厘米,三角形的面积是( )平方厘米。
6.一个等边三角形的周长是18厘米,高是5.2厘米,这个等边三角形的面积是( )平方厘米。
7.一个三角形和一个平行四边形的底相等,高是平行四边形的2倍,如果三角形的面积是8平方分米,那么平行四边形的面积是( )平方分米;一个三角形和一个平行四边形的底和面积都相等,三角形的高是10厘米,平行四边形的高是( )厘米。
8.一张长5分米、宽4分米的长方形可以剪成( )个底和高都是2厘米的直角三角形。
9.如图,甲的面积是20平方厘米,乙的面积是( )平方厘米。
10. 一个直角三角形三条边长分别是5厘米,13厘米,12厘米,它的面积是( )平方厘米。
二、判断快车
1.两个完全一样的三角形一定能拼成一个长方形。
( )
2.两个面积相等的三角形,底和高也相等。
( )
3.三角形的面积等于平行四边形面积的一半。
( )
4.三角形的高不变,底越长,面积越大。
( )
5.一个三角形底不变,高扩大4倍,面积也扩大4倍。
( )
6.三角形的底和高各减少一半,面积也减少一半。
( )
7.平行四边形的面积一定大于三角形的面积。
( )
8.下边三个三角形的面积相等。
( )
三、选择超市
1.三角形的面积和平行四边形的面积相比,三角形的面积( )
A.比平行四边形大B.比平行四边形小
C.是平行四边形的一半D.可能大、可能小、可能相等
2.图中三角形的面积相等的是( )
A.①②③B.②③④C.①②④
3.在一个长方形内画一个最大的三角形,这个三角形的面积( )长方形面积的一半。
A .大于
B .小于
C .等于
4.三角形的底扩大到原来的6倍,高缩小到原来的31,它的面积( )
A .扩大到原来的3倍
B .扩大到原来的2倍
c .缩小到原来的31 D .缩小到原来的21
5.一个三角形与一个平行四边形的底相等,面积也相等。
平行四边形的高是3厘米,三角形的高是( )厘米。
A .3
B .1.5
C .6
D .9
四、应用题天地
1.安装一块三角形的镜子,底18分米,高10.6分米。
如果每平方分米0.8元,买这块玻璃要多少钱?
2.一块三角形花圃底长88 m ,高35 m ,花圃中栽种3080株玫瑰花苗,平均每株玫瑰花苗占地面积是多少?
3.一个三角形的面积是34平方厘米,它的一条底边是17厘米,这条底边上的高是多少厘米?
4.一块三角形果园的底是80米,高比底短20米,如果平均每棵树占地12平方米,这个果园一共有果树多少棵?
5.等腰直角三角形的面积是4.5平方厘米,用8个这样的三角形组成一个正方形,这个正方形的周长是多少厘米?
6.用长80厘米、宽48厘米的长方形彩纸剪小旗,小旗是两条直角边分别为20厘米和12厘米的直角三角形,每张彩纸最多能剪多少面小旗?
一、开放探究
1.如图,大正方形和小正方形的边长分别是6厘米和5厘米,求阴影部分的面积。
2.下图是两个等腰直角三角形,试求阴影部分的面积。
(单位:厘米)
3.下图中三角形ABE 、三角形AFD 和四边形AECF 的面积相等,求三角形AEF 的面积。
(单位:厘米)
二、尖子生竞赛闯关
1.如图,BD=2AD,CE=3AE,三角形ABC的面积是18平方厘米,求三角形ADE的面积。
2.平行四边形ABCD的边长BC=10厘米,直角三角形BCE的直角边EC长8厘米.已知阴影部分的面积比三角形EFG的面积大10平方厘米。
求CF的长。
3.如图,三角形ABC的面积为5平方厘米,AE=DE,BD=2DC.求阴影部分的面积。
1.在一块长15米、宽9.5米的长方形花坛中种花(如图,图中的阴影部分要种花),种花的面积是多少平方米?
2.如图.两块阴影部分的面积相差多少平方厘米?
3.把一块边长9.5分米的正方形铁板切割成两条直角边分别为4.5分米和1分米的直角三角形小铁板,最后可以切成多少块?
2.三角形的面积
一、1.完全一样底高2倍 2.6平方分米 3. 14 4.10.4 5.10 6.15.6 7.8 5
8. 1000 9.10 10. 30
二、1.×2.×3.× 4.√5.√6.×7.×8.√
三、1.D 2.C 3.C 4.B 5.C
四、1. 18x10.6÷2x0.8=76.32(元) 2.88x35÷2÷3080=0.5 (m ²) 3. 34x2÷17=4(厘米)
4. 80×( 80 -20) ÷2 =2400(平方米) 2400÷12=200(棵)
5. 4.5x8=36(平方厘米) 正方形边长为6厘米,6x4=24(厘米)
6. (80x48)÷ (20x12÷2)=32(面)
一、1. 6x6+5 x5 =61(平方厘米) 5x5÷2=12.5(平方厘米) (5+6) x6÷2=33(平方厘米) 61-( 33+12.5 )=15.5(平方厘米)
2.(12+8)x(12+8)÷2÷2-8x8÷2=68(平方厘米)
3. 15平方厘米 提示:18369S 31S S S
AECF AFD ABE =÷⨯====∆∆长方形四边形(平方厘米),BE=18x2÷6=6(厘米),FD=18x2÷9=4(厘米),EC=BC-BE=9-6=3(厘米),FC=DC-FD=2厘米,FEC S ∆=3x2÷2=3(平方厘米),FEC AEC F AEF S S S ∆∆-=四边形=18-3=15(平方厘米)
二、1. 18 -12 =1.5(平方厘米) 提示:如图,连接DF ,DG ,DC ,HC ,则△ADE ,△DEF .△DFG .△DGC
面积相等,即ADE
ADC S 4S ∆∆=, 由于△ADC .△DCH ,△CHB 等底等高,面积也相等,则 ADC AB C S 3S ∆∆=,因此ADE
AB C S 12S ∆∆=。
2. 10x8÷2=40 (cm ²) 40+10=50 (cm ²) 50÷10=5 (cm)
3.5÷(1+1+0.5)=2(平方厘米) 提示:连接FD ,DEF AEF S S ∆∆=,BED ABE S S ∆∆=,FC D S ∆等于BDF S ∆的一半。
1. 15x9.5÷2=71.25(平方米) 提示:在一个长方形中任意点一点,连接四个顶点,形成四个三角形,上下两个三角形面积的和等于左右两个三角形的面积和。
2. 15 x15÷2 =112.5(平方厘米)……三角形ADC 的面积
30x15÷2=225(平方厘米)……三角形BDC 的面积
225 -112.5 =112.5(平方厘米)……阴影面积之差
提示:阴影部分的面积之差即ADC B C D S S ∆∆-
3. 9.5÷
4.5=2(块)……0.5(分米) 9.5÷1=9(块)……0.5(分米) 2x9x2=36(块)。
