最值问题(定弦定角定线段)教学提纲
第三讲 定点、定值、最值问题

【互动探究】若本例(1)中抛物线方程为y2=2px(p>0),且弦 AB的中点到直线x-2y=0的距离的最小值为 2 5 且 OA OB =0,
5
求抛物线的方程.
x1 x 2 x , 2 【解析】设AB中点C(x,y),则 y y1 y 2 , 2
3.易错提醒 (1)忽略判别式致误:在解决直线和曲线的相交问题时,要考虑 Δ ≥0,否则易出现错误. (2)不能正确区分变量:在处理定点、定值问题时,要分清变量 与常量,选择正确的消元方向.
【考题回顾】
1.(2013·重庆高考)设双曲线C的中心为点O,若有且只有一
对相交于点O、所成的角为60°的直线A1B1和A2B2,使|A1B1|=
3
只有一对相交于点O、所成的角为60°的直线A1B1和A2B2,使 |A1B1|=|A2B2|,所以渐近线斜率满足 3 b 3 ,解得 2 3 <e
3 a 3
≤2.故选A.
2 2 x y 2.(2014·潮州模拟)已知P(x,y)为椭圆C: 1 上一点,F 25 16
为椭圆C的右焦点,若点M满足 | MF | =1且 MP MF =0,则 | PM |的 最小值为(
△A1B1C1相似于△A2B2C2,
A1B1 2 AB S1 p 因此 ( ) ,又由(1)中的 A1B1 p1 A 2 B2 知 1 1 1 , S2 A 2 B2 p 2 A 2 B2 p2 2 S p 1 1 故 2. S2 p 2
热点考向一
定点的探究与证明问题
【考情快报】
难度:中、高档 命题指数:★★☆
微课教案--最值问题

初中数学线段最值问题---中考专题在平面几何的动态问题中,当某几何元素在给定条件变动时,求某几何量(如线段的长度、图形的周长或面积、角的度数以及它们的和与差)的最大值或最小值问题,称为最值问题。
解决平面几何最值问题的常用的方法有:(1)应用两点间线段最短的公理(含应用三角形的三边关系)求最值;(2)应用垂线段最短的性质求最值;(3)应用轴对称的性质求最值;(4)应用二次函数求最值;(5)应用其它知识求最值。
第一部分:开篇---几何模型第一部分:两条线段的和与差的最值(1)在直线L 上找一点P ,使PA+PB 的值最小 (2)在直线a 上找一点P,使PA+PB 的值最小 (3)在直线a 上找一点Q ,使︱QB-QA ︱的值最大 (4)在直线a 上找一点Q ,使︱QB-QA ︱的值最大P ´A PBA´AQLB· QAB ´L第二部分:点到直线距离和圆外一点到圆的距离第二部分:立体图形中的最短路径第一课时正方体在棱长为5cm 的立方体纸盒A 处有一只蚂蚁,在H 处有一粒蜜糖,蚂蚁想吃到蜜糖,那它沿立方体表面所走的最短路程是_____cm .变式:如图是一个棱长为4厘米的正方体盒子,一只蚂蚁在AE 的中点M 处,它到CD 的中点N 的最短路线是多少?ABLBOAP【长方体】如图是一块长,宽,高分别是4厘米、5厘米、3厘米的长方体木块,一只瓢虫要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是?变式:如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点B处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?圆柱体如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是母线BC上一点,且PC=2BC.一只蚂蚁从A3点出发沿着圆柱体的表面爬行到点P的最短距离是【】立体图形中的最短路径第二课时圆柱体如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为▲ cm.圆柱的展开,矩形的性质,轴对称的性质,三角形三边关系,勾股定理。
(完整版)定弦定角最值问题(含答案)

定弦定角最值问题【定弦定角题型的识别】有一个定弦,一个主动点,一个从动点,定弦所对的张角固定不变。
【题目类型】图形中一般求一个从动点到一个定点线段长度最值问题,一般涉及定弦定角最值问题【解题原理】同弧所对的圆周角相等,定弦的同侧两个圆周角相等,则四点共圆,因此动点的轨迹是圆。
(线段同侧的两点对线段的张角相等,则这两点以及线段的两个端点共圆。
)【一般解题步骤】①让主动点动一下,观察从动点的运动轨迹,发现从动点的运动轨迹是一段弧。
②寻找不变的张角(这个时候一般是找出张角的补角,这个补角一般为45°、60°或者一个确定的三角函数的对角等)③找张角所对的定弦,根据三点确定隐形圆。
④确定圆心位置,计算隐形圆半径。
⑤求出隐形圆圆心至所求线段定点的距离。
⑥计算最值:在此基础上,根据点到圆的距离求最值(最大值或最小值)。
【例1】(2016·新观察四调模拟1)如图,△ABC 中,AC =3,BC =24,∠ACB =45°,D 为△ABC 内一动点,⊙O 为△ACD 的外接圆,直线BD 交⊙O 于P 点,交BC 于E 点,弧AE =CP ,则AD 的最小值为( )A .1B .2C .2D .2441-解:∵∠CDP =∠ACB =45°∴∠BDC =135°(定弦定角最值)如图,当AD 过O ′时,AD 有最小值∵∠BDC =135°∴∠BO ′C =90°∴△BO ′C 为等腰直角三角形∴∠ACO ′=45°+45°=90°∴AO ′=5又O ′B =O ′C =4∴AD =5-4=1【例2】如图,AC =3,BC =5,且∠BAC =90°,D 为AC 上一动点,以AD 为直径作圆,连接BD 交圆于E 点,连CE ,则CE 的最小值为( )A .213-B .213+C .5D .916解:连接AE∵AD 为⊙O 的直径∴∠AEB =∠AED =90°∴E 点在以AB 为直径的圆上运动当CE 过圆心O ′时,CE 有最小值为213-【练】(2015·江汉中考模拟1)如图,在△ABC 中,AC =3,BC =24,∠ACB =45°,AM ∥BC ,点P 在射线AM 上运动,连BP 交△APC 的外接圆于D ,则AD 的最小值为( )A .1B .2C .2D .324-解:连接CD∴∠P AC =∠PDC =∠ACB =45°∴∠BDC =135°如图,当AD 过圆心O ′时,AD 有最小值∵∠BDC =135°∴∠BO ′C =90°∴O ′B =O ′C =4又∠ACO ′=90°∴AO ′=5∴AD 的最小值为5-4=1【例3】(2016·勤学早四调模拟1)如图,⊙O 的半径为2,弦AB 的长为32,点P 为优弧AB 上一动点,AC ⊥AP 交直线PB 于点C ,则△ABC 的面积的最大值是( )A .3612+B .336+C .3312+D .346+【练】(2014·洪山区中考模拟1)如图,⊙O 的半径为1,弦AB =1,点P 为优弧AB 上一动点,AC ⊥AP 交直线PB 于点C ,则△ABC 的最大面积是( )A .21 B .22 C .23 D .43【例5】如图,A (1,0)、B (3,0),以AB 为直径作⊙M ,射线OF 交⊙M 于E 、F 两点,C 为弧AB 的中点,D 为EF 的中点.当射线绕O 点旋转时,CD 的最小值为__________解:连接DM∵D 是弦EF 的中点∴DM ⊥EF∴点D 在以A 为圆心的,OM 为直径的圆上运动当CD 过圆心A 时,CD 有最小值连接CM∵C 为弧AB 的中点∴CM ⊥AB∴CD 的最小值为12-【练】如图,AB 是⊙O 的直径,AB =2,∠ABC =60°,P 是上一动点,D 是AP 的中点,连接CD ,则CD 的最小值为__________解:连接OD∵D 为弦AP 的中点∴OD ⊥AP∴点D 在以AO 为直径的圆上运动当CD 过圆心O ′时,CD 有最小值过点C 作CM ⊥AB 于M∵OB =OC ,∠ABC =60°∴△OBC 为等边三角形∴OM =21,CM =23 ∴O ′C =47 ∴CD 的最小值为2147-。
线段最值系列之(一)——定弦定角,定最值
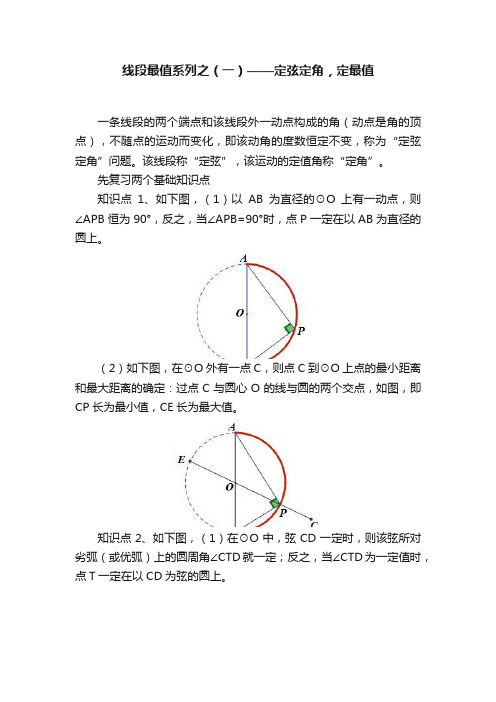
线段最值系列之(一)——定弦定角,定最值一条线段的两个端点和该线段外一动点构成的角(动点是角的顶点),不随点的运动而变化,即该动角的度数恒定不变,称为“定弦定角”问题。
该线段称“定弦”,该运动的定值角称“定角”。
先复习两个基础知识点知识点1、如下图,(1)以AB为直径的⊙O上有一动点,则∠APB恒为90°,反之,当∠APB=90°时,点P一定在以AB为直径的圆上。
(2)如下图,在⊙O外有一点C,则点C到⊙O上点的最小距离和最大距离的确定:过点C与圆心O的线与圆的两个交点,如图,即CP长为最小值,CE长为最大值。
知识点2、如下图,(1)在⊙O中,弦CD一定时,则该弦所对劣弧(或优弧)上的圆周角∠CTD就一定;反之,当∠CTD为一定值时,点T一定在以CD为弦的圆上。
(2)如下图,在⊙O外有一点A,射线AO与圆的交点分别为点T和点E,则点A到圆的最小距离是AT的长,最大距离是AE的长。
下面,以两道典型例题来说明定弦定角在解一类线段最值题目中的应用。
例1:如图,在Rt△ABC ,∠ABC=90° ,AB=4, BC=6 ,P是△ABC 内部的一个动点,且满足∠PAB=∠PBC , 则线段CP的长度的最小值是 .(您的点赞,就是给予作者一份信心,别忘了,给作者一个鼓励,点个赞哦!)下面还有,继续……变式练习:如图,在Rt△ABC ,∠ABC=90° ,AB=4,BC=6, P是△ABC所在平面上的一个动点,且满足∠APB=90° , 则线段CP长度的取值范围是 .例2:如图,已知点E , F为等边△ABC边AB 、AC上的两动点,且AF=BE ,:连接CE , BF交于点T, 若等边△ABC的边长为6 ,则AT的长度的最小值是 .。
初中数学精品教案:几何最值问题

微设计《破解中考数学压轴题(一)0107几何最值问题》学习目标:1、学会怎样通过平行线和直角三角形构造相似三角形.2、理解并会运用二次函数的性质解决几何最值问题.3、学会通过求2x的最值来求x的最值的方法.4、体会数形结合在解决压轴题中的重要作用.学习重点:1、做辅助线构造相似的过程.2、借助变量表示线段长度,建立等量关系的过程.3、运用二次函数求2x的最小值的过程.学习难点:先求2x的最小值,再求x的最小值的过程.学习过程:一、问题背景几何中最值问题是指在一定条件下,求平面几何图形中某个确定的量(如线段长度,角度大小,图形面积)等的最大值或最小值。
几何最值问题近年来广泛出现在中考中,这是由于这类问题具有很强的探索性(目标不明确)。
解题时,需要运用动态思维,数形结合,特殊与一般相结合,逻辑推理与合情想象相结合等思想。
二、例题解析16.(5分)如图1,直线l1∥l2∥l3,A,B,C分别为直线l1,l2,l3上的动点,连接AB,BC,AC,线段AC交直线l2于点D.设直线l1,l2之间的距离为m,直线l2,l3之间的距离为n,若∠ABC=90°,BD=4,且=,则m+n的最大值为.图11. 思路探究问题一:题中所给的已知条件有哪些呢?这些条件可以分为几大类呢?(设计意图:分析题目之前,首先让学生自主理清题目条件,并归类.)问题二:由l 1∥l 2∥l 3 ,你能想到什么?结合∠ABC =90° ,你会做怎样的构造?(设计意图:让学生自主通过角相等联想到三角形相似,自主想到添加辅助线的办法.) 问题三:对于条件4=n m 通常情况下怎么处理? (设计意图:引导学生常用结论的固定处理方式.让学生联想已有结论表示出线段的长度.) 问题四:在⊿AEB ∽⊿BFC 中,能否尽可能多的表示出线段长?(引导学生二次设元,在相似三角形中表示出更多的线段.)问题五:如何能将BD=4这一条件运用到解题中?你能表示出更多的线段吗?(设计意图:引导学生作出另外两条辅助线,构造出另一组相似三角形⊿AGD ∽⊿CHD ,表示出相应的线段长.从而得到关于两个未知数的等式.) 问题六:结合原题所问,你认为怎样处理236442=--yx y 这一条件会更好? (设计意图:引导学生分离变量,为后面求x 的最小值做好铺垫.)问题七:观察等式91022y y x -=的左边和右边,你认为怎样与求x 的最小值联系起来? (设计意图:引导学生尝试先求2x 的最小值,再求x 的最小值.)2.解法展示解:如图2,EABCBF ABE EAB CBF ABE ABC BFC AEB Fl E l EF B ∠=∠︒=∠+∠︒=∠+∠∴︒=∠︒=∠=∠⊥则又则于点,交于点作过点9090909031 E G HDB A 1l 2l 3l 图2∵m+n=5x ∴当x 最大时,m+n 最大 .由二次函数的性质可知:当y=5时,2x 有最大值为925,则x 的最大值为 35,m+n 的最大值为325 . 3.方法小结 本题最主要的解题模型是添加了3条辅助线,构造两组三角形相似,这两个相似三角形是常见的“三垂相似型”,“8字相似型”,课件灵活运用基本图形在解决综合题中的起到关键的作用。
定弦定角最值问题(含答案)

定弦定角最值问题【定弦定角题型的识别】有一个定弦,一个主动点,一个从动点,定弦所对的张角固定不变。
【题目类型】图形中一般求一个从动点到一个定点线段长度最值问题,一般涉及定弦定角最值问题【解题原理】同弧所对的圆周角相等,定弦的同侧两个圆周角相等,则四点共圆, 因此动点的轨迹是圆。
(线段同侧的两点对线段的张角相等,则这两点以及线段的两个端点共圆。
)【一般解题步骤】①让主动点动一下,观察从动点的运动轨迹,发现从动点的运动轨迹是一段弧。
②寻找不变的张角(这个时候一般是找出张角的补角,这个补角一般为45°、60°或者一个确定的三角函数的对角等)③找张角所对的定弦,根据三点确定隐形圆。
④确定圆心位置,计算隐形圆半径。
⑤求出隐形圆圆心至所求线段定点的距离。
⑥计算最值:在此基础上,根据点到圆的距离求最值(最大值或最小值)。
CD OBEC A259EBC)B 2 ■_wCD DB . 2A . 1A . 1 D . .414.2D .16【例1】(2016 •新观察四调模拟 1)如图,△ ABC 中,AC = 3 , BC = 4^2,/ ACB = 45° D 为△ ABC 内一动点,O O ACD 的外接圆,直线 BD 交O O 于P 点,交BC 于E 点,弧AE = CP , 则AD 的最小值为( ) AD = 5 — 4= 1 \丿【例2】如图,AC = 3,BC = 5,且/ BAC = 90° D 为AC 上一动点,以 为直径作圆,连接BD 交圆于E 点,连CE ,则CE 的最小值为( ) ----- "解:连接AE•/ AD 为O O 的直径•••/ AEB = / AED = 90 .E 点在以AB 为直径的圆上运动 当CE 过圆心O 时,CE 有最小值为-132【练】(2015 •江汉中考模拟1)如图,在△ ABC 中,AC = 3,BC = 4 .. 2,/ ACB = 45° AM II BC , 点P 在射线AM 上运动,连 严 ----------- ------解:•••/ CDP = / ACB = 45°•••/ BDC = 135 ° (定弦定角最值) 如图,当AD 过O 时,AD 有最小值•••/ BDC = 135• / BO'C = 90• △ BO C 为等腰直角三角形:丄 ACO = 45 °+ 45 °= 90 • AO = 5 又 O B = O 'C =4BP 交厶APC 的外接圆于 D ,贝0 AD 的最小值为(4 23O6.2 B 223 *0CD244 ..3B . 6 3 73 A . 12 6,3C . 12 3.3D . 6 A.- ••• AD 的最小值为 5 — 4= 1%/【例3】(2016 •勤学早四调模拟 1)如图,O O 的半径为2,弦AB 的长为2... 3,点P 为优弧AB 上一动点,AC 丄AP 交直线PB 于点C ,则△ ABC 的面积的最大值是(.⑼M 救学早呵H 權®L Tl^l, 00的平栓肖3花初的民育2再,点尸为优那M 上一歐钛啕诂目隹丹呂it 按丿E ・宴罠厶乂肚的叢丸丽希 则点芒駆腼閉壯MfiA- \ AB=2^, ^ACB=KT,・当点C 朗烦胡旳中屯肘* 点闭肋睡琥大.此01氐册?两梅三肃惑CV^l^+3> |X 2M 5 XpJJ+5)-6+5^,放说3,【练】(2014 •洪山区中考模拟 1)如图,O O 的半径为1,弦AB = 1,点P 为优弧AB 上一动点, 又/ ACO = 90°• AO = 5AC± AP 交宜线PB 干桓U 刚色仙匚用I 面理的審丈:A. )2+6 J!R 什 C 口+3 唐 D. 6+4n/3解:连接CD•••/ FAC = Z PDC = Z ACB = 45 •••/ BDC = 135如图,当AD 过圆心O 时,AD 有最小值 •••/ BDC = 135° •••/ BO C = 90° • O 'B = O C = 4AC 丄AF 交直线 FB 于点C , 则△ ABC 的最大面积是(【例5】如图,A(1 , 0)、B(3, 0),以AB 为直径作O M ,射线OF 交O M 于E 、F 两点,C 为弧 AB 的中点,D 为EF 的中点•当射线绕 O 点旋转时,CD 的最小值为 _________________4'1//解: 连接DM••• D 是弦EF 的中点• DM 丄 EF1•点D 在以A 为圆心的,OM 为直径的圆上运动C当CD 过圆心A 时,CD 有最小值连接CMx ••• C 为弧AB 的中点 0 '、A\ 阿• CM 丄 AB\ V /『/••• CD 的最小值为 .2 1【练】如图,AB 是O O 的直径,AB = 2,/ ABC = 60° P 是上一动点,D 是AP 的中点,连接解:连接OD •/ D 为弦AP 的中点CD ,贝U CD 的最小值为• OD 丄AP•••点D在以AO为直径的圆上运动当CD过圆心O 时,CD有最小值过点C作CM丄AB于M•/ OB = OC,/ ABC = 60°• △ OBC为等边三角形1 J3•OM = -,CM =2•O'C= —74• CD的最小值为。
(完整版)定弦定角最值问题(含答案)

定弦定角最值问题【定弦定角题型的鉴别】有一个定弦,一个主动点,一个从动点,定弦所对的张角固定不变。
【题目种类】图形中一般求一个从动点到一个定点线段长度最值问题,一般涉及定弦定角最值问题【解题原理】同弧所对的圆周角相等,定弦的同侧两个圆周角相等,则四点共圆,因此动点的轨迹是圆。
(线段同侧的两点对线段的张角相等,则这两点以及线段的两个端点共圆。
)【一般解题步骤】①让主动点动一下,观察从动点的运动轨迹,发现从动点的运动轨迹是一段弧。
②搜寻不变的张角(这个时候一般是找出张角的补角,这个补角一般为 45°、 60°也许一个确定的三角函数的对角等)③找张角所对的定弦,依照三点确定隐形圆。
④确定圆心地址,计算隐形圆半径。
⑤求出隐形圆圆心至所求线段定点的距离。
⑥计算最值:在此基础上,依照点到圆的距离求最值(最大值或最小值)。
【例 1】(2016 ·新观察四调模拟1) 如图,△ ABC 中, AC= 3,BC= 42 ,∠ ACB = 45°,D 为△ABC 内一动点,⊙ O 为△ ACD 的外接圆,直线BD 交⊙ O 于 P 点,交BC 于 E 点,弧 AE= CP,则 AD 的最小值为()A . 1B. 2C.2D.41 4 2解:∵∠ CDP =∠ ACB = 45°∴∠ BDC =135 °(定弦定角最值)如图,当AD 过 O′时, AD 有最小值∵∠ BDC =135 °∴∠ BO′C= 90 °∴ △ BO′C 为等腰直角三角形∴∠ ACO ′= 45 °+ 45 °= 90 °∴AO′= 5又O′B=O′C= 4∴AD =5- 4=1【例 2】如图, AC= 3, BC = 5,且∠ BAC =90°,D 为 AC 上一动点,以AD 为直径作圆,连接BD 交圆于 E 点,连 CE,则 CE 的最小值为()A . 13 2B. 13 2C. 516 D.9解:连接 AE∵AD 为⊙ O 的直径∴∠AEB=∠ AED = 90 °∴ E 点在以 AB 为直径的圆上运动当 CE 过圆心O′时, CE 有最小值为13 2【练】(2015 ·江汉中考模拟1) 如图,在△ ABC 中, AC = 3,BC = 4 2 ,∠ ACB = 45°,AM ∥ BC,点 P 在射线 AM 上运动,连BP 交△ APC 的外接圆于D,则 AD 的最小值为()A . 1B. 2C.2 D . 4 2 3解:连接 CD∴∠ PAC =∠ PDC =∠ ACB= 45 °∴∠ BDC =135 °如图,当AD 过圆心 O′时, AD 有最小值∵∠ BDC =135°∴∠ BO′C= 90°∴O′B= O′C= 4又∠ ACO ′= 90°∴AO′= 5∴AD 的最小值为 5-4= 1【例3】 (2016 ·勤学早四调模拟1) 如图,⊙ O的半径为2,弦AB的长为 2 3 ,点 P 为优弧AB 上一动点, AC ⊥ AP交直线 PB 于点C,则△ ABC的面积的最大值是()A . 12 6 3B. 6 33C. 12 33D. 6 4 3【练】 (2014·洪山区中考模拟1)如图,⊙ O 的半径为1,弦 AB= 1,点 P 为优弧 AB 上一动点,AC ⊥ AP 交直线 PB 于点 C,则△ ABC 的最大面积是()A .1B.2 22C.3D .3 24【例 5】如图, A(1 , 0) 、 B(3, 0) ,以 AB 为直径作⊙ M,射线 OF 交⊙ M 于 E 、 F 两点, C 为弧AB 的中点, D 为 EF 的中点.当射线绕 O 点旋转时, CD 的最小值为 __________解:连接 DM∵D 是弦 EF 的中点∴DM ⊥ EF∴点 D 在以 A 为圆心的,OM 为直径的圆上运动当CD 过圆心 A 时, CD 有最小值连接 CM∵C 为弧 AB 的中点∴ CM⊥ AB∴ CD 的最小值为 2 1【练】如图, AB 是⊙ O 的直径, AB= 2,∠ ABC= 60°, P 是上一动点, D 是 AP 的中点,连接CD ,则 CD 的最小值为 __________解:连接 OD∵ D 为弦 AP 的中点∴OD⊥ AP∴点 D 在以 AO 为直径的圆上运动当CD 过圆心 O′时, CD 有最小值过点 C 作 CM ⊥ AB 于 M∵OB=OC ,∠ ABC = 60°∴△ OBC 为等边三角形∴OM =1, CM =3 22∴O′C=747 1∴ CD 的最小值为42。
巧用几何画板探究中考数学中的定弦定角问题教学设计宝鸡高新第一

巧用几何画板探究中考数学中的定弦定角问题教学设计宝鸡高新第一中学党莉娜教学对象:九年级学生教学内容:九年级下册中考复习教学目标1.利用几何画板作图探究定弦定角问题,求最值;2.会使用几何画板的思维方式体会动点和次动点的关系;3.通过观察次动点的轨迹,求解最值。
教学重难点重点:如何使用几何画板作图,采用度量和画次动点轨迹的方式观察最值位置难点:观察次动点的轨迹将定弦定角问题转化为求圆弧外(或者上)一点到圆弧的最值。
教学方法:微课学习+自主学习教学过程一、问题引入圆弧外一点到圆弧的最小值和最大值如何计算?设计意图:通过问题的引入让学生明确处理这类问题的方式。
二、新知探究定弦定角问题中考备考复习中的难点,多数同学在遇到这类问题时感到无从下手,这里通过几何画板作图演示让学生体会定弦定角问题问题一(定角)在矩形ABCD中,AB=4,BC=6,E是BC上一动点,连接AE,过B作BF⊥AE交于点G,连接CG,则CG的最小值。
画板作图:1. 画矩形,用文本工具标记ABCD,得到矩形ABCD,在BC上取一点E,连接AE,过B作BF⊥AE交于点G, 连接CG,2.拖动点E,观察动点E和次动点G,画出次动点G的轨迹。
3.度量CG的长度。
拖动点E观察CG的长度变化。
问题分析:通过观察画板中的次动点G的轨迹可以得出,次动点G轨迹在以点O为圆心,AB长为直径的一段圆弧,所求问题线段CG的最小值可以转化成求点C到圆弧的上一点的最小值,观察图形发现当点O,G,C三点共线时,线段CG最小,在三角形OBC中,根据勾股定理得OC=2√10,所以CG=OC-OG=2√10-2.问题二(定弦对定角)三角形ABC是等边三角形,BC=2,∠BDC=45°,求AD的最大值和最小值。
画板作图1.画等边三角形ABC,分别以B,C为中心,将线段BC旋转90°,得到点M,N,则∠BMC=45°, ∠BNC=45°.2.分别以点B,M,C画弧,点B,N,C画弧,分别在圆弧上取一点D, D',根据同弧所对的圆周角相等,得到∠BDC=∠BMC=45°;∠B D'C=∠BNC=45°。
九年级讲义:定弦定角最值问题秘籍

九年级讲义:定弦定角最值问题【定弦定角题型的识别】有一个定弦,一个主动点,一个从动点,定弦所对的张角固定不变。
【题目类型】图形中一般求一个从动点到一个定点线段长度最值问题,一般涉及定弦定角最值问题【解题原理】同弧所对的圆周角相等,定弦的同侧两个圆周角相等,则四点共圆,因此动点的轨迹是圆。
(线段同侧的两点对线段的张角相等,则这两点以及线段的两个端点共圆。
)【一般解题步骤】①让主动点动一下,观察从动点的运动轨迹,发现从动点的运动轨迹是一段弧。
②寻找不变的张角(这个时候一般是找出张角的补角,这个补角一般为45°、60°或者一个确定的三角函数的对角等)③找张角所对的定弦,根据三点确定隐形圆。
④确定圆心位置,计算隐形圆半径。
⑤求出隐形圆圆心至所求线段定点的距离。
⑥计算最值:在此基础上,根据点到圆的距离求最值(最大值或最小值)。
【例1】如图,△ABC 中,AC =3,BC =24,∠ACB =45°,D 为△ABC 内一动点,⊙O 为△ACD 的外接圆,直线BD 交⊙O 于P 点,交BC 于E 点,弧AE =CP ,则AD 的最小值为( )A .1B .2C .2D .2441-【例2】如图,AC =3,BC =5,且∠BAC =90°,D 为AC 上一动点,以AD 为直径作圆,连接BD 交圆于E 点,连CE,则CE 的最小值为( )A .213-B .213+C .5D .916 【练】如图,在△ABC 中,AC =3,BC =24,∠ACB =45°,AM ∥BC ,点P 在射线AM 上运动,连BP 交△APC 的外接圆于D,则AD 的最小值为( )A .1B .2C .2D .324-【例3】如图,⊙O 的半径为2,弦AB 的长为32,点P 为优弧AB 上一动点,AC ⊥AP 交直线PB 于点C,则△ABC 的面积的最大值是( )A .3612+B .336+C .3312+D .346+【练】如图,⊙O 的半径为1,弦AB =1,点P 为优弧AB 上一动点,AC ⊥AP 交直线PB 于点C ,则△ABC 的最大面积是( )A .21 B .22 C .23 D .43 【例4】如图,边长为3的等边△ABC ,D 、E 分别为边BC 、AC 上的点,且BD =CE ,AD 、BE 交于P 点,则CP 的最小值为_________例题4 例题5 图8【例5】如图,A(1,0)、B(3,0),以AB 为直径作⊙M ,射线OF 交⊙M 于E 、F 两点,C 为弧AB 的中点,D 为EF 的中点.当射线绕O 点旋转时,CD 的最小值为__________【练】如图8,AB 是⊙O 的直径,AB =2,∠ABC =60°,P 是上一动点,D 是AP 的中点,连接CD ,则CD 的最小值为__________针对练习:1.如图,在动点C 与定长线段AB 组成的△ABC 中,AB =6,AD ⊥BC 于点D,BE ⊥AC 于点E ,连接DE .当点C 在运动过程中,始终有22 AB DE ,则点C 到AB 的距离的最大值是_________2.如图,已知以BC 为直径的⊙O ,A 为弧BC 中点,P 为弧AC 上任意一点,AD ⊥AP 交BP 于D ,连CD .若BC =8,则CD 的最小值为___________。
轨迹问题之定角对定边 定弦定角最值问题(含答案) (PDF版)

定弦定角最值问题----20190828【定弦定角题型的识别】有一个定弦,一个主动点,一个从动点,定弦所对的张角固定不变。
【题目类型】图形中一般求一个从动点到一个定点线段长度最值问题,一般涉及定弦定角最值问题【解题原理】同弧所对的圆周角相等,定弦的同侧两个圆周角相等,则四点共圆,因此动点的轨迹是圆。
(线段同侧的两点对线段的张角相等,则这两点以及线段的两个端点共圆。
)【一般解题步骤】①让主动点动一下,观察从动点的运动轨迹,发现从动点的运动轨迹是一段弧。
②寻找不变的张角(这个时候一般是找出张角的补角,这个补角一般为45°、60°或者一个确定的三角函数的对角等)③找张角所对的定弦,根据三点确定隐形圆。
④确定圆心位置,计算隐形圆半径。
⑤求出隐形圆圆心至所求线段定点的距离。
⑥计算最值:在此基础上,根据点到圆的距离求最值(最大值或最小值)。
【例1】(2019·模拟)如图,△ABC中,AC=3,BC=24,∠ACB=45°,D为△ABC内一动点,⊙O为△ACD的外接圆,直线BD交⊙O于P点,交BC于E 点,弧AE=CP,则AD的最小值为()A.1 B.2 C.2D.241-4解:∵∠CDP=∠ACB=45°∴∠BDC=135°(定弦定角最值)如图,当AD过O′时,AD有最小值∵∠BDC=135°∴∠BO′C=90°∴△BO′C为等腰直角三角形∴∠ACO′=45°+45°=90°∴AO′=5又O′B=O′C=4∴AD=5-4=1【例2】如图,AC=3,BC=5,且∠BAC=90°,D为AC上一动点,以AD为直径作圆,连接BD交圆于E点,连CE,则CE的最小值为16()A.213-B.213+C.5 D.9解:连接AE∵AD为⊙O的直径∴∠AEB=∠AED=90°∴E点在以AB为直径的圆上运动当CE过圆心O′时,CE有最小值为213-【练】(2015·江汉中考模拟1)如图,在△ABC 中,AC =3,BC =24,∠ACB =45°,AM ∥BC ,点P 在射线AM 上运动,连BP 交△APC 的外接圆于D ,则AD 的最小值为( )A .1B .2C .2D .324-解:连接CD∴∠P AC =∠PDC =∠ACB =45°∴∠BDC =135°如图,当AD 过圆心O ′时,AD 有最小值∵∠BDC =135°∴∠BO ′C =90°∴O ′B =O ′C =4又∠ACO ′=90°∴AO ′=5∴AD 的最小值为5-4=1【例3】(2016·勤学早四调模拟1)如图,⊙O 的半径为2,弦AB 的长为32,点P 为优弧AB 上一动点,AC ⊥AP 交直线PB 于点C ,则△ABC 的面积的最大值是( )A .3612+B .336+C .3312+D .346+2019【练】(·洪山区中考模拟 1)如图,⊙O 的半径为 1,弦 AB =1,点 P 为优弧 AB 上一动点, AC ⊥AP 交直线 PB 于点 C ,则△ABC 的最大面积是( )A .21B .22C .23D .43【例5】如图,A (1,0)、B (3,0),以AB 为直径作⊙M ,射线OF 交⊙M 于E 、F 两点,C 为弧AB 的中点,D 为EF 的中点.当射线绕O 点旋转时,CD 的最小值为__________解:连接DM∵D 是弦EF 的中点∴DM ⊥EF∴点D 在以A 为圆心的,OM 为直径的圆上运动当CD 过圆心A 时,CD 有最小值连接CM∵C 为弧AB 的中点∴CM ⊥AB∴CD 的最小值为12-【练】如图,AB 是⊙O 的直径,AB =2,∠ABC =60°,P 是上一动点,D 是AP 的中点,连接CD ,则CD 的最小值为__________解:连接OD ∵D 为弦AP 的中点∴OD ⊥AP ∴点D 在以AO 为直径的圆上运动当CD 过圆心O ′时,CD 有最小值 过点C 作CM ⊥AB 于M∵OB =OC ,∠ABC =60° ∴△OBC 为等边三角形∴OM =21,CM =23∴O ′C =47∴CD 的最小值为2147-定弦定角1.(安徽)如图,Rt △ABC 中,AB ⊥BC ,AB=6,BC=4,P 是△ABC 内部的一个动点,且满足∠PAB=∠PBC ,则线段CP 长的最小值为()A .23B .2C .13138D .131312故选B.3.(宜兴模拟)如图,半径为2cm,圆心角为90°的扇形OAB的弧AB上有一运动的点P从点P向半径OA引垂线PH交OA于点H,设△OPH的内心为I,当点P在弧AB上从点A 运动到点B时,内心I所经过的路径长为.4.等腰直角△ABC 中,∠C =90°,AC =BC =4,D 为线段AC 上一动点,连接BD ,过点C 作CH ⊥BD 于H ,连接AH ,则AH 的最小值为.答案:2-52(点H 在以BC 为直径的圆上)5.直线y =x +4分别与x 轴、y 轴相交与点M 、N ,边长为2的正方形OABC 一个顶点O 在坐标系的原点,直线AN 与MC 相交与点P ,若正方形绕着点O 旋转一周,则点P 到点(0,2)长度的最小值是.A.1B.2C.332 D.3答案:D (点C 在以AB 为弦的圆上)8.(外国语模拟)如图,以正方形ABCD 的边BC 为一边向内部做一等腰△BCE ,BE=BC ,过E 做EH ⊥BC ,点P 是Rt △BEH 的内心,连接AP ,若AB=2,则AP 的最小值为________.答案:22π(点P 在以BC 为弦的圆上)9.(江阴期中)如图,以G (0,1)为圆心,半径为2的圆与x 轴交于A 、B 两点,与y 轴交于C 、D 两点,点E 为⊙G 上一动点,CF ⊥AE 于F ,当点E 从点B 出发顺时针运动到点D 时,点F 所经过的路径长为________.答案:π33(点F 在以AC 为直径的圆上)10.(南长区二模)如图,矩形OABC 的边OA 、OC分别在x 轴、y 轴上,点B 的坐标为(7,3),点E 在边AB 上,且AE=1,已知点P 为y 轴上一动点,连接EP ,过点O 作直线EP 的垂线段,垂足为点H ,在点P 从点F(0,254)运动到原点O 的过程中,点H 的运动路径长为________.答案:π425(点H 在以OE 为直径的圆上)。
九年级讲义:定弦定角最值问题秘籍

九年级道义:定弦定角最值问题之阳早格格创做【定弦定角题型的辨别】有一个定弦,一个主动面,一个从动面,定弦所对于的弛角牢固没有变.【题目典型】图形中普遍供一个从动面到一个定面线段少度最值问题,普遍波及定弦定角最值问题【解题本理】共弧所对于的圆周角相等,定弦的共侧二个圆周角相等,则四面共圆,果此动面的轨迹是圆.(线段共侧的二面对于线段的弛角相等,则那二面以及线段的二个端面共圆.)【普遍解题步调】①让主动面动一下,瞅察从动面的疏通轨迹,创造从动面的疏通轨迹是一段弧.②觅找没有变的弛角(那个时间普遍是找出弛角的补角,那个补角普遍为45°、60°大概者一个决定的三角函数的对于角等)③找弛角所对于的定弦,根据三面决定隐形圆.④决定圆心位子,估计隐形圆半径.⑤供出隐形圆圆心至所供线段定面的距离.⑥估计最值:正在此前提上,根据面到圆的距离供最值(最大值大概最小值).【例1】如图,△ABC中,AC=3,BC=,∠ACB=45°,D为△ABC内一动面,⊙O为△ACD的中接圆,曲线BD接⊙O于P面,接BC于E面,弧AE=CP,则AD的最小值为()A.1B.2C.D.【例2】如图,AC=3,BC=5,且∠BAC=90°,D为AC 上一动面,以AD为曲径做圆,对接BD接圆于E面,连CE,则CE的最小值为()A.B.C.5D.【练】如图,正在△ABC中,AC=3,BC=,∠ACB=45°,AM∥BC,面P正在射线AM上疏通,连BP接△APC的中接圆于D,则AD的最小值为()A.1B.2C.D.【例3】如图,⊙O的半径为2,弦AB的少为,面P为劣弧AB上一动面,AC⊥AP接曲线PB于面C,则△ABC 的里积的最大值是()A.B.C.D.【练】如图,⊙O的半径为1,弦AB=1,面P为劣弧AB 上一动面,AC⊥AP接曲线PB于面C,则△ABC的最大里积是()A.B.C.D.【例4】如图,边少为3的等边△ABC,D、E分别为边BC、AC上的面,且BD=CE,AD、BE接于P面,则CP 的最小值为_________例题4 例题5 图8 【例5】如图,A(1,0)、B(3,0),以AB为曲径做⊙M,射线OF接⊙M于E、F二面,C为弧AB的中面,D为EF 的中面.当射线绕O面转动时,CD的最小值为__________【练】如图8,AB是⊙O的曲径,AB=2,∠ABC=60°,P是上一动面,D是AP的中面,对接CD,则CD的最小值为__________针对于训练:1.如图,正在动面C取定少线段AB组成的△ABC中,AB=6,AD⊥BC于面D,BE⊥AC于面E,对接DE.当面C正在疏通历程中,末究有,则面C到AB的距离的最大值是_________2.如图,已知以BC为曲径的⊙O,A为弧BC中面,P为弧AC上任性一面,AD⊥AP接BP于D,连CD.若BC=8,则CD的最小值为___________。
定弦定角最值问题(含答案)

定弦定角最值问题【定弦定角题型的识别】有一个定弦,一个主动点,一个从动点,定弦所对的张角固定不变。
【题目类型】图形中一般求一个从动点到一个定点线段长度最值问题,一般涉及定弦定角最值问题【解题原理】同弧所对的圆周角相等,定弦的同侧两个圆周角相等,则四点共圆,因此动点的轨迹是圆。
(线段同侧的两点对线段的张角相等,则这两点以及线段的两个端点共圆。
)【一般解题步骤】①让主动点动一下,观察从动点的运动轨迹,发现从动点的运动轨迹是一段弧。
②寻找不变的张角(这个时候一般是找出张角的补角,这个补角一般为45°、60°或者一个确定的三角函数的对角等)③找张角所对的定弦,根据三点确定隐形圆。
④确定圆心位置,计算隐形圆半径。
⑤求出隐形圆圆心至所求线段定点的距离。
⑥计算最值:在此基础上,根据点到圆的距离求最值(最大值或最小值)。
【例1】(2016·新观察四调模拟1)如图,△ABC 中,AC =3,BC =24,∠ACB =45°,D 为△ABC 内一动点,⊙O 为△ACD 的外接圆,直线BD 交⊙O 于P 点,交BC 于E 点,弧AE =CP ,则AD 的最小值为( )A .1B .2C .2D .2441解:∵∠CDP =∠ACB =45°∴∠BDC =135°(定弦定角最值)如图,当AD 过O ′时,AD 有最小值∵∠BDC =135°∴∠BO ′C =90°∴△BO ′C 为等腰直角三角形∴∠ACO ′=45°+45°=90°∴AO ′=5又O ′B =O ′C =4∴AD =5-4=1【例2】如图,AC =3,BC =5,且∠BAC =90°,D 为AC 上一动点,以AD 为直径作圆,连接BD 交圆于E 点,连CE ,则CE 的最小值为( )A .213-B .213+C .5D .916 解:连接AE∵AD 为⊙O 的直径∴∠AEB =∠AED =90°∴E 点在以AB 为直径的圆上运动当CE 过圆心O ′时,CE 有最小值为213-【练】(2015·江汉中考模拟1)如图,在△ABC 中,AC =3,BC =24,∠ACB =45°,AM ∥BC ,点P 在射线AM 上运动,连BP 交△APC 的外接圆于D ,则AD 的最小值为( )A .1B .2C .2D .324-解:连接CD ∴∠PAC =∠PDC =∠ACB =45°∴∠BDC =135°如图,当AD 过圆心O ′时,AD 有最小值∵∠BDC =135°∴∠BO ′C =90°∴O ′B =O ′C =4又∠ACO ′=90°∴AO ′=5∴AD 的最小值为5-4=1【例3】(2016·勤学早四调模拟1)如图,⊙O 的半径为2,弦AB 的长为32,点P 为优弧AB 上一动点,AC ⊥AP 交直线PB 于点C ,则△ABC 的面积的最大值是( )A .3612+B .336+C .3312+D .346+【练】(2014·洪山区中考模拟1)如图,⊙O 的半径为1,弦AB =1,点P 为优弧AB 上一动点,AC ⊥AP 交直线PB 于点C ,则△ABC 的最大面积是( )A .21 B .22 C .23 D .43 【例5】如图,A (1,0)、B (3,0),以AB 为直径作⊙M ,射线OF 交⊙M 于E 、F 两点,C 为弧AB 的中点,D 为EF 的中点.当射线绕O 点旋转时,CD 的最小值为__________解:连接DM∵D 是弦EF 的中点∴DM ⊥EF∴点D 在以A 为圆心的,OM 为直径的圆上运动当CD 过圆心A 时,CD 有最小值连接CM∵C 为弧AB 的中点∴CM ⊥AB∴CD 的最小值为12-【练】如图,AB 是⊙O 的直径,AB =2,∠ABC =60°,P 是上一动点,D 是AP 的中点,连接CD ,则CD 的最小值为__________解:连接OD∵D 为弦AP 的中点∴OD ⊥AP∴点D 在以AO 为直径的圆上运动 当CD 过圆心O ′时,CD 有最小值 过点C 作CM ⊥AB 于M ∵OB =OC ,∠ABC =60° ∴△OBC 为等边三角形 ∴OM =21,CM =23 ∴O ′C =47 ∴CD 的最小值为2147。
最新初三中考复习二次函数最值问题教学提纲

二次函数之最值问题基本解题步骤:1.审题.读懂问题.分析问题各个量之间的关系;2.列数学表达式.用数学方法表示它们之间的关系.即写出变量与常量之间的二次函数关系式;3.求值.利用二次函数关系式的顶点坐标公式24,24b ac b a a ⎛⎫-- ⎪⎝⎭或配方法求得最值;配方法:将二次函数2y ax bx c =++转化为2()y a x h k =-+的形式.顶点坐标为(),h k .对称轴为x h =.当0a >时.y 有最小值.即当x h =时.=y k 最小值;当0a <时.y 有最大值.即当x h =时.=y k 最大值.4.检验.检验结果的合理性.(函数求最值需考虑实际问题的自变量的取值范围)解题策略−−−→−−−→−−−→转化数学检验解答实际问题数学问题解问题答案利润最值问题例1、一玩具厂去年生产某种玩具.成本为10元/件.出厂价为12元/件.年销售量为2万件.今年计划通过适当增加成本来提高产品的档次.以拓展市场.若今年这种玩具每件的成本比去年成本增加0.7x倍.今年这种玩具每件的出厂价比去年出厂价相应提高0.5x倍.则预计今后年销售量将比去年年销售量增加x倍(本题中01<≤).x(1)用含x的代数式表示:今年生产的这种玩具每件的成本为_______元.今年生产的这种玩具每件的出厂价为______元.(2)求今年这种玩具每件的利润y元与x之间的函数关系式;(3)设今年这种玩具的年销售利润为w万元.求当x为何值时.今年的年销售利润最大?最大年销售利润是多少万元?注:年销售利润=(每件玩具的出厂价-每件玩具的成本)×年销售量.解:(1)10+7x;12+6x;(2)y=(12+6x)-(10+7x).∴y=2-x (0<x≤11);(3)∵w=2(1+x)•y=2(1+x)(2-x)=-2x2+2x+4.∴w=-2(x-0.5)2+4.5∵-2<0.0<x≤11.∴w有最大值.∴当x=0.5时.w最大=4.5(万元).答:当x为0.5时.今年的年销售利润最大.最大年销售利润是4.5万元.例2、新星电子科技公司积极应对2008年世界金融危机.及时调整投资方向.瞄准光伏产业.建成了太阳能光伏电池生产线.由于新产品开发初期成本高.且市场占有率不高等因素的影响.产品投产上市一年来.公司经历了由初期的亏损到后来逐步盈利的过程(公司对经营的盈亏情况每月最后一天结算1次).公司累积获得的利润y (万元)与销售时间第x (月)之间的函数关系式(即前x 个月的利润总和y 与x 之间的关系)对应的点都在如下图所示的图象上.该图象从左至右.依次是线段OA 、曲线AB 和曲线BC.其中曲线AB 为抛物线的一部分.点A 为该抛物线的顶点.曲线BC 为另一抛物线252051230y x x =-+-的一部分.且点A.B.C 的横坐标分别为4.10.12.(1)求该公司累积获得的利润y (万元)与时间第x (月)之间的函数关系式;(2)直接写出第x 个月所获得S (万元)与时间x (月)之间的函数关系式(不需要写出计算过程); (3)前12个月中.第几个月该公司所获得的利润最多?最多利润是多少万元?解:(1)设直线OA 的解析式为y=kx. ∵点O (0.0).A (4.-40)在该直线上. ∴-40=4k. 解得k=-10.∴y=-10x ;∵点B 在抛物线y=-5x 2+205x-1230上. 设B (10.m ).则m=320. ∴点B 的坐标为(10.320). ∵点A 为抛物线的顶点.∴设曲线AB 所在的抛物线的解析式为y=a (x-4)2-40. ∴320=a(10-4)2-40. 解得a=10.即y=10(x-4)2-40=10x 2-80x+120.月)(2)利用第x个月的利润应该是前x个月的利润之和减去前x-1个月的利润之和:(3)由(2)知当x=1.2.3.4时.s的值均为-10.当x=5.6.7.8.9时.s=20x-90.即当x=9时s有最大值90.而在x=10.11.12时.s=-10x+210.当x=10时.s有最大值110.因此第10月公司所获利润最大.它是110万元.试一试:1、某水果批发商销售每箱进价为40元的的苹果.物价部门规定每箱售价不得高于55元.市场调查发现.若每箱以50元的价格销售.平均每天销售90箱.价格每提高1元.平均每天少销售3箱.(1)求平均每天销售量y(箱)与销售价x(元/箱)之间的函数关系式.(2)求该批发商平均每天销售利润w(元)与销售价x(元/箱)之间的函数关系式.(3)当每箱苹果的售价为多少元时.可以获得最大利润?最大利润是多少?解:(1)设y=kx+b.把已知(45.105).(50.90)代入得.故平均每天销售量y(箱)与销售价x(元/箱)之间的函数关系式为:y=-3x+240;(2)∵水果批发商销售每箱进价为40元的苹果.销售价x 元/箱.∴该批发商平均每天的销售利润w (元)与销售价x (元/箱)之间的函数关系式为: W=(x-40)(-3x+240)=-3x 2+360x-9600.(3)W=-3x 2+360x-9600=-3(x-60)2+1200. ∵a=-3<0.∴抛物线开口向下.又∵对称轴为x=60.∴当x <60.W 随x 的增大而增大. 由于50≤x≤55.∴当x=55时.W 的最大值为1125元.∴当每箱苹果的销售价为55元时.可以获得最大利润.为1125元.2、我市 某镇的一种特产由于运输原因.长期只能在当地销售.当地政府对该特产的销售投资收益为:每投入x 万元.可获得利润()216041()100P x =--+万元.当地政府拟在“十二·五”规划中加快开发该特产的销售.其规划方案为:在规划前后对该项目每年最多可投入100万元的销售投资.在实施规划5年的前两年中.每年都从100万元中拨出50万元用于修建一条公路.两年修成.通车前该特产只能在当地销售;公路通车后的3年中.该特产既在本地销售.也在外地销售.在外地销售的投资收益为:每投入x 万元.可获利润()()2992941001001601005Q x x =--+-+(万元). (1)若不进行开发.求5年所获利润的最大值是多少?(2)若按规划实施.求5年所获利润(扣除修路后)的最大值是多少? (3)根据(1).(2).该方案是否具有实施价值?解:(1)∵每投入x 万元.可获得利润∴当x=60时.所获利润最大.最大值为41万元.∴若不进行开发.5年所获利润的最大值是:41×5=205(万元);(2)前两年:0≤x≤50.此时因为P 随x 的增大而增大. 所以x=50时.P 值最大.即这两年的获利最大为后三年:设每年获利y.设当地投资额为a.则外地投资额为100-a.∴当a=30时.y 最大且为1065.∴这三年的获利最大为1065×3=3195(万元).∴5年所获利润(扣除修路后)的最大值是:80+3195-50×2=3175(万元).线段和(或三角形周长)最值问题复习:如图.正方形ABCD 的边长为4.点P 在DC 边上且DP=1.点Q 是AC 上一动点.则DQ+PQ 的最小值为 .例1、已知二次函数2y x bx c =++的图象过点()3,0A -和点()1,0B .且与y 轴交于点C .D 点在抛物线上且横坐标是2-.(1)求抛物线的解析式;(2)抛物线的对称轴上有一动点P.求出PA PD +的最小值.例2、如图.在平面直角坐标系xOy中.直线32y x=-+分别交x轴、y轴于C、A两点.将射线AM绕着点A顺时针旋转45°得到射线AN.点D为AM上的动点.点B为AN上的动点.点C在∠MAN的内部.(1)求线段AC的长;(2)当AM∥x轴.且四边形ABCD为梯形时.求△BCD的面积;(3)求△BCD周长的最小值;(4)当△BCD的周长取得最小值.且52BD=时.△BCD的面积为________.例3、已知.如图.二次函数()2230y ax ax a a =+-≠图像的顶点为H.与x 轴交于A 、B 两点(B 在A 点右侧).点H.B 关于直线l :33yx=+对称. (1)求A 、B 两点坐标.并证明点A 在直线l 上; (2)求二次函数解析式;(3)过点B 作直线BK ∥AH 交直线l 于K 点.M 、N 分别为直线AH 和直线l 上的两个动点.连接HN.NM.MK.求HN NM MK ++和的最小值.yA xO BHK试一试:1、已知抛物线21y ax bx =++经过点()1,3A 和点()2,1B . (1)求此抛物线解析式;(2)点C 、D 分别是x 轴和y 轴上的动点.求四边形ABCD 周长的最小值;(3)过点B 作x 轴的垂线.垂足为E 点.点P 从抛物线的顶点出发.先沿抛物线的对称轴到达F 点.再沿FE到达E 点.若P 点在对称轴上的运动速度是它在直线FE 倍.试确定点F 的位置.使得点P 按照上述要求到达E 点所用的时间最短.(要求:简述确定F 点位置的方法.但不要求证明)二次函数中字母替换例1、如图.已知A (a.m )、B (2a.n )是反比例函数)0(>=k x k y 与一次函数b x y +-=34图像上的两个不同的交点.分别过A 、B 两点作x 轴的垂线.垂足分别为C 、D 。
13、定弦定角最值问题

22九年级讲义:定弦定角最值问题主要是体现在题目中出现了固定度数的角对着固定长度的线段时隐含着一个固定大小的圆,此时定线段为隐圆的一条弦,定角为弦所对的一个圆周角,借助隐圆来分析问题极其方便,关键是要先发现隐含着的特殊度数的角。
【例1】如图,△ABC中,AC=3,BC=4 ,∠ACB=45°,D 为△ABC内一动点,⊙O为△ACD的外接圆,直线BD 交⊙O于P 点,交BC 于E 点,弧AE=CP,则AD 的最小值为()【例2】如图,AC=3,BC=5,且∠BAC=90°,D 为AC 上一动点,以AD 为直径作圆,连接BD 交圆于E 点,连CE,则CE 的最小值为()【练】如图,在△ABC中,AC=3,BC=4 ,∠ACB=45°,AM∥BC,点P 在射线AM 上运动,连BP 交△APC的外接圆于D,则AD 的最小值为()【例3】如图,⊙O的半径为2,弦AB 的长为2 ,点P 为优弧AB 上一动点,AC3⊥AP交直线PB 于点C,则△ABC的面积的最大值是()【练】如图,⊙O的半径为1,弦AB=1,点P 为优弧AB 上一动点,AC⊥AP交直线PB 于点C,则△ABC的最大面积是()【例4】如图,边长为3 的等边△ABC,D、E 分别为边BC、AC 上的点,且BD=CE,AD、BE 交于P 点,则CP 的最小值为【例 5】如图,A(1,0)、B(3,0),以 AB 为直径作⊙M,射线 OF 交⊙M 于E、F 两点,C 为弧AB 的中点,D 为EF 的中点.当射线绕 O 点旋转时,CD 的最小值为【练】如图,AB 是⊙O的直径,AB=2,∠ABC=60°,P 是上一动点,D 是AP 的中点,连接CD,则CD 的最小值为针对练习:1.如图,在动点 C 与定长线段 AB 组成的△ABC 中,AB=6,AD⊥BC于点 D,BE⊥AC于点E,连接 DE.当点 C 在运动过程中,始终有DEAB 2 ,则点 C 到 AB 的2距离的最大值是3332.如图,已知以BC 为直径的⊙O,A 为B C 中点,P 为 AC上任意一点,A D⊥AP 交BP 于D,连CD.若BC=8,则CD 的最小值为3.如图,在⊙O中,弦AD 等于半径,B 为优弧AD 上的一动点,等腰△ABC的底边BC 所在直线经过点D,若⊙O的半径为1,则OC 的长不可能为()A. 2- B. -1 C.2 D. +13.如图,E,F是正方形A B C D的边A D上两个动点,满足A E=D F.连接C F交B D 于G,连接B E交A G于点H.若正方形的边长为2,则线段D H长度的最小值是( ).23.如图,在Rt⊿ABC中,∠BAC=90º,AB=AC,BC=4 ,点D 是AC 边上一动点,连接BD,以AD 为直径的圆交BD 于E,连接CE,则线段CE 长的最小值为( )4.如图,直径 AB、CD 的夹角为 60 º,P 为⊙O一的个动点(不与点 A、B、C、D 重合)。
定弦定角最值问题

定弦定角最值问题【定弦定角题型的识别】有一个定弦,一个主动点,一个从动点,定弦所对的张角固定不变。
【题目类型】图形中一般求一个从动点到一个定点线段长度最值问题,一般涉及定弦定角最值问题【解题原理】同弧所对的圆周角相等,定弦的同侧两个圆周角相等,则四点共圆,因此动点的轨迹是圆。
(线段同侧的两点对线段的张角相等,则这两点以及线段的两个端点共圆。
)【一般解题步骤】①让主动点动一下,观察从动点的运动轨迹,发现从动点的运动轨迹是一段弧。
②寻找不变的张角(这个时候一般是找出张角的补角,这个补角一般为45°、60°或者一个确定的三角函数的对角等)③找张角所对的定弦,根据三点确定隐形圆。
④确定圆心位置,计算隐形圆半径。
⑤求出隐形圆圆心至所求线段定点的距离。
⑥计算最值:在此基础上,根据点到圆的距离求最值(最大值或最小值)。
【例1】(2016 ·新观察四调模拟1)如图,△ABC中,AC=3,BC=4 2 ,∠ACB=45°,D为△ABC内一动点,⊙O为△ACD的外接圆,直线BD交⊙O于P点,交BC于E点,弧AE=CP,则AD 的最小值为()A.1 B.2 C.2 D.41 4 2解:∵∠CDP=∠ACB=45°∴∠BDC=135°(定弦定角最值)如图,当AD过O′时,AD有最小值∵∠BDC=135°∴∠BO′ C=90°∴△BO′C为等腰直角三角形∴∠ACO′=45 °+45°=90°∴AO′=5又O′ B=O′C=4 ∴AD=5-4=1【例2】如图,AC=3,BC=5,且∠BAC=90°,D为AC上一动点,以AD为直径作圆,连接BD 交圆于E 点,连CE,则CE的最小值为()A.13 2 B.13 2 C.5 D.169解:连接AE∵AD为⊙O的直径∴∠AEB=∠AED=90°∴E点在以AB为直径的圆上运动当CE过圆心O′时,CE有最小值为13 2【练】(2015 ·江汉中考模拟1)如图,在△ABC中,AC=3,BC=4 2 ,∠ACB=45°,AM∥BC,点P 在射线AM上运动,连BP 交△APC的外接圆于D,则AD的最小值为()A.1 B.2C.2 D.4 2 3解:连接CD∴∠PAC=∠PDC=∠ACB=45°∴∠BDC=135°如图,当AD过圆心O′时,AD有最小值∵∠BDC=135°∴∠BO′ C=90°∴O′ B=O′ C=4又∠ACO′=90 °∴ AO ′= 5∴AD 的最小值为 5- 4= 1【例 3】(2016 ·勤学早四调模拟 1) 如图,⊙ O 的半径为 2,弦 AB 的长为 2 3 ,点 P 为优弧 AB 上一动点, AC ⊥ AP 交直线 PB 于点 C ,则△ ABC 的面积的最大值是() A .12 6 3 B . 6 3 3 C .12 3 3 D . 6 4 3【练】(2014 ·洪山区中考模拟 1)如图,⊙ O 的半径为 1,弦 AB =1,点 P 为优弧 AB 上一动点, AC ⊥ AP 交直线 PB 于点 C ,则△ ABC 的最大面积是( )A .【例 5】如图,A (1,0)、B (3,0),以 AB 为直径作⊙ M ,射线 OF 交⊙ M 于E 、 F 两点, C 为弧 AB 的中点, D 为 EF 的中点.当射线绕 O 点旋转时, CD 的最小值为 ______ 解 :连接 DM∵ D 是弦 EF 的中点∴DM ⊥EF∴点 D 在以 A 为圆心的, OM 为直径的圆上运动 当 CD 过圆心 A 时, CD 有最小值 连接 CM∵ C 为弧 AB 的中点∴ CM ⊥ AB∴ CD 的最小值为 2 1练 】如图, AB 是⊙ O 的直径, AB =2,∠ABC =60°, P 是上一动点, D 是 AP 的中点,连接 CD ,则 CD 的最小值为 _________ 解 :连接 OD∵ D 为弦 AP 的中点∴OD ⊥AP∴点 D 在以 AO 为直径的圆上运动 当 CD 过圆心 O ′时, CD 有最小值 过点 C 作 CM ⊥ AB 于 M ∵OB =OC ,∠ ABC =60°∴△ OBC 为等边三角形∴ OM = 1 , CM = 322∴ O ′ C = 74∴ CD 的最小值为 7 142 B . C .D . 2。
初中数学线段最值教案

初中数学线段最值教案1. 让学生理解线段的基本概念和性质,掌握线段的表示方法。
2. 培养学生运用线段解决实际问题的能力,提高学生的数学素养。
3. 引导学生通过合作、探究、交流,培养学生的团队精神和创新能力。
二、教学内容1. 线段的基本概念和性质2. 线段的表示方法3. 线段在实际问题中的应用三、教学重点与难点1. 重点:线段的基本概念、性质和表示方法。
2. 难点:运用线段解决实际问题。
四、教学过程1. 导入:利用实物或图片,引导学生观察并说出线段的特点,从而引出线段的概念。
2. 新课讲解:a. 线段的基本概念:线段是有两个端点的直线段,表示为AB,其中A和B为线段的两个端点。
b. 线段的性质:线段有两个端点,有限长,可以度量。
c. 线段的表示方法:用大写字母表示线段的两个端点,如AB;用小写字母表示线段的长度,如AB=5cm。
d. 线段的画法:用直尺和圆规画线段,注意线段的两个端点要清晰标出。
3. 实例讲解:通过实际问题,让学生运用线段的知识解决问题,如计算两点的距离、设计路线等。
4. 练习与巩固:设计一些练习题,让学生独立完成,检验学生对线段知识的掌握程度。
5. 课堂小结:回顾本节课所学内容,让学生总结线段的基本概念、性质和表示方法。
6. 作业布置:布置一些有关线段的练习题,让学生课后巩固所学知识。
五、教学反思本节课通过观察实物、讲解、实例和练习,让学生掌握了线段的基本概念、性质和表示方法。
在教学过程中,要注意引导学生运用线段解决实际问题,提高学生的数学素养。
同时,要关注学生的学习反馈,及时调整教学方法和策略,使学生在轻松愉快的氛围中学习数学。
定弦定角模型的最值问题

课题:定弦定角模型的最值问题
准
备
教学过程设计
〔设计意图:这道题综合性很强,包含三大类型问题:定弦定角问题,双动点最值问题,点圆之间距离最值问题,通过这道题的分析让学生掌握定弦定角模型的最值问题〕
教学反思
1、本节课是九年级总复习中的“定弦定角模型的最值问题〞专题,综合性很强,通过这道题的分析,让学生了解定弦定角模型,并从中找到隐形圆,这是重点和难点,也是解决这类题的关键入口
2、学生对双动点问题不熟悉,学生可以从这道题当中体验转化的思想把不熟悉的双动点问题转化为我们熟悉的单动点问题最终转化点圆距离问题
3、定弦定角模型有关问题是一个难点,学生们要学会从题目中构造出模型,以后也还要多加练习。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最值问题(定弦定角定
线段)
最值问题专题训练
一、定弦定角最值问题
【例1】如图,△ABC中,AC=3,BC=2
4,∠ACB=45°,D为△ABC内一动点,⊙O为△ACD的外接圆,直线BD交⊙O于P点,交BC于E点,弧AE=CP,则AD的最小值为()
A.1 B.2 C.2
D.2
41-
4
【例2】如图,AC=3,BC=5,且∠BAC=90°,D为AC上一动点,以AD为直径作圆,连接BD交圆于E点,连CE,则CE的最小值为()
A.2
13+C.5
13-B.2
16
D.
9
【练习1】如图,在△ABC中,AC=3,BC=2
4,∠ACB=45°,AM∥BC,点P 在射线AM上运动,连BP交△APC的外接圆于D,则AD的最小值为()A.1 B.2 C.2
D.3
4-
2
【例3】如图,⊙O 的半径为2,弦AB 的长为32,点P 为优弧AB 上一动点,AC ⊥AP 交直线PB 于点C ,则△ABC 的面积的最大值是( )
A .3612+
B .336+
C .3312+
D .346+
【练习2】如图,⊙O 的半径为1,弦AB =1,点P 为优弧AB 上一动点,AC ⊥AP 交直线PB 于点C ,则△ABC 的最大面积是( )
A .21
B .22
C .23
D .43
【例4】如图,边长为3的等边△ABC ,D 、E 分别为边BC 、AC 上的点,且BD =CE ,AD 、BE 交于P 点,则CP 的最小值为_________
A B C D P 【例5】如图,A(1,0)、B(3,0),以AB 为直径作⊙M ,射线OF 交⊙M 于E 、F 两点,C 为弧AB 的中点,D 为EF 的中点.当射线绕O 点旋转时,CD 的最小值为__________
【练习3】如图,AB 是⊙O 的直径,AB =2,∠ABC =60°,P 是上一动点,D 是AP 的中点,连接CD ,则CD 的最小值为__________
4.如图,在动点C 与定长线段AB 组成的△ABC 中,AB =6,AD ⊥BC 于点D ,BE ⊥AC 于点E ,连接DE .当点C 在运动过程中,始终有
2
2 AB DE ,则点C 到AB 的距离的最大值是_________
5.如图,已知以BC 为直径的⊙O ,A 为BC 中点,P 为AC 上任意一点,AD ⊥AP 交BP 于D ,连CD .若BC =8,则CD 的最小值为___________
二、定角、定线段与定圆问题
主要是体现在题目中出现了固定度数的角对着固定长度的线段时隐含着一个固定大小的圆,此时定线段为隐圆的一条弦,定角为弦所对的一个圆周角,借助隐圆来分析问题极其方便,关键是要先发现隐含着的特殊度数的角。
举例如下:
例1: 如图,在△ABC中,∠BAC=45°,AH⊥BC于H(H在边BC上),若BH=1,CH=2,则AH=.
例2:如图,扇形AOD中, ∠AOD=90º,OA=6,点P为弧AD上任意一点(不与点A
和D重合),PQ⊥OD于点Q,点I为△OPQ的内心,过O,I和D三点的圆的半径为r.则当点P在弧AD上运动时,r的值满足()
A.0<r<3
B.r=3
C.3<r<32
D. r=32
练习1.如图,在⊙O中,弦AD等于半径,B为优弧AD上的一动点,等腰△ABC 的底边BC所在直线经过点D,若⊙O的半径为1,则OC的长不可能为
()
A. 2-3
B. 3-1
C.2
D. 3+1
2.如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD
于G,
连接BE 交AG 于点H .若正方形的边长为2,则线段DH 长度的最小值是
( ).
3. 如图,在Rt ⊿ABC 中,∠BAC=90º,AB=AC ,BC=42,点D 是AC 边上一动点,连接BD ,以AD 为直径的圆交BD 于E ,连接CE ,则线段CE 长的最小值为
( )
4.如图,△ABC 中,AC=3,BC=42,∠ACB=45º,AM ∥BC ,点P 在射线AM 上运动,连BP 交△ABC 的外接圆于D ,则AD 的最小值为( ) A.1 B.2 C.2 D.2441
5.如图,直径AB 、CD 的夹角为60 º,P 为⊙O 一的个动点(不与点A 、B 、C 、
D 重
合)。
PM ,PN 分别垂直于CD ,AB ,垂足分别为M ,N 。
若⊙O 的半径长为2,则MN 的长 ( ) A. 随P 点运动而变化,最大值为3 B. 等于3 C. 随P 点运动而变化,最小值为3 D. 随P 点运动而变化,没有最值。
6、如图,⊙O的半径为2,弦AB的长为23,以AB为直径作⊙M,点C是优
弧AB上的一个动点,连结AC、BC分别交⊙M于点D、E,则线段CD的最大值为。
A 3
B 2
C 23-2
D 4-23
7. 如图,边长为2的正方形ABCD中,F为CD上一动点,E为AF上一点,且BE=BA, ∠CBE的角平分线交AF的延长线于点G,则G到CD距离的最大值
为。
2,若点P在优弧BAC上由点B向点C移8. 如图,弓形图中, ∠BAC=60°,BC=3
动,记⊿PBC的内心为I,点I随点P的移动所经过的路程为m,则m的取值范围
为()
10. 如图,点C是⊙O上一动点,弦AB=6,∠ACB=120°,⊿ABC内切圆半径r
的最大值为( ) 。
A 6-23
B 4-33
C 6-33
D 6。
