微分几何(宋卫东编著)PPT模板
合集下载
微分几何课件

3、向量函数 r (t )的微商 r (t )仍为 t 的一个向量函数,如果函数 r (t ) 也是连续和可微的,则 r (t )的微商r (t ) 称为 r (t )的二阶微商。
( n) 类似可定义三阶、四阶微商。如r (t ), r (t ).
4、在区间 [t1,t2]上有直到 k 阶连续微商的函数称为这区间上的 k次
微分几何
第一节
向量函数
向量函数的概念:给出一点集 G ,如果对于G 中的每一个 点 x ,有一 个确定的向量 r 和它对应,则说在 G上给定了一个向 量函数,记作 r r ( x), x G, 例如 设G是实数轴上一区间 [t0 , t ] ,则得一元向量函数 r r (t ). 设G是一平面域, (u, v) G,则得二元向量函数 r r (u, v). ( x, y, z ) G,得三元向量函数 r r ( x, y, z) 设G是空间一区域, 1、1 向量函数的极限
例书中的开圆和圆柱螺线。
z
3、曲线的参数方程
坐标式
M
x x(t ) y y (t ) z z (t )
at b
x
o
y
向量式 r (t ) x(t )e1 y(t )e2 z(t )e3
例1、 开圆弧
x a cos t y a sin t
t (0, 2 )
1、5 向量函数的积分
c b (1)当a<c<b时有 a r (t )dt a r (t )dt c r (t )dt b b (2)m 是常数时有 mr (t )dt m r (t )dt
a
b
a (3)如果 m 是常向量,则有
【精品PPT】微分学课件

u v,
(u+v+…+ω)′=
u vω .
(2)积的导数:(uv)′= uv uv,
特例:(cu)′= cu (c为常数).
(3)商的导数: u =
uv - uv v2 (v≠0).
v
例1 设 y x4,则 y '
例2 求 y x3 2x2 sin x 的导数 .
f (x0 )
f(x0 )
lim
x0
y x
lim x0
f (x0 x) x
f (x0 )
注意 函数在一点可导的充分必要条件为:
f' (x0 ) f' (x0 )
导函数
(1)如果函数 y f (x)在开区间(a,b)内的每一点都可导,
就称函数 f (x)在开区间(a,b) 内可导.
y
y f (x)
T
M
o
x0
x
在(x0, f (x0 ))处的
切线方程为 y y0 f ( x0 )( x x0 ). 每年都考、重点掌握!
法线方程为
y y0
f
1 ( x0
)
(
x
x0
)
(f (x0 ) 0).
例1、曲线 y 2x2在点(1,2)处的切线方程为:.
A. y x 1 B. y x C. y x 1 D. y x
例. 曲线 y 3 x 在点 (0,0) 处的切线方程为(
)
A、 x 0
B、 y 0
C、 x y
例. 设 y (1 x2 ) arctan x, 求 y/
D、不存在
微分几何office2003

返回章首
1.2 向量分析-向量函数极限的计算
定理. 设 r(t) = (x(t), y(t), z(t)),a = (x0, y0, z0) , lim r (t ) a 当且仅当 则
t t0
lim x(t ) x0 , lim y (t ) y0 ,
t t0 t t0
lim z (t ) z0 .
t t0
这个定理表明对向量函数求极限就是对它的 每个分量求极限.这样,向量函数的极限就转 化成普通函数的极限.
返回章首
1.2 向量分析-向量函数的极限的性质
推论. (极限的运算性质)设当 t→t0 时, 有 r(t) → a ,s(t) → b ,l(t) → c ,则我们 有: r(t)±s(t) → a±b,l(t)r(t) → ca. r(t) ⋅ s(t) → a ⋅ b. r(t)×s(t) → a×b.
返回章首
1.1 向量代数-两个不等式
定理. 对任意的两个向量 a、b∈R3 有下 面两个不等式成立: 许瓦滋不等式 a ⋅ b ≤ |a| ⋅ |b|. 闵可夫斯基不等式 |a + b| ≤ |a| + |b|. 这两个不等式中的等式成立的充分必要条 件是 a∥b.
返回章首
1.1 向量代数-两向量的夹角
返回章首
1.2 向量分析-具有固定长度和固定方向的向量函数
可导的向量函数 r(t) 具有固定长度的充要条 件是 r' (t) 垂直于 r(t). 可导的向量函数 r(t) 具有固定方向的充要条 件是 r' (t) 平行于 r(t).
看证明
返回章首
1.2 向量分析-一元向量函数的链式法则
定理. (一元向量函数的链式法则)设 r(u) 可微的向量函数,u = u(t) 是可微的普通函 数,则复合函数 r(t) = r(u(t)) 也可微,并 且
多元函数微分学的几何应用ppt课件

9.6 多元函数微分学的几何应用
2. 空间曲线的方程为 两个柱面 的交线
x
设曲线直角坐标方程为
x0 y y0 z z0
y z
y( x) ,
z( x)
x(t0 ) y(t0 ) z(t0 )
x x
令
x为参数,
曲线的参数方程是
y
y(
x)
z z( x) 由前面得到的结果, 在M(x0, y0, z0)处,
5
9.6 多元函数微分学的几何应用
(3)向量值函数的图像
设向量 r 的起点在坐标原点,则终
点M随t的改变而移动,点M的轨迹 Γ
称为向量值函数 r=f(t) 的终端曲 x
线,也称为该函数的图像,记作Γ
反过来,向量值函数
z
•M
rf
(t)
o
y
r f (t) ( f1(t), f2 (t), f3 (t))
f (2) (4,4,2), f (2) 42 42 22 6.
所求单位切向量一个是:(4,4,2) 2 , 2 , 1 6 3 3 3
另一个是: 2 , 2 , 1
其指向与t的增长方向一致
3 3 3 其指向与t的增长方向相反
16
9.6 多元函数微分学的几何应用
二、空间曲线的切线与法平面
lim
t t0
f
(t)
r0
7
9.6 多元函数微分学的几何应用
说明 设 f (t) ( f1(t), f2(t), f3(t))
r 0 (m, n, p),
则lim f (t) t t0
r0
lltt iimmtt00
f1(t) f3(t)
m,
《微分的概念》课件

《微分的概念》ppt课 件
目录 CONTENT
• 引言 • 微分的定义 • 微分的性质 • 微分法则 • 微分的应用 • 习题与答案
01
引言
微分的重要性和应用
微分是数学分析中的基本概念,对于理解函数的变化规律和解决实际问题 具有重要意义。
在科学、工程、经济等领域,微分被广泛应用于优化问题、预测模型、控 制系统等方面。
04
微分法则
和差法则
总结词
和差法则是指函数和差运算的微分规则,即 两个函数的和或差的微分等于它们各自微分 的和或差。
详细描述
设函数$u(x)$和$v(x)$在某点$x$处可导, 则$(u+v)'=u'+v'$,$(u-v)'=u'-v'$。
幂的微分法则
总结词
幂的微分法则是表示幂函数导数的规 则,即幂函数的导数等于该函数的指 数乘以自变量的导数。
03
微分的性质
线性性质
总结词
பைடு நூலகம்线性性质是微分学中的一个基本性质,它表明函数的一阶导数在一定条件下具有线性性质。
详细描述
如果函数y=f(x)在某点的导数f'(x)存在,且常数a和b都存在,那么函数a*f(x)+b的导数等于a*f'(x)。这 个性质在求复杂函数的导数时非常有用,因为它可以将复杂的函数拆分成几个简单的部分来分别求导 。
详细描述
设函数$x^n$在某点$x$处可导,则 $(x^n)'=n x^{n-1}$。
常数微分法则
要点一
总结词
常数微分法则是表示常数函数导数的规则,即常数函数的 导数为0。
要点二
详细描述
设常数$c$在某点$x$处可导,则$(c)'=0$。
目录 CONTENT
• 引言 • 微分的定义 • 微分的性质 • 微分法则 • 微分的应用 • 习题与答案
01
引言
微分的重要性和应用
微分是数学分析中的基本概念,对于理解函数的变化规律和解决实际问题 具有重要意义。
在科学、工程、经济等领域,微分被广泛应用于优化问题、预测模型、控 制系统等方面。
04
微分法则
和差法则
总结词
和差法则是指函数和差运算的微分规则,即 两个函数的和或差的微分等于它们各自微分 的和或差。
详细描述
设函数$u(x)$和$v(x)$在某点$x$处可导, 则$(u+v)'=u'+v'$,$(u-v)'=u'-v'$。
幂的微分法则
总结词
幂的微分法则是表示幂函数导数的规 则,即幂函数的导数等于该函数的指 数乘以自变量的导数。
03
微分的性质
线性性质
总结词
பைடு நூலகம்线性性质是微分学中的一个基本性质,它表明函数的一阶导数在一定条件下具有线性性质。
详细描述
如果函数y=f(x)在某点的导数f'(x)存在,且常数a和b都存在,那么函数a*f(x)+b的导数等于a*f'(x)。这 个性质在求复杂函数的导数时非常有用,因为它可以将复杂的函数拆分成几个简单的部分来分别求导 。
详细描述
设函数$x^n$在某点$x$处可导,则 $(x^n)'=n x^{n-1}$。
常数微分法则
要点一
总结词
常数微分法则是表示常数函数导数的规则,即常数函数的 导数为0。
要点二
详细描述
设常数$c$在某点$x$处可导,则$(c)'=0$。
《大学数学解析几何》PPT课件

➢笛卡尔的《几何》虽然不像现在的解析几何那样,给读者展现 出一个从建立坐标系和方程到研究方程的循序过程,但是他通过 具体的实例,确定表达了他的新思想和新方法.这种思想和方法 尽管在形式上没有现在的解析几何那样完整,但是在本质上它却 是地道的解析几何.
➢笛卡尔的解析几何有两个基本思想: (1)用有序数对表示点的坐标; (2)把互相关联的两个未知数的代数方程,看成平面上的一 条曲线。
Back
四、学习要求
1、课前预习. 2、课上认真听讲,积极思考,记好笔记. 3、课后及时复习,独立认真地完成作业. 4、课外适当阅读课外参考书,拓宽知识面,加深对课本内 容的理解.
Back
五、考核方式及成绩评定
考核方式:闭卷考试 总评成绩=平时成绩×30%
+期末考试成绩70%
《解析几何》
-Chapter 1
Back
3.解析几何创立的意义
➢ 笛卡尔和费马创立解析几何,在数学史上具有划时代的意义。
➢解析几何沟通了数学内数与形、代数与几何等最基本对象之间 的联系,从此,代数与几何这两门学科互相吸取营养而得到迅速 发展,并结合产生出许多新的学科,近代数学便很快发展起来了。
➢恩格斯高度评价了笛卡尔的革新思想。他说:“数学中的转折 点是笛卡儿的变数。有了变数,运动进入了数学;有了变数,辩 证法进入了数学;有了变数,微分和积分也就立刻成为必要的 了。”
关于解析几何产生的历史,可以查阅数学史方面的 书,例 如李文林的《数学史概论》(高等教育出版社),或 上网查阅 查关的内容,网址:
/2/22/07/0641.htm
Back
二、本课程的主要内容及基本要求
本课程在中学平面向量和平面解析几何的基础上,进一步 学习空间向量和空间解析几何。主要内容有:
➢笛卡尔的解析几何有两个基本思想: (1)用有序数对表示点的坐标; (2)把互相关联的两个未知数的代数方程,看成平面上的一 条曲线。
Back
四、学习要求
1、课前预习. 2、课上认真听讲,积极思考,记好笔记. 3、课后及时复习,独立认真地完成作业. 4、课外适当阅读课外参考书,拓宽知识面,加深对课本内 容的理解.
Back
五、考核方式及成绩评定
考核方式:闭卷考试 总评成绩=平时成绩×30%
+期末考试成绩70%
《解析几何》
-Chapter 1
Back
3.解析几何创立的意义
➢ 笛卡尔和费马创立解析几何,在数学史上具有划时代的意义。
➢解析几何沟通了数学内数与形、代数与几何等最基本对象之间 的联系,从此,代数与几何这两门学科互相吸取营养而得到迅速 发展,并结合产生出许多新的学科,近代数学便很快发展起来了。
➢恩格斯高度评价了笛卡尔的革新思想。他说:“数学中的转折 点是笛卡儿的变数。有了变数,运动进入了数学;有了变数,辩 证法进入了数学;有了变数,微分和积分也就立刻成为必要的 了。”
关于解析几何产生的历史,可以查阅数学史方面的 书,例 如李文林的《数学史概论》(高等教育出版社),或 上网查阅 查关的内容,网址:
/2/22/07/0641.htm
Back
二、本课程的主要内容及基本要求
本课程在中学平面向量和平面解析几何的基础上,进一步 学习空间向量和空间解析几何。主要内容有:
微分ppt课件

微分PPT课件
目录
微分的定义与性质导数的概念与性质导数在研究函数中的应用微分中值定理微分的应用
01
CHAPTER
微分的定义与性质
总结词
微分是一种数学运算,表示函数在某一点的局部变化率。
详细描述
微分是微积分的基本概念之一,它表示函数在某一点的切线的斜率。具体来说,如果函数在某一点的导数存在,那么这个导数就是函数在该点的微分。微分可以看作是函数值的增量与自变量增量的比的极限。
极值点是函数的重要特征点,利用导数研究函数的极值有助于找到这些关键点。
1
2
3
4
通过求二阶导数,可以找到函数的拐点。
二阶导数为0的点可能是拐点,需要进一步判断三阶导数的符号来确定是向上凸还是向下凸。
对于函数$f(x) = x^4$,其二阶导数$f''(x) = 12x^2$,令其为0得到拐点$x=0$,进一步求三阶导数$f'''(x) = 24x$,在$x=0$处为非正值,因此$x=0$为向下凸的拐点。
举例
单调性是函数的一个重要性质,利用导数研究函数的单调性有助于理解函数的述
举例
应用
通过求导数,可以找到函数的极值点。
一阶导数为0的点可能是极值点,需要进一步判断二阶导数的符号来确定是极大值还是极小值。
对于函数$f(x) = x^3$,其一阶导数$f'(x) = 3x^2$,令其为0得到极值点$x=0$,进一步求二阶导数$f''(x) = 6x$,在$x=0$处为非负值,因此$x=0$为极小值点。
罗尔定理是数学分析中的一个基本定理,由法国数学家罗尔发现。该定理在微分学、积分学等领域有着广泛的应用。它提供了一个判断函数是否存在导数为零的点的方法,对于研究函数的极值和拐点等问题具有重要的意义。
目录
微分的定义与性质导数的概念与性质导数在研究函数中的应用微分中值定理微分的应用
01
CHAPTER
微分的定义与性质
总结词
微分是一种数学运算,表示函数在某一点的局部变化率。
详细描述
微分是微积分的基本概念之一,它表示函数在某一点的切线的斜率。具体来说,如果函数在某一点的导数存在,那么这个导数就是函数在该点的微分。微分可以看作是函数值的增量与自变量增量的比的极限。
极值点是函数的重要特征点,利用导数研究函数的极值有助于找到这些关键点。
1
2
3
4
通过求二阶导数,可以找到函数的拐点。
二阶导数为0的点可能是拐点,需要进一步判断三阶导数的符号来确定是向上凸还是向下凸。
对于函数$f(x) = x^4$,其二阶导数$f''(x) = 12x^2$,令其为0得到拐点$x=0$,进一步求三阶导数$f'''(x) = 24x$,在$x=0$处为非正值,因此$x=0$为向下凸的拐点。
举例
单调性是函数的一个重要性质,利用导数研究函数的单调性有助于理解函数的述
举例
应用
通过求导数,可以找到函数的极值点。
一阶导数为0的点可能是极值点,需要进一步判断二阶导数的符号来确定是极大值还是极小值。
对于函数$f(x) = x^3$,其一阶导数$f'(x) = 3x^2$,令其为0得到极值点$x=0$,进一步求二阶导数$f''(x) = 6x$,在$x=0$处为非负值,因此$x=0$为极小值点。
罗尔定理是数学分析中的一个基本定理,由法国数学家罗尔发现。该定理在微分学、积分学等领域有着广泛的应用。它提供了一个判断函数是否存在导数为零的点的方法,对于研究函数的极值和拐点等问题具有重要的意义。
微分几何的ppt

射影微分几何起始于1878年阿尔方的学位论文,后来1906年 起经以威尔辛斯基为代表的美国学派所发展,1916年起又经 以富比尼为首的意大利学派所发展。
二十世纪二、三十年代E.Cartan开创并发展了外微分形式与 活动标架法,建立起李群与微分几何之间的联系,从而为微 分几何的发展奠定了重要基础且开辟了广阔的园地,影响极 为深远。陈省身将Cartan的方法发扬光大,他关于纤维丛和 示性类的理论,建立了微分几何与拓扑的联系,是一个光辉 的里程碑。
0下载券文档一键搜索 VIP用户可在搜索时使用专有高级功能:一键搜索0下载券文档,下载券不够用不再有压力!
内容特 无限次复制特权 权 文档格式转换
VIP有效期内可以无限次复制文档内容,不用下载即可获取文档内容 VIP有效期内可以将PDF文档转换成word或ppt格式,一键转换,轻松编辑!
阅读页去广告
如果考虑洛伦茨流形到黎曼流形的调和映射,就归结为双曲型偏微 分方程的整体解的存在性问题,这方面成果国际上较少,谷超豪证 明了闵科夫斯基平面到完备黎曼流形的调和映射的柯西问题的整体 存在性定理,某些调和映射在物理学中称为非线性σ模型,是物理 学家独立地提出的。
有些微分几何学问题还必须求解“真正”非线性偏 微分方程,这是比拟线性方程的非线性程度更高 的偏微分方程,其难度更大,突出的事项是丘成 桐解决了由卡拉皮所提出的一个猜想,证明了某 种爱因斯坦-凯勒流形的存在定理,这需要求解复 蒙日-安培方程,它的非线性程度更高,需要有高 度的分析技巧。丘成桐还解决了一系列的其他的 与买的VIP时长期间,下载特权不清零。
100W优质文档免费下 载
VIP有效期内的用户可以免费下载VIP免费文档,不消耗下载特权,非会员用户需要消耗下载券/积分获取。
《微分几何》PPT课件

3点到平面的距离:
点M 0 x0 , y0 , z0 到平面Ax By Cz D 0的距离
d Ax0 By0 Cz0 D A2 B2 C 2
结论:
平面
1:A1x B1 y C1z D1 0 2:A2 x B2 y C2 z D2 0
1 // 2
n1 // n2
n A, B, C为平面的法向量 , D 0平面过坐标原点,A=0
平面过x轴,A B 0平面平行于xoy面.
2 两平面的夹角
1:A1x B1 y C1z D1 0
2:A2 x B2 y C2 z D2 0
cos n1 n2
n1 n2
A1 A2 B1B2 C1C2 A12 B12 C12 A22 B22 C22
椭
球
面:
x2 a2
y2 b2
z2 c2
1
y
o x
z
椭圆抛物面:
x2 a2
y2 b2
2z
y
o
x
双曲抛物面:- x2 a2
y2 b2
2z
单叶双曲面:x 2 a2
y2 b2
z2 c2
1
双叶双曲面:x2 y2 z 2 1 a2 b2 c2
二
次
锥面:x 2 a2
y2 b2
z2 c2
0
z
o x
z
o x
a b a b sin a b
a b的方向垂直于 a与 b决定的平面,a b的指向 按右手规则,从 a转向 b,大拇指的指向即 a b 的方向.
i jk a b ax ay az
bx by bz
aybz azby i azbx axbz j axby aybx k
微分几何-§3-曲面的第二基本形式PPT优秀课件

k
n
f
( p,
du ) dv
S上点p的切方向d和曲面的法向确定的平面称为曲面 上一点处沿切方向的法截面 ,法截面 和曲面的交线 就是P点处沿切方向的法截线 对法曲率,是否存在一条曲线使得这条曲线的曲率就 是法曲率呢?只要 cos 1即可,这就是法截线
n
7
梅尼埃定理:曲面上曲线 在给定点p处的曲率中
证明:因为直线的曲率 k 0 ,所以沿直线方向的 法曲率 kn kcos0,即
Ld u22M d u d vNd v20
因而直线是曲面的渐近曲线.
13
命题2 曲面在渐进线上一点的切平面一定是渐进曲 线的密切平面
证明:沿渐近曲线有 kn kcos0得到
k0或 cos0.
当 k 0 时, 渐近曲线是直线,这时曲面的切平面
计算公式2:因为 n d r 0 d n d r n d 2 r 0
所以 IIdndr 可得
L n u r u , M r u n v , N n v r v
3
例1 求球面 r { R c o sc o s,R c o ss i n ,R s i n }
的第二基本形式
解:n {cos cos , cos sin , sin }
I Ed2 u2FduG dvd2 v
只要在p点及与C相切的曲线,这个值不变,这就是曲面 在P点沿C方向的法曲率 定义3.4.2 设点P是曲面上曲线C上一点, k是C在点p 的曲率,. 则称 k 为C在点p的曲率向量, 称 k n 为在 曲面S上的点P处沿曲线C的切方向的法曲率.记为 k n
6
曲面法曲率是曲面上点P和方向 (d ) 的函数 同一点只要方向相同,则法曲率相同
所以第二基本形式 II (R co s2d 2R d 2)
【精品PPT】微分学课件

解 y eu,u x3,
dy dy du dx du dx
eu 3x2 ex3 3x2.
例2 求函数 y ln sin x 的导数.
解 y ln u, u sin x.
dy dy du 1 cos x cos x cot x
y
y f (x)
T
M
o
x0
x
在(x0, f (x0 ))处的
切线方程为 y y0 f ( x0 )( x x0 ). 每年都考、重点掌握!
法线方程为
y y0
f
1 ( x0
)
(
x
x0
)
(f (x0 ) 0).
例1、曲线 y 2x2在点(1,2)处的切线方程为:.
x
2
1
1 2
2x x2
1
y
x
2
1
1 2
2x x2
1
(
x 1)2 x2 1
说明:
对幂指函数 y uv 可用对数求导法求导 :
ln y v lnu
1 y vln u uv
y
u
y uv ( vln u uv ) u
解: y' 4 x
y' |x1 4
根据导数的几何意义, 得切线斜率为 k y x1 4 故曲线 y 2x2在点(1,2)处的切线方程为
y 2 4(x 1)
即 y 4x 2
4、 函数的可导性与连续性的关系
可导的函数一定是连续的.
微分的概念ppt课件
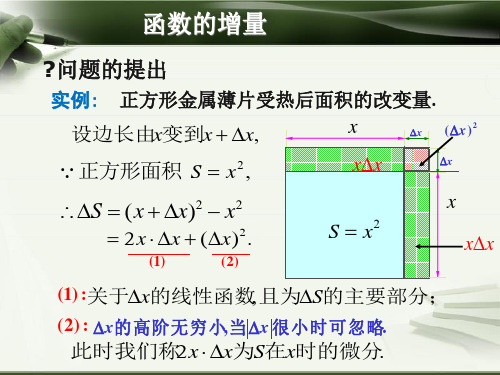
例2 求函数 y x3 当 x 2, x 0.02时的y以及微分. 解: y (x x)3 x3 (2 0.02 )3 23 0.242408
dy ( x3 )x 3x2x.
dy x2 3 x 2x x2 0.24.
x 0.02
x 0.02
y dy o(x), 可见y, dy虽然近似但是还是有差 异
即 y f (x) ,
x
从而 y f (x) x (x), 0 (x 0),
f (x) x o(x),
函数 f (x)在点 x可微, 且 f (x) A.
可微 可导. A f (x).
函数 y f ( x)在任意点x的微分, 称为函数的 微分, 记作 dy或 df ( x), 即 dy f ( x)x.
PQ
MQ tanx
f
'(x0 )dx
从图可见y是函数的纵坐标增量,
dy.
dy就是切线纵坐标对应的增量.
2.3.3 微分的基本公式
一阶微分形式的不变性 dy f ( x)dx 基本求法: 计算函数的导数, 乘以自变量的微分.
1.基本初等函数的微分公式
d(C) 0
d( x ) x1dx
d(sin x) cos xdx
当x x0 x,则有: f (x) f (x0 ) f '(x0 )(x x0 ).
该公式可以用于近似计算。
例7 求 9.09的近似值. 解 设函数f (x) x , x0 9, x 9.09,则
f (x0 ) 3,f '(x0 ) 1/6,x x0 0.09 f (x) f (x0 ) f '(x0 )( x x0 )
可导性是等价的,所以有人说“微分就是导 数,导数就是微分”,这说法对吗?
微分几何第二章

返回章首
2.1 曲线的概念
一元向量函数 r(t) 所描绘的图形 C 叫曲线, r(t)叫曲线 C 的参数化,或者叫曲线的向量函 数,t 叫曲线的参数.曲线 C 连同它的参数化 r(t) 一起叫参数曲线.
参数曲线用 C : r = r(t) 表示.如果对某个 t0 使得 r'(t0) ≠ 0,就称 r(t0)(或者简称 t0)是曲 线的正则点.如果曲线上处处是正则点,就称 该曲线是正则曲线,相应的参数叫正则参数.
解:直接计算得
r' (t) = (– sint, cost, 1),
r'' (t) = (– cost, – sint, 0). 在给定点 P 处的参数 t = 0,所以有 r' (0) = (0,1,1),r'' (0) = (– 1,0,0). 代入上面的基本向量计算公式得
α 1 (0,1,1), β (1, 0, 0), γ 1 (0, 1,1).
k ( x)
1
| y | ( y)2
3/ 2
.
平面曲线为直线的充分必要条件是其曲率
为零.
返回章首
2.2 平面曲线-例子
例. 求椭圆 (x2/a2) + (y2/b2) = 1 的曲率.
解:椭圆可参数化为 r(t) = (a cost, b sint), 参数方程为 x = acost, y = bsint,所以有
t O cost
返回章首
2.1 曲线的概念 -曲线的例子抛物线
抛物线. 曲线 C: r = (x, x2), x∈(–∞, +∞) 也 是一条正则曲线,它是抛物线.
返回章首
2.1 曲线的概念 -曲线的例子圆柱螺线
2.1 曲线的概念
一元向量函数 r(t) 所描绘的图形 C 叫曲线, r(t)叫曲线 C 的参数化,或者叫曲线的向量函 数,t 叫曲线的参数.曲线 C 连同它的参数化 r(t) 一起叫参数曲线.
参数曲线用 C : r = r(t) 表示.如果对某个 t0 使得 r'(t0) ≠ 0,就称 r(t0)(或者简称 t0)是曲 线的正则点.如果曲线上处处是正则点,就称 该曲线是正则曲线,相应的参数叫正则参数.
解:直接计算得
r' (t) = (– sint, cost, 1),
r'' (t) = (– cost, – sint, 0). 在给定点 P 处的参数 t = 0,所以有 r' (0) = (0,1,1),r'' (0) = (– 1,0,0). 代入上面的基本向量计算公式得
α 1 (0,1,1), β (1, 0, 0), γ 1 (0, 1,1).
k ( x)
1
| y | ( y)2
3/ 2
.
平面曲线为直线的充分必要条件是其曲率
为零.
返回章首
2.2 平面曲线-例子
例. 求椭圆 (x2/a2) + (y2/b2) = 1 的曲率.
解:椭圆可参数化为 r(t) = (a cost, b sint), 参数方程为 x = acost, y = bsint,所以有
t O cost
返回章首
2.1 曲线的概念 -曲线的例子抛物线
抛物线. 曲线 C: r = (x, x2), x∈(–∞, +∞) 也 是一条正则曲线,它是抛物线.
返回章首
2.1 曲线的概念 -曲线的例子圆柱螺线
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
微分几何(宋卫东编著)
演讲人
2 0 2 X - 11 - 11
目录
01. 第一章 预备知识
02. 第二章 曲线论
03. 第三章 曲面的局部性质 04. 第四章 联络
05. 第五章 曲面的一些整体 性质
06. 第六章 微分流形初步
07. 主要参考文献
第一章 预备 知识
第一章 预备知识
0 1
1.1 欧氏空 间的基本概念
5.5.1 全平均曲率
5.5.2 环面的全平 均曲率
第六章 微分 流形初步
第六章 微 分流形初步
0 1
6.1 微分流 形的定义
0 4
6.4 流形上 的切向量场
0 2
6.2 流形在 一点的切空间
0 5
6.5 仿射联 络
0 3
6.3 Riemann空间
0 6
习题
第六章 微 分流形初步
6.4 流形上的切向量 场
1.1.4 连通集
0 5
1.1.5 紧致性
第一章 预备知识
1.2 向量函数
01 1 .2 .1 向 量 函 数 的
极限
02 1 .2 .2 向 量 函 数 的
连续性
03 1 .2 .3 向 量 函 数 的
微 导 , Ta y l o r 公 式
04 1 .2 .4 向 量 函 数 的
05 1 .2 .5 向 量 函 数 的
0 4
1.4 Grassmann积
0 2
1.2 向量函 数
0 5
1.5 p-形式 及外代数
0 3
1.3 一次形 式
0 6
1.6 外微分d
第一章 预备知识
习题
第一章 预 备知识
1.1 欧氏空间的基本概 念
0 1
1.1.1 n维欧
氏空间
0 2
1.1.2 邻域
开集 闭集
0 3
1.1.3
同胚
连续性
0 4
3.2.3 等距对 应
3.2.2 第一基 本形式
3.2.4 共形对 应
第三章 曲面的局部性质
3.4 曲面上的曲率
3.4.2 主曲 率 主方向
3.4.1 法 曲率
3.4.3 Gauss曲率 平均曲率
第三章 曲面 的局部性质
3.5 曲面上的一些重要曲线
1 3.5.1 曲 率线
3 3.5.3 测 地线
2.6.4 空间曲 线的球面像
第二章 曲 线论
2.7 曲线的一些整体性 质
2.7.2 平面 曲线的几个 整体性质
2.7.1 曲线 的有关概念
2.7.3 空间 曲线的某些 整体性质
第三章 曲面 的局部性质
第三章 曲面 的局部性质
3.1 曲面 的概念
3.6 特殊
01
曲 面 06
3.2 曲面 的第一基 02 本 形 式
V<sup>p</sup>
0 3 1.5.3 外代数(Grassmann代数)
第二章 曲线 论
第二章 曲线论
2.1 曲线的一般概念
2.3 空间曲线的基本 公式
2.5 曲线论的基本定 理
2.2 空间曲线的活动 标架(基本三棱形)
2.4 曲率和挠率
2.6 几种特殊曲线
第二章 曲线论
2.7 曲线的一些整体性质 习题
06
习题
第五章 曲面的一些整体性质
5.3 Gauss-Bonnet公式
5.3.1 局部 的GaussBonnet公式
5.3.2 整体 的GaussBonnet公式
第五章 曲面的一些整体性质
5.4 凸曲面与积分公式
5.4.1 凸 曲面
1
5.4.2 积 分公式
2
第五章 曲面的 一些整体性质
5.5 全平均曲率与Willmove猜 想
第二章 曲线论
2.1 曲线的一般概念
2.1.1 曲线的概念
2.1.2 曲线的弧长 自然参数
第二章 曲线论
2.4 曲率和挠率
2.4.1 曲 率和挠率的 计算
2.4.2 曲 率和挠率的 几何意义
第二章 曲线论
2.6 几种特殊曲线
2.6.1 平面曲 线
2.6.3 曲线在 一点的密切圆
2.6.2 球面曲 线
积分
几个常用性质
第一章 预备知识
1.3 一次形式
1.3.1 一 次形式的定 义
1.3.2 一 次形式组成 的空间
第一章 预备知识
1.4 Grassman引
理
01
1.4.1 Grassmann积的
定义及其简单性质
第一章 预备知识
1.5 p-形式及外代数
0 1 1.5.1 V<sup>2</sup>-空间 0 2 1.5.2 p-形式及空间
3.5 曲
05
面上的一
些重要曲
线
04
3.4 曲面 上的曲率
03 3 . 3 曲 面的第二 基本形式
第三章 曲面的局部性质
3.7 曲面论的基本定理 习题
第三章 曲面的局部性质
3.1 曲面的概念
3.1.1 曲面的表示
3.1.2 切平面与法 向量
第三章 曲面 的局部性质
3.2 曲面的第一基本形 式
3.2.1 曲面上 的光滑函数
3.5.5 三
5 种重要曲 线之间的 关系
2 3.5.2 渐 近曲线
3.5.4 三
4 种重要曲 线的等价 命题
第三章 曲面的局部性质
3.6 特殊曲面
3.6.1 极小曲 面
3.6.3 可展曲 面
3.6.2 常曲率 曲面
3.6.4 单参数 平面族的包络面
第三章 曲面 的局部性质
3.7 曲面论的基本定 理
04 4.4
4.2
02 络
测地线
曲面上的联
05 习题
4.3 联络的曲率
03 张量
第五章 曲面的 一些整体性质
一第 些五 整章 体 性曲 质面
的
01
5.1 整体 曲面
04
5.4 凸曲 面与积分公
式
02
5.2 球面 的刚性
05
5.5 全平均 曲率与
Willmove猜 想
03 5.3 GaussBonnet公式
6.4.1 基本 概念
6.4.2 Poisson括号积
6.4.3 光滑切 向量场的积分曲
线
第六章 微分流形初步
6.5 仿射联络
0 1 6.5.1 仿射联络的定义及局部表示 0 2 6.5.2 仿射联络的存在性定理 0 3 6.5.3 仿射联络的挠率和曲率
主要参考文献
主要参考文献
感谢聆听
3.7.2 曲面 的基本方程
3.7.1 曲面 的基本公式
3.7.3 曲面 论的基本定 理
第四章 联络
第四章 联络
4.1 曲面上的向
01 量场
4.1.1 曲面上的光滑函数 4.1.2 曲面S在点p∈S的切向量 X<sub>p</sub> 4.1.3 曲面S上的切向量场 4.1.2 曲面S在点p∈S的切向量 X<sub>p</sub> 4.1.3 曲面S上的切向量场
演讲人
2 0 2 X - 11 - 11
目录
01. 第一章 预备知识
02. 第二章 曲线论
03. 第三章 曲面的局部性质 04. 第四章 联络
05. 第五章 曲面的一些整体 性质
06. 第六章 微分流形初步
07. 主要参考文献
第一章 预备 知识
第一章 预备知识
0 1
1.1 欧氏空 间的基本概念
5.5.1 全平均曲率
5.5.2 环面的全平 均曲率
第六章 微分 流形初步
第六章 微 分流形初步
0 1
6.1 微分流 形的定义
0 4
6.4 流形上 的切向量场
0 2
6.2 流形在 一点的切空间
0 5
6.5 仿射联 络
0 3
6.3 Riemann空间
0 6
习题
第六章 微 分流形初步
6.4 流形上的切向量 场
1.1.4 连通集
0 5
1.1.5 紧致性
第一章 预备知识
1.2 向量函数
01 1 .2 .1 向 量 函 数 的
极限
02 1 .2 .2 向 量 函 数 的
连续性
03 1 .2 .3 向 量 函 数 的
微 导 , Ta y l o r 公 式
04 1 .2 .4 向 量 函 数 的
05 1 .2 .5 向 量 函 数 的
0 4
1.4 Grassmann积
0 2
1.2 向量函 数
0 5
1.5 p-形式 及外代数
0 3
1.3 一次形 式
0 6
1.6 外微分d
第一章 预备知识
习题
第一章 预 备知识
1.1 欧氏空间的基本概 念
0 1
1.1.1 n维欧
氏空间
0 2
1.1.2 邻域
开集 闭集
0 3
1.1.3
同胚
连续性
0 4
3.2.3 等距对 应
3.2.2 第一基 本形式
3.2.4 共形对 应
第三章 曲面的局部性质
3.4 曲面上的曲率
3.4.2 主曲 率 主方向
3.4.1 法 曲率
3.4.3 Gauss曲率 平均曲率
第三章 曲面 的局部性质
3.5 曲面上的一些重要曲线
1 3.5.1 曲 率线
3 3.5.3 测 地线
2.6.4 空间曲 线的球面像
第二章 曲 线论
2.7 曲线的一些整体性 质
2.7.2 平面 曲线的几个 整体性质
2.7.1 曲线 的有关概念
2.7.3 空间 曲线的某些 整体性质
第三章 曲面 的局部性质
第三章 曲面 的局部性质
3.1 曲面 的概念
3.6 特殊
01
曲 面 06
3.2 曲面 的第一基 02 本 形 式
V<sup>p</sup>
0 3 1.5.3 外代数(Grassmann代数)
第二章 曲线 论
第二章 曲线论
2.1 曲线的一般概念
2.3 空间曲线的基本 公式
2.5 曲线论的基本定 理
2.2 空间曲线的活动 标架(基本三棱形)
2.4 曲率和挠率
2.6 几种特殊曲线
第二章 曲线论
2.7 曲线的一些整体性质 习题
06
习题
第五章 曲面的一些整体性质
5.3 Gauss-Bonnet公式
5.3.1 局部 的GaussBonnet公式
5.3.2 整体 的GaussBonnet公式
第五章 曲面的一些整体性质
5.4 凸曲面与积分公式
5.4.1 凸 曲面
1
5.4.2 积 分公式
2
第五章 曲面的 一些整体性质
5.5 全平均曲率与Willmove猜 想
第二章 曲线论
2.1 曲线的一般概念
2.1.1 曲线的概念
2.1.2 曲线的弧长 自然参数
第二章 曲线论
2.4 曲率和挠率
2.4.1 曲 率和挠率的 计算
2.4.2 曲 率和挠率的 几何意义
第二章 曲线论
2.6 几种特殊曲线
2.6.1 平面曲 线
2.6.3 曲线在 一点的密切圆
2.6.2 球面曲 线
积分
几个常用性质
第一章 预备知识
1.3 一次形式
1.3.1 一 次形式的定 义
1.3.2 一 次形式组成 的空间
第一章 预备知识
1.4 Grassman引
理
01
1.4.1 Grassmann积的
定义及其简单性质
第一章 预备知识
1.5 p-形式及外代数
0 1 1.5.1 V<sup>2</sup>-空间 0 2 1.5.2 p-形式及空间
3.5 曲
05
面上的一
些重要曲
线
04
3.4 曲面 上的曲率
03 3 . 3 曲 面的第二 基本形式
第三章 曲面的局部性质
3.7 曲面论的基本定理 习题
第三章 曲面的局部性质
3.1 曲面的概念
3.1.1 曲面的表示
3.1.2 切平面与法 向量
第三章 曲面 的局部性质
3.2 曲面的第一基本形 式
3.2.1 曲面上 的光滑函数
3.5.5 三
5 种重要曲 线之间的 关系
2 3.5.2 渐 近曲线
3.5.4 三
4 种重要曲 线的等价 命题
第三章 曲面的局部性质
3.6 特殊曲面
3.6.1 极小曲 面
3.6.3 可展曲 面
3.6.2 常曲率 曲面
3.6.4 单参数 平面族的包络面
第三章 曲面 的局部性质
3.7 曲面论的基本定 理
04 4.4
4.2
02 络
测地线
曲面上的联
05 习题
4.3 联络的曲率
03 张量
第五章 曲面的 一些整体性质
一第 些五 整章 体 性曲 质面
的
01
5.1 整体 曲面
04
5.4 凸曲 面与积分公
式
02
5.2 球面 的刚性
05
5.5 全平均 曲率与
Willmove猜 想
03 5.3 GaussBonnet公式
6.4.1 基本 概念
6.4.2 Poisson括号积
6.4.3 光滑切 向量场的积分曲
线
第六章 微分流形初步
6.5 仿射联络
0 1 6.5.1 仿射联络的定义及局部表示 0 2 6.5.2 仿射联络的存在性定理 0 3 6.5.3 仿射联络的挠率和曲率
主要参考文献
主要参考文献
感谢聆听
3.7.2 曲面 的基本方程
3.7.1 曲面 的基本公式
3.7.3 曲面 论的基本定 理
第四章 联络
第四章 联络
4.1 曲面上的向
01 量场
4.1.1 曲面上的光滑函数 4.1.2 曲面S在点p∈S的切向量 X<sub>p</sub> 4.1.3 曲面S上的切向量场 4.1.2 曲面S在点p∈S的切向量 X<sub>p</sub> 4.1.3 曲面S上的切向量场
