2018-2019学年北师大版必修二-1.7.1简单几何体的侧面积-(18张)PPT课件
1.7.1 简单几何体的侧面积

h
d
b
h
h
b
a
a
d
S直棱柱侧=(a + b + d ) ⋅ h = ch
1 S正棱锥侧 = ch' 2
h'
h'
C′
h'
1 S正棱台侧 (c + c' )h' = 2
h'
C
思考:将直棱柱、正棱锥、正棱台的侧面积公式进行比较, 思考:将直棱柱、正棱锥、正棱台的侧面积公式进行比较, 你能发现它们的联系和区别吗? 你能发现它们的联系和区别吗?
2
答:锅炉的表面积约为 8.8m 2.
例2
圆台的上下底面半径分别是10cm和20cm,它的侧面 圆台的上下底面半径分别是10cm和20cm,它的侧面 10cm
展开图的扇环的圆心角是180° 展开图的扇环的圆心角是180°,那么圆台的侧面积是多 180 少?(结果中保留 π ) ?(结果中保留 解 如图,设上底面周长为c,因为扇环 如图,设上底面周长为c,因为扇环 c, 的圆心角是180° 所以c= 的圆心角是180°,所以c= π·SA 180
r1 = r2
S圆柱侧 = 2p rl
例1.一个无上盖圆柱形的锅炉,底面直径 d = 1m , 1.一个无上盖圆柱形的锅炉, 一个无上盖圆柱形的锅炉 求锅炉的表面积(保留2个有效数字) 高 h = 2.3m ,求锅炉的表面积(保留2个有效数字)
骣÷ çd ÷ 解: S = S侧面积 + 2S底面积 = p dh + 2p ç ÷ ç2 桫 1 = p 创 2.3 + 2p 椿 1 4 8.8 (m 2 )
又因为c=2 ,所以SA=20.同理 所以SA=20. 又因为c=2 π×10=20 π ,所以SA=20.同理 SB=40.所以,AB=SBSB=40.所以,AB=SB-SA=20,S圆台侧= 所以
北师大版高中数学必修二课件1.7.1简单几何体的侧面积

S圆锥侧 = p rl
r1 = 0
S圆台侧 = p (r1 + r2 )l
r1 = r2
S圆柱侧 = 2p rl
例1.一个无上盖圆柱形的锅炉,底面直径,高,求锅炉的 d = 1m
h = 2.3m 表面积(保留2个有效数字)
骣 d÷ 解: S = S侧面积 + 2S ç ÷ 底面积 = p dh + 2p ç ç 桫 2÷ 1 = p创 1 2.3 + 2p 椿 4 8.8(m 2 )
§7简单几何体的面积和体积
7.1简单几何体的侧面积
1.掌握柱体、锥体、台体的侧面积公式; 2.能应用公式求柱体、锥体、台体的侧面积,熟悉台体
与柱体、锥体之间的转换关系;
3.感受几何体的侧面积求解过程,培养空间想象和空间
思维.
在初中已经学过了正方体和长方体的表面积,您知道正方
体和长方体的展开图与其表面积的关系吗?
2
2 答:锅炉的表面积约为 8.8m .
例2圆台的上下底面半径分别是10cm和20cm,它的侧面展 开图的扇环的圆心角是180°,那么圆台的侧面积是多少? (结果中保留)
解如图,设上底面周长为c,因为扇环
的圆心角是180°,所以c=· SA
又因为c=2× SA=20.同理 10=20,所以 SB=40.所以,AB=SB-SA=20,S圆台侧=
(r1 r2 ) AB
(10 20) 20 600 (cm )
2
2 答:圆台的侧面积为600cm
思考:圆台的上、下底面半径分别为2和4,高为, 2 3
求其侧面展开图扇环所对的圆心角. 分析:抓住相似三角形中的相似比是解题的关键 答:180°
2018_2019高中数学第一章立体几何初步1.7.1简单几何体的侧面积课件北师大版必修2ppt版本

PE21=PO21+O1E21=122+32=32×17, 在 Rt△POE 中, PE2=PO2+OE2=242+62=62×17, 所以 E1E=PE-PE1=6 17-3 17=3 17. 所以 S 侧=4×12×(BC+B1C1)×E1E =2×(12+6)×3 17=108 17.
互动 探究
2.若圆台的高是 3,一个底面半径是另一个底面半径的 2 倍,母线
与下底面成 45°角,则这个圆台的侧面积是
()
A.27π
B.27 2π
C.9 2π
D.36 2π
解析 ∵上底半径 r′=3,下底半径 r=6,母线长 l=3 2, ∴S 侧=π(r′+r)l=π(3+6)×3 2=27 2π.
答案 B
• 单击此处编辑母版文本样式
解 过 C 点作 CD⊥AB 于点 D.如图所示,△ABC 以 AB 所在直线为 轴旋转一周,所得 到的旋转体是两个底面重合的圆锥,这两个圆锥的高的和为 AB=5, 底面半径 DC=ACA·BBC=152, 故 S 表=π·DC·(BC+AC)=854π.
• 单击解此处如编题图辑所母示,版所文得本几何样体式为一个圆柱除去一个圆锥.
方法二 如图,正四棱台的侧棱延长交于一点 P. 取 B1C1、BC 的中点 E1、E,则 EE1 的延长线必过 P 点(以后可以证 明).O1、O 分别是正方形 A1B1C1D1 与正方形 ABCD 的中心.由正 棱锥的定义,CC1 的延长线过 P 点,且有 O1E1=12A1B1=3,OE=12AB =6, 则有PPOO1=OO1EE1=36, 即PO1P+OO1 1O=12,所以 PO1=O1O=12. 在 Rt△PO1E1 中,
2 ∴圆台的侧面积 S 侧=π(r+R)l=π(2 3+ 3)×2 3=18π. 即圆台的侧面积是 18π.
2018学年北师大版高中数学必修2课件:1.7.1简单几何体

简单几何体的面积和体积
7.1 简单几何体的侧面积
自主学习· 新知突破
1.初中阶段我们学习过长方体、正方体的表面积计算,长、宽、高分别为 a、 b、c 的长方体的表面积公式和棱长为 a 的正方体的表面积公式,你还记得吗?
[提示] S长方体=2(ab+bc+ca),S正方体=6a2.
2.有一节用铁皮卷成的圆柱形烟囱,你知道如何求出做这节烟囱所用的铁 皮的面积吗? [提示] 将烟囱沿母线剪开,展开所得的矩形的面积便是.
[自主练习] 1.矩形的边长分别为 1 和 2,分别以这两边为轴旋转,所形成的几何体的侧 面积之比为( A.1∶2 C.1∶4 ) B.1∶1 D.4∶1
解析:
S1=2π·1·2=4π,S2=2π·2·1=4π, B
∴S1=S2. 答案:
2. 若圆台的上下底面半径分别是 1 和 3, 它的侧面积是两底面面积和的 2 倍, 则圆台的母线长是( A. 2 C. 5
圆柱、圆锥、圆台的侧面积 圆锥的高和底面半径相等, 它的一个内接圆柱的高和圆柱底面半径 也相等.求圆柱的表面积和圆锥的表面积之比.
[思路探究] 设出圆柱和圆锥的底面半径,利用相似三角形,得半径之间关
系和圆锥母线与半径的关系,写出圆柱、圆锥的表面积求其比值.
[边听边记]
如图,设圆柱和圆锥的底面半径分别为 r、R,圆锥母线长为 l,
④这三种几何体侧面积之间的关系
(2)关于正棱柱、正棱锥、正棱台的侧面积 ①这三种几何体侧面积之间的关系
②求这三种几何体侧面积的常见策略 a.正棱柱、正棱锥、正棱台的所有侧面都全等,因此求侧面积时,可先求一 个侧面的面积,然后乘以侧面的个数. b. 棱台是由棱锥所截得到的, 因此棱台的侧面积可由大小棱锥侧面积作差得 到.
北师大版必修2-1.7.1简单几何体的侧面积1

10cm 7.5cm
1000 cm2 0.1 m2
涂100个花盆需油漆:0.1100 100 1000 毫升
答:涂100个这样的花盆需油漆1000毫升。
练习:
1、若一个圆柱的侧面展开图是一个正方形,且正方形的
边长为2,则这个圆柱的全面积与侧面积的比是___A___
A. 1 2 2
1 4
B.
盆外观,需要涂油漆,已知每平方米用100毫升油漆,涂100
个这样的花盆需多少油漆?(结果精确到1cm2)
分析:只要求出花盆的表面积.花盆的表面 积等于花盆的侧面面积加上底面面积,再 减去底面圆孔的面积。
解:由圆台的表面积公式得
s
15
2
15
15
20
15
1.5
2
2 2
2 2
1.5cm
圆台表面积:S r 2 r,2 rl r,l r2 r,2 rl r,l
点评:圆柱、圆锥可以看成圆台的特例,它们的表面积 公式可以由圆台的表面积公式得到
例2 如图,一个圆台形花盆盆口直径为20cm,盆底直径为15
cm,底部渗水圆孔直径为1. 5cm,盆壁长15cm,为了美化花
下
1、粉碎机上的下料斗是正四棱台形(图4), 它的两底面边长分别是80mm和440mm , 高是200mm。计算制造这样一个下料斗所 需铁板的面积(保留两位有效数字)。
解:上底面周长c’=4×80=320(mm)
下底面周长c=4 ×440=1760(mm)
斜高h`=
2002
44080 2 2
D
(二)、正棱台的侧面积
d问题:在研究直棱柱和棱锥的侧面积
时,我们采用什么方法分别得到它们的 侧面 积的计算公式?
高中数学 1.7.1 简单几何体的侧面积多媒体教学优质课件 北师大版必修2

第五页,共28页。
特别(tèbié) 提醒
将空间图形问题转化(zhuǎnhuà)为平面图形问题,是解立 体几何 问题基本、常用的方法.
第六页,共28页。
思考:把圆锥的侧面沿着一条母线展开,得到什么图形? 展开的图形与原图(yuán tú)有什么关系?
第七页,共28页。
扇形 (shàn
l xínɡ)
第二页,共28页。
在初中已经学过了正方体和长方体的表面积,您知道正方 体和长方体的展开图与其(yǔqí)表面积的关系吗?
第三页,共28页。
思考: 把圆柱的侧面沿着(yán zhe)一条母线展开,得到什么图形? 展开的图形与原图有什么关系?
第四页,共28页。
r
l
长方形
宽= l
长=2r
S圆柱侧
S长方形=2 rl
答:180°
第十六页,共28页。
思考:圆柱、圆台、圆锥表面积公式
圆柱(yuánzhù)的表 面积为:
S圆柱表 2 r 2
2 rl
2rr l
圆锥(yuánzhuī)的表面 积为:
S圆锥表 r 2 rl r r l
圆台(yuántái)的表 面积为:
S圆台表
r12 r22 r1l r2l
第十七页,共28页。
r
S圆锥侧=S扇=
n l2 360
1 2 l扇l rl
第八页,共28页。
思考:把圆台(yuántái)的侧面沿着一条母线展开,得到 什么图形?
展开的图形与原图有什么关系?
第九页,共28页。
S圆台侧=S扇环
扇环 =(r1 r2 )l
r1
l
r2
第十页,共28页。
S
在S0A 和S0B 中 ∵
《1.7.1 简单几何体的侧面积》课件 3-优质公开课-北师大必修2精品

∴R=2r,l= 2R.
当 堂
案
双
设 计
课
∴SS圆 圆柱 锥表 表=πR2π·r22+R+2ππrR2 2
基 达 标
前
自 主 导
= 4
2π4rπ2+r2 4πr2=4
4πr2 2+1πr2
课 时 作
学
业
课 堂
= 21+1= 2-1.
互
动
探
究
教 师 备 课 资 源
菜单
BS ·数学 必修2
教
学
易
教
教
学
易
教
错
法
易
分
误
析
辨
教
●教学建议
析
学
当
方
教学时从学生熟悉的正方体和长方体的展开图入手,分 堂
案
双
设
计 析展开图与其侧面积的关系,类比正、长方体侧面讨论棱
基 达
标
课 前
柱、棱锥、棱台的侧面问题,进一步探究圆柱、圆锥、圆台
自
课
主 导
的侧面积问题,在教学时教师可以以实物进行侧面展开让学
时 作
学
业
生直观认识其侧面展开图,从而增强记忆.
学
当
方 案
S全=6π×4π+π×4×2=24π2+8π=8π(3π+1).
堂 双
设
基
计
当长为4π的边为高时,底面半径r=3.
达 标
课
前 自
S全=24π2+2×9π=6π(4π+3).
课
主
时
导
作
学
业
【答案】 C
课 堂 互 动 探 究
教 师 备 课 资 源
2018版高中数学北师大版必修二学案:第一章7.1简单几何体的侧面积

7.1简单几何体的侧面积学习目标 1.通过对柱体、锥体、台体的研究,把握柱体、锥体、台体的表面积的求法.2.了解柱体、锥体、台体的表面积计算公式;能运用柱体、锥体、台体的表面积公式进行计算和解决有关实际问题.3.培育空间想象能力和思维能力.知识点一圆柱、圆锥、圆台的表面积试探1 圆柱OO′及其侧面展开图如下,那么其侧面积为多少?表面积为多少?试探2 圆锥SO及其侧面展开图如下,那么其侧面积为多少?表面积为多少?试探3 圆台OO′及其侧面展开图如下,那么其侧面积为多少?表面积为多少?梳理圆柱、圆锥、圆台的侧面积公式知识点二直棱柱、正棱锥、正棱台的侧面积试探1 类比圆柱侧面积的求法,你以为如何求直棱柱的侧面积?若是直棱柱底面周长为c,高为h,那么直棱柱的侧面积是什么?试探2 正棱锥的侧面展开图如图,设正棱锥底面周长为c,斜高为h′,如何求正棱锥的侧面积?试探3 以下图是正四棱台的展开图,设下底面周长为c,上底面周长为c′,你能依照展开图,归纳出正n棱台的侧面面积公式吗?梳理棱柱、棱锥、棱台侧面积公式类型一旋转体的侧面积(表面积)例1 (1)一个几何体的三视图如下图,那么该几何体的表面积为( )A.3πB.4πC.2π+4 D.3π+4(2)圆台的上、下底面半径别离为10 cm和20 cm.它的侧面展开图扇环的圆心角为180°,那么圆台的表面积是________cm2.(结果中保留π)反思与感悟圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将那个曲面展为平面图形计算,而表面积是侧面积与底面圆的面积之和.跟踪训练1 (1)圆柱的侧面展开图是两边长别离为6π和4π的矩形,那么圆柱的表面积为( )A.6π(4π+3)B.8π(3π+1)C.6π(4π+3)或8π(3π+1)D.6π(4π+1)或8π(3π+2)(2)圆锥的中截面把圆锥侧面分成两部份,那么这两部份侧面积的比为( )A.1∶1B.1∶2C.1∶3D.1∶4类型二多面体的侧面积(表面积)及应用例2 某几何体的三视图如下图,那么该几何体的表面积等于( )A.8+2 2 B.11+22C.14+2 2 D.15反思与感悟多面体中的有关计算通常转化为平面图形(三角形或特殊的四边形)来计算,关于棱锥中的计算问题往往要构造直角三角形,即棱锥的高、斜高和斜高在底面上的投影组成的直角三角形,或由棱锥的高、侧棱和侧棱在底面上的投影组成的直角三角形.跟踪训练2 已知正四棱台上底面边长为4 cm,侧棱和下底面边长都是8 cm,求它的侧面积.类型三组合体的侧面积(表面积)命题角度1 由三视图求组合体的表面积例3 某几何体的三视图(单位:cm)如下图,那么此几何体的表面积是________cm2.反思与感悟关于此类题目:(1)将三视图还原为几何体;(2)组合体的表面积应注意重合部份的处置.跟踪训练3 一个几何体的三视图如下图(单位:m),那么该几何体的表面积为________m2.命题角度2 由旋转形成的组合体的表面积例4 已知在梯形ABCD中,AD∥BC,∠ABC=90°,AD=a,BC=2a,∠DCB=60°,在平面ABCD内,过C作l⊥CB,以l为轴将梯形ABCD旋转一周,求此旋转体的表面积.反思与感悟 (1)关于由大体几何体拼接成的组合体,要注意拼接面重合对组合体表面积的阻碍.(2)关于从大体几何体中切掉或挖掉的部份组成的组合体,要注意新产生的截面和原几何体表面的转变.跟踪训练4 已知△ABC 的三边长别离是AC =3,BC =4,AB =5,以AB 所在直线为轴,将此三角形旋转一周,求所得旋转体的表面积.1.一个圆锥的表面积为πa m 2,且它的侧面展开图是一个半圆,那么圆锥的底面半径为( ) A.2a 2 m B.3a 3 m C.a 2 m D.5a 5m 2.一个正三棱台的上、下底面边长别离为3 cm 和6 cm ,高是32 cm.那么三棱台的侧面积为( ) A .27 3 cm 2B.2732cm 2C.32cm 2D. 3 cm 23.一个几何体的三视图(单位长度:cm)如下图,那么此几何体的表面积是( )A .(80+162)cm 2B .84 cm 2C .(96+162)cm 2D .96 cm 24.假设圆台的上下底面半径别离是1和3,它的侧面积是两底面面积和的2倍,那么圆台的母线长是________.5.正三棱锥S -ABC 的侧面积是底面积的2倍,它的高SO =3,求此正三棱锥的侧面积.1.多面体的表面积为围成多面体的各个面的面积之和.2.有关旋转体的表面积的计算要充分利用其轴截面,确实是说将已知条件尽可能归结到轴截面中求解.而关于圆台有时需要将它还原成圆锥,再借助相似的相关知识求解. 3.S 圆柱表=2πr (r +l );S 圆锥表=πr (r +l );S 圆台表=π(r 2+rl +Rl +R 2).答案精析问题导学 知识点一试探1 S 侧=2πrl ,S 表=2πr (r +l ). 试探2 底面周长是2πr ,利用扇形面积公式得S 侧=12×2πrl =πrl , S 表=πr 2+πrl =πr (r +l ).试探3 圆台的侧面展开图是扇环,内弧长等于圆台上底周长,外弧长等于圆台下底周长,xx +l =r R,解得x =rR -rl . S 扇环=S 大扇形-S 小扇形=12(x +l )×2πR -12x ·2πr =π[(R -r )x +Rl ]=π(r +R )l ,因此,S 圆台侧=π(r +R )l ,S 圆台表=π(r 2+rl +Rl +R 2).梳理 2πr 22πrl 2πr (r +l ) πr 2πrl πr (r +l ) πr ′2πr 2π(r ′l +rl ) π(r ′2+r 2+r ′l +rl ) 知识点二 试探1利用直棱柱的侧面展开图求棱柱的侧面积.展开图如图,不难求得S 直棱柱侧=ch . 试探 2 正棱锥的侧面积确实是展开图中各个等腰三角形面积之和,不宝贵到S正棱锥侧=12ch ′.试探3 S 正棱台侧=12n (a +a ′)h ′=12(c +c ′)h ′.题型探讨例1 (1)D (2)1 100π 解析 (1)由三视图可知, 该几何体为:故表面积为πr 2+2πr 2l +l 2=π+2π+4=3π+4. (2) 如下图,设圆台的上底面周长为c , 因为扇环的圆心角是180°, 故c =π·SA =2π×10, 因此SA =20,同理可得SB =40, 因此AB =SB -SA =20, 因此S 表面积=S 侧+S 上+S 下 =π(r 1+r 2)·AB +πr 21+πr 22 =π(10+20)×20+π×102+π×202=1 100π(cm 2).故圆台的表面积为1 100π cm 2.跟踪训练1 (1)C [由题意,圆柱的侧面积S 侧=6π×4π=24π2. ①当以边长为6π的边为母线时,4π为圆柱底面周长,那么2πr =4π, 即r =2,因此S 底=4π, 因此S 表=S 侧+2S 底=24π2+8π =8π(3π+1).②当以边长为4π的边为母线时,6π为圆柱底面周长,那么2πr =6π, 即r =3,因此S 底=9π, 因此S 表=S 侧+2S 底=24π2+18π =6π(4π+3).](2)C [如下图,PB 为圆锥的母线,O 1,O 2别离为截面与底面的圆心.因为O 1为PO 2的中点,因此PO 1PO 2=PA PB =O 1A O 2B =12, 因此PA =AB ,O 2B =2O 1A . 又因为S 圆锥侧=π·O 1A ·PA ,S 圆台侧=π·(O 1A +O 2B )·AB ,则S 圆锥侧S 圆台侧=O 1A ·PA O 1A +O 2B ·AB =13.] 例2 B[该几何体为底面是直角梯形的直四棱柱.S 表=2×12×(1+2)×1+2×1+2×1+2×2+2×2=11+22,应选B.]跟踪训练2 解 方式一在Rt△B 1FB 中,B 1F =h ′,BF =12(8-4)=2(cm), B 1B =8 cm ,∴B 1F =82-22=215(cm),∴h ′=B 1F =215 cm.∴S 正棱台侧=12×4×(4+8)×215=4815(cm 2).方式二 延长正四棱台的侧棱交于点P ,如图,设PB 1=x cm , 则xx +8=48, 得x =8 cm. ∴PB 1=B 1B =8 cm , ∴E 1为PE 的中点.∴PE 1=82-22=215(cm).PE =2PE 1=415 cm.∴S 正棱台侧=S 大正棱锥侧-S 小正棱锥侧 =4×12×8×PE -4×12×4×PE 1=4×12×8×415-4×12×4×215=4815(cm 2). 例3 138解析 将三视图还原为长方体与直三棱柱的组合体,再利用表面积公式求解.该几何体如下图,长方体的长,宽,高别离为6 cm ,4 cm,3 cm ,直三棱柱的底面是直角三角形,边长别离为 3 cm ,4 cm,5 cm ,因此表面积S =[2×(4×6+4×3)+3×6+3×3]+⎝ ⎛⎭⎪⎫5×3+4×3+2×12×4×3=99+39=138(cm 2).跟踪训练3 12π+42π例4 解 如下图,该几何体是由一个圆柱挖去一个圆锥组成的.在直角梯形ABCD 中,AD =a ,BC =2a ,AB =(2a -a )tan 60°=3a ,DC =2a -a cos 60°=2a , 又DD ′=DC =2a ,则S 表=S 圆柱表+S 圆锥侧-S 圆锥底=2π·2a ·3a +2π·(2a )2+π·a ·2a -πa 2=(9+43)πa 2.跟踪训练4 解 如图,在△ABC 中,过C 作CD ⊥AB ,垂足为点D .由AC =3,BC =4,AB =5,知AC 2+BC 2=AB 3,则AC ⊥BC .因此BC ·AC =AB ·CD ,因此CD =125, 记为r =125, 那么△ABC 以AB 为轴旋转所得旋转体是两个同底的圆锥,且底面半径r =125,母线长别离是AC =3,BC =4,因此S 表面积=πr ·(AC +BC )=π×125×(3+4)=845π. 当堂训练1.B2.B [如图,O 1,O 别离是上、下底面中心,那么O 1O =32cm ,连接A 1O 1并延长交B 1C 1于点D 1,连接AO 并延长交BC 于点D ,过D 1作D 1E ⊥AD 于点E .在Rt△D 1ED 中,D 1E =O 1O =32cm , DE =DO -OE =DO -D 1O 1=13×32×(6-3) =32 (cm), DD 1=D 1E 2+DE 2=⎝ ⎛⎭⎪⎫322+⎝ ⎛⎭⎪⎫322= 3 (cm), 因此S 正三棱台侧=12(c +c ′)·DD 1=2732(cm 2).] 3.A5.解设正三棱锥底面边长为a ,斜高为h ′,如下图,过O 作OE ⊥AB ,连接SE , 则SE ⊥AB ,且SE =h ′. 因为S 侧=2S 底, 因此12×3a ×h ′=34a 2×2. 因此a =3h ′.因为SO ⊥OE ,因此SO 2+OE 2=SE 2.因此32+(36×3h ′)2=h ′2. 因此h ′=23,因此a =3h ′=6.因此S底=34a2=34×62=9 3.因此S侧=2S底=18 3.。
2018学年北师大版高中数学必修2课件:1.7.1简单几何体的侧面积 精品

=48+8 17. 答案: C
与表面积有关的综合问题
正四棱台两底面边长分别为 3 和 9. (1)若侧棱所在直线与上、下底面正方形中心的连线所成的角为 45°,求棱台 的侧面积; (2)若棱台的侧面积等于两底面面积之和,求它的高. [思路探究] 侧棱 C1C 与上、下底面正方形中心连线以及 CO 和 C1O1 可构成 直角梯形,从而可知∠C1CA=45°.从而求 h=C1E 以及斜高 C1F.
简单几何体的侧面积
几何体
侧面展开图
圆柱
圆锥
侧面积公式
S 圆柱侧=__2_π_r_l__ r 为__底__面__半__径___ l 为_侧__面__母__线__长__
S 圆锥侧=__π_rl__ r 为__底__面__半__径___ l 为_侧__面__母__线__长__
圆台 直棱柱
S 圆台侧=__π__(r_1_+__r_2)_l___ r1 为__上__底__面__半__径___ r2 为__下__底__面__半__径___ l 为__侧__面__母__线__长___ S 直棱柱侧=__c_h___ c 为_底__面__周___长___ h 为__高___
l
R
l
母线长为2,截得圆台的上底半径为2,下底面半径为 R,母线长为2.
ห้องสมุดไป่ตู้
Rlπ S 圆锥=πrl=π×2×2=4Rl.
R l 3π S 圆台=π(r+r′)l=π(R+2)·2= 4 Rl.
π S圆锥 4Rl 1 S圆台=3 =3.
4πRl
答案: (1)C (2)C
直棱柱、正棱锥、正棱台的表面积
(北师大版)高中数学必修2检测1.7.1简单几何体的侧面积 Word版含解析
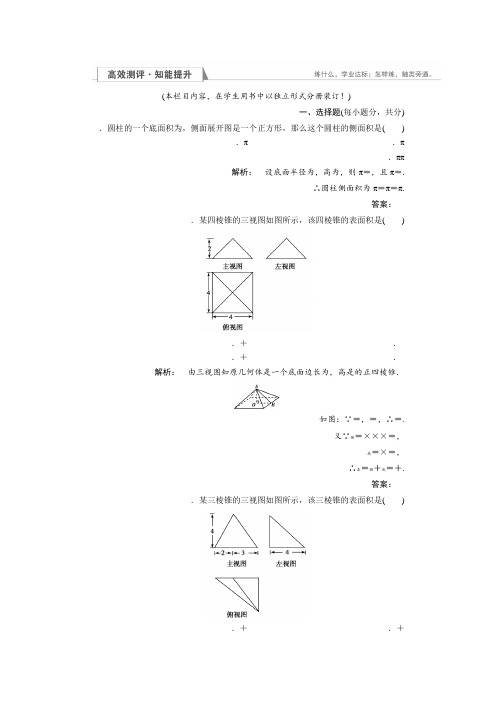
(本栏目内容,在学生用书中以独立形式分册装订!)一、选择题(每小题分,共分).圆柱的一个底面积为,侧面展开图是一个正方形,那么这个圆柱的侧面积是( ).π.π.ππ解析:设底面半径为,高为,则π=,且π=.∴圆柱侧面积为π=π=π.答案:.某四棱锥的三视图如图所示,该四棱锥的表面积是( ).+..+.解析:由三视图知原几何体是一个底面边长为,高是的正四棱锥.如图:∵=,=,∴=.又∵侧=×××=,底=×=,∴表=侧+底=+.答案:.某三棱锥的三视图如图所示,该三棱锥的表面积是( ).+.+.+.+解析:从所给的三视图可以得到该几何体的直观图,如图所示,结合图中的数据,利用勾股定理计算出各边的长度,进而求出面积.表=底+侧=××+××+××+××=+.答案:.一个圆台的母线长等于上、下底面半径和的一半,且侧面积是π,则母线长为( )....解析:设圆台的上、下底面圆半径分别为,,母线长为,则π(+)=π,即(+)=.又∵=(+),∴=,即=,∴=.答案:二、填空题(每小题分,共分).如图,在一个几何体的三视图中,主视图和左视图都是矩形,俯视图是等腰直角三角形(如下图),根据图中标注的长度,可以计算出该几何体的表面积是.解析:如图,该几何体为底面为等腰直角三角形的直棱柱.由图知=,=,⊥.∴表=·+××+×=+.答案:+.如图所示,一个正方体的棱长为,以相对两个面的中心连线为轴,钻一个直径为的圆柱。
高中数学第一章立体几何初步1.7.1简单几何体的侧面积课时作业北师大版必修2(2021年整理)

2018-2019学年高中数学第一章立体几何初步1.7.1 简单几何体的侧面积课时作业北师大版必修2编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018-2019学年高中数学第一章立体几何初步1.7.1 简单几何体的侧面积课时作业北师大版必修2)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018-2019学年高中数学第一章立体几何初步1.7.1 简单几何体的侧面积课时作业北师大版必修2的全部内容。
1。
7.1 简单几何体的侧面积[学业水平训练]错误!圆锥的底面直径为6,高是4,则它的侧面积为( )A.12πB.24πC.15πD.30π解析:选C.作圆锥截面如图,高AD=4,底面半径CD=3,则母线AC=5,得S侧=π×3×5=15π。
错误!已知圆锥的侧面展开图为半圆,半圆的面积为S,则圆锥的底面面积是() A.2S B。
错误!C.错误!SD.错误!S解析:选B.设圆锥的母线长为l,则侧面展开图半圆的半径R=l.∴S=12πR2=错误!πl2,∴l=错误!,∴圆锥的底面周长C=πR=πl=错误!,∴圆锥的底面半径r=错误!=错误!=错误!,∴圆锥的底面积为S′=πr2=错误!,故选B.错误!若一个底面是正三角形的三棱柱的主视图如图所示,则其侧面积等于()A.6 B.2错误!C。
错误!D.2解析:选A。
由主视图可知底面边长为2,高为1,因为三棱柱底面为等边三角形,所以其侧面积S=6×1=6.错误!正三棱锥的底面边长为a,高为错误!a,则三棱锥的侧面积等于()A。
错误!a2B。
错误!a2C.错误!a2D。
2018-2019数学北师大版必修2课件:第一章7.1简单几何体的侧面积 (41张)

因此 S 棱锥侧=1Ch′=1×4×4×4=32(cm2),
2
2
S = 表面积 S 侧+S 底=32+16=48(cm2).
方法归纳 (1)求直棱柱的侧面积,即求底面周长和高的乘积,因此解题 时可逐个求解,也可以把积作为一个整体求解. (2) 对 于 正 棱 锥 , 正 棱 台 的 表 面 积 , 求 侧 面 的 高 是 解 题 的 关 键. (3)特殊的多面体: ①侧棱与底面垂直的棱柱叫做直棱柱. ②底面为正多边形的直棱柱叫做正棱柱. ③底面是正多边形,顶点在底面的正投影是底面中心的棱锥 叫做正棱锥.
侧面积公式及其关系是: S正 = 棱柱侧 Ch ―C′―=→C
S正 棱台侧=1( C+ C′) h′ 2 ―C′―=→0
S正 棱锥侧=1Ch′ 2
其中 C,C′为底面周长,h 是正棱柱的高,h′是正棱台或正 棱锥的斜高(斜高指侧面等腰三角形或等腰梯形的高).
2.已知棱长为 a,各面均为等边三角形的四面体 S-ABC,求它 的表面积. 解:先求△SBC 的面积,如图,过点 S 作 SD⊥BC,交 BC 于 点 D.
如图①,在矩形 OO1BA 中,OO1=AB=h=l,AO=r. 圆柱的侧面展开图是一个矩形,在矩形 ABCD 中,AD=BC= 2π r,BD= l2+4π 2r2 .BD 是从 B 点绕圆柱侧面一周到 A 点 的最短距离. ②圆锥:
如图②,在 Rt△OPA 中,l2=h2+r2.
︵ 圆锥的侧面展开图是一个扇形,在扇形 PAA′中,AA′=C=2 π r. AA′为从 A 点出发绕圆锥侧面一周再回到 A 点的最短距离. ③圆台:
∴AM1=2 89,即绳子的最短长度为 2 89.
︵ (2)过点 S 作 SQ⊥AM1,交BB1于点 P,交 AM1 于点 Q,则 PQ 的长度即为所求.
【三维设计】高中数学 第一部分 第一章§7 7.1 简单几何体的侧面积配套课件 北师大版必修2
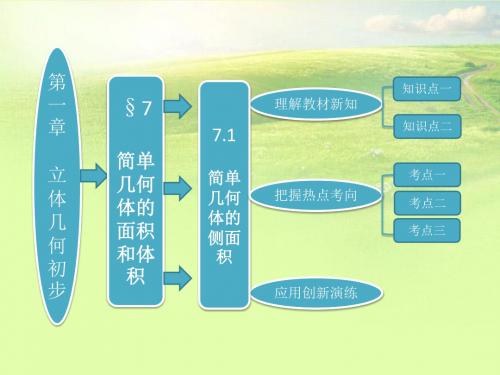
(2)∵S 圆柱侧的表示式中 x2 的系数小于零, ∴这个二次函数有最大值, 当 x=--22×πR2HπR=H2 时,S 圆柱侧最大. ∴当圆柱的高是已知圆锥的高的一半时,它的侧面积最大.
1.对于旋转体的表面积,处理好两个方面的问题 (1)利用轴截面平面化; (2)在轴截面中建立高、母线、底面半径的数量关系. 2.对于正棱锥、正棱台的表面积,求侧面的高是 解题的关键,这就要求在几个特殊直角三角形或直角梯 形中建立高、斜高、底边长的数量关系.
S 圆台=π(r+r′)l=π(R+R2)·2l =34πRl.
π SS圆 圆锥 台=344πRRll=13.
答案:C
3.如图,圆台的上底半径为3 cm,下底 半径为6 cm,母线长为6 cm,则圆台的侧面 积为________ 解析:S侧=π(3+6)×6=54π (cm2) 答案:54 π (cm2)
因为 SO⊥OE,所以 SO2+OE2=SE2. 所以 32+( 63× 3h′)2=h′2. 所以 h′=2 3.所以 a= 3 h′=6. 所以 S 底= 43a2= 43×62=9 3. 所以 S 侧=2S 底=18 3.
[一点通] 1.正棱锥和正棱台的侧面分别是等腰三角形和等 腰梯形,只要弄清相对应的元素求解很简单. 2.多面体的表面积等于各侧面与底面的面积之和, 对正棱锥中的计算问题往往要构造直角三角形求解,对 正棱台则需要构造直角梯形或等腰梯形求解.
[例1] 圆锥的高和底面半径相等,它的一个内接 圆柱的高和圆柱底面半径也相等.求圆柱的表面积和 圆锥的表面积之比.
[思路点拨] 设出圆柱和圆锥的底面半径,利用 相似三角形,得半径之间关系和圆锥母线与半径的关 系,写出圆柱、圆锥的表面积求其比值.
[精解详析] 如图,设圆柱和圆锥的底面半径
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
扇环
r1
l
r2
S 圆= 台 S 扇 侧 = 环 ( r1 r2)l
思考: 圆柱、圆锥、圆台的侧面积公式间 的联系与区别
rO
r 1 O’
r1=r2
l r1=0
l
l 上底扩大
O
r2 O
上底缩小
rO
S柱侧 2rl
S台侧(r1r2)l
S锥侧 rl
棱柱:
直棱柱:侧棱和底面垂直的棱柱叫直棱柱.
正棱柱:底面是正多边形的直棱柱叫正棱柱.
分析: 可以把圆柱沿这条母线展开,将问题转化为平面几何的问题.
随堂练习:
• 1、已知正四棱柱的底面边长是3,侧面的对角 线长是3 5 ,求这个正四棱柱的侧面积。72 3 3
• 2、求底面边长为2,高为1的正三棱锥的全面积。 • 3、下列图形中,不是正方体的展开图的是( C )
A
B
C
D
随堂练习:
4.如图,E,F分别为正方形ABCD的边BC,CD的中 点,沿图中虚线折起来,它能围成怎样的几何体?
C1 A1
C A
B1
棱柱两底面的距离叫做棱柱 的高.
B
把直(正)三棱柱侧面沿一条侧棱展开,得到 什么图形?侧面积怎么求?
h
cb
a
h
a
h
bc
S直棱 = 柱 a ( 侧 bc)hch
棱锥、棱台
正棱锥:底面是正多边形,顶点在底面的射
影是底面中心的棱锥.
正棱台:正棱锥被平行于底面的平面所截,截
P 面和底面之间的部分叫正棱台.
h' h'
思考:
正棱柱、正棱锥和正棱台的侧面积的关系:
c’=c
上底扩大
c’=0
上底缩小
S柱侧 ch '
S台侧
1c'ch'
2
S锥侧
1 2
ch '
数学运用
例1 设计一个正四棱锥形冷水塔塔顶,高是0.85m, 底面的边长是1.5m,制造这种塔顶需要多少平方米的 铁板?(保留两位有效数字)
S
解:如图,S表示塔的顶点,O表示底
3.圆台的上、下底半径分别是10cm和20cm,它的侧 面展开图的扇环的圆心角是1800,那么圆台的表面积 是多少?(结果中保留π)
将立方体纸盒沿某些棱剪开, 并使六个面连在一起,然后铺平。 你能画出铺平后的图形吗? (看谁画最多)
A
D
三棱锥
F
B
E
C
5.用半径为r的半圆形铁皮卷成一个圆锥筒, 3 r
那么这个圆锥筒的高是多少?
2
6.一个正三棱台的两个底面的边长分别等于8cm和
18cm,侧棱长等于13cm,求它的侧面积. 468cm2
小结:
1、弄清楚柱、锥、台的侧面展开图的形状是关键; 2、对应的侧面积公式
S三棱锥 =12 ch'
S圆锥=πrl
C’=0
r1=0
S正 棱 = 台 1 2(c+c')h'
C’=C
S直棱= 柱ch'ch
S圆台=π(r1+r2)l
r1=r2
S圆柱=2πrl
作业:
1.一个正三棱柱的底面是边长为5的正三角形,侧棱 长为4,求其侧面积.
2.正四棱锥底面边长为6 ,高是4,中截面把棱锥截成一 个小棱锥和一个棱台,求棱台的侧面积.
7.1空间几何体的表面积
把圆柱的侧面沿着一条母线展开,得到什么图 形?展开的图形与原图有什么关系?
r
l
矩形
宽= l
长= 2r
S圆柱 侧 S矩= 形 2rl
把圆锥的侧面沿着一条母线展开,得到什么图 形?展开的图形与原图=S扇=12cl rl
把圆台的侧面沿着一条母线展开,得到什么图 形?展开的图形与原图有什么关系?
面中心,则SO是高,设SE是斜高。 在Rt△SOE中,由勾股定理得
SE=
1.52 2
0.852
1.13(m)
E O
S 正 棱 锥 侧 1 2 c h ' 1 2 1 .5 4 1 .1 3 3 .4m 2
数学运用
例2 有一根长为5cm,底面半径为1cm的圆柱形铁 管,用一段铁丝在铁管上缠绕4圈,并使铁丝的 两个端点落在圆柱的同一母线的两端,则铁丝的 最短长度为多少厘米?(精确到0.1cm)
A1
C1
D1
B1 h' C
h'
A
C
B
OD
OD
B
A 斜高:侧面等腰三角形底边上的高.
注:只有正棱锥和正棱台才有斜高.
把正三棱锥侧面沿一条侧棱展开,得到什么图 形?侧面积怎么求?
h' h'
S正棱锥= 侧 12ch'
把正三棱台侧面沿一条侧棱展开,得到什么图 形?侧面积怎么求?
S正 棱 台 =侧 12(cc')h'
