机械优化设计经典实例PPT页
合集下载
八章机械优化设计实例PPT课件

第22页/共25页
2)曲柄摇杆机构的传动角应在 和 之间,可得 min
max
g7
x
arccos
l2
2
l32 l1
2l2l3
l4
2
max
0
g8
x
min
arccos
l22
l32 l1
2l2l3
l4
2
0
二、曲柄摇杆机构再现已知运动轨迹的优化设计
所谓再现已知运动轨迹:是指机构的连杆曲线尽可能 地接近某一给定曲线。
第15页/共25页
不同的设计要求,目标函数不同。若减速器的中心距没有要求时,可取减速器 最大尺寸最小或重量最轻作为目标函数。
第16页/共25页
f x m min f x l r1 a r4 min
若中心距固定,可取其承载能力为目标函数。
f x 1/ min
减速器类型、结构形式不同,约束函数也不完全相同。 (1)边界约束
第14页/共25页
不同类型的减速器,选取的设计变量使不同的。
展开式圆柱齿轮减速器:齿轮齿数、模数、齿宽、 螺旋角及变位系数等。
行星齿轮减速器:除此之外,还可加行星轮个数。 设计变量应是独立参数,非独立参数不可列为设计 变量。例如齿轮齿数比为已知,一对齿轮传动中,只 能取Z1或Z2一个为设计变量。
又如中心距不可取为设计变量,因为齿轮齿数确定 后,中心距就随之确定了。
(2)性能约束
第17页/共25页
一、单级圆柱齿轮减速器的优化设计
第18页/共25页
第四节 平面连杆机构的优化设计 连杆机构的类型很多,这里只以曲柄摇杆机构两类 运动学设计为例来说明连杆机构优化设计的一般步骤 和方法。 一、曲柄摇杆机构再现已知运动规律的优化设计
2)曲柄摇杆机构的传动角应在 和 之间,可得 min
max
g7
x
arccos
l2
2
l32 l1
2l2l3
l4
2
max
0
g8
x
min
arccos
l22
l32 l1
2l2l3
l4
2
0
二、曲柄摇杆机构再现已知运动轨迹的优化设计
所谓再现已知运动轨迹:是指机构的连杆曲线尽可能 地接近某一给定曲线。
第15页/共25页
不同的设计要求,目标函数不同。若减速器的中心距没有要求时,可取减速器 最大尺寸最小或重量最轻作为目标函数。
第16页/共25页
f x m min f x l r1 a r4 min
若中心距固定,可取其承载能力为目标函数。
f x 1/ min
减速器类型、结构形式不同,约束函数也不完全相同。 (1)边界约束
第14页/共25页
不同类型的减速器,选取的设计变量使不同的。
展开式圆柱齿轮减速器:齿轮齿数、模数、齿宽、 螺旋角及变位系数等。
行星齿轮减速器:除此之外,还可加行星轮个数。 设计变量应是独立参数,非独立参数不可列为设计 变量。例如齿轮齿数比为已知,一对齿轮传动中,只 能取Z1或Z2一个为设计变量。
又如中心距不可取为设计变量,因为齿轮齿数确定 后,中心距就随之确定了。
(2)性能约束
第17页/共25页
一、单级圆柱齿轮减速器的优化设计
第18页/共25页
第四节 平面连杆机构的优化设计 连杆机构的类型很多,这里只以曲柄摇杆机构两类 运动学设计为例来说明连杆机构优化设计的一般步骤 和方法。 一、曲柄摇杆机构再现已知运动规律的优化设计
机械优化设计范例(共9张PPT)

设计变量
现设 甲矿运往东站x万吨
乙矿运往东站y万吨
则甲矿运往西站200-x万吨
乙矿运往西站260-y万吨 令x=x1,y=x2
所以:X43;1.5(200-x1)+0.8x2+1.6(260-x2) =716-0.5x1-0.8x2(万元)
所以:Min f(X)= 716-0.5x1-0.8x2
约束条件
- x1 ≤0 X1-200 ≤0 -x2 ≤0 x2 - 260 ≤ 0
x1+x2-280≤ 0 100-x1-x2≤0
求解结果
x2 280 260
100
Z
(20,260)
x1=20 x2=260
Minf(X)= 498万元
100
200 280
x1
所以: 乙矿运往西站260-y万吨
Mx2in-f(26X0)≤ =0 498万元 则令甲x=矿x1运,y=往x2西站200-x万吨
最少的运费为498万元 x令1x+=xx21-2,y8=0x≤20
己 x1知+x甲2-、28乙0≤两0煤矿每年的产量分别为200万吨和260万吨,需经过东、西两个车站运外地。 M甲i煤nf(矿X运)往=东49站8和万西元车站的运费价格分别为1元/吨和1.5元/吨,乙煤矿运往东车站和西车站的运费价格分别为0.8元/吨和1.6元/吨 所。以:Min f(X)= 716-0. 煤乙矿应 运怎往样东编站制y万调吨运方案才能使总运费最少? 己x1知+x甲2-、28乙0≤两0煤矿每年的产量分别为200万吨和260万吨,需经过东、西两个车站运外地。 xM1i+nfx(2-X2)80=≤ 4098万元 现甲设煤矿甲运矿往运东往站东和站西x万车吨站的运费价格分别为1元/吨和1.5元/吨,乙煤矿运往东车站和西车站的运费价格分别为0.8元/吨和1.6元/吨 所 。以:X = [ x1, x2 ]T
机械优化设计方法ppt课件

目标函数的一般表示式为:
f (x) f (x1, x2,...xn )
23
优化设计的目的就是要求所选择的设计变
量使目标函数达到最佳值,即使 f (x) Opt
通常 f (x) min
单目标设计问题
目标函数
多目标设计问题
目前处理多目标设计问题的方法是组合成一个 复合的目标函数,如采用线性加权的形式,即
f (x) W1 f1(x) W2 f2 (x) ... Wq fq (x)
24
四、优化问题的数学模型
优化设计的数学模型是对优化设计问题的数 学抽象。 优化设计问题的一般数学表达式为:
min f (x) x Rn
s.t. gu (x) 0 u 1, 2,..., m
hv (x) 0 v 1, 2,..., p n
4
图1-3 机械优化设计过程框图
5
优化设计与传统设计相比,具有如下三个特点:
(1)设计的思想是最优设计; (2)设计的方法是优化方法; (3)设计的手段是计算机。
二、机械优化设计的发展概况
1ቤተ መጻሕፍቲ ባይዱ优化设计的应用领域 近几十年来,随着数学规划论和电子计算机的迅 速发展而产生的,它首先在结构设计、化学工程、 航空和造船等部门得到应用。
架的高h和钢管平均直径D,使钢管总质量m为最小。
11
图2-2 人字架的受力
12
人字架的优化设计问题归结为:
x D H T 使结构质量
mx min
但应满足强度约束条件 x y 稳定约束条件 x e
13
1
钢管所受的压力
F1
FL h
F(B2 h
25
f (x) f (x1, x2,...xn )
23
优化设计的目的就是要求所选择的设计变
量使目标函数达到最佳值,即使 f (x) Opt
通常 f (x) min
单目标设计问题
目标函数
多目标设计问题
目前处理多目标设计问题的方法是组合成一个 复合的目标函数,如采用线性加权的形式,即
f (x) W1 f1(x) W2 f2 (x) ... Wq fq (x)
24
四、优化问题的数学模型
优化设计的数学模型是对优化设计问题的数 学抽象。 优化设计问题的一般数学表达式为:
min f (x) x Rn
s.t. gu (x) 0 u 1, 2,..., m
hv (x) 0 v 1, 2,..., p n
4
图1-3 机械优化设计过程框图
5
优化设计与传统设计相比,具有如下三个特点:
(1)设计的思想是最优设计; (2)设计的方法是优化方法; (3)设计的手段是计算机。
二、机械优化设计的发展概况
1ቤተ መጻሕፍቲ ባይዱ优化设计的应用领域 近几十年来,随着数学规划论和电子计算机的迅 速发展而产生的,它首先在结构设计、化学工程、 航空和造船等部门得到应用。
架的高h和钢管平均直径D,使钢管总质量m为最小。
11
图2-2 人字架的受力
12
人字架的优化设计问题归结为:
x D H T 使结构质量
mx min
但应满足强度约束条件 x y 稳定约束条件 x e
13
1
钢管所受的压力
F1
FL h
F(B2 h
25
机械优化设计课件2

用如下二维问题来说明有约束优化问题的几何解释 可知该问题的最优点为目标函数等值线 与可行域边界 g2 ( x) 0 的切点
( x1* , x2* ) (1.34,0.58)
* * 最优值为: f ( x1 , x2 ) 3.8
该问题的目标函数及等值线
该问题的设计空间及可行域
有约束的二维优化问题极值点所处位置的不同情况:
等式约束
---要求设计点同时在n维设计空间l个约束曲面上
不等式约束
---要求设计点在设计空间约束曲面的一侧(包括曲面本身)
在设计空间中,满足所有约束条件的区域称为可行域。
在设计空间中,至少不满足一个约束条件的区域称为非可行域。 可行域可记为: D x g j ( x) 0 ( j 1, 2,
在优化过程中,通过设计变量的不断向F(X)值改善的方向自动调整,最 后求得F(X)值最好或最满意的X值。
在实际优化问题中,对目标函数有两种要求形式
目标函数极小化 目标函数极大化
等价
所以,今后优化问题的数学表达一律采用目标函数的极小化形式
目标函数在设计空间的图像描述
一般地,n维目标函数可以在n+1维空间中描述其图像。 为了在n维设计空间中反映目标函数的变化情况,常采用 目标函数等值面的方法。其数学表达式:
1、
2、
采用作图法进行人字架的优化设计
3、数值迭代法(数学规划法):
xk
k 从一个初始设计 x 出发,按如下迭代公式:
x k 1 x k x k k 1 x 得到一个改进的设计 。
( x k ——修改量)
k 在这类方法中,许多算法是沿着某个搜索方向 ,以适当步长 k 的方式 d k 实现对 x 的修改,以获得x k 的值。
机械优化设计PPT

二、离散变量优化的主要方法及其特点、思路和步骤
表7-3 离散变量优化的主要方法及其特点和步骤
图7-8 两个目标函数的等值线和约束边界
三、协调曲线法
图7-9 协调曲线
四、分层序列法及宽容分层序列法
四、分层序列法及宽容分层序列法
采用分层序列法,在求解过程中可能会出现中断现象,使求解过程 无法继续进行下去。当求解到第k个目标函数的最优解是惟一时, 则再往后求第(k+1),(k+2),…,l个目标函数的解就完全没有意义 了。这时可供选用的设计方案只是这一个,而它仅仅是由第一个至 第k个目标函数通过分层序列求得的,没有把第k个以后的目标函数 考虑进去。尤其是当求得的第一个目标函数的最优解是唯一时,则 更失去了多目标优化的意义了。为此引入“宽容分层序列法”。这 种方法就是对各目标函数的最优值放宽要求,可以事先对各目标函 数的最优值取给定的宽容量,即ε1>0,ε2>0,…。这样,在求后一 个目标函数的最优值时,对前一目标函数不严格限制在最优解内, 而是在前一些目标函数最优值附近的某一范围内进行优化,因而避 免了计算过程的中断。
5.组合型算法终止准则
6.组合型算法的辅助功能
(1) 直线加速与二次曲线加速 当目标函数严重非线性时,即若
函数具有尖峰脊线,即存在“谷”时,则希望能沿着脊线方向进 行搜索,可迅速提高算法的寻优效率,该算法称为具有脊线加速 能力。 (2) 网格搜索法技术 将离散空间视为一网格空间,每个离散点 就是一个网格节点。 (3) 变量分解策略 将目标函数中的变量分成若干个子集合,若
离散复合形,重新进行调优搜索,直到前后两次离散复合形运算
的优化点重合,算法才最终结束。
6.组合型算法的辅助功能
图7-24 有脊线目标函数 寻优过程示意图
机械创新设计实例分析课件PPT(共 36张)
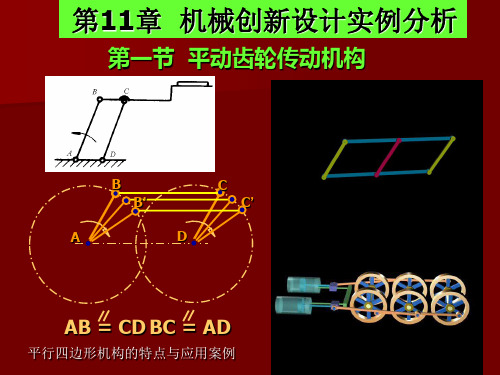
第一节 平动齿轮传动机构
1. 应用了平行四边形机构和齿轮机构的串 行连接;
平动齿轮创新设计方法总结: 2. 应用了三套机构的并行连接;
3. 应用了转动副的销钉扩大和尺寸变化等 演化与变异设计。
第一节 平动齿轮传动机构
二、平动齿轮传动的关键技术
使齿轮实现圆平动运动的机构称为圆平动机构。常用的圆平动机构有: 1.用平行四边形机构实现齿轮圆平动
第一节 平动齿轮传动机构
2.用正弦机构实现齿轮圆平动 3.用孔销机构实现齿轮圆平动
应用“机构同性异形变换原理”,还可以演化出多种圆平动机构。它 的性能决定了平动齿轮传动的性能,所以每综合出一种圆平动机构,就得 到一种新型平动齿轮传动。
第一节 平动齿轮传动机构
三、平动齿轮机构的演化
平动发生器是平动齿轮机构的关键技术。不同的平动发生器,会演化出 结构不同的平动齿轮机构,相同的平动发生器,结构不同,也会演化出性能 差异很大的平动齿轮传动装置。
•
13、要相信,这个世界上永远能够依靠的只有你自己。所以,管别人怎么看,坚持自己的坚持,直到坚持不下去为止。
•
14、也许你想要的未来在别人眼里不值一提,也许你已经很努力了可还是有人不满意,也许你的理想离你的距离从来没有拉近过......但请你继续向前走,因为别人看不到你的努力,你却始终看得见自己。
•
第二节 机构应用创新设计案例分析
三.Stewart机构的应用创新设计
Stewart平台机构
Stewart平台机构用于运动模拟器
第二节 机构应用创新设计案例分析
三.Stewart机构的应用创新设计
俄罗斯Lapic 公司的KNM-750
世界上第一台并联机床
第二节 机构应用创新设计案例分析
机械优化设计实例.pptx

用梯度投影法,对函数易于求导的问题,以可利 用导数信息的方法为好,例如可行方向法;对求导 非常困难的问题则应选用直接解法,例如复合形 法;对于高度非线性的函数,则应选用计算稳定性 较好的方法,例如BFGS变尺度法和内点惩罚函 数法相结合的方法。
• 编写计算机程序对于使用者来说,已经没 有多少工作要做了,因为已有许多成熟的 优化方法程序可供选择。使用者只需要将 数学模型按要求编写成子程序嵌入已有的 优化程序即可。
• 对于一般的机械,可按重量最轻或体积最小的要 求建立目标函数;对应力集中现象尤其突出的构件, 则以应力集中系数最小作为追求的目标,对于精 密仪器,应按其精度最高或误差最小的要求建立 目标函数。在机构设计中,当对所设计的机构的 运动规律有明确的要求时,可针对其运动学参数 建立目标函数;若对机构的动态特性有专门要求, 则应针对其动力学参数建立目标函数;而对于要求 再现运动轨迹的机构设计,则应根据机构的轨迹 误差最小的要求建立目标函数。
第一节 应用技巧
• 一、机械优化设计的一般过程 • 机械优化设计的全过程一般可分为如下几个步骤: • 1)建立优化设计的数学模型。 • 2)选择适当的优化方法。 • 3)编写计算机程序。 • 4)准备必要的初始数据并上机计算。 • 5)对计算机求得的结果进行必要的分析。 • 其中建立优化设计数学模型是首要的和关键的一
• 例如一架好的飞机,应该具有自重轻、净 载重量大,航程长,使用经济,价格便宜, 跑道长度合理等性能,显然这些都是设计 时追求的指标。但并不需要把它们都列为 目标函数,在这些指标中最重要的指标是 飞机的自重。因为采用轻的零部件建造的 自身重量最轻的飞机只会促进其它几项指 标,而不会损害其中任何一项。因此选择 飞机自重作为优化设计的目标函数应该是 最合适的了。
• 编写计算机程序对于使用者来说,已经没 有多少工作要做了,因为已有许多成熟的 优化方法程序可供选择。使用者只需要将 数学模型按要求编写成子程序嵌入已有的 优化程序即可。
• 对于一般的机械,可按重量最轻或体积最小的要 求建立目标函数;对应力集中现象尤其突出的构件, 则以应力集中系数最小作为追求的目标,对于精 密仪器,应按其精度最高或误差最小的要求建立 目标函数。在机构设计中,当对所设计的机构的 运动规律有明确的要求时,可针对其运动学参数 建立目标函数;若对机构的动态特性有专门要求, 则应针对其动力学参数建立目标函数;而对于要求 再现运动轨迹的机构设计,则应根据机构的轨迹 误差最小的要求建立目标函数。
第一节 应用技巧
• 一、机械优化设计的一般过程 • 机械优化设计的全过程一般可分为如下几个步骤: • 1)建立优化设计的数学模型。 • 2)选择适当的优化方法。 • 3)编写计算机程序。 • 4)准备必要的初始数据并上机计算。 • 5)对计算机求得的结果进行必要的分析。 • 其中建立优化设计数学模型是首要的和关键的一
• 例如一架好的飞机,应该具有自重轻、净 载重量大,航程长,使用经济,价格便宜, 跑道长度合理等性能,显然这些都是设计 时追求的指标。但并不需要把它们都列为 目标函数,在这些指标中最重要的指标是 飞机的自重。因为采用轻的零部件建造的 自身重量最轻的飞机只会促进其它几项指 标,而不会损害其中任何一项。因此选择 飞机自重作为优化设计的目标函数应该是 最合适的了。
机械优化设计经典实例PPT课件

x1
x2 x1
3/ 2
0
g3 (X ) 3 l 3 x3 0
g4 (X ) d x2 0
g5 ( X ) D d x1 x2 0
设计实例2: 平面连杆机构优化设计
一曲柄摇杆机构, M为连秆BC上一点, mm为预期的运动 轨迹,要求设计该 曲柄摇杆机构的有 关参数,使连杆上 点M在曲柄转动一 周中,其运动轨迹 (即连杆曲线)MM 最佳地逼近预期轨 迹mm。
6.12(x12 x22 )x3 106
设计实例1:
g1 ( X ) d 4 D 4 1.27 D 10 5 x2 4 x14 1.27 10 5 0
g2 ()
154.34D D4 d 4
Dd D
3/ 2
154.34x1 x14 x2 4
设计实例2:
设计一再现预期轨迹mm的曲柄摇杆机构。已知xA= 67mm,yA=10mm,等分数s=12,对应的轨迹mm 上12个点的坐标值见表,许用传动角[γ]=300。
设计实例2:
一、建立优化设计的数学模型
点M的坐标: xM xA l1 cos( ) l5 cos( ) yM yA l1 sin( ) l5 sin( )
( ) arccosl12 l22 l32 l42 2l1l4 cos
2l2 l12 l42 2l1l4 cos arctg l1 sin
l4 l1 cos
设计实例2:
点M的坐标: xM xA l1 cos( ) l5 cos( ) yM yA l1 sin( ) l5 sin( )
机械优化设计NO.5.ppt

凸函数的基本性质
⑴、设f(X)为定义在D上的凸函数,λ为任意正
实数,则λf(X)也是凸集D上的凸函数
⑵、若函数 f1( X )和 f2 ( X )为凸集D上的两个凸
函数,则对任意正实数a和b,函数
f ( X ) af1( X ) bf2 ( X )仍为D集上的凸函数
⑶、若f(X)为凸集D上的凸函数,则f(X)在D上的 一个极小点也就是在D上的“全域最小点”
总返回
思考题:
1、何谓凸集、凸函数、凸规划? 2、如何判断函数的凸性? 3、写出第三章内容之间的相互联系以及在求优中
的意义。
预 习: 4 一维优化方法
4.1 概 述 4.2 初始搜索区间的确定 4.3 黄金分割法
Φ(X)
a X(1) X
X(2) b
X
f(X) ≤ Φ(X)
f(X)
f(X)
Φ (X)
0a
b
cX
定义:设f (X) 为定义在Rn 中凸集D上的函数,X (1) 和 X (2)
为D上任意两点,若对于任意实数 [0,1],恒
有: f(X) ≤ Φ(X) ,即: f (X (1) (1 ) X (2) ) ≤ f ( X (1) ) (1 ) f ( X (2) )成立,则称 f(X)为 定义在凸集D上的一个凸函数
f xi
(
X
(k
)
)
2
2
二、函数的二阶导数矩阵(Hesse矩阵)
H
(
X
)
2
f
(
X
)
简写为:
机械优化设计(张翔,陈建能编著)PPT模板

2.6优化设 计的约束极
值条件
2.4函数的 凸性
2.5目标函 数的无约束
极值条件
2.1本章导 读
2.2向量、 矩阵的若干
概念
2.3目标函 数的性态分
析基础
第2章优化设计的 理论基础
2.7优化设计的数值解法及终止 准则 2.8习题
第3章一维优化 方法
第3章一维优化方 法
3.1引言 3.2确定搜索区间的进退法 3.3黄金分割法 3.4二次插值法 3.5习题
第9章优化设计实例
9.1复演预期函数机构的
1
设计
9.2圆柱齿轮减速器的优
化设计
2
9.3圆柱螺旋压缩弹簧的
3
优化设计
9.4椭圆齿轮-曲柄摇杆-
轮系引纬机构的设计
4
9.5手脚联控机构的多目
5
标优化设计
9.6应用的扩展——两个
非工程设计的应用实例
6
第9章优化设计实 例
9.7习题
参考文献
参考文献
附录混合罚函数优化 程 序 与 M AT L A B 使 用 示例
附录混合罚函数优化程序 与 M AT L A B 使 用 示 例
F1混合罚函数调用Powell法求 优参考程序
F 2 M AT L A B 优 化 工 具 使 用 示 例
2020
感谢聆听
换
05
7.5优化计 算结果的分
析
03
7.3建模中 数表和图线
的程序化
06
7.6习题
第8章现代优化计算 方法与优化工具软件 应用概述
第8章现代优化计算方法与优化 工具软件应用概述
8.1现代优化计算方法 8 . 2 M AT L A B 优 化 工 具 应 用 概 述 8.3习题
机械创新设计实例分析 PPT(共 46张)

4.外平动齿轮传动的特点 (1)传动比大、分级密集,单级传动比在11~99之间,双级
传动比可达9801。 (2)承载能力大 啮合时几乎是面接触,齿面赫兹应力小。单
个转臂轴承变换为多个转臂轴承分担载荷,转臂轴承的寿命
可达两万小时,且转臂轴承等基本构件不受内齿轮尺寸的限 制,可以按强度要求确定,利于按强度进行优化设计。
平动齿轮减速滚筒具有:传动比大、机械效率高、结构紧凑、 尺寸和重量轻、均载性能好等优点。
3.双曲柄平动齿轮机构 多曲柄平动齿轮机构。如图
9-11所示。 多曲柄平动齿轮机构的传动
原理:输入轴的转速经第一级减 速后,由平动发生器传递给平动 齿轮ZG,同时限制了平动齿轮 ZG的自转,再经第二级减速后, 由内齿中心轮Zb输出。其传动比 统一表达式为
式中 d0——内齿轮根圆直径; d2e——偏心轴距。
外平动齿轮机构的尺寸难以缩小,而且提供内齿轮作平动 的曲柄轴只能有两个,限制了输入功率的分流,不利于传递过 大的功率。
6.内平动齿轮机构的基本型及其演化 图9-4所示为内平动齿轮机构的基本型。图9-5所示的内二环
减速器和内三环减速器。 内平动齿轮机构可获得较小尺寸和重量,其整机性能优于外
2)必须满足一定的装配条件能装配起来。同时也为精度 设计增加了限制条件。
3)传动机构的振动大、噪声高,并随着转速的提高迅速 增加。
上述存在的问题是这种传动的基本原理所决定的,改进
传动原理,开发新的传动类型是平动齿行星轮传动发展 的重要途径。
外平动齿轮机构的A、D两轴之距离受结构的限制
LADd0d2e
(1)组成结构及传动原理 图912所示
外激波摆动活齿传动的传动原 理;当驱动力输入后,输入轴以等 角速度带动外激波器H绕固定主轴 线转动,由于外激波器内轮廓径向 尺寸的变化,产生向心的推力,推 动摆动活齿绕其在活齿架上的铰链 点摆动,通过摆动活齿中心轮高副 啮合运动,摆动活齿推动外齿中心 轮K以等角速度绕主轴线转动,使 与其固联的输出轴获得输出转速, 于是外激波摆动活齿传动完成了转 速变换运动。
机械优化设计方法ppt课件

现在举典型实例来说明优化设计的基本问 题。
图1-1所示的人字架由两个钢管构成,其顶点受外力
2F=3×1 0 5 N。人字架的跨度2B=152cm,钢管壁厚T=0.25cm,
钢管材料的弹性模量E=2.1 ×1 0 5 Mpa,材料密度ρ=7.8 ×
1不0 3超k g过/m许3,用许压用应压力应 力y 和 失y =稳4临20界MP应a。力求e 在的钢条管件压下应,力人 字
A TDh
钢管的临界应力
e
Fe
2E
T2
D2
A 8 B2h2
强度约束条件 x y 可以写成 1 F B2 h2 2 TDh y
稳定约束条件 x e 可以写成
1
F B2h2 2 2E T2 D2
TDh
8 B2 h2
人字架的总质量
1
m D ,h2A L2 T D B 2h22
h v ( x ) 0 v 1, 2,..., p n
数学模型的分类: (1)按数学模型中设计变量和参数的性质分:
确定型模型
设计变量和参数取值确定
随机型模型
设计变量和参数取值随机
(2)按目标函数和约束函数的性质分:
a.目标函数和约束函数都是设计变量的线形函数 称为线性规划问题,其数学模型一般为:
架的高h和钢管平均直径D,使钢管总质量m为最小。
图2-2 人字架的受力
人字架的优化设计问题归结为:
x D HT 使结构质量
mxmin
但应满足强度约束条件 x y
稳定约束条件 x e
1
钢管所受的压力
F1
FL h
F(B2 h2)2 h
失稳的临界力
Fe
2EI L2
1
钢管所受的压应力 F1 F B2 h2 2
图1-1所示的人字架由两个钢管构成,其顶点受外力
2F=3×1 0 5 N。人字架的跨度2B=152cm,钢管壁厚T=0.25cm,
钢管材料的弹性模量E=2.1 ×1 0 5 Mpa,材料密度ρ=7.8 ×
1不0 3超k g过/m许3,用许压用应压力应 力y 和 失y =稳4临20界MP应a。力求e 在的钢条管件压下应,力人 字
A TDh
钢管的临界应力
e
Fe
2E
T2
D2
A 8 B2h2
强度约束条件 x y 可以写成 1 F B2 h2 2 TDh y
稳定约束条件 x e 可以写成
1
F B2h2 2 2E T2 D2
TDh
8 B2 h2
人字架的总质量
1
m D ,h2A L2 T D B 2h22
h v ( x ) 0 v 1, 2,..., p n
数学模型的分类: (1)按数学模型中设计变量和参数的性质分:
确定型模型
设计变量和参数取值确定
随机型模型
设计变量和参数取值随机
(2)按目标函数和约束函数的性质分:
a.目标函数和约束函数都是设计变量的线形函数 称为线性规划问题,其数学模型一般为:
架的高h和钢管平均直径D,使钢管总质量m为最小。
图2-2 人字架的受力
人字架的优化设计问题归结为:
x D HT 使结构质量
mxmin
但应满足强度约束条件 x y
稳定约束条件 x e
1
钢管所受的压力
F1
FL h
F(B2 h2)2 h
失稳的临界力
Fe
2EI L2
1
钢管所受的压应力 F1 F B2 h2 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
154.34D D4 d4
Dd D
3/ 2
0
(3)结构尺寸
l l min d 0
Dd 0
设计实例1:
设:
x1
D
x2
d
x3
l
则数学模型为:
min f () 6.12(D 2 d 2 )l 106
6.12(x12 x 2 2 )x3 106
设计实例1:
g1 ( X ) d 4 D 4 1.27D 105 x24 x14 1.27 105 0
1.3 数组
2)域表定义数组 变量=初值:增量:终值|初值:终值 变量=(初值:增量:终值)*常数 例如: x=0:0.02:10 y=1:80
1.3 数组
1.3.2、 数组的访问(一维)
数组名
表示全体元素
数组名(k)
表示第k元素
数组名(k1:k2)
表示第k1到k2元素
1.3.3 数组运算
1). 纯量与数组的算术运算 a ω c1 或 c1 ω a 其中ω可为+、-、* 结果为[a1ωc1 a2ωc1 … anωc1] 或[c1ωa1 c1ωa2 … c1ωan]
2.3 约束优化函数
[函数] fmincon [格式] x=
fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon) x=
fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon, options) [x,fval] = fmincon(…)
2.3 约束优化函数—盖板优化实例:
s
f ( x) ( xMi xmi )2 ( yMi ymi )2
i 1
设计实例2:
3)确定约束条件
(1)由曲柄存在条件,可得:
g1(x) l1 l2 l3 l4 0 g2 (x) l1 l3 l2 l4 0 g3(x) l1 l4 l2 l3 0
(2)由杆长必须大于零及曲柄1为最短杆,可得:
l4 l1 cos 0 ' 其中 ' 将由设计的已知条件给出。
设计实例2:
该问题有8个设计变量,记为:
x x1, x2 , , x8 T
l1, l2 , l3, l4 , l5, , ,0 T
设计实例2:
2)确定目标函数
将曲柄一周转角分为s等分,要求连秆曲线最佳地逼近 预期轨迹mm,具体可由连杆曲线上的s个点M最佳地逼 近预期轨迹上的s个点m予以实现。由此可按点距和最 小的原则建立如下目标函数:
设计实例2:
设计一再现预期轨迹mm的曲柄摇杆机构。已知xA= 67mm,yA=10mm,等分数s=12,对应的轨迹mm 上12个点的坐标值见表,许用传动角[γ]=300。
设计实例2:
一、建立优化设计的数学模型
点M的坐标: xM xA l1 cos( ) l5 cos( ) yM yA l1 sin( ) l5 sin( ) ( ) arccos l12 l22 l32 l42 2l1l4 cos 2l2 l12 l42 2l1l4 cos arctg l1 sin l4 l1 cos
2). 数组加(减) 使两数组的对应各元素相加(减)
1.3.3 数组运算
3). 数组点乘 两数组的对应元素相乘a.*b 结果: [a1*b1 a2*b2…an*bn]
(a与b的维数必须相同)
1.3.3 数组运算
4). 数组点正除(右除) 使两数组的对应元素正除 a./b 结果为:
(a、b维数必须相同)
数字、下划线组成,长度≤19)。可以合 法出现而定义。
区分大小写字母,以当前值定义其类型。 2、函数名
函数名用标识符表示。
1.3 数组
行向量、列向量、矩阵 1.3.1 创建数组的常用方法
1)直接列表定义数组 例如:
x=[1 2 3 4 5 6 7 8 9 0] y=[1,2,3,4,5,6,7,8,9,0] z=[1,2,3,4,5;2,3,4,5,6,7]
1.4 源文件(M-文件)
分为两类: 函数文件和非函数文件 都用扩展名.M
1.4.1 函数文件(相当于子程序)
格式 function [输出表]=函数名(输入表) 函数体
1.4.2 非函数文件
无函数头的M文件,由若干命令和注释构成。 相当于主程序 如: % is a sine.m
x = 0:0.1:2*pi; y = sin(x); plot(x,y)
设计实例2:
点M的坐标: xM xA l1 cos( ) l5 cos( ) yM yA l1 sin( ) l5 sin( )
( ) arccos l12 l22 l32 l42 2l1l4 cos
2l2 l12 l42 2l1l4 cos arctg l1 sin
g4 (x) e l1 0
设计实例2:
(3)由满足传动角条件γ>[γ],可得:
g5 ( x)
[ ] arccos l22
l32 (l4 2l2l3
l1)2
0
g6
(
x)
[
]
[180。
arccos
l22
l32
(l4 2l2l3
l1 ) 2
]
0
优化设计工具
优化设计工具
第1部分 MATLAB基础 第2部分 优化计算工具
目标函数:
f (x) 2 60t 2 0.5h 120x1 x2
约束:
g1 ( x)
[ ] max
1
1 4 x2
1 0
g2 (x)
[ ] max
1
7 45
x1 x2
1
0
g3 (x)
c max
1
7 45
x13
x2
1
0
g4 (x)
1.5 f max
1
1 321
x1 x22
1
1.4.3 M-文件的操作
1.4.3 M-文件的操作
sin( x 2 y 2 ) z
x2 y2
(7.5 x 7.5,7.5 y 7.5)
1.4.3 M-文件的操作
1.4.3 M-文件的操作
第2部分 优化计算工具
2.1 线性规划优化函数 2.2 无约束非线性优化函数 2.3 约束优化函数
机械优化设计实例 及matlab优化工具
机械优化设计实例
➢ 机械优化设计的一般过程 ➢ 建立数学模型的基本原则 ➢ 机械优化设计实例
机械优化设计的一般过程
机械优化设计全过程一般可分为:
1)建立优化设计的数学模型。 2)选择适当的优化方法。 3)编写计算机程序。 4)准备必要的初始数据并上机计算。 5)对计算机求得的结果进行必要的分析。
[τ]=60MPa。轴所受扭矩为M=1.5×106N·mm。
分析
设计变量:外径D、内径d、长度l
设计要求:满足强度,稳定性和结构尺寸要 求外,还应达到重量最轻目的。
设计实例1:
所设计的空心传动轴应满足以下条件: (1)扭转强度
空心传动轴的扭转切应力不得超过许用值,即
空心传动轴的扭转切应力:
16D (D4 d 4)
fval = 0.1787
exitflag = 4
output = iterations: 7 funcCount: 39 stepsize: 1 algorithm: 'medium-scale: SQP, Quasi-Newton, line-search'
g6 (x) x2 0
盖板优化实例
盖板优化实例
运行结果:
x = 0.6332 25.3264 fval = 101.3056
前面空心轴的问题:
clear all
x0=[23,19,4];
options=optimset('largescale','off','display','iter','tolx',1e-6);
设计实例1:
空心传动轴的扭切应力:
16D (D4 d 4)
经整理得:
d 4 D 4 1.27 105 D 0
设计实例1:
(2)抗皱稳定性 扭转切应力不得超过扭转稳定得临界切应力:
' 空心传动轴的扭转稳定的临界切应力为:
' 0.7E( D d )3/ 2
2D
设计实例1:
整理得:
0
g5 (x) x1 0
g6 (x) x2 0
盖板优化实例
f (x) 2 60t 2 0.5h 120x1 x2
盖板优化实例
g1 ( x)
1
1 4
x2
0
g2 ( x)
1
7 45
x1x2
0
g3 ( x)
1
7 45
x13 x2
0
g4 ( x)
1
1 321
x1x22
0
g5 (x) x1 0
g2 ()
154.34D D4 d4
Dd D
3 / 2
154.34x1 x14 x2 4
x1
x2 x1
3/ 2
0
g3 (X ) 3 l 3 x3 0
g4 (X ) d x2 0
g5 ( X ) D d x1 x2 0
设计实例2: 平面连杆机构优化设计
一曲柄摇杆机构, M为连秆BC上一点, mm为预期的运动 轨迹,要求设计该 曲柄摇杆机构的有 关参数,使连杆上 点M在曲柄转动一 周中,其运动轨迹 (即连杆曲线)MM 最佳地逼近预期轨 迹mm。
[结果] x = 0.0000 15.0000 3.0000
fval = -78.0000
