椭圆中焦点三角形的性质含答案
椭圆的性质二 焦点三角形的性质

||PF|2 |PF|1
a
ex
(a
ex)
2ex
2
4 5
x
,
5
x
0
,
∴0<|F2N|<8,∴0<|OM|<4.
若 P 在椭圆的右半部分时,同样可得出 0<|OM|<4,故选:B.
方法二 极限法,当 P 在左端点时,|OM|=4,在 P 上顶点时,|OM|=0,∴0<|OM|<4.
三 课后练习:
1.(2019·郑州第二次质量预测)已知椭圆 C:ax22+by22=1(a>b>0)的左、右焦点分别为 F1,F2,离心率为23,
x2
令椭圆方程为
a2
y2 b2
1(a b 0)
则由椭圆的定义有 | PF1 | | PF2 | 2a , | F1F2 | 2c ,
∴
| PF1 | | PF2 |
| F1F2 | 2c
sin PF2F1 sin PF1F2 sin F1PF2
又 ∵ PF1F2 5PF2F1 , ∴ PF1F2 750 , PF2F1 150 ,
4.(2019
南昌模拟)P
为椭圆 x2 +y2=1 25 9
上一点,F1,F2
分别是椭圆的左、右焦点,过
P
点作
PH⊥F1F2
于
点 H,若 PF1⊥PF2,则|PH|=( )
A.25
B.8
4
3
C.8
D.9
4
解析:选 D 由椭圆 x2 +y2=1 得 a2=25,b2=9, 25 9
则 c= a2-b2= 25-9=4,∴|F1F2|=2c=8.由椭圆的定义可得|PF1|+|PF2|=2a=10,
A. (0, 3 ] 2
椭圆中焦点三角形的性质及应用探究

2 . 故 答 案 为 D.
2 、f 2
所以 l P F . 1 『 P F 。 I = ( 『 P F 『 +『 P F 。 I ) -4 c
2 ( 1 +C O S 0 )
4n 2— 4c 2 b
性质 四: 已 知 椭 圆 方 程 为 + 一 l ( n> 6> o) ・ 两 焦 点 分 别 为 F , Fz , 设 焦 点 三 角 形 PF F 中 F PF 一 0, 则
( 异 于 长 轴 的 端 点) ,则 称
△F PF 为 椭 圆 的 焦 点 三
证明 : 设 P( 。 , Y 。 ) , 由焦 半 径公 式可 知 : l P F l 一口+
e o , l PF1 口一e 1 . T o .
角形 .
性质一 : 过椭圆焦点 的所 有弦 中通 径 ( 垂 直于焦 点的 弦 ) 最短。 通 径 为 .
y a
在
一
一
刚一
一 4 b
半
一 一
例 1 设 椭 圆x z
十
一1 ( c £ >6 >0 ) 的右 焦点 为 F , 右 准
( 1 P F I +l P F : { ) 。 一2 I P F I I P F l 一4 c 2 l P F I l P F
6 z t a n 要一 t a n , 所 以 当 △ F P F 的 面 积 最 大 时 , 0 为 最 大 ,
这 时 点 P 为 椭 圆 短 轴 的端 点 , 0 —1 2 0 。 .
所 以P Fl ・PF 2 一l P Fl I・f P F z J C O S 0 一Ⅱ C O S 1 2 0 。 一
c o s 8 ≥1 —2 e 。 .
椭圆焦点三角形的几个性质

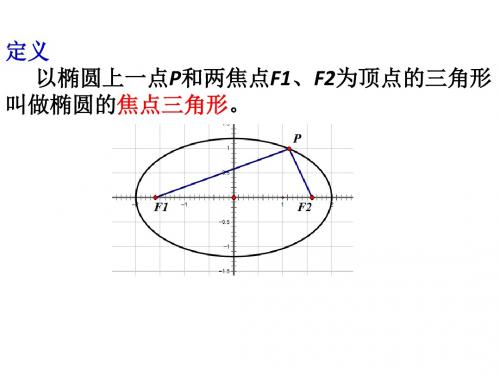
学科纵横幸福生活指南223幸福生活指南椭圆焦点三角形的几个性质张春梅招远第一中学 山东 招远 265400椭圆的两个焦点与椭圆上任一点(非长轴端点)所构成的三角形,我们称之为椭圆的焦点三角形。
焦点三角形是椭圆中的一个基本图形,在它当中很好的体现了椭圆中的一些基本量之间的关系,也很好的体现了解决椭圆问题常用到的方法,下面我们就通过几个例题来研究一下椭圆的焦点三角形的几条性质:在椭圆22221(0)x y a b a b +=>>中,12,F F 是它的两个焦点,P是椭圆上非长轴端点的任一点。
性质一:若椭圆的长轴为2a ,焦距为2c ,则△12F PF 的周长为2a+2c.证明:由椭圆的定义得到1||PF + 2||PF =2a ,又|F 1F 2|=2c ,进而得出焦点三角形的周长=1||PF +2||PF +|F 1F 2|=2a+2c性质二:当P点位在椭圆的短轴端点处时,∠12F PF 最大,且1||PF •2||PF 最大,最大值等于a 2证明:设1||PF =1r ,2||PF =2r ,则1r +2r =2a 。
在△12F PF 中,由余弦定理可得cos ∠12F PF =222121242r r c r r +−=22121212()422r r c r r r r +−−=2212124422a c r r r r −−=212412b r r −22221244112()2b b r r a ≥−=−+。
当且仅当1r =2r 时取得等号。
即1||PF =2||PF 时∠12F PF 最大,所以当P点在椭圆的短轴端点处时,∠12F PF 最大。
由椭圆定义得和式1||PF +2||PF =2a(定值),结合基本不等式得到积式1||PF 2||PF 有最大值,当且仅当1||PF =2||PF 时取等号。
即P 位于短轴端点时,1||PF 2||PF 取得最大值a2。
点评:在该性质的证明过程中,用到了椭圆的定义和基本不等式的有关知识,要灵活应用。
椭圆中焦点三角形的性质及应用

椭圆中焦点三角形的性质及应用
又,故满足:故为直角三角形、说明:考查定义、利用已知、发挥联想,从而解题成功、性质一:已知椭圆方程为两焦点分别为设焦点三角形中则。
性质二:已知椭圆方程为左右两焦点分别为设焦点三角形,若最大,则点P为椭圆短轴的端点。
证明:设,由焦半径公式可知:,在中, = 性质三:过椭圆焦点的所有弦中通径(垂直于焦点的弦)最短,通径为性质四:已知椭圆方程为两焦点分别为设焦点三角形中则证明:设则在中,由余弦定理得:
命题得证。
(2000年高考题)已知椭圆的两焦点分别为若椭圆上存在一点使得求椭圆的离心率的取值范围。
简解:由椭圆焦点三角形性质可知即 ,于是得到的取值范围是性质五:已知椭圆方程为两焦点分别为设焦点三角形,则椭圆的离心率。
由正弦定理得:由等比定理得:而,∴。
已知椭圆的焦点是F1(-1,0)、F2(1,0),P为椭圆上一点,且|F1F2|是|PF1|和|PF2|的等差中项.(1)求椭圆的方程;(2)若点P在第三象限,且∠PF1F2=120,求tanF1PF2.解:(1)由题设2|F1F2|=|PF1|+|PF2|∴2a=4,又2c=2,∴b=∴椭圆的方程为=1.(2)设∠F1PF2=θ,则∠PF2F1=60-θ椭圆的离心率则,整理得:5sinθ=(1+cosθ)∴故,tanF1PF2=tanθ=.
第 1 页共 1 页。
椭圆焦点三角形的性质

椭圆的焦点三角形 基础再现: 已知椭圆22122:1(0)x y C a b a b+=>>的焦点为21,F F ,长轴端点为21,A A ,短轴端点为21,B B ,P 为椭圆上任意一点,O 为坐标原点.1. 焦半径1PF 的范围:[]c a c a +-,.类似的:OP 的范围:[]a b ,.2. 焦点三角形的周长:c a L 22+=.3.[]22221,b c b PF PF -∈⋅,当且仅当P 位于短轴端点时取得22c b -,长轴端点时取得2b . 4. 21PF F ∠在点P 位于短轴端点时取得最大值.类似的:21PA A ∠在点P 位于短轴端点时取得最大值.特别的:过焦点的所有弦中通径通径最短,通径:ab L 22= 5. 焦点三角形的面积: ⅰ.2121sin 21PF F PF PF S ∠⋅⋅=. ⅱ.p y c b b S =⋅=+⋅=2tan cos 1sin 22θθθ,当且仅当点P 位于短轴端点时面积取得最大值bc . 6.22121cos e PF F -≥∠,其中e 为椭圆离心率. 7. PF F F PF PF F e 212121sin sin sin ∠+∠∠=,其中e 为椭圆离心率. 实战演练1.已知椭圆()()221:1,3,0,3,02516x y C A C +=-,B 为椭圆上一点,则在ABC ∆中BC A sin sin sin +的值为 .2.已知21,F F 为椭圆221:12516x y C +=的两个焦点,过1F 的直线交椭圆于B A ,,且1222=+B F A F ,则=AB .3.如图,把椭圆2212516x y +=的长轴AB 分成8分,过每个分点作x 轴的垂线交椭圆的上半部分于1P ,2P ,……7P 七个点,F 是椭圆的一个焦点,则127......PF P F P F +++= .4.已知椭圆()012222>>=+b a b y a x 的左右焦点分别为F ₁(-c ,0)、F ₂(c,0),且椭圆上存在一点P 使得∠F ₁PF ₂ =90°,则椭圆离心率e 的取值范围是: .5.若P 是椭圆16410022=+y x 上的一点,1F 、2F 分别是其左右焦点,且︒=∠6021PF F ,则△21PF F 的面积=S ,点P 的坐标为 .6.已知椭圆1:222=+y ax C (a >1)的左右焦点分别为1F 、2F ,P 为椭圆上一点,且︒=∠6021PF F ,则||||21PF PF ⋅的值为 .7.已知椭圆14:22=+y x C 的左右焦点分别为1F 、2F , P 是椭圆上一点,当△21PF F 的面积为1时,21PF PF ⋅的值为 .8.已知椭圆22194x y +=的左右焦点分别为1F 、2F ,点P 为其上的动点,当12F PF ∠为钝角时,点P 横坐标的取值范围是 .9.已知椭圆221164x y +=的左右焦点分别为1F 、2F ,点M 为其上的动点,当12F MF ∆为直角三角形时,12F MF ∆的面积=S .若将第9题椭圆方程变为2212516x y +=,则12F MF ∆的面积=S . 10.已知椭圆221259x y +=的左右焦点分别为1F 、2F ,点P 为其上的动点,且1260PF F ∠= ,则12F PF ∆的面积=S .11.已知椭圆221259x y +=的左右焦点分别为1F 、2F ,点P 为其上的动点,直线1PF 的斜率为73,则12F PF ∆的面积=S .。
椭圆中与焦点三角形有关的问题

椭圆中与焦点三角形有关的问题性质一:当点P 从右至左运动时,21PF F ∠由锐角变成直角,又变成钝角,过了Y 轴之后,对称地由钝角变成直角再变成锐角,并且发现当点P 与短轴端点重合时,21PF F ∠达到最大。
3.“性质一”是为什么呢?你能证明吗?(面对cos 21PF F ∠=||||2||||||212212221PF PF F F PF PF ⋅-+ 如何求最小值,有的同学尝试后发现若用两次均值不等式,则两次不等号方向相反,达不到目的。
能否少用一次均值不等式求出最值呢?学生们发现分子变化的部分是2221||||PF PF +,分母变化的部分是||||221PF PF ⋅,二者的关系是 ()||||24||||2||||||||212212212221PF PF a PF PF PF PF PF PF ⋅-=⋅++=+ ,于是目标式可分成两部分1||||2212-⋅PF PF b ,最后对||||21PF PF ⋅ 利用均值不等式,即可大功告成。
问题5:由上面的分析,你能得出cos 21PF F ∠与离心率e 的关系吗?性质二:已知椭圆方程为),0(12222>>=+b a by a x 两焦点分别为,,21F F 设焦点三角形21F PF 中,21θ=∠PF F ________.21cos 2e -≥θ_______________(当且仅当动点为短轴端点时取等号)设计意图:进一步的挖掘,可以让问题简单化,应用价值就更高,“看似一小步,其实一大步”!题2:已知1F 、2F 是椭圆)0(12222>>=+b a by a x 的两个焦点,椭圆上一点P 使︒=∠9021PF F ,求椭圆离心率e 的取值范围。
1由椭圆定义,有212a PF PF =+|||| 平方后得42228212221212221222a PF PF PF PF PF PF F F c =++⋅≤+==||||||||(||||)||得c a2212≥ 所以有,)e ∈[221 2⇒22≤e <1 变式1:已知椭圆)0(12222>>=+b a by a x 的两焦点分别为,,21F F 若椭圆上存在一点,P 使得,120021=∠PF F 求椭圆的离心率e 的取值范围。
椭圆焦点三角形的性质

一
。
一
1 f P F1
PF 2 l S i n 一
0
0
t an
两个 交 点 ( O , 一6 ) 、 ( 0 , 6 ) 。若 点 P 的 横 坐标 为 0 , 则 点 P在圆 z +Y 一C 上 , 故 /F PF 2为直 角 ; 若 点
P 的横 坐标 ∈( 一a , 0 ) U( 0 , a ) , 则 点 P在圆 z 。 + Y 。 一C 外 , 故 F PF 为锐 角 。 当c >6时 , 椭 导 。
例 2 已知 F 1 、 F z 是椭圆 c: x z T y Z —l ( 口 >6
P F 2 。若 △PF F z的面积 为 9 , 则6 一
四个 交点 。联 立 +西 Y 一 1和 。 +Y 一c , 得 一
,, n 。
。
—
—
解: 由椭 圆焦 点三 角形 的性 质 2 , 知 9 —6 z t d , n
性质 1 : 设以原点为圆心, 以 椭 圆 的 两 个 焦 点 的
由c >b , 知 在 椭 圆 上 存 在 点 P, 使
F P F 是锐角、 直角、 钝角。 设点 P的横 坐标 为 。 由椭 圆焦 点 三 角 形 的 性 质 1及 其 探 究 , 知: 当 F PF 为 直 角 时 , z 一 ± 二 一 ± 3 ;当
2 r l
z ∈ f 一 互 , — - b 2 1 , 则 点P 在 圆 z z + z 一 ≥ 羔 2 ( 字) 一
f 内 , 故 F P F。 为钝 角 。
中学生数理亿. 赢I l 赢三使用
椭 园 焦 点 三 角 开 乡 白 勺J } 生质
一 甘 肃
秒杀题型 焦点三角形(椭圆与双曲线)

2020年高考数学试题调研之秒杀圆锥曲线压轴题之秒杀题型三:椭圆、双曲线焦点三角形椭圆的焦点三角形:椭圆上任意一点P 与两焦点1F 、2F 构成的三角形:12PF F ∆。
秒杀题型一:性质:1.周长为定值:2()a c +。
2.12,F PF θ∠=当点P 靠近短轴端点时θ增大,当点P 靠近长轴端点时θ减小;与短轴端点重合时θ最大。
类比:(注:椭圆中端点三角形(长轴两端点与椭圆上一点构成)当P 在短轴端点时顶角最大。
)。
1.(2017年新课标全国卷I 文12)设A 、B 是椭圆C 1323=+m y x 长轴的两个端点,若C 上存在点M 满足︒=∠120AMB ,则m 的取值范围是()A.(][)+∞,91,0 B.(][)+∞,93,0 C.(][)+∞,41,0 D.(][)+∞,43,0【解析】:当03m <<时,椭圆的焦点在x 轴上,要使C 上存在点M 满足120AMB ∠=,则tan 60ab≥= ,即≥.得01m <≤;当3m >时,椭圆的焦点在y 轴上,要使C 上存在点M 满足120AMB ∠= ,则tan 60ab ≥= ,≥,得9m ≥,故m 的取值范围为(][)+∞,91,0 ,选A.秒杀题型二:3.三角形面积:212tan 22S c y c y b θ=⨯⨯=⨯=,max ,S bc =即P 与短轴端点重合时面积最大。
1.(高考题)已知1F ,2F 是椭圆1:2222=+by a x C )0(>>b a 的两个焦点,P 为椭圆C 上一点,21PF PF ⊥.若21F PF ∆的面积为9,则b =.【解析】:由椭圆焦点三角形面积公式得:94tanb 22==b π,3=∴b 。
〖母题1〗已知12,F F 是椭圆22195x y +=的焦点,点P 在椭圆上且123F PF π∠=,求12F PF ∆的面积.【解析】:由椭圆定义及余弦定理得:533。
椭圆中与焦点三角形有关的问题

椭圆中与焦点三角形有关的问题2y1的焦点为 F l 、F 2,点 P 为其上动点,当4点 P 横坐标的取值范围是 ______二)问题的分析点 P 的横坐标是 _____ 。
问题 2. 而此题为钝角,究竟钝角和直角有何联系?解题的关键在于点动,发现 F 1PF 2 的大小与点 P 的位置有关,究竟有何联系。
性质一: 当点 P 从右至左运动时, F 1PF 2 由锐角变成直角,又变成钝角,过了 Y 轴之 后,对称地由钝角变成直角再变成锐角, 并且发现当点 P 与短轴端点重合时, F 1PF 2达到 最大。
3. “性质一”是为什么呢?你能证明吗?问题 3: 解三角形中我们常用的理论依据是什么?问题 4:究竟转化为求哪种三角函数的最值,经演算、试验,悟出“欲求 F 1PF 2 的最 大值,只需求 cos F 1PF 2 的最小值”问题 1. x2椭圆9 2 y1的焦点为 F l 、 F 2,点 P 为其上一点,当4F 1PF 2 为直角时,例 1 :椭圆F 1 PF 2 为钝角时,问题5:由上面的分析,你能得出cos F1 PF2与离心率 e 的关系吗?性质二:已知椭圆方程为2x2a2y2 1(a b 0), 两焦点分别为F1, F2 ,设焦点三角形b2PF1F 2 中F1PF22,则cos 1 2e2. (当且仅当动点为短轴端点时取等号)题2:已知F1、F2是椭圆2x2a2y2 1(a b 0) 的两个焦点,椭圆上一b2点P 使F1PF290 ,求椭圆离心率e 的取值范围。
变式1:已知椭圆2x2a2y2 1(a b 0)的两焦点分别为F1, F2 ,若椭圆上存在一点P, 使b得F1PF2 1200,求椭圆的离心率e 的取值范围。
22变式2:若椭圆x y 1 的两个焦点F14 31F 2 ,试问:椭圆上是否存在点P ,使F1PF2 90 ?存在,求出点P 的纵坐标;否则说明理由。
三)问题引入2x2题3:P 是椭圆52y1 上的点,F l ,F2是椭圆的焦点,若F1PF2 ,则PF1F 2 41 231 2的面积等于2 x 问题1:已知椭圆C: 2 a22b y221(a>b>0),F1、F2 是两个焦点,对于给定的角探求在 C 上存在点P,使F1PF2的条件。
《椭圆的焦点三角形》专题1

《椭圆的焦点三角形》专题2018年( )月( )日 班级 姓名 从善如登,从恶如崩。
——《国语》椭圆的焦点三角形是指以椭圆的两个焦点12,F F 与椭圆上任意一点P 为顶点组成的三角形。
)0(12222>>=+b a by a x性质有:(1)12||||2PF PF a +=(2)2221212124||||2||||cos c PF PF PF PF F PF =+-∠(3)椭圆上的点与两焦点连线的夹角以椭圆短轴顶点与两焦点连线的夹角最大.证明:设P 是椭圆22221x y a b+= (0a b >>,c 为半焦距)上的一点 ,O 为原点,E 、F 是椭圆的两焦点,PE m =,PF n = 则222222244222cos 1122m n c b mn b b EPF mn mn mn a+--∠===-≥-, 由余弦函数图象性质知EPF ∠有最大值,当且仅当P 在短轴端点时取到该最大值。
(4)设P 为椭圆上的任意一点,角12F F P α∠=,21F F P β∠=,21F PF θ∠=, 则有离心率sin()sin sin e αβαβ+=+,122sin 1cos PF F S b θθ∆=+2=b tan 2θ 证明:由正弦定理得:βαβαsin sin )180sin(1221PF PF F F o ==-- 由等比定理得:βαβαsin sin )sin(2121++=+PF PF F F 而)sin(2)sin(21βαβα+=+c F F ,βαβαsin sin 2sin sin 21+=++a PF PF ∴βαβαsin sin )sin(++==a c e 。
例题:1、椭圆22221(,0)x y a b a b+=>的两个焦点12,F F ,点P 在椭圆上,且1212414,||,||33PF PF PF PF ⊥==.求椭圆的方程22194x y +=2、设P 为椭圆12222=+by a x )0(>>b a 上一点,F 1、F 2为焦点,如果 7521=∠F PF , 1512=∠F PF ,则椭圆的离心率为( )A .22 B .23 C .32 D .363、1F 、2F 是椭圆17922=+y x 的两个焦点,A 为椭圆上一点,且∠02145=F AF ,则 12AF F ∆的面积为( )A .7B .47 C .27 D .2574、1F 、2F 是椭圆2212516x y +=的两个焦点,A 为椭圆上一点,且1290,F AF ∠=,则A 到x 轴的距离为A .163B .165C .161635or D .非上述答案5、设21F F ,分别是椭圆1162522=+y x 的左、右焦点,P 为椭圆上一点,12,F F P , 是直角三角形的一个顶点,则P 点到x 轴的距离是 A.163 B . 165 C. 161653或 D. 非上述答案6、设21F F ,分别是椭圆221259x y +=的左、右焦点,P 为椭圆上一点,12,F F P , 是是直角三角形的三个顶点,则P 点到x 轴的距离是 A.94 B. 95 C . 9954或 D. 非上述答案7、过椭圆左焦点F ,倾斜角为3π的直线交椭圆于A ,B 两点,若FB FA 2=,则椭圆的离心率为 (构造焦点三角形,两次应用余弦定理,整体处理余弦定理的结果)8、已知Rt ABC ∆,1,AB AC ==点C 为椭圆22221(0)x y a b a b+=>>的右焦点,且AB 为经过椭圆左焦点的弦,求椭圆的离心率。
椭圆焦点三角形(解析版)

椭圆焦点三角形(解析版)椭圆焦点三角形(解析版)在数学几何学中,椭圆焦点三角形是一个有趣且有着独特性质的三角形。
本文将介绍椭圆焦点三角形的定义、性质以及相关定理证明。
定义椭圆焦点三角形是指一个三角形的三个顶点分别位于给定椭圆的两个焦点和一个点上的三角形。
性质1. 椭圆焦点三角形的三边和三个内角有特定的关系设椭圆的两个焦点分别为F1和F2,三角形的三个顶点分别为A、B、C。
那么有以下性质成立:① AF1 + AF2 = BF1 + BF2 = CF1 + CF2②∠F1AF2 + ∠F1BF2 + ∠F1CF2 = 360°2. 椭圆焦点三角形的内角和有一定范围设椭圆的离心率为e,且e < 1。
那么椭圆焦点三角形的内角和满足以下条件:π / 2 < ∠A + ∠B + ∠C < 3π / 2定理证明定理1:椭圆焦点三角形的三边与三个内角的关系假设AF1 + AF2 = BF1 + BF2 = CF1 + CF2 = 2a,并且AF1 < AF2 < BF1 < BF2 < CF1 < CF2。
由于椭圆的几何性质可知,AF1 + AF2 + BF1 + BF2 + CF1 + CF2 = 2a + 2a + 2a = 6a。
根据三角形内角和的性质可知,∠A + ∠B + ∠C = π,其中∠A = ∠F1AF2,∠B = ∠F1BF2,∠C = ∠F1CF2。
由于∠A、∠B、∠C都在同一个三角形内,所以∠A + ∠B + ∠C = π。
因此,AF1 + AF2 + BF1 + BF2 + CF1 + CF2 = 6a = 2π。
得到结论:AF1 + AF2 + BF1 + BF2 + CF1 + CF2 = 2π,即AF1 + AF2 = BF1 + BF2 = CF1 + CF2。
定理2:椭圆焦点三角形的内角和的范围由于e < 1,所以根据椭圆的性质可知,AF1 + AF2 > 2a, BF1 + BF2 > 2a, CF1 + CF2 > 2a。
椭圆中焦点三角形的性质(含答案)

椭圆中焦点三角形的性质(含答案)案场各岗位服务流程销售大厅服务岗:1、销售大厅服务岗岗位职责:1)为来访客户提供全程的休息区域及饮品;2)保持销售区域台面整洁;3)及时补足销售大厅物资,如糖果或杂志等;4)收集客户意见、建议及现场问题点;2、销售大厅服务岗工作及服务流程阶段工作及服务流程班前阶段1)自检仪容仪表以饱满的精神面貌进入工作区域2)检查使用工具及销售大厅物资情况,异常情况及时登记并报告上级。
班中工作程序服务流程行为规范迎接指引递阅资料上饮品(糕点)添加茶水工作要求1)眼神关注客人,当客人距3米距离时,应主动跨出自己的位置迎宾,然后侯客迎询问客户送客户注意事项15度鞠躬微笑问候:“您好!欢迎光临!”2)在客人前方1-2米距离领位,指引请客人向休息区,在客人入座后问客人对座位是否满意:“您好!请问坐这儿可以吗?”得到同意后为客人拉椅入座“好的,请入座!”3)若客人无置业顾问陪同,可询问:请问您有专属的置业顾问吗?,为客人取阅项目资料,并礼貌的告知请客人稍等,置业顾问会很快过来介绍,同时请置业顾问关注该客人;4)问候的起始语应为“先生-小姐-女士早上好,这里是XX销售中心,这边请”5)问候时间段为8:30-11:30 早上好11:30-14:30 中午好 14:30-18:00下午好6)关注客人物品,如物品较多,则主动询问是否需要帮助(如拾到物品须两名人员在场方能打开,提示客人注意贵重物品);7)在满座位的情况下,须先向客人致歉,在请其到沙盘区进行观摩稍作等待;阶段工作及服务流程班中工作程序工作要求注意事项饮料(糕点服务)1)在所有饮料(糕点)服务中必须使用托盘;2)所有饮料服务均已“对不起,打扰一下,请问您需要什么饮品”为起始;3)服务方向:从客人的右面服务;4)当客人的饮料杯中只剩三分之一时,必须询问客人是否需要再添一杯,在二次服务中特别注意瓶口绝对不可以与客人使用的杯子接触;5)在客人再次需要饮料时必须更换杯子;下班程序1)检查使用的工具及销售案场物资情况,异常情况及时记录并报告上级领导;2)填写物资领用申请表并整理客户意见;3)参加班后总结会;4)积极配合销售人员的接待工作,如果下班时间已经到,必须待客人离开后下班;1.3.3.3吧台服务岗1.3.3.3.1吧台服务岗岗位职责1)为来访的客人提供全程的休息及饮品服务;2)保持吧台区域的整洁;3)饮品使用的器皿必须消毒;4)及时补充吧台物资;5)收集客户意见、建议及问题点;1.3.3.3.2吧台服务岗工作及流程阶段工作及服务流程班前阶段1)自检仪容仪表以饱满的精神面貌进入工作区域2)检查使用工具及销售大厅物资情况,异常情况及时登记并报告上级。
椭圆中的“焦点三角形”性质及应用

性质一 : ( 焦点三角形面积 ) 已知椭 圆方程 为 +
一1 ( 口 >6 >0 ) ,两焦点 分别 为 F 、 F 2 , P为椭 圆上任 意
一
F I P G 的取值范 围
. ( 答案 : [ 0 , ] )
点( 除长轴端点外) , 设 焦点三角形 P F F 2 中 F P F 2
一
一
1 — 1 — 2 P 2
a。
通过性质三 , 可得应用三 :
~
( 答案 : 2 0 )
2
.
.
2
2 . 若P 为 椭圆 + 等一 1 上的 一点, F 、 F 。 为 左 右
焦点, 若 F I P G一号 , 求点 P到z轴的距离. ( 答案:
)
1 . ( 2 0 0 0年全国高考题) 已知椭 圆方程 为 + 一
‘ 。
.
一n < z0 < 口, . ‘ . <以 ,
“ 焦点三角形” 的定 义为 : 椭 圆上 的任 意一 点 ( 除长 轴端 点外) 与两个焦 点构 成 的三角 形. 通常“ 焦 点三 角形 ” 的 问题都 有 意地考 查 了椭 圆的定义 、 三角 形 中的正 弦 、 余 弦定理 、 三角形 的面积 、 内角 大小 等知识 , 现 笔者就 椭 圆
“ 焦点三角形” 的 性 质 及 应 用 举 例 分 析 如 一0时 , c o s O取 最 小 值 , 此 时 0最 大 , 即若
F 1 P F 2 最大 , 则点 P为椭圆短轴的端点.
通过性质二 , 可得 应 用 二 :
1 . 点 P 在 椭 圆 +y 。 一 1上 , F 1 、 F 2 为焦点, 则
一
( 1 P F 1 f +I P G( ) 。 一2 l P F 1 c .1 P G l -4 c 2 I P F 1 .f P G J
12.4.3焦点三角形的性质及椭圆中的最值问题
F1
O
F2
x
x2 (2)已知直线l : x y m 0与椭圆C : y 2 1, 4 交于A, B两点,求|AB | 的最大值.
4 10 5
(2)当F 1PF 2 60 时,求F 1PF 2的面积;
4 3 3
y
F1
o
F2
x
x2 y 2 变式:已知椭圆 2 2 1 (a b 0), 焦点坐标为F1 , F2 , 点P为椭圆上的动点, a b 2 S△ PF1F2 b tan 若F1PF2 时,求F1PF2的面积; 2
2
xp2
yp2
F1
o
P F2
x
PF1 PF2 2 cos F1PF2 0 PF1 PF2 0 ( 5 x p )( 5 x p ) y p 0 | PF1 || PF2 |
4 2 9 3 5 3 5 2 x ( , ) xp 5 y p 0 x p 5 4 x p 0 x p p 9 5 5 5
3. 椭圆上一点到定直线的距离的最值问题
x2 y 2 例1:已知椭圆 1,直线L : 4 x 5 y 40 0, 25 9 椭圆上是否存在一点,它到直线L的距离最小? 最小距离是多少?
解:设直线m平行于l, 则l可写成: 4x 5 y k 0
4 x 5 y k 0 2 2 由方程组 x y 1 25 9 2 2 消去y,得25x 8kx k - 225 0
x2 y 2 2.在椭圆 C: 2 2 1( a b 0 )中, F1 和 F2 是椭圆的两个焦 a b
椭圆焦点三角形性质探究

椭圆焦点三角形的性质探究在椭圆的定义中,焦点占有举足轻重的地位,在椭圆的定义性质考查中,或多或少都会和椭圆的焦点联系考查,而椭圆的焦点三角形(椭圆上一点与两焦点所构成的三角形称为焦点三角形。
)又包含了两个焦点作为顶点,因此在高考模考中经常以焦点三角形为背景进行命题。
本文就焦点三角形的一些常见性质进行归纳总结,并在性质背景下对19年的文数高考题进行旧题新解,希望对大家的学习所帮助。
形21F PF 的周长为定值c a 22+.【例1】已知椭圆22221(0)x y a b a b +=>>的左右焦点分别为21,F F ,离心率为43,点P 为椭圆上一点,若 9021=∠PF F ,且21F PF ∆内切圆的半径为1,则椭圆C 的方程为______.【答案】171622=+y x【解析】因为21F PF ∆的周长为c a 22+则1)22(214tan221⨯+==∆c a b S F PF π,即2b c a =+ 又43=a c ,且222c b a +=,解得7,4==b a 即椭圆方程为171622=+y x【证明】记2211||,||r PF r PF ==,由椭圆定义得a r r 2||21=+ ①在△21PF F 中,由余弦定理得:.)2(cos 22212221c r r r r =-+θ 即.4cos 22)(22121221c r r r r r r =--+θ ② 将①式代入②式得.4)cos 1(242212c r r a =+-θ.cos 12cos 1)(222221θθ+=+-=∴b c a r r所以2tan 2cos 22cos2sin2cos 1sin sin 2122222121θθθθθθθ⋅=⋅=+⋅==∆b b b r r S PF F .即.2tan 221θ⋅=∆b S PF F【例2】已知12,F F 为椭圆22221(0)x y a b a b+=>>的左右焦点,P 为椭圆上一点(异于左、右顶点),若存在以c 22为半径的圆内切于21F PF ∆,则椭圆离心率的取值范围是( )A. ]31,0( B.]32,0( C.]32,31( D.)1,32[ 【答案】A 【解析】存在以c 22为半径的圆内切于21F PF ∆,即焦点三角形面积满足: b c r c a S PF F ⨯⨯≤⋅+=∆221)22(2121 即bc c a c ≤+)(22,所以b c a 2)(≤+ 即)(22)(2222c a b c a -=≤+,化简得0)3)((≥-+c a c a 即c a 3≥,故有310≤<e 【2020∙全国Ⅰ卷∙文∙11】设21,F F 是双曲线13:22=-y x C 的两个焦点,O 为坐标原点,点P 在C 上且2=OP ,则21F PF ∆的面积为A.27 B.3 C. 25D.2 【答案】B【解析】在双曲线C 中,易得2=c所以221===OF OF OP ,即21F PF ∆为直角三角形 由引理2易得345cot 2cot2221==⋅=∆ b b S F PF θ(其中θ为21PF F ∠)【2019∙全国Ⅱ卷∙文∙20】已知12,F F 是椭圆2222:1(0)x y C a b a b+=>>的两个焦点,P 为C 上一点,O 为坐标原点.(1)若2POF △为等边三角形,求C 的离心率;(2)如果存在点P ,使得12PF PF ⊥,且12F PF △的面积等于16,求b 的值和a 的取值范围.【解析】(1)连结1PF ,由2POF △为等边三角形可知在12F PF △中,1290F PF ∠=︒,2PF c =,1PF =1221)a PF PF c =+=,故C 的离心率是1ce a==. (2)【解法一】设点为(,)P x y ,则1||2162y c ⋅= ① 222x y c +=,②22221x y a b+=,③ 由②③及222a b c =+得422b y c=,又由①知22216y c =,故4b =.由②③得()22222a x c b c=-,所以22c b ≥,从而2222232,a b c b =+≥=故a ≥所以4b =,a 的取值范围为)+∞.【解法二】由性质二(需要证明)得,1645tan 2tan 2221221===∠⋅=∆b b PF F b S F PF ,所以4b = 又因为y c PFF b S F PF =∠⋅=∆2tan 21221,所以当且仅当点P 位于椭圆上下顶点时,21PF F ∠达到最大,即9021≥∠PF F依题需要12tan21≥=∠bcPF F ,即b c ≥ 所以2222232,a b c b =+≥=故42a ≥.性质三:已知12,F F 为椭圆22221(0)x y a b a b+=>>的两个焦点,P 为椭圆上任意一点,则当点P 为椭圆短轴的端点时,12F PF ∠最大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
焦点三角形习题性质一:过椭圆焦点的所有弦中通径(垂直于焦点的弦)最短,通径为ab 22性质二:已知椭圆方程为),0(12222>>=+b a b y a x 两焦点分别为,,21F F 设焦点三角形21F PF 中,21θ=∠PF F 则2tan221θb S PF F =∆.证明:记2211||,||r PF r PF ==,由椭圆的第一定义得.4)(,2222121a r r a r r =+∴=+在△21PF F 中,由余弦定理得:.)2(cos 22212221c r r r r =-+θ配方得:.4cos 22)(22121221c r r r r r r =--+θ 即.4)cos 1(242212c r r a =+-θ.cos 12cos 1)(222221θθ+=+-=∴b c a r r由任意三角形的面积公式得:2tan 2cos 22cos2sin2cos 1sin sin 2122222121θθθθθθθ⋅=⋅=+⋅==∆b b b r r S PF F ..2tan 221θb S PF F =∴∆同理可证,在椭圆12222=+bx a y (a >b >0)中,公式仍然成立.性质三:已知椭圆方程为),0(12222>>=+b a by a x 两焦点分别为,,21F F 设焦点三角形21F PF 中,21θ=∠PF F 则.21cos 2e -≥θ性质三证明:设,,2211r PF r PF ==则在21PF F ∆中,由余弦定理得:1222242)(2cos 212221221221212212221--=--+=-+=r r c a r r c r r r r r r F F r r θ.2112221)2(222222222122e a c a r r c a -=--=-+-≥ 命题得证。
例1. 若P 是椭圆16410022=+y x 上的一点,1F 、2F 是其焦点,且︒=∠6021PF F , 求△21PF F 的面积.例1.解法一:在椭圆16410022=+y x 中,,6,8,10===c b a 而.60︒=θ 记.||,||2211r PF r PF ==Θ点P 在椭圆上,∴由椭圆的第一定义得:.20221==+a r r在△21PF F 中,由余弦定理得:.)2(cos 22212221c r r r r =-+θ配方,得:.1443)(21221=-+r r r r.144340021=-∴r r 从而.325621=r r .336423325621sin 212121=⨯⨯==∆θr r S PF F 解法二:在椭圆16410022=+y x 中,642=b ,而.60︒=θ.336430tan 642tan221=︒==∴∆θb S PF F例2.已知P 是椭圆192522=+y x 上的点,1F 、2F 分别是椭圆的左、右焦点,212121=,则△21PF F 的面积为( ) A. 33 B. 32 C. 3 D.33 解:设θ=∠21PF F ,则21cos 2121==θ,.60︒=∴θ .3330tan 92tan221=︒==∴∆θb S PF F 故选答案A.例3.已知椭圆191622=+y x 的左、右焦点分别是1F 、2F ,点P 在椭圆上. 若P 、1F 、2F 是一个直角三角形的三个顶点,则点P 到x 轴的距离为( ) A.59 B. 779 C. 49 D. 49或779解:若1F 或2F 是直角顶点,则点P 到x 轴的距离为半通径的长492=a b ;若P 是直角顶点,设点P 到x 轴的距离为h ,则945tan 92tan221=︒==∆θb S PF F ,又,7)2(2121h h c S PF F =⋅⋅=∆ 97=∴h ,.779=h 故选D.1. 椭圆1244922=+x y 上一点P 与椭圆两个焦点1F 、2F 的连线互相垂直,则△21PF F 的面积为( )A. 20B. 22C. 28D. 24 解:24,90221=︒==∠b PF F θ,∴2445tan 242tan 221=︒==∆θb S PF F .故选D.2. 椭圆1422=+y x 的左右焦点为1F 、2F , P 是椭圆上一点,当△21PF F 的面积为1时,21PF PF ⋅的值为( )A. 0B. 1C. 3D. 6 解:设θ=∠21PF F ,Θ12tan2tan221===∆θθb S PF F ,∴︒=︒=90,452θθ,021=⋅PF PF .故选A.3. 椭圆1422=+y x 的左右焦点为1F 、2F , P 是椭圆上一点,当△21PF F 的面积最大时,21PF PF ⋅的值为( )A. 0B. 2C. 4D. 2- 解:3,1,2===c b a ,设θ=∠21PF F ,Θ 2tan 2tan 221θθ==∆b S PF F ,∴当△21PF F 的面积最大时,θ为最大,这时点P 为椭圆短轴的端点,︒=120θ, ∴2120cos cos ||||22121-=︒=⋅=⋅a PF PF PF PF θ.故答案选D. 4.已知椭圆1222=+y ax (a >1)的两个焦点为1F 、2F ,P 为椭圆上一点,且︒=∠6021PF F ,则||||21PF PF ⋅的值为( )A .1B .31C .34D .32 解:︒==∠6021θPF F ,1=b ,3330tan 2tan221=︒==∆θb S PF F , 又Θ||||43sin ||||21212121PF PF PF PF S PF F ⋅=⋅=∆θ, ∴33||||4321=⋅PF PF ,从而34||||21=⋅PF PF . 故答案选C.5. 已知椭圆的中心在原点,对称轴为坐标轴,1F 、2F 为焦点,点P 在椭圆上, 直线1PF 与2PF 倾斜角的差为︒=∠9021PF F ,△21PF F 的面积是20,且c/a=√5/3, 求椭圆的标准方程.解:设θ=∠21PF F ,则︒=90θ. Θ 2045tan 2tan 22221==︒==∆b b b S PF F θ,又Θ3522=-==a b a ace , ∴95122=-ab ,即952012=-a .解得:452=a .∴所求椭圆的标准方程为1204522=+y x 或1204522=+x y .专题2:离心率求法:1.若椭圆的两个焦点与它的短轴的两个端点是一个 正方形的四个顶点,则椭圆的离心率为( )A.22B.32C.53D.631.解析:选A.如图所示,四边形B 1F 2B 2F 1为正方形,则△B 2OF 2为等腰直角三角形, ∴c a =22.2.若一个椭圆长轴的长度、短轴的长度和焦距 成等差数列,则该椭圆的离心率是( ) A.45 B.35 C.25 D.15 2.解析:选B.由题意知2b =a +c ,又b 2=a 2-c 2, ∴4(a 2-c 2)=a 2+c 2+2ac .∴3a 2-2ac -5c 2=0.∴5c 2+2ac -3a 2=0.∴5e 2+2e -3=0.∴e =35或e =-1(舍去).3.若椭圆的短轴长为6,焦点到长轴的一个端点的最近距离是1,则椭圆的离心率为________.3.解析:依题意,得b =3,a -c =1. 又a 2=b 2+c 2,解得a =5,c =4,∴椭圆的离心率为e =c a =45. 答案:454.已知A 为椭圆x 2a 2+y 2b2=1(a >b >0)上的一个动点,直线AB 、AC 分别过焦点F 1、 F 2,且与椭圆交于B 、C 两点,若当AC 垂直于x 轴时,恰好有|AF 1|∶|AF 2|=3∶1, 求该椭圆的离心率.4.解:设|AF 2|=m ,则|AF 1|=3m ,∴2a =|AF 1|+|AF 2|=4m . 又在Rt △AF 1F 2中,|F 1F 2|=|AF 1|2-|AF 2|2=22m .∴e =2c 2a =|F 1F 2|2a =22m 4m =22.5.如图所示,F 1、F 2分别为椭圆的左、右焦点,椭圆上点M 的横坐标等于右焦点的横坐标,其纵坐标等于短半轴长的23,求椭圆的离心率.5. 解:法一:设椭圆的长半轴、短半轴、半焦距长分别为a 、b 、c .则焦点为F 1(-c,0),F 2(c,0),M 点的坐标为(c ,23b ),则△MF 1F 2为直角三角形. 在Rt △MF 1F 2中,|F 1F 2|2+|MF 2|2=|MF 1|2,即4c 2+49b 2=|MF 1|2.而|MF 1|+|MF 2|=4c 2+49b 2+23b =2a ,整理得3c 2=3a 2-2ab .又c 2=a 2-b 2,所以3b =2a .所以b 2a 2=49.∴e 2=c 2a 2=a 2-b 2a 2=1-b 2a 2=59, ∴e =53.法二:设椭圆方程为 x 2a 2+y 2b 2=1(a >b >0), 则M (c ,23b ).代入椭圆方程,得c 2a 2+4b 29b 2=1,所以c 2a 2=59,所以c a =53,即e =53.椭圆中焦点三角形的性质及应用(答案)性质二Array离心率求法:。
