初中数学 第三章 三角形 全章导学案
北师大版七年级下册第三章 三角形 导学案-3.1.4认识三角形导学案
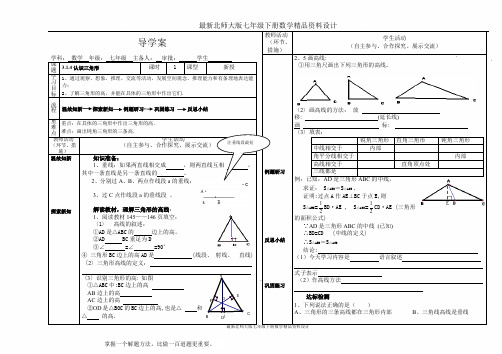
jO EC D B F A 导学案教师活动(环节、措施) 学生活动(自主参与、合作探究、展示交流)学科: 数学 年级: 七年级 主备人: 审批: 学生例题研习反思小结 巩固练习2、5画高线:①用三角尺画出下列三角形的高线。
〈2〉画高线的方法: 放移: (延长线)画 标: 〈3〉填表:锐角三角形 直角三角形 钝角三角形 中线相交于 内部 角平分线相交于 内部 高线相交于 直角顶点处 三线都是例:已知:AD 是三角形ABC 的中线, 求证: S △ABD =S △ACD .证明:过点A 作AE ⊥BC 于点E,则S △ABD =21BD ·AE , S △ACD =21CD ·AE (三角形的面积公式)∵AD 是三角形ABC 的中线 (已知) ∴BD=CD (中线的定义) ∴S △ABD =S △ACD结论: (1)今天学习内容是 语言叙述 式子表示(2)作高线方法达标检测1、下列说法正确的是( )A 、三角形的三条高线都在三角形内部B 、三角线高线是垂线课题 3.1.4认识三角形课时 1 课型 新授学习目标 1、通过观察、想象、推理、交流等活动,发展空间观念、推理能力和有条理地表达能力;2、了解三角形的高,并能在具体的三角形中作出它们. 流程温故知新 探索新知 例题研习 巩固练习 反思小结重难点 重点:在具体的三角形中作出三角形的高. 难点:画出钝角三角形的三条高. 教师活动 (环节、措施)学生活动 (自主参与、合作探究、展示交流)温故知新探索新知知识准备:1、垂线:如果两直线相交成 ,则两直线互相 ,其中一条直线是另一条直线的 。
2、分别过A 、B 、两点作线段a 的垂线;3、过C 点作线段a 的垂线段 。
解读教材,理解三角形的高线: 1、阅读教材145——146页填空: 〈1〉 高线的叙述: ①AD 是△ABC 的 边上的高。
②AD BC 垂足为D ③∠ =∠ =90° ④ 三角形BC 边上的高AD 是 (线段、 射线、 直线) 〈2〉三角形高线的定义: 〈3〉识别三角形的高: 如图 ①△ABC 中:BC 边上的高 AB 边上的高 AC 边上的高②OD 是△BOC 的BC 边上的高,也是△ 和△ 的高.注垂线段最短B DAC CD E B AC 、三角形的高线、中线、角平分线都是线段D 、三角形角平分线是射线教师活动 (环节、措施) 学生活动 (自主参与、合作探究、展示交流) 教师活动(环节、措施) 学生活动 (自主参与、合作探究、展示交流)巩固练习 2、.下列说法:①钝角三角形有两条高在三角形内部;②三角形三条高至多有两条不在三角形内部;③三角形的三条高的交点不在三角形内部,就在三角形外部;④钝角三角形三内角的平分线的交点一定不在三角形内部.其中正确的个数为 ( ) A 1个 B 2个 C 3个 D 4个 3、如下图1,AD 、AE 分别是△ABC 的角平分线和高,∠B=50°,∠C=70°,则∠EAD= . 4、如图2所示,CD 是△ABC 的高,且CD =5,S △ABC =25,则AB =________. 5、如图3所示,在△ABC 中,CD ⊥AB ,∠ACB =86°,∠B =20°,则∠ACD =________. 6、在△ABC 中,已知∠ABC =66°,∠ACB =54°,BE 是AC 上的高,CF 是AB 上的高,H 是BE 和CF 的交点,求∠ABE 、∠ACF 和 ∠BHC 的度数.7、如图,已知:CF ⊥AB 于F ,ED ⊥AB 于D ,∠1=∠2,求证:FG ∥BC巩固练习小结8、已知:∠ACB=90°,CD 是△ABC 的高线∠A=30° 求:∠ACD 、 ∠BCD9、已知:∠ACB=90° CD ⊥AB AB=13 BC=12 AC=5求:(1)S △ABC ,(2)CD 长。
XX年春新版七年级数学下册第三章三角形教学案导学案

XX年春新版七年级数学下册第三章三角形教学案导学案XX年春新版七年级数学下册第三章三角形教学案导学案3.4用尺规作三角形学习目标:一、了解尺规作图的含义及其历史背景。
二、会作一个角等于已知角,并了解作法理由。
3、在别离给出的两角夹边、两边夹角和三边的条件下,能够利用尺规作三角形。
4、作已知线段的垂直平分线,并了解作法理由。
五、能结合三角形全等的条件与同伴交流作图进程和结果的合理性。
学习重点:大体尺规作图学习难点:作一个角等于已知角,作已知线段的垂直平分线的作法分析进程。
四、学习设计:(一)预习预备(1)预习书169~172页(2)学具:圆规、直尺(3)预习作业:已知:a求作:AB,使AB=a已知:∠求作:∠AOB,使∠AOB=∠(二)学习进程:1.作一个三角形与已知三角形全等(1)已知三角形的两边及其夹角,求作那个三角形.已知:线段a,c,∠α。
求作:ΔABC,使得BC= a,AB=c,∠ABC=∠α。
作法与进程:1.作一条线段BC=a,2.以B为极点,BC为一边,作角∠DBC=∠a;3.在射线BD上截取线段BA=c;3.连接AC,ΔABC确实是所求作的三角形。
给出示范和作法,让学生仿照,教师能够在黑板上做一次示范,让学生随着一路操作,并在画完图后,让学生再自己操作一遍.而在下面的作图中,就让学生小组内讨论、交流,通过集体的力量完成,教师再给以必然的指导。
(2)已知三角形的两角及其夹边,求作那个三角形.已知:线段∠α,∠β,线段c 。
求作:ΔABC,使得∠A=∠α,∠B=∠β,AB=c。
作法:1.作____________=∠α;2.在射线______上截取线段_________=c;3.以______为极点,以_________为一边,作∠______=∠β,________交_______于点_______.ΔABC确实是所求作的三角形.先让学生独立试探,探讨作图的进程,对能够自己作出图形的学生,要求他们在小组内交流,用自己的语言表述作图进程。
新北师大版七年级数学下-第三章--三角形学案

第三章 三角形学案认识三角形(1)学习目标:1、通过观察、想象、推理、交流等活动,发展空间观念、推理能力和有条理地表达能力;2、能证明出“三角形内角和等于180°”,能发现“直角三角形的两个锐角互余”;3、按角将三角形分成三类。
学习重难点:三角形内角和定理推理和应用。
学习设计: (一) 预习准备 (1)预习书62-65页(2)思考①三角形的角之间的关系②三角形的分类 (3)预习作业三角形中角的关系:(1)三角形的三个内角之和是 ;(2)直角三角形的两个锐角 三角形的分类:按角分为三类: 三角形; 三角形和 三角形。
(二) 学习过程例1 证明三角形的内角和为180°例2 在△ABC 中,(1)082,42,C A B ∠=∠=∠则= (2)5,A B C C ∠+∠=∠∠那么=(3)在△ABC 中,C ∠的外角是120°,B ∠的度数是A ∠度数的一半,求△ABC 的三个内角的度数变式训练:在△ABC 中(1)078,25,B A C ∠=∠=∠则= (2)若C ∠=55°,010B A ∠-∠=,那么A ∠= ,B ∠=例3 已知△ABC 中,::1:2:3A B C ∠∠∠=,试判断此三角形是什么形状变式训练:已知△ABC 中,090,2,A B B C ∠-∠=∠=∠试判断此三角形是什么形状例4 如图,在△ABC 中,090ACB ∠=,CD ⊥AB 于点D ,1,2?A B ∠∠∠∠与有何关系与呢例5 如图,已知060,30,20,A B C BOC ∠=∠=∠=∠求的度数。
变式训练:如图在锐角三角形ABC 中,BE 、CD 分别垂直AC 、AB ,若040A ∠=,求BHC ∠的度数。
21DC AOCBA拓展:1、如图所示,求A B C D E ∠+∠+∠+∠+∠的度数。
2、如图在△ABC 中,已知1,2,,A B ABC ACB ACB ∠=∠∠=∠∠=∠∠求的度数。
北师大版七年级下册第三章 三角形 导学案-3.1.3认识三角形导学案
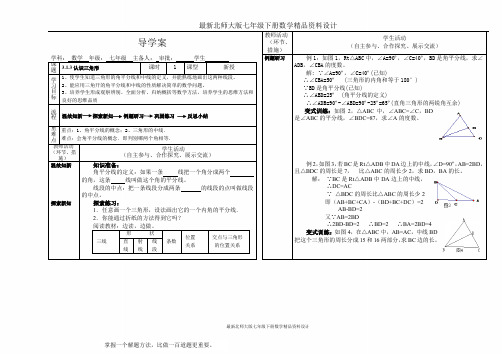
导学案教师活动 (环节、措施)学生活动(自主参与、合作探究、展示交流)学科: 数学 年级: 七年级 主备人: 审批: 学生 例题研习例1:如图1,Rt △ABC 中,∠A=90º,∠C=40º,BD 是角平分线,求∠ADB ,∠CBA 的度数。
解: ∵∠A=90º,∠C=40º(已知)∴∠CBA=50º (三角形的内角和等于180°) ∵BD 是角平分线(已知)∴∠ABD=25º (角平分线的定义)∴∠ADB=90º-∠ABD=90º-25º=65º(直角三角形的两锐角互余) 变式训练:如图2,△ABC 中,∠ABC=∠C ,BD 是∠ABC 的平分线,∠BDC=87,求∠A 的度数。
例2,如图3,若BC 是Rt △ADB 中DA 边上的中线,∠D=90º,AB=2BD ,且△BDC 的周长是7, 比△ABC 的周长少2,求BD ,BA 的长。
解: ∵BC 是Rt △ADB 中DA 边上的中线, ∴DC=AC∵ △BDC 的周长比△ABC 的周长少2 即(AB+BC+CA )-(BD+BC+DC )=2 AB-BD=2 又∵AB=2BD∴2BD-BD=2 ∴BD=2 ∴BA=2BD=4 变式训练:如图4,在△ABC 中,AB=AC ,中线BD 把这个三角形的周长分成15和16两部分,求BC 边的长。
课题 3.1.3认识三角形课时 1 课型 新授学习目标 1、使学生知道三角形的角平分线和中线的定义,并能熟练地画出这两种线段。
2、能应用三角开的角平分线和中线的性质解决简单的数学问题。
3、培养学生形成观察辨别、全面分析、归纳概括等数学方法,培养学生的思维方法和良好的思维品质流程温故知新 探索新知 例题研习 巩固练习 反思小结重难点 重点:1、角平分线的概念;2、三角形的中线.难点:会角平分线的概念.即判别哪两个角相等. 教师活动 (环节、措施)学生活动 (自主参与、合作探究、展示交流)温故知新 探索新知 知识准备:角平分线的定义:如果一条 线把一个角分成两个 的角,这条 线叫做这个角的平分线。
初一数学教案新版第三章三角形导学案

第三章 三角形 3.1 认识三角形(1)学习设计:(一) 预习准备 (1)预习书62-65页(2)思考①三角形的角之间的关系②三角形的分类 (3)预习作业三角形中角的关系:(1)三角形的三个内角之和是;(2)直角三角形的两个锐角 三角形的分类:按角分为三类:三角形;三角形和三角形。
(二) 学习过程例1 证明三角形的内角和为180°例2 在△ABC 中,(1)0082,42,C A B ∠=∠=∠则= (2)5,A B C C ∠+∠=∠∠那么=变式训练:在△ABC 中(1)0078,25,B A C ∠=∠=∠则= (2)若C ∠=55°,010B A ∠-∠=,那么A ∠=,B ∠=例3 已知△ABC 中,::1:2:3A B C ∠∠∠=,试判断此三角形是什么形状?变式训练:已知△ABC 中,090,2,A B B C ∠-∠=∠=∠试判断此三角形是什么形状?例4 如图,在△ABC 中,90ACB ∠=,CD ⊥AB 于点D ,1,2?A B ∠∠∠∠与有何关系与呢例5 如图,已知00060,30,20,A B C BOC ∠=∠=∠=∠求的度数。
变式训练:如图在锐角三角形ABC 中,BE 、CD 分别垂直AC 、AB ,若040A ∠=,求BHC ∠的度数。
拓展:1、如图所示,求A B C D E ∠+∠+∠+∠+∠的度数。
21DC AOCBAHE DCB AHED CBA3.1认识三角形(2)学习设计(一)预习准备(1)预习书66-67页(2)思考①什么叫三角形?②三角形的基本构造③三角形的三边关系 (3)预习作业:如图,已知AD ⊥BC 于点D ,DE ⊥AB 于点E ,点F 是AE 的中点,则图中有个三角形,个直角三角形,个锐角三角形,个钝角三角形;以B 为内角的三角形有个,它们分别是;以BE 为一边的三角形是。
(二)学习过程1、三角形的有关概念(1)三角形的定义:由不在上的三条线段首尾相连所组成的图形。
新版北师大版七年级数学下册第三章 三角形导学案

第三章三角形第一节认识三角形(1)【学习目标】1.认识三角形的定义及相关概念和表示方法2.理解并能运用三角形的内角和定理.3.掌握三角形的分类.4.掌握直角三角形的表示方法及内角的性质.【学习方法】自主探究与小组合作交流相结合.【学习过程】模块一预习反馈一、学习准备1.观察下面的屋顶框架(1)你能从图中找出四个不同的三角形吗?(2)这些三角形有什么共同的特点?解:(1)能(2)都有条边,内角,个顶点。
2.多边形的概念:由若干条不在上的线段相连组成的封闭平面图形。
3.(1)什么叫做三角形?解:由不在同一直线上的线段首尾相接所组成的图形叫做三角形。
(2)如何表示三角形?解:三角形可用符号“△”表示,如右图三角形记作:(3)三角形的边可以怎么表示?解:如图三角形中三边可表示为AB,BC,AC,顶点A所对的边BC也可表示为a,顶点B所对的边表示为b,顶点C所对的边AB表示。
4.如果我说三角形有三要素,你能猜出是哪三要素吗?解:角:三角形中有个角:∠A,,∠C顶点:三角形中有个顶点,顶点,顶点B,顶点边:三角形中三边 AB,,AC二、教材精读1.你能用学过的知识解释“三角形的三个内角和是180˚”吗?解:小明只撕下三角形的一个角,得到了结论,他是这样做的:(1)如图所示,剪一个三角形纸片,它的三个内角分别为∠1, ,∠3.(2)将∠1撕下,按图所示摆放,其中∠1的顶点与∠2的顶点重合,它的一条边与∠2的一条边重合。
由 相等可知∠1的另一边b 与∠3的一边a 平行。
(3)将∠3与∠2的公共边延长,它与b 所夹的角为 ,由∠1的另一边b 与∠3的一边a 平行可知∠3=所以∠1+∠2+∠3=∠1+∠2+ =︒180,即三角形内角和为 。
2.下面的图⑴、图⑵、图⑶中的三角形被遮住的两个内角是什么角?请说明理由。
解:图1,图2露出的角分别是 , ,由三角形三个内角和等于可以得到被遮住的两个角都是 ;当图3露出的一个角是锐角时,另外两个角有 中可能,即 个锐角, 、一直角, 、一钝角。
七年级数学下册精品导学案第三章三角形

第四章三角形第一节认识三角形(1)【学习目标】1.认识三角形的定义及相关概念和表示方法2.理解并能运用三角形的内角和定理.3.掌握三角形的分类.4.掌握直角三角形的表示方法及内角的性质.【学习方法】自主探究及小组合作交流相结合.【学习过程】模块一预习反馈一、学习准备1.观察下面的屋顶框架(1)你能从图中找出四个不同的三角形吗?(2)这些三角形有什么共同的特点?解:(1)能(2)都有条边,内角,个顶点。
2.多边形的概念:由若干条不在上的线段相连组成的封闭平面图形。
3.(1)什么叫做三角形?解:由不在同一直线上的线段首尾相接所组成的图形叫做三角形。
(2)如何表示三角形?解:三角形可用符号“△”表示,如右图三角形记作:(3)三角形的边可以怎么表示?解:如图三角形中三边可表示为AB,BC,AC,顶点A所对的边BC也可表示为a,顶点B所对的边表示为b,顶点C所对的边AB表示。
4.如果我说三角形有三要素,你能猜出是哪三要素吗?解:角:三角形中有个角:∠A,,∠C顶点:三角形中有个顶点,顶点,顶点B,顶点边:三角形中三边 AB,,AC二、教材精读1.你能用学过的知识解释“三角形的三个内角和是180˚”吗?解:小明只撕下三角形的一个角,得到了结论,他是这样做的:(1)如图所示,剪一个三角形纸片,它的三个内角分别为∠1,,∠3.(2)将∠1撕下,按图所示摆放,其中∠1的顶点及∠2的顶点重合,它的一条边及∠2的一条边重合。
由 相等可知∠1的另一边b 及∠3的一边a 平行。
(3)将∠3及∠2的公共边延长,它及b 所夹的角为 ,由∠1的另一边b 及∠3的一边a 平行可知∠3=所以∠1+∠2+∠3=∠1+∠2+ = 180,即三角形内角和为 。
2.下面的图⑴、图⑵、图⑶中的三角形被遮住的两个内角是什么角?请说明理由。
解:图1,图2露出的角分别是 , ,由三角形三个内角和等于可以得到被遮住的两个角都是 ;当图3露出的一个角是锐角时,另外两个角有 中可能,即 个锐角, 、一直角, 、一钝角。
全等三角形全章导学案
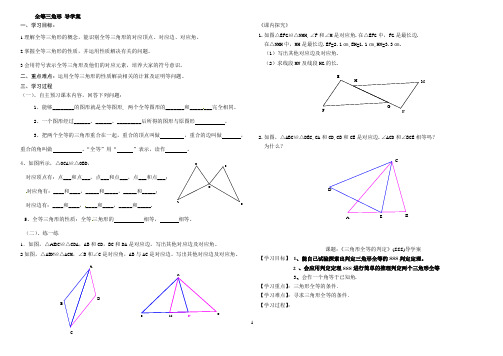
1全等三角形 导学案 一、学习目标:1.理解全等三角形的概念,能识别全等三角形的对应顶点、对应边、对应角。
2.掌握全等三角形的性质,并运用性质解决有关的问题。
3.会用符号表示全等三角形及他们的对应元素,培养大家的符号意识。
二、重点难点:运用全等三角形的性质解决相关的计算及证明等问题。
三、学习过程(一)、自主预习课本内容,回答下列问题:1、能够________的图形就是全等图形, 两个全等图形的_______和________完全相同。
2、一个图形经过______、______、_________后所得的图形与原图形 。
3、把两个全等的三角形重合在一起,重合的顶点叫做 ,重合的边叫做 ,重合的角叫做 。
“全等”用“ ”表示,读作 。
4、如图所示,△OCA ≌△OBD ,对应顶点有:点___和点___,点___和点___,点___和点___; 对应角有:____和____,_____和_____,_____和_____; 对应边有:____和____,____和____,_____和_____.5、全等三角形的性质:全等三角形的 相等, 相等。
(二)、练一练1.如图,△AB C ≌△CDA ,AB 和CD ,BC 和DA 是对应边。
写出其他对应边及对应角。
2如图,△ABN ≌△ACM ,∠B 和∠C 是对应角,AB 与AC 是对应边。
写出其他对应边及对应角。
《课内探究》1.如图△EFG ≌△NMH,∠F 和∠M 是对应角.在△EFG 中,FG 是最长边. 在△NMH 中,MH 是最长边.EF=2.1㎝,EH=1.1㎝,HN=3.3㎝. (1)写出其他对应边及对应角. (2)求线段MN 及线段HG 的长.2.如图,△ABC ≌△DEC,CA 和CD,CB 和CE 是对应边.∠ACD 和∠BCE 相等吗? 为什么?课题:《三角形全等的判定》(SSS)导学案【学习目标】 1、能自己试验探索出判定三角形全等的SSS 判定定理。
新北师大版七年级数学下《第三章三角形》导学案

新北师大版七年级数学下《第三章三角形》导学案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第四章 三角形 4.1 认识三角形(1)三角形中角的关系:(1)三角形的三个内角之和是 ;(2)直角三角形的两个锐角 三角形的分类:按角分为三类: 三角形; 三角形和 三角形。
变式训练:已知△ABC 中,090,2,A B B C ∠-∠=∠=∠试判断此三角形是什么形状?例5 如图,已知00060,30,20,A B C BOC ∠=∠=∠=∠求的度数。
变式训练:如图在锐角三角形ABC 中,BE 、CD 分别垂直AC 、AB ,若040A ∠=,求BHC ∠的度数。
2、如图在△ABC 中,已知1,2,,A B ABC ACB ACB ∠=∠∠=∠∠=∠∠求的度数。
4.1认识三角形(2)变式训练:1、已知两条线段的长为5cm 和8cm ,要订成一个三角形,试求: (1) 第三条线段的长度范围;(2) 若第三条线段的长度为奇数,求此时三角形的周长。
2、已知等腰三角形中,有两边长为3和7,求此等腰三角形的底边和腰长 拓展:1、若设,,a b c 是△ABC 的三边,则a b c a b c +++--= 回顾小结:掌握三角形三边关系:“三角形任意两边之和大于第三边;三角形任意两边之差小于第三边”。
4.1认识三角形(3)OCAHE DCBA21D CBA画出下图三角形的三条高(一)学习过程1、在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫做2、在三角形中, 的线段,叫做这个三角形的中线。
3、从三角形的一个顶点向它的对边所在直线作垂线, 之间的线段叫做三角形的高。
例1 (1)如图1,D 为S △ABC 的变BC 边的中点,若S △ADC =15, 那么S △ABC =(2)如图2,已知AD 、BE 分别是△ABC 中BC 、AC 边上的高,若0070,120,2C ∠=∠=∠=那么D CBA21EDCBA图1 图2变式训练:如图在△ABC 中,BD 平分00,66,24,ABC C ABD A ∠∠=∠=∠那么=例2 如图,已知在△ABC 中,ABC ACB ∠∠与的平分线交于点O ,试说明:01902BOC A ∠=+∠DCB AOCBAIA变式训练:如图在△ABC 中,已知I 是△ABC 三个内角平分线的交点,0130BIC BAC ∠=∠,则为( )A 、40°B 、50°C 、65°D 、80°2、如图1在△ABC 中,AD ⊥BC 于点D ,AE 平分∠BAC ,∠B=40°,∠C=65°,求∠EAD 的度数.回顾小结:(1)三角形的角平分线、中线、高线的定义; (2) 三角形的角平分线、中线、高线是线段.4.3 探索三角形全等的条件(1)[例1]如图,1、如图,△ABC 中 AB=AC , D 为BC 中点求证:①△ABD ≌△ACD .②∠BAD=∠CAD ③AD ⊥BC变式训练:如图,已知AC=FE 、BC=DE ,点A 、D 、B 、F 在一条直线上,AD=FB .要用“边边边”证明△ABC ≌△FDE ,除了已知中的AC=FE ,BC=DE 以外,还应该有什么条件怎样才能得到这个条件例2、如图,已知AB=CD ,AC=BD ,求证:∠A=∠DFDCBEA图1E D CBA拓展延伸1、如图,AC 与BD 交于点O ,AD=CB ,E 、F 是BD 上两点,且AE=CF ,DE=BF. 请推导下列结论:⑴∠D=∠B ;⑵AE ∥CF .2、已知如图,A 、E 、F 、C 四点共线,BF=DE ,AB=CD.⑴请你添加一个条件,使△DEC ≌△BFA ;⑵在⑴的基础上,求证:DE ∥BF.3、 已知:AB =AC, D 为△ABC 内部一点, 且BD = CD,连接AD 并延长,交BC 于点E. 试找出图中的一对全等的三角形,并证明你的结论。
七年级数学下册第三章三角形导学案新版北师大版

2014七年级数学下册第三章三角形导学案(新版北师大版)第五节三角形全等测距离【学习目标】能利用三角形全等解决实际问题,体会数学与实际生活的联系。
2、能在解决问题的过程中进行有条理的思考和表达。
【学习方法】自主探究与小组合作交流相结合.【学习重难点】有条理的思考和表达【学习过程】模块一预习反馈学习准备1.请你在下列各图中,以最快的速度画出一个三角形,使它与△ABC全等,比比看谁快!教材精读1.战士面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部;然后,他转过一个角度,保持刚才的姿势,这时视线落在了自己所在岸的某一点上;接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡的距离。
你觉得他测的距离准确吗?2.小明在上周末游览风景区时,看到了一个美的池塘,他想知道最远两点A、B之间的距离,但是他没有船,不能直接去测。
手里只有一根绳子和一把尺子,他怎样才能测出A、B之间的距离呢?把你的设计方案在图上画出来,并与你的同伴交流你的方案,看看谁是方案更便捷。
方案一:在能够到达A、B的空地上取一适当点C,连接AC,并延长AC到D,使CD=AC,连接BC,并延长BC 到E,使CE=BC,连接ED。
则只要测ED的长就可以知道AB的长了理由: 在△ACB与△DCE中,AC=CD∠BCA=∠ECDBAB=DE (全等三角形的相等)方案二:如图,找一点D,使AD⊥BD,延长AD至C,使CD=AD,连结BC,量BC的长即得AB的长。
解:在Rt∆ADB与Rt∆CDB中BD=BD (同一条线段)∠ADB=∠CDB (都是)CD=AD ()≌∆CDB ( )∴ BA = BC ()模块二合作探究05年,法军在拿破仑的率领下与德军在莱茵河畔激战,德军在莱茵河北岸Q处,如图所示,因不知河宽,法军大炮很难瞄准敌兵营,聪明的拿破仑站在南岸的点O处,调整好自己的帽子,使视线恰好擦着帽舌边缘看到对面德军营Q处,然后他一步一步后退,一直退到自己的视线恰好落在他刚刚站立的点O处,让士兵丈量他所站位置B与O点的距离,并下令按这个距离炮轰敌兵营,试问:法军能命中目标吗?请说明理由,用帽舌边缘视线法还可以怎样测量,也能测出河岸两边OQ的距离?模块三形成提升1.如图,某人要测量河中浅滩B和对岸A的距离,先在岸边定出点C,使C、A、B在一直线上,再依AC的垂直方向在岸边画线段CD,取它的中点O,又画DF垂直CD,观测得E、O、B在一直线上,同时F、O、A也在一直线上,那么EF的长就是AB的距离,为什么?模块四小结反思本课知识1.三角形全等的判定方法1:三边分别______的两个三角形,简称为“边边边”或“ ”。
章三角形的初步认识全章导学案(浙教版七年级下)

章三角形的初步认识全章导学案(浙教版七年级下)1认识三角形-----导学案一、学习目标三角形的概念..用符号、字母表示三角形..三角形任何两边之和大于第三边的性质。
二、学习重点:“三角形任何两边之和大于第三边”的性质学习难点:判断三条线段能否组成三角形三、过程性学习学前准备:定义:由不在直线上的三条首尾顺次连结所组成的图形,叫做三角形。
三角形的三要素是、、。
如图,三角形记为,三角形的边,三角形的顶点为,三角形的内角为注意:表示三角形时,字母没有先后顺序,但通常按逆时针来排列。
探索新知如图,在三角形中,比较任意两边的和与第三边的大小,并填空:a+bc→c–aba+cb→b-acb+ca→c-ba结论:①②.应用新知例1:判断下列各组线段中,哪些能组成三角形,哪些不能组成三角形,并说明理由。
a=3c,b=4c,c=8ce=5.7c,f=6.2c,g=11.9c:当堂练:下列哪组线段能组成三角形?并说明理由A1c,2c,3.5cB4c,5c,9cc6c,8c,13c如图,在三角形ABc中,D是AB上一点,且AD=Ac请比较大小:ABAc+Bc2ADcD四、评价性学习基础性练习如图三角形ABc中,∠B的对边是,夹∠B的两边是、。
图中有几个三角形?请分别把它们表示出来。
已知四组线段:第①组长度分别为5,6,11;第②组长度分别为1,4,4;;第③组长度分别为4,4,4;第④组长度分别为3,4,5,其中不能成为一个三角形的三条边的是A、①B、②c、③D、④已知一个三角形的两边长分别是1和5,则第三边c的取值范围是A.1或∠1>三角形的外角与不相邻内角的关系:①,②。
运用新知例:如图,在⊿ABc中,∠A=450,∠B=300,求∠c和它的外角的度数四、评价性学习基础性评价在△ABc中若∠A=45°,∠B=30°,则∠c=.变式1:在△ABc中,∠A=45°,∠B=2∠c,求∠B、∠c的度数。
新北师大版七年级数学下-第三章--三角形学案

新北师大版七年级数学下-第三章--三角形学案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第三章 三角形学案3.1 认识三角形(1)学习目标:1、通过观察、想象、推理、交流等活动,发展空间观念、推理能力和有条理地表达能力;2、能证明出“三角形内角和等于180°”,能发现“直角三角形的两个锐角互余”;3、按角将三角形分成三类。
学习重难点:三角形内角和定理推理和应用。
学习设计: (一)预习准备(1)预习书62-65页(2)思考①三角形的角之间的关系②三角形的分类 (3)预习作业三角形中角的关系:(1)三角形的三个内角之和是 ;(2)直角三角形的两个锐角三角形的分类:按角分为三类: 三角形; 三角形和 三角形。
(二)学习过程例1 证明三角形的内角和为180°例2 在△ABC 中,(1)0082,42,C A B ∠=∠=∠则= (2)5,A B C C ∠+∠=∠∠那么=(3)在△ABC 中,C ∠的外角是120°,B ∠的度数是A ∠度数的一半,求△ABC 的三个内角的度数变式训练:在△ABC 中(1)0078,25,B A C ∠=∠=∠则= (2)若C ∠=55°,010B A ∠-∠=,那么A ∠= ,B ∠=例3 已知△ABC 中,::1:2:3A B C ∠∠∠=,试判断此三角形是什么形状?变式训练:已知△ABC 中,090,2,A B B C ∠-∠=∠=∠试判断此三角形是什么形状?例4 如图,在△ABC 中,090ACB ∠=,CD ⊥AB 于点D ,1,2?A B ∠∠∠∠与有何关系与呢 例5 如图,已知00060,30,20,A B C BOC ∠=∠=∠=∠求的度数。
变式训练:如图在锐角三角形ABC 中,BE 、CD 分别垂直AC 、AB ,若040A ∠=,求BHC ∠的度数。
21DC AOCBADA拓展:1、如图所示,求A B C D E ∠+∠+∠+∠+∠的度数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 三角形 4.1 认识三角形(1)学习目标:1、通过观察、想象、推理、交流等活动,发展空间观念、推理能力和有条理地表达能力; 2、能证明出“三角形内角和等于180°”,能发现“直角三角形的两个锐角互余”; 3、按角将三角形分成三类。
学习重难点:三角形内角和定理推理和应用。
学习设计:(一) 预习准备(1)预习书62-65页(2)思考①三角形的角之间的关系①三角形的分类 (3)预习作业三角形中角的关系:(1)三角形的三个内角之和是 ;(2)直角三角形的两个锐角 三角形的分类:按角分为三类: 三角形; 三角形和 三角形。
(二) 学习过程例1 证明三角形的内角和为180°例2 在①ABC 中,(1)082,42,C A B ∠=∠=∠则= (2)5,A B C C ∠+∠=∠∠那么=(3)在①ABC 中,C ∠的外角是120°,B ∠的度数是A ∠度数的一半,求①ABC 的三个内角的度数变式训练:在①ABC 中(1)0078,25,B A C ∠=∠=∠则= (2)若C ∠=55°,010B A ∠-∠=,那么A ∠= ,B ∠=例3 已知①ABC 中,::1:2:3A B C ∠∠∠=,试判断此三角形是什么形状?变式训练:已知①ABC 中,090,2,A B B C ∠-∠=∠=∠试判断此三角形是什么形状?例4 如图,在①ABC 中,090ACB ∠=,CD ①AB 于点D ,1,2?A B ∠∠∠∠与有何关系与呢例5 如图,已知060,30,20,A B C BOC ∠=∠=∠=∠求的度数。
21DC BAOCBA变式训练:如图在锐角三角形ABC 中,BE 、CD 分别垂直AC 、AB ,若040A ∠=,求BHC ∠的度数。
拓展:1、如图所示,求A B C D E ∠+∠+∠+∠+∠的度数。
2、如图在①ABC 中,已知1,2,,A B ABC ACB ACB ∠=∠∠=∠∠=∠∠求的度数。
回顾小结:1、三角形的三个内角的和等于180°; 2、三角形按角分为三类:(1)锐角三角形 (2)直角三角形 (3)钝角三角形 3、直角三角形的两个锐角互余HE DCBAHED CB A 21D C BA4.1认识三角形(2)一、学习目标:1、通过观察、操作、想象、推理、交流等活动,发掌空间观念、推理能力和有条理地表达能力;2、结合具体实例,进一步认识三角形的概念及其基本要素,掌握三角形三边关系:“三角形任意两边之和大于第三边;三角形任意两边之差小于第三边”。
二、学习重点:三角形三边关系:“三角形任意两边之和大于第三边;三角形任意两边之差小于第三边”。
三、学习难点: 灵活运用三角形三边关系解决一些实际问题。
四、学习设计 (一)预习准备(1)预习书66-67页(2)思考①什么叫三角形?①三角形的基本构造①三角形的三边关系 (3)预习作业:如图,已知AD ①BC 于点D ,DE ①AB 于点E ,点F 是AE 的中点,则图中有 个三角形, 个直角三角形, 个锐角三角形, 个钝角三角形;以B 为内角的三角形有 个,它们分别是 ;以BE 为一边的三角形是 。
(二)学习过程1、三角形的有关概念(1)三角形的定义:由不在 上的三条线段首尾 相连所组成的图形。
(2)三角形的基本构造:①组成三角形的三条线段叫做三角形的 ①两条边相接的点叫做三角形的 ①相邻两边组成的角叫做三角形的 2、三角形的三边关系: (1)三角形任意两边之和 第三边 (2)三角形任意两边之差 第三边例1 图中共有几个三角形?并把它们用符号表示出来。
例2 下面各组数分别表示三条线段的长度,试判断以它们为边是否能组成三角形。
(1)1 ;4 ;5 (2)3 ;3 ;5(3)3x ;5x ;7x (x 为正数) (4)三条线段长度之比为4:7:6 变式训练:有下列长度的三条线段能否构成三角形?为什么? (1)3 ;4 ;8 (2)5 ;6 ;11 (3)5 ;7 ;10 (4)4 ;4 ;9 (5)5 ;5 ;5例3 小明要制作一个三角形铁丝架,已知有两根铁丝长度分别是3cm ,5cm (1) 他该如何选择第三根铁丝?你能帮助小明确定它的长度或范围吗? (2) 如果要求第三根铁丝的长度是整数,那么小明有几种选择?G FE D CBA变式训练:1、已知两条线段的长为5cm 和8cm ,要订成一个三角形,试求: (1) 第三条线段的长度范围;(2) 若第三条线段的长度为奇数,求此时三角形的周长。
2、已知等腰三角形中,有两边长为3和7,求此等腰三角形的底边和腰长例4 如图所示,在小河的同侧有A ,B ,C 三个村庄,图中的线段表示道路,某邮递员从A 村送信到B 村,总是走经过C 村的道路,不走经过D 村的道路,这是为什么呢? 请利用你所学的数学知识加以证明。
拓展:1、若设,,a b c 是①ABC 的三边,则a b c a b c +++--=2、已知,,a b c 是①ABC 的三边,2,5a b ==,且三角形的周长是偶数,(1)求c 的值;(2)判断①ABC 的形状。
回顾小结:掌握三角形三边关系:“三角形任意两边之和大于第三边;三角形任意两边之差小于第三边”。
4.1认识三角形(3)学习目标:1、通过观察、想象、推理、交流等活动,发展空间观念、推理能力和有条理地表达能力;2、了解三角形的角平分线、中线、高线,并能在具体的三角形中作出高线。
学习重点:1、角平分线的概念2、三角形的中线、高线。
学习难点:高线的画法以及三个定义做计算 学习设计:(一) 预习准备(1) 预习书68-72(2) 思考:什么是三角形的角平分线?中线?高线? (3) 预习作业画出下图三角形的三条高(二) 学习过程1、在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫做2、在三角形中, 的线段,叫做这个三角形的中线。
3、从三角形的一个顶点向它的对边所在直线作垂线, 之间的线段叫做三角形的高。
例1 (1)如图1,D 为S ①ABC 的变BC 边的中点,若S ①ADC =15, 那么S ①ABC = (2)如图2,已知AD 、BE 分别是①ABC 中BC 、AC 边上的高,若0070,120,2C ∠=∠=∠=那么图1 图2变式训练:如图在①ABC 中,BD 平分0,66,24,ABC C ABD A ∠∠=∠=∠那么=D CBA21EDCBA DCB A例2 如图,已知在①ABC 中,ABC ACB ∠∠与的平分线交于点O ,试说明: (1)01180()2BOC ABC ACB ∠=-∠+∠ (2)01902BOC A ∠=+∠变式训练:如图在①ABC 中,已知I 是①ABC 三个内角平分线的交点,0130BIC BAC ∠=∠,则为( )A 、40°B 、50°C 、65°D 、80°例3 如图,已知在①ABC 中,CF 、BE 分别是AB 、AC 边上的中线,若AE =2,AF =3,且①ABC 的周长为15,求BC 的长。
变式训练:如图,在①ABC 中,AB =AC ,AC 边上的中线BD 把三角形的周长分为12和15两部分,求①ABC 各边的长。
拓展:1、(1)如图,若AD 为①ABC 底边BC 的中线,则ABDS= =12; OCBAICBAOF E CB A DC BA(2)两个等底(同底)三角形面积之比等于它们的 之比;两个等高(同高)三角形面积之比等于它们的 之比;(3)如图,在四边形ABCD 中,点E 、F 分别在BC 、CD 上,DF =FC ,CE =2EB 。
已知,SDFAECF Sm S n ==四边形(其中n >m ),则ABCD S 四边形=2、如图1在①ABC 中,AD ①BC 于点D ,AE 平分()BAC C B ∠∠>∠ (1)试探究,EAD C B ∠∠∠与的关系;(2)若F 是AE 上一动点①若F 移动到AE 之间的位置时,FD ①BD ,如图2所示,此时EFD C B ∠∠∠与与的关系如何?①当F 继续移动到AE 延长线上时,如图3所示FD ①BC ,①中的结论是否还成立,如果成立说明理由,如果不成立,写出新的结论。
回顾小结:(1)三角形的角平分线、中线、高线的定义;(2) 三角形的角平分线、中线、高线是线段.FEDC BA图1E D CBAF 图2E D CB A F 图3E DC B A4.2 图形的全等一、学习目标:1.了解全等图形、全等多边形、全等三角形.2.平移、旋转、翻折等图形基本运动对全等图形的影响.3.掌握全等多边形性质与识别方法,全等三角形的性质.4.简单应用全等多边形性质、全等三角形的性质解决实际问题.二、学习重点:全等多边形的性质与识别方法;全等三角形的性质应用.三、学习难点:平移、旋转、翻折等图形基本运动对全等图形的影响.四、学习设计:(一)引入观察教材P73 图3-21几组图形。
(二)学习过程阅读课本P73-75填空:_________________两个图形就是全等图形。
全等图形的________和______都相同。
下面,我们看看图形的运动对全等图形有何影响?活动请同学们在方格纸中任意画一个多边形,先将这个多边形沿某一方向平移一定距离(与原图形无重叠);再将原多边形绕形外一点顺时针(或逆时针)旋转一定角度(与原图形无重叠);然后将原图形沿形外某格线对称;最后将这些图形剪下来,将其叠合.你能发现什么?通过这个活动过程,说明了什么问题?说明图形经过平移、旋转、翻折的图形运动,位置发生了变化,但形状和大小却没有改变,图形运动前后的两个图形是全等的;反过来,也就是说,两个全等的图形经过图形运动一定能重合.请你说说什么是全等多边形?什么是全等多边形的对应顶点、对应角、对应边?你认为全等多边形有何特征?全等多边形对应边、对应角分别相等.如图1,四边形ABCD与四边形EFGH全等,可记为四边形ABCD①四边形EFGH,请指出对应顶点、对应角、对应边.全等多边形的识别方法:如果两个多边形对应边、对应角分别相等,那么这两个多边形全等.三角形是特殊的多边形,所以,全等三角形的对应边、对应角分别相等;如果两个三角形的___________、__________分别相等,那么这两个多边形全等.例1 如图2,已知将①ABC绕其顶点A顺时针方向旋转20°后得到①ADE.(1)①ABC与①ADE的关系如何?(2)求①BAD的度数.分析:将①ABC绕其顶点A旋转得到①ADE,故①ADE是由①ABC旋转得到的,若将①ADE 逆时针方向旋转20°,则能与①ABC重合,所以①ABC与①ADE是全等的.由学生自主思考、分析解答.探索:请同学们将两张纸叠起来,剪下两个全等三角形,然后将叠合的两个三角形纸片放在桌面上,从平移、旋转、对称几个方面进行摆放,看看两个三角形有一些怎样的特殊位置关系?并画出这些位置关系的代表性图形.4.3 探索三角形全等的条件(1)一、学习目标:1.经历探索三角形全等的“边边边”的条件的过程.2.了解三角形的稳定性.3.经历探索三角形全等条件的过程,体会利用操作、①归纳获得数学结论的过程. 二、学习重点: 三角形全等的条件. 三、学习难点:寻求三角形全等的条件 四、学习设计: (一)、预习准备(1)回忆前面研究过的全等三角形. (2)预习课本P 157-158 (二)、学习过程已知①ABC ①①A ′B ′C ′,找出其中相等的边与角.图中相等的边是:AB =A ′B 、BC =B ′C ′、AC =A ′C . 相等的角是:①A =①A ′、①B =①B ′、①C =①C ′.(1)提出问题:你能画一个三角形与它全等吗?怎样画? (提示:可以先量出三角形纸片的各边长和各个角的度数,再作出一个三角形使它的边、角分别和已知的三角形纸片的对应边、对应角相等.这样作出的三角形一定与已知的三角形纸片全等).这是利用了全等三角形的定义来作图.那么是否一定需要六个条件呢?条件能否尽可能少呢?现在我们就来探究这个问题.(2)小明家衣橱上两块全等的三角形玻璃装饰物,其中一块被打碎了,妈妈让小明快速配一块回来,如果只有一把尺子,小明该怎么办?讨论下面几种情况: 1.给一个条件: 只给定一条边时:只给定一个角时:2.给出两个条件可能是:①一边一内角;①两内角;①两边.C 'B 'A 'C BA可以发现按这些条件画出的三角形都_______________保证一定全等. 给出三个条件画三角形,你能说出有几种可能的情况吗?归纳:有四种可能.即:三内角、三条___、两边一内角、两_____一边. 在刚才的探索过程中,我们已经发现三内角不能保证三角形全等.下面我们就来逐一探索其余的三种情况.已知一个三角形的三条边长分别为6cm 、8cm 、10cm .你能画出这个三角形吗?把你画的三角形剪下与同伴画的三角形进行比较,它们全等吗?1.作图方法:先画一线段AB ,使得AB =6cm ,再分别以A 、B 为圆心,8cm 、10cm 为半径画弧,①两弧交点记作C ,连结线段AC 、BC ,就可以得到三角形ABC ,使得它们的边长分别为AB =6cm ,AC =8cm ,BC =10cm .2.以小组为单位,把剪下的三角形重叠在一起,发现都能够重合.①这说明这些三角形都是全等的.这反映了一个规律:_______________的两个三角形全等,简写为_________或_________.用三根木条钉成三角形框架,它的大小和形状是固定不变的,①而用四根木条钉成的框架,它的形状是可以改变的.三角形的这个性质叫做三角形的__________.[例1]如图,1、如图,①ABC 中 AB =AC , D 为BC 中点求证:①①ABD ①①ACD . ①①BAD =①CAD①AD ①BC证明:①3cm3cm3cm30︒30︒30︒②50︒50︒30︒30︒③6cm4cm4cm6cm变式训练:如图,已知AC =FE 、BC =DE ,点A 、D 、B 、F 在一条直线上,AD =FB .要用“边边边”证明①ABC ①①FDE ,除了已知中的AC =FE ,BC =DE 以外,还应该有什么条件?怎样才能得到这个条件?例2、如图,已知AB =CD ,AC =BD ,求证:①A =①D拓展延伸1、如图,AC 与BD 交于点O ,AD =CB ,E 、F 是BD 上两点,且AE =CF ,DE =BF .请推导下列结论:①①D =①B ;①AE ①CF .FDCBEA2、已知如图,A 、E 、F 、C 四点共线,BF =DE ,AB =CD . ①请你添加一个条件,使①DEC ①①BF A ; ①在①的基础上,求证:DE ①BF .3、 已知:AB =AC , D 为①ABC 内部一点, 且BD = CD , 连接AD 并延长,交BC 于点E . 试找出图中的一对全等的三角形,并证明你的结论。
