历年中考数学难题及答案.pptx
浙江省中考数学压轴题分类及解析.pptx

在△ABD 和△BCE 中,
,
∴△ABD≌△BCE(ASA); 2 △DEF 是正三角形;理由如下: ∵△ABD≌△BCE≌△CAF, ∴∠ADB=∠BEC=∠CFA, ∴∠FDE=∠DEF=∠EFD, ∴△DEF 是正三角形; 3 作 AG⊥BD 于 G,如图所示: ∵△DEF 是正三角形, ∴∠ADG=60°,
,
答:a 的值为 0.04,b 的值为 30;
(2)①当 0≤t≤50 时,设 y 与 t 的函数解析式为 y=k1t+n1,
将(0,15)、(50,25)代入,得:
,
解得:
,
∴y 与 t 的函数解析式为 y= t+15; 当 50<t≤100 时,设 y 与 t 的函数解析式为 y=k2t+n2,
路段流量 q 与速度 v 之间的部分数据如下表:[来源:学科网 ZXXK]
速度 v(千米/小时) …[来源:学科网] 5 10 20 32 40 48 …
流量 q(辆/小时) …
550 1000 1600 1792 1600 1152 …
(1) 根据上表信息,下列三个函数关系式中,刻画 q,v 关系最准确的是
(只需填上
正确答案的序号)①
②
③
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速为多少时,流量达到最大?最
大流量是多少?
(3) 已知 q,v,k 满足
,请结合(1)中选取的函数关系式继续解决下列问题:
①市交通运行监控平台显示,当
时道路 出现轻度拥堵,试分析当车流密度 k
在什么范围时,该路段出现轻度拥堵;
在 Rt△ADG 中,DG= b,AG= b,
在 Rt△ABG 中,c2=(a+ b)2+( b)2,
超难的中考数学试题及答案

超难的中考数学试题及答案一、选择题1. 已知等差数列{an}的公差为5,首项为3,若a1+a2+a3+a4=150,求a5的值。
A. -10B. 10C. 15D. 20答案:A. -10解析:根据已知条件,可以列出等差数列的通项公式an = a1 + (n-1)d,其中d为公差。
a1+a2+a3+a4 = 4a1 + 6d = 150由a1 = 3和d = 5,代入得到:12 + 30 = 15042 = 150解得d=-10。
因此,a5 = a1 + (5-1)d = 3 + 4(-10) = -37.2. 已知函数y = ax^2 + bx + c的图像经过点(1, 4),(2, 9),(3, 16),求a, b, c的值。
A. a=1, b=2, c=2B. a=1, b=2, c=3C. a=2, b=3, c=4D. a=2, b=2, c=1答案:A. a=1, b=2, c=2解析:将给定的三个点分别代入函数,可以得到以下三个方程:a(1)^2 + b(1) + c = 4a(2)^2 + b(2) + c = 9a(3)^2 + b(3) + c = 16化简并解方程可得:a +b +c = 44a + 2b + c = 99a + 3b + c = 16求解该方程组,得到a=1,b=2,c=2。
二、填空题1. 设正整数a、b、c满足a<b<c,且满足c的立方减去b的立方等于a的立方减去b的立方,求a、b、c的最小值。
答案:a=6,b=7,c=8解析:根据题意,可以列出方程c^3 - b^3 = a^3 - b^3。
根据立方差公式(a^3 - b^3 = (a-b)(a^2 + ab + b^2)),可以得到:(a-b)(a^2 + ab + b^2) = (c-b)(c^2 + cb + b^2)由于a<b<c,令a-b=1和c-b=2,代入方程得到:(1)(a^2 + ab + b^2) = (2)(c^2 + cb + b^2)化简并整理得:a^2 - 2b + b^2 = 4c + 2ba^2 + b^2 = 4c + 4b根据a<b<c,我们可以假设最小的三个数分别为6、7和8,代入方程验证:6^2 + 7^2 = 4(8) + 4(7)36 + 49 = 32 + 28因此,a=6,b=7,c=8是满足条件的最小值。
中考数学压轴题及答案(2020年整理).pptx
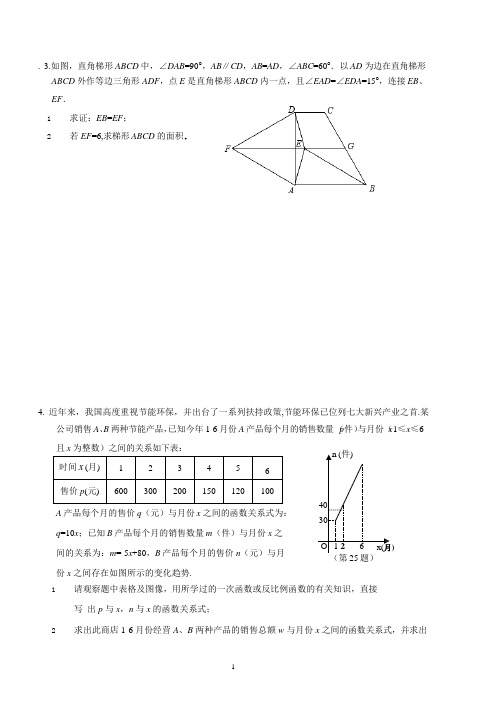
写 出 p 与 x,n ห้องสมุดไป่ตู้ x 的函数关系式;
2 求出此商店 1-6 月份经营 A、B 两种产品的销售总额 w 与月份 x 之间的函数关系式,并求出
1
在哪个月时获得最大销售总额; (3)今年 7 月份,商店调整了 A、B 两种产品的价格,A 产品价格在 6 月份基础上减少 0.5a%,B
产品价格在 6 月份基础上增加 0.5a%,结果 7 月份 A 产品的销售数量比 6 月份增加 0.6a%, B 产品的销售数量比 6 月份减少 1.5a%.若调整价格后 7 月份的销售总额比 6 月份的销售总 额少(1000―20a)元,请根据以下参考数据估算 a 的正整数值.
的函数关系式; 2 若该品种金银花的折干率为 20%(即每 100 千克鲜花蕾,干燥后可得 20 千克干花蕾),去年
每千克干花蕾售价为 200 元,则当每亩种苗数 x 为多少时,每亩销售利润W 可获得最大值, 并求出该最大利润;(利润=收入 成本)
3 若该花农按照(2)中获得最大利润的方案种植,并不断改善养植技术,今年每亩鲜花蕾产
(1)求当等边 △PMN 的顶点 M 运动到与点 O 重合时 t 的值;
(2)求等边 PMN △ 的边长(用 t 的代数式表示); (3)设等边△PMN 和矩形 ODE F 重
AP
叠部分的面积为 S,请求你直接
写出当 0≤t≤2 秒时 S 与 t 的函
F
E
数关系式,并写出对应的自变量 t 的取值范围;
M
O
ND
B
2
C (第 24 题)
(4) 点 P 在运动过程中,是否 存在点 M ,使得△EFM 是等腰 三角形? 若存在,求出对应的 t 的值;若不存在,请说明理由.
中考专题训练 阿氏圆(2020年整理).pptx
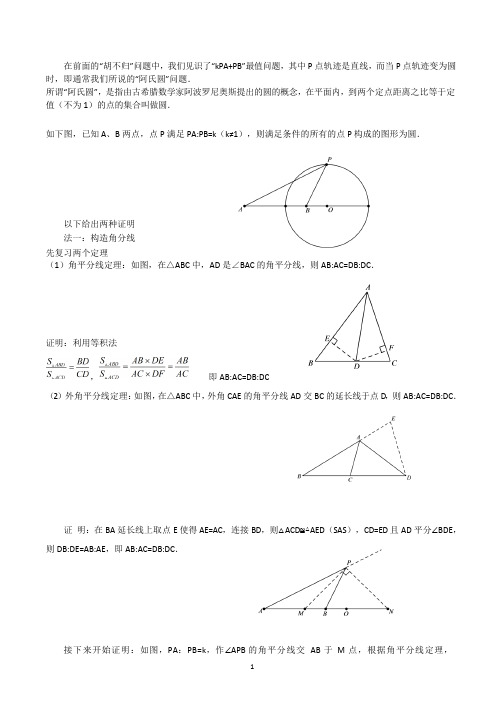
证 明:在 BA 延长线上取点 E 使得 AE=AC,连接 BD,则△ACD≌△AED(SAS),CD=ED 且 AD 平分∠BDE, 则 DB:DE=AB:AE,即 AB:AC=DB:DC.
接下来开始证明:如图,PA:PB=k,作∠APB 的角平分线交 AB 于 M 点,根据角平分线定理,
1
MA:MB=PA:PB=k,故 M 点为定点,即∠APB 的角平分线交 AB 于定点;
2
4.如图 1,抛物线 y=ax2+(a+3)x+3(a≠0)与 x 轴交于点 A(4,0),与 y 轴交于点 B,在 x 轴上有一动点 E(m, 0)(0<m<4),过点 E 作 x 轴的垂线交直线AB 于点N,交抛物线于点 P,过点 P 作 PM⊥AB 于点 M.
(1)求 a 的值和直线 AB 的函数表达式;
在前面的“胡不归”问题中,我们见识了“kPA+PB”最值问题,其中 P 点轨迹是直线,而当 P 点轨迹变为圆 时,即通常我们所说的“阿氏圆”问题. 所谓“阿氏圆”,是指由古希腊数学家阿波罗尼奥斯提出的圆的概念,在平面内,到两个定点距离之比等于定 值(不为 1)的点的集合叫做圆.
如下图,已知 A、B 两点,点 P 满足 PA:PB=k(k≠1),则满足条件的所有的点 P 构成的图形为圆.
一动点,且∠BPA=135°,则 2PD+PC 的最小值是
.
5.已知⊙O 半径为 1,AC、BD 为切线,AC=1,BD=2,P 为弧 AB 上一动点, 试求 2 PC PD 的最小值. 2
4
巩固练习:
1.如图,在△ABC 中,∠B﹦90°,AB﹦CB﹦2,以点 B 为圆心作⊙B 与 AC 相切,点 P 为圆 B 上任一动点,
§2.1 一元一次方程、二元一次方程(组)(试题部分).pptx

•
3.(2014苏州,16,3分)某地准备对一段长120 m的河道进行清淤疏通.若甲工程队先用4天单独完
成其中一部分河道的疏通任务,则余下的任务由乙工程队单独完成需要9天;若甲工程队先单
2x 3 y,① 3x 2y 2.②
解析 由①得y=3-2x,③ 把③代入②得3x+2(3-2x)=2,解得x=4. 把x=4代入③得y=-5,
所以原方程组的解是
x y
4, 5
.
5.(2017镇江,19(1),5分)解方程组
x 2
x
y
y
4
, 5
.
解析
解法一:
x 2
y 4, ① x y 5, ②
解析 设中型汽车有x辆,小型汽车有y辆.
根据题意,得 1x2解xy得8y50, 480.
x 20,
y
3
0
.
答:中型汽车有20辆,小型汽车有30辆.
6.(2017徐州,24,8分)4月9日上午8时,2017徐州国际马拉松赛鸣枪开跑,一名34岁的男子带着他 的两个孩子一同参加了比赛,下面是两个孩子与记者的对话:
中考数学 (江苏专用)
第二章 方程(组)与不等式(组)
§2.1 一元一次方程、二元一次方程(组)
五年中考
A组 2014-2018年江苏中考题组
考点1 解一元一次方程、二元一次方程(组)
1.(2018淮安,12,3分)若关于x、y的二元一次方程3x-ay=1有一个解是
x 则 a3 ,=
九年级数学难题精选(有答案)

一、如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N,其顶点为D.(1)抛物线及直线AC的函数关系式;(2)设点M(3,m),求使MN+MD的值最小时m的值;(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF ∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E 的坐标;若不能,请说明理由;(4)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值.解:(1)由抛物线y=﹣x2+bx+c过点A(﹣1,0)及C(2,3)得,,解得,故抛物线为y=﹣x2+2x+3又设直线为y=kx+n过点A(﹣1,0)及C(2,3)得,解得故直线AC为y=x+1;(2)作N点关于直线x=3的对称点N',则N'(6,3),由(1)得D(1,4),故直线DN'的函数关系式为y=﹣x+,当M(3,m)在直线DN'上时,MN+MD的值最小,则m=﹣×=;(3)由(1)、(2)得D(1,4),B(1,2)∵点E在直线AC上,设E(x,x+1),①当点E在线段AC上时,点F在点E上方,则F(x,x+3),∵F在抛物线上,∴x+3=﹣x2+2x+3,解得,x=0或x=1(舍去)∴E(0,1);②当点E在线段AC(或CA)延长线上时,点F在点E下方,则F(x,x﹣1)由F在抛物线上∴x﹣1=﹣x2+2x+3解得x=或x=∴E(,)或(,)综上,满足条件的点E为E(0,1)、(,)或(,);(4)方法一:过点P作PQ⊥x轴交AC于点Q;过点C作CG⊥x轴于点G,如图1设Q(x,x+1),则P(x,-x2+2x+3)∴PQ=(-x2+2x+3)-(x﹣1)=-x2+x+2又∵S△APC=S△APQ+S△CPQ=PQ·AG=(-x2+x+2)×3=-(x﹣)2+∴面积的最大值为.二、已知:直角梯形OABC中,BC∥OA,∠AOC=90°,以AB为直径的圆M交OC于D、E,连结AD、BD、BE。
中考数学重点难点(附答案)
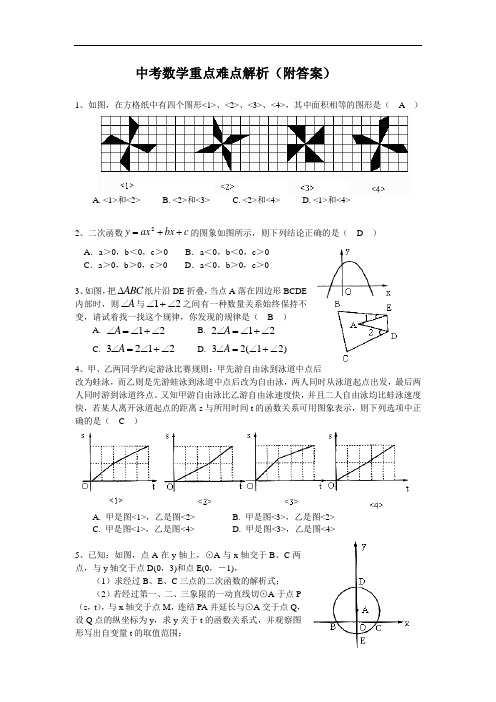
中考数学重点难点解析(附答案)1、如图,在方格纸中有四个图形<1>、<2>、<3>、<4>,其中面积相等的图形是( A )A. <1>和<2>B. <2>和<3>C. <2>和<4>D. <1>和<4>2、二次函数y ax bx c =++2的图象如图所示,则下列结论正确的是( D ) A .a >0,b <0,c >0 B .a <0,b <0,c >0 C .a >0,b >0,c >0 D .a <0,b >0,c >0 3、如图,把∆ABC 纸片沿DE 折叠,当点A 落在四边形BCDE 内部时,则∠A 与∠+∠12之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( B ) A. ∠=∠+∠A 12B. 212∠=∠+∠AC. 3212∠=∠+∠AD. 3212∠=∠+∠A ()4、甲、乙两同学约定游泳比赛规则:甲先游自由泳到泳道中点后改为蛙泳,而乙则是先游蛙泳到泳道中点后改为自由泳,两人同时从泳道起点出发,最后两人同时游到泳道终点。
又知甲游自由泳比乙游自由泳速度快,并且二人自由泳均比蛙泳速度快,若某人离开泳道起点的距离s 与所用时间t 的函数关系可用图象表示,则下列选项中正确的是( C )A. 甲是图<1>,乙是图<2>B. 甲是图<3>,乙是图<2>C. 甲是图<1>,乙是图<4>D. 甲是图<3>,乙是图<4>5、已知:如图,点A 在y 轴上,⊙A 与x 轴交于B 、C 两点,与y 轴交于点D(0,3)和点E(0,-1),(1)求经过B 、E 、C 三点的二次函数的解析式; (2)若经过第一、二、三象限的一动直线切⊙A 于点P (s ,t ),与x 轴交于点M ,连结PA 并延长与⊙A 交于点Q ,设Q 点的纵坐标为y ,求y 关于t 的函数关系式,并观察图形写出自变量t 的取值范围;(3)在(2)的条件下,当y =0时,求切线PM 的解析式,并借助函数图象,求出(1)中抛物线在切线PM 下方的点的横坐标x 的取值范围。
中考巨难数学试卷及答案

一、选择题(每题5分,共50分)1. 已知函数f(x) = 2x^3 - 3x^2 + 4x + 1,若f(x)在x=1处的切线斜率为k,则k的值为:A. 1B. 2C. 3D. 4答案:B解析:由导数的定义,f'(x) = 6x^2 - 6x + 4,代入x=1得f'(1) = 6 - 6 + 4= 4,所以切线斜率k=4。
2. 在等差数列{an}中,a1=1,公差d=2,则第10项an的值为:A. 19B. 20C. 21D. 22答案:A解析:由等差数列的通项公式an = a1 + (n-1)d,代入a1=1,d=2,n=10,得an= 1 + (10-1)×2 = 1 + 18 = 19。
3. 已知三角形ABC中,AB=AC,BC=4,则角A的正弦值为:A. 1/2B. √2/2C. √3/2D. 1答案:C解析:由勾股定理,AB=AC=√(BC^2/4) = √(4^2/4) = √4 = 2。
在直角三角形ABC中,sinA = 对边/斜边 = BC/AB = 4/2 = 2。
4. 若复数z满足|z-1|+|z+1|=4,则复数z对应的点在复平面上的轨迹是:A. 矩形B. 等腰梯形C. 矩形D. 等腰梯形答案:B解析:由复数的几何意义,|z-1|表示点z到点(1,0)的距离,|z+1|表示点z到点(-1,0)的距离。
因为|z-1|+|z+1|=4,所以点z到这两个点的距离之和为4,对应的轨迹是一个等腰梯形。
5. 已知函数f(x) = ax^2 + bx + c,若f(1) = 2,f'(2) = 6,则a+b+c的值为:A. 2B. 3C. 4D. 5答案:B解析:由导数的定义,f'(x) = 2ax + b,代入x=2得f'(2) = 4a + b = 6。
又因为f(1) = a + b + c = 2,解得a+b+c=3。
二、填空题(每题5分,共25分)6. 已知函数f(x) = x^2 - 4x + 3,则f(x)的图像与x轴的交点坐标为______。
最难中考数学试卷真题答案

最难中考数学试卷真题答案Ⅰ. 选择题(共15小题,每小题2分,满分30分)1. D2. C3. A4. B5. A6. D7. C8. B9. D 10. A11. C 12. D 13. A 14. B 15. DⅡ. 非选择题(共10小题,每小题6分,满分60分)16. 解:设几何平均数为x,则有:\[2x^3-12x^2+18x=0\]\[2x(x-3)^2=0\]得出x=0或x=3,由于几何平均数必须大于0,所以x=3。
故几何平均数为3。
17. 解:数列的前n项和公式为:\[S_n=\frac{n}{2}(2a+(n-1)d)\]代入已知条件解得:\[S_n=\frac{n}{2}(a+5d)=150\]联立求解方程组:\[\begin{cases}a+5d=30 \\ a+11d=66\end{cases}\]解得a=6,d=4。
故该等差数列的首项为6,公差为4。
18. 解:根据Vieta定理,二次方程\[ax^2+bx+c=0\]的两个根之和为\(-\frac{b}{a}\),两个根的乘积为\(\frac{c}{a}\)。
由已知条件可得:\[\begin{cases}r_1+r_2=5 \\ r_1r_2=-1\end{cases}\]解得\(r_1=1,r_2=4\)。
故满足题意的二次方程为\[x^2-5x+4=0\]。
19. 解:由已知条件得:\[\begin{cases}x+y=16 \\ xy=60\end{cases}\]将第一个等式变形为\(x=16-y\),代入第二个等式得:\[(16-y)y=60\]解得\(y=6\),代入第一个等式得\(x=10\)。
故原方程的两个整数解为6和10。
20. 解:将$f(x)=\log_a{(x^2+2x+1)}$转化为指数形式得:\[a^{f(x)}=x^2+2x+1\]代入已知条件可得:\[a^2=a+2\]解得\(a=2\)或\(a=-1\)。
初三数学总复习资料分专题试题及答案(90页)(2020年整理).pptx

A. 12
B. 3x
C. 2x3
) 5
D. 3
2、 下列根式与 8 是同类二次根式的是( )
A. 2
B. 3
C. 5
D. 6
3、 二次根式 3x 4 有意义,则 x 的取值范围
4、 若 3x 6 ,则 x=
5、 计算:3 2 3 2 2 3 3
6、 计算:5 a2 4a2 (a 0)
7、 计算: 20 1 5
2、 当 x
时,分式 x 2 4 的值为零 x 2
3、 下列分式是最简分式的是( )
2a 2 a A.
ab
6xy B.
3a
x2 1 C.
x 1
4、 下列各式是分式的是(
A. 1
B. a
a
3
5、 计算: 1 1 1 x 1 x
)
C. 1 2
x2 1 D
x 1 D6
6、 计算: a2 a 1 a 1
知识结构及内容:
1 几个概念
2 一元一次方程
(一)方程与方程组
3 一元二次方程
4 方程组
5 分式方程
6 应用
1、 概念:方程、方程的解、解方程、方程组、方程组的解 2、 一元一次方程:
解方程的步骤:去分母、去括号、移项、合并同类项、系数化一(未知项系数不能为零)
例题:.解方程:
(1) x 1 x 1 33
形 式(如 )。
1、 把下列各数填入相应的集合内:
7.5, 15, 4,
有理数集{ 正实数集{
8 , 2 , 3 8, , 0.25, 0.15
13 3
},无理数集{
}
}
2、 在实数 4,
3 , 0, 2
人教版初中数学中考经典好题难题有答案

数学难题一.填空题(共2小题)1.如图,矩形纸片ABCD中,AB=,BC=.第一次将纸片折叠,使点B与点D 重合,折痕与BD交于点O1;O1D的中点为D1,第二次将纸片折叠使点B与点D1重合,折痕与BD交于点O2;设O2D1的中点为D2,第三次将纸片折叠使点B与点D2重合,折痕与BD交于点O3,….按上述方法折叠,第n次折叠后的折痕与BD交于点O n,则BO1= _________ ,BO n= _________ .2.如图,在平面直角坐标系xoy中,A(﹣3,0),B(0,1),形状相同的抛物线C n(n=1,2,3,4,…)的顶点在直线AB上,其对称轴与x轴的交点的横坐标依次为2,3,5,8,13,…,根据上述规律,抛物线C2的顶点坐标为_________ ;抛物线C8的顶点坐标为_________ .二.解答题(共28小题)3.已知:关于x的一元二次方程kx2+2x+2﹣k=0(k≥1).(1)求证:方程总有两个实数根;(2)当k取哪些整数时,方程的两个实数根均为整数.4.已知:关于x的方程kx2+(2k﹣3)x+k﹣3=0.(1)求证:方程总有实数根;(2)当k取哪些整数时,关于x的方程kx2+(2k﹣3)x+k﹣3=0的两个实数根均为负整数5.在平面直角坐标系中,将直线l:沿x轴翻折,得到一条新直线与x 轴交于点A,与y轴交于点B,将抛物线C1:沿x轴平移,得到一条新抛物线C2与y轴交于点D,与直线AB交于点E、点F.(1)求直线AB的解析式;(2)若线段DF∥x轴,求抛物线C2的解析式;(3)在(2)的条件下,若点F在y轴右侧,过F作FH⊥x轴于点G,与直线l 交于点H,一条直线m(m不过△AFH的顶点)与AF交于点M,与FH交于点N,如果直线m既平分△AFH的面积,又平分△AFH的周长,求直线m的解析式.6.已知:关于x的一元二次方程﹣x2+(m+4)x﹣4m=0,其中0<m<4.(1)求此方程的两个实数根(用含m的代数式表示);(2)设抛物线y=﹣x2+(m+4)x﹣4m与x轴交于A、B两点(A在B的左侧),若点D的坐标为(0,﹣2),且ADBD=10,求抛物线的解析式;(3)已知点E(a,y1)、F(2a,y2)、G(3a,y3)都在(2)中的抛物线上,是否存在含有y1、y2、y3,且与a无关的等式如果存在,试写出一个,并加以证明;如果不存在,说明理由.7.点P为抛物线y=x2﹣2mx+m2(m为常数,m>0)上任一点,将抛物线绕顶点G 逆时针旋转90°后得到的新图象与y轴交于A、B两点(点A在点B的上方),点Q为点P旋转后的对应点.(1)当m=2,点P横坐标为4时,求Q点的坐标;(2)设点Q(a,b),用含m、b的代数式表示a;(3)如图,点Q在第一象限内,点D在x轴的正半轴上,点C为OD的中点,QO 平分∠AQC,AQ=2QC,当QD=m时,求m的值.8.关于x的一元二次方程x2﹣4x+c=0有实数根,且c为正整数.(1)求c的值;(2)若此方程的两根均为整数,在平面直角坐标系xOy中,抛物线y=x2﹣4x+c 与x轴交于A、B两点(A在B左侧),与y轴交于点C.点P为对称轴上一点,且四边形OBPC为直角梯形,求PC的长;(3)将(2)中得到的抛物线沿水平方向平移,设顶点D的坐标为(m,n),当抛物线与(2)中的直角梯形OBPC只有两个交点,且一个交点在PC边上时,直接写出m的取值范围.9.如图,已知AD为△ABC的角平分线,EF为AD的垂直平分线.求证:FD2=FBFC.10.如图,AD是△ABC的角平分线,EF是AD的垂直平分线.求证:(1)∠EAD=∠EDA.(2)DF∥AC.(3)∠EAC=∠B.11.已知:关于x的一元二次方程(m﹣1)x2+(m﹣2)x﹣1=0(m为实数)(1)若方程有两个不相等的实数根,求m的取值范围;(2)在(1)的条件下,求证:无论m取何值,抛物线y=(m﹣1)x2+(m﹣2)x ﹣1总过x轴上的一个固定点;(3)关于x的一元二次方程(m﹣1)x2+(m﹣2)x﹣1=0有两个不相等的整数根,把抛物线y=(m﹣1)x2+(m﹣2)x﹣1向右平移3个单位长度,求平移后的解析式.12.已知△ABC,以AC为边在△ABC外作等腰△ACD,其中AC=AD.(1)如图1,若∠DAC=2∠ABC,AC=BC,四边形ABCD是平行四边形,则∠ABC= _________ ;(2)如图2,若∠ABC=30°,△ACD是等边三角形,AB=3,BC=4.求BD的长;(3)如图3,若∠ACD为锐角,作AH⊥BC于H.当BD2=4AH2+BC2时,∠DAC=2∠ABC 是否成立若不成立,请说明你的理由;若成立,证明你的结论.13.已知关于x的方程mx2+(3﹣2m)x+(m﹣3)=0,其中m>0.(1)求证:方程总有两个不相等的实数根;(2)设方程的两个实数根分别为x1,x2,其中x1>x2,若,求y与m的函数关系式;(3)在(2)的条件下,请根据函数图象,直接写出使不等式y≤﹣m成立的m的取值范围.14.已知:关于x的一元二次方程x2+(n﹣2m)x+m2﹣mn=0①(1)求证:方程①有两个实数根;(2)若m﹣n﹣1=0,求证:方程①有一个实数根为1;(3)在(2)的条件下,设方程①的另一个根为a.当x=2时,关于m的函数y1=nx+am与y2=x2+a(n﹣2m)x+m2﹣mn的图象交于点A、B(点A在点B的左侧),平行于y轴的直线L与y1、y2的图象分别交于点C、D.当L沿AB由点A平移到点B时,求线段CD的最大值.15.如图,已知抛物线y=(3﹣m)x2+2(m﹣3)x+4m﹣m2的顶点A在双曲线y=上,直线y=mx+b经过点A,与y轴交于点B,与x轴交于点C.(1)确定直线AB的解析式;(2)将直线AB绕点O顺时针旋转90°,与x轴交于点D,与y轴交于点E,求sin∠BDE的值;(3)过点B作x轴的平行线与双曲线交于点G,点M在直线BG上,且到抛物线的对称轴的距离为6.设点N在直线BG上,请直接写出使得∠AMB+∠ANB=45°的点N的坐标.16.如图,AB为⊙O的直径,AB=4,点C在⊙O上,CF⊥OC,且CF=BF.(1)证明BF是⊙O的切线;(2)设AC与BF的延长线交于点M,若MC=6,求∠MCF的大小.17.如图1,已知等边△ABC的边长为1,D、E、F分别是AB、BC、AC边上的点(均不与点A、B、C重合),记△DEF的周长为p.(1)若D、E、F分别是AB、BC、AC边上的中点,则p= _________ ;(2)若D、E、F分别是AB、BC、AC边上任意点,则p的取值范围是_________ .小亮和小明对第(2)问中的最小值进行了讨论,小亮先提出了自己的想法:将△ABC以AC边为轴翻折一次得△AB1C,再将△AB1C以B1C为轴翻折一次得△A1B1C,如图2所示.则由轴对称的性质可知,DF+FE1+E1D2=p,根据两点之间线段最短,可得p≥DD2.老师听了后说:“你的想法很好,但DD2的长度会因点D的位置变化而变化,所以还得不出我们想要的结果.”小明接过老师的话说:“那我们继续再翻折3次就可以了”.请参考他们的想法,写出你的答案.18.已知关于x的方程x2﹣(m﹣3)x+m﹣4=0.(1)求证:方程总有两个实数根;(2)若方程有一个根大于4且小于8,求m的取值范围;(3)设抛物线y=x2﹣(m﹣3)x+m﹣4与y轴交于点M,若抛物线与x轴的一个交点关于直线y=﹣x的对称点恰好是点M,求m的值.19.在Rt△ABC中,∠ACB=90°,ta n∠BAC=.点D在边AC上(不与A,C重合),连接BD,F为BD中点.(1)若过点D作DE⊥AB于E,连接CF、EF、CE,如图1.设CF=kEF,则k= _________ ;(2)若将图1中的△ADE绕点A旋转,使得D、E、B三点共线,点F仍为BD中点,如图2所示.求证:BE﹣DE=2CF;(3)若BC=6,点D在边AC的三等分点处,将线段AD绕点A旋转,点F始终为BD中点,求线段CF长度的最大值.20.我们给出如下定义:如果四边形中一对顶点到另一对顶点所连对角线的距离相等,则把这对顶点叫做这个四边形的一对等高点.例如:如图1,平行四边形ABCD中,可证点A、C到BD的距离相等,所以点A、C是平行四边形ABCD的一对等高点,同理可知点B、D也是平行四边形ABCD的一对等高点.(1)如图2,已知平行四边形ABCD,请你在图2中画出一个只有一对等高点的四边形ABCE(要求:画出必要的辅助线);(2)已知P是四边形ABCD对角线BD上任意一点(不与B、D点重合),请分别探究图3、图4中S1,S2,S3,S4四者之间的等量关系(S1,S2,S3,S4分别表示△ABP,△CBP,△CDP,△ADP的面积):①如图3,当四边形ABCD只有一对等高点A、C时,你得到的一个结论是_________ ;②如图4,当四边形ABCD没有等高点时,你得到的一个结论是_________ .21.已知:关于x的一元一次方程kx=x+2 ①的根为正实数,二次函数y=ax2﹣bx+kc(c≠0)的图象与x轴一个交点的横坐标为1.(1)若方程①的根为正整数,求整数k的值;(2)求代数式的值;(3)求证:关于x的一元二次方程ax2﹣bx+c=0 ②必有两个不相等的实数根.22.已知抛物线经过点A(0,4)、B(1,4)、C(3,2),与x轴正半轴交于点D.(1)求此抛物线的解析式及点D的坐标;(2)在x轴上求一点E,使得△BCE是以BC为底边的等腰三角形;(3)在(2)的条件下,过线段ED上动点P作直线PF∥BC,与BE、CE分别交于点F、G,将△EFG沿FG翻折得到△E′FG.设P(x,0),△E′FG与四边形FGCB 重叠部分的面积为S,求S与x的函数关系式及自变量x的取值范围.23.已知二次函数y=ax2+bx+c的图象分别经过点(0,3),(3,0),(﹣2,﹣5).求:(1)求这个二次函数的解析式;(2)求这个二次函数的最值;(3)若设这个二次函数图象与x轴交于点C,D(点C在点D的左侧),且点A 是该图象的顶点,请在这个二次函数的对称轴上确定一点B,使△ACB是等腰三角形,求出点B的坐标.24.根据所给的图形解答下列问题:(1)如图1,△ABC中,AB=AC,∠BAC=90°,AD⊥BC于D,把△ABD绕点A旋转,并拼接成一个与△ABC面积相等的正方形,请你在图中完成这个作图;(2)如图2,△ABC中,AB=AC,∠BAC=90°,请你设计一种与(1)不同的方法,将这个三角形拆分并拼接成一个与其面积相等的正方形,画出利用这个三角形得到的正方形;(3)设计一种方法把图3中的矩形ABCD拆分并拼接为一个与其面积相等的正方形,请你依据此矩形画出正形,并根据你所画的图形,证明正方形面积等于矩形ABCD的面积的结论.25.例.如图①,平面直角坐标系xOy中有点B(2,3)和C(5,4),求△OBC 的面积.解:过点B作BD⊥x轴于D,过点C作CE⊥x轴于E.依题意,可得S△OBC=S梯形BDEC+S△OBD﹣S△OCE==×(3+4)×(5﹣2)+×2×3﹣×5×4=.∴△OBC的面积为.(1)如图②,若B(x1,y1)、C(x2,y2)均为第一象限的点,O、B、C三点不在同一条直线上.仿照例题的解法,求△OBC的面积(用含x1、x2、y1、y2的代数式表示);(2)如图③,若三个点的坐标分别为A(2,5),B(7,7),C(9,1),求四边形OABC的面积.26.阅读:①按照某种规律移动一个平面图形的所有点,得到一个新图形称为原图形的像.如果原图形每一个点只对应像的一个点,且像的每一个点也只对应原图形的一个点,这样的运动称为几何变换.特别地,当新图形与原图形的形状大小都不改变时,我们称这样的几何变换为正交变换.问题1:我们学习过的平移、_________ 、_________ 变换都是正交变换.②如果一个图形绕着一个点(旋转中心)旋转n° (0<n≤360)后,像又回到原图形占据的空间(重合),则称该变换为该图形的 n度旋转变换.特别地,具有180旋转变换的图形称为中心对称图形.例如,图A中奔驰车标示意图具有120°,240°,360°的旋转变换.图B的几何图形具有180°的旋转变换,所以它是中心对称图形.问题2:图C和图D中的两个几何图形具有n度旋转变换,请分别写出n的最小值.答:(图C)_________ ;答:(图D)_________ .问题3:如果将图C和图D的旋转中心重合,组合成一个新的平面图形,它具有n 度旋转变换,则n的最小值为_________ .问题4:请你在图E中画出一个具有180°旋转变换的正多边形.(要求以O为旋转中心,顶点在直线与圆的交点上)27.已知:点P为线段AB上的动点(与A、B两点不重合).在同一平面内,把线段AP、BP分别折成△CDP、△EFP,其中∠CDP=∠EFP=90°,且D、P、F三点共线,如图所示.(1)若△CDP、△EFP均为等腰三角形,且DF=2,求AB的长;(2)若AB=12,tan∠C=,且以C、D、P为顶点的三角形和以E、F、P为顶点的三角形相似,求四边形CDFE的面积的最小值.28.在平面直角坐标系xOy中,已知直线y=﹣x+交x轴于点C,交y轴于点A.等腰直角三角板OBD的顶点D与点C重合,如图A所示.把三角板绕着点O 顺时针旋转,旋转角度为α(0°<α<180°),使B点恰好落在AC上的B'处,如图B所示.(1)求图A中的点B的坐标;(2)求α的值;(3)若二次函数y=mx2+3x的图象经过(1)中的点B,判断点B′是否在这条抛物线上,并说明理由.29.已知:如图,AC是⊙O的直径,AB是弦,MN是过点A的直线,AB等于半径长.(1)若∠BAC=2∠BAN,求证:MN是⊙O的切线.(2)在(1)成立的条件下,当点E是的中点时,在AN上截取AD=AB,连接BD、BE、DE,求证:△BED是等边三角形.30.在一个夹角为120°的墙角放置了一个圆形的容器,俯视图如图,在俯视图中圆与两边的墙分别切于B、C两点.如果用带刻度的直尺测量圆形容器的直径,发现直尺的长度不够.(1)写出此图中相等的线段.(2)请你设计一种可以通过计算求出直径的测量方法.(写出主要解题过程)2012年初中难题数学组卷参考答案与试题解析一.填空题(共2小题)1.如图,矩形纸片ABCD中,AB=,BC=.第一次将纸片折叠,使点B与点D 重合,折痕与BD交于点O1;O1D的中点为D1,第二次将纸片折叠使点B与点D1重合,折痕与BD交于点O2;设O2D1的中点为D2,第三次将纸片折叠使点B与点D2重合,折痕与BD交于点O3,….按上述方法折叠,第n次折叠后的折痕与BD交于点O n,则BO1= 2 ,BO n= .考点:翻折变换(折叠问题);矩形的性质。
中考数学压轴题含解答及几何画板课件

中考数学阅读理解类专题〔市〕25.如图,在平面直角坐标系xOy 中,△ABC 三个顶点的坐标分别为A (-6,0),B (6,0),C (0,4 3 )延长AC 到点D ,使CD =12AC ,过点D 作DE ∥AB 交BC 的延长线于点E .〔1〕求D 点的坐标;〔2〕作C 点关于直线DE 的对称点F ,分别连结DF 、EF ,假设过B 点的直线y =kx +b 将四边形CDFE 分成周长相等的两个四边形,确定此直线的解析式;〔3〕设G 为y 轴上一点,点P 从直线y =kx +b 与y 轴的交点出发,先沿y 轴到达G 点,再沿GA 到达A 点,假设P 点在y 轴上运动的速度是它在直线GA 上运动速度的2倍,试确定G点的位置,使P 点按照上述要求到达A 点所用的时间最短.〔要求:简述确定G 点位置的方法,但不要求证明〕.〔市〕26.如图,在平面直角坐标系xOy 中,矩形OABC 的边OA 在y 轴的正半轴上,OC 在x 轴的正半轴上,OA =2,OC =3.过原点O 作∠AOC 的平分线交AB 于点D ,连接DC ,过点D 作DE ⊥DC ,交OA 于点E .〔1〕求过点E 、D 、C 的抛物线的解析式;〔2〕将∠EDC 绕点D 按顺时针方向旋转后,角的一边与y 轴的正半轴交于点F ,另一边与线段OC 交于点G .如果DF 与〔1〕中的抛物线交于另一点M ,点M 的横坐标为 65,那么EF=2GO 是否成立?假设成立,请给予证明;假设不成立,请说明理由;〔3〕对于〔2〕中的点G ,在位于第一象限的该抛物线上是否存在点Q ,使得直线GQ 与AB 的交点P 与点C 、G 构成的△PCG 是等腰三角形?假设存在,请求出点Q 的坐标;假设不存在,请说明理由.(省)26.如图,直线l 1:y =23x +83与直线l 2:y =-2x +16相交于点C ,l 1、l 2分别交x 轴于A 、B两点.矩形DEFG的顶点D、E分别在直线l1、l2上,顶点F、G都在x轴上,且点G与点B 重合.〔1〕求△ABC的面积;〔2〕求矩形DEFG的边DE与EF的长;〔3〕假设矩形DEFG从原点出发,沿x轴的反方向以每秒1个单位长度的速度平移,设移动时间为t(0≤t≤12)秒,矩形DEFG与△ABC重叠局部的面积为S,求S关于的t函数关系式,并写出相应的t的取值围.〔綦江县〕26.如图,抛物线y=a(x-1)2+33(a≠0)经过点A(-2,0),抛物线的顶点为D,过O 作射线OM∥AD.过顶点D平行于x轴的直线交射线OM于点C,B在x轴正半轴上,连结BC.〔1〕求该抛物线的解析式;〔2〕假设动点P从点O出发,以每秒1个长度单位的速度沿射线OM运动,设点P运动的时间为t(s).问当t为何值时,四边形DAOP分别为平行四边形?直角梯形?等腰梯形?〔3〕假设OC=OB,动点P和动点Q分别从点O和点B同时出发,分别以每秒1个长度单位和2个长度单位的速度沿OC和BO运动,当其中一个点停顿运动时另一个点也随之停顿运动.设它们的运动的时间为t(s),连接PQ,当t为何值时,四边形BCPQ的面积最小?并求出最小值及此时PQ的长.〔省〕26.如图,在Rt△ABC中,∠C=90°,AC=3,AB=5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A 出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.点P、Q同时出发,当点Q到达点B时停顿运动,点P也随之停顿.设点P、Q运动的时间是t秒〔t>0〕.〔1〕当t=2时,AP=,点Q到AC的距离是;〔2〕在点P从C向A运动的过程中,求△APQ的面积S与t的函数关系式;〔不必写出t 的取值围〕〔3〕在点E从B向C运动的过程中,四边形QBED能否成为直角梯形?假设能,求t的值.假设不能,请说明理由;写出t的值.〔4〕当DE经过点C时,请直接..〔2021年省〕23.如图,在平面直角坐标系中,矩形ABCD的三个顶点B〔4,0〕、C〔8,0〕、D 〔8,8〕.抛物线y=ax2+bx过A、C两点.(1)直接写出点A的坐标,并求出抛物线的解析式;(2)动点P从点A出发.沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动.速度均为每秒1个单位长度,运动时间为t秒.过点P作PE⊥AB交AC于点E①过点E作EF⊥AD于点F,交抛物线于点G.当t为何值时,线段EG最长?②连接EQ.在点P、Q运动的过程中,判断有几个时刻使得△CEQ是等腰三角形?请直接写出相应的t值.〔省市〕29. 如左图,将正方形纸片ABCD 折叠,使点B 落在CD 边上一点E 〔不与点C ,D重合〕,压平后得到折痕MN .当CE CD =12时,求AMBN的值.方法指导:为了求得AMBN的值,可先求BN 、AM 的长,不妨设:AB =2. 类比归纳:在左图中,假设CE CD =13那么AM BN 的值等于;假设CE CD =14那么AM BN 的值等于;假设CECD=1n(n为整数),那么AMBN的值等于.(用含n的式子表示〕联系拓广:如右图将矩形纸片ABCD 折叠,使点B 落在CD 边上一点E 〔不与点C ,D 重合〕,压平后得到折痕MN ,设 AB BC =1m (m >1)CE CD =1n ,那么AM BN的值等于.〔用含m ,n 的式子表示〕〔省〕25.如图1,在等腰梯形ABCD中,AD∥BC,E是AB的中点,过点E作EF∥BC交CD于点F.AB=4,BC=6,∠B=60°.〔1〕求点E到BC的距离;〔2〕点P为线段EF上的一个动点,过P作PM⊥EF交BC于点M,过M作MN∥AB交折线ADC于点N,连结PN,设EP=x.①当点N在线段AD上时〔如图2〕,△PMN的形状是否发生改变?假设不变,求出△PMN 的周长;假设改变,请说明理由;②当点N在线段DC上时〔如图3〕,是否存在点P,使△PMN为等腰三角形?假设存在,请求出所有满足要求的x的值;假设不存在,请说明理由.〔〕25. 如图,二次函数y=x2+px+q(p<0)的图象与x轴交于A、B两点,与y轴交于点C〔0,-1〕,△ABC的面积为5 4.〔1〕求该二次函数的关系式;〔2〕过y轴上的一点M〔0,m〕作y轴的垂线,假设该垂线与△ABC的外接圆有公共点,求m的取值围;〔3〕在该二次函数的图象上是否存在点D,使四边形ABCD为直角梯形?假设存在,求出点D的坐标;假设不存在,请说明理由.〔省市〕22.正方形ABCD边长为4,M、N分别是BC、CD上的两个动点,当M点在BC 上运动时,保持AM和MN垂直.〔1〕证明:Rt△ABM∽Rt△M;〔2〕设BM=x,梯形AB的面积为y,求y与x之间的函数关系式;当M点运动到什么位置时,四边形AB面积最大,并求出最大面积;〔3〕当M点运动到什么位置时Rt△ABM∽Rt△AMN,求此时x的值.〔市〕28.如图,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为〔-3,4〕,点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H.〔1〕求直线AC的解析式;〔2〕连接BM,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S〔S≠0〕,点P的运动时间为t秒,求S与t之间的函数关系式〔要求写出自变量t的取值围〕;〔3〕在〔2〕的条件下,当t为何值时,∠MPB与∠BCO互为余角,并求此时直线OP与直线AC所夹锐角的正切值.(省市)26.如下列图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,CE⊥BD.〔1〕求证:BE=AD;〔2〕求证:AC是线段ED的垂直平分线;〔3〕△DBC是等腰三角形吗?并说明理由.〔市〕26.如图,抛物线y=a2+bx-3与x轴交于A,B两点,与y轴交于C点,且经过点(2,-3a),对称轴是直线x=1,顶点是M.(1)求抛物线对应的函数表达式;(2)经过C,M两点作直线与x轴交于点N,在抛物线上是否存在这样的点P,使以点P,A,C,N 为顶点的四边形为平行四边形?假设存在,求出点P的坐标;假设不存在,说明理由;(3)设直线y=-x+3与y轴的交点是D,在线段BD上任取一点E〔不与B,D重合〕,经过A,B,E三点的圆交直线BC于点F,试判断△AEF的形状,并说明理由;(4)当E是直线y=-x+3上任意一点时,〔3〕中的结论是否成立?〔请直接写出结论〕.〔省日照〕24.正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.〔1〕求证:EG=CG;〔2〕将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.问〔1〕中的结论是否仍然成立?假设成立,请给出证明;假设不成立,请说明理由.〔3〕将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问〔1〕中的结论是否仍然成立?通过观察你还能得出什么结论?〔均不要求证明〕〔潍坊市〕24.如图,在平面直角坐标系xOy中,半径为1的圆的圆心O在坐标原点,且与两坐标轴分别交于A、B、C、D四点.抛物线y=a2+bx+c与y轴交于点D,与直线y=x 交于点M、N,且MA、NC分别与圆O相切于点A和点C.〔1〕求抛物线的解析式;〔2〕抛物线的对称轴交x轴于点E,连结DE,并延长DE交圆O于F,求EF的长.〔3〕过点B作圆O的切线交DC的延长线于点P,判断点P是否在抛物线上,说明理由.〔市〕26.如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.〔1〕求出抛物线的解析式;〔2〕P是抛物线上一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以A,P,M为顶点的三角形与△OAC相似?假设存在,请求出符合条件的点P的坐标;假设不存在,说明理由;〔3〕在直线AC上方的抛物线上有一点D,使得△DCA的面积最大,求出点D的坐标.(省市)26.在平面直角坐标中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y =x上时停顿旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N〔如图〕. 〔1〕求边OA在旋转过程中所扫过的面积;〔2〕旋转过程中,当MN和AC平行时,求正方形OABC旋转的度数;〔3〕设△MBN的周长为p,在旋转正方形OABC的过程中,p值是否有变化?请证明你的结论.〔市〕25.如图,二次函数的图象经过点D (0,793),且顶点C 的横坐标为4,该图象在x 轴上截得的线段AB 的长为6.〔1〕求二次函数的解析式;〔2〕在该抛物线的对称轴上找一点P ,使PA +PD 最小,求出点P 的坐标;〔3〕在抛物线上是否存在点Q ,使△QAB 与△ABC 相似?如果存在,求出点Q 的坐标;如果不存在,请说明理由.〔市〕21.如图9,正比例函数和反比例函数的图象都经过点A (3,3).〔1〕求正比例函数和反比例函数的解析式; 〔2〕把直线OA 向下平移后与反比例函数的图象交于点B (6,m ),求m 的值和这个一次函数的解析式;〔3〕第〔2〕问中的一次函数的图象与x 轴、y 轴分别交于C 、D ,求过A 、B 、D 三点的二次函数的解析式;〔4〕在第〔3〕问的条件下,二次函数的图象上是否存在点E ,使四边形OECD 的面积S 1与四边形OABD 的面积S 满足:S 1=23S ?假设存在,求点E 的坐标;假设不存在,请说明理由.〔凉山州〕26.如图,抛物线y=a2+bx+c经过A(1,0),B(0,2)两点,顶点为D.〔1〕求抛物线的解析式;〔2〕将△OAB绕点A顺时针旋转90°后,点B落到点C的位置,将抛物线沿y轴平移后经过点C,求平移后所得图象的函数关系式;〔3〕设〔2〕中平移后,所得抛物线与y轴的交点为B1,顶点为D1,假设点N在平移后的抛物线上,且满足△NBB1的面积是△NDD1面积的2倍,求点N的坐标.〔市〕27.如下列图,将矩形OABC沿AE折叠,使点O恰好落在BC上F处,以CF为边作正方形CFGH,延长BC至M,使CM=|CE—EO|,再以CM、CO为边作矩形CMNO.(1)试比较EO、EC的大小,并说明理由.(2)令m =S 四边形CFGH S 四边形MO,请问m 是否为定值?假设是,请求出m 的值;假设不是,请说明理由 (3)在(2)的条件下,假设CO =1,CE =13,Q 为AE 上一点且QF =23,抛物线y =mx 2+bx +c 经过C 、Q 两点,请求出此抛物线的解析式.(4)在(3)的条件下,假设抛物线y =mx 2+bx +c 与线段AB 交于点P ,试问在直线BC 上是否存在点K ,使得以P 、B 、K 为顶点的三角形与△AEF 相似?假设存在,请求直线KP 与y 轴的交点T 的坐标?假设不存在,请说明理由.〔市〕27.如图,抛物线与x 交于A (-1,0)、E (3,0)两点,与y 轴交于点B (0,3).(1)求抛物线的解析式;(2)设抛物线顶点为D ,求四边形AEDB 的面积;(3)△AOB 与△DBE 是否相似?如果相似,请给以证明;如果不相似,请说明理由.〔省市〕24、如图甲,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连结AD,以AD 为一边且在AD的右侧作正方形ADEF.〔1〕如果AB=AC,∠BAC=90°,①当点D在线段BC上时〔与点B不重合〕,如图乙,线段CF、BD之间的位置关系为,数量关系为.②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?〔2〕如果AB≠AC,∠BAC≠90°点D在线段BC上运动.试探究:当△ABC满足一个什么条件时,CF⊥BC〔点C、F重合除外〕?画出相应图形,并说明理由.〔画图不写作法〕〔3〕假设AC=42,BC=3,在〔2〕的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.〔市〕25.如图,抛物线y=a2+bx-4a经过A(-1,0)、C(0,4)两点,与x轴交于另一点B. 〔1〕求抛物线的解析式;〔2〕点D(m,m+1)在第一象限的抛物线上,求点D关于直线BC对称的点的坐标;〔3〕在〔2〕的条件下,连接BD,点P为抛物线上一点,且∠DBP=45°,求点P的坐标.〔省市〕25.一开口向上的抛物线与x轴交于A(m-2,0),B(m+2,0)两点,记抛物线顶点为C,且AC⊥BC.(1)假设m为常数,求抛物线的解析式;(2)假设m为小于0的常数,那么(1)中的抛物线经过怎么样的平移可以使顶点在坐标原点?(3)设抛物线交y轴正半轴于D点,问是否存在实数m,使得△BOD为等腰三角形?假设存在,求出m的值;假设不存在,请说明理由.〔省市〕25.点P是双曲线(k1<0,x<0)上一动点,过点P作x轴、y轴的垂线,分别交x轴、y 轴于A、B两点,交双曲线〔0<k2<|k1|〕于E、F两点.〔1〕图1中,四边形PEOF的面积S1=▲ (用含k1、k2的式子表示);〔2〕图2中,设P点坐标为〔-4,3〕.①判断EF与AB的位置关系,并证明你的结论;②记S2=S△PEF-S△OEF,S2是否有最小值?假设有,求出其最小值;假设没有,请说明理由.〔襄樊市〕26.如图,在梯形ABCD中,AD∥BC,AD=2,BC=4点M是AD的中点,△MBC 是等边三角形.〔1〕求证:梯形ABCD是等腰梯形;〔2〕动点P、Q分别在线段BC和MC上运动,且∠MPQ=60°保持不变.设PC=x,MQ=y,求y与x的函数关系式;〔3〕在〔2〕中:①当动点P、Q运动到何处时,以点P、M和点A、B、C、D中的两个点为顶点的四边形是平行四边形?并指出符合条件的平行四边形的个数;②当y取最小值时,判断△PQC的形状,并说明理由.〔省株洲市〕23.如图,△ABC为直角三角形,∠ACB=90°,AC=BC,点A、C在x轴上,点B 坐标为〔3,m〕〔m>0〕,线段AB与y轴相交于点D,以P〔1,0〕为顶点的抛物线过点B、D.〔1〕求点A的坐标〔用m表示〕;〔2〕求抛物线的解析式;〔3〕设点Q为抛物线上点P至点B之间的一动点,连结PQ并延长交BC于点E,连结BQ 并延长交AC于点F,试证明:FC(AC+EC)为定值.〔市〕26.如图,直线y=-x+4与两坐标轴分别相交于A、B点,点M是线段AB上任意一点〔A、B两点除外〕,过M分别作MC⊥OA于点C,MD⊥OB于D.〔1〕当点M在AB上运动时,你认为四边形OCMD的周长是否发生变化?并说明理由;〔2〕当点M运动到什么位置时,四边形OCMD的面积有最大值?最大值是多少?〔3〕当四边形OCMD为正方形时,将四边形OCMD沿着x轴的正方向移动,设平移的距离为a(0<a<4),正方形OCMD与△AOB重叠局部的面积为S.试求S与a的函数关系式并画出该函数的图象.〔市〕25.如图在△ABC中,∠C=90°,BC=8,AC=6,另有一直角梯形DEFH〔HF∥DE,∠HDE=90°〕的底边DE落在CB上,腰DH落在CA上,且DE=4,∠DEF=∠CBA,AH:AC=2:3.〔1〕延长HF交AB于G,求△AHG的面积.〔2〕操作:固定△ABC,将直角梯形DEFH以每秒1个单位的速度沿CB方向向右移动,直到点D与点B重合时停顿,设运动的时间为t秒,运动后的直角梯形为DEFH'〔如图2〕.探究1:在运动中,四边形CDH'H能否为正方形?假设能,请求出此时t的值;假设不能,请说明理由.探究2:在运动过程中,△ABC与直角梯形DEFH'重叠局部的面积为y,求y与t的函数关系.〔省〕25.问题探究:〔1〕请在图①的正方形ABCD,画出使∠APB=90°的一个点P,并说明理由...的点P,并说明理由. 〔2〕在图②的正方形ABCD〔含边〕,画出使∠APB=60°的所有..问题解决:〔3〕如图③,现在一块矩形钢板ABCD,AB=4,BC=3.工人师傅想用它裁出两块全等的、面积最大的△APB和△CP'D钢板,且∠APB=∠CP'D=60°.请你在图③中画出符合要求的点P和P',并求出△APB的面积〔结果保存根号〕.〔市第26题〕如图,抛物线C1:y=a(x+2)2-5的顶点为P,与x轴相交于A、B两点〔点A在点B的左边〕,点B的横坐标是1.〔1〕求P点坐标及a的值;〔2〕如图〔1〕,抛物线C2与抛物线C1关于x轴对称,将抛物线C2向右平移,平移后的抛物线记为C3,C3的顶点为M,当点P、M关于点B成中心对称时,求C3的解析式;〔3〕如图〔2〕,点Q是x轴正半轴上一点,将抛物线C1绕点Q旋转180°后得到抛物线C.抛物线C4的顶点为N,与x轴相交于E、F两点〔点E在点F的左边〕,当以点P、N、4F为顶点的三角形是直角三角形时,求点Q的坐标.(省黔东南苗族侗族自治州)26.二次函数22-++=a ax x y .〔1〕求证:不管a 为何实数,此函数图象与x 轴总有两个交点.〔2〕设a <0,当此函数图象与x 轴的两个交点的距离为13时,求出此二次函数的解析式. 〔3〕假设此二次函数图象与x 轴交于A 、B 两点,在函数图象上是否存在点P ,使得△PAB的面积为2133,假设存在求出P 点坐标,假设不存在请说明理由.(省市第20题)阅读材料:如图,过△ABC 的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC 的“水平宽〞(a ),中间的这条直线在△ABC 部线段的长度叫△B铅垂高水平宽ha 图1AABC 的“铅垂高(h )〞.我们可得出一种计算三角形面积的新方法:ah S ABC 21=∆,即三角形面积等于水平宽与铅垂高乘积的一半. 解答以下问题:如图2,抛物线顶点坐标为点C (1,4),交x 轴于点A (3,0),交y 轴于点B . (1)求抛物线和直线AB 的解析式;(2)点P 是抛物线(在第一象限)上的一个动点,连结PA ,PB ,当P 点运动到顶点C 时,求△CAB 的铅垂高CD 及S △CAB ; (3)是否存在一点P ,使S △PAB =89S △CAB ,假设存在,求出P 点的坐标;假设不存在,请说明理由.〔省〕28.如图,射线DE 与x 轴和y 轴分别交于点D (3,0)和点E (0,4).动点C 从点M (5,0)出发,以1个单位长度/秒的速度沿x 轴向左作匀速运动,与此同时,动点P 从点D 出发,也以1个单位长度/秒的速度沿射线DE 的方向作匀速运动.设运动时间为t 秒. 〔1〕请用含t 的代数式分别表示出点C 与点P 的坐标;〔2〕以点C 为圆心、12t 个单位长度为半径的⊙C 与x 轴交于A 、B 两点〔点A 在点B 的左侧〕,连接PA 、PB .①当⊙C 与射线DE 有公共点时,求t 的取值围; ②当△PAB 为等腰三角形时,求t 的值.图2xCOy AB D1 1(省市)24. 平行于x 轴的直线y =a (a ≠0)与函数y =x 和函数y =1x的图象分别交于点A 和点B ,又有定点P 〔2,0〕.〔1〕假设a >0,且tan ∠POB =19,求线段AB 的长;〔2〕在过A ,B 两点且顶点在直线y =x 上的抛物线中,线段AB =83,且在它的对称轴左边时,y随着x 的增大而增大,试求出满足条件的抛物线的解析式;〔3〕经过A ,B ,P 三点的抛物线,平移后能得到y =95x 2的图象,求点P 到直线AB 的距离.〔市〕24.如图,直线121+-=x y 交坐标轴于A ,B 两点,以线段AB 为边向上作正方形ABCD ,过点A ,D ,C 的抛物线与直线另一个交点为E . 〔1〕请直接写出点C ,D 的坐标; 〔2〕求抛物线的解析式;〔3〕假设正方形以每秒5个单位长度的速度沿射线AB下滑,直至顶点D落在x轴上时停顿.设正方形落在x轴下方局部的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值围;〔4〕在〔3〕的条件下,抛物线与正方形一起平移,同时D停顿,求抛物线上C,E两点间的抛物线弧所扫过的面积.〔市〕24. 直角坐标系中菱形ABCD的位置如图,C,D两点的坐标分别为(4,0),(0,3).现有两动点P,Q分别从A,C同时出发,点P沿线段AD向终点D运动,点Q沿折线CBA向终点A 运动,设运动时间为t秒.(1)填空:菱形ABCD的边长是▲、面积是▲、高BE的长是▲;(2)探究以下问题:①假设点P的速度为每秒1个单位,点Q的速度为每秒2个单位.当点Q在线段BA上时,求△APQ的面积S关于t的函数关系式,以及S的最大值;②假设点P的速度为每秒1个单位,点Q的速度变为每秒k个单位,在运动过程中,任何时刻都有相应的k值,使得△APQ沿它的一边翻折,翻折前后两个三角形组成的四边形为菱形.请探究当t=4秒时的情形,并求出k的值.〔省市〕24.抛物线y =x 2-2x +a (a <0)与y 轴相交于点A ,顶点为M .直线a x y -=21分别与x 轴,y 轴相交于B ,C 两点,并且与直线AM 相交于点N .(1)填空:试用含a 的代数式分别表示点M 与N 的坐标,那么M ( , ), N ( , ); (2)如图,将△NAC 沿y 轴翻折,假设点N 的对应点N '恰好落在抛物线上, AN '与x 轴交于点D ,连结CD ,求a 的值和四边形AD 的面积;(3)在抛物线y =x 2-2x +a (a <0)上是否存在一点P ,使得以P ,A ,C ,N 为顶点的四边形是平行四边形?假设存在,求出P 点的坐标;假设不存在,试说明理由.〔省市自选题〕25.假设P 为△ABC 所在平面上一点,且∠APB =∠BPC =∠CPA =120°,那么点P 叫做△ABC 的费马点.(1)假设点P 为锐角△ABC 的费马点,且∠ABC =60°,PA =3,PC =4,那么PB 的值为_____;(2)如图,在锐角△ABC 外侧作等边△ACB '连结BB '. 求证:BB '过△ABC 的费马点P ,且BB '=PA +PB +PC .B(省市)29.〔此题总分值9分〕如左图,正方形ABCD中,点A、B的坐标分别为〔0,10〕,〔8,4〕,点C在第一象限.动点P在正方形ABCD的边上,从点A出发沿A→B→C→D匀速运动,同时动点Q以一样速度在x轴正半轴上运动,当P点到达D点时,两点同时停顿运动,设运动的时间为t秒.(1)当P点在边AB上运动时,点Q的横坐标x〔长度单位〕关于运动时间t〔秒〕的函数图象如右图所示,请写出点Q开场运动时的坐标及点P运动速度;(2)求正方形边长及顶点C的坐标;(3)在〔1〕中当t为何值时,△OPQ的面积最大,并求此时P点的坐标;(4)如果点P、Q保持原速度不变,当点P沿A→B→C→D匀速运动时,OP与PQ能否相等,假设能,写出所有符合条件的t的值;假设不能,请说明理由.t〔威海市〕25.一次函数y =ax +b 的图象分别与x 轴、y 轴交于点M ,N ,与反比例函数y =kx的图象相交于点A ,B .过点A 分别作AC ⊥x 轴,AE ⊥y 轴,垂足分别为C ,E ;过点B 分别作BF ⊥x 轴,BD ⊥y 轴,垂足分别为F ,D ,AC 与BD 交于点K ,连接CD .〔1〕假设点A ,B 在反比例函数y =k x的图象的同一分支上,如左图,试证明: ①S 四边形AEDK =S 四边形CFBK ;②AN =BM .〔2〕假设点A ,B 分别在反比例函数y =kx的图象的不同分支上,如右图,那么AN 与BM 还相等吗?试证明你的结论.- .word.zl.(省市)24.如图,A 、B 是线段MN 上的两点,MN =4,MA =1,MB >1.以A 为中心顺时针旋转点M ,以B 为中心逆时针旋转点N ,使M 、N 两点重合成一点C ,构成△ABC ,设AB =x . 〔1〕求x 的取值围;〔2〕假设△ABC 为直角三角形,求x 的值; 〔3〕探究:△ABC 的最大面积?〔省〕23.某种水果的批发单价与批发量的函数关系如图〔1〕所示.金额w 〔元〕O批发量m 〔kg 〕300 20010020 40 60- .word.zl.〕 第23题图〔1〕第23题图〔2〕〔1〕请说明图中①、②两段函数图象的实际意义.〔2〕写出批发该种水果的资金金额w 〔元〕与批发量m 〔kg 〕之间的函数关系式;在以下列图的坐标系中画出该函数图象;指出金额在什么围,以同样的资金可以批发到较多数量的该种水果.〔3〕经调查,某经销商销售该种水果的日最高销量与零售价之间的函数关系如图〔2〕所示,该经销商拟每日售出60kg 以上该种水果,且当日零售价不变,请你帮助该经销商设计进货和销售的方案,使得当日获得的利润最大.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
应用题
20.(本小题满分 8 分) 北京奥运会开幕前,某体育用品商场预测某品牌运动服能够畅销,就用 32000 元购进了一批 这种运动服,上市后很快脱销,商场又用 68000 元购进第二批这种运动服,所购数量是第一 批购进数量的 2 倍,但每套进价多了 10 元. 1 该商场两次共购进这种运动服多少套? 2 如果这两批运动服每套的售价相同,且全部售完后总利润率不低于 20%,那么每套售 价至少是多少元?(利润率 利成润本100% ) 22.(本小题满分 10 分) 某水产品养殖企业为指导该企业某种水产品的养殖和销售,对历年市场行情和水产品养殖情
2
2
学海无 涯
21.(本小题满分 8 分)
已知:如图,在 ABCD 中,AE 是 BC 边上的高,将 △ABE 沿 BC 方向平移,使点 E 与 点 C 重合,得 △GFC .
1 求证: BE DG ;
2 若 B 60°,当 AB 与 BC 满足什么数量关系时,四边形 ABFG 是菱形?证明你的
交于点 E,点 B 的坐标是(-1,0),P 点是 AC 上的动点(P 点与
A、C 两点不重合). (1) (2 分)写出点A、点 E 的坐标.
y A
P E
(2) (2 分)若抛物线 y 6 3 x2 bx c 7
过 A、E 两点,求抛物线的解析式.
BO D
(3) (5 分)连结 PB、PD.设 l 为△PBD 的周长,当 l 取最小值时, 求点 P 的坐标及l 的 图 10
y2(元)
y2
1 x2 8
bx
c
21.(本题满分
10
分)星期天,小明和七名同学共
8
人去郊游,途中,他用 25
20
元钱去买饮料,
商店只有可乐和奶茶,已知可乐 2 元一杯,奶茶 3 元24一杯,如果 20 元钱刚好用完.
(1)有几种购买方式?每种方式可乐和奶茶各多少杯?
(2)每人至少一杯饮料且奶茶至少二杯时,有几种购买方式? 20.(9 分)某项工程,甲工程队单独完成任务需要 40 天O.1若2 3 4 5 6 7 8 9 10 11 12 x(月) 乙队先做 30 天后,甲、乙两队一起合做 20 童装不再销售。
(1)请建立销售价格 y(元)与周次 x 之间的函数关系;
(2)若该品牌童装于进货当周售完,且这种童装每件进价 z(元)与周次 x 之间的关系为
z 1 (x 8)2 12 , 1≤ x ≤11,且 x 为整数,那么该品牌童装在第几周售出后,每 8
件获得利润最大?并求最大利润为多少?
出自变量 x 的取值范围;
2 当降价多少元时,每星期的利润最大?最大利润是多少?
几何题
20.(本题满分 8 分)如图,在□ABCD 中,∠BAD 为钝角,且 AE⊥BC,AF⊥CD.
(1)求证:A、E、C、F 四点共圆; (2)设线段 BD 与(1)中的圆交于 M、N.求证:BM=ND.
A
D
N
M
F
BE
5、某商品的进价为每件 40 元.当售价为每件 60 元时,每星期可卖出 300 件,现需降价处 理,且经市场调查:每降价 1 元,每星期可多卖出 20 件.在确保盈利的前提下,解答下列
问题:
1
学海无涯
1若设每件降价 x 元、每星期售出商品的利润为 y 元,请写出 y 与 x 的函数关系式,并 求
请问:
(1)(5 分)乙队单独做需要多少天才能完成任务?
(2)(4 分)现将该工程分成两部分,甲队做其中一部分工程用了 x 天,乙队做另一部分 工程用了 y 天.若 x、y 都是正整数,且甲队做的时间不到 15 天,乙队做的时间不到
70 天,那么两队实际各做了多少天? 3、某商场在销售旺季临近时 ,某品牌的童装销售价格呈上升趋势,假如这种童装开始时的 售价为每件 20 元,并且每周(7 天)涨价 2 元,从第 6 周开始,保持每件 30 元的稳定价格
C
第 20 题图
23.(本题满分 10 分)如图,半径为 2 5 的⊙O 内有互相垂直的两条弦 AB、CD 相交于 P 点.
(1)求证:PA·PB=PC·PD;
(2)设 BC 的中点为 F,连结 FP 并延长交 AD 于 E,求证:EF⊥AD:
(3)若 AB=8,CD=6,求 OP 的长.
C
F
AP
B
况进行了调查.调查发现这种水产品的每千克售价 y1 (元)与销售月份 x (月)满足关系
式
y
3 8
x
36
,而其每千克成本
y2(元)与销售月份
x (月)满足的函数关系如图所示.
(1)试确定b、c 的值;
2 求出这种水产品每千克的利润 y (元)与销售月份 x (月)之间的函数关系式;
3 “五·一”之前,几月份出售这种水产品每千克的利润最大?最大利润是多少?
结论.
A
G
D
二次函数结合图像题
(本题满分 12 分)一开口向上的抛物线与 顶点为 C,且 AC⊥BC.
x
轴交于
A(m-2B,0),BE(m+2,F0)两点,C记抛物线
(1)若 m 为常数,求抛物线的解析式;
第 21题图
(2)若 m 为小于 0 的常数,那么(1)中的抛物线经过怎么样的平移可以使顶点在坐标原点?
△CBM.
(2)若 AB=CD,△ADM 与△CBM 是否全等?为什么?
A :△ADM≌C
图8
21.(本题 10 分)如图,已知 AB 是⊙O的直径,过点作弦 BC 的平行线,交过点的切线 AP 于点,连结 AC .
(1)求证: △ABC ∽△POA ;
(2)若 OB 2 , OP 7 ,求 BC 的长.
(3)设抛物线交 y 轴正半轴于 D 点,问是否存在实数 m,使得△BOD 为等腰三角形?若存在,
求出 m 的值;若不存在,请说明理由.
y
D
OA
Bx
C
第 25 题图
21.(9 分)如图 10,已知:△ABC 是边长为 4 的等边三角形,BC 在 x 轴上,点 D 为 BC 的中点,点 A 在第一象限内,AB 与 y 轴正半轴 相
E
O
D
第 23 题图
18.(8 分)如图 8,大楼 AD 的高为 10m,远处有一塔 BC. 某人在楼底A 处测得塔顶B 点处的仰角为 60°,爬到楼顶 D 点处测得塔顶B 点的仰角为 30°.求塔 BC 的高度.
B
D 30°
E
60°
22.已知:如图,在⊙O 中,弦 AB 与 CD 相交于点 M.(1)若 AD=CB,求证
