解三角形应用举例
解直角三角形应用举例

海洋100海里以内的区域,如图,设A、B
是我们的观察站,A和B 之间的距离为
157.73海里,海岸线是过A、B的一条直
线,一外国船只在P点,在A点测得
∠BAP=450,同时在B点测得∠ABP=600,
问此时是否要向外国船只发出警告,令
其退出我国海域.
P
A
B
——坡度、坡角
学习目标
1、知道坡角、坡比(坡度)的意义。 2、能将h、l、c、i各量的计算问题转化 为解直角三角形的问题,这些量中若已知 两个量,可求其他量. 3、在有些实际问题中没有直角三角形, 学会添加辅助线构造直角三角形.
Ex
x
100 2xD
1、解直角三角形的关键是找到与已知和未知 相关联的直角三角形,当图形中没有直角三角 形时,要通过作辅助线构筑直角三角形(作某 边上的高是常用的辅助线);当问题以一个实 际问题的形式给出时,要善于读懂题意,把实 际问题化归为直角三角形中的边角关系。
2、一些解直角三角形的问题往往与其他知识联 系,所以在复习时要形成知识结构,要把解直 角三角形作为一种工具,能在解决各种数学问 题时合理运用。
65° P
C 34°
B
例4.海中有一个小岛A,它的周围8海里范围内 有暗礁,渔船跟踪鱼群由西向东航行,在B点测 得小岛A在北偏东60°方向上,航行12海里到达 D点,这时测得小岛A在北偏东30°方向上,如 果渔船不改变航线继续向东航行,有没有触礁 的危险?
A
60°
B 12
30°
DF
3.国外船只,除特许外,不得进入我国
___1 :__3__。
h
α
L
例1.水库大坝的横断面是梯形,坝顶宽6m,坝高
23m,斜坡AB的坡度i=1∶3,斜坡CD的坡度
2019年§3 解三角形的实际应用举例语文

6.
2
所以海监船接到通知时,距离岛 A 5 6 海里.
栏目 导引
第二章 解三角形
(2)设海监船航行时间为 t 小时,则 BD=10 3t,CD=10t,又 因为∠BCD=180°-∠ACB=180°-60°=120°, 所以 BD2=BC2+CD2-2BC·CDcos 120°, 所以 300t2=100+100t2-2×10×10t·-12, 所以 2t2-t-1=0, 解得 t=1 或 t=-12(舍去).
第二章 解三角形
§3 解三角形的实际应用举例
第二章 解三角形
1.常见的几种角 (1)坡角:坡向与水平向的 夹角 ,如图①.
栏目 导引
第二章 解三角形
(2)仰角和俯角:在视线和水平线所成角中,视线在水平线上方 的角叫 仰角 ,在水平线 下方 的角叫俯角,如图②.
栏目 导引
第二章 解三角形
(3)方位角:指从 正北方向 顺时针转到目标方向线所成的 角,如图③,B 点的方位角为 α.
栏目 导引
第二章 解三角形
2.(1)为了测量水 田两侧 A,B 两点间的距离(如图所 示),某观测者在 A 的同侧选定一点 C,测得 AC=8 m,∠BAC=30°,∠BCA=45°,则 A,B 两点间的距离为________ m.
栏目 导引
第二章 解三角形
(2)如图,A、B 两点都在河的对岸(不可到达),若在河岸选取相 距 20 米的 C、D 两点,测得∠BCA=60°,∠ACD=30°,∠ CDB=45°,∠BDA=60°,那么此时 A、B 两点间的距离是 多少?
栏目 导引
第二章 解三角形
在△ABC 中,由余弦定理得 AB= AC2+BC2-2AC×BCcos∠BCA =10 6(米). 所以 A、B 两点间的距离为 10 6米.
解三角形的实际应用举例

第二章 解三角形
(2)由正弦定理得 AC=sin[180°20-sin((3405°°++4650°°+)60°)] =20ssiinn4150°5°=20sisnin4575°° =10(1+ 3)(米), BC=sin[180°-(206s0i°n 4+5°30°+45°)] =20sisnin4455°°=20(米).
栏目 导引
第二章 解三角形
测量高度问题 如图,一辆汽车在一条水平的公路上向 正西行驶,到 A 处时测得公路北侧一山顶 D 在 西偏北 30°的方向上,行驶 600 m 后到达 B 处, 测得此山顶在西偏北 75°的方向上,仰角为 30°,则此山的 高度 CD=________m.
栏目 导引
第二章 解三角形
栏目 导引
第二章 解三角形
若 P 在 Q 的北偏东 44°,则 Q 在 P 的( )
A.东偏北 46°
B.东偏北 44°
C.南偏西 44°
D.西偏南 44°
解析:选 C.如图,因为 P 在 Q 的北偏东 44°,则 Q 在 P 的南 偏西 44°.
栏目 导引
第二章 解三角形
A,B 两点间有一小山,选定能直接到达点 A,B 的点 C, 测得 AC=60 m,BC=160 m,∠ACB=60°,则 A,B 两点间 的距离为________m. 解析:在△ABC 中,由余弦定理得 AB2=AC2+BC2-2·AC·BC·cos 60° =602+1602-2×60×160cos 60°=196 00, 所以 AB=140 m,即 A、B 两点间的距离为 140 m. 答案:140
栏目 导引
第二章 解三角形
1.(1)在 200 m 高的山顶上,测得山下一塔顶
解三角形(4)---解三角形应用举例

解三角形(4)---解三角形应用举例例1、如图,设A 、B 两点在河的两岸,要测量两点之间的距离,测量者在A 的同侧,在所在的河岸边选定一点C ,测出AC 的距离是55m ,∠BAC=︒51,∠ACB=︒75.求A 、B 两点的距离(精确到0.1m )启发提问1:∆ABC 中,根据已知的边和对应角,运用哪个定理比较适当?启发提问2:运用该定理解题还需要那些边和角呢?分析:这是一道关于测量从一个可到达的点到一个不可到达的点之间的距离的问题,题目条件告诉了边AB 的对角,AC 为已知边,再根据三角形的内角和定理很容易根据两个已知角算出AC 的对角,应用正弦定理算出AB 边。
解:根据正弦定理,得ACB AB ∠sin = ABCAC ∠sin AB =ABC ACB AC ∠∠sin sin =ABC ACB ∠∠sin sin 55 = )7551180sin(75sin 55︒-︒-︒︒ =︒︒54sin 75sin 55 ≈ 65.7(m) 答:A 、B 两点间的距离为65.7米变式练习:两灯塔A 、B 与海洋观察站C 的距离都等于a km ,灯塔A 在观察站C 的北偏东30︒,灯塔B 在观察站C 南偏东60︒,则A 、B 之间的距离为多少?(画图建立数学模型。
答案:2a km )例2、如图,A 、B 两点都在河的对岸(不可到达),设计一种测量A 、B 两点间距离的方法。
分析:这是例1的变式题,研究的是两个不可到达的点之间的距离测量问题.首先需要构造三角形,所以需要确定C 、D 两点.根据正弦定理中已知三角形的任意两个内角与一边既可求出另两边的方法,分别求出AC 和BC ,再利用余弦定理可以计算出AB 的距离.解:测量者可以在河岸边选定两点C 、D ,测得CD=a ,并且在C 、D 两点分别测得∠BCA=α,∠ACD=β,∠CDB=γ,∠BDA =δ,在∆ADC 和∆BDC 中,应用正弦定理得:AC = )](180sin[)sin(δγβδγ++-︒+a = )sin()sin(δγβδγ+++a BC = )](180sin[sin γβαγ++-︒a = )sin(sin γβαγ++a 计算出AC 和BC 后,再在∆ABC 中,应用余弦定理计算出AB 两点间的距离AB =αcos 222BC AC BC AC ⨯-+ 分组讨论:还没有其它的方法呢?变式训练:若在河岸选取相距40米的C、D两点,测得∠BCA=60︒,∠ACD=30︒,∠CDB=45︒,∠BDA =60︒(画图建立数学模型。
解三角形应用举例

B C
α β
A
D
BC AB = sin(α β ) sin(90 + β )
BC sin(90 + β ) BC cos β = 所以,AB = sin(α β ) sin(α β )
解RtABD, 得 BC cos β sin α BD = AB sin ∠BAD = sin(α β ) 28 cos 30 sin 60 = sin(60 30 ) = 42(m)
视 线
N 仰角 俯角
水平线
方位角 60度
目标方向线
视 线
二、例 题 讲 解
例2、如图,要测底部不能到达的烟囱的高 ,从与烟囱底部在 、如图,要测底部不能到达的烟囱的高AB, 间的距离是12m.已知测角仪器高 已知测角仪器高1.5m,求烟囱的高。 求烟囱的高。 , 间的距离是 求烟囱的高 β = 60° CD间的距离是 已知测角仪器高 想一想 图中给出了怎样的一个 几何图形?已知什么, 几何图形?已知什么, 求什么? 求什么?
a sin β AC = sin(α β ) a sin α sin β AB = AE + h = AC sin α + h = +h sin(α β )
ห้องสมุดไป่ตู้
练习: 在山顶铁塔上B处测得地面 练习 在山顶铁塔上 处测得地面 上一点A的俯角 的俯角α= ° 上一点 的俯角 = 60° ,在塔底 C处测得 处的俯角 =30°。已 处测得A处的俯角 处测得 处的俯角β= ° 知铁塔BC部分的高为 部分的高为28m,求出 知铁塔 部分的高为 , 山高CD. 山高 分析:根据已知条件, 分析:根据已知条件,应该设 法计算出AB或 的长 法计算出 或AC的长 解:在⊿ABC中, 中 ∠BCA=90°+β, ° ∠ABC=90°-α, ∠BAC=α° β, ∠BAD=α.根据正弦定理, 根据正弦定理, 根据正弦定理
解三角形应用举例

3 .
14
在Rt HAO中,AH=350米,cos HAO=11, 14
所以OA= AH =4900 445(米). cos HAO 11
答:扇形的半径OA的长约为445米.
测量角度问题
【例5】 缉私艇发现在北偏东45°方向,距离12 n mile的海面上有一走私船正以10 n mile/h的 速度沿东偏南15°方向逃窜.缉私艇的速度 为14 n mile/h.若要在最短的时间内追上该走 私船,缉私艇应沿北偏东45°+α的方向去 追.求追及所需的时间和角α的正弦值.
方法2:连结AC, 作OH AC,交AC于H. 由题意,得 CD=500米,AD=300米,CDA=120. 在 ACD中, AC 2=CD 2+AD 2-2?CD·AD·cos120 =5002+3002+2 500 300 1=7002,
2 所以AC=700(米).
则cos CAD= AC2 AD2 CD2 =11. 2 AC AD 14
44
得A+ ,故A= .
42
4
2由S=1 AC·ABsinA=3 2 AB=3,得AB=2 2.
2
4
由此及余弦定理得BC2=AC2+AB2-2AC ABcosA
=9+8-2 3 2 2 2 =5,故BC= 5. 2
测量距离问题
【例1】 如图,某住宅小区的平面图呈 扇形AOC.小区的两个出入口设 置在点A及点C处,小区里有两 条笔直的小路AD,DC,且拐弯处的转角为120°. 已知某人从C沿CD走到D用了10分钟,从D沿DA走 到A用了6分钟.若此人步行的速度为每分钟50米, 求该扇形的半径OA的长(精确到1米).
【解析】方法1:设该扇形的半径为r米. 由题意,得 CD=500米,DA=300米,CDO=60. 在 CDO中, CD2+OD2-2 CD OD cos60=OC2,
高中数学必修5《解三角形应用举例》教案(4)

《解三角形应用举例》教案(4)教学目标1.能够运用正弦定理、余弦定理等知识和方法进一步解决有关三角形的问题, 掌握三角形的面积公式的简单推导和应用;2.通过综合训练强化学生的相应能力,让学生有效、积极、主动地参与到探究问题的过程中来,逐步让学生自主发现规律,举一反三.3.进一步提高利用正弦定理、余弦定理解斜三角形的能力,提高运用数学知识解决实际问题的能力4.让学生进一步巩固所学的知识,加深对所学定理的理解,提高创新能力;进一步培养学生研究和发现能力,让学生在探究中体验愉悦的成功体验.教学重点难点1.重点:推导三角形的面积公式并解决简单的相关题目.2.难点:利用正弦定理、余弦定理来求证简单的证明题.教法与学法1.教法选择:教学形式采用自主探究与尝试指导相结合,引导学生通过分析实践、自主探究、合作交流得出转化问题方法.2.学法指导:学生通过数学建模,自主探究、合作交流,在实践中体验过程,在过程中感受应用,在交流中升华.教学过程一、设置情境,激发学生探索的兴趣三、思维拓展,课堂交流 3AB AC ⋅=.(II )若b c +=,253AB AC ⋅=cos 3,A =bc ∴1sin 2bc A ==)对于5bc =,又5,1b c∴==或1,5b c==,由余弦定理得2222cos20a b c bc A=+-=,25a∴=四、归纳小结,课堂延展教学环节教学过程设计意图师生活动归纳小结利用正弦定理或余弦定理将已知条件转化为只含边的式子或只含角的三角函数式,然后化简并考察边或角的关系,从而确定三角形的形状.特别是有些条件既可用正弦定理也可用余弦定理甚至可以两者混用.回顾解斜三角形的一般题型,便于学生在复习中更深入的思考,更广泛的研究解三角形.由学生谈体会,师生共同归纳总结.巩固创新课堂延展1 .△ABC中,a=2bcosC,则此三角形一定是( )A.等腰三角形B.直角三角形C.等腰直角三角形D.等腰或直角三角形答案:A2.某城市有一条公路,自西向东经过A点到市中心O点后转向东北方向OB,现要修建一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,现要求市中心O与AB的距离为10 km,问把A、B分别设在公路上离中心O多远处才能使|AB|最短?并求其最短距离.(不要求作近似计算)答案:当AB分别在OA、OB上离O点既能保证全体学生的巩固应用,又兼顾学有余力的学生,同时将探究的空间由课堂延伸到课外.学生课下通过练习,巩固正余弦定理的理解.1.教材地位分析解三角形应用举例(4)是在学习了正弦定理、余弦定理的基础上安排的一节应用举例课程,是在学习了测量距离、高度、角度问题后,有了解三角形方法的初步体验,本节主要介绍了正弦定理和余弦定理在计算三角形面积、判断三角形形状、证明恒等式中的应用.本节课是解三角形应用举例第四阶段,为前面学习测量距离、高度、角度问题做了总结,是前面问题的进一步深化.2.学生现实状况分析通过正弦定理、余弦定理的学习,学生对解斜三角形已经有了直观地认识,能够从图形中找到解三角形的方法.但学生对正弦定理和余弦定理应用范围、应注意的问题缺乏清晰的概念.因此,本节课补充了三角形新的面积公式,巧妙设疑,引导学生证明,同时总结出该公式的特点,循序渐进地具体运用于相关的题型.另外本节课的证明题体现了前面所学知识的生动运用,要放手让学生摸索,使学生在具体的论证中灵活把握正弦定理和余弦定理的特点,能不拘一格,一题多解.只要学生自行掌握了两定理的特点,就能很快开阔思维,有利地进一步突破难点.。
解三角形应用举例
B
例4:如图,在山顶铁塔上B处测得地面上一 点A的俯角,在塔底C处测得A处的俯角.已 知铁塔BC部分的高为27.3米,求出山高 CD.
例5:一辆汽车在一条水平的公路上向正 东行驶,到A处时测得公路南侧远处一山 顶D在东偏南15°的方向上,行驶5KM后 到达B处,测得此山顶在东偏南25°的方 向上,仰角为8° ,求此山的高度CD.
(1)已知a=14.8cm,c=23.5cm,B=148.5° (2)已知B=62.7°C=65.8° ,b=3.16cm; (3)已知三边的长分别为 a=41.4cm,b=27.3cm,c=38.7cm.
例8:在某市进行城市环境建设中,要把 一个三角形的区域改造城市内公园,经 过测量得到这个三角形区域的三条边长 分别为68m,88m,127m,这个区域的面 积是多少? (精确到0.1cm2)
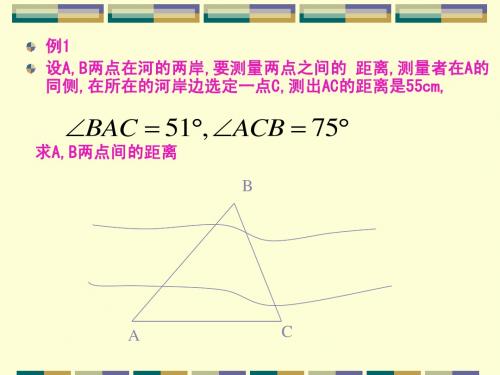
例1 设A,B两点在河的两岸,要测量两点之间的 距离,测量者在A的 同侧,在所在的河岸边选定一点C,测出AC的距离是55cm,
BAC 51, ACB 75
求A,B两点间的距离
B
A
C
例 2 如图A,B两点都在河的对岸(不可到达),设 计一种测量A,B两点距离的方法
A B
例3 : AB是底部B不可到达的一个建筑物,A 为建筑物的最高点,设计一种测量建筑物高 度AB的方法. A
例6:如图一艘海轮从A出发,沿北偏东75°的方 向航行67.5海里后到达海岛B,然后从B出发,沿 北偏东32°的方向航向54海里后到达海岛C. 如果下次航行直接从A出发到达C,此船应该沿 怎样的方向航行,需要航行多少距离?,根据下列条件,求三角 形的面积S(精确到0.1cm2)
解三角形的实际应用举例

小结:
1、解决应用题的思想方法是什么? 答:把实际问题转化为数学问题,即数学建模思想。 2、解决应用题的步骤是什么? 实际问题 分析转化
数学问题(画出图形)
检 验
数学结论 解三角形问题
布置作业:课本P.70 习题B 1、2
课外探究:
如果要测量某铁塔的高度,但不能到达铁塔 的底部,在只能使用简单的测量工具的前提 下,你能设计出哪些测量方法?并提供每种 方法的计算公式。
思考与交流:
1、你能设计出别的测量方法吗?把你设 计的方案与本小组的同学讨论,看看是否 B 可行。
CD
C
90o
D
A
例2:如图,一辆汽车在一条水平的公路上向西行 750 驶,到A处时测得公路北侧远处一山顶D在北偏西 的 方向上,行驶5km后到达B处,测得此山顶在北偏 0 西 的方向上,仰角为 8 ,求此山的高度CD.
B
C1
C
D1
D
A1 A
49028 35012
11.12 m
1.52m
B
49028
35 12
0
求A1B
D1
C1
A1
C 11.12 m D
A
1.52m
B
49028
35012
C1
求A1B
D1
A1
C1D1B 180 0 130 032,
解:
A C 11.12 m D 在BC1D1中,已知BC1D1 35012,
0 56
D
北
西
B
0 56
C
750
A
0 解:在⊿ABC中 A 15,0ACB 250 150 10, 根 据正弦定理,
解三角形应用举例

3:某人在塔的正东沿着南偏 600的方向前进40米后,看见 西 塔在东北方向,若沿途测得塔 300 ,求塔高为多 的最大仰角为 米?
4:已知在河的一侧可测有关 的距离,以及观测点及河对面 测量目标M和N的有关角度, 请设计测量对岸目标M和N之 间距离的方案,并用有关公式 给出计算步骤。
Hale Waihona Puke 本节小结: 1:对于平面图形,解三角形的关键在于确定三 角关系,选择恰当工具进行合理运算与转化。 2:对于空间图形,解三角形的关键在于确定空 间关系,建立空间的架构,进而确立已未知的 转化路径。 3:注意正余弦定理与均值定理等知识点的综合 运用。 4:注意生活中一些常见的角的表述及其意义。 5:注意建模类问题的训练,及其解答与表述。
解三角形应用举例
银川一中 蔡炜
1:为了竖一块广告牌,要制造三 角形支架,三角形支架如图所示: 0 60 要求∠ACB= BC的长度大于1 米,且AC比AB长0.5米,为了使 广告牌稳固,要求AC的长越短越 好,求AC最短为多少米?AC最 短时BC的长为多少米?
2:已知海军在海岸A处发现北偏东 0 45 方向距离A( 3 -1)Km的B处有一 0 艘敌舰,在A北偏西 75 方向距A 2Km 处有我军一驱逐舰奉命以 10 3 的 速度追截敌舰,此时敌舰以10的速度 0 从B处向北偏东30 方向逃窜,问驱逐 舰沿什么方向能最快追上敌舰?
解三角形应用举例

解三角形应用举例一、选择题1.在相距2 km的A,B两点处测量目标点C,若∠CAB=75°,∠CBA=60°,则A,C两点之间的距离为( )A. 6 kmB. 2 kmC. 3 kmD.2 km解析如图,在△ABC中,由已知可得∠ACB=45°,∴AC sin 60°=2sin 45°,∴AC=22×32=6(km).答案 A2.一艘海轮从A处出发,以每小时40海里的速度沿南偏东40°的方向直线航行,30分钟后到达B处,在C处有一座灯塔,海轮在A处观察灯塔,其方向是南偏东70°,在B处观察灯塔,其方向是北偏东65°,那么B,C两点间的距离是( )A.102海里B.103海里C.203海里D.202海里解析如图所示,易知,在△ABC中,AB=20,∠CAB=30°,∠ACB=45°,根据正弦定理得BCsin 30°=ABsin 45°,解得BC=102(海里).答案 A3.(2017·合肥调研)如图所示,已知两座灯塔A和B与海洋观察站C的距离都等于a km,灯塔A在观察站C的北偏东20°,灯塔B在观察站C的南偏东40°,则灯塔A与B的距离为( )A.a kmB. 3 a kmC.2a kmD.2a km解析由题图可知,∠ACB=120°,由余弦定理,得AB2=AC2+BC2-2AC·BC·cos∠ACB=a 2+a 2-2·a ·a ·⎝ ⎛⎭⎪⎫-12=3a 2,解得AB =3a (km). 答案 B 4.如图,一条河的两岸平行,河的宽度d =0.6 km ,一艘客船从码头A 出发匀速驶往河对岸的码头B .已知AB =1km ,水的流速为2 km/h ,若客船从码头A 驶到码头B 所用的最短时间为6 min ,则客船在静水中的速度为( )A.8 km/hB.6 2 km/hC.234 km/hD.10 km/h 解析 设AB 与河岸线所成的角为θ,客船在静水中的速度为v km/h ,由题意知,sin θ=0.61=35,从而cos θ=45,所以由余弦定理得⎝ ⎛⎭⎪⎫110v 2=⎝ ⎛⎭⎪⎫110×22+12-2×110×2×1×45,解得v =6 2.选B. 答案 B5.如图,测量河对岸的塔高AB 时可以选与塔底B 在同一水平面内的两个测点C 与D ,测得∠BCD =15°,∠BDC =30°,CD =30,并在点C 测得塔顶A 的仰角为60°,则塔高AB 等于( )A.5 6B.15 3C.5 2D.15 6解析 在△BCD 中,∠CBD =180°-15°-30°=135°.由正弦定理得BCsin 30°=30sin 135°,所以BC =15 2. 在Rt △ABC 中,AB =BC tan ∠ACB =152×3=15 6.答案 D二、填空题6.如图所示,一艘海轮从A 处出发,测得灯塔在海轮的北偏东15°方向,与海轮相距20海里的B 处,海轮按北偏西60°的方向航行了30分钟后到达C 处,又测得灯塔在海轮的北偏东75°的方向,则海轮的速度为________海里/分. 解析由已知得∠ACB=45°,∠B=60°,由正弦定理得ACsin B=ABsin∠ACB,所以AC=AB·sin Bsin∠ACB=20×sin 60°sin 45°=106,所以海轮航行的速度为10630=63(海里/分).答案6 37.江岸边有一炮台高30 m,江中有两条船,船与炮台底部在同一水平面上,由炮台顶部测得俯角分别为45°和60°,而且两条船与炮台底部连线成30°角,则两条船相距________m.解析如图,OM=AO tan 45°=30(m),ON=AO tan 30°=33×30=103(m),在△MON中,由余弦定理得,MN=900+300-2×30×103×3 2=300=103(m).答案10 38.在200 m高的山顶上,测得山下一塔顶和塔底的俯角分别是30°,60°,则塔高为________m.解析如图,由已知可得∠BAC=30°,∠CAD=30°,∴∠BCA=60°,∠ACD=30°,∠ADC=120°.又AB=200 m,∴AC=40033(m).在△ACD中,由余弦定理得,AC2=2CD2-2CD2·cos 120°=3CD2,∴CD=13AC=4003(m).答案400 3三、解答题9.如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12海里,渔船乙以10海里/时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上.(1)求渔船甲的速度;(2)求sin α的值.解(1)依题意知,∠BAC=120°,AB=12,AC=10×2=20,∠BCA=α. 在△ABC中,由余弦定理,得BC2=AB2+AC2-2AB·AC·cos∠BAC=122+202-2×12×20×cos 120°=784.解得BC=28.所以渔船甲的速度为BC2=14海里/时.(2)在△ABC中,因为AB=12,∠BAC=120°,BC=28,∠BCA=α,由正弦定理,得ABsin α=BCsin 120°,即sin α=AB sin 120°BC=12×3228=3314.10.(2015·安徽卷)在△ABC中,A=3π4,AB=6,AC=32,点D在BC边上,AD=BD,求AD的长.解设△ABC的内角A,B,C所对边的长分别是a,b,c,由余弦定理,得a2=b2+c2-2bc cos∠BAC=(32)2+62-2×32×6×cos 3π4=18+36-(-36)=90,所以a=310.又由正弦定理,得sin B=b sin∠BACa=3310=1010,由题设知0<B<π4,所以cos B=1-sin2B=1-110=31010.在△ABD中,因为AD=BD,所以∠ABD=∠BAD,所以∠ADB=π-2B.由正弦定理,得AD=AB·sin Bsin(π-2B)=6sin B2sin B cos B=3cos B=10.11.(2016·全国Ⅲ卷)在△ABC中,B=π4,BC边上的高等于13BC,则cos A=( )A.31010B.1010C.-1010D.-31010解析设BC边上的高AD交BC于点D,由题意B=π4,BD=13BC,DC=23BC,tan∠BAD=1,tan∠CAD=2,tan A=1+21-1×2=-3,所以cos A=-1010.答案 C12.如图所示,D,C,B三点在地面同一直线上,DC=a,从D,C两点测得A点仰角分别为α,β(α<β),则点A离地面的高AB等于( )A.a sin α·sin βsin(β-α)B.a sin α·sin βcos(β-α)C.a cos α·cos βsin(β-α)D.a cos α·cos βcos(β-α)解析结合题图示可知,∠DAC=β-α.在△ACD中,由正弦定理得:DCsin∠DAC=ACsin α,∴AC=a sin αsin∠DAC=a sin αsin(β-α).在Rt△ABC中,AB=AC sin β=a sin αsin βsin(β-α).答案 A13.如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为75°,30°,此时气球的高是60 m,则河流的宽度BC等于________m.解析如图,∠ACD=30°,∠ABD=75°,AD=60 m,在Rt△ACD中,CD=ADtan∠ACD=60tan 30°=603(m),在Rt△ABD中,BD=ADtan∠ABD=60tan 75°=602+3=60(2-3)(m),∴BC=CD-BD=603-60(2-3)=120(3-1)(m).答案120(3-1)14.如图,在海岸A处,发现北偏东45°方向距A为(3-1)海里的B处有一艘走私船,在A处北偏西75°方向,距A为2海里的C处的缉私船奉命以103海里/时的速度追截走私船.此时走私船正以10海里/时的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船?并求出所需要的时间(注:6≈2.449). 解设缉私船应沿CD方向行驶t小时,才能最快截获(在D点)走私船,则有CD=103t(海里),BD=10t(海里).在△ABC中,∵AB=(3-1)海里,AC=2海里,∠BAC=45°+75°=120°,根据余弦定理,可得BC=(3-1)2+22-2×2×(3-1)cos 120°=6(海里).根据正弦定理,可得sin∠ABC=AC sin 120°BC=2×326=22.∴∠ABC=45°,易知CB方向与正北方向垂直,从而∠CBD=90°+30°=120°.在△BCD中,根据正弦定理,可得sin∠BCD=BD sin∠CBDCD=10t·sin 120°103t=12,∴∠BCD=30°,∠BDC=30°,∴BD=BC=6(海里),则有10t=6,t=610≈0.245小时=14.7分钟.故缉私船沿北偏东60°方向,需14.7分钟才能追上走私船.。
1.2解三角形应用举例(一)

1.2解三角形应用举例(一)班级_______姓名________ 1、自动卸货汽车的车厢采用液压机构,设计时需要计算油泵顶杆BC的长度,已知车箱的最大仰角是60°,油泵顶点B与车箱支点A之间的距离为1.95m,AB与水平线之间的夹角为6°20′,AC长为1.40m,计算BC的长(精确到0.01m)。
2、如图,在山脚A测得山顶P的仰角为,α沿倾斜角为β的斜坡向上走a米到B,在B处测得山顶P的仰角为,γ求证:山高sin sin().sin()ahαγβγβ-=-3、勘探队员朝一座山行进,在前后两处观察山顶的仰角分别是29°和38°,两个观察点之间的距离是200m,求此山的高度。
4、飞机的航线和山顶在同一个铅垂平面内,已知飞机的高度为海拔20 250m,速度为1 000km/h,飞行员先看到山顶的俯角为18°30′,经过150s后又看到山顶的俯角为81°,求山顶的海拔高度(精确到1 m)。
5、测山上石油钻井的井架BC 的高,从山脚A 测得AC=65.3m ,塔顶B 的仰角a 是25°25′。
已知山坡的倾斜角β是17°38′,求井架的高BC 。
6、在△ABC 中,根据下列条件,求三角形的面积S (精确到0.01cm 2):(1)已知 45,33,28===B cm c cm a ;(2)已知cm a C A 36,5.66,8.32=== ;(3)已知三边的长分别为cm c cm b cm a 71,61,54===。
7、证明三角形的面积公式AC B a S sin sin sin 212=8、有一块四边形土地的形状如图所示,它的三条边的长分别是50m ,60m ,70m ,两个内角是127°和132°,求四边形的面积(精确到0.01m 2)。
9、货轮在海上以35n mile/h 的速度沿着方位角(从指北方向顺时针转到目标方向线的水平角)为148°的方向航行。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解三角形应用举例
一、测量距离问题
例1(1)如图,A,B两点在河的同侧,且A,B两点均不可到达,要测出A,B 的距离,测量者可以在河岸边选定两点C,
D,若测得CD=
3
2km,∠ADB=∠CDB
=30°,∠ACD=60°,∠ACB=45°,则A,B两点间的距离为km.
答案
6 4
解析∵∠ADC=∠ADB+∠CDB=60°,∠ACD=60°,
∴∠DAC=60°,∴AC=DC=
3
2km.
在△BCD中,∠DBC=180°-∠CDB-∠ACD-∠ACB=45°,
由正弦定理,得BC=DC
sin∠DBC
·sin∠BDC
=
3
2
sin 45°·sin 30°=
6
4(km).
在△ABC中,由余弦定理,得AB2=AC2
+BC2-2AC·BCcos 45°=3
4+3
8
-2×3
2
×
6
4×
2
2
=3
8.
∴AB=
6
4km.
∴A,B两点间的距离为
6
4km.
(2)如图,为了测量两座山峰上P,Q两点之间的距离,选择山坡上一段长度为300 3 m且和P,Q两点在同一平面内的路段AB的两个端点作为观测点,现测得∠PAB=90°,∠PAQ=∠PBA=∠PBQ=
60°,则P,Q两点间的距离为m.
答案900
解析由已知,得∠QAB=∠PAB-
∠PAQ=30°.
又∠PBA=∠PBQ=60°,
∴∠AQB=30°,∴AB=BQ.
又PB为公共边,∴△PAB≌△PQB,∴PQ =PA.
在Rt△PAB中,AP=AB·tan 60°=900(m),故PQ=900 m,∴P,Q两点间的距离为900 m.
二、测量高度问题
例2如图所示,为测量一树的高度,在地面上选取A,B两点,从A,B两点分别测得树尖的仰角为30°,45°,且A,B 两点间的距离为60 m,则树的高度为
m.
答案30+30 3
解析在△PAB中,∠PAB=30°,∠APB =15°,AB=60 m,
sin 15°=sin(45°-30°)=sin 45°cos 30°-
cos 45°sin 30°=
2
2×
3
2
-2
2×
1
2
=
6-2 4
,
由正弦定理得PB sin 30°=AB sin 15°
, 所以PB =12×606-2
4
=30(6+2), 所以树的高度为PB ·sin 45°=30(6+
2)×
22
=(30+303)(m ). 三、测量角度问题
例3 已知岛A 南偏西38°方向,距岛A 3海里的B 处有一艘缉私艇.岛A 处的一艘走私船正以10海里/小时的速度向岛北偏西22°方向行驶,问缉私艇朝何方向以多大速度行驶,恰好用0.5小时能截住该走私船?
⎝⎛⎭⎫参考数据:sin 38°≈5314,sin 22°≈3314 解 如图,设缉私艇在C 处截住走私船,D 为岛A 正南方向上一点,缉私艇的速度为x 海里/小时,结合题意知BC =0.5x ,AC =5,∠BAC =180°-38°-22°=120°.
由余弦定理可得BC 2=AB 2+AC 2-
2AB ·ACcos 120°,
所以BC 2=49,所以BC =0.5x =7, 解得x =14.
又由正弦定理得
sin ∠ABC =AC ·sin ∠BAC BC
=5×327=5314
, 所以∠ABC =38°,
又∠BAD =38°,所以BC ∥AD ,
故缉私艇以14海里/小时的速度向正北方向行驶,恰好用0.5小时截住该走私船. 素养提升 数学抽象是指舍去事物的一切物理属性,得到数学研究对象的思维过程,主要包括:从数量与数量关系、图形
与图形关系中抽象出数学概念及概念之间的关系,从事物的具体背景中抽象出一般规律和结构,并且用数学符号或数学术语予以表征.从实际问题中抽象出距离、高度、角度等数学问题,然后利用正弦定理、余弦定理求解,很好地体现了数学抽象的数学素养.。
