万能解题模型(六) 圆中常见辅助线的作法
圆中辅助线做法和解题策略

《圆》常用辅助线作法1、弧有中点:圆心连。
利用等弧所对的圆心角相等、弦相等、圆周角相等可得到一系列的相等关系的量2、弦有中点:圆心连。
利用垂径定理的推论可得,所连半径垂直于弦。
如果再把圆心和弦的一端连起来,就可以得到由半径、半弦、弦心距构成的直角三角形。
3、弦和直径同时现:过圆心作弦的垂线。
利用垂径定理构建由半径、半弦、弦心距构成的直角三角形4、两条半径同时现:半径外端用线连。
此时就构建了一个等腰三角形,可以进一步用等腰三角形性质解题5、条件中有直径和与直径有公共端点的弦:把弦的另一端点与直径的另一端点连起来。
利用直径所对的圆周角是直角,可得到一个直角三角形6、条件中有90°的圆周角:把圆周角所对的弦做出来。
利用90°的圆周角所对的弦是直径,可得所作的弦是直径,同时得到一个直角三角形7、证明直线是圆的切线:当直线与圆有明确的公共点时,连接圆心和公共点,证明所连半径与直线垂直即可;当直线与圆没有明确的公共点时,过圆心作直线的垂线,证明所做垂线段等于半径即可。
8、条件中有切线,有切点:连结圆心和切点。
利用切线的性质---圆的切线垂直于过切点的半径——可得到所连半径与切线垂直。
《圆》解题规律1、“圆内接四边形”往往是隐含条件,要注意分析观察,自觉应用圆内接四边形的性质解决问题2、连结半径外端构建等腰三角形,往往忽计,要善于用等腰三角形性质解决问题3、有弦有直径,要构建半径、半弦、弦心距构成的直角三角形,利用勾股定理和垂径定理解决问题4、圆中主要学了两种特殊的角,圆心角和圆周角,它们不仅在解题时用的多,而且它们之间的关系很特殊,要主动利用5、圆中得“线段相等、角相等”的方法比直线型问题要多得多,垂径定理,圆周角定理,弧、弦、圆心角关系定理,切线长定理都可以用。
6、垂径定理和三线合一定理既有联系又有区别,在做题时要分清(是弦时,直接用垂径定理,否则要用三线合一定理)7、三角形中位线定理和垂径定理的综合比较常见8、作出恰当的辅助线很关键,而辅助线的作法如前8条9、要注意多解的问题:(1)平形弦间的距离(2)圆周角的计算时,顶点位置不明确(优弧上、劣弧上)(3)点到圆的最大距离和最小距离问题(点在圆内、点在圆外)(4) 两圆相切(内切、外切)(5)弦所在弓形高(弦对的弧为优弧、劣弧)。
《圆》常用辅助线构造技巧

《圆》常用辅助线构造技巧圆是数学中非常重要的一个几何形状,对于圆的构造和分析,辅助线构造技巧是不可或缺的工具之一、辅助线的引入可以帮助我们简化问题、找到关键信息、发现隐藏的特性和关系,从而更好地解决问题。
在本文中,我将介绍一些常用的辅助线构造技巧,希望能对大家的圆的学习有所帮助。
1.划分弧长和角度:当需要将圆上的弧划分成等长的部分时,可以引入辅助线。
例如,要将一个给定的圆上的弧ACB分成5等份。
我们可以在弧上选择两点D和E,并通过D、E和圆心O分别画两条半径,使其与弧ACB交于点F和G。
然后通过直线OF、OG将圆分成5个等弧。
2.寻找垂直角:当我们需要判断两条线段是否垂直时,可以通过引入垂直辅助线来判断。
例如,当我们需要判断线段AB和CD是否垂直时,可以通过引入半径OC和OD,然后判断角AOC和角COD是否互为垂直角来判断。
3.寻找平行线段:当我们需要判断两条线段是否平行时,可以通过引入平行辅助线来判断。
例如,当我们需要判断线段AB和CD是否平行时,可以通过引入直径AC和BD,然后判断角ABC和角CDA是否互为对应角来判断。
4.寻找相等线段和角:当我们需要证明两条线段或两个角相等时,可以通过引入相等辅助线来证明。
例如,当我们需要证明线段AB和CD相等时,可以通过引入直径AC和BD,然后通过三角形ABC和三角形CDA的相似性来证明。
5.寻找点的位置关系:当我们需要判断一个点与一条线段或一条弧的位置关系时,可以通过引入辅助线来判断。
例如,当我们需要判断点P是否在线段AB上时,可以通过引入半径OP,然后判断角AOP和角BOP是否相等来判断。
6.寻找三角形的性质:圆与三角形的关系是数学中一个重要的研究领域,通过引入辅助线可以有助于研究三角形的特性。
例如,当我们需要研究圆内接三角形的性质时,可以通过引入辅助线将圆分成若干个等弧,然后通过引入半径和垂直辅助线来研究三角形的边长和角度。
除了以上的常用辅助线构造技巧外,还有许多其他的技巧可以应用于解决圆的问题。
圆中常用的作辅助线的八种方法

证明:1 如图;过点D作⊙O的直径DE;连接AE;EC;AC ∵DE是⊙O的直径; ∴∠ECD=∠EAD=90° 又∵CD⊥AB;∴EC∥AB ∴∠BAC=∠ACE ∴B︵C=A︵E ∴BC=AE 在Rt△AED中;AD2+AE2=DE2; ∴AD2+BC2=4R2
2若弦AD;BC的长是方程x26x+5=0的两个根 AD>BC;求⊙O的半径及点O到AD的距离
1求证:PB是⊙O的切线; 证明:1 如图;连接OB;∵OA=OB;
∴∠OAB=∠OBA ∵PA=PB; ∴∠PAB=∠PBA ∴∠OAB+∠PAB=∠OBA+∠PBA
即∠PAO=∠PBO 又∵PA是⊙O的切线;∴∠PAO=90° ∴∠PBO=90° ∴OB⊥PB 又∵OB是⊙O的半径; ∴PB是⊙O的切线
︵ 2求由弦CD;BD与BC所围成的阴影部分的面积
结果保留π
解:2∵OE⊥DB;∴EB=
D1 B=3 2
c3m
在Rt△EOB中;∵∠OBD=30°;
∴OE=
1 2
OB
∵EB=3 3 cm;
∴由勾股定理可求得OB=6 cm
又∵∠CDB=∠DBO;DE=BE;
∠CED=∠OEB;
∴△CDE≌△OBE
方法 8 巧添辅助线计算阴影部分的面积
9 中考·自贡如图所示;点B;C;D都在⊙O上; 过点C作AC∥BD交OB的延长线于点A;连接CD; 且∠CDB=∠OBD=30°;DB=6 3cm
1求证:AC是⊙O的切线;
证明:1如图;连接CO;交DB于点E; ∴∠O=2∠CDB=60° 又∵∠OBE=30°; ∴∠BEO=180°60°30°=90° ∵AC∥BD;∴∠ACO=∠BEO=90° 即OC⊥AC 又∵点C在⊙O上; ∴AC是⊙O的切线
圆中常用辅助线的画法

圆中常用辅助线的添法圆是初中数学重点内容,属中考必考内容,中考中有关圆的问题,大部分需添辅助线解之,那么圆问题中常用的辅助线有哪些呢?现就圆中常用辅助线的添法作一归纳,以期对同学们的学习有所帮助.1.作弦心距.在解决有关弦的问题时,常常作弦心距,以利用垂经定理或圆心角、弦、弦心距之间的关系定理及推论.例1.如图,AB是⊙O 的直径,PO ⊥AB 交⊙O 于P 点,弦PN 与AB 相交于点M , 求证:PM •PN=2PO 2.分析:过O 点作OC ⊥PN 于C ,根据垂经定理 NC=PC ,要证明PM •PN=2PO 2,即证明PM •PC =PO 2,只需证明PM •PC=PO 2,要证明PM •PC=PO 2只需证明Rt △POC ∽Rt △PMO.证明: 过圆心O 作OC ⊥PN 于C ,∴PC= 21PN∵PO ⊥AB, OC ⊥PN ,∴∠MOP=∠OCP=90°.又∵∠OPC=∠MPO ,∴Rt △POC ∽Rt △PMO. ∴PO PC PM PO 即∴PO 2= PM •PC. ∴PO 2= PM •21PN ,∴PM •PN=2PO 2. 2.作直径所对的圆周角在解决有关直径的问题时,常常作直径所对的圆周角,以利用直径所对的圆周角是直角的性质。
例2 如图,在△ABC 中,∠C=90°,以BC 上一点O 为圆心,以OB 为半径的圆交AB 于点M ,交BC 于点N .(1) 求证:BA ·BM=BC ·BN ;(2) 如果CM 是⊙O 的切线,N 为OC 的中点,当AC=3时,求AB 的值.分析:要证BA ·BM=BC ·BN ,需证△ACB ∽△NMB ,而∠C=90°,所以需要△NMB 中有个直角,而BN 是圆O 的直径,所以连结MN 可得∠BMN=90°。
(1) 证明:连结MN ,则∠BMN=90°=∠ACB∴△ACB ∽△NMB ∴BN AB BM BC ∴AB ·BM=BC ·BN(2) 解:连结OM ,则∠OMC=90°∵N 为OC 中点∴MN=ON=OM ,∴∠MON=60°∵OM=OB ,∴∠B=21∠MON=30°∵∠ACB=90°,∴AB=2AC=2×3=63、连结半径 圆的半径是圆的重要元素,圆中的许多性质如:“同圆的半径相等”和“圆的切线垂直于过切点的半径”等都与圆的半径有关,连结半径是常用的方法之一. 例3.已知:如图,△ABC 中,∠B=90°,O 是AB 上一点,以O 为圆心,以OB 为半径的圆切AC 于D 点,交AB 与E 点,AD=2,AE=1.求CD 的长.分析:D 为切点,连结DO ,则∠ODA=90°.根据切线长定理,有CD=CB.DO=EO=半径r ,在Rt △ADO 中根据勾股定理或Rt △ADO~ Rt △ABC ,即可求出CD.证明: 连结DO ∴OD ⊥AC 于D, ∴∠ODA =90°.B∵AB过O点, ∠B=90°. ∴BC为⊙O的切线, ∴CD=CB 设CD=CB=x,DO=EO=y在Rt△ADO中,AO2 =AD2+ DO2,AD=2,AE=1∴2222)1(yy+=+, 解得 y=23在Rt△ABC中,AC2 =AB2+ BC2,即(2+x)2=(1+ y + y)2+x2, ∴x=3 ∴CD=3.4、连结公共弦在处理有关两圆相交的问题时,公共弦像一把“钥匙”,常常可以打开相应的“锁”,因此“遇到相交圆,连接公共弦.”。
解题技巧专题:圆中辅助线的作法
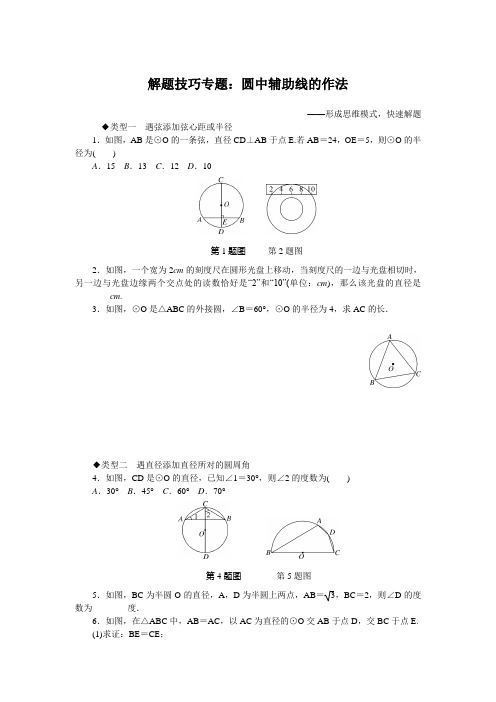
解题技巧专题:圆中辅助线的作法——形成思维模式,快速解题◆类型一遇弦添加弦心距或半径1.如图,AB是⊙O的一条弦,直径CD⊥AB于点E.若AB=24,OE=5,则⊙O的半径为()A.15 B.13 C.12 D.10第1题图第2题图2.如图,一个宽为2cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:cm),那么该光盘的直径是________cm.3.如图,⊙O是△ABC的外接圆,∠B=60°,⊙O的半径为4,求AC的长.◆类型二遇直径添加直径所对的圆周角4.如图,CD是⊙O的直径,已知∠1=30°,则∠2的度数为()A.30°B.45°C.60°D.70°第4题图第5题图5.如图,BC为半圆O的直径,A,D为半圆上两点,AB=3,BC=2,则∠D的度数为________度.6.如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.(1)求证:BE=CE;(2)若∠B =70°,求DE ︵的度数;(3)若BD =2,BE =3,求AC 的长.◆类型三 遇切线连接圆心和切点7.如图,四边形ABCD 内接于⊙O ,AB 是直径,过C 点的切线与AB 的延长线交于P 点,若∠P =40°,则∠D 的度数为________.8.如图,在矩形ABCD 中,AB =4,AD =5,AD ,AB ,BC 分别与⊙O 相切于E ,F ,G 三点,过点D 作⊙O 的切线交BC 于点M ,切点为N ,求DM 的长.参考答案与解析1.B 2.104.C 5.1506.(1)证明:连接AE .∵AC 为⊙O 的直径,∴∠AEC =90°,∴AE ⊥BC .∵AB =AC ,∴BE =CE .(2)解:连接OD ,OE .在Rt △ABE 中,∠BAE =90°-∠B =90°-70°=20°,∴∠DOE =2∠DAE =40°,∴DE ︵的度数为40°.(3)解:连接CD .由(1)可知BE =CE ,∴BC =2BE =6.设AB =AC =x ,则AD =AB -BD =x -2.∵AC 为⊙O 的直径,∴∠ADC =90°.在Rt △BCD 中,CD 2=BC 2-BD 2=62-22=32.在Rt △ADC 中,AD 2+CD 2=AC 2,即(x -2)2+32=x 2,解得x =9,即AC 的长为9.7.115°8.解:连接OE ,OF ,ON ,OG .∵四边形ABCD 是矩形,∴∠A =∠B =90°,CD =AB =4.∵AD ,AB ,BC 分别与⊙O 相切于E ,F ,G 三点,∴∠AEO =∠AFO =∠OFB =∠BGO =90°,OE =OF =OG ,∴四边形AFOE ,FBGO 是正方形,∴AF =BF =AE =BG =2,∴DE =3.∵DM 是⊙O 的切线,∴DN =DE =3,MN =MG ,∴CM =BC -BG -MG =5-2-MN=3-MN .在Rt △DMC 中,DM 2=CD 2+CM 2,∴(3+MN )2=42+(3-MN )2,∴MN =43,∴DM =3+43=133.。
例谈圆中常见作辅助线的方法

例谈圆中常见作辅助线的方法圆是初中几何局部的重要内容之一,与圆有关的大局部几何题型都需要添加辅助线来解决。
只要添上适宜的辅助线,不仅会使问题迎刃而解,而且还会有效地培养学生的解题能力与创造性思维能力。
通过对实践教学中的归纳与总结,发现添加辅助线的方法有很多,本文就圆中常见作辅助线的方法归纳如下:一、作弦心距(在与弦有关的计算或证明题时,常作辅助线的方法是作弦心距)例1:如图1,AB为O的直径,PQ切O于T,ACPQ于C,交O于D,AD=2,TC=.求O的半径。
解:过点O作OMAC于M,AM=MD=AD/2=1.PQ切O于T,OTPQ.又ACPQ,OMAC,∠OTC=∠ACT=∠OMC=90°,四边形OTCM为矩形.OM=TC=,在RtAOM中,.即O的半径为2.例2:如图2,已知在以O为圆心的两个同心圆中,大圆的弦AB 交小圆于C、D两点.求证:AC=BD.证明:过点O作OEAB于E,那么AE=BE,CE=DE,AECE=BEDE.AC=AECE,BD=BEDE.AC=BD.二、连半径(与半径和弦有关的简单计算、已知圆中有切线的有关计算和证明时,常作辅助线的方法是连半径)例3:如图3,O的直径CD=20cm,直线lCO,垂足为H,交O于A、B两点,AB=16 cm,直线l平移多少厘米时能于O相切?解:连接OA,lCO,OC平分ABAH=8cm.在RtAHO中,OH=6cm.CH=4cm,DH=16 cm.答:直线l向左平移4cm,或向右平移16cm时能于O相切。
例4:如图4,PA是O的切线,切点是A,过点A作AHOP于点H,交O于点B.求证:PB是O的切线.证明:连接OA、OB.PA是O的切线,∠OAP=90°.OA=OB,ABOP,∠AOP=∠BOP.又OA=OB,OP=OP,AOP≌BOP.∠OPB=∠OAP=90°.PB是O的切线.三、既作弦心距又连半径(与半径和弦都有关的计算时,常作辅助线的方法是既作弦心距又连半径,利用勾股定理来解决)例5:直径为52厘米的圆柱形油槽内装入一些油后,截面如图5,假设油最大深度为16厘米.那么油面宽度AB的长是多少厘米?解:连接OA,作OCAB于C,那么AC=BC=AB.在RtOAC中,OA=×52=26厘米,OC=2616=10厘米,AC=24厘米.AB=2AC=48厘米.四、连弦构造相似三角形或直角三角形(在圆中与弦或其他有关的计算或证明时,常作辅助线的方法是连弦,利用同弧所对的圆周角相等连弦构造相似三角形或利用直径所对的圆周角为直角这个性质连弦构造出直角三角形,从而将问题转化到相似三角形或直角三角形中去计算或证明)例6:已知,如图6,在半径为4的O中,AB,CD是两条直径,M为OB的中点,CM的延长线交O于点E,且EM>MC.连结DE,DE=.(1)求证:AM・MB=EM・MC;(2)求EM的长;(3)求sin∠EOB的值.解:(1)连接AC,EB,那么∠CAM=∠BEM.又∠AMC=∠EMB,AMC∽EMB.,即AM・MB=EM・MC.(2) DC为O的直径,∠DEC=90°,EC=OA=OB=4,M为OB的中点,AM=6,BM=2.设EM=x,那么CM=7x.代入(1),得6×2=x(7x).解得x1=3,x2=4.但EM>MC,EM=4.(3)由(2)知,OE=EM=4,作EFOB于F,那么OF=MF=OB=1.在RtEOF中,sin∠EOB=.例7:如图7所示,ABC是直角三角形,∠ABC=90°,以AB为直径的O交AC于点E,点D是BC边的中点,连结DE.(1)求证:DE与O相切;(2)假设O的半径为,DE=3,求AE.(1)证明:连结OE,BE,AB是直径,BEAC.D是BC的中点, DE=DB,∠DBE=∠DEB.又OE=OB,∠OBE=∠OEB,∠DBE+∠OBE=∠DBE+∠OEB.即∠ABD=∠OED.又∠ABC=90°,∠OED=90°,DE是O的切线.(2)解:,,.五、作直径构造直角三角形(在圆中牵涉到三角函数的运算或与直径的计算与证明时,常作辅助线的方法是作直径,利用直径所对的圆周角是直角构造直角三角形,从而将问题转化到直角三角形中去解决)例8:如图8,点A、B、C在O上(AC不过O点),假设∠ACB=60°,AB=6,求O半径的长。
园中常做辅助线的做法

几何证明一般都离不开作辅助线,能否迅速、准确地作出所需的辅助线,往往成为成败的关键。
本文就圆中常见辅助线的作法归纳如下,供参考。
一、作弦心距证明圆中与弦有关的问题,常需作弦心距(即垂直于弦的直径或半径),其目的在于利用垂径定理来沟通弦、弦、弦心距之间的关系,或构造半径、弦心距、弦为边的直角三角形。
例1:求证:经过相交两圆的一个交点的那些直线,被两圆所截得的线段中,平行于连心线的那一条线段最长。
分析:如图1,PQ ∥OO′,要证明PQ 最长,只须证明PQ 大于过A 点的任意一条不平行于OO ′的割线P′Q′,这是证明与圆的弦有关的问题,因此过O 、O′分别作PQ 、P′Q′的垂线,垂足分别为C 、D ;C′、D′。
由垂径定理知AC= AP 、AD= AQ ,所以CD=PQ 。
同理C′D′= P′Q′,又OO′=CD ,于是问题转化为证明OO′> C′D′,而OO′D′C′为直角梯形,显然有OO′> C′D′。
从而问题可证。
图1二、作过切点的半径或弦当所证问题含有圆的切线时,常常需要作出过切点的半径或弦,利用该半径与切线垂直或弦切角定理来沟通题设与结论之间的联系。
例2:已知AB 是⊙O 的直径,AC ⊥MN ,BD ⊥MN ,MN 切⊙O 于K ,求证:(1)AC+BD=AB(2)BK2=AB·BD分析:(1)AC 、BD 为直角梯形的上、下底边,其和必与梯形的中位线有关,由MN切⊙O 于K ,想到需连结OK ,则OK 为梯形的中位线且OK= (AC+BD ),而AB=2OK ,所以有AC+BD=AB 。
(2)要证BK =AB·BD ,即AB :BK=BK :BD ,所以需连结AK ,由弦切角定理知∠KAB=∠BKD ,又∠AKB=∠KDB=90°,所以△AKB ∽△KDB,故问题可以获证。
图2 三、过已知点作圆的切线过已知点作圆的切线是圆中常作的辅助线之一,其目的在于利用切线的性质来沟通题中各元素间的联系。
圆中常见的辅助线

计算弧长
利用半径和直径,可以计算圆中的 弧长,如半圆、四分之一圆等。
证明定理
半径和直径在证明圆的定理中起到 关键作用,如垂径定理、切线长定 理等。
半径和直径的作法
作半径
从圆心出发,用直尺或圆规画出到圆上任意一点的线段。
作直径
通过圆心,用直尺或圆规画出穿过圆上任意两点的线段。
02 弦
定义与性质
弦的作法
01
02
03
04
通过作弦的中垂线来找到弦的 中点;
通过连接圆心和弦的一个端点 来找到弦;
通过作经过圆上两点的切线来 找到弦;
通过作经过圆心的直线来找到 弦。
03 切线
定义与性质
定义
切线是指与圆只有一个公共点的直线。
性质
切线与半径垂直,切线长度与半径相等,切线到圆心的距离为0。
切线在解题中的作用
定义
连接圆上任意两点的线段被称为圆的 弦。
性质
弦与直径垂直时,弦平分直径;同弦 所对的圆周角相等;弦长与半径成正 比。
弦在解题中的作用
利用弦的性质求角度
利用弦的性质证明定理
通过利用弦所对的圆周角相等,可以 求出某些角度。
通过利用弦的性质,可以证明一些与 圆有关的定理。
利用弦的性质求长度
利用弦长与半径的比例关系,可以求 出某些长度。
圆中常见的辅助线
目 录
• 半径和直径 •弦 • 切线 • 割线
01 半径和直径
定义与性质
定义
半径是连接圆心和圆上任意一点 的线段,直径是穿过圆心且两端 点在圆上的线段。
性质
半径长度等于圆的半径,直径长 度等于圆的直径。
半径和直径在解题中的作用
3-方法技巧突破(六) 圆中常见辅助线的作法

类型六:遇到要证切线时,若无交点,则作垂直,证半径 如图,在 Rt△ABC 中,∠B=90°,∠BAC 的
平分线交 BC 于点 D,E 为 AB 上的一点,DE=DC,以 D 为 圆心,DB 长为半径作⊙D,AB=5,EB=3.
(1)求证:AC 是⊙D 的切线; (2)求线段 AC 的长.
上一页
目录
2021版 甘肃 数学
(2)解:连接 AE,如图. ∵AD=DE,∠ADE=60°, ∴△ADE 是等边三角形, ∴AE=DE,∠AED=60°, ∴EAC=∠AED-∠C=30°,∴∠EAC=∠C. ∴AE=CE=2 3 .∴DE=2 3 . ∴⊙D 的半径为 2 3 .
上一页
目录
下一页
2021版 甘肃 数学
上一页
目录
下一页
2021版 甘肃 数学
(2)解:设 EF 交 OP 于 G.
∵∠C=90°,∴BF 是⊙O 的直径.∴∠BEF=90°.
∴四边形 BCFE 是矩形.∴EF=BC.
∵tan ∠FBC=34 ,设 FC=3x,BC=4x,则 BF=5x,OP=12 BF=52 x.
∵OG=52 x- 5 ,在 Rt△OGF 中,OG2+GF2=OF2,
点,若∠ABC=30°,则弦 AB 的长为
(D )
1
53
A.2
B.5
C. 2
D.5 3
上一页
目录
下一页
2021版 甘肃 数学
类型二:遇到直径时,常作直径所对的圆周角,得到直角三角形
(1)如图①,在半径为 3 的⊙O 中,直径 AB
与弦 CD 相交于点 E,连接 AC,BD.若 AC=2,则 tan
上一页
目录
圆中常用辅助线的作法

圆中常用辅助线的作法1.圆中作辅助线的常用方法:(1)作弦心距,以便利用弦心距与弧、弦之间的关系与垂径定理。
(2)若题目中有“弦的中点”和“弧的中点”条件时,一般连接中点和圆心,利用垂径定理的推论得出结果。
(3)若题目中有“直径”这一条件,可适当选取圆周上的点,连结此点与直径端点得到90度的角或直角三角形。
(4)连结同弧或等弧的圆周角、圆心角,以得到等角。
(5)若题中有与半径(或直径)垂直的线段。
(6)若题目中有“切线”条件时,一般是:对切线引过切点的半径,(7)若题目中有“两圆相切”(内切或外切),往往过切点作两圆的切线或作出它们的连心线(连心线过切点)以沟通两圆中有关的角的相等关系。
(8)若题目中有“两圆相交”的条件,经常作两圆的公共弦,使之得到同弧上的圆周角或构成圆内接四边形解决,有时还引两连心线以得到结果。
(9)有些问题可以先证明四点共圆,借助于辅助圆中角之间的等量关系去证明。
(10)对于圆的内接正多边形的问题,往往添作边心距,抓住一个直角三角形去解决。
1.有弦,可作弦心距在解决与弦、弧有关的问题时,常常需要作出弦心距、半径等辅助线,以便应用于垂径定理和勾股定理解决问题。
2.有直径,可作直径上的圆周角对于关系到直径的有关问题时,可作直径上的圆周角,以便利用直径所对的圆周角是直角这个性质。
说明,由直径及等腰三角形想到作直径上的圆周角。
3. 当圆中有切线常连结过切点的半径或过切点的弦说明,由过切点的半径垂直于切线想到连结半径说明,由有切线且在同圆中等弧所对的圆周角相等想到连结弦。
4.当两圆相切,可作公切线或连心线说明,由需证弦平行且弦切角等于其所夹弧对的圆周角想到作公切线和作弦。
说明,由连心线必过切点可构造三角形证全等想到作连心线。
5.当两圆相交,可作公共弦或连心线。
说明,由两圆相交及用到弦切角和圆内接四边形想到作公共弦。
说明,由两圆相交连心线垂直于公共弦想到作连心线。
6.有半圆,可作整圆说明,由平分弦的直径必平分弦所对的弧想到补全圆。
解题技巧专题圆中辅助线的作法

解题技巧专题圆中辅助线的作法在解题过程中,我们经常会遇到一些问题,例如如何构造等腰三角形、正方形、平行四边形等几何图形,以及如何构造垂直线、角平分线、中位线等几何线段。
这些问题在解决数学问题时非常常见,而圆中辅助线的作法就是一种常用的解决这类问题的技巧。
圆中辅助线的作法是指在解决圆相关的问题时,通过添加一些辅助线来辅助解决问题。
这些辅助线可以增强我们对图形的理解,简化问题的分析过程,使问题更易于解决。
下面将介绍一些常见的圆中辅助线的作法:1.构造圆的切线如果需要构造一条圆的切线,可以先连接圆心与切点,然后再从切点向圆外引一条与半径垂直的线段,两条线段的交点就是切线的切点。
利用这条切线可以帮助我们解决一些关于切线的性质问题。
2.构造垂直线如果需要构造一条与圆上特定点垂直的直线,可以连接该点与圆心,并在圆上引一条经过该点的切线,然后从圆心引一条与切线垂直的线段,两条线段的交点就是所求直线与圆的交点。
利用这条直线可以帮助我们解决一些关于圆的性质问题。
3.构造角平分线如果需要构造一条角的平分线,可以先连接角的两个顶点与圆心,然后再从圆心引一条与角平分线相垂直的线段,两条线段的交点就是所求角的平分线与圆的交点。
利用这条角平分线可以帮助我们解决一些关于角平分线的性质问题。
4.构造中位线如果需要构造一条线段的中位线,可以将线段的两个端点连接到圆心,并在圆上引一条经过中点的切线,然后再从圆心引一条与切线垂直的线段,两条线段的交点就是所求线段的中点。
利用这条中位线可以帮助我们解决一些关于线段中点的性质问题。
5.构造等腰三角形如果需要构造一个等腰三角形,可以先在圆上确定一个顶点,然后连接圆心与该点,并延长线段到圆的另一侧,再将圆切割成两个等弧,然后以切割点为顶点连接圆心,就可以得到一个等腰三角形。
利用这个等腰三角形可以帮助我们解决一些关于等腰三角形的性质问题。
这些是一些常见的圆中辅助线的作法,通过添加这些辅助线,我们可以更好地理解和解决与圆相关的问题。
初中数学圆的辅助线八种作法

中考数学圆的辅助线在平面几何中,与圆有关的许多题目需要添加辅助线来解决。
百思不得其解的题目,添上合适的辅助线,问题就会迎刃而解,思路畅通,从而有效地培养学生的创造性思维。
添加辅助线的方法有很多,本文只通过分析探索归纳几种圆中常见的辅助线的作法。
下面以几道题目为例加以说明。
1.有弦,可作弦心距在解决与弦、弧有关的问题时,常常需要作出弦心距、半径等辅助线,以便应用于垂径定理和勾股定理解决问题。
例1 如图1, ⊙O 的弦AB 、CD 相交于点P , 且AC=BD 。
求证:PO 平分∠APD 。
分析1:由等弦AC=BD 可得出等弧 = 进一步得出 = ,从而可证等弦AB=CD ,由同圆中 等弦上的弦心距相等且分别垂直于它们所对应的弦,因此可作辅助线OE ⊥AB ,OF ⊥CD ,易证△OPE ≌△OPF ,得出PO 平分∠APD 。
证法1:作OE ⊥AB 于E ,OF ⊥CD 于FAC=BD => = => ==> AB=CD => OE=OF∠OEP=∠OFP=90° => △OPE ≌△OPF0OP=OP=>∠OPE=∠OPF => PO 平分∠APD 分析2:如图1-1,欲证PO 平分∠APD ,即证AB(BD , (CD (D 图 1AC(AC (BD (AB (CD(∠OPA=∠OPD ,可把∠OPA 与∠OPD 构造在两个 三角形中,证三角形全等,于是不妨作辅助线即半径OA ,OD ,因此易证△ACP ≌△DBP ,得AP=DP ,从而易证△OPA ≌△OPD 。
证法2:连结OA ,OD 。
∠CAP=∠BDP∠APC=∠DPB =>△ACP ≌△DBP AC=BD=>AP=DPOA=OD =>△OPA ≌△OPD =>∠OPA=∠OPD =>PO 平分∠APD OP=OP2.有直径,可作直径上的圆周角对于关系到直径的有关问题时,可作直径上的圆周角,以便利用直径所对的圆周角是直角这个性质。
初中数学《圆》常用辅助线构造技巧

初中数学《圆》常用辅助线构造技巧圆是初中数学中的重要内容,常常会涉及到圆的基本性质、切线、切点、弦、弦长、弧、弧长等概念。
为了更好地解题,我们可以使用一些常用的辅助线构造技巧。
下面,我将介绍几种常用的辅助线构造技巧。
1.直径是圆的特殊弦,通过任意两点连接圆心,可以得到直径。
在解题中,如果涉及到圆心和两点的位置关系,可以考虑构造直径。
2.过圆心的直线与圆的切线垂直。
当我们需要求解两个垂直的线段或角度时,可以考虑构造一条过圆心的直径,使其与需要垂直的线段或角度相交。
3.过圆心的直线将弧等分为两个等长的弧。
当我们需要将一个弧等分为两个等长的弧时,可以考虑构造一条过圆心的直线,将这个弧分割为两个等长的弧。
1.过切点的切线与圆的半径垂直。
当我们需要求解两个垂直的线段或角度时,可以考虑构造一条过切点的切线,并将其延伸至圆心,使其与需要垂直的线段或角度相交。
2.过切点的切线等于切点至圆心的半径。
当我们需要求解两个等长的线段或角度时,可以考虑构造一条过切点的切线,并将其延伸至圆心,使其与另一条需要等长的线段或角度相交。
1.弦的中点与圆心以及两个端点可以构成一个等腰三角形。
当我们需要求解与等腰三角形相关的线段或角度时,可以考虑构造一条连接弦的中点与圆心以及两个端点的直线。
2.以弦的中点为顶点的直角三角形。
当我们需要求解与直角三角形相关的线段或角度时,可以考虑构造一条连接弦的中点与两个端点的直线,并通过调整弦的位置,使其与这条直线构成一个直角。
1.弦的垂直平分线同时也是弦的中垂线。
在解题中,如果需要求解弦的垂直平分线或者弦的中垂线,可以考虑构造一条连接弦的两个端点的直线,并将其垂直平分或中垂。
2.连接弦的两个端点与圆心的线段是一个等角二段线。
当我们需要求解与等角二段线相关的线段或角度时,可以考虑构造一条连接弦的两个端点与圆心的直线。
以上是一些常用的圆的辅助线构造技巧,通过合理地运用这些技巧,可以帮助我们更好地理解和解题。
圆的常用辅助线

圆中常见的辅助线的作法1.遇到弦时(解决有关弦的问题时)常常添加弦心距,或者作垂直于弦的半径(或直径)或再连结过弦的端点的半径。
作用:①利用垂径定理;②利用圆心角及其所对的弧、弦和弦心距之间的关系;③利用弦的一半、弦心距和半径组成直角三角形,根据勾股定理求有关量。
2.遇到有直径时常常添加(画)直径所对的圆周角。
作用:利用圆周角的性质得到直角或直角三角形。
3.遇到90度的圆周角时常常连结两条弦没有公共点的另一端点。
作用:利用圆周角的性质,可得到直径。
4.遇到弦时常常连结圆心和弦的两个端点,构成等腰三角形,还可连结圆周上一点和弦的两个端点。
作用:①可得等腰三角形;②据圆周角的性质可得相等的圆周角。
5.遇到有切线时(1)常常添加过切点的半径(连结圆心和切点)作用:利用切线的性质定理可得OA⊥AB,得到直角或直角三角形。
(2)常常添加连结圆上一点和切点作用:可构成弦切角,从而利用弦切角定理。
6.遇到证明某一直线是圆的切线时(1)若直线和圆的公共点还未确定,则常过圆心作直线的垂线段。
作用:若OA=r,则l为切线。
(2)若直线过圆上的某一点,则连结这点和圆心(即作半径)作用:只需证OA⊥l,则l为切线。
(3)有遇到圆上或圆外一点作圆的切线7.遇到两相交切线时(切线长)常常连结切点和圆心、连结圆心和圆外的一点、连结两切点。
作用:据切线长及其它性质,可得到:①角、线段的等量关系;②垂直关系;③全等、相似三角形。
8.遇到三角形的内切圆时连结内心到各三角形顶点,或过内心作三角形各边的垂线段。
作用:利用内心的性质,可得:①内心到三角形三个顶点的连线是三角形的角平分线;②内心到三角形三条边的距离相等。
9.遇到三角形的外接圆时,连结外心和各顶点作用:外心到三角形各顶点的距离相等。
10.遇到两圆外离时(解决有关两圆的外、内公切线的问题)常常作出过切点的半径、连心线、平移公切线,或平移连心线。
作用:①利用切线的性质;②利用解直角三角形的有关知识。
圆中常见辅助线作法例析

弦心 距是 惯 用 的辅 助 线.
二、 当题 目 中 出 现 直 径 时 。 作 出 直 径 上 的 圆周 角 。 常 构 造 出直 角 , 者 说 明 两 直 线 垂 直 . 时 图 中 无 直 径 , 可 根 或 有 还
.
C为 切 点 ,
OC _AB , = 曰c = L AC 旭
・ . .
分 析 : 问题 需要 结合 题 意 画 出 示 意 图进 行 分 析 , 以 本 可 画 出 两种 图形 如 图 9 图 l 同 时 需要 添 加 适 当的 辅 助 线. 、 0,
在 R ZA C中 , C=6m,A=1 c tk O O c O 0 m.
分 析 : 据 切 线 的 性 质 , 圆 的 切 线 垂 直 于 过 切 点 的 半 根 “ 径 ” 作 出半 径 , 据 垂径 定理 、 , 根 勾股 定 理 相 结 合 解 决.
五 、 圆 相 交 时 。 接 公 共弦 ( 圆 相 切 时 。 过 切 点 的 两 连 两 作 公切 线)利用公共弦 ( 切线 ) , 公 沟通 两 圆 的角 或 线 段 .
・
麓题思路 ・
新课 哥 覃导 学 23 口.己 11 1
在 R AA M 中 , M = ~ 『 : (m) t O O 二 3c 故点 m 圆 中 常 见 辅 助 线 作 法 例 析 P到 圆心 O 的最 短距 离是 3c .
说 明: 本题考查 了图形运 动 的特 点, 涉及 到 垂径定 理 、
・ . .
A =、 C 伍
AB =2 AC = 1 m. 6c
:、 i = (m) ( 8c ,
2020年数学中考 专题复习 万能解题模型(六) 圆中常见辅助线的作法

万能解题模型(六)圆中常见辅助线的作法前言:“一学就会,一考就废?”,正是因为考试后缺少了这个环节从小学到初中,学生们经历了无数次考试。
通过考试可以检测同学们对知识的理解、掌握情况,提高应试能力。
但对待考试,部分同学只关注自己的分数,而对试卷的分析和总结缺乏重视。
结果常常出现一些题在考试中屡次出现,但却一错再错的情况。
这样,学生们无法从考试中获益,考试也就失去了它的重要意义。
做好试卷分析和总结是十分有必要的。
那么,怎样做好试卷分析呢?我认为,应从下面两点做起:一.失分的原因主要有如下四方面:(1)考试心理:心理紧张,马虎大意;(2)知识结构:知识面窄,基础不扎实;(3)自身能力:审题不清,读不懂题意;(4)解题基本功:答题规范性差。
只有查出、找准原因,才能对症下药,从弱项方面加强训练,以提高成绩。
二.“扭转乾坤”的方法做题的过程中对每一道题要试图问如下几个问题?(1)怎样做出来的?——想解题方法;(2)为什么这样做?——思考解题原理;(3)怎样想到这种方法?——想解题的基本思路;(4)题目体现什么样的思想?——揭示本质,挖掘规律;(5)是否可将题目变化?——一题多变,拓宽思路;(6)题目是否有创新解法?——创新、求异思维。
转变,让我们从一轮复习开始。
按照上面两点认真完成后面练习题。
希望每一位同学经过一轮复习后,能够扭转“一考就废”的局面,最后决胜中考。
类型1 连半径——构造等腰三角形作圆的半径,利用“同圆的半径相等”构造等腰三角形,这样就把有关线段或角的问题转化到三角形中来解答.1.如图,△ABC 内接于⊙O.若∠A =α,则∠OBC 等于(D) A .180°-2α B .2α C .90°+α D .90°-α2.如图,⊙O 的直径AB 与弦CD 的延长线交于点E.若DE =OB ,∠AOC =84°,则∠E 等于(B) A .42° B .28° C .21° D .20°类型2 与垂径定理有关的辅助线在圆中,求弦长、半径或圆心到弦的距离时,常过圆心作弦的垂线段或连接弧的中点与圆心,再连接半径构成直角三角形,利用勾股定理或锐角三角函数进行计算.3.(2018·枣庄)如图,AB 是⊙O 的直径,弦CD 交AB 于点P ,AP =2,BP =6,∠APC =30°,则CD 的长为(C) A.15 B .2 5 C .215 D .84.(2018·威海)如图,⊙O 的半径为5,AB 为弦,点C 为AB ︵的中点.若∠ABC =30°,则弦AB 的长为(D) A.12 B .5 C.532D .5 3类型3 与圆周角定理及其推论有关的辅助线(1)利用圆周角定理求角度时,常构造同弧或等弧所对的圆周角或者圆心角;(2)遇到直径时,常构造直径所对的圆周角,这是圆中常用的辅助线作法,可充分利用“半圆(或直径)所对的圆周角是直角”这一性质;(3)遇90°的圆周角时,常连接圆周角的两边与圆的交点,得到直径.5.如图,在半径为3的⊙O 中,直径AB 与弦CD 相交于点E ,连接AC ,BD.若AC =2,则tanD 的值是(A)A .2 2B.223C.24D.136.(2019·辽阳)如图,A ,B ,C ,D 是⊙O 上的四点,且点B 是AC ︵的中点,BD 交OC 于点E ,∠AOC =100°,∠OCD =35°,那么∠OED =60°.7.(2019·连云港)如图,点A ,B ,C 在⊙O 上,BC =6,∠BAC =30°,则⊙O 的半径为6.类型4 与切线的性质有关的辅助线已知圆的切线时,常把切点与圆心连接起来,得半径与切线垂直,从而构造出直角三角形,再利用直角三角形的有关性质解题.8.如图,在⊙O 中,AD ,CD 是弦,连接OC 并延长,交过点A 的切线于点B.若∠ADC =30°,则∠ABO 的度数为(B)A .20°B .30°C .40°D .50°类型5 与切线的判定有关的辅助线证明一条直线是圆的切线,当直线与圆有公共点时,只需“连半径、证垂直”即可;当已知条件中没有指出圆与直线有公共点时,则需要过圆心作已知直线的垂线,证明垂线段的长等于半径.9.(2019·齐齐哈尔)如图,以△ABC 的边BC 为直径作⊙O ,点A 在⊙O 上,点D 在线段BC 的延长线上,AD =AB ,∠D =30°.(1)求证:直线AD 是⊙O 的切线;(2)若直径BC =4,求图中阴影部分的面积.解:(1)证明:连接OA. ∵AD =AB ,∠D =30°, ∴∠B =∠D =30°.∵OA =OB ,∴∠OAB =∠B =30°. ∴∠AOD =60°. ∴∠OAD =180°-30°-60°=90°. ∴OA ⊥AD.又∵OA 是⊙O 的半径, ∴AD 是⊙O 的切线. (2)∵BC =4,∴OA =2. ∴AD =OA·tan60°=2 3.∴S △AOD =12AD·OA =2 3.又∵S 扇形AOC =60π×4360=2π3,∴S 阴影=23-2π3.10.如图,在梯形ABCD 中,AD ∥BC ,AE ⊥BC 于点E ,∠ADC 的平分线交AE 于点O ,以点O 为圆心,OA 为半径的圆经过点B ,交BC 于另一点F.(1)求证:CD 与⊙O 相切;(2)若BF =24,OE =5,求tan ∠ABC 的值.解:(1)证明:过点O 作OG ⊥DC ,垂足为G. ∵AD ∥BC ,AE ⊥BC , ∴OA ⊥AD.又∵DO 平分∠ADC ,OG ⊥DC , ∴OA =OG.∴OG 是⊙O 的半径. ∴DC 是⊙O 的切线. (2)连接OF. ∵OA ⊥BC ,∴BE =EF =12BF =12.在Rt △OEF 中,OE =5,EF =12. ∴OF =OE 2+EF 2=13.∴AE =OA +OE =13+5=18.∴tan ∠ABC =AE BE =32.类型6 与三角形内切圆有关的辅助线 11.(2019·娄底)如图,边长为23的等边△ABC 的内切圆的半径为(A)A .1 B. 3 C .2 D .2 312.(2018·河北)如图,点I为△ABC的内心,AB=4,AC=3,BC=2,将∠ACB平移使其顶点与I重合,则图中阴影部分的周长为(B)A.4.5 B.4C.3 D.2类型7与圆中阴影部分面积的计算有关的辅助线13.(2019·南充)如图,在半径为6的⊙O中,点A,B,C都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为(A)A.6πB.33πC.23πD.2π。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)∵BC=4,∴OA=2. ∴AD=OA·tan60°=2 3. ∴S△ AOD=12AD·OA=2 3. 又∵S 扇形 AOC=603π6×04=23π, ∴S 阴影=2 3-23π.
10.如图,在梯形 ABCD 中,AD∥BC,AE⊥BC 于点 E,∠ADC 的 平分线交 AE 于点 O,以点 O 为圆心,OA 为半径的圆经过点 B,交 BC 于 另一点 F.
7.(2019·连云港)如图,点 A,B,C 在⊙O 上,BC=6,∠BAC=30°, 则⊙O 的半径为 6 .
类型 4 与切线的性质有关的辅助线
已知圆的切线时,常把切点与圆心连接起来,得半径与切线垂直,从 而构造出直角三角形,再利用直角三角形的有关性质解题.
8.如图,在⊙O 中,AD,CD 是弦,连接 OC 并延长,交过点 A 的切 线于点 B.若∠ADC=30°,则∠ABO 的度数为( B )
(1)求证:直线 AD 是⊙O 的切线; (2)若直径 BC=4,求图中阴影部分的面积.
解:(1)证明:连接 OA. ∵AD=AB,∠D=30°, ∴∠B=∠D=30°. ∵OA=OB, ∴∠OAB=∠B=30°. ∴∠AOD=60°. ∴∠OAD=180°-30°-60°=90°. ∴OA⊥AD. 又∵OA 是⊙O 的半径, ∴AD 是⊙O 的切线.
1 A.2
B.5
53 C. 2
D.5 3
类型 3 与圆周角定理及其推论有关的辅助线
(1)利用圆周角定理求角度时,常构造同弧或等弧所对的圆周角或者圆 心角;(2)遇到直径时,常构造直径所对的圆周角,这是圆中常用的辅助线 作法,可充分利用“半圆(或直径)所对的圆周角是直角”这一性质;(3)遇 90° 的圆周角时,常连接圆周角的两边与圆的交点,得到直径.
类型 6 与三角形内切圆有关的辅助线
11.(2019·娄底)如图,边长为 2 3的等边△ ABC 的内切圆的半径为(A )
A.1
B. 3
C.2
D.2 3
12.(2018·河北)如图,点 I 为△ ABC 的内心,AB=4,AC=3,BC=2,
将∠ACB 平移使其顶点与 I 重合,则图中阴影部分的周长为( B )
第六单元 圆 万能解题模型(六) 圆中常见辅助线的作法
类型 1 连半径——构造等腰三角形
作圆的半径,利用“同圆的半径相等”构造等腰三角形,这样就把有关 线段或角的问题转化到三角形中来解答.
1.如图,△ ABC 内接于⊙O.若∠A=α,则∠OBC 等于( D )
A.180°-2α
B.2α
C.90°+α
3.(2018·枣庄)如图,AB 是⊙O 的直径,弦 CD 交 AB 于点 P,AP=2,
BP=6,∠APC=30°,则 CD 的长为(C )
A. 15
B.2 5
C.2 15
D.8
4.(2018·威海)如图,⊙O 的半径为 5,AB 为弦,点 C 为A︵B的中点.若
∠ABC=30°,则弦 AB 的长为(D )
(1)求证:CD 与⊙O 相切; (2)若 BF=24,OE=5,求 tan∠ABC 的值.
解:(1)证明:过点 O 作 OG⊥DC,垂足为 G. ∵AD∥BC,AE⊥BC, ∴OA⊥AD. 又∵DO 平分∠ADC,OG⊥DC, ∴OA=OG. ∴OG 是⊙O 的半径. ∴DC 是⊙O 的切线.
(2)连接 OF. ∵OA⊥BC, ∴BE=EF=12BF=12. 在 Rt△ OEF 中,OE=5,EF=12. ∴OF= OE2+EF2=13. ∴AE=OA+OE=13+5=18. ∴tan∠ABC=ABEE=23.
A.20° B.30° C.40° D.50°
类型 5 与切线的判定有关的辅助线
证明一条直线是圆的切线,当直线与圆有公共点时,只需“连半径、证 垂直”即可;当已知条件中没有指出圆与直线有公共点时,则需要过圆心作 已知直线的垂线,证明垂线段的长等于半径.
9.(2019·齐齐哈尔)如图,以△ ABC 的边 BC 为直径作⊙O,点 A 在⊙O 上,点 D 在线段 BC 的延长线上,AD=AB,∠D=30°.
5.如图,在半径为 3 的⊙O 中,直径 AB 与弦 CD 相交于点 E,连接
AC,BD.若 AC=2,则 tanD 的值是(A ) A.2 2
B.2
2 3
2 C. 4
1 D.3
6.(2019·辽阳)如图,A,B,C,D 是⊙O 上的四点,且点 B 是A︵C的 中点,BD 交 OC 于点 E,∠AOC=100°,∠OCD=35°,那么∠OED=60°.
D.90°-α
2.如图,⊙O 的直径 AB 与弦 CD 的延长线交于点 E.若 DE=OB,∠AOC
=84°,则∠E 等于( B )
A.42°
B.28°
C.21°
D.20°
类型 2 与垂径定理有关的辅助线
在圆中,求弦长、半径或圆心到弦的距离时,常过圆心作弦的垂线段 或连接弧的中点与圆心,再连接半径构成直角三角形,利用勾股定理或锐 角三角函数进行算.
A.4.5
B.4
C.3
D.2
类型 7 与圆中阴影部分面积的计算有关的辅助线 13.(2019·南充)如图,在半径为 6 的⊙O 中,点 A,B,C 都在⊙O 上, 四边形 OABC 是平行四边形,则图中阴影部分的面积为(A ) A.6π B.3 3π C.2 3π D.2π
