大学物理-电势
合集下载
大学物理-电势

Va E dl a E dl
讨论
a
a
1)电势零点的选择(参考点)
任意 视分析问题方便而定
参考点不同电势不同
10
通常:
理论计算有限带电体电势时选无限远为参考点
实际应用中或研究电路问题时取大地、仪器外 壳等
2)电势的量纲
SI制:单位 V (伏特)
量纲
V
W q
L2 MT
3I
1
3)电势是一个长程物理量
b b
a
f dl q E dl Wa Wb
a
a
b E dl
Wa
Wb
a
q
q 与试验电荷无关
根据静电场 Wa Wb 的环路定理 q q
E dl Va Vb
a
称 a b两点电势差
若选b点的势能为参考零点 则
a点的电势:
势能零点
势能零点
VA VB
11
rB rA
E
dr
Q 4πε0
rB dr rA r 2
()
4πε0 rA rB
(2)r R
VA VB
rB rA
E
dr
0
o A B A dr B
R
drrA r
r
rB
20
(3)r R 令 rB V 0
Q 1 1
VA VB
(4)r R
()
4πε0
rA R
q
x2 R2
x
R,VP
q 4πε0 x
V
dl
q
q
4πε0 R
4πε0 x2 R2
R
r
xo x
Px
o
x
大学物理第三章电势

2 π AR + 3 λ e E3 = 6 πε 0 r
方向沿径向向外
18
(2)选距离轴线的距离为 l ( l > R ) 处为电势 零点,计算圆柱体内、 零点,计算圆柱体内、外各点的电势分 布。 注意: 求各点电势(电势分布) 注意: 求各点电势(电势分布)时,要分 区域讨论,分区方式与场强相同。 区域讨论,分区方式与场强相同。 电势零点位置选择: 电势零点位置选择: “无限长”柱状带电 无限长” 对 体产生的电场, 体产生的电场,绝对不 能选无穷远处为电势零 点,只能选其它任一点 为电势零点。 为电势零点。
qo =∫ ⋅
5
静电场的保守性(静电场环路定理) 二、 静电场的保守性(静电场环路定理)
L2
∫
L
E ⋅ dl = 0
a
.
qo
L1
b
.
在静电场中,场强沿任意闭合路径的线积 在静电场中, 分等于零。 对任何静电场, 分等于零。即:对任何静电场,电场强度的 线积分都只取决于起点和终点的位置, 线积分都只取决于起点和终点的位置,而与连 接起点和终点间的路径无关。 接起点和终点间的路径无关。
15
例2(1197)一半径为R的“无限长”圆柱形带 1197)一半径为 的 无限长” 电体, 电体,其电荷体密度为 ρ = A r ( r ≤ R ) 式中A为常数 为常数。 式中 为常数。在此圆柱体外再罩一半 径为R 无限长” 径为 1 、线电荷密度为 λ e 的“无限长”圆 试求: 筒,试求: 圆柱体内、 (1)圆柱体内、外各点的电场强度分布 (2)选距离轴线的距离为 l ( l > R ) 处为电势零点,计算圆柱体内、 处为电势零点,计算圆柱体内、 外各点的电势分布。 外各点的电势分布。 (3)柱表面与柱壳之间的电势差。 柱表面与柱壳之间的电势差。
大学物理电势ppt课件

电势定义
$V = frac{kQ}{r}$,其中$k$为静电力常量,$Q$为场源电荷量,$r$为到场源电荷的距离。
点电荷电势公式
点电荷电势计算
对于多个点电荷或连续分布电荷产生的电势,可应用叠加原理进行求解。
叠加原理
对于连续分布电荷,需采用积分方法计算电势,如线积分、面积分或体积分。
积分方法
均匀带电直线、均匀带电平面、均匀带电球体等。
大学物理电势ppt课件
目录
电势基本概念与性质 点电荷与连续分布电荷电势 导体与绝缘体在电场中电势特性 电势能、电势差及等势面 电场力做功与路径无关性讨论 总结回顾与拓展延伸
01
CHAPTER
电势基本概念与性质
电势定义及物理意义
电势定义
描述电场中某点电势能的性质,反映单位正电荷在该点所具有的电势能。
实际应用举例
04
CHAPTER
电势能、电势差及等势面
电荷在电场中具有的势能,与电荷量及所在位置有关。
电势能定义
通过电场力做功来计算,公式为W=qU,其中W为电势能,q为电荷量,U为电势差。
电势能计算
电势能具有相对性,与零电势点的选择有关。
电势能性质
电势能概念及计算
电场中两点间电势的差值,等于单位正电荷从一点移动到另一点时电场力所做的功。
常见连续分布电荷
连续分布电荷电势求解方法
均匀带电直线电势
通过高斯定理和积分方法求解,结果与观察点到直线的垂直距离和线电荷密度有关。
均匀带电平面电势
利用高斯定理和叠加原理,可求得电势与观察点到平面的距离和平面电荷密度之间的关系。
均匀带电球体电势
采用高斯定理和积分方法,可得到球体内外任意一点的电势表达式。
$V = frac{kQ}{r}$,其中$k$为静电力常量,$Q$为场源电荷量,$r$为到场源电荷的距离。
点电荷电势公式
点电荷电势计算
对于多个点电荷或连续分布电荷产生的电势,可应用叠加原理进行求解。
叠加原理
对于连续分布电荷,需采用积分方法计算电势,如线积分、面积分或体积分。
积分方法
均匀带电直线、均匀带电平面、均匀带电球体等。
大学物理电势ppt课件
目录
电势基本概念与性质 点电荷与连续分布电荷电势 导体与绝缘体在电场中电势特性 电势能、电势差及等势面 电场力做功与路径无关性讨论 总结回顾与拓展延伸
01
CHAPTER
电势基本概念与性质
电势定义及物理意义
电势定义
描述电场中某点电势能的性质,反映单位正电荷在该点所具有的电势能。
实际应用举例
04
CHAPTER
电势能、电势差及等势面
电荷在电场中具有的势能,与电荷量及所在位置有关。
电势能定义
通过电场力做功来计算,公式为W=qU,其中W为电势能,q为电荷量,U为电势差。
电势能计算
电势能具有相对性,与零电势点的选择有关。
电势能性质
电势能概念及计算
电场中两点间电势的差值,等于单位正电荷从一点移动到另一点时电场力所做的功。
常见连续分布电荷
连续分布电荷电势求解方法
均匀带电直线电势
通过高斯定理和积分方法求解,结果与观察点到直线的垂直距离和线电荷密度有关。
均匀带电平面电势
利用高斯定理和叠加原理,可求得电势与观察点到平面的距离和平面电荷密度之间的关系。
均匀带电球体电势
采用高斯定理和积分方法,可得到球体内外任意一点的电势表达式。
大学物理静电场3(电势)ppt课件
最新课件
9
单个点电荷的场的电势 U q
2)电势叠加原理(标量叠加)
q
Up Edl
Eidl
1
4
0r r1 r2
p
p
P Ei dl
qi
q2
4 0ri
或对连续分布带电体
U p
dq
4 0r
q
最新课件
dq
r
p
r3
ri
q3
qi
p
Up=?
10
Ua
i
qi
40ri
一个点电荷系的电场中,任一点的电势等于每一个点电 荷单独存在时在该点所产生电势的代数和。——电势 叠加原理
电势叠加原理 习题最指新课导件 P65 16
34
形状如图所示的绝缘细线,其上均匀分布着
正电荷。已知电荷线密度为λ,两段直线长 均为a,半圆环的半径为a。求环心O点的电 势?
电势叠加原理
求电势能和电力
习题指导P65 17
最新课件
35
3.有一边长为a的正方形平面,在其中垂线上距 中心O点a/2处,有一电量为q的正点电荷,如图所 示,则通过该平面的电场强度通量为:
b
W a W bA a bq 0 aE d r
二、电势差:
移动单位正电荷从电场中a 点到b点,静电力所做 的功,为静电场中两点的电势差:
U abU aU ba bEdr最 新W 课q 件aW qb 描只述与电电场场的有性关质6
➢某点 (a点) 的电势:
首先设定电势0点(b点):
Ua
b
Edr
积分与路径无关
最新课件
4
对任何静电场,电场强度的线积分都只取决于起 点和终点的位置而与积分路径无关--静电场的
大学物理电势

Q
+ r+ rA
r
rB
Q
4π 0
rB rA
dr r2
er
er
Q (1 1)
4π 0 rA rB
8 –7 电势
第八章静电场
(2) r R
VA VB
rB rA
E1
dr
0
(3) r R
令 rB , V 0
r +
+ +
R
o
+
+
Q
++
+ e+
+ r+ rA
A
r
dr
rB
B
由
VA
VB
A
iA
VA
VAi
i
i
qi
4π 0ri
电荷连续分布
VP
dq
4π 0r
第八章静电场
q1 q2
r1 r2
q3
r3
E3
E2
A
E1
dqqdrqP
dV
dE
8 –7 电势
第八章静电场
讨论
求电势 的方法
➢ 利用
VP
dq
4π 0r
(利用了点电荷电势 V q / 4π 0r,
这一结果已选无限远处为电势零点,即使
E dl
AB
8 –7 电势
电势差
第八章静电场
U AB VA VB
E dl
AB
(将单位正电荷从 A移到 B电场力作的功.)
注意 电势差是绝对的,与电势零点的选择无关; 电势大小是相对的,与电势零点的选择有关.
静电场力的功 WAB q0VA q0VB q0U BA
+ r+ rA
r
rB
Q
4π 0
rB rA
dr r2
er
er
Q (1 1)
4π 0 rA rB
8 –7 电势
第八章静电场
(2) r R
VA VB
rB rA
E1
dr
0
(3) r R
令 rB , V 0
r +
+ +
R
o
+
+
Q
++
+ e+
+ r+ rA
A
r
dr
rB
B
由
VA
VB
A
iA
VA
VAi
i
i
qi
4π 0ri
电荷连续分布
VP
dq
4π 0r
第八章静电场
q1 q2
r1 r2
q3
r3
E3
E2
A
E1
dqqdrqP
dV
dE
8 –7 电势
第八章静电场
讨论
求电势 的方法
➢ 利用
VP
dq
4π 0r
(利用了点电荷电势 V q / 4π 0r,
这一结果已选无限远处为电势零点,即使
E dl
AB
8 –7 电势
电势差
第八章静电场
U AB VA VB
E dl
AB
(将单位正电荷从 A移到 B电场力作的功.)
注意 电势差是绝对的,与电势零点的选择无关; 电势大小是相对的,与电势零点的选择有关.
静电场力的功 WAB q0VA q0VB q0U BA
大学物理课件电势梯度

大学物理课件-电势梯度
contents
目录
• 电势梯度的定义 • 电势梯度的性质 • 电势梯度在物理中的应用 • 电势梯度的计算实例 • 电势梯度与物理学其他概念的关系
01 电势梯度的定义
定义与公式
定义
电势梯度是描述电场中电势随位置变 化的物理量,表示为▽Φ。
公式
▽Φ = -E,其中E是电场强度矢量,Φ 是电势。
物理意义
电势梯度的方向表示电场强度矢量场的方向,即电场线方向。
计算方法
在标量场中,梯度的方向可以通过求导数的方法得到,即▽ = grad 。
电势梯度的计算方法
计算公式
电势梯度的计算公式为▽·E = ρ/ε0, 其中▽表示哈密顿算子,E表示电场强 度矢量,ρ表示电荷密度,ε0表示真 空电容率。
计算步骤
时,需要考虑这些元件的影响。
复杂电场的电势梯度计算
总结词:非线性关系 总结词:方向判断
详细描述:在复杂电场中,电势梯度与电场强度 之间的关系可能变得非线性。例如,在点电荷产 生的电场中,电势梯度随距离的增加而减小,但 仍然与电场强度成正比。
详细描述:在复杂电场中,判断电势梯度的方向 需要考虑电场线的分布和方向。通常,电势梯度 的方向与电场线增加的方向一致。
02 电势梯度的性质
电势梯度的标量性质
标量性质
电势梯度是一个标量,表示电势在空间中的变化率,没有方向。
计算公式
电势梯度等于电场强度在三维空间中的散度,计算公式为▽·E = ρ/ε0。
物理意义
电势梯度表示单位距离内的电势变化量,可用于描述电场中电势的 变化趋势。
电势梯度的方向
方向判定
电势梯度的方向由负梯度的方向确定,即电势降低的方向。
contents
目录
• 电势梯度的定义 • 电势梯度的性质 • 电势梯度在物理中的应用 • 电势梯度的计算实例 • 电势梯度与物理学其他概念的关系
01 电势梯度的定义
定义与公式
定义
电势梯度是描述电场中电势随位置变 化的物理量,表示为▽Φ。
公式
▽Φ = -E,其中E是电场强度矢量,Φ 是电势。
物理意义
电势梯度的方向表示电场强度矢量场的方向,即电场线方向。
计算方法
在标量场中,梯度的方向可以通过求导数的方法得到,即▽ = grad 。
电势梯度的计算方法
计算公式
电势梯度的计算公式为▽·E = ρ/ε0, 其中▽表示哈密顿算子,E表示电场强 度矢量,ρ表示电荷密度,ε0表示真 空电容率。
计算步骤
时,需要考虑这些元件的影响。
复杂电场的电势梯度计算
总结词:非线性关系 总结词:方向判断
详细描述:在复杂电场中,电势梯度与电场强度 之间的关系可能变得非线性。例如,在点电荷产 生的电场中,电势梯度随距离的增加而减小,但 仍然与电场强度成正比。
详细描述:在复杂电场中,判断电势梯度的方向 需要考虑电场线的分布和方向。通常,电势梯度 的方向与电场线增加的方向一致。
02 电势梯度的性质
电势梯度的标量性质
标量性质
电势梯度是一个标量,表示电势在空间中的变化率,没有方向。
计算公式
电势梯度等于电场强度在三维空间中的散度,计算公式为▽·E = ρ/ε0。
物理意义
电势梯度表示单位距离内的电势变化量,可用于描述电场中电势的 变化趋势。
电势梯度的方向
方向判定
电势梯度的方向由负梯度的方向确定,即电势降低的方向。
大学物理第2章 电势能 电势

4
Wa b
q0 q 4 0
b
a
q0 q r dr 3 r 4 0
b
a
1 d(r r ) 2 r3
q0 q 4 0
b
a
q0 q 1 dr 2 3 2 r 4 0
b
a
q0 q 1 2rdr 3 2 r 4 0
b
b
a
dr r2
q0 q 4 0
rR 0 Er Q 4 r 2 r R 0
球面内部任意一点的电势为
V (r )
r
r R
R E dl E dl E dl
r R
沿电场线积分
dr
Q 4 0 R
15
E dl Er dr
求电场的空间分布,并求在点(2,3,3)处的电 场强度。解:根据公式得
E V (2x+3y)i (3x z) j yk
代入x,y,z坐标便得到在处的电场强度为 r r r r E 2 , 3 , 3 13i 6 j 3k SI
27
沿电场线积分
(r Ra17 )
V (r )
Rb
Ra
E dl
Rb
Ra
1 1 Er dr ( ) 4 0 Ra Rb
Q
(2)两球面之间一点b的电势为
V (r )
V (r ) E dl
r Rb
Rb
r
Rb
E dl E dl
21
2.3.2 电势梯度
Va Vb E dl
《大学物理》第三章电势S

i
" p"
或: d
40 ri dq d 40 r
z • 你能否迅速算出“非均匀带电球面(只知道总电量)”
在球心处的电势? • 如果用“路径积分法”,本题应如何解?
例计算均匀带电q 的园环轴线上任一点的电势。 解: 用“电势叠加法” y (以无穷远处 先考虑点电荷dq对电势的贡献 dq 的电势为0) dq d 4 0 r r q dq q R d 0 4 r 40 r 0 x o x Q 2 2 4 0 x 2 R 2 r x R
球面A 产生的电势分布
球面B 产生的电势分布
qA r R A A 4 0 RA q r RA A A 4 0 r
r RB r RB
qB B 4 0 RB qB B 4 0 r
A B
qB
qA R A
r RA
qA qB 4 0 RA 4 0 RB
E
●
●
dr
P2
2
空间变化率:
d E cos dr d E ( d dr dr ) Max
当
0
时
E
●
有最大值
沿电场方向电势随空间的变化率最大,就把这一最大值称为
1
P 1
dr
●
P2
2
该点的电势梯度 d ( ) Max 定义电势梯度--- grad
则:E dl a b
dl
a
E
E dl
0
dl
b
——场强与等势面正交。
若再取小位移 dl 与电场同向(由点 a到点b′) 则:E dl a b 0 , a b
" p"
或: d
40 ri dq d 40 r
z • 你能否迅速算出“非均匀带电球面(只知道总电量)”
在球心处的电势? • 如果用“路径积分法”,本题应如何解?
例计算均匀带电q 的园环轴线上任一点的电势。 解: 用“电势叠加法” y (以无穷远处 先考虑点电荷dq对电势的贡献 dq 的电势为0) dq d 4 0 r r q dq q R d 0 4 r 40 r 0 x o x Q 2 2 4 0 x 2 R 2 r x R
球面A 产生的电势分布
球面B 产生的电势分布
qA r R A A 4 0 RA q r RA A A 4 0 r
r RB r RB
qB B 4 0 RB qB B 4 0 r
A B
qB
qA R A
r RA
qA qB 4 0 RA 4 0 RB
E
●
●
dr
P2
2
空间变化率:
d E cos dr d E ( d dr dr ) Max
当
0
时
E
●
有最大值
沿电场方向电势随空间的变化率最大,就把这一最大值称为
1
P 1
dr
●
P2
2
该点的电势梯度 d ( ) Max 定义电势梯度--- grad
则:E dl a b
dl
a
E
E dl
0
dl
b
——场强与等势面正交。
若再取小位移 dl 与电场同向(由点 a到点b′) 则:E dl a b 0 , a b
大学物理静电场2电势

各电势的零点应是同一点)
用“点电荷电势叠加的方法”:
对点电荷系:
对有限的 连续电荷分布:
qi
4 π ori
(选
0)
d q
q 4πor
(选 0)
例. 求半径为 R、带电量为 q 的细圆环 轴线上任意点的电势。
【解】 这是连续带电体, 任取一电荷元dq,
用“点电荷电势叠加法”
dq
R 0
r R2 x2 取轴线上任一点 P,电势:
x
x
P
d q
(q)4 π0r
所以
4π 0
q R2 x2
1/ 2
1
dq
4 π0r (q)
思考: 环上电荷均匀或不均匀结果一样吗?
等势面:
电场中电势相等的点组成的面称为等势面。 等势面是形象描述电场的一种表示方法。 画法:相邻等势面的电势差为常数。
例1. 正点电荷电场的等势面。
等势面有如下特点:
2π0 r
r > r0 的点,电势为负,
r = r0 的点,电势为零,
r < r0 的点,电势为正。
r
可以看到,若选无限远为 电势零点,
会使积分发散。
8.4.5 电势叠加原理
由
po
E
d
l
及
E
p
Ei
得 ( po p
Ei ) d l
po p
i Ei
d
l
i
i
i
i
(注意:用电势叠加原理时,
静电势能是属于电荷 q0 和场源所共有的 (正如重力势能是属于物体和地球),
也叫电荷之间的相互作用能。
例 1. 氢原子中的电子在原子核电场中的 静电势能为
大学物理电动势

v
O
A
dl
解: 在铜棒上距O点为 l 处取线元 d l ,其方向 沿O指向A,其运动速度 的大小为 v 。 l 显然 d l相互垂直, B、 v、 所以 d l 上的动生电动势为
v
O
A
dl
d i (v B ) d l vB d l
L 0 1 2
如果是铜盘转动,等效于无数铜棒并联,因此,铜盘 中心与边缘电势差仍为0.39V。此为一种简易发电机 模型。
Example7-3 例2 如图,长直导线中电流为I=10A,在其附近有一 长为l=0.2m的金属棒MN,以速度v=2m/s平行于导线 做匀速运动,如果靠近导线的一端M 距离导线为 a=0.1m,求金属棒中的动生电动势。 解: 金属棒上取长度元dx,每一 dx处磁场可看作均匀的
e
B
+ + + -+ + +
+ + + O+ +
+ + + Fm - -
+ v
+
+
+ + + +
OP
( v B ) dl
P
设杆长为 l i 0 vBdl vBl
O
i
思考: 洛仑兹力不对运动电荷做功
洛仑兹力充当非静电力 矛盾?
Fm
y
fm
f
' m
P
由此可得金属棒上总电动势为
2
由图可知,v B 的方向由A指向O,此即电动势的方向 Vo VA 0.39V
0.01100 0.5 i Bl d l BL 0.39V 2
大学物理电磁学部分04-环路定理电势

Ua
Ub
Epa Epb q0
Aab q0
b E dl
a
意义:把单位正电荷从a点沿任意路径移到b点时电
场力所作的功。
电势差和电势的单位相同,在国际单位制中,电势 的单位为:焦耳/库仑(记作J/C),也称为伏特(V) ,即1V=1J/C。
7
注意几点:
1.电势是标量,只有正负之分。U a
E pa q0
设在静电场中,将检验电荷 q0 从 a 点沿任意路 径移动到 b 点,电场力作功为Aab。
因为保守力所作的功等于势能增量的负值。
电荷 q0 在静电场中从 a 点沿任意路径移动到 b 点时, 电场力所作的作功Aab与这两点电势能Ea、Eb的关系为:
Aab
E p
b
(E
pb
E pa
b
Aab
F dl
(2)连续带电体:将带电体分割成无限多个电荷元,
将每个电荷元看成点电荷,根据点电荷电势公式求电
荷元的电势,迭加归结于积分。
U
dU
dq
4 0r
注意电荷元的选取!
11
例1:均匀带电圆环,半径为 R,带电为 q,求 圆环轴线上一点的电势 U。
解:将圆环分割成无限多个电荷元:
dU dq
4 0r
环上各点到轴线等距。
一、静电场的保守性——环路定理
1.电场力的功
1.点电荷的场
点电荷q0所受电场力为:F q0E 点电荷的场中移动点电荷q0从 r
到 r dr,电场做的功:
dA F dl q0E dl
q
q0Edl dr dl c
dA q0
cos
os , E
q
4 0r 2
大学物理第三章电势

电势零点
8
P
电荷分布在有限空间, 取无穷远为 U= 0 点。
电位零点的选取: 电荷分布在无限空间, 取有限远点为U= 0 点。 一般工程上, 选大地或设备外壳为U=0点。
9
解题技巧:当场源带电体是球状带电体和柱状带 电体时,无论电势零点取在什么位置, 积分路径都应沿径向向外。此时,
dl dr
19
本题令 U r l 0 电场中任一点的电势 U P P 柱体内 ( r R)
U P1
电势零点 P 1
电势零点
E cosdr
U P E cosdr
电势零点
P
E cosdr E1dr E2 dr R
R r
l
柱外筒内 ( R r R1 )
7
五、电势 (Electric Potential) *场中任一点P的电势
U P E cos dl
P c
当取电场中某一点c为电势零点(即:令Uc = 0)时,
电势零点
P
E cos dl
即:电场中任意一点P的电势等于电场强度从P点 经任一路径到电势零点的积分。
U P E cos dl
qo
5
二、 静电场的保守性(静电场环路定理)
L
E dl 0
a
L2
.
qo
L1
b
.
在静电场中,场强沿任意闭合路径的线积 分等于零。即:对任何静电场,电场强度的 线积分都只取决于起点和终点的位置,而与连 接起点和终点间的路径无关。
6
三、电势能差
Aab Wa Wb qo a 实验电荷qo 在静电场中从a运动到b时,静电场力
8
P
电荷分布在有限空间, 取无穷远为 U= 0 点。
电位零点的选取: 电荷分布在无限空间, 取有限远点为U= 0 点。 一般工程上, 选大地或设备外壳为U=0点。
9
解题技巧:当场源带电体是球状带电体和柱状带 电体时,无论电势零点取在什么位置, 积分路径都应沿径向向外。此时,
dl dr
19
本题令 U r l 0 电场中任一点的电势 U P P 柱体内 ( r R)
U P1
电势零点 P 1
电势零点
E cosdr
U P E cosdr
电势零点
P
E cosdr E1dr E2 dr R
R r
l
柱外筒内 ( R r R1 )
7
五、电势 (Electric Potential) *场中任一点P的电势
U P E cos dl
P c
当取电场中某一点c为电势零点(即:令Uc = 0)时,
电势零点
P
E cos dl
即:电场中任意一点P的电势等于电场强度从P点 经任一路径到电势零点的积分。
U P E cos dl
qo
5
二、 静电场的保守性(静电场环路定理)
L
E dl 0
a
L2
.
qo
L1
b
.
在静电场中,场强沿任意闭合路径的线积 分等于零。即:对任何静电场,电场强度的 线积分都只取决于起点和终点的位置,而与连 接起点和终点间的路径无关。
6
三、电势能差
Aab Wa Wb qo a 实验电荷qo 在静电场中从a运动到b时,静电场力
大学物理电势
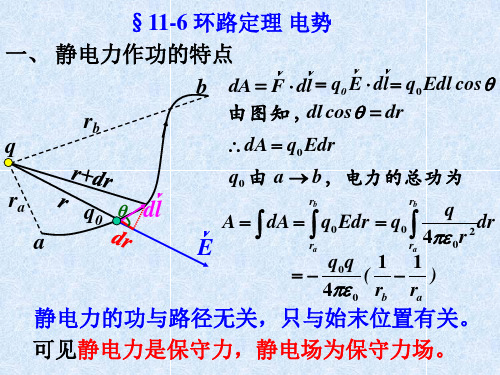
Aab q0 E dl ( Wb Wa )
a
c
b
W——电势能
电势能的值与参考点(W=0的点)的选择有关。
选c点为参考点,q0 E dl (Wc Wa ) 且 Wc 0.
a
Wa q0 E dl (Wc 0 )
a
c
某点(a)的电势能等于将q0由a →参考点c电力所作 的功,它为q0 和产生电场的源电荷系统所共有。
练习:学习指导“静电学” 一、5-7 二、24-32 三、44-47、49、52 五、63、65、66
E dl 0
L
静电场的环流为0. ——环路定理 (circuital theorem) ▲物理意义:单位正电荷在静电场中沿任意闭 合路径绕行一周,电力作功为零。说明静电场 为保守力场。
思考 电场线∥但不均匀分布是否可能?
静电场的 E 线?
反 证 法
三、电势能(electric potential energy) 保守力的功=势能增量的负值
2、电势是标量,但有正负。 3、单位:J / C = V . 4、上面的线积分和作功均与路径无关。
五、电势差(electric potential difference) 两点电势之差:
c b U a U b U ab E dl - E dl E dl
U E dr (沿径向积分)
r
(1) r>R时, U
r
q
(2) r=R 时,
U q 40 r R
40 r q q dr 2 4 0 r 40 r r e dr 2 r e dr 2 r
q q 40 R
a
c
b
W——电势能
电势能的值与参考点(W=0的点)的选择有关。
选c点为参考点,q0 E dl (Wc Wa ) 且 Wc 0.
a
Wa q0 E dl (Wc 0 )
a
c
某点(a)的电势能等于将q0由a →参考点c电力所作 的功,它为q0 和产生电场的源电荷系统所共有。
练习:学习指导“静电学” 一、5-7 二、24-32 三、44-47、49、52 五、63、65、66
E dl 0
L
静电场的环流为0. ——环路定理 (circuital theorem) ▲物理意义:单位正电荷在静电场中沿任意闭 合路径绕行一周,电力作功为零。说明静电场 为保守力场。
思考 电场线∥但不均匀分布是否可能?
静电场的 E 线?
反 证 法
三、电势能(electric potential energy) 保守力的功=势能增量的负值
2、电势是标量,但有正负。 3、单位:J / C = V . 4、上面的线积分和作功均与路径无关。
五、电势差(electric potential difference) 两点电势之差:
c b U a U b U ab E dl - E dl E dl
U E dr (沿径向积分)
r
(1) r>R时, U
r
q
(2) r=R 时,
U q 40 r R
40 r q q dr 2 4 0 r 40 r r e dr 2 r e dr 2 r
q q 40 R
(大学物理ppt)第 2 章 电势

ra
静电力作功与具体路径无关,只取决于检验电
荷的始末位置。 定义 电势差
rb A a b E dl ra q0
二、电势差和电势
2.电势
b a E dl ra d E dl
rb
即 若
称为电势零点 rb 则:电场中 a 点的电势 a r E dl
r rb 时, b 0,
a
通常
rb 时,b 0,
电势
a
ra
E dl
二、电势差和电势 电势
Biblioteka r E dl上式表明,电场中某点的电势大小,等于把单 位正电荷从该点经任意路径移到无限远处电场力 所作的功的大小。 电 势 单 位 : 焦 尔 / 库 仑 , 称 为 伏 特 , 简 称 伏
A dA q0 Edr
L ra rb
q0q 1 1 ( ) 40 ra rb
一、静电场环路定理
2.静电场的保守性
在点电荷电场中,电场力对检验电荷所作的
功,只取决于检验电荷 q0 及其始末位置,与连 接始末位置的具体路径无关。这个性质称为静电 场的保守性。
一、静电场环路定理
二、电势差和电势
3.单个点电荷在空间的电势
点电荷在空间任意一点的电势 E dl
r
q
r
p
r
q dr 2 40 r
1
E
1 q 40 r
q e 2 r 40 r 1
积分路径沿位矢方向
二、电势差和电势
1 q 40 r
在正电荷的电场中,各点的电势均为正 值,离电荷越远的点,电势越低; 在负电荷的电场中 ,各点的电势均为负 值,离电荷越远的点,电势越高。
静电力作功与具体路径无关,只取决于检验电
荷的始末位置。 定义 电势差
rb A a b E dl ra q0
二、电势差和电势
2.电势
b a E dl ra d E dl
rb
即 若
称为电势零点 rb 则:电场中 a 点的电势 a r E dl
r rb 时, b 0,
a
通常
rb 时,b 0,
电势
a
ra
E dl
二、电势差和电势 电势
Biblioteka r E dl上式表明,电场中某点的电势大小,等于把单 位正电荷从该点经任意路径移到无限远处电场力 所作的功的大小。 电 势 单 位 : 焦 尔 / 库 仑 , 称 为 伏 特 , 简 称 伏
A dA q0 Edr
L ra rb
q0q 1 1 ( ) 40 ra rb
一、静电场环路定理
2.静电场的保守性
在点电荷电场中,电场力对检验电荷所作的
功,只取决于检验电荷 q0 及其始末位置,与连 接始末位置的具体路径无关。这个性质称为静电 场的保守性。
一、静电场环路定理
二、电势差和电势
3.单个点电荷在空间的电势
点电荷在空间任意一点的电势 E dl
r
q
r
p
r
q dr 2 40 r
1
E
1 q 40 r
q e 2 r 40 r 1
积分路径沿位矢方向
二、电势差和电势
1 q 40 r
在正电荷的电场中,各点的电势均为正 值,离电荷越远的点,电势越低; 在负电荷的电场中 ,各点的电势均为负 值,离电荷越远的点,电势越高。
2020年大学物理 第12章 电势

ra
qo
4
0r 2
dr
r
a qq0
4 0
(
1 ra
q0 1 rb
)
推广
b
Aab q0 ( E1 E2 En ) dl
p2
qn ri2
dr E qo
a
q1
b b
b
q0E1 dl q0E2 dl q0En dl qi
r R
V
qdl
q
rR 80rR 40r
rR
qdl dV
8 0 rR
Rr
V
qdl
q
Rr 80rR 40R
方法二 定义法
q
由高斯定理求出场强分布 E 4 0r 2 r R
由电势定义 V E dl
0
rR
P
rR
rR
R
V E dl E dl
对称性 以q为球心的同一球面上的点电势相等
点电荷的电势:
VP
q 4 0r
二、 点电荷系的电势
由电势叠加原理,P 点的电势为 q2
V Vi
qi 4 0ri
r1 q1
r2 P
qnrn
三、 连续带电体的电势
由电势叠加原理
V
dV
dq 4 0r
dq
r P
问题:谁是能量的携带者?是电荷 还是电场? 例1 均匀带电橡皮气球的能量
由于电荷之间的相互排斥,当 气球体积膨胀时,能量改变
R dR
原来储存在球壳中电场 的能量
大学物理学第11章电势

38
例1 求电矩为 p=ql 的电偶极子在均匀外电场 E 中的电势能
l A
-q
B +q
θ
E
讨论:
39
§11.7 静电场的能量 电场能量密度
电场总能量
积分遍及整个空间
注意:电场能量存在于场强所在的全部空间
40
例2 在真空中一个均匀带电球体,半径为R,总电量为q,试利用电 场 能量公式求此带电系统的静电能。 思路分析: (1)确定电场分布;
R
(2)确定能量密度; (3)从电场能量定义出发求电场能量;
41
++
+
+
+R + +
+
+
+ +r
+ +
+ +
+ +
o +
+ dr +
+
+
+ + +
+++ +
42
期末复习.doc
解:思路分析:
+++ +
+R
o
+
(1)确定电势零点——无穷远处;
q+ (2)用高斯定律确定电场分布;
+ +
+
+ ++
+
+ + (3)确定电势分布;
10
++ +
+
+R
+
o
+ +++
例1 求电矩为 p=ql 的电偶极子在均匀外电场 E 中的电势能
l A
-q
B +q
θ
E
讨论:
39
§11.7 静电场的能量 电场能量密度
电场总能量
积分遍及整个空间
注意:电场能量存在于场强所在的全部空间
40
例2 在真空中一个均匀带电球体,半径为R,总电量为q,试利用电 场 能量公式求此带电系统的静电能。 思路分析: (1)确定电场分布;
R
(2)确定能量密度; (3)从电场能量定义出发求电场能量;
41
++
+
+
+R + +
+
+
+ +r
+ +
+ +
+ +
o +
+ dr +
+
+
+ + +
+++ +
42
期末复习.doc
解:思路分析:
+++ +
+R
o
+
(1)确定电势零点——无穷远处;
q+ (2)用高斯定律确定电场分布;
+ +
+
+ ++
+
+ + (3)确定电势分布;
10
++ +
+
+R
+
o
+ +++
大学物理第23章_电势

电场力做正功,电势能减少
U Ua Ub 0
Vab
V
Va
Vb
Ua
Ub q
因为q<0,所以电势增大
沿着电场线方向,电势降低。
VP VQ
P dl
Q
VP VQ
P
dl Q
思考(1)把电荷 +q 从P点移动到Q点,电场力 是作正功还是负功?P,Q两点哪点的电势高?
(2)如果移动的是负电荷呢?
Va
Ua q
已知电场分布可计算电势
电势差
Br r
ò VA - VB = E ?dl
A
记住!
A、B 两点间的电势差=将单位正电荷从A点 经任意路径移到B点的过程中电场力所做的功。
如何求电场中某点的电势?
设无穷远处电势为零
VA VA V VA
E dl
A
物理意义是什么?
将单位正电荷在电场中从A点经任意路径到达无 穷远处,静电场力所做的功。
电场力所作的功如何用电势差表示出来?
AAB q0 (VA VB )
沿着电场线方向,电势降低。A点电势高,B点
电势低。
对于正电荷:高电势 低电势
B
A 电场力做正功还是负功?
电势能如何变化?
负电荷呢?
例题 23-1 一负电荷(如电子)被放置在图中负极板附近的b 点。如果电子可以自由移动,问:电子的电势能是增加还是减 小?电势将如何变化? 负电荷受力方向与电场方向相反, 在b点释放的电子将朝正极板运动。
例题23-4 一半径为 r0、总电荷为Q的带电导体球,试确定 距离球心为 r处的电势(a)r > r0,(b)r =r0,(c) r < r0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a
注意:电势差是绝对的,电势大小是相对的,与
电势零点的选择有关。
b
Va a E dl Vb
为了确定 a 点的电势值,可以选定 b 点的电势
值为零,则 a 点的电势值为:
令
Vb 0 ,
b
Va
E dl
a
V 0点
Va a E dl
电场中某点的电势等于将单位正电荷从该点经
任意路径移到零势点时电场力所作的功;也等于单
q
4 π 0r
P dr
r
q
V q
4 π 0r
q 0, V 0 q 0, V 0
15
(2)电势叠加原理
点电荷系 E Ei
i
Vp E dl Ei dl
p
iP
VP
VPi
i
i
qi
4 π 0ri
q1
q2 q3
r1 r2 r3
E3
p
E2
E1
表明:一个点电荷系的电场中任一点的电势,等于每
8
Aab (Wb Wa )
电势能的参考点选择是任意的,
若取 b 点为电势能的零点 (零势点Wa ab q0E dl
势能零点
Wa q0 A
E dl
试验电荷 q0在电场中某点的电势能,在数值上等
于把它从该点移到零势能处静电场力所作的功。
9
点电荷的电场中
rdA dlq0Erddllcos4θπqεq00rr3drr
dl
dA
4
qq0
π 0r 2
dr
Aab
qq0
4 π 0
rb dr r ra 2
qq0 ( 1 1 )
4 π 0 ra rb
结果: Aab 仅与 q0 的始末位置有关,与路径无关。 3
任意带电体的电场(视为点电荷系)中
q0
b
E
b
E dl
(Wb
Wa
)
a
q0 q0
a
(积分大小与 q0无关,反映了电场在 a、b 两点的性质。)
b
E
dl
Wa
a
q0
Wb q0
Va
Vb
称为 a、b两点的电势差。
意义:把单位正电荷从A点沿任意路径移到B点的过
程中,静电场力所做的功。
11
电势差
b
Uab Va Vb
E dl
L
s
7
二、电 势 差 与 电 势 1、电势能 ( Electric Potential Energy )
静电场是保守场,静电场力是保守力。静电场力所做的功 就等于电荷电势能增量的负值。
Aab ab q0 E dl
(Wb Wa ) W
Aab
0, Wb Wa
0, Wb Wa
电势能的大小是相对的, 电势能的差是绝对的。
Va a E dl
Va
P0
E
dl
a
(选无穷远为电势零点) (选 P0 为电势零点)13
电势差
b
Uab Va Vb
E dl
a
当已知电势分布时,可用电势差求出点电荷在 电场中移动时电场力所做的功。
静电场力的功
Aab q0Va q0Vb q0Uab
公式小结:
零势点
b
一个点电荷单独存在时在该点所产生的电势的代数和。
这一结论称作电势叠加原理。
16
电荷连续分布带电体电场中的电势
第一种方法:将带电体分为许
多电荷元dq(点电荷),利用点电 荷的电势公式积分:
qr VP
dq
(电势叠加法)
4π 0r
d+q
dq
P
dV
dE
第二种方法:按电势的定义式进行计算:(场强积分法)
3)环路定理反映了静电场是保守场(或叫无旋场),
可引入电势能的概念。
6
静电场的两条基本定理:
静电场的环路定理: E dl 0 L
静电场是保守场 (或无旋场)
静电场的高斯定理:
E dS
1
S
ε0
qi (内)
静电场是有源场
静电场是有源、无旋(保守)场
E dl ( E ) dS 0 E 0 无旋场
(Circuital Theorem of Electrostatic Field)
q0 E dl q0 E dl
a1b
a2b
q0( E dl E dl ) 0
1
b
a
2E
a1b
b2a
l E dl 0
静电场中,场强沿任意闭合环路的线积分恒等于零 。
静电场力是保守力,静电场是保守场。
5
7.4 静电场力的功 电势
1
静电场的性质: 1)电荷在电场中受到电场力
电场强度 E
2)当电荷在电场中移动时, 电场力要对电荷作功。
电势 V
先从库仑定律和场强叠加原理出发,证明静电 场力的功与路径无关,说明静电场是保守场,然后 引入描述静电场的另一个物理量 —— 电势。
一、静电场的环路定理
2
1、 静电场力所做的功
E Ei
b •
i b
Aab q0 a E dl b
q0 a Ei dl
L a•
q1 q2 qi qn1
i
q0qi ( 1 1 )
i 4 0 ria rib
qn
结论:试验电荷在任何静电场中移动时,静电场力
所作的功,仅与试验电荷的电量、起始与终了位置
有关,而与路径无关。
4
2、 静电场的环路定理
位正电荷在该点的电势能。
12
电势零点的选择:
• 对有限带电体一般选 无穷远为电势零点。
Va a E dl
物理意义 把单位正试验电荷从点A移到无穷远 时,静电场力所作的功。
• 在实际问题中,常选地球或仪器外壳的电势为零。
• 对无限带电体不宜选无穷远为电势零点,只能选 有限区域的某一位置为电势零点。
Va a E dl Va Vb a E dl
Wa q0Va
Aab q0 (Va Vb )
14
电势的计算
Va a E dl
零势点 & Va a E dl
3、电势叠加原理
(1)点电荷电场中的电势
取无穷远为电势零点,由定义式有
VP
E dl
P
r
Edr
qdr r 4 πε0r 2
说明:
E dl 0
l
1)环路定理是静电场的另一重要定理,可用环路
定理检验一个电场是不是静电场。
b c d a
E dl a E dl b E dl c E dl d E dl
b
d
a
a E1dl c E2dl
0 不是静电场!
d
b
cE
2)环路定理要求电场线不能闭合。
VP
例:若选择无限远处为电
势能零点,试验电荷 q0 在 点电荷 q 的电场中,A 点 处的电势能为:
Wa a q0 E dl
0
q0
1
4 0
q dr r2
q0q
4 0ra 10
2、电势 电势差
b
Aab a q0 E dl (Wb Wa )
Wa
b a q0 E dl
(Wb 0)
注意:电势差是绝对的,电势大小是相对的,与
电势零点的选择有关。
b
Va a E dl Vb
为了确定 a 点的电势值,可以选定 b 点的电势
值为零,则 a 点的电势值为:
令
Vb 0 ,
b
Va
E dl
a
V 0点
Va a E dl
电场中某点的电势等于将单位正电荷从该点经
任意路径移到零势点时电场力所作的功;也等于单
q
4 π 0r
P dr
r
q
V q
4 π 0r
q 0, V 0 q 0, V 0
15
(2)电势叠加原理
点电荷系 E Ei
i
Vp E dl Ei dl
p
iP
VP
VPi
i
i
qi
4 π 0ri
q1
q2 q3
r1 r2 r3
E3
p
E2
E1
表明:一个点电荷系的电场中任一点的电势,等于每
8
Aab (Wb Wa )
电势能的参考点选择是任意的,
若取 b 点为电势能的零点 (零势点Wa ab q0E dl
势能零点
Wa q0 A
E dl
试验电荷 q0在电场中某点的电势能,在数值上等
于把它从该点移到零势能处静电场力所作的功。
9
点电荷的电场中
rdA dlq0Erddllcos4θπqεq00rr3drr
dl
dA
4
qq0
π 0r 2
dr
Aab
qq0
4 π 0
rb dr r ra 2
qq0 ( 1 1 )
4 π 0 ra rb
结果: Aab 仅与 q0 的始末位置有关,与路径无关。 3
任意带电体的电场(视为点电荷系)中
q0
b
E
b
E dl
(Wb
Wa
)
a
q0 q0
a
(积分大小与 q0无关,反映了电场在 a、b 两点的性质。)
b
E
dl
Wa
a
q0
Wb q0
Va
Vb
称为 a、b两点的电势差。
意义:把单位正电荷从A点沿任意路径移到B点的过
程中,静电场力所做的功。
11
电势差
b
Uab Va Vb
E dl
L
s
7
二、电 势 差 与 电 势 1、电势能 ( Electric Potential Energy )
静电场是保守场,静电场力是保守力。静电场力所做的功 就等于电荷电势能增量的负值。
Aab ab q0 E dl
(Wb Wa ) W
Aab
0, Wb Wa
0, Wb Wa
电势能的大小是相对的, 电势能的差是绝对的。
Va a E dl
Va
P0
E
dl
a
(选无穷远为电势零点) (选 P0 为电势零点)13
电势差
b
Uab Va Vb
E dl
a
当已知电势分布时,可用电势差求出点电荷在 电场中移动时电场力所做的功。
静电场力的功
Aab q0Va q0Vb q0Uab
公式小结:
零势点
b
一个点电荷单独存在时在该点所产生的电势的代数和。
这一结论称作电势叠加原理。
16
电荷连续分布带电体电场中的电势
第一种方法:将带电体分为许
多电荷元dq(点电荷),利用点电 荷的电势公式积分:
qr VP
dq
(电势叠加法)
4π 0r
d+q
dq
P
dV
dE
第二种方法:按电势的定义式进行计算:(场强积分法)
3)环路定理反映了静电场是保守场(或叫无旋场),
可引入电势能的概念。
6
静电场的两条基本定理:
静电场的环路定理: E dl 0 L
静电场是保守场 (或无旋场)
静电场的高斯定理:
E dS
1
S
ε0
qi (内)
静电场是有源场
静电场是有源、无旋(保守)场
E dl ( E ) dS 0 E 0 无旋场
(Circuital Theorem of Electrostatic Field)
q0 E dl q0 E dl
a1b
a2b
q0( E dl E dl ) 0
1
b
a
2E
a1b
b2a
l E dl 0
静电场中,场强沿任意闭合环路的线积分恒等于零 。
静电场力是保守力,静电场是保守场。
5
7.4 静电场力的功 电势
1
静电场的性质: 1)电荷在电场中受到电场力
电场强度 E
2)当电荷在电场中移动时, 电场力要对电荷作功。
电势 V
先从库仑定律和场强叠加原理出发,证明静电 场力的功与路径无关,说明静电场是保守场,然后 引入描述静电场的另一个物理量 —— 电势。
一、静电场的环路定理
2
1、 静电场力所做的功
E Ei
b •
i b
Aab q0 a E dl b
q0 a Ei dl
L a•
q1 q2 qi qn1
i
q0qi ( 1 1 )
i 4 0 ria rib
qn
结论:试验电荷在任何静电场中移动时,静电场力
所作的功,仅与试验电荷的电量、起始与终了位置
有关,而与路径无关。
4
2、 静电场的环路定理
位正电荷在该点的电势能。
12
电势零点的选择:
• 对有限带电体一般选 无穷远为电势零点。
Va a E dl
物理意义 把单位正试验电荷从点A移到无穷远 时,静电场力所作的功。
• 在实际问题中,常选地球或仪器外壳的电势为零。
• 对无限带电体不宜选无穷远为电势零点,只能选 有限区域的某一位置为电势零点。
Va a E dl Va Vb a E dl
Wa q0Va
Aab q0 (Va Vb )
14
电势的计算
Va a E dl
零势点 & Va a E dl
3、电势叠加原理
(1)点电荷电场中的电势
取无穷远为电势零点,由定义式有
VP
E dl
P
r
Edr
qdr r 4 πε0r 2
说明:
E dl 0
l
1)环路定理是静电场的另一重要定理,可用环路
定理检验一个电场是不是静电场。
b c d a
E dl a E dl b E dl c E dl d E dl
b
d
a
a E1dl c E2dl
0 不是静电场!
d
b
cE
2)环路定理要求电场线不能闭合。
VP
例:若选择无限远处为电
势能零点,试验电荷 q0 在 点电荷 q 的电场中,A 点 处的电势能为:
Wa a q0 E dl
0
q0
1
4 0
q dr r2
q0q
4 0ra 10
2、电势 电势差
b
Aab a q0 E dl (Wb Wa )
Wa
b a q0 E dl
(Wb 0)
