半角模型课件电子教案
初二上学期全等三角形专题之半角模型教案(有答案)
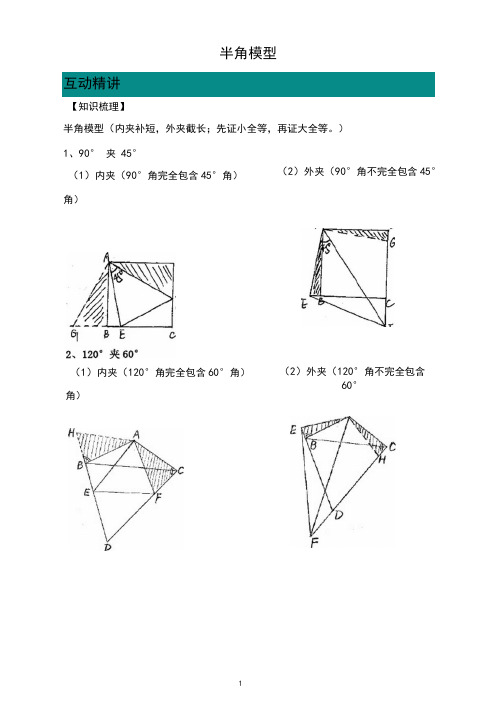
半角模型互动精讲【知识梳理】半角模型(内夹补短,外夹截长;先证小全等,再证大全等。
)1、90° 夹45°(1)内夹(90°角完全包含45°角)角)(2)外夹(90°角不完全包含45°(1)内夹(120°角完全包含60°角)角)(2)外夹(120°角不完全包含60°A【例题精讲】例1、正方形ABCD中,M, N分别是直线CB、DC上的动点,ZMAN=45°。
(1)当ZMAN交边CB、DC于点H、N (如图①)时,线段B\I、DN和MN之间有怎样的数量关系?请写出你的猜想,并加以证明;(2)当ZMAN分别交边CB, De的延长线于点M/N时(如图②),线段BH, DN和MN 之间的乂有怎样的数量关系?请写出你的猜想,并加以证明。
MΛr(2)DN一BAI = MN.理由如下:如图,在DC上截取DF = BM ,连接AF.VAB=AD,Bxf =^ADF = 90ΛI・・・ ^ABM^^ADF(SAS):.AM = AF t ZAfAB = ZFAD・・・.ΔMA13 + ZZ?/IF = ΔFAD ^BAF = 9O c .即 ZMAF = ZBAD = 9(『・又 ZMTIN = 45。
,.∖^NAF = ΛMAN = 45∖・・・AN = AN J・・・ΔFAN・・・.MN = FN I即 MN = DN 一DF = DN- BM;在厶MDN 与厶EDy 中: (D-W = DE< ZΛ∕D.V 二 AEDN t I DN = DN 所以V 空I)X(SAS)-所以对.\「= NE = .VC+ 〃対・ Δ.43∕.V 的周长 Q = AM + AN + MN=AM + AN + (NC+ ΠM)=(∕LV/ + BM) + (/LV + NC) =AB+AC =2A1L而等边△ ABCm 长L = 3.4B.因为= CD I S. DC = 120°所以 ZDBC =厶 DCB = 30° 又因为Δ.1BC 是等边三角形, 所以 ΛMΓ3D= ZLNCD = 90°.在厶MBD 与厶ECD 中:(BM = CE< Δ∖il3D - AECUI BD = Dc所以△ MliL) ≤ ^ECD(SAS)- 所以 D.” = DE^BDM = ACDE 1 所以ZEZZY =乙BDC-ZA/P.V = 60°例2、在等边AABC 的两边AB 、AC 所在直线上分别有两点M 、X, D 为AABC 外一 点,且ZMDN 二60° , ZBDC=I20o, BD=DC.探究:当M 、N 分别在直线AB 、AC 上移 动时,BM 、NC 、MN 之间的数量关系及AAMN 的周长Q 与等边AABC 的周长L 的关 系. (I) 如图1,当点M 、N 边AB 、Ae 上,且DM 二DN 时,BM 、NC. MN 之间的数量关 系是 _______ ; 此时—= ____________ ; L (II) 如图2,点M 、\边AB 、AC ±,且当DM≠DN 时,猜想(I)问的两个结论 还成立吗?写出你的猜想并加以证明; (IlI)如图3,当M 、N 分别在边AB 、CA 的延长线上时,若AN=Λ,则Q 二(用八L 表示)•(3)如图,当M-V 分别在AB. CT 的延长线上时,若.LV = z,SMQ = 2了+話(用八Z 表示)・3解:⑴如图,BAf 、NC 、M 之间的数屋关系DM + NC =此时Q=?L 3(2)猜想:结论仍然成立.证明:如图,延长.1C 至&使CE= I3M.连接DE【课堂练习】1、如图,正方形ABCD 中,E 和F 分别是边BC 和CD 上的点,AG 丄EF 于G,若Z EAF=45o ,求证:AG=ADO延长CD 到使DM=BE I 连接AM I ∙.∙四边形ABCD^AE 方形,・•・ AB=AD y ΔB= ZADF = ^ADM = ZBAD = 90° r ・・・ZEAF = 45° . .∖ΛBAE+^DAF = 45QT在MBE 和ZXADF 中AB=AD^B=ΔADF BE=DF.∖ΔABE 丝 ΔADF I••• ZDAM = ZBAE t AE = AM ,・•・ ZFAM = ZDAF + ZDAM = ZjDAF + ΔBAE = 45° = Z.EAF^ΔEAF 和 ZkMAF 中 AE=AMLEAF = AMAF AF=AF.∖ΔEAF ^ΔMAF t.∙∙ EF = MF, SbEAF= SIMAFF{{.∖^EF×AG≈^MF× AD t Z 厶.∖AG=AD.2、已知:∆ABC 是等边三角形,ΔBDC 是等腰三角形,其中ZBDC=I20° ,过点 D 作ZEDF=60° ,分别交AB 于E,交AC 于F,连接EF.(1) 若BE 二CF,求证:①Z ∖DEF 是等边三角形;②BE+CF 二EF.(2) 若BE≠CF,即E 、F 分别是线段AB, AC 上任意一点,BE+CF=EF 还会成立吗?ΛA NBD^∙FCD (SAS), /-DN=DF r ZNDB=ZFDC r ∙.zEDB=ZFDC ZΛZ EDB=Z BDN=Z FDC,∙.zBDC=120o f ZEDF=60%ΛZ EDB÷Z FDC=60% ΛZ EDB÷Z BDN=60% 即ZEDF=ZEDN, 在AEDN 和、ED F 中ΛΔ∈D N^EDF (SAS),.∙.EF=EN=BE+BN=BE+CF,请说明理山.IZNBD = ZFCD = 90°BN = CFBD = DC(1)证明:延长AB到N•使BN=CF Z连接DN,VMBC是等边三角形,∙∙.Z ABC=ZACB=60。
初二上学期全等三角形专题之半角模型教案(有答案)
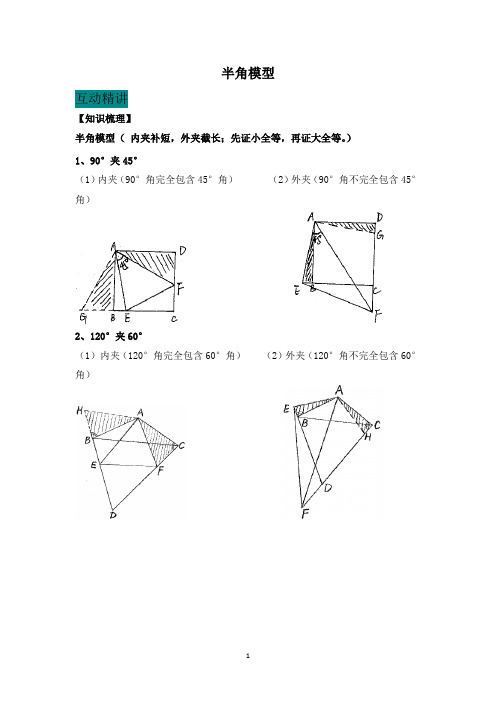
半角模型互动精讲【知识梳理】半角模型(内夹补短,外夹截长;先证小全等,再证大全等。
)1、90°夹45°(1)内夹(90°角完全包含45°角)(2)外夹(90°角不完全包含45°角)2、120°夹60°(1)内夹(120°角完全包含60°角)(2)外夹(120°角不完全包含60°角)【例题精讲】例1、正方形ABCD中,M,N分别是直线CB、DC上的动点,∠MAN=45°。
(1)当∠MAN交边CB、DC于点M、N(如图①)时,线段BM、DN和MN之间有怎样的数量关系?请写出你的猜想,并加以证明;(2)当∠MAN分别交边CB,DC的延长线于点M/N时(如图②),线段BM,DN和MN之间的又有怎样的数量关系?请写出你的猜想,并加以证明。
例2、在等边△ABC 的两边AB 、AC 所在直线上分别有两点M 、N ,D 为△ABC 外一点,且∠MDN=60°,∠BDC=120°,BD=DC. 探究:当M 、N 分别在直线AB 、AC 上移动时,BM 、NC 、MN 之间的数量关系及△AMN 的周长Q 与等边△ABC 的周长L 的关系.(I )如图1,当点M 、N 边AB 、AC 上,且DM=DN 时,BM 、NC 、MN 之间的数量关系是 ; 此时=LQ; (II )如图2,点M 、N 边AB 、AC 上,且当DM ≠DN 时,猜想(I )问的两个结论还成立吗?写出你的猜想并加以证明;(III ) 如图3,当M 、N 分别在边AB 、CA 的延长线上时,若AN=x ,则Q= (用x 、L 表示).【课堂练习】1、如图,正方形ABCD中,E和F分别是边BC和CD上的点,AG⊥EF于G,若∠EAF=45°,求证:AG=AD。
2、已知:△ABC是等边三角形,△BDC是等腰三角形,其中∠BDC=120°,过点D作∠EDF=60°,分别交AB于E,交AC于F,连接EF.(1)若BE=CF,求证:①△DEF是等边三角形;②BE+CF=EF.(2)若BE≠CF,即E、F分别是线段AB,AC上任意一点,BE+CF=EF还会成立吗?请说明理由.课堂检测1、(1)如图1、在四边形ABCD 中,AB=AD ,∠BAD=120°,∠B=∠ADC=90°,E 、F 分别是BC 、CD 上的点,且∠EAF=60°,探究图中的线段BE 、EF 、FD 之间的数量关系(2)如图2,在四边形ABCD 中,AB=AD ,∠B+∠ADC=180°,且∠EAF=21∠BAD ,探究图中的线段BE 、EF 、FD 之间的数量关系(1)延长FD 至G,使得GD=BE,再连接AG2、如图,在正方形ABCD中,点E,F分别为BC、DC边上的点,且满足DF+BE=EF。
中考数学专题复习 正方形之“半角”模型 课件

也相当于翻折法、 (或轴对称)
“截长”: 在EF上截取一点H,使BE=EH
EF=BE+DF
“补短”
“截长”
“旋转” “翻折”或(轴对称)
几何主要包括线与角,既然可以从“线段”上考虑, 那能否从“角”上考虑呢?
二、模型讲解
1.在正方形中,E、F分别是BC,CD上的点,且∠EAF=45°,连接EF.
三、变式训练
1、如图,在四边形中ABCD,AB=AD,∠B=∠D=90°,E、 F分别是BC,CD上的点,且∠EAF= 12∠BAD, 求证:EF=BE+DF;
三、变式训练
2.如图,在四边形中ABCD,AB=AD,∠B+∠D=180°,E、 F分别是BC,CD上的点,且∠EAF= 12∠BAD, 变式1中的结论 是否仍然成立?请写出证明过程.
能否通过翻折来解决问题?
二、模型讲解
1.在正方形中,E、F分别是BC,CD上的点,且∠EAF=45°,连接EF. (1)求证:EF=BE+DF
延长
“补短” 全等变换-- 旋转、翻折
方法归一
既然可以“补短”,那可以“截长”吗?
二、模型讲解 1.在正方形中,E、F分别是BC,CD上的点,且∠EAF=45°, 连接EF.(1)求证:EF=BE+DF
同理: 延长CD到点H,使BE=DH,连接AH
二、模型讲解 1.在正方形中,E、F分别是BC,CD上的点,且∠EAF=45°, 连接EF.(1)求证:EF=BE+DF 分析: 除了延长得到△ABG, 还可以如何得到?
将△ADF绕点A顺时针旋转90°
二、模型讲解 1.在正方形中,E、F分别是BC,CD上的点,且∠EAF=45°, 连接EF.(1)求证:EF=BE+DF 分析: 旋转是全等变换,还可以利用其它全等变换吗? 平移与翻折
几何模型——半角模型

9
精选课件ห้องสมุดไป่ตู้
10
精选课件
其实,世上最温暖的语言,“ 不是我爱你,而是在一起。” 所以懂得才是最美的相遇!只有彼此以诚相待,彼此尊重,
相互包容,相互懂得,才能走的更远。 相遇是缘,相守是爱。缘是多么的妙不可言,而懂得又是多么的难能可贵。否则就会错过一时,错过一世! 择一人深爱,陪一人到老。一路相扶相持,一路心手相牵,一路笑对风雨。在平凡的世界,不求爱的轰轰烈烈;不求誓
你越渴望的东西,也许越是无情无义地弃你而去。所以美好的愿望,就会像肥皂泡一样破灭,只能在错误的时间遇到错的人。 岁月匆匆像一阵风,有多少故事留下感动。愿曾经的相遇,无论是锦上添花,还是追悔莫及;无论是青涩年华的懵懂赏
识,还是成长岁月无法躲避的经历……愿曾经的过往,依然如花芬芳四溢,永远无悔岁月赐予的美好相遇。 其实,人生之路的每一段相遇,都是一笔财富,尤其亲情、友情和爱情。在漫长的旅途上,他们都会丰富你的生命,使
8
精选课件
爱是什么? 一个精灵坐在碧绿的枝叶间沉思。 风儿若有若无。 一只鸟儿飞过来,停在枝上,望着远处将要成熟的稻田。 精灵取出一束黄澄澄的稻谷问道:“你爱这稻谷吗?” “爱。” “为什么?” “它驱赶我的饥饿。” 鸟儿啄完稻谷,轻轻梳理着光润的羽毛。 “现在你爱这稻谷吗?”精灵又取出一束黄澄澄的稻谷。 鸟儿抬头望着远处的一湾泉水回答:“现在我爱那一湾泉水,我有点渴了。” 精灵摘下一片树叶,里面盛了一汪泉水。 鸟儿喝完泉水,准备振翅飞去。 “请再回答我一个问题,”精灵伸出指尖,鸟儿停在上面。 “你要去做什么更重要的事吗?我这里又稻谷也有泉水。” “我要去那片开着风信子的山谷,去看那朵风信子。” “为什么?它能驱赶你的饥饿?” “不能。” “它能滋润你的干渴?” “不能。”爱是什么? 一个精灵坐在碧绿的枝叶间沉思。 风儿若有若无。 一只鸟儿飞过来,停在枝上,望着远处将要成熟的稻田。 精灵取出一束黄澄澄的稻谷问道:“你爱这稻谷吗?” “爱。” “为什么?” “它驱赶我的饥饿。” 鸟儿啄完稻谷,轻轻梳理着光润的羽毛。 “现在你爱这稻谷吗?”精灵又取出一束黄澄澄的稻谷。 鸟儿抬头望着远处的一湾泉水回答:“现在我爱那一湾泉水,我有点渴了。” 精灵摘下一片树叶,里面盛了一汪泉水。 鸟儿喝完泉水,准备振翅飞去。 “请再回答我一个问题,”精灵伸出指尖,鸟儿停在上面。 “你要去做什么更重要的事吗?我这里又稻谷也有泉水。” “我要去那片开着风信子的山谷,去看那朵风信子。” “为什么?它能驱赶你的饥饿?” “不能。” “它能滋润你的干渴?” “不能。”
半角模型课件

2、如图,有一块三角形空地,AC=BC,∠ACB=90°,
∠DCE=45°,AD=3m,BE=4m,那么这块三角形空地
的面积为
.
C
A
D
E
B
学习交流PPT
16
学习交流PPT
17
解答:
学习交流PPT
18
五、课堂小结 升华模型
畅谈本节课的收获,和同学分享交流
学习交流PPT
19
六、链接中考 实战模型
4
一、探究规律 创建模型
A
45°
1
F′ B E
D 解:延长CB,使BF'=DF,连接AF'。
∵四边形ABCD是正方形,
∴AB=AD, ∠ABF ′ =∠ADF,
F∴△ADF≌△ABF′ ∴AF=AF′,∠1=∠2. ∴∠1+∠3=∠2+∠3=45° 即∠EAF′=∠EAF
∵AE=AE ∴△AEF′≌△AEF
学习交流PPT
14
四、当堂检测 巩固模型
1、如图,△ABC是正三角形,△BDC是顶角为120°的等
腰三角形,DB=DC,以D为顶点作一个60°角,角的两
边分别交AB、AC边于M、N两点,连接MN. 则BM、CN、
MN之间的数量关系为
。 BM+CN=MN.
A
N M
B
C
D
学习交流PPT
15
四、当堂检测 巩固模型
2
则BD、CE、DE之间的数量关系为 BD+CE=D。E
A
B D
C E
学习交流PPT
9
三、拓展提高 延伸模型
【变式一】如图,正方形ABCD中,点E、F分别在边
专题3.1 半角模型-2021年中考数学第二轮总复习课件(全国通用)

∴DE=GF=b-3,CE=7-b.
4.在Rt△BCE中求出b=25/7
E
DБайду номын сангаас
拓展提高
2.如图,在△ABC中,AB=BC,∠ABC=90º,D是AB上一动点,连接CD,以
CD为直径的⊙M交AC于点E,连接BM并延长交AC于点F,交⊙M于点
G,连接BE.
(1)求证:点B在⊙M上;
(2)当点D移动到使CD⊥BE时,求BC:BD的值; 2 +1
A
【思路点拨】
D
先将△ADF绕点A旋转得△ABF´
再证△AEF≌△AEF´
F
结论:EF=BE+DF
F´
BE C
半角信息——带形旋转——轴对称的全等三角形.
当堂训练一
2.如图,已知△ABC是等腰直角三角形,
A
点D,E在BC上,且满足∠DAE=45º. E´
求证:DE2=BD2+CE2
【思路点拨】
【一】将△ACE绕点A旋转到△ADE´,连
F´
EB
C
半角信息——带形旋转——轴对称的全等三角形.
F
类型2 小角不全在大角内部
1.如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180º,E,F分别是BC,
CD上的点,且∠EAF=0.5∠BAD,BE,DF,EF三条线段之间的数量关系
是否仍然成立,若不成立,写出它们之间的数量关系并证明.
C
=AB+AC=2
D
E
基础训练
4.如图,在正方形ABCD内作∠EAF=45º,AE交BC于点E,AF交CD于点F,连接EF,
过点A作AH⊥EF,垂足为H.
(1)将△ADF绕点A顺时针旋转90º得到△ABG. 求证:△AGE≌△AFE;
旋转的应用-半角模型教案鲁教版(五四制)数学八年级上册

《旋转的应用—半角模型》教学设计【教学目标】结合数学课程标准和学科德育一体化要求,围绕“目标—--评价—--教学”一致性原则,确定本课教学目标如下:半角模型的特点,掌握用旋转的方法解决半角问题的一般思路和方法。
2.在解决问题的过程中体会旋转的作用,归纳总结解决半角模型问题的基本方法。
3. 通过讨论交流、合作探究等活动,积累数学活动经验,培养数学学科的严谨思维和理性精神。
【教学重点】明确半角模型的特点,掌握用旋转的方法解决半角问题的一般思路和方法。
【教学难点】在解决问题的过程中体会旋转的作用,归纳总结解决半角模型问题的基本方法。
【教学过程】之前,我们学习过图形的变换主要有哪些形式?平移、旋转和轴对称。
其中旋转式我们解决几何问题的一大利器。
今天我们就来探究如何利用旋转来解决半角模型问题(板书课题)。
教学目标1、认识半角模型,能在复杂的图形当中找到半角模型;2、会利用旋转的知识解决半角模型的相关问题。
知识回顾△ABC为等边三角形,D是△ABC内一点,将△ABD经过逆时针旋转后到△ACP位置,则旋转中是,旋转角等于°AD与AP的夹角是°△ADP是三角形。
设计意图:同学们通过这道题的练习,熟悉旋转的性质,为后续的探究夯实基础。
典例探究在正方形ABCD中,E、F分别是CB、DC上的点,且∠EAF=45°,探究BE、FD、EF三条线段的数量关系。
(1)大胆猜测,独立思考,找出解决问题的方法。
(2)小组讨论,各抒己见,让思维撞击出火花。
(3)集体讨论,质疑问难,探讨解决问题的方案。
(4)几何画板演示旋转的意义所在,教师语言要注意引导半角模型的特点。
设计意图:教育本质是一棵树摇动另一棵树,一朵云推动另一朵云,一个灵魂唤醒另一个灵魂。
通过个人探究、小组讨论和集体讨论,激发学生对问题的深入思考。
几何画板的动态演示直观的展示了旋转的过程中,变与不变的量,变与不变的关系,加深学生对利用旋转解半角模型题目的认知。
2024成都中考数学第一轮专题复习之第五章 微专题 半角模型 教学课件

微专题 半角模型
解法二:
证明:如解图②,将△ABD和△ACE分别沿AD,AE翻折,使得AB,AC
重合在AH上.
由折叠的性质得,BD=DH,CE=HE.
∵△ABC和△AGF都是等腰直角三角形,
∴∠ABC=∠ACB=45°,
∴∠AHD=∠AHE=45°,∴∠DHE=90°.
例2题解图②
在Rt△DHE中,根据勾股定理得,DH2+EH2=DE2,
AB AD, ABE ADG , BE DG,
∴△ABE≌△ADG(SAS), ∴∠BAE=∠DAG,AE=AG.
G
例1题图
微专题 半角模型
∵∠BAE+∠EAD=90°, ∴∠DAG+∠EAD=90°,即∠EAG=90°. ∵∠EAF=45°,∴∠FAG=∠EAF=45°. 在△AFE和△AFG中,
微专题 半角模型
例1
一题多解法 如图,E,F分别是正方形ABCD边BC,CD上
的点,∠EAF=45°,求证:EF=BE+DF. 解法一:
一题多解 证明:如解图①,将△ADF绕点A顺时针旋转90°得到
△ABG,使AD与AB重合. ∵四边形ABCD是正方形,
例1题图
∴∠ABC=∠BAD=∠D=90°,
∵四边形ABCD是正方形,
∴AD=AB,∠BAD=∠D=∠ABM=90°.
E
在△ABM与△ADE中,
AB AD, ABM D , BM DE,
∴BD2+CE2=DE2.
微专题 半角模型
例3 如图,在四边形ABCD中,∠B=∠D=90°,E,F分别是四边形
ABCD的边BC,CD上的点,其中AB=AD,∠BAD=120°,∠EAF=
60°,求证:EF=BE+DF.
半角模型ppt课件

精品课件
21
感谢亲观看此幻灯片,此课件部分内容来源于网络, 如有侵权请及时联系我们删除,谢谢配合!
感谢亲观看此幻灯片,此课件部分内容来源于网络, 如有侵权请及时联系我们删除,谢谢配合!
8x
E
4
B
C
精品课件
14
2、(1)探究:
如图,已知Rt△ABC中, ∠ACB=90°,AC=BC,点D、E在斜边AB上, 且—∠——D—C—E—=— 45—°——,探——究— BE、DF、EF三条线段之
———————
间的数量关系.
AD
精品课件
E
B
15
13
D′
AD
E
B
结论: D2E A2 D B2E
பைடு நூலகம்
A
D
EB
18
C
D′
A
D
E
B
结论: 当AD=BE时,线段DE、AD、EB
能构成一个等腰三角形且顶角
∠DFE为120°.
精品课件
19
(3)应用:
在探究问题的条件下,如果AB=10,求 BD·AE的值.
AD
E
精品课件
20
一、知识与技能:
1、“半角模型” 特征: ①共端点的等线段; ②共顶点的倍半角;
———————————————
CD上的点,且∠EAF=45°,探究BE、DF、
————————
EF三条线段之间的数量关系.
A
D
人教版九年级数学上册《半角模型专题探究》优质课教案_10

通过上面两道题的解决,变式(2)学生可以轻松的猜想出结论.
基本模型(2)——等腰直角三角形内含半角
如图,已知Rt△ABC中,∠BAC=90°,AB=AC,点D、E在斜边BC上,且∠DAE=45°,探究BD、DE、EC三条线段之间的数量关系,并对你的猜想给予证明.
∠BDC=120°,BD=DC.
求证:BM+CN=MN
分析已知条件,此题是120°夹60°问题,而且题中也有一组有公共端点的线段,因此此题仍可以使用截长补短法或旋转法解决.
让学生自由选择方法解决此题,发现多数学生采用的仍是旋转法,因为他们发现旋转法可简化证明步骤,但仍需注意要证明三点共线.
由于时间有限,课堂上我们不能把所有的半角模型题都练到,但通过前面几道题的探究此时请学生来总结:
学生B;旋转法
对于学生在叙述过程中出现的问题需要及时纠正,对于学生可能会犯的错误要特别注意,如旋转的三要素,三点共线的证明.
之后通过课件演示动画,展示两种解决方法,使学生能更直观的体会两种方法的优缺点.
变式(1):已知:如图,在正方形ABCD中,E、F分别是CB、DC的延长线上的点,且∠EAF=45°.
猜想:线段BE,DF,EF之间有什么关系并证明.
将基本模型(1)进行变式,首先让生猜想结论,继续探究解决方法.
学生A:截长法.
学生B:旋转法.
通过两道题的训练,学生能够体会,解决此类半角问题,采用截长补短法或旋转法.但对于半角模型的特征还没有明确掌握.
变式(2)已知:如图,在正方形ABCD中,E、F分别是BC、CD延长线上的点,且∠EAF=45°.
基本模型(1)——正方形内含半角
已知:如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45°.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D 解:延长CB,使BF'=DF,连接AF
∵四边形ABCD是正方形,
∴AB=AD, ∠ABF ′ =∠ADF,
F∴△ADF≌△ABF′ ∴AF=AF′,∠1=∠2. ∴∠1+∠3=∠2+∠3=45° 即∠EAF′=∠EAF
∵AE=AE ∴△AEF′≌△AEF
C ∴EF'=EF ∴BE+DF=BE+BF′=EF′=EF
一、探究规律 创建模型
E'
A
D
A
D
F
F
F' B
E
C
B
E
C
辅助线方法一
辅助线方法二
一、探究规律 创建模型
【探究二】 如图,四边形ABCD中,AB⊥BC,AD⊥CD,AB=AD, 点E、F分别在边BC、CD上,∠BAD=120°,∠EAF=60°, 猜想BE、EF、DF之间有什么关系? BE+DF=EF
MN、DN之间的数量关系为
。
A
D
NF M
B
E
C
三、拓展提高 延伸模型
小组合作要求; 1、先独立思考。 2、小组内互相交流方法、思路、疑惑,互相帮助。 3、选出代表,向全班同学展示。
三、拓展提高 延伸模型
【变式二】如图,正方形ABCD中,点E、F
分别在边BC、CD上,∠EAF=45°,连接
BD,分别交AE、AF于点M、N,则BM、
MN、DN之间的数量关系为
。
A
D
A
D
NF M
B
E
C
N' B
NF M
E
C
三、拓展提高 延伸模型
A
D
A
D
F
NF
M N'
F' B
E
C
B
E
C
★总结:对于正方形中的半角模型存在那些数量关系?
四、当堂检测 巩固模型
1、如图,△ABC是正三角形,△BDC是顶角为120°
的等腰三角形,DB=DC,以D为顶点作一个60°角 ,角的两边分别交AB、AC边于M、N两点,连接MN. 则BM、CN、MN之间的数量关系为 BM+CN=。MN.
试着说明理由。
D
A
F
D
A
F
BE
C
F'
B
E
C
一、探究规律 创建模型
A
D
D
F
A
F
F' B
E
C
F'
B
E
C
★观察以上两个题目,你发现了什么?
二、一试身手 体验模型
【从特殊到一般】1、如图,已知AB=AC,在∠BAC内部∠BAC 共顶点的一个角∠DAE= 1∠BAC,并且有∠B+∠C=180°.
2
则BD、CE、DE之间的数量关系为BD+CE=DE。
学习重点:“半角”模型的辨别(一)及灵活应 用
学习难点:辅助线的添加及说明能力(一)。
一、探究规律 创建模型
【探究一】 在正方形ABCD中,E、F分别是BC、CD上的点, 且∠EAF=45°,探究BE、DF、EF三条线段之间的数量关系.
A
D
F
B究规律 创建模型
A
45°
1
F′ B E
A
N M
B
C
D
四、当堂检测 巩固模型
2、如图,有一块三角形空地,AC=BC,∠ACB=90°,
∠DCE=45°,AD=3m,BE=4m,那么这块三角形空地
的面积为
.
C
A
D
E
B
解答:
五、课堂小结 升华模型
畅谈本节课的收获,和同学分享交流
六、链接中考 实战模型
A
B D
C E
三、拓展提高 延伸模型
【变式一】如图,正方形ABCD中,点E、F分别在 边BC、CD上,∠EAF=45°.若正方形边长为2, 则△FEC的周长为 4 .
A
D
F
B
E
C
三、拓展提高 延伸模型
【变式二】如图,正方形ABCD中,点E、F
分别在边BC、CD上,∠EAF=45°,连接
BD,分别交AE、AF于点M、N,则BM、
商河县郑路中学
杨春利
学习目标:
(1)理解掌握“半角”模型,明确符合半角模型的特征(一); (2)用心经历探究模型演变过程,体会“从特殊到一般”(二)、
“分类”、 “化归”的研究思想,发展自己观察、比较、分析 推理能力(一二三); (3)明确辅助线的构造原理(一),进一步培养综合 运用知识 解决问题的能力。
