数列与数学文化专题 9
高三数学传统文化

教育部考试中心要求“增加中华优秀传统文化的考核内容,积极培育和践行社会主义核心价值观,充分发挥高考命题的育人功能和积极导向作用.比如,在数学中增加数学文化的内容”.因此,我们特别编写了此课时,将数学文化与数学知识相结合.考点一立体几何中的数学传统文化题[典例1]“牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体,它由完全相同的四个曲面构成,相对的两个曲面在同一个圆柱的侧面上,好似两个扣合(牟合)在一起的方形伞(方盖).其直观图如图1,图2中四边形是为体现其直观性所作的辅助线,当其主视图和左视图完全相同时,它的主视图和俯视图分别可能是()A.a,b B.a,cC.c,b D.b,d[解析]A[当主视图和左视图完全相同时,“牟合方盖”相对的两个曲面正对前方,主视图为一个圆,俯视图为一个正方形,且两条对角线为实线,故选A.]“牟合方盖”是我国古代利用立体几何模型和数学思想方法解决数学问题的代表之一.本题取材于“牟合方盖”,通过加工改造,添加解释和提供直观图的方式降低了理解题意的难度.解题从识“图”到想“图”再到构“图”,考生要经历分析、判断的逻辑过程.另外,我国古代数学中的其他著名几何体,如“阳马”“鳖臑”和“堑堵”等的三视图问题都有可能在高考中考查.[跟踪训练1]《九章算术》商功章有题:一圆柱形谷仓,高1丈3尺313寸,容纳米2 000斛(1丈=10尺,1尺=10寸,斛为容积单位,1斛≈1.62立方尺,π≈3),则圆柱底面圆周长约为( )A .1丈3尺B .5丈4尺C .9丈2尺D .48丈6尺解析:B [设圆柱底面圆半径为r 尺,高为h 尺,依题意,圆柱体积为V =πr 2h =2 000×1.62≈3×r 2×13.33,所以r 2≈81,即r ≈9,所以圆柱底面圆周长为2πr ≈54,54尺=5丈4尺,则圆柱底面圆周长约为5丈4尺,故选B.]考点二 数列中的数学传统文化题[典例2] 中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其意思为:有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地,请问第二天走了( )A .192里B .96里C .48里D .24里[解析] B [设等比数列{a n }的首项为a 1,公比为q =12,依题意有a 1⎝⎛⎭⎫1-1261-12= 378,解得a 1=192,则a 2=192×12= 96,即第二天走了96里,故选B.]与等差数列一样,我国古代数学涉及等比数列问题也有很多,因此,涉及等比数列的数学文化题也频繁出现在各级各类考试试卷中.解决这类问题的关键是将古代实际问题转化为现代数学问题,掌握等比数列的概念、通项公式和前n 项和公式.[跟踪训练2]《周髀算经》是中国古代的天文学和数学著作.其中一个问题大意为:一年有二十四个节气,每个节气晷长损益相同(即太阳照射物体影子的长度增加和减少大小相同).若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(注:一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长为( )A .五寸B .二尺五寸C.三尺五寸D.一丈二尺五寸解析:B[设晷长为等差数列{a n},公差为d,a1=15,a13=135,则15+12d=135,解得d=10.∴a2=15+10=25,∴《易经》中所记录的惊蛰的晷影长是2尺5寸.故选B.]考点三算法中的数学传统文化题[典例3]如图所示算法框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该算法框图,若输入的a,b分别为8,12,则输出的a=()A.4B.2C.0 D.14[解析]A[由算法框图输入的a=8,b=12,按算法框图所示依次执行,可得b=12-8=4,a=8;a=8-4=4,b=4,a=b,所以输出a=4.故选A.]《九章算术》系统总结了我国古代人民的优秀数学思想,开创了构造算法以解决各类问题的东方数学发展的光辉道路,这与当今计算机科学的飞速发展对数学提出的要求不谋而合.本题算法框图的算法思路源于《九章算术》中计算两个正整数的最大公约数的“更相减损术”算法.[跟踪训练3](2019·益阳、湘潭调研)秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数学九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的算法框图给出了利用秦九韶算法求某多项式值的一个实例.若输入n,x的值分别为3,3.则输出v的值为()A. 15B. 16C. 47D. 48解析:D [执行算法框图:输入n =3,x =3,v =1,i =2,i ≥0,是 i ≥0,是, v =1×3+2=5,i =1; i ≥0,是, v =5×3+1=16,i =0; i ≥0,是, v =16×3+0=48,i =-1; i ≥0,否,输出v =48.]考点四 概率统计中的传统文化题[典例4] (2018·全国Ⅰ卷)下图来自古希腊数学家希波克拉底所研究的几何图形.此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC 的斜边BC ,直角边AB ,AC .△ABC 的三边所围成的区域记为Ⅰ,黑色部分记为Ⅱ,其余部分记为Ⅲ.在整个图形中随机取一点,此点取自Ⅰ,Ⅱ,Ⅲ的概率分别记为p 1,p 2,p 3,则( )A .p 1=p 2B .p 1=p 3C .p 2=p 3D .p 1=p 2+p 3[解析] A [法一:设直角三角形ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,则区域Ⅰ的面积即△ABC 的面积为S 1=12bc ,区域Ⅱ的面积S 2=12π×⎝⎛⎭⎫c 22+12π×⎝⎛⎭⎫b 22-⎣⎢⎡⎦⎥⎤π×⎝⎛⎭⎫a 222-12bc =18π(c 2+b 2-a 2)+12bc =12bc ,所以S 1=S 2,由几何概型的知识知p 1=p 2,故选A.法二:不妨设△ABC 为等腰直角三角形,AB =AC =2,则BC =22,所以区域Ⅰ的面积即△ABC 的面积,为S 1=12×2×2=2,区域Ⅱ的面积S 2=π×12-⎣⎢⎡⎦⎥⎤π×(2)22-2=2,区域Ⅲ的面积S 3=π×(2)22-2=π-2.根据几何概型的概率计算公式,得p 1=p 2=2π+2,p 3=π-2π+2,所以p 1≠p 3,p 2≠p 3,p 1≠p 2+p 3,故选A.]从中国古代文学作品中选取素材考查数学问题,丰富了数学文化题的取材途径.试题插图的创新是本题的一个亮点,其一,增强了数学问题的生活化,使数学的应用更贴近考生的生活实际;其二,有利于考生分析问题和解决问题,这对稳定考生在考试中的情绪和心态起到了较好的效果;其三,探索了数学试题插图的新形式,给出了如何将抽象的数学问题直观化的范例.[跟踪训练4](理科)(2018·全国Ⅱ卷)我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30=7+23.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是( )A.112B.114C.115D.118解析:C [不超过30的素数有2,3,5,7,11,13,17,19,23,29,共10个,从中随机选取两个不同的数有C 210种不同的取法,这10个数中两个不同的数的和等于30的有3对,所以所求概率p =3C 210=115,故选C.](文科)2017年8月1日是中国人民解放军建军90周年纪念日,中国人民银行发行了以此为主题的金银纪念币.如图所示的是一枚8克圆形金质纪念币,直径22毫米, 面额100元.为了测算图中军旗部分的面积,现向硬币内随机投掷100粒芝麻,已知恰有30粒芝麻落在军旗内,据此可估计军旗的面积大约是( )A. 726π5mm 2 B. 363π10mm 2C.363π5mm 2 D.363π20mm 2 解析:B [利用古典概型近似几何概型可得,芝麻落在军旗内的概率为p =30100=310,设军旗的面积为S ,由题意可得:S π×112=310,∴S =310×π×112=36310π()mm 2,故选B.] 考点五 三角函数中的数学传统文化题[典例5] 第24届国际数学家大会会标是以我国古代数学家赵爽的弦图为基础进行设计的.如图,会标是由四个全等的直角三角形与一个小正方形拼成的一个大正方形.如果小正方形的面积为1,大正方形的面积为25,直角三角形中较大的锐角为θ,那么tan ⎝⎛⎭⎫θ+π4= ________ .[解析] 依题意得大、小正方形的边长分别是5,1,于是有5sin θ-5cos θ=1(0<θ<π2),即有sin θ-cos θ=15.从而(sin θ+cos θ)2=2-(sin θ-cos θ)2=4925,则sin θ+cos θ=75,因此sin θ=45,cos θ=35,tan θ=43,故tan ⎝⎛⎭⎫θ+π4=tan θ+11-tan θ=-7. [答案] -71700多年前,赵爽绘制了极富创意的弦图,采用“出入相补”原理使得勾股定理的证明不证自明.该题取材于第24届国际数学家大会会标,题干大气,设问自然,流露出丰富的文化内涵.既巧妙地考查了三角函数的相关知识,又丰富了弦图的内涵,如正方形四边相等寓言各国及来宾地位平等,小正方形和三角形紧紧簇拥在一起,表明各国数学家要密切合作交流,等等.[跟踪训练5](2019·沈阳监测)刘徽是一个伟大的数学家,他的杰作《九章算术注》和《海岛算经》是中国最宝贵的文化遗产,他所提出的割圆术可以估算圆周率π,理论上能把π的值计算到任意的精度.割圆术的第一步是求圆的内接正六边形的面积.若在圆内随机取一点,则此点取自该圆内接正六边形的概率是( )A. 334π B. 332π C.12πD. 14π解析:B [设圆的半径为R ,则圆的内接正六边形可以分解为6个全等的三角形,且每个三角形的边长为R ,据此可得,圆的面积为S 1=πR 2,其内接正六边形的面积为S 2=6×⎝⎛⎭⎫12×R 2×sin 60°=332R 2,利用几何概型计算公式可得:此点取自该圆内接正六边形的概率是p =S 2S 1=332π.故选B.]特色专题 数学文化[基础训练组]1.二十四节气(The 24 Solar Terms)是指中国农历中表示季节变迁的24个特定节令,是根据地球在黄道(即地球绕太阳公转的轨道)上的位置变化而制定的,每一个分别相应于地球在黄道上每运动15°所到达的一定位置。
以《数列》为例谈数学文化在教材中的引入

以《数列》为例谈数学文化在教材中的引入作者:谢晨明来源:《中学课程辅导·教师通讯》2018年第06期【内容摘要】十九大提出了“发展素质教育,推进教育公平,培养德智体美全面发展的社会主义建设者和接班人”的核心素养,明确把数学文化纳入到新课程标准中,那么如何把握教材中的文化资源,把数学文化素养纳入课堂之中,一直是高中老师的一大困惑,本文结合《数列》苏教版教材,界定出高中教材中主要的数学文化内容,为教材中数学文化的研究提供新的方向。
【关键词】数列数学文化苏教教材刚刚结束的党的十九大明确提出:“要全面贯彻党的教育方针,落实立德树人根本任务,发展素质教育,推进教育公平,培养德智体美全面发展的社会主义建设者和接班人。
”教育部于近日刚刚发布的《普通高中课程方案于标准》中更加明确的数学学科的核心素养是“学生学习该学科课程后应形成正确价值观念、必备品格和关键能力,并围绕学科核心素养的落实,精选、重组教学内容,设计教学活动,提出考试评价建议”明确了要把数学文化融入到课程内容,在前段时间教育部考试中心函件《关于2018年普通高考考试大纲修订内容的通知》再次要求“增加中华优秀传统文化的考核内容,积极培育和践行社会主义核心价值观,充分发挥高考命题的育人功能和积极导向作用。
”针对数学文化的考查,相信大家一定会比较迷惑:考什么?怎样考?怎么教?正如冯光庭在《基于“体现数学的文化价值”的数学教学策略探究》中所提到的:“要在数学教学过程中有效地体现数学的文化价值,并使数学教育真正成为数学文化的教育,第一要素是教师的认识问题,第二才是具体的操作问题”。
本文结合高中苏教必修五数列一章界定出高中教材中主要的数学文化内容,为教材中数学文化的研究提供新的方向。
一、首先了解“数学文化”的含义美国学者怀尔德在《作为文化系统的数学》一书中最早提出数学文化的概念,其特点在于:注重问题解决、数学应用、数学交流、数学思想方法和学生的情感态度。
(完整word版)高考数学中国传统文化题专项突破

高考数学中国传统文化题专项突破教育部考试中心函件《关于2017年普通高考考试大纲修订内容的通知》要求“增加中华优秀传统文化的考核内容,积极培育和践行社会主义核心价值观,充分发挥高考命题的育人功能和积极导向作用.比如,在数学中增加数学文化的内容.”因此,我们特别策划了此专题,将数学文化与数学知识相结合,选取典型样题深度解读,希望能够给予广大师生的复习备考以专业的帮助与指导.一、算法问题1.用更相减损术求294和84的最大公约数时,需要做减法的次数为()A.2 B.3C.4 D.5答案 C解析(84,294)→(84,210)→(84,126)→(84,42)→(42,42),一共做了4次减法.2.如图所示的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为14,18,则输出的a为()A.4 B.2C.0 D.14答案 B解析由题意输出的a是18,14的最大公约数2,故选B.3.用辗转相除法求459和357的最大公约数,需要做除法的次数是()A.1 B.2C.3 D.4答案 C解析∵459÷357=1…102,357÷102=3…51,102÷51=2,∴459和357的最大公约数是51,需要做除法的次数是3.4.秦九韶算法是中国南宋时期的数学家秦九韶提出的一种多项式简化算法,对于求一个n次多项式函数f n(x)=a n x n+a n-1x n-1+…+a1x+a0的具体函数值,运用常规方法计算出结果最多需要n次加法和n(n+1)2次乘法,而运用秦九韶算法由内而外逐层计算一次多项式的值的算法至多需要n次加法和n次乘法.对于计算机来说,做一次乘法运算所用的时间比做一次加法运算要长得多,所以此算法极大地缩短了CPU运算时间,因此即使在今天该算法仍具有重要意义.运用秦九韶算法计算f(x)=0.5x6+4x5-x4+3x3-5x当x=3时的值时,最先计算的是()A.-5×3=-15B.0.5×3+4=5.5C.3×33-5×3=66D.0.5×36+4×35=1 336.6答案 B解析f(x)=0.5x6+4x5-x4+3x3-5x=(((((0.5x+4)x-1)x+3)x+0)x-5)x,然后由内向外计算,最先计算的是0.5×3+4=5.5.5.若用秦九韶算法求多项式f(x)=4x5-x2+2当x=3时的值,则需要做乘法运算和加减法运算的次数分别为()A.4,2 B.5,3C.5,2 D.6,2答案 C解析∵f(x)=((((4x)x)x-1)x)x+2,∴乘法要运算5次,加减法要运算2次.6.已知函数f(x)=6x6+5,当x=x0时,用秦九韶算法求f(x0)的值,需要进行乘方、乘法、加法的次数分别为()A.21,6,2 B.7,1,2C.0,1,2 D.0,6,1答案 D解析∵f(x)=6x6+5,多项式的最高次项的次数是6,∴要进行乘法运算的次数是6.要进行加法运算的次数是1,运算过程中不需要乘方运算.7.中国古代有计算多项式值的秦九韶算法,下图是实现该算法的程序框图.执行该程序框图,若输入的a依次为2,2,5,x,n均为2,则输出的s等于()A.7 B.12C.17 D.34答案 C解析第一次运算,a=2,s=2,n=2,k=1,不满足k>n;第二次运算,a=2,s=2×2+2=6,k=2,不满足k>n;第三次运算,a=5,s=6×2+5=17,k=3,满足k>n,输出s=17,故选C.8.用秦九韶算法求多项式f(x)=x3-3x2+2x-11的值时,应把f(x)变形为()A.x3-(3x+2)x-11 B.(x-3)x2+(2x-11)C.(x-1)(x-2)x-11 D.((x-3)x+2)x-11答案 D解析f(x)=x3-3x2+2x-11=((x-3)x+2)x-119.用秦九韶算法求函数f(x)=3x5-2x4+2x3-4x2-7当x=2的值时,v3的结果是()A.4 B.10C.16 D.33答案 C解析函数f(x)=3x5-2x4+2x3-4x2-7=((((3x-2)x+2)x-4)x)x-7,当x=2时,v0=3,v1=3×2-2=4,v2=4×2+2=10,v3=10×2-4=16.10.用秦九韶算法求多项式f(x)=x6-5x5+6x4+x2+0.3x+2的值,当x=-2时,v1的值为()A.1 B.7C.-7 D.-5答案 C解析∵f(x)=x6-5x5+6x4+x2+0.3x+2=(((((x-5)x+6)x+0)x+1)x+0.3)x+2,∴v0=a6=1, v1=v0x+a5=1×(-2)-5=-7.11.利用秦九韶算法求多项式f(x)=-6x4+5x3+2x+6的值,当x=3时,v3的值为() A.-486 B.-351C.-115 D.-339答案 C解析f(x)=-6x4+5x3+2x+6=(((-6x+5)x+0)x+2)x+6,∴v0=a4=-6,v1=v0x+a3=-6×3+5=-13,v2=v1x+a2=-13×3+0=-39,v3=v2x+a1=-39×3+2=-115.12.秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例.若输入n,x的值分别为4,3,则输出v的值为()A.20 B.61C.183 D.548答案 C解析由程序框图知,初始值:n=4,x=3,v=1,i=3,第一次循环:v=6,i=2;第二次循环:v=20,i=1;第三次循环:v=61,i=0;第四次循环:v=183,i=1.结束循环,输出当前v的值183.13.原始社会时期,人们通过在绳子上打结来计算数量,即“结绳计数”,当时有位父亲,为了准确记录孩子的成长天数,在粗细不同的绳子上打结,由细到粗,满七进一,那么孩子已经出生多少天?()A.1 326 B.510 C.429 D.336答案 B解析由题意满七进一,可得该图示为七进制数,化为十进制数为1×73+3×72+2×7+6=510.14.用秦九韶算法计算多项式f(x)=5x5+4x4+3x3+2x2+x+1,乘法运算次数为____________.加法运算次数为________.答案5 5解析∵f(x)=((((5x+4)x+3)x+2)x+1)x+1,∴乘法要运算5次,加法要运算5次15.若f(x)=x4+3x3+x+1,用秦九韶算法计算f(π)时,需要乘法m次,加法n次,则m+n=________.答案 6解析f(x)=x4+3x3+x+1=(((x+3)x)x+1)x+1,用秦九韶算法计算f(π)时,乘法运算与加法运算的次数和等于6.16.我国南北朝数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法,其理论依据是:设实数x的不足近似值和过剩近似值分别为ba和dc(a,b,c,d∈N*),则b+da+c是x的更为精确的不足近似值或过剩近似值.我们知道π=3.141 59…,若令3110<π<4915,则第一次用“调日法”后得165是π的更为精确的过剩近似值,即3110<π<165,若每次都取最简分数,那么第四次用“调日法”后可得π的近似分数为________.答案22 717.我国古代数学名著《九章算术》中割圆术有:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”其体现的是一种无限与有限的转化过程,比如在222…中“…”即代表无限次重复,但原式却是个定值x .这可以通过方程2+x =x 确定x =2,则1+11+11+…=________. 答案 1+52解析 由题意,可令1+11+11+…=x ,即1+1x =x ,即x 2-x -1=0,解得x =1+52(x =1-52舍),故1+11+11+…=1+52. 18.用辗转相除法求840与1 764的最大公约数.答案 1 764=840×2+84,840=84×10+0,∴840与1 764的最大公约数是84.19.用更相减损术求440 与556的最大公约数.答案 556-440=116,440-116=324,324-116=208,208-116=92,116-92=24,92-24=68,68-24=44,44-24=20,24-20=4,20-4=16,16-4=12,12-4=8,8-4=4,∴440与556的最大公约数4.20.用秦九韶算法求多项式f (x )=7x 7+6x 6+5x 5+4x 4+3x 3+2x 2+x 当x =3时的值. 答案 f (x )=((((((7x +6)x +5)x +4)x +3)x +2)x +1)xv 0=7,v 1=7×3+6=27,v 2=27×3+5=86,v 3=86×3+4=262,v 4=262×3+3=789,v 5=789×3+2=2 369,v 6=2 369×3+1=7 108,v 7=7 108×3+0=21 324,∴f (3)=21 324,即当x =3时,函数值是21 324.21.(1)用辗转相除法求840与1 785的最大公约数;(2)用秦九韶算法计算函数f (x )=2x 4+3x 3+5x -4在x =2时的函数值.答案 (1)1 785=840×2+105,840=105×8+0,∴840与1 785的最大公约数是105.(2)秦九韶算法如下:f(x)=2x4+3x3+5x-4=x(2x3+3x2+5)-4=x[x(2x2+3x)+5]-4=x{x[x(2x +3)]+5}-4,故当x=2时,f(x)=2×{2×[2×(2×2+3)]+5}-4=62.22.(1)用辗转相除法求779与247的最大公约数;(2)利用秦九韶算法求多项式f(x)=2x5+4x4-2x3+8x2+7x+4当x=3时的值.答案(1)779=247×3+38,247=38×6+19,38=19×2.故779与247的最大公约数是19;(2)把多项式改成如下形式:f(x)=2x5+4x4-2x3+8x2+7x+4=((((2x+4)x-2)x+8)x+7)x+4.按照从内到外的顺序,依次计算一次多项式当x=3时的值:v0=2,v1=v0x+4=2×3+4=10,v2=v1x-2=10×3-2=28,v3=v2x+8=28×3+8=92,v4=v3x+7=92×3+7=283,v5=v4x+4=283×3+4=853.所以当x=3时,多项式f(x)的值是853.23.(1)用辗转相除法求228与1 995的最大公约数;(2)用秦九韶算法求多项式f(x)=3x5+2x3-8x+5在x=2时的值.答案(1)1 995=228×8+171,228=171×1+57,171=57×3,因此57是1 995与228的最大公约数.(2)f(x)=3x5+2x3-8x+5=((((3x+0)x+2)x+0)x-8)x+5当x=2时,v0=3,v1=3×2=6,v2=6×2+2=14,v3=14×2=28,v4=28×2-8=48,v5=48×2+5=101,所以当x=2时,多项式的值是101.24.(1)用“更相减损术”求72和168的最大公约数;(2)用“辗转相除法”求98和280的最大公约数.答案(1)∵168-72=96,96-72=24,72-24=48,48-24=24,故72和168的最大公约数是24.(2)∵280=2×98+84,98=1×84+14,84=6×14,故98和280的最大公约数是14.25.用秦九韶算法求函数f(x)=x5+x3+x2+x+1当x=3时的函数值.答案f(x)=x5+x3+x2+x+1=((((x+0)x+1)x+1)x+1)x+1,当x=3时,v0=1,v1=v0×3+0=3;v2=v1×3+1=10;v3=v2×3+1=31;v4=v3×3+1=94;v5=v4×3+1=283,即x=3时的函数值为283.二、数列问题1.《九章算术》是我国古代的数学名著,书中有如下问题:“今有五人分五钱,令上二人所得与下三人等.问各得几何.”其意思为“已知甲、乙、丙、丁、戊五人分5钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列.问五人各得多少钱?”(“钱”是古代的一种重量单位).这个问题中,甲所得为()A.54钱 B.43钱C.32钱 D.53钱答案 B解析依题意设甲、乙、丙、丁、戊所得钱分别为a-2d,a-d,a,a+d,a+2d,则由题意可知,a-2d+a-d=a+a+d+a+2d,即a=-6d,又a-2d+a-d+a+a+d+a+2d=5a=5,∴a=1,则a -2d =a -2×(-a 6)=43a =43. 2.南北朝时期的数学古籍《张邱建算经》有如下一道题:“今有十等人,每等一人,宫赐金以等次差(即等差)降之,上三人,得金四斤,持出;下四人后入得三斤,持出;中间三人未到者,亦依等次更给.问:每等人比下等人多得几斤?”( )A.439 B.778 C.776D.581 答案 B解析 设第十等人得金a 1斤,第九等人得金a 2斤,以此类推,第一等人得金a 10斤, 则数列{a n }构成等差数列,设公差为d ,则每一等人比下一等人多得d 斤金,由题意得⎩⎨⎧ a 1+a 2+a 3+a 4=3a 8+a 9+a 10=4,即⎩⎨⎧4a 1+6d =3,3a 1+24d =4,解得d =778, ∴每一等人比下一等人多得778斤金. 3.《张丘建算经》是公元5世纪中国古代内容丰富的数学著作,书中卷上第二十三问:“今有女善织,日益功疾,初日织五尺,今一月织九匹三丈.问日益几何?”其意思为“有个女子织布,每天比前一天多织相同量的布,第一天织五尺,一个月(按30天计)共织390尺.问:每天多织多少布?”已知1匹=4丈,1丈=10尺,估算出每天多织的布约有( )A .0.55尺B .0.53尺C .0.52尺D .0.5尺答案 A解析 设每天多织d 尺,由题意a 1=5,{a n }是等差数列,公差为d ,∴S 30=30×5+30×292d =390, 解得d ≈0.55.4.《张丘建算经》有这样一个问题:今有女子善织,日增等尺,七日织二十一尺,第二日,第五日,第八日所织之和为十五尺,问第九日所织尺数为( )A .7B .9C .11D .13 答案 D解析 设第一天织a 1尺,从第二天起每天比第一天多织d 尺,由已知得⎩⎪⎨⎪⎧7a 1+7×62d =21,a 1+d +a 1+4d +a 1+7d =15,解得a 1=-3,d =2,∴第九日所织尺数为a 9=a 1+8d =-3+8×2=13.5.古代数学著作《九章算术》有如下问题:“今有女子善织,日自倍,五日织五尺,问日织几何?” 意思是:“一女子善于织布,每天织的布都是前一天的2倍,已知她5天共织布5尺,问这女子每天分别织布多少?”根据已知条件,可求得该女子第3天所织布的尺数为( ) A.23B.815C.2031D.35 答案 C解析 由题意可得:每天织布的量组成了等比数列{a n },S 5=5,公比q =2 ,a 1(1-25)1-2=5, 计算可得a 1=531,所以a 3=531×22=2031. 6.在《张邱建算经》中有一道题:“今有女子不善织布,逐日所织的布比同数递减,初日织五尺,末一日织一尺,计织三十日”,由此推断,该女子到第10日时,大约已经完成三十日织布总量的( )A .33%B .49%C .62%D .88%答案 B解析 由题意可得:每日的织布量形成等差数列{a n },且a 1=5,a 30=1,设公差为d ,则1=5+29d ,解得d =-429. ∴S 10=5×10+10×92×(-429)=1 27029. S 30=30×(5+1)2=90. ∴该女子到第10日时,大约已经完成三十日织布总量的1 27029×190≈0.49=49%. 7.《张丘建算经》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有女不善织,日减功迟,初日织五尺,末日织一尺,今三十织迄,问织几何.”其意思为:有个女子不善于织布,每天比前一天少织同样多的布,第一天织五尺,最后一天织一尺,三十天织完,问三十天共织布()A.30尺B.90尺C.150尺D.180尺答案 B解析由题意可得,每日的织布量形成等差数列{a n},且a1=5,a30=1,所以S30=30×(5+1)2=90.8.在我国古代著名的数学专著《九章算术》里有一段叙述:今有良马与驽马发长安至齐,齐去长安一千一百二十五里,良马初日行一百零三里,日增十三里;驽马初日行九十七里,日减半里;良马先至齐,复还迎驽马,二马相逢.问:几日相逢?()A.9日B.8日C.16日D.12日答案 A解析由题意知,良马每日行的距离成等差数列,记为{a n},其中a1=103,d=13;驽马每日行的距离成等差数列,记为{b n},其中b1=97,d=-0.5;设第m天相逢,则a1+a2+…+a m+b1+b2+…+b m=103m+m(m-1)×132+97m+m(m-1)×(-0.5)2=2×1 125,解得m=9(负值舍去).9.《九章算术》是我国古代第一部数学专著,全书收集了246个问题及其解法,其中一个问题为“现有一根九节的竹子,自上而下各节的容积成等差数列,上面四节容积之和为3升,下面三节的容积之和为4升,求中间两节的容积各为多少?”该问题中第2节,第3节,第8节竹子的容积之和为()A.176升 B.72升 C.11366升 D.10933升答案 A解析自上而下依次设各节容积为a1,a2, (9)由题意得⎩⎨⎧ a 1+a 2+a 3+a 4=3a 7+a 8+a 9=4,即⎩⎨⎧2(a 2+a 3)=33a 8=4,得⎩⎨⎧a 2+a 3=32,a 8=43,所以a 2+a 3+a 8=32+43=176(升).10.中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其意思为:有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地,请问第二天走了( ) A .24里 B .48里 C .96里 D .192里答案 C解析 由题意可知此人每天走的步数构成以12为公比的等比数列,由题意和等比数列的求和公式可得a 1[1-(12)6]1-12=378,解得a 1=192,∴第二天此人走了192×12=96里.11.中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初步健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其大意为:“有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地.”则该人最后一天走的路程为( ) A .24里 B .12里 C .6里 D .3里答案 C解析 记每天走的路程里数为{a n },可知{a n }是公比q =12的等比数列,由S 6=378,得S 6=a 1(1-126)1-12=378,解得a 1=192,∴a 6=192×125=6.12.我国古代数学著作《九章算术》有如下问题:“今有金箠,长五尺,斩本一尺,重四斤,斩末一尺,重二斤,问次一尺各重几何?”意思是:“现有一根金箠,一头粗,一头细,在粗的一段截下一尺,重四斤;在细的一端截下一尺,重二斤.问依次每一尺各重几斤?”根据已知条件,若金箠由粗到细是均匀变化的,中间三尺的重量为( ) A .6斤 B .9斤 C .10斤D .12斤解析此问题构成一个等差数列{a n},设首项为2,则a5=4,∴中间3尺的重量为3a3=a1+a52×3=2+42×3=9(斤),故选B.13.我国古代数学著作《九章算术》有如下问题:“今有金箠,长五尺,斩本一尺,重四斤,斩末一尺,重二斤,问次一尺各重几何?”意思是:“现有一根金箠,长五尺,一头粗,一头细,在粗的一端截下1尺,重4斤;在细的一端截下1尺,重2斤;问依次每一尺各重多少斤?”根据上题的已知条件,若金箠由粗到细是均匀变化的,问第二尺与第四尺的重量之和为()A.6斤B.9斤C.9.5斤D.12 斤答案 A解析依题意,金箠由粗到细各尺构成一个等差数列,设首项a1=4,则a5=2,由等差数列性质得a2+a4=a1+a5=6,所以第二尺与第四尺的重量之和为6斤.14.《算法通宗》是我国古代内容丰富的数学名书,书中有如下问题:“远望巍巍塔七层,红灯向下倍加增,共灯三百八十一,请问塔顶几盏灯?”其意思为“一座塔共七层,从塔顶至塔底,每层灯的数目都是上一层的2倍,已知这座塔共有381盏灯,请问塔顶有几盏灯?”() A.3 B.4C.5 D.6答案 A解析由题意设塔顶有a盏灯,由题意由上往下数第n层就有2n-1·a盏灯,∴共有(1+2+4+8+16+32+64)a=381盏灯,即1×(1-27)1-2a=381.解得a=3.15.我国古代数典籍《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”上述问题中,两鼠在第几天相逢.()A.3 B.4C.5 D.6解析 由题意可知,大老鼠每天打洞的距离是以1为首项,以2为公比的等比数列, 前n 天打洞之和为1-2n 1-2=2n -1,同理,小老鼠前n 天打洞之和为1-(12)n1-12=2-12n -1,∴2n -1+2-12n -1=10,解得n ∈(3,4),取n =4. 即两鼠在第4天相逢.16.如图是谢宾斯基(Sierpinsiki)三角形,在所给的四个三角形图案中,着色的小三角形个数构成数列{a n }的前4项,则{a n }的通项公式可以是( )A .a n =3n -1 B .a n =2n -1 C .a n =3n D .a n =2n -1答案 A解析 着色的小三角形个数构成数列{a n }的前4项,分别为a 1=1,a 2=3,a 3=3×3=32,a 4=32×3,因此{a n }的通项公式可以是a n =3n -1.17.《九章算术》“竹九节”问题:现有一根9节的竹子,自上而下各节的容积成等差数列.上面4节的容积共3升,下面3节的容积共4升,则第5节的容积为________升. 答案6766解析 设该数列{a n }的首项为a 1,公差为d ,依题意⎩⎨⎧a 1+a 2+a 3+a 4=3,a 7+a 8+a 9=4,即⎩⎨⎧4a 1+6d =3,3a 1+21d =4,解得⎩⎨⎧a 1+7d =43,d =766,则a 5=a 1+4d =a 1+7d -3d =43-2166=6766.18.华罗庚数学小组的同学们在图书馆发现一块古代楔形文字泥板的图片,同学们猜测它是一种乘法表的记录,请你根据这个猜测,判定表示________?(如图)答案395解析图片中记录的是自然数乘以9的运算结果,左列是被乘数,右列是该数乘以9的积数,经过分析可知:其中▽代表1,⊲代表10,代表60.所以表示60×6+10×3+5×1=395.19.在我国南宋数学家杨辉所著的《详解九章算法》(1261年)一书中,用如图A所示的三角形,解释二项和的乘方规律.在欧洲直到1623年以后,法国数学家布莱士·帕斯卡的著作(1655年)介绍了这个三角形.近年来国外也逐渐承认这项成果属于中国,所以有些书上称这是“中国三角形”(Chinese triangle),如图 A.17世纪德国数学家莱布尼茨发现了“莱布尼茨三角形”如图B.在杨辉三角中相邻两行满足关系式:C r n+C r+1n =C r+1n+1,其中n是行数,r∈N.请类比上式,在莱布尼茨三角形中相邻两行满足的关系式是________.1 112 1133 11464 11510105 1…C0n C1n…C r n…C n-1n C n n图A1 21 21 316131 41121121415 120 130 120 15 16 130 160 160 130 16 1C 1n +1C 0n 1C 1n +1C 1n (1)C 1n +1C r n…1C 1n +1C n -1n 1C 1n +1C n n 图B答案1C 1n +1C r n =1C 1n +2C r n +1+1C 1n +2C r +1n +1 解析 类比观察得,莱布尼茨三角形的每一行都能提出倍数1C 1n +1,而相邻两项之和是上一行的两者相拱之数,所以类比式子C r n +C r +1n =C r +1n +1,有1C 1n +1C r n =1C 1n +2C r n +1+1C 1n +2C r +1n +1. 20.传说古希腊毕达哥拉斯学派的数学家经常在沙滩上面用点或用小石子表示数.他们研究过如图所示的三角形数,将三角形数1,3,6,10,…记为数列{a n },将可被5整除的三角形数按从小到大的顺序组成一个新数列{b n }.可以推测:(1)b 2 012是数列{a n }中的第________项; (2)b 2k -1=________.(用k 表示) 答案 (1)5 030 (2)5k (5k -1)2解析 由题意可得a n =1+2+3+…+n =n (n +1)2,n ∈N *, 故b 1=a 4,b 2=a 5,b 3=a 9,b 4=a 10,b 5=a 14,b 6=a 15, 由上述规律可知:b 2k =a 5k =5k (5k +1)2(k ∈N *), b 2k -1=a 5k -1=(5k -1)(5k -1+1)2=5k (5k -1)2,故b 2 012=b 2×1 006=a 5×1 006=a 5 030, 即b 2 012是数列{a n }中的第5 030项. 21.请认真阅读下列材料:“杨辉三角” (1261年)是中国古代重要的数学成就,它比西方的“帕斯卡三角”(1653年)早了300多年(如图1).在“杨辉三角”的基础上德国数学家莱布尼兹发现了下面的单位分数三角形(单位分数是分子为1,分母为正整数的分数),称为莱布尼兹三角形(如图2)11 112 1133 11464 1 1510105 1……图1111 21 21 316131 4112112141 512013012015……图2请回答下列问题:(1)记S n为图1中第n行各个数字之和,求S4,S7,并归纳出S n;(2)根据图2前5行的规律依次写出第6行的数.答案(1)S4=8=23;S7=64=26;Sn=2n-1.(2)图中每个数字都是其两脚的数字和,故第6行为1613016016013016.三、空间几何体1.我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水.天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平地降雨量是()寸.(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸)A.1 B.2 C.3 D.4答案 C解析如图,由题意可知,天池盆上底面半径为14寸,下底面半径为6寸,高为18寸.∵积水深9寸,∴水面半径为12(14+6)=10寸,则盆中水的体积为13π×9(62+102+6×10)=588π(立方寸).∴平地降雨量等于588ππ×142=3(寸). 故选C.2.《九章算术》卷5《商功》记载一个问题“今有圆堡瑽,周四丈八尺,高一丈一尺.问积几何?答曰:二千一百一十二尺.术曰:周自相乘,以高乘之,十二而一”.这里所说的圆堡瑽就是圆柱体,它的体积为“周自相乘,以高乘之,十二而一.”就是说:圆堡瑽(圆柱体)的体积为:V =112×(底面的圆周长的平方×高).则由此可推得圆周率π的取值为(注:1丈=10尺)( ) A .3 B .3.14 C .3.2 D .3.3答案 A解析 由题意,圆柱体底面的圆周长48尺,高11尺, ∵圆堡瑽(圆柱体)的体积V =112×(底面的圆周长的平方×高), ∴V =112×(482×11)=2 112, 设底面圆的半径为R ,∴⎩⎨⎧2πR =48,πR 2×11=2 112,∴π=3.3.《九章算术》商功章有题:一圆柱形谷仓,高1丈3尺313寸,容纳米2000斛(1丈=10尺,1尺=10寸,斛为容积单位,1斛≈1.62立方尺,π≈3),则圆柱底圆周长约为( ) A .1丈3尺 B .5丈4尺 C .9丈2尺 D .48丈6尺答案 B解析设圆柱形谷仓底面半径为r尺,由题意得,谷仓高h=403尺.于是谷仓的体积V=πr2·h≈2 000×1.62,解得r≈9.∴圆柱底圆周长约为2πr≈54尺=5丈4尺.4.《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“囷盖”的术:“置如其周,令相乘也.又以高乘之,三十六成一”.该术相当于给出了由圆锥的底面周长L与高h,计算其体积V的近似公式V≈136L2h.它实际上是将圆锥体积公式中的圆周率π近似取为3.那么,近似公式V≈275L2h相当于将圆锥体积公式中的π近似取为()A.227 B.258C.15750 D.355113答案 B解析由题意知275L2h≈13πr2h⇒275L2≈13πr2,而L=2πr,代入得π≈258.5.在《九章算术》中,将有三条棱互相平行且有一个面为梯形的五面体称之为羡除,现有一个羡除如图所示,面ABCD、面ABFE、面CDEF均为等腰梯形,AB∥CD∥EF,AB=6,CD=8,EF=10,EF到面ABCD的距离为3,CD与AB间的距离为10,则这个羡除的体积是()A.110 B.116C.118 D.120答案 D解析过A作AP⊥CD,AM⊥EF,过B作BQ⊥CD,BN⊥EF,垂足分别为P,M,Q,N,将一侧的几何体放到另一侧,组成一个直三棱柱,底面积为12×10×3=15.棱柱的高为8,∴V=15×8=120.故选D.6.刘徽在他的《九章算术注》中提出一个独特的方法来计算球体的体积:他不直接给出球体的体积,而是先计算另一个叫“牟合方盖”的立体的体积.刘徽通过计算,“牟合方盖”的体积与球的体积之比应为4π.后人导出了“牟合方盖”的18体积计算公式,即18V牟=r3-V方盖差,r为球的半径,也即正方形的棱长均为2r,从而计算出V球=43πr3.记所有棱长都为r的正四棱锥的体积为V正,棱长为2r的正方形的方盖差为V方盖差,则V方盖差V正等于()A.12 B.22C. 2D. 3 答案 C解析由题意,V方盖差=r3-18V牟=r3-18×4π×43×π×r3=13r3,所有棱长都为r的正四棱锥的体积为V正=13×r×r×r2-(22r)2=26r3,∴V方盖差V正=13r326r3= 2.7.“牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体.它由完全相同的四个曲面构成,相对的两个曲面在同一个圆柱的侧面上,好似两个扣合(牟合)在一起的方形伞(方盖).其直观图如图所示,图中四边形是为体现其直观性所作的辅助线,当其正视图与侧视图完全相同时,它的正视图和俯视图分别可能是()A.a,b B.a,cC.c,b D.b,d答案 A解析由直观图可知,其正视图与侧视图完全相同,则其只能是圆,这时其俯视图就是正方形加对角线(实线).故选A.8.刘徽在他的《九章算术注》中提出一个独特的方法来计算球体的体积:他不直接给出球体的体积,而是先计算另一个叫“牟合方盖”的立体的体积.刘徽通过计算,“牟合方盖”的体积与球的体积之比应为4∶π,即V牟:V球=4∶π.也导出了“牟合方盖”的18体积计算公式,即18V牟=r3-V方盖差,从而计算出V球=43πr3.记所有棱长都为r的正四棱锥的体积为V正,则()A.V方盖差>V正B.V方盖差=V正C.V方盖差<V正D.以上三种情况都有可能答案 A解析由题意,V方盖差=r3-18V牟=r3-18×4π×43πr3=13r3,所有棱长都为r的正四棱锥的体积为V正=13×r×r×r2-(22r)2=26r3,∴V方盖差>V正.9.我国古代数学名著《数学九章》中有云:“今有木长二丈四尺,围之五尺.葛生其下,缠木两周,上与木齐,问葛长几何?”其意思为“圆木长2丈4尺,圆周为5尺,葛藤从圆木的底部开始向上生长,绕圆木两周,刚好顶部与圆木平齐,问葛藤最少长多少尺(注:1丈等于10尺)()A.29尺B.24尺C.26尺D.30尺21答案 C解析由题意,圆柱的侧面展开图是矩形,一条直角边(即木棍的高)长24尺,另一条直角边长5×2=10(尺),因此葛藤长242+102=26(尺).10.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为9尺,米堆的高为5尺,米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米有()A.14斛B.28斛C.36斛D.66斛答案 B解析设圆锥的底面半径为r,则π2r=9,解得r=18π,故米堆的体积为14×13×π×(18π)2×5≈45,∵1斛米的体积约为1.62立方,∴堆放的米有45÷1.62≈28斛.11.《九章算术》是我国古代著名数学经典.其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺.问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示(阴影部分为镶嵌在墙体内的部分).已知弦AB=1尺,弓形高CD=1寸,估算该木材镶嵌在墙中的体积约为()(注:1丈=10尺=100寸,π≈3.14,sin 22.5°≈5 13)22A.600立方寸B.610立方寸C.620立方寸D.633立方寸答案 D解析如图,AB=10(寸),则AD=5(寸),CD=1(寸),设圆O的半径为x(寸),则OD=(x-1)(寸),在Rt△ADO中,由勾股定理可得52+(x-1)2=x2,解得x=13(寸).∴sin∠AOD=ADAO=513,即∠AOD≈22.5°,则∠AOB=45°.则弓形¼ACB的面积S=12×π4×132-12×10×12≈6.33(平方寸).则该木材镶嵌在墙中的体积约为V=6.33×100=633(立方寸).故选D.12.鲁班锁是中国传统的智力玩具,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称.从外表上看,六根等长的正四棱柱体分成三组,经90°榫卯起来,如图,若正四棱柱体的高为6,底面正方形的边长为1,现将该鲁班锁放进一个球形容器内,则该球形容器的表面积的最小值为________.(容器壁的厚度忽略不计)23答案41π解析由题意,该球形容器的半径的最小值为1236+4+1=412,∴该球形容器的表面积的最小值为4π·414=41π.13.沙漏是古代的一种计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时.如图,某沙漏由上下两个圆锥组成,圆锥的底面直径和高均为8 cm,细沙全部在上部时,其高度为圆锥高度的23(细管长度忽略不计).(1)如果该沙漏每秒钟漏下0.02 cm3的沙,则该沙漏的一个沙时为多少秒(精确到1秒)?(2)细沙全部漏入下部后,恰好堆成一个盖住沙漏底部的圆锥形沙堆,求此锥形沙堆的高度(精确到0.1cm).答案(1)开始时,沙漏上部分圆锥中的细沙的高为H=23×8=163,底面半径为r=23×4=83,V=13πr2H=13π×(83)2×163=39.71,V÷0.02=1 986(秒).所以沙全部漏入下部约需1 986秒.24。
数列中包含的数学文化

数列中包含的数学文化数学家的故事———数学王子高斯高斯(Carl Fried rich Gauss,1777~1855)德国数学家、天文学家和物理学家,被誉为历史上伟大的数学家之一,和阿基米德、牛顿并列,同享盛名。
1777年4月30日生于不伦瑞克的一个工匠家庭,1855年2月23日卒于格丁根。
幼时家境贫困,但聪敏异常,受一贵族资助才进学校受教育。
1795~1798年在格丁根大学学习1798年转入黑尔姆施泰特大学,翌年因证明代数基本定理获博士学位。
从1807年起担任格丁根大学教授兼格丁根天文台台长直至逝世。
高斯是近代数学奠基者之一,在历史上影响之大,可以和阿基米德、牛顿、欧拉并列,有“数学王子”之称。
高斯的成就遍及数学的各个领域,在数论、非欧几何、微分几何、超几何级数、复变函数论以及椭圆函数论等方面均有开创性贡献。
他十分注重数学的应用,并且在对天文学、大地测量学和磁学的研究中也偏重于用数学方法进行研究。
幼年时,他在数学方面就显示出了非凡的才华。
3岁能纠正父亲计算中的错误;10岁便独立发现了算术级数的求和公式;11岁发现了二项式定理。
少年高斯的聪颖早慧,得到了很有名望的布瑞克公爵的垂青与资助,使他得以不断深造。
19岁的高斯在进大学不久,就发明了只用圆规和直尺作出正17边形的方法,解决了两千年来悬而未决的几何难题。
1801年,他发表的《算术研究》,阐述了数论和高等代数的某些问题。
他对超几何级数、复变函数、统计数学、椭圆函数论都有重大贡献。
作为一个物理学家,他与威廉.韦伯合作研究电磁学,并发明了电极。
为了进行实验,高斯还发明了双线磁力计,这是他对电磁学问题研究的一个很有实际意义的成果。
高斯30岁时担任了德国著名高等学府天文台台长,并一直在天文台工作到逝世。
他平生还喜欢文学和语言学,懂得十几门外语。
他一生共发表323篇(种)著作,提出了404项科学创见,完成了4项重要发明。
数学文化网课新版答案

数学文化数学文化(一)12002年,为中国少年数学论坛活动题词“数学好玩”的是(D)。
A、邓东皋B、钱学森C、齐民友D、陈省身2“数学文化”一词最早进入官方文件,是出现在中华人民共和国教育部颁布的(C)。
A、《小学数学课程标准》B、《初中数学课程标准》C、《高中数学课程标准》D、《大学数学课程标准》3数学的研究对象是从众多物质形态种抽象出来的人脑的产物,这是它与其他自然科学研究的一个共同点。
()正确答案:×4广义的数学文化,是指数学的思想、精神、方法、观点、语言,以及他们的形成和发展。
()正确答案:×数学文化(二)11998年以后,教育部的专业目录里规定了数学学科专业,包括数学与应用数学专业、(C)。
A、统计学B、数理统计学C、信息与计算科学专业D、数学史与数学文化2数学目前仅仅是一种重要的工具,要上升至思维模式的高度,还需学者们的探索。
()正确答案:×3数学素养的通俗说法,是指在经过数学学习后,将所学的数学知识都排除或忘掉后,剩下的东西。
()正确答案:√数学文化(三)1“数学文化”课是以数学问题为载体,以教授数学系统知识及其应用为目的。
()正确答案:×2反证法是解决数学难题的一种有效方法。
()正确答案:√数学文化(四)1“哥尼斯堡七桥问题”最后是被谁解决的?(B)A、阿基米德B、欧拉C、高斯D、笛卡尔2在解决“哥尼斯堡七桥问题”时,数学家先做的第一步是(D)。
A、分析B、概括C、推理D、抽象3数学是研究现实世界中的数量关系与空间形式的一门科学。
这句话出自(C)。
A、阿基米德B、欧拉C、恩格斯D、马克思4从牛顿的著作《自然哲学之数学原理》可以看出,他是不支持数学定义中的“哲学说”的。
()正确答案:×5罗素关于数学概念的描述,是从数学的公理体系角度而言的。
()正确答案:√数学文化(六)1一堆20粒的谷粒,甲乙两个人轮流抓,每次可以抓一粒到五粒,规定谁抓到最后一把谁赢。
2024年高考数学专项复习数列考查的九个热点(解析版)

数列考查的九个热点热点题型速览热点一等差数列的基本计算热点二等比数列的基本计算热点三等差数列与等比数列的综合计算热点四数列与函数的交汇热点五数列与不等式交汇热点六数列与解析几何交汇热点七数列与概率统计交汇热点八等差数列、等比数列的判断与证明热点九数列中的“新定义”问题热点一等差数列的基本计算1(2023春·河南开封·高三通许县第一高级中学校考阶段练习)已知等差数列a n 为递增数列,S n 为其前n 项和,a 3+a 7=34,a 4⋅a 6=280,则S 11=()A.516B.440C.258D.2202(2022秋·黑龙江哈尔滨·高三哈师大附中校考期中)某种卷筒卫生纸绕在圆柱形盘上,空盘时盘芯直径为60mm ,满盘时直径为120mm ,已知卫生纸的厚度为0.1mm ,则满盘时卫生纸的总长度大约( )(π≈3.14,精确到1m )A.65mB.85mC.100mD.120m3(2020·全国高考真题(理))北京天坛的圜丘坛为古代祭天的场所,分上、中、下三层,上层中心有一块圆形石板(称为天心石),环绕天心石砌9块扇面形石板构成第一环,向外每环依次增加9块,下一层的第一环比上一层的最后一环多9块,向外每环依次也增加9块,已知每层环数相同,且下层比中层多729块,则三层共有扇面形石板(不含天心石)()A.3699块B.3474块C.3402块D.3339块2024年高考数学专项复习数列考查的九个热点(解析版)4(2022·全国·统考高考真题)记S n为等差数列a n的前n项和.若2S3=3S2+6,则公差d=.【规律方法】1.等差数列中的基本量a1,a n,d,n,S n,“知三可求二”,在求解过程中主要运用方程思想.要注意使用公式时的准确性与合理性,更要注意运算的准确性.在遇到一些较复杂的方程组时,要注意运用整体代换思想,使运算更加便捷.2. 在等差数列{a n}中,若出现a m-n,a m,a m+n等项时,可以利用等差数列的性质将其转化为与a m有关的条件;若求a m项,可由a m=12(a m-n+a m+n)转化为求a m-n,a m+n或a m-n+a m+n的值.3.数列的基本计算,往往以数学文化问题为背景.热点二等比数列的基本计算5(2020·全国·统考高考真题)设{a n}是等比数列,且a1+a2+a3=1,a2+a3+a4=2,则a6+a7+a8= ()A.12B.24C.30D.326(2023·广东揭阳·惠来县第一中学校考模拟预测)在《增减算法统宗》中有这样一则故事:“三百七十八里关,初行健步不为难;次日脚痛减一半,如此六日过其关”.其大意是:有人要去某关口,路程为378里,第一天健步行走,从第二天起由于脚痛,每天走的路程都为前一天的一半,一共走了六天,才到目的地.则此人后3天共走的里程数为()A.6B.12C.18D.427(2023·全国高考真题)已知a n为等比数列,a2a4a5=a3a6,a9a10=-8,则a7=.【规律方法】1.等比数列运算问题的一般求法是设出首项a1和公比q,然后由通项公式或前n项和公式转化为方程(组)求解.2.等比数列的通项公式及前n项和公式,共涉及五个量a1,a n,q,n,S n,知其中三个就能求另外两个,体现了用方程的思想解决问题.3.根据题目特点,可选用等比数列的性质.热点三等差数列与等比数列的综合计算8(2019·北京·高考真题)设{an}是等差数列,a1=-10,且a2+10,a3+8,a4+6成等比数列.(Ⅰ)求{an}的通项公式;(Ⅱ)记{an}的前n项和为Sn,求Sn的最小值.9(2022·全国·统考高考真题)记S n为数列a n的前n项和.已知2S nn+n=2a n+1.(1)证明:a n是等差数列;(2)若a4,a7,a9成等比数列,求S n的最小值.10(2023·天津·统考高考真题)已知a n是等差数列,a2+a5=16,a5-a3=4.(1)求a n的通项公式和2n-1i=2n-1a i .(2)已知b n为等比数列,对于任意k∈N*,若2k-1≤n≤2k-1,则b k<a n<b k+1,(Ⅰ)当k≥2时,求证:2k-1<b k<2k+1;(Ⅱ)求b n 的通项公式及其前n 项和.热点四数列与函数的交汇11(2018·浙江·高考真题)已知a 1,a 2,a 3,a 4成等比数列,且a 1+a 2+a 3+a 4=ln (a 1+a 2+a 3).若a 1>1,则A.a 1<a 3,a 2<a 4B.a 1>a 3,a 2<a 4C.a 1<a 3,a 2>a 4D.a 1>a 3,a 2>a 412(2023秋·湖南长沙·高三雅礼中学校考阶段练习)如图1所示,古筝有多根弦,每根弦下有一个雁柱,雁柱用于调整音高和音质.图2是根据图1绘制的古筝弦及其雁柱的简易平面图.在图2中,每根弦都垂直于x 轴,相邻两根弦间的距离为1,雁柱所在曲线的方程为y =1.1x ,第n 根弦(n ∈N ,从左数首根弦在y 轴上,称为第0根弦)分别与雁柱曲线和直线l :y =x +1交于点A n x n ,y n 和B n x n,y n,则20n =0y n y n=.(参考数据:取1.122=8.14.)13(2023秋·福建厦门·高三厦门一中校考阶段练习)已知数列a n 满足a 1>0,a n +1=log 2a n ,n =2k -1,k ∈N ∗2a n+2,n =2k ,k ∈N ∗.(1)判断数列a 2n -1 是否是等比数列?若是,给出证明;否则,请说明理由;(2)若数列a n 的前10项和为361,记b n =1log 2a 2n +1 ⋅a 2n +2,数列b n 的前n 项和为T n ,求证:T n <12.14(2023·全国·高三专题练习)已知A x 1,y 2 、B x 2,y 2 是函数f x =2x 1-2x ,x ≠12-1,x =12的图象上的任意两点,点M 在直线x =12上,且AM =MB .(1)求x 1+x 2的值及y 1+y 2的值;(2)已知S 1=0,当n ≥2时,S n =f 12 +f 2n +f 3n +⋅⋅⋅+f n -1n,设a n =2Sn,T n 数列a n 的前n 项和,若存在正整数c ,m ,使得不等式T m -c T m +1-c <12成立,求c 和m 的值;热点五数列与不等式交汇15(2022·浙江·统考高考真题)已知数列a n 满足a 1=1,a n +1=a n -13a 2n n ∈N ∗,则()A.2<100a 100<52 B.52<100a 100<3 C.3<100a 100<72 D.72<100a 100<416(2023·浙江嘉兴·统考模拟预测)如图,在一个单位正方形中,首先将它等分成4个边长为12的小正方形,保留一组不相邻的2个小正方形,记这2个小正方形的面积之和为S 1;然后将剩余的2个小正方形分别继续四等分,各自保留一组不相邻的2个小正方形,记这4个小正方形的面积之和为S 2.以此类推,操作n 次,若S 1+S 2+⋅⋅⋅+S n ≥20232024,则n 的最小值是()A.9B.10C.11D.1217(2023秋·四川绵阳·高三绵阳中学校考阶段练习)已知等差数列a n 的前n 项和为S n ,且S 4=4S 2,a 3n =3a n +2n ∈N *(1)求a n 的通项公式,(2)设b n =1a n a n +1,且b n 的前n 项和为T n ,证明,13≤T n <12.18(2022·全国·统考高考真题)记S n 为数列a n 的前n 项和,已知a 1=1,S n a n 是公差为13的等差数列.(1)求a n 的通项公式;(2)证明:1a 1+1a 2+⋯+1a n<2.19(2021·全国·统考高考真题)设a n 是首项为1的等比数列,数列b n 满足b n =na n3.已知a 1,3a 2,9a 3成等差数列.(1)求a n 和b n 的通项公式;(2)记S n 和T n 分别为a n 和b n 的前n 项和.证明:T n <S n2.20(2023·河南郑州·统考模拟预测)已知数列a n 与b n 的前n 项和分别为A n 和B n ,且对任意n ∈N *,a n +1-a n =32b n +1-b n 恒成立.(1)若A n =3n 2+3n2,b 1=2,求B n ;(2)若对任意n ∈N *,都有a n =B n 及b 2a 1a 2+b 3a 2a 3+b 4a 3a 4+⋯+b n +1a n a n +1<13恒成立,求正整数b 1的最小值.21(2023秋·云南·高三云南师大附中校考阶段练习)已知a n 为等差数列,b n 为等比数列,b 1=2a 1=2,a 5=5a 4-a 3 ,b 5=4b 4-b 3 ,数列c n 满足c n =1a n a n +2,n 为奇数b n,n 为偶数.(1)求a n 和b n 的通项公式;(2)证明:2ni =1c i ≥133.热点六数列与解析几何交汇22(2022·全国·统考高考真题)图1是中国古代建筑中的举架结构,AA ,BB ,CC ,DD 是桁,相邻桁的水平距离称为步,垂直距离称为举,图2是某古代建筑屋顶截面的示意图.其中DD 1,CC 1,BB 1,AA 1是举,OD 1,DC 1,CB 1,BA 1是相等的步,相邻桁的举步之比分别为DD 1OD 1=0.5,CC 1DC 1=k 1,BB 1CB 1=k 2,AA 1BA 1=k 3.已知k 1,k 2,k 3成公差为0.1的等差数列,且直线OA 的斜率为0.725,则k 3=()A.0.75B.0.8C.0.85D.0.923(重庆·高考真题)设A x 1,y 1 ,B 4,95 ,C x 2,y 2 是右焦点为F 的椭圆x 225+y 29=1上三个不同的点,则“|AF |,|BF |,|CF |成等差数列”是“x 1+x 2=8”的()A.充要条件B.必要而不充分条件C.充分而不必要条件D.既不充分也不必要条件24(2021·浙江·统考高考真题)已知a ,b ∈R ,ab >0,函数f x =ax 2+b (x ∈R ).若f (s -t ),f (s ),f (s +t )成等比数列,则平面上点s ,t 的轨迹是()A.直线和圆B.直线和椭圆C.直线和双曲线D.直线和抛物线热点七数列与概率统计交汇25(2023秋·江西·高三校联考阶段练习)甲同学现参加一项答题活动,其每轮答题答对的概率均为13,且每轮答题结果相互独立.若每轮答题答对得5分,答错得0分,记第i 轮答题后甲同学的总得分为X i ,其中i =1,2,⋅⋅⋅,n .(1)求E X 99 ;(2)若乙同学也参加该答题活动,其每轮答题答对的概率均为23,并选择另一种答题方式答题:从第1轮答题开始,若本轮答对,则得20分,并继续答题;若本轮答错,则得0分,并终止答题,记乙同学的总得分为Y .证明:当i >24时,E X i >E Y .26(2023秋·湖北荆州·高三沙市中学校考阶段练习)在正三棱柱ABC -A 1B 1C 1中,点A 处有一只小蚂蚁,每次随机等可能地沿各条棱或侧面对角线向另一顶点移动,设小蚂蚁移动n 次后仍在底面ABC 的顶点处的概率为P n .(1)求P1,P2的值.(2)求P n.27(2019·全国·高考真题(理))为了治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得-1分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得-1分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X.(1)求X的分布列;(2)若甲药、乙药在试验开始时都赋予4分,p i(i=0,1,⋯,8)表示“甲药的累计得分为i时,最终认为甲药比乙药更有效”的概率,则p0=0,p8=1,p i=ap i-1+bp i+cp i+1(i=1,2,⋯,7),其中a=P(X=-1),b=P(X=0),c=P(X=1).假设α=0.5,β=0.8.(i)证明:{p i+1-p i}(i=0,1,2,⋯,7)为等比数列;(ii)求p4,并根据p4的值解释这种试验方案的合理性.热点八等差数列、等比数列的判断与证明28【多选题】(2022·广东茂名·模拟预测)已知数列a n的前n项和为S,a1=1,S n+1=S n+2a n+1,数列2na n⋅a n+1的前n项和为Tn,n∈N*,则下列选项正确的为()A.数列a n+1是等比数列 B.数列a n+1是等差数列C.数列a n的通项公式为a n=2n-1 D.T n>129(2021·全国·统考高考真题)记S n为数列a n的前n项和,b n为数列S n的前n项积,已知2S n+1b n=2.(1)证明:数列b n是等差数列;(2)求a n的通项公式.热点九数列中的“新定义”问题30(2020·全国·统考高考真题)0-1周期序列在通信技术中有着重要应用.若序列a1a2⋯a n⋯满足a i∈{0,1}(i=1,2,⋯),且存在正整数m,使得a i+m=a i(i=1,2,⋯)成立,则称其为0-1周期序列,并称满足a i+m=a i(i=1,2,⋯)的最小正整数m为这个序列的周期.对于周期为m的0-1序列a1a2⋯a n⋯,C(k)=1 mmi=1a i a i+k(k=1,2,⋯,m-1)是描述其性质的重要指标,下列周期为5的0-1序列中,满足C(k)≤15(k=1,2,3,4)的序列是()A.11010⋯B.11011⋯C.10001⋯D.11001⋯31【多选题】(2023秋·湖南长沙·高三周南中学校考阶段练习)古希腊毕达哥拉斯学派的数学家用沙粒和小石子来研究数,他们根据沙粒或小石子所排列的形状,把数分成许多类,如图中第一行图形中黑色小点个数:1,3,6,10,⋯称为三角形数,第二行图形中黑色小点个数:1,4,9,16,⋯称为正方形数,记三角形数构成数列a n,正方形数构成数列b n,则下列说法正确的是()A.1b 1+1b 2+1b 3+⋯+1b n<2;B.1225既是三角形数,又是正方形数;C.10i =11b i +1-a i +1=95;D.∀m ∈N *,m ≥2总存在p ,q ∈N *,使得b m =a p +a q 成立;32(2022秋·山东·高三校联考阶段练习)若项数为n 的数列a n 满足:a i =a n +1-i i =1,2,3,⋯,n 我们称其为n 项的“对称数列”.例如:数列1,2,2,1为4项的“对称数列”;数列1,2,3,2,1为5项的“对称数列”.设数列c n 为2k +1项的“对称数列”,其中c 1,c 2⋯c k +1是公差为2的等差数列,数列c n 的最大项等于8,记数列c n 的前2k +1项和为S 2k +1,若S 2k +1=32,则k =.数列考查的九个热点热点题型速览热点一等差数列的基本计算热点二等比数列的基本计算热点三等差数列与等比数列的综合计算热点四数列与函数的交汇热点五数列与不等式交汇热点六数列与解析几何交汇热点七数列与概率统计交汇热点八等差数列、等比数列的判断与证明热点九数列中的“新定义”问题热点一等差数列的基本计算1(2023春·河南开封·高三通许县第一高级中学校考阶段练习)已知等差数列a n 为递增数列,S n 为其前n 项和,a 3+a 7=34,a 4⋅a 6=280,则S 11=()A.516 B.440C.258D.220【答案】D【分析】根据给定条件,利用等差数列性质求出a 4,a 6,再利用前n 项和公式求解作答.【详解】等差数列a n 为递增数列,则a 4<a 6,由a 3+a 7=34,得a 4+a 6=34,而a 4⋅a 6=280,解得a 4=14,a 6=20,所以S 11=11(a 1+a 11)2=11a 6=220.故选:D2(2022秋·黑龙江哈尔滨·高三哈师大附中校考期中)某种卷筒卫生纸绕在圆柱形盘上,空盘时盘芯直径为60mm ,满盘时直径为120mm ,已知卫生纸的厚度为0.1mm ,则满盘时卫生纸的总长度大约( )(π≈3.14,精确到1m )A.65m B.85mC.100mD.120m【答案】B【分析】依题意,可以把绕在盘上的卫生纸长度,近似看成300个半径成等差数列的圆周长,然后分别计算各圆的周长,再借助等差数列前n 项和公式求总和即可.【详解】因为空盘时盘芯直径为60mm ,则半径为30mm ,周长为2π×30=60πmm ,又满盘时直径为120mm ,则半径为60mm ,周长为2π×60=120πmm ,又因为卫生纸的厚度为0.1mm ,则60-300.1=300,即每一圈周长成等差数列,项数为300,于是根据等差数列的求和公式,得:S300=300×60π+120π2=27000πmm ,又27000πmm≈84780mm≈85m,即满盘时卫生纸的总长度大约为85m,故选:B.3(2020·全国高考真题(理))北京天坛的圜丘坛为古代祭天的场所,分上、中、下三层,上层中心有一块圆形石板(称为天心石),环绕天心石砌9块扇面形石板构成第一环,向外每环依次增加9块,下一层的第一环比上一层的最后一环多9块,向外每环依次也增加9块,已知每层环数相同,且下层比中层多729块,则三层共有扇面形石板(不含天心石)()A.3699块B.3474块C.3402块D.3339块【答案】C【解析】设第n环天石心块数为a n,第一层共有n环,则a n是以9为首项,9为公差的等差数列,a n=9+n-1×9=9n,设S n为a n的前n项和,则第一层、第二层、第三层的块数分别为S n,S2n-S n,S3n-S2n,因为下层比中层多729块,所以S3n-S2n=S2n-S n+729,即3n9+27n2-2n9+18n2=2n9+18n2-n9+9n2+729即9n2=729,解得n=9,所以S3n=S27=279+9×272=3402.故选:C4(2022·全国·统考高考真题)记S n为等差数列a n的前n项和.若2S3=3S2+6,则公差d=.【答案】2【分析】转化条件为2a1+2d=2a1+d+6,即可得解.【详解】由2S3=3S2+6可得2a1+a2+a3=3a1+a2+6,化简得2a3=a1+a2+6,即2a1+2d=2a1+d+6,解得d=2.故答案为:2.【规律方法】1.等差数列中的基本量a1,a n,d,n,S n,“知三可求二”,在求解过程中主要运用方程思想.要注意使用公式时的准确性与合理性,更要注意运算的准确性.在遇到一些较复杂的方程组时,要注意运用整体代换思想,使运算更加便捷.2. 在等差数列{a n}中,若出现a m-n,a m,a m+n等项时,可以利用等差数列的性质将其转化为与a m有关的条件;若求a m 项,可由a m =12(a m -n +a m +n)转化为求a m -n ,a m +n 或a m -n +a m +n 的值.3.数列的基本计算,往往以数学文化问题为背景.热点二等比数列的基本计算5(2020·全国·统考高考真题)设{a n }是等比数列,且a 1+a 2+a 3=1,a 2+a 3+a 4=2,则a 6+a 7+a 8=()A.12B.24C.30D.32【答案】D【分析】根据已知条件求得q 的值,再由a 6+a 7+a 8=q 5a 1+a 2+a 3 可求得结果.【详解】设等比数列a n 的公比为q ,则a 1+a 2+a 3=a 11+q +q 2 =1,a 2+a 3+a 4=a 1q +a 1q 2+a 1q 3=a 1q 1+q +q 2 =q =2,因此,a 6+a 7+a 8=a 1q 5+a 1q 6+a 1q 7=a 1q 51+q +q 2 =q 5=32.故选:D .6(2023·广东揭阳·惠来县第一中学校考模拟预测)在《增减算法统宗》中有这样一则故事:“三百七十八里关,初行健步不为难;次日脚痛减一半,如此六日过其关”.其大意是:有人要去某关口,路程为378里,第一天健步行走,从第二天起由于脚痛,每天走的路程都为前一天的一半,一共走了六天,才到目的地.则此人后3天共走的里程数为()A.6B.12C.18D.42【答案】D【分析】设第n n ∈N ∗ 天走a n 里,其中1≤n ≤6,由题意可知,数列a n 是公比为12的等比数列,利用等比数列的求和公式求出a 1的值,然后利用等比数列的求和公式可求得此人后3天共走的里程数.【详解】设第n n ∈N ∗ 天走a n 里,其中1≤n ≤6,由题意可知,数列a n 是公比为12的等比数列,所以,a 11-12 6 1-12=6332a 1=378,解得a 1=378×3263=192,所以,此人后三天所走的里程数为a 4+a 5+a 6=192×181-1231-12=42.故选:D .7(2023·全国高考真题)已知a n 为等比数列,a 2a 4a 5=a 3a 6,a 9a 10=-8,则a 7=.【答案】-2【分析】根据等比数列公式对a 2a 4a 5=a 3a 6化简得a 1q =1,联立a 9a 10=-8求出q 3=-2,最后得a 7=a 1q ⋅q 5=q 5=-2.【解析】设a n 的公比为q q ≠0 ,则a 2a 4a 5=a 3a 6=a 2q ⋅a 5q ,显然a n ≠0,则a 4=q 2,即a 1q 3=q 2,则a 1q =1,因为a 9a 10=-8,则a 1q 8⋅a 1q 9=-8,则q 15=q 5 3=-8=-2 3,则q 3=-2,则a 7=a 1q ⋅q 5=q 5=-2,故答案为:-2.【规律方法】1.等比数列运算问题的一般求法是设出首项a 1和公比q ,然后由通项公式或前n 项和公式转化为方程(组)求解.2.等比数列的通项公式及前n 项和公式,共涉及五个量a 1,a n ,q ,n ,S n ,知其中三个就能求另外两个,体现了用方程的思想解决问题.3.根据题目特点,可选用等比数列的性质.热点三等差数列与等比数列的综合计算8(2019·北京·高考真题)设{an }是等差数列,a 1=-10,且a 2+10,a 3+8,a 4+6成等比数列.(Ⅰ)求{an }的通项公式;(Ⅱ)记{an }的前n 项和为Sn ,求Sn 的最小值.【答案】(Ⅰ)a n =2n -12;(Ⅱ)-30.【分析】(Ⅰ)由题意首先求得数列的公差,然后利用等差数列通项公式可得a n 的通项公式;(Ⅱ)首先求得S n 的表达式,然后结合二次函数的性质可得其最小值.【详解】(Ⅰ)设等差数列a n 的公差为d ,因为a 2+10,a 3+8,a 4+6成等比数列,所以(a 3+8)2=(a 2+10)(a 4+6),即(2d -2)2=d (3d -4),解得d =2,所以a n =-10+2(n -1)=2n -12.(Ⅱ)由(Ⅰ)知a n =2n -12,所以S n =-10+2n -122×n =n 2-11n =n -112 2-1214;当n =5或者n =6时,S n 取到最小值-30.9(2022·全国·统考高考真题)记S n 为数列a n 的前n 项和.已知2S nn+n =2a n +1.(1)证明:a n 是等差数列;(2)若a 4,a 7,a 9成等比数列,求S n 的最小值.【答案】(1)证明见解析;(2)-78.【分析】(1)依题意可得2S n +n 2=2na n +n ,根据a n =S 1,n =1S n-Sn -1,n ≥2,作差即可得到a n -a n -1=1,从而得证;(2)法一:由(1)及等比中项的性质求出a 1,即可得到a n 的通项公式与前n 项和,再根据二次函数的性质计算可得.【详解】(1)因为2S nn+n =2a n +1,即2S n +n 2=2na n +n ①,当n ≥2时,2S n -1+n -1 2=2n -1 a n -1+n -1 ②,①-②得,2S n +n 2-2S n -1-n -1 2=2na n +n -2n -1 a n -1-n -1 ,即2a n +2n -1=2na n -2n -1 a n -1+1,即2n -1 a n -2n -1 a n -1=2n -1 ,所以a n -a n -1=1,n ≥2且n ∈N *,所以a n 是以1为公差的等差数列.(2)[方法一]:二次函数的性质由(1)可得a 4=a 1+3,a 7=a 1+6,a 9=a 1+8,又a 4,a 7,a 9成等比数列,所以a 72=a 4⋅a 9,即a 1+6 2=a 1+3 ⋅a 1+8 ,解得a 1=-12,所以a n=n-13,所以S n=-12n+n n-12=12n2-252n=12n-2522-6258,所以,当n=12或n=13时,S nmin=-78.[方法二]:【最优解】邻项变号法由(1)可得a4=a1+3,a7=a1+6,a9=a1+8,又a4,a7,a9成等比数列,所以a72=a4⋅a9,即a1+62=a1+3⋅a1+8,解得a1=-12,所以a n=n-13,即有a1<a2<⋯<a12<0,a13=0.则当n=12或n=13时,S nmin=-78.【整体点评】(2)法一:根据二次函数的性质求出S n的最小值,适用于可以求出S n的表达式;法二:根据邻项变号法求最值,计算量小,是该题的最优解.10(2023·天津·统考高考真题)已知a n是等差数列,a2+a5=16,a5-a3=4.(1)求a n的通项公式和2n-1i=2n-1a i .(2)已知b n为等比数列,对于任意k∈N*,若2k-1≤n≤2k-1,则b k<a n<b k+1,(Ⅰ)当k≥2时,求证:2k-1<b k<2k+1;(Ⅱ)求b n的通项公式及其前n项和.【答案】(1)a n=2n+1,2n-1i=2n-1a i=3⋅4n-1;(2)(Ⅰ)证明见解析;(Ⅱ)b n=2n,前n项和为2n+1-2.【分析】(1)由题意得到关于首项、公差的方程,解方程可得a1=3,d=2,据此可求得数列的通项公式,然后确定所给的求和公式里面的首项和项数,结合等差数列前n项和公式计算可得2n-1i=2n-1a i=3⋅4n-1.(2)(Ⅰ)利用题中的结论分别考查不等式两侧的情况,当2k-1≤n≤2k-1时,b k<a n,取n=2k-1,当2k-2≤n≤2k-1-1时,a n<b k,取n=2k-1-1,即可证得题中的不等式;(Ⅱ)结合(Ⅰ)中的结论,利用极限思想确定数列的公比,进而可得数列的通项公式,最后由等比数列前n 项和公式即可计算其前n项和.【详解】(1)由题意可得a2+a5=2a1+5d=16a5-a3=2d=4,解得a1=3d=2,则数列a n的通项公式为a n=a1+n-1d=2n+1,求和得2n-1i=2n-1a i=2n-1i=2n-12i+1=22n-1i=2n-1i+2n-1-2n-1+1=22n-1+2n-1+1+2n-1+2+⋯+2n-1+2n-1=22n-1+2n-1⋅2n-12+2n-1=3⋅4n-1.(2)(Ⅰ)由题意可知,当2k-1≤n≤2k-1时,b k<a n,取n=2k-1,则b k<a2k-1=2×2k-1+1=2k+1,即b k<2k+1,当2k-2≤n≤2k-1-1时,a n<b k,取n=2k-1-1,此时a n=a2k-1-1=22k-1-1+1=2k-1,据此可得2k-1<b k,综上可得:2k-1<b k<2k+1.(Ⅱ)由(Ⅰ)可知:2k-1<bk<2k+1,2k+1-1<b k+1<2k+1+1则数列b n的公比q满足2k+1-12k+1=2-32k+1<q=b k+1b k<2k+1+12k-1=2+32k-1,当k∈N*,k→+∞时,2-3 2k+1→2,2+32k-1→2,所以q=2,所以2k-1<b12k-1<2k+1,即2k-12k-1=2-12k-1<b1<2k+12k-1=2+12k-1,当k∈N*,k→+∞时,2-1 2k-1→2,2+12k-1→2,所以b1=2,所以数列的通项公式为b n=2n,其前n项和为:S n=2×1-2n1-2=2n+1-2.热点四数列与函数的交汇11(2018·浙江·高考真题)已知a1,a2,a3,a4成等比数列,且a1+a2+a3+a4=ln(a1+a2+a3).若a1>1,则A.a1<a3,a2<a4B.a1>a3,a2<a4C.a1<a3,a2>a4D.a1>a3,a2>a4【答案】B【分析】先证不等式x≥ln x+1,再确定公比的取值范围,进而作出判断.【详解】令f(x)=x-ln x-1,则f (x)=1-1x,令f(x)=0,得x=1,所以当x>1时,f (x)>0,当0<x<1时,f (x)<0,因此f(x)≥f(1)=0,∴x≥ln x+1,若公比q>0,则a1+a2+a3+a4>a1+a2+a3>ln(a1+a2+a3),不合题意;若公比q≤-1,则a1+a2+a3+a4=a1(1+q)(1+q2)≤0,但ln(a1+a2+a3)=ln[a1(1+q+q2)]>ln a1>0,即a1+a2+a3+a4≤0<ln(a1+a2+a3),不合题意;因此-1<q<0,q2∈(0,1),∴a1>a1q2=a3,a2<a2q2=a4<0,选B.【点睛】构造函数对不等式进行放缩,进而限制参数取值范围,是一个有效方法.如x≥ln x+1,e x≥x+1,e x≥x2+1(x≥0).12(2023秋·湖南长沙·高三雅礼中学校考阶段练习)如图1所示,古筝有多根弦,每根弦下有一个雁柱,雁柱用于调整音高和音质.图2是根据图1绘制的古筝弦及其雁柱的简易平面图.在图2中,每根弦都垂直于x轴,相邻两根弦间的距离为1,雁柱所在曲线的方程为y=1.1x,第n根弦(n∈N,从左数首根弦在y轴上,称为第0根弦)分别与雁柱曲线和直线l:y=x+1交于点A n x n,y n和B n x n ,y n,则20n=0y n y n=.(参考数据:取1.122=8.14.)【答案】914【分析】根据题意可得y n =n +1,y n=1.1n ,进而利用错位相减法运算求解.【详解】由题意可知:y n =n +1,y n =1.1n ,则20n =0y n y n=20n =0n +1 1.1n =1×1.10+2×1.11+⋯+20×1.119+21×1.120,可得1.1×20n =0y n y n =1×1.11+2×1.12+⋯+20×1.120+21×1.121,两式相减可得:-0.1×20n =0y n y n=1.10+1.11+⋯+1.120-21×1.121=1-1.1211-1.1-21×1.121=1-1.121+0.1×21×1.121-0.1=1+1.122-0.1=1+8.14-0.1=-91.4,所以20n =0y n y n=914.故答案为:914.13(2023秋·福建厦门·高三厦门一中校考阶段练习)已知数列a n 满足a 1>0,a n +1=log 2a n ,n =2k -1,k ∈N ∗2a n+2,n =2k ,k ∈N ∗.(1)判断数列a 2n -1 是否是等比数列?若是,给出证明;否则,请说明理由;(2)若数列a n 的前10项和为361,记b n =1log 2a 2n +1 ⋅a 2n +2,数列b n 的前n 项和为T n ,求证:T n <12.【答案】(1)数列a 2n -1 成等比数列,证明见解析(2)证明见解析【分析】(1)推导出a 2n +1=2a 2n +2=2log 2a 2n -1+2=4a 2n -1,得到结论;(2)先得到a 2n -1=a 1⋅4n -1,a 2n =2(n -1)+log 2a 1,从而得到S 10=341a 1+5log 2a 1+20,令f (x )=341x +5log 2x +20,得到函数单调递增,且由特殊点函数值得到a 1=1,b n =14n2,求出T 1=14<74,当n ≥2时,利用裂项相消法求和,得到T n <12.【详解】(1)数列a 2n -1 成等比数列,证明如下:根据a n +1=log 2a n ,n =2k -1,k ∈N ∗2a n+2,n =2k ,k ∈N ∗得,a 2n +1=2a 2n +2=2log 2a 2n -1+2=22a 2n -1=4a 2n -1;∵a 1>0,∴a 2n -1>0,a2n +1a 2n -1=4,即数列a 2n -1 成等比数列.(2)由(1)得,a 2n -1=a 1⋅4n -1,a 2n =log 2a 2n -1=2(n -1)+log 2a 1,故S 10=a 140+41+42+43+44 +5log 2a 1+2×(0+1+2+3+4)=341a 1+5log 2a 1+20,由S 10=361,得341a 1+5log 2a 1+20=361.令f (x )=341x +5log 2x +20,当x >0时,f (x )=341x +5log 2x +20单调递增,且f (1)=361=f a 1 ,故a 1=1,a 2n +1=4n =22n ,a 2n +2=log 2a 1+2n =2n ,∴b n =1log 2a 2n +1 ⋅a 2n +2=14n 2,T 1=b 1=14<12,当n ≥2时,b n =14n2<14(n -1)n =141n -1-1n∴T n =b 1+b 2+⋯+b n <141+1-12+12-13+⋯+1n -1-1n=142-1n <14×2=12,综上,知T n <1214(2023·全国·高三专题练习)已知A x 1,y 2 、B x 2,y 2 是函数f x =2x 1-2x,x ≠12-1,x =12的图象上的任意两点,点M 在直线x =12上,且AM =MB .(1)求x 1+x 2的值及y 1+y 2的值;(2)已知S 1=0,当n ≥2时,S n =f 12 +f 2n +f 3n +⋅⋅⋅+f n -1n,设a n =2Sn,T n 数列a n 的前n 项和,若存在正整数c ,m ,使得不等式T m -c T m +1-c <12成立,求c 和m 的值;【答案】(1)x 1+x 2=1,y 1+y 2=-2(2)存在,c =1,m =1【分析】(1)根据点M 在直线x =12上,设M 12,y M ,利用AM =MB ,可得x 1+x 2=1,分类讨论:①x 1=12,x 2=12;②x 1≠12时,x 2≠12,利用函数解析式,可求y 1+y 2的值;(2)由(1)知,当x 1+x 2=1时,y 1+y 2=-2,∴f k n +f n -kn=-2,代入k =0,1,2,⋯,n -1,利用倒序相加法可得S n =1-n ,从而可得数列a n 的通项与前n 项和,利用T m -c T m +1-c <12化简即可求得结论.【详解】(1)根据点M 在直线x =12上,设M 12,y M ,则AM =12-x 1,y M -y 1 ,MB =x 2-12,y 2-y M ,∵AM =MB ,∴x 1+x 2=1.①当x 1=12时,x 2=12,y 1+y 2=f x 1 +f x 2 =-1-1=-2;②当x 1≠12时,x 2≠12,y 1+y 2=2x 11-2x 1+2x 21-2x 2=2x 11-2x 2 +2x 21-2x 1 1-2x 1 1-2x 2 =2(x 1+x 2)-8x 1x 21-2(x 1+x 2)+4x 1x 2=2(1-4x 1x 2)4x 1x 2-1=-2;综合①②得,y 1+y 2=-2.(2)由(1)知,当x 1+x 2=1时,y 1+y 2=-2.∴f k n +f n -k n=-2,k =0,1,2,⋯,n -1,∴n ≥2时,S n =f 1n +f 2n +f 3n +⋯+f n -1n①S n =f n -1n +f n -2n +f n -3n +⋯+f 1n ②①+②得,2S n =-2(n -1),则S n =1-n .又n =1时,S 1=0满足上式,∴S n =1-n .∴a n =2S n=21-n ,∴T n =1+12+⋯+12n -1=1×1-12 n1-12=2-22n.∵T m -c T m +1-c <12,∴2T m -c -T m +1-c 2T m +1-c<0,∴c -2T m -T m +1c -T m +1<0,∵Tm +1=2-12m ,2T m -T m +1=4-42m -2+12m =2-32m ,∴12≤2-32m <c <2-12m <2,c ,m 为正整数,∴c =1,当c =1时,2-32m<12-12m >1,∴1<2m <3,∴m =1.【点评】作为高考热点,数列与函数的交汇问题,等差数列易于同二次函数结合,研究和的最值问题,而等比数列易于同指数函数结合,利用指数函数的单调性解决问题,递推、通项问题往往与函数的单调性、周期性相结合.热点五数列与不等式交汇15(2022·浙江·统考高考真题)已知数列a n 满足a 1=1,a n +1=a n -13a 2n n ∈N ∗,则()A.2<100a 100<52 B.52<100a 100<3 C.3<100a 100<72 D.72<100a 100<4【答案】B【分析】先通过递推关系式确定a n 除去a 1,其他项都在0,1 范围内,再利用递推公式变形得到1a n +1-1a n =13-a n >13,累加可求出1a n >13(n +2),得出100a 100<3,再利用1a n +1-1a n =13-a n<13-3n +2=131+1n +1 ,累加可求出1a n -1<13n -1 +1312+13+⋯+1n ,再次放缩可得出100a 100>52.【详解】∵a 1=1,易得a 2=23∈0,1 ,依次类推可得a n ∈0,1由题意,a n +1=a n 1-13a n ,即1a n +1=3a n 3-a n=1a n +13-a n ,∴1a n +1-1a n =13-a n >13,即1a 2-1a 1>13,1a 3-1a 2>13,1a 4-1a 3>13,⋯,1a n -1a n -1>13,(n ≥2),累加可得1a n -1>13n -1 ,即1a n >13(n +2),(n ≥2),∴a n <3n +2,n ≥2 ,即a 100<134,100a 100<10034<3,又1a n +1-1a n =13-a n <13-3n +2=131+1n +1 ,(n ≥2),∴1a 2-1a 1=131+12 ,1a 3-1a 2<131+13 ,1a 4-1a 3<131+14 ,⋯,1a n -1a n -1<131+1n,(n≥3),累加可得1a n -1<13n -1 +1312+13+⋯+1n ,(n ≥3),∴1a 100-1<33+1312+13+⋯+1100 <33+1312×4+16×96 <39,即1a 100<40,∴a 100>140,即100a 100>52;综上:52<100a 100<3.故选:B .16(2023·浙江嘉兴·统考模拟预测)如图,在一个单位正方形中,首先将它等分成4个边长为12的小正方形,保留一组不相邻的2个小正方形,记这2个小正方形的面积之和为S 1;然后将剩余的2个小正方形分别继续四等分,各自保留一组不相邻的2个小正方形,记这4个小正方形的面积之和为S 2.以此类推,操作n 次,若S 1+S 2+⋅⋅⋅+S n ≥20232024,则n 的最小值是()A.9B.10C.11D.12【答案】C【分析】由题意可知操作n 次时有2n 个边长为12n 的小正方形,即S n =2n ×12n2=12n,结合等比数列前n 项和解不等式即可.【详解】由题意可知操作1次时有21=2个边长为121=12的小正方形,即S 1=21×1212=121=12,操作2次时有22=4个边长为122=14的小正方形,即S 2=22×122 2=122=14,操作3次时有23=8个边长为123=18的小正方形,即S 3=23×1232=123=18,以此类推可知操作n 次时有2n 个边长为12n 的小正方形,即S n =2n ×12n2=12n ,由等比数列前n 项和公式有S 1+S 2+⋅⋅⋅+S n =12+12 2+⋅⋅⋅+12 n =12×1-12 n1-12=1-12 n,从而问题转换成了求1-12 n ≥20232024不等式的最小正整数解,将不等式变形为12 n ≤12024,注意到12 10=11024>12024,1211=12048<12024,且函数y =12x在R 上单调递减,所以n 的最小值是11.故选:C .17(2023秋·四川绵阳·高三绵阳中学校考阶段练习)已知等差数列a n 的前n 项和为S n ,且S 4=4S 2,a 3n =3a n +2n ∈N *(1)求a n 的通项公式,(2)设b n =1a n a n +1,且b n 的前n 项和为T n ,证明,13≤T n <12.【答案】(1)a n =2n -1(2)证明见解析【分析】(1)利用等差数列的通项公式以及前n 项和公式,列方程求解首项和公差,即得答案;(2)由(1)结论可得b n =1a n a n +1的表达式,利用裂项求和可得T n 表达式,即可证明结论.【详解】(1)设a n 的公差为d ,由S 4=4S 2得,4a 1+6d =42a 1+d ,解得d =2a 1,∵a 3n =3a n +2,即a 1+3n -1 d =3a 1+n -1 d +2,∴2d =2a 1+2,结合d =2a 1,∴d =2,a 1=1,∴a n =1+2n -1 =2n -1;(2)证明:由b n =12n -1 2n +1=1212n -1-12n +1 .∴T n =b 1+b 2+⋯+b n =121-13+13-15+⋯+12n -1-12n +1,即∴T n =121-12n +1 ,又T n 随着n 的增大增大,当n =1时,T n 取最小值为T 1=13,又n →+∞时,12n +1>0,且无限趋近于0,故T n =121-12n +1 <12,故13≤T n <12.18(2022·全国·统考高考真题)记S n 为数列a n 的前n 项和,已知a 1=1,S n a n 是公差为13的等差数列.(1)求a n 的通项公式;(2)证明:1a 1+1a 2+⋯+1a n<2.【答案】(1)a n =n n +12(2)见解析【分析】(1)利用等差数列的通项公式求得S n a n =1+13n -1 =n +23,得到S n =n +2 a n 3,利用和与项的关系得到当n ≥2时,a n =S n -S n -1=n +2 a n 3-n +1 a n -13,进而得:a n a n -1=n +1n -1,利用累乘法求得a n =n n +1 2,检验对于n =1也成立,得到a n 的通项公式a n =n n +1 2;(2)由(1)的结论,利用裂项求和法得到1a 1+1a 2+⋯+1a n =21-1n +1 ,进而证得.【详解】(1)∵a 1=1,∴S 1=a 1=1,∴S1a 1=1,又∵S n a n 是公差为13的等差数列,∴S n a n =1+13n -1 =n +23,∴S n =n +2 a n 3,∴当n ≥2时,S n -1=n +1 a n -13,∴a n =S n -S n -1=n +2 a n 3-n +1 a n -13,整理得:n -1 a n =n +1 a n -1,即a na n-1=n+1n-1,∴a n=a1×a2a1×a3a2×⋯×a n-1a n-2×a na n-1=1×31×42×⋯×nn-2×n+1n-1=n n+12,显然对于n=1也成立,∴a n的通项公式a n=n n+12;(2)1a n =2n n+1=21n-1n+1,∴1 a1+1a2+⋯+1a n=21-12+12-13+⋯1n-1n+1=21-1n+1<219(2021·全国·统考高考真题)设a n是首项为1的等比数列,数列b n满足b n=na n3.已知a1,3a2,9a3成等差数列.(1)求a n和b n的通项公式;(2)记S n和T n分别为a n和b n的前n项和.证明:T n<S n 2.【答案】(1)a n=13n-1,b n=n3n;(2)证明见解析.【分析】(1)利用等差数列的性质及a1得到9q2-6q+1=0,解方程即可;(2)利用公式法、错位相减法分别求出S n,T n,再作差比较即可.【详解】(1)因为a n是首项为1的等比数列且a1,3a2,9a3成等差数列,所以6a2=a1+9a3,所以6a1q=a1+9a1q2,即9q2-6q+1=0,解得q=13,所以a n=13n-1,所以b n=na n3=n3n.(2)[方法一]:作差后利用错位相减法求和T n=13+232+⋯+n-13n-1+n3n,S n 2=12130+131+132+⋯+13n-1 ,T n-S n2=13+232+333+⋯+n3n-12130+131+132+⋯+13n-1 =0-1230+1-1231+2-1232+⋯+n-1-123n-1+n3n.设Γn=0-1230+1-1231+2-1232+⋯+n-1-123n-1, ⑧则13Γn=0-1231+1-1232+2-1233+⋯+n-1-123n. ⑨由⑧-⑨得23Γn=-12+131+132+⋯+13n-1-n-323n=-12+131-13n-11-13-n-323n.所以Γn=-14×3n-2-n-322×3n-1=-n2×3n-1.因此T n-S n2=n3n-n2×3n-1=-n2×3n<0.故T n<S n 2.[方法二]【最优解】:公式法和错位相减求和法证明:由(1)可得S n=1×1-13n1-13=321-13n,T n=13+232+⋯+n-13n-1+n3n,①1 3T n=132+233+⋯+n-13n+n3n+1,②①-②得23T n=13+132+133+⋯+13n-n3n+1=131-13n1-13-n3n+1=121-13n-n3n+1,所以T n=341-13n-n2⋅3n,所以T n-S n2=341-13n-n2⋅3n-341-13n=-n2⋅3n<0,所以T n<S n 2 .[方法三]:构造裂项法由(Ⅰ)知b n=n13n,令c n=(αn+β)13 n,且b n=c n-c n+1,即n13 n=(αn+β)13 n-[α(n+1)+β]13n+1,通过等式左右两边系数比对易得α=32,β=34,所以c n=32n+34 ⋅13 n.则T n=b1+b2+⋯+b n=c1-c n+1=34-34+n2 13 n,下同方法二.[方法四]:导函数法设f(x)=x+x2+x3+⋯+x n=x1-x n1-x,由于x1-x n1-x'=x1-x n'1-x-x1-x n×1-x'1-x2=1+nx n+1-(n+1)x n(1-x)2,则f (x)=1+2x+3x2+⋯+nx n-1=1+nx n+1-(n+1)x n(1-x)2.又b n=n13n=13n13 n-1,所以T n=b1+b2+b3+⋯+b n=131+2×13+3×132+⋯+n⋅13n-1 =13⋅f 13 =13×1+n13n+1-(n+1)13 n1-132=341+n13n+1-(n+1)13n =34-34+n213 n,下同方法二.20(2023·河南郑州·统考模拟预测)已知数列a n与b n的前n项和分别为A n和B n,且对任意n∈N*,a n +1-a n =32b n +1-b n 恒成立.(1)若A n =3n 2+3n2,b 1=2,求B n ;(2)若对任意n ∈N *,都有a n =B n 及b 2a 1a 2+b 3a 2a 3+b 4a 3a 4+⋯+b n +1a n a n +1<13恒成立,求正整数b 1的最小值.【答案】(1)n (n +1);(2)3【分析】(1)利用a n ,S n 求通项公式,再求证{b n }是首项、公差均为2的等差数列,进而求B n ;(2)由题设易得b n +1=3b n ,等比数列前n 项和公式求B n ,进而可得b n +1a n a n +1=1B n -1B n +1,裂项相消法化简已知不等式左侧,得b 1>31-23n +1-1恒成立,进而求最小值.【详解】(1)由题设,a n =A n -A n -1=32[n 2+n -(n -1)2-n +1]=3n 且n ≥2,而a 1=A 1=3,显然也满足上式,故a n =3n ,由a n +1-a n =32b n +1-b n ⇒b n +1-b n =2,又b 1=2,所以{b n }是首项、公差均为2的等差数列.综上,B n =2×(1+...+n )=n (n +1).(2)由a n =B n ,a n +1-a n =32b n +1-b n ,则B n +1-B n =b n +1=32(b n +1-b n ),所以b n +1=3b n ,而b 1≥1,故bn +1b n=3,即{b n }是公比为3的等比数列.所以B n =b 1(1-3n )1-3=b 12(3n -1),则B n +1=b12(3n +1-1),b n +1a n a n +1=B n +1-B n B n +1B n =1B n -1B n +1,而b 2a 1a 2+b 3a 2a 3+b 4a 3a 4+⋯+b n +1a n a n +1<13,所以1B 1-1B 2+1B 2-1B 3+...+1B n -1B n +1=1B 1-1B n +1=1b 1-2b 1(3n +1-1)<13,所以1b 11-23n +1-1 <13⇒b 1>31-23n +1-1对n ∈N *都成立,所以1-23n +1-1<1,故b 1≥3,则正整数b 1的最小值为3.21(2023秋·云南·高三云南师大附中校考阶段练习)已知a n 为等差数列,b n 为等比数列,b 1=2a 1=2,a 5=5a 4-a 3 ,b 5=4b 4-b 3 ,数列c n 满足c n =1a n a n +2,n 为奇数b n,n 为偶数.(1)求a n 和b n 的通项公式;(2)证明:2ni =1c i ≥133.【答案】(1)a n =n ;b n =2n (2)证明见解析【分析】(1)设等差数列a n 的公差为d ,等比数列b n 的公比为q ,根据题意列式求d ,q ,进而可得结果;(2)利用分组求和以及裂项相消法求得T n =-14n +2+4n +13-56,进而根据数列单调性分析证明.【详解】(1)设等差数列a n 的公差为d ,等比数列b n 的公比为q ,由a 1=1,a 5=5a 4-a 3 ,可得1+4d =5d ,解得d =1。
中考数学总复习讲义课件:核心素养专题九 数学文化

B.160
256 C. 3
D.64
【解析】 作出几何体的直观图如答图所示:
跟踪训练 3 答图 沿上棱两端向底面作垂面,且使垂面与上棱垂直, 则将几何体分成两个四棱锥和 1 个直三棱柱, 则三棱柱的体积 V1=12×4×4×4=32, 四棱锥的体积 V2=13×2×4×4×1=332, 由三视图可知两个四棱锥大小相等, ∴V=V1+2V2=1630.
跟踪训练 1.[2018·孝义期末]公元前 5 世纪古希腊的毕达哥拉斯学派有一种观点,
即“万物皆数”,一切量都可以用整数或整数比(分数)表示,后来,当这一学派中
的希帕索斯发现,边长为 1 的正方形的对角线的长度不能用整数或整数的比表示
时,毕达哥拉斯学派感到惊恐不安,由此,引发了第一次数学危机,这儿“不能
3.[2019·汉阳区模拟]我国古代数学名著《九章算术》记载:刍甍者,下有袤有广, 而上有袤无丈.刍,草也;甍,屋盖也.翻译为:底面有长有宽为矩形,顶部只 有长没有宽为一条棱.刍甍字面意思为茅草屋顶.图 6 为一刍甍的三视图,其中 正视图为等腰梯形,侧视图为等腰三角形.则它的体积为( A )
图6
160 A. 3
类型一 以科技或数学时事为题材 典例 [2019·广元]我国古代数学家刘徽用“牟合方盖”找到了球体体积的计算方 法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公 共部分形成的几何体.如图 1 所示的几何体是可以形成“牟合方盖”的一种模型, 它的俯视图是( A )
跟踪训练 1.[2019·宜昌]古希腊几何学家海伦和我国宋代数学家秦九韶都曾提出利
用整数或整数的比表示的数”指的是( B )
A.有理数
B.无理数
C.合数
D.质数
数列与离散型随机变量相结合问题-高考数学大题精做之解答题题型全覆盖高端精品

高考数学大题精做之解答题题型全覆盖高端精品第四篇概率与统计专题09数列与离散型随机变量相结合问题类型对应典例数列递推公式与离散型随机变量的分布列和数学期望典例1数列通项公式与离散型随机变量的分布列和数学期望典例2等比数列的证明与离散型随机变量的分布列和数学期望典例3等比数列求和与离散型随机变量的分布列和数学期望典例4数列的综合问题与离散型随机变量的分布列和数学期望典例5【典例1】某游戏棋盘上标有第0、1、2、 、100站,棋子开始位于第0站,选手抛掷均匀硬币进行游戏,若掷出正面,棋子向前跳出一站;若掷出反面,棋子向前跳出两站,直到跳到第99站或第100站时,游戏结束.设游戏过程中棋子出现在第n 站的概率为nP .(1)当游戏开始时,若抛掷均匀硬币3次后,求棋子所走站数之和X 的分布列与数学期望;(2)证明:()()1111982n n n n P P P P n +--=--≤≤;(3)若最终棋子落在第99站,则记选手落败,若最终棋子落在第100站,则记选手获胜.请分析这个游戏是否公平.【思路引导】(1)由题意得出随机变量X 的可能取值有3、4、5、6,求出相应的概率,由此可得出随机变量X 的分布列,并计算出随机变量X 的数学期望;(2)棋子要到第()1n +站,分两种情况讨论:一是由第n 站跳1站得到,二是由第()1n -站跳2站得到,可得出111122n n n P P P +-=+,变形后可得出结论;(3)根据(2)中的{}n P 的递推公式得出100P 和99P 的大小关系,从而得出结论.【典例2】11月,2019全国美丽乡村篮球大赛在中国农村改革的发源地-安徽凤阳举办,其间甲、乙两人轮流进行篮球定点投篮比赛(每人各投一次为一轮),在相同的条件下,每轮甲乙两人在同一位置,甲先投,每人投一次球,两人有1人命中,命中者得1分,未命中者得-1分;两人都命中或都未命中,两人均得0分,设甲每次投球命中的概率为12,乙每次投球命中的概率为23,且各次投球互不影响.(1)经过1轮投球,记甲的得分为X ,求X 的分布列;(2)若经过n 轮投球,用i p 表示经过第i 轮投球,累计得分,甲的得分高于乙的得分的概率.①求,,p p p 123;②规定00p =,经过计算机计算可估计得11(1)i i i i p ap bp cp b +-=++≠,请根据①中,,p p p 123的值分别写出a ,c 关于b 的表达式,并由此求出数列{}n p 的通项公式.【思路引导】(1)经过1轮投球,甲的得分X 的取值为1,0,1-,记一轮投球,甲投中为事件A ,乙投中为事件B ,,A B 相互独立,计算概率后可得分布列;(2)由(1)得1p ,由两轮的得分可计算出2p ,计算3p 时可先计算出经过2轮后甲的得分Y 的分布列(Y的取值为2,1,0,1,2--),然后结合X 的分布列和Y 的分布可计算3p ,由00p =,代入11(1)i i i i p ap bp cp b +-=++≠,得两个方程,解得,a c ,从而得到数列{}n p 的递推式,变形后得1{}n n p p --是等比数列,由等比数列通项公式得1n n p p --,然后用累加法可求得n p .【典例3】某产品自生产并投入市场以来,生产企业为确保产品质量,决定邀请第三方检测机构对产品进行质量检测,并依据质量指标Z 来衡量产品的质量.当8Z ≥时,产品为优等品;当68Z ≤<时,产品为一等品;当26Z ≤<时,产品为二等品.第三方检测机构在该产品中随机抽取500件,绘制了这500件产品的质量指标Z 的条形图.用随机抽取的500件产品作为样本,估计该企业生产该产品的质量情况,并用频率估计概率.(1)从该企业生产的所有产品中随机抽取1件,求该产品为优等品的概率;(2)现某人决定购买80件该产品.已知每件成本1000元,购买前,邀请第三方检测机构对要购买的80件产品进行抽样检测.买家、企业及第三方检测机构就检测方案达成以下协议:从80件产品中随机抽出4件产品进行检测,若检测出3件或4件为优等品,则按每件1600元购买,否则按每件1500元购买,每件产品的检测费用250元由企业承担.记企业的收益为X 元,求X 的分布列与数学期望;(3)商场为推广此款产品,现面向意向客户推出“玩游戏,送大奖”活动.客户可根据抛硬币的结果,操控机器人在方格上行进,已知硬币出现正、反面的概率都是12,方格图上标有第0格、第1格、第2格、……、第50格.机器人开始在第0格,客户每掷一次硬币,机器人向前移动一次,若掷出正面,机器人向前移动一格(从k 到1k +),若掷出反面,机器人向前移动两格(从k 到2k +),直到机器人移到第49格(胜利大本营)或第50格(失败大本营)时,游戏结束,若机器人停在“胜利大本营”,则可获得优惠券.设机器人移到第n 格的概率为()*050,N n P n n ≤≤∈,试证明{}()*1149,N nn P P n n --≤≤∈是等比数列,并解释此方案能否吸引顾客购买该款产品.【思路引导】(1)根据条形图,可得优等品的频率为1218742500++,进而可得其概率;(2)计算出X 的值可以为47000,39000,计算出其分别对应的概率,得到分布列,进而可得期望;(3)首先易得01P =,112P =,根据题意可得121122n n n P P P --=+,化简即可得()11212n n n n P P P P ----=--,即{}1n n P P --为等比数列,利用累加法可得()12110,1,,4932n n P n +⎡⎤⎛⎫=--=⋅⋅⋅⎢⎥ ⎪⎝⎭⎢⎥⎣⎦,再分别计算出获胜和失败的概率,比较大小即可得结果.【典例4】抚州不仅有着深厚的历史积淀与丰富的民俗文化,更有着许多旅游景点.每年来抚州参观旅游的人数不胜数.其中,名人园与梦岛被称为抚州的两张名片,为合理配置旅游资源,现对已游览名人园景点的游客进行随机问卷调查.若不去梦岛记1分,若继续去梦岛记2分.每位游客去梦岛的概率均为23,且游客之间的选择意愿相互独立.(1)从游客中随机抽取3人,记总得分为随机变量X ,求X 的分布列与数学期望;(2)若从游客中随机抽取m 人,记总分恰为m 分的概率为m A ,求数列{}m A 的前6项和;(3)在对所有游客进行随机问卷调查的过程中,记已调查过的累计得分恰为n 分的概率为n B ,探讨n B 与1n B -之间的关系,并求数列{}n B 的通项公式.【思路引导】(1)根据n 次独立重复试验模型可求解(2)总分恰为m 的概率13mm A ⎛⎫= ⎪⎝⎭,求前6项和即可(3)已调查过的累计得分恰为n 分的概率为n B ,得不到n 分的情况只有先得1n -分,再得2分,概率为123n B -,可得递推关系1213n n B B -=-+,构造等比数列求解即可.【典例5】为了治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得1-分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得1-分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X .(1)求X 的分布列;(2)若甲药、乙药在试验开始时都赋予4分,(0,1,,8)i p i = 表示“甲药的累计得分为i 时,最终认为甲药比乙药更有效”的概率,则00p =,81p =,11i i i i p ap bp cp -+=++(1,2,,7)i = ,其中(1)a P X ==-,(0)b P X ==,(1)c P X ==.假设0.5α=,0.8β=.(i)证明:1{}i i p p +-(0,1,2,,7)i = 为等比数列;(ii)求4p ,并根据4p 的值解释这种试验方案的合理性.【思路引导】(1)首先确定X 所有可能的取值,再来计算出每个取值对应的概率,从而可得分布列;(2)(i )求解出,,a b c 的取值,可得()110.40.50.11,2,,7i i i i p p p p i -+=++=⋅⋅⋅,从而整理出符合等比数列定义的形式,问题得证;(ii )列出证得的等比数列的通项公式,采用累加的方式,结合8p 和0p 的值可求得1p ;再次利用累加法可求出4p .1.棋盘上标有第0、1、2、 、100站,棋子开始位于第0站,棋手抛掷均匀硬币走跳棋游戏,若掷出正面,棋子向前跳出一站;若掷出反面,棋子向前跳出两站,直到调到第99站或第100站时,游戏结束.设棋子位于第n 站的概率为nP .(1)当游戏开始时,若抛掷均匀硬币3次后,求棋手所走步数之和X 的分布列与数学期望;(2)证明:()()1111982n n n n P P P P n +--=--≤≤;(3)求99P 、100P的值.2.随着科学技术的飞速发展,网络也已经逐渐融入了人们的日常生活,网购作为一种新的消费方式,因其具有快捷、商品种类齐全、性价比高等优势而深受广大消费者认可.某网购公司统计了近五年在本公司网购的人数,得到如下的相关数据(其中“x =1”表示2015年,“x =2”表示2016年,依次类推;y 表示人数):x 12345y (万人)2050100150180(1)试根据表中的数据,求出y 关于x 的线性回归方程,并预测到哪一年该公司的网购人数能超过300万人;(2)该公司为了吸引网购者,特别推出“玩网络游戏,送免费购物券”活动,网购者可根据抛掷骰子的结果,操控微型遥控车在方格图上行进.若遥控车最终停在“胜利大本营”,则网购者可获得免费购物券500元;若遥控车最终停在“失败大本营”,则网购者可获得免费购物券200元.已知骰子出现奇数与偶数的概率都是12,方格图上标有第0格、第1格、第2格、…、第20格。
十年(2014-2023)高考数学真题分项汇编文科专题5 数列小题(文科)(解析版)

n 项和
Sn,公差
d≠0, a1 d
1 .记
b1=S2,
bn+1=Sn+2–S2n, n N ,下列等式不可能成立的是
( )
A.2a4=a2+a6
B.2b4=b2+b6
C. a42 a2a8
D. b42 b2b8
【答案】D
解析:对于 A,因为数列an 为等差数列,所以根据等差数列的下标和性质,由 4 4 2 6 可得,
由 an
a1
n
1 d
0
可得 n
1
a1 d
,取
N0
1
a1 d
1 ,则当 n
N0
时, an
0,
所以,“an 是递增数列” “存在正整数 N0 ,当 n N0 时, an 0 ”;
若存在正整数 N0 ,当 n N0 时, an 0 ,取 k N 且 k N0 , ak 0 ,
假设 d
0 ,令 an
Sn =
1 2
An An+1 ×tan q Bn Bn+1 ,都为定值,所以 Sn+1 - Sn 为定值.故选 A.
3.(2022 高考北京卷·第 15 题)己知数列an 各项均为正数,其前 n 项和 Sn 满足 an Sn 9(n 1, 2,) .给
出下列四个结论:
①an 的第 2 项小于 3; ②an 为等比数列;
2a4 a2 a6 ,A 正确;
对于 B,由题意可知, bn1 S2n2 S2n a2n1 a2n2 , b1 S2 a1 a2 ,
∴ b2 a3 a4 , b4 a7 a8 , b6 a11 a12 , b8 a15 a16 .
∴ 2b4 2 a7 a8 , b2 b6 a3 a4 a11 a12 .
数学文化在高中数学教学渗透研究——以数列为例优秀课例

《数学文化在高中数学教学渗透研究——以数列为例》是一篇关于数学教学中融入数学文化元素的研究论文。
在该论文中,作者以数列作为例子,探讨了如何通过融入数学文化来提升高中数学教学的质量和效果。
在这篇论文中,优秀的课例可以通过以下方式展示:
引入历史背景:通过介绍数列的历史背景,如斐波那契数列的发现历程、数列在数学发展中的重要性等,让学生了解数列在数学领域的起源和发展。
数学文化的艺术表达:通过介绍数列在艺术中的应用,如黄金分割、音乐中的节奏等,引发学生对数列的兴趣,增强他们对数学的美感和创造力。
数学文化的实际应用:通过举例数列在实际生活中的应用,如金融领域中的利息计算、物理学中的运动描述等,帮助学生理解数列在实际问题中的重要性和应用价值。
数学文化的探索和发现:通过引导学生发现数列中的规律和性质,培养他们的探索和发现能力,同时提高他们的数学思维能力。
数学文化的交流和讨论:通过小组活动、讨论或展示,让学生分享自己对数列的理解和应用,促进彼此之间的交流和合作。
这些课例通过将数学与文化相结合,帮助学生更好地理解数列的概念和性质,增强他们对数学的兴趣和学习动力。
同时,融入数学文化元素可以提升课堂的趣味性和互动性,使学生更积极地参与数学学习和思考。
注意,上述的课例仅为一般性的指导,实际的优秀课例需要根据具体教学目标、学生特点和教学资源进行调整和设计。
高考数学文化题目的命制背景-数列中的数学文化

高考数学文化题目的命制背景-数列中的数学文化背景:高考数学文化题目常以等差数列、等比数列为背景,考查读题、分析问题能力和逻辑推理能力。
预测:本文将以等差数列为题材,考查数列中的文化。
回顾:以2017年高考数学文化题目为例,考查了古代数学名著《算法统宗》中的问题,要求求解一座7层塔顶层的灯数,利用等比数列的知识进行计算。
典例分析:以2017江西红色七校联考为例,考查了《张丘建算经》中的问题,要求求解一个女子每天织布的数量,利用等差数列的知识进行计算。
另一道题目则考查了《算法统宗》中的问题,要求求解一个人走378里路后第二天走了多少里程,利用等比数列的知识进行计算。
规律总结:我国古代数学注重算理算法,很多问题可转化为等差数列、等比数列问题。
数学文化题目考查的是将古代实际问题转化为现代数学问题,建立数列模型,进行数列的基本计算,利用方程思想求解。
1.XXX是明代的一位著名音乐家、数学家和天文历算家。
他在著作《律学新说》中制定了十二平均律,这是目前世界上通用的将一组音分成十二个半音音程的律制。
这些音程之间的频率比完全相等,因此也被称为十二等程律。
具体来说,一个八度包含13个音,相邻两个音之间的频率比相等,而最后一个音的频率是最初那个音的2倍。
如果设第三个音的频率为f1,第七个音的频率为f2,则f2/f1=2^(2/12)=1.1228.2.《孙子算经》是我国古代的一部数学名著。
其中有一个问题是:“今有五个诸侯,共分60个橘子,每人加三个。
问:五人各得几何?”这个问题的意思是:五个人要分60个橘子,他们分得的橘子数构成一个公差为3的等差数列。
得到橘子最少的人所得的橘子个数是6.3.《九章算术》是我国古代一部重要的数学著作。
其中有一个问题是:“现在有良马和驽马同时从长安出发到齐去。
已知长安和齐的距离是3000里,良马第一天行193里,之后每天比前一天多行13里;驽马第一天行97里,之后每天比前一天少行0.5里。
以数学文化史为背景的专题训练

专题1 以数学文化史为背景的专题训练题型一渗透数学文化的数列题1.【2017届安徽省池州市东至县高三12月联考】《九章算术》是我国古代的数学名著,书中有如下问题:“今有五人分五钱,令上二人所得与下三人等,问各得几何?”其意思为“已知甲、乙、丙、丁、戊五人分五钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列,问五人各得多少钱?”(“钱”是古代一种重量单位),这个问题中,甲所得为()钱A. B. C. D.2.【2017届甘肃天水一中高三理12月月考】《张丘建算经》是我国南北朝时期的一部重要数学著作,书中系统的介绍了等差数列,同类结果在三百多年后的印度才首次出现.书中有这样一个问题,大意为:某女子善于织布,后一天比前一天织的快,而且每天增加的数量相同,已知第一天织布5尺,一个月(按30天计算)总共织布390尺,问每天增加的数量为多少尺?该问题的答案为()A.829尺 B.1629尺 C.3229尺 D.12尺3.【2017届湖南长沙一中高三月考五】“珠算之父”程大位是我国明代伟大是数学家,他的应用数学巨著《算法统综》的问世,标志着我国的算法由筹算到珠算转变的完成.程大位在《算法统综》中常以诗歌的形式呈现数学问题,其中有一首“竹筒容米”问题:“家有九节竹一茎,为因盛米不均平,下头三节三升九,上梢四节贮三升,唯有中间两节竹,要将米数次第盛,若有先生能算法,也教算得到天明.”([注释]三升九:3.9升.次第盛:盛米容积依次相差同一数量.)用你所学的数学知识求得中间两节的容积为()A.1.9升 B.2.1升C.2.2升D.2.3升4.【2017届山西省临汾一中、忻州一中、长治二中等五校高三上学期第五次联考】在我刚明代数学家吴敬所著的《九章算术比类大全》中,有一道数学命题叫“宝塔装灯”,内容为“远望魏巍塔七层,红灯点点倍加增;共灯三百八十一,请问顶层几盏灯?”(“倍加增”指灯的数量从塔的顶层到底层按公比为的等比数列递增),根据此诗,可以得出塔的顶层和底层共有()A. 盏灯B. 盏灯C. 盏灯D. 盏灯5.【2017届湖北孝感市高三上学期第一次统考试】《九章算术》中有一个“两鼠穿墙”问题:“今有垣(墙,读音)厚五尺,两鼠对穿,大鼠日(第一天)一尺,小鼠也日(第一天)一尺.大鼠日自倍(以后每天加倍),小鼠日自半(以后每天减半).问何日相逢,各穿几何?”在两鼠“相逢”时,大鼠与小鼠“穿墙”的“进度”之比是: .6.【2017届河南漯河高级中学高三12月月考】“中国剩余定理”又称“孙子定理”.1852年,英国来华传教士伟烈亚力将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年,英国数学家马西森指出此法符合1801年由高斯得到的关于问余式解法的一般性定理,因而西方称之为“中国剩余定理”.“中国剩余定理”讲的是一个关于整除的问题,现有这样一个整除问题:将1到2016这2016个数中,能被3除余1且被5整除余1的数按从小到大的顺序排成一列,构成数列{}n a,则此数列的项数为_____________.7.【2017届湖北省荆、荆、襄、宜四地七校考试联盟高三2月联考】“斐波那契”数列由十三世纪意大利数学家斐波那契发现.数列中的一系列数字常被人们称之为神奇数.具体数列为:,即从该数列的第三项数字开始,每个数字等于前两个相邻数字之和.已知数列为“斐波那契”数列,为数列的前项和,则(Ⅰ)__________;(Ⅱ)若,则__________.(用表示)8.【2017届吉林省吉林市普通中学高三毕业班第二次调研测试】艾萨克·牛顿(1643年1月4日----1727年3月31日)英国皇家学会会长,英国著名物理学家,同时在数学上也有许多杰出贡献,牛顿用“作切线”的方法求函数零点时给出一个数列:满足,我们把该数列称为牛顿数列.如果函数有两个零点1,2,数列为牛顿数列,设,已知,,则的通项公式__________.题型二渗透数学文化的立体几何题9.【2017届福建省漳州市七校高三联考】我国古代数学名著《九章算术》中“开立圆术”曰:置积尺数,以十六乘之,九而一,所得开立方除之,即立圆径. “开立圆术”相当于给出了已知球的体积V,求其直径d的一个近似公式3169d V人们还用过一些类似的近似公式. 根据π =3.14159判断,下列近似公式中最精确的一个是()A.3169d V B.32d V C.3300157d V≈D.32111d V≈10.【2017届河北唐山市高三理上学期期末】《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的表面积为()A.4B.642+C.442+D.211.【2017届湖南郴州市高三理第二次质监】我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水.天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平地降雨量是(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸;③台体的体积公式1()3V S S S S h =++下下上上•). A . 2寸 B .3寸 C. 4寸 D .5寸12.【2017届湖南长沙雅礼中学高三文月考】“牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体. 它由完全相同的四个曲面构成,相对的两个曲面在同一个圆柱的侧面上,好似两个扣和(牟和)在一起的方形伞(方盖). 其直观图如下左图,图中四边形是为体现其直观性所作的辅助线. 其实际直观图中四边形不存在,当正视图和侧视图完全相同时,它的的正视图和俯视图分别可能是( )A .b a ,B .c a ,C. b c , D .d b ,13.【2017届湖南师大附中高三理上学期月考四】《九章算术》是我国古代内容记为丰富的数学名著,书中有如下问题:“今有圆堡壔,周四丈八尺,高一丈一尺,问积几何?答曰:二千一百一十二尺.术曰:周自相乘,以高乘之,十二而一”.这里所说的圆堡壔就是圆柱体,它的体积为“周自相乘,以高乘之,十二而一.”就是说:圆堡壔(圆柱体)的体积112V=⨯(底面的圆周长的平方⨯高),则该问题中圆周率π的取值为.题型三渗透数学文化的程序框图题14.【2017届三省高三上学期百校大联考】下边程序框图的算法思路来源于我国古代数学名著《数书九章》中的“秦九韶算法”求多项式的值.执行程序框图,若输入01a=,11a=,20a=,31a=-,则输出u的值为()A.2 B.1 C.0 D.-115.【2017届云南大理州高三理上学期统测一】下边程序框图的算法思路源于欧几里得名著《几何原本》中的“辗转相除法”,执行该程序框图,若输入,m n分别为225、135,则输出的m=()A.5 B.9C.45 D.9016.【2017届云南省师范大学附属中学高三高考适应性月考】秦九韶算法是南宋时期数学家秦九韶提出的一种多项式简化算法,即使在现代,它依然是利用计算机解决多项式问题的最优算法,即使在现代,它依然是利用计算机解决多项式问题的最优算法,其算法的程序框图如图所示,若输入的分别为,若,根据该算法计算当时多项式的值,则输出的结果为()A. 248B. 258C. 268D. 278题型四 渗透数学文化的函数题17.【2017届甘肃天水一中高三理12月月考】德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数1,()0,x f x x ⎧=⎨⎩为有理数为无理数称为狄利克雷函数,则关于函数()f x 有以下四个命题:①(())1f f x =;②函数()f x 是偶函数;③任意一个非零有理数T ,()()f x T f x +=对任意x R ∈恒成立;④存在三个点11(,())A x f x ,22(,())B x f x , 33(,())C x f x ,使得ABC ∆为等边三角形.其中真命题的个数是( )A .4B .3C .2D .1题型五 渗透数学文化的复数题18.【2017届四川双流中学高三文必得分训练8】欧拉公式cos sin ixe x i x =+(i 为虚数单位)是由瑞士著名数学家欧拉发明的,它将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,它在复变函数论里非常重要,被誉为“数学中的天桥”,根据欧拉公式可知,2i e 表示的复数在复平面中位于( )A .第一象限B .第二象限C .第三象限D .第四象限 题型六 渗透数学文化的概率题19.【2017届重庆巴蜀中学高三12月月考】“勾股定理”在西方被称为“华达哥拉斯定理”,三国时期吴国的数学家赵爽创制了一幅“勾股圆方图”,用形数结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角6πα=,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内的概率是( )A. 31 343- 3 20.【2017届广东潮阳黄图盛中学高三月考】数学与文学有许多奇妙的联系,如诗中有回文诗:“儿忆父兮妻忆夫”,既可以顺读也可以逆读.数学中有回文数,如343、12521等,两位数的回文数有11、22、33、…、99共9个,则三位数的回文数中,偶数的概率是 .题型七 渗透数学文化的推理题21.【2017届四川成都市高三理一诊】我国南北朝时代的数学家祖恒提出体积的计算原理(祖恒原理):“幂势既同,则积不容异”.“势”即是高,“幂”是面积.意思是:如果两等高的几何体在同高处截得两几何体的截面积恒等,那么这两个几何体的体积相等.类比祖恒原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个上底为1的梯形,且当实数t 取[]0,3上的任意值时,直线y t =被图1和图2所截得的两线段长始终相等,则图1的面积为 ____________.22.【2017届湖南省长沙市雅礼中学高三月考】如图所示,将平面直角坐标系的格点(横、纵坐标均为整数的点)按如下规则标上数字标签:原点处标数字0,点()1,0处标数字1,点(1)1-,处标数字2,点(0)1-,处标数字3,点(11)--,处标数字4,点(10)-,处标数字5,点()11-,处标数字6,点(0)1,处标数字7,…以此类推:记格点坐标为()m n ,的点(m n ,均为正整数)处所标的数字为()f m n =,,若n m >,则()f m n =, .题型七 渗透现代科技或数学时事的创新题23.【2017福建莆田二十四中高三理月考】把11化为二进制数为( ).A.1 011(2)B.11 011(2)C.10 110(2)D.0 110(2)。
尔雅通识课数学文化问题详解

数学文化(一)12002年,为中国少年数学论坛活动题词“数学好玩”的是()。
A、邓东皋B、钱学森C、齐民友D、陈省身正确答案:D2“数学文化”一词最早进入官方文件,是出现在中华人民共和国教育部颁布的()。
A、《小学数学课程标准》B、《初中数学课程标准》C、《高中数学课程标准》D、《大学数学课程标准》正确答案:C3数学的研究对象是从众多物质形态种抽象出来的人脑的产物,这是它与其他自然科学研究的一个共同点。
()正确答案:×4广义的数学文化,是指数学的思想、精神、方法、观点、语言,以及他们的形成和发展。
()正确答案:×数学文化(二)11998年以后,教育部的专业目录里规定了数学学科专业,包括数学与应用数学专业、()。
A、统计学B、数理统计学C、信息与计算科学专业D、数学史与数学文化正确答案:C2数学目前仅仅是一种重要的工具,要上升至思维模式的高度,还需学者们的探索。
()正确答案:×3数学素养的通俗说法,是指在经过数学学习后,将所学的数学知识都排除或忘掉后,剩下的东西。
()正确答案:√数学文化(三)1“数学文化”课是以数学问题为载体,以教授数学系统知识及其应用为目的。
()正确答案:×2反证法是解决数学难题的一种有效方法。
()正确答案:√数学文化(四)1“哥尼斯堡七桥问题”最后是被谁解决的?()A、阿基米德B、欧拉C、高斯D、笛卡尔正确答案:B2在解决“哥尼斯堡七桥问题”时,数学家先做的第一步是()。
A、分析B、概括C、推理D、抽象正确答案:D3数学是研究现实世界中的数量关系与空间形式的一门科学。
这句话出自()。
A、阿基米德B、欧拉C、恩格斯D、马克思正确答案:C4从牛顿的著作《自然哲学之数学原理》可以看出,他是不支持数学定义中的“哲学说”的。
()正确答案:×5罗素关于数学概念的描述,是从数学的公理体系角度而言的。
()正确答案:√数学文化(六)1一堆20粒的谷粒,甲乙两个人轮流抓,每次可以抓一粒到五粒,规定谁抓到最后一把谁赢。
数学文化试题答案

一、简单题(9选6,36分)1、什么是可数集?为什么说全体奇数与自然数一样多?答:如果一个集合能与正整数集建立一一对应的映射,则称集合A是可数集。
之所以说全体奇数与自然数一样多,是因为全体奇数能与自然数建立一一对应的关(1→0,3→1,5→2。
),用康托集合论的观点来看,这两个集合的势是相等的。
因为奇数有正奇数也有负奇数,因为负奇数没有什么用处,一般情况下都不提,负奇数的个数当然与自然数中正偶数的个数相同,所以全体奇数与自然数一样多。
2、7座房子,每座房里养7只猫,每只猫抓7只老鼠,每只老鼠吃7颗麦穗,每颗麦穗可产7赫卡特粮食,问房子,猫,老鼠,麦穗和粮食各数值总和。
这一问题产生于哪个国家?哪个时代?7座房子,49只猫,343只老鼠,2401颗麦穗,16807赫卡特。
产生于古埃及的莱茵德草书(阿姆士纸草书);产生时间大约在公元前1650年左右。
.3、万物皆数是哪个学派的口号?如何理解这一口号?古希腊毕达哥拉斯学派,“他们认为,‘数’乃万物之源”“数的要素即万物的要素”,用数来解释一切./毕达哥拉斯学派主张:数是万物之本源,有了数才有点,有了点才有线、面、体,有了这些几何形体才有宇宙万物. 总之,万物皆数!4、勾股定理最早在何时、何地发现?最早的证明又出现在哪个时代,哪个国家?古希腊的毕达哥拉斯发现大禹治水中国5、《几何原本》的作者是谁?他是哪个国家、哪个时代的人?323年-前283年)时期的亚历山大里亚.6、《圆锥曲线》的作者是谁?作者大概生于哪个时期?《圆锥曲线论》是由阿波罗尼奥斯所写的一部经典巨著;托勒密四世。
7、中国最早出现的数学书叫什么?大约成于何时?《算数书》秦或先秦8、中国古代“十部算经”中最重要的是什么?它大概成书于什么时期?《九章算术》, 约公元1世纪的汉代9、朱世杰是哪个时代的人,他在数学上的主要贡献是什么?朱世杰(1249年-1314年)元代对数学的主要贡献是1.创造了一套完整的消未知数方法(多元高次方程列式与消元解法“四元术”)、2.高阶等差数列求和方法(“垛积法”)、3.高次内插法(“招差术”)。
数学文化中的数列(解析版)

第05讲 数列一、单选题1.(2021·江苏常州市·高三一模)天干地支纪年法源于中国,中国自古便有十天干与十二地支,十天干即甲、乙、丙、丁、戊、己、庚、辛、壬、癸;十二地支即子、丑、寅、卯、辰、已、午、未、申、酉、戌、亥.天干地支纪年法是按顺序以一个天干和一个地支相配,排列起来,天干在前,地支在后,天干由“甲”起,地支由“子”起,例如,第一年为“甲子”,第二年为“乙丑”,第三年为“丙寅”,以此类推,排列到“癸酉”后,天干回到“甲”重新开始,即“甲戌”,“乙亥”,然后地支回到“子”重新开始,即“丙子”,以此类推.今年是辛丑年,也是伟大、光荣、正确的中国共产党成立100周年,则中国共产党成立的那一年是( ) A .辛酉年B .辛戊年C .壬酉年D .壬戊年 【答案】A【分析】推导出1921年的天干与地支,由此可得出结果.【详解】由题意知,天干是公差为10的等差数列,地支为公差为12的等差数列,且1001010=⨯,1008124=⨯+,因为2021年为辛丑年,则100年前的天干为“辛”,地支为“酉”,可得到1921年为辛酉年, 故选:A.2.(2021·山东高三专题练习)九连环是我国从古至今广泛流传的一种益智游戏,它用九个圆环相连成串,以解开为胜.据明代杨慎《丹铅总录》记载:“两环互相贯为一,得其关捩,解之为二,又合面为一”.在某种玩法中,用n a 表示解下()9,n n n *≤∈N 个圆环所需的移动最少次数,若11a =,且1121,22,n n n a n a a n ---⎧=⎨+⎩为偶数为奇数,则解下5个环所需的最少移动次数为( )A .7B .13C .16D .22【答案】C【分析】根据数列{}n a 的递推公式逐项计算可得出5a ,即为所求.【详解】数列{}n a 满足11a =.且1121,22,n n n a n a a n ---⎧=⎨+⎩为偶数为奇数,所以,21211a a =-=,32224a a =+=,43217a a =-=,542216a a =+=.所以解下5个环所需的最少移动次数为16.故选:C .3.(2021·全国高三专题练习(理))“中国剩余定理”又称“孙子定理”,讲的是关于整除的问题.现有这样一个整除问题:将1到2021这2021个正整数中能被3除余1且被5除余1的数按从小到大的顺序排成一列,构成数列{}n a ,则数列{}n a 各项的和为( )A .137835B .137836C .135809D .135810【答案】D【分析】由题意知n a 被15除余1,它们成等差数列,公差为15,由此只要确定不大于2021的项数即可得求和.【详解】由题意n a 被15除1,{}n a 是等差数列,公差15d =,首项为11a =, 115(1)1514n a n n =+-=-,由15142021n -≤得,21353n ≤.因此135n ≤, 1351351341351151358102S ⨯=⨯+⨯=. 故选:D .4.5.(2021·南京市宁海中学高二期末)意大利数学家斐波那契()17701250,以兔子繁殖为例,引入“兔子数列”:即1、1、2、3、5、8、13、21、34、55、89、144、233、,在实际生活中,很多花朵(如梅花,飞燕草,万寿简等)的瓣数恰是斐波那契数列中的数,斐波那契数列在物理及化学等领域也有着广泛得应用.已知斐波那契数列{}n a 满足:11a =,21a =,21n n n a a a ++=+,若2357959k a a a a a a a ++++++=,则k =( ) A .2020B .2021C .59D .60 【答案】D【分析】 利用21n n n a a a ++=+化简得出235795960a a a a a a a ++++++=,即可得出结果. 【详解】由于21n n n a a a ++=+,则2357959795945a a a a a a a a a a a +++++=++++++67959585960a a a a a a a ++++==+==,因此,60k =.故选:D. 6.(2021·全国高三专题练习(文))我国古代数学论著中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯二百五十四,请问底层几盏灯?意思是:一座7层塔共挂了254盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的底层共有灯( )A .32盏B .64盏C .128盏D .196盏 【答案】C【分析】根据等比数列前n 项和公式,计算首项.【详解】设最底层的灯数为1a ,公比12q =, 177112254112a S ⎛⎫- ⎪⎝⎭∴==-,解得:1128a =.故选:C7.(2021·江苏苏州市·苏州中学高二开学考试)我国古代数学名著《九章算术》中有如下“两鼠穿墙”问题:有两只老鼠同时从墙的两面相对着打洞穿墙.大老鼠第一天打进11尺,以后每天进度是前一天的2倍.小老鼠第一天也打进1尺,以后每天进度是前一天的一半.如果墙的厚度为10尺,则两鼠穿透此墙至少在第()A.3天B.4天C.5天D.6天【答案】B【分析】设两只老鼠在第n天相遇,利用等比数列的求和公式列方程可求得2n的范围,即可得解.【详解】设两只老鼠在第n天相遇,则大老鼠第n天打洞的厚度成以2为公比的等比数列,小老鼠第n天打洞的厚度成以12为公比的等比列,由等比数列的求和公式可得111221011212n n--+≥--,整理得()229220n n-⋅-≥,可得2n≤(舍去)或()28,16n≥,所以,两鼠穿透此墙至少在第4天.故选:B.8.(2020·四川成都市·北大附中成都为明学校高三月考(文))电影《刘三姐》中有一个“舟妹分狗”的片段.其中,罗秀才唱道:三百条狗交给你,一少三多四下分,不要双数要单数,看你怎样分得匀?舟妹唱道;九十九条圩上卖,九十九条腊起来,九十九条赶羊走,剩下三条,财主请来当奴才(讽刺财主请来对歌的三个奴才).事实上,电影中罗秀才提出了一个数学问题:把300条狗分成4群,每群都是单数,1群少,3群多,数量多的三群必须都是一样的,否则就不是一少三多,问你怎样分舟妹已唱出其中一种分法,即{}3,99,99,99,那么,所有分法的种数为()A.6B.9C .10D .12【答案】D【分析】 设少的1群狗有n 条,多的3群狗每群有m 条,m 、n *∈N ,且m n >,由已知条件可得出3300n m +=,分析出n 为3的倍数,设()*3n t t N=∈,求出t 的可能取值,然后列举出所有的分法,由此可得出结果. 【详解】设少的1群狗有n 条,多的3群狗每群有m 条,m 、n *∈N ,且m n >.根据题意,3300n m +=,则n 一定是3的倍数,可设()*3n t t N =∈,由m n >,得075n <<,则0375t <<,即025t <<.由n 为奇数,则t 为奇数,即{}1,3,5,7,9,11,13,15,17,19,21,23t ∈,于是分配方法有以下12种:{}3,99,99,99、{}9,97,97,97、{}15,95,95,95、{}21,93,93,93、{}27,91,91,91、{}33,89,89,89、{}39,87,87,87、{}45,85,85,85、{}51,83,83,83、{}57,81,81,81、{}63,79,79,79、{}69,77,77,77.故选:D.【点睛】关键点点睛:本题考查分配问题,根据题意得出m 、n 的等式以及n 的可能取值是解题的关键,本题是数学文化题,在解题时要充分理解题中的信息,将题意转化为等式或不等式来求解.9.(2020·重庆高三月考)我国古代数学家著作《九章算术》有如下问题:“今有人持金出五关,前关二而税一,次关三而税一,次关四而税一,次关五而税一,次关六而税一,并五关所税,适重一斤.问本持金几何.”,其意思是“今有人持金出五关,第一关收税金为持金的12,第2关收税金为剩余的13,第3关收税金为剩余税金的14,第4关收税金为剩余税金的15,第5关收税金为剩余税金的16”5关所税金之和,恰好重1斤.则在此问题中,第3关收税金为( )斤A.110B.310C.13D.910【答案】A【分析】依题意求出最初持有金子数量,即可得解;【详解】解:第一关后,剩余金为原来的一半,第二关后,剩余金为原来的三分之一,第三关后,剩余金为原来的四分之一,第四关后,剩余金为原来的五分之一,第五关后,剩余金为原来的六分之一,故最初持有金子的六分之五是1斤,最初持有金子1.2斤,第三关使得整体持有金子从原来的三分之一变到四分之一,减少了0.1斤,故选:A.10.(2020·六盘山高级中学高三月考(理))天干地支纪年法源于中国,中国自古便有十天干与十二地支,十天干即甲、乙、丙、丁、戊、己、庚、辛、壬、癸;十二地支即子、丑、寅、卯、辰、已、午、未、申、酉、戌、亥天干地支纪年法是按顺序以一个天干和一个地支相配,排列起来,天干在前,地支在后,天干由“甲”起,地支由“子”起,例如,第一年为“甲子”,第二年为“乙丑”,第三年为“丙寅”,…,以此类推,排列到“癸酉”后,天于回到“甲”重新开始,即“甲戌”,“乙亥”,然后地支回到“子”重新开始,即“丙子”,以此类推已知1949年为“己丑”年,那么2021年时为()A.己亥年B.戊申年C.庚子年D.辛丑年【答案】D【分析】根据题意,天干和地支的年份分别是以10和12为公差的等差数列,根据等差数列的性质即可求解.【详解】由题意可知,天干是以10为公差的等差数列,地支是以12为公差的等差数列,从1949到2021经历72年,且1949年为“己丑”年,以1949年的天干和地支分别为首项,则7210=7 (2)÷,则2021年的天干为辛,7212=6÷,则2021年的地支为丑。
与数学文化相关的数学专题

与数学文化相关的数学专题【方法综述】关注学生数学文化的意识的养成,努力推进数学文化的教育,已经成为当今数学教师与改革的一个重要特征,在新课改的数学命题中,数学文化已经得到足够的重视,但并没由得到应有的落实,造成数学文化教学的缺失的根本原因在于教师自身数学文化素养的缺乏,令人欣喜的是在近几年的高考试题中已经开始有意识的进行尝试和引导,在众多的经典试题中,湖北卷的数学文化题更超凡脱俗和出类拔萃,因此,我们特别策划了此专题,将数学文化与数学知识相结合,选取典型样题深度解读,希望能够给予广大师生的复习备考以专业的帮助与指导.【解答策略】类型一、取材数学游戏游戏可以让数学更加好玩,在游戏中运用数学知识,或蕴含着数学原理的智力游戏可笼统地称为数学游戏,把数学游戏改编为高考试题,既不失数学型,又能增加了考题的趣味性,充分体现了素质教育与大众数学的理念.例1、五位同学围成一圈依次循环报数,规定:①第一位同学首次报出的数为1,第二位同学首次报出的数也为1,之后每位同学所报出的数都是前两位同学所报出的数之和;②若报出的数是3的倍数,则报该数的同学需拍手一次.已知甲同学第一个报数,当五位同学依次循环报到第100个数时,甲同学拍手的总次数为 .【答案】【解析】由题意可知:将每位同学所报的数排列起来,即是“斐波那契数列”:1,1,2,3,5,8,13,21,34,55,89,44,233,377,610,987,……该数列的一个规律是,第4,8,12,16,……4n项是3的倍数;甲同学报数的序数是1,6,11,16,……,5m-4;甲同学报的数为3的倍数,依次为第15,35,55,75,95位数,共5个,所以,甲同学拍手的总次数是5次.【指点迷津】以数学游戏为素材的命制高考题目,创造了既宽松又竞争的环境,拉近了考生与数学的心理距离,但要注意游戏素材的选择应与考生的实际生活密切相关,便于考生更好地理解游戏.例如:2012年高考湖北卷第13题“回文数”,考查排列、组合和归纳推理等知识.本题以此为背景,以简单的游戏为分析计算对象,考查学生的阅读理解能力和合情推理能力.【举一反三】回文数是指从左到右与从右到左读都一样的正整数.如22,,11,3443,94249等.显然2位回文数有9个:11,22,33…,99.3位回文数有90个:101,111,121,…,191,202,…,999.则(Ⅰ)4位回文数有______个;(Ⅱ)2n +1(n ∈N+)位回文数有______个.【答案】910n ⨯ ()21n n ++∈N 位回文数与()22n n ++∈N 位回文数个数相等,均为910n ⨯个. 类型二、取材数学名著如数学家的传记、数学演讲报告、数学讲义等,这些都是命制考题好的素材,从中选取一段有关的数学素材,突出索要考查的数学知识,在引导中学数学教学知能并重的同时,有意识地培养学生的数学素养.例2、我国古代数学著作《九章算术》有如下问题:“今有金箠,长五尺,斩本一尺,重四斤,斩末一尺,重二斤,问次一尺各重几何?”意思是:“现有一根金杖,长5尺,一头粗,一头细,在粗的一端截下1尺,重4斤;在细的一端截下1尺,重2斤;问依次每一尺各重多少斤?”设该金杖由粗到细是均匀变化的,其重量为M ,现将该金杖截成长度相等的10段,记第i 段的重量为()1,2,,10i a i =,且1210a a a <<<,若485i a M =,则i =( )A. 4B. 5C. 6D. 7【答案】C【解析】【指点迷津】本题主要考查阅读能力、等差数列的通项公式、等差数列的前n项和公式以及转化与划归思想,属于中档题.等差数列基本量的运算是等差数列的一类基本题型,数列中的五个基本量1,,,,,n na d n a S,一般可以“知二求三”,通过列方程组所求问题可以迎刃而解,解决此类问题的关键是熟练掌握等差数列的有关性质和公式,并灵活应用,在运算过程中,还应善于运用整体代换思想简化运算过程.学*科网【举一反三】我国明代伟大数学家程大位在《算法统综》中常以诗歌的形式呈现数学问题,其中有一首“竹筒容米”问题:“家有九节竹一茎,为因盛米不均平,下头三节三升九,上梢四节贮三升,唯有中间两节竹,要将米数次第盛,若有先生能算法,也教算得到天明”意思是:九节竹的盛米容积成等差数列,其中的“三升九”指3.9升,则九节竹的中间一节的盛米容积为()A.0.9升B.1升C.1.1升D.2.1升【答案】B【解析】依题意得,故,即,解得,故升.故选B.类型三、取材数学名题数学名题具有非凡的魅力,它常常蕴涵深刻的数学内容、经典的数学方法或与一些数学大师相关联,数学名题能持续地是命制试题的重点取材之一.例3、我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表,即杨辉三角,这是数学史上的一个伟大成就.在“杨辉三角”中,第行的所有数字之和为,若去除所有为1的项,依次构成数列,则此数列的前55项和A.4072 B.2026 C.4096 D.2048【答案】A【解析】解:由题意可知:每一行数字和为首项为1,公比为2的等比数列,则杨辉三角形的前n项和为S n2n﹣1,若去除所有的为1的项,则剩下的每一行的个数为1,2,3,4,……,可以看成构成一个首项为1,公差为1的等差数列,则T n,可得当n=10,所有项的个数和为55,则杨辉三角形的前12项的和为S12=212﹣1,则此数列前55项的和为S12﹣23=4072,故选:A.【指点迷津】利用n次二项式系数对应杨辉三角形的第n+1行,然后令x=1得到对应项的系数和,结合等比数列和等差数列的公式进行转化求解即可.【举一反三】 2018年9月24日,英国数学家M.F阿帝亚爵在“海德堡论坛”展示了他“证明”黎曼猜想的过程,引起数学界震动,黎曼猜想来源于一些特殊数列求和.记无穷数列的各项的和,那么下列结论正确的是()A. B. C. D.【答案】C由时,,可得,时,,可得,排除,由,可排除,故选C.类型四、取材数学推理数学猜想是推动数学发展的强大动力之一,是数学发展中最活跃、最主动、最积极的因素,也是人类理性中最富有创造性的部分,数学猜想一旦被证明,就将转化为定理,从而丰富数学理论,即使被否定或不能被证实,也常常能给数学带来不可预期的成果,数学猜想是命制考题的好素材,它包含丰富的数学知识和思想方法.例4、古希腊人常用小石子在沙滩上摆成各种性状来研究数,例如:他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似地,称图2中的1,4,9,16…这样的数成为正方形数.下列数中及时三角形数又是正方形数的是A.289B.1024C.1225D.1378【答案】C【指点迷津】合情推理主要包括归纳推理和类比推理.数学研究中,在得到一个新结论前,合情推理能帮助猜测和发现结论,在证明一个数学结论之前,合情推理常常能为证明提供思路与方向.合情推理仅是“合乎情理”的推理,它得到的结论不一定正确.而演绎推理得到的结论一定正确(前提和推理形式都正确的前提下).【举一反三】朱世杰是历史上最伟大的数学家之一,他所著的《四元玉鉴》卷中“如像招数”五问中有如下问题:今有官司差夫一千八百六十四人筑堤,只云初日差六十四人,次日转多七人.”其大意为“官府陆续派遣1864人前往修筑堤坝,第一天派出64人,从第二天开始每天派出的人数比前一天多7人.”在该问题中的1864人全部派遣到位需要的天数为()A.9 B.16 C.18 D.20【答案】B【解析】根据题意设每天派出的人数组成数列,分析可得数列是首项,公差的等差数列,该问题中的1864人全部派遣到位的天数为,则,依次将选项中的值代入检验得,满足方程,故选B.类型五、取材数学图形例5、一幅图胜过一千字,“数缺形时少直观,形少数时难入微;数形结合百般好,隔离分家万事休”,图形不仅包含大量信息,而且形象直观,生动绚丽,还能展示数学之美,图形是数学总要的组成部分,高考试题中自然少不了这样的试题,同时能较好的体现数学文化,甚至富有诗意的数学图形.【贵州省凯里市第一中学2019届高三下学期模拟考试《黄金卷二》】如图,是我国古代数学家赵爽的弦图,它是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如果大正方形的面积为,小正方形的面积为,直角三角形较小的锐角为,则()A.B.C.D.【答案】D【解析】大正方形的面积为,小正方形的面积为,大正方形的边长为,小正方形边长为.设四个全等的直角三角形的长直角边为,则短直角边为由勾股定理得,解得为直角三角形较小的锐角,所以所以【举一反三】1.中国古代数学名著《九章算术》中记载了公元前344年商鞅督造的一种标准量器——商鞅铜方升,其三视图如图所示(单位:寸),若取,立方寸=升,则商鞅铜方升的容积约为()A.升B.升C.升D.升【答案】B【解析】由三视图得,商鞅铜方升由一圆柱和一长方体组合而成,(如图所示)故其体积(立方寸),(升),故选:B2.牛顿迭代法亦称切线法,它是求函数零点近似解的另一种方法,若定义是函数零点近似解的初始值,过点的切线为,切线与轴交点的横坐标,即为函数零点近似解的下一个初始值,以此类推,满足精度的初始值即为函数零点的近似解,设函数,满足应用上述方法,则()A.B.C.D.【答案】D【解析】,,切线斜率,切线方程,令,得,切线斜率,切线方程,令,得,切线斜率,切线方程,令,得,故选D项类型六、取材数学文化与现代科学:数学文化与现代科学泛指最近一段时间国内外发生的数学方面的大事,被广大媒体和公众共同关注,具有方向性和短暂性和聚焦性等特点,命题专家从一段时事材料中甄选一个角度,简明扼要的交代时事背景,抽象出数学模型,突出索要考查的数学问题,类似于文科综合卷中的时事材料,既能达到一般试题的考查效果,又能融入肥厚的数学文化,平添点滴生活气息.例6、习总书记在十九大报告中指出:必须树立和践行绿水青山就是金山银山的理念.某市为贯彻落实十九大精神,开展植树造林活动,拟测量某座山的高.如图,勘探队员在山脚A测得山顶B的仰角为,他沿着倾斜角为的斜坡向上走了40米后到达C,在C 处测得山顶B的仰角为,则山高约为______米.(结果精确到个位,在同一铅垂面).参考数据:.【答案】【解析】过C做CM⊥BD于M,CN⊥AD于N,设BM=h,则CM=,解得h=20(),∴BD=h+20【指点迷津】 1.命题者抓住“嫦娥奔月”这个古老而又现代的浪漫话题,以探测卫星轨道为背景,抽象出共一条对称轴、一个焦点和一个顶点的两个椭圆的几何性质,并以加减乘除的方式构造两个等式和两个不等式,考查椭圆的几何性质,可谓匠心独运.2.注意到椭圆轨道Ⅰ和Ⅱ共一个顶点P和一个焦点F,题目所给四个式子涉及长半轴长和半焦距,从焦距入手,这是求解的关键,本题对考生的数学能力进行了比较全面的考查,是一道名副其实的小中见大、常中见新、蕴文化于现代科学技术应用之中的好题.【举一反三】中国最早的天文学和数学著作《周髀算经》里提到了七衡,即七个等距的同心圆.七衡的直径和周长都是等差数列,最里面的一圆叫内一衡,外面的圆依次叫次二衡,次三衡,….设内一衡直径为,衡间距为,则次二衡直径为,次三衡直径为,…,执行如下程序框图,则输出的中最大的一个数为()A.B.C.D.【答案】D【解析】由题意可知题中所给的程序框图功能为计算并输出的值,由等差数列通项公式有:,且易知恒成立,则:,当且仅当,即时等号成立.综上可得,输出的中最大的一个数为.本题选择D选项.【强化训练】一、选择题1.《九章算术》中有一题:今有牛、马、羊食人苗苗主责之粟五斗羊主曰:“我羊食半马”马主曰:“我马食半牛”今欲衰偿之,问各出几何其意思是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿五斗粟羊主人说:“我羊所吃的禾苗只有马的一半”马主人说:“我马所吃的禾苗只有牛的一半”若按此比例偿还,牛、马、羊的主人各应赔偿多少?设牛、马、羊的主人分别应偿还x斗、y斗、z斗,则下列判断正确的是()A.且B.且C.且D.且【答案】B【解析】由题意可知x,y,z依次成公比为的等比数列,则,解得,由等比数列的性质可得.故选:B.3.《算法统宗》是中国古代数学名著,由明代数学家程大位编著,它对我国民间普及珠算和数学知识起到了很大的作用,是东方古代数学的名著.在这部著作中,许多数学问题都是以歌诀形式呈现的,“九儿问甲歌”就是其中一首:一个公公九个儿,若问生年总不知,自长排来差三岁,共年二百又零七,借问长儿多少岁,各儿岁数要详推.在这个问题中,记这位公公的第个儿子的年龄为,则( )A.23 B.32 C.35 D.38【答案】C【解析】由题意可得儿子的岁数成等差数列,设公差为,其中公差,,即,解得,故选C.4.我国古代数学著作算法统宗中有这样一个问题意为:“有一个人要走378里路,第一天健步行走,从第二天起因脚痛每天走的路程为前一天的一半,走了6天后到达目的地“那么,此人第4天和第5天共走路程是A.24里 B.36里 C.48里 D.60里【答案】B【解析】记每天走的路程里数为,可知是公比的等比数列,由,得,解得:,.所以此人第4天和第5天共走了里,故选B.5.中国最早的天文学和数学著作《周髀算经》里提到了七衡,即七个等距的同心圆.七衡的直径和周长都是等差数列,最里面的一圆叫内一衡,外面的圆依次叫次二衡,次三衡,….设内一衡直径为,衡间距为,则次二衡直径为,次三衡直径为,…,执行如下程序框图,则输出的中最大的一个数为()A.B.C.D.【答案】D【解析】由题意可知题中所给的程序框图功能为计算并输出的值,由等差数列通项公式有:,且易知恒成立,则:,当且仅当,即时等号成立.综上可得,输出的中最大的一个数为.本题选择D选项.6.“垛积术”(隙积术)是由北宋科学家沈括在《梦溪笔谈》中首创,南宋数学家杨辉、元代数学家朱世杰丰富和发展的一类数列求和方法,有茭草垛、方垛、刍童垛、三角垛等等.某仓库中部分货物堆放成如图所示的“菱草垛”:自上而下,第一层1件,以后每一层比上一层多1件,最后一层是件.已知第一层货物单价1万元,从第二层起,货物的单价是上一层单价的.若这堆货物总价是万元,则的值为()A.7 B.8 C.9 D.10【答案】D【解析】由题意,第一层货物总价为1万元,第二层货物总价为万元,第三层货物总价为万元,…,第层货物总价为万元,设这堆货物总价为万元,则,,两式相减得,则,解得,故选D.7.在《九章算术》中,将四个面都是直角三角形的四面体称为鳖臑,在鳖臑中,平面,,且,为AD的中点,则异面直线与夹角的余弦值为()A.B.C.D.【答案】C【解析】设是中点,连接,由于分别是中点,是三角形的中位线,故,所以是两条异面直线所成的角.根据鳖臑的几何性质可知.故,在三角形中,由余弦定理得,故选C.8.我国南北朝时的数学著作《张邱建算经》有一道题为:“今有十等人,每等一人,宫赐金以等次差降之,上三人先入,得金四斤,持出,下三人后入得金三斤,持出,中间四人未到者,亦依次更给,问各得金几何?”则在该问题中,中等级中的五等人与六等人所得黄金数()A.B.C.D.【答案】C【解析】设为第等人的得金数,则为等差数列,由题设可知,,故,而,故选C.9.中国宋代的数学家秦九韶曾提出“三斜求积术”,即假设在平面内有一个三角形,边长分别为,三角形的面积可由公式求得,其中为三角形周长的一半,这个公式也被称为海伦-秦九韶公式,现有一个三角形的边长满足,则此三角形面积的最大值为( )A.B.C.D.【答案】C【解析】由题意,p=10,S8,∴此三角形面积的最大值为8.故选:C.10.赵爽是我国古代数学家、天文学家,大约在公元222年,赵爽为《周髀算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽弦图”(以弦为边长得到的正方形由4个全等的直角三角形再加上中间的一个小正方形组成的),类比“赵爽弦图”,可类似地构造如图所示的图形,它是由3个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形,设,则()A.B.C.D.【答案】D【解析】设,因此,又由题意可得,所以,因此;延长交于,记,,则,所以;又由题意易知,则,在三角形中,由正弦定理可得,即,因此,,所以,因为,所以,即,整理得,所以.故选D11.我国南北朝时期的数学家祖暅提出了计算体积的祖暅原理:“幂势既同,则积不容异.”意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.已知曲线,直线为曲线在点处的切线.如图所示,阴影部分为曲线、直线以及轴所围成的平面图形,记该平面图形绕轴旋转一周所得的几何体为.给出以下四个几何体:①②③④图①是底面直径和高均为的圆锥;图②是将底面直径和高均为的圆柱挖掉一个与圆柱同底等高的倒置圆锥得到的几何体;图③是底面边长和高均为的正四棱锥;图④是将上底面直径为,下底面直径为,高为的圆台挖掉一个底面直径为,高为的倒置圆锥得到的几何体.根据祖暅原理,以上四个几何体中与的体积相等的是()A.①B.②C.③D.④【答案】A【解析】几何体是由阴影旋转得到,所以横截面为环形,且等高的时候,抛物线对应的点的横坐标为,切线对应的横坐标为,切线为,即,横截面面积图①中的圆锥高为1,底面半径为,可以看成由直线绕轴旋转得到横截面的面积为.所以几何体和①中的圆锥在所有等高处的水平截面的面积相等,所以二者体积相等,故选A项.12.孔明锁,也叫鲁班锁,起源于中国古代建筑中首创的榫卵结构,它是用6根木条制作的一件可拼可拆的、广泛流传于中国民间的智力玩具.如图,网格纸上小正方形的边长为1,粗线画出的是其中3根木条的三视图,记这3根木条的体积分别为,则()A.B.C.D.【答案】C【解析】解:由题意可知几何体是正四棱柱去掉部分棱柱的几何体,由题意可知V1=32﹣8=24;V2=32﹣10=22;V3=32﹣6=26,这3根木条的体积分别为V1,V2,V3,满足V2<V1<V3.故选:C.二、填空题12. 我国古代数学家祖暅提出原理:“幂势既同,则积不容异”.其中“幂”是截面积,“势”是几何体的高.该原理的意思是:夹在两个平行平面间的两个几何体,被任一平行于这两个平行平面的平面所截,若所截的两个截面的面积恒相等,则这两个几何体的体积相等.如图,在空间直角坐标系中的平面内,若函数的图象与轴围成一个封闭的区域,将区域沿轴的正方向平移8个单位长度,得到几何体如图一,现有一个与之等高的圆柱如图二,其底面积与区域的面积相等,则此圆柱的体积为__________.【答案】【解析】【分析】利用四分之一圆的面积和直角三角形面积公式求得阴影部分的面积,进而求得圆柱的体积. 【详解】表示的是四分之一的圆的面积,且圆的半径是,所以区域的面积为,所以圆柱的体积.13.九章算术中有一题:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马,”马主曰:“我马食半牛”,今欲衰偿之,问各出几何?其意:今有牛、马、羊吃了别人的禾苗,苗主人要求赔偿五斗粟,羊主人说:“我羊所吃的禾苗只有马的一半”马主人说:“我马所吃的禾苗只有牛的一半”打算按此比例偿还,问羊的主人应赔偿______斗粟,在这个问题中牛主人比羊主人多赔偿______斗粟.【答案】【解析】设牛、马、羊的主人应赔偿的斗栗分别为x,y,z.由题意可知x,y,z依次成公比为的等比数列,则,解得,则,羊的主人应赔偿斗粟;牛主人比羊主人多赔偿斗粟.故答案为:;.14.中国古代数学专家(九章算术)中有这样一题:今有男子善走,日增等里,九日走里,第一日,第四日,第七日所走之和为里,则该男子的第三日走的里数为__________.【答案】120【解析】因为男子善走,日增等里,可知每天走的里数符合等差数列,设这个等差数列为,其公差为,前项和为.根据题意可知,,法一:,,.法二:,解得所以15.太极图被称为“中华第一图”.从孔庙大成殿粱柱,到楼观台、三茅宫、白外五观的标记物;从道袍、卦摊、中医、气功、武术到南韩国旗、新加坡空军机徽……,太极图无不跃居其上.这种广为人知的太极图,其形状如阴阳两鱼互抱在一起,因而被称为“阴阳鱼太极图”.在如图所示的阴阳鱼图案中,阴影部分的区域可用小等式组或来表示,设是阴影中任意一点,则的最大值为___________.【答案】【解析】如图,作出直线:,当直线往上平移至与阴影部分的圆的边界相切时,最大,此时圆心到直线的距离等于半径1,即:.解得:16.《孙子算经》是我国古代内容极其丰富的数学名著,书中有如下问题:“今有圆窖,周五丈四尺,深一丈八尺,问受粟几何?”其意思为:“有圆柱形容器,底面圆周长五丈四尺,高一丈八尺,求此容器能装多少斛米.”则该圆柱形容器能装米__________斛.(古制1丈=10尺,1斛=1.62立方尺,圆周率)【答案】【解析】,圆柱形容器体积为 ,所以此容器能装斛米.16.对于直角三角形的研究,中国早在商朝时期商高就提出了“勾三股四玄五”勾股定理的特例,而西方直到公元前6世纪,古希腊的毕达哥拉斯才提出并证明了勾股定理如果一个直角三角形的斜边长等于5,那么这个直角三角形面积的最大值等于______.【答案】【解析】设直角三角形的斜边为c,直角边分别为a,b,由题意知,则,则三角形的面积,,,则三角形的面积,当且仅当a=b=取等即这个直角三角形面积的最大值等于,故答案为:.。
高中数学文化情景题专题9 牛顿 (以牛顿为背景的高中数学考题题组训练)解析版
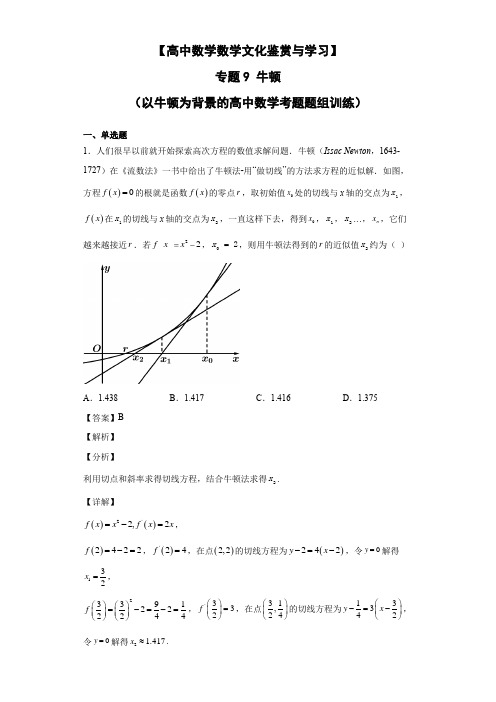
【高中数学数学文化鉴赏与学习】专题9 牛顿(以牛顿为背景的高中数学考题题组训练)一、单选题1.人们很早以前就开始探索高次方程的数值求解问题.牛顿(Issac Newton ,1643-1727)在《流数法》一书中给出了牛顿法-用“做切线”的方法求方程的近似解.如图,方程()0f x =的根就是函数()f x 的零点r ,取初始值0x 处的切线与x 轴的交点为1x ,()f x 在1x 的切线与x 轴的交点为2x ,一直这样下去,得到0x ,1x ,2x …,n x ,它们越来越接近r .若22f xx ,02x =,则用牛顿法得到的r 的近似值2x 约为( )A .1.438B .1.417C .1.416D .1.375【答案】B 【解析】 【分析】利用切点和斜率求得切线方程,结合牛顿法求得2x . 【详解】()()2'2,2f x x f x x =-=,()2422f =-=,()'24f =,在点()2,2的切线方程为()242y x -=-,令0y =解得132x =, 23391222244f ⎛⎫⎛⎫=-=-= ⎪ ⎪⎝⎭⎝⎭,'332f ⎛⎫= ⎪⎝⎭,在点31,24⎛⎫ ⎪⎝⎭的切线方程为13342y x ⎛⎫-=- ⎪⎝⎭,令0y =解得2 1.417x ≈.故选:B2.牛顿冷却定律描述物体在常温环境下的温度变化:如果物体的初始温度为0T ,则经过一定时间t 分钟后的温度T 满足()012tha a T T T T ⎛⎫-=- ⎪⎝⎭,h 称为半衰期,其中a T 是环境温度.若25a T =℃,现有一杯80℃的热水降至75℃大约用时1分钟,那么水温从75℃降至45℃大约还需要( )(参考数据:lg 20.30≈,lg11 1.04≈) A .8分钟 B .9分钟 C .10分钟 D .11分钟【答案】C 【解析】 【分析】由题意可得1110()211h=,代入14525()(7525)2th -=-,得510112t⎛⎫= ⎪⎝⎭,两边取常用对数得:10lglg 1152t =,再利用对数的运算性质即可求出t 的值. 【详解】解:根据题意得:117525(8025)2h⎛⎫-=- ⎪⎝⎭,∴1110211h⎛⎫= ⎪⎝⎭, ()14525()75252t h∴-=-,112050()2th ⎡⎤∴=⨯⎢⎥⎣⎦,∴510112t⎛⎫= ⎪⎝⎭, 两边取常用对数得:10lglg 1152t =, 2lglg 2lg52lg 2120.31510101lg111lg111 1.04lg 11t --⨯-∴===≈=---,∴水温从75℃降至45℃大约还需要10分钟, 故选:C .3.牛顿切线法是牛顿在十七世纪提出的一种在实数域和复数域上近似求解方程的方法.比如求解方程323410x x x -+-=,先令32()341f x x x x =-+-,然后对()y f x =的图象持续实施下面的步骤:第一步,在点(1,1)处作曲线的切线,交x 轴于()1,0x ; 第二步,在点()()11,x f x 处作曲线的切线,交x 轴于()2,0x ; 第三步,在点()()22,x f x 处作曲线的切线,交x 轴于()3,0x ; ……利用该方法可得方程近似解3x (保留三位有效数字)是( ) A .0.313 B .0.314 C .0.315 D .0.316【答案】B 【解析】 【分析】根据导数的几何意义先求解点(1,1)处的切线,进而得到()1,0x ,再按题意继续计算得到3x 即可 【详解】2()364(1)1f x x x f ''=-+∴=所以()y f x =在(1,1)处的切线方程11,y x y x -=-=,则10x =;同理(0)4f '=,()y f x =在(0,1)-处的切线方程41y x =-,令0y =,得214x =,又143()416f '=,()y f x =在111,464⎛⎫- ⎪⎝⎭处的切线方程4311116464y x ⎛⎫=-- ⎪⎝⎭,令0y =,得3270.31486x =≈. 故选:B .4.牛顿曾经提出了常温环境下的温度冷却模型:0101ln t k θθθθ-=--(t 为时间,单位为分钟,0θ为环境温度,1θ为物体初始温度,θ为冷却后温度),假设一杯开水温度190C θ=,环境温度010C θ=,常数16k =,大约经过多少分钟水温降为40(参考数据:ln 20.7≈,ln3 1.1≈}( ) A .8 B .7C .6D .5【答案】C 【解析】【分析】根据题意,将数据代入温度冷却模型,即可求解. 【详解】由题意知:代入冷却模型,()401036ln 6ln 6ln 3ln890108t -=-=-=---即()6ln33ln 26t =--≈ 故选:C.5.中国茶文化博大精深,某同学在茶艺选修课中了解到,茶水的口感与茶叶类型和水的温度有关,某种绿茶用80℃左右的水泡制可使茶汤清澈明亮,营养也较少破坏.为了方便控制水温,该同学联想到牛顿提出的物体在常温环境下温度变化的冷却模型:如果物体的初始温度是1θ℃,环境温度是0θ℃,则经过t 分钟后物体的温度θ℃将满足()010e kt θθθθ-=+-,其中k 是一个随着物体与空气的接触状况而定的正常数.该同学通过多次测量平均值的方法得到初始温度为100℃的水在20℃的室温中,12分钟以后温度下降到50℃.则在上述条件下,100℃的水应大约冷却( )分钟冲泡该绿茶(参考数据:ln 20.7≈,ln3 1.1≈) A .3 B .3.6 C .4 D .4.8【答案】B 【解析】 【分析】根据题意求出k 的值,再将θ=80℃,1θ=100℃,0θ=20℃代入()010e ktθθθθ-=+-即可求得t 的值. 【详解】由题可知:()()112121233502010020e e e 88k k k ---⎛⎫=+-⇒=⇒= ⎪⎝⎭, 冲泡绿茶时水温为80℃, 故()()33802010020ee ln e ln 44tktkk t ---=+-⋅⇒=⇒⋅= ()()1123ln12ln32ln2121.120.743.6ln33ln21.130.73ln 8t --⨯⇒==≈=--⨯⎛⎫⎪⎝⎭.故选:B.6.牛顿流体符合牛顿黏性定律,在一定温度和剪切速率范围内黏度值是保持恒定的:τηγ=,其中τ为剪切应力,η为黏度,γ为剪切速率;而当液体的剪切应力和剪切速率存在非线性关系时液体就称为非牛顿流体.非牛顿流体会产生很多非常有趣的现象,如人陷入沼泽越挣扎将会陷得越深;也有很多广泛的应用,如某些高分子聚合物还可以做成“液体防弹衣”.如图是测得的某几种液体的流变τγ-曲线,则其中属于沼泽和液体防弹衣所用液体的曲线分别是( )A .℃和℃B .℃和℃C .℃和℃D .℃和℃【答案】C 【解析】 【分析】根据所给定义,分析出图象中牛顿流体和非牛顿流体对应的曲线,即可得答案. 【详解】由题意得牛顿流体黏度η恒定,即在τγ-曲线中,图象为直线,即℃和℃为牛顿流体,℃和℃为非牛顿流体,又属于沼泽和液体防弹衣所用液体为非牛顿流体, 所以对应曲线为℃和℃. 故选:C7.牛顿曾经提出了常温环境下的温度冷却模型:()100e ktθθθθ-=-+,其中为时间(单位:min ),0θ为环境温度,1θ为物体初始温度,θ为冷却后温度),假设在室内温度为20C 的情况下,一桶咖啡由100C 降低到60C 需要20min .则k 的值为( ) A .ln 220B .ln 320C .ln 210-D .ln 310-【答案】A 【解析】 【分析】把020θ=,1100θ=,60θ=,20t =代入()100e ktθθθθ-=-+可求得实数k 的值.【详解】由题意,把020θ=,1100θ=,60θ=,20t =代入()100e ktθθθθ-=-+中得2080e 2060k -+=,可得201e2k-=, 所以,20ln 2k -=-,因此,ln 220k =. 故选:A.8.人们很早以前就开始探索高次方程的数值求解问题.牛顿(1643—1727)给出了牛顿法——用“作切线”的方法求方程的近似解.如图,方程()0f x =的根就是函数()f x 的零点r ,取初始值0x 处的切线与x 轴的交点为1x ,()f x 在1x 处的切线与x 轴的交点为2x ,一直这样下去,得到0x ,1x ,2x ,…,n x ,它们越来越接近r .若22f x x ,02x =,则用牛顿法得到的r 的近似值2x 约为( )A .1.438B .1.417C .1.415D .1.375【答案】B 【解析】 【分析】利用切点和斜率求得切线方程,结合牛顿法求得2x . 【详解】由题意,得()2f x x '=,()2422f =-=,()24f '=, 所以曲线()y f x =在点()2,2处的切线方程为()242y x -=-, 令0y =,得132x =.又23312224f ⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭,332f ⎛⎫'= ⎪⎝⎭,所以曲线()y f x =在点31,24⎛⎫⎪⎝⎭处的切线方程为13342y x ⎛⎫-=- ⎪⎝⎭,令0y =,解得2 1.417x ≈. 故选:B.9.著名数学家、物理学家牛顿曾提出:物体在空气中冷却,如果物体的初始温度为1θ℃,空气温度为0θ℃,则t 分钟后物体的温度θ(单位:℃)满足:()010e kt θθθθ-=+-.若常数0.05k =,空气温度为25℃ ,某物体的温度从85℃ 下降到45℃ ,大约需要的时间为( )(参考数据:ln3 1.1≈)A .25分钟B .24分钟C .23分钟D .22分钟【答案】D 【解析】 【分析】由题意可得,025θ=,185θ=,45θ=,故0.054525(8525)e t -=+-,再结合对数函数的公式,即可求解. 【详解】由题意可得,025θ=,185θ=,45θ=, 故0.054525(8525)e t -=+-,0.0531e t -∴=,即0.05n 31l t -=,ln3220.05001.1.5t ∴=≈=(分钟),即大约需要的时间为22分钟, 故选:D .10.牛顿曾经提出了常温环境下的温度冷却模型:0101ln t k θθθθ-=--(t 为时间,单位为分钟,0θ为环境温度,1θ为物体初始温度,θ为冷却后温度),假设一杯开水温度190θ=℃,环境温度010θ=℃,常数16k =,大约经过多少分钟水温降为40℃?(参考数据:ln20.7,ln3 1.1≈≈)( ) A .8 B .7C .6D .7【答案】C 【解析】【分析】根据题设的温度冷却模型有40106ln 9010t -=--,应用对数的运算性质即可求值.【详解】由题意知:401036ln 6ln 6(ln 3ln8)6(ln 33ln 2)690108t -=-=-=--=--≈-分钟,故选:C.11.英国著名物理学家牛顿用“作切线”的方法求函数零点时,给出的“牛顿数列”在航空航天中应用广泛,若数列{}n x 满足()()n 1n n n f x x x f x +'=-,则称数列{}n x 为牛顿数列.如果函数2()2f x x x =--,数列{}n x 为牛顿数列,设n n 2ln 1n x a x -=+且11a =-,2n x >,数列{}n a 的前n 项和为n S ,则2021S =( ) A .202121-B .202112-C .20211122⎛⎫- ⎪⎝⎭D .2021122⎛⎫- ⎪⎝⎭【答案】B 【解析】 【分析】先由题设得到:221222121n n n n n n n x x x x x x x +--+=-=--,从而得到12n n a a +=,即可说明数列{}n a 是以-1为首项,2为公比的等比数列,再利用等比数列前n 项和求和公式得到结果. 【详解】解:由题知()21f x x '=-221'()22()2121n n n n n n n n n n f x x x x x x x f x x x +--+=-=-=--22121222212211121n n n n n n n n x x x x x x x x +++-⎛⎫---∴== ⎪+++⎝⎭+-两边取对数得:1122ln 2ln 11n n n n x x x x ++--=++令2ln1n n n x a x -=+即12n n a a +=,所以数列{}n a 是以-1为首项,2为公比的等比数列,()1202120211121n a q S q-∴==--故选:B12.英国著名物理学家牛顿用“作切线”的方法求函数零点时,给出的“牛顿数列”在航空航天中应用广泛.若数列{}n x 满足()()1n n n n f x x x f x +=-',则称数列{}n x 为牛顿数列.如果函数()22f x x x =--,数列{}n x 为牛顿数列,设2ln1n n n x a x -=+.且11,2n a x =>,数列{}n a 的前n 项和为n S ,则2022S =( )A .202221- B .202222-C .20221122⎛⎫- ⎪⎝⎭D .2022122⎛⎫- ⎪⎝⎭【答案】A 【解析】 【分析】得到()f x ',计算()()1n n n n f x x x f x +=-',然后计算1121n n x x ++-+,最后可得数列{}n a 为等比数列,最后根据公式计算即可. 【详解】由题可知:()21f x x '=-,212222121n n n n n n n x x x x x x x +--+-==--所以22121222121121212n n n n n n n nx x x x x x x x +++⎛⎫---== ⎪+++⎝⎭--+,则两边取对数可得1122ln2ln 11n n n n x x x x ++--=++,即12n n a a +=所以数列{}n a 是以1为首项2为公比的等比数列,所以()2022202220221122112S ⨯-==--故选:A13.牛顿冷却定律描述一个事物在常温环境下的温度变化:如果物体的初始温度为0T ,则经过一定时间t 后的温度T 满足()012t ha aT T T T ⎛⎫-=- ⎪⎝⎭,其中a T 是环境温度,h称为半衰期,现有一杯80℃的热水用来泡茶,研究表明,此茶的最佳饮用口感会出现在55℃.经测量室温为25℃,茶水降至75℃大约用时1分钟,那么为了获得最佳饮用口感,从泡茶开始大约需要等待( )(参考数据:lg30.4771≈,lg50.6990≈,lg11 1.0414≈)A .4分钟B .5分钟C .6分钟D .7分钟【答案】C 【解析】 【分析】根据已知条件代入公式计算得到1101112h⎛⎫= ⎪⎝⎭,再把该值代入,利用对数的运算即可求得结果. 【详解】根据题意,()11752580252h⎛⎫-=- ⎪⎝⎭,即1101112h⎛⎫= ⎪⎝⎭ 设茶水从75℃降至55℃大约用时t 分钟,则()1552575252ht ⎛⎫-=- ⎪⎝⎭,即3152h t⎛⎫= ⎪⎝⎭,即310511t⎛⎫= ⎪⎝⎭ 两边同时取对数:()31010lg lg lg 1lg1151111tt t ⎛⎫⎛⎫===- ⎪ ⎪⎝⎭⎝⎭解得lg 3lg 551lg11t -=≈-,所以从泡茶开始大约需要等待516+=分钟故选:C 【点睛】关键点点睛:本题考查了函数的实际应用,考查了对数的运算性质,解题的关键是熟练运用对数的运算公式,考查学生的审题分析能力与运算求解能力,属于基础题. 二、多选题14.牛顿在《流数法》一书中,给出了高次代数方程的一种数值解法一牛顿法.首先,设定一个起始点0x ,如图,在0x x =处作()f x 图象的切线,切线与x 轴的交点横坐标记作1x :用1x 替代0x 重复上面的过程可得2x ;一直继续下去,可得到一系列的数0x ,1x ,2x ,…,n x ,…在一定精确度下,用四舍五入法取值,当1n x -,()*n x n ∈N 近似值相等时,该值即作为函数()f x 的一个零点r .的近似值r (精确到0.1),我们可以先构造函数()36f x x =-,再用“牛顿法”求得零点的近似值r的近似值,则下列说法正确的是( )A .对任意*n ∈N ,1n n x x -<B .若0x ∈Q ,且00x ≠,则对任意*n N ∈,121223n n n x x x --=+ C .当02x =时,需要作2条切线即可确定r 的值 D .无论0x 在()2,3上取任何有理数都有 1.8r = 【答案】BCD 【解析】 【分析】利用特殊情况判断选项A ;求出曲线在1n x x -=处的切线方程与x 轴的交点横坐标,即可判断选项B ;求出1x ,2x ,即可判断选项C 、D 【详解】A ,因为()36f x x =-,则()23f x x '=,设01x =,则切线方程为()531y x +=-, 切线与x 轴的交点横坐标为182.73x =≈,所以10x x >,故A 错误; B ,1n x x -=处的切线方程为()()2311136n n n y x x x x ---=-+-, 所以与x 轴的交点横坐标为121223n n n x x x --=+,故B 正确; C ,因为1222112 1.8236x =+⨯=≈,221211 1.836116x =+⨯≈⎛⎫⎪⎝⎭, 所以两条切线可以确定r 的值,故C 正确;D ,由选项C 可知, 1.8r =,所以无论0x 在()2,3上取 任何有理数都有 1.8r =,故D 正确. 故选:BCD15.若函数()f x 的图象是连续的平滑曲线,且在区间[],a b 上恒非负,则其图象与直线x a x b x ==、、轴围成的封闭图形的面积称为()f x 在区间[],a b 上的“围面积”.根据牛顿-莱布尼茨公式,计算面积时,若存在函数()F x 满足()()',F x f x =则()()F b F a -为()f x 在区间[],a b 上的围面积.下列围面积计算正确的是( )A .函数()2xf x =在区间[]0,2上的围面积是2ln 2B .函数()2cos f x x =在区间0,4⎡⎤⎢⎥⎣⎦π上的围面积是148π+C .函数()1f x x=在区间[]1,2上的围面积是ln 2D .函数()ln f x x =在区间2,e e ⎡⎤⎣⎦上的围面积是2e【答案】BCD 【解析】 【分析】根据定积分的定义和性质逐个分析求解即可 【详解】对于A ,函数()2xf x =在区间[]0,2上是连续的非负函数,且存在2()ln 2x F x =满足()()F x f x =',所以函数()2x f x =在区间[]0,2上的围面积是2213(2)(0)ln 2ln 2ln 2F F -=-=,所以A 错误,对于B ,函数()2cos f x x =在区间0,4⎡⎤⎢⎥⎣⎦π上是连续的非负函数,且存在1()sin 224x F x x =+满足()()F x f x =',所以函数()2cos f x x =在区间0,4⎡⎤⎢⎥⎣⎦π上围面积是11(0)sin 484248F F ππππ⎛⎫-=+=+ ⎪⎝⎭,所以B 正确,对于C ,函数()1f x x=在区间[]1,2上是连续的非负函数,且存在()ln F x x =,满足()()F x f x =',所以函数()1f x x=在区间[]1,2上的围面积是(2)(1)ln 2ln1ln 2F F -=-=,所以C 正确,对于D ,函数()ln f x x =在区间2e,e ⎡⎤⎣⎦上是连续的非负函数,且存在()ln F x x x x =-,满足()()F x f x =',所以函数()ln f x x =在区间2,e e ⎡⎤⎣⎦上的围面积是22222(e )(e)e ln e e (eln e e)e F F -=---=,所以D 正确,故选:BCD16.英国数学家牛顿在17世纪给出了一种近似求方程根的方法—牛顿迭代法.做法如下:如图,设r 是()0f x =的根,选取0x 作为r 初始近似值,过点()()00,x f x 作曲线()y f x =的切线l ,l 与x 轴的交点的横坐标()()()()010000f x x x f x f x ''=-≠,称1x 是r 的一次近似值,过点()()11,x f x 作曲线()y f x =的切线,则该切线与x 轴的交点的横坐标为()()()()121110f x x x f x f x '=-≠',称2x 是r 的二次近似值.重复以上过程,得到r 的近似值序列,其中()()()()10n n n n n f x x x f x f x +'=-≠',称1n x +是r 的1n +次近似值,这种求方程()0f x =近似解的方法称为牛顿迭代法.若使用该方法求方程22x =的近似解,则( )A .若取初始近似值为1,则该方程解得二次近似值为1712B .若取初始近似值为2,则该方程近似解的二次近似值为1712C .()()()()()()()()0123400123f x f x f x f x x x f x f x f x f x =----'''' D .()()()()()()()()0124300123f x f x f x f x x x f x f x f x f x '=-+-+''' 【答案】ABC 【解析】【分析】根据牛顿迭代法求方程()0f x =近似解的方法,将初始值代入公式计算即可求解. 【详解】令2()2f x x =-,则()2f x x '=,当01x =,1(1)1311(1)22f x f -=-=-=',()()12111712f x x x f x =-=',故A 正确; 当02x =,1(2)2322(2)42f x f =-=-=',()()12111712f x x x f x =-=',故B 正确; 因为()()0100f x x x f x '=-;()()1211f x x x f x '=-;()()3222f x x x f x =-';()()3433f x x x f x =-', ℃()()()()()()()()0123400123f x f x f x f x x x f x f x f x f x =----'''',故C 正确,D 错误. 故选:ABC17.牛顿曾提出了物体在常温环境下温度变化的冷却模型:如果物体的初始温度是1θ(单位:C ︒),环境温度是0θ(单位:C ︒),其中10θθ>.则经过t 分钟后物体的温度θ将满足()010()ktf t e θθθθ-==+-⋅,其中k 为正常数.现有一杯80C ︒的热红茶置于20C︒的房间里,根据这一模型研究红茶冷却,正确的结论是( )A .()'0f t <B .若()365C f =︒,则()650C f =︒C .若()'34f =-,则其实际意义是在第3分钟附近,红茶温度大约以每分钟4C ︒的速率下降D .红茶温度从80C ︒下降到60C ︒所需的时间比从60C ︒下降到40C ︒所需的时间少 【答案】ACD 【解析】 【分析】由题知200(6)kt f t e θ-==+,进而根据导数的几何意义,导数运算等依次讨论各选项求解即可. 【详解】解:由题知200(6)kt f t e θ-==+,对于A 选项,因为k 为正常数,所以'600()kt f k t e -=-<,故A 选项正确; 对于B 选项,若()365C f =︒,即3206506k e -=+,所以334k e -=,则()()2639620602*********.75C 16k k f e e --=+=+=+⨯=︒,故B 选项错误; 对于C 选项,()'3f 表示3t =处的函数值的变化情况,若()'340f =-<,所以实际意义是在第3分钟附近,红茶温度大约以每分钟4C ︒的速率下降,故C 选项正确;对于D 选项,令()'()60kt g k x f t e -==-,则()2'600ktg k x e ->=,故'()f t 是定义域内的单调递增函数,由于'()0f t <,所以()f t 随着时间的增加,下降速度再减小,由于8060604020-=-=,故当下降温度相同的时候,下降所需时间相对增加,故红茶温度从80C ︒下降到60C ︒所需的时间比从60C ︒下降到40C ︒所需的时间少, 故D 选项正确. 故选:ACD18.众所周知,组合数(1)(2)(1)!m nn n n n m C m ---+=,这里*,m N n N ∈∈,并且m n ≤.牛顿在研究广义二项式定理过程中把二项式系数m n C 中的下标n 推广到任意实数,规定广义组合数(1)(1)!mx x x x m C m --+=是组合数的一种推广,其中(,)m N x R ∈∈,且定义01x C =,比如522(21)(22)(23)(24)05!C ----==.下列关于广义组合数的性质说法正确的有( )A .47210C -=-B .当m ,n 为正整数且m n >时,0m n C =C .当m 为正奇数时,11mC -=-D .当n 为正整数时,1(1)m m mn n m C C -+-=-【答案】BCD 【解析】 【分析】选项A. 由定义直接求出47C -的值,可判断;选项B. 由定义有(1)(2)(1)!m n n n n n m C m ---+=,根据条件121n n n n m ---+,,,,这m 个数中,一定有某个数为0,从而可判断;选项C. 由定义直接求出1mC -的不等式,结合条年可判断;选项D. 由定义分别得出1m mn n m C C -+-,从而可判断.【详解】选项A. 由题意()()()()4777172732105!C --⨯--⨯--⨯--==,故选项A 不正确.选项B. 由(1)(2)(1)!mn n n n n m C m ---+=,当m ,n 为正整数且m n >时,则1n m -≤-,所以10n m -+≤所以121n n n n m ---+,,,,这m 个数中,一定有某个数为0, 所以(1)(2)(1)0!mn n n n n m C m ---+==,故选项B 正确.选项C. 当m 为正奇数时,11(2)(11)1(2)()1!!mm m C m m -----+---===-,故选项C正确.选项D. 当n 为正整数时,()(1)(2)(1)(1)(2)(1)1!!m m n n n n n m n n n n m C m m --------++++-==-()()()11(2)(11)1(2)1!!mn m n m n m n m m n m n m n n C m m +-+-+-+--++-+-+== 所以1(1)m m mn n m C C -+-=-,故选项D 正确故选:BCD19.英国数学家牛顿在17世纪给出了一种求方程近似根的方法—牛顿迭代法,做法如下:如图,设r 是0f x的根,选取0x 作为r 的初始近似值,过点()()00,x f x 作曲线()y f x =的切线()()()000:l y f x f x x x '-=-,则l 与x 轴的交点的横坐标()()0100f x x x f x '=-()()00f x '≠,称1x 是r 的一次近似值;过点()()11,x f x 作曲线()y f x =的切线,则该切线与x 轴的交点的横坐标为2x ,称2x 是r 的二次近似值;重复以上过程,得r 的近似值序列,其中()()1n n n n f x x x f x +=-'()()0nf x '≠,称1n x+是r 的1n +次近似值,这种求方程0f x 近似解的方法称为牛顿迭代法.若使用该方法求方程23x =的近似解,则( )A .若取初始近似值为1,则过点()()1,1f 作曲线()y f x =的切线:24=-l y xB .若取初始近似值为1,则该方程解的三次近似值为9756C .()()()()()()01230012f x f x f x x x f x f x f x =-+-''' D .()()()()()()()()01210012n n n f x f x f x f x x x f x f x f x f x +=-----'''' 【答案】ABD 【解析】 【分析】根据条件介绍的牛顿迭代法求近似解即可. 【详解】解:构造函数()23f x x =-,则()2f x x '=,取初始近似值01x =,()02f x =-,()02f x '=,则()()221y x --=-,即24y x =-,则A 正确; ()()001001311221f x x x x f x -=⇒=-=-='⨯,()()12114372224f x x x f x -=-=-='⨯, ()()232249379716745624f x x x f x -=-=-='⨯,则B 正确;根据题意,可知()()()()()()()()0121021321012,,,,n n n n f x f x f x f x x x x x x x x x f x f x f x f x +=-=-=-=-'''', 上述式子相加,得()()()()()()()()01210012n n n f x f x f x f x x x f x f x f x f x +=-----'''',C 不正确,则D 正确.故选:ABD. 三、双空题20.中国茶文化博大精深.小明在茶艺选修课中了解到,不同类型的茶叶由于在水中溶解性的差别,达到最佳口感的水温不同.为了方便控制水温,小明联想到牛顿提出的物体在常温环境下温度变化的冷却模型:如果物体的初始温度是1θ,环境温度是0θ,则经过时间t (单位:分)后物体温度θ将满足:()010kte θθθθ-=+-⋅,其中k 为正的常数.小明与同学一起通过多次测量求平均值的方法得到200ml 初始温度为98C ︒的水在19C ︒室温中温度下降到相应温度所需时间如表所示:(1)k 的值约为___________;(填序号) ℃0.04;℃0.05;℃;0.06℃0.07.(2)“碧螺春”用75C ︒左右的水冲泡可使茶汤清澈明亮,口感最佳.在(1)的条件下,200mL 水煮沸后在19C ︒室温下为获得最佳口感大约冷却___________.(精确到个位)分钟左右冲泡.(参考数据:ln79 4.369=,ln71 4.263=,ln66 4.190=,ln61 4.111=,ln56 4.025=)【答案】 ℃ 7 【解析】 【分析】℃根据题目中给的三组数据,代入()010kt e θθθθ-=+-⋅,即可得到k 的值. ℃将得到k 的值以及0θ,1θ代入公式中,即可得t 值【详解】由()010kte θθθθ-=+-⋅得010=kt e θθθθ---,故010=ln kt θθθθ---,当环境温度是019C θ=,物体的初始温度是198θ=,经过约两分钟下降到90θ=这组数据有9019712=lnln ln71ln79 4.263 4.369981979k --==-≈--,0.05k ∴≈ 当环境温度是019C θ=,物体的初始温度是198θ=,经过3.4分钟下降到85θ=这组数据有8519663.4=lnln ln 66ln 79 4.190 4.369981979k --==-≈--,0.05k ∴≈ 当环境温度是019C θ=,物体的初始温度是198θ=,经过5分钟下降到80θ=这组数据有8019615=lnln ln61ln79 4.111 4.369981979k --==-≈--,0.05k ∴≈ 故0.05k ≈ 故答案为:℃0.05当环境温度是019C θ=,物体的初始温度是198θ=,经过k 分钟下降到75θ=有75190.05=lnln56ln 799819t --=--,ln 79ln 56 6.880.05t -∴=≈,所以取7t =. 故答案为:721.令函数2()1f x x x =+-,对抛物线()y f x =,持续实施下面牛顿切线法的步骤:在点(1,1)处作抛物线的切线,交x 轴于()1,0x ;在点()()11,x f x 处作抛物线的切线,交x 轴于()2,0x ;在点()()22,x f x 处作抛物线的切线,交x 轴于(),0n x ;……由此能得到一个数列{}n x 随着n 的不断增大,n x 会越来越接近函数()f x 的一个零在点0x ,因此我们可以用这种方法求()f x 零点0x 的近似值.℃设()1n n x g x +=,则()n g x =___________;℃用二分法求方程210x x +-=在区间(0,1)上的近似解,根据前4步结果比较,可以得到牛顿切线法的求解速度___________(快于、等于、慢于)二分法.【答案】2121n n x x ++ 快于 【解析】 【分析】由直线与抛物线相切求出()n g x ,然后利用()n g x 和二分法对零点进行四次计算后比较可得. 【详解】2()1f x x x =+-,()21f x x '=+,()21n n f x x '=+,所以切线方程为2(1)(21)()n n n n y x x x x x -+-=+-,令0y =,得2121n n x x x +=+,所以211()21n n n n x x g x x ++==+,二分法计算:101122x +==,11()024f =-<,(1)10f =>;2113224x +==,35()0416f =>;3135240.62528x +===, 51()0864f =>,4159280.5625216x +===,430.0625x x -= 用切线逼近法:1112(1)213x g +'===+,'2412139432113x g +⎛⎫=== ⎪⎝⎭+,2'313113210.61802621121x g ⎛⎫+ ⎪⎛⎫⎝⎭==≈ ⎪⎝⎭+,2'40.61810.6180320.6181x +=≈⨯+,430.0001x x ''-<<0.0625,因此牛顿切线法的求解速度快于二分法.故答案为:2121n n x x ++;快于.22.牛顿迭代法是牛顿在17世纪提出的一种近似求方程根的方法.如图,设r 是()0f x =的根,选取0x 作为r 初始近似值,过点()()00,x f x 作曲线()y f x =的切线l ,则l 与x 轴的交点的横坐标()()()()010000f x x x f x f x ''=-≠,称1x 是r 的一次近似值,过点()()11,x f x 作曲线()y f x =的切线,则该切线与x 轴的交点的横坐标()()()()121110f x x x f x f x '=-≠',称2x 是r 的二次近似值.重复以上过程,得到r 的近似值序列.(1)请选出r 的n 次近似值与r 的1n -次近似值的关系式____________(请填正确的关系式序号).℃()()()12n n n n f x x x n f x -=-≥';℃()()()1112n n n n f x x x n f x ---=-≥';℃()()()1112n n n n f x x x n f x +-+=-≥'.(2)若()23f x x =-,取02x =作为r 的初始近似值,则()0f x =的正根的二次近似值为______. 【答案】 ℃; 9756【解析】 【分析】(1)根据题中的两个表达式,选出公式即可; (2)根据(1)中的公式代入数据计算可得出结果. 【详解】 (1)由()()()()010000f x x x f x f x ''=-≠,()()1211f x x x f x '=-,推得r 的n 次近似值与r 的1n -次近似值的关系式为()()()1112n n n n f x x x n f x ---=-≥'.所以公式②正确;(2)()2f x x '=,()()21313222n n n n n n n n nf x x x x x x f x x x +-=-=-=+', 02x =时,100133712244x x x =+=+=,21113176972224756x x x =+=⨯+=.四、填空题23.物体在常温下的温度变化可以用牛顿冷却规律来描述:设物体的初始温度是0T ,经过一定时间t (单位:min )后的温度是T ,则()012t ha a T T T T ⎛⎫-=- ⎪⎝⎭,其中a T 称为环境温度,h 为常数,现有一杯用85℃热水冲的速溶咖啡,放在21℃的房间中,如果咖啡降到37℃需要16min ,那么这杯咖啡要从37℃降到25℃,还需要______min . 【答案】16 【解析】 【分析】根据所给函数模型,由Ta =21℃.令T 0=85℃,T =37℃,求得h ,然后令T 0=37℃,T =25℃,求得t .【详解】由题意知Ta =21℃.令T 0=85℃,T =37℃,得161(8521)23721h⎛⎫-⋅ ⎪⎝-⎭=, ℃h =8.令T 0=37℃,T =25℃,则812521(3721)2t ⎛⎫-=- ⎪⎝⎭, ℃16t =. 故答案为:16.24.英国著名物理学家牛顿用“作切线”的方法求函数零点时,给出的“牛顿数列”在航空航天中应用广泛,若数列{}n x 满足()()1n n n n f x x x f x +=-',则称数列{}n x 为牛顿数列.如果函数()228f x x =-,数列{}n x 为牛顿数列,设2ln2n n n x a x +=-,且11a =,2n x >.数列{}n a 的前n 项和为n S ,则n S =______. 【答案】21n -##12n -+ 【解析】 【分析】先由题设得到:12+24n n n x x x +=,进而求得1212222n n n n x x x x ++⎛⎫+ ⎪--⎝=⎭-,从而有12n n a a +=,即可得数列数列{}n a 是首项为1,公比为2的等比数列,再利用等比数列的前n 项和公式求得结果. 【详解】℃()228f x x =-,℃()4f x x '=,又℃()()2128+4242n n n n n n n n n f x x x x x x f x x x +=-=-='-, ℃()21222nn nx x x +++=,()21222nn nx x x +--=,℃1212222n n n n x x x x ++⎛⎫+ ⎪--⎝=⎭-,又2n x >℃211222ln ln 2ln 222n n n n n n x x x x x x ++⎛⎫⎛⎫⎛⎫+++== ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭,又2ln2n n n x a x +=-,且11a =, 所以12n n a a +=,℃数列{}n a 是首项为1,公比为2的等比数列, ℃{}n a 的前n 项和为n S ,则()1122112n n n S ⨯-==--.故答案为:21n -.25.2019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆,我国航天事业取得又一重大成就.实现月球背面软着陆需要解决的一个关键技术问题是地面与探测器的通讯联系.为解决这个问题,发射了嫦娥四号中继星“鹊桥”,鹊桥沿着围绕地月拉格朗日2L 点的轨道运行.2L 点是平衡点,位于地月连线的延长线上.设地球质量为M 1,月球质量为M 2,地月距离为R ,2L 点到月球的距离为r ,根据牛顿运动定律和万有引力定律,r 满足方程:121223()()M M M R r R r r R +=++.设rRα=,由于α的值很小,因此在近似计算中34532333(1)ααααα++≈+,则r 的近似值为_________.【解析】 【分析】由r Rα=推导出3453221333(1)M M ααααα++=≈+,进而可得r R α==. 【详解】 由rRα=,得r R α=, 由121223()()M M M R r R r r R +=++,得21212221(1)12R r M M M r r r RR R⋅+⋅=++⋅+, 将rRα=代入,得1212211(1)(1)M M M ααα⋅+⋅=++, 有32211122221(1)1(33)[(1)](1)(1)(1)M M M M ααααααααα+-++=+-=⋅=⋅+++, 所以3453221333(1)M M ααααα++=≈+,则α=,所以r R α==.. 26.人们很早以前就开始探索高次方程的数值求解问题.牛顿(1643-1727)给出了牛顿法——用“作切线”的方法求方程的近似解如图,方程()0f x =的根就是函数()f x 的零点r ,取初始值0x 处的切线与x 轴的交点为1,()x f x 在1x 处的切线与x 轴的交点为2x ,一直这样下去,得到012,,,n x x x x ⋯,它们越来越接近r .若30()1,1f x x x x =-+=-,则用牛顿法得到的r 的近似值2x 约为___________(结果保留两位小数).【答案】 1.35- 【解析】 【分析】根据导数的几何意义求出切线方程进行求解即可. 【详解】由3'2()1()31f x x x f x x =-+⇒=-,''00()(1)2,()(1)1f x f f x f =-==-=,所以在0x 处的切线方程为:12(1)y x -=+,令10 1.5y x =⇒=-,可得:''10()( 1.5) 5.75,()( 1.5)0.875f x f f x f =-==-=-,所以在1x 处的切线方程为:0.875 5.75( 1.5)y x +=+,令20 1.35y x =⇒≈-,故答案为: 1.35-27.牛顿迭代法又称牛顿-拉夫逊方法,它是牛顿在17世纪提出的一种在实数集上近似求解方程根的一种方法.具体步骤如下:设r 是函数()y f x =的一个零点,任意选取0x 作为r 的初始近似值,作曲线()y f x =在点0(x ,0())f x 处的切线1l ,设1l 与x 轴交点的横坐标为1x ,并称1x 为r 的1次近似值;作曲线()y f x =在点1(x ,1())f x 处的切线2l ,设2l 与x 轴交点的横坐标为2x ,并称2x 为r 的2次近似值.一般的,作曲线()y f x =在点(n x ,())(N)n f x n ∈处的切线1n l +,记1n l +与x 轴交点的横坐标为1n x +,并称1n x +为r 的1n +次近似值.设3()1f x x x =+-的零点为r ,取00x =,则r 的2次近似值为 _____.【答案】34##0.75【解析】 【分析】首先对()f x 求导,进而写出切线方程,再求0y =处对应的x 值,结合题设中r 的1n +次近似值的定义求r 的2次近似值. 【详解】由题设2()31f x x '=+,设切点为(n x ,31)n n x x +-,则切线斜率231n k x =+, ∴切线方程为23(31)()1n n n n y x x x x x =+-++-,令0y =,可得331221213131n n n n n n n x x x x x x x ++-+=-+=++,若00x =,则11x =,234x =,即r 的2次近似值为34. 故答案为:34.28.中国古代近似计算方法源远流长,早在八世纪,我国著名数学家、天文学家张隧(法号:一行)为编制《大衍历》发明了一种近似计算的方法——二次插值算法(又称一行算法,牛顿也创造了此算法,但是比我国张隧晚了上千年):对于函数()y f x =在()123123,,x x x x x x <<处的函数值分别为()11y f x =,()22y f x =,()33y f x =,则在区间[]13,x x 上()f x 可以用二次函数()()()()111212f x y k x x k x x x x =+-+--来近似代替,其中21121y y k x x -=-,3232y y k x x -=-,1231k k k x x -=-.若令10x =,22x π=,3x π=,请依据上述算法,估算2sin 5π的近似值是_______. 【答案】2425##0.96 【解析】 【分析】根据题意先求出123,,y y y ,进而求出12,,k k k ,然后求得()f x ,最后求得2sin 5π的近似值. 【详解】函数()sin y f x x ==在10x =,22x π=,3x π=处的函数值分别为()100y f ==,212y f π⎛⎫== ⎪⎝⎭,()30y f π==,故211212y y k x x π-==-,32322y y k x x π-==--,122314k k k x x π-==--, 故()22224442f x x x x x x πππππ⎛⎫=--=-+ ⎪⎝⎭, 即2244sin x x x ππ≈-+,所以2224242sin 555πππππ⎛⎫≈-⨯+⨯=⎪⎝⎭2425. 故答案为:2425. 29.艾萨克·牛顿在17世纪提出了一种求方程近似解的方法,这种方法是通过迭代,依次得到方程的根的一系列近似值1x ,2x ,3x ,…,这样得到的数列{}n x 称为“牛顿数列”.例如,对于方程240x -=,已知牛顿数列{}n x 满足2142n n n nx x x x +-=-,且2n x >,设22log 2n n n x a x +=-,若34528++=a a a ,则1x =___________. 【答案】6 【解析】 【分析】结合已知条件求出{}n a 是以公比为2的等比数列,进而求出1a ,再利用22log 2n n n x a x +=-可得到1x . 【详解】因为2142n n n nx x x x +-=-,且2n x >,所以2214(2)2222n n n n n n x x x x x x +-+=-+=+;2214(2)2222n n n n n nx x x x x x +--=--=-, 故211222112(2)22log 2log 2(2)22n n n n n n n n x x x x x x x x ++++++++=⇒=----, 即1122n n n na a a a ++⇒==,从而数列{}n a 是以公比为2的等比数列,故23453411112222828a a a a a a a =⨯+⨯+⨯=++=,即11a =,由11122log 12x a x +==-,解得16x =. 故答案为:6.30.艾萨克·牛顿(1642—1727)被称为有史以来最有影响力的思想家之一,在数学方面,牛顿“明显地推进了当时数学的每一个分支”.牛顿在给莱布尼茨的信中描述了他的一个发现——广义二项式展开,即)(122012k k x y x x y x y x y k ααααααααα---⎛⎛⎛⎛⎫⎫⎫⎫+=+++⋅⋅⋅++⋅⋅⋅ ⎪⎪⎪⎪⎭⎭⎭⎭⎝⎝⎝⎝,其中广义二项式系数10α⎛⎫= ⎪⎭⎝,)()()(121!k k k ααααα--⋅⋅⋅-+⎛⎫=⎪⎭⎝,α∈R ,k *∈N .根据以上信息,若对任意12x <都有)()(320122112n n x a a x a x a x x -=+++⋅⋅⋅++⋅⋅⋅+,则3a =___________. 【答案】81- 【解析】 【分析】方法一:利用广义二项式展开可得()212x -+展开,同时确定()31x -的展开,两式相除后,整理可得结果,由结果中3x 的系数可得3a ;方法二:利用)()()(322012112nn x x a a x a x a x -=++++⋅⋅⋅++⋅⋅⋅,对比两侧n x 的系数,依次可判断出对应的值. 【详解】 方法一:)()()(223234522221211212120123x x x x -----⎛⎛⎛⎛----⎫⎫⎫⎫+=++⋅++⋅⋅⋅ ⎪⎪⎪⎪⎭⎭⎭⎭⎝⎝⎝⎝)()()()()(232323421248123!x x x ------=+⋅+++⋅⋅⋅ )(3231133x x x x -=-+-)()()()(3232234421133413312133212x x x x x x x x x x a x x -=-+---++--++⋅⋅⋅+23172781x x x =-+-∴381a =- 方法二:)()()(322012112n n x x aa x a x a x -=++++⋅⋅⋅++⋅⋅⋅,显然01a =,比较两边x 的系数)(13101147C a a a ⇒⋅-=+⇒=-;比较两边2x 的系数2321024427C a a a a ⇒=++⇒=;比较两边3x 的系数)(33321314481C a a a a ⇒⋅-=++⇒=-.故答案为:81-. 【点睛】关键点点睛:本题考查二项式定理中的新定义运算的问题,解题关键是能够充分理解广义二项式展开的定义,将其变为熟知的二项式运算问题.。
基于数学文化的高中数学教学案例——以“数列”为例

教育·现场基于数学文化的高中数学教学案例———以“数列”为例文|王洋洋一、背景数学文化涵盖了数学知识、思想、方法,以及它们在社会历史进程中的应用和影响,这包含了数学在历史、科学、艺术和哲学等领域的应用和影响。
因此,高中数学教学的重心不再只是解题技巧和公式定理的灌输,而是要让学生在掌握数学知识之余,能够深度理解并体验到数学的历史沿革和文化内涵,从而激发他们的创新思维。
在这个背景下,这套教学案例设计独特而新颖。
案例不再是一道道简单的数学题目,而是具有真实性、历史性和文化性的问题,如金字塔的建造问题、哥德巴赫猜想等,这些都是数学历史上的重大问题,是数学文化的重要组成部分。
二、教学过程(一)引入数列概念在初步接触数列概念的阶段,教师会通过举例来引入数列的定义和特性。
在数学的领域里,数列是一项基本且关键的概念,特别是对高中生来说。
为了让学生掌握这一概念,教学过程中教师应结合实际例子帮助学生感受数列的实用性。
例如,可以用人口增长、金融投资收益等现实情境来说明数列如何在社会和经济领域内发挥作用。
数列的定义涵盖一组按照一定顺序排列的数,这些数称为项,它们按照位置排列形成第一项、第二项等序列。
探索数列时,会发现它们可能遵循某种规律,像等差数列中项与项之间的差是恒定的,等比数列中每一项都是其前一项的固定倍数。
这些规律反映了数列的结构特点,为深入数学研究提供了线索。
教师:同学们知道数列是什么吗?学生1:数列就是按照一定规律排列的一串数字。
教师:非常好,这是数列的基本理解。
数列确实是一系列按照特定规律排列的数字。
谁能说出一个生活中的例子呢?学生2:我们考试成绩表上的成绩由高到低排列,可以看作是一个数列。
教师:很好的例子,每次考试的成绩确实可以形成一个数列。
大家知道人口增长怎么算吗?学生3:人口增长,是不是每年的人口数量会有变化,这个变化可以用数字表示出来。
教师:正是如此。
想象一下,如果我们有一个城市从2000年到2020年每年人口的数据,这些数据会形成怎样的数列呢?学生4:这应该是一个时间序列的数列,可能是递增的,因为人口一般会增长。
数学文化巧融合 数列求和妙应用——以一道高考数学题为例

㊀㊀㊀数学文化巧融合㊀数列求和妙应用以一道高考数学题为例◉安徽省太和县第二中学㊀谭续续1引言数学文化问题作为新课标高考中比较常见的一类创新应用问题,在试卷中以各种方式出现,不仅能够反映古今中外劳动人民的聪明才智和数学家探索数学科学的精神与品质,而且能够让学生体验数学产生与发展的过程,体会数学的本质特征.特别是,结合中华优秀传统文化情境,展现我国古代劳动人民的智慧与创造,形成民族自豪感和远大理想,在高考数学试卷中倍受关注.2真题呈现高考真题㊀(2021年高考数学新高考Ⅰ卷第16题)某校学生在研究民间剪纸艺术时,发现剪纸时经常会沿纸的某条对称轴把纸对折.规格为20d mˑ12d m的长方形纸,对折1次共可以得到10d mˑ12d m,20d mˑ6d m两种规格的图形,它们的面积之和S1=240d m2,对折2次共可以得到5d mˑ12d m,10d mˑ6d m,20d mˑ3d m三种规格的图形,它们的面积之和S2=180d m2,以此类推.则对折4次共可以得到不同规格图形的种数为;如果对折n次,那么ðn k=1S k=d m2.3真题剖析此题以我国传统文化剪纸艺术为背景,通过两小问的设置,借助穷举法解决第一小问,再进一步归纳整理并计算得到第二小问的结果,让考生体验从特殊到一般探索数学问题的过程,体现了数学中的归纳思想方法,带领学生从有穷走向无穷,是思维上的一个飞跃与拓展,重点考查考生灵活运用数学知识分析与解决问题的能力.此题依次呈现高中数学核心素养中的直观想象㊁数学建模㊁逻辑推理以及数学运算等四个方面,对学生的能力与素养进行了全方位的考查.4真题破解解法1:(穷举法+错位相减法)由条件可知:对折1次得到2种规格:10d mˑ12d m,20d mˑ6d m;对折2次得到3种规格:5d mˑ12d m,10d mˑ6d m,20d mˑ3d m;对折3次得到4种规格:5d mˑ6d m,52d mˑ12d m,10d mˑ3d m,20d mˑ32d m;对折4次得到5种规格:20d mˑ34d m,10d mˑ32d m,5d mˑ3d m,52d mˑ6d m,54d mˑ12d m;猜想对折n次得到n+1种不同规格的图形,且这n+1个长方形的面积相等,等于240ˑ12æèçöø÷n,故面积和S n=(n+1)ˑ240ˑ12æèçöø÷n,所以S=ðn k=1S k=S1+S2+ +S n=2ˑ240ˑ12æèçöø÷1+3ˑ240ˑ12æèçöø÷2+ +nˑ240ˑ12æèçöø÷n-1+(n+1)ˑ240ˑ12æèçöø÷n,则有S=ðn k=1S k=240ðn k=1k+12k.记T n=ðn k=1k+12k,则12T n=ðn k=1k+12k+1,故12T n=ðn k=1k+12k-ðn k=1k+12k+1=1+ðn-1k=1k+22k+1-ðn k=1k+22k+1æèçöø÷-n+12n+1=1+141-12n-1æèçöø÷1-12-n+12n+1=32-n+32n+1,则T n=3-n+32n.故S=ðnk=1S k=2403-n+32næèçöø÷.48教育纵横数学文化㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀2022年6月上半月Copyright©博看网. All Rights Reserved.㊀㊀㊀故填答案:(1)5;(2)2403-n +32n æèçöø÷.点评:此解法是绝大多数考生在考场上采用的基本破解方案,第一问难度不大,学生多会用穷举法;在第二问中,错位相减法是平时解决数学问题时练习比较多的解决数列求和问题的基本方案.解法2:(穷举法+裂项相消法)以上部分同解法1.猜想对折n 次得到n +1种不同规格的图形,且这n +1个长方形的面积相等,都等于240ˑ12æèçöø÷n,故面积之和为S n =(n +1)ˑ240ˑ12æèçöø÷n.因为n +12n =n +22n -1-n +32n,所以S =ðnk =1S k =S 1+S 2+ +S n =240320-421æèçöø÷+240421-522æèçöø÷+ +240n +22n -1æèç-n +32nöø÷=2403-n +32n æèçöø÷.故填答案:(1)5;(2)2403-n +32n æèçöø÷.点评:此解法对数列求和的能力要求比较高,在第二问中,利用数列中通项关系式的变形与转化,合理通过待定系数法来进行裂项相消的工作,进而达到数列求和的目的,此方法对数列通项的推理与代数变形的技巧与要求比较高,在平时的教学中可以视学生情况进行选讲㊁拓展.解法3:(归纳推理法+数列求和法)显然对折n 次后,得到矩形的规格为:长20ˑ12æèçöø÷m,宽12ˑ12æèçöø÷n -m,0ɤm ɤn ,m ,n ɪN ,当m 取遍从0到n 的整数时,长20ˑ12æèçöø÷m的数值呈现严格单调递减的变化趋势,宽12ˑ12æèçöø÷n -m的数值呈现严格单调递增的变化趋势,但面积保持不变,每个小矩形的面积为20ˑ12æèçöø÷mˑ12ˑ12æèçöø÷n -m=240ˑ12æèçöø÷n,假设当m 取遍从0到n 的整数时,即长20ˑ12æèçöø÷m单调递减,宽12ˑ12æèçöø÷n -m单调递增的变化过程中,存在出现相同小矩形的特殊情况,即存在整数i ,且i ʂm ,使得20ˑ12æèçöø÷m=12ˑ12æèçöø÷n -i,可得m +i -n =l og 35,又m ,i ,n ɪN ,则m +i -n ɪN ,这与l og35∉N 矛盾,舍去.故不存在出现相同小矩形,即每个小矩形的规格必须互不相同,于是当k 取遍从0到n 的整数时,长20ˑ12æèçöø÷m会出现n +1种不同的数值,必须会出现n +1种不同的小矩形.以下具体计算可以通过解法1或解法2中的数列求和加以处理.故填答案:(1)5;(2)2403-n +32n æèçöø÷.点评:对于解决第一小问,往往直接穷举法就可以达到列举与应用的目的,此归纳推理法有些牛刀宰鸡的感觉,一般学生不会从这个推理角度来分析与应用,但从对学生严密逻辑思维能力的训练角度来看,学优生还是需要这样严密的推理过程的,助其养成良好的严谨的数学思维品质.解法4:(穷举法+高观点下的数学求和法)以上部分同解法1.对折n 次后各图形的面积之和为S n =(n +1)ˑ240ˑ12æèçöø÷n=240ˑ(n +1)ˑ12æèçöø÷n,构造函数f (x )=(n +1)x n ,则F (x )=ʏf (x )d x =x n +1,g (x )=ðnk =1f (x )=d d x ðnk =1F (x )()=d d x(x 2+x 3+ +x n +1)=d d x x 2-x n +21-x æèçöø÷=(n +1)x n +2-(n +2)x n +1-x 2+2x (1-x )2,所以S n =240ˑf 12æèçöø÷,ðn k =1S k =240ˑðnk =1f 12æèçöø÷=240ˑg 12æèçöø÷=2403-n +32n æèçöø÷.故填答案:(1)5;(2)2403-n +32n æèçöø÷.点评:此法只供教师参考,从高观点视角来剖析数学求和问题,供有一定高等数学基础的学生观摩,不作要求.从高等数学的角度,降维打击数列求和中的大量繁杂运算,开拓学生的视野,对少部分有兴趣㊁有能力的学生展示了高等数学的强大,激发学生探求新知的热情与欲望.5解后反思作为填空题的最后一题,有一点压轴的味道,其中数学文化情境的合理设置,很好地考查考生的阅读理解能力,并在充分理解题目情境与背景的条件下,融合相应的数学知识㊁数学思想方法和数学能力等,同时需要解题者有较好的数学核心素养,直观想象㊁数学建模㊁逻辑推理㊁数学运算等核心素养,一个都不能少.582022年6月上半月㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀数学文化教育纵横Copyright ©博看网. All Rights Reserved.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学中国传统文化专题
1.“中国剩余定理”又称“孙子定理”.1852年,英国来华传教士伟烈亚力将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年,英国数学家马西森指出此法复合1801年由高斯得到的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.“中国剩余定理”讲的是一个关于整除的问题,现有这样一个整除问题:将1至2 018这2 018个数中,能被3除余1且被7除余1的数按从小到大的顺序排成一列,构成数列{a n},则此数列共有()
A.98项
B.97项
C.96项
D.95项
解析能被3除余1且被7除余1的数就只能是被21除余1的数,故a n=21n-20,由1≤a n≤2 018得1≤n≤97,又n∈N*,故此数列共有97项.
答案 B
2.(数学文化)著名的斐波那契数列{a n}:1,1,2,3,5,8,…,满足a1=a2=1,a n+2=a n+1+a n,n∈N*,那么1+a3+a5+a7+a9+…+a2 017是斐波那契数列的第________项.
解析1+a3+a5+a7+a9+…+a2 017=a2+a3+a5+a7+a9+…+a2 017=a4+a5+a7+a9+…+a2 017=a6+a7+a9+…+a2 017=a8+a9+…+a2 017=…=a2 016+a2 017=a2 018,即为第2
018项.
答案 2 018
3.\中国古诗词中,有一道“八子分绵”的数学名题:“九百九十六斤绵,赠分八子作盘缠,次第每人多十七,要将第八数来言”.题意是:把996斤绵分给8个儿子作盘缠,按照年龄从大到小的顺序依次分绵,年龄小的比年龄大的多17斤绵,那么第8个儿子分到的绵是()
A.174斤
B.184斤
C.191斤
D.201斤
解析用a1,a2,…,a8表示8个儿子按照年龄从大到小得到的绵数,
由题意得数列a1,a2,…,a8是公差为17的等差数列,且这8项的和为996,
∴8a1+8×7
2×17=996,解之得a1=65.
∴a8=65+7×17=184,即第8个儿子分到的绵是184斤. 答案 B
4.\“十二平均律”是通用的音律体系,明代朱载堉最早用数学方法计算出半音比例,为这个理论的发展做出了重要贡献.十二平均律将一个纯八度音程分成十二份,依次得到十三个单音,从第二个单音起,每一个单音的频率与它的前一个单
音的频率的比都等于12
2.若第一个单音的频率为f,则第八个
单音的频率为()
A.3
2f B.
3
22f C.
12
25f D.
12
27f
解析由题意知十三个单音的频率依次构成首项为f,公比为122的等比数列,设此数列为{a n},则a8=1227f,即第八个单音的频率为1227f.
答案 D
5.我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯() A.1盏 B.3盏 C.5盏 D.9盏
解析设塔的顶层的灯数为a1,七层塔的总灯数为S7,公比
为q,则依题意S7=381,公比q=2.∴a1(1-27)
1-2
=381,
解得a1=3.
答案 B
6. 某同学利用暑假时间到一家商场勤工俭学.该商场向他提供了三种付酬方案:第一种,每天支付38元;第二种,第一天付4元,第二天付8元,第三天付12元,依此类推;第三种,第一天付0.4元,以后每天比前一天翻一番(即增加1倍).他应该选择哪种方式领取报酬呢?
解设该学生工作n天,每天领工资a n元,共领工资S n元,
则第一种方案a n(1)=38,S n(1)=38n;
第二种方案a n(2)=4n,S n(2)=4(1+2+3+…+n)=2n2+2n;
第三种方案a n(3)=0.4×2n-1,S n(3)=0.4(1-2n)
1-2
=0.4(2n-1).
令S n(1)≥S n(2),即38n≥2n2+2n,解得n≤18,即小于或等于18天时,第一种方案比第二种方案报酬高(18天时一样高). 令S n(1)≥S n(3),即38n≥0.4×(2n-1),
利用计算器计算得小于或等于9天时,第一种方案报酬高,所以少于10天时,选择第一种方案.
比较第二、第三种方案,S10(2)=220,S10(3)=409.2,S10(3)>S10(2),…,S n(3)>S n(2).
所以等于或多于10天时,选择第三种方案.
7.某厂2019年投资和利润逐月增加,投入资金逐月增长的百分率相同,利润逐月增加值相同.已知1月份的投资额与利润值相等,12月份投资额与利润值相等,则全年的总利润ω与总投资N的大小关系是()
A.ω>N
B.ω<N
C.ω=N
D.不确定
解析 投入资金逐月值构成等比数列{b n },利润逐月值构成等差数列{a n },等比数列{b n }可以看成关于n 的指数式函数,它是凹函数,等差数列{a n }可以看成关于n 的一次式函数.由于a 1=b 1,a 12=b 12,相当于图象有两个交点,且两交点间指数式函数图象在一次函数图象下方,所以全年的总利润ω=a 1+a 2+…+a 12比总投资N =b 1+b 2+…+b 12大,故选A. 答案 A
8.我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯
( )
A .1盏
B .3盏
C .5盏
D .9盏
解析:选B 每层塔所挂的灯数从上到下构成等比数列,记为{a n },则前7项的和S 7=381,公比q =2,依题意,得S 7
=a 1(1-27)1-2
=381,解得a 1=3.
9.[数学建模]一种专门占据内存的计算机病毒开机时占据内存1 KB,然后每3分钟自身复制一次,复制后所占内存是原来的2倍,那么开机________分钟,该病毒占据内存64 MB(1 MB=210 KB).
解析:由题意可知,病毒每复制一次所占内存的大小构成一等比数列{a n},且a1=2,q=2,∴a n=2n,∵2n=64×210=216,∴n=16,即病毒共复制了16次.
∴所需时间为16×3=48(分钟).
答案:48
10.(1)中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其大意为:“有一个人走了378里路,第一天健步行走,从第二天起因脚痛每天走的路程为前一天的一半,走了6天后到达目的地.”则此人第4天和第5天共走了()
A .60里
B .48里
C .36里
D .24里
(2)为了观看2022年的冬奥会,小明打算从2018年起,每年的1月1日到银行存入a 元 的一年期定期储蓄,若年利率为p ,且保持不变,并约定每年到期存款本息均自动转为新一年的定期.到2022年的1月1日不再存钱而是将所有的存款和利息全部取出,则可取回________元.
[解析] (1)由题意知,此人每天走的里数构成公比为12
的等比数列{a n },
设等比数列的首项为a 1,则a 1⎝ ⎛⎭⎪⎫1-1261-12=378,
解得a 1=192,所以a 4=192×18=24,a 5=24×12
=12, 则a 4+a 5=24+12=36,即此人第4天和第5天共走了36里.
(2)2022年1月1日可取出钱的总数为
a (1+p )4+a (1+p )3+a (1+p )2+a (1+p )
=a ·(1+p )[1-(1+p )4]1-(1+p )。
