毕奥萨伐尔定律的应用
.毕奥-萨伐尔定律

.毕奥-萨伐尔定律摘要:1.引言2.毕奥- 萨伐尔定律的定义3.毕奥- 萨伐尔定律的公式表示4.毕奥- 萨伐尔定律的应用领域5.我国在毕奥- 萨伐尔定律研究方面的贡献6.结论正文:1.引言毕奥- 萨伐尔定律是电磁学中的一个基本定律,它描述了电流在磁场中的作用力。
这个定律是由法国物理学家毕奥和萨伐尔在19 世纪初提出的,为电磁学的发展奠定了基础。
2.毕奥- 萨伐尔定律的定义毕奥- 萨伐尔定律指出,一个电流在磁场中受到的磁场力与电流的大小、磁场的强度和电流与磁场之间的夹角有关。
具体来说,磁场力F 的大小与电流I、磁感应强度B 以及电流与磁场之间的夹角θ的关系可以表示为:F = I * (Bl * sinθ)。
3.毕奥- 萨伐尔定律的公式表示毕奥- 萨伐尔定律可以用数学公式表示为:F = I * (Bl * sinθ),其中F 表示磁场力,I 表示电流,B 表示磁感应强度,l 表示电流元的长度,θ表示电流与磁场之间的夹角。
4.毕奥- 萨伐尔定律的应用领域毕奥- 萨伐尔定律在许多领域都有广泛的应用,如电磁制动、电磁起重机、磁悬浮列车等。
此外,这个定律还为研究电磁波、电磁感应和磁流体等现象提供了理论基础。
5.我国在毕奥- 萨伐尔定律研究方面的贡献我国科学家在毕奥- 萨伐尔定律研究方面取得了举世瞩目的成果。
例如,中国科学院物理研究所的科学家们通过对磁性材料的研究,为理解毕奥- 萨伐尔定律提供了新的视角。
此外,我国在磁悬浮列车、电磁制动等领域的研究也取得了重要突破,为国民经济的发展做出了巨大贡献。
6.结论毕奥- 萨伐尔定律是电磁学的基本定律之一,它对电磁学的发展产生了深远的影响。
毕奥——萨伐尔定律在极坐标系中的表达式及其应用

毕奥——萨伐尔定律在极坐标系中的表达式及其应用萨伐尔定律是一条重要的物理学定律,它表明在极坐标系中,线性磁场与磁力线紧密联系。
在此定律的影响下,较小的磁场并非总是比较複杂的磁力线模式。
萨伐尔定律的具体表达式是:Bθ=-∂Φ/∂z,其中Bθ为放射状波函数,Φ为磁力函数。
萨伐尔定律在极坐标系中能广泛地应用于物理领域,作用涉及磁场跃迁、电离层静电场、星际磁力场等各方面。
比如,针对电离层的放射现象,在极坐标系中,萨伐尔定律可用来量化磁力线紊乱程度,即把磁力线画化为一条定义其强度大小的简单曲线;在星际磁力场中,萨伐尔定律可用来量化磁场并推导出磁矩变化规律,磁场和磁矩变化会受连续性和格林函数影响。
总之,萨伐尔定律是一条重要且关键的物理学定律,它对于我们研究物理领域有重要意义。
在极坐标系中,萨伐尔定律的表达式为Bθ=-∂Φ/∂z,且其应用远不止这里所述,而是渗透于各个新兴学科中,通过它可以深入了解物理性质,探索出许多未知的现象。
11-3毕奥-萨伐尔定律及应用

真空的磁导率: π×10 真空的磁导率:o=4π× -7 π× 点的距离. (2) r是电流元 到P点的距离. ) 是电流元Idl 点的距离 r是从电流元 指向 点的单位矢量. 是从电流元Idl 指向P点的单位矢量 点的单位矢量. 是从电流元
上页 下页
(3)磁场的大小: )磁场的大小:
o Idl sin θ dB = 2 θ是Idl与r 之间的夹角 与 之间的夹角. 4π r
在薄片中取弧长为dl的窄条, 在薄片中取弧长为 的窄条, 的窄条 其中通过的微元电流为: 其中通过的微元电流为:
I
I I dI = dl = dθ πR π
上页 下页
y
在俯视图上建立如图坐标, 在俯视图上建立如图坐标, 电流元在O点激发的磁感应 电流元在 点激发的磁感应 强度为: 强度为:
o
dB
θ
毕奥-萨伐尔定律及应用 §11-3 毕奥 萨伐尔定律及应用
毕奥-萨伐尔定律 一, 毕奥 萨伐尔定律
d 真空中,电流元 真空中,电流元Idl 在P点产 B 点产 生的磁场为
o Idl ×r dB = 2 4π r
说明
P
r
θ
I
Idl
上式称为毕奥 萨伐尔定律 上式称为毕奥-萨伐尔定律 毕奥
(1)公式中的系数是 制要求的. 制要求的. )公式中的系数是SI制要求的
x R
0 0 I dB = dI = 2 dθ 2πR 2π R
所以: 所以:
π
dθ
方向如图所示. 方向如图所示.
0 I Bx = dBx = 2 ∫0 π R
即:
0 I dBx = dBsinθ = 2 sinθdθ 2π R
By = ∫ dB = 0
毕奥-萨伐尔定律

将实验结果与毕奥-萨伐尔定律的理论值进行对比,评估定律的准确性。
结果分析
分析实验误差来源,如设备精度、环境干扰等,提高实验的可靠性和准确性。
05
毕奥-萨伐尔定律的扩展与 推广
对三维空间的推广
总结词
毕奥-萨伐尔定律最初是在二维空间中 推导出来的,但通过引入矢量运算, 该定律可以扩展到三维空间中。
Idl
电流元,表示电流的一 部分。
r
观察点到电流元的径矢 ,表示观察点与电流元
之间的距离。
03
毕奥-萨伐尔定律的应用场 景
电场与磁场的关系
磁场是由电流产生的,而电场是由电 荷产生的。毕奥-萨伐尔定律描述了 电流和磁偶极子产生的磁场,以及变 化的电场产生的磁场。
毕奥-萨伐尔定律揭示了电场和磁场之 间的相互关系,表明它们是电磁场的 两个方面,而不是独立存在的。
THANKS
对微观尺度的适用性问题
毕奥-萨伐尔定律在描述微观尺度的电磁场时,其精确度受 到限制。在量子尺度下,电磁场的涨落和量子效应可能导 致定律的不适用。
未来研究需要进一步探索毕奥-萨伐尔定律在微观尺度下 的适用性和修正,以更好地描述量子电磁场的行为。
对超导态物质的适用性问题
毕奥-萨伐尔定律在描述超导态物质的 电磁场时,可能存在局限性。超导态 物质的电磁行为与常规物质有所不同, 需要更复杂的理论模型来描述。
电流与磁场的相互作用
根据毕奥-萨伐尔定律,电流产生磁场,而磁场对电流有作用 力。这种作用力被称为洛伦兹力,它描述了电流在磁场中所 受到的力。
毕奥-萨伐尔定律是电动机和发电机等电气设备工作的基础, 它解释了电流如何在磁场中受到作用力,从而产生旋转或线 性运动。
磁力线的描绘
11.2_毕奥-萨伐尔定律及应用
第十一章 稳恒磁场
B=
µ0 nI
2
(cos β 2 − cos β1 )
β1 = π − β 2
l/2
点位于管内轴线中点 (1)P点位于管内轴线中点 ) 点位于管内
cos β1 = − cos β 2
B = µ0 nI cos β 2 =
若
cos β2 =
(l / 2)
l
2
+ R2
µ0 nI
2
(l
2
毕奥—萨伐尔定律 11.2 毕奥 萨伐尔定律
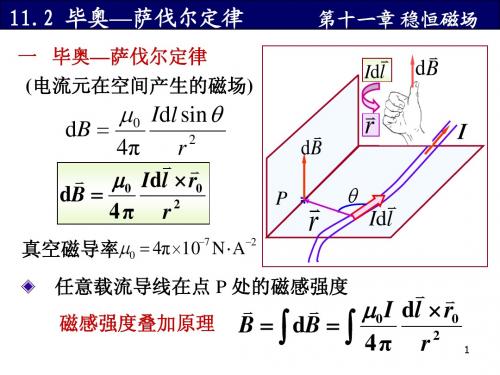
毕奥—萨伐尔定律 一 毕奥 萨伐尔定律 (电流元在空间产生的磁场 电流元在空间产生的磁场) 电流元在空间产生的磁场
第十一章 稳恒磁场
Idl
dB
4π r µ0 Idl × r0 dB = 4π r2
−7 −2 真空磁导率µ0 = 4π ×10 N ⋅ A
dB =
µ0 Idl sin θ
2
r
dB
P *
I
r
θ
Idl
任意载流导线在点 P 处的磁感强度 磁感强度叠加原理
B = ∫ dB = ∫
µ0 I dl × r0
4π r
2
1
毕奥—萨伐尔定律 11.2 毕奥 萨伐尔定律
第十一章 稳恒磁场 毕奥—萨伐尔定律 毕奥 萨伐尔定律
dB =
µ0 Idl × r0
4π
1
r
1 B = µ 0 nI 2
B=
µ0nI
2
(cos β2 − cos β1 )
B
1 µ 0 nI 2
µ0nI
x
24
O
毕奥—萨伐尔定律 11.2 毕奥 萨伐尔定律
毕奥-萨伐尔定律及应用

B x = ∫ dB x B y = ∫ dB y Bz = ∫ dBz
}Байду номын сангаас
⇒
v v v v B = Bx i + B y j + Bz k
设有长为L的载流直导 例1 载流长直导线的磁场 设有长为 的载流直导 线,其中电流为I。计算距离直导线为a处的 点的磁 其中电流为 。计算距离直导线为 处的P点的磁 处的 感应强度。 感应强度。 I 解:任取电流元 Idl 据毕奥-萨伐尔定律 萨伐尔定律, r 据毕奥 萨伐尔定律,此电 α Idl 流元在P 流元在P点磁感应强度dB为 r r L r
I dl
R
r
x
d B⊥
θ
θ
r dB
I
O
P
r d B//
µ0 I d l B = ∫ dB// = ∫ dB sin θ = ∫L r 2 sin θ L L 4π µ 0 I sin θ 2πR µ 0 I sin θ = 2 ∫0 d l = 4πr 2 2πR 4πr
µ0 I sin θ B= 2πR 2 4πr
单位矢量
真空中的磁导率
大小: 大小: dB =
4π
µ0 Idl sin θ
r2
Idl vθ
P
v B
方向: 方向:右螺旋法则
v r
r dB
r dB
r Id l
P
r r
α
r dl
I
电流元在给定点所产生的磁感应强度的大小与 I d l 成正比 , 与到电流元的距离平方成反比 ,与电 r 成正比,与到电流元的距离平方成反比, r 流 元 r 矢 径 夹 角 的 正 弦 成 正 比 。 dB 方 向 垂 直 于 r 和 r r 组成的平面, 与 Idl 组成的平面,指向为由 Idl 经 α 角转向 r 时 右螺旋前进方向。 右螺旋前进方向。 r
高二物理竞赛毕奥-萨伐尔定律应用举例PPT(课件)
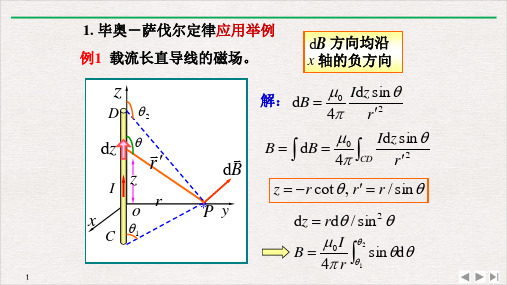
由右手螺旋关系可知每个电流元在圆心处产生的磁感 强度的方向相同。
◆ 在载流圆线圈轴线以外的空间,其磁感强度的分 布大致如下图所示:
I
思考2:
I
R o
B0
x
B0
0I
2R
I R o
B0
0I
4R
I
R o
B0
0I
8R
BA
0I 4d
d *A
I
R1
R2
*o
B0
讨 (1) 若线圈有 N 匝
论 二
B
N 0IR 2
2(x2 R2)3/ 2
xP x
(2) x 0,B 的方向不变 ( I 和 B 成右螺旋关系)
(3) x 0 , B 0I 圆环形电流中心的磁场
2R
思考1:圆弧形电流在圆心处的磁场为多少?
B 0I 2R 2
方向
I
R
O
提示:将该平面载流线圈在圆心处产生的磁感强度看
(3) 半无限长螺线管
B 0nI
或由 1 , 2 0 代入
B
0nI
2
cos2
c os 1
1
,
2
2
B
1 2
0nI
I
1 2
0
nI
B 0nI
O
x
磁感应线的绕向与电流满足右螺旋定则
在沿电流方向的延长线上任一点处,
引入磁矩:
(与磁场方向一致)
例2 圆形载流导线的磁场。
例3 载流直螺线管轴上的磁场
毕奥-萨伐尔定律应用举例
R 载流直导线延长线上任一点的磁感强度为零。
例3 载流直螺线管轴上的磁场 提示:将该平面载流线圈在圆心处产生的磁感强度看成是由 设把螺线管放在真空中,求管内轴线上一点处的磁感强度。 设把螺线管放在真空中,求管内轴线上一点处的磁感强度。
毕奥——萨伐尔定律在极坐标系中的表达式及其应用

毕奥——萨伐尔定律在极坐标系中的表达式及其应用
毕奥萨伐尔定律是世界上最经典的物理定律之一,它可以描述磁场在极坐标系中的表达式及其应用,是物理学中不可缺少的重要组成部分。
本文主要介绍毕奥萨伐尔定律在极坐标系中的表达式及其应用。
首先,我们来介绍毕奥萨伐尔定律在极坐标系中的表达式。
首先,毕奥萨伐尔定律定义了磁场从磁极出发的表达式,它表示磁场受到磁极强度的影响而产生,而且它的值取决于磁极的强度与磁极之间的距离,而这个距离关系可以用一个抛物线表达:即磁场强度随着距离的减小而增大,而随着距离的增加而减小,用公式表示为:B=B0*(1/r^2),其中B0为磁极强度,r为两磁极之间的距离。
此外,毕奥萨伐尔定律还可以描述磁场的产生方向,即它的向量表达式,它表明磁场是从磁极出发的,具体来说,磁场的方向是从磁极的正极指向负极的方向。
用公式表示为:B=B0*(1/r)*对应的单位
向量,其中B0为磁极强度,r为两磁极之间的距离,对应的单位向
量表示磁场方向。
接着,我们来讨论毕奥萨伐尔定律在极坐标系中的应用,首先,它可以用于研究磁性材料,因为磁性材料向外施加磁极的时候,磁场的变化遵循毕奥萨伐尔定律。
其次,毕奥萨伐尔定律可以用于研究空间磁场的变化,这对于放射性核物质的研究有着重要意义,因为空间磁场变化可以影响核子间的相互作用,从而影响放射性核物质的结构和品质,从而不同的空间磁场可以调节放射性核物质表现出不同的性质。
总而言之,毕奥萨伐尔定律可以描述磁场在极坐标系中的表达式及其应用,是物理学中不可缺少的重要组成部分。
它的表达式可以用简单的数学公式来描述,而它的应用范围也包括磁性材料和放射性核物质的研究。
毕奥萨伐尔定律

磁力发电机
磁力发电机是一种利用磁场产生电能的装置。根据毕奥萨 伐尔定律,当导体在磁场中运动时,会在导体中产生感应 电流。磁力发电机通过转子产生的旋转磁场与定子绕组相 对运动,使定子绕组中产生感应电流,实现发电的目的。
磁力发电机广泛应用于风力发电、水力发电、汽车发动机 等领域,为可再生能源的开发和节能减排做出了重要贡献 。
06
毕奥萨伐尔定律的未来研 究与展望
磁场产生的原因与机制
磁场产生的原因
毕奥-萨伐尔定律指出,运动电荷或电流会产生磁场,这是磁场产生的根本原因。
磁场产生的机制
磁场的产生与电荷或电流的运动有关,当电荷或电流运动时,会激发周围的磁场 ,磁场的大小和方向与电荷或电流的运动状态有关。
磁场对物质的作用与影响
核磁共振成像等磁现象在医疗领域具有广泛的应用前景,同时磁 约束核聚变等前沿技术也在积极探索中。
磁现象在太阳能领域的应用
太阳能电池板在吸收太阳能时,利用磁性原理可以提高太阳能利 用率。
感谢您的观看
THANKS
磁场强度的方向与单位
磁场强度的方向
在右手螺旋定则中,拇指指向电流的方向 ,四指环绕的方向就是磁场的方向。
VS
磁场强度的单位
安培/米(A/m),国际单位制中,磁场强度 的单位是安培/米。
03
毕奥萨伐尔定律的实验验 证
实验设计思路
确定实验目标
验证毕奥萨伐尔定律在特定情况下 的适用性,即通过实验手段测量物 理量以验证理论的准确性。
总结词
描述电磁场基本规律的方程组。
详细描述
麦克斯韦方程组是描述电磁场基本规律的方程组,其 中包括了电场、磁场和电荷密度等物理量的关系。毕 奥萨伐尔定律是麦克斯韦方程组的一个推论,它描述 了磁场与电流之间的关系。此外,麦克斯韦方程组还 预言了电磁波的存在,即光、无线电波等。
毕奥—萨伐尔定律及其应用

0 I
4a
sin d
0 I
4a
(cos1
cos2 )
上式中,1 和2 分别是直导线两端的电流元与它们到 P 点的矢径之间的夹角。
毕奥—萨伐尔定律及其应用
, ,
,
,
例题讲解 1
设长为 L 的直导线通有电流 I,求距离导线为 a 处一点 P 的磁感应强度。
若导线长度远大于点 P 到直导线的垂直距离( L a ),则导线可视为无限长。
dB,Idl,r 这 3 个矢量的方向符合右手螺旋法则。
因此,矢量形式
dB
0 4
Idl r2
er
er ——由电流元指向点 P 的单位矢量。
整个载流导线在空间某点 P 的磁感应强度 B,等于导线上所有电流元在该点所产生的磁感应强度
dB
的矢量和,即
B
L
dB
L
0 4
Idl r2
er
积分是对整个载流导线进行矢量积分。
r2
式中,0 称为真空磁导率,其值为 0 4π 10–7 N A2 。磁感应强度 dB 的方向垂直于 Idl 和 r 所组
成的平面,并沿 Idl r 的方向,即当右手弯曲,四指从 Idl 方向沿小于 π 的角转向 r 时,伸直的大拇指所
指的方向为 dB 的方向。
毕奥—萨伐尔定律及其应用
1.1 毕奥—萨伐尔定律
大学物理
毕奥—萨伐尔定律及其应用
1.1 毕奥—萨伐尔定律
毕奥—萨伐尔定律指出:电流元 Idl 在真空中某点 P 所产生的磁感应强度 dB 的大小,与电流元的
大小 Idl 成正比,与电流元和从电流元到 P 点的矢径 r 之间夹角的正弦成正比,与电流元到点 P 的距离 r
8-3 毕奥-萨伐尔定律

B
ad d
o I ad o I d x ln 2 a d 2 ax
a
[小结 ]
1.毕奥—萨伐尔定律:
0 Idl r dB 4π r 3
大 小:dB
2.几种常见载流导线的磁感强 度(记住结论): (1)载流长直导线的磁场:
0 Idl sin
4π r2 方 向:与 dl r ˆ一致
N 0 IR2 ( 2 x R )2
2 2 3
2) x 0 , B 的方向不变( I 和 B 成右手螺旋关系)
3)x 0 B
0 I
2R
4)x R
B
0 IR
2x
3
2
, B
0 IS
2π x
3
三 磁矩
如图所示,有一平面圆电流,其面积 为S,电流为I 取元电流平面的单位正法线矢量为 en , 它与电流I的流向遵守右手螺旋定则
4π R1
例3 圆形载流导线的磁场
Y
Id l
R
O
I Z
x
r
dB dB
dl r
X
建立坐标,取 电流元。
p dB// p
o I dB dl 2 4 r dB// dB cos
dB dB sin
sin 1
o Idl r dB 3 4 r
0 I 解: B B B B 1 2 3 B 2 R 2 向里为正参考方向 R b a B 0 B2 B3 方向 0 I 0 I 0 (cos cos ) 2r 2 4r 2 0 I d l dB 0 I 0 I 4 R 2 4r 4r
11-2.3 毕奥-萨伐尔定律及其应用
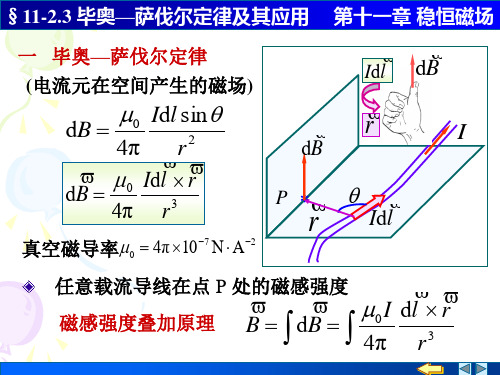
毕奥—萨伐尔定律及其应用 §11-2.3 毕奥 萨伐尔定律及其应用 例3 载流直螺线管的磁场
第十一章 稳恒磁场
如图所示,有一长为 半径为R的载流密绕直螺 如图所示,有一长为l , 半径为 的载流密绕直螺 线管,螺线管的总匝数为N,通有电流I. 线管,螺线管的总匝数为 ,通有电流 设把螺线管 放在真空中,求管内轴线上一点处的磁感强度. 放在真空中,求管内轴线上一点处的磁感强度
判断下列各点磁感强度的方向和大小. 例 判断下列各点磁感强度的方向和大小
8 2
d 1、5 点 : B = 0 、
3、7点 :dB 、 点 +3
+
=
µ 0 Id l
4π R
2
7
Idl
R
6 5
2、4、6、8 点 : 、 、 、
+4
dB =
µ 0 Idl
4π R
sin 450 2
毕奥—萨伐尔定律及其应用 §11-2.3 毕奥 萨伐尔定律及其应用 毕奥---萨伐尔定律 萨伐尔定律应用举例 二 毕奥 萨伐尔定律应用举例 载流长直导线的磁场. 例1 载流长直导线的磁场
dB =
µ0
2
B = ∫ dB =
µ 0 nI
2
(R
R In d x
2
2
+x
x2 x1
2 3/2
)
B=−
µ 0 nI
2
∫ (R
2
R 2 dx
2
x = R ctg β 2 dx = − R csc βdβ
+x
2 3/ 2
∫β
β
1
R 3 csc 2 β d β R 3 csc 3 β
复习 毕奥萨伐尔定律的应用ppt课件

无限长载流长直导线的磁场.
B
0
4π
Ir0(cos1
cos
)
2
I
o
1 0 2 π
B 0I
2π r0
x 1
C
B
+
P
y
3
毕奥—萨伐尔定律的应用
也可表示为:
B
0I 4d
sin
2
sin
1
导线无限长时,即
I
第八章
1 2
2
2
B 0I 2 ddl Llr NhomakorabeaO
1
d
Pr 2 dB
4
毕奥—萨伐尔定律的应用 无限长载流长直导线的磁场
o
x
*p x
B 0I
4π
cosdl
l r2
dB 0
4π
Idl r2
dBx
0
4π
I cosdl
r2
B
0IR
4π r3
2π R
dl
0
B
0 IR2
(2 x2 R2)32
7
毕奥—萨伐尔定律的应用
第八章
I
R
ox
B
*x
B
0IR2
(2 x2 R2)32
讨 1)若线圈有 N 匝
论
B
N (2 x2
0 IR2
B
0nI
2
cos2
c os 1
B
1 2
0nI
14
毕奥—萨伐尔定律的应用
第八章
例 如图载流长直导线的电流为 I
形面积的磁通量.
解 先求
, 试求通过矩 B ,对变磁场
B
第十九讲:§6.3 毕奥—萨伐尔定律及其应用

第十九讲: §6.3 毕奥—萨伐尔定律及其应用引课:大家知道通电导线周围有磁场,那某一点的磁场如何来求解? 一、稳恒电流的磁场:通过实验来确定1、表述:电流元 Id 在空间某一点(P 点)处产生的磁场 的强度dB 与Id 成正比;与θsin 成正比; 与r 2成反比。
2、Id 在P 点产生的磁场:2sin dB r Id θ∝20sin 4rId dB θπμ =⇒标量式 204re Id B d r⨯=πμ矢量式 3、任意载流导线的磁场:204B r e Id B d r⨯==⎰⎰πμ二、运动电荷的磁场 1、Id 与其他量的关系nSd q υ==S d j Id ⎪⎭⎫ ⎝⎛===υυqn S S qn dS I2、 Id 在P 点处产生的磁场202020444r qdN r qnSd r Id d rr r ⨯=⨯=⨯=υπμυπμπμ3、单个运动电荷产生的磁场204rq dN d r⨯==υπμ 讨论:①o B ⇒0q 满足右手螺旋关系②o B ⇒0q 满足左手螺旋关系三、载流线圈的磁矩(磁偶极矩m ):表示载流线圈磁场性质的物理量。
如任意电流回路的磁场:IS I m == 对任意形状的载流回路都是适用的。
若是N 匝线圈,其面积是一样的,则:N N IS I m ==四、毕奥—萨伐尔定律及其应用 例题1:载流直导线的磁场Id :20sin z 4r Id dB θπμ=⇒CD :()120020DCD Csin -sin a 4Id cos a 4I zsin 4B B 21ββπμββπμθπμββ====⎰⎰⎰rId d 讨论:① 无限长:2-1πβ→22πβ+→ 00r 2IB πμ=②半无限长: 01→β 22πβ+→0r 4IB πμ=ββββd a dz a z a z 2sec tan tan =⇒=⇒=ββsec sec a r ar=⇒= βθcos sin =例题2:圆电流在其轴线上的磁场Id :204rId dBπμ=⇒ ()0901sin ==θθ, 圆电流:()23222203020x 2d r 4IR r R 4dBcos B B XRIR r Id d R +=====⎰⎰⎰⎰μπμπμαπ讨论:①0X = R2IB 0μ=②R X320XR 2B I μ= 课堂练习:练习1:RIR I 8241B 00μμ== ⊙练习:2:RIR I πμμ22B 00-= ×练习3:R I R Iπμμ42221B 00+= ⊙小结:电流P 点处产生磁场公式—毕-萨定律作业:P253预习:§6.4磁场的安培环路定理第十九讲: §6.3 毕奥—萨伐尔定律及其应用 作业:P253:6-1 由毕—沙定律30d 4r rl I B d⨯=πμ可得 ),,(o o a 点,k a l I i j a l I B20204d )(4d d πμπμ-=⨯=),,(o a o 点,0)(4d d 20=⨯=j j al I Bπμ),,(a o o 点,i a l I k j a l I B20204d )(4d d πμπμ-=⨯=),,(a a 点,)()2(4d d 020a j a l I B ⨯=μ k a l I j i j a Idl202016d 2)(228πμπμ-=+⨯=),,(a o a 点,)(22)2(4d d 20k i j a l I B+⨯=πμ )(16d 220k i a l I-=πμ6-2 在X 轴上P 点的磁感应强度如图示,可得i x d I i r r I i B B)(d d 22cos 22201101+=⨯⨯==πμπμα 显然x =0处为B 的最大值d0πμIB m =6-4 2002104422R IlR I B B B πμπμ+⨯=+= ⎪⎭⎫⎝⎛+=+=ππμαπμ4324)2(400R I R L )38(160ππμ+=RI方向垂直纸面向外。
毕奥萨伐尔定律的应用

毕奥萨伐尔定律的应用
毕奥萨伐尔定律是一个广泛应用于物理学和工程学的原理,以下是一些其应用的例子:
1. 电动机理论:毕奥萨伐尔定律可以用来确定电动机所产生的力矩和电流之间的关系。
这可以用于电动机的设计和性能优化。
2. 磁共振成像(MRI):MRI利用了毕奥萨伐尔定律,通过物体中的原子核自旋与外加磁场之间的相互作用来产生图像。
由此可以用于医学成像、生命科学、材料科学等方面。
3. 电力工程:毕奥萨伐尔定律可以用于变压器和发电机的设计。
通过探索磁场的作用,我们可以优化电力系统的性能和效率。
4. 磁选分离技术:通过应用毕奥萨伐尔定律来制造强磁场,在该磁场中将由特定元素组成的粒子分离出来,以帮助提取或清洁物质。
这种技术可以应用于生产、环保和化学制药等领域。
5. 磁浮列车:使用毕奥萨伐尔定律可以制造出磁浮飞行的草图。
由于磁场中的气垫,磁浮列车可以悬浮在轨道上,并以高速运行,相比于传统的火车安全和效率相对提高。
6. 鸽派派论争:在哲学中,毕奥萨伐尔定律常用于指导对归因于自然色素或者文化习俗的某些现象占主导地位的讨论。
总而言之,毕奥萨伐尔定律不仅是一个理论上有趣的原则,而且在科学,工程和医学方面具有非常广泛的应用。
毕奥–萨伐尔定律可以用于

毕奥–萨伐尔定律可以用于
毕奥-萨伐尔定律适用于计算一个稳定电流所产生的磁场。
该定律在静磁近似中是有效的,并且与Ampère的电路规律和磁性高斯定律一致,以Jean-BaptisteBiot和FélixSavart命名。
基本内容:
电流元Idl在空间某点P处产生的磁感应强度dB的大小与电流元Idl的大小成正比,与电流元Idl所在处到P点的位置矢量和电流元Idl之间的夹角的正弦成正比,而与电流元Idl到P点的距离的平方成反比。
毕奥-萨伐尔定律定律是由H.C.奥斯特实验(见电流磁效应)引起的,这个实验表明,长直载流导线对磁极的作用力是横向力。
为了揭示电流对磁极作用力的普遍定量规律,J.B.毕奥和F.萨伐尔认为电流元对磁极的作用力也应垂直于电流元与磁极构成的平面,即也是横向力。
他们通过长直和弯折载流导线对磁极作用力的实验,得出了作用力与距离和弯折角的关系。
在P.S.M.拉普拉斯的帮助下,经过适当的分析,得到了电流元对磁极作用力的规律。
根据近距作用观点,它现在被理解为电流元产生磁场的规律。
毕萨定律及其应用

Idl
p1
2) dB与 r 和 Idl 的夹角的有关: 在与电流元垂直的方向上,磁场最强; 在与电流元重合的方向上,磁场为零; 2. 关于dB 的方向: 垂直于电流元和矢径构成的平面。
(下一页)
二、 毕奥---萨伐尔定律的应用 计算各种电流分布产生的磁场的磁感强度 基本步骤: p 1)任取电流元Idl, 求出其在 ==场点 P 产生的磁感dB的 dB p r ==大小与方向; α 2 ) 分 析 dB方 向 是 否 变 化 : ==若不变,直接积分; Idl ===若变化, 则要将dB适当= 的分解, 对各分量分别积分, 然后再合成起来.
B
dB
L
L
0 Idl r 4 r 3
(下一页)
例1. 直电流的磁场 已知:真空中, I、1、 2、a 求 p点的磁感强度. 建立坐标系OXY
Y
I
2
dl l
O
1
r
dB
任取电流元 Idl
0 Idl sin 大小: dB 2 4 r
m Pm NISn
S
n
大小: B
0 IR 2
2( R 2 x 2 )3 2
则 B 0m 3 2x
方向: 右手螺旋法则
(下一页)
2.) 圆心处: x
0 IR B 2( R 2 x 2 )3 2 0 I B 2R
2
0
0 Idl sin =900 Bx dBx I 2 = R2 4 r 0 I 0 IR 0 IR d dl Rd 3 3 4R 2 4R 2R 4R 2
I
0 I 0 I Bo 2R 4 R
毕奥-萨伐尔定律及毕奥-萨伐尔定律应用举例
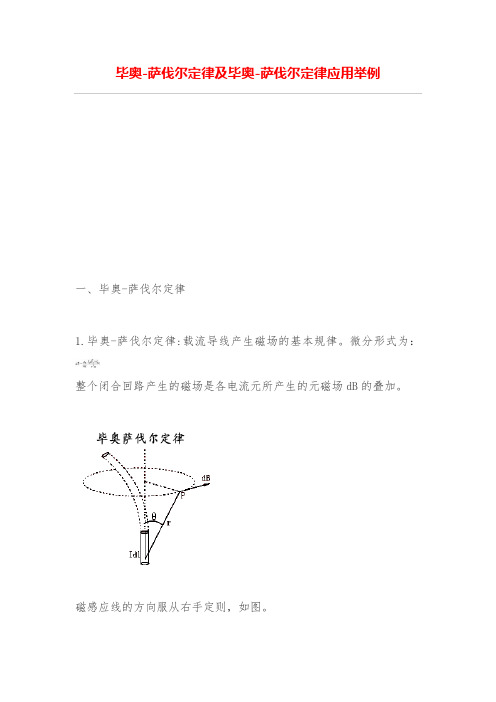
毕奥-萨伐尔定律及毕奥-萨伐尔定律应用举例一、毕奥-萨伐尔定律1.毕奥-萨伐尔定律:载流导线产生磁场的基本规律。
微分形式为:整个闭合回路产生的磁场是各电流元所产生的元磁场dB的叠加。
磁感应线的方向服从右手定则,如图。
二、毕奥-萨伐尔定律应用举例两种基本电流周围的磁感应强度的分布:载流直导线;圆电流。
例1.载流长直导线的磁场解:建立如图坐标系,在载流直导线上,任取一电流元Idz,由毕-萨定律得元电流在P点产生的磁感应强度大小为:方向为垂直进入纸面。
所有电流元在P点产生的磁场方向相同,所以求总磁感强度的积分为标量积分,即:(1)由图得:,即:此外:,代入(1)可得:讨论:(1)无限长直通电导线的磁场:(2)半无限长直通电导线的磁场:(3)其他例子例2:圆形载流导线轴线上的磁场:设在真空中,有一半径为 R ,通电流为 I 的细导线圆环,求其轴线上距圆心 O 为 x 处的P点的磁感应强度。
解:建立坐标系如图,任取电流元,由毕-萨定律得:,方向如图:,所有dB形成锥面。
将dB进行正交分解:,则由由对称性分析得:,所以有:,因为: ,r=常量,所以:,又因为:所以:,方向:沿x轴正方向,与电流成右螺旋关系。
讨论:(1)圆心处的磁场:x=0 ,。
(2)当即P点远离圆环电流时,P点的磁感应强度为:。
例3:设有一密绕直螺线管。
半径为 R ,通电流 I。
总长度L,总匝数N(单位长度绕有n 匝线圈),试求管内部轴线上一点 P 处的磁感应强度。
解:建立坐标系,在距P 点 x 处任意截取一小段 dx ,其线圈匝数为: 电流为:。
其相当于一个圆电流,它在P点的磁感应强度为:。
因为螺线管各小段在P点的磁感应强度的方向均沿轴线向右,所以整个螺线管在P点的磁感应强度的大小为:因为:代入上式得:所以:讨论:(1)管内轴线上中点的磁场:(2)当 L>>R时,为无限长螺线管。
此时,,管内磁场。
即无限长螺线管轴线上及内部为均匀磁场,方向与轴线平行满足右手定则。
大学物理 毕奥-萨伐尔定律的应用

各电流元的磁场方向不相同,可分解为 d B
逐对抵消,所以P 点B 的大小为:
0 B dB// dB sin L L 4
I dl L r 2 sin
I dl
R
r x
2R
d B
dB
d B//
I
O
P
0 I sin 2R d l 2 0 4r 0 I d l B dB// dB sin sin 2 L L 4 L r 0 I sin 2 4r
磁感应强度的方向与电流方向满足右手 螺旋定则。 考虑三种情况: dl (1)导线无限长,即 1 , 2 L 2 2
r
1
0I B 2 d (2)导线半无限长,场点与一端 0I 的连线垂直于导线
l
4 d (3)P点位于导线延长线上,B=0
B
O
d
P 2 dB
3. 载流直螺线管内部的磁场
设螺线管的半径为 R ,电流为 I ,每单位长度 有线圈n匝。
1
A 1
r
dB
R
p
2
A2ldl源自作业题习题(P266) 11-5 11-6 11-10 11-17
所有dB的方向相同, 所以P 点的 B 的大小为:
I
L
dl l
r
0 I d l sin B d B 2 L L 4 r
O
d
P dB
0 I d l sin B d B 2 L L 4 r
由几何关系有:
I
sin cos
r d sec
0 IS IS 3 x 2 r 3 pm r3
13-3 毕奥—萨伐尔定律

dB
0
R 2 Indx
2 3/ 2
x Rcot
讨 论
0 nI cos 2 cos 1 B 2
1)P点位于管内轴线中点
1 π 2
l/2
cos 1 cos 2
B 0 nI cos 2
若
cos 2
l / 2
1、载流长直导线的磁场.
z
D
dB
2
0 Idz sin
4π r
2
dz
I
z
1
r
r0
0 Idz sin B dB 4π CD r 2 dB z r cot , r r / sin 0 0
* y P
x
C
o
dz r0d / sin 2
B
B0 方向垂直于纸面向外。
R
I
o B0
(c )
I
习题13-5 如图所示,电流I沿着长度方向均匀地流过 b的无限长导体薄板。试求在薄板的平面内,距板的一 边为r的点P的磁感强度。 解:取坐标ox,
I 取电流元 dI jdx dx b
I
B
x
dx
b
r
x
P
o
由无限长直导线产生的磁 场得 0 dI 0 I dx dB 2 x 2 b x
B 2π r0
0 I
2)半无限长载流长直导线的磁场
π 1 , 2 π 2
BP
0 I
4 π r0
3) P点在载流直导线延长线上
1 2 0( )
Bp 0
2、圆形载流导线的磁场. 真空中 , 半径为R 的载流导线 , 通有电流I , 称圆 电流. 求其轴线上一点 p 的磁感强度的方向和大小.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
dB
0 R nI d l
2
l R cot
d l R csc d
2 2 2 2 2
1
A1
r
dB
p
2
R
A2
又 R l R csc
B L
0 R nI d l
2
l
dl
2( R l )
2
2 3/ 2
0
0
2
2
nI
0 nI
0 nI
2
B
A1
O
A2
通电螺线管的磁场
B
I
B 0 nI
I
0 I B 2 r
【例】载流圆线圈轴线上的磁场
电流元 Idl 在P点磁场
Idl
Id l r 0 dB dB// dB 3 4r
R
r
x
dB dB
I
由圆对称性得
B dB 0
o
P
dB//
所以
B dB//
B B // dB// dB sin
dl
L
r
l d tan
d l d sec d
2
l
P 0 I d l sin d B O 2 dB L 4 r 0 I 0 I cos d sin 2 sin 1 4 d 4d
1
2
2
1
考虑三种情况:
按毕奥—萨伐尔定律有:
I
0 I d l r dB 4 r3
所有dB的方向相同, 所以P点的 的大小为 : B
dl
L
r
l
0 I d l sin B d B L L 4 r2
O
d
1
2
P
dB
I
由几何关系有:
sin cos
r d sec
0 I sin 2 sin 1 B 4d
1 2 2
2
(1)导线无限长,即
I
(2) 导线半无限长,场点与一端 的连线垂直于导线
0 I B 2d 0 I B 4d
dl
L
r
(3)P点位于导线延长线上,B=0
O
d
1
2
P
dB
I
无限长直线电流的磁场
设螺线管的半径为R,电流为I,每单位长度有 线圈n匝。
1
A1
r
dB
R
p
2
A2
dl
l
1
A1
r
dB
p
2
R
A2
l
dl
由于每匝可作平面线圈处理, ndl匝线圈可作 Indl的一个圆电流,在P点产生的磁感应强度:
2( R l ) 2 0 R nI d l B L dB L 2 2 3/ 2 2( R l )
0 4
sindl 0 I sin r 2 4r 2 2R
r 2 R2 x2 sin R r R (x R )
2 2
1 2
B
0 IR 2
2( x 2 R 2 ) 3 2
讨论: 1.x=0处,即圆电流中心,磁场最大:
I 0 B
2R
2.x>>R,x≈r:
推广至 I 0 任意圆 B 2 2R 弧中心
2 2 IR I R IS 0 0 0 B 3 3 2x 2x 2x 3
I
pm
p B 0 m 3 2x
电流磁矩 pm ISe n
圆电流的磁场
I
【例】密绕长直载流螺线管轴线上的磁场
2
1
sin d
nI (cos 2 cos 1 )
B
0 nI
2
(cos 2 cos 1 )
讨论:
(1)螺线管无限长
1 , 2 0 B 0 nI
(2)半无限长螺线管的端点圆心处
B 0 nI / 2
实际上, L>>R 时, 螺 线管 内 部的 磁场 近 似均 匀 ,大 小为 0 nI
