江苏省南京市江宁高级中学2020届高三数学周周练(3)
江苏省南京市2020届高三第三次模拟考试(6月) 数学 Word版含答案

2020届高三模拟考试试卷数 学(满分160分,考试时间120分钟)2020.6一、 填空题:本大题共14小题,每小题5分,共70分.1. 已知集合A ={x|2<x <4},B ={x|1<x <3},则A ∪B________.2. 若z =a1+i+i(i 是虚数单位)是实数,则实数a 的值为________.3. 某校共有教师300人,男学生1 200人,女学生1 000人,现用分层抽样从所有师生中抽取一个容量为125的样本,则从男学生中抽取的人数为________.4. 如图是一个算法的伪代码,其输出的结果为________. S ←0For i From 1 To 4 S ←S +i End For Print S(第 4 题) (第6题)5. 将甲、乙、丙三人随机排成一行,则甲、乙两人相邻的概率为________.6. 已知函数f(x)=2sin (ωx +φ)(其中ω>0,-π2<φ<π2)的部分图象如图所示,则f(π2)的值为________.7. 已知数列{a n }为等比数列.若a 1=2,且a 1,a 2,a 3-2成等差数列,则{a n }的前n 项和为________.8. 在平面直角坐标系xOy 中,已知双曲线 x 2a 2-y 2b 2=1(a >0,b >0)的右焦点为F.若以F为圆心,a 为半径的圆交该双曲线的一条渐近线于A ,B 两点,且AB =2b ,则该双曲线的离心率为________.9. 若正方体ABCDA 1B 1C 1D 1的棱长为2,则三棱锥AB 1CD 1的体积为________.10. 已知函数f(x)=⎩⎪⎨⎪⎧x +2,x ≤0,f (-x ),x >0,g(x)=f(x -2).若g(x -1)≥1,则实数x 的取值范围是________.11. 在平面直角坐标系xOy 中,A ,B 是圆O :x 2+y 2=2上两个动点,且OA →⊥OB →.若A ,B 两点到直线l :3x +4y -10=0的距离分别为d 1,d 2,则d 1+d 2的最大值为________.12. 若对任意a ∈[e ,+∞)(e 为自然对数的底数),不等式x ≤e ax +b 对任意x ∈R 恒成立,则实数b 的取值范围是________.13. 已知点P 在边长为4的等边三角形ABC 内,满足AP →=λAB →+μAC →,且2λ+3μ=1,延长AP 交边BC 于点D.若BD =2DC ,则PA →·PB →的值为________.14. 在△ABC 中,∠A =π3,点D 是BC 的中点.若AD ≤22BC ,则sin Bsin C 的最大值为________.二、 解答题:本大题共6小题,共90分. 解答时应写出必要的文字说明、证明过程或演算步骤.15. (本小题满分14分)如图,在四棱锥PABCD 中,底面ABCD 为矩形,平面PAD ⊥平面ABCD ,PA ⊥PD ,点E ,F 分别为AD ,PB 的中点.求证:(1) EF ∥平面PCD ;(2) 平面PAB ⊥平面PCD.16.(本小题满分14分)已知向量m =(cos x ,sin x),n =(cos x ,-sin x),函数f(x)=m·n +12.(1) 若f(x2)=1,x ∈(0,π),求tan(x +π4)的值;(2) 若f(α)=-110,α∈(π2,3π4),sin β=7210,β∈(0,π2),求2α+β的值.17. (本小题满分14分)如图,港口A 在港口O 的正东100海里处,在北偏东方向有一条直线航道OD ,航道和正东方向之间有一片以B 为圆心,半径为85海里的圆形暗礁群(在这片海域行船有触礁危险),其中OB =2013海里,tan ∠AOB =23,cos ∠AOD =55.现有一艘科考船以105海里/小时的速度从O 出发沿OD 方向行驶,经过2个小时后,一艘快艇以50海里/小时的速度准备从港口A 出发,并沿直线方向行驶与科考船恰好相遇.(1) 若快艇立即出发,判断快艇是否有触礁的危险,并说明理由; (2) 在无触礁危险的情况下,若快艇再等x 小时出发,求x 的最小值.18. (本小题满分16分)如图,在平面直角坐标系xOy 中,椭圆C :x 2a 2+y 2b 2=1(a >b >0)经过点(-2,0)和(1,32),椭圆C 上三点A ,M ,B 与原点O 构成一个平行四边形AMBO.(1) 求椭圆C 的方程;(2) 若点B 是椭圆C 左顶点,求点M 的坐标;(3) 若A ,M ,B ,O 四点共圆,求直线AB 的斜率.19. (本小题满分16分)已知函数f(x)=e xx 2-ax +a(a ∈R ),其中e 为自然对数的底数.(1) 若a =1,求函数f(x)的单调减区间;(2) 若函数f(x)的定义域为R ,且f(2)>f(a),求a 的取值范围;(3) 求证:对任意a ∈(2,4),曲线y =f(x)上有且仅有三个不同的点,在这三点处的切线经过坐标原点.20. (本小题满分16分)若数列{a n }满足n ≥2,n ∈N *时,a n ≠0,则称数列⎩⎨⎧⎭⎬⎫a n a n +1(n ∈N *)为{a n }的“L 数列”.(1) 若a 1=1,且{a n }的“L 数列”为⎩⎨⎧⎭⎬⎫12n ,求数列{a n }的通项公式;(2) 若a n =n +k -3(k >0),且{a n }的“L 数列”为递增数列,求k 的取值范围;(3) 若a n =1+p n -1,其中p >1,记{a n }的“L 数列”的前n 项和为S n ,试判断是否存在等差数列{c n },对任意n ∈N *,都有c n <S n <c n +1成立,并证明你的结论.2020届高三模拟考试试卷(十九)数学附加题(满分40分,考试时间30分钟)21. 【选做题】 在A ,B ,C 三小题中只能选做两题,每小题10分,共20分.若多做,则按作答的前两题计分.解答时应写出必要的文字说明、证明过程或演算步骤.A. (选修42:矩阵与变换)已知矩阵A =⎣⎢⎡⎦⎥⎤1-1a 0,a ∈R .若点P(1,1)在矩阵A 的变换下得到点P′(0,-2).(1) 求矩阵A ;(2) 求点Q(0,3)经过矩阵A 的2次变换后对应点Q′的坐标.B. (选修44:坐标系与参数方程)在平面直角坐标系xOy 中,曲线C 的参数方程为⎩⎪⎨⎪⎧x =1+cos θ,y =sin θ(θ为参数),直线l 的参数方程为⎩⎨⎧x =3t ,y =1+t (t 为参数),求曲线C 上的点到直线l 的距离的最大值.C. (选修45:不等式选讲)已知a ,b 为非负实数,求证:a 3+b 3≥ab(a 2+b 2).【必做题】 第22,23题,每小题10分,共20分.解答时应写出必要的文字说明、证明过程或演算步骤.22. 如图,在直三棱柱ABCA 1B 1C 1中,AB ⊥AC ,AB =3,AC =4,B 1C ⊥AC 1. (1) 求AA 1的长;(2) 试判断在侧棱BB 1上是否存在点P ,使得直线PC 与平面AA 1C 1C 所成角和二面角BA 1CA 的大小相等,并说明理由.23. 口袋中有大小、形状、质地相同的两个白球和三个黑球.现有一抽奖游戏规则如下:抽奖者每次有放回的从口袋中随机取出一个球,最多取球2n +1(n ∈N *)次.若取出白球的累计次数达到n +1时,则终止取球且获奖,其他情况均不获奖.记获奖概率为P n .(1) 求P 1;(2) 求证:P n +1<P n .2020届高三模拟考试试卷(十九)(南京)数学参考答案及评分标准1. {x|1<x <4}2. 23. 604. 105. 236. 37. 2n +1-2 8. 62 9. 83 10. [2,4]11. 6 12. [-2,+∞) 13. -94 14. 3815. 证明:(1) 取PC 的中点G ,连结DG ,FG .在△PBC 中,因为点F ,G 分别为PB ,PC 的中点,所以GF ∥BC ,GF =12BC.因为底面ABCD 为矩形,且点E 为AD 的中点, 所以DE ∥BC ,DE =12BC ,(2分)所以GF ∥DE ,GF =DE ,所以四边形DEFG 为平行四边形, 所以EF ∥DG.(4分)因为EF ⊄平面PCD ,DG ⊂平面PCD , 所以EF ∥平面PCD.(6分)(2) 因为底面ABCD 为矩形,所以CD ⊥AD.因为平面PAD ⊥平面ABCD ,平面PAD ∩平面ABCD =AD ,CD ⊂平面ABCD , 所以CD ⊥平面PAD.(10分)因为PA ⊂平面PAD ,所以CD ⊥PA.(12分)因为PA ⊥PD ,PD ⊂平面PCD ,CD ⊂平面PCD ,PD ∩CD =D ,所以PA ⊥平面PCD. 因为PA ⊂平面PAB ,所以平面PAB ⊥平面PCD.(14分)16. 解:(1) 因为向量m =(cos x ,sin x),n =(cos x ,-sin x), 所以 f(x)=m·n +12=cos 2x -sin 2x +12=cos 2x +12.(2分)因为f(x 2)=1,所以cos x +12=1,即cos x =12.因为x ∈(0,π),所以x =π3,(4分)所以tan(x +π4)=tan(π3+π4)=tan π3+tan π41-tan π3·tanπ4=-2- 3.(6分)(2) 若f(α)=-110,则cos 2α+12=-110,即cos 2α=-35.因为α∈(π2,3π4),所以2α∈(π,3π2),所以sin 2α=-1-cos 22α=-45.(8分)因为sin β=7210,β∈(0,π2),所以cos β=1-sin 2β=210,(10分)所以cos (2α+β)=cos 2αcos β-sin 2αsin β=(-35)×210-(-45)×7210=22.(12分)因为2α∈(π,3π2),β∈(0,π2),所以2α+β∈(π,2π),所以2α+β的值为7π4.(14分)17. 解:如图,以O 为原点,正东方向为x 轴,正北方向为y 轴,建立直角坐标系xOy. 因为OB =2013,tan ∠AOB =23,OA =100,所以点B(60,40),且A(100,0).(2分)(1) 设快艇立即出发经过t 小时后两船相遇于点C , 则OC =105(t +2),AC =50t. 因为OA =100,cos ∠AOD =55, 所以AC 2=OA 2+OC 2-2OA·OC·cos ∠AOD , 即(50t)2=1002+[105(t +2)]2-2×100×105(t +2)×55. 化简得t 2=4,解得t 1=2,t 2=-2(舍去),(4分) 所以OC =40 5. 因为cos ∠AOD =55,所以sin ∠AOD =255,所以C(40,80), 所以直线AC 的方程为y =-43(x -100),即4x +3y -400=0.(6分)因为圆心B 到直线AC 的距离d =|4×60+3×40-400|42+32=8,而圆B 的半径r =85,所以d <r ,此时直线AC 与圆B 相交,所以快艇有触礁的危险. 答:若快艇立即出发有触礁的危险.(8分)(2) 设快艇所走的直线AE 与圆B 相切,且与科考船相遇于点E. 设直线AE 的方程为y =k(x -100),即kx -y -100k =0.因为直线AE 与圆B 相切,所以圆心B 到直线AC 的距离d =|60k -40-100k|12+k 2=85,即2k 2+5k +2=0,解得k =-2或k =-12.(10分)由(1)可知k =-12舍去.因为cos ∠AOD =55,所以tan ∠AOD =2,所以直线OD 的方程为y =2x. 由⎩⎪⎨⎪⎧y =2x ,y =-2(x -100),解得⎩⎪⎨⎪⎧x =50,y =100,所以E(50,100), 所以AE =505,OE =505,(12分)此时两船的时间差为505105-50550=5-5,所以x ≥5-5-2=3- 5.答:x 的最小值为(3-5)小时.(14分)18. 解:(1) 因为椭圆x 2a 2+y 2b 2=1(a >b >0)过点(-2,0)和(1,32),所以a =2,1a 2+34b 2=1,解得b 2=1,所以椭圆C 的方程为x 24+y 2=1.(2分)(2) 因为B 为左顶点,所以B (-2,0).因为四边形AMBO 为平行四边形,所以AM ∥BO ,且AM =BO =2.(4分) 设点M(x 0,y 0),则A(x 0+2,y 0).因为点M ,A 在椭圆C 上,所以⎩⎨⎧x 204+y 20=1,(x 0+2)24+y 2=1,解得⎩⎪⎨⎪⎧x 0=-1,y 0=±32,所以M(-1,±32).(6分) (3) 因为直线AB 的斜率存在,所以设直线AB 的方程为y =kx +m ,A(x 1,y 1),B(x 2,y 2).由⎩⎪⎨⎪⎧y =kx +m ,x 24+y 2=1,消去y ,得(4k 2+1)x 2+8kmx +4m 2-4=0, 则有x 1+x 2=-8km 1+4k 2,x 1x 2=4m 2-41+4k 2.(8分)因为平行四边形AMBO ,所以OM →=OA →+OB →=(x 1+x 2,y 1+y 2).因为x 1+x 2=-8km 1+4k 2,所以y 1+y 2=k(x 1+x 2)+2m =k·-8km 1+4k 2+2m =2m1+4k 2, 所以M(-8km 1+4k 2,2m 1+4k 2).(10分)因为点M 在椭圆C 上,所以将点M 的坐标代入椭圆C 的方程, 化简得4m 2=4k 2+1 ①.(12分)因为A ,M ,B ,O 四点共圆,所以平行四边形AMBO 是矩形,且OA ⊥OB , 所以OA →·OB →=x 1x 2+y 1y 2=0. 因为y 1y 2=(kx 1+m)(kx 2+m)=k 2x 1x 2+km(x 1+x 2)+m 2=m 2-4k 21+4k 2,所以x 1x 2+y 1y 2=4m 2-41+4k 2+m 2-4k 21+4k 2=0,化简得5m 2=4k 2+4 ②.(14分) 由①②解得k 2=114,m 2=3,此时Δ>0,因此k =±112.所以所求直线AB 的斜率为±112.(16分) 19. (1) 解:当a =1时,f(x)=e xx 2-x +1,所以函数f(x)的定义域为R ,f ′(x)=e x (x -1)(x -2)(x 2-x +1)2.令f′(x)<0,解得1<x <2,所以函数f(x)的单调减区间为(1,2).(2分)(2) 解:由函数f(x)的定义域为R ,得x 2-ax +a ≠0恒成立, 所以a 2-4a <0,解得0<a <4.(4分)(解法1)由f(x)=e xx 2-ax +a ,得f′(x)=e x (x -a )(x -2)(x 2-ax +a )2.①当a =2时,f(2)=f(a),不符题意.②当0<a <2时,因为当a <x <2时,f ′(x)<0,所以f(x)在(a ,2)上单调递减, 所以f(a)>f(2),不符题意.(6分) ③当2<a <4时,因为当2<x <a 时,f ′(x)<0,所以f(x)在(2,a)上单调递减, 所以f(a)<f(2),满足题意.综上,a 的取值范围是(2,4).(8分)(解法2)由f(2)>f(a),得e 24-a >e aa .因为0<a <4,所以不等式可化为e 2>e aa(4-a). 设函数g(x)=e xx (4-x)-e 2,0<x <4.(6分)因为g′(x)=e x ·-(x -2)2x 2≤0恒成立,所以g(x)在(0,4)上单调递减.因为g(2)=0,所以g(x)<0的解集为(2,4). 所以a 的取值范围是(2,4).(8分) (3) 证明:设切点为(x 0,f(x 0)),则f′(x 0)=ex 0(x 0-2)(x 0-a )(x 20-ax 0+a )2, 所以切线的方程为y -ex 0x 20-ax 0+a =ex 0(x 0-2)(x 0-a )(x 20-ax 0+a )2×(x -x 0). 由0-ex 0x 20-ax 0+a =ex 0(x 0-2)(x 0-a )(x 20-ax 0+a )2×(0-x 0), 化简得x 30-(a +3)x 20+3ax 0-a =0.(10分) 设h(x)=x 3-(a +3)x 2+3ax -a ,a ∈(2,4), 则只要证明函数h(x)有且仅有三个不同的零点.由(2)可知a ∈(2,4)时,函数h(x)的定义域为R ,h ′(x)=3x 2-2(a +3)x +3a.因为Δ=4(a +3)2-36a =4(a -32)2+27>0恒成立,所以h′(x)=0有两不相等的实数根x 1和x 2,不妨设x 1<x 2. 列表如下:所以函数h(x)最多有三个零点.(12分)因为a ∈(2,4),所以h(0)=-a <0,h(1)=a -2>0,h(2)=a -4<0,h(5)=50-11a >0, 所以h(0)h(1)<0,h(1)h(2)<0,h(2)h(5)<0.因为函数的图象不间断,所以函数h(x)在(0,1),(1,2),(2,5)上分别至少有一个零点. 综上所述,函数h(x)有且仅有三个零点.(16分)20. 解: (1) 因为{a n }的“L 数列”为{12n },所以a n a n +1=12n ,n ∈N *,即a n +1a n =2n ,所以n ≥2时,a n =a n a n -1·a n -1a n -2·…·a 2a 1·a 1=2n -1·2n -2·…·2·1=2(n-1)+(n -2)+…+1=2n (n -1)2.又a 1=1符合上式,所以{a n }的通项公式为a n =2n (n -1)2,n ∈N *.(2分)(2) 因为a n =n +k -3(k >0),且n ≥2,n ∈N *时,a n ≠0,所以k ≠1. (解法1)设b n =a n a n +1,n ∈N *,所以b n =n +k -3(n +1)+k -3=1-1n +k -2. 因为{b n }为递增数列,所以b n +1-b n >0对n ∈N *恒成立,即1n +k -2-1n +k -1>0对n ∈N *恒成立.(4分) 因为1n +k -2-1n +k -1=1(n +k -2)(n +k -1),所以1n +k -2-1n +k -1>0等价于(n +k -2)(n +k -1)>0.当0<k <1时,因为n =1时,(n +k -2)(n +k -1)<0,不符合题意.(6分) 当k >1时,n +k -1>n +k -2>0,所以(n +k -2)(n +k -1)>0. 综上,k 的取值范围是(1,+∞). (8分)(解法2)令f(x)=1-1x +k -2,所以f(x)在区间(-∞,2-k)和区间(2-k ,+∞)上单调递增.当0<k <1时,f(1)=1-1k -1>1,f(2)=1-1k <1,所以b 2<b 1,不符合题意.(6分)当k >1时,因为2-k <1,所以f(x)在[1,+∞)上单调递增,所以{b n }单调递增,符合题意.综上,k 的取值范围是(1,+∞).(8分)(3) 存在满足条件的等差数列{c n },证明如下:因为a k a k +1=1+p k -11+p k =1p +1-1p 1+pk ,k ∈N *,(10分) 所以S n =n p +(1-1p )·(11+p +11+p 2+…+11+p n -1+11+p n).因为p >1,所以1-1p >0,所以n p <S n <n p +(1-1p ).(1p +1p 2+ (1)n -1+1p n ), 即n p <S n <n p +1p ·[1-(1p)n ].(14分) 因为1p ·[1-(1p )n ]<1p ,所以n p <S n <n +1p. 设c n =n p ,则c n +1-c n =n +1p -n p =1p,且c n <S n <c n +1, 所以存在等差数列{c n }满足题意. (16分)2020届高三模拟考试试卷(南京)数学附加题参考答案及评分标准21. A. 解:(1) ⎣⎢⎡⎦⎥⎤1-1a 0⎣⎢⎡⎦⎥⎤11=⎣⎢⎡⎦⎥⎤0a .(2分) 因为点P(1,1)在矩阵A 的变换下得到点P′(0,-2),所以a =-2,所以A =⎣⎢⎡⎦⎥⎤ 1-1-2 0.(4分) (2) 因为A =⎣⎢⎡⎦⎥⎤ 1-1-2 0,所以A 2=⎣⎢⎡⎦⎥⎤ 1-1-2 0⎣⎢⎡⎦⎥⎤ 1-1-2 0=⎣⎢⎡⎦⎥⎤ 3-1-2 2,(6分) 所以A 2⎣⎢⎡⎦⎥⎤03=⎣⎢⎡⎦⎥⎤ 3-1-2 2⎣⎢⎡⎦⎥⎤03=⎣⎢⎡⎦⎥⎤-3 6, 所以点Q′的坐标为(-3,6).(10分)B. 解:由直线l 的参数方程⎩⎨⎧x =3t ,y =1+t(t 为参数),得直线l 的方程为x -3y +3=0.(2分)曲线C 上的点到直线l 的距离d =|1+cos θ-3sin θ+3|2(4分) =⎪⎪⎪⎪2cos (θ+π3)+1+32.(6分) 当θ+π3=2k π,即θ=-π3+2k π(k ∈Z )时,(8分) 曲线C 上的点到直线l 的距离取最大值3+32.(10分) C. 证明:因为a ,b 为非负实数,所以a 3+b 3-ab(a 2+b 2)=a 2a(a -b)+b 2b(b -a)=(a -b)[(a)5-(b)5].(4分)若a ≥b 时,a ≥b ,从而(a)5≥(b)5,得(a -b)·[(a)5-(b)5]≥0.(6分)若a <b 时,a <b ,从而(a)5<(b)5,得(a -b)·[(a)5-(b)5]>0.(8分)综上,a 3+b 3≥ab(a 2+b 2).(10分)22. 解:(1) 因为三棱柱ABCA 1B 1C 1为直三棱柱,所以AA 1⊥平面ABC , 所以AA 1⊥AB ,AA 1⊥AC.又AB ⊥AC ,所以以{AB →,AC →,AA 1→}为正交基底建立如图所示的空间直角坐标系Axyz.设AA 1=t(t >0),又AB =3,AC =4,则A(0,0,0),C 1(0,4,t),B 1(3,0,t),C(0,4,0),所以AC 1→=(0,4,t),B 1C →=(-3,4,-t).(2分)因为B 1C ⊥AC 1,所以B 1C →·AC 1→=0,即16-t 2=0,解得t =4,所以AA 1的长为4.(4分)(2) 由(1)知B(3,0,0),C(0,4,0),A 1(0,0,4),所以A 1C →=(0,4,-4),BC →=(-3,4,0).设n =(x ,y ,z)为平面A 1CB 的法向量,则n ·A 1C →=0,n ·BC →=0,即⎩⎪⎨⎪⎧4y -4z =0,-3x +4y =0. 取y =3,解得z =3,x =4,所以n =(4,3,3)为平面A 1CB 的一个法向量.因为AB ⊥平面AA 1C 1C ,所以AB →=(3,0,0)为平面A 1CA 的一个法向量,则cos 〈n ,AB →〉=AB →·n |AB →|·|n |=123×42+32+32=434,(6分)所以sin 〈n ,AB →〉=317. 设P(3,0,m),其中0≤m ≤4,则CP →=(3,-4,m).因为AB →=(3,0,0)为平面A 1CA 的一个法向量,所以cos 〈CP →,AB →〉=AB →·CP →|AB →|·|CP →|=93·32+(-4)2+m 2=3m 2+25, 所以直线PC 与平面AA 1C 1C 所成角的正弦值为3m 2+25.(8分) 因为直线PC 与平面AA 1C 1C 所成角和二面角BA 1CA 的大小相等, 所以3m 2+25=317,此时方程无解, 所以侧棱BB 1上不存在点P ,使得直线PC 与平面AA 1C 1C 所成角和二面角BA 1CA 的大小相等 .(10分)23. (1) 解:根据题意,每次取出的球是白球的概率为25,取出的球是黑球的概率为35, 所以P 1=25×25+C 12×(25)2×35=425+24125=44125.(2分) (2) 证明:累计取出白球次数是n +1的情况有:前n 次取出n 次白球,第n +1次取出的是白球,概率为C n n ×(25)n +1; 前n +1次取出n 次白球,第n +2次取出的是白球,概率为C n n +1×(25)n +1×35;(4分) ……前2n -1 次取出n 次白球,第2n 次取出的是白球,概率为C n 2n -1×(25)n +1×(35)n -1; 前2n 次取出n 次白球,第2n +1次取出的是白球,概率为C n 2n ×(25)n +1×(35)n ; 则P n =C n n ×(25)n +1+C n n +1×(25)n +1×35+…+C n 2n -1×(25)n +1×(35)n -1+C n 2n ×(25)n +1×(35)n =(25)n +1×[C n n +C n n +1×35+…+C n 2n -1×(35)n -1+C n 2n ×(35)n ] =(25)n +1×[C 0n +C 1n +1×35+…+C n -12n -1×(35)n -1+C n 2n ×(35)n ],(6分) 因此P n +1-P n =(25)n +2×[C 0n +1+C 1n +2×35+…+C n 2n +1×(35)n +C n +12n +2×(35)n +1] -(25)n +1×[C 0n +C 1n +1×35+…+C n -12n -1×(35)n -1+C n 2n ×(35)n ]=(25)n +1×{25×[C 0n +1+C 1n +2×35+…+C n 2n +1×(35)n +C n +12n +2×(35)n +1] -[C 0n +C 1n +1×35+…+C n -12n -1×(35)n -1+C n 2n ×(35)n ]} =(25)n +1×{(1-35)×[C 0n +1+C 1n +2×35+…+C n 2n +1×(35)n +C n +12n +2×(35)n +1] -[C 0n +C 1n +1×35+…+C n -12n -1×(35)n -1+C n 2n ×(35)n ]} =(25)n +1×{[C 0n +1+C 1n +2×35+…+C n 2n +1×(35)n +C n +12n +2×(35)n +1] -[C 0n +1×35+C 1n +2×(35)2+…+C n 2n +1×(35)n +1+C n +12n +2×(35)n +2] -[C 0n +C 1n +1×35+…+C n -12n -1×(35)n -1+C n 2n ×(35)n ]}(8分) =(25)n +1×{[C 0n +1+C 1n +2×35+…+C n 2n +1×(35)n +C n +12n +2×(35)n +1] -[C 0n +C 1n +2×35+…+C n 2n +1×(35)n +C n 2n +1×(35)n +1+C n +12n +2×(35)n +2]}, 则P n +1-P n =(25)n +1×[C n +12n +2×(35)n +1-C n 2n +1×(35)n +1-C n +12n +2×(35)n +2] =(25)n +1×(35)n +1×(C n +12n +2-C n 2n +1-35C n +12n +2) =(25)n +1×(35)n +1×(C n +12n +1-35C n +12n +2). 因为C n +12n +1-35C n +12n +2=C n +12n +1-35(C n +12n +1+C n 2n +1)=25C n +12n +1-35C n 2n +1=-15C n 2n +1, 所以P n +1-P n =(25)n +1×(35)n +1×(-15)×C n 2n +1<0, 因此P n +1<P n .(10分)。
【试题】江苏省南京市2020届高三年级第三次模拟考试数学试题含附加题(解析版)

【试题】江苏省南京市2020届高三年级第三次模拟考试数学试题2020.6一、填空题(本大题共14小题,每小题5分,共计70分.不需要写出解答过程,请将答案填写在答题卡相应的位置上..........) 1.已知集合A ={}24x x <<,B ={}13x x <<,则A U B = . 2.若i 1iaz =++(i 是虚数单位)是实数,则实数a 的值为 . 3.某校共有教师300人,男学生1200人,女学生1000人,现用分层抽样从所有师生中抽取一个容量为125的样本,则从男学生中抽取的人数为 . 4.如图是一个算法的伪代码,其输出的结果为 .第4题第6题5.将甲、乙、丙三人随机排成一行,则甲、乙两人相邻的概率为 . 6.已知函数()2sin()f x x ωϕ=+(其中ω>0,22ππϕ-<≤)部分图象如图所示,则()2f π的值为 .7.已知数列{}n a 为等比数列,若12a =,且1a ,2a ,32a -成等差数列,则{}n a 的前n 项和为 .8.在平面直角坐标系xOy 中,已知双曲线22221x y a b-=(a >0,b >0)的右焦点为F .若以F 为圆心,a 为半径的圆交该双曲线的一条渐近线于A ,B 两点,且AB =2b ,则该双曲线的离心率为 .9.若正方体ABCD —A 1B 1C 1D 1的棱长为2,则三棱锥A —B 1CD 1的体积为 . 10.已知函数2, 0()(), 0x x f x f x x +≤⎧=⎨->⎩,()(2)g x f x =-,若(1)1g x -≥,则实数x 的取值范围为 .11.在平面直角坐标系xOy 中,A ,B 是圆O :x 2+y 2=2上两个动点,且OA u u u r ⊥OB uuu r,若A ,B 两点到直线l :3x +4y ﹣10=0的距离分别为d 1,d 2,则d 1+d 2的最大值为 . 12.若对任意a ∈[e ,+∞)(e 为自然对数的底数),不等式eax bx +≤对任意x ∈R 恒成立,则实数b 的取值范围为 .13.已知点P 在边长为4的等边三角形ABC 内,满足AP AB AC λμ=+u u u r u u u r u u u r ,且231λμ+=,延长AP 交边BC 于点D ,若BD =2DC ,则PA PB ⋅u u u r u u u r的值为 .14.在△ABC 中,∠A =3π,D 是BC 的中点.若AD BC ,则sinBsinC 的最大值为.二、解答题(本大题共6小题,共计90分.请在答题纸指定区域.......内作答,解答应写出文字说明,证明过程或演算步骤.) 15.(本题满分14分)如图,在四棱锥P —ABCD 中,底面ABCD 为矩形,平面PAD ⊥平面ABCD ,PA ⏊PD ,E , F 分别为AD ,PB 的中点.求证:(1)EF//平面PCD ;(2)平面PAB ⏊平面PCD .16.(本题满分14分)已知向量m u r =(cos x ,sin x ),n r=(cos x ,﹣sin x ),函数1()2f x m n =⋅+u r r .(1)若()12x f =,x ∈(0,π),求tan(x +4π)的值;(2)若1()10f α=-,α∈(2π,34π),sin 10β=,β∈(0,2π),求2αβ+的值.17.(本题满分14分)如图,港口A 在港口O 的正东100海里处,在北偏东方向有条直线航道OD ,航道和正东方向之间有一片以B 为圆心,半径为危险),其中OB =tan ∠AOB =23,cos ∠AOD =5,现一艘科考船以海里/小时的速度从O 出发沿OD 方向行驶,经过2个小时后,一艘快艇以50海里/小时的速度准备从港口A 出发,并沿直线方向行驶与科考船恰好相遇.(1)若快艇立即出发,判断快艇是否有触礁的危险,并说明理由; (2)在无触礁危险的情况下,若快艇再等x 小时出发,求x 的最小值.18.(本题满分16分)如图,在平面直角坐标系xOy 中,椭圆C :22221x y a b+=(a >b >0)经过点(﹣2,0)和(1,2),椭圆C 上三点A ,M ,B 与原点O 构成一个平行四边形AMBO . (1)求椭圆C 的方程;(2)若点B 是椭圆C 左顶点,求点M 的坐标;(3)若A ,M ,B ,O 四点共圆,求直线AB 的斜率.19.(本题满分16分)已知函数2e ()xf x x ax a=-+(a ∈R),其中e 为自然对数的底数.(1)若a =1,求函数()f x 的单调减区间;(2)若函数()f x 的定义域为R ,且(2)()f f a >,求a 的取值范围;(3)证明:对任意a ∈(2,4),曲线()y f x =上有且仅有三个不同的点,在这三点处的切线经过坐标原点. 20.(本题满分16分)若数列{}n a 满足n ≥2时,0n a ≠,则称数列1n n a a +⎧⎫⎨⎬⎩⎭(n N *∈)为{}n a 的“L 数列”. (1)若11a =,且{}n a 的“L 数列”为12n ⎧⎫⎨⎬⎩⎭,求数列{}n a 的通项公式; (2)若3n a n k =+-(k >0),且{}n a 的“L 数列”为递增数列,求k 的取值范围; (3)若11n n a p-=+,其中p >1,记{}n a 的“L 数列”的前n 项和为n S,试判断是否存在等差数列{}n c ,对任意n N *∈,都有1n n n c S c +<<成立,并证明你的结论.江苏省南京市2020届高三年级第三次模拟考试数学附加题本试卷共40分,考试时间30分钟. 21.【选做题】本题包括A ,B ,C 三小题,请选定其中两题作答,每小题10分共计20分,解答时应写出文字说明,证明过程或演算步骤. A .选修4—2:矩阵与变换已知矩阵A =1 1 0a -⎡⎤⎢⎥⎣⎦,a ∈R .若点P(1,1)在矩阵A 的变换下得到点P′(0,﹣2). (1)求矩阵A ;(2)求点Q(0,3)经过矩阵A 的2次变换后对应点Q′的坐标.B .选修4—4:坐标系与参数方程在平面直角坐标系xOy 中,曲线C 的参数方程为1cos sin x y θθ=+⎧⎨=⎩(θ为参数),直线l的参数方程为1x y t⎧=⎪⎨=+⎪⎩(t 为参数),求曲线C 上的点到直线l 的距离的最大值.C .选修4—5:不等式选讲已知为a ,b 非负实数,求证:3322)a b a b +≥+.【必做题】第22题、第23题,每题10分,共计20分,解答时应写出文字说明,证明过程或演算步骤. 22.(本小题满分10分)如图,在直三棱柱中ABC —A 1B 1C 1,AB ⏊AC ,AB =3,AC =4,B 1C ⏊AC 1. (1)求AA 1的长;(2)试判断在侧棱BB 1上是否存在点P ,使得直线PC 与平面AA 1C 1C 所成角和二面角B —A 1C —A 的大小相等,并说明理由.23.(本小题满分10分)口袋中有大小、形状、质地相同的两个白球和三个黑球.现有一抽奖游戏规则如下:抽奖者每次有放回的从口袋中随机取出一个球,最多取球2n +1(n N *∈)次.若取出白球的累计次数达到n +1时,则终止取球且获奖,其它情况均不获奖.记获奖概率为n P .(1)求1P ;(2)证明:1n n P P +<.江苏省南京市2020届高三年级第三次模拟考试数学试题2020.6一、填空题(本大题共14小题,每小题5分,共计70分.不需要写出解答过程,请将答案填写在答题卡相应的位置上..........) 1.已知集合A ={}24x x <<,B ={}13x x <<,则A U B = . 答案:(1,4)考点:集合的并集运算解析:∵集合A ={}24x x <<,B ={}13x x <<, ∴A U B =(1,4). 2.若i 1iaz =++(i 是虚数单位)是实数,则实数a 的值为 . 答案:2 考点:复数 解析:∵(2)i i 1i 2a a a z +-=+=+是实数,∴实数a 的值为2. 3.某校共有教师300人,男学生1200人,女学生1000人,现用分层抽样从所有师生中抽取一个容量为125的样本,则从男学生中抽取的人数为 . 答案:60考点:分层抽样 解析:12512006030012001000⨯=++.4.如图是一个算法的伪代码,其输出的结果为 .答案:10 考点:伪代码解析:第一步:i =1,S =1;第一步:i =2,S =3; 第一步:i =3,S =6;第一步:i =4,S =10;故输出的结果为10.5.将甲、乙、丙三人随机排成一行,则甲、乙两人相邻的概率为 . 答案:23考点:随机事件的概率解析:22223323A A P A ==. 6.已知函数()2sin()f x x ωϕ=+(其中ω>0,22ππϕ-<≤)部分图象如图所示,则()2f π的值为 .考点;三角函数的图像与性质 解析:首先222[()]33πππω=--,解得ω=1, 又222326k k πππϕπϕπ+=+⇒=-+,k Z ∈,∵22ππϕ-<≤, ∴6πϕ=-,故()2sin()6f x x π=-,所以()2sin()226f πππ=-=.7.已知数列{}n a 为等比数列,若12a =,且1a ,2a ,32a -成等差数列,则{}n a 的前n 项和为 . 答案:122n +-考点:等比数列的前n 项和公式,等差中项解析:∵1a ,2a ,32a -成等差数列,∴22a =1a +32a -=3a ,故q =2,∴12(21)2221n n n S +-==-- 8.在平面直角坐标系xOy 中,已知双曲线22221x y a b-=(a >0,b >0)的右焦点为F .若以F 为圆心,a 为半径的圆交该双曲线的一条渐近线于A ,B 两点,且AB =2b ,则该双曲线的离心率为 .答案:2考点:双曲线的简单性质解析:由题意知a =,则c =,离心率e =2c a ==. 9.若正方体ABCD —A 1B 1C 1D 1的棱长为2,则三棱锥A —B 1CD 1的体积为 . 答案:83考点:正四面体的体积计算解析:可知三棱锥A —B 1CD 1是以V =38123⨯=. 10.已知函数2, 0()(), 0x x f x f x x +≤⎧=⎨->⎩,()(2)g x f x =-,若(1)1g x -≥,则实数x 的取值范围为 . 答案:[2,4]考点:函数与不等式 解析:首先2, 0()2, 0x x f x x x +≤⎧=⎨-+>⎩,由()(2)g x f x =-知(1)(3)g x f x -=-,当()1f x ≥,解得11x -≤≤,故(1)(3)1g x f x -=-≥,得131x -≤-≤, ∴24x ≤≤,故实数x 的取值范围为[2,4].11.在平面直角坐标系xOy 中,A ,B 是圆O :x 2+y 2=2上两个动点,且OA u u u r ⊥OB uuu r,若A ,B 两点到直线l :3x +4y ﹣10=0的距离分别为d 1,d 2,则d 1+d 2的最大值为 . 答案:6考点:直线与圆综合解析:取AB 中点D ,设D 到直线l 的距离为d ,易知:d 1+d 2=2dOA u u u r ⊥OB ⇒u u u r D 轨迹为:22max 13x y d +=⇒=⇒d 1+d 2的最大值为6.12.若对任意a ∈[e ,+∞)(e 为自然对数的底数),不等式e ax bx +≤对任意x ∈R 恒成立,则实数b 的取值范围为 . 答案:[﹣2,+∞)考点:函数与不等式(恒成立问题) 解析:当0x ≤时,显然成立,b R ∈; 当0x >时,[,)a e ∀∈+∞,ln ln ()ax bx e x ax b b x ex f x +≤⇒≤+⇒≥-=1()ex f x x -'=,易知:max 1()()2f x f e==-,故2b ≥-; 综上,实数b 的取值范围为[﹣2,+∞).13.已知点P 在边长为4的等边三角形ABC 内,满足AP AB AC λμ=+u u u r u u u r u u u r,且231λμ+=,延长AP 交边BC 于点D ,若BD =2DC ,则PA PB ⋅u u u r u u u r的值为 .答案:94-考点:平面向量数量积解析:A ,P ,D 共线,不妨令3AP mAD =u u u r u u u r又2BD DC =u u u r u u u r,故12233AD AB AC AP mAB mAC AB AC λμ=+⇒=+=+u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r ,因此121182311844AP AB AC λμλλμμ⎧=⎪=⎧⎪⇒⇒=+⎨⎨+=⎩⎪=⎪⎩u u u r u u u r u u u r , 则7184PB AB AP AB AC =-=-u u u r u u u r u u u r u u u r u u u r,故11719()()84844PA PB AB AC AB AC ⋅=-+⋅-=-u u u r u u u r u u u r u u u r u u u r u u u r .14.在△ABC 中,∠A =3π,D 是BC 的中点.若AD ≤2BC ,则sinBsinC 的最大值为. 答案:38考点:解三角形综合解析:22222213222a bcbc AD a a +=+=+≤ 22113sin sin sin 228bc a B C A ⇒≤⇒≤=. 二、解答题(本大题共6小题,共计90分.请在答题纸指定区域.......内作答,解答应写出文字说明,证明过程或演算步骤.) 15.(本题满分14分)如图,在四棱锥P —ABCD 中,底面ABCD 为矩形,平面PAD ⊥平面ABCD ,PA ⏊PD ,E ,F 分别为AD ,PB 的中点.求证:(1)EF//平面PCD ;(2)平面PAB ⏊平面PCD .证明:(1)取PC 中点G ,连接DG 、FG .在△PBC 中,因为F ,G 分别为PB ,PC 的中点,所以GF ∥BC ,GF =12BC .因为底面ABCD 为矩形,且E 为AD 的中点, 所以DE ∥BC ,DE =12BC ,所以GF ∥DE ,GF =DE ,所以四边形DEFG 为平行四边形, 所以EF ∥DG .又因为EF ⊄平面PCD ,DG ⊂平面PCD , 所以EF ∥平面PCD .(2)因为底面ABCD 为矩形,所以CD ⊥AD .又因为平面P AD ⊥平面ABCD ,平面P AD ∩平面ABCD =AD ,CD ⊂平面ABCD , 所以CD ⊥平面P AD .因为P A ⊂平面P AD ,所以CD ⊥P A .又因为P A ⊥PD ,PD ⊂平面PCD ,CD ⊂平面PCD ,PD ∩CD =D ,所以P A ⊥平面PCD .因为P A ⊂平面P AB ,所以平面P AB ⊥平面PCD .16.(本题满分14分)已知向量m u r =(cos x ,sin x ),n r=(cos x ,﹣sin x ),函数1()2f x m n =⋅+u r r .(1)若()12x f =,x ∈(0,π),求tan(x +4π)的值;(2)若1()10f α=-,α∈(2π,34π),sin 10β=,β∈(0,2π),求2αβ+的值.解:(1) 因为向量m =(cos x ,sin x ),n =(cos x ,-sin x ),所以 f (x )=m ·n +12=cos 2x -sin 2x +12=cos2x +12.因为f (x 2)=1,所以cos x +12=1,即cos x =12.又因为x ∈(0,π) ,所以x =π3,所以tan(x +π4)=tan(π3+π4)=tan π3+ tan π41-tan π3tanπ4=-2-3.(2)若f (α)=-110,则cos2α+12=-110,即cos2α=-35.因为α∈(π2,3π4),所以2α∈(π,3π2),所以sin2α=-1-cos 22α=-45.因为sin β=7210,β∈(0,π2),所以cos β=1-sin 2β=210,所以cos(2α+β)=cos2αcos β-sin2αsin β=(-35)×210-(-45)×7210=22.又因为2α∈(π,3π2),β∈(0,π2),所以2α+β∈(π,2π),BEA COD xy所以2α+β的值为7π4.17.(本题满分14分)如图,港口A 在港口O 的正东100海里处,在北偏东方向有条直线航道OD ,航道和正东方向之间有一片以B 为圆心,半径为5危险),其中OB =2013tan ∠AOB =23,cos ∠AOD 55海里/小时的速度从O 出发沿OD 方向行驶,经过2个小时后,一艘快艇以50海里/小时的速度准备从港口A 出发,并沿直线方向行驶与科考船恰好相遇.(1)若快艇立即出发,判断快艇是否有触礁的危险,并说明理由; (2)在无触礁危险的情况下,若快艇再等x 小时出发,求x 的最小值.解:如图,以O 为原点,正东方向为x 轴,正北方向为y 轴,建立直角坐标系xOy . 因为OB =2013,tan ∠AOB =23,OA =100,所以点B (60,40),且A (100,0).(1)设快艇立即出发经过t 小时后两船相遇于点C , 则OC =105(t +2),AC =50t .因为OA =100,cos ∠AOD =55, 所以AC 2=OA 2+OC 2-2OA ·OC ·cos ∠AOD ,即(50t )2=1002+[105(t +2)]2-2×100×105(t +2)×55.化得t 2=4,解得t 1=2,t 2=-2(舍去), 所以OC =405.因为cos ∠AOD =55,所以sin ∠AOD =255,所以C (40,80),所以直线AC 的方程为y =-43(x -100),即4x +3y -400=0.因为圆心B 到直线AC 的距离d =|4×60+3×40-400| 42+32=8,而圆B 的半径r =85,所以d <r ,此时直线AC 与圆B 相交,所以快艇有触礁的危险. 答:若快艇立即出发有触礁的危险.(2)设快艇所走的直线AE 与圆B 相切,且与科考船相遇于点E . 设直线AE 的方程为y =k (x -100),即kx -y -100k =0.因为直线AE 与圆B 相切,所以圆心B 到直线AC 的距离d =|60k -40-100k | 12+k 2=85,即2k 2+5k +2=0,解得k =-2或k =-12.由(1)可知k =-12舍去.因为cos ∠AOD =55,所以tan ∠AOD =2,所以直线OD 的方程为y =2x . 由⎩⎨⎧y =2x , y =-2(x -100),解得⎩⎨⎧x =50,y =100,所以E (50,100),所以AE =50 5,OE =505,此时两船的时间差为50 5105-50 550=5- 5,所以x ≥5- 5-2=3-5.答:x 的最小值为(3-5)小时. 18.(本题满分16分)如图,在平面直角坐标系xOy 中,椭圆C :22221x y a b+=(a >b >0)经过点(﹣2,0)和(1,,椭圆C 上三点A ,M ,B 与原点O 构成一个平行四边形AMBO . (1)求椭圆C 的方程;(2)若点B 是椭圆C 左顶点,求点M 的坐标;(3)若A ,M ,B ,O 四点共圆,求直线AB 的斜率.解:(1)因为椭圆x 2a 2+y 2b 2=1(a >b >0)过点(-2,0)和 (1,32),所以a =2,1a 2+34b 2=1,解得b 2=1,所以椭圆C 的方程为x 24+y 2=1.(2)因为B 为左顶点,所以B (-2,0).因为四边形AMBO 为平行四边形,所以AM ∥BO ,且AM =BO =2. 设点M (x 0,y 0),则A (x 0+2,y 0).因为点M ,A 在椭圆C 上,所以⎩⎨⎧x 024+y 02=1, (x 0+2)24+y 02=1,解得⎩⎪⎨⎪⎧x 0=-1, y 0=±32,所以M (-1,±32). (3) 因为直线AB 的斜率存在,所以设直线AB 的方程为y =kx +m ,A (x 1,y 1),B (x 2,y 2). 由⎩⎪⎨⎪⎧y =kx +m ,x 24+y 2=1,消去y ,得(4k 2+1)x 2+8kmx +4m 2-4=0, 则有x 1+x 2=-8km 1+4k 2,x 1x 2=4m 2-41+4k 2. 因为平行四边形AMBO ,所以OM →=OA →+OB →=(x 1+x 2,y 1+y 2).因为x 1+x 2=-8km 1+4k 2,所以y 1+y 2=k (x 1+x 2)+2m =k ·-8km 1+4k 2+2m =2m1+4k 2, 所以M (-8km 1+4k 2,2m1+4k 2).因为点M 在椭圆C 上,所以将点M 的坐标代入椭圆C 的方程, 化得4m 2=4k 2+1.①因为A ,M ,B ,O 四点共圆,所以平行四边形AMBO 是矩形,且OA ⊥OB , 所以OA →·OB →=x 1x 2+y 1y 2=0.因为y 1y 2=(kx 1+m )(kx 1+m )=k 2x 1x 2+km (x 1+x 2)+m 2=m 2-4 k 21+4k 2,所以x 1x 2+y 1y 2=4m 2-41+4k 2+m 2-4k 21+4k2=0,化得5m 2=4k 2+4.② 由①②解得k 2=114,m 2=3,此时△>0,因此k =±112.所以所求直线AB 的斜率为±112. 19.(本题满分16分)已知函数2e ()xf x x ax a=-+(a ∈R),其中e 为自然对数的底数.(1)若a =1,求函数()f x 的单调减区间;(2)若函数()f x 的定义域为R ,且(2)()f f a >,求a 的取值范围;(3)证明:对任意a ∈(2,4),曲线()y f x =上有且仅有三个不同的点,在这三点处的切线经过坐标原点.解:(1)当a =1时,f (x )=e xx 2-x +1,所以函数f (x )的定义域为R ,f'(x )=e x (x -1)(x -2)(x 2-x +1)2.令f'(x )<0,解得1<x <2,所以函数f (x )的单调减区间为(1,2).(2)由函数f (x )的定义域为R ,得x 2-ax +a ≠0恒成立, 所以a 2-4a <0,解得0<a <4. 方法1由f (x )=e xx 2-ax +a ,得f'(x )=e x (x -a )(x -2)(x 2-ax +a )2.①当a =2时,f (2)=f (a ),不符题意. ②当0<a <2时,因为当a <x <2时,f ′(x )<0,所以f (x )在(a ,2)上单调递减, 所以f (a )>f (2),不符题意. ③当2<a <4时,因为当2<x <a 时,f ′(x )<0,所以f (x )在(2,a )上单调递减, 所以f (a )<f (2),满足题意. 综上,a 的取值范围为(2,4).方法2由f (2)>f (a ),得e 24-a >e aa .因为0<a <4,所以不等式可化为e 2>e a a(4-a ).设函数g (x )=e xx(4-x )-e 2, 0<x <4.因为g'(x )=e x·-(x -2)2x 2≤0恒成立,所以g (x )在(0,4)上单调递减.又因为g (2)=0,所以g (x )<0的解集为(2,4). 所以,a 的取值范围为(2,4).(3)证明:设切点为(x 0,f (x 0)),则f'(x 0)=e x 0(x 0-2)(x 0-a )(x 02-ax 0+a )2,所以切线方程为y -ex 0x 02-ax 0+a =e x 0(x 0-2)(x 0-a )(x 02-ax 0+a )2×(x -x 0).由0-ex 0x 02-ax 0+a =e x 0(x 0-2)(x 0-a )(x 02-ax 0+a )2×(0-x 0),化简得x 03-(a +3)x 02+3ax 0-a =0. 设h (x )=x 3-(a +3)x 2+3ax -a ,a ∈(2,4), 则只要证明函数h (x )有且仅有三个不同的零点.由(2)可知a ∈(2,4)时,函数h (x )的定义域为R ,h'(x )=3x 2-2(a +3)x +3a . 因为△=4(a +3)2-36a =4(a -32)2+27>0恒成立,所以h'(x )=0有两不相等的实数根x 1和x 2,不妨x 1<x 2. 因为所以函数h (x )最多有三个零点.因为a ∈(2,4),所以h (0)=-a <0,h (1)=a -2>0,h (2)=a -4<0,h (5)=50-11a >0,所以h (0)h (1)<0,h (1)h (2)<0,h (2)h (5)<0.因为函数的图象不间断,所以函数h (x )在(0,1),(1,2),(2,5)上分别至少有一个零点.综上所述,函数h (x )有且仅有三个零点. 20.(本题满分16分)若数列{}n a 满足n ≥2时,0n a ≠,则称数列1n n a a +⎧⎫⎨⎬⎩⎭(n N *∈)为{}n a 的“L 数列”. (1)若11a =,且{}n a 的“L 数列”为12n ⎧⎫⎨⎬⎩⎭,求数列{}n a 的通项公式; (2)若3n a n k =+-(k >0),且{}n a 的“L 数列”为递增数列,求k 的取值范围; (3)若11n n a p-=+,其中p >1,记{}n a 的“L 数列”的前n 项和为n S ,试判断是否存在等差数列{}n c ,对任意n N *∈,都有1n n n c S c +<<成立,并证明你的结论. 解:(1)由题意知,112n n n a a +=,所以12n n na a +=, 所以(1)121123(1)1221121222122n n n n n n n n n n a a a a a a a a ---++++----=⋅⋅⋅⋅=⋅⋅⋅⋅==L L L即数列{}n a 的通项公式为(1)22n n n a -=(2)因为a n =n +k -3(k >0),且n ≥2,n ∈N *时,a n ≠0,所以k ≠1. 方法1设b n =a n a n +1,n ∈N *,所以b n =n +k -3(n +1)+k -3=1-1n +k -2.因为{b n }为递增数列,所以b n +1-b n >0对n ∈N*恒成立, 即1n +k -2-1n +k -1>0对n ∈N*恒成立.因为1n +k -2-1n +k -1=1(n +k -2)(n +k -1),所以1n +k -2-1n +k -1>0等价于(n +k -2)(n +k -1)>0.当0<k <1时,因为n =1时,(n +k -2)(n +k -1)<0,不符合题意. 当k >1时,n +k -1>n +k -2>0,所以(n +k -2)(n +k -1)>0, 综上,k 的取值范围是(1,+∞). 方法2令f (x )=1-1x +k -2,所以f (x )在区间(-∞,2-k )和区间(2-k ,+∞)上单调递增.当0<k <1时,f (1)=1-1k -1>1,f (2)=1-1k <1,所以b 2<b 1,不符合题意.当k >1时,因为2-k <1,所以f (x )在[1,+∞)上单调递增,所以{b n }单调递增,符合题意. 综上,k 的取值范围是(1,+∞).(3)存在满足条件的等差数列{}n c ,证明如下:因为11111111k k kkk a p p a p p p-+-+==+++,k N *∈, 所以2111111(1)()1111n n nn S p p p p p p -=+-++++++++L , 又因为1p >,所以110p->, 所以2111111(1)()n n n n n S p p p p p p p-<<+-++++L , 即11(1)n n n n S p p p p<<+-, 因为111(1)n p p p -<,所以1n n n S p p+<<, 设n n c p=,则111n n n n c c p p p ++-=-=,且1n n n c S c +<<, 所以存在等差数列{}n c 满足题意.江苏省南京市2020届高三年级第三次模拟考试数学附加题本试卷共40分,考试时间30分钟. 21.【选做题】本题包括A ,B ,C 三小题,请选定其中两题作答,每小题10分共计20分,解答时应写出文字说明,证明过程或演算步骤. A .选修4—2:矩阵与变换已知矩阵A =1 1 0a -⎡⎤⎢⎥⎣⎦,a ∈R .若点P(1,1)在矩阵A 的变换下得到点P′(0,﹣2). (1)求矩阵A ;(2)求点Q(0,3)经过矩阵A 的2次变换后对应点Q′的坐标.解:(1) ⎣⎢⎡⎦⎥⎤1 -1a 0 ⎣⎢⎡⎦⎥⎤11=⎣⎢⎡⎦⎥⎤0a .因为点P (1,1)在矩阵A 的变换下得到点P ′(0,-2),所以a =-2, 所以A =⎣⎢⎡⎦⎥⎤1 -1-2 0.(2)因为A =⎣⎢⎡⎦⎥⎤1 -1-2 0,所以A 2=⎣⎢⎡⎦⎥⎤1 -1-2 0 ⎣⎢⎡⎦⎥⎤1 -1-2 0=⎣⎢⎡⎦⎥⎤3 -1-2 2,所以A 2⎣⎡⎦⎤03=⎣⎢⎡⎦⎥⎤3 -1-2 2 ⎣⎡⎦⎤03=⎣⎢⎡⎦⎥⎤-36, 所以,点Q ′的坐标为(-3,6).B .选修4—4:坐标系与参数方程在平面直角坐标系xOy 中,曲线C 的参数方程为1cos sin x y θθ=+⎧⎨=⎩(θ为参数),直线l的参数方程为1x y t⎧=⎪⎨=+⎪⎩(t 为参数),求曲线C 上的点到直线l 的距离的最大值.解:曲线C :(x ﹣1)2+y 2=1,直线l :0x +=圆心C(1,0)到l 的距离设为d ,12d =故曲线C 上的点到直线l 的距离的最大值为112++,即32+.C .选修4—5:不等式选讲已知a ,b 为非负实数,求证:3322)a b a b +≥+.证明:因为a ,b 为非负实数,3322)a b a b ab +-+=+55]-若a b ≥≥,从而55≥,得55]0-≥,若a b <<,从而55<,得55]0->,综上,3322)a b a b +≥+.【必做题】第22题、第23题,每题10分,共计20分,解答时应写出文字说明,证明过程或演算步骤. 22.(本小题满分10分)如图,在直三棱柱中ABC —A 1B 1C 1,AB ⏊AC ,AB =3,AC =4,B 1C ⏊AC 1. (1)求AA 1的长;(2)试判断在侧棱BB 1上是否存在点P ,使得直线PC 与平面AA 1C 1C 所成角和二面角B —A 1C —A 的大小相等,并说明理由.解:(1)直三棱柱ABC —A 1B 1C 1中,AA 1⊥平面ABC ,又AB ,AC ⊂平面ABC ,故AA 1⊥AB ,AA 1⊥AC ,又AB ⊥AC故以A 为原点,{AB uuu r ,AC u u u r ,1AA u u ur }为正交基底建立空间直角坐标系设AA 1=a >0,则A 1(0,0,a ),C(0,4,0),B 1(3,0,a ),C 1(0,4,a ),1B C u u u r =(﹣3,4,﹣a ),1AC u u u u r=(0,4,a )因为B 1C ⊥AC 1,故11=0B C AC ⋅u u u r u u u u r ,即2160a -=,又a >0,故a =4,即AA 1的长为4;(2)由(1)知:B(3,0,0),B 1(3,0,4),假设存在,设1BP BB λ==u u u r u u u r(0,0,4λ),(0,1)λ∈, 则P(3,0,4λ),则CP u u u r=(3,﹣4,4λ)AB ⊥AC ,AB ⊥AA 1,又AC I AA 1=A ,AC ,AA 1⊂平面AA 1C 1C所以AB ⊥平面AA 1C 1C ,故平面AA 1C 1C 的法向量为AB uuu r=(3,0,0) 设PC 与平面AA 1C 1C 所成角为α,则sin cos ,CP AB α=<>=u u u r u u u r,设平面BA 1C 的法向量为n r=(x ,y ,z ),平面AA 1C 的法向量为AB uuu r =(3,0,0)由(1)知:1AC u u u r=(0,4,﹣4),BC uuu r =(﹣3,4,0),AC u u u r =(0,4,0), 1340440n BC x y n AC y z ⎧⋅=-+=⎪⎨⋅=-=⎪⎩r u u u r r u u u r,令3y =,则n r =(4,3,3) 设二面角B —A 1C —A 的大小为β,则cos cos ,n AB β=<>=r u u u r ,因为αβ=,则22298sincos 1162517αβλ+=+=+,无解,故侧棱BB 1上不存在符合题意的点P .23.(本小题满分10分)口袋中有大小、形状、质地相同的两个白球和三个黑球.现有一抽奖游戏规则如下:抽奖者每次有放回的从口袋中随机取出一个球,最多取球2n +1(n N *∈)次.若取出白球的累计次数达到n +1时,则终止取球且获奖,其它情况均不获奖.记获奖概率为n P .(1)求1P ;(2)证明:1n n P P +<.解:(1)根据题意,每次取出的球是白球的概率为25,取出的球是黑球的概率为35, 所以1212222344()5555125P C =⨯+⨯⨯=; (2)证明:累计取出白球次数是n +1的情况有:前n 次取出n 次白球,第n +1次取出的是白球,概率为12()5nn n C +⨯前n+1次取出n 次白球,第n +2次取出的是白球,概率为1123()55nn n C ++⨯⨯ 前2n ﹣1次取出n 次白球,第2n 次取出的是白球,概率为112123()()55nn n n C +--⨯⨯ 前2n 次取出n 次白球,第2n +1次取出的是白球,概率为1223()()55nn n n C +⨯⨯ 则111112122323()()()()55555nn n n nn n n n n n P C C C +++-+-=⨯+⨯⨯++⨯⨯+L 11011121212232333()()()[()()]555555n n n n n n nn n n n n nC C C C C ++--+-⨯⨯=⨯+⨯++⨯+⨯L 因此2011111221222333()[()()]5555n n n n n n n n n n n P P C C C C ++++++++-=⨯+⨯++⨯+⨯L 1011112122333()[()()]5555n n n nn n n n nC C C C +--+--⨯+⨯++⨯+⨯L 101111221222333(){[()()]5555n n n n n n n n n C C C C +++++++=⨯+⨯++⨯+⨯L01+1+1+222+12+12+23333[()()+()]}5555n n n n n n n n n n n C C C C C +-+⨯++⨯+⨯⨯L 则11111212221222333()[()()()]5555n n n n n n n n n n n n P P C C C ++++++++++-=⨯⨯-⨯-⨯ 1111222122233()()()555n n n nn n n n C C C +++++++=⨯-- 11112122233()()()555n n n n n n C C ++++++=⨯- 因为11111212221212121212133231()55555n n n n nn n n n n n n n n n n C C C C C C C C +++++++++++++-=-+=-=-, 所以11121231()()()0555n n n n n n P P C ++++-=⨯⨯-<,因此1n n P P +<.。
2020年6月江苏省南京市普通高中2020届高三下学期第三次高考模拟考试数学试题(含附加题)答案

1 绝密★启用前
江苏省南京市普通高中
2020届高三毕业班下学期第三次高考模拟考试
数学试题参考答案
2020年6月
说明:
1.本解答给出的解法供参考.如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.
2.对计算题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.
3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.
4.只给整数分数,填空题不给中间分数.
一、填空题(本大题共14小题,每小题5分,计70分. 不需写出解答过程,请把答案写在答题纸的指定位置上)
1.{x |1<x <4} 2.2 3.60 4.10 5.23
6. 3 7.2n +1-2 8.62 9.83
10.[2,4] 11.6 12. [-2,+∞) 13.-94
14.38
二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内)
15.(本小题满分14分)
证明:(1)取PC 中点G ,连接DG 、FG .
在△PBC 中,因为F ,G 分别为PB ,PC 的中点,所以GF ∥BC ,GF =12
BC . 因为底面ABCD 为矩形,且E 为AD 的中点,。
【数学解析版】南京2020届高三年级三模数学卷(解析版)

EF 平面 PCD , DG 平面 PCD EF / / 平面 PCD (2)四边形 ABCD 是矩形 AB AD 平面 PAD 平面 ABCD 平面 PAD 平面 ABCD AD AB 平面 ABCD AB 平面 PAD PD 平面 PAD AB PD PA PD AB PA A AB, PA 平面 PAB PD 平面 PAB PD 平面 PCD 平面 PAB 平面 PCD 【点评】第一问考查线面平行的判定定理,第二问考查面面垂直的性质定理,以及面面垂直的判定定理, 属于基础题型。(优能中学教育)
S 0 For i From 1 To 4
S S i End For Pr int S
第4题 5. 将甲、乙、丙三人随机排成一行,则甲、乙两人相邻的概率为_______. 【答案】 2
3 【解析】列举法:甲乙丙,甲丙乙,乙甲丙,乙丙甲,丙甲乙,丙乙甲,共 6 种排列方式,甲乙相邻的排 列方式有 4 种,故概率为 2
【解析】(1)取 PC 中点G,并连接 DG , FG 在 PBC 中, F,G 分别为 PB, PC 中点 FG / /BC, FG 1 BC
2 四边形 ABCD 是矩形 AD / /BC, AD BC FG / / AD, FG 1 AD
2 E 为 AD 中点 FG / /ED, FG ED 四边形 DEFG 为平行四边形 EF //DG
2 10
5
2
,
3 4
2
,
3 2
sin 2 1 cos2 2 4 5
sin
72 10
,
且
0,
2
cos 1 sin 2 2 10
sin 2 sin 2 cos cos 2 sin 4 2 ( 3 7 2) 2
南京2020届高三三模数学卷

南京市2020届高三年级第三次模拟考试数 学2020.06注意事项:1.本试卷共4页,包括填空题(第1题~第14题)、解答题(第15题~第20题)两部分.本试卷满分为160分,考试时间为120分钟.2.答题前,请务必将自己的姓名、学校、考试号写在答题纸内.试题的答案写在答题..纸.上对应题目的答案空格内.考试结束后,交回答题卡.一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应位置上.1. 已知集合{}{}24,13A x x B x x =<<=<<,则AB =_______. 2. 若1a z i i=++(i 为虚数单位)是实数,则实数a 的值为_______. 3. 某校共有教师300人,男学生1200人,女学生1000人.现用分层抽样从所有师生中抽取一个容量为125的样本,则从男学生中抽取的人数为_______.4. 如图是一个算法的伪代码,其输出的结果为_______.5. 将甲、乙、丙三人随机排成一行,则甲、乙两人相邻的概率为_______.6. 已知函数()2sin()f x x ωϕ=+(其中0,22ππωϕ>-<<)的部分图像如图所示,则()2f π的值为_______. 7. 已知数列{}n a 为等比数列,若12a =,且123,,2a a a -成等差数列,则{}n a 的前n 和为_______.8. 在平面直角坐标系xOy 中,已知双曲线()222210,0x y a b a b-=>>的右焦点为F ,若以F 为圆心,a 为半径的圆交该双曲线的一条渐近线于,A B 两点,且2AB b =,则该双曲线的离心率为_________.9. 若正方体1111ABCD A B C D -的棱长为2,则三棱锥11A B CD -的体积为_________.0S ←For i From 1 To 4S S i ←+End ForPr int S 第6题第4题10. 已知函数()()()()2,0,2,0x x f x g x f x f x x +≤⎧⎪==-⎨->⎪⎩.若()11g x -≥,则实数x 的取值范围为_________. 11. 在平面直角坐标系xOy 中,,A B 是圆22:2O x y +=上两个动点,且OA OB ⊥ 若,A B 两点到直线:34100l x y +-=的距离分别为12,d d ,则12d d +的最大值为__________.12. 若对任意[),a e ∈+∞,(e 为自然对数的底数),不等式ax b x e +≤对任意x R ∈恒成立,则实数b 的取值范围为 ___________.13. 已知点P 在边长为4的等边三角形ABC 内,满足AP AB AC λμ=+,且231λμ+=,延长AP 交边BC 于点D ,若2BD DC =,则PA PB ⋅的值为___________.14. 在ABC ∆中 3A π∠=,D 是BC 的中点,若2AD BC ≤,则sin sin B C 的最大值为_________. 二、解答题:本大题共6小题,共90分.解答题写出必要的文字说明,证明过程或演算步骤,请把答案填写在答题卡相应位置上.15.(本小题满分14分)如图,在四棱锥ABCD P -中,底面ABCD 为矩形,平面⊥PAD 平面ABCD ,F E PD PA ,,⊥分别为PB AD ,的中点.求证:(1)//EF 平面PCD ;(2)平面⊥PAB 平面.PCD16. (本小题满分14分)已知向量m ()x x sin ,cos =,n ()x x sin ,cos -=,函数()=x f n m ⋅21+. (1)若()π,0,12∈=⎪⎭⎫ ⎝⎛x x f ,求⎪⎭⎫ ⎝⎛+4tan πx 的值; (2)若()1372,,,sin ,0,,1024102f πππααββ⎛⎫⎛⎫=-∈=∈ ⎪ ⎪⎝⎭⎝⎭求βα+2的值.如图,港口A 在港口O 的正东100海里处,在北偏东方向有一条直线航道OD ,航道和正东方向之间有一片以B 为圆心,半径为58海里的圆形暗礁群(在这片海域行船有触礁危险),其中1320=OB 海里,55cos ,32tan =∠=∠AOD AOB ,现一艘科考船以510海里/小时的速度从O 出发沿OD 方向行驶,经过2个小时后,一艘快艇以50海里/小时的速度准备从港口A 出发,并沿直线方向行驶与科考船恰好相遇.(1)若快艇立即出发,判断快艇是否有触礁的危险,并说明理由;(2)在无触礁危险的情况下,若快艇再等x 小时出发,求x 的最小值.18.(本小题满分16分)如图,在平面直角坐标系xOy 中,椭圆C :22221(0)x y a b a b+=>>经过点(2,0)-和3(1,)2.椭圆C 上三点,,A M B 与原点O 构成一个平行四边形AMBO .(1) 求椭圆C 的方程;(2) 若点B 是椭圆C 左顶点,求点M 的坐标;(3) 若,,,A M B O 四点共圆,求直线AB 的斜率.已知函数2()()xe f x a R x ax a=∈-+,其中e 为自然对数的底数. (1) 若1a =,求函数()f x 的单调减区间;(2) 若函数()f x 的定义域为R ,且(2)()f f a >,求a 的取值范围;(3) 证明:对任意的(2,4)a ∈,曲线()y f x =上有且仅有三个不同的点,在这三点处的切线经过坐标原点.20.(本小题满分16分)若数列{}n a 满足*2,n n N ≥∈时,0n a ≠,则称数列1()n n a n N a *+⎧⎫∈⎨⎬⎩⎭为{}n a 的“L 数列”. (1) 若11a =,且{}n a 的“L 数列”为12n ⎧⎫⎨⎬⎩⎭,求数列{}n a 的通项公式; (2) 若3(0)n a n k k =+->,且{}n a 的“L 数列”为递增数列,求k 的取值范围;(3) 若11n n a p -=+,其中1p >,记{}n a 的“L 数列”的前n 项和为n S ,试判断是否存在等差数列{}n c ,对任意n N *∈,都有1n n n c S c +<<成立,并证明你的结论.南京市2020届高三年级第三次模拟考试数学附加题2020.06注意事项:1.附加题供选修物理的考生使用.2.本试卷共40分,考试时间30分钟.3.答题前,考生务必将自己的姓名、学校写在答题卡上.试题的答案写在答题卡上对应题目的答案空格内.考试结束后,交回答题卡.21.【选做题】在A 、B 、C 、D 四小题中只能选做2题,每小题10分,共计20分.请在答卷卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤.A. 选修4-2:矩阵与变换已知矩阵11,0A a R a -⎡⎤=∈⎢⎥⎣⎦.若点(1,1)P 在矩阵A 的变换下得到点(0,2)P '-. (1) 求矩阵A ;(2) 求点(0,3)Q 经过矩阵A 的2次变换后对应点Q '的坐标.B. 选修4-4:坐标系与参数方程在平面直角坐标系xOy 中,曲线C 的参数方程为⎩⎨⎧=+=θθsin cos 1y x ,(θ为参数),直线l 的参数方程为,13⎪⎩⎪⎨⎧+==ty t x (t 为参数),求曲线C 上的点到直线l 的距离的最大值.22.【必做题】第22题、第23题,每题10分,共20分.请在答卷卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤.22.(本小题满分10分)如图,在直棱柱中111ABC A B C -,11,3,4,.AB AC AB AC B C AC ⊥==⊥(1) 求1AA 的长;(2) 试判断在侧棱1BB 上是否存在点P ,使得直线PC 与平面11AAC C 所成角和二面角1B AC A --的大小相等,并说明理由.23.(本小题满分10分)口袋中有大小、形状、质地相同的两个白球和三个黑球,现有一抽奖游戏规则如下:抽奖者每次有放回的从口袋中随机取出一个球,最多取球()*21n n N+∈次.若取出白球的累计次数达到1+n 时,则终止取球且获奖,其他情况均不获奖.记获奖概率为n P .(1)求1P ;(2)证明:n n P P <+1.。
2020年5月江苏省南京市普通高中2020届高三下学期高考模拟考试数学试题(解析版)

绝密★启用前江苏省南京市普通高中2020届高三毕业班下学高考模拟考试数学试题(解析版)2020年5月一、填空题(本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上)1.设集合M ={m |﹣3<m <2,m ∈Z },N =R ,则M ∩N =_____.【答案】{﹣2,﹣1,0,1}【解析】【分析】可以求出集合M ,然后进行交集的运算即可.【详解】∵M ={﹣2,﹣1,0,1},N =R ,∴M ∩N ={﹣2,﹣1,0,1}.故答案为:{﹣2,﹣1,0,1}.【点睛】本题考查了描述法、列举法的定义,交集的定义及运算,考查了计算能力,属于基础题.2.复数z 1i i=+复平面上对应的点位于第_____象限. 【答案】一【解析】【分析】首先进行复数的除法运算,分子和分母同乘以分母的共轭复数,分母变成一个实数,分子进行复数的乘法运算,整理成复数的标准形式,写出对应点的坐标,看出所在的象限. 【详解】∵复数()()()1111111222i i i i i i i i -+===+++-,∴复数对应的点的坐标是(12,12) ∴复数1i i+在复平面内对应的点位于第一象限, 故答案为:一【点睛】本题考查复数的实部和虚部的符号,是一个概念题,考查了复数的四则运算,属于简单题.3.某次测验,将20名学生平均分为两组,测验结果两组学生成绩的平均分和标准差分别为90,6;80,4.则这20名学生成绩的方差为_____.【答案】51【解析】【分析】由方差定义可得n 个数与其平均数,方差间关系x 21+x 22++x 2n =nS 2+n x 2,利用此关系可结合条件把20 个数据中的前10个数,后10个数分别找出其平方和,及平均数,进而求出20名学生成绩的方差.【详解】设x 1,x 2…x n 的方差S 21n =[(x 1x -)2+(x 2x -)2+…+(x n x -)2]1n=[x 21+x 22++x 2n -2x (x 1+x 2+…+x n )+n x 2]1n =[x 12+x 22++x 2n -n x 2] ∴x 21+x 22++x 2n =nS 2+n x 2, 则x 21+x 22++x 210=10×36+10×902=81360,x 211+x 212++x 220=10×16+10×802=64160, 1220109010802020x x x +++⨯+⨯==85. ∴S 2120=[x 21+x 22++x 220-20x 2]120=[81360+64160﹣20×852]=51, 故答案:51.【点评】本题依托平均数,方差,标准差的定义关系,考查学生的数据处理能力和计算能力,属于中低档题.4.执行如图所示的程序框图,输出的S 值为_____.。
江苏省南京市2020届高三第三次模拟考试(6月)数学试题含答案
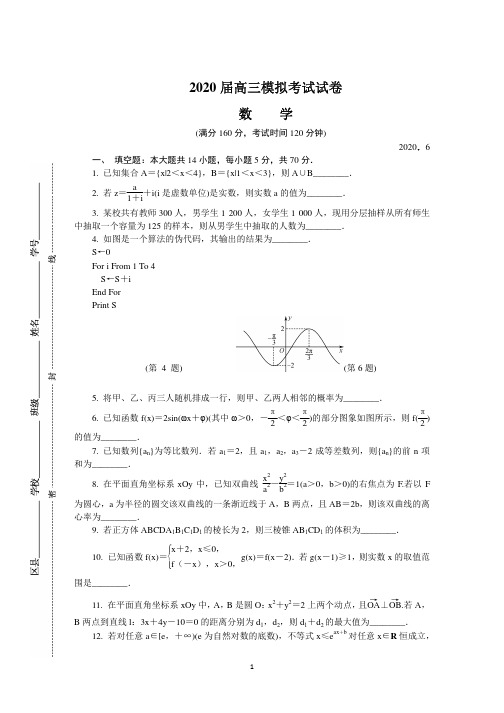
(第 4 题)
(第 6 题)
5. 将甲、乙、丙三人随机排成一行,则甲、乙两人相邻的概率为________.
ππ
π
6. 已知函数 f(x)=2sin(ωx+φ)(其中 ω>0,- 2 <φ< 2 )的部分图象如图所示,则 f( 2 )
的值为________. 7. 已知数列{an}为等比数列.若 a1=2,且 a1,a2,a3-2 成等差数列,则{an}的前 n 项
x2 y2
3
如图,在平面直角坐标系 xOy 中,椭圆 C:a2+b2=1(a>b>0)经过点(-2,0)和(1,2 ),
椭圆 C 上三点 A,M,B 与原点 O 构成一个平行四边形 AMBO.
(1) 求椭圆 C 的方程;
(2) 若点 B 是椭圆 C 左顶点,求点 M 的坐标;
(3) 若 A,M,B,O 四点共圆,求直线 AB 的斜率.
1
则实数 b 的取值范围是________. 13. 已知点 P 在边长为 4 的等边三角形 ABC 内,满足A→P=λA→B+µA→C,且 2λ+3µ=1,
延长 AP 交边 BC 于点 D.若 BD=2DC,则P→A·P→B的值为________.
π
2
14. 在△ABC 中,∠A= 3 ,点 D 是 BC 的中点.若 AD≤ 2 BC,则 sin Bsin C 的最大
值为________.
二、 解答题:本大题共 6 小题,共 90 分. 解答时应写出必要的文字说明、证明过程或
演算步骤. 15. (本小题满分 14 分) 如图,在四棱锥 PABCD 中,底面 ABCD 为矩形,平面 PAD⊥平面 ABCD,PA⊥PD,
点 E,F 分别为 AD,PB 的中点.求证: (1) EF∥平面 PCD; (2) 平面 PAB⊥平面 PCD.
江苏省南京市江宁高级中学2020届高三数学周周练(3)

高三数学周周练(3)一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题..卡.相应位置....上.. 1.在复平面内,复数对应的点位于第 四 象限.2. 命题“若,则”的否命题是 若,则 ;3.某大学对1000名学生的自主招生水平测试成绩进行统计,得到样本频率分布直方图如下图所示,现规定不低于70分为合格,则合格人数是 600 .4.在区间上随机取一个实数,使得成立的概率为 ;5. 向量的夹角为120°,= 7 .6. 执行上面的框图,若输入的是6,则输出的值是 720 .7. 过双曲线的一个焦点引它到渐进线的垂线,垂足为,延长交轴于,若,则该双曲线离心率为 3 ;8.计算,可以采用以下方法:k s *5u构造恒等式,两边对x 求导,得,在上式中令,得.类比上述计算方法,计算 .9. 若函数()在P 处的切线平行于函数在Q 处的切线,则直线PQ 的斜率为10. 已知,则的值为 ;11.点A 、B 、C 、D 在同一个球的球面上,AB = BC =,AC = 2,若四面体ABCD 体积的最大值为,则这个球的表面积为 ;12. 已知数列中,,对任意,都成立,则 102413. 已知,点的坐标满足,则的取值范围为 .14.已知函数存在整数零点的恰有3个,则的取值范围是 。
二、解答题:本大题共6小题,共90分.请在答题卡指定区域内........作答,解答时应写出文字说明、证明过程或演算步骤.15. 在中,角A ,B ,C 的对边分别为a ,b ,c ,且(1)求角C 的大小;(2)求的最大值.15.解:(1)sin A +3cos A =2sin B 即2sin (A + π 3)=2sin B ,则sin (A + π 3)=sin B . 因为0<A ,B <π,又a ≥b 进而A ≥B ,所以A + π 3=π-B ,故A +B =2π3,C = π 3. (2)由正弦定理及(Ⅰ)得a +bc =sin A +sin B sin C =23[sin A +sin (A + π 3)]=3sin A +cos A =2sin (A + π 6). 当A = π 3时,a +b c取最大值2.16. (本小题满分14分) 在四棱锥P -ABCD 中,∠ABC =∠ACD =90°,∠BAC =∠CAD =60°,PA ⊥平面ABCD ,E 为PD 的中点,PA =2AB =2.(1)求证:PC ⊥;(2)求证:CE ∥平面PAB ;(3)求三棱锥P -ACE 的体积V .解析:(1)在Rt △ABC 中,AB =1,∠BAC =60°,∴BC =,AC =2.取中点,连,则∵PA =AC =2,∴PC ⊥. (1分)∵PA ⊥平面ABCD ,平面ABCD ,∴PA ⊥,又∠ACD =90°,即,∴,∴,∴. (3分)∴. (4分)∴PC ⊥. (5分)(2)证法一:取AD 中点M ,连EM ,CM .则EM ∥PA .∵EM 平面PAB ,PA 平面PAB ,∴EM ∥平面PAB . (7分)在Rt △ACD 中,∠CAD =60°,AC =AM =2,∴∠ACM =60°.而∠BAC =60°,∴MC ∥AB .∵MC 平面PAB ,AB 平面PAB ,∴MC ∥平面PAB . (9分)∵EM ∩MC =M ,∴平面EMC ∥平面PAB .∵EC 平面EMC ,∴EC ∥平面PAB . (10分) 证法二:延长DC 、AB ,设它们交于点N ,连PN .∵∠NAC =∠DAC =60°,AC ⊥CD ,∴C 为ND 的中点. (7分) ∵E 为PD 中点,∴EC ∥PN . (9分) ∵EC 平面PAB ,PN 平面PAB ,∴EC ∥平面PAB . (10分)(3)由(1)知AC =2,.在Rt △ACD 中,AC =2,∠CAD =60°,∴CD =2,得. (12分)则V =. (14分)17. 如图,2020年春节,摄影爱好者S 在某公园A 处,发现正前方B 处有一立柱,测得立柱顶端O 的仰角和立柱底部B 的俯角均为,已知S 的身高约为米(将眼睛距地面的距离按米处理)(1) 求摄影者到立柱的水平距离和立柱的高度;(2) 立柱的顶端有一长2米的彩杆MN绕中点O在S与立柱所在的平面内旋转.摄影者有一视角范围为的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由.17.(1) 如图,不妨将摄影者眼部设为S点,做SC垂直OB于C,又故在中,可求得BA=3,即摄影者到立柱的水平距离为3米……… 3分由SC=3,在中,可求得又故即立柱高为米. -------------------------- ------ ------ - 6分(2) (注:若直接写当时,最大,并且此时,得2分)连结SM,SN, 在△SON和△SOM中分别用余弦定理,故摄影者可以将彩杆全部摄入画面. (14)分18. 已知中心在原点,焦点在坐标轴上的椭圆的方程为它的离心率为,一个焦点是(-1,0),过直线上一点引椭圆的两条切线,切点分别是A、B.(Ⅰ)求椭圆的方程;(Ⅱ)若在椭圆上的点处的切线方程是.求证:直线AB恒过定点C,并求出定点C的坐标; (Ⅲ)是否存在实数使得恒成立?(点C为直线AB恒过的定点)若存在,求出的值;若不存在,请说明理由..解:(I)设椭圆方程为的焦点是,故,又,所以,所以所求的椭圆方程为. ………………………4分(II)设切点坐标为, ,直线上一点M的坐标,则切线方程分别为,,又两切线均过点M,即,即点A,B的坐标都适合方程,故直线AB的方程是,显然直线恒过点(1,0),故直线AB恒过定点.…………………………………10分(III)将直线AB的方程,代入椭圆方程,得,即,所以,不妨设,,同理,…………13分所以,即,故存在实数,使得. ……………………………16分19. (1) 设函数,且数列满足= 1, (n∈N,);求数列的通项公式.(2)设等差数列、的前n项和分别为和,且,,;求常数A的值及的通项公式.(3)若,其中、即为(1)、(2)中的数列、的第项,试求.19.(1) 由题意:,变形得:,(1分)∴数列是以为公比,为首项的等比数列. (3分)∴,即.(5分)(2) ∵由等差数列、知:;∴由得:,(6分)∴,∵,∴,解得;(8分)∴,和分别是等差数列、的前n项和;∴可设;∵,∴,即. (10分)当时,,当n≥2时,.综上得:. (12分) (3)当(N*)时,(14分)当(N*)时,.(16分)20. (本小题满分15分)记函数.(1)若函数在处取得极值,试求的值;(2)若函数有两个极值点,且,试求的取值范围;(3)若函数对任意恒有成立,试求的取值范围.(参考:)20解:(1),由……3分(3)……10分记则,又……11分记当时,上单调递减,故可得上单调递减,故……12分可得上单调递减,故可得上单调递减,……13分即在上单调递减,由题意……16分数学Ⅱ(附加题)21(1) 选修4—2 矩阵与变换已知矩阵有特征值及对应的一个特征向量.(1)求矩阵;(2)求曲线在的作用下的新曲线的方程.解:(1)由已知,即,,所以; …………………………4分(2)设曲线上任一点P,P在M作用下对应点,则即,解之得,代入得,即曲线在的作用下的新曲线的方程是.………10分21. (2) 选修4-4:坐标系与参数方程已知曲线C的极坐标方程为.以极点为平面直角坐标系的原点,极轴为轴的正半轴,建立平面直角坐标系,直线的参数方程为,若直线与曲线C相切,求的值.解析:曲线化为直角坐标方程为,即,(3分)直线的参数方程化为普通方程为.(6分)由题设条件,有:,∴, (8分)∴(舍去)或,∴. (10分)22.(本小题满分10分)如图,已知三棱柱的侧面与底面垂直,,分别是,,的中点.(1)求证:;(2)若直线与平面所成的角为,求的值.22.解:(1)建立如图所示直角坐标系,则, , , , , , , , , , ,因为,所以.………………4分, ,则令,得,所以.又,所以.……………………10分23.(本小题满分10分)在平面直角坐标系中,为坐标原点,点满足,.(1)当变化时,求点的轨迹的方程;(2)若过点的直线交曲线于A,B两点,求证:直线TA,TF,TB的斜率依次成等差数列.解析:(1)设点的坐标为,由,得点是线段的中点,则,,, (2分)由,得,―――――――――――① (3分)由,得∴t=y ――――② (4分)由①②消去,得即为所求点的轨迹的方程. (5分)(2)设直线的斜率依次为,并记,,则有.(6分)设直线方程为,由,得,∴,(8分)∴,∴,∴成等差数列.(10分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三数学周周练(3)一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题..卡.相应位置....上..1.在复平面内,复数21ii-+对应的点位于第四象限.2. 命题“若1x>,则0x>”的否命题是若1x≤,则0x≤ ;3.某大学对1000名学生的自主招生水平测试成绩进行统计,得到样本频率分布直方图如下图所示,现规定不低于70分为合格,则合格人数是 600 .4.在区间)2,2(ππ-上随机取一个实数x,使得21xcos>成立的概率为32;5. 向量,的夹角为120°,|5|,3||,1||baba-==则= 7 .6. 执行上面的框图,若输入的N是6,则输出p的值是 720 .7. 过双曲线)0,0(12222>>=-babyax的一个焦点F引它到渐进线的垂线,垂足为M,延长FM交y轴于E,若MEFM2=,则该双曲线离心率为 3 ;8.计算12323nn n n nC C C nC++++L,可以采用以下方法:k s*5u(第3题图)11(第6题图)11构造恒等式0122(1)n nn n n n n C C x C x C x x ++++=+L ,两边对x 求导,得12321123(1)n n n n n n n C C x C x nC x n x --++++=+L ,在上式中令1x =,得1231232n n n n n n C C C nC n -++++=⋅L .类比上述计算方法,计算12223223n n n n n C C C n C ++++=L 22)1(-+n n n .9. 若函数12sin y x =([0,2)x π∈)在P 处的切线平行于函数2(1)3xy =+在Q 处的切线,则直线PQ 的斜率为3810. 已知)2,0(,1010)4cos(π∈θ=π+θ,则)42sin(π-θ的值为 102 ; 11.点A 、B 、C 、D 在同一个球的球面上,AB = BC,AC = 2,若四面体ABCD 体积的最大值为23,则这个球的表面积为 4; 12. 已知数列{}n a 中,121,3a a ==,对任意*n N ∈,2132,21n n n n n a a a a ++≤+⋅≥+都成立,则1110a a -= 102413. 已知,点),(y x P的坐标满足0200y x y -<-+<⎨⎪≥⎪⎩,则223y x y x ++的取值范围为)3,3[- .14.已知函数)M a 0(1ax x )x (f 023≤≤--=存在整数零点的a 恰有3个,则0M 的取值范围是 )1663,926[。
二、解答题:本大题共6小题,共90分.请在答题卡指定区域内........作答,解答时应写出文字说明、证明过程或演算步骤. 15. 在ABC ∆中,角A ,B ,C 的对边分别为a ,b ,c ,且,sin 2sin .a b A A B ≥+= (1)求角C 的大小;(2)求a bc+的最大值. 15.解:(1)sin A +3cos A =2sin B 即2sin (A + π 3)=2sin B ,则sin (A + π3)=sin B .因为0<A ,B <π,又a ≥b 进而A ≥B ,所以A + π 3=π-B ,故A +B =2π3,C = π3.(2)由正弦定理及(Ⅰ)得 a +b c =sin A +sin B sin C =23[sin A +sin (A + π 3)]=3sin A +cos A =2sin (A + π6). 当A = π3时,a +b c 取最大值2.16. (本小题满分14分)在四棱锥P -ABCD 中,∠ABC =∠ACD =90°,∠BAC =∠CAD =60°,PA ⊥平面ABCD ,E 为PD 的中点,PA =2AB =2.(1)求证:PC ⊥AE ;(2)求证:CE ∥平面PAB ; (3)求三棱锥P -ACE 的体积V . 解析:(1)在Rt △ABC 中,AB =1,∠BAC =60°, ∴BC AC =2.取PC 中点F ,连,AF PF ,则∵PA =AC =2,∴PC ⊥AF . (1分)∵PA ⊥平面ABCD ,CD ⊂平面ABCD , ∴PA ⊥CD ,又∠ACD =90°,即CD AC ⊥, ∴CD PAC ⊥平面,∴CD PC ⊥,∴EF PC ⊥. (3分) ∴PC AEF ⊥平面. (4分)∴PC ⊥AE . (5分)(2)证法一:取AD 中点M ,连EM ,CM .则 EM ∥PA .∵EM ⊄平面PAB ,PA ⊂平面PAB ,∴EM ∥平面PAB . (7分) 在Rt △ACD 中,∠CAD =60°,AC =AM =2, ∴∠ACM =60°.而∠BAC =60°,∴MC ∥AB . ∵MC ⊄平面PAB ,AB ⊂平面PAB , ∴MC ∥平面PAB . (9分)∵EM ∩MC =M ,∴平面EMC ∥平面PAB . ∵EC ⊂平面EMC ,∴EC ∥平面PAB . (10分) 证法二:延长DC 、AB ,设它们交于点N ,连PN . P ADBCE PA D BCE F M∵∠NAC =∠DAC =60°,AC ⊥CD ,∴C 为ND 的中点. (7分) ∵E 为PD 中点,∴EC ∥PN . (9分) ∵EC ⊄平面PAB ,PN ⊂平面PAB ,∴EC ∥平面PAB . (10分)(3)由(1)知AC =2,1,2EF CD EF PAC =⊥且平面. 在Rt △ACD 中,AC =2,∠CAD =60°,∴CD =EF =(12分)则V=112232E PAC V -=⨯⨯⨯ (14分)17. 如图,2020年春节,摄影爱好者S 在某公园A 处,发现正前方B 处有一立柱,测得立柱顶端O 的仰角和立柱底部B 的俯角均为30︒,已知S(1) 求摄影者到立柱的水平距离和立柱的高度;(2) 立柱的顶端有一长2米的彩杆MN 绕中点O 在S 与立柱所在的平面内旋转.摄影者有一视角范围为60︒的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由.17.(1) 如图,不妨将摄影者眼部设为S 点,做SC 垂直OB 于C ,,60,30οο=∠=∠ASB CSB又,3=SA 故在SAB Rt ∆中,可求得BA =3,即摄影者到立柱的水平距离为3米……… 3分由SC =3,,30ο=∠CSO 在SCO Rt ∆中,可求得,3=OC又,3==SA BC 故,32=OB 即立柱高为32米. -------------------------------- ------ - 6分(2) (注:若直接写当SO MN ⊥时,MSN ∠最大,并且此时ο60<∠MSN ,得2分) 连结SM ,SN , 在△SON 和△SOM 中分别用余弦定理,13221)32(13221)32(222222⋅⋅-+-=⋅⋅-+a b 2622=+∴b a211311221122cos 22222>=+≥=-+=∠b a ab ab b a MSN ο60<∠∴MSN 故摄影者可以将彩杆全部摄入画面. (14)分18. 已知中心在原点,焦点在坐标轴上的椭圆Ω的方程为22221(0),x y a b a b+=>>它的离心率为12,一个焦点是(-1,0),过直线4x =上一点引椭圆Ω的两条切线,切点分别是A 、B.(Ⅰ)求椭圆Ω的方程;(Ⅱ)若在椭圆Ω22221(0)x y a b a b +=>>上的点00(,)x y 处的切线方程是00221x x y ya b+=.求证:直线AB 恒过定点C ,并求出定点C 的坐标;(Ⅲ)是否存在实数λ使得||||||||AC BC AC BC λ+=⋅恒成立?(点C 为直线AB 恒过的定点)若存在,求出λ的值;若不存在,请说明理由..解:(I )设椭圆方程为()222210x y a b a b +=>>的焦点是()1,0-,故1c =,又12c a =,所以2,a b ===,所以所求的椭圆Ω方程为22143x y +=. ………………………4分(II )设切点坐标为()11,A x y ,()22,B x y ,直线l 上一点M 的坐标()4,t ,则切线方程分别为11143x x y y +=,22143x x y y +=,又两切线均过点M ,即11221,133t tx y x y +=+=,即点A,B 的坐标都适合方程13t x y +=,故直线AB 的方程是13t x y +=,显然直线13tx y +=恒过点(1,0),故直线AB 恒过定点()1,0C .…………………………………10分 (III )将直线AB 的方程13t x y =-+,代入椭圆方程,得223141203t y y ⎛⎫-++-= ⎪⎝⎭,即2242903t y ty ⎛⎫+--= ⎪⎝⎭,所以121222627,1212t y y y y t t -+==++,不妨设120,0y y ><,1AC y ===,同理2BC y =,…………13分所以211212121111y y AC BC y y y y ⎛⎫-+=-= ⎪⎝⎭24312t ===+, 即43AC BC AC BC +=⋅,故存在实数43λ=,使得AC BC AC BC λ+=⋅. ……………………………16分19. (1) 设函数)(21)(R x x x g ∈-=,且数列}{n c 满足1c = 1,)(1-=n n c g c (n ∈N ,1>n );求数列}{n c 的通项公式.(2)设等差数列}{n a 、}{n b 的前n 项和分别为n S 和n T ,且827643b b a b b a +++ 52=,721++=n An T S n n , 62=S ;求常数A 的值及}{n a 的通项公式. (3)若⎪⎩⎪⎨⎧=)()(为正偶数为正奇数n c n a d nn n ,其中n a 、n c 即为(1)、(2)中的数列}{n a 、}{n c 的第n 项,试求n d d d +++Λ21. 19.(1) 由题意:)1(211-=-n n c c ,变形得:)1(2111+=+-n n c c , (1分) ∴数列}1{+n c 是以21为公比,211=+c 为首项的等比数列. (3分) ∴1)21(21-⋅=+n n c ,即1)21(2-=-n n c . (5分)(2) ∵由等差数列}{n a 、}{n b 知:573582642,2a a a b b b b b =+=+=+;∴由52827643=+++b b a b b a 得:5255=b a , (6分)∴52929255919199==⨯+⨯+=b a b b a a T S ,∵721++=n An T S n n ,∴5279219=+⨯+A ,解得1=A ;(8分)∴)72()1(721++=++=n n n n n n T S n n ,n S 和n T 分别是等差数列}{n a 、}{n b 的前n 项和; ∴可设)72()1(+=+=n kn T n kn S n n ,; ∵62=S , ∴1=k ,即n n S n +=2. (10分) 当1=n 时,211==S a ,当n ≥2时,n n n n n S S a n n n 2)]1()1[(221=-+--+=-=-.综上得:n a n 2=. (12分) (3)当12+=k n (∈k N *)时,)()(242123121k k n c c c a a a d d d +++++++=++++ΛΛΛ])21(1[3422])41(1[34)1(2122--+++=--++=n k n n k k(14分)当k n 2= (∈k N *)时,)()(242123121k k n c c c a a a d d d +++++++=+++-ΛΛΛ])21(1[342])41(1[34222n k n n k k -+-=--+=. (16分)20. (本小题满分15分)记函数()ln(1),()f x x g x x =+=.(1)若函数2()()()F x af x g x =+在1x =处取得极值,试求a 的值;(2)若函数2()()()()G x af x g x b g x =+-⋅有两个极值点12,x x ,且[]1243,,0,155x x ⎡⎤∈--∈⎢⎥⎣⎦,试求a 的取值范围;(3)若函数11()()()H x f x g x =-对任意[]12,1,3x x ∈恒有12()()H x H x a -≤成立,试求a 的取值范围.(参考:ln 20.7≈)20解:(1)2()ln(1),(1)F x a x x x =++>-,'()21aF x x x=++ 由'(1)04F a =⇒=-……3分(3)222211(1)ln (1)(),'()ln(1)(1)ln (1)x x x H x H x x x x x x ++-=-=+++……10分记22()(1)ln (1),(1)m x x x x x =++->-则2'()ln (1)2ln(1)2m x x x x =+++-,又2ln(1)2''()1x xm x x+-=+……11分记2()2ln(1)2(1),'()1xn x x x x n x x-=+->-=+ 当0x ≥时,'()0()[0,)n x n x <⇒+∞在上单调递减,故()(0)0n x n ≤= 可得''()0'()[0,)m x m x ≤⇒+∞在上单调递减,故'()'(0)0m x m ≤=……12分 可得()[0,)m x +∞在上单调递减,故()(0)0m x m ≤= 可得'()0()[0,)H x H x ≤⇒+∞在上单调递减,……13分即()H x 在[]1,3上单调递减,由题意max min |()()||(1)(3)|a H x H x H H ≥-=-11112121ln 2ln 432ln 232ln 23=--+=-=-……16分 数学Ⅱ(附加题)21(1) 选修4—2 矩阵与变换已知矩阵12b c ⎡⎤=⎢⎥⎣⎦M 有特征值41=λ及对应的一个特征向量123⎡⎤=⎢⎥⎣⎦e . (1)求矩阵M ;(2)求曲线225841x xy y ++=在M 的作用下的新曲线的方程.解:(1)由已知1283122b c ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,即238,2612b c +=+=,2,3b c ==, 所以1232M ⎡⎤=⎢⎥⎣⎦; …………………………4分(2)设曲线上任一点P (,)x y ,P 在M 作用下对应点///(,)P x y ,则//1232x x y y ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦即{//232x x y y x y =+=+,解之得////234y x x x y y ⎛-= - =⎝,代入225841x xy y ++=得222x y ''+=, 即曲线225841x xy y ++=在M 的作用下的新曲线的方程是222x y +=.………10分 21. (2) 选修4-4:坐标系与参数方程已知曲线C 的极坐标方程为()cos 0a a ρθ=>.以极点为平面直角坐标系的原点,极轴为x 轴的正半轴,建立平面直角坐标系,直线l的参数方程为1(2x t y t ⎧=⎪⎪⎨⎪=⎪⎩为参数),若直线l 与曲线C 相切,求a 的值.解析:曲线C 化为直角坐标方程为220x y ax +-=,即22222a a x y ⎛⎫⎛⎫-+= ⎪ ⎪⎝⎭⎝⎭,(3分)直线l 的参数方程化为普通方程为10x y --=. (6分)由题设条件,|1|2a a -=,∴|1|22a a -=, (8分)∴122a a =+(舍去)或122a =-,∴)21a =. (10分)22.(本小题满分10分)如图,已知三棱柱111C B A ABC -的侧面与底面垂直,11,AA AB AC AB AC ===⊥,,,M N P 分别是1CC ,BC ,11B A 的中点.(1)求证:AM PN ⊥;(2)若直线MB 与平面PMN 所成的角为θ,求sin θ的值. 22.解:(1)建立如图所示直角坐标系,则(0,0,0)A ,(1,0,0)B ,(0,1,0)C ,1(0,0,1)A ,1(1,0,1)B ,1(0,1,1)C , 1(,0,1)2P ,1(0,1,)2M , 11(,,0)22N ,1(0,,1)2=-,1(0,1,)2=,因为⋅PN 11001(1)022=⨯+⨯+-⨯=,所以AM PN ⊥. ………………4分(2)设平面PMN 的一个法向量为1111(,,)n x y z =u u r,1(0,,1)2NP =-u u u r ,111(,,)222NM =-u u u u r ,则1100n NP n NM ⎧⋅=⎪⎨⋅=⎪⎩u u r u u u r u u r u u u u r⇒1111110,21110.222y z x y z ⎧-+=⎪⎪⎨⎪-++=⎪⎩ 令12y =,得11z =,13x =所以1(3,2,1)n =u u r. …………………………………………………6分又1(1,1,)2MB =--u u u r ,所以1112sin 342||||2n MB n MB θ⋅===⨯u u r u u u ru u r u u u u r . ……………………10分B A 1AB 1C 1CM P(第22题图)23. (本小题满分10分)在平面直角坐标系中,O 为坐标原点,点F T M P 、、、满足(1,0),(1,)OF OT t ==-uuu r uuu r ,,,//FM MT PM FT PT OF =⊥u u u u r u u u r u u u u r u u u r u u u r u u u r .(1)当t 变化时,求点P 的轨迹C 的方程;(2)若过点F 的直线交曲线C 于A ,B 两点,求证:直线TA ,TF ,TB 的斜率依次成等差数列.解析:(1)设点P 的坐标为(,)x y ,由FM MT =u u u u r u u u r ,得点M 是线段FT 的中点,则(0,)2t M ,(,)2t PM x y =--u u u u r ,(2,),(1,)FT OT OF t PT x t y =-=-=---u u u r u u u r u u u r u u u r , (2分) 由PM FT ⊥u u u u r u u u r ,得2()02t x t y +-=,―――――――――――① (3分) 由//PT OF u u u r u u u r ,得(1)0()10,x t y --⨯+-⨯= ∴t=y ――――② (4分)由①②消去t ,得24y x =即为所求点P 的轨迹C 的方程. (5分)(2)设直线,,TA TF TB 的斜率依次为12,,k k k ,并记11(,)A x y ,22(,)B x y ,则有2t k =-. (6分) 设直线AB 方程为1x my =+,由241y x x my ⎧=⎨=+⎩,得2440y my --=,∴121244y y m y y +=⎧⎨⋅=-⎩,(8分) ∴2222121212()2168y y y y y y m +=+-=+,∴12121211y t y t k k x x --+=+++ 2221122212()(1)()(1)44(1)(1)44y y y t y t y y -++-+=++ 2212121212222212124()4()16()3224()16y y y y t y y y y t t k y y y y +-+++-==-=+++,∴12,,k k k 成等差数列.(10分)。
