初二数学----几何证明初步经典习题(和答案)
初中数学几何证明经典题(含答案)

初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得==,又CO=EO,所以CD=GF得证。
2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得==,又CO=EO,所以CD=GF得证。
.如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得==,又CO=EO,所以CD=GF得证。
3、如图,已知四边形ABCD、A1B1D1都是正方形,A2、B2、C2、D2分别是AA1、BB1、CC1、DD1的中点.求证:四边形A2B2D2是正方形.(初二)4、已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.求证:∠DEN=∠F.经典题(二)1、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于M.(1)求证:AH=2OM;(2)若∠BAC=600,求证:AH=AO.(初二)2、设MN是圆O外一直线,过O作OA⊥MN于A,自A引圆的两条直线,交圆于B、C 及D、E,直线EB及CD分别交MN于P、Q.求证:AP=AQ.(初二)3、如果上题把直线MN由圆外平移至圆内,则由此可得以下命题:设MN是圆O的弦,过MN的中点A任作两弦BC、DE,设CD、EB分别交MN 于P、Q.求证:AP=AQ.(初二)4、如图,分别以△ABC的AC和BC为一边,在△ABC的外侧作正方形ACDE和正方形CBFG,点P是EF的中点.求证:点P到边AB的距离等于AB的一半.(初二)经典题(三)1、如图,四边形ABCD为正方形,DE∥AC,AE=AC,AE与CD相交于F.求证:CE=CF.(初二)2、如图,四边形ABCD为正方形,DE∥AC,且CE=CA,直线EC交DA延长线于F.求证:AE=AF.(初二)3、设P是正方形ABCD一边BC上的任一点,PF⊥AP,CF平分∠DCE.求证:PA=PF.(初二)4、如图,PC切圆O于C,AC为圆的直径,PEF为圆的割线,AE、AF与直线PO相交于B、D.求证:AB=DC,BC=AD.(初三)经典题(四)1、已知:△ABC是正三角形,P是三角形内一点,PA=3,PB=4,PC=5.求:∠APB的度数.(初二)2、设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.(初二)3、设ABCD为圆内接凸四边形,求证:AB·CD+AD·BC=AC·BD.(初三)4、平行四边形ABCD中,设E、F分别是BC、AB上的一点,AE与CF相交于P,且AE=CF.求证:∠DPA=∠DPC.(初二)经典难题(五)1、设P是边长为1的正△ABC内任一点,L=PA+PB+PC,求证:≤L<2.2、已知:P是边长为1的正方形ABCD内的一点,求PA+PB+PC的最小值.3、P为正方形ABCD内的一点,并且PA=a,PB=,PC=,求正方形的边长.4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
初中数学几何证明经典题(含答案)
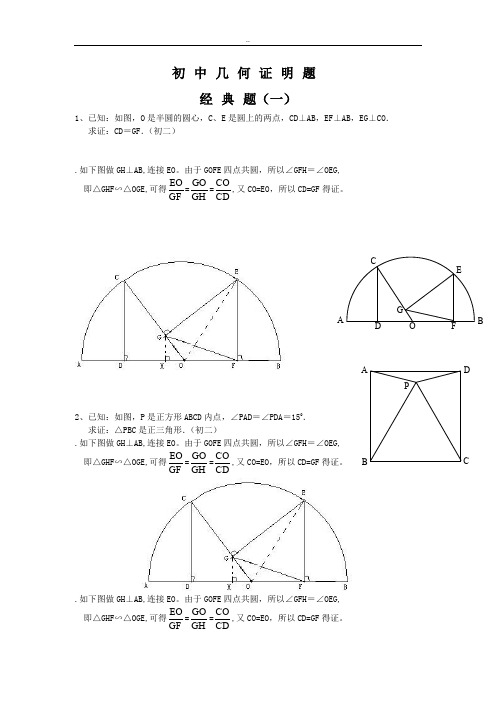
初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
.如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
APCDBAFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 BF2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC点P 是EF 的中点.求证:点P 到边AB 的距离等于AB的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、证:AB =DC ,BC =AD .(初三)经典1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC 求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA =200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
初中数学-几何证明经典试题(含答案)

初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A F G CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1F经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD .(初三)E经典题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)D经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC , 求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.APCBACBPDEDCB AA CBPD经典题(一)1.如下图做GH⊥AB,连接EO。
初中数学几何证明经典试题(含答案)
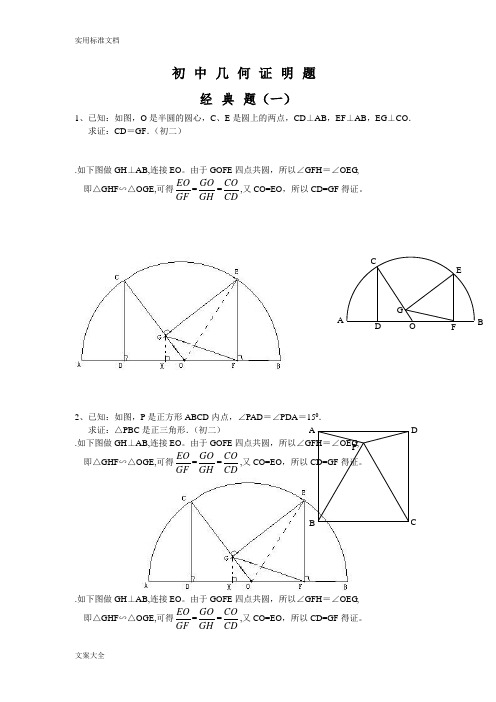
初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
.如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
APCDBAFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 BF2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD.(初三)经典1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
初中数学几何证明经典试题(含答案)
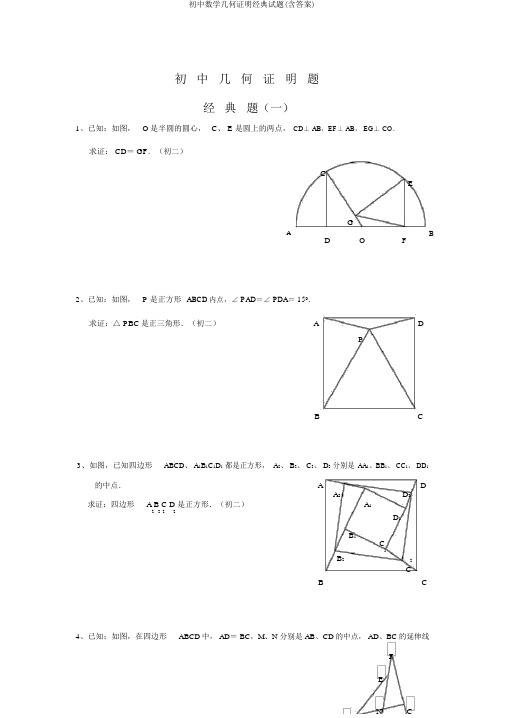
初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、 E 是圆上的两点,CD⊥ AB,EF⊥ AB, EG⊥ CO.求证: CD= GF.(初二)CEGA BD O F2、已知:如图,P 是正方形ABCD内点,∠ PAD=∠ PDA= 150.求证:△ PBC是正三角形.(初二)A DPB C3、如图,已知四边形ABCD、 A1B1C1D1都是正方形, A2、 B2、 C2、 D2分别是AA1、BB1、 CC1、 DD1的中点.A DA2D2求证:四边形 A B C D 是正方形.(初二)A12222D1B1C1B22CB C4、已知:如图,在四边形ABCD中, AD= BC,M、N 分别是 AB、CD的中点, AD、BC的延伸线FEN C交 MN于 E、 F.求证:∠ DEN=∠ F.经典题(二)1、已知:△ ABC中, H 为垂心(各边高线的交点), O为外心,且 OM⊥ BC于M.( 1)求证: AH=2OM;A( 2)若∠ BAC= 600,求证: AH= AO.(初二)O·H EB M D C2、设 MN是圆 O外向来线,过 O作 OA⊥ MN于 A,自 A引圆的两条直线,交圆于B、C及D、E,直线 EB及 CD分别交 MN于 P、 Q.GE求证: AP= AQ.(初二)O·CB DMP A Q N3、假如上题把直线MN由圆外平移至圆内,则由此可得以下命题:设 MN是圆 O的弦,过 MN的中点 A 任作两弦 BC、DE,设 CD、 EB分别交 MN于 P、 Q.求证: AP=AQ.(初二)CEA M Q·P N·O B D4、如图,分别以△ABC的 AC和 BC为一边,在△ ABC的外侧作正方形ACDE和正方形 CBFG,点 P是 EF的中点.求证:点P 到边 AB的距离等于AB的一半.(初二)DGCEPFA Q B经典题(三)1、如图,四边形ABCD为正方形, DE∥AC, AE=AC, AE与 CD订交于 F.求证: CE=CF.(初二)AB2、如图,四边形ABCD为正方形, DE∥AC,且 CE= CA,直线 EC交 DA延伸线于求证: AE= AF.(初二)DF ECF.F A DB C3、设 P 是正方形ABCD一边 BC上的任一点,PF⊥ AP, CF均分∠ DCE.求证: PA= PF.(初二)AE DFBP C E4、如图, PC切圆 O于 C,AC为圆的直径, PEF为圆的割线, AE、AF 与直线 PO订交于 B、D.求证: AB= DC, BC= AD.(初三)AB O DPEFC经典题(四)A1、已知:△ ABC是正三角形, P 是三角形内一点,PA=3, PB= 4, PC= 5.P 求:∠ APB的度数.(初二)B C2、设 P 是平行四边形ABCD内部的一点,且∠PBA=∠ PDA.求证:∠ PAB=∠ PCB.(初二)A DPB C3、设 ABCD为圆内接凸四边形,求证:AB· CD+AD· BC=AC· BD.(初三)ADB C4、平行四边形ABCD中,设 E、 F 分别是 BC、 AB上的一点, AE 与 CF订交于 P,且AE= CF.求证:∠ DPA=∠ DPC.(初二)A DFPB E C经典难题(五)A1、设 P 是边长为 1 的正△ ABC内任一点, L= PA+ PB+ PC,PB C求证:≤ L<2.2、已知: P 是边长为 1 的正方形ABCD内的一点,求PA+ PB+ PC的最小值.A DPCB3、 P 为正方形ABCD内的一点,而且PA= a, PB= 2a, PC= 3a,求正方形的边长.A DPCB4、如图,△ ABC中,∠ ABC=∠ ACB= 800, D、 E 分别是 AB、 AC上的点,∠ DCA= 300,∠ EBAAE= 200,求∠ BED的度数.经典题(一)1.以下列图做 GH⊥ AB,连结 EO。
初中数学几何证明经典题(含答案)

F初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二).如下图做GH ⊥AB,连接EO 。
由于GOFE 四点共圆,所以∠GFH =∠OEG, 即△GHF ∽△OGE,可得EO GF =GO GH =COCD,又CO=EO ,所以CD=GF 得证。
2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二).如下图做GH ⊥AB,连接EO 。
由于GOFE 四点共圆,所以∠GFH =∠OEG, 即△GHF ∽△OGE,可得EO GF =GO GH =COCD,又CO=EO ,所以CD=GF 得证。
.如下图做GH ⊥AB,连接EO 。
由于GOFE 四点共圆,所以∠GFH =∠OEG, 即△GHF ∽△OGE,可得EO GF =GO GH =COCD,又CO=EO ,所以CD=GF 得证。
3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点. 求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N MN 于E 、F .求证:∠DEN =∠F . 经典1、已知:△ABC 中,H 为垂心(各边高线的交点),O (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二) 3、如果上题把直线MN 设MN 是圆O 的弦,过MN 的中点A 任作两弦、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC ,点P 是EF 的中点. 求证:点P 到边AB 的距离等于AB 的一半.经典1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC APCDB AFGCEBOD求证:CE =CF .(初二)2、如图,四边形ABCD求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC AB =DC ,BC =AD .(初三)1、已知:△ABC 是正三角形,求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 求证:∠PAB =∠PCB .3、设ABCD4、平行四边形ABCD 中,设E AE =CF .求证:∠DPA 1、 设P 是边长为1的正△ABC 求证:≤L <2.2、已知:P 是边长为13、P 为正方形ABCD4、如图,△ABC 中,∠ABC =200,求∠BED 的度数. 1.如下图做GH ⊥AB,连接EO 即△GHF ∽△OGE,可得EO GF 2. .如下图做GH ⊥AB,连接EO 即△GHF ∽△OGE,可得EO GF 3.如下图连接BC 1和AB 1连接EB 2并延长交C 2Q 于H 点,连接FB 2并延长交A 2Q 于G 点,由A 2E=12A 1B 1=12B 1C 1= FB 2 ,EB 2=12AB=12BC=F C 1 ,又∠GFQ+∠Q=900和∠GE B 2+∠Q=900,所以∠GE B 2=∠GFQ 又∠B 2FC 2=∠A 2EB 2 , 可得△B 2FC 2≌△A 2EB 2 ,所以A 2B 2=B 2C 2 ,又∠GFQ+∠HB 2F=900和∠GFQ=∠EB 2A 2 , 从而可得∠A 2B 2 C 2=900 , 同理可得其他边垂直且相等,从而得出四边形A 2B 2C 2D 2是正方形。
初中数学几何证明经典试题(含答案)
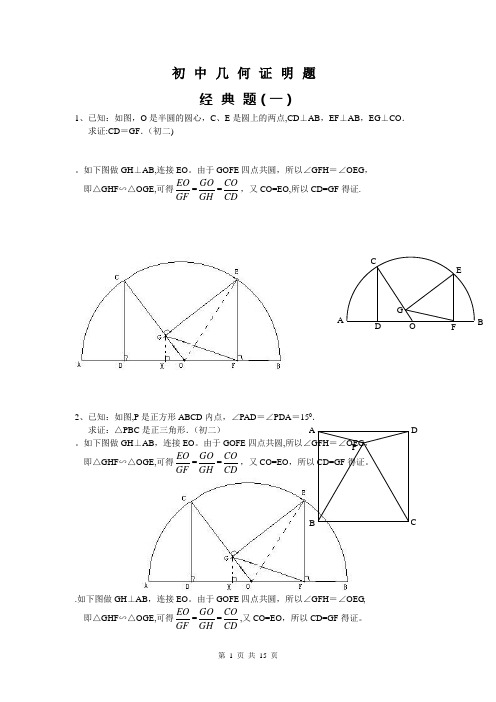
初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二)。
如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证.2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二)。
如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
.如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
APCDBAFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM; (2)若∠BAC =600,求证:AH =AO .(初二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 A N FE CDMB · A HEOF2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线D .求证:AB =DC,BC =AD .(初三)经典 1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC 求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.C BD A F PD E CB A APCBACPDA CBPD4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
初中数学几何证明经典题(含答案)
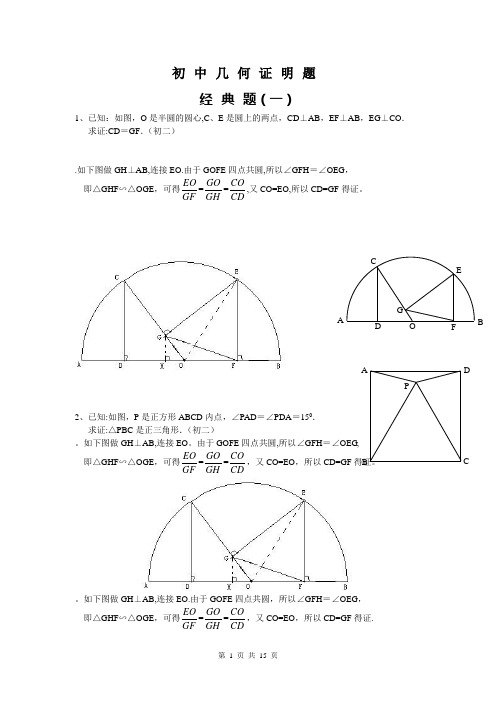
初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二).如下图做GH⊥AB,连接EO.由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE ,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二)。
如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
如下图做GH⊥AB,连接EO.由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证.APCDBAFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 AN FE CDMB· A HEOF2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线D .求证:AB =DC ,BC =AD .(初三)经典1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC 求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.C BD A F PD E CB A APCBACPDA CBPD4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
初中数学几何证明经典题(含答案)

初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二).如下图做GH ⊥AB,连接EO 。
由于GOFE 四点共圆,所以∠GFH =∠OEG ,即△GHF ∽△OGE,可得EO GF =GO GH =COCD,又CO=EO ,所以CD=GF 得证。
APDAFGCEBOD2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF =GOGH=COCD,又CO=EO,所以CD=GF得证。
.如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF =GOGH=COCD,又CO=EO,所以CD=GF得证。
3、如图,已知四边形ABCD、A1B1C1D1都是正方形,A2、B2、C2、D2分别是AA1、BB1、CC1、DD1的中点.求证:四边形A2B2C2D2是正方形.(初二)4、已知:如图,在四边形ABCD中,AD=、CD的中点,AD、BC的延长线交求证:∠DEN=∠F.D2C2B2A2D1C1B1C BD AA1经典题(二)1、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于M.(2)若∠BAC=600,求证:AH=AO.F2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于条直线,交圆于B 、C 及D 、E ,直线EB 及Q .求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A CD 、EB 分别交MN 于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点. 求证:点P 到边AB 的距离等于AB经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F . 求证:AE =AF .3、设P是正方形ABCD一边BC上的任一点,PF⊥AP,CF平分∠DCE.求证:PA=PF.(初二)4、如图,PC切圆O于C,ACAF与直线PO相交于B、D经典题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PC =5.求:∠APB的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA. 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD中,设E、F分别是BC、AB上的一点,AE与CF相交于P,且AE=CF.求证:∠DPA=∠DPC.(初二)经典难题(五)1、设P是边长为1的正△ABC内任一点,L求证:≤L<2.2、已知:P 是边长为1的正方形ABCD的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
初中数学几何证明经典试题(含答案)
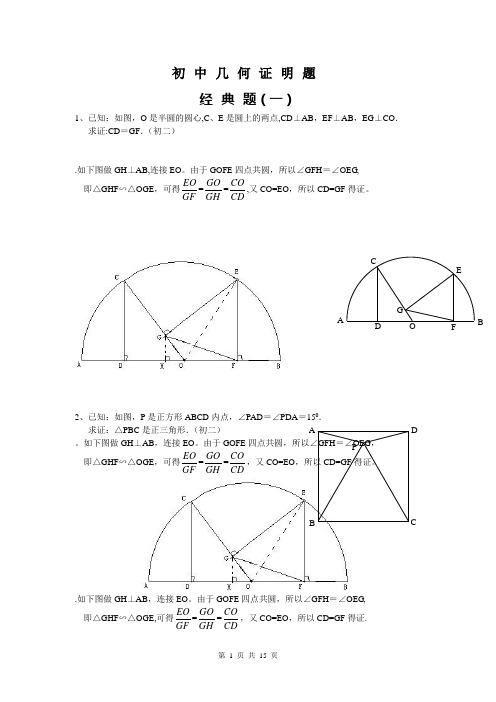
初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE ,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二)。
如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
.如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证.APCDBAFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 A N FE CDMB · A HEOF 2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC,BC =AD .(初三)经典 1、已知:△ABC 是正三角形,P是三角形内一点,PA =3,PB =4,求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.C BD A F PD E CB A APCBACPDA CBPD4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
初中数学几何证明经典试题(含答案)
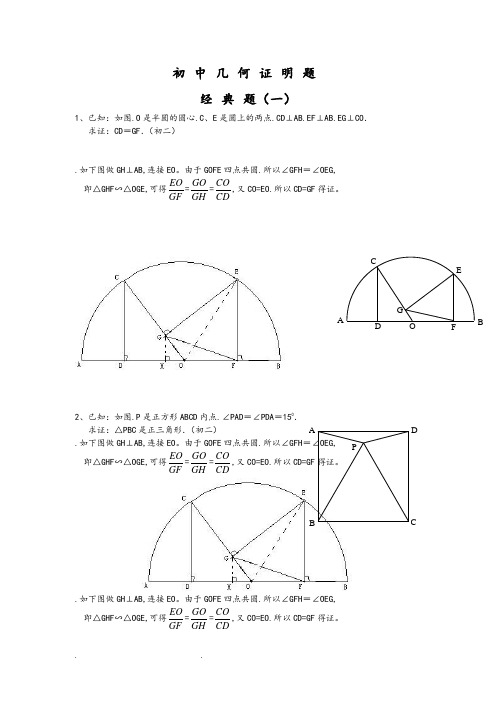
初中几何证明题经典题(一)1、已知:如图.O是半圆的圆心.C、E是圆上的两点.CD⊥AB.EF⊥AB.EG⊥CO.求证:CD=GF.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆.所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO.所以CD=GF得证。
2、已知:如图.P是正方形ABCD内点.∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆.所以∠GFH =∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO.所以CD=GF得证。
.如下图做GH⊥AB,连接EO。
由于GOFE四点共圆.所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO.所以CD=GF得证。
APCDBAFGCEBOD3、如图.已知四边形ABCD 、A 1B 1C 1D 1都是正方形.A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图.在四边形ABCD 中.AD =BC.M 、N 分别是AB 、CD 的中点.AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中.H 为垂心(各边高线的交点).O 为外心.且(1)求证:AH =2OM ;(2)若∠BAC =600.求证:AH =AO .(初二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 BF2、设MN 是圆O 外一直线.过O 作OA ⊥MN 于A.自A 引圆的两条直线.交圆于B 、C 及D 、E.直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内.则由此可得以下命题:设MN 是圆O 的弦.过MN 的中点A 任作两弦BC 、DE.设CD 、EB 分别交MN 于P 、Q .求证:AP =AQ .(初二)4、如图.分别以△ABC 的AC 和BC 为一边.在△ABC 的外侧作正方形是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图.四边形ABCD 为正方形.DE ∥AC.AE =AC.AE 与CD 相交于F .求证:CE =CF .(初二)2、如图.四边形ABCD 为正方形.DE ∥AC.且CE =CA.直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC求证:PA =PF .(初二)4、如图.PC 切圆O 于C.AC 为圆的直径.PEF 为圆的割线.AE 、证:AB =DC.BC =AD .(初三)经典1、已知:△ABC 是正三角形.P 是三角形内一点.PA =3.PB =4.PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点.且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形.求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中.设E 、F 分别是BC 、AB 上的一点.AE 与CF 相交于P.且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点.L =PA +PB +PC.求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点.求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点.并且PA =a.PB =2a.PC =3a.求正方形的边长.4、如图.△ABC中.∠ABC=∠ACB=800.D、E分别是AB、AC上的点.∠DCA=300.∠EBA=200.求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
初中数学几何证明经典题含答案

初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
.如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
APCDBAFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 BF2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD.(初三)经典1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
最新初中二年级数学几何证明初步经典练习题(含答案).doc

一、选择题(本大题共6小题,每小题2分,满分12分)1.下列条件不能推出两个直角三角形全等的是--------------------------()(A)两条直角边对应相等(B)一个锐角和一条直角边对应相等(C)一条直角边和斜边对应相等 (D)两个锐角对应相等2.下列命题中, 逆命题正确的是--------------------------------------()(A)对顶角相等 (B)直角三角形两锐角互余(C)全等三角形面积相等 (D)全等三角形对应角相等3.如图,⊿ABC是等腰直角三角形,点D在边AC上,且2=,BD AD则CBD∠是---------------------------------------------------- ()(A)5o(B)10o(C)15o(D)45o4.在直角三角形中,若有一个角等于45o,那么三角形三边的比为------- ()(A)1:2(B)1:2(C)3(D)1:15.下列各组数中不能作为直角三角形的三边长的是-------------------- ()(A)6、8、10(B)1、1、2(C)2、6D)7、24、256.如图,AD是⊿ABC的中线,45∠=o,将⊿ADC沿直线ADADC翻折,点C 落在点'C 的位置上,如果10BC =,求'BC 的长为---------( ) (A )10 (B )5( C)(D)二、填空题:(本大题共12小题,每小题3分,满分36分)7.命题“等腰三角形两腰相等”的逆命题是____________ ___.8.到定点A 的距离为9cm 的点的轨迹是____________ ____________. 9.如图,已知14AB BC cm ==, DE 是AB 的中垂线,则AE EC +是__________cm .10.如图,已知点P 是ABC ∠的角平分线BD 上的点,PH BA ⊥,如果5PH cm =,那么点P 到BC 的距离是 cm .11.若直角三角形的两个锐角的比是2:7,则这个直角三角形的较大的锐角是___________度.12.若Rt ⊿ABC 的两条直角边分别为1和2,则斜边为___________. 13.在Rt ⊿ABC 中,90A ∠=o ,30C ∠=o ,2AB cm =,则BC = cm . 14.已知点(3,4)P -,(3,4)Q -,则线段PQ 的长为_____________.15.如果一个三角形的三条边长分别为5,12,13cm cm cm ,那么这个三角形的面积为_____________2cm .DCBA第3题图CBA'C第6题图 EDCBA第9题图HPDCBA 第10题图16.如图,以直角三角形三边向外作正方形,三个正方形的面积分别是1S 、2S 、3S ,且115S =,2136S =,则3S =_________.17.如图,90C D ∠=∠=︒,请你再添加一个条件: ,使ABC BAD ∆≅∆.18. 等腰三角形腰上的高是腰长的一半,那么它的顶角等于_______. 三、解答题:(本大题共4小题,第19,20题每题5分,第21,22题每题6分,满分22分)19. 如图,求作一点P ,使PC PD =,并且P 到AOB ∠两边的距离相等. 20. 如图,已知BD CD =,B C ∠=∠.求证:AB AC =.21. 已知直角坐标平面的两点分别为(3,3),(6,1)A B ,设点P 在y 轴上,且PA PB =,求点P 的坐标.S 3S 2S 1第16题图DCBA第17题图第19题图A CBD第20题图22.已知⊿ABC 的三个顶点分别是(2,0)A -、(2,4)B 、(6,0)C ,试判断⊿ABC 的形状.四、解答题:(本大题共4小题,第23、24题每题7分,第25、26题每题8分,满分30分)23. 如图,在△ABC 中,已知120C ∠=o ,边AC 的垂直平分线DE 与AC 、AB 分别交于点D 和点E .(1) 作出边AC 的垂直平分线DE ; (2) 当AE BC =时,求A ∠的度数.BCA第23题图24.已知:如图,在⊿ABC 中,D 是BC 边的中点,DE AB ⊥,DF AC ⊥,垂足分别是E 、F ,且BE CF =.求证:AD 平分BAC ∠.25. 在⊿ABC 中,60B ∠=o ,AD BC ⊥,垂足为D ,若3AD cm =,5AC cm =,求⊿ABC 的面积.26.已知:如图,在⊿ABC 中,90C ∠=o ,30B ∠=o ,6AC =,点D 、E 、F 分别在边BC 、AC 、AB 上(点E 、F 与⊿ABC 顶点不重合),AD 平分CAB ∠,EF AD ⊥,垂足为H .(1) 求证:AE AF =;(2) 设CE x =,BF y =,求y 与x 之间的函数解析式,并写出定义域; (3) 当⊿DEF 是直角三角形时,求出BF 的长.BACD第25题图F E DCBA第24题图第26题图C备用图一、选择题(本大题共6小题,每小题2分,满分12分) 1. D 2.B 3.C 4. D 5.C 6.C二、填空题(本大题共12小题,每小题3分,满分36分)7.两条边相等的三角形是等腰三角形 8.以点A 为圆心,9cm 为半径的圆9.14 10.5 11.70o 4 14.10 15.30 16.121 17.AD BC =,BD AC =,DBA CAB ∠=∠,CBA DAB ∠=∠四个答案任选一个 18.30o 或150o三、解答题(本大题共4小题,第19,20题每题5分,第21,22题每题6分,满分22分)19.作图略 (中垂线2分,角平分线2分,结论1分) 20.证明:联结BC . BD CD =Q DBC DCB ∴∠=∠.(2分)ABD ACD ∠=∠Q ABC ACD ∴∠=∠(2分).AB AC ∴=.(1分)21. 解:点P 在y 轴上,可设点P 的坐标为(0,)m , (1分)得PA ==(1分)PB == (两点距离公式).(1分)PA PB =Q (已知),22PA PB ∴=, 即 29(3)m +-=236(1)m +-.(1分)解得194m =-. (1分) ∴P 的坐标为19(0,)4-.(1分)22. 解:AB ==,(1分)8AC == , (1分)BC ==(两点距离公式). (1分) 得AB BC =. (1分)2264AB BC +=Q ,264AC = 222AB BC AC ∴+=.得90A ∠=o (勾股定理的逆定理). (1分)∴⊿ABC 是等腰直角三角形. (1分)四、解答题(本大题共4小题,第23、24题每题7分,第25、26题每题8分,满分30分)23. 证明:(1)作出垂直平分线DE .(2分)(2)联结CE . ∵DE 垂直平分AC ,∴CE AE = .(1分) ∵AE BC =,∴CE BC =.(1分)设A x ∠=,则ECA A x ∠=∠=.∴2B CEB x ∠=∠=.(1分) ∵180A B ACB ∠+∠+∠=o ,∴2120180x x ++=o o .(1分) ∴20x =o ,即20A ∠=o .(1分) 24.,DE AB DF AC ⊥⊥Q ,90BED CFD ∴∠=∠=o .(1分)D Q 是AB 的中点,BD CD ∴=.(1分)在Rt ⊿BDE 和Rt ⊿CDF 中,,,BD CD BE CF =⎧⎪⎨⎪=⎩∴Rt BDE Rt CDF ∆≅∆(HL ). (2分)DE DF ∴=.(1分),,DE DF DE AB DF AC =⊥⊥Q (已知),AD ∴平分BAC ∠(在一个角的内部且到角的两边距离相等的点,在这个角的角平分线上). (2分) 25. AD BC ⊥Q ,90ADB ∴∠=o .(1分)60B ∠=o Q ,30BAD ∴∠=o .(1分) 12BD AB ∴=.(1分) 设BD =x ,则2AB x =.90ADB ∠=o Q ,222AD BD AB ∴+=,(1分)求得BD =.(1分) 同理可得4DC =.(1分)4BC ∴=+.(1分) ABC S ∴V 6=(1分) 26 .(1)证明:∵EF AD ⊥,∴90AHE AHF ∠=∠=o .在△AHE 和△AHF 中,,,,EAH FAH AH AH AHE AHF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△AHE ≌△AHF (A.S.A ). (1分)∴AE AF =.(1分)(2)解:在△ABC 中,∵90C ∠=o ,30B ∠=o ,∴212AB AC ==. (1分) ∵6AF AE AC CE x ==-=-,∴6BF x =+,∴x y +=6.(1分) 函数定义域为60<<x . (1分)(3)解:∵AE AF =,EAD FAD ∠=∠,∴AD 垂直平分EF . ∴DE DF =.∵△DEF 是直角三角形,∴90EDF ∠=o .∴45ADF ∠=o .又∵1302BAD CAD CAB ∠=∠=∠=o ,∴75BFD FDA FAD ∠=∠+∠=o , ∴FDB BFD ∠=∠,∴BF BD =. (1分)设CD m =,则2AD m =, 32,6)2(222==-m m m .(1分)∵30DAB B ∠=∠=o ,BF BD AD ===(1分)赠送相关资料考试答题的技巧拿到试卷之后,可以总体上浏览一下,根据以前积累的考试经验,大致估计一下试卷中每部分应该分配的时间。
初中数学几何证明经典试题(含答案)

初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE ,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证.2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二)。
如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证.。
如下图做GH⊥AB,连接EO.由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
APCDBAFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM; (2)若∠BAC =600,求证:AH =AO .(初二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 A N FE CDMB · A HEOF2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C,AC 为圆的直径,PEF 为圆的割线,D .求证:AB =DC ,BC =AD .(初三)经典1、已知:△ABC是正三角形,P 是三角形内一点,PA =3,PB =4,PC 求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a,PB =2a ,PC =3a ,求正方形的边长.C BD A F PD E CB A APCBACPDA CBPD4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO.由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE ,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
(完整版)初二数学----几何证明初步经典练习题(含答案)

(完整版)初二数学----几何证明初步经典练习题(含答案)几何证明初步测验题(1)一、选择题(每空3 分,共36 分)1、使两个直角三角形全等的条件是()A、一组锐角对应相等B、两组锐角分别对应相等C、一组直角边对应相等D、两组直角边分别对应相等2、如图,已知AB∥CD,∠A=50°,∠C=∠E.则∠C =()A.20°B.25°C.30°D.40°第2题图第4题图第6题图第7题图3、用反证法证明命题“一个三角形中不能有两个角是直角”,应先假设这个三角形中()A.有两个角是直角B.有两个角是钝角C.有两个角是锐角D.一个角是钝角,一个角是直角4、如图,直线AB、CD相交于点O,∠BOE=90°,OF平分∠AOE,∠1=15°30’,则下列结论不正确的是( )A.∠2=45°B.∠1=∠3 C.∠AOD+∠1=180°D.∠EOD=75°30’5、下列说法中,正确的个数为()①三角形的三条高都在三角形内,且都相交于一点②三角形的中线都是过三角形的某一个顶点,且平分对边的直线③在△ABC中,若∠A=12∠B=13∠C,则△ABC是直角三角形④一个三角形的两边长分别是8和10,那么它的最短边的取值范围是2<b<18< p="">A.1个B.2个C.3个D.4个6、如图,在AB=AC的△ABC中,D是BC边上任意一点,DF⊥AC于F,E在AB边上,使ED ⊥BC于D,∠AED=155°,则∠EDF等于()A、50°B、65°C、70°D、75°7、如图,已知△ABC是等腰直角三角形,∠A=90°,BD是∠ABC 的平分线,DE⊥BC于E,若BC=10cm,则△DEC的周长为()A.8cm B.10cm C.12cm D.14cm8、如图,已知△ABC中,∠ABC=45°,AC=4,H是高AD和BE 的交点,则线段BH的长度为()A. B. C.5 D.49、如图,正方形ABCD内有两条相交线段MN、EF,M、N、E、F分别在边AB、CD、AD、BC 上.小明认为:若MN = EF,则MN⊥EF;小亮认为: 若MN⊥EF,则MN = EF.你认为()A.仅小明对B.仅小亮对C.两人都对D.两人都对第9题图第10题图第11题图第12题图10、如图,△ABC为等边三角形,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,?则四个结论正确的是().①点P在∠A的平分线上; ②AS=AR; ③QP∥AR; ④△BRP≌△QSP.A.全部正确; B.仅①和②正确; C.仅②③正确; D.仅①和③正确11、如图,△ABC中,CD⊥AB于D,一定能确定△ABC为直角三角形的条件的个数是()①∠1=∠②③∠+∠2=90°④=3:4:5 ⑤A.1 B.2 C.3 D.412、如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC 于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为()A.13B.12C.23D.不能确定二、填空题(每空3 分,共15 分)13、命题“对顶角相等”中的题设是_________ ,结论是___________ 。
初中数学几何证明经典题(含答案)
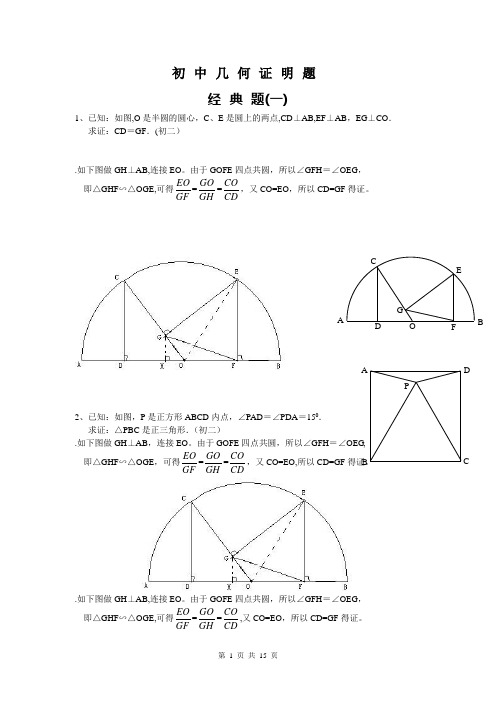
初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
.如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
APCDBAFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM; (2)若∠BAC =600,求证:AH =AO .(初二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 AN FE CDMB· A HEOF2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C,AC 为圆的直径,PEF 为圆的割线,AE 、证:AB =DC,BC =AD .(初三)经典1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a,PC =3a ,求正方形的边长.C BD A F PD E CB A APCBACPDA CBPD4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几何证明初步练习题编辑整理:临朐王老师1、三角形的角和定理:三角形的角和等于180°.推理过程:○1 作CM ∥AB ,则∠A= ,∠B= ,∵∠ACB +∠1+∠2=1800( ,∴∠A+∠B+∠ACB=1800. ○2 作MN ∥BC ,则∠2= ,∠3= ,∵∠1+∠2+∠3=1800,∴∠BAC+∠B+∠C=1800.2.求证:在一个三角形中,至少有一个角大于或者等于60°。
3、.如图,在△ABC 中,∠C >∠B,求证:AB >AC 。
4. 已知,如图,AE//DC ,∠A=∠C ,求证:∠1=∠B.5. 已知:如图,EF ∥AD ,∠1 =∠2. 求证:∠AGD +∠BAC = 180°.反证法经典例题6.求证:两条直线相交有且只有一个交点.7.如图,在平面,AB 是L 的斜线,CD 是L 的垂线。
求证:AB 与CD 必定相交。
8.2一.角平分线--轴对称9、已知在ΔABC 中,E为BC的中点,AD 平分BAC ∠,BD ⊥AD 于D .AB =9,AC=13求DE的长第9题图 第10题图 第11题图分析:延长BD交AC于F.可得ΔABD ≌ΔAFD .则BD =DF .又BE =EC ,即D E为ΔBCF 的中位线.∴DE=12FC=12(AC-AB)=2. 10、已知在ΔABC 中,108A ∠=,AB =AC ,BD 平分ABC ∠.求证:BC =AB +CD .分析:在BC上截取BE=BA,连接DE.可得ΔBAD ≌ΔBED .由已知可得:18ABD DBE ∠=∠=,108A BED ∠=∠=,36C ABC ∠=∠=.∴72DEC EDC ∠=∠=,∴CD =CE ,∴BC =AB +CD .11、如图,ΔABC 中,E是BC 边上的中点,DE ⊥BC 于E ,交BAC ∠的平分线AD 于D ,过D 作DM ⊥AB 于M,作DN ⊥AC 于N .求证:BM =CN .分析:连接DB 与DC .∵DE 垂直平分BC ,∴DB =DC .易证ΔAMD ≌ΔAND . ∴有DM =DN .∴ΔBMD ≌ΔCND (HL).∴BM =CN .二、旋转12、如图,已知在正方形ABCD 中,E在BC 上,F在DC 上,BE +DF C B A D E F D AB C B A E D N M B D A C=EF .求证:45EAF ∠=.分析:将ΔADF 绕A顺时针旋转90得ABG .∴GAB FAD ∠=∠.易证ΔAGE≌ΔAFE .∴ 1452FAE GAE FAG ∠=∠=∠=13、如图,点E 在ΔABC 外部,D 在边BC 上,DE 交AC 于F .若123∠=∠=∠,AC=AE.求证:ΔABC ≌ΔADE .分析:若ΔABC ≌ΔADE ,则ΔADE 可视为ΔABC 绕A逆时针旋转1∠所得.则有B ADE ∠=∠.∵12B ADE ∠+∠=∠+∠,且12∠=∠.∴B ADE ∠=∠.又∵13∠=∠.∴BAC DAE ∠=∠.再∵AC=AE.∴ΔABC ≌ΔADE .14、如图,点E为正方形ABCD的边CD上一点,点F为CB的延长线上的一点,且EA⊥AF.求证:DE=BF.分析:将ΔABF视为ΔADE 绕A顺时针旋转90即可. ∵90FAB BAE EAD BAE ∠+∠=∠+∠=.∴FBA EDA ∠=∠. 又∵90FBA EDA ∠=∠=,AB=AD.∴ΔABF ≌ΔADE .(ASA)∴DE=DF.平移第14题图 第15题图 第16题图 第17题图三、平移15、如图,在梯形ABCD 中,BD ⊥AC ,AC =8,BD =15.求梯形ABCD 的中位线长.分析:延长DC到E使得CE=AB.连接BE.可得ACEB .可视为将AC平移到BE.AB平移到CE.由勾股定理可得DE=17.∴梯形ABCD中位线长为8.5.16、已知在ΔABC 中,AB =AC ,D 为AB 上一点,E为AC 延长线一点,且BD =CE .求证:DM =EM 分析:作DF∥AC交BC于F.易证DF=BD=CE.则DF可视为CE平移所得.∴四边形DCEF为DCEF .∴DM=EM.线段中点的常见技巧 --倍长四、倍长17、已知,AD为ABC 的中线.求证:AB+AC>2AD.分析:延长AD到E使得AE=2AD.连接BE易证ΔBDE ≌ΔCDA .∴BE=AC.∴AB+AC>2AD.E18、如图,AD 为ΔABC 的角平分线且BD =CD .求证:AB =AC .分析:延长AD到E使得AD=ED.易证ΔABD ≌ΔECD .∴EC=AB.∵BAD CAD ∠=∠.∴E CAD ∠=∠.∴AC=EC=AB.19、已知在等边三角形ABC中,D和E分别为BC与AC上的点,且AE=CD.连接AD与BE交于点P,作BQ⊥AD于Q.求证:BP=2PQ.分析:延长PD到F使得FQ=PQ.在等边三角形ABC中AB=BC=AC,60ABD C ∠=∠=.又∵AE=CD,∴BD=CE.∴ΔABD ≌ΔBCE . ∴CBE BAD ∠=∠.∴60BPQ PBA PAB PBA DBP ∠=∠+∠=∠+∠=.易证ΔBPQ ≌ΔBFQ .得BP=BF,又60BPD ∠=.∴ΔBPF 为等边三角形.∴BP=2PQ.中位线五、中位线、中线:20、已知在梯形ABCD 中,AD ∥BC ,E和F分别为BD 与AC 的中点, 求证:1()2EF BC AD =-. 分析:取DC中点G,连接EG与FG.则EG为ΔBCD 中位线,FG为ΔACD 的中位线. ∴EG∥=12BC ,FG ∥=12AD .∵AD ∥BC .∴过一点G有且只有一条直线平行于已知直线BC,即E、F、G共线.∴1()2EF BC AD =-.直角三角形斜边上的中线等于斜边的一半21、已知,在ABCD 中BD AB 21=.E为OA的中点,F为OD中点,G为BC中点. 求证:EF=EG.分析:连接BE .∵BD AB 21=,AE=O E.∴BE⊥CE,∵BG=CG. ∴BD EG 21=.又EF为ΔAOD 的中位线.∴AD EF 21=.∴EF=EG. 22、在ΔABC 中,AD是高,CE是中线,DC=BE,DG⊥CE于G.求证:(1)CG=EG.(2)2B BCE ∠=∠.分析:(1)连接DE.则有DE=BE=DC.∴Rt ΔCDG ≌Rt ΔEDG (HL).∴EG=CG. ∵DE=BE.∴B BDE DEC BCE ∠=∠=∠+∠.∵DE=CD.∴DEC BCE ∠=∠.∴2B BCE ∠=∠.几何证明初步测验题(1) 一、选择题(每空3 分,共36 分)1、使两个直角三角形全等的条件是( ) A 、一组锐角对应相等 B 、两组锐角分别对应相等C 、一组直角边对应相等D 、两组直角边分别对应相等2、如图,已知AB ∥CD ,∠A =50°,∠C =∠E .则∠C =( )A.20°B.25°C.30°D.40°第2题图第4题图第6题图第7题图3、用反证法证明命题“一个三角形中不能有两个角是直角”,应先假设这个三角形中()A.有两个角是直角B.有两个角是钝角C.有两个角是锐角D.一个角是钝角,一个角是直角4、如图,直线AB、CD相交于点O,∠BOE=90°,OF平分∠AOE,∠1=15°30’,则下列结论不正确的是( )A.∠2=45°B.∠1=∠3 C.∠AOD+∠1=180°D.∠EOD=75°30’5、下列说法中,正确的个数为()①三角形的三条高都在三角形,且都相交于一点②三角形的中线都是过三角形的某一个顶点,且平分对边的直线③在△ABC中,若∠A=12∠B=13∠C,则△ABC是直角三角形④一个三角形的两边长分别是8和10,那么它的最短边的取值围是2<b<18A.1个B.2个C.3个D.4个6、如图,在AB=AC的△ABC中,D是BC边上任意一点,DF⊥AC于F,E在AB边上,使ED ⊥BC于D,∠AED=155°,则∠EDF等于()A、50°B、65°C、70°D、75°7、如图,已知△ABC是等腰直角三角形,∠A=90°,BD是∠ABC的平分线,DE⊥BC于E,若BC=10cm,则△DEC的周长为()A.8cm B.10cm C.12cm D.14cm8、如图,已知△ABC中,∠ABC=45°,AC=4,H是高AD和BE的交点,则线段BH的长度为()A. B. C.5 D.49、如图,正方形ABCD有两条相交线段MN、EF,M、N、E、F分别在边AB、CD、AD、BC上.小明认为:若MN = EF,则MN⊥EF;小亮认为: 若MN⊥EF,则MN = EF.你认为()A.仅小明对B.仅小亮对C.两人都对D.两人都对第9题图第10题图第11题图第12题图10、如图,△ABC为等边三角形,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,•则四个结论正确的是().①点P在∠A的平分线上; ②AS=AR; ③QP∥AR; ④△BRP≌△QSP.A.全部正确; B.仅①和②正确; C.仅②③正确; D.仅①和③正确11、如图,△ABC中,CD⊥AB于D,一定能确定△ABC为直角三角形的条件的个数是()①∠1=∠②③∠+∠2=90°④=3:4:5 ⑤A.1 B.2 C.3 D.412、如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为()A.13B.12C.23D.不能确定二、填空题(每空3 分,共15 分)13、命题“对顶角相等”中的题设是_________ ,结论是___________ 。
14、请写出“等腰三角形的两个底角相等”的逆命题:15、如图,已知∠1=∠2,请你添加一个条件:___________,使△ABD≌△ACD。
16、对于同一平面的三条直线、、,给出下列五个论断:①∥;②∥;③⊥;④∥;⑤⊥.以其中两个论断为条件,一个论断为结论,组成一个你认为正确的命题:_____.17、如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.恒成立的结论有______________(把你认为正确的序号都填上).三、计算、简答题18、已知:如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,E、F分别为垂足.求证:AD垂直平分EF.19、如图7,已知A、B、C在一条直线上,分别以AB、BC为边在AC同侧作等边三角形ABD 和等边三角形BCE,AE交BD于点F,DC交BE于点G。
