初二几何证明经典难题.

合集下载

初二几何证明高难度题目

初二几何证明高难度题目题目描述给定一个三角形ABC，其中AB = AC，角BAC = 90°。

点D 是BC边上的一个点，使得角ADC = 90°。

点E是AC边上的一个点，使得AE = AD。

证明：角BCE = 45°。

证明过程我们可以通过以下步骤来证明角BCE = 45°：1.连接BE和CD两条线段。

2.由题目给定，AC = AB，所以ACB是一个等腰直角三角形。

3.角ADC = 90°，所以ADC是一个直角三角形。

4.由于AE = AD，所以AE也等于AC，即AE = AC。

5.角EAC = 角CAE，因为AE = AC。

6.角EAC + 角CAE + 角AEC = 180°，根据三角形内角和定理。

7.角EAC + 角CAE + 90° = 180°，因为ACB是一个直角三角形。

8.角EAC + 角CAE = 90°。

9.角BEC = 角EAC + 角CAE，根据相邻角的性质。

10.角BEC = 90°，根据步骤8.11.角CBE = 180° - 角BEC - 角BCE = 180° - 90° - 角BCE。

12.角CBE = 90° - 角BCE。

13.角CBE = 角BCE，因为CBE = 45°。

14.90° - 角BCE = 角BCE，根据步骤13.15.角BCE = 45°。

结论通过以上证明过程可以得出结论：在给定的三角形ABC中，当点D是BC边上的一个点，使得角ADC = 90°，点E是AC边上的一个点，使得AE = AD时，角BCE = 45°。

初二几何证明挑战难题

初二几何证明挑战难题引言初二几何证明是中学数学的重要内容之一，是培养学生逻辑思维能力和推理能力的关键环节。

然而，有些几何证明问题对于学生来说是具有一定难度的，需要一些挑战性的问题来激发学生的研究兴趣和思考能力。

本文将介绍一些初二几何证明的挑战难题，旨在帮助学生提升自己的证明能力。

难题1：平行线性质证明题目描述给定平行线l1和l2，证明两个平行线的截线与这两条平行线的交点共线。

证明思路1.根据平行线的定义，我们知道两条平行线的截线是平行的。

2.假设截线AB与平行线l1和l2的交点分别为C和D。

3.通过截线AB，可以构造三角形ACD。

4.观察三角形ACD，可以发现AC和AD与平行线l1和l2平行。

5.根据平行线的性质，可以得出AC和AD平行。

6.根据平行线的性质，如果两条线分别与另外一条直线平行，那么这两条线也是平行的。

7.因此，AC和AD是平行的。

8.综上所述，截线AB与平行线l1和l2的交点共线。

难题2：等腰三角形性质证明题目描述给定等腰三角形ABC，证明等腰三角形的顶角的平分线与底边中点重合。

证明思路1.根据等腰三角形的定义，我们知道等腰三角形的两个底角相等。

2.设顶角A的平分线与底边BC的交点为D。

3.因为顶角A的平分线，所以∠BAD=∠CAD。

4.此外，因为等腰三角形ABC，所以∠BAC=∠ABC。

5.根据三角形内角和等于180度的性质，我们可以得知∠BAC+∠ABC+∠ACB=180度。

6.由于∠___∠ABC，所以∠BAC+∠BAC+∠ACB=180度。

7.综上所述，2∠BAC+∠ACB=180度。

8.因为∠BAC=∠CAD，所以2∠CAD+∠ACB=180度。

9.再考虑三角形ACD，我们可以得出∠CAD+∠CAD+∠ACD=180度。

10.综上所述，2∠CAD+∠ACD=180度。

11.由于2∠CAD+∠ACD=2∠CAD+∠ACB，所以2∠BAC+∠ACB=2∠CAD+∠___。

12.可以推导出∠BAC=∠CAD，即顶角A的平分线与底边BC 的交点D重合。

初二数学平面几何经典难题

初二数学平面几何经典难题
以下是初二数学平面几何的一些经典难题：
1. 直角三角形中的勾股定理：在一个直角三角形中，直角边的平方和等于斜边的平方。

这是勾股定理的基本形式，但是有许多变种和证明方法。

2. 三角形中的角度和定理：一个三角形的三个内角之和等于180度。

这个定理有许多证明方法和应用，例如在几何作图和计算面积时。

3. 平行线的性质和判定：平行线在几何中非常重要，因为它们有一些特殊的性质，例如同位角相等、内错角相等、同旁内角互补等。

同时，也有一些判定平行线的方法，例如同位角相等、内错角相等、同旁内角互补等。

4. 圆中的基本定理：圆中的基本定理包括圆心角定理、圆周角定理、弦心距定理等。

这些定理是圆的基础，并且对于解决关于圆的问题非常重要。

5. 立体几何初步：立体几何是平面几何的扩展，它研究三维空间中的图形和几何体。

立体几何有许多经典问题，例如计算几何体的表面积和体积、证明空间中的角度和距离等。

以上难题仅供参考，建议查阅数学教辅或资料书获取更多经典难题。

源于经典而高于经典的初二几何难题解答概要

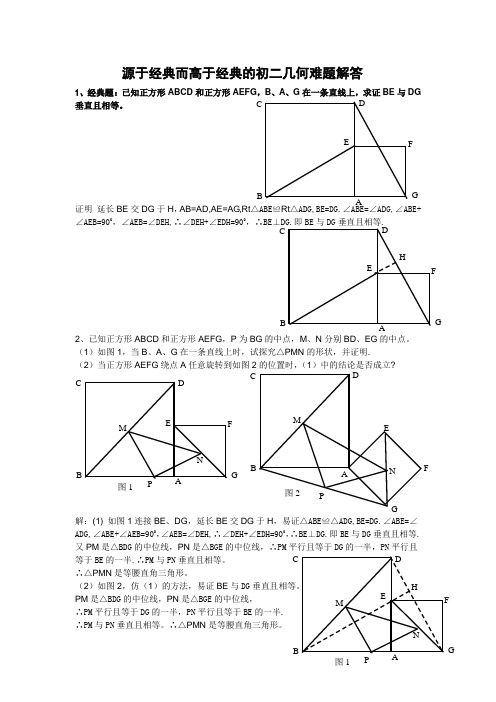
源于经典而高于经典的初二几何难题解答1、经典题：已知正方形ABCD 和正方形AEFG ，B 、A 、G 在一条直线上，求证BE 与DG垂直且相等。

证明延长BE 交DG 于H ，AB=AD,AE=AG,Rt △ABE ≌Rt △ADG,BE=DG.∠ABE=∠ADG,∠ABE+∠AEB=900，∠AEB=∠DEH,∴∠DEH+∠EDH=900，∴BE ⊥DG.即BE 与DG 垂直且相等.2、已知正方形ABCD 和正方形AEFG ，P 为BG 的中点，M 、N 分别BD 、EG 的中点。

（1）如图1，当B 、A 、G 在一条直线上时，试探究△PMN 的形状，并证明. （2）当正方形AEFG 绕点A 任意旋转到如图2的位置时，（1）中的结论是否成立?解：(1) 如图1连接BE 、DG ，延长BE 交DG 于H ，易证△ABE ≌△ADG,BE=DG.∠ABE=∠ADG,∠ABE+∠AEB=900，∠AEB=∠DEH,∴∠DEH+∠EDH=900，∴BE ⊥DG.即BE 与DG 垂直且相等. 又PM 是△BDG 的中位线，PN 是△BGE 的中位线，∴PM 平行且等于DG 的一半，PN 平行且等于BE 的一半.∴PM 与PN 垂直且相等。

∴△PMN 是等腰直角三角形。

（2）如图2，仿（1）的方法，易证BE 与DG 垂直且相等。

PM 是△BDG 的中位线，PN 是△BGE 的中位线，∴PM 平行且等于DG 的一半，PN 平行且等于BE 的一半. ∴PM 与PN 垂直且相等。

∴△PMN 是等腰直角三角形。

N图1 D M E CPBA F G P 图2 A D M E N CB F G图1HD MEC PBAFGND E C B AF G H D E C B AF G说明：本题的第（2）小题也可看成以△ABG 边AB 、AG 向外作正方形ABCD 和正方形AEFG 。

可得以上结论。

3、分别以任意四边形ABCD 的各边向外作正方形ABEF 、AGHD 、DIJC 、CKLB 。

【几何突破】初二证明难题汇总详细解析

【几何突破】初二证明难题汇总详细解析成才路上特级教师与奥数国家一级教练联手执教。

1、证明线段相等或角相等两条线段或两个角相等是平面几何证明中最基本也是最重要的一种相等关系。

很多其它问题最后都可化归为此类问题来证。

证明两条线段或两角相等最常用的方法是利用全等三角形的性质，其它如线段中垂线的性质、角平分线的性质、等腰三角形的判定与性质等也经常用到。

说明：利用三角形全等证明线段求角相等。

常须添辅助线，制造全等三角形，这时应注意：（1）制造的全等三角形应分别包括求证中一量；（2）添辅助线能够直接得到的两个全等三角形。

说明：当一个三角形中出现角平分线、中线或高线重合时，则此三角形必为等腰三角形。

我们也可以理解成把一个直角三角形沿一条直角边翻折（轴对称）而成一个等腰三角形。

说明：有等腰三角形条件时，作底边上的高，或作底边上中线，或作顶角平分线是常用辅助线。

证明二：如图5所示，延长ED到M，使DM＝ED，连结FE，FM，BM说明：证明两直线垂直的方法如下：（1）首先分析条件，观察能否用提供垂直的定理得到，包括添常用辅助线，见本题证二。

（2）找到待证三直线所组成的三角形，证明其中两个锐角互余。

（3）证明二直线的夹角等于90°。

2. 分析：本题从已知和图形上看好象比较简单，但一时又不知如何下手，那么在证明一条线段等于两条线段之和时，我们经常采用“截长补短”的手法。

“截长”即将长的线段截成两部分，证明这两部分分别和两条短线段相等；“补短”即将一条短线段延长出另一条短线段之长，证明其和等于长的线段。

来源网络，尊重原创，如侵权则删。

本学期全部原创文章：八上第25讲十题突破八上代数重难点八上第24讲十题突破八上几何重难点八上第23讲一次函数利润，方案类问题大汇总八上第22讲一次函数行程类问题大汇总八上第21讲《一次函数》必考知识点(下)八上第20讲《一次函数》必考知识点(中)八上第19讲《函数、一次函数》必考知识点(上)八上第18讲《直角坐标系》典题大集合(下)八上第17讲《直角坐标系》典题大集合(上)八上第16讲《平面直角坐标系》全章知识点融合八上第15讲《实数近似数》必考知识点汇总八上14讲《平方根算术平方根立方根》典型易错辨析八上第13讲 4大类，9小题突破期中冲刺难点八上12讲《勾股定理》解题方法(下)——从立体到平面八上11讲《勾股定理》解题方法汇总(上)八上第10讲等腰三角形，你都掌握了吗？(下) 模型篇【期中特辑】八上考前冲刺易错题大汇总！八上第9讲等腰三角形，你都掌握了吗？(中) 方法篇八上第8讲等腰三角形，你都掌握了吗？(上)八上第7讲你必须学会的《线段、角的轴对称性》书写格式！八上第6讲你真的弄懂轴对称了吗？八上第5讲再谈全等辅助线—截长补短&半角八上第4讲全等动点问题&再谈倍长中线八上第3讲“一线三等角”型全等都在这了！八上第2讲 SAS、 ASA 、AAS 型全等典型易错分析八上第1讲怎样分割全等图形&再谈图形变化中的“对应”如何关注QQ端：将本文直接分享到微信好友聊天页面，点击蓝字即可关注．点击最右下留言，期待您的宝贵意见！您的分享和转发，是对我最大的支持！如能在文中GG位轻点一次，或者为文章点一次在看！不仅对我是莫大的鼓励，更是我长期更新的动力！最后附上成为尊贵星标用户的方法，你再也不会担心错过消息啦！笔者主编的《领跑数学二轮专题复习》，新版年后上市，敬请期待．。

初二几何经典难题集锦(含答案)

初二几何经典训练题1、如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=2DC,对角线AC⊥BD,垂足为F,过点F作EF∥AB,交AD于点E,CF=4cm.⑴求证：四边形ABFE是等腰梯形;⑵求AE的长.2、如图，矩形ABCD的对角线AC、BD相交于点O，E、F分别是OA、OB的中点．（1）求证：△ADE≌△BCF；（2）若AD=4cm，AB=8cm，求CF和OF的长。

3、如图，已知直角梯形ABCD中，AD∥BC，∠B=90°，AB=12cm，BC=8cm，DC=13cm，动点P沿A→D→C线路以2cm/秒的速度向C运动，动点Q沿B→C线路以1cm/秒的速度向C运动．P、Q两点分别从A、B同时出发，当其中一点到达C点时，另一点也随之停止．设运动时间为t秒，△PQB的面积为ycm2．（1）求A D的长及t的取值范围；（2）当1.5≤t≤t0（t0为（1）中t的最大值）时，求y关于t的函数关系式；（3）请具体描述：在动点P、Q的运动过程中，△PQB的面积随着t的变化而变化的规律。

4、如图,AB与CD相交于E,AE=EB,CE=ED,D为线段FB的中点,GF与AB相交于点G,若CF=15cm,求GF 之长。

5、如图所示，在平行四边形ABCD中，过点B作BE⊥CD，垂足为E，连接AE，F为AE上的一点，且∠BFE =∠C。

（1）求证：△ABF∽△EAD；（2）若AB=4，∠BAE=30°，求AE的长；（3）在（1）、（2）的条件下，若AD=3，求BF的长（计算结果可含根号）。

6、如图是一个常见铁夹的侧面示意图，OA，OB表示铁夹的两个面，C是轴，CD⊥OA于点D，已知DA ＝15mm，DO＝24mm，DC＝10mm，我们知道铁夹的侧面是轴对称图形，请求出A、B两点间的距离。

7、如图，用三个全等的菱形ABGH、BCFG、CDEF拼成平行四边形ADEH，连接AE与BG、CF分别交于P、Q，（1）若AB=6，求线段BP的长；（2）观察图形，是否有三角形与△ACQ全等？并证明你的结论．8、如图已知点E、F在△ABC的边AB所在的直线上，且AE=BF，FH∥FG∥AC，FH、EG分别交边BC所在的直线于点H、G。

(完整版)初中几何证明题五大经典(含答案)

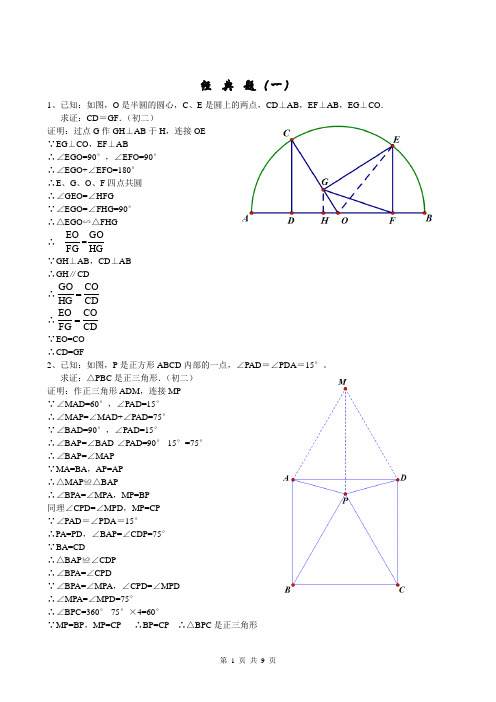
经典题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．（初二）证明：过点G 作GH ⊥AB 于H ，连接OE ∵EG ⊥CO ，EF ⊥AB∴∠EGO=90°，∠EFO=90° ∴∠EGO+∠EFO=180° ∴E 、G 、O 、F 四点共圆 ∴∠GEO=∠HFG∵∠EGO=∠FHG=90° ∴△EGO ∽△FHG ∴FG EO =HGGO∵GH ⊥AB ，CD ⊥AB ∴GH ∥CD∴CD COHG GO =∴CDCO FG EO = ∵EO=CO ∴CD=GF2、已知：如图，P 是正方形ABCD 内部的一点，∠PAD ＝∠PDA ＝15°。

求证：△PBC 是正三角形．（初二）证明：作正三角形ADM ，连接MP ∵∠MAD=60°，∠PAD=15° ∴∠MAP=∠MAD+∠PAD=75° ∵∠BAD=90°，∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75° ∴∠BAP=∠MAP ∵MA=BA ，AP=AP ∴△MAP ≌△BAP∴∠BPA=∠MPA ，MP=BP 同理∠CPD=∠MPD ，MP=CP ∵∠PAD ＝∠PDA ＝15°∴PA=PD ，∠BAP=∠CDP=75° ∵BA=CD∴△BAP ≌∠CDP ∴∠BPA=∠CPD∵∠BPA=∠MPA ，∠CPD=∠MPD ∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP ，MP=CP ∴BP=CP ∴△BPC 是正三角形3、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC 的延长线交MN于E 、F ．求证：∠DEN ＝∠F ．证明:连接AC ，取AC 的中点G ,连接NG 、MG ∵CN=DN ，CG=DG ∴GN ∥AD ，GN=21AD ∴∠DEN=∠GNM ∵AM=BM ，AG=CG ∴GM ∥BC ，GM=21BC ∴∠F=∠GMN ∵AD=BC ∴GN=GM∴∠GMN=∠GNM ∴∠DEN=∠F经典题（二）1、已知：△ABC 中，H 为垂心（各边高线的交点），O 为外心，且OM ⊥BC 于M ．（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）证明：（1）延长AD 交圆于F ，连接BF ，过点O 作OG ⊥AD 于G ∵OG ⊥AF ∴AG=FG ∵AB⌒ =AB ⌒ ∴∠F=∠ACB又AD ⊥BC ，BE ⊥AC ∴∠BHD+∠DBH=90° ∠ACB+∠DBH=90° ∴∠ACB=∠BHD ∴∠F=∠BHD∴BH=BF 又AD ⊥BC ∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2（GH+DH ）=2GD 又AD ⊥BC ，OM ⊥BC ，OG ⊥AD ∴四边形OMDG 是矩形 ∴OM=GD ∴AH=2OM （2）连接OB 、OC∵∠BAC=60∴∠BOC=120° ∵OB=OC ，OM ⊥BC ∴∠BOM=21∠BOC=60°∴∠OBM=30° ∴BO=2OM由（1）知AH=2OM ∴AH=BO=AO2、设MN 是圆O 外一条直线，过O 作OA ⊥MN 于A ，自A 引圆的两条割线交圆O 于B 、C 及D 、E ，连接CD 并延长交MN 于Q ，连接EB 并延长交MN 于P. 求证：AP ＝AQ ．证明：作点E 关于AG 的对称点F ，连接AF 、CF 、QF ∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF 即∠PAE=∠QAF∵E 、F 、C 、D 四点共圆 ∴∠AEF+∠FCQ=180° ∵EF ⊥AG ，PQ ⊥AG ∴EF ∥PQ∴∠PAF=∠AFE ∵AF=AE∴∠AFE=∠AEF ∴∠AEF=∠PAF ∵∠PAF+∠QAF=180° ∴∠FCQ=∠QAF ∴F 、C 、A 、Q 四点共圆 ∴∠AFQ=∠ACQ 又∠AEP=∠ACQ ∴∠AFQ=∠AEP3、设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）证明：作OF ⊥CD 于F ，OG ⊥BE 于G ，连接OP 、OQ 、OA 、AF 、AG ∵C 、D 、B 、E 四点共圆 ∴∠B=∠D ，∠E=∠C ∴△ABE ∽△ADC ∴DFBGFD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF ∴∠AGB=∠AFD ∴∠AGE=∠AFC ∵AM=AN ， ∴OA ⊥MN 又OG ⊥BE ，∴∠OAQ+∠OGQ=180° ∴O 、A 、Q 、E 四点共圆 ∴∠AOQ=∠AGE 同理∠AOP=∠AFC ∴∠AOQ=∠AOP又∠OAQ=∠OAP=90°，OA=OA ∴△OAQ ≌△OAP ∴AP=AQ 在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQ4、如图,分别以△ABC 的AB 和AC 为一边,在△ABC 的外侧作正方形ABFG 和正方形ACDE ，点O 是DF 的中点，OP ⊥BC求证：BC=2OP （初二）证明：分别过F 、A 、D 作直线BC 的垂线，垂足分别是L 、M 、N ∵OF=OD ，DN ∥OP ∥FL ∴PN=PL∴OP 是梯形DFLN 的中位线 ∴DN+FL=2OP ∵ABFG 是正方形∴∠ABM+∠FBL=90° 又∠BFL+∠FBL=90° ∴∠ABM=∠BFL又∠FLB=∠BMA=90°，BF=AB ∴△BFL ≌△ABM ∴FL=BM同理△AMC ≌△CND ∴CM=DN∴BM+CN=FL+DN ∴BC=FL+DN=2OP经典题（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）证明：连接BD 交AC 于O 。

很难证明的几何题

很难证明的几何题一、那些让人头疼的几何题。

几何题啊，真的是像一个个小怪兽，有些时候特别难搞定。

就像那种证明三角形全等或者相似的题目，条件给得模模糊糊的，你得像个侦探一样在图里找线索。

比如说有一道题，给了一个三角形，里面几条线段交叉着，然后告诉你一些线段的长度关系，让你证明这个三角形和另一个三角形相似。

那图看起来就像一团乱麻，你得先把那些线段关系捋清楚。

有时候呢，是角度的问题。

那些角度隐藏在图形的各个角落，就像调皮的小精灵，你得把它们一个个找出来。

像在多边形里，求某个内角的度数，又要用到内角和公式，又要找互补角、对顶角之类的关系，一个不小心就会掉进陷阱里。

我记得有一次考试，有个几何题是关于四边形的，它的对角线把四边形分成了好几个三角形，然后要根据这些三角形的角度关系来证明四边形的一些性质。

我当时看着那图，眼睛都花了，那些角度感觉就像在跟我捉迷藏一样。

二、圆相关的证明题——弯弯绕绕的难题。

圆的几何题也是难搞的主儿。

圆里面的切线、割线、圆周角、圆心角这些概念，单独看都还好，一旦放在一道题里，就变得超级复杂。

比如说要证明一条直线是圆的切线，你得想办法证明这条直线和圆只有一个交点，或者证明这条直线垂直于过切点的半径。

这就需要你在图里找到各种隐藏的直角三角形，利用勾股定理或者三角形的相似性来证明垂直关系。

还有那种关于圆内接四边形的题目，什么对角互补啦，外角等于内对角啦。

这些性质要在证明题里灵活运用，真的不容易。

我有个同学，他在做一道圆内接四边形的证明题时，被那些角的关系绕晕了。

他说感觉自己就像走进了一个迷宫，在那些角之间转来转去，怎么也找不到出口。

三、立体几何——从平面到空间的挑战。

立体几何就更上一层楼了，难度直接升级。

从平面图形到立体图形，多了一个维度，我们的脑袋有时候就转不过来这个弯儿。

像证明两个立体图形之间的关系，比如证明一个三棱柱和一个四棱锥的某些面平行或者垂直。

你得先把立体图形拆分成平面图形来看，找到那些关键的平面，然后再用平面几何的知识去证明。

初中数学几何证明经典试题(含答案)

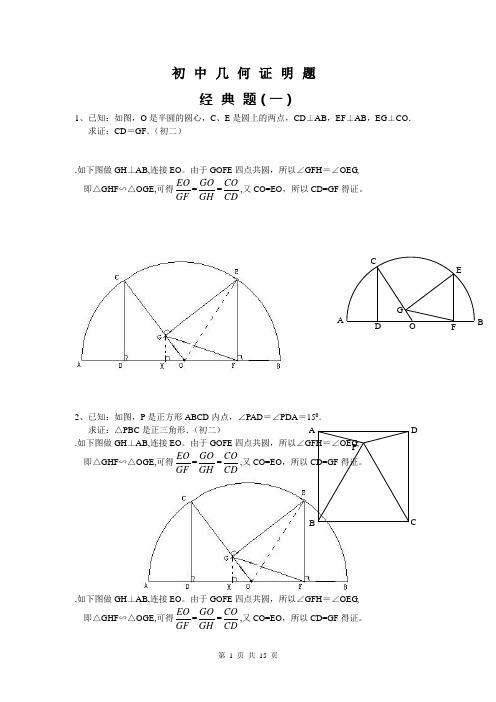
初中几何证明题经典题（一）1、已知：如图，O是半圆的圆心，C、E是圆上的两点，CD⊥AB，EF⊥AB，EG⊥CO．求证：CD＝GF．（初二）.如下图做GH⊥AB,连接EO。

由于GOFE四点共圆，所以∠GFH＝∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO，所以CD=GF得证。

2、已知：如图，P是正方形ABCD内点，∠PAD＝∠PDA＝150．求证：△PBC是正三角形．（初二）.如下图做GH⊥AB,连接EO。

由于GOFE四点共圆，所以∠GFH＝∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO，所以CD=GF得证。

.如下图做GH⊥AB,连接EO。

由于GOFE四点共圆，所以∠GFH＝∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO，所以CD=GF得证。

APCDBAFGCEBOD3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．经典题（二）1、已知：△ABC 中，H 为垂心（各边高线的交点），O 为外心，且OM ⊥BC 于M ．（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 A N FE CDMB · A HEOF2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 引圆的两条直线，交圆于B 、C 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．经典题（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边求证：PA ＝PF ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PEFB 、D ．求证：AB ＝DC ，BC ＝AD．（初三）经典1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）3、设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）经典难题（五）1、设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．2、已知：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．C BD A F PD E CB A APCBACPDA CBPD4、如图，△ABC中，∠ABC＝∠ACB＝800，D、E分别是AB、AC上的点，∠DCA＝300，∠EBA＝200，求∠BED的度数．经典题（一）1.如下图做GH⊥AB,连接EO。

八年级几何难题精选(含解析)

经典难题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．（初二）2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．（初二）APCDB AFGCEBOD3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 的中点，AD BC的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．经典难题（二）D 2 C 2B 2A 2 D 1C 1B 1CBDA A 1ANFECDMB1、已知：△ABC 中，H 为垂心（各边高线的交点），O 为外心，且OM ⊥BC 于M ．（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 引圆的两条直线，交圆于B C 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）· ADHE M CBO· GA O DB ECQP NMP C GFBQADE 3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE 分别交于P 、Q ．求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．（初二）经典难题（三）· O QPB DECNM · A1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边BC 上的任一点，PF ⊥AP ，CF 平分∠DCE ．AFDECBEDACBF求证：PA ＝PF ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PO 相交于B 、D ．求证：AB ＝DC ，BC ＝AD ．（初三）经典难题（四）1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC ＝5．FEP C BA OD BFAECP求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）3、设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）APCBP A DCBCBDA4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）经典难题（五）1、设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．FP DE CBAAP2、已知：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．A CBPDA CBPD4、如图，△ABC 中，∠ABC ＝∠ACB ＝800，D 、E 分别是AB 、AC上的点，∠DCA ＝300，∠EBA ＝200，求∠BED 的度数．经典难题（一）1.如下图做GH ⊥AB,连接EO 。

初二几何证明经典难题

初二几何证明经典难题1、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．如下图做△DGC 使与△ADP 全等，可得△PDG 为等边△，从而可得 △DGC ≌△APD ≌△CGP,得出PC=AD=DC,和∠DCG=∠PCG ＝150 所以∠DCP=300 ，从而得出△PBC 是正三角形2、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．如下图连接AC 并取其中点Q ，连接QN 和QM ，所以可得∠QMF=∠F ，∠QNM=∠DEN 和∠QMN=∠QNM ，从而得出∠DEN ＝∠F 。

A PCDB AN FE CDMBPCGFBQADE3、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．3.过E,C,F 点分别作AB 所在直线的高EG ，CI ，FH 。

可得PQ=2EG FH+。

由△EGA ≌△AIC ，可得EG=AI ，由△BFH ≌△CBI，可得FH=BI 。

从而可得PQ=2AI BI += 2AB，从而得证。

4、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．顺时针旋转△ADE ，到△ABG ，连接CG . 由于∠ABG=∠ADE=900+450=1350从而可得B ，G ，D 在一条直线上，可得△AGB ≌△CGB 。

推出AE=AG=AC=GC ，可得△AGC 为等边三角形。

∠AGB=300，既得∠EAC=300，从而可得∠A EC=750。

又∠EFC=∠DFA=450+300=750. 可证：CE=CF 。

5、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．连接BD 作CH ⊥DE ，可得四边形CGDH 是正方形。

初二几何证明经典难题研究

初二几何证明经典难题研究初二几何证明经典难题是学生在几何学研究中经常遇到的挑战。

这些问题不仅能够帮助学生提高几何证明的能力，而且能够培养他们的逻辑思维和问题解决能力。

下面将介绍几个常见的初二几何证明经典难题及其解决方法：1. 两角和（角和角差）公式的证明两角和（角和角差）公式是初二阶段研究几何证明的重点之一。

通过证明这个公式，学生能够加深对角度和角差概念的理解，并且掌握角的基本运算规则。

证明过程如下：假设角A和角B的大小分别为x和y，则角A和B的和的大小为x+y。

然后，将角A和角B的大小用角度的定义表示出来，例如，角A和角B的和的大小可以表示为：x+y = （180 - α） + （180 - β）接下来，根据角度和的定义和等式性质，将相同的项合并并进行简化：x+y = 360 -（α+β）最后，根据等式性质将角度和的结果重新表示为角度的定义：x+y = （180 - α） + （180 - β） = 360 -（α+β）因此，两角和（角和角差）公式得到证明。

2. 相似三角形的证明相似三角形是初二几何研究中的另一个重要概念。

证明相似三角形的过程可以帮助学生理解相似三角形的性质和判断两个三角形是否相似的方法。

证明过程如下：假设有两个三角形ABC和DEF，且它们的对应角度相等，即∠A = ∠D，∠B = ∠E，∠C = ∠F。

我们需要证明这两个三角形相似。

首先，根据角度的定义，将∠A、∠D、∠B、∠E、∠C和∠F 表示为对应角度的定义：∠A = ∠D = α∠B = ∠E = β∠C = ∠F = γ接下来，根据相等角的性质，将三角形ABC和DEF的对应边等式表示为：AB/DE = BC/EF = AC/DF最后，根据等式性质和相似三角形的定义，可以得出结论：三角形ABC和DEF是相似的。

3. 三角形内角和公式的证明三角形内角和公式是初二几何研究的基本知识之一。

通过证明这个公式，学生可以更好地理解三角形内角和的性质和计算方法。

初中数学经典几何难题及答案

经典难题（一）之蔡仲巾千创作1、已知：如图, O 是半圆的圆心, C 、E 是圆上的两点, CD ⊥AB, EF ⊥AB, EG ⊥CO ．求证：CD ＝GF ．（初二）第1题图第2题图2、已知：如图, P 是正方形ABCD 内点, ∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．（初二）3、如图, 已知四边形ABCD 、A 1B 1C 1D 1都是正方形, A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）第3题图第4题图4、已知：如图, 在四边形ABCD 中, AD ＝BC, M 、N 分别是AB 、CD 的中点, AD 、BC 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．经典难题（二）1、已知：△ABC 中, H 为垂心（各边高线的交点）, O 为外心, 且OM ⊥BC 于M ．（1）求证：AH ＝2OM ；AFGCEBODAPC DBD 2C 2B 2A 2D 1C 1B 1C BDAA 1B（2）若∠BAC ＝600, 求证：AH ＝AO ．（初二）第1题图第2题图2、设MN 是圆O 外一直线, 过O 作OA ⊥MN 于A, 自A 引圆的两条直线, 交圆于B 、C 及D 、E 直线EB 及CD分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二） 3、如果上题把直线MN 由圆外平移至圆内, 则由此可得以下命题：设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE, 设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）第4题图4、如图, 分别以△ABC 的AC 和BC 为一边, 在△ABC 的外侧作正方形ACDE 和正方形CBFG, 点P 是EF 的中点．求证：点P 到边AB 的距离即是AB 的一半．（初二）经典难题（三）1、如图, 四边形ABCD 为正方形, DE ∥AC, AE ＝AC, AE 与CD 相交于F ．求证：CE ＝CF ．（初二）NF第2题图2、如图, 四边形ABCD 为正方形, DE ∥AC,且CE ＝CA, 直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边BC 上的任一点, PF ⊥AP, CF 平分∠DCE ．求证：PA ＝PF ．（初二）第3题图 4、如图, PC切圆O 于C, AC 为圆的直径, PEF 为圆的割线, AE 、AF 与直线PO 相交于B 、D ．求证：AB ＝DC, BC ＝AD ．（初三）经典难题（四）1、已知：△ABC 是正三角形, P 是三角形内一点, PA ＝3, PB ＝4, PC ＝5．求：∠APB 的度数．（初二）第1题图第2题图2、设P 是平行四边形ABCD 内部的一点, 且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）E3、设ABCD 为圆内接凸四边形, 求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）第3题图第4题图4、平行四边形ABCD 中, 设E 、F 分别是BC 、AB 上的一点, AE 与CF 相交于P, 且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）经典难题（五）1、设P 是边长为1的正△ABC 内任一点, L ＝PA ＋PB ＋PC, 求证：≤L ＜2．第1题图第2题图2、P 是边长为1的正方形ABCD 内的一点, 求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 内的一点, 而且PA ＝a, PB ＝2a, PC ＝3a, 求正方形的边长．第3题图4、如图, △ABC 中, ∠ABC ＝∠ACB ＝800, D 、E 分别是AB 、AC 上的点, ∠DCA ＝300, ∠EBA ＝200, 求∠BED 的度数．C BDAFPDE CBAA PCBAC B PDEDCBAACBPD经典难题（一）1、已知：如图, O 是半圆的圆心, C 、E 是圆上的两点, CD ⊥AB, EF ⊥AB, EG ⊥CO ．求证：CD ＝GF.（初二）证一：连接OE.∵EG ⊥CO , EF ⊥AB, ∴O 、G 、E 、F 四点共圆, 且OE 为直径.∴GF=OE ·sin ∠GOF.又△OCD 中, CD=OC ·sin ∠COD.∵∠GOF+∠COD=180°, OC= OE 为⊙O 半径, ∴CD ＝GF. 证二：连接OE, 过G 作GH ⊥AB 于H.∵EG ⊥CO , EF ⊥AB, ∴O 、G 、E 、F 四点共圆, 且OE 为直径.∴∠GEO=∠HFG.又∠EGO=∠FHG=Rt ∠, ∴△GEO ∽△HFG.∴GF:OE=GH:OG.又GH∥CD,∴GH:CD=OG:OC, 即GH:OG=CD:OC, ∴GF:OE=CD:OC, 而OE=OC, ∴CD ＝GF.2、已知：如图, P 是正方形ABCD 内点, ∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．（初二）证明：3、如图, 已知四边形ABCD 、A 1B 1C 1D 1都是正方形, A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）AFGCEBODAFG CEBO DAPCDB EH4、已知：如图, 在四边形ABCD 中, AD ＝BC, M 、N 分别是AB 、CD 的中点, AD 、BC 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．经典难题（二）1、已知：△ABC 中, H 为垂心（各边高线的交点）, O 为外心, 且OM ⊥BC 于M ．（1）求证：AH ＝2OM ；（2）若∠BAC ＝600, 求证：AH ＝AO ．（初二）D 2C 2 B 2A 2D 1C 1B 1CBDAA 1B2、设MN 是圆O 外一直线, 过O 作OA ⊥MN 于A, 自A 引圆的两条直线, 交圆于B 、C 及D 、E 直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内, 则由此可得以下命题：设MN 是圆O 的弦, 过MN 的中点A 任作两弦BC 、DE, 设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）4、如图, 分别以△ABC 的AC 和BC 为一边, 在△ABC 的外侧作正方形ACDE 和正方形CBFG, 点P 是EF 的中点．求证：点P 到边AB 的距离即是AB 的一半．（初二）NF经典难题（三）1、如图, 四边形ABCD 为正方形, DE ∥AC, AE ＝AC, AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图, 四边形ABCD 为正方形, DE ∥AC, 且CE ＝CA, 直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边BC 上的任一点, PF ⊥AP, CF 平分∠DCE ．求证：PA ＝PF ．（初二）E4、如图, PC切圆O于C, AC为圆的直径, PEF为圆的割线, AE、AF与直线PO相交于B、D．求证：AB＝DC, BC＝AD．（初三）经典难题（四）1、已知：△ABC是正三角形, P是三角形内一点, PA＝3, PB＝4, PC＝5．求：∠APB的度数．（初二）2、设P是平行四边形ABCD内部的一点, 且∠PBA＝∠PDA．求证：∠PAB＝∠PCB．（初二）3、设ABCD为圆内接凸四边形, 求证：AB·CD＋AD·BC＝AC·BD．（初三）4、平行四边形ABCD 中, 设E 、F 分别是BC 、AB 上的一点, AE 与CF 相交于P, 且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）经典难题（五）1、设P 是边长为1的正△ABC 内任一点, L ＝PA ＋PB ＋PC, 求证：≤L ＜2．CBDAFPDE CBA A PCB2、已知：P是边长为1的正方形ABCD内的一点, 求PA＋PB＋PC的最小值．3、P为正方形ABCD内的一点, 而且PA＝a, PB＝2a, PC＝3a, 求正方形的边长．4、如图, △ABC中, ∠ABC＝∠ACB＝800, D、E分别是AB、AC上的点, ∠DCA＝300,∠EBA＝200, 求∠BED的度数．经典难题（一）⊥AB,连接EO.由于GOFE四点共圆, 所以∠GFH＝∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO, 所以CD=GF得证.2. 如下图做△DGC使与△ADP全等, 可得△PDG为等边△, 从而可得△DGC≌△APD≌△CGP,得出PC=AD=DC,和∠DCG=∠PCG＝150所以∠DCP=300 , 从而得出△PBC是正三角形3.如下图连接BC1和AB12F与A2E并延长相交于Q点,连接EB2并延长交C2Q于H点, 连接FB2并延长交A2Q于G点,由A2E=12A1B1=12B1C1= FB2 , EB2=12AB=12BC=F C1 , 又∠GFQ+∠Q=900和∠GE B2+∠Q=900,所以∠GE B2=∠GFQ又∠B2FC2=∠A2EB2 ,可得△B2FC2≌△A2EB2 , 所以A2B2=B2C2 ,又∠GFQ+∠HB2F=900和∠GFQ=∠EB2A2 ,从而可得∠A2B2 C2=900 ,同理可得其他边垂直且相等,从而得出四边形A2B2C2D2是正方形.4.如下图连接AC并取其中点Q, 连接QN和QM, 所以可得∠QMF=∠F, ∠QNM=∠DEN 和∠QMN=∠QNM, 从而得出∠DEN＝∠F.经典难题（二）1.(1)延长AD到F连BF, 做OG⊥AF,又∠F=∠ACB=∠BHD,可得BH=BF,从而可得HD=DF,又AH=GF+HG=GH+HD+DF+HG=2(GH+HD)=2OM (2)连接OB, OC,既得∠BOC=1200,从而可得∠BOM=600,所以可得OB=2OM=AH=AO,得证.⊥CD, OG⊥BE, 连接OP, OA, OF, AF, OG, AG, OQ.由于22AD AC CD FD FD AB AE BE BG BG,由此可得△ADF≌△ABG, 从而可得∠AFC=∠AGE.又因为PFOA与QGOA四点共圆, 可得∠AFC=∠AOP和∠AGE=∠AOQ, ∠AOP=∠AOQ, 从而可得AP=AQ.4.过E,C,F 点分别作AB 所在直线的高EG, CI, FH.可得PQ=2EGFH.由△EGA ≌△AIC, 可得EG=AI, 由△BFH ≌△CBI, 可得FH=BI.从而可得PQ=2AIBI =2AB, 从而得证.经典难题（三）△ADE, 到△ABG, 连接CG.由于∠ABG=∠ADE=900+450=1350从而可得B, G, D在一条直线上, 可得△AGB≌△CGB.推出AE=AG=AC=GC, 可得△AGC为等边三角形.∠AGB=300, 既得∠EAC=300, 从而可得∠A EC=750.又∠EFC=∠DFA=450+300=750.可证：CE=CF.⊥DE, 可得四边形CGDH是正方形.由AC=CE=2GC=2CH,可得∠CEH=300, 所以∠CAE=∠CEA=∠AED=150,又∠FAE=900+450+150=1500,从而可知道∠F=150, 从而得出AE=AF.⊥CD, FE⊥BE, 可以得出GFEC为正方形.令AB=Y , BP=X ,CE=Z ,可得PC=Y-X .tan∠BAP=tan∠EPF=XY=ZY X Z, 可得YZ=XY-X2+XZ,即Z(Y-X)=X(Y-X) , 既得X=Z , 得出△ABP≌△PEF , 获得PA＝PF , 得证 .经典难题（四）1.顺时针旋转△ABP 600 , 连接PQ , 则△PBQ是正三角形. 可得△PQC是直角三角形.所以∠APB=1500 .2.作过P点平行于AD的直线, 并选一点E, 使AE∥DC, BE∥PC. 可以得出∠ABP=∠ADP=∠AEP, 可得：AEBP共圆（一边所对两角相等）.可得∠BAP=∠BEP=∠BCP, 得证.3.在BD取一点E, 使∠BCE=∠ACD, 既得△BEC∽△ADC, 可得：BEBC=ADAC, 即AD•BC=BE•AC, ①又∠ACB=∠DCE, 可得△ABC∽△DEC, 既得ABAC =DEDC , 即AB •CD=DE •AC, ②由①+②可得: AB •CD+AD •BC=AC(BE+DE)= AC ·BD , 得证.⊥AE , AG ⊥CF , 由ADES=2ABCDS=DFCS, 可得：2AE PQ =2AE PQ , 由AE=FC.可得DQ=DG, 可得∠DPA ＝∠DPC （角平分线逆定理）.经典难题（五）1.（1）顺时针旋转△BPC 600 , 可得△PBE为等边三角形.既得PA+PB+PC=AP++PE+EF要使最小只要AP, PE, EF在一条直线上, 即如下图：可得最小L=；（2）过P点作BC的平行线交AB,AC与点D, F.由于∠APD>∠ATP=∠ADP,推出AD>AP ①又BP+DP>BP ②和PF+FC>PC ③又DF=AF ④由①②③④可得：最年夜L< 2 ；由（1）和（2）既得：≤L＜2 .△BPC 600 , 可得△PBE为等边三角形.既得PA+PB+PC=AP+PE+EF要使最小只要AP, PE, EF在一条直线上, 即如下图：可得最小PA+PB+PC=AF.既得AF=213(1)42=23=4232=2(31)2 =2(31)2=622 .△ABP 900 , 可得如下图：既得正方形边长L =2222(2)()22a=522a.4.在AB上找一点F, 使∠BCF=600 ,连接EF, DG, 既得△BGC为等边三角形,可得∠DCF=100 , ∠FCE=200 ,推出△ABE≌△ACF , 获得BE=CF , FG=GE .推出：△FGE为等边三角形 , 可得∠AFE=800 ,既得：∠DFG=400①又BD=BC=BG , 既得∠BGD=800 , 既得∠DGF=400②推得：DF=DG ,获得：△DFE≌△DGE ,从而推得：∠FED=∠BED=300 .经典难题（一）⊥AB,连接EO.由于GOFE四点共圆, 所以∠GFH＝∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO, 所以CD=GF得证.2. 如下图做△DGC使与△ADP全等, 可得△PDG为等边△, 从而可得△DGC≌△APD≌△CGP,得出PC=AD=DC,和∠DCG=∠PCG＝150所以∠DCP=300 , 从而得出△PBC是正三角形3.如下图连接BC1和AB12F与A2E并延长相交于Q点,连接EB2并延长交C2Q于H点, 连接FB2并延长交A2Q于G点,由A2E=12A1B1=12B1C1= FB2 , EB2=12AB=12BC=F C1 , 又∠GFQ+∠Q=900和∠GE B2+∠Q=900,所以∠GE B2=∠GFQ又∠B2FC2=∠A2EB2 , 可得△B2FC2≌△A2EB2 , 所以A2B2=B2C2 ,又∠GFQ+∠HB2F=900和∠GFQ=∠EB2A2 ,从而可得∠A2B2 C2=900 ,同理可得其他边垂直且相等,从而得出四边形A2B2C2D2是正方形.4.如下图连接AC并取其中点Q, 连接QN和QM, 所以可得∠QMF=∠F, ∠QNM=∠DEN 和∠QMN=∠QNM, 从而得出∠DEN＝∠F.经典难题（二）1.(1)延长AD到F连BF, 做OG⊥AF,又∠F=∠ACB=∠BHD,可得BH=BF,从而可得HD=DF,又AH=GF+HG=GH+HD+DF+HG=2(GH+HD)=2OM(2)连接OB, OC,既得∠BOC=1200,从而可得∠BOM=600,所以可得OB=2OM=AH=AO,得证.⊥CD, OG⊥BE, 连接OP, OA, OF, AF, OG, AG, OQ.由于22AD AC CD FD FD AB AE BE BG BG,由此可得△ADF≌△ABG, 从而可得∠AFC=∠AGE.又因为PFOA与QGOA四点共圆, 可得∠AFC=∠AOP和∠AGE=∠AOQ, ∠AOP=∠AOQ, 从而可得AP=AQ.4.过E,C,F 点分别作AB 所在直线的高EG, CI, FH.可得PQ=2EGFH.由△EGA ≌△AIC, 可得EG=AI, 由△BFH ≌△CBI, 可得FH=BI.从而可得PQ=2AIBI =2AB, 从而得证.经典难题（三）△ADE, 到△ABG, 连接CG.由于∠ABG=∠ADE=900+450=1350从而可得B, G, D在一条直线上, 可得△AGB≌△CGB.推出AE=AG=AC=GC, 可得△AGC为等边三角形.∠AGB=300, 既得∠EAC=300, 从而可得∠A EC=750.又∠EFC=∠DFA=450+300=750.可证：CE=CF.⊥DE, 可得四边形CGDH是正方形.由AC=CE=2GC=2CH,可得∠CEH=300, 所以∠CAE=∠CEA=∠AED=150,又∠FAE=900+450+150=1500,从而可知道∠F=150, 从而得出AE=AF.⊥CD, FE⊥BE, 可以得出GFEC为正方形.令AB=Y , BP=X ,CE=Z ,可得PC=Y-X .tan∠BAP=tan∠EPF=XY=ZY X Z, 可得YZ=XY-X2+XZ,即Z(Y-X)=X(Y-X) , 既得X=Z , 得出△ABP≌△PEF , 获得PA＝PF , 得证 .经典难题（四）2.顺时针旋转△ABP 600 , 连接PQ , 则△PBQ是正三角形. 可得△PQC是直角三角形.所以∠APB=1500 .2.作过P点平行于AD的直线, 并选一点E, 使AE∥DC, BE∥PC. 可以得出∠ABP=∠ADP=∠AEP, 可得：AEBP共圆（一边所对两角相等）.可得∠BAP=∠BEP=∠BCP, 得证.3.在BD取一点E, 使∠BCE=∠ACD, 既得△BEC∽△ADC, 可得：BEBC=ADAC, 即AD•BC=BE•AC, ①又∠ACB=∠DCE, 可得△ABC∽△DEC, 既得ABAC =DEDC , 即AB •CD=DE •AC, ②由①+②可得: AB •CD+AD •BC=AC(BE+DE)= AC ·BD , 得证.⊥AE , AG ⊥CF , 由ADES=2ABCDS=DFCS, 可得：2AE PQ =2AE PQ , 由AE=FC.可得DQ=DG, 可得∠DPA ＝∠DPC （角平分线逆定理）.经典难题（五）1.（1）顺时针旋转△BPC 600 , 可得△PBE为等边三角形.既得PA+PB+PC=AP++PE+EF要使最小只要AP, PE, EF在一条直线上,即如下图：可得最小L=；（2）过P点作BC的平行线交AB,AC与点D, F.由于∠APD>∠ATP=∠ADP,推出AD>AP ①又BP+DP>BP ②和PF+FC>PC ③又DF=AF ④由①②③④可得：最年夜L< 2 ；由（1）和（2）既得：≤L＜2 .△BPC 600 , 可得△PBE为等边三角形.既得PA+PB+PC=AP+PE+EF要使最小只要AP, PE, EF在一条直线上, 即如下图：可得最小PA+PB+PC=AF.既得AF=213(1)42=23=4232=2(31)2 =2(31)2=622 .△ABP 900 , 可得如下图：既得正方形边长L =2222(2)()22a=522a.4.在AB上找一点F, 使∠BCF=600 ,连接EF, DG, 既得△BGC为等边三角形,可得∠DCF=100 , ∠FCE=200 ,推出△ABE≌△ACF , 获得BE=CF , FG=GE .推出：△FGE为等边三角形 , 可得∠AFE=800 ,既得：∠DFG=400①又BD=BC=BG , 既得∠BGD=800 , 既得∠DGF=400②推得：DF=DG ,获得：△DFE≌△DGE ,从而推得：∠FED=∠BED=300 .创作时间：二零二一年六月三十日。

初中几何证明的经典难题

初中几何证明的经典难题一．割补法：1.（全等）如图，点E 是BC 中点，CDE BAE ∠=∠，求证：CD AB =（相似）如图，点E 是BC 上一点，EC k BE ⋅=，CDE BAE ∠=∠，猜想AB 、CD 的数量关系.2. （全等）如图，在ABC ∆中，︒=∠90BAC ，AC AB =，BA CD //，点P 是BC 上一点，连结AP ，过点P 做AP PE ⊥交CD 于E .探究PE 与PA 的数量关系.（相似）如图，在ABC ∆中，︒=∠90BAC ，AC k AB ⋅=，BA CD //，点P 是BC 上一点，连结AP ，过点P 做AP PE ⊥交CD 于E .探究PE 与PA 的数量关系.3. （全等）如图，在ABC ∆中，AC AB =，点D 在AB 上，点E（相似）如图，在ABC ∆中，AC k AB ⋅=，点D 在AB 上，点E 在AC 的延长线上，且CE BD =，DE 交BC 于点P .探究PE 与PD 的数量关系.4. （全等）如图，在ABC ∆中，A ECB DBC ∠=∠=∠21，BD 、CE 交于点P . 探究BE 与CD 的数量关系.（相似）如图，在ABC ∆中，A ECB DBC ∠=∠+∠，BD 、CE 交于点P ，PC k PB ⋅=. 探究BE 与CD 的数量关系.5．（全等）如图，在EBC ∆中，BD 平分EBC ∠，延长DE 至点A ，使得ED EA =，且C ABE ∠=∠. 探究AB 与CD 的数量关系.（相似）如图，BD 平分EBC ∠，D '是BD 上一点，且D B k BD '⋅=，连结C D '、DE ，并延长DE 至点A ，使得ED EA =，且C ABE ∠=∠.探究AB 与D C '的数量关系.6.（全等）如图，在ABC ∆中，︒=∠90C ，BC AC =，P 为AB 的中点，PF PE ⊥分别交AC 、BC 于E 、F .探究PE 、PF 的数量关系.（相似）如图，在ABC ∆中，︒=∠90C ，BC AC =，P 为AB 上一点，且PB k AP ⋅=，PF PE ⊥分别交AC 、BC 于E 、F .探究PE 、PF 的数量关系.（相似）如图，在ABC ∆中，BC AC =，P 为AB 上一点，且PB k AP ⋅=，︒=∠+∠180C EPF ，EPF ∠的两边分别交AC 、BC 于E 、F .探究PE 、PF 的数量关系.7. （全等）如图，CD CB =，︒=∠+∠180CDE ABC ，DE AB =. 探究：AF 与EF 之间的数量关系9（相似）如图，CD CB =，︒=∠+∠180CDE ABC ，DE k AB ⋅=. 探究：AF 与EF 之间的数量关系10如图，直线1l 、2l 相交于点A ，点B 、点C 分别在直线1l 、2l 上，AC k AB ⋅=，连结BC ，点D 是线段AC 上任意一点（不与A 、C 重合），作α=∠=∠BAC BDE ，与ECF ∠的一边交于点E ，且ABC ECF ∠=∠.⑴如图1，若1=k ，且︒=∠90α时，猜想线段BD 与DE 的数量关系，并加以证明； ⑵如图2，若1≠k ，时，猜想线段BD 与DE 的数量关系，并加以证明.二．倍长中线法：11. （全等）如图，点E 是BC 中点，CDE BAE ∠=∠，求证：CD AB =12（相似）如图，AD 是ABC ∆的中线，AC k AB ⋅=，点E 是AC 延长线上一点，且BAD AEF ∠=∠，EF 交BA 延长线于点F .探究AE 、AF 的数量关系.13 （全等）如图，在ABC ∆中，AB CD =，BDA BAD ∠=∠，AE 是BD 边的中线.求证：AE AC 2=14（相似）如图，在ABC ∆中，AD k AB ⋅=，BDA BAD ∠=∠，AE 是BD 边的中线，且C EAD ∠=∠. 探究AE 、AC 的数量关系.15. （全等）如图，在ABC ∆中，AD 平分BAC ∠，G 为BC 的中点，AD EG //交CA 延长线于E . 求证：EC BF =17（全等）如图，等腰直角ABC ∆与等腰直角BDE ∆，P 为CE 中点，连接PA 、PD . 探究PA 、PD 的关系.18（相似）如图，ABC ∆与BDE ∆中，︒=∠=∠90BDE CAB ，AB k AC ⋅=，DB k DE ⋅=，P 为CE 中点，连接PA 、PD .探究PA 、PD 的数量关系.19（全等）如图，两个正方形ABDE 和ACGF ，点P 为BC 的中点，连接PA 交EF 于点Q . 探究AP 与EF 的关系.20（相似）⑴如图1，两个矩形ABDE 和ACGF 相似，AB k AE ⋅=，点P 为BC 的中点，连接PA 交EF 于点Q .探究AP 与EF 的关系.⑵如图2，若将“两个矩形ABDE和ACGF相似”改为“两个平行四边形ABDE和ACGF相似”，且α∠EAB.探究AP与EF的关系.=21．已知：如图，正方形ABCD和正方形EBGF，点M是线段DF的中点.⑴试说明线段ME与MC的关系.α），其他条件不变，上述结论还⑵如图，若将上题中正方形EBGF绕点B顺时针旋转α度数（︒<90正确吗？若正确，请你证明；若不正确，请说明理由.22.如图1，正方形ABCD中，对角线AC、BD交于点O.⑴操作：将三角板中的︒90角的顶点与点O重合，使这个角落在ABC∆的内部，两边分别与正方形ABCD的边AB、BC交于F、E.当F、E的位置发生变化时，请你通过测量并回答，每组AF、FE、EC三条线段中，哪一条线段是中始终最长.⑵以AF、FE、EC这三条线段能否组成以FE为斜边的直角三角形？若能，请你证明；若不能，请你说明理由.结论是否仍然成立？请你证明.23⑴如图1，操作：把正方形CGEF的对角线CE放在正方形ABCD的边BC的延长线上（BCCG ）取线段AE的中点P.探究：线段PD、PF的关系，并加以证明.⑵如图2，将正方形CGEF绕点C旋转任意角度后，其他条件不变. 探究：线段PD、PF的关系，并加以证明.。

初二几何证明经典难题集

初二几何证明经典难题集
一、等腰三角形的垂直平分线相等证明
问题描述：在等腰三角形ABC中，AD是边BC上的高，M是AB的中点，N是AC的中点，证明DM=DN。

证明步骤：
1. 连接AM和AN，得到垂直平分线MN。

2. 由于AM和AN分别是AB和AC的中线，所以AM=AN。

3. 由三角形的等腰性质可知，AD是BC的高，所以AM=MB 和AN=NC。

4. 由于AM=AN，所以BN=CM。

5. 由步骤3和4可知，DM=BM和DN=NC。

6. 由于BM=NC，所以DM=DN。

证毕。

二、相交线段的垂直角相等证明
问题描述：在平面内，直线AB和直线CD相交于点E，证明∠AEC=∠BED。

证明步骤：
1. 由直线交叉引理可知，AE和CD是平行的，同理，EC和
BD也是平行的。

2. 因此，∠AEC和∠CED是同位角，由同位角性质可知
∠AEC=∠CED。

3. 同样地，∠BED和∠BEC也是同位角，所以∠BED=∠BEC。

4. 由步骤2和3可知，∠AEC=∠CED=∠BED。

证毕。

以上是初二几何中的两个经典难题的证明过程，通过严谨的推
理和应用基本几何性质，我们可以得到结论，并验证了几何问题的
正确性。

希望这些例题可以帮助你更好地理解几何证明的方法和思路。

(以上内容仅供参考，切勿照抄照搬，建议自己动手尝试，理
解证明的精髓。

)。

初二数学上册几何难题

1、：如图，Rt ABC ∆中，=90ACB ∠，AC=BC ，将直角三角板中45角的顶点放在点C 处．并将三角板绕点C 旋转，三角板的两边分别交AB 边于D 、E 两点(点D 在点E 的左侧，并且点D 不与点A 重合，点E 不与点B 重合)，设AD=m,DE=x,BE=n.(1)判断以m 、x 、n 为三边长组成的三角形的形状，并说明理由；(2)当三角板旋转时，找出AD DE BE 、、三条线段中始终最长的线段，并说明理由．2、直角三角形纸片ABC 中，∠ACB=90°,AC ≤BC,如图，将纸片沿某条直线折叠，使点A 落在直角边BC 上，记落点为D,设折痕与AB 、AC 边，分别交与点E 、点F.探究：如果折叠后的△CDF 与BDE 均为等腰三角形，那么纸片中∠B 的度数是多少？写出你的计算过程，并画出符合条件的折叠后．．．的图形。

解：3、如图，△ABC 中，AB=AC ，∠A=120°，DE 垂直平分仙于D ，交BC 于E 点．求证：CE=2BE ．4、：如图，△ABC 中，AB=AC ，∠BAC=90°，假设CD ⊥BD 于D 点，且BD 交AC 于E 点，问当BD 满足什么条件时CD=12BE 并证明你的判断．5、如图，在直角坐标系xOy 中，直线y=kx+b 交x 轴正半轴于A(-1,0),交y 轴正半轴于B,C 是x 轴负半轴上一点，且CA=43CO,△ABC 的面积为6。

〔1〕求C 点的坐标。

〔2〕求直线AB 的解析式。

〔3〕D 是第二象限内一动点，且OD ⊥BD,直线BE 垂直射线CD 于额，OF ⊥CD 交直线BE 于F .当线段OD,BD 的长度发生改变时，∠BDF 的大小是否发生改变？假设改变，请说明理由；假设不变，请证明并求出其值。

ABCOxy COxFEDy6、某研究性学习小组在探究矩形的折纸问题时，将一块直角三角板的直角顶点绕着矩形ABCD 〔AB ＜BC 〕的对角线交点O 旋转〔如图①→②→③〕，图中M 、N 分别为直角三角板的直角边与矩形ABCD 的边CD 、BC 的交点.〔1〕该学习小组中一名成员意外地发现：在图①〔三角板的一直角边与OD 重合〕中，BN 2＝CD 2＋CN 2；在图③〔三角板的一直角边与OC 重合〕中，CN 2＝BN 2＋CD 2.请你对这名成员在图①和图③中发现的结论选择其一．．．．说明理由. 〔2〕试探究图②中BN 、CN 、CM 、DM 这四条线段之间的关系，写出你的结论，并说明理由.→图①图②图③→7、如图，射线CB ∥OA ，∠C=∠OAB=100 ,E 、F 在CB 上，且满足∠FOB=∠AOB ，OE 平分∠COF. 〔1〕求∠EOB 的度数；〔2〕假设平行移动AB ，那么∠OBC ∶∠OFC 的值是否随之变化？假设变化，找出变化规律；假设不变，求出这个比值；〔3〕在平行移动AB 的过程中，是否存在某种情况，使∠OEC=∠OBA ？假设存在，求出其度数；假设不存在，说明理由；FO ECBA。

初二几何难题大全

初二几何难题大全篇一：初二几何典型题1、已知：在△ABC中，BC=10, D是AC上一点且AB=BD, E, F 分别是AD、BC的中点.求:EF的长如图,已知∠ABC=∠ADC=90°,P、Q分别是AC、BD的中心。

AC=10,BD=8,求PQ的长在线等，答得快和好，追加分连结DP和BP,∵∠ABC=∠ADC=90°,△ADC和△ABC是RT△,∴DP=AC/2,BP=AC/2,(斜边的中线等于斜边的一半)∴DP=BP,∴△PDB是等腰△,∵DQ=BQ,∴PQ也是BD边上的高,∴PQ⊥BD.∵BP=5 QB=4∴PQ^2=BP^2-QB^2=9∵PQ >0∴PQ=3已知；如图，在△ABC中，∠BAC=90°, AB=AC, BD⊥AE, CE⊥AE.求证：BD=DE+CEBD⊥AE, CE⊥AE则BD//CE，∠DBC=∠BCEAB=AC，则∠ACB=∠ABD+∠DBC=45度RT三角形AC0 E中∠EAC=90-∠ACB-∠BCE=45-∠BCE=45-∠DBC=∠ABD又AB=AC所以RTABD与RT三角形CAE全等即AD=CE，BD=AE因为AE=AD+DE所以BD=AE=AD+DE=CE+DE连接BE，因为AB=BD，E是AD的中点，所以BE垂直于AD又因为F是BC的中点，且在直角△BEC中，斜边的中线等于其长度的一半所以EF=BC/2=5如图,在五边形ABCDE中,∠BAE=120°，∠B=∠E=90°。

AB=BC，AE=DE，在BC，DE上分别找一点M，N，使得△AMN的周长最小时，则∠AMN+∠ANM的度数为？A.100°B.110°C.120°D.130°（2011?日照）如图，已知点D为等腰直角△ABC内一点，∠CAD=∠CBD=15°，E为AD延长线（1）求证：DE平分∠BDC；上的一点，且CE=CA．（2）若点M在DE上，且DC=DM，求证：ME=BD满意回答回答者：莪昰呓伿貓2012-07-28 17:17解：作A关于BC和ED的对称点A′，A″，连接A′A″，交BC 于M，交CD于N，则A′A″即为△AMN的周长最小值．作DA 延长线AH，∵∠EAB=120°，∴∠HAA′=60°，∴∠AA′M+∠A″=∠HAA′=60°，∵∠MA′A=∠MAA′，∠NAD=∠A″，且∠MA′A+∠MAA′=∠AMN，∠NAD+∠A″=∠ANM，∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2（∠AA′M+∠A″）=2×60°=120证∴∠BAC=∠ABC=45°，∵∠CAD=∠CBD=15°，∴∠BAD=∠ABD=45°-15°=30°，∴BD=AD．在△BDC与△ADC中，明：（1）∵△ABC是等腰直角三角形，BD=AD∠CBD=∠CADBC=AC，∴△BDC≌△ADC（SAS），∴∠DCB=∠DCA，又∵∠DCB+∠DCA=90°，∴∠DCB=∠DCA=45°．由∠BDM=∠ABD+∠BAD=30°+30°=60°，∠EDC=∠DAC+∠DCA=15°+45°=60°，∴∠BDM=∠EDC，∴DE平分∠BDC；（2）如图，连接MC．∵DC=DM，且∠MDC=60°，∴△MDC是等边三角形，即CM=CD．又∵∠EMC=180°-∠DMC=180°-60°=120°，∠ADC=180°-∠MDC=180°-60°=120°，∴∠EMC=∠ADC．又∵CE=CA，∴∠DAC=∠CEM．在△ADC与△EMC中，∠ADC=∠EMC篇二：初一几何难题_练习题(含答案)1、证明线段相等或角相等两条线段或两个角相等是平面几何证明中最基本也是最重要的一种相等关系。