高考数学异构异模复习第八章立体几何8.4直线平面垂直的判定与性质撬题文

合集下载

2023年新高考数学一轮复习8-4 直线、平面平行的判定及性质(知识点讲解)含详解

专题8.4 直线、平面平行的判定及性质（知识点讲解）【知识框架】【核心素养】以立体几何的定义、公理和定理为出发点，认识和理解空间中线面平行的有关性质与判定定理，运用公理、定理和已获得的结论证明一些有关空间图形的平行关系的简单命题，凸显逻辑推理、直观想象、数学运算的核心素养．【知识点展示】（一）空间平行关系1.直线与平面平行的判定与性质a∥α，a⊂β，2.利用线面平行的定义，一般用反证法；利用线面平行的判定定理(a ⊄α，b ⊂α，a ∥b ⇒a ∥α)，其关键是在平面内找(或作)一条直线与已知直线平行，证明时注意用符号语言的叙述；)利用面面平行的性质定理(α∥β，a ⊂α⇒a ∥β)；利用面面平行的性质(α∥β，a ⊄β，a ∥α⇒a ∥β)．（二）平行关系中的三个重要结论(1)垂直于同一条直线的两个平面平行，即若a ⊥α，a ⊥β，则α∥β. (2)垂直于同一个平面的两条直线平行，即若a ⊥α，b ⊥α，则a ∥b. (3)平行于同一个平面的两个平面平行，即若α∥β，β∥γ，则α∥γ.【常考题型剖析】题型一：与线、面平行相关命题的判定例1. （2023·全国·高三专题练习）已知m ，n 为两条不同的直线，α，β为两个不同的平面，则下列结论中正确的是（） A ．若m //α，m //n ，则n //α B ．若m //α，n //α，则m //n C ．若m //α，n ⊂α，则m //nD ．若m //α，m ⊂β，αβ＝n ，则m //n例2.（2022·上海静安·二模）在下列判断两个平面α与β平行的4个命题中，真命题的个数是（）. （1）α、β都垂直于平面r ，那么α∥β. （2）α、β都平行于平面r ，那么α∥β. （3）α、β都垂直于直线l ，那么α∥β.（4）如果l 、m 是两条异面直线，且l ∥α，m ∥α，l ∥β，m ∥β，那么α∥β A ．0B ．1C ．2D ．3例3．（四川·高考真题（文））下列命题正确的是（） A ．若两条直线和同一个平面所成的角相等，则这两条直线平行 B ．若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行 C ．若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行D ．若两个平面都垂直于第三个平面，则这两个平面平行例4. （2022·云南师大附中模拟预测（理））若α，β是两个不同平面，m ，n 是两条不同直线，则下列4个推断中正确的是（）A ．m α∥，m β∥，n ⊂α，n m n β⊂⇒∥B ．m α⊂，n β⊂，m n αβ⇒∥∥C ．m α∥，n α∥，m β⊂，n βαβ⊂⇒∥D ．m α⊂，n β⊂，m n αβ⇒∥∥ 【方法技巧】直线、平面间平行的判定方法(1)关注是否符合判定定理与性质定理，并注意定理中易忽视的条件． (2)结合题意构造或绘制图形，结合图形作出判断． (3)利用实物进行空间想象，比较判断．(4)熟记一些常见结论，如垂直于同一条直线的两个平面平行等．题型二：直线与平面平行的判定例5.（2023·全国·高三专题练习）在直三棱柱111ABC A B C -中，D 、E 、F 、M 、N 分别是BC 、11B C 、1AA 、1CC 、1A C 的中点，给出下列四个判断：①//EF 平面1ADB ；②//EM 平面1ADB ； ③//EN 平面1ADB ； ④1//A M 平面1ADB ，错误的序号为___________.例6.【多选题】（2017·全国·高考真题（文））如图，在下列四个正方体中，A ，B 为正方体的两个顶点，M ，N ，Q 为所在棱的中点，则在这四个正方体中，直线AB 与平面MNQ 平行的是（）A．B．C．D．例7.（2023·全国·高三专题练习）如图，AB是圆O的直径，点C是圆O上异于,A B的点，直线PC 平面ABC，,E F分别是PA，PC的中点.记平面BEF与平面ABC的交线为l，求证：直线l//平面PAC【总结提升】证明直线与平面平行的方法(1)线面平行的定义：一条直线与一个平面无公共点(不相交)．(2)线面平行的判定定理：关键是找到平面内与已知直线平行的直线．常利用三角形的中位线、平行四边形的对边、成比例线段出现平行线或过已知直线作一平面找其交线．注意内外平行三条件，缺一不可．题型三：线面平行性质定理的应用例8.（福建·高考真题（文））如图，在正方体ABCD-A1B1C1D1中，AB＝2，点E为AD的中点，点F在CD 上．若EF∥平面AB1C，则线段EF的长度等于________．例9.(2019·全国卷Ⅰ改编)如图，直四棱柱ABCD A 1B 1C 1D 1的底面是菱形，AA 1＝4，AB ＝2，∠BAD ＝60°，E ，M ，N 分别是BC ，BB 1，A 1D 的中点．证明：MN ∥平面C 1DE .例10.如图，在直四棱柱ABCD A 1B 1C 1D 1中，E 为线段AD 上的任意一点(不包括A ，D 两点)，平面CEC 1∩平面BB 1D ＝FG .证明：FG ∥平面AA 1B 1B ．【总结提升】 1.思路方法：(1)通过线面平行可得到线线平行，其中一条线应是两平面的交线，要树立这种应用意识． (2)利用线面平行性质必须先找出交线． 2.易错提醒（1）在推证线面平行时，一定要强调直线不在平面内，否则，会出现错误.（2）线面平行关系证明的难点在于辅助面和辅助线的添加，在添加辅助线、辅助面时一定要以某一性质定理为依据，绝不能主观臆断.（3）解题中注意符号语言的规范应用. 题型四：平面与平面平行的判定与性质例11.（2023·全国·高三专题练习）已知长方体1111ABCD A B C D -中，4AB AD ==，12AA =，E ，F 分别为棱11A B 和11A D 的中点，M 为长方体表面上任意一点．若BM ∥平面AEF ，则BM 的最大值为（）A．B ．C ．D ．6例12.（2020·全国·高三专题练习（文））如图，平面//α平面β，PAB △所在的平面与α，β分别交于CD 和AB ，若2PC =，3CA =，1CD =，则AB =______．例13.（2023·全国·高三专题练习）如图，在正方体1111ABCD A B C D -中，E ，F分别为棱11,DD CC 的中点.求证：平面1//AEC 平面BDF例14.（陕西·高考真题（文））如图,四棱柱ABCD －A 1B 1C 1D 1的底面ABCD 是正方形, O 为底面中心, A 1O∥平面ABCD, 12AB AA ==.（1）证明: 平面A 1BD // 平面CD 1B 1;（2）求三棱柱ABD －A 1B 1D 1的体积.【规律方法】 1.证明面面平行的常用方法 (1)利用面面平行的定义．(2)利用面面平行的判定定理：如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行． (3)利用“垂直于同一条直线的两个平面平行”．(4)利用“如果两个平面同时平行于第三个平面，那么这两个平面平行”． (5)利用“线线平行”“线面平行”“面面平行”的相互转化．2.面面平行的应用(1)两平面平行，构造与之相交的第三个平面，可得交线平行．(2)两平面平行，其中一个平面内的任意一条直线与另一个平面平行，可用于证明线面平行．3.三种平行关系之间的转化其中线面平行是核心，线线平行是基础，要注意它们之间的灵活转化．专题8.4 直线、平面平行的判定及性质（知识点讲解）【知识框架】【核心素养】以立体几何的定义、公理和定理为出发点，认识和理解空间中线面平行的有关性质与判定定理，运用公理、定理和已获得的结论证明一些有关空间图形的平行关系的简单命题，凸显逻辑推理、直观想象、数学运算的核心素养．【知识点展示】（一）空间平行关系1.直线与平面平行的判定与性质a∥α，a⊂β，2.利用线面平行的定义，一般用反证法；利用线面平行的判定定理(a ⊄α，b ⊂α，a ∥b ⇒a ∥α)，其关键是在平面内找(或作)一条直线与已知直线平行，证明时注意用符号语言的叙述；)利用面面平行的性质定理(α∥β，a ⊂α⇒a ∥β)；利用面面平行的性质(α∥β，a ⊄β，a ∥α⇒a ∥β)．（二）平行关系中的三个重要结论(1)垂直于同一条直线的两个平面平行，即若a ⊥α，a ⊥β，则α∥β. (2)垂直于同一个平面的两条直线平行，即若a ⊥α，b ⊥α，则a ∥b. (3)平行于同一个平面的两个平面平行，即若α∥β，β∥γ，则α∥γ.【常考题型剖析】题型一：与线、面平行相关命题的判定例1. （2023·全国·高三专题练习）已知m ，n 为两条不同的直线，α，β为两个不同的平面，则下列结论中正确的是（） A ．若m //α，m //n ，则n //α B ．若m //α，n //α，则m //n C ．若m //α，n ⊂α，则m //n D ．若m //α，m ⊂β，αβ＝n ，则m //n【答案】D 【解析】【分析】举例说明判断A ，B ，C ；利用线面平行的性质判断D 作答. 【详解】如图，长方体1111ABCD A B C D -中，平面1111D C B A 视为平面α，对于A ，直线AB 视为m ，直线11A B 视为n ，满足m //α，m //n ，而n ⊂α，A 不正确；对于B，直线AB视为m，直线BC视为n，满足m//α，n//α，而m与n相交，B不正确；A D视为n，满足m//α，n⊂α，显然m与n是异面直线，C不正确；对于C，直线AB视为m，直线11对于D，由直线与平面平行的性质定理知，D正确.故选：D例2.（2022·上海静安·二模）在下列判断两个平面α与β平行的4个命题中，真命题的个数是（）.（1）α、β都垂直于平面r，那么α∥β.（2）α、β都平行于平面r，那么α∥β.（3）α、β都垂直于直线l，那么α∥β.（4）如果l、m是两条异面直线，且l∥α，m∥α，l∥β，m∥β，那么α∥βA．0B．1C．2D．3【答案】D【解析】【分析】由面面平行的判定定理及其相关结论分析可得结果.【详解】由面面平行的判定定理分析可知（1）错，（2），（3），（4）正确.故选：D例3．（四川·高考真题（文））下列命题正确的是（）A．若两条直线和同一个平面所成的角相等，则这两条直线平行B．若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行C．若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行D．若两个平面都垂直于第三个平面，则这两个平面平行【答案】C【解析】【详解】若两条直线和同一平面所成角相等，这两条直线可能平行，也可能为异面直线，也可能相交，所以A错；一个平面不在同一条直线的三点到另一个平面的距离相等，则这两个平面平行，故B错；若两个平面垂直同一个平面两平面可以平行，也可以垂直；故D错；故选项C正确.例4. （2022·云南师大附中模拟预测（理））若α，β是两个不同平面，m ，n 是两条不同直线，则下列4个推断中正确的是（）A ．m α∥，m β∥，n ⊂α，n m n β⊂⇒∥B ．m α⊂，n β⊂，m n αβ⇒∥∥C ．m α∥，n α∥，m β⊂，n βαβ⊂⇒∥D ．m α⊂，n β⊂，m n αβ⇒∥∥【答案】A【解析】【分析】利用线面，面面位置关系逐项分析即得.【详解】对于A ，如图，n ⊂α，n n βαβ⊂⇒⋂=，结合m α，m β，可知m n ∥，故A 正确；对于B ，如图，m ，n 可能异面，故B 错误；对于C ，如图，α，β可能相交，故C 错误；对于D ，如图，αβ，可能相交，故D 错误.故选：A ．【方法技巧】直线、平面间平行的判定方法(1)关注是否符合判定定理与性质定理，并注意定理中易忽视的条件．(2)结合题意构造或绘制图形，结合图形作出判断．(3)利用实物进行空间想象，比较判断．(4)熟记一些常见结论，如垂直于同一条直线的两个平面平行等．题型二：直线与平面平行的判定例5.（2023·全国·高三专题练习）在直三棱柱111ABC A B C -中，D 、E 、F 、M 、N 分别是BC 、11B C 、1AA 、1CC 、1A C 的中点，给出下列四个判断：①//EF 平面1ADB ；②//EM 平面1ADB ；③//EN 平面1ADB ；④1//A M 平面1ADB ，错误的序号为___________.【答案】①②④【解析】【分析】连接DE 、1A E 、CE 、EF 、EM 、EN 、1A M 、FM ，证明出平面1//A CE 平面1AD B ，利用面面平行的性质结合假设法可判断①②③④的正误.【详解】连接DE 、1A E 、CE 、EF 、EM 、EN 、1A M 、FM ，在三棱柱111ABC A B C -中，因为11//BB CC 且11BB CC =，所以，四边形11BB C C 为平行四边形，则11//BC B C 且11BC B C =，D 、E 分别为BC 、11B C 的中点，则1//CD B E 且1CD B E =，故四边形1CDB E 为平行四边形，则1//CE B D ，CE ⊄平面1ADB ，1B D ⊂平面1ADB ，故//CE 平面1ADB ，同理可证四边形1BB ED 为平行四边形，则11////DE BB AA ，11DE BB AA ==，则四边形1AA ED 为平行四边形，所以，1//A E AD ，1A E ⊄平面1ADB ，AD ⊂平面1ADB ，则1//A E 平面1ADB ，1CE A E E =，故平面1//A CE 平面1AD B ，EN ⊂平面1A CE ，则//EN 平面1ADB ，③对；对于①，若//EF 平面1ADB ，EF EN E =，则平面//EFN 平面1ADB ，因为过点E 且与平面1ADB 平行的平面只有一个，矛盾，故①错，同理可知，②④均错.故答案为：①②④.例6.【多选题】（2017·全国·高考真题（文））如图，在下列四个正方体中，A ，B 为正方体的两个顶点，M ，N ，Q 为所在棱的中点，则在这四个正方体中，直线AB 与平面MNQ 平行的是（）A ．B ．C ．D ．【答案】BCD【解析】【分析】利用线面平行判定定理逐项判断可得答案．【详解】对于选项A，OQ∥AB，OQ与平面MNQ是相交的位置关系，故AB和平面MNQ不平行，故A错误；对于选项B，由于AB∥CD∥MQ，结合线面平行判定定理可知AB∥平面MNQ，故B正确；对于选项C，由于AB∥CD∥MQ，结合线面平行判定定理可知AB∥平面MNQ：故C正确；对于选项D，由于AB∥CD∥NQ，结合线面平行判定定理可知AB∥平面MNQ：故D正确；故选：BCD例7.（2023·全国·高三专题练习）如图，AB 是圆O 的直径，点C 是圆O 上异于,A B 的点，直线PC ⊥平面ABC ，,E F 分别是PA ，PC 的中点.记平面BEF 与平面ABC 的交线为l ，求证：直线l //平面PAC【答案】证明见解析【解析】【分析】先通过//EF AC 可得出//EF 平面ABC ，再利用线面平行的性质即可证明.【详解】因为,E F 分别是,PA PC 的中点，所以//EF AC ，又因为AC ⊂平面ABC ，EF ⊄平面ABC ，所以//EF 平面ABC ，又EF ⊂平面BEF ，平面BEF 与平面ABC 的交线为l ，所以//EF l ，而l ⊄平面PAC ，EF ⊂平面PAC ，所以//l 平面P AC .【总结提升】证明直线与平面平行的方法(1)线面平行的定义：一条直线与一个平面无公共点(不相交)．(2)线面平行的判定定理：关键是找到平面内与已知直线平行的直线．常利用三角形的中位线、平行四边形的对边、成比例线段出现平行线或过已知直线作一平面找其交线．注意内外平行三条件，缺一不可．题型三：线面平行性质定理的应用例8.（福建·高考真题（文））如图，在正方体ABCD -A 1B 1C 1D 1中，AB ＝2，点E 为AD 的中点，点F 在CD 上．若EF ∥平面AB 1C ，则线段EF 的长度等于________．【解析】【分析】根据直线与平面平行的性质定理可得//EF AC ,再根据E 为AD 的中点可得F 为CD 的中点,从而根据三角形的中位线可得.【详解】如图:因为//EF 平面1AB C ,EF ⊂平面DABC ,且平面1A C B 平面ABCD AC =,所以//EF AC ,又因为E 为AD 的中点,所以F 为CD 的中点, 所以12EF AC =,因为正方体的棱长为2.所以AC =所以EF =故答案为.例9.(2019·全国卷Ⅰ改编)如图，直四棱柱ABCD A 1B 1C 1D 1的底面是菱形，AA 1＝4，AB ＝2，∠BAD ＝60°，E ，M，N分别是BC，BB1，A1D的中点．证明：MN∥平面C1DE.【答案】见解析【解析】证明:连接B1C，ME.因为M，E分别为BB1，BC的中点，所以ME∥B1C，且ME＝12B1C．又因为N为A1D的中点，所以ND＝12A1D．由题设知A1B1//=DC，可得B1C//=A1D，故ME//=ND，因此四边形MNDE为平行四边形，所以MN∥ED．又MN⊄平面C1DE，ED⊂平面C1DE，所以MN∥平面C1DE.例10.如图，在直四棱柱ABCDA1B1C1D1中，E为线段AD上的任意一点(不包括A，D两点)，平面CEC1∩平面BB1D＝FG.证明：FG∥平面AA1B1B．【答案】见解析【解析】证明：在直四棱柱ABCDA1B1C1D1中，BB1∥CC1，BB1⊂平面BB1D，CC1⊄平面BB1D，所以CC1∥平面BB1D．又CC1⊂平面CEC1，平面CEC1∩平面BB1D＝FG，所以CC1∥FG.因为BB1∥CC1，所以BB1∥FG.而BB1⊂平面AA1B1B，FG⊄平面AA1B1B，所以FG∥平面AA1B1B．【总结提升】1.思路方法：(1)通过线面平行可得到线线平行，其中一条线应是两平面的交线，要树立这种应用意识．(2)利用线面平行性质必须先找出交线．（1）在推证线面平行时，一定要强调直线不在平面内，否则，会出现错误.（2）线面平行关系证明的难点在于辅助面和辅助线的添加，在添加辅助线、辅助面时一定要以某一性质定理为依据，绝不能主观臆断.（3）解题中注意符号语言的规范应用.题型四：平面与平面平行的判定与性质例11.（2023·全国·高三专题练习）已知长方体1111ABCD A B C D -中，4AB AD ==，12AA =，E ，F 分别为棱11A B 和11A D 的中点，M 为长方体表面上任意一点．若BM ∥平面AEF ，则BM 的最大值为（）A．B ．C ．D ．6【答案】C【解析】【分析】由面面平行的性质结合题意可确定点M 所在的平面，再由平面几何的性质即可确定BM 的值为最大值时的位置，即可求解【详解】如图所示，取G ，H 分别为棱11B C 和11D C 的中点，连接11,,,BG DH BD B D ,由题意易知1111,BF B D GH B D ∥∥，所以BF GH ∥；又易知AF BG ∥，故可以证明平面BGHD ∥平面AEF ；又BM ∥平面AEF ，由面面平行的性质可知M ∈平面BGHD ，所以由题意可知M 在等腰梯形BGHD 四条边上运动，过点H 作HQ BD ⊥，交BD 于点Q ，由题意可知BD GH DH BG DQ ====所以HQ BQ BD DQ =-=所以BH又BD BH ==，所以故当M 与D 点重合时，BM 的值为最大值，此时BM BD ==例12.（2020·全国·高三专题练习（文））如图，平面//α平面β，PAB △所在的平面与α，β分别交于CD 和AB ，若2PC =，3CA =，1CD =，则AB =______．【答案】52【解析】【分析】根据面面平行的性质，证得//CD AB ，结合CD PC AB PA =，即可求解. 【详解】由题意，平面//α平面β，PAB △所在的平面与α，β分别交于CD 和AB ，根据面面平行的性质，可得//CD AB ，所以CD PC AB PA =，因为2PC =，3CA =，1CD =，所以15522CD PA AB PC ⋅⨯===.故答案为：52. 例13.（2023·全国·高三专题练习）如图，在正方体1111ABCD A B C D -中，E ，F 分别为棱11,DD CC 的中点.求证：平面1//AEC 平面BDF【答案】证明见解析【解析】【分析】根据1//DF EC ，可证明1//EC 平面BDF ；又//BF AE ，可得//AE 平面BDF .进而根据线面平行证明面面平行.【详解】证明：在正方体1111ABCD A B C D -中，E ，F 分别为棱11,DD CC 的中点，所以11111,22DE DD C F CC ==. 因为11CC DD =，且11//CC DD ，所以1DE C F =，且1//DE C F ，所以四边形1DEC F 是平行四边形，所以1//DF EC 又DF ⊂平面BDF ，1EC ⊄平面BDF ，所以1//EC 平面BDF .同理，//BF AE ，又BF ⊂平面BDF ，AE ⊄平面BDF ，所以//AE 平面BDF .又1AE EC E ⋂=，1,AE EC ⊂平面1AEC ，所以平面1//AEC 平面BDF 例14.（陕西·高考真题（文））如图,四棱柱ABCD －A 1B 1C 1D 1的底面ABCD 是正方形, O 为底面中心, A 1O∥平面ABCD, 1AB AA =（1）证明: 平面A 1BD // 平面CD 1B 1;（2）求三棱柱ABD －A 1B 1D 1的体积.【答案】（1）证明见解析；（2）1.【解析】【详解】试题分析：（1）要证明1A C ⊥平面11BB D D ，只要证明1A C 垂直于平面11BB D D 内的两条相交直线即可，由已知可证出1A C ⊥BD ，取11B D 的中点为1E ，通过证明四边形11A OCE 为正方形可证1A C ⊥1E O ．由线面垂直的判定定理问题得证；（2）由已知1A O 是三棱柱ABD ﹣A 1B 1D 1的高，由此能求出三棱柱ABD ﹣A 1B 1D 1的体积试题解析：（Ⅰ）∵四棱柱ABCD ﹣A 1B 1C 1D 1的底面ABCD 是正方形，O 为底面中心，A 1O ⊥平面ABCD ，AB=AA 1=，由棱柱的性质可得BB 1和DD 1平行且相等，故四边形BB 1D 1D 为平行四边形，故有BD 和B 1D 1平行且相等．而BD 不在平面CB 1D 1内，而B 1D 1在平面CB 1D 1内，∴BD ∥平面CB 1D 1．同理可证，A 1BCD 1为平行四边形，A 1B ∥平面CB 1D 1．而BD 和A 1B 是平面A 1BD 内的两条相交直线，故有平面A 1BD ∥平面CD 1B 1 ．（Ⅱ）由题意可得A 1O 为三棱柱ABD ﹣A 1B 1D 1的高．三角形A 1AO 中，由勾股定理可得A 1O===1，∴三棱柱ABD ﹣A 1B 1D 1的体积V=S △ABD •A 1O=•A 1O=×1=1．【规律方法】1.证明面面平行的常用方法 (1)利用面面平行的定义．(2)利用面面平行的判定定理：如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行．(3)利用“垂直于同一条直线的两个平面平行”．(4)利用“如果两个平面同时平行于第三个平面，那么这两个平面平行”．(5)利用“线线平行”“线面平行”“面面平行”的相互转化．2.面面平行的应用(1)两平面平行，构造与之相交的第三个平面，可得交线平行．(2)两平面平行，其中一个平面内的任意一条直线与另一个平面平行，可用于证明线面平行．3.三种平行关系之间的转化其中线面平行是核心，线线平行是基础，要注意它们之间的灵活转化．。

2020届高考数学一轮复习第八章立体几何8.4直线、平面垂直的判定与性质课件文

∵PO⊥平面ABC,∴PO⊥AC,又PO∩PE=P,∴AC⊥平面POE,∴AC⊥OE,同理有BC⊥OF,∴四边形OECF为矩形, ∵PC=PC且PE=PF, ∴Rt△PEC≌Rt△PFC,∴EC=FC= PC2 PE2 =1,
∴四边形OECF是边长为1的正方形,∴OC= 2 , 在Rt△POC中,PO= PC2 OC2 = 2 .
连接OB,因为AB=BC= 2 AC, 2
所以△ABC为等腰直角三角形,
且OB⊥AC,OB= 1 AC=2.
2
由OP2+OB2=PB2知,OP⊥OB. 由OP⊥OB,OP⊥AC且OB∩AC=O知PO⊥平面ABC.
(2)作CH⊥OM,垂足为H. 又由(1)可得OP⊥CH,
所以CH⊥平面POM.
故CH的长为点C到平面POM的距离.
可得四棱锥P-ABCD的侧面积为 1 PA·PD+ 1 PA·AB+ 1 PD·DC+1 BC2sin 60°=6+2 3 .
2
2
2
2
解法二:由题设条件和(1)可知四棱锥P-ABCD是一个正方体的一部分,底面ABCD是正方体的
一个对角面,P是正方体的一个顶点(如图),
设正方体的棱长为a,
则V = P-ABCD
由题设可知OC= 1 AC=2,CM= 2 BC= 4 2 ,∠ACB=45°.
2
3
3
所以OM= 2 5 ,CH= OC MC sin ACB = 4 5 .
3
OM
5
所以点C到平面POM的距离为 4 5 . 5
解题关键认真分析三棱锥各侧面和底面三角形的特殊性,利用线面垂直的判定方法及等积
法求解是关键.

高考数学异构异模复习第八章立体几何 8.3 直线、平面平行的判定与性质撬题文-人教版高三全册数

2018高考数学异构异模复习考案第八章立体几何 8.3 直线、平面平行的判定与性质撬题文1.已知m ，n 是两条不同直线，α，β是两个不同平面，则下列命题正确的是( ) A ．若α，β垂直于同一平面，则α与β平行 B ．若m ，n 平行于同一平面，则m 与n 平行C ．若α，β不平行，则在α内不存在与β平行的直线D ．若m ，n 不平行，则m 与n 不可能垂直于同一平面答案 D解析 A 中，垂直于同一个平面的两个平面可能相交也可能平行，故A 错误；B 中，平行于同一个平面的两条直线可能平行、相交或异面，故B 错误；C 中，若两个平面相交，则一个平面内与交线平行的直线一定和另一个平面平行，故C 错误；D 中，若两条直线垂直于同一个平面，则这两条直线平行，所以若两条直线不平行，则它们不可能垂直于同一个平面，故D 正确．2．如图，三棱锥P －ABC 中，平面PAC ⊥平面ABC ，∠ABC ＝π2，点D ，E 在线段AC 上，且AD ＝DE ＝EC ＝2，PD ＝PC ＝4，点F 在线段AB 上，且EF ∥BC .(1)证明：AB ⊥平面PFE ；(2)若四棱锥P －DFBC 的体积为7，求线段BC 的长．解 (1)证明：如图，由DE ＝EC ，PD ＝PC 知，E 为等腰△PDC 中DC 边的中点，故PE ⊥AC .又平面PAC ⊥平面ABC ，平面PAC ∩平面ABC ＝AC ，PE ⊂平面PAC ，所以PE ⊥平面ABC ，从而PE ⊥AB .因∠ABC ＝π2，EF ∥BC ，故AB ⊥EF .从而AB 与平面PFE 内两条相交直线PE ，EF 都垂直，所以AB ⊥平面PFE . (2)设BC ＝x ，则在Rt △ABC 中，AB ＝AC 2－BC 2＝36－x 2，从而S △ABC ＝12AB ·BC ＝12x 36－x 2.由EF ∥BC 知，AF AB ＝AE AC ＝23，得△AFE ∽△ABC ，故S △AFE S △ABC ＝⎝ ⎛⎭⎪⎫232＝49，即S △AFE ＝49S △ABC .由AD ＝12AE ，得S △AFD ＝12S △AFE ＝12·49S △ABC ＝29S △ABC ＝19x 36－x 2，从而四边形DFBC 的面积为S DFBC ＝S △ABC －S △AFD ＝12x 36－x 2－19x 36－x 2＝718x 36－x 2.由(1)知，PE ⊥平面ABC ，所以PE 为四棱锥P －DFBC 的高．在Rt △PEC 中，PE ＝PC 2－EC 2＝42－22＝2 3. 体积V P －DFBC ＝13·S DFBC ·PE ＝13·718x 36－x 2·23＝7，故得x 4－36x 2＋243＝0，解得x 2＝9或x 2＝27，由于x >0，可得x ＝3或x ＝3 3. 所以，BC ＝3或BC ＝3 3.3．如图，在直三棱柱ABC－A1B1C1中，已知AC⊥BC，BC＝CC1.设AB1的中点为D，B1C∩BC1＝E.求证：(1)DE∥平面AA1C1C；(2)BC1⊥AB1.证明(1)由题意知，E为B1C的中点，又D为AB1的中点，因此DE∥AC.又因为DE⊄平面AA1C1C，AC⊂平面AA1C1C，所以DE∥平面AA1C1C.(2)因为棱柱ABC－A1B1C1是直三棱柱，所以CC1⊥平面ABC.因为AC⊂平面ABC，所以AC⊥CC1.又因为AC⊥BC，CC1⊂平面BCC1B1，BC⊂平面BCC1B1，BC∩CC1＝C，所以AC⊥平面BCC1B1.又因为BC1⊂平面BCC1B1，所以BC1⊥AC.因为BC＝CC1，所以矩形BCC1B1是正方形，因此BC1⊥B1C.因为AC，B1C⊂平面B1AC，AC∩B1C＝C，所以BC1⊥平面B1AC.又因为AB1⊂平面B1AC，所以BC1⊥AB1.4．一个正方体的平面展开图及该正方体的直观图的示意图如图所示．(1)请将字母F，G，H标记在正方体相应的顶点处(不需说明理由)；(2)判断平面BEG与平面ACH的位置关系，并证明你的结论；(3)证明：直线DF⊥平面BEG.解(1)点F，G，H的位置如图所示．(2)平面BEG∥平面ACH，证明如下：因为ABCD－EFGH为正方体，所以BC∥FG，BC＝FG，又FG∥EH，FG＝EH，所以BC∥EH，BC＝EH，于是四边形BCHE为平行四边形，所以BE∥CH.又CH⊂平面ACH，BE⊄平面ACH，所以BE∥平面ACH.同理BG∥平面ACH.又BE∩BG＝B，所以平面BEG∥平面ACH.(3)证明：连接FH.因为ABCD－EFGH为正方体，所以DH⊥平面EFGH.因为EG⊂平面EFGH，所以DH⊥EG.又EG⊥FH，DH∩FH＝H，所以EG⊥平面BFHD.又DF⊂平面BFHD，所以DF⊥EG.同理DF⊥BG.又EG∩BG＝G，所以DF⊥平面BEG.5．如图，三棱台DEF－ABC中，AB＝2DE，G，H分别为AC，BC的中点．(1)求证：BD∥平面FGH；(2)若CF⊥BC，AB⊥BC，求证：平面BCD⊥平面EGH.证明(1)证法一：连接DG，CD，设CD∩GF＝M，连接MH.在三棱台DEF－ABC中，AB＝2DE，G为AC的中点，可得DF∥GC，DF＝GC，所以四边形DFCG为平行四边形，则M为CD的中点，又H为BC的中点，所以HM∥BD.又HM⊂平面FGH，BD⊄平面FGH，所以BD∥平面FGH.证法二：在三棱台DEF－ABC中，由BC＝2EF，H为BC的中点，可得BH∥EF，BH＝EF，所以四边形HBEF为平行四边形，可得BE∥HF.在△ABC中，G为AC的中点，H为BC的中点，所以GH∥AB.又GH∩HF＝H，所以平面FGH∥平面ABED.因为BD⊂平面ABED，所以BD∥平面FGH.(2)连接HE，GE.因为G，H分别为AC，BC的中点，所以GH∥AB，由AB⊥BC，得GH⊥BC.又H为BC的中点，所以EF∥HC，EF＝HC，因此四边形EFCH是平行四边形，所以CF∥HE.又CF⊥BC，所以HE⊥BC.又HE，GH⊂平面EGH，HE∩GH＝H，所以BC⊥平面EGH.又BC⊂平面BCD，所以平面BCD⊥平面EGH.6. 如图，三棱柱ABC－A1B1C1中，侧面BB1C1C为菱形，B1C的中点为O，且AO⊥平面BB1C1C.(1)证明：B1C⊥AB；(2)若AC⊥AB1，∠CBB1＝60°，BC＝1，求三棱柱ABC－A1B1C1的高．解(1)证明：连接BC 1，则O 为B 1C 与BC 1的交点．因为侧面BB 1C 1C 为菱形，所以B 1C ⊥BC 1. 又AO ⊥平面BB 1C 1C ，所以B 1C ⊥AO ，AO ∩BC 1＝0，故B 1C ⊥平面ABO . 由于AB ⊂平面ABO ，故B 1C ⊥AB .(2)作OD ⊥BC ，垂足为D ，连接AD .作OH ⊥AD ，垂足为H . 由于BC ⊥AO ，BC ⊥OD ，故BC ⊥平面AOD ，所以OH ⊥BC . 又OH ⊥AD ，所以OH ⊥平面ABC .因为∠CBB 1＝60°，所以△CBB 1为等边三角形，又BC ＝1，可得OD ＝34. 由于AC ⊥AB 1，所以OA ＝12B 1C ＝12.由OH ·AD ＝OD ·OA ，且AD ＝OD 2＋OA 2＝74，得OH ＝2114. 又O 为B 1C 的中点，所以点B 1到平面ABC 的距离为217，故三棱柱ABC －A 1B 1C 1的高为217. 7．如图，四棱锥P －ABCD 中，AP ⊥平面PCD ，AD ∥BC ，AB ＝BC ＝12AD ，E ，F 分别为线段AD ，PC 的中点．(1)求证：AP ∥平面BEF ； (2)求证：BE ⊥平面PAC .证明 (1)设AC ∩BE ＝O ，连接OF ，EC .由于E 为AD 的中点，AB ＝BC ＝12AD ，AD ∥BC ，所以AE ∥BC ，AE ＝AB ＝BC ，因此四边形ABCE 为菱形，所以O 为AC 的中点．又F 为PC 的中点，因此在△PAC 中，可得AP ∥OF . 又OF ⊂平面BEF ，AP ⊄平面BEF ，所以AP ∥平面BEF .(2)由题意知ED ∥BC ，ED ＝BC ，所以四边形BCDE 为平行四边形，因此BE ∥CD . 又AP ⊥平面PCD ，所以AP ⊥CD ，因此AP ⊥BE .因为四边形ABCE 为菱形，所以BE ⊥AC . 又AP ∩AC ＝A ，AP ，AC ⊂平面PAC ，所以BE ⊥平面PAC .8．如图，在三棱锥P －ABC 中，D ，E ，F 分别为棱PC ，AC ，AB 的中点．已知PA ⊥AC ，PA ＝6，BC ＝8，DF ＝5.求证：(1)直线PA ∥平面DEF ； (2)平面BDE ⊥平面ABC .证明 (1)因为D ，E 分别为棱PC ，AC 的中点，所以DE ∥PA . 又因为PA ⊄平面DEF ，DE ⊂平面DEF ，所以直线PA ∥平面DEF . (2)因为D ，E ，F 分别为棱PC ，AC ，AB 的中点，PA ＝6，BC ＝8，所以DE ∥PA ，DE ＝12PA ＝3，EF ＝12BC ＝4.又因为DF ＝5，故DF 2＝DE 2＋EF 2，所以∠DEF ＝90°，即DE ⊥EF . 又PA ⊥AC ，DE ∥PA ，所以DE ⊥AC .因为AC ∩EF ＝E ，AC ⊂平面ABC ，EF ⊂平面ABC ，所以DE ⊥平面ABC .又DE ⊂平面BDE ，所以平面BDE ⊥平面ABC .。

高考数学总复习第8章立体几何第4节直线、平面垂直的判定与性质课件文新人教A版

文字语言垂直于同一个平性质定理面的两条直线
图形语言
符号语言 ab⊥⊥αα⇒a∥b
直二面角 3.如图，PA⊥⊙O 所在平面，AB 是⊙O 的直径，C 是⊙O 上一点，AE⊥PC，AF⊥PB，给出下列结论：①AE⊥BC；②EF⊥ PB；③AF⊥BC；④AE⊥平面 PBC，其中真命题的序号是
解析：①AE⊂平面 PAC，BC⊥AC，BC⊥PA⇒AE⊥BC，故①正确；②AE⊥PC，AE⊥BC，PB⊂平面 PBC⇒AE⊥ PB，AF⊥PB，EF⊂平面 AEF⇒EF⊥PB，故②正确；③AF ⊥PB，若 AF⊥BC⇒AF⊥平面 PBC，则 AF∥AE 与已知矛盾，故③错误；由①可知④正确．
ABE.
交线
(1)证明直线和平面垂直的常用方法： ①判定定理；②垂直于平面的传递性(a∥b，a⊥α⇒b⊥α)；③面面平行的性质(a⊥α， α∥β⇒a⊥β)；④面面垂直的性质．
(2)证明线面垂直的核心是证线线垂直，而证明线线垂直则需借助线面垂直的性质．因此，判定定理与性质定理的合理转化是证明线面垂直的基本思想．
PBC⊥平面
PDC，共
7
对．
[听前试做] (1)在四棱锥 P-ABCD 中， ∵PA⊥底面 ABCD，CD⊂平面 ABCD， ∴PA⊥CD.∵AC⊥CD，PA∩AC＝A， ∴CD⊥平面 PAC. 而 AE⊂平面 PAC，∴CD⊥AE.
(2016·深圳模拟)如图，在四棱锥 P-ABCD 中，底面 ABCD 为菱形， PB⊥平面 ABCD.
(3)线面垂直的性质，常用来证明线线垂直．
平行
(2)判定定理和性质定理
文字语言
一个平面过另一个
判定定理
平面的一条，则这两个
平面互相垂直

高考数学一轮复习第八章立体几何8.4直线、平面垂直的判定与性质文

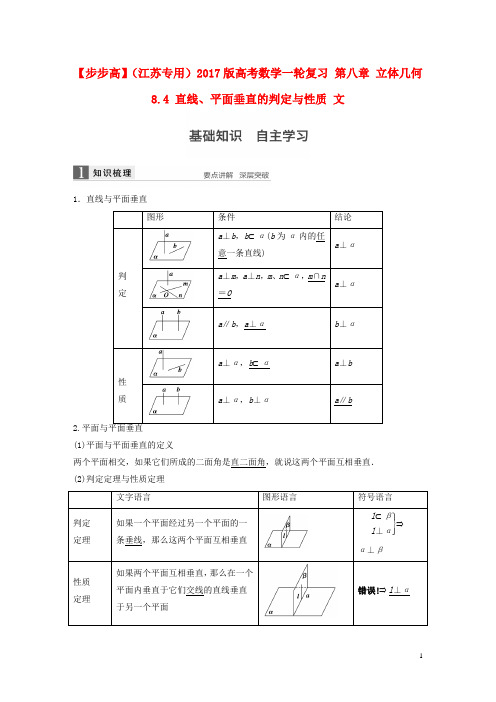
【步步高】（江苏专用）2017版高考数学一轮复习第八章立体几何8.4 直线、平面垂直的判定与性质文1．直线与平面垂直2.(1)平面与平面垂直的定义两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面互相垂直． (2)判定定理与性质定理【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”)(1)直线l与平面α内的无数条直线都垂直，则l⊥α.( ×)(2)若直线a⊥平面α，直线b∥α，则直线a与b垂直．( √)(3)直线a⊥α，b⊥α，则a∥b.( √)(4)若α⊥β，a⊥β⇒a∥α.( ×)(5)a⊥α，a⊂β⇒α⊥β.( √)(6)若两平面垂直，则其中一个平面内的任意一条直线垂直于另一个平面．( ×)1．(教材改编)下列条件中，能判定直线l⊥平面α的是____________．①l与平面α内的两条直线垂直；②l与平面α内无数条直线垂直；③l与平面α内的某一条直线垂直；④l与平面α内任意一条直线垂直．答案④解析由直线与平面垂直的定义，可知④正确．2．设平面α与平面β相交于直线m，直线a在平面α内，直线b在平面β内，且b⊥m，则“α⊥β”是“a⊥b”的____________条件．答案充分不必要解析若α⊥β，因为α∩β＝m，b⊂β，b⊥m，所以根据两个平面垂直的性质定理可得b⊥α，又a⊂α，所以a⊥b；反过来，当a∥m时，因为b⊥m，且a，m共面，一定有b⊥a，但不能保证b⊥α，所以不能推出α⊥β.3．已知平面α⊥β，α∩β＝l，P是空间一点，且P到平面α、β的距离分别是1、2，则点P到l的距离为________．答案 5解析如图，∵PO⊂平面PAB，∴l⊥PO.∴PO就是P到直线l的距离，∵α⊥β，∴四边形PAOB为矩形，PO＝12＋22＝ 5.4．(教材改编)PD垂直于正方形ABCD所在的平面，连结PB，PC，PA，AC，BD，则一定互相垂直的平面有________________________________________________________________________对．答案7解析由于PD⊥平面ABCD，故平面PAD⊥平面ABCD，平面PDB⊥平面ABCD，平面PDC⊥平面ABCD，平面PDA⊥平面PDC，平面PAC⊥平面PDB，平面PAB⊥平面PAD，平面PBC⊥平面PDC，共7对．5．(教材改编)在三棱锥P－ABC中，点P在平面ABC中的射影为点O，(1)若PA＝PB＝PC，则点O是△ABC的________心．(2)若PA⊥PB，PB⊥PC，PC⊥PA，则点O是△ABC的________心．答案(1)外(2)垂解析(1)如图1，连结OA，OB，OC，OP，在Rt△POA、Rt△POB和Rt△POC中，PA＝PC＝PB，所以OA＝OB＝OC，即O为△ABC的外心．(2)如图2，延长AO、BO、CO分别交对边于H、D、G点，∵PC⊥PA，PB⊥PC，PA∩PB＝P，∴PC⊥平面PAB，AB⊂平面PAB，∴PC⊥AB，又AB⊥PO，PO∩PC＝P，∴AB⊥平面PGC，又CG⊂平面PGC，∴AB⊥CG，即CG为△ABC边AB的高．同理可证BD，AH为△ABC底边上的高，即O为△ABC的垂心．题型一直线与平面垂直的判定与性质例1 (2014·辽宁)如图，△ABC和△BCD所在平面互相垂直，且AB＝BC＝BD＝2，∠ABC＝∠DBC＝120°，E，F，G分别为AC，DC，AD的中点．(1)求证：EF⊥平面BCG；(2)求三棱锥D －BCG 的体积． (1)证明由已知得 △ABC ≌△DBC ，因此AC ＝DC .又G 为AD 的中点，所以CG ⊥AD .同理BG ⊥AD ，又BG ∩CG ＝G ，因此AD ⊥平面BGC . 又因E ，F 分别为AC ，DC 的中点，所以EF ∥AD ，所以EF ⊥平面BCG .(2)解在平面ABC 内，作AO ⊥BC ，交CB 的延长线于O ，如图由平面ABC ⊥平面BCD ，知AO ⊥平面BDC .又G 为AD 中点，因此G 到平面BDC 的距离h 是AO 长度的一半．在△AOB 中，AO ＝AB ·sin 60°＝3，所以V D －BCG ＝V G －BCD ＝13S △DBC ·h＝13×12BD ·BC ·sin 120°·32＝12. 思维升华 (1)证明直线和平面垂直的常用方法：①判定定理；②垂直于平面的传递性(a ∥b ，a ⊥α⇒b ⊥α)；③面面平行的性质(a ⊥α，α∥β⇒a ⊥β)；④面面垂直的性质．(2)证明线面垂直的核心是证线线垂直，而证明线线垂直则需借助线面垂直的性质．因此，判定定理与性质定理的合理转化是证明线面垂直的基本思想． (3)线面垂直的性质，常用来证明线线垂直．如图所示，已知AB 为圆O 的直径，点D 为线段AB 上一点，且AD ＝13DB ，点C 为圆O 上一点，且BC ＝3AC ，PD ⊥平面ABC ，PD ＝DB .求证：PA ⊥CD .证明因为AB 为圆O 的直径，所以AC ⊥CB ，在Rt△ABC 中，由3AC ＝BC 得， ∠ABC ＝30°，设AD ＝1，由3AD ＝DB 得，DB ＝3，BC ＝23，由余弦定理得CD 2＝DB 2＋BC 2－2DB ·BC cos 30°＝3，所以CD 2＋DB 2＝BC 2，即CD ⊥AO . 因为PD ⊥平面ABC ，CD ⊂平面ABC ，所以PD ⊥CD ，由PD ∩AO ＝D 得，CD ⊥平面PAB ，又PA ⊂平面PAB ，所以PA ⊥CD . 题型二平面与平面垂直的判定与性质例2 如图所示，四边形ABCD 中，AD ∥BC ，AD ＝AB ，∠BCD ＝45°，∠BAD ＝90°.将△ABD 沿对角线BD 折起，记折起后A 的位置为点P ，且使平面PBD ⊥平面BCD .求证：(1)CD ⊥平面PBD . (2)平面PBC ⊥平面PDC .证明 (1)∵AD ＝AB ，∠BAD ＝90°， ∴∠ABD ＝∠ADB ＝45°，又∵AD ∥BC ，∴∠DBC ＝45°，又∠DCB ＝45°，∴∠BDC ＝90°，即BD ⊥DC .∵平面PBD ⊥平面BCD ，平面PBD ∩平面BCD ＝BD ， ∴CD ⊥平面PBD .(2)由CD ⊥平面PBD 得CD ⊥BP . 又BP ⊥PD ，PD ∩CD ＝D ， ∴BP ⊥平面PDC . 又BP ⊂平面PBC ， ∴平面PBC ⊥平面PDC .思维升华面面垂直的性质应用技巧(1)两平面垂直，在一个平面内垂直于交线的直线必垂直于另一个平面．这是把面面垂直转化为线面垂直的依据，运用时要注意“平面内的直线”．(2)两个相交平面同时垂直于第三个平面，那么它们的交线也垂直于第三个平面，此性质在不是很复杂的题目中，要对此进行证明．(2015·重庆)如图，三棱锥PABC 中，平面PAC ⊥平面ABC ，∠ABC ＝π2，点D ，E 在线段AC 上，且AD ＝DE ＝EC ＝2，PD ＝PC ＝4，点F在线段AB 上，且EF ∥BC . (1)证明：AB ⊥平面PFE ；(2)若四棱锥PDFBC 的体积为7，求线段BC 的长．(1)证明由DE ＝EC ，PD ＝PC 知，E 为等腰△PDC 中DC 边的中点，故PE ⊥AC .又平面PAC ⊥平面ABC ，平面PAC ∩平面ABC ＝AC ，PE ⊂平面PAC ，PE ⊥AC ，所以PE ⊥平面ABC ，从而PE ⊥AB . 因∠ABC ＝π2，EF ∥BC ，故AB ⊥EF .又PE ∩EF ＝E ，所以AB ⊥平面PFE . (2)解设BC ＝x ，则在Rt△ABC 中，AB ＝AC 2－BC 2＝36－x 2，从而S △ABC ＝12AB ·BC ＝12x 36－x 2.由EF ∥BC 知，AF AB ＝AE AC ＝23，得△AFE ∽△ABC ，故S △AFE S △ABC ＝⎝ ⎛⎭⎪⎫232＝49，即S △AFE ＝49S △ABC .由AD ＝12AE ，S △AFD ＝12S △AFE ＝12·49S △ABC＝29S △ABC ＝19x 36－x 2. 从而四边形DFBC 的面积为S DFBC ＝S △ABC －S △AFD ＝12x 36－x 2－19x 36－x 2＝718x 36－x 2. 由(1)知，PE ⊥平面ABC ，所以PE 为四棱锥PDFBC 的高．在Rt△PEC 中，PE ＝PC 2－EC 2＝42－22＝2 3. 体积V PDFBC ＝13·S DFBC ·PE＝13·718x 36－x 2·23＝7，故得x 4－36x 2＋243＝0，解得x 2＝9或x 2＝27，由于x ＞0，可得x ＝3或x ＝3 3. 所以，BC ＝3或BC ＝3 3. 题型三垂直关系中的探索性问题例3 (2015·合肥质量检测)如图，在三棱台ABC －DEF 中，CF ⊥平面DEF ，AB ⊥BC .(1)设平面ACE ∩平面DEF ＝a ，求证：DF ∥a ；(2)若EF ＝CF ＝2BC ，试问在线段BE 上是否存在点G ，使得平面DFG ⊥平面CDE ？若存在，请确定G 点的位置；若不存在，请说明理由．(1)证明在三棱台ABC －DEF 中，AC ∥DF ，AC ⊂平面ACE ，DF ⊄平面ACE ， ∴DF ∥平面ACE .又∵DF ⊂平面DEF ，平面ACE ∩平面DEF ＝a ， ∴DF ∥a .(2)解线段BE 上存在点G ，且BG ＝13BE ，使得平面DFG ⊥平面CDE .证明如下：取CE 的中点O ，连结FO 并延长交BE 于点G ，连结GD ，∵CF ＝EF ，∴GF ⊥CE .在三棱台ABC －DEF 中，AB ⊥BC ⇒DE ⊥EF . 由CF ⊥平面DEF ⇒CF ⊥DE .又CF ∩EF ＝F ，∴DE ⊥平面CBEF ，∴DE ⊥GF .⎭⎪⎬⎪⎫GF ⊥CEGF ⊥DE CE ∩DE ＝E ⇒GF ⊥平面CDE . 又GF ⊂平面DFG ，∴平面DFG ⊥平面CDE .此时，如平面图所示，延长FO 与CB 交于点H ，∵O 为CE 的中点，EF ＝CF ＝2BC ，由平面几何知识易证△HOC ≌△FOE ， ∴HB ＝BC ＝12EF .由△HGB ∽△FGE 可知BG GE ＝12，即BG ＝13BE .思维升华同“平行关系中的探索性问题”的规律方法一样，一般是先探求点的位置，多为线段的中点或某个三等分点，然后给出符合要求的证明．如图(1)所示，在Rt△ABC 中，∠C ＝90°，D ，E 分别为AC ，AB 的中点，点F为线段CD 上的一点，将△ADE 沿DE 折起到△A 1DE 的位置，使A 1F ⊥CD ，如图(2)所示． (1)求证：DE ∥平面A 1CB ； (2)求证：A 1F ⊥BE ；(3)线段A 1B 上是否存在点Q ，使A 1C ⊥平面DEQ ？说明理由．(1)证明因为D，E分别为AC，AB的中点，所以DE∥BC.又因为DE⊄平面A1CB，BC⊂平面A1CB，所以DE∥平面A1CB.(2)证明由已知得AC⊥BC且DE∥BC，所以DE⊥AC，所以DE⊥A1D，DE⊥CD，所以DE⊥平面A1DC.而A1F⊂平面A1DC，所以DE⊥A1F.又因为A1F⊥CD，CD∩DE＝D，所以A1F⊥平面BCDE，又BE⊂平面BCDE，所以A1F⊥BE.(3)解线段A1B上存在点Q，使A1C⊥平面DEQ. 理由如下：如图所示，分别取A1C，A1B的中点P，Q，则PQ∥BC.又因为DE∥BC，所以DE∥PQ，所以平面DEQ即为平面DEP.由(2)知，DE⊥平面A1DC，所以DE⊥A1C.又因为P是等腰三角形DA1C底边A1C的中点，所以A1C⊥DP，因为DE∩DP＝D，所以A1C⊥平面DEP，从而A1C⊥平面DEQ.故线段A1B上存在点Q，使得A1C⊥平面DEQ.17．立体几何证明问题中的转化思想典例(14分)如图所示，M，N，K分别是正方体ABCD—A1B1C1D1的棱AB，CD，C1D1的中点．求证：(1)AN∥平面A1MK；(2)平面A1B1C⊥平面A1MK.思维点拨(1)要证线面平行，需证线线平行．(2)要证面面垂直，需证线面垂直，要证线面垂直，需证线线垂直．规范解答证明(1)如图所示，连结NK.在正方体ABCD—A1B1C1D1中，∵四边形AA1D1D，DD1C1C都为正方形，∴AA1∥DD1，AA1＝DD1，C1D1∥CD，C1D1＝CD.[2分]∵N，K分别为CD，C1D1的中点，∴DN∥D1K，DN＝D1K，∴四边形DD1KN为平行四边形．[3分]∴KN∥DD1，KN＝DD1，∴AA1∥KN，AA1＝KN.∴四边形AA1KN为平行四边形．∴AN∥A1K.[4分]∵A1K⊂平面A1MK，AN⊄平面A1MK，∴AN∥平面A1MK.[6分](2)如图所示，连结BC1.在正方体ABCD—A1B1C1D1中，AB∥C1D1，AB＝C1D1.∵M，K分别为AB，C1D1的中点，∴BM∥C1K，BM＝C1K.∴四边形BC1KM为平行四边形．∴MK∥BC1.[8分]在正方体ABCD—A1B1C1D1中，A1B1⊥平面BB1C1C，BC1⊂平面BB1C1C，∴A1B1⊥BC1.∵MK∥BC1，∴A1B1⊥MK.∵四边形BB1C1C为正方形，∴BC1⊥B1C.∴MK⊥B1C.[12分]∵A1B1⊂平面A1B1C，B1C⊂平面A1B1C，A1B1∩B1C＝B1，∴MK⊥平面A1B1C.又∵MK⊂平面A1MK，∴平面A1B1C⊥平面A1MK.[14分]温馨提醒(1)线面平行、垂直关系的证明问题的指导思想是线线、线面、面面关系的相互转化，交替使用平行、垂直的判定定理和性质定理；(2)线线关系是线面关系、面面关系的基础．证明过程中要注意利用平面几何中的结论，如证明平行时常用的中位线、平行线分线段成比例；证明垂直时常用的等腰三角形的中线等； (3)证明过程一定要严谨，使用定理时要对照条件、步骤书写要规范．[方法与技巧] 1．三类论证(1)证明线线垂直的方法①定义：两条直线所成的角为90°； ②平面几何中证明线线垂直的方法； ③线面垂直的性质：a ⊥α，b ⊂α⇒a ⊥b ； ④线面垂直的性质：a ⊥α，b ∥α⇒a ⊥b . (2)证明线面垂直的方法①线面垂直的定义：a 与α内任何直线都垂直⇒a ⊥α； ②判定定理1：⎭⎪⎬⎪⎫m 、n ⊂α，m ∩n ＝A l ⊥m ，l ⊥n⇒l ⊥α；③判定定理2：a ∥b ，a ⊥α⇒b ⊥α； ④面面平行的性质：α∥β，a ⊥α⇒a ⊥β；⑤面面垂直的性质：α⊥β，α∩β＝l ，a ⊂α，a ⊥l ⇒a ⊥β. (3)证明面面垂直的方法①利用定义：两个平面相交，所成的二面角是直二面角； ②判定定理：a ⊂α，a ⊥β⇒α⊥β. 2．转化思想：垂直关系的转化线线垂直判定性质线面垂直判定性质面面垂判定性质直在证明两平面垂直时一般先从现有的直线中寻找平面的垂线，若这样的直线图中不存在，则可通过作辅助线来解决． [失误与防范]1．在解决直线与平面垂直的问题过程中，要注意直线与平面垂直的定义、判定定理和性质定理的联合交替使用，即注意线线垂直和线面垂直的互相转化．2．面面垂直的性质定理是作辅助线的一个重要依据．我们要作一个平面的一条垂线，通常是先找这个平面的一个垂面，在这个垂面中，作交线的垂线即可．A组专项基础训练(时间：40分钟)1．已知平面α⊥平面β，α∩β＝l，点A∈α，AD/∈l，直线AB∥l，直线AC⊥l，直线m∥α，m∥β，则下列四种位置关系中，不一定成立的是________．①AB∥m; ②AC⊥m；③AB∥β；④AC⊥β.答案④解析如图所示，AB∥l∥m；AC⊥l，m∥l⇒AC⊥m；AB∥l⇒AB∥β，只有④不一定成立．2．(2014·浙江改编)设m、n是两条不同的直线，α、β是两个不同的平面，则下列命题正确的是________．①若m⊥n，n∥α，则m⊥α；②若m∥β，β⊥α，则m⊥α；③若m⊥β，n⊥β，n⊥α，则m⊥α；④若m⊥n，n⊥β，β⊥α，则m⊥α.答案③解析①中，由m⊥n, n∥α，可得m⊂α或m∥α或m与α相交，错误；②中，由m∥β，β⊥α，可得m⊂α或m∥α或m与α相交，错误；③中，由m⊥β，n⊥β，可得m∥n，又n⊥α，则m⊥α，正确；④中，由m⊥n，n⊥β，β⊥α，可得m与α相交或m⊂α或m∥α，错误．3．(2015·天津滨海新区模拟)如图，以等腰直角三角形ABC的斜边BC上的高AD为折痕，把△ABD和△ACD折成互相垂直的两个平面后，某学生得出下列四个结论：①BD⊥AC；②△BAC是等边三角形；③三棱锥D－ABC是正三棱锥；④平面ADC⊥平面ABC.其中正确的是________．答案①②③解析由题意知，BD⊥平面ADC，故BD⊥AC，①正确；AD为等腰直角三角形斜边BC上的高，平面ABD⊥平面ACD，所以AB＝AC＝BC，△BAC是等边三角形，②正确；易知DA＝DB＝DC，又由②知③正确；由①知④错．4．(2015·福建改编)若l ，m 是两条不同的直线，m 垂直于平面α，则“l ⊥m ”是“l ∥α”的____________条件．答案必要而不充分解析 m 垂直于平面α，当l ⊂α时，也满足l ⊥m ，但直线l 与平面α不平行，∴充分性不成立，反之，l ∥α，一定有l ⊥m ，必要性成立．5．(2015·镇江模拟)如图所示，在四棱锥P －ABCD 中，PA ⊥底面ABCD ，且底面各边都相等，M 是PC 上的一动点，当点M 满足________时，平面MBD ⊥平面PCD .(只要填写一个你认为是正确的条件即可)答案 DM ⊥PC (或BM ⊥PC 等)解析由定理可知，BD ⊥PC .∴当DM ⊥PC (或BM ⊥PC )，即有PC ⊥平面MBD .而PC ⊂平面PCD ，∴平面MBD ⊥平面PCD .6.如图，直三棱柱ABC －A 1B 1C 1中，侧棱长为2，AC ＝BC ＝1，∠ACB ＝90°，D 是A 1B 1的中点，F 是BB 1上的动点，AB 1，DF 交于点E .要使AB 1⊥平面C 1DF ，则线段B 1F 的长为________．答案 12解析设B 1F ＝x ，因为AB 1⊥平面C 1DF ，DF ⊂平面C 1DF ，所以AB 1⊥DF .由已知可得A 1B 1＝2，设Rt△AA 1B 1斜边AB 1上的高为h ，则DE ＝12h . 由面积相等得2×2＝h 22＋22，所以h ＝233，DE ＝33. 在Rt△DB 1E 中， B 1E ＝ 222－332＝66. 由面积相等得66× x 2＋222＝22x ，得x ＝12.7．如图，PA ⊥圆O 所在的平面，AB 是圆O 的直径，C 是圆O 上的一点，E ，F 分别是点A在PB，PC上的射影，给出下列结论：①AF⊥PB；②EF⊥PB；③AF⊥BC；④AE⊥平面PBC.其中正确结论的序号是________．答案①②③解析由题意知PA⊥平面ABC，∴PA⊥BC.又AC⊥BC，且PA∩AC＝A，∴BC⊥平面PAC，∴BC⊥AF.∵AF⊥PC，且BC∩PC＝C，∴AF⊥平面PBC，∴AF⊥PB，又AE⊥PB，AE∩AF＝A，∴PB⊥平面AEF，∴PB⊥EF.故①②③正确．8．点P在正方体ABCD－A1B1C1D1的面对角线BC1上运动，则下列四个命题：①三棱锥A－D1PC的体积不变；②A1P∥平面ACD1；③DP⊥BC1；④平面PDB1⊥平面ACD1.其中正确的命题序号是________．答案①②④解析由题意可得直线BC1平行于直线AD1，并且直线AD1⊂平面AD1C，直线BC1⊄平面AD1C，所以直线BC1∥平面AD1C.所以点P到平面AD1C的距离不变，VA－D1PC＝VP－AD1C，所以体积不变．故①正确；如图，连结A1C1，A1B，可得平面AD1C∥平面A1C1B.又因为A1P⊂平面A1C1B，所以A1P∥平面ACD1，故②正确；当点P运动到B点时，△DBC1是等边三角形，所以DP不垂直于BC1.故③不正确；连结DB1，因为直线AC⊥平面DB1，DB1⊂平面DB1.所以AC⊥DB1.同理可得AD1⊥DB1.所以可得DB1⊥平面AD1C.又因为DB1⊂平面PDB1.所以可得平面PDB1⊥平面ACD1.故④正确．综上，正确的序号为①②④.9．(2014·湖北)如图，在正方体ABCD－A1B1C1D1中，E，F，P，Q，M，N分别是棱AB，AD，DD1，BB1，A1B1，A1D1的中点．求证：(1)直线BC1∥平面EFPQ；(2)直线AC1⊥平面PQMN.证明(1)如图，连结AD1，由ABCD－A1B1C1D1是正方体，知AD1∥BC1，因为F，P分别是AD，DD1的中点，所以FP∥AD1，从而BC1∥FP.而FP⊂平面EFPQ，且BC1⊄平面EFPQ，故直线BC1∥平面EFPQ.(2)连结AC，BD，则AC⊥BD.由CC1⊥平面ABCD，BD⊂平面ABCD，可得CC1⊥BD.又AC∩CC1＝C，所以BD⊥平面ACC1.而AC1⊂平面ACC1，所以BD⊥AC1.因为M，N分别是A1B1，A1D1的中点，所以MN∥BD，从而MN⊥AC1.同理可证PN⊥AC1.又PN∩MN＝N，所以直线AC1⊥平面PQMN.10.如图，在四棱锥P－ABCD中，AB∥CD，AB⊥AD，CD＝2AB，平面PAD⊥底面ABCD，PA⊥AD.E和F分别是CD、PC的中点．求证：(1)PA⊥底面ABCD；(2)BE∥平面PAD；(3)平面BEF⊥平面PCD.证明(1)∵平面PAD∩平面ABCD＝AD.又平面PAD⊥平面ABCD，且PA⊥AD.∴PA⊥底面ABCD.(2)∵AB∥CD，CD＝2AB，E为CD的中点，∴AB∥DE，且AB＝DE.∴四边形ABED为平行四边形．∴BE∥AD.又∵BE⊄平面PAD，AD⊂平面PAD，∴BE∥平面PAD.(3)∵AB⊥AD，且四边形ABED为平行四边形．∴BE⊥CD，AD⊥CD.由(1)知PA⊥底面ABCD，则PA⊥CD，又PA∩AD＝A，∴CD⊥平面PAD，从而CD⊥PD，又E、F分别为CD、CP的中点，∴EF∥PD，故CD⊥EF.由(2)知BE∥平面PAD，∴BE⊥CD，又EF，BE在平面BEF内，且EF∩BE＝E，∴CD⊥平面BEF.又∵CD⊂平面PCD，∴平面BEF⊥平面PCD.B组专项能力提升(时间：30分钟)11．如图，在斜三棱柱ABC－A1B1C1中，∠BAC＝90°，BC1⊥AC，则C1在底面ABC上的射影H必在________________________________________________________________________．①直线AB上；②直线BC上；③直线AC上；④△ABC内部．答案①解析由AC⊥AB，AC⊥BC1，∴AC⊥平面ABC1.又∵AC⊂面ABC，∴平面ABC1⊥平面ABC.∴C1在面ABC上的射影H必在两平面交线AB上．12．设α，β是空间两个不同的平面，m，n是平面α及β外的两条不同直线．从“①m⊥n；②α⊥β；③n⊥β；④m⊥α”中选取三个作为条件，余下一个作为结论，写出你认为正确的一个命题：________(用代号表示)．答案①③④⇒②(或②③④⇒①)解析逐一判断．若①②③成立，则m与α的位置关系不确定，故①②③⇒④错误；同理①②④⇒③也错误；①③④⇒②与②③④⇒①均正确．13．已知α，β，γ是三个不同的平面，命题“α∥β，且α⊥γ⇒β⊥γ”是真命题，如果把α，β，γ中的任意两个换成直线，另一个保持不变，在所得的所有新命题中，真命题有________个．答案 2解析若α，β换为直线a ，b ，则命题化为“a ∥b ，且a ⊥γ⇒b ⊥γ”，此命题为真命题；若α，γ换为直线a ，b ，则命题化为“a ∥β，且a ⊥b ⇒b ⊥β”，此命题为假命题；若β，γ换为直线a ，b ，则命题化为“a ∥α，且b ⊥α⇒a ⊥b ”，此命题为真命题．14．如图，四边形ABCD 和ABEF 为直角梯形，平面ABCD ⊥平面ABEF ，且AD ∥BC ，AF ∥BE ，∠ABC ＝∠ABE ＝90°，AF ＝AB ＝12BE ＝1，M ，N 分别为BC ，AF 的中点．(1)证明：EM ∥平面ADF ；(2)证明：平面BMN ⊥平面MAE .证明 (1)由题意知BC ∥AD ，∵BC ⊂平面BCE ，AD ⊄平面BCE ，∴AD ∥平面BCE .同理可得AF ∥平面BCE .∵AD ，AF ⊂平面ADF ，AD ∩AF ＝A ，∴平面ADF ∥平面BCE .∵EM ⊂平面BCE ，∴EM ∥平面ADF .(2)在底面ABEF 中，易知△ABN ∽△BEA ，∴AE ⊥BN .∵平面ABCD ⊥平面ABEF ，平面ABCD ∩平面ABEF ＝AB ，AB ⊥BM ，∴BM ⊥平面ABEF . ∵AE ⊂平面ABEF ，∴BM ⊥AE .∵BN ∩BM ＝B ，∴EA ⊥平面BMN .∵AE ⊂平面MAE ，∴平面BMN ⊥平面MAE .15．(2015·湖北)《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑．在如图所示的阳马PABCD 中，侧棱PD ⊥底面ABCD ，且PD ＝CD ，点E 是PC 的中点，连结DE 、BD 、BE .(1)证明：DE ⊥平面PBC .试判断四面体EBCD 是否为鳖臑．若是，写出其每个面的直角(只需写出结论)；若不是，请说明理由；(2)记阳马PABCD 的体积为V 1，四面体EBCD 的体积为V 2，求V 1V 2的值．(1)证明因为PD ⊥底面ABCD ，所以PD ⊥BC ，由底面ABCD 为长方形，有BC ⊥CD ，而PD ∩CD ＝D ，所以BC ⊥平面PCD .而DE ⊂平面PCD ，所以BC ⊥DE .又因为PD ＝CD ，点E 是PC 的中点，所以DE ⊥PC .而PC ∩BC ＝C ，所以DE ⊥平面PBC .由BC ⊥平面PCD ，DE ⊥平面PBC ，可知四面体EBCD 的四个面都是直角三角形，即四面体EBCD 是一个鳖臑，其四个面的直角分别是∠BCD ，∠BCE ，∠DEC ，∠DEB .(2)解由已知得，PD 是阳马PABCD 的高，所以V 1＝13S ABCD ·PD ＝13BC ·CD ·PD . 由(1)知，DE 是鳖臑DBCE 的高，BC ⊥CE ，所以V 2＝13S △BCE ·DE ＝16BC ·CE ·DE . 在Rt△PDC 中，因为PD ＝CD ，点E 是PC 的中点，所以DE ＝CE ＝22CD ，于是V 1V 2＝13BC ·CD ·PD 16BC ·CE ·DE ＝2CD ·PD CE ·DE ＝4.。

高考数学专题八立体几何 4 直线、平面垂直的判定与性质课件理

2.利用面面垂直的判定定理:a⊥β,a⊂α⇒α⊥β.
利用面面垂直的判定定理证明面面垂直的一般方法:先从现有的直线中
寻找平面的垂线,若这样的直线在图中存在,则可通过线面垂直来证明
面面垂直;若这样的直线在图中不存在,则可通过作辅助线来解决.作辅
助线应有理论根据并有利于证明,不能随意添加.
证明两个平面垂直,通常是通过证明线线垂直→线面垂直→面面垂直来
∴EO⊥平面ABCD.
由(1)知△ABD,△EBD都是直角三角形,
∴BD= A
=2
, AD2
B2
∴S△EBD= 1
2
3
ED·BD=2 3 . (10分)
设点C到平面EBD的距离为h,
由VC-EBD=VE-BCD,得 1
3
又S△BCD= 1
2
S△EBD·h=1
S△BCD·EO,
3
BC·CDsin 120°= 3 ,
(2)过一点有且只有一个平面与已知直线垂直.
12/10/2021
考向突破
考向一证明空间直线与平面垂直
例1 (2018广东东莞模拟,18)如图1,矩形ABCD中,AB=12,AD=6,E、F分
别为CD、AB边上的点,且DE=3,BF=4,将△BCE沿BE折起至△PBE的位
置(如图2所示),连接AP、PF,其中PF=2 5.
又AC∩AB=A,∴SD⊥平面ABC.
(2)由于AB=BC,则BD⊥AC,
由(1)可知,SD⊥平面ABC,又BD⊂平面ABC,∴SD⊥BD,
又SD∩AC=D,∴BD⊥平面SAC.
12/10/2021
方法2
证明平面与平面垂直的方法
1.利用面面垂直的定义(作出两平面构成的二面角的平面角,计算平面

高考数学考点第八章立体几何与空间向量 8.4 直线、平面垂直的判定与性质(理)-人教版高三全册

考点8.4 直线、平面垂直的判定与性质1．直线与平面垂直 (1)定义如果直线l 与平面α内的任意一条直线都垂直，则直线l 与平面α互相垂直，记作l ⊥α，直线l 叫做平面α的垂线，平面α叫做直线l 的垂面． (2)判定定理与性质定理2.直线和平面所成的角 (1)定义平面的一条斜线和它在平面上的射影所成的锐角，叫做这条直线和这个平面所成的角．若一条直线垂直于平面，它们所成的角是直角，若一条直线和平面平行，或在平面内，它们所成的角是0°的角．(2)X 围：⎣⎢⎡⎦⎥⎤0，π2.3．平面与平面垂直 (1)二面角的有关概念①二面角：从一条直线出发的两个半平面所组成的图形叫做二面角；②二面角的平面角：在二面角的棱上任取一点，以该点为垂足，在两个半平面内分别作垂直于棱的两条射线，这两条射线所构成的角叫做二面角的平面角． (2)平面和平面垂直的定义两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面互相垂直．(3)平面与平面垂直的判定定理与性质定理概念方法微思考1．若两平行线中的一条垂直于一个平面，则另一条也垂直于这个平面吗？提示垂直．若两平行线中的一条垂直于一个平面，那么在平面内可以找到两条相交直线与该直线垂直，根据异面直线所成的角，可以得出两平行直线中的另一条也与平面内的那两条直线成90°的角，即垂直于平面内的这两条相交直线，所以垂直于这个平面．2．两个相交平面同时垂直于第三个平面，它们的交线也垂直于第三个平面吗？提示垂直．在两个相交平面内分别作与第三个平面交线垂直的直线，则这两条直线都垂直于第三个平面，那么这两条直线互相平行．由线面平行的性质定理可知，这两个相交平面的交线与这两条垂线平行，所以该交线垂直于第三个平面．1．（2017•新课标Ⅲ）在正方体1111ABCD A B C D -中，E 为棱CD 的中点，则() A ．11A E DC ⊥B ．1A E BD ⊥C ．11A E BC ⊥D ．1A E AC ⊥ 【答案】C【解析】法一：连1B C ，由题意得11BC B C ⊥， 11A B ⊥平面11B BCC ，且1BC ⊂平面11B BCC ，111A B BC ∴⊥， 1111A B B C B =，1BC ∴⊥平面11A ECB ， 1A E ⊂平面11A ECB ， 11A E BC ∴⊥．故选C ．法二：以D 为原点，DA 为x 轴，DC 为y 轴，1DD 为z 轴，建立空间直角坐标系，设正方体1111ABCD A B C D -中棱长为2，则1(2A ，0，2)，(0E ，1，0)，(2B ，2，0)，(0D ，0，0)，1(0C ，2，2)，(2A ，0，0)，(0C ，2，0)，1(2A E =-，1，2)-，1(0DC =，2，2)，(2BD =-，2-，0)， 1(2BC =-，0，2)，(2AC =-，2，0)，112A E DC =-，12A E BD =，110A E BC =，16A E AC =， 11A E BC ∴⊥．故选C ．2．（2016•某某）已知互相垂直的平面α，β交于直线l ，若直线m ，n 满足//m α，n β⊥，则() A ．//m l B ．//m n C ．n l ⊥D ．m n ⊥ 【答案】C【解析】互相垂直的平面α，β交于直线l ，直线m ，n 满足//m α，//m β∴或m β⊂或m 与β相交，l β⊂， n β⊥， n l ∴⊥．故选C ．3．（2019•）已知l ，m 是平面α外的两条不同直线．给出下列三个论断： ①l m ⊥；②//m α；③l α⊥．以其中的两个论断作为条件，余下的一个论断作为结论，写出一个正确的命题：__________．【答案】若l α⊥，l m ⊥，则//m α．（或若l α⊥，//m α，则)l m ⊥ 【解析】由l ，m 是平面α外的两条不同直线，知：由线面平行的判定定理得：若l α⊥，l m ⊥，则//m α．若l α⊥，//m α，则由线面垂直的性质和线面平行的性质得l m ⊥，∴若l α⊥，//m α，则l m ⊥故答案为：若l α⊥，l m ⊥，则//m α．（或若l α⊥，//m α，则)l m ⊥．4．（2019•某某）如图，在直三棱柱111ABC A B C -中，D ，E 分别为BC ，AC 的中点，AB BC =．求证：（1）11//A B 平面1DEC ；（2）1BE C E ⊥．【解析】（1）在直三棱柱111ABC A B C -中，D ，E 分别为BC ，AC 的中点， //DE AB ∴，11//AB A B ，11//DE A B ∴，DE ⊂平面1DEC ，11A B ⊂/平面1DEC ，11//A B ∴平面1DEC ．解：（2）在直三棱柱111ABC A B C -中，E 是AC 的中点，AB BC =． BE AC ∴⊥，直三棱柱111ABC A B C -中，1AA ⊥平面ABC ，BE ⊂平面ABC ， 1BE AA ∴⊥，又1AA AC A =，BE ∴⊥平面11ACC A ，1C E ⊂平面11ACC A ，1BE C E ∴⊥．5．（2017•某某）如图，在三棱锥A BCD -中，AB AD ⊥，BC BD ⊥，平面ABD ⊥平面BCD ，点E 、(F E 与A 、D 不重合）分别在棱AD ，BD 上，且EF AD ⊥．求证：（1）//EF 平面ABC ；（2）AD AC ⊥．【解析】（1）AB AD ⊥，EF AD ⊥，且A 、B 、E 、F 四点共面，//AB EF ∴，又EF ⊂/平面ABC ，AB ⊂平面ABC ，//EF ∴平面ABC ；（2）在线段CD 上取点G ，连结FG 、EG 使得//FG BC ，则//EG AC ， BC BD ⊥，//FG BC ，FG BD ∴⊥，又平面ABD ⊥平面BCD ，平面ABD ⋂平面BCD BD =，FG ⊂平面BCD ， FG ∴⊥平面ABD ，AD ⊂平面ABD ，FG AD ∴⊥，AD EF ⊥，且EFFG F =，AD ∴⊥平面EFG ，EG ⊂平面EFG ，AD EG ∴⊥，//EG AC ，AD AC ∴⊥．6．（2020•某某）在三棱柱111ABC A B C -中，AB AC ⊥，1B C ⊥平面ABC ，E ，F 分别是AC ，1B C的中点．（1）求证：//EF 平面11AB C ；（2）求证：平面1AB C ⊥平面1ABB ．【解析】（1）E ，F 分别是AC ，1B C 的中点．所以1//EF AB ，因为EF ⊂/平面11AB C ，1AB ⊂平面11AB C ，所以//EF 平面11AB C ；（2）因为1B C ⊥平面ABC ，AB ⊂平面1ABB ，所以1B C AB ⊥，又因为AB AC ⊥，1AC B C C =，AC ⊂平面1AB C ，1B C ⊂平面1AB C ，所以AB ⊥平面1AB C ，因为AB ⊂平面1ABB ，所以平面1AB C ⊥平面1ABB ．7．（2020•新课标Ⅰ）如图，D 为圆锥的顶点，O 是圆锥底面的圆心，ABC ∆是底面的内接正三角形，P 为DO 上一点，90APC ∠=︒．（1）证明：平面PAB ⊥平面PAC ；（2）设DO ，求三棱锥P ABC -的体积．【解析】（1）连接OA ，OB ，OC ，ABC ∆是底面的内接正三角形，所以AB BC AC ==．O 是圆锥底面的圆心，所以：OA OB OC ==，所以222222AP BP CP OA OP OB OP OC OP ===+=+=+，所以APB BPC APC ∆≅∆≅∆，由于90APC ∠=︒，所以90APB BPC ∠=∠=︒，所以AP BP ⊥，CP BP ⊥，由于APCP P =，所以BP ⊥平面APC ，由于BP ⊂平面PAB ，所以：平面PAB ⊥平面PAC ．（2）设圆锥的底面半径为r ，圆锥的母线长为l ，所以l =，所以22rr π+=，整理得22(3)(1)0r r +-=，解得1r =．所以AB =由于222AP BP AB +=，解得AP =则：1132P ABC V -=⨯=8．（2019•）如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，底面ABCD 为菱形，E 为CD 的中点．（Ⅰ）求证：BD ⊥平面PAC ；（Ⅱ）若60ABC ∠=︒，求证：平面PAB ⊥平面PAE ；（Ⅲ）棱PB 上是否存在点F ，使得//CF 平面PAE ？说明理由．【解析】（Ⅰ）四棱锥P ABCD -中，PA ⊥平面ABCD ，底面ABCD 为菱形，BD PA ∴⊥，BD AC ⊥，∴⊥平面PAC．=，BDPA AC A（Ⅱ）在四棱锥P ABCD-中，PA⊥平面ABCD，底面ABCD为菱形，E为CD的中点，60∠=︒，ABC∴⊥，PA AEAB AE⊥，∴⊥平面PAB，=，AEPA AB AAE⊂平面PAE，∴平面PAB⊥平面PAE．解：（Ⅲ）棱PB上是存在中点F，使得//CF平面PAE．理由如下：取AB中点G，连结GF，CG，在四棱锥P ABCD-中，PA⊥平面ABCD，底面ABCD为菱形，E为CD的中点，//FG PA，∴，//CG AE=，AE PA ACG FG G=，CFG平面PAE，∴平面//∴平面PAE．CF⊂平面CFG，//CF9．（2018•新课标Ⅲ）如图，矩形ABCD所在平面与半圆弧CD所在平面垂直，M是CD上异于C，D的点．（1）证明：平面AMD⊥平面BMC；（2）在线段AM上是否存在点P，使得//MC平面PBD？说明理由．【解析】（1）矩形ABCD 所在平面与半圆弦CD 所在平面垂直，所以AD ⊥半圆弦CD 所在平面，CM ⊂半圆弦CD 所在平面， CM AD ∴⊥，M 是CD 上异于C ，D 的点．CM DM ∴⊥，DM AD D =，CM ∴⊥平面AMD ，CM ⊂平面CMB ，∴平面AMD ⊥平面BMC ；（2）存在P 是AM 的中点，理由：连接BD 交AC 于O ，取AM 的中点P ，连接OP ，可得//MC OP ，MC ⊂/平面BDP ，OP ⊂平面BDP ，所以//MC 平面PBD ．10．（2018•）如图，在四棱锥P ABCD -中，底面ABCD 为矩形，平面PAD ⊥平面ABCD ，PA PD ⊥，PA PD =，E ，F 分别为AD ，PB 的中点．（Ⅰ）求证：PE BC ⊥；（Ⅱ）求证：平面PAB ⊥平面PCD ；（Ⅲ）求证：//EF 平面PCD ．【解析】（Ⅰ）PA PD =，E 为AD 的中点，可得PE AD ⊥，底面ABCD 为矩形，可得//BC AD ，则PE BC ⊥；（Ⅱ）由于平面PAB 和平面PCD 有一个公共点P ，且//AB CD ，在平面PAB 内过P 作直线//PG AB ，可得//PG CD ，即有平面PAB ⋂平面PCD PG =，由平面PAD ⊥平面ABCD ，又AB AD ⊥，可得AB ⊥平面PAD ，即有AB PA ⊥， PA PG ⊥；同理可得CD PD ⊥，即有PD PG ⊥，可得APD ∠为平面PAB 和平面PCD 的平面角，由PA PD ⊥，可得平面PAB ⊥平面PCD ；（Ⅲ）取PC 的中点H ，连接DH ，FH ，在三角形PBC 中，FH 为中位线，可得//FH BC ， 12FH BC =，由//DE BC ，12DE BC =，可得DE FH =，//DE FH ，四边形EFHD 为平行四边形，可得//EF DH ，EF ⊂/平面PCD ，DH ⊂平面PCD ，即有//EF 平面PCD ．11．（2017•新课标Ⅰ）如图，在四棱锥P ABCD -中，//AB CD ，且90BAP CDP ∠=∠=︒．（1）证明：平面PAB ⊥平面PAD ；（2）若PA PD AB DC ===，90APD ∠=︒，且四棱锥P ABCD -的体积为83，求该四棱锥的侧面积．【解析】（1）在四棱锥P ABCD -中，90BAP CDP ∠=∠=︒，AB PA ∴⊥，CD PD ⊥，又//AB CD ，AB PD ∴⊥， PAPD P =，AB ∴⊥平面PAD ，AB ⊂平面PAB ，∴平面PAB ⊥平面PAD ．解：（2）设PA PD AB DC a ====，取AD 中点O ，连结PO ， PA PD AB DC ===，90APD ∠=︒，平面PAB ⊥平面PAD ，PO ∴⊥底面ABCD ，且AD =，PO =，四棱锥P ABCD -的体积为83，由AB ⊥平面PAD ，得AB AD ⊥， 13P ABCD ABCD V S PO -∴=⨯⨯四边形311183333AB AD PO a a =⨯⨯⨯=⨯==，解得2a =，2PA PD AB DC ∴====，AD BC ==，PO =，PB PC ∴==∴该四棱锥的侧面积：PAD PAB PDC PBC S S S S S ∆∆∆∆=+++侧11112222PA PD PA AB PD DC BC =⨯⨯+⨯⨯+⨯⨯+⨯11112222222222=⨯⨯+⨯⨯+⨯⨯+⨯6=+12．（2017•某某）由四棱柱1111ABCD A B C D -截去三棱锥111C B CD -后得到的几何体如图所示，四边形ABCD 为正方形，O 为AC 与BD 的交点，E 为AD 的中点，1A E ⊥平面ABCD ，（Ⅰ）证明：1//A O 平面11B CD ；（Ⅱ）设M 是OD 的中点，证明：平面1A EM ⊥平面11B CD ．【解析】（Ⅰ）取11B D 中点G ，连结1A G 、CG ，四边形ABCD 为正方形，O 为AC 与BD 的交点，∴四棱柱1111ABCD A B C D -截去三棱锥111C B CD -后，1//AG OC =，∴四边形1OCGA 是平行四边形，1//AO CG ∴， 1AO ⊂/平面11B CD ，CG ⊂平面11B CD ， 1//AO ∴平面11B CD ．（Ⅱ）四棱柱1111ABCD A B C D -截去三棱锥111C B CD -后，11//BD B D =，M 是OD 的中点，O 为AC 与BD 的交点，E 为AD 的中点，1A E ⊥平面ABCD ，又BD ⊂平面ABCD ，1BD A E ∴⊥，四边形ABCD 为正方形，O 为AC 与BD 的交点， AO BD ∴⊥，M 是OD 的中点，E 为AD 的中点，EM BD ∴⊥，1A EEM E =，BD ∴⊥平面1A EM ，11//BD B D ，11B D ∴⊥平面1A EM ， 11B D ⊂平面11B CD ，∴平面1A EM ⊥平面11B CD ．1．（2020•某某模拟）已知α，β是空间两个不同的平面，m ，n 是空间两条不同的直线，则给出的下列说法中正确的是()①//m α，//n β，且//m n ，则//αβ； ②//m α，//n β，且m n ⊥，则αβ⊥； ③m α⊥，n β⊥，且//m n ，则//αβ； ④m α⊥，n β⊥、且m n ⊥，则αβ⊥． A ．①②③B ．①③④C ．②④D ．③④ 【答案】D【解析】对于①，当//m α，//n β，且//m n 时，有//αβ或α、β相交，所以①错误；对于②，当//m α，//n β，且m n ⊥时，有αβ⊥或//αβ或α、β相交且不垂直，所以②错误；对于③，当m α⊥，n β⊥，且//m n 时，得出m β⊥，所以//αβ，③正确；对于④，当m α⊥，n β⊥、且m n ⊥时，αβ⊥成立，所以④正确．综上知，正确的命题序号是③④．故选D ．2．（2020•某某四模）已知直线a 和平面α、β有如下关系：①αβ⊥，②//αβ，③a β⊥，④//a α，则下列命题为真的是()A ．①③⇒④B ．①④⇒③C ．③④⇒①D ．②③⇒④ 【答案】C【解析】对于A ，由αβ⊥，a β⊥，可得//a α或a α⊂，故A 错误；对于B ，由αβ⊥，//a α，可得a β⊂或//a β或a 与β相交，故B 错误；对于C ，由//a α，过a 作平面γ与α相交，交线为b ，则//a b ， a β⊥，b β∴⊥，而b α⊂，可得αβ⊥，故C 正确；对于D ，由//αβ，a β⊥，可得a α⊥，故D 错误．故选C ．3．（2020•五华区校级模拟）在长方体1111ABCD A B C D -中，AB =，E 为棱CD 的中点，则() A ．11A E DD ⊥B ．1A E DB ⊥C ．111A E D C ⊥D ．11A E DB ⊥ 【答案】B【解析】连结AE ，BD ，因为AB =，所以AB ADAD DE=，所以ABD DAE ∆∆∽，所以DAE ABD ∠=∠，所以90EAB ABD ∠+∠=︒，即AE BD ⊥，所以BD ⊥平面1A AE ，所以1A E DB ⊥．故选B ．4．（2020•海淀区二模）如图，正方体1111ABCD A B C D -的棱长为2，点O 为底面ABCD 的中心，点P 在侧面11BB C C 的边界及其内部运动．若1D O OP ⊥，则△11D C P 面积的最大值为()A B C D ．【答案】C 【解析】如图，由正方体性质知，当P 位于C 点时，1D O OC ⊥，当P 位于1BB 的中点1P 时，由已知得，12DD =，DO BO ==1111BP B P ==，11B D =求得1OD =1OP ==113D P ==．∴2221111OD OP D P +=，得11OD OP ⊥．又1OP OC O =，1D O ∴⊥平面1OP C ，得到P 的轨迹在线段1PC 上．由111C P CP ==11C CP ∠为锐角，而12CC =< 知P 到棱11C D 的最大值为5．则△11D C P 面积的最大值为122⨯．故选C ．5．（2020•某某模拟）已知四棱锥S ABCD -中，四边形ABCD 为等腰梯形，//AD BC ，120BAD ∠=︒，SAD ∆是等边三角形，且SA AB ==若点P 在四棱锥S ABCD -的外接球面上运动，记点P到平面ABCD 的距离为d ，若平面SAD ⊥平面ABCD ，则d 的最大值为()A 1B 2+C 1D 2 【答案】A【解析】依题意，3MBC π∠=，取BC 的中点E ，则E 是等腰梯形ABCD 外接圆的圆心，F 是SAD ∆的外心，作OE ⊥平面ABCD ，OF ⊥平面SAB ，则O 是人锥S ABCD -的外接球的球心，且3OF DE ==，2AF =，设四棱锥S ABCD -的外接球半径为R ，则22213R SF OF =+=，则1OE DF ==，∴当四棱锥S ABCD -的体积最大时，1max d R OE =+=．故选A ．6．（2020•某某模拟）已知AB是圆柱上底面的一条直径，C是上底面圆周上异于A，B的一点，D 为下底面圆周上一点，且AD⊥圆柱的底面，则必有()A．平面ABC⊥平面BCD B．平面BCD⊥平面ACDC．平面ABD⊥平面ACD D．平面BCD⊥平面ABD【答案】B【解析】因为AB是圆柱上底面的一条直径，所以AC BC⊥，又AD垂直圆柱的底面，所以AD BC=，⊥，因为AC AD A所以BC⊥平面ACD，因为BC⊂平面BCD，所以平面BCD⊥平面ACD．故选B．7．（2020•婺城区校级模拟）在正四面体ABCD中，已知E，F分别是AB，CD上的点（不含端点），则()A．不存在E，F，使得EF CD⊥B．存在E，使得DE CD⊥C ．存在E ，使得DE ⊥平面ABCD ．存在E ，F ，使得平面CDE ⊥平面ABF 【答案】D【解析】（1）对于A ，D 选项，取E ，F 分别为AB ，CD 的中点如图：因为A BCD -是正四面体，所以它的各个面是全等的等边三角形．所以CE DE =，所以EF CD ⊥，同理可证EF AB ⊥．故A 错误；又因为AB CE ⊥，AB DE ⊥，且CEDE E =，故AB ⊥平面CED ，又AB ⊂平面ABF ，所以平面ABF ⊥平面CED ．故D 正确．（2）对于B 选项，将C 看成正三棱锥的顶点，易知当E 在AB 上移动时，CDE ∠的最小值为直线CD 与平面ABD 所成的角，即（1）中的CDE ∠，显然为锐角，最大角为60CDB CDA ∠=∠=︒，故当E 在AB 上移动时，不存在E ，使得DE CD ⊥．故B 错误．（3）对于C 选项，将D 看成顶点，则由D 向底面作垂线，垂足为底面正三角形ABC 的中心，不落在AB 上，又因为过空间中一点有且只有一条直线与已知平面垂直，故不存在E ，使得DE ⊥平面ABC ，故C 错误．故选D ．8．（2020•兖州区模拟）如图，在四棱锥P ABCD -中，底面ABCD 为菱形，60DAB ∠=︒，侧面PAD 为正三角形，且平面PAD ⊥平面ABCD ，则下列说法正确的是()A ．在棱AD 上存在点M ，使AD ⊥平面PMB B ．异面直线AD 与PB 所成的角为90︒C ．二面角P BC A --的大小为45︒D ．BD ⊥平面PAC 【答案】ABC【解析】如图所示，A ．取AD 的中点M ，连接PM ，BM ，连接对角线AC ，BD 相较于点O ．侧面PAD 为正三角形，PM AD ∴⊥．又底面ABCD 为菱形，60DAB ∠=︒，ABD ∴∆是等边三角形．AD BM ∴⊥．又PM BM M =．AD ∴⊥平面PMB ，因此A 正确．B ．由A 可得：AD ⊥平面PMB ，AD PB ∴⊥，∴异面直线AD 与PB 所成的角为90︒，正确．C ．平面PBC ⋂平面ABCD BC =，//BC AD ，BC ∴⊥平面PBM ，BC PB ∴⊥，BC BM ⊥．PBM ∴∠是二面角P BC A --的平面角，设1AB =，则BM PM ==，在Rt PBM ∆中，tan 1PMPBM BM∠==，45PBM ∴∠=︒，因此正确． D ．BD 与PA 不垂直，BD ∴与平面PAC 不垂直，因此D 错误．故选ABC ．9．（2020•某某模拟）如图所示，在四个正方体中，l 是正方体的一条体对角线，点M ，N ，P 分别为其所在棱的中点，能得出l ⊥平面MNP 的图形为()A ．B ．C ．D ．【答案】AD【解析】对于AD ．根据正方体的性质可得：l MN ⊥，l MP ⊥，可得l ⊥平面MNP ．而BC 无法得出l ⊥平面MNP ．故选AD ．10．（2020•某某市模拟）在三棱锥P ABC -中，4AB AC ==，120BAC ∠=︒，PB PC ==，平面PBC ⊥平面ABC ，则三棱锥P ABC -外接球的表面积为__________．【答案】80π【解析】如图，设ABC ∆的外接圆的圆心为1O ，连接1O C ，1O A ，1BCO A H =，连接PH ．由题意可得AH BC ⊥，且1122AH O A ==，12BH BC ==因为平面PBC ⊥平面ABC ，且PB PC =，所以PH ⊥平面ABC ，且6PH ．设O 为三棱锥P ABC -外接球的球心，连接1OO ，OP ，OC ，过O 作OD PH ⊥，垂足为D ，则外接球的半径R 满足222221114(6)R OO OO O H =+=-+，即221116(6)4OO OO +=-+，解得12OO =，从而220R =，故三棱锥P ABC -外接球的表面积为2480R ππ=．故答案为：80π．12．（2020•某某三模）已知四边长均为的空间四边形ABCD 的顶点都在同一个球面上，若3BAD π∠=，平面ABD ⊥平面CBD ，则该球的体积为__________．【解析】如图所示，设E 是ABD ∆的外心，F 是BCD ∆的外心，过E ，F 分别作平面ABD 与平面BCD 的垂线OE 、OF ，相交于O ；由空间四边形ABCD 的边长为3BAD π∠=，所以ABD ∆与BCD ∆均为等边三角形；又平面ABD ⊥平面CBD ，所以O 为四面体ABCD 外接球的球心；又2AE =，1OE =，所以外接球的半径为R =所以外接球的体积为334433R V ππ==⨯=． 13．（2020•某某模拟）在四棱锥S ABCD -中，底面四边形ABCD 为矩形，SA ⊥平面ABCD ，P ，Q 别是线段BS ，AD 的中点，点R 在线段SD 上．若4AS =，2AD =，AR PQ ⊥，则AR =__________．【解析】取SA 的中点E ，连接PE ，QE ．SA ⊥平面ABCD ，AB ⊂平面ABCD ，SA AB ∴⊥，而AB AD ⊥，AD SA A =，AB ∴⊥平面SAD ，故PE ⊥平面SAD ，又AR ⊂平面SAD ，PE AR ∴⊥．又AR PQ ⊥，PEPQ P =，AR ∴⊥平面PEQ ，EQ ⊂平面PEQ ，AR EQ ∴⊥．E ，Q 分别为SA ，AD 的中点，//EQ SD ∴，则AR SD ⊥，在直角三角形ASD 中，4AS =，2AD =，可求得SD =由等面积法可得AR ．．14．（2020•某某模拟）如图所示，在四棱锥P ABCD -中，底面ABCD 是菱形，3DAB π∠=，侧面PAD是等边三角形，且平面PAD ⊥平面ABCD ，E 为棱PC 上一点，若平面EBD ⊥平面ABCD ，则PEEC=__________．【答案】12【解析】取AD 的中点O ，连接OC 交BD 于F 点，连结EF ， //OD BC ，2BC OD =，2FC OF ∴=．平面PAD ⊥平面ABCD ，PO AD ⊥， PO ∴⊥平面ABCD ，又平面BDE ⊥平面ABCD ， //OP EF ∴，∴12PE OF EC FC ==．故答案为：12．15．（2020•某某二模）在几何体P ABC -中，PAB ∆是正三角形，平面PAB ⊥平面ABC ，且2AB BC ==，AB BC ⊥，则P ABC -外接球的表面积等于__________．【答案】283π【解析】PAB ∆是正三角形，所以三棱锥的外接球的球心一定在三角形PAB 的中心的垂线上，因为平面PAB ⊥平面ABC ，所以作GO ⊥平面PAB ，AB BC ⊥，外接球的球心也在平面ABC 的重心的垂线上，作OE ⊥平面ABC 交AC 于E ，O 为外接球的球心，由题意可知EC 123GD ==，外接球的半径为：OC ==外接球的表面积为：22843ππ⨯=．故答案为：283π．16．（2020•市中区校级模拟）如图，在四棱柱1111ABCD A B C D -中，底面ABCD 是边长为2的菱形，11AB CB =．（1）证明：平面11BDD B ⊥平面ABCD ；（2）若60DAB ∠=︒，△1DB B 是等边三角形，求点1D 到平面1C BD 的距离．【解析】（1）设AC 交BD 于E ，连接1B E ，如图四边形ABCD 为菱形，AC BD ∴⊥且点E 为AC 中点，在△1AB C 中，11AB CB =，AE CE =， 1B E AC ∴⊥， 1DBB E E =，BD ，1B E ⊂平面11BDD B ，AC ∴⊥平面11BDD B ， AC ⊂平面ABCD ，∴平面ABCD ⊥平面11BDD B ；（2）连接1BD ，11A C ，1C E ，在四棱柱1111ABCD A B C D -中，平面//ABCD 平面1111A B C D ，又由（1）可知，平面ABCD ⊥平面11BDD B ，∴平面1111A B C D ⊥平面11BDD B ，则1DD ⊥平面ABCD ，又BD ⊂平面ABCD ， 1DD BD ∴⊥，11AC ⊂平面1111A B C D ， 11AC ∴⊥平面11BDD B ，2AD AB ==，60DAB ∠=︒， DAB ∴∆为等边三角形， 2BD AB ∴==，△1DB B 为等边三角形，2BD AB ∴==，△1DB B 为等边三角形，12BB BD ∴==，又112DD BB ==，∴112222BDD S ∆=⨯⨯=，∴11111||132C BDD BDD AC V S -∆=⨯⨯=又1BB ⊥平面ABCD ，BC ⊂平面ABCD ， 1BB BC ∴⊥，12BB BD AB ===，2AB BC ==， 1BB BC ∴=，又因为四边形11BCC B 为平行四边形，∴四边形11BCC B 为正方形，11BC B C ∴=， 11C D BC ∴=，又E 为BD 中点，1C E BD ⊥，∴111||||2C BDSBD C E =111||||222BD C E ==⨯， ∴11112333D C BD C BDV S d -==，∴7d =所以点1D 到平面1C BD17．（2020•龙凤区校级模拟）如图，四棱锥P ABCD -中，//AB CD ，33AB CD ==，2PA PD BC ===，90ABC ∠=︒，且PB PC =．（1）求证：平面PAD ⊥平面ABCD ；（2）求点D 到平面PBC 的距离．【解析】（1）取AD 、BC 的中点分别为M 、E ，连结PM ，PE ，ME ，//AB CD ，33AB CD ==，∴四边形ABCD 为梯形，又M 、E 为AD 、BC 的中点，ME ∴为梯形的中位线，//ME AB ∴，又90ABC ∠=︒， ME BC ∴⊥，PB PC =，E 为BC 的中点 PE BC ∴⊥，又PE M E E =，PE ⊂平面PME ，ME ⊂平面PME ，BC ∴⊥平面PME ，又PM ⊂平面PME ，故PM BC ⊥，由PA PD =，M 为AD 中点，PM AD ∴⊥，又AD ，BC 不平行，必相交于某一点，且AD ，BC 都在平面ABCD 上，PM ∴⊥平面ABCD ，由PM ⊂平面PAD ，则平面PAD ⊥平面ABCD ．（2）由（1）及题意知，PM 为三棱锥P BCD -的高，AD =，2ME =，PM =故PE = 11222PBC S BC PE ∆=⨯=⨯1121122BCD S BC CD ∆=⨯=⨯⨯=，设点D 到平面PBC 的距离为h ，∴由等体积法知：111113333P BCD D BCP BCD PBC V V S PM S h h --∆∆==⨯=⨯=⨯=，解得h ，所以点D 到平面PBC ．18．（2020•某某模拟）如图，菱形ABCD 与正三角形BCE 的边长均为2，它们所在平面互相垂直，FD ⊥平面ABCD ．（1）求证：平面ACF ⊥平面BDF ；（2）若60CBA ∠=︒，求三棱锥E BCF -体积．【解析】（1）证明：在菱形ABCD 中，AC BD ⊥，FD ⊥平面ABCD ，FD AC ∴⊥．又BDFD D =，AC ∴⊥平面BDF ．而AC ⊂平面ACF ，∴平面ACF ⊥平面BDF ；（2）解：取BC 中点O ，连接EO ，OD ， BCE ∆为正三角形，EO BC ∴⊥，平面BCE ⊥平面ABCD 且交线为BC ，EO ∴⊥平面ABCD ．FD ⊥平面ABCD ，//EO FD ∴，得//FD 平面BCE ．E BCF F BCE D BCE E BCD V V V V ----∴===．122sin1202BCD S ∆=⨯⨯⨯︒EO =11133E BCF BCD V S EO -∆=⨯=．19．（2020•某某模拟）图1是直角梯形ABCD ，//AB CD ，90D ∠=︒，2AB =，3,2DC AD CE ED ===，以BE 为折痕将BCE ∆折起，使C 到达1C 的位置，且1AC =图2．（Ⅰ）证明：平面1BC E ⊥平面ABED ；（Ⅱ）求点B 到平面1AC D 的距离．【解析】（Ⅰ）证明：在直角梯形ABCD 中，由2,1,AB DE AD ===2EB EC BC ===．连接AC 交EB 与M 点，则ECM BAM ∆≅，M ∴为BE 的中点，则CM BE ⊥．∴1C M MA ==，又1C A =1C M MA ∴⊥，又1C M BE ⊥，BEAM M =，1C M ∴⊥平面ABED ，又1C M ⊂平面1C EB ，∴平面ABED ⊥平面1C EB ；（Ⅱ）解：设B 到平面1AC D 的距离为d ，则1113B AC DAC D V d S -=，又11111121332B AC D C ABD ABD V V S C M --∆==⨯=⨯⨯．DM AM ==1C M =，∴1C D =∴112AC DS==∴1113B AC D AC D V d S -====．即点B 到平面1AC D20．（2020•某某模拟）如图，在长方体ABCD HKLE -中，底面ABCD 是边长为3的正方形，对角线AC 与BD 相交于点O ，点F 在线段AH 上且20AF HF +=，BE 与底面ABCD 所成角为3π．（1）求证：AC BE ⊥；（2）M 为线段BD 上一点，且BM =AM 与BF 所成角的余弦值．【解析】（1）证明：因为在长方体ABCD HKLE -中，有DE ⊥平面ABCD ，所以DE AC ⊥，因为四边形ABCD 是正方形，所以AC BD ⊥，又BD DE D =，从而AC ⊥平面BDE ．而BE ⊂平面BDE ，所以AC BE ⊥．（2）因为在长方体ABCD HKLE -中，有BE 与平面ABCD 所成角为3π，由（1）知DBE ∠为直线BE 与平面ABCD 所成的角，所以3DBE π∠=，所以ED DB3AD =可知DE =所以AH =20AF HF +=，即13AF AH =，故AF =DE 上取一点G ，使13DG DE =，连接FG ，则在长方体ABCD HKLE -中，有////FG AD BC ，且FG AD BC ==，所以四边形FBCG 为平行四边形，所以//BF CG ，在BD 上取一点N ，使DN BM =，因为BM =BD =13DN BM BD ==，所以在正方形ABCD 中，ON OM =，所以CON AOM ∆≅∆，所以CNO AMO ∠=∠，所以//AM CN ，所以GCN ∠（或其补角）为异面直线AM 与BF 所成的角，在GNC ∆中，GC BF ==在AMB ∆中，由余弦定理得AM ==，则CN AM =GN ==在GNC ∆中，由余弦定理得：222cos 2GC NC GN GCN GC NC +-∠==．故异面直线AM 与BF ．21．（2020•某某模拟）如图所示，菱形ABCD 与正方形CDEF 所在平面相交于CD ．（1）求作平面ACE 与平面BCF 的交线l ．并说明理由；（2）若BD CF ⊥，求证：平面BDE ⊥平面ACE ．【解析】（1）过点C 作BF 的平行线l 即可，下面予以证明．由已知得，AB 和EF 都与CD 平行且相等，∴四边形ABFE 是平行四边形，//AE BF ∴，BF ⊂/平面ACE ，且AE ⊂平面ACE ，//BF ∴平面ACE ， BF ⊂平面BCE ，且平面ACE ⋂平面BCF l =，//BF l ∴．（2）证明：由CF BD ⊥，CF CD ⊥，且BD CD D =，CF ∴⊥平面ABCD ，AC ⊂平面ABCD ，CF AC ∴⊥，//DE CF ，DE AC ∴⊥，在菱形ABCD 中，BD AC ⊥，又DE BD D =，AC ∴⊥平面BDE ，AC ⊂平面ACE ，∴平面BDE ⊥平面ACE ．22．（2020•某某一模）如图，四棱锥E ABCD -中，底面ABCD 是平行四边形，60ADC ∠=︒，2CD AD =，EC ⊥底面ABCD ．（Ⅰ）求证：平面ADE ⊥平面ACE ；（Ⅱ）若2AD CE ==，求点C 到面ADE 的距离．【解析】（Ⅰ）证明：EC ⊥平面ABCD ，EC AD ∴⊥，又60ADC ∠=︒，2CD AD =，AD AC ∴⊥，AD ∴⊥平面ACE ，又AD ⊂平面ADE ，故平面ADE ⊥平面ACE ．（Ⅱ）设点C 到面ADE 的距离为h ，又C ADE F ACD V V --=，由（Ⅰ）可知AD ⊥平面ACE ，则AD AE ⊥，所以，111124223232h ⨯⨯⨯⨯=⨯⨯⨯，所以h =C 到面ADE。

高考数学专题八立体几何 4 直线、平面垂直的判定与性质课件文

B.平面ACD⊥平面BCD D.平面ACD⊥平面ABC
12/10/2021
解析 ∵在四边形ABCD中,AD∥BC,∠BCD=45°, ∴∠ADC=135°, ∵AD=AB,∠BAD=90°,∴∠ADB=45°, ∴∠BDC=90°,∴BD⊥CD. 又在四面体ABCD中,平面ABD⊥平面BCD,且平面ABD∩平面BCD=BD, ∴CD⊥平面ABD,∴CD⊥AB, 又AD⊥AB,AD∩CD=D,∴AB⊥平面ACD, 又AB⊂平面ABC,∴平面ABC⊥平面ADC.故选D.
α
a α
b
α
⇒a∥b
12/10/2021
2.面面垂直的判定和性质
类别
文字语言
判定两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直
图形语言
符号语言
∠AOB是二面角α-l-β的平面角,且∠AOB=90°, 则α⊥β
如果一个平面过另一个平面的垂线,则这两个平面互相垂直(即线面垂直⇒面面垂直)
l l
αβ⇒ α⊥β
12/10/2021
性质如果两个平面垂直,则其中一个平面内垂直于交线的直线垂直于另一个平面
如果两个相交平面同时垂直于第三个平面,那么它们的交线垂直于第三个平面
α α
β β
⇒ al⊥ α
l β
l a
α β⇒ l⊥l γ
α γ
β γ
12/10/2021
3.直线与平面所成的角 (1)斜线与平面所成的角的定义:平面的一条斜线和它在这个平面内的射影所成的锐角,叫做这条直线和这个平面所成的角. (2)当一条直线垂直于平面时,规定它们所成的角是直角;当一条直线和平面平行或在平面内时,规定它们所成的角大小为0°. (3)直线l与平面α所成角θ意得△ABC为等腰直角三角形,所以AE⊥BC,

2021高考数学一轮复习第8章立体几何8.5直线、平面垂直的判定和性质课件文

答案：B
4．[2020·郑州一中测试]已知两条不重合的直线 m，n 和两个不重合的平面 α，β，m⊥α，n⊂β.给出下列四个命题：
①若 α∥β，则 m⊥n；②若 m⊥n，则 α∥β；③若 m∥n，则 α⊥β； ④若 α⊥β，则 m∥n.
其中正确命题的个数是( ) A．0 B．1 C．2 D．3
解析：依题意，对于①，由“若一条直线与两个平行平面中的
6.垂直关系中的两个重要结论 (1)若两平行线中的一条垂直于一个平面，则另一条也垂直于这个平面． (2)若一条直线垂直于一个平面，则它垂直于这个平面内的任何一条直线(证明线线垂直的一个重要方法)．
二、必明 3 个易误点 1．证明线面垂直时，易忽视面内两条线为相交线这一条件． 2．面面垂直的判定定理中，直线在面内且垂直于另一平面易忽视． 3．面面垂直的性质定理在使用时易忘面内一线垂直于交线而盲目套用造成失误．
【知识重温】
一、必记 6 个知识点 1．直线与平面垂直 (1)定义：直线 l 与平面 α 内的①_任__意__一条直线都垂直，就说直线 l 与平面 α 互相垂直．
(2)判定定理与性质定理文字语言
图形语言
一条直线与一个平
判定定理
面内的两条相交直线都垂直，则该直线
与此平面垂直
性质定理
垂直于同一个平面的两条直线平行
符号语言
a，b⊂α
②a_∩__b_＝__O__
l⊥a
l⊥b
⇒l⊥α
③___ab__⊥ ⊥____αα___⇒ a∥b
2.直线和平面所成的角 (1)定义：平面的一条斜线和它在平面上的射影所成的④_锐__角__ 叫做这条直线和这个平面所成的角，一条直线垂直于平面，则它们所成的角是直角；一条直线和平面平行或在平面内，则它们所成的角是 0°的角． (2)范围：0，2π.

2020届高考数学一轮复习第八章立体几何8.4直线、平面垂直的判定和性质教师用书(PDF,含解析)

＝
｜
｜Ｂ→Ｄ·ｎ｜Ｂ→Ｄ｜ · ｜ｎ
｜
＝
２３
，
２ ∴ 直线ＢＤ与平面ＡＤＦ所成角的正弦值为３．
（１５分）
１－１（２０１８浙江绍兴高三３月适应性模拟，１９）如图，在三
第八章立体几何９５
§ ８．４直线、平面垂直的判定和性质
��
（１３分）
设直线
ＢＤ
与平面
ＡＤＦ
所成的角为
θ，则ｓｉｎ
θ＝
２３
．
（
１５
分）
解法二：以Ａ为原点，建立如图所示的空间直角坐标系，设
ＡＤ＝ＡＢ＝ＢＣ＝
１２
ＤＣ
＝
１，则Ａ（
０，０，０）
，Ｂ
（
０，１，０
）
，
Ｃ
æ
ç
Hale Waihona Puke è３２，
３２
，０
ö
÷
，
ø
Ｄ
æ
ç
３，－
１
，０
ö
÷
．
è２２ ø
（８分）
＝
即０，
í îïï
３３
ａ＋
６３
ｃ
＝
０，
令ａ＝２，则ｂ＝６，ｃ＝－１，即ｎ＝（２，６，－１），（１３分）

浙江专用2021届高考数学一轮复习专题八立体几何8.4直线平面垂直的判定与性质试题含解析

§8。

4 直线、平面垂直的判定与性质基础篇固本夯基【基础集训】考点一直线与平面垂直的判定与性质1。

已知m和n是两条不同的直线,α和β是两个不重合的平面,下面给出的条件中一定能推出m⊥β的是()A。

α⊥β且m⊂α B.α⊥β且m∥αC。

m∥n且n⊥β D.m⊥n且n∥β答案C2.下列命题中错误的是（）A.如果平面α外的直线a不平行于平面α，则平面α内不存在与a平行的直线B.如果平面α⊥平面γ，平面β⊥平面γ,α∩β=l,那么直线l⊥平面γC。

如果平面α⊥平面β,那么平面α内所有直线都垂直于平面βD.一条直线与两个平行平面中的一个平面相交，则必与另一个平面相交答案C3.如图，PA⊥圆O所在的平面,AB是圆O的直径，C是圆O上一点，E、F分别是A在PB、PC上的射影，给出下列结论：①AF⊥PB；②EF⊥PB;③AF⊥BC;④AE⊥平面PBC.其中正确命题的序号是.答案①②③4.《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑。

如图，在阳马P-ABCD中，侧棱PD⊥底面ABCD,且PD=CD，过棱PC的中点E，作EF⊥PB交PB于点F，连接DE,DF,BD，BE。

证明：PB⊥平面DEF.试判断四面体DBEF是不是鳖臑，若是,写出其每个面的直角（只需写出结论）;若不是，说明理由.解析因为PD⊥底面ABCD，所以PD⊥BC，由底面ABCD为长方形,得BC⊥CD,因为PD∩CD=D,所以BC⊥平面PCD,因为DE⊂平面PCD,所以BC⊥DE。

又因为PD=CD，点E是PC的中点,所以DE⊥PC.因为PC∩BC=C，所以DE⊥平面PBC。

因为PB⊂平面PBC,所以PB⊥DE.又PB⊥EF,DE∩EF=E，所以PB⊥平面DEF.由DE⊥平面PBC,PB⊥平面DEF，可知四面体BDEF的四个面都是直角三角形,即四面体DBEF是一个鳖臑,其四个面的直角分别为∠DEB,∠DEF，∠EFB,∠DFB.考点二平面与平面垂直的判定与性质5.如图，四棱锥P-ABCD中，PA⊥底面ABCD,底面ABCD为正方形，给出下列结论:①AD∥平面PBC;②平面PAC⊥平面PBD；③平面PAB⊥平面PAC；④平面PAD⊥平面PDC.其中正确结论的序号是.答案①②④6.如图，在三棱锥P-ABC中，PA⊥AB,PA⊥BC，AB⊥BC，PA=AB=BC=2,D为线段AC的中点，E为线段PC上一点.（1)求证：PA⊥BD；（2）求证:平面BDE⊥平面PAC;（3）当PA∥平面BDE时,求三棱锥E-BCD的体积。

高考数学复习第八章立体几何8.4直线平面垂直的判定与性质文市赛课公开课一等奖省名师优质课获奖PPT课

1 2 3 4 5 6 7 8 9 10 11 12 13 49/72
2.(·常州模拟)设m、n是两条不一样直线，α、β是两个不一样平面，则以下命题正确是_____.③ ①若m⊥n，n∥α，则m⊥α； ②若m∥β，β⊥α，则m⊥α； ③若m⊥β，n⊥β，n⊥α，则m⊥α； ④若m⊥n，n⊥β，β⊥α，则m⊥α.
证实
27/72
引申探究 1.在本例条件下，证实：平面EMN⊥平面PAC. 证实
因为AB⊥PA，AB⊥AC，且PA∩AC＝A，PA⊂平面PAC，AC⊂平面PAC，所以AB⊥平面PAC. 又MN∥CD，CD∥AB，所以MN∥AB，所以MN⊥平面PAC. 又MN⊂平面EMN，所以平面EMN⊥平面PAC.
12/72
4.(·徐州模拟)α、β是两个不一样平面，m、n是平面α及平面β之外两条不一样直线，给出四个论断：①m⊥n；②α⊥β；③n⊥β；④m⊥α，以其中三个论断作为条件，剩下一个论断作为结论，写出你认为正确一个命题：_________可__填__①__③__④__⇒_②__与__②__③__④__⇒__①__中_.一个
19/72
跟踪训练 1 (·江苏 ) 如图，在直三棱柱 ABCA1B1C1中，已知AC⊥BC，BC＝CC1.设AB1中点为D，B1C∩BC1＝E. 求证：(1)DE∥平面AA1C1C；
证实
由题意知，E为B1C中点，又D为AB1中点，所以DE∥AC. 又因为DE⊄平面AA1C1C，AC⊂平面AA1C1C，所以DE∥平面AA1C1C.
1 2 3 4 5 6 7 8 9 10 11 12 13 51/72
4.如图，三棱柱ABC－A1B1C1中，侧棱AA1垂直底面A1B1C1，底面三角形A1B1C1是正三角形，E是BC中点，则以下叙述正确是___③_. ①CC1与B1E是异面直线； ②AC⊥平面ABB1A1； ③AE与B1C1是异面直线，且AE⊥B1C1； ④A1C1∥平面AB1E.

高考数学复习第八章立体几何8.5直线平面垂直的判定与性质文新人教B版市赛课公开课一等奖省名师优质课获

√5.
故三棱锥 E-ACD 的侧面积为 3+2√5.
21/45
-22考点1
考点2
考点3
解题心得1.两个平面相互垂直是两个平面相交特殊情形.
2.由平面和平面垂直判定定理可知,要证实平面与平面垂直,可转
化为从现有直线中寻找平面垂线,即证实线面垂直.
3.平面和平面垂直判定定理两个条件:l⊂α,l⊥β,缺一不可.
-26考点1
考点2
考点3
考点 3
平行与垂直的综合问题(多考向)
考向一平行与垂直关系证实
例3如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC中点,点F在
侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.
求证:(1)直线DE∥平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
思索处理平行与垂直关系综合问题主要数学思想是什么?
(1)若P到△ABC三边距离相等,且O在△ABC内部,则O是△ABC
心;
(2)若PA⊥BC,PB⊥AC,则O是△ABC
心;
(3)若PA,PB,PC与底面所成角相等,则O是△ABC
心.
关闭
(1)P到△ABC三边距离相等,且O在△ABC内部,可知O到△ABC三边距离
相等,即O是△ABC内心;(2)由PO⊥平面ABC且BC⊂平面ABC,得PO⊥BC,
形,∠DAB=45°,PD⊥平面ABCD,PD=AD=1,点E为AB上一点,且
由 BE⊥平面 ABCD,知△EBG 为直角三角形,可得
√2
BE= x.
2
20/45
-21考点1
考点2
考点3
由已知得,三棱锥 E-ACD 的体积
1 1
√6 3 √6

高考数学异构异模复习第八章立体几何课时撬分练8.4直线平面垂直的判定与性质文

2018高考数学异构异模复习考案第八章立体几何课时撬分练8.4直线、平面垂直的判定与性质文时间：45分钟基础组1.[2016·冀州中学猜题]设m，n是两条不同的直线，α，β是两个不同的平面，则下列命题正确的是( )A．m∥α，n∥β，且α∥β，则m∥nB．m⊥α，n⊥β，且α⊥β，则m⊥nC．m∥α，n⊂β，m⊥n，则α⊥βD．m⊂α，n∥α，m∥β，n∥β，则α∥β答案B解析对于A，m，n的位置关系应该是平行、相交或异面，故A不正确；对于B，由面面垂直及线面垂直的性质知，m⊥n，故B正确；对于C，α与β还可以平行或相交，故C不正确；对于D，α与β还可以相交，所以D不正确．故选B.2．[2016·武邑中学仿真]已知不同直线m、n及不重合平面α、β给出下列结论：①m⊂α，n⊂β，m⊥n⇒α⊥β②m⊂α，n⊂β，m∥n⇒α∥β③m⊂α，n⊂β，m∥n⇒α∥β④m⊥α，n⊥β，m⊥n⇒α⊥β其中的假命题有( )A．1个 B．2个C．3个 D．4个答案C解析①为假命题，m不一定与平面β垂直，所以平面α与β不一定垂直．命题②与③为假命题，②中两平面可以相交，③α与β可能相交．只有④是真命题，因为两平面的垂线所成的角与两平面所成的角相等或互补．3．[2016·衡水中学模拟]设l、m、n均为直线，其中m、n在平面α内，则“l⊥α”是“l⊥m且l⊥n”的( )A．充分不必要条件 B．必要不充分条件C．充要条件 D．既不充分也不必要条件答案A解析当l⊥α时，l⊥m且l⊥n.但当l⊥m，l⊥n时，若m、n不是相交直线，则得不到l⊥α.即l⊥α是l⊥m且l⊥n的充分不必要条件．故选A. 4．[2016·冀州中学期中]已知m和n是两条不同的直线，α和β是两个不重合的平面，那么下面给出的条件中一定能推出m⊥β的是( )A．α⊥β，且m⊂α B．m∥n，且n⊥βC．α⊥β，且m∥α D．m⊥n，且n∥β答案B解析根据定理、性质、结论逐个判断．因为α⊥β，m⊂α，则m，β的位置关系不确定，可能平行、相交、m在β面内，故A错误；由线面垂直的性质定理可知B正确；若α⊥β，m∥α，则m，β的位置关系也不确定，故C错误；若m⊥n，n∥β，则m，β的位置关系也不确定，故D错误．5．[2016·衡水中学仿真]设平面α与平面β相交于直线m，直线a在平面α内，直线b在平面β内，且b⊥m，则“α⊥β”是“a⊥b”的( )A．充分不必要条件 B．必要不充分条件C．充分必要条件 D．既不充分也不必要条件答案A解析若α⊥β，因为α∩β＝m，b⊂β，b⊥m，所以根据两个平面垂直的性质定理可得b⊥α，又a⊂α，所以a⊥b；反过来，当a∥m时，因为b⊥m，一定有b⊥a，但不能保证b⊥α，所以不能推出α⊥β. 6．[2016·枣强中学预测]PA垂直于正方形ABCD所在平面，连接PB，PC，PD，AC，BD，则下列垂直关系正确的是( )①平面PAB⊥平面PBC；②平面PAB⊥平面PAD；③平面PAB⊥平面PCD；④平面PAB⊥平面PAC.A．①② B．①③C．②③ D．②④答案A解析易证BC⊥平面PAB，则平面PAB⊥平面PBC.又AD∥BC，故AD⊥平面PAB，则平面PAD⊥平面PAB. 7．[2016·冀州中学一轮检测]如图所示，在四棱锥P－ABCD中，PA⊥底面ABCD，且底面各边都相等，M是PC上的一动点，当点M满足________时，平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可)答案DM⊥PC(答案不唯一)解析由定理可知，BD⊥PC.∴当DM⊥PC时，即有PC⊥平面MBD，而PC⊂平面PCD，∴平面MBD⊥平面PCD. 8．[2016·武邑中学一轮检测]已知a、b、l表示三条不同的直线，α、β、γ表示三个不同的平面，有下列四个命题：。

高考数学异构异模复习第八章立体几何8.4直线平面垂直的判定与性质课件文

① 根据课堂提问抓住老师的思路。老师在讲课过程中往往会提出一些问题，有的要求回答，有的则是自问自答。一般来说，老师在课堂上提出的问题都是学习中的关键，若能抓住老师提出的问题深入思考，就可以抓住老师的思路。
② 根据自己预习时理解过的逻辑结构抓住老师的思路。老师讲课在多数情况下是根据教材本身的知识结构展开的，若把自己预习时所理解过的知识逻辑结构与老师的讲解过程进行比较，便可以抓住老师的思路。
(2)证明：①因为平面 PAD⊥底面 ABCD，且 PA 垂直于这两个平面的交线 AD，所以 PA⊥底面 ABCD.
②因为 AB∥CD，CD＝2AB，E 为 CD 的中点，所以 AB∥DE，且 AB＝DE. 所以四边形 ABED 为平行四边形．所以 BE∥AD. 又因为 BE⊄平面 PAD， AD⊂平面 PAD，所以 BE∥平面 PAD. ③因为 AB⊥AD，而且四边形 ABED 为平行四边形，所以 BE⊥CD，AD⊥CD. 由①知 PA⊥底面 ABCD.
由题设知△AHB≌△DHB，所以 AH＝DH，∴∠ADH＝45°，
所以直线 AD 与平面 BCD 所成的角为 45°. (2)过 H 作 HR⊥BD，垂足为 R，连接 AR，因为 AH⊥平面 BCD，所以 AH⊥BD，AH∩HR＝H，所以 BD⊥平面 AHR，所以 BD⊥AR.
故∠ARH 为二面角 A－BD－C 的平面角的补角，
(3)垂直问题的转化关系
命题法 2 求线面角、二面角典例 2 已知△ABC 和△DBC 所在的平面互相垂直，且 AB＝BC＝BD，∠CBA＝∠DBC＝120°，求：
(1)直线 AD 与平面 BCD 所成角的大小； (2)二面角 A－BD－C 的余弦值． [解] (1)如图，在平面 ABC 内，过 A 作 AH⊥BC，交 CB 的延长线于 H，连接 DH，则 AH⊥平面 DBC，所以∠ADH 即直线 AD 与平面 BCD 所成的角，

高考数学一轮总复习专题8 立体几何 8.4 直线、平面垂

5.平面与平面垂直
(1)定义:一般地,平面α和β相交,如果它们所成的二面角是③直二面角 ,
就说这两个平面互相垂直.记作α⊥β.
(2)判定定理:一个平面经过另一个平面的④ 一条垂线 ,则这两个平
a α
面互相垂直.符号表示为
a

β
⇒β⊥α.

二、线面、面面垂直的性质 1.直线与平面垂直的性质定理同⑤ 垂直于一个平面的两直线平行. 2.直线与平面所成的角(设为θ) (1)斜线与平面所成的角的定义:平面的一条斜线和它在这个平面内的 ⑥ 射影所成的锐角,叫做这条直线和这个平面所成的角. (2)当一条直线垂直于平面时,规定它们所成的角是⑦ 直角 ;当一条直线和平面平行或在平面内时,规定它们所成的角为⑧ 0° 的角.
高考数学（浙江专用）
8.4 直线、平面垂直的判定和性质
考点
考点清单
垂直的判定和性质
考向基础一、线面、面面垂直的判定 1.直线与平面垂直 (1)定义:如果一条直线和一个平面相交,并且和这个平面内的①任意一条直线都垂直,则称这条直线和这个平面互相垂直. (2)判定定理:如果一条直线和一个平面内的② 两条相交直线都垂直,那么这条直线垂直于这个平面;用数学符号表示为:已知m⊂α,n⊂α,m ∩n=B,l⊥m,l⊥n,则l⊥α.
αβ
直.符号表示为αa βα

l

⇒a⊥β.
a l
4.二面角的概念及计算
ቤተ መጻሕፍቲ ባይዱ
(1)从一条直线出发的两个半平面所组成的图形叫做二面角 .这
条直线叫做二面角的棱,这两个半平面叫做二面角的面.
棱为AB,面分别为α、β的二面角记作二面角α-AB-β,如果棱为l,那么这个