2020届神州智达高三诊断性大联考一理综试题答案解析
2.2020届高三第一次在线大联考(新课标I卷)物理(全解全析)

2020届高三第一次在线大联考(新课标I 卷)理科综合(物理) 全解全析1.B 【解析】I 轴左侧的图线表示电场力对逸出的光电子做负功,A 极接的是电池的负极,即开关S 应扳向2,选项A 错误;逸出功W 0仅由阴极金属本身的性质决定,与入射光频率v 无关,选项C 错误;根据动能定理有:–eU c =0–E km ,根据光电效应方程有:E km =hv –W 0,得:光子能量hv=W 0+eU c ,由图乙知:b 光照射时的遏止电压U c1大于a 光照射时的遏止电压U c2,则b 光的光子能量大于a 光的光子能量,b 光照射阴极时逸出的光电子最大初动能大于a 光照射阴极时逸出的光电子最大初动能,选项B 正确,D 错误。
2.D 【解析】0~3 s 内,质点运动的路程为3.27 m+(3.27–2) m =4.54 m ,选项A 错误;根据“位移–时间图象切线的斜率表示速度”知:0~1 s 内,质点做匀速运动,1~3 s 内,质点先做减速运动后做加速运动,选项B 错误;1~5 s 内,质点的位移为零,平均速度为零,选项C 错误;根据对称性知:1 s 末的速度与3 s 末的速度等值反向,由于1 s 末,质点的速度大小为2 m/s ,故3 s 末质点的速度大小为2 m/s ,选项D 正确。
3.D 【解析】只有静止同步轨道卫星是相对于地面静止的,选项A 错误;卫星环绕速度v =半径越大线速度越小,除近地卫星外,运行速度均小于第一宇宙速度,选项B 错误;静止同步轨道卫星绕地心运行,相对地面静止(同周期,与赤道共面,且自西向东转),有向心加速度,选项C 错误;卫星的向心加速度2GMa r=,当r R =地球时,a g =,r R >地球,a g <,选项D 正确。
4.B 【解析】物体刚滑上传送带时做减速运动,加速度大小为1sin cos 78mg mg a g m θμθ+==,当物体的速度与传送带的速度相等时,摩擦力方向改变,由于mg sin θ>μmg cos θ,物体继续做减速运动,加速度大小为21sin cos 18mg mg a g a m θμθ-==<,“恰能到达传送带顶端B ”表明物块到达顶端B 时的速度大小为零,综上分析可知选项B 正确。
2020届神州智达高三诊断性大联考英语试题解析(高清)

t#yMNE{|> )$%$* b R xI}z#IL~I}%
!
"#$ %&'()*+,'$-.$+./010234&56+ N15A6;04205,I065;42=EK/2<>2=E3#30/<A4/653,6.,=/.5=43KB0;6D2=E=;4/6;<6,0@230;<<5> )J,0@X0/4;60124504/65*#;46;>242,= -241,D56'#"""B5;63$F,.5I;.,/3#,41563<244<5@=,-=#
,=5,I415 E65;4534465;3/653 ,I %/>>1234;642= 415 -,6<> I6,. -1201 B,/ 0;= 46;05415 >5D5<,A.5=4,I*12=535;64,D56##"""B5;63I6,. ,=5>B=;34B4,415=5?4K50;/355;01>B=;34B
)$N,5=0,/6;E5012<>65=4,65;>$
%$N,A6,45044155=D26,=.5=4$
*$N,3;D5.,=5BI,6415A,,6$ !"$:1;423415A6535=4324/;42,=,I415.,K2<5<2K6;6B
)$W41;3E,4415E,D56=.5=4O33/AA,64$
[ I J E K ; 6 O C D 6 E F G C D \ ] 1 G ^ _
&$- ] ` a P ; \ ] 1 b 6 E F . c d H
理科综合-2020年3月高三第一次在线大联考(新课标Ⅰ卷)(全解全析)

糖体的组成部分,C 选项错误;蛋白质中氨基酸发生改变也包括氨基酸的种类发生变化,D 选项错误。
4.A 【解析】由图可知,竞争性抑制剂与底物的结构有的部位相同,A 选项错误;酶只能催化一种或一类
化学反应,B 选项正确;正是因为有酶的存在,细胞代谢才能在温和条件下快速进行,C 选项正确;由
图可以判断,非竞争性抑制剂可以改变酶的结构,D 选项正确。
数酶是蛋白质,少数酶是 RNA,少数酶的形成只需通过转录即可,C 选项正确;细胞凋亡是有关调亡的
基因选择性表达的过程,所以有转运 RNA 参与,D 选项错误。
3.B 【解析】碱基对的增添、缺失、替换都可以导致基因突变,A 选项错误;a2 和 a1 分布在一对同源染色
体的同一位置,控制相对性状,是一对等位基因,B 选项正确;a1 基因表达时需要核糖体,rRNA 是核
11.B 【解析】钙与水能够剧烈反应,所以,左室中的 LiPF6−LiAsF6 电解质一定为非水电解质,Li2SO4 溶 液为右室中的电解质溶液,它们的主要作用都是传递离子,形成电流,构成闭合回路,A 正确;放电 时,负极反应为:Ca−2e−===Ca2+,使左室中正电荷数目增多,锂离子导体膜只允许 Li+通过,使 LiPF6−LiAsF6 电 解 质 中 的 Li+ 通 过 锂 离 子 导 体 膜 移 入 右 室 , 正 极 反 应 为 : Li1−xFePO4 + xLi+ + xe−===LiFePO4,电极发生 Li+嵌入,B 错误;充电时,阳极发生:LiFePO4−xe−===xLi++Li1−xFePO4,电 极发生 Li+脱嵌,阴极发生:Ca2++2e−===Ca,转移 0.2 mol 电子时,有 0.2 mol Li+从右室通过锂离子导 体膜移入左室,左室电解质中有 0.1 mol Ca2+得电子生成 Ca 沉积在钙电极上,故左室中电解质的质量 减轻 40×0.1 g −7×0.2 g =2.6 g,C、D 正确。
2020届全国大联考高三联考-理科综合(A)物理试题(带答案解析)

2020届全国大联考高三1月联考理科综合(A)物理试题第I卷(选择题)一、单选题1.“复兴号”动车组在京沪高铁率先实现350公里时速运营,我国成为世界上高铁商业运营速度最高的国家。
一列“复兴号”正在匀加速直线行驶途中,某乘客在车厢里相对车厢以一定的速度竖直向上抛出一个小球,则小球()A.在最高点对地速度为零B.在最高点对地速度最大C.落点位置与抛出时车厢的速度大小无关D.抛出时车厢速度越大,落点位置离乘客越远2.一跳伞运动员从悬停的直升飞机上跳下,2s时开启降落伞,运动员跳伞过程中的v-t 图象如图所示,根据图象可知运动员()A.在2~6s内速度方向先向上后向下B.在2~6s内加速度方向先向上后向下C.在2~6s内先处于失重状态后处于超重状态D.在0~20s内先匀加速再匀减速最终匀速直线运动3.如图,△abc中bc=4cm,∠acb=30°。
匀强电场的电场线平行于△abc所在平面,且a、b、c点的电势分别为3V、-1V、3V。
下列说法中正确的是()A.电场强度的方向沿ac方向B.电场强度的大小为2 V/cmC.电子从a点移动到b点,电势能减少了4 eVD.电子从c点移动到b点,电场力做功为4 eV4.用两根细线系住一小球悬挂于小车顶部,小车在水平面上做直线运动,球相对车静止。
细线与水平方向的夹角分别为α和β(α>β),设左边细线对小球的拉力大小为T1,右边细线对小球的拉力大小为T2,重力加速度为g,下列说法正确的是()A.若T1=0,则小车可能在向右加速运动B.若T2=0,则小车可能在向左减速运动C.若T1=0,则小车加速度大小为gtanβD.若T2=0,则小车加速度大小为gsinα5.两物体分别在某行星表面和地球表面上由静止开始自由下落相同的高度,它们下落的时间之比为2:3.已知该行星半径约为地球的2倍,则该行星质量与地球质量之比约为()A.9:1 B.2:9 C.3:8 D.16:9二、多选题6.如图,C为中间插有电介质的电容器,b极板与静电计金属球连接,a极板与静电计金属外壳都接地。
高考试题1-20三联考(一-理科综合参考答案_高考试题1

间连丝是高等植物细胞间信息交流的通道,而不是遗传信息交流的通道,
B 错误;多细胞生物体
内细胞间的功能协调不仅依赖于信息交流,还依赖于物质交换和能量供应,
C 错误;细胞骨架位
于细胞内,不属于细胞间的信息交流,
D 错误.
2.
D ② 为 mRNA,在真核细胞内基因上存在非编 码 区 和 内 含 子 等 非 编 码 序 列,所 以 ② 的 碱 基 总
息,
两
个
原电池左
2 mo
lL
i
a
2 mo
lL
i
Cl
D
侧均为正极,所以二者外电路中电子流动方向均为从右到左,正确.
-
-
-
OH )和c(
CH3COO )越 大、
CH3COOH)越 小,则 l
13
C pH 越大c(
c(H+ )和 c(
gc(OH )、
-
-
+
l
c(
c(H+ )、
c(
c(
CH3COO )增大,
辐射出的光的能量,根据光电效应发生的条件可 知,若 氢 原 子 从 n=6 能 级 向 n=1 能 级 跃 迁
时辐射出的光不能使某金属发生光电效应,则氢原子从 n=6 能级向 n=2 能级跃迁时辐射 出
的光也不能使该金属发生光电效应,故 D 错误.
15
C 物体在 A 点处于平衡状态,从 B 到 A 过 程 中,弹 簧 弹 力 大 于 重 力,根 据 牛 顿 第 二 定 律 可
子核内发生β 衰变,其中的中子转化为质子而放出的电子,故 B 错误;根据量子说守 恒 与 电 荷
37
137
数守恒可知,核反应方程式1
2020届神州智达高三诊断性大联考(一)数学(理)质检卷解析

绝密★启用前2020届神州智达高三诊断性大联考(一)数学(理)质检卷注意事项:1、答题前填写好自己的姓名、班级、考号等信息 2、请将答案正确填写在答题卡上 一、单选题1.已知集合{}{}*2,1,0,1,2N 129xA B x =--=∈<<,,则A B =I ( )A .{}1,0,1,2-B .{}1,0,1-C .{}1,1,2-D .{}1,2答案D由题意{}1,2,3B =,再由集合交集的概念可直接得解. 解:{}{}*N 1291,2,3x B x =∈<<=,∴{}{}{}2,1,0,1,21,21,32,A B --==I I . 故选:D. 点评:本题考查了指数不等式的求解,考查了集合交集的概念,属于基础题. 2.已知命题p :复数121i z i-=+的虚部是32-,命题q :复数()()21243i i i +-=-,以下命题真假判断正确的是( ) A .p 真q 真 B .p 真q 假C .p 假q 真D .p 假q 假答案A由复数的除法法则和虚部的概念可判断命题p ,由复数的乘法运算法则可判断命题q ,即可得解. 解:因为()()()()121121311122i i i z i i i i ----===-++-,所以其虚部为32-,所以p 为真命题; 因为()()221224243i i i i i i +-=-+-=-,所以q 为真命题.故选:A. 点评:本题考查了复数的运算和虚部的概念,考查了命题真假性的判断,属于基础题. 3.已知各项均为正数的等比数列{}n a 中,12a =,前三项的和为26,则4a =( )A .36B .48C .54D .64答案C设等比数列{}n a 的公比为q ,由题意可得222226q q ++=,解方程求得3q =即可得解. 解:Q 数列{}n a 为各项均为正数等比数列,12a =,前三项的和为26,设等比数列{}n a 的公比为q ,∴222226q q ++=,解得3q =或4q =-(舍),所以34154a a q ==. 故选:C. 点评:本题考查了利用等比数列的通项公式进行基本量计算,属于基础题.4.已知0.50.50.70.50.3log 0.2a b c ===,,,则a b c ,,的大小关系是( ) A .c a b << B .b a c << C .c b a << D .a b c <<答案B由对数函数和幂函数的单调性可得1b a c <<<,即可得解. 解: 因为0.5y x=在(0,)+∞上是增函数,所以0.50.50.50.30.51<<,即1b a <<,因为0.7log y x =在(0,)+∞上是减函数,所以0.70.7log 0.2log 0.71c =>= 所以1b a c <<<. 故选:B. 点评:本题考查了利用对数函数和幂函数的单调性比较大小,属于基础题.5.阳马,中国古代算数中的一种几何形体,是底面长方形,两个三角面与底面垂直的四棱锥体,在阳马P ABCD -中,PC 为阳马P ABCD -中最长的棱,1,2,3AB AD PC ===,若在阳马P ABCD -的外接球内部随机取一点,则该点位阳马内的概率为( ) A .127πB .427πC .827πD .49π答案C由题意知PC 的长等于其外接球的直径,可知2PA =,计算棱锥的体积,球的体积,根据古典概型即可求解. 解:根据题意,PC 的长等于其外接球的直径,因为222PC PA AB AD =++,∴2314PA =++,∴2PA =,又PA ⊥平面ABCD ,所以314431223332P ABCDV V π-⎛⎫=⨯⨯⨯==⨯ ⎪⎝⎭球,, ∴3483274332P ππ==⎛⎫⨯ ⎪⎝⎭. 点评:本题主要考查了棱锥的外接球,棱锥的体积,球的体积,古典概型,属于中档题.6.已知1sin 63πα⎛⎫+= ⎪⎝⎭,则sin 26πα⎛⎫-= ⎪⎝⎭( )A .89B .89-C .79D .79-答案C利用诱导公式和余弦的二倍角公式可得2sin 212sin 66ππαα⎛⎫⎛⎫-=-+ ⎪ ⎪⎝⎭⎝⎭,即可得解.解:由题意227sin 2sin 2cos 212sin 16233699πππππαααα⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫-=-+=+=-+=-= ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦.故选:C 点评:本题考查了三角函数的以值求值,考查了诱导公式和余弦的二倍角公式的应用,属于基础题.7.函数()21x xe ef x x --=-的图象大致是( )A .B .C .D .答案C根据函数的性质对比图象的特征,逐项排除即可得解. 解:由()()2121x x x xe e e ef x f x x x -----==-=---,∴()f x 为奇函数,排除选项B ; 当14x =时,11440x x e e e e ---=->,210x -<,∴()0f x <,排除选项D ; 当()2,x ∈+∞时,()21x xe ef x x --=-,则()()()()()()()()22212230222111xx x xxxe e x e e e x ef x x x x ---+----+'==>--+∴()f x 在()2,x ∈+∞时单调递增,排除选项A. 故选:C. 点评:本题考查了函数图象的识别,考查了函数奇偶性和利用导数判断函数单调性的应用,属于中档题.8.执行如图所示的程序框图,若输出的10232512iS S S -==+,则判断框内可以为( )A .10?i <B .10?i ≤C .11?i <D .11?i ≤答案A根据程序框图,注意变量取值的变化,可得1023512S =时10i =,即可得解. 解:第一次运行时,13122S -=+=,2i =; 第二次运行时,1271224S --=++=,3i =;第三次运行时,1231512228S ---=+++=,4i =;第四次运行时,1234311222216S ----=++++=,5i =;…,以此类推,第九次运行时,1012349112102312222212512S --------=+++++⋅⋅⋅+==-,10i =,依题意,此时刚好不满足判断条件,因此判断条件可以为10i <. 故选:A. 点评:本题考查了当型循环结构程序框图的应用,属于基础题. 9.()5221x x --的展开式中2x 的系数为( ) A .400 B .120C .80D .0答案D变形已知为()525521(1)(21)x x x x --=-+,分别写出两个二项式展开式的通项55(1)r r r C x --,55C (2)kk x -,可知()525521(1)(21)x x x x --=-+的通项为510()55(1)2r k r k k r C C x --+-,即可求解.解: ∵()525521(1)(21)x x x x --=-+,二项展开式5(1)x -的通项为55(1)r r r C x --,二项展开式5(21)x +的通项式为5555C (2)(1)(21)kkx x x --+,的通项为510()55(1)2r k r k k r C C x --+-,所以8k r +=,所以展开式中2x 的系数为5253444355555553(1)2(1)2(1)0C C C C C C -+-+-=.点评:本题主要考查了二项展开式的通项,利用通项求二项式的特定项,属于难题. 10.如图,在棱长为1的正方体1111ABCD A B C D -中,P 为线段1BC 上的动点(不含端点),则下列结论错误的是( )A .平面11D C P ⊥平面1C CPB .三棱锥1A D DP -的体积为定值C .11AD D P ⊥ D .DP ⊥平面11D C P答案D由面面垂直的判定可判断A ;由11A D DP P D DA V V --=,再利用三棱锥体积公式可判断B ;由1A D ⊥平面11D C P ,再利用线面垂直的性质可判断C ;由反证法可判断D ;即可得解.解:在正方体中,显然有11D C ⊥平面1C CP ,又11D C ⊂平面11D C P , 所以平面11D C P ⊥平面1C CP ,故A 正确;三棱锥1A D DP -的体积满足11A D DP P D DA V V --=,因为P 到平面1D DA 的距离不变,1D DA △的面积不变,三棱锥1A D DP 一的体积为定值,故B 正确;在正方体中,显然有111A D D C ⊥,11A D BC ⊥,所以1A D ⊥平面11D C P ,。
2020届高三一模检测理综试题及答案

2019—2020学年度第一学期期末教学质量检测高三理科综合试卷注意事项:1.答卷前,考生务必将自己的姓名、考号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
可能用到的相对原子质量:H 1 C 12 N 14 O 16 Na 23 Fe 56一、选择题:本题共13个小题,每小题6分,共78分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列有关化合物的说法正确的是A.腺苷是构成ATP、DNA和RNA的组成成分B.多糖、脂肪和核酸都是由许多单体连接而成的生物大分子C.线粒体和叶绿体中的核酸彻底水解后得到6种有机小分子物质D.由C、H、O、N、S元素构成的化合物不能为胞吞和胞吐的过程直接供能2.2019年诺贝尔生理学或医学奖颁给揭示细胞感知和适应氧气供应机制的研究者,这种特殊的分子机制能调节基因的活性来响应不同水平的氧气,调节过程如下图。
下列说法错误的是A.在不缺氧的情况下缺氧诱导因子蛋白HIF-1α通过过程[3][4][2]快速被降解B.缺氧时HIF-1α进入细胞核中与ARNT结合,启动红细胞生成因子基因的表达C.开发新型药物激活氧气调节机制促进过程[3][4][2]可使红细胞数量增加D.机体进行剧烈运动时肌肉可以通过[1]过程适应缺氧环境3.有丝分裂和减数分裂是遗传变异的细胞学基础,下列说法正确的是A.可以通过解离、漂洗、染色和制片观察植物根尖分生区细胞两种分裂中的染色体变异现象B.有丝分裂中着丝点的分裂伴随着相同基因的分离,减数分裂中着丝点的分裂伴随着等位基因的分离C.在两种分裂过程中,发生在非同源染色体之间的部分片段交换都会导致染色体结构变异D.在细胞分裂中AaBb变为AaB的原因是发生了基因突变中碱基对的缺失4.野生水稻植株高达2.5米,孕穗后种子发育期容易倒伏、造成减产,在水稻遗传育种的过程中,降低植株高度是育种面临的一个重要课题。
神州智达2020届高三诊断性大联考(一)理科数学质检卷I试题及答案

神州智达2020届高三诊断性大联考(一)理科数学(质检卷Ⅰ)班级___________ 姓名___________注意事项:1.考试时间120分钟,总共150分.2.答卷前,考生务必将自己的姓名、考号填涂在答题卡上.3.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上,写在本试卷上无效.4.考试结束后,将本试卷和答题卡一并交回.一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}{}*2,1,0,1,2N 129x A B x =--=∈<<,,则A B =I ( ) A.{}1,0,1,2-B.{}1,0,1-C.{}1,1,2-D.{}1,22.已知命题p :复数121i z i-=+的虚部是32-,题q :复数()()21243i i i +-=-,以下命题真假判断正确的是( ) A.p 真q 真B.p 真q 假C.p 假q 真D.p 假q 假3.已知各项均为正数的等比数列{}n a 中,12a =,前三项的和为26,则4a =( ) A.36B.48C.54D.644.已知0.50.50.70.50.3log 0.2a b c ===,,,则a b c ,,的大小关系是( ) A.c a b <<B.b a c <<C.c b a <<D. a b c <<5.阳马,中国古代算数中的一种几何形体,是底面为长方形,两个三角面与底面垂直的四棱锥体,在阳马P ABCD -中,PC 为阳马中最长的棱,123AB AD PC ===,,,若在阳马P ABCD -的外接球内部随机取一点P ,则P 位于阳马内的概率为( )A.127πB.427πC.827πD.49π6.已知1sin 63πα⎛⎫+= ⎪⎝⎭,则sin 26πα⎛⎫-= ⎪⎝⎭( )A.89B.89-C.79 D.79-7.函数()21x xe ef x x --=-的图象大致是( )A. B. C. D.8.执行如图所示的程序框图,若输出的1023512S =,则判断框内可以为( )A.10?i <B.10?i ≤C.11?i <D.11?i ≤9.()5221x x --的展开式中2x 的系数为( ) A.400B.120C.80D.010.如图,在棱长为1的正方体1111ABCD A B C D -中,P 为线段1BC 上的动点(不含端点),则下列结论错误的是( )A.平面11D C P ⊥平面1C CPB.三棱锥1A D DP -的体积为定值C.11A D D P ⊥D.DP ⊥平面11D C P11.已知点A B ,为抛物线()220x py p =>上的两个动点,以AB 为直径的圆经过焦点F ,面积为2π,若过圆心C 作该抛物线准线的垂线CD ,垂足为D ,则的最大值为( )A.2D.1212.已知函数()2ln f x mx x x =++,若存在00(),x ∈+∞使得()00f x >,则m 的取值范围是( )A.1,2⎛⎫-∞- ⎪⎝⎭B.()0,+∞C.()1,-+∞D.1,2⎛⎫-+∞ ⎪⎝⎭二、填空题:本题共4小题,每小题5分,共20分.13.已知向量a r 与b r的夹角为60︒,1a a b =-=r r r ,则b =r __________.14.在直角坐标系xOy 中,实数x y ,满足不等式组20,10,30,y x y x y -≤⎧⎪--≤⎨⎪+-≥⎩则yx 的取值范围为__________.15.在ABC △中,角A B C ,,所对的边分别为a b c ,,,且cos cos b c B C a +=+,8sin bcA=,则ABC △的 周长的最小值为__________.16.已知双曲线()()()2222:10,0,02,0x y C a b A a B a a b -=>>,,,点P 为双曲线C 右支上一点(异于点A ),满足222PA PB a +=u u u r u u u r ,则该双曲线离心率e 的取值范围为__________.三、解答题:共70分.解答应写岀文字说眀、证眀过程或演算步骤.第17~21题为必考题,第22、23题为选考题,考生根据要求作答. (一)必考题:共60分 17.已知数列{}n a 满足112nn n a a a +-=,且11a =. (1)求数列{}n a 的通项公式;(2)设数列{}1n n a a +的前n 项和为n T ,求证:12n T <. 18.如图,三棱柱111ABC A B C -中,侧面11AA B B 是边长为2的菱形,AC ⊥平面11AA B B ,且2AC =,点E 为11A C 的中点.(1)证明:平面1ACB ⊥平面1B CE ;(2)若160ABB ∠=︒,求直线BC 与平面1B CE 所成角的正弦值.19.为了调查某公司员工的饮食习惯与月收入之间的关系,随机抽取30名员工,调查他们的饮食习惯和月收人的关系,并制作了30人的月平均收入的频率分布直方图和饮食指数表(说明:表中饮食指数不高于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主).其中月收入4000元以上员工中饮食指数高于70的有11人.(1)填表,并判断是否有95%的把握认为饮食习惯与月收入有关系.若有,请说明理由,若没有明理由,并分析原因;(2)以上面的统计数据为参考,从该公司主食蔬菜的员工中随机抽取3人,设这3人中月收入4000元以上的人数为X ,求X 的分布列与期望.(3)经调查该公司员工的月收入x (百元)和月饮食支出y (百元)具有线性相关关系,并得到y 关于x 的回归直线方程:$0.245 3.210y x =+,若一个员工的月收入恰好为这30人的月平均收人,求该人的月饮食支出费用.(结果保留到小数点后三位) 附:参考公式及临界值表:()()()()()22n ad bc K a b c d a c b c -=++++,其中n a b c d =+++.20.如图,一张坐标纸上已作出圆22(16:E x y +=及点)Q ,折叠此纸片,使Q 与圆周上某点Q '重合,每次折叠都会留下折痕,设折痕与直线EQ 的交点为N ,点N 的轨迹为曲线C . (1)求曲线C 的方程;(2)若曲线C 与y 轴的负半轴交于点D ,过D 作两条互相垂直的直线分别与曲线C 相交于点P M 、,求证:直线PM 经过一定点,并求出该定点的坐标.21.已知函数()ln f x x x a =-+有两个不同的零点. (1)求实数a 的取值范围;(2)若函数()f x 的两个不同的零点为12x x ,,且12x x <,当22x ≥时,证明:2212x x ⋅<.(二)选考题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题记分,在答题卡选答区域指定位置答题,并用2B 铅笔在答题卡上把所选题目对应的题号涂黑.注意所做题目的题号必须与所涂题目题号一致. 22.[选修4-4:坐标系与参数方程]在平面直角坐标系xOy 中,已知曲线22:14x C y +=,将C 的横坐标变为原来的12,纵坐标不变得到曲线1C ,再将曲线1C 向右平移一个单位得到曲线2C ,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,直线l 的极坐标方程为cos sin 3ρθθ=.(1)求曲线2C 的极坐标方程;(2)若射线22ππθαα⎛⎫=-<< ⎪⎝⎭与直线l 和曲线2C 分别交于A B ,两点,求OB OA 的最大值. 23.[选修4-5:不等式选讲] 已知函数()4f x x x =-+. (1)解关于x 的不等式()12f x <;(2)对任意的R x ∈,都有不等式()()+1(49R )f x t m t t ⎛⎫ +⎪⎝⎭≥--∈恒成立,求实数m 的取值范围.神州智达2020届高三诊断性大联考(一)理科数学参考答案(质检卷Ⅰ)一、选择题1.D {}{}2,1,0,1,21,2,3A B =--=,,∴{}1,2A B =I ,故选D.2.A 因为()()()()12112131112i i i i z i i i -----===++-,所以其虚部为32-,所以p 为真命题; 因为()()221224243i i i i i i +-=-+-=-所以q 为真命题,所以选A.3.C 设等比数列{}n a 的公比为q ,则222226q q ++=,解得3q =或4q =-(舍),所以34154a a q ==.4.B 因为0.5y x =在(0,)+∞上是增函数,且0.50.3>,所以0.50.50.50.3>,即0.70.7log 0.2log 0.71a b c >=>=,,而00.510.50.5=>,所以b a c <<.5.C 根据题意,PC 的长等于其外接球的直径,因为PC =3=,∴2PA =,又PA ⊥平面ABCD ,所以1412233P ABCD V -=⨯⨯⨯=,V 球=34332π⎛⎫⨯ ⎪⎝⎭,∴3483274332P ππ==⎛⎫⨯ ⎪⎝⎭. 6.C 27sin 2sin 2cos 21sin 623369πππππαααα⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫-=-+=+=-+= ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦.7.C ()()2121x x x x e e e e f x f x x x -----==-=---,()f x 为奇函数,排除选项B ;当14x =时:11440,x x e e e e ---=-> 210x -<,∴()0f x <,排除选项D ;当x →+∞时,()f x →+∞,排除选项A ,故选C.8.A 第一次运行时,13122S -=+=,2i =;第二次运行时,1271224S --=++=,3i =;第三次运行时,1231512228S ---=+++=,4i =;第四次运行时,1234311222216S ----=++++=,5i =;…,以此类推,第九次运行时,1012349112102312222212512S --------=+++++⋅⋅⋅+==-,10i =,依题意,此时刚好不满足判断条件,因此判断条件可以为10i <.9.D ()2521x x --的展开式中2x 的系数为()()4311423545321110100C C C C -+-=-=.故选D.10.D 在正方体中,显然有11D C ⊥平面1C CP ,又11D C ⊂平面11D C P ,所以平面11D C P ⊥平面1C CP ,故A 正确;三棱锥1A D DP -的体积11A D DP P D DA V V --=,因为P 到平面1D DA 的距离不变,1D DA △的面积不变,所以三棱锥1P D DA 一的体积为定值,故三棱锥1A D DP 一的体积也为定值,故B 正确;在正方体中,显然有11111A D D C A D BC ⊥⊥,,所以1A D ⊥平面11D C P ,因为1D P ⊂平面11D C P ,所以11A D D P ⊥,故C 正确;由图形易得DP 与平面11D C P 不垂直,故D 不正确,故选D.11.A 根据题意得,222AB ππ⎛⎫= ⎪⎝⎭,∴AB =. 设AF a =,BF b =,由抛物线定义,得AF AQ =,BF BP =,在梯形ABPQ 中,2CD AQ BP a b =+=+,由勾股定理得,228a b =+,∵ 22222228222424424a b a b ab ab ab a b CD +++++⎛⎫====+≤+= ⎪⎝⎭, 所以2CD ≤ (当且仅当a b =时,等号成立) 故选A.12.C ()212121mx x f x mx x x++'=++=,当0m ≥时,()()0f x f x '>,在(0,)+∞上单调递增,显然存在00(),x ∈+∞使得()00f x >,当0m <时,令()0f x '=,即221010mx x m ++=>,△=-8,设两根分别为()1212x x x x <,,易得120x x <<,即只需要满足()20f x >,则有222210mx x ++=,2222ln 0x mx x ++>,消元得221ln 02x x -+>,构造函数()()1ln 102x g x x g -=+=,,则()1102g x x '=+>,所以()g x 单调递增,则1x >,即21x >,又因为222112m x x ⎛⎫=-+ ⎪⎝⎭,则2210m m >--<<,.综上1m >-,故选C. 二、填空题13.2 22223a b a a b b -=-⋅+=r r r r r r ,由题意得1cos602a b a b b ⋅=︒=r r r r r,所以220b b --=r r ,解得2b =r .14.1,22⎡⎤⎢⎥⎣⎦ 如图,不等式组120300y x x y y -≤--≤⎧⎪⎨⎪+-≥⎩,表示的平面区域为ABC △ (包括边界),所以表示点(),x y 与()0,0连线的斜率,因为()()1,22,1A B ,,所以2OA k =,12OB k =,故1,22y x ⎡⎤∈⎢⎥⎣⎦.15.4+因为cos cos b a B C a +=+,根据余弦定理可得22222222b c a c b a b c a ac ab++-+-=+, 整理得2222322322b c bc a b bc b a c b c c +=+-++-,即()222233b c bc a b a c b c +=+-+,因式分解得()()2220b c b c a +-=+,所以222b c a +=,即90A =︒,sin 1A =,则8bc =,所以()4a b c b c +++≥+,当且仅当b c =时,取等号, 综上ABC △的周长的最小值为4+16.⎛ ⎝⎭ 由222PA PB a +=u u u r u u u r ,得222PA PB AB +=,故PA PB ⊥.设(),P m n ,可得(),AP m a n =-u u u r , ()2,PB a m n =--u u u r ,所以()()220AP PB m a a m n ⋅=---=u u u r u u u r ①.又因为点P 在双曲线上,所以22221m n a b-=,整理得22221m n b a ⎛⎫=- ⎪⎝⎭②,将②式代入①式得()()222102mb a m a a m ⎛⎫-- ⎝-=⎪⎭-,化简整理得22222330c m am c a a -++-=,此方程的根为321223a ac m a m c -==,,因为点P 是双曲线右支上异于右顶点A 的一点,所以3223a ac a c ->,得2232a c>,即232e <,又1e >,∴1e <<C 的离线率e的取值范围是⎛ ⎝⎭. 三、解答题17.解:(1)因为112n n n a a a +-=,所以1112n n a a +-=. 则有()()111111221n n d n n a a =+-=+-⨯=-. 所以121n a n =-. (2)设()()11111212122121n n n b a a n n n n +⎛⎫===- ⎪-+-+⎝⎭12n n T b b b =++⋅⋅⋅+ ()()11113352121n n =++⋅⋅⋅+⨯⨯-+ 11111111111123352121221242n n n n ⎛⎫⎛⎫=-+-+⋅⋅⋅+-=-=- ⎪ ⎪-+++⎝⎭⎝⎭, 因为1042n >+,所以12n T <. 综上,12n T <. 18.证明:(1)连接1BA ,交1AB 于点O ,设1B C 中点为F ,连接OF EF ,. 因为O F ,分别为11B A B C ,的中点, 所以OF AC ∥,且12OF AC =, 因为111AC AC AC AC =∥,,且11112A E AC =, 所以1OF A E ∥且1OF A E =. 所以四边形1OFEA 为平行四边形, 所以1OA EF ∥,即1BA EF ∥.因为AC ⊥平面111AA B B BA ⊂,平面11AA B B ,所以1AC BA ⊥. 因为四边形11AA B B 是菱形,所以11BA AB ⊥. 因为1AB AC A =I ,所以1BA ⊥平面1ACB .因为1BA EF ∥,所以EF ⊥平面1ACB .因为FE ⊂平面1B CE 所以平面1ACB ⊥平面1B CE .(2)因为160ABB ∠=︒,四边形11AA B B 是边长为2的菱形, 故1ABB △为等边三角形.设1BB 的中点为M ,连接AM ,则1AM BB ⊥.以A 为原点,1AM AA AC ,,所在直线分别为x y z ,,轴,建立空间直角坐标系A xyz -.则()()1)0,0,20,2,11,0)C B E B -,,,,)()112()1,2CB B E BC =-==u u u r u u u u r u u u r,,.设平面1B CE 的法向量为(),,n x y z =r ,则110,0,n CB n B E ⎧⋅=⎪⎨⋅=⎪⎩r u u u rr u u u u r即20,0.y z y z +-=++=⎪⎩令1y =,则 2.x z ⎧=⎪⎨=⎪⎩所以)n =r .设直线BC 与平面1B CE 所成角为θ,则1sin cos ,4BC n BC n BC nθ⋅===⋅u u u r r u u u r r u u ur r , 即直线BC 与平面1B CE 所成角的正弦值为14. 19.解:(1)根据频率分布直方图,月收入4000元以上的人数为()300.030.0250.0151021⨯++⨯=, 所以2×2列联表如下:所以2230811110 4.471 3.841921(2)118K ⨯⨯-⨯=≈>⨯⨯⨯,故有95%的把握认为饮食习惯与月收入有关系. (2)从主食蔬菜的员工中任选1人,该人月收入4000元以上的概率105189p ==.X 可取0,1,2,3,所以()335499iii P X i C -⎛⎫⎪⎝⎭⎛⎫== ⎪⎝⎭,0,1,2,3i =.X 的分布列为∵~3,9X B ⎛⎫⎪⎝⎭,∴()53E X np == (人).(3)根据频率分布直方图,得0.1250.2350.3450.25550.156546.5⨯+⨯+⨯+⨯+⨯=(百元), 所以$0.24546.5 3.21014.602514.603y =⨯+=≈ (百元),故该人的月饮食支出费用为14.603百元.20.解:(1)折痕为QQ '的垂直平分线,则NQ NQ '=,由题意知圆E 的半径为4, 所以4NE NQ NE NQ EQ +'+==>,所以N 的轨迹是以E Q 、为焦点的椭圆,且2a c ==, 所以2221b a c =-=,所以N 的轨迹C 的方程为2214x y +=.(2)解法1:由题意知直线PD MD ,的斜率存在且不为0, 设直线PD 的斜率为k ,则:1PD y kx =-, 由22114y kx x y =-⎧⎪⎨+=⎪⎩,得222841,1441k k P k k ⎛⎫- ⎪++⎝⎭, 用1k -去替换k ,得22284,44k k M k k ⎛⎫-- ⎪++⎝⎭, 作直线PM 关于y 轴的对称直线P M '',此时得到点P M 、关于y 轴对称的点P M '',,则PM 与P M ''相 交于y 轴,可知定点y y 轴上, 当1k =时,8383,,5555P M ⎛⎫ ⎪⎛-⎝⎪⎭⎫⎝⎭,,此时直线PM 经过y 轴上的点30,5T ⎛⎫⎪⎝⎭,因为222241314158514PT k k k k k kk ---+==+, 222243145854MT k k k k k kk ---+==-+, 所以PT MT k k =,所以P M T 、、三点共线,即直线PM 经过点T ,故直线PM 经过定点30,5T ⎛⎫ ⎪⎝⎭. 解法2:由题意知直线PD MD 、的斜率存在且不为0,设直线PD 的斜率为k ,则:1PD y kx =-. 由22114y kx x y =-⎧⎪⎨+=⎪⎩,得222841,1441k k P k k ⎛⎫- ⎪++⎝⎭, 用1k -去替换k ,得22284,44k k M k k ⎛⎫-- ⎪++⎝⎭所以22222224141414885144PM k k k k k k k k k k k ----++==+++, 所以2222418454k k k y x k k k --⎛⎫-=+ ⎪++⎝⎭即21355k y x k -=+, 所以直线PM 经过定点30,5T ⎛⎫ ⎪⎝⎭. 21.解:(1)函数()ln f x x x a =-+有两个不同的零点,即ln 0x x a -+=在(0,)+∞上有两个不同的实根, 而()11f x x'=-, 当01x <<时,()0f x '<,此时()f x 在()0,1上递减;当1x >时,()0f x '>,此时()f x 在(1,)+∞上递增;所以()f x 在(0,)+∞的最小值为()11f a =+.易知10a +<,1a <-,()0a f e >,()2a a f e e a --=+, 令t a =-,()()21t g t e t t =->,则()20t g t e '=->,所以()g t 在(1,)+∞上单调递增,所以()()120g t g e >=->,所以当1a <-时,ln 0x x a -+=在()0,1和(1,)+∞上各有一个实根, 故实数a 的取值范围为(),1∞--.(2)由(1)可得()()12120110x x f x f x <<>==,,,而()()111222222222ln ln f x f x x a a x x x ⎛⎫⎛⎫-=-+--+ ⎪ ⎪⎝⎭⎝⎭()2222222222222ln ln 3ln ln 2x x a a x x x x x ⎛⎫=-+--+=--+ ⎪⎝⎭, 设2t x =,令()223ln ln 2g t t t t =--+,于是()()()23321341t t g t t t t-+'=-+=, 由于2t ≥,故()0g t '≥,即()g t 在[)2,+∞上单调递增, ∴()()322ln 202g t g ≥=->. ∴当22x ≥时,()12220f x f x ⎛⎫-> ⎪⎝⎭,即()1222f x f x ⎛⎫> ⎪⎝⎭, 又()f x 在()0,1上递减,而101x <<,22201x <<, 所以1222x x <,即2122x x ⋅<. 22解:(1)由平移变换和伸缩变换得曲线2C 的直角坐标方程为()2211x y -+=, 由cos sin x y ρθρθ==,得曲线2C 的极坐标方程为2cos ρθ=.(2)由cos sin 3ρθθθα⎧=-=⎪⎨⎪⎩,得OA =, 由2cos ρθθα=⎧⎨=⎩,得2cos OB α=,所以2221cos cos cos 23332OBOA παααα⎛⎫===++ ⎪⎝⎭, 当且仅当6πα=-时,OBOA 取得最大值,为1.23.解:(1)不等式()12f x <,即412x x -+<等价于0,412x x x <⎧⎨--<⎩或04412x x x ≤<⎧⎨-+<⎩或4,412,x x x ≥⎧⎨-+<⎩整理可得48x -<<, 故不等式()12f x <的解集为()4,8-. (2)由于()444x x x x -+≥--=,而()1444919363793725t t t t t t ⎛⎫--=--+=-+≤- ⎪⎝⎭⎛⎫ ⎪⎝⎭, 当且仅当49t t =,即249t =,23t =时,等号成立. 要使不等式()()1449R x x t m t t +⎛⎫ ⎪⎝⎭-+≥--+∈恒成立, 则254m +≤,解得21m ≤-, 实数m 的取值范围为(],21-∞-.。
2020年神州智达高三诊断性大联考理科数学质检卷及答案

【解析】由题意可知 ,设 ,可得 ,再与方程 联立,令 即可得解.
【详解】
由 ,得 ,故 .
设 ,可得 , ,
所以 ①.
又因为点 在双曲线上,所以 ,整理得 ②,
将②式代入①式得 ,
化简整理得 ,
此方程的根为 , ,
因为点 是双曲线右支上异于右顶点 的一点,
所以 ,得 ,即 ,
又 ,∴ ,
故答案为: .
【详解】
(1)因为 ,所以 ,
所以数列 是首项为 ,公差为2的等差数列,
则有 ,
所以 .
(2)证明:设 ,
,
因为 ,所以 .
综上, .
【点睛】
本题考查了构造新数列求原数列的通项,考查了裂项相消法求数列前n项和的应用,属于中档题.
18.如图,三棱柱 中,侧面 是边长为2的菱形, 平面 ,且 ,点 为 的中点.
在正方体中,显然有 , ,所以 平面 ,
因为 平面 ,所以 ,故C正确;
若 平面 ,则 ,结合 可得 平面 ,所以 ,但 不是一直成立,故D不正确.
故选:D.
【点睛】
本题考查了线面、面面关系的判定和性质,考查了三棱锥体积公式的应用,属于中档题.
11.已知 为抛物线 上的两个动点,以 为直径的圆 经过抛物线的焦点 ,且面积为 ,若过圆心 作该抛物线准线 的垂线 ,垂足为 ,则 的最大值为()
本题考查了利用等比数列的通项公式进行基本量计算,属于基础题.
4.已知 ,则 的大小关系是()
A. B. C. D.
【答案】B
【解析】由对数函数和幂函数的单调性可得 ,即可得解.
【详解】
因为 在 上是增函数,所以 ,即 ,
因为 在 上是减函数,所以
2020届高三第一次联考理综试题含答案解析
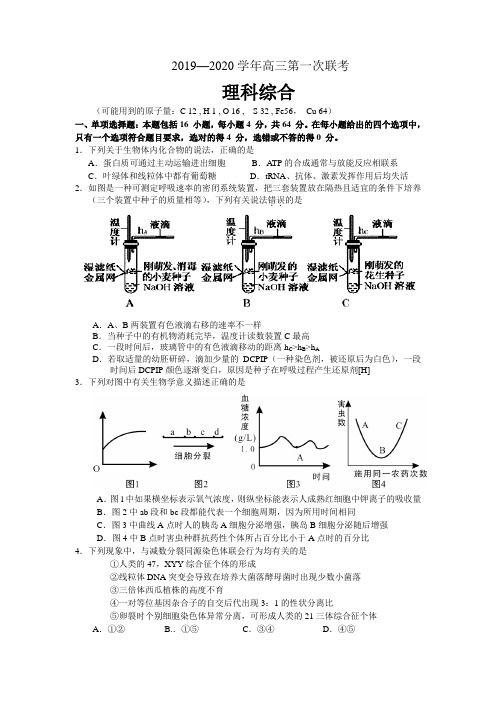
2019—2020学年高三第一次联考理科综合(可能用到的原子量:C 12 , H 1 , O 16 , S 32 , Fe56,Cu 64)一、单项选择题:本题包括16 小题,每小题4 分,共64 分。
在每小题给出的四个选项中,只有一个选项符合题目要求,选对的得4 分,选错或不答的得0 分。
1.下列关于生物体内化合物的说法,正确的是A.蛋白质可通过主动运输进出细胞B.ATP的合成通常与放能反应相联系C.叶绿体和线粒体中都有葡萄糖D.tRNA、抗体、激素发挥作用后均失活2.如图是一种可测定呼吸速率的密闭系统装置,把三套装置放在隔热且适宜的条件下培养(三个装置中种子的质量相等),下列有关说法错误..的是A.A、B两装置有色液滴右移的速率不一样B.当种子中的有机物消耗完毕,温度计读数装置C最高C.一段时间后,玻璃管中的有色液滴移动的距离h C>h B>h AD.若取适量的幼胚研碎,滴加少量的DCPIP(一种染色剂,被还原后为白色),一段时间后DCPIP颜色逐渐变白,原因是种子在呼吸过程产生还原剂[H]3.下列对图中有关生物学意义描述正确的是A.图l中如果横坐标表示氧气浓度,则纵坐标能表示人成熟红细胞中钾离子的吸收量B.图2中ab段和bc段都能代表一个细胞周期,因为所用时间相同C.图3中曲线A点时人的胰岛A细胞分泌增强,胰岛B细胞分泌随后增强D.图4中B点时害虫种群抗药性个体所占百分比小于A点时的百分比4.下列现象中,与减数分裂同源染色体联会行为均有关的是①人类的47,XYY综合征个体的形成②线粒体DNA突变会导致在培养大菌落酵母菌时出现少数小菌落③三倍体西瓜植株的高度不育④一对等位基因杂合子的自交后代出现3:1的性状分离比⑤卵裂时个别细胞染色体异常分离,可形成人类的21三体综合征个体A.①② B..①⑤C.③④D.④⑤5.图表示人体神经元的结构。
以下相关叙述中,正确的是A.突触一般不含有Ⅰ部位的结构B.发生反射时,神经冲动在Ⅱ上以局部电流的形式双向传导C.只有兴奋时,Ⅲ才能合成神经递质D.神经冲动传到Ⅲ部位时,电信号转变为化学信号6.在一段新建公路的边坡(甲)上移栽灌木和草本植物以保护边坡,另一段边坡(乙)不进行移栽,其他实验条件相同,1年后两段边坡的检测结果如下表。
2020届高三一诊理科综合测试物理题和答案

高中2020级一诊试题物 理 试 卷二、选择题(本题共8个小题,每小题6分,共48分。
在每小题给出的四个选项中,第14~18题只有一项符合题目要求,第19~21题有多项符合题目要求。
全部选对的得6分,选对但不全的得3分, 有选错的得0分)14.高空中竖直下落的物体,若阻力与速度成正比,则下列说法中正确的是( )A .下落过程,物体的机械能守恒B .重力对物体做的功等于物体动能的增加量C .若物体做加速运动,必是匀加速运动D .物体落地前有可能做匀速直线运动 15.如图所示,长为d 质量为m 的细金属杆ab ,用长为L 的细线悬挂后,恰好与水平光滑的平行金属导轨接触,平行金属 导轨间距为d ,导轨平面处于竖直向下的磁感应强度为B 的匀强 磁场中。
闭合开关S ,细金属杆ab 向右摆起,悬线的最大偏角 为θ,重力加速度为g ,则闭合开关的短时间内通过细金属杆ab 的电量为( )A .)cos 1(2θ-gL BL m B .)cos 1(θ-gL Bd mC .)cos 1(2θ-gL Bd mD .θsin 2gL Bdm16.如图所示,直角三角形框架由两根光滑细杆构成,左侧杆与水平 地面成θ角,细杆上分别穿有两个小球A 和B , 两个小球A 、B 用轻质细线相连。
当两个小球都静止时,细线与左侧杆成α角, 已知θ=45°,α=30°。
则小球A 与小球B 的质量之比为( ) A .3:1 B .1:3 C .2:1 D .1:217.两颗质量相同的卫星P 、Q 均绕地球做匀速圆周运动,卫星P 的动能是卫星Q 动能的4倍。
把地球视 为半径为R 的球体,卫星P 、Q 距地高度为h P 、h Q ,卫星P 、Q 做匀速圆周运动的周期分别为T P 、T Q 。
下列说法中正确的是( )A .h Q =4h P ,T Q =4T PB .h Q =4h P +3R ,T Q =4T PC .h Q =4h P ,T Q =8T PD .h Q =4h P +3R ,T Q =8T P18.如图所示,倾角为θ,足够长的光滑斜面体固定在地面上。
2020届 神州智达高三诊断性大联考(一)数学(理)质检卷(解析版)

2020届神州智达高三诊断性大联考(一)数学(理)质检卷一、单选题1.已知集合{}{}*2,1,0,1,2N 129xA B x =--=∈<<,,则A B =I ( )A .{}1,0,1,2-B .{}1,0,1-C .{}1,1,2-D .{}1,2【答案】D【解析】由题意{}1,2,3B =,再由集合交集的概念可直接得解.【详解】{}{}*N 1291,2,3x B x =∈<<=,∴{}{}{}2,1,0,1,21,21,32,A B --==I I .故选:D.【点睛】本题考查了指数不等式的求解,考查了集合交集的概念,属于基础题.2.已知命题p :复数121i z i-=+的虚部是32-,命题q :复数()()21243i i i +-=-,以下命题真假判断正确的是( ) A .p 真q 真B .p 真q 假C .p 假q 真D .p 假q 假【答案】A【解析】由复数的除法法则和虚部的概念可判断命题p ,由复数的乘法运算法则可判断命题q ,即可得解.【详解】因为()()()()121121311122i i i z i i i i ----===-++-,所以其虚部为32-,所以p 为真命题; 因为()()221224243i i i i i i +-=-+-=-,所以q 为真命题.故选:A.【点睛】本题考查了复数的运算和虚部的概念,考查了命题真假性的判断,属于基础题. 3.已知各项均为正数的等比数列{}n a 中,12a =,前三项的和为26,则4a =( )A .36B .48C .54D .64【答案】C【解析】设等比数列{}n a 的公比为q ,由题意可得222226q q ++=,解方程求得3q =即可得解.【详解】Q 数列{}n a 为各项均为正数等比数列,12a =,前三项的和为26,设等比数列{}n a 的公比为q ,∴222226q q ++=,解得3q =或4q =-(舍),所以34154a a q ==.故选:C.【点睛】本题考查了利用等比数列的通项公式进行基本量计算,属于基础题.4.已知0.50.50.70.50.3log 0.2a b c ===,,,则a b c ,,的大小关系是( )A .c a b <<B .b a c <<C .c b a <<D .a b c <<【答案】B【解析】由对数函数和幂函数的单调性可得1b a c <<<,即可得解.【详解】因为0.5y x=在(0,)+∞上是增函数,所以0.50.50.50.30.51<<,即1b a <<,因为0.7log y x =在(0,)+∞上是减函数,所以0.70.7log 0.2log 0.71c =>= 所以1b a c <<<.故选:B.【点睛】本题考查了利用对数函数和幂函数的单调性比较大小,属于基础题.5.阳马,中国古代算数中的一种几何形体,是底面长方形,两个三角面与底面垂直的四棱锥体,在阳马P ABCD -中,PC 为阳马P ABCD -中最长的棱,1,2,3AB AD PC ===,若在阳马P ABCD -的外接球内部随机取一点,则该点位阳马内的概率为( )A .127πB .427πC .827πD .49π【答案】C【解析】由题意知PC 的长等于其外接球的直径,可知2PA =,计算棱锥的体积,球的体积,根据古典概型即可求解.【详解】根据题意,PC 的长等于其外接球的直径,因为222PC PA AB AD =++,∴2314PA =++,∴2PA =,又PA ⊥平面ABCD ,所以314431223332P ABCDV V π-⎛⎫=⨯⨯⨯==⨯ ⎪⎝⎭球,, ∴3483274332P ππ==⎛⎫⨯ ⎪⎝⎭. 【点睛】本题主要考查了棱锥的外接球,棱锥的体积,球的体积,古典概型,属于中档题.6.已知1sin 63πα⎛⎫+= ⎪⎝⎭,则sin 26πα⎛⎫-= ⎪⎝⎭( ) A .89B .89-C .79D .79-【答案】C【解析】利用诱导公式和余弦的二倍角公式可得2sin 212sin 66ππαα⎛⎫⎛⎫-=-+ ⎪ ⎪⎝⎭⎝⎭,即可得解.【详解】由题意227sin 2sin 2cos 212sin 16233699πππππαααα⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫-=-+=+=-+=-= ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦.故选:C【点睛】本题考查了三角函数的以值求值,考查了诱导公式和余弦的二倍角公式的应用,属于基础题.7.函数()21x xe ef x x --=-的图象大致是( )A .B .C .D .【答案】C【解析】根据函数的性质对比图象的特征,逐项排除即可得解.【详解】由()()2121x x x xe e e ef x f x x x -----==-=---,∴()f x 为奇函数,排除选项B ;当14x =时,11440x x e e e e ---=->,210x -<,∴()0f x <,排除选项D ; 当()2,x ∈+∞时,()21x xe ef x x --=-,则()()()()()()()()22212230222111xx x xxxe e x e e e x ef x x x x ---+----+'==>--+∴()f x 在()2,x ∈+∞时单调递增,排除选项A.故选:C.【点睛】本题考查了函数图象的识别,考查了函数奇偶性和利用导数判断函数单调性的应用,属于中档题.8.执行如图所示的程序框图,若输出的10232512iS S S -==+,则判断框内可以为( )A .10?i <B .10?i ≤C .11?i <D .11?i ≤【答案】A【解析】根据程序框图,注意变量取值的变化,可得1023512S =时10i =,即可得解. 【详解】第一次运行时,13122S -=+=,2i =; 第二次运行时,1271224S --=++=,3i =; 第三次运行时,1231512228S ---=+++=,4i =; 第四次运行时,1234311222216S ----=++++=,5i =;…,以此类推,第九次运行时,1012349112102312222212512S --------=+++++⋅⋅⋅+==-,10i =,依题意,此时刚好不满足判断条件,因此判断条件可以为10i <.故选:A.【点睛】本题考查了当型循环结构程序框图的应用,属于基础题.9.()5221x x --的展开式中2x 的系数为( )A .400B .120C .80D .0【答案】D【解析】变形已知为()525521(1)(21)x x x x --=-+,分别写出两个二项式展开式的通项55(1)rrr C x--,55C (2)k k x -,可知()525521(1)(21)x x x x --=-+的通项为510()55(1)2r k r k k r C C x --+-,即可求解.【详解】∵()525521(1)(21)x x x x --=-+,二项展开式5(1)x -的通项为55(1)r r r C x --,二项展开式5(21)x +的通项式为5555C (2)(1)(21)kkx x x --+,的通项为510()55(1)2r k r k k r C C x --+-,所以8k r +=,所以展开式中2x 的系数为5253444355555553(1)2(1)2(1)0C C C C C C -+-+-=.【点睛】本题主要考查了二项展开式的通项,利用通项求二项式的特定项,属于难题.10.如图,在棱长为1的正方体1111ABCD A B C D -中,P 为线段1BC 上的动点(不含端点),则下列结论错误的是( )A .平面11D C P ⊥平面1C CPB .三棱锥1A D DP -的体积为定值C .11AD D P ⊥D .DP ⊥平面11D C P【答案】D【解析】由面面垂直的判定可判断A ;由11A D DP P D DA V V --=,再利用三棱锥体积公式可判断B ;由1A D ⊥平面11D C P ,再利用线面垂直的性质可判断C ;由反证法可判断D ;即可得解.【详解】在正方体中,显然有11D C ⊥平面1C CP ,又11D C ⊂平面11D C P ,所以平面11D C P ⊥平面1C CP ,故A 正确;三棱锥1A D DP -的体积满足11A D DP P D DA V V --=,因为P 到平面1D DA 的距离不变,1D DA △的面积不变,三棱锥1A D DP 一的体积为定值,故B 正确;在正方体中,显然有111A D D C ⊥,11A D BC ⊥,所以1A D ⊥平面11D C P ,因为1D P ⊂平面11D C P ,所以11A D D P ⊥,故C 正确;若DP ⊥平面11D C P ,则1DP BC ^,结合1DC BC ⊥可得1BC ⊥平面DCP ,所以1BC CP ⊥,但1BC CP ⊥不是一直成立,故D 不正确.故选:D.【点睛】本题考查了线面、面面关系的判定和性质,考查了三棱锥体积公式的应用,属于中档题.11.已知,A B 为抛物线22(0)x py p =>上的两个动点,以AB 为直径的圆C 经过抛物线的焦点F ,且面积为2π,若过圆心C 作该抛物线准线l 的垂线CD ,垂足为D ,则||CD 的最大值为( )A .2B 2C .22D .12【答案】A【解析】由圆的面积可得22AB =设||||AF a BF b ==,,过点A 作AQ l ⊥于Q ,过点B 作BP l ⊥于P ,利用抛物线定义得AF AQ BF BP ==,,根据梯形中位线可知2CD AQ BP a b =+=+,利用均值不等式即可求出最大值.【详解】根据题意,222AB ππ⎛⎫= ⎪⎝⎭,∴22AB =设||||AF a BF b ==,,过点A 作AQ l ⊥于Q ,过点B 作BP l ⊥于P , 由抛物线定义,得AF AQ BF BP ==,,在梯形ABPQ 中,∴2CD AQ BP a b =+=+,由勾股定理得,228a b =+,∵2222282244a b a b ab CD ab++++⎛⎫==== ⎪⎝⎭2222424ab a b +++=…, 所以2CD ≤(当且仅当a b =时,等号成立).【点睛】本题主要考查了抛物线的定义,梯形的中位线,均值不等式,属于难题.12.已知函数()2ln f x mx x x =++,若存在0(0,)x ∈+∞使得()00f x >,则m 的取值范围是( )A .1,2⎛⎫-∞-⎪⎝⎭B .()0,∞+C .()1,-+∞D .1,2⎛⎫-+∞ ⎪⎝⎭【答案】C【解析】由题意可得2ln x x m x-->在(0,)+∞有解,令()()2ln 0x xg x x x --=>,求导判断()g x 的单调性后,求出()g x 的最小值即可得解.【详解】Q 存在0(0,)x ∈+∞使得()00f x >,∴2ln mx x x >--即2ln x xm x -->在(0,)+∞有解, 令()()2ln 0x x g x x x --=>,则()()243112ln 2ln 1x x x x x x x g x x x ⎛⎫--++ ⎪+-⎝⎭'==,()10g '=,当()0,1x ∈时,2ln 10x x +-<,则()0g x '<,函数()g x 单调递减;当()1,x ∈+∞时,2ln 10x x +->,则()0g x '>,函数()g x 单调递增;∴当0(0,)x ∈+∞时,()()11g x g ≥=-, ∴1m >-.故选:C.【点睛】本题考查了利用导数解决能成立问题,考查了转化化归思想,属于中档题.二、填空题13.已知向量a r 与b r 的夹角为60︒,1a =v ,3a b -=v v a =v__________.【答案】2【解析】由题意22223a b a a b b -=-⋅+=v v v v v v ,计算出a b ⋅r r 的值后即可得解.【详解】Q 22223a b a a b b -=-⋅+=v v v v v v ,1a =v ,向量a r 与b r 的夹角为60o , ∴1cos602a b a b b ⋅==ov v v v v ,21a =v ,∴220b b --=v v,解得2b =v 或1b =-v (舍去).故答案为:2.【点睛】本题考查了利用向量数量积解决向量模的问题,属于基础题.14.已知实数,x y满足不等式组201030yx yx y-≤⎧⎪--≤⎨⎪+-≥⎩,则yx的取值范围为__________.【答案】1,22⎡⎤⎢⎥⎣⎦【解析】作出可行域,yx表示(),x y与(0,0)连线的斜率,结合图形求出斜率的最小值,最大值即可求解.【详解】如图,不等式组201030yx yx y-⎧⎪--⎨⎪+-⎩„„…表示的平面区域ABCV(包括边界),所以yx表示(),x y 与(0,0)连线的斜率,因为()()1,22,1A B,,所以122OA OBk k==,,故1,22yx⎡⎤∈⎢⎥⎣⎦. 【点睛】本题主要考查了简单的线性规划问题,涉及斜率的几何意义,数形结合的思想,属于中档题.15.在ABC V 中,角A B C ,,所对的边分别为a b c ,,,且cos cos b cB C a+=+,8sin bcA=,则ABC V 的周长的最小值为__________. 【答案】442+【解析】由余弦定理化简可得()()2220b c b c a++-=,即可得222bc a +=,进而可得8bc =,再利用基本不等式即可得解.【详解】因为cos cos b a B C a +=+,根据余弦定理可得22222222b c a c b a b c a ac ab++-+-=+, 整理得()222233b c bc a b a c b c+=+-+,因式分解得()()2220b c bc a ++-=,由0b c +≠可得222b c a +=,即90A =o ,sin 1A =,则8bc =,所以()2222442a b c b c b c bc bc +++++,当且仅当b c =时,取等号, 综上ABC V 的周长的最小值为442+.故答案为:442+.【点睛】本题考查了余弦定理解三角形的应用,考查了利用基本不等式求最值,属于中档题.16.已知双曲线()()()2222:10,0,02,0x y C a b A a B a a b-=>>,,,点P 为双曲线C 右支上一点(异于点A ),满足222PA PB a +=u u u r u u u r ,则该双曲线离心率e 的取值范围为__________.【答案】61,2⎛⎫⎪ ⎪⎝⎭【解析】由题意可知PA PB ⊥,设()P m n ,,可得()()220m a a m n ---=,再与方程22221m n a b-=联立,令32223a ac m a c -=>即可得解. 【详解】由222PA PB a +=u u u r u u u r ,得222PA PB AB +=,故PA PB ⊥.设()P m n ,,可得(),AP m a n =-u u u r ,()2,PB a m n =--u u u r, 所以()()220AP PB m a a m n ⋅=---=u u u r u u u r ①.又因为点P 在双曲线上,所以22221m n a b -=,整理得22221mn b a ⎛⎫=- ⎪⎝⎭②,将②式代入①式得()()222102m b a m a a m ⎛⎫-- ⎝-=⎪⎭-,化简整理得22222330c m am c a a-++-=,此方程的根为1m a =,32223a ac m c -=,因为点P 是双曲线右支上异于右顶点A 的一点,所以3223a ac a c ->,得2232a c>,即232e <,又1e >,∴61e <<, 故答案为:61,2⎛ ⎝⎭. 【点睛】本题考查了双曲线离心率的求解,考查了计算能力,属于中档题.三、解答题17.已知数列{}n a 满足112nn n a a a +-=,且11a =. (1)求数列{}n a 的通项公式;(2)设数列{}1n n a a +的前n 项和为n T ,求证:12n T <. 【答案】(1)121n a n =-;(2)详见解析. 【解析】(1)由题意可得1112n n a a +-=,利用等差数列的通项公式求出1na 后即可得解; (2)设()()112121n n n b a a n n +==-+,利用裂项相消法求出n T 后即可得证.【详解】(1)因为112nn n a a a +-=,所以1112n na a +-=,所以数列1n a ⎧⎫⎨⎬⎩⎭是首项为111a =,公差为2的等差数列,则有()112121nn n a =+-=-, 所以121n a n =-. (2)证明:设()()11111212122121n n n b a a n n n n +⎛⎫===- ⎪-+-+⎝⎭,12n n T b b b =++⋅⋅⋅+()()11113352121n n =++⋅⋅⋅+⨯⨯-+11111111111123352121221242n n n n ⎛⎫⎛⎫=-+-+⋅⋅⋅+-=-=- ⎪ ⎪-+++⎝⎭⎝⎭, 因为1042n >+,所以12n T <. 综上,12n T <. 【点睛】本题考查了构造新数列求原数列的通项,考查了裂项相消法求数列前n 项和的应用,属于中档题.18.如图,三棱柱111ABC A B C -中,侧面11AA B B 是边长为2的菱形,AC ⊥平面11AA B B ,且2AC =,点E 为11A C 的中点.(1)证明:平面1ACB ⊥平面1B CE ;(2)若160ABB ∠=︒,求直线BC 与平面1B CE 所成角的正弦值.【答案】(1)详见解析;(2)14. 【解析】(1)连接1BA ,交1AB 于点O ,取1B C 中点为F ,连接OF ,EF ,由中位线和平行四边形的性质可得1//BA EF ,再由线面垂直的性质和菱形的性质可得1BA ⊥平面1ACB ,进而可得EF ⊥平面1ACB ,由面面垂直的判定即可得证;(2)由题意建立空间直角坐标系后,求出各点坐标后,求出平面1B CE 的一个法向量为n r 和直线BC 方向向量BC uuu r,利用sin cos ,BC n θ=u u u v v 即可得解.【详解】(1)证明:连接1BA ,交1AB 于点O ,取1B C 中点为F ,连接OF ,EF . 因为O ,F 分别为1B A ,1B C 的中点,所以//OF AC ,且12OF AC =, 因为11//A C AC ,1AC AC =,且11112A E AC =, 所以1//OF A E 且1OF A E =,所以四边形1OFEA 为平行四边形,所以1//OA EF ,即1//BA EF .因为AC ⊥平面11AA B B ,1BA ⊂平面11AA B B ,所以1AC BA ⊥.因为四边形11AA B B 是菱形,所以11BA AB ⊥.因为1AB AC A =I ,所以1BA ⊥平面1ACB .因为1//BA EF ,所以EF ⊥平面1ACB .因为FE ⊂平面1B CE ,所以平面1ACB ⊥平面1B CE .(2)因为160ABB ∠=︒,四边形11AA B B 是边长为2的菱形,故1ABB △为等边三角形.取1BB 的中点为M ,连接AM ,则1AM BB ⊥.以A 为原点,AM ,1AA ,AC 所在直线分别为x ,y ,z 轴,建立空间直角坐标系A xyz -.则()0,0,2C ,13,()1,0B ,()0,2,1E ,3,1,0)B -, )13,1,2CB =-u u u r ,()13,1,1B E =-u u u u r ,(3,1,2)BC =u u u r,设平面1B CE 的一个法向量为(),,n x y z =r,则110,0,n CB n B E ⎧⋅=⎪⎨⋅=⎪⎩u u u v v u u u v v 即320,30.x y zx y z ⎧+-=⎪⎨-++=⎪⎩,令1y =,则()3,1,2n =r .设直线BC 与平面1B CE 所成角为θ,则1sin cos ,42222BC n BC n BC nθ⋅====⨯⋅u u u v vu u u v v u u u v v, 即直线BC 与平面1B CE 所成角的正弦值为14. 【点睛】本题考查了面面垂直的证明和利用空间向量求线面角,考查了运算能力,属于中档题.19.为了调查某公司员工的饮食习惯与月收入之间的关系,随机抽取30名员工,调查他们的饮食习惯和月收人的关系,并制作了30人的月平均收入的频率分布直方图和饮食指数表(说明:表中饮食指数不高于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主).其中月收入4000元以上员工中饮食指数高于70的有11人.(1)填表,并判断是否有95%的把握认为饮食习惯与月收入有关系.若有,请说明理由,若没有明理由,并分析原因;月收入4000元及以下 月收入4000元以上 合计主食蔬菜主食肉类合计(2)以上面的统计数据为参考,从该公司主食蔬菜的员工中随机抽取3人,设这3人中月收入4000元以上的人数为X ,求X 的分布列与期望.(3)经调查该公司员工的月收入x (百元)和月饮食支出y (百元)具有线性相关关系,并得到y 关于x 的回归直线方程:$0.245 3.210y x =+,若一个员工的月收入恰好为这30人的月平均收人,求该人的月饮食支出费用.(结果保留到小数点后三位)附:参考公式及临界值表:()()()()()22n ad bc K a b c d a c b c -=++++,其中n a b c d =+++.()20P K k ≥0.15 0.10 0.05 0.025 0.0100k2.072 2.7063.841 5.024 6.635【答案】(1)表格详见解析,有95%的把握认为饮食习惯与月收入有关系,理由详见解析;(2)分布列详见解析,期望值为53;(3)14.603百元. 【解析】(1)由频率分布直方图可得月收入4000元以上的人数为21,即可完成列联表;代入数值计算出2K 后与3.841比较即可得解;(2)由题意5~3,9X B ⎛⎫⎪⎝⎭,由二项分布概率公式计算即可得分布列;由二项分布的期望公式可直接求得期望,即可得解;(3)由频率分布直方图求出这30人的月平均收入,代入线性回归方程即可得解.【详解】(1)根据频率分布直方图,月收入4000元以上的人数为()300.030.0250.0151021⨯++⨯=,所以2×2列联表如下:月收入4000元及以下 月收入4000元以上 合计主食蔬菜 8 10 18主食肉类 1 11 12合计 9 21 30所以2230(811110) 4.471 3.8419211218K ⨯⨯-⨯=≈>⨯⨯⨯,故有95%的把握认为饮食习惯与月收入有关系.(2)从主食蔬菜的员工中任选1人,该人月收入4000元以上的概率105189p ==.X 可取0,1,2,3,所以()0335464099729P X C ⎛⎫=== ⎪⎝⎭⎛⎫ ⎪⎝⎭,()121354240199729P X C ⎛⎫===⎛⎫ ⎪⎭⎭⎝⎪⎝,()22354297293009P X C ⎛⎫=== ⎪⎝⎭⎛⎫ ⎪⎝⎭,()303354125399729P X C ⎛⎫===⎛⎫ ⎪⎭⎭⎝⎪⎝, 所以X 的分布列为X 01 23P64729 240729 300729 125729∵5~3,9X B ⎛⎫⎪⎝⎭,∴()53E X np ==(人). (3)由频率分布直方图得这30人的月平均收入为0.1250.2350.3450.25550.156546.5⨯+⨯+⨯+⨯+⨯=(百元), 所以$0.24546.5 3.21014.602514.603y =⨯+=≈(百元),故该人的月饮食支出费用为14.603百元.【点睛】本题考查了独立性检验的应用和二项分布分布列与期望的求解,考查了线性回归方程的应用,属于中档题.20.如图,一张坐标纸上已作出圆22(316):E x y ++=及点(3,0)Q ,折叠此纸片,使Q 与圆周上某点Q '重合,每次折叠都会留下折痕,设折痕与直线EQ '的交点为N ,点N 的轨迹为曲线C .(1)求曲线C 的方程;(2)若曲线C 与y 轴的负半轴交于点D ,过D 作两条互相垂直的直线分别与曲线C 相交于点P M 、,求证:直线PM 经过一定点,并求出该定点的坐标.【答案】(1)2214x y +=;(2)证明详见解析,过定点30,5T ⎛⎫ ⎪⎝⎭. 【解析】(1)由题意转化条件得4NE NQ EQ +=>,由椭圆定义即可得解; (2)设直线:1PD y kx =-,联立方程组得222841,1441k k P k k ⎛⎫- ⎪++⎝⎭,22284,44k k M k k ⎛⎫-- ⎪++⎝⎭, 进而可求得直线PM 的直线方程,即可得解.【详解】(1)折痕为QQ '的垂直平分线,则NQ NQ =',由题意知圆E 的半径为4,所以4NE NQ NE NQ EQ +=+=>',所以N 的轨迹是以E Q 、为焦点的椭圆,且2a =,3c =,所以2221b a c =-=,所以N 的轨迹C 的方程为2214xy +=.(2)由题意知直线PD 、MD 的斜率存在且不为0,点()0,1D -,设直线PD 的斜率为k ,则:1PD y kx =-.由22114y kx x y =-⎧⎪⎨+=⎪⎩,消去y 得()224180k x kx +-=,0>V , 可得222841,1441k k P k k ⎛⎫- ⎪++⎝⎭, 用1k -去替换k ,得22284,44k k M k k ⎛⎫-- ⎪++⎝⎭, 所以()()()22222222224148111414885401144PMk k k k k k k k k k k k k k k ---+--++===++++, 所以直线:PM 2222418454k k k y x k k k --⎛⎫-=+ ⎪++⎝⎭即21355k y x k -=+, 所以直线PM 经过定点30,5T ⎛⎫⎪⎝⎭.【点睛】本题考查了与椭圆有关的轨迹问题,考查了直线与椭圆的综合,属于中档题. 21.已知函数()ln f x x x a =-+有两个不同的零点.(1)求实数a 的取值范围;(2)若函数()f x 的两个不同的零点为12x x ,,且12x x <,当22x ≥时,证明:2212x x ⋅<.【答案】(1)(),1∞--;(2)详见解析. 【解析】(1)求导得()f x 在(0,)+∞的最小值为()11f a =+,即可得10+<a ,由()0a a f e e =>,并通过构造新函数求导证明()0a f e ->即可得解;(2)由题意得()1222222223ln ln 2f x f x x x x ⎛⎫-=--+ ⎪⎝⎭,设2t x =,令()()223ln ln 22h t t t t t =--+≥,求导后可得()0h t >即()1222f x f x ⎛⎫> ⎪⎝⎭,由函数()f x 在()0,1上的单调性即可得证.【详解】(1)由题意得ln 0x x a -+=在(0,)+∞上有两个不同的实根,而()11f x x'=-, 当01x <<时,()0f x '<,此时()f x 在()0,1上单调递减; 当1x >时,()0f x '>,此时()f x 在(1,)+∞上单调递增; 所以()f x 在(0,)+∞的最小值为()11f a =+.所以10+<a 即1a <-,易得01a e <<,()0aaf ee=>,1a e ->,()2a af e e a --=+,令t a =-,()()21t g t e t t =->,则()20tg t e '=->,所以()g t 在(1,)+∞上单调递增,所以()()120g t g e >=->,所以()20a af e e a --=+>所以当1a <-时,ln 0x x a -+=在()0,1和(1,)+∞上各有一个实根,故实数a 的取值范围为(),1∞--.(2)证明:由(1)可得101x <<,21>x ,()()120f x f x ==,而()()111222222222ln ln f x f x x a a x x x ⎛⎫⎛⎫-=-+--+ ⎪ ⎪⎝⎭⎝⎭()2222222222222ln ln 3ln ln 2x x a a x x x x x ⎛⎫=-+--+=--+ ⎪⎝⎭,设2t x =,令()()223ln ln 22h t t t t t =--+≥,于是()()()23321341t t h t t t t -+'=-+=, 由于2t ≥,故()0h t '≥,即()h t 在[)2,+∞上单调递增,∴()()322ln 202h t h ≥=->. ∴当22x ≥时,()12220f x f x ⎛⎫-> ⎪⎝⎭,即()1222f x f x ⎛⎫> ⎪⎝⎭, 又()f x 在()0,1上递减,而101x <<,22201x <<, 所以1222x x <,即2122x x ⋅<. 【点睛】本题考查了利用导数研究函数的零点个数问题,考查了利用导数证明不等式,考查了推理能力和转化化归思想,属于难题.22.在平面直角坐标系xOy 中,已知曲线22:14x C y +=,将C 的横坐标变为原来的12,纵坐标不变得到曲线1C ,再将曲线1C 向右平移一个单位得到曲线2C ,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,直线l 的极坐标方程为cos 3sin 3ρθρθ=.(1)求曲线2C 的极坐标方程;(2)若射线22ππθαα⎛⎫=-<< ⎪⎝⎭与直线l 和曲线2C 分别交于A B ,两点,求OB OA的最大值.【答案】(1)2cos ρθ=;(2)1. 【解析】(1)由题意可得曲线2C 的直角坐标方程为()2211x y -+=,利用直角坐标方程和极坐标方程的转化公式即可得解;(2)由题意联立方程组可得3cos 3sin OA αρα=-、2cos OB α=,代入并化简得21cos 2332OB OAπα⎛⎫=++ ⎪⎝⎭,利用三角函数的性质即可得解. 【详解】(1)由平移变换和伸缩变换得曲线2C 的直角坐标方程为()2211x y -+=,由cos x ρθ=,sin y ρθ=得曲线2C 的极坐标方程为2cos ρθ=.(2)由cos 3sin 3ρθρθθα⎧-=⎪⎨=⎪⎩得3cos 3sin OA αρα=-,由2cos ρθθα=⎧⎨=⎩得2cos OB α=,所以22cos 221cos 3cos cos 233323cos 3sin OBOAαπαααααα⎛⎫===++ ⎪⎝⎭-, 由22ππα-<<可得242,333παππ⎛⎫+∈- ⎪⎝⎭, 所以当且仅当6πα=-时,OB OA取得最大值1.【点睛】本题考查了函数图象的变换与直角坐标和极坐标的转化,考查了极坐标的应用,属于中档题.23.已知函数()4f x x x =-+. (1)解关于x 的不等式()12f x <;(2)对任意的R x ∈,都有不等式()()+1(49R )f x t m t t ⎛⎫ +⎪⎝⎭≥--∈恒成立,求实数m 的取值范围.【答案】(1)()4,8-;(2)(],21-∞-. 【解析】(1)由题意()24,44,0442,0x x f x x x x -≥⎧⎪=≤<⎨⎪-<⎩,分类讨论即可得解; (2)利用绝对值三角不等式求出()min f x ,利用基本不等式求出()max 149t t ⎡⎤⎛⎫ ⎪⎢⎥⎝⎭⎣⎦--,利用恒成立问题的解决办法即可得解.【详解】(1)由题意()24,444,0442,0x x f x x x x x x -≥⎧⎪=-+=≤<⎨⎪-<⎩,则不等式()12f x <可转化为4212x x <⎧⎨-<⎩或04412x ≤<⎧⎨<⎩或42412x x ≥⎧⎨-<⎩, 整理可得48x -<<,故不等式()12f x <的解集为()4,8-.(2)由于()444x x x x -+≥--=,当04x ≤≤时,等号成立;而()1444491936379372925t t t t t t t t ⎛⎫--=--+=-+≤-⋅ ⎪⎝⎭⎛⎫ ⎪⎝⎭,当且仅当49t t =,即249t =,23t =时,等号成立.要使不等式()()1449R x x t m t t +⎛⎫ ⎪⎝⎭-+≥--+∈恒成立,则254m +≤,解得21m ≤-, 实数m 的取值范围为(],21-∞-.【点睛】本题考查了绝对值不等式的解法,考查了绝对值三角不等式和基本不等式的应用,考查了恒成立问题的解决,属于中档题.旗开得胜31 读万卷书行万里路。
2020届高三联考理科综合试题及答案

绝密★启用前2020届高三联考理科综合试题本试卷分选择题和非选择题两部分,共12页,满分300分,考试用时150分钟。
注意事项:1.答卷前,考生务必用2B铅笔在“准考证号”处填涂准考证号。
用黑色字迹的钢笔或签字笔将自己姓名、班级、考场号、座位号、准考证号填写在答题卷指定区域内。
2.选择题每小题选出答案后,用2B铅笔把答题卷上对应题目的答案标号涂黑:如需改动,用橡皮擦干净后,再选涂其它答案:不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卷各题目指定区域内的相应位置上:如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液:必须保持答题卷的整洁。
不按以上要求作答的答案无效。
可能用到的原子量:H 1 C 12 N 14 O 16 Cu 64第一部分选择题(共126分)1.下列关于细胞结构与成分的叙述,正确的是( )A.线粒体膜上有葡萄糖的载体,没有氧气的载体B.细胞中的色素不是分布在叶绿体中,就是分布在液泡中C.含有蛋白质的细胞器不一定含有核酸,含核酸的细胞器一定含有蛋白质D.微量元素可参与某些复杂化合物的组成,如下Fe、Mg分别参与蛋白质和叶绿素的组成2.SGLT2是肾小管细胞膜上重吸收葡萄糖的一种载体蛋白,SGLT2可以与肾小管腔中葡萄糖和结合,形成-载体-葡萄糖复合物,将顺浓度梯度运入细胞,同时将葡萄糖逆浓度梯度运入细胞,下列叙述错误的是( )A.氧气的含量变化会直接影响SGLT2参与的葡萄糖的运输速率B.SGLT2将肾小管腔中的葡萄糖运入细胞属于主动运输C.细胞通过SGLT2运输葡萄糖的动力来自的浓度差D.肾小管细胞中SGLT2合成不足可能导致人尿液中含有葡萄糖3.蝗虫的决定为XO型,正常雄虫的体细胞中有23条染色体,仅有一条性染色体(X染色体)。
如图表示某雄虫精巢中某一细胞染色体的行为,染色体A和B为一对同源染色体。
以下叙述正确的是( )A.图示细胞处于减数第二次分裂后期B.若对该种蝗虫进行基因组测序,则应该测定I2条染色体的DNA序列C.该细胞所处的时期染色体高度螺旋化难以解旋,细胞内不能合成新的蛋白质D.萨顿通过观察雄蝗虫体细胞和精子细胞的染色体数,提出了基因在染色体上的假说4.2017年诺贝尔生理学或医学奖颁给了美国的三位科学家,他们发现果蝇的昼夜节律与PER 蛋白浓度的变化有关,如图表示PER蛋白作用部分过程,有关叙述错误的是( )A.PER蛋白可反馈抑制per基因的转录B.permRNA的合成过程发生在细胞核内C.图中核糖体移动的方向是从a→bD.PER蛋白与TIM蛋白结合后穿过核膜进入细胞核5.下列关于生物变异、育种和进化的叙述,正确的是A.B基因可突变成、基因反映了基因突变的随机性B.单倍体育种中常用一定浓度的秋水仙素处理萌发的种子或幼苗C.生物产生的变异个体都属于可遗传的变异,都可以作为生物进化的原材料D.地理隔离可阻止种群间的基因交流,种群基因库的明显差异导致种群间产生生殖隔离6.如图为人体体液物质交换示意图,下列叙述正确的是A.体液①含有尿素、氨基酸、糖原、等物质B.体液①和②之间进行物质交换,可以等量地相互转化C.④能回流血浆,是淋巴细胞和吞噬细胞的直接生活环境D.③若产生乳酸会引起①②④内pH剧烈变化7.下列说法中错误的是()A. 采煤工业爆破时把干冰和炸药放在一起,既能增强爆炸威力,又能预防火灾B. 国产大型飞机C919使用的碳纤维是一种新型的无机非金属材料C. 《肘后急备方》“青蒿一握,以水二升渍,取绞汁”,该过程属于物理变化D. 高级脂肪酸乙酯是生物柴油的一种成分,它属于油脂8.国际计量大会第26次会议新修订了阿伏加德罗常数(N A=6.02214076×1023mol-1),并于2019年5月20日正式生效。
