《点群和空间群》PPT课件
合集下载
第九讲—点式空间群
6 (S35)
S3, S32(C32), S33(σh), S34(C3), S35, S36(E)
65, 64,
63,
62,
6, 66
对称条件
1(E)或1(i)
晶系
特点
三 斜 a≠ b≠ c, ≠≠
2(C2)或2(m)
单 斜 a≠b≠c, = = 90o≠
两个2(C2)或2(m) 正 交 a≠b≠c, = = = 90o
1(C) m(P) mm2 4/m
(L22P) (L4PC)
6/m
(L6PC)
3m
(L33P)
m3
(3L24L33PC)
32 2/m mmm 4mm 6mm 32(L33L2) 43m
种 (L2PC) (3L23PC) (L44P)
(L66P)
(3Li44L36P)
点 群
4/mmm 6/mmm 3(Li3)
2或2沿a±b
三方 3或3沿c 2或2沿a、b和a+b 2或2a、b和a+b
六方 6或6沿c 2或2沿a、b和a+b 2或2a、b和a+b
立方 4、4、2或2
沿<100>
3或3沿<111>
2或2沿<110>
1(L1) 2(L2) 222(3L2) 4(L4)
6(L6)
3(L3)
23(3L24L3)
P
P2, Pm, P2/m
B B2, Bm, B2/m
正交
222, mm2, mmm
P C I
F
P222, Pmm2, Pmmm C222, Cmm2, Cmmm, I222, Imm2, Immm F222, Fmm2, Fmmm
点群格子及空间群
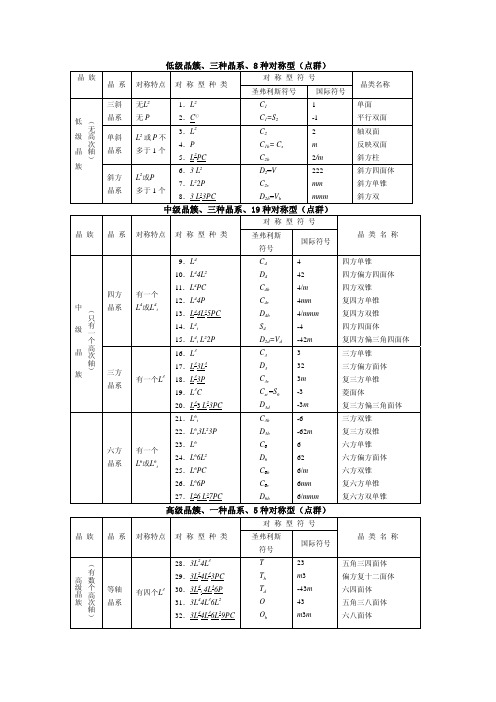
单面 平行双面 轴双面 反映双面 斜方柱 斜方四面体 斜方单锥 斜方双
对称型符号
对称特点 对 称 型 种 类
圣弗利斯 符号
国际符号
晶类名称
9．L4
C4
4
10．L44L2
D4
42
有一个 L4或L4i
11．L4PC 12．L44P 13．L44L25PC
C4h
4/m
C4v
4mm
D4h
4/mmm
14．L4i
Oh5
226
228
Oh8
229
Oh9
230
Oh10
P31 m P3 c 1 P31 c R3 m R3 c
P23 F23 I23 P213 I213 Pm3 Pn3 Fm3 Fd3 Im3 Pa3 Ia3 P432 P4232 F 432 F4132 I 432 P4332 P4132 I 4132 P-43m F-43m I-43m P-43n F-43c I-43d Pm3m Pn3n Pm3n Pn3m Fm3m Fm3c Fd3m Fd3c Im3m Ia3d
对称型符号
对称特点 对 称 型 种 类
圣弗利斯 符号
国际符号
晶类名称
28．3L24L3
T
29．3L24L33PC
Th
有四个L3 30．3L4i 4L36P
Td
31．3L44L36L2
O
32．3L44L36L29PC
Oh
23 m3 -43m 43 m3m
五角三四面体 偏方复十二面体 六四面体 五角三八面体 六八面体
C6
6
D6
62
C6h
6/m
26．L66P
2.2.3点群和空间群
该图形显然具有一个对称中心
因此 3 次倒转轴相当于 1 条 3 次旋转轴加上一个对称中心
3 3i
4 次倒转轴
相当于旋转90后再对中 心反演而图形不变。
这是一个独立的对称操 作。它既没有 4 次旋转 轴也没有对称中心，不 能分解成其他基本对称 要素的组合。
注意这里的 2、6、4、 8 这四个点是不存在的， 也是过渡点。
对称面
对称面是一个假想的平面，相应 的对称操作为对此平面的反映。对 称面就像一面镜子，把物体的两个 相同的部分以互成镜像反映的关系 联系起来。 垂直于对称面作任意直线，位于 直线两侧等距离的两点是性质完全 相同的对应点 晶体中如果存在有对称面，则必 定通过晶体的几何中心并将晶体分 为互成镜像反映的两个相同部分 在结晶学中，对称面一般用符号 “m” 表示。
倒转轴
倒转轴是一种复合对称 要素，由一根假想的直线 和在此直线上的一个定点 组成。相应的对称操作是 绕此直线旋转一定角度以 及对此定点的倒反。 根据晶体对称轴定律，倒 转轴也只有 1 次、2 次、 3 次、4 次和 6 次 5 种
倒反类倒转轴 中，只有 4 次倒转轴是一个独立的基本对称操
点群：在宏观晶体中存在的所有对称要素都必定 通过晶体的中心，因此不论如何进行对称操作，晶
体中至少有一个点是不变的，因此对称型也称为点
群。32点群
特征对称元素与7 大晶系
在32晶体学点群中，某些点群均含有一种相同的对称元素， 这样的对称元素叫做特征对称元素。
根据相应的对称性特征，晶体结构可以分为 7 类， 称为 7 大晶系。这 7 大晶系按对称程度增加的次序
在旋转操作中，使物体复原所需的最小旋转角 称为基转角。轴次 n 可以写成
5+点群格子及空间群
C2v20
C2v21
C2v22
Fdd2
Imm2
Iba2
Ima2(Ibm2)
2
C11
P-1
1 Ci
3
4
5
C12
C22
C32
P2
P21
C2（A2，Ⅰ2）
2
C2
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
D2h1
D2h2
D2h3
D2h4
D2h5
D2h6
D2h7
D2h8
D2h9
D2h10
D2h11
D2h12
D2h13
D2h14
D2h15
D2h16
D2h17
D2h18
D192h
D202h
D212h
D222h
D232h
D242h
D252h
D2h26
D2h27
D2h28
Pmmm
Pnnn
Pccm(Pbmb,Pmaa)
Pban(Pcna, Pncb)
mmm
D2h
6
7
8
9
Cs1
Cs2
Cs3
Cs4
Pm
Pc(Pa,Pn)
Cm(Am,Im)
Cc(Aa,Ia)
m
Cs
10
11
12
13
14
15
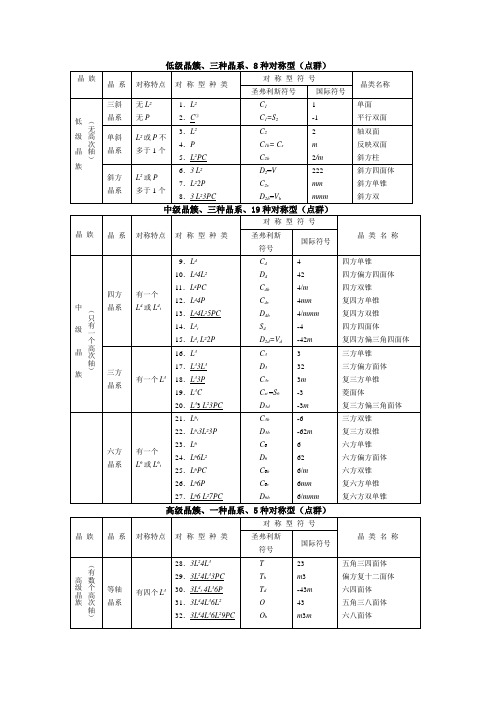
C2v21
C2v22
Fdd2
Imm2
Iba2
Ima2(Ibm2)
2
C11
P-1
1 Ci
3
4
5
C12
C22
C32
P2
P21
C2（A2，Ⅰ2）
2
C2
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
D2h1
D2h2
D2h3
D2h4
D2h5
D2h6
D2h7
D2h8
D2h9
D2h10
D2h11
D2h12
D2h13
D2h14
D2h15
D2h16
D2h17
D2h18
D192h
D202h
D212h
D222h
D232h
D242h
D252h
D2h26
D2h27
D2h28
Pmmm
Pnnn
Pccm(Pbmb,Pmaa)
Pban(Pcna, Pncb)
mmm
D2h
6
7
8
9
Cs1
Cs2
Cs3
Cs4
Pm
Pc(Pa,Pn)
Cm(Am,Im)
Cc(Aa,Ia)
m
Cs
10
11
12
13
14
15
点群和空间群
国际符号 international symbol
采用国际符号，不仅可以表示出各种晶类 中有那些对称元素，而且还能表示出这 些对称元素在空间的方向。国际符号根 据各种晶类的对称性可以是三项、或二 项、或一项符号组成，它分别表示晶体 某三个、或二个、或一个方向上的对称 元素。如果在某一个方向上，同时具有 对称轴和垂直于此轴的对称面，则写成 分数形式。
8
小结 summary
❖ 密勒指数（Miller indices） ❖ 对称元素和对称操作 ❖ 晶体的三十二个点群 ❖ 对称性和点群对于压电铁电体非常重要！ ❖ 只有晶体才会有压电铁电性，不存在非
晶压电铁电体。但是有非晶半导体和非 晶磁性材料。
wangcl@
9
晶体中的点群
❖ 由于无限大周期性的限制，晶体中的对称 操作只能有：1，2，3，4，6，i，m,4 ；
wangcl@
17
wangcl@
18
宏观对称元素的组合，可以导出32
种点群；宏观对称元素与微观对称元
素的组合，可以导出230种空间群。
空间群的国际符号由两部分组成，第
一部分为大写字母P、C、I、F，表
示14种布喇菲格子中的原始格子
（P）、底心格子（C）、体心格子
❖ 由于分子没有无限周期性的限制，所以 分子点群的数目要多于晶体中的点群数 目32个；
❖ 自然界对称性很多，例如：五度对称性， 足球，富勒烯C60, buckministerfullerence，碳管
wangcl@
6
wangcl@
7
wangcl@
❖ 由这些对称操作所构成的集合就是晶体中 的点群；
❖ 点：所有这些对称操作下，肯定有一个点 是不变的；
❖ 晶体中一共有32个这样的点群；
采用国际符号，不仅可以表示出各种晶类 中有那些对称元素，而且还能表示出这 些对称元素在空间的方向。国际符号根 据各种晶类的对称性可以是三项、或二 项、或一项符号组成，它分别表示晶体 某三个、或二个、或一个方向上的对称 元素。如果在某一个方向上，同时具有 对称轴和垂直于此轴的对称面，则写成 分数形式。
8
小结 summary
❖ 密勒指数（Miller indices） ❖ 对称元素和对称操作 ❖ 晶体的三十二个点群 ❖ 对称性和点群对于压电铁电体非常重要！ ❖ 只有晶体才会有压电铁电性，不存在非
晶压电铁电体。但是有非晶半导体和非 晶磁性材料。
wangcl@
9
晶体中的点群
❖ 由于无限大周期性的限制，晶体中的对称 操作只能有：1，2，3，4，6，i，m,4 ；
wangcl@
17
wangcl@
18
宏观对称元素的组合，可以导出32
种点群；宏观对称元素与微观对称元
素的组合，可以导出230种空间群。
空间群的国际符号由两部分组成，第
一部分为大写字母P、C、I、F，表
示14种布喇菲格子中的原始格子
（P）、底心格子（C）、体心格子
❖ 由于分子没有无限周期性的限制，所以 分子点群的数目要多于晶体中的点群数 目32个；
❖ 自然界对称性很多，例如：五度对称性， 足球，富勒烯C60, buckministerfullerence，碳管
wangcl@
6
wangcl@
7
wangcl@
❖ 由这些对称操作所构成的集合就是晶体中 的点群；
❖ 点：所有这些对称操作下，肯定有一个点 是不变的；
❖ 晶体中一共有32个这样的点群；
刘胜新-第三章点群、空间群和晶体结构PPT课件
上述的推导过程完全可以推广到其它晶系的空间群。把上述办
法依次用于7种晶系，共导出66种空间群。如果再考虑点群元素与
布喇菲点阵之间的取向关系，又能得到另一些空间群，结果总共得
出7320种20/1点0/9式空间群。
1
附表3 73种点式空间群
1 2020/10/9
3.4.2 非点式空间群
非点式空间群必包含1个非初基平移T的非点式操作，引入了 这种非点式操作，又可以导出157种非点式空间群。
石英的基本结构可以看成是硅氧四面体在三和六次螺旋轴 附近的螺旋链。左边为其中一个三次螺旋，右方显示的是螺旋连 接构成晶体框架。
1 2020/10/9
滑移面
由镜面和平移组合产生的对称元素称为滑移反映面，简称滑移
1 2020/10/9
子群、母群及生殖元素
子群：若群GA的全部元素是群G中的元素，并且两者的结合律 相同，称GA是群G的子群，而G是群GA的母群。如果对称元素GA和 GB能够得到G的全部对称元素，则称这两个对称元素为群G中的两 个生殖元素(Generating Element).
3.2点群的描述及图示
的全2对020/称10/点9 群。
1
从上述两种点群的极射投影再一次说明在投影图上一般位置的 正规点系的数目和点群具有对称操作的数目相同，即与点群的阶数 相同。
1 2020/10/9
立方系各晶类的投影图
在(e)所示：在投影面上{111)位置4个3轴，单胞3个轴为4次轴， 过单胞3个轴两两构成3个镜面及6个{110}的镜面。一般位置点的等效 点系共有48个点。
230种
对称操作全部作用于同一个公共点上的，至少包
含一个比初基平移还要小的平移τ。 157种
1
第八讲 点群符号空间群
Crystal System
Primary
Symmetry Direction Secondary
Tertiary
Triclinic
None
Monoclinic
[010]
Orthorhombic Tetragonal Hexagonal/ Trigonal
Cubic
[100] [001]
[001]
[100]/[010]/ [001]
以点群为m3m的晶体为例： CsCl 垂直于a方向为m
NaCl 垂直于a方向m，b，c，n共存
金刚石 垂直于a方向为d
CsCl结构沿c方向投影 垂直于a方向为m
NaCl结构沿c方向的投影
垂直于a方向m，b，c，n共存
金刚石结构沿c方向的投影 垂直于a方向为d
属于同一点群的晶体，可以属于不同的空间群。属于同 一宏观点群的所有空间群，称为与该点群同形的空间群。
27
8
圣佛里斯符号——Schoenflies notation
主要规则：
只有一个旋转轴：Cn 多个二次轴：Dn 多个高次轴：T
(Cyclic group) (Dihedra group) (Tetrahedral group)
八面体（等轴）：O
(Octahedral group)
与轴平行的反映面：v （vertical）
点群的国际符号和圣佛里斯符号
对称型的一般符号（也即对称型的全面符号）： 按一定顺序将对称型中所有的对称要素都书写出来， 不管方向性，且比较烦琐。
国际符号——一种比较简明的符号，也称HM符号。
（International notation 或者 Hermann-Mauguin notation）
第一章 课时六 点群 空间群 晶格对称性
13
四面体点群
E+8C3 + 3C2； 绕3个立方轴（红色）旋转π/2, 3π/2，接着做水平面镜像，共6 个对称操作，记为6S4； 对立方体相对面的对角线形成截 面作镜像，共6个对称操作，记 为6σd； 共12+6+6=24个对称操作；
由如上所示的24个点对称操作{E, 3C2, 8C3, 6S4, 6σd}组成的点群，用T d表示，称为正四面体点群。
47
钙钛矿(BaTiO3)结构
布拉维格子是？ 基元是？ 空间群？
48
钙钛矿(BaTiO3)结构
Barium titanate can exist in five phases, listing from high temperature to low temperature: (1) hexagonal (2) Cubic (Pm-3m, 221) (3) Tetragonal (P4mm, 99) (4) Orthorhombic (5) Rhombohedral
1.12
63
64
65
66
67
68
69
C1群：只含有一个元素（不动），表示没有任何对称性
Cn群：只含有一个旋转轴的点群，共4个，C2, C3, C4, C6 Cnv群：Cn群加上包含n重轴的镜面，共4个 Cnh群：Cn群加上垂直于n重轴的镜面，共4个 Cs群：C1群加上镜面
Ci群：C1群加上中心反演
horizontal vertical inversion
space group table: /wiki/Space_group#Table_of_space_groups_in_3_dimension4s0
41
点群、空间群和晶体结构介绍
群是某些具有相互联系规律的一些元素的组合，群的元素可 以是字母、数字、对称操作、点阵等。
任何一个群都应具有以下4个基本性质：
封闭性（Closure）
群G的n个不等效元素中，任两个元素组合或一个同类元素自 身组合都是群中的一个元素。
群中所有元素都遵循组合律，但组合次序不能变。
有唯一的单位元素（E）。它和群中任何一个元素的组合是元素 本身。 群中每一个元素，必有一个相应的逆元素（Inverse Element） 使得两者相乘为其本身。 以一个4次对称轴C4的全部操作所构成的群G来说明4个基本性 质。 两个独立群的直接积 设有两个独立群 GA和GB，其中GA是n阶群，GB是m阶群。两个 群中除了恒等元素外，没有其它共有元素，两个群的元素间相乘有 ai · bj=bj · ai 交换律，即 两个群的直接积G以 G G A G B 表示：
立方系各晶类的投影图
在(e)所示：在投影面上{111)位置4个3轴，单胞3个轴为4次轴， 过单胞3个轴两两构成3个镜面及6个{110}的镜面。一般位置点的等 效点系共有48个点。 5种点群中(e) 是该晶系的全对称点群。从这5种点群可以看 到立方晶系不一定有4次轴，例如点群(a) 和(b) 就没有4次轴。另 外，立方晶系并不一定总是具有最高的对称性，例如四方晶系的 点群D4h-4／mmm(16阶)和六方晶系的点群D6h-6／mmm(24阶)就 比立方晶系的点群T-23(12阶)的对称性高。
这两种类型的对称操作正是描述整个晶体结构对称性的基本操作。 图 (a)是正交点阵的阵 点 上 放 上 对 称 性 为 C2vmm2 的物体的空间群的俯 视图。
(a)正交晶系的Pmm2空间群
图中画出单胞的轮廓，原点选在左上角，a轴指向页底，b 轴指向右， c 轴从页面指出来。以圆圈排列来表示它的对称性 ，在左边的图中每个阵点的对称性用一般位置点的等效点系表 示。其中每一个圆圈既可以代表晶体中单个原子，也可以代表 原子集团。在右边的图上给出对称元素的配置。在原点有一个 沿 c 方向的2次轴和 2个镜面 (用粗线表示 )。 P- 初基点阵， mm2基本操作。非基本操作（附加的2次轴和镜面）未表示。
第5讲、点群、空间群和表面几何结构
3
单位元素 —— 不动操作
第一章 晶体结构
任意元素的逆元素 ——绕转轴角度，其逆操作 为绕转轴角度－ ； 中心反演的逆操作仍是中心反演； A 操作 —— 绕OA轴转动/2 —— S点转到T'点
B 操作 —— 绕OC轴转动/2 —— T'点转到S点 —— T点转到T'点
连续进行A和B操作 —— 相当于C操作
t 为一非完整格矢。
10
n度螺旋及其轴
绕轴每转2π/n角度后，再沿该轴的方向平移 T/n的l 倍，则晶体中的
原子与相同的原子重合。
第一章 晶体结构
(l为小于 n 的整数， 为沿轴方向上的周期矢量) T
晶体只能有1、2、3、4和6度螺旋轴。
例1：4度螺旋轴
A4
例2： 金刚石结构
上下底心的连线就是4度螺旋轴
可以证明8个基本的点对称操作可组合成32个点群。
空间群 (space group) ——包含点群的对称操作和平移对称操作的所 有组合方式。 (布喇菲格子和复式格子)
可以证明有230个空间群。
6
第一章 晶体结构
(一)、点群 —由点对称操作作为元素构成的群。
从宏观上看晶体是有限的，有限物体的对称群不能包含 平移操作，所以晶体的宏观对称性质用点群描写。
n12346由6种对称素可以组成10种二维点群按照点群对基矢的要求划分二维格子有4个晶系5种布拉伐格子25晶系轴和角度布拉伐格子简单斜方长方简单长方中心长方正方简单正方六角简单六方二维晶格的晶系和布拉伐格子26晶体表面相对于晶体表面结构的研究表明晶体表面的结构不完全是晶体内部相应结构的面的延续晶体表面是晶体三维周期性结构和真空之间的过渡层可以将它看作是特殊的相表面相晶体内部与表面平行的平面基矢晶体表面二维晶格基矢这两族基矢有可能是不同的表面的再构27典型表面再构之一晶体表面平面的密勒指数例如111si面原子排列的周期为体内相应平面的7倍28典型表面再构之二不同的方法可以获得不同的再构表面表面的再构现象与表面原子的驰豫原子的吸附有关通常可由低能电子衍射leed获得表面再构的几何规其中s为表面吸附原子29预告
单位元素 —— 不动操作
第一章 晶体结构
任意元素的逆元素 ——绕转轴角度，其逆操作 为绕转轴角度－ ； 中心反演的逆操作仍是中心反演； A 操作 —— 绕OA轴转动/2 —— S点转到T'点
B 操作 —— 绕OC轴转动/2 —— T'点转到S点 —— T点转到T'点
连续进行A和B操作 —— 相当于C操作
t 为一非完整格矢。
10
n度螺旋及其轴
绕轴每转2π/n角度后，再沿该轴的方向平移 T/n的l 倍，则晶体中的
原子与相同的原子重合。
第一章 晶体结构
(l为小于 n 的整数， 为沿轴方向上的周期矢量) T
晶体只能有1、2、3、4和6度螺旋轴。
例1：4度螺旋轴
A4
例2： 金刚石结构
上下底心的连线就是4度螺旋轴
可以证明8个基本的点对称操作可组合成32个点群。
空间群 (space group) ——包含点群的对称操作和平移对称操作的所 有组合方式。 (布喇菲格子和复式格子)
可以证明有230个空间群。
6
第一章 晶体结构
(一)、点群 —由点对称操作作为元素构成的群。
从宏观上看晶体是有限的，有限物体的对称群不能包含 平移操作，所以晶体的宏观对称性质用点群描写。
n12346由6种对称素可以组成10种二维点群按照点群对基矢的要求划分二维格子有4个晶系5种布拉伐格子25晶系轴和角度布拉伐格子简单斜方长方简单长方中心长方正方简单正方六角简单六方二维晶格的晶系和布拉伐格子26晶体表面相对于晶体表面结构的研究表明晶体表面的结构不完全是晶体内部相应结构的面的延续晶体表面是晶体三维周期性结构和真空之间的过渡层可以将它看作是特殊的相表面相晶体内部与表面平行的平面基矢晶体表面二维晶格基矢这两族基矢有可能是不同的表面的再构27典型表面再构之一晶体表面平面的密勒指数例如111si面原子排列的周期为体内相应平面的7倍28典型表面再构之二不同的方法可以获得不同的再构表面表面的再构现象与表面原子的驰豫原子的吸附有关通常可由低能电子衍射leed获得表面再构的几何规其中s为表面吸附原子29预告
点群和空间群ppt课件
❖ 宏观对称要素和微观对称要素在三维空间的组合，称为空 间群。
❖ 经过严格证明可以得出，晶体中可能存在230种空间群，任 何一种晶体的微观结构属于且只属于230种空间群之一。
50
点群与空间群的关系
晶体外形的对称性仅有32个点群，而晶体结构的对称性却有320
种空间群。晶体外形的对称性是晶体结构对称性的反映。 属于同一点群的晶体不一定属于同一空间群。换言之，空间群
59
60
61
62
63
64
重要对称元素的书写与图形记号
65
5
3
3
5
1
1
4
6
2
4
6 2
19
20
(3) 6 象转轴——实际上就是3度转轴＋对称面(m)
5 5
3
3
1
1
2
6
2
4
6
4
21
22
(3) 4 象转轴
3
1 2
2
3
1 4
4
23
24
结论： 晶体的宏观对称性中有以下八种基本的对称
操作：1，2，3，4，6，1, m, 4 。 这些基本的操
作组合起来，就可以得到32种不包括平移的宏观 操作类型。
12
二、中心反演(中心反映)
1.中心反演
如图所示，有对称心i，晶体中
iA
任一点A过中心 i 连线Ai并延长到A'，
使Ai = A' i, A与A'是等同点， i点称
A
为对称心。
2.表示方式
x, y, z
(1)熊夫利符号表示——i;
x, y,z
(2)国际符号表示—— 1
❖ 经过严格证明可以得出，晶体中可能存在230种空间群，任 何一种晶体的微观结构属于且只属于230种空间群之一。
50
点群与空间群的关系
晶体外形的对称性仅有32个点群，而晶体结构的对称性却有320
种空间群。晶体外形的对称性是晶体结构对称性的反映。 属于同一点群的晶体不一定属于同一空间群。换言之，空间群
59
60
61
62
63
64
重要对称元素的书写与图形记号
65
5
3
3
5
1
1
4
6
2
4
6 2
19
20
(3) 6 象转轴——实际上就是3度转轴＋对称面(m)
5 5
3
3
1
1
2
6
2
4
6
4
21
22
(3) 4 象转轴
3
1 2
2
3
1 4
4
23
24
结论： 晶体的宏观对称性中有以下八种基本的对称
操作：1，2，3，4，6，1, m, 4 。 这些基本的操
作组合起来，就可以得到32种不包括平移的宏观 操作类型。
12
二、中心反演(中心反映)
1.中心反演
如图所示，有对称心i，晶体中
iA
任一点A过中心 i 连线Ai并延长到A'，
使Ai = A' i, A与A'是等同点， i点称
A
为对称心。
2.表示方式
x, y, z
(1)熊夫利符号表示——i;
x, y,z
(2)国际符号表示—— 1
点群和空间群
国际符号international symbol 采用国际符号，不仅可以表示出各种晶类中有那些对称元素，而且还能表示出这些对称元素在空间的方向。
国际符号根据各种晶类的对称性可以是三项、或二项、或一项符号组成，它分别表示晶体某三个、或二个、或一个方向上的对称元素。
如果在某一个方向上，同时具有对称轴和垂直于此轴的对称面，则写成分数形式。
熊夫利斯（Sch öenfles ）符号C n ：字母表示旋转的意思，组标n 表示旋转的次数，n=1、2、3、4、6。
例如C 2代表二次旋转轴。
C nh ：表示除了n 次旋转轴外，还包括一个与此轴垂直的对称面。
C nv ：表示除了n 次旋转轴外，还包括一个与此轴重合（即平行）的对称面。
C ni ：表示除了n 次旋转轴外，还包括一个对称中心。
C i：表示有一个对称中心。
S4：表示有一个四次旋转倒反轴。
D n：表示除了n次主旋转轴外，还包括n 个与之轴垂直的二次旋转轴。
D nh：表示除了D n的对称性外，还包括一个与主旋转轴垂直的对称面，和n个与二次旋转轴重合（即平行）的对称面。
D nd：表示除了D n的对称性外，还包括n个T：除了四个三次旋转轴外，还包括三个正交的二次旋转轴。
T h：除了T的对称性外，还包括与二次旋转轴垂直的三个对称面。
T d：除了T的对称性外，还包括六个平分两个二次旋转轴夹角的对称面。
O：包括三个互相垂直的四次旋转轴，六个二次旋转轴，和四个三次旋转轴。
O h：除了O的对称性外，还包括T d与T h的对国际符号与熊氏符号对比国际符号熊氏符号1C 12C 23C 34C 46C 6m C sC i ，S 2S 14其它注意事项由于分子没有无限周期性的限制，所以分子点群的数目要多于晶体中的点群数目32个； 自然界对称性很多，例如：五度对称性，足球，富勒烯C 60,buckministerfullerence ，碳管小结summary密勒指数（Miller indices）对称元素和对称操作晶体的三十二个点群对称性和点群对于压电铁电体非常重要！ 只有晶体才会有压电铁电性，不存在非晶压电铁电体。
第九讲—点式空间群 ppt课件
全对称点群 1 2/m
mmm 4/mmm 3m 6/mmm m3m
点群各符号的顺序
晶系
在国际符号中的位置
1
2
3
三斜 只用一个符号
单斜 第一种定向：c是唯一轴；第二种定向：b是唯一轴
正交 2或2沿a
四方 4或4沿c
2或2沿b 2或2沿a和b
2或2沿c 2或2沿a±b
三方 3或3沿c 2或2沿a、b和a+b 2或2a、b和a+b
222 32 422 622
D2 D3 D4 D6 二面体点群
11种中心对称点群：
23 432
TO 立方点群
1 2/m 3 4/m 6/m mmm 3m 4/mmm 6/mmm m3 m3m
S2 C2h S6 C4h C6h D2h D3d D4h
D6h
Th Oh
10种新子群：
1 2/m 3 4/m 6/m mmm 3m 4/mmm 6/mmm m3 m3m
六方 6或6沿c 2或2沿a、b和a+b 2或2a、b和a+b
立方 4、4、2或2
沿<100>
3或3沿<111>
第九讲—点式空间群
2或2沿<110>
1(L1) 2(L2) 222(3L2) 4(L4)
6(L6)
3(L3)
23(3L24L3)
1(C) m(P) mm2 4/m
(L22P) (L4PC)
6 (S35)
第S九3讲, —S点32式(空C间32群), S33(σh), S34(C3), S35, S36(E)
65, 64,
63,
62,
6, 66
点群空间群和晶体结构
点群空间群和晶体结构
一、点群
点群是模拟物体在实际应用中的一种常用方法，它可以使用离散的点
来模拟物体的形状，形成空间网格。
它比传统三维建模技术更易于实现，
更少的信息就可以获得一个物体的完整几何描述。
点群可以被用来快速创建几何模型，而且可以利用点的位置和位置关
系来描述一个物体的形状特征，例如法向量和曲率，这对于计算机视觉、
求解机器人运动规划任务等都是非常有用的信息。
点群技术也被用来提取
复杂物体的特征，比如可以通过计算点群中局部点的法向量和曲率等特征
来识别物体的形状。
点群技术的另一个重要应用是三维重构，也就是把两个点群之间的关
系映射为3D模型，这样可以根据点群之间的变换关系或者任意点群之间
的距离来精确恢复模型的几何形状和位置变换。
点群技术的另一个作用就是可以将点群视为物体制作模型的基础构件，如通过点群文件可以构建3D打印、CAD和CAM模型。
二、空间群
空间群是由含有三维空间元素的群体组成的，是用来描述三维物体的
空间结构的一种技术。
空间群可以帮助科学家和工程师深入理解物体的表
面结构，从而更好地控制物体的生长和变化。
点群和空间群
7
六方晶系 正交晶系 三斜晶系
59
60
61
62
63
64
重要对称元素的书写与图形记号
A4
A3
4
3
A2
A1
A
整数；T为沿u轴方向上的周期矢量)。
晶体只能有1，2，3，4，6度螺旋轴。
如图所示，为4度螺旋轴。晶体绕
轴转900后，再沿该轴平移a/4，能自身
2 1
26
重合。
2.滑移反映面 经过该面的镜象操作
A2
M
A2
以后,再沿平行于该面的某
个方向平移T/n的距离(T是 该方向上的周期矢量，n为 2或4)，晶体中的原子和相 同的原子重合。
47
49
230种晶体学空间群
除了宏观对称要素之外，还有平移、平移与旋转结合形成
的螺旋对称轴、平移和反映结合形成的滑移面等微观对称
要素。 宏观对称要素和微观对称要素在三维空间的组合，称为空 间群。 经过严格证明可以得出，晶体中可能存在230种空间群，任
何一种晶体的微观结构属于且只属于230种空间群之一。
单胞中结点数目： 简单(原始)点阵: 1 面心点阵： 4 底心点阵： 2 体心点阵： 2
按照结点在7大种晶系上的不同分布方式，可形成14种布拉菲点阵。
简单点阵 : 1 ［［000］］
体心点阵: 2 [000] [1/2 1/2 1/2 ]
底心点阵:2 [000] [1/2 1/2 0 ]
面心点阵: 4 [000] [1/2 1/2 0] [1/2 0 1/2] [ 0 1/2 1/2]
点群和空间群
1
晶体对称性
2
3
4
5
§1 晶体的特殊对称性——对称操作
空间群、点群
一些物理对象能够在一定的操作下保持不变，这种性质称为对称性，使物理对象保持不变的操作O叫做对称操作。
按顺序先做对称操作O1，再做对称操作O2，显然物理对象保持不变，因此连做两次对称操作是一个新的对称操作O3，可以记为O3 O2O1，O2O1称为对称操作的乘积。
对称操作O的逆操作也保持物理对象不变，因此也是一个对称操作，记为O−1，按照数学上的定义，对称操作全体关于前面定义的乘法成为一个群，称为对称群，对称操作O称为对称元素。
使晶体保持不变的空间变换构成的群称为空间群。
空间群的元素一般写成 R| ，其中R是一个3 3矩阵，代表对称操作的旋转部分（包括空间反演）， 是一个矢量， R| 把空间矢量r 变为 R| r Rr 。
乘法规则R2| 2 R1| 1 r R2| 2 R1r 1R2R1r R2 1 2R2R1|R2 1 2 r就是说R2| 2 R1| 1 R2R1|R2 1 2因此R−1|−R−1 R| I|0R| −1 R−1|−R−1一般来说即使 R| 是一个对称操作，单纯的转动R也不是对称操作，但是按照上面的乘法和取逆规则，空间群元素的旋转部分全体也构成一个群，这个群叫做点群。
晶体的点群的元素R一般不能保持晶体不变，点群一般不是晶体的空间群的子群。
下面证明几个基本事实：1.对任意格矢l 和对称操作 R| ，都有Rl l ′，也就是说虽然 R|0 一般不能保持晶体不变，但是 R|0 可以保持空间点阵不变。
证明： R| 、 I|l 和 R| −1 R−1|−R−1 都是对称操作，因此它们的乘积也是对称操作，按照上面的乘法规则，我们有R| I|l R−1|−R−1R|Rl R−1|−R−1I|Rl这是一个单纯的平移，因此Rl l ′必定是一个格矢。
2.对称操作的旋转角只能取0，60∘，90∘，120∘，180∘及其整数倍。
证明：首先任取一个不平行于转轴的格矢l ，按照上面的结论，Rl 也是格矢，因此非零矢量Rl −l （如果det R −1，R包含空间反演或镜面反射，则取Rl l ）也是格矢，且从几何关系易知格矢Rl −l （如果det R −1，R包含空间反演或镜面反射，则取Rl l ）垂直于转轴。
点群空间群
[111]
[100]([010])
[110] [110] [001]
[010]
a
2a+b
[001]
[100]
[210]
空间群
利用空间群信息,可以确定原子,离子,分子,原子团的具体排 列位置!尤其对于确定未知相的晶体结构具有重要意义!
空间群的国际符号符号格子类型123pnmapnma第一章晶体几何学基础第六节微观对称与空间群晶系三个位所表示的方向依次列出等轴cabcab001111110四方cabab001100010110斜方abc100010001单斜b010三斜任意方向任意方向三或六方ca2ab001100210123123第一章晶体几何学基础第六节微观对称与空间群空间群利用空间群信息可以确定原子离子分子原子团的具体排列位置
第一章
晶体几何学基础
第五节
晶系与32 晶系与32点群 32点群
7个晶系的划分和 晶体学点群 个晶系的划分和32晶体学点群 个晶系的划分和
第一章
晶体几何学基础
第五节
晶系与32 晶系与32点群 32点群
第一章
晶体几何学基础
第五节
晶系与32 晶系与32点群 32点群
第一章
晶体几何学基础
第六节
微观对称与空间群
空间群的符号 包含了空间格子类型, 对称元素及其相互之间的关系。 包含了空间格子类型, 对称元素及其相互之间的关系。 国际符号分两个部分：前半部分是平移群的符号， 国际符号分两个部分：前半部分是平移群的符号，即布拉 维格子的符号，按格子类型的不同而分别用字母P 维格子的符号，按格子类型的不同而分别用字母P、R、I、 等表示之。后半部分则是其他对称要素之集合的符号， C、F等表示之。后半部分则是其他对称要素之集合的符号， 类似于点群符号的表达, 但有的被微观对称要素取代。 类似于点群符号的ห้องสมุดไป่ตู้达, 但有的被微观对称要素取代。 空间群的国际符号
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
能作周期性
重复排列。
2021/3/26
11
晶体中不可能出现5次轴或高于6次的对称轴。这是由于它们不符合空间格子
构造规律。 只有1、2、3、4、6次五种对称轴才能按空间格子中结点分布要求构成面网 网孔，不留间隙地排满整个平面。
2021/3/26
12
二、中心反演(中心反映)
1.中心反演 如图所示，有对称心i，晶体中
(4)2度轴垂直的对称面
2021/3/26
31
例题2：金刚石的对称性简析—正四面体的对称操作
四个原子 位于正四 面体的四 个顶角上
2021/3/26
32
1.绕三个立方轴转动
2021/3/26
33
2. 绕4个立方体对角线轴转动 2 , 4
33
2021/3/26
点群和空间群
2021/3/26
1
晶体对称性
2021/3/26
2
2021/3/26
3
2021/3/26
4
2021/3/26
5
§1 晶体的特殊对称性——对称操
作
四种基本的操作——转动（旋转）、反演、镜象（反映
）、象转轴（旋转反映）。
一、转动
1.转动对称操作
设晶体外形为一立方体，沿图中
所示转轴转动900，外形与原来重合。
操作：1，2，3，4，6，1, m, 4 。 这些基本的操
作组合起来，就可以得到32种不包括平移的宏观 操作类型。
熊夫利符号：C1 ,C2 ,C3 ,C4 ,C6 ,i, , S4
2021/3/26
25
五、晶体的微观对称操作
A4
1.n度螺旋轴
晶体绕u轴每转2/n角度后，再沿
4
A3
该轴的方向平移T/n的 l 倍，则晶体中的
这样的转动称为转动对称操作。该轴
称为转动轴。如果转动1800等晶体都
保持外形重合。
2021/3/26
转动轴
6
2.转动对称操作的种类 由于受晶格周期性的限制，转动对称操作所转动的
角度并不是任意的。而是遵循一定的规律。
B
A
B1
A
B
A1
AB是晶列上最近邻两格点的距离。
BA nAB AB AB cos BAcos AB(1 2cos )
A1
该方向上的周期矢量，n为
2或4)，晶体中的原子和相
A
同的原子重合。
2021/3/26
M A2
A1
A
M
27
例题1：立方系的对称性简析。
(1) 三 个 相 互 垂 直 的 四 度 轴
2021/3/26
28
(2)四个三度轴(空间对角线)
2021/3/26
29
(3)六个2度轴
2021/3/26
30
O(对称心)
y
际上即为中心反演
x
2021/3/26
x, y,z
A
16
(2) 2 象转轴——实际上就是对镜象m。
z(u轴)
A
Ax, y, z
x, y, z
和O-xy对称面 的操作相当。
O(对称心)
y
2021/3/26
x
x, y,z
A 17
2021/3/26
18
(3) 3 象转轴——实际上就是3度转轴＋对称心(i)
3.n度旋转对称轴(rotation about an axis)
(1)定义
晶体绕某一固定轴u旋转角度2/n以后，能自身重
合，则称u为n度(或n次)旋转对称轴。n只能取1，2，3
，4，6。
晶体不能有5度或6度以上的转轴。
(2)对称轴表示方式
①熊夫利(Schoenflies notation)符号表示
5
3
3
5
1
1
4
6
2
4
6
2
2021/3/26
19
2021/3/26
20
(3) 6 象转轴——实际上就是3度转轴＋对称面(m)
5 5
3
3
1
1
2
6
2
4
6
4
2021/3/26
21
2021/3/26
22
(3) 4 象转轴
3
1 2
2
2021/3/26
3
1 4
4
23
2021/3/26
24
结论： 晶体的宏观对称性中有以下八种基本的对称
34
3. 绕三个立方轴转动 , 3
22
加中心反演
2021/3/26
35
4. 绕6条面对角线轴转动 加上中心反演
2021/3/26
36
例题3 正六面柱的对称性分析
合，则称u轴为n度旋转—反演轴，又称为n度象转轴。
只有1，2，3，4，6。
(2)符号表示
1，2，3， 4， 6
2.象转轴解析
2021/3/26
15
(1) 1 象转轴——实际上就是对称心i。
A点绕旋转轴(z轴)
z(u轴)
Ax, y, z
旋 转 3600 ， 在 经 过
中 心 反 演 到 A' 点 ， 晶体完全重合。实
iA
任一点A过中心 i 连线Ai并延长到A'
，使Ai = A' i, A与A'是等同点， i点
A
称为对称心。
2.表示方式
x, y, z
(1)熊夫利符号表示——i;
x, y,z
(2)国际符号表示—— 1
例：立方体的中心就是对称中心。如果将对称心放在坐
标2原021/3点/26 上，则有(x,y,z)点与(-x,-y,-z)点等同。
cos n 1
n是整数。
2021/3/26
2
7
cos n 1，且1 cos 1， n只能取值：3，2，1，0， 1。
2
n : 3 2 1 0 -1;
cos : 1
:0
2
1
0.5 0 - 0.5 -1
2
323
2 2 2 2
643
2
2
2021/3/26
n
n 1，2，3，4，6。 分别称 为1，2，3，4，6次( 度 )转轴。 8
C1、C2、C3、C4、C6。 ②国际符号(International notation)表示
1、 2、 3、 4、 6。
2021/3/26
9
4.对称轴度数 度数 n 2
3
4
6
符号表示
符号
2021/3/26
10
5. 长方形、
正三角形、
正方形和正
六方形可以
在平面内周
期性重复排
列。正五边
形及其它正
n 边形则不
3
原子和相同的原子重合(其中l为小于n的
整数；T为沿u轴方向上的周期矢量)。
A2
晶体只能有1，2，3，4，6度螺旋轴。 A1
如图所示，为4度螺旋轴。晶体绕 A
2
轴转900后，再沿该轴平移a/4，能自身
1
重合。 2021/3/26
26
2.滑移反映面
经过该面的镜象操作
A2
以后,再沿平行于该面的某
个方向平移T/n的距离(T是
13
三、镜象(镜面反映、对称面)
1.镜象 如图所示，A和A’等同，如同镜子一样。
2.表示方式
(1)熊夫利符号表示—— ;
(2)国际符号表示——m。
z A x, y, z
A
A
O
y
x2021/3/26
A x, y,z O-xy 相当于镜面。
14
四、n度旋转—反演轴(象转轴)
1.象转轴
(1)定义
先绕u轴转动2/n，再经过中心反演，晶体自动重