河北省容城中学2014-2015学年高二11月月考数学(理)试题

合集下载

河北省容城中学高二11月月考数学文试题 Word版无答案

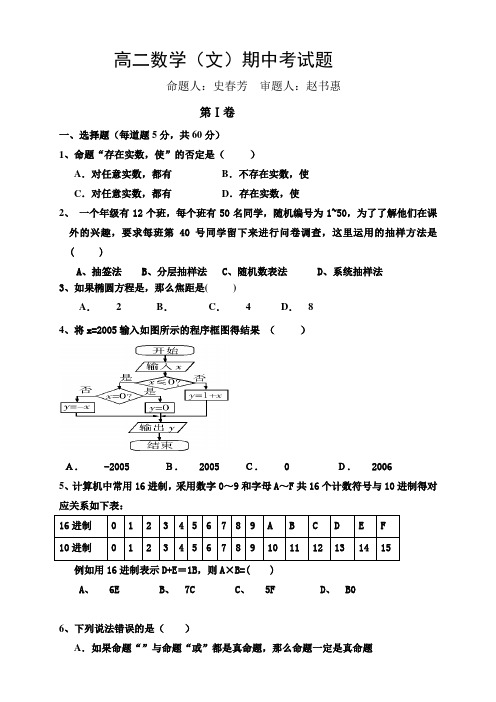
高二数学（文）期中考试题命题人：史春芳审题人：赵书惠第Ⅰ卷一、选择题（每道题5分，共60分）1、命题“存在实数，使”的否定是（）A．对任意实数，都有B．不存在实数，使C．对任意实数，都有D．存在实数，使2、一个年级有12个班，每个班有50名同学，随机编号为1~50，为了了解他们在课外的兴趣，要求每班第40号同学留下来进行问卷调查，这里运用的抽样方法是( )A、抽签法B、分层抽样法C、随机数表法D、系统抽样法3、如果椭圆方程是，那么焦距是()A．2B．C．4D．84、将x=2005输入如图所示的程序框图得结果（）Ａ． -2005 Ｂ． 2005 Ｃ． 0 Ｄ． 20065、计算机中常用16进制，采用数字0～9和字母A～F共16个计数符号与10进制得对应关系如下表：例如用16进制表示D+E＝1B，则A×B=( )A、 6EB、 7CC、 5FD、 B06、下列说法错误的是（）A．如果命题“”与命题“或”都是真命题，那么命题一定是真命题B ．命题“若，则”的逆否命题是：“若，则”C ．命题：存在，使，则：对任意的D ．特称命题“存在，使”是真命题7、一个质地均匀的正四面体玩具的四个面上分别标有1,2,3,4这四个数字．若连续两次抛掷这个玩具，则两次向下的面上的数字之积为偶数的概率是( )A 、B 、 34C 、D 、 588、命题“（2x+1）（x-3）<0”的一个必要不充分条件是（）Ａ．Ｂ．Ｃ．Ｄ．9、已知两点，且是与的等差中项，则动点的轨迹方程是（） A ． B ． C ． D ．10、200辆汽车通过某一段公路时的时速频率分布图如图所示，则时速在分汽车大约有多少辆？（）A 、 30B 、 40C 、 50D 、 60 11、已知椭圆C 的短轴长为6，离心率为45，则椭圆C的焦点F 到长轴的一个端点的距离为( )A ．9B ．1C ．1或9D ．以上都不对12、已知为椭圆上的一个点, ,分别为圆和圆上的点，则的最小值为（）A ． 5B ． 7C ． 13D ． 15 第Ⅱ卷二、填空题（每小题5分，共20分）13、利用计算机产生0～1之间的均匀随机数a ，则事件“3a －1＞0”发生的概率为__________．14、将某选手的9个得分去掉1个最高分，去掉1个最低分，7个剩余分数的平均分为91，现场作的9个分数的茎叶图后来有1个数据模糊，无法辨认，在图中以x 表示：则7个剩余分数的方差为__________。

高二数学试题(含答案)

A C
B1E BC1
B
又 EF BC1 ，所以 BC1 平面 B1EF ，即 B1F BC1 ，
所以 B1FE 就是平面 A1BC1 与平面 B1BC1 所成的锐二面角的平面角。…………8 分
在 B1EF 中， B1EF 90 0 ， B1E
2 2
，
B1 F
1
2 3
,
sin B1FE
从某校随机抽取 100 名学生，获得了他们一周课外阅读时间(单位：小时)的数据，整理得到
组号
分组
频数
数据分组及频数分布和频率分布直方图
1 2 3 4 5 6 7 8 9 合计
[0,2) [2,4) [4,6) [6,8) [8,10) [10,12) [12,14) [14,16) [16,18) 100
河北容城中学 2014～2015 学年度题（共 12 小题，每题 5 分，共 60 分）只有一个答案符合题目要求，多选、不选或错选均不得分. 1. 一个人打靶时连续射击两次,事件“至少有一次中靶”的互斥事件是
A. 至多有一次中靶 B. 两次都中靶 C. 只有一次中靶 D. 两次都不中靶
④连接四面体 ABCD 每组对棱中点的线段互垂直平分 ⑤从四面体 ABCD 每个顶点出发的三条棱的长可作为一个三角形的三边长 16. 已知正方体 ABCD A1B1C1D1 中，E 、F 分别为 BB1、CC1 的中点，那么异面直线 AE 与
D1F 所成角的余弦值为____________.
三．解答题（本大题共 6 个小题，共 70 分）. 17. (本小题满分 10 分)
B1
2
（2）设向量 n (x, y, z) 且 n 平面 A1BC1
于是 n A1B 且 n A1C1 ，即 n A1B 0 且 n A1C1 0 ，

河北省容城中学2014-2015学年高二11月月考化学试卷 Word版含答案.pdf

高二年级11月月考化学试题命题人胡欣阁审题人阴增彬考试时间：90分钟；总分：100分。

可能用到的相对原子质量：H-l C-40 N-14 O-16 S-32 Al-27 Cl-35.5 Cu-64 Ag-108 Pb-207 C-12 第I卷（选择题，每小题2分，共60分） 1.国际巴黎车展示上，世界各大汽车商纷纷推出环保动力小汽车,使用的新型环保电池为? （? ）氢氧燃料电池 B锌锰电池 C镍镉电池 D铅蓄电池.0mol/L，经过20s后，它的浓度变成了0.2mol/L，在这20s内它的反应速率为 ( )A、0.04B、0.04mol / (L.s)C、0.08mol / (L.s)D、0.04mol / L 3.将纯水加热至较高温度，下列叙述正确的是A?、水的离子积变大、pH变小、呈酸性B?、水的离了积不变、pH不变、呈中性 C? 水的离子积变小、pH变大、呈碱性D?、水的离子积变大、pH变小、呈中性）．汽车的启动电源常用铅蓄电池，放电时的电池反应如下：PbO2 + Pb + 2H2SO4=2PbSO4↓+ 2H2O，根据此反应判断下列叙述中正确是? ? （? ） ?A．PbO2是电池的负极 ?B．负极的电极反应式为：Pb + SO - 2e -=PbSO4↓ C．PbO2得电子，被氧化 D．电池放电时，溶液酸性增强、下列说法正确的是 A．钢铁发生电化腐蚀的正极反应式：Fe－2e－===Fe2＋ B．氢氧燃料电池的负极反应式：O2 ＋2H2O ＋4e-===4OH－ C．粗铜精炼时，与电源正极相连的是纯铜 D．用惰性电极电解饱和食盐水时，阳极的电极反应式为：2Cl－2e－===Cl2.①②③ B.②③④⑤C.②③④⑤⑥D.①②③④⑤⑥ 9.一种新型燃料电池，以铂板为电极插入KOH溶液中，分别向两极通乙烷和氧气，电极反应为C2H6 + 18OH-=2CO + 12H2O + 14e-； 14H2O + 7O2 + 28e-=28 OH-，有关推断错误的是（） A．通氧气的电极为正极 B．在电解质溶液中CO向正极移动 C．放电一段时间后，KOH的物质的量浓度将下降 D．参加反应的氧气和乙烷的物质的量之比为7:2 10.一定条件下，在体积为10 L的密闭容器中，1 mol X和1 mol Y进行反应： 2X(g)＋Y(g)Z(g)，经60 s达到平衡，生成0.3 mol Z，下列说法正确的是（） A．以X浓度变化表示的反应速率为0.001 mol/(L·s) B．将容器体积变为20 L，Z的平衡浓度变为原来的1/2 C．若升高温度Y的转化率减小，则正反应为吸热反应 D．达到平衡时，X与Y 的浓度相等 11.25℃时，水的电离达到平衡：H2OH＋＋OH-；ΔH＞0，下列叙述正确的是A、向水中加稀氨水，平衡逆向移动，c(OH)降低 B 向水中加入少量固体硫酸氢钠，c(H＋)增大，Kw不变 C 向水中加入少量固体CH3COONa，平衡逆向移动，c(H＋)降低 D 将水加热，Kw增大，pH不变在25、101 kPa下，1 g甲醇燃烧生成CO2和液态水时放热22.68 kJ,下列热化学方程式正确的是（? ） A.CH3OH（l）+O2（g）===CO2（g）+2H2O（l）；ΔH=+725.8 kJ/mol B.2CH3OH（l）+3O2（g）===2CO2（g）+4H2O（l）；ΔH=－1452 kJ/mol C.2CH3OH（l）+3O2（g）===2CO2（g）+4H2O（l）；ΔH=－725.8 kJ/mol D.2CH3OH（l）+3O2（g）===2CO2（g）+4H2O（l）；ΔH=+1452 kJ/mol 13．在0.1mol/L的CH3COOH溶液中，要促进醋酸电离，且氢离子浓度增大，应采取的措施是（）A. 升温B. 降温C. 加入NaOH溶液D. 加入稀HCl 14．在同温同压下，下列各组热化学方程式中Q2 > Q1的是（） A、2H2(g)+O2(g)=2H2O(g) ΔH==- Q1 2H2(g)+O2(g)=2H2O(l) ΔH==- Q2 B、S(g)+O2(g)=SO2(g) ΔH==- Q1 S(s)+O2(g)=SO2(g) ΔH==- Q2 C、C(s)+O2(g)=CO2(g) ΔH==- Q1 C(s)+1/2O2(g)=CO(g) ΔH==- Q2 D、H2(g)+Cl2(g)=2HCl(g) ΔH==- Q1 1/2H2(g)+1/2Cl2(g)=HCl(g) ΔH==- Q2 15. 以下现象与电化腐蚀无关的是? A? 黄铜（铜锌合金）制作的铜锣不易产生铜绿（铜锈） B? 生铁比软铁芯（几乎是纯铁）容易生锈? C? 质器件附有铜质配件，在接触处易生铁锈D? 银质奖牌久置后表面变暗．用铂电极电解下列溶液时，阴极和阳极上的主要产物分别为H2和O2的是（　）A、稀NaOH溶液? ?B、HCl溶液C、CuSO4溶液?D、AgNO3溶液．某原电池总反应离子方程式为.2Fe3++Fe=3Fe2+ ，不能实现该反应的原电池是(　) A．正极为Cu，负极为Fe，电解质溶液为FeCl3 溶液 B．正极为C，负极为Fe，电解质溶液为Fe(NO3)3 溶液 C．正极为Ag，负极为Fe，电解质溶液为Fe2(SO4)3 溶液 D．正极为Ag,负极为Fe,电解质溶液为CuSO4溶液NH4Cl与Ba(OH)2.8H2OA.(1) (2) (6)B.(1) (2) (4) (6)C.(2) (6)D.(2) (4) (6) 19.已知：H2(g)＋F2(g)===2HF(g) H＝－270kJ，下列说法正确的是A．1个氢气分子与1个氟气分子反应生成2个氟化氢分子放出270kJ B．1mol氢气与1mol氟气反应生成2mol液态氟化氢放出的热量小于270kJ C．相同条件下，1mol氢气与1mol氟气的能量总和大于2mol氟化氢气体的量 D．2氟化氢气体分解成1的氢气和1的氟气270kJ热量H＞0已知：298K时，2SO2(g) + O2(g) 2SO3(g)；H=—Q1KJ/mol，在相同温度下，向密闭容器中通入2molSO2和1molO2，达到平衡时放出热量Q2KJ，则下列关系式正确的是（） A．无法比较 B．Q1＜Q2 C．Q1＝Q2 D．Q1＞Q2 可逆反应N2＋3H22NH3的正、逆反应速率可用各反应物或生成物浓度的变化来表示。

河北省容城中学2014-2015学年高二下学期第一次月考数学(理)试题 Word版含答案

1．用三段论推理：“指数函数x a y =是增函数，因为x y )21(=是指数函数，所以x y )21(=是增函数”，你认为这个推理( ) A ．大前提错误 B 小前提错误C ．推理形式错误D ．是正确的2．若'0()3f x =-，则000()(3)limh f x h f x h h→+--=（）A ．3-B ．6-C ．9-D ．12-3.定积分⎠⎜⎛01(2x ＋e x )d x 的值为( ) A ．e ＋2 B ．e ＋1 C ．e D ．e －14．函数xxy ln =的最大值为（） A ．1-e B ．e C ．2e D ．310 5．数列2,5,11,20,,47,x …中的x 等于（） A ．28 B ．32 C ．33 D ．276．直线y ＝4x 与曲线y ＝x 3在第一象限内围成的封闭图形的面积为( )A. 2 2B. 4 2C. 2D. 4 7．曲线y ＝x e x －1在点(1，1)处切线的斜率等于( )A ．2eB ．eC ．2D ．18．设曲线y ＝ax －ln(x ＋1)在点(0，0)处的切线方程为y ＝2x ，则a ＝( )A ．0B ．1C ．2D ．39.已知32()32f x x x x a =-++，若()f x 在R 上的极值点分别为,m n ，则m n +的值为（）A ．2 B ．3 C ．4 D ．610．函数)(x f 的定义域为开区间),(b a ，导函数)(x f '在),(b a 内的图象如图所示，则函数)(x f 在开区间),(b a 内有极小值点（）A ．1个B ．2个C ．3个D ．4个 11．设△ABC 的三边长分别为,,,c b a △ABC 的面积为S ，内切圆半径为r ，则cb a Sr ++=2.类比这个结论可知：四面体ABC P -的四个面的面积分别为,1S ,2S ,3S ,4S 内切球的半径为r ，四面体ABC P -的体积为V ，则r＝( )A.VS 1＋S 2＋S 3＋S 4 B.2V S 1＋S 2＋S 3＋S 4C.3V S 1＋S 2＋S 3＋S 4D.4VS 1＋S 2＋S 3＋S 412．对于R 上可导的任意函数()f x ，若满足'(1)()0x f x -≥，则必有（）A ． (0)(2)2(1)f f f +< B. (0)(2)2(1)f f f +≤ C. (0)(2)2(1)f f f +≥ D. (0)(2)2(1)f f f +>二、填空题.( 本题共4个小题，每小题5分，满分20分)13. 220sin 2xdx π=⎰14. 若函数x a x x f sin 2cos )(+=在区间)2,6(ππ是减函数，则a 的取值范围是_15．)(131211)(+∈+⋅⋅⋅+++=N n nn f ，经计算的27)32(,3)16(,25)8(,2)4(,23)2(>>>>=f f f f f ，推测当2≥n 时，有__________________________.16.如图14，在边长为e(e 为自然对数的底数)的正方形中随机撒一粒黄豆，则它落到阴影部分的概率为________．三、解答题：17．(10分)已知函数32()39f x x x x a =-+++ （1）求函数()y f x =的单调递减区间（2）函数()y f x =在区间[]2,2-上的最大值是20，求它在该区间上的最小值18．（12分）已知函数23bx ax y +=，当1x =时，有极大值3；（1）求,a b 的值；（2）求函数y 的极小值。

河北省保定市容城中学2014-2015学年高二数学下学期第二次月考试题理

河北省保定市容城中学2014-2015学年高二数学下学期第二次月考试题理第I 卷（选择题）一、选择题（每题5分）1．在复平面内，复数32i 1i --对应的点位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限2．用三段论推理：“任何实数的平方大于0，因为a 是实数，所以02>a ”，你认为这个推理（）A ．大前提错误B ．小前提错误C ．推理形式错误D ．是正确的 3．命题“x ∀∈R ，xe －x ＋1≥0”的否定是（） A ．x ∀∈R ，lnx ＋x ＋1＜0 B ．x ∃∈R ，xe －x ＋1＜0 C ．x ∀∈R ，xe －x ＋1＞0 D ．x ∃∈R ，x e －x ＋1≥04．设随机变量X 服从正态分布N （3，4），若P （X ＜2a+3）=P （X ＞a ﹣2），则a 的值为（）. A ． B ．3 C ．5 D ．5．已知盒中装有3个红球、2个白球、5个黑球，它们大小形状完全相同，现需一个红球，甲每次从中任取一个不放回，在他第一次拿到白球的条件下，第二次拿到红球的概率（）. A ． B ． C ． D ．6．某人上班途中要经过三个有红绿灯的路口，设遇到红灯的事件相互独立，且概率都是0.3，则此人上班途中遇到红灯的次数的期望为（）.A ．0.3B ．0.33C ．0.9D ．0.7 7．设（x ﹣）6的展开式中x3的系数为a ，二项式系数为b ，则的值为（）.A ．B ．C ．16D ．48．甲，乙，丙，丁四位同学各自对A ，B 两变量的线性相关试验，并用回归分析方法分别求得相关系数r 如表：甲乙丙丁 r0.820.780.690.85则这四位同学的试验结果能体现出A ，B 两变量有更强的线性相关性的是（）. A ．甲 B ．乙 C ．丙 D ．丁9．用数学归纳法证明12+22+…+（n ﹣1）2+n2+（n ﹣1）2+…+22+12═时，由n=k的假设到证明n=k+1时，等式左边应添加的式子是（）A.（k+1）2+2k2B.（k+1）2+k2C.（k+1）2D.10．某城市有3个演习点同时进行消防演习，现将4个消防队分配到这3个演习点，若每个演习点至少安排1个消防队，则不同的分配方案种数为（）.A．12 B．36 C．72 D．10811．函数f（x）=（x2﹣2x）ex（e为自然数的底数）的图象大致是（）.12．已知函数2(0)()(0)x xf xx x⎧≥⎪=⎨-<⎪⎩则1x=是()2f x=成立的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件13．已知()24f x x x=++-的最小值为n，则2()nxx-的展开式中常数项为（）A．20 B．160 C．-160 D．-20[来源:学&科&网]14．若函数1()e(0,)axf x a bb=-＞＞0的图象在0x=处的切线与圆221x y+=相切，则a b+的最大值是（）A.4B.22C.2D.2二、填空题（每题5分）15．若（x+m）9=a0+a1（x+1）+a2（x+1）2+…+a9（x+1）9，且a0﹣a1+a2﹣a3+…+a8﹣a9=39，则实数m的值为．16．已知函数f（x）=x3+ax2﹣a（a∈R），若存在x0，使f（x）在x=x0处取得极值，且f （x0）=0，则a的值为．17．22sin2xdxπ=⎰．18．计算12323n n n n n C C C nC +++⋅⋅⋅+，可以采用以下方法：构造等式：0122n nn n n n C C x C x C x +++⋅⋅⋅+()1nx =+，两边对x 求导，得()112321231n n n n n n n C C x C x nC x n x --+++⋅⋅⋅+=+，在上式中令1x =，得1231232n n n n n n C C C nC n -+++⋅⋅⋅+=⋅．类比上述计算方法，计算12223223n n n n n C C C n C +++⋅⋅⋅+= ．三、解答题（19题10分，20题12分，21、22题各14分）19．在平面直角坐标系中，以原点为极点，x 轴为极轴建立极坐标系，曲线1C 的方程为sin x y θθ⎧=⎪⎨=⎪⎩（θ为参数），曲线2C 的极坐标方程为2:cos sin 1C ρθρθ+=,若曲线1C 与2C 相交于A 、B 两点．(1)求||AB 的值；(2)求点(1,2)M -到A 、B 两点的距离之积．20．某次考试中，从甲、乙两个班各随机抽取10名学生的成绩进行统计分析，学生成绩的茎叶图如图所示，成绩不小于90分为及格．（1）从每班抽取的学生中各随机抽取一人，求至少有一人及格的概率（2）从甲班10人中随机抽取一人，乙班10人中随机抽取两人，三人中及格人数记为X ，求X 的分布列和期望．21．设数列{an}满足a1=3，an+1=an2﹣2nan+2，n∈N*．（1）求出a2，a3，a4的值，并猜想数列{an}的通项公式（不需证明）；（2）记Sn为数列{an}的前n项和，试求使得2n＞Sn成立的最小正整数n，并给出证明．22．已知函数f（x）=alnx﹣ax﹣3（a＜0）．（1）求函数f （x ）的单调区间；（2）若函数y=f （x ）的图象在点（2，f （2））处的切线的倾斜角为45°，对于任意的t ∈[0，1]，函数g （x ）=x3+x2[f ′（x ）+m]在区间（t ，2）上总不是单调函数，其中f ′（x ）为f （x ）的导函数，求实数m 的取值范围．参考答案 1．A 【解析】试题分析：ii i 21123+=--,对应的点()2,1，因此是第一象限。

河北省保定市满城中学2014-2015学年高二10月月考数学(理)试题(无答案)

一、选择题（本大题共12个小题，每小题5分，共60分）二、1. 某商场有四类食品,其中粮食类、植物油类、动物性食品类及果蔬类分别有40种、10种、30种、20种,现从中抽取一个容量为20的样本进行食品安全检测,若采用分层抽样的方法抽取样本,则抽取的植物油类与果蔬类食品种数之和是( ) A.4 B.5 C.6 D.72.命题p :若a ·b <0,则a 与b 的夹角为钝角.命题q :定义域为R 的函数f (x )在(-∞,0)及(0,+∞)上都是增函数,则f (x )在(-∞,+∞)上是增函数.下列说法正确的是( )A.“p 或q”是真命题B.“p 且q”是假命题C.“p ⌝”是假命题D.“q ⌝”是假命题3.已知p : “a=”,q :“直线x+y=0与圆x 2+(y-a )2=1相切”,则p 是q的( )A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件4.执行如图所示的程序框图，输入m=828,n=345,则输出的实数m 的值是A.68B.69C. 138D. 1395.与圆222212:26260,:4240C x y x y C x y x y ++--=+-++=都相切的直线有( )A 、1条B 、2条C 、3条D 、4条6. 下列判断正确的是( )A.命题“负数的平方是正数”不是全称命题7882466792B.命题“任意的x ∈N ,x 3>x 2”的否定是“存在x 0∈N ,”C.“a=1”是“函数f(x)=cos 2ax-sin 2ax 的最小正周期是π”的必要不充分条件D.“b=0”是“函数f(x)=ax 2+bx+c 是偶函数”的充要条件 7.已知F 1,F 2是椭圆=1的两焦点,过点F 2的直线交椭圆于A ,B 两点.在△AF 1B 中,若有两边之和是10,则第三边的长度为( ) A.6 B.5 C.4 D.3 8.若右面的程序框图输出的S 是126,则①应为()A.n ≤5?B.n ≤6?C.n ≤7?D.n ≤8?9.为了了解某地区10 000名高三男生的身体发育情况,抽查了该地区100名年龄为17~18岁的高三男生体重(kg),得到频率分布直方图如图.根据图示,请你估计该地区高三男生中体重在[56.5,64.5] kg 的学生人数是()A.40B.400C.4 000D.4 400 10. 已知条件p:x ≤1,条件q:1x ＜1，则q 是⌝p 的成立的( ) A ．充分不必要条件 B.必要不充分条件 C. 充要条件 D. 非充分非必要条件11.已知直线m x y l +=:与曲线21x y -=有两个公共点，则实数m 的取值范围是（）A ．（－2，2）B ．（－1，1）C ．D ．]22[，- 12.已知A={1,2,3},B={x ∈R |x 2-ax+b=0,a ∈A ,b ∈A },则A ∩B=B 的概率是( )A. B. C. D.1二、填空题（本在题共4小题，每小题5分，共20分．） 13.如图是2013年元旦歌咏比赛，七位评委为某班打出的分数的茎叶统计图，去掉一个最高分和一个最低分后，所剩数据的方差为_ _．14. 把“二进制”数)2(1011001化为“五进制”数是15. 已知动点(,)P x y4=,则点P 的轨迹的方程是_________. 16．在区域M=内随机撒一把黄豆,落在区域N=内的概率是 .三、解答题（本大题共6小题，70分．）17. （10分）（1）写出命题05末位数字是的多位数是“的倍数”的否命题，并判断其真假；（2）写出命题“所有的偶数都能被2整除”的否定，并判断其真假. 18. （12分）已知下面两个命题：命题:p R x ∈∃,使012=+-ax x ；命题:q R x ∈∀,都有012>+-ax ax若“p ⌝”为真命题，“q p ∨”也是真命题，求实数a 的取值范围.19、（12分）已知过点)2,1(P 的直线l 和圆622=+y x 交于B A ,两点.（1）若点P 恰好为线段AB 的中点，求直线l 的方程；（2）若52=AB ，求直线l 的方程.20. （12分）某大型养鸡场在本年度的第x 月的盈利y （万元）与x 的对应值如下表：注：∑∑==Λ--=ni i nii i xn x yx n y x b 1221(1)依据这些数据求出x ,y 之间的回归直线方程ˆˆˆybx a =+； (2)依据此回归直线方程预测第五个月大约能盈利多少万元.21. （12分）有两枚大小相同、质地均匀的正四面体玩具，每个玩具的各个面上分别写着数字1，2，3，5. 同时投掷这两枚玩具一次，记m 为两个朝上的面上的数字之和.（要求列出基本事件）（1）求事件“m 不小于6”的概率；（2）“m 为奇数”的概率和“m 为偶数”的概率是不是相等？证明你作出的结论.。

河北省容城中学2014-2015学年高二11月月考数学理试题 Word版含答案

河北容城中学高二年级2014年11月份月考数学（理）试题命题人段美英审题人段飞华一、选择题（每小题5分，共60分）1．已知椭圆2214x y +=，则椭圆的焦距长为（）(A). 1 (B). 2 (C). (D). 232. 一个年级有12个班，每个班有50名同学，随机编号为1-50，为了了解他们在课外的兴趣，要求每班第40号同学留下来进行问卷调查，这里运用的抽样方法是( )（A ）抽签法 (B)系统抽样法 (C)随机数表法 (D)分层抽样法 3.若命题“p ∨q ”为真，“﹁p ”为真，则（） (A) p 真q 真 (B) p 假q 假 (C)p 真q 假 (D)p 假q 真4.从区间()0,1内任取一个实数，则这个数小于56的概率是( )（A ）35 (B) 45 (C)56 (D)16255.已知椭圆C 1、C 2的离心率分别为e 1、e 2，若椭圆C 1比C 2更圆，则e 1与e 2的大小关系正确的是 ( )（A ）e 1＜e 2 (B) e 1=e 2 (C) e 1＞e 2 (D) e 1、e 2大小不确定 6.计算机中常用16进制，采用数字0～9和字母A ～F 共16个计数符号与10进制得对应关系如下表：例如用16进制表示D+E ＝1B ，则A×B=( )（A ） 6E (B) 7C (C)5F (D) B07.某产品分为甲、乙、丙三级，其中乙、丙两级均属次品，若生产中出现乙级品的概率为0.03,出现丙级品的概率为0.01,则对产品抽查一次抽得正品的概率是( )(A)0.99 (B)0.98 (C)0.97 (D)0.968．将x=2005输入如图所示的程序框图得结果（）（A ）-2005 (B) 2005 (C) 0(D) 20069.已知|x|≤2，|y|≤2，点P 的坐标为(x ，y)，则当x ，y ∈Z 时，P 满足(x －2)2＋(y －2)2≤4的概率为( )(A)225 (B) 425 (C) 625 (D) 82510．已知椭圆22143x y +=的长轴的左、右端点分别为A 、B ，在椭圆上有一个异于点A 、B 的动点P ，若直线PA 的斜率k PA ＝12，则直线PB 的斜率k PB 为( )(A)32 (B) －32 (C)34 (D) －3411.下列说法正确的是( )（A ）“1>a ”是“)1,0(log )(≠>=a a x x f a 在),0(+∞上为增函数”的充要条件（B ）命题“R x ∈∃使得0322<++x x ”的否定是：“032,2>++∈∀x x R x ” （C ）“1-=x ”是“0322=++x x ”的必要不充分条件（D ）命题:p “2cos sin ,≤+∈∀x x R x ”，则p ⌝是真命题12.已知椭圆2222:1(0)x y C a b a b+=>>的左焦点为F,C 与过原点的直线相交于A,B 两点,连接AF,BF. 若AB 10=,BF 8=,4cos ABF 5∠=,则C 的离心率为 ( )（A ） (B) (C) (D)二、填空题(每题5分，共20分)13.如图阴影部分是圆O 的内接正方形，随机撒314粒黄豆，则预测黄豆落在正方形内的约_____粒.14．已知x,y 的取值如下表所示，若y 与x 线性相关，且0.95,y x a a ∧=+=则15. 表示椭圆，则k 的取值范围为___________16.已知2214x y +=，1F ,2F 分别为其左右焦点,P 为椭圆上一点,则12F PF ∠的取值范围是三、解答题：（共70分）17. （10分）求椭圆9x 2+25y 2=900的长轴和短轴的长、离心率、焦点和顶点的坐标. .18. （12分）为了对某课题进行研究，用分层抽样方法从三所高校A 、B 、C 的相关人员中，抽取若干人组成研究小组，有关数据如下表（单位：人）（1）求x 、y ；（2）若从高校B 、C 抽取的人中选2人作专题发言，求这二人来自高校C 的概率。

河北省容城中学14—15学年高二升级考试数学(理)(附答案)

高二年级升级考试数学试题（理科）（考试时间：120分钟分值：150分）一、选择题（本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1、集合{}{}202,0A x x B x x x A B =≤≤=->⋂=，则 ( )A.RB. ()()012-∞⋃，，C.∅D. (]12，2、已知复数1z i =-，则21z z =- ( ) A.2 B.-2 C.2i D.-2i3、若0<a ，01<<-b ，那么下列不等式中正确的是 ( ) A. 2ab ab a << B. ab a ab <<2C.ab ab a <<2D ．a ab ab <<24、给定函数①12yx = ②12log (1)y x =+ ③1y x =- ④12x y +=，其中在区间()0,1上单调递减的函数序号是（） A ．①② B ．②③ C ．③④ D ．①④5、类比平面内“垂直于同一条直线的两条直线互相平行”的性质，可得出空间内的下列结论： ( ) ①垂直于同一个平面的两条直线互相平行； ②垂直于同一条直线的两条直线互相平行； ③垂直于同一个平面的两个平面互相平行； ④垂直于同一条直线的两个平面互相平行； A.①②B.②③C.③④D.①④6、一个几何体的俯视图是半径为l 的圆，其主视图和侧视图如图所示，则该几何体的表面积为 ( )A ．3πB ．4πC ．5πD ．7π7、如图是一个算法的流程图．若输入x 的值为2，则输出y 的值是（） A ．0 B ．1-C ．2-D ．3-8、已知53)4cos(=-x π，那么sin 2x ＝ ( ) A. 2518 B. 2524±C. 257-D ． 2579、在等差数列{}n a 中，912162a a =+，则数列{}n a 的前11项和S 11等于( ) A.132B.66C.48D ．2410、已知函数()()21cos ,4f x x x f x '=+是函数()f x 的导函数，则()f x '的图象大致是（）11、已知,x y 满足约束条件133x x y ay x ≥⎧⎪+≤⎨⎪≥-⎩,若2z x y =+的最小值为1,则实数a 的值是（）A.4B.12C.1D.2 12、已知函数()0()210x e a x f x a R x x ⎧+≤=∈⎨->⎩，若函数()f x 在R 上有两个零点，则a 的取值范围是（） A ．(),1-∞- B ．(),0-∞ C ．()1,0- D ．[)1,0-二、填空题（每题5分，满分20分，将答案填在答题纸上）13、某校对全校1600名男女学生的视力状况进行调查，现用分层抽样的方法抽取一个容量是200的样本，已知女生比男生少抽10人，则该校的女生人数是人. 14、已知21k π-=⎰，直线1y kx =+交圆22:1P xy +=于,A B 两点，则AB = ．15、已知向量()1,2=，()1,0-=．若()⊥+λ，则实数λ＝．16、设函数222(1)()log (1)x x f x x x ⎧+≤=⎨>⎩，则((0))f f ＝三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17、（本小题满分10分）在ABC ∆中，角A ，B ，C 的对边分别是a ，b ，c ，已知5c =，23B π=，ABC ∆的面积是（1）求b 的值；（2）求cos 2A 的值．18、(本小题满分12分)已知函数21()cos cos2222xxxf x ωωω=-(0)ω>的最小正周期为π．（1）求ω的值及函数()f x 的最大值和最小值；（2）求函数()f x 的单调递增区间．19、(本小题满分12分)如图，在四棱锥P -ABCD 中，底面ABCD 是菱形，∠DAB ＝45°，PD ⊥平面ABCD ，PD =AD =1，点E 为AB 上一点，且k ABAE=，点F 为PD 中点. (1)若21=k ，求证：直线AF //平面PEC ； (2)是否存在一个常数k ，使得平面PED ⊥平面P AB ，若存在，求出k 的值；若不存在，说明理由，20、(本小题满分12分)观察下列等式:1=1 2+3+4=9 3+4+5+6+7=25 4+5+6+7+8+9+10=49……照以上式子规律．．．．．．．：（1）写出第5个等式，并猜想第n 个等式； (n ∈N *) （2）用数学归纳法证明上述所猜想的第n 个等式成立. (n ∈N *)21、(本小题满分12分)已知数列{}n a 前n 项和n S 满足：21n n S a +=（1）求数列{}n a 的通项公式；（2）设()()11211n n n n a b a a ++=++，数列{}n b 的前n 项和为n T ，求证：14n T <.22、(本小题满分12分)已知函数1()ln ,()(0)af x x a xg x a x+=-=->． (1)若1a =，求函数()f x 的极值；(2)设函数()()()h x f x g x =-，求函数()h x 的单调区间；(3)若存在0[1,]x e ∈，使得00()()f x g x <成立，求a 的取值范围．高二年级升级考试数学参考答案（理科）（考试时间： 120分钟分值：150分）一、1、D2、A3、C4、B5、D6、C7、C8、 C9、A 10、A 11、D 12、D二、13、760 14、17178 15、5 16、1三、17、解：（1）因为ABC ∆，5c =，23B π=，所以1sin 2ac B =4 即1522a ⋅⋅=4所以 3.a = …………… 3分由余弦定理2222cos b a c ac B =+-，得22259253cos49.3b π=+-⨯⨯⨯= 所以7.b = …………………… 5分（2）由正弦定理.sin sin a b A B =所以3sin 7214A =⨯= …………… 8分所以2271cos 212sin 12.1498A A ⎛=-=-⨯= ⎝⎭……………… 10分18、解析：（1）21()coscos2222xxxf x ωωω=-21sin 232cos 1-++=x x ωω x x ωωc o s 21s i n 23+=)6s i n (πω+=x ． ……… 3分因为πωπ==2T ，0>ω，所以2=ω． 5分因为)62sin()(π+=x x f ，R x ∈，所以1)62sin(1≤+≤-πx ．所以函数()f x 的最大值为1，最小值为-1． ……8分（2）令226222πππππ+≤+≤-k x k )(Z k ∈，得322322ππππ+≤≤-k x k )(Z k ∈，所以63ππππ+≤≤-k x k )(Z k ∈．所以函数()f x 的单调递增区间为3[ππ-k ，]6ππ+k )(Z k ∈．……………………12分19、解：(1)证明：作FM ∥CD 交PC 于M . ∵点F 为PD 中点，∴CD FM 21=. ∵21=k ，∴FM AB AE ==21，又FM ∥CD ∥AB ∴AEMF 为平行四边形，∴AF ∥EM ，∵AF PEC EM PEC ⊄⊂平面，平面，∴直线AF //平面PEC . ……………6分(2)存在常数22=k ，使得平面PED ⊥平面P AB ．…………8分 ∵k AB AE =，1AB =，22=k，∴AE =，又∵∠DAB ＝45°，∴AB ⊥DE . 又∵PD ⊥平面ABCD ，∴PD ⊥AB . 又∵PD DE D ⋂=，∴AB ⊥平面PDE ，∵PAB AB 平面⊂，∴平面PED ⊥平面P AB . …………………12分 20、解：（1）第5个等式为: 5+6+7+8+9+10+11+12+13=92 (2)分第n 个等式为:2)12()23()2()1(-=-++++++n n n n n ，*n N ∈ (5)分（2）①当1n =时，等式左边=1，等式右边=(2-1)2=1,所以等式成立． (6)分②假设n k=*()k N ∈时，等式成立，即),1()12()23()2()1(2*∈≥-=-++++++N k k k k k k k那么，当1n k =+时，2222]1)1(2[)12(81448)12()13(3)13()23()2()1()13()3()2()1(]2)1(3[]2)1[(]1)1[()1(-+=+=++-=+-=-+++-+-++++++=++++++++=-++++++++++k k k k k kk k k k k k k k k k k k k k k k k 即1n k =+时等式成立．……………… 11分根据（1）和（2），可知对任何*n N ∈，等式都成立．……… 12分 21、22、解：（1）()ln f x x a x =-的定义域为(0,)+∞． ………1分当1a =时，1()x f x x-'=． ………2分由()0f x '=，解得1x =.当01x <<时，()0,()f x f x '<单调递减；当1x >时，()0,()f x f x '>单调递增；所以当1x =时，函数()f x 取得极小值，极小值为(1)1ln11f =-=； ……..4分（2）1()()()ln ah x f x g x x a x x+=-=-+，其定义域为(0,)+∞．又222(1)(1)[(1)]()x ax a x x a h x x x--++-+'==． …………..6分由0a >可得10a +>，在(0,1)x a ∈+上()0h x '<，在(1,)x a ∈++∞上()0h x '>，所以()h x 的递减区间为(0,1)a +；递增区间为(1,)a ++∞． ……..……7分（3）若在[1,]e 上存在一点0x ，使得00()()f x g x <成立，即在[1,]e 上存在一点0x ，使得0()0h x <．即()h x 在[1,]e 上的最小值小于零． …8分 ①当1a e +≥，即1a e ≥-时，由（II ）可知()h x 在[1,]e 上单调递减．故()h x 在[1,]e 上的最小值为()h e ，由1()0a h e e a e +=+-<，可得211e a e +>-． ………9分因为2111e e e +>--．所以211e a e +>-； ………10分 ②当11a e <+<，即01a e <<-时，由（II ）可知()h x 在(1,1)+a 上单调递减，在(1,)a e +上单调递增．()h x 在[1,]e 上最小值为(1)2ln(1)h a +a a a +=-+． ………11分因为0ln(1)1a <+<，所以0ln(1)a a a <+<．2ln(1)2+a a a ∴-+>，即(1)2h a +>不满足题意，舍去．综上所述:a ∈21(,)1e e ++∞-． ………12分。

河北省保定市容城中学高二化学上学期11月月考试卷(含解析)

河北省保定市容城中学2014-2015 学年高二上学期月考化学试卷（11月份）一、选择题（共30小题，每小题2分，满分60分）1．（2分）国际巴黎车展示上，世界各大汽车商纷纷推出环保动力小汽车，使用的新型环保电池为（）A．氢氧燃料电池B．锌锰电池C．镍镉电池D．铅蓄电池2．（2分）某一反应物的浓度是1.0mol/L，经过20s后，它的浓度变成了0.2mol/L，在这20s 内它的反应速率为（）A．0.04 B．0.04mol/（L•s）C．0.08mol/（L•s）D．0.04mol/L3．（2分）将纯水加热至较高温度，下列叙述正确的是（）A．水的离子积变大、pH变小、呈酸性B．水的离了积不变、pH不变、呈中性C．水的离子积变小、pH变大、呈碱性D．水的离子积变大、pH变小、呈中性4．（2分）下列各组物质的燃烧热相等的是（）A．碳和二氧化碳B．1mol碳和3mol碳C．3mol乙炔（C2H2）和1mol苯D．淀粉和纤维素5．（2分）已知：C（s）+CO2（g）═2CO（g）△H＞0，该反应达到平衡后，改变下列条件都有利于反应向正方向进行的是（）A．升高温度和减小压强B．降低温度和减小压强C．降低温度和增大压强D．升高温度和增大压强6．（2分）汽车的启动电源常用铅蓄电池，放电时的电池反应如下：PbO2+Pb+2H2SO4=2PbSO4↓+2H2O，根据此反应判断下列叙述中正确是（）A．PbO2是电池的负极B．负极的电极反应式为：Pb+SO42﹣﹣2e ﹣=PbSO4↓C．PbO2得电子，被氧化D．电池放电时，溶液酸性增强7．（2分）下列说法正确的是（）A．钢铁发生电化腐蚀的正极反应式：Fe→Fe2++2e﹣B．氢氧燃料电池的负极反应式：O2+2H2O+4e﹣→4OH﹣C．粗铜精炼时，与电源正极相连的是纯铜D．用惰性电极电解饱和食盐水时，阳极的电极反应式2Cl﹣﹣2e﹣→Cl2↑8．（2分）氨水中所含有的分子和离子有（）①②H2O ③NH3④NH3•H2O ⑤H+⑥OH﹣．A．①②③B．①②③④⑤⑥C．②③④⑤⑥D．②③④⑤9．（2分）一种新型燃料电池，以镍板为电极插入KOH溶液中，分别向两极通乙烷和氧气，电极反应为C2H6+18OH﹣→2CO32﹣+12H2O+14e﹣；14H2O+7O2+28e﹣→28OH﹣，有关推断错误的是（）A．通氧气的电极为正极B．在电解质溶液中CO32﹣向正极移动C．放电一段时间后，KOH的物质的量浓度将下降D．参加反应的氧气和乙烷的物质的量之比为7：210．（2分）一定条件下，在体积为10L的密闭容器中，1mol X和1mol Y进行反应：2X（g）+Y（g）⇌Z（g），经60s达到平衡，生成0.3mol Z，下列说法正确的是（）A．以X浓度变化表示的反应速率为0.001mol/（L•s）B．将容器体积变为20L，Z的平衡浓度变为原来的C．若升高温度Y的转化率减小，则正反应为吸热反应D．达到平衡时，X与Y 的浓度相等11．（2分）25℃时，水的电离达到平衡：H2O⇌H++OH﹣△H＞0，下列叙述正确的是（）A．向水中加入氨水，平衡逆向移动，c（OH﹣）降低B．向水中加入少量固体硫酸氢钠，c（H+）增大，K W不变C．向水中加入少量固体CH3COONa，平衡逆向移动，c（H+）降低D．将水加热，K W增大，pH不变12．（2分）在25℃、101kPa下，1g甲醇燃烧生成CO2和液态水时放热22.68kJ，下列热化学方程式正确的是（）A．CH3OH（l）+O2（g）═CO2（g）+2H2O（l）；△H=+725.8 kJ/molB．2CH3OH（l）+3O2（g）═2CO2（g）+4H2O（l）；△H=﹣1452 kJ/molC．2CH3OH（l）+3O2（g）═2CO2（g）+4H2O（l）；△H=﹣725.8 kJ/molD．2CH3OH（l）+3O2（g）═2CO2（g）+4H2O（l）；△H=+1452 kJ/mol13．（2分）在0.1mol/L的CH3COOH溶液中，要促进醋酸电离，且氢离子浓度增大，应采取的措施是（）A．升温B．降温C．加入NaOH溶液D．加入稀HCl14．（2分）在同温同压下，下列各组热化学方程式Q2＞Q1的是（）A．2H2（g）+O2（g）=2H2O（l）△H=﹣Q1 2H2（g）+O2（g）=2H2O（g）△H=﹣Q2B．S（s）+O2（g）=SO2（g）△H=﹣Q1 S（g）+O2（g）=SO2（g）△H=﹣Q2C．C（s）+O2（g）=CO2（g）△H=﹣Q1 C（s）+O2（g）=CO（g）△H=﹣Q2D．H2（g）+Cl2（g）=2HCl（g）△H=﹣Q1 H2（g）+Cl2（g）=HCl（g）△H=﹣Q215．（2分）以下现象与电化学腐蚀无关的是（）A．黄铜（铜锌合金）制作的铜锣不易产生铜绿B．生铁比纯铁容易生锈C．铁质器件附有铜质配件，在接触处易生铁锈D．银质物品久置表面变暗16．（2分）用铂电极电解下列溶液时，阴极和阳极上的主要产物分别为H2和O2的是（）A．稀NaOH溶液B．HCl溶液C．CuSO4溶液D．AgNO3溶液17．（2分）某原电池总反应的离子方程式为：2Fe3++Fe=3Fe2+，不能实现该反应的原电池是（）A．正极为Cu，负极为Fe，电解质为FeCl3溶液B．正极为C，负极为Fe，电解质为Fe（NO3）3溶液C．正极为Cu，负极为Fe，电解质为Fe2（SO4）3溶液D．正极为Ag，负极为Fe，电解质为CuSO4溶液18．（2分）下列变化过程，属于吸热反应的是（）（1）液氨汽化（2）将胆矾加热变为白色粉末（3）浓硫酸稀释（4）氨催化氧化生成一氧化氮（5）酸碱中和生成水（6）NH4Cl与Ba（OH）2.8H2O．A．（1）（2）（6）B．（1）（2）（4）（6）C．（2）（6）D．（2）（4）（6）19．（2分）已知：H2（g）+F2（g）═2HF（g）△H=﹣270kJ，下列说法正确的是（）A．1个氢气分子与1个氟气分子反应生成2个氟化氢分子放出270kJB．1mol氢气与1mol氟气反应生成2mol液态氟化氢放出的热量小于270kJC．相同条件下，1mol氢气与1mol氟气的能量总和大于2mol氟化氢气体的能量D．2mol氟化氢气体分解成1mol的氢气和1mol的氟气放出270kJ热量20．（2分）已知反应2CO（g）=2C（s）+O2（g）的△H为正值，△S为负值．设△H和△S不随温度改变，下列说法中正确的是（）A．低温下能自发进行B．高温下能自发进行C．低温下不能自发进行，高温下能自发进行D．任何温度下都不能自发进行21．（2分）如图是温度和压强对X+Y⇌2Z 反应影响的示意图．图中横坐标表示温度，纵坐标表示平衡混合气体中Z的体积分数．下列叙述正确的是（）A．上述可逆反应的正反应为放热反应B．X、Y、Z均为气态C．X和Y中只有一种是气态，Z为气态D．上述反应的正反应的△H＞022．（2分）把 0.6molX气体和0.4molY气体混合于2L的密闭容器中，使它们发生如下反应 3X （g）+Y（g）⇌nZ（g）+2W（g），5min末已生成 0.2molW，若测知以 Z 表示的平均反应速率为0.01mol•L﹣1•min﹣1，则 n是（）A．2 B．4 C．1 D．323．（2分）已知：298K时，2SO2（g）+O2（g）⇌2SO3（g）△H=﹣Q1kJ/mol，在相同温度下，向密闭容器中通入2mol SO2和1mol O2，达到平衡时放出热量Q2kJ，则下列关系式正确的是（）A．无法比较B．Q1＜Q2C．Q1=Q2D．Q1＞Q224．（2分）可逆反应N2+3H2⇌2NH3的正逆反应速率可用各反应物或生成物浓度的变化来表示．下列关系中能说明反应已达到平衡状态的是（）A．2υ正（N2）=υ逆（NH3）B．3υ正（N2）=υ正（H2）C．υ正（H2）=3υ逆（NH3）D．υ正（N2）=3υ逆（H2）25．（2分）已知反应A2（g）+2B2（g）⇌2AB2（g）△H＜0，下列说法正确的是（）A．升高温度，正向反应速率增加，逆向反应速率减小B．升高温度有利于反应速率增加，从而缩短达到平衡的时间C．达到平衡后，升高温度或增大压强都有利于该反应平衡正向移动D．达到平衡后，降低温度或减小压强都有利于该反应平衡正向移动26．（2分）某温度下的定容密闭容器中，进行可逆反应：A（s）+2B（g）⇌C（g）+D（g），当下列物理量不发生变化时：①混合气体的密度②容器内气体的压强③混合气体的平均相对分子质量④B的物质的量浓度则能表明该反应一定已达到平衡状态的是（）A．只有④B．②③C．②③④D．①③④27．（2分）电子表所用的某种纽扣电池的电极材料为Zn和Ag2O，电解质溶液是KOH溶液．电池总反应式为：Zn+Ag2O=ZnO+2Ag，下列说法错误的是（）A．该电池的正极是Zn，负极是Ag2OB．该电池负极的电极反应式为：Zn+2OH=ZnO+H2OC．理论上该电池工作一段时间后，溶液中KOH的浓度不变D．该电池工作时，电解质中的阴离子向负极移动28．（2分）下列物质的水溶液能导电，但属于非电解质的是（）A．CH3CH2COOH B．Cl2C．NH4HCO3D．SO229．（2分）下列电离方程式书写正确的是（）A．HS﹣在水溶液中的电离方程式：HS﹣+H2O⇌H3O++S2﹣B．H3PO4在水溶液中的电离方程式：H3PO4⇌3H++PC．NaHSO4在水溶液中的电离方程式：NaHSO4=Na++HSO4﹣D．CaCO3在水溶液中的电离方程式：CaCO3⇌Ca2++CO32﹣30．（2分）反应H2（g）+I2（g）⇌2HI（g）在450℃时，化学平衡常数是49．则反应：HI（g）⇌H2（g）+I2（g）在450℃时的化学平衡常数是（）A．B．C．7 D．二、解答题（共4小题，满分40分）31．（11分）全球气候变暖已经成为全世界人类面临的重大问题，温家宝总理在“哥本哈根会议”上承诺到2020年中国减排温室气体40%．（1）地球上的能源主要源于太阳，绿色植物的光合作用可以大量吸收CO2以减缓温室效应，主要过程可以描述分为下列三步（用“C5”表示C5H10O4，用“C3”表示C3H6O3）：Ⅰ、H2O（l）=2H+（aq）+1/2O2（g）+2e﹣△H=+284kJ/molⅡ、CO2（g）+C5（s）+2H+（aq）=2C3+（s）△H=+396kJ/molⅢ、12C3+（s）+12e﹣=C6H12O6（葡萄糖、s）+6C5（s）+3O2（g）△H=﹣1200kJ/mol写出绿色植物利用水和二氧化碳合成葡萄糖并放出氧气的热化学方程式．（2）降低大气中CO2的含量及有效地开发利用CO2，目前工业上有一种方法是用CO2来生产燃料甲醇．为探究反应原理，现进行如下实验，在体积为1L的恒容密闭容器中，充入1mol CO2和3mol H2，一定条件下发生反应：CO2（g）+3H2（g）⇌CH3OH（g）+H2O（g）△H=﹣49.0kJ/mol．测得CO2和CH3OH（g）的浓度随时间变化如图1所示．①从反应开始到平衡，氢气的平均反应速率v（H2）=mol/（L•min）；②氢气的转化率=；③该反应的平衡常数为（保留小数点后2位）；④下列措施中能使平衡体系中n（CH3OH）/n（CO2）增大的是．A．升高温度B．充入He（g），使体系压强增大C．将H2O（g）从体系中分离出去D．再充入1mol CO2和3mol H2⑤当反应达到平衡时，H2的物质的量浓度为c1，然后向容器中再加入一定量H2，待反应再一次达到平衡后，H2的物质的量浓度为c2．则c1c2的关系（填＞、＜、=）．（3）减少温室气体排放的关键是节能减排，大力开发利用燃料电池就可以实现这一目标．如图2所示甲烷燃料电池就是将电极表面镀一层细小的铂粉，铂吸附气体的能力强，性质稳定．将其插入KOH溶液从而达到吸收CO2的目的．请回答：①通入甲烷一极的电极反应式为；②随着电池不断放电，电解质溶液的pH（填“增大”、“减小”或“不变”）．③通常情况下，甲烷燃料电池的能量利用率（填“大于”、“小于”或“等于”）甲烷燃烧的能量利用率．32．（14分）如图表示一个电解池，装有电解质溶液a；X、Y是两块电极板，通过导线与直流电源相连．请回答以下问题：（1）若X、Y都是惰性电极，a是饱和NaCl溶液，实验开始时，同时在两边各滴入几滴酚酞试液，则①Y电极上的电极反应式．②在X电极附近观察到的现象是．（2）若X、Y都是惰性电极，a是浓度均为2mol•L﹣1的AgNO3与Cu（NO3）2的混合溶液1L，电解一段时间后，X电极上有3.2g铜析出，写出电解过程中有关反应的离子方程式此时直流电源已输出mol电子．（3）如果要用电解的方法精炼粗铜（含有Fe、Zn、Pt、C等杂质），电解质溶液a选用CuSO4溶液，则：①X电极的材料是，电极反应式．②精炼完成后，硫酸铜溶液的浓度（填“变大”、“变小”或“不变”）（4）铅蓄电池反应的化学方程式是Pb+PbO2+2H2SO4=2PbSO4+2H2O．若以铅蓄电池为电源，用惰性电极电解CuSO4溶液，在电解过程中生成11.2LO2（标准状况），则铅蓄电池中消耗的硫酸的物质的量为．33．（9分）铝和氢氧化钠都是重要的工业产品．请回答：（1）工业冶炼铝的化学方程式是．（2）可用阳离子交换膜法电解饱和食盐水制NaOH，其工作原理如图2所示．①请写出A、B两处物质的名称：A、B②请写出电解食盐水的离子方程式（3）以镁条、铝片为电极，以NaOH溶液为电解质溶液设计的原电池如图2．①负极材料为（填Mg或Al）．②该原电池的总反应式为34．（6分）在5L的密闭容器中充入2mol A气体和1mol B气体，在一定条件下发生反应：2A （g）+B（g）⇌2C（g），10min后达平衡时，在相同温度下测得容器内混合气体的物质的量是反应前的，试计算：（1）A的转化率（2）平衡常数K（3）10min内生成物C的反应速率．河北省保定市容城中学2014-2015学年高二上学期月考化学试卷（11月份）参考答案与试题解析一、选择题（共30小题，每小题2分，满分60分）1．（2分）国际巴黎车展示上，世界各大汽车商纷纷推出环保动力小汽车，使用的新型环保电池为（）A．氢氧燃料电池B．锌锰电池C．镍镉电池D．铅蓄电池考点：化学电源新型电池．分析：环保电池应为不产生污染性物质的电池，锌锰电池、镍镉电池、铅蓄电池中都含有重金属离子，污染环境．解答：解：A．氢氧燃料电池产物为水，对环境无污染，为环保电池，故A选；B．锌锰电池中含有重金属锰离子，对环境有污染，故B不选；C．镍镉电池中镍、镉离子都为重金属离子，对环境有污染，故C不选；D．铅蓄电池中含有重金属铅，对环境有污染，故D不选．故选A．点评：本题考查环保电池，题目难度不大，注意常见重金属对环境的污染．2．（2分）某一反应物的浓度是1.0mol/L，经过20s后，它的浓度变成了0.2mol/L，在这20s 内它的反应速率为（）A．0.04 B．0.04mol/（L•s）C．0.08mol/（L•s）D．0.04mol/L考点：反应速率的定量表示方法．专题：化学反应速率专题．分析：根据v=计算20s内该物质的反应速率．解答：解：20s内该物质的浓度变化为△c=1.0mol/L﹣0.2mol/L=0.8mol/L．所以20s内该物质的反应速率为=0.04mol/（L•s）．故选：B．点评：考查学生运用定义计算反应速率，难度不大，旨在考查学生对基础知识的掌握，注意反应速率为单位时间内浓度的变化量．3．（2分）将纯水加热至较高温度，下列叙述正确的是（）A．水的离子积变大、pH变小、呈酸性B．水的离了积不变、pH不变、呈中性C．水的离子积变小、pH变大、呈碱性D．水的离子积变大、pH变小、呈中性考点：水的电离．分析：依据纯水是呈中性的，一定温度下水中的氢离子浓度和氢氧根离子浓度乘积是常数，温度升高促进水的电离，水的离子积增大分析．解答：解：水的电离是吸热过程，将纯水加热至较高温度，促进了水的电离，生成的氢离子和氢氧根离子浓度增大，pH减小，水的离子积增大，水的离子积只随温度的改变而改变；但电离出的氢离子和氢氧根离子相等，所以水仍是中性．综上所述，给纯水加热时水的离子积增大、pH减小、呈中性；故选：D．点评：本题考查了水的电离平衡及影响因素，主要考查水的离子积的应用，加热促进水的电离，水的pH大小判断．4．（2分）下列各组物质的燃烧热相等的是（）A．碳和二氧化碳B．1mol碳和3mol碳C．3mol乙炔（C2H2）和1mol苯D．淀粉和纤维素考点：燃烧热．分析：燃烧热是指1 mol物质完全燃烧生成稳定氧化物时所放出的热量．燃烧热是物质的性质，可燃物的物质的量为1mol，产物为稳定氧化物，据此分析即可解答．解答：解：A．碳和二氧化碳是不同的物质，具有不同的能量，所以燃烧热不相等，故A错误；B．燃烧热是指1 mol物质完全燃烧生成稳定氧化物时所放出的热量，与量的多少无关，可燃物相同，该组物质的燃烧热相等，故B正确；C．乙炔和苯物质是不同的物质，物质不同，具有不同的能量，燃烧热不相等，故C错误；D．淀粉和纤维素是不同的物质，物质不同，具有不同的能量，燃烧热不相等，故D错误；故选：B．点评：本题考查燃烧热的概念，难度较小，注意把握燃烧热的含义可燃物为1mol，生成物质为稳定的氧化物．5．（2分）已知：C（s）+CO2（g）═2CO（g）△H＞0，该反应达到平衡后，改变下列条件都有利于反应向正方向进行的是（）A．升高温度和减小压强B．降低温度和减小压强C．降低温度和增大压强D．升高温度和增大压强考点：化学平衡的影响因素．分析：根据升温时平衡正向移动，减小压强化学平衡向正反应方向移动来分析能使平衡向正反应方向移动的措施．解答：解：对于反应A（g）+B（s）⇌2C（g）△H＞0，反应是气体体积增大的吸热反应，升高温度和减小压强促进反应正向进行，故选A．点评：本题考查了化学平衡移动原理的应用，注意反应特征的分析判断，掌握基础是关键，题目较简单．6．（2分）汽车的启动电源常用铅蓄电池，放电时的电池反应如下：PbO2+Pb+2H2SO4=2PbSO4↓+2H2O，根据此反应判断下列叙述中正确是（）A．PbO2是电池的负极B．负极的电极反应式为：Pb+SO42﹣﹣2e ﹣=PbSO4↓C．PbO2得电子，被氧化D．电池放电时，溶液酸性增强考点：原电池和电解池的工作原理．分析：该原电池放电时，电池反应中Pb元素化合价由0价、+4价变为+2价，所以Pb作负极、PbO2作正极，负极反应式为Pb+SO42﹣﹣2e ﹣=PbSO4↓，正极反应式为PbO2+SO42﹣+2e﹣+4H+═PbSO4+2H2O，据此分析解答．解答：解：A．根据电池反应式知，PbO2在反应中得电子化合价由+4价变为+2价，所以二氧化铅作正极，故A错误；B．Pb失电子作负极，负极反应式为：Pb+SO42﹣﹣2e ﹣=PbSO4↓，故B正确；C．PbO2得电子，被还原，故C错误；D．放电时，硫酸参加反应，导致溶液中氢离子浓度减小，则溶液的酸性减弱，pH增大，故D 错误；故选B．点评：本题考查原电池原理，为2015届高考高频点，明确原电池正负极与元素化合价的关系是解本题关键，会正确书写电极反应式，知道各个电极上反应类型，题目难度不大．7．（2分）下列说法正确的是（）A．钢铁发生电化腐蚀的正极反应式：Fe→Fe2++2e﹣B．氢氧燃料电池的负极反应式：O2+2H2O+4e﹣→4OH﹣C．粗铜精炼时，与电源正极相连的是纯铜D．用惰性电极电解饱和食盐水时，阳极的电极反应式2Cl﹣﹣2e﹣→Cl2↑考点：原电池和电解池的工作原理．专题：电化学专题．分析：A．钢铁发生电化学腐蚀时，Fe为负极，正极反应可能为析氢或吸氧的反应；B．氢氧燃料电池负极为氢气，正极为氧气；C．粗铜精炼时，粗铜作阳极，与电源正极相连；D．用惰性电极电解饱和食盐水时，阳极上阴离子放电．解答：解：A．钢铁发生电化学腐蚀时，Fe为负极，则负极反应式为Fe→Fe2++2e﹣，正极反应可能为析氢或吸氧的反应，故A错误；B．氢氧燃料电池负极为氢气，正极为氧气，则正极反应式为O2+2H2O+4e﹣→4OH﹣，故B错误；C．粗铜精炼时，粗铜作阳极，与电源正极相连，则与电源负极相连的是纯铜，故C错误；D．用惰性电极电解饱和食盐水时，阳极上阴离子放电，所以阳极的电极反应式2Cl﹣﹣2e﹣→Cl2↑，故D正确；故选D．点评：本题考查原电池及电解池的工作原理，明确电化学腐蚀、燃料电池、粗铜精炼、电解食盐水的电极反应、正负极即可解答，题目难度不大．8．（2分）氨水中所含有的分子和离子有（）①②H2O ③NH3④NH3•H2O ⑤H+⑥OH﹣．A．①②③B．①②③④⑤⑥C．②③④⑤⑥D．②③④⑤考点：氨的化学性质．专题：元素及其化合物．分析：根据氨水中存在化学平衡：H2O⇌H++OH﹣，NH3+H2O⇌NH3•H2O⇌NH4++OH﹣分析；解答：解：氨水中存在化学平衡：H2O⇌H++OH﹣，NH3+H2O⇌NH3•H2O⇌NH4++OH﹣；溶液中存在三种分子：NH3、H2O、NH3•H2O；三种离子：NH4+、OH﹣、H+；故选：B；点评：本题考查了氨气的性质应用，主要考查氨气溶于水的反应特征和平衡分析，题目难度中等．9．（2分）一种新型燃料电池，以镍板为电极插入KOH溶液中，分别向两极通乙烷和氧气，电极反应为C2H6+18OH﹣→2CO32﹣+12H2O+14e﹣；14H2O+7O2+28e﹣→28OH﹣，有关推断错误的是（）A．通氧气的电极为正极B．在电解质溶液中CO32﹣向正极移动C．放电一段时间后，KOH的物质的量浓度将下降D．参加反应的氧气和乙烷的物质的量之比为7：2考点：化学电源新型电池．专题：电化学专题．分析：原电池中，负极发生氧化反应，正极发生还原反应，根据电极反应式判断电解质溶液的变化以及参加反应物的物质的量之间的关系．解答：解：A、在燃料电池中，通入氧气的一极为原电池的正极，发生还原反应，故A正确；B、在原电池中，电解质中的阴离子移向原电池的负极，故B错误；C、电池工作过程中，电池总反应为2C2H6+8OH﹣+7O2=4CO32﹣+10H2O，反应消耗OH﹣离子，溶液的pH值逐渐减小，故C正确；原电池中两极上转移的电子相等，当有28mol电子转移时，正极上消耗7molO2，负极上消耗2molC2H6，正极与负极上参加反应的气体的物质的量之比为7：2，故D正确．故选B．点评：本题考查原电池知识，题目难度中等，注意电极反应式的书写和电解质溶液的酸碱性变化．10．（2分）一定条件下，在体积为10L的密闭容器中，1mol X和1mol Y进行反应：2X（g）+Y（g）⇌Z（g），经60s达到平衡，生成0.3mol Z，下列说法正确的是（）A．以X浓度变化表示的反应速率为0.001mol/（L•s）B．将容器体积变为20L，Z的平衡浓度变为原来的C．若升高温度Y的转化率减小，则正反应为吸热反应D．达到平衡时，X与Y 的浓度相等考点：化学平衡的计算．专题：化学平衡专题．分析：2X（g）+Y（g）⇌Z（g），开始1mol 1mol 0转化0.6mol 0.3mol 0.3mol平衡0.4mol 0.7mol 0.3mol结合反应速率的计算及平衡移动的影响因素来解答．解答：解：2X（g）+Y（g）⇌Z（g），开始1mol 1mol 0转化0.6mol 0.3mol 0.3mol平衡0.4mol 0.7mol 0.3molA．以X浓度变化表示的反应速率为=0.001mol/（L•s），故A正确；B．将容器体积变为20L，压强减小，平衡逆向移动，则Z的平衡浓度小于原来的，故B错误；C．若升高温度Y的转化率减小，则升高温度，平衡逆向移动，故C错误；D．达到平衡时，X的浓度为0.04mol/L，Y的浓度为0.07mol/L，二者不相等，故D错误；故选A．点评：本题考查化学平衡的计算，明确化学平衡的三段法计算及影响平衡的因素即可解答，题目难度中等．11．（2分）25℃时，水的电离达到平衡：H2O⇌H++OH﹣△H＞0，下列叙述正确的是（）A．向水中加入氨水，平衡逆向移动，c（OH﹣）降低B．向水中加入少量固体硫酸氢钠，c（H+）增大，K W不变C．向水中加入少量固体CH3COONa，平衡逆向移动，c（H+）降低D．将水加热，K W增大，pH不变考点：水的电离．专题：电离平衡与溶液的pH专题．分析：A、氨水溶液显碱性，纯水显中性，碱中氢氧根浓度大于水中的；B、硫酸氢钠能完全电离出钠离子、氢离子和硫酸根离子；C、醋酸根水解对水的电离起到促进作用；D、温度升高，水的离子积常数增大，则pH值减小．解答：解：A、向水中加入氨水，溶液由中性到碱性，碱对水的电离起抑制作用，所以平衡逆向移动，c（OH﹣）增大，故A错误；B、NaHSO4═Na++SO42﹣+H+，其中电离出的氢离子使c（H+）增大，但是温度不变，K W不变，故B 正确；C、CH3COONa中的醋酸根水解对水的电离起到促进作用，电离平衡右移，c（H+）降低，故C错误；D、温度升高，水的离子积常数K W增大，则pH值减小，故D错误．故选：B．点评：本题考查学生水的电离知识，酸、碱对水的电离起抑制作用，水解的盐对水的电离起促进作用．12．（2分）在25℃、101kPa下，1g甲醇燃烧生成CO2和液态水时放热22.68kJ，下列热化学方程式正确的是（）A．CH3OH（l）+O2（g）═CO2（g）+2H2O（l）；△H=+725.8 k J/molB．2CH3OH（l）+3O2（g）═2CO2（g）+4H2O（l）；△H=﹣1452 kJ/molC．2CH3OH（l）+3O2（g）═2CO2（g）+4H2O（l）；△H=﹣725.8 kJ/molD．2CH3OH（l）+3O2（g）═2CO2（g）+4H2O（l）；△H=+1452 kJ/mol考点：热化学方程式．专题：化学反应中的能量变化．分析：A、根据反应吸时焓变值为正值，放热时焓变值为负值来分析；B、根据热化学方程式的书写原则以及方程式系数的含义来分析；C、根据甲醇燃烧时的用量和放出的热量之间的关系进行回答；D、根据反应吸时焓变值为正值，放热时焓变值为负值来分析．解答：解：A、反应吸热时焓变值为正值，放热时焓变值为负值，甲醇燃烧是放热反应，故△H＜0，故A错误；B、1g甲醇燃烧生成CO2和液态水时放热22.68kJ，则64g甲醇即2mol甲醇燃烧放的热量为1452kJ，则热化学方程式为2CH3OH（l）+3O2（g）2CO2（g）+4H2O（l）△H=﹣1452kJ/mol，故B正确；C、1g甲醇燃烧生成CO2和液态水时放热22.68kJ，则64g甲醇即2mol甲醇燃烧放的热量为1452kJ，焓变的数值与化学计量数不成正比，故C错误；D、反应吸时焓变值为正值，放热时焓变值为负值，甲醇燃烧是放热反应，故△H＜0，故D错误；故选B．点评：本题主要考查学生热化学方程式的书写方法及系数的含义，注意焓变的正负和单位问题，该题型是考试的热点．13．（2分）在0.1mol/L的CH3COOH溶液中，要促进醋酸电离，且氢离子浓度增大，应采取的措施是（）A．升温B．降温C．加入NaOH溶液D．加入稀HCl考点：弱电解质在水溶液中的电离平衡．专题：电离平衡与溶液的pH专题．分析：根据题意知，加入的物质和醋酸根离子反应或升高温度才能使醋酸的电离平衡向右移动且c（H+）增大，据此分析解答．解答：解：A、醋酸的电离是吸热反应，升高温度能促进醋酸的电离，且氢离子浓度增大，故A正确；B、醋酸的电离是吸热反应，降低温度抑制醋酸的电离，氢离子浓度减小，故B错误；C、加入氢氧化钠溶液，氢氧化钠和氢离子反应生成水，能促进醋酸的电离，但氢离子浓度减小，故C错误；D、加入稀盐酸，氢离子浓度增大但抑制醋酸的电离，故D错误．故选A．点评：本题考查了影响弱电解质电离的因素，难度不大，注意：如果加入含有相同离子的物质就抑制其电离，如果加入和弱电解质电离的离子发生反应的物质就促进其电离．14．（2分）在同温同压下，下列各组热化学方程式Q2＞Q1的是（）A．2H2（g）+O2（g）=2H2O（l）△H=﹣Q1 2H2（g）+O2（g）=2H2O（g）△H=﹣Q2B．S（s）+O2（g）=SO2（g）△H=﹣Q1 S（g）+O2（g）=SO2（g）△H=﹣Q2C．C（s）+O2（g）=CO2（g）△H=﹣Q1 C（s）+O2（g）=CO（g）△H=﹣Q2D．H2（g）+Cl2（g）=2HCl（g）△H=﹣Q1 H2（g）+Cl2（g）=HCl（g）△H=﹣Q2考点：反应热的大小比较．专题：化学反应中的能量变化．分析：A、液态水变为气态水的过程要吸收能量；B、固体硫燃烧时要先变为气态硫，过程吸热；C、一氧化碳是碳单质不完全燃烧的产物，完全燃烧时生成二氧化碳，完全燃烧放热更多；D、热化学方程式中，物质的量越多，伴随的能量变化越大．解答：解：A、两个反应时都是氢气和氧气生成水，但第2个式子是生成气体，第1个是液态，从气态变为液态还要放出一定的热量，所以Q2＜Q1，故A错误；B、固体硫燃烧时要先变为气态硫，过程吸热，气体与气体反应生成气体比固体和固体反应生气气体产生热量多，所以Q1＜Q2，故B正确；C、第1个反应是完全燃烧反应，第2个反应是不完全燃烧反应，那么放出的热量很明显是完全燃烧比不完全燃烧放出的多，所以Q2＜Q1，故C错误；D、反应的能量变化和反应中各物质的量成正比，故 Q2=Q1，所以Q2＜Q1，故D错误．故选：B．点评：本题考查反应热的大小比较，题目难度中等，本题注意比较反应热的角度，化学反应中，反应的程度、物质的量以及物质的聚集状态不同，反应放出或吸收的热量是不同的．15．（2分）以下现象与电化学腐蚀无关的是（）A．黄铜（铜锌合金）制作的铜锣不易产生铜绿B．生铁比纯铁容易生锈C．铁质器件附有铜质配件，在接触处易生铁锈。

河北省容城中学2014-2015学年高二下学期第一次月考物理试题 Word版含答案

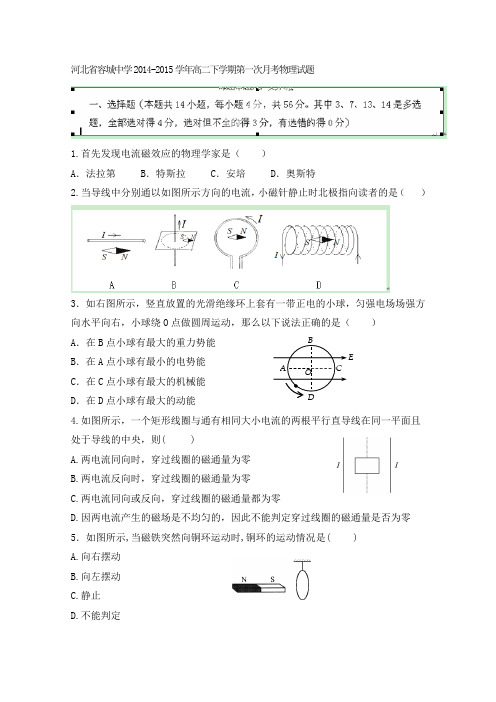
河北省容城中学2014-2015学年高二下学期第一次月考物理试题1.首先发现电流磁效应的物理学家是（）A ．法拉第B ．特斯拉C ．安培D ．奥斯特2.当导线中分别通以如图所示方向的电流，小磁针静止时北极指向读者的是（）3．如右图所示，竖直放置的光滑绝缘环上套有一带正电的小球，匀强电场场强方向水平向右，小球绕O 点做圆周运动，那么以下说法正确的是（） A ．在B 点小球有最大的重力势能 B ．在A 点小球有最小的电势能 C ．在C 点小球有最大的机械能 D ．在D 点小球有最大的动能4.如图所示，一个矩形线圈与通有相同大小电流的两根平行直导线在同一平面且处于导线的中央，则( )A.两电流同向时，穿过线圈的磁通量为零B.两电流反向时，穿过线圈的磁通量为零C.两电流同向或反向，穿过线圈的磁通量都为零D.因两电流产生的磁场是不均匀的，因此不能判定穿过线圈的磁通量是否为零 5．如图所示,当磁铁突然向铜环运动时,铜环的运动情况是( ) A.向右摆动B.向左摆动C.静止D.不能判定E6．如图所示电路中，电源电动势为E，内阻为r，当变阻器的滑动触头P向上移动时，电压表V的示数U和电流表的示数I的变化情况是（）A．U变大，I变小B．U变小， I变小C．U变大，I变大D．U变小，I变大7．单匝矩形线圈在匀强磁场中匀速转动，转轴垂直于磁场，若线圈所围面积里磁通量随时间变化的规律如图所示，则OD时间范围内( )A．线圈中O时刻感应电动势最大B．线圈中D时刻感应电动势为零C．线圈中D时刻感应电动势最大D．线圈中O到D时间内平均感应电动势为0.4 V8.如图所示，闭合金属圆环沿垂直于磁场方向放置在匀强磁场中，将它从匀强磁场中匀速拉出，以下说法中正确的是( )A．向左拉出和向右拉出时，环中的感应电流方向相反B．向左或向右拉出时，环中的感应电流方向都是沿顺时针方向C．向左或向右拉出时，环中的感应电流方向都是沿逆时针方向D．环穿出磁场之前，就已经有了电流9.如图所示，A是一边长为 l的正方形线框，电阻为R。

河北省容城中学高二数学上学期第一次月考试题理(无答案)

河北容城中学高二第一次月考数学（理）试题一、选择题(本大题共12小题，每小题5分，共60分)1．已知以点A (2，－3)为圆心，半径长等于5的圆O ，则点M (5，－7)与圆O 的位置关系是( )A ．在圆内B ．在圆上C ．在圆外D ．无法判断2．方程y ＝9－x 2表示的曲线是( )A ．一条射线B ．一个圆C ．两条射线D ．半个圆3．圆2x 2＋2y 2＋6x －4y －3＝0的圆心坐标和半径分别为( )A ．⎝ ⎛⎭⎪⎫－32，1和194B ．(3,2)和192C ．⎝ ⎛⎭⎪⎫－32，1和192D ．⎝ ⎛⎭⎪⎫32，－1和192 4．方程x 2＋y 2＋4x －2y ＋5m ＝0表示圆的条件是( )A ．14<m <1B ．m >1C ．m <14D ．m <1 5．直线3x ＋4y ＋12＝0与⊙C ：(x －1) 2＋(y －1)2＝9的位置关系是( )A ．相交并且过圆心B ．相交不过圆心C ．相切D ．相离6．两圆(x ＋3)2＋(y －2)2＝4和(x －3)2＋(y ＋6)2＝64的位置关系是( )A ．外切B ．内切C ．相交D ．相离7．结晶体的基本单位称为晶胞，如图是食盐晶胞的示意图(可看成是八个棱长为12的小正方体堆积成的正方体)．其中实圆•代表钠原子，空间圆代表氯原子．建立空间直角坐标系Oxyz 后，图中最上层中间的钠原子所在位置的坐标是( ) A ．⎝ ⎛⎭⎪⎫12，12，1 B ．(0,0,1) C ．⎝ ⎛⎭⎪⎫1，12，1 D ．⎝ ⎛⎭⎪⎫1，12，12 8．长方体ABCD －A 1B 1C 1D 1中，若AB →＝3i ，AD →＝2j ，AA 1→＝5k ，则AC 1→＝( )A ．i ＋j ＋k B.13i ＋12j ＋15k C ．3i ＋2j ＋5k D ．3i ＋2j －5k 9．若A (1,3，－2)、B (－2,3,2)，则A 、B 两点间的距离为( ) A ．61 B ．25 C ．5 D ．5710．直线a,b 的方向向量分别为(1,2,2),(2,3,2)e n =--=--,则a 与b 的位置关系是( )A.平行B.重合C.垂直D.夹角等于3π 11．对于向量a 、b 、c 和实数λ，下列正确的是( )A ．若a ·b ＝0，则a ＝0或b ＝0B ．若λa ＝0，则λ＝0或a ＝0C ．若a 2＝b 2，则a ＝b 或a ＝－bD ．若a ·b ＝a ·c ，则b ＝c12．已知ABCD 是平行四边形,且A(4,1,3),B(2,-5,1),C(3,7,-5),则顶点D 的坐标为（）A. (1,1,-7)B. (5,13, -3)C. (-3,1,5)D. (5,3,1)二、填空题(本大题共4小题，每小题5分，共20分)13.圆O 的方程为(x －3)2＋(y －4)2＝25，点(2,3)到圆上的最大距离为________14.空间向量a ＝(－1,1，－2)、b ＝(1，－2，－1)、n ＝(x ，y ，－2)，且n ∥b ，则a·n ＝__________________.15.已知A （-4， 2，3）关于xoz 平面的对称点为__________________．16.已知(3,2,1),(1,0,2)a b →→=-=-，向量a →与a b λ→→-垂直，则实数λ的值为_____三、解答题(本大题共6小题，共70分)17.(10分)已知一个圆与y 轴相切，圆心在直线x －3y ＝0上，且该圆经过点A (6,1)，求这个圆的方程．18.(10分)求过点P (－1,5)的圆(x －1)2＋(y －2)2＝4的切线方程．19.(12分)如图，已知正方体ABCD －A ′B ′C ′D ′，点E 是上底面A ′B ′C ′D ′的中心，取向量AB →、AD →、AA ′→为基底的基向量，在下列条件下，分别求x 、y 、z 的值．(1)BD ′→＝xAD →＋yAB →＋zAA ′→；(2)AE →＝xAD →＋yAB →＋zAA ′→.20.(12分)如图，正方体ABCD—A1B1C1D1中，M、N分别为AB、B1C的中点．(1)用向量法证明平面A1BD∥平面B1CD1；(2)用向量法证明MN⊥面A1BD.21.(12分)10．如图5所示，在正方体ABCD－A1B1C1D1中，E是棱DD1的中点．(1)求直线BE和平面ABB1A1所成的角的正弦值；(2)在棱C1D1上是否存在一点F，使B1F∥平面A1BE？22.(14分)如图，PA⊥平面ABCD，四边形ABCD是正方形，PA＝AD＝2，M、N分别是AB、PC的中点．(1)求二面角P—CD—B的大小；(2)求证：平面MND⊥平面PCD；(3)求点P到平面MND的距离．姓名班级考号 ……………………………………………………………………装………………………………订………………………………线……………………………………… 河北容城中学高二第一次月考数学（理）答题纸二、填空题(本大题共4小题，每小题5分，共20分) 13.___________________ 14._____________________ 15.___________________ 16._____________________ 三、解答题(本大题共6小题，共70分) 17.(10分) 18..(10分)19.(12分)20.(12分)22.( 14分)。

河北省保定市容城中学高二数学下学期第二次月考试题理

河北省保定市容城中学2014-2015学年高二数学下学期第二次月考试题理第I 卷（选择题）一、选择题（每题5分）1．在复平面内，复数32i 1i --对应的点位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限2．用三段论推理：“任何实数的平方大于0，因为a 是实数，所以02>a ”，你认为这个推理（）A ．大前提错误B ．小前提错误C ．推理形式错误D ．是正确的3．命题“x ∀∈R ，xe －x ＋1≥0”的否定是（）A ．x ∀∈R ，lnx ＋x ＋1＜0B ．x ∃∈R ，xe －x ＋1＜0C ．x ∀∈R ，xe －x ＋1＞0 D ．x ∃∈R ，x e －x ＋1≥04．设随机变量X 服从正态分布N （3，4），若P （X ＜2a+3）=P （X ＞a ﹣2），则a 的值为（）.A ．B ．3C ．5D ．5．已知盒中装有3个红球、2个白球、5个黑球，它们大小形状完全相同，现需一个红球，甲每次从中任取一个不放回，在他第一次拿到白球的条件下，第二次拿到红球的概率（）.A ．B ．C ．D ．6．某人上班途中要经过三个有红绿灯的路口，设遇到红灯的事件相互独立，且概率都是0.3，则此人上班途中遇到红灯的次数的期望为（）.A ．0.3B ．0.33C ．0.9D ．0.7 7．设（x ﹣）6的展开式中x3的系数为a ，二项式系数为b ，则的值为（）.A ．B ．C ．16D ．48．甲，乙，丙，丁四位同学各自对A ，B 两变量的线性相关试验，并用回归分析方法分别求得相关系数r 如表：则这四位同学的试验结果能体现出A ，B 两变量有更强的线性相关性的是（）. A ．甲 B ．乙 C ．丙 D ．丁9．用数学归纳法证明12+22+…+（n ﹣1）2+n2+（n ﹣1）2+…+22+12═时，由n=k的假设到证明n=k+1时，等式左边应添加的式子是（）A.（k+1）2+2k2B.（k+1）2+k2C.（k+1）2D.10．某城市有3个演习点同时进行消防演习，现将4个消防队分配到这3个演习点，若每个演习点至少安排1个消防队，则不同的分配方案种数为（）.A．12 B．36 C．72 D．10811．函数f（x）=（x2﹣2x）ex（e为自然数的底数）的图象大致是（）.12．已知函数2(0)()0)x xf xx⎧≥⎪=<则1x=是()2f x=成立的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件13．已知()24f x x x=++-的最小值为n，则2()nxx-的展开式中常数项为（）A．20 B．160 C．-160 D．-2014．若函数1()e(0,)axf x a bb=-＞＞0的图象在0x=处的切线与圆221x y+=相切，则a b+的最大值是（）A.4B. C.2二、填空题（每题5分）15．若（x+m）9=a0+a1（x+1）+a2（x+1）2+…+a9（x+1）9，且a0﹣a1+a2﹣a3+…+a8﹣a9=39，则实数m的值为．16．已知函数f（x）=x3+ax2﹣a（a∈R），若存在x0，使f（x）在x=x0处取得极值，且f（x0）=0，则a的值为．17．22sin2xdxπ=⎰．18．计算12323n n n n n C C C nC +++⋅⋅⋅+，可以采用以下方法：构造等式：0122n nn n n n C C x C x C x +++⋅⋅⋅+()1nx =+，两边对x 求导，得()112321231n n n n n n n C C x C x nC x n x --+++⋅⋅⋅+=+，在上式中令1x =，得123232n n n n n n C C CnC n -+++⋅⋅⋅+=⋅．类比上述计算方法，计算12223223nn n n n C C C n C +++⋅⋅⋅+= ．三、解答题（19题10分，20题12分，21、22题各14分）19．在平面直角坐标系中，以原点为极点，x 轴为极轴建立极坐标系，曲线1C 的方程为sin x y θθ⎧=⎪⎨=⎪⎩（θ为参数），曲线2C 的极坐标方程为2:cos sin 1C ρθρθ+=,若曲线1C 与2C 相交于A 、B 两点．(1)求||AB 的值；(2)求点(1,2)M -到A 、B 两点的距离之积．20．某次考试中，从甲、乙两个班各随机抽取10名学生的成绩进行统计分析，学生成绩的茎叶图如图所示，成绩不小于90分为及格．（1）从每班抽取的学生中各随机抽取一人，求至少有一人及格的概率（2）从甲班10人中随机抽取一人，乙班10人中随机抽取两人，三人中及格人数记为X ，求X 的分布列和期望．21．设数列{an}满足a1=3，an+1=an2﹣2nan+2，n∈N*．（1）求出a2，a3，a4的值，并猜想数列{an}的通项公式（不需证明）；（2）记Sn为数列{an}的前n项和，试求使得2n＞Sn成立的最小正整数n，并给出证明．22．已知函数f（x）=alnx﹣ax﹣3（a＜0）．（1）求函数f （x ）的单调区间；（2）若函数y=f （x ）的图象在点（2，f （2））处的切线的倾斜角为45°，对于任意的t ∈[0，1]，函数g （x ）=x3+x2[f ′（x ）+m]在区间（t ，2）上总不是单调函数，其中f ′（x ）为f （x ）的导函数，求实数m 的取值范围．参考答案 1．A 【解析】试题分析：ii i 21123+=--,对应的点()2,1，因此是第一象限。

高二年级11月月考理科答案

河北容城中学高二年级2014年11月份月考语文答案1. D【解析】原文是说抗战精神“变作掩护暴力刺激的一张虎皮”，而非抗战精神本身是“暴力刺激”，且原文并无递进意味。

2. B【解析】根据文中“乍一看”可知“剧中体现出的乐观、无畏的精神和非凡的想象力还是有价值的”判断错误。

3. A【解析】反推错误，“情爱、武打、警匪与色情、暴力、凶杀之间有着内在的共通性”是不可变更的前提。

4．B【解析】因为5．D6．C 【解析】没有因果关系7．（1）他倚仗自己的才华，凌辱怠慢他人，被他们共同嫉恨。

（陵藉、省略句、被动句各1分，文意2分）（2）勃曾经说过作为儿子不可不懂医术，当时长安曹元有秘传的医术，王勃跟随他学习，完全掌握其中的精要。

（秘术、游、要各1分，文意2分）8.答：三四句用了反衬手法，以乐景写哀情，衬托得梁园更加萧条。

（反衬1分，以乐写哀2分，结合内容2分）9.答：这首诗抒发了物是人非，盛衰无常的感慨。

（物是人非2分，盛衰无常2分，结合内容2分）10. 【答案】（1）悟已往之不谏（2）生物之以息相吹也（3）则其负大舟也无力（4）烟光凝而暮山紫（5）气息奄奄，人命危浅（6）历职郎署，本图宦达，不矜名节。

11.（1）答E给3分，答B给2分。

答A给1分。

答C,D不给分。

【解析】A,原文说“真正使他步上研红之路的，是著名学者胡适先生。

C, “这说明《红楼梦》大受欢迎”错，应是说明了周汝昌先生的研究成果被人认可。

D,文中没有关于“周汝昌和胡适研究《红楼梦》的不同方法的内容。

”（2）①治学初以语言，诗词理论，笺注，赏析和中外文翻译为主。

②国学基础博厚，研究领域涉及古典文学和诗词等多个方面。

③极善诗词。

④擅长书法，极有造诣。

⑤擅长京剧。

（第1点2分，其它各1分）（3）①对学术研究的认真、勤奋、刻苦精神，56年成一书。

②身体多病却依然坚持研究与写作，执着于追求。

③轻物质，重精神。

（每点2分，共6分。

意思对即可）（4）【解析】对于本题，要围绕周汝昌先生面对恶劣的条件却以一颗执着的心去快乐地做研究来探究。

河北省容城中学2014-2015学年高二1月月考数学(理)试题 Word版含答案

河北省容城中学2014-2015学年高二1月月考数学（理）试题一、选择题共小题每小题5分，共0分=2的焦点坐标是A.（，0）B.（0，）C.（0，）D.（，0） 2.运行右面方框内的程序，若输入=4,则输出的结果是A.12B.3C.4D.5 3.设A是半径为1的圆周上一定点，P是圆周上一动点，则弦PA＜1的概率是 A. B. C. D. 4.已知条件p:≤1,条件q:＜1，则q是?p的成立的 A．充分不必要条件 B.必要不充分条件C. 充要条件D. 非充分非必要条件 5. 的展开式中的常数项为A.56B.70C. 28D. 60 6. 已知实数，随机输入，执行如右图所示的程序框图，则输出的不小于的概率为_______．B. C. D. 7.某班级有50名学生，期中考试数学成绩X～N(120，σ2)，已知 P（X＞140）=0.2，则X∈[100,140]的人数为A.5B. 10C.20D.30 8.双曲线左支上一点P到其左、右两焦点F1、F2的距离之和为8，则点P到左焦点F1的距离是A. 9B. 7C. 4D. 1 9. 右图是某公司个销售店某月销售某产品数量(单位台)的茎叶图则数据落在区间，内的概率为 1 2 3 8 9 0 2 3 7 9 0 1 3 A．B． C．D．共焦点且过点（,）A. B. C. D. 11.把5名师范大学生安排到一、二、三3个不同的班级实习，要求每班至少有一名且甲必须安排在一班，则所有不同的安排种数有A.24B.36C.48D.50 12. 已知点是上的动点，为椭圆的左、右焦点，是坐标原点，若是平分线上一点，且，则的取值范围是 A． B． C． D．二、填空题：（本大题共4小题，每小题5分，满分20分.） 13．二进制数110110（2）化为十进制数是_____________. 14.已知动点满足：,则点P的轨迹的离心率是_________. 15.对任意实数,都有，则的值为 . 16.双曲线和具有相同的：①焦点；②焦距；③离心率；④渐近线.其中正确的结论序号是_________（填上你认为正确的所有序号）. 三、解答题（共 6 小题，每小题要写出必要的文字说明和步骤。

河北省保定市容城中学高二数学下学期第二次月考试题文

2014-2015学年度容城中学4月月考数学（文）试卷第I卷（选择题）一、选择题（每题5分，共60分）1．满足条件M∪{1}={1，2，3}的集合M的个数是（）A．1B．2C．3D．42．设集合{1,0,1}A=-，{|0}B x R x=∈>，则A B=I（）A．{1,0}-B．{1}-C．{0,1}D．{1}3．已知集合{}{}2104 M x x,N xx,=+≥=<则M N=I( )A.(],1-∞-B.[)1,2-C.(]1,2-D.()2,+∞4．设全集U＝{1，2，3，4}，集合S＝{1，3}，T＝{4}，则等于( )A、{2，4}B、{4}C、ΦD、{1，3，4}5．函数f(x)＝12x-＋3x+的定义域为( )．A．(－3,0] B．(－3,1]C．(－∞，－3)∪(－3,0] D．(－∞，－3)∪(－3,1]6．已知函数||5)(xxf=，)()(2Raxaxxg∈-=，若1)]1([=gf，则=a（）A.1B. 2C. 3D. -17．已知函数y=ax2+bx﹣1在（﹣∞，0]是单调函数，则y=2ax+b的图象不可能是（）8．函数()()01xf x a a=<<在区间[0，2]上的最大值比最小值大43，则a的值为（）A.12B.7C.2D.39．已知函数()xx f =，则下列哪个函数与()x f y =表示同一个函数( )A ．()()2x x g = B ．()2x x h = C ．()x x s = D ．⎩⎨⎧<->=00x x x x y ，，10．已知2log 3a =，12log 3b =，123c -=，则A.c b a >> B ．c a b >> C.a b c >> D.a c b >>11．函数f （x ）= +lg （1+x ）的定义域是（）A.（﹣∞，﹣1）B.（1，+∞）C.（﹣1，1）∪（1，+∞）D.（﹣∞，+∞）12．已知函数()f x 是定义在区间[-2，2]上的偶函数，当[0,2]x ∈时，()f x 是减函数，如果不等式(1)()f m f m -<成立，则实数m 的取值范围（）A.1[1,)2- B. 1，2 C. (,0)-∞ D.(,1)-∞第II 卷（非选择题）13.）时，（是幂函数，且）（已知函数0x )1(x f 322∞+∈--=-+m m xm m ，则m 的值是___ ．14．幂函数 f （x ）=xα（α∈R ）过点2)，则 f （4）= ．15．已知函数()x x x x e e f x e e ---=+，若1()2f a =-，则()f a -= . 16．已知函数()535f x ax x bx =++-，若()1008f -=，那么()100f =______二、填空题（每题5分，共20分）三、解答题（共70分） 17．（共10分）已知二次函数f(x)满足f(2)＝－1,f(－1)＝－1，且f(x)的最大值为8，求二次函数f(x)的解析式． 18．（共12分）二次函数f(x)满足f(x+1)-f(x)=2x,且f(0)=1. （1）求f(x)的解析式；（2）在区间[－1，1]上，y=f(x)的图象恒在y=2x+m 的图象上方，求实数m 的取值范围19．（共12分）命题p ：实数x 满足22430x ax a -+<，其中0a <，命题q ：实数x 满足 260x x --≤或2280x x +->，且 q 是p 的必要不充分条件，求a的取值范围.20．（共12分）已知函数()f x 在定义域]1,1[-上单调递减，又当]1,1[,-∈b a ，且0=+b a 时，()()0f a f b +=．（Ⅰ）证明()f x 是奇函数；（Ⅱ）求不等式2(1)(1)0f m f m -+->的解集．21．（共12分）已知函数()|2||1|f x x a x =-+-。

河北省容城中学2014-2015学年高二数学升级考试试题文

河北省容城中学2014-2015学年高二升级考试试题（数学文）（考试时间：120分钟分值：150分）一、选择题（本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1、设集合{1,2,3,4,5,6}U =，{|13}A x N x =∈≤≤，则U C A = （） A ．U B ．{1，2，3} C ．{4，5，6} D ．{1，3，4，5，6}2、已知命题:,sin 1,p x x ∀∈≤R 则p ⌝是（） A ．,sin 1x x ∃∈≥R B ．,sin 1x x ∃∈>R C ．,sin 1x x ∀∈≥RD ．,sin 1x x ∀∈>R3、下列函数中，在区间(0,)+∞上存在最小值的是（）A ．2(1)y x =-B ．y =．2x y = D ．2log y x =4、记函数)(x f 的导函数为)(x f '，若()f x 对应的曲线在点))(,(00x f x 处的切线方程为1y x =-+，则（）A.0()=2f x 'B.0()=1f x 'C.0)(0='x fD.0()=1f x '-5、已知函数()f x 是奇函数，且当0x >时，()e x f x =，则(1)f -= （）A.1eB.1e-C.eD.e - 6、若抛物线22(0)y px p =>的焦点与双曲线222x y -=的右焦点重合，则p 的值为（）A ．2 C ．4 D ．7、设1a =-，32log b m =，那么“a b =”是“3m =”的（）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件8、函数32()34f x x x =-+-的图象在1x =处的切线方程为（） A ．350x y ++= B ．350x y --= C ．310x y +-= D ．370x y --=9、函数ππ()2sin()cos()66f x x x =--图象的一条对称轴方程是（）A ．π6x =B. π3x =C. 5π12x =D. 2π3x = 10、一个几何体的三视图如图所示，则该几何体的体积的是（）A.7B.152C.233D.47611、函数321xx y =-的图像大致是（）12、已知定义域为R 的奇函数()y f x =的导函数为()y f x '=，当0x ≠时，()()0f x f x x '+>，若()1111,22,ln ln 2222a f b f c f ⎛⎫⎛⎫⎛⎫==--= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，则,,a b c 的大小关系正确的是（） A. a b c <<B. b c a <<C. a c b <<D. c a b <<二、填空题（每题5分，满分20分，将答案填在答题纸上） 13、若复数iia z +=，且z ∈R ,则实数a =_____．侧(左)视图正(主)视图俯视图14、已知平面向量,a b满足(1,1)=-a，()()+⊥-a b a b，那么|b|= ____.15、已知,x y满足不等式组22y xx yx≤⎧⎪+≥⎨⎪≤⎩，则2z x y=+的最大值与最小值的比为 .16、如图，()y f x=是可导函数，直线l是曲线)(xfy=在4=x处的切线，令()()f xg xx=，则(4)g'=；三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17、（本小题满分10分）在科普知识竞赛前的培训活动中，将甲、乙两名学生的6次培训成绩（百分制）制成如图所示的茎叶图：(1)若从甲、乙两名学生中选择1人参加该知识竞赛，你会选哪位？请运用统计学的知识说明理由；(2)若从学生甲的6次培训成绩中随机选择2个，求选到的分数中至少有一个大于85分的概率．18、(本小题满分12分)已知向量,1cos)x x=m，(1sin,cos)x x=-n，函数()f x=⋅m n+（1）求函数()f x的零点；（2）若8()5fα=，且π(,π)2α∈，求cosα的值．19、（本小题满分12分）如图，在四棱锥ABCDE-中，底面ABCD为正方形，⊥AE平面CDE，已知2AE DE==，F为线段DE的中点．（1）求证：//BE平面ACF；（2）求四棱锥ABCDE-的体积．AB20、（本小题满分12分）已知数列{}n a 是公差不为0的等差数列，12a =，且1a ，3a ，11a 成等比数列.（1）求数列{}n a 的通项公式；（2）若122n n n b a =--，求数列{}n b 的前n 项和n T .21、（本小题满分12分）已知函数()()2f 4xx e ax b x x =+--，曲线y ＝f (x )在点(0，f (0))处的切线方程为y ＝4x ＋4． (1)求a ，b 的值；(2)若对任意实数),0(+∞∈m ，不等式x x m x e x f x2)2()1(4)(2-+-+>恒成立，求x 的取值范围．22、（本小题满分12分）已知函数()e x f x ax a =--（其中a ∈R ，e 是自然对数的底数，e ＝2.71828…）．(1)当e a =时，求函数()f x 的极值；(2)若()0f x ≥恒成立，求实数a 的取值范围．高二年级升级考试数学参考答案（文科）一、1、C 2、B 3、A 4、D 5、D 6、C 7、C 8、B 9、C 10、 D 11、C 12、C二、13、0． 14、1:2 16、316- 三、17、解：(1)学生甲的平均成绩687679868895826x +++++==甲，学生乙的平均成绩717582848694826x +++++==乙，又22222221[(6882)(7682)(7982)(8682)(8882)(9582)]776s =-+-+-+-+-+-=甲，22222221167[(7182)(7582)(8282)(8482)(8682)(9482)]63s =-+-+-+-+-+-=乙，则x x =甲乙，22s s >甲乙，说明甲、乙的平均水平一样，但乙的方差小，则乙发挥更稳定，故应选择学生乙参加知识竞赛.5分注：(1)由茎叶图的分布可知应选择乙同学.（可给2分）(2)由茎叶图可以看到甲的平均成绩在80分左右，其分布对称，乙的平均成绩在80分左右，但总体成绩稳定性较好，故应选择乙同学.（可给4分）(2) 从学生甲的成绩中随机选择2个，其基本事件有(68,76)，(68,79)，(68,86)，(68,88)，(68,95)，(76,79)，(76,86)，(76,88)，(76,95)，(79,86)，(79,88)，(79,95)，(86,88)，(86,95)，(88,95)，共有15个，其中选到的分数中至少有一个大于85分的事件有12个，故所求的概率124155P ==．···················· 10分18、．解：（1）22()cos f x x x x x =⋅+mcos x x =+π2sin()6x =+，…………（3分）由π2sin()06x +=，得ππ()6x k k +=∈Z ，所以ππ()6x k k =-∈Z ，所以函数()f x 的零点为ππ()6x k k =-∈Z ．………………（6分）（1）由（2）知π8()2sin()65f αα=+=，所以π4sin()65α+=，……（8分）因为π(,π)2α∈，所以2ππ7π366α<+<，则π3cos()65α+=-，………（10分）所以ππππππcos cos[()]cos()cos sin()sin 666666αααα=+-=+++341552=-⋅=． …………（12分） 19、证明：（1）连结BD 和AC 交于O ，连结OF ，………………………1分ABCD 为正方形，∴O 为BD 中点，F 为DE 中点，BE OF //∴， ………4分BE ⊄ 平面ACF ，OF ⊂平面ACF//BE ∴平面ACF ．……………………………5分（2）作EG AD ⊥于G⊥AE 平面CDE ，⊂CD 平面CDE ，CD AE ⊥∴， ABCD 为正方形，CD AD ∴⊥，,,AE AD A AD AE =⊂ 平面DAE ，⊥∴CD 平面D A E ，……………7分 CD EG ∴⊥，AD CD D = ，EG ∴⊥平面ABCD ………8分⊥AE 平面CDE ，DE ⊂平面CDE ，AE DE ∴⊥，2AE DE == ，AD ∴=，EG …10分∴四棱锥ABCD E -的体积211333ABCD V S EG =⨯=⨯=………12分20、解：（1）因为数列{}n a 是等差数列，设公差为d ，所以31222.a a d d =+=+ 11210.a d =+ ………… 2分因为1a ，3a ，11a 成等比数列，所以23111.a a a =⋅ ……………… 3分即()()2222210.d d +=⨯+所以230.d d -=所以0d =，或 3.d = ………… 4分因为0d ≠，所以 3.d = 5分所以()2313 1.n a n n =+-=- ………… 6分(2) 因为122nn n b a =--，所以332.2nn b n =-- ………… 7分所以12n n T b b b =+++ 2333326232222nn ⎛⎫⎛⎫⎛⎫=--+--++-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ ()()233632222n n n =+++-+++- …………… 10分()213332222n n n n +⎛⎫+=--- ⎪⎝⎭2132 2.2n n +=-+ O AC BEFG所以数列{}n b 的前n 项和2132 2.2n n T n +=-+ …………… 12分 21、解：(1)f ′(x )＝e x(ax ＋a ＋b )－2x －4．…………………………………2分由已知得f (0)＝4，f ′(0)＝4．故b ＝4，a ＋b ＝8． ………4分从而a ＝4，b ＝4． …………………………………6分 (2)由(1)知，f (x )＝4e x (x ＋1)－x 2－4x ，所以4e x(x ＋1)－x 2－4x x x m x e x 2)2()1(42-+-+>，即02)2(22>--+x x x m 对任意实数),0(+∞∈m 恒成立．…… 7分令x x m x m g 2)2()(22--+=，则函数)(m g 是关于m 的一次函数，…8分由022>+x ，故)(x g 在),0(+∞上为增函数．只需,02)0(2≥--=x x g …10分得02≤≤-x ，故使原不等式恒成立的x 的取值范围是[]0,2-．…………12分22、解：(1) 当e a =时，()e e e x f x x =--，()e e x f x '=-，当1x <时，()0f x '<；当1x >时，()0f x '>．所以函数()f x 在(,1)-∞上单调递减，在(1,)+∞上单调递增，所以函数()f x 在1x =处取得极小值(1)e f =-，函数()f x 无极大值． ······ 5分 (2)由()e x f x ax a =--，()e x f x a '=-，若0a <，则()0f x '>，函数()f x 单调递增，当x 趋近于负无穷大时，()f x 趋近于负无穷大；当x 趋近于正无穷大时，()f x 趋近于正无穷大，故函数()f x 存在唯一零点0x ，当0x x <时，()0f x <；当0x x >时，()0f x >．故0a <不满足条件． ············ 8分若0a =，()e 0x f x =≥恒成立，满足条件． ················· 9分若0a >，由()0f x '=，得ln x a =，当ln x a <时，()0f x '<；当ln x a >时，()0f x '>，所以函数()f x 在(,ln )a -∞上单调递减，在(ln ,)a +∞上单调递增，所以函数()f x 在ln x a =处取得极小值(ln )f a ln e ln ln a a a a a a =-⋅-=-⋅，由(ln )0f a ≥得ln 0a a -⋅≥，解得01a <≤．综上，满足()0f x ≥恒成立时实数a 的取值范围是[0,1]． ··········· 12分。

高三数学月考试题及答案-容城中学2014届高三上学期第二次月考(理)2

河北省容城中学2014届高三上学期第二次月考（理）时量：120分钟满分：150分一、选择题（本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）1.设集合{}{}{}1,2,3,4,1,2,3,2,3,4U M N ===，则()U C MN =（ A ）{}{}{}.1,4.2,3.2,4.A B C D φ2.设集合{}{}03,02M x x N x x =<≤=<≤，则a M ∈“”是a N ∈“”的（ B ） ....A B C D 充分不必要条件必要不充分条件充要条件不充分也既不必要条件3.若函数2log ,0()2,0x x x f x a x ⎧>⎪=⎨-≤⎪⎩有且只有一个零点，则a 的取值范围是（ C ）.0.0.0.0A a B a C a D a >≥≤<4.已知函数()sin(2),2f x x x R π=-∈，则()f x 是（ B ）.A π最小正周期为的奇函数 .B π最小正周期为的偶函数.2C π最小正周期为的奇函数 .2D π最小正周期为的偶函数 5.已知tan 2θ=，则22sinsin cos 2cos θθθθ+-=（ D ）4534....3445A B C D --6.若11222(21)(1)m m m +>+-，则实数m 的取值范围是（ D ）.().(1,2)2)A B C D -∞+∞- 7. 已知函数1(),4,()2(1),4,xx f x f x x ⎧≥⎪=⎨⎪+<⎩则2(2log 3)f +的值为（ A ）1111....241263A B C D 8.已知()f x 是R 上最小正周期为2的周期函数，且当02x ≤<时，3()f x x x =-，则函数()f x 的图像在区间[0,6]上与x 轴的交点个数为（ B ）.6.7.8.9A B C D二、填空题（本大题共7小题，每小题5分，共35分.把答案填在答题卡中对应题号后的横线上） 9.120(1)x dx -+⎰=3. 解:131202(1)()33x x dx x -+=-+=⎰10. 已知函数()f x =,则()f x 的定义域为 5(,2]3 .解：125log (35)0035123x x x -≥⇒<-≤⇒<≤，所以定义域为5(,2]311.若曲线22y x =的一条切线与直线480x y +-=垂直，则切线的方程为 420x y --=解：设切点为00(,)x y ，4y x '=，则000441,2x x y =⇒=∴=，所以切线方程为：24(1)420y x x y -=-⇒--=12.已知35cos ,cos(),,513ααβαβ=+=-都是锐角，则cos β=65解：因为,αβ都是锐角，且35cos ,cos(),513ααβ=+=- 所以412sin ,sin(),513ααβ=+= 则 5312433cos cos[()]cos()cos sin()sin 13513565βαβααβααβα=+-=+++=-⨯+⨯=13．函数f (x )＝2sin(ωx ＋φ)(ω>0，－π2<φ<π2)的部分图象如图所示，则(0)f 的值是解：353(),,2 41234T Tππππω=--=∴=∴=把5(,2)12π代入，得552sin()22662kππϕπϕπ+=⇒+=+2,,3223k k Zππππϕπϕϕ∴=-+∈-<<∴=-()2sin(2)(0)2sin()33f x x fππ∴=-∴=-=14.对任意两个实数12,x x，定义11212212,,max(,),.x x xx xx x x⎧≥⎪=⎨<⎪⎩若2()2,()f x xg x x=-=-，则max((),())f xg x的最小值为-1 .解：22,21max((),()),21x x xf xg xx x⎧-≤-≥⎪=⎨--<<⎪⎩或，所以max((),())f xg x的最小值为-115.已知集合{}(,)()M x y y f x==，若对于任意实数11(,)x y M∈，存在22(,)x y M∈，使得1212x x y y+=成立，则称集合M是“垂直对点集”.给出下列四个集合：①1(,)M x y yx⎧⎫==⎨⎬⎩⎭；②{}(,)2xM x y y e==-；③{}(,)cosM x y y x==④{}(,)lnM x y y x==.其中是“垂直对点集”的序号是②③.解：对于①，注意到12121x xx x+=无实数解，因此①不是“垂直对点集”；对于②，注意到过原点任意作一条直线与曲线2xy e=-相交，过原点与该直线垂直的直线必与曲线2xy e=-相交，因此②是“垂直对点集”；对于③，与②同理；对于④，注意到对于点（1,0），不存在22(,)x y M ∈，使得2210ln 0x x ⨯+⨯=，因为20x =与20x >矛盾，因此④不是“垂直对点集”. 答案：②③三、解答题（本大题共6小题，共75分.解答应写出文字说明、证明过程或演算步骤） 16. （本小题满分12分）已知向量(sin ,1),(3cos ,cos 2)(0)2A x A x x A ==>m n ，函数()f x =⋅m n 的最大值为4．（1）求A ；（2）求()f x 在[0,]2x π∈上的值域．17. （本小题满分12分）已知函数13()sin()cos(),44f x x x x R ππ=-+-∈ （1）求()f x 的最小正周期和最小值；（2）已知44cos(),cos(),(0)552a πββααβ-=+=-<<≤，求证：2[()]20f β-=．18．（本小题满分12分）已知函数()ln f x x x =-， ()ln ag x x x=+，（0a >）．（1）求函数()g x 的极值；（2）已知10x >，函数11()()()f x f x h x x x -=-，1(,)x x ∈+∞，判断并证明()h x 的单调性．19. （本小题满分13分）旅行社为某旅行团包飞机去旅游，其中旅行社的包机费为16000元.旅行团中的每个人的飞机票按以下方式与旅行社结算：若旅行团的人数不超过35人时，飞机票每张收费800元；若旅行团的人数多于35人时，则予以优惠，每多1人，每个人的机票费减少10元，但旅行团的人数最多不超过60人.设旅行团的人数为x 人，飞机票价格为y 元，旅行社的利润为Q 元.（1）写出飞机票价格y 元与旅行团人数x 之间的函数关系式；（2）当旅行团人数x 为多少时，旅行社可获得最大利润？求出最大利润.20. （本小题满分13分）已知函数f (x ) =3ln ,()2(0).x g x x x=-> （1）试判断当()()f x g x 与的大小关系；（2）试判断曲线()y f x =和()y g x =是否存在公切线，若存在，求出公切线方程，若不存在，说明理由.21. （本小题满分13分）已知函数2()2ln f x x x =-(1)若方程()0f x m +=在1[,]e e内有两个不等的实根，求实数m 的取值范围；（e 为自然对数的底数）（2）如果函数()()g x f x ax =-的图象与x 轴交于两点1(,0)A x 、2(,0)B x 且120x x <<.求证：12()0g px qx '+<（其中正常数,1,p q p q q p +=≥满足且）.。