历年初三数学中考函数复习试题
初三数学函数的试卷含答案

一、选择题(每题5分,共25分)1. 下列函数中,自变量x的取值范围是实数集的是()A. y = √(x - 2)B. y = 1/xC. y = log2(x + 3)D. y = |x|2. 函数y = -2x + 5的图像是()A. 一次函数的图像是一条直线B. 一次函数的图像是一条斜率为负的直线C. 一次函数的图像是一条斜率为正的直线D. 一次函数的图像是一条经过原点的直线3. 若函数y = kx + b(k≠0)的图像与x轴、y轴都相交,则k、b的取值范围是()A. k > 0, b > 0B. k > 0, b < 0C. k < 0, b > 0D. k < 0, b < 04. 函数y = (1/2)^x的图像是()A. 递增函数B. 递减函数C. 非单调函数D. 周期函数5. 若函数y = 3x - 1在x=2时取得最小值,则该函数的图像是()A. 递增函数B. 递减函数C. 非单调函数D. 周期函数二、填空题(每题5分,共25分)6. 函数y = 2x - 3的图像与y轴的交点坐标是______。
7. 若函数y = 3x^2 - 4x + 5在x=1时取得最大值,则该函数的图像是______。
8. 函数y = -5x + 10的图像在y轴上的截距是______。
9. 函数y = (1/4)^x的图像是______。
10. 函数y = x^3 - 3x的图像是______。
三、解答题(每题15分,共45分)11. (10分)已知函数y = -3x + 4,求以下问题:(1)当x=1时,函数的值是多少?(2)函数的图像与x轴、y轴的交点坐标分别是什么?12. (15分)已知函数y = 2x^2 - 5x + 2,求以下问题:(1)函数的图像与x轴的交点坐标。
(2)函数在x=2时的值。
(3)函数的最大值是多少?13. (15分)已知函数y = (1/2)^x,求以下问题:(1)当x=3时,函数的值是多少?(2)函数的图像是否经过第一象限?(3)函数的图像是否关于y轴对称?答案:一、选择题1. C2. B3. B4. B5. A二、填空题6. (0, -3)7. 递减8. 109. 递减函数10. 递增函数三、解答题11. (1)当x=1时,y = -31 + 4 = 1。
中考数学复习专题训练精选试题及答案

中考数学复习专题训练精选试题及答案一、选择题1. 以下哪一个数是最小的无理数?A. √2B. πC. 3.14D. √9答案:A2. 若一个等差数列的首项是2,公差是3,则第8项是多少?A. 17B. 18C. 19D. 20答案:A3. 一个二次函数的图像开口向上,顶点坐标为(3,-4),则该二次函数的一般式为:A. y = x² + 6x - 13B. y = x² - 6x + 13C. y = -x² + 6x - 13D. y = -x² - 6x + 13答案:B4. 在三角形ABC中,a = 5,b = 7,C = 60°,则边c 的长度等于:A. 6B. 8C. 10D. 12答案:C二、填空题1. 已知a = 3,b = 4,则a² + b² = _______。
答案:252. 已知一个等差数列的前5项和为35,首项为7,求公差d = _______。
答案:23. 在梯形ABCD中,AB // CD,AB = 6,CD = 8,AD = BC = 5,求梯形的高h = _______。
答案:34. 若函数f(x) = x² - 2x + 1的最小值为m,求m =_______。
答案:0三、解答题1. 已知一元二次方程x² - 4x - 12 = 0,求解该方程。
解:首先,将方程因式分解为(x - 6)(x + 2) = 0。
然后,解得x = 6或x = -2。
答案:x = 6或x = -22. 已知一个长方体的长为a,宽为b,高为c,且a、b、c成等差数列。
若长方体的体积为V,求V的表达式。
解:由题意可知,a + c = 2b,所以c = 2b - a。
长方体的体积V = abc = ab(2b - a)。
答案:V = ab(2b - a)3. 已知三角形ABC,AB = AC,∠BAC = 40°,BC = 6,求三角形ABC的周长。
初三数学常考试题及答案

初三数学常考试题及答案一、选择题1. 已知一个二次函数的图像经过点A(-1,0)和点B(3,0),且函数的开口向上,则该二次函数的对称轴是()。
A. x = 0B. x = 1C. x = 2D. x = -1答案:B解析:二次函数的对称轴是其顶点的x坐标,由于函数图像经过点A(-1,0)和点B(3,0),且开口向上,根据二次函数的性质,对称轴是这两点x坐标的平均值,即x = (-1 + 3) / 2 = 1。
2. 下列哪个选项是不等式2x - 3 > 0的解集?A. x > 3/2B. x < 3/2C. x > 3D. x < 3答案:A解析:将不等式2x - 3 > 0移项得到2x > 3,再除以2得到x > 3/2,因此选项A是正确的。
二、填空题3. 计算绝对值:|-7| = _______。
答案:7解析:绝对值表示一个数距离0的距离,因此|-7|表示-7距离0的距离,即7。
4. 计算平方根:√9 = _______。
答案:±3解析:平方根是一个数的平方等于给定数的那个数,9的平方根是3,因为3的平方是9。
同时,-3的平方也是9,所以9的平方根是±3。
三、解答题5. 已知一个直角三角形的两条直角边长分别为3和4,求斜边的长度。
答案:5解析:根据勾股定理,直角三角形的斜边长度等于两直角边长度的平方和的平方根。
即斜边长度= √(3² + 4²) = √(9 + 16) = √25 = 5。
6. 某工厂生产一种零件,每件成本为10元,售价为15元,若该工厂希望获得的利润不低于1000元,问至少需要生产多少件零件?答案:100件解析:设需要生产的零件数量为x件,则总利润为(15 - 10)x = 5x元。
根据题意,5x ≥ 1000,解得x ≥ 200。
因此,至少需要生产200件零件。
四、证明题7. 证明:如果一个三角形的两边之和大于第三边,那么这个三角形是存在的。
历年初三数学中考函数经典试题集锦及答案

中考数学函数经典试题集锦1、已知:m n 、是方程2650x x -+=的两个实数根,且m n <,抛物线2y x bx c=-++的图像经过点A(,0m )、B(0n ,).(1) 求这个抛物线的解析式;(2) 设(1)中抛物线与x 轴的另一交点为C,抛物线的顶点为D ,试求出点C 、D 的坐标和△BCD 的面积;(注:抛物线2y ax bx c =++(0)a ≠的顶点坐标为24(,)24b ac b a a--) (3) P 是线段OC 上的一点,过点P 作PH ⊥x 轴,与抛物线交于H点,若直线BC 把△PCH 分成面积之比为2:3的两部分,请求出P 点的坐标.[解析] (1)解方程2650,x x -+=得125,1x x == 由m n <,有1,5m n ==所以点A 、B 的坐标分别为A (1,0),B (0,5).将A (1,0),B (0,5)的坐标分别代入2y x bx c =-++.得105b c c -++=⎧⎨=⎩解这个方程组,得45b c =-⎧⎨=⎩所以,抛物线的解析式为245y x x =--+(2)由245y x x =--+,令0y =,得2450x x --+=解这个方程,得125,1x x =-=所以C 点的坐标为(-5,0).由顶点坐标公式计算,得点D (-2,9). 过D 作x 轴的垂线交x 轴于M.则1279(52)22DMC S ∆=⨯⨯-= 12(95)142MDBO S =⨯⨯+=梯形,1255522BOC S ∆=⨯⨯=所以,2725141522BCD DMC BOC MDBO S S S S ∆∆∆=+-=+-=梯形. (3)设P 点的坐标为(,0a )因为线段BC 过B 、C 两点,所以BC 所在的值线方程为5y x =+.那么,PH 与直线BC 的交点坐标为(,5)E a a +,PH 与抛物线245y x x =--+的交点坐标为2(,45)H a a a --+.由题意,得①32EH EP =,即23(45)(5)(5)2a a a a --+-+=+ 解这个方程,得32a =-或5a =-(舍去)②23EH EP =,即22(45)(5)(5)3a a a a --+-+=+解这个方程,得23a =-或5a =-(舍去)P 点的坐标为3(,0)2-或2(,0)3-.2、某工厂用一种自动控制加工机制作一批工件,该机器运行过程分为加油过程和加工过程:加工过程中,当油箱中油量为10升时,机器自动停止加工进入加油过程,将油箱加满后继续加工,如此往复.已知机器需运行185分钟才能将这批工件加工完.下图是油箱中油量y(升)与机器运行时间x(分)之间的函数图象.根据图象回答下列问题: (1)求在第一个加工过程中,油箱中油量y(升)与机器运行时间x(分)之间的函数关系式(不必写出自变量x 的取值范围);(2)机器运行多少分钟时,第一个加工过程停止? (3)加工完这批工件,机器耗油多少升?[解析] (1)设所求函数关系式为y=kx+b .由图象可知过(10,100),(30,80)两点,得101003080k b k b +=⎧⎨+=⎩解得1110k b =-⎧⎨=⎩∴ y=-x+llO(2)当y=10时,-x+110=10,x=100机器运行100分钟时,第一个加工过程停止(3)第一个加工过程停止后再加满油只需9分钟 加工完这批工件,机器耗油166升3、已知抛物线y x x c 122=-+的部分图象如图1所示。
中考数学总复习之列函数关系式专项训练(选填题)

中考数学总复习之列函数关系式专项训练(选填题)一.选择题(共20小题)1.某商场为了增加销售额,推出了“春节期间大酬宾”活动,活动内容是:“凡春节期间在该商场一次性购物超过100元者,超过100元的部分按八折优惠.”在酬宾活动中,小张到该商场为单位购买了单价为30元的办公用品x件(x>4),则应付款y与商品件数x 的关系式为()A.y=24x B.y=24x+2C.y=24x+20D.y=24x+22 2.为打造“比、学、赶、帮、超”良好的班风和浓厚的学风,数学白老师为8班孩子购买了5包卡通橡皮和x包表扬信,卡通橡皮每包12元,表扬信每包30元,共花费y元,则关系式为()A.y=5x+6B.y=12x+30C.y=8x+12D.y=30x+60 3.甲、乙两地相距320km,一货车从甲地出发以80km/h的速度匀速向乙地行驶,则货车距离乙地的路程S(km)与时间t(h)之间的函数表达式是()A.S=320t B.S=80t C.S=320﹣80t D.S=320﹣4t 4.一粒石子落入湖面,形成一个如圆周样的涟漪,在圆周长C与半径r的关系式C=2πr 中,变量是()A.C,r B.C,πC.π,r D.C,2π5.矩形周长为20cm,其长和宽分别为x cm和y cm,当x在一定范围内变化时,y随x的变化而变化.则y与x满足的函数关系是()A.正比例函数关系B.一次函数关系C.二次函数关系D.反比例函数关系6.在烧开水时,水温达到100℃水就会沸腾.下表是小红同学做“观察水的沸腾”试验时所记录的时间t(min)和水温T(℃)的数据:时间t/min024********…温度T/℃3044587286100100100…在水烧开之前(即t<10),水温T与时间t之间的关系式为()A.T=7t+30B.T=16t+30C.T=14t﹣16D.T=30t﹣16 7.小明的妈妈给了小明50元去买作业本,已知作业本的单价是2.5元,小明购买x本作业本,剩余费用为y元,则y与x的表达式为()A.y=﹣2.5x+50B.y=2.5xC.y=(50﹣2.5)x D.y=50x﹣2.58.若等腰三角形的周长为60cm,底边长为x cm,一腰长为y cm,则y与x的函数关系式及自变量x的取值范围是()A.y=60﹣2x(0<x<60)B.y=60﹣2x(0<x<30)C.y=(60﹣x)(0<x<60)D.y=(60﹣x)(0<x<30)9.某品牌的自行车链条每节长为2.5cm,每两节链条相连部分重叠的圆的直径为0.8cm,按照这种连接方式,n节链条总长度为y cm,则y与n的关系式是()A.y=2.5n B.y=1.7nC.y=1.7n+0.8D.y=2.5n﹣0.810.一个长方形的周长为30cm,其中一条边长为x cm,面积为y cm2,则y与x的关系式为()A.y=30﹣x B.y=15﹣x C.y=﹣x2+30x D.y=﹣x2+15x 11.清明假期,刘老师乘车从学校到井冈山观赏映山红,缅怀革命先烈.已知学校距离井冈山150km,车行驶的平均速度为60km/h,x h后刘老师距离井冈山y km,则y与x之间的关系式是()A.y=150﹣60x B.y=150+60x C.y=60﹣150x D.y=60+150x 12.小军用50元钱去买单价是8元的笔记本,则他剩余的钱Q(元)与他买这种笔记本的本数x之间的关系是()A.Q=8x B.Q=8x﹣50C.Q=50﹣8x D.Q=8x+5013.一个正方形的边长为5cm,它的各边边长减少x cm后,得到的新正方形的周长为y cm,y与x之间的函数解析式是()A.y=3x﹣20B.y=20﹣3x C.y=﹣4x+20D.y=4x14.已知球的表面积S(cm2)与它的半径R(cm)之间的关系式是S=4πR2,其中S随R 的变化而变化,则在这个公式中变量是()A.π,R B.S,R C.S D.S,π,R 15.我们知道,互相垂直且有公共原点的两条数轴构成平面直角坐标系.如果坐标系中两条坐标轴不垂直,那么这样的坐标系称为“斜坐标系”.如图1,P是斜坐标系xOy中的任意一点,与直角坐标系相类似,过点P分别作两坐标轴的平行线,分别与x轴、y轴交于M、N两点,若M、N两点在x轴、y轴上分别对应实数a、b,则有序实数对(a,b)叫做点P在斜坐标系xOy中的坐标.如图2,在斜坐标系xOy中,已知点B(4,0)、点C (0,3),P(x,y)是线段BC上的任意一点,则x、y之间一定满足的等量关系式为()A.B.C.D.16.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂重物的质量x(kg)有下面的关系,那么弹簧总长y(cm)与所挂重物x(kg)之间的关系式为()x(kg)0123456y(cm)1212.51313.51414.515A.y=x+12B.y=0.5x+12C.y=0.5x+10D.y=x+10.5 17.下列关于两个变量的关系,表述不正确的是()A.圆的面积公式S=πr2中,S是r的函数B.同一物质,物体的体积是质量的函数C.光线照到平面镜上,入射角为α,反射角为β,则β是α的函数D.表达式(x≥0)中y是x的函数18.在一次运动会的100米比赛中,小明以8米/秒速度奔跑,设小明离终点的距离为y (米),则y 与奔跑时间t (秒)之间的关系式是( ) A .y =8tB .C .y =100﹣8tD .y =8t ﹣10019.某链条每节长为3.7cm ,每两节链条相连部分重叠的圆的直径为1.2cm ,按照这种连接方式,x 节链条总长度为y cm ,则y 与x 的关系式是( )A .y =3.7xB .y =2.5xC .y =2.5x ﹣1.2D .y =2.5x +1.220.一根高18厘米的蜡烛点燃后剩余的高度h (厘米)与燃烧时间t (时)(0≤t ≤6)的关系如表,已知平均每小时蜡烛燃掉3厘米,则蜡烛点燃后剩余的高度h (厘米)与燃烧时间t (时)(0≤t ≤6)之间的关系式是( ) 燃烧时间t (时) 01234剩余的高度h (厘米) 18151296A .h =18﹣tB .h =18+tC .h =18﹣3tD .h =18+3t二.填空题(共20小题)21.长方形的周长为20cm ,其中一边为x cm (其中x >0),面积为y cm 2,则y 关于x 的关系式为 .22.如图,要围一个长方形ABCD 的菜园,菜园的一边利用足够长的墙,用35米长的篱笆围成另外三边.为了方便进出,在BC 边上留了一个2米宽的小门.设AB 边的长为x 米,BC 边的长为y 米,则y 与x 之间的关系式是 .23.高山地区海拔高,空气稀薄,所以大气压低于一个标准大气压,水的沸点随高原气压的减小而降低.下表是各个城市的海拔高度及水的沸点统计情况,请根据表中的数据,请写出y与x的关系式为.城市A地B地C地D地海拔x(米)03006001500沸点y(度)100999895 24.2024世界泳联跳水世界杯总决赛4月19﹣21日在西安奥体中心游泳跳水馆举行,小陆同学和家人一同从家出发观赛,由于距离较远,决定打车前往.已知西安市出租车的收费标准是起步价8.5元(行程小于或等于3公里),超过3公里每增加1公里(不足1公里按1公里计算)加收2元,则出租车费y(元)与行程x(公里)(x是大于3的整数)之间的关系式为.25.小丽给新办的饭卡充值100元,学校餐厅每顿午饭均为5元,则饭卡余额y(元)与购买午饭的次数x(次)之间的关系是.26.某工程队承建一条长为60km的乡村公路,预计工期为120天,若每天修建公路的长度保持不变,则还未完成的公路长度y(km)与施工时间x(天)之间的关系式为y =.27.已知一根弹簧秤不挂物体时弹簧的长度为7cm,在弹性限度内,每挂重1kg物体,弹簧伸长0.5cm,则挂重后弹簧的长度y(cm)与所挂物体的质量x(kg)之间的函数表达式是.28.某电器进价为250元/台,售价为400元/台,若售出x台,售出x台的总利润为y元,则y与x之间的关系式为.29.某出租车的收费标准是:3千米以内(包括3千米)收费8元,超过3千米,每增加1千米加收2元,则路程为x(x>3)时,车费y(元)与路程x(千米)之间的关系式为:.30.晋商博物院位于太原市府东街101号,是一座集文物古建、园林景观,展览展示于一体的人文历史性质的博物馆.今年六一,某校4名老师带领初一x名学生到晋商博物院参观研学,已知成人票每张38元,学生票按成人票价给予半价优惠,设门票的总费用为y 元,则y与x的关系式为.31.一名老师带领x名学生到动物园参观,已知成人票每张30元,学生票每张10元,设门票的总费用为y元,则y与x的函数关系式为.32.长方形的周长为36cm,其中一边长为x(cm),面积为y(cm2),则y与x的关系可表示为.33.中国齐笔历史悠久,盛产于大王镇西营一带,东营一书法爱好者驱车前往离家30km的西营购买,速度为60km/h,则他离西营的路程s(km)与行驶时间t(h)之间的表达式为.34.佳佳的爸爸计划用一根长为10m的铁丝围成一个长方形,那么这个长方形的长y(m)与宽x(m)之间的关系式为.35.声音在空气中传播的速度简称音速,实验测得音速与气温的一些数据如下表:用x表示y的关系式为.气温x/°C05101520331334337340343音速y/(米/秒)36.某电影院地面的一部分为扇形,观众席的座位数按下列方式设置:排数(x)1234……座位数(y)40434649……若排数x是自变量,y是因变量,则y与x之间的函数关系式为.37.一支18cm长的蜡烛点燃后每小时燃烧掉2cm,用y(cm)表示燃烧后蜡烛的长度,t (h)表示燃烧的时间,那么y与t(0≤t≤9)之间的关系式是.38.西安市出租车的收费标准是起步价9元(行程小于或等于3千米),超过3千米每增加1千米(不足1千米按1千米计算)加收2元,则出租车费y(元)与行程x(千米)(x >3)之间的关系式为.39.某超市“6.18”期间做促销优惠活动,凡一次性购物超过100元以上者,超过100元的部分按8.5折优惠.小宇在此期间到该超市为单位购买单价为60元的办公用品x件(x >2),则应付款y元(元)与商品件数x的关系式是.40.兴平市出租车白天的收费起步价为5元,即路程不超过3公里时收费5元,超过部分每公里收费1.5元,若乘客白天乘坐出租车的路程为x(x>3)公里,乘车费为y元,则y 与x之间的关系式为.。
初中函数测试题及答案

初中函数测试题及答案一、选择题(每题3分,共30分)1. 函数y=2x+3中,当x=1时,y的值为()A. 5B. 4C. 3D. 22. 下列哪个函数的图像是一条直线?()A. y=x^2B. y=2x+1C. y=x/(x-1)D. y=√x3. 函数y=-2x+1的斜率是多少?()A. 2B. -2C. 1D. -14. 函数y=3x-5与y轴的交点坐标是()A. (0, -5)B. (0, 3)C. (5, 0)D. (-5, 0)5. 如果函数y=kx+b的图像经过点(2, 6)和(3, 9),那么k的值是()A. 3B. 2C. 1D. 06. 函数y=4x+5的图像与x轴的交点坐标是()A. (-5/4, 0)B. (5/4, 0)C. (0, 5)D. (0, -5)7. 函数y=x^2-4x+3的顶点坐标是()A. (2, -1)B. (2, 1)C. (-2, 1)D. (-2, -1)8. 函数y=1/x的图像在哪个象限?()A. 第一象限和第三象限B. 第二象限和第四象限C. 第一象限和第二象限D. 第三象限和第四象限9. 函数y=|x|的图像关于哪个轴对称?()A. x轴B. y轴C. 原点D. 都不是10. 下列哪个函数是奇函数?()A. y=x^2B. y=x^3C. y=x+1D. y=x-1二、填空题(每题4分,共20分)11. 函数y=2x-1的图像与x轴的交点坐标是______。
12. 函数y=-3x+4的斜率是______。
13. 函数y=x^2-6x+8的顶点坐标是______。
14. 函数y=1/x的图像在第一象限的斜率是______。
15. 函数y=|x-2|的图像与y轴的交点坐标是______。
三、解答题(每题10分,共50分)16. 已知函数y=5x-2,求当x=-1时,y的值。
17. 已知函数y=-4x+7,求该函数与y轴的交点坐标。
18. 已知函数y=2x^2-3x+1,求该函数的顶点坐标。
中考函数复习题及答案

中考函数复习题及答案一、选择题1. 函数y = 2x + 3的斜率是()A. 2B. 3C. -2D. -32. 下列哪个是一次函数的图象?A. 直线B. 曲线C. 抛物线D. 双曲线3. 函数f(x) = x^2 - 4x + 4的顶点坐标是()A. (2, 0)B. (-2, 0)C. (0, 4)D. (2, 4)4. 函数y = 1/x的图象不经过哪个象限?A. 第一象限B. 第二象限C. 第三象限D. 第四象限5. 函数y = |x|的图象是()A. 直线B. V形C. U形D. 抛物线答案:1. A 2. A 3. A 4. D 5. B二、填空题6. 函数y = 3x - 2的截距是______。
7. 如果一个函数的图象与x轴交于点(1,0),则该函数可以表示为y = ______。
8. 函数y = x^2 + 2x + 1可以化简为y = (x + ______)^2。
9. 函数y = 1/x的图象在x轴的正半轴上,y的值随着x的增大而______。
10. 函数y = kx + b,当k > 0时,图象从左向右上升;当k < 0时,图象从左向右______。
答案:6. -2 7. x - 1 8. 1 9. 减小 10. 下降三、解答题11. 已知函数f(x) = 2x - 5,求f(3)的值。
12. 已知二次函数y = ax^2 + bx + c的顶点坐标为(-1, -4),求a的值。
13. 函数y = 3x + 7与x轴的交点坐标是什么?14. 函数y = x^2 - 6x + 9的最大值是多少?15. 已知函数y = |x - 2| + 3,求x = 2时的函数值。
答案:11. f(3) = 2 * 3 - 5 = 6 - 5 = 112. 顶点坐标(-1, -4),根据顶点公式,-b/2a = -1,b = 2a,又因为顶点的y坐标是-4,所以有a(-1)^2 + b(-1) + c = -4,代入b =2a,解得a = -4。
初三函数测试题目及答案

初三函数测试题目及答案一、选择题(每题3分,共30分)1. 下列哪个选项是一次函数的图象?A. 一条直线B. 一个圆C. 一个椭圆D. 一个抛物线答案:A2. 函数y=2x+3的斜率是多少?A. 2B. 3C. -2D. -3答案:A3. 如果一个函数的图象经过点(2,5),那么这个点一定在函数的:A. 定义域内B. 值域内C. 函数图象上D. 函数图象外答案:C4. 函数y=x^2的反函数是:A. y=√xB. y=x^2C. y=1/xD. y=-x^2答案:A5. 函数y=1/x的图象不经过哪个象限?A. 第一象限B. 第二象限C. 第三象限D. 第四象限答案:D6. 函数y=3x-2的零点是多少?A. 0.5B. 1C. 2D. 3答案:B7. 函数y=2x+1的图象与y轴的交点坐标是:A. (0, 1)B. (0, 2)C. (1, 0)D. (1, 2)答案:A8. 函数y=x^2-4x+3的最大值是多少?A. -1B. 0C. 1D. 3答案:B9. 函数y=|x|的图象是:A. 一条直线B. 一个V形C. 一个W形D. 一个倒V形答案:B10. 如果函数y=f(x)是奇函数,那么f(-x)等于:A. f(x)B. -f(x)C. xD. -x答案:B二、填空题(每题4分,共20分)11. 函数y=3x+5的图象与x轴的交点坐标是________。
答案:(-5/3, 0)12. 函数y=x^2-6x+9的最小值是________。
答案:013. 函数y=1/x的图象在x=2处的斜率是________。
答案:1/414. 函数y=x^3-3x^2+3x-1的零点是________。
答案:115. 函数y=2x^2-4x+1的顶点坐标是________。
答案:(1, -1)三、解答题(每题10分,共50分)16. 已知函数y=2x^2-4x+3,求该函数的顶点坐标。
答案:顶点坐标为(1, 1)。
初中函数专题试题及答案

初中函数专题试题及答案一、选择题(每题3分,共30分)1. 下列函数中,哪一个是一次函数?A. \( y = x^2 \)B. \( y = 2x + 3 \)C. \( y = \frac{1}{x} \)D. \( y = x^3 - 2x \)答案:B2. 函数 \( y = 3x - 5 \) 的图象与x轴的交点坐标是:A. \( (0, -5) \)B. \( (5, 0) \)C. \( (-5, 0) \)D. \( (0, 5) \)答案:C3. 如果函数 \( y = 2x + 1 \) 在 \( x = 2 \) 时的值为5,那么\( x = 1 \) 时的值是:A. 3B. 4C. 2D. 1答案:A4. 函数 \( y = -\frac{1}{2}x + 3 \) 的斜率是:A. \( \frac{1}{2} \)B. \( -\frac{1}{2} \)C. \( \frac{3}{2} \)D. \( -3 \)答案:B5. 函数 \( y = 4x^2 \) 的顶点坐标是:A. \( (0, 0) \)B. \( (0, 4) \)C. \( (2, 0) \)D. \( (0, -4) \)答案:A6. 函数 \( y = x^2 - 6x + 9 \) 可以写成完全平方的形式:A. \( (x - 3)^2 \)B. \( (x + 3)^2 \)C. \( (x - 3)^2 + 3 \)D. \( (x + 3)^2 - 3 \)答案:A7. 函数 \( y = 2x^2 - 8x + 7 \) 的最小值是:A. 1B. 3C. 7D. 无法确定答案:A8. 函数 \( y = \frac{1}{x} \) 的图象是:A. 一条直线B. 两条直线C. 一个双曲线D. 一个抛物线答案:C9. 函数 \( y = 3x^2 + 2x - 5 \) 的对称轴是:A. \( x = -\frac{2}{3} \)B. \( x = \frac{2}{3} \)C. \( x = -1 \)D. \( x = 1 \)答案:B10. 函数 \( y = 2x + 3 \) 和 \( y = -x + 1 \) 的交点坐标是:A. \( (-2, -1) \)B. \( (2, 5) \)C. \( (-1, 1) \)D. \( (1, 3) \)答案:C二、填空题(每题4分,共20分)11. 函数 \( y = 2x + 1 \) 在 \( x = -1 \) 时的值为 _______。
初三数学函数必刷题试卷

1. 下列函数中,定义域为实数集R的是()A. f(x) = √(x-1)B. f(x) = |x-1|C. f(x) = 1/xD. f(x) = x^22. 函数f(x) = x^2 + 1的值域是()A. [1, +∞)B. (-∞, 1]C. (-∞, +∞)D. [1, +∞) ∪ (-∞, 1]3. 若函数f(x) = ax^2 + bx + c的图像开口向上,则a的取值范围是()A. a > 0B. a < 0C. a ≥ 0D. a ≤ 04. 函数f(x) = 2x + 1在R上单调递增,则k的取值范围是()A. k > 0B. k < 0C. k ≥ 0D. k ≤ 05. 函数f(x) = 3x - 2的图像关于y轴对称,则f(-x)的图像是()A. 关于x轴对称B. 关于y轴对称C. 关于原点对称D. 无对称性二、填空题(每题5分,共25分)6. 函数f(x) = (x-1)^2 + 2的顶点坐标是______。
7. 函数f(x) = 2x - 1在x=1时取得最小值,最小值为______。
8. 若函数f(x) = x^2 + kx + 1的图像开口向上,且与x轴有两个交点,则k的取值范围是______。
9. 函数f(x) = 3x - 4的图像向右平移2个单位后的函数解析式是______。
10. 函数f(x) = |x-1|的图像关于x=1对称。
三、解答题(每题10分,共30分)11. (10分)已知函数f(x) = x^2 - 2x + 1,求:(1)函数f(x)的图像的顶点坐标;(2)函数f(x)在x=1时的值。
12. (10分)已知函数f(x) = 2x^2 - 3x + 1,求:(1)函数f(x)的图像的对称轴;(2)函数f(x)在x=2时的值。
13. (10分)已知函数f(x) = 3x^2 - 2x + 1,求:(1)函数f(x)的图像的开口方向;(2)函数f(x)在x=0时的值。
九年级函数专题试卷及答案

九年级函数专题试卷及答案专业课原理概述部分一、选择题(每题1分,共5分)1. 下列函数中,哪个是正比例函数?A. y = 2x + 3B. y = 3x 2C. y = x^2 + 1D. y = 1/x2. 如果函数y = kx + b的图像是一条经过原点的直线,那么k和b的关系是?A. k = 0, b ≠ 0B. k ≠ 0, b = 0C. k = 0, b = 0D. k ≠ 0, b ≠ 03. 下列函数中,哪个是反比例函数?A. y = 2/xB. y = x^2C. y = 3x + 1D. y = 1/x^24. 如果函数y = kx的图像是一条经过原点的直线,那么k的值是?A. k = 0B. k > 0C. k < 0D. k ≠ 05. 下列函数中,哪个是一次函数?A. y = x^2B. y = 2/xC. y = 3x + 1D. y = 1/x^2二、判断题(每题1分,共5分)1. 正比例函数的图像是一条经过原点的直线。
()2. 反比例函数的图像是一条经过原点的直线。
()3. 一次函数的图像是一条直线。
()4. 二次函数的图像是一条抛物线。
()5. 函数y = kx + b是一次函数当且仅当b = 0。
()三、填空题(每题1分,共5分)1. 如果函数y = kx的图像是一条经过原点的直线,那么k的值是______。
2. 如果函数y = kx + b的图像是一条经过原点的直线,那么b的值是______。
3. 反比例函数的一般形式是______。
4. 二次函数的一般形式是______。
5. 一次函数的图像是一条______。
四、简答题(每题2分,共10分)1. 请简述正比例函数的定义。
2. 请简述反比例函数的定义。
3. 请简述一次函数的定义。
4. 请简述二次函数的定义。
5. 请简述函数图像的斜率是什么。
五、应用题(每题2分,共10分)1. 如果函数y = 2x的图像是一条经过原点的直线,那么当x = 3时,y的值是多少?2. 如果函数y = 3/x的图像是一条经过原点的直线,那么当x = 2时,y的值是多少?3. 如果函数y = kx + b的图像是一条经过原点的直线,那么当x = 1时,y的值是多少?4. 如果函数y = x^2的图像是一条抛物线,那么当x = 2时,y的值是多少?5. 如果函数y = 1/x^2的图像是一条经过原点的直线,那么当x = 3时,y的值是多少?六、分析题(每题5分,共10分)1. 请分析一次函数和二次函数的图像有什么不同。
中考数学总复习《函数》专项测试卷-附参考答案

中考数学总复习《函数》专项测试卷-附参考答案一、单选题(共12题;共24分)1.如图所示,抛物线L:y=ax2+bx+c(a<0)的对称轴为x=5,且与x轴的左交点为(1,0)则下列说法正确的有()①C(9,0);②b+c>-10;③y的最大值为-16a;④若该抛物线与直线y=8有公共交点,则a的取值范围是a≤ 1 2.A.①②③④B.①②③C.①③④D.①④2.若y+3与x-2成正比例,则y是x的()A.正比例函数B.不存在函数关系C.一次函数D.以上都有可能3.关于函数y=2x﹣1,下列结论成立的是()A.当x<0时,则y<0B.当x>0时,则y>0C.图象必经过点(0,1)D.图象不经过第三象限4.关于一次函数y=x+2,下列说法正确的是()A.y随x的增大而减小B.经过第一、三、四象限C.与y轴交于(0,2)D.与x轴交于(2,0)5.点P(3,y1)、Q (4,y2)是二次函数y=x2−4x+5的图象上两点,则y1与y2的大小关系为()A.y1>y2B.y1<y2C.y1=y2D.无法确定6.快、慢两车分别从甲、乙两地同时出发,相向匀速行驶,两车在途中相遇时都停留了一段时间,然后分别按原速度原方向匀速行驶,快车到达乙地后休息半小时后,再以另一速度原路匀速返回甲地(掉头的时间忽略不计),慢车到达甲地以后即停在甲地等待快车.如图所示为快、慢两车间的距离y (千米)与快车的行驶时间x(小时)之间的函数图象.则下列说法:①两车在途中相遇时都停留了1小时;②快车从甲地去乙地时每小时比慢车多行驶40km;③快车从乙地返回甲地的速度为120km/h;④当慢车到达甲地的时候,快车与甲地的距离为400km.其中正确的有()A.4B.3C.2D.17.如图,动点A在抛物线y=−x2+2x+3(0≤x≤3)上运动,直线l经过点(0,6),且与y轴垂直,过点A做AC⊥ l于点C,以AC为对角线作矩形ABCD,则另一对角线BD的取值范围正确的是()A.2≤BD≤3B.3≤BD≤6C.1≤BD≤6D.2≤BD≤68.如图,在平面直角坐标系中,函数y=kx,y=−2x的图像交于A,B两点,过A作y轴的垂线,交函数y=3x的图像于点C,连接BC,则ΔABC的面积为()A.2B.3C.5D.69.如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点是A,对称轴是直线x=1,且抛物线与x轴的一个交点为B(4,0);直线AB的解析式为y2=mx+n(m≠0).下列结论:①2a+b=0;②abc>0;③方程ax2+bx+c=mx+n有两个不相等的实数根;④抛物线与x轴的另一个交点是(﹣1,0);⑤当1<x<4时,则则y1>y2,其中正确的是()A.①②B.①③⑤C.①④D.①④⑤10.如图,矩形ABCD中,AB=3,BC=4,点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数大致图象是()A.B.C.D.11.如图,在平面直角坐标系中,ΔA1A2A3,ΔA3A4A5,ΔA5A6A7,…都是等边三角形,其边长依次为2,4,6,…,其中点A1的坐标为(2,0),点A2的坐标为(1,−√3),点A3的坐标为(0,0),点A4的坐标为(2,2√3),…,按此规律排下去,则点A2020的坐标为()A.(1,−1009√3)B.(1,−1010√3)C.(2,1009√3)D.(2,1010√3)12.如图,二次函数y=-x2+bx+c 图象上有三点A(-1,y1 )、B(1,y2) 、C(2,y3),则y1,y2,y3大小关系为()A.y1<y3<y2B.y3<y1<y2C.y1<y2<y3D.y2<y1<y3二、填空题(共6题;共6分)13.点P(1,1)向左平移两个单位后恰好位于双曲线y=k x上,则k=.14.将二次函数y=−x2+3的图像向下平移5个单位长度,所得图像对应的函数表达式为.15.如图,已知A1(1,0),A2(1,1),A3(﹣1,1),A4(﹣1,﹣1),A5(2,﹣1)…,则点A2021的坐标为.16.请写出一个二次函数,使它的图象同时满足下列两个条件:①开口向下,②与y轴的交点是(0,1),你写出的函数表达式是.17.若点P(n,1),Q(n+6,3)在正比例函数图象上,请写出正比例函数的表达式. 18.在−3,−2,−1,4,5五个数中随机选一个数作为一次函数y=kx−3中k的值,则一次函数y=kx−3中y随x的增大而减小的概率是.三、综合题(共6题;共67分)19.3−√(−3)2+|√3−2|(1)计算:(−1)2021+√16+√−27(2)如图所示的是某学校的平面示意图,已知旗杆的位置是(−1,2),实验室的位置是(2,3).①根据所给条件建立适当的平面直角坐标系,并用坐标表示食堂,宿舍楼和大门的位置.②已知办公楼的位置是(−2,1),教学楼的位置是(3,1),在①中所画的图中标出办公楼和教学楼的位置.20.汽车出发1小时后油箱里有油40L,继续行驶若干小时后,在加油站加油若干升(加油时间忽略不计).图象表示出发1小时后,油箱中剩余测量(y)与行驶时间t(h)之间的关系.(1)汽车行驶h后加油,中途加油L;(2)求加油前油箱剩余量y与行驶时间t的函数关系式;(3)若加油前后汽车都以80km/h匀速行驶,则汽车加油后最多能行驶多远?21.凤凰单丛(枞)茶,是潮汕的名茶,已有九百余年的历史.潮汕人将单丛茶按香型分为黄枝香、芝兰香、桃仁香、玉桂香、通天香、鸭屎香等多种.清明采茶季后,某茶叶店准备购买通天香和鸭屎香两种单丛茶进行销售,已知若购买4千克通天香单丛和3千克鸭屎香单丛需要2500元,购买2千克通天香单丛和5千克鸭屎香单丛需要2300元.(1)求通天香、鸭屎香两种茶叶的单价分别为多少元?(2)茶叶专卖店计划购买通天香、鸭屎香两种单丛茶共80千克,总费用不多于26000元,并且要求通天香茶叶数量不能低于10千克,那么应如何安排购买方案才能使总费用最少,最少费用应为多少元?22.为落实“双减”政策,丰富课后服务的内容,某学校计划到甲、乙两个体育专卖店购买一批新的体育用品,两个商店的优惠活动如下:甲:所有商品按原价8.5折出售;乙:一次购买商品总额不超过300元的按原价付费,超过300元的部分打7折.设需要购买体育用品的原价总额为x元,去甲商店购买实付y甲元,去乙商店购买实付y乙元,其函数图象如图所示.(1)分别求y甲,y乙关于x的函数关系式;(2)两图象交于点A,求点A坐标;(3)请根据函数图象,直接写出选择去哪个体育专卖店购买体育用品更合算.23.直线y=kx+b经过A(0,-3))和B(-3,0)两点.(1)求这个一次函数的解析式;(2)画出图象,并根据图象说明不等式kx+b<0的解集.24.“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场,下面的函数图象表示“龟兔再次赛跑”时,则乌龟所走路程y1(米)和兔子所走的路程y2(米)分别与乌龟从起点出发所用的时间x(分)之间的函数图象,根据图象解答下列问题:(1)“龟兔再次赛跑”的路程是米,兔子比乌龟晚走了分钟,乌龟在途中休息了分钟,“龟兔再次赛跑”获胜的是.(2)分别求出乌龟在途中休息前和休息后所走的路程y1关于时间x的函数解析式,并写出自变量x的取值范围.(3)乌龟和兔子在距离起点米处相遇.参考答案1.【答案】B 2.【答案】C 3.【答案】A 4.【答案】C 5.【答案】B 6.【答案】B 7.【答案】D 8.【答案】C 9.【答案】B 10.【答案】C 11.【答案】D 12.【答案】A 13.【答案】-114.【答案】y =−x 2−2 15.【答案】(506,﹣505)16.【答案】y =−x 2+x +1 (不唯一) 17.【答案】y =13x 18.【答案】3519.【答案】(1)解:原式=−1+4−3−3+2−√3=−1−√3(2)解:①根据题意,建立如图所示的平面直角坐标系,如下:∴食堂(−4,4),宿舍楼(-5,1),大门(1,−1) ②办公楼和教学楼的位置如图所示.20.【答案】(1)4;35(2)解:设y 与x 的函数关系式为y =kt+b 把(1,40)和(4,10)代入得{k +b =404k +b =10解得 {k =−10b =50∴加油前油箱剩余油量y 与行驶时间t 的函数关系式y =﹣10t+50(3)解:由图象知,汽车加油前行驶了3小时,则用油40﹣10=30(L ) ∴汽车行驶1小时耗油量为 303=10(L/h )加油后邮箱中剩余油量45L ,可以行驶 4510 ×80=360(km ).∴汽车加油后最多能行驶360km .21.【答案】(1)解:设通天香茶叶每千克为x 元,鸭屎香茶叶每千克为y 元,根据题意,得{4x +3y =25002x +5y =2300解得{x =400y =300∴通天香茶叶每千克为400元,鸭屎香茶叶每千克为300元.(2)解:设购买通天香茶叶m 千克,鸭屎香茶叶(80-m )千克,总费用w 元 根据题意,得400m +300(80−m)≤26000 解得m ≤20 ∵m ≥10∴m 的取值范围是:10≤m ≤20总费用w =400m +300(80−m)=100m +24000 ∵100>0∴w 随着m 的增大而增大∴当m =10时,则w 最少,w 最少=1000+24000=25000(元)∴通天香茶叶购进10千克,鸭屎香茶叶购进70千克,总费用最少为25000元.22.【答案】(1)解:由题意可得,y 甲=0.85x ;乙商店:当0≤x≤300时,则y 乙与x 的函数关系式为y 乙=x ; 当x >300时,则y 乙=300+(x-300)×0.7=0.7x+90 由上可得,y 乙与x 的函数关系式为y 乙={x(0≤x ≤300)0.7x +90(x >300)(2)解:由{y 甲=0.85xy 乙=0.7x +90,解得{x =600y 乙=510点A 的坐标为(600,510);(3)解:由点A 的意义,当买的体育商品标价为600元时,则甲、乙商店优惠后所需费用相同,都是510元 结合图象可知当x <600时,则选择甲商店更合算; 当x=600时,则两家商店所需费用相同; 当x >600时,则选择乙商店更合算.23.【答案】(1)解:将A(0,−3),B(−3,0)代入y =kx +b 得{b =−3−3k +b =0解得:k =−1,b =−3∴y =−x −3一次函数的解析式为:y =−x −3. (2)解:作图如下:由图象可知:直线从左往右逐渐下降,即y 随x 的增大而减小 当x =−3时∴kx +b <0的解集为:x >−3.24.【答案】(1)1000;40;10;兔子(2)解:设乌龟在途中休息前所走的路程y 1关于时间x 的函数解析式为y 1=kx ∴600=30k ,解得k =20∴乌龟在途中休息前所走的路程y 1关于时间x 的函数解析式为y 1=20x (0≤x≤30) 设乌龟在途中休息后所走的路程y 1关于时间x 的函数解析式为y 1=k′x+b∴{40k ′+b =60060k ′+b =1000,解得{k ′=20b =−200∴乌龟在途中休息后所走的路程y1关于时间x的函数解析式为y1=20x﹣200(40≤x≤60);(3)750第11页共11。
初三-中考中的函数真题100题
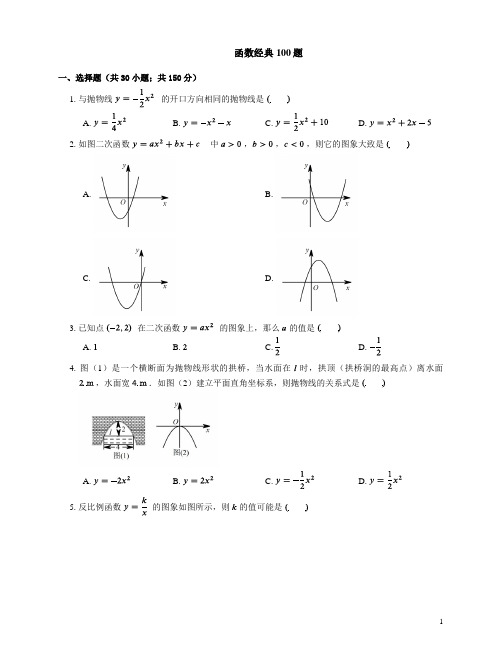
函数经典100题一、选择题(共30小题;共150分)1. 与抛物线的开口方向相同的抛物线是A. B. C. D.2. 如图二次函数中,,,则它的图象大致是A. B.C. D.3. 已知点在二次函数的图象上,那么的值是A. B.4. 图(1)是一个横断面为抛物线形状的拱桥,当水面在时,拱顶(拱桥洞的最高点)离水面.如图(2)建立平面直角坐标系,则抛物线的关系式是A. B. C. D.5. 反比例函数的图象如图所示,则的值可能是B. C.6. 一件工艺品的进价为元,标价元出售,每天可售出件,根据销售统计,一件工艺品每降价元,则每天可多售出件,要使每天获得的利润最大,则每件需降价A. 元B. 元C. 元D. 元7. 如图,是一次函数与反比例函数的图象,则关于的方程的解为A. ,B. ,C. ,D. ,8. 已知,那么函数的最大值是C. D.9. 已知反比例函数,当时,的取值范围是A. B. C. D.10. 二次函数的部分图象如图所示,对称轴为直线,与轴的一个交点为,与轴的交点为,则方程的解为A. B. C. , D. ,11. 已知二次函数的图象如图,则其解析式为A. B. C. D.12. 已知蓄电池的电压为定值,使用蓄电池时,电流(单位:)与电阻(单位:)是反比例函数关系,它的图象如图所示.则用电阻表示电流的函数表达式为A. B. C. D.13. 反比例函数的图象经过点,那么这个函数的解析式为A. B. C. D.14. 如图,以原点为圆心的圆与反比例函数的图象交于,,,四点,已知点的横坐标为,则点的横坐标为15. 已知是关于的二次函数,当的取值范围在时,在时取得最大值,则实数的取值范围是A. B. C. D.16. 抛物线与抛物线关于轴对称,则抛物线的解析式为A. B. C. D.17. 已知正比例函数的图象与反比例函数的图象交于,两点,若点的坐标为,则关于的方程的两个实数根分别为A. ,B. ,C. ,D. ,18. 函数的图象经过一组平移后,得到函数的图象,这组平移正确的是A. 先向上平移个单位,再向左平移个单位B. 先向右平移个单位,再向上平移个单位C. 先向左平移个单位,再向下平移个单位D. 先向下平移个单位,再向右平移个单位19. 如图,在平面直角坐标系中,抛物线经过平移得到抛物线,其对称轴与两段抛物线所围成的阴影部分的面积为A. B. C. D.20. 在同一平面直角坐标系中,函数与的图象可能是A. B.C. D.21. 如果,两点都在反比例函数的图象上,那么与的大小关系是A. B. C. D.22. 抛物线与轴交于点和,且与轴交于点,则该抛物线对应的函数表达式为A. B.C. D.23. 在平面直角坐标系中,将抛物线先向上平移个单位长度,再向左平移个单位长度,所得的抛物线的解析式是A. B.C. D.24. 已知二次函数与轴交于,两点,则线段的最小值为A. B. C. D. 无法确定25. 已知二次函数(为常数),在自变量的值满足的情况下,与其对应的函数值的最小值为,则的值是或 C.26. 某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为米的小正方形组成,且每个小正方形的种植方案相同,其中的一个小正方形如图乙所示,米,,在五边形区域上种植花卉,则大正方形花坛种植花卉的面积与的函数图象大致是A. B.C. D.27. 如图,一次函数与二次函数的图象相交于,两点,则函数的图象可能是A. B.C. D.28. 如图,的顶点在抛物线上,将绕点顺时针旋转,得到,边与该抛物线交于点,则点的坐标为B. D.29. 下列关于二次函数的图象与轴交点的判断,正确的是A. 没有交点B. 只有一个交点,且它位于轴右侧C. 有两个交点,且它们均位于轴左侧D. 有两个交点,且它们均位于轴右侧30. 如图,是直角三角形,,,点在反比例函数的图象上.若点在反比例函数的图象上,则的值为B. D.二、填空题(共30小题;共150分)31. 下列函数:①;②;③;④.其中属于二次函数的有(只要写出正确答案的序号).32. 写出一个反比例函数,使它的图象经过第二、四象限,它是.33. 点关于原点对称的点的坐标是.34. 抛物线的顶点坐标是.35. 已知二次函数中,函数与自变量的部分对应值如下表:则此二次函数的对称轴为.36. 若函数是反比例函数,则.37. 在平面直角坐标系中,以原点为旋转中心,将顺时针旋转得到,其中点与点对应,点与点对应.若点,,则点的坐标为,点的坐标为.38. 若抛物线的图象与抛物线的图象关于轴对称,则函数的解析式为.39. 下列各题中,成反比例关系的是.A、每公顷的产量一定,总产量和总的公顷数B、一根绳子,剪去的一段和剩下的一段C、平行四边形的面积一定,底和高40. 已知点与都在反比例函数的图象上,则.41. 二次函数的图象与轴只有一个公共点,则的值为.42. 将二次函数化为的形式为.43. 如图,是抛物线上的一点,以点为圆心、个单位长度为半径作,当与直线相切时,点的坐标为.44. 二次函数中,当时,函数值最大,.45. 抛物线的形状大小、开口方向都与相同且顶点为,则该抛物线的解析式为.46. 抛物线不经过第象限.47. 点,在二次函数的图象上,若,则与的大小关系是.(用“ ”、“ ”、“ ”填空)48. 若反比例函数的图象在同一象限内,随的增大而减小,则的取值范围是.49. 如图,反比例函数在第一象限的图象上有两点,,它们的横坐标分别是,,则的面积是.50. 已知二次函数,当时,随的增大而减小,则的取值范围是.51. 将抛物线绕原点旋转,则旋转后抛物线的解析式为.52. 如图,已知函数的图象与二次函数(,)的图象交于点,点的纵坐标为,则关于的方程的解为.53. 如图,抛物线与直线的两个交点坐标分别为,,则关于的方程的解为.54. 二次函数的图象如图所示,那么关于的方程的近似解为(精确到).55. 在直角坐标系中,有如图所示的,轴于点,斜边,,反比例函数的图象经过的中点,且与交于点,则点的坐标为.56. 如图,在曲线与两坐标轴之间的区域内,最多可以水平排放边长为的正方形个.57. 如图,抛物线与轴的一个交点在点和之间(包括这两点),顶点是矩形上(包括边界和内部)的一个动点,则的取值范围是.58. 如图,在平面直角坐标系中,点,的坐标分别为.点在抛物线上,设点的横坐标为.当时,的面积的取值范围是.59. 如图,在中,,,动点从点出发沿运动,动点从点出发沿运动.如果,两点同时出发,速度均为个单位/秒.设出发时间为秒,记的面积的函数图象为.若直线与只有一个交点,则的取值范围为.60. 如图,经过原点的抛物线与轴的另一交点为,过点作直线轴于点,交抛物线于点.点关于抛物线对称轴的对称点为.连接,,,要使得,则的值为.三、解答题(共40小题;共520分)61. 如图,已知二次函数的图象与轴交于一点,与轴交于点,对称轴与轴交于点,连接,,求的面积.62. 已知函数是二次函数,求该二次函数的解析式.63. 已知与成反比例,且时,,当时,求的值.64. 已知和是反比例函数图象上的两点,且,,,当时,求的取值范围.65. 求二次函数的图象的顶点坐标,并在所给坐标系中画出它的图象.66. 已知二次函数的图象是.(1)求关于成中心对称的图象的函数解析式;(2)设曲线与轴的交点分别为,当时,求的值.67. 请按要求画出函数的图象:(1)列表;(2)描点;(3)连线;(4)请你判断点是否在函数图象上,答:.68. 心理学家发现,在一定的时间范围内,学生对概念的接受能力与提出概念所用的时间(单位:分钟)之间满足函数关系式,的值越大,表示接受能力越强.(1)若用分钟提出概念,学生的接受能力的值是多少?(2)如果改用分钟或分钟来提出这一概念,那么与用分钟相比,学生的接受能力是增强了还是减弱了?通过计算来回答.69. 画出反比例函数的图象,并根据图象回答问题:(1)根据图象指出当时的值;(2)根据图象指出当且时的取值范围;(3)根据图象指出当且时的取值范围.70. 如图,已知三个顶点的坐标分别是,,.(1)画出绕点逆时针旋转后的,并写出点的坐标;(2)画出绕点逆时针旋转后的,并写出点的坐标;(3)直接回答:与有什么关系?71. 已知抛物线.(1)求证:此抛物线与轴必有两个不同的交点;(2)若此抛物线与直线的一个交点在轴上,求的值.72. 已知二次函数.(1)求证:此二次函数的图象与轴总有交点;(2)如果此二次函数的图象与轴两个交点的横坐标都是整数,求正整数的值.73. 若是反比例函数,试求其函数解析式.74. 如图,已知一次函数与反比例函数的图象交于点和.(1)求反比例函数的解析式和点的坐标;(2)根据图象回答,当在什么范围内时,一次函数的值大于反比例函数的值?75. 已知函数是反比例函数,且在每一个象限内,随的增大而减小,求其函数解析式.76. 如图,反比例函数的图象与相交.某同学在内做随机扎针试验,求针头落在阴影区域内的概率.77. 已知,在同一平面直角坐标系中,反比例函数与二次函数的图象交于点.(1)求,的值;(2)求二次函数图象的对称轴和顶点坐标.78. 科技馆是少年儿童节假日游玩的乐园.如图所示,图中的横坐标表示科技馆从开门后经过的时间(分钟),纵坐标表示到达科技馆的总人数.图中曲线对应的函数解析式为,之后来的游客较少可忽略不计.(1)请写出图中曲线对应的函数解析式;(2)为保证科技馆内游客的游玩质量,馆内人数不能超过人,后来的人需在馆外休息区等待.从开始到馆内陆续有人离馆,平均每分钟离馆人,直到馆内人数减少到人时,馆外等待的游客可全部进入.请问馆外游客最多等待多少分钟?79. 如图(1)是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是,拱桥的跨度为,桥洞与水面的最大距离是距离水面的景观灯.现把拱桥的截面图放在平面直角坐标系中,如图(2).求(1)抛物线的解析式;(2)两盏景观灯,之间的水平距离.80. 已知:抛物线.(1)写出抛物线的开口方向和它与轴交点的坐标;(2)若抛物线的对称轴为直线,求的值,并画出抛物线的草图(不必列表);(3)如图,若,过抛物线上一点作直线轴,垂足为,交抛物线于另一点,且,求这条抛物线所对应的二次函数的解析式.81. 实验数据显示,一般成人喝半斤低度白酒后,小时内其血液中酒精含量(毫克/百毫升)与时间(时)的关系可近似地用二次函数刻画;小时后(包括小时)与可近似地用反比例函数刻画(如图所示).(1)根据上述数学模型计算:①当时,,求的值.②喝酒后血液中的酒精含量不低于毫克的时间持续了多长?(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上在家喝完半斤低度白酒,第二天早上能否驾车去上班?请说明理由.82. 在平面直角坐标系中,抛物线的对称轴为.(1)求的值及抛物线与轴的交点坐标;(2)若抛物线与轴有交点,且交点都在点,之间,求的取值范围.83. 已知,是反比例函数图象上的两点,且,.(1)在图中用“描点”的方法作出此反比例函数的图象;(2)求的值及点的坐标;(3)若,依据图象写出的取值范围.84. 已知:如图,二次函数的图象经过原点,.(1)写出该函数图象的对称轴;(2)若将线段绕点逆时针旋转到,试判断点是否为该函数图象的顶点?请说明理由.85. 阅读下面解题过程,解答相关问题.求一元二次不等式的解集的过程.①构造函数,画出图象:根据不等式特征构造二次函数;并在坐标系中画出二次函数的图象(如图1).②求得界点,标示所需:当时,求得方程的解为,;并用锯齿线标示出函数图象中的部分(如图 2).③借助图象,写出解集:由所标示图象,可得不等式的解集为.请你利用上面求一元二次不等式解集的过程,求不等式的解集.86. 在平面直角坐标系中,已知抛物线:与抛物线:,(1)抛物线与轴交于点,其对称轴与轴交于点.求点,的坐标;(2)若抛物线在这一段位于下方,并且抛物线在这一段位于上方,求抛物线的解析式.87. 如图,在直角坐标系中,点的坐标是,抛物线经过原点和点,已知正方形的三个顶点为,,.(参考公式:的顶点坐标是)(1)若当时求,并写出抛物线对称轴及的最大值;(2)求证:抛物线的顶点在函数的图象上;(3)若抛物线与直线交于点,求为何值时,的面积为;(4)若抛物线经过正方形区域(含边界),请直接写出的取值范围.88. 已知抛物线经过点.(1)求的值;(2)若此抛物线的顶点为,用含的式子分别表示和,并求与之间的函数关系式;(3)若一次函数,且对于任意的实数,都有,直接写出的取值范围.89. 已知:关于的一元二次方程(为实数).(1)若方程有两个不相等的实数根,求的取值范围;(2)在(1)的条件下,求证:无论取何值,抛物线总过轴上的一个固定点;(3)若是整数,且关于的一元二次方程有两个不相等的整数根,把抛物线向右平移个单位长度,求平移后的解析式.90. 已知反比例函数.(1)若该反比例函数的图象与直线只有一个公共点,求的值;(2)如图,反比例函数的图象记为曲线,将向左平移个单位长度,得曲线,请在图中画出,并直接写出平移至处所扫过的面积.91. 已知:二次函数的图象与轴的交点为,.(1)如果与重合,求的值;(2)横、纵坐标都是整数的点叫做整点;①当时,求线段上整点的个数;②若设抛物线在点,之间的部分与线段所围成的区域内(包括边界)整点的个数为,当时,结合函数的图象,求的取值范围.92. 如图,在平面直角坐标系中,,,,反比例函数的图象经过点.(1)求的值;(2)将绕点逆时针旋转,得到,其中点与点对应,试判断点是否在该反比例函数的图象上?93. 如图,点,在反比例函数图象上,轴于点,轴于点,.(1)求,的值并写出该反比例函数的解析式.(2)点在线段上,,求点的坐标.94. 已知常数(是整数)满足下面两个要求:①关于的一元二次方程有两个不相等的实数根;②反比例函数的图象在二,四象限.(1)求的值;(2)在所给直角坐标系中用描点法画出的图象,并根据图象写出:当时,的取值范围是;当时,的取值范围是.95. 如图,在平面直角坐标系中,为坐标原点,是反比例函数图象上任意一点,以为圆心,为半径的圆与轴交于点,与轴交于点,连接.(1)求证:为线段的中点;(2)求的面积.96. 在平面直角坐标系中,二次函数的图象过、两点.(1)求此二次函数的解析式;(2)点是轴上的一个动点,过点作轴的垂线交直线于点,交二次函数的图象于点.当点位于点的上方时,直接写出的取值范围.97. 在平面直角坐标系中,反比例函数的图象过点.(1)求反比例函数的表达式;(2)过点的直线与反比例函数的图象的另一个交点为,与轴交于点,若,求点的坐标.98. 某种商品每天的销售利润(元)与销售单价(元)之间满足关系:,其图象如图所示.(1)销售单价为多少元时,该种商品每天的销售利润最大?最大利润为多少元?(2)销售单价在什么范围时,该种商品每天的销售利润不低于元?99. 企业的污水处理有两种方式,一种是输送到污水厂进行集中处理,另一种是通过企业的自身设备进行处理.某企业去年每月的污水量均为吨,由于污水厂处于调试阶段,污水处理能力有限,该企业投资自建设备处理污水,两种处理方式同时进行.1 至 6 月,该企业向污水厂输送的污水量(吨)与月份(,且取整数)之间满足的函数关系如下表:7 至 12 月,该企业自身处理的污水量(吨)与月份(,且取整数)之间满足二次函数关系式,其图象如图所示.1 至 6 月,污水厂处理每吨污水的费用(元)与月份之间满足函数关系式,该企业自身处理每吨污水的费用(元)与月份之间满足函数关系式;7 至 12 月,污水厂处理每吨污水的费用均为元,该企业自身处理每吨污水的费用均为元.(1)请观察题中的表格和图象,用所学过的一次函数、反比例函数或二次函数的有关知识,分别直接写出,与之间的函数关系式;(2)请你求出该企业去年哪个月用于污水处理的费用(元)最多,并求出这个最多费用;(3)今年以来,由于自建污水处理设备的全面运行,该企业决定扩大产能并将所有污水全部自身处理,估计扩大产能后今年每月的污水量都将在去年每月的基础上增加,同时每吨污水处理的费用将在去年12 月份的基础上增加.为鼓励节能降耗,减轻企业负担,财政对企业处理污水的费用进行的补助.若该企业每月的污水处理费用为元,请计算出的整数值.(参考数据:,,)100. 在平面直角坐标系中,对于双曲线和双曲线,如果,则称双曲线和双曲线为“倍半双曲线”,双曲线是双曲线的“倍双曲线”,双曲线是双曲线“”的“半双曲线”.(1)请你写出双曲线的“倍双曲线”是;双曲线的“半双曲线”是;(2)如图,在平面直角坐标系中,已知点是双曲线在第一象限内任意一点,过点与轴平行的直线交双曲线的“半双曲线”于点,求的面积;(3)如图,已知点是双曲线在第一象限内任意一点,过点与轴平行的直线交双曲线的“半双曲线”于点,过点与轴平行的直线交双曲线的“半双曲线”于点,若的面积记为,且,求的取值范围.答案第一部分1. B2. A3. C4. C5. A6. B7. C8. B9. D 10. C11. B 12. D 13. D 14. B 15. D16. D 17. D 18. B 19. B 20. A21. B 22. D 23. A 24. C 【解析】设,.依题意得,,则故线段的最小值为.25. B26. A 27. A【解析】点在抛物线上,设点,又因点在直线上,,;由图象可知一次函数与二次函数交于第一象限的,两点,方程有两个正实数根.函数与轴有两个交点,又,,,函数的对称轴为直线,A 符合条件.28. C 29. D 【解析】一元二次方程的判别式为.二次函数的图象与轴有两个交点,设方程的两个根为和,则,,二次函数的图象与轴的两个交点均位于轴右侧.30. A【解析】过点作轴于点,过点作轴于点,,.,,.第二部分31. ①32. (答案不唯一,满足即可)33.34.35.37. ,38.39. C40.41.42.43. 、、、.【解析】当半径为的与直线相切时,此时点纵坐标为或,当时,,解得:,,此时点坐标为,;当时,,解得:,,此时点坐标为,.44.45.46. 四47.48.49.【解析】根据反比例函数的性质,可知,的面积等于梯形的面积.50.51.52.【解析】方程的解就是函数的图象与二次函数(,)的图象的交点的横坐标.已知点的纵坐标为,把代入中得.53. 或54. ,【解析】当时,,当时,,当时,,方程的一个近似根在之间,当时,,方程的一个近似根为,同理可得方程的另一个近似根为.55.56.【解析】提示:令函数的值分别等于,直到所得的函数值小于等于把每列可放的正方形的个数相加即可.57.【解析】顶点是矩形上,当顶点与点重合,顶点坐标为,则抛物线解析式,由.当顶点与点重合,顶点坐标为,则抛物线解析式,由题意得:解得.顶点可以在矩形内部,的取值范围是.58.59. 或或【解析】当时,;当时,,将两个函数解析式分别与联立,当,时,,,即;当,,,即;当时,,综上,结合图象可知若直线与函数只有一个交点,则或或.60.第三部分61. 将代入函数,得:,解得:,二次函数解析式为.当时,,,抛物线对称轴为直线,,.62. 依题意得:且.即且,解得,则该二次函数的解析式为.63. 由与成反比例,可设解析式为: .时,,,即 ..当时,.64. 把,代入,得,.,,.,,,解得.反比例函数解析式为.当时,;当时,,当时,的取值范围为.65. ,顶点坐标为,其图象如图所示:66. (1)(2)或67. (1)列表;(2)描点,如图所示;(3)连线,如图所示;(4)点在函数图象上,点不在函数图象上.68. (1)当时,..(2)时,,减弱;时,,增强.69. (1)图略.由观察可知:当时.(2)当且时,或.(3)当且时,或.70. (1)如图所示,.(2)如图所示,.(3).71. (1)此抛物线与轴必有两个不同的交点.(2)此抛物线与直线的一个交点在轴上,,,,.的值为或.72. (1),,.此二次函数的图象与轴总有交点.(2)解:令,得,解得,.二次函数的图象与轴交点的横坐标都是整数,为正整数,正整数的值为或.又当时,,此时二次函数的图象与轴只有一个交点.不合题意,舍去.正整数的值为.73. 由反比例函数的定义可知.此反比例函数的解析式为.74. (1)设反比例函数的解析式为,反比例函数图象经过点,,,反比例函数的解析式为,在的图象上,,,点的坐标为;(2)根据图象得,当或时,一次函数的值大于反比例函数的值.75. 由题意,得解得.此函数的解析式是.76. 因为反比例函数的图象关于原点对称,且圆关于原点对称,所以阴影部分的面积占77. (1)将点的坐标代入反比例函数解析式可得..将点的坐标代入二次函数解析式可得.(2)由(1)知,二次函数的解析式为.配方得.对称轴直线,顶点.78. (1)由图象可知,,解得,,,解得,.(2)由题意,解得或(舍去).,,馆外游客最多等待分钟.答:馆外游客最多等待分钟.79. (1)抛物线的顶点坐标为,与轴交点坐标是.设抛物线的解析式是.把代入得,()..(2)由已知得两景观灯的纵坐标都是,,,解得,,.两景观灯间的距离为米.80. (1),抛物线开口向上,当时,,它与轴的交点坐标为.(2)抛物线的对称轴为直线,,解得,故抛物线的解析式为,图象如图.(3),抛物线的对称轴直线,对称轴在点的左侧,直线轴,且,,点的坐标为,点,,的中点在抛物线的对称轴上,,解得.抛物线所对应的二次函数的解析式为.81. (1)①当时,,则满足,.②把代入,解得;把代入得,或(大于舍去),(小时),喝酒后血液中的酒精含量不低于毫克的时间持续了小时.(2)不能驾车上班,理由如下:晚上到第二天早上,一共有小时,将代入,则,第二天早上不能驾车去上班.82. (1)因为抛物线的对称轴为,所以,解得,所以.令,则,解得, .所以抛物线与轴的交点坐标为,.(2)因为抛物线抛物线的二次项系数相同,所以抛物线可以由抛物线上下平移得到.因为抛物线与轴的交点坐标为,都在点,之间,且点比点离对称轴近.所以把点代入中,得,把点代入中,得,所以 .83. (1)反比例函数的图象如图.(2),..由得,代入得:.或,当时,;当时,.所以点的坐标或.(3)当时,的取值范围为.84. (1)二次函数的图象经过原点,.抛物线的对称轴为直线.(2)点是该函数图象的顶点.理由如下:如图,作轴于点,线段绕点逆时针旋转到,,,在中,,.点的坐标为,由(1)得,把代入得..抛物线顶点坐标为.点为抛物线的顶点.85. ①构造函数,画出图象:根据不等式特征构造二次函数并在坐标系中画出二次函数的图象.②求得界点,标示所需:当时,求得方程的解为,;并用锯齿线标示出函数图象中的部分(如图).③借助图象,写出解集:不等式的解集为或.86. (1)根据:,,可得点,.(2)根据对称,抛物线在这一段位于下方,相当于抛物线在这一段位于下方.抛物线在这一段位于上方,两条抛物线的交点横坐标:,把代入,,抛物线经过点,,抛物线的解析式:.87. (1)当时,则,抛物线经过原点和点,解得抛物线解析式为,抛物线对称轴为直线,,当时,有最大值.(2)把,的坐标代入抛物线解析式可得解得抛物线解析式为,抛物线顶点坐标为,在中,当时,,抛物线的顶点在函数的图象上.。
初中函数综合试题及答案

初中函数综合试题及答案一、选择题(每题3分,共30分)1. 函数y=2x+3的图象是一条直线,其斜率k和截距b分别是()A. k=2, b=3B. k=3, b=2C. k=-2, b=3D. k=-3, b=22. 若函数y=x^2-4x+3的最小值是-1,则x的值是()A. 2B. 3C. 4D. 53. 函数y=-2x+1与y=-x-1的交点坐标是()A. (0,1)B. (1,-1)C. (-1,-3)D. (2,-3)4. 函数y=x+1/x的值域是()A. (-∞,-2]∪[2,+∞)B. (-∞,-1]∪[1,+∞)C. (-∞,0)∪(0,+∞)D. (-∞,-1)∪(1,+∞)5. 函数y=x^3-3x^2+2在区间(1,2)上是()A. 增函数B. 减函数C. 先增后减D. 先减后增6. 若函数y=x^2+2x-3与x轴有两个交点,则这两个交点的横坐标之和是()A. -2B. 2C. -4D. 47. 函数y=1/x的图象关于()A. 原点对称B. y轴对称C. x轴对称D. 直线y=x对称8. 函数y=x^2-6x+8的顶点坐标是()A. (3, -1)B. (3, 1)C. (-3, 1)D. (-3, -1)9. 函数y=2x-1与直线y=3x+2平行的条件是()A. 斜率不相等B. 斜率相等C. 截距不相等D. 截距相等10. 函数y=x^2-4x+m的图象与x轴有两个交点,则m的取值范围是()B. m<4C. m≥4D. m≤4二、填空题(每题3分,共15分)1. 函数y=x^2-6x+8的对称轴是直线x=______。
2. 若函数y=x^2-4x+3的图象向上平移2个单位,则新的函数解析式为y=______。
3. 函数y=-2x+1与y=-x-1的交点坐标是(1,-1),因此函数y=-2x+1的图象经过点______。
4. 函数y=x+1/x在x=1处的导数为______。
初三数学函数试题及答案

初三数学函数试题及答案一、选择题(每题3分,共30分)1. 下列函数中,是一次函数的是()A. y = 3x + 2B. y = x^2 + 1C. y = 1/xD. y = √x2. 若函数y = 2x - 3的图象经过点(2,1),则该函数的解析式为()A. y = 2x - 5B. y = 2x - 3C. y = 2x + 1D. y = 2x - 13. 函数y = 3x + 1与y = -2x + 5的交点坐标是()A. (-1, 4)B. (1, 2)C. (-1, 2)D. (1, 4)4. 函数y = 4x - 1的图象在y轴上的截距为()A. 1B. -1C. 4D. -45. 函数y = 5x + 2的图象在x轴上的截距为()A. 0.4B. -0.4C. 2/5D. -2/56. 若一次函数y = kx + b的图象经过原点,则()A. k ≠ 0,b = 0B. k = 0,b ≠ 0C. k = 0,b = 0D. k ≠ 0,b ≠ 07. 函数y = 3x + 2的图象在x轴上的截距为()A. 2/3B. -2/3C. 2D. -28. 函数y = 2x - 3与x轴的交点坐标为()A. (1.5, 0)B. (-1.5, 0)C. (3, 0)D. (-3, 0)9. 函数y = -x + 4的图象在y轴上的截距为()A. 4B. -4C. 0D. -010. 函数y = x^2 - 4x + 3的顶点坐标为()A. (2, -1)B. (2, 1)C. (-2, 1)D. (-2, -1)二、填空题(每题4分,共20分)1. 函数y = 2x + 3的图象在x轴上的截距为______。
2. 函数y = -3x + 4的图象在y轴上的截距为______。
3. 函数y = 4x - 2的图象与x轴的交点坐标为______。
4. 函数y = 5x - 6的图象与y轴的交点坐标为______。
初中数学九年级总复习《函数》专题复习卷含答案

中考《函数》总复习检测试题含答案时间: 120分钟 满分: 150分一. 选择题(每小题3分, 共30分)1.点P 关于 轴的对称点P1的坐标是(3, -2), 则点P 关于 轴的对称点P2的坐标是( ) A.(-3,-2) B.(-2,3) C.(-3,2 ) D.(3,-2)2.若一次函数 的图象经过第一、二、四象限, 则下列不等式中总是成立的是( ) A. ab >0 B. b -a >0 C. a +b >0 D. a -b >03.对于二次函数 , 下列说法正确的是( )A.当x>0时, y 随x 的增大而增大B.图象的顶点坐标为(-2, -7)C.图象与x 轴有两个交点D.当x=2时,y 有最大值-3.4.如图, 一次函数 与反比例函数 的图象在第一象限 交于点A, 与y 轴交于点M, 与x 轴交于点N, 若AM:MN=1:2, 则k =( ) A.2 B.3 C.4 D.55.若将抛物线 沿着x 轴向左平移1个单位, 再沿y 轴向下平移2个单位, 则得到的新抛物线的顶点坐标是( )A. (0, -2 )B. (0, 2)C. (1, 2)D. (-1, 2) 6.如图, 直线 相交于点P, 已知点P 的坐标为(1, -3), 则关于x 的不等式 的解集是( ) A. x>1 B.x<1 C.x>-3 D.x<-37.向最大容量为60升的热水器内注水, 每分钟注水10升, 注水2分钟后停止注水1分钟, 然后继续注水, 直至注满.则能反映注水量与注水时间函数关系的图象是( )A. B. C. D.8.如图, 将函数 的图象沿y 轴向上平移得到一条新函数的图象, 其中点A (1, m ), B (4, n )平移后的对应点分别为点A'、B'. 若曲线段AB 扫过的面积为9(图中的阴影部分), 则新图象的函数表达式是( ) A. B.C. D.9.如图, 菱形ABCD 边AD 与x 轴平行, A.B 两点的横坐标分别为1和3, 反比例函数 的图象经过A.B 两点, 则菱形ABCD 的面积是( ) A.4 B. C. D.210.如图,抛物线 与x 轴交于点(-3,0),其对称轴为直线 ,结合图象分析下列结论: (abc>0 ; (3a+c>0; (当x<0时,y 随x 的增大而增大;④一元二次方程 的两根分别为 ;⑤ ,其中正确的结论有( )个. A.2 B.3 C.4 D.5填空题(每小题4分, 共24分) 11.函数13-+=x x y 中自变量x 的取值范围是_________________.第8题图12.二次函数 图象先沿x 轴水平向左平移3个单位, 再向上平移4个单位后得到的表达式为_________________.13.如图, 在平面直角坐标系中, 的顶点A.C 的坐标分别为(0, 3)和(3, 0), , AC=2BC,函数 的图象经过点B, 则k 的值为_______.14.二次函数 的部分图象如图所示, 若关于x 的一元二次方程 的一根为 , 则另一个根为________.15.如图, 直线 与坐标轴交于A 、B 两点, 在射线AO 上有一点P, 当 是以AP 为腰的等腰三角形时, 点P 的坐标是_________.16.如图, 平面直角坐标系中, 点A ( , 1)在射线OM 上, 点B ( , 3)在射线ON 上, 以AB 为直角边做 , 以BA1为直角边作第二个 , 以A1B1为直角边作第三个 ……依此规律, 得到 , 则点B2018的纵坐标为___________.(1)三、解答题(17题8分, 18-22题每题10分, 23.24题每题12分, 25题14分, 共96分) (2)17.(8分)在平面直角坐标系中, 点O 为坐标原点, 如图摆放, 按要求回答下列问题. (3)将 沿y 轴向下平移3个单位, 得到 , 并写出B1的坐标. (4)将111B O A ∆作关于原点O 成中心对称图形222B O A ∆.在第三象限做 , 与 关于原点O 位似, 相似比为1: 2.18.(10分)在平面直角坐标系中, 若点 在坐标系象限角平分线上, 求a 的值及点的坐标.第13题图A 第14题图 第15题图19.(10分)如图, 在平面直角坐标系中, 点A.B的坐标分别为, , 连接AB, 以AB为边向上作等边三角形ABC.(1)求点C的坐标.(2)求线段BC所在直线的解析式.20.(10分)已知A.B 两地之间有一条270 千米的公路, 甲、乙两车同时出发, 甲车以60千米/时的速度沿此公路从 A 地匀速开往 B 地, 乙车从 B 地沿此公路匀速开往 A 地, 两车分别到达目的地后停止.甲、乙两车相距的路程y(千米)与甲车的行驶时间x(时)之间的函数关系如图所示.(1)乙车的速度为_____ 千米/时, a=____b=_____.(2)求甲、乙两车相遇后y 与x 之间的函数关系式.(3)当甲车到达距B 地70 千米处时, 求甲、乙两车之间的路程.21.(10分)某演唱会购买门票的方式有两种: 方式一, 若单位赞助广告费10万元, 则该单位所购门票的价格为每张0.02万元;方式二, 如图所示.设购买门票x张, 总费用为y 万元.问题: (1)求方式一中y与x 的函数关系式;(总费用=广告费+门票费)(2)若甲乙两个公司分别采用方式一和方式二购买本场演唱会门票共400张, 且乙单位购买门票超过100张, 两单位共花费27.2万元, 求甲乙两公司各购买多少张门票?(1)22.(10分)如图, 抛物线与x轴交于A(-1, 0)、B(3, 0)两点, 与y轴交于点C, OB=OC, 连接BC, 抛物线的顶点为D, 连接BD.(2)求抛物线的解析式.的正弦值.(3)求CBD(1)23.(12分)如图, 在平面直角坐标系中, 反比例函数 的图象过等边三角形BOC 的顶点B, OC=2, 点A 在反比例函数图象上, 连接AC.AO. (2)求反比例函数)0(≠=k xky 的表达式. 若四边形ACBO 的面积是 , 求点A 的坐标.24.(12分)某游泳馆每年夏季推出两种游泳付费方式.方式一: 先购买会员证, 每张会员证100元, 只限本人当年使用, 凭证游泳每次再付费5元;方式二: 不购买会员证, 每次游泳付费9元.设小明计划今年夏季游泳次数为x(x为正整数).(2)若小明计划今年夏季游泳的总费用为270元, 选择哪种付费方式, 他游泳的次数比较多?(3)当x>20时, 小明选择哪种付费方式更合算?并说明理由.25.(14分)如图, 一次函数的图象分别交y轴、x轴于A.B两点, 抛物线过A.B两点.(1)求这个抛物线的解析式.(2)作垂直于x轴的直线x=t, 在第一象限交直线AB于M, 交这个抛物线于N.当t取何值时, MN有最大值?最大值为多少?(3)在(2)的情况下, 以点AMND为顶点作平行四边形, 直接写出第四个顶点D的坐标.参考答案一.选择题(每小题3分, 共30分)1.C2.B3.D4.C5.A6.A7.D8.D9.B 10.C 备用图二.填空题(每小题4分, 共24分)11.13≠-≥x x 且 12.1)2(22++-=x y 或7822---=x x y 13.427 14. 15. 16. 三.解答题 17.(8分)(1) 如图 即为所求, B1(4, -1).…… (3分) (2)如图222B O A ∆即为所求.……(5分)(3)如图33OB A ∆即为所求.……(8分)18.解: (10分)当点在第一、三象限角平分线上时, …… (1分) 即 1-2a=a-2∴ a=1 ……(3分) 此时, 点的坐标为(-1, -1). …… (5分)当点在第二、四象限角平分线上时, …… (6分) 即 1-2a= -(a-2)∴ a=-1 …… (8分) 此时, 点的坐标为(3, -3). ……(9分) 因此, 当a 的值为1时, 点的坐标为(-1, -1);当a 的值为-1时, 点的坐标为(3, -3) ……(10分) 19.(10分)解: 过点B 作BE ⊥x 轴, 交x 轴于点E, ……(1分) ∵点A.B 的坐标分别为 , ∴AE= , BE=1……(2分) 在 中, 根据勾股定理可得, AB=2…… ∵sin ∠BAE=AB BE =21∴∠BAE=30°……(4分) ∵⊿ABC 是等边三角形 ∴∠CAE=90°……(5分) ∴点C )2,23(-.……(6分) (2)设BC 所在直线表达式为)0(≠+=k b kx y ……(7分)∵直线过点C )2,23(-和点B )1,23(代入得∴{b k b k +-=+=232231……(8分)解得 ⎪⎪⎩⎪⎪⎨⎧=-=2333b k ……(9分) ∴BC 所在直线表达式为2333+-=x y ……(10分) 20.(10分)(1)乙车的速度为75 千米/时, a=3.6 ,b= 4.5.……(3分) (2)60×3.6=216(千米)当2<x ≤3.6时, 设 , 根据题意得:⎩⎨⎧=+=+2166.3021111b x b k 解得⎩⎨⎧-==27013511b k);6.32(270135≤<-=x x y ……(5分)当3.6<x ≤4.5时, 设 , 根据题意得:⎩⎨⎧=+=+2705.42166.32222b k b k 解得⎩⎨⎧==06022b k∴)5.46.3(60≤<=x x y ……(7分)因此⎩⎨⎧≤<≤<-=)5.46.3(60)6.32(270135x x x x y ……(8分)甲车到达距B 地70千米处时行驶的时间为: , 将x =620代入得千米)(180270620135=-⨯=y ……(9分)21.因此, 甲车到达距B 地70千米处时, 甲乙两车之间的路程为180千米。
初中数学九年级总复习《函数》专项试卷含详解答案

AP,当点 P 满足 DP+AP的值最小时, P 点坐标为
.
第 11 题图
第 12 题图
第 13 题图
第 14 题图
12. 如图,在平面直角坐标系中,正方形 ABOC和正方形 DOFE的顶点 B,F 在 x
轴上,顶点
C,D 在 y 轴上,且
S△ADF= 4,反比例函数
??=
??
(
x>
0)的图象经
??
《函数》总复习试卷含答案
一、选择题 (本大题共 10 小题,每小题 3 分,共 30 分)
1.在函数 ??= √??+1中,自变量 x 的取值范围是(
)
??-2
A. x>﹣ 1 B .x≥﹣ 1 C .x>﹣ 1 且 x≠2 D .x≥﹣ 1 且 x≠ 2
2.如图,若一次函数 y=kx+b 的图象与两坐标轴分别交于 A,B 两点,点 A 的坐
22. (本小题满分 10 分) 某实验学校为开展研究性学习, 准备购买一定数量的两人学习桌和三人学习 桌,如果购买 3 张两人学习桌和 1 张三人学习桌需 220 元;如果购买 2 张两 人学习桌和 3 张三人学习桌需 310 元.
(1)求两人学习桌和三人学习桌的单价; (2)学校欲投入资金不超过 6000 元,购买两种学习桌共 98 张,以至少满足
第 23-24 题每小题 12 分, 25 题 14 分,共 96 分)
17. (本小题满分 8 分)
对于给定的两个函数,任取自变量 x 的一个值,当 x<1 时,它们对应的函
数值互为相反数:当 x≥1 时,它们对应的函数值相等,我们称这样的两个
函 数 互 为 相 关 函 数 , 例 如 : 一 次 函 数 y=x-4 , 它 的 相 关 函 数 为 ??=
九年级数学中考复习:函数专题训练(含答案)

中考复习函数专题训练(含答案解析)1. 如图,已知A、B是反比例面数kyx=(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C.动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C.过P作PM⊥x轴,PN⊥y轴,垂足分别为M、N.设四边形0MPN 的面积为S,P点运动时间为t,则S关于t的函数图象大致为【答案】A2.坐标平面上,二次函数362+-=xxy的图形与下列哪一个方程式的图形没有交点?A. x=50 B. x=-50 C. y=50 D. y=-50【答案】D3. 某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=-x2+4(单位:米)的一部分,则水喷出的最大高度是( )A.4米B.3米 C.2米 D.1米【答案】D4. 某公园草坪的防护栏是由100段形状相同的抛物线组成的.为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为()A .50mB .100mC .160mD .200m【答案】C5. 一小球被抛出后,距离地面的高度h (米)和飞行时间t (秒)满足下列函数关系式:61t 5h 2+--=)(,则小球距离地面的最大高度是( )A .1米B .5米C .6米D .7米【答案】C二、填空题 1. 出售某种手工艺品,若每个获利x 元,一天可售出(8-x )个,则当x=________元时,一天出售该种手工艺品的总利润y 最大.【答案】42. 如图,已知函数x y 3-=与bx ax y +=2(a>0,b>0)的图象交于点P ,点P 的纵坐标为1,则关于x 的方程bx ax +2x 3+=0的解为【答案】-3三、解答题1. 如图,某广场设计的一建筑物造型的纵截面是抛物线的一部分,抛物线的顶点O 落在水平面上,对称轴是水平线OC 。
初三函数试题及答案

初三函数试题及答案一、选择题(每题3分,共30分)1. 函数y=2x-3的图象经过第几象限?A. 第一、二、三象限B. 第一、三、四象限C. 第一、二、四象限D. 第二、三、四象限答案:B2. 函数y=-3x+6与x轴的交点坐标为:A. (2, 0)B. (-2, 0)C. (0, 6)D. (0, -6)3. 函数y=x^2-4x+4的顶点坐标为:A. (2, 0)B. (-2, 0)C. (2, 4)D. (-2, 4)答案:A4. 若一次函数y=kx+b的图象经过点(1, 2)和(2, 3),则k的值为:A. 1B. 2C. 3D. 4答案:A5. 函数y=-2x+1的图象与y轴的交点坐标为:B. (0, -1)C. (1, 0)D. (-1, 0)答案:A6. 函数y=x^2+2x-3与x轴有两个交点,则这两个交点的横坐标之和为:A. -2B. 2C. -4D. 4答案:B7. 函数y=3x-5的图象与y=-2x+6的图象相交于点(a, b),则a+b 的值为:A. 1B. 2C. 3D. 4答案:B8. 函数y=x^2-6x+8的图象开口方向为:A. 向上B. 向下C. 向左D. 向右答案:A9. 函数y=-x+1的图象与x轴的交点坐标为:A. (1, 0)B. (-1, 0)C. (0, 1)D. (0, -1)答案:A10. 函数y=x^2-4x+4的最小值为:A. 0B. 4C. -4D. 1答案:A二、填空题(每题3分,共30分)11. 函数y=2x+3的图象与y轴的交点坐标为______。
答案:(0, 3)12. 函数y=-3x+6与x轴的交点坐标为______。
答案:(2, 0)13. 函数y=x^2-4x+4的顶点坐标为______。
答案:(2, 0)14. 函数y=-2x+1的图象经过点(0, 1)和(1, -1),则该函数的解析式为______。
答案:y=-2x+115. 函数y=x^2-6x+8的顶点坐标为______。
初三数学函数中考试卷

一、选择题(每题4分,共40分)1. 下列函数中,是奇函数的是()A. y = x^2B. y = x^3C. y = x^4D. y = |x|2. 函数y = 2x - 3的图像是()A. 一次函数的图像B. 反比例函数的图像C. 二次函数的图像D. 指数函数的图像3. 已知函数y = kx + b(k ≠ 0),若k > 0,则函数图像()A. 过一、二、三象限B. 过一、二、四象限C. 过一、三、四象限D. 过二、三、四象限4. 函数y = -x^2 + 4x - 3的顶点坐标是()A. (1, 2)B. (2, 3)C. (1, -2)D. (2, -3)5. 已知函数y = ax^2 + bx + c(a ≠ 0),若a > 0,则函数图像()A. 顶点在x轴上方B. 顶点在x轴下方C. 顶点在y轴上方D. 顶点在y轴下方6. 函数y = √x的图像是()A. 对称于x轴B. 对称于y轴C. 对称于原点D. 对称于直线y = x7. 函数y = 2^x的图像()A. 在y轴上B. 在x轴上C. 在第一象限D. 在第二象限8. 已知函数y = log2x的图像()A. 在x轴上B. 在y轴上C. 在第一象限D. 在第二象限9. 函数y = (1/2)^x的图像()A. 在x轴上B. 在y轴上C. 在第一象限D. 在第二象限10. 函数y = k/(x - 1)(k ≠ 0)的图像()A. 过点(1, k)B. 过点(1, 0)C. 过点(0, 1)D. 过点(0, k)二、填空题(每题4分,共20分)11. 函数y = -2x + 5的图像与x轴的交点坐标是__________。
12. 函数y = x^2 - 4x + 4的顶点坐标是__________。
13. 函数y = 3x^2 - 12x + 9的图像的对称轴是__________。
14. 函数y = 2^x在x = 2时的函数值是__________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
)中考数学函数复习第11课 函数的基本概念(含直角坐标系)1.函数是研究( )A .常量之间的对应关系的B .常量与变量之间的对应关系的C .变量与常量之间对应关系的 D.变量之间的对应关系的 2.点M (-3,-5)向上平移7个单位到点M 1的坐标为( ) A.(-3,2) B.(-2,-12) C.(4,-5 ) D.(-10,-5)3.点M 在y 轴的左侧,到x 轴、y 轴的距离分别是3和5,则点M 的坐标是( ) A.(-5,3) B .(-5,-3)C .(5,3)或(-5,3) D.-5,3)或(-5,-3)4.△DEF 是由△ABC 平移得到的,点A (-1,-4)的对应点为D (1,-1),则点B (1,1)的对应点E 、点C (-1,4)的对应点F 的坐标分别为( ) A .(2,2),(3,4) B .(3,4),(1,7) C .(-2,2),(1,7) D .(3,4),(2,-2)5.已知M (1,-2),N(-3,-2)则直线MN 与x 轴,y 轴的位置关系分别为( )A.相交,相交B.平行,平行C.垂直相交,平行D.平行,垂直相交 6.点A (m ,n )满足=mn 0,则点A 在( )上A .原点B .坐标轴C .x 轴D .y 轴7.在匀速运动公式vt s =中,v 表示速度,t 表示时间,s 表示在时间t 内所走的路程,则变量是________,常量是_______. 8.函数y =x 的取值范围是___________.9.拖拉机开始工作时,油箱中有油40升,如果每小时耗油5升,如图是拖拉机工作时,油箱中的余油量Q (升)与工作时间 t (小时)的函数关系图像,那么图中?应是______. 10.王华和线强同学在合作电学实验时,记录下电流I (安培)与电阻R (欧)有如下对应关系.观察下表:你认为I 与R 间的函数关系式为________;当电阻R =5欧时,电流I =____安培. 11.在某公用电话亭打电话时,需付电话费y (元)与通话时间 x (分钟)之间的函数关系用图象表示如图.小明打了2分钟需付费______元;小莉打了8分钟需付费_______元.第11题图)12.线段AB中,点A(-2,3), 点B(1,3),现把线段AB平移到A’B’,使A’(0,2),B’(3,2),则直线AB、A’B’间的距离为13.以0为原点,正东、正北方向为x轴、y轴正方向建立平面直角坐标系,一个机器人从原点O点出发,向正东方向走3米到达A1点,再向正北方向走6米到达A2,再向正西方向走9米到达A3,再向正南方向走12米到达A4,再向正东方向走15米到达A5,按此规律走下去,当机器人走到A6时, A6的坐标是_____________14.在某城市中,体育场在火车站以西4000m再往北2000m处,华侨宾馆在火车站以西3000m 再往南2000m处,百佳超市在火车站以南3000m再往东2000m处,请建立适当的平面直角坐标系,分别写出各地的坐标。
15.一天上午8时,小华去县城购物,到下午14时返回家,结合图象回答:(1)小华何时第一次休息?(2)小华离家最远的距离时多少?(3)返回时平均速度是多少?(4)请你描述一下小华购物的情况.第12课 一次函数1.一次函数的图象经过点(-2,3)与(1 ,-1),它的解析式是___ _____. 2.将直线y =3x 向上平移5个单位,得到直线 ;将直线y =-x -5向下平移5个单位,得到直线 .3.平行四边形相邻的两边长为x 、y ,周长是50,则y 与x 的函数关系式是__________. 4.出租车收费按路程计算,3km 内(包括3km )收费10元;超过3km 每增加1km 加收1元,则路程x ≥3km 时,车费y (元)与x (km )之间的函数关系式是________________. 5.已知点P (3a +1,a + 3)是第二象限内坐标为整数的点,则整数a 的值是_______. 6.若直线a x y +-=和直线b x y +=的交点坐标为(,6m ),则=+b a ____________. 7.下列函数中,与y =x 表示同一个函数的是 ( ) A.y =x 2xB.2y x = C.y =(x )2 D.y =3x 38.下列关系式中,不是函数关系的是 ( )A.y =-x (x <0) B.y =±x (x >0) C.y =x (x >0) D.y =-x (x>0) 9.若m <0, n >0, 则一次函数y=mx+n 的图象不经过 ( )A .第一象限B .第二象限C .第三象限D .第四象限 10.已知函数y =2x +1,当自变量增加m 时,相应的函数值增加 ( ) A.2 m +1 B.2 m C.m D.2m -111.汽车由A地驶往相距360km 的B 地,它的平均速度是60km /h ,则汽车距B地路程s(km )与行驶时间t (h )的函数关系式及自变量t 的取值范围是( ) A.S =360-60t (0≤t ≤6) B.S =360-60t (t >0) C.S =60t (0≤t ≤6) D.S =60t (t <6) 12.已知函数221+-=x y ,当11≤<-x 时,y 的取值范围是 ( ) A .2325≤<-y B .2523<<y C .2523<≤y D .2523≤<y13.小平的父亲散步,从家中走20分钟到一个离家900米的报亭看10分钟的报纸后,用15分钟返回家中,下列图形中表示小平父亲离家的时间与距离之间的关系是( )A .B .C .D .14.当00><b ,a 时,函数y =a x+b 与a bx y +=在同一坐标系中的图象大致是( )A .B .C .D .15.已知3y +与x 成正比例,且2=x 时,7=y .(1)求y 与x 的函数关系式;(2)当21-=x时,求y 的值; (3)将所得函数图象平移,使它过点(4,-3) .求平移后直线的解析式.16.王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上,然后追赶爷爷.图中两条线段分别表示小强和爷爷离开山脚的距离(米)与爬山所用时间(分)的关系(从小强开始爬山时计时). (1)小强让爷爷先走多少米再出发?(2)山顶离山脚的距离有多少米?谁先爬上山顶? (3)小强经过多少时间追上爷爷?17. 如图,在边长为4的正方形ABCD 的一边BC 上,一点P 从B 点运动到C 点,设BP=x ,四边形APCD 的面积为y .⑴ 写出y 与x 之间的函数关系式及x 的取值范围; ⑵ 说明是否存在点P ,使四边形APCD 的面积为3?18. k 在为何值时,直线2k +1=4x+5y 与直线 k =3x+2y 的交点在第二象限?19.有一条直线y=kx+b ,它与直线132y x =+交点的纵坐标为5,而与直线y =3x -9的交点的横坐标也是5.求该直线与两坐标轴围成的三角形面积.AB CDP第13课 反比例函数1.若反比例函数y=xm的图像经过点A(-2,3) ,那么m= . 2.△ABC 的面积为6,BC 边的长度为x ,BC 边上的高为y ,则y 与x 之间的函数关系式为 . 3.如图所示,点A 在反比例函数y=xk图像上, 且AB ⊥x 轴,垂足为B ,若S △AOB =6,则k= .4.若y -3与x+5成反比例,且x=3时y=5,那么当y=7时,x= . 5.已知反比例函数y=(2k-5)x k 2-10的图像在所在像限内,y 随x 的增大而减小,则k= .6.反比例函数y=x2(x>0)在平面直角坐标系中,绕着坐标原点O 逆时针旋转90°后,所得到的图像解析式是(注明自变量的取值范围) . 7.如图所示,A 、C 是函数y=xk图像上任意两点, 过A 作x 轴垂线,垂足为B ,过C 点作y 轴的垂线,垂足为D ,且Rt △AOB ,Rt △OCD 的面积分别记为 S 1和S 2,则S 1S 2 (比较大小关系)8.下面哪个点在反比例函数y=x3的图像上( ). A .(3,1) B .(-3,1) C .(3,31) D .(31,3)9.已知一次函数y=-x+4与反比例函数y=xk在同一平面直角坐标系内的图像没有交点,则k 的取值范围是( )A .k > 0B .k < 0C .k > - 4D .k > 4 10.直线y=x+4与双曲线y=x5的交点为A 、B ,O 为坐标原点,求△AOB 面积.x11.如图所示,在平面直角坐标系中,射线OM 与反比例函数的图像相交于点A ,且∠MOx=45°,OA=32,求:(1)点A 的坐标;(2)此反比例函数的解析式.12.已知反比例函数y=xk和一次函数y=ax+b 的图像的一个交点A 的坐标为(-3,4)且一次函数的图像与x 轴的交点到原点的距离为5,求反比例函数和一次函数的解析式.13.已知:y=y 1 – y 2 ,y 1与x 成正比例,y 2与x 2成反比例,且当x=1时y= -2;x= -1时y=-6,求y 与x 之间的函数关系式.14.设x 1、x 2是关于x 的一元二次方程kx 2+2(k -3)x+k -3 = 0的两个不相等实数根(k 为非负整数),一次函数y=(k -2)x+m 与反比例函数y =xn的图像都经过点(x 1,x 2), 试求:(1)k 的值;(2)一次函数与反比例函数的解析式.15.已知反比例函数y=xk(k<0)的图像经过点A (-3,m ),过点A 作AB ⊥x 轴于点B ,且S △AOB =3. (1)求k 和m 的值;(2)若一次函数y=ax+1的图像经过点A ,并且与x 轴相交于 点C,求∠ACO 的度数和∣AO ∣:∣AC ∣的值.O Ay Mx第11题图 第15题图第14课 二次函数1.抛物线y=x 2+5x- 6与x 轴的交点坐标为 ,与y 轴的交点坐标为 . 2.若抛物线y=(m - 1)x m 2- m 的开口向上,则m 的值为 .3.将二次函数y =3x 2+6x+12 化为y=a(x- h)2+k 的形式则y= .顶点坐标 ,对称轴 ,当x 时函数值y 随x 的增大而减小. 4.抛物线y=ax 2+bx+c 与抛物线y=x 2- 3x-4关于x 轴对称,则abc = . 5.抛物线y =2x 2 – 3x – 1的图像在x 轴上截得的线段的长为 .6.抛物线y=ax 2+bx+c 与x 轴有两个交点,一个交点为(2,0),对称轴直线x = 4,则另个一交点坐标为 .7.已知二次函数y = ax 2-bx+c 的图像如图所示,则点P (a,bc)在 ( ) A .第一像限 B .第二像限 C .第三像限 D .第四像限8.在同一直角坐标系中,如图所示直线y= ax+b 和抛物线y= ax 2+bx 的图像只可能是( )9.二次函数y = x 2的图像向上平移2个单位再向右平移3个单位,得到新图像的二次函数解析式为( )A .y = (x+2)2 – 3B .y =(x+2)2 + 3C .y = (x - 2)2+3D .y=(x-2)2 – 3 10.下列哪两条抛物线关于x 轴对称( )A .y =-x 2 +2x +5 与 y =-x 2+2x -5B .y = -x 2 +2x +5 与 y =-x 2 - 2x +5C .y =-x 2 +2x +5 与 y =-x 2 -2x -5D .y = -x 2 +2x +5 与 y =x 2 -2x -5 11.已知抛物线和直线L 在同一直角坐标系中的图像如图所示,抛物线的对称轴为直线x = -1 ,P 1(x 1 , y 1 )、P 2(x 2 , y 2 )线上的点,P 3(x 3, y 3 )是直线L 上的点,且 -1<x 1 <x 2,x 3<-则y 1、y 2、y 3的大小关系是( )A .y 1<y 2<y 3B .y 3<y 1<y 2C .y 3<y 2<y 1D .y 2<y 1<y 3A DC B12.二次函数y=ax 2+bx+c 的图像如图所示,则下列 不等式成立的个数是( ) ①a bc <0 ② a+b+c <0 ③a+c > b ④ a <2bc A .1 B .2 C .3 D .4 13.根据下列条件求二次函数的解析式;(1)二次函数图像经过点(0,3)、(-2 ,-5)、(1,4); (第12题图) (2)二次函数图像经过点(4,1),且顶点为(3,-1);(3)二次函数图像经过点(0,0)、(12,0),且顶点到x 轴的距离为3;14.已知二次函数y = ax 2+bx-5的图像的对称轴为直线x=3,图像与y 轴交于点B ,设x 1、x 2是方程ax 2+bx – 5 = 0的两根,且x 12 +x 22 =26,求: (1)二次函数的解析式和顶点A 的坐标; (2)原点O 到直线AB 的距离.15.已知抛物线y = ax 2+bx+c (a ≠0)与x 轴交于不同的两点A 和B (4,0),与y 轴交于点C (0,8),其对称轴为x =1; (1)求此抛物线的解析式;(2)过A 、B 、C 三点作⊙O ′与y 轴的负半轴交于点D ,求经过原点O 且与直线AD 垂直(垂足为E )的直线OE 的方程.第15课 函数的应用(1)1.如右图,是某生物实验室的温度自动描点记录仪所录绘该室2004年4月8日的气温随时间变化的图象. 请你结合下表观察图象记录中的7个点,大致估计表中缺失的数据并补写出来:________.2.南通市与庄河两地之间的距离是160千米,若汽车以平均每小时80千米的速度从南通开往庄河,则汽车距庄河的路程s (千米)与行驶的速度t (小时)之间的函数关系式为_________________.3.我们学习过反比例函数. 例如,当矩形面积S 一定时,长a 是宽b 的反比例函数,其函数关系式可以写为aSa =(S 为常数,S ≠0). 请你仿照上例另举一个在日常生活、生产或学习中具有反比例函数关系的量的实例,并写出它的函数关系式.实例:_________________________________________________; 函数关系式:___________________________________________. 4.点)6,1(在双曲线xky =上,则k =______________. 5.已知抛物线c bx ax y ++=2与x 轴有两个交点,那么一元二次方程02=++c bx ax 的根的情况是______________________.6.已知二次函数的图象开口向上,且与y 轴的正半轴相交,请你写出一个满足条件的二次函数的解析式:_____________________.7.某闭合电路中,电源的电压为定值,电流I (A )与电阻R (Ω)成反比例.右图表示的是该电路中电流I 与电阻R 之间的图象,则用电阻R 表示电流I 的函数解析式为( ) A . RI 2= B . R I 3=C .RI 6=D . RI 6-= 8.抛物线322+-=x x y 的对称轴是直线( )时刻t (时) 04812162024温度T (℃)16 18.1 19.9 221917.2O R (Ω)I (A)(3,2)3 2A . 2-=xB .2=xC .1-=xD . 1=x9.强在劳动技术课中要制作一个周长为80cm 的等腰三角形,请你写出底边长y (cm )与一腰长x (cm )的函数关系式,并求出自变量x 的取值范围.10.某农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售, 售出土豆千克数与他手持有的钱数(含备用零钱)的关系如右图所示,结合图象回答下列问题: (1)农民自带的零钱是多少?(2)降价前他每千克土豆出售的价格是多少?(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?11.环岛高速公路上,一辆轿车和一辆货车沿相同路线从A 地到B 地,所经过的路程y (千米)与时间x (小时)的函数关系如图所示,试根据图象回答下列问题:(1)货车比轿车早出发__________小时,轿车追上货车时行驶了__________千米,A地到B 地的距离为_________千米. (2)轿车追上货车需要多小时? (3)轿车比货车早到多少时间?.(千克)第16课 函数的应用(2)1.在平面直角坐标系中,直线b kx y +=(k ,b 为常数k ≠0,b >0)可以看成是将直线kx y = 沿y 轴向上平行移动b 个单位得到的,那么将直线kx y =沿x 轴向右平行移动m 个单位(m >0得到的直线方程是____________. 2.若一次函数m x m y +-=)2(的图象经过第一、二、四象限,则m 的取值范围是________. 3.近视眼镜的度数y (度)与镜片焦距x (米)成反比例. 已知400度近视眼镜镜片的焦距为0.25米,则眼镜度数y 与镜片焦距x 之间的函数关系式是____________. 4.有一个二次函数的图象,三位同学分别说出它的一些特点:甲:对称轴是直线4=x ;乙:与x 轴两个交点的横坐标都是整数;丙:与y 轴交点的纵坐标也是整数,且以这三个交点为顶点的三角形面积为3. 请你写出满足上述全部特点的一个二次函数解析式: 5.两条直线121y x =+与22y x =+在同一坐标系中的图象可能是下图中的( )6.如果反比例函数的图象经过点)2,3(,那么下列各点在此函数图象上的是( )A . )23,2(-B . )32,9( C . )32,3(-D . )23,6(7.南通市某中学环保兴趣小组对南胡清除淤泥工程进行调查,并从《南通晚报》上收集到下列数据:根据上表解答下列问题:(1)请你按体积=面积×高来估算,南胡的淤泥量大约有多少万立方米?(2)设清除淤泥x 天后,剩余的淤泥量为y (万米3),求y 与x 的函数关系(不要求写出自变量x 的取值范围).(3)为了使南胡的生物链不遭到破坏,仍需保留一定量的淤泥. 若需保留的淤泥量约为22万米3,求清除淤泥所需天数.8.某地举办乒乓球比赛的费用y (元)包括两部分:一部分是租用比赛场地等固定不变的费用b (元),另一部分与参加比赛的人数x (人)成正比例. 当x =20时,y =1600;当x=30时,y=2000.(1)求y与x之间的函数关系式;(2)如果有50名运动员参加比赛,且全部费用由运动员分摊,那么没2名运动员需要支付多少元?9.在压力不变的情况下,某物承受的压强P(Pa)是它的受力面积S(m2)的反比例函数,其图象如右图所示:(1)求P与S之间的函数关系式;(2)求当S=0.5m2时物体所受的压强P.10.卢浦大桥拱形可以近似地看作抛物线的一部分,在大桥截面1:11000的比例图上去,跨度AB=5cm,拱高OC=0.9cm,线段DE表示大桥拱内桥长,DE∥AB,如图(1),在比例图上,以直线AB为x轴,抛物线的对称轴为y轴,以1cm作为数轴的单位长度,建立平面直角坐标系,如图(2),(1)求出图(2)上以这一部分抛物线为图象的函数解析式,写出函数定义域;(2)如果DE与AB的距离OM=0.45cm,求卢浦大桥拱内实际桥长(备用数据:2≈1.4,计算结果精确到1米).(1)A BCD EMO(2)第三单元 函数检测卷 (总分100分,时间60分钟)一.填空题(本题共6小题,每小题3分,共18分.) 1.如果反比例函数xk y 3-=的图象位于第二、第四象限内,那么满足条件的正整数k 可能的值是 .2.若一次函数y=a x+1―a 中,y 随x 的增大而增大,且它的图像与y 轴交于正半轴,则 |a ―1|+2a = . 3.请写出一个开口向上,与y 轴交点纵坐标为-1,且经过点(1,3)的抛物线的解析式 . 4.一次函数5y x =+的图象经过点P (),a b 和Q (),c d ,则()()a c d b c d --- 的值为____________.5.矩形AOCB 的两边OC 、OA 分别位于x 轴、y 轴上,点B 的坐标为B (20,53-),D 是AB 边上的一点.将△ADO 沿直线OD 翻折,使A 点恰好落在对角线OB 上的点E 处,若点E 在一反比例函数的图像上,那么该函数的解析式是_______.6.如图,△P 1OA 1、△P 2OA 2是等腰直角三角形,点1P 、2P 在函数4(0)y x x=>的图象上,斜边1OA 、12A A 都在x 轴上,则点2A 的坐标是________________.二.选择题(每题3分,共33分) 7.若代数式1xx -在实数范围内有意义,则x 的取值范围为( ) A .x>0 B .x≥0 C .x ≠0 D.x≥0且x ≠1 8.反比例函数xy 1-=的图象位于( ) A .第一、三象限 B .第二、四象限 C .第一、四象限 D .第二、三象限9.如图,一次函数b kx y +=的图像经过A 、B 两点,则0>+b kx 解集是 ( )A .0>xB .3>xC .2>xD .23<<-x 10.抛物线y=3(x-1)+1的顶点坐标是( )A .(1,1)B .(-1,1)C .(-1,-1)D .(1,-1)(第6第5题图 (- 3 ,0)xy O(0,2)B A 第9题图11.直线323+-=x y 与x 轴、y 轴所围成的三角形的面积为( ) A .3 B .6 C .43 D .2312.小亮早晨从家骑车到学校,先上坡后下坡,行程情况如图所示.若返回时上坡、下坡的速度仍保持不变,那么小明从学校骑车回家用的时间是( )A .37.2分钟B .48分钟C .30分钟D .33分钟13m 等于( )A .-1B .0C .21D .2 14.下列四个函数中,y 随x 增大而减小的是( ) A .y=2x B .y=―2x+5 C .y=―3xD .y=―x 2+2x ―115. 在同一平面直角坐标系中,一次函数y ax b =+和二次函数2y ax bx =+的图象可能为( )16.根据下列表格中二次函数2y ax bx c =++的自变量x 与函数值y 的对应值,判断方程20ax bx c ++=(0a a b c ≠,,,为常数)的一个解x 的范围是( )A .6 6.17x <<B .6.17 6.18x <<C .6.18 6.19x <<D .6.19 6.20x <<x -1 0 1 y1m-1x6.17 6.18 6.19 6.202y ax bx c =++0.03-0.01- 0.02 0.04O xyO x yO xyO xyABCD第12题图三.解答题17.( 6分)如图,直线l 经过点A (-3,1)、B (0,- 2),将该直线向右平移2个单位得到直'l .(1)在图(7)中画出直线'l 的图象; (2)求直线'l 的解析式.18. (7分)已知函数241y x x =-+ (1) 求函数的最小值;(2) 在给定坐标系中,画出函数的图象;(3) 设函数图象与x 轴的交点为A (x 1,0)、B (x 2,0),求2212x x +的值.19. (8分)如图,一次函数b kx y +=的图象与反比例函数xmy =图象交于A (-2,1)、B (1,n )两点.(1)求反比例函数和一次函数的解析式;(2)根据图象写出使一次函数的值大于反比例函数的值的x 的取值范围.20.(8分)为了鼓励市民节约用水,自来水公司特制定了新的用水收费标准,每用水量,x(吨)与应付水费(元)的函数关系如图.(1)求出当月用水量不超过5吨时,y与x之间的函数关系式;(2)某居民某月用水量为8吨,求应付的水费是多少?21.(10分)某企业信息部进行市场调研发现:信息一:如果单独投资A种产品,则所获利润y A(万元)与投资金额x(万元)之间存在正比例函数关系:y A=kx,并且当投资5万元时,可获利润2万元;信息二:如果单独投资B种产品,则所获利润y B(万元)与投资金额x(万元)之间存在二次函数关系:y B=ax2+bx,并且当投资2万元时,可获利润2.4万元;当投资4万元,可获利润3.2万元.(1)请分别求出上述的正比例函数表达式与二次函数表达式;(2)如果企业同时对A、B两种产品共投资10万元,请你设计一个能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少.22.(10分)某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC 为0.6米.(1)以O为原点,OC所在的直线为y轴建立平面直角坐标系,请根据以上的数据,求出抛物线y=ax2的解析式;(2)计算一段栅栏所需立柱的总长度.(精确到0.1米)数与代数综合测试(一) (时间100分 满分100分)一.填空题:(每小题2分,共20分)1.用代数式表示:a 的相反数的平方与b 的绝对值的和是__________.2.用科学计数法表示:(1)-0.0000015=_________;(2)125000000=___________.3.计算:43x x ⋅=_________.4.分解因式:12-a =__________________.5.已知函数12-=x y ,当x=1时,y=_________.6.把抛物线()22-=x y 向左平移2个单位,再向下平移1个单位,得到的解析式是_______.7.不等式3x -4≥4+2(x -2)的最小整数解是__________. 8.函数y =8632+--x x x 的自变量x 的取值范围是___________. 9.当a ____________时,关于x 的方程(a -2)x 2+(-2a +1)x +a =0有两实数根. 10.样本2,4,1,2,1的平均数为_____,方差为_____. 二.选择题:(每小题2分,共20分)11.下列各式中,一定正确的是 ( )A.x+2x=x 2B.x 2÷x=x C. (1+x)2=1+x 2D. (xy)2=xy 2. 12.二次函数y=ax 2+bx+c 中,b 2=4ac 且x=0时y=-4,则 ( ) A.y 最大值=-4 B.y最小值=-4 C. y最大值=-3 D. y 最小值=-313.下列说法正确的是 ( )A.负数和零没有平方根B. -2002的倒数是2002C.0.5是分数D.0和1的相反数是它本身 14.设(x +y)(x +2+y)-15=0,则x +y 的值是 ( ) A.-5或3 B.-3或5 C.3 D.515.二次函数y =x 2+x +a -2的图象与x 轴只有一个交点,则a 的值为( )A.2B.-2C. 49D.4 16.在同一直角坐标系中,函数y=3x 与y=1-图象大致是 ( )17.如果分式2312+--x x x 的值为零,那么x 等于( )A .-1B .1C .-2或1D .1或218.某餐厅共有7名员工,所有员工的工资情况如下所示:则餐厅所有员工工资的众数、中位数是 ( ) A.340 520 B.520 340 C.340 560 D.560 3402019.生物学指出:生态系统中,每输入一个营养级的能量,大约只有10%的能量能够流动到下一个营养级,在M 1→M 2→M 3→M 4→M 5→M 6 这条生物链中(Mn 表示第n 个营养级,n=1,2,...,6),要使M 6获得10千焦的能量,那么需要M 1提供的能量约为( ) A.104千焦 B.105千焦 C.106千焦 D.107千焦 20.下列函数中,自变量x 的取值范围为x ≤1的是 ( ) A.y=x-1 B.y=x-1 C.y=1-x D.y=1x-1三.计算题:(每小题4分,共16分)21.( 3 –1)-1+12 -(7 - 2 )0-3·tan30022.n n n n n xy y x y x ])[(]7)2[(2225241-÷+++23.(31)-1-sin300-(2π)024.化简求值:22222ba b ab a -++.其中a=2+1,b=2-1四.解方程:(6分) 25. xx x --=--31132五.(本题6分) 26.解不等式组:六.(每小题10分,共20分)27.已知一次函数y =kx +b 图象不经过第四象限,而过点(1,3),又知系数k 是方程3x 2-5x -2=0的一个根,求这一次函数的解析式.28.若二次函数y =ax 2+bx +c 中,c =3,图象的顶点坐标为(2,-1),求二次函数的解析式.七.(本题12分)29 .某商场经营一批进价为2元一件的小商品,在市场营销中发现下商品的日销售单价x 元与日销售量y 件之间有如下关系:(1)在所给的直角坐标系①中①根据表中提供的数据描出实数对(x, y)的对应点;②猜测并确定日销售量y 件与日销售单价x 元之间的函数关系式,并画出图像。
