2022-2023学年江苏省苏州市姑苏区第十六中学九年级上学期12月月考数学试卷带讲解
江苏省G4联盟(苏州中学、扬州中学、盐城2022-2023学年高三上学期12月联考数学试题
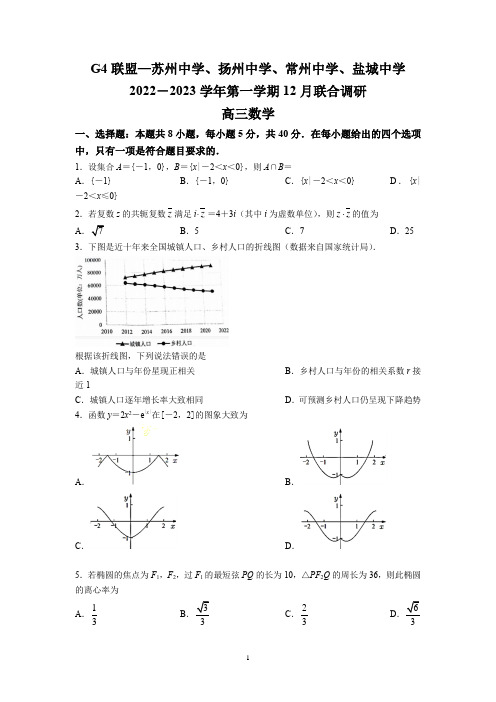
G4联盟—苏州中学、扬州中学、常州中学、盐城中学2022-2023学年第一学期12月联合调研高三数学一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合A={-1,0},B={x|-2<x<0},则A∩B=A.{-1} B.{-1,0} C.{x|-2<x<0} D.{x|-2<x≤0}2.若复数z的共轭复数z满足i⋅z=4+3i(其中i为虚数单位),则z z⋅的值为A7B.5C.7D.25 3.下图是近十年来全国城镇人口、乡村人口的折线图(数据来自国家统计局).根据该折线图,下列说法错误的是A.城镇人口与年份星现正相关B.乡村人口与年份的相关系数r接近1C.城镇人口逐年增长率大致相同D.可预测乡村人口仍呈现下降趋势4.函数y=2x2-e|x|在[-2,2]的图象大致为A.B.C.D.5.若椭圆的焦点为F1,F2,过F1的最短弦PQ的长为10,△PF2Q的周长为36,则此椭圆的离心率为A.13B.33C.23D636.南宋时期,秦九韶就创立了精密测算雨量、雨雪的方法,他在《数学九章》载有“天池盆测雨”题,使用一个圆台形的天池盆接雨水.观察发现体积一半时的水深大于盆高的一半,体积一半时的水面面积大于盆高一半时的水面面积,若盆口半径为a ,盆地半径为b (0<b <a ),根据如上事实,可以抽象出的不等关系为A 33322a ba b+<B 22a ba b+< C .22222a b a b ++⎛⎫< ⎪⎝⎭D .33322a b a b ++⎛⎫<⎪⎝⎭7.在数列{a n }中,()()111sin sin 10n n n n a a a a ++-⋅+=,则该数列项数的最大值为 A .9B .10C .11D .128.在△ABC 中,AB =4,BC =3,CA =2,点P 在该三角形的内切圆上运动,若AP mAB nAC =+(m ,n 为实数),则m +n 的最小值为A .518B .13C .718D .49二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.已知a >0,b >0,a +b =1,则 A .114a b+≤B .2222a b+≥C .log 2a +log 2b ≤-2D .1sin sin 2sin2a b +≤ 10.已知函数()x a a x f x e e --=+,()x a a x g x e e --=-,则 A .函数y =g (x )有且仅有一个零点B .f ′(x )=g (x )且g ′(x )=f (x )C .函数y =f (x )g (x )的图象是轴对称图形D .函数()()g x y f x =在R 上单调递增11.乒乓球(tabletennis ),被称为中国的“国球”,是一种世界流行的球类体育项目,是推动外交的体育项目,被誉为“小球推动大球”.某次比赛采用五局三胜制,当参赛甲、乙两位中有一位赢得三局比赛时,就由该选手晋级而比赛结束.每局比赛皆须分出胜负,且每局比赛的胜负不受之前已赛结果影响.假设甲在任一局赢球的概率为p (0≤p ≤1),实际比赛局数的期望值记为f (p ),下列说法正确的是 A .三局就结束比赛的概率为p 3+(1-p )3B .f (p )的常数项为3C .1435f f ⎛⎫⎛⎫< ⎪⎪⎝⎭⎝⎭D .13328f ⎛⎫=⎪⎝⎭ 12.在四棱锥P -ABCD 中,底面ABCD 为正方形,P A ⊥底面ABCD ,P A =AB =1.G 为PC的中点,M 为平面PBD 上一点下列说法正确的是 A .MG 的最小值为36B .若MA +MG =1,则点M 的轨迹是椭圆C .若156MA =M 的轨迹围成图形的面积为12π D .存在点M ,使得直线BM 与CD 所成角为30°三、填空题:本题共4小题,每小题5分,共20分.13.在6x x ⎛- ⎝的展开式中,常数项为 .14.如图,将绘有函数()sin 2f x M πϕ⎛⎫=+⎪⎝⎭(M >0,0<φ<π)部分图象的纸片沿x 轴折成直二面角,此时A ,B 10φ= .15.我们利用“错位相减”的方法可求等比数列的前n 项和,进而可利用该法求数列{(2n -1)⋅3n }的前n 项和S n ,其操作步骤如下: 由于S n =1×31+3×32+…+(2n -1)⋅3n ,()23131333213n n S n +=⨯+⨯++-⋅,从而()()21232323213n n n S n +=--⨯++⨯+-⋅,所以()1133n n S n +=-⋅+,始比如上方法可求数列{n 2⋅3n }的前n 项和T n ,则2T n +3= .16.已知函数f (x )是定义在R 上的偶函数,且当x ≥0时,f (x )=2x .若对任意x ∈[1,3],不等式f (x +a )≤f 2(x )恒成立,则实数a 的取值范围是 .四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(本小题满分10分)在数列{a n }中,a =1,其前n 项和S n 满足2S n =(n +1)a n ,n ∈N *. (1)求数列{a n }的通项公式a n ; (2)若m 为正整数,记集合22n nn a a m a ⎧⎫⎪⎪+⎨⎬⎪⎪⎩⎭≤的元素个数为b m ,求数列{b m }的前20项和.18.(本小题满分12分)在轴截面为正方形ABCD 的圆柱中,M ,N 分别为弧AD ,弧BC 的中点,且在平面ABCD 的两侧.(1)求证:四边形ANCM 是矩形; (2)求二面角B -MN -C 的余弦值.19.(本小题满分12分)文化月活动中,某班级在宣传栏贴出标语“学好数学好”,可以不同断句产生不同意思,“学/好数学/好”指要学好的数学,“学好/数学/好”强调数学学习的重要性,假设一段时间后,随机有N 个字脱落.(1)若N =3,用随机变量X 表示脱落的字中“学”的个数,求随机变量X 的分布列及期望;(2)若N =2,假设某同学检起后随机贴回,求标语恢复原样的概率. 20.(本小题满分12分)记△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知b =1,c =2. (1)若2CD DB =,2AD CB ⋅=,求A ; (2)若23C B π-=,求△ABC 的面积. 21.(本小题满分12分)在平面直角坐标系xOy 中,已知点P 在抛物线C 1:y 2=4x 上,圆C 2:(x -2)2+y 2=r 2(0<r <2).(1)若r =1,Q 为圆C 2上的动点,求线段PQ 长度的最小值;(2)若点P 的纵坐标为4,过P 的直线m ,n 与圆C 2相切,分别交抛物线C 1于A ,B (异于点P ),求证:直线AB 过定点. 22.(本小题满分12分)若对实数x 0,函数f (x ),g (x )满足f (x 0)=g (x 0)且f ′(x 0)=g ′(x 0),则称()()()00,,f x x x F x g x x x <⎧⎪=⎨⎪⎩≥为“平滑函数”,x 0为该函数的“平滑点”.已知()323122x f x ax x x =-+,g (x )=bx ln x . (1)若1是平滑函数F (x )的“平滑点”, (ⅰ)求实数a ,b 的值;(ⅱ)若过点P (2,t )可作三条不同的直线与函数y =F (x )的图象相切,求实数t的取值范围;(2)对任意b >0,判断是否存在a ≥1,使得函数F (x )存在正的“平滑点”,并说明理由.G4联盟—苏州中学、扬州中学、常州中学、盐城中学2022-2023学年第一学期12月联合调研高三数学答案及其解析一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.【答案】A 2.【答案】D【解析】4334i z i z i ⋅=+⇒=-,所以25z z ⋅= 3.【答案】B【解析】因为乡村人口与年份望负线性相关关系,所以r 接近-1,故选B 4.【答案】D 5.【答案】C【解析】由题意得22245109436b b a a a ⎧⎧==⎪⇒⎨⎨=⎩⎪=⎩,所以226c a b =-=,故椭圆离心率为23c e a == 6.【答案】D 7.【答案】C 【解析】()()()()()()11112111cos cos sin sin sin 2n n n n n n n n n n n n n a a a a a a a a a a a a a +++++++--+--++⎡⎤⎡⎤⎣⎦⎣⎦-⋅+==-21sin 10n a =,所以{}2sin n a 为等差数列,公差为110,所以()2211sin sin 1110n a a n =+-⨯≤,所以110n -211sin 111a n -⇒≤≤≤,故选C 8.【答案】B【解析】()m n AP mAB nAC m n AB AC m n m n ⎛⎫=+=++⎪++⎝⎭,由P 在内切圆上,故APm n m n AB AC m n m n +=⎛⎫+ ⎪++⎝⎭,则11cos 16A =,所以BC 边上高为15h =圆半径15r =,故由平行线等比关系,可得213h r m n h -+=≥,故选B 二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.【答案】BCD 【解析】选项A ,应该是114a b+≥,B :22221a ba b+++≥,B 正确;C :222log log 2log 22a ba b ++=-≤,C 正确;D :1sin sin 2sincos 2sin 222a b a b a b +-+=⋅≤,D 正确;答案为BCD 10.【答案】ABD【解析】AB 正确,因为()f x 关于x a =轴对称,()g x 关于(),0a 中心对称,故()()f xg x 为中心对称图形,C 错误:而()()()()()220'g x f x q x f x B x ⎡⎤-=>⎢⎥∠⎣⎦或根据一般得分离常数变形可知D 正确;答案为:ABD 11.【答案】ABD 【解析】 显然A 正确;()()()()()323131223343141151f p p p C p p C p p C p p ⎡⎤⎡⎤=+-+-+-+⨯-⎣⎦⎣⎦()03f =,13328f B ⎛⎫=⇒ ⎪⎝⎭,D 正确; 求导或根据()f p 关于12对称,且p 越极端,越可能快结束,有11412352--≤,得1435f f ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭, 故答案为:ABD 12.【答案】ABC 【解析】A 选项判断:应用等体积法,可()()min min 11223MG AG =≥,A 正确; B 选项:因为面PBD 不与AG 垂直,也不平行,故轨迹不可能时圆,即为椭圆,B 正确; C 选项判断:设MH ⊥面PBD ,H ∈面PBD ,2151612MA HM =⇒=,故C 正确;D 选项判断:由于CD 与面PBD 夹角θ满足1sin 23θ=>,故[],6πθπθ∉-,D 错误; 综上所述,答案为ABC三、填空题:本题共4小题,每小题5分,共20分.13.【答案】15【解析】展开式的通项为()()36621661rr rr Tr C x C x x --+⎛==- ⎝,当31602r -=,4r =时,为常数项15 14.【答案】56π【解析】如图,因为()f x 的周期为242T ππ==,所以22T CD ==,22TCD ==,所以22AB AC BC +22410M =+=解得3M =所以()32f x x πϕ⎛⎫=+ ⎪⎝⎭,所以()3032f ϕ==,1sin 2ϕ=,因为0ϕπ<<,所以6πϕ=或56π,又因为函数()f x 在y 轴右侧单调递减,所以56πϕ=. 15.【答案】()2113n n n +-+⋅【解析】2122213233n n T n =⨯+⨯+⋯+⋅① 222321313233n n T n +=⨯+⨯+⨯+⋅②②-①()()()222222322123123233133n n n T n n n +⎡⎤=-+-⋅+-⋅++--⋅+⋅⎣⎦()()3321333532133n n n n +=--⋅+⋅++-⋅+⋅()()212112333313n n n n n S n S n n n +++=---+⋅=-+⋅=-+⋅所以()212313n n T n n ++=-+⋅16.【答案】[]3,1-. 【解析】()()()()[]2221,3f x a fx f x f x x +==⇒∀∈≤,[]23,1x a a +⇒∈-≤四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(本小题满分10分) 解析:(1)()()()()()111212221212nn n n n n n n n n a S n a a S S n a na n n a na n n---=+⇒=-=+-⇒-=⇒=≥≥11111n n a a a n n -===⇒=- (2)2214222n n a n m m n m a n n ⎛⎫+⇒+⇒-+ ⎪⎝⎭≤≤≤, 因为1422n n ⎛⎫+ ⎪⎝⎭≥,当且仅当2n =时成立, 所以10b =,21b =,当3n ≥,35b =,47b =,59b =,611b =,…,2339b = 所以{}m b 的前20项和为()135739378+++++=.18.(本小题满分12分) 【解析】(1)设轴截面正方形ABCD 边长为2a ,取弧BC 另一侧的中点Q , 则BC 与NQ 垂直平分,且2BC NQ a ==, 所以四边形BNCQ 为正方形,2BQ NC a ==,因为M 为弧AD 中点,所以MQ AB ∥,四边形ABQM 为矩形, 所以AM BQ ∥,所以AM CN ∥,所以四边形AMCN 为平行四边形, 因为226AN AB BN a =+,2222MN MQ QN a =+=,所以22228AM AN MN a +==,所以AM ⊥AN ,所以四边形ANCM 为矩形; (2)由(1)知,226MB MC MQ QB a ==+=,2BN CN a ==,22MN a =,所以2MNB MNC π∠=∠=所以MNB MNC ∆∆≌,Rt △MBN 斜边MN 上的高626222a a h a==, 作BP ⊥MN ,则CP ⊥MN ,∠BPC 即为二面角B -MN -C 的平面角,6BP CP ==,2BC a =, 在△BPC 中,由余弦定理得222222341cos 233BP CP BC a a BPC BP CP a +--∠===-⨯, 二面角B -MN -C 的余弦值为13- 19.(本小题满分12分) 【解析】(1)随机变量X 的可能取值为0,1,2,12C()33351010C P X C ===,()1223356110C C P X C ===,()2123353210C C P X C ===,随机变量X 的分布列如下表:X 012P110 610 310随机变量X 的期望为()012 1.2101010E X =⨯+⨯+⨯= 法二:随机变量X 服从超几何分布X ~H (3,2,5),所以()26355E X =⨯= (2)设脱落一个“学”为事件A ,脱落一个“好”为事件B ,脱落一个“数”为事件C ,事件M 为脱落两个字M AA BB AB AC BC =++++,()2225110C P AA C ==,()2225110C P BB C ==,()112225410C C P AB C ⋅==,()112125210C C P AC C ⋅==,()112125210C C P BC C ⋅==, 所以某同学捡起后随机贴回,标语恢复原样的概率为()()()()()()()11413125525P P AA P BB P AB P AC P BC =+⨯+++⨯=+⨯=,法二:掉下的两个字不同的概率为1020.810p -==, 所以标语恢复原样的概率为()110.62p p -+=. 20.(本小题满分12分) 解:(1)()112123333CD DB AD AB BD AB BC AB AC AB AB AC =⇒=+=+=+-=+ 所以()22212118112cos 233333333AD CB AB AC AB AC AB AC AB AC A ⎛⎫⋅=+-=--⋅=--⨯⨯=⇒⎪⎝⎭1cos 2A =,因为()0,A π∈,所以3A π=(2)法一:因为23C B π-=,所以562A C π=-,62AB π=-, 因为2c b =,sin 2sinC B =,则5sin 2sin 6262A A ππ⎛⎫⎛⎫-=-⎪ ⎪⎝⎭⎝⎭化简整理得3tan 29A =, 所以22tan332sin 141tan 2AA A ==+ 故面积为133sin 2S bc A == 法二:因为2sin 2sin c b C B =⇒=, 因为23C B π-=, 所以23sin 2sin sin 3B B B B π⎛⎫+=⇒=⎪⎝⎭①, 联立22sin cos 1B B +=②解得3sin 27cos 27B B ⎧=⎪⎪⎨⎪=⎪⎩, 所以3sin 2sin 7C B ==232C B ππ=+> 所以cos 0C <,则2cos 1sin 7C C =-=所以()33sin sin sin cos cos sin 14A B C B C B C =+=+=所以△ABC 的面积为133sin 214ABC S bc A ∆==. 21.(本小题满分12分)【解析】 (1)设()2,2P t t ,则()222212411PQ PC t t --+-≥,当()0,0P ,Q 为2PC 线段与圆2C 的交点时,min 1PQ = (2)题意可知()4,4P ,过P 点直线()44y k x -=-与圆2C 相切, 2241k r k -=+,即()222416160r k k r --+-=,① 设直线AB 为:()()441m x n y -+-=,则与抛物线C 的交点方程可化为: ()()()()()()24844444(4)4y y m x n y x m x n y -+--+-=--+-⎡⎤⎡⎤⎣⎦⎣⎦, 令44y z x -=-,则:()()2188440n z m n z m ++--=,② 题意有,①②方程同解,故有()()()[]()2233164164818444y r r m n m n -⎡⎤⎣=---+⨯=--+-⎦-, 即:2111m n -=,故:直线AB 恒过()6,7-.22.(本小题满分12分)【解析】 (1)(ⅰ)()21'332f x ax a =-+,()[]'1lng x b x =+, 由题意可知10a -=,且532a b -=, 故解得:1a =,12b =, (ⅱ)进一步()323,122ln ,12x x x x F x x x ⎧-+<⎪⎪=⎨⎪⎪⎩≥,过点()2,P t 作()F x 的切线,切点()(),x F x 满足方程:()()()2F x t F x x -=-,故题意等价于方程:()()()'2t F x F x x =--有3个不同根,()()()()'2p x F x F x x =--,()()()''2p x F x x =--,代入得1,2x ⎛⎫∈-∞ ⎪⎝⎭时,()p x 单调递减,1,22x ⎡⎫∈⎪⎢⎣⎭时,()p x 单调递增,[)2,x ∈+∞时,()p x 单调递减, 故()13,2,ln 228t p x x ⎧⎫⎛⎫⎛⎫∈∈=-⎨⎬ ⎪ ⎪⎝⎭⎝⎭⎩⎭ (2)题意等价于:0b ∀>,是否1a ∃≥,使得[]3223ln 221331ln 2x ax x bx x ax x b x ⎧-+=⎪⎪⎨⎪-+=+⎪⎩有解 消a 有:()313212ln 122ln 1x x b x b x ---=-⇒=-,其中由0b >,可得23x e ⎛∈ ⎝, 故题意进一步化简23x e ⎛∀∈ ⎝,是否1a ∃≥,使得()3ln 3122ln 1x x x a x x -+=-成立, 23x e ⎛⇔∀∈ ⎝,()23ln 3122ln 1x x x x x -+-≤是否恒成立 设()()2243ln 231q x x x x x x =--+-,()()'83ln q x x x =-, 故2,13x ⎛⎫∈ ⎪⎝⎭时,单调递减,(x e ∈,()q x 单调递增,故:()()10q x q =≥得证,即0b ∀>,31a ≥,使得()F x 存在的“平滑点”.。
江苏省苏州市苏苑高级中学2023-2024学年高一上学期12月月考数学试题

江苏省苏州市苏苑高级中学2023-2024学年高一上学期
12月月考数学试题
学校:___________姓名:___________班级:___________考号:___________
二、多选题
9.函数()f x 是定义在R 上的奇函数,下列说法正确的是( )A .()00
f =B .若()f x 在[0,)+¥上有最小值1-,则()f x 在(,0]-¥上有最大值1C .若()f x 在[1,)+¥上为增函数,则()f x 在(,1]-¥-上为减函数D .若0x >时,()22f x x x =-,则0x <时,()22f x x x
=--10.已知扇形的周长是12,面积是8,则扇形的圆心角的弧度数可能是( )
A .1
B .4
C .2
D .3
11.在同一直角坐标系中,函数23y x ax a =++-与x y a =的图象可能是( )
六、问答题
20.已知函数44()log (1)log (3)f x x x =++-.
(1)求f (x )的定义域及单调区间.
(2)求f (x )的最大值,并求出取得最大值时x 的值.
(3)设函数4
()log [(2)4]g x a x =++,若不等式f (x )£g (x )在(0,3)x Î上恒成立,求实数a。
江苏省南京市2023~2024学年九年级上学期12月月考数学试卷

数学(满分120分,考试时间120分钟)一、选择题(本大题共6小题,每小题2分,共12分.在每个小题所给出的四个选项中,恰有一项符合题目要求,请将正确选项前的字母代号填涂在答题卡相应位置上)1.一元二次方程x (x -1)=0的根是A .x =1B .x =0C .x 1=2,x 2=1D .x 1=0,x 2=12.平面内,若⊙O 的半径为2,OPP 在⊙OA .内B .上C .外D .内或外3.若二次函数y =ax 2的图象经过点P (-2,4),则该图象必经过点A .(-4,2)B .(-2,-4)C .(2,4)D .(4,-2)4.某班9名学生参加定点投篮测试,每人投篮10次,投中的次数统计如下:3,6,4,6,4,3,6,5,7.这组数据的中位数和众数分别是A .5,4B .5,6C .6,5D .6,65.如图,二次函数y =ax 2+bx +c 的图象经过A (1,0),B (5,0),下列说法正确的是A .c <0B .b 2-4ac <0C .a -b +c <0D .图象的对称轴是直线x =36.如图,已知点C 为圆锥母线SB 的中点,AB 为底面圆的直径,SB =6,AB =4.一只蚂蚁沿着圆锥的侧面从A 点爬到C 点,则蚂蚁爬行的最短路程为A .5B.C.D.二、填空题(本大题共10小题,每小题2分,共20分.不需要写出解答过程,请把答案直接填写在答题卡相应位置上)7.二次函数y =(x +1)2+2图象的顶点坐标为▲.8.一组数据:2,3,-1,5的极差为▲.9.已知x 1、x 2是方程x 2-2x -4=0的两个根,则x 1+x 2-x 1x 2的值为▲.10.在平面直角坐标系中,将二次函数y =2x 2的图象向右平移3个单位,再向上平移1个单位,则平移后的图象所对应的函数表达式为▲.(第5题)(第6题)11.如图,若甲、乙比赛成绩平均数相等,则2S 甲▲2S 乙(填“>”、“<”或“=”).12.已知圆锥的底面半径为6cm ,母线长为8cm ,它的侧面积为▲2cm .13.某产品原来每件成本是100元,连续两次降低成本后,现在成本是81元,设平均每次降低成本的百分率为x ,可得方程▲.14.如图,四边形ABCD 内接于⊙O ,延长AD 至点E ,已知∠AOC =140°,那么∠CDE=▲°.15.如图,点E 在y 轴上,⊙E 与x 轴交于点A 、B ,与y 轴交于点C 、D ,若C (0,9),D (0,-1),则线段AB 的长度为▲.16.如图,△ABC 为等腰直角三角形,∠BAC =90°,AB =AC =22,点D 为平面内一点,且∠BDC =90°,以AC 、CD 为边作□ACDE ,则CE 的最小值为▲.三、解答题(本大题共11小题,共88分.请在答题卡指定区域内作答,解答时应写出必要的文字说明、证明过程或演算步骤)17.(8分)解下列方程:(1)x 2+4x -1=0;(2)2x (x -3)=x -3.(第11题)(第14题)(第15题)(第16题)18.(8分)为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,5次打靶命中的环数如下:甲:8,7,10,7,8;乙:9,5,10,9,7(1)将下表填写完整:平均数极差方差甲▲3▲乙8▲ 3.2(2)根据以上信息,若你是教练,你会选择谁参加射击比赛,理由是什么?(3)若乙再射击一次,命中8环,则乙这六次射击成绩的方差会▲(填“变大”或“变小”或“不变”).19.(8分)已知一个二次函数图象上部分点的横坐标x与纵坐标y的对应值如表所示:x…-3-2-101…y…0-3-4-30…(1)这个二次函数的表达式是▲;(2)在给定的平面直角坐标系中画出这个二次函数的图象;(3)观察图象,当-4<x<0时,y的取值范围为▲.20.(7分)如图,在⊙O 中,AB =AC .(1)若∠BOC =100°,则⌒AB 的度数为▲°;(2)若AB =13,BC =10,求⊙O 的半径.21.(6分)如图,已知线段a 及∠ACB .请仅用直尺..和.圆规..作⊙O ,使⊙O 在∠ACB 的内部,CO =a ,且⊙O 与∠ACB 的两边分别相切.(不写作法,保留.......作.图痕迹...).22.(8分)若关于x 的方程x 2+bx +c =0有两个实数根,且其中一个根比另一个根大2,那么称这样的方程为“隔根方程”.例如,方程x 2+2x =0的两个根是x 1=0,x 2=-2,则方程x 2+2x =0是“隔根方程”.(1)方程x 2-x -20=0是“隔根方程”吗?判断并说明理由;(2)若关于x 的方程x 2+mx +m -1=0是“隔根方程”,求m 的值.23.(8分)如图,四边形ABCD是⊙O的内接四边形,AB是直径,C是⌒BD的中点,过点C 作CE⊥AD交AD的延长线于点E.(1)求证:CE是⊙O的切线;(2)若BC=6,AC=8,求CE、DE的长.24.(9分)某淘宝网店销售台灯,成本为每个30元.销售大数据分析表明:当每个台灯售价为40元时,平均每月售出600个;若售价每下降1元,其月销售量就增加200个.(1)若售价下降1元,每月能售出▲个台灯,若售价下降x元(x>0),每月能售出▲个台灯;(2)为迎接“双十一”,该网店决定降价促销,在库存为1210个台灯的情况下,若预计月获利恰好为8400元,求每个台灯的售价.25.(8分)已知二次函数y=(x-m)2-1(m为常数).(1)求证:不论m为何值,该函数图象与x轴总有两个公共点;(2)当-1≤x≤3时,y的最小值为3,求m的值.26.(8分)掷实心球是南京市高中阶段学校招生体育考试的选考项目.如图1,一名女生投掷实心球,实心球行进路线是一条抛物线,行进高度y (m )与水平距离x (m )之间的函数关系如图2所示,已知掷出时起点处高度为35m ,当水平距离为3m 时,实心球行进至最高点3m 处.(1)求y 关于x 的函数表达式;(2)根据南京市高中阶段学校招生体育考试评分标准(女生),投掷过程中,实心球从起点到落地点的水平距离大于等于6.9m ,此项考试得分为满分.该女生在此项考试中是否得满分,请说明理由.27.(10分)在探究“四点共圆的条件”的数学活动课上,小霞小组通过探究得出:在平面内,一组对角互补的四边形的四个顶点共圆.请运用..此结论...,解决以下问题:如图1,△ABC 中,AB =AC ,∠BAC =α(60°<α<180°).点D 是BC 边上的一动点(点D 不与B 、C 重合),将线段AD 绕点A 顺时针旋转α到线段AE ,连接BE .(1)求证:A 、E 、B 、D 四点共圆;(2)如图2,当AD =CD 时,⊙O 是四边形AEBD 的外接圆,求证:AC 是⊙O 的切线;(3)已知α=120°,BC =6,点M 是边BC 的中点,此时⊙P 是四边形AEBD 的外接圆,直接写出圆心P 与点M 距离的最小值.图1图2图1图2备用图。
2022-2023学年江苏省苏州中学高二年级上册学期12月阶段质量评估数学试题【含答案】

2022-2023学年江苏省苏州中学高二上学期12月阶段质量评估数学试题一、单选题1.若方程2220x y y m +--=表示圆,则实数m 的取值范围为( ) A .(),1-∞ B .()1,+∞ C .(),1-∞- D .()1,-+∞【答案】D【分析】将方程化为标准式即可计算求解.【详解】解:方程2220x y y m +--=可变形为()2211x y m +-=+, 因为方程表示圆,则10m +>,所以1m >-. 故选:D.2.若直线4mx ny 与圆224x y +=没有交点,则过点(),P m n 的直线与椭圆22194x y+=的交点的个数为( ) A .0或1 B .2 C .1 D .0【答案】B【分析】由直线与圆相离得到P 点位置后判断 222m n>+,得224m n +<,故点(),P m n 在以原点为圆心,2为半径的圆内,即在椭圆内部,过P 点的直线与该椭圆必有2个交点. 故选:B3.过点(3,1)A 的圆C 与直线0x y -=相切于点(1,1)B ,则圆C 的方程为( ) A .22(2)2x y -+= B .22(2)(1)1x y -+-= C .22(3)(4)9x y -+-= D .22()(31)8x y -++=【答案】A【分析】求得圆心和半径,由此求得圆的方程. 【详解】设圆心为(),a b ,半径为r , 则()()()()22223111111a b a b b a ⎧-+-=-+-⎪⎨-=-⎪-⎩,解得2,0a b ==,所以圆心为()2,0, 半径r ==所以圆C 的方程为22(2)2x y -+=. 故选:A4.如果方程222x ky +=表示焦点在y 轴上的椭圆,那么实数k 的取值范围是( ) A .()1,+∞ B .()1,2C .1(2,1)D .()0,1【答案】D【分析】化曲线方程为椭圆的标准方程,由题意可得22k>,求解此不等式可得k 的取值范围. 【详解】由方程222x ky +=,可得22122x y k+=, 因为方程222x ky +=表示焦点在y 轴上的椭圆,可得22k>,解得01k <<. 所以实数k 的取值范围是0,1. 故选:D.5.已知等比数列{}n a 满足12a =,23564a a a ⋅=,则3a 的值为( )A .14B .12C .1D .2【答案】C【解析】根据23564a a a ⋅=,利用等比数列的性质求得2q ,再利用通项公式求解.【详解】在等比数列{}n a 中,12a =,23564a a a ⋅=,所以46224a a =,所以4211,42q q ==,所以2311a a q ==,故选:C6.已知数列{}n a 的前n 项和122n n S +=-,若()*5,p q p q +=∈N ,则p q a a =( )A .8B .16C .32D .64【答案】C【分析】当1n =时,由122n n S +=-可得1a ,当2n ≥时,1n n n a S S -=-,验证1a 是否适合可得通项公式,代入通项公式求解可得结果.【详解】解:当1n =时,211222a S ==-=,当2n ≥时,()1122222n n nn n n a S S +-=-=---=,12a =,符合上式,∴数列{}n a 的通项公式为:2n n a =5222232p q q p q p a a +=⋅===,故选:C.7.如图,已知抛物线22y x =,过点()10P ,和()3,0Q 分别作斜率大于0的两平行直线,交抛物线于A ,B 和C ,D ,连接AD 交x 轴于点3,02M ⎛⎫ ⎪⎝⎭,则直线AB 的斜率是( )A .1B 2C 3D .2【答案】D【分析】由题知3D A y y =-,进而设直线AD 的方程为()302x my m =+>,与抛物线联立方程得2,3A D A D y y m y y +=⋅=-,进而可得113A D m y y =⎧⎪=-⎨⎪=⎩,1,12A ⎛⎫- ⎪⎝⎭,再求斜率即可.【详解】解:因为()10P ,,()3,0Q ,3,02M ⎛⎫⎪⎝⎭,所以13,22PM QM ==, 因为//AB CD , 所以AMP ∽DMQ △, 所以13A D PM AM y MQ MQ y ===,即3D A y y =-,因为过点()10P ,和()3,0Q 两平行直线,AB CD 斜率大于0 所以,直线AD 斜率大于0, 故设直线AD 的方程为()302x my m =+>, 联立方程2322x my y x ⎧=+⎪⎨⎪=⎩得2230y my --=, 所以2,3A D A D y y m y y +=⋅=-所以,233A D A D A D y y my y y y +=⎧⎪⋅=-⎨⎪-=⎩,解得113A D m y y =⎧⎪=-⎨⎪=⎩所以1,12A ⎛⎫- ⎪⎝⎭,所以102112AB AP k k --===-,即直线AB 的斜率是2. 故选:D8.已知双曲线C :()222210,0x y a b a b-=>>的右焦点为F ,左顶点为A ,M 为C 的一条渐近线上一点,延长FM 交y 轴于点N ,直线AM 经过ON (其中O 为坐标原点)的中点B ,且2ON BM =,则双曲线C 的离心率为( ) A .2 BC .52D.【答案】A【分析】由中点B ,且2ON BM =得NF OM ⊥,由点到直线距离公式得FM b =,从而得OM OA a ==,通过三角形全等证得△MNB 为等边三角形,然后得ba ,从而计算出离心率.【详解】记M 为双曲线C :()222210,0x y a b a b-=>>的渐近线0bx ay -=上的点,因为2ON BM =,且OB BN =,所以BOM BMO ∠=∠,BMN BNM ∠=∠.所以NF OM ⊥.因为右焦点(),0F c 到渐近线0bx ay -=的距离MF b ==,所以OM OA a ==.所以BMO BAO ∠=∠,所以BOM BAO ∠=∠, 所以Rt AOB Rt OMN ≌,所以ABO ONM ∠=∠, 又因为MNB NMB ∠=∠,ABO NBM ∠=∠.所以△MNB 为等边三角形,所以60FNO ∠=︒,所以30MFO ∠=︒,即tan 603b a =︒=,所以2212be a=+=. 故选:A .二、多选题9.已知等差数列{}n a 的前n 项和为*()n S n N ∈,公差0d ≠,690S =,a 7是a 3与a 9的等比中项,则下列选项正确的是( ) A .122a =B .2d =-C .当且仅当10n =时,n S 取得最大值D .当0n S >时,n 的最大值为20【答案】BD【分析】先求出2d =-,120a =,从而可判断AB 的正误,再求出通项公式,根据其符号可判断C 的正误,求出n S 并解不等式0n S >,故可判断D 的正误.【详解】因为690S =,故161590a d +=,又()()()2111628a d a d a d +=++,整理得到:12125301000a d a d d d +=⎧⎪+=⎨⎪≠⎩,故2d =-,120a =,故A 错,B 正确.又222n a n =-,当12n ≥时,0n a <;当110n ≤≤时,0n a >;当11n =时,0n a =, 故当且仅当10n =、11n =时,n S 取得最大值,故C 错误. 又()21202212n n n S n n n -=-⨯=-+,令0n S >,则021n <<即n 的最大值为20,故D 正确 故选:BD.10.已知数列{}n a 的前n 项和为n S ,11a =,23a =,且111(2)n n n n a a S S n +--=-+≥,则下列说法正确的是( )A .数列{}n a 的通项公式为21n n a =-B .若1n n b a =+,则2202221012b b b =C .数列{}n S n +为等比数列D .11n n S n a +++= 【答案】ABD【分析】对于选项A ,因为11,2,1n n n S S n a S n --≥⎧=⎨=⎩,所以112(1)(2)n n a a n ++=+≥,从而判断出{}1n a +为等比数列,从而求出{}n a 的通项公式;对于选项B ,通过选项A 中{}1n a +为等比数列,判断出{}n b 为等比数列,从而得到答案;对于选项C ,因为{}n a 的通项公式已知,通过分组求和得到n S ,从而判断出{}n S n +是否为等比数列; 对于选项D ,通过选项A 和D 可以得到n a 和n S ,从而判断11n n S n a +++=是否正确. 【详解】对于选项A ,111(2)n n n n a a S S n +--=-+≥,则112(1)(2)n n a a n ++=+≥,又21121a a +=+,故数列{}1n a +是以首项为2,公比为2的等比数列,所以12n n a +=,即21nn a =-,故A 正确;对于选项B ,12n n n b a =+=,则{}n b 为等比数列,所以2202221012b b b =,故B 正确;对于选项C ,由1122nn n i i S a n +===--∑,得122n n S n ++=-,又2132(1)(3)(2)S S S ++≠+,则数列{}n S n +不是等比数列,故C 错误;对于选项D ,易得11222(21)21n nn n n S n n a n a n ++=--=--=-=--,即11n n S n a +++=,故D 正确.故选:ABD11.已知点O 为坐标原点,直线1y x =-与抛物线2:4C y x =相交于,A B 两点,则( ) A .||8AB =B .OA OB ⊥C .AOB的面积为D .线段AB 的中点到直线0x =的距离为2【答案】AC【分析】先判断直线过焦点,联立方程组214y x y x =-⎧⎨=⎩结合韦达定理得两根关系,再根据选项一一判断即可.【详解】设()()1122,,,A x y B x y ,抛物线2:4C y x =,则2P = ,焦点为()1,0,则直线1y x =-过焦点;联立方程组214y x y x=-⎧⎨=⎩ 消去y 得2610x x -+=, 则12126,1x x x x +==, ()()()121212121114y y x x x x x x =--=-++=-所以12628AB x x P =++=+= ,故A 正确;由12121430OA OB x x y y ⋅=+=-=-≠,所以OA 与OB 不垂直,B 错;原点到直线1y x =-的距离为d ==,所以AOB 的面积为11822S d AB =⨯⨯==,则C 正确;因为线段AB 的中点到直线0x =的距离为126322x x +==,故D 错 故选:AC【点睛】(1)直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似,一般要用到根与系数的关系;(2)有关直线与抛物线的弦长问题,要注意直线是否过抛物线的焦点,若过抛物线的焦点,可直接使用公式|AB |=x 1+x 2+p ,若不过焦点,则必须用一般弦长公式.12.已知1F 、2F 分别为双曲线()222210,0x y a b a b-=>>的左、右焦点,过点2F 的直线与双曲线的右支交于A 、B 两点,记12AF F △的内切圆1I 的半径为1r ,12BF F △的内切圆2I 的半径为2r .若212r r a =,则( )A .1I 、2I 在直线x a =上B .双曲线的离心率e =C .1ABF 内切圆半径最小值是32aD .12r r +的范围是2a ⎡⎤⎢⎥⎣⎦【答案】AC【分析】对于A ,由切线长定理结合双曲线定义可判断正误;对于B ,由A 分析,结合212r r a =可判断正误;对于C ,联立直线AB 方程与双曲线方程,利用韦达定理表示出内切圆半径,后可判断正误;对于D ,利用几何知识得到12r r +表达式,后利用函数知识可判断正误.【详解】设()()12,0,0F c F c -,,其中222c a b =+. 设()()112212,,,I I I I I x y I x y ,()()1122,,A x y B x y ,.对于A ,过1I 分别作1AF 、2AF 、12F F 的垂线,垂足分别为D 、E 、F ,所以由切线长定理有1122,,AD AE F D F F F E F F ===,则121212122AF AF AD DF AE EF DF EF F F FF a -=+--=-=-=, 又因为12122F F FF FF c =+=,所以1FF a c =+.又()1,0F c -,所以1I x a =,同理可得2I x a =.则1I 、2I 在直线x a =上,故A 正确; 对于B ,因21F I 平分2FF A ∠,22F I 平分2FF B ∠,2πAF B ∠=,则122π2I F I ∠=. 在122I I F △中,122π2I F I ∠=,2F F c a =-.由射影定理可得2122I F I F F F ⋅=, 即2212()r r c a a =-=2202c ac c a ⇒-=⇒=,则双曲线离心率为2,故B 错误;对于C ,因112ABF S lr =,则内切圆半径12ABF S r l=. 其中112121211222ABF SF F y y c y y =⋅⋅-=⋅⋅-, 又由B 分析可知2c a =.则1122ABF Sa y y =-.其中1122l AF F B AF BF =+++,又12122AF AF BF BF a -=-=, 则42l a AB =+.故12442a y y r a AB-=+.设直线AB 方程为2xmy a ,将其与双曲线联立有:2222132x y a a x my a ⎧-=⎪⎨⎪=+⎩,消去x 得:()222311290m y may a -++=,则21212221293131,am a y y y y m m -+==--,()()222221212121212224344243131,a a m a x x m y y a x x m y y am y y a m m ---+=++==+++=--.又A B ,两点在双曲线右支,则1221203100x x m m x x ⎛+>⎧⇒-<⇒∈ ⎨ >⎩⎝⎭.又12y y -===()()()2222121212261113a m AB xx y y m y y m +=-+-=+⋅-=-.代入12442a y y r a AB -=+,有()2222222614241313132211246113a m a a m a m m r a a a m m a -+⋅++-===≥++. 当且仅当0m =,即直线AB 与x 轴垂直时取等号.故C 正确;对于D ,设12I F F ∠α=,又由对称性设直线AB 的倾斜角为θ,其中π0,2θ⎡⎤∈⎢⎥⎣⎦.则2112π2πFF I I F A θαθ∠+∠+=⇒+=.又由C 分析知,1303,tan m θ⎡⎫=∈⎪⎢⎪⎢⎣⎭,则πππ2,32θα⎛⎤=-∈ ⎥⎝⎦,所以ππ,43α⎡⎫∈⎪⎢⎣⎭,得)tan 1,3α⎡∈⎣,则112tan tan r I F FF a ===αα, 2222πtan tan 2tan a r FF I F F a αα⎛⎫=∠=-= ⎪⎝⎭,所以121tan tan r r a ⎛⎫+=+ ⎪⎝⎭αα,又()1f x a x x ⎛⎫=+ ⎪⎝⎭在)1,3⎡⎣上单调递增, 则12143tan 2,tan 3r r a a a αα⎡⎫⎛⎫+=+∈⎪⎢ ⎪⎪⎝⎭⎣⎭.故D 错误. 故选:AC.【点睛】关键点点睛:本题涉及双曲线焦点三角形的内切圆,难度较大. 对于A 选项,关键为利用切线长定理得到122F F FF a -=; 对于B 选项,关键为利用射影定理; 对于C 选项,关键为利用112ABF Slr =结合双曲线定义得到12442a y y r a AB -=+.对于D 选项,关键为找到12I F F ∠α=范围,后表示出121tan tan r r a ⎛⎫+=+ ⎪⎝⎭αα.三、填空题13.设P 为椭圆M :22110x y +=和双曲线N :2218y x -=的一个公共点,且P 在第一象限,F 是M 的左焦点,则PF =______.1##1+【分析】先求出F 点坐标,再联立椭圆和双曲线方程,求出P 点坐标,运用两点距离公式即可.【详解】对于椭圆M ,()2222210,1,9,3,0a b c a b F ==∴=-=- ;联立方程222211018x y y x ⎧+=⎪⎪⎨⎪-=⎪⎩ ,解得22108,99x y == , 因为P在第一象限,P ∴⎝⎭,1PF =;1 .14.n S 是公差为2的等差数列{}n a 的前n项和,若数列也是等差数列,则1a =________. 【答案】1-或3【解析】可由特殊值求出1a ,再验证对所有正整数n,都有数列是等差数列 【详解】由题意211(1)2(1)2n n n S na n a n -=+⨯=+-, ∵数列是等差数列∴11a =-或13a =,11a =-1n -,13a =1n +,均为n 的一次函数,数列是等差数列, 故答案为:1-或3.【点睛】本题考查等差数列的前n 项和公式,考查等差数列的证明,如果数列的通项公式是n 的一次函数,则数列一定是等差数列.15.3D 打印是快速成型技术的一种,它是一种以数字模型文件为基础,运用粉末状金属或塑料等可粘合材料,通过逐层打印的方式来构造物体的技术.如图所示的塔筒为3D 打印的双曲线型塔筒,该塔筒是由离心率为5的双曲线的一部分围绕其旋转轴逐层旋转打印得到的,已知该塔筒(数据均以外壁即塔筒外侧表面计算)的上底直径为6cm ,下底直径为9cm ,高为9cm ,则喉部(最细处)的直径为______cm .【答案】42【分析】由已知,根据题意,以最细处所在的直线为x 轴,其垂直平分线为y 轴建立平面直角坐标系,设出双曲线方程,并根据离心率表示出,a b 之间的关系,由题意底直径为6cm ,所以双曲线过点()3,m ,下底直径为9cm ,高为9cm ,所以双曲线过点9,92m ⎛⎫- ⎪⎝⎭,代入双曲线方程即可求解方程从而得到喉部(最细处)的直径.【详解】由已知,以最细处所在的直线为x 轴,其垂直平分线为y 轴建立平面直角坐标系, 设双曲线方程为()222210,0x y a b a b -=>>,由已知可得,5ce a==222c a b =+,所以224a b =,所以双曲线方程为222214x y a a-=,底直径为6cm ,所以双曲线过点()3,m ,下底直径为9cm ,高为9cm ,所以双曲线过点9,92m ⎛⎫- ⎪⎝⎭,代入双曲线方程得:()222222914819414m aa m aa ⎧-=⎪⎪⎨⎪--=⎪⎩,解得:2m a =⎧⎪⎨=⎪⎩所以喉部(最细处)的直径为cm.故答案为:四、双空题16.设n S 是数列{}n a 的前n 项和,1332n n n S a +=-,则n a =______;若不等式2n a ≥对任意+N n ∈恒成立,则k 的最小值为______.【答案】 ()423nn + 136k ≥【分析】利用题设条件可得1132322nn n a a -=+⨯,化简后可得1122323n n n n a a --=+⨯⨯,从而可求{}n a 的通项,再利用数列单调性求出3n n ⎧⎫⎨⎬⎩⎭的最大项,从而可求参数的取值范围.【详解】因为1332n n n S a +=-,故11932a a =-即118a =.因为1332n n n S a +=-,故当2n ≥时,11332nn n S a --=-,故11333322n n n n n a a a +--=+-,整理得到1132322nn n a a -=+⨯,所以1122323n n n n a a --=+⨯⨯,故23n na ⎧⎫⎨⎬⨯⎩⎭为等差数列且首项为1233a ⨯=,公差为2, 故()3212123n na n n =+-=+⨯,故()423nna n =+.又2n a ≥即为()2423nn +≥3n n .设()3n nf n =,则当2n ≥时,()()113210333n n nn n n f n f n -----=-=<, 故(){}f n 为单调递减数列,故()max 13f n =,故13即136k ≥. 故答案为:()423nn +,136k ≥.五、解答题17.已知数列{}n a 满足:112a =,21a =,2145n n n a a a +++=(*n ∈N ).(1)证明:数列{}1n n a a +-是等比数列; (2)求数列{}n a 的通项公式. 【答案】(1)证明见解析 (2)n a 23*1(21)()3n n N -=+∈【分析】(1)结合递推公式利用等比数列的定义证明即可; (2)结合(1)中结论,利用累加法和等比数列求和公式即可求解. 【详解】(1)证明:∵*2145n n n a a a n +++=∈N ,, ∴*2114(),n n n n a a a a n +++-=-∈N , ∵12112,a a ==,∴2112a a -=, ∴数列{1n n a a +-}是以12为首项,4为公比的等比数列.(2)由(1)知,12311422n-n n n a a -+-=⨯=, 当2n ≥时,112211()()()+n n n n n a a a a a a a a ---=-+-++-2527291122222n n n -----=+++++()()123114112212143n n ---=+=+-当n =1时,1111(21)32a -=+=满足上式.所以,n a 23*1(21)()3n n N -=+∈. 18.在ABC ∆中,已知(1,1)A ,(3,5)B --.(1)若直线l 过点(2,0)M ,且点A ,B 到l 的距离相等,求直线l 的方程; (2)若直线:260m x y --=为角C 的内角平分线,求直线BC 的方程. 【答案】(1)2340x y --=或3260x y --= (2)270x y --=【分析】(1)因为点A ,B 到l 的距离相等,所以直线l 过线段AB 的中点或//l AB ,分直线l 过线段AB 的中点和//l AB 两种情况讨论即可;(2)因为直线m 为角C 的内角平分线,所以点A 关于直线m 的对称点A '在直线BC 上,求出点A '的坐标,即可求出直线方程.【详解】(1)解:因为点A ,B 到l 的距离相等,所以直线l 过线段AB 的中点或//l AB , 当直线l 过线段AB 的中点时,线段AB 的中点为(1,2)--,l 的斜率202123k --==--,则l 的方程为2(2)3y x =-,即2340x y --=, 当//l AB 时,l 的斜率513312AB k k --===--, 则l 的方程为3(2)2y x =-,即3260x y --=,综上:直线l 的方程为2340x y --=或3260x y --=;(2)因为直线m 为角C 的内角平分线,所以点A 关于直线m 的对称点A '在直线BC 上, 设(,)A s t ',则有11260221112s t t s ++⎧⨯--=⎪⎪⎨-⎪=-⎪-⎩,得51s t =⎧⎨=-⎩,即(5,1)A '-,所以直线BC 的斜率为151532k -+==+, 则直线BC 的方程为11(5)2y x +=-,即270x y --=.19.如图,在平面直角坐标系xoy 中,点(0,3)A ,直线:24l y x =-,设圆C 的半径为1, 圆心在l 上.(1)若圆心C 也在直线1y x =-上,过点A 作圆C 的切线,求切线方程; (2)若圆C 上存在点M ,使2MA MO =,求圆心C 的横坐标a 的取值范围. 【答案】(1)3y =或34120x y +-=;(2)12[0,]5. 【分析】(1)两直线方程联立可解得圆心坐标,又知圆C 的半径为1,可得圆的方程,根据点到直线距离公式,列方程可求得直线斜率,进而得切线方程;(2)根据圆C 的圆心在直线l :24y x =-上可设圆C 的方程为[]22()(24)1x a y a -+--=,由2MA MO =,可得M 的轨迹方程为22(1)4x y ++=,若圆C 上存在点M ,使2MA MO =,只需两圆有公共点即可. 【详解】(1)由24,{1,y x y x =-=-得圆心()3,2C ,∵圆C 的半径为1,∴圆C 的方程为:22(3)(2)1x y -+-=,显然切线的斜率一定存在,设所求圆C 的切线方程为3y kx =+,即30kx y -+=.1=,∴2(43)0k k +=,∴0k =或34k =-.∴所求圆C 的切线方程为3y =或34120x y +-=.(2)∵圆C 的圆心在直线l :24y x =-上,所以,设圆心C 为(,24)a a -, 则圆C 的方程为[]22()(24)1x a y a -+--=. 又∵2MA MO =,∴设M 为(,)x y =22(1)4x y ++=,设为圆D . 所以点M 应该既在圆C 上又在圆D 上,即圆C 和圆D 有交点,∴2121-≤+, 由251280a a -+≥,得a R ∈, 由25120a a -≤,得1205a ≤≤. 综上所述,a 的取值范围为120,5⎡⎤⎢⎥⎣⎦.【解析】1、圆的标准方程及切线的方程;2、圆与圆的位置关系及转化与划归思想的应用. 【方法点睛】本题主要考查圆的标准方程及切线的方程、圆与圆的位置关系及转化与划归思想的应用.属于难题.转化与划归思想是解决高中数学问题的一种重要思想方法,是中学数学四种重要的数学思想之一,尤其在解决知识点较多以及知识跨度较大的问题发挥着奇特功效,大大提高了解题能力与速度.运用这种方法的关键是将题设条件研究透,这样才能快速找准突破点.以便将问题转化为我们所熟悉的知识领域,进而顺利解答,希望同学们能够熟练掌握并应用于解题当中.本题(2)巧妙地将圆C 上存在点M ,使2MA MO =问题转化为,两圆有公共点问题是解决问题的关键所在.20.已知数列{}n a ,{}n b 满足1n n n b a a +=-,其中,*N n ∈. (1)若12a =,2n n b =.①求证:{}n a 为等比数列; ②试求数列{}n n a ⋅的前n 项和.(2)若2n n b a +=,数列{}n a 的前6291项之和为1926,前77项之和等于77,试求前2024项之和是多少?【答案】(1)①证明见解析;②1(1)22+=-⋅+n n S n(2)20241849=T【分析】(1)①,利用累加法求解n a 即可;②由①得2n n a =,令2nn n c na n ==⋅,{}n c 的前n 项和为n S ,利用错位相减法求解数列的和即可;(2)推出数列{}n a 是一个周期为6的周期数列,然后求解数列{}n a 的任意连续6项之和为0,然后利用其周期和相关值求出12,a a ,则得到答案.【详解】(1)①证明:12nn n a a +-=,当2n ≥时累加得()()()112211n n n n n a a a a a a a a ---=-+-++-+1212222n n --=++++()12122212n n --=+=-11222n n n n a a ++∴==,()2n ≥,又211212,2,4,2a a b a a ===∴=所以{}n a 为首项为2,公比为2的等比数列.②由①得2n n a =,令2nn n c na n ==⋅,{}n c 的前n 项和为n S ,则2311231122232(1)22n nn n n S c c c c c n n --=+++⋯++=⋅+⋅+⋅+⋯+-⋅+⋅,A23412122232(1)22n n n S n n +=⋅+⋅+⋅+⋯+-⋅+⋅,BA B -得23122222n n n S n +-=+++⋯+-⋅()211121222(1)2212n n n n n -++-=+-⋅=-⋅--1(1)22n n S n +∴=-⋅+(2)若21n n n n b a a a ++==-,则32163n n n n n n n a a a a a a a +++++=-=-⇒=-=,所以数列{}n a 是周期为6的周期数列,设1a m =,2a t =,则3a t m =-,4a m =-,5a t =-,6a m t =-,1234560a a a a a a ∴+++++=设数列{}n a 的前n 项和为n T ,则60n T =. 所以629110486332221926963T T T a a ⨯+====⇒=, 7712655377T T T a ⨯+====,所以123886a a a =-=所以2024337622128869631849T T T a a ⨯+===+=+=.21.已知椭圆2214x y +=的左右顶点为A 、B ,直线l :1x =.已知O 为坐标原点,圆G 过点O 、B 交直线l 于M 、N 两点,直线AM 、AN 分别交椭圆于P 、Q .(1)记直线AM ,AN 的斜率分别为1k 、2k ,求12k k ⋅的值; (2)证明直线PQ 过定点,并求该定点坐标. 【答案】(1)1219k k ⋅=-(2)证明见解析,10,013⎛⎫⎪⎝⎭【分析】(1)首先设出点,M N 的坐标,根据OM ON ⊥,利用斜率公式表示12k k ⋅; (2)当直线PQ 的斜率存在时,设直线方程y kx m =+,与椭圆方程联立,利用韦达定理表示()()12121229AP AQ y y k k x x ⋅==-++,从而得到k 与m 的关系,计算定点坐标,并验证当直线的斜率不存在时,也过此定点.【详解】(1)由已知可得MN 为圆G 的直径,所以OM ON ⊥,则1OM ON k k ⋅=-, 根据题意不妨设()1,M m ,()1,N n ,()2,0A - 则1mn =-,所以()()11212339AM AN m n m n k k ⋅=⋅=⋅=-----,所以1219k k ⋅=-.(2)证明:当直线PQ 的斜率存在时,设直线PQ 的方程为y kx m =+,()11,P x y ,()22,Q x y ,联立2244y kx m x y =+⎧⎨+=⎩,得()()222148440k x kmx m +++-=,所以122814km x x k +=-+,21224414m x x k -=+, ()()()222121212122414m k y y kx m kx m k x x km x x k -=++=++=+, 所以()()()121212121219240229AP AQ y y k k y y x x x x x x ⋅==-⇒++++=++, 所以22222222444892401316200141414m k m km m km k k k k --⎛⎫⨯++-+=⇒--= ⎪+++⎝⎭, ()()131020m k m k +-=即1013m k =-,或2m k =, 当1013m k =-时,直线l 的方程为1013y k x ⎛⎫=- ⎪⎝⎭,过定点10,013⎛⎫⎪⎝⎭,当2m k =时,直线l 的方程为()2y k x =+,过定点()2,0A -,舍去. 当直线PQ 斜率不存在时,()1,1M ,()1,1N -,()2,0A -,直线AM 方程是()123y x =+与椭圆方程2214x y +=联立得1012,1313P ⎛⎫ ⎪⎝⎭,同理得1012,1313Q ⎛⎫- ⎪⎝⎭,此时直线PQ 的方程是1013x =,过定点10,013⎛⎫ ⎪⎝⎭, 综上可知,直线PQ 过定点,该定点坐标是10,013⎛⎫⎪⎝⎭.22.已知{}n a 为等比数列,124a a +=,记数列{}n b 满足31log n n b a +=,且11n n b b +-=. (1)求{}n a 和{}n b 的通项公式;(2)对任意的正整数n ,设()228,,n nn n n n n b a n c b b a b n +⎧-⎪=⎨⎪⎩为奇数为偶数,求{}n c 的前2n 项的和2n S .【答案】(1)13n n a -=,n b n =;(2)22431359322132n n n S n -⎛⎫=-+ ⎪+⎝⎭. 【分析】(1)设等比数列{}n a 的公比为q ,分析可知0q >,根据已知条件可求得q 的值,金额可求得1a 的值,利用等比数列的通项公式可求得等比数列{}n a 的通项公式,在利用对数的运算性质可求得数列{}n b 的通项公式;(2)分析可得出11133,23,n n n n n c n n n n -+-⎧-⎪=+⎨⎪⋅⎩为奇数为偶数,利用裂项相消法可求得奇数项的和,利用错位相减法可求得偶数项的和,由此化简可得2n S 的表达式.【详解】(1)设等比数列{}n a 的公比为q ,对任意的n N *∈,则31log n n b a +=,则0n a >,所以,0q >, 因为21323131log log log 1n n n n n n a b b a a a +++++-=-==,可得213n n a q a ++==, 因为1211144a a a a q a +=+==,则11a =,1113n n n a a q --∴==,所以,3log 3nn b n ==;(2)当n 为奇数时,()()()()111129283333222n n n n n n n n c n n n n n n --+-+-⎡⎤-⎣⎦==⨯=-+++,前2n 项中所有的奇数项的和为022422223333333911133521212121n n n nS n n n n -=-+-+⋅⋅⋅+-=-=--+++奇 当n 为偶数时,13n n c n -=⋅,记213523436323n S n -=⨯+⨯+⨯+⋅⋅⋅+⋅偶,()2121359234322323n n S n n -+=⨯+⨯+⋅⋅⋅+-⋅+⋅偶,两式相减得()()()2212135212161381338232333323194n n n n n n S n n ++-+--⋅+=⋅-++++=⋅-=-偶, 所以,()2439332n n S -⋅+=偶. 故数列{}n c 的前2n 项和22431359322132n n n S S S n -⎛⎫=+=-+⎪+⎝⎭奇偶.。
2022-2023学年江苏省苏州市苏州中学九年级上学期期中考数学试卷含详解

A.点P在圆内B.点P在圆上C.点P在圆外D.无法确定
【答案】C
【解析】
【分析】由⊙O的半径分别是2,点P到圆心O的距离为4,根据点与圆心的距离与半径的大小关系即可确定点P与⊙O的位置关系.
【详解】解:∵⊙O的半径是2,点P到圆心O的距离为4,
∴点P与⊙O的位置关系是:点在圆外.
∴当x=m时,y取得最小值,即 =-2,
解得m= 或m=- (不在范围内,舍去);
当m>2时,
∵二次函数 ( 为常数)中,a=1>0,
∴在对称轴的左侧,y随x的增大而减小,
∴当x=2时,函数y取得最小值,即4-4m=-2,解得m= ,(不在范围内,舍去)
综上所述,m的值为 或 ,
故选D.【点睛】本题考查了二次函数的对称轴,最值,函数的增减性,利用分类思想,灵活运用二次函数的增减性确定最值是解题的关键.
令 ,则
,
解得: ,
故选A.
【点睛】本题考查了二次函数与坐标轴交点问题,转化为一元二次方程根的判别式是解题的关键.
5.半径相等的圆的内接正三角形、正方形、正六边形的边长之比为( )
A.1: : B. : :1C.3:2:1D.1:2:3
【答案】B
【解析】
【分析】设圆的半径为R,分别画出圆的内接正三角形、正方形、正六边形,根据锐角三角函数的定义,等腰直角三角形的性质和等边三角形的性质,求出边长即可.
故选:C.
【点睛】考查了切线的性质和正方形的判定、性质,解题关键是理解和掌握切线的性质.
7.如图, 是半圆 的直径, , 是 上两点,连接 , 并延长交于点 ,连接 , ,如果 ,那么 的度数为( )
A B. C. D.
2022-2023学年度上期九年级月考(二)数学考试试卷

2022-2023学年度上期九年级月考(二)考试试卷数 学一、选择题(本大题共10小题,每小题3分,共30分)1.在Rt △ABC 中,∠C=90°,BC=3,AB=5,则sinA 的值为( ) A.35 B.45 C.34 D.以上都不对 2.在Rt △ABC 中,∠C =90°,cos A =35,那么tan B =( ) A .35B .45C .43D .343.在△ABC 中,已知∠A 、∠B 都是锐角,|sinA ﹣12|+(1﹣tanB)2=0,则∠C 度数为( )A.75°B.90°C.105°D.120°4.一个不透明的口袋中,装有5个红球,2个黄球,1个白球,这些球除颜色外其余都相同,从口袋中随机摸一个球,则摸到红球的概率为( ) A .18B .38C .58D .345.如图,在4×4正方形网格中,黑色部分的图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是( ) A .B .C .D .6.抛物线22(3)1y x =++的顶点坐标是( )A .()3,1B .()3,1-C .()3,1-D .()3,1--7.二次函数y=3x 2的图象向左平移2个单位,得到新的图象的二次函数表达式是( )A.B.C.D.8.已知点(-2,y1),(0,y2),(1,y3)都在函数2y x=的图象上,则( )A.y2>y3>y1B.y1>y3>y2C.y3>y2>y1D.y2>y1>y39.在同一坐标系中,一次函数y=ax+2与二次函数y=x2+a的图象可能是()A.B.C.D.10.已知二次函数2y ax bx c=++的图象如图所示,分析下列四个结论:①abc<0;②b2-4ac>0;③20a b-=;④a+b+c<0.其中正确的结论有()A.1个B.2个C.3个D.4个二、填空题(本大题共5小题,每小题3分,共15分)11.如果一个三角形的三个内角之比是1:2:3,则它们所对的边的比是_________.12.如图所示,小明从坡角为30°的斜坡的山底(A)到山顶(B)共走了200米,则山坡的高度BC为_____米.第12题图第14题图13.小明同学平时不用功学习,某次数学测验做选择题时,他有1道题不会做,于是随意选了一个答案(每小题4个项),他选对的概率是__________.14.已知二次函数y=−x2+2x+m的部分图象如图所示,则该图象在y轴的左侧与x轴的交点坐标为________.15.已知抛物线y=-x2+2x+3与x轴交于A、B两点,与y轴交于点C,P是抛物线对称轴l上的一个动点,则PA+PC的最小值是__________.三、解答题(本大题共8小题,共75分)16.(10分)计算:(1)2﹣2﹣2cos30°+con245°﹣|3﹣2|; (2) 6tan230∘-√3sin60∘-2sin45∘17.(9分)一个不透明的口袋中装有三个除所标数字外完全相同的小球,小球上分别标有数字﹣1,0,1.从袋中一次随机摸出两个小球,把上面标注的两个数字分别作为点M的横、纵坐标.(1)请用列表或画树状图的方法列出点M所有可能的坐标;(2)求点M在直线y=﹣x﹣1上的概率.18.(8分)在美化校园的活动中,某兴趣小组用总长为28米的围栏材料,一面靠墙,围成一个矩形花园,墙长8米,设AB的长为x米,矩形花园的面积为S平方米,当x为多少时,S取得最大值,最大值是多少?、19.(9分)已知二次函数的图象以A(-1,4)为顶点,且过点B(2,-5).(1)求该函数的表达式;(2)求该函数图象与坐标轴的交点坐标;20.(9分)如图,在△ABC中,AB=AC,∠BAC=120°,AD⊥AC交BC于点D,AD =3cm,求BC的长.21.(9分)如图,在矩形ABCD中,E是BC边上的点,AE=BC,DF⊥AE,垂足为F,连接DE.(1)求证:AB=DF;(2)若AD=10,AB=6,求tan∠EDF的值.22.(10分)如图,某建筑物BC上有一旗杆AB,小明在F处,由E点观察到旗杆顶部A的仰角为52︒,底部B的仰角为45︒,小明的观测点与地面距离EF为1.6m,(1)若F与BC相距12m,求建筑物BC的高度;(2)若旗杆AB长3.15m,求建筑物BC的高度.(结果精确到0.1m)(参考数据: 4 tan52 1.280︒≈,).23.(11分)如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.(1)求此抛物线的解析式;(2)直接写出点C和点D的坐标;=4S(3)若点P在第一象限内的抛物线上,且S△ABP,求P点坐标.△COE。
2022-2023学年苏科版九年级数学上册第一次月考(1

2022-2023学年苏科版九年级数学上册第一次月考(1.1—2.8)数学测试题(附答案)一、选择题(24分)1.下列方程是一元二次方程的是()A.x2+2y=1B.x3﹣2x=3C.x2+=5D.x2=02.如图,⊙O是△ABC的内切圆,则点O是△ABC的()A.三条边的垂直平分线的交点B.三条角平分线的交点C.三条中线的交点D.三条高的交点3.已知半径为5的圆,其圆心到直线的距离是3,此时直线和圆的位置关系为()A.相离B.相切C.相交D.无法确定4.关于x的一元二次方程x2+ax﹣1=0的根的情况是()A.有两个相等的实数根B.有两个不相等的实数根C.只有一个实数根D.没有实数根5.某厂家2020年1~5月份的口罩产量统计如图所示.设从2月份到4月份,该厂家口罩产量的平均月增长率为x,根据题意可得方程()A.180(1﹣x)2=461B.180(1+x)2=461C.368(1﹣x)2=442D.368(1+x)2=4426.如图,点I是△ABC的内心,∠BIC=130°,则∠BAC=()A.60°B.65°C.70°D.80°7.如图,已知正五边形ABCDE内接于⊙O,连接BD,CE相交于点F,则∠BFC的度数是()A.60°B.70°C.72°D.90°8.如图,“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何.”用几何语言可表述为:CD为⊙O的直径,弦AB⊥CD于E,CE=1寸,AB=10寸,则直径CD的长为()A.12.5寸B.13寸C.25寸D.26寸二、填空题(24分)9.一元二次方程x2=x的根.10.关于x的一元二次方程(m﹣2)x2+3x+m2﹣4=0有一个解是0,则m的值为.11.如图,已知AB是△ABC外接圆的直径,∠A=35°,则∠B的度数是.12.如图,P为⊙O外一点,P A、PB分别切⊙O于A、B,CD切⊙O于点E,分别交P A、PB于点C、D,若P A=5,则△PCD的周长为.13.对于实数a,b,定义运算“*”如下:a*b=(a+b)2﹣(a﹣b)2.若(m﹣2)*(m﹣3)=80,则m=.14.已知三角形的三边分别为3cm、4cm、5cm,则这个三角形内切圆的半径是.15.若关于x的一元二次方程(k﹣1)x2+x+2=0有两个实数根,则k的取值范围是.16.如图,Rt△ABC中,∠ACB=90°,AC=4,BC=6,D为线段AC上一动点,连接BD,过点C作CH⊥BD于H,连接AH,则AH的最小值为.三、解答题(72分)17.用适当方法解下列方程:(1)x2﹣25=0;(2)x2﹣4x﹣3=0.(配方法)18.如图,在平面直角坐标系中,A(0,4)、B(4,4)、C(6,2).(1)在图中画出经过A、B、C三点的圆弧所在圆的圆心M的位置;(2)点M的坐标为;⊙M的半径为;(3)点D(5,﹣2)与⊙M的位置关系是点D在⊙M;(4)若画出该圆弧所在圆,则在整个平面直角坐标系网格中该圆共经过个格点.19.已知关于x的一元二次方程(k+1)x2﹣3x﹣k2﹣2=0有一个根为﹣1,求k的值及方程的另一个根.20.如图,已知:AC、BD是⊙O的两条弦,且AC=BD,求证:AB=CD.21.已知关于x的一元二次方程x2﹣(2m+3)x+m2+2=0.(1)若方程有实数根,求实数m的取值范围;(2)若方程两实数根分别为x1、x2,且满足x12+x22=31+|x1x2|,求实数m的值.22.如图,已知AB是⊙O的直径,C是⊙O上的点,点D在AB的延长线上,∠BCD=∠BAC.(1)求证:CD是⊙O的切线;(2)若∠D=30°,BD=2,求图中阴影部分的面积.23.如图,四边形ABCD是正方形,以边AB为直径作⊙O,点E在BC边上,连结AE交⊙O于点F,连结BF并延长交CD于点G.(1)求证:△ABE≌△BCG;(2)若∠AEB=50°,OA=3,求劣弧BF的长.(结果保留π)24.某商场销售一批鞋子,平均每天可售出20双,每双盈利50元.为了扩大销售,增加盈利,商场决定采取降价措施,调查发现,每双鞋子每降价1元,商场平均每天可多售出2双.(1)若每双鞋子降价5元,商场平均每天可售出多少双鞋子?(2)若商场每天要盈利1600元,且让顾客尽可能多得实惠,每双鞋子应降价多少元?25.解某些高次方程或具有一定结构特点方程时,我们可以通过整体换元的方法,把方程转化为一元二次方程进行求解,从而达到降次或变复杂为简单的目的.例如:解方程(x2﹣3)2﹣5(3﹣x2)+2=0,如果设x2﹣3=y,∵x2﹣3=y,∴3﹣x2=﹣y,用y表示x后代入(x2﹣3)2﹣5(3﹣x2)+2=0得:y2+5y+2=0.应用:请用换元法解下列各题:(1)已知(x2+y2+1)(x2+y2+3)=8,求x2+y2的值;(2)解方程:;(3)已知a2+ab﹣b2=0(ab≠0),求的值.26.【特例感知】(1)如图①,∠ABC是⊙O的圆周角,BC为直径,BD平分∠ABC交⊙O于点D,CD =5,BD=12,则点D到直线BC的距离为,点D到直线AB的距离为.【类比迁移】(2)如图②,∠ABC是⊙O的圆周角,BC为⊙O的弦,BD平分∠ABC交⊙O于点D,过点D作DE⊥BC,垂足为E,探索线段AB、BE、BC之间的数量关系,并说明理由.【问题解决】(3)如图③,四边形ABCD为⊙O的内接四边形,∠ABC=90°,BD平分∠ABC,BD =,AB=12,则△ABC的内心与外心之间的距离为.参考答案一、选择题(24分)1.解:A、x2+2y=1是二元二次方程,故A错误;B、x3﹣2x=3是一元三次方程,故B错误;C、x2+=5是分式方程,故C错误;D、x2=0是一元二次方程,故D正确;故选:D.2.解:∵⊙O是△ABC的内切圆,则点O到三边的距离相等,∴点O是△ABC的三条角平分线的交点;故选:B.3.解:半径r=5,圆心到直线的距离d=3,∵5>3,即r>d,∴直线和圆相交,故选:C.4.解:Δ=a2﹣4×1×(﹣1)=a2+4.∵a2≥0,∴a2+4>0,即Δ>0,∴方程x2+ax﹣1=0有两个不相等的实数根.故选:B.5.解:从2月份到4月份,该厂家口罩产量的平均月增长率为x,根据题意可得方程:180(1+x)2=461,故选:B.6.解:∵点I是△ABC的内心,∴∠ABC=2∠IBC,∠ACB=2∠ICB,∵∠BIC=130°,∴∠IBC+∠ICB=180°﹣∠CIB=50°,∴∠ABC+∠ACB=2×50°=100°,∴∠BAC=180°﹣(∠ACB+∠ABC)=80°.故选:D.7.解:如图所示:∵五边形ABCDE为正五边形,∴BC=CD=DE,∠BCD=∠CDE=108°,∴∠CBD=∠CDB=∠CED=∠DCE==36°,∴∠BFC=∠BDC+∠DCE=72°.故选:C.8.解:设直径CD的长为2x,则半径OC=x,∵CD为⊙O的直径,弦AB⊥CD于E,AB=10寸,∴AE=BE=AB=×10=5寸,连接OA,则OA=x寸,根据勾股定理得x2=52+(x﹣1)2,解得x=13,CD=2x=2×13=26(寸).故选:D.二、填空题(24分)9.解:由原方程得x2﹣x=0,整理得x(x﹣1)=0,则x=0或x﹣1=0,解得x1=0,x2=1.故答案是:x1=0,x2=1.10.解:把x=0代入方程(m﹣2)x2+3x+m2﹣4=0中,得m2﹣4=0,解得m=﹣2或2,当m=2时,原方程二次项系数m﹣2=0,舍去,故答案是:﹣2.11.解:∵AB是△ABC外接圆的直径,∴∠ACB=90°,∴∠B=90°﹣∠A=90°﹣35°=55°.故答案为55°.12.解:∵P A、PB切⊙O于A、B,∴P A=PB=5;同理,可得:EC=CA,DE=DB;∴△PDC的周长=PC+CE+DE+DP=PC+AC+PD+DB=P A+PB=2P A=10.即△PCD的周长是10.13.解:由题意,得(m﹣2+m﹣3)2﹣(m﹣2﹣m+3)2=80,即(2m﹣5)2﹣1=80,(2m﹣5)2=81,2m﹣5=±9,解得m=7或﹣2.故答案为:7或﹣2.14.解:∵32+42=52,∴这个三角形为直角三角形,∴这个三角形内切圆的半径==1.故答案为1.15.解:根据题意得k﹣1≠0且Δ=12﹣4(k﹣1)×2≥0,解得k≤且k≠1.故答案为k≤且k≠1.16.解:∵∠CHB=90°,BC是定值,∴H点是在以BC为直径的半圆上运动(不包括B点和C点),连接HO,则HO=BC=3.∵∠ACB=90°,AC=4,BC=6,∴AO===5,当A、H、O三点共线时,AH最短,此时AH=AO﹣HO=5﹣3=2.故答案为:2.三、解答题(72分)17.解:(1)移项得:x2=25,两边开方得:x=±5,解得:x1=5,x2=﹣5;(2)移项得到x2﹣4x=3,配方得:(x﹣2)2=7,∴x﹣2=或x﹣2=﹣,解得:x1=2+,x2=2﹣.18.解:(1)如图,点M即为所求.(2)M(2,0),MA= .故答案为:(2,0),2.(3)点D(5﹣2)在⊙M内部.故答案为:内部.(4)如图,满足条件的点有8个.故答案为:8.19.解:将x=﹣1代入(k+1)x2﹣3x﹣k2﹣2=0得,k+1+3﹣k2﹣2=0,整理得k2﹣k﹣2=0,∴k=2或﹣1,∵k+1≠0,∴k=2,∴该方程为3x2﹣3x﹣6=0,设另外一根为x=m,由根与系数的关系可知:﹣m=﹣2,∴m=2,∴k的值2,方程的另一个根为2.20.证明:∵AC=BD,∴=,∴﹣=﹣,∴=,∴AB=CD.21.解:(1)根据题意得(2m+3)2﹣4(m2+2)≥0,解得m≥﹣;(2)根据题意x1+x2=2m+3,x1x2=m2+2,因为x1x2=m2+2>0,所以x12+x22=31+x1x2,即(x1+x2)2﹣3x1x2﹣31=0,所以(2m+3)2﹣3(m2+2)﹣31=0,整理得m2+12m﹣28=0,解得m1=﹣14,m2=2,而m≥﹣;所以m=2.22.解:(1)连接OC,∵OA=OC,∴∠BAC=∠OCA,∵∠BCD=∠BAC,∴∠BCD=∠OCA,∵AB是直径,∴∠ACB=90°,∴∠OCA+∠OCB=∠BCD+∠OCB=90°∴∠OCD=90°∵OC是半径,∴CD是⊙O的切线(2)设⊙O的半径为r,∴AB=2r,∵∠D=30°,∠OCD=90°,∴OD=2r,∠COB=60°∴r+2=2r,∴r=2,∠AOC=120°∴BC=2,∴由勾股定理可知:AC=2易求S△AOC=×2×1=S扇形OAC==∴阴影部分面积为﹣23.(1)证明:∵四边形ABCD是正方形,AB为⊙O的直径,∴∠ABE=∠BCG=∠AFB=90°,∴∠BAF+∠ABF=90°,∠ABF+∠EBF=90°,∴∠EBF=∠BAF,在△ABE与△BCG中,,∴△ABE≌△BCG(ASA);(2)解:连接OF,∵∠ABE=∠AFB=90°,∠AEB=50°,∴∠BAE=90°﹣50°=40°,∴∠BOF=2∠BAE=80°,∵OA=3,∴的长=.24.解:(1)由题意得:商场平均每天可售出的鞋子数量为:20+2×5=30(双);答:若每双鞋子降价5元,商场平均每天可售出30双鞋子;(2)设每双鞋子应降价x元,根据题意,得(50﹣x)(20+2x)=1600,整理,得x2﹣40x+300=0,解得:x1=10,x2=30,∵让顾客尽可能多得实惠,∴x应取30元.答:鞋子的单价应降30元.25.解:(1)设x2+y2=m,原方程化为:(m+1)(m+3)=8,m2+4m﹣5=0,b2﹣4ac=36>0,∴方程有两个不想等的实数根,解得m1=﹣5,m2=1,∵x2+y2≥0,∴x2+y2=1.(2)设x+=m,原方程化为:m2+m﹣2=0,(m+2)(m﹣1)=0,m+2=0或m﹣1=0,m1=﹣2或m2=1.∴x+=﹣2,x2+2x+1=0,(x+1)2=0,x1=x2=﹣1,经检验是原方程的解,∴x=﹣1.x+=1,x2+x+1=0,b2﹣4ac<0,∴此方程无解.综上所述,x=﹣1.(3)原方程化为:+﹣1=0,+﹣1=0,∴=,∴=,=.26.解:(1)如图,过点D作DF⊥BA,交BA的延长线于点F,作DE⊥BC于点E,∵BD平分∠ABC,DF⊥AB,DE⊥BC,∴DF=DE,∵BC是直径,∴∠BDC=90°,∴BC==5,在△BCD中,BC•DE=BD•DC,∴DE=,∴DF=DE=;(2)AB+BC=2BE,理由如下:如图,过点D作DF⊥BA,交BA的延长线于点F,连接AD,DC,∵BD平分∠ABC,DE⊥BC,DF⊥BA,∴DF=DE,∠DFB=∠DEB=90°,∴∠DFB=90°,∠DEB=90°,∴∠ABC+∠EDF=180°,又∵∠ABC+∠ADC=180°,∴∠ADC=∠EDF,∴∠FDA=∠CDE,∵∠DF A=∠DEC=90°,∴△DF A≌△DEC(ASA),∴AF=CE,∵BD=BD,DF=DE,∴Rt△BDF≌Rt△BDE(HL),∴BF=BE,∴AB+BC=BF﹣AF+BE+CE=2BE;(3)如图,过点D作DF⊥BA,交BA的延长线于点F,DE⊥BC,交BC于点E,连接AC,作△ABC的内切圆,圆心为M,N为切点,连接MN,OM,由(1)(2)可知,四边形BEDF是正方形,BD是对角线,∵BD=14,正方形BEDF的边长为:=14,由(2)可知BC=2BE﹣AB=16,∴AC==20,由切线长定理可知AN=,∴ON==2,设内切圆的半径为r,则,解得r=4,即MN=4,在Rt△OMN中,OM=.。
苏科版2022-2023学年第一学期九年级数学第二次月考测试题(附答案)

2022-2023学年第一学期九年级数学第二次月考测试题(附答案)一、选择题1.下列方程中,关于x的一元二次方程是()A.x2+2x=x2﹣1B.ax2+bx+c=0C.3(x+1)2=2(x+1)D.+﹣2=02.用配方法解方程x2﹣2x﹣5=0时,原方程应变形为()A.(x+1)2=6B.(x+2)2=9C.(x﹣1)2=6D.(x﹣2)2=9 3.如图,已知A,B,C为⊙O上三点,若∠AOB=80°,则∠ACB度数为()A.80°B.70°C.60°D.40°4.如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC的度数为()A.70°B.90°C.110°D.120°5.若关于x的一元二次方程x2+x+m=0有实数根,则m的最大整数值是()A.﹣1B.0C.1D.26.如图,AB是⊙O的直径,C、D是⊙O上一点,∠CDB=25°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于()A.35°B.40°C.45°D.50°7.如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,4),(5,4),(1,﹣2),则以A,B,C为顶点的三角形外接圆的圆心坐标是()A.(2,3)B.(3,2)C.(3,1)D.(1,3)8.某超市一月份的营业额为200万元,已知第一季度的总营业额共1000万元,如果平均每月增长率为x,则由题意列方程应为()A.200(1+x)2=1000B.200+200×2x=1000C.200+200×3x=1000D.200[1+(1+x)+(1+x)2]=1000二、填空题9.方程x2=2x的解是.10.若a是方程x2﹣2x﹣2=0的一个根,则2a2﹣4a=.11.写出一个以和﹣3为根,且二次项系数为1的一元二次方程为.12.如图,△ABC内接于⊙O,∠BAC=30°,BC=2,则⊙O的直径等于.13.在⊙O中,直径AB=4,弦CD⊥AB于P,OP=,则弦CD的长为.14.如图,在△ABC中,AB=AC,∠B=30°,以点A为圆心,以3cm为半径作⊙A,当AB=cm时,BC与⊙A相切.15.若关于x的一元二次方程x2﹣(k+2)x+2k=0的两根的和与积相等,则k的值为.16.如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在直线AB 上,且与点O的距离为6cm.如果⊙P以1cm∕s的速度,沿由A向B的方向移动,那么秒钟后⊙P与直线CD相切.三、解答题17.用适当的方法解下列方程:(1)(2x﹣1)2﹣25=0;(2)x2﹣2x﹣1=0(配方法);(3)2(x2﹣2)=7x;(4)3(x﹣2)2=x(x﹣2).18.已知:关于x的方程x2﹣6x+m﹣5=0的一个根是﹣1,求m值及另一根.19.已知一元二次方程x2﹣4x+k=0有两个不相等的实数根(1)求k的取值范围;(2)如果k是符合条件的最大整数,且一元二次方程x2﹣4x+k=0与x2+mx﹣1=0有一个相同的根,求此时m的值.20.如图,CD是⊙O的直径,∠EOD=84°,AE交⊙O于点B,且AB=OC,求∠A的度数.21.如图,AB是⊙O的直径,CE是⊙O上的两点,CD⊥AB于D,交BE于F,,求证:BF=CF.22.如图,在△ABC中,∠CAB=90°,∠CBA=50°,以AB为直径作⊙O交BC于点D,点E在边AC上,且满足ED=EA.(1)求∠DOA的度数;(2)求证:直线ED与⊙O相切.23.如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.(1)若∠CBD=39°,求∠BAD的度数;(2)求证:∠1=∠2.24.文通小商店经销甲、乙两种商品,现有如下信息:信息1:甲乙两种商品的进货单价之和是3元.信息2:甲商品零售单价比进货单价多2元,乙商品零售单价比进货单价的2倍少1元.信息3:按零售单价购买甲商品3件和乙商品2件,共付了15元.请根据以上信息,解答请根据以上信息,解答下列问题:(1)求甲、乙两种商品的零售单价;(2)该商店平均每天卖出甲商品500件和乙商品400件.经调查发现,甲种商品零售单价每降0.1元,甲种商品每天可多销售100件.商店决定把甲种商品的零售单价下降m (m>0)元.在不考虑其他因素的条件下,当m为多少时,商店每天销售甲、乙两种商品获取的总利润为1900元?25.实践操作:如图,△ABC是直角三角形,∠ABC=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法).(1)作∠BCA的平分线,交AB于点O;(2)以O为圆心,OB为半径作圆.综合运用:在你所作的图中,(1)AC与⊙O的位置关系是(直接写出答案)(2)若BC=6,AB=8,求⊙O的半径.26.阅读理解:(1)【学习心得】小刚同学在学习完“圆”这一章内容后,感觉到一些几何问题,如果添加辅助圆,运用圆的知识解决,可以使问题变得非常容易.例如:如图1,在△ABC中,AB=AC,∠BAC=46°,D是△ABC外一点,且AD=AC,求∠BDC的度数,若以点A为圆心,AB为半径作辅助圆⊙A,则点C、D必在⊙A上,∠BAC是⊙A的圆心角,而∠BDC是圆周角,从而可容易得到∠BDC=°.(2)【问题解决】如图2,在四边形ABCD中,∠BAD=∠BCD=90°,∠BDC=28°,求∠BAC的度数.小刚同学认为用添加辅助圆的方法,可以使问题快速解决,他是这样思考的:△ABD的外接圆就是以BD的中点为圆心,BD长为半径的圆;△BCD的外接圆也是以BD的中点为圆心,BD长为半径的圆.这样A、B、C、D四点在同一个圆上,进而可以利用圆周角的性质求出∠BAC的度数,请运用小刚的思路解决这个问题.(3)【问题拓展】如图3,在△ABC的三条高AD、BE、CF相交于点H,求证:∠EFC=∠DFC.参考答案一、选择题1.解:A、x2+2x=x2﹣1是一元一次方程,故A错误;B、ax2+bx+c=0,a=0时是一元一次方程,故B错误;C、3(x+1)2=2(x+1)是一元二次方程,故C正确;D、+﹣2=0是分式方程,故D错误;故选:C.2.解:由原方程移项,得x2﹣2x=5,方程的两边同时加上一次项系数﹣2的一半的平方1,得x2﹣2x+1=6∴(x﹣1)2=6.故选:C.3.解:∵∠AOB=80°,∴∠ACB=∠AOB=40°,故选:D.4.解:∵∠A=50°,∴∠BOC=2∠A=100°,∵∠B=30°,∠BOC=∠B+∠BDC,∴∠BDC=∠BOC﹣∠B=100°﹣30°=70°,∴∠ADC=180°﹣∠BDC=110°,故选:C.5.解:由题意知,Δ=12﹣4m≥0,∴m≤,∴m的最大整数值是0.故选:B.6.解:连接OC,∵CE为圆O的切线,∴OC⊥CE,∴∠COE=90°,∵∠CDB与∠BAC都对,且∠CDB=25°,∴∠BAC=∠CDB=25°,∵OA=OC,∴∠OAC=∠OCA=25°,∵∠COE为△AOC的外角,∴∠COE=50°,则∠E=40°.故选:B.7.解:根据垂径定理的推论,则作弦AB、AC的垂直平分线,交点O1即为圆心,且坐标是(3,1).故选:C.8.解:∵一月份的营业额为200万元,平均每月增长率为x,∴二月份的营业额为200×(1+x),∴三月份的营业额为200×(1+x)×(1+x)=200×(1+x)2,∴可列方程为200+200×(1+x)+200×(1+x)2=1000,即200[1+(1+x)+(1+x)2]=1000.故选:D.二、填空题9.解:∵x2﹣2x=0,∴x(x﹣2)=0,∴x=0或x﹣2=0,∴x1=0,x2=2.故答案为x1=0,x2=2.10.解:把x=a代入方程得a2﹣2a﹣2=0,则a2﹣2a=2,所以2a2﹣4a=2(a2﹣2a)=2×2=4.故答案为4.11.解:∵+(﹣3)=﹣3,×(﹣3)=﹣3,∴以和﹣3为根,且二次项系数为1的一元二次方程为x2﹣(﹣3)x﹣3=0.故答案为:x2﹣(﹣3)x﹣3=0.12.解:作直径BD,连接CD,由圆周角定理得,∠D=∠BAC=30°,∠BCD=90°,∴BD=2BC=4,故答案为:4.13.解:连接OC,∵在⊙O中,直径AB=4,∴OA=OC=AB=2,∴弦CD⊥AB于P,OP=,∴CP==1,∴CD=2CP=2.故答案为:2.14.解:如图,过点A作AD⊥BC于点D.∵AB=AC,∠B=30°,∴AD=AB,即AB=2AD.又∵BC与⊙A相切,∴AD就是圆A的半径,∴AD=3cm,则AB=2AD=6cm.故答案是:6.15.解:∵关于x的一元二次方程x2﹣(k+2)x+2k=0的两根的和与积相等,∴x1+x2=x1x2k+2=2k,解得:k=2.故答案为:2.16.解:当点P在射线OA时⊙P与CD相切,如图,过P作PE⊥CD与E,∴PE=1cm,∵∠AOC=30°,∴OP=2PE=2cm,∴⊙P的圆心在直线AB上向右移动了(6﹣2)cm后与CD相切,∴⊙P移动所用的时间==4(秒);当点P在射线OB时⊙P与CD相切,如图,过P作PE⊥CD与F,∴PF=1cm,∵∠AOC=∠DOB=30°,∴OP=2PF=2cm,∴⊙P的圆心在直线AB上向右移动了(6+2)cm后与CD相切,∴⊙P移动所用的时间==8(秒).故答案为4或8.三、解答题17.解:(1)(2x﹣1)2﹣25=0,(2x﹣1)2=25,2x﹣1=±5,2x﹣1=5或2x﹣1=﹣5,x1=3,x2=﹣2;(2)x2﹣2x﹣1=0,x2﹣2x=1,x2﹣2x+1=1+1,(x﹣1)2=2,x﹣1=±,x﹣1=或x﹣1=﹣,x1=1+,x2=1﹣;(3)2(x2﹣2)=7x,2x2﹣7x﹣4=0,(x﹣4)(2x+1)=0,x﹣4=0或2x+1=0,x1=4,x2=﹣;(4)3(x﹣2)2=x(x﹣2),3(x﹣2)2﹣x(x﹣2)=0,(x﹣2)[3(x﹣2)﹣x]=0,(x﹣2)(3x﹣6﹣x)=0,(x﹣2)(2x﹣6)=0,x﹣2=0或2x﹣6=0,x1=2,x2=3.18.解:设方程的另一个根为n,∵方程x2﹣6x+m﹣5=0的两个根为﹣1和n,∴,解的:.∴m的值为﹣2,方程的另一根是7.19.解:由一元二次方程x2﹣4x+k=0有两个不相等的实数根,得Δ=b2﹣4ac=(﹣4)2﹣4k>0,解得k<4;(2)由k是符合条件的最大整数,且一元二次方程x2﹣4x+k=0,得x2﹣4x+3=0,解得x1=1,x2=3,一元二次方程x2﹣4x+k=0与x2+mx﹣1=0有一个相同的根,当x=1时,把x=1代入x2+mx﹣1=0,得1+m﹣1=0,解得m=0,当x=3时,把x=3代入x2+mx﹣1=0,得9+3m﹣1=0,解得m=﹣,综上所述:如果k是符合条件的最大整数,且一元二次方程x2﹣4x+k=0与x2+mx﹣1=0有一个相同的根,.20.解:连接OB,如图,∵AB=OC,∴AB=BO,∴∠BOC=∠A,∴∠EBO=∠BOC+∠A=2∠A,而OB=OE,得∠E=∠EBO=2∠A,∴∠EOD=∠E+∠A=3∠A,而∠EOD=84°,∴3∠A=84°,∴∠A=28°.21.证明:延长CD交⊙O于点G,连接BC,∵AB是⊙O的直径,CD⊥AB于D∴=,∵=,∴=,∴∠BCF=∠CBF,∴BF=CF.22.(1)解;∵∠DBA=50°,∴∠DOA=2∠DBA=100°,(2)证明:连接OE.在△EAO与△EDO中,,∴△EAO≌△EDO,∴∠EDO=∠EAO,∵∠BAC=90°,∴∠EDO=90°,∴DE与⊙O相切.23.(1)解:∵CB=CD,∴∠CDB=∠CBD=39°,由圆周角定理得,∠CAB=∠CDB=39°,∠CAD=∠CBD=39°,∴∠BAD=39°+39°=78°;(2)证明:∵CE=CB,∴∠CBE=∠CEB,∴∠1+∠CDB=∠2+∠CAB,∵∠BAC=∠BDC=∠CBD,∴∠1=∠2.24.解:(1)设甲商品的零售单价为x元,乙商品的零售单价为y元,则甲商品的进价为(x﹣2)元,乙商品的进价为,由题意得,,解得:.答:甲商品的零售单价为3元,乙商品的零售单价为3元;(2)把甲种商品的零售单价下降m,可多卖甲商品100×件,则利润为:(500+100×)×(3﹣m﹣1)+400(3﹣2)=1900,解得:m1=0.5,m2=1.答:当m为0.5或1时,商店每天销售甲、乙两种商品获取的总利润为1900元.25.解:实践操作:(1)如图所示:CO即为所求;(2)如图所示:⊙O即为所求;综合运用:(1)AC与⊙O的位置关系是:相切;故答案为:相切;(2)过点O连接AC与⊙O的切点E,∵BC=6,AB=8,∠ABC=90°,∴AC==10,由题意可得出:CB⊙O的切点为B,则CE=CB=6,设BO=x,则EO=x,AO=6﹣x,AE=10﹣6=4,∴在Rt△AOE中,AE2+EO2=AO2,即42+x2=(8﹣x)2,解得:x=3,∴⊙O的半径为:3.26.解:(1)如图1,∵AB=AC,AD=AC,∴以点A为圆心,点B、C、D必在⊙A上,∵∠BAC是⊙A的圆心角,而∠BDC是圆周角,∴∠BDC=∠BAC=23°,故答案是:23°;(2)取BD中点O,连接AO、CO,在Rt△BAO中,AO=BD,同理:CO=BD,∴AO=DO=CO=BO,∴点A、B、C、D在以O为圆心的同一个圆上,∴∠BAC=∠BDC=28°;(3)∵CF⊥AB,BE⊥AC,∴点A、F、H、E在以AH为直径的同一个圆上,∴∠EFC=∠DAC,同理:点B、D、H、E在以BH为直径的同一个圆上,∠DFC=∠CBE,又∵∠DAC=∠EBC,∴∠EFC=∠DFC.。
苏州市姑苏区南环实验中学校2022-2023学年九年级上学期12月月考化学试题(含解析)

苏州市姑苏区南环实验中学校2022-2023学年九年级上学期12月月考化学试题可能用到的相对原子质量:H-1 C-12 O-16 K-39 I-127 Fe-56选择题(共40分)单项选择题(包括25题,每题2分,共40分。
每题只有一个选项符合题意.)1. 2018年“世界环境日”中国的主题是“美丽中国,我是行动者”。
每位公民都应当具有节能环保意识,成为建设“美丽中国”的行动者。
下列做法与之相违背的是()A. 离开房间随手关灯B. 布袋购物重复利用C. 生活垃圾分类处理D. 燃放烟花庆祝节日2. 下列工艺制作过程包含化学变化的是()A. 烧制陶瓷B. 裁剪窗花C. 雕刻玉石D. 编织竹篮3. 下列化学用语既能表示一种元素,又能表示一个原子,还能表示一种物质的是A. FeB. H2C. HD. CO4. 人体缺乏下列哪种元素会引起甲状腺疾病A. 钙B. 铁C. 锌D. 碘5. 同种元素在不同的物质中可能会表现出不同的化合价,O2、H2O和H2O2三种物质中氧元素的化合价依次为A. -2、0、-1B. 0、-2、-1C. 0、-1、-2D. -1、0、-26. 下列化学用语书写不.正确的是A. 2个钙离子:2Ca2+B. 钠原子的结构示意图:C. 氯化铜:CuClD. 氧化镁中镁元素显+2价:7. 下列有关物质的性质与用途不.具有对应关系的是A. 氮气性质稳定,可用作灯泡填充气B. 铝合金能导电,可用作飞机机身材料C. 干冰升华吸热,可用于冷藏食品D. 金刚石质地坚硬,可用于切割玻璃8. 下列关于二氧化碳的说法正确的是A. 光合作用需要二氧化碳,说明人类生活离不开二氧化碳B. 用排水法能收集到二氧化碳,说明二氧化碳不溶于水C. 空气中二氧化碳含量达6%以上会致人死亡,说明二氧化碳有毒D. 水中通入二氧化碳后仍为无色,说明二氧化碳与水未发生反应9. 我国化学家张青莲精确测定了铈(Ce)等元素的相对原子质量数值。
江苏省苏州市苏州工业园区星湾学校2023-2024学年九年级上册12月月考数学试题(含解析)

A .4B .108.二次函数中,自变量0()20y ax bx c a =++≠x L 2-1-yL4.5m -2m -0.5m -A .二、填空题(本大题共11.若是关于12.若方程13.如图,四边形322x =x 2ax bx ++ABCO16.如图,在网格中,每个小正方形的边长均为则.17.如图,在中,作交于点则折叠后所得到的四边形18.如图,二次函数点B 的横坐标为2,二次函数图象的对称轴是直线的两根为三、解答题(本大题共10小题,共19.计算:20.解方程:.21.如图,在6×6的正方形网格中,sin ABC ∠=Rt ABC △D DE BC ⊥AB E AEDF 2y ax bx =+2ax bx c kx ++=13x =-114sin6023-⎛⎫︒++- ⎪⎝⎭2890x x -+=(1)在图1中以线段AB 为边画一个,使其与(2)在图2中画一个,使其与相似,且面积为22.已知关于的方程.(1)求证:无论取何值,这个方程总有实数根;(2)若等腰三角形的一边长,另两边、恰好是这个方程的两个根,求(1)求线段的长;(2)求的值.24.如图,在中,分.(1)判断与的位置关系,并说明理由;(2)若,,求25.根据素材解决问题.ABD △ABC EFG ABC x ()2121402x k x k ⎛⎫-++-= ⎪⎝⎭k ABC 4a =b c CD cos BDE ∠ABC CAD ∠BC O 10AC =8DC =.(1)求抛物线的解析式;(2)是线段上的一个动点,过点坐标;(3)在轴上是否存在一点,使得E AC y P参考答案与解析1.C【分析】根据特殊角的三角函数值进行解答即可.3∵,∴.∵,,∴.在中,故最小值为90APB ∠=︒132PD AB ==3BD =4BC =22345CD =+=PCD PC DC ≥PC 53-∵正三角形顶点离圆柱边缘不少于∴当正三角形边长最大时,则∵半径为10cm ,∴cm ,5OB =,又点是的中点,,221310,AC BC =+= AC BC ∴= D AB CD AB ∴⊥②时,点在的延长线上...又,90EAF ∠=︒F BC 30EFA ∴∠=︒EFD EFA ∴∠=∠,ED BF EA AF ⊥⊥(2)如图,△EFG即为所求.【点睛】本题考查作图-相似变换,想解决问题,属于中考常考题型.22.(1)见解析10(2)【分析】(1)运用根的判别式,根与系数的关系,平方数的非负性进行判断即可求证;∵是的平分线,∴,又∵,AB CAD ∠BAD BAO ∠=∠OB OA =如图,过点作于点,,P PG AC ⊥60OAP OAC ∠︒∠+= 160,2PAG AG PA ︒∴∠==221322PG PA PA ⎛⎫∴=-= ⎪⎝⎭2224,42PA n AC =+=+由图可知,,一次函数图象的∴当直线经过点时,时,,此时图象的()()2,2,2,2C D - 41y ax a =-+()2,2C -122412a a a =-+⇒=-,当点运动到点处时,设,将代入,得,解得:,,,在中,,当点运动到点处时,22622,1832BC BD CD AD ∴=-=-===∴P B 2t =()242S a t =-+()2,6426a +=1a =()2242818S t t t ∴=-+=-+32242AC AD CD ∴=+=+=Rt ABC △()22224226AB AC BC =+=+=∴P A 268t =+=。
江苏省苏州市2022-2023学年第一学期初三数学期末试卷及参考答案

2022~2023学年第一学期初三期末试卷数 学本卷由选择题、填空题和解答题组成,共27题,满分130分,调研时间120分钟. 注意事项:1.答题前,考生务必将学校、班级、姓名、调研号等信息填写在答题卡相应的位置上. 2.答选择题必须用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,请用橡皮擦干净后,再选涂其他答案;答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡指定的位置上,不在答题区域内的答案一律无效;如需作图,先用2B 铅笔画出图形,再用0.5毫米黑色墨水签字笔描黑,不得用其他笔答题.3.考生答题必须答在答题卡相应的位置上,答在试卷和草稿纸上一律无效.一、选择题(本大题共8小题,每小题3分,共24分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将答案填涂在答题卡相应位置.......上) 1.有一组数据:11,11,12,15,16,则这组数据的中位数是A .11B .12C .15D .162.方程24x =的根是AB .2C或D .2或2-3.已知⊙O 的半径是4,点A 到圆心O 的距离为3,则点A 与⊙O 的位置关系是A .点A 在圆内B .点A 在圆上C .点A 在圆外D .无法确定4.若抛物线y =x 2+ax +2的对称轴是y 轴,则a 的值是A .2-B .1-C .0D .25.如图,点A ,B ,C 在⊙O 上,若∠AOB =100°,则∠ACB 的度数为A .40︒B .50︒C .80︒D .100︒6.我们可用“斜尺”测量管道的内径(如图),若玻璃管的内径DE 正对“30”刻度线,已知AB 长为5mm ,DE ∥AB ,则玻璃管内径DE 的长度等于 A .2.5mm B .3mm C .3.5mm D .4mm(第5题)(第6题)0EDCBA504030OCBA7.如图,C 为⊙O 上一点,AB 是⊙O 的直径,AB =4,∠ABC =30°,现将△ABC 绕点B 按顺时针方向旋转30°后得到△A BC '',BC '交⊙O 于点D ,则图中阴影部分的面积为 A .3πB.3πC .23π D.23π+8.如图,已知抛物线2y ax c =+与直线y kx m =+交于1(3)A y -,,2(1)B y ,两点,则关于x 的不等式2ax kx c ++≥m 的解集是 A .3x -≤或1x ≥ B .1x -≤或3x ≥ C .31x -≤≤ D .13x -≤≤二、填空题(本大题共8小题,每小题3分,共24分.不需写出解答过程,请把答案直接填写在答题卡相应位置.......上) 9.某体育用品专卖店在一段时间内销售了20双男生运动鞋,各种尺码运动鞋的销售量如下表.则由这20双运动鞋尺码组成的数据的众数是 ▲ cm .10 11.一只蚂蚁在一块黑白两色的正六边形地砖上任意爬行,并随机停留在地砖上某处,则蚂蚁停留在黑色区域的概率是 ▲ .12.已知1x ,2x 是一元二次方程2560x x +-=的两个根,则1211x x +的值为 ▲ . BA(第8题)(第7题)CBA(第10题)(第11题)13.如图,MN 与⊙O 相切于点A ,AB 是⊙O 的弦,且AB =1,30BAN ∠=︒,则⊙O 的半径长为 ▲ .14.如图,四边形ABCD 中,点E 在AD 上,且EC ∥AB ,EB ∥DC ,已知△ABE 的面积为3,△ECD 的面积为1,则△BCE 的面积为 ▲ .15.在△ABC 中,AB =2,BC,则∠A 度数的最大值为 ▲ °.16.已知抛物线2y x bx c =++过(10)A -,,(0)B m ,两点.若2<m <3,则下列四个结论中正确的是 ▲ .(请将所有正确结论的序号都填写到横线上): ①b >0; ②0c <;③点11()M x y ,,22()N x y ,在抛物线上,若x 1<x 2,x 1+x 2=1,则y 1>y 2; ④关于x 的一元二次方程220x bx c +++=必有两个不相等的实数根.三、解答题(本大题共11小题,共82分.请在答题卡指定区域内........作答,解答时应写出文字说明、证明过程或演算步骤) 17.(本题满分5分)计算:2cos30tan 60sin 45︒-︒+︒.18.(本题满分5分)解方程:2450x x --=.ANME DCBA(第13题)(第14题)为落实“双减”政策,某中学在课后服务时间开设了四个兴趣小组,分别为A :机器人,B :交响乐,C :油画,D :古典舞.为了解学生的报名情况(每名学生只报一个兴趣小组),现随机抽取部分学生进行调查,并根据调查结果绘制了如下两幅不完整的统计图.请根据以上图文信息回答下列问题: (1)此次调查共抽取 ▲ 名学生; (2)请将条形统计图补充完整;(3)扇形统计图中,项目A 所对应的扇形圆心角的度数为 ▲ °.20.(本题满分6分)为深入学习贯彻党的二十大精神,我市某中学决定举办“青春心向党,奋进新征程”主题演讲比赛.该校九年级有二男二女共4名学生报名参加演讲比赛.(1)若从报名的4名学生中随机选1名,则所选的这名学生是女生的概率是 ▲ ; (2)若从报名的4名学生中随机选2名,用树状图或表格列出所有可能的情况,并求出这2名学生都是男生的概率.21.(本题满分6分)如图,测绘飞机在同一高度沿直线BC 由B 向C 飞行,且飞行路线经过观测目标A 的正上方.在第一观测点B 处测得目标A 的俯角为60°,航行1000米后在第二观测点C 处测得目标A 的俯角为75°.求第二观测点C 与目标A 之间的距离.CBA60°75°(第21题)把一根长8米的绳子剪成两段,并把每一段绳子围成一个正方形. (1)要使这两个正方形面积的和等于2平方米,应该怎么剪? (2)这两个正方形面积的和可能等于418平方米吗?请说明理由.23.(本题满分8分)60°的扇形(图中的阴影部分). (1)求这个扇形的半径;(2)若用剪得的扇形纸片围成一个圆锥的侧面,求所围成圆锥的底面圆半径.24.(本题满分8分)已知二次函数244y ax ax =-+的图像与x 轴有唯一公共点(1)求a 的值;(2)当0≤x ≤m 时(0m >),函数的最大值为4,且最小值为0,则实数m 的取值范围是 ▲ .25.(本题满分10分)如图,矩形ABCD 中,AD =3,CD =4,点P 从点A 出发,以每秒1个单位长度的速度在射线AB 上向右运动,运动时间为t 秒,连接DP 交AC 于点Q .(1)求证:DCQ PAQ △∽△;(2)若△ADQ 是以AD 为腰的等腰三角形,求运动时间t 的值.(第25题)如图,以AB 为直径的⊙O 经过△ABC 的顶点C ,AE ,BE 分别平分∠BAC 和∠ABC ,AE 的延长线交BC 于点F ,交⊙O 于点D ,连接BD .(1)求证:CBD BAD ∠=∠; (2)求证:BD =DE ;(3)若AB=BE=BC 的长.27.(本题满分10分)在平面直角坐标系中,O 为坐标原点,直线3y x =-+与x 轴交于点B ,与y 轴交于点C .二次函数y =ax 2+2x +c 的图像过B ,C 两点,且与x 轴交于另一点A ,点M 为线段OB 上的一个动点(不与端点O ,B 重合).(1)求二次函数的表达式;(2)如图①,过点M 作y 轴的平行线l 交BC 于点F ,交二次函数y =ax 2+2x +c 的图像于点E .记CEF △的面积为1S ,BMF △的面积为2S ,当1212S S =时,求点E 的坐标; (3)如图②,连接CM ,过点M 作CM 的垂线1l ,过点B 作BC 的垂线2l ,1l 与2l 交于点G .试探究CG CM 的值是否为定值?若是,请求出CGCM的值;若不是,请说明理由.(第26题)苏州市阳光指标学业水平调研测试初三数学参考答案及评分标准2023.019.25 10.1211.1312.5613.1 1415.45︒16.②③④三、解答题(共11小题,共82分)17.(本题满分5分)················································································ 3分. ························································································· 5分18.(本题满分5分)解:原方程可化为:(5)(1)0x x-+=······························································· 3分∴原方程的解为:15x=,21x=-. ··························································· 5分19.(本题满分6分)解:(1)100;··························································································· 2分(2)图(略); ······················································································· 4分(3)144.····························································································· 6分20.(本题满分6分)解:(1)12; ····························································································· 2分(2)树状图或表格(略); ······································································ 4分2名学生都是男生的概率为16. ································································· 6分答:这两名学生都是男生的概率为16.21.(本题满分6分)解:如图,过点C作CH AB⊥,垂足为H. ····························· 1分CH AB⊥90CHB CHA∴∠=∠=︒.在Rt△CHB中,60B∠=︒,1000BC=CH∴=.······· 3分在Rt△CHA中,∵45A∠=︒,CH=AC∴=··························· 5分答:第二观测点C与目标A之间的距离为 ···································· 6分22.(本题满分8分)解:设剪成的两段绳子长分别为x米,(8)x-米.CHBA60°75°(1)由题意可得:228()()244x x -+=. ····················································· 2分 解得:124x x ==.················································································· 4分 ∴应该剪成两段长度均为4米的绳子,可使得两个正方形的面积和为2平方米. (2)由题意可得:22841()()448x x -+=. ······················································ 5分 解得:11x =-,29x =. ·········································································· 7分 经检验,11x =-,29x =均不符合题意.∴两个正方形的面积和不可能为418平方米. ················································ 8分 23.(本题满分8分)解:(1)连接OA ,OB ,过点O 作OH AB ⊥,垂足为H .由图形的轴对称性可得:30OAB ∠=︒. ············ 1分OA OB =.在等腰三角形OAB中,OA OB =30OAB ∠=︒,OH AB ⊥∴32AH =且H 为AB 中点. ····································································· 3分 ∴23AB AH ==,即扇形ABC 的半径为3. ················································ 4分 (2)设圆锥的底面圆半径为r .603=180180n R l ππ⨯==π扇形. ······································································· 6分 又2r π=π,12r ∴=. ··········································································· 8分 ∴圆锥底面圆的半径为12. 24.(本题满分8分)解:(1)由题意得:2=16160a a -=△. ························································· 2分解得:10a =,21a =. ············································································ 4分 ∵0a ≠,∴1a =. ················································································· 5分 (2)24m ≤≤. ·················································································· 8分 25.(本题满分10分)解:(1)∵矩形ABCD ,∴DC ∥AP . ······························································· 1分 ∴∠CDQ =∠APQ ,∠DCQ =∠P AQ . ·························································· 2分 DCQ PAQ ∴△∽△. ··············································································· 3分 (2)设点P 运动的时间为t 秒.①如图1,若AQ AD =.矩形ABCD ,3AD =,4DC =,90ADC ∠=︒,∴5AC =.AQ AD =,3AD =,3AQ ∴=,CQ =2. ·················································· 4分DCQ PAQ △∽△,DC CQ PA AQ ∴=,即:423t =. ·········································· 5分 解得:6t =. ························································································ 6分②如图2,若AD DQ =.过点D 作DH AC ⊥,垂足为H .DH AC ⊥,90AHD ∴∠=︒,又矩形ABCD ,90ADC ∴∠=︒,∴.AHD ADC ∠=∠ 又∵DAH CAD ∠=∠,ADH ACD ∴△∽△. AH AD AD AC ∴=,335AH ∴=,95AH ∴=.DA DQ =,DH AC ⊥,1825AQ AH ∴==,75CQ ∴=. ····························· 8分又DCQ PAQ △∽△,DC QC PA QA ∴=,∴47/518/5t =. ···································· 9分 解得:727t =. ···················································································· 10分综上所述:6t =或727. 26.(本题满分10分) 解:(1)AE 平分BAC ∠,BAD CAD ∴∠=∠. ················································ 1分DBC DAC ∠=∠. ················································································ 2分CBD BAD ∴∠=∠. ················································································ 3分 (2)BE 平分ABC ∠,ABE CBE ∴∠=∠. ················································ 4分 DBE DBC EBC ∠=∠+∠,DEB BAE EBA ∠=∠+∠.DBE DEB ∴∠=∠. ············ 5分 ∴BD =DE . ··························································································· 6分 (3)解法一:如图①,延长BD , 交AC 的延长线于点G . AB 是直径,=90BDA ∴∠︒,=90GDA ∠︒.在ABD △和AGD △中,∵BDA GDAAD AD BAD GAD ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴ABD AGD △≌△.∴=BD DG ,AB =AG . ················· 7分 在△BDE中,∵BE =90BDA ∠︒,BD DE =,∴=2BD . ····················· 8分 在△ABD 中,∠BDA =90°,AB=,BD=2,由勾股定理可得:4AD =. 在△ABG 中,AB =AG=,=BD DG =2,4AD =,∠BDA=∠BCA =90°.由等面积法可得:BG AD AG BC ⋅=⋅,即44BC ⨯=. ··························· 9分解得:BC =. ··············································································· 10分B Q P DC B A (图1) (图2)解法二:如图②,连接CD ,过D 作DH ⊥BC 于H . ∵∠BAD =∠CAD ,∴BD =CD ,即△BDC 为等腰三角形. ································································· 7分 又∵DH ⊥BC ,∴H 为BC 中点. 在△BHD 和△ADB 中:∠BAD =∠BCD =∠DBH ;∠BDA =∠DHB =90°. ∴△ABD ∽△BDH ,∴AB BDAD BH=. ·················· 8分 同解法一可得:=2BD ,4AD =. ··················· 9分2BH =,解得:BH =∴2BC BH ==. ··································· 10分 27.(本题满分10分) 解:(1)直线3y x =-+与x 轴交于点B ,与y 轴交于点C ,(3,0)B ∴,(0,3)C . ·· 1分将B ,C 两点的坐标代入22y ax x c =++可得:9603a c c ++=⎧⎨=⎩. ······················ 2分解得:1a =-,3c =.∴二次函数的解析式为:223y x x =-++. ··················· 3分 (2)EM y ∥轴,EM x ∴⊥轴.设(,0)M t (03t <<),则(,3)F t t -,2(,23)E t t t -++,23EF t t ∴=-+,3FM t =-+. ∴211(3)2S t t =-,221(3)2S t =-,2122(3)1(3)2S t t S t -∴==-. ·································· 5分 2230t t ∴+-=,1t ∴=或32t =-(舍去).·················································· 6分(1,4)E ∴. ···························································································· 7分(3)如图,在线段OC 上取点N ,使得ON OM = 3OB OC ==,ON OM =,CN BM ∴=. CM MG ⊥,90OMC GMB ∴∠+∠=︒. 90BOC ∠=︒,90OMC NCM ∴∠+∠=︒. 90OMC GMB ∠+∠=︒,90OMC NCM ∠+∠=︒, NCM BMG ∴∠=∠.135MBG CBG CBO ∠=∠+∠=︒, 180135CNM MNO ∠=︒-∠=︒,CNM MBG ∴∠=∠. ··············································································· 8分在CNM △和MBG △中CNM MBGCN BMNCM BMG ∠=∠⎧⎪=⎨⎪∠=∠⎩,CNM MBG ∴△≌△. ··············································· 9分 CM MG ∴=.90CMG ∠=︒,CG ∴=.CGCM∴=····················· 10分图② 图①。
江苏省南通市部分学校2023-2024学年九年级上学期12月月考数学试题

A. 7
B.3
C. 3 2
D.5
10.如图,在平面直角坐标系中,点 A,B 的坐标分别为 (3,0),(0,6) ,过 A、O、B 三点
作圆,点 C 在第一象限部分的圆上运动,连接 CO ,过点 O 作 CO 的垂线交 CB 的延长线
试卷第 2 页,共 7 页
于点 D,下列说法:① AOC BOD ;② tan ODB 1 ;③ CD 的最大值为 15.其中 2
对应点 D , E , F ),且 VABC 与 VDEF 的相似比为 2:1.其中点 B 坐标为 4, 2 .
(1)画出 VDEF ; (2)点 E 坐标为________;
(3)线段 AC 上一点 x, y 经过变换后对应的点的坐标为________.
试卷第 4 页,共 7 页
21.如图,一扇窗户垂直打开,即 OM OP , AC 是长度不变的滑动支架,其中一端 固定在窗户的点 A 处,另一端在 OP 上滑动,将窗户 OM 按图示方向向内旋转 45 到达 ON 位置,此时,点 A 、 C 的对应位置分别是点 B 、 D .测量出 ODB 为 30 ,点 D 到 点 O 的距离为 40cm .
B. 20
C. 22.5
D. 30
6.如图,点 P 是 VABC 的 AB 边上一点,下列条件不一定保证△ ACP ∽△ ABC 的是( )
A. ACP B B. APC ACB C. AC AP AB AC
D. PC AC BC AB
7.如图,两个相邻的直角三角形,恰好能组合得到四边形 OABC .若 AB BC 1,
(1)求 B 点到 OP 的距离; (2)求滑动支架 AC 的长.(结果保留根号). 22.如图, AB 与 e O 相切于点 A,半径 OC∥ AB , BC 与 e O 相交于点 D,连接 AD .
2022-2023学年度第一学期第三次数学月考

九年级数学月考试卷 第 1 页,共 10 页 九年级数学月考试卷 第 2 页,共 10 页2022-2023学年第一学期12月份月考 九年级数学试卷(满分120分)3分,10小题,共计30分).下列四个图形中是中心对称图形但不是轴对称图形的是( ) A .B .C .D .关于二次函数y =(x +1)2的图象,下列说法正确的是( ) A .开口向下 B .经过原点C .对称轴右侧的部分是下降的D .顶点坐标是(﹣1,0) 抛物线y =(x ﹣3)2+4的顶点坐标是( )A .(﹣1,2)B .(﹣1,﹣2)C .(1,﹣2)D .(3,4) 关于x 的方程2x 2+mx+n =0的两个根是﹣2和1,则n m 的值为( ) A .﹣8B .8C .16D .﹣16时钟的时针在不停的旋转,时针从上午的6时到9时,时针旋转的旋转角是 ( )A.30° B .60° C.90° D.9°如图,⊙O 是△ABC 的外接圆,连接OA 、OB ,∠OBA =50°,则∠C 的度数为( ) A .30°B .40°C .50°D .80°7.已知x =2是关于x 的方程x 2﹣(m +4)x +4m =0的一个实数根,并且这个方程的两个实数根恰好是等腰三角形ABC 的两条边长,则△ABC 的周长为( ) A.6 B.8 C.10D.8或108.已知⊙O 的面积是9πc ㎡。
点0到直线p 的距离为πcm ,则直线p 与⊙O 的位置关系是( ) A.相交B.相切C.相离D.无法确定9.某药品经过两次降价,每瓶零售价由112元降为63元.已知两次降价的百分率相同.要求每次降价的百分率,若设每次降价的百分率为x ,则得到的方程为( )A .112(1﹣x )2=63B .112(1+x )2=63C .112(1﹣x )=63D .112(1+x )=6310.已知二次函数)0(2≠++=acbx ax y 的图象如图所示,有下列4个结论,其中正确的结论是( )A.0>abcB.02=-b aC.c a b +>D.042<-ac b九年级数学月考试卷 第 3 页,共 10 页 九年级数学月考试卷 第 4 页,共 10 页----------------请---------------------二、填空题(共10小题,每小题3分,共30分)11.在平面直角坐标系中,点A (1,2)关于原点对称的点为B (a ,b ),则a +b = .12.如果关于x 的方程x 2﹣5x +k =0没有实数根,那么k 的值为 . 13.已知某抛物线向左平移4个单位,再向下平移2个单位后所得抛物线的解析式为y =3x 2那么原抛物线的解析式是 .14.若关于x 的一元二次方程(m +2)x 2+3x +m 2﹣4=0的一个根为0,则m 的值为= .15.如图,⊙O 的半径为10cm ,AB 是⊙O 的弦,OC ⊥AB 于D ,交⊙O 于点C ,且CD =4cm ,弦AB 的长为 cm .16.已知圆锥的母线长5,底面半径为3,则圆锥的侧面积为 17.我市体育局要组织一次篮球赛,赛制为单循环形式(每两队之间都赛一场),计划安排28场比赛,应邀请多少支球队参加比赛?若设应邀请x 支球队参赛,根据题意,可列出方程 。
2022-2023学年江苏省苏州市姑苏区振华中学校九年级上学期12月月考数学试卷含详解

B、由一次函数 图象可知 ,由二次函数的图象知道 ,即 ,且两图象交于同一点,故选项正确;
C、抛物线的对称轴在 轴的左侧,故选项错误;
D、抛物线的对称轴在 轴的左侧,故选项错误;
故选:B.
【点睛】本题考查一次函数和二次函数图象与系数的关系,解题关键是明确函数图象与系数的关系,树立数形结合思想,准确进行判断推理.
(1)求点A、B、C三点的坐标;
(2)点P是抛物线上的一动点且在直线AC的上方,过点P作x轴垂线交直线AC于点D,当点P运动到什么位置时,线段PD的长度最大?求出此时点P的坐标和线段PD的最大值;
(3)将抛物线L: 的图像向下平移得到新的抛物线 ,直线AC与抛物线 交于M,N两点,满足 ,在抛物线 上有且仅有三个点 , , 使得△ ,△ , 的面积均为定值S,求出定值S及 , , 的坐标.
16.一个小球从水平面开始竖直向上发射,小球的高度h(m)关于运动时间t(s)的函数表达式为 ,其图象如图所示.若小球在发射后第2 s与第6 s时的高度相等,则小球从发射到回到水平面共需时间________(s).
17.同学将如图所示的三条水平直线 的其中一条记为x轴(向右为正方向),三条竖直直线 的其中一条记为y轴(向上为正方向),并在此坐标平面内画出了二次函数 的图像,那么她所选择的x轴和y轴分别为直线_________.
【详解】解:∵二次函数 的图象经过点 ,
∴ ,故A选项错误,不符合题意;
∵二次函数的图象的对称轴为直线 ,
∴二次函数图象与x轴的另一个交点为 ,
∵二次函数的开口向下,
∴当 时, ,
∴当 时, ,故B选项正确,符合题意;
∵二次函数的图象的对称轴为直线 ,
2022-2023学年江苏省苏州市昆山市、太仓市、常熟市、张家港市九年级上学期期中数学试题

2022-2023学年江苏省苏州市昆山市、太仓市、常熟市、张家港市九年级上学期期中数学试题1.下列方程中,一元二次方程的是()A.B.C.D.2.用配方法解一元二次方程的过程中,配方正确的是()A.B.C.D.3.关于的方程的一个解为,则该方程的另一个解是()A.B.C.D.4.“杂交水稻之父”袁隆平培育的超级杂交稻在全世界推广种植.某种植户为了考察所种植的杂交水稻苗的长势,从稻田中随机抽取株水稻苗,测得苗高(单位:)分别是:,,,,,,.则这组数据的众数和中位数分别是()A.,B.,C.,D.,5.已知的直径为,线段,那么点与的位置关系是()A.点在外B.点在上C.点在内D.不能确定6.如图,是的直径,,是上位于两侧的点,若,则度数为()A.B.C.D.7.如图,是的直径,半径于点,平分,交于点,交于点,连接,,给出以下四个结论:①;②;③;④.其中结论正确的序号是()A.①②③B.①②④C.②③④D.①③④8.如图,半圆的直径,弦,平分,则的长为()A.B.C.D.9.一元二次方程x2﹣2x=0的解是_____.10.若关于的方程有一个根是,则______.11.若,是方程的两个实数根,则代数式的值等于______.12.如图,在的正方形网格纸中,每个小正方形的边长均为1,点O,A,B为格点,即是小正方形的顶点,若将扇形围成一个圆锥,则这个圆锥的底面圆半径为______.13.已知,有一量角器如图摆放,中心在边上,为刻度线,为刻度线,角的另一边与量角器半圆交于,两点,点,对应的刻度分别为,,则______14.如图,等边内接于,若,则图中阴影部分的面积为______.(结果保留)15.平面直角坐标系中,以点为圆心的,若该圆上有且仅有两个点到轴的距离等于,则的半径的取值范围是______.16.如图,在平面直角坐标系中,半径为的与轴交于点,,与轴交于点,,连接,已知轴上一点,点是上一动点,连接,点为的中点,连接,,则面积的最小值为______.17.解方程:(1);(2).18.已知,求的值.19.已知关于的方程.(1)若方程有两个不相等的实数根,求的取值范围;(2)如果方程的两个实数根为,且,求的值.20.如图,有一块破碎的圆形玻璃边缘残片,现需要配制一块同样大小的圆形玻璃.请用圆规和无刻度的直尺确定该玻璃残片所在圆的圆心,并补全该残缺的圆.(保留作图痕迹,不写作法)21.某射箭俱乐部准备从甲,乙两位射箭运动员中选出一人参加俱乐部联赛.现两人在选拔赛中各射了箭,甲,乙两人的比赛成绩如下(单位:环):甲:,,,,,,,,,;乙:,,,,,,,,,.教练组根据两人的比赛成绩绘制了如下不完整的数据分析表:根据以上数据解答下列问题:(1)由上表填空:______,______,______;(2)根据本次选拔赛结果,请你从平均数和方差的角度分析,应选择其中哪一位参加俱乐部联赛更好些?22.为丰富学生课外活动,各校积极开展各类社团活动.某校开设了“健美操”社团项目,某班级名有舞蹈基础的学生准备报名参加“健美操”社团,其中名男生,名女生,由于该社团名额有限,只能从中随机选取部分学生进入“健美操”社团.(1)若只能从这名学生中随机选取人进入“健美操”社团,则选中的学生是男生的概率为______;(2)若从这名学生中随机选取人进入“健美操”社团,请用画树状图或列表格的方法,求选中的名学生中恰好是男女的概率.23.阅读理解以下内容,解决问题:解方程:.解:,方程即为:,设,原方程转化为:解得,,,当时,即,,;当时,即,不成立.综上所述,原方程的解是,.以上解方程的过程中,将其中作为一个整体设成一个新未知数,从而将原方程化为关于的一元二次方程,像这样解决问题的方法叫做“换元法”(“元”即未知数).(1)已知方程:,若设,则利用“换元法”可将原方程化为关于的方程是______;(2)仿照上述方法,解方程:.24.某社区在开展“美化社区,幸福家园”活动中,计划利用如图所示的直角墙角(阴影部分,两边足够长),用米长的篱笆围成一个矩形花园(篱笆只围,两边),设米.(1)若花园的面积为平方米,求的值;(2)若在直角墙角内点处有一棵桂花树,且与墙,的距离分别是米,米,要将这棵树围在矩形花园内(含边界,不考虑树的粗细),则花园的面积能否为平方米?若能,求出的值;若不能,请说明理由.25.如图,中,,以为直径作,分别交,于点,,过点作,交于点,垂足为,连接.(1)若,求的度数;(2)若,,求弦的长.26.如图,在中,,平分,交于点,以上一点为圆心的经过点,,分别交,于点,.(1)求证:是的切线;(2)若,,求的半径;(3)试探究线段,,三者之间满足的数量关系,并证明你的结论.27.已知矩形中,,,点是上一动点,的半径为(为定值),当经过点时,此时恰与对角线相切于点,如图所示.(1)求的半径;(2)若从点出发(圆心与点重合),沿方向向点平移,速度为每秒个单位长度,同时,动点,分别从点,点出发,其中点沿着方向向点运动,速度为每秒个单位长度,点沿着射线方向运动,速度为每秒个单位长度,连接,如图所示.当平移至点(圆心与点重合)时停止运动,点,也随之停止运动.设运动时间为秒.①在整个运动过程中,是否存在某一时刻,与相切?若存在,请求出此时的值;若不存在,请说明理由;②在运动过程中,当直线与相交时,直线被截得的线段长度记为,且满足,则运动时间的取值范围是______.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∵x=1时,y1=a+b+c<2,
∴-(a+b+c)>-2
∴x=1时,y2=-a-b-c+2=-(a+b+c)+2>0,故D错误,
故选C.
【点睛】本题考查二次函数图象上点的坐标特征、与x轴的交点、二次函数与系数的关系,能根据图象确定与系数有关的式子的符号是解题关键.
(3)根据抛物线的对称轴,开口方向确定最小值,再根据离对称轴越远,函数值越大,确定最大值,进而即可求解.
【小问1详解】
解:设二次函数关系式为 ,
图象过点 ,
,解得 ,
二次函数关系式为 .
【小问2详解】
∵二次函数关系式为 .
当 时, ,
∴抛物线与 轴的交点坐标为: .
又抛物线经过 ,
∴抛物线与坐标轴的交点为: , ;
【详解】解:∵ ,
此时抛物线的顶点坐标为 ,
函数的图象向上平移1个单位长度后的顶点坐标为 ,即 ,
∵平移后所得抛物线与坐标轴有且只有一个公共点(抛物线开口向上,即与 轴有交点),
∴ ,
解得: ,
故答案: .
【点睛】本题考查了二次函数图象与几何变换,二次函数的性质,解决本题的关键是得到新抛物线的顶点坐标.
(1)画出该二次函数的图象;
(2)连接AC、CD、BD,求ABCD的面积
(1)见解析;(2)9
【分析】(1)先求出抛物线的顶点坐标、抛物线与坐标轴的交点坐标,然后利用描点法画二次函数图象;
(2)连接OD,如图,根据三角形面积公式,利用四边形ABDC的面积=S△AOC+S△OCD+S△OBD进行计算.
【详解】解:抛物线 中, ,开口向上,顶点坐标为 ,对称轴为 ,有最小值为 ,故D选项正确;
故选:D.
【点睛】本题考查了二次函数图象与性质,掌握二次函数的图象与性质是解题的关键.
4.抛物线y=a(x+1)(x-3)(a≠0)的对称轴是直线()
A. x=1B. x=-1C. x=-3D. x=3
A
【分析】已知抛物线解析式为交点式,通过解析式可求抛物线与x轴的两交点坐标;两交点的横坐标的平均数就是对称轴.
11.抛物线 的图像向右平移2个单位,再向下平移3个单位后的解析式为_____.
【分析】根据抛物线的平移规律:上加下减,左加右减解答即可.
【详解】解:抛物线 的图像向右平移2个单位,再向下平移3个单位后的解析式为
故答案为:
【点睛】本题考查了二次函数的平移,掌握二次函数的平移规律是解题的关键.
12.二次函数 的图象经过点 ,则代数式 的值为_____.
D.当 时是一次函数,不是二次函数,故此选项错误;
故选:C.
【点睛】本题考查了二次函数的定义,一般地,形如 ( 是常数, )的函数,叫做二次函数.其中 是变量, 是常量, 是二次项系数, 是一次项系数, 是常数项.
2.若二次函数 的图象经过点P(-2,4),则该图象必经过点()
A.(2,4)B.(-2,-4)C.(-4,2)D.(4,-2)
【详解】抛物线的对称轴为直线 ,
∵ ,
∴当 , 随 的增大而增大,∵ 关于直线 的对称点是 ,
且 ,
∴ .
故选:A.
【点睛】本题考查了二次函数图象上点的坐标特征,主要利用了二次函数的增减性和对称性,求出对称轴是解题的关键.
6.已知:M,N两点关于y轴对称,且点M在双曲线 上,点N在直线y=x+3上,设点M的坐标为(a,b),则二次函数y=﹣abx2+(a+b)x【】
【详解】∵-1,3是方程a(x+1)(x-3)=0的两根,
∴抛物线y=a(x+1)(x-3)与x轴交点横坐标是-1,3.
∵这两个点关于对称轴对称,
∴对称轴是 .
故选A.
5.已知 是抛物线 上的点,则( )
A. B. C. D.
A
【分析】求出抛物线的对称轴为直线 ,然后根据二次函数的增减性和对称性解答即可.
【详解】解:依题意, 是方程 的两个解,
∴ ,
∴
,
故答案为: .
【点睛】本题考查了二次函数与 轴交点问题,一元二次方程根与系数的关系,理解题意是解题的关键.
14.把二次函数 的图象向上平移1个单位长度,如果平移后所得抛物线与坐标轴有且只有一个公共点,那么m应满足条件:_____.
【分析】先求得原抛物线的顶点坐标为 ,再求得平移后的顶点坐标为 ,根据题意得到不等式 ,据此即可求解.
【详解】∵y1的图象开口向上,与y轴交点在(0,2)上方,
∴a>0,c>2,
∵y1+y2=2,
∴y2=-y1+2=-ax2-bx-c+2,
∵-a<0,
∴函数y2的图像开口向下,故A错误,
∴y2的最大值为 =- +2,
∵ <1,
∴- +2>1
∴函数y2的图像与x轴有两个交点,故B错误,
∵对称轴直线在1和2之间,图象开口向下,
15.已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表:
x
…
-1
0
1
2
3
…
y
…
10
5
2
1
2
…
则当y<5时,x的取值范围是_______.
【分析】根据表格数据可知:利用二次函数 对称性判断出对称轴x=2,在对称轴的左边y随着x的增大而减小,在对称轴的右边y随着x的增大而增大,进一步得出x=4时,y=5,然后写出y<5时,x的取值范围即可.
∵二次项系数为 <0,∴函数有最大值,最大值为y= .故选B.
7.二次函数y1=ax2+bx+c(a,b,c为常数)的图象如图所示,若y1+y2=2,则下列关于函数y2的图象与性质描述正确的是:( )
A.函数y2的图象开口向上
B.函数y2的图象与x轴没有公共点
C.当x>2时,y2随x的增大而减小
D.当x=1时,函数y2的值小于0C
8.如图①,E为矩形ABCD的边AD上一点,点P从点B出发沿折线B﹣E﹣D运动到点D停止,点Q从点B出发沿BC运动到点C停止,它们的运动速度都是1cm/s.现P,Q两点同时出发,设运动时间为x(s),△BPQ的面积为y(cm2),若y与x的对应关系如图②所示,则矩形ABCD的面积是( )
A.96cm2B.84cm2C.72cm2D.56cm2
【详解】解:令 ,则 ,
解得 , ,
, ,
, ,
令 ,则 , ,
,
,
为 中点,
,
由 沿 折叠所得,
,
在以 为圆心, 为半径的圆弧上运动,
当 , , 在同一直线上时, 最小,
过点 作 ,垂足为 ,
, ,
,
,
又 ,
的最小值为 ,
故答案为: .
【点睛】本题考查了抛物线与 轴的交点,翻折变换、勾股定理以及求线段最小值等知识,关键是根据抛物线的性质求出 , , 的坐标.
【详解】由表可知,
∵二次函数的两个对称点为(1,2),(3,2)对称轴为直线x=2,
∴当x<2时,y随着x的增大而减小,当x>2时,y随着x的增大而增大,
∴x=4时,y=5,
∴y<5时,x的取值范围为0<x<4.
故答案为:0<x<4.
【点睛】此题考查二次函数的性质,利用表格发现数据的对应计算规律得出对称点,求得对称轴是解决问题的关键.
【详解】解:∵二次函数 的图象开口向下,
∴ ,
故答案为: .
【点睛】本题考查了二次函数的性质,二次项系数决定了开口方向,大于零开口向上,小于零开口向下.
10.二次函数 的顶点坐标_____.
【分析】将解析式化为顶点式即可求解.
【详解】解: ,
∴顶点坐标为 ,
故答案为: .
【点睛】本题考查了二次函数顶点式 的顶点坐标为 ,掌握顶点式求顶点坐标是解题的关键.
(1)
(2)
(3)一次函数的表达式为 ,当 或 时,一次函数值大于二次函数值
16.如图,抛物线 交 轴于 、 两点( 在 的左侧),交 轴于点 ,点 是线段 的中点,点 是线段 上一个动点, 沿 折叠得 ,则线段 的最小值是_____.
##
【分析】先根据抛物线解析式求出点 , , 坐标,从而得出 , , ,再根据勾股定理求出 的长度,然后根据翻折的性质得出 在以 为圆心, 为半径的圆弧上运动,当 , , 在同一直线上时, 最小;过点 作 ,垂足为 ,由中位线定理得出 , 的长,然后由勾股定理求出 ,从而得出结论.
【详解】解:(1)y=x2-2x-3=(x-1)2-4,
抛物线的顶点坐标为(1,-4),
解方程x2-2x-3=0,解得x1=-1,x2=3,
抛物线与x轴的交点坐标为(-1,0),(3,0),
当x=0时,y=x2-2x-3=-3,则抛物线与y轴的交点坐标为(0,-3),
如图,
(2)连接OD,四边形ABDC的面积=S△AOC+S△OCD+S△OBD= ×1×3+ ×3×1+ ×3×4=9.
故答案为9.
【点睛】本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化解.关于x的一元二次方程即可求得交点横坐标.也考查了二次函数的性质.
19.已知二次函数图象经过点 .
(1)求该二次函数解析式;
(2)当 时, 的取值范围是;
(3)若该二次函数的图象与一次函数 图象交于点( ,?),( ,?),求一次函数的表达式并直接回答 取何值时,一次函数值大于二次函数值.
【分析】将点 代入 得出 ,得到 ,整体代入代数式即可求解.
