1晶体结构III

合集下载

晶体晶胞结构讲解

物质结构要点1、核外电子排布式外围核外电子排布式价电子排布式价电子定义：1、对于主族元素，最外层电子2、第四周期，包括3d与4S 电子电子排布图熟练记忆 Sc Fe Cr Cu2、S能级只有一个原子轨道向空间伸展方向只有1种球形P能级有三个原子轨道向空间伸展方向有3种纺锤形d能级有五个原子轨道向空间伸展方向有5种一个电子在空间就有一种运动状态例1：N 电子云在空间的伸展方向有4种N原子有5个原子轨道电子在空间的运动状态有7种未成对电子有3个 ------------------------结合核外电子排布式分析例23、区的划分按构造原理最后填入电子的能级符号如Cu最后填入3d与4s 故为ds区 Ti 最后填入能级为3d 故为d区4、第一电离能：同周期从左到右电离能逐渐增大趋势（反常情况：S2与P3 半满或全满较稳定，比后面一个元素电离能较大）例3、比较C、N、O、F第一电离能的大小 --------------- F ＞N＞O＞C例4、某元素的全部电离能(电子伏特)如下：回答下列各问：(1)I6到I7间，为什么有一个很大的差值?这能说明什么问题? _________________________(2)I4和I5间，电离能为什么有一个较大的差值_________________________________(3)此元素原子的电子层有 __________________层。

最外层电子构型为 ______________ 5、电负性：同周期从左到右电负性逐渐增大（无反常）------------F＞ O ＞N ＞C6、对角线规则：某些主族元素与右下方的主族元素的性质有些相似，被称为“对角线规则”如：锂和镁在空气中燃烧的产物，铍和铝的氢氧化物的酸碱性以及硼和硅的含氧酸酸性的强弱7、共价键：按原子轨道重叠形式分为：σ键和π键 (具有方向性和饱和性)单键 -------- 1个σ键双键------1个σ键和1个π键三键---------1个σ键和2个π键8、等电子体：原子总数相等，价电子总数相等----------具有相似的化学键特征例5、N2 CO CN-- C22-互为等电子体CO2 CS2 N2O SCN-- CNO-- N3- 互为等电子体从元素上下左右去找等电子体，左右找时及时加减电荷，保证价电子相等。

1-2 第一章晶体的结构(配位数、几种重要的晶体结构)

11
体积和配位数(举例体积和配位数举例) 举例
• • • • •
简立方体心立方面心立方氯化铯（氯化铯（CsCl））氯化钠
12
简立方
配位数：? 配位数：6
V= a3
13
体心立方
V = ？ /2 a3 原胞？原胞？
配位数：？配位数：？ 8
14
面心立方
a3 V = ？ /4 原胞？原胞？
8 c/a = ? 3 7
fcc（立方密堆）（立方密堆）
8 c/a = ? 3
A B C ABCABC
8
堆积比（结构结构）堆积比（fcc结构）
a
• fcc：每个晶胞共个原子：每个晶胞共4个原子 • 顶角原子：共8个原子，每个原子，顶角原子：个原子个顶角原子8个晶胞共享个晶胞共享，个顶角原子个晶胞共享，相当于每个晶胞1个顶角原相当于每个晶胞个顶角原子 • 面上原子：共6个原子，每面上原子：个原子，个原子 2a 个面上原子2个晶胞共享个晶胞共享，个面上原子个晶胞共享， rmax = 4 相当于每个晶胞3个原子相当于每个晶胞个原子 4 3 4 × πrmax • 堆积比：硬球体积与整个体堆积比： 2π 3 堆积比 = = 积之比 3 a 6
c
πa 3 / 3 2a 3 = 2π / 6 堆积比= 堆积比 ?
3 2 V = 6 × ( a )× 4 8 a = 3 3
3
a
2a
3
4 a 刚球所占体积 = (3 + 2 + 1)× π = πa 3 3 2
27
Structures: hcp
• Crystals c/a • He 1.633 • Be 1.581 • Mg 1.623 • Ti 1.586 • Crystals c/a • Zn 1.861 • Co 1.622 • Cd 1.996 • Zr 1.594

第一章晶体结构(四晶体的结构与性质--无机化合物结构 )

纤锌矿型结构的晶体，纤锌矿型结构的晶体，如ZnS、CdS、GaAs等和、、等和其它II与族族化合物，其它与IV族，III与V族化合物，制成半导体器件，可与族化合物制成半导体器件，以用来放大超声波。这样的半导体材料具有声电效应。以用来放大超声波。这样的半导体材料具有声电效应。通过半导体进行声电相互转换的现象称为声电效应。通过半导体进行声电相互转换的现象称为声电效应。声电效应
二、AX2型结构
AX2型结构主要有萤石（CaF2，fluorite）型，金红石型结构主要有萤石（）（TiO2，rutile）型和方石英（SiO2，α-cristobalite）型结构。）型和方石英（）型结构。其中CaF2为激光基质材料，在玻璃工业中常作为助熔剂和晶其中为激光基质材料，核剂，在水泥工业中常用作矿化剂。核剂，在水泥工业中常用作矿化剂。TiO2为集成光学棱镜材料，SiO2为光学材料和压电材料。AX2型结构中还有一种层为光学材料和压电材料。型的CdI2和CdCl2型结构，这种材料可作固体润滑剂。AX2 型结构，这种材料可作固体润滑剂。型的型晶体也具有按r 选取结构类型的倾向，型晶体也具有按 +/r-选取结构类型的倾向，见表1-7。。
型化合物的结构类型与r 表1-4 AX型化合物的结构类型与 +/r-的关系型化合物的结构类型与
结构类型 CsCl 型 NaCl 型 r+/r1.000~0.732 0.732~0.414 KF RbCl PbBr SrS SrSe MgO NaBr LiCl 1.00 0.82 0.76 0.73 0.66 0.59 0.50 0.43 实例（右边数据为 r+/r-比值） CsCl 0.91 CsBr 0.84 CsI 0.75 SrO 0.96 BaS 0.82 BaSe 0.75 RbI 0.68 CaS 0.62 LiF 0.59 CaTe 0.50 MgSe 0.41 BaO 0.96 RbF 0.89 CaO 0.80 CsF 0.80 NaF 0.74 KCl 0.73 KBr 0.68 BaTe 0.68 KI 0.61 SrTe 0.60 CaSe 0.56 NaCl 0.54 MgS 0.49 NaI 0.44 LiBr 0.40 LiF 0.35 0.20 BeSe 0.18

晶体结构与性质的关系研究

晶体结构与性质的关系研究引言：晶体是固体中最常见的形态之一，它们具有有序排列的原子、离子或分子结构。

这种有序性使得晶体在性质上表现出一系列独特的特征，因此，晶体结构与性质的关系一直是材料科学领域的热门研究方向。

本文将探讨晶体结构与性质之间的关系，并介绍一些相关的研究进展。

I. 晶体结构对物理性质的影响晶体的结构决定了它们的物理性质。

例如，各向同性的晶体（如立方晶体）具有均匀分布的原子结构，导致它们具有各向同性的物理性质。

然而，一些晶体会因为其结构的非均匀性而表现出各向异性的性质。

例如，石墨的层状晶体结构使其在平面上具有很高的导电性，而在垂直于平面方向上则导电性非常差。

II. 晶体结构对化学性质的影响晶体的结构还会影响其化学性质。

晶体中的原子排列方式决定了它们与其他物质的反应性。

例如，钙钛矿结构的晶体由具有不同电荷的离子构成，这使得它们具有良好的光电性能和催化活性。

此外，晶体结构中的孔道和缺陷也会影响其化学性质。

孔道结构可以增加晶体的吸附性能和储能性能，而缺陷结构可能导致晶体的导电性和热稳定性发生变化。

III. 晶体结构对热学性质的影响晶体的结构还会对其热学性质产生影响。

晶体中原子或分子的排列方式决定了其导热性能、热膨胀性和热导率等特性。

例如，金刚石的均匀排列的碳原子结构使其具有极高的热导率。

此外，晶体结构中的缺陷也会对热学性质产生影响。

一个例子是材料中的点状缺陷能够降低晶体的热导率。

IV. 晶体结构对光学性质的影响晶体的结构还可以影响其光学性质。

晶体中的原子或分子的排列方式决定了其对不同波长的光的吸收、反射和透射能力。

例如，金属结构的晶体对可见光具有很强的反射能力，而透明晶体则对可见光有较高的透射性。

此外，晶体的缺陷结构和掺杂物也会对光学性质产生重要影响。

掺杂不同元素可以使晶体发生光致发光或变色等现象。

结论：晶体结构与性质之间的关系是一个复杂而又有趣的研究领域。

通过对晶体结构进行系统的分析和研究，我们可以揭示晶体的各种性质特征，并为制备具有特定性能的新型材料提供指导。

晶体结构.01

2
1.1 几种常见的晶体结构
一、晶体的定义
晶体: 组成固体的原子（或离子）在微观上的排列具有长程周期性结构
非晶体：组成固体的粒子只有短程序（在近邻或次近邻原子间的键合：如配位数、键长和键角等具有一定的规律性），无长程周期性准晶: 有长程的取向序，沿取向序的对称轴方向有准周期性，但无长程周期性
第一章晶体结构(crystal structure)
1-1 几种常见的晶体结构 1-2 晶格的周期性 1-3 晶向、晶面和它们的标志 1-4 对称性和Brawais点阵
1-5 倒点阵及其基本性质
1-6 晶体衍射物理基础
1
1-1几种常见的晶体结构
主要内容
1.1简立方晶格结构(cubic)
1) NaCl晶体的结构氯化钠由Na+和Cl－结合而成 —— 一种典型的离子晶体 Na+构成面心立方格子；Cl－也构成面心立方格子
20
2) CsCl晶体的结构 CsCl结构 —— 由两个简单立方子晶格彼此沿立方体空间对角线位移1／2 的长度套构而成
21
CsCl晶体
22
3) ZnS晶体的结构 —— 闪锌矿结构立方系的硫化锌 —— 具有金刚石类似的结构化合物半导体 —— 锑化铟、砷化镓、磷化铟
六角密排晶格的原胞基矢选取 —— 一个原胞中包含A层和B层原子各一个 —— 共两个原子 k
定义：
i
j
原胞基矢为：
a1 , a2 , a3
a1 a2 a3
（四）晶格周期性的描述 —— 布拉伐格子
Bravais lattices
由于组成晶体的组分和组分的原子排列方式的多样性，使得实际的晶体结构非常复杂。

晶体结构,配合物结构知识点与习题1-1

117晶体结构一、基本概念（The Basic Concepts ）： 1．晶体（Crystals ）：(1)物质的质点（分子、离子或原子）在空间有规则地排列而成的、具有整齐外形的、以多面体出现的固体物质，称为晶体。

(2) 晶体有同质多象性由同样的分子（或原子）可以以不同的方式堆积成不同的晶体，这种现象叫做同质多象性。

但同一种物质的气态、液态只存在一种结构。

(3) 晶体的几何度量和物理效应常随方向不同而表现出量上的差异，这种性质称为各向异性。

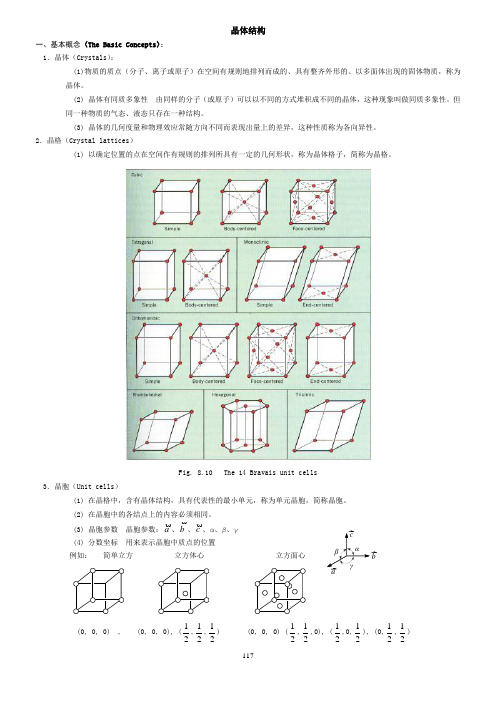
2．晶格（Crystal lattices ）(1) 以确定位置的点在空间作有规则的排列所具有一定的几何形状，称为晶体格子，简称为晶格。

Fig. 8.10 The 14 Bravais unit cells3．晶胞（Unit cells ）(1) 在晶格中，含有晶体结构，具有代表性的最小单元，称为单元晶胞，简称晶胞。

(2) 在晶胞中的各结点上的内容必须相同。

(3) 晶胞参数晶胞参数：a、b、c、α、β、γ (4) 分数坐标用来表示晶胞中质点的位置例如：简单立方立方体心立方面心(0, 0, 0) , (0, 0, 0), (21,21,21) (0, 0, 0) (21,21,0), (21,0,21), (0,21,21) αβγbc a118在分数坐标中，绝对不能出现1，因为1即0。

这说明晶胞是可以前后、左右、上下平移的。

等价点只需要一个坐标来表示即可，上述三个晶胞中所含的质点分别为1、2、4，所以分数坐标分别为1组、2组和4组。

(5) 晶面指数晶面在三维空间坐标上的截距的倒数（h 、k 、l ）来表示晶体中的晶面，称为晶面指数，如立方晶系中(100),(110),(111)面分别为(100) (110)(111)lFig. 8.12 Selected planes and their Miller indices for cubic system用X-ray 的衍射可以测量晶体中的面间距，2d ·sin θ = n ·λ。

晶体结构的基本结构单元

晶体结构的基本结构单元
晶体结构的基本结构单元主要有三种：原子、分子和离子。

这些基本结构单元在空间中按照一定的规律排列，形成了具有周期性的三维结构。

1.原子：原子是构成物质的基本粒子，它们按照一定的顺序排列在晶体中，形
成一种重复的模式。

原子的排列方式直接决定了晶体的物理和化学性质。

例如，金属原子按照一种被称为“金属键”的强力键合排列，这使得金属具有良好的导电性和导热性。

2.分子：分子是由两个或更多原子通过共价键结合在一起的。

在晶体中，分子
可以是链状、网状或者层状排列。

分子的排列方式会影响分子的化学性质和物理性质。

例如，在石墨中，碳原子以层状排列，每层之间的相互作用很弱，因此石墨可以轻易地在层之间滑动。

3.离子：离子是带有电荷的原子或分子。

在晶体中，离子通常通过离子键或者
共价键结合在一起。

离子的排列方式会影响晶体的离子导电性和耐压性。

例如，在食盐（NaCl）中，钠离子和氯离子通过离子键结合，这种键合方式使得食盐具有良好的导电性和耐压性。

晶体结构

§3 晶体结构一、晶体与非晶体1、晶体的特征：⑴有一定的几何外形，非晶体如玻璃等又称无定形体；⑵有固定的熔点；⑶各向异性：晶体在不同方向上表现出不同的物理性质。

一块晶体的某些性质，如光学性质、力学性质、导电导热性质、机械强度等，从晶体的不同方向去测定，常不同。

⑷晶体具有平移对称性：在晶体的微观空间中，原子呈现周期性的整齐排列。

对于理想的完美晶体，这种周期性是单调的，不变的，这是晶体的普遍特征，叫做平移对称性。

⑸自范性：在适宜条件下，晶体能够自发地呈现封闭的、规则的多面体外形。

2、晶体的内部结构⑴晶格：把晶体中规则排列的微粒抽象成几何学中的点，并称为结点。

这些点的结合称为点阵，沿着一定的方向按某种规则把结点连结起来，则得到描述各种晶体内部结构的几何图像——晶体的空间格子，称为晶格。

⑵晶胞：在晶格中，能表现出其结构的一切特征的最小部分称为晶胞。

（晶体中最有代表性的重复单位）⑶晶胞基本特征：晶胞有二个要素：①是晶胞的大小、型式，②是晶胞的内容。

晶胞的大小、型式由a、b、c三个晶轴及它们间的夹角α.β.γ所确定。

晶胞的内容由组成晶胞的原子或分子及它们在晶胞中的位置所决定。

3、单晶体和多晶体⑴单晶体——由一个晶核（微小的晶体）各向均匀生成而成，其内部的粒子基本上按某种规律整齐排列。

如冰糖、单晶硅等。

⑵多晶体——由很多单晶体杂乱聚结而成，失去了各二、离子晶体及其性质1、离子晶体的特征和性质⑴由阳离子和阴离子通过静电引力结合成的晶体——离子晶体。

⑵性质：静电作用力较大，故一般熔点较高，硬度较大、难挥发，但质脆，一般易溶于水，其水溶液或熔融态能导电。

2、离子键⑴定义：阳离子和阴离子通过静电作用形成的化学键。

⑵离子键的形成条件：元素的电负性差要比较大。

⑶离子键的本质特征：是①静电作用力，②没有方向性和饱和性。

⑷影响离子键强度的因素①离子电荷数的影响。

②离子半径的影响：半径大, 导致离子间距大, 所以作用力小; 相反, 半径小, 则作用力大。

无机化学《晶体结构》教案

无机化学《晶体结构》教案[ 教学要求]1 ．了解晶体与非晶体的区别，掌握晶体的基本类型及其性质特点。

2 ．了解离子极化的基本观点及其对离子化合物的结构和性质变化的解释。

3 ．了解晶体的缺陷和非整比化合物。

[ 教学重点]1 ．晶胞2 ．各种类型晶体的结构特征3 ．离子极化[ 教学难点]晶胞的概念[ 教学时数] 4 学时[ 主要内容]1 ．晶体的基本知识2 ．离子键和离子晶体3 ．原子晶体和分子晶体4 ．金属键和金属晶体5 ．晶体的缺陷和非整比化合物6 ．离子极化[ 教学内容]3-1 晶体3-1-1 晶体的宏观特征晶体有一定规则的几何外形。

不论在何种条件下结晶，所得的晶体表面夹角（晶角）是一定的。

晶体有一定的熔点。

晶体在熔化时，在未熔化完之前，其体系温度不会上升。

只有熔化后温度才上升。

3-1-2 晶体的微观特征晶体有各向异性。

有些晶体，因在各个方向上排列的差异而导致各向异性。

各向异性只有在单晶中才能表现出来。

晶体的这三大特性是由晶体内部结构决定的。

晶体内部的质点以确定的位置在空间作有规则的排列，这些点本身有一定的几何形状，称结晶格子或晶格。

每个质点在晶格中所占的位置称晶体的结点。

每种晶体都可找出其具有代表性的最小重复单位，称为单元晶胞简称晶胞。

晶胞在三维空间无限重复就产生晶体。

故晶体的性质是由晶胞的大小、形状和质点的种类以及质点间的作用力所决定的。

3-2 晶胞3-2-1 晶胞的基本特征平移性3-2-2 布拉维系十四种不拉维格子类型说明单斜底心格子（ N ）单位平行六面体的三对面中有两对是矩形，另一对是非矩形。

两对矩形平面都垂直于非矩形平面，而它们之间的夹角为β，但∠β≠ 90°。

a 0≠ b 0 ≠ c 0 ，α = γ =90°， β≠ 90°正交原始格子（ O ）属于正交晶系，单位平行六面体为长、宽、高都不等的长方体，单位平行六面体参数为： a 0 ≠ b 0 ≠ c 0 α = β = γ =90 °正交体心格子（ P ）属于正交晶系，单位平行六面体为长、宽、高都不等的长方体，单位平行六面体参数为： a 0 ≠ b 0 ≠ c 0 α = β = γ =90 °正交底心格子（ Q ）属于正交晶系，单位平行六面体为长、宽、高都不等的长方体，单位平行六面体参数为： a 0 ≠ b 0 ≠ c 0 α = β = γ =90 °正交面心格子（ S ）属于正交晶系，单位平行六面体为长、宽、高都不等的长方体，单位平行六面体参数为： a 0 ≠ b 0 ≠ c 0 α = β = γ =90 °立方体心格子（ B ）属于等轴晶系，单位平行六面体是一个立方体。

晶体学基础PPT课件

➢ 单位格子：只包含一个点阵点的格子叫单位格子。
➢ 复单位：即每一个格子单位分摊到一个以上的点阵点。
点阵
图1-4 平面点阵单位上图所示，平行四边形I和II都只分摊到一个点阵点，故它们都是单位格子；平行四边形III 分摊到两个点阵点，故它是复单位。
点阵
3.三维点阵(空间点阵)
➢分布在三维空间的点阵叫空间点阵。 ➢空间点阵对应的平移群可用下式表示：
T m n m p n a p b ,m c ,n ,p 0 , 1 , 2 (1 .
图1-5 空间点阵单位
点阵
➢空间格子：空间点阵按确定的平行六面体单位划分后所形成的格子称为空间格子。
➢基本单位：每个平行六面体格子单位只分摊到1个点阵点，称为空间点阵的基本单位。
我们把所有阵点可用位矢(1.1)、(1.2)或(1.3) 来描述的点阵称为布拉菲点阵。
➢ 点阵的这两条基本性质也正是判断一组点是否为点阵的依据。
点阵
三.直线点阵、平面点阵与空间点阵
点阵和平移群
➢ 能使一个点阵复原的全部平移矢量组成的一个平移群(它符合数学上群的定义) 称为该点阵对应的平移群。
➢ 点阵和平移群有一一对应的关系。一个点阵所对应的平移群能够反映出该点阵的全部特征。
第一章晶体学基础
内容提要
晶体的基本性质晶体结构几何理论的历史发展简况点阵平面点阵与空间点阵的性质晶体的点阵结构晶胞典型晶体结构举例晶向指数与面指数晶体结构的对称性
第一节晶体的基本性质
一.晶体与非晶体在宏观性质上的区别
➢晶体具有固定的外形，各向异性，固定的熔点。 • 微细单晶体的集合体，称为多晶体 • 取向杂乱的单晶体集合成的多晶体，显示出各向同性 • 择优取向的多晶体呈现出各向异性

晶体结构

(a) (b)
(c)
(d)
图 4.9 C60(a)、C70(b)、C84(c)和纳米管(d) 的晶体结构模型
碳６０
碳６０
碳７０
碳２４０
碳８０
碳管
Si、 Ge、属金刚石型与白锡型两种结构。 Sn 19 D 4 h I 41 / amd 。每个 Sn 原子白锡的空间群为有四个配位（扁四面体）Sn-Sn=0.3002nm，另外两个配位 Sn-Sn=0.3182nm， CN=6，如图 4.10 所示。
典型实例
(1).铜的晶体结构属 A1 型，空间群为 Fm3m ， a0=0.3608nm,CN=12,晶胞中原子数目Z=4。晶体结构如图4.1所示。属铜型结构的有Au、Ag、Pb、Ni、 Co、Pt、γ-Fe、Al、Sc、Ca、Sr等单质晶体。
(2).α -Fe的晶体结构属 A2 型，空间群 Im3m ， a0=0.2860nm,CN=8,Z=2, 结构图如图 4.2 所示。属α-Fe型结构的有W、Mo、Li、Na、 K、Rb、Cs、Ba等。
3.考虑到以上方法的优缺点，同时考虑到晶胞的形状与大小和晶体生长习性间的相互关系的分类法。将晶体结构分为等向型、层型和链型三种主要类型，而这三种类型又以等大球的六方和立方最紧密堆积为基础。
晶体结构的研究方法
• 衍射法
– X射线衍射、电子衍射、中子衍射
• 谱学方法
– 红外光谱（研究基团振动）、核磁共振谱（磁场作用下核能级间的跃迁，研究水、质子、某种离子的行为和配位性况，结构有序－无序情况）、拉曼光谱（通过测定分子极化率的变化研究分子结构，与红外光谱互补）、穆斯堡尔谱（研究铁等离子在结构中的分布和配位）、电子顺磁共振谱（研究与顺磁性离子有关的结构现象）

半导体物理第1章半导体的晶体结构与价键模型

电作用形成
•成键的条件：成键原子得失电子的能力相当或是差别较小 •非极性共价键：元素半导电体子科的技大相学邻刘诺原子吸引电子的能力一样，
共用电子对不会发生偏移
共价键的特征
方向性
原子只在特定方向形成共价键键之间的夹角都是109°28´
饱和性
每个原子的价电子层都是满的
离子键：原子首先转变为正、负离子，然后正、负离
例：晶面指数？
晶面指数（1/2, 1/2, 1/1）-> （112）
电子科技大学刘诺
弥勒（Miller）指数:晶向指数
晶向指数描述特定的晶向
电子科技大学刘诺
第1章半导体的晶体结构与价键模型
1.1 材料和晶体的分类 1.2 晶面、晶向和勒指数 1.3 原子价键 1.4三维晶体结构的定性描述 1.5π电子体系晶体结构简介 1.6小结
• 晶向指数：[hkl] • 等效晶向指数：<hkl> • 等效晶面指数：{hkl}
电子科技大学刘诺
弥勒（Miller）指数:晶面指数
(110)面
电子科技大学刘诺
晶面指数
确定方法
(110)面
晶面与坐标轴相交
确定晶面在三个坐标轴上的截距（1, 1, ∞ ）的数值取截距的倒数（1/x, 1/y, 1/z）= （110）（1/x, 1/y, 1/z）乘以电子最科技小大学公刘诺分母= （110）
[2] 黄昆，谢希德.半导体物理学。北京：科学出版社，1965.
[3] 黄昆，韩汝琦.半导体物理基础。北京：科学出版社，1979.
[4] 刘恩科，朱秉升，罗晋生. 半导体物理学。北京：电子工业出版社，2005.
[5] 萨支唐. 固态电子学基础。上海：复旦大学出版社，2002.

晶体的结构

石英晶体（长程有序）
硅酸盐玻璃（长程无序）
几个基本概念
晶体结构
点阵（晶格lattice)：晶体中的重复单元，
用抽象的点表示，一组无限的点，有平移对称性
点阵点:
结构基元 = 点阵 + 结构基元
晶体结构
NaCl的晶胞
NaCl的面心立方点阵
点阵结构人为抽象的数学模型点阵点的摆放无限素单位(含一个点阵点) 复单位
从逆向思维你已明白，立方面心晶胞确实满足ABCABC……堆积。那么, 再把思路正过来: ABCABC……堆积形成立方面心晶胞也容易理解吧? 将视线逐步移向体对角线，沿此线观察:
你看到的正是ABCABC……堆积！
最密堆积结构中的空隙类型
球堆积决不可能将空间完全填满, 必然要留下空隙. 下面将由简到繁地讨论空隙数
特别注意: 四配位的多面体是正四面体而不是正方形. 由于正离子被包在正四面体
中难以看清正负离子的大小关系, 故简化成平面结构用作示意图, 这并不是真实结构!
对于几种确定的CN+，理论上要求的r+/r-临界值(最小值)如下:
r+ + r−
三配位的正三角形空隙
= 2 r − ⋅ sin 60 = 2 r− ⋅ 3 2 ⋅ 2 3
空间利用率
空间利用率=晶胞中原子总体积 / 晶胞体积用公式表示: P0=Vatoms/Vcell
A1 空间利用率的计算
4r = 2 2r 2a = 4 r → a = 2 4 3 16 3 Vatoms = πr × 4 = πr 3 3 Vcell = a 3 = 16 2r 3 Vatoms π = = 74.05% Po = Vcell 3 2

第二章晶体结构(3)-无机单质及化合物晶体结构

CaF2——激光基质材料，在玻璃工业中常作为助熔剂
和晶核剂，在水泥工业中常用作矿化剂；
TiO2——集成光学棱镜材料；
SiO2——光学材料和压电材料。
此外还有层状CdI2和CdCl2型结构，可作固体润滑剂。
AX2型晶体也具有按r+/r-选取结构类型的倾向。第二章晶体结构——2.3~4无机单质及化合物晶体结构
第二章晶体结构——2.3~4无机单质及化合物晶体结构
纤锌矿结构中六方柱晶胞
纤锌矿结构中平行六面体晶胞
资源加工与生物工程学院
（2）纤锌矿结构与热释电性及声电效应
某些纤锌矿型结构，其结构中无对称中心存在，使得晶体具有热释电性，可产生声电效应。
热释电性是指加热使晶体温度变化时，在与该晶体c轴平行
一、AX型结构，二、AX2型结构，三、A2X3型结构，四、 ABO3型结构，五、 AB2O4型（尖晶石）结构，六、无机化合物结构与鲍林规则（Pauling’s rule）
第二章晶体结构——2.3~4无机单质及化合物晶体结构
资源加工与生物工程学院
一、AX型结构
有CsCl，NaCl，ZnS，NiAs等类型结构，其中：
第二章晶体结构——2.3~4无机单质及化合物晶体结构
资源加工与生物工程学院
r AX型化合物的结构类型与的关系 r
结构类型 CsCl型 NaCl型
r r
1.000~0.732 0.732~0.414
实例（右边数据为
r r 比值）
CsCl 0.91 CsBr 0.84 CsI 0.75 KF 1.00 SrO 0.96 BaO 0.96 RbF 0.89 RbCl 0.82 BaS 0.82 CaO 0.80 CsF 0.80 PbBr 0.76 BaSe 0.75 NaF 0.74 KCl 0.73 SrS 0.73 RbI 0.68 KBr 0.68 BaTe 0.68 SrSe 0.66 CaS 0.62 KI 0.61 SrTe 0.60 MgO 0.59 LiF 0.59 CaSe 0.56 NaCl 0.54 NaBr 0.50 CaTe 0.50 MgS 0.49 NaI 0.44 LiCl 0.43 MgSe 0.41 LiBr 0.40 LiF 0.35 MgTe 0.37 BeO 0.26 BeS 0.20 BeSe 0.18 BeTe 0.17

固体物理学第一章晶体的结构(1)

1.3 晶向、晶面和它们的标志晶体周期性的描述通常还要用到：晶列、晶向、晶面和密勒指数、面间距等概念。
（1）晶列
• 通过Bravias格子的任意两点连一条直线，该直线上包括无限多个格点,这样的直线称晶列.晶体外观上所见的晶棱为个别晶列。
• 通过其它任一格点可引出与原晶列平行的晶列，这些
相互平行的晶列族将包含全部的格点。 • 晶列的性质：同一晶列族上，格点具有相同的周期分布 • 通过一个格点可以引出无数晶列，晶列数目是无限的，（晶列的性质）。
固体由大量原子（离子）组成，1022—1023/cm3。晶体中原子、离子的排列是有规律的，这种排列方式称固体晶体的结构。固体的宏观物理性质是由组成材料的[原子、分子和离子]成分和原子分子的排列方式共同决定的。
可以将固体分为：晶体和非晶体。晶体：原子严格按一定周期性的规则排列，具有周期性和平移对称性，即长程有序。非晶：原子排列短程有序，长程无序。何为长程有序呢？主要是与原子的尺寸相比。晶体分为：单晶：理想的大块晶体多晶：有许多晶粒组成的晶体 1984年 D.Shechtman等从实验上发现了具有五重旋转对称性的不同于晶体和非晶体的固体，称准晶。准晶从结构上讲，其有序程度是介于晶体和非晶之间的。
(2) 体心立方结构(bcc) • 排列方式：ABABAB….. • a为原子间的距离，称为晶格常数。对角线距离
0.31ro
a
ro
• 体心立方结构晶体自然界中很多：Li, Na, K,ro 2ro 3
(3)六角密排结构(主要是金属晶体) • 排列方式：ABABAB….. • 层内原子密排列，层之间原子紧密接触。 • 自然界中。碱土金属Be, Mg 及Zn, Cd, Ti等三十多种晶体

常见的晶体结构-PPT

Octahedral sites:
6
×
×
晶体结构中得空隙位(3): hcp
Tetrahedral sites
×
×
7c 8
1c
××
8
2 6 2 1 2 3 12 3
5c 8
3c 8
棱与中心线得1/4与3/4处
3、点阵常数与原子半径
R 2R
R RR
a0
a0 2R
a0
a0
2 2R 3
R 2R
图2-48 NaCL晶胞
图2-49 CsCL晶胞
Zn
0 75
(0, 0, 0), (1 , 1 , 0), (1 , 0, 1), (0, 1 , 1) 22 2 2 22
50 25
0
(1 , 1 , 1), ( 3 , 3 , 1), (1 , 3 , 3), ( 3 , 1 , 3) 444 444 444 444
(2
R
fcc
)
Center of tetrahedron, o,
oD = (3/4)DE
A D
B
rin
oD
R fcc
3 4
DE
R fcc
2Rfcc
rin
3 2
2 3
R
fcc
R fcc
(
3 2
1)R
fcc
o
C
A
E
B
rin 3 1 0.225
R fcc
2
晶体结构中得空隙位(2): bcc
Octahedral sites: Face and edge center sites
6 1 12 1 6
2
4

晶体晶胞结构

物质结构要点1、核外电子排布式外围核外电子排布式价电子排布式价电子定义：1、对于主族元素,最外层电子2、第四周期,包括3d与4S 电子电子排布图熟练记忆 Sc Fe Cr Cu2、S能级只有一个原子轨道向空间伸展方向只有1种球形P能级有三个原子轨道向空间伸展方向有3种纺锤形d能级有五个原子轨道向空间伸展方向有5种一个电子在空间就有一种运动状态例1：N 电子云在空间的伸展方向有4种N原子有5个原子轨道电子在空间的运动状态有7种未成对电子有3个 ------------------------结合核外电子排布式分析例23、区的划分按构造原理最后填入电子的能级符号如Cu最后填入3d与4s 故为ds区 Ti 最后填入能级为3d 故为d区4、第一电离能：同周期从左到右电离能逐渐增大趋势反常情况：S2与P3 半满或全满较稳定,比后面一个元素电离能较大例3、比较C、N、O、F第一电离能的大小 --------------- F ＞N＞O＞C例4、某元素的全部电离能电子伏特如下：回答下列各问：1I6到I7间,为什么有一个很大的差值这能说明什么问题 _________________________2I4和I5间,电离能为什么有一个较大的差值_________________________________3此元素原子的电子层有 __________________层;最外层电子构型为 ______________ 5、电负性：同周期从左到右电负性逐渐增大无反常------------F＞ O ＞N ＞C6、对角线规则：某些主族元素与右下方的主族元素的性质有些相似,被称为“对角线规则”如：锂和镁在空气中燃烧的产物,铍和铝的氢氧化物的酸碱性以及硼和硅的含氧酸酸性的强弱7、共价键：按原子轨道重叠形式分为：σ键和π键具有方向性和饱和性单键 -------- 1个σ键双键------1个σ键和1个π键三键---------1个σ键和2个π键8、等电子体：原子总数相等,价电子总数相等----------具有相似的化学键特征例5、N2 CO CN-- C22-互为等电子体CO2 CS2N2O SCN-- CNO-- N3- 互为等电子体从元素上下左右去找等电子体,左右找时及时加减电荷,保证价电子相等;9、应用VSEPR理论判断下表中分子或离子的构型;化学式σ键电子对数中心原子含有孤对电子对数VSEPR模型分子立体构型杂化类型ABnSO3对于给出结构的分子或离子,根据中心原子成四个价键8个电子,直接判断.B原子六个电子例6、N原子的杂化类型2- P的杂化类型 _________________PO4CHO C原子的杂化类型____________CH3NiCO中心原子的杂化_________________410、配合物配位键也是共价键,属于σ键 ;例7、中心原子或离子配体配位原子或离子配位数FeCO5FeSCN3--ZnCN4--Al F611、分子间作用力:①一般分子间作用力—范德华力②氢键例8、晶体中存在的作用力________________________________________12、氢键①存在：一个分子的X-H中的H原子与另外的X原子相结合而成X表示N、O、F②表示方法：A━H┄B例9、写出氨水中氢键的种类N━H┄N N━H┄O O━H┄O O━H┄N 共4种③H2O分子中氢键的数目 ---1个水分子形成4个氢键---1mol H2O分子含氢键2NAHF分子中氢键的数目---1个HF分子形成2个氢键---1molHF分子含氢键NA④氢键对某些现象的解释i．解释分子熔沸点的大小II．解释物质溶解性的大小III．解释冰融化为水密度减小,体积增大：氢键的存在使处于中心的水分子与其他水分子呈四面体,空间利用率较低,溶化后空隙减小iv．解释邻羟基苯甲醛与对羟基苯甲醛沸点的高低v．解释接近水的沸点的水蒸气的Mr测定值比用化学式计算的值大一些：13、比较物质熔沸点的大小⑴先考虑晶体类型;原子晶体＞离子晶体＞分子晶体⑵对于属于同种晶型,再具体分析①离子晶体：含有离子键---金属和NH4+的出现,晶格能电荷,半径②原子晶体：从共价键的键长分析③分子晶体：优先考虑氢键的存在,存在氢键的分子相对熔沸点高对于不存在氢键的分子晶体,再从Mr来比较;例10、比较Si 、SiC、NacL 、KcL、H2O、H2S、HCL沸点高低14、无机含氧酸①属于几元酸,看结构中所含━OH的数目,或者看与NaOH生成盐的种类②同一元素的含氧酸,该元素的化合价越高显正价则正电性高,则含氧酸酸性强该元素的化合价高与含氧酸的氧化性无直接联系对于跟多含氧酸,中心元素不同,━OH的数目也不同,HOm ROn, 非羟基氧原子数目越多,含氧酸酸性越强;NaCl型一个晶胞中四个Na +,四个Cl-CsCl型正负离子配位数均为8与铯离子等距离且最近的铯离子有6个、氯离子有8个CaF2型•CaF2晶体属立方面心点阵,F－作简单立方堆积,Ca2＋数目比F－少一半,所以填了一半的立方体空隙,每一个Ca2＋由八个F－配位,而每个F－有4个Ca2＋配位ZnS型TiO2金红石型AB2型晶体中,最常见的重要结构是四方金红石TiO2结构;在此结构中Ti4＋处在略有变形的氧八面体中,即氧离子作假六方堆积,Ti4＋填在它的准八面体空隙中一、分子晶体的一般宏观性质①较低的熔沸点②较小的硬度③固态或熔融状态下都不导电构成分子晶体的粒子是分子,粒子间的相互作用是分子间作用力或氢键二、.晶体分子结构特征１只有范德华力,无分子间氢键－分子密堆积每个分子周围有12个紧邻的分子,如：C60、干冰、I2、O2----晶胞结构都属于面心立方２有分子间氢键－不具有分子密堆积特征如：HF 、冰、NH3与CO2分子距离最近的CO2分子共有12个原子晶体晶体中每个C原子和4个C原子形成4个共价键,成为正四面体结构,C原子与碳碳键个数比为1：2,最小环由6个C原子组成,每个C原子被12个最小环所共用；平均每个最小环含有1/2个C原子;每个C原子被4个碳碳键所共用；每个碳碳键含有2个C原子,平均每个碳碳键含有1/2个C原子; 故平均每个最小环含有1个碳碳键金刚石是立体网状结构,每个碳原子形成4个共价键,任意抽出2个共价键, 每两个单键归两个六元环所有,而不是只归一个六元环所有如图所示,红色的两个碳碳单键,可以构成蓝色和紫红色的两个六元环;每个碳原子连出4个共价键,任意抽出2个共价键能决定两个6元环,4个共价键总共能抽出6组;所以6组碳碳键实际上可以构成12个六元环,所以一个碳归十二个六元环共用;6 × 1/12 = 1/2晶体中的最小环为十二元环,其中有6个Si原子和6个O原子,含有12个Si-O键；每个Si原子被12个十二元环共有,每个O原子被6个十二元环共有,每个Si-O键被6个十二元环共有；2015年全国理综能力测试卷中第37题是物质结构与性质选考题,其中有一个小题的内容是：“在金刚石晶体中,C原子所连接的最小环也为六元环,每个C原子连接个六元环,六元环中最多有个C原子在同一平面;”从不同观察和分析角度的观察金刚石的晶体结构模型,可以对上述问题的第1问做如下两种盘判断：1晶体中每个C原子和它周围的4个C原子以共价键相连,金刚石晶体结构的观察分析形成空间正四面体结构,晶体中每个碳原子都和其他碳原子构成空间正六边形的碳环;由于每个C原子和它周围的4个C原子连接,因此它必然同处于4个六元环上,而与之相连的4个C原子的每一个又和另外3个C原子相连;因而,它必然又在另外3个碳原子所在的环上;所以这个碳原子连接3×4=12个六元环;2晶体中每个碳原子以四个碳碳单键分别其他碳原子连接,这个碳原子上的每两个碳碳单键可以分属于两个六元环右图中用红色描出的环;每个碳原子的四个碳碳单键,每两个键组合成环,依据组合排列规律,可以知道有C42种即6种组合,因此,每个碳原子可以处于2×C42=12个六元环;金属晶体面心立方：在立方体顶点的微粒为8个晶胞共有,在面心的为2个晶胞共有;微粒数为：8×1/8 + 6×1/2 = 4晶体密度=m晶胞/v晶胞m晶胞=摩尔质量除以阿伏伽德罗常数乘以晶胞中所含的原子或离子数体心立方晶胞四点间的夹角均为60°C60的形状类似于足球,1个顶点引出3条边其中1个是双键,另2个是单键,1条边被两个顶点共用,因此1个C60有60个顶点和90个边;假设1mol C60有x mol碳碳双键C=C,y mol碳碳单键C-C从每个顶点来看,y=2x从边的数量来看,x+y=90解得x=30,y=60因此1mol C60有60mol碳碳单键C-C ,30mol碳碳双键C=C设正六边形x个正五边形y个由欧拉公式60+x+y-6x+5y/2=2 欧拉公式顶点+面—棱=2每个正五边形有5个键每个正六边形有6个键6x/2+5y/2=60×3÷2 有一个双键解得x=20,y=12习题1、最近科学家发现一种由钛原子和碳原子构成的气态分子,如右图所示;顶角和面心的原于是钛原子,棱的中心和体心的原子是碳原子,则它的分子式是A．TiC B．Ti4C4, C．Ti14C13D．Ti13C142、硼砂是含结晶水的四硼酸钠,其阴离子X m—含B、O、H三种元素的球棍模型如右下图所示：①在X m—中,硼原子轨道的杂化类型有；配位键存在于原子之间填原子的数字标号；m= 填数字;②硼砂晶体由Na+、X m—和H2O构成,它们之间存在的作用力有 ;A．离子键 B.共价键 C.金属键D.范德华力E.氢键4①1,3,5,6代表氧原子,2,4代表B原子,2号B形成3个键,则B原子为SP2杂化, 4号B 形成4个键,则B原子为SP3杂化； B一般是形成3个键,4号B形成4个键,其中1个键很可能就是配位键,配位键存在4号与5号之间;观察模型,可知X m—是H4B4O9m—,依据化合价H为+1,B为+3,O为—2,可得m=2,这问有一定难度,思维能力,空间能力要求比较高;②钠离子与X m—形成离子键,结晶水分子间存在氢键和范德华力题目是问钠离子、X m—、水分子之间的作用力,而不是硼砂晶体中的作用力,可能会多选B;3、下列关于金属及金属键的说法正确的是_;a.金属键具有方向性与饱和性b.金属键是金属阳离子与自由电子间的相互作用c.金属导电是因为在外加电场作用下产生自由电子d.金属具有光泽是因为金属阳离子吸收并放出可见光1金属键没有方向性和饱和性,a错；金属键是金属阳离子和自由电子间的相互作用,b 对；金属导电是因为在外加电场作用下发生定向移动,c错；金属具有光泽是因为自由电子能够吸收并放出可见光,d错;4、过渡金属配合物NiCOn的中心原子价电子数与配体提供电子总数之和为18,则n= ;5、ZnS在荧光体、光导体材料、涂料、颜料等行业中应用广泛;立方ZnS晶体结构如下图所示,其晶胞边长为,其密度为列式并计算,a位置S2-离子与b位置Zn2+离子之间的距离为pm列式表示;7、肼能与硫酸反应生成N2H6SO4;N2H6SO4晶体类型与硫酸铵相同,则N2H6SO4的晶体内不存在__________填标号a. 离子键b. 共价键c. 配位键d. 范德华力8、图1表示某种含氮有机化合物的结构,其分子内4个氮原子分别位于正四面体的4个顶点见图2,分子内存在空腔,能嵌入某离子或分子并形成4个氢键予以识别;下列分子或离子中,能被该有机化合物识别的是_________填标号;a. CF4 b. CH4c. NH4＋ d. H2O解析③N2H6SO4晶体类型与硫酸铵相同,可见它是离子晶体,晶体内肯定不存在范德华力;4要形成氢键,就要掌握形成氢键的条件：一是要有H原子,二是要电负性比较强,半径比较小的原子比如F、O、N等构成的分子间形成的特殊的分子间作用力;符合这样的选项就是c和d,但题中要求形成4个氢键,氢键具有饱和性,这样只有选c;9、钛酸钡的热稳定性好,介电常数高,在小型变压器、话筒和扩音器中都有应用;钛酸钡晶体的结构示意图为右图,它的化学式是。

冰的18种晶体结构

冰的18种晶体结构冰是一种常见的物质，它存在于我们生活的各个角落中。

然而，你是否知道冰实际上存在着不同的晶体结构？下面我们将一一介绍冰的18种晶体结构。

1. 冰Ih：冰Ih是最常见的冰的结构，也是我们平常所说的冰块。

它具有六方晶体结构，每个水分子都与其他四个水分子相邻，形成一个六边形的结构。

2. 冰II：冰II是在高压下形成的一种冰的结构。

它具有四方晶体结构，水分子排列更加紧密，形成一个立方体的结构。

3. 冰III：冰III是在更高的压力下形成的一种冰的结构。

它具有同样的六方晶体结构，但水分子的排列更加紧密，相邻的水分子之间的距离更近。

4. 冰IV：冰IV是在更高压力下形成的一种冰的结构。