一阶系统
第四章 一阶系统

4.4.3
寻的负反馈系统的行为的三 种模式
(1)GL> 0,LEV≥0,(LEV(0)-GL)< 0; ) , , ; (2)GL> 0,LEV≥0,(LEV(0)-GL)> 0; ) , , ; (3)GL=0,LEV> 0。 ) = , 。 • 模式 如教材 模式3如教材 如教材P105 图5.25所示 所示 • 模式 称为零目标结构。目标值 为“0”, 模式3称为零目标结构 目标值GL为 称为零目标结构。 , 状态值由LEV(0)指数衰减至“0”。 状态值由 ( )指数衰减至“ 。
• 4.5.1 S形增长的系统内部结构 形增长的系统内部结构
LEV 状状 RT 速速
RTV 速 速率
图
S形形形形形形形图
• 方程式: P111 方程式:
4.4.2 负反馈系统的特性
LEV 状态 过渡区 稳定区
时间
状态随时间变化曲线包括两个区段: 状态随时间变化曲线包括两个区段:瞬 过渡区)和稳态(稳定区)两个部分。 态(过渡区)和稳态(稳定区)两个部分。 • 在过渡区段, 值与目标值GL不相 在过渡区段,LEV值与目标值 不相 值与目标值 此时LEV具有寻的与瞬变的特点;在 具有寻的与瞬变的特点; 等。此时 具有寻的与瞬变的特点 稳定区, 值接近或近似地达到目标值, 稳定区,LEV值接近或近似地达到目标值, 值接近或近似地达到目标值 稳定不变。 也最终近似地达到 也最终近似地达到“ 。 稳定不变。RT也最终近似地达到“0”。 • • •
• 求新的目标值 求新的目标值NGL: : • 方法 : 方法1: • 200×20%= %=40 × %= • GL=DINV=200 • NGL=200-40=160 • 方法 : 方法2: • NGL=GL+T*SR=200-1/0.5*20=20040=160
一阶系统

Automatic Control Theory
1
第2章 要 点
建模,化简
建模:输入—输出模型 微分方程,传递函数
化简: 结构图,信号流图
2
第3章 线性系统的时域分析
分析和设计控制系统的首要工作是建立系统的 数学模型。在获得系统的数学模型后,就可以 采用不同的数学方法去分析系统的性能。
控制系统的主要分析方法 时域分析法 根轨迹分析法 频域(率)分析法 ……
3
第3章 线性系统的时域分析
时域法是一种直接又比较准确的分析方 法,它通过拉氏反变换求出系统输出量 的表达式,提供系统时间响应的全部信 息。
时域分析法得到的结果直观,但其计算 量随系统阶次的升高而急剧增加。
4
第3章 线性系统的时域分析
为了衡量系统的动态性能,同时便于对不同系 统的性能进行比较,通常采用单位阶跃函数作 为测试试验信号。相应地,系统的响应称为单 位阶跃响应。
14
3.1 典型试验信号与系统性能指标
系统性能指标
y(t)
ymax
1.05 y () 1.00 y () 0.95 y() 0.90 y()
0.50y()
方程
.
..
y(0), y(0), y(0), y(n1) (0)
.
..
u(0),u(0),u(0), u(m1) (0)
初始条件
y(t) yt (t) yss (t)
解的结果
12
3.1 典型试验信号与系统性能指标
时域响应的构成
暂态响应(自由分量)和稳态响应(强迫分量 )
y(t) yt (t) yss (t)
r(t) 1 at 2 2
一阶系统传递函数

一阶系统传递函数一阶系统是指系统的阶次为1的系统,其传递函数一般形式为:G(s) = K / (τs + 1)其中,G(s)为系统的传递函数,K为系统的增益,τ为系统的时间常数,s为复变量。
一阶系统是控制系统理论中最简单的系统之一,它具有较为简单的数学模型和动态特性。
在现实生活中,许多物理系统和电气系统都可以近似地看作是一阶系统,如机械阻尼系统、电路RC电路等。
一阶系统的传递函数可以用来描述系统的输入与输出之间的关系。
传递函数的分子部分表示输出对输入的比例关系,分母部分表示系统对输入的响应速度。
增益K表示输出与输入之间的比例关系,时间常数τ则决定了系统的响应速度。
一阶系统的动态特性主要体现在其单位阶跃响应上。
单位阶跃响应是指输入信号为单位阶跃函数时,系统的输出响应。
对于一阶系统,其单位阶跃响应可以通过拉普拉斯逆变换得到。
一阶系统的单位阶跃响应的形式为:y(t) = K * (1 - e^(-t/τ))其中,y(t)为系统的输出,t为时间。
从单位阶跃响应的表达式可以看出,一阶系统的单位阶跃响应具有指数衰减的特性。
随着时间的推移,系统的输出将逐渐趋于稳定值K。
根据一阶系统的传递函数和单位阶跃响应,可以进一步分析系统的稳态误差和动态响应特性。
对于稳态误差,一阶系统的单位阶跃响应在稳定状态下会达到稳态值K。
当输入信号发生变化时,系统的输出将逐渐趋向于新的稳态值。
稳态误差可以通过比较输出与输入的差异来评估系统的准确性。
对于动态响应特性,一阶系统的时间常数τ决定了系统的响应速度。
时间常数越小,系统的响应速度越快;反之,时间常数越大,系统的响应速度越慢。
在实际应用中,需要根据系统的需求来选择合适的时间常数。
除了单位阶跃响应,一阶系统还可以对其他输入信号进行分析和建模。
常见的输入信号包括阶跃信号、脉冲信号、正弦信号等。
通过对不同输入信号的分析,可以得到系统的频率响应和幅频特性,从而更好地了解系统的动态性能。
总结起来,一阶系统是控制系统中最简单的系统之一,其传递函数可以用来描述系统的输入与输出之间的关系。
一阶系统和二阶系统区分方法

一阶系统和二阶系统是控制系统中常见的两种类型,它们可以通过以下几个方面进行区分: 1. 数学模型形式:一阶系统的数学模型通常由一个一阶微分方程描述,例如 RC 电路。而二 阶系统的数学模型则由一个二阶微分方程描述,例如振动系统或者 RLC 电路。
2. 阶数:一阶系统的阶数为1,即系统的最高导数为一阶导数。而二阶系统的阶数为2,即 系统的最高导数为二阶导数。
3. 动态响应:一阶系统的动态响应相对简单,通常具有指数衰减的特点。例如,一阶惯性 系统的响应可以用指数函数来描述。而二阶系统的动态响应则更加复杂,通常具有振荡、超调 和稳定性等特点。
一阶系统和二阶系统区分方法
4. 频率响应:一阶系统的频率响应通常是单调递减的,即随着频率的增加,系统的增益逐 渐减小。而二阶系统的频率响应则可能具有共振现象,即在某个特定频率处,系统的增益达 到最大值。
ቤተ መጻሕፍቲ ባይዱ
5. 控制器设计:由于其较简单的动态特性,一阶系统的控制器设计相对简单。而二阶系统 的控制器设计则需要考虑更多的因素,例如稳定性、超调和振荡等。
通过对以上方面的观察和分析,可以较为准确地区分一阶系统和二阶系统。但需要注意的 是,实际系统可能具有更复杂的特性,可能不严格符合一阶或二阶系统的定义,因此在实际 应用中需要综合考虑多种因素。
一阶系统

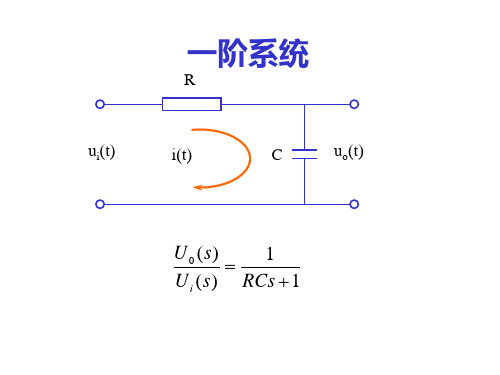
3-3 一 阶 系 统图3-5所示系统。
其输入-输出关系为11111)()(+=+=Ts s Ks R s C (3-3) 式中KT 1=,因为方程(3-3)对应的微分方程的最高阶次是1,故称一阶系统。
实际上,这个系统是一个非周期环节,T 为系统的时间常数。
一、一阶系统的单位阶跃响应因为单位阶跃函数的拉氏变换为s 1,将s s R 1)(=代入方程(3-3),得 sTs s C 111)(+=将)(s C 展开成部分分式,有11()1C s ss T=-+(3-4)对方程(3-4)进行拉氏反变换,并用)(t h 表示阶跃响应)(t C ,有 t Te t h 11)(--= 0t ≥ (3-5)由方程(3-5)可以看出,输出量)(t h 的初始值等于零,而最终将趋于1。
常数项“1”是由s 1反变换得到的,显然,该分量随时间变化的规律和外作用相似(本例为相同),由于它在稳态过程中仍起作用,故称为稳态分量 (稳态响应)。
方程(3-5)中第二项由11/()s T+反变换得到,它随时间变化的规律取决于传递函数1/(1)Ts +的极点,即系统特征方程()10D s Ts =+=的根(1/)T -在复平面中的位置,若根处在复平面的左半平面如图3-6(a)所示,则随着时间 t 的增加, 它将逐渐衰减, 最后趋于零 (如图3-6(b) 所示),称为瞬态响应。
可见,阶跃响应曲线具有非振荡特性,故也称为非周期响应。
显然,这是一条指数响应曲线,其初始斜率等于1/T ,即Te T dt dh t t T t 1|1|010===-= (3-6)这就是说,假如系统始终保持初始响应速度不变,那么当T t =时,输出量就能达到稳态值。
实际上从方程(3-6)可以看出,响应曲线)(t h 的斜率是不断下降的,从0=t 时的T1一直下降到∞=t 时的零值。
因此,当T t =时,指数响应曲线将从零上升到稳态值的63.2%;当T t 2=时,响应曲线将上升到稳态值的86.5%;当T t 3=,T 4和T 5时,响应曲线分别达到稳态值的95%,98.2%和99.3%。
一阶系统分析

5. 当ξ<0时,系统有一对实部为正的共扼复根, 系统时间响应具有发散振荡的特性,称为 负阻尼状态。
15
二、二阶系统的单位阶跃响应 s1,2 n n 2 1
下面根据不同ξ值的条件来讨论对应的阶跃响应。
过阻尼ξ>1 的情况 式中:
于是闭环传递函数为
s2
2n s n2
(s
1 )(s T1
1) T2
0
T1
n (
1
2
1)
T2
n (
1
2
1)
C(s)
1 / T1T2
1
R(s) (s 1 )(s 1 ) (T1s 1)(T2 s 1)
T1
T2
则系统在单位阶跃信号作用时,系统的输出
C(s)
1 / T1T2
1
(s 1 )(s 1 ) s
T1
T2
16
取C(s)的拉氏反变换,得到单位阶跃响应
n K , 2n 1 KA
29
首先,由要求的求出相应的阻尼比 ,即由
ln 1 1.61
1 2
0.456
再根据要求条件t p 1s求取无阻尼自振频率n :
n
tp
3.53rad / s
1 2
R(s)
K s(s 1)
另由 n K 解得:K n2 12.5
1 As
C(s)
n2
1 s
1
s n
n
s (s n )2 d2 (s n )2 d2
取C(s)的拉氏反变换,得到单位阶跃响应:
c(t) 1 ent (cosd t
1 2
sin d t)
(t 0)
1
一阶系统的数学模型

n 称 称为阻尼系数, ( s )称为典型二阶系统的传递函数,
为无阻尼振荡圆频率或自然频率。这两个参数称为二阶系统特 征参数。T称为二阶系统的时间常数。
二阶系统的特征方程为: s 2 n s n 0
2 2
其特征根为: p1, 2 n n 2 1
p1, 2 n n 2 1
1,临界阻尼
s1,2 n (重根) 一对负实重根
s1, 2 n n 2 1
1,过阻尼
两个互异负实根
3.3.3
典型二阶系统的性能指标(衰减振荡瞬态过程)
最大超调量 %
1 2
%e
2、调节时间 t s :
100%
4 ,当Δ 2时 n ts 3 ,当Δ 5时 n
n Y ( s) ( s ) 2 R( s) s 2 n s n 2
2
n K / T 4 /1 2
1/ 2n 0.25
% e
/ 1 2
100% 44.4%
ts 4 / n 8
(4)当要求在=0.707时,n=1/2= 0.707,则K=n2=0.5。 可见要满足二阶工程最佳参数的要求(该例中为增加阻尼 系数),必须降低开环放大系数 K的值。
注意:当 不同时,特征根有不同的形式,系统的阶跃响 应形式也不同。它的阶跃响应有振荡和非振荡两种情况。
⒈ 当 0 时,特征方程有一对共轭的虚根,称为零 (无)阻尼系统,系统的阶跃响应为持续的等幅振荡。 ⒉ 当 0 1 时,特征方程有一对实部为负的共轭复 根,称为欠阻尼系统,系统的阶跃响应为衰减的振荡过程。 ⒊ 当 1 时,特征方程有一对相等的实根,称为临界 阻尼系统,系统的阶跃响应为非振荡过程。 ⒋ 当 1 时,特征方程有一对不等的实根,称为过阻 尼系统,系统的阶跃响应为非振荡过程。
第三章一阶系统

3.1.1 典型试验信号 Typical test signals
(1) 实际系统的输入信号不可知性 (2) 典型试验信号的响应与系统的实际响应,存在某种关系 (3) 电压试验信号是时间的简单函数,便于分析。 突然受到恒定输入作用或突然的扰动。如果控制系统的输入量是随时间逐步变化的 函数,则斜坡时间函数是比较合适的。 (单位)阶跃函数(Step function) 1(t ) , t ≥ 0 室温调节系统和水位调节系统 (单位)斜坡函数(Ramp function) 速度
t , t≥0
1 2 t , t≥0 2
(单位)加速度函数(Acceleration function)抛物线 (单位)脉冲函数(Impulse function)
δ (t ) , t = 0
正弦函数(Simusoidal function)Asinut ,当输入作用具有周期性变化时。 通常运用阶跃函数作为典型输入作用信号,这样可在一个统一的基础上对各种控 制系统的特性进行比较和研究。本章讨论系统对非周期信号(Step、Ramp、对 正弦试验信号响应,将在第五章频域分析法,第六章校正方法中讨论)
3.1.2动态过程和稳态过程 在典型信号作用下,控制系统的时间响应是由动态过程 和稳态过程两部分组成。 1.动态过程(过渡过程、暂态过程):在典型输入信号 作用下,系统从初态到终态的响应过程。 动态响应过程有三种情况:衰减型、发散型、等幅振荡 型 2.稳态响应过程:在输入信号作用下,当时间t趋向无穷 大时,系统输出的表现形式。稳态误差是稳态性能描述 的指标。
1
1 T T2 T2 = + 1 S3 S2 1 S S+ S+ T T D
t 1 2 2 c(t ) = t Tt + T (1 e T ) 2
一阶系统的定义

一阶系统的定义
嘿,咱来说说一阶系统是啥定义。
有一次我开车的时候,发现踩下油门后,车子不是马上就加速到很快,而是慢慢地速度才提起来。
这时候我就想到了一阶系统。
一阶系统呢,简单来说就是反应不是特别快,有个逐渐变化的过程。
比如说我那车,油门踩下去,速度得一点点地变,不会一下子就飞出去。
就像你往杯子里倒热水,水温不是一下子就变热了,而是慢慢升高。
这也是一种一阶系统的表现。
在生活中,一阶系统还挺常见的。
比如你开灯,灯也不是瞬间就亮到最亮,而是有个过程。
就像我开车那次经历,让我对一阶系统有了更直观的认识。
嘿嘿。
一阶系统的时域分析

数T之间的关系。
时间t
0
T
2T 3T
…
输出量 0 0.632 0.865 0.950 … 1.0
斜率 1/T 0.368/T 0.135/T 0.050/T … 0.0
根据这一特点,可用实验的方法测定一阶系统的时间常 数,或测定系统是否属于一阶系统。
时间常数T是一阶系统的一个重要参数。 当t=3T时,响应输出可达稳态值的95%;
输出量和输入量之间的位置误差: t ess (t) 1(t) c(t) e T
稳态误差 :
t
lim
t
ess
(t
)
lim
t
e
T
0
三 一阶系统的单位斜坡响应
当一阶系统的输入信号为单位斜坡信号r(t)=t,其拉氏变 换为R(s)=1/s2,则系统的输出为:
C(s)
R(s) Ts 1
1 Ts 1
S tep R esponse 10
9
8
7
k 0.1
6
A m plitude
5
4
3
k 0.3
2
1
0
0
0.1
0.2
0.3
0.4
0.5
0.6
T im e (sec)
小结
• 一阶系统的传递函数和典型方块图 • 一阶系统的单位阶跃响应(单调上升曲线,性
能指标常用调整时间) • 系统对输入信号导数的响应等于对输入信号响
五.三种响应之间的关系
比较一阶系统对单位脉冲、单位阶跃和单位斜 坡输入信号的响应,就会发现它们的输入信号 有如下关系:
d (t) d [1(t)];
dt
1(t) d [t 1(t)]; dt
一阶二阶系统的动态响应1汇总

一阶二阶系统的动态响应1汇总一阶系统和二阶系统是控制系统中常见的两种动态响应模型。
它们在自然科学、工程技术等领域中具有重要的应用价值。
本文将对一阶系统和二阶系统的动态响应进行详细的介绍和分析,并对其特性进行总结和比较。
一、一阶系统的动态响应一阶系统是指系统的微分方程中只含有一阶导数的控制系统。
一阶系统的动态响应通常由一阶微分方程表示。
一般而言,一阶系统的微分方程可以表示为:$ \frac{dy(t)}{dt} = -ay(t) + bx(t) $其中,$y(t)$表示系统的输出,$x(t)$表示系统的输入,$a$和$b$为系统的参数。
根据方程的特性,可以推导出一阶系统的动态响应的数学表达式。
1.1零输入响应当系统处于零输入状态(即$x(t)=0$)时,系统的输出仅由初始条件决定。
一阶系统的零输入响应表达式为:$ y(t) = y(0)e^{-at} $其中,$y(0)$表示系统初始时刻的输出。
可以看出,在没有输入信号的情况下,一阶系统的输出会随着时间的推移而指数级衰减。
1.2零状态响应当系统处于零状态(即初始条件$y(0)$为0)时,系统的输出完全由输入信号决定。
一阶系统的零状态响应表达式为:$ y(t) = \frac{b}{a}(1 - e^{-at})x(t) $其中,$x(t)$表示系统的输入。
可以看出,在没有初始条件的情况下,一阶系统的输出将随着时间的推移而趋近于输入信号。
1.3一阶系统的阶跃响应阶跃响应是指当输入信号为单位阶跃函数时,系统的输出响应。
一阶系统的阶跃响应表达式为:$ y(t) = b(1 - e^{-at})\cdot u(t) $其中,$u(t)$表示单位阶跃函数。
可以看出,在单位阶跃输入信号的作用下,一阶系统的输出会随时间的推移而逐渐趋近于输入信号的幅值。
二、二阶系统的动态响应二阶系统是指系统的微分方程中含有二阶导数的控制系统。
二阶系统的动态响应通常由二阶微分方程表示。
一阶系统的时间响应

定义
能用一阶微分方程描述的系统称为一阶系统。
系统传递函数中分母多项式中s的最高幂数为1的系统称为一阶系统。
一阶系统的典型形式是惯性环节。
数学模型
一阶系统的数学模型为 a dct bct rt
dt
传递函数
传递函数的一般形式为
Gs
Cs RS
K Ts 1
为时间常数。
因为输入信号是单位阶跃信号,所以 Rs 1
s
又因为
Gs
Cs RS
1 Ts 1
所以,输出信号的拉氏变换为 Cs GsRS 1 1 1 1
查拉氏变换对照表得
Ts 1 s
s
s
1 T
ct
1
e
t T
此即为一阶系统的单位阶跃响应。式中T称为系统的时间常数,具有时间量纲,是 一阶系统的重要特征参数,表征了系统过渡过程的品质,T越小,系统响应越快。
现在分析三个典型输入信号的时间 响应。
一阶单位斜坡信号的时间响应为
ct
t
t
T
Te
t T
,t
0
一阶单位阶跃信号的时间响应为
cI
t
1
e
t T
一阶单位脉冲信号的时间响应为
c
t
1 T
e
t T
,t
0
显然,
d
ct
t
1
e
t T
dt
cI t
dcI t 1
dt T
e
t T
c t
即单位阶跃响应是单位斜坡响 应的导数,单位脉冲响应是单 位阶跃响应的导数。
一阶系统的单位阶跃响应曲线
结论
一阶系统的不失真条件

一阶系统的不失真条件一阶系统是一种简单的线性时不变系统模型,通常用来描述输入信号通过一个惯性元件的传递过程。
一阶系统的不失真条件主要可以归纳为以下几点:1. 线性:不失真条件要求系统满足线性性质,即系统的输入和输出之间存在线性关系。
这意味着系统对于输入信号的响应是可加的,即输入信号的线性组合对应的输出信号是这些输入信号对应输出信号的线性组合。
2. 时不变:时不变是指系统的特性不随时间而变化。
一阶系统的不失真条件要求系统的传递函数或差分方程在给定输入下的输出不随时间推移而变化。
3. 无记忆性:无记忆性是指系统的输出仅取决于当前的输入信号,而与过去的输入信号和输出信号无关。
一阶系统的不失真条件要求系统的传递函数或差分方程只依赖于当前时刻的输入信号,没有引入延迟项或状态变量。
4. 因果性:因果性是指系统的输出仅取决于当前和过去的输入信号,而不依赖于未来的输入信号。
一阶系统的不失真条件要求系统的传递函数或差分方程只包含正时间的项,并且没有出现未来时刻的输入信号。
在一阶系统的不失真条件下,系统的传递函数可以表示为一个比例项和一个惯性项的乘积。
具体而言,一阶系统的传递函数可以表示为:H(s) = K / (sT + 1)其中,H(s)是系统的传递函数,K是系统的增益,T是系统的时间常数。
一阶系统的差分方程则可以表示为:y[n] = K * (x[n] - x[n-1]) + (1 - T) * y[n-1]其中,y[n]是系统的输出信号,x[n]是系统的输入信号,y[n-1]和x[n-1]分别是上一时刻的输出信号和输入信号。
不失真条件下的一阶系统具有许多重要的特性。
首先,系统的零点位于负实轴,因此系统不会引入频率失真。
其次,系统的相位响应为-90度,即输入信号的相位滞后90度,这是一阶系统的固有特性。
此外,在一阶系统的不失真条件下,系统的幅频响应为1/(sqrt(1 +(fT)^2)),其中f是输入信号的频率。
自动控制原理系统的型次

自动控制原理系统的型次自动控制原理系统的型次指的是系统的阶次或者等效阶次。
在自动控制中,我们常常使用阶次的概念来描述系统的复杂程度和动态响应的性质。
型次是指系统传递函数中最高阶导数的次数。
简而言之,这是描述系统动态响应能力的一个度量标准。
阶次越高,系统的动态响应能力越强。
在自动控制原理中,系统的型次主要由系统的传递函数决定。
传递函数可以是一个或多个函数相乘得到的。
下面我们来介绍几种常见的型次:1. 一阶系统:系统传递函数中只有一个一阶导数,例如1/(s+a)。
一阶系统是最简单的系统,具有较低的复杂度和动态响应能力。
2. 二阶系统:系统传递函数中有一个二阶导数项,例如1/(s^2+as+b)。
二阶系统比一阶系统更复杂,具有更强的动态响应能力。
许多机械和电子系统可以近似为二阶系统。
3. 三阶系统:系统传递函数中有一个三阶导数项,例如1/(s^3+as^2+bs+c)。
三阶系统比二阶系统更为复杂,通常用于模拟更复杂的物理系统。
4. 高阶系统:系统传递函数中有更高阶的导数项。
高阶系统具有更复杂的动态响应能力,可以用于描述更复杂的物理现象。
高阶系统在实际应用中比较常见,如电力系统、化学过程控制等。
不同型次的系统具有不同的动态响应特性。
一阶系统具有较慢的动态响应速度和较大的超调量;二阶系统具有较快的动态响应速度和较小的超调量;高阶系统具有更高的动态响应速度和更小的超调量。
在进行自动控制系统设计时,理解系统的型次是非常重要的。
通过研究系统的型次,可以选择合适的控制策略和参数,以实现期望的动态性能。
总之,自动控制原理系统的型次是衡量系统复杂程度和动态响应能力的重要指标。
了解不同型次系统的特点和性能对于系统设计和实际应用都具有重要意义。
一阶系统.ppt
m
k(s zj)
q
j 1 r
(s si )
(s2
2nk
s
2 nk
)
i 1
k 1
m
Y (s)
q
k (s zj )
j 1
1
r
(s si )
(s2
2nk
s
2 nk
)
s
i 1
k 1
1 s
q i 1
Ai s si
r k 1
Bk (s
k nk ) Cknk
1
2 k
s2
2
k nk s
二阶系统的单位脉冲响应曲线
nt
(t) d [1(t)] , k(t) d [ y(t)]
dt
dt
t
tp
y(t) k(t)dt , y(tp ) k(t)dt 1 p
0
0
二阶系统的单位斜坡响应
1
r(t)
1.欠阻尼
0
t
R(s)
1
s2
Y
(s)
s2
n2 2ns
n2
1 s2
y(t)=t- 2 n1 iaRaeb Nhomakorabeaey
y
r
y
电动机力矩平衡方程式
J0
d 2
dt 2
b0
d
dt
M
其中 M K2ia 电磁转矩
(s) 1
M (s) s(J0s b0 )
ia K2 M
M
1 1
J0s b0
s
ey
y
r
y
电机转角 与负载转角 y 间的转速比n y n
y
n
G(s)
3.3 一阶系统的时间响应一、一阶系统可用一阶微分方程表示的

Xi (s) 1/ s
X
ou
(
s)
G(s).X
i
(s)
G(s).
1 s
xou
(t)
L1[
X
o
(s)]
L1[G(s).
1] s
L1[ 1 Ts
. 1
1 s
]
L1[1 1 ] s s 1 T
所以,
xou (t) 1 et /T
(t 0)
xou (t) 1 et /T
输入
输出
(t)
1
t
eT
T
t
u(t)
1e T
t
r(t)
t T Te T
如果输入函数等于某个函数的导数,则该输入函数所引起的输 出等于这个函数所引起的输出的导函数;如果输入函数等于某 个函数的积分,则该输入函数所引起的输出等于这个函数所引 起的输出的积分。
例:已知xi
(t
)
t,
xor
3.3 一阶系统的时间响应
一、一阶系统
可用一阶微分方程表示的系统,称为一阶系统。其微分方程的
一般形式为
T
dx0 (t) dt
x0 (t)
xi (t)
G(s) X0(s) 1 X i (s) Ts 1
其中,T称为一阶系统的时间常数,是一阶系统的特征参数。
二、一阶系统的单位脉冲响应 当系统的输入信号是理想的脉冲函数时,系统的输出称为 系统的单位脉冲响应函数(或单位脉冲响应),记为 w(t)
(t 0)
显然,xo (t)瞬态项为 Tet /T,稳态项为 t T
t 0时,xo (t) 0.
一、二阶系统的动态特性 - 机电一体化

一、二阶系统的动态特性 - 机电一体化1.一阶测量装置的特性一阶系统:包括液柱式温度计,RC滤波电路,弹簧、阻尼振子。
传递函数是,, R=热阻,电阻;C=热容,电容;幅频特性是,相频特性是从公式可看出,输出的幅值是降低的,相位是滞后的.一阶系统的特性:(1).一阶测量装置适用用于测量缓变或低频的被测量。
(2).当激励频率ω远小于1/τ时, 其A(ω)值接近于1(误差不超过2%),输入和输出幅值几乎相等。
(3).时间常数是反映一阶系统特性的重要参数。
时间常数实际上决定了该装置适用的频率范围。
(4).一阶系统的伯德图表明在频率为 1/τ处(称为转折频率),该点折线偏离实际曲线的误差最大。
2.二阶测量装置的特性:包括动圈式振子中,固定的永久磁铁形成的磁场和通电线圈形成的动圈磁场相互作用,形成的电磁转矩,该转矩使线圈偏转运动,运动规律可用二阶系统描述。
弹簧、质量、阻尼振子系统;RLC电路;其中,系统的固有频率和系统的阻尼比需要根据具体情况判断。
系统组成后,或调整完成后,其阻尼比、固有频率、灵敏度也随之而定。
二阶系统的特性:(1).当ωωn时,H(ω)≈1;当ωωm 时,H(ω)→0。
(2).影响二阶系统动态特性的参数是:固有频率和阻尼比。
(3).在ω=ωn 附近,系统的幅频特性受阻尼比影响最大,当ω≈ωn时,系统发生共振。
(4).根据二阶系统的脉冲响应函数:在ωωn时,φ(ω)很小,且与频率近似成正比增加。
在ωωn时,接近-180度,输出信号与输入信号反相。
在ω靠近ωn区间时,φ(ω) 随频率的变化而剧烈变化,当ζ越小,这种变化越剧烈。
二阶系统是一个震荡环节。
要选择一个恰当的固有频率与阻尼比的组合,从而获得较小的误差与较较宽的工作频率范围。
一般取ω=(0.6~0.8)ωn,ζ=(0.65~0.7)。
测试装置对任意输入的响应实现不失真测量的条件(1).A(ω)=Ao= 常数,φ(ω) =-toω。
(2).若测试的结果用作反馈控制信号,则相位误差应力求小。
一阶系统时间响应分析

一阶系统时间响应分析一阶系统是指具有一个自由度的线性系统,它的传递函数可以表示为H(s)=K/(τs+1),其中K表示系统的增益,τ表示系统的时间常数。
一阶系统常见于许多实际应用中,包括温度控制、物体的加速度、放电过程等。
在进行一阶系统的时间响应分析时,可以通过单位阶跃响应或冲激响应等方法来研究系统的动态特性。
首先,考虑单位阶跃响应,即在t=0时刻输入信号从0跃迁到1的情况。
对于一阶系统,单位阶跃响应可以表示为y(t)=K(1-e^(-t/τ)),其中y(t)表示系统的输出。
可以看出,单位阶跃响应的特征是在初始时刻输出信号从0逐渐上升,最终趋于K。
其中,时间常数τ决定了系统的时间响应速度。
当τ较大时,单位阶跃响应的上升时间较长,系统的响应较为缓慢。
当τ较小时,单位阶跃响应的上升时间较短,系统的响应较为迅速。
另外,增益K决定了单位阶跃响应的最终稳定值。
当增益K较大时,单位阶跃响应的稳定值也较大;当K较小时,单位阶跃响应的稳定值也较小。
除了单位阶跃响应,冲激响应也是研究系统时间响应特性的重要方法之一、冲激响应可以表示为h(t)=K/τ*e^(-t/τ),其中h(t)表示系统的输出。
冲激响应的特征是系统在接收到一个冲激信号(即瞬间施加一次激励)后的输出情况。
可以看出,冲激响应的形式与单位阶跃响应相似,只是其幅度除以了时间常数τ。
冲激响应的峰值位于t=0时刻,由于单位冲激信号具有单位面积,因此冲激响应的峰值等于系统的增益K。
通过对冲激响应的分析,可以得到系统的频率响应。
频率响应是指系统对各种频率输入信号的响应特性,通常用幅频特性和相频特性来表示。
幅频特性表示了系统对不同频率输入信号的幅度传递特性。
对于一阶系统,幅频特性可以表示为,H(jω),=K/√(1+(ωτ)^2),其中ω为频率。
幅频特性的曲线呈现出一个低通滤波器的形状,即在低频时幅度较大,而在高频时幅度逐渐减小。
该特性说明了一阶系统的低频增益和高频截止频率的关系。
一阶系统和二阶系统

0,t 0
A,
t
0
A阶跃幅度,A=1 x(t)
称为单位阶跃函数,A
记为1(t)。
t
其拉氏变换后旳像函数为: L[x(t)] A
s
斜坡函数(速度阶跃函数):
0,t 0 x(t) Bt,t 0
B=1时称为单位 斜坡函数。
其拉氏变换后旳像函数为:
L[x(t)]
B s2
x(t) x(t) Bt
⒍ 振荡次数N:
在调整时间内,y(t)偏离 旳y(振) 荡次数。或在
0<t<ts时间内,单位阶跃响应穿越其稳态值次数旳二 分之一,定义为振荡次数。
y
ymax
0.05 y()
y()
或
0.02 y()
y() 2
0
td tr tp
t ts
在上述几种性能指标中,t p , tr , ts表达瞬态过程进行旳快慢,是 迅速性指标;而 %, N 反应瞬态过程旳振荡程度,是振荡性指
时域分析是一种在时间域中对系统进行分析旳措施,具 有直观和精确旳优点。因为系统旳输出量旳时域体现式是时 间旳函数,所以系统旳输出量旳时域体现式又称为系统旳时 间响应。
系统输出量旳时域表达可由微分方程得到,也可由传递函 数得到。在初值为零时,可利用传递函数进行研究,用传递 函数间接旳评价系统旳性能指标。
3.1.4 稳态过程旳性能指标
稳态过程旳性能指标
当响应时间t>ts时,系统旳输出响应进入稳态过程。稳 态过程旳性能指标主要是稳态误差。当初间趋于无穷大时, 若系统旳输出量不等于输入量,则系统存在稳态误差,稳态 误差是控制系统精度或抗干扰能力旳一种度量。
ess
lim e(t)
t
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一阶系统:凡是能够用一阶微分方程描述的系统。
典型环节:比例环节,惯性环节,微分环节,积分环节,震荡环节。
时间相应的组成:按振动性质分为自由响应强迫响应,按振动源分为零输入响应零状态响应。
时间响应:是指控制系统在输入作用下,被控变量(即系统的输入)随时间的变化情况。
传递函数:为当系统初始条件为零时,输出量(响应函数)的拉普拉斯变换与输入量(激励函数)的拉普拉斯变换之比。
频率响应:系统对正弦输入信号的稳定响应称为。
稳定性:是指系统受到扰动作用偏离平衡状态后,当扰动消失,系统经过自身调节能否以一定的准确度恢复到原平衡状态的性能。
2-1什么是线性系统?其最重要特性是什么?答:如果系统的数学模型是线性的,这种系统就叫做线性系统。
线性系统最重要的特性,是适用于叠加原理。
叠加原理说明,两个不同的作用函数(输入),同时作用于系统所产生的响应(输出),等于两个作用函数单独作用的响应之和因此,线性系统对几个输入量同时作用而产生的响应,可以一个一个地处理,然后对它们的响应结果进行叠加。
3-1 时间响应由哪两个部分组成?各部分的定义是什么?答:根据工作状态的不同,把系统的时间响应分为瞬态响应和稳态响应。
系统稳定时,它的自由响应称为瞬态响应,即系统在某一输入信号的作用下其输出量从初始状态到稳定状态的响应过程。
而稳态响应一般就是指强迫响应,即当某一信号输入时,系统在时间趋于无穷大时的输出状态。
2-7证明图(题2-7)所示两系统是相似系统(即证明两系统的传递函数具有相同形式)。
Cou 2R 1R iu1C2ox ix k 1c 1c 2k 2()a (b )解:根据图)(a 的已知内容可得:11R C I I I += ① 011V IR R V i += ② ⎰+=idt C i R V 2201③ ⎰=dti C IR R C 11111④由②有:11R V V i iR -= ③求导:220C i i R V +=②求导:10111V c i V R i R V C i +=+=10)(1C V V i i C -=101)(11C V V R V V i i i i i C R -+-=+=⎪⎪⎭⎫ ⎝⎛-+-+⎪⎪⎭⎫ ⎝⎛-+-=10102101020)(1)(C V V R V V C C V V R V V R V i i i i ∴1)(1)()()(1122212121221121210+++++++==s C R C R C R s R R C C s C R s C R s R R C C s V s V s G i根据图b)可得:⎩⎨⎧=--=-+-1110101002)()()()(x k x x C x x C x x k x x C i i i1)(1)()()()()()(21221122121221122121211112212212112212210+++++++=+++++++==s k C k C k C s k k C C s k C k C s k k C C k k s k C k C k C s C C k k s k C k C s C C s X s X s G i1-1 试举日常生活工程中开环和闭环控制系统的两个例子,说明其工作原理。
答:(1)控制系统的输出量不影响系统的控制作用,即系统中输出端与输入端之间无反馈通道时称开环系统。
如普通的车削加工或没有反馈通道的控制车床进给系统。
其工作原理为:指令(系统输入)(系统输出)工作台控制装置 输入装置伺服装置工作台位置(2)控制系统的输出与输入间存在着反馈通道,即系统的输出对控制作用有直接影响的系统,称为闭环系统。
因此,反馈系统也就是闭环控制系统。
如数控机床进给系统(采用闭环系统时)。
系统的输出(工作台的移动)通过检测装置(同步感应器或光栅等)把信号反馈到输入端,与输入信号一起通过控制装置对工作台的移动进行控制。
其工作原理为:工作台控制装置指令输入装置驱动装置工作台位置检测装置1-2 图(题1-2)是控制导弹发射架方位的电位器式随动系统原理图。
图中电位器P1,P2并联后跨接到同一电源E0的两端,其滑臂分别与输入轴和输出轴相联结,组成方位角的给定元件和测量反馈元件。
输入轴由手轮操纵;输出轴则由直流电动机经减速后带动,电动机采用电枢控制的方式工作。
手轮输入轴输出轴放大器发射架iθoE oθoE 2P 1P eu au ou 1u u +-题 1-2 导弹发射架方位角控制系统原理图试分析系统的工作原理,指出系统的被控对象、被控量和给定量,画出系统的方框图。
解 当导弹发射架的方位角与输入轴方位角一致时,系统处于相对静止状态。
当摇动手轮使电位器P1的滑臂转过一个输入角i θ的瞬间,由于输出轴的转角i o θθ≠,于是出现一个误差角o i e θθθ-=,该误差角通过电位器1P、2P 转换成偏差电压o i e u u u -=,e u经放大后驱动电动机转动,在驱动导弹发射架转动的同时,通过输出轴带动电位器2P 的滑臂转过一定的角度o θ,直至i o θθ=时,o i u u =,偏差电压0=e u ,电动机停止转动。
这时,导弹发射架停留在相应的方位角上。
只要o i θθ≠,偏差就会产生调节作用,控制的结果是消除偏差e θ,使输出量o θ严格地跟随输入量i θ的变化而变化。
系统中,导弹发射架是被控对象,发射架方位角o θ是被控量,通过手轮输入的角度i θ是给定量。
系统方框图如图解1-4所示。
1-3 许多机器,像车床、铣床和磨床,都配有跟随器,用来复现模板的外形。
图(题1-3)就是这样一种跟随系统的原理图。
在此系统中,刀具能在原料上复制模板的外形。
试说明其工作原理,画出系统方框图。
跟随控制器命令输入Z 轴直流伺服马达跟随刀头触针切割刀具原料X 轴直流伺服马达Y 轴直流伺服马达题1-3跟随系统原理图模板解 模板与原料同时固定在工作台上。
X 、Y 轴直流伺服马达接受控制器的指令,按输入命令带动工作台做X 、Y 方向运动。
模板随工作台移动时,触针会在模板表面滑动,跟随刀具中的位移传感器将触针感应到的反映模板表面形状的位移信号送到跟随控制器,控制器的输出驱动Z 轴直流伺服马达带动切削刀具连同刀具架跟随触针运动,当刀具位置与触针位置一致时,两者位置偏差为零,Z 轴伺服马达停止。
系统中,刀具是被控对象,刀具位置是被控量,给定量是由模板确定的触针位置。
系统方框图如图解1-9所示。
最终原料被切割加工成模板的形状。
2-2 分别求出图(题2-2)所示各系统的微分方程。
)()(t f t y km(a ))(t y )(t f 21k k m(b )c c 12m x x io(c )1k 2k oix x c(d )1k 2k x ix oc(e )解:)(a )()()(t f t ky t y m =+)(b )()()()(21t f t y k k t y m =++⋅⋅⋅⋅+=-02010))((x c xm c x x c i212110)()()()(K K s K K c csK s X s X d i ++=02010)())((x K c x xK x x e i i =-+-⋅⋅2-3 求图(题2-3)所示的传递函数,并写出两系统的无阻尼固有频率n ω及阻尼比ξ的表达式。
x ix ockm(a )Cu u oiLR(b )解:图)(a 有:m ks m c s mk s G ++=2)(m k n =ωmk C2=ξ 图)(b 有:⎪⎪⎩⎪⎪⎨⎧=++=⎰⎰idt C V idt C R L V i i i 110∴LC s L R s LC s G 11)(2++=LC n 1=ω L CR 2=ξ2-4 求图(题2-4)所示机械系统的传递函数。
图中M 为输入转矩,mC 为圆周阻尼,J 为转动惯量。
(应注意消去θθ ,及θ )xmkRcMm,C J题2-4解:由已知可知输入量M 与输出量θ之间的关系为:Mk C J m =++θθθ经拉氏变换后为:)()()(2s M k s s C s Js m =++θθθ∴ 222222/11)()()(n n n m m s J k s J C s J k s C Js s M s s G ωξωωθ++=++=++==其中,J k n =ωJk C m 2=ξ 3-2 设温度计能在1分钟内指示出实际温度值的98%,并且假设温度计为一阶系统,求时间常数。
如果将温度计放在澡盆内,澡盆的温度依10℃/min 的速度线性变化,求温度计示值的误差是多大? 解1:依题意可得已知条件为1=t 分,98.0)(=t C 而一阶系统的传递函数为 11)()(+=Ts t R t C 即)(11)(s R Ts s C += 在上述第一问中,要求温度计在1分钟内指示出响应值的98%,这相当于对温度计输入一个单位阶跃。
亦即 )(1)(t t r = 则s s R 1)(=11111)(+-=⋅+=Ts Ts s Ts s C即]11[)]([)(11+-==--Ts Ts L t C L t cTte T s L s L ----=+-=1]11[]1[11将1=t分及98.0)(=t C 代入上式可得Te1198.0--=即 02.098.011=-=-Te将上式两端取自然对数化简后得秒分36.15256.09.3102.0lg 3.21==--=-=T解2:在第二问中已知澡盆温度以分/10线性变化,说明输入函数t At t r 10)(==,为斜坡函数,此时温度计的误差为 )()()()(t c At t c t r t e -=-=而当At t r =)( 时2)(s As R =即]11[11)(11)(222++-=⋅+=+=Ts T s T s A s A Ts s R Ts s C则]11[)()(211211++-==----Ts T L s T L s L A s C L t C)(]1111[1121T tTe T t A T s TL s TL s L A ----+-=++-=即)1()()(T tTte AT TeT t A At t e ---=+--=将已知和已求得之值数1=t 分、256.0=t 分、10=A 代入上式即可求得温度计的误差为)(53.298.0256.010)(上式为近似计算=⨯⨯=t e 。
3-3 已知系统的单位阶跃响应为10tt 02.12.01)(---+=e e t x ,试求:(1)该系统的闭环传递函数;(2)系统的阻尼比ξ和无阻尼固有频率n ω。
解:(1)求解闭环传递函数)(s Φ由已知条件,当输入为单位阶跃信号时]2.12.01[)]([1)()(106000t t e e t x ss s X ---+℘=℘=Φ=1012.16012.01+⨯-+⨯+=s s s则)10)(60()60(2.1)10(2.0)10)(60(102.1602.01)()(0+++-++++=+-++==Φs s s s s s s s s s s s s sX s 6007060060070722.122.06007022222++=++--++++=s s s s s s s s s s(2)求解阻尼比ζ和无阻尼固有频率n ω 将闭环传递函数化为二阶振荡环节的标准形式2222260070600)(n n ns s s s s ωζωω++=++=Φ根据对应关系可得⎪⎩⎪⎨⎧==7026002n n ζωω解得 sra d n /5.24=ω,43.1=ζ。
