2、磁场的高斯定理和安培环路定理
合集下载
磁场的高斯定理和安培环路定理

L
解:
Bp
发生变化. 发生变化.
I2 I1
∫
L
B dl 不发生变化 P
L
例如: 例如: I1 >0 L I2<0 I1 I2 I3 L I L
I3
∫
L
B dl = o ( I1 I 2 )
∫
L
B dl = o ( I1 + I 3 )
∫ B dl
l
= 4 0 I
二,安培环路定理
∑Ii
i =0
§8-4
稳恒磁场的高斯定理与 安培环路定理
一,稳恒磁场的高斯定理
由磁感应线的闭合性可知, 对任意闭合曲面, 由磁感应线的闭合性可知 , 对任意闭合曲面 , 穿入的磁感应线条数与穿出的磁感应线条数相同, 穿入的磁感应线条数与穿出的磁感应线条数相同 , 因此,通过任何闭合曲面的磁通量为零. 因此,通过任何闭合曲面的磁通量为零.
Φ = BS 2 = (6i + 3 j + 1.5k ) (0.15) i = 0.135Wb ( 2) z Φ = ∫∫ B dS = 0
S
O l
x
l
l
一长直导线通有电流I 距其d 例,一长直导线通有电流I,距其d处有 一长为a 宽为b的长方形, 一长为a,宽为b的长方形,求通过这个 长方形的磁通量. 长方形的磁通量.
n
闭合回路所包围的所有电流 的代数和. 的代数和. 所取的闭合路径上各点的磁 感强度值, 感强度值,是由闭合路径内 外所有的电流产生的. 外所有的电流产生的.即是 由空间所有的电流产生的. 由空间所有的电流产生的.
B
二,安培环路定理
定理的物理意义 由安培环路定理可以看出, 由安培环路定理可以看出,由于 磁场中的磁感强度的环流一般不 为零,所以磁场是非保守场 非保守场. 为零,所以磁场是非保守场.
解:
Bp
发生变化. 发生变化.
I2 I1
∫
L
B dl 不发生变化 P
L
例如: 例如: I1 >0 L I2<0 I1 I2 I3 L I L
I3
∫
L
B dl = o ( I1 I 2 )
∫
L
B dl = o ( I1 + I 3 )
∫ B dl
l
= 4 0 I
二,安培环路定理
∑Ii
i =0
§8-4
稳恒磁场的高斯定理与 安培环路定理
一,稳恒磁场的高斯定理
由磁感应线的闭合性可知, 对任意闭合曲面, 由磁感应线的闭合性可知 , 对任意闭合曲面 , 穿入的磁感应线条数与穿出的磁感应线条数相同, 穿入的磁感应线条数与穿出的磁感应线条数相同 , 因此,通过任何闭合曲面的磁通量为零. 因此,通过任何闭合曲面的磁通量为零.
Φ = BS 2 = (6i + 3 j + 1.5k ) (0.15) i = 0.135Wb ( 2) z Φ = ∫∫ B dS = 0
S
O l
x
l
l
一长直导线通有电流I 距其d 例,一长直导线通有电流I,距其d处有 一长为a 宽为b的长方形, 一长为a,宽为b的长方形,求通过这个 长方形的磁通量. 长方形的磁通量.
n
闭合回路所包围的所有电流 的代数和. 的代数和. 所取的闭合路径上各点的磁 感强度值, 感强度值,是由闭合路径内 外所有的电流产生的. 外所有的电流产生的.即是 由空间所有的电流产生的. 由空间所有的电流产生的.
B
二,安培环路定理
定理的物理意义 由安培环路定理可以看出, 由安培环路定理可以看出,由于 磁场中的磁感强度的环流一般不 为零,所以磁场是非保守场 非保守场. 为零,所以磁场是非保守场.
12磁场的高斯定理和安培环路定理解读

穿过一面元的磁通量:
d m BdS BdS cos B dS 式中:dS dSn ˆ 称为面元矢量。 ˆ 为法线方向单位矢量。 n
4
2.穿过某一曲面的磁通量
m d m B dS
d m
B
BdS cos
dS
ˆ n
S
3.穿过闭合曲面的磁通量
m d m B dS
规定:取闭合面外法线方向为正向。 磁力线穿出闭合面为正通量, 磁力线穿入闭合面为负通量。
2
B
磁通量单位:韦伯,Wb
2
ˆ n
Байду номын сангаас
B
5
3.磁场中的高斯定理 定理表述:穿过任意闭合面的磁通量等于 0。
dB
dB ' dB' '
dl '
p
d
dl ' '
l
c
B
结果
o j
2
o
方向如图所示。
a
b
在无限大均匀平面电流的两侧的磁场都为 均匀磁场,并且大小相等,但方向相反。
15
例5 一矩形截面的空心环形螺线管,尺寸如图所示, 其上均匀绕有N匝线圈,线圈中通有电流I。试求: (1)环内距轴线为r 远处的磁感应强度;(2)通过 螺线管截面的磁通量。 I
解:在管内作环路半径为 r的圆环 ,
环路内电流代数和为: I NI
rR
o R1
2
当 r >> ( R2 – R1) 时N n 为沿轴向线圈密度;
0 NI B 2r 0 NI B 2r
磁介质中的高斯定理和安培环路定理.

B 0(H M ) 0(H mH) 0(1 m)H
在各B向0H同r0H性r H介质r中H10B.rH为m磁相关导对系 率磁:B导 率。0D r电H介0质rHE中
E
在真空 中 r 1, B0 0H
3.明确几点:
①. H 是 一辅助物理量,描述磁场的基本物理量仍然
是 B。H是 为消除磁化电流的影响而引入的,
B 和H 的名字张冠李戴了。
4
②. H 既与磁感应强度B 有关,又与磁化强度M 有
关,所以H 又是混合物理量。
③.磁场强度 的单 位与磁化强度相同,安培/米,A/m
④.若 H dl 0不一定环路内无电流。
或由 I s (r 1)I c
求 Is;
9
例1:长直螺线管半径为 R ,通有电流 I,线圈密度 为 n , 管内插有半径为 r ,相对磁导率为 r 磁介质, 求介质内和管内真空部分的磁感应强度 B 。
解: 由螺线管的磁场分布 可知,管内的场各处均匀
R
r
a Bb
一致,管外的场为0;
H
1.介质内
10
H dl H dl 0
bc
da
因为 cd 段处在真空中,真
a
B ab H b
空中的 M = 0;B = 0 ,
有 H dl 0
d
c d
Ic
cd H dl
H dl
Hdl cos H dl H ab I c
§12.2 磁介质中的高斯定理和安培环路定理
1
一、磁介质中的高斯定理
磁介质放在磁场中,磁介质受到磁场的作用要产
第2、3次_磁场高斯定理_安培环路定律讲解

通过曲面S的磁通量为
在国际单位制中,磁通量 的单位是Wb(韦伯)。
dm B dS BdS cos
m
BdS
s
BdS cos
s
二、磁场的高斯定理
对一封闭曲面来说,一般取向外的指向为正法线的指向。 这样从闭合面穿出的磁通量为正 ( / 2),穿入的磁通量为 负 ( / 2) ,由于磁感线是闭合线,那么穿过任一封闭曲 面的磁通量一定为零。
0 I
(r R) (r R)
0 (r R)
B
0
I
2 r
(r R)
0I B 2 R
O
I R
Rr
练 同轴的两筒状导线通有等值反向的电流 I , 习 求 B 的分布。
(1) r R2, B 0
R2
R1
(2)
R1
r
R2 ,
B
0 I 2 r
I
I
r
(3) r R1, B 0
电场、磁场中典型结论的比较
长直线
长 直
内
圆
柱 面
外
长 直
内
圆
柱 体
外
电荷均匀分布
E
2 0r
E0
E
2 0r r
E 2 0 R2 E
环 等于该闭合曲线所包围(套链)的电流的代数和与
路 定
真空中的磁导率的乘积。即
理
B dl 0 Ii
说 明
电流与环路成右旋关系
I4
I1 I 2
I3
如图 B dl 0 Ii
l
0 (I2 I3)
说
B dl 0 Ii 0 (I2 I3)
明
由环
环路
路上
磁场中的高斯定理和安培环路定理
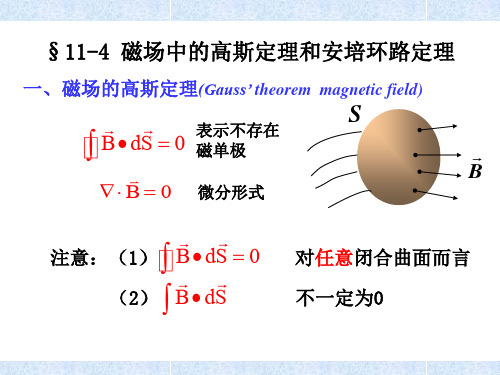
规定:
与L 绕向成右旋关系 与L 绕向成左旋关系
Ii 0 Ii 0
例如:
Ii I1 2I2
(穿 过L )
注意:
L
B dl
0 Ii
(穿 过L)
B:
与空间所有电流有关
B 的环流:只与穿过环路的电流代数和有关
穿过 L的电流:对 B 和 B dl 均有贡献 L
2
r1
2
d r1 r2
2.26 106 wb
二、安培环路定理(Ampere’s circulation theorem)
1.导出: 可由毕 — 沙定律出发严格推证
采用: 以无限长直电流的磁场为例验证
推广到任意稳恒电流磁场(从特殊到一般)
1)选在垂直于长直载流导线的平面内,以导线与 平面交点o为圆心,半径为 r 的圆周路径 L,其指向 与电流成右旋关系。
B 0I 2r
练习:同 求轴B的的两分筒布状。导线通有等值反向的电流I,
(1) r R2 , B 0
R2
R1
(2)
R1
r
R2 ,
B
0I 2r
I
rI
(3) r R1, B 0
2.长直载流螺线管的磁场分布
已知:I、n(单位长度导线匝数) 分析对称性 管内磁力线平行于管轴 管外靠近管壁处磁场为零
dl
0I
2π
2π
0
d
0I
对任意形状的回路
B dl
0I
rd
0I
d
2π r
2π
磁场的高斯定理和安培环路定理

电流 正负的规定 : 与 成右螺旋时, 为正; 即在真空的稳恒磁场中,磁感应强度 沿任一闭合路径的积分的值,等于
乘以该闭合路径所包围的各电流的代数和.
B d l B d l B d l B d l B d l 二 安培环路定理的应用举例
二 磁通量 磁场的高斯定理
l 无限长载流螺线管内部磁场处处相等 ,M 外部磁场为零. N NO O P PM
oR
l
B dl0I dl
l 2πRl
设闭合回路 l 为圆形
lBdl0I
回路(l 与 I成右螺旋)
I
o
B
dl
R
若回路绕向化为逆时针时,则
lB dl 20 π I0 2πd0I
l
I
d
dl
B
r
对任意形状的回路
B dl0Ird0Id
2πr 2π
l
l 与 I成右螺旋
Bdl
l
0I
电流在回路之外
d
( 0 I1I2)
I1
I1
I2 I3
L
I1
问 1)B是否与回路 L外电流有关?
2)若 Bdl 0,是否回路 L上各处 B0? L
是否回路 L内无电流穿过?
以上结果对任意形状的闭合电流(伸向无限远的电流)均成立.
二 安培环路定理的应用举例 电流 正负的规定 : 与 成右螺旋时, 为正;
设闭合回路 为圆形回路( 与 成右螺旋)
I
B1
r1
B2
dl1
dl2
r2
l
B12π0Ir1,B22π0Ir2
B 1dl1B 2dl2 20 πId
B 1 d l 1 B 2 d l 2 0
lBdl 0
乘以该闭合路径所包围的各电流的代数和.
B d l B d l B d l B d l B d l 二 安培环路定理的应用举例
二 磁通量 磁场的高斯定理
l 无限长载流螺线管内部磁场处处相等 ,M 外部磁场为零. N NO O P PM
oR
l
B dl0I dl
l 2πRl
设闭合回路 l 为圆形
lBdl0I
回路(l 与 I成右螺旋)
I
o
B
dl
R
若回路绕向化为逆时针时,则
lB dl 20 π I0 2πd0I
l
I
d
dl
B
r
对任意形状的回路
B dl0Ird0Id
2πr 2π
l
l 与 I成右螺旋
Bdl
l
0I
电流在回路之外
d
( 0 I1I2)
I1
I1
I2 I3
L
I1
问 1)B是否与回路 L外电流有关?
2)若 Bdl 0,是否回路 L上各处 B0? L
是否回路 L内无电流穿过?
以上结果对任意形状的闭合电流(伸向无限远的电流)均成立.
二 安培环路定理的应用举例 电流 正负的规定 : 与 成右螺旋时, 为正;
设闭合回路 为圆形回路( 与 成右螺旋)
I
B1
r1
B2
dl1
dl2
r2
l
B12π0Ir1,B22π0Ir2
B 1dl1B 2dl2 20 πId
B 1 d l 1 B 2 d l 2 0
lBdl 0
磁场的高斯定理和安培环路定理

. . . . . . . . ..
第4节
. . . .. . .. B . ∮H ·dl = 2rH = NI . . . . . H = NI/2r, r . . . . R 1 . . B = o NI/2r . . R 2 . . .. . 环管截面 r R, . .. . . ... B o NI/2R = o n I 解:1、环管内:
第八章
I
R
r B
R
r
第4节
第八章
直线电流的磁力线
I
I B
第4节
例8-5 求通电螺绕环的磁场分布。设环管 的轴线半径为 R,环上均匀密绕 N 匝线圈, 线圈中通有电流 I,管内磁导率为 o 。
第八章
I
I
. . . . . . ..
. . . .. . .. . . R1 R2
..
. . . ...
第八章
第4节
第八章
通电螺线管的模型
I
第4节
思考题: 如果通电螺线管的磁力线如下所示,图 中环路积分 ∮H ·dl = ?
第八章
I
L
I
二、磁场的安培环路定理 1、真空中 根据闭合电流产生的磁场公式,即安 培 — 拉普拉氏定律,可证明真空中磁场 B 沿闭合回路 L 的积分,即环流为: ∮L B ·dl =μoΣI 此式称为真空中磁场的安培环流定理,式 中ΣI 是闭合回路 L 所包围的所有闭合电流 I 的代数和。 物理意义:磁场 B 是有旋场,非保守场
第八章
I
R
o dS
B
Io
r
第4节
2、r>R ∮H ·dl =∮H dl = 2rH ΣIo = I H = I /2r ,B = oI /2r 上式表明,从导线外部看, 磁场分布与全部电流 I 集中 在轴线上相同。 μ I B H 2 πR I μ 0I 2 R π 2 πR 0 r 0
133磁场的基本特征 高斯定理和安培环路定理
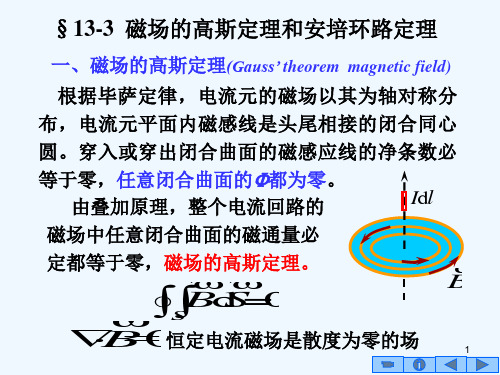
S 恒定电流磁场是散度为零的场 B = 0
B d S = 0
1
1.磁感线
切线方向—— B 的方向; 疏密程度—— B 的大小.
I I I
2
I S N S I N
3
直线电流的磁感应线
I I B
4
圆电流的磁感应线
I
5
通电螺线管的磁感应线
I
I
6
各种典型的磁感应线的分布:
围绕单根载流导线的任一回路 L
L2
对L每个线元 d l 以过垂直导线平面作参考分解 为分量 dl// 和垂直于该平面的分量 d l d l B 0 B d l B d l B d l //
L
B d l B d l I 证明步骤同上 // 0 L L //
直线电流的磁感线
圆形电流的磁感线
7
直螺线管电流的磁感线
环形螺线管电流的磁感线
8
1.磁力线的特征 无头无尾 与电流套连 与电流成右手螺旋关系 闭合曲线
I
2. 磁通量
B d s 单位:韦伯(Wb) m S
9
2. 磁通量 磁场的高斯定理
S B
ΔN B ΔS
磁场中某点处垂直 B 矢量的单位面积上 通过的磁感线数目等于该点 B 的数值.
讨论
S 0 1)Bd
S
磁场的基本性质方程
2)关于磁单极:
将电场和磁场对比: 由电场的高斯定理
d Sq 0 D
S
可把磁场的高斯定理写成 与电场类似的形式
BdS qm
S
q0 -自由电荷
qm - 磁荷
磁场的高斯定理和安培环路定律

0I
是否成立???
设任意回路L在垂直于导线的平面内,与电流
成右手螺旋。
l B dl Bdl cos
0I
2πr
dlc
os
d
B
I
dl
r
0I
2πr
rd
0I
2π
d
l
B dl
l
0I
dl cos rd
闭合回路不环绕电流时
B1
0I
2 π r1
B2
0I
2 π r2
B1
B2
d
I
dl1
r1
dl2
I
I
解:取垂直纸面向里为法
B
线方向,以导线1所在位
置为坐标原点,建立如图 所示的坐标轴。
x
l
取细长条面元,面元内为
均匀磁场
a aa
B
0I 2x
2
0I
3a
x
o
x
窄条形面元的元磁通为
dm B dS BdS Bldx I
通过矩形面积内的磁通量
m
dm
2a
Bldx
a1
2a
a
0I 2x
2
0I
o
B 0I
2π x
B // S
x
方向垂直于纸面向里
dΦ BdS 0I ldx I
2π x
B
Φ
S
B dS
0Il
2π
d2
d1
dx x
l
Φ 0Il ln d2
2π d1
d1 d2
o
x
例2 两平行的无限长直导线通有电流 I , 相距3a,
矩形线框宽为a,高为l与直导线共面,求通过线框的
磁场的高斯定理和安培环路定理.
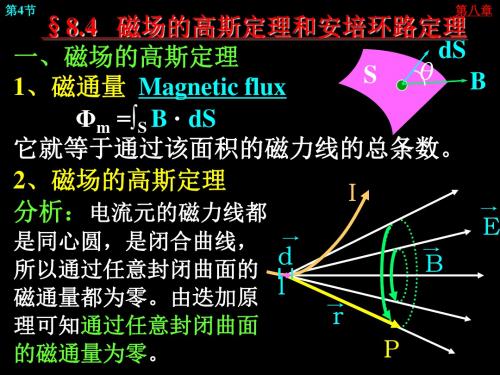
第二4节 、磁场的安培环路定理
第八章
1、真空中
根据闭合电流产生的磁场公式,即安
培 — 拉普拉氏定律,可证明真空中磁场 B
沿闭合回路 L
∮L B ·dl =μoΣI 此式称为真空中磁场的安培环流定理,式
中ΣI 是闭合回路 L 所包围的所有闭合电流
I 的代数和。
物理意义:磁场 B 是有旋场,非保守场
第4节
第八章
电流正负符号按右手螺旋定则:
电流方向与 L 的绕行方向符合右手螺
旋关系时,此电流为正,否则为负。
举例说明:
+I I
+ I1 + I2
- I3
L
第24、节 有磁介质
第八章
∮L B ·dl =μoΣI = μoΣIo +μoΣI’
式中ΣIo 和ΣI’ 分别是穿过安培环路 L 的自 由电流和束缚电流的总和。
其中 n = N/2R 为螺绕环单位长度的匝数。
2、环管外:ΣIo = 0,H// = 0,B// = 0 此式说明密绕螺绕环外部无磁场。
第特4节 例:当
R
第八章
时,即为无限长螺线管。
因此,长直螺线管内磁感应强度公式为:
B = o n I 此式表明,理想长直螺线管内部的磁感应强
注意:螺绕环和螺线管的外部磁场为零的结 论是在假定它们由许多不相连的圆环密集排 列组成的模型下得出的。实际上圆环以螺旋 线形式相连形成螺绕环和螺线管,沿螺绕环 和螺线管有一电流分量通过,即等效一圆电 流和长直载流导线,因此它们的外部磁场不 为零。但相比内部磁场而言,则相对很小。
2π R
μ 0I
2π R
第八章
I R
r
13-2-磁场的高斯定理-安培环路定理

L1
电流在闭合回路内
n B dl 0 I i L i 1
电流在闭合回路外
——安培环路定理
路径的积分的值,等于 0 乘以该闭合路径所穿过 的各电流的代数和.
在真空的恒定磁场中,磁感强度 B 沿任一闭合
二、安培环路定理
说明:
n B dl 0 I i i 1
解方程求出B的大小,指出B的方向。
二、安培环路定理
例2.无限大载流薄平板的磁场
d B1
j
d
dB
P
dB 2
d l1
O
c
d l2
结论:
B
1 2
0 j
a
L
b
在无限大均匀平面电流的两侧的磁场都为均匀 磁场,大小相等,但方向相反。
二、安培环路定理
例3.载流螺线环内的磁场 一环形载流螺线管,匝数为 N ,内径为 R1 ,外径为 R2 ,通有电流 I ,求管内 磁感应强度。
计2 有两半径分别为 R 和 2 R 的金属球壳同心放置
分析:(1) 内球壳接地,电势为零,但电量未必为零
(方法一:定义式求电势) 设内球壳带电为 q ,由高斯定理得
r
R
2R
q 4 r 2 0 r E q q0 40 r 2
2R R R
R r 2R r 2R
q
q q0 外球壳 (q q0 ) 无穷远
2R
C C1 C2 4 π 0 r 1 R 1 2R 4 π 0 2 R
24 π 0 R
L
(3)若 B d l 0 ,则回路内无电流穿过。
L
二、安培环路定理
磁场中的高斯定理及安培环路定理
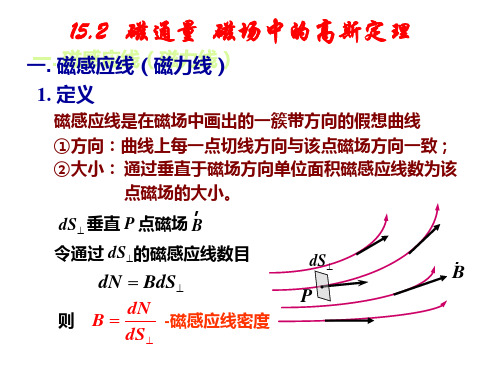
P
r B
则 B dN -磁感应线密度
dS
2. 几种典型的磁感应线
I
直线电流
圆电流
载流长螺线管
3. 磁感应线特性
磁感应线是环绕电流的无头尾的闭合曲线,无起点无终点; 磁感应线不相交。
二. 磁通量(magnetic flux)
1. 定义 通过磁场中任一给定面的
磁感线数目称为通过该面的 磁通量,用 表示。 2. 磁通量的计算 ① 磁场不均匀,S 为任意曲面
a
b
B
eeeeeeeeeeeee
Ñ B dl μ0 NI
l
B 0 NI
2 r
Amperian loop
B
o R1 R2 r
若 R1、R2 R2 R1
n N N
2 R1 2 r
则
B
μ 0
nI
B 0 NI 2 r
I
R2
R1
例题3 :
设在无限大导体薄板中有均匀电流沿平面流动, 在垂直于电流方向的单位长度上流过的电流为i (电流密度)。求此电流产生的磁场。
因而,同静电场中利用高斯定理确定已知电荷分 布的电场分布一样,需要满足一定的对称性。
例题1 :
已知:I 、R,电流沿轴向在截面上均匀分布, 求“无限长”载流圆柱导体内外磁场的分布
解: 首先分析对称性
电流分布——轴对称
I
磁场分布——轴对称
R
r
dS1
dB
dB2 dB1
O
l
P
dS2
电流及其产生的磁场具有轴对称分布时
B 0I 2 x
方向:
I
a
阴影部分通过的磁通量为:
rr B dS
6-2磁场的高斯定理和安培环路定理
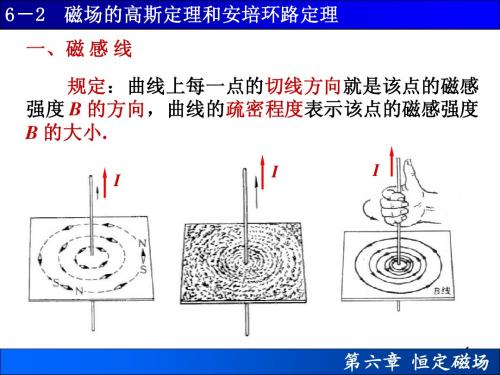
例6-3 如图所示,载流长直导线上的电流强度为 I , 它与边长分别为 a 和 b 矩形共面,边与长直导线平 行,两者之间的距离 d .求载流长直导线的磁场穿过 该平面的磁通量. 0 I 解 B 2π x B C B I
dΦ BdS
0
I
b
A dx D
2π x
bdx
o
x
d
a
0 Ib d a dx Φ 2 π d x 0 Ib d a ln 2π d
I2 I 3
l
B B1 B2 B3 B d l 0 ( I 2 I 3 )
l
L
I1
B d l 0 (I1 I1 I1 I 2 )
L
0 I1 I2) (
第六章 恒定磁场
11
6-2
磁场的高斯定理和安培环路定理
即在真空的稳恒磁场中,磁感应强度 B 沿任
0 乘以该闭合路径
I
电流 I 正负的规定 :I 与 为正;反之为负.
L 成右螺旋时,
第六章 恒定磁场
9
6-2
磁场的高斯定理和安培环路定理
注意
(1)环路定理中的磁感强度 B
为闭合路径 L 上的 磁感强度,它是由空间所有电流产生的。 (2)磁感强度沿闭合路径的环流,仅与闭合路径所包
6-2
磁场的高斯定理和安培环路定理
一、磁 感 线 规定:曲线上每一点的切线方向就是该点的磁感 强度 B 的方向,曲线的疏密程度表示该点的磁感强度 B 的大小.
I I I
第六章 恒定磁场
1
6-2
磁场的高斯定理和安培环路定理
I S S N I
N
磁场的高斯定理和安培环路定理

磁场是无源场 磁场是 无源场 比较 静电场 稳恒 磁场 磁感应线闭合成环,无头无尾 不存在磁单极。 磁感应线闭合成环,或两端伸向 不存在磁单极(?) 高斯定理 环路定理
内
3. 磁场的高斯定理
1 E dS
S
0
q
有源场 无源场
E dl 0
L
保守场
B dS 0
三.安培环路定理的应用
—— 求解具有某些对称性的磁场分布
LB dl 0 I i
( 穿过L )
适用条件:稳恒电流的磁场 求解条件:电流分布(磁场分布)具有某些对称性,
以便可以找到恰当的安培环路L,使 LB dl 能积
出,从而方便地求解 B 。
[例一] 无限长均匀载流圆柱体 I , R 内外磁场.
无限长直螺线管内为均匀磁场
思考: 如果要计管外磁场(非线密绕)对以上结果有无影响?
I
n
B内 0nI
外
B
I //
0 //
I B 2r
练习: 半径 R 无限长均匀带电圆筒绕轴线匀速旋转
.R. 求: 内部 B ?
已知:
解:
R
等效于长直螺线管 B 0 nI 单位长度上电流 nI ?
I
i
I1 I 2 I 3
(穿过L )
I
i
注意:
LB dl 0 I i
( 穿过L )
B 的环流:只与穿过环路的电流代数和有关 穿过 L 的电流:对 B 和 B dl 均有贡献
L
B : 与空间所有电流有关
不穿过 L 的电流:对 L 上各点 B有贡献; 对 LB dl 无贡献
内
3. 磁场的高斯定理
1 E dS
S
0
q
有源场 无源场
E dl 0
L
保守场
B dS 0
三.安培环路定理的应用
—— 求解具有某些对称性的磁场分布
LB dl 0 I i
( 穿过L )
适用条件:稳恒电流的磁场 求解条件:电流分布(磁场分布)具有某些对称性,
以便可以找到恰当的安培环路L,使 LB dl 能积
出,从而方便地求解 B 。
[例一] 无限长均匀载流圆柱体 I , R 内外磁场.
无限长直螺线管内为均匀磁场
思考: 如果要计管外磁场(非线密绕)对以上结果有无影响?
I
n
B内 0nI
外
B
I //
0 //
I B 2r
练习: 半径 R 无限长均匀带电圆筒绕轴线匀速旋转
.R. 求: 内部 B ?
已知:
解:
R
等效于长直螺线管 B 0 nI 单位长度上电流 nI ?
I
i
I1 I 2 I 3
(穿过L )
I
i
注意:
LB dl 0 I i
( 穿过L )
B 的环流:只与穿过环路的电流代数和有关 穿过 L 的电流:对 B 和 B dl 均有贡献
L
B : 与空间所有电流有关
不穿过 L 的电流:对 L 上各点 B有贡献; 对 LB dl 无贡献
14-2磁场高斯定理和安培环路定理

环路L上的 B 与 L 相切或垂直,且相切部 分的 B 相等。这样才有可能将 B 提到积 分号外。积分环路一般为同心圆周和矩形。
步骤:
(1)分析磁场对称性
(2)选择合适回路通过待求的 B 场点
(3)求L内包围的电流的代数和 I内 (4)用安培环路定理求B;并说明方向 有时还可灵活应用叠加原理和“补偿 法”。
I
o
B d l
L
L
r
B
o I dl cos 0 L 2 r
o I 2 r dl 0 I 2 r 0
以无限长直电流的磁场为例验证 若电流反向
I
o
2 r 0 I dlcos LB dl 0 2 r
L
r B
可证: 对任何形式的电流所激 发的磁场、对任何形状的闭 合路径(环路), 安培环路定理 都成立。
S
B dS B cos d S 0
S
磁场是“无源场” 磁场是“涡旋场”
例:无限长直导线通以电流I,求通过如图所示的矩
形面积的磁通量。
解: a
I
非均匀场
b
面积元
l
x
元通量
0 I B 2x dS ldx dΦm B dS
I 0 O d B d S l d x m x dx 2x 0 Il a b 1 0 Il a b m d m dx ln S 2 a x 2 b
I内: 环路内,穿过以L为边界的所有曲面的电流。
规定:与L绕向成右旋的电流为正,反之为负。
I1
B d l I 2 I 0 1 2
L
I2
L
步骤:
(1)分析磁场对称性
(2)选择合适回路通过待求的 B 场点
(3)求L内包围的电流的代数和 I内 (4)用安培环路定理求B;并说明方向 有时还可灵活应用叠加原理和“补偿 法”。
I
o
B d l
L
L
r
B
o I dl cos 0 L 2 r
o I 2 r dl 0 I 2 r 0
以无限长直电流的磁场为例验证 若电流反向
I
o
2 r 0 I dlcos LB dl 0 2 r
L
r B
可证: 对任何形式的电流所激 发的磁场、对任何形状的闭 合路径(环路), 安培环路定理 都成立。
S
B dS B cos d S 0
S
磁场是“无源场” 磁场是“涡旋场”
例:无限长直导线通以电流I,求通过如图所示的矩
形面积的磁通量。
解: a
I
非均匀场
b
面积元
l
x
元通量
0 I B 2x dS ldx dΦm B dS
I 0 O d B d S l d x m x dx 2x 0 Il a b 1 0 Il a b m d m dx ln S 2 a x 2 b
I内: 环路内,穿过以L为边界的所有曲面的电流。
规定:与L绕向成右旋的电流为正,反之为负。
I1
B d l I 2 I 0 1 2
L
I2
L
06磁场的高斯定理和安培环路定理

∫
∑
(4)安培环路定理说明磁场性质 磁场定理说明磁场性质 磁场是有旋场。
6
特例:以无限长载流直导线为例。 特例:以无限长载流直导线为例。 长直导线周围的磁力 线为一系列的同心圆, 长直导线周围的磁力 线为一系列的同心圆,选 取路径方向与磁感应强度方向相同; 感应强度方向相同 取路径方向与磁感应强度方向相同; 左边= 左边
dB ' '
dl '
o dl ' '
点的总磁场方向平行于电流平面。 无数对称元在 p点的总磁场方向平行于电流平面。 因为电流平面是无限大,故与电流平面等距离的各点 因为电流平面是无限大,故与电流平面等距离的各点B 的大小相等。在该平面两侧的磁场方向相反。 的大小相等。在该平面两侧的磁场方向相反。
13
. .. . .. . .. . .. . ..
a
b
B
B外 = 0
d
d a c d
c
∫ B ⋅ dl = ∫
b
a
B ⋅ dl + ∫ B ⋅ dl + ∫ B ⋅ dl + ∫ B ⋅ dl
b
c
∵ B ⊥ d l , cosθ = 0
B 螺线管外: 螺线管外: 外 = 0,
b
∫
c
b
B ⋅ dl = ∫ B ⋅ dl = 0,
∫ dl
B ⊥ dl , cosθ = 0
∫ B⋅ dl = 0
L
8
例1:长直密绕载流螺线管通有电流为 I,线圈密度 : 线圈密度 为 n,求管内一点的磁感应强度 。 ,求管内一点的磁感应强度 解:理想密绕螺线管,管内的磁 理想密绕螺线管, 场是均匀的, 场是均匀的,管外的磁场为 0 ; 作闭合环路 abcda,环路内的 环路内的 电流代数和为: 电流代数和为:∑ I = nabI
磁场的高斯定理和安培环路定理
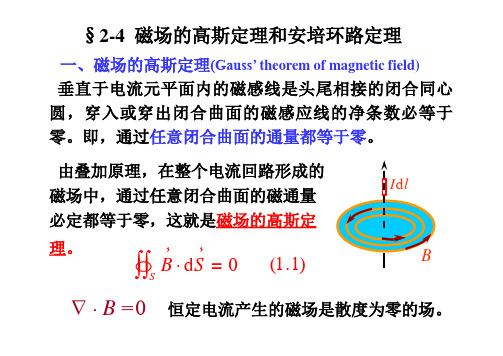
§2-4 磁场的高斯定理和安培环路定理
一、磁场的高斯定理(Gauss’ theorem of magnetic field) 垂直于电流元平面内的磁感线是头尾相接的闭合同心 圆,穿入或穿出闭合曲面的磁感应线的净条数必等于 零。即,通过任意闭合曲面的通量都等于零。
由叠加原理,在整个电流回路形成的
磁场中,通过任意闭合曲面的磁通量
L Bn dl 0In ,
L Bnk dl 0
任意回路
¸¸
n
B dl L
0
Ii
i1
穿过回路 的电流
闭合路径包围的电流为电
流 密度沿所包围的曲面的
¸
Ii
j dS
S
i
积分 安培环路定理说明磁场不是保守场,不存在标
量势函数。这是恒磁场不同于静电场的一个十分
重要的性质。
安培环路定理可以用来处理电流分布具有一定 对称性的恒磁场问题。
设 I1 , I 2 , … , I n电流过回路L,In 1 , I n 2 , … , I n k
电流不穿过回路L。令 B1 , B2 , … , Bn k 分别为单根
导线
I1
,
I
2
,
L
…
¸ B1
,
In
dl
பைடு நூலகம்
k产生的磁场,则有
¸
0I1 ,
L Bn1
dl
0
¸ #¸
# 所有电流的总¸ 场 ¸
小结
应用环路定理求解磁感应强度的步骤:
(1)根据通电电流产生的磁场的对称性,选 择合适的闭合曲线L,并规定计算方向;
(2)计算磁感应强度的环流以及通过曲线L 所包围的平面的电流的代数和;
一、磁场的高斯定理(Gauss’ theorem of magnetic field) 垂直于电流元平面内的磁感线是头尾相接的闭合同心 圆,穿入或穿出闭合曲面的磁感应线的净条数必等于 零。即,通过任意闭合曲面的通量都等于零。
由叠加原理,在整个电流回路形成的
磁场中,通过任意闭合曲面的磁通量
L Bn dl 0In ,
L Bnk dl 0
任意回路
¸¸
n
B dl L
0
Ii
i1
穿过回路 的电流
闭合路径包围的电流为电
流 密度沿所包围的曲面的
¸
Ii
j dS
S
i
积分 安培环路定理说明磁场不是保守场,不存在标
量势函数。这是恒磁场不同于静电场的一个十分
重要的性质。
安培环路定理可以用来处理电流分布具有一定 对称性的恒磁场问题。
设 I1 , I 2 , … , I n电流过回路L,In 1 , I n 2 , … , I n k
电流不穿过回路L。令 B1 , B2 , … , Bn k 分别为单根
导线
I1
,
I
2
,
L
…
¸ B1
,
In
dl
பைடு நூலகம்
k产生的磁场,则有
¸
0I1 ,
L Bn1
dl
0
¸ #¸
# 所有电流的总¸ 场 ¸
小结
应用环路定理求解磁感应强度的步骤:
(1)根据通电电流产生的磁场的对称性,选 择合适的闭合曲线L,并规定计算方向;
(2)计算磁感应强度的环流以及通过曲线L 所包围的平面的电流的代数和;
6-4稳恒磁场的高斯定理与安培环路定理

16
轴线 Bab: 0nI 管内 Bdc: 0nI D
L(>>D)
a Pb
d
c
管 外B: fe0
a Pb
f
e
17
设螺线管长度为l,共有N匝B 。dl
Bdl B0
Bdl Bdl ab bc
Bdl
Bdl Bdl
cd
da
I
Bdl ab
Bab
0abnI
B0nI
0
N l
安培环路定理仅仅适用于恒定电流产生的恒 定磁场,恒定电流本身总是闭合的,因此安 培环路定理仅仅适用于闭合的载流导线。
静电场的高斯定理说明静电场为有源场,环 路定理又说明静电场无旋;稳恒磁场的环路 定理反映稳恒磁场有旋,高斯定理又反映稳 恒磁场无源。
10
静电场
Edl0无旋
电场有保守性,它是 保守场,或有势场
§6-4 稳恒磁场的高斯定理与 安培环路定理
一、稳恒磁场的高斯定理
由磁感应线的闭合性可知,对任意闭合曲面, 穿入的磁感应线条数与穿出的磁感应线条数相同, 因此,通过任何闭合曲面的磁通量为零。
BdS0
S
磁场的高斯定 理
穿过任意闭合曲面S的总磁通必然为零,这就 是稳恒磁场的高斯定理。
1
激发静电场的场源(电荷)是电场线的源头或尾闾 ,所以静电场是属于发散式的场,可称作有源场; 而磁场的磁感线无头无尾,恒是闭合的,所以磁场 可称作无源场。
SEdS10 qi
电力线起于正电荷、 止于负电荷。
静电场是有源场
稳恒磁场
Bdl 0 Ii 有旋 i
磁场没有保守性,它是 非保守场,或无势场
BdS0
S
磁力线闭合、 无自由磁荷
轴线 Bab: 0nI 管内 Bdc: 0nI D
L(>>D)
a Pb
d
c
管 外B: fe0
a Pb
f
e
17
设螺线管长度为l,共有N匝B 。dl
Bdl B0
Bdl Bdl ab bc
Bdl
Bdl Bdl
cd
da
I
Bdl ab
Bab
0abnI
B0nI
0
N l
安培环路定理仅仅适用于恒定电流产生的恒 定磁场,恒定电流本身总是闭合的,因此安 培环路定理仅仅适用于闭合的载流导线。
静电场的高斯定理说明静电场为有源场,环 路定理又说明静电场无旋;稳恒磁场的环路 定理反映稳恒磁场有旋,高斯定理又反映稳 恒磁场无源。
10
静电场
Edl0无旋
电场有保守性,它是 保守场,或有势场
§6-4 稳恒磁场的高斯定理与 安培环路定理
一、稳恒磁场的高斯定理
由磁感应线的闭合性可知,对任意闭合曲面, 穿入的磁感应线条数与穿出的磁感应线条数相同, 因此,通过任何闭合曲面的磁通量为零。
BdS0
S
磁场的高斯定 理
穿过任意闭合曲面S的总磁通必然为零,这就 是稳恒磁场的高斯定理。
1
激发静电场的场源(电荷)是电场线的源头或尾闾 ,所以静电场是属于发散式的场,可称作有源场; 而磁场的磁感线无头无尾,恒是闭合的,所以磁场 可称作无源场。
SEdS10 qi
电力线起于正电荷、 止于负电荷。
静电场是有源场
稳恒磁场
Bdl 0 Ii 有旋 i
磁场没有保守性,它是 非保守场,或无势场
BdS0
S
磁力线闭合、 无自由磁荷
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
L
B dl o I i
L
S
B dS 0 j dS
S
B 0 j
安培环路定理的物理意义 磁场是有旋场(或磁场是非保守场,磁感应线 是闭合曲线)。
三、安培环路定理的应用
O
R
r
例3、求长直螺线管内的磁场。设螺线管的长度为 L,共有N匝线圈,单位长度上有 n = N/L匝线圈, 通过每匝线圈电流为I。管内中间部分的磁场是均 匀的,方向与管的轴线平行,在管的外侧磁场很 弱,可以忽略不计。
B
a
b
c d [解]: 若螺线管很长,则边缘效应可以忽略,螺 线管可看成是无限长,由对称性可知管内磁场是 均匀的,方向与管的轴线平行,并由右手螺旋定 则确定。在管的外侧磁场很弱,可以忽略不计。
B dl B 2πr μ0 I ,
j I / R2
且 I j s jπr 2 (r <R)
B
1 B μ0 jr 2
μ0 Ir B 2π R 2
0 I B 2R
μ0 I r = R处 B 2π R
B
0 Ir 1 0 jr, ( r R) 2 2 R 2 0 I 1 R2 0 j , r R ) ( 2 r 2 r
例2、求均匀载流无限长圆柱导体内外的磁场分布。
[解]:当r R时 B dl B 2r 0 I
L
I
R
μ0 I B 2π r
I 由 j πR 2
1 R2 B μ0 j 2 r
(r >R)
I jπR2
r
L
L
(r >R)
当r R时
L
r
O
μ0 NI N I B μ0 I μ0 nI 2π r 2πR 上式表明,对于细 式中n=N/2R为单位长度的匝数。
螺绕环,管内的B近似为常数。但各处磁感的方向均 沿切线方向,并非匀强磁场。但当R→∞时,任一段都 可看成长直螺线管,内部磁场为均匀的。
则有 (2)在螺绕环外部,环形积分回路为L'、L" ,
2、磁通量
3、磁场的高斯定理 规定:对于闭合曲面由里向外为法线的正方向。 由闭合曲面穿出的磁通量为正,进入闭合 曲面的磁通量为负。由于磁感应线是闭合线, 因此穿入闭合曲面的磁感应线数必然等于穿出 闭合曲面的磁感应线数,所以通过任一闭合曲 面的总磁通量必然为零。即: B dS 0 磁场高斯定理 的积分形式
例 1.
I2
I1
I
L
I
I
L ② ① ① B dl 0 I1 I 2
L
L ③ ② B dl 0
L
③ B dl o I I 0
L
2、证明 ①、同心圆 B 0 I 2r B dl Bdl B dl
L L
I
L
0 I 2r 0 I 2r
②、同一平面任意闭合环路 B dl B cosdl Brd
L
I
B
r
d
L
dl
2
0
0 I 2 0 I rd 0 d o I 2 2r
L
S
B dS BdV 0
S
V
B 0
微分形式
磁场的高斯定理的物理意义 磁场为无源场,磁单极子(磁荷)不存在。
二、安培环路定理
1、定理 在恒定磁场中,磁感应强度 B 沿任一闭合 环路的线积分,等于穿过该环路的所有电流的 代数和的 0倍。
B
L R2 R1
r
O
I
(1)在螺绕环内部,环形积分回路为L, 的方向如图 B
L B dl L Bdl B L dl B 2πr μ0 NI
根据安培环路定理
μ0 NI , ∴ B 2π r
( R1 r R2 )
B
R2 R1
可见螺绕环内各处的磁场强 L 弱不同,r越小处,即越靠近螺 绕环内侧,B越大。当螺绕环很 细时, R1–R2<<R= (R1+R2)/2, 即R1R2 R,则有
b
B dl 或B 0
B 0 nI
( L)
例4、求均匀密绕环形螺线管 (螺绕环)的磁场。设螺线管内 半径为R1,外半径为R2,共有 N匝线圈,通有电流I。 [解]: 根据对称性分析可知螺 线管的磁感应线应为以O为中 心的同心圆环,每一圆环处的 磁感大小相等。以O为中心作 一系列半径为r的环形积分回 路,沿逆时针方向绕行。则有
对r < R1的L': L B dl L Bdl B L dl B 2πr 0
∴ B0,
( r R1 )
根据安培环路定理
L B dl L Bdl B L dl
B 2πr 0
根据安培环路定理
对r > R2的L":
B
L R2 R1 L' O
r r
L"
r
∴ B0,
( r R2 )
I
0,
通电螺绕环 的磁场分布
( r R1 )
B
μ0 NI , ( R1 r R2 ) 2π r 0, ( r R2 )
以上计算表明,螺绕环的磁场集中在管内的 空间里,若在环管上截开一小段空隙,便可得到相 当均匀的较强的磁场。
L
B dl o I i
L
说明: ①、积分的回路方向与电流方向满足右手螺旋 关系时,电流取正;相反则电流取负。
②、 I i为穿过闭合曲线L为边界的任意曲面的电流。
L
③、 是空间所有电流产生的磁感应强度的矢量和, B 其中也包括不穿过L的电流产生的磁场,只不过后者 产生的磁场沿L积分后的总效果等于零。
B1
dl2
2
B2
r2
B1 dl1 B2 dl2 0
B dl 0
L
B dl B dS
L S
3、微分形式
I i j dS
L S
§8.4 磁场的高斯定理和安培环路定理
一、磁通量 磁场的高斯定理 1、磁感应线 磁感应线的性质: ①、磁感应线上任一点的切线方向都与该点 处的磁感应强度方向一致; ②、磁感应强度较大的地方,磁感应线较密, 反之,磁感应线较疏; ③、磁感应线是无头无尾的闭合曲线。
④、磁感应线与激发磁场的电流互相套合,磁感
应线的绕行方向和电流流向成右手螺旋关系。
穿过面元dS的磁通量 d M B dS B cos dS 式中 为 B与 dS 的法向单位矢量 n 之间的夹 角,dS ndS为面元矢量。 穿过任意曲面 的磁通量 S M S d M S B dS S B cos dS M单位:韦伯(Wb) n B可看成是单位面积 B dS 的磁通量,称为磁通密度。 Wb m 2 其单位是
③、不在同一平面任意闭合环路 B dl B dl dl//
B cos 900dl B cos dl// 0 Brd 0 I
④、闭合环路中没有包括电流 r1 1 B1 dl1 B1 cos 1dl1 d dl1 0 I d B1r1d 2 I I B2 r2d 0 d B2 dl2 B2 cos 2dl2 2
小结:
1、磁场中的高斯定理 B 0 B dS 0
2、安培环路定理 B dl o I i
L L
B 0 j
B
a
d B // dl
b
B dl 或B 0
c
B0
b c d a B dl a B dl b B dl c B dl d B dl
( L)
a Bdl B ab 根据安培环路定理有 B dl μ0 nabI
