第27届中国数学奥林匹克(CMO)竞赛试题(图片版,含答案)
1986年第二十七届IMO试题(不含答案)

第二十七届(1986年)波兰华沙(Warsaw,Poland)1. 设d是不等于2,5,13的任意整数。
说明在集合{2,5,13,d}可以找到两个不同的数a、b,使得ab-1不是完全平方数。
(联邦德国)2. 平面上有一个三角形A1A2A3和一点P0。
我们定义对于所有的s≥4都有A s=A s-3。
我们构造一组点P1,P2,P3,…,使得P k+1是P k绕点A k+1顺时针旋转120°得到的(k=0,1,2,…)。
证明如果P1986=P0,那么三角形A1A2A3是等边三角形。
(中国)3. 给正五边形的每个顶点赋值一个整数,使五个整数的和为正。
如果三个连续的顶点分别被赋值为x、y、z且y<0,那么执行下面的操作:数字x、y、z分别被x+y、-y、z+y代替。
只要五个数中有一个数是负的,就重复执行操作。
判断是否可以在有限步后结束操作。
(民主德国)4. 设A、B是平面上一个中心为O的正n边形(n≥5)的相邻顶点。
一个三角形XYZ,开始与三角形OAB重合,现用如下的方式移动三角形XYZ:保持Y、Z始终在多边形的边界上、X在多边形的内部。
试求出当Y、Z都走遍多边形的边界时X点所形成的轨迹。
(以色列)5. 找到所有满足条件的函数f,它定义在非负实数上,取值也为非负实数,且满足:i) 对于所有的x,y≥0,都有f(xf(y))=f(x+y);ii) f(2)=0;iii) 对于0≤x<2有f(x)≠0。
(英国)6. 给定平面上一个有限的点集,每个点的坐标值都为整数。
试问有没有可能用红色给点集中的一些点上色,并用白色给其它点上色,使得任何一条与坐标轴平行的直线L上,白点个数和红点个数的差不大于1?(民主德国)。
2021年中国数学奥林匹克(CMO)试题(完整)

2021年12月21日1.给定正实数,a b 和平面上两个点,A B ,满足AB a =.平面上取两个点,C D 满足ABCD 是一个非退化点凸四边形,并且,BC CD b AD a ===.易知四边形ABCD 有内切圆,求内切圆圆心的轨迹.2.求最大的实数λ,使得对任意,,,p q r s +∈ ,都存在一个复数z a bi =+满足b a λ≥,并且z 是如下方程的根:3232(22)(22)0pz qz rz s qz pz sz r ++++++=3.求所有a ∈ ,使得存在一个六元集合X 满足对1,2,,36k = ,方程0(mod 37)ax y k +−≡均存在解(,)x y 满足,x y X ∈.2021年12月22日4.n (3n >)个科学家一同参加会议.在会议上,每个科学家都有一些朋友(朋友关系是相互的,且每个人都不是自己的朋友).已知无论怎样将这些科学家分成两个非空的群体,总存在两个来自同一群体的科学家是朋友,也存在两个来自不同群体的科学家是朋友.在会议的第一天提出了一项提案,每个科学家对该提案的意见均用一个非负整数表示.从第二天起,每个科学家对该提案的意见改为前一天其所有朋友对该提案意见的平均值的整数部分.证明:经过一段时间,所有科学家对该提案都有相同的意见.5.我们知道,在尺规作图结构中,只有两种类型的一维结构:圆和直线.最开始时,白纸上只有两个距离为1的点.证明:可以用无刻度直尺和圆规在纸上作出一条直线和直线上距离的两点,且在构造过程中,出现的圆和直线的总数不超过10.注:请给出明确的作图步骤.并按照圆和直线出现的顺序贴上标签.如果作图步骤中出现的圆和直线的总数超过10,则根据总数可能会得到部分分数.6.对整数0a n ≤≤,设(,)f n a 为多项式(1)(2)a n a x x −++的展开式系数中,3的倍数的个数.例如:31432(1)(2)5972x x x x x x ++=++++,则(4,3)1f =.对任意正整数n ,设()F n 为(,0),(,1),,(,)f n f n f n n 中的最小值.(1)求证:存在无穷多个正整数n ,使得1()3n F n −≥. (2)求证:对任意正整数n ,1()3n F n −≤.。
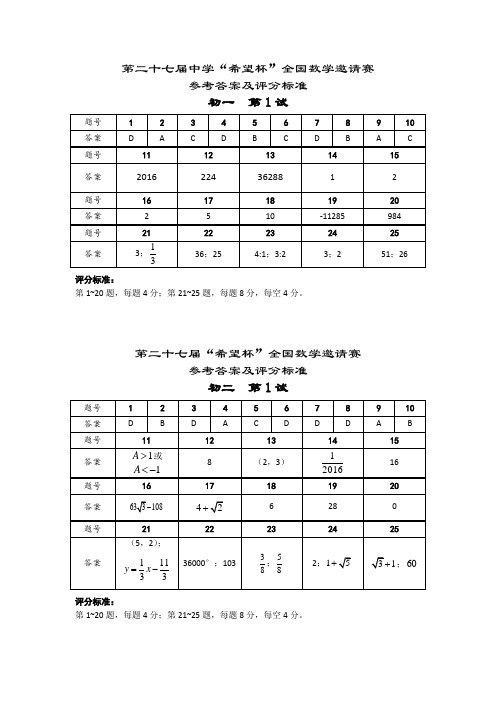
第二十七届“希望杯”全国数学邀请赛参考答案及评分标准初一第2试

第二十七届“希望杯”全国数学邀请赛参考答案及评分标准初一 第2试一、选择题(每题4分。
)题号 1 2 3 4 5 6 7 8 9 10 答案CDCDBBCCAD二、填空题(每题4分。
)题号 11 12 131415 答案 四 35 3:21-900 题号 16 17 181920 答案473112016- 5:3:25三、解答题21 解:设:有x 次跳绳的个数是18,有y 次跳绳的个数是20,有z 次跳绳 的个数是24. 则8,182024168,x y z x y z ++=⎧⎨++=⎩(5分)消去y ,得 24x z =-,由题可知,16x ≤≤,27x z ≤+≤,且,,x y z 均为整数. 当1x =,52z =;(不合题意) 当2x =,3z =,3y =;其中182203243168,⨯+⨯+⨯=(符合题意);当3x =,72z =;(不合题意); 当4x =,4z =;(不合题意) 当5x =,92z =;(不合题意); 当6x =,5z =;(不合题意).综上可知,当2x =,3z =,3y =时符合题意,所以她有3次跳绳的个数是20. (10分) 22. 证明:由于△ABD 与△ACD 的角分别对应相等,由三角形外角定理,得 ,,BAD ADC ABC ADC ∠>∠∠>∠ 所以只能 ADB ADC ∠=∠,但 ο180=∠+∠ADB ADC ,所以 .90ο=∠=∠ADB ADC于是 .BC AD ⊥ (5分) 由于 ,C B ∠≠∠因此 ,CAD B ∠=∠.BAD C ∠=∠相加得 ,BAC BAD CAD C B ∠=∠+∠=∠+∠ 但 ,180ο=∠+∠+∠BAC C B所以 90.BAC ∠=o即 △ABC 是直角三角形. (10分) AD 为斜边BC 上的高. 用两种方法计算直角三角形ABC 的面积,得11.22ABC AD BC S AB AC ∆⋅==⋅ 所以 .AD BC AB AC ⋅=⋅ (15分)23. 证明:不存在正整数,x y ,使222016x y +=. (2分) 假设存在正整数x y ,,使222016x y +=成立.因为 奇数的平方是被4除余1的数,偶数的平方为4的倍数,两个奇数的平方和为被4除余2的数,一个奇数的平方与一个偶数的平方之和是被4除余3的数, 只有两个偶数的平方和是4的倍数,而 2016是4的倍数, 故 2016是两个偶数的平方和. 即 ,x y 必同时为偶数. 不妨设22x a y b ==,.(,a b 为正整数)则有 ()()22222016a b +=, 整理得 22504a b +=成立. 同理,因为 504是4的倍数, 故 ,a b 同时为偶数. 不妨设22a c b d ==,.(,c d 为正整数)则有 ()()2222504c d +=, 整理得 存在正整数,c d 使得22126c d +=成立. 因为 126被4除余2,故 c d ,必同时为奇数. (10分) 不妨设 c d ≤, 则 2126632c =≤, 故 c 只能取1,3,5和7.当7c =时,21264977d =-=,而77不是完全平方数,故d 非正整数; 当5c =时,212625101d =-=,而101不是完全平方数,故d 非正整数; 当3c =时,21269117d =-=,而117不是完全平方数,故d 非正整数; 当1c =时,21261125d =-=,而125不是完全平方数,故d 非正整数. 所以不存在正整数c 和,d 使得22126c d +=成立.所得矛盾表明,“存在正整数x y ,,使222016x y +=”成立的假设不成立.综上所述,不存在正整数,x y ,使得222016x y +=成立. (15分)。
第 27届“希望杯”全国数学邀请赛初二1试解析

第27届“希望杯”全国数学邀请赛初二1试解析一、选择题1、【解析】A ,B 选项SSA 不能判定全等;C 明显不是判定全等的条件,D 项正确,选D .2、【解析】由3-=x y 与k kx y -=,得ky k x -+-=-+=122121,,∵交点为整点,∴k 可取1-,0,2,3,共计4个不同的值,故选B .3、【解析】由题可得混合后男女生的比为23:22)1112(:)1210(=++,故选D .4、【解析】解不等式2|1|>+x ,得1>x 或3-<x ;解不等式)0(||≥≤a a x ,得a x a ≤≤-,∵它们的解集没有公共部分,∴1≤a 且3-≥-a ,∴10≤≤a ,故选A .5、【解析】解不等式组,得5<x 且21m x ->,∵要满足不等式组只有四个整数解,∴需要满足以下关系:1210<m -≤,解得11≤-m <,故选C .6、【解析】∵ED AE =,∴A EDA ∠=∠,∴A A EDA DEB ∠=∠+∠=∠2;∵DB ED =,∴A DEB DBE ∠=∠=∠2,∴A DBE A CDB ∠=∠+∠=∠3;∵CD BC =,∴A CBD CDB ∠=∠=∠3,∴A CBD DBE ABC ∠=∠+∠=∠5;∵AC AB =,∴A ABC C ∠=∠=∠5,∴︒=∠=∠+∠+∠18011A ABC C A ,∴11180︒=∠A ,故选D .7、【解析】当0=n 时,4205==A ;当1=n 时,44411==A ;当2=n 时,47619==A ;当3=n 时,411629==A ……,要使得p A +的平方根是有理数,需满足p A +是一个平方数,观察发现,有且仅有各项的分子加上5,就使各数均成为平方数,故45=p ,答案是D .8、【解析】∵504201625.0=⨯,63)42(504=⨯÷,∴动点p 回到A 点;∵7251820151⋯=÷⨯,即动点p 再从A 往原方向移动7个单位到AD 中点,故选D .9、【解析】不妨从1开始,取1,2,3,5,8,13共六个数,其中没有任何3条线段可以构成三角形,如果往其中加入任意一个141-的其它数,那么必有3可以构成一个三角形;故n 最小可取值为7,选A .10、【解析】不妨设)(2x k a C ,)00(>,>k a ,则ak BC BC a OB 2'===,,设'AA 的中点为D ,延长'AA 交'BC 于E ;∵A 点在xy 1=上,∴1=⋅DO AD ;易证CBO Rt ODA Rt △∽△,∴有22a k OB BC AD DO ==,∴222ak DO =,∴a k DO =,k a D A AD ==',∴k a a D A OB E A -=-='',a k a OB AD AE +=+=,a k a k BC DO BC EB EC 2+=+=+=,ak a k EB BC EC -=-=2'';∴10'=+ECA AEC S S △△,即10))((21))((2122=--+++a k a k k a a a k a k a k a ,整理得20222=+k ,∴92=k ,∵0>k ,∴3=k ,∴6)(21)(212122=+=+⋅=⋅=k k a k a a k AE BC S ABC△,故选B .二、A 组填空题11、【解析】∵1>ab ,1>bc ,1>ca ,∴1)(2>abc ,∴1>abc 或1-<abc ,∴1)(2016>abc A =,故1>A .12、【解析】∵A ,B 关于原点对称,∴21x x -=,21y y -=,∴221221253y x y x y x =-;∵422=y x ,∴8222=y x ,即8531221=-y x y x .13、【解析】∵0)11()3()12(=--+--k y k x k ,∴0)113()12(=-+---y x y x k ∴⎩⎨⎧=-+=--0113012y x y x ,解得⎩⎨⎧==32y x ,∵无论k 取何值,当32==y x ,时,关于x 的一次函数的值恒为零,∴不论k 取何值,关于x 的一次函数0)11()3()12(=--+--k y k x k 的图象必经过点)32(,.14、【解析】设a =+⋯⋯+++2016131211,原式20161)201611()20161)(1(=-----=a a a a .15、【解析】根据题意,三角形三边长可以有以下情形:16153,,,16144,,,15145,,,16135,,,15136,,,16126,,,14137,,,15127,,,16117,,,14128,,,15118,,,16108,,,13129,,,14119,,15109,,,131110,,,故有16个.16、【解析】原式2223223)1)(1()1)(1(1)1(+-+=+-+=+-++-=a a a a a a a a a a a ,∵31131=+-=+a ,33663)113324()1(222-=++--=+-a a ,∴108363)33663(3)1)(1(22-=-=+-+a a a ,∴10836312345-=+-++-a a a a a .17、【解析】易证BCE Rt AFE Rt △≌△,∴1==CE FE ,∴2222=-==AE AF AE BE ,∴122+=+=CE AE AC ,∴2422)122(2121+=⨯+⨯=⋅=BE AC S ABC △.18、【解析】40722⋯=÷,617)32(22⋯=÷+,147)432(222⋯=÷++,577)5432(2222⋯=÷+++,6127)65432(22222⋯=÷++++677)765432(222222⋯=÷+++++,297)8765432(2222222=÷++++++4407)98765432(22222222⋯=÷+++++++,∵62877)12016(⋯=÷-,∴a 除以7所得的余数是6.19、【解析】设梯形两条对角线分别为a ,b ,根据题意有16=+b a ,14422=+b a ,∴56=ab ∴28562121=⨯==ab S 梯形.20、【解析】∵20162016)2016)(2016(2222=-+=-+++x x x x x x ,∴y y x x ++=-+2016201622,∴y x -=,∴0=+y x .三、B 组填空题21、【解析】如图,易证BEC Rt ADB Rt △≌△,∴2==AD BE ,1==DB EC ,∴)25(,C ;∴)25(')32('--,,,C A ,设直线''C A 的解析式为b kx y +=,则有⎩⎨⎧-=+-=+2532b x b x ,解得⎪⎪⎩⎪⎪⎨⎧-==31131b k ,∴直线''C A 的解析式为31131-=x y .22、【解析】所有多边形的内角和是︒=︒⨯+36000360)199(;边数最多的多边形最多有103499=+条边.23、【解析】依题意有⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=+++=+++=+++=+++4141664313927212481d c b a d c b a d c b a d c b a ,解得241-=a ,125=b ,∴83=+b a ,∴85)(1=+-=+b a d c .24、【解析】∵ABC △是△Rt ,∴①222c b a =+,∵0111=+--ba b a ,∴②ab a b =-22,②①+得③ab c b +=222,①②-得④ab c a -=222;④③⨯得2222245210(b a b a =-+,∴252+=ab 或252--=ab 舍去,将252+=ab 代入④解得2=a 或2-=a 舍去;∴1521+==ab S ABC △.25、【解析】如图,将CDM △绕点D 顺时针旋转︒60得到EDN △,连接AM ,MN ,则EN CM =,∵ND MD =,︒=∠60MDN ,∴MDN △是等边三角形,∴MN MD =;∵CM 与AM 关于BD 对称,∴CM AM =,∴当E 、N 、M 、A 共线时,AE NE AM MN MC MD =++=+2(最小),此时︒=∠=∠=∠60DMN BMA BMC ,作DA EF ⊥交AD 的延长线于F ,则︒=∠90F ,由旋转可得︒=∠60CDE ,2==ED CD ,∴︒=︒-︒=∠306090EDF ,∴在DEF Rt △中,2221==DE FE ,∴2622=-=EF DE DF ,∴262+=+=DF AD AF ;∴AEF Rt △中,22EF AF AE +=22)22()262(++=13+=.故答案为:13+,︒60.。
中国数学奥林匹克竞赛试题【CMO】[1987-2003]
![中国数学奥林匹克竞赛试题【CMO】[1987-2003]](https://img.taocdn.com/s3/m/3dc2f4630b1c59eef8c7b4ea.png)
CMO 中国数学奥林匹克竞赛试题1987第二届年中国数学奥林匹克1.设n为自然数,求方程z n+1-z n-1=0有模为1的复根的充份必要条件是n+2可被6整除。
2.把边长为1的正三角形ABC的各边都n等分,过各分点平行于其它两边的直线,将这三角形分成小三角形,和小三角形的顶点都称为结点,在第一结点上放置了一个实数。
已知i.A、B、C三点上放置的数分别为a、b、c。
ii.在每个由有公共边的两个最负三角形组成的菱形之中,两组相对顶点上放置的数之和相等。
试求3.放置最大数的点积放置最小数的点之间的最短距离。
4.所有结点上数的总和S。
3.某次体育比赛,每两名选手都进行一场比赛,每场比赛一定决出胜负,通过比赛确定优秀选手,选手A被确定为优秀选手的条件是:对任何其它选手B,或者A胜B,或者存在选手C,C胜B,A胜C。
结果按上述规则确定的优秀选手只有一名,求证这名选手胜所有其它选手。
4.在一个面积为1的正三角形内部,任意放五个点,试证:在此正三角形内,一定可以作三个正三角形盖住这五个点,这三个正三角形的各边分别平行于原三角形的边,并且它们的面积之和不超过0.64。
5.设A1A2A3A4是一个四面体,S1, S2, S3, S4分别是以A1, A2, A3, A4为球心的球,它们两两相切。
如果存在一点O,以这点为球心可作一个半径为r的球与S1, S2, S3, S4都相切,还可以作一个半径为R的球积四面体的各棱都相切,求证这个四面体是正四面体。
6.m个互不相同的正偶数与n个互不相同的正奇数的总和为1987,对于所有这样的m与n,问3m+4的最大值是多少?请证明你的结论。
1.设a1, a2, ... , a n是给定的不全为零的实数,r1, r2, ... , r n为实数,如果不等式r1(x1-a1)+r2(x2-a2)+...+r n(x n-a n)≦√(x12+ x22+ ... + x n2) + √(a12+ a22+ ... + a n2)对任何实数x1, x2, ... , x n成立,求r1, r2, ... , r n的值。
高中数学竞赛-历届IMO试题(1-46届)及答案

1.求证(21n+4)/(14n+3) 对每个自然数 n都是最简分数。
2.设√(x+√(2x-1))+√(x-√(2x-1))=A,试在以下3种情况下分别求出x的实数解:(a) A=√2;(b)A=1;(c)A=2。
3.a、b、c都是实数,已知 cos x的二次方程a cos2x +b cos x +c = 0,试用a,b,c作出一个关于 cos 2x的二次方程,使它的根与原来的方程一样。
当a=4,b=2,c=-1时比较 cos x和cos 2x的方程式。
4.试作一直角三角形使其斜边为已知的 c,斜边上的中线是两直角边的几何平均值。
5.在线段AB上任意选取一点M,在AB的同一侧分别以AM、MB为底作正方形AMCD、MBEF,这两个正方形的外接圆的圆心分别是P、Q,设这两个外接圆又交于M、N,(a.) 求证 AF、BC相交于N点;(b.) 求证不论点M如何选取直线MN 都通过一定点 S;(c.) 当M在A与B之间变动时,求线断 PQ的中点的轨迹。
6.两个平面P、Q交于一线p,A为p上给定一点,C为Q上给定一点,并且这两点都不在直线p上。
试作一等腰梯形ABCD(AB平行于CD),使得它有一个内切圆,并且顶点B、D分别落在平面P和Q上。
1.找出所有具有下列性质的三位数 N:N能被11整除且 N/11等于N的各位数字的平方和。
2.寻找使下式成立的实数x:4x2/(1 - √(1 + 2x))2< 2x + 93.直角三角形ABC的斜边BC的长为a,将它分成 n 等份(n为奇数),令α为从A点向中间的那一小段线段所张的锐角,从A到BC边的高长为h,求证:tan α = 4nh/(an2 - a).4.已知从A、B引出的高线长度以及从A引出的中线长,求作三角形ABC。
5.正方体ABCDA'B'C'D'(上底面ABCD,下底面A'B'C'D')。
(完整版)第27届全国奥林匹克化学竞赛决赛理论试题WORD

第27届中国化学奥林匹克〔决赛〕理论试题2021年11月29日北京营员号__________ 测试须知竞赛时间4小时,迟到超过半小时者不能进考场,开始测试后1小时内不得离场.时间到,把试卷、做题纸和草稿纸装入信封,放于桌面,听到指令前方可离开考场.将营员号写在试卷首页及每页答卷指定位置,写于其他位置按废卷论处.说有解答必须写于答卷指定框内,写于其他位置无效.凡要求计算或推演的,须给出计算或推演过程,无计算或推演过程,即使结果正确也不得分.用铅笔解答的局部〔包括作图〕无效.禁用涂改液和修正带,否那么,整个答卷无效.试卷已装订成册,不得拆散.允许使用非编程计算器及直尺等文具,不得携带铅笔盒和任何通讯工具入场,否那么取消测试资格.用黑色墨水笔或黑色圆珠笔做题.不得携带任何其他纸张进入考场.假设另需草稿纸,可举手向监考教师索取.写有与试题内容无关的任何文字的答卷均无效.H1.008元素周期表He4.003Li Be B C N O F Ne 6.9419.01210.8112.0114.0116.0019.0020.18 Na Mg Al Si P S Cl Ar 22.9924.3126.9828.0930.9732.0735.4539.95 K Ca Sc Ti V Cr Mn Fe Co Ni Cu Zn Ga Ge As Se Br Kr 39.1040.0844.9647.8850.9452.0054.9455.8558.9358.6963.5565.3969.7272.6174.9278.9679.9083.80 Rb Sr Y Zr Nb Mo Tc Ru Rh Pd Ag Cd In Sn Sb Te I Xe 85.4787.6288.9191.2292.9195.96[98]101.07102.91106.42107.87112.41114.82118.71121.76127.60126.90131.29 Cs Ba La Hf Ta W Re Os Ir Pt Au Hg Tl Pb Bi Po At Rn 132.91137.33138.91178.49180.95183.84186.21190.23192.22195.08196.97200.59204.38207.2208.98(209)(210)(222) Fr Ra Ac Rf Db(223)(226)(227)(261)(262)Ce Pr Md Pm S TI Eu GO lb Dy Ho Er Tfl»Yb LuHO Tz! 140 91144 24 1 5036151157 25i能第诩工61M93njoe ir4.97Ps U rup Pu Ain Cm Bk Cf Fm MO No Lf23Q 03237.0£(244)(243)(247)(247>(2S1)四〕37](256)(254)网有关常量N A = 6.022 1023 mol-1R = 8.314 J?mol-1K-1 F = 9.647 104C?mol-1第1题〔7分〕氮与其他元素可形成多种化合物, 如二元氮化物Li3N、GaN、Ge3N4、P3N5,叠氮化物NaN3、Ca〔N3〕2等.这些氮化物在发光、平安气囊等方面有重要应用.1-1 NaN3受热产生气体,写出反响方程式.1-2在二元氮化物Ga3N2、GaN和Ge3N4结构中,金属与氮采用四面体配位方式结合, N原子只有一种化学环境,写出这三种氮化物中N的配位数.1-3 P3N5晶体结构中,P的配位数为4,指出N有几种配位方式、配位数和不同配位方式的N的比例.1-4 Ca〔N3〕2中,Ca与N3-中两端的N相连,Ca的配位数为8,指出N3-两端的N与几个Ca相连.第二题〔9分〕光合作用是自然界最重要的过程之一,其总反响一半表示为6CO2+6H2— C 6H12O6+6O2实际反响分多步进行.其中,水的氧化过程是一个很重要的环节,此过程在光系统II 〔简称PSII〕中发生, 使水氧化的活性中央是含有4个镒原子的配位簇〔成为镒氧簇〕.初始状态的镒氧簇〔S0〕在光照下依次失去电子变为S1、S2、S3和S4, S4氧化H2O生成02.该过程简示如下:2-1光合作用中,水的氧化是几个电子转移的过程?2-2 25C,标态下,以下电极反响的电极电势分别为:a)M nO43-+4H++e- - MnO2+2H2Ob)M nO2+4H++e- - Mn3++2H2Oc)O2+4H ++4e-- 2H 2O计算上述半反响在中性条件下的电极电势.假定??e= 2.90V??e= 0.95 V??e= 1.23VMnO43-和Mn3+的浓度均为0.10mol • L-1,氧分压等于其在空气中的分压.答复此条件下MnO43-和MnO2能否氧化水. .M 产圄|2-3在模拟镒氧簇的人工光合作用研究中,研究者注意到了如下Mn(III)/Mn(II)体系(25C):d) Mn3++e- - Mn2+?? = 1.51Ve) 在[H 2P2O72-]=0.40mol • L-1, [Mn(H 2P2O7)33-]=[Mn(H 2P2.7)22-]的溶液中:Mn(H 2P2O7)33-+2H++e-- Mn(H 2P2O7)22-+H4P2O7 ?? = 1.15V2-3-1计算e〕中的半反响的标准电极电势.(H4P2.7 的酸解离常数:K a1 = 1.2X 10-1, K a2=7.9X 10-3, K a3=2.0 X 10-7, K a4=4.5 X 10-10)2-3-2 计算Mn〔H 2P2.7〕22-和Mn〔H 2P2.7〕33-的稳定常数之比. 第3题〔13分〕X、Y、Z均为非金属元素〔X的原子序数小于Y的原子序数〕,三者形成多种化合物.其中分子式为XYZ 6的化合物被认为是潜在的储氢材料,氢的质量分数达19.6%.3-1通过计算说明X、Y、Z各是说明元素3-2以下图示出XYZ 6及相关化合物的生成与转化的流程图:I.尸・.但.其中,实线箭头表示在一定条件的转化过程,虚线仅表示分子式的关联关系;由A和B制备XYZ 6的过程中给出了所有的反响物和产物, 而其他过程仅给出了所有的反响物及其参与反响的计量系数的比例〔例如, A - C,箭头上的1/2B表示“2A+B〞反响,产物为C或者C和其他可能的物质,计量系数比未给出〕;B 和D的结构中均含有正四面体构型的负离子基团, E、F和G均为六元环结构.根据图中的关系与所述条件,写出化合物A、B、C、D、E、F、G、H和I的化学式;画出D和G的结构式;写出D与A产生C的反响方程式.第4题〔10分〕工业漂白剂由次氯酸钙、氢氧化钙、氯化钙和水组成,有效成分为次氯酸钙.准确称取7.630g研细试样,用蒸储水溶解,定容于1000ml容量瓶.移取25.00ml该试样溶液至250ml锥形瓶中,缓慢参加过量的KI水溶液,以足量的1:1乙酸水溶液酸化,以0.1076mol • L-1的Na2s2O3标准溶液滴定至终点,消耗18.54ml.移取25.00ml试样溶液至250ml锥形瓶中,缓慢参加过足量的3%出.2水溶液,搅拌至不再产生气泡.以0.1008mol . L-1的AgNO3标准溶液滴定至终点,消耗20.36ml.移取25.00ml试样溶液至100ml容量瓶中,一蒸储水稀释至刻度. 移取25.00ml试样溶液至250ml锥形瓶中,以足量的3%H2O2水溶液处理至不再产生气泡.于氨性缓冲液中以0.01988mol • L-1的EDTA标准溶液滴定至终点,消耗24.43ml.4-1计算该漂白粉中有效氯的百分含量〔以Cl2计〕4-2计算总氯百分含量4-3计算总钙百分含量第5题〔7分〕稀溶液的一些性质只取决于所含溶质的分子数目而与溶质本性无关,所谓的分子的数目必须是独立运动的质点数目,此即稀溶液的依数性. 1912年McBain在研究脂肪酸纳水溶液的时发现,与一般电解质〔如NaCl〕水溶液不同,脂肪酸纳体系在浓度到达一定值后,其电导率、外表张力等依数性质严重偏离该浓度前的线T规律,依数性 -浓度曲线上呈现一个明显的拐点.而密度等非依数性质那么符合一般电解质溶液的规律.通过对多种 =脂肪酸盐的实验,他发现这是一个普遍的规律.他认为在浓度大于拐点值时, 脂肪酸盐在溶液中并非以单分子形式存在,而是发生了分子聚集.他将这些聚集体成为缔合胶体.5-1根据上述事实,你认为McBain的推论是否合理?说明理由.5-2 McBain对脂肪酸纳体系进行了量热实验,发现在拐点浓度附近,由拐点前到拐点后体系的标准始变几乎为零,这让他百思不得其解.经过长期的研究和思考,他鼓起勇气在国际学术会上宣讲了自己的研究结果,认为脂肪酸盐在拐点浓度后的缔合胶体形成是热力学稳定的.当时的会议主席对此勃然大怒,没有等报告讲完就以“ McBain ,胡说! ",将NcBain 轰下讲台.假设在脂肪酸盐拐点浓度前、后体系中水的结构性之没有发生变化, 结合根底热力学和嫡的统计意义,简单说明会议主席认为McBain的观点“荒唐〞的原因.5-3然而,大量研究结果证实了McBain的结论是正确的,原因是“在脂肪酸盐拐点浓度前、后水的结构性质没有变化〞这一假设是错误的.如果认为“在脂肪酸盐拐点浓度前、后对溶剂水的结构会产生不同影响〞那么请基于嫡的统计意义,推测水的结构在拐点浓度前和拐点后哪个更有序,说明理由.5-4除脂肪酸盐外还有很多物质具有类似的变化规律. 这些物质〔外表活性剂〕的分子结构具有一个共同的特点,都具有亲水头基和疏水尾链〔如以下图所示〕.请给出外表活性剂在水中形成的“缔合胶体〞的结构示意图.假设外表活性剂的分子长度为1.0n m,估算“缔合胶体〞在刚过拐点浓度时的最大尺寸.第六题〔9分〕将1mol水在100C, 101.3kPa下全部蒸发为水蒸气, 再沿着p/V= a 〔常数〕的可逆过程压缩,终态压力为152.0kPa,设水蒸气为理想气体,在此过程温度范围内,它的摩尔等压热容C p,m=33.20J mol-1K -1.水的气化热为40.66kJ • mol-1〔假设一定温度范围内水的气化热不变〕6-1计算整个过程终态的热力学温度T2.6-2通过计算,判断终态时体系中是否含有液态水,假设存在,液态水的量是多少.6-3计算整个过程发生后,体系的焰变^H.6-4假设整个过程的嫡变为132.5J- K-1,推算可逆过程的嫡变AS.第7题〔5分〕某酸碱催化反响〔E和S是反响物,P是产物〕机理如下:HE, +3'HES.T PE + S A ES・ r pk i=1.0x 107mol-1• dm3 - s-1, k2=1.0x 102mol-1• dm3 . s-1, pK a=5.0,反响决速步骤为中间产物HES〞和ES之生成.7-1推倒表观反响速率常数k exp的表达式,式中只能含有基元反响的速率常数k1和k2以及氢离子浓度[H+]和E的电离平衡常数K ao7-2推断上述反响属于酸催化还是碱催化.假设限制此反响缓慢进行,通过计算,判断根本不随pH在什么范围,k exp pH发生变化〔1%以内〕.第8题〔11分〕金属氢化物是储氢和超导领域的一个研究热点.在70GPa下榻的氢化物可形成四方晶系晶体:晶胞参数a=305.2pm , b=305.2pm , c=383.1pm;通过晶胞顶点有4次旋转轴,通过顶点垂直于a, b, c 方向均有镜面;在晶胞顶点处有Ba2+离子,在〔0.500,0.500,0.237〕处有H-离子,在〔0.132,0.500,0.500〕处有H原子.8-1写出一个正当晶胞中各离子〔原子〕的坐标及结构基元〔须指明具体的原子或离子种类及数目〕8-2画出一个正当晶胞沿a方向的投影图,标出坐标方向.8-3计算该晶体中H原子之间的最短距离.8-4该晶体可看作由H 2分子填入Ba 2+离子和H -离子组成的多面体中央而形成,说明此多面体的连接方式.8-5假设常压脱氢后氢化物骨架不变,计算最大储氢密度.第9题〔6分〕9-3局部丙烷与卤素自由基发生的反响及其相应的反响始变如下:CH 3CH 2CH 3 + Cl • CH 3CHCH 3 + HCl CH 3CH 2CH 3 + Cl - CH13cH 2cH 2+ HClCH 3CH 2CH 3 + Br ♦ CH 3CH 2CH 2 + HBr 当反响温度升高,上述反响的速率将 A.都降低; B.都升高; C.反响〔1〕和〔2〕降低,反响 ⑶升高; D.反响〔1〕和〔2〕升高,反响〔3〕降低;9-4 25C,以下反响的两种产物的比例已经给出CH 3CH 2CH 3 + Cl • CH 3CH 2CH 2 + CH 3CHCH 3 + HCl43% 57%结合9-3题中所给的信息,预测当反响温度升高而其他反响条件不变时,1级自由基产物比例将A.降低;B.升高;C.不变;D.无法判断△ H e = -34kJ/mol △ H e = -22kJ/mol △ H 0 = +44kJ/mol⑴(2)⑶9-1以下化合物中碱性最强的是AB C D第10题〔10分〕根据以下化学反响答复以下问题10-1在以下化学反响中10-1-1试齐【J NH4C1在反响中白^作用为____________________________________________________10-1-2画出产物D的稳定的湖边异构体的结构简式.10-1-3产物D中碱性最强的氮原子是.10-2以下两个反响在相同条件下发生,分别画出两根反响的产物的结构简式.第11题〔13分〕11-1画出以下反响的中间体结构简式.RCHO11-2画出以下两个反响的所有产物结构简式.Me3OBF4上述反响含苯环的产物A。
中国数学奥林匹克(CMO)历届试题及解答(1986-2005)

过P2 作 平 行 于BC 的 直 线
EP2 P3 . ABC .证毕.
DP2 P3 ,也就不大于S
5.能否把1,1,2,2,. . . ,1986,1986这些数排成一行, 使得两个1之间夹着1个数,两个2之间夹着2个数,. . . , 两 个1986之间夹着1986个数.请证明你的结论. 解:不能.假设可以做出这样的排列,将已排好的数按顺序编号为1,2,. . . ,3972. 当n为奇数时,两个n的编号奇偶性相同;当n为偶数时,两个n的编号奇偶性不同. 而1到1986之间有993个 偶数,所以一共有2k + 993个编号为偶数的数.(k ∈ N∗ ) 但是1到3972之间有1986个偶数,k = 496.5.矛 盾.所以不能按要求排成这样一行. √ 6.用任意的方式,给平面上的每一点染上黑色或白色. 求证:一定存在一个边长为1或 3的正三角形,它的
3
第二届中国数学奥林匹克(1987年)
北京 北京大学
1.设n为自然数,求证方程z n+1 − z n − 1 = 0有模为1的复根的充分必要条件是 n + 2可被6整除. 证明:当6|n + 2时,令z = ei 3 = ∴ z n+1 − z n − 1 = e ∴z
n+1 n −i π 3
π
1 2
2 2 a1 x2 1 + a2 x2 + · · · + an xn ; 2 2 a1 x2 1 + a2 x2 + · · · + an xn
0(i = 1, 2, . . . , n),则显然有a1 x1 + a2 x2 + · · · + an xn 0, ai −a1 > 0(i = 2, 3, . . . , n). ∴
数学奥林匹克高中训练题(27)及答案

数学奥林匹克高中训练题(27)第一试、选择题(本题满分 36分,每小题6分)1 •(训练题57)若f (x )是R 上的减函数,且f (x )图像经过点 A (0,3)和点B (3, - 1),则不等式f (x 1^12的解集为(D) •4.(训练题57) f (x )是定义在R 上的函数,且对任意的x 满足f (x ,1) = -f (x ) •已知当(2,3]时,f (x )=x •那么,当(-2,0]时,f (x )的表达式为(C ) •(B)f(xJ 仆 WI-x + 2,x^(-1,0](C)f(x)二x 4,x"Tx-3,x (-1,0](D)f(X“「XJX (-2,-1]x-3,x (-1,0]5.(训练题57)已知ABCD -AB 1G D 1是边长为1的正方体,P 为线段AB 1上的动点,Q 为底面ABCD 上动点•则PC 1 PQ 的最小值为(A ) •6.(训练题57)已知在数列{a n }中,a 1 =1,S n 为前n 项的和,且满足 &二n 匕(n=1,2』l ) •则a .的 表达式为(D ) •(B )(」:,2)(C)(0,3) (D) (-1,2)2 •(训练题57)若函数 2f (x) = a sin 2x (a - 2) cos 2x 的图像关于直线 Jix 对称,则a 的值等于8(C) • (B)1 或-1 (C)1 或- 2(D) -1 或 22x23.(训练题57)设椭圆的方程为 y=1,A (0, -1)为短轴的一个端点,M , N 为椭圆上相异两点, 若总存在以MN 为底边的等腰■ AMN ,则直线MN 的斜率k 的取值范围是(C ) •(A)(-1,0](B)[0,1](C)(-1,1)(A) f (x)二 x 4(A)V(B) 3(C)22二、填空题(本题满分 54分,每小题9分)AD 1AC AB1 (训练题57)在 ABC 中,AD _ BC 于D ,且•则的最大值为13 .BC 3 AB AC————a - x2.(训练题57)已知函数y 的反函数图像关于点(-1,4)成中心对称.则实数 a 的值 3 •x —a -13. (训练题 57)集合 A ={x | Ja 2 +4x -x 2 >a (x+1)}, B={x|x —丄<丄},当 A 匸 B 时,a 的取值范2 2围为 1_a_.. 2 .4. (训练题57)已知线段 AD//平面〉,且到平面:的距离等于8,点 B 是平面〉内的一动点,且满 足AB =10 •若AD =21,则点D 与B 距离的最小值为17 .2545. (训练题57)已知多项式x -x-1整除多项式ax bx • 1 .则实数a =3 ___ , b=_-5—6.(训练题57)设S 二[..1] 1、2] 1、3]咽| [ . 2002],其中[「n ]表示不超过n 的最大整数。
第 27届“希望杯”全国数学邀请赛初一1试解析

第27届“希望杯”全国数学邀请赛初一1试解析一、选择题1、【解析】基础题,选D.2、【解析】每人每天的效率为mn 1,)(n m +个人每天的总效率为mnn m +,因此这项工程需要的天数为mn n m +=+÷ 1,故选A.3、【解析】考查基本概念,选C.4、【解析】∵c b a 543==,∴,,c b c a 4535==∴,c c c b a 12354535=+=+∵,kc b a =+∴1235=k ,故选D.5、【解析】设两非零自然数),,,.(互质为正整数,,n m x n m nx b mx a ==,依题意得,x mnx nx mx +=⋅∴mn x 11+=∵互质为正整数,n m x n m ,,,,∴,1==n m ∴,2=x ∴,2==b a ∴.1024210102222==⎪⎪⎭⎫ ⎝⎛+b a b a 故选B.6、【解析】如图,连接AD、BD、CD,设小方格的边长为1,则,52122=+===CD BD AD 103122=+==CD AB ,∴222222CD BD BC AB BD AD =+=+,,∴︒=∠=∠90DBC ABD ,∴︒=︒-︒=∠=∠45)90180(1A ABD ,∴︒=︒+︒=∠+∠=∠1359045DBC ABD ABC ,故选C.7、【解析】由已知得,084238146222=--++-++-a c c b b a ,整理得,0)4()3()2(222=-+-+-c b a ,∴432===c b a ,,,∴9=++c b a ,故选D.8、【解析】∵502100=÷,1333100⋯=÷,205100=÷,4166100⋯=÷,1010100=÷,10615100⋯=÷,10330100⋯=÷,∴26361016203350100=-+++---=k ,故选B.9、【解析】201652121212<时,当=++⨯=*=n ,2016233535353<时,当=++⨯=*=n ,20161194234234234<时,当=++⨯=*=n ,20167195119511951195<时,当=++⨯=*=n ,201650396719671967196>时,当=++⨯=*=n ,∴满足2016>x 的最小整数是6,故选A.10、【解析】当积木藏在内部的重叠的面最多时,表面积最小。
第27届中学(第1试答案,含初三)
2;
;
评分标准:
第1~20题,每题4分;第21~25题,每题8分,每空4分。
第27届“希望杯”全国数学邀请赛第1试
参考答案及评分标准
初中三年级
题号
1
2
3
4
5
6
7
8
9
10
答案
C
A
C
A
A
C
B
C
C
A
题号
11
12
13
14
15
答案
5
2
4
2
题号
16
17
18
19
20
答案
6
882
题号
21
22
23
24
25
答案
2;
;5
第二十七届中学“希望杯”全国数学邀请赛
参考答案及评分标准
初一第1试
题号
1
2
3
4
5
6
7
8
9
10
答案
D
A
C
D
B
C
D
B
A
C
题号
11
12
13
14
15
答案
2016
224
36288
1
2
题号
16
17
18
19
20
答案
2
5
10
-11285
984
题号
21
22
23
24
25
答案
3;
36;25
4:1:
第1~20题,每题4分;第21~25题,每题8分,每空4分。
