六步教你备考华杯赛!

合集下载

备考华杯赛需要哪些复习资料？.doc

备考华杯赛需要哪些复习资料？
备考华杯赛需要哪些复习资料：
准备华杯赛的考试，应该用哪些资料呢?哪些数学资料对备战华杯赛有帮助?做华杯赛历年真题有用吗?针对这些问题，济南奥数编辑整理了备考华杯赛应该学习哪些资料。

一、华杯赛历年真题
这个不用多说，最能体现华杯赛命题难度和方向的珍贵资料。

建议学生成套按考试时间把近五年真题完成，并且把所有涉及的知识点和方法完全掌握。

二、华杯赛赛前教程
组委会官方出版的材料。

部分题目难度等同于总决赛，所以在使用的时候，不用花太多时间在最难的题目上。

每年决赛中都会有一两道题《教程》中的题目通过改编或者更改数据结构出现在试卷上。

三、数学思维训练汇编
华杯赛组委会推荐参考书。

目前最新、最全的汇编题集。

书中题目逻辑关系更清楚，更贴近杯赛命题，解析非常清楚。

通过对以上华杯赛资料的学习，相信你一定能在华杯赛的考试中取得优秀的成绩。

【备考】华杯赛：想要获奖你必须做到的事

【备考】华杯赛：想要获奖你必须做到的事长沙2015赛备考冲刺迫在眉睫，现在已经是4月份，杯赛复赛马上就开始。

接下来最重要的要数华杯赛了。

下面为大家说一说冲刺华杯赛一、二、三等奖必须做到的事。

首先，华杯赛重要的考察模块为：计算、数论、几何、计数、行程、组合等。

对于学生的
奥数解题技巧上要求比较高。

当然，每年华杯赛对于各知识模块中的细分知识点侧重都会有所变化，但是大的模块不会
变动，这要求同学们对于每一个细小的知识点都有所掌握，切忌以偏概全。

下面是知识模块逐个突破的大体规划：
其次，真题当练习。

做完就完了吗？你还差得远呢！真题的作用除了查缺补漏，还有一点
最重要也是最容易被很多人忽略的作用——帮你摸清出题思路。

华杯赛考试时间上比较紧张，
往年考试总有人为了不会的题目左思右想、畏葸不前，而耽误拿下后面应该拿到的分数，最终
和获奖擦肩而过。

所以，摸清出题人的出题风格，对症下药，是给那些会做的题争取更多的时间。

对于试卷风格的熟悉程度，一定程度上可能决定了答卷的速度，同样也决定了学生本身对
考试的信心。

华杯赛试题原创性非常高，历年的试题经常成为下一年其它杯赛命题的来源！
与华杯赛初赛相比，决赛考试时间一个半小时，满分150分。

决赛考点相对初赛有所偏重，从题型的难易程度来分析，基础题占50分，中档题60分，难题40分，基础中档题超过70%。

所以，打好基础非常重要。

从历届获奖学生的得分情况来看，能获得二、三等奖的孩子不一定会做最难的题目，而是
把会做的题目都做对了。

当然如果想拿一等奖，攻破难题是孩子们需要努力的。

2021小升初华杯赛夺冠全攻略(参考)

2021小升初华杯赛夺冠全攻略(参考)2021小升初华杯赛夺冠全攻略(参考)华杯赛作为奥数的权威和经典赛事，在升学领域发挥了很大的作用。

今天，我们一起走进华杯赛。

给xxxx小升初的家长和孩子一些参考的意见。

1、华杯赛的考试时间及如何报考？时间：初赛在每年3月的第二个星期六；复赛在每年4月的第二个星期六。

总决赛在7月进行；进入总决赛的另一途径：报名参加华杯赛冬令营（在每年1月份进行，一等奖可以直接进入华杯赛全国个人总决赛）2、华杯赛到底有多难？国内的所有杯赛都来自于民间组织。

一个杯赛的价值取决于试题的含金量和举办形式的正规程度，从这两方面来看，华杯赛可以说是行业内的标杆。

在国内风行的几大赛事有：希望杯、华杯赛、迎春杯。

其中希望杯是一种普及型比赛，考试难度低、按地区评奖使得更多的人能参与，更多的人能获奖；迎春杯在xxxx年左右初势头正旺，一奖在手，红遍京城；现在的华杯有一样的势头，其试题和迎春杯类型相仿，知识点覆盖全，非常经典。

其试题不完全是难，而是巧妙，真正能学懂的人不但能开阔思路，对中学的理科学习也有极大帮助。

与之形成对比的是，日本算术奥林匹克竞赛（绝大多数试题由中国提供）则让很多华杯选手郁闷，因为很多试题无处下手，与复习方向有关，不再一一赘述。

3、如何准备华杯赛？首先从时间上来看，最迟的准备时间是五升六的暑假。

这个意思是说，在9月之前之前已经有一些奥数基础，对和差、和倍、差倍、年龄、植树、鸡兔、盈亏、行程工程、百分比、数论、几何、抽屉等知识点有个基本的了解。

那么对xxxx年小升初的学生而言，在华杯考试之前的复习思路如何呢？暑假是一个节点，首先在暑假的时候要对五年级和之前的知识点进行系统复习，查找漏洞。

比如：数字迷、数论里的同余、抽屉原理的多个类型等（涉及华杯赛初赛的难度）；秋季进行专题复习：结合华杯赛考察的知识点和华杯复赛的考察难度进行讲解，寒假进行真题演练，这样下来，如果把前面的题目搞清楚，华杯赛得奖是情理之中的事情。

华杯一等奖备考策略

华杯一等奖备考策略全文共四篇示例，供读者参考第一篇示例：华杯一等奖备考策略备考华杯一等奖需要提前进行充分的准备。

在备考之前，考生应该了解竞赛的规则和考试科目，对每一科目的考试大纲和要求有清晰的了解。

要认真分析自己的优势和劣势，制定合理的学习计划，科学安排每一科目的复习时间和重点，确保每个科目的复习都得到充分的准备。

不要等到考试前才临时抱佛脚，这样很难取得好成绩。

备考华杯一等奖需要注重综合能力的培养。

华杯一等奖考试不仅要求考生在各科目中取得高分，还要求考生具备较强的综合能力，包括逻辑思维能力、分析问题能力、解决问题能力等。

备考的过程中要注重培养这些能力，而不是单纯的死记硬背。

可以通过做题、模拟考试等方式来提高综合能力，在实战中不断提升自己的应试能力。

备考华杯一等奖也需要注重提高学习的效率。

在备考的过程中，很多考生会遇到时间不够用的问题，这时就需要提高学习的效率，合理安排时间，有效利用每一分钟。

可以采用番茄工作法、碎片时间学习等方法，把时间利用到最大，确保每一次学习都有收获。

还要注重课外阅读和实践，扩大知识面，提高文化素养和综合能力。

备考华杯一等奖需要保持良好的心态和自信心。

备考期间很可能会遇到各种各样的困难和挑战，考生要保持乐观积极的心态，坚持不懈地努力。

同时要相信自己，相信自己的实力和潜力，相信只要努力就一定会取得好成绩。

不要因为一时的挫折而灰心丧气，要坚信自己的能力，坚定地向着目标迈进。

备考华杯一等奖需要考生有充分的准备和综合能力，提高学习的效率，保持良好的心态和自信心。

只有这样，才能在竞争激烈的竞赛中脱颖而出，取得好成绩。

希望广大考生在备考的过程中能够按照这些策略认真努力，最终实现自己的梦想，获得华杯一等奖的荣誉。

祝大家考试顺利，取得优异成绩！第二篇示例：【华杯一等奖备考策略】华杯是一个著名的英语演讲比赛，参加这个比赛需要经历多轮激烈的竞争，而获得一等奖更是需要具备优秀的英语表达能力和深厚的知识储备。

如何准备华杯赛

如何准备华杯赛?首先从时间上来看，最迟的准备时间是五升六的暑假。

除了知识点的掌握，参加杯赛还要重视那些方面的准备?1)强化数学思想的训练。

“华杯赛”的题目来源于我们体系中的基本题目但又高于基本题目，有花样繁多的变形，但其本质是不变的，作为学生，解题能力的强弱取决于能否在考场上及时精准的把遇到的复杂题目转化为学过的基本数学模型。

此外，华杯赛的题目一般都是把一些经典的数学背景经过综合改造而成适合小学生思维模式的较为开放的题目。

因此要求学生不仅对知识体系更扎实的掌握，探索解决问题的常用方法和思想也相当重要，比如从简单情况思考、从反面情况思考、从特殊情况思考、分类有序思考、图表与数形结合方法等。

2)培养好的解答习惯。

华杯赛与其它杯赛不同，强调数学逻辑思维的考察，题目具有很强的学术性与严谨性。

因此，考生务必做到概念清楚，基础问题考不倒;习惯优秀，解答题过程不失分。

良好的审题、分析、答题习惯表现如下：能找到题目的关键词“题眼”;能读懂题意，分析清楚题目出现的数量关系、逻辑关系;能通过自己的语言或者数学符号清晰、完整并且简洁的解答问题。

那么对2014年小升初的学生而言，在华杯考试之前的复习思路如何呢?暑假是一个节点，首先在暑假的时候要对五年级和之前的知识点进行系统复习，查找漏洞。

比如：数字迷、数论里的同余、抽屉原理的多个类型等(涉及华杯赛初赛的难度);秋季进行专题复习：结合华杯赛考察的知识点和华杯复赛的考察难度进行讲解，寒假进行真题演练，这样下来，如果把前面的题目搞清楚，华杯赛得奖是情理之中的事情。

答题时的有什么注意事项?建议注意以下几点：1、填空题一定要注意单位，分清题目问的是分钟还是小时，条件给的是米还是千米;2、草稿纸一定要写明题号，像答题一样写草稿纸，尽量避免从草稿到答题过程中的出错，也更方便检查;3、解答题一定要尽可能的清楚，突出关键步骤，简答题也要写清关键步骤，必要的文字叙述;4、不要列综合算式，分部的去计算，过程分的细一些增加自己得分的机会。

华杯赛赛前教程

前言“华罗庚金杯”少年数学邀请赛（简称华杯赛）是以华罗庚名字命名的数学竞赛，始于1986年，是为了纪念我国著名数学家华罗庚，由中国优选法统筹法和经济数学研究会、中国少年报社、中国数学会和中央电视台青少中心等单位发起和组织的一项全国少年学生数学竞赛，至2008年，“华杯赛”共举行了十三届，已经成为一项重要的、有影响的和全国性的少年科技教育和普及活动.为了配合第十四届“华杯赛”，帮助学生提高数学的水平和素质，在“华杯赛”中取得优秀成绩，华杯赛主试委员会组织编写了第十四届“华罗庚金杯少年数学邀请赛”赛前教程(小学册)，简称为“赛前教程”.“赛前教程”共有五章，第一章是数的运算，由卢振虎主笔；第二章是整除和带余除法，由王世坤、卢振虎、赵小峰和陈平等编写，王世坤和陶小勇主编.“赛前教程”每一章有三节和一套练习题，每一节大致包含三部分内容：第一部分简要地介绍一些基本概念和知识；第二部分是“说明”，主要介绍一些扩展的知识、与该节有关的数学的思想和应当注意的问题，个别内容较深，仅供辅导老师和家长参考；第三部分是“例题讲解”，是该节的核心部分，含有本书作者精心选择和编制的十个例题，其中多数是“华杯赛”常见和典型的问题，并且做了细致的解答，有的例题附有“说明和评注”，更深入地介绍了解题的方法和思想.“赛前教程”每一章均有30道练习题，它们选自“华杯赛”的试题、其它数学竞赛的试题和辅导材料，其中有一些是本书作者编制的新题. “赛前教程”附有三套初赛测试题和三套决赛测试题，由“华杯赛”主试委员会卢振虎、朱华伟、那吉生、余其煌、连四请、周春荔和闫桂英编制，由闫桂英统编，是本书非常重要的内容. 全书由主编王世坤做了适当的修改和编辑.“华杯赛”主试委员会主试委员秉承“华杯赛”普及性、趣味性和新颖性命题的原则，编排了六套测试题，它们连同精心选择的各节的例题以及各章练习题，基本上覆盖了“华杯赛”命题的思想和试题的类型，是第十四届“华杯赛”命题重要的参考. 一般而言，多做练习题是学好数学和在数学竞赛中取得优异成绩必须做的努力. 但是，“题海训练”，过多的赛前“冲刺”等，既消耗了学生过多的时间和精力，效果也未必令人满意. 而且，有的“模拟试题”或者“练习题”粗制滥造，偏离学习数学基本的规律，会误导学生，对学生没有太多的益处.我们相信，只要细致阅读本书，认真完成“赛前教程”中的练习题和测试题，读者会加深对课堂知识的理解，会增长应用数学知识去解决实际问题的能力和提高数学的素质，会在“华杯赛”中取得优秀成绩.这本“赛前教程”虽然是为了配合第十四届“华杯赛”，但是，其内容基本上覆盖了小学数学的主要知识，可以作为一本小学数学的复习教程.一般而言，一本优秀的数学的复习教程，应当以更高的角度来归纳和总结数学的知识，就像登山，途中，只能看到局部的风景，登至山顶，从高处浏览周围的风景，就会更深地了解，你走过的路和周围“景致”的关系，就会有“一览众山小”的感觉.复习就要做到登高望远，能够梳理出原来学过的数学知识之间的内在的联系，发现这些知识原来很“简单”.这本教程遵循这个原则，对小学数学知识做了深入的归纳和总结，提供了许多典型的例题和练习题.所以，即使不参加“华杯赛”，如果能认真阅读本书，细细体会其中的精髓，定有收获.学习数学，既要学习数学的知识，同时，也要特别注意数学的思想和方法对人的智力的巨大的影响.这本教程无论是从小学数学知识的总结和归纳，例题的认真选择和讲解，还是练习题的安排，都特别注重启迪同学们的数学兴趣和开发他们的智力，都非常强调帮助学生建立和提高应用数学知识去解决实际问题的能力，增强他们数学的能力.所以，将这本教程作为一册数学课外的读物，细致地钻研，初步理解一些数学的思想和方法，就能提高数学的素质和水平，为进一步的学习奠定扎实的基础.第十四届“赛前教程”和十三届“赛前教程”比较，书中不仅提供了全新的测试题，而且，修改了十三届“赛前教程”部分内容、大多数的例题和练习题，焕然一新了.虽然“赛前教程”的编写者是“华杯赛”主试委员和华杯赛教练员，他们具有扎实的数学的修养和造诣，又有从事数学教育和数学竞赛丰富的经历、经验和成就，他们编写的这本教程会受到读者的欢迎.但是，限于他们的水平和时间，书中仍然有许多不完善和考虑欠周的地方，也难免有错误.十三届“赛前教程”出版后，受到广大读者的欢迎，一些热心的读者也指出了一些错误和疏漏漏，“赛前教程”编著者向他们表示感谢，同时，诚挚地希望和欢迎读者一如既往，指出本书的不足和错误，提供修改的宝贵意见.本书由包善贤老师做了二校，他非常细心和认真的工作使本书增益不少，“赛前教程”编著者表示忠心的感谢.“华罗庚金杯”少年数学邀请赛的宗旨和目的是弘扬华罗庚教授的爱国主义精神，引导少年学生学习华罗庚教授勤奋学习、献身科学的优秀品质，激发他们学习数学的兴趣、开发他们的智力，提高他们的数学素质. 我们希望本书，即“第十四届华罗庚金杯少年数学邀请赛赛前教程”能体现这个宗旨，对读者有所帮助.第十三届“华杯赛”主试委员会，2008年7月目录第一章数的运算第1节整数、分数和小数第2节四则运算第3节数字谜和数阵图第一章练习题第二章整除和带余除法第1节整数和整除第2节带余数除法（1）第3节带余数除法（2）第二章练习题第三章应用问题第1节应用问题（1）第2节从算术到代数第3节方程的概念和解法第4节应用问题（2）第三章练习题第四章图形知识第1节简单平面图形第2节平面几何图形第3节简单立体图形第四章练习题第五章综合问题选讲第1节最大和最小第2节分类和计数第3节整数综合问题第五章练习题模拟测试题初赛测试题（1）初赛测试题（2）初赛测试题（3）决赛测试题（1）决赛测试题（2）决赛测试题（3）附录1练习题参考答案和提示附录2 模拟测试题答案和提示第一章数的运算数是人类长期实践活动中产生和发展的，整数、小数和分数及其四则混合运算是小学数学的重要内容，这些知识及相应的扩展是“华杯赛”和一些数学竞赛必考的部分. 这一章将复习这些知识，举例说明一些运算的技巧、相关思维的方法，并且渗透一些简单的数学思想.第1节整数、分数和小数（一）基本知识1．整数 ● 整数的认识我们在数物体的时候，用来表示物体个数的1，2，3，4，5 ……都是自然数. 一个物体也没有，可以用0表示，0也是自然数. 自然数可以用来表示事物的多少，也可以用来编号，表示事物的次序. 当用来表示事物的数量，即被数的物体有“多少个”时，叫做自然数的基数意义；当用来表示事物的次序，即最后被数的物体是“第几个”时，叫做自然数的序数意义.引入负数后，“1，2，3，4，5 ……”叫做正整数，“-1，-2，-3，-4，-5 …………”叫做负整数. 非负整数是0和正整数的统称，也就是自然数. 整数是正整数，负整数和零的统称.在这本书中，整数特指是正整数和零. ● 整数的大小位数越多的整数越大；如果两个整数位数相同，就从最高位依次比起.2．分数 ● 分数的概念把单位“1”平均分成若干份，表示这样一份或几份的数叫做分数. 把单位“1”等分后，表示其中一份的数，叫做这个分数的分数单位. 两个整数相除，它们的商可以用分数表示，即：a ÷b =)0(≠b b a. 也可以直接把符号m n（m 、n 都是整数，且n ≠0）定义为分数，其中符号“－”称为分数线.当n =1时，m n=1m =m ，即任何整数m 都可以用分数1m 表示. ● 百分数表示一个数是另一个数百分之几的数，叫做百分数，也叫百分率或百分比. 百分数通常不写成分数形式，而用百分号“%”来表示. 如百分之九十六写作96%，百分之零点6写为0.6%. 由于百分数便于比较，所以在生产和日常生活中有着广泛的应用.● 分数的分类分子小于分母的分数叫做真分数，真分数比1小. 分子大于或等于分母的分数，叫做假分数，假分数大于或者等于1. 一个整数和一个真分数合成的数，叫做带分数，带分数只是假分数的另一种形式. 严格的说，分数只能分为真分数、假分数两类.一个分数，如果分子和分母除了1之外，没有其他公共的约数（见37页约数），则称为最简分数.● 分数的运算一个分数，总是可以约分为最简分数；一个带分数可以转化为假分数，假分数也可化为带分数或整数；两个分数，通过通分做加法，通过转化为假分数做乘法.● 分数的性质和大小分数的分子和分母同时乘以或除以相同的不为0的数，分数的大小不变.分母相同，分子越小的分数值越小；分子相同，分母越小的分数值越大. 任何假分数都大于真分数.3．小数 ● 小数的概念分母是10、100、1000…… 的分数，改写成不带分母形式的数就是小数，如，把103改写成0.3. 符号“.”称为小数点，小数点左端的数是整数部分，右端是小数部分.整数部分为0的小数叫做纯小数，纯小数比1小.● 小数的分类及性质小数部分的位数有限时，称为有限小数. 另外还有一些小数的小数部分位数是无限多的，叫做无限小数. 无限小数又可分为循环小数和非循环小数. 在一个数的小数部分中，从某一位起，一个数字或几个数字依次不断地重复出现，这样的小数叫做循环小数. 例如，0.888……、3.15353……都是循环小数. 其中，0.888……的循环节是“8”，可以记作08.∙，它是纯循环小数. 3.15353……的循环节是“53”，可以记作3153.∙∙，它是混循环小数. 一个无限小数，从小数部分起各位数字的排列没有一定的规律，这样的无限小数叫做非循环小数. 例如圆周率π就是非循环小数.在小数的末尾添上“0”或者去掉“0”，小数的大小不变.整数部分越大的小数越大. 如果整数部分相同，则从十分位依次比起. 4．小数和分数的互化● 分数化小数：直接用分子除以分母，除不尽时，可以化为循环小数，或者根据需要用四舍五入法取近似值.● 小数化分数：有限小数化为分数. 原来有几位小数，就在1后面写几个零作为分母，原来的小数去掉小数点作分子，能约分的要约分. 例如：0.37 =37100，14652931.4651000200==.纯循环小数化为分数. 分子是一个循环节的数字所组成的数；分母的各位数字都是9，9的个数与循环节的数字的个数相同. 例如：310.393∙==，4730.473999∙∙=；混循环小数化为分数. 分子是小数点后面第一个数字到第一个循环节末端的数字所组成的数减去不循环数字所组成的数的差；分母的头几位上的数字是9，末几位上的数字是0，9的个数与循环节中的数字的个数相同，0的个数和不循环部分的数字的个数相同. 例如：1311220.13909015∙-===，1759117582930.1759999099901665∙∙-===. 由此可知，任何一个循环小数都可化为分数.非循环小数无法化为分数.（二）说明1．负数在小学阶段所说的整数、小数及分数主要指正数和0，在以后的学习中数的范围会扩大到负数. 因为人们在生活中经常会遇到各种相反意义的量. 比如,记帐时，有余有亏;在计算粮仓库存米时,有时要记进库粮食,有时要记出库粮食. 为了方便，人们就考虑了用相反意义的数来表示. 于是人们引入了负数这个概念，把余钱、进库粮食记为正，把亏钱、出库粮食记为负. 为了使“数”能蕴涵相反的含义，就在前面添加一个符号“-”，称为负数，符号“-”称为负号. 如果原来的“数”是整数，但不是零，添加负号之后，称为负整数，原来的整数则称为正整数. 如果原来的“数”是分数，添加负号之后，则称为负分数，原来的分数则称为正分数. 正整数和正分数统称为正数，用符号“+”来表示正数，例如：+5、+16，符号“+”称为正号，有时候省略正号“+”不写.2．用字母表示数用字母表示数，是对数的认识的一个飞跃，既可以表示一些不好写出和表达的数（例如圆周率π），也可以表示一类数或具有某种相同性质的数（例如字母v 代表速度，N 表示自然数等），为计算和解决问题带来了极大的方便.3．繁分数本书将分子和分母中还含有分数、小数或四则混合运算的“分数”叫做繁分数. 繁分数是分数形式的数，但不是分数. 前面在介绍分数的概念时提到可以直接把符号m n（m 、n 都是整数，且n ≠0）定义为分数，显然繁分数并不满足这一定义，所以说繁分数不是分数. 在一个繁分数里，最长的分数线叫做繁分数的主分数线，主分数线上下不管有多少个数或运算，都把它们分别看作是繁分数的分子和分母.把繁分数化为最简分数或整数的过程，叫做繁分数的化简. 繁分数的化简一般采用以下两种方法.（1）先找出主分数线，确定分子部分和分母部分，然后这两部分分别进行计算，每部分的计算结果能约分的要约分，最后形成“分子部分÷分母部分”的形式，再求出结果.（2）根据分数的基本性质，将繁分数的分子部分和分母部分同时扩大相同的倍数（这个倍数可以是分子部分与分母部分所有分母的最小公倍数），从而去掉分子部分和分母部分的分母，然后通过计算化为最简分数或整数.4．取整运算当只关心某数的整数部分时，规定][x 表示不超过x 的最大整数，称为高斯符号，或称为取整运算.又记][}{x x x -=，即{}x 为x 的小数或真分数部分，如3]14.3[=，14.0}14.3{=.显然有{}01x ≤<，当x 为整数时，等号成立.5．数的表示形式和转化可以将分数、带分数、假分数、小数、百分数甚至繁分数和字母代表数等等，理解为数的各种不同的表达“形式”, 例如：1可以表达为循环小数09.∙，2可以表达为假分数42，等等.至于整数是否是特殊的分数和小数，并不太重要，重要的是深入理解数的各种表达“形式”蕴涵的数学意义和掌握它们相互转化的方法，例如：2和2.0, 在科学和技术中，它们是有重大区别的.因为科学和技术的测量总是有误差的，2.0可能是2.03要求精确到小数点后1位，舍弃了0.03后, 这样，2.0就蕴涵了精确度，所以2和2.0是不同的.但是，在小学数学中，它们是相同的数，依照数学表达简洁化的原则，2最好不要写成2.0, 0.3一般不要表达为030.∙.尽管小学阶段遇到数学概念比较少，但是，准确理解数学概念和相近数学概念细小的差别还是比较重要的.唯有如此，养成良好的数学习惯，现在和将来，才能学好数学.（三）例题讲解1. 选择题例1下面是6个等式： ① 0301230423...∙∙∙∙+=； ② 6255062510008.==；③533581142142162++===+；④ 102 1314 2235 323 4546.,.,,.,.,.∙∙∙∙∙∙中有2个纯循环小数； ⑤ 1991.∙∙＝9999911；⑥ 31334127535⨯=；其中正确的命题是（）.（A ）①与② （B ）②、④与⑤ （C ）①与④ （D ）②、⑤和⑥ 答案：B.理由：①不正确，因为03012304231...∙∙∙∙+=；②正确；③不正确，因为521521136114141477++===；④正确，因为10166.∙=，是混循环小数；⑤正确；⑥不正确，因为31242150414341475753535⨯=⨯==.例2下面是6个命题：① 两个真分数之间至少有1个真分数； ② 两个分数之间至少有1个真分数； ③ 两个分数之间有无穷多个分数； ④ 圆周率π可以化为一个分数； ⑤ 总可以将一个分数化为有限小数； ⑥ 无限循环小数不能化为分数；其中正确的命题是（）.（A ）①与③ （B ）②与③ （C ）①与④ （D ）⑤与⑥答案：A .理由：①正确，理由是：设ab 和c d是真分数，并且a c bd<，则有a a c c bb dd+<<+；②不正确，因为真分数小于1，例如：32和52之间没有真分数；③正确，理由是：如①所述理由，两个不同的分数之间有1个分数，则可以推出有无穷多个分数；④不正确，因为圆周率π是无限不循环小数，不能化为分数；⑤不正确，例如17化为小数时，是无限循环小数；⑥不正确，无限循环小数能化为分数，例如：10.33∙=.2. 填空题例3在混循环小数9617472.∙的某一位上再添上一个表示循环的圆点，使新产生的循环小数尽可能大. 这个新的循环小数是（）.答案：9617472.∙∙.理由：要求新产生的循环小数尽可能大，实际上是要求组成循环节的前几位数字尽可能大.首先，要选择好循环节的首位数，一定要是小数点以后最大的一个数字.在这道题里，最大的数是7，表示循环的圆点应该点在7上. 可是，题目里有两个7，点在哪个7上呢？哪个7后面的数字大，就点在哪个7上，所以，新的循环小数是9617472.∙∙.例4分母为2009的所有最简真分数之和为（）. 答案：740.理由：因为20097741=⨯⨯，所以分母是2009的最简真分数，分子不能是7、41和它们的倍数. 因此，分母为2009的所有最简真分数之和为()()()()1741S=122008122861248200920092009741 1262009+++-+++-+++⨯++++ ，因为()()()12200812008220071004100520091004122862871431248492412673,,,,+++=++++++=⨯+++=⨯+++=⨯+++=⨯所以2009100472872434149247417320092009200920091004243243740S ⨯⨯⨯⨯⨯⨯⨯⨯=--+=--+=例5 记1111112021223839S =+++++，[]S ＝（）.答案：1.理由：先估算分母的大小，因为111120120213920+++<⨯=…，且111120202021393939+++>⨯=…，所以1<原式<3920=1.95，[]S =1.说明和评注：解决这种估算类题目的关键是放缩，即找到所求值的范围，这一方法在比较分数大小时也经常会用到.3．解答题例6计算：123369714211453121572835⨯⨯+⨯⨯+⨯⨯⨯⨯+⨯⨯+⨯⨯＝？解答：原式=)541(7)541(3541)321(7)321(33213333⨯⨯⨯+⨯⨯⨯+⨯⨯⨯⨯⨯+⨯⨯⨯+⨯⨯=)731(541)731(3213333++⨯⨯⨯++⨯⨯⨯=123145⨯⨯⨯⨯=310.例7 有红、蓝、黄、绿4种卡片，每种3张，相同颜色的卡片上写有相同的整数，不同颜色卡片上的整数互不相同，由小到大依次为红、蓝、黄、绿. 现在把这些卡片分给6名同学，每人得到颜色不同的两张，六名同学分别求和，得到6个和数：88，121，129，143，154，187. 其中一个错了，则这4个整数分别是多少？解答：设这四个整数分别为a <b <c <d ，因为6个和数分别为88，121，129，143，154，187，显然a+b =88，a+c =121，b+d =154，c+d =187而a+b+c+d =88+187=121+154≠129+143，所以错误的和数为129或143，a+b+c+d =275. 又因为c -b =187-154=33，所以b+c 为奇数.若错误的和数为129，则实际应为275-143=132，即b+c =143，a+d =132，解得a =33，b =55，c =88，d =99；若错误的和数为143，则实际应为275-129=146，即b+c==129，a+d =146，解得a =40，b =48，c =81，d =106.例8 将2009个分数21，31，41，…，12009,12010化成小数，共有多少个有限小数？解答：一个有限小数化为最简分数时，其分母只含质因数2或5.反之，也成立.1011882627343544245220102 5220105252201052 5220105252201052 520105,,,,,,<<⨯<<⨯⨯<<⨯⨯<<⨯⨯<<⨯<< 上面的六个不等式意味着：小于2011的整数中，只含质因数2的整数有10个；只含质因数2和仅有1个质因数5的整数有8个；只含质因数2和仅有2个质因数5的整数有6个；只含质因数2和仅有3个质因数5的整数有4个；只含质因数2和仅有4个质因数5的整数有1个；只含质因数5的整数有4个，所以，共有10＋8＋6＋4＋1＋4＝33个有限小数. 例9 A ，B ，C 为正整数，满足算式111524+++=C B A ，则C B A 32++的值是多少.解答：将245表示为连分数形式：131114411144514544524+++=++=+=+=,则有：A =4，B =1，C =3，所以，153312432=⨯+⨯+=++C B A .例10求1411421497149833333333⨯⨯⨯⨯⎡⎤⎡⎤⎡⎤⎡⎤++++⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦的和. 解答：已知：对121004k ,,,= ，()()()141414333333149914991499, 333333k k k ,k k k ⨯⨯⨯⎧⎫⎡⎤=+⎨⎬⎢⎥⎩⎭⎣⎦⨯-⨯-⨯-⎧⎫⎡⎤=+⎨⎬⎢⎥⎩⎭⎣⎦所以，()()()14991499149914141442333333333333k k k k k k ⨯-⨯-⨯-⎧⎫⎡⎤⨯⨯⨯⎧⎫⎡⎤=+=+++⎨⎬⎨⎬⎢⎥⎢⎥⎩⎭⎣⎦⎩⎭⎣⎦，并且上式中，()1499143333k k ⨯-⎡⎤⨯⎡⎤+⎢⎥⎢⎥⎣⎦⎣⎦的和是整数，所以，()1499143333k k ⨯-⎧⎫⨯⎧⎫+⎨⎬⎨⎬⎩⎭⎩⎭的和应当是整数.并且，既然对于任何整数n ，{}1n <，就有()149914013333k k ⨯-⎧⎫⨯⎧⎫<+=⎨⎬⎨⎬⎩⎭⎩⎭.所以，()149914413333k k ⨯-⎡⎤⨯⎡⎤+=⎢⎥⎢⎥⎣⎦⎣⎦1411421497149833333333141149814214971449145033333333333341492009.⨯⨯⨯⨯⎡⎤⎡⎤⎡⎤⎡⎤++⋯++⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⨯⨯⨯⨯⨯⨯⎛⎫⎛⎫⎛⎫⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=++++++ ⎪⎪ ⎪⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎝⎭⎝⎭⎝⎭=⨯= .第2节四则运算（一）基本知识1．四则混合运算●运算法则在一个算式里，如果含有两种或两种以上的运算，通常就称为混合运算. 加、减、乘、除的混合运算也叫四则混合运算.在数的运算中，加法和减法叫做第一级运算，乘法和除法叫做第二级运算，乘方和开方叫做第三级运算. 第三级运算是第二级运算的高级运算，第二级运算是第一级运算的高级运算；反之，第一级运算是第二级运算的低级运算，第二级运算是第三级运算的低级运算.如果一个算式里含有不同级的运算，那么就先做高级运算，后做低级运算. 在有括号的情况下，要按照从里到外的顺序，先算小括号里的，再算中括号里的，然后算大括号里的，最后算括号外面的.●运算定律加法交换律. 两个数相加，交换加数的位置，它们的和不变. 即a+b=b+a.加法结合律. 三个数相加，先把前两个数相加，再加上第三个数；或者先把后两个数相加，再和第一个数相加，它们的和不变. 即（a+b）+c=a+（b+c）.加法交换律和结合律的推广：几个数相加，任意交换加数的位置，或者先把其中几个数结合成一组相加，它们的和不变.乘法交换律. 两个数相乘，交换因数的位置，它们的积不变. 即a×b=b×a.乘法结合律. 三个数相乘，先把前两个数相乘，再乘以第三个数；或者先把后两个数相乘，再和第一个数相乘，它们的积不变. 即（a×b）×c=a×（b×c）.乘法交换律和结合律的推广：几个数相乘，任意交换因数的位置，或者先把其中几个数结合成一组相乘，它们的积不变.乘法分配律. 两个数的和与某个数相乘，可以把两个加数分别与这个数相乘，再把两个积相加，所得的结果不变. 即（a+b）×m=a×m+b×m.2．速算法在进行数的运算时，根据数的特点，结合和、差、积、商的变化，运用运算定律、性质，进行简便、迅速的运算，叫做速算，常用的速算法有：（1）分组法. 把算式中能凑成整十、整百、整千的数先算，以便于后面的计算. 例如：869+27+131+73=（869+131）+（27+73）=1000+100=1100； 167-（89+67）=167-67-89 =100-89=11.（2）补数法. 对接近整百、整千的数，可以补上一个数使它成为整百、整千数，使计算简便. 例如：1453-397=1453-（400-3）=1453-400+3 =1056.（3）分解法. 有些乘除计算，可把已知数适当进行分解，然后应用运算性质，使计算简便. 例如：25×32=25×4×8=100×8=800.此外还有基准数加法、公式法等，其本质都是对数的特征和运算定律的灵活运用.（二）说明1．数列按照一定顺序排列的一列数叫做数列，通常记作a 1，a 2，… a n ， …，简记为{ a n }. 数列中的每一个数都叫做这个数列的项，其中a n 表示数列{ a n }的通项. 如果一个数列{ a n }的第n 项a n 与项数n 之间的关系可以用一个关于n 的公式来表示，我们就把这个公式叫做这个数列的通项公式. 如数列1，4，9，16，…，通项公式为a n =n 2. 如果数列只有有限个项，将第一项称为首项，最后一项称为末项（a n ），项的总数叫做项数，求数列中所有的项的和，称为数列求和.“华杯赛”和其他一些重要的小学数学竞赛中常常出现两类数列：等差和等比数列. 等差数列是从第二项起，每一项减去它的前一项，所得的差为定值的数列，这个差叫做公差，记作d ，即21321n n a a a a a a d --=-==-= . 由公差的定义，可以推出等差数列{ a n }的通项公式：a n =1a +（n-1）×d ，或a n = a m +（n-m ）×d . 用两种方法求等差数列{ a n }前n 项的和：121121n n n n n n S a a a a S a a a a ,--=++++=++++将上面两个式子相加，因为121112n n n n a a a a a a a a --+=+==+=+ ，得等差数列{ a n }前n 项求和公式：S n =（a 1+ a n ）×n ÷2. 这种求和方法叫做倒序相加法.⏹ 等比数列是后一项与前一项的商（后一项除以前一项）为一个固定的数的数列，这个商叫做公比，记作q ，即a 2÷1a = a 3÷a 2= a 4÷a 3=……= a n ÷1n a -=q . 由公比的定义，可以推出等比数列{ a n }的通项公式：11n n a a q -=. 等比数列的前n 项和：S n =1(1)1na q q--等比数列{ a n }的前n 项和：S n =a 1+a 2+……+a n ①等号两边同时乘以公比q ，得到qS n =qa 1+qa 2+…+qa n ，即qS n =a 2+a 3+……+a n +a n+1 ②①-②得（1-q ）S n = a 1- a n+1，而a n+1=q n a 1，得到等比数列{ a n }前n 项求和公式：（1-q ）S n =（1- q n）a 1，即S n =1(1)1na q q--.这种求和方法叫做错位相减法. ⏹ 数列求和除了前面介绍的倒序相加法和错位相减法外，在求数列和时，经常应用“裂项法”.“裂项法”的基本思想是()()()112211n n n n n a a a a a a a a ---=-+-++-+ . 这个方法可以简化计算过程，其最基本的形式是111(1)1n n n n =-+-，例如：11111 122334899101111111111()()()()()12233489910191.1010+++++⨯⨯⨯⨯⨯=-+-+-++-+-=-= 2．新的运算以四则运算为基础，可以定义新的运算，例如：用符号&表示一个二元运算：35a &b a b b =⨯⨯⨯+,对于这个&运算，446577337&3=+⨯⨯⨯=.可以验证，当a b ≠时，a&b b&a≠，即没有交换律.3．运算能力做有理数四则运算题目，当运算式子中有带分数、假分数、小数甚至百分数、大小括号和繁分数，即式子比较复杂时，有些同学很难给出正确解答. 做这种题目，需要多练习，细心严谨，才能正确和快速给出答案. 除此之外，如何避免出错呢？这里介绍几个注意要点，供读者参考.●先乘（除）后加（减），是指运算式子中，只有一个“加”和一个“乘”时应当遵守的规则，例如：3124491136111121107878-⨯=-⨯=-=-先做乘运算. 当算式同时有括号、多个乘和多个加时，在同级运算中，如何确定运算次序呢？建议的原则是：第一，使运算和随后的运算尽量“整数化”，遇到分数，尽量转化为分母更小一些的分数；第二，使运算式子尽量“简洁化”，如将有的除法转换为乘法，或者将带分数、小数等转化为既约分数等，但是注意不要增加后面运算的难度；第三，建立你自已的原则来确定运算的顺序，例如：你的原则是先将所有的带分数都化为假分数，哪怕实际运算时要复杂一些，也没有关系. 因为运算时“心中有序”了，习惯了，就不易出现错误，这点很重要.●计算的每一步骤，即每个等号后为一个步骤，所做运算不易太多，确保每个步骤的运算都是比较简单的运算，步步为营，稳答稳扎. 计算一道较为复杂的四则计算题时，要大致浏览一下，看看题目有何特点，以便确定计算的顺序和策略.●做计算题，难免出现错误，重要的是需要掌握一些查错法，例如“估值”和“消9”查错法等，很简单，多数情况很起作用. 但需要注意，它们仅仅是查错法，不是查对法.四则运算是小学数学重要内容，是其他复杂运算的基础，计算要准确和快速，是小学学好数学和在“华杯赛”中取得好成绩的要求.小学高年级学生要善于根据数的特征，灵活运用运算定律和性质，选择恰当的方法进行计算. 长此以往，可以全面提高学生的计算能力. 计算能力不仅是学生学好数学的基础，更是学好数学的保证（三）例题讲解1．选择题。

华杯赛备考

4、如果你朝着华杯赛一等奖而去参赛的，那么在做题时，就不可以放过高难度题啦！
华杯赛复习重点知识点：数论、几何、组合、应用题
2013年1月：综合练习，查漏补缺（这是最后的大量做题练习的时间）
这段时间，建议多做一些综合练习，例如华杯模拟题、真题，或者是一些其他比赛的题目，检查自己薄弱的知识点，查漏补缺，整理公式定理，重做错题本上的题目。必做试题就是华杯赛官网的历年真题，点击下载真题>>
备考2013年“华杯赛”教你如何规划时间
据“华杯赛”官方网站显示：第十八届“华杯赛”2013年3月23日开赛，想要在华杯赛中拿到一个合理的成绩，利用剩下的时间做好合理的时间规划是非常有必要的，下面是华杯赛的备考时间规划。
2012年10月~2012年12月：考题攻破，第一轮总复习
我们需要完整的过一遍华杯赛所涉及的全部知识点，保证自己知识体系的完整性，做到在知识点上无盲区。
2013年2月:考试临近，考前冲刺。
考试临近，考前冲刺。此时应该停止大量的练习，是自己错题本上的不懂按照考试的时间进行，当成一次真正的考试，才是高质量的模拟练习。
2013年3月：看看公式及定理，加深自己的印象
此时千万不要再继续大量做题了，我们该做的是：看看公式及定理，加深自己的印象。同时，要扔掉自己的错题本，不要再纠结上面的题目了。如果报了官网的网络课程，可以好好利用上面免费的网络工具，网上笔记本、错题本、在线答疑等等。
具体做法：
1、复习学过的专题：如数论，行程，几何，应用题，计数问题，计算题等等。（推荐：官网有配套网络课程可以学，每周学几节课，是挺不错测，点击学习>>）
2、整理所有学过的讲义，整理自己的错题本
3、在做题时，要注重难度的提升，挑战难题，突破自我。（推荐：《思维导引》3~4星题要注重练习，每天2道，一定要写过程。）

第22届华杯赛备考三大注意事项介绍

第22届华杯赛备考三大注意事项介绍
第_届华杯赛备考三大注意事项介绍
一、以解决实际问题为重点，以提升数学趣味性为目标
本次大赛主试委员会将以解决实际问题为重点，以提升数学趣味性为目标。

数学的趣味性，绝大部分情况是出现数学的本身上，数学作为我们认识世界或理解世界，改造世界的一个基础学科，从本质上讲它本身是一个具有趣味性的学科，所以数学的趣味性不应当体现在它的包装，在它的问题来源、它的问题的根本上，趣味性就蕴含在数学的内容里。

二、第_届“华杯赛”初赛、决赛、总决赛赛程安排及试题分布情况
本次大赛分为初赛、决赛、总决赛三个阶段，初赛采取笔试的形式，共_道题，考试时间为一个小时，6道选择题，4道填空题，决赛也采取笔试形式，每个组别共_道题，8道填空题，4道简答题，2道详细解答题(要求有详细的解答思路)。

小学中年级，稍有变化，8道填空题，4道简答题。

总决赛分为笔试一，笔试二，以及团体决赛。

笔试一和笔试二是由每个选手参加，共6道题，分为3道填空题和3道解答题。

团体决赛是由八个代表队参加，团体比赛的阶段的题目，与往年稍有变化，回答题目的方式分为：选答题，抢答题，必答题;
三、牢记杯赛宗旨，弘扬数学精神
为了第_届“华杯赛”的公平、公正、公开的进行，每一位主试委员会的成员在华杯赛结束之前不得进行“华杯赛”的授课工作。

请各位老师，各机构进行监督和检查。

同时，本次比赛的目的是弘扬华罗庚教授的数学精神，它不仅仅是比赛，同时也是对于数学趣味性的普及和数学认识的深入。

第_届华杯赛备考三大注意事项介绍.到电脑，方便收藏和打印：。

华赛杯的考点

华赛杯考点
摘要：重点掌握九大题型和五大方法，只有掌握了正确的方法才能有效地解决复杂多变的题型。

秋季我们会重点学习两大方法的应用：公式法和图示法。

让孩子熟记各类行程公式，且拿到题目能够画图分析，一目了然。

华杯赛常考的知识点有哪些呢?参加华杯赛的同学要注意行程问题、组合、几何问题、数论问题等知识点的掌握与突破。

1、行程问题重点掌握九大题型和五大方法，只有掌握了正确的方法才能有效地解决复杂多变的题型。

秋季我们会重点学习两大方法的应用：公式法和图示法。

让孩子熟记各类行程公式，且拿到题目能够画图分析，一目了然。

2、组合根据对华杯赛和创新杯一等奖学生的考试情况调查，在组合模块得分率高的学生往往冲击一等奖的可能性会增大许多。

3、几何问题六年级孩子最为生疏的模块在于几何中的曲线型面积和立体几何，而秋季是唯一能够学习且熟练掌握这两个新模块的时间。

4、数论问题常考内容，而且可以应用于策略问题，数字谜问题，计算问题等其他专题中，相当重要，应重点掌握以下内容掌握被特殊数整除的性质、掌握约数倍数的性质、分解质因数，短除法，辗转相除法求两个数的最大公因数和最小公倍数、求约数个数、了解同余的概念，学会把余数问题转化成整除问题。

。

五年级数学华杯赛书

五年级数学华杯赛书
摘要：
1.华杯赛的简介
2.五年级数学华杯赛的内容
3.如何准备五年级数学华杯赛
4.五年级数学华杯赛的重要性
正文：
【华杯赛的简介】
华杯赛，全名为全国小学数学奥林匹克竞赛，是我国小学阶段最具权威和影响力的数学竞赛之一。

该竞赛旨在激发学生学习数学的兴趣，培养学生的数学思维能力和创新意识，选拔和培养优秀的数学人才。

【五年级数学华杯赛的内容】
五年级数学华杯赛的内容主要包括小学五年级数学的全部课程，包括四则运算、方程与不等式、几何图形、计量与统计等。

比赛形式一般为个人赛和团体赛，分为初赛、复赛和决赛三个阶段。

【如何准备五年级数学华杯赛】
1.扎实掌握基础知识：学生需要对小学五年级的全部数学知识有深入的理解和掌握，这是解决华杯赛题目的基础。

2.提高解题速度和准确度：学生在日常学习中要注意提高解题速度和准确度，这样才能在比赛中取得好成绩。

3.培养数学思维能力：华杯赛不仅需要学生掌握数学知识，更需要学生有良好的数学思维能力，能够在遇到新问题时迅速找到解决方法。

4.做模拟题和真题：学生在准备华杯赛时，可以做一些模拟题和真题，熟悉比赛形式和题目类型，提高应赛能力。

【五年级数学华杯赛的重要性】
五年级数学华杯赛对于学生的学习和成长具有重要意义。

首先，参加华杯赛可以激发学生学习数学的兴趣，提高学生的学习积极性。

其次，通过比赛，学生可以检验自己的数学水平，了解自己在数学方面的优势和劣势。

第十八届华杯赛赛事安排及备考攻略

来源：华杯赛官网 2012-11-12 23:35:23[标签：华杯赛参赛方法复习指导]初赛时间：2013年3月23日(星期六)上午10:00—11:00形式：笔试，由“华杯赛”组委会办公室统一提供试题，各参赛单位组织比赛和阅卷。

决赛时间：2013年4月20日(星期六)上午10:00—11:30形式：笔试，由“华杯赛”组委会办公室统一提供试题。

选手：从参加初赛选手中选拔不超过30%的优胜者进入决赛，获奖名单将在“华杯赛”网站()上公布。

总决赛时间：2013年7月下旬(具体时间另行通知)地点：广东省惠州市形式：笔试和口试笔试：所有参赛选手参加相应组别的笔试1、笔试2。

口试：8支代表队同台竞技。

参赛原则所有一年级到初中二年级的学生，均可自愿报名参加第十八届华罗庚金杯少年数学邀请赛。

组别设置设立以下四个组别：1、小学中年级组：2013年9月前不高于小学四年级的学生;2、小学高年级组：2013年9月前不高于小学六年级的学生;3、初中一年级组：2013年9月前不高于初中一年级的学生;4、初中二年级组：2013年9月前不高于初中二年级的学生。

奖项设置笔试决赛：(1) 设个人一、二、三等奖。

(2) 获决赛一、二等奖选手的基层辅导教师荣获“优秀教练员”奖，获决赛三等奖选手的基层辅导教师荣获“优秀辅导员”奖。

注：竞赛结果将在“华杯赛”网站()和《“华杯赛”第十八届专辑》等媒体中公布。

总结赛：(1) 设个人金、银、铜牌奖。

由“华杯赛”组委会颁发奖牌和证书。

(2) 团体总分前20名的代表队由组委会颁发奖牌和证书。

(3) 团体总分第一名的代表队将“华罗庚金杯”捧回保存至下届。

(4) 对组织参赛工作做出突出成绩的单位授予优秀组织工作奖。

(5) 设金牌教练员奖，总决赛获金牌选手的主要教练员1人，颁发证书。

第十八届“华杯赛”2013年3月23日开赛第十八届华罗庚金杯少年数学邀请赛参赛办法看完了华杯赛的赛事安排，不少家长心里肯定惦记着该如何去备考，也想看看有没有一些考场经验可分享，广州奥数网特意把之前的资料整理了如下，让家长们心里有个底做好万全准备，一起来接着往下看哦。

【考试技巧大分享】让你在华杯赛中拿到更多分数！

【考试技巧大分享】让你在华杯赛中拿到更多分数！
一、写好姓名、准考证号等信息
二、审题别偷懒、用时不吝啬
三、优化做题策略、合理安排时间
四、保证正确率、勇于“舍弃”难题
五、选择、填空巧方法
六、不留空白、全部填满
以上这六点，就是大刚老师针对华杯赛初赛、决赛总结出的相关
考试技巧，希望能帮助大家在华杯赛中取得更好的成绩！如果大家还有其他关于考试的小技巧，也可以来分享一下，让我们共同进步吧！
明天大刚老师将针对考试心态进行分享，敬请期待！
如何获取更多杯赛信息？
方式一：
方式二：。

快速提分的华杯赛初赛内部应考攻略(五年级)

快速提分的华杯赛初赛内部应考攻略1、五年级参加华杯赛需注意事项：很多家长以为五年级同学比六年级同学少学一年，考出来一定会比六年级差，其实不然，华杯赛初赛的难度不大，重视对基础知识的掌握程度，五年级同学由于一些知识点刚学，对基础知识的掌握相对来说有时还会比六年级还要牢固一些（仅限初赛），比如对比较大小这一块，学而思安排在第一讲。

我五六年级同时教，同是一个班次的同学，同是讲五大模型的一道题，五年级同学接受起来反而比六年级快。

当然，五年级同学也是有一定劣势的，主要是体现在两块：一个是对分数以及比和比例的掌握不是很牢固，尤其是使用北师版教材的同学更是如此；二是部分同学还没有接触过一些知识点，如：曲线型面积如圆的面积、扇形的面积等的求法；勾股定理；几何变换中的平移；立体图形的体积的计算等几何知识。

而两点是华杯赛初赛考试的大热门。

2、华杯赛历年考点归纳：几何：几何是华杯赛初赛考察的重中之重，所考察知识点包括了轴对称与中心对称图形认知、直线型面积基本图形计算、曲线形面积基本图形计算、几何变换之平移、立体图形体积的计算，其他变相对几何的考察包括几何图形的计数、几何操作。

计数:华杯赛对计数考察的非常多，尤其是几何计数，计数的方法以枚举为主，但是要求同学有很强的有序枚举能力，应用乘法原理计算也会出现，但不多。

计算：从第1到第14届华杯赛初赛，共考了21道计算题，这些计算题总体来说比较简单，没有六年级已经或即将学过的较难的裂项、拆分、换元与通向归纳这些知识点，考察的除了一些极为简单的简便运算之外，比较有难度的主要集中在分数、小数的混合运算以及比较大小这两块。

数论，数论从整体来说，出现的试题较少，出现的试题比重从高到低有：约数倍数、余数、质数与合数、带余除法、同余。

应用题：华杯赛对应用题的考察比重从高到低有：经济利润浓度、行程问题、工程问题、鸡兔同笼、年龄问题。

在方法上经常要用到列方程解应用题。

数阵图与数字谜:这类题出现的也比较多，替代性数字谜较多，但都较简单，比较有难度的是填充型的数字谜。

(完整版)华杯赛考试大纲及备考攻略

华杯赛考试大纲及备考攻略一．华杯赛常考考点总结计算：分数小数互化、循环小数化分数、约分、运算级别、加法、乘法运算律常用公式、常用数据记忆裂项(整数、分数裂项;分数拆分)、通项公式、换元法估算、取整、取小数论：奇偶数质数、合数整除及位值原理约数、(最大)公约数、(最小)公倍数余数及同余完全平方数数字迷进制(常考二进制)几何：平面几何的周长及面积规则图形：掌握公式、高不规则图形：割补法、转化为规则的常用模型：同底等高模型、四边形定理、蝴蝶定理、鸟头定理、燕尾定理、容斥定理立体几何的体积及表面积圆柱、圆锥等公式 (挖洞后)立体的体积表面积与体积图形的染色与切割平面图形的旋转圆形的滚动应用题：行程问题：多次相遇、多次追及、环形行程、走走停停、变速行驶工程问题：多人合作、中途请假、做做停停、工资分配、工作交换经济、浓度问题：概念转换、利润计算、浓度计算、利润最大化、溶液配比、溶液装置变换最值问题：最短时间、最大利润、最大乘积、最小损耗容斥原理：集合的交集、并集与补集抽屉原理(构造抽屉是难点) 抽屉原理一：告诉苹果和抽屉，求最值抽屉原理二：告诉抽屉和最值，求苹果(最不利) 抽屉原理三：整数分组其他问题：决赛中约考察15分构造与染色：奇偶染色、证明问题加乘原理排列组合捆绑与插空枚举与树形图容斥与排除归纳与递推标数法对应法重要：线分面，面分体。

如果怒了用枚举二、如何备考各大杯赛1、第一阶段：奥数各大专题复习。

杯赛考察的是孩子的综合实力，几乎涉及奥数所有专题，孩子平时的学习情况基本决定了孩子的竞赛成绩。

有计划有准备的奥数学习的孩子去参加各大杯赛考试，获奖的概率将大大增加。

因此，有必要为了每一种杯赛而制定学习计划，否则将会得不偿失。

现阶段可以把老师讲过的知识整理一遍，把每个知识模块都画一张脑图。

以一本参考书为蓝本进行练习，这本书一定要是按知识模块分类的书，不是综合性题型的书，每天晚上拿出30分钟做几道题。

注意：薄弱的知识点一定要记下来！以便后期薄弱知识模块学习更有针对性！2、第二阶段：薄弱知识模块突破。

【备战华杯赛】近五年华杯赛小高初赛真题解读

【备战华杯赛】近五年华杯赛小高初赛真题解读为了帮助大家更有效地准备初赛，今天我们针对华杯赛初赛考点和大家进行分享。

1 初赛考什么？初赛一共十道题（六道选择题四道填空题），共100分，都不用写过程，用时60分钟。

大家首先一定要知道华杯赛的所有考点：计算、应用题、行程问题、数论、几何、计数、组合杂题。

而这正好对应于我们小学奥数核心知识体系里面的七大模块。

华杯赛其实就是对学生所学奥数知识的一个测试。

那其中哪些模块是我们的重难点呢？哪些是我们在这段时间里需要重点关注的呢？看下面！2 初赛怎么考？想要通过华杯赛初赛，我们第一步先要了解一下华杯赛初赛的命题规律，在这里我们对近五年的所有华杯赛初赛试题做了一份详细的考点分析。

通过把所有的数据整合到一起，我们发现每年的考点是这样的：通过这个图我们发现：华杯赛涉及的知识点都很全面，七个模块均会考察，只不过每年对模块中的细分知识点有所变化，这就要求我们对各个知识模块的完整体系有所掌握与研究。

然而考试重点在哪里呢？哪些是我们需要关注的重中之重呢？我们通过一个饼图来观察分析一下。

我们可以发现初赛考试侧重点在于：数论、组合杂题、应用题这几个模块。

数论一直最受华杯赛组委会所青睐，小高华杯赛考察数论方面是一个重点！因为2015年华杯赛主试委员会委员陶晓永教授讲过：“华杯赛主要目的是要学习华罗庚先生的精神，而华罗庚先生在数学方面最大的成就就在数论这一块。

” 在数论这一个模块上，考察知识点较多，综合性也比较强，这就要求孩子们对于数论里面的知识点要有一定的了解和灵活运用的能力。

组合杂题一般难度系数比较大点，有的题目需要孩子具有很强的分析、空间、逻辑思维能力。

但不要慌张，大部分学生都做不出来，所以这个不是学生前期备考的重点。

想再冲刺华杯赛一等奖的孩子，组合杂题一定需要被重视起来的。

应用题这个模块，一般考察浓度问题、经济问题、工程问题、比例问题（份数思想、量率对应）、列方程解应用题等，基本上难度系数不高，加把劲，一定可以拿得下来！3 初赛难易度分析上述部分，我们对于模块进行了详细的分析。

华杯赛备考

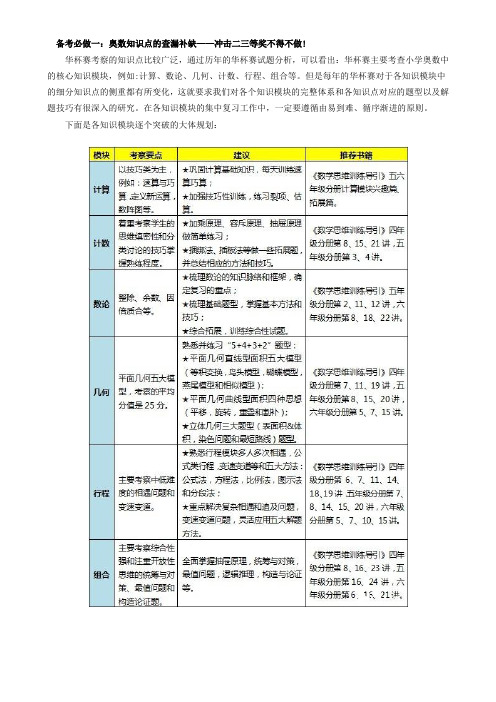
备考必做一：奥数知识点的查漏补缺——冲击二三等奖不得不做!华杯赛考察的知识点比较广泛，通过历年的华杯赛试题分析，可以看出：华杯赛主要考查小学奥数中的核心知识模块，例如:计算、数论、几何、计数、行程、组合等。

但是每年的华杯赛对于各知识模块中的细分知识点的侧重都有所变化，这就要求我们对各个知识模块的完整体系和各知识点对应的题型以及解题技巧有很深入的研究。

在各知识模块的集中复习工作中，一定要遵循由易到难、循序渐进的原则。

下面是各知识模块逐个突破的大体规划：备考必做二：真题全接触——冲击二三等奖不得不做!在做题过程中要注意以下三点：规定完成试卷的时间，建议和考试时间相同或者略少;做的时候切忌边做题边对答案;做错的题目最好拿一个错题本记录下来，认真分析错误原因，查漏补缺，总结关键解题思路。

通过做历届的杯赛试题需要达到两个目的：第一、检测和评价自己目前的奥数功底;第二、查漏补缺，为备战的第二步打下铺垫。

备考必做三：突破难点，冲刺一等奖不得不做!(一)突破数论模块备战建议：数论的难度就毋庸多说了，它占了总分值的将近40%，是想拿一等奖的学生必争之地!在上述梳理基础和综合拓展的基础上，顶尖的学生要做的就是拔高难度，勇于挑战。

参考书推荐：《仁华学校思维导引》五六年级分册，五年级第4、5、7、14、15、19讲;六年级第4、5、8、14、15讲。

(二)战胜几何难关备战建议：几何的难度偏中高，它占了总分值的将近20%，多以详答题的形式出现，在上述梳理“5+4+3+2”和全面提高解题能力的基础上，顶尖的学生要做的仍然是拔高难度，勇于挑战综合性强、灵活多变的较难题目。

参考书推荐：《仁华学校思维导引》五六年级分册，五年级第6、16、17讲;六年级第6、7、16讲。

(三)拿下组合问题备战建议：组合类题目的难度偏中等，它占了总分值的将近20%，多以简答题的形式出现，在上述梳理基础题型和全面查漏补缺的基础上，顶尖的学生要做的是养成良好的解题习惯，勇于挑战综合性强、背景新颖的较难题目，要保证在组合问题上不丢冤枉分、习惯分。

华杯初赛的考试规则及答题注意事项

•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
华杯初赛的考试规则及答题注意事项
华杯初赛的考试规则及答题注意事项
华杯赛堪称国内小学阶段规模最大、最正式也是难度最高的比赛。

下面和小编一起来看华杯初赛的'考试规则及答题注意事项，希望有所帮助!
考试时间：
12月10号周六上午10:00-11:00
考试必带：
带上准考证、身份证或有效证件(含学生证、户口本等)准时到场参加考试。

考前注意事项：
1.准备好必要的文具，带上准考证等有效证件;
2.提前到达考试地点，熟悉考场和座位;
3.进考场前上一次洗手间;
4.考前深呼吸，保持平和的心态。

考场注意事项：
1.答题前通览全卷;
2.做题时先易后难;
3.认真审题;
4.复看试卷防止缺漏;
5.字迹清晰;
6.答题规范;
考场小贴士：
答题使用中性笔，不需要带草稿纸(可自带无标签水壶)。

(1)考前15分钟凭准考证和有效身份证件进入考场，对号入座。

(2)考试15分钟后，迟到人员不能进入考场，开考45分钟内考生不得退场。

(3)只携带中性笔，2B铅笔(可带入但不使用铅笔作答)、直尺、橡皮、铅笔刀等规定之内的应试用品进入考场。

与考试无关的物品，按规定存放在考场指定位置(移动电话等电子产品须关机)
(4)遵守考场规则，考试时不准旁窥、交谈、吸烟、传递物品，严禁作弊。

交卷后不得在考场附近逗留或谈论。

(5)考试结束后，立即停止答卷，不得将试卷、答题卡和草稿纸带出考场。

“华杯赛”决赛高分备考方法

“华杯赛”决赛高分备考方法华杯赛作为国内中小学数学奥林匹克的权威赛事，是杭州优秀中小学生必参与重点中学必关注小升初必参考的重大赛事之一。

华杯赛试题知识点覆盖全，非常经典。

试题不完全是难，而是巧妙，能帮助孩子开阔思路，对中学的理科学习也有极大帮助。

在此从15届（2010年）华杯赛的决赛试题入手，着力就华杯赛命题特点与大家进行探讨并介绍一下备考华杯赛的策略。

华杯赛题型及试题特点解析试卷难度分为三类：基础题、中档题和高档题，其中基础题和中档题的比重超过三分之二，只要将基础和中档题全部做对，就可以在华杯赛中得奖！一．华杯赛命题浅析按难度分类：其中基础题和中档题的比重超过三分之二，只要将基础和中档题全部做对，就可以在华杯赛中得奖！华杯赛的试题近年来主要有一下几个特点：A.强调数学题概念清晰、过程清楚和答案明确三个要求并重，强调逻辑分析与解答的严密性。

这一点在笔者参与阅卷过程中体会非常深刻。

以第一个解答题为例，只写得数仅得5分；把图形处理为正六边形没有过程分。

B.考点上侧重数论、几何和组合问题（构造、论证、染色、计数）——即传统意义上的杂题。

但是由于种种原因，华杯赛对于几何模块的考察难度还没有其他模块那么大，所以大家可以根据个人情况进行备考。

C.解答题中特别重视对代数思维的考察。

这一点在数论模块体现非常明显，笔者归纳了数论的三大解题法宝：一是遇到具体数字未知的情况以位值原理的形式展现出来并对应做分类讨论；二是位值原理展开和分解质因数是数论问题的两大救命稻草；三是冲刺高端数论题目需要牢牢掌握公式变形。

其中第三点正是应对华杯赛这样的题目的良方。

想在华杯赛中取得好成绩，培养缜密的代数思维至关重要，要将算术的精妙技巧与代数的清晰逻辑结合起来。

整体而言，学生想要在华杯赛中取得不俗的成绩，需要重点对数论和组合（构造论证、染色、计数）进行专题击破，并且在平时要非常注重对代数思维的培养，在具体解答过程中一定要注意步骤清晰和答案明确。

第二十二届华杯赛决赛考前注意事项（附往年决赛真题）

第二十二届华杯赛决赛考前注意事项（附往年决赛真题）
为了帮助各位家长做好说教工作，分享下
我的经验：
(1)每道解答题一定要“答”！否则老师
连答案都找不到（P.S.判卷老师是绝对没有心
情去帮你找答案的，第一眼没看到，基本就当
不存在了）；
(2)解答题一定要从最左边开始写，否则
地方根本不够！这就是很多孩子解题过程忽左
忽右的原因，其实本质上就是哪有空地方，下
一步就写在哪，完全不考虑判卷老师的感受。

所以判卷老师也不会考虑你的感受了！书写是
个大问题，有时一个好的书写甚至能够躲过一
些小错误。

一般一张书写工整的试卷，尤其是
在小学，基本就是答案对就是对了，答案错了，
老师还会有一种想找点过程分的冲动。

其实字
不在优雅，过程不在诗意，清晰明了是关键。

(3)答案一定要一笔一划写。

有时从头到
尾一笔一划真的很难做到，但是答案一定要好
好写！！在这个问题上有多少人发生过多少痛
彻心扉的惨案啊……
(4)最后，不要纠结在某道题上，不要刻
板地做完一道题再做下一道题。

华杯赛做对一
半就能一等奖，何必纠结在一两道题上？先挑
选最有把握的题做完，再按顺序看能多解决一
个题算一个题。

【2016年决赛真题】。

六步教你备考华杯赛!

备考华杯赛需要哪些复习资料？.doc

【备考】华杯赛：想要获奖你必须做到的事

2021小升初华杯赛夺冠全攻略(参考)

华杯一等奖备考策略

如何准备华杯赛

华杯赛赛前教程

华杯赛备考

第22届华杯赛备考三大注意事项介绍

华赛杯的考点

五年级 数学 华杯赛 书

第十八届华杯赛赛事安排及备考攻略

【考试技巧大分享】让你在华杯赛中拿到更多分数！

快速提分的华杯赛初赛内部应考攻略(五年级)

(完整版)华杯赛考试大纲及备考攻略

【备战华杯赛】近五年华杯赛小高初赛真题解读

华杯赛备考

华杯初赛的考试规则及答题注意事项

“华杯赛”决赛高分备考方法

第二十二届华杯赛决赛考前注意事项（附往年决赛真题）

五年级数学华杯赛书