正等轴测投影图
正等测轴测图的画法

新课:4.2 正等测轴测图的画法
一、正等轴测投影图的形成
P
Z1
正等轴测投影图
O1 X1
Y1 X
Z
S O
Y
二、 轴间角和轴向伸缩系数
投影线方向 轴向伸缩系数
特 简化轴向伸缩系数
投影线与轴测投影面垂直 p1=q1=r1=0.82 p=q=r=1
Z1
性
轴间角
120° O1 120°
X1
120°
Y1
L 0.82L
1、平行H面的圆的画法:四心圆法
Z o4
o2
o3
o5
2. 圆柱体的正等测图的画法
3. 圆角的正等测图的画法
O'
X' O1
Z' O
Z1 X
Y
X1
Y1 Z1 X1
Y1
整理、完成作图
O'
X'
O1 Z'
O
X Z1
Y
X1 Y1
(三)、 组合体的正等测轴测图的画法
(1)切割法
例1:已知三视图,画轴测图。
边长为L的正 方形的轴测图
按简化轴向伸缩系数绘制
按实际轴向伸缩系数绘制
三、正等测轴测图的基本作图方法
(1) 在三视图上建立坐标系
(2) 画出正等测轴测轴
(3) 从三视图上直接量取与坐标轴平行的 线段画到相应的轴测轴的对应位置,从而 画出物体的轴测图
(一) 平面立体正等测轴测图的画法
(二) 曲面立体正等测轴测图的画法
Z
X O
X
Y
例2
Z
Z
18
10
25
16 8
8
X
轴测投影图画法详解

例5
简便画法:
1.截取 O1D1= O1G1= A1E1 = A1F1 =圆角半径
2.作 O2D1⊥O1A1、 O2G1⊥O1C1 O3 E1⊥O1A1 、O3F1⊥A1B1
E2 D2 G2
● ● ● ● ● ● ●
O E1
5
A1
O3
●
F1
3.分别以 O2、 O3为圆心, O2D1、 O3E1为半径画圆弧
1Z1、∠Y1O1Z1
P
Z1
S⊥P:正轴测图 S倾斜于P:斜轴 测图
Z X1 S Y1
X
Y12ຫໍສະໝຸດ 轴测轴上某线段长度与它的实长之比,称 为轴向变形系数。
O1X1/OX= p ——称为X轴 向变形系数
O1Y1/OY= r
P
Z1
Z ——称为Y轴 X1 S Y1
向变形系数
O1Z1/OZ= q ——称为Z轴 向变形系数
的形体平面(图纸1) 用硫酸纸将建筑的形体平面再
描一次(图纸2)
在图2上作各个体块的高度线。 (高度平行线的角度要控制好) 沿平行方向移动图纸1,使之 达到各个体块的高度位置,并 把轮廓描绘一次。 再拿一张新硫酸纸,描绘建筑 的体块轮廓,略去遮挡线。 最后,增加女儿墙、窗洞等细 节。
工程制图
2012.5
3
Part 3
轴测图
2
学习目的及要求
了解轴测图的形成、性质及作用 掌握正等、斜二测(正面及水平)的作图方法 掌握圆的正等、斜二测作图方法
3
本章内容:
前言 基本知识 正等轴测图 斜二等轴测图
4
前言
5
6
7
8
9
10
11
第五章,轴测投影图

例2-2
画轴测轴 画 沿轴测量画动平面 各顶点沿Y方向画20 画动平面(终止位置) 画 检查、描深
*
例3 画出给定形体的正等轴测图
画空间轴 画轴测轴 画长方体 画五棱柱 检查、描深
例4 画出圆锥的正等轴测图
确定坐标轴 画轴测轴 画圆锥底面(侧平圆) 画锥顶 画转向线 判别可见性、描深
例5 根据已知的两面投影,画出正等轴测图
三、斜二轴测图画法
例13:已知两视图,画斜二轴测图。
第五章 轴测投影图
[例14] 作出如图所示带孔圆锥台的斜二轴测图。
z′
z〞
x′
o′
o〞
a″ y〞
L
Z1
X1
O1
L2
A
O1 A
Y1
圆弧公切线
[例15] 作出如图所示物体的斜二轴测图。
z′
z〞
x′
o′
L1
L
o〞 y〞圆弧公切线
Z1
X1 L1/2 L/2
2 平行于H面的圆为椭圆,长 轴对O1X1轴偏转7°, 长轴≈1.06d, 短轴≈0.33d。
3 平行于W面的圆与平行于H 面的圆的椭圆形状相同,长 轴对O1Z1轴偏转7°。
由于两个椭圆的作图相当繁,所以当物体这 两个方向上有圆时,一般不用斜二轴测图,而采 用正等轴测图。 斜二轴测图的最大优点:
物体上凡平行于V面的平面都反映实形。
x′
x1
2
z′
Z1
圆弧公切线
A
o′ o4
A1 41
o
31
11
3
X1
21
Y1
圆
弧
y
公 切
线
[例12] 作出如图所示支架的正等轴测。
正等测轴测图的画法

(2) 画出正等测轴测轴
(3) 从三视图上直接量取与坐标轴平行的 线段画到相应的轴测轴的对应位置,从而 画出物体的轴测图
(一) 平面立体正等测轴测图的画法
(二) 曲面立体正等测轴测图的画法
1、平行H面的圆的画法:四心圆法 Z
o4
o2
o5
o3
2. 圆柱体的正等测图的画法
3、 轴测投影的基本性质
(1)物体上相互平行的线段的轴测投影仍相互平行;
(2)物体上平行于坐标轴的直线段的轴测投影仍与相应 的轴测轴平行;
(3)物体上原来平行于坐标轴的线段,在轴测图中可以 按其原来的尺寸乘以轴向伸缩系数后,再沿着相应的轴测 轴定出其投影的长短。
凡是与坐标轴平行的直线,就可以在轴测图 上沿轴向进行度量和作图。
(2)能熟练地根据实物或投影图绘制物体的正等 轴测图。 六、作业:习题集P26
4、轴测图的种类
正轴测图 轴测图 正等轴测图 正二轴测图 正三轴测图 p=q=r p=rq pqr
斜轴测图
斜等轴测图 p = q = r 斜二轴测图 p = r q 斜三轴测图 p q r
正等轴测图
斜二轴测图
新课:4.2 正等测轴测图的画法
一、正等轴测投影图的形成
P
Z1 Z
正等轴测投影图
X1 O1 Y1 X O
S
Y
二、 轴间角和轴向伸缩系数
投影线方向 轴向伸缩系数 投影线与轴测投影面垂直 p1=q1=r1=0.82
特
简化轴向伸缩系数
p=q=r=1
Z1 性
轴间角
120°O
1
120°
X1
120°
Y1
边长为L的正 方形的轴测图
正等轴测图
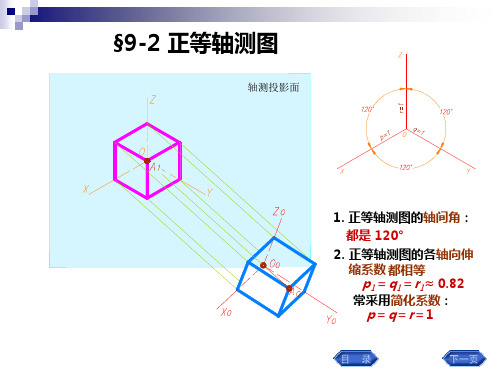
例5-2:作垫块的正等轴测图
例5-3:作轴套的正等轴测图
例5-4:作支架的正等轴测图
§9-2 正等轴测图
轴测投影面
1. 正等轴测图的轴间角: 都是 120°
2. 正等轴测图的各轴向伸 缩系数都相等 p1=q1=r1≈ 0.82 常采用简化系数: p=q=r=1
二、平行于坐标面的圆的正等轴测图
比较圆柱的两 面投影图和正等 轴测图,可见圆 柱的顶圆和底圆 都是椭圆。
用四段圆弧 连成的近似椭圆 可画平行于坐标 平面的圆的正等 轴测图。
两面投影图
正等轴测图
平行于坐标面的圆的正等轴测图——近似椭圆的作法
立方体表面上的圆的正等轴测图
平行于水平面的 圆的轴测图
O
平行于侧面的 圆的轴测图
平行于正面的 圆的轴测图
注意:
椭圆的长轴: 垂直于与圆平面垂
直的坐标轴的ห้องสมุดไป่ตู้测图 (轴测轴。
椭圆的短轴: 平行于这条轴测轴。
三、画法举例
例5-1:根据正六棱柱的两视图作其正等轴测图
轴测图基本知识及正等测图
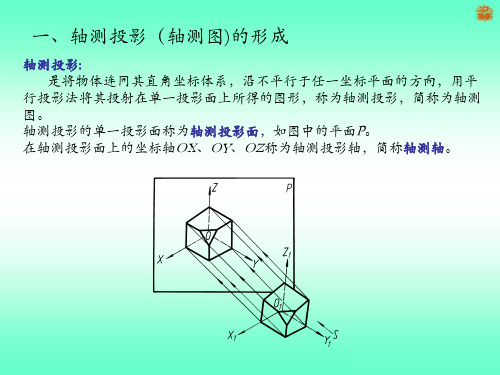
2.正等轴测图的画法
(1)平面立体正等轴测图的画法
例1已知长方体的三视图,画出它的正等轴测图。
解 分析:长方体共有八个顶点,用坐标确定各顶点在其轴 测图中的位置,然后连接各顶点间的棱线即为所求。作图 步骤如图:
例2已知垫块的三视图,画出它的正等轴测图。
解 分析:垫块为一简单组合体,是由两个长方体与一个三棱柱组合而
一、轴测投影(轴测图)的形成
轴测投影: 是将物体连同其直角坐标体系,沿不平行于任一坐标平面的方向,用平
行投影法将其投射在单一投影面上所得的图形,称为轴测投影,简称为轴测 图。
轴测投影的单一投影面称为轴测投影面,如图中的平面P。 在轴测投影面上的坐标轴OX、OY、OZ称为轴测投影轴,简称轴测轴。
二、正等轴测图的画法
0.75d
1.22d
1. 轴间角和轴向伸缩系数 轴测投影中,任两根轴测轴之间的夹角称为轴间角。
轴测轴上的单位长度与相应直角坐标轴上的单位长度的比值 称为轴向伸缩系数。
OX、OY、OZ轴上的轴向伸缩系数分别用p1、q1、r1表
示。 为了便于作图,绘制轴测图时,对轴向伸缩系数进行简
化,以使其比值成为简单的数值。简化伸缩系数分别用p、 q、r表示。
成。只要画出底部长方体后,应用叠加法就可得到它的正等轴测图。 作图步骤如图:
图3-4切割法画正等测
返回
(2)回转体正等轴测图的画法
例已知圆柱体的二视图,画出它的正等轴测图。
(1)圆柱正等轴测图的画法
Z
O
X
Y
图3-5平行坐标面的正等轴测图
返回
三向正平方向椭圆
正等轴测图

映实形。 平行于H面的圆为椭圆,长
轴对O1X1轴偏转7°,长轴 ≈1.06d, 短轴≈0.33d
平行于W面的圆与平行于H 面的圆的椭圆形状相同,长 轴对O1Z1轴偏转7°。
由于两个椭圆的作图相当繁,所以当物体这 两个方向上有圆时,一般不用斜二轴测图,而采 用正等轴测图。
例1:画三棱锥的正等轴测图
s
Z Z s
S Z1 ●
X a b a
X
s
b
c OOcOca
Y
b
Y
A●
X1
●CO1
Y1
●B
⑵ 切割法
例2:已知三视图,画轴测图。
⑶ 叠加法 例3:已知三视图,画轴正等测图。
⒉ 回转体的正等轴测图画法
⑴ 平行于各个坐标面的椭圆的画法
平行于W面的椭
Z1
圆长轴⊥O1X1轴
平行于H面的椭 圆长轴⊥O1Z1轴
O E1 ●
●
5
O●
3
A1 F●
1
●
D1 O●4
B1
O●
2
C1
1.截取 O1D1=O1G1=A1E1=A1F1 =圆角半径
2.作 O2D1⊥O1A1 , O2G1⊥O1C1 O3 E1⊥O1A1 , O3F1⊥A1B1
3.分别以 O2、 O3为圆心, O2D1、 O3E1为半径画圆弧
4.定后端面的圆心,画后端面 的圆弧
平行于V面 的椭圆长轴 ⊥O1Y1轴
X1
Y1
画法:四心椭圆法
(以平行于H面的圆为例)
e
●
E1 ●
B● 1
a
b
●
●
A● 1
正等测轴测图的画法课件

18
10
25
16
8
X
36
O
O
O X
20
Y X
O Y
16
Y
•正等测轴测图的画法
•14
完成
18
10
25
36
16
8
20
•正等测轴测图的画法
•15
(2) 叠加法
例1:已知三视图,画正等轴测图。
•正等测轴测图的画法
•16
例2 24 Z 6
步骤1
Z 6
28
20
X
32
O
O
X
O
8
Z Y
O
24
Y X
Y
•正等测轴测图的画法
2、三视图与轴测图的比较
三视图可以较完整地确切地表达出零件各部分的形状,且作图方便,但这
种图样直观性差;
轴测图能同时反映形体长、宽、高三个方向的形状,具有立体感强,形
象直观的优点,但不能确切地表达零件原来的形状与大小.且作图较复杂,
因而轴测图在工程上一般仅用作辅助图样。
•正等测轴测图的画法
•1
3、 轴测投影的基本性质
(1)物体上相互平行的线段的轴测投影仍相互平行;
(2)物体上平行于坐标轴的直线段的轴测投影仍与相应 的轴测轴平行;
(3)物体上原来平行于坐标轴的线段,在轴测图中可以 按其原来的尺寸乘以轴向伸缩系数后,再沿着相应的轴测 轴定出其投影的长短。
凡是与坐标轴平行的直线,就可以在轴测图 上沿轴向进行度量和作图。
•正等测轴测图的画法
•2
4、轴测图的种类
正轴测图 轴测图
斜轴测图
正等轴测图 p = q = r 正二轴测图 p = r q 正三轴测图 p q r
正等轴测图

由于两个椭圆的作图相当繁,所以当物体这 两个方向上有圆时,一般不用斜二轴测图,而采 用正等轴测图。 斜二轴测图的最大优点: 物体上凡平行于V面的平面都反映实形。
例:已知两视图,画斜二轴测图。
7.4 轴测剖视图
为了表示零件的内部结构和形状,常用 两个剖切平面沿两个坐标面方向切掉零件的 四分之一。
凡是与坐标轴平行的线段,就可以在轴测图上 沿轴向进行度量和作图。 轴测含义 注意:与坐标轴不平行的线段其伸缩系数与之不同, 不能直接度量与绘制,只能根据端点坐标,作 出两端点后连线绘制。
四、轴测图的分类
正轴测图 轴测图 正等轴测图 p = q = r 正二轴测图 p = r q 正三轴测图 p q r 斜等轴测图 p = q = r 斜二轴测图 p = r q 斜三轴测图 p q r
X1O1Y1, X1O1Z1, Y1O1Z1
轴测轴
2. 轴向伸缩系数 物体上平行于坐标轴的线段在轴测图上 的长度与实际长度之比叫做轴向伸缩系数。
投影面
X1 A 1 C Z C1 Z1 X O1 B1 A Y O B A1 X1 O1 B1 C Z1
投影面
C1
Z
Y1
Y1
O
X A
正轴测
B Y
二、轴测轴、轴间角和轴向伸缩系数
1. 轴测轴和轴间角 建立在物体上的坐标轴在投影面上的投影 叫做轴测轴,轴测轴间的夹角叫做轴间角。
投影面
X1 Z Z1 X O1 Y1 Y O Z1
投影面
O1
X1 Y1
Z O X
正轴测
Y
斜轴测
轴间角
物体上 投影面上
OX, OY, OZ O1X1,O1Y1,O1Z1
机械制图轴测投影图

❖
安全象只弓,不拉它就松,要想保安 全,常 把弓弦 绷。20.12.2000:13:0800:13Dec-2020-Dec-20
❖
加强交通建设管理,确保工程建设质 量。00:13:0800:13:0800:13Sunday, December 20, 2020
❖
安全在于心细,事故出在麻痹。20.12.2020.12.2000:13:0800:13:08December 20, 2020
❖
弄虚作假要不得,踏实肯干第一名。00:13:0800:13:0800:1312/20/2020 12:13:08 AM
❖
安全象只弓,不拉它就松,要想保安 全,常 把弓弦 绷。20.12.2000:13:0800:13Dec-2020-Dec-20
❖
重于泰山,轻于鸿毛。00:13:0800:13:0800:13Sunday, December 20, 2020
2
§12-1 概述
轴测图是由平 行光线投射而形 成的,如右图所 示。
光线垂直与投 影面投射所得到 的轴测图叫正轴 测图;光线倾斜 于投影面投射所 得的轴测图叫斜 轴测图。
2020/12/20
轴测投影的形成
3
用平行投影法所获得的轴测图,具有下列投影 特性:
❖ 1) 物体上互相平行的线段,在轴测图上仍互相 平行。
27
(3) 用30º三角板过B1和A1点,画与水平线成60º的直线交 短轴延长线于O1和O2点。交长轴于O3和O4点。再连O1 B1、 O1 C1和O2 A1、O2 D1。则O1、O2、O3、O4是四段圆弧的中心 ,C1、 B1、 A1、 D1为四段圆弧的分界点(切点)。
2020/12/20
28
(4) 以O1、O2为圆心,以O1B1为半径,分别画B1C1弧 和A1D1弧,再以O3、O4为圆心,以O3B1为半径,分别画 B1D1弧和A1C1弧, 四段圆弧组成近似椭圆。
正等轴测图
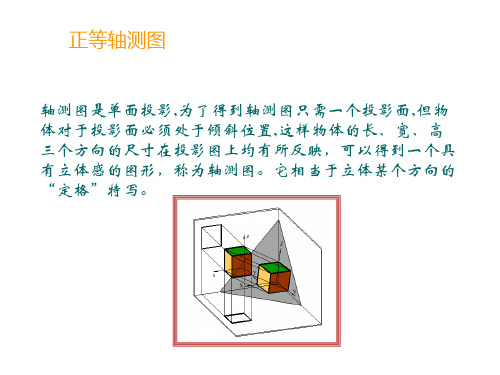
(1)画圆
基本图形的画法
“正等测圆”的画法 类似,只是把画“正 方形”改为画“菱形” 而已
(2)画圆柱体
①画两个正等测圆
②用两条平行线连接两个正 等测圆
(3)画立方体
①画正等测正方形(两条虚线)
②确定立方体的高,画四角 垂线(内侧垂线为虚线)
③画一个平行于底面的正等 测正方形
(4)画锥体
①画两条与水平面成30°角的射 线
正等轴测图
轴测图是单面投影,为了得到轴测图只需一个投影面,但物 体对于投影面必须处于倾斜位置,这样物体的长、宽、高 三个方向的尺寸在投影图上均有所反映,可以得到一个具 有立体感的图形,称为轴测图。它相当于立体某个方向的 “定格”特写。
轴测图示例
投影图无立体感,度量性好; 轴测图立体感强,度量性差。
正等轴测图
• 正等轴测图是一种表现物体三维结构的 图,、Y、Z三维,与数学的坐标系一致!
Z
13200度度
120度 30度
X
Y
Z
X
Y
Z
X
Y
画法小结
1、画出三维; 2、继续画出长80mm,宽50mm,高40mm 的长方体的正等轴测图; 3、画出长方体削去两刀的绘制,最后剩余的 部分用铅笔把轮廓线加深、加粗凸显出来;
②画一条垂线
③连接线(内侧为虚线)
正等测轴测图画法
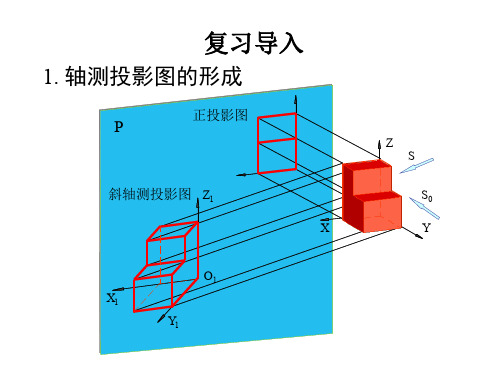
Z o4
o2
o3
o5
2. 圆柱体的正等测图的画法
3. 圆角的正等测图的画法
X1
O'
X' O1
Z' O
Z1 X
Y1 Z1
X1 Y
Y1
整理、完成作图
X1
O'
X'
O1 Z'
O
X Z1
Y1 Y
(三)、 组合体的正等测轴测图的画法
(1)切割法
例1:已知三视图,画轴测图。
X Y
Z
O Y
24 Z 6
步骤2
Z 6
28
20
8
Y
X
32
OOXO Nhomakorabea24
X
Y
Z
O Y
24 Z 6
步骤3
Z 6
28
20
8
Y
X
32
O
O
X
O
24
X Y
Z
O Y
完成
24 Z
Z
6
6
28
20
8
Y
X
32
O
O
X
O
24
Y
四、练习:习题集P25
五、小结:
(1)知道正等轴测图是如何形成的,知道轴向伸 缩系数和轴间角的几何意义;
(2)能熟练地根据实物或投影图绘制物体的正等 轴测图。
六、作业:习题集P26
凡是与坐标轴平行的直线,就可以在轴测图 上沿轴向进行度量和作图。
4、轴测图的种类
正轴测图 轴测图
斜轴测图
正等轴测图 p = q = r 正二轴测图 p = r q 正三轴测图 p q r
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、正等轴测投影的形成
正等轴测投影的投射方向S垂直于轴测投影间P,如图7-2 a所示,且确定物体空间位置的三个坐标平面与轴测投影面均倾斜,其上的三根直角坐标轴与轴测投影面的倾角均相等,物体上平行于三个坐标平面的平面图形的正等轴测投影的形状和大小的变化均相同,因此,物体的正等轴投影的立体感颇强。
二、正等轴测投影的轴间角和轴向伸缩系数
(一)轴间角
正等轴测投影,由于物体上的三根直角坐标轴与轴测投影面的倾角均相等,因此,与之相对应的轴测轴之间的轴间角也必须相等,即∠XOY=∠YOZ=∠XOZ=120°,如图7-3a 所示。
(二) 轴相伸缩系数
正等轴测投影中OX、OY、OZ轴的轴向伸缩系数相等,即 p=q=r。
经数学推导得:p=q=r≈0.82。
为作图方便,取简化轴向伸缩系数p=q=r=1,这样,画出的图形,在沿各轴向长度上均分别放大到1/0.82≈1.22倍,如图7-3c所示。
三、平面立体的正等轴测图画法
由多面正投影图画轴测图时,应先选好适当的坐标体系,画出对应的轴测轴,然后,按一定方法作图,画平面立体轴测图的基本方法是按坐标画出各顶点的轴测图,称为坐标法,见以下两例。
[例7-1] 根据三棱锥的三面投影图,画出它的正等轴测图。
作图步骤,如图7-4所示。
[例7-2] 根据六棱柱的三面投影图,画出它的正等轴测图。
作图步骤,如图7-5所示。
本题关键在于选定坐标轴和坐标圆点,如先确定顶面各点的坐标,可避免画不必要的作图线。
四、曲面立体的正等轴测图的画法
(一)坐标平面(或其平面)上的圆的正等轴测投影
坐标平面(或其平行面)上圆的正等轴测投影为椭圆。
立方体平行于坐标平面的各表面上的内切圆的正等轴测投影,如图7-6所示。
从图7-6中可以看出:
(1)分别平行于坐标平面的圆的正等轴测投影均为形状和大小完全相同的椭圆,但其长轴和短轴方向各不相同。
(2)各椭圆的长轴方向垂直于不属于轴测投影(即轴测轴),且在菱形(圆的外切正方形的轴测投影)的长对角线上;短轴方向平行于不属于此坐标平面的那根坐标轴的轴测投影(即轴测轴),且在菱形的短对角线上。
(3)各椭圆的长轴等于圆的直径d,短轴等于0.58d,如图7-6a。
按简化轴向伸缩系数作图,长轴等于1.22d,短轴等于0.7d,如图7-6b。
为作图方便,一般采用轴向伸缩系数。
(二)圆的正等轴测投影(椭圆)的画法
椭圆常用的近似画法是菱形法,现以坐标平面XOY上的圆(或其平行圆)的正等轴测投影为例,说明作图方法,如图7-7所示。
(三)常见曲面立体的正等轴测投影画法
(1)圆柱的画法,如图7-8所示。
(2)圆锥台的画法,如图7-9所示。
(3)圆球的画法,如图7-10所示。
(四)圆角正等轴测投影的画法
从图7-7用菱形法近似画椭圆可以看出,菱形的钝角与大圆弧相对,锐角与小圆弧相对,菱形相邻两边的中垂线的交点就是大圆弧(或小圆弧0的圆心,由此可得出圆角的正等轴测投影的近似画法:画圆角正等轴测投影时,只要在作圆角的两边上量取圆角半径R,自量得的点作边线的垂线,然后以两垂线交点为圆心,以交点至垂足的距离为半径画弧,所得的弧即为圆角的正等轴测投影。
图7-11a是带圆角的四棱柱底版,其正等轴测投影的作图步骤,如图
7-11b~f所示。
五、组合体的正等轴测图的画法
画组合体的轴测图,常用堆叠法、挖切法、综合法作图。
对于堆叠式的组合体,可按各基本形体逐一叠加画出其轴测图,称为挖切法。
对于既有堆叠又有挖切的组合体,可综合采用上述两种方法画轴测图,称为综合法。
[例7-3]根据图7-12a所示物体(支撑)的三视图,画出它的正等轴测投影。
根据支撑的形体特点,可用堆叠法作图,其作图步骤如图7-12b~e所示。
该支撑用形体分析法可看作由四棱柱底版、四棱柱竖板和直角三棱柱肋板组成。
(1)在三视图图上定坐标轴,原点定在后、中、下(在对称平面与后下方底棱线的交点)处,如图7-12a所示。
(2)画轴测轴并画底版沿OX轴向由O点左、右各量a/2。
沿OY轴向量b,画出底版的下底面,沿OZ轴向量c,即可画出底版,如图7-16b 所示。
(3)画竖板在底版的后、上方(后面平齐),沿OY轴向自后向前量e,沿OZ轴自下而上量h-c,即可画出竖板,如图7-12c所示。
(4)画肋板在底版、竖板的居中位置上,沿OX轴向左、右各量d/2,沿OZ轴向自上而下量f,即可画出肋板,如图7-12d所示。
(5)通常不画物体的不可见轮廓,擦出多余线,然后加深,既完成作图,如图7-13e所示。
[例7-5] 根据图7-14a所示物体(支撑座)的三示图,画出它的正等轴测投影。
根据支撑座的形体特点,可用综合法作图,一般先作堆叠型的形体,后作挖切型的形体,其作图步骤如图7-14b~f所示。
六、截交线、相贯线的正等轴测投影的画法
在画组合体的轴测投影时,常需作出其上的截交线和相贯线的轴测投影,一般可用坐标法或辅助平面法求出交线上的一系列的轴测投影,然后,光滑连接各点即可。
(一)截交线的正等轴测投影画法
一般采用坐标法,如图7-15所示。
(二)相贯线的正等轴测投影画法
1.坐标法
先在多面正投影图上定出属于相贯线上一系列的点,再根据这些点的坐标,在轴测投影上定出诸点的位置,并连成圆滑的曲线,如图7-16所示。
2.辅助平面法
在轴测投影上,直接用辅助平面来求属于相贯线上的点,然后,连成圆滑的曲线,如图7-17所示。
