图形的面积知识结构图

1 建筑识图与房屋构造

识
一、施工图组成
图
弱电图包括目录、设计说明、电话站设计图、广播。电视、火警、信号、通讯等设计图、计算书等。采暖通风图包括目录、设计说明、采暖平面图、通风除尘平面图、空调平面图、制冷机房平面图、空调机房平面图、及其相应的剖面图、系统图，以及各系统控制原理图、计算书等。动力图包括目录、设计说明、区域总平面图、系统图，管道平面、剖面布置图，管道横截面图，详图及计算书等。
综上所述：基础、主体、屋顶是组成房屋骨架的主要承重结构，其中外墙、屋顶即是承重结构又是围护结构，具有双重作用，而门窗仅是分隔和围护作用。一幢房屋除这些组成部分外，还有人们生活所必须的其他附属构配件和设施，如阳台、雨篷、壁橱、台阶、各种饰面、装修等等。
建筑构造
二、工业建筑的基本组成
供人们进行工业生产活动使用的建筑工程为工业建筑，又称工业厂房。工业建筑按层数分为单层和多层。工业建筑按主体承重结构组成不同，分为排架结构和框架结构。排架结构是指由柱与屋架组成的平面骨架，其间用连系梁拉结；框架结构是指由柱与梁组成的立体骨架。单层工业建筑多采用排架结构，多层工业建筑常采用框架结构。
图
识
图
识
图
识
图
识
图
识
图
识
图
识
图
识
图
识
图
识
图
识
图
识
图
识
图
识
图
识
（2）符号
图
①剖面剖切符号:剖面剖切符号是由位置及剖视方向线组成。剖面剖切符号的编号，采用阿拉伯数字，注写在剖视方向线的端部。需要转折的剖切为直线，在转折处如与其他图线发生混淆，应在转角的外侧加注与该符号相同的编号（图1-4)。

人教版小学数学六年级小升初总复习知识点结构图 ppt课件

解方程的应用题
人教版小学数学六年级小升初总复
11
习知识点结构图
1-1-4A：
概念
长度、面积、地积、体积、容积单位进率
长度单位与面积、体积单位的区别和联系
常见的量
面积单位和地积单位的区别和联系体积单位和容积单位的区别和联系名数的改写
常用的质量、时间、人民币单位常用的质量、时间、人民币单位和它们之间的进率 “时间”（小时）和“时刻”（时）的区四边形s=ah
三角形
s 1 ah 2
s r S人=教a版b小学数圆学六年级小升初总2复
各图面积的推导过程习知识点结构图
8
习知识点结构图
1-1-2A：
四则运算的意义四则运算的关系
加法：一个加数+另一个加数=和
减法
被减数=减数+差减数=被减数-差
乘法：一个因数=积÷另一个因数
四则运算的法则
被除数=商×除数除法除数=被除数÷商
“0”和“1”在四则运算中的特殊性
数的运算运算定律
运算性质
和、差、积、商的变化规律
四则混合运算的顺序
人教版小学数学总复习知识点结构图
人教版小学数学六年级小升初总复
1
习知识点结构图
知识结构体系1：
数与代数小学数学知识空间与图形（分为四类）统计与概率
综合运用
人教版小学数学六年级小升初总复
2
习知识点结构图
1-1：
数的认识数的运算数与代数式与方程常见的量比和比例数学思考
人教版小学数学六年级小升初总复
“季度”与“人季教版节小学”数学的六区年级别小升初总复
12
习知识点结构图
1-1-4B：

二年级数学上册知识结构图(全册)

经过时间
三年级
数学
知识树
下册
计算经过的时间
分段法减法计算法
1日星期日
1日星期日
1日是星期四
二月份的月历三月份的月历
一月份的月历
1日星期二
2007年历
2009年历 2008年历
展示年历
观察月历
十二月份的月历
年历的的样式
制作方法
2行6列 3行4列 4行3列
2000年年历
制
12张
作
年
历
年历的制作方法
例1 横向条形统计图
例2起始格与其他格代表的单位量不一致
的条形统计图
简单的数据分析
简单的数据分析知识树
例1平均数的含义和求法
例2用平均数来比较两组数据的总体情况
求平均数
求平均数知识树
四个四六九冬
365天
2月28天
366天
2月29天
平年小月
闰年
七个一三五七八十蜡
大月
里圈和外圈的关系
里圈1——12时
钟面的认识
12时与24时的转换
12小时记时法
（上午：AM
24
下午：PM）
时
记时法
24小时记时法
记
时
法
三年级数学
知识树下册
24时计时法
开始时间结束时间
经过时间=结束时间-开始时间
经过时间
应用
开始时间=结束时间-经过时间
求经过时间的方法
结束时间=开始时间+经过时间
乘加(减) 解决问题
集合
等量代换思想
被除数是两口算
位数的除法

结构力学图乘法

EI
E1I1 E2 I 2 E3 I3
Ei Ii
对于等直杆有
Δ

1 EI
l M ( x)M ( x)dx
M(x)
MC
EI
ω
C
即积分可用M(x)图的面积 ω 和与M(x)
xc
x
图形心C对应的 Mc 的乘积来代替
M(x)
当M图为正弯矩时，
Δ MC
EI
ω应代以正号. 当M图为负弯矩时， ω应代以负号.
EI
EI
y3=4 ω2 2m MP图(kN.m)
ω3 y2
M图
4B 4
ω1
C 2
y1
1
作业：
4-3 (a)；(c)
§4-5 互等定理
互等定理适用于线性变形体系，即体系产生的是小变形，且杆件材料服从虎克定律。
一、功的互等定理
功的互等本质上是虚功互等。
下图给出状态I和状态II。
FP1 FP2

(c
2d) 3
b c取负值
A
a A1
C
y1 c
B A2 b
D y2
d
MK 图 M图
（3）一般形式的二次抛物线图形相乘
（4）曲线图形与折线图形相乘
M i M K dx A1 y1 A2 y2 A3 y3 Ai yi
（5）阶形杆件图形相乘
M i M K dx A1 y1 A2 y2 A3 y3 Ai yi
12 22
1） δij也称为柔度系数，即单位力产生的位移。
I 产生位移的方位；j 产生位移的原因。
2） FP1和FP2可以是集中力也可以是集中力偶，则相应的δ12和δ21就是线位移影响系数或角位移影响系数。

2022届新教材高考数学一轮复习第7章7.1基本立体图形直观图表面积和体积课件新人教A版

体叫做棱锥
记作棱锥 S-ABCD 记作棱台 ABCD-A'B'C'D'
名称棱柱
底面:两个互相平行
的面;
侧面:底面以外的其
相关余各面;
概念侧棱:相邻侧面的公
共边;
顶点:侧面与底面的
公共顶点
棱锥
棱台
底面:多边形面; 上底面:平行于原棱锥底
侧面:有公共顶
面的截面;
点的各个三角
下底面:原棱锥的底面;
④过任意两条母线
的截面是矩形
圆锥
①圆锥有无数条母线,
它们有公共点即圆锥
的顶点,且长度相等.
②平行于底面的截面
都是圆.
③过轴的截面是全等
的等腰三角形.
④过任意两条母线的
截面是等腰三角形
圆台
①圆台有无数条母
线,且长度相等,延
长后相交于一点.
②平行于底面的截
面是圆.
③过轴的截面是全
等的等腰梯形.
④过任意两条母线
2.紧扣结构特征是判断的关键,熟悉空间几何体的结构特征,依据条件构建
S 圆锥侧=πrl
S 圆台侧=π(r1+r2)l
6.柱、锥、台、球的表面积与体积公式
几何体
表面积
柱体(棱柱和圆柱)
S 表面积=S 侧+2S 底
锥体(棱锥和圆锥)
台体(棱台和圆台)
球
体积
V= Sh
1
Sh
3
S 表面积=S 侧+S 底
V=
S 表面积=S 侧+S 上+S 下
1
V= (S
3
S= 4πR
2
V=
吗?
不一定,因为“其余各面都是平行四边形”并不等价于“相邻两个四边形的

2023高考数学基础知识综合复习第18讲简单几何体的表面积与体积课件(共24张PPT)

分叫作棱台
(2)旋转体的形成
几何体
旋转图形
圆柱
矩形
旋转轴
矩形一边所在的直线
圆锥
直角三角形
一直角边所在的直线
圆台
直角梯形或等腰梯形
球
半圆或圆
直角腰所在的直线或等腰梯形
上下底中点连线所在的直线
直径所在的直线
2.空间几何体的直观图
空间几何体的直观图常用斜二测画法来画,其画法步骤为:
①画轴:在平面图形上取互相垂直的x轴和y轴,作出与之对应的x'轴
3
4
3 = .故选 D.
考点一
考点二
考点三
本题考查四面体的体积的最大值的求法,涉及空间中线线、线面、
面面间的位置关系等基础知识,考查运算求解能力,属于难题.处理
此类问题时,往往先去找到不变的量,再根据题中的所给条件的变
化规律找到最值,从而得到体积的最值.
和y'轴,使得它们正方向的夹角为45°(或135°);
②画线(取长度):平面图形中与x轴平行(或重合)的线段画出与x'轴
平行(或重合)的线段,且长度不变,平面图形中与y轴平行(或重合)的
线段画出与y'轴平行(或重合)的线段,且长度为原来长度的一半;
③连线(去辅助线):连接有关线段,擦去作图过程中的辅助线.
径,从而进一步求解.
考点一
考点二
考点三
◆角度3.体积最值问题
例5(1)(2019年1月浙江学考)如图,线段AB是圆的直径,圆内一条动
弦CD与AB交于点M,且MB=2AM=2,现将半圆沿直径AB翻折,则三
棱锥C-ABD体积的最大值是(
)
2
3
1
3
A.

结构力学-图乘法

实例分析：圆轴扭转内力计算
第一段
M1 = (T1 + T2) × L/2
第二段
M2 = (T2 + T1) × L/2
实例分析：圆轴扭转内力计算
01
4. 比较M1和M2的大小，取较大者作为圆轴内的最大扭矩。
02
5. 根据扭矩的正负号，绘制扭矩图。
Part
04
组合变形图乘法
组合变形基本概念及分类
者联系起来，从而求解结构位移。
图乘法适用条件及限制
适用条件Βιβλιοθήκη 01载荷作用下，结构的变形是线性的，即变形量与载荷成正比。
03
02
结构变形符合小变形假设，即变形量与结构尺寸相比很小。
04 限制
图乘法只适用于线性弹性问题，对于非线性问题或塑性变形问题不适用。
05
06
在应用图乘法时，需要保证图形函数的准确性，否则会影响计算结果的精度。
Part
02
弯曲内力图乘法
弯曲内力基本概念
01
02
03
弯曲内力
指构件在受到外力作用时，其内部产生的抵抗弯曲变形的力。
剪力
作用于构件横截面上的内力，其方向与构件轴线垂直。
弯矩
作用于构件横截面上的内力偶矩，其大小等于该截面左侧或右侧所有外力对截面形心的力矩之和。
弯曲内力图乘法求解步骤
图乘法优点总结
直观性
图乘法通过图形表示结构中的力学元素和它们之间的关系，使得分析结果更直观，易于理解和解释。
高效性
相较于数值分析方法，图乘法能够更快地给出结构分析的近似解，适用于初步设计和快速评估。
适用性广
图乘法可应用于各种不同类型的结构，包括静定结构和超静定结构，具有较广泛的适用性。

初一至初二上册课本内结构图及知识点总结

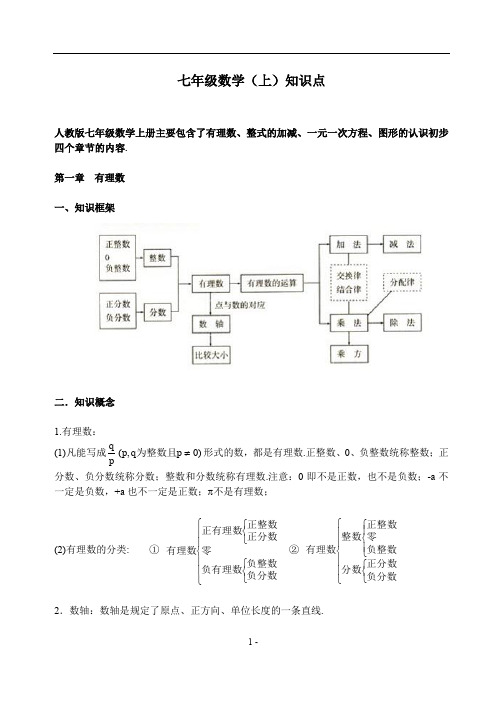
七年级数学（上）知识点人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容.第一章有理数一、知识框架二．知识概念1.有理数：(1)凡能写成)0p q ,p (p q≠为整数且形式的数，都是有理数.正整数、0、负整数统称整数；正分数、负分数统称分数；整数和分数统称有理数.注意：0即不是正数，也不是负数；-a 不一定是负数，+a 也不一定是正数；π不是有理数；(2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数2．数轴：数轴是规定了原点、正方向、单位长度的一条直线.3．相反数：(1)只有符号不同的两个数，我们说其中一个是另一个的相反数；0的相反数还是0； (2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数.4.绝对值：(1)正数的绝对值是其本身，0的绝对值是0，负数的绝对值是它的相反数；注意：绝对值的意义是数轴上表示某数的点离开原点的距离；(2) 绝对值可表示为：⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或⎩⎨⎧<-≥=)0a (a )0a (aa ；绝对值的问题经常分类讨论；5.有理数比大小：（1）正数的绝对值越大，这个数越大；（2）正数永远比0大，负数永远比0小；（3）正数大于一切负数；（4）两个负数比大小，绝对值大的反而小；（5）数轴上的两个数，右边的数总比左边的数大；（6）大数-小数＞ 0，小数-大数＜ 0.6.互为倒数：乘积为1的两个数互为倒数；注意：0没有倒数；若 a ≠0，那么a 的倒数是a1；若ab=1⇔ a 、b 互为倒数；若ab=-1⇔ a 、b 互为负倒数.7. 有理数加法法则：（1）同号两数相加，取相同的符号，并把绝对值相加；（2）异号两数相加，取绝对值较大的符号，并用较大的绝对值减去较小的绝对值；（3）一个数与0相加，仍得这个数.8．有理数加法的运算律：（1）加法的交换律：a+b=b+a ；（2）加法的结合律：（a+b ）+c=a+（b+c ）.9．有理数减法法则：减去一个数，等于加上这个数的相反数；即a-b=a+（-b ）.10 有理数乘法法则：（1）两数相乘，同号为正，异号为负，并把绝对值相乘；（2）任何数同零相乘都得零；（3）几个数相乘，有一个因式为零，积为零；各个因式都不为零，积的符号由负因式的个数决定.11 有理数乘法的运算律：（1）乘法的交换律：ab=ba ；（2）乘法的结合律：（ab ）c=a （bc ）；（3）乘法的分配律：a （b+c ）=ab+ac .12．有理数除法法则：除以一个数等于乘以这个数的倒数；注意：零不能做除数，无意义即0a.13．有理数乘方的法则：（1）正数的任何次幂都是正数；（2）负数的奇次幂是负数；负数的偶次幂是正数；注意：当n 为正奇数时: (-a)n =-a n 或(a -b)n =-(b-a)n , 当n 为正偶数时: (-a)n =a n 或 (a-b)n =(b-a)n .14．乘方的定义：（1）求相同因式积的运算，叫做乘方；（2）乘方中，相同的因式叫做底数，相同因式的个数叫做指数，乘方的结果叫做幂； 15．科学记数法：把一个大于10的数记成a ×10n 的形式，其中a 是整数数位只有一位的数，这种记数法叫科学记数法.16.近似数的精确位：一个近似数，四舍五入到那一位，就说这个近似数的精确到那一位.17.有效数字：从左边第一个不为零的数字起，到精确的位数止，所有数字，都叫这个近似数的有效数字.18.混合运算法则：先乘方，后乘除，最后加减.第二章整式的加减一．知识框架二.知识概念1．单项式：在代数式中，若只含有乘法（包括乘方）运算。

第八章-立体几何初步复习课图文课件

简单说，斜二测画法的规则是：横竖不变，纵减半，平行
性不变．
复习回顾结合正八棱柱的直观图，说出用斜二测画法画空间几何体的直观图的基本步骤．
横竖不变，纵减半，平行性不变
复习回顾
问题3 对于空间几何体，可以有不同的分类，你能选择不同的分类标准对柱、锥、台、球等空间几何体进行分类吗？如何计算柱、锥、台、球的表面积和体积？你能说出柱、锥、台、球的体积公式之间的联系吗？
，得 α ∩ γ ＝a；又γ ∩ β ＝直线b，故a与b
重合，
α ， β ， γ相交于同一条直线．
复习回顾
探究3 已知三个不同的平面 α， β， γ两两相交，设 α ∩ β＝直线 c，
β ∩ γ ＝直线a， γ ∩ α ＝直线b，试问a，b，c有怎样的位置关系？
说明理由并画出相应图形． ②当a与c相交时，设a∩c＝点O，由 α ∩ β ＝直线c， β ∩ γ
复习回顾探究4 怎样求图中的四个四面体的外接球与内切球的半径？
四个四面体的外接球与正方体的
类比
外接球相同，其一条直径为正方
体的体对角线，半径
．
复习回顾
问题4 刻画平面的三个基本事实是立体几何公理体系的基石，是研究空间图形、进行逻辑推理的基础．实际上，三个基本事实刻画了平面的“平”、平面的“无限延展”，你能归纳一下刻画的方法
探究1 说明作出点H的过程．点H在线段DB1的什么位置？
设B1D1 ∩A1C1＝P，点P为线段B1D1的中点，且平面
A1BC1 ∩平面BB1D1D＝BP．
在矩形BB1D1D中， BP∩B1D＝H．
由△B1HP∽△DHB，且．
，知
复习回顾
探究1 说明作出点H的过程．点H在线段DB1的什么位置？

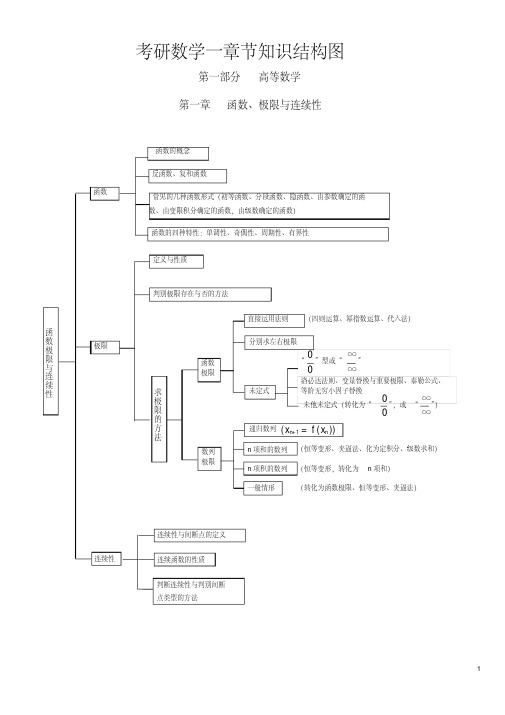
考研数学一章节知识结构图

重积分
计算公式二重积分的极坐标变换面积微元重积分变量替换三重积分柱坐标变换，体积微元
d σ= rdrd θ dV = rdrd θ dz
三重积分球坐标变换、体积微元
几何应用应用物理应用多元函数积分学平面图形面积、体积质量、质心、转动惯量
dV = ρ sin ? dρ d? dθ
2
基本概念、性质
8
第九章
常微分方程
基本概念一阶微分方程基本类型变量可分离方程一阶线性方程全微分方程伯努力方程可化为基本类型齐次方程用某些简单的变量代换求解某些微分方程
常微分方程
解的叠加原理性质通解的结构可降阶的高阶微分方程基本概念可降阶的类型二阶，高阶微分方程
基本概念二阶线性常系数方程高阶线性微分方程二阶微分方程（含某些高阶情形）特殊的二阶线性变系数方程可化为求解微分方程的情形（含变限积分的方程）
奇偶性与周期函数的导数性质隐函数与反函数求导法分阶函数求导法基本求导法则含参数方程所确定的函数的求导对数求导法及幂指数求导法导数的计算与高阶导数高阶导数
导数与微分
高阶导数的定义
极大值、极小值
微分中值定理与导数的应用
几种微分中值定理
（费马定理、罗尔定理、拉格朗日中值定理、泰勒公定、柯西定理）
17
第三章
多维随机变量及其概率分布
基本概念
多维，二维随机变量离散型
考研数学一章节知识结构图
第一部分第一章高等数学函数、极限与连续性
函数的概念反函数、复和函数函数常见的几种函数形式（初等函数、分段函数、隐函数、由参数确定的函数、由变限积分确定的函数，由级数确定的函数）函数的四种特性：单调性、奇偶性、周期性、有界性

小学数学知识结构图(知识树PPT)

ቤተ መጻሕፍቲ ባይዱ
工程问题
浓度问题
溶液=溶剂+溶质
浓度=溶质÷溶液×100%
解决问题----列方程解决问题
*弄清题意，找出要求的的未知数用X表示 *找出题中数量间的等量关系，列出方程 *解方程 *检验或验算，写出答案
列方程解决问题
一般步骤
找等量关系常用方法
关键语句常见的加、减、乘、除的数量关系常用的等量关系利用图形周长、面积、体积公式
分数问题类型
利息
*求a的几分之几（或百分之几）是多少 *一个数的几分之几（或百分之几）是a，求这个数 *求a是b的几分之几（或百分之几） *比a多（少）几分之几（或百分之几）的数是多少 *a比b多（少）几分之几（或百分之几），求b *求a比b多（少）几分之几（或百分之几）。
利息=本金×利率×时间
图形的认识
测量空间与图形图形与位置
图形与变换
基本图形
线：直线，射线，线段，平行线，垂线。（相交，垂直，平行）角：角的概念，角的分类平行四边形，长方形，正方形三角形梯形圆和圆环长方体，正方体圆柱
图形的认识
平面图形
立体图形
圆锥
球
基本图形
线角平行四边形，长方形，正方形的周长和面积三角形的周长和面积
一般不给出具体的的工作总量用单位1表示用分数表示工效工作效率工作时间工作总量工作总量工作效率工作时间工作总量工作时间工作效率数量关系浓度问题溶液溶剂溶质浓度溶质溶液100解决问题列方程解决问题列方程解决问题题弄清题意找出要求的的未知数用x表示找出题中数量间的等量关系列出方程解方程检验或验算写出答案找等量关系常用方法关键语句常见的加减乘除的数量关系常用的等量关系利用图形周长面积体积公式一般步骤典型应用题平均数问题归一问题归总问题和差问题差倍问题和倍问题倍比问题行程问题流水问题还原问题植树问题盈亏问题年龄问题鸡兔同笼问题解决问题行程问题行程问题一般行程问题火车过桥问题相遇问题追及问题路程速度时间速度路程时间时间路程速度路程桥长车长车速桥长车长通过时间通过时间桥长车长车速桥长车速通过时间车长车长车速通过时间桥长相遇路程速度和相遇时间相遇时间相遇路程速度和速度和相遇路程相遇时间速度差追及时间追及路程追及路程速度差追及时间追及路程追及时间速度差量与计量常见的量计量进率与换算度量衡名数与名数的改写常见的量量计量单位及进率率长度

2025届高考一轮复习《基本立体图形、简单几何体的表面积与体积》课件

可知 AC1⊥O1M，O1M＝0.6，那么 tan∠CAC1＝CACC1＝OAO1M1 ，
高考一轮总复习•数学
第27页
即 12＝A0O.61，解得 AO1＝0.6 2，根据对称性可知圆柱的高为 3－2×0.6 2≈1.732－1.2×1.414＝0.035 2>0.01，所以能够被整体放入正方体内，故 D 符合题意．故选 ABD.
高考一轮总复习•数学
第26页
设 OE∩AC＝E，可知 AC＝ 2，CC1＝1，AC1＝ 3，OA＝ 23，
那么
tan∠CAC1＝CACC1＝OAOE，即
1 ＝OE， 23
2
解得 OE＝ 46，且 462＝38＝294>295＝0.62，
即 46>0.6，
所以以 AC1 为轴可能对称放置底面直径为 1.2 m 圆柱，若底面直径为 1.2 m 的圆柱与正方体的上下底面均相切，设圆柱的底面圆心为 O1，与正方体的下底面的切点为 M，
圆台
体积 V＝ Sh ＝πr2h
V＝
1 3Sh
＝13πr2h＝13πr2
l2－r2
V＝13(S 上＋S 下＋ S上S下)h
＝13π(r21＋r22＋r1r2)h
第11页
高考一轮总复习•数学
名称棱柱棱锥棱台球
体积 V＝ Sh
1 V＝ 3Sh V＝13(S 上＋S 下＋ S上S下)h V＝43πR3
＝直观图
2 4S
原图形．
高考一轮总复习•数学
以三角形为例说明原因：
第36页
S
直观图＝12B′C′·O′A′·sin
高考一轮总复习•数学
第24页
解析：(1)由圆台定义知，以直角梯形垂直于底边的腰为旋转轴，其余三边旋转一周形成的面围成的旋转体是圆台，故 A 错误；

空间几何体的结构特征及三视图和直观图经典课件(最新)

图 12
高中数学课件
【反思·升华】三视图的正(主)视图、侧(左)视图、俯视图分别是从几何体的正前方、正左方、正上方观察几何体画出的轮廓线，主视图反映了物体的长度和高度；俯视图反映了物体的长度和宽度；左视图反映了物体的宽度和高度，由此得到：主俯长对正，主左高平齐，俯左宽相等．
(1)由几何体的直观图画三视图需注意的事项：①注意正视图、侧视图和俯视图对应的观察方向；②注意能看到的线用实线画，被挡住的线用虚线画；③画出的三视图要符合“长对正、高平齐、宽相等”的基本特征；
高中数学课件
空间几何体的结构特征及三视图和直观图课件
高中数学课件
1．空间几何体
【最新考纲】
(1)认识柱、锥、台、球及其简单组合体的结构特征，并能运用这些特征描述现实生
活中简单物体的结构．
Hale Waihona Puke (2)能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图，
能识别上述三视图所表示的立体模型，会用斜二侧画法画出它们的直观图．
高中数学课件
(3)旋转体的展开图 ①圆柱的侧面展开图是矩形，矩形的长(或宽)是底面圆周长，宽(或长)是圆柱的母线长； ②圆锥的侧面展开图是扇形，扇形的半径长是圆锥的母线长，弧长是圆锥的底面周长； ③圆台的侧面展开图是扇环，扇环的上、下弧长分别为圆台的上、下底面周长．
注：圆锥和圆台的侧面积公式 S 圆锥侧＝21cl 和 S 圆台侧＝21(c′＋c)l 与三角形和梯形的面积公式在形式上相同，可将二者联系起来记忆．
答案：D
高中数学课件
高频考点 2 空间几何体的三视图【例 2.1】 (2018 年高考·课标全国卷Ⅲ)中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫榫头，凹进部分叫卯眼，图 8 中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是( )